Mathematica jest bardzo zaawansowanym narz dziem do tworzenia 2D and 3D grafiki. W pewnym
|
|
|
- Franciszek Marek
- 8 lat temu
- Przeglądów:
Transkrypt
1 . Grafika Mathematica jest bardzo zaawansowanym narz dziem do tworzenia D and D grafiki. W pewnym sensie jest to najprostsza a w innym najbardziej skomplikowana cz tego skryptu. Jest ona prosta bo wszystkie instrukcje i cechy mo na znale w Documentation Center. Jednak e, dosy skomplikowanym zadaniem jest znalezienie potrzebnych cech w rod setek podobnych. Poni ej podajemy tyko przy ady najcz ciej u ywanych cech graficznych. Wszystkie poni sze ilustracje zosta y stworzone w Mathematice 7. We wcze niejszych wersji Mathematiki niektóre z nich nie b d dzia a lub b d dzia a inaczej. Wi kszo obrazków t umaczy si sama a z pytaniami o sposób u ywania ró nych funkcji graficznych odsy amy czytelnika do dokumentacji. PlotASinAx E, 8x,, <, PlotRange 8,.<E
2 z<, 8z, - Π, Π<, 8t,, Π<, PlotRange 88, <, 8, <, 8, <<D PlotAx -. x +. x - 7, 8x, -, <, PlotRange AllE - - -
3 <, D, PlotLabel "circle"d circle <, D, AspectRatio, PlotLabel "ellipse"d ellipse
4 <, D, Axes AutomaticD Π Π PlotBSin@xD, 8x,, Π<, Ticks ::,, Π,, Π>, Automatic>F. Π - -. Π Π Π
5 8x,, Π<, AxesStyle D, Plot@Sin@xD, 8x,, Π<, Frame TrueD PlotBLog@xD + SinBx + Sin@xDF, 8x,, <, GridLines AutomaticF - 6 8
6 6 data = Table@Sin@xD + Random@Real, 8-.,.<D, 8x,, Π,.<D 8.876,.87,.6,.689, 6, 769,.6989, 6,.689,.77,.89788,.989,.98,.86898,.,.9796,.77,.79,.67,.996,.88,.8887,.87,.7899,.69, 778, 7,.986,.,.69,.8, -.776, -.976, -., , -.678, , -.6, , -.78, , , , , -.866, -.979, -.987, -.96, -.966, -.997, -.86, -.97, -.998, , , -.788, -.7, -.76, , -.97, -., -.76, - 787< ListPlot@dataD ListLinePlot@dataD. - -.
7 zd, zd, zd<, 8z, -, 6<, PlotStyle PlotD@Sin@x yd, 8x,, Π<, 8y,, Π<, PlotPoints D
8 yd, 8x,, Π<, 8y,, Π<, PlotPoints D
9 9 ViewPoint -> 8.,.,.<D z y x PlotDA ã-hx-l -Hy-L, 8x, -, <, 8y, -, <, PlotRange -> All, AxesLabel -> 8"x", "y", "z"<e z x y
10 ViewVertical 8,, <D y - x - - z Plot@Sin@xD, 8x,, Π<, Background GrayLevel@DD Quit@D PolyhedronData@"Dodecahedron"D ListPlotD@Table@Mod@y, xd, 8x,, <, 8y,, <DD plot = Plot@Sin@xD, 8x, - Pi, Π<, PlotStyle RedD; plot = Plot@Sin@ xd, 8x, - Pi, Π<, PlotStyle GreenD; plot = Graphics@8Yellow, Circle@8, <, D<D;
11 plot, plot, AspectRatio AutomaticD vertices = 88, - <, 8, <, 8, <, 8-, <, 8, - <<; p = Graphics@8RGBColor@,, D, Polygon@verticesD<D; l = Graphics@8Thickness@.D, RGBColor@,, D, Line@verticesD<D; Show@p, ld p = Plot@Sin@xD, 8x,, Π<D p = Plot@Sin@ xd, 8x,, Π<D; GraphicsGrid@88p, p<<d GraphicsGrid@88p<, 8p<<D RandomReal@8, <, 8, <D Graphics@Line@RandomReal@8, <, 8, <DDD Graphics@ 8Hue@.77D, Rectangle@8, <, 8, <D, Hue@.7D, Rectangle@8, <, 8, <D<D GraphicsD@ 8Cuboid@8,, <D, Cuboid@8,, <D, Cuboid@8,, <D, Cuboid@8,, <D<D GraphicsB:Circle@8, <, D, Circle@8, <, 8, <D, CircleB:, - >,, :, >F>, AspectRatio -> Automatic, Axes -> AutomaticF InscribedCircleData@pA : 8_, _<, pb : 8_, _<, pc : 8_, _<D := ModuleB 8AB, BC, AC, a, b, c, s, pp, pq, AP, BQ, p, q, ps, qs, pqs, incenter, inradius<, AB = pb - pa; BC = pc - pb; AC = pc - pa; a = BC.BC ; b = AC.AC ; c = AB.AB ; AP.AB AP.AC AP = pb + p BC - pa; BQ = pa + q AC - pb; ps = SolveB ==, pf@@, DD; c b BQ.BC BQ.H- ABL qs = SolveB ==, qf@@, DD; pp = pb + p BC.ps; a c pq = pa + q AC.qs; pqs = Solve@pA + p HpP - pal == pb + q HpQ - pbl, 8p, q<d@@dd; incenter = pa + p HpP - pal.pqs; s = Ha + b + cl; inradius =, H shs - al Hs - bl Hs - cll; 8incenter, inradius<f InscribedCircle@pA : 8_, _<, pb : 8_, _<, pc : 8_, _<D := Graphics@ 8Line@8pA, pb, pc, pa<d, Circle@Sequence InscribedCircleData@pA, pb, pcdd<, AspectRatio -> Automatic, PlotRange -> All, Frame -> TrueD InscribedCircle@8.8, 6.8<, 8.,.<, 86.,.<D
12 D, <, 8, <D<, D, <, D<, D, <,, 8, <D<<, AspectRatio Automatic, Axes AutomaticD 8-, <, 8-, <D, 8, <, 8, <D, 8, <, 8, - <D, Text@"Below", 8, - <, 8, <D, 8PointSize@.7D, RGBColor@,, D, Point@8, <D<<, PlotRange AllD ListPlot@Table@8x, EulerPhi@xD<, 8x, <D, PlotStyle PointSize@.DD Graphics@8Dashing@8,.<D, Circle@8, <, D<, AspectRatio AutomaticD PlayASinAt E, 8t,, <E Animate[Plot[Sin[n x], {x,, Pi}, Axes -> False], {n,,, }] g = ParametricPlotD[ {x, Cos[t] Sin[x], Sin[t] Sin[x]}, {x, -Pi, Pi}, {t,, Pi}, Axes -> False, Boxed -> False] Quit@D Graphics[{Arrow[{{, },{, }}], Hue[], Arrow[{{.7,.},{.,.7}}]}] Plot[Sin[x], {x,, Pi}, Epilog -> {Arrow[{{,.}, {Pi/, }}], Text["Here", {,.}, {, -}]} ] ContourPlot[x^ + y^ ==, {x, -, },{y,-,}] ContourPlot[{(x^ + y^)^ == (x^ - y^), (x^ + y^)^ == x y}, {x,-,},{y,-,} ] RegionPlotA Hx + yl + y, 8x, -, <, 8y, -, < E RegionPlotDB x + y + z í x + y z, 8x, -, <, 8y, -, <, 8z, -, <F VectorPlot@8Sin@xD, Cos@yD<, 8x,, Pi<, 8y,, Pi<D RevolutionPlotD[ Sin[x], {x,, Pi}] RevolutionPlotD[{. Sin[u], u^}, {u,, Pi/}, BoxRatios -> {,, }] RevolutionPlotD[x^, {x,, }, RevolutionAxis -> {,, }] FinancialData@"GE", "Price"D DateListLogPlot@FinancialData@"^DJI", AllD, Joined True, Filling BottomD Plot@Table@BesselJ@n, xd, 8n, <D, 8x,, <, Filling Axis, Evaluated -> TrueD
13 xd + yd, 8x,, <, 8y,, <, ContourLabels Automatic, ColorFunction "Pastel"D 8Cos@vD +. ud +. vd, u, +. ud +. vd<, 8u, - Π, Π<, 8v, - Π, Π<, PlotPoints, PlotStyle 8Orange, Specularity@White, D<, Axes None, Mesh NoneD Graphics@8LightGray, Disk@D, Inset@Plot@Tan@xD, 8x, -, <DD<D Graphics@8Circle@D, Inset@X ^ + Y ^, 8, <D<D solution = NDSolve@8x ''@td + x@td ^ Sin@tD, x@d x '@D <, x, 8t,, <D ParametricPlot@8x@tD, x '@td<. solution, 8t,, <D Block@8f = Cos@x + I yd<, ParametricPlot@Evaluate@8Re@fD, Im@fD<D, 8x, - Pi, Pi<, 8y, -, <DD
Plotki. Wstęp. Wybrane wbudowane funkcje graficzne:
 Plotki Wstęp Wybrane wbudowane funkcje graficzne: funkcja Plot@y, 8x, x min, x max
Plotki Wstęp Wybrane wbudowane funkcje graficzne: funkcja Plot@y, 8x, x min, x max
Kurs komputerowy S - Mathematica - cz. 2
 OBLICZENIA SYMBOLICZNE, Karolina MikulskaRuminska Kurs komputerowy S Mathematica cz. zmienna = wartosc Set[zmienna,wartosc] x = 7 7 x = x ^ x = 5 5 x Inaczej.. y = y ^ y y = 5 y 5 5 y = 0 y 0 000 KursS_cz.nb
OBLICZENIA SYMBOLICZNE, Karolina MikulskaRuminska Kurs komputerowy S Mathematica cz. zmienna = wartosc Set[zmienna,wartosc] x = 7 7 x = x ^ x = 5 5 x Inaczej.. y = y ^ y y = 5 y 5 5 y = 0 y 0 000 KursS_cz.nb
Kurs komputerowy S - Mathematica - cz. 3 Suma i iloczyn elementow ciagu NSum[wyr, {zm, w_pocz, w_konc}], NProduct[wyr, {zm, w_pocz, w_konc}]
![Kurs komputerowy S - Mathematica - cz. 3 Suma i iloczyn elementow ciagu NSum[wyr, {zm, w_pocz, w_konc}], NProduct[wyr, {zm, w_pocz, w_konc}] Kurs komputerowy S - Mathematica - cz. 3 Suma i iloczyn elementow ciagu NSum[wyr, {zm, w_pocz, w_konc}], NProduct[wyr, {zm, w_pocz, w_konc}]](/thumbs/65/53823904.jpg) OBLICZENIA NUMERYCZNE, Karolina Mikulska-Ruminska Kurs komputerowy S - Mathematica - cz. Suma i iloczyn elementow ciagu NSum[wyr, {zm, w_pocz, w_konc}], NProduct[wyr, {zm, w_pocz, w_konc}]? *Sum* System`
OBLICZENIA NUMERYCZNE, Karolina Mikulska-Ruminska Kurs komputerowy S - Mathematica - cz. Suma i iloczyn elementow ciagu NSum[wyr, {zm, w_pocz, w_konc}], NProduct[wyr, {zm, w_pocz, w_konc}]? *Sum* System`
Wprowadzanie wyrazen w Mathematice
 1 z 52 2006-11-12 14:07 Wprowadzanie wyrazen w Mathematice Greckie litery Greckie litery jako nazwy zmiennych In[1]:= Expand[(α + β)^3] Out[1]= In[2]:= Out[2]= Expand[(\[Alpha] + \[Beta])^3] In[3]:= Out[3]=
1 z 52 2006-11-12 14:07 Wprowadzanie wyrazen w Mathematice Greckie litery Greckie litery jako nazwy zmiennych In[1]:= Expand[(α + β)^3] Out[1]= In[2]:= Out[2]= Expand[(\[Alpha] + \[Beta])^3] In[3]:= Out[3]=
Mathematica od zera. Paulina Suchanek, IFT Wroclaw. Factor x 2 2 x 1. Series Log 1 x, x, 0, 5. 1. Wprowadzenie. Start. Struktura notatnika
 Mathematica od zera Paulina Suchanek, IFT Wroclaw 1. Wprowadzenie Start Struktura notatnika Notatnik edytujemy uzywajac opcji z zakladki Format. Strukture rozdzialow wprowadzamy wybierajac opcje z okienka
Mathematica od zera Paulina Suchanek, IFT Wroclaw 1. Wprowadzenie Start Struktura notatnika Notatnik edytujemy uzywajac opcji z zakladki Format. Strukture rozdzialow wprowadzamy wybierajac opcje z okienka
Mathematica (1) Organizacja Mathematica Notebooks. Style dokumentów
 Mathematica (1) Organizacja Mathematica Notebooks Dokument Mathematica zorganizowany jest w tzw. komórki. KaŜda komórka zawiera materiał określonego rodzaju: tekst, grafikę, dane wejściowe, dane wyjściowe
Mathematica (1) Organizacja Mathematica Notebooks Dokument Mathematica zorganizowany jest w tzw. komórki. KaŜda komórka zawiera materiał określonego rodzaju: tekst, grafikę, dane wejściowe, dane wyjściowe
Witam! Czym jest Mathematica?
 Witam! Nazywam się Jacek Golak Pracuję w Zakładzie Fizyki Jądrowej Instytutu Fizyki UJ Moja dziedzina to teoretyczna fizyka jądrowa Numer pokoju: B2-32 e-mail: jacek.golak@uj.edu.pl strona WWW: http://users.uj.edu.pl/~golak/zestawynof.html
Witam! Nazywam się Jacek Golak Pracuję w Zakładzie Fizyki Jądrowej Instytutu Fizyki UJ Moja dziedzina to teoretyczna fizyka jądrowa Numer pokoju: B2-32 e-mail: jacek.golak@uj.edu.pl strona WWW: http://users.uj.edu.pl/~golak/zestawynof.html
Witam Państwa na wykładzie dotyczącym narzędzi obliczeniowych fizyki!
 Witam Państwa na wykładzie dotyczącym narzędzi obliczeniowych fizyki! Nazywam się Jacek Golak Pracuję w Zespole Zakładów Fizyki Jądrowej Instytutu Fizyki UJ i jestem kierownikiem Zakładu Teorii Układów
Witam Państwa na wykładzie dotyczącym narzędzi obliczeniowych fizyki! Nazywam się Jacek Golak Pracuję w Zespole Zakładów Fizyki Jądrowej Instytutu Fizyki UJ i jestem kierownikiem Zakładu Teorii Układów
Mathematica III Równania różniczkowe, układy równań różniczkowych, wykresy, badanie funkcji, importowanie danych, instrukcje warunkowe, pętle
 Mathematica III Równania różniczkowe, układy równań różniczkowych, wykresy, badanie funkcji, importowanie danych, instrukcje warunkowe, pętle na podstawie materiałów wolfram.com Równania różniczkowe: Równanie
Mathematica III Równania różniczkowe, układy równań różniczkowych, wykresy, badanie funkcji, importowanie danych, instrukcje warunkowe, pętle na podstawie materiałów wolfram.com Równania różniczkowe: Równanie
wiczenia (z przyk adami i cz ciowymi rozwi zaniami)
 wiczenia (z przyk adami i cz ciowymi rozwi zaniami) 1. Narysuj wykresy funkcji z x 2 y 2, z 2 x 2 y 9 w R 3. Narysuj linie x 1 2 t, y 1 2 t, z 2 t. Poka wszystkie wykresy na jednym obrazku. Rozwi zanie
wiczenia (z przyk adami i cz ciowymi rozwi zaniami) 1. Narysuj wykresy funkcji z x 2 y 2, z 2 x 2 y 9 w R 3. Narysuj linie x 1 2 t, y 1 2 t, z 2 t. Poka wszystkie wykresy na jednym obrazku. Rozwi zanie
Zadanie1. (* parametryzacja okręgu r'= x',y',0 *) xp = R * Cos fp ; yp = R * Sin fp ; vecrp = xp, yp, 0 ; vecr = r * Cos f, r * Sin f, z ;
 Zadanie1 (* parametryzacja okręgu r'= x',y',0 *) Z ogólnego twierdzenia o rozwiązaniach równania Laplace a wynika, że potencjał elektryczny nie może mieć w tym punkcie ekstremum lokalnego. Warto się jednak
Zadanie1 (* parametryzacja okręgu r'= x',y',0 *) Z ogólnego twierdzenia o rozwiązaniach równania Laplace a wynika, że potencjał elektryczny nie może mieć w tym punkcie ekstremum lokalnego. Warto się jednak
Wykład 6. Prawo Hooke a. Robert Hooke
 Wykład 6 Równania różniczkowe, funkcje DSolve oraz NDSolve. Wykres fazowy. Prawo Hooke a, drgania sprężyn. Ruch z oporem powietrza. In[1]:= ClearAll["Global`*"] wyczyść wszystko Prawo Hooke a Robert Hooke
Wykład 6 Równania różniczkowe, funkcje DSolve oraz NDSolve. Wykres fazowy. Prawo Hooke a, drgania sprężyn. Ruch z oporem powietrza. In[1]:= ClearAll["Global`*"] wyczyść wszystko Prawo Hooke a Robert Hooke
(4) (b) m. (c) (d) sin α cos α = sin 2 k = sin k sin k. cos 2 m = cos m cos m. (g) (e)(f) sin 2 x + cos 2 x = 1. (h) (f) (i)
 (3) (e) sin( θ) sin θ cos( θ) cos θ sin(θ + π/) cos θ cos(θ + π/) sin θ sin(θ π/) cos θ cos(θ π/) sin θ sin(θ ± π) sin θ cos(θ ± π) cos θ sin(θ ± π) sin θ cos(θ ± π) cos θ (f) cos x cos y (g) sin x sin
(3) (e) sin( θ) sin θ cos( θ) cos θ sin(θ + π/) cos θ cos(θ + π/) sin θ sin(θ π/) cos θ cos(θ π/) sin θ sin(θ ± π) sin θ cos(θ ± π) cos θ sin(θ ± π) sin θ cos(θ ± π) cos θ (f) cos x cos y (g) sin x sin
Kurs z matematyki - zadania
 Kurs z matematyki - zadania Miara łukowa kąta Zadanie Miary kątów wyrażone w stopniach zapisać w radianach: a) 0, b) 80, c) 90, d), e) 0, f) 0, g) 0, h), i) 0, j) 70, k), l) 80, m) 080, n), o) 0 Zadanie
Kurs z matematyki - zadania Miara łukowa kąta Zadanie Miary kątów wyrażone w stopniach zapisać w radianach: a) 0, b) 80, c) 90, d), e) 0, f) 0, g) 0, h), i) 0, j) 70, k), l) 80, m) 080, n), o) 0 Zadanie
= 1, = = + 1D, + 2D<,
 'Przypadkowe bladzenie' jako przyklad prostego problemu, ktory moze byc pierwszym zadaniem, dla studiujacych 'Mathematica', zwiazanychm z rozwiazaniem 'rzeczywistego' problemu. Rozwazmy ruch jednowymiarowy
'Przypadkowe bladzenie' jako przyklad prostego problemu, ktory moze byc pierwszym zadaniem, dla studiujacych 'Mathematica', zwiazanychm z rozwiazaniem 'rzeczywistego' problemu. Rozwazmy ruch jednowymiarowy
 123456 782923456 6 22336 46466 6 6 6 783863658386 6 6 6 6 4!"! 468983#84636434$4636 6 6 6 %&6 '5626 ()68'546 6 6 &6 6 82845469234548*+6 %6 6 6 %6 '56268'546"'844$$6 %6 6 6 %&6 '5626 ()68'546,6 6 6 6 -*386
123456 782923456 6 22336 46466 6 6 6 783863658386 6 6 6 6 4!"! 468983#84636434$4636 6 6 6 %&6 '5626 ()68'546 6 6 &6 6 82845469234548*+6 %6 6 6 %6 '56268'546"'844$$6 %6 6 6 %&6 '5626 ()68'546,6 6 6 6 -*386
Liczby zespolone to (uporządkowane) pary liczb rzeczywistych, dla których dodawanie i mnożenie jest określone wzorami:
 Przytaczając definicję liczb zespolonych, wyznacznika, wypowiedź twierdzenia Cramera oraz Kroneckera-Capelliego, korzystałem z I tomu wykładów Prof. Andrzeja Staruszkiewicza dla fizyków: ALGEBRA I GEOMETRIA,
Przytaczając definicję liczb zespolonych, wyznacznika, wypowiedź twierdzenia Cramera oraz Kroneckera-Capelliego, korzystałem z I tomu wykładów Prof. Andrzeja Staruszkiewicza dla fizyków: ALGEBRA I GEOMETRIA,
n 2 1. lim n 3 sin 2. lim k 2 + n 2 3. lim 8 k n + 2 k + 5 n 2 Oblicz granice n lim n 2 3 π + log(8) x π + log(64) lim sin sin lim
 . Oblicz graice. k= k 3 + 3. 3. si k= k + 8 k + k + 5 k= k= k 3 + 3 9 3 π + log(8) 3 k= k 3 + 3 k= k 3 + 3 k= 3 + k 3 Itegrate, {,, } 3 + 8 3 π + log(64) k 3 k= k= si si k + k + k + - LimitSum π 4 k +
. Oblicz graice. k= k 3 + 3. 3. si k= k + 8 k + k + 5 k= k= k 3 + 3 9 3 π + log(8) 3 k= k 3 + 3 k= k 3 + 3 k= 3 + k 3 Itegrate, {,, } 3 + 8 3 π + log(64) k 3 k= k= si si k + k + k + - LimitSum π 4 k +
Wstęp do chemii kwantowej - laboratorium. Zadania
 Wstęp do chemii kwantowej - laboratorium. Zadania 2 października 2012 1 Wstęp Używanie maximy jako kalkulatora Zadanie 1 1. Oblicz 2+2*2 2. Oblicz 18769 3. Oblicz 2 10 4. Oblicz 7/8 i 7.0/8.0 5. Oblicz
Wstęp do chemii kwantowej - laboratorium. Zadania 2 października 2012 1 Wstęp Używanie maximy jako kalkulatora Zadanie 1 1. Oblicz 2+2*2 2. Oblicz 18769 3. Oblicz 2 10 4. Oblicz 7/8 i 7.0/8.0 5. Oblicz
.<=->./?-> 0 A " #($" $' $ "./ F / % 6789 G HIJKLMNO 2 #$ ab]^[ #$ P 6 c_`ab b ]^FG&H+ IJ K LMNO P$QR SU^I T T+ UV? cwxky N ` ]^ Z[\]^ _
![.<=->./?-> 0 A #($ $' $ ./ F / % 6789 G HIJKLMNO 2 #$ ab]^[ #$ P 6 c_`ab b ]^FG&H+ IJ K LMNO P$QR SU^I T T+ UV? cwxky N ` ]^ Z[\]^ _ .<=->./?-> 0 A #($ $' $ ./ F / % 6789 G HIJKLMNO 2 #$ ab]^[ #$ P 6 c_`ab b ]^FG&H+ IJ K LMNO P$QR SU^I T T+ UV? cwxky N ` ]^ Z[\]^ _](/thumbs/94/118621653.jpg) F / % 6789 G HIJKLMNO 2 #$ ab]^[ #$ P 6 c_`ab b ]^FG&H+ IJ K LMNO P$QR SU^I T T+ UV? cwxky N ` ]^ Z[\]^ _` a/r c9 bc ) &HSU]^ IJ S P. ) # P IJ c _`ab]^ ]^ +c T N _`ab]^ \(c a cg QRS _`ab ]^ + ^I )T U/
F / % 6789 G HIJKLMNO 2 #$ ab]^[ #$ P 6 c_`ab b ]^FG&H+ IJ K LMNO P$QR SU^I T T+ UV? cwxky N ` ]^ Z[\]^ _` a/r c9 bc ) &HSU]^ IJ S P. ) # P IJ c _`ab]^ ]^ +c T N _`ab]^ \(c a cg QRS _`ab ]^ + ^I )T U/
Kurs Komputerowy S System Symboliczny Mathematica
 Kurs Komputerowy S System Symboliczny Mathematica Obliczenia numeryczne Dokladnosc i precyzja Precision[wartosc] SetPrecision[wartosc, precyzja] Accuracy[wartosc] SetAccuracy[wartosc, dokladnosc] MachinePrecision
Kurs Komputerowy S System Symboliczny Mathematica Obliczenia numeryczne Dokladnosc i precyzja Precision[wartosc] SetPrecision[wartosc, precyzja] Accuracy[wartosc] SetAccuracy[wartosc, dokladnosc] MachinePrecision
M P A P S - 50 X 100
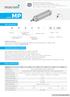 ul. Hauke Bosaka 15, 25-217 Kielce; e-mail: marketing@obreiup.com.pl MP seria Jak zamawiać? M P A P S - 50 X 100 M: Marani A: Dwustronnego działania (typ podstawowy) S: Magnes na tłoku Średnica x Skok
ul. Hauke Bosaka 15, 25-217 Kielce; e-mail: marketing@obreiup.com.pl MP seria Jak zamawiać? M P A P S - 50 X 100 M: Marani A: Dwustronnego działania (typ podstawowy) S: Magnes na tłoku Średnica x Skok
1 Wizualizacja danych - wykresy 2D
 1 Wizualizacja danych - wykresy 2D Funkcje sterujące tworzeniem wykresów plot(x,y, KSL ) tworzy wykres 2D wraz z specyfikatorem lini K - kolor, S - symbol, L - linia figure(nr) subplot(m,n,active) hold
1 Wizualizacja danych - wykresy 2D Funkcje sterujące tworzeniem wykresów plot(x,y, KSL ) tworzy wykres 2D wraz z specyfikatorem lini K - kolor, S - symbol, L - linia figure(nr) subplot(m,n,active) hold
Stałe = Infinity, π = Pi, E = e, Deg = π/180
 ( Notatki, w opracowaniu M. Szurka do Seminarium Modelowanie matematyczne : wersja 25 października 2004) De computer is niet de steen, maar de slijpsteen der wijzen. Komputer nie jest kamieniem filozoficznym,
( Notatki, w opracowaniu M. Szurka do Seminarium Modelowanie matematyczne : wersja 25 października 2004) De computer is niet de steen, maar de slijpsteen der wijzen. Komputer nie jest kamieniem filozoficznym,
Pakiety matematyczne. Matematyka Stosowana. dr inż. Krzysztof Burnecki
 Pakiety matematyczne Matematyka Stosowana dr inż. Krzysztof Burnecki 22.05.2013 Wykład 12 Mathematica. Wprowadzenie Obliczenia w Mathematice Wolfram Alpha Slajdy powstały na podstawie strony www.mathematica.pl
Pakiety matematyczne Matematyka Stosowana dr inż. Krzysztof Burnecki 22.05.2013 Wykład 12 Mathematica. Wprowadzenie Obliczenia w Mathematice Wolfram Alpha Slajdy powstały na podstawie strony www.mathematica.pl
pobrano z (A1) Czas GRUDZIE
 EGZAMIN MATURALNY OD ROKU SZKOLNEGO 014/015 MATEMATYKA POZIOM ROZSZERZONY PRZYK ADOWY ZESTAW ZADA (A1) W czasie trwania egzaminu zdaj cy mo e korzysta z zestawu wzorów matematycznych, linijki i cyrkla
EGZAMIN MATURALNY OD ROKU SZKOLNEGO 014/015 MATEMATYKA POZIOM ROZSZERZONY PRZYK ADOWY ZESTAW ZADA (A1) W czasie trwania egzaminu zdaj cy mo e korzysta z zestawu wzorów matematycznych, linijki i cyrkla
Liczby i działania na liczbach
 Na tym wykładzie chciałbym przekonać Państwa, że Mathematica może być pomocna w studiowaniu analizy matematycznej. Liczby i działania na liczbach (* liczby całkowite *) Element[-, Integers] należy do zbiór
Na tym wykładzie chciałbym przekonać Państwa, że Mathematica może być pomocna w studiowaniu analizy matematycznej. Liczby i działania na liczbach (* liczby całkowite *) Element[-, Integers] należy do zbiór
Szkielet skryptu z AM II - wersja 2 października 2015
 Szkielet skryptu z AM II - wersja października 015 Sławomir Kolasiński, Michał Jóźwikowski października 015 1 Wstęp W niniejszym dodatku chcielibyśmy zaprezentować Czytelnikowi zestaw sytuacji, w których
Szkielet skryptu z AM II - wersja października 015 Sławomir Kolasiński, Michał Jóźwikowski października 015 1 Wstęp W niniejszym dodatku chcielibyśmy zaprezentować Czytelnikowi zestaw sytuacji, w których
(naci nij SHIFT + ENTER po ustawieniu kursora w dowolnym miejscu w komórce zawieraj cej formu )
 1. Podstawowe Zasady 1. Przegl d funkcjonalno ci. Mathematica jako kalkulator. Praktycznie wszyskie potrzebne informacje o Mathematice mo na uzyska z Centrum Dokumentacji (aby do niego dotrze nale y nacisn
1. Podstawowe Zasady 1. Przegl d funkcjonalno ci. Mathematica jako kalkulator. Praktycznie wszyskie potrzebne informacje o Mathematice mo na uzyska z Centrum Dokumentacji (aby do niego dotrze nale y nacisn
Strategia rozwoju kariery zawodowej - Twój scenariusz (program nagrania).
 Strategia rozwoju kariery zawodowej - Twój scenariusz (program nagrania). W momencie gdy jesteś studentem lub świeżym absolwentem to znajdujesz się w dobrym momencie, aby rozpocząć planowanie swojej ścieżki
Strategia rozwoju kariery zawodowej - Twój scenariusz (program nagrania). W momencie gdy jesteś studentem lub świeżym absolwentem to znajdujesz się w dobrym momencie, aby rozpocząć planowanie swojej ścieżki
Modele odpowiedzi do arkusza Próbnej Matury z OPERONEM. Matematyka Poziom rozszerzony
 Pobrno ze strony www.sqlmedi.pl Modele odpowiedzi do rkusz Próbnej Mtury z OPERONEM Mtemtyk Poziom rozszerzony Listopd 9 W kluczu sà prezentowne przyk dowe prwid owe odpowiedzi. Nle y równie uznç odpowiedzi
Pobrno ze strony www.sqlmedi.pl Modele odpowiedzi do rkusz Próbnej Mtury z OPERONEM Mtemtyk Poziom rozszerzony Listopd 9 W kluczu sà prezentowne przyk dowe prwid owe odpowiedzi. Nle y równie uznç odpowiedzi
REDUKTORY ŒLIMAKOWE PRZEK ADNIE ŒLIMAKOWE NMRV 050 NRV 050 NMRV 090 NRV 090 NRV 030/040 NRV 040/090
 REDUKTORY ŒLIMAKOWE PRZEK ADNIE ŒLIMAKOWE 0 NRV 0 00 NRV 00 NRV 0/0 NRV 0/00 2 NRV PRZY CZA DO SILNIKA IEC Oferowane reduktory musz¹ byæ zespolone z silnikami za pomoc¹ ko³nierzy adaptacyjnych odpowiadaj¹cych
REDUKTORY ŒLIMAKOWE PRZEK ADNIE ŒLIMAKOWE 0 NRV 0 00 NRV 00 NRV 0/0 NRV 0/00 2 NRV PRZY CZA DO SILNIKA IEC Oferowane reduktory musz¹ byæ zespolone z silnikami za pomoc¹ ko³nierzy adaptacyjnych odpowiadaj¹cych
Zadania. SiOD Cwiczenie 1 ;
 1. Niech A będzie zbiorem liczb naturalnych podzielnych przez 6 B zbiorem liczb naturalnych podzielnych przez 2 C będzie zbiorem liczb naturalnych podzielnych przez 5 Wyznaczyć zbiory A B, A C, C B, A
1. Niech A będzie zbiorem liczb naturalnych podzielnych przez 6 B zbiorem liczb naturalnych podzielnych przez 2 C będzie zbiorem liczb naturalnych podzielnych przez 5 Wyznaczyć zbiory A B, A C, C B, A
ZADANIA OTWARTE KRÓTKIEJ ODPOWIEDZI
 Zadanie 51. ( pkt) Rozwi równanie 3 x 1. 1 x Zadanie 5. ( pkt) x 3y 5 Rozwi uk ad równa. x y 3 Zadanie 53. ( pkt) Rozwi nierówno x 6x 7 0. ZADANIA OTWARTE KRÓTKIEJ ODPOWIEDZI Zadanie 54. ( pkt) 3 Rozwi
Zadanie 51. ( pkt) Rozwi równanie 3 x 1. 1 x Zadanie 5. ( pkt) x 3y 5 Rozwi uk ad równa. x y 3 Zadanie 53. ( pkt) Rozwi nierówno x 6x 7 0. ZADANIA OTWARTE KRÓTKIEJ ODPOWIEDZI Zadanie 54. ( pkt) 3 Rozwi
n p 2 i = R 2 (8.1) i=1
 8.9 Rozkład Maxwella Jest to rozkład prędkości cząstek w gazie doskonałym. Wielkość f (p) jest gęstością prawdopodobieństwa znalezienia cząstki o pędzie p. Różnica pomiędzy rozkładem Maxwella i rozkładem
8.9 Rozkład Maxwella Jest to rozkład prędkości cząstek w gazie doskonałym. Wielkość f (p) jest gęstością prawdopodobieństwa znalezienia cząstki o pędzie p. Różnica pomiędzy rozkładem Maxwella i rozkładem
Funkcje Andrzej Musielak 1. Funkcje
 Funkcje Andrzej Musielak 1 Funkcje Funkcja liniowa Funkcja liniowa jest postaci f(x) = a x + b, gdzie a, b R Wartość a to tangens nachylenia wykresu do osi Ox, natomiast b to wartość funkcji w punkcie
Funkcje Andrzej Musielak 1 Funkcje Funkcja liniowa Funkcja liniowa jest postaci f(x) = a x + b, gdzie a, b R Wartość a to tangens nachylenia wykresu do osi Ox, natomiast b to wartość funkcji w punkcie
I Konkurencja: Webmaster to ja! bran a elektrycznoelektroniczna/administracyjno-usługowa
 Zał cznik nr 1 do Regulaminu I Konkurencja: Webmaster to ja! bran a elektrycznoelektroniczna/administracyjno-usługowa Miejsce: Zespół Szkół Technicznych im. Ignacego Mo cickiego w Tarnowie, ul. Kwiatkowskiego
Zał cznik nr 1 do Regulaminu I Konkurencja: Webmaster to ja! bran a elektrycznoelektroniczna/administracyjno-usługowa Miejsce: Zespół Szkół Technicznych im. Ignacego Mo cickiego w Tarnowie, ul. Kwiatkowskiego
#$%&"!' ()*+$,% -$)%.)/ 01! *0,,2* %2, 40,-7 $$$
 M NM O *+ 62-3B6 8 -C 6-B7 6 * *+5 2 B9 A: 6:!"#$% '!"#$%' ()* +,-. $/0(1()*$ +,!' + -.+ -/ (* +,!' + - / +,!'0!" $(1 234.56789: $(1 ;. *; ' +,!' 1 $% )# ?@ABCDE!6 9: $(1 FGH IJ!" $/0(1 IJKL
M NM O *+ 62-3B6 8 -C 6-B7 6 * *+5 2 B9 A: 6:!"#$% '!"#$%' ()* +,-. $/0(1()*$ +,!' + -.+ -/ (* +,!' + - / +,!'0!" $(1 234.56789: $(1 ;. *; ' +,!' 1 $% )# ?@ABCDE!6 9: $(1 FGH IJ!" $/0(1 IJKL
Arkusz zawiera informacje prawnie chronione do momentu rozpocz cia egzaminu.
 Centralna Komisja Egzaminacyjna Arkusz zawiera informacje prawnie chronione do momentu rozpocz cia egzaminu. Uk ad graficzny CKE 010 KOD WPISUJE ZDAJ CY PESEL Miejsce na naklejk z kodem dysleksja EGZAMIN
Centralna Komisja Egzaminacyjna Arkusz zawiera informacje prawnie chronione do momentu rozpocz cia egzaminu. Uk ad graficzny CKE 010 KOD WPISUJE ZDAJ CY PESEL Miejsce na naklejk z kodem dysleksja EGZAMIN
Egzamin maturalny z matematyki Poziom podstawowy ZADANIA ZAMKNI TE. W zadaniach od 1. do 25. wybierz i zaznacz na karcie odpowiedzi poprawn odpowied.
 Egzamin maturalny z matematyki ZADANIA ZAMKNI TE W zadaniach od 1. do 5. wybierz i zaznacz na karcie odpowiedzi poprawn odpowied. Zadanie 1. (1 pkt) Cen nart obni ono o 0%, a po miesi cu now cen obni ono
Egzamin maturalny z matematyki ZADANIA ZAMKNI TE W zadaniach od 1. do 5. wybierz i zaznacz na karcie odpowiedzi poprawn odpowied. Zadanie 1. (1 pkt) Cen nart obni ono o 0%, a po miesi cu now cen obni ono
L.Kowalski zadania z rachunku prawdopodobieństwa-zestaw 4 ZADANIA - ZESTAW 4
 ZADANIA - ZESTAW 4 Zadanie 4. 0-0,4 c 0 0, 0, Wznacz c. Wznacz rozkład brzegowe. Cz, są niezależne? (odp. c = 0,3 Zadanie 4.- 0-0,4 0,3 0 0, 0, Wznaczć macierz kowariancji i korelacji. Cz, są skorelowane?
ZADANIA - ZESTAW 4 Zadanie 4. 0-0,4 c 0 0, 0, Wznacz c. Wznacz rozkład brzegowe. Cz, są niezależne? (odp. c = 0,3 Zadanie 4.- 0-0,4 0,3 0 0, 0, Wznaczć macierz kowariancji i korelacji. Cz, są skorelowane?
W. Guzicki Próbna matura, grudzień 2014 r. poziom rozszerzony 1
 W. Guzicki Próbna matura, grudzień 01 r. poziom rozszerzony 1 Próbna matura rozszerzona (jesień 01 r.) Zadanie 18 kilka innych rozwiązań Wojciech Guzicki Zadanie 18. Okno na poddaszu ma mieć kształt trapezu
W. Guzicki Próbna matura, grudzień 01 r. poziom rozszerzony 1 Próbna matura rozszerzona (jesień 01 r.) Zadanie 18 kilka innych rozwiązań Wojciech Guzicki Zadanie 18. Okno na poddaszu ma mieć kształt trapezu
Funkcje: wielomianowa, wykładnicza, logarytmiczna wykład 3
 Funkcje: wielomianowa, wykładnicza, logarytmiczna wykład 3 dr Mariusz Grzadziel Katedra Matematyki, Uniwersytet Przyrodniczy we Wrocławiu semestr zimowy 2016/2017 Potęgowanie Dla dowolnej liczby dodatniej
Funkcje: wielomianowa, wykładnicza, logarytmiczna wykład 3 dr Mariusz Grzadziel Katedra Matematyki, Uniwersytet Przyrodniczy we Wrocławiu semestr zimowy 2016/2017 Potęgowanie Dla dowolnej liczby dodatniej
Finansowanie inwestycji w OZE - PO Infrastruktura i Środowisko
 Finansowanie inwestycji w OZE - PO Infrastruktura i Środowisko Dofinansowanie projektów związanych z inwestycjami w OZE w ramach Polskich Narodowych Strategicznych Ram Odniesienia na lata 2007 2013 moŝe
Finansowanie inwestycji w OZE - PO Infrastruktura i Środowisko Dofinansowanie projektów związanych z inwestycjami w OZE w ramach Polskich Narodowych Strategicznych Ram Odniesienia na lata 2007 2013 moŝe
Raport, został przygotowany na podstawie 42 wypełnionych przez uczestników kursu ankiet ewaluacyjnych przeprowadzonych w dniach:
 Raport z analizy ankiet ewaluacyjnych kursu Gender Mainstreaming przeprowadzonego w dniach : 15-16.10.2009r., 22-23.10.2009r., 24 25.10.2009r., 05-06.11.2009r. w Wydziale Nauk Społecznych WSP TWP w Warszawie
Raport z analizy ankiet ewaluacyjnych kursu Gender Mainstreaming przeprowadzonego w dniach : 15-16.10.2009r., 22-23.10.2009r., 24 25.10.2009r., 05-06.11.2009r. w Wydziale Nauk Społecznych WSP TWP w Warszawie
Zbigniew Krzysiak. Projektowanie 2D w programie AutoCAD
 Zbigniew Krzysiak Projektowanie 2D w programie AutoCAD Recenzenci Dr hab. inż. Józef Drewniak, prof. ATH w Bielsku-Białej Dr inż. Kamil Sybilski Projekt okładki Andrzej Leśkiewicz Redakcja Krzysztof Janus
Zbigniew Krzysiak Projektowanie 2D w programie AutoCAD Recenzenci Dr hab. inż. Józef Drewniak, prof. ATH w Bielsku-Białej Dr inż. Kamil Sybilski Projekt okładki Andrzej Leśkiewicz Redakcja Krzysztof Janus
SzeregFouriera-Legendre a
 SzeregFouriera-Legendre a Szereg Fouriera-Legendre a : n=0 P n (t) f n Współczynniki f n = Pn (t) f (t) dt - Pn (t) 2 dt - = 2 n + Pn 2 - (t) f (t) dt Pn - (t) 2 dt = 2 2 n + Zadanie Policz kwadrat normy
SzeregFouriera-Legendre a Szereg Fouriera-Legendre a : n=0 P n (t) f n Współczynniki f n = Pn (t) f (t) dt - Pn (t) 2 dt - = 2 n + Pn 2 - (t) f (t) dt Pn - (t) 2 dt = 2 2 n + Zadanie Policz kwadrat normy
Mathematica - organizacja. czyli sztuka obliczeń symbolicznych. Możliwości. Mathematica do czego można ją użyć. Możliwości, cd. Mathematica publikacje
 czyli sztuka obliczeń symbolicznych Mathematica - organizacja Dokument Mathematica zorganizowany jest w tzw. komórki. Ręczne zerowanie zmiennych Clear[variables] (* czyści wartości zmiennych*) x=. (* to
czyli sztuka obliczeń symbolicznych Mathematica - organizacja Dokument Mathematica zorganizowany jest w tzw. komórki. Ręczne zerowanie zmiennych Clear[variables] (* czyści wartości zmiennych*) x=. (* to
MATERIAŁY DIAGNOSTYCZNE Z MATEMATYKI
 MATERIAŁY DIAGNOSTYCZNE Z MATEMATYKI LUTY 01 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla zdającego 1. Sprawdź, czy arkusz zawiera strony (zadania 1 ).. Arkusz zawiera 4 zadania zamknięte i 9
MATERIAŁY DIAGNOSTYCZNE Z MATEMATYKI LUTY 01 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla zdającego 1. Sprawdź, czy arkusz zawiera strony (zadania 1 ).. Arkusz zawiera 4 zadania zamknięte i 9
DANE MAKROEKONOMICZNE (TraderTeam.pl: Rafa Jaworski, Marek Matuszek) Lekcja V
 DANE MAKROEKONOMICZNE (TraderTeam.pl: Rafa Jaworski, Marek Matuszek) Lekcja V Inflacja (CPI, PPI) Wszelkie prawa zastrze one. Kopiowanie i rozpowszechnianie ca ci lub fragmentu niniejszej publikacji w
DANE MAKROEKONOMICZNE (TraderTeam.pl: Rafa Jaworski, Marek Matuszek) Lekcja V Inflacja (CPI, PPI) Wszelkie prawa zastrze one. Kopiowanie i rozpowszechnianie ca ci lub fragmentu niniejszej publikacji w
Sin[Pi / 4] Log[2, 1024] Prime[10]
![Sin[Pi / 4] Log[2, 1024] Prime[10] Sin[Pi / 4] Log[2, 1024] Prime[10]](/thumbs/64/50895785.jpg) In[1]:= (* WSTĘP DO PAKIETU MATHEMATICA *) (* autorzy: Łukasz Płociniczak,Marek Teuerle*) (* Składnia: nazwy funkcji z wielkiej litery a argumenty w kwadratowych nawiasach. Wywołujemy wartość SHIFT+ENTER
In[1]:= (* WSTĘP DO PAKIETU MATHEMATICA *) (* autorzy: Łukasz Płociniczak,Marek Teuerle*) (* Składnia: nazwy funkcji z wielkiej litery a argumenty w kwadratowych nawiasach. Wywołujemy wartość SHIFT+ENTER
Główne wyniki badania
 1 Nota metodologiczna Badanie Opinia publiczna na temat ubezpieczeń przeprowadzono w Centrum badania Opinii Społecznej na zlecenie Urzędu Ochrony Konkurencji i Konsumentów w dniach od 13 do 17 maja 2004
1 Nota metodologiczna Badanie Opinia publiczna na temat ubezpieczeń przeprowadzono w Centrum badania Opinii Społecznej na zlecenie Urzędu Ochrony Konkurencji i Konsumentów w dniach od 13 do 17 maja 2004
KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM. Matematyka Poziom rozszerzony
 KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM Matematyka Poziom rozszerzony Listopad 0 Zadania zamknięte Za każdą poprawną odpowiedź zdający otrzymuje punkt. Poprawna odpowiedź Wskazówki do rozwiązania.
KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM Matematyka Poziom rozszerzony Listopad 0 Zadania zamknięte Za każdą poprawną odpowiedź zdający otrzymuje punkt. Poprawna odpowiedź Wskazówki do rozwiązania.
Blok III: Funkcje elementarne. e) y = 1 3 x. f) y = x. g) y = 2x. h) y = 3x. c) y = 3x + 2. d) y = x 3. c) y = x. d) y = x.
 Blok III: Funkcje elementarne III. Narysuj wykres funkcji: a) y = x y = x y = x y = x III. Narysuj wykres funkcji: a) y = x + y = 4 x III. Znajdź miejsca zerowe funkcji: a) y = 6 x y = x e) y = x f) y
Blok III: Funkcje elementarne III. Narysuj wykres funkcji: a) y = x y = x y = x y = x III. Narysuj wykres funkcji: a) y = x + y = 4 x III. Znajdź miejsca zerowe funkcji: a) y = 6 x y = x e) y = x f) y
Korekta jako formacja cenowa
 Korekta jako formacja cenowa Agenda Co to jest korekta i jej cechy Korekta a klasyczne formacje cenowe Korekta w teorii fal Geometria Czas - jako narzędzie Przykłady Korekta To ruch ceny na danym instrumencie
Korekta jako formacja cenowa Agenda Co to jest korekta i jej cechy Korekta a klasyczne formacje cenowe Korekta w teorii fal Geometria Czas - jako narzędzie Przykłady Korekta To ruch ceny na danym instrumencie
Mathematica jako narz dzie badawcze Cz ± pi ta. Fraktale
 Mathematica jako narz dzie badawcze Cz ± pi ta. Fraktale Czy koªa s pi kne? Mo»na udowodni wiele teorii na ich temat, wiele ich cech jest interesuj cych, ale»eby koªo miaªo by pi kne? Jest nudne, wsz dzie
Mathematica jako narz dzie badawcze Cz ± pi ta. Fraktale Czy koªa s pi kne? Mo»na udowodni wiele teorii na ich temat, wiele ich cech jest interesuj cych, ale»eby koªo miaªo by pi kne? Jest nudne, wsz dzie
Optyka geometryczna i falowa
 Pojęcie podstawowe: promień świetlny. Optyka geometryczna i alowa Podstawowa obserwacja: jeżeli promień świetlny pada na granicę dwóch ośrodków to: ulega odbiciu na powierzchni granicznej za!amaniu przy
Pojęcie podstawowe: promień świetlny. Optyka geometryczna i alowa Podstawowa obserwacja: jeżeli promień świetlny pada na granicę dwóch ośrodków to: ulega odbiciu na powierzchni granicznej za!amaniu przy
Przekształcenia wykresów funkcji
 Przekształcenia wykresów funkcji Przekształcenia wykresów funkcji Jerzy Rutkowski Teoria Niech f : R R będzie dowolną funkcją i niech liczby a, k R spełniają warunki: a > 0 i k 0 Związek między funkcją
Przekształcenia wykresów funkcji Przekształcenia wykresów funkcji Jerzy Rutkowski Teoria Niech f : R R będzie dowolną funkcją i niech liczby a, k R spełniają warunki: a > 0 i k 0 Związek między funkcją
Funkcje: wielomianowa, wykładnicza, logarytmiczna wykład 2
 Funkcje: wielomianowa, wykładnicza, logarytmiczna wykład 2 dr Mariusz Grządziel semestr zimowy 2013 Potęgowanie Dla dowolnej liczby dodatniej a oraz liczy wymiernej w = p/q definiujemy: a w (a 1/q ) p.
Funkcje: wielomianowa, wykładnicza, logarytmiczna wykład 2 dr Mariusz Grządziel semestr zimowy 2013 Potęgowanie Dla dowolnej liczby dodatniej a oraz liczy wymiernej w = p/q definiujemy: a w (a 1/q ) p.
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM ROZSZERZONY 25 LUTEGO 2017 CZAS PRACY: 180 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Liczba 15! jest podzielna
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM ROZSZERZONY 25 LUTEGO 2017 CZAS PRACY: 180 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Liczba 15! jest podzielna
O SPIRALI ARCHIMEDESA I JEJ INTERPRETACJI PRZYRODNICZEJ ILUSTRUJĄCEJ BUDOWĘ PAJĘCZYN
 Polska Problemy Nauk Stosowanych, 016, Tom 4, s. 19 4 Szczecin dr Grzegorz Paweł SKORNY, dr Andrzej Antoni CZAJKOWSKI, mgr Jakub ŚLEDZIOWSKI Wyższa Szkoła Techniczno-Ekonomiczna w Szczecinie, Wydział Transportu
Polska Problemy Nauk Stosowanych, 016, Tom 4, s. 19 4 Szczecin dr Grzegorz Paweł SKORNY, dr Andrzej Antoni CZAJKOWSKI, mgr Jakub ŚLEDZIOWSKI Wyższa Szkoła Techniczno-Ekonomiczna w Szczecinie, Wydział Transportu
Korzy ci wynikaj ce ze standaryzacji procesów w organizacjach publicznych a zarz dzanie jako ci
 Roman Batko Korzy ci wynikaj ce ze standaryzacji procesów w organizacjach publicznych a zarz dzanie jako ci Uniwersytet Jagiello ski wypracowanie i upowszechnienie najbardziej skutecznej i efektywnej dobrej
Roman Batko Korzy ci wynikaj ce ze standaryzacji procesów w organizacjach publicznych a zarz dzanie jako ci Uniwersytet Jagiello ski wypracowanie i upowszechnienie najbardziej skutecznej i efektywnej dobrej
Postrzeganie reklamy zewnętrznej - badania
 Według opublikowanych na początku tej dekady badań Demoskopu, zdecydowana większość respondentów (74%) przyznaje, że w miejscowości, w której mieszkają znajdują się nośniki reklamy zewnętrznej (specjalne,
Według opublikowanych na początku tej dekady badań Demoskopu, zdecydowana większość respondentów (74%) przyznaje, że w miejscowości, w której mieszkają znajdują się nośniki reklamy zewnętrznej (specjalne,
1 Przypomnienie wiadomo±ci ze szkoªy ±redniej. Rozwi zywanie prostych równa«i nierówno±ci
 Zebraª do celów edukacyjnych od wykªadowców PK, z ró»nych podr czników Maciej Zakarczemny 1 Przypomnienie wiadomo±ci ze szkoªy ±redniej Rozwi zywanie prostych równa«i nierówno±ci dotycz cych funkcji elementarnych,
Zebraª do celów edukacyjnych od wykªadowców PK, z ró»nych podr czników Maciej Zakarczemny 1 Przypomnienie wiadomo±ci ze szkoªy ±redniej Rozwi zywanie prostych równa«i nierówno±ci dotycz cych funkcji elementarnych,
Wyznaczanie statycznego i kinetycznego współczynnika tarcia przy pomocy równi pochyłej
 Wyznaczanie statycznego i kinetycznego współczynnika tarcia przy pomocy równi pochyłej Równia pochyła jest przykładem maszyny prostej. Jej konstrukcja składa się z płaskiej powierzchni nachylonej pod kątem
Wyznaczanie statycznego i kinetycznego współczynnika tarcia przy pomocy równi pochyłej Równia pochyła jest przykładem maszyny prostej. Jej konstrukcja składa się z płaskiej powierzchni nachylonej pod kątem
POSTANOWIENIE. SSN Henryk Pietrzkowski (przewodniczący) SSN Anna Kozłowska SSN Dariusz Zawistowski (sprawozdawca)
 Sygn. akt II CSK 35/13 POSTANOWIENIE Sąd Najwyższy w składzie: Dnia 30 października 2013 r. SSN Henryk Pietrzkowski (przewodniczący) SSN Anna Kozłowska SSN Dariusz Zawistowski (sprawozdawca) w sprawie
Sygn. akt II CSK 35/13 POSTANOWIENIE Sąd Najwyższy w składzie: Dnia 30 października 2013 r. SSN Henryk Pietrzkowski (przewodniczący) SSN Anna Kozłowska SSN Dariusz Zawistowski (sprawozdawca) w sprawie
Redukcja płaskiego układu wektorów, redukcja w punkcie i redukcja do najprostszej postaci
 Redukcja płaskiego układu wektorów, redukcja w punkcie i redukcja do najprostszej postaci Twierdzenie o redukcji: Każdy układ wektorów równoważny jest układowi złożonemu ze sumy o początku w dowolnym punkcie
Redukcja płaskiego układu wektorów, redukcja w punkcie i redukcja do najprostszej postaci Twierdzenie o redukcji: Każdy układ wektorów równoważny jest układowi złożonemu ze sumy o początku w dowolnym punkcie
Kratownice Wieża Eiffel a
 Kratownice Wieża Eiffel a Kratownica jest to konstrukcja nośna, składająca się z prętów połączonch ze sobą w węzłach. Kratownica może bć: 1) płaska, gd wszstkie pręt leżą w jednej płaszczźnie, 2) przestrzenna,
Kratownice Wieża Eiffel a Kratownica jest to konstrukcja nośna, składająca się z prętów połączonch ze sobą w węzłach. Kratownica może bć: 1) płaska, gd wszstkie pręt leżą w jednej płaszczźnie, 2) przestrzenna,
DANE MAKROEKONOMICZNE (TraderTeam.pl: Rafa Jaworski, Marek Matuszek) Lekcja IV
 DANE MAKROEKONOMICZNE (TraderTeam.pl: Rafa Jaworski, Marek Matuszek) Lekcja IV Stopa procentowa Wszelkie prawa zastrze one. Kopiowanie i rozpowszechnianie ca ci lub fragmentu niniejszej publikacji w jakiejkolwiek
DANE MAKROEKONOMICZNE (TraderTeam.pl: Rafa Jaworski, Marek Matuszek) Lekcja IV Stopa procentowa Wszelkie prawa zastrze one. Kopiowanie i rozpowszechnianie ca ci lub fragmentu niniejszej publikacji w jakiejkolwiek
Zamiana sumowania po stanach jednocząstkowych na całkowanie
 TiFS, Ćwiczenia nr 11 Zamiana sumowania po stanach jednocząstkowych na całkowanie Gęstość stanów kwantowych na osi energii f (E) określa liczbę stanów N(E) w określonym przedziale energii de: f (E) de
TiFS, Ćwiczenia nr 11 Zamiana sumowania po stanach jednocząstkowych na całkowanie Gęstość stanów kwantowych na osi energii f (E) określa liczbę stanów N(E) w określonym przedziale energii de: f (E) de
MATEMATYKA EiT. (studia drugiego stopnia, drugi semestr) 3 2i, 2i44 i i )12, (cos 15 + i sin 15 ) 15, ( p 3 i) i)17, (i 1) 9, ( 1 i
 MATEMATYKA EiT (studia drugiego stopnia, drugi semestr) ) Wyznaczyć Re z; Im z; jzj ; z dla z = ( + i)(3 i), ( + i)( i) + (3 5i), (+i) 3 i, i44 i 45 i 46 +3i, 47 (cos 33 + i sin 33 ), ( + p 3 i)7, (i )
MATEMATYKA EiT (studia drugiego stopnia, drugi semestr) ) Wyznaczyć Re z; Im z; jzj ; z dla z = ( + i)(3 i), ( + i)( i) + (3 5i), (+i) 3 i, i44 i 45 i 46 +3i, 47 (cos 33 + i sin 33 ), ( + p 3 i)7, (i )
TO TRZEBA ROZWIĄZAĆ-(I MNÓSTWO INNYCH )
 Kujawsko-Pomorskie Centrum Edukacji Nauczycieli w Bydgoszczy PLACÓWKA AKREDYTOWANA TO TRZEBA ROZWIĄZAĆ-(I MNÓSTWO INNYCH ) PAKIET ZADAŃ (zadania wybrano ze zbiorów autorów i wydawnictw: Kiełbasa, Res Polona,
Kujawsko-Pomorskie Centrum Edukacji Nauczycieli w Bydgoszczy PLACÓWKA AKREDYTOWANA TO TRZEBA ROZWIĄZAĆ-(I MNÓSTWO INNYCH ) PAKIET ZADAŃ (zadania wybrano ze zbiorów autorów i wydawnictw: Kiełbasa, Res Polona,
EGZAMIN MATURALNY Z MATEMATYKI
 ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZ CIA EGZAMINU! Miejsce na naklejk MMA-P1_1P-092 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2009 Czas pracy 120 minut Instrukcja
ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZ CIA EGZAMINU! Miejsce na naklejk MMA-P1_1P-092 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2009 Czas pracy 120 minut Instrukcja
Instrukcja instalacji programu Plantator oraz transferu pliku danych z/do PC kolektor danych PT-20
 BEXLAB RYSZARD MATUSZYK UL. BRZOZOWA 14 05-311 DĘBE WIELKIE TEL. KOM. 512-019-590 Instrukcja instalacji programu Plantator oraz transferu pliku danych z/do PC kolektor danych PT-20 http://bexlab.pl BEXLAB
BEXLAB RYSZARD MATUSZYK UL. BRZOZOWA 14 05-311 DĘBE WIELKIE TEL. KOM. 512-019-590 Instrukcja instalacji programu Plantator oraz transferu pliku danych z/do PC kolektor danych PT-20 http://bexlab.pl BEXLAB
Zadania z analizy matematycznej - sem. I Liczby i funkcje
 Zadania z analizy matematycznej - sem. I Liczby i funkcje Definicja 1. Mówimy że: liczba m Z jest dzielnikiem liczby n Z gdy istnieje l Z takie że n = l m. Zapisujemy to symbolem m n; liczba m Z jest wspólnym
Zadania z analizy matematycznej - sem. I Liczby i funkcje Definicja 1. Mówimy że: liczba m Z jest dzielnikiem liczby n Z gdy istnieje l Z takie że n = l m. Zapisujemy to symbolem m n; liczba m Z jest wspólnym
ODLEGŁOŚĆ NA PŁASZCZYŹNIE - SPRAWDZIAN
 ODLEGŁOŚĆ NA PŁASZCZYŹNIE - SPRAWDZIAN Gr. 1 Zad. 1. Dane są punkty: P = (-, 1), R = (5, -1), S = (, 3). a) Oblicz odległość między punktami R i S. b) Wyznacz współrzędne środka odcinka PR. c) Napisz równanie
ODLEGŁOŚĆ NA PŁASZCZYŹNIE - SPRAWDZIAN Gr. 1 Zad. 1. Dane są punkty: P = (-, 1), R = (5, -1), S = (, 3). a) Oblicz odległość między punktami R i S. b) Wyznacz współrzędne środka odcinka PR. c) Napisz równanie
Analiza Matematyczna MAEW101 MAP1067
 1 Analiza Matematyczna MAEW101 MAP1067 Wydział Elektroniki Przykłady do Listy Zadań nr 14 Funkcje wielu zmiennych. Płaszczyzna styczna. Ekstrema Opracowanie: dr hab. Agnieszka Jurlewicz Przykłady do zadania
1 Analiza Matematyczna MAEW101 MAP1067 Wydział Elektroniki Przykłady do Listy Zadań nr 14 Funkcje wielu zmiennych. Płaszczyzna styczna. Ekstrema Opracowanie: dr hab. Agnieszka Jurlewicz Przykłady do zadania
EGZAMIN MATURALNY Z MATEMATYKI
 pobrano z www.sqlmedia.pl ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZ CIA EGZAMINU! Miejsce na naklejk MMA-P1_1P-092 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2009 Czas
pobrano z www.sqlmedia.pl ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZ CIA EGZAMINU! Miejsce na naklejk MMA-P1_1P-092 EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MAJ ROK 2009 Czas
Podstawy analizy matematycznej II
 Podstawy analizy matematycznej II Andrzej Marciniak Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii informatycznych i ich zastosowań
Podstawy analizy matematycznej II Andrzej Marciniak Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii informatycznych i ich zastosowań
Jakub Dzionek, Zygmunt Kalinowski Nowe logo i nowy system identyfikacji Muzeum Pierwszych Piastów na Lednicy. Studia Lednickie 12, 199-202
 Jakub Dzionek, Zygmunt Kalinowski Nowe logo i nowy system identyfikacji Muzeum Pierwszych Piastów na Lednicy Studia Lednickie 12, 199-202 2013 Jakub Dzionek, Zygmunt Kalinowski Muzeum Pierwszych Piastów
Jakub Dzionek, Zygmunt Kalinowski Nowe logo i nowy system identyfikacji Muzeum Pierwszych Piastów na Lednicy Studia Lednickie 12, 199-202 2013 Jakub Dzionek, Zygmunt Kalinowski Muzeum Pierwszych Piastów
OFERTA UPOMINKÓW Z OKAZJI DNIA KOBIET
 OFERTA UPOMINKÓW Z OKAZJI DNIA KOBIET 2011 Kwiaty w puszce Puszki zawierające nasiona lub cebulki roślin wraz ze specjalnie spreparowanymi składnikami gwarantującymi optymalne warunki wzrostu, przeobrażają
OFERTA UPOMINKÓW Z OKAZJI DNIA KOBIET 2011 Kwiaty w puszce Puszki zawierające nasiona lub cebulki roślin wraz ze specjalnie spreparowanymi składnikami gwarantującymi optymalne warunki wzrostu, przeobrażają
2010 W. W. Norton & Company, Inc. Nadwyżka Konsumenta
 2010 W. W. Norton & Company, Inc. Nadwyżka Konsumenta Pieniężny Pomiar Korzyści z Handlu Możesz kupić tyle benzyny ile chcesz, po cenie 2zł za litr. Jaka jest najwyższa cena, jaką zapłacisz za 1 litr benzyny?
2010 W. W. Norton & Company, Inc. Nadwyżka Konsumenta Pieniężny Pomiar Korzyści z Handlu Możesz kupić tyle benzyny ile chcesz, po cenie 2zł za litr. Jaka jest najwyższa cena, jaką zapłacisz za 1 litr benzyny?
Marii. Skłodowskiej-Curie. Ekspozycja-warsztaty Lekcje
 Epyj-y Lj M.--.-v.f L M 2011 j- Epyj-y p L M NR (b M) p Mé, Uy P-D, Uy. P M j- Uy P 11 Oy. y yp M j- phą ąż Lj M j- Ib hv, yj p E EDP 2003. Zję M j- ą ć Mé. L M 386, v Dv L 92290 hây-mby - FRANJA (33)
Epyj-y Lj M.--.-v.f L M 2011 j- Epyj-y p L M NR (b M) p Mé, Uy P-D, Uy. P M j- Uy P 11 Oy. y yp M j- phą ąż Lj M j- Ib hv, yj p E EDP 2003. Zję M j- ą ć Mé. L M 386, v Dv L 92290 hây-mby - FRANJA (33)
Przekształcenia wykresów funkcji
 Przekształcenia wykresów funkcji Przekształcenia wykresów funkcji Jerzy Rutkowski Teoria Niech f : R R będzie dowolną funkcją i niech liczby a, k R spełniają warunki: a > 0 i k 0. Związek między funkcją
Przekształcenia wykresów funkcji Przekształcenia wykresów funkcji Jerzy Rutkowski Teoria Niech f : R R będzie dowolną funkcją i niech liczby a, k R spełniają warunki: a > 0 i k 0. Związek między funkcją
Zadania zamknięte. A) 3 pierwiastki B) 1 pierwiastek C) 4 pierwiastki D) 2 pierwiastki. C) a 4 = 2 3
 Zadania zamknięte ZADANIE 1 (1 PKT) Równanie x2 3x+2 = 0 ma: x 2 4 A) 3 pierwiastki B) 1 pierwiastek C) 4 pierwiastki D) 2 pierwiastki ZADANIE 2 (1 PKT) Liczba b jest 3 razy większa od liczby a. Wtedy
Zadania zamknięte ZADANIE 1 (1 PKT) Równanie x2 3x+2 = 0 ma: x 2 4 A) 3 pierwiastki B) 1 pierwiastek C) 4 pierwiastki D) 2 pierwiastki ZADANIE 2 (1 PKT) Liczba b jest 3 razy większa od liczby a. Wtedy
 Ę Ć Ę Ó Ą ź Ó Ń Ń Ć Ó Ó Ł Ź Ł Ą Ł ć Ł ć Ź Ź ź Ń Ń Ź ć ć Ó Ą ź ć ć Ż ć ć Ź ć Ą ź Ł Ł Ę ć ć Ł Ś ć Ź ć Ł ć ć ć Ż Ó Ś Ł ć ź ć Ć ć ź ć Ź Ź Ł ć ć ć ź ź Ż Ą ź Ł ć ć ć Ó Ś Ć Ń ć Ń ć ć ź ć ć ć ć Ą Ł Ń ć Ł ć Ę Ą
Ę Ć Ę Ó Ą ź Ó Ń Ń Ć Ó Ó Ł Ź Ł Ą Ł ć Ł ć Ź Ź ź Ń Ń Ź ć ć Ó Ą ź ć ć Ż ć ć Ź ć Ą ź Ł Ł Ę ć ć Ł Ś ć Ź ć Ł ć ć ć Ż Ó Ś Ł ć ź ć Ć ć ź ć Ź Ź Ł ć ć ć ź ź Ż Ą ź Ł ć ć ć Ó Ś Ć Ń ć Ń ć ć ź ć ć ć ć Ą Ł Ń ć Ł ć Ę Ą
 Ć ń ń Ę Ó ń Ę ć ć ź Ę ć Ź ć ń ń ń ń ć ń ń ń Ę ć Ą Ę Ź ć ć ń Ą ź Ó ź ń Ę ć ć ń Ó Ą Ą ź ź Ę Ć Ę ć Ó ź Ą ć ć Ę ź ć Ź ć Ę ć Ź Ź ć ć ć ć Ł Ę ć Ć Ę Ź ć Ż Ę ń Ź Ę ć ń ć ń Ź Ź ń Ę ń ć Ó Ó Ź ć ń Ź ń Ż ć ź ź Ą Ć
Ć ń ń Ę Ó ń Ę ć ć ź Ę ć Ź ć ń ń ń ń ć ń ń ń Ę ć Ą Ę Ź ć ć ń Ą ź Ó ź ń Ę ć ć ń Ó Ą Ą ź ź Ę Ć Ę ć Ó ź Ą ć ć Ę ź ć Ź ć Ę ć Ź Ź ć ć ć ć Ł Ę ć Ć Ę Ź ć Ż Ę ń Ź Ę ć ń ć ń Ź Ź ń Ę ń ć Ó Ó Ź ć ń Ź ń Ż ć ź ź Ą Ć
 Ą Ą ć Ż ć ć ź ć ć ć ć ć ć ć ć ć Ą ć ć Ą ć ć Ó Ź ć Ą ć ć ć ć ć Ą ć ć Ą Ź ć ć ć ć ć ć ć ć ć ć ć ć ć Ą ć Ą Ż ć Ź ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć Ż ć ć Ż ć ć ć ć ć Ą ź ć Ę ć ć ć ć Ź ć ć ź ć ć ć
Ą Ą ć Ż ć ć ź ć ć ć ć ć ć ć ć ć Ą ć ć Ą ć ć Ó Ź ć Ą ć ć ć ć ć Ą ć ć Ą Ź ć ć ć ć ć ć ć ć ć ć ć ć ć Ą ć Ą Ż ć Ź ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć Ż ć ć Ż ć ć ć ć ć Ą ź ć Ę ć ć ć ć Ź ć ć ź ć ć ć
 Ą Ą Ą ń ż Ę Ż ż ń ż ć ż ż ć Ń Ż ż ż Ź Ą ń Ż Ę Ń ż Ą ń ż ć Ź ć ć ż ć ż ć ż Ż ż ż ż ć ż ń ż ć ń ż ż ż ć ć ń ń ż ć ż ćż ż ż ń ż ń ż ż Ę ż Ę Ą ż ż Ęć ż ż Ę ż ć ć ć ż ń ź ń ń Ź ż Ę Ę ń Ź Ź ć Ż ć ź ż ż ż ź Ę
Ą Ą Ą ń ż Ę Ż ż ń ż ć ż ż ć Ń Ż ż ż Ź Ą ń Ż Ę Ń ż Ą ń ż ć Ź ć ć ż ć ż ć ż Ż ż ż ż ć ż ń ż ć ń ż ż ż ć ć ń ń ż ć ż ćż ż ż ń ż ń ż ż Ę ż Ę Ą ż ż Ęć ż ż Ę ż ć ć ć ż ń ź ń ń Ź ż Ę Ę ń Ź Ź ć Ż ć ź ż ż ż ź Ę
 Ę Ę Ń ć Ź ć Ź Ń Ę Ó Ź Ę Ź Ń Ń ć Ź ź Ą Ź ć Ę Ą Ę Ź Ź Ź Ę Ź Ą Ź Ź Ą Ó Ó Ź Ą ć Ń Ą ć ć ć Ż Ą Ą Ż Ą Ą Ą ć Ź Ź Ę Ą Ą Ę Ź Ń ź Ś ź Ż Ż Ż Ą ć Ś Ą ć Ą Ż Ń Ż Ą Ź Ź ć Ń Ś Ń Ź Ź Ą Ź Ż Ą ź ć ć Ę Ź Ź Ź ź Ę ź Ę Ń Ź Ę
Ę Ę Ń ć Ź ć Ź Ń Ę Ó Ź Ę Ź Ń Ń ć Ź ź Ą Ź ć Ę Ą Ę Ź Ź Ź Ę Ź Ą Ź Ź Ą Ó Ó Ź Ą ć Ń Ą ć ć ć Ż Ą Ą Ż Ą Ą Ą ć Ź Ź Ę Ą Ą Ę Ź Ń ź Ś ź Ż Ż Ż Ą ć Ś Ą ć Ą Ż Ń Ż Ą Ź Ź ć Ń Ś Ń Ź Ź Ą Ź Ż Ą ź ć ć Ę Ź Ź Ź ź Ę ź Ę Ń Ź Ę
 Ł Ł Ś Ł Ń Ń Ł Ę ć ć Ż ć Ż Ę ć ć ć Ę Ę ć Ż ź Ż ć Ż Ą Ę Ę Ż Ę ź Ś ć ć Ę ź Ą ć Ł Ę Ę ź Ż ć ć Ę Ę Ż Ż ć Ż Ę ć Ę Ę ć ź Ą ć ć ć Ę ć ć ź ć ć ź ć Ś Ż ć ć Ż ć Ż ć Ż ć ź Ż Ż Ę Ę ź Ę ć Ż Ż Ę Ż Ę Ż Ą ć ć ć Ż ź Ż ć
Ł Ł Ś Ł Ń Ń Ł Ę ć ć Ż ć Ż Ę ć ć ć Ę Ę ć Ż ź Ż ć Ż Ą Ę Ę Ż Ę ź Ś ć ć Ę ź Ą ć Ł Ę Ę ź Ż ć ć Ę Ę Ż Ż ć Ż Ę ć Ę Ę ć ź Ą ć ć ć Ę ć ć ź ć ć ź ć Ś Ż ć ć Ż ć Ż ć Ż ć ź Ż Ż Ę Ę ź Ę ć Ż Ż Ę Ż Ę Ż Ą ć ć ć Ż ź Ż ć
 ć ź ć ź ć ć Ź ć ć ć ć ź ć ć ź ć ć Ź Ł ć ć ć Ż ć Ż ć ć Ź ź Ć Ą Ź Ż Ż Ź Ż Ć Ł Ł Ź Ź ź Ą ź Ą Ć Ź Ł Ź ć Ź ćź Ź Ź Ą Ź ć Ź ć Ł ć Ł ć ć Ł ć Ą ć ć ć ź ź ć ć ć ć ź ć ć ć ź ć ć ć ć ć ć ć ć Ł Ź ć ź ć Ą ć ć Ą Ć
ć ź ć ź ć ć Ź ć ć ć ć ź ć ć ź ć ć Ź Ł ć ć ć Ż ć Ż ć ć Ź ź Ć Ą Ź Ż Ż Ź Ż Ć Ł Ł Ź Ź ź Ą ź Ą Ć Ź Ł Ź ć Ź ćź Ź Ź Ą Ź ć Ź ć Ł ć Ł ć ć Ł ć Ą ć ć ć ź ź ć ć ć ć ź ć ć ć ź ć ć ć ć ć ć ć ć Ł Ź ć ź ć Ą ć ć Ą Ć
 Ł Ł Ń Ń Ś Ń Ń ź Ń Ą Ż Ł Ę Ł Ś Ą Ą Ś Ł Ń Ś Ą Ń ć Ą Ą Ą Ą Ł Ś Ę Ś Ń Ż Ż Ś Ć Ź ć Ę Ś Ą Ź Ś Ś Ś Ś Ż Ś Ź Ą Ż Ć Ą Ś Ź Ż Ź Ź Ź Ś Ą ć Ś Ść Ś Ść Ż Ź Ź ć Ź Ź Ź Ż Ż Ź Ś Ś Ż Ż ć Ź Ż Ż ć Ś Ś Ą Ź ć Ś ć ć Ś Ś ć Ż Ż Ą
Ł Ł Ń Ń Ś Ń Ń ź Ń Ą Ż Ł Ę Ł Ś Ą Ą Ś Ł Ń Ś Ą Ń ć Ą Ą Ą Ą Ł Ś Ę Ś Ń Ż Ż Ś Ć Ź ć Ę Ś Ą Ź Ś Ś Ś Ś Ż Ś Ź Ą Ż Ć Ą Ś Ź Ż Ź Ź Ź Ś Ą ć Ś Ść Ś Ść Ż Ź Ź ć Ź Ź Ź Ż Ż Ź Ś Ś Ż Ż ć Ź Ż Ż ć Ś Ś Ą Ź ć Ś ć ć Ś Ś ć Ż Ż Ą
Poniżej instrukcja użytkowania platformy
 Adres dostępowy: http://online.inter-edukacja.wsns.pl/ Poniżej instrukcja użytkowania platformy WYŻSZA SZKOŁA NAUK SPOŁECZNYCH z siedzibą w Lublinie SZKOLENIA PRZEZ INTERNET Instrukcja użytkowania platformy
Adres dostępowy: http://online.inter-edukacja.wsns.pl/ Poniżej instrukcja użytkowania platformy WYŻSZA SZKOŁA NAUK SPOŁECZNYCH z siedzibą w Lublinie SZKOLENIA PRZEZ INTERNET Instrukcja użytkowania platformy
Raport zrównoważonego rozwoju Kompanii Piwowarskiej 2012
 Raport zrównoważonego rozwoju Kompanii Piwowarskiej 2012 Raport obejmuje dane za rok finansowy F12 (12 miesięcy od 1 kwietnia 2011 r. do 31 marca 2012 r.), chyba że w treści wskazano inaczej. Raport został
Raport zrównoważonego rozwoju Kompanii Piwowarskiej 2012 Raport obejmuje dane za rok finansowy F12 (12 miesięcy od 1 kwietnia 2011 r. do 31 marca 2012 r.), chyba że w treści wskazano inaczej. Raport został




