III. Dvojný a trojný integrál
|
|
|
- Filip Pietrzak
- 6 lat temu
- Przeglądów:
Transkrypt
1 III. vojný a trojný integrál III.. Eistence Necht je měřitelná v Jordanově smslu množina v E resp. E a funkce f je omezená na. Necht množina bodů nespojitosti funkce f v má míru. Potom f je integrovatelná v, tj. integrál f,dd resp. f,,zdddz eistuje. poznámka : alší podrobnosti najdete ve skriptech J.Neustupa: Matematika II. Příklad 7. Rozhodněte, zda daný integrál dd eistuje, jestliže : + a {[, E : + }; b {[, E : + }; c {[, E : + }. Budeme vcházet z toho, že dvojný a trojný integrál vlastní je definován pouze pro funkce omezené na omezené množině a dále budeme používat větu o eistenci. a Množina je měřitelná, ted je omezená a její hranice má míru a f, je spojitá a + omezená na. Integrál eistuje. b Množina je měřitelná, ale f, není omezená v, protože [, a lim [, [, +. Integrál neeistuje. c f, opět není omezená na [,, integrál neeistuje. 5
2 Příklad8.Je dána množina {[, E : + }. Všetřete, zda eistují dvojné integrál : sin + dd dd a dd, b + +, c + +, d dd, e + a eistuje, lim [, [, b neeistuje, lim [, [, c eistuje, d neeistuje, protože např. lim + dd. sin + < funkce je omezená, + +, + + je spojitá v E, [, [,, + e neeistuje, protože např. lim [, [, +. / Příklad 9. Všetřete, zda eistují trojné integrál : dddz a W ++z, W {[,,z E :,, z }, b +zdddz, W {[,,z E :, z }, W c + +z 9 dddz, W {[,,z E : < + +z < }. W a neeistuje, protože funkce neníomezenánaw,{++z } W, ++z b neeistuje, protože množina W není omezená v E, c eistuje; W je měřitelná množina v E ; + +z 9 ve W, ted integrovaná funkce je spojitá na W; 8 < + +z 9 < pro každý bod [,,z W, 5 ted funkce je omezená na W. III.. Fubiniova Fubiniho věta pro dvojný integrál Množinu M {[, E ; a b, φ φ }, kde funkce φ, φ jsou spojité na < a,b > a φ φ, nazýváme elementárním oborem integrace vzhledem k ose. Necht M je elementární obor integrace vzhledem k ose. Necht funkce f, je spojitá v M. Pak b φ f,dd f,d d. a 6 φ
3 poznámka: Analogick pro elementární obor vzhledem k ose Vpočítejte dvojné integrál na daných obdélníkových množinách : Příklad. I I ln dd +, {[, E :, } d d ln. Příklad. I d [ Obdélník je ohraničen křivkami,,,. d [ ln ln + d ln ln ln+ln dd +, {[, E :, } [ I + d d d d 5 [ d ln 5 ln ln 9 5. Příklad. I sin dd, {[, E : π, } I [ sin / π/ sin d 8 / cos d π 7 7π. [ d poznámka: Je-li funkce tpu f, g h a množina je obdélník b d < a, b > < c, d >, pak f,dd gd h d. Příklad. I I [ e t e d ln ln e + dd, {[, E :, } + d t d dt a c e t dt [ ln + e ln e ln e ln. 7
4 Množina E je omezená zadanými křivkami. Načrtněte ji a vjádřete jako elementární obor integrace. Příklad., 5,, 5 { : 5 - Šipka označuje možný směr vnitřní integrace při výpočtu dvojného integrálu na pomocí Fubiniov vět. -5 Množina je elementárním oborem integrace vzhledem k ose. Příklad 5.,, : nebo { : je elementární oblast integrace vzhledem k ose i k ose Příklad 6. 8, , ± : { 8 8
5 Příklad 7.,,, [, [, { : : [, Zaměňte pořadí integrace : Příklad 8. I f,d d { { I f,d d. Příklad 9. I { f,d d [, { I f,d d. 9
6 Příklad 5. I { f,d d Množina E je omezená křivkami :, což je rovnice horní polovin kružnice +,, což je rovnice horní větve parabol,,. Ve směru os rozdělíme množinu na tři části tak, ab tto části bl elementárními obor integrace. [, : : : { + I Příklad 5. I f,d d+ { : { 6 : 6 I 6 f,d d. f,d d + 6 f,d d f,d d f,d d. + Nový směr vnitřní integrace dovoluje vjádřit celou množinu bez předcházejícího dělení : { : 6 5
7 Pomocí Fubiniho vět převed te dvojný integrál f,dd na dvojnásobné integrál pro oba směr integrace, jestliže množina E je omezená křivkami : Příklad 5.,, + f,dd f,d d [, + f,d d + f,d d. Příklad 5., { Vřešením soustav dostaneme průsečík parabol s přímkou o rovnici. f,dd f,d d [, + f,d d+ + + f,d d. [, + Načrtněte množinu E omezenou zadanými křivkami a vpočítejte dané integrál : Příklad 5. I dd, :,, I / / / [ 8 d d + d / 5 6 / [ d / / d 5
8 Příklad 55. I a a a Příklad 56. I dd, : + a, I a a a d d a d a [ a d a a + d [a a a 7 a a7 dd +, :, neboli je rovnice parabol s vrcholem [,. Průsečík parabol s přímkou najdeme tak, že zjistíme jejich -ové souřadnice: { po dosazení, Příklad 57. I I d d + + +d + + d + d + + [ d + ln + arctg je rovnice hperbol. ln+arctg +dd, :,,, I + +d d d [ d+ }{{} lichá funkce d }{{} sudá funkce d [+ 5
9 Příklad 58. I +dd, :,, Stanovíme -ové souřadnice průsečíků parabol s přímkou : {. Po dosazení +, I +d d + [ d d - [ Příklad 59. +dd, :,, [, Příklad [, +9 d +dd [ + d [ dd, :,,, dd ln ln u ln, v u, v [ d 8 / +d d + 8 d [ / d d ln d / d lnd per partes [ ln 8ln 6 dd +, :,,, [ ln 5 cos+dd, :, π, [- + dd, :,, + +dd, :, 5 [5, 5 [
10 dd, :, [9 + dd, :,,, dd, :,, +dd, :,,, [ +ln 5 [ 5 [ +8ln 69. Převed te dvojný integrál oběma způsob na dvojnásobný tj. obě pořadí integrace a integrál vpočítejte. {[, E ; ln,, },f, / [ Omezená množina E je zadána nerovnicemi nebo hraničními křivkami a je dána funkce f, a Načrtněte množinu s popisem os, měřítkem, popisem křivek a vznačením bodů, které jsou pro řešení úloh důležité. b Ověřte splnění předpokladů pro použití Fubiniho vět. c Množinu vjádřete ve tvaru elementárního oboru integrace vzhledem ke vhodně zvolené ose. d Vpočítejte f, dd. 7. {[, E ;, +}, f, c,,+ d {[, E ; + π, π, } f, sin+ [π c, π, +π dπ 7. E je ohraničena křivkami: /,, f, c, /, d 9 7. {[, E ;, +, } f, c,, d 7 5
11 7. {[, E ;, } f, c 6 6 d6 75. E je ohraničena křivkami:,, f, c d 76. E je ohraničena křivkami:, /, f, c / d 5 III.. Substituční metoda pro dvojný integrál Necht eistuje vzájemně jednoznačné regulární zobrazení oblasti Bu,v E na oblast E definované rovnicemi φ u,v, φ u,v. Pak f,dd Bu,v f φ u,v, φ u,v J dudv, kde J φ u φ u φ v φ v Příklad 77. Rozhodněte, zda eistuje integrál +,, }. Pokud ano, spočítejte jej. Zde použijeme transformaci do polárních souřadnic. arctg dd rcosϕ r rsinϕ ϕ π J r arctg dd, kde {[, E : Množina je měřitelná v E. Funkce f, arctg není definována na množině {[, E : }. Množina bodů nespojitosti funkce f v, tj. {[, :, <, >} je množina mír nula v E. ále platí, že funkce f je omezená na množině \, proto daný integrál eistuje. ϕ rdr dϕ 55
12 ϕdϕ [ ϕ rdr π [ r π 6. Vpočítejte integrál : Příklad 78. : + dd, {[, E : + b }, b > b + b b + dd / π/ bcosϕ rcosϕ rsinϕ J r r rdr dϕ / π/ [ r + b r brcosϕ r bcosϕ cosϕ π ϕ π bcosϕ dϕ / π/ b cos ϕdϕ / b cos ϕdϕ b 9 b. Příklad 79. ln+ + dd, {[, E : + a, } ln+ + dd / π/ π +a Příklad 8.* ln+r rdrdϕ lntdt π rcosϕ rsinϕ J r / [ tlnt t π/ +a dϕ π r a π ϕ π ln+r rdr [ +r t rdr dt +a ln+a a. dd, kde E je množina ohraničená křivkami,,,. 56 Použijeme transformaci, kde { u v {[u,v E : u, v }.
13 Nní spočítáme a pomocí u a v a dále Jakobián u, u v, v u u u v, v v v u v ; J u u u v u v v v u v u v 9 v + 9 v v. Užitím vět o substituci dostaneme u dd J dudv v / u v dv v du / v dv udu [ [ u v. Příklad 8.* dd, E je omezená přímkami +, +, + +, 5 5 Nejvhodnější substituce bude následující } + u v,, kde {[u,v E : u, v 5}. Potom u +v uv +v ; J +v v +v u +v u +v u +v + uv +v u +v ; u dd +v uv 5 u J dudv +v +v uv u +v +v du 5 u v [ u 5 du +v dv v + 5 dv +v +v + +v [ +v 5 +v Příklad dd, {[, E : +9 6, } Použijeme transformaci do zobecněných polárních souřadnic eliptických : rcosϕ rsinϕ 57 }, J r, r, ϕ π. dv dv
14 dd dϕ +6r 6rdr π + 9r cos ϕ+9 r sin ϕ 6rdr dϕ [ +6r / π dd, {[, E : + a } [πa dd, {[, E : + } Použijte souřadnice +rcosϕ, +rsinϕ. + dd, {[, E : + } [π [ 9 +dd, {[, E :,,, 9} Použijte souřadnice u, [ v. J v, 9 Vpočtěte integrál 87. {[, E ; f,dd, je-li dána množina a funkce f, 9 +, } f, 88. {[, E ; +9 9, }, f, [ π {[, E ; +, }, f, + [ 9. {[, E ; 6 + 9,, }, f, 9. {[, E ; +, }, f, 9. {[, E ; +, }, f, e [π e [ 8 5 [ 9 [ 58
15 III.6. Aplikace dvojných integrálů Určete plošný obsah rovinného obrazce E ohraničeného danými křivkami : Příklad 9., +, + P dd d d d [ [ d. Příklad 9.,,, 8 8 P dd 8 d d+ 8 d d d+ [ d ln + [ 8 + ln ln +ln8 ln +ln. +ln 8 Příklad 95. Určete plošný obsah rovinného obrazce omezeného osou a jedním obloukem ckloid o parametrických rovnicích at sint, a cost. P ϕ πa dd πa ϕ Jeden oblouk ckloid opíše bod kružnice, která se kotálí po přímce, tj. t,π. a substituce : t at sint d a costdt t a cost,πa t,π a cost dt a +a +cost dt a π + a a ϕ d d ϕd a cost a costdt cost+cos t [ t+ sint π [ dt a t sint πa +a π πa. π + 59
16 Příklad 96. Určete plošný obsah rovinného obrazce omezeného asteroidou / + / a /. a P dd rcos Použijeme transformace do souřadnic : ϕ rsin ϕ / / rcos ϕ + rsin ϕ a / r / a / r a ϕ π P, J cos ϕ rcos ϕsinϕ sin ϕ rsin ϕcosϕ rsin ϕcos ϕ. rsin ϕcos ϕdr dϕ sin ϕ a π 8 πa. [ r dϕ a rsin ϕcos ϕ+rsin ϕcos ϕ cosϕ sin ϕcos ϕdϕ dϕ a a [ rdr ϕ sinϕ π Určete plošný obsah rovinného obrazce omezeného uzavřenou křivkou : Příklad a Bernoulliova lemniskáta a P dd rcosϕ rsinϕ J r. Podosazenídozadánídostávámepostupně:r a r cos ϕ sin ϕ,r a cosϕ, r a cosϕ cosϕ, ϕ π, π π, 5π. P a [ sinϕ Příklad 98.* P cosϕ π a. rdr dϕ +9 dd rcosϕ r sinϕ J r [ r a cosϕ dϕ a cosϕdϕ r r cos ϕ r sinϕ cos ϕsinϕ ϕ π r cos ϕsinϕ 6
17 P 6 7 cos ϕsinϕ dϕ rdr 9 cos ϕsin ϕdϕ 5 [ r cos ϕsinϕ dϕ cos ϕ cos ϕdϕ cos ϕ cos 6 ϕdϕ Wallisova formule 7 π 5 6 π π 86. Příklad 99.* + a escartesův list a a P dd J r ϕ rϕ rdr dϕ ϕ rcosϕ rsinϕ ϕ r rϕ ϕ ϕ ϕ ϕ r ϕdϕ. Nní určíme rϕ a dosadíme do posledního integrálu. + a r cos ϕ+r sin ϕ ar cosϕsinϕ, takže rϕ acosϕsinϕ cos ϕ+sin ϕ, ϕ π, r rπ. dϕ 9a P acosϕsinϕ cos ϕ+sin ϕ čitatel a jmenovatel vdělíme cos 6 ϕ 9a C a lim C + a. tg ϕ tg ϕ+ dϕ cos ϕ u a du u + tgϕ u dϕ du cos ϕ cos ϕsin ϕ dϕ cos ϕ+sin ϕ 9a [ C lim a C + u + Příklad. Určete plošný obsah rovinného obrazce omezeného křivkami + +, + +,, u u + du lim C + C + + P dd rcosϕ rsinϕ J r + + r cosϕ + + r cosϕ cosϕ r cosϕ π ϕ 5 π 6
18 5 π π 5 5 cosϕ 5 π cosϕ cos ϕdϕ 5 π 5 π + sin 5π rdr dϕ 5 5 π π π sinπ π π cosϕ [r dϕ cosϕ +cosϕ dϕ 5 [ 5 π + 5 π π ϕ+ sinϕ 5π cos ϕ cos ϕ dϕ Příklad.Je dána parabolická úseč s tětivou kolmou k ose. élka tětiv je a, výška úseče h, a plošná hustota. Určete : a moment setrvačnosti úseče vzhledem k tětivě, b těžiště úseče. h a 5 π Analtické vjádření této parabol bude h p. [ a Použijeme-li bod,, pak h p a h p a h h. a a Moment setrvačnosti k tětivě je nní momentem setrvačnosti vzhledem k ose. J : h h dd a h h a d d h h a [ h h a d a a a a h h d h a h d a a a6 a a + a a h a 5 7 b T [, T, T M m h h a m dd a M T a a d h dd a d d a π a d [ a a 67 6h a 5. h h a d [ a a h a a 6 ha, h h a d d 5 h a, 5 h a ha [, 5 h, T 5 h. a 7a 6 6
19 Příklad.Určete těžiště rovinné desk omezené křivkami +, +, je-li plošná hustota T [ T,, T M m, m P m P π π π, kde P je plocha dané desk M π 56 dd cosϕ cosϕ dd r cosϕdr dϕ cos ϕdϕ π rcosϕ rsinϕ J r [ r cosϕ π 7π, cosϕ cosϕ T 7π π, T [ 7,. + r cosϕ + r cosϕ cosϕ r cosϕ π ϕ π dϕ π 56cos ϕdϕ Příklad. Určete souřadnice těžiště kruhové výseče viz obrázek, je-li konst. α α rcosϕ rsinϕ J r a r a α ϕ α T [ T,, m πa π α a α, M dd a sinα, T asinα α α α [ r r cosϕdr dϕ [ T asinα α, a [ α sinϕ α Příklad. Určete moment setrvačnosti vzhledem k počátku soustav souřadnic homogenní rovinné desk s plošnou hustotou k omezené křivkami +, +. J k +,dd polární souřadnice k + dd r drdϕ 5 kπ. 6
20 Příklad 5. Určete polohu těžiště obrazce omezeného kardioidou r a + cos ϕ, ϕ,π, a >,. a r a+cosϕ T [ T,, T M m ϕ rϕ m dd ϕ +cosϕ rdr dϕ rdr dϕ a+cosϕ [r dϕ a +cosϕ dϕ a +cosϕ+cos ϕdϕ π [ϕ+sinϕ a + +cosϕ a dϕ a π +a π a π, [ +cosϕ M dd polární souř. r cosϕdr dϕ cosϕ a +cosϕ dϕ a cosϕ+cos ϕ+cos ϕ+cos ϕ 5 a π, T 5a 6, T [ 5 6 a, dϕ Je dána omezená množina E a funkce f, a Načrtněte množinu. b Ověřte splnění předpokladů pro použití Fubiniov vět c Uved te alespoň dva příklad možného fzikálního významu daného integrálu. Uved te, zda se jedná o hmotnost při jaké hustotě, statický moment nebo moment setrvačnosti při jaké hustotě a vzhledem k jakému bodu nebo přímce. d Vpočítejte f, dd. 6. je ohraničena křivkami:, +,,, f, / cm pro / m pro / d 6 7. je ohraničena křivkami:,, f,, cm pro m pro d 6
21 8. je ohraničena křivkami:,, f, cm pro m pro J pro d {[, E ;, +, }, f, + cm pro + m pro + d 5. je ohraničena křivkami:, /,, f, cm pro m pro m pro J pro d 6 5. je ohraničena křivkami:, /,, f, cm pro d {[, E ; +,, }, f, cm pro m pro m pro d Určete plošný obsah P rovinného obrazce E ohraničeného danými křivkami :., 8, 5., +,, 5.,,, ln,, 8., 8 + [ 875 [ 6 [ ln [ 9 8 [ e [ π 65
22 Určete hmotnost m rovinné desk omezené křivkami : 9., +, je-li hustota,. + a, je-li, +, a >.,,, je-li,. +,,, je-li, [ 5 8 [ 9 a [ 9 5 [. +, +,,, je-li hustota, v libovolném bodě rovna vzdálenosti tohoto bodu od počátku soustav souřadnic. Určete hmotnost m rovinné desk při dané plošné hustotě,. [ 7 9. {[, E ; +,, },, [6 5. {[, E ;,, /},, 6. {[, E ; +, + },, [ 9 5 [ 6 Určete těžiště T rovinné desk omezené křivkami : 7.,, je-li, 8. sin,,,π, je-li, 9. +, +, je-li, [ [ T 5, [ [ π T, π 8 [ [ T 5,. + a,,, je-li, jde o čtvrtinu asteroid ležící v I. kvadrantu, použijte souřadnice rcos ϕ, rsin ϕ Určete moment setrvačnosti :. kruhu o poloměru a vzhledem k jeho tečně,,,. množin ohraničené elipsou + vzhledem k ose,,,. čtvrtin kruhu o poloměru a vzhledem k jeho ose souměrnosti,,, Zvolte polohu tak, ab osa bla osou souměrnosti.. čtverce o straně a vzhledem k jeho vrcholu,,, [ T T 56a 5π [ 5 πa [ [ a π 6 [ a 5. části mezikruží +, +, omezeného přímkami, v I. kvadrantu s hustotou, k, k > vzhledem ke středu mezikruží. [5kπ Je dána omezená množina E a funkce f, a Načrtněte těleso, jehož objem bude roven hodnotě spočítaného integrálu. b Načrtněte průmět tělesa do rovin z. c Napište název ploch z f,. d Vpočítejte f, dd. 6 66
23 6. je ohraničena křivkami:,,, f, + z [ crovina d 7. {[, E ; +, + }, f, + z [ crotační paraboloid d 8. {[, E ;,, }, f, z [ crovina d 7 9. {[, E ;,, }, f, z [ cválcová plocha d 6. {[, E ;, +, }, f, z [ chperbolický paraboloid d 7. {[, E ; + 9, }, f, 9 z [ ckulová plocha d9π 67
Kristýna Kuncová. Matematika B3
 (10) Vícerozměrný integrál II Kristýna Kuncová Matematika B3 Kristýna Kuncová (10) Vícerozměrný integrál II 1 / 30 Transformace Otázka Jaký obrázek znázorňuje čtverec vpravo po transformaci u = x + y a
(10) Vícerozměrný integrál II Kristýna Kuncová Matematika B3 Kristýna Kuncová (10) Vícerozměrný integrál II 1 / 30 Transformace Otázka Jaký obrázek znázorňuje čtverec vpravo po transformaci u = x + y a
Kristýna Kuncová. Matematika B2 18/19
 (6) Určitý integrál Kristýna Kuncová Matematika B2 18/19 Kristýna Kuncová (6) Určitý integrál 1 / 28 Newtonův integrál Zdroj: https://kwcalculus.wikispaces.com/integral+applications Kristýna Kuncová (6)
(6) Určitý integrál Kristýna Kuncová Matematika B2 18/19 Kristýna Kuncová (6) Určitý integrál 1 / 28 Newtonův integrál Zdroj: https://kwcalculus.wikispaces.com/integral+applications Kristýna Kuncová (6)
Určitý (Riemannův) integrál a aplikace. Nevlastní integrál. 19. prosince 2018
 Určitý (Riemnnův) integrál plikce. Nevlstní integrál Seminář 9. prosince 28 Určitý integrál Existence: Necht funkce f (x) je definovná n uzvřeném intervlu, b. Necht je splněn n tomto intervlu kterákoliv
Určitý (Riemnnův) integrál plikce. Nevlstní integrál Seminář 9. prosince 28 Určitý integrál Existence: Necht funkce f (x) je definovná n uzvřeném intervlu, b. Necht je splněn n tomto intervlu kterákoliv
5. a 12. prosince 2018
 Integrální počet Neurčitý integrál Seminář 9, 0 5. a. prosince 08 Neurčitý integrál Definice. Necht funkce f (x) je definovaná na intervalu I. Funkce F (x) se nazývá primitivní k funkci f (x) na I, jestliže
Integrální počet Neurčitý integrál Seminář 9, 0 5. a. prosince 08 Neurčitý integrál Definice. Necht funkce f (x) je definovaná na intervalu I. Funkce F (x) se nazývá primitivní k funkci f (x) na I, jestliže
Úvodní informace. 18. února 2019
 Úvodní informace Funkce více proměnných Cvičení první 18. února 2019 Obsah 1 Úvodní informace. 2 Funkce více proměnných Definiční obor Úvodní informace. Komunikace: e-mail: olga@majling.eu nebo olga.majlingova@fs.cvut.cz
Úvodní informace Funkce více proměnných Cvičení první 18. února 2019 Obsah 1 Úvodní informace. 2 Funkce více proměnných Definiční obor Úvodní informace. Komunikace: e-mail: olga@majling.eu nebo olga.majlingova@fs.cvut.cz
Matematika 2, vzorová písemka 1
 Matematika 2, vzorová písemka Pavel Kreml 9.5.20 Přesun mezi obrazovkami Další snímek: nebo Enter. Zpět: nebo Shift + Enter 2 3 4 Doporučení Pokuste se vyřešit zadané úlohy samostatně. Pokud nebudete vědět
Matematika 2, vzorová písemka Pavel Kreml 9.5.20 Přesun mezi obrazovkami Další snímek: nebo Enter. Zpět: nebo Shift + Enter 2 3 4 Doporučení Pokuste se vyřešit zadané úlohy samostatně. Pokud nebudete vědět
(1) Derivace. Kristýna Kuncová. Matematika B2 17/18. Kristýna Kuncová (1) Derivace 1 / 35
 (1) Derivace Kristýna Kuncová Matematika B2 17/18 Kristýna Kuncová (1) Derivace 1 / 35 Růst populací Zdroj : https://www.tes.com/lessons/ yjzt-cmnwtvsq/noah-s-ark Kristýna Kuncová (1) Derivace 2 / 35 Růst
(1) Derivace Kristýna Kuncová Matematika B2 17/18 Kristýna Kuncová (1) Derivace 1 / 35 Růst populací Zdroj : https://www.tes.com/lessons/ yjzt-cmnwtvsq/noah-s-ark Kristýna Kuncová (1) Derivace 2 / 35 Růst
Co nám prozradí derivace? 21. listopadu 2018
 Co nám prozradí derivace? Seminář sedmý 21. listopadu 2018 Derivace základních funkcí Tečna a normála Tečna ke grafu funkce f v bodě dotyku T = [x 0, f (x 0 )]: y f (x 0 ) = f (x 0 )(x x 0 ) Normála: y
Co nám prozradí derivace? Seminář sedmý 21. listopadu 2018 Derivace základních funkcí Tečna a normála Tečna ke grafu funkce f v bodě dotyku T = [x 0, f (x 0 )]: y f (x 0 ) = f (x 0 )(x x 0 ) Normála: y
Necht je funkce f spojitá v intervalu a, b a má derivaci v (a, b). Pak existuje bod ξ (a, b) tak, že f(b) f(a) b a. Geometricky
 Monotónie a extrémy funkce Diferenciální počet - průběh funkce Věta o střední hodnotě (Lagrange) Necht je funkce f spojitá v intervalu a, b a má derivaci v (a, b). Pak existuje bod ξ (a, b) tak, že f (ξ)
Monotónie a extrémy funkce Diferenciální počet - průběh funkce Věta o střední hodnotě (Lagrange) Necht je funkce f spojitá v intervalu a, b a má derivaci v (a, b). Pak existuje bod ξ (a, b) tak, že f (ξ)
Funkce zadané implicitně. 4. března 2019
 Funkce zadané implicitně 4. března 2019 Parciální derivace druhého řádu Parciální derivace druhého řádu funkce z = f (x, y) jsou definovány: Parciální derivace 2 f 2 = ( ) f 2 f 2 = ( ) f 2 f a 2 f 2 f
Funkce zadané implicitně 4. března 2019 Parciální derivace druhého řádu Parciální derivace druhého řádu funkce z = f (x, y) jsou definovány: Parciální derivace 2 f 2 = ( ) f 2 f 2 = ( ) f 2 f a 2 f 2 f
MATEMATIKA 3. Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci
 MATEMATIKA 3 Dana Černá http://www.fp.tul.cz/kmd/ Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci Osnova: Komplexní funkce - definice, posloupnosti, řady Vybrané komplexní funkce
MATEMATIKA 3 Dana Černá http://www.fp.tul.cz/kmd/ Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci Osnova: Komplexní funkce - definice, posloupnosti, řady Vybrané komplexní funkce
x y (A)dy. a) Určete a načrtněte oblasti, ve kterých je funkce diferencovatelná. b) Napište diferenciál funkce v bodě A = [x 0, y 0 ].
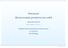
![x y (A)dy. a) Určete a načrtněte oblasti, ve kterých je funkce diferencovatelná. b) Napište diferenciál funkce v bodě A = [x 0, y 0 ]. x y (A)dy. a) Určete a načrtněte oblasti, ve kterých je funkce diferencovatelná. b) Napište diferenciál funkce v bodě A = [x 0, y 0 ].](/thumbs/94/121813288.jpg) II.4. Totální diferenciál a tečná rovina Značení pro funkci z = f,: totální diferenciál funkce f v bodě A = 0, 0 ]: dfa = A 0+ A 0 Označme d = 0, d = 0. Pak dfa = A d+ A d Příklad91.Je dána funkce f, =.
II.4. Totální diferenciál a tečná rovina Značení pro funkci z = f,: totální diferenciál funkce f v bodě A = 0, 0 ]: dfa = A 0+ A 0 Označme d = 0, d = 0. Pak dfa = A d+ A d Příklad91.Je dána funkce f, =.
Obsah. Aplikovaná matematika I. Vlivem meze Vlivem funkce Bernhard Riemann. Mendelu Brno. 3 Vlastnosti určitého integrálu
 Určitý integrál Aplikovná mtemtik I Dn Říhová Mendelu Brno Obsh Zákldní úloh integrálního počtu Definice určitého integrálu 3 Vlstnosti určitého integrálu 4 Výpočet určitého integrálu 5 Geometrické plikce
Určitý integrál Aplikovná mtemtik I Dn Říhová Mendelu Brno Obsh Zákldní úloh integrálního počtu Definice určitého integrálu 3 Vlstnosti určitého integrálu 4 Výpočet určitého integrálu 5 Geometrické plikce
Vybrané kapitoly z matematiky
 Vybrané kapitoly z matematiky VŠB-TU Ostrava 2018-2019 Vybrané kapitoly z matematiky 2018-2019 1 / 11 Křivkový integrál Vybrané kapitoly z matematiky 2018-2019 2 / 11 Parametricky zadaná křivka v R 3 :
Vybrané kapitoly z matematiky VŠB-TU Ostrava 2018-2019 Vybrané kapitoly z matematiky 2018-2019 1 / 11 Křivkový integrál Vybrané kapitoly z matematiky 2018-2019 2 / 11 Parametricky zadaná křivka v R 3 :
x2 + 2x 15 x 2 + 4x ) f(x) = x 2 + 2x 15 x2 + x 12 3) f(x) = x 3 + 3x 2 10x. x 3 + 3x 2 10x x 2 + x 12 10) f(x) = log 2.
 Příklady k 1 zápočtové písemce Definiční obor funkce Určete definiční obor funkce: x + x 15 1 f(x x + x 1 ( x + x 1 f(x log x + x 15 x + x 1 3 f(x x 3 + 3x 10x ( x 3 + 3x 10x f(x log x + x 1 x3 + 5x 5
Příklady k 1 zápočtové písemce Definiční obor funkce Určete definiční obor funkce: x + x 15 1 f(x x + x 1 ( x + x 1 f(x log x + x 15 x + x 1 3 f(x x 3 + 3x 10x ( x 3 + 3x 10x f(x log x + x 1 x3 + 5x 5
Komplexní analýza. Martin Bohata. Katedra matematiky FEL ČVUT v Praze Martin Bohata Komplexní analýza Úvod 1 / 32
 Komplexní analýza Úvod Martin Bohata Katedra matematiky FEL ČVUT v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Úvod 1 / 32 Základní informace Stránky předmětu: http://math.feld.cvut.cz/bohata/kan.html
Komplexní analýza Úvod Martin Bohata Katedra matematiky FEL ČVUT v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Úvod 1 / 32 Základní informace Stránky předmětu: http://math.feld.cvut.cz/bohata/kan.html
1 Soustava lineárních rovnic
 Soustavy lineárních rovnic Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Soustava lineárních rovnic 2 Řešitelnost soustavy lineárních rovnic 3 Gaussova eliminační metoda 4 Jordanova eliminační
Soustavy lineárních rovnic Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Soustava lineárních rovnic 2 Řešitelnost soustavy lineárních rovnic 3 Gaussova eliminační metoda 4 Jordanova eliminační
Inverzní Z-transformace
 Modelování systémů a procesů (11MSP) Bohumil Kovář, Jan Přikryl, Miroslav Vlček Ústav aplikované matematiky ČVUT v Praze, Fakulta dopravní 9. přednáška 11MSP úterý 16. dubna 2019 verze: 2019-04-15 12:25
Modelování systémů a procesů (11MSP) Bohumil Kovář, Jan Přikryl, Miroslav Vlček Ústav aplikované matematiky ČVUT v Praze, Fakulta dopravní 9. přednáška 11MSP úterý 16. dubna 2019 verze: 2019-04-15 12:25
Kristýna Kuncová. Matematika B2
 (3) Průběh funkce Kristýna Kuncová Matematika B2 Kristýna Kuncová (3) Průběh funkce 1 / 26 Monotonie (x 2 ) = 2x (sin x) = cos x Jak souvisí derivace funkce a fakt, zda je funkce rostoucí nebo klesající?
(3) Průběh funkce Kristýna Kuncová Matematika B2 Kristýna Kuncová (3) Průběh funkce 1 / 26 Monotonie (x 2 ) = 2x (sin x) = cos x Jak souvisí derivace funkce a fakt, zda je funkce rostoucí nebo klesající?
Zadání: Vypočítejte hlavní momenty setrvačnosti a vykreslete elipsu setrvačnosti na zadaných
 Příklad k procvičení : Průřeové charakteristik Zadání: Vpočítejte hlavní moment setrvačnosti a vkreslete elipsu setrvačnosti na adaných obracích. Příklad. Zadání: Rokreslení na jednoduché obrace: 500 T
Příklad k procvičení : Průřeové charakteristik Zadání: Vpočítejte hlavní moment setrvačnosti a vkreslete elipsu setrvačnosti na adaných obracích. Příklad. Zadání: Rokreslení na jednoduché obrace: 500 T
Obsah. 1 Konstrukce (definice) Riemannova integrálu Výpočet Newtonova Leibnizova věta Aplikace výpočet objemů a obsahů 30
 Určitý integrál Robert Mřík 6. září 8 Obsh 1 Konstrukce (definice) Riemnnov integrálu. Výpočet Newtonov Leibnizov vět. 18 3 Numerický odhd Lichoběžníkové prvidlo 19 4 Aplikce výpočet objemů obshů 3 c Robert
Určitý integrál Robert Mřík 6. září 8 Obsh 1 Konstrukce (definice) Riemnnov integrálu. Výpočet Newtonov Leibnizov vět. 18 3 Numerický odhd Lichoběžníkové prvidlo 19 4 Aplikce výpočet objemů obshů 3 c Robert
(2) Funkce. Kristýna Kuncová. Matematika B2. Kristýna Kuncová (2) Funkce 1 / 25
 (2) Funkce Kristýna Kuncová Matematika B2 Kristýna Kuncová (2) Funkce 1 / 25 Sudá a lichá funkce Určete, které funkce jsou sudé a které liché: liché: A, D, E sudé: B Kristýna Kuncová (2) Funkce 2 / 25
(2) Funkce Kristýna Kuncová Matematika B2 Kristýna Kuncová (2) Funkce 1 / 25 Sudá a lichá funkce Určete, které funkce jsou sudé a které liché: liché: A, D, E sudé: B Kristýna Kuncová (2) Funkce 2 / 25
Kristýna Kuncová. Matematika B2 18/19. Kristýna Kuncová (1) Vzorové otázky 1 / 36
 (1) Vzorové otázky Kristýna Kuncová Matematika B2 18/19 Kristýna Kuncová (1) Vzorové otázky 1 / 36 Limity - úlohy Otázka Určete lim x 0 f (x) A -3 B 0 C 5 D 7 E D Zdroj: Calculus: Single and Multivariable,
(1) Vzorové otázky Kristýna Kuncová Matematika B2 18/19 Kristýna Kuncová (1) Vzorové otázky 1 / 36 Limity - úlohy Otázka Určete lim x 0 f (x) A -3 B 0 C 5 D 7 E D Zdroj: Calculus: Single and Multivariable,
(13) Fourierovy řady
 (13) Fourierovy řady Kristýna Kuncová Matematika B3 Kristýna Kuncová (13) Fourierovy řady 1 / 22 O sinech a kosinech Lemma (O sinech a kosinech) Pro m, n N 0 : 2π 0 2π 0 2π 0 sin nx dx = sin nx cos mx
(13) Fourierovy řady Kristýna Kuncová Matematika B3 Kristýna Kuncová (13) Fourierovy řady 1 / 22 O sinech a kosinech Lemma (O sinech a kosinech) Pro m, n N 0 : 2π 0 2π 0 2π 0 sin nx dx = sin nx cos mx
Komplexní analýza. Martin Bohata. Katedra matematiky FEL ČVUT v Praze Martin Bohata Komplexní analýza Mocninné řady 1 / 18
 Komplexní analýza Mocninné řady Martin Bohata Katedra matematiky FEL ČVUT v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Mocninné řady 1 / 18 Posloupnosti komplexních čísel opakování
Komplexní analýza Mocninné řady Martin Bohata Katedra matematiky FEL ČVUT v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Mocninné řady 1 / 18 Posloupnosti komplexních čísel opakování
Euklidovský prostor. Funkce dvou proměnných: základní pojmy, limita a spojitost.
 Euklidovský prostor. Funkce dvou proměnných: základní pojmy, limita a spojitost. Vyšší matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU
Euklidovský prostor. Funkce dvou proměnných: základní pojmy, limita a spojitost. Vyšší matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU
Numerické metody 8. května FJFI ČVUT v Praze
 Obyčejné diferenciální rovnice Numerické metody 8. května 2018 FJFI ČVUT v Praze 1 Úvod Úvod Základní metody Pokročilejší metody Soustava Vyšší řád Program 1 Úvod Úvod - Úloha Základní úloha, kterou řešíme
Obyčejné diferenciální rovnice Numerické metody 8. května 2018 FJFI ČVUT v Praze 1 Úvod Úvod Základní metody Pokročilejší metody Soustava Vyšší řád Program 1 Úvod Úvod - Úloha Základní úloha, kterou řešíme
Kapitola 4: Soustavy diferenciálních rovnic 1. řádu
 Sbírka příkladů Matematika II pro strukturované studium Kapitola 4: Soustavy diferenciálních rovnic 1 řádu Chcete-li ukončit prohlížení stiskněte klávesu Esc Chcete-li pokračovat stiskněte klávesu Enter
Sbírka příkladů Matematika II pro strukturované studium Kapitola 4: Soustavy diferenciálních rovnic 1 řádu Chcete-li ukončit prohlížení stiskněte klávesu Esc Chcete-li pokračovat stiskněte klávesu Enter
Całka krzywoliniowa niezorientowana Niech R 3 będzie krzywą prostowalną opisywaną parametryzacją r:,α, β- γ taką, że
 Całka krzywoliniowa niezorientowana Niech R będzie krzywą prostowalną opisywaną parametryzacją r:,α, β- taką, że t α, β : r t = ( t, y t, z t ) ef. Mówimy, że krzywa jest kawałkami gładka funkcja r t ma
Całka krzywoliniowa niezorientowana Niech R będzie krzywą prostowalną opisywaną parametryzacją r:,α, β- taką, że t α, β : r t = ( t, y t, z t ) ef. Mówimy, że krzywa jest kawałkami gładka funkcja r t ma
Operace s funkcemi [MA1-18:P2.1] funkční hodnota... y = f(x) (x argument)
![Operace s funkcemi [MA1-18:P2.1] funkční hodnota... y = f(x) (x argument) Operace s funkcemi [MA1-18:P2.1] funkční hodnota... y = f(x) (x argument)](/thumbs/95/126221157.jpg) KAPITOLA : Funkce - úvod [MA-8:P.] reálná funkce (jedné) reálné proměnné... f : A R...... zobrazení množin A R do množin reálných čísel R funkční hodnota... = f() ( argument) ( tj. reálná funkce f : A
KAPITOLA : Funkce - úvod [MA-8:P.] reálná funkce (jedné) reálné proměnné... f : A R...... zobrazení množin A R do množin reálných čísel R funkční hodnota... = f() ( argument) ( tj. reálná funkce f : A
Numerické metody minimalizace
 Numerické metody minimalizace Než vám klesnou víčka - Stříbrnice 2011 12.2. 16.2.2011 Emu (Brkos 2011) Numerické metody minimalizace 12.2. 16.2.2011 1 / 19 Obsah 1 Úvod 2 Základní pojmy 3 Princip minimalizace
Numerické metody minimalizace Než vám klesnou víčka - Stříbrnice 2011 12.2. 16.2.2011 Emu (Brkos 2011) Numerické metody minimalizace 12.2. 16.2.2011 1 / 19 Obsah 1 Úvod 2 Základní pojmy 3 Princip minimalizace
Teorie. kuncova/ Definice 1. Necht f je reálná funkce a a R. Jestliže existuje.
 8. cvičení http://www.karlin.mff.cuni.cz/ kuncova/ kytaristka@gmail.com Teorie Definice. Necht f je reálná funkce a a R. Jestliže eistuje h 0 fa + h) fa), h pak tuto itu nazýváme derivací funkce f v bodě
8. cvičení http://www.karlin.mff.cuni.cz/ kuncova/ kytaristka@gmail.com Teorie Definice. Necht f je reálná funkce a a R. Jestliže eistuje h 0 fa + h) fa), h pak tuto itu nazýváme derivací funkce f v bodě
Matematická analýza II pro kombinované studium. Konzultace první a druhá. RNDr. Libuše Samková, Ph.D. pf.jcu.cz
 Učební texty ke konzultacím předmětu Matematická analýza II pro kombinované studium Konzultace první a druhá RNDr. Libuše Samková, Ph.D. e-mail: lsamkova@ pf.jcu.cz webová stránka: home.pf.jcu.cz/ lsamkova/
Učební texty ke konzultacím předmětu Matematická analýza II pro kombinované studium Konzultace první a druhá RNDr. Libuše Samková, Ph.D. e-mail: lsamkova@ pf.jcu.cz webová stránka: home.pf.jcu.cz/ lsamkova/
Jednoduchá zobrazení. Podpořeno z projektu FRVŠ 584/2011.
 Podpořeno z projektu FRVŠ 584/2011. Obsah 1 2 Obsah 1 2 Společné vlastnosti jednoduchých zobrazení: Zobrazovací ref. plocha je rovina - souřadnice X, Y, případně ρ, ɛ Zobrazovaná ref. plocha je eliposid
Podpořeno z projektu FRVŠ 584/2011. Obsah 1 2 Obsah 1 2 Společné vlastnosti jednoduchých zobrazení: Zobrazovací ref. plocha je rovina - souřadnice X, Y, případně ρ, ɛ Zobrazovaná ref. plocha je eliposid
Stavový popis Stabilita spojitých systémů (K611MSAP) Katedra aplikované matematiky Fakulta dopravní ČVUT. čtvrtek 20. dubna 2006
 Modelování systémů a procesů (K611MSAP) Přednáška 4 Katedra aplikované matematiky Fakulta dopravní ČVUT Pravidelná přednáška K611MSAP čtvrtek 20. dubna 2006 Obsah 1 Laplaceova transformace Přenosová funkce
Modelování systémů a procesů (K611MSAP) Přednáška 4 Katedra aplikované matematiky Fakulta dopravní ČVUT Pravidelná přednáška K611MSAP čtvrtek 20. dubna 2006 Obsah 1 Laplaceova transformace Přenosová funkce
Obsah. Limita posloupnosti a funkce. Petr Hasil. Limita posloupnosti. Pro a R definujeme: Je-li a < 0, pak a =, a ( ) =. vlastní body.
 Obsah a funkce Petr Hasil Přednáška z Matematické analýzy I Úvod 2 c Petr Hasil (MUNI) a funkce Matematická analýza / 90 c Petr Hasil (MUNI) a funkce Matematická analýza 2 / 90 Úvod Úvod Pro a R definujeme:
Obsah a funkce Petr Hasil Přednáška z Matematické analýzy I Úvod 2 c Petr Hasil (MUNI) a funkce Matematická analýza / 90 c Petr Hasil (MUNI) a funkce Matematická analýza 2 / 90 Úvod Úvod Pro a R definujeme:
Geometrická nelinearita: úvod
 Geometrická nelinearita: úvod Opakování: stabilita prutů Eulerovo řešení s využitím teorie 2. řádu) Stabilita prutů Ritzovou metodou Stabilita tenkých desek 1 Geometrická nelinearita Velké deformace průhyby,
Geometrická nelinearita: úvod Opakování: stabilita prutů Eulerovo řešení s využitím teorie 2. řádu) Stabilita prutů Ritzovou metodou Stabilita tenkých desek 1 Geometrická nelinearita Velké deformace průhyby,
Sb ırka pˇr ıklad u z matematick e anal yzy II Petr Tomiczek
 Sbírka příkladů z matematické analýzy II Petr Tomiczek Obsah 0 Diferenciální rovnice. řádu 0. Separace proměnných Příklad : Najděte obecné řešení (obecný integrál) diferenciální rovnice y = tg x tg y.
Sbírka příkladů z matematické analýzy II Petr Tomiczek Obsah 0 Diferenciální rovnice. řádu 0. Separace proměnných Příklad : Najděte obecné řešení (obecný integrál) diferenciální rovnice y = tg x tg y.
Edita Pelantová, katedra matematiky / 16
 Edita Pelantová, katedra matematiky seminář současné matematiky, září 2010 Axiomy reálných čísel Axiomy tělesa Axiom 1. x + y = y + x a xy = yx (komutativní zákon). Axiom 2. x + (y + z) = (x + y) + z a
Edita Pelantová, katedra matematiky seminář současné matematiky, září 2010 Axiomy reálných čísel Axiomy tělesa Axiom 1. x + y = y + x a xy = yx (komutativní zákon). Axiom 2. x + (y + z) = (x + y) + z a
Jednoduchá zobrazení. Podpořeno z projektu FRVŠ 584/2011.
 Podpořeno z projektu FRVŠ 584/2011. Obsah 1 2 Obsah 1 2 Společné vlastnosti jednoduchých zobrazení: Zobrazovací ref. plocha je rovina - souřadnice X, Y, případně ρ, ɛ Zobrazovaná ref. plocha je eliposid
Podpořeno z projektu FRVŠ 584/2011. Obsah 1 2 Obsah 1 2 Společné vlastnosti jednoduchých zobrazení: Zobrazovací ref. plocha je rovina - souřadnice X, Y, případně ρ, ɛ Zobrazovaná ref. plocha je eliposid
Obsah. 1.2 Integrály typu ( ) R x, s αx+β
 Sbírka úloh z matematické analýzy. Čížek Jiří Kubr Milan. prosince 006 Obsah Neurčitý integrál.. Základní integrály...................................... Integrály typu ) R, s α+β γ+δ d...........................
Sbírka úloh z matematické analýzy. Čížek Jiří Kubr Milan. prosince 006 Obsah Neurčitý integrál.. Základní integrály...................................... Integrály typu ) R, s α+β γ+δ d...........................
Aproximace funkcí 1,00 0,841 1,10 0,864 1,20 0,885. Body proložíme lomenou čarou.
 Příklad Známe následující hodnoty funkce Φ: u Φ(u) 1,00 0,841 1,10 0,864 1,20 0,885 Odhadněte přibližně hodnoty Φ(1,02) a Φ(1,16). Možnosti: Vezmeme hodnotu v nejbližším bodě. Body proložíme lomenou čarou.
Příklad Známe následující hodnoty funkce Φ: u Φ(u) 1,00 0,841 1,10 0,864 1,20 0,885 Odhadněte přibližně hodnoty Φ(1,02) a Φ(1,16). Možnosti: Vezmeme hodnotu v nejbližším bodě. Body proložíme lomenou čarou.
Příklad 1.2 Nalezněte obsah oblasti ohraničené křivkami y =lnx, y =ln 2 x.
 Kpitol Aplikce určitého integrálu. Délk, obsh, objem Příkld. Nlezněte obsh oblsti ohrničené křivkmi xy 4, x + y 5. Návod. Soustv rovnice xy 4,x + y 5mádvěřešení[, 4] [4, ]. (viz obr.) Oblst ohrničená křivkmi
Kpitol Aplikce určitého integrálu. Délk, obsh, objem Příkld. Nlezněte obsh oblsti ohrničené křivkmi xy 4, x + y 5. Návod. Soustv rovnice xy 4,x + y 5mádvěřešení[, 4] [4, ]. (viz obr.) Oblst ohrničená křivkmi
Diferenciální rovnice základní pojmy. Rovnice se
 Diferenciální rovnice základní pojmy. Rovnice se separovanými proměnnými. Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské
Diferenciální rovnice základní pojmy. Rovnice se separovanými proměnnými. Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské
Cauchyova úloha pro obyčejnou diferenciální rovnici
 Řešení ODR v MATLABu Přednáška 3 15. října 2018 Cauchyova úloha pro obyčejnou diferenciální rovnici y = f (x, y), y(x 0 ) = y 0 Víme, že v intervalu a, b existuje jediné řešení. (f (x, y) a f y jsou spojité
Řešení ODR v MATLABu Přednáška 3 15. října 2018 Cauchyova úloha pro obyčejnou diferenciální rovnici y = f (x, y), y(x 0 ) = y 0 Víme, že v intervalu a, b existuje jediné řešení. (f (x, y) a f y jsou spojité
Průvodce studiem V této kapitole se budeme zabývat diferenciálním počtem pro funkce více
 5 Diferenciální počet funkcí více proměnných Průvodce studiem V této kapitole se budeme zabývat diferenciálním počtem pro funkce více proměnných, především budeme pracovat s funkcemi dvou proměnných Ukážeme
5 Diferenciální počet funkcí více proměnných Průvodce studiem V této kapitole se budeme zabývat diferenciálním počtem pro funkce více proměnných, především budeme pracovat s funkcemi dvou proměnných Ukážeme
kontaktní modely (Winklerův, Pasternakův)
 TÉMA 7: Pružný poloprostor, modely podloží pružný poloprostor základní předpoklady pružný poloprostor Boussinesqueovo řešení kontaktní modely (Winklerův, Pasternakův) 1 Pružný poloprostor (1) vychází z
TÉMA 7: Pružný poloprostor, modely podloží pružný poloprostor základní předpoklady pružný poloprostor Boussinesqueovo řešení kontaktní modely (Winklerův, Pasternakův) 1 Pružný poloprostor (1) vychází z
Matematika I (KMI/PMATE) Co se naučíme? x = a a x = b. rozumět pojmu střední hodnota funkce na daném intervalu. Obrázek 1.
 Mtemtik I (KMI/PMATE). Integrální počet funkcí jedné proměnné.. Co se nučíme? Po sérii přednášek věnovných integrálům byste měli být schopni: rozumět definici pojmu neurčitý integrál používt metodu přímé
Mtemtik I (KMI/PMATE). Integrální počet funkcí jedné proměnné.. Co se nučíme? Po sérii přednášek věnovných integrálům byste měli být schopni: rozumět definici pojmu neurčitý integrál používt metodu přímé
Petr Hasil. c Petr Hasil (MUNI) Nekonečné řady MA III (M3100) 1 / 187
 Nekonečné řady Petr Hasil Přednáška z Matematické analýzy III c Petr Hasil (MUNI) Nekonečné řady MA III (M3100) 1 / 187 Obsah 1 Nekonečné číselné řady Základní pojmy Řady s nezápornými členy Řady s libovolnými
Nekonečné řady Petr Hasil Přednáška z Matematické analýzy III c Petr Hasil (MUNI) Nekonečné řady MA III (M3100) 1 / 187 Obsah 1 Nekonečné číselné řady Základní pojmy Řady s nezápornými členy Řady s libovolnými
lim = 0, gdzie d n oznacza najdłuższą przekątną prostokątów
 9. CAŁKA POWÓJNA 9.. Całka podwójna w prostokącie Niech P będzie prostokątem opisanm na płaszczźnie OXY nierównościami: a < < b, c < < d, a f(,) funkcją określoną i ograniczoną w tm prostokącie. Prostokąt
9. CAŁKA POWÓJNA 9.. Całka podwójna w prostokącie Niech P będzie prostokątem opisanm na płaszczźnie OXY nierównościami: a < < b, c < < d, a f(,) funkcją określoną i ograniczoną w tm prostokącie. Prostokąt
Analiza Matematyczna. Zastosowania Całek
 Analiza Matematyczna. Zastosowania Całek Aleksander Denisiuk denisiuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 8-45 Gdańsk 9 maja 217
Analiza Matematyczna. Zastosowania Całek Aleksander Denisiuk denisiuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 8-45 Gdańsk 9 maja 217
Rovnice proudění Slapový model
 do oceánského proudění Obsah 1 2 3 Co způsobuje proudění v oceánech? vyrovnávání rozdílů v teplotě, salinitě, tlaku, ρ = ρ(p, T, S) vítr - wind stress F wind = ρ air C D AU 2 10 slapy produkují silné proudy,
do oceánského proudění Obsah 1 2 3 Co způsobuje proudění v oceánech? vyrovnávání rozdílů v teplotě, salinitě, tlaku, ρ = ρ(p, T, S) vítr - wind stress F wind = ρ air C D AU 2 10 slapy produkují silné proudy,
Statistika (KMI/PSTAT)
 Statistika (KMI/PSTAT) Cvičení deváté aneb Důležitá rozdělení pravděpodobnosti spojité náhodné veličiny Statistika (KMI/PSTAT) 1 / 15 Spojitá náhodná veličina Spojitá náhodná veličina Spojitá náhodná veličina
Statistika (KMI/PSTAT) Cvičení deváté aneb Důležitá rozdělení pravděpodobnosti spojité náhodné veličiny Statistika (KMI/PSTAT) 1 / 15 Spojitá náhodná veličina Spojitá náhodná veličina Spojitá náhodná veličina
Stochastické modelování v ekonomii a financích Konzistence odhadu LWS. konzistence OLS odhadu. Předpoklady pro konzistenci LWS
 Whitův pro heteroskedasticitě pro heteroskedasticitě Stochastické modelování v ekonomii a financích 7. 12. 2009 Obsah Whitův pro heteroskedasticitě pro heteroskedasticitě 1 Whitův 2 pro 3 heteroskedasticitě
Whitův pro heteroskedasticitě pro heteroskedasticitě Stochastické modelování v ekonomii a financích 7. 12. 2009 Obsah Whitův pro heteroskedasticitě pro heteroskedasticitě 1 Whitův 2 pro 3 heteroskedasticitě
fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného základu (reg. č. CZ.1.07/2.2.00/28.
 Extrémy Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného
Extrémy Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného
Obsah. Zobrazení na osmistěn. 1 Zobrazení sféry po částech - obecné vlastnosti 2 Zobrazení na pravidelný konvexní mnohostěn
 Obsah 1 2 3 Použití Zobrazení rozsáhlého území, ale hodnoty zkreslení nesmí přesáhnout určitou hodnotu Rozdělením území na menší části a ty pak zobrazíme zvlášť Nevýhodou jsou však samostatné souřadnicové
Obsah 1 2 3 Použití Zobrazení rozsáhlého území, ale hodnoty zkreslení nesmí přesáhnout určitou hodnotu Rozdělením území na menší části a ty pak zobrazíme zvlášť Nevýhodou jsou však samostatné souřadnicové
Obsah. Petr Hasil. (konjunkce) (disjunkce) A B (implikace) A je dostačující podmínka pro B; B je nutná podmínka pro A A B: (A B) (B A) A (negace)
 Množiny, číselné obory, funkce Petr Hasil Přednáška z Matematické analýzy I c Petr Hasil (MUNI) Množiny, číselné obory, funkce Matematická analýza / 5 Obsah Množinové operace Operace s funkcemi Definice
Množiny, číselné obory, funkce Petr Hasil Přednáška z Matematické analýzy I c Petr Hasil (MUNI) Množiny, číselné obory, funkce Matematická analýza / 5 Obsah Množinové operace Operace s funkcemi Definice
Referenční plochy. Podpořeno z projektu FRVŠ 584/2011.
 Podpořeno z projektu FRVŠ 584/2011. Obsah 1 2 Souřadnice na elipsoidu Zeměpisné souřadnice Kartografické souřadnice Izometrické (symetrické) souřadnice Pravoúhlé a polární souřadnice 3 Ortodroma Loxodroma
Podpořeno z projektu FRVŠ 584/2011. Obsah 1 2 Souřadnice na elipsoidu Zeměpisné souřadnice Kartografické souřadnice Izometrické (symetrické) souřadnice Pravoúhlé a polární souřadnice 3 Ortodroma Loxodroma
Matematická analýza 2. Kubr Milan
 Matematická analýza. Kubr Milan. února 008 Obsah Vektorové funkce jedné reálné proměnné. 3. Základní pojmy...................................... 3. Křivky v R n........................................
Matematická analýza. Kubr Milan. února 008 Obsah Vektorové funkce jedné reálné proměnné. 3. Základní pojmy...................................... 3. Křivky v R n........................................
7. Aplikace derivace
 7. Aplikace derivace 7A. Taylorův polynom 7. Aplikace derivace Verze 20. července 207 Derivace funkce se využívá při řešení úloh technické prae i teorie. Uvedeme několik z nich: vyčíslení hodnot funkce,
7. Aplikace derivace 7A. Taylorův polynom 7. Aplikace derivace Verze 20. července 207 Derivace funkce se využívá při řešení úloh technické prae i teorie. Uvedeme několik z nich: vyčíslení hodnot funkce,
Linea rnı (ne)za vislost
 [1] Lineární (ne)závislost Skupiny, resp. množiny, vektorů mohou být lineárně závislé nebo lineárně nezávislé... a) zavislost, 3, b) P. Olšák, FEL ČVUT, c) P. Olšák 2010, d) BI-LIN, e) L, f) 2009/2010,
[1] Lineární (ne)závislost Skupiny, resp. množiny, vektorů mohou být lineárně závislé nebo lineárně nezávislé... a) zavislost, 3, b) P. Olšák, FEL ČVUT, c) P. Olšák 2010, d) BI-LIN, e) L, f) 2009/2010,
(a). Pak f. (a) pro i j a 2 f
 Připomeň: 1. Necht K R n. Pak 1. Funkce více proměnných II 1.1. Parciální derivace vyšších řádů K je kompaktní K je omezená a uzavřená. 2. Necht K R n je kompaktní a f : K R je spojitá. Pak f nabývá na
Připomeň: 1. Necht K R n. Pak 1. Funkce více proměnných II 1.1. Parciální derivace vyšších řádů K je kompaktní K je omezená a uzavřená. 2. Necht K R n je kompaktní a f : K R je spojitá. Pak f nabývá na
Matematika II. Ing. Radek Fučík, Ph.D. WikiSkriptum. verze: 25. října 2019
 Mtemtik II Ing. Rdek Fučík, Ph.D. WikiSkriptum verze: 25. říjn 209 Obsh Integrce rcionálních funkcí 4 2 Zobecněný Riemnnův integrál 5 2. Definice........................................ 5 2.2 Kritéri konvergence.................................
Mtemtik II Ing. Rdek Fučík, Ph.D. WikiSkriptum verze: 25. říjn 209 Obsh Integrce rcionálních funkcí 4 2 Zobecněný Riemnnův integrál 5 2. Definice........................................ 5 2.2 Kritéri konvergence.................................
Funkce více proměnných: limita, spojitost, derivace
 Matematika III 2. přednáška Funkce více proměnných: limita, spojitost, derivace Michal Bulant Masarykova univerzita Fakulta informatiky 22. 9. 2014 Obsah přednášky 1 Literatura 2 Zobrazení a funkce více
Matematika III 2. přednáška Funkce více proměnných: limita, spojitost, derivace Michal Bulant Masarykova univerzita Fakulta informatiky 22. 9. 2014 Obsah přednášky 1 Literatura 2 Zobrazení a funkce více
Tvarová optimalizace pro 3D kontaktní problém
 Tvarová optimalizace pro 3D kontaktní problém s Coulombovým třením Petr Beremlijski, Jaroslav Haslinger, Michal Kočvara, Radek Kučera a Jiří V. Outrata Katedra aplikované matematik Fakulta elektrotechnik
Tvarová optimalizace pro 3D kontaktní problém s Coulombovým třením Petr Beremlijski, Jaroslav Haslinger, Michal Kočvara, Radek Kučera a Jiří V. Outrata Katedra aplikované matematik Fakulta elektrotechnik
Matematika prˇedna sˇka Lenka Prˇibylova 7. u nora 2007 c Lenka Prˇibylova, 200 7
 Matematika přednáška Lenka Přibylová 7. února 2007 Obsah Základy matematické logiky 9 Základní množinové pojmy 13 Množina reálných čísel a její podmnožiny 16 Funkce 18 Složená funkce 20 Vlastnosti funkcí
Matematika přednáška Lenka Přibylová 7. února 2007 Obsah Základy matematické logiky 9 Základní množinové pojmy 13 Množina reálných čísel a její podmnožiny 16 Funkce 18 Složená funkce 20 Vlastnosti funkcí
FAKULTA STAVEBNÍ. Stavební statika. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ Stavební statika Úvod, opakování, soustavy sil Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.broovsky@vsb.c WWW:
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ Stavební statika Úvod, opakování, soustavy sil Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.broovsky@vsb.c WWW:
Laplaceova transformace
 Laplaceova transformace Modelování systémů a procesů (11MSP) Bohumil Kovář, Jan Přikryl, Miroslav Vlček Ústav aplikované matematiky ČVUT v Praze, Fakulta dopravní 5. přednáška 11MSP 219 verze: 219-3-17
Laplaceova transformace Modelování systémů a procesů (11MSP) Bohumil Kovář, Jan Přikryl, Miroslav Vlček Ústav aplikované matematiky ČVUT v Praze, Fakulta dopravní 5. přednáška 11MSP 219 verze: 219-3-17
1 Definice. A B A B vlastní podmnožina. 4. Relace R mezi množinami A a B libovolná R A B. Je-li A = B relace na A
 1 Definice 1. Množiny: podmnožina: A B x(x A x B) průnik: A B = {x A x B} sjednocení: A B = {x x A x B} rozdíl: A B = {x A x B} A B A B vlastní podmnožina 2. uspořádaná dvojice: (x, y) = {{x}, {x, y}}
1 Definice 1. Množiny: podmnožina: A B x(x A x B) průnik: A B = {x A x B} sjednocení: A B = {x x A x B} rozdíl: A B = {x A x B} A B A B vlastní podmnožina 2. uspořádaná dvojice: (x, y) = {{x}, {x, y}}
Matematika (KMI/PMATE)
 Matematika (KMI/PMATE) Úvod do matematické analýzy Limita a spojitost funkce Matematika (KMI/PMATE) Osnova přednášky lineární funkce y = kx + q definice lineární funkce význam (smysl) koeficientů lineární
Matematika (KMI/PMATE) Úvod do matematické analýzy Limita a spojitost funkce Matematika (KMI/PMATE) Osnova přednášky lineární funkce y = kx + q definice lineární funkce význam (smysl) koeficientů lineární
Analiza Matematyczna 3 Całki wielowymiarowe
 [wersja z 6 X 9] Analiza Matematczna 3 Całki wielowmiarowe Konspekt wkładu dla studentów II r. fizki Uniwerstet Jana Kochanowskiego 9/ Wojciech Broniowski Powierzchnie kawałkami gładkie RYS Sfera Aleandra
[wersja z 6 X 9] Analiza Matematczna 3 Całki wielowmiarowe Konspekt wkładu dla studentów II r. fizki Uniwerstet Jana Kochanowskiego 9/ Wojciech Broniowski Powierzchnie kawałkami gładkie RYS Sfera Aleandra
Funkce více proměnných: limita, spojitost, parciální a směrové derivace, diferenciál
 Matematika III 2. přednáška Funkce více proměnných: limita, spojitost, parciální a směrové derivace, diferenciál Michal Bulant Masarykova univerzita Fakulta informatiky 29. 9. 2010 Obsah přednášky 1 Literatura
Matematika III 2. přednáška Funkce více proměnných: limita, spojitost, parciální a směrové derivace, diferenciál Michal Bulant Masarykova univerzita Fakulta informatiky 29. 9. 2010 Obsah přednášky 1 Literatura
DFT. verze:
 Výpočet spektra signálu pomocí DFT kacmarp@fel.cvut.cz verze: 009093 Úvod Signály můžeme rozdělit na signály spojité v čase nebo diskrétní v čase. Další možné dělení je na signály periodické nebo signály
Výpočet spektra signálu pomocí DFT kacmarp@fel.cvut.cz verze: 009093 Úvod Signály můžeme rozdělit na signály spojité v čase nebo diskrétní v čase. Další možné dělení je na signály periodické nebo signály
Přijímací zkouška na navazující magisterské studium 2018
 Přijímací zkouška na navazující magisterské studium 28 Studijní program: Studijní obory: Fyzika FFUM Varianta A Řešení příkladů pečlivě odůvodněte. Příklad 25 bodů Nechť {x n } je posloupnost, f : R R
Přijímací zkouška na navazující magisterské studium 28 Studijní program: Studijní obory: Fyzika FFUM Varianta A Řešení příkladů pečlivě odůvodněte. Příklad 25 bodů Nechť {x n } je posloupnost, f : R R
Matematika III Stechiometrie stručný
 Matematika III Stechiometrie stručný matematický úvod Miroslava Dubcová, Drahoslava Janovská, Daniel Turzík Ústav matematiky Přednášky LS 2015-2016 Obsah 1 Zápis chemické reakce 2 umožňuje jednotný přístup
Matematika III Stechiometrie stručný matematický úvod Miroslava Dubcová, Drahoslava Janovská, Daniel Turzík Ústav matematiky Přednášky LS 2015-2016 Obsah 1 Zápis chemické reakce 2 umožňuje jednotný přístup
Elementární funkce. Edita Pelantová. únor FJFI, ČVUT v Praze. katedra matematiky, FJFI, ČVUT v Praze
 Elementární funkce Edita Pelantová FJFI, ČVUT v Praze Seminář současné matematiky katedra matematiky, FJFI, ČVUT v Praze únor 2013 c Edita Pelantová (FJFI) Elementární funkce únor 2013 1 / 19 Polynomiální
Elementární funkce Edita Pelantová FJFI, ČVUT v Praze Seminář současné matematiky katedra matematiky, FJFI, ČVUT v Praze únor 2013 c Edita Pelantová (FJFI) Elementární funkce únor 2013 1 / 19 Polynomiální
cos(ωt) ω ( ) 1 cos ω sin(ωt)dt = sin(ωt) ω cos(ωt)dt i 1 = sin ω i ( 1 cos ω ω 1 e iωt dt = e iωt iω II sposób: ˆf(ω) = 1 = e iω 1 = i(e iω 1) i ω
 Rachunk prawdopodobiństwa MAP6 Wydział Elktroniki, rok akad. 8/9, sm. ltni Wykładowca: dr hab. A. Jurlwicz Przykłady do listy : Transformata Fourira Przykłady do zadania. : Korzystając z dfinicji wyznaczyć
Rachunk prawdopodobiństwa MAP6 Wydział Elktroniki, rok akad. 8/9, sm. ltni Wykładowca: dr hab. A. Jurlwicz Przykłady do listy : Transformata Fourira Przykłady do zadania. : Korzystając z dfinicji wyznaczyć
Matematika 1 Jiˇr ı Fiˇser 24. z aˇr ı 2013 Jiˇr ı Fiˇser (KMA, PˇrF UP Olomouc) KMA MAT1 24. z aˇr ı / 52
 í150doc-start í251doc-start Jiří Fišer (KMA, PřF UP Olomouc) KMA MAT1 24. září 2013 1 / 52 Matematika 1 Jiří Fišer 24. září 2013 Jiří Fišer (KMA, PřF UP Olomouc) KMA MAT1 24. září 2013 1 / 52 Zimní semestr
í150doc-start í251doc-start Jiří Fišer (KMA, PřF UP Olomouc) KMA MAT1 24. září 2013 1 / 52 Matematika 1 Jiří Fišer 24. září 2013 Jiří Fišer (KMA, PřF UP Olomouc) KMA MAT1 24. září 2013 1 / 52 Zimní semestr
(A B) ij = k. (A) ik (B) jk.
 Příklady z lineární algebry Michael Krbek 1 Opakování 1.1 Matice, determinanty 1. Je dána matice 1 2 0 M = 3 0 1. 1 0 1 Určete M 2, MM T, M T M a vyjádřete M jako součet symetrické a antisymetrické matice!
Příklady z lineární algebry Michael Krbek 1 Opakování 1.1 Matice, determinanty 1. Je dána matice 1 2 0 M = 3 0 1. 1 0 1 Určete M 2, MM T, M T M a vyjádřete M jako součet symetrické a antisymetrické matice!
Katedra aplikované matematiky FEI VŠB Technická univerzita Ostrava
 Lineární algebra 5. přednáška: Báze a řešitelnost soustav Dalibor Lukáš Katedra aplikované matematiky FEI VŠB Technická univerzita Ostrava email: dalibor.lukas@vsb.cz http://www.am.vsb.cz/lukas/la1 Text
Lineární algebra 5. přednáška: Báze a řešitelnost soustav Dalibor Lukáš Katedra aplikované matematiky FEI VŠB Technická univerzita Ostrava email: dalibor.lukas@vsb.cz http://www.am.vsb.cz/lukas/la1 Text
Paradoxy geometrické pravděpodobnosti
 Katedra aplikované matematiky 1. června 2009 Úvod Cíle práce : Analýza Bertrandova paradoxu. Tvorba simulačního softwaru. Osnova 1 2 3 4 Osnova 1 2 3 4 Osnova 1 2 3 4 Osnova 1 2 3 4 V rovině je zadán kruh
Katedra aplikované matematiky 1. června 2009 Úvod Cíle práce : Analýza Bertrandova paradoxu. Tvorba simulačního softwaru. Osnova 1 2 3 4 Osnova 1 2 3 4 Osnova 1 2 3 4 Osnova 1 2 3 4 V rovině je zadán kruh
Katedra aplikované matematiky FEI VŠB Technická univerzita Ostrava
 Lineární algebra 8. přednáška: Kvadratické formy Dalibor Lukáš Katedra aplikované matematiky FEI VŠB Technická univerzita Ostrava email: dalibor.lukas@vsb.cz http://www.am.vsb.cz/lukas/la Text byl vytvořen
Lineární algebra 8. přednáška: Kvadratické formy Dalibor Lukáš Katedra aplikované matematiky FEI VŠB Technická univerzita Ostrava email: dalibor.lukas@vsb.cz http://www.am.vsb.cz/lukas/la Text byl vytvořen
Internetová matematická olympiáda 8. ročník, Baví se student Fakulty strojního inženýrství VUT v Brně (FSI) s kamarádem:
 Internetová matematická olympiáda 8. ročník, 24. 11. 2015 1. Baví se student Fakulty strojního inženýrství VUT v Brně (FSI) s kamarádem: Kamarád: Co jsi tak veselý? Něco slavíš? Student FSI: Já přímo ne,
Internetová matematická olympiáda 8. ročník, 24. 11. 2015 1. Baví se student Fakulty strojního inženýrství VUT v Brně (FSI) s kamarádem: Kamarád: Co jsi tak veselý? Něco slavíš? Student FSI: Já přímo ne,
Zastosowania geometryczne całek
 Matematyka Zastosowania geometryczne całek Aleksander Denisiuk denisjuk@euh-e.edu.pl Elblaska Uczelnia Humanistyczno-Ekonomiczna ul. Lotnicza 2 82-3 Elblag Matematyka p. 1 Zastosowania geometryczne całek
Matematyka Zastosowania geometryczne całek Aleksander Denisiuk denisjuk@euh-e.edu.pl Elblaska Uczelnia Humanistyczno-Ekonomiczna ul. Lotnicza 2 82-3 Elblag Matematyka p. 1 Zastosowania geometryczne całek
Robotika. Kinematika 13. dubna 2017 Ing. František Burian Ph.D.
 Robotika Kinematika 13. dubna 2017 Ing. František Burian Ph.D., Řízení stacionárních robotů P P z q = f 1 (P) q z Pøímá úloha q U ROBOT q P R q = h(u) P = f (q) DH: Denavit-Hartenberg (4DOF/kloub) A i
Robotika Kinematika 13. dubna 2017 Ing. František Burian Ph.D., Řízení stacionárních robotů P P z q = f 1 (P) q z Pøímá úloha q U ROBOT q P R q = h(u) P = f (q) DH: Denavit-Hartenberg (4DOF/kloub) A i
Algebra I Cvičení. Podstatná část příkladů je převzata od kolegů, jmenovitě Prof. Kučery, Doc. Poláka a Doc. Kunce, se
 Algebra I Cvičení Podstatná část příkladů je převzata od kolegů, jmenovitě Prof. Kučery, Doc. Poláka a Doc. Kunce, se kterými jsem při přípravě cvičení spolupracoval. Sbírka vznikla modifikací některých
Algebra I Cvičení Podstatná část příkladů je převzata od kolegů, jmenovitě Prof. Kučery, Doc. Poláka a Doc. Kunce, se kterými jsem při přípravě cvičení spolupracoval. Sbírka vznikla modifikací některých
MATEMATIKA 1 ALEŠ NEKVINDA. + + pokud x < 0; x. Supremum a infimum množiny.
 MATEMATIKA ALEŠ NEKVINDA DIFERENCIÁLNÍ POČET Přednáška Označíme jako na střední škole N, Z, Q, R a C postupně množinu přirozených, celých, racionálních, reálných a komplexních čísel R = R { } { } Platí:
MATEMATIKA ALEŠ NEKVINDA DIFERENCIÁLNÍ POČET Přednáška Označíme jako na střední škole N, Z, Q, R a C postupně množinu přirozených, celých, racionálních, reálných a komplexních čísel R = R { } { } Platí:
Komplexní analýza. Příklad Body. Nepište obyčejnou tužkou ani červeně, jinak písemka nebude přijata. Soupis vybraných vzorců. 4a.
 Komplexí aalýa Písemá část koušky (XX.XX.XXXX) Jméo a příjmeí:... Podpis:... Příklad.. 3.. 5. Body Před ahájeím práce Vyplňte čitelě rubriku Jméo a příjmeí a podepište se. Během písemé koušky smíte mít
Komplexí aalýa Písemá část koušky (XX.XX.XXXX) Jméo a příjmeí:... Podpis:... Příklad.. 3.. 5. Body Před ahájeím práce Vyplňte čitelě rubriku Jméo a příjmeí a podepište se. Během písemé koušky smíte mít
GEOMETRIE. Vytvořeno v rámci projektu Operačního programu Rozvoje lidských zdrojů CZ / /0016. základu studia.
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA GEOMETRIE Jiří Doležal Vytvořeno v rámci projektu Operačního programu Rozvoje lidských zdrojů CZ.04.1.03/3.2.15.1/0016 Studijní opory s převažujícími distančními
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA GEOMETRIE Jiří Doležal Vytvořeno v rámci projektu Operačního programu Rozvoje lidských zdrojů CZ.04.1.03/3.2.15.1/0016 Studijní opory s převažujícími distančními
Speciální funkce, Fourierovy řady a Fourierova transformace
 1 Speciální funkce, Fourierovy řady a Fourierova transformace Při studiu mnoha přírodních jevů se setkáváme s veličinami, které jsou všude nulové s výjimkou malého časového intervalu I, ale jejich celková
1 Speciální funkce, Fourierovy řady a Fourierova transformace Při studiu mnoha přírodních jevů se setkáváme s veličinami, které jsou všude nulové s výjimkou malého časového intervalu I, ale jejich celková
Analiza Matematyczna 3 Całki wielowymiarowe
 [wersja z X 008] Analiza Matematyczna 3 Całki wielowymiarowe Konspekt wykładu dla studentów II r. fizyki Uniwersytet Jana Kochanowskiego 008/009 Wojciech Broniowski Powierzchnie kawałkami gładkie RYS Sfera
[wersja z X 008] Analiza Matematyczna 3 Całki wielowymiarowe Konspekt wykładu dla studentów II r. fizyki Uniwersytet Jana Kochanowskiego 008/009 Wojciech Broniowski Powierzchnie kawałkami gładkie RYS Sfera
(4) (b) m. (c) (d) sin α cos α = sin 2 k = sin k sin k. cos 2 m = cos m cos m. (g) (e)(f) sin 2 x + cos 2 x = 1. (h) (f) (i)
 (3) (e) sin( θ) sin θ cos( θ) cos θ sin(θ + π/) cos θ cos(θ + π/) sin θ sin(θ π/) cos θ cos(θ π/) sin θ sin(θ ± π) sin θ cos(θ ± π) cos θ sin(θ ± π) sin θ cos(θ ± π) cos θ (f) cos x cos y (g) sin x sin
(3) (e) sin( θ) sin θ cos( θ) cos θ sin(θ + π/) cos θ cos(θ + π/) sin θ sin(θ π/) cos θ cos(θ π/) sin θ sin(θ ± π) sin θ cos(θ ± π) cos θ sin(θ ± π) sin θ cos(θ ± π) cos θ (f) cos x cos y (g) sin x sin
Metody, s nimiž se seznámíme v této kapitole, lze použít pro libovolnou
 2. Řešení nelineárních rovnic Průvodce studiem Budeme se zabývat výpočtem reálných kořenů nelineární rovnice f(x) =0, (2.0.1) kde f je v jistém smyslu rozumná reálná funkce. Pro některé funkce (kvadratické,
2. Řešení nelineárních rovnic Průvodce studiem Budeme se zabývat výpočtem reálných kořenů nelineární rovnice f(x) =0, (2.0.1) kde f je v jistém smyslu rozumná reálná funkce. Pro některé funkce (kvadratické,
Uniwersytet Warmińsko-Mazurski w Olsztynie
 Uniwersytet Warmińsko-Mazurski w Olsztynie ZETAW II Całka podwójna.. Obliczyć całki iterowane (a 4 4 2 ( (x + y ( 2 4 ( y x y dy dx y 3 x 2 + y 2 dx dy. 2. Zmienić kolejność całkowania (a (d 2 e ( 2x x
Uniwersytet Warmińsko-Mazurski w Olsztynie ZETAW II Całka podwójna.. Obliczyć całki iterowane (a 4 4 2 ( (x + y ( 2 4 ( y x y dy dx y 3 x 2 + y 2 dx dy. 2. Zmienić kolejność całkowania (a (d 2 e ( 2x x
Logika V. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı BI-MLO, ZS 2011/12
 Logika V. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Logika V. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
GEM a soustavy lineárních rovnic, část 2
 GEM a soustavy lineárních rovnic, část Odpřednesenou látku naleznete v kapitole 6 skript Abstraktní a konkrétní lineární algebra. Jiří Velebil: B6B0LAG 8.3.09: GEM a soustavy, část / Minulá přednáška Gaussova
GEM a soustavy lineárních rovnic, část Odpřednesenou látku naleznete v kapitole 6 skript Abstraktní a konkrétní lineární algebra. Jiří Velebil: B6B0LAG 8.3.09: GEM a soustavy, část / Minulá přednáška Gaussova
22. CAŁKA KRZYWOLINIOWA SKIEROWANA
 CAŁA RZYWOLINIOWA SIEROWANA Niech łuk o równaniach parametrycznych: x x(t), y y(t), a < t < b, będzie łukiem regularnym skierowanym, tzn łukiem w którym przyjęto punkt A(x(a), y(a)) za początek łuku, zaś
CAŁA RZYWOLINIOWA SIEROWANA Niech łuk o równaniach parametrycznych: x x(t), y y(t), a < t < b, będzie łukiem regularnym skierowanym, tzn łukiem w którym przyjęto punkt A(x(a), y(a)) za początek łuku, zaś
podle přednášky doc. Eduarda Fuchse 16. prosince 2010
 Jak souvisí plochá dráha a konečná geometrie? L ubomíra Balková podle přednášky doc. Eduarda Fuchse Trendy současné matematiky 16. prosince 2010 (FJFI ČVUT v Praze) Konečná geometrie 16. prosince 2010
Jak souvisí plochá dráha a konečná geometrie? L ubomíra Balková podle přednášky doc. Eduarda Fuchse Trendy současné matematiky 16. prosince 2010 (FJFI ČVUT v Praze) Konečná geometrie 16. prosince 2010
Definice Řekneme, že PDA M = (Q,Σ,Γ,δ,q 0,Z 0,F) je. 1. pro všechna q Q a Z Γ platí: kdykoliv δ(q,ε,z), pak δ(q,a,z) = pro všechna a Σ;
 Deterministické zásobníkové automaty Definice 3.72. Řekneme, že PDA M = (Q,Σ,Γ,δ,q 0,Z 0,F) je deterministický (DPDA), jestliže jsou splněny tyto podmínky: 1. pro všechna q Q a Z Γ platí: kdykoliv δ(q,ε,z),
Deterministické zásobníkové automaty Definice 3.72. Řekneme, že PDA M = (Q,Σ,Γ,δ,q 0,Z 0,F) je deterministický (DPDA), jestliže jsou splněny tyto podmínky: 1. pro všechna q Q a Z Γ platí: kdykoliv δ(q,ε,z),
Mendelova univerzita v Brně user.mendelu.cz/marik
 INŽNÝRSKÁ MATMATIKA Robert Mařík Mendelova univerzita v Brně marik@mendelu.cz user.mendelu.cz/marik ABSTRAKT. Učební text k mým přednáškám z předmětu Inženýrská matematika. Text je poměrně hutný a není
INŽNÝRSKÁ MATMATIKA Robert Mařík Mendelova univerzita v Brně marik@mendelu.cz user.mendelu.cz/marik ABSTRAKT. Učební text k mým přednáškám z předmětu Inženýrská matematika. Text je poměrně hutný a není
