W η φ. Rys.1. To same. A B r1 A G F. B pionowej. To same. E E koło w pozycji pionowej. L2 Obwód koła K K K K K
|
|
|
- Liliana Kuczyńska
- 6 lat temu
- Przeglądów:
Transkrypt
1 RUCHOME SZKIELETY KONSTRUKCI PRZYSTOSOWANE DO KAŻDEGO PRZEKROU KRZYWYCH STOŻKOWYCH. SZTUKA PRZEKAZU w (). str.1 W η φ Rys.1 Stożek prosty o zrysie trójkąt: (DGC), do którego wprowdziłem ELIPSOIDĘ (oskrd), C pod kątem β do pionu. C ξ = 180,000 [ ] β A H A r1 To sme Hβ β r1 H odchyl.koło r1 koło w pozycji B r1 B B 90 od pionu B pionowej A B r1 A G A A L1 Obwód koł L1= 2*π*r1 F odchyl.koło F r2 od pionu E r2 To sme E E E koło w pozycji pionowej G F E r2 F E (H) F F r2 L2 Obwód koł K D D L2= 2*π*r2 K K K K k Pństwo pmiętcie wszystko, co jest w () robię w większości pierwszy rz. Byw, że wykonłem coś, co zwier błąd i ujrzło świtło dzienne w Internecie. Nie od rzu dostrzegm ten błąd. Byw, że rozwijm dny sposób interpretcji geometrii w rysunkch, który od niedwn nzywm "sztuką przekzu". Kiedy tworzyłem do UKŁAD-u (XYZ) rzuty prostopdłe punktów; odcinków; łuków; figur; brył n płszczyżnie poziomej (XY) MAPA; n płszczyznch pionowych, będących w pozycjch leżących: (XZ); (YZ), nie od rzu wszystko głdko mi wychodziło. Cły czs musiłem wszystko regulowć, by wreszcie swoje oprzyrządownie () zgrć. Udło mi się to wykonć, z cłą pewnością, w skrypcie poświęconym TEORII KRZYWYCH STOŻKOWYCH. Po modyfikcji. W tym pliku nie korzystm z UKŁAD-u, lecz jest coś, co jest wrte uwgi. Po lewej stronie w rmce jest rysunek ELIPSOIDY - bryły o ksztłcie oskrdu (młot do rozkuwni skł). Cł brył jest odchylow od płszczyzny pionowej pod kątem β. Brył styk się od góry z poprzeczką poziomą. Pełni rolę ogrnicznik ruchu bryły. N rysunku uwidoczniłem zielone strzłki, świdczące o ruchu obrotowym bryły. Istnieje tylko jeden punkt A, który styk się z płszczyzną prostopdłą ściny szrej. Po wprowdzeniu bryły w ruch, powstnie zbiór wszystkich punktów A n obwodzie kołowym ELIPSOIDY o promieniu r1. W punkcie centrlnym E bryły wpisuję koło o promieniu r2. Terz dot.ww uwgi. N osi wzdłużnej ELIPSOIDY są punkty: H, B, E, K,. Żeby je przemieścić do pionu i zchowć te sme odległości między nimi, użyłem z progrmu komput. "łuk". A tk nprwdę dopsowuję okrąg przy użyciu średnicy (lini pionow lub poziom), któr po obrocie (w prwo lub w lewo) spełni rolę średnicy. Punktem centr.łuku koł jest pkt C. Dopsowuję okrąg w tki sposób by pkt E znlzł się n tym okręgu. Terz rysuję łuk - lini 0,5 czerwon z grotmi. Łuk wyzncz mi pkt E n ścinie pionowej. Przez punkty: E i E przeprowdzm linię czerwoną prostą, przerywną. To jej kierunek n rysunku ndje kierunki pozostłym punktom oznczonych litermi dużymi, niebieskimi. Od tych punktów odchodzą linie poziome przerywne 0,25 do przekroju ELIPSOIDY z prwej str. W ten sposób otrzymłem w pionie obrz przekroju - rzutu prostopdłego n płszczyznę ELIPSOIDY. Przy okzji wykonłem przekroje płszczyzn bryły w osich: A-A; F-F. Poz tym wykonłem rysunki dwóch kół w pozycji pionowej z punktmi centrlnymi: B i E wrz z obliczeniem długości toru jzdy obu kół. Po przeprowdzeniu linii skośnej 0,25 przez groty strzłek obu kół z linią pionową przechodzącą przez punkty: B i E otrzymłem trójkąt, który m prwe rmię odchylone od pionu o kąt ξ =180[ ]-β. N rys.1 nrysowłem linią czerwoną 0,25 szkielet konstrukcji przekroju, który powstł z linii krzywej progrmu komp. M.Excel. Żeby tki szkielet uzyskć, musiłem wszystkie punkty zznczyć jko nrożne. W ten sposób powstł wspomniny szkielet. Krzyw z której powstł szkielet jest n rys.2 i rys.3. Do wykonni szkieletów n przekrojch krzywych stożkowych posłużyłem się przekrojmi z pliku: Skrypt (R).009.A. T Ruchomy szkielet konstr.przystos.do kżdego przekr. ELIPSY
2 RUCHOME SZKIELETY KONSTRUKCI PRZYSTOSOWANE DO KAŻDEGO PRZEKROU ELIPSY. SZTUKA PRZEKAZU w (). H Linie krzywych, grficznych progrmu komput.m.excel. Rys.2 = b < b < b b b b b b b ψ ψ < b str.2 liniły czerwone Szkielet ruchomy konstrukcji ELIPSOIDY (przekrój) = b przekrój koł Rys.3 H ψ ψ < b b b b b b b b b b b b b przekrój koł < b I. < b Szkielet ruchomy konstrukcji ELIPSOIDY (przekrój) b b b b T Ruchomy szkielet konstr.przystos.do kżdego przekr. ELIPSY
3 RUCHOME SZKIELETY KONSTRUKCI PRZYSTOSOWANE DO KAŻDEGO PRZEKROU ELIPSY. SZTUKA PRZEKAZU w (). 3h str.3 O O O O O Rys.4 TARCZA ZEGARA 2 2; 3h 18h O O O 17h h 1 T Ruchomy szkielet konstr.przystos.do kżdego przekr. ELIPSY
4 RUCHOME SZKIELETY KONSTRUKCI PRZYSTOSOWANE DO KAŻDEGO PRZEKROU PARABOLI. SZTUKA PRZEKAZU w (). Rys.5b Rys.5c Rys.5d Rys.5e Rys.5 Rys.5 Rys.5g str.4 Rys. Constns Rusztownie n prboli Ruchomy szkielet n prboli Rys.5f Constns Szkielet prboli (smukły) Rys.6 Rys.6 Rys.6b Rys.6c Rys.6d Rys.6e T Ruchomy szkielet konstr.przystos.do kżdego przekr.paraboli
5 RUCHOME SZKIELETY KONSTRUKCI PRZYSTOSOWANE DO KAŻDEGO PRZEKROU PARABOLI. SZTUKA PRZEKAZU w (). Rys.6f Rys.6g Rys. 3h Rys.6i str.5 2; Rys.6j 3h Rys.6k 18h O 17h h 1 TARCZA ZEGARA 2 Rys.6m T Ruchomy szkielet konstr.przystos.do kżdego przekr.paraboli
6 RUCHOME SZKIELETY KONSTRUKCI PRZYSTOSOWANE DO KAŻDEGO PRZEKROU HIPERBOLI. SZTUKA PRZEKAZU w (). str.6 Rys.7 Rys.7 Rys.7b Rys.7c constns Rys.7d Rusztownie n hiperboli Rys.7e Rys.7f Rys.7g Rys.7h Rys.7i Rys.7j Rys.7m constns Rys.7k Rys.7n T Ruchomy szkielet konstr.przystos.do kżdego przekr.hiperboli Koszlin dni r
7 RUCHOME SZKIELETY KONSTRUKCI PRZYSTOSOWANE DO KAŻDEGO PRZEKROU HIPERBOLI. SZTUKA PRZEKAZU w (). str.7 3h Rys.7o Rys.7p Rys.7r Rys.7s TARCZA ZEGARA 2 2; 3h 18h O 17h Rys.7t 13h 1 Rys.7u Rys.7w Z pewnością spytcie Pństwo, po co zrobiłem tkie szkielety? Odpowiem. Po pierwsze, nbrłem pewności, że kżdą krzywą możn swobodnie obrcć pod kżdym kątem n trczy zegr (2). Po drugie, mogę stożek prosty przystosowć do elstycznego, ruchomego szkieletu krzywej. Po trzecie, nic tk nie przyspiesz prcę, jk ściąg. W prktyce nie trzeb pokzywć szkieletu n rysunkch. est zintegrowny z figurą krzywej stożkowej. Po czwrte, ściąg w M.Excel może być stosown w (). T Ruchomy szkielet konstr.przystos.do kżdego przekr.hiperboli Koszlin dni r
Rys.5a. Grot stożka widziany jako trójkąt równoram. Dwa rysunki w jednym. W' 1h na kole Pkt W najbardziej. 23h na kole w4 2h na kole Ø3
 BRÓT KÓŁ SI (Z) GRTA STŻKEG SKRĘTNEG Z PLIKU SKRYPT (R).009.N NA GDZINIE (24h). Grot turbiny stożkowo-skrętny, ośmiołukowy.rys.powiększony 2*.Ruch obrotowy równoleżnikowy grota wokół osi (X) Rys.6a Rys.5a
BRÓT KÓŁ SI (Z) GRTA STŻKEG SKRĘTNEG Z PLIKU SKRYPT (R).009.N NA GDZINIE (24h). Grot turbiny stożkowo-skrętny, ośmiołukowy.rys.powiększony 2*.Ruch obrotowy równoleżnikowy grota wokół osi (X) Rys.6a Rys.5a
(a) (b) (c) o1" o2" o3" o1'=o2'=o3'
 Zad.0. Odwzorowanie powierzchni stożka, walca, sfery oraz punktów leżących na tych powierzchniach. Przy odwzorowaniu powierzchni stożka, walca, sfery przyjmiemy reprezentację konturową, co oznacza, że
Zad.0. Odwzorowanie powierzchni stożka, walca, sfery oraz punktów leżących na tych powierzchniach. Przy odwzorowaniu powierzchni stożka, walca, sfery przyjmiemy reprezentację konturową, co oznacza, że
Rys.1 pomocniczy. Okrąg z którego powstały łuki na rys.1b.
 OBRÓT OKÓŁ OSI (Z) GROTA STOŻKOEGO SKRĘTNEGO Z PLIKU SKRYPT (R).9.N NA GOZINIE h(24h). str.1 Grot skrętny turbiny, ośmiołukowy, powiększony 2*. Rysunki pokazują wcześniej poznane metody przekazu wiedzy,
OBRÓT OKÓŁ OSI (Z) GROTA STOŻKOEGO SKRĘTNEGO Z PLIKU SKRYPT (R).9.N NA GOZINIE h(24h). str.1 Grot skrętny turbiny, ośmiołukowy, powiększony 2*. Rysunki pokazują wcześniej poznane metody przekazu wiedzy,
Projekt Era inżyniera pewna lokata na przyszłość jest współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Mteriły dydktyczne n zjęci wyrównwcze z mtemtyki dl studentów pierwszego roku kierunku zmwinego Biotechnologi w rmch projektu Er inżynier pewn lokt n przyszłość Projekt Er inżynier pewn lokt n przyszłość
Mteriły dydktyczne n zjęci wyrównwcze z mtemtyki dl studentów pierwszego roku kierunku zmwinego Biotechnologi w rmch projektu Er inżynier pewn lokt n przyszłość Projekt Er inżynier pewn lokt n przyszłość
TABELA PRZELICZENIOWA
 Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował: inż. Kazimierz arski Romana - imię
Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował: inż. Kazimierz arski Romana - imię
gk T Okrąg z punktami wg tarczy zegara (24h), przerobiony na turbinę obrotową. Uruchomienie fantazji. Rys.1 Rys.2
 krąg z punktami wg tarczy zegara (24h), przerobiony na turbinę obrotową. Uruchomienie fantazji. Rys.1 23h 1h 22h 2h str.1 21h 3h 20h 4h 19h 5h 18h 6h 17h 7h 16h 8h 15h 9h 14h 10h 13h 11h Rys.2 Szablon
krąg z punktami wg tarczy zegara (24h), przerobiony na turbinę obrotową. Uruchomienie fantazji. Rys.1 23h 1h 22h 2h str.1 21h 3h 20h 4h 19h 5h 18h 6h 17h 7h 16h 8h 15h 9h 14h 10h 13h 11h Rys.2 Szablon
gk T Jak wykorzystać poznaną wiedzę na przyrządach geometrii kulowej (gk), w sposób praktyczny. Rys.2a
 Jak wykorzystać poznaną wiedzę na przyrządach geometrii kulowej (), w sposób praktyczny. str.1 Wpadłem na pomysł, by opracować schemat bryły biurowieca o ciekawej konstrukcji architektonicznej. Najciekawszą
Jak wykorzystać poznaną wiedzę na przyrządach geometrii kulowej (), w sposób praktyczny. str.1 Wpadłem na pomysł, by opracować schemat bryły biurowieca o ciekawej konstrukcji architektonicznej. Najciekawszą
Rys.1. Rys.1. str.1. 19h 20h 21h 22h 23h 24h 0h 1h 2h 3h 4h 5h 6h. kopia. Nr1
 niewidoczny 18h skrypt Romny (R) dl wszystkich ludzi świt Romn imię mojej młżonki Nr NIESAMWITE MŻLIWŚCI SZABLNÓW LISTWWYCH: "A"; "B", "C" ZWIĄZANE Z ŁUKAMI, PDZIAŁEM RÓWNMIERNIE RZŁŻNYM. KPIA FRAGMENTU
niewidoczny 18h skrypt Romny (R) dl wszystkich ludzi świt Romn imię mojej młżonki Nr NIESAMWITE MŻLIWŚCI SZABLNÓW LISTWWYCH: "A"; "B", "C" ZWIĄZANE Z ŁUKAMI, PDZIAŁEM RÓWNMIERNIE RZŁŻNYM. KPIA FRAGMENTU
MECHANIKA 2 KINEMATYKA. Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 KINEMATYKA Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY Prowadzący: dr Krzysztof Polko Określenie położenia ciała sztywnego Pierwszy sposób: Określamy położenia trzech punktów ciała nie leżących
MECHANIKA 2 KINEMATYKA Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY Prowadzący: dr Krzysztof Polko Określenie położenia ciała sztywnego Pierwszy sposób: Określamy położenia trzech punktów ciała nie leżących
MECHANIKA 2. Wykład Nr 3 KINEMATYKA. Temat RUCH PŁASKI BRYŁY MATERIALNEJ. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Wykład Nr 3 KINEMATYKA Temat RUCH PŁASKI BRYŁY MATERIALNEJ Prowadzący: dr Krzysztof Polko Pojęcie Ruchu Płaskiego Rys.1 Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie
MECHANIKA 2 Wykład Nr 3 KINEMATYKA Temat RUCH PŁASKI BRYŁY MATERIALNEJ Prowadzący: dr Krzysztof Polko Pojęcie Ruchu Płaskiego Rys.1 Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie
Rok akademicki 2005/2006
 GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2005/2006 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2005/2006 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
- Wydział Fizyki Zestaw nr 5. Powierzchnie 2-go stopnia
 1 Algebr Liniow z Geometri - Wydził Fizyki Zestw nr 5 Powierzchnie -go stopni 1 N sferze 1 + + 3 = 4 znleźć punkt, którego odległość od punktu p = (, 6, 3) byłby njmniejsz Wyznczyć osie elipsy powstłej
1 Algebr Liniow z Geometri - Wydził Fizyki Zestw nr 5 Powierzchnie -go stopni 1 N sferze 1 + + 3 = 4 znleźć punkt, którego odległość od punktu p = (, 6, 3) byłby njmniejsz Wyznczyć osie elipsy powstłej
400% Rys.2a Negatyw *** ZASADA *** Rys.1a Pozytyw pł.(yz) Zabawa "włosem" musi być oparta na OPIS WYKONYWANYCH CZYNNOŚCI.
 Szkic 1. `````2 2 str.1 PWIĘKSZ! 00% Rys.2a *** ZSD *** Rys.1a Pozytyw pł.(yz) Zabawa "włosem" musi być oparta na 0h() 12 dwóch rzutach prostokątnych, na dwie 12 płaszczyzny tj. MPĘ (XY) i pł.(yz). Powyższe
Szkic 1. `````2 2 str.1 PWIĘKSZ! 00% Rys.2a *** ZSD *** Rys.1a Pozytyw pł.(yz) Zabawa "włosem" musi być oparta na 0h() 12 dwóch rzutach prostokątnych, na dwie 12 płaszczyzny tj. MPĘ (XY) i pł.(yz). Powyższe
gk T Przenik.wzajem.brył obr.hiperboloidy z paraboloidą
 Przeniknie wzjemne brył obrot.hiperboloid dwupowłokową cz.górn z prboloidą eliptyczną. Do tego zdni wykorzystm krzywe zmknięte z pliku krypt (R).009.38(Ukryt bud.apoloniusz z Pregi). Chodzi o hiperbolę
Przeniknie wzjemne brył obrot.hiperboloid dwupowłokową cz.górn z prboloidą eliptyczną. Do tego zdni wykorzystm krzywe zmknięte z pliku krypt (R).009.38(Ukryt bud.apoloniusz z Pregi). Chodzi o hiperbolę
Płaszczyzny, Obrót, Szyk
 Płaszczyzny, Obrót, Szyk Zagadnienia. Szyk kołowy, tworzenie brył przez Obrót. Geometria odniesienia, Płaszczyzna. Wykonajmy model jak na rys. 1. Wykonanie korpusu pokrywki Rysunek 1. Model pokrywki (1)
Płaszczyzny, Obrót, Szyk Zagadnienia. Szyk kołowy, tworzenie brył przez Obrót. Geometria odniesienia, Płaszczyzna. Wykonajmy model jak na rys. 1. Wykonanie korpusu pokrywki Rysunek 1. Model pokrywki (1)
Rys.1. Rys.1. str.1. 19h 20h 21h 22h 23h 24h 0h 1h 2h 3h 4h 5h 6h. kopia. Nr1
 niewidoczny skrypt Romny (R) dl wszystkich ludzi świt NIESAMWITE MŻLIWŚCI SZABLNÓW LISTWWYCH: "A"; "B", "C" ZWIĄZANE Z ŁUKAMI, PDZIAŁEM RÓWNMIERNIE RZŁŻNYM. KPIA FRAGMENTU PLIKU: SKRYPT (R).001. STRNA
niewidoczny skrypt Romny (R) dl wszystkich ludzi świt NIESAMWITE MŻLIWŚCI SZABLNÓW LISTWWYCH: "A"; "B", "C" ZWIĄZANE Z ŁUKAMI, PDZIAŁEM RÓWNMIERNIE RZŁŻNYM. KPIA FRAGMENTU PLIKU: SKRYPT (R).001. STRNA
Zestaw Obliczyć objętość równoległościanu zbudowanego na wektorach m, n, p jeśli wiadomo, że objętość równoległościanu zbudowanego na wektorach:
 Zestaw 9. Wykazać, że objętość równoległościanu zbudowanego na przekątnych ścian danego równoległościanu jest dwa razy większa od objętości równoległościanu danego.. Obliczyć objętość równoległościanu
Zestaw 9. Wykazać, że objętość równoległościanu zbudowanego na przekątnych ścian danego równoległościanu jest dwa razy większa od objętości równoległościanu danego.. Obliczyć objętość równoległościanu
gk T GEOMETRIA WYKREŚLNA PRZESTRZENNA T (GK) W PRAKTYCE. SZTUKA TRASOWANIA CZ.1. Rys.3. Rys.4. Rysunek jest zbyt duży, zmniejszę go na str.2.
 GEOMERIA WYKREŚLNA PRZESRZENNA (GK) W PRAKYCE. SZUKA RASOWANIA CZ.1. str.1 Kiedyś od jakiegoś gościa otrzymałem emaila. Pytał mnie jakie należy stosować linie i jakie grubości tych linii. W końcu zapytał
GEOMERIA WYKREŚLNA PRZESRZENNA (GK) W PRAKYCE. SZUKA RASOWANIA CZ.1. str.1 Kiedyś od jakiegoś gościa otrzymałem emaila. Pytał mnie jakie należy stosować linie i jakie grubości tych linii. W końcu zapytał
TABELA PRZELICZENIOWA
 Romana - imię mojej małżonki 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
Romana - imię mojej małżonki 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
Mechanical 2000 Power Pack
 Autoryzowane Centrum Szkolenia Autodesk ID No 80057559 Instytut Podstaw Budowy Maszyn Politechnika Warszawska 02-524 Warszawa ul. Narbutta 84 tel. 849-03-07 Mechanical 2000 Power Pack Ćwiczenia rysunkowe
Autoryzowane Centrum Szkolenia Autodesk ID No 80057559 Instytut Podstaw Budowy Maszyn Politechnika Warszawska 02-524 Warszawa ul. Narbutta 84 tel. 849-03-07 Mechanical 2000 Power Pack Ćwiczenia rysunkowe
SZa 98 strona 1 Rysunek techniczny
 Wstęp Wymiarowanie Rodzaje linii rysunkowych i ich przeznaczenie 1. linia ciągła cienka linie pomocnicze, kreskowanie przekrojów, linie wymiarowe, 2. linia ciągła gruba krawędzie widoczne 3. linia kreskowa
Wstęp Wymiarowanie Rodzaje linii rysunkowych i ich przeznaczenie 1. linia ciągła cienka linie pomocnicze, kreskowanie przekrojów, linie wymiarowe, 2. linia ciągła gruba krawędzie widoczne 3. linia kreskowa
Projekt Era inżyniera pewna lokata na przyszłość jest współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Mteriły dydktyczne n zjęci wyrównwcze z mtemtyki dl studentów pierwszego roku kierunku zmwinego Inżynieri Środowisk w rmch projektu Er inżynier pewn lokt n przyszłość Projekt Er inżynier pewn lokt n przyszłość
Mteriły dydktyczne n zjęci wyrównwcze z mtemtyki dl studentów pierwszego roku kierunku zmwinego Inżynieri Środowisk w rmch projektu Er inżynier pewn lokt n przyszłość Projekt Er inżynier pewn lokt n przyszłość
Moja geometria kulowa (sferyczna) w praktyce (gk) powoli Rzutnie: (XZ); (YZ); (XY).
 CZ.II. Przenikanie dwóch róŝnych stoŝków obrot.w (gk). Mimośród osi stoŝków leŝących na pł.równoległych. str.1 Rys.1 pł.(xz) pionowa. Osie obu stoŝków obrotowych znajdują się na dwóch płaszczyznach pionowych,
CZ.II. Przenikanie dwóch róŝnych stoŝków obrot.w (gk). Mimośród osi stoŝków leŝących na pł.równoległych. str.1 Rys.1 pł.(xz) pionowa. Osie obu stoŝków obrotowych znajdują się na dwóch płaszczyznach pionowych,
Rozwiązania maj 2017r. Zadania zamknięte
 Rozwiązni mj 2017r. Zdni zmknięte Zd 1. 5 16 5 2 5 2 Zd 2. 5 2 27 2 23 2 2 2 2 Zd 3. 2log 3 2log 5log 3 log 5 log 9 log 25log Zd. 120% 8910 1,2 8910 2,2 8910 $%, 050 Zd 5. Njłtwiej jest zuwżyć że dl 1
Rozwiązni mj 2017r. Zdni zmknięte Zd 1. 5 16 5 2 5 2 Zd 2. 5 2 27 2 23 2 2 2 2 Zd 3. 2log 3 2log 5log 3 log 5 log 9 log 25log Zd. 120% 8910 1,2 8910 2,2 8910 $%, 050 Zd 5. Njłtwiej jest zuwżyć że dl 1
Geometria wykreślna. 5. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław. Politechnika Gdańska, Wydział Architektury
 Geometria wykreślna 5. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Architektura, semestr I 1 5. Obroty i
Geometria wykreślna 5. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Architektura, semestr I 1 5. Obroty i
Zadanie I. 2. Gdzie w przestrzeni usytuowane są punkty (w której ćwiartce leży dany punkt): F x E' E''
 GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2012/2013 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2012/2013 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
Rys.1. str.1. 48h;0h 18h 19h 20h 21h 22h 46h. 44h r1 4h. 10h. 38h. 34h 14h. 32h 16h. 24h jest linią do przenoszenia szablonów
 Moje własne opracowanie torusa na przyrządach: tarczy zegara (48h); szablonu listwowego A. en rysunek ORUSA, będzie miał ostatecznie 48 promieni. str.1 Rys.1 N 48h;0h 18h 19h 20h 21h 22h 46h 2h 4h 6h 8h
Moje własne opracowanie torusa na przyrządach: tarczy zegara (48h); szablonu listwowego A. en rysunek ORUSA, będzie miał ostatecznie 48 promieni. str.1 Rys.1 N 48h;0h 18h 19h 20h 21h 22h 46h 2h 4h 6h 8h
Przykład Łuk ze ściągiem, obciążenie styczne. D A
 Przykład 1.4. Łuk ze ściągiem, obciążenie styczne. Rysunek przedstawia łuk trójprzegubowy, kołowy, ze ściągiem. Łuk obciążony jest obciążeniem stycznym do łuku, o stałej gęstości na jednostkę długości
Przykład 1.4. Łuk ze ściągiem, obciążenie styczne. Rysunek przedstawia łuk trójprzegubowy, kołowy, ze ściągiem. Łuk obciążony jest obciążeniem stycznym do łuku, o stałej gęstości na jednostkę długości
Definicja obrotu: Definicja elementów obrotu:
 5. Obroty i kłady Definicja obrotu: Obrotem punktu A dookoła prostej l nazywamy ruch punktu A po okręgu k zawartym w płaszczyźnie prostopadłej do prostej l w kierunku zgodnym lub przeciwnym do ruchu wskazówek
5. Obroty i kłady Definicja obrotu: Obrotem punktu A dookoła prostej l nazywamy ruch punktu A po okręgu k zawartym w płaszczyźnie prostopadłej do prostej l w kierunku zgodnym lub przeciwnym do ruchu wskazówek
ZADANIA Z GEOMETRII RÓŻNICZKOWEJ NA PIERWSZE KOLOKWIUM
 ZADANIA Z GEOMETRII RÓŻNICZKOWEJ NA PIERWSZE KOLOKWIUM. Koło o promieniu n płszczyźnie Oxy oczy się bez poślizgu wzdłuż osi Ox. Miejsce geomeryczne opisne przez punk M leżący n obwodzie ego koł jes cykloidą.
ZADANIA Z GEOMETRII RÓŻNICZKOWEJ NA PIERWSZE KOLOKWIUM. Koło o promieniu n płszczyźnie Oxy oczy się bez poślizgu wzdłuż osi Ox. Miejsce geomeryczne opisne przez punk M leżący n obwodzie ego koł jes cykloidą.
Projekt Era inżyniera pewna lokata na przyszłość jest współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Mteriły dydktyczne n zjęci wyrównwcze z mtemtyki dl studentów pierwszego roku kierunku zmwinego Inżynieri i Gospodrk Wodn w rmch projektu Er inżynier pewn lokt n przyszłość Projekt Er inżynier pewn lokt
Mteriły dydktyczne n zjęci wyrównwcze z mtemtyki dl studentów pierwszego roku kierunku zmwinego Inżynieri i Gospodrk Wodn w rmch projektu Er inżynier pewn lokt n przyszłość Projekt Er inżynier pewn lokt
Zadania nadobowiązkowe KRZYWE STOŻKOWE OKRĄG
 OKRĄG Przykład 1. W układzie współrzędnych XOY narysujmy okrąg o środku w punkcie (0,0) i promieniu 1: Współrzędne dowolnego punktu P(x,y) leżącego na okręgu spełniają równanie + y =1, natomiast współrzędne
OKRĄG Przykład 1. W układzie współrzędnych XOY narysujmy okrąg o środku w punkcie (0,0) i promieniu 1: Współrzędne dowolnego punktu P(x,y) leżącego na okręgu spełniają równanie + y =1, natomiast współrzędne
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH
 STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
KONKURS MATEMATYCZNY dla uczniów gimnazjów w roku szkolnym 2012/13. Propozycja punktowania rozwiązań zadań
 KONKURS MATEMATYCZNY dl uczniów gimnzjów w roku szkolnym 0/ II etp zwodów (rejonowy) 0 listopd 0 r. Propozycj punktowni rozwiązń zdń Uwg: Z kżde poprwne rozwiąznie inne niż przewidzine w propozycji punktowni
KONKURS MATEMATYCZNY dl uczniów gimnzjów w roku szkolnym 0/ II etp zwodów (rejonowy) 0 listopd 0 r. Propozycj punktowni rozwiązń zdń Uwg: Z kżde poprwne rozwiąznie inne niż przewidzine w propozycji punktowni
wymagania programowe z matematyki kl. II gimnazjum
 wymagania programowe z matematyki kl. II gimnazjum Umie obliczyć potęgę liczby wymiernej o wykładniku naturalnym. 1. Arytmetyka występują potęgi o wykładniku naturalnym. Umie zapisać i porównać duże liczby
wymagania programowe z matematyki kl. II gimnazjum Umie obliczyć potęgę liczby wymiernej o wykładniku naturalnym. 1. Arytmetyka występują potęgi o wykładniku naturalnym. Umie zapisać i porównać duże liczby
Projekcje (rzuty) Sferyczna, stereograficzna, cyklograficzna,...
 Projekcje (rzuty) Sferyczna, stereograficzna, cyklograficzna,... Rzut sferyczny (projekcja sferyczna) Kryształ zastępuje się zespołem płaszczyzn i prostych równoległych do odpowiadających im płaszczyzn
Projekcje (rzuty) Sferyczna, stereograficzna, cyklograficzna,... Rzut sferyczny (projekcja sferyczna) Kryształ zastępuje się zespołem płaszczyzn i prostych równoległych do odpowiadających im płaszczyzn
I. DYNAMIKA PUNKTU MATERIALNEGO
 I. DYNAMIKA PUNKTU MATERIALNEGO A. RÓŻNICZKOWE RÓWNANIA RUCHU A1. Bryła o masie m przesuwa się po chropowatej równi z prędkością v M. Podać dynamiczne równania ruchu bryły i rozwiązać je tak, aby wyznaczyć
I. DYNAMIKA PUNKTU MATERIALNEGO A. RÓŻNICZKOWE RÓWNANIA RUCHU A1. Bryła o masie m przesuwa się po chropowatej równi z prędkością v M. Podać dynamiczne równania ruchu bryły i rozwiązać je tak, aby wyznaczyć
1 Definicja całki oznaczonej
 Definicj cłki oznczonej Niech dn będzie funkcj y = g(x) ciągł w przedzile [, b]. Przedził [, b] podzielimy n n podprzedziłów punktmi = x < x < x
Definicj cłki oznczonej Niech dn będzie funkcj y = g(x) ciągł w przedzile [, b]. Przedził [, b] podzielimy n n podprzedziłów punktmi = x < x < x
ROZWINIĘCIA POWIERZCHNI STOPNIA DRUGIEGO W OPARCIU O MIEJSCA GEOMETRYCZNE Z ZA- STOSOWANIEM PROGRAMU CABRI II PLUS.
 Anna BŁACH, Piotr DUDZIK, Anita PAWLAK Politechnika Śląska Ośrodek Geometrii i Grafiki Inżynierskiej ul. Krzywoustego 7 44-100 Gliwice tel./ fax: 0-32 237 26 58, e-mail: anna.blach@polsl.pl, piotr.dudzik@polsl.pl,
Anna BŁACH, Piotr DUDZIK, Anita PAWLAK Politechnika Śląska Ośrodek Geometrii i Grafiki Inżynierskiej ul. Krzywoustego 7 44-100 Gliwice tel./ fax: 0-32 237 26 58, e-mail: anna.blach@polsl.pl, piotr.dudzik@polsl.pl,
Co należy zauważyć Rzuty punktu leżą na jednej prostej do osi rzutów x 12, którą nazywamy prostą odnoszącą Wysokość punktu jest odległością rzutu
 Oznaczenia A, B, 1, 2, I, II, punkty a, b, proste α, β, płaszczyzny π 1, π 2, rzutnie k kierunek rzutowania d(a,m) odległość punktu od prostej m(a,b) prosta przechodząca przez punkty A i B α(1,2,3) płaszczyzna
Oznaczenia A, B, 1, 2, I, II, punkty a, b, proste α, β, płaszczyzny π 1, π 2, rzutnie k kierunek rzutowania d(a,m) odległość punktu od prostej m(a,b) prosta przechodząca przez punkty A i B α(1,2,3) płaszczyzna
str 1 WYMAGANIA EDUKACYJNE ( ) - matematyka - poziom podstawowy Dariusz Drabczyk
 str 1 WYMAGANIA EDUKACYJNE (2017-2018) - matematyka - poziom podstawowy Dariusz Drabczyk Klasa 3e: wpisy oznaczone jako: (T) TRYGONOMETRIA, (PII) PLANIMETRIA II, (RP) RACHUNEK PRAWDOPODOBIEŃSTWA, (ST)
str 1 WYMAGANIA EDUKACYJNE (2017-2018) - matematyka - poziom podstawowy Dariusz Drabczyk Klasa 3e: wpisy oznaczone jako: (T) TRYGONOMETRIA, (PII) PLANIMETRIA II, (RP) RACHUNEK PRAWDOPODOBIEŃSTWA, (ST)
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO. dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury
 KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
Skrypt 13. Koło i okrąg. Opracowanie: GIM3. 1. Okrąg i koło - podstawowe pojęcia (promień, średnica, cięciwa) 2. Wzajemne położenie dwóch okręgów
 Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 13 Koło i okrąg 1. Okrąg i koło - podstawowe
Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 13 Koło i okrąg 1. Okrąg i koło - podstawowe
Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych
 Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych Wydział Matematyki Politechniki Wrocławskiej Okrąg Okrąg jest szczególną krzywą stożkową. Wyznacza nam koło, które jest podstawą
Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych Wydział Matematyki Politechniki Wrocławskiej Okrąg Okrąg jest szczególną krzywą stożkową. Wyznacza nam koło, które jest podstawą
Analiza Matematyczna MAEW101 MAP1067
 Analiza Matematyczna MAEW MAP67 Wydział Elektroniki Przykłady do Listy Zadań nr 4 Funkcje wielu zmiennych. Pochodne cząstkowe Opracowanie: dr hab. Agnieszka Jurlewicz Przykłady do zadania 4.: Wyznaczyć
Analiza Matematyczna MAEW MAP67 Wydział Elektroniki Przykłady do Listy Zadań nr 4 Funkcje wielu zmiennych. Pochodne cząstkowe Opracowanie: dr hab. Agnieszka Jurlewicz Przykłady do zadania 4.: Wyznaczyć
Pokrywka. Rysunek 1. Projekt - wynik końcowy. Rysunek 2. Pierwsza linia łamana szkicu
 Pokrywka Rysunek 1. Projekt - wynik końcowy Projekt rozpoczynamy od narysowania zamkniętego szkicu. 1. Narysujemy i zwymiarujmy linię łamaną jako część szkicu (nie zamknięty), rys. 2. Uwaga: a) Dodajmy
Pokrywka Rysunek 1. Projekt - wynik końcowy Projekt rozpoczynamy od narysowania zamkniętego szkicu. 1. Narysujemy i zwymiarujmy linię łamaną jako część szkicu (nie zamknięty), rys. 2. Uwaga: a) Dodajmy
O kula. w (gks). Rzutnie: (XZ); (YZ); (XY). A B (YZ) (XY) D sześciana
 Zad.nr 14 zastępcze.dwa stoŝki cięte odchyl.od pionu w jednej pł.z rozwin.w ().Wzór uŝykt. W 116814 UP RP. Format.Ark.A4 12,75*1,75 str.1 Rys.1 pł.( X Z )pn.w () Oba rzuty zawierają pełny zakres danych
Zad.nr 14 zastępcze.dwa stoŝki cięte odchyl.od pionu w jednej pł.z rozwin.w ().Wzór uŝykt. W 116814 UP RP. Format.Ark.A4 12,75*1,75 str.1 Rys.1 pł.( X Z )pn.w () Oba rzuty zawierają pełny zakres danych
Krzywe stożkowe Lekcja I: Wprowadzenie
 Krzywe stożkowe Lekcja I: Wprowadzenie Wydział Matematyki Politechniki Wrocławskiej Powierzchnia stożkowa Zaczniemy od przyjrzenia się powierzchni stożkowej. Jest ona wyznaczona przez linię prostą (tworzącą)
Krzywe stożkowe Lekcja I: Wprowadzenie Wydział Matematyki Politechniki Wrocławskiej Powierzchnia stożkowa Zaczniemy od przyjrzenia się powierzchni stożkowej. Jest ona wyznaczona przez linię prostą (tworzącą)
Zestaw zadań z Analizy Matematycznej II 18/19. Konwencja: pierwsze litery alfabetu są parametrami, do tego zazwyczaj dodatnimi
 Literatura pomocnicza Zestaw zadań z Analizy Matematycznej II 8/9 G.M. Fichtenholz - Rachunek różniczkowy i całkowy. B. Demidowicz - Zbiór zadań z analizy matematycznej. T 2,3 Krysicki, Włodarski - Analiza
Literatura pomocnicza Zestaw zadań z Analizy Matematycznej II 8/9 G.M. Fichtenholz - Rachunek różniczkowy i całkowy. B. Demidowicz - Zbiór zadań z analizy matematycznej. T 2,3 Krysicki, Włodarski - Analiza
Projekt połowicznej, prostej endoprotezy stawu biodrowego w programie SOLIDWorks.
 1 Projekt połowicznej, prostej endoprotezy stawu biodrowego w programie SOLIDWorks. Rysunek. Widok projektowanej endoprotezy według normy z wymiarami charakterystycznymi. 2 3 Rysunek. Ilustracje pomocnicze
1 Projekt połowicznej, prostej endoprotezy stawu biodrowego w programie SOLIDWorks. Rysunek. Widok projektowanej endoprotezy według normy z wymiarami charakterystycznymi. 2 3 Rysunek. Ilustracje pomocnicze
Spis treści. Podstawowe definicje. Wielokąty. Trójkąty. Czworokąty. Kąty
 Mrt Compny Ksprowicz LOGO Spis treści. 1 Podstwowe definicje 2 Wielokąty 3 Trójkąty 4 Czworokąty 5 Kąty Podstwowe definicje w geometrii. 1.Punkt 2.Prost 3.Proste prostopdłe 4.Proste równoległe 5.Półprost
Mrt Compny Ksprowicz LOGO Spis treści. 1 Podstwowe definicje 2 Wielokąty 3 Trójkąty 4 Czworokąty 5 Kąty Podstwowe definicje w geometrii. 1.Punkt 2.Prost 3.Proste prostopdłe 4.Proste równoległe 5.Półprost
Grafika inżynierska geometria wykreślna. 5a. Obroty i kłady. Rozwinięcie wielościanu.
 Grafika inżynierska geometria wykreślna 5a. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Gospodarka przestrzenna,
Grafika inżynierska geometria wykreślna 5a. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Gospodarka przestrzenna,
MECHANIKA 2. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Prowadzący: dr Krzysztof Polko PLAN WYKŁADÓW 1. Podstawy kinematyki 2. Ruch postępowy i obrotowy bryły 3. Ruch płaski bryły 4. Ruch złożony i ruch względny 5. Ruch kulisty i ruch ogólny bryły
MECHANIKA 2 Prowadzący: dr Krzysztof Polko PLAN WYKŁADÓW 1. Podstawy kinematyki 2. Ruch postępowy i obrotowy bryły 3. Ruch płaski bryły 4. Ruch złożony i ruch względny 5. Ruch kulisty i ruch ogólny bryły
TABELA PRZELICZENIOWA
 Romana - imię mojej małżonki Nr 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
Romana - imię mojej małżonki Nr 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
w jednym kwadrat ziemia powietrze równoboczny pięciobok
 Wielościany Definicja 1: Wielościanem nazywamy zbiór skończonej ilości wielokątów płaskich spełniających następujące warunki: 1. każde dwa wielokąty mają bok lub wierzchołek wspólny albo nie mają żadnego
Wielościany Definicja 1: Wielościanem nazywamy zbiór skończonej ilości wielokątów płaskich spełniających następujące warunki: 1. każde dwa wielokąty mają bok lub wierzchołek wspólny albo nie mają żadnego
KWADRYKI PARABOLOIDA HIPERBOLICZNA ELIPSOIDA HIPERBOLOIDA DWUPOWŁOKOWA HIPERBOLOIDA JEDNOPOWŁOKOWA PARABOLOIDA ELIPTYCZNA
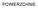 POWIERZCHNIE 1. Powierzchnia jedno z podstawowych pojęć geometrii. 1.1. W geometrii elementarnej powierzchnię opisuje się jako pewne zbiory punktów lub prostych o określonych własnościach np.: - sfera
POWIERZCHNIE 1. Powierzchnia jedno z podstawowych pojęć geometrii. 1.1. W geometrii elementarnej powierzchnię opisuje się jako pewne zbiory punktów lub prostych o określonych własnościach np.: - sfera
Kolektor. Zagadnienia. Wyciągnięcia po profilach, Lustro, Szyk. Wykonajmy model kolektora jak na rys. 1.
 Kolektor Zagadnienia. Wyciągnięcia po profilach, Lustro, Szyk Wykonajmy model kolektora jak na rys. 1. Rysunek 1 Składa się on z grubszej rury, o zmiennym przekroju, leżącej w płaszczyźnie symetrii kolektora
Kolektor Zagadnienia. Wyciągnięcia po profilach, Lustro, Szyk Wykonajmy model kolektora jak na rys. 1. Rysunek 1 Składa się on z grubszej rury, o zmiennym przekroju, leżącej w płaszczyźnie symetrii kolektora
Wykład 2. Granice, ciągłość, pochodna funkcji i jej interpretacja geometryczna
 1 Wykłd Grnice, ciągłość, pocodn unkcji i jej interpretcj geometryczn.1 Grnic unkcji. Grnic lewostronn i grnic prwostronn unkcji Deinicj.1 Mówimy, że liczb g jest grnicą lewostronną unkcji w punkcie =,
1 Wykłd Grnice, ciągłość, pocodn unkcji i jej interpretcj geometryczn.1 Grnic unkcji. Grnic lewostronn i grnic prwostronn unkcji Deinicj.1 Mówimy, że liczb g jest grnicą lewostronną unkcji w punkcie =,
Plan wykładu. Wykład 3. Rzutowanie prostokątne, widoki, przekroje, kłady. Rzutowanie prostokątne - geneza. Rzutowanie prostokątne - geneza
 Plan wykładu Wykład 3 Rzutowanie prostokątne, widoki, przekroje, kłady 1. Rzutowanie prostokątne - geneza 2. Dwa sposoby wzajemnego położenia rzutni, obiektu i obserwatora, metoda europejska i amerykańska
Plan wykładu Wykład 3 Rzutowanie prostokątne, widoki, przekroje, kłady 1. Rzutowanie prostokątne - geneza 2. Dwa sposoby wzajemnego położenia rzutni, obiektu i obserwatora, metoda europejska i amerykańska
Skrypt 20. Planimetria: Opracowanie L6
 Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 20 Planimetria: 1. Kąty w
Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 20 Planimetria: 1. Kąty w
Skrypt 20. Bryły: 24. Obliczanie pól powierzchni walców w sytuacjach praktycznych. 26. Zastosowanie tw. Pitagorasa do obliczania objętości walców
 Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 20 Bryły: 21. Przykłady brył obrotowych 22.
Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 20 Bryły: 21. Przykłady brył obrotowych 22.
ZADANIE.Nr 1. Z GEOMETRII KULOWEJ (SFERYCZNEJ) W PRAKTYCE (gk).
 ZADANIE.Nr 1. Z GEOMETRII KULOWEJ (SFERYCZNEJ) W PRAKTYCE (). str.1 patrzymy Stożek prosty nr1 Rys.1 m k ELIPSA jest cieniem, czyli rzutem prostopadłym na. Zatem nie podlega odchyleniom od pionu. Co nie
ZADANIE.Nr 1. Z GEOMETRII KULOWEJ (SFERYCZNEJ) W PRAKTYCE (). str.1 patrzymy Stożek prosty nr1 Rys.1 m k ELIPSA jest cieniem, czyli rzutem prostopadłym na. Zatem nie podlega odchyleniom od pionu. Co nie
3. Model Kosmosu A. Einsteina
 19 3. Model Kosmosu A. Einsteina Pierwszym rozwiązaniem równań pola grawitacyjnego w 1917 r. było równanie hiperpowierzchni kuli czterowymiarowej, przy założeniu, że materia kosmiczna tzw. substrat jest
19 3. Model Kosmosu A. Einsteina Pierwszym rozwiązaniem równań pola grawitacyjnego w 1917 r. było równanie hiperpowierzchni kuli czterowymiarowej, przy założeniu, że materia kosmiczna tzw. substrat jest
Skrypt dla ucznia. Geometria analityczna część 3: Opracowanie L3
 Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt dla ucznia Geometria analityczna
Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt dla ucznia Geometria analityczna
wymiarowanie1 >>> wymiarowanie2 >>> wymiarowanie3 >>> wymiarowanie >>> wymiarowanie >>> Co to jest wymiarowanie?
 wymiarowanie1 >>> wymiarowanie2 >>> wymiarowanie3 >>> wymiarowanie >>> wymiarowanie >>> Co to jest wymiarowanie? Jedną z najważniejszych części rysunku technicznego jest wymiarowanie. Jest to podanie pełnej
wymiarowanie1 >>> wymiarowanie2 >>> wymiarowanie3 >>> wymiarowanie >>> wymiarowanie >>> Co to jest wymiarowanie? Jedną z najważniejszych części rysunku technicznego jest wymiarowanie. Jest to podanie pełnej
WYKŁAD IV BRYŁY OBROTOWE PRZEKROJE BRYŁ OBROTOWYCH DR INŻ. ELŻBIETA RUDCZYK-MALIJEWSKA
 WYKŁAD IV BRYŁY OBROTOWE PRZEKROJE BRYŁ OBROTOWYCH DR INŻ. ELŻBIETA RUDCZYK-MALIJEWSKA WALEC powstaje w wyniku obrotu prostokąta wokół prostej zawierającej jeden z jego boków WALEC oś obrotu podstawa wysokość
WYKŁAD IV BRYŁY OBROTOWE PRZEKROJE BRYŁ OBROTOWYCH DR INŻ. ELŻBIETA RUDCZYK-MALIJEWSKA WALEC powstaje w wyniku obrotu prostokąta wokół prostej zawierającej jeden z jego boków WALEC oś obrotu podstawa wysokość
Ćwiczenie 9. Rzutowanie i wymiarowanie Strona 1 z 5
 Ćwiczenie 9. Rzutowanie i wymiarowanie Strona 1 z 5 Problem I. Model UD Dana jest bryła, której rzut izometryczny przedstawiono na rysunku 1. (W celu zwiększenia poglądowości na rysunku 2. przedstawiono
Ćwiczenie 9. Rzutowanie i wymiarowanie Strona 1 z 5 Problem I. Model UD Dana jest bryła, której rzut izometryczny przedstawiono na rysunku 1. (W celu zwiększenia poglądowości na rysunku 2. przedstawiono
Katalog wymagań programowych na poszczególne stopnie szkolne
 rozpoznaje figury podobne zna własności figur podobnych rozpoznaje trójkąty prostokątne podobne Rozdział 6. Figury podobne zna cechy podobieństwa trójkątów prostokątnych podobnych podaje skalę podobieństwa
rozpoznaje figury podobne zna własności figur podobnych rozpoznaje trójkąty prostokątne podobne Rozdział 6. Figury podobne zna cechy podobieństwa trójkątów prostokątnych podobnych podaje skalę podobieństwa
Wymagania edukacyjne na poszczególne stopnie szkolne klasa III
 Wymagania edukacyjne na poszczególne stopnie szkolne klasa III Rozdział 1. Bryły - wie, czym jest graniastosłup, graniastosłup prosty, graniastosłup prawidłowy - wie, czym jest ostrosłup, ostrosłup prosty,
Wymagania edukacyjne na poszczególne stopnie szkolne klasa III Rozdział 1. Bryły - wie, czym jest graniastosłup, graniastosłup prosty, graniastosłup prawidłowy - wie, czym jest ostrosłup, ostrosłup prosty,
Katalog wymagań programowych na poszczególne stopnie szkolne
 rozpoznaje figury podobne zna własności figur podobnych rozpoznaje trójkąty prostokątne podobne Rozdział 6. Figury podobne zna cechy podobieństwa trójkątów prostokątnych podobnych podaje skalę podobieństwa
rozpoznaje figury podobne zna własności figur podobnych rozpoznaje trójkąty prostokątne podobne Rozdział 6. Figury podobne zna cechy podobieństwa trójkątów prostokątnych podobnych podaje skalę podobieństwa
PODSTAWY > Figury płaskie (1) KĄTY. Kąt składa się z ramion i wierzchołka. Jego wielkość jest mierzona w stopniach:
 PODSTAWY > Figury płaskie (1) KĄTY Kąt składa się z ramion i wierzchołka. Jego wielkość jest mierzona w stopniach: Kąt możemy opisać wpisując w łuk jego miarę (gdy jest znana). Gdy nie znamy miary kąta,
PODSTAWY > Figury płaskie (1) KĄTY Kąt składa się z ramion i wierzchołka. Jego wielkość jest mierzona w stopniach: Kąt możemy opisać wpisując w łuk jego miarę (gdy jest znana). Gdy nie znamy miary kąta,
Przedmiotowy system oceniania Wymagania na poszczególne oceny,,liczy się matematyka
 Przedmiotowy system oceniania Wymagania na poszczególne oceny,,liczy się matematyka I. Potęgi i pierwiastki. Klasa II 1. Zapisuje w postaci potęgi iloczyn tych samych czynników i odwrotnie. 2. Oblicza
Przedmiotowy system oceniania Wymagania na poszczególne oceny,,liczy się matematyka I. Potęgi i pierwiastki. Klasa II 1. Zapisuje w postaci potęgi iloczyn tych samych czynników i odwrotnie. 2. Oblicza
Analiza Matematyczna. Zastosowania Całek
 Analiza Matematyczna. Zastosowania Całek Aleksander Denisiuk denisiuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 8-45 Gdańsk 9 maja 217
Analiza Matematyczna. Zastosowania Całek Aleksander Denisiuk denisiuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 8-45 Gdańsk 9 maja 217
Przykładowe zadania/problemy egzaminacyjne. Wszystkie bezwymiarowe wartości liczbowe występujące w treści zadań podane są w jednostkach SI.
 Przykładowe zadania/problemy egzaminacyjne. Wszystkie bezwymiarowe wartości liczbowe występujące w treści zadań podane są w jednostkach SI. 1. Ładunki q 1 =3,2 10 17 i q 2 =1,6 10 18 znajdują się w próżni
Przykładowe zadania/problemy egzaminacyjne. Wszystkie bezwymiarowe wartości liczbowe występujące w treści zadań podane są w jednostkach SI. 1. Ładunki q 1 =3,2 10 17 i q 2 =1,6 10 18 znajdują się w próżni
Uniwersytet Warmińsko-Mazurski w Olsztynie
 Uniwersytet Warmińsko-Mazurski w Olsztynie ZETAW II Całka podwójna.. Obliczyć całki iterowane (a 4 4 2 ( (x + y ( 2 4 ( y x y dy dx y 3 x 2 + y 2 dx dy. 2. Zmienić kolejność całkowania (a (d 2 e ( 2x x
Uniwersytet Warmińsko-Mazurski w Olsztynie ZETAW II Całka podwójna.. Obliczyć całki iterowane (a 4 4 2 ( (x + y ( 2 4 ( y x y dy dx y 3 x 2 + y 2 dx dy. 2. Zmienić kolejność całkowania (a (d 2 e ( 2x x
3.3. dwie płaszczyzny równoległe do siebie α β Dwie płaszczyzny równoległe do siebie mają ślady równoległe do siebie
 Widoczność A. W rzutowaniu europejskim zakłada się, że przedmiot obserwowany znajduje się między obserwatorem a rzutnią, a w amerykańskim rzutnia rozdziela przedmiot o oko obserwatora. B. Kierunek patrzenia
Widoczność A. W rzutowaniu europejskim zakłada się, że przedmiot obserwowany znajduje się między obserwatorem a rzutnią, a w amerykańskim rzutnia rozdziela przedmiot o oko obserwatora. B. Kierunek patrzenia
KGGiBM GRAFIKA INŻYNIERSKA Rok III, sem. VI, sem IV SN WILiŚ Rok akademicki 2011/2012
 Rysowanie precyzyjne 7 W ćwiczeniu tym pokazane zostaną wybrane techniki bardzo dokładnego rysowania obiektów w programie AutoCAD 2012, między innymi wykorzystanie punktów charakterystycznych. Narysować
Rysowanie precyzyjne 7 W ćwiczeniu tym pokazane zostaną wybrane techniki bardzo dokładnego rysowania obiektów w programie AutoCAD 2012, między innymi wykorzystanie punktów charakterystycznych. Narysować
Końcoworoczne kryteria oceniania dla klasy II z matematyki przygotowały mgr Magdalena Murawska i mgr Iwona Śliczner
 Końcoworoczne kryteria oceniania dla klasy II z matematyki przygotowały mgr Magdalena Murawska i mgr Iwona Śliczner Semestr I Rozdział: Potęgi i pierwiastki zapisuje w postaci potęgi iloczyn tych samych
Końcoworoczne kryteria oceniania dla klasy II z matematyki przygotowały mgr Magdalena Murawska i mgr Iwona Śliczner Semestr I Rozdział: Potęgi i pierwiastki zapisuje w postaci potęgi iloczyn tych samych
OBLICZENIE PRZEKROJU WALCA PO CIĘCIU SKOŚNYM. Rysunki i obliczenia dotyczą walca
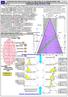 Kolejna metoda obliczania rzędnych i odciętych także obrazowa, przy stosowaniu tzw.przyrostów (trójkątów prostokątnych) różniącymi się kolorami żółtym i zielonym. Przy każdym poziomie koła jest mała tabelka
Kolejna metoda obliczania rzędnych i odciętych także obrazowa, przy stosowaniu tzw.przyrostów (trójkątów prostokątnych) różniącymi się kolorami żółtym i zielonym. Przy każdym poziomie koła jest mała tabelka
ZADANIA OTWARTE. Są więc takie same. Trzeba jeszcze pokazać, że wynoszą one 2b, gdyż taka jest długość krawędzi dwudziestościanu.
 ZADANIA OTWARTE ZADANIE 1 DWUDZIESTOŚCIAN FOREMNY Wiemy, że z trzech złotych prostokątów możn skonstruowć dwudziestościn foremny. Wystrczy wykzć, że długości boków trójkąt ABC n rysunku obok są równe.
ZADANIA OTWARTE ZADANIE 1 DWUDZIESTOŚCIAN FOREMNY Wiemy, że z trzech złotych prostokątów możn skonstruowć dwudziestościn foremny. Wystrczy wykzć, że długości boków trójkąt ABC n rysunku obok są równe.
TYCZENIE OSI TRASY W 2 R 2 SŁ KŁ W 1 W 3
 TYCZENIE TRAS W procesie projektowania i realizacji inwestycji liniowych (autostrad, linii kolejowych, kanałów itp.) materiałem źródłowym jest mapa sytuacyjno-wysokościowa w skalach 1:5 000; 1:10 000 lub
TYCZENIE TRAS W procesie projektowania i realizacji inwestycji liniowych (autostrad, linii kolejowych, kanałów itp.) materiałem źródłowym jest mapa sytuacyjno-wysokościowa w skalach 1:5 000; 1:10 000 lub
Wymagania edukacyjne niezbędne do uzyskania poszczególnych śródrocznych ocen klasyfikacyjnych z matematyki klasa 2 (oddział gimnazjalny)
 edukacyjne niezbędne do uzyskania poszczególnych śródrocznych ocen klasyfikacyjnych z matematyki klasa 2 (oddział gimnazjalny) Stopień Rozdział 1. Potęgi i pierwiastki zapisuje w postaci potęgi iloczyn
edukacyjne niezbędne do uzyskania poszczególnych śródrocznych ocen klasyfikacyjnych z matematyki klasa 2 (oddział gimnazjalny) Stopień Rozdział 1. Potęgi i pierwiastki zapisuje w postaci potęgi iloczyn
Kąty, trójkąty i czworokąty.
 Kąty, trójkąty i czworokąty. str. 1/5...... imię i nazwisko lp. w dzienniku...... klasa data 1. Do kartonu wstawiono 3 garnki (zobacz rysunek), których dna mają promienie:13 cm, 15 cm i 11 cm. Podaj długość
Kąty, trójkąty i czworokąty. str. 1/5...... imię i nazwisko lp. w dzienniku...... klasa data 1. Do kartonu wstawiono 3 garnki (zobacz rysunek), których dna mają promienie:13 cm, 15 cm i 11 cm. Podaj długość
Klasa 3.Graniastosłupy.
 Klasa 3.Graniastosłupy. 1. Uzupełnij nazwy odcinków oznaczonych literami: a........................................................... b........................................................... c...........................................................
Klasa 3.Graniastosłupy. 1. Uzupełnij nazwy odcinków oznaczonych literami: a........................................................... b........................................................... c...........................................................
Rozdział 2. Krzywe stożkowe. 2.1 Elipsa. Krzywe stożkowe są zadane ogólnym równaniem kwadratowym na płaszczyźnie
 Rozdział Krzywe stożkowe Krzywe stożkowe są zadane ogólnym równaniem kwadratowym na płaszczyźnie x + By + Cxy + Dx + Ey + F = 0. (.) W zależności od relacji pomiędzy współczynnikami otrzymujemy elipsę,
Rozdział Krzywe stożkowe Krzywe stożkowe są zadane ogólnym równaniem kwadratowym na płaszczyźnie x + By + Cxy + Dx + Ey + F = 0. (.) W zależności od relacji pomiędzy współczynnikami otrzymujemy elipsę,
Tik Z wiadomości wstępne
 Tik Z wiadomości wstępne Zofia Walczak 17 lutego 2014 1 Co należy wiedzieć na początku Aby rozpocząć pracę z TikZ -em należy w preambule dokumentu wczytać pakiet używając polecenia \usepackage{tikz}. Tik
Tik Z wiadomości wstępne Zofia Walczak 17 lutego 2014 1 Co należy wiedzieć na początku Aby rozpocząć pracę z TikZ -em należy w preambule dokumentu wczytać pakiet używając polecenia \usepackage{tikz}. Tik
Równania prostych i krzywych; współrzędne punktu
 Równania prostych i krzywych; współrzędne punktu Zad 1: Na paraboli o równaniu y = 1 x znajdź punkt P leŝący najbliŝej prostej o równaniu x + y = 0 Napisz równanie stycznej do tej paraboli, poprowadzonej
Równania prostych i krzywych; współrzędne punktu Zad 1: Na paraboli o równaniu y = 1 x znajdź punkt P leŝący najbliŝej prostej o równaniu x + y = 0 Napisz równanie stycznej do tej paraboli, poprowadzonej
11. Znajdż równanie prostej prostopadłej do prostej k i przechodzącej przez punkt A = (2;2).
 1. Narysuj poniższe figury: a), b), c) 2. Punkty A = (0;1) oraz B = (-1;0) należą do okręgu którego środek należy do prostej o równaniu x-2 = 0. Podaj równanie okręgu. 3. Znaleźć równanie okręgu przechodzącego
1. Narysuj poniższe figury: a), b), c) 2. Punkty A = (0;1) oraz B = (-1;0) należą do okręgu którego środek należy do prostej o równaniu x-2 = 0. Podaj równanie okręgu. 3. Znaleźć równanie okręgu przechodzącego
Bryła sztywna Zadanie domowe
 Bryła sztywna Zadanie domowe 1. Podczas ruszania samochodu, w pewnej chwili prędkość środka przedniego koła wynosiła. Sprawdź, czy pomiędzy kołem a podłożem występował poślizg, jeżeli średnica tego koła
Bryła sztywna Zadanie domowe 1. Podczas ruszania samochodu, w pewnej chwili prędkość środka przedniego koła wynosiła. Sprawdź, czy pomiędzy kołem a podłożem występował poślizg, jeżeli średnica tego koła
WOJEWÓDZKI KONKURS MATEMATYCZNY
 Kod ucznia Liczba punktów WOJEWÓDZKI KONKURS MATEMATYCZNY DLA UCZNIÓW DOTYCHCZASOWYCH GIMNAZJÓW W ROKU SZKOLNYM 08/09.0.09 R.. Test konkursowy zawiera zadania. Są to zadania zamknięte i otwarte. Na ich
Kod ucznia Liczba punktów WOJEWÓDZKI KONKURS MATEMATYCZNY DLA UCZNIÓW DOTYCHCZASOWYCH GIMNAZJÓW W ROKU SZKOLNYM 08/09.0.09 R.. Test konkursowy zawiera zadania. Są to zadania zamknięte i otwarte. Na ich
Analiza Matematyczna Praca domowa
 Analiza Matematyczna Praca domowa J. de Lucas Zadanie 1. Pokazać, że dla wszystkich n naturalnych ( n ) exp kx k dx 1 dx n = 1 n (e k 1). (0,1) n k=1 n! k=1 Zadanie. Obliczyć dla dowolnego n. (0,1) n (x
Analiza Matematyczna Praca domowa J. de Lucas Zadanie 1. Pokazać, że dla wszystkich n naturalnych ( n ) exp kx k dx 1 dx n = 1 n (e k 1). (0,1) n k=1 n! k=1 Zadanie. Obliczyć dla dowolnego n. (0,1) n (x
PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1
 PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1 Planimetria to dział geometrii, w którym przedmiotem badań są własności figur geometrycznych leżących na płaszczyźnie (patrz określenie płaszczyzny). Pojęcia
PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1 Planimetria to dział geometrii, w którym przedmiotem badań są własności figur geometrycznych leżących na płaszczyźnie (patrz określenie płaszczyzny). Pojęcia
Matematyka II. Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 2018/2019 Wykład 1
 Mtemtyk II Bezpieczeństwo jądrowe i ochron rdiologiczn Semestr letni 2018/2019 Wykłd 1 Zsdy współprcy przypomnienie Wykłdy są nieobowiązkowe, le Egzmin: pytni teoretyczne z łtwymi ćwiczenimi (będzie list)
Mtemtyk II Bezpieczeństwo jądrowe i ochron rdiologiczn Semestr letni 2018/2019 Wykłd 1 Zsdy współprcy przypomnienie Wykłdy są nieobowiązkowe, le Egzmin: pytni teoretyczne z łtwymi ćwiczenimi (będzie list)
Całka oznaczona i całka niewłaściwa Zastosowania rachunku całkowego w geometrii
 Wydził Mtemtyki Stosownej Zestw zdń nr 6 Akdemi Górniczo-Hutnicz w Krkowie WFiIS, informtyk stosown, I rok Elżbiet Admus 9 listopd 8r. Cłk oznczon i cłk niewłściw Zstosowni rchunku cłkowego w geometrii
Wydził Mtemtyki Stosownej Zestw zdń nr 6 Akdemi Górniczo-Hutnicz w Krkowie WFiIS, informtyk stosown, I rok Elżbiet Admus 9 listopd 8r. Cłk oznczon i cłk niewłściw Zstosowni rchunku cłkowego w geometrii
GEOMETRIA PRZESTRZENNA (STEREOMETRIA)
 GEOMETRIA PRZESTRZENNA (STEREOMETRIA) WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. Na początek omówimy
GEOMETRIA PRZESTRZENNA (STEREOMETRIA) WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. Na początek omówimy
- Wydział Fizyki Zestaw nr 2. Krzywe stożkowe
 1 Algebra Liniowa z Geometria - Wydział Fizyki Zestaw nr 2 Krzywe stożkowe 1 Znaleźć współrze dne środka i promień okre gu x 2 8x + y 2 + 6y + 20 = 0 2 Znaleźć zbiór punktów płaszczyzny R 2, których odległość
1 Algebra Liniowa z Geometria - Wydział Fizyki Zestaw nr 2 Krzywe stożkowe 1 Znaleźć współrze dne środka i promień okre gu x 2 8x + y 2 + 6y + 20 = 0 2 Znaleźć zbiór punktów płaszczyzny R 2, których odległość
Pytania do spr / Własności figur (płaskich i przestrzennych) (waga: 0,5 lub 0,3)
 Pytania zamknięte / TEST : Wybierz 1 odp prawidłową. 1. Punkt: A) jest aksjomatem in. pewnikiem; B) nie jest aksjomatem, bo można go zdefiniować. 2. Prosta: A) to zbiór punktów; B) to zbiór punktów współliniowych.
Pytania zamknięte / TEST : Wybierz 1 odp prawidłową. 1. Punkt: A) jest aksjomatem in. pewnikiem; B) nie jest aksjomatem, bo można go zdefiniować. 2. Prosta: A) to zbiór punktów; B) to zbiór punktów współliniowych.
Zad.3. Jakub Trojgo i Jakub Wieczorek. 14 grudnia 2013
 Zad.3 Jakub Trojgo i Jakub Wieczorek 14 grudnia 2013 W pierwszej części naszej pracy będziemy chcieli zbadać ciągłość funkcji f(x, y) w przypadku gdy płaszczyzna wyposażona jest w jedną z topologii: a)
Zad.3 Jakub Trojgo i Jakub Wieczorek 14 grudnia 2013 W pierwszej części naszej pracy będziemy chcieli zbadać ciągłość funkcji f(x, y) w przypadku gdy płaszczyzna wyposażona jest w jedną z topologii: a)
Geometria. Hiperbola
 Geometria. Hiperbola Definicja 1 Dano dwa punkty na płaszczyźnie: F 1 i F 2 oraz taką liczbę d, że F 1 F 2 > d > 0. Zbiór punktów płaszczyzny będących rozwiązaniami równania: XF 1 XF 2 = ±d. nazywamy hiperbolą.
Geometria. Hiperbola Definicja 1 Dano dwa punkty na płaszczyźnie: F 1 i F 2 oraz taką liczbę d, że F 1 F 2 > d > 0. Zbiór punktów płaszczyzny będących rozwiązaniami równania: XF 1 XF 2 = ±d. nazywamy hiperbolą.
