MECHANIZMY ROBOTÓW M A N I P U L A T O R Y
|
|
|
- Andrzej Czerwiński
- 7 lat temu
- Przeglądów:
Transkrypt
1 MECHANIZMY ROBOTÓW M A N I P U L A T O R Y
2 sterowanie Manipulator mechaniczny uład przeznaczony do realizaci nietórych funci ręi ludzie. Manus (łacina) - ręa uład mechaniczny Karel Cape R.U.R. (Roboty Universalna Rossuma) 9
3 Prawa robotów : Isaac Asimov w rou 94 stworzył trzy prawa robotów i przedstawił e w fantastycznym opowiadaniu Zabawa w bera (Runaround).. Robot nie może srzywdzić człowiea, ani przez zaniechanie działania dopuścić, aby człowie doznał rzywdy.. Robot musi być posłuszny rozazom człowiea, chyba że stoą one w sprzeczności z Pierwszym Prawem.. Robot musi chronić sam siebie, eśli tylo nie stoi to w sprzeczności z Pierwszym lub Drugim Prawem.
4 Ewoluca MANIPULATOR KOPIUJĄCY -małe siły (napędza operator), - małe odległości (długi łańcuch inemat błędy) servo computer
5 Ewoluca operator sterue za pomocą przycisów (bra czucia ) servo computer
6 Ewoluca Serwonapędy operator czue siłę servo computer
7 Ewoluca servo computer Robot współczesny
8 ZASTOSOWANIA: PRACA W SRODOWISKU NIEBEZPIECZNYM: PROMIENIOWANIE, SKAŻENIE ZAGROŻENIE EKSPLOZJĄ WYSOKIE CIŚNIENIE GŁĘBIA UCIĄŻLIWE I POWTARZALNE OPERACJE TECHNOLOGICZNE MONTAZOWE, SPAWALNICZE, OBRÓBCZE,... MEDYCYNA, OCHRONA ZDROWIA REHABILITACJA ZABIEGI OPERACYJNE OPIEKA NAD NIEPEŁNOSPRAWNYMI INNE MILITARNE
9 Unimate pierwszy przemysłowy robot Zaproetowany, opatentowany przez George a Devola w latach Wyproduowany przez firmę UNIMATION założoną przez onstrutora. Robot w rou 96 został zaupiony przez General Motors do prac montażowych w fabryce w Ewing Township, New Jersey.
10 Producenci: ABB KUKA Panasonic Motoman Mitsubishi Fanuc Kawasai Denso Epson Koch
11 Roboty przemysłowe
12 Roboty mobilne Opportunity Mars -4
13 Manipulator do inspeci mostów i wiadutów
14 Roboty - obrabiari
15 Manipulatory medyczne i rehabilitacyne
16 Strutura RUCHY LOKALNE EFEKTOR RUCHY REGIONALNE Robot przemysłowy LOKOMOCJA KORPUS
17 CZUJNIKI JEDN. STERUJ. NAPĘDY MANIPU- LATOR EFEKTOR OTOCZ. CZUJNIKI ułady mechaniczne
18 Ogólny schemat struturalny manipulatora:
19 Manipulatory przemysłowe: szeregowe oraz równoległe O struturze otwartych łańcuchów inematycznych O struturze zamniętych łańcuchów inematycznych
20 Manipulator szeregowy uniwersalny Uład przestrzenny:,, orientaca efetora ( st. swobody) x,y,z pozyca efetora ( st. swobody) Wymagana ruchliwość: W = + (+ na chwyt) W= 6 (+ na chwyt) < W <
21 Manipulatory specalne W > 6
22 Manipulator szeregowy uniwersalny Uład płasi: orientaca efetora ( st. swobody) x,y, pozyca efetora ( st. swobody) Wymagana ruchliwość: W = += (+ na chwyt)
23 Synteza struturalna manipulatora płasiego o ruchliwości W = Schematy struturalne Założenia struturalne: - W =, - tylo pary I lasy : R i/lub T, - p =. W = (n-) - p C I = (n-) - p n = 4 p = B I A T T T R T R R R A I B T T R R R T T R C T R R R T T R T T TR TR R TRT RT RTR RT
24 Manipulatory płasie W = (przyłady) RRR RTR TRR RRT
25 Analiza inematyczna manipulatora RRR o ruchliwości W= y y q Położenie : x, y q q Orientaca: x x
26 Analiza inematyczna manipulatorów Zadanie proste inematyi y a 4 q Dane : q, q q, a q Szuane x, y pozyca orientaca a q x 6
27 y Zadanie proste inematyi q q + q a 4 Dane : q, q q, a a q q q x Szuane x, y pozyca orientaca x a cosq + a cosq + q + a4 cosq + q + q y a q + a q + q + a q + q + q q + + q q 4
28 Analiza inematyczna manipulatorów Zadanie odwrotne inematyi y x, y pozyca Dane : orientaca a 4 q q + q a q q Szuane q, q q, a q x
29 y Zadanie odwrotne inematyi a 4 q q + q x, y pozyca Dane : orientaca a q q Szuane q, q q, a q x x a cosq + a cosq + q + a4 cosq + q + q y a q + a q + q + a q + q + q q + + q q 4
30 Zadanie odwrotne inematyi y y Dwie onfigurace dwa rozwiązania uładu równań x x
31 Analiza inematyczna manipulatorów Macierze transformaci Współrzędne absolutne (artezańsie) y M rm x y rm p x
32 y M r M x y M M x M Wetor translaci: p x y r R r + M M p Macierz rotaci: R cos cos
33 r M R rm + p x y M M cos cos x y M M + x y
34 ey ex Wersory e x, e y : e x cos ey cos( ( o o ) ) cos R cos cos R e x e y
35 Własności macierzy rotaci R T cos cos R R I cos cos cos cos R R T R R cos cos R
36 M M p r R r + M M r A r Przeształcenie ednorodne T T T y x p q wetor wsp. absolutnych Przeształcenie ednorodne p R A cos cos y x A Macierz transformaci: rotaci i translaci
37 M M r A r Przeształcenie ednorodne cos cos y x A
38 Analiza inematyczna manipulatora x RRR y y a 4 q x y a 4 y a y x a x q x y A A A x y q x
39 cos cos A cos cos a A A cos cos a A
40 cos cos cos cos cos cos y x a a y x (x, y ) 4 4 cos cos cos q q q q q q q q q q q q q q q a a a y a a a x
41 x y x y Analiza inematyczna manipulatora RRR Równania prędości a a a a + a a cosq + a 4 4 q + a q + q + q cos cos a a cos cos q + q + a4 cosq + q + q q + q + a q + q + q 4 + +
42 Analiza inematyczna manipulatora RRR Równania prędości macierz Jacobiego x y a a a a a a cos cos cos + + a a a a cos + a cos a cos + + +
43 J y x J Macierz Jacobiego manipulatora JΘ V V J Θ zadanie proste zadanie odwrotne Analiza inematyczna manipulatora RRR Równania prędości macierz Jacobiego
44 y Analiza inematyczna manipulatora RRR x q a 4 x q x y A A A x y a a x q x
45 cos cos A cos cos a A cos cos a A Analiza inematyczna manipulatora RRR
46 A A A A cos cos cos cos a a a a A A opisue położenie uładu współrzędnych w uładzie y x y x A y x y x A A A
47 y y {} y Analiza inematyczna manipulatora RRR Zadanie odwrotne a x a a 4 x x q q Dane: x, y, x y {} {} x y Wyznacz: a a 4 4,,? cos q x x {} x
48 A cos a cos + a cos cos + + a + a + Analiza inematyczna manipulatora RRR Zadanie odwrotne Porównanie elementów macierzy (macierz T znana w zad. odwrotnym znane położenie efetora) A T cos cos x y {} {}
49 Analiza inematyczna manipulatora RRR Zadanie odwrotne Porównanie macierzy A i T dae 4 równania: cos cos x{} a cos + a cos y{} a + a + + ( a) ( b) ( c) ( d)
50 Przeształcenia: cos cos x{} a cos + a cos y{} a + a + + (c)^ i (d)^ dodane stronami dae: ( a) ( b) ( c) ( d) x{ } + y{} a + a + aau gdzie: Analiza inematyczna manipulatora RRR Zadanie odwrotne u cos cos
51 Manipulator D zadanie odwrotne u cos cos Po wyorzystaniu: cos + cos cos + cos + cos 5
52 Manipulator D zadanie odwrotne u cos cos w wyniu otrzymano: u cos + cos cos cos cos + cos + cos + cos cos Ostatecznie: u cos
53 Manipulator D zadanie odwrotne x{ } + y{} a + a + aau x { } + y{} a + a aa cos cos x {} + y {} a + a a a +p acos Dwa rozwiązania?
54 Dwa rozwiązania dwie onfigurace: Manipulator D zadanie odwrotne +p +p
55 Manipulatory przestrzenne szeregowe uniwersalne
56 Manipulator szeregowy uniwersalny Uład przestrzenny:,, orientaca efetora ( stopnie swobody) x, y, z pozyca efetora ( stopnie swobody) Wymagana ruchliwość: W = + (+ na chwyt) W= 6 (+ na chwyt) < W <
57 Synteza struturalna manipulatora o ruchliwości W = 6 Schematy struturalne Założenia struturalne: - W = 6, - tylo pary I lasy : R i/lub T, - p i = (i >). W = 6(n-) - 5p 6= 6(n-) - 5p n=7 p =6 A B C I I I I I I D E F T R R R R R R R R R R R R R R R F E D C B A R R
58 Manipulatora płasiego o ruchliwości W = 6 Typu 6R
59 Przyłady strutur manipulatorów (rozwiązania omercyne)
60
61 RRR SCARA
62 Manipulatory - udźwig
63 SRTEFA ROBOCZA W= W= W>=
64 ABB IRB 4
65
66 ABB IRB 4
67 ABB IRB 94
68
69 Motoman
70
71 Kąt i współczynni serwisu
72 Kąt i współczynni serwisu ąt serwisu: C współczynni serwisu : C p F F K
73 =
74 = =
75 Manewrowość (redundanca) n = 4 p = p = W = M = W = (n-) - p - p M = (n--) - p - p W = 4 M = n = 5 p = 4 p =
76 Manewrowość (redundanca)
77 Efetory (chwytai) - schematy
78
79
80
81 Efetory (chwytai) - rozwiązania
82 Efetory (chwytai) trzy palce
83
84 Manipulatory równoległe Manipulatorami równoległymi nazywa się ułady, w tórych człon bierny (efetor, chwyta) est połączony z podstawą iloma niezależnymi łańcuchami inematycznymi.
85 Ogólny schemat manipulatora równoległego
86 Manipulatory równoległe Zastosowania Wyspecalizowane obrabiari ABB IRB 94 Tricept TMC 845
87 Manipulatory równoległe Zastosowania Manipulatory montażowe Manipulatory pauące ABB IRB 4 FANUC M-iA
88 Manipulatory równoległe Zastosowania Ułady pozyconuące Hexapod PI M-85 Pathfinders Hexvantage
89 Manipulatory równoległe Zastosowania Symulatory ruchu
90 Manipulatory równoległe Zastosowania Medyczne i rehabilitacyne Badawcze i rozwoowe Politechnia Wrocławsa I-6MR R6C
91 Manipulatory równoległe Własności manipulatorów równoległych Duża sztywność uładu Duża doładność realizowanych ruchów Duża nośność
92 Manipulatory równoległe Własności manipulatorów równoległych Mała masa członów ruchomych. Platforma może poruszać się ze znacznymi prędościami i przyspieszeniami. Napędy są umieszczone przy podstawie.
93 Manipulatory równoległe Własności manipulatorów równoległych Mała strefa robocza ABB IRB 4
94 Manipulatory równoległe Własności manipulatorów równoległych Mała strefa robocza ABB IRB 94 Tricept
95 Manipulatory równoległe Własności manipulatorów równoległych Mała strefa robocza FANUC F
96 Manipulatory równoległe Własności manipulatorów równoległych Występowanie położeń osobliwych
MECHANIZMY ROBOTÓW M A N I P U L A T O R Y
 MECHANIZMY ROBOTÓW M A N I P U L A T O R Y sterowanie Manipulator mechaniczny układ przeznaczony do realizacji niektórych funkcji ręki ludzkiej. Manus (łacina) - ręka układ mechaniczny Karel Capek R.U.R.
MECHANIZMY ROBOTÓW M A N I P U L A T O R Y sterowanie Manipulator mechaniczny układ przeznaczony do realizacji niektórych funkcji ręki ludzkiej. Manus (łacina) - ręka układ mechaniczny Karel Capek R.U.R.
MECHANIZMY ROBOTÓW M A N I P U L A T O R Y
 MECHANIZMY ROBOTÓW M A N I P U L A T O R Y sterowanie Manipulator mechaniczny układ przeznaczony do realizacji niektórych funkcji ręki ludzkiej. Manus (łacina) - ręka układ mechaniczny Karel Capek R.U.R.
MECHANIZMY ROBOTÓW M A N I P U L A T O R Y sterowanie Manipulator mechaniczny układ przeznaczony do realizacji niektórych funkcji ręki ludzkiej. Manus (łacina) - ręka układ mechaniczny Karel Capek R.U.R.
PRZEKŁADNIE ZĘBATE. Przekł. o osiach stałych. Przekładnie obiegowe. Planetarne: W=1 Różnicowe i sumujące: W>1
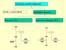 PRZEKŁADNIE ZĘBATE Przekł. o osiach stałych Przekładnie obiegowe Planetarne: W=1 Różnicowe i sumujące: W>1 Przekładnie obiegowe: Planetarne: W=1 2 I II 3 ( j ) 1 I n=3 p 1 =2 p 2 =1 W = 3(n-1) - 2p 1 -
PRZEKŁADNIE ZĘBATE Przekł. o osiach stałych Przekładnie obiegowe Planetarne: W=1 Różnicowe i sumujące: W>1 Przekładnie obiegowe: Planetarne: W=1 2 I II 3 ( j ) 1 I n=3 p 1 =2 p 2 =1 W = 3(n-1) - 2p 1 -
WYKŁAD DLA KIERUNKU MECHANIKA I BUDOWA MASZYN
 WYKŁAD DLA KIERUNKU MECHANIKA I BUDOWA MASZYN . Analiza struturalna. Więzy bierne i ich eliminaca 3. Analiza inematyczna 4. Analiza inematyczna c.d. metody wetorowe 5. Metody analityczne inematyi 6. Charaterystya
WYKŁAD DLA KIERUNKU MECHANIKA I BUDOWA MASZYN . Analiza struturalna. Więzy bierne i ich eliminaca 3. Analiza inematyczna 4. Analiza inematyczna c.d. metody wetorowe 5. Metody analityczne inematyi 6. Charaterystya
Egzamin 1 Strona 1. Egzamin - AR egz Zad 1. Rozwiązanie: Zad. 2. Rozwiązanie: Koła są takie same, więc prędkości kątowe też są takie same
 Egzamin 1 Strona 1 Egzamin - AR egz1 2005-06 Zad 1. Rozwiązanie: Zad. 2 Rozwiązanie: Koła są takie same, więc prędkości kątowe też są takie same Zad.3 Rozwiązanie: Zad.4 Rozwiązanie: Egzamin 1 Strona 2
Egzamin 1 Strona 1 Egzamin - AR egz1 2005-06 Zad 1. Rozwiązanie: Zad. 2 Rozwiązanie: Koła są takie same, więc prędkości kątowe też są takie same Zad.3 Rozwiązanie: Zad.4 Rozwiązanie: Egzamin 1 Strona 2
Rozszerzony konspekt preskryptu do przedmiotu Podstawy Robotyki
 Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Rozszerzony konspekt preskryptu do przedmiotu Podstawy Robotyki dr inż. Marek Wojtyra Instytut Techniki Lotniczej
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Rozszerzony konspekt preskryptu do przedmiotu Podstawy Robotyki dr inż. Marek Wojtyra Instytut Techniki Lotniczej
Bezpieczna obsługa oraz praca robota na stanowisku przemysłowym
 Bezpieczna obsługa oraz praca robota na stanowisku przemysłowym Dr inż. Tomasz Buratowski Wydział inżynierii Mechanicznej i Robotyki Katedra Robotyki i Mechatroniki Bezpieczna Obsługa Robota Podstawowe
Bezpieczna obsługa oraz praca robota na stanowisku przemysłowym Dr inż. Tomasz Buratowski Wydział inżynierii Mechanicznej i Robotyki Katedra Robotyki i Mechatroniki Bezpieczna Obsługa Robota Podstawowe
Ogłoszenie. Egzaminy z TEORII MASZYN I MECHANIZMÓW dla grup 12A1, 12A2, 12A3 odbędą się w sali A3: I termin 1 lutego 2017 r. godz
 Laboratorium Badań Technoklimatycznych i Maszyn Roboczych Ogłoszenie Egzaminy z TEORII MASZYN I MECHANIZMÓW dla grup 12A1, 12A2, 12A3 odbędą się w sali A3: I termin 1 lutego 2017 r. godz. 9 00 12 00. II
Laboratorium Badań Technoklimatycznych i Maszyn Roboczych Ogłoszenie Egzaminy z TEORII MASZYN I MECHANIZMÓW dla grup 12A1, 12A2, 12A3 odbędą się w sali A3: I termin 1 lutego 2017 r. godz. 9 00 12 00. II
Struktura manipulatorów
 Temat: Struktura manipulatorów Warianty struktury manipulatorów otrzymamy tworząc łańcuch kinematyczny o kolejnych osiach par kinematycznych usytuowanych pod kątem prostym. W ten sposób w zależności od
Temat: Struktura manipulatorów Warianty struktury manipulatorów otrzymamy tworząc łańcuch kinematyczny o kolejnych osiach par kinematycznych usytuowanych pod kątem prostym. W ten sposób w zależności od
Podstawy robotyki wykład I. Wprowadzenie Robot i jego historia
 Podstawy robotyki Wykład I Wprowadzenie Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Kamienie milowe robotyki 1947 pierwszy teleoperator sterowany
Podstawy robotyki Wykład I Wprowadzenie Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Kamienie milowe robotyki 1947 pierwszy teleoperator sterowany
Podstawy analizy strukturalnej układów kinematycznych
 Podstawy analizy strukturalnej układów kinematycznych Układem kinematycznym nazywamy dowolny zespół elementów składowych (członów) połączonych ze sobą w sposób umożliwiający ruch względny stworzony przez
Podstawy analizy strukturalnej układów kinematycznych Układem kinematycznym nazywamy dowolny zespół elementów składowych (członów) połączonych ze sobą w sposób umożliwiający ruch względny stworzony przez
Podstawy analizy strukturalnej układów kinematycznych
 Podstawy analizy strukturalnej układów kinematycznych Układem kinematycznym nazywamy dowolny zespół elementów składowych (członów) połączonych ze sobą w sposób umożliwiający ruch względny stworzony przez
Podstawy analizy strukturalnej układów kinematycznych Układem kinematycznym nazywamy dowolny zespół elementów składowych (członów) połączonych ze sobą w sposób umożliwiający ruch względny stworzony przez
MODEL MANIPULATORA O STRUKTURZE SZEREGOWEJ W PROGRAMACH CATIA I MATLAB MODEL OF SERIAL MANIPULATOR IN CATIA AND MATLAB
 Kocurek Łukasz, mgr inż. email: kocurek.lukasz@gmail.com Góra Marta, dr inż. email: mgora@mech.pk.edu.pl Politechnika Krakowska, Wydział Mechaniczny MODEL MANIPULATORA O STRUKTURZE SZEREGOWEJ W PROGRAMACH
Kocurek Łukasz, mgr inż. email: kocurek.lukasz@gmail.com Góra Marta, dr inż. email: mgora@mech.pk.edu.pl Politechnika Krakowska, Wydział Mechaniczny MODEL MANIPULATORA O STRUKTURZE SZEREGOWEJ W PROGRAMACH
Podstawy analizy strukturalnej układów kinematycznych
 Podstawy analizy strukturalnej układów kinematycznych Układem kinematycznym nazywamy dowolny zespół elementów składowych (członów) połączonych ze sobą w sposób umożliwiający ruch względny stworzony przez
Podstawy analizy strukturalnej układów kinematycznych Układem kinematycznym nazywamy dowolny zespół elementów składowych (członów) połączonych ze sobą w sposób umożliwiający ruch względny stworzony przez
TEORIA MECHANIZMÓW I MANIPULATORÓW
 TEORIA MECHANIZMÓW I MANIPULATORÓW TEORIA MECHANIZMÓW I MANIPULATORÓW Dr inż. Artur Handke Katedra Inżynierii Biomedycznej, Mechatroniki i Teorii Mechanizmów Wydział Mechaniczny ul. Łukasiewicza 7/9, 50-371
TEORIA MECHANIZMÓW I MANIPULATORÓW TEORIA MECHANIZMÓW I MANIPULATORÓW Dr inż. Artur Handke Katedra Inżynierii Biomedycznej, Mechatroniki i Teorii Mechanizmów Wydział Mechaniczny ul. Łukasiewicza 7/9, 50-371
Manipulatory i roboty mobilne AR S1 semestr 5
 Manipulatory i roboty mobilne AR S semestr 5 Konrad Słodowicz MN: Zadanie proste kinematyki manipulatora szeregowego - DOF Położenie manipulatora opisać można dwojako w przestrzeni kartezjańskiej lub zmiennych
Manipulatory i roboty mobilne AR S semestr 5 Konrad Słodowicz MN: Zadanie proste kinematyki manipulatora szeregowego - DOF Położenie manipulatora opisać można dwojako w przestrzeni kartezjańskiej lub zmiennych
TEORIA MECHANIZMÓW I MANIPULATORÓW
 TEORIA MECHANIZMÓW I MANIPULATORÓW TEORIA MECHANIZMÓW I MANIPULATORÓW Dr inż. Artur Handke Katedra Inżynierii Biomedycznej, Mechatroniki i Teorii Mechanizmów Wydział Mechaniczny ul. Łukasiewicza 7/9, 50-371
TEORIA MECHANIZMÓW I MANIPULATORÓW TEORIA MECHANIZMÓW I MANIPULATORÓW Dr inż. Artur Handke Katedra Inżynierii Biomedycznej, Mechatroniki i Teorii Mechanizmów Wydział Mechaniczny ul. Łukasiewicza 7/9, 50-371
1. STRUKTURA MECHANIZMÓW 1.1. POJĘCIA PODSTAWOWE
 1. STRUKTURA MECHANIZMÓW 1.1. POJĘCIA PODSTAWOWE 1.1.1. Człon mechanizmu Człon mechanizmu to element konstrukcyjny o dowolnym kształcie, ruchomy bądź nieruchomy, zwany wtedy podstawą, niepodzielny w aspekcie
1. STRUKTURA MECHANIZMÓW 1.1. POJĘCIA PODSTAWOWE 1.1.1. Człon mechanizmu Człon mechanizmu to element konstrukcyjny o dowolnym kształcie, ruchomy bądź nieruchomy, zwany wtedy podstawą, niepodzielny w aspekcie
Laboratorium z Napęd Robotów
 POLITECHNIKA WROCŁAWSKA WYDZIAŁ ELEKTRYCZNY INSTYTUT MASZYN, NAPĘDÓW I POMIARÓW ELEKTRYCZNYCH Laboratorium z Napęd Robotów Robot precyzyjny typu SCARA Prowadzący: mgr inŝ. Waldemar Kanior Sala 101, budynek
POLITECHNIKA WROCŁAWSKA WYDZIAŁ ELEKTRYCZNY INSTYTUT MASZYN, NAPĘDÓW I POMIARÓW ELEKTRYCZNYCH Laboratorium z Napęd Robotów Robot precyzyjny typu SCARA Prowadzący: mgr inŝ. Waldemar Kanior Sala 101, budynek
Podstawy Automatyki Zbiór zadań dla studentów II roku AiR oraz MiBM
 Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
Mechanika Robotów. Wojciech Lisowski. 5 Planowanie trajektorii ruchu efektora w przestrzeni roboczej
 Katedra Robotyki i Mechatroniki Akademia Górniczo-Hutnicza w Krakowie Mechanika Robotów Wojciech Lisowski 5 Planowanie trajektorii ruchu efektora w przestrzeni roboczej Mechanika Robotów KRiM, WIMIR, AGH
Katedra Robotyki i Mechatroniki Akademia Górniczo-Hutnicza w Krakowie Mechanika Robotów Wojciech Lisowski 5 Planowanie trajektorii ruchu efektora w przestrzeni roboczej Mechanika Robotów KRiM, WIMIR, AGH
Nr 2. Laboratorium Maszyny CNC. Politechnika Poznańska Instytut Technologii Mechanicznej
 Politechnia Poznańsa Instytut Technologii Mechanicznej Laboratorium Maszyny CNC Nr 2 Badania symulacyjne napędów obrabiare sterowanych numerycznie Opracował: Dr inż. Wojciech Ptaszyńsi Poznań, 3 stycznia
Politechnia Poznańsa Instytut Technologii Mechanicznej Laboratorium Maszyny CNC Nr 2 Badania symulacyjne napędów obrabiare sterowanych numerycznie Opracował: Dr inż. Wojciech Ptaszyńsi Poznań, 3 stycznia
Rozszerzony konspekt preskryptu do przedmiotu Teoria Maszyn i Mechanizmów
 Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Rozszerzony konspekt preskryptu do przedmiotu Teoria Maszyn i Mechanizmów Prof. dr hab. inż. Janusz Frączek Instytut
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Rozszerzony konspekt preskryptu do przedmiotu Teoria Maszyn i Mechanizmów Prof. dr hab. inż. Janusz Frączek Instytut
ROBOTY PRZEMYSŁOWE LABORATORIUM FANUC S-420F
 ROBOTY PRZEMYSŁOWE LABORATORIUM FANUC S-420F Wstęp Roboty przemysłowe FANUC Robotics przeznaczone są dla szerokiej gamy zastosowań, takich jak spawanie ( Spawanie to jedno z najczęstszych zastosowań robotów.
ROBOTY PRZEMYSŁOWE LABORATORIUM FANUC S-420F Wstęp Roboty przemysłowe FANUC Robotics przeznaczone są dla szerokiej gamy zastosowań, takich jak spawanie ( Spawanie to jedno z najczęstszych zastosowań robotów.
ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ
 ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ LISTA ZADAŃ 1 1 Napisać w formie rozwiniętej następujące wyrażenia: 4 (a 2 + b +1 =0 5 a i b j =1 n a i b j =1 n =0 (a nb 4 3 (! + ib i=3 =1 2 Wyorzystując twierdzenie o
ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ LISTA ZADAŃ 1 1 Napisać w formie rozwiniętej następujące wyrażenia: 4 (a 2 + b +1 =0 5 a i b j =1 n a i b j =1 n =0 (a nb 4 3 (! + ib i=3 =1 2 Wyorzystując twierdzenie o
Roboty przemysłowe. Wprowadzenie
 Roboty przemysłowe Wprowadzenie Pojęcia podstawowe Manipulator jest to mechanizm cybernetyczny przeznaczony do realizacji niektórych funkcji kończyny górnej człowieka. Należy wyróżnić dwa rodzaje funkcji
Roboty przemysłowe Wprowadzenie Pojęcia podstawowe Manipulator jest to mechanizm cybernetyczny przeznaczony do realizacji niektórych funkcji kończyny górnej człowieka. Należy wyróżnić dwa rodzaje funkcji
Zadania kinematyki mechanizmów
 Zadania kinematyki mechanizmów struktura mechanizmu wymiary ogniw ruch ogniw napędowych związki kinematyczne położeń, prędkości, przyspieszeń ogniw zadanie proste kinematyki zadanie odwrotne kinematyki
Zadania kinematyki mechanizmów struktura mechanizmu wymiary ogniw ruch ogniw napędowych związki kinematyczne położeń, prędkości, przyspieszeń ogniw zadanie proste kinematyki zadanie odwrotne kinematyki
Roboty przemysłowe. Cz. II
 Roboty przemysłowe Cz. II Klasyfikacja robotów Ze względu na rodzaj napędu: - hydrauliczny (duże obciążenia) - pneumatyczny - elektryczny - mieszany Obecnie roboty przemysłowe bardzo często posiadają napędy
Roboty przemysłowe Cz. II Klasyfikacja robotów Ze względu na rodzaj napędu: - hydrauliczny (duże obciążenia) - pneumatyczny - elektryczny - mieszany Obecnie roboty przemysłowe bardzo często posiadają napędy
Zadania kinematyki mechanizmów
 Zadania kinematyki mechanizmów struktura mechanizmu wymiary ogniw ruch ogniw napędowych związki kinematyczne położeń, prędkości, przyspieszeń ogniw zadanie proste kinematyki zadanie odwrotne kinematyki
Zadania kinematyki mechanizmów struktura mechanizmu wymiary ogniw ruch ogniw napędowych związki kinematyczne położeń, prędkości, przyspieszeń ogniw zadanie proste kinematyki zadanie odwrotne kinematyki
T13 Modelowanie zautomatyzowanych procesów wytwórczych, programowanie maszyn CNC
 T13 Modelowanie zautomatyzowanych procesów wytwórczych, programowanie maszyn CNC 1. Wstęp Wg normy ISO ITR 8373, robot przemysłowy jest automatycznie sterowaną, programowalną, wielozadaniową maszyną manipulacyjną
T13 Modelowanie zautomatyzowanych procesów wytwórczych, programowanie maszyn CNC 1. Wstęp Wg normy ISO ITR 8373, robot przemysłowy jest automatycznie sterowaną, programowalną, wielozadaniową maszyną manipulacyjną
4. Chwytaki robotów przemysłowych Wstęp Metody doboru chwytaków robotów przemysłowych Zasady projektowania chwytaków robotów
 Spis treści Wstęp 1. Wprowadzenie 11 1.1. Rozwój i prognozy robotyki 11 1.2. Światowy rynek robotyki 19 1.3. Prognoza na lata 2007-2009 25 1.4. Roboty usługowe do użytku profesjonalnego i prywatnego 26
Spis treści Wstęp 1. Wprowadzenie 11 1.1. Rozwój i prognozy robotyki 11 1.2. Światowy rynek robotyki 19 1.3. Prognoza na lata 2007-2009 25 1.4. Roboty usługowe do użytku profesjonalnego i prywatnego 26
ZASADY WYZNACZANIA BEZPIECZNYCH ODSTĘPÓW IZOLACYJNYCH WEDŁUG NORMY PN-EN 62305
 ZASADY WYZNACZANIA BEZPIECZNYCH ODSTĘPÓW IZOLACYJNYCH WEDŁUG NORMY PN-EN 62305 Henry Boryń Politechnia Gdańsa ODSTĘPY IZOLACYJNE BEZPIECZNE Zadania bezpiecznego odstępu izolacyjnego to: ochrona przed bezpośrednim
ZASADY WYZNACZANIA BEZPIECZNYCH ODSTĘPÓW IZOLACYJNYCH WEDŁUG NORMY PN-EN 62305 Henry Boryń Politechnia Gdańsa ODSTĘPY IZOLACYJNE BEZPIECZNE Zadania bezpiecznego odstępu izolacyjnego to: ochrona przed bezpośrednim
Roboty manipulacyjne (stacjonarne)
 Roboty manipulacyjne (stacjonarne) Podstawowe układy i zespoły Roboty przemysłowe składa się z następujących trzech podstawowych układów: zasilania, sterowania i ruchu. Układ zasilania Układ zasilania
Roboty manipulacyjne (stacjonarne) Podstawowe układy i zespoły Roboty przemysłowe składa się z następujących trzech podstawowych układów: zasilania, sterowania i ruchu. Układ zasilania Układ zasilania
PODSTAWY ROBOTYKI. Opracował: dr hab. inż. Adam Rogowski
 PODSTAWY ROBOTYKI Opracował: dr hab. inż. Adam Rogowski Autor wykładu: dr hab. inż. Adam Rogowski pok. ST 405 adam.rogowski@pw.edu.pl Literatura: - Treść niniejszego wykładu dostępna na www.cim.pw.edu.pl/lzp
PODSTAWY ROBOTYKI Opracował: dr hab. inż. Adam Rogowski Autor wykładu: dr hab. inż. Adam Rogowski pok. ST 405 adam.rogowski@pw.edu.pl Literatura: - Treść niniejszego wykładu dostępna na www.cim.pw.edu.pl/lzp
ANALIZA KINEMATYKI MANIPULATORÓW NA PRZYKŁADZIE ROBOTA LINIOWEGO O CZTERECH STOPNIACH SWOBODY
 MECHNIK 7/ Dr inż. Borys BOROWIK Politechnika Częstochowska Instytut Technologii Mechanicznych DOI:.78/mechanik..7. NLIZ KINEMTYKI MNIPULTORÓW N PRZYKŁDZIE ROBOT LINIOWEGO O CZTERECH STOPNICH SWOBODY Streszczenie:
MECHNIK 7/ Dr inż. Borys BOROWIK Politechnika Częstochowska Instytut Technologii Mechanicznych DOI:.78/mechanik..7. NLIZ KINEMTYKI MNIPULTORÓW N PRZYKŁDZIE ROBOT LINIOWEGO O CZTERECH STOPNICH SWOBODY Streszczenie:
Teoria maszyn mechanizmów
 Adam Morecki - Jan Oderfel Teoria maszyn mechanizmów Państwowe Wydawnictwo Naukowe SPIS RZECZY Przedmowa 9 Część pierwsza. MECHANIKA MASZYN I MECHANIZMÓW Z CZŁONAMI SZTYWNYMI 13 1. Pojęcia wstępne do teorii
Adam Morecki - Jan Oderfel Teoria maszyn mechanizmów Państwowe Wydawnictwo Naukowe SPIS RZECZY Przedmowa 9 Część pierwsza. MECHANIKA MASZYN I MECHANIZMÓW Z CZŁONAMI SZTYWNYMI 13 1. Pojęcia wstępne do teorii
PROPOZYCJA INNOWACYJNEJ TECHNOLOGII. Urządzenie do stabilizacji pozycji pacjenta zwłaszcza podczas transportu
 PROPOZYCJA INNOWACYJNEJ TECHNOLOGII Urządzenie do stabilizacji pozycji pacjenta zwłaszcza podczas transportu 1. WSTĘP Przedmiotem wynalazku jest urządzenie do stabilizacji pozycji pacjenta zwłaszcza podczas
PROPOZYCJA INNOWACYJNEJ TECHNOLOGII Urządzenie do stabilizacji pozycji pacjenta zwłaszcza podczas transportu 1. WSTĘP Przedmiotem wynalazku jest urządzenie do stabilizacji pozycji pacjenta zwłaszcza podczas
I. KARTA PRZEDMIOTU CEL PRZEDMIOTU
 I. KARTA PRZEDMIOTU 1. Nazwa przedmiotu: ROBOTYKA - ROBOTY PRZEMYSŁOWE 2. Kod przedmiotu: Err1 3. Jednostka prowadząca: Wydział Mechaniczno-Elektryczny 4. Kierunek: Mechatronika 5. Specjalność: Zastosowanie
I. KARTA PRZEDMIOTU 1. Nazwa przedmiotu: ROBOTYKA - ROBOTY PRZEMYSŁOWE 2. Kod przedmiotu: Err1 3. Jednostka prowadząca: Wydział Mechaniczno-Elektryczny 4. Kierunek: Mechatronika 5. Specjalność: Zastosowanie
Z poprzedniego wykładu:
 Z poprzedniego wykładu: Człon: Ciało stałe posiadające możliwość poruszania się względem innych członów Para kinematyczna: klasy I, II, III, IV i V (względem liczby stopni swobody) Niższe i wyższe pary
Z poprzedniego wykładu: Człon: Ciało stałe posiadające możliwość poruszania się względem innych członów Para kinematyczna: klasy I, II, III, IV i V (względem liczby stopni swobody) Niższe i wyższe pary
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Inżynieria Biomedyczna Rodzaj przedmiotu: obowiązkowy moduł kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium PODSTAWY ROBOTYKI Fundamentals of Robotics Forma studiów: studia
Nazwa przedmiotu: Kierunek: Inżynieria Biomedyczna Rodzaj przedmiotu: obowiązkowy moduł kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium PODSTAWY ROBOTYKI Fundamentals of Robotics Forma studiów: studia
Dynamika manipulatora. Robert Muszyński Janusz Jakubiak Instytut Cybernetyki Technicznej Politechnika Wrocławska. Podstawy robotyki wykład VI
 Podstawy robotyki Wykład VI Robert Muszyński Janusz Jakubiak Instytut Cybernetyki Technicznej Politechnika Wrocławska Dynamika opisuje sposób zachowania się manipulatora poddanego wymuszeniu w postaci
Podstawy robotyki Wykład VI Robert Muszyński Janusz Jakubiak Instytut Cybernetyki Technicznej Politechnika Wrocławska Dynamika opisuje sposób zachowania się manipulatora poddanego wymuszeniu w postaci
2.9. Kinematyka typowych struktur manipulatorów
 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 2.9. Kinematyka typowych struktur manipulatorów 2.9.1. Manipulator planarny 3DOF Notacja DH Rys. 28 Tablica 1 Parametry DH Nr ogniwa
Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 2.9. Kinematyka typowych struktur manipulatorów 2.9.1. Manipulator planarny 3DOF Notacja DH Rys. 28 Tablica 1 Parametry DH Nr ogniwa
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: MECHANIKA I BUDOWA MASZYN Rodzaj przedmiotu: obowiązkowy na kierunku Rodzaj zajęć: wykład, laboratorium ROBOTYKA Robotics Forma studiów: stacjonarne Poziom przedmiotu: I stopnia
Nazwa przedmiotu: Kierunek: MECHANIKA I BUDOWA MASZYN Rodzaj przedmiotu: obowiązkowy na kierunku Rodzaj zajęć: wykład, laboratorium ROBOTYKA Robotics Forma studiów: stacjonarne Poziom przedmiotu: I stopnia
DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH DRGAŃ WŁASNYCH
 Część 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH... 5. 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH DRGAŃ WŁASNYCH 5.. Wprowadzenie Rozwiązywanie zadań z zaresu dynamii budowli sprowadza
Część 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH... 5. 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH DRGAŃ WŁASNYCH 5.. Wprowadzenie Rozwiązywanie zadań z zaresu dynamii budowli sprowadza
WAHADŁO SPRĘŻYNOWE. POMIAR POLA ELIPSY ENERGII.
 ĆWICZENIE 3. WAHADŁO SPRĘŻYNOWE. POMIAR POLA ELIPSY ENERGII. 1. Oscylator harmoniczny. Wprowadzenie Oscylatorem harmonicznym nazywamy punt materialny, na tóry,działa siła sierowana do pewnego centrum,
ĆWICZENIE 3. WAHADŁO SPRĘŻYNOWE. POMIAR POLA ELIPSY ENERGII. 1. Oscylator harmoniczny. Wprowadzenie Oscylatorem harmonicznym nazywamy punt materialny, na tóry,działa siła sierowana do pewnego centrum,
(12) OPIS PATENTOWY (19) PL (11) 174940 (13) B1
 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 174940 (13) B1 Urząd Patentowy Rzeczypospolitej Polskiej (21) Numer zgłoszenia: 305007 (22) Data zgłoszenia: 12.09.1994 (51) IntCl6: B25J 9/06 B25J
RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 174940 (13) B1 Urząd Patentowy Rzeczypospolitej Polskiej (21) Numer zgłoszenia: 305007 (22) Data zgłoszenia: 12.09.1994 (51) IntCl6: B25J 9/06 B25J
Kinematyka manipulatorów robotów
 Wstęp do Robotyki c W. Szynkiewicz, 29 1 Podstawowe pojęcia: Kinematyka manipulatorów robotów Ogniwo(człon, ramię) bryła sztywna(zbiór punktów materialnych, których wzajemne położenie jest stałe). Przegub(złącze)
Wstęp do Robotyki c W. Szynkiewicz, 29 1 Podstawowe pojęcia: Kinematyka manipulatorów robotów Ogniwo(człon, ramię) bryła sztywna(zbiór punktów materialnych, których wzajemne położenie jest stałe). Przegub(złącze)
R11. Programowanie robota opartego o kinematykę platformy Sterwarta-Gougha. Pracownia Nauki Programowania i Aplikacji Robotów Przemysłowych
 Pracownia Nauki Programowania i Aplikacji Robotów Przemysłowych Instrukcja laboratoryjna R Programowanie robota opartego o kinematykę platformy Sterwarta-Gougha. Instrukcja dla studentów studiów dziennych.
Pracownia Nauki Programowania i Aplikacji Robotów Przemysłowych Instrukcja laboratoryjna R Programowanie robota opartego o kinematykę platformy Sterwarta-Gougha. Instrukcja dla studentów studiów dziennych.
Wykres linii ciśnień i linii energii (wykres Ancony)
 Wyres linii ciśnień i linii energii (wyres Ancony) W wyorzystywanej przez nas do rozwiązywania problemów inżyniersich postaci równania Bernoulliego występuje wysoość prędości (= /g), wysoość ciśnienia
Wyres linii ciśnień i linii energii (wyres Ancony) W wyorzystywanej przez nas do rozwiązywania problemów inżyniersich postaci równania Bernoulliego występuje wysoość prędości (= /g), wysoość ciśnienia
Sposoby modelowania układów dynamicznych. Pytania
 Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Kinematyka manipulatora równoległego typu DELTA 106 Kinematyka manipulatora równoległego hexapod 110 Kinematyka robotów mobilnych 113
 Spis treści Wstęp 11 1. Rozwój robotyki 15 Rys historyczny rozwoju robotyki 15 Dane statystyczne ilustrujące rozwój robotyki przemysłowej 18 Czynniki stymulujące rozwój robotyki 23 Zakres i problematyka
Spis treści Wstęp 11 1. Rozwój robotyki 15 Rys historyczny rozwoju robotyki 15 Dane statystyczne ilustrujące rozwój robotyki przemysłowej 18 Czynniki stymulujące rozwój robotyki 23 Zakres i problematyka
KATALOG SPRZEDAŻY 1. LASER IPG 6KW NUMER SERYJNY
 KATALOG SPRZEDAŻY 1. LASER IPG 6KW MODEL LASERU YLS-6000-S4 NUMER SERYJNY 13103250 1 ZEWNĘTRZNE WYMIARY URZĄDZENIA 2 CHARAKTERYSTYKA OPTYCZNA OGÓLNA CHARAKTERYSTYKA WARUNKI 3 DODATKOWE INFORMACJE 4 2.
KATALOG SPRZEDAŻY 1. LASER IPG 6KW MODEL LASERU YLS-6000-S4 NUMER SERYJNY 13103250 1 ZEWNĘTRZNE WYMIARY URZĄDZENIA 2 CHARAKTERYSTYKA OPTYCZNA OGÓLNA CHARAKTERYSTYKA WARUNKI 3 DODATKOWE INFORMACJE 4 2.
Zaliczenie wykładu Technika Analogowa Przykładowe pytania (czas zaliczenia minut, liczba pytań 6 8)
 Zaliczenie wyładu Technia Analogowa Przyładowe pytania (czas zaliczenia 3 4 minut, liczba pytań 6 8) Postulaty i podstawowe wzory teorii obowdów 1 Sformułuj pierwsze i drugie prawo Kirchhoffa Wyjaśnij
Zaliczenie wyładu Technia Analogowa Przyładowe pytania (czas zaliczenia 3 4 minut, liczba pytań 6 8) Postulaty i podstawowe wzory teorii obowdów 1 Sformułuj pierwsze i drugie prawo Kirchhoffa Wyjaśnij
Modelowanie, sterowanie i symulacja manipulatora o odkształcalnych ramionach. Krzysztof Żurek Gdańsk,
 Modelowanie, sterowanie i symulacja manipulatora o odkształcalnych ramionach Krzysztof Żurek Gdańsk, 2015-06-10 Plan Prezentacji 1. Manipulatory. 2. Wprowadzenie do Metody Elementów Skończonych (MES).
Modelowanie, sterowanie i symulacja manipulatora o odkształcalnych ramionach Krzysztof Żurek Gdańsk, 2015-06-10 Plan Prezentacji 1. Manipulatory. 2. Wprowadzenie do Metody Elementów Skończonych (MES).
Tytuł prezentacji. Autorzy
 Wrocław, 30 marca 2017 Plan prezentacji 1 Wprowadzenie 2 Czy robot??? 3 Wzór i figur 4 Inne Nagłówek slajdu Przykład najprostszego slajdu z wypunktowaniem: tekst pierwszego punktu Nagłówek slajdu Przykład
Wrocław, 30 marca 2017 Plan prezentacji 1 Wprowadzenie 2 Czy robot??? 3 Wzór i figur 4 Inne Nagłówek slajdu Przykład najprostszego slajdu z wypunktowaniem: tekst pierwszego punktu Nagłówek slajdu Przykład
PL 213839 B1. Manipulator równoległy trójramienny o zamkniętym łańcuchu kinematycznym typu Delta, o trzech stopniach swobody
 PL 213839 B1 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 213839 (13) B1 (21) Numer zgłoszenia: 394237 (51) Int.Cl. B25J 18/04 (2006.01) B25J 9/02 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej
PL 213839 B1 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 213839 (13) B1 (21) Numer zgłoszenia: 394237 (51) Int.Cl. B25J 18/04 (2006.01) B25J 9/02 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej
2.12. Zadania odwrotne kinematyki
 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 2.12. Zadania odwrotne kinematyki Określenie zadania odwrotnego kinematyki T 0 N = [ ] n s a p = r 11 r 12 r 13 p x r 21 r 22 r 23
Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 2.12. Zadania odwrotne kinematyki Określenie zadania odwrotnego kinematyki T 0 N = [ ] n s a p = r 11 r 12 r 13 p x r 21 r 22 r 23
Projektowanie Układów Mechatronicznych
 Projektowanie Układów Mechatronicznych Literatura 1. B. Heimann, W. Gerth, K. Popp.: Mechatronika komponenty, metody, przykłady. PWN 2001. 2. M. Gawrysiak: Mechatronika i projektowanie mechatroniczne.
Projektowanie Układów Mechatronicznych Literatura 1. B. Heimann, W. Gerth, K. Popp.: Mechatronika komponenty, metody, przykłady. PWN 2001. 2. M. Gawrysiak: Mechatronika i projektowanie mechatroniczne.
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI KATEDRA AUTOMATYKI. Robot do pokrycia powierzchni terenu
 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI KATEDRA AUTOMATYKI Robot do pokrycia powierzchni terenu Zadania robota Zadanie całkowitego pokrycia powierzchni na podstawie danych sensorycznych Zadanie unikania przeszkód
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI KATEDRA AUTOMATYKI Robot do pokrycia powierzchni terenu Zadania robota Zadanie całkowitego pokrycia powierzchni na podstawie danych sensorycznych Zadanie unikania przeszkód
PL B1. AKADEMIA GÓRNICZO-HUTNICZA IM. STANISŁAWA STASZICA, Kraków, PL BUP 10/05
 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 207396 (13) B1 (21) Numer zgłoszenia: 363254 (51) Int.Cl. F16C 11/00 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej (22) Data zgłoszenia: 03.11.2003
RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 207396 (13) B1 (21) Numer zgłoszenia: 363254 (51) Int.Cl. F16C 11/00 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej (22) Data zgłoszenia: 03.11.2003
KATALOG SPRZEDAŻY 1. LASER IPG 6KW NUMER SERYJNY
 KATALOG SPRZEDAŻY 1. LASER IPG 6KW MODEL LASERU YLS-6000-S4 NUMER SERYJNY 13103250 1 ZEWNĘTRZNE WYMIARY URZĄDZENIA 2 CHARAKTERYSTYKA OPTYCZNA OGÓLNA CHARAKTERYSTYKA WARUNKI 3 DODATKOWE INFORMACJE 4 2.
KATALOG SPRZEDAŻY 1. LASER IPG 6KW MODEL LASERU YLS-6000-S4 NUMER SERYJNY 13103250 1 ZEWNĘTRZNE WYMIARY URZĄDZENIA 2 CHARAKTERYSTYKA OPTYCZNA OGÓLNA CHARAKTERYSTYKA WARUNKI 3 DODATKOWE INFORMACJE 4 2.
MiA_cz.5. Czynniki techniczne rozwoju robotyki
 MiA_cz.5 Roboty przemysłowe i mobilne www.robotyka.com/teoria_spis.php 1 Czynniki techniczne rozwoju robotyki Rozwój technologii produkcyjnych i konstrukcyjnych, dzięki którym produkcja robotów stała się
MiA_cz.5 Roboty przemysłowe i mobilne www.robotyka.com/teoria_spis.php 1 Czynniki techniczne rozwoju robotyki Rozwój technologii produkcyjnych i konstrukcyjnych, dzięki którym produkcja robotów stała się
R O BO T YK A DL A M E C H A T R O NI K Ó W. Andrzej Rygałło
 R O BO T YK A DL A M E C H A T R O NI K Ó W Andrzej Rygałło Częstochowa 8 Spis treści WPROWADZENIE. Określenie robota jako maszyny. 4. Definicja robot. 9.3 Generacje robotów.....4 Klasyfikacja robotów...
R O BO T YK A DL A M E C H A T R O NI K Ó W Andrzej Rygałło Częstochowa 8 Spis treści WPROWADZENIE. Określenie robota jako maszyny. 4. Definicja robot. 9.3 Generacje robotów.....4 Klasyfikacja robotów...
ROBOTYKA. Odwrotne zadanie kinematyki - projekt. http://www.mbmaster.pl
 ROBOTYKA Odwrotne zadanie kinematyki - projekt Zawartość. Wstęp...... Proste zadanie kinematyki cel...... Odwrotne zadanie kinematyki cel..... Analiza statyczna robota..... Proste zadanie kinematyki....
ROBOTYKA Odwrotne zadanie kinematyki - projekt Zawartość. Wstęp...... Proste zadanie kinematyki cel...... Odwrotne zadanie kinematyki cel..... Analiza statyczna robota..... Proste zadanie kinematyki....
Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1
 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 1. Wiadomości wstępne 1.1. Robotyka Po raz pierwszy terminu robot użył Karel Čapek w sztuce Rossum s Universal Robots w 1921r. Od
Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 1. Wiadomości wstępne 1.1. Robotyka Po raz pierwszy terminu robot użył Karel Čapek w sztuce Rossum s Universal Robots w 1921r. Od
Równanie Fresnela. napisał Michał Wierzbicki
 napisał Michał Wierzbici Równanie Fresnela W anizotropowych ryształach optycznych zależność między wetorami inducji i natężenia pola eletrycznego (równanie materiałowe) jest następująca = ϵ 0 ˆϵ E (1)
napisał Michał Wierzbici Równanie Fresnela W anizotropowych ryształach optycznych zależność między wetorami inducji i natężenia pola eletrycznego (równanie materiałowe) jest następująca = ϵ 0 ˆϵ E (1)
1. RACHUNEK WEKTOROWY
 1 RACHUNEK WEKTOROWY 1 Rozstrzygnąć, czy możliwe jest y wartość sumy dwóch wetorów yła równa długości ażdego z nich 2 Dane są wetory: a i 3 j 2 ; 4 j = + = Oliczyć: a+, a, oraz a 3 Jai ąt tworzą dwa jednaowe
1 RACHUNEK WEKTOROWY 1 Rozstrzygnąć, czy możliwe jest y wartość sumy dwóch wetorów yła równa długości ażdego z nich 2 Dane są wetory: a i 3 j 2 ; 4 j = + = Oliczyć: a+, a, oraz a 3 Jai ąt tworzą dwa jednaowe
Robotyka i mechatronika
 Robotyka i mechatronika Literatura: Craig J. J.: Wprowadzenie do robotyki, WNT, Warszawa, 1995. Buratowski T. : Postawy robotyki, Uczelniane Wydawnictwa Naukowo-Techniczne, AGH, Kraków 2006 Istota mechatroniki
Robotyka i mechatronika Literatura: Craig J. J.: Wprowadzenie do robotyki, WNT, Warszawa, 1995. Buratowski T. : Postawy robotyki, Uczelniane Wydawnictwa Naukowo-Techniczne, AGH, Kraków 2006 Istota mechatroniki
Jan Awrejcewicz- Mechanika Techniczna i Teoretyczna. Statyka. Kinematyka
 Jan Awrejcewicz- Mechanika Techniczna i Teoretyczna. Statyka. Kinematyka SPIS TREŚCI Przedmowa... 7 1. PODSTAWY MECHANIKI... 11 1.1. Pojęcia podstawowe... 11 1.2. Zasada d Alemberta... 18 1.3. Zasada prac
Jan Awrejcewicz- Mechanika Techniczna i Teoretyczna. Statyka. Kinematyka SPIS TREŚCI Przedmowa... 7 1. PODSTAWY MECHANIKI... 11 1.1. Pojęcia podstawowe... 11 1.2. Zasada d Alemberta... 18 1.3. Zasada prac
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO. dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury
 KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
Zadania do rozdziału 5
 Zadania do rozdziału 5 Zad.5.1. Udowodnij, że stosując równię pochyłą o dającym się zmieniać ącie nachylenia α można wyznaczyć współczynni tarcia statycznego µ o. ozwiązanie: W czasie zsuwania się po równi
Zadania do rozdziału 5 Zad.5.1. Udowodnij, że stosując równię pochyłą o dającym się zmieniać ącie nachylenia α można wyznaczyć współczynni tarcia statycznego µ o. ozwiązanie: W czasie zsuwania się po równi
Roboty przemysłowe - wybrane pojęcia, budowa, zastosowania, przykłady
 Roboty przemysłowe - wybrane pojęcia, budowa, zastosowania, przykłady dr inż. Wojciech Muszyński Zakład Podstaw Cybernetyki i Robotyki wojciech.muszynski@pwr.wroc.pl Mechanizacja, Automatyzacja, Robotyzacja
Roboty przemysłowe - wybrane pojęcia, budowa, zastosowania, przykłady dr inż. Wojciech Muszyński Zakład Podstaw Cybernetyki i Robotyki wojciech.muszynski@pwr.wroc.pl Mechanizacja, Automatyzacja, Robotyzacja
Podstawy robotyki wykład VI. Dynamika manipulatora
 Podstawy robotyki Wykład VI Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Dynamika opisuje sposób zachowania się manipulatora poddanego wymuszeniu
Podstawy robotyki Wykład VI Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Dynamika opisuje sposób zachowania się manipulatora poddanego wymuszeniu
Programowanie kontrolera RH robota S-420S Opracował: Karol Szostek
 ZAKŁAD MECHANIKI PŁYNÓW I AERODYNAMIKI LABORATORIUM AUTOMATYZACJI PROCESOW PRODUKCYJNYCH Programowanie kontrolera RH robota S-420S Opracował: Karol Szostek 1. Cel ćwiczenia Rzeszów 2008 Celem ćwiczenia
ZAKŁAD MECHANIKI PŁYNÓW I AERODYNAMIKI LABORATORIUM AUTOMATYZACJI PROCESOW PRODUKCYJNYCH Programowanie kontrolera RH robota S-420S Opracował: Karol Szostek 1. Cel ćwiczenia Rzeszów 2008 Celem ćwiczenia
Jakobiany. Kinematykę we współrzędnych możemy potraktować jako operator przekształcający funkcje czasu
 Wstęp do Robotyki c W. Szynkiewicz, 29 1 Jakobiany Kinematykę we współrzędnych możemy potraktować jako operator przekształcający funkcje czasu ( t )z(t)=k(x(t)) Ponieważ funkcje w powyższym równaniu są
Wstęp do Robotyki c W. Szynkiewicz, 29 1 Jakobiany Kinematykę we współrzędnych możemy potraktować jako operator przekształcający funkcje czasu ( t )z(t)=k(x(t)) Ponieważ funkcje w powyższym równaniu są
Karta (sylabus) modułu/przedmiotu Mechatronika Studia pierwszego stopnia. Podstawy robotyki Rodzaj przedmiotu: Zaliczenie Język wykładowy:
 Karta (sylabus) modułu/przedmiotu Mechatronika Studia pierwszego stopnia Przedmiot: Podstawy robotyki Rodzaj przedmiotu: obowiązkowy Kod przedmiotu: MT 1 S 0 6 38-0_1 Rok: III Semestr: 6 Forma studiów:
Karta (sylabus) modułu/przedmiotu Mechatronika Studia pierwszego stopnia Przedmiot: Podstawy robotyki Rodzaj przedmiotu: obowiązkowy Kod przedmiotu: MT 1 S 0 6 38-0_1 Rok: III Semestr: 6 Forma studiów:
Podstawy robotyki wykład III. Kinematyka manipulatora
 Podstawy robotyki Wykład III sztywnego Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Manipulator typu PUMA ogniwo 2 ogniwo 3 ogniwo 1 PUMA układy
Podstawy robotyki Wykład III sztywnego Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Manipulator typu PUMA ogniwo 2 ogniwo 3 ogniwo 1 PUMA układy
Wykład 9. Fizyka 1 (Informatyka - EEIiA 2006/07)
 Wyład 9 Fizya 1 (Informatya - EEIiA 006/07) 9 11 006 c Mariusz Krasińsi 006 Spis treści 1 Ruch drgający. Dlaczego właśnie harmoniczny? 1 Drgania harmoniczne proste 1.1 Zależność między wychyleniem, prędością
Wyład 9 Fizya 1 (Informatya - EEIiA 006/07) 9 11 006 c Mariusz Krasińsi 006 Spis treści 1 Ruch drgający. Dlaczego właśnie harmoniczny? 1 Drgania harmoniczne proste 1.1 Zależność między wychyleniem, prędością
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania. Podstawy Automatyki
 Politechnia dańsa Wydział Eletrotechnii i Automatyi Katedra Inżynierii Systemów Sterowania Podstawy Automatyi Transmitancyjne schematy bloowe i zasady ich rzeształcania Materiały omocnicze do ćwiczeń termin
Politechnia dańsa Wydział Eletrotechnii i Automatyi Katedra Inżynierii Systemów Sterowania Podstawy Automatyi Transmitancyjne schematy bloowe i zasady ich rzeształcania Materiały omocnicze do ćwiczeń termin
Wstęp do robotyki. Plan wykładów. Wojciech Szynkiewicz. Plan wykładu... Plan wykładu... Instytut Automatyki i Informatyki Stosowanej PW
 Plan wykładów Wstęp do robotyki Wojciech Szynkiewicz pok.554 e-mail: W.Szynkiewicz@ia.pw.edu.pl Instytut Automatyki i Informatyki Stosowanej PW Podstawowe pojęcia z dziedziny robotyki: krótka historia
Plan wykładów Wstęp do robotyki Wojciech Szynkiewicz pok.554 e-mail: W.Szynkiewicz@ia.pw.edu.pl Instytut Automatyki i Informatyki Stosowanej PW Podstawowe pojęcia z dziedziny robotyki: krótka historia
I. KARTA PRZEDMIOTU CEL PRZEDMIOTU
 I. KARTA PRZEDMIOTU. Nazwa przedmiotu: PODSTAWY ROBOTYKI 2. Kod przedmiotu: Sr 3. Jednostka prowadząca: Wydział Mechaniczno-Elektryczny 4. Kierunek: Automatyka i Robotyka 5. Specjalność: Elektroautomatyka
I. KARTA PRZEDMIOTU. Nazwa przedmiotu: PODSTAWY ROBOTYKI 2. Kod przedmiotu: Sr 3. Jednostka prowadząca: Wydział Mechaniczno-Elektryczny 4. Kierunek: Automatyka i Robotyka 5. Specjalność: Elektroautomatyka
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnia Gdańsa Wydział Eletrotechnii i Autoatyi Katedra Inżynierii Systeów Sterowania MODELOWANIE I PODSTAWY IDENTYFIKACJI Systey ciągłe budowa odeli enoenologicznych z praw zachowania Materiały poocnicze
Politechnia Gdańsa Wydział Eletrotechnii i Autoatyi Katedra Inżynierii Systeów Sterowania MODELOWANIE I PODSTAWY IDENTYFIKACJI Systey ciągłe budowa odeli enoenologicznych z praw zachowania Materiały poocnicze
Modelowanie przez zjawiska przybliżone. Modelowanie poprzez zjawiska uproszczone. Modelowanie przez analogie. Modelowanie matematyczne
 Modelowanie rzeczywistości- JAK? Modelowanie przez zjawisa przybliżone Modelowanie poprzez zjawisa uproszczone Modelowanie przez analogie Modelowanie matematyczne Przyłady modelowania Modelowanie przez
Modelowanie rzeczywistości- JAK? Modelowanie przez zjawisa przybliżone Modelowanie poprzez zjawisa uproszczone Modelowanie przez analogie Modelowanie matematyczne Przyłady modelowania Modelowanie przez
Lista projektów. Roboty Fanuc. VW Pamplona (SP)
 VW Pamplona (SP) Roboty Fanuc Programowanie robotów Fanuc. Optymalizacja czasu pracy linii. Standaryzacja programów. Aplikacje: zgrzewanie punktowe, nakładanie kleju. Cornaglia (PL) Robot Kuka KRC1 Diagnostyka
VW Pamplona (SP) Roboty Fanuc Programowanie robotów Fanuc. Optymalizacja czasu pracy linii. Standaryzacja programów. Aplikacje: zgrzewanie punktowe, nakładanie kleju. Cornaglia (PL) Robot Kuka KRC1 Diagnostyka
ANALIZA KINEMATYCZNA PALCÓW RĘKI
 MODELOWANIE INŻYNIERSKIE ISSN 1896-771X 40, s. 111-116, Gliwice 2010 ANALIZA KINEMATYCZNA PALCÓW RĘKI ANTONI JOHN, AGNIESZKA MUSIOLIK Katedra Wytrzymałości Materiałów i Metod Komputerowych Mechaniki, Politechnika
MODELOWANIE INŻYNIERSKIE ISSN 1896-771X 40, s. 111-116, Gliwice 2010 ANALIZA KINEMATYCZNA PALCÓW RĘKI ANTONI JOHN, AGNIESZKA MUSIOLIK Katedra Wytrzymałości Materiałów i Metod Komputerowych Mechaniki, Politechnika
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw udowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2016/2017
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw udowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2016/2017
PRACA DYPLOMOWA MAGISTERSKA
 KATEDRA WYTRZYMAŁOSCI MATERIAŁÓW I METOD KOMPUTEROWYCH MACHANIKI PRACA DYPLOMOWA MAGISTERSKA Analiza kinematyki robota mobilnego z wykorzystaniem MSC.VisualNastran PROMOTOR Prof. dr hab. inż. Tadeusz Burczyński
KATEDRA WYTRZYMAŁOSCI MATERIAŁÓW I METOD KOMPUTEROWYCH MACHANIKI PRACA DYPLOMOWA MAGISTERSKA Analiza kinematyki robota mobilnego z wykorzystaniem MSC.VisualNastran PROMOTOR Prof. dr hab. inż. Tadeusz Burczyński
Pomiar prędkości i natęŝenia przepływu za pomocą rurek spiętrzających
 Pomiar prędości i natęŝenia przepływu za pomocą rure spiętrzających Instrucja do ćwiczenia nr 8 Miernictwo energetyczne - laboratorium Opracowała: dr inŝ. ElŜbieta Wróblewsa Załad Miernictwa i Ochrony
Pomiar prędości i natęŝenia przepływu za pomocą rure spiętrzających Instrucja do ćwiczenia nr 8 Miernictwo energetyczne - laboratorium Opracowała: dr inŝ. ElŜbieta Wróblewsa Załad Miernictwa i Ochrony
Numeryczna algebra liniowa. Krzysztof Banaś Obliczenia Wysokiej Wydajności 1
 Numeryczna algebra liniowa Krzysztof Banaś Obliczenia Wysokiej Wydajności 1 Numeryczna algebra liniowa Numeryczna algebra liniowa obejmuje szereg algorytmów dotyczących wektorów i macierzy, takich jak
Numeryczna algebra liniowa Krzysztof Banaś Obliczenia Wysokiej Wydajności 1 Numeryczna algebra liniowa Numeryczna algebra liniowa obejmuje szereg algorytmów dotyczących wektorów i macierzy, takich jak
GEOMETRIA ANALITYCZNA W PRZESTRZENI
 Wykład z Podstaw matematyki dla studentów Inżynierii Środowiska Wykład 13. Egzaminy I termin wtorek 31.01 14:00 Aula A Wydział Budownictwa II termin poprawkowy czwartek 9.02 14:00 Aula A Wydział Budownictwa
Wykład z Podstaw matematyki dla studentów Inżynierii Środowiska Wykład 13. Egzaminy I termin wtorek 31.01 14:00 Aula A Wydział Budownictwa II termin poprawkowy czwartek 9.02 14:00 Aula A Wydział Budownictwa
METODY OBLICZENIOWE. Projekt nr 3.4. Dariusz Ostrowski, Wojciech Muła 2FD/L03
 METODY OBLICZENIOWE Projekt nr 3.4 Dariusz Ostrowski, Wojciech Muła 2FD/L03 Zadanie Nasze zadanie składało się z dwóch części: 1. Sformułowanie, przy użyciu metody Lagrange a II rodzaju, równania różniczkowego
METODY OBLICZENIOWE Projekt nr 3.4 Dariusz Ostrowski, Wojciech Muła 2FD/L03 Zadanie Nasze zadanie składało się z dwóch części: 1. Sformułowanie, przy użyciu metody Lagrange a II rodzaju, równania różniczkowego
Koła rowerowe malują fraktale
 Koła rowerowe malują fratale Mare Berezowsi Politechnia Śląsa Rozważmy urządzenie sładającego się z n ół o różnych rozmiarach, obracających się z różnymi prędościami. Na obręczy danego oła, obracającego
Koła rowerowe malują fratale Mare Berezowsi Politechnia Śląsa Rozważmy urządzenie sładającego się z n ół o różnych rozmiarach, obracających się z różnymi prędościami. Na obręczy danego oła, obracającego
NOWE METODY SYNTEZY STRUKTURALNEJ ŁAŃCUCHÓW KINEMATYCZNYCH O ZEROWEJ LICZBIE STOPNI SWOBODY
 MODELOWANIE INŻYNIERSKIE ISSN 1896-771X 8, s. 18-19, Gliwice 2009 NOWE METODY SYNTEZY STRUKTURALNEJ ŁAŃCUCHÓW KINEMATYCZNYCH O ZEROWEJ LICZBIE STOPNI SWOBODY KRYSTYNA ROMANIAK Wydział Architektury, Politechnika
MODELOWANIE INŻYNIERSKIE ISSN 1896-771X 8, s. 18-19, Gliwice 2009 NOWE METODY SYNTEZY STRUKTURALNEJ ŁAŃCUCHÓW KINEMATYCZNYCH O ZEROWEJ LICZBIE STOPNI SWOBODY KRYSTYNA ROMANIAK Wydział Architektury, Politechnika
PL B1. HIKISZ BARTOSZ, Łódź, PL BUP 05/07. BARTOSZ HIKISZ, Łódź, PL WUP 01/16. rzecz. pat.
 PL 220905 B1 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 220905 (13) B1 (21) Numer zgłoszenia: 376878 (51) Int.Cl. F16H 7/00 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej (22) Data zgłoszenia:
PL 220905 B1 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 220905 (13) B1 (21) Numer zgłoszenia: 376878 (51) Int.Cl. F16H 7/00 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej (22) Data zgłoszenia:
9. Sprzężenie zwrotne własności
 9. Sprzężenie zwrotne własności 9.. Wprowadzenie Sprzężenie zwrotne w uładzie eletronicznym realizuje się przez sumowanie części sygnału wyjściowego z sygnałem wejściowym i użycie zmodyiowanego w ten sposób
9. Sprzężenie zwrotne własności 9.. Wprowadzenie Sprzężenie zwrotne w uładzie eletronicznym realizuje się przez sumowanie części sygnału wyjściowego z sygnałem wejściowym i użycie zmodyiowanego w ten sposób
Podstawy Robotyki Określenie kinematyki oraz dynamiki manipulatora
 Podstawy Robotyki Określenie kinematyki oraz dynamiki manipulatora AiR V sem. Gr. A4/ Wicher Bartłomiej Pilewski Wiktor 9 stycznia 011 1 1 Wstęp Rysunek 1: Schematyczne przedstawienie manipulatora W poniższym
Podstawy Robotyki Określenie kinematyki oraz dynamiki manipulatora AiR V sem. Gr. A4/ Wicher Bartłomiej Pilewski Wiktor 9 stycznia 011 1 1 Wstęp Rysunek 1: Schematyczne przedstawienie manipulatora W poniższym
IRB PODSUMOWANIE:
 IRB 2400 - PODSUMOWANIE: Rysunki obrazujące wymiary, udźwig i zasięg znajdują się na kolejnych stronach. Zdjęcia robota opisywanego tutaj są dostępne na dysku sieciowym pod adresem: https://drive.google.com/open?id=0b0jqhp-eodqgcfrhctlual9tauu
IRB 2400 - PODSUMOWANIE: Rysunki obrazujące wymiary, udźwig i zasięg znajdują się na kolejnych stronach. Zdjęcia robota opisywanego tutaj są dostępne na dysku sieciowym pod adresem: https://drive.google.com/open?id=0b0jqhp-eodqgcfrhctlual9tauu
Rok akademicki: 2015/2016 Kod: RME s Punkty ECTS: 12. Poziom studiów: Studia I stopnia Forma i tryb studiów: Stacjonarne
 Nazwa modułu: Roboty przemysłowe Rok akademicki: 2015/2016 Kod: RME-1-504-s Punkty ECTS: 12 Wydział: Inżynierii Mechanicznej i Robotyki Kierunek: Mechatronika Specjalność: Poziom studiów: Studia I stopnia
Nazwa modułu: Roboty przemysłowe Rok akademicki: 2015/2016 Kod: RME-1-504-s Punkty ECTS: 12 Wydział: Inżynierii Mechanicznej i Robotyki Kierunek: Mechatronika Specjalność: Poziom studiów: Studia I stopnia
Autor: mgr inż. Robert Cypryjański METODY KOMPUTEROWE
 METODY KOMPUTEROWE PRZYKŁAD ZADANIA NR 1: ANALIZA STATYCZNA KRATOWNICY PŁASKIEJ ZA POMOCĄ MACIERZOWEJ METODY PRZEMIESZCZEŃ Polecenie: Wykonać obliczenia statyczne kratownicy za pomocą macierzowej metody
METODY KOMPUTEROWE PRZYKŁAD ZADANIA NR 1: ANALIZA STATYCZNA KRATOWNICY PŁASKIEJ ZA POMOCĄ MACIERZOWEJ METODY PRZEMIESZCZEŃ Polecenie: Wykonać obliczenia statyczne kratownicy za pomocą macierzowej metody
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM
 TEOR OBWODÓW SGNŁÓW LBORTORM KDEM MORSK Katedra Telekomunikacji Morskiej ĆWCENE BDNE ÓW PSWNCH RESTNCJNCH. Cel ćwiczenia Doświadczalne wyznaczenie parametrów macierzowych pasywnych czwórników rezystancyjnych
TEOR OBWODÓW SGNŁÓW LBORTORM KDEM MORSK Katedra Telekomunikacji Morskiej ĆWCENE BDNE ÓW PSWNCH RESTNCJNCH. Cel ćwiczenia Doświadczalne wyznaczenie parametrów macierzowych pasywnych czwórników rezystancyjnych
