2.9. Kinematyka typowych struktur manipulatorów
|
|
|
- Halina Zalewska
- 7 lat temu
- Przeglądów:
Transkrypt
1 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str Kinematyka typowych struktur manipulatorów Manipulator planarny 3DOF Notacja DH Rys. 28 Tablica 1 Parametry DH Nr ogniwa α i a i d i θ i σ i σ i 1 0 a 1 0 ϑ a 2 0 ϑ a 3 0 ϑ c 123 s a 1 c 1 + a 2 c 12 + a 3 c 123 T 0 s 123 c a 1 s 1 + a 2 s 12 + a 3 s = (67)
2 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 2 Notacja ZDH y x 4 p y y 1 p y 4 y 0 y 2 y 3 a 3 a 2 x 3 q 3 q 2 x 2 a 1 x 1 q 1 x 0 p x x Rys. 29 Tablica 2 Parametry ZDH Nr ogniwa α i 1 a i 1 d i θ i = q i σ i σ i q a 1 0 q a 2 0 q T 0 3 = c 123 s a 1 c 1 + a 2 c 12 s 123 c a 1 s 1 + a 2 s (68)
3 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str Manipulator o strukturze równoległej Rys. 30 Tablica 3 Parametry DH Nr ogniwa α i a i d i θ i σ i σ i 1 0 a 1 0 ϑ a 2 0 ϑ a 3 0 ϑ a 1 0 ϑ a 4 T 0 3 (q ) = c s a 1 c 1 + a 2 c a 3 c s c a 1 s 1 + a 2 s a 3 s
4 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 4 T 0 1 (q ) = T 3 4 = c 1 s 1 0 a 1 c 1 s 1 c 1 0 a 1 s a R 3 0 (o 0 3 o0 1 ) = 0 a 1 (c 1 + c ) + a 1 (c 1 2 c 1 ) = 0 a 1 (s 1 + s ) + a 1 (s 1 2 s 1 ) = 0 ϑ 2 = ϑ 1 ϑ 1 ϑ 3 = π ϑ 2 = π ϑ 1 + ϑ 1 c 1 s 1 0 a 1 c 1 a 4c 1 T 0 s 1 c 1 0 a 4(q) = 1 s 1 a 4s (69)
5 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str Manipulator sferyczny Rys. 31 Tablica 4 Parametry DH Nr ogniwa α i a i d i θ i σ i σ i 1 π/2 0 0 ϑ π/2 0 d 2 ϑ d T 0 1(ϑ 1 ) = c 1 0 s 1 0 s 1 0 c
6 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 6 c 2 0 s 2 0 T 1 s 2 0 c 2 0 2(ϑ 2 ) = d T (d 3 ) = d 3 c 1 c 2 s 1 c 1 s 2 c 1 s 2 d 3 s 1 d 2 T 0 s 1 c 2 c 1 s 1 s 2 s 1 s 2 d 3 + c 1 d 2 3(q) = s 2 0 c 2 c 2 d 3 (70)
7 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str Manipulator antropomorficzny 3R - notacja DH Rys. 32 Tablica 5 Parametry DH Nr ogniwa α i a i d i θ i σ i σ i 1 π/2 0 0 ϑ a 2 0 ϑ a 3 0 ϑ T 0 1 = c 1 0 s 1 0 s 1 0 c (71)
8 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 8 dla i = 2, 3 T 0 3 = T i 1 i = c i s i 0 a i c i s i c i 0 a i s i c 1 c 23 c 1 s 23 s 1 c 1 (a 2 c 2 + a 3 c 23 ) s 1 c 23 s 1 s 23 c 1 s 1 (a 2 c 2 + a 3 c 23 ) s 23 c 23 0 a 2 s 2 + a 3 s 23 (72) (73)
9 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str Nadgarstek sferyczny 3R - notacja DH Rys. 33 Tablica 6 Parametry DH Nr ogniwa α i a i d i θ i σ i σ i 4 π/2 0 0 ϑ π/2 0 0 ϑ d 6 ϑ c 4 0 s 4 0 T 3 s 4 0 c = c 5 0 s 5 0 T 4 s 5 0 c = (74) (75)
10 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 10 T 3 6 = T 5 6 = c 6 s s 6 c d 6 c 4 c 5 c 6 s 4 s 6 c 4 c 5 c 6 s 4 c 6 c 4 s 5 c 4 s 5 d 6 s 4 c 5 c 6 c 4 s 6 s 4 c 5 s 6 + c 4 c 6 s 4 s 5 s 4 s 5 d 6 s 5 c 6 s 5 s 6 c 5 c 5 d 6 (76) (77)
11 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str Manipulator Stanford Rys. 34 Tablica 7 Parametry DH Nr ogniwa α i a i d i θ i σ i σ i 1 π/2 0 0 ϑ π/2 0 d 2 ϑ d π/2 0 0 ϑ π/2 0 0 ϑ d 6 ϑ 6 0 1
12 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 12 T 0 6 = T 0 3T 3 6 = n0 s 0 a 0 p 0 = r 11 r 12 r 13 p x r 21 r 22 r 23 p y r 31 r 32 r 33 p z r 11 = c 1 (c 2 (c 4 c 5 c 6 s 4 s 6 ) s 2 s 5 c 6 ) s 1 (s 4 c 5 c 6 + c 4 s 6 ), r 21 = s 1 (c 2 (c 4 c 5 c 6 s 4 s 6 ) s 2 s 5 c 6 ) + c 1 (s 4 c 5 c 6 + c 4 s 6 ), r 31 = s 2 (c 4 c 5 c 6 s 4 s 6 ) c 2 s 5 c 6, r 12 = c 1 ( c 2 (c 4 c 5 s 6 + s 4 c 6 ) + s 2 s 5 s 6 ) s 1 ( s 4 c 5 s 6 + c 4 c 6 ), r 22 = s 1 ( c 2 (c 4 c 5 s 6 + s 4 c 6 ) + s 2 s 5 s 6 ) + c 1 ( s 4 c 5 s 6 + c 4 c 6 ), r 32 = s 2 (c 4 c 5 s 6 + s 4 c 6 ) + c 2 s 5 s 6, r 13 = c 1 (c 2 c 4 s 5 + s 2 c 5 ) s 1 s 4 s 5, r 23 = s 1 (c 2 c 4 s 5 + s 2 c 5 ) + c 1 s 4 s 5, r 33 = s 2 c 4 s 5 + c 2 c 5, p x = c 1 s 2 d 3 + s 1 d 2 + (c 1 (c 2 c 4 s 5 + s 2 c 5 ) s 1 s 4 s 5 )d 6, p y = s 1 s 2 d 3 + c 1 d 2 + (s 1 (c 2 c 4 s 5 + s 2 c 5 ) + c 1 s 4 s 5 )d 6, p z = c 2 d 3 + ( s 2 c 4 s 5 + c 2 c 5 )d 6,. (78) (79)
13 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str Manipulator antropomorficzny z nadgarstkiem sferycznym 6R Rys. 35 Tablica 8 Parametry DH Nr ogniwa α i a i d i θ i σ i σ i 1 π/2 0 0 ϑ a 2 0 ϑ π/2 0 0 ϑ π/2 0 d 4 ϑ π/2 0 0 ϑ d 6 ϑ 6 0 1
14 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 14 T 2 3 = T 3 4 = c 3 0 s 3 0 s 3 0 c c 4 0 s 4 0 s 4 0 c d 4 (80) (81) T 0 6 = r 11 r 12 r 13 p x r 21 r 22 r 23 p y r 31 r 32 r 33 p z. (82)
15 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 15 r 11 = c 1 (c 23 (c 4 c 5 c 6 s 4 s 6 ) s 23 s 5 c 6 ) + s 1 (s 4 c 5 c 6 + c 4 s 6 ), r 21 = s 1 (c 23 (c 4 c 5 c 6 s 4 s 6 ) s 23 s 5 c 6 ) c 1 (s 4 c 5 c 6 + c 4 s 6 ), r 31 = s 23 (c 4 c 5 c 6 s 4 s 6 ) + c 23 s 5 c 6, r 12 = c 1 ( c 23 (c 4 c 5 s 6 + s 4 c 6 ) + s 23 s 5 s 6 ) + s 1 ( s 4 c 5 s 6 + c 4 c 6 ), r 22 = s 1 ( c 23 (c 4 c 5 s 6 + s 4 c 6 ) + s 23 s 5 s 6 ) c 1 ( s 4 c 5 s 6 + c 4 c 6 ), r 32 = s 23 (c 4 c 5 s 6 + s 4 c 6 ) c 23 s 5 s 6, r 13 = c 1 (c 23 c 4 s 5 + s 23 c 5 ) + s 1 s 4 s 5, r 23 = s 1 (c 23 c 4 s 5 + s 23 c 5 ) c 1 s 4 s 5, r 33 = s 23 c 4 s 5 c 23 c 5, p x = a 2 c 1 c 2 + d 4 c 1 s 23 + d 6 (c 1 (c 23 c 4 s 5 + s 23 c 5 ) + s 1 s 4 s 5 ), p y = a 2 s 1 c 2 + d 4 s 1 s 23 + d 6 (s 1 (c 23 c 4 s 5 + s 23 c 5 ) c 1 s 4 s 5 ), p z = a 2 s 2 d 4 c 23 + d 6 (s 23 c 4 s 5 c 23 c 5 ), (83)
16 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str Przestrzeń konfiguracyjna a przestrzeń operacyjna (zadania) Przestrzeń operacyjna to zbiór punktów określajacych położenie i orientację efektora manipulatora opisany m-elementowym wektorem x (m N): x = Ω p (84) gdzie Ω jest minimalna reprezentacja katow a (orientacji), zaś p jest wektorem położenia (pozwalaja opisywać zadanie wykonywane przez efektor robota). Przestrzeń konfiguracyjna opisana jest N-elementowym wektorem współrzędnych uogólnionych q = q 1.. (85) q N Zatem k jest nieliniowa funkcja wektorowa zależna od q x = k(q) (86)
17 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str Przetrzeń robocza Przetrzeń robocza manipulatora jest całkowicie określona przez jego geometrię i zakres zmienności współrzędnych uogólnionych q im q i q im dla i = 1, 2,.., N spowodowany ograniczeniami mechanicznymi i określana jest wektorem p = p(q). Pojęcia: przestrzeń robocza osiagalna, przestrzeń robocza manipulacyjna, dokładność, powtarzalność Przykład: manipulator planarny 2R Rys. 36
18 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 18 Przetrzeń robocza obliczana jest z zadania prostego kinematyki na podstawie określonych ograniczeń Rys Redundancja kinematycza Manipulator nazywamy kinematycznie redundantnym, jeżeli liczba jego stopni swobody jest większa niż liczba zmiennych potrzebnych do opisu konkretnego zadania, czyli wymiar przestrzeni operacyjnej jest mniejszy niż wymiar przestrzeni złaczy tj. m < N. (Redundancja jest zatem pojęciem względnym zależnym od zadania.)
19 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str Kalibracja kinematyki Niech x = k(a, α, d, ϑ) (87) x = k k k k a + α + d + ϑ (88) a α d ϑ γ = [ a T α T d T ϑ T] T [ Φ = k a k α k d k ϑ ] γ = γ m γ n Zatem x = Φ(γ n ) γ Dla l położeń (pomiary) x = x 1.. = Φ 1.. γ = Φ(γ) γ (89) x l Φ l γ = (Φ T Φ) 1 Φ T x (90) γ = γ n + γ
2.12. Zadania odwrotne kinematyki
 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 2.12. Zadania odwrotne kinematyki Określenie zadania odwrotnego kinematyki T 0 N = [ ] n s a p = r 11 r 12 r 13 p x r 21 r 22 r 23
Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 2.12. Zadania odwrotne kinematyki Określenie zadania odwrotnego kinematyki T 0 N = [ ] n s a p = r 11 r 12 r 13 p x r 21 r 22 r 23
3.1. Jakobian geometryczny
 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 3. Kinematyki różniczkowa i statyka 3.1. Jakobian geometryczny Pozycja i orientacja x manipulatora o n stopniach swobody zależy od
Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 3. Kinematyki różniczkowa i statyka 3.1. Jakobian geometryczny Pozycja i orientacja x manipulatora o n stopniach swobody zależy od
Jakobiany. Kinematykę we współrzędnych możemy potraktować jako operator przekształcający funkcje czasu
 Wstęp do Robotyki c W. Szynkiewicz, 29 1 Jakobiany Kinematykę we współrzędnych możemy potraktować jako operator przekształcający funkcje czasu ( t )z(t)=k(x(t)) Ponieważ funkcje w powyższym równaniu są
Wstęp do Robotyki c W. Szynkiewicz, 29 1 Jakobiany Kinematykę we współrzędnych możemy potraktować jako operator przekształcający funkcje czasu ( t )z(t)=k(x(t)) Ponieważ funkcje w powyższym równaniu są
Podstawy robotyki wykład III. Kinematyka manipulatora
 Podstawy robotyki Wykład III sztywnego Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Manipulator typu PUMA ogniwo 2 ogniwo 3 ogniwo 1 PUMA układy
Podstawy robotyki Wykład III sztywnego Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Manipulator typu PUMA ogniwo 2 ogniwo 3 ogniwo 1 PUMA układy
Kinematyka manipulatorów robotów
 Wstęp do Robotyki c W. Szynkiewicz, 29 1 Podstawowe pojęcia: Kinematyka manipulatorów robotów Ogniwo(człon, ramię) bryła sztywna(zbiór punktów materialnych, których wzajemne położenie jest stałe). Przegub(złącze)
Wstęp do Robotyki c W. Szynkiewicz, 29 1 Podstawowe pojęcia: Kinematyka manipulatorów robotów Ogniwo(człon, ramię) bryła sztywna(zbiór punktów materialnych, których wzajemne położenie jest stałe). Przegub(złącze)
Rozszerzony konspekt preskryptu do przedmiotu Podstawy Robotyki
 Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Rozszerzony konspekt preskryptu do przedmiotu Podstawy Robotyki dr inż. Marek Wojtyra Instytut Techniki Lotniczej
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Rozszerzony konspekt preskryptu do przedmiotu Podstawy Robotyki dr inż. Marek Wojtyra Instytut Techniki Lotniczej
Metody Lagrange a i Hamiltona w Mechanice
 Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 9 M. Przybycień (WFiIS AGH) Metody Lagrange a i Hamiltona... Wykład
Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 9 M. Przybycień (WFiIS AGH) Metody Lagrange a i Hamiltona... Wykład
Mechanika Robotów. Wojciech Lisowski. 5 Planowanie trajektorii ruchu efektora w przestrzeni roboczej
 Katedra Robotyki i Mechatroniki Akademia Górniczo-Hutnicza w Krakowie Mechanika Robotów Wojciech Lisowski 5 Planowanie trajektorii ruchu efektora w przestrzeni roboczej Mechanika Robotów KRiM, WIMIR, AGH
Katedra Robotyki i Mechatroniki Akademia Górniczo-Hutnicza w Krakowie Mechanika Robotów Wojciech Lisowski 5 Planowanie trajektorii ruchu efektora w przestrzeni roboczej Mechanika Robotów KRiM, WIMIR, AGH
Podstawy robotyki wykład V. Jakobian manipulatora. Osobliwości
 Podstawy robotyki Wykład V Jakobian manipulatora i osobliwości Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Metoda bezpośrednia uzyskania macierzy
Podstawy robotyki Wykład V Jakobian manipulatora i osobliwości Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Metoda bezpośrednia uzyskania macierzy
Roboty przemysłowe. Cz. II
 Roboty przemysłowe Cz. II Klasyfikacja robotów Ze względu na rodzaj napędu: - hydrauliczny (duże obciążenia) - pneumatyczny - elektryczny - mieszany Obecnie roboty przemysłowe bardzo często posiadają napędy
Roboty przemysłowe Cz. II Klasyfikacja robotów Ze względu na rodzaj napędu: - hydrauliczny (duże obciążenia) - pneumatyczny - elektryczny - mieszany Obecnie roboty przemysłowe bardzo często posiadają napędy
PODSTAWY ROBOTYKI. Opracował: dr hab. inż. Adam Rogowski
 PODSTAWY ROBOTYKI Opracował: dr hab. inż. Adam Rogowski Autor wykładu: dr hab. inż. Adam Rogowski pok. ST 405 adam.rogowski@pw.edu.pl Literatura: - Treść niniejszego wykładu dostępna na www.cim.pw.edu.pl/lzp
PODSTAWY ROBOTYKI Opracował: dr hab. inż. Adam Rogowski Autor wykładu: dr hab. inż. Adam Rogowski pok. ST 405 adam.rogowski@pw.edu.pl Literatura: - Treść niniejszego wykładu dostępna na www.cim.pw.edu.pl/lzp
Notacja Denavita-Hartenberga
 Notacja DenavitaHartenberga Materiały do ćwiczeń z Podstaw Robotyki Artur Gmerek Umiejętność rozwiązywania prostego zagadnienia kinematycznego jest najbardziej bazową umiejętność zakresu Robotyki. Wyznaczyć
Notacja DenavitaHartenberga Materiały do ćwiczeń z Podstaw Robotyki Artur Gmerek Umiejętność rozwiązywania prostego zagadnienia kinematycznego jest najbardziej bazową umiejętność zakresu Robotyki. Wyznaczyć
Dynamika manipulatora. Robert Muszyński Janusz Jakubiak Instytut Cybernetyki Technicznej Politechnika Wrocławska. Podstawy robotyki wykład VI
 Podstawy robotyki Wykład VI Robert Muszyński Janusz Jakubiak Instytut Cybernetyki Technicznej Politechnika Wrocławska Dynamika opisuje sposób zachowania się manipulatora poddanego wymuszeniu w postaci
Podstawy robotyki Wykład VI Robert Muszyński Janusz Jakubiak Instytut Cybernetyki Technicznej Politechnika Wrocławska Dynamika opisuje sposób zachowania się manipulatora poddanego wymuszeniu w postaci
METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ
 METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ Wykład 3 Elementy analizy pól skalarnych, wektorowych i tensorowych Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 1 Analiza
METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ Wykład 3 Elementy analizy pól skalarnych, wektorowych i tensorowych Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 1 Analiza
Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1
 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 1. Wiadomości wstępne 1.1. Robotyka Po raz pierwszy terminu robot użył Karel Čapek w sztuce Rossum s Universal Robots w 1921r. Od
Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 1. Wiadomości wstępne 1.1. Robotyka Po raz pierwszy terminu robot użył Karel Čapek w sztuce Rossum s Universal Robots w 1921r. Od
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO. dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury
 KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
MECHANIKA OGÓLNA (II)
 MECHNIK GÓLN (II) Semestr: II (Mechanika I), III (Mechanika II), rok akad. 2013/2014 Liczba godzin: sem. II *) - wykład 30 godz., ćwiczenia 30 godz. sem. III *) - wykład 30 godz., ćwiczenia 30 godz., ale
MECHNIK GÓLN (II) Semestr: II (Mechanika I), III (Mechanika II), rok akad. 2013/2014 Liczba godzin: sem. II *) - wykład 30 godz., ćwiczenia 30 godz. sem. III *) - wykład 30 godz., ćwiczenia 30 godz., ale
Podstawy robotyki. Wykład II. Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska
 Podstawy robotyki Wykład II Ruch ciała sztywnego w przestrzeni euklidesowej Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Preliminaria matematyczne
Podstawy robotyki Wykład II Ruch ciała sztywnego w przestrzeni euklidesowej Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Preliminaria matematyczne
Mechanika Teoretyczna Kinematyka
 POLITECHNIKA RZESZOWSKA Wydział Budownictwa i Inżynierii Środowiska Katedra Mechaniki Konstrukcji Materiały pomocnicze do zajęć z przedmiotu: Mechanika Teoretyczna Kinematyka dr inż. Teresa Filip tfilip@prz.edu.pl
POLITECHNIKA RZESZOWSKA Wydział Budownictwa i Inżynierii Środowiska Katedra Mechaniki Konstrukcji Materiały pomocnicze do zajęć z przedmiotu: Mechanika Teoretyczna Kinematyka dr inż. Teresa Filip tfilip@prz.edu.pl
Definiowanie układów kinematycznych manipulatorów
 Definiowanie układów kinematycznych manipulatorów Definicja Robota Według Encyklopedii Powszechnej PWN: robotem nazywa się urządzenie służące do wykonywania niektórych funkcji manipulacyjnych, lokomocyjnych,
Definiowanie układów kinematycznych manipulatorów Definicja Robota Według Encyklopedii Powszechnej PWN: robotem nazywa się urządzenie służące do wykonywania niektórych funkcji manipulacyjnych, lokomocyjnych,
Roboty manipulacyjne (stacjonarne)
 Roboty manipulacyjne (stacjonarne) Podstawowe układy i zespoły Roboty przemysłowe składa się z następujących trzech podstawowych układów: zasilania, sterowania i ruchu. Układ zasilania Układ zasilania
Roboty manipulacyjne (stacjonarne) Podstawowe układy i zespoły Roboty przemysłowe składa się z następujących trzech podstawowych układów: zasilania, sterowania i ruchu. Układ zasilania Układ zasilania
Metody Lagrange a i Hamiltona w Mechanice
 Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 8 M. Przybycień (WFiIS AGH) Metody Lagrange a i Hamiltona... Wykład
Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 8 M. Przybycień (WFiIS AGH) Metody Lagrange a i Hamiltona... Wykład
Egzamin 1 Strona 1. Egzamin - AR egz Zad 1. Rozwiązanie: Zad. 2. Rozwiązanie: Koła są takie same, więc prędkości kątowe też są takie same
 Egzamin 1 Strona 1 Egzamin - AR egz1 2005-06 Zad 1. Rozwiązanie: Zad. 2 Rozwiązanie: Koła są takie same, więc prędkości kątowe też są takie same Zad.3 Rozwiązanie: Zad.4 Rozwiązanie: Egzamin 1 Strona 2
Egzamin 1 Strona 1 Egzamin - AR egz1 2005-06 Zad 1. Rozwiązanie: Zad. 2 Rozwiązanie: Koła są takie same, więc prędkości kątowe też są takie same Zad.3 Rozwiązanie: Zad.4 Rozwiązanie: Egzamin 1 Strona 2
Wprowadzenie do robotyki
 Wprowadzenie do robotyki Robotyka to nauka i technologia projektowania, budowy i zastosowania sterowanych komputerowo urządzeń mechanicznych popularnie zwanych robotami. Robot urządzenie mechaniczne, które
Wprowadzenie do robotyki Robotyka to nauka i technologia projektowania, budowy i zastosowania sterowanych komputerowo urządzeń mechanicznych popularnie zwanych robotami. Robot urządzenie mechaniczne, które
Wprowadzenie do robotyki
 Wprowadzenie do robotyki Robotyka to nauka i technologia projektowania, budowy i zastosowania sterowanych komputerowo urządzeń mechanicznych popularnie zwanych robotami. Robot urządzenie mechaniczne, które
Wprowadzenie do robotyki Robotyka to nauka i technologia projektowania, budowy i zastosowania sterowanych komputerowo urządzeń mechanicznych popularnie zwanych robotami. Robot urządzenie mechaniczne, które
MECHANIKA 2. Wykład Nr 3 KINEMATYKA. Temat RUCH PŁASKI BRYŁY MATERIALNEJ. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Wykład Nr 3 KINEMATYKA Temat RUCH PŁASKI BRYŁY MATERIALNEJ Prowadzący: dr Krzysztof Polko Pojęcie Ruchu Płaskiego Rys.1 Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie
MECHANIKA 2 Wykład Nr 3 KINEMATYKA Temat RUCH PŁASKI BRYŁY MATERIALNEJ Prowadzący: dr Krzysztof Polko Pojęcie Ruchu Płaskiego Rys.1 Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie
1 Charakterystyka ustrojów powierzchniowych. Anna Stankiewicz
 1 Charakterystyka ustrojów powierzchniowych Anna Stankiewicz e-mail: astankiewicz@l5.pk.edu.pl Tematyka zajęć Przykłady konstrukcji inżynierskich Klasyfikacja ustrojów powierzchniowych Podstawowe pojęcia
1 Charakterystyka ustrojów powierzchniowych Anna Stankiewicz e-mail: astankiewicz@l5.pk.edu.pl Tematyka zajęć Przykłady konstrukcji inżynierskich Klasyfikacja ustrojów powierzchniowych Podstawowe pojęcia
Kinematyka manipulatora równoległego typu DELTA 106 Kinematyka manipulatora równoległego hexapod 110 Kinematyka robotów mobilnych 113
 Spis treści Wstęp 11 1. Rozwój robotyki 15 Rys historyczny rozwoju robotyki 15 Dane statystyczne ilustrujące rozwój robotyki przemysłowej 18 Czynniki stymulujące rozwój robotyki 23 Zakres i problematyka
Spis treści Wstęp 11 1. Rozwój robotyki 15 Rys historyczny rozwoju robotyki 15 Dane statystyczne ilustrujące rozwój robotyki przemysłowej 18 Czynniki stymulujące rozwój robotyki 23 Zakres i problematyka
Podstawy robotyki wykład VI. Dynamika manipulatora
 Podstawy robotyki Wykład VI Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Dynamika opisuje sposób zachowania się manipulatora poddanego wymuszeniu
Podstawy robotyki Wykład VI Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Dynamika opisuje sposób zachowania się manipulatora poddanego wymuszeniu
MODEL MANIPULATORA O STRUKTURZE SZEREGOWEJ W PROGRAMACH CATIA I MATLAB MODEL OF SERIAL MANIPULATOR IN CATIA AND MATLAB
 Kocurek Łukasz, mgr inż. email: kocurek.lukasz@gmail.com Góra Marta, dr inż. email: mgora@mech.pk.edu.pl Politechnika Krakowska, Wydział Mechaniczny MODEL MANIPULATORA O STRUKTURZE SZEREGOWEJ W PROGRAMACH
Kocurek Łukasz, mgr inż. email: kocurek.lukasz@gmail.com Góra Marta, dr inż. email: mgora@mech.pk.edu.pl Politechnika Krakowska, Wydział Mechaniczny MODEL MANIPULATORA O STRUKTURZE SZEREGOWEJ W PROGRAMACH
ANALIZA KINEMATYKI MANIPULATORÓW NA PRZYKŁADZIE ROBOTA LINIOWEGO O CZTERECH STOPNIACH SWOBODY
 MECHNIK 7/ Dr inż. Borys BOROWIK Politechnika Częstochowska Instytut Technologii Mechanicznych DOI:.78/mechanik..7. NLIZ KINEMTYKI MNIPULTORÓW N PRZYKŁDZIE ROBOT LINIOWEGO O CZTERECH STOPNICH SWOBODY Streszczenie:
MECHNIK 7/ Dr inż. Borys BOROWIK Politechnika Częstochowska Instytut Technologii Mechanicznych DOI:.78/mechanik..7. NLIZ KINEMTYKI MNIPULTORÓW N PRZYKŁDZIE ROBOT LINIOWEGO O CZTERECH STOPNICH SWOBODY Streszczenie:
Mechanika Analityczna
 Mechanika Analityczna Wykład 2 - Zasada prac przygotowanych i ogólne równanie dynamiki Politechnika Wrocławska, Wydział Mechaniczny, Katedra Mechaniki i Inżynierii Materiałowej 29 lutego 2016 Plan wykładu
Mechanika Analityczna Wykład 2 - Zasada prac przygotowanych i ogólne równanie dynamiki Politechnika Wrocławska, Wydział Mechaniczny, Katedra Mechaniki i Inżynierii Materiałowej 29 lutego 2016 Plan wykładu
Podstawy Robotyki Określenie kinematyki oraz dynamiki manipulatora
 Podstawy Robotyki Określenie kinematyki oraz dynamiki manipulatora AiR V sem. Gr. A4/ Wicher Bartłomiej Pilewski Wiktor 9 stycznia 011 1 1 Wstęp Rysunek 1: Schematyczne przedstawienie manipulatora W poniższym
Podstawy Robotyki Określenie kinematyki oraz dynamiki manipulatora AiR V sem. Gr. A4/ Wicher Bartłomiej Pilewski Wiktor 9 stycznia 011 1 1 Wstęp Rysunek 1: Schematyczne przedstawienie manipulatora W poniższym
Laboratorium Podstaw Robotyki ĆWICZENIE 5
 Laboratorium Podstaw Robotyki Politechnika Poznańska Katedra Sterowania i Inżynierii Systemów ĆWICZENIE 5 Rotacje 3D, transformacje jednorodne i kinematyka manipulatorów. Celem ćwiczenia jest analiza wybranych
Laboratorium Podstaw Robotyki Politechnika Poznańska Katedra Sterowania i Inżynierii Systemów ĆWICZENIE 5 Rotacje 3D, transformacje jednorodne i kinematyka manipulatorów. Celem ćwiczenia jest analiza wybranych
Więzy i ich klasyfikacja Wykład 2
 Więzy i ich klasyfikacja Wykład 2 Karol Kołodziej (przy współpracy Bartosza Dziewita) Instytut Fizyki Uniwersytet Śląski, Katowice http://kk.us.edu.pl Karol Kołodziej Mechanika klasyczna i relatywistyczna
Więzy i ich klasyfikacja Wykład 2 Karol Kołodziej (przy współpracy Bartosza Dziewita) Instytut Fizyki Uniwersytet Śląski, Katowice http://kk.us.edu.pl Karol Kołodziej Mechanika klasyczna i relatywistyczna
D l. D p. Rodzaje baz jezdnych robotów mobilnych
 ERO Elementy robotyki 1 Rodzaje baz jezdnych robotów mobilnych Napęd różnicowy dwa niezależnie napędzane koła jednej osi, dla zachowania równowagi dodane jest trzecie koło bierne (lub dwa bierne koła)
ERO Elementy robotyki 1 Rodzaje baz jezdnych robotów mobilnych Napęd różnicowy dwa niezależnie napędzane koła jednej osi, dla zachowania równowagi dodane jest trzecie koło bierne (lub dwa bierne koła)
Bezpieczna obsługa oraz praca robota na stanowisku przemysłowym
 Bezpieczna obsługa oraz praca robota na stanowisku przemysłowym Dr inż. Tomasz Buratowski Wydział inżynierii Mechanicznej i Robotyki Katedra Robotyki i Mechatroniki Bezpieczna Obsługa Robota Podstawowe
Bezpieczna obsługa oraz praca robota na stanowisku przemysłowym Dr inż. Tomasz Buratowski Wydział inżynierii Mechanicznej i Robotyki Katedra Robotyki i Mechatroniki Bezpieczna Obsługa Robota Podstawowe
ANALIZA KINEMATYCZNA PALCÓW RĘKI
 MODELOWANIE INŻYNIERSKIE ISSN 1896-771X 40, s. 111-116, Gliwice 2010 ANALIZA KINEMATYCZNA PALCÓW RĘKI ANTONI JOHN, AGNIESZKA MUSIOLIK Katedra Wytrzymałości Materiałów i Metod Komputerowych Mechaniki, Politechnika
MODELOWANIE INŻYNIERSKIE ISSN 1896-771X 40, s. 111-116, Gliwice 2010 ANALIZA KINEMATYCZNA PALCÓW RĘKI ANTONI JOHN, AGNIESZKA MUSIOLIK Katedra Wytrzymałości Materiałów i Metod Komputerowych Mechaniki, Politechnika
KINEMATYKA ODWROTNA TRIPODA Z NAPĘDEM MIMOŚRODOWYM
 4-2007 PROBLEMY EKSPLOATACJI 275 Andrzej ZBROWSKI Instytut Technologii Eksploatacji PIB, Radom Krzysztof ZAGROBA Politechnika Warszawska, Warszawa KINEMATYKA ODWROTNA TRIPODA Z NAPĘDEM MIMOŚRODOWYM Słowa
4-2007 PROBLEMY EKSPLOATACJI 275 Andrzej ZBROWSKI Instytut Technologii Eksploatacji PIB, Radom Krzysztof ZAGROBA Politechnika Warszawska, Warszawa KINEMATYKA ODWROTNA TRIPODA Z NAPĘDEM MIMOŚRODOWYM Słowa
MECHANIKA PRĘTÓW CIENKOŚCIENNYCH
 dr inż. Robert Szmit Przedmiot: MECHANIKA PRĘTÓW CIENKOŚCIENNYCH WYKŁAD nr Uniwersytet Warmińsko-Mazurski w Olsztynie Katedra Geotechniki i Mechaniki Budowli Opis stanu odkształcenia i naprężenia powłoki
dr inż. Robert Szmit Przedmiot: MECHANIKA PRĘTÓW CIENKOŚCIENNYCH WYKŁAD nr Uniwersytet Warmińsko-Mazurski w Olsztynie Katedra Geotechniki i Mechaniki Budowli Opis stanu odkształcenia i naprężenia powłoki
ROZWIĄZANIE PROBLEMU NIELINIOWEGO
 Budownictwo, studia I stopnia, semestr VII przedmiot fakultatywny rok akademicki 2012/2013 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Jerzy Pamin Tematyka zajęć 1 Dyskretyzacja
Budownictwo, studia I stopnia, semestr VII przedmiot fakultatywny rok akademicki 2012/2013 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Jerzy Pamin Tematyka zajęć 1 Dyskretyzacja
KATEDRA AUTOMATYKI, BIOMECHANIKI I MECHATRONIKI. Laboratorium Mechaniki technicznej
 KATEDRA AUTOMATYKI, BIOMECHANIKI I MECHATRONIKI Laboratorium Mechaniki technicznej Ćwiczenie 1 Badanie kinematyki czworoboku przegubowego metodą analitycznonumeryczną. 1 Cel ćwiczenia Celem ćwiczenia jest
KATEDRA AUTOMATYKI, BIOMECHANIKI I MECHATRONIKI Laboratorium Mechaniki technicznej Ćwiczenie 1 Badanie kinematyki czworoboku przegubowego metodą analitycznonumeryczną. 1 Cel ćwiczenia Celem ćwiczenia jest
Zadania kinematyki mechanizmów
 Zadania kinematyki mechanizmów struktura mechanizmu wymiary ogniw ruch ogniw napędowych związki kinematyczne położeń, prędkości, przyspieszeń ogniw zadanie proste kinematyki zadanie odwrotne kinematyki
Zadania kinematyki mechanizmów struktura mechanizmu wymiary ogniw ruch ogniw napędowych związki kinematyczne położeń, prędkości, przyspieszeń ogniw zadanie proste kinematyki zadanie odwrotne kinematyki
MECHANIZMY ROBOTÓW M A N I P U L A T O R Y
 MECHANIZMY ROBOTÓW M A N I P U L A T O R Y sterowanie Manipulator mechaniczny układ przeznaczony do realizacji niektórych funkcji ręki ludzkiej. Manus (łacina) - ręka układ mechaniczny Karel Capek R.U.R.
MECHANIZMY ROBOTÓW M A N I P U L A T O R Y sterowanie Manipulator mechaniczny układ przeznaczony do realizacji niektórych funkcji ręki ludzkiej. Manus (łacina) - ręka układ mechaniczny Karel Capek R.U.R.
PODSTAWY RACHUNKU WEKTOROWEGO
 Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Skalar Definicja Skalar wielkość fizyczna (lub geometryczna)
Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Skalar Definicja Skalar wielkość fizyczna (lub geometryczna)
Manipulatory i roboty mobilne AR S1 semestr 5
 Manipulatory i roboty mobilne AR S semestr 5 Konrad Słodowicz MN: Zadanie proste kinematyki manipulatora szeregowego - DOF Położenie manipulatora opisać można dwojako w przestrzeni kartezjańskiej lub zmiennych
Manipulatory i roboty mobilne AR S semestr 5 Konrad Słodowicz MN: Zadanie proste kinematyki manipulatora szeregowego - DOF Położenie manipulatora opisać można dwojako w przestrzeni kartezjańskiej lub zmiennych
MECHANIZMY ROBOTÓW M A N I P U L A T O R Y
 MECHANIZMY ROBOTÓW M A N I P U L A T O R Y sterowanie Manipulator mechaniczny układ przeznaczony do realizacji niektórych funkcji ręki ludzkiej. Manus (łacina) - ręka układ mechaniczny Karel Capek R.U.R.
MECHANIZMY ROBOTÓW M A N I P U L A T O R Y sterowanie Manipulator mechaniczny układ przeznaczony do realizacji niektórych funkcji ręki ludzkiej. Manus (łacina) - ręka układ mechaniczny Karel Capek R.U.R.
Mechanika Analityczna
 Mechanika Analityczna Wykład 1 - Organizacja wykładu (sprawy zaliczeniowe, tematyka). Więzy i ich klasyfikacja Politechnika Wrocławska, Wydział Mechaniczny, Katedra Mechaniki i Inżynierii Materiałowej
Mechanika Analityczna Wykład 1 - Organizacja wykładu (sprawy zaliczeniowe, tematyka). Więzy i ich klasyfikacja Politechnika Wrocławska, Wydział Mechaniczny, Katedra Mechaniki i Inżynierii Materiałowej
Statystyka matematyczna. Wykład III. Estymacja przedziałowa
 Statystyka matematyczna. Wykład III. e-mail:e.kozlovski@pollub.pl Spis treści Rozkłady zmiennych losowych 1 Rozkłady zmiennych losowych Rozkład χ 2 Rozkład t-studenta Rozkład Fischera 2 Przedziały ufności
Statystyka matematyczna. Wykład III. e-mail:e.kozlovski@pollub.pl Spis treści Rozkłady zmiennych losowych 1 Rozkłady zmiennych losowych Rozkład χ 2 Rozkład t-studenta Rozkład Fischera 2 Przedziały ufności
LASERY I ICH ZASTOSOWANIE W MEDYCYNIE
 LASERY I ICH ZASTOSOWANIE W MEDYCYNIE Laboratorium Instrukcja do ćwiczenia nr 4 Temat: Modulacja światła laserowego: efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą
LASERY I ICH ZASTOSOWANIE W MEDYCYNIE Laboratorium Instrukcja do ćwiczenia nr 4 Temat: Modulacja światła laserowego: efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą
Roboty przemysłowe. Wprowadzenie
 Roboty przemysłowe Wprowadzenie Pojęcia podstawowe Manipulator jest to mechanizm cybernetyczny przeznaczony do realizacji niektórych funkcji kończyny górnej człowieka. Należy wyróżnić dwa rodzaje funkcji
Roboty przemysłowe Wprowadzenie Pojęcia podstawowe Manipulator jest to mechanizm cybernetyczny przeznaczony do realizacji niektórych funkcji kończyny górnej człowieka. Należy wyróżnić dwa rodzaje funkcji
LASERY I ICH ZASTOSOWANIE
 LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 3 Temat: Efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą modulowania zmiany polaryzacji światła oraz
LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 3 Temat: Efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą modulowania zmiany polaryzacji światła oraz
Układy fizyczne z więzami Wykład 2
 Układy fizyczne z więzami Wykład 2 Karol Kołodziej (przy współpracy Bartosza Dziewita) Instytut Fizyki Uniwersytet Śląski, Katowice http://kk.us.edu.pl Karol Kołodziej Mechanika klasyczna i relatywistyczna
Układy fizyczne z więzami Wykład 2 Karol Kołodziej (przy współpracy Bartosza Dziewita) Instytut Fizyki Uniwersytet Śląski, Katowice http://kk.us.edu.pl Karol Kołodziej Mechanika klasyczna i relatywistyczna
Rok akademicki: 2013/2014 Kod: RAR s Punkty ECTS: 5. Poziom studiów: Studia I stopnia Forma i tryb studiów: -
 Nazwa modułu: Roboty przemysłowe Rok akademicki: 2013/2014 Kod: RAR-1-604-s Punkty ECTS: 5 Wydział: Inżynierii Mechanicznej i Robotyki Kierunek: Automatyka i Robotyka Specjalność: - Poziom studiów: Studia
Nazwa modułu: Roboty przemysłowe Rok akademicki: 2013/2014 Kod: RAR-1-604-s Punkty ECTS: 5 Wydział: Inżynierii Mechanicznej i Robotyki Kierunek: Automatyka i Robotyka Specjalność: - Poziom studiów: Studia
Kinematyka robotów mobilnych
 Kinematyka robotów mobilnych Maciej Patan Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Adaptacja slajdów do wykładu Autonomous mobile robots R. Siegwart (ETH Zurich Master Course:
Kinematyka robotów mobilnych Maciej Patan Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Adaptacja slajdów do wykładu Autonomous mobile robots R. Siegwart (ETH Zurich Master Course:
Idea. θ = θ 0, Hipoteza statystyczna Obszary krytyczne Błąd pierwszego i drugiego rodzaju p-wartość
 Idea Niech θ oznacza parametr modelu statystycznego. Dotychczasowe rozważania dotyczyły metod estymacji tego parametru. Teraz zamiast szacować nieznaną wartość parametru będziemy weryfikowali hipotezę
Idea Niech θ oznacza parametr modelu statystycznego. Dotychczasowe rozważania dotyczyły metod estymacji tego parametru. Teraz zamiast szacować nieznaną wartość parametru będziemy weryfikowali hipotezę
METODY KOMPUTEROWE W MECHANICE
 METODY KOMPUTEROWE W MECHANICE wykład dr inż. Paweł Stąpór laboratorium 15 g, projekt 15 g. dr inż. Paweł Stąpór dr inż. Sławomir Koczubiej Politechnika Świętokrzyska Wydział Zarządzania i Modelowania
METODY KOMPUTEROWE W MECHANICE wykład dr inż. Paweł Stąpór laboratorium 15 g, projekt 15 g. dr inż. Paweł Stąpór dr inż. Sławomir Koczubiej Politechnika Świętokrzyska Wydział Zarządzania i Modelowania
Ogłoszenie. Egzaminy z TEORII MASZYN I MECHANIZMÓW dla grup 12A1, 12A2, 12A3 odbędą się w sali A3: I termin 1 lutego 2017 r. godz
 Laboratorium Badań Technoklimatycznych i Maszyn Roboczych Ogłoszenie Egzaminy z TEORII MASZYN I MECHANIZMÓW dla grup 12A1, 12A2, 12A3 odbędą się w sali A3: I termin 1 lutego 2017 r. godz. 9 00 12 00. II
Laboratorium Badań Technoklimatycznych i Maszyn Roboczych Ogłoszenie Egzaminy z TEORII MASZYN I MECHANIZMÓW dla grup 12A1, 12A2, 12A3 odbędą się w sali A3: I termin 1 lutego 2017 r. godz. 9 00 12 00. II
Bezpośrednie sterowanie momentem silnika indukcyjnego zasilanego z 3-poziomowego. przekształtnika MSI z kondensatorami o zmiennym potencjale
 Bezpośrednie sterowanie momentem silnika indukcyjnego zasilanego z 3-poziomowego przekształtnika MSI z kondensatorami o zmiennym potencjale przekształtnika MSI z kondensatorami o zmiennym potencjale 1
Bezpośrednie sterowanie momentem silnika indukcyjnego zasilanego z 3-poziomowego przekształtnika MSI z kondensatorami o zmiennym potencjale przekształtnika MSI z kondensatorami o zmiennym potencjale 1
II. POSTULATY MECHANIKI KWANTOWEJ W JĘZYKU WEKTORÓW STANU. Janusz Adamowski
 II. POSTULATY MECHANIKI KWANTOWEJ W JĘZYKU WEKTORÓW STANU Janusz Adamowski 1 1 Przestrzeń Hilberta Do opisu stanów kwantowych używamy przestrzeni Hilberta. Przestrzenią Hilberta H nazywamy przestrzeń wektorową
II. POSTULATY MECHANIKI KWANTOWEJ W JĘZYKU WEKTORÓW STANU Janusz Adamowski 1 1 Przestrzeń Hilberta Do opisu stanów kwantowych używamy przestrzeni Hilberta. Przestrzenią Hilberta H nazywamy przestrzeń wektorową
Modelowanie i Wizualizowanie 3W grafiki. Łańcuchy kinematyczne
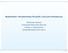 Modelowanie i Wizualizowanie 3W grafiki. Łańcuchy kinematyczne Aleksander Denisiuk Uniwersytet Warmińsko-Mazurski Olsztyn, ul. Słoneczna 54 denisjuk@matman.uwm.edu.pl 1 / 31 Łańcuchy kinematyczne Najnowsza
Modelowanie i Wizualizowanie 3W grafiki. Łańcuchy kinematyczne Aleksander Denisiuk Uniwersytet Warmińsko-Mazurski Olsztyn, ul. Słoneczna 54 denisjuk@matman.uwm.edu.pl 1 / 31 Łańcuchy kinematyczne Najnowsza
VIII. VIII.1. ORBITALNY MOMENT MAGNETYCZNY ELEKTRONU, L= r p (VIII.1.1) p=m v (VIII.1.2) L= L =mvr (VIII.1.1a) r v. r=v (VIII.1.3)
 VIII. VIII.1. ORBITALNY MOMENT MAGNETYCZNY ELEKTRONU, L= r p (VIII.1.1) p=m v (VIII.1.2) Z (VIII.1.1) i (VIII.1.2) wynika (VIII.1.1a): L= L =mvr (VIII.1.1a) r v r=v (VIII.1.3) Z zależności (VIII.1.1a)
VIII. VIII.1. ORBITALNY MOMENT MAGNETYCZNY ELEKTRONU, L= r p (VIII.1.1) p=m v (VIII.1.2) Z (VIII.1.1) i (VIII.1.2) wynika (VIII.1.1a): L= L =mvr (VIII.1.1a) r v r=v (VIII.1.3) Z zależności (VIII.1.1a)
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania KOMPUTEROWE SYSTEMY STEROWANIA I WSPOMAGANIA DECYZJI Rozproszone programowanie produkcji z wykorzystaniem
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania KOMPUTEROWE SYSTEMY STEROWANIA I WSPOMAGANIA DECYZJI Rozproszone programowanie produkcji z wykorzystaniem
Przekształcenia liniowe
 Przekształcenia liniowe Zadania Które z następujących przekształceń są liniowe? (a) T : R 2 R 2, T (x, x 2 ) = (2x, x x 2 ), (b) T : R 2 R 2, T (x, x 2 ) = (x + 3x 2, x 2 ), (c) T : R 2 R, T (x, x 2 )
Przekształcenia liniowe Zadania Które z następujących przekształceń są liniowe? (a) T : R 2 R 2, T (x, x 2 ) = (2x, x x 2 ), (b) T : R 2 R 2, T (x, x 2 ) = (x + 3x 2, x 2 ), (c) T : R 2 R, T (x, x 2 )
WYKŁAD 6 KINEMATYKA PRZEPŁYWÓW CZĘŚĆ 2 1/11
 WYKŁAD 6 KINEMATYKA PRZEPŁYWÓW CZĘŚĆ 1/11 DEFORMACJA OŚRODKA CIĄGŁEGO Rozważmy dwa elementy płynu położone w pewnej chwili w bliskich sobie punktach A i B. Jak zmienia się ich względne położenie w krótkim
WYKŁAD 6 KINEMATYKA PRZEPŁYWÓW CZĘŚĆ 1/11 DEFORMACJA OŚRODKA CIĄGŁEGO Rozważmy dwa elementy płynu położone w pewnej chwili w bliskich sobie punktach A i B. Jak zmienia się ich względne położenie w krótkim
Całki powierzchniowe w R n
 Całki powierzchniowe w R n Na początek małe uzupełnienie z algebry liniowej. Niech R n k oznacza przestrzeń liniową macierzy o n wierszach i k kolumnach. Dla dowolnej macierzy A R n k, gdzie k n, połóżmy
Całki powierzchniowe w R n Na początek małe uzupełnienie z algebry liniowej. Niech R n k oznacza przestrzeń liniową macierzy o n wierszach i k kolumnach. Dla dowolnej macierzy A R n k, gdzie k n, połóżmy
Rozkłady wielu zmiennych
 Rozkłady wielu zmiennych Uogólnienie pojęć na rozkład wielu zmiennych Dystrybuanta, gęstość prawdopodobieństwa, rozkład brzegowy, wartości średnie i odchylenia standardowe, momenty Notacja macierzowa Macierz
Rozkłady wielu zmiennych Uogólnienie pojęć na rozkład wielu zmiennych Dystrybuanta, gęstość prawdopodobieństwa, rozkład brzegowy, wartości średnie i odchylenia standardowe, momenty Notacja macierzowa Macierz
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż.
 Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
MECHANIKA 2 KINEMATYKA. Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 KINEMATYKA Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY Prowadzący: dr Krzysztof Polko Określenie położenia ciała sztywnego Pierwszy sposób: Określamy położenia trzech punktów ciała nie leżących
MECHANIKA 2 KINEMATYKA Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY Prowadzący: dr Krzysztof Polko Określenie położenia ciała sztywnego Pierwszy sposób: Określamy położenia trzech punktów ciała nie leżących
KATEDRA AUTOMATYKI, BIOMECHANIKI I MECHATRONIKI. Laboratorium Mechaniki technicznej
 KATEDRA AUTOMATYKI, BIOMECHANIKI I MECHATRONIKI Laboratorium Mechaniki technicznej Ćwiczenie 1 Badanie kinematyki czworoboku przegubowego metodą analitycznonumeryczną. 1 Cel ćwiczenia Celem ćwiczenia jest
KATEDRA AUTOMATYKI, BIOMECHANIKI I MECHATRONIKI Laboratorium Mechaniki technicznej Ćwiczenie 1 Badanie kinematyki czworoboku przegubowego metodą analitycznonumeryczną. 1 Cel ćwiczenia Celem ćwiczenia jest
Fuzja sygnałów i filtry bayesowskie
 Fuzja sygnałów i filtry bayesowskie Roboty Manipulacyjne i Mobilne dr inż. Janusz Jakubiak Katedra Cybernetyki i Robotyki Wydział Elektroniki, Politechnika Wrocławska Wrocław, 10.03.2015 Dlaczego potrzebna
Fuzja sygnałów i filtry bayesowskie Roboty Manipulacyjne i Mobilne dr inż. Janusz Jakubiak Katedra Cybernetyki i Robotyki Wydział Elektroniki, Politechnika Wrocławska Wrocław, 10.03.2015 Dlaczego potrzebna
I. KARTA PRZEDMIOTU CEL PRZEDMIOTU
 I. KARTA PRZEDMIOTU. Nazwa przedmiotu: PODSTAWY ROBOTYKI 2. Kod przedmiotu: Sr 3. Jednostka prowadząca: Wydział Mechaniczno-Elektryczny 4. Kierunek: Automatyka i Robotyka 5. Specjalność: Elektroautomatyka
I. KARTA PRZEDMIOTU. Nazwa przedmiotu: PODSTAWY ROBOTYKI 2. Kod przedmiotu: Sr 3. Jednostka prowadząca: Wydział Mechaniczno-Elektryczny 4. Kierunek: Automatyka i Robotyka 5. Specjalność: Elektroautomatyka
Wykład 4 Zastosowanie robotyki w chirurgii
 Zastosowanie Robotyki w Medycynie Wykład 4 (3) Piotr Sauer Katedra Sterowania i Inżynierii Systemów Wymagania telemanipulatorów Kinematyka umożliwiająca penetrację przez powłoki skórne pacjenta Odpowiednia
Zastosowanie Robotyki w Medycynie Wykład 4 (3) Piotr Sauer Katedra Sterowania i Inżynierii Systemów Wymagania telemanipulatorów Kinematyka umożliwiająca penetrację przez powłoki skórne pacjenta Odpowiednia
Wykład 2 - zagadnienie dwóch ciał (od praw Keplera do prawa powszechnego ciążenia i z powrotem..)
 Wykład 2 - zagadnienie dwóch ciał (od praw Keplera do prawa powszechnego ciążenia i z powrotem..) 24.02.2014 Prawa Keplera Na podstawie obserwacji zgromadzonych przez Tycho Brahe (głównie obserwacji Marsa)
Wykład 2 - zagadnienie dwóch ciał (od praw Keplera do prawa powszechnego ciążenia i z powrotem..) 24.02.2014 Prawa Keplera Na podstawie obserwacji zgromadzonych przez Tycho Brahe (głównie obserwacji Marsa)
UKŁADY WIELOCZŁONOWE Z WIĘZAMI JEDNOSTRONNYMI W ZASTOSOWANIU DO MODELOWANIA ZŁOŻONYCH UKŁADÓW MECHANICZNYCH
 POLITECHNIKA GDAŃSKA KRZYSZTOF LIPIŃSKI UKŁADY WIELOCZŁONOWE Z WIĘZAMI JEDNOSTRONNYMI W ZASTOSOWANIU DO MODELOWANIA ZŁOŻONYCH UKŁADÓW MECHANICZNYCH GDAŃSK 2012 PRZEWODNICZĄCY KOMITETU REDAKCYJNEGO WYDAWNICTWA
POLITECHNIKA GDAŃSKA KRZYSZTOF LIPIŃSKI UKŁADY WIELOCZŁONOWE Z WIĘZAMI JEDNOSTRONNYMI W ZASTOSOWANIU DO MODELOWANIA ZŁOŻONYCH UKŁADÓW MECHANICZNYCH GDAŃSK 2012 PRZEWODNICZĄCY KOMITETU REDAKCYJNEGO WYDAWNICTWA
MECHANIKA 2. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Prowadzący: dr Krzysztof Polko PLAN WYKŁADÓW 1. Podstawy kinematyki 2. Ruch postępowy i obrotowy bryły 3. Ruch płaski bryły 4. Ruch złożony i ruch względny 5. Ruch kulisty i ruch ogólny bryły
MECHANIKA 2 Prowadzący: dr Krzysztof Polko PLAN WYKŁADÓW 1. Podstawy kinematyki 2. Ruch postępowy i obrotowy bryły 3. Ruch płaski bryły 4. Ruch złożony i ruch względny 5. Ruch kulisty i ruch ogólny bryły
T13 Modelowanie zautomatyzowanych procesów wytwórczych, programowanie maszyn CNC
 T13 Modelowanie zautomatyzowanych procesów wytwórczych, programowanie maszyn CNC 1. Wstęp Wg normy ISO ITR 8373, robot przemysłowy jest automatycznie sterowaną, programowalną, wielozadaniową maszyną manipulacyjną
T13 Modelowanie zautomatyzowanych procesów wytwórczych, programowanie maszyn CNC 1. Wstęp Wg normy ISO ITR 8373, robot przemysłowy jest automatycznie sterowaną, programowalną, wielozadaniową maszyną manipulacyjną
Wykład 3 Zastosowanie robotyki w chirurgii
 Zastosowanie Robotyki w Medycynie Wykład 3 (2) Piotr Sauer Katedra Sterowania i Inżynierii Systemów Chirurg nie ma bezpośredniej styczności z operowaną tkanką - możliwość operowania na odległość czyli
Zastosowanie Robotyki w Medycynie Wykład 3 (2) Piotr Sauer Katedra Sterowania i Inżynierii Systemów Chirurg nie ma bezpośredniej styczności z operowaną tkanką - możliwość operowania na odległość czyli
Kinematyka: opis ruchu
 Kinematyka: opis ruchu Fizyka I (B+C) Wykład IV: Ruch jednostajnie przyspieszony Ruch harmoniczny Ruch po okręgu Klasyfikacja ruchów Ze względu na tor wybrane przypadki szczególne prostoliniowy, odbywajacy
Kinematyka: opis ruchu Fizyka I (B+C) Wykład IV: Ruch jednostajnie przyspieszony Ruch harmoniczny Ruch po okręgu Klasyfikacja ruchów Ze względu na tor wybrane przypadki szczególne prostoliniowy, odbywajacy
OPISY PRZESTRZENNE I PRZEKSZTAŁCENIA
 OPISY PRZESTRZENNE I PRZEKSZTAŁCENIA Wprowadzenie W robotyce przez pojęcie manipulacji rozumiemy przemieszczanie w przestrzeni przedmiotów i narzędzi za pomocą specjalnego mechanizmu. W związku z tym pojawia
OPISY PRZESTRZENNE I PRZEKSZTAŁCENIA Wprowadzenie W robotyce przez pojęcie manipulacji rozumiemy przemieszczanie w przestrzeni przedmiotów i narzędzi za pomocą specjalnego mechanizmu. W związku z tym pojawia
Algorytm kinematyki odwrotnej typu jakobianu pseudoodwrotnego dla manipulatorów mobilnych. Mariusz Janiak 1
 Na prawach rękopisu INSTYTUT INFORMATYKI AUTOMATYKI I ROBOTYKI POLITECHNIKI WROCŁAWSKIEJ Raport serii??? nr??/26 Algorytm kinematyki odwrotnej typu jakobianu pseudoodwrotnego dla manipulatorów mobilnych.
Na prawach rękopisu INSTYTUT INFORMATYKI AUTOMATYKI I ROBOTYKI POLITECHNIKI WROCŁAWSKIEJ Raport serii??? nr??/26 Algorytm kinematyki odwrotnej typu jakobianu pseudoodwrotnego dla manipulatorów mobilnych.
1. Zbadać liniową niezależność funkcji x, 1, x, x 2 w przestrzeni liniowej funkcji ciągłych na przedziale [ 1, ).
 B 2 Suma Zbadać, czy liniowo niezależne wektory u, v, w stanowią bazę przestrzeni liniowej lin { u + 2 v + w, u v + 2 w, 3 u + 5 w } 2 Współrzędne wektora (, 4, 5, 4 ) w pewnej bazie podprzestrzeni U R
B 2 Suma Zbadać, czy liniowo niezależne wektory u, v, w stanowią bazę przestrzeni liniowej lin { u + 2 v + w, u v + 2 w, 3 u + 5 w } 2 Współrzędne wektora (, 4, 5, 4 ) w pewnej bazie podprzestrzeni U R
Planowanie przejazdu przez zbiór punktów. zadania zrobotyzowanej inspekcji
 dla zadania zrobotyzowanej inspekcji Katedra Sterowania i Inżynierii Systemów, Politechnika Poznańska 3 lipca 2014 Plan prezentacji 1 Wprowadzenie 2 3 4 Postawienie problemu Założenia: Rozpatrujemy kinematykę
dla zadania zrobotyzowanej inspekcji Katedra Sterowania i Inżynierii Systemów, Politechnika Poznańska 3 lipca 2014 Plan prezentacji 1 Wprowadzenie 2 3 4 Postawienie problemu Założenia: Rozpatrujemy kinematykę
Elementy geometrii analitycznej w R 3
 Rozdział 12 Elementy geometrii analitycznej w R 3 Elementy trójwymiarowej przestrzeni rzeczywistej R 3 = {(x,y,z) : x,y,z R} możemy interpretować co najmniej na trzy sposoby, tzn. jako: zbiór punktów (x,
Rozdział 12 Elementy geometrii analitycznej w R 3 Elementy trójwymiarowej przestrzeni rzeczywistej R 3 = {(x,y,z) : x,y,z R} możemy interpretować co najmniej na trzy sposoby, tzn. jako: zbiór punktów (x,
Roboty manipulacyjne i mobilne. Roboty przemysłowe zadania i elementy
 Roboty manipulacyjne i mobilne Wykład II zadania i elementy Janusz Jakubiak IIAiR Politechnika Wrocławska Informacja o prawach autorskich Materiały pochodzą z książek: J. Honczarenko.. Budowa i zastosowanie.
Roboty manipulacyjne i mobilne Wykład II zadania i elementy Janusz Jakubiak IIAiR Politechnika Wrocławska Informacja o prawach autorskich Materiały pochodzą z książek: J. Honczarenko.. Budowa i zastosowanie.
Rozkład napięcia na łańcuchu izolatorów wiszących
 POLITECHNIKA LBELSKA WYDZIAŁ ELEKTROTECHNIKI I INFORMATYKI KATEDRA RZĄDZEŃ ELEKTRYCZNYCH I TWN LABORATORIM TECHNIKI WYSOKICH NAPIĘĆ Ćw. nr 13 Rozkład napięcia na łańcuchu izolatorów wiszących Grupa dziekańska...
POLITECHNIKA LBELSKA WYDZIAŁ ELEKTROTECHNIKI I INFORMATYKI KATEDRA RZĄDZEŃ ELEKTRYCZNYCH I TWN LABORATORIM TECHNIKI WYSOKICH NAPIĘĆ Ćw. nr 13 Rozkład napięcia na łańcuchu izolatorów wiszących Grupa dziekańska...
Wektor, prosta, płaszczyzna; liniowa niezależność, rząd macierzy
 Wektor, prosta, płaszczyzna; liniowa niezależność, rząd macierzy Justyna Winnicka Na podstawie podręcznika Matematyka. e-book M. Dędys, S. Dorosiewicza, M. Ekes, J. Kłopotowskiego. rok akademicki 217/218
Wektor, prosta, płaszczyzna; liniowa niezależność, rząd macierzy Justyna Winnicka Na podstawie podręcznika Matematyka. e-book M. Dędys, S. Dorosiewicza, M. Ekes, J. Kłopotowskiego. rok akademicki 217/218
Iloczyn wektorowy. Autorzy: Michał Góra
 Iloczyn wektorowy Autorzy: Michał Góra 019 Iloczyn wektorowy Autor: Michał Góra DEFINICJA Definicja 1: Iloczyn wektorowy Iloczynem wektorowym wektorów v = ( v x, v y, v z ) R 3 oraz w = ( w x, w y, w z
Iloczyn wektorowy Autorzy: Michał Góra 019 Iloczyn wektorowy Autor: Michał Góra DEFINICJA Definicja 1: Iloczyn wektorowy Iloczynem wektorowym wektorów v = ( v x, v y, v z ) R 3 oraz w = ( w x, w y, w z
WPŁYW KINEMATYCZNYCH CHARAKTERYSTYK RUCHU CHWYTAKA NA POŁOśENIA, PRĘDKOŚCI I PRZYSPIESZENIA OGNIW AGROROBOTA
 InŜynieria Rolnicza 11/006 Andrzej Graboś, Marek Boryga Katedra Podstaw Techniki Akademia Rolnicza w Lublinie WPŁYW KINEMATYCZNYCH CHARAKTERYSTYK RUCHU CHWYTAKA NA POŁOśENIA, PRĘDKOŚCI I PRZYSPIESZENIA
InŜynieria Rolnicza 11/006 Andrzej Graboś, Marek Boryga Katedra Podstaw Techniki Akademia Rolnicza w Lublinie WPŁYW KINEMATYCZNYCH CHARAKTERYSTYK RUCHU CHWYTAKA NA POŁOśENIA, PRĘDKOŚCI I PRZYSPIESZENIA
PRZEKŁADNIE ZĘBATE. Przekł. o osiach stałych. Przekładnie obiegowe. Planetarne: W=1 Różnicowe i sumujące: W>1
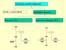 PRZEKŁADNIE ZĘBATE Przekł. o osiach stałych Przekładnie obiegowe Planetarne: W=1 Różnicowe i sumujące: W>1 Przekładnie obiegowe: Planetarne: W=1 2 I II 3 ( j ) 1 I n=3 p 1 =2 p 2 =1 W = 3(n-1) - 2p 1 -
PRZEKŁADNIE ZĘBATE Przekł. o osiach stałych Przekładnie obiegowe Planetarne: W=1 Różnicowe i sumujące: W>1 Przekładnie obiegowe: Planetarne: W=1 2 I II 3 ( j ) 1 I n=3 p 1 =2 p 2 =1 W = 3(n-1) - 2p 1 -
Seria zadań z Algebry IIR nr kwietnia 2017 r. i V 2 = B 2, B 4 R, gdzie
 Seria zadań z Algebry IIR nr 29 kwietnia 207 r Notacja: We wszystkich poniższych zadaniach K jest ciałem, V wektorow a nad K zaś jest przestrzeni a Zadanie Niechaj V = K 4 [t] Określmy podprzestrzenie
Seria zadań z Algebry IIR nr 29 kwietnia 207 r Notacja: We wszystkich poniższych zadaniach K jest ciałem, V wektorow a nad K zaś jest przestrzeni a Zadanie Niechaj V = K 4 [t] Określmy podprzestrzenie
STATYSTYKA MATEMATYCZNA WYKŁAD 4. WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH X - cecha populacji, θ parametr rozkładu cechy X.
 STATYSTYKA MATEMATYCZNA WYKŁAD 4 WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH X - cecha populacji, θ parametr rozkładu cechy X. Wysuwamy hipotezy: zerową (podstawową H ( θ = θ i alternatywną H, która ma jedną z
STATYSTYKA MATEMATYCZNA WYKŁAD 4 WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH X - cecha populacji, θ parametr rozkładu cechy X. Wysuwamy hipotezy: zerową (podstawową H ( θ = θ i alternatywną H, która ma jedną z
Drgania układu o wielu stopniach swobody
 Drgania układu o wielu stopniach swobody Rozpatrzmy układ składający się z n ciał o masach m i (i =,,..., n, połączonych między sobą i z nieruchomym podłożem za pomocą elementów sprężystych o współczynnikach
Drgania układu o wielu stopniach swobody Rozpatrzmy układ składający się z n ciał o masach m i (i =,,..., n, połączonych między sobą i z nieruchomym podłożem za pomocą elementów sprężystych o współczynnikach
ANALIZA OBCIĄŻEŃ JEDNOSTEK NAPĘDOWYCH DLA PRZESTRZENNYCH RUCHÓW AGROROBOTA
 Inżynieria Rolnicza 7(105)/2008 ANALIZA OBCIĄŻEŃ JEDNOSTEK NAPĘDOWYCH DLA PRZESTRZENNYCH RUCHÓW AGROROBOTA Katedra Podstaw Techniki, Uniwersytet Przyrodniczy w Lublinie Streszczenie. W pracy przedstawiono
Inżynieria Rolnicza 7(105)/2008 ANALIZA OBCIĄŻEŃ JEDNOSTEK NAPĘDOWYCH DLA PRZESTRZENNYCH RUCHÓW AGROROBOTA Katedra Podstaw Techniki, Uniwersytet Przyrodniczy w Lublinie Streszczenie. W pracy przedstawiono
Manipulator OOO z systemem wizyjnym
 Studenckie Koło Naukowe Robotyki Encoder Wydział Automatyki, Elektroniki i Informatyki Politechnika Śląska Manipulator OOO z systemem wizyjnym Raport z realizacji projektu Daniel Dreszer Kamil Gnacik Paweł
Studenckie Koło Naukowe Robotyki Encoder Wydział Automatyki, Elektroniki i Informatyki Politechnika Śląska Manipulator OOO z systemem wizyjnym Raport z realizacji projektu Daniel Dreszer Kamil Gnacik Paweł
1. STRUKTURA MECHANIZMÓW 1.1. POJĘCIA PODSTAWOWE
 1. STRUKTURA MECHANIZMÓW 1.1. POJĘCIA PODSTAWOWE 1.1.1. Człon mechanizmu Człon mechanizmu to element konstrukcyjny o dowolnym kształcie, ruchomy bądź nieruchomy, zwany wtedy podstawą, niepodzielny w aspekcie
1. STRUKTURA MECHANIZMÓW 1.1. POJĘCIA PODSTAWOWE 1.1.1. Człon mechanizmu Człon mechanizmu to element konstrukcyjny o dowolnym kształcie, ruchomy bądź nieruchomy, zwany wtedy podstawą, niepodzielny w aspekcie
R o z d z i a ł 2 KINEMATYKA PUNKTU MATERIALNEGO
 R o z d z i a ł KINEMATYKA PUNKTU MATERIALNEGO Kinematyka zajmuje się opisem ruchu ciał bez uwzględniania ich masy i bez rozpatrywania przyczyn, które ten ruch spowodowały. Przez punkt materialny rozumiemy
R o z d z i a ł KINEMATYKA PUNKTU MATERIALNEGO Kinematyka zajmuje się opisem ruchu ciał bez uwzględniania ich masy i bez rozpatrywania przyczyn, które ten ruch spowodowały. Przez punkt materialny rozumiemy
ALGEBRA Z GEOMETRIĄ BAZY PRZESTRZENI WEKTOROWYCH
 ALGEBRA Z GEOMETRIĄ 1/10 BAZY PRZESTRZENI WEKTOROWYCH Piotr M. Hajac Uniwersytet Warszawski Wykład 11, 18.12.2013 Typeset by Jakub Szczepanik. Istnienie bazy Tak jak wśród wszystkich pierścieni wyróżniamy
ALGEBRA Z GEOMETRIĄ 1/10 BAZY PRZESTRZENI WEKTOROWYCH Piotr M. Hajac Uniwersytet Warszawski Wykład 11, 18.12.2013 Typeset by Jakub Szczepanik. Istnienie bazy Tak jak wśród wszystkich pierścieni wyróżniamy
MECHANIKA II. Dynamika ruchu obrotowego bryły sztywnej
 MECHANIKA II. Dynamika ruchu obrotowego bryły sztywnej Daniel Lewandowski Politechnika Wrocławska, Wydział Mechaniczny, Katedra Mechaniki i Inżynierii Materiałowej http://kmim.wm.pwr.edu.pl/lewandowski/
MECHANIKA II. Dynamika ruchu obrotowego bryły sztywnej Daniel Lewandowski Politechnika Wrocławska, Wydział Mechaniczny, Katedra Mechaniki i Inżynierii Materiałowej http://kmim.wm.pwr.edu.pl/lewandowski/
Rozkład napięcia na łańcuchu izolatorów wiszących
 Politechnika Lubelska Wydział Elektrotechniki i Informatyki Katedra rządzeń Elektrycznych i TWN 20-618 Lublin, ul. Nadbystrzycka 38A www.kueitwn.pollub.pl LABORATORIM TECHNIKI WYSOKICH NAPIĘĆ Instrukcja
Politechnika Lubelska Wydział Elektrotechniki i Informatyki Katedra rządzeń Elektrycznych i TWN 20-618 Lublin, ul. Nadbystrzycka 38A www.kueitwn.pollub.pl LABORATORIM TECHNIKI WYSOKICH NAPIĘĆ Instrukcja
