TEORETYCZNE PODSTAWY PROGNOZOWANIA USZKADZALNOŚCI SIECI WODOCIĄGOWEJ

Transkrypt

1 RYSZARDA IWANEJKO, JAROSŁAW BAJER* TEORETYCZNE PODSTAWY PROGNOZOWANIA USZKADZALNOŚCI SIECI WODOCIĄGOWEJ THEORETICAL BASIS OF PROGNOSING THE FAILURES IN WATER SUPPLY SYSTEMS Streszczee Abstract Sec wodocągowe wody staową jede z elemetów strategczej frastruktury mejskej. Są systemam złożoym dyamczym. Optymala stratega eksploatacj sec powa uwzględać sta aktualy progozy. Aktualy sta sec może być charakteryzoway przez tzw. uszkadzalość. Parametr te może być wyzaczoy przez eksploatatora sec jako średa lczba uszkodzeń przypadająca a jedostkę długośc a jedostkę czasu. W artykule przedstawoo podstawy teoretycze wybraych model matematyczych, które mogą być zastosowae do progoz krótko- średotermowych. Słowa kluczowe: seć wodocągowa, seć dystrybucj wody, uszkadzalość, progoza Water supply systems are a mportat elemet of a strategc urba frastructure. Ther cofguratos are usually complex ad dyamc. The optmal operato strategy of the water supply system should cosder both curret codtos as well as the future progoss. Curret codtos of the water supply system may be characterzed by so called: falure rate. The parameter may be determed drectly by the water system operator ad defed as the average umber of falures per the ut legth of ppe ad the tme ut. The work presets a theoretcal backgroud for the selected mathematcal models, that may be appled for the both short-term ad md-term predctos. Keywords: water supply system, water dstrbuto system, falures, predctos * Dr Ryszarda Iwaejko, dr ż. Jarosław Bajer, Istytut Zaopatrzea w Wodę Ochroy Środowska, Wydzał Iżyer Środowska, Poltechka Krakowska.

2 Wstęp Zadaem sec wodocągowej (sec dystrybucj wody) jest zapewee cągłej dostawy do odborców wody w potrzebej lośc, o odpowedej jakośc pod wymagaym cśeem. Skutk eprawdłowej pracy sec są odczuwae przez odborców jako ucążlwośc, a przez eksploatatora jako straty fasowe (m.. usuwae awar, straty wody w sec). Optymala stratega eksploatacj sec wodocągowej, mmalzująca straty ucążlwośc, powa uwzględać zarówo sytuację aktualą, jak odpowede progozy. Sytuacja aktuala, charakteryzowaa m.. przez tzw. uszkadzalość sec l 0 (rocza lczba uszkodzeń odesoa do długośc sec) welkość strat wody, jest wykem stau techczego sec, struktury materałowej wekowej, beżących prac prowadzoych a sec sposobu eksploatacj. Sec wodocągowe to złożoe systemy ejedorodych przewodów, uzbrojea ych obektów towarzyszących. Były rozbudowywae wraz z rozwojem mast, a w cągu lat zmae mogły ulegać struktura sec, fukcje poszczególych przewodów, ch obcążee waruk pracy. Gromadzoe przez każdego eksploatatora sec wodocągowej formacje dotyczące uszkodzeń pozwalają wyzaczyć uszkadzalość sec l 0. Te wartośc uzyskae dla poszczególych lat tworzą szereg dyamcze {l 0, } =1, gdze lczba daych (w kokretych przypadkach jest to lczba lat, mesęcy, kwartałów, dób). Na zmeość w czase każdego zjawska, a węc zjawska uszkadzalośc sec, mają wpływ: tedecja rozwojowa, wahaa okresowe wahaa przypadkowe [6]. Tedecja rozwojowa (tred) to powole, regulare systematycze zmay określoego zjawska obserwowae w dostatecze długm okrese (ajlepej co ajmej 10 lat) będące rezultatem dzałaa tzw. przyczy główych. W przypadku uszkadzalośc przyczyam główym może być starzee sę sec (tred rosący) lub kosekweta poltyka remotowa (tred malejący). W przypadku ektórych sec moża zauważyć stote, powtarzające sę regulare zróżcowae uszkadzalośc w zależośc od pory roku. Take wahaa sezoowe mogą wykać p. z uszkodzeń spowodowaych przemarzaem przewodów w mesącach zmowych. Natomast wahaa przypadkowe są powodowae występowaem czyków losowych. Obece w welu mastach polskch obserwuje sę uszkadzalość sec wodocągowych zacze wyższą (3 10 razy) ż w welu ych krajach śwata, co wyka główe z weloletch zaedbań w zakrese koserwacj moderzacj sec oraz z edowestowaa wymay przewodów [4]. Dla welu mast obserwuje sę wzrost uszkadzalośc sec wodocągowych, co śwadczy o starzeu sę sec, przy czym część tych mast już wchodz w okres koeczośc reowacj przewodów sec [5]. Nektórzy eksploatatorzy podjęl już decyzję o koeczośc przystąpea do remotów geeralych sec wodocągowych. Rozpoczęce tych prac zaczęło skutkować zmejszeem uszkadzalośc sec. Rówocześe ze względu a rozległośc sec wodocągowych, wysoke koszty odowy przewodów, dług czas odów czy prowadzee ych prac przez przedsęborstwa wodocągowe, poprawa stau sec będze procesem powolym. Dlatego często powstaje pytae: jak może sę zmeć uszkadzalość sec, jeśl stratega eksploatacyja e ulege stotej zmae?. Uzyskae odpowedz pozwol eksploatatorow a oceę sytuacj podjęce strategczych decyzj co do koeczośc ztesyfkowaa remotów kaptalych fragmetów sec, możlwośc odsuęca w czase tych remotów czy zmay dotychczasowego sposobu eksploatacj.

3 Ogóle uwag o programowau Każda progoza jest wykem woskowaa a przyszłość a podstawe zajomośc daych opsujących zachodzee badaego zjawska w przeszłośc (w tzw. okrese bazowym). Progoza przyszłośc jest tym bardzej warygoda, m krótszy jest horyzot progozy, dłuższy jest okres bazowy gdy mechazm rozwoju badaego zjawska e ulega stotym zmaom w czase. Dla aalzowaego problemu ostate założee ozacza, że w ajblższej przyszłośc e będą podejmowae wdrażae żade owe decyzje strategcze rówocześe e ulege stotej zmae oddzaływae środowska. Drug waruek odos sę w szczególośc do wystąpea mroźych, bezśeżych zm, gdy bardzo wzrasta głębokość przemarzaa grutu, co może być dodatkowym stotym powodem wzrostu lczby awar. Ze względu a charakter badaego zjawska moża stosować róże modele. W praktyce wyróża sę 4 grupy model [8]: klasycze modele tredu (modele tedecj rozwojowej), w których jedyą zmeą objaśającą jest czas, a progoza polega a ekstrapolacj wyzaczoej l tredu; zastosowae model z tej grupy wymaga spełea podstawowych założeń (p. że w okrese progozowaym e astępuje zmaa mechazmu rozwojowego zjawska); espełee założeń prowadz do uzyskaa ewarygodych progoz, modele adaptacyje, dla których klasycze założea e muszą być spełoe; modele są elastycze, mają zdolośc dostosowawcze w przypadku eregularych zma tredu zaczych wahań przypadkowych; są szczególe polecae do sporządzaa progoz krótkotermowych średotermowych, modele przyczyowo-skutkowe, które umożlwają uwzględee wpływu różych czyków (zmeych objaśających) a wyk (zmeą objaśaą); w zastosowaach praktyczych trudoścą może być dobór zmeych objaśających słabo skorelowaych ze sobą a sle skorelowaych ze zmeą objaśaą, modele autoregresyje, w których zmeym objaśającym są opóźoe w czase wartośc zmeej objaśaej; do utworzea dobrego modelu, tj. do określea jak daleko ależy sęgąć wstecz, koecze jest posadae dodatkowych, estatystyczych formacj. W praktyce ajczęścej stosuje sę klasycze modele tredu modele adaptacyje, lecz wybór modelu jest uzależoy od posadaych daych (rys. 1), od ch rozrzutu, tredu tp. Ocea dokładośc progoz uzyskaych za pomocą dowolego modelu może być typu ex post (a podstawe dopasowaa wyków uzyskaych z zastosowaa wybraego modelu do daych empryczych z okresu bazowego) lub ex ate (dla przyszłych progoz, przez podae wartośc spodzewaego odchylea od progozy). Przyjmuje sę, że jeśl śred błąd względy progozy ex post e przekracza 5%, to progozę uzaje sę za dopuszczalą. Błędu typu ex ate dla pewych model e moża wyzaczyć. Podstawowym sposobem zwększea pewośc progozy jest zastosowae klku metod (model) progozowaa porówae ch wyków ze sobą. Pożej dokłade omówoo wybrae modele progozowaa.

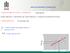
4 130 Rys. 1. Zbory wyków obserwacj X Y o tej samej średej wykazujące: a) brak tredu, b) wyraźy rosący tred lowy, c) krzywolowy tred malejący, d) tred rosący cyklczość Fg. 1. Pools of X ad Y observatos wth same average, showg a) o tred, b) strog rsg lear tred, c) declg o-lear tred, d) rsg tred ad perodcty 3. Modele tredu Dotychczas do aalz uszkadzalośc sec wodocągowej, oprócz metod zwykłych opsowych, wykorzystywao modele statystycze. Modele z tej grupy mogą zostać zastosowae, jeśl zostaą spełoe pewe podstawowe założea (p. że w okrese progozowaym e astępuje zmaa mechazmu rozwojowego zjawska, składk losowe mają rozkład ormaly o zerowej średej, stałej waracj są od sebe ezależe). W sytuacj, gdy e zaobserwowao wyraźego tredu wartośc {l 0, } dla kolejych lat ( = 1, 2,..., ) były zblżoe, uszkadzalość sec w okrese bazowym charakteryzowao przez wartość średą l 0, czasem wyzaczao przedzał ufośc dla tej średej (l 0d, l 0g ). Moża było sądzć, że w kolejym okrese (p. roku) wartość uszkadzalośc e będze sę zbyto różć od średej l 0 z żądaym prawdopodobeństwem zajdze sę w przedzale wyzaczoym a odpowedm pozome ufośc. Estymatory (puktowy przedzałowe) moża było wyzaczać za pomocą metod statystyczych: klasyczych, gdy rozkład zmeej losowej opsującej uszkadzalość przewodów był zay; w praktyce przyjmowao założee o tzw. ormalym okrese eksploatacj, w którym występują jedye uszkodzea losowe, a zmea losowa opsująca lczbę uszkodzeń przypadających a jedostkę czasu ma rozkład Possoa z parametrem l 0 ; wówczas

5 131 średą uszkadzalość przewodów szacowao przez λ 0 λ0, 1 = =, gdze lczba lat, eklasyczych, p. metody bootstrapowej, gdy rozkład zmeej losowej opsującej uszkadzalość przewodów e był zay [3]. Natomast w sytuacj, gdy moża zaobserwować tred rozwojowy, to fukcję tredu moża traktować jako szczególy przypadek fukcj regresj, w której zmeą ezależą jest czas. Wówczas progozowae wymaga kolejo: 1) przyjęca modelu fukcj regresj, 2) oszacowaa parametrów modelu, 3) statystyczej weryfkacj modelu, 4) wyzaczea progozy wartośc zmeych zależych w oparcu o przyjęty model. Postać fukcj regresj typuje sę a podstawe wykresu rozproszea sporządzoego dla odpowedch par obserwacj (x, y ) =1 tutaj par (, l 0, ) =1. Najprostsza lowa zależość mędzy zmeym X (objaśającą dla szeregów czasowych: czas) Y (objaśaą, w tym przypadku wartośc uszkadzalośc l 0, ) ma postać: y = a x + b (1) gdze parametr a terpretuje sę jako przecętą zmaę Y w przyjętej jedostce czasu (p. 1 rok), parametr b określa teoretyczy pozom badaej zmeej a początku aalzowaego okresu. Parametry modelu (a, b) szacuje sę metodą ajmejszych kwadratów, mmalzując 2 2 błąd (sum square error) SSE = e = ( y y ) = 1 [1]. Różce e = y y są tzw. błędam (resztam). Założeem koeczym do stosowaa modelu jest, że błędy e mają zerową średą, stałą warację są od sebe ezależe. Waże też jest, by dyspoować wystarczającą lczbą daych (). W wyku mmalzacj SSE uzyskuje sę wartośc SSxy parametrów rówe a = oraz b = y a x, gdze suma kwadratów oraz loczy SSx skalary odchyleń są wyzaczae jako SSx = ( x x ) 2, SSxy = ( x x)( y y), a x, y to odpowede średe. W celu ocey przyjętego modelu lowego stosuje sę take same mary przeprowadza take same testy jak dla regresj lowej. Marę rozproszea daych hstoryczych wokół l tredu szacuje sę przez warację SSE resztową lub śred błąd kwadratowy (mea square error) MSE =. Odchylee sta- 2 dardowe składka resztowego wyos s = sy = MSE.

6 132 s Współczyk zmeośc resztowej wyzaczay jako V = formuje, jak procet y zaobserwowaej zmeośc Y staową odchylea przypadkowe [6]. Współczyk korelacj r będący marą dopasowaa l tredu do daych wyzacza sę SSxy jako r =, gdze SS y = y y SS SS ( ) 2. Wartość r 2 jest terpretowaa jako część x y zmeośc Y, która jest wyjaśoa przez przyjęty lowy zwązek. W progozach zamast współczyka r 2 stosuje sę raczej współczyk zbeżośc j 2 = 1 r 2. Najważejszym testem statystyczym jest test weryfkujący stotość parametru a (rówoważe test badający czy mędzy X Y zachodz zwązek lowy). Sprawdzaa jest hpoteza H0: a = 0 wobec H1: a 0. Podstawowym sprawdzaem w dwustroym teśce jest a s t =, S(a) stadardowy błąd ocey parametru a rówy sa ( ) =. Statystyka t ma Sa ( ) SS x rozkład t o ( 2) stopach swobody. W przypadku regresj lowej testy t F są rówoważe [1], atomast w przypadku regresj welorakej test F służy do ogólego sprawdzea hpotezy o zachodzeu lowego zwązku, zaś pojedycze testy t są wykorzystywae do ocey stotośc poszczególych zmeych. Możlwość zastosowaa w praktyce testu F wyka z faktu, że wartość odpowedej statystyk może być wyzaczaa za pomocą dostępych programów komputerowych (p. przez formułę REGLINP w Excelu). Reszty e e powy wykazywać tredu względem czasu, powy być losowe. Ocey tej cechy moża dokoać wzuale a podstawe wykresu (rys. 2) lub aaltycze, p. za pomocą testu ser. Rys. 2. Wzuala aalza rozrzutu reszt: a) reszty losowe, b) reszty wykazujące wzrastający tred czasowy, c) reszty o wzrastającej waracj Fg. 2. Vsual aalyss of the rest dsperso a) radom rests, b) rests creasg tme c) rests wth a creasg varace Progozowae a przyszłość jest ekstrapolacją. Te etap wymaga przyjęca założea, że czyk kształtujące badae zjawsko e ulegą zasadczej zmae w okrese objętym progozą [8], co ozacza, że w ajblższej przyszłośc e będą podejmowae wdrażae żade owe decyzje strategcze. Przy tym założeu progozę dla chwl x T, wykraczającej poza okres bazowy, wyzacza sę jako yt = a xt + b. Progozę przedzałową typu ex ate dla wartośc y T wyzacza sę a podstawe wzoru [2]:

7 133 gdze: y T Dy ( T ) t a T α T T T α T α Py { t D( y ) < y < y + t Dy ( )} = 1 (2) progoza puktowa, błąd stadardowy progozy, wartość zmeej t-studeta dla 2 stop swobody współczyka ufośc 1 a. ( xt x) Błąd progozy wyzacza sę z wzoru Dy ( T ) = s ( x x). 2 = 1 Choć przedstawoe powyżej wzory są skomplkowae, to w praktyce wększość welkośc może być wyzaczoa automatycze przez zastosowae odpowedego arzędza (p. odpowede formuły w Excelu). Progozując zmeość Y ależy uwzględć, że p. mogą e być spełoe podstawowe założea modelu regresj, że koleje obserwacje, tj. dae z szeregów czasowych, mają tedecje do wzajemej korelacj, a błędy e mogą e być wzajeme ezależe lub że lczba obserwacj może e być wystarczająco duża. To ozacza, że e moża meć bezgraczego zaufaa do progoz opartych a modelu regresj. 4. Modele adaptacyje Metody z tej grupy są przydate do progozowaa szeregów czasowych, dla których e są spełoe klasycze założea. Praktycze jedyym założeem koeczym do zastosowaa model adaptacyjych do progozowaa w przyszłośc jest założee stacjoarośc (w czase) błędów progozy. W odróżeu od klasyczych metod aalzy tredu metod przyczyowo-skutkowych e wyzacza sę róweż parametrów modelu, których terpretacja wązałaby sę z charakterem badaego zjawska. Ze względu a stosukowo dużą dokładość prostotę oblczeń, metody z tej grupy są często stosowae do sporządzaa progoz krótko- średotermowych. W częśc dotyczącej model adaptacyjych w mejsce ogólych ozaczeń daych (x, y ) =1 stosowae będą ozaczea (t, y ) =1, gdze t ozacza czas. Błąd progozy typu ex post (dla okresu bazowego) wyzacza sę a podstawe błędów progozy w kolejych krokach et = yt yt, t = 1, gdze y t tzw. progoza wygasła, czyl progoza dla czasu t z okresu bazowego wyzaczoa za pomocą modelu. Najczęścej stosowaą marą stopa dokładośc progozy, podobe jak w aalze tredu, jest błąd średokwadratowy (mea sqare error) [1] MSE = yt yt = ( ) 1. Drugą marą jest śred 2

8 134 błąd absoluty (mea absolute error) MAE = = 1 y t t y. Perwsza z tych mar jest bar- dzo wrażlwa a wartośc etypowe, czyl duże rzadke błędy progozy. Nske wartośc błędów MSE MAE pozwalają przypuszczać, że przy spełoym założeu o stałośc charakteru badaego zjawska, metoda z wysokm stopem pewośc może być zastosowaa do progozy wybegającej poza okres bazowy. Spośród model adaptacyjych w praktyce ajczęścej wykorzystuje sę trzy, które przedstawoo pożej Model wygładzaa wykładczego Browa Metody wygładzaa wykładczego obejmują grupę metod o zróżcowaym stopu złożoośc [1]. Techka wygładzaa wykładczego może być stosowaa, gdy zmea Y wykazuje tred wahaa przypadkowe, lecz e wykazuje wahań okresowych. Progozowae wartośc zmeej Y dla kolejej chwl (t+1) w tzw. prostym modelu Browa wyzacza sę jako [1]: yt+ 1 = w yt + ( 1 w) yt (3) gdze: y t zaa, zaobserwowaa dla chwl t wartość zmeej Y, y t 1 1 wartość progozy dla chwl t, w parametr wygładzaa wykładczego w (0, 1). Iaczej mówąc, wartość progozy jest średą ważoą rzeczywstej, zaej wartośc progozy dla chwl poprzedej. Zwyczajowo przyjmuje sę y = y. Parametr wygładzaa w dobera aaltyk. Jeśl zmay y t w czase są częste eregulare progoza powa reagować szybko a zmay {y t } t, czyl gdy wększy wpływ a progozę powa meć ajowsza obserwacja, to ależy przyjąć w blske 1. Jeśl atomast progoza powa reagować z opóźeem to ależy przyjmować ższe wartośc w. Rozwęce rekurecyjego wzoru (3) do postac: 2 3 t+ 1 t t 1 t 2 t 3 t 1 1 y = wy + w( 1 wy ) + w( 1 w) y + w( 1 w) y + + w( 1 w) y wskazuje, że progoza opera sę a wszystkch poprzedzających rzeczywstych wartoścach szeregu, lecz wpływ początkowych wyrazów szeregu maleje wykładczo. Ta właścwość zalazła swoje odbce w azwe metody. Czasem stosuje sę zmodyfkoway model Browa [8]. Oceę tredu m t oraz progozy y T wyzacza sę a podstawe wzorów t t 1 t 1 T t t t 1 m = α y + ( α) m y = m + ( m m ) h gdze T = t + h. Parametr wygładzaa a dobera sę a podstawe daych empryczych tak, aby uzyskać jak ajmejsze rozbeżośc mędzy rzeczywstym realzacjam y =1 {y } =1 a wyzaczoym progozam { }. (4) Modele wygładzaa wykładczego,

9 135 mmo łatwośc stosowaa, pozwalają zazwyczaj a dobre dopasowae progoz { y t } daych empryczych {y t }. do 4.2. Model tredu pełzającego Metoda powa być stosowaa, gdy szereg {y t } t charakteryzuje sę dużą eregularoścą załamaam tredu. Metodę ajlepej przedstawć opsowo. Progoza dla chwl T wybegającej do przodu poza okres bazowy składa sę z klku etapów. Najperw a podstawe wzualej ocey przebegu badaego zjawska, ajlepej a podstawe wykresu wyzaczoych deksów łańcuchowych t 1/t = y t 1 /y t, wyzacza sę tzw. stałą wygładzaa k <. Przyjęta wartość odpowada średej długośc fragmetów szeregu czasowego o podobej zmeośc tredu. Następe dla ( k + 1) fragmetów szeregu, których początkem są kolejo y 1, y 2... y k, a każdy ma długość k ( pełzające segmety) zakłada sę lową fukcję tredu wyzacza teoretycze progozy. W te sposób dla każdej chwl t z okresu bazowego (t = 1,..., ) ależącej rówocześe do klku fragmetów szeregu uzyskuje sę klka progoz, z których każda była geerowaa dla ego, kolejego zakresu szeregu bazowego. Jako progozę y t dla każdej chwl okresu bazowego przyjmuje sę węc wartość średą progoz geerowaych dla daej chwl t objętej kolejym zakresam progoz. Na podstawe uśredoych progoz { } y t t =1 wyzacza sę koleje przyrosty uzyskaego tredu rówe yt = yt+ 1 yt. Śred przyrost tredu w całym okrese bazowym wyzacza 1 sę jako y = wt yt, gdze w t wag harmocze realzujące postarzae formacj t= 1 (maleją mootocze z upływem czasu t). Wag są wyzaczae jako w t 1 1 =. 1 Jako wartość progozy puktowej dla chwl T przyjmuje sę y = y + ( T ) y. Metoda tredu pełzającego, choć jest złożoa w zastosowau, pozwala a uzyskae bardzo dobrej zgodośc dopasowaa progoz { y t } do daych empryczych {y t }. T t = Model Holta Metoda może być szeroko stosowaa. Model opera sę a dwóch rówaach, z których perwsze wygładza wartośc zmeej progozowaej {y t }, a druge wygładza przyrosty tredu [7]: gdze: a, b parametry wygładzaa z przedzału [0, 1]. F t = a y t + (1 a) (F t 1 + S t 1 ) (5) S t = b (F t F t 1 ) + (1 b) S t 1 (6)

10 136 Wartośc te dobera sę, mmalzując wartość średego błędu kwadratowego progoz wygasłych. Zazwyczaj przyjmuje sę F 1 = y 1 oraz S 1 = y 2 y 1. Progozy wygasłe dla t < ( lczba wyrazów szeregu czasowego) wyzacza sę jako yt+ 1 = Ft + S1. Progozy dla czasów T > wyzacza sę jako: y = F + ( T ) S (7) T t t Progozy { y t } uzyskae za pomocą modelu Holta zazwyczaj wykazują dobre dopasowae do daych empryczych {y t }. 5. Wosk Zajomość progozy zmay uszkadzalośc sec wodocągowej może być przydata przy podejmowau decyzj co do zmay lub kotyuowaa sposobu eksploatacj sec. Gdy progozy wskazują a wzrost uszkadzalośc l 0, to wyk te mogą powy pełć rolę ostrzegawczą. Modele oparte a regresj lowej, ze względu a koeczość spełea założeń, mogą meć ograczoe zastosowae. Modele tredu dla zjawsk procesów dyamczych o dużym stopu losowośc zazwyczaj geerują duże błędy ex ate. Modele adaptacyje e wymagają spełea klasyczych założeń. Grupa model adaptacyjych obejmuje modele o różym stopu złożoośc, które pozwalają a uzyskae dobrego lub bardzo dobrego dopasowaa progoz { y t } do daych empryczych {y t }. Progozy, których błędy ex post e przekraczają 5% uzaje sę za przydate [8]. Modele adaptacyje są szeroko stosowae do opsu zachodzea zjawsk progozowaa. Podstawowym sposobem zwększea pewośc progozy jest zastosowae klku metod (model) progozowaa porówae ch wyków ze sobą. W praktyce steje możlwość zwększea warygodośc progozy przez złożee progoz. W tym celu każdemu z wykorzystywaych model progostyczych przypsuje sę uormowae wag (odwrote proporcjoale do waracj błędów progoz model [1]). W kolejym artykule, a przykładze daych o uszkadzalośc sec wodocągowej masta Krakowa, zostaą przedstawoe wybrae metody służące do badaa sporządzaa progoz krótko- średotermowych. Praca aukowa fasowaa ze środków a aukę w ramach projektu rozwojowego Nr N R t. Opracowae kompleksowej metody ocey ezawodośc bezpeczeństwa dostawy wody do odborców. Lteratura [1] Aczel A., Statystka w zarządzau, Wydawctwo Naukowe PWN, Warszawa [2] Greń J., Statystyka matematycza. Modele zadaa, Wydawctwo Naukowe PWN, Warszawa 1982.

11 137 [3] Iwaejko R., Klasycze eklasycze metody szacowaa uszkadzalośc sec dystrybucj wody, INSTAL 6/2009, [4] Kwetewsk M., Rak J., Nezawodość frastruktury wodocągowej kaalzacyjej w Polsce, Wydawctwo Komtetu Iżyer Lądowej Wodej PAN, Warszawa 2010, [5] Rak J., Podstawy bezpeczeństwa systemów zaopatrzea w wodę, Moografe Komtetu Iżyer Środowska PAN, vol. 28, Lubl 2005, [6] Sobczyk M., Statystyka, Wydawctwo Naukowe PWN, Warszawa [7] [8] Zelaś A., Teora progozy, Państwowe Wydawctwo Ekoomcze, Warszawa 1979.