Przejścia optyczne w cząsteczkach
|
|
|
- Martyna Szewczyk
- 7 lat temu
- Przeglądów:
Transkrypt
1 Przejścia optyczne w cząsteczkach Jacek.Szczytko@fuw.edu.pl Podziękowania za pomoc w przygotowaniu zajęć: Prof. dr hab. Paweł Kowalczyk Prof. dr hab. Dariusz Wasik Uniwersytet Warszawski 011
2 Cząsteczki Przybliżenie Borna Oppenheimera Max Born ( ) Jacob R. Oppenheimer ( )
3 Powtórzenie Przybliżenia Cząsteczki n n n [ Tˆ + E ( R)] χ ( R) = Eχ ( R) N el Ostatecznie więc ruch jąder odbywa się w potencjale wyznaczonym przez energię stanu elektronowego i dlatego mówi się zwykle, że zależność E eln (R) wyznacza powierzchnię energii potencjalnej. Przybliżenie Borna-Oppenheimera nie jest spełnione gdy powierzchnie energii potencjalnej dwóch stanów elektronowych zbliżają się.
4 Powtórzenie Przybliżenia Cząsteczki n n n [ Tˆ + E ( R)] χ ( R) = Eχ ( R) N Energia kinetyczna drgań (oscylacji) i rotacji (obrotów) separują się, ponieważ zakładamy małe drgania i powolne obroty. [ Tˆ + Tˆ + E ( R)] χ ( R) = E χ( R) osc rot el Operatory działają na różne współrzędne: możemy rozdzielić zmienne. E E N E E el el osc el χ ( R ) = χ ( R) χ ( θ, ϕ) Ψ = = = Ψ χ + osc osc E + E χ osc rot rot + N rot E rot
5 Przykład: cząsteczka HF Cząsteczki F: (1s) (s) (p) 5 1. Zbliżone wartości energii mają orbital p dla fluoru oraz 1s dla wodoru.. Tylko orbital p z daje różną całkę nakrywania z orbitalem 1s (orbital wiążący σ). 3. elektrony fluoru z orbitalu p x i elektrony z orbitalu p y nie uczestniczą w wiązaniu cząsteczki HF i są nazywane wolnymi parami elektronowymi. 4. Podobnie 1s i s fluoru nie tworzą wiązania z elektronem 1s wodoru ze względu na dużą różnicę energii. 5. Stan podstawowy: 1 Σ + P. Kowalczyk
6 Cząsteczki Hybrydyzacja i całki przykrycia P. Kowalczyk
7 Cząsteczki Hybrydyzacja sp i całki przykrycia Kąty między wiązaniami wodoru wynoszą 180. Hybrydyzacja sp Wodorek Berylu BeH h h = s 1 1 = s + p p x x
8 Cząsteczki Hybrydyzacja sp i całki przykrycia P. Kowalczyk Kąty między wiązaniami wodoru wynoszą 10. Hybrydyzacja sp z z x z x p s h p p s h p p s h = + = = Etylen C H 4
9 Cząsteczki Hybrydyzacja sp 3 i całki przykrycia P. Kowalczyk Kąty między wiązaniami wodoru wynoszą 109,5. Hybrydyzacja sp 3 ) ( 1 ) ( 1 ) ( 1 ) ( z y x z y x z y x z y x p p p s h p p p s h p p p s h p p p s h + = + = + = = Metan CH 4
10 Cząsteczki Hybrydyzacja i całki przykrycia Kąty między wiązaniami wodoru wynoszą 109,5. Hybrydyzacja sp 3 ) ( 1 ) ( 1 ) ( 1 ) ( z y x z y x z y x z y x p p p s h p p p s h p p p s h p p p s h + = + = + = = Metan CH 4 Amoniak NH 3 Woda H O
11 Cząsteczki Hybrydyzacja i całki przykrycia Kąty między wiązaniami wodoru wynoszą 109,5. Hybrydyzacja sp 3 ) ( 1 ) ( 1 ) ( 1 ) ( z y x z y x z y x z y x p p p s h p p p s h p p p s h p p p s h + = + = + = = CuO
12 Cząsteczki Hybrydyzacja i całki przykrycia Węgiel
13 Cząsteczki Hybrydyzacja i całki przykrycia
14 Cząsteczki Cząsteczka benzenu Wiązania σ (sp ) są zlokalizowane i tworzą sztywny szkielet, natomiast elektrony tworzące wiązania π są zdelokalizowane. Ψ E k k 1 6 (πi / 6) kn = e p 6 n= 1 = α + β cos(πk / z, n 6) k = 0, ±1, ±, 3 Benzen Funkcje falowe tej postaci pokazują, że sześć orbitali atomowych p z daje równoprawny wkład do wszystkich orbitali molekularnych. Funkcje te odpowiadają falom biegnącym wokół pierścienia atomów węgla, w przeciwnych kierunkach dla dodatnich i ujemnych wartości k
15 Wiązanie rezonansowe sp Friedrich August Kekule Rys. Wikipedia
16
17 dr hab. Andrzej Wysmołek dr inż. Włodzimierz Strupiński,
18 dr hab. Andrzej Wysmołek dr inż. Włodzimierz Strupiński,
19 dr Jacek Szczytko Michał Kluz Izabela Rytarowska
20 dr Jacek Szczytko Michał Kluz Izabela Rytarowska
21 dr Jacek Szczytko Michał Kluz Izabela Rytarowska
22 Nanorurki Nanorurki można sobie wyobrazić jako warstwy atomów węgla (takie jak w graficie), które zostały zrolowane. Rozróżniamy orientacje: Armchair Zig-zag Chiral Orientacja jest zdefiniowana przez wektor chiralny (n,m) c h = n a + m b J.Basak, D.Mitra, S.Sinha Carbon nanotube: the next generation sensors presentation Paweł Tomasz Pęczkowski
23 Ogród Zoologiczny nanorurek Single Wall Nanotube (Zig-Zag Type) Uprolling a Graphene (Zig-Zag Type) Single Wall Nanotube (Arm-Chair Type) Uprolling a Graphene (Arm-Chair Type) Single Wall Nanotube (Chiral Type) φ = 0.46 (n +nm+m ) 1/ / π (nm)
24 Nanomaszyny 1. Najsilniejsze u najbardziej giętkie wiązanie molekularne (wiązanie kowalencyjne C-C). Moduł Younga ponad 1TPa (w porównaniu do 70 GPa dla Al, 700 GPa dla włókien węglowych) 3. Odporność na rozciąganie 45 GPa (najbardziej odporna stal pęka przy GPa) 4. Stosunek wytrzymałości do wagi 500 większy niż Al, podobnie dla stali i tytanu. Jeden rząd wielkości więcej niż dla grafitu / żywic epoxy 5. Maksymalne naprężenia ok. 10% większe niż dla znanych materiałów 6. Przewodnictwo cieplne ok W/mK wzdłuż osi (i małe w poprzek) 7. Przewodność elektryczna większa niż Cu!
25 Nanomaszyny Single twist
26 Nanomaszyny Single bend
27 Nanomaszyny Single compress
28 Nanomaszyny Multi twist
29 Nanomaszyny Multi bend
30 Nanomaszyny Multi compress
31 Winda do nieba
32 Winda do nieba
33 Winda do nieba
34 Fullereny Buckminster Fuller pour un exposition en 1967 à Montréal
35
36 Roztwory w toluenie
37
38 C 60 kryształy fcc
39 C 60 kryształy złożone
40 Paweł Tomasz Pęczkowski C 60 kryształy złożone Nadprzewodnictwo K 3 C 60 X.D. Xiang, J.G. Hou, et al. Nature 361, 54, 1993 Zależność oporu właściwego K 3 C 60 od temperatury Zależność Tc od stałej sieci
41 Nanomaszyny Benzen + C 60 Za wolno Za szybko W sam raz
42 Benzen + CN Nanomaszyny Za wolno Gear Rotation in a Vacuum 00 rot/ns W sam raz Powered Sharf
43 Nanomaszyny Gear Rotation at RT 50/70/100 rot/ns Too fast > 100 rot/ns Gear Rotation at RT 50 rot/ns
44 Nanomaszyny Large Gear Drives Small Gear Gear and Shaft Operation Powered Sharf Powered Gear
45 Nanomaszyny Rotation of Gears with Two Off-line Rows of Teeth Zbyt szybko Long Gear Rotation at Room Temperature Startup Rotating
46 plumber s nightmare
47 Szwarcyty
48
49 Cząsteczki Cząsteczka benzenu Wiązania σ (sp ) są zlokalizowane i tworzą sztywny szkielet, natomiast elektrony tworzące wiązania π są zdelokalizowane. Ψ E k k 1 6 (πi / 6) kn = e p 6 n= 1 = α + β cos(πk / z, n 6) k = 0, ±1, ±, 3 Benzen Funkcje falowe tej postaci pokazują, że sześć orbitali atomowych p z daje równoprawny wkład do wszystkich orbitali molekularnych. Funkcje te odpowiadają falom biegnącym wokół pierścienia atomów węgla, w przeciwnych kierunkach dla dodatnich i ujemnych wartości k
50 Cząsteczki Cząsteczki polimerów Wiązania σ (sp ) są zlokalizowane i tworzą sztywny szkielet, natomiast elektrony tworzące wiązania π są zdelokalizowane. N Ψ E k k 1 (πi / N ) = e N n= 1 = α + β cos(πk kn / p z, n N) Polimery W polimerach sekwencje C=C-C=C-C=C- to także wiązania rezonansowe elektrony są zdelokalizowane. P. Kowalczyk
51 State-of-the-Art: Electronic Circuits Kees Hummelen - University of Groningen From macroscopic to nanoscale electronics copper ( 1 μm) organic molecules ( nm) wire: X Y CH diode: CH Y X Source transistor: (FET) Gate CH C H 5 C H 5 C H 5 barrier: - CH - - CH CH terminal complex logic elements 3- and 4-terminal junction Drain Jaszowiec
52 Nanoprzełączniki
53 Nanoprzełączniki
54 State-of-the-Art: Electronic Circuits Kees Hummelen - University of Groningen From macroscopic to nanoscale electronics copper ( 1 μm) organic molecules ( nm) wire: X Y CH diode: CH Y X Source transistor: (FET) Gate CH C H 5 C H 5 C H 5 barrier: - CH - - CH CH terminal complex logic elements 3- and 4-terminal junction Drain Jaszowiec
55 State-of-the-Art: Electronic Circuits Kees Hummelen - University of Groningen 3-terminal junctions: Tour wires [1] M.A. Ratner et. al. [] failure to measure transport when built on meta-positions 4-terminal: junctions no examples logic elements, AND-gate: C H 5 * * * C H 5 C H 5 A CN CH 3 O C CN O CH 3 B CN CN CH 3 O O CH 3 7 C. Joachim et. al. [3] molecules remain based on 3-branch molecules [1] J.Am.Chem.Soc., 1998, 10, [] Ann. NY. Acad. Sci., 00, 960, 153. V+ [3] Chem. Phys. Lett., 003, 367, 66.
56 Nano i bio (DNA)
57 Nano i bio (DNA)
58 Nano i bio (DNA)
59 Nano i bio (DNA)
60 Nano i bio (DNA)
61 Od cząsteczki do ciała stałego P. Atkins
62 Czy dwa półprzewodniki dadzą cały przewodnik? Co to jest izolator, półprzewodnik, przewodnik? J. Ginter Mała odległość między atomami pasma Duża odległość między atomami poziomy W. Ibach Dr hab. Darek Wasik
63 Czy dwa półprzewodniki dadzą cały przewodnik? Co to jest izolator, półprzewodnik, przewodnik? E g J. Ginter Mała odległość między atomami pasma Duża odległość między atomami poziomy Przerwa energetyczna Energy gap
64 Od cząsteczki do ciała stałego P. Atkins
65 Cząsteczki Przybliżenie Borna Oppenheimera Max Born ( ) Jacob R. Oppenheimer ( )
66 Powtórzenie Przybliżenia Cząsteczki n n n [ Tˆ + E ( R)] χ ( R) = Eχ ( R) N el Ostatecznie więc ruch jąder odbywa się w potencjale wyznaczonym przez energię stanu elektronowego i dlatego mówi się zwykle, że zależność E eln (R) wyznacza powierzchnię energii potencjalnej. Przybliżenie Borna-Oppenheimera nie jest spełnione gdy powierzchnie energii potencjalnej dwóch stanów elektronowych zbliżają się.
67 Powtórzenie Przybliżenia Cząsteczki n n n [ Tˆ + E ( R)] χ ( R) = Eχ ( R) N Energia kinetyczna drgań (oscylacji) i rotacji (obrotów) separują się, ponieważ zakładamy małe drgania i powolne obroty. [ Tˆ + Tˆ + E ( R)] χ ( R) = E χ( R) osc rot el Operatory działają na różne współrzędne: możemy rozdzielić zmienne. E E N E E el el osc el χ ( R ) = χ ( R) χ ( θ, ϕ) Ψ = = = Ψ χ + osc osc E + E χ osc rot rot + N rot E rot
68 Cząsteczki Przybliżenia Cząsteczka dwuatomowa w układzie środka masy: Operatory działają na różne współrzędne, możemy rozdzielić zmienne. ( ) ( ) ( ) R E R R E n n n el R χ χ µ = + ( ) ( ) R E R R E R L R R R R n n n el χ χ µ µ = + + ) ( ˆ ( ) ( ) ( ) ϕ θ χ χ χ, 1 n rot n osc n R R R = n rot n rot n osc n osc n el n osc L E R R E dr d λχ χ χ χ µ λ χ µ = = + + ˆ ) ( Radialne Kątowe
69 Rotacja Widma rotacyjne Cząsteczka dwuatomowa w układzie środka masy: L ˆ n χ χ = λχ rot n rot n rot n = χ ( θ, ϕ) = Y ( θ, ϕ) J=0, 1,... M = -J,...,+J rot JM Operatory działają na różne współrzędne, możemy rozdzielić zmienne. λ = E J rot = J ( J + 1) J ( J + 1) µ R = J ( J I + 1) I moment bezwładności jąder względem osi przechodzącej przez środek masy i prostopadłej do osi cząsteczki
70 Widma rotacyjne Przybliżenie sztywnego rotatora Stała rotacyjna B = E J rot µ R e Kolejne poziomy energetyczne = BJ ( J + 1) Energia 4B 30B J = 6 J = 5 E J = B[ J ( J E J rot + 1) E ( J J 1 rot = 1) J ] = BJ 0B J = 4 0,1-10 cm -1 1B 6B B 0 J = 3 J = J = 1 J = 0
71 Widma rotacyjne Przybliżenie sztywnego rotatora Przejścia optyczne: Cząsteczka musi być polarna, tj. musi mieć trwały moment dipolowy. Homojądrowe cząsteczki dwuatomowe oraz symetryczne cząsteczki liniowe, np. CO są nieaktywne. Aktywne są cząsteczki heterojądrowe oraz np. H O, OCS Reguły wyboru: ΔJ = ±1 Energia 4B 30B 0B 1B 6B B 0 J = 6 J = 5 J = 4 J = 3 J = J = 1 J = 0
72 Widma rotacyjne Przybliżenie sztywnego rotatora Przejścia optyczne: Energia 4B J = 6 30B J = 5 B 4B 6B 8B 10B 1B Energia Reguły wyboru: ΔJ = ±1 0B 1B 6B B 0 J = 4 J = 3 J = J = 1 J = 0
73 Widma rotacyjne Przybliżenie sztywnego rotatora Przejścia optyczne: Po uwzględnieniu siły odśrodkowej Energia 4B J = 6 30B J = 5 B 4B 6B 8B 10B 1B Energia Reguły wyboru: ΔJ = ±1 1 Stała Bν = B αe ν + odkształcenia J E = B J ( J + 1) D [ J ( J + 1)] rot ν odśrodkowego v 0B 1B 6B B 0 J = 4 J = 3 J = J = 1 J = 0
74 Widma rotacyjne Przybliżenie sztywnego rotatora Przejścia optyczne: Po uwzględnieniu siły odśrodkowej Cząsteczka B (mev) R 0 Å OH,341 0,97 HCl 1,3 1,7 NO 0,11 1,15 CO 0,39 1,13 B 4B 6B 8B 10B 1B Energia Reguły wyboru: ΔJ = ±1 1 Stała Bν = B αe ν + odkształcenia J E = B J ( J + 1) D [ J ( J + 1)] rot ν odśrodkowego v KBr 0,01,94
75 Obsadzenie stanów Widma rotacyjne P. Kowalczyk P. Atkins
76 Widma rotacyjne Rotacyjne widma Ramanowskie Ogólna reguła: Polaryzowalność cząsteczki musi być anizotropowa. Dla rotatorów liniowych oznacza to: ΔJ = 0, ± P. Atkins
77 Powtórzenie Stany elektronowe Opis stanów elektronowych Energia elektronowa zależy silnie od odległości między jądrami. E(R) - zwykle w postaci numerycznej. Przybliżenia potencjał Morse a Np. Lit V [ ] 1 V ( r ) α ( r r0 ) ( R) = D e e + Przybliżenia potencjał Lenarda-Jonesa 1 6 σ σ V + r r ( R) = 4ε V 0 P. Kowalczyk
78 Powtórzenie Stany elektronowe Opis stanów elektronowych Energia elektronowa zależy silnie od odległości między jądrami. E(R) - zwykle w postaci numerycznej. Przybliżenia potencjał Morse a Np. Lit V [ ] 1 V ( r ) α ( r r0 ) ( R) = D e e + Przybliżenia potencjał Lenarda-Jonesa 1 6 σ σ V + r r ( R) = 4ε V 0 Wikipedia
79 Widma oscylacyjne Energia elektronowa a rotacja cząsteczki d n J J ( + 1) + Eel ( R) + χ µ dr µ R V ef ( R) = E n el ( R) + J ( J + 1) µ R nνj osc = Eχ nνj osc KLi P. Kowalczyk Energia elektronowa zależy NIE TYLKO od odległości między jądrami, ale też od tego jak szybko cząsteczka ROTUJE.
80 Widma oscylacyjne Przybliżenie harmoniczne Oscylator harmoniczny: Rozwijamy potencjał wokół położenia równowagi ) ( 1 ) ( e n n el R R k R E ) 1 ( ) ( + = = ν ω χ ν ν ν ν e x osc E x H e N cm -1
81 Widma oscylacyjne Przybliżenie harmoniczne Rozwijamy potencjał wokół położenia równowagi E n el 1 ( R) kn( R Re Oscylator harmoniczny: ) Cząsteczka Energia hν (ev) χ E ν osc ν = N ν x = ω ( ν + e e Anharmoniczność: E ν H ν 1 ) ( x) cm -1 1 = ωe( ν + ) ωexe( ν + 1 ) C 0,04 N 0,93 O 0,196 HCl 0,357 HBr 0,316 HJ 0,491
82 Widma oscylacyjne Przybliżenie harmoniczne Poziomy energetyczne oscylacyjno-rotacyjne Energia J = 6 E = E n el + BJ ( J + 1) + ω e ν + 1 J = 5 J = 4 J = 3 J = J = 1 J = 0
83 Przybliżenie harmoniczne Poziomy energetyczne oscylacyjno-rotacyjne Widma oscylacyjne Energia J = 6 J = 5 E = E n el + BJ ( J + 1) + ω e ν + 1 J = 6 J = 5 J = 4 J = 3 J = J = 1 J = 6 J = 4 J = 3 J = 0 ν = J = 5 J = 4 J = J = 1 J = 0 ν = 1 J = 3 n E el J = J = 1 J = 0 ν = 0
84 Przybliżenie harmoniczne Poziomy energetyczne oscylacyjno-rotacyjne Reguła wyboru: Δν = ±1 Z reguły dla przejść oscylacyjno-rotacyjnych: B ν B ν Gałąź R ΔJ = J J = +1 E = ωe + Bν ' + (3Bν ' Bν ") J" + ( Bν ' Bν ") J" Gałąź Q ΔJ = 0 Widma oscylacyjne E = ωe + ( Bν ' Bν ") J" + ( Bν ' Bν ") J" Gałąź P ΔJ = J J = 1 E = ωe + ( Bν ' + Bν ") J" + ( Bν ' Bν ") J" BŁĄD! We wzorze! P. Kowalczyk
85 Przybliżenie harmoniczne Poziomy energetyczne oscylacyjno-rotacyjne Reguła wyboru: Δν = ±1 Z reguły dla przejść oscylacyjno-rotacyjnych: B ν B ν Gałąź R ΔJ = J J = +1 E = ωe + Bν ' + (3Bν ' Bν ") J" + ( Bν ' Bν ") J" Gałąź Q ΔJ = 0 Widma oscylacyjne E = ωe + ( Bν ' Bν ") J" + ( Bν ' Bν ") J" Gałąź P ΔJ = J J = 1 E = ωe + ( Bν ' + Bν ") J" + ( Bν ' Bν ") J" P. Kowalczyk
86 Przybliżenie harmoniczne Poziomy energetyczne oscylacyjno-rotacyjne E = E n el + BJ ( J + 1) + ω e ν + Widma oscylacyjne 1 Energia n+1 E el J = 6 J = 5 J = 4 J = 3 J = J = 1 J = 0 J = 6 J = 5 J = 4 J = 3 J = J = 1 J = 0 J = 6 J = 5 J = 4 J = 3 J = J = 1 ν = J = 0 ν = 1 ν = 0 J = 6 J = 5 J = 6 J = 4 n E el J = 6 J = 5 J = 4 J = 3 J = J = 1 J = 0 J = 5 J = 4 J = 3 J = J = 1 J = 0 J = 3 J = J = 1 ν = J = 0 ν = 1 ν = 0
87 Zasada Francka-Condona Ψ' M el " µ Ψ ν ( R) = = χ χ dr ν ' " M Ψ' ( r, R) µ Ψ" * el Widma elektronowe el el el χ' rot χ" ( r, R) dτ rot el dω Ponieważ jądra są znacznie cięższe od elektronów, przejścia elektronowe zachodzą znacznie szybciej, niż jądra są w stanie na nie zareagować. P. Atkins
88 Zasada Francka-Condona Widma elektronowe James Franck Edward U. Condon Widma rotacyjne związane są tylko ze zmianą ruchu obrotowego λ~ cm (mikrofale) Widma oscylacyjno-rotacyjne odpowiadają jednocześnie zmianie stanu drgań i rotacji cząsteczki λ ~ μm (podczerwień) Widma elektronowo-oscylacyjno-rotacyjne związane są ze zmianą stanu chmury elektronowej, której towarzyszy też zmiana oscylacji i rotacji λ ~ 100 nm 1 μm (zakres widzialny i nadfioletu)
89 Fluorescencja Fluorescencja i fosforesnecja Zanik natychmiastowy po wyłączeniu promieniowania wzbudzającego ( s) Przejścia niepromieniste s P. Atkins
90 Fluorescencja Fluorescencja i fosforesnecja Emisja spontaniczna, może utrzymywać się przez długi czas (od 10-4 s do godzin) P. Atkins
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 10 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2015/16
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 10 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2015/16
Zad Sprawdzić, czy dana funkcja jest funkcją własną danego operatora. Jeśli tak, znaleźć wartość własną funkcji.
 Zad. 1.1. Sprawdzić, czy dana funkcja jest funkcją własną danego operatora. Jeśli tak, znaleźć wartość własną funkcji. Zad. 1.1.a. Funkcja: ϕ = sin2x Zad. 1.1.b. Funkcja: ϕ = e x 2 2 Operator: f = d2 dx
Zad. 1.1. Sprawdzić, czy dana funkcja jest funkcją własną danego operatora. Jeśli tak, znaleźć wartość własną funkcji. Zad. 1.1.a. Funkcja: ϕ = sin2x Zad. 1.1.b. Funkcja: ϕ = e x 2 2 Operator: f = d2 dx
Model wiązania kowalencyjnego cząsteczka H 2
 Model wiązania kowalencyjnego cząsteczka H 2 + Współrzędne elektronu i protonów Orbitale wiążący i antywiążący otrzymane jako kombinacje orbitali atomowych Orbital wiążący duża gęstość ładunku między jądrami
Model wiązania kowalencyjnego cząsteczka H 2 + Współrzędne elektronu i protonów Orbitale wiążący i antywiążący otrzymane jako kombinacje orbitali atomowych Orbital wiążący duża gęstość ładunku między jądrami
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 9 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 9 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Przejścia optyczne w cząsteczkach
 -4-8 Pzejścia optycze w cząsteczkac Pzybliżeie Boa Oppeeimea acek.szczytko@fuw.edu.pl ttp://www.fuw.edu.pl/~szczytko/t ttp://www.sciececatoosplus.com/ Podziękowaia za pomoc w pzygotowaiu zajęć: Pof. d
-4-8 Pzejścia optycze w cząsteczkac Pzybliżeie Boa Oppeeimea acek.szczytko@fuw.edu.pl ttp://www.fuw.edu.pl/~szczytko/t ttp://www.sciececatoosplus.com/ Podziękowaia za pomoc w pzygotowaiu zajęć: Pof. d
że w wyniku pomiaru zmiennej dynamicznej A, której odpowiada operator αˆ otrzymana zostanie wartość 2.41?
 TEST. Ortogonalne i znormalizowane funkcje f i f są funkcjami własnymi operatora αˆ, przy czym: α ˆ f =. 05 f i α ˆ f =. 4f. Stan pewnej cząstki opisuje 3 znormalizowana funkcja falowa Ψ = f + f. Jakie
TEST. Ortogonalne i znormalizowane funkcje f i f są funkcjami własnymi operatora αˆ, przy czym: α ˆ f =. 05 f i α ˆ f =. 4f. Stan pewnej cząstki opisuje 3 znormalizowana funkcja falowa Ψ = f + f. Jakie
Wykład 5 Widmo rotacyjne dwuatomowego rotatora sztywnego
 Wykład 5 Widmo rotacyjne dwuatomowego rotatora sztywnego W5. Energia molekuł Przemieszczanie się całych molekuł w przestrzeni - Ruch translacyjny - Odbywa się w fazie gazowej i ciekłej, w fazie stałej
Wykład 5 Widmo rotacyjne dwuatomowego rotatora sztywnego W5. Energia molekuł Przemieszczanie się całych molekuł w przestrzeni - Ruch translacyjny - Odbywa się w fazie gazowej i ciekłej, w fazie stałej
Diagnostyka plazmy - spektroskopia molekularna. Ewa Pawelec wykład dla pracowni specjalistycznej
 Diagnostyka plazmy - spektroskopia molekularna Ewa Pawelec wykład dla pracowni specjalistycznej Plazma Różne rodzaje plazmy: http://www.ipp.cas.cz/mi/index.html http://www.pro-fusiononline.com/welding/plasma.htm
Diagnostyka plazmy - spektroskopia molekularna Ewa Pawelec wykład dla pracowni specjalistycznej Plazma Różne rodzaje plazmy: http://www.ipp.cas.cz/mi/index.html http://www.pro-fusiononline.com/welding/plasma.htm
SPEKTROSKOPIA IR I SPEKTROSKOPIA RAMANA JAKO METODY KOMPLEMENTARNE
 SPEKTROSKOPIA IR I SPEKTROSKOPIA RAMANA JAKO METODY KOMPLEMENTARNE Promieniowanie o długości fali 2-50 μm nazywamy promieniowaniem podczerwonym. Absorpcja lub emisja promieniowania z tego zakresu jest
SPEKTROSKOPIA IR I SPEKTROSKOPIA RAMANA JAKO METODY KOMPLEMENTARNE Promieniowanie o długości fali 2-50 μm nazywamy promieniowaniem podczerwonym. Absorpcja lub emisja promieniowania z tego zakresu jest
Stany skupienia materii
 Stany skupienia materii Ciała stałe - ustalony kształt i objętość - uporządkowanie dalekiego zasięgu - oddziaływania harmoniczne Ciecze -słabo ściśliwe - uporządkowanie bliskiego zasięgu -tworzą powierzchnię
Stany skupienia materii Ciała stałe - ustalony kształt i objętość - uporządkowanie dalekiego zasięgu - oddziaływania harmoniczne Ciecze -słabo ściśliwe - uporządkowanie bliskiego zasięgu -tworzą powierzchnię
Inżynieria Biomedyczna. Wykład XII
 Inżynieria Biomedyczna Wykład XII Plan Wiązania chemiczne Teoria Lewisa Teoria orbitali molekularnych Homojądrowe cząsteczki dwuatomowe Heterojądrowe cząsteczki dwuatomowe Elektroujemność Hybrydyzacja
Inżynieria Biomedyczna Wykład XII Plan Wiązania chemiczne Teoria Lewisa Teoria orbitali molekularnych Homojądrowe cząsteczki dwuatomowe Heterojądrowe cząsteczki dwuatomowe Elektroujemność Hybrydyzacja
Cząsteczki. 1.Dlaczego atomy łącz. 2.Jak atomy łącz. 3.Co to jest wiązanie chemiczne? Jakie sąs. typy wiąza
 Cząsteczki 1.Dlaczego atomy łącz czą się w cząsteczki?.jak atomy łącz czą się w cząsteczki? 3.Co to jest wiązanie chemiczne? Co to jest rząd d wiązania? Jakie sąs typy wiąza zań? Dlaczego atomy łącz czą
Cząsteczki 1.Dlaczego atomy łącz czą się w cząsteczki?.jak atomy łącz czą się w cząsteczki? 3.Co to jest wiązanie chemiczne? Co to jest rząd d wiązania? Jakie sąs typy wiąza zań? Dlaczego atomy łącz czą
SPEKTROSKOPIA IR I SPEKTROSKOPIA RAMANA JAKO METODY KOMPLEMENTARNE
 1 SPEKTROSKOPIA IR I SPEKTROSKOPIA RAMANA JAKO METODY KOMPLEMENTARNE 2 Promieniowanie o długości fali 2-50 μm nazywamy promieniowaniem podczerwonym. Absorpcja lub emisja promieniowania z tego zakresu jest
1 SPEKTROSKOPIA IR I SPEKTROSKOPIA RAMANA JAKO METODY KOMPLEMENTARNE 2 Promieniowanie o długości fali 2-50 μm nazywamy promieniowaniem podczerwonym. Absorpcja lub emisja promieniowania z tego zakresu jest
Podstawy chemii obliczeniowej
 Podstawy chemii obliczeniowej Anna Kaczmarek Kędziera Katedra Chemii Materiałów, Adsorpcji i Katalizy Wydział Chemii UMK, Toruń Elementy chemii obliczeniowej i bioinformatyki 2015 Plan wykładu 15 godzin
Podstawy chemii obliczeniowej Anna Kaczmarek Kędziera Katedra Chemii Materiałów, Adsorpcji i Katalizy Wydział Chemii UMK, Toruń Elementy chemii obliczeniowej i bioinformatyki 2015 Plan wykładu 15 godzin
Orbitale typu σ i typu π
 Orbitale typu σ i typu π Dwa odpowiadające sobie orbitale sąsiednich atomów tworzą kombinacje: wiążącą i antywiążącą. W rezultacie mogą powstać orbitale o rozkładzie przestrzennym dwojakiego typu: σ -
Orbitale typu σ i typu π Dwa odpowiadające sobie orbitale sąsiednich atomów tworzą kombinacje: wiążącą i antywiążącą. W rezultacie mogą powstać orbitale o rozkładzie przestrzennym dwojakiego typu: σ -
Mechanika kwantowa. Jak opisać atom wodoru? Jak opisać inne cząsteczki?
 Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Elektron fala stojąca wokół jądra Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkowy
Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Elektron fala stojąca wokół jądra Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkowy
Wstęp do Optyki i Fizyki Materii Skondensowanej. Mateusz Goryca
 Wstęp do Optyki i Fizyki Materii Skondensowanej Mateusz Goryca mgoryca@fuw.edu.pl Uniwersytet Warszawski 2015 Materia skondensowana OC 6 H 13 H 13 C 6 O OC 6 H 13 H 17 C 8 O H 17 C 8 O N N Cu O O H 21
Wstęp do Optyki i Fizyki Materii Skondensowanej Mateusz Goryca mgoryca@fuw.edu.pl Uniwersytet Warszawski 2015 Materia skondensowana OC 6 H 13 H 13 C 6 O OC 6 H 13 H 17 C 8 O H 17 C 8 O N N Cu O O H 21
Wykład 5: Cząsteczki dwuatomowe
 Wykład 5: Cząsteczki dwuatomowe Wiązania jonowe i kowalencyjne Ograniczenia teorii Lewisa Orbitale cząsteczkowe Kombinacja liniowa orbitali atomowych Orbitale dwucentrowe Schematy nakładania orbitali Diagramy
Wykład 5: Cząsteczki dwuatomowe Wiązania jonowe i kowalencyjne Ograniczenia teorii Lewisa Orbitale cząsteczkowe Kombinacja liniowa orbitali atomowych Orbitale dwucentrowe Schematy nakładania orbitali Diagramy
WYKŁAD 2 Podstawy spektroskopii wibracyjnej, model oscylatora harmonicznego i anharmonicznego. Częstość oscylacji a struktura molekuły Prof. dr hab.
 WYKŁAD 2 Podstawy spektroskopii wibracyjnej, model oscylatora harmonicznego i anharmonicznego. Częstość oscylacji a struktura molekuły Prof. dr hab. Halina Abramczyk POLITECHNIKA ŁÓDZKA Wydział Chemiczny
WYKŁAD 2 Podstawy spektroskopii wibracyjnej, model oscylatora harmonicznego i anharmonicznego. Częstość oscylacji a struktura molekuły Prof. dr hab. Halina Abramczyk POLITECHNIKA ŁÓDZKA Wydział Chemiczny
1. Przesłanki doświadczalne mechaniki kwantowej.
 1 Pytania egzaminacyjne: 1. Przesłanki doświadczalne mechaniki kwantowej. 2. Efekt fotoelektryczny- interpretacja Einsteina. 3. Efekt fotoelektryczny: jak skorelowana jest liczba wybijanych elektronów
1 Pytania egzaminacyjne: 1. Przesłanki doświadczalne mechaniki kwantowej. 2. Efekt fotoelektryczny- interpretacja Einsteina. 3. Efekt fotoelektryczny: jak skorelowana jest liczba wybijanych elektronów
3. Cząsteczki i wiązania
 3. Cząsteczki i wiązania Elektrony walencyjne Wiązania jonowe i kowalencyjne Wiązanie typu σ i π Hybrydyzacja Przewidywanie kształtu cząsteczek AX n Orbitale zdelokalizowane Cząsteczki związków organicznych
3. Cząsteczki i wiązania Elektrony walencyjne Wiązania jonowe i kowalencyjne Wiązanie typu σ i π Hybrydyzacja Przewidywanie kształtu cząsteczek AX n Orbitale zdelokalizowane Cząsteczki związków organicznych
c) prawdopodobieństwo znalezienia cząstki między x=1.0 a x=1.5 jest równe
 TEST 1. Ortogonalne i znormalizowane funkcje f 1 i f są funkcjami własnymi operatora, przy czym: f 1 =1.05 f 1 i f =.41 f. Stan pewnej cząstki opisuje znormalizowana funkcja 1 3 falowa = f1 f. Jakie jest
TEST 1. Ortogonalne i znormalizowane funkcje f 1 i f są funkcjami własnymi operatora, przy czym: f 1 =1.05 f 1 i f =.41 f. Stan pewnej cząstki opisuje znormalizowana funkcja 1 3 falowa = f1 f. Jakie jest
Mechanika kwantowa. Erwin Schrödinger ( ) Werner Heisenberg
 Mechanika kwantowa Erwin Schrödinger (1887-1961) Werner Heisenberg 1901-1976 Falowe równanie ruchu (uproszczenie: przypadek jednowymiarowy) Dla fotonów Dla cząstek Równanie Schrödingera y x = 1 c y t y(
Mechanika kwantowa Erwin Schrödinger (1887-1961) Werner Heisenberg 1901-1976 Falowe równanie ruchu (uproszczenie: przypadek jednowymiarowy) Dla fotonów Dla cząstek Równanie Schrödingera y x = 1 c y t y(
SPEKTROSKOPIA MOLEKULARNA 2015/16 nazwa przedmiotu SYLABUS A. Informacje ogólne
 SPEKTROSKOPIA MOLEKULARNA 2015/16 nazwa SYLABUS A. Informacje ogólne Elementy składowe sylabusu Nazwa jednostki prowadzącej kierunek Nazwa kierunku studiów Poziom kształcenia Profil studiów Forma studiów
SPEKTROSKOPIA MOLEKULARNA 2015/16 nazwa SYLABUS A. Informacje ogólne Elementy składowe sylabusu Nazwa jednostki prowadzącej kierunek Nazwa kierunku studiów Poziom kształcenia Profil studiów Forma studiów
Właściwości kryształów
 Właściwości kryształów Związek pomiędzy właściwościami, strukturą, defektami struktury i wiązaniami chemicznymi Skład i struktura Skład materiału wpływa na wszystko, ale głównie na: właściwości fizyczne
Właściwości kryształów Związek pomiędzy właściwościami, strukturą, defektami struktury i wiązaniami chemicznymi Skład i struktura Skład materiału wpływa na wszystko, ale głównie na: właściwości fizyczne
i elektronów w czasteczkach (laboratoryjnym) operator Hamiltona dla czasteczki dwuatomowej (jadra 2M b a i b; m -masa elektronu e 2 r ij
 Notatki do wyk ladu IX Rozdzielenie ruchu jader i elektronów w czasteczkach W dowolnym uk ladzie wspó lrzednych (laboratoryjnym) operator Hamiltona dla czasteczki dwuatomowej (jadra a i b)ma postać: Ĥ
Notatki do wyk ladu IX Rozdzielenie ruchu jader i elektronów w czasteczkach W dowolnym uk ladzie wspó lrzednych (laboratoryjnym) operator Hamiltona dla czasteczki dwuatomowej (jadra a i b)ma postać: Ĥ
na dnie (lub w szczycie) pasma pasmo jest paraboliczne, ale masa wyznaczona z krzywizny niekoniecznie = m 0
 Koncepcja masy efektywnej swobodne elektrony k 1 1 E( k) E( k) =, = m m k krzywizna E(k) określa masę cząstek elektrony prawie swobodne - na dnie pasma masa jest dodatnia, ale niekoniecznie = masie swobodnego
Koncepcja masy efektywnej swobodne elektrony k 1 1 E( k) E( k) =, = m m k krzywizna E(k) określa masę cząstek elektrony prawie swobodne - na dnie pasma masa jest dodatnia, ale niekoniecznie = masie swobodnego
Zasady obsadzania poziomów
 Zasady obsadzania poziomów Model atomu Bohra Model kwantowy atomu Fala stojąca Liczby kwantowe -główna liczba kwantowa (n = 1,2,3...) kwantuje energię elektronu (numer orbity) -poboczna liczba kwantowa
Zasady obsadzania poziomów Model atomu Bohra Model kwantowy atomu Fala stojąca Liczby kwantowe -główna liczba kwantowa (n = 1,2,3...) kwantuje energię elektronu (numer orbity) -poboczna liczba kwantowa
Podczerwień bliska: cm -1 (0,7-2,5 µm) Podczerwień właściwa: cm -1 (2,5-14,3 µm) Podczerwień daleka: cm -1 (14,3-50 µm)
 SPEKTROSKOPIA W PODCZERWIENI Podczerwień bliska: 14300-4000 cm -1 (0,7-2,5 µm) Podczerwień właściwa: 4000-700 cm -1 (2,5-14,3 µm) Podczerwień daleka: 700-200 cm -1 (14,3-50 µm) WIELKOŚCI CHARAKTERYZUJĄCE
SPEKTROSKOPIA W PODCZERWIENI Podczerwień bliska: 14300-4000 cm -1 (0,7-2,5 µm) Podczerwień właściwa: 4000-700 cm -1 (2,5-14,3 µm) Podczerwień daleka: 700-200 cm -1 (14,3-50 µm) WIELKOŚCI CHARAKTERYZUJĄCE
Fizyka atomowa r. akad. 2012/2013
 r. akad. 2012/2013 wykład VII - VIII Podstawy Procesów i Konstrukcji Inżynierskich Fizyka atomowa Zakład Biofizyki 1 Spin elektronu Elektrony posiadają własny moment pędu L s. nazwany spinem. Wartość spinu
r. akad. 2012/2013 wykład VII - VIII Podstawy Procesów i Konstrukcji Inżynierskich Fizyka atomowa Zakład Biofizyki 1 Spin elektronu Elektrony posiadają własny moment pędu L s. nazwany spinem. Wartość spinu
Chemia kwantowa. Pytania egzaminacyjne. 2010/2011: 1. Przesłanki doświadczalne mechaniki kwantowej.
 1 Chemia kwantowa. Pytania egzaminacyjne. 21/211: 1. Przesłanki doświadczalne mechaniki kwantowej. 2. Efekt fotoelektryczny - interpretacja Einsteina. 3. Efekt fotoelektryczny: jak skorelowana jest licza
1 Chemia kwantowa. Pytania egzaminacyjne. 21/211: 1. Przesłanki doświadczalne mechaniki kwantowej. 2. Efekt fotoelektryczny - interpretacja Einsteina. 3. Efekt fotoelektryczny: jak skorelowana jest licza
Geometria cząsteczek wieloatomowych. Hybrydyzacja orbitali atomowych.
 Geometria cząsteczek wieloatomowych. Hybrydyzacja orbitali atomowych. Geometria cząsteczek Geometria cząsteczek decyduje zarówno o ich właściwościach fizycznych jak i chemicznych, np. temperaturze wrzenia,
Geometria cząsteczek wieloatomowych. Hybrydyzacja orbitali atomowych. Geometria cząsteczek Geometria cząsteczek decyduje zarówno o ich właściwościach fizycznych jak i chemicznych, np. temperaturze wrzenia,
ZASADY ZALICZENIA PRZEDMIOTU MBS
 ZASADY ZALICZENIA PRZEDMIOTU MBS LABORATORIUM - MBS 1. ROZWIĄZYWANIE WIDM kolokwium NMR 25 kwietnia 2016 IR 30 maja 2016 złożone 13 czerwca 2016 wtorek 6.04 13.04 20.04 11.05 18.05 1.06 8.06 coll coll
ZASADY ZALICZENIA PRZEDMIOTU MBS LABORATORIUM - MBS 1. ROZWIĄZYWANIE WIDM kolokwium NMR 25 kwietnia 2016 IR 30 maja 2016 złożone 13 czerwca 2016 wtorek 6.04 13.04 20.04 11.05 18.05 1.06 8.06 coll coll
OGÓLNE PODSTAWY SPEKTROSKOPII
 WYKŁAD 8 OGÓLNE PODSTAWY SPEKTROSKOPII E E0 sn( ωt kx) ; k π ; ω πν ; λ T ν E (m c 4 p c ) / E +, dla fotonu m 0 p c p hk Rozkład energ w stane równowag: ROZKŁAD BOLTZMANA!!!!! P(E) e E / kt N E N E/
WYKŁAD 8 OGÓLNE PODSTAWY SPEKTROSKOPII E E0 sn( ωt kx) ; k π ; ω πν ; λ T ν E (m c 4 p c ) / E +, dla fotonu m 0 p c p hk Rozkład energ w stane równowag: ROZKŁAD BOLTZMANA!!!!! P(E) e E / kt N E N E/
= a (a c-c )x(3) 1/2. Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową. Metody wytwarzania
 Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową a 1 = a (a c-c )x(3) 1/ ( 3 a, ), ( 3 a a a = a, ) wektory bazowe sieci odwrotnej definiuje się inaczej niż w 3D musi zachodzić
Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową a 1 = a (a c-c )x(3) 1/ ( 3 a, ), ( 3 a a a = a, ) wektory bazowe sieci odwrotnej definiuje się inaczej niż w 3D musi zachodzić
CZĄSTECZKA. Do opisu wiązań chemicznych stosuje się najczęściej metodę (teorię): metoda wiązań walencyjnych (VB)
 CZĄSTECZKA Stanislao Cannizzaro (1826-1910) cząstki - elementy mikroświata, termin obejmujący zarówno cząstki elementarne, jak i atomy, jony proste i złożone, cząsteczki, rodniki, cząstki koloidowe; cząsteczka
CZĄSTECZKA Stanislao Cannizzaro (1826-1910) cząstki - elementy mikroświata, termin obejmujący zarówno cząstki elementarne, jak i atomy, jony proste i złożone, cząsteczki, rodniki, cząstki koloidowe; cząsteczka
Pasmowa teoria przewodnictwa. Anna Pietnoczka
 Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Atom wodoru. Model klasyczny: nieruchome jądro +p i poruszający się wokół niego elektron e w odległości r; energia potencjalna elektronu:
 ATOM WODORU Atom wodoru Model klasyczny: nieruchome jądro +p i poruszający się wokół niego elektron e w odległości r; energia potencjalna elektronu: U = 4πε Opis kwantowy: wykorzystując zasadę odpowiedniości
ATOM WODORU Atom wodoru Model klasyczny: nieruchome jądro +p i poruszający się wokół niego elektron e w odległości r; energia potencjalna elektronu: U = 4πε Opis kwantowy: wykorzystując zasadę odpowiedniości
Oddziaływanie atomu z kwantowym polem E-M: C.D.
 Oddziaływanie atomu z kwantowym polem E-M: C.D. 1 atom jakoźródło 1 fotonu. Emisja spontaniczna wg. złotej reguły Fermiego. Absorpcja i emisja kolektywna ˆ E( x,t)=i λ Powtórzenie d 3 ω k k 2ǫ(2π) 3 e
Oddziaływanie atomu z kwantowym polem E-M: C.D. 1 atom jakoźródło 1 fotonu. Emisja spontaniczna wg. złotej reguły Fermiego. Absorpcja i emisja kolektywna ˆ E( x,t)=i λ Powtórzenie d 3 ω k k 2ǫ(2π) 3 e
Różne typy wiązań mają ta sama przyczynę: energia powstającej stabilnej cząsteczki jest mniejsza niż sumaryczna energia tworzących ją, oddalonych
 Wiązania atomowe Atomy wieloelektronowe, obsadzanie stanów elektronowych, układ poziomów energii. Przykładowe konfiguracje elektronów, gazy szlachetne, litowce, chlorowce, układ okresowy pierwiastków,
Wiązania atomowe Atomy wieloelektronowe, obsadzanie stanów elektronowych, układ poziomów energii. Przykładowe konfiguracje elektronów, gazy szlachetne, litowce, chlorowce, układ okresowy pierwiastków,
Struktura elektronowa czasteczek. przybliżenie Borna-Oppenheimera. równania Schrödingera dla elektronów przy ustalonym po lożeniu jader
 Notatki do wyk ladu VII Struktura elektronowa czasteczek przybliżenie Borna-Oppenheimera rozwiazanie równania Schrödingera dla elektronów przy ustalonym po lożeniu jader przybliżenie jednoelektronowe metoda
Notatki do wyk ladu VII Struktura elektronowa czasteczek przybliżenie Borna-Oppenheimera rozwiazanie równania Schrödingera dla elektronów przy ustalonym po lożeniu jader przybliżenie jednoelektronowe metoda
WYKŁAD 3 CZĄSTECZKI WIELOATOMOWE ZWIĄZKI WĘGLA
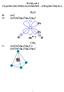 WYKŁAD 3 ZĄSTEZKI WIELOATOMOWE ZWIĄZKI WĘGLA O : (s) O: (s) (s) (p z ) (p x ) (p y ) px py s 90 o? s 4 : (s) (s) (p x ) (p y ) (s) (s) (p x ) (p y ) (p z ) s pz px py s so : (s) s s.orbital MOLEKULARNY
WYKŁAD 3 ZĄSTEZKI WIELOATOMOWE ZWIĄZKI WĘGLA O : (s) O: (s) (s) (p z ) (p x ) (p y ) px py s 90 o? s 4 : (s) (s) (p x ) (p y ) (s) (s) (p x ) (p y ) (p z ) s pz px py s so : (s) s s.orbital MOLEKULARNY
FALOWA I KWANTOWA HASŁO :. 1 F O T O N 2 Ś W I A T Ł O 3 E A I N S T E I N 4 D Ł U G O Ś C I 5 E N E R G I A 6 P L A N C K A 7 E L E K T R O N
 OPTYKA FALOWA I KWANTOWA 1 F O T O N 2 Ś W I A T Ł O 3 E A I N S T E I N 4 D Ł U G O Ś C I 5 E N E R G I A 6 P L A N C K A 7 E L E K T R O N 8 D Y F R A K C Y J N A 9 K W A N T O W A 10 M I R A Ż 11 P
OPTYKA FALOWA I KWANTOWA 1 F O T O N 2 Ś W I A T Ł O 3 E A I N S T E I N 4 D Ł U G O Ś C I 5 E N E R G I A 6 P L A N C K A 7 E L E K T R O N 8 D Y F R A K C Y J N A 9 K W A N T O W A 10 M I R A Ż 11 P
Spektroskopia charakterystycznych strat energii elektronów EELS (Electron Energy-Loss Spectroscopy)
 Spektroskopia charakterystycznych strat energii elektronów EELS (Electron Energy-Loss Spectroscopy) Oddziaływanie elektronów ze stałą, krystaliczną próbką wstecznie rozproszone elektrony elektrony pierwotne
Spektroskopia charakterystycznych strat energii elektronów EELS (Electron Energy-Loss Spectroscopy) Oddziaływanie elektronów ze stałą, krystaliczną próbką wstecznie rozproszone elektrony elektrony pierwotne
Atomy wieloelektronowe i cząsteczki
 Atomy wieloelektronowe i cząsteczki 1 Atomy wieloelektronowe Wodór ma liczbę atomową Z=1 i jest prostym atomem. Zawiera tylko jeden elektron i jeden proton stąd potencjał opisuje oddziaływanie kulombowskie
Atomy wieloelektronowe i cząsteczki 1 Atomy wieloelektronowe Wodór ma liczbę atomową Z=1 i jest prostym atomem. Zawiera tylko jeden elektron i jeden proton stąd potencjał opisuje oddziaływanie kulombowskie
Wykład V Wiązanie kowalencyjne. Półprzewodniki
 Wykład V Wiązanie kowalencyjne. Półprzewodniki Wiązanie kowalencyjne molekuła H 2 Tworzenie wiązania kowalencyjnego w molekule H 2 : elektron w jednym atomie przyciągany jest przez jądro drugiego. Wiązanie
Wykład V Wiązanie kowalencyjne. Półprzewodniki Wiązanie kowalencyjne molekuła H 2 Tworzenie wiązania kowalencyjnego w molekule H 2 : elektron w jednym atomie przyciągany jest przez jądro drugiego. Wiązanie
WYKŁAD NR 3 OPIS DRGAŃ NORMALNYCH UJĘCIE KLASYCZNE I KWANTOWE.
 1 WYKŁAD NR 3 OPIS DRGAŃ NORMALNYCH UJĘCIE KLASYCZNE I KWANTOWE. Współrzędne wewnętrzne 2 F=-fq q ξ i F i =-f ij x j U = 1 2 fq2 U = 1 2 ij f ij ξ i ξ j 3 Najczęściej stosowaną metodą obliczania drgań
1 WYKŁAD NR 3 OPIS DRGAŃ NORMALNYCH UJĘCIE KLASYCZNE I KWANTOWE. Współrzędne wewnętrzne 2 F=-fq q ξ i F i =-f ij x j U = 1 2 fq2 U = 1 2 ij f ij ξ i ξ j 3 Najczęściej stosowaną metodą obliczania drgań
Optyczna spektroskopia oscylacyjna. w badaniach powierzchni
 Optyczna spektroskopia oscylacyjna w badaniach powierzchni Zalety oscylacyjnej spektroskopii optycznej uŝycie fotonów jako cząsteczek wzbudzających i rejestrowanych nie wymaga uŝycia próŝni (moŝliwość
Optyczna spektroskopia oscylacyjna w badaniach powierzchni Zalety oscylacyjnej spektroskopii optycznej uŝycie fotonów jako cząsteczek wzbudzających i rejestrowanych nie wymaga uŝycia próŝni (moŝliwość
Spektroskopia molekularna. Spektroskopia w podczerwieni
 Spektroskopia molekularna Ćwiczenie nr 4 Spektroskopia w podczerwieni Spektroskopia w podczerwieni (IR) jest spektroskopią absorpcyjną, która polega na pomiarach promieniowania elektromagnetycznego pochłanianego
Spektroskopia molekularna Ćwiczenie nr 4 Spektroskopia w podczerwieni Spektroskopia w podczerwieni (IR) jest spektroskopią absorpcyjną, która polega na pomiarach promieniowania elektromagnetycznego pochłanianego
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 2, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 17.02.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Równania Maxwella r-nie falowe
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 17.02.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Równania Maxwella r-nie falowe
H H 2.5 < H H CH 3 N O O H C N ŁADUNEK FORMALNY. 2.5 dla atomu węgla C C 2.5 H 2.1. Li 1.0. liczba e - walencyjnych w atomie wolnym C 2.5 H 2.
 .5 dla atomu węgla ŁADUNEK RMALNY pierwiastek o mniejszej elektroujemności od węgla
.5 dla atomu węgla ŁADUNEK RMALNY pierwiastek o mniejszej elektroujemności od węgla
Mechanika kwantowa. Jak opisać atom wodoru? Jak opisać inne cząsteczki?
 Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkow Hamiltona energia funkcja falowa h d d d + + m d d dz
Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkow Hamiltona energia funkcja falowa h d d d + + m d d dz
Księgarnia PWN: Krzysztof Pigoń, Zdzisław Ruziewicz Chemia fizyczna. T. 2
 Księgarnia PWN: Krzysztof Pigoń, Zdzisław Ruziewicz Chemia fizyczna. T. 2 Przedmowa XIII 8. PODSTAWY MECHANIKI KWANTOWEJ I STRUKTURA ELEKTRONOWA ATOMÓW 1 8.1. Podstawy doświadczalne teorii kwantów 1 8.1.1.
Księgarnia PWN: Krzysztof Pigoń, Zdzisław Ruziewicz Chemia fizyczna. T. 2 Przedmowa XIII 8. PODSTAWY MECHANIKI KWANTOWEJ I STRUKTURA ELEKTRONOWA ATOMÓW 1 8.1. Podstawy doświadczalne teorii kwantów 1 8.1.1.
WIĄZANIA. Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE
 WIĄZANIA Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE Przyciąganie Wynika z elektrostatycznego oddziaływania między elektronami a dodatnimi jądrami atomowymi. Może to być
WIĄZANIA Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE Przyciąganie Wynika z elektrostatycznego oddziaływania między elektronami a dodatnimi jądrami atomowymi. Może to być
Elektryczne własności ciał stałych
 Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Atomy wieloelektronowe
 Wiązania atomowe Atomy wieloelektronowe, obsadzanie stanów elektronowych, układ poziomów energii. Przykładowe konfiguracje elektronów, gazy szlachetne, litowce, chlorowce, układ okresowy pierwiastków,
Wiązania atomowe Atomy wieloelektronowe, obsadzanie stanów elektronowych, układ poziomów energii. Przykładowe konfiguracje elektronów, gazy szlachetne, litowce, chlorowce, układ okresowy pierwiastków,
S. Baran - Podstawy fizyki materii skondensowanej Wiązania chemiczne w ciałach stałych. Wiązania chemiczne w ciałach stałych
 Wiązania chemiczne w ciałach stałych Wiązania chemiczne w ciałach stałych typ kowalencyjne jonowe metaliczne Van der Waalsa wodorowe siła* silne silne silne pochodzenie uwspólnienie e- (pary e-) przez
Wiązania chemiczne w ciałach stałych Wiązania chemiczne w ciałach stałych typ kowalencyjne jonowe metaliczne Van der Waalsa wodorowe siła* silne silne silne pochodzenie uwspólnienie e- (pary e-) przez
TEORIA ORBITALI MOLEKULARNYCH (MO) dr Henryk Myszka - Uniwersytet Gdański - Wydział Chemii
 TERIA RBITALI MLEKULARNYCH (M) Metoda (teoria) orbitali molekularnych (M) podstawy metody M - F. Hund, R.S. Mulliken Teoria M zakłada, że zachowanie się elektronu w cząsteczce opisuje orbital molekularny
TERIA RBITALI MLEKULARNYCH (M) Metoda (teoria) orbitali molekularnych (M) podstawy metody M - F. Hund, R.S. Mulliken Teoria M zakłada, że zachowanie się elektronu w cząsteczce opisuje orbital molekularny
Spektrometria w bliskiej podczerwieni - zastosowanie w cukrownictwie. Radosław Gruska Politechnika Łódzka Wydział Biotechnologii i Nauk o Żywności
 Spektrometria w bliskiej podczerwieni - zastosowanie w cukrownictwie Radosław Gruska Politechnika Łódzka Wydział Biotechnologii i Nauk o Żywności Spektroskopia, a spektrometria Spektroskopia nauka o powstawaniu
Spektrometria w bliskiej podczerwieni - zastosowanie w cukrownictwie Radosław Gruska Politechnika Łódzka Wydział Biotechnologii i Nauk o Żywności Spektroskopia, a spektrometria Spektroskopia nauka o powstawaniu
SPEKTROSKOPIA ROTACYJNA
 SPEKTROSKOPIA ROTACYJNA Co to jest spektroskopia mikrofalowa Obejmuje obszar częstości od 3GHz do 300GHz czyli od 0.1 do 10 cm -1 Wykrywa przejścia pomiędzy skwantowanymi poziomami energetycznymi obracającej
SPEKTROSKOPIA ROTACYJNA Co to jest spektroskopia mikrofalowa Obejmuje obszar częstości od 3GHz do 300GHz czyli od 0.1 do 10 cm -1 Wykrywa przejścia pomiędzy skwantowanymi poziomami energetycznymi obracającej
Elektronowa struktura atomu
 Elektronowa struktura atomu Model atomu Bohra oparty na teorii klasycznych oddziaływań elektrostatycznych Elektrony mogą przebywać tylko w określonych stanach, zwanych stacjonarnymi, o określonej energii
Elektronowa struktura atomu Model atomu Bohra oparty na teorii klasycznych oddziaływań elektrostatycznych Elektrony mogą przebywać tylko w określonych stanach, zwanych stacjonarnymi, o określonej energii
Elementy chemii obliczeniowej i bioinformatyki Zagadnienia na egzamin
 Elementy chemii obliczeniowej i bioinformatyki Zagadnienia na egzamin 1. Zapisz konfigurację elektronową dla atomu helu (dwa elektrony) i wyjaśnij, dlaczego cząsteczka wodoru jest stabilna, a cząsteczka
Elementy chemii obliczeniowej i bioinformatyki Zagadnienia na egzamin 1. Zapisz konfigurację elektronową dla atomu helu (dwa elektrony) i wyjaśnij, dlaczego cząsteczka wodoru jest stabilna, a cząsteczka
Spis treści. Metoda VSEPR. Reguły określania struktury cząsteczek. Ustalanie struktury przestrzennej
 Spis treści 1 Metoda VSEPR 2 Reguły określania struktury cząsteczek 3 Ustalanie struktury przestrzennej 4 Typy geometrii cząsteczek przykłady 41 Przykład 1 określanie struktury BCl 3 42 Przykład 2 określanie
Spis treści 1 Metoda VSEPR 2 Reguły określania struktury cząsteczek 3 Ustalanie struktury przestrzennej 4 Typy geometrii cząsteczek przykłady 41 Przykład 1 określanie struktury BCl 3 42 Przykład 2 określanie
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 8 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Aneta Drabińska, Barbara Piętka, Paweł Kowalczyk Wydział Fizyki Uniwersytet
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 8 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Aneta Drabińska, Barbara Piętka, Paweł Kowalczyk Wydział Fizyki Uniwersytet
Podstawy chemii obliczeniowej
 Podstawy chemii obliczeniowej Anna Kaczmarek Kędziera Katedra Chemii Materiałów, Adsorpcji i Katalizy Wydział Chemii UMK, Toruń Elementy chemii obliczeniowej i bioinformatyki 2015 Plan wykładu 15 godzin
Podstawy chemii obliczeniowej Anna Kaczmarek Kędziera Katedra Chemii Materiałów, Adsorpcji i Katalizy Wydział Chemii UMK, Toruń Elementy chemii obliczeniowej i bioinformatyki 2015 Plan wykładu 15 godzin
CZĄSTECZKA. Do opisu wiązań chemicznych stosuje się najczęściej jedną z dwóch metod (teorii): metoda wiązań walencyjnych (VB)
 CZĄSTECZKA Stanislao Cannizzaro (1826-1910) cząstki - elementy mikroświata, termin obejmujący zarówno cząstki elementarne, jak i atomy, jony proste i złożone, cząsteczki, rodniki, cząstki koloidowe; cząsteczka
CZĄSTECZKA Stanislao Cannizzaro (1826-1910) cząstki - elementy mikroświata, termin obejmujący zarówno cząstki elementarne, jak i atomy, jony proste i złożone, cząsteczki, rodniki, cząstki koloidowe; cząsteczka
Opis kwantowy cząsteczki jest bardziej skomplikowany niż atomu. Hamiltonian przy zaniedbaniu oddziaływań związanych ze spinem ma następującą postać:
 Cząsteczki. Kwantowy opis stanów enegetycznych cząsteczki. Funkcje falowe i enegia ektonów 3. Ruchy jąde oscylacje i otacje 4. Wzbudzenia cząsteczek Opis kwantowy cząsteczki jest badziej skomplikowany
Cząsteczki. Kwantowy opis stanów enegetycznych cząsteczki. Funkcje falowe i enegia ektonów 3. Ruchy jąde oscylacje i otacje 4. Wzbudzenia cząsteczek Opis kwantowy cząsteczki jest badziej skomplikowany
KARTA PRZEDMIOTU. Informacje ogólne WYDZIAŁ MATEMATYCZNO-PRZYRODNICZY. SZKOŁA NAUK ŚCISŁYCH UNIWERSYTET KARDYNAŁA STEFANA WYSZYŃSKIEGO W WARSZAWIE
 1 3 4 5 6 7 8 8.0 Kod przedmiotu Nazwa przedmiotu Jednostka Punkty ECTS Język wykładowy Poziom przedmiotu Symbole efektów kształcenia Symbole efektów dla obszaru kształcenia Symbole efektów kierunkowych
1 3 4 5 6 7 8 8.0 Kod przedmiotu Nazwa przedmiotu Jednostka Punkty ECTS Język wykładowy Poziom przedmiotu Symbole efektów kształcenia Symbole efektów dla obszaru kształcenia Symbole efektów kierunkowych
Przewodność elektryczna ciał stałych. Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki
 Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
Zadania powtórkowe do egzaminu maturalnego z chemii Wiązania chemiczne, budowa cząsteczek
 strona 1/11 Zadania powtórkowe do egzaminu maturalnego z chemii Wiązania chemiczne, budowa cząsteczek Monika Gałkiewicz Zad. 1 () Podaj wzory dwóch dowolnych kationów i dwóch dowolnych anionów posiadających
strona 1/11 Zadania powtórkowe do egzaminu maturalnego z chemii Wiązania chemiczne, budowa cząsteczek Monika Gałkiewicz Zad. 1 () Podaj wzory dwóch dowolnych kationów i dwóch dowolnych anionów posiadających
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 2, Mateusz Winkowski, Jan Szczepanek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 06.10.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Jan Szczepanek Radosław Łapkiewicz Równania Maxwella r-nie
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 06.10.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Jan Szczepanek Radosław Łapkiewicz Równania Maxwella r-nie
struktura atomowa 9 grudnia 2016 struktura atomowa
 9 grudnia 2016 układ okresowy 1869 - układ Mendelejewa (60 znanych pierwiatków), układ według mas atomowych, z periodycznie powtarzającymi się własnościami chemicznymi, przewidział istnienie: galu (odkrycie
9 grudnia 2016 układ okresowy 1869 - układ Mendelejewa (60 znanych pierwiatków), układ według mas atomowych, z periodycznie powtarzającymi się własnościami chemicznymi, przewidział istnienie: galu (odkrycie
Budowa atomu Poziom: rozszerzony Zadanie 1. (2 pkt.)
 Budowa atomu Poziom: rozszerzony Zadanie 1. (2 pkt.) Zadanie 1 2 3 4 5 6 7 8 9 10 Punkty Okres połowiczego rozpadu pewnego radionuklidu wynosi 16 godzin. a) Określ, ile procent atomów tego izotopu rozpadnie
Budowa atomu Poziom: rozszerzony Zadanie 1. (2 pkt.) Zadanie 1 2 3 4 5 6 7 8 9 10 Punkty Okres połowiczego rozpadu pewnego radionuklidu wynosi 16 godzin. a) Określ, ile procent atomów tego izotopu rozpadnie
Wykład przygotowany w oparciu o podręczniki:
 Slajd 1 Wykład przygotowany w oparciu o podręczniki: Organic Chemistry 4 th Edition Paula Yurkanis Bruice Slajd 2 Struktura elektronowa wiązanie chemiczne Kwasy i zasady Slajd 3 Chemia organiczna Związki
Slajd 1 Wykład przygotowany w oparciu o podręczniki: Organic Chemistry 4 th Edition Paula Yurkanis Bruice Slajd 2 Struktura elektronowa wiązanie chemiczne Kwasy i zasady Slajd 3 Chemia organiczna Związki
Spektroskopowe metody identyfikacji związków organicznych
 Spektroskopowe metody identyfikacji związków organicznych Wstęp Spektroskopia jest metodą analityczną zajmującą się analizą widm powstających w wyniku oddziaływania promieniowania elektromagnetycznego
Spektroskopowe metody identyfikacji związków organicznych Wstęp Spektroskopia jest metodą analityczną zajmującą się analizą widm powstających w wyniku oddziaływania promieniowania elektromagnetycznego
Uniwersytet Śląski w Katowicach str. 1 Wydział Matematyki, Fizyki i Chemii
 Uniwersytet Śląski w Katowicach str. 1 Kierunek i poziom studiów: Chemia, pierwszy poziom Sylabus modułu: Chemia kwantowa 021 Nazwa wariantu modułu (opcjonalnie): 1. Informacje ogólne koordynator modułu
Uniwersytet Śląski w Katowicach str. 1 Kierunek i poziom studiów: Chemia, pierwszy poziom Sylabus modułu: Chemia kwantowa 021 Nazwa wariantu modułu (opcjonalnie): 1. Informacje ogólne koordynator modułu
Teorie wiązania chemicznego i podstawowe zasady mechaniki kwantowej Zjawiska, które zapowiadały nadejście nowej ery w fizyce i przybliżały
 WYKŁAD 1 Teorie wiązania chemicznego i podstawowe zasady mechaniki kwantowej Zjawiska, które zapowiadały nadejście nowej ery w fizyce i przybliżały sformułowanie praw fizyki kwantowej: promieniowanie katodowe
WYKŁAD 1 Teorie wiązania chemicznego i podstawowe zasady mechaniki kwantowej Zjawiska, które zapowiadały nadejście nowej ery w fizyce i przybliżały sformułowanie praw fizyki kwantowej: promieniowanie katodowe
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki
 OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania (3.7), pomimo swojej prostoty, nie posiadają poza nielicznymi przypadkami ścisłych rozwiązań,
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania (3.7), pomimo swojej prostoty, nie posiadają poza nielicznymi przypadkami ścisłych rozwiązań,
I. PROMIENIOWANIE CIEPLNE
 I. PROMIENIOWANIE CIEPLNE - lata '90 XIX wieku WSTĘP Widmo promieniowania elektromagnetycznego zakres "pokrycia" różnymi rodzajami fal elektromagnetycznych promieniowania zawartego w danej wiązce. rys.i.1.
I. PROMIENIOWANIE CIEPLNE - lata '90 XIX wieku WSTĘP Widmo promieniowania elektromagnetycznego zakres "pokrycia" różnymi rodzajami fal elektromagnetycznych promieniowania zawartego w danej wiązce. rys.i.1.
1. Określ liczbę wiązań σ i π w cząsteczkach: wody, amoniaku i chloru
 1. Określ liczbę wiązań σ i π w cząsteczkach: wody, amoniaku i chloru 2. Na podstawie struktury cząsteczek wyjaśnij dlaczego N 2 jest bierny a Cl 2 aktywny chemicznie? 3. Które substancje posiadają budowę
1. Określ liczbę wiązań σ i π w cząsteczkach: wody, amoniaku i chloru 2. Na podstawie struktury cząsteczek wyjaśnij dlaczego N 2 jest bierny a Cl 2 aktywny chemicznie? 3. Które substancje posiadają budowę
Podstawy chemii. dr hab. Wacław Makowski. Wykład 1: Wprowadzenie
 Podstawy chemii dr hab. Wacław Makowski Wykład 1: Wprowadzenie Wspomnienia ze szkoły Elementarz (powtórka z gimnazjum) Układ okresowy Dalsze wtajemniczenia (liceum) Program zajęć Podręczniki Wydział Chemii
Podstawy chemii dr hab. Wacław Makowski Wykład 1: Wprowadzenie Wspomnienia ze szkoły Elementarz (powtórka z gimnazjum) Układ okresowy Dalsze wtajemniczenia (liceum) Program zajęć Podręczniki Wydział Chemii
WŁASNOŚCI CIAŁ STAŁYCH I CIECZY
 WŁASNOŚCI CIAŁ STAŁYCH I CIECZY Polimery Sieć krystaliczna Napięcie powierzchniowe Dyfuzja 2 BUDOWA CIAŁ STAŁYCH Ciała krystaliczne (kryształy): monokryształy, polikryształy Ciała amorficzne (bezpostaciowe)
WŁASNOŚCI CIAŁ STAŁYCH I CIECZY Polimery Sieć krystaliczna Napięcie powierzchniowe Dyfuzja 2 BUDOWA CIAŁ STAŁYCH Ciała krystaliczne (kryształy): monokryształy, polikryształy Ciała amorficzne (bezpostaciowe)
Elektronowa struktura atomu
 Elektronowa struktura atomu Model atomu Bohra oparty na teorii klasycznych oddziaływań elektrostatycznych Elektrony mogą przebywać tylko w określonych stanach, zwanych stacjonarnymi, o określonej energii
Elektronowa struktura atomu Model atomu Bohra oparty na teorii klasycznych oddziaływań elektrostatycznych Elektrony mogą przebywać tylko w określonych stanach, zwanych stacjonarnymi, o określonej energii
Spis treści. Przedmowa redaktora do wydania czwartego 11
 Mechanika kwantowa : teoria nierelatywistyczna / Lew D. Landau, Jewgienij M. Lifszyc ; z jęz. ros. tł. Ludwik Dobrzyński, Andrzej Pindor. - Wyd. 3. Warszawa, 2012 Spis treści Przedmowa redaktora do wydania
Mechanika kwantowa : teoria nierelatywistyczna / Lew D. Landau, Jewgienij M. Lifszyc ; z jęz. ros. tł. Ludwik Dobrzyński, Andrzej Pindor. - Wyd. 3. Warszawa, 2012 Spis treści Przedmowa redaktora do wydania
EFEKT SOLWATOCHROMOWY. WYZNACZANIE MOMENTU DIPOLOWEGO CZĄSTECZKI W STANIE WZBUDZONYM METODĄ SOLWATOCHROMOWĄ
 Ćwiczenie EFEKT SOLWATOCHROMOWY. WYZNACZANIE MOMENTU DIPOLOWEGO CZĄSTECZKI W STANIE WZBUDZONYM METODĄ SOLWATOCHROMOWĄ Zagadnienia: typy przejść elektronowych, orbitale atomowe (s, p, d) i molekularne (σ,
Ćwiczenie EFEKT SOLWATOCHROMOWY. WYZNACZANIE MOMENTU DIPOLOWEGO CZĄSTECZKI W STANIE WZBUDZONYM METODĄ SOLWATOCHROMOWĄ Zagadnienia: typy przejść elektronowych, orbitale atomowe (s, p, d) i molekularne (σ,
Fizyka 2. Janusz Andrzejewski
 Fizyka 2 wykład 14 Janusz Andrzejewski Atom wodoru Wczesne modele atomu -W czasach Newtona atom uważany była za małą twardą kulkę co dość dobrze sprawdzało się w rozważaniach dotyczących kinetycznej teorii
Fizyka 2 wykład 14 Janusz Andrzejewski Atom wodoru Wczesne modele atomu -W czasach Newtona atom uważany była za małą twardą kulkę co dość dobrze sprawdzało się w rozważaniach dotyczących kinetycznej teorii
Bryła sztywna. Fizyka I (B+C) Wykład XXIII: Przypomnienie: statyka
 Bryła sztywna Fizyka I (B+C) Wykład XXIII: Przypomnienie: statyka Moment bezwładności Prawa ruchu Energia ruchu obrotowego Porównanie ruchu obrotowego z ruchem postępowym Przypomnienie Równowaga bryły
Bryła sztywna Fizyka I (B+C) Wykład XXIII: Przypomnienie: statyka Moment bezwładności Prawa ruchu Energia ruchu obrotowego Porównanie ruchu obrotowego z ruchem postępowym Przypomnienie Równowaga bryły
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 1 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2015/16
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 1 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2015/16
3. Cząsteczki i wiązania
 20161020 3. Cząsteczki i wiązania Elektrony walencyjne Wiązania jonowe i kowalencyjne Wiązanie typu σ i π Hybrydyzacja Przewidywanie kształtu cząsteczek AX n Orbitale zdelokalizowane Cząsteczki związków
20161020 3. Cząsteczki i wiązania Elektrony walencyjne Wiązania jonowe i kowalencyjne Wiązanie typu σ i π Hybrydyzacja Przewidywanie kształtu cząsteczek AX n Orbitale zdelokalizowane Cząsteczki związków
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 1 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 1 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Początek XX wieku. Dualizm korpuskularno - falowy
 Początek XX wieku Światło: fala czy cząstka? Kwantowanie energii promieniowania termicznego postulat Plancka efekt fotoelektryczny efekt Comptona Fale materii de Broglie a Dualizm korpuskularno - falowy
Początek XX wieku Światło: fala czy cząstka? Kwantowanie energii promieniowania termicznego postulat Plancka efekt fotoelektryczny efekt Comptona Fale materii de Broglie a Dualizm korpuskularno - falowy
TEORIA PASMOWA CIAŁ STAŁYCH
 TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
Budowa atomów. Atomy wieloelektronowe Układ okresowy pierwiastków
 Budowa atomów Atomy wieloelektronowe Układ okresowy pierwiastków Model atomu Bohra atom zjonizowany (ciągłe wartości energii) stany wzbudzone jądro Energia (ev) elektron orbita stan podstawowy Poziomy
Budowa atomów Atomy wieloelektronowe Układ okresowy pierwiastków Model atomu Bohra atom zjonizowany (ciągłe wartości energii) stany wzbudzone jądro Energia (ev) elektron orbita stan podstawowy Poziomy
n n 1 2 = exp( ε ε ) 1 / kt = exp( hν / kt) (23) 2 to wzór (22) przejdzie w następującą równość: ρ (ν) = B B A / B 2 1 hν exp( ) 1 kt (24)
 n n 1 2 = exp( ε ε ) 1 / kt = exp( hν / kt) (23) 2 to wzór (22) przejdzie w następującą równość: ρ (ν) = B B A 1 2 / B hν exp( ) 1 kt (24) Powyższe równanie określające gęstość widmową energii promieniowania
n n 1 2 = exp( ε ε ) 1 / kt = exp( hν / kt) (23) 2 to wzór (22) przejdzie w następującą równość: ρ (ν) = B B A 1 2 / B hν exp( ) 1 kt (24) Powyższe równanie określające gęstość widmową energii promieniowania
Temat Ocena dopuszczająca Ocena dostateczna Ocena dobra Ocena bardzo dobra Ocena celująca. Uczeń:
 Chemia - klasa I (część 2) Wymagania edukacyjne Temat Ocena dopuszczająca Ocena dostateczna Ocena dobra Ocena bardzo dobra Ocena celująca Dział 1. Chemia nieorganiczna Lekcja organizacyjna. Zapoznanie
Chemia - klasa I (część 2) Wymagania edukacyjne Temat Ocena dopuszczająca Ocena dostateczna Ocena dobra Ocena bardzo dobra Ocena celująca Dział 1. Chemia nieorganiczna Lekcja organizacyjna. Zapoznanie
Dwie lub więcej cząstek poza zamkniętą powłoką
 Dwie lub więcej cząstek poza zamkniętą powłoką Rozważmy dwa (takie same) nukleony (lub dwie dziury) na orbitalu j poza zamkniętymi powłokami. Te dwie cząstki mogą sprzęgać się do momentu pędu J = j + j,
Dwie lub więcej cząstek poza zamkniętą powłoką Rozważmy dwa (takie same) nukleony (lub dwie dziury) na orbitalu j poza zamkniętymi powłokami. Te dwie cząstki mogą sprzęgać się do momentu pędu J = j + j,
SPEKTROSKOPIA RAMANA. Laboratorium Laserowej Spektroskopii Molekularnej PŁ
 SPEKTROSKOPIA RAMANA Laboratorium Laserowej Spektroskopii Molekularnej PŁ WIDMO OSCYLACYJNE Zręby atomowe w molekule wykonują oscylacje wokół położenia równowagi. Ruch ten można rozłożyć na 3n-6 w przypadku
SPEKTROSKOPIA RAMANA Laboratorium Laserowej Spektroskopii Molekularnej PŁ WIDMO OSCYLACYJNE Zręby atomowe w molekule wykonują oscylacje wokół położenia równowagi. Ruch ten można rozłożyć na 3n-6 w przypadku
gęstością prawdopodobieństwa
 Funkcja falowa Zgodnie z hipotezą de Broglie'a, cząstki takie jak elektron czy proton, mają własności falowe. Własności falowe cząstki (lub innego obiektu) w mechanice kwantowej opisuje tzw. funkcja falowa(,t)
Funkcja falowa Zgodnie z hipotezą de Broglie'a, cząstki takie jak elektron czy proton, mają własności falowe. Własności falowe cząstki (lub innego obiektu) w mechanice kwantowej opisuje tzw. funkcja falowa(,t)
Przejścia optyczne w strukturach niskowymiarowych
 Współczynnik absorpcji w układzie dwuwymiarowym można opisać wyrażeniem: E E gdzie i oraz f są energiami stanu początkowego i końcowego elektronu, zapełnienie tych stanów opisane jest funkcją rozkładu
Współczynnik absorpcji w układzie dwuwymiarowym można opisać wyrażeniem: E E gdzie i oraz f są energiami stanu początkowego i końcowego elektronu, zapełnienie tych stanów opisane jest funkcją rozkładu
