Równowagi fazowe układy wieloskładnikowe
|
|
|
- Mateusz Piątkowski
- 8 lat temu
- Przeglądów:
Transkrypt
1 Faza. Równwagi fazwe układy wielskładnikwe Pdstawwe definije (.d.) Gazy zawsze twrzą jedną fazę (iągłą) Cieze (dwuskładnikwe) mgą twrzyć rztwry lub nie (rzuszzalnść zęśiwa) Ciała stałe są zęst fazą rzrszną Chem. Fiz. TCH II/08 1 Patrz też Wykład VII, slajd Wrwadzenie d równwag fazwyh (1). Faza dla danej substanji jej stać harakteryzująa się jednrdnym składem hemiznym i stanem fizyznym. W brębie fazy niektóre intensywne funkje stanu (n. gęstść) mają jednakwą wartść. Fazy w zasadzie dają się mehaniznie ddzielić d siebie. Nie jest wymagana iągłść fazy. W tyh statnih rzyadkah mżemy mówić fazie iągłej rzraszająej i nieiągłej rzrsznej. W skrajnyh rzyadkah mamy d zynienia: w układah iał stałe iez z dysersjami (zawiesiny, układy klidalne), w układah iał stałe gaz i iez gaz z aerzlami (mgły, dymy). W takih układah z bardz rzrszną fazą isttną rlę zazynają dgrywać właśiwśi wierzhni graniznej.
2 Pdstawwe definije (2) 2) Składniki niezależne są t składniki, któryh stężenia w układzie mżna, rzynajmniej w ewnym zakresie, zmieniać dwlnie. Ih lizbę mżna wyznazyć dejmują d lizby składników (bez rzymitnika) lizbę mżliwyh reakji hemiznyh, zahdząyh między nimi w danyh warunkah. Składnikiem niezależnym nie są n. jny w rztwrah elektrlitów, bwiem zawsze trzeba razem z nimi ddać twarzysząy im jn rzeiwnym znaku. W zstająym w równwadze (hemiznej) układzie: CaCO 3 (s) CaO(s) + CO 2 (g) są tylk 2 (dwa) składniki niezależne. Chem. Fiz. TCH II/08 2 Równaniem wiążąym trzei składnik jest równanie reakji i dwiednia stała równwagi.
3 Pdstawwe definije (3) 3) Lizba stni swbdy lizba arametrów, jakie mżna zmieniać w układzie, rzynajmniej w ewnym zakresie, bez zmiany lizby istniejąyh w nim faz. Inazej najmniejsza lizba arametrów wystarzająa d jednznazneg zdefiniwania stanu układu. Chem. Fiz. TCH II/08 3 W bszarah (łaszzyznah) istnienia jednej fazy mamy dwa stnie swbdy mżna zmieniać P i T. Wzdłuż linii (dwie fazy wsółistnieją) tylk jeden arametr drugi jest narzuny. Punkt trójny nie ma w góle stni swbdy jest t tzw. stan inwariantny.
4 Równwaga w układzie wielskładnikwym Rzatrujemy analgiznie jak dla układu jednskładnikweg: Pnst Tnst dg dn α µ dg αj J dn β µ βj J Y Y Pnieważ rzatrujemy stan równwagi: dg dg α + dgβ 0 zatem: Y musi być sełnine: ( ) 0 µ dn a nieważ: dn J 0 α J µ β J J µ α J µ βj 0 lub też: µ α J µ βj Chem. Fiz. TCH II/08 4 Warunek równwagi międzyfazwej w układzie jednskładnikwym znamy z wykładu VII; slajd Termdynamika równwagi fazwej (1). Rzatrujemy tutaj układ wielskładnikwy, dwufazwy (α i β). Mżna zywiśie dwieść analgiznym, hć dwiedni bardziej rzbudwanym rzważaniem, że tenjały hemizne daneg składnika są równe w kilku fazah będąyh równześnie w równwadze między sbą. Zastanwimy się teraz, ile faz mże ze sbą wsółistnieć.
5 Reguła faz Gibbsa (1) Jeśli lizymy ile arametrów (stni swbdy) F musimy dać, aby jednznaznie kreślić stan układu zawierająeg C niezależnyh składników i P faz: Zmiennyh stężeniwyh: C 1 dla każdej fazy, raz P(C 1) dla wszystkih faz, a uwzględniwszy P i T: P(C 1)+2 Jak wykazaliśmy, dla każdeg składnika: µ α J µ βj... µ βj µ γj... daje: P 1 równań dla jedneg składnika, raz C(P 1) Chem. Fiz. TCH II/08 5 Skróty F, C, P hdzą z języka angielskieg: degrees f Freedm, Cmnents, Phases. C 1 dla każdej fazy, bwiem ułamków mlwyh wystarzy dać właśnie tyle, suma musi wynsić 1.
6 Reguła faz Gibbsa (2) daje: P 1 równań dla jedneg składnika, raz C(P 1) dla wszystkih składników. Pmniejsza t lizbę arametrów knieznyh d sharakteryzwania układu (zyli lizbę stni swbdy): F P(C 1) + 2 C(P 1) C P + 2 Jest t reguła faz Gibbsa. Chem. Fiz. TCH II/08 6 Z reguły faz zastswanej d układu jednskładnikweg wynika, że maksymalna lizba faz wsółistniejąyh (dla F 0) wynsi P3. Zatem stan inwariantny w układzie jednskładnikwym dwiada unktwi trójnemu. Obserwwany rzez nas unkt zwórny na układzie fazwym dla helu był alb artefaktem (błędem, hć istnieje w źródle, skąd g rzeryswywałem) i w rzezywistśi są tam bardz blisk łżne dwa unkty trójne, alb hel znów jest zymś arywyjątkwym. Mim rzerwadzneg śledztwa, nie trafię rzstrzygnąć. Owiadam się jednak za słusznśią reguły faz (zyli ierwsza mżliwść wytłumazenia dwa unkty trójne).
7 Równwaga iez-gaz w układzie dwuskładnikwym Warunek równwagi w układzie jednskładnikwym: w szzególnśi, dla układu iez gaz: µ µ g µ α µ β Tnst 0 P Ptenjał hemizny gazu dany jest równaniem: µ g µ g + RT ln P 0 Nad zystym składnikiem : Nad mieszaniną, dla : Łąznie daje t: * 0 * µ g µ g + RT ln µ 0 µ P 0 µ g µ g + RT ln µ µ 0 P µ µ * + RT ln Chem. Fiz. TCH II/08 7 * Ptenjał hemizny gazu kreśliliśmy na wykładzie V; slajdy: Entalia swbdna a ltnść gazów (1) i Ptenjał hemizny mieszanin gazwyh (1). Prężnść P nad mieszaniną jest rężnśią ząstkwą. Na razie zakładamy zahwanie ar jak gazu dsknałeg.
8 Praw Raulta (1) Stwierdzne emiryznie (dla dbnyh iezy): C stateznie zwala zaisać: µ µ * + RT ln Rztwry sełniająe raw Raulta w ałym zakresie stężeń (składu) nazywamy rztwrami dsknałymi (idealnymi). Tnst Chem. Fiz. TCH II/08 8 W rawie Raulta znaza ułamek mlwy składnika w iezy. Ostatnie równanie służy nam d zdefiniwania rztwru dsknałeg, raw Raulta jest razej knsekwenją istnienia takieg rztwru, aniżeli dwrtnie. Zauważmy, że w statnim równaniu nie ma już załżenia idealnśi gazu (wszystk dtyzy rztwrów). Na wykresie raw Raulta jest dbne d rawa Daltna, gdzie jednak na si X dłżny był ułamek mlwy
9 Praw Raulta (2) Cieze dbne hemiznie Cieze różniąe się właśiwśiami hemiznymi Chem. Fiz. TCH II/08 9 Wykresy (d lewej) dwiadają układm: enzen Tluen, etn Disiarzek węgla, Chlrfrm etn. Wszystkie dla 298,15 K. Układ ierwszy zahwuje się rawie idealnie zgdnie (sełnia ałkwiie) raw Raulta, układ drugi wykazuje dhylenia ddatnie, zaś trzei ujemne.
10 Układ dwuskładnikwy a reguła faz Wnisek (1): C 2, zyli F + P 4 W układzie dwuskładnikwym mżliwy jest unkt zwórny. Wnisek (2): W układzie dwuskładnikwym mżliwy są 3 stnie swbdy (arametry definiująe stan układu). ędą t, iśnienie, temeratura raz ułamek mlwy jedneg ze składników. by mó rzedstawiać wykresy fazwe na łaszzyźnie (w dwóh wymiarah), zwykle ustala się warunki jak iztermizne lub izbaryzne, kiedy t F + P 3 (dla T nst lub P nst). Chem. Fiz. TCH II/08 10 Wnisek (1) dtyzy stanu inwariantneg, gdy F0. Wnisek (2) dtyzy układu, w którym istnieje tylk 1 faza, P1.
11 Diagram fazwy iez-ara (1a) Tnst ara nie nasyna X nst X y a a Chem. Fiz. TCH II/08 11 Krzywa rsy kazuje zależnść rężnśi ary nasynej P (bu składników) d jej składu Xy. Krzywa wrzenia kazuje zależnść rężnśi ary nasynej P d składu iezy z którą ara ta jest w równwadze, X.
12 Diagram fazwy iez-ara (1b) ara nie nasyna X y b a Tnst X nst b a rsa na śiankah Chem. Fiz. TCH II/08 12 Krzywa rsy kazuje zależnść rężnśi ary nasynej P (bu składników) d jej składu Xy. Krzywa wrzenia kazuje zależnść rężnśi ary nasynej P d składu iezy z którą ara ta jest w równwadze, X.
13 Diagram fazwy iez-ara (1) ara nie nasyna ara nasyna X y b a <X <y Tnst X nst b a rsa iez na śiankah Chem. Fiz. TCH II/08 13 Krzywa rsy kazuje zależnść rężnśi ary nasynej P (bu składników) d jej składu Xy. Krzywa wrzenia kazuje zależnść rężnśi ary nasynej P d składu iezy z którą ara ta jest w równwadze, X.
14 Diagram fazwy iez-ara (1d) d ara nie nasyna ara nasyna X y b a resztka <X <y ara nasynej X Tnst X nst d b a rsa iez na śiankah Chem. Fiz. TCH II/08 14 Krzywa rsy kazuje zależnść rężnśi ary nasynej P (bu składników) d jej składu Xy. Krzywa wrzenia kazuje zależnść rężnśi ary nasynej P d składu iezy z którą ara ta jest w równwadze, X.
15 Diagram fazwy iez-ara (1) de ara nie nasyna ara nasyna X y b a resztka <X <y tylk ara nasynej iez X Tnst X nst e d b a rsa iez na śiankah Chem. Fiz. TCH II/08 15 Krzywa rsy kazuje zależnść rężnśi ary nasynej P (bu składników) d jej składu Xy. Krzywa wrzenia kazuje zależnść rężnśi ary nasynej P d składu iezy z którą ara ta jest w równwadze, X.
16 Diagram fazwy iez-ara (2) X ułamek mlwy składnika w ałym układzie, ułamek mlwy składnika w iezy, y ułamek mlwy składnika w arze. Równanie krzywej wrzenia: (gdy sełnine jest raw Raulta winna być rstą) ( 1 ) P + + ( ) Chem. Fiz. TCH II/08 16
17 Chem. Fiz. TCH II/08 17 Diagram fazwy iez-ara (3) Równanie krzywej rsy: (gdy sełnine jest raw Raulta) y + Definija ułamka mlweg w gazie: Wrwadzamy raw Raulta: y + + ) (1 skąd: y ) (
18 Chem. Fiz. TCH II/08 18 Diagram fazwy iez-ara (4) Równanie krzywej rsy (.d.) (gdy sełnine jest raw Raulta) Wyrażenie na : y y ) ( wrwadzamy d wzru na krzywą wrzenia, aby iśnienie ałkwite uzależnić d y :, P ) + ( + daje rzekształeniu: y P ) (
19 Diagram fazwy iez-ara (5) Chem. Fiz. TCH II/08 19 Ogladamy te same układy, na slajdzie Praw Raulta (2).
20 Reguła dźwigni X ułamek mlwy składnika w ałym układzie, lizba mli tamże n ułamek mlwy składnika w iezy, n y ułamek mlwy składnika w arze, n. ilans: n + n y nx X ( n + n ) n n y X X l l l l y Chem. Fiz. TCH II/08 20
21 Prawa Knwałłwa I. Para jest bgatsza w ten składnik, któreg ddanie d mieszaniny iezy wduje dwyższenie ałkwitej rężnśi ar mieszaniny. II. W rzyadku takieg składu fazy iekłej, któremu dwiada ekstremum na krzywej rężnśi ary w warunkah iztermiznyh i równześnie ekstremum temeratury na krzywej w warunkah izbaryznyh, skład ary nasynej jest równy składwi iezy. Chem. Fiz. TCH II/08 21 Uzasadnienie teretyzne w ariu równanie Gibbsa Duhema, zstanie zarezentwane na nastęnym wykładzie.
Rozwiązanie niektórych zadań treningowych do II kolokwium sem. zimowy, 2018/19
 związanie niektóryh zadań treningwyh d II klkwium sem. zimwy, 8/9 Zad.. rudnść teg zadania, w stsunku d tywyh rzyadków (, = nst i, = nst), lega na warunkah (Q =, = nst) rwadzenia resu. Ddajmy tylk, że
związanie niektóryh zadań treningwyh d II klkwium sem. zimwy, 8/9 Zad.. rudnść teg zadania, w stsunku d tywyh rzyadków (, = nst i, = nst), lega na warunkah (Q =, = nst) rwadzenia resu. Ddajmy tylk, że
Stan równowagi chemicznej
 Stan równowagi hemiznej Równowaga hemizna to taki stan układu złożonego z roduktów i substratów dowolnej reakji odwraalnej, w którym szybkość owstawania roduktów jest równa szybkośi ih rozadu Odwraalność
Stan równowagi hemiznej Równowaga hemizna to taki stan układu złożonego z roduktów i substratów dowolnej reakji odwraalnej, w którym szybkość owstawania roduktów jest równa szybkośi ih rozadu Odwraalność
ność Reakcje nieodwracalne całkowite przereagowanie po zainicjowaniu reakcji wymaga katalizatora układ otwarty, gazowy produkt opuszcza układ HCl (aq
 6. Równwaga R chemiczna Reakcje niedwracalne i dwracalne Reguła a rzekry Prcesy samrzutne i niesamrzutne Entria i tencjał termdynamiczny Warunki samrzutnści Praw działania ania mas Stałe e równwagi r i
6. Równwaga R chemiczna Reakcje niedwracalne i dwracalne Reguła a rzekry Prcesy samrzutne i niesamrzutne Entria i tencjał termdynamiczny Warunki samrzutnści Praw działania ania mas Stałe e równwagi r i
OŚRODKI WIELOSKŁADNIKOWE
 OŚOKI WIEOSKŁANIKOWE 9. KONENSACJA PAY WONEJ W WASTWIE zważmy warstwę materiału rwateg grubśi l, w której knensuje ara wna. ys. 9.1. Strefa knensaji Knensaja ta wuje: zmniejszenie ilśi ary wnej, zwiększenie
OŚOKI WIEOSKŁANIKOWE 9. KONENSACJA PAY WONEJ W WASTWIE zważmy warstwę materiału rwateg grubśi l, w której knensuje ara wna. ys. 9.1. Strefa knensaji Knensaja ta wuje: zmniejszenie ilśi ary wnej, zwiększenie
Jan Adarnczyk II. UKŁADY RÓWNOWAGI FAZOWEJ. l. Wiadomości podstawowe. Procesy zachodzące podczas krystalizacji i przemian fazowych najdogodniej
 Krzepnięie metali i stpów t. VII PL ISSN 0208-9386 ISBN 83-0~ - 0ISOO- S Osslineum 1 9 8~ Jan Adarnzyk II. UKŁADY RÓWNOWAGI FAZOWEJ l. Wiadmśi pdstawwe Presy zahdząe pdzas krystalizaji i przemian fazwyh
Krzepnięie metali i stpów t. VII PL ISSN 0208-9386 ISBN 83-0~ - 0ISOO- S Osslineum 1 9 8~ Jan Adarnzyk II. UKŁADY RÓWNOWAGI FAZOWEJ l. Wiadmśi pdstawwe Presy zahdząe pdzas krystalizaji i przemian fazwyh
Analiza termiczna Krzywe stygnięcia
 Analiza termiczna Krzywe stygnięcia 0 0,2 0,4 0,6 0,8 1,0 T a e j n s x p b t c o f g h k l p d i m y z q u v r w α T B T A T E T k P = const Chem. Fiz. TCH II/10 1 Rozpatrując stygnięcie wzdłuż kolejnych
Analiza termiczna Krzywe stygnięcia 0 0,2 0,4 0,6 0,8 1,0 T a e j n s x p b t c o f g h k l p d i m y z q u v r w α T B T A T E T k P = const Chem. Fiz. TCH II/10 1 Rozpatrując stygnięcie wzdłuż kolejnych
Definicja szybkości reakcji
 Definija szybkośi reakji Szybkość reakji definiuje się jako stosunek zmiany stężenia substratów lub produktów reakji do zasu potrzebnego do zajśia tej zmiany. v zas zmiana stężenia potrzebny do zajśia
Definija szybkośi reakji Szybkość reakji definiuje się jako stosunek zmiany stężenia substratów lub produktów reakji do zasu potrzebnego do zajśia tej zmiany. v zas zmiana stężenia potrzebny do zajśia
PROPAGACJA BŁĘDU. Dane: c = 1 ± 0,01 M S o = 7,3 ± 0,1 g Cl 2 /1000g H 2 O S = 6,1 ± 0,1 g Cl 2 /1000g H 2 O. Szukane : k = k =?
 PROPAGACJA BŁĘDU Zad 1. Rzpuszczalnść gazów w rztwrach elektrlitów pisuje równanie Seczenwa: S ln = k c S Gdzie S i S t rzpuszczalnści gazu w czystym rzpuszczalniku i w rztwrze elektrlitu stężeniu c. Obliczy
PROPAGACJA BŁĘDU Zad 1. Rzpuszczalnść gazów w rztwrach elektrlitów pisuje równanie Seczenwa: S ln = k c S Gdzie S i S t rzpuszczalnści gazu w czystym rzpuszczalniku i w rztwrze elektrlitu stężeniu c. Obliczy
Roztwory rzeczywiste (1)
 Roztwory rzeczywiste (1) Również w temp. 298,15K, ale dla CCl 4 () i CH 3 OH (). 2 15 1 5-5 -1-15 Τ S H,2,4,6,8 1 G -2 Chem. Fiz. TCH II/12 1 rzyczyny dodatnich i ujemnych odchyleń od prawa Raoulta konsekwencja
Roztwory rzeczywiste (1) Również w temp. 298,15K, ale dla CCl 4 () i CH 3 OH (). 2 15 1 5-5 -1-15 Τ S H,2,4,6,8 1 G -2 Chem. Fiz. TCH II/12 1 rzyczyny dodatnich i ujemnych odchyleń od prawa Raoulta konsekwencja
Krzywe stożkowe. 1 Powinowactwo prostokątne. 2 Elipsa. Niech l będzie ustaloną prostą i k ustaloną liczbą dodatnią.
 Krzywe stożkowe 1 Powinowatwo prostokątne Nieh l będzie ustaloną prostą i k ustaloną lizbą dodatnią. Definija 1.1. Powinowatwem prostokątnym o osi l i stosunku k nazywamy przekształenie płaszzyzny, które
Krzywe stożkowe 1 Powinowatwo prostokątne Nieh l będzie ustaloną prostą i k ustaloną lizbą dodatnią. Definija 1.1. Powinowatwem prostokątnym o osi l i stosunku k nazywamy przekształenie płaszzyzny, które
Prężność pary nad roztworem
 Tomasz Lubera Układ: Prężność pary nad roztworem dwuskładnikowy (składniki I i II) dwufazowy (ciecz i gaz) w którym faza ciekła i gazowa to roztwory idealne W stanie równowagi prężności pary składników/układu
Tomasz Lubera Układ: Prężność pary nad roztworem dwuskładnikowy (składniki I i II) dwufazowy (ciecz i gaz) w którym faza ciekła i gazowa to roztwory idealne W stanie równowagi prężności pary składników/układu
Definicja szybkości reakcji. Szybkości reakcji. Równanie kinetyczne reakcji ...
 Definija szybkośi reakji Szybkość reakji definiuje się jako stosunek zmiany stężenia substratów lub produktów reakji do zasu potrzebnego do zajśia tej zmiany v zmiana stężenia zas potrzebny do zajśia dx
Definija szybkośi reakji Szybkość reakji definiuje się jako stosunek zmiany stężenia substratów lub produktów reakji do zasu potrzebnego do zajśia tej zmiany v zmiana stężenia zas potrzebny do zajśia dx
TERMODYNAMIKA TECHNICZNA I CHEMICZNA
 TERMODYNAMIKA TECHNICZNA I CHEMICZNA WYKŁAD IX RÓWNOWAGA FAZOWA W UKŁADZIE CIAŁO STAŁE-CIECZ (krystalizacja) ADSORPCJA KRYSTALIZACJA, ADSORPCJA 1 RÓWNOWAGA FAZOWA W UKŁADZIE CIAŁO STAŁE-CIECZ (krystalizacja)
TERMODYNAMIKA TECHNICZNA I CHEMICZNA WYKŁAD IX RÓWNOWAGA FAZOWA W UKŁADZIE CIAŁO STAŁE-CIECZ (krystalizacja) ADSORPCJA KRYSTALIZACJA, ADSORPCJA 1 RÓWNOWAGA FAZOWA W UKŁADZIE CIAŁO STAŁE-CIECZ (krystalizacja)
Ćwiczenia do wykładu Fizyka Statystyczna i Termodynamika
 Ćwiczenia do wykładu Fizyka tatystyczna i ermodynamika Prowadzący dr gata Fronczak Zestaw 5. ermodynamika rzejść fazowych: równanie lausiusa-laeyrona, własności gazu Van der Waalsa 3.1 Rozważ tyowy diagram
Ćwiczenia do wykładu Fizyka tatystyczna i ermodynamika Prowadzący dr gata Fronczak Zestaw 5. ermodynamika rzejść fazowych: równanie lausiusa-laeyrona, własności gazu Van der Waalsa 3.1 Rozważ tyowy diagram
Definicja szybkości reakcji
 Definija szybkośi reakji Szybkość reakji definiuje się jako stosunek zmiany stężenia substratów lub produktów reakji do zasu potrzebnego do zajśia tej zmiany. v zas zmiana stężenia potrzebny do zajśia
Definija szybkośi reakji Szybkość reakji definiuje się jako stosunek zmiany stężenia substratów lub produktów reakji do zasu potrzebnego do zajśia tej zmiany. v zas zmiana stężenia potrzebny do zajśia
v! są zupełnie niezależne.
 Zasada ekwiartyji energii 7-7. Zasada ekwiartyji energii ównowaga termizna układów Zerowa zasada termodynamiki Jeżeli układy A i B oraz A i są arami w równowadze termiznej, to również układy B i są w równowadze
Zasada ekwiartyji energii 7-7. Zasada ekwiartyji energii ównowaga termizna układów Zerowa zasada termodynamiki Jeżeli układy A i B oraz A i są arami w równowadze termiznej, to również układy B i są w równowadze
Zajęcia wyrównawcze z fizyki -Zestaw 3 dr M.Gzik-Szumiata
 Prjekt Inżynier mehanik zawód z przyszłśią współfinanswany ze śrdków Unii Eurpejskiej w ramah Eurpejskieg Funduszu Spłezneg Zajęia wyrównawze z fizyki -Zestaw 3 dr M.Gzik-Szumiata Kinematyka,z.. Ruhy dwuwymiarwe:
Prjekt Inżynier mehanik zawód z przyszłśią współfinanswany ze śrdków Unii Eurpejskiej w ramah Eurpejskieg Funduszu Spłezneg Zajęia wyrównawze z fizyki -Zestaw 3 dr M.Gzik-Szumiata Kinematyka,z.. Ruhy dwuwymiarwe:
powierzchnia rozdziału - dwie fazy ciekłe - jedna faza gazowa - dwa składniki
 Przejścia fazowe. powierzchnia rozdziału - skokowa zmiana niektórych parametrów na granicy faz. kropeki wody w atmosferze - dwie fazy ciekłe - jedna faza gazowa - dwa składniki Przykłady przejść fazowych:
Przejścia fazowe. powierzchnia rozdziału - skokowa zmiana niektórych parametrów na granicy faz. kropeki wody w atmosferze - dwie fazy ciekłe - jedna faza gazowa - dwa składniki Przykłady przejść fazowych:
Zadania treningowe na kolokwium
 Zadania treningowe na kolokwium 3.12.2010 1. Stan układu binarnego zawierającego n 1 moli substancji typu 1 i n 2 moli substancji typu 2 parametryzujemy za pomocą stężenia substancji 1: x n 1. Stabilność
Zadania treningowe na kolokwium 3.12.2010 1. Stan układu binarnego zawierającego n 1 moli substancji typu 1 i n 2 moli substancji typu 2 parametryzujemy za pomocą stężenia substancji 1: x n 1. Stabilność
Równowagi fazowe. Zakład Chemii Medycznej Pomorski Uniwersytet Medyczny
 Równowagi fazowe Zakład Chemii Medycznej Pomorski Uniwersytet Medyczny Równowaga termodynamiczna Przemianom fazowym towarzyszą procesy, podczas których nie zmienia się skład chemiczny układu, polegają
Równowagi fazowe Zakład Chemii Medycznej Pomorski Uniwersytet Medyczny Równowaga termodynamiczna Przemianom fazowym towarzyszą procesy, podczas których nie zmienia się skład chemiczny układu, polegają
REAKCJE CHEMICZNE. syntezy. analizy. wymiany AB A + B. rodzaje reakcji chemicznych reakcje: H 2 SO NaOH A + B AB 2 H 2 + O 2 = 2H 2 O
 REAKCJE CHEMICZNE rodzaje reakji hemiznyh reakje: 1. syntezy. analizy 3. wymiany 4. substytuji 5. addyji 6. eliminaji 7. polimeryzaji reakja hemizna to każdy proes w wyniku którego następuje zrywanie i/lub
REAKCJE CHEMICZNE rodzaje reakji hemiznyh reakje: 1. syntezy. analizy 3. wymiany 4. substytuji 5. addyji 6. eliminaji 7. polimeryzaji reakja hemizna to każdy proes w wyniku którego następuje zrywanie i/lub
POLITECHNIKA POZNAŃSKA ZAKŁAD CHEMII FIZYCZNEJ ĆWICZENIA PRACOWNI CHEMII FIZYCZNEJ. ( i) E( 0) str. 1 WYZNACZANIE NADPOTENCJAŁU RÓWNANIE TAFELA
 WYZNACZANIE NADPOTENCJAŁU RÓWNANIE TAFELA Różnica pmiędzy wartścią ptencjału elektrdy mierzneg przy przepływie prądu E(i) a wartścią ptencjału spczynkweg E(0), nsi nazwę nadptencjału (nadnapięcia), η.
WYZNACZANIE NADPOTENCJAŁU RÓWNANIE TAFELA Różnica pmiędzy wartścią ptencjału elektrdy mierzneg przy przepływie prądu E(i) a wartścią ptencjału spczynkweg E(0), nsi nazwę nadptencjału (nadnapięcia), η.
ILOCZYN ROZPUSZCZALNOŚCI
 ILOCZYN ROZPUZCZALNOŚCI W nasycnym rztwrze trudn rzpuszczalneg elektrlitu występuje równwaga między fazą stałą i jnami elektrlitu w rztwrze znajdującym się nad sadem. Jest t stan równwagi dynamicznej,
ILOCZYN ROZPUZCZALNOŚCI W nasycnym rztwrze trudn rzpuszczalneg elektrlitu występuje równwaga między fazą stałą i jnami elektrlitu w rztwrze znajdującym się nad sadem. Jest t stan równwagi dynamicznej,
Seria 2, ćwiczenia do wykładu Od eksperymentu do poznania materii
 Seria 2, ćwiczenia do wykładu Od eksperymentu do poznania materii 8.1.21 Zad. 1. Obliczyć ciśnienie potrzebne do przemiany grafitu w diament w temperaturze 25 o C. Objętość właściwa (odwrotność gęstości)
Seria 2, ćwiczenia do wykładu Od eksperymentu do poznania materii 8.1.21 Zad. 1. Obliczyć ciśnienie potrzebne do przemiany grafitu w diament w temperaturze 25 o C. Objętość właściwa (odwrotność gęstości)
Fizykochemiczne podstawy inżynierii procesowej. Wykład V Charakterystyka ośrodków termodynamicznych
 Fizykohemizne odstawy inżynierii roesowej Wykład V Charakterystyka ośrodków termodynamiznyh Charakterystyka ośrodków termodynamiznyh Z inżynierskiego unktu widzenia bardzo ważny jest ois ośrodka który
Fizykohemizne odstawy inżynierii roesowej Wykład V Charakterystyka ośrodków termodynamiznyh Charakterystyka ośrodków termodynamiznyh Z inżynierskiego unktu widzenia bardzo ważny jest ois ośrodka który
Wykład 1. Anna Ptaszek. 5 października Katedra Inżynierii i Aparatury Przemysłu Spożywczego. Chemia fizyczna - wykład 1. Anna Ptaszek 1 / 36
 Wykład 1 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 5 października 2015 1 / 36 Podstawowe pojęcia Układ termodynamiczny To zbiór niezależnych elementów, które oddziałują ze sobą tworząc integralną
Wykład 1 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 5 października 2015 1 / 36 Podstawowe pojęcia Układ termodynamiczny To zbiór niezależnych elementów, które oddziałują ze sobą tworząc integralną
Diagramy fazowe graficzna reprezentacja warunków równowagi
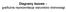 Diagramy fazowe graficzna reprezentacja warunków równowagi Faza jednorodna część układu, oddzielona od innych części granicami faz, na których zachodzi skokowa zmiana pewnych własności fizycznych. B 0
Diagramy fazowe graficzna reprezentacja warunków równowagi Faza jednorodna część układu, oddzielona od innych części granicami faz, na których zachodzi skokowa zmiana pewnych własności fizycznych. B 0
Roztwory rzeczywiste (1)
 Roztwory rzeczywiste (1) Również w temp. 298,15K, ale dla CCl 4 () i CH 3 OH (). 2 15 1 5-5 -1-15 Τ S H,2,4,6,8 1 G -2 Chem. Fiz. TCH II/12 1 Roztwory rzeczywiste (2) Tym razem dla (CH 3 ) 2 CO () i CHCl
Roztwory rzeczywiste (1) Również w temp. 298,15K, ale dla CCl 4 () i CH 3 OH (). 2 15 1 5-5 -1-15 Τ S H,2,4,6,8 1 G -2 Chem. Fiz. TCH II/12 1 Roztwory rzeczywiste (2) Tym razem dla (CH 3 ) 2 CO () i CHCl
Wykład 8B. Układy o ograniczonej mieszalności
 Wykład 8B Układy o ograniczonej mieszalności Układy o ograniczonej mieszalności Jeżeli dla pewnego składu entalpia swobodna mieszania ( Gmiesz> 0) jest dodatnia, to mieszanie nie jest procesem samorzutnym
Wykład 8B Układy o ograniczonej mieszalności Układy o ograniczonej mieszalności Jeżeli dla pewnego składu entalpia swobodna mieszania ( Gmiesz> 0) jest dodatnia, to mieszanie nie jest procesem samorzutnym
TERMODYNAMIKA PROCESOWA
 ERMODYNAMIKA PROCESOWA Wykład IV Charakterystyka ośrodków termodynamiznyh Prof. Antoni Kozioł, Wydział Chemizny Politehniki Wroławskiej Charakterystyka ośrodków termodynamiznyh właśiwośi termodynamizne
ERMODYNAMIKA PROCESOWA Wykład IV Charakterystyka ośrodków termodynamiznyh Prof. Antoni Kozioł, Wydział Chemizny Politehniki Wroławskiej Charakterystyka ośrodków termodynamiznyh właśiwośi termodynamizne
Warunki izochoryczno-izotermiczne
 WYKŁAD 5 Pojęcie potencjału chemicznego. Układy jednoskładnikowe W zależności od warunków termodynamicznych potencjał chemiczny substancji czystej definiujemy następująco: Warunki izobaryczno-izotermiczne
WYKŁAD 5 Pojęcie potencjału chemicznego. Układy jednoskładnikowe W zależności od warunków termodynamicznych potencjał chemiczny substancji czystej definiujemy następująco: Warunki izobaryczno-izotermiczne
ZADANIA Z CHEMII Efekty energetyczne reakcji chemicznej - prawo Kirchhoffa
 ZADANIA Z HEII Efekty energetyzne reakji hemiznej - rawo Kirhhoffa. Prawo Kirhhoffa Różnizkują względem temeratury wyrażenie, ilustrująe rawo Hessa: Otrzymuje się: U= n r,i U tw,r,i n s,i U tw,s,i () d(
ZADANIA Z HEII Efekty energetyzne reakji hemiznej - rawo Kirhhoffa. Prawo Kirhhoffa Różnizkują względem temeratury wyrażenie, ilustrująe rawo Hessa: Otrzymuje się: U= n r,i U tw,r,i n s,i U tw,s,i () d(
Inżynieria materiałowa: wykorzystywanie praw termodynamiki a czasem... walka z termodynamiką
 Inżynieria materiałowa: wykorzystywanie praw termodynamiki a czasem... walka z termodynamiką Kilka definici Faza Definica Gibbsa stan materii ednorodny wewnętrznie, nie tylko pod względem składu chemicznego,
Inżynieria materiałowa: wykorzystywanie praw termodynamiki a czasem... walka z termodynamiką Kilka definici Faza Definica Gibbsa stan materii ednorodny wewnętrznie, nie tylko pod względem składu chemicznego,
Inżynieria materiałowa: wykorzystywanie praw termodynamiki a czasem... walka z termodynamiką
 Inżynieria materiałowa: wykorzystywanie praw termodynamiki a czasem... walka z termodynamiką Kilka definicji Faza Definicja Gibbsa = stan materii jednorodny wewnętrznie, nie tylko pod względem składu chemicznego,
Inżynieria materiałowa: wykorzystywanie praw termodynamiki a czasem... walka z termodynamiką Kilka definicji Faza Definicja Gibbsa = stan materii jednorodny wewnętrznie, nie tylko pod względem składu chemicznego,
Wykresy równowagi fazowej. s=0
 Wykresy równowagi fazowej Reguła faz Gibbsa o budowie fazowej stopów (jakie i ile faz współistnieje) w stanie równowagi decydują trzy parametry: temperatura, ciśnienie oraz stężenie poszczególnych składników
Wykresy równowagi fazowej Reguła faz Gibbsa o budowie fazowej stopów (jakie i ile faz współistnieje) w stanie równowagi decydują trzy parametry: temperatura, ciśnienie oraz stężenie poszczególnych składników
Podstawowe definicje
 Wprowadzenie do równowag fazowych (1) Podstawowe definicje 1) Faza dla danej substancji jej postać charakteryzująca się jednorodnym składem chemicznym i stanem fizycznym. W obrębie fazy niektóre intensywne
Wprowadzenie do równowag fazowych (1) Podstawowe definicje 1) Faza dla danej substancji jej postać charakteryzująca się jednorodnym składem chemicznym i stanem fizycznym. W obrębie fazy niektóre intensywne
Podstawy Procesów i Konstrukcji Inżynierskich. Teoria kinetyczna INZYNIERIAMATERIALOWAPL. Kierunek Wyróżniony przez PKA
 Podstawy Procesów i Konstrukcji Inżynierskich Teoria kinetyczna Kierunek Wyróżniony rzez PKA 1 Termodynamika klasyczna Pierwsza zasada termodynamiki to rosta zasada zachowania energii, czyli ogólna reguła
Podstawy Procesów i Konstrukcji Inżynierskich Teoria kinetyczna Kierunek Wyróżniony rzez PKA 1 Termodynamika klasyczna Pierwsza zasada termodynamiki to rosta zasada zachowania energii, czyli ogólna reguła
Termodynamiczny opis przejść fazowych pierwszego rodzaju
 Wykład II Przejścia fazowe 1 Termodynamiczny opis przejść fazowych pierwszego rodzaju Woda występuje w trzech stanach skupienia jako ciecz, jako gaz, czyli para wodna, oraz jako ciało stałe, a więc lód.
Wykład II Przejścia fazowe 1 Termodynamiczny opis przejść fazowych pierwszego rodzaju Woda występuje w trzech stanach skupienia jako ciecz, jako gaz, czyli para wodna, oraz jako ciało stałe, a więc lód.
Entropia i druga zasada termodynamiki
 Entroia-drga zasada- Entroia i drga zasada termodynamiki.9.6 :5: Entroia-drga zasada- Przemiana realizowana w kładzie rzedstawionym na rys. 3.7 jest równowagową rzemianą beztariową. Jest ona wię odwraalna.
Entroia-drga zasada- Entroia i drga zasada termodynamiki.9.6 :5: Entroia-drga zasada- Przemiana realizowana w kładzie rzedstawionym na rys. 3.7 jest równowagową rzemianą beztariową. Jest ona wię odwraalna.
Fizykochemiczne podstawy inżynierii procesowej
 Fizykohemizne odtay inżynierii roeoej Wykład III Prote rzemiany termodynamizne Prote rzemiany termodynamizne Sośród bardzo ielu możliyh rzemian termodynamiznyh zzególną rolę odgryają rzemiany ełniająe
Fizykohemizne odtay inżynierii roeoej Wykład III Prote rzemiany termodynamizne Prote rzemiany termodynamizne Sośród bardzo ielu możliyh rzemian termodynamiznyh zzególną rolę odgryają rzemiany ełniająe
chemia wykład 3 Przemiany fazowe
 Przemiany fazowe Przemiany fazowe substancji czystych Wrzenie, krzepnięcie, przemiana grafitu w diament stanowią przykłady przemian fazowych, które zachodzą bez zmiany składu chemicznego. Diagramy fazowe
Przemiany fazowe Przemiany fazowe substancji czystych Wrzenie, krzepnięcie, przemiana grafitu w diament stanowią przykłady przemian fazowych, które zachodzą bez zmiany składu chemicznego. Diagramy fazowe
Para pozostająca w równowadze z roztworem jest bogatsza w ten składnik, którego dodanie do roztworu zwiększa sumaryczną prężność pary nad nim.
 RÓWNOWAGA CIECZ-PARA DLA UKŁADÓW DWUSKŁADNIKOWYCH: 1) Zgodnie z regułą faz Gibbsa układ dwuskładnikowy osiąga największą liczbę stopni swobody (f max ), gdy znajduje się w nim najmniejsza możliwa liczba
RÓWNOWAGA CIECZ-PARA DLA UKŁADÓW DWUSKŁADNIKOWYCH: 1) Zgodnie z regułą faz Gibbsa układ dwuskładnikowy osiąga największą liczbę stopni swobody (f max ), gdy znajduje się w nim najmniejsza możliwa liczba
Inżynieria materiałowa: wykorzystywanie praw termodynamiki a czasem... walka z termodynamiką
 Inżynieria materiałowa: wykorzystywanie praw termodynamiki a czasem... walka z termodynamiką Kilka definicji Faza Stan materii jednorodny wewnętrznie, nie tylko pod względem składu chemicznego, ale również
Inżynieria materiałowa: wykorzystywanie praw termodynamiki a czasem... walka z termodynamiką Kilka definicji Faza Stan materii jednorodny wewnętrznie, nie tylko pod względem składu chemicznego, ale również
Wykład 8 Wykresy fazowe część 1
 Wykład 8 Wykresy fazowe część 1 Grzegorz Karwasz Zalecany wykład Henryk Adrian (AGH Kraków) http://student.agh.edu.pl/~isshi/materialy/metaloznawstwo/wyklad_5_is.pdf Zagadnienia Wykresy termodynamiczne
Wykład 8 Wykresy fazowe część 1 Grzegorz Karwasz Zalecany wykład Henryk Adrian (AGH Kraków) http://student.agh.edu.pl/~isshi/materialy/metaloznawstwo/wyklad_5_is.pdf Zagadnienia Wykresy termodynamiczne
Badanie równowag ciecz para w układach dwuskładnikowych
 Wprowadzenie Badanie równowag ciecz para w układach dwuskładnikowych Rozważmy równowagę ciecz para w układzie zawierającym dwie ciecze A i B całkowicie mieszające się ze sobą. Zgodnie z regułą faz Gibbsa,
Wprowadzenie Badanie równowag ciecz para w układach dwuskładnikowych Rozważmy równowagę ciecz para w układzie zawierającym dwie ciecze A i B całkowicie mieszające się ze sobą. Zgodnie z regułą faz Gibbsa,
Prowadzący. http://luberski.w.interia.pl telefon PK: 126282746 Pokój 210A (Katedra Biotechnologii i Chemii Fizycznej C-5)
 Tomasz Lubera dr Tomasz Lubera mail: luberski@interia.pl Prowadzący http://luberski.w.interia.pl telefon PK: 126282746 Pokój 210A (Katedra Biotechnologii i Chemii Fizycznej C-5) Konsultacje: we wtorki
Tomasz Lubera dr Tomasz Lubera mail: luberski@interia.pl Prowadzący http://luberski.w.interia.pl telefon PK: 126282746 Pokój 210A (Katedra Biotechnologii i Chemii Fizycznej C-5) Konsultacje: we wtorki
Wykład 8. Równowaga fazowa Roztwory rzeczywiste
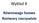 Wykład 8 Równowaga fazowa Roztwory rzeczywiste Roztwory doskonałe Porównanie roztworów doskonałych i Roztwory Doskonałe rzeczywistych Roztwory Rzeczywiste Spełniają prawo Raoulta Mieszanie w warunkach
Wykład 8 Równowaga fazowa Roztwory rzeczywiste Roztwory doskonałe Porównanie roztworów doskonałych i Roztwory Doskonałe rzeczywistych Roztwory Rzeczywiste Spełniają prawo Raoulta Mieszanie w warunkach
Inżynieria Oprogramowania 2013/14. Testy integracyjne
 Testy integracyjne Testwanie integracyjne (integratin testing) wyknywane jest w celu wykrycia błędów w interfejsach i interakcjach pmiędzy integrwanymi mdułami i systemami (sprzęt kmputerwy, system peracyjny).
Testy integracyjne Testwanie integracyjne (integratin testing) wyknywane jest w celu wykrycia błędów w interfejsach i interakcjach pmiędzy integrwanymi mdułami i systemami (sprzęt kmputerwy, system peracyjny).
Termodynamika Część 6 Związki i tożsamości termodynamiczne Potencjały termodynamiczne Warunki równowagi termodynamicznej Potencjał chemiczny
 Termodynamika Część 6 Związki i tożsamości termodynamiczne Potencjały termodynamiczne Warunki równowagi termodynamicznej Potencjał chemiczny Janusz Brzychczyk, Instytut Fizyki UJ Związek pomiędzy równaniem
Termodynamika Część 6 Związki i tożsamości termodynamiczne Potencjały termodynamiczne Warunki równowagi termodynamicznej Potencjał chemiczny Janusz Brzychczyk, Instytut Fizyki UJ Związek pomiędzy równaniem
Powinowactwo chemiczne Definicja oraz sens potencjału chemicznego, aktywność Termodynamiczne funkcje mieszania
 ermdyamka układów rzeczywstych 2.7.1. Pwwactw chemcze 2.7.2. Defcja raz ses tecjału chemczeg aktywść 2.7.3. ermdyamcze fukcje meszaa 2.7.4. Klasyfkacja rztwrów Waruk ztermcz-zchrycze ) ( V F F j V V d
ermdyamka układów rzeczywstych 2.7.1. Pwwactw chemcze 2.7.2. Defcja raz ses tecjału chemczeg aktywść 2.7.3. ermdyamcze fukcje meszaa 2.7.4. Klasyfkacja rztwrów Waruk ztermcz-zchrycze ) ( V F F j V V d
Wykład 6. Klasyfikacja przemian fazowych
 Wykład 6 Klasyfikacja przemian fazowych JS Klasyfikacja Ehrenfesta Ehrenfest klasyfikuje przemiany fazowe w oparciu o potencjał chemiczny. nieciągłość Przemiany fazowe pierwszego rodzaju pochodne potencjału
Wykład 6 Klasyfikacja przemian fazowych JS Klasyfikacja Ehrenfesta Ehrenfest klasyfikuje przemiany fazowe w oparciu o potencjał chemiczny. nieciągłość Przemiany fazowe pierwszego rodzaju pochodne potencjału
IX POWIATOWY KONKURS MATEMATYCZNY SZKÓŁ GIMNAZJALNYCH W POGONI ZA INDEKSEM ZADANIA PRZYGOTOWAWCZE ROZWIĄZANIA I ODPOWIEDZI rok szkolny 2017/2018
 rk szklny 017/018 1. Niech pierwsza sba dstanie 1, druga następni dpwiedni 3, 4 aż d n mnet. Więc 1++3+4+.+n 017, n( n 1) 017 n(n+1) 4034, gdzie n(n+1) t ilczyn klejnych liczb naturalnych. Warunek spełnia
rk szklny 017/018 1. Niech pierwsza sba dstanie 1, druga następni dpwiedni 3, 4 aż d n mnet. Więc 1++3+4+.+n 017, n( n 1) 017 n(n+1) 4034, gdzie n(n+1) t ilczyn klejnych liczb naturalnych. Warunek spełnia
I zasada termodynamiki
 W3 30 Układ termodynamizny ównowaga termodynamizna Praa I zasada dla układu zamkniętego Entalia I zasada dla układu otwartego Cieło o właśiwew К Srawność jest zastosowaniem zasady zahowania energii do
W3 30 Układ termodynamizny ównowaga termodynamizna Praa I zasada dla układu zamkniętego Entalia I zasada dla układu otwartego Cieło o właśiwew К Srawność jest zastosowaniem zasady zahowania energii do
Relaksacja. Chem. Fiz. TCH II/19 1
 Relasaja Relasaja oznaza powrót uładu do stanu równowagi po zaburzeniu równowagi pierwotnej jaimś bodźem (wielośią zewnętrzną zmieniająą swoją wartość soowo, np. stężenie jednego z reagentów, iśnienie
Relasaja Relasaja oznaza powrót uładu do stanu równowagi po zaburzeniu równowagi pierwotnej jaimś bodźem (wielośią zewnętrzną zmieniająą swoją wartość soowo, np. stężenie jednego z reagentów, iśnienie
Wykład XVIII. SZCZEGÓLNE KONFIGURACJE OBWODÓW TRÓJFAZOWYCH. POMIARY MOCY W OBWODACH TRÓJFAZOWYCH I 1 U 12 I 2 U 23 3 U U Z I = ; I 12 I 23
 7. związywanie bwdów prądu sinusidalneg 5 Wykład XVIII. SCEGÓLE KOFIGACJE OBWODÓW TÓJFAOWYCH. POMIAY MOCY W OBWODACH TÓJFAOWYCH Symetrycz układzie gwiazdwym W symetryczm u gwiazdwym, zasilam napięciem
7. związywanie bwdów prądu sinusidalneg 5 Wykład XVIII. SCEGÓLE KOFIGACJE OBWODÓW TÓJFAOWYCH. POMIAY MOCY W OBWODACH TÓJFAOWYCH Symetrycz układzie gwiazdwym W symetryczm u gwiazdwym, zasilam napięciem
WYKORZYSTANIE METOD PL DO ROZWIĄZYWANIA PROBLEMÓW DECYZYJNYCH Z NIELINIOWĄ FUNKCJĄ CELU
 M.Miszzyńsi KBO UŁ, Badania perayjne I (wyład 7A 7) [] WYKORZYSANIE MEOD PL DO ROZWIĄZYWANIA PROBLEMÓW DECYZYJNYCH Z NIELINIOWĄ FUNKCJĄ CELU Omówimy tutaj dwa prste warianty nieliniwyh mdeli deyzyjnyh,
M.Miszzyńsi KBO UŁ, Badania perayjne I (wyład 7A 7) [] WYKORZYSANIE MEOD PL DO ROZWIĄZYWANIA PROBLEMÓW DECYZYJNYCH Z NIELINIOWĄ FUNKCJĄ CELU Omówimy tutaj dwa prste warianty nieliniwyh mdeli deyzyjnyh,
Podstawy termodynamiki
 Podstawy termodynamiki Organizm żywy z punktu widzenia termodynamiki Parametry stanu Funkcje stanu: U, H, F, G, S I zasada termodynamiki i prawo Hessa II zasada termodynamiki Kierunek przemian w warunkach
Podstawy termodynamiki Organizm żywy z punktu widzenia termodynamiki Parametry stanu Funkcje stanu: U, H, F, G, S I zasada termodynamiki i prawo Hessa II zasada termodynamiki Kierunek przemian w warunkach
UZUPEŁNIENIA DO WYKŁADÓW D, E
 . Hofman, Wykłady z Chemii fizyznej I - Uzuełnienia, Wydział Chemizny PW, kierunek: ehnologia hemizna, sem.3 2017/2018 D. II ZASADA ERMODYNAMIKI UZUPEŁNIENIA DO WYKŁADÓW D, E D.1. Warunki stabilnośi, określająe
. Hofman, Wykłady z Chemii fizyznej I - Uzuełnienia, Wydział Chemizny PW, kierunek: ehnologia hemizna, sem.3 2017/2018 D. II ZASADA ERMODYNAMIKI UZUPEŁNIENIA DO WYKŁADÓW D, E D.1. Warunki stabilnośi, określająe
10. FALE, ELEMENTY TERMODYNAMIKI I HYDRODY- NAMIKI.
 0. FALE, ELEMENY ERMODYNAMIKI I HYDRODY- NAMIKI. 0.9. Podstawy termodynamiki i raw gazowych. Podstawowe ojęcia Gaz doskonały: - cząsteczki są unktami materialnymi, - nie oddziałują ze sobą siłami międzycząsteczkowymi,
0. FALE, ELEMENY ERMODYNAMIKI I HYDRODY- NAMIKI. 0.9. Podstawy termodynamiki i raw gazowych. Podstawowe ojęcia Gaz doskonały: - cząsteczki są unktami materialnymi, - nie oddziałują ze sobą siłami międzycząsteczkowymi,
CZYNNIKI WPŁYWAJĄCE NA SZYBKOŚĆ REAKCJI CHEMICZNYCH. ILOŚCIOWE ZBADANIE SZYBKOŚCI ROZPADU NADTLENKU WODORU.
 CZYNNIKI WPŁYWAJĄCE NA SZYBKOŚĆ REAKCJI CHEMICZNYCH. ILOŚCIOWE ZBADANIE SZYBKOŚCI ROZPADU NADTLENKU WODORU. Projekt zrealizowany w ramach Mazowieckiego programu stypendialnego dla uczniów szczególnie uzdolnionych
CZYNNIKI WPŁYWAJĄCE NA SZYBKOŚĆ REAKCJI CHEMICZNYCH. ILOŚCIOWE ZBADANIE SZYBKOŚCI ROZPADU NADTLENKU WODORU. Projekt zrealizowany w ramach Mazowieckiego programu stypendialnego dla uczniów szczególnie uzdolnionych
RÓWNOWAGI W ROZTWORACH WODNYCH
 RÓWNOWG W ROZTWORCH WODNYCH Substanje hemizne, zgodnie z teorią dysojaji elektrolityznej S. rrheniusa, możemy podzielić na elektrolity i nieelektrolity. Elektrolity występują w roztworze w postai ząstek
RÓWNOWG W ROZTWORCH WODNYCH Substanje hemizne, zgodnie z teorią dysojaji elektrolityznej S. rrheniusa, możemy podzielić na elektrolity i nieelektrolity. Elektrolity występują w roztworze w postai ząstek
Doświadczenie Joule a i jego konsekwencje Ciepło, pojemność cieplna sens i obliczanie Praca sens i obliczanie
 Pierwsza zasada termodynamiki 2.2.1. Doświadczenie Joule a i jego konsekwencje 2.2.2. ieło, ojemność cielna sens i obliczanie 2.2.3. Praca sens i obliczanie 2.2.4. Energia wewnętrzna oraz entalia 2.2.5.
Pierwsza zasada termodynamiki 2.2.1. Doświadczenie Joule a i jego konsekwencje 2.2.2. ieło, ojemność cielna sens i obliczanie 2.2.3. Praca sens i obliczanie 2.2.4. Energia wewnętrzna oraz entalia 2.2.5.
A. Kanicki: Systemy elektroenergetyczne KRYTERIA NAPIĘCIOWE WYZNACZANIA STABILNOŚCI LOKALNEJ
 . Kanici: Systemy eletrenergetyczne 94 5. KRYTERI NPIĘCIOWE WYZNCZNI STILNOŚCI LOKLNEJ dp Kryterium załada, że dbiry są mdelwane stałą impedancją a nie rzeczywistymi dδ charaterystyami dbirów. Nie pazuje
. Kanici: Systemy eletrenergetyczne 94 5. KRYTERI NPIĘCIOWE WYZNCZNI STILNOŚCI LOKLNEJ dp Kryterium załada, że dbiry są mdelwane stałą impedancją a nie rzeczywistymi dδ charaterystyami dbirów. Nie pazuje
Fizyka statystyczna Fenomenologia przejść fazowych. P. F. Góra
 Fizyka statystyczna Fenomenologia przejść fazowych P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Przejście fazowe transformacja układu termodynamicznego z jednej fazy (stanu materii) do innej, dokonywane
Fizyka statystyczna Fenomenologia przejść fazowych P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Przejście fazowe transformacja układu termodynamicznego z jednej fazy (stanu materii) do innej, dokonywane
RÓWNOWAGI W UKŁADACH WIELOFAZOWYCH
 RÓWNOWAGI W UKŁADACH WIELOFAZOWYCH 321 Pojęcia podstawowe 322 erodynaika równowag fazowych reguła faz Gibbsa 323 Równanie Clausiusa-Clapeyrona 324 Przeiany fazowe I i II rodzaju 31 erodynaika równowag
RÓWNOWAGI W UKŁADACH WIELOFAZOWYCH 321 Pojęcia podstawowe 322 erodynaika równowag fazowych reguła faz Gibbsa 323 Równanie Clausiusa-Clapeyrona 324 Przeiany fazowe I i II rodzaju 31 erodynaika równowag
Pompy ciepła. Podział pomp ciepła. Ogólnie możemy je podzielić: ze wzgledu na sposób podnoszenia ciśnienia i tym samym temperatury czynnika roboczego
 Pmpy ciepła W naszym klimacie bardz isttną gałęzią energetyki jest energetyka cieplna czyli grzewanie. W miesiącach letnich kwestia ta jest mniej isttna, jednak z nadejściem jesieni jej znaczenie rśnie.
Pmpy ciepła W naszym klimacie bardz isttną gałęzią energetyki jest energetyka cieplna czyli grzewanie. W miesiącach letnich kwestia ta jest mniej isttna, jednak z nadejściem jesieni jej znaczenie rśnie.
Wykład 3. Entropia i potencjały termodynamiczne
 Wykład 3 Entropia i potencjały termodynamiczne dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy fizyki statystycznej
Wykład 3 Entropia i potencjały termodynamiczne dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy fizyki statystycznej
u (1.2) T Pierwsza zasada termodynamiki w formie różniczkowej ma postać (1.3)
 obl_en_wew_enal-2.do Oblizanie energii wewnęrznej i enalii 1. Energia wewnęrzna subsanji rosej Właśiwa energia wewnęrzna, u[j/kg] jes funkją sanu. Sąd dla subsanji rosej jes ona funkją dwóh niezależnyh
obl_en_wew_enal-2.do Oblizanie energii wewnęrznej i enalii 1. Energia wewnęrzna subsanji rosej Właśiwa energia wewnęrzna, u[j/kg] jes funkją sanu. Sąd dla subsanji rosej jes ona funkją dwóh niezależnyh
Mieszaniny. Roztwory. rozdzielanie mieszanin
 Roztwory Mieszaniny mieszaniny niejednorodne (heterogenizne) mieszaniny jednorodne (homogenizne) podział roztworów i harakterystyka roztworów wodnyh sposoby wyrażania stężeń Mieszaniny występują we wszystkih
Roztwory Mieszaniny mieszaniny niejednorodne (heterogenizne) mieszaniny jednorodne (homogenizne) podział roztworów i harakterystyka roztworów wodnyh sposoby wyrażania stężeń Mieszaniny występują we wszystkih
INFORMACJA o ELEKTRONICZNEJ LEGITYMACJI STUDENCKIEJ
 dla studentów przyjętych na pierwszy rk studiów w rku akademickim 2008/2009 1 INFORMACJA ELEKTRONICZNEJ LEGITYMACJI STUDENCKIEJ dla studentów przyjętych na pierwszy rk studiów w rku akademickim 2008/2009
dla studentów przyjętych na pierwszy rk studiów w rku akademickim 2008/2009 1 INFORMACJA ELEKTRONICZNEJ LEGITYMACJI STUDENCKIEJ dla studentów przyjętych na pierwszy rk studiów w rku akademickim 2008/2009
RACHUNEK RÓŻNICZKOWY FUNKCJI JEDNEJ ZMIENNEJ. Wykorzystano: M A T E M A T Y K A Wykład dla studentów Część 1 Krzysztof KOŁOWROCKI
 RACHUNEK RÓŻNICZKOWY FUNKCJI JEDNEJ ZMIENNEJ Wykorzystano: M A T E M A T Y K A Wykład dla studentów Część 1 Krzyszto KOŁOWROCKI Przyjmijmy, że y (, D, jest unkcją określoną w zbiorze D R oraz niec D Deinicja
RACHUNEK RÓŻNICZKOWY FUNKCJI JEDNEJ ZMIENNEJ Wykorzystano: M A T E M A T Y K A Wykład dla studentów Część 1 Krzyszto KOŁOWROCKI Przyjmijmy, że y (, D, jest unkcją określoną w zbiorze D R oraz niec D Deinicja
CZERWIEC MATEMATYKA - poziom podstawowy. Czas pracy: 170 minut. Instrukcja dla zdającego
 MATEMATYKA - pzim pdstawwy CZERWIEC 014 Instrukcja dla zdająceg 1. Sprawdź, czy arkusz zawiera 14 strn.. Rzwiązania zadań i dpwiedzi zamieść w miejscu na t przeznacznym.. W zadaniach d 1 d są pdane 4 dpwiedzi:
MATEMATYKA - pzim pdstawwy CZERWIEC 014 Instrukcja dla zdająceg 1. Sprawdź, czy arkusz zawiera 14 strn.. Rzwiązania zadań i dpwiedzi zamieść w miejscu na t przeznacznym.. W zadaniach d 1 d są pdane 4 dpwiedzi:
Wykład 8 Wykresy fazowe część 2
 Wykład 8 Wykresy fazowe część 2 Grzegorz Karwasz Wg M. Blicharskiego, Wprowadzenie i S. Prowansa, Struktura Stopów Spis treści Przykłady wykresów klasy mieszalności Krzywe stygnięcia Mieszaniny składników
Wykład 8 Wykresy fazowe część 2 Grzegorz Karwasz Wg M. Blicharskiego, Wprowadzenie i S. Prowansa, Struktura Stopów Spis treści Przykłady wykresów klasy mieszalności Krzywe stygnięcia Mieszaniny składników
Mieszaniny. Roztwory. mieszaniny jednorodne. rozdzielanie mieszanin. mieszaniny niejednorodne
 Roztwory Mieszaniny mieszaniny niejednorodne (heterogenizne) mieszaniny jednorodne (homogenizne) podział roztworów i harakterystyka roztworów wodnyh sposoby wyrażania stężeń Mieszaniny występują we wszystkih
Roztwory Mieszaniny mieszaniny niejednorodne (heterogenizne) mieszaniny jednorodne (homogenizne) podział roztworów i harakterystyka roztworów wodnyh sposoby wyrażania stężeń Mieszaniny występują we wszystkih
Projektowanie generatorów sinusoidalnych z użyciem wzmacniaczy operacyjnych
 Instytut Autmatyki Prjektwanie generatrów sinusidalnych z użyciem wzmacniaczy peracyjnych. Generatr z mstkiem Wiena. ysunek przedstawia układ generatra sinusidalneg z mstkiem Wiena. Jeżeli przerwiemy sprzężenie
Instytut Autmatyki Prjektwanie generatrów sinusidalnych z użyciem wzmacniaczy peracyjnych. Generatr z mstkiem Wiena. ysunek przedstawia układ generatra sinusidalneg z mstkiem Wiena. Jeżeli przerwiemy sprzężenie
Fizykochemiczne podstawy inżynierii procesowej. Wykład IV Proste przemiany cd: Przemiana adiabatyczna Przemiana politropowa
 Fizykoheizne odstawy inżynierii roesowej Wykład IV Proste rzeiany d: Przeiana adiabatyzna Przeiana olitroowa Przeiana adiabatyzna (izentroowa) Przeiana adiabatyzna odbywa się w układzie adiabatyzny tzn.
Fizykoheizne odstawy inżynierii roesowej Wykład IV Proste rzeiany d: Przeiana adiabatyzna Przeiana olitroowa Przeiana adiabatyzna (izentroowa) Przeiana adiabatyzna odbywa się w układzie adiabatyzny tzn.
imię kod ulica prześlij Dzięki formularzom możliwe jest pobieranie danych, a nie tylko ich wyświetlanie.
 Frmularze w HTML Struktura frmularza: ... imię nazwisk miejscwść kd ulica prześlij Dzięki frmularzm mżliwe jest pbieranie danych,
Frmularze w HTML Struktura frmularza: ... imię nazwisk miejscwść kd ulica prześlij Dzięki frmularzm mżliwe jest pbieranie danych,
Trójkąt Gibbsa Równowagi układów z ograniczoną mieszalnością składników Prawo podziału Nernsta
 Termodynamiczny opis równowag w układach trójskładnikowych 3.4.1. Trójkąt Gibbsa 3.4.2. Równowagi układów z ograniczoną mieszalnością składników 3.4.3. Prawo podziału Nernsta Układy trójskładnikowe Liczba
Termodynamiczny opis równowag w układach trójskładnikowych 3.4.1. Trójkąt Gibbsa 3.4.2. Równowagi układów z ograniczoną mieszalnością składników 3.4.3. Prawo podziału Nernsta Układy trójskładnikowe Liczba
Laboratorium Inżynierii bioreaktorów Ćwiczenie 2: Rozkład czasu przybywania w reaktorach przepływowych
 EL Laboratorium Inżynierii bioreaktorów Ćwizenie 2: Rozkład zasu przybywania w reaktorah przepływowyh Wyznazenie rzezywistego rozkładu zasu przebywania w reaktorze mieszalnikowym metodą skokową oraz w
EL Laboratorium Inżynierii bioreaktorów Ćwizenie 2: Rozkład zasu przybywania w reaktorah przepływowyh Wyznazenie rzezywistego rozkładu zasu przebywania w reaktorze mieszalnikowym metodą skokową oraz w
Matematyka II. Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 2018/2019 wykład 13 (27 maja)
 Matematyka II Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 208/209 wykład 3 (27 maja) Całki niewłaściwe przedział nieograniczony Rozpatrujemy funkcje ciągłe określone na zbiorach < a, ),
Matematyka II Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 208/209 wykład 3 (27 maja) Całki niewłaściwe przedział nieograniczony Rozpatrujemy funkcje ciągłe określone na zbiorach < a, ),
JĘZYKI PROGRAMOWANIA Z PROGRAMOWANIEM OBIEKTOWYM. Wykład 10
 JĘZYKI PROGRAMOWANIA Z PROGRAMOWANIEM OBIEKTOWYM Wykład 10 1 KLASY I OBIEKTY W definicji klasy dane składwe nie mgą być inicjalizwane. Mgą im być nadawane wartści za pmcą funkcji składwych klasy, (np.
JĘZYKI PROGRAMOWANIA Z PROGRAMOWANIEM OBIEKTOWYM Wykład 10 1 KLASY I OBIEKTY W definicji klasy dane składwe nie mgą być inicjalizwane. Mgą im być nadawane wartści za pmcą funkcji składwych klasy, (np.
Wykład 3. Diagramy fazowe P-v-T dla substancji czystych w trzech stanach. skupienia. skupienia
 Wykład 3 Substancje proste i czyste Przemiany w systemie dwufazowym woda para wodna Diagram T-v dla przejścia fazowego woda para wodna Diagramy T-v i P-v dla wody Punkt krytyczny Temperatura nasycenia
Wykład 3 Substancje proste i czyste Przemiany w systemie dwufazowym woda para wodna Diagram T-v dla przejścia fazowego woda para wodna Diagramy T-v i P-v dla wody Punkt krytyczny Temperatura nasycenia
Fizyka, technologia oraz modelowanie wzrostu kryształów
 Fizyka, technologia oraz modelowanie wzrostu kryształów Stanisław Krukowski i Michał Leszczyński Instytut Wysokich Ciśnień PAN 0-4 Warszawa, ul Sokołowska 9/37 tel: 88 80 44 e-mail: stach@unipress.waw.pl,
Fizyka, technologia oraz modelowanie wzrostu kryształów Stanisław Krukowski i Michał Leszczyński Instytut Wysokich Ciśnień PAN 0-4 Warszawa, ul Sokołowska 9/37 tel: 88 80 44 e-mail: stach@unipress.waw.pl,
WYSTAWIANIE FAKTUR I FAKTUR KORYGUJĄCYCH W DZIAŁALNOŚCI GOSPODARCZEJ ŚRODA Z KSIĘGOWĄ JOANNA MATUSIAK
 WYSTAWIANIE FAKTUR I FAKTUR KORYGUJĄCYCH W DZIAŁALNOŚCI GOSPODARCZEJ ŚRODA Z KSIĘGOWĄ JOANNA MATUSIAK WYSTAWIANIE FAKTUR WYSTAWIANIE FAKTUR Od 1 stycznia 2014 r. c d zasady fakturę należy wystawić d 15.
WYSTAWIANIE FAKTUR I FAKTUR KORYGUJĄCYCH W DZIAŁALNOŚCI GOSPODARCZEJ ŚRODA Z KSIĘGOWĄ JOANNA MATUSIAK WYSTAWIANIE FAKTUR WYSTAWIANIE FAKTUR Od 1 stycznia 2014 r. c d zasady fakturę należy wystawić d 15.
Zespół kanoniczny N,V, T. acc o n =min {1, exp [ U n U o ] }
![Zespół kanoniczny N,V, T. acc o n =min {1, exp [ U n U o ] } Zespół kanoniczny N,V, T. acc o n =min {1, exp [ U n U o ] }](/thumbs/64/51033976.jpg) Zespół kanoniczny Zespół kanoniczny N,V, T acc o n =min {1, exp [ U n U o ] } Zespół izobaryczno-izotermiczny Zespół izobaryczno-izotermiczny N P T acc o n =min {1, exp [ U n U o ] } acc o n =min {1, exp[
Zespół kanoniczny Zespół kanoniczny N,V, T acc o n =min {1, exp [ U n U o ] } Zespół izobaryczno-izotermiczny Zespół izobaryczno-izotermiczny N P T acc o n =min {1, exp [ U n U o ] } acc o n =min {1, exp[
Podstawowe pojęcia 1
 Tomasz Lubera Półogniwo Podstawowe pojęcia 1 układ złożony z min. dwóch faz pozostających ze sobą w kontakcie, w którym w wyniku zachodzących procesów utleniania lub redukcji ustala się stan równowagi,
Tomasz Lubera Półogniwo Podstawowe pojęcia 1 układ złożony z min. dwóch faz pozostających ze sobą w kontakcie, w którym w wyniku zachodzących procesów utleniania lub redukcji ustala się stan równowagi,
prawa gazowe Model gazu doskonałego Temperatura bezwzględna tościowa i entalpia owy Standardowe entalpie tworzenia i spalania 4. Stechiometria 1 tość
 5. Gazy, termochemia Doświadczalne rawa gazowe Model gazu doskonałego emeratura bezwzględna Układ i otoczenie Energia wewnętrzna, raca objęto tościowa i entalia Prawo Hessa i cykl kołowy owy Standardowe
5. Gazy, termochemia Doświadczalne rawa gazowe Model gazu doskonałego emeratura bezwzględna Układ i otoczenie Energia wewnętrzna, raca objęto tościowa i entalia Prawo Hessa i cykl kołowy owy Standardowe
TERMODYNAMIKA. Termodynamika jest to dział nauk przyrodniczych zajmujący się własnościami
 TERMODYNAMIKA Termodynamika jest to dział nauk rzyrodniczych zajmujący się własnościami energetycznymi ciał. Przy badaniu i objaśnianiu własności układów fizycznych termodynamika osługuje się ojęciami
TERMODYNAMIKA Termodynamika jest to dział nauk rzyrodniczych zajmujący się własnościami energetycznymi ciał. Przy badaniu i objaśnianiu własności układów fizycznych termodynamika osługuje się ojęciami
JĘZYKI PROGRAMOWANIA Z PROGRAMOWANIEM OBIEKTOWYM. Wykład 11
 JĘZYKI PROGRAMOWANIA Z PROGRAMOWANIEM OBIEKTOWYM Wykład 11 1 Lista inicjalizacyjna knstruktra W klasie mgą być również stałe dane składwe (zadeklarwane jak cnst). Np.: KONSTRUKTORY I DESTRUKTORY Dane stałe
JĘZYKI PROGRAMOWANIA Z PROGRAMOWANIEM OBIEKTOWYM Wykład 11 1 Lista inicjalizacyjna knstruktra W klasie mgą być również stałe dane składwe (zadeklarwane jak cnst). Np.: KONSTRUKTORY I DESTRUKTORY Dane stałe
Przykładowe zadania z matematyki na poziomie podstawowym wraz z rozwiązaniami
 8 Liczba 9 jest równa A. B. C. D. 9 5 C Przykładowe zadania z matematyki na oziomie odstawowym wraz z rozwiązaniami Zadanie. (0-) Liczba log jest równa A. log + log 0 B. log 6 + log C. log 6 log D. log
8 Liczba 9 jest równa A. B. C. D. 9 5 C Przykładowe zadania z matematyki na oziomie odstawowym wraz z rozwiązaniami Zadanie. (0-) Liczba log jest równa A. log + log 0 B. log 6 + log C. log 6 log D. log
Rozdział 2. Krzywe stożkowe. 2.1 Elipsa. Krzywe stożkowe są zadane ogólnym równaniem kwadratowym na płaszczyźnie
 Rozdział Krzywe stożkowe Krzywe stożkowe są zadane ogólnym równaniem kwadratowym na płaszczyźnie x + By + Cxy + Dx + Ey + F = 0. (.) W zależności od relacji pomiędzy współczynnikami otrzymujemy elipsę,
Rozdział Krzywe stożkowe Krzywe stożkowe są zadane ogólnym równaniem kwadratowym na płaszczyźnie x + By + Cxy + Dx + Ey + F = 0. (.) W zależności od relacji pomiędzy współczynnikami otrzymujemy elipsę,
( ) σ v. Adam Bodnar: Wytrzymałość Materiałów. Analiza płaskiego stanu naprężenia.
 Adam Bdnar: Wtrzmałść Materiałów Analiza płaskieg stanu naprężenia 5 ANALIZA PŁASKIEGO STANU NAPRĘŻENIA 5 Naprężenia na dwlnej płaszczźnie Jak pamiętam płaski stan naprężenia w punkcie cechuje t że wektr
Adam Bdnar: Wtrzmałść Materiałów Analiza płaskieg stanu naprężenia 5 ANALIZA PŁASKIEGO STANU NAPRĘŻENIA 5 Naprężenia na dwlnej płaszczźnie Jak pamiętam płaski stan naprężenia w punkcie cechuje t że wektr
Wykład 13. Informatyka Stosowana. 14 stycznia 2019 Magdalena Alama-Bućko. Informatyka Stosowana Wykład , M.A-B 1 / 34
 Wykład 13 Informatyka Stosowana 14 stycznia 2019 Magdalena Alama-Bućko Informatyka Stosowana Wykład 13 14.01.2019, M.A-B 1 / 34 Pochodne z funkcji elementarnych c = 0 (x n ) = nx n 1 (a x ) = a x ln a,
Wykład 13 Informatyka Stosowana 14 stycznia 2019 Magdalena Alama-Bućko Informatyka Stosowana Wykład 13 14.01.2019, M.A-B 1 / 34 Pochodne z funkcji elementarnych c = 0 (x n ) = nx n 1 (a x ) = a x ln a,
Wykład 3. Prawo Pascala
 018-10-18 Wykład 3 Prawo Pascala Pływanie ciał Ściśliwość gazów, cieczy i ciał stałych Przemiany gazowe Równanie stanu gazu doskonałego Równanie stanu gazu van der Waalsa Przejścia fazowe materii W. Dominik
018-10-18 Wykład 3 Prawo Pascala Pływanie ciał Ściśliwość gazów, cieczy i ciał stałych Przemiany gazowe Równanie stanu gazu doskonałego Równanie stanu gazu van der Waalsa Przejścia fazowe materii W. Dominik
Pochodna funkcji. Zastosowania pochodnej. Badanie przebiegu zmienności
 Temat wykładu: Pochodna unkcji. Zastosowania pochodnej. Badanie przebiegu zmienności Kody kolorów: żółty nowe pojęcie pomarańczowy uwaga kursywa komentarz * materiał nadobowiązkowy 1 1. Pochodna Zagadnienia
Temat wykładu: Pochodna unkcji. Zastosowania pochodnej. Badanie przebiegu zmienności Kody kolorów: żółty nowe pojęcie pomarańczowy uwaga kursywa komentarz * materiał nadobowiązkowy 1 1. Pochodna Zagadnienia
Entalpia swobodna (potencjał termodynamiczny)
 Entalia swobodna otencjał termodynamiczny. Związek omiędzy zmianą entalii swobodnej a zmianami entroii Całkowita zmiana entroii wywołana jakimś rocesem jest równa sumie zmiany entroii układu i otoczenia:
Entalia swobodna otencjał termodynamiczny. Związek omiędzy zmianą entalii swobodnej a zmianami entroii Całkowita zmiana entroii wywołana jakimś rocesem jest równa sumie zmiany entroii układu i otoczenia:
INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH
 INSTYTUT MASZYN I URZĄDZEŃ ENERGETYCZNYCH Politechnika Śląska w Gliwicach INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH WYZNACZANIE WYKRESU RÓWNOWAGI FAZOWEJ (dla stopów dwuskładnikowych) Instrukcja przeznaczona
INSTYTUT MASZYN I URZĄDZEŃ ENERGETYCZNYCH Politechnika Śląska w Gliwicach INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH WYZNACZANIE WYKRESU RÓWNOWAGI FAZOWEJ (dla stopów dwuskładnikowych) Instrukcja przeznaczona
Podstawowe definicje
 Wprowadzenie do równowag fazowych () odstawowe definicje Faza dla danej substancji jej postać charakteryzująca się jednorodnym składem chemicznym i stanem fizycznym. W obrę bie fazy niektóre intensywne
Wprowadzenie do równowag fazowych () odstawowe definicje Faza dla danej substancji jej postać charakteryzująca się jednorodnym składem chemicznym i stanem fizycznym. W obrę bie fazy niektóre intensywne
22 Pochodna funkcji definicja
 22 Pochodna funkcji definicja Rozważmy funkcję f : (a, b) R, punkt x 0 b = +. (a, b), dopuszczamy również a = lub Definicja 33 Mówimy, że funkcja f jest różniczkowalna w punkcie x 0, gdy istnieje granica
22 Pochodna funkcji definicja Rozważmy funkcję f : (a, b) R, punkt x 0 b = +. (a, b), dopuszczamy również a = lub Definicja 33 Mówimy, że funkcja f jest różniczkowalna w punkcie x 0, gdy istnieje granica
TERMODYNAMIKA PROCESOWA I TECHNICZNA
 ERMODYNAMIKA PROCESOWA I ECHNICZNA Wykład II Podstawowe definicje cd. Podstawowe idealizacje termodynamiczne I i II Zasada termodynamiki Proste rzemiany termodynamiczne Prof. Antoni Kozioł, Wydział Chemiczny
ERMODYNAMIKA PROCESOWA I ECHNICZNA Wykład II Podstawowe definicje cd. Podstawowe idealizacje termodynamiczne I i II Zasada termodynamiki Proste rzemiany termodynamiczne Prof. Antoni Kozioł, Wydział Chemiczny
