OCENA WYTRZYMAŁOŚCI KOMORY SPALANIA SILNIKA RAKIETOWEGO NA PALIWO STAŁE
|
|
|
- Maksymilian Dąbrowski
- 8 lat temu
- Przeglądów:
Transkrypt
1 mg inŝ. Jey NOWICKI Wojskoy Instytut echnicny Ubojenia OCENA WYRZYMAŁOŚCI KOMORY SPALANIA SILNIKA RAKIEOWEGO NA PALIWO SAŁE W atykule estaiono analię ytymałości mechanicnej komoy salania silnika akietoego na alio stałe. Poano obciąŝenia na jakie naaŝona jest komoa casie acy silnika akietoego oa iąane nimi naęŝenia ostające ściance komoy. Pestaiono aleŝności na ostaie, któych oblica się te naęŝenia. Poano uoscony sosób saenia ytymałości komoy. W oaciu o tę metoę estaiono ocenę ytymałości komoy salania ocisku akietoego M-1OF. 1. Wstę Silnik ocisku akietoego na alio stałe skłaa się asaie komoy salania, tylnego na ysą oa na eniego łącącego komoę cęścią bojoą ocisku. W komoe umiescany jest łaunek naęoy, elementy ałonu (osyka ochoa, słonka) oa ust. Kous komoy salania aycaj ykonuje się kstałcie cylinycnej uy. Niekiey sotyka się konstukcje innego oaju, jenak ich ykonanie i montaŝ są nacnie tuniejse. Dla konstuktoa silnika akietoego ostaoym oblemem ytymałościoym jest okeślenie gubości ścianki komoy salania. Z jenej stony gubość ścianki oinna być tak obana, aby komoa mogła ytymać naęŝenia ostałe casie acy silnika tj. naę- Ŝenia o ciśnienia gaó (salanie łaunku naęoego) oa naęŝenia temicne ostałe na skutek nageania się ścianki (óŝnicy temeatuy enętnej i enętnej oiechni). Jenoceśnie gubość ścianki oinna być jak najmniejsa, aby aenić minimalną masę silnika, co y yjętej masie łaunku naęoego umoŝliia uyskanie ięksej ękości maksymalnej (asięgu) ocisku. W celu ogoenia tych ymagań (scególnie la silnikó o casie acy oyŝej 1 sekuny) oiechnię enętną komoy okya się astą temoiolacyjną, co ioluje ściankę e iałaniem ysokiej temeatuy i nacne mniejsa naęŝenia cielne. Na skutecność tego oiąania skaują ytocone [1] ane la niemieckiego ocisku ecilotnicego, któego silnik acoał na aliie akietoym o kaloycności około. 850 kcal/kg casie 1,5 sekuny. Ścianka komoy salania tego ocisku ostała okyta oma astami temoiolacji, co ooliło mniejsyć jej gubość o δ = mm i y takiej gubości agaantoać ytymałość komoy na ciśnienie oboce max = 13 MPa. Kontolne salania na hamoni silnikó ocisku be okycia iolacją cielną oooało oyanie się komoy salania. Aby achoać ytymałość komoy salania, teba było oięksyć gubość ścianki ona ukotnie. Py tym masa silnika niemal oajała się, co oaiło o obniŝenia maksymalnej ękości ocisku o m/s, ocas gy ocisk iolacją cielną komoy i δ = mm miał V max = 1500 m/s. 99
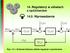
2 Ze glęu na okeśloną oyŝej agę otymalnego oiąania e konstuktoa oblemu ytymałości komoy salania silnika akietoego, yaje się celoym estaienie oaju obciąŝeń na jakie naaŝona jest komoa casie acy silnika akietoego i iąanych nimi naęŝeń ostających ściance komoy. Pokaano, któe naęŝenia są najbaiej niebeiecne la komoy, gie na gubości ścianki osiągają maksimum oa cy są to naęŝenia ściskające cy ociągające. Oceniono ilościoo i jakościoo te naęŝenia i na tej ostaie oano oste aleŝności umoŝliiające stęne oblicenie gubości ścianki komoy silnika oa końcoe saenie ytymałości komoy. Na ich ostaie eoaono ocenę ytymałości komoy salania ocisku akietoego M-1OF.. ObciąŜenia komoy salania i iąane nimi naęŝenia ostające ściance komoy Postaoym ytymałościoym elementem komoy salania jest jej uoy kous. W casie acy silnika kous musi ytymać ee systkim obciąŝenia o ciśnienia gaó ostających e salenia łaunku naęoego oa obciąŝenia temicne iąane ysoką temeatuą ełyających łuŝ ścianki gaó. Ocyiście ocas statu akiety na kous iałają takŝe obciąŝenia iąane iałaniem sił bełaności yołanych ysieseniami osioymi oa oecnymi (jeśli akieta stabiliuje się obotoo) akiety. W yaku akiet ysiesenia te są nieielkie, latego atykule ich nie uglęniono. ObciąŜenia te yołują ściance komoy salania okeślony stan naęŝeń uaunkoany iałaniem ciśnienia i temeatuy. W ybliŝeniu moŝna yjąć, Ŝe naęŝenia te są niealeŝne i oatyać je oielnie, a nastęnie okeślić naęŝenia sumaycne jako sumę ooienich (n. omienioych) naęŝeń: = + t (1) gie: t - omienioe naęŝenie sumaycne o ciśnienia i temeatuy, - omienioe naęŝenie skłaoe tylko o ciśnienia, - omienioe naęŝenie skłaoe tylko o temeatuy..1. NaęŜenia o ciśnienia Na kous komoy salania casie acy silnika iała ciśnienie gaó ob. ónomienie ołoŝone na jego oiechni enętnej oa osioa siła ociągająca ostająca na skutek iałania ciśnienia na na komoy (enie i ysoe). Ciśnienie oboce ob. jest ciśnieniem chiloym, natomiast o obliceń ytymałościoych yjmuje się t. ciśnienie oblicenioe obl. ( ys. 1 oa kt 3.1.). Po iałaniem tego obciąŝenia ściance komoy salania ostaje okeślone ole naęŝeń. Roatując ekój oecny i łuŝny komoy (ys. 1) iimy, Ŝe kaŝy unkt ekoju (ola naęŝeń) chaakteyuje się na ogół tema naęŝeniami: omienioym (kieunek omienia), obooym łuŝnym (kieunek ónoległy o osi komoy salania). l (kieunek ostoały o omienia) i 100
3 Rys. 1. Schemat oblicenioy obciąŝeń i naęŝeń ścianki komoy salania NaęŜenia omienioe oa naęŝenia omienioe na gubości ścianki, omijając ciśnienie atmosfeycne, okeśla się oó, któe są ynikiem oiąania t. aganienia Lame go: = ob. 1 () = ob. 1 + (3) gie: ob. - ciśnienie oboce komoe salania, - omień enętny komoy salania, - omień enętny komoy salania, - omień bieŝący komoy salania. Z oyŝsych oó ynika, Ŝe atość naęŝeń aleŝy o ołoŝenia oatyanego unktu glęem osi komoy salania. Na ich ostaie oa na ostaie obliceń ytymałościoych silnikó akietoych oaonych e autoa moŝna stieić, Ŝe: naęŝenia omienioe są naęŝeniami ściskającymi (atość mniejsa o ea); osiągają maksymalną atość, óną ciśnieniu anującemu komoe salania, na enętnej oiechni komoy: = max ob. i mniejsają się o ea na enętnej ( = ) oiechni komoy. Beglęna atość tych naęŝeń jest ięc stosunkoo nieielka. naęŝenia obooe są ociągające (atość oatnia) e systkich unktach ekoju oecnego komoy; maksymalną atość osiągają one tak jak naęŝenia omienioe na oiechni enętnej ścianki i a e ostem omienia nienacnie maleją (ok. 5 %). NaęŜenia te są nacnie iękse (co najmniej o ą ielkości) niŝ naęŝenia omienioe. Na ykła la silnika o ob. = 3 MPa, = 57,5 mm i = 60 mm naęŝenia te mieniają się o 80 o 768 MPa. 101
4 NaęŜenia łuŝne l nie aleŝą o omienia i mają atość stałą. NaęŜenia te ostają ekoju oecnym kousu komoy na skutek iałania osioej siły ociągającej. Na komoę amkniętą nem enim i nem tylnym ysą kieunku łuŝnym iałają ie siły: π P1 = ob. - na enie no () π P = ob. ς ob. Fk - na no tylne ysą (5) gie: ς ob. Fk = R - ciąg silnika, ς = 1, 1,6 - sółcynnik ciągu, - ekój kytycny ysy, F k - śenica enętna komoy salania. Na komoę iałają atem kieunku ecinym ie nieóne siły. Onaca to, Ŝe komoa bęie się emiescać i ociągać. Py tym siłą ociągającą jest siła mniejsa iałających sił cyli siła P, aś esuającą óŝnica iałających sił cyli siła ciągu silnika. Po iałaniem siły P oecnym ekoju komoy ostają naęŝenia ynosące: ob. F k P ς ς k = = = ob. (6) π π ( ) ( ) π gie: - śenica enętna komoy salani, - śenica kytycna ysy. k Poónując algebaicne ielkości, i głónym jest naęŝenie obooe ; najmniejsym naęŝenie omienioe iimy, e najięksym naęŝeniem,a najiękse ytęŝenie mateiału komoy y oatyaniu tylko naęŝeń o ciśnienia ystąi na enętnej oiechni komoy... NaęŜenia o temeatuy Pocas acy silnika akietoego ścianki komoy salania nageają się o goących gaó o temeatue ęu C. PonieaŜ ścianki nageają się nieónomienie ostają nich naęŝenia cielne. NaęŜenia te, scególnie gy ścianki nie są okyte temoiolacja, naleŝy uglęnić y obliceniach ytymałości komoy. NaęŜenia cielne aleŝą ee systkim o saku temeatuy na ściance silnika oa o geometycnych chaakteystyk oecnego ekoju kousu komoy. Woy na oblicanie tych naęŝeń są nastęujące: 10
5 E α max = f1 (7) 1 µ E α max = f (8) 1 µ = + (9) gie: E - mouł sęŝystości Younga mateiału ścianki, α - sółcynnik linioej osealności cielnej mateiału ścianki, max - saek temeatuy na gubości ścianki komoy, µ - sółcynnik Poissona, f 1, f - funkcje uglęniające ły geometycnych chaakteystyk ekoju komoy na naęŝenia cielne. Postaoą tunością iąaną obliceniem naęŝeń temicnych jest okeślenie saku temeatuy na gubości ścianki cyli óŝnicy temeatuy enętnej i enętnej oiechni komoy salania. Wymaga to oiąania ónania eonicta cielnego omięy gaem a ścianką yaŝającego aleŝność mięy temeatuą, casem i sółęnymi oatyanego unktu ekoju komoy. NaęŜenia temicne omienioe są ase ujemne (ściskające) yjątkiem enętnej i enętnej oiechni komoy salania gie są óne eu. Wielkość tych naęŝeń jest nieielka. NaęŜenia obooe i łuŝne l osiągają se najiękse ujemne atości na enętnej oiechni komoy (są ściskające) nastęnie okolicach ołoy gubości ścianki naęŝenia te eują się i osiągają na oiechni enętnej atość oatnią (są ociągające)..3. Sumaycne naęŝenia o ciśnienia i temeatuy Sumaycne naęŝenia o ciśnienia i temeatuy oblica się na ostaie ou (1). W liteatue fachoej tuno naleźć ane otycące atości algebaicnych naęŝeń o ciśnienia, a scególnie o temeatuy na gubości ścianki la ecyistego silnika. Dlatego la oceny ilościoej tych naęŝeń oa naęŝeń sumaycnych oano (tabela 1) ane oblicenioe la silnika ytoconego y omaianiu naęŝeń o ciśnienia ( max = 98,3 C - ścianka okyta temoiolacją o gubości 0,5 mm, cas acy silnika τ = 0,6 s.). abela 1 Pomień NaęŜenia omienioe NaęŜenia obooe NaęŜenia łuŝne [mm] [MPa] [MPa] [MPa] [MPa] [MPa] [MPa] [MPa] [MPa] [MPa] = 57,5-3,1 0-3,1 +801,7-1,3 +587, -1,3 +83,6 = 58,15-5, -1,5-6,7 +79,8-78, +71,6-79,7 +18, = 57,75-16,5-1,8-18,3 +78,1 +19,3 +803, +97,9 +17,5 +315, = 57,375-8,1-1,1-9, +775,7 +77,9 +853,6 +76,8 +37,7 = ,6 +96,9 +86,5 +96,
6 3. Ocena ytymałości komoy salania W yaku oatyania ieloosioego stanu naęŝeń la oceny ytymałości komoy salania koysta się ojęcia naęŝenia eukoanego. Pe naęŝenie to oumie się astęce naęŝenie ociągające, któego iałanie anym unkcie yołuje taki sam stan naęŝenia, jak iałanie ecyistych naęŝeń głónych. Do oblicenia koysta się hiotey ytymałościoej Hubea (hiotea enegii okstałcenia ostacioego), co oala na naisanie aunku ytymałościoego la komoy ostaci: = 1 [( ) ( ) ( ) ] + + o. (10) gie: o. - naęŝenia ouscalne la mateiału komoy. W yaku analioanego silnika oblicone naęŝenie eukoane na gubości ścianki okaano tabeli. abela Pomień [mm] = 57,5 = 58,15 = 58,75 = 59,375 = 60 [MPa] Z tabeli 1 i ynika, Ŝe y oatyaniu tylko naęŝeń o ciśnienia maksymalne ytęŝenie mateiału komoy ystęuje na enętnej oiechni komoy. Natomiast y uglęnieniu takŝe naęŝeń o temeatuy najbaiej obciąŝona jest oiechnia enętna Paktycne saenie ytymałości komoy salania (gubości ścianki) silnika; oblicenia la ocisku akietoego M-1OF. W ocątkoej faie konstuoania silnika akietoego (na ostaie Z na ocisk) okeśla się jego aamety balistycne (ojekt balistycny) tn. ustala się ciśnienie oboce silnika ob., cas acy silnika, kstałt i ymiay łaunku naęoego oa aamety konstukcyjne tj. śenicę enętną komoy salania i stęną gubość ścianki silnika δ. W aktyce y ojektoaniu silnika akietoego bao tuno jest ocenić ytymałość yjętej komoy salania (gubości ścianki silnika) uglęniając tójosioy stan naęŝeń oa atość naęŝeń cielnych. Dlatego, co takŝe ynika analiy oanych atości naęŝeń (tabela 1 i ) taką ocenę la silnika temoiolacją lub kótkim casem salania łaunku moŝna eoaić nastęujący nacne uoscony sosób: a) oblicenia eoaa się la oiechni enętnej komoy salania; maksymalne ytęŝenie mateiału, b) naęŝenia omienioe aóno o ciśnienia jak i temeatuy na oiechni enętnej komoy się eują, latego naęŝenia te obliceniach omija się, c) naęŝenia obooe o ciśnienia okeśla się yjmując, Ŝe gubość ścianki komoy oónaniu e śenicą jest stosunkoo mała i moŝna ałoŝyć, Ŝe naęŝenie jest stałe na całej gubości ścianki i okłaa się niej ónomienie. W takim yaku oblica się ostej aleŝności: 10
7 obl. = (11) δ ostaiając amiast ob. t. ciśnienie oblicenioe, któe okeśla się jako: = k k (1) obl. 1 o max( + 50 C) gie: - maksymalne ciśnienie oboce oblicone ciśnienia ónoagi [3] o max( + 50 C) la skajnej oatniej tem. eksloatacyjnej; eguły jest to +50 C, k 1, k - sółcynniki uglęniające toleancję na out ciśnienia la atii oukcyjnej łaunku naęoego oa skok (ik) ciśnienia y ałonie łaunku. ) onieaŝ naęŝenia temicne na oiechni enętnej komoy salania ooują ost naęŝeń obooych o ok. 10%, naęŝenia oblicone ou (11) ięksa się o taką atość i taktuje jako sumaycne naęŝenia obooe o ciśnienia i temeatuy, e) naęŝenia łuŝne l ynaca się uosconego ou (6): = obl R o. max( + 50 C) δ π δ (13) gie: R o max( 50 C) - ciąg maksymalny la skajnej oatniej tem. eksloatacyjnej; eguły jest to +50 C (ooiaający + obl. ), f) onieaŝ naęŝenia temicne na oiechni enętnej komoy salania ooują ost naęŝeń łuŝnych o ok. 30%, naęŝenia oblicone ou (13) ięksa się o taką atość i taktuje jako sumaycne naęŝenia łuŝne o ciśnienia i temeatuy, g) o ynaceniu sumaycnych naęŝeń obooych i łuŝnych saa się ostatecnie aunek ytymałościoy (10), któy la eoych naęŝeń omienioych moŝna aisać ostaci: = + (1) o. Jako naęŝenie ouscalne o. yjmuje się eguły ganicę lastycności mateiału, któego jest ykonana komoa uglęnieniem sółcynnika beieceństa ónego ykle 1,. WaŜne jest ónieŝ, aby uglęnić y okeślaniu mianę (obniŝenie) chaakteystyk ytymałościoych mateiału aleŝności o. o ostu temeatuy ścianki komoy. Peoaone estaiony sosób oblicenia ytymałościoe la silnika ocisku M-1OF tj. la obl. = 0,6 MPa, = 113,5 mm, δ = 3,3 mm, R obl. = 5500 N ały nastęujące yniki: = 335MPa ; = 35,5MPa ; 390MPa = 131MPa ; = 39, 3MPa ; 170MPa 105
8 = 339MPa Kałub tylny silnika (maksymalne nageanie) ykonany jest e stali stooej 8W13N, la któej ganica lastycności ynosi 850 MPa. W końcu lat osiemiesiątych eoaono baania stacjonane silnikó akietoych yobu M-1OF temostatoanych tem. +50 C omiaem temeatuy tylnej cęści komoy (y ysy). W miejscach umiescenia cujnikó temeatuy usunięto astę temoiolacji na enętnej oiechni komoy ostokątach o ymiaach 0x0 mm. Stieono, e śenia temeatua ścianki silnika ocas jego acy ynosi tych miejscach ś o +600 C. ZałoŜono, Ŝe stal stooa 8W13N bęie miała tej temeatue ganicę lastycności óna ok. 60% jej atości tem. +0 C. Pyjmując sółcynnik beieceństa óny 1, ynacono naęŝenia ouscalne MPa i ostatecnie stieono, Ŝe: o. = 5 = 339MPa < o. = 5MPa Onaca to, e ytymałość komoy salania jest ystacająca, a gubość ścianki ostała obana e nacnym aasem ytymałości, gyŝ y uglęnieniu temoiolacji i aunkach ynamicnych ( locie) temeatua ścianki bęie uŝo niŝsa. Oacoany oaciu o oyŝsą metoę ukła naęoy imitatoa celu oietnego GROM (cas acy 0,6 s., ścianka be temoiolacji) eseł omyślnie baania oligonoe stelaniem, co skauje, Ŝe moŝna ją aktycnie stosoać.. Posumoanie Oblicanie ytymałości komoy salania silnika akietoego na alio stale olega na kolejnym oiąaniu óch ostaoych aań. Piese nich oblicenia balistycne i konstukcyjne soaa się o stęnego okeślenia gubości ścianki komoy, któa la yjętego mateiału komoy oinna abeiecyć ooienim aasem ytymałość komoy na obciąŝenia ostałe o ciśnienia gaó enąt komoy oa obciąŝenia temicne iąane nieónomienym nageaniem się ścianki ocas acy silnika. Py oiąaniu tego aania uglęnia się ykle tylko najiękse iałających naęŝeń cyli naęŝenia obooe o ciśnienia i okeśla się niebęną gubość ścianki ekstałconego ou (11). Ustalenie gubości ścianki oala okeślić masę konstukcji silnika. JeŜeli masa jest byt uŝa naleŝy mienić mateiał na baiej ytymały, eiieć temoiolację komoy lub elicyć otónie balistykę enętną silnika (mniejsyć ciśnienie komoe). Po skoygoaniu gubości ścianki komoy oiąuje się ugie aanie oblicenia ytymałości oblicenia saające, któe eoaa się gonie metoyka oaną kt Py obliceniach ytymałościoych silnika naleŝy uglęnić saek łasności mechanicnych mateiału komoy iąany temeatuą ścianki (mniejsenie naęŝeń ouscalnych). NaleŜy auaŝyć, Ŝe okeślona na ostaie obliceń ytymałościoych gubość ścianki komoy salania jest gubością minimalną, abeiecająca ytymałość komoy o iałających obciąŝeń. W ysunku konstukcyjnym komoy o tej gubości naleŝy oać nastęujące naatki technologicne: - naatek na toleancję ykonania śenicy enętnej i enętnej komoy (toleuje się głąb mateiału), - naatek na óŝnicę gubości ścianki na ługości komoy, któy aktyce ustala się jako oloa toleancji na śenicy. 106
9 Liteatua [1] W. Kuo, J. DołŜański Zasay ojektoania ociskó akietoych na alio stałe, Wyanicto MON, Wasaa 196. [] J. Noicki Ciśnienie acy siniku akietoym na alio stałe, PU N /00. [3] J. Weiss, S. oecki, S. Majeski Postay teoii i konstukcji silnikó akietoych na alio stałe, WA, Wasaa [] I. H. Fahutino Rakietnyje igateli tieoo tolia, MASZINOSROJENIE, Moska [5] J. M. Saio, G. J. Maing, H.E. Puniko Osnoy ojektioanja akiet na tieom toliie, WOJENNOJE IZDAELSWO MINISERSWA OBORONY SSSR, Moska [6] A. M. Siniuko Balisticeskaja akieta na tieom toliie, WOJENNOJE IZ- DAELSWO MINISERSWA OBORONY SSSR, Moska
PIŚMIENNICTWO. Dotychczas Pro Novum wykonało ocenę stanu technicznego i naprawę kilkudziesięciu walczaków produkcji krajowej i zagranicznej
 Dotychcas Pro Novum ykonało ocenę stanu technicnego i naraę kilkuiesięciu alcakó roukcji krajoej i agranicnej PIŚMIENNICTWO [1] Ea Zbroińska-Scechura Prycyny uskoeń otoró rur oaoych alcakó niektórych tyach
Dotychcas Pro Novum ykonało ocenę stanu technicnego i naraę kilkuiesięciu alcakó roukcji krajoej i agranicnej PIŚMIENNICTWO [1] Ea Zbroińska-Scechura Prycyny uskoeń otoró rur oaoych alcakó niektórych tyach
11.0. Zadania konstrukcyjne. 11.1. Wytyczne wykonania
 ostay Konstukcji Masyn - pojektoanie.0. Zaania konstukcyjne estaione poniżej aania konstukcyjne osta Konstukcji Masyn mają a cel aponanie stuentó pebiegiem typoych obliceń elementó konstukcyjnych ykoystaniem
ostay Konstukcji Masyn - pojektoanie.0. Zaania konstukcyjne estaione poniżej aania konstukcyjne osta Konstukcji Masyn mają a cel aponanie stuentó pebiegiem typoych obliceń elementó konstukcyjnych ykoystaniem
WYBRANE ZAGADNIENIA ODKSZTAŁCEŃ NAPĘDOWEGO KOŁA PNEUMATYCZNEGO CIĄGNIKA ROLNICZEGO. Bronisław Kolator
 MOTROL, 26, 8, 118 124 WBRANE ZAGADNIENIA ODKSZTAŁCEŃ NAPĘDOWEGO KOŁA PNEUMATCZNEGO CIĄGNIKA ROLNICZEGO Bonisław Kolato Kateda Eksploatacji Pojadów i Masyn, Uniwesytet Wamińsko-Mauski w Olstynie Stescenie.
MOTROL, 26, 8, 118 124 WBRANE ZAGADNIENIA ODKSZTAŁCEŃ NAPĘDOWEGO KOŁA PNEUMATCZNEGO CIĄGNIKA ROLNICZEGO Bonisław Kolato Kateda Eksploatacji Pojadów i Masyn, Uniwesytet Wamińsko-Mauski w Olstynie Stescenie.
Rozciąganie i ściskanie prętów projektowanie 3
 Rozciąganie i ściskanie pętó pojektoanie 3 Sposób oziązyania pętó ozciąganych/ściskanych został omóiony ozziale. Zaania pojektoe spoazają się o okeślenia ymiaó pzekoju popzecznego pęta na postaie aunku
Rozciąganie i ściskanie pętó pojektoanie 3 Sposób oziązyania pętó ozciąganych/ściskanych został omóiony ozziale. Zaania pojektoe spoazają się o okeślenia ymiaó pzekoju popzecznego pęta na postaie aunku
14. Pole elektryczne, kondensatory, przewodniki i dielektryki. Wybór i opracowanie zadań 14.1. 14.53.: Andrzej Kuczkowski.
 III Elektycność i magnetym 4. Pole elektycne, konensatoy, pewoniki i ielektyki. Wybó i opacowanie aań 4.. 4.5.: Anej Kuckowski. 4.. Dwie niewielkie, pewoące kulki o masach ównych opowienio m i m nałaowane
III Elektycność i magnetym 4. Pole elektycne, konensatoy, pewoniki i ielektyki. Wybó i opacowanie aań 4.. 4.5.: Anej Kuckowski. 4.. Dwie niewielkie, pewoące kulki o masach ównych opowienio m i m nałaowane
Wycena europejskiej opcji kupna model ciągły
 Henyk Kogie Uniesytet ceciński Wycena euopejskiej opcji kupna model ciągły tescenie elem tego atykułu jest ukaanie paktycnego ykoystania metody matyngałoej dla pocesó ciągłych do yceny euopejskiej opcji
Henyk Kogie Uniesytet ceciński Wycena euopejskiej opcji kupna model ciągły tescenie elem tego atykułu jest ukaanie paktycnego ykoystania metody matyngałoej dla pocesó ciągłych do yceny euopejskiej opcji
Badanie kotła parowego
 Badanie kotła aoego Instukcja do ćiczenia n 14 Badanie maszyn - laboatoium Oacoał: d inŝ. Andzej Tataek Zakład Mienicta i Ochony Atmosfey Wocła, gudzień 2006. 1. Cel i zakes ćiczenia Celem ćiczenia jest
Badanie kotła aoego Instukcja do ćiczenia n 14 Badanie maszyn - laboatoium Oacoał: d inŝ. Andzej Tataek Zakład Mienicta i Ochony Atmosfey Wocła, gudzień 2006. 1. Cel i zakes ćiczenia Celem ćiczenia jest
Maria Dems. T. Koter, E. Jezierski, W. Paszek
 Sany niesalone masyn synchonicnych Maia Dems. Koe, E. Jeieski, W. Pasek Zwacie aowe pąnicy synchonicnej San wacia salonego, wany akże waciem nomalnym lb pomiaowym yskje się pe wacie acisków wonika (j (sojana
Sany niesalone masyn synchonicnych Maia Dems. Koe, E. Jeieski, W. Pasek Zwacie aowe pąnicy synchonicnej San wacia salonego, wany akże waciem nomalnym lb pomiaowym yskje się pe wacie acisków wonika (j (sojana
Ścianki szczelne. Rozwiązanie ogólne pojedynczo zakotwionej ścianki szczelnej w jednorodnym, idealnie sypkim gruncie zawodnionym
 Ścinki scene Roiąnie ogóne ojeynco kotionej ścinki scenej jenoonym, ienie sykim guncie onionym Micł oski - GiBS Ścink scen jenoonym guncie onionym WPROWADZNI Rotmy siły iłjące n ścinkę sceną umiesconą
Ścinki scene Roiąnie ogóne ojeynco kotionej ścinki scenej jenoonym, ienie sykim guncie onionym Micł oski - GiBS Ścink scen jenoonym guncie onionym WPROWADZNI Rotmy siły iłjące n ścinkę sceną umiesconą
1) Cechy geometryczne: bez współpracy przekroju belki (rys. 3.9) i szyny Pole przekroju:
 .. Pład licbo Ocenić nośność i stność beli podsunicoej jednopęsłoej o peoju popecnm monosmetcnm spaanm blach: pas gón 00 x 0 pas doln 00 x 0 śodni 0 x 5 sna 50 x 0 połącona pasem gónm ołącnie. Długość
.. Pład licbo Ocenić nośność i stność beli podsunicoej jednopęsłoej o peoju popecnm monosmetcnm spaanm blach: pas gón 00 x 0 pas doln 00 x 0 śodni 0 x 5 sna 50 x 0 połącona pasem gónm ołącnie. Długość
Laboratorium z Badania Maszyn
 Politechnika Wocłaska Instytut Techniki Cielnej i Mechaniki Płynó Zakła Mienicta i Eksloatacji Maszyn i Uzązeń Enegetycznych Laboatoiu z Baania Maszyn Ćiczenie n 5. Poia bilansoy ukłau ciełoniczego Poazący:
Politechnika Wocłaska Instytut Techniki Cielnej i Mechaniki Płynó Zakła Mienicta i Eksloatacji Maszyn i Uzązeń Enegetycznych Laboatoiu z Baania Maszyn Ćiczenie n 5. Poia bilansoy ukłau ciełoniczego Poazący:
Rozwiązanie ogólne pojedynczo zakotwionej ścianki szczelnej w jednorodnym, idealnie sypkim gruncie zawodnionym Dr inż.
 Roiąnie ogóne ojeynco kotionej ścinki scenej jenoonym, ienie sykim guncie onionym D inż. Micł oski N yiłu: Gónict i Geoinżynieii N ktey: Geomecniki, Buonict i Geotecniki Woenie Rotmy siły iłjące n ścinkę
Roiąnie ogóne ojeynco kotionej ścinki scenej jenoonym, ienie sykim guncie onionym D inż. Micł oski N yiłu: Gónict i Geoinżynieii N ktey: Geomecniki, Buonict i Geotecniki Woenie Rotmy siły iłjące n ścinkę
Podstawy Konstrukcji Maszyn
 Podstay Konstukcji Maszyn Wykład 8 Pzekładnie zębate część D inŝ. Jacek zanigoski Klasyfikacja pzekładni zębatych. Ze zględu na miejsce zazębienia O zazębieniu zenętznym O zazębieniu enętznym Klasyfikacja
Podstay Konstukcji Maszyn Wykład 8 Pzekładnie zębate część D inŝ. Jacek zanigoski Klasyfikacja pzekładni zębatych. Ze zględu na miejsce zazębienia O zazębieniu zenętznym O zazębieniu enętznym Klasyfikacja
Przykładowe zadania zaliczeniowe z Mechaniki Płynów
 Pykładoe adania alicenioe Mechaniki Płynó kieunek: Inżynieia Biomedycna 1. Wynacyć atość oa kieunek całkoitego napou hydostatycnego, jaki yiea ciec o ciężae łaściym γ = 9810 [N/m 3 ], na ścianę ABCD bionika.
Pykładoe adania alicenioe Mechaniki Płynó kieunek: Inżynieia Biomedycna 1. Wynacyć atość oa kieunek całkoitego napou hydostatycnego, jaki yiea ciec o ciężae łaściym γ = 9810 [N/m 3 ], na ścianę ABCD bionika.
Belki złożone i zespolone
 Belki łożone i espolone efinicja belki łożonej siła rowarswiająca projekowanie połąceń prkła obliceń efinicja belki espolonej ałożenia echnicnej eorii ginania rokła naprężeń normalnch prkła obliceń Belki
Belki łożone i espolone efinicja belki łożonej siła rowarswiająca projekowanie połąceń prkła obliceń efinicja belki espolonej ałożenia echnicnej eorii ginania rokła naprężeń normalnch prkła obliceń Belki
Metodyka obliczenia natężenia przepływu za pomocą anemometru skrzydełkowego.
 ZAŁĄCZNIK Metoyka obliczenia natężenia rzełyu za omocą anemometru skrzyełkoego. Prękość oietrza osi symetrii kanału oblicza się ze zoru: S max τ gzie: S roga rzebyta rzez gaz ciągu czasu trania omiaru
ZAŁĄCZNIK Metoyka obliczenia natężenia rzełyu za omocą anemometru skrzyełkoego. Prękość oietrza osi symetrii kanału oblicza się ze zoru: S max τ gzie: S roga rzebyta rzez gaz ciągu czasu trania omiaru
Wykład 3. Wymiana ciepła
 Wykład 3 Wymiana cieła. Woadenie Poce ymiany cieła jet oceem fiycnym iąanym oetenianiem ię enegii cielnej. Można yóżnić ty ooby, y omocy któych cieło może być ymieniane a) eodenie i enikanie kondukcja,
Wykład 3 Wymiana cieła. Woadenie Poce ymiany cieła jet oceem fiycnym iąanym oetenianiem ię enegii cielnej. Można yóżnić ty ooby, y omocy któych cieło może być ymieniane a) eodenie i enikanie kondukcja,
Uproszczony ilościowy opis procesu wymiany ciepła w otworze wiertniczym pomiędzy cyrkulującą płuczką a górotworem
 NAFTA-GAZ, OK LXIX, N / 03 Tadeus Spuna, Paeł Budak Instytut Nafty i Gau Uposcony ilościoy opis pocesu ymiany ciepła otoe ietnicym pomiędy cykulującą płucką a góotoem W atykule podano opis modelu matematycnego
NAFTA-GAZ, OK LXIX, N / 03 Tadeus Spuna, Paeł Budak Instytut Nafty i Gau Uposcony ilościoy opis pocesu ymiany ciepła otoe ietnicym pomiędy cykulującą płucką a góotoem W atykule podano opis modelu matematycnego
Uwagi: LABORATORIUM WYTRZYMAŁOŚCI MATERIAŁÓW. Ćwiczenie nr 16 MECHANIKA PĘKANIA. ZNORMALIZOWANY POMIAR ODPORNOŚCI MATERIAŁÓW NA PĘKANIE.
 POLITECHNIKA KRAKOWSKA WYDZIAŁ MECHANZNY INSTYTUT MECHANIKI STOSOWANEJ Zakład Mechaniki Doświadczalnej i Biomechaniki Imię i nazwisko: N gupy: Zespół: Ocena: Uwagi: Rok ak.: Data ćwicz.: Podpis: LABORATORIUM
POLITECHNIKA KRAKOWSKA WYDZIAŁ MECHANZNY INSTYTUT MECHANIKI STOSOWANEJ Zakład Mechaniki Doświadczalnej i Biomechaniki Imię i nazwisko: N gupy: Zespół: Ocena: Uwagi: Rok ak.: Data ćwicz.: Podpis: LABORATORIUM
1. Podstawy rachunku wektorowego
 1 Postaw rachunku wektorowego Wektor Wektor est wielkością efiniowaną pre ługość (mouł) kierunek iałania ora wrot Dwa wektor o tm samm moule kierunku i wrocie są sobie równe Wektor presunięt równolegle
1 Postaw rachunku wektorowego Wektor Wektor est wielkością efiniowaną pre ługość (mouł) kierunek iałania ora wrot Dwa wektor o tm samm moule kierunku i wrocie są sobie równe Wektor presunięt równolegle
BADANIE SILNIKA WYKONAWCZEGO PRĄDU STAŁEGO
 LABORATORIUM ELEKTRONIKI I ELEKTROTECHNIKI BADANIE SILNIKA WYKONAWCZEGO PRĄDU STAŁEGO Opacował: d inŝ. Aleksande Patyk 1.Cel i zakes ćwiczenia. Celem ćwiczenia jest zapoznanie się z budową, właściwościami
LABORATORIUM ELEKTRONIKI I ELEKTROTECHNIKI BADANIE SILNIKA WYKONAWCZEGO PRĄDU STAŁEGO Opacował: d inŝ. Aleksande Patyk 1.Cel i zakes ćwiczenia. Celem ćwiczenia jest zapoznanie się z budową, właściwościami
23. CAŁKA POWIERZCHNIOWA NIEZORIENTOWANA
 . CAŁKA POWIERZCHNIOWA NIEZORIENTOWANA Płat powiechniow o ównaniach paametcnch: ( ) ( ) ( ) () gdie oba jet obaem eglanm nawam płatem gładkim (płatem eglanm) gd w każdm pnkcie tego płata itnieje płacna
. CAŁKA POWIERZCHNIOWA NIEZORIENTOWANA Płat powiechniow o ównaniach paametcnch: ( ) ( ) ( ) () gdie oba jet obaem eglanm nawam płatem gładkim (płatem eglanm) gd w każdm pnkcie tego płata itnieje płacna
ANALIZA ROZDZIAŁU SIŁ HAMOWANIA POJAZDU HYBRYDOWEGO Z NAPĘDEM NA KOŁA TYLNE W ASPEKCIE REKUPERACJI ENERGII
 Zesyty Problemowe Masyny Elektrycne Nr 9/211 15 Marcin Fice, Rafał Setlak Politechnika Śląska, Gliwice ANALIZA ROZDZIAŁU SIŁ HAMOWANIA POJAZDU HYBRYDOWEGO Z NAPĘDEM NA KOŁA TYLNE W ASPEKCIE REKUPERACJI
Zesyty Problemowe Masyny Elektrycne Nr 9/211 15 Marcin Fice, Rafał Setlak Politechnika Śląska, Gliwice ANALIZA ROZDZIAŁU SIŁ HAMOWANIA POJAZDU HYBRYDOWEGO Z NAPĘDEM NA KOŁA TYLNE W ASPEKCIE REKUPERACJI
OBLICZENIA CIEPLNE WYMIENNIKA STANOWIĄCEGO UJĘCIE DOLNEGO ŹRÓDŁA CIEPŁA POWIETRZNEJ POMPY CIEPŁA
 CZASOPISMO INŻYNIERII LĄDOWEJ, ŚRODOWISKA I ARCHITEKTURY JOURNAL OF CIVIL ENGINEERING, ENVIRONMENT AND ARCHITECTURE JCEEA, t. XXXIII,. 63 (3/16), liiec-resień 2016, s. 543-552 Wojciech ZALEWSKI 1 OBLICZENIA
CZASOPISMO INŻYNIERII LĄDOWEJ, ŚRODOWISKA I ARCHITEKTURY JOURNAL OF CIVIL ENGINEERING, ENVIRONMENT AND ARCHITECTURE JCEEA, t. XXXIII,. 63 (3/16), liiec-resień 2016, s. 543-552 Wojciech ZALEWSKI 1 OBLICZENIA
DZIAŁ: HYDRODYNAMIKA ĆWICZENIE B: Wyznaczanie oporów przy przepływie płynów [OMÓWIENIE NAJWAŻNIEJSZYCH ZAGADNIEŃ] opracowanie: A.W.
![DZIAŁ: HYDRODYNAMIKA ĆWICZENIE B: Wyznaczanie oporów przy przepływie płynów [OMÓWIENIE NAJWAŻNIEJSZYCH ZAGADNIEŃ] opracowanie: A.W. DZIAŁ: HYDRODYNAMIKA ĆWICZENIE B: Wyznaczanie oporów przy przepływie płynów [OMÓWIENIE NAJWAŻNIEJSZYCH ZAGADNIEŃ] opracowanie: A.W.](/thumbs/24/4265481.jpg) DZIAŁ: HYDRODYNAMIKA ĆWICZENIE B: Wynacanie ooró ry rełyie łynó [OMÓWIENIE NAJWAŻNIEJSZYCH ZAGADNIEŃ] oracoanie: A.W. rys.. Rokład rędkości rekroju rury dla rełyu laminarnego i turbulentnego LICZBY KRYTERIALNE:
DZIAŁ: HYDRODYNAMIKA ĆWICZENIE B: Wynacanie ooró ry rełyie łynó [OMÓWIENIE NAJWAŻNIEJSZYCH ZAGADNIEŃ] oracoanie: A.W. rys.. Rokład rędkości rekroju rury dla rełyu laminarnego i turbulentnego LICZBY KRYTERIALNE:
= ± Ne N - liczba całkowita.
 POL LKTRYCZN W PRÓŻNI Ładunek - elementany Nieodłączna własność niektóych cząstek elementanych, [n. elektonu (-e), otonu (+e)], zejawiająca się w oddziaływaniu elektomagnetycznym tych cząstek. e =,6-9
POL LKTRYCZN W PRÓŻNI Ładunek - elementany Nieodłączna własność niektóych cząstek elementanych, [n. elektonu (-e), otonu (+e)], zejawiająca się w oddziaływaniu elektomagnetycznym tych cząstek. e =,6-9
dr inż. Zbigniew Szklarski
 ykład 6: Paca i enegia d inż. Zbigniew Szklaski szkla@agh.edu.l htt://laye.uci.agh.edu.l/z.szklaski/ negia a aca negia jest to wielkość skalana, okeślająca stan, w jakim znajduje się jedno lub wiele ciał.
ykład 6: Paca i enegia d inż. Zbigniew Szklaski szkla@agh.edu.l htt://laye.uci.agh.edu.l/z.szklaski/ negia a aca negia jest to wielkość skalana, okeślająca stan, w jakim znajduje się jedno lub wiele ciał.
DODATEK 6. Pole elektryczne nieskończenie długiego walca z równomiernie rozłożonym w nim ładunkiem objętościowym. Φ = = = = = π
 DODATEK 6 Pole elektycne nieskońcenie długiego walca ównomienie ołożonym w nim ładunkiem objętościowym Nieskońcenie długi walec o pomieniu jest ównomienie naładowany ładunkiem objętościowym o stałej gęstości
DODATEK 6 Pole elektycne nieskońcenie długiego walca ównomienie ołożonym w nim ładunkiem objętościowym Nieskońcenie długi walec o pomieniu jest ównomienie naładowany ładunkiem objętościowym o stałej gęstości
Wyznaczanie profilu prędkości płynu w rurociągu o przekroju kołowym
 1.Wpowadzenie Wyznaczanie pofilu pędkości płynu w uociągu o pzekoju kołowym Dla ustalonego, jednokieunkowego i uwastwionego pzepływu pzez uę o pzekoju kołowym ównanie Naviea-Stokesa upaszcza się do postaci
1.Wpowadzenie Wyznaczanie pofilu pędkości płynu w uociągu o pzekoju kołowym Dla ustalonego, jednokieunkowego i uwastwionego pzepływu pzez uę o pzekoju kołowym ównanie Naviea-Stokesa upaszcza się do postaci
4πε0ε w. q dl. a) V m 2
 Rozwiązania są moje, Batka i jeszcze te któe znaazłem w A. Niestety nie mogę zagwaantować, że są popawne :( Jeżei twoje opowiezi óżnią się o tych, to napisz o mnie (najepiej z wyjaśnienie ską bieze się
Rozwiązania są moje, Batka i jeszcze te któe znaazłem w A. Niestety nie mogę zagwaantować, że są popawne :( Jeżei twoje opowiezi óżnią się o tych, to napisz o mnie (najepiej z wyjaśnienie ską bieze się
5.1 Połączenia gwintowe
 5.0 Połączenia Połączenia służą o pzenoszenia obciążeń mięzy elementami konstukcyjnymi uniemożliwiając ich wzajemne pzemieszczenia. POŁĄCZENIA NIEROZŁĄCZNE ROZŁĄCZNE PLASTYCZNE - nitowe - zawijane - zaginane
5.0 Połączenia Połączenia służą o pzenoszenia obciążeń mięzy elementami konstukcyjnymi uniemożliwiając ich wzajemne pzemieszczenia. POŁĄCZENIA NIEROZŁĄCZNE ROZŁĄCZNE PLASTYCZNE - nitowe - zawijane - zaginane
Wyznaczanie współczynnika wnikania ciepła dla konwekcji swobodnej
 Kateda Silników Salinowych i Pojazdów ATH ZAKŁAD TERMODYNAMIKI Wyznaczanie wsółczynnika wnikania cieła dla konwekcji swobodnej - - Pojęcia odstawowe Konwekcja- zjawisko wymiany cieła między owiezchnią
Kateda Silników Salinowych i Pojazdów ATH ZAKŁAD TERMODYNAMIKI Wyznaczanie wsółczynnika wnikania cieła dla konwekcji swobodnej - - Pojęcia odstawowe Konwekcja- zjawisko wymiany cieła między owiezchnią
Endogenous tariffs, the Political Economy of Trade Restrictions, and Welfare, R. Findlay, S. Wellisz
 Endoenous tais the Political Economy o ade Restictions and Welae 198. R. Findlay S. Wellisz Założenia modelu Findleya-Wellisza Pionieski zykład zastosoania endoenicznej tayy celnej do modelu HOS (acto
Endoenous tais the Political Economy o ade Restictions and Welae 198. R. Findlay S. Wellisz Założenia modelu Findleya-Wellisza Pionieski zykład zastosoania endoenicznej tayy celnej do modelu HOS (acto
Katedra Silników Spalinowych i Pojazdów ATH ZAKŁAD TERMODYNAMIKI. Pomiar ciepła spalania paliw gazowych
 Katedra Silników Salinowych i Pojazdów ATH ZAKŁAD TERMODYNAMIKI Pomiar cieła salania aliw gazowych Wstę teoretyczny. Salanie olega na gwałtownym chemicznym łączeniu się składników aliwa z tlenem, czemu
Katedra Silników Salinowych i Pojazdów ATH ZAKŁAD TERMODYNAMIKI Pomiar cieła salania aliw gazowych Wstę teoretyczny. Salanie olega na gwałtownym chemicznym łączeniu się składników aliwa z tlenem, czemu
1. SZCZEGÓLNE PRZYPADKI ŁUKÓW.
 Olga Kopacz, Aam Łoygowski, Kzysztof Tymbe, ichał Płotkowiak, Wojciech Pawłowski Konsultacje naukowe: pof. hab. Jezy Rakowski Poznań /. SZCZEGÓLNE PRZYPADKI ŁUKÓW.. Łuk jenopzegubowy kołowy. Dla łuku jak
Olga Kopacz, Aam Łoygowski, Kzysztof Tymbe, ichał Płotkowiak, Wojciech Pawłowski Konsultacje naukowe: pof. hab. Jezy Rakowski Poznań /. SZCZEGÓLNE PRZYPADKI ŁUKÓW.. Łuk jenopzegubowy kołowy. Dla łuku jak
pionowe od kół suwnic, zgodnie z warunków równowagi statecznej (rys. 6.4) dla
 6.7. Prkład oblicania słupa pełnościennego esakad podsuwnicowej Pełnościenne słup esakad podsuwnicowej podpierają or podsuwnicowe na kórch pracują suwnice pomosowe naorowe o udźwigach i paramerach echnicnch
6.7. Prkład oblicania słupa pełnościennego esakad podsuwnicowej Pełnościenne słup esakad podsuwnicowej podpierają or podsuwnicowe na kórch pracują suwnice pomosowe naorowe o udźwigach i paramerach echnicnch
POLE ELEKTROSTATYCZNE W PRÓŻNI - CD. Dipol charakteryzuje się przez podanie jego dipolowego momentu elektrycznego p (5.1)
 POL LKTROTATYCZN W PRÓŻNI - CD Dio ktyczny q + q Dio ktyczny to ukła ównych co o watości unktowych łaunków ktycznych zciwngo znaku ozmiszczonych w stałj ogłości o sibi Dio chaaktyzuj się zz oani jgo ioowgo
POL LKTROTATYCZN W PRÓŻNI - CD Dio ktyczny q + q Dio ktyczny to ukła ównych co o watości unktowych łaunków ktycznych zciwngo znaku ozmiszczonych w stałj ogłości o sibi Dio chaaktyzuj się zz oani jgo ioowgo
2. Określenie składowych tensora naprężenia i odkształcenia
 Górnicto i Geoinżynieria ok Zesyt /1 9 Marek Cała*, Marian Paluch*, Antoni Tajduś* NIELINIWA DEFMACJA IZTPWEJ SFEY GUBŚCIENNEJ 1. Wproadenie Palia ciekłe i gaoe lub inne płyny mogą być magaynoane naiemnych
Górnicto i Geoinżynieria ok Zesyt /1 9 Marek Cała*, Marian Paluch*, Antoni Tajduś* NIELINIWA DEFMACJA IZTPWEJ SFEY GUBŚCIENNEJ 1. Wproadenie Palia ciekłe i gaoe lub inne płyny mogą być magaynoane naiemnych
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektotechniki i utomatyki Kateda Inżynieii Systemów Steowania KOMPUTEROWE SYSTEMY STEROWNI (sem. 6) Steowanie otymalizacyjne. Mateiały omocnicze Temin T8 Oacowanie: Tomasz
Politechnika Gdańska Wydział Elektotechniki i utomatyki Kateda Inżynieii Systemów Steowania KOMPUTEROWE SYSTEMY STEROWNI (sem. 6) Steowanie otymalizacyjne. Mateiały omocnicze Temin T8 Oacowanie: Tomasz
Ćw. 4. Określenie momentu i pracy tarcia w złącznych sprzęgłach ciernych. 1. Wprowadzenie do zagadnienia.
 aboaoium Podsaw Konsukcji asyn Ćw. 4. Okeślenie momenu i pacy acia w łącnych spęgłach cienych. 1. Wpowadenie do agadnienia. Spęgłem naywamy espół słuŝący do łącenia wałów. Dięki asosowaniu spęgła moŝna
aboaoium Podsaw Konsukcji asyn Ćw. 4. Okeślenie momenu i pacy acia w łącnych spęgłach cienych. 1. Wpowadenie do agadnienia. Spęgłem naywamy espół słuŝący do łącenia wałów. Dięki asosowaniu spęgła moŝna
dr inż. Zbigniew Szklarski
 ykład 5: Paca i enegia d inż. Zbigniew Szklaski szkla@agh.edu.pl http://laye.uci.agh.edu.pl/z.szklaski/ Enegia a paca Enegia jest to wielkość skalana, okeślająca stan, w jakim znajduje się jedno lub wiele
ykład 5: Paca i enegia d inż. Zbigniew Szklaski szkla@agh.edu.pl http://laye.uci.agh.edu.pl/z.szklaski/ Enegia a paca Enegia jest to wielkość skalana, okeślająca stan, w jakim znajduje się jedno lub wiele
Informacje uzupełniające: Wyboczenie z płaszczyzny układu w ramach portalowych. Spis treści
 S032a-PL-EU Informacje uupełniające: Wybocenie płascyny układu w ramach portalowych Ten dokument wyjaśnia ogólną metodę (predstawioną w 6.3.4 E1993-1-1 sprawdania nośności na wybocenie płascyny układu
S032a-PL-EU Informacje uupełniające: Wybocenie płascyny układu w ramach portalowych Ten dokument wyjaśnia ogólną metodę (predstawioną w 6.3.4 E1993-1-1 sprawdania nośności na wybocenie płascyny układu
MECHANIKA BUDOWLI 2 PRACA SIŁ WEWNĘTRZNYCH W PRĘTACH
 Oga Kopac, am Łogowski, Wojciech Pawłowski, ichał Płotkowiak, Krstof mber Konsutacje naukowe: prof. r hab. JERZY RKOWSKI Ponań /3 ECHIK BUDOWI Praca sił normanch Siła normana prpomnienie (): Jest to siła
Oga Kopac, am Łogowski, Wojciech Pawłowski, ichał Płotkowiak, Krstof mber Konsutacje naukowe: prof. r hab. JERZY RKOWSKI Ponań /3 ECHIK BUDOWI Praca sił normanch Siła normana prpomnienie (): Jest to siła
Analiza uchybowa układów dyskretnych
 Akademia Moska w Gdyni ateda Automatyki Okętowej eoia steowania Analia uchybowa układów dysketnych Miosław omea. WPOWADZENIE Analia uchybowa eowadona w tym oacowaniu oganicona jest tylko do układów jednostkowym
Akademia Moska w Gdyni ateda Automatyki Okętowej eoia steowania Analia uchybowa układów dysketnych Miosław omea. WPOWADZENIE Analia uchybowa eowadona w tym oacowaniu oganicona jest tylko do układów jednostkowym
 Ą Ś Ś ż Ż ć Ś Ż Ś Ń Ó Ż ć Ź ć ć Ż Ź Ś Ą Ą Ż Ś Ą ĘĄ Ś Ę ŚĘ Ę Ó Ś Ą ć Ś ź Ś ż Ż Ź ć ć ć Ą ć ć Ź ć ć ć ć Ś ć Ż ć ć Ą ć Ż ć Ż ć Ż Ż Ż ć Ż ć Ż ć Ż ż ź Ą ż ć Ż Ź Ż Ś Ż Ś Ą ż Ą Ż ź Ż ż ć Ż Ż Ą Ś Ź ć Ś ż Ź ż Ł
Ą Ś Ś ż Ż ć Ś Ż Ś Ń Ó Ż ć Ź ć ć Ż Ź Ś Ą Ą Ż Ś Ą ĘĄ Ś Ę ŚĘ Ę Ó Ś Ą ć Ś ź Ś ż Ż Ź ć ć ć Ą ć ć Ź ć ć ć ć Ś ć Ż ć ć Ą ć Ż ć Ż ć Ż Ż Ż ć Ż ć Ż ć Ż ż ź Ą ż ć Ż Ź Ż Ś Ż Ś Ą ż Ą Ż ź Ż ż ć Ż Ż Ą Ś Ź ć Ś ż Ź ż Ł
Konstrukcja i wymiary wybranych gwintów znormalizowanych
 Rozział 4 Konstrukcja i wymiary wybranych gwintów znormalizowanych Kazimierz Łyczko 4.1. y metryczne 4.1.1. y metryczne ISO ogólnego przeznaczenia zwykłe i robnozwojne y metryczne ISO ogólnego przeznaczenia
Rozział 4 Konstrukcja i wymiary wybranych gwintów znormalizowanych Kazimierz Łyczko 4.1. y metryczne 4.1.1. y metryczne ISO ogólnego przeznaczenia zwykłe i robnozwojne y metryczne ISO ogólnego przeznaczenia
ĆWICZENIE 5. Badanie przekaźnikowych układów sterowania
 ĆWICZENIE 5 Badanie zekaźnikowych układów steowania 5. Cel ćwiczenia Celem ćwiczenia jest badanie zekaźnikowych układów steowania obiektem całkującoinecyjnym. Ćwiczenie dotyczy zekaźników dwu- i tójołożeniowych
ĆWICZENIE 5 Badanie zekaźnikowych układów steowania 5. Cel ćwiczenia Celem ćwiczenia jest badanie zekaźnikowych układów steowania obiektem całkującoinecyjnym. Ćwiczenie dotyczy zekaźników dwu- i tójołożeniowych
ObciąŜenia układu kierowniczego w granicznych stanach ruchu samochodu osobowego
 JANCZUR Robert KURANOWSKI Aleksander ObciąŜenia układu kieronicego granicnych stanach ruchu samochodu osoboego WSTĘP Układ kieronicy ojadu samochodoego oinien sełniać odoiednie ymagania iąane komfortem
JANCZUR Robert KURANOWSKI Aleksander ObciąŜenia układu kieronicego granicnych stanach ruchu samochodu osoboego WSTĘP Układ kieronicy ojadu samochodoego oinien sełniać odoiednie ymagania iąane komfortem
dr inż. Zbigniew Szklarski
 Wykład 6: Paca i enegia d inż. Zbigniew Szklaski szkla@agh.edu.l htt://laye.uci.agh.edu.l/z.szklaski/ negia a aca negia jest to wielkość skalana, okeślająca stan, w jakim znajduje się jedno lub wiele ciał.
Wykład 6: Paca i enegia d inż. Zbigniew Szklaski szkla@agh.edu.l htt://laye.uci.agh.edu.l/z.szklaski/ negia a aca negia jest to wielkość skalana, okeślająca stan, w jakim znajduje się jedno lub wiele ciał.
POMIAR PĘTLI HISTEREZY MAGNETYCZNEJ
 POMAR PĘTL STEREZ MAGNETZNEJ 1. Opis teoetyczny do ćwiczenia zamieszczony jest na stonie www.wtc.wat.edu.pl w dziale DDAKTKA FZKA ĆZENA LABORATORJNE.. Opis układu pomiaowego Mateiały feomagnetyczne (feyt,
POMAR PĘTL STEREZ MAGNETZNEJ 1. Opis teoetyczny do ćwiczenia zamieszczony jest na stonie www.wtc.wat.edu.pl w dziale DDAKTKA FZKA ĆZENA LABORATORJNE.. Opis układu pomiaowego Mateiały feomagnetyczne (feyt,
Funkcje analityczne. Wykład 13. Zastosowanie rachunku residuów do rozwiązywania problemów analizy rzeczywistej. Paweł Mleczko
 Funkcje analitycne Wykład 3. Zastosowanie achunku esiduów do owiąywania poblemów analiy ecywistej Paweł Mlecko Funkcje analitycne ok akademicki 8/9 Plan wykładu W casie wykładu omawiać będiemy astosowanie
Funkcje analitycne Wykład 3. Zastosowanie achunku esiduów do owiąywania poblemów analiy ecywistej Paweł Mlecko Funkcje analitycne ok akademicki 8/9 Plan wykładu W casie wykładu omawiać będiemy astosowanie
Przejmowanie ciepła przy konwekcji swobodnej w przestrzeni ograniczonej (szczeliny)
 inż. Michał Stzeszewski 0-006 Pzejowanie ciepła pzy konwekcji swobonej w pzestzeni oganiczonej (szczeliny) Zaania o saozielnego ozwiązania v. 0.. powazenie celu uposzczenia achunkowego ozwiązania zjawiska
inż. Michał Stzeszewski 0-006 Pzejowanie ciepła pzy konwekcji swobonej w pzestzeni oganiczonej (szczeliny) Zaania o saozielnego ozwiązania v. 0.. powazenie celu uposzczenia achunkowego ozwiązania zjawiska
Powłoki osiowosymetryczne
 yymałść maeiałów i knsukcji ykład 1 Pwłki siwsymeycne Pykłady D inż. Pi Maek Zad.1. Zbinik łżny cęści sżkwej, walcwej i kulisej, day na ieścieniu, wyełniny jes ciecą d imu łącenia walca kulą. Pwyżej ciecy
yymałść maeiałów i knsukcji ykład 1 Pwłki siwsymeycne Pykłady D inż. Pi Maek Zad.1. Zbinik łżny cęści sżkwej, walcwej i kulisej, day na ieścieniu, wyełniny jes ciecą d imu łącenia walca kulą. Pwyżej ciecy
METEMATYCZNY MODEL OCENY
 I N S T Y T U T A N A L I Z R E I O N A L N Y C H w K i e l c a c h METEMATYCZNY MODEL OCENY EFEKTYNOŚCI NAUCZNIA NA SZCZEBLU IMNAZJALNYM I ODSTAOYM METODĄ STANDARYZACJI YNIKÓ OÓLNYCH Auto: D Bogdan Stępień
I N S T Y T U T A N A L I Z R E I O N A L N Y C H w K i e l c a c h METEMATYCZNY MODEL OCENY EFEKTYNOŚCI NAUCZNIA NA SZCZEBLU IMNAZJALNYM I ODSTAOYM METODĄ STANDARYZACJI YNIKÓ OÓLNYCH Auto: D Bogdan Stępień
Instalacje pompowe. Zadania do samodzielnego rozwiązania v ,1. dr inż. Michał Strzeszewski,
 dr inż. Michał Stresewski, 00-008 Instalacje omowe Zadania do samodielnego rowiąania v. 1.5 Zadanie 1 Obli wymaganą wydajność omy obiegowej ry nastęujących ałożeniach: oblieniowa moc cielna instalacji
dr inż. Michał Stresewski, 00-008 Instalacje omowe Zadania do samodielnego rowiąania v. 1.5 Zadanie 1 Obli wymaganą wydajność omy obiegowej ry nastęujących ałożeniach: oblieniowa moc cielna instalacji
ANALIZA KONSTRUKCJI POWŁOKOWEJ. CIENKOŚCIENNY ZBIORNIK CIŚNIENIOWY
 Cw3_biornik.doc ANALIZA KONTRUKCJI POWŁOKOWEJ. CIENKOŚCIENNY ZBIORNIK CIŚNIENIOWY 1. W P R O W A D Z E N I E Ciało utworone pre dwie akrwione powierchnie nawane jest powłoką, jeśli preciętna odlełość pomięd
Cw3_biornik.doc ANALIZA KONTRUKCJI POWŁOKOWEJ. CIENKOŚCIENNY ZBIORNIK CIŚNIENIOWY 1. W P R O W A D Z E N I E Ciało utworone pre dwie akrwione powierchnie nawane jest powłoką, jeśli preciętna odlełość pomięd
Propagacja impulsu. Literatura. B.E.A. Saleh i M.C. Teich: Fundamentals of Photonics. John Wiley & Sons, Inc. New York 1991, rozdział 5 ( 5.
 Literatura Propagacja impulsu B.E.A. Saleh i M.C. Teich: Funamentals of Photonics. John Wiley & Sons, Inc. New York 99, roiał 5 ( 5.6) pomocnica alecana naukowa Propagacja impulsu w ośroku yspersyjnym
Literatura Propagacja impulsu B.E.A. Saleh i M.C. Teich: Funamentals of Photonics. John Wiley & Sons, Inc. New York 99, roiał 5 ( 5.6) pomocnica alecana naukowa Propagacja impulsu w ośroku yspersyjnym
TEMAT: Próba statyczna rozciągania metali. Obowiązująca norma: PN-EN 10002-1:2002(U) Zalecana norma: PN-91/H-04310 lub PN-EN10002-1+AC1
 ĆWICZENIE NR 1 TEMAT: Próba statycna rociągania metali. Obowiąująca norma: PN-EN 10002-1:2002(U) Zalecana norma: PN-91/H-04310 lub PN-EN10002-1+AC1 Podać nacenie następujących symboli: d o -.....................................................................
ĆWICZENIE NR 1 TEMAT: Próba statycna rociągania metali. Obowiąująca norma: PN-EN 10002-1:2002(U) Zalecana norma: PN-91/H-04310 lub PN-EN10002-1+AC1 Podać nacenie następujących symboli: d o -.....................................................................
Władcy Skandynawii opracował
 W Ł~ D C Y S K~ N D Y N~ W I I K R Ó L O W I E D ~ N I IW. K J S O L D U N G O W I E 1 K R Ó L O W I E D ~ N I IW. K J S O L D U N G O W I E 2 Władcy Skandynawii G E N E~ L O G I~ K R Ó L Ó W D~ N O R
W Ł~ D C Y S K~ N D Y N~ W I I K R Ó L O W I E D ~ N I IW. K J S O L D U N G O W I E 1 K R Ó L O W I E D ~ N I IW. K J S O L D U N G O W I E 2 Władcy Skandynawii G E N E~ L O G I~ K R Ó L Ó W D~ N O R
14. Regulatory w układach z opóźnieniem Wprowadzenie. Hs () Ws () Es () Ys () Us () Vs ()
 4. Regulatoy układach opóźnieniem 4.0. Wpoadenie Z s u( ) Z s y( ) Ws () Es () G s ( ) Us () G s o( ) Ys () Vs () Hs () Rys. 4.. Schemat blokoy układu egulacji opóźnieniem Ped omóieniem egulatoó stosoanych
4. Regulatoy układach opóźnieniem 4.0. Wpoadenie Z s u( ) Z s y( ) Ws () Es () G s ( ) Us () G s o( ) Ys () Vs () Hs () Rys. 4.. Schemat blokoy układu egulacji opóźnieniem Ped omóieniem egulatoó stosoanych
Własności koligatywne
 Własności koligatyne Własnościami koligatynymi nazyamy łasności roztorach rozcieńczonych zależne yłącznie od liczby cząsteczek (a naet szerzej indyiduó chemicznych) substancji rozuszczonej a nie od ich
Własności koligatyne Własnościami koligatynymi nazyamy łasności roztorach rozcieńczonych zależne yłącznie od liczby cząsteczek (a naet szerzej indyiduó chemicznych) substancji rozuszczonej a nie od ich
5b. Obliczanie grubości okrągłych den płaskich
 5b. Obliczanie ubści ąłych den łaskich Śednice śednic, zaówn zewnętnych z jak i wewnętnych w, są znmalizwane i zdnie z nmą BN-64/01-01 wynszą: 0.19, 0.73, 0.34, 0.356, 0.406, 0.457 lub 0.508 [m]. w 0.6,
5b. Obliczanie ubści ąłych den łaskich Śednice śednic, zaówn zewnętnych z jak i wewnętnych w, są znmalizwane i zdnie z nmą BN-64/01-01 wynszą: 0.19, 0.73, 0.34, 0.356, 0.406, 0.457 lub 0.508 [m]. w 0.6,
PRAWA ZACHOWANIA Prawa zachowania najbardziej fundamentalne prawa:
 PRW ZCHOWNI Pawa achowania nabadie fundamentalne pawa: o ewnętne : pawo achowania pędu, pawo achowania momentu pędu, pawo achowania enegii; o wewnętne : pawa achowania np. całkowite licb nukleonów w eakci
PRW ZCHOWNI Pawa achowania nabadie fundamentalne pawa: o ewnętne : pawo achowania pędu, pawo achowania momentu pędu, pawo achowania enegii; o wewnętne : pawa achowania np. całkowite licb nukleonów w eakci
A - przepływ laminarny, B - przepływ burzliwy.
 PRZEPŁYW CZYNNIK ŚCIŚLIWEGO. Definicje odstaoe Rys... Profile rędkości rurze. - rzeły laminarny, B - rzeły burzliy. Liczba Reynoldsa Re D [m/s] średnia rędkość kanale D [m] średnica enętrzna kanału ν [m
PRZEPŁYW CZYNNIK ŚCIŚLIWEGO. Definicje odstaoe Rys... Profile rędkości rurze. - rzeły laminarny, B - rzeły burzliy. Liczba Reynoldsa Re D [m/s] średnia rędkość kanale D [m] średnica enętrzna kanału ν [m
Document: Exercise-03-manual --- 2014/12/10 --- 8:54--- page 1 of 8 INSTRUKCJA DO ĆWICZENIA NR 3. Optymalizacja wielowarstwowych płyt laminowanych
 Document: Exercise-03-manual --- 2014/12/10 --- 8:54--- page 1 of 8 PRZEDMIOT TEMAT KATEDRA MECHANIKI STOSOWANEJ Wydiał Mechanicny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 3 1. CEL ĆWICZENIA Wybrane
Document: Exercise-03-manual --- 2014/12/10 --- 8:54--- page 1 of 8 PRZEDMIOT TEMAT KATEDRA MECHANIKI STOSOWANEJ Wydiał Mechanicny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 3 1. CEL ĆWICZENIA Wybrane
Rys. 29. Schemat obliczeniowy płyty biegowej i spoczników
 Przykład obliczeniowy schodów wg EC-2 a) Zebranie obciąŝeń Szczegóły geometryczne i konstrukcyjne przedstawiono poniŝej: Rys. 28. Wymiary klatki schodowej w rzucie poziomym 100 224 20 14 9x 17,4/28,0 157
Przykład obliczeniowy schodów wg EC-2 a) Zebranie obciąŝeń Szczegóły geometryczne i konstrukcyjne przedstawiono poniŝej: Rys. 28. Wymiary klatki schodowej w rzucie poziomym 100 224 20 14 9x 17,4/28,0 157
MODEL MATEMATYCZNY PROCESU EKSPLOATACJI POJAZDÓW MECHANICZNYCH
 Stanisła NIZIŃSKI Słaomir IERZBICKI MODEL MATEMATYCZNY PROCESU EKSPLOATACJI POJAZDÓ MECHANICZNYCH Model of exloatation rocess of mechanical vehicles stę fazie eksloatacji ojazdó mechanicznych zachodzą
Stanisła NIZIŃSKI Słaomir IERZBICKI MODEL MATEMATYCZNY PROCESU EKSPLOATACJI POJAZDÓ MECHANICZNYCH Model of exloatation rocess of mechanical vehicles stę fazie eksloatacji ojazdó mechanicznych zachodzą
Prawo powszechnego ciążenia Newtona
 Pawo powszechnego ciążenia Newtona m M FmM Mm =G 2 Mm FMm = G 2 Stała gawitacji G = 6.67 10 11 2 Nm 2 kg Wielkość siły gawitacji z jaką pzyciągają się wzajemnie ciała na Ziemi M = 100kg N M = Mg N m =
Pawo powszechnego ciążenia Newtona m M FmM Mm =G 2 Mm FMm = G 2 Stała gawitacji G = 6.67 10 11 2 Nm 2 kg Wielkość siły gawitacji z jaką pzyciągają się wzajemnie ciała na Ziemi M = 100kg N M = Mg N m =
9. 1. KOŁO. Odcinki w okręgu i kole
 9.. KOŁO Odcinki w okęgu i kole Cięciwa okęgu (koła) odcinek łączący dwa dowolne punkty okęgu d Śednica okęgu (koła) odcinek łączący dwa dowolne punkty okęgu pzechodzący pzez śodek okęgu (koła) Pomień
9.. KOŁO Odcinki w okęgu i kole Cięciwa okęgu (koła) odcinek łączący dwa dowolne punkty okęgu d Śednica okęgu (koła) odcinek łączący dwa dowolne punkty okęgu pzechodzący pzez śodek okęgu (koła) Pomień
Przykład: Projektowanie poŝarowe nieosłoniętego słupa stalowego według standardowej krzywej temperatura-czas
 Dokument Ref: SX043a-PL-EU Strona 1 5 Prykład: Projektowanie poŝarowe nieosłoniętego słupa stalowego według standardowej krywej temperatura-cas Wykonał Z. Sokol Data styceń 006 Sprawdił F. Wald Data styceń
Dokument Ref: SX043a-PL-EU Strona 1 5 Prykład: Projektowanie poŝarowe nieosłoniętego słupa stalowego według standardowej krywej temperatura-cas Wykonał Z. Sokol Data styceń 006 Sprawdił F. Wald Data styceń
11. DYNAMIKA RUCHU DRGAJĄCEGO
 11. DYNAMIKA RUCHU DRGAJĄCEGO Ruchem dgającym nazywamy uch, któy powtaza się peiodycznie w takcie jego twania w czasie i zachodzi wokół położenia ównowagi. Zespół obiektów fizycznych zapewniający wytwozenie
11. DYNAMIKA RUCHU DRGAJĄCEGO Ruchem dgającym nazywamy uch, któy powtaza się peiodycznie w takcie jego twania w czasie i zachodzi wokół położenia ównowagi. Zespół obiektów fizycznych zapewniający wytwozenie
TEORIA SPRĘŻYSTOŚCI 10
 W YKŁ ADY Z T EOII S ĘŻYSTOŚCI ZADANIE BOUSSINESQA I FLAMANTA olitechnika onańska Kopac, Kawck, Łodgowski, łotkowiak, Świtek, Tmpe Olga Kopac, Kstof Kawck, Adam Łodgowski, Michał łotkowiak, Agnieska Świtek,
W YKŁ ADY Z T EOII S ĘŻYSTOŚCI ZADANIE BOUSSINESQA I FLAMANTA olitechnika onańska Kopac, Kawck, Łodgowski, łotkowiak, Świtek, Tmpe Olga Kopac, Kstof Kawck, Adam Łodgowski, Michał łotkowiak, Agnieska Świtek,
Wykład 10 I zasada termodynamiki; perpetuum mobile I rodzaju Układy i procesy zgodne z I zasadą ale niezachodzące ( praca z ciepła i ciepło z zimna )
 ykła 10 I zasaa termoynamiki; perpetuum mobile I rozaju Ukłay i procesy zone z I zasaą ale niezachozące ( praca z ciepła i ciepło z zimna ) Silniki cieplne, chłoziarki i pompy cieplne II zasaa termoynamiki
ykła 10 I zasaa termoynamiki; perpetuum mobile I rozaju Ukłay i procesy zone z I zasaą ale niezachozące ( praca z ciepła i ciepło z zimna ) Silniki cieplne, chłoziarki i pompy cieplne II zasaa termoynamiki
dr inż. Zbigniew Szklarski
 ykład 5: Paca i enegia d inż. Zbigniew Szklaski szkla@agh.edu.pl http://laye.uci.agh.edu.pl/z.szklaski/ Enegia a paca Enegia jest to wielkość skalana, okeślająca stan, w jakim znajduje się jedno lub wiele
ykład 5: Paca i enegia d inż. Zbigniew Szklaski szkla@agh.edu.pl http://laye.uci.agh.edu.pl/z.szklaski/ Enegia a paca Enegia jest to wielkość skalana, okeślająca stan, w jakim znajduje się jedno lub wiele
KINEMATYKA. Pojęcia podstawowe
 KINEMTYK Pojęcia podstawowe Kinematka jest diałem mechaniki ajmującm się badaniem uchu ciał be uwględniania pcn wwołującch ten uch. Jej celem jest opis tego uchu. Ruchem nawam mianę położenia ciała w odniesieniu
KINEMTYK Pojęcia podstawowe Kinematka jest diałem mechaniki ajmującm się badaniem uchu ciał be uwględniania pcn wwołującch ten uch. Jej celem jest opis tego uchu. Ruchem nawam mianę położenia ciała w odniesieniu
Cieplne Maszyny Przepływowe. Temat 8 Ogólny opis konstrukcji promieniowych maszyn wirnikowych. Część I Podstawy teorii Cieplnych Maszyn Przepływowych.
 Temat 8 Ogólny opis konstkcji 06 8. Wstęp Istnieje wiele typów i ozwiązań konstkcyjnych. Mniejsza wiedza dotycząca zjawisk pzepływowych Niski koszt podkcji Kótki cykl pojektowy Solidna konstkcja pod względem
Temat 8 Ogólny opis konstkcji 06 8. Wstęp Istnieje wiele typów i ozwiązań konstkcyjnych. Mniejsza wiedza dotycząca zjawisk pzepływowych Niski koszt podkcji Kótki cykl pojektowy Solidna konstkcja pod względem
W płaszczowo-rurowych wymiennikach ciepła pęczek rur umieszczany jest w płaszczu najczęściej o przekroju kołowym.
 Wnikanie ciepła pry opłyie pęcka rur 1. Wdłużny opły pęcka W płascoo-ruroych ymiennikach ciepła pęcek rur umiescany jest płascu najcęściej o prekroju kołoym. Rys. 1-1. Wymiennik płascoo-ruroy, rónoległo
Wnikanie ciepła pry opłyie pęcka rur 1. Wdłużny opły pęcka W płascoo-ruroych ymiennikach ciepła pęcek rur umiescany jest płascu najcęściej o prekroju kołoym. Rys. 1-1. Wymiennik płascoo-ruroy, rónoległo
Rozdział 1. Nazwa i adres Zamawiającego Gdyński Ośrodek Sportu i Rekreacji jednostka budżetowa Rozdział 2.
 Z n a k s p r a w y G O S I R D Z P I 2 7 1 03 3 2 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f U d o s t p n i e n i e t e l e b i m ó w i n a g ł o n i e n i
Z n a k s p r a w y G O S I R D Z P I 2 7 1 03 3 2 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f U d o s t p n i e n i e t e l e b i m ó w i n a g ł o n i e n i
ANALIZA ZALEśNOŚCI KĄTA PODNIESIENIA LUFY OD WZAJEMNEGO POŁOśENIA CELU I STANOWISKA OGNIOWEGO
 ZESZYTY NAUKOWE WSOWL Nr (148) 8 ISSN 1731-8157 Sławomir KRZYśANOWSKI ANALIZA ZALEśNOŚI KĄTA PODNIESIENIA LUFY OD WZAJEMNEGO POŁOśENIA ELU I STANOWISKA OGNIOWEGO Jednym z ierwszych etaów nauczania rzedmiotu
ZESZYTY NAUKOWE WSOWL Nr (148) 8 ISSN 1731-8157 Sławomir KRZYśANOWSKI ANALIZA ZALEśNOŚI KĄTA PODNIESIENIA LUFY OD WZAJEMNEGO POŁOśENIA ELU I STANOWISKA OGNIOWEGO Jednym z ierwszych etaów nauczania rzedmiotu
III. POSADOWIENIE 1. OBLICZENIA POSADOWIENIA FILARA POŚREDNIEGO
 III. POSADOWIENIE 1. OBLICZENIA POSADOWIENIA FILARA POŚREDNIEGO 1.1. Schemat podpory 1.2. Zestawienie obciąŝeń długość przęseł : l t1 = 10.15 m l t2 = 9.44 m l t3 = 9.3 m długość całkowita : l c = 28.89
III. POSADOWIENIE 1. OBLICZENIA POSADOWIENIA FILARA POŚREDNIEGO 1.1. Schemat podpory 1.2. Zestawienie obciąŝeń długość przęseł : l t1 = 10.15 m l t2 = 9.44 m l t3 = 9.3 m długość całkowita : l c = 28.89
Podstawy Konstrukcji Maszyn
 Podsta Konstrukcji Masn kład Podsta oliceń elementó masn Dr inŝ. acek Carnigoski OciąŜenia elementu OciąŜeniem elementu (cęści lu całej masn) są oddiałania innc elementó, środoiska ora ociąŝeń enętrnc
Podsta Konstrukcji Masn kład Podsta oliceń elementó masn Dr inŝ. acek Carnigoski OciąŜenia elementu OciąŜeniem elementu (cęści lu całej masn) są oddiałania innc elementó, środoiska ora ociąŝeń enętrnc
PROJEKTOWANIE I BUDOWA
 ObciąŜenia usterzenia PROJEKTOWANIE I BUDOWA OBIEKTÓW LATAJĄCYCH I ObciąŜenia usterzenia W. BłaŜewicz Budowa samolotów, obciąŝenia St. Danilecki Konstruowanie samolotów, wyznaczanie ociąŝeń R. Cymerkiewicz
ObciąŜenia usterzenia PROJEKTOWANIE I BUDOWA OBIEKTÓW LATAJĄCYCH I ObciąŜenia usterzenia W. BłaŜewicz Budowa samolotów, obciąŝenia St. Danilecki Konstruowanie samolotów, wyznaczanie ociąŝeń R. Cymerkiewicz
OSCYLATOR HARMONICZNY
 OSCYLTOR HRMONICZNY Dgania swobone oscylaoa haonicznego negia oencjalna sęŝysości Dgania łuione oscylaoa haonicznego Dgania wyuszone oscylaoa haonicznego Rezonans aliuowy Rezonans ocy Doboć ukłau gającego
OSCYLTOR HRMONICZNY Dgania swobone oscylaoa haonicznego negia oencjalna sęŝysości Dgania łuione oscylaoa haonicznego Dgania wyuszone oscylaoa haonicznego Rezonans aliuowy Rezonans ocy Doboć ukłau gającego
Arkusze maturalne poziom podstawowy
 Akusze matualne poziom postawowy zaania zamknięte N zaania 5 7 8 9 0 Pawiłowa opowieź a c a b c b a Liczba punktów zaania otwate N zaania Pawiłowa opowieź Punkty Q mg 00 N Z III zasay ynamiki wynika, że
Akusze matualne poziom postawowy zaania zamknięte N zaania 5 7 8 9 0 Pawiłowa opowieź a c a b c b a Liczba punktów zaania otwate N zaania Pawiłowa opowieź Punkty Q mg 00 N Z III zasay ynamiki wynika, że
- ---Ą
 Ą ż ą ą ą Ą ó ą ł ą ł Ąą ż ś Ę ÓŁ Ę Ó ŁĄ ŁŚĆ ł ż ł ż ó ł Ó Ć Ą Ł ŁÓ ŁŚ Ą ż Ó ŁÓ Ę ś ś ł ż ł Ą ęś Ą ń ź ć ą ą ę ń ż ąń ę ę ć óź ŁĄ ą ł ę ę ł ę ń Ą Ęł ą Ł ł ł ż ó ą ł ęę ĘĘ ęć ó ą ń ł ą Ą ęś ł ś ÓŁ Ą ę ę
Ą ż ą ą ą Ą ó ą ł ą ł Ąą ż ś Ę ÓŁ Ę Ó ŁĄ ŁŚĆ ł ż ł ż ó ł Ó Ć Ą Ł ŁÓ ŁŚ Ą ż Ó ŁÓ Ę ś ś ł ż ł Ą ęś Ą ń ź ć ą ą ę ń ż ąń ę ę ć óź ŁĄ ą ł ę ę ł ę ń Ą Ęł ą Ł ł ł ż ó ą ł ęę ĘĘ ęć ó ą ń ł ą Ą ęś ł ś ÓŁ Ą ę ę
[ ] 1. Zabezpieczenia instalacji ogrzewań wodnych systemu zamkniętego. 1. 2. Przeponowe naczynie wzbiorcze. ν dm [1.4] 1. 1. Zawory bezpieczeństwa
![[ ] 1. Zabezpieczenia instalacji ogrzewań wodnych systemu zamkniętego. 1. 2. Przeponowe naczynie wzbiorcze. ν dm [1.4] 1. 1. Zawory bezpieczeństwa [ ] 1. Zabezpieczenia instalacji ogrzewań wodnych systemu zamkniętego. 1. 2. Przeponowe naczynie wzbiorcze. ν dm [1.4] 1. 1. Zawory bezpieczeństwa](/thumbs/39/18677346.jpg) . Zabezieczenia instalacji ogrzewań wodnych systemu zamkniętego Zabezieczenia te wykonuje się zgodnie z PN - B - 0244 Zabezieczenie instalacji ogrzewań wodnych systemu zamkniętego z naczyniami wzbiorczymi
. Zabezieczenia instalacji ogrzewań wodnych systemu zamkniętego Zabezieczenia te wykonuje się zgodnie z PN - B - 0244 Zabezieczenie instalacji ogrzewań wodnych systemu zamkniętego z naczyniami wzbiorczymi
Temperatura i ciepło E=E K +E P +U. Q=c m T=c m(t K -T P ) Q=c przem m. Fizyka 1 Wróbel Wojciech
 emeratura i cieło E=E K +E P +U Energia wewnętrzna [J] - ieło jest energią rzekazywaną między układem a jego otoczeniem na skutek istniejącej między nimi różnicy temeratur na sosób cielny rzez chaotyczne
emeratura i cieło E=E K +E P +U Energia wewnętrzna [J] - ieło jest energią rzekazywaną między układem a jego otoczeniem na skutek istniejącej między nimi różnicy temeratur na sosób cielny rzez chaotyczne
MAXPOL P.W. PRACOWNIA PROJEKTOWA O B L I C Z E NIA S TATY C Z N O -WYTRZY M A ŁOŚCIOWE
 P.W. PRACOWNIA PROJEKTOWA MAXPOL Raom ul. śeromskiego 51a tel./fax. (0-48) 385-09-57 O B L I C Z E NIA S TATY C Z N O -WYTRZY M A ŁOŚCIOWE Lokalizacja: Kierzyń z. Nr 100/1, 101/1 gm. Góz Inwestor: Gmina
P.W. PRACOWNIA PROJEKTOWA MAXPOL Raom ul. śeromskiego 51a tel./fax. (0-48) 385-09-57 O B L I C Z E NIA S TATY C Z N O -WYTRZY M A ŁOŚCIOWE Lokalizacja: Kierzyń z. Nr 100/1, 101/1 gm. Góz Inwestor: Gmina
Kształty żłobków stojana
 Kztałty żłobów tojana Kztałty żłobów winia: a), b), c) lati olewane Al. ) - i) lati lutowane z pętów Cu Wymiay żłoba oplowego Kąt zbieżności ściane żłoba: Śenica mniejza: = π + h )in in ( b Śenica więza:
Kztałty żłobów tojana Kztałty żłobów winia: a), b), c) lati olewane Al. ) - i) lati lutowane z pętów Cu Wymiay żłoba oplowego Kąt zbieżności ściane żłoba: Śenica mniejza: = π + h )in in ( b Śenica więza:
Pompa hydrauliczna dwustopniowa ręczna typ UPTR 12-1,6
 Pompa hydrauliczna dustopnioa ręczna typ UPTR -, V = cm /skok ; p =max 4 MPa V =, cm /skok ; p =max MPa WK 49 0.00 ZASTOSOWANIE Dustopnioa pompa ręczna typ UPTR -, jest stosoana do zasilania urządzeń pracujących
Pompa hydrauliczna dustopnioa ręczna typ UPTR -, V = cm /skok ; p =max 4 MPa V =, cm /skok ; p =max MPa WK 49 0.00 ZASTOSOWANIE Dustopnioa pompa ręczna typ UPTR -, jest stosoana do zasilania urządzeń pracujących
Pola siłowe i ich charakterystyka
 W-6 (Jaosewic) 10 slajdów Pola siłowe i ich chaaktestka Pola siłowe: pojęcie i odaje pól siłowch, wielkości chaakteujące pola siłowe Pola achowawce Pole gawitacjne: uch w polu gawitacjnm 3/10 L.R. Jaosewic
W-6 (Jaosewic) 10 slajdów Pola siłowe i ich chaaktestka Pola siłowe: pojęcie i odaje pól siłowch, wielkości chaakteujące pola siłowe Pola achowawce Pole gawitacjne: uch w polu gawitacjnm 3/10 L.R. Jaosewic
Załącznik Nr:.. KROKWIE POŁACI STROMEJ-poz.1 ;
 Załącnik Nr:.. KROKWIE POŁACI STROMEJ-po.1 ; I. Element 1-krokiew frontowa-połaci stromej krycie blachą na deskowaniu: Krokiew _prekrój nominalny-14/15 cm KROKIEW UKOSNA -prekrój nie skorodowany Serokość
Załącnik Nr:.. KROKWIE POŁACI STROMEJ-po.1 ; I. Element 1-krokiew frontowa-połaci stromej krycie blachą na deskowaniu: Krokiew _prekrój nominalny-14/15 cm KROKIEW UKOSNA -prekrój nie skorodowany Serokość
DWUCZĘŚCIOWE ŁOŻYSKO POROWATE
 PROBLEMY NIEKONWENCJONALNYCH UKŁADÓW ŁOŻYSKOWYCH Łódź, 1 14 maja 1999 r. Karol Kremiński Politechnika Warsawska DWUCZĘŚCIOWE ŁOŻYSKO POROWATE SŁOWA KLUCZOWE: łożysko śligowe, tuleja porowata, prepuscalność
PROBLEMY NIEKONWENCJONALNYCH UKŁADÓW ŁOŻYSKOWYCH Łódź, 1 14 maja 1999 r. Karol Kremiński Politechnika Warsawska DWUCZĘŚCIOWE ŁOŻYSKO POROWATE SŁOWA KLUCZOWE: łożysko śligowe, tuleja porowata, prepuscalność
Sterowanie Procesami Ciągłymi
 Poltechnka Gdańska Wydzał Elektotechnk Automatyk Kateda Inżyne Systemów Steowana Steowane Pocesam Cągłym Laboatoum temn T2a Oacowane: Meczysław A. Bdyś, o. d hab. nż. Wojcech Kuek, mg nż. Tomasz Zubowcz,
Poltechnka Gdańska Wydzał Elektotechnk Automatyk Kateda Inżyne Systemów Steowana Steowane Pocesam Cągłym Laboatoum temn T2a Oacowane: Meczysław A. Bdyś, o. d hab. nż. Wojcech Kuek, mg nż. Tomasz Zubowcz,
PROCES SEPARACJI MIESZANINY TECHNOLOGICZNEJ NA GÓRCE PALCOWEJ KOMBAJNU DO ZBIORU ZIEMNIAKÓW
 InŜynieria Rolnica 1/006 Wojciech Tanaś, Marcin Zawierucha Katedra Masynonawstwa Rolnicego Akademia Rolnica w Lublinie PROCES SEPARACJI MIESZANINY TECHNOLOGICZNEJ NA GÓRCE PALCOWEJ KOMBAJNU DO ZBIORU ZIEMNIAKÓW
InŜynieria Rolnica 1/006 Wojciech Tanaś, Marcin Zawierucha Katedra Masynonawstwa Rolnicego Akademia Rolnica w Lublinie PROCES SEPARACJI MIESZANINY TECHNOLOGICZNEJ NA GÓRCE PALCOWEJ KOMBAJNU DO ZBIORU ZIEMNIAKÓW
Wydział Budownictwa Lądowego i Wodnego, Politechnika Wrocławska, Wrocław **
 Górnictwo i Geoinżynieria Rok 33 Zesyt 1 2009 Adrian Różański*, Maciej Sobótka** WARUNKI OPTYMALIZACJI KSZTAŁTU WYROBISK PODZIEMNYCH 1. Wstę Zagadnienie otymaliacji kstałtu wyrobisk odiemnych o ra ierwsy
Górnictwo i Geoinżynieria Rok 33 Zesyt 1 2009 Adrian Różański*, Maciej Sobótka** WARUNKI OPTYMALIZACJI KSZTAŁTU WYROBISK PODZIEMNYCH 1. Wstę Zagadnienie otymaliacji kstałtu wyrobisk odiemnych o ra ierwsy
ROZDZIAŁ 12 PRZYKŁAD ZASTOSOWANIA METOD WAP DO ANALIZY PROCESÓW GOSPODAROWANIA ZASOBAMI LUDZKIMI W PRZEDSIĘBIORSTWIE
 Marek Kunas ROZDZIAŁ 2 PRZYKŁAD ZASTOSOWANIA METOD WAP DO ANALIZY PROCESÓW GOSPODAROWANIA ZASOBAMI LUDZKIMI W PRZEDSIĘBIORSTWIE. Wprowaenie Celem głównym niniejsego opracowania jest prestawienie wybranych
Marek Kunas ROZDZIAŁ 2 PRZYKŁAD ZASTOSOWANIA METOD WAP DO ANALIZY PROCESÓW GOSPODAROWANIA ZASOBAMI LUDZKIMI W PRZEDSIĘBIORSTWIE. Wprowaenie Celem głównym niniejsego opracowania jest prestawienie wybranych
Gdyńskim Ośrodkiem Sportu i Rekreacji jednostką budżetową Zamawiającym Wykonawcą
 W Z Ó R U M O W Y n r 1 4 k J Bk 2 0 Z a ł» c z n i k n r 5 z a w a r t a w G d y n i w d n i u 1 4 ro ku p o m i 2 0d z y G d y s k i m O r o d k i e m S p o r t u i R e k r e a c j ei d n o s t k» b
W Z Ó R U M O W Y n r 1 4 k J Bk 2 0 Z a ł» c z n i k n r 5 z a w a r t a w G d y n i w d n i u 1 4 ro ku p o m i 2 0d z y G d y s k i m O r o d k i e m S p o r t u i R e k r e a c j ei d n o s t k» b
POMIAR PĘTLI HISTEREZY MAGNETYCZNEJ
 POMIAR PĘTLI ITEREZY MAGNETYZNEJ 1. Opis teoetyczny do ćiczenia zamieszczony jest na stonie.tc.at.edu.pl dziale DYDAKTYKA FIZYKA ĆWIZENIA LAORATORYJNE.. Opis układu pomiaoego Mateiały feomagnetyczne (feyt,
POMIAR PĘTLI ITEREZY MAGNETYZNEJ 1. Opis teoetyczny do ćiczenia zamieszczony jest na stonie.tc.at.edu.pl dziale DYDAKTYKA FIZYKA ĆWIZENIA LAORATORYJNE.. Opis układu pomiaoego Mateiały feomagnetyczne (feyt,

