Dobór optymalnego sygnału wejściowego w zadaniu identyfikacji parametrów układu inercyjnego
|
|
|
- Krzysztof Kurek
- 6 lat temu
- Przeglądów:
Transkrypt
1 Symulacja w Badaniach i Rozwoju Vol. No. /0 Państwowa Wyższa Szkoła Informatyki i Przedsiębiorczości ul. Akademicka Łomża wjakowluk@pwsip.edu.pl Dobór optymalnego sygnału wejściowego w zadaniu identyfikacji parametrów układu inercyjnego Wprowadzenie Identyfikacja parametrów obiektu regulacji jest ważnym etapem budowy dokładnego modelu matematycznego na podstawie przeprowadzonego eksperymentu identyfikacyjnego oraz dostępnej wiedzy [ ]. Dokładność uzyskiwanych estymat parametrów modelu matematycznego zależy przede wszystkim od doboru odpowiedniego sygnału który wzbudza starannie wybrane wejście obiektu regulacji [ 4]. Stwierdzono iż opracowanie dokładnego modelu matematycznego rozpatrywanego procesu pochłania 75% kosztów związanych z zaawansowanymi projektami automatyki [5]. W wielu praktycznych zastosowaniach identyfikacja przeprowadzana jest w czasie rzeczywistym podczas normalnej pracy obiektu (procesu technologicznego). Z tego względu preferowane są metody doboru optymalnego sygnału wejściowego przyjaznego dla obiektu [6 7]. Dobór optymalnego sygnału przyjaznego dla obiektu wiąże się z uwzględnieniem ograniczeń procesu technologicznego (tj. czasu trwania eksperymentu amplitudy sygnału wejściowego i wyjściowego oraz szybkości zmian pobudzenia) [8]. Pobudzanie wejścia identyfikowanego modelu sygnałem przyjaznym zabezpiecza obiekt przed gwałtownymi zmianami sygnału sterującego które mogą mieć wpływ nie tylko na wskaźniki ekonomiczne procesu ale również na stabilność obiektu. Identyfikacja przyjazna dla obiektu powinna zapewniać akceptowalne wartości estymat jego parametrów [9]. Optymalizacja eksperymentu polega na wyborze kryterium optymalności i wyznaczeniu takich zmiennych eksperymentu (np. postaci sygnału pobudzającego czasu trwania eksperymentu schematu próbkowania wariancji dokładności pomiarów) dla których to kryterium jest spełnione. Po sprecyzowaniu kryterium optymalności planowanie eksperymentu sprowadza się do zadania optymalizacji z ograniczeniami. Wektor dopuszczalnych eksperymentów może podlegać ograniczeniom jakościowym ze względu na liczbę i rodzaj wielkości wejściowych i wyjściowych oraz ograniczeniom ilościowym dotyczącym energii pobudzenia dopuszczalnych wejść czasu trwania eksperymentu fizycznych ograniczeń zmiennych eksperymentu minimalnego odstępu czasu pomiędzy kolejnymi pomiarami itp. Dobór optymalnego sygnału wejściowego w zadaniu estymacji wektora parametrów badanego systemu polega na optymalizacji funkcji celu zdefiniowanej na macierzy informacyjnej Fishera M [0]. Często wykorzystywanym kryterium w zadaniu doboru optymalnego sterowania jest 8
2 maksymalizacja sumy elementów diagonalnych macierzy informacyjnej M. Inne wskaźniki optymalnego rozwiązania przedstawiono poniżej: A-optymalność: tr(m - ) minimalizuje średnią wariancję estymowanych parametrów E-optymalność: λ ma (M - ) minimalizuje maksymalną wartość własną macierzy M - D-optymalność: minimalizuje objętość elipsoidalnych obszarów ufności estymowanych parametrów. Wybór kryterium optymalności jest istotny ze względu na cel przeprowadzanego eksperymentu identyfikacyjnego. Weryfikację wybranego kryterium można przeprowadzić na podstawie odpowiednio zdefiniowanego wskaźnika efektywności. Wskaźnik ten umożliwia stwierdzenie o ile optymalny wektor eksperymentu jest lepszy od wektora początkowego []. Celem niniejszej pracy jest dobór optymalnego sygnału pobudzającego w zadaniu identyfikacji parametrów układu jednoinercyjnego. Optymalizowany funkcjonał celu zdefiniowano w postaci kanonicznej Mayera. Dobór optymalnego sygnału sterującego układem inercyjnym W niniejszym rozdziale rozważano liniowy obiekt dynamiczny pierwszego rzędu o następującej transmitancji operatorowej G ( s) k p = () Ts + W przypadku układu liniowego pierwszego rzędu o jednej zmiennej wejściowej u i jednej zmiennej stanu działanie układu można przedstawić w postaci opisu w przestrzeni stanu gdzie ( t; a b) ( t) a( t) + bu( t) ( 0) ( t) = ( t) y = = 0 = przy czym parametry modelu a i b są stałe. Esencją planowania eksperymentów optymalnych jest spełnienie warunków wynikających z twierdzenia Cramera-Rao tj. macierz kowariancji estymat parametrów jest ograniczona od dołu przez odwrotność macierzy informacyjnej Fishera (FIM) ([ ab] ) M () cov () Macierz informacyjną FIM modelu układu jednoinercyjnego () można przedstawić w postaci T T T adt abdt T a a ab M ( T ) = [ ] = a b dt dt = 0 0 (4) T T 0 b 0 ab b abdt b dt
3 Dobór optymalnego sygnału wejściowego w zadaniu identyfikacji parametrów układu inercyjnego gdzie a = / a oraz b = / b. Różniczkując obie strony równania () względem jego parametrów a i b można dokonać konwersji równania stanu na równania wrażliwościowe systemu w następującej postaci ( 0) 0 ( 0) 0 + a = (5) a = a a a + u = (6) b = b b W celu doboru optymalnego sygnału sterującego układem inercyjnym maksymalizacji poddano wskaźnik jakości w postaci wyznacznika macierzy informacyjnej FIM (kryterium D-optymalności). t a d M ( t) = [ a b ] dτ // (7) b dt Po sprowadzeniu równania (7) do postaci kanonicznej otrzymujemy Przyjmując że otrzymujemy 0 M& a ( t) = [ a b ] M( 0) = 0 (8) b ( t) m ( t) ( ) ( ) t m t m M ( t) = (9) m m ( t) = a ( t) m ( 0) = 0 ( t) = m& ( t) = ( t) ( t) m ( 0) 0 & (0) m& () a b = ( t) = ( t) m ( 0) 0 m& () b = Układ równań stanu poszerzony o równania wrażliwościowe przyjmuje postać = = a = m = m = b = m = m = a = = + a = = a = + bu + u ( 0) = ( 0) = 0 ( 0) = 0 ( 0) = 0 ( 0) = 0 ( 0) = 0 Maksymalizacji poddano funkcjonał celu w formie kanonicznej Mayera. W celu wygładzenia charakteru przebiegu sygnału sterującego (rys. ) do kryterium dodano człon odpowiadający całce z kwadratu sterowania przemnożonej przez założoną stałą q (tj. koszt energetyczny) która powinna być tak dobrana aby nie zdominować członu z wyznacznikiem macierzy informacyjnej Fishera []. Maksymalizowany wskaźnik jakości przyjmuje postać () 85
4 J = T f ( ( T f ) 6 ( T f ) 5 ( T f ) q 4 ) 0 T u ( t) u( t dt (4) Powyższy problem może zostać rozwiązany z wykorzystaniem istniejących bibliotek narzędziowych przeznaczonych do rozwiązywania problemów optymalnego sterowania takich jak: RIOTS_95 [] DIRCOL [4] oraz MISER[5]. Obliczenia i symulacje przeprowadzono z wykorzystaniem komputera osobistego (Pentium 4 00 GHz 5 MB RAM) systemu operacyjnego Windows XP oraz programu Matlab 7 (R4). Optymalne i suboptymalne sygnały wejściowe zostały wyznaczone przyjmując nominalne wartości parametrów modelu układu inercyjnego a = - b = funkcję kryterialną określono na stanie końcowym T f = 0 [s] wykorzystano algorytm SQP. Przedział wartości sterowań dobrano arbitralnie - u(t) założono warunek początkowy systemu 0 (0) = 5 oraz wartość początkową sygnału sterującego u(0) =. Optymalny sygnał sterujący wyznaczono na podstawie gradientu wskaźnika jakości uzyskanego w wyniku całkowania równań różniczkowych krokową metodą Runge-Kutty z siatką całkowania 0 [s]. Wyniki doboru D-optymalnych sygnałów wejściowych dla różnych wartości współczynnika kosztu energetycznego q przedstawiono na poniższych rysunkach. Rys.. Optymalny sygnał wejściowy dla współczynnika q = 0 Fig.. Optimal input signal for coefficient q = 0 86
5 Dobór optymalnego sygnału wejściowego w zadaniu identyfikacji parametrów układu inercyjnego Rys.. Optymalny sygnał wejściowy dla współczynnika q = 5 Fig.. Optimal input signal for coefficient q = 5 Rys.. Optymalny sygnał wejściowy dla współczynnika q = 95 (wartość krytyczna) Fig.. Optimal input signal for coefficient q = 95 (critical value) 87
6 Rys. 4. Optymalny sygnał wejściowy dla współczynnika q = 7 Fig. 4. Optimal input signal for coefficient q = 7 W celu uniknięcia lokalnych maksimów wszystkie obliczenia powtórzono kilkukrotnie przyjmując różne warunki początkowe. Wyznaczanie optymalnego sygnału sterującego zajmowało około sześćdziesięciu sekund. Optymalny sygnał pobudzający wyznaczony na podstawie maksymalizacji wskaźnika jakości (4) bez ograniczenia na energię sygnału wejściowego (tj. q = 0) przedstawiono na rysunku. Następnie zwiększano współczynnik opłaty za energię sterowania (rys. ) aż do uzyskania wartości krytycznej q = 95 przekroczenie której powoduje dominację funkcjonału odpowiadającego za koszt energetyczny nad maksymalizowanym wyznacznikiem FIM. W celu porównania na rysunku przedstawiono D-optymalny sygnał wejściowy wyznaczony dla wartości krytycznej współczynnika energetycznego oraz zamieszczono wizualizację sygnału nieoptymalnego (rys. 4) uzyskanego dla q = 7. Opłata za energię sterowania jest w tym przypadku tak duża że obiektem nie opłaca się sterować. Funkcjonał celu przedstawiony równaniem (4) może zostać zapisany w następującej postaci J = J qj (5) gdzie: J oznacza wyznacznik FIM J jest całką z kwadratu sygnału wejściowego. Eksperyment D-optymalny e * maksymalizuje wyznacznik macierzy informacyjnej Fishera M(e) lub minimalizuje wyznacznik macierzy odwrotnej M - (e). Każde kryterium optymalności J(.) może być weryfikowane na podstawie odpowiednio zdefiniowanego wskaźnika efektywności. Wskaźnik ten umożliwia wyznaczenie względnej miary wydajności dowolnego wektora eksperymentu e w stosunku do wektora eksperymentu optymalnego e *. D-efektywność która określa ilościową miarę suboptymalności trajektorii sygnału wejściowego zdefiniowano za pomocą poniższej zależności 88
7 Dobór optymalnego sygnału wejściowego w zadaniu identyfikacji parametrów układu inercyjnego E D ( ) ( Mθ ( e) ) / k det e = * (6) det( Mθ ( e ) gdzie: k - ilość identyfikowanych parametrów θ - wektor estymowanych parametrów oraz e * - wektor eksperymentu D optymalnego. Wyniki obliczeń dla różnych wartości współczynnika kosztu energetycznego q oraz odpowiadających im wartości D-efektywności zamieszczono w tabeli. Tabela. Porównanie komponentów wskaźnika jakości oraz D-efektywności Table. Comparison of the performance inde components and D-efficiency q J J E D (e) e- 78e- 9e-7 Jak można było się spodziewać ograniczenie na energię sygnału wejściowego ma znaczny wpływ na postać optymalnego sterowania. Wartość wyznacznika det(m) = oznacza iż odpowiadająca mu macierz informacyjna Fishera jest praktycznie osobliwa (dla q = 8). Przeprowadzono identyfikację parametrów modelu układu inercyjnego poddając go pobudzeniu różnymi sygnałami wejściowymi. W celu weryfikacji dokładności uzyskiwanych estymat parametrów modelu system poddano wymuszeniu: sygnałem optymalnym (rys. ) skokiem jednostkowym sygnałem sinusoidalnym wolnym o częstotliwości f = 0 [Hz] oraz sygnałem sinusoidalnym szybkim o częstotliwości f = [Hz]. Symulacje przeprowadzono z wykorzystaniem obiektu opisanego równaniem () przyjmując nominalne wartości parametrów równe: a = - oraz b =. Obiekt poddano zakłóceniu losowemu o rozkładzie normalnym wartości średniej równej zero i ograniczonej wariancji. Schemat blokowy procesu identyfikacji przedstawiono na rysunku 5. Identyfikowano parametry modelu poszukując minimum zmiennej wyjściowej y(t) wykorzystując metodę poszukiwań prostych Neldera - Meada. Minimalnych wartości zmiennej y(t) poszukiwano wprowadzając węzły siatki warunku początkowego 5 0 (0) 5 zmieniającego się skokowo o jeden i wariancji zakłóceń 0 σ 07 zmieniającej się skokowo o jedną dziesiątą. Wyznaczono optymalne estymaty parametrów modelu dla wszystkich kombinacji wartości warunku początkowego oraz wariancji zakłóceń. Poszczególne elementy macierzy kowariancji parametrów określają wybrane wymiary elipsy niepewności. Szerokość elipsy wzdłuż poszczególnych osi współrzędnych jest określona przez wariancję estymat elementów diagonalnych macierzy kowariancji. Spłaszczenie elipsy zależy od współczynnika korelacji estymat tj. stosunku odpowiednich elementów pozadiagonalnych do diagonalnych macierzy kowariancji parametrów. Wartości własne macierzy kowariancji określają długości poszczególnych osi elipsy. Kwadrat pola powierzchni elipsy jest proporcjonalny do wyznacznika macierzy kowariancji który jest również iloczynem wartości własnych tej macierzy. Na rysunku 6 wykreślono obszary ufności estymat parametrów modelu. 89
8 b b b b Szum bialy + Obiekt + u( t) + y( t) Model Rys. 5. Przepływ informacji w procesie identyfikacji Fig. 5. Flow of information in identification Wymuszenie sygnałem optymalnym Wymuszenie skokiem jednostkowym a a Wymuszenie sygnałem sinusoidalnym (f = 0. Hz) a Wymuszenie sygnałem sinusoidalnym (f = Hz) a Rys. 6. Elipsoidalne obszary ufności estymat parametrów modelu inercyjnego pobudzanego różnymi sygnałami wejściowymi Fig. 6. Ellipsoidal confidence regions of the inertial model parameters estimates which was perturbed using different input signals Optymalny sygnał sterujący układem inercyjnym różni się od skoku jednostkowego przełączeniem występującym w początkowej fazie przebiegu sterowania (rys. ). Różnice te wpływają jednak w zauważalny sposób na niepewność otrzymywanych estymat parametrów. Najmniejszą niepewność wyznaczonych parametrów uzyskano pobudzając system optymalnym sygnałem wejściowym o czym świadczy obszar ufności wyznaczonych estymat (rys. 6). Nieco większą niepewność wyników estymacji zaobserwowano przy pobudzeniu systemu skokiem jednostkowym. Można zauważyć że niepewność estymowanych parametrów modelu sterowanego sygnałem sinusoidalnym rośnie wraz ze wzrostem jego częstotliwości. 90
9 Dobór optymalnego sygnału wejściowego w zadaniu identyfikacji parametrów układu inercyjnego Podsumowanie W pracy przedstawiono problem wielokryterialnego doboru optymalnego sygnału wejściowego w zadaniu identyfikacji parametrów modelu układu inercyjnego. Wyniki doboru optymalnego sygnału pobudzającego oraz jego weryfikację zamieszczono w postaci graficznej. Istotne znaczenie ma fakt iż maksymalizowany wskaźnik jakości może zostać zapisany w postaci kanonicznej Mayera co umożliwia rozwiązanie zadania z wykorzystaniem istniejących bibliotek narzędziowych do optymalizacji układów dynamicznych. Literatura. Ljung L. System identification Theory for the user nd Edition Prentice Hall USA 999. Pintelon R. Schoukens J. System identification: A frequency domain approach John Wiley & Sons USA 00. Kalaba R. Spingarn K. Control identification and input optimization: Plenum Press New York Mehra R. Choice of input signals. In trends and progress in systems identification Eykhoff Ed Pergamon Press New York Hussain M. Review of the applications of neural networks in chemical process control-simulation and on-line implementation Artificial Intelligence in Engineering Narasimhan S. Rengaswamy R. Multi-objective input signal design for plant friendly identification of process systems Proceeding of the American Control Conference Boston Massachusetts Narasimhan S. Rengaswamy R. Multi-objective optimal input design for plant friendly identification Proceeding of the American Control Conference Seattle Washington Rivera D. Braun M. Mittelmann H. Constrained multisine inputs for plant friendly identification of chemical process In IFAC World Congress Barcelona Spain Rivera D. Lee H. Braun M. Mittelmann H. Plant friendly system identification: A challenge for the process industries In SYSID 00 Rotterdam Netherlands Atkinson A. Donev A. Tobias R. Optimum eperimental design with SAS Oford University Press Oford 007. Jakowluk W. Design of an optimal input signal for plant-friendly identification of inertial systems Electrical Review n Jakowluk W. Design of an optimal ecitation signal for identification of inertial systems in time domain Electrical Review n Schwartz A. Polak E. Chen Y. A Matlab toolbo for solving optimal control problems. Version.0 for Windows May 997. Available at: 4. Stryk O. User s quide for DIRCOL a direct collocation method for the numerical solution of optimal control problems. Version.. Technische Universität Darmstadt November 999. Available at: 9
10 5. Jennings L. Fisher M. Teo K. Goh C. MISER : Optimal control software Version.0. Theory and user manual. Dept. of Mathematics University of Western Australia Nedlands (00). Available at: Streszczenie Dokładność uzyskiwanych estymat parametrów identyfikowanego modelu zależy przede wszystkim od doboru odpowiedniego sygnału wejściowego który wzbudza wybrane wejście obiektu regulacji. W pracy przedstawiono wyniki doboru optymalnego sygnału pobudzającego układem jednoinercyjnym. Celem takiego eksperymentu jest minimalizacja wariancji uzyskiwanych estymat parametrów. Maksymalizowano funkcjonał celu określony jako wyznacznik macierzy informacyjnej Fishera uwzględniając nałożone ograniczenia na amplitudę sygnału wejściowego. Stwierdzono że optymalne pobudzenie identyfikowanego obiektu minimalizuje elipsoidalne obszary ufności estymowanych parametrów. Design of an optimal input signal for identification of inertial system parameters Summary The choice of an input signal used for actuation of the system is critical in the task of model building and parameter identification. In the paper the optimal ecitation signal was generated for an inertial model. The objective of this kind of eperiment design is to minimise the variance of the parameters to be estimated. In this case the objective function was formulated through maimisation of the Fisher information matri determinant in the form of a conventional integral criterion with amplitude constraints. It was shown that the optimal input signal used for system ecitation minimises the volume of the ellipsoidal confidence region of parameters estimates. 9
Transmitancje układów ciągłych
 Transmitancja operatorowa, podstawowe człony liniowe Transmitancja operatorowa (funkcja przejścia, G(s)) stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego
Transmitancja operatorowa, podstawowe człony liniowe Transmitancja operatorowa (funkcja przejścia, G(s)) stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego
ZASTOSOWANIE ZASADY MAKSIMUM PONTRIAGINA DO ZAGADNIENIA
 ZASTOSOWANIE ZASADY MAKSIMUM PONTRIAGINA DO ZAGADNIENIA DYNAMICZNYCH LOKAT KAPITAŁOWYCH Krzysztof Gąsior Uniwersytet Rzeszowski Streszczenie Celem referatu jest zaprezentowanie praktycznego zastosowania
ZASTOSOWANIE ZASADY MAKSIMUM PONTRIAGINA DO ZAGADNIENIA DYNAMICZNYCH LOKAT KAPITAŁOWYCH Krzysztof Gąsior Uniwersytet Rzeszowski Streszczenie Celem referatu jest zaprezentowanie praktycznego zastosowania
Automatyka i robotyka ETP2005L. Laboratorium semestr zimowy
 Automatyka i robotyka ETP2005L Laboratorium semestr zimowy 2017-2018 Liniowe człony automatyki x(t) wymuszenie CZŁON (element) OBIEKT AUTOMATYKI y(t) odpowiedź Modelowanie matematyczne obiektów automatyki
Automatyka i robotyka ETP2005L Laboratorium semestr zimowy 2017-2018 Liniowe człony automatyki x(t) wymuszenie CZŁON (element) OBIEKT AUTOMATYKI y(t) odpowiedź Modelowanie matematyczne obiektów automatyki
przy warunkach początkowych: 0 = 0, 0 = 0
 MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
Plan wykładu. Własności statyczne i dynamiczne elementów automatyki:
 Plan wykładu Własności statyczne i dynamiczne elementów automatyki: - charakterystyka statyczna elementu automatyki, - sygnały standardowe w automatyce: skok jednostkowy, impuls Diraca, sygnał o przebiegu
Plan wykładu Własności statyczne i dynamiczne elementów automatyki: - charakterystyka statyczna elementu automatyki, - sygnały standardowe w automatyce: skok jednostkowy, impuls Diraca, sygnał o przebiegu
ZAJĘCIA IX. Granice dokładności identyfikacji
 ZAJĘCIA IX Granice dokładności identyfikacji Macierz informacyjna Fishera Ograniczenie Rao-Craméra Dokładność funkcją parametrów Elipsoida niepewności estymatora (ufności estymat) Katedra Metrologii AGH
ZAJĘCIA IX Granice dokładności identyfikacji Macierz informacyjna Fishera Ograniczenie Rao-Craméra Dokładność funkcją parametrów Elipsoida niepewności estymatora (ufności estymat) Katedra Metrologii AGH
Przekształcanie równań stanu do postaci kanonicznej diagonalnej
 Przekształcanie równań stanu do postaci kanonicznej diagonalnej Przygotowanie: Dariusz Pazderski Liniowe przekształcenie równania stanu Rozważmy liniowe równanie stanu i równanie wyjścia układu niesingularnego
Przekształcanie równań stanu do postaci kanonicznej diagonalnej Przygotowanie: Dariusz Pazderski Liniowe przekształcenie równania stanu Rozważmy liniowe równanie stanu i równanie wyjścia układu niesingularnego
Podstawy Automatyki. wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak. Politechnika Wrocławska. Instytut Technologii Maszyn i Automatyzacji (I-24)
 Podstawy Automatyki wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak Politechnika Wrocławska Instytut Technologii Maszyn i Automatyzacji (I-24) Laboratorium Podstaw Automatyzacji (L6) 105/2 B1 Sprawy organizacyjne
Podstawy Automatyki wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak Politechnika Wrocławska Instytut Technologii Maszyn i Automatyzacji (I-24) Laboratorium Podstaw Automatyzacji (L6) 105/2 B1 Sprawy organizacyjne
Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów
 Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Sterowania Procesami Ciągłych Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów. Obliczanie
Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Sterowania Procesami Ciągłych Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów. Obliczanie
Sposoby modelowania układów dynamicznych. Pytania
 Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Podstawy Automatyki. Wykład 7 - obiekty regulacji. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania MODELOWANIE I IDENTYFIKACJA Studia niestacjonarne Estymacja parametrów modeli, metoda najmniejszych kwadratów.
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania MODELOWANIE I IDENTYFIKACJA Studia niestacjonarne Estymacja parametrów modeli, metoda najmniejszych kwadratów.
1. Regulatory ciągłe liniowe.
 Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
PROGRAMOWANIE DYNAMICZNE W ROZMYTYM OTOCZENIU DO STEROWANIA STATKIEM
 Mostefa Mohamed-Seghir Akademia Morska w Gdyni PROGRAMOWANIE DYNAMICZNE W ROZMYTYM OTOCZENIU DO STEROWANIA STATKIEM W artykule przedstawiono propozycję zastosowania programowania dynamicznego do rozwiązywania
Mostefa Mohamed-Seghir Akademia Morska w Gdyni PROGRAMOWANIE DYNAMICZNE W ROZMYTYM OTOCZENIU DO STEROWANIA STATKIEM W artykule przedstawiono propozycję zastosowania programowania dynamicznego do rozwiązywania
Sterowanie optymalne
 Sterowanie optymalne Sterowanie Procesami Ciągłymi 2017 Optymalizacja statyczna funkcji Funkcja celu/kryterialna/kosztów Ograniczenie Q(x) min x x = arg min Q(x) x x X, gdzie X zbiór rozwiązań dopuszczalnych
Sterowanie optymalne Sterowanie Procesami Ciągłymi 2017 Optymalizacja statyczna funkcji Funkcja celu/kryterialna/kosztów Ograniczenie Q(x) min x x = arg min Q(x) x x X, gdzie X zbiór rozwiązań dopuszczalnych
Ćwiczenie 3 Badanie własności podstawowych liniowych członów automatyki opartych na biernych elementach elektrycznych
 Ćwiczenie 3 Badanie własności podstawowych liniowych członów automatyki opartych na biernych elementach elektrycznych Cel ćwiczenia Celem ćwiczenia jest poznanie podstawowych własności członów liniowych
Ćwiczenie 3 Badanie własności podstawowych liniowych członów automatyki opartych na biernych elementach elektrycznych Cel ćwiczenia Celem ćwiczenia jest poznanie podstawowych własności członów liniowych
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE
 CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
Sterowanie napędów maszyn i robotów
 Wykład 7b - Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Instytut Automatyki i Robotyki Warszawa, 2014 Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Zadanie przestawiania Postać modalna
Wykład 7b - Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Instytut Automatyki i Robotyki Warszawa, 2014 Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Zadanie przestawiania Postać modalna
Metoda największej wiarygodności
 Metoda największej wiarygodności Próbki w obecności tła Funkcja wiarygodności Iloraz wiarygodności Pomiary o różnej dokładności Obciążenie Informacja z próby i nierówność informacyjna Wariancja minimalna
Metoda największej wiarygodności Próbki w obecności tła Funkcja wiarygodności Iloraz wiarygodności Pomiary o różnej dokładności Obciążenie Informacja z próby i nierówność informacyjna Wariancja minimalna
Algebra liniowa. Macierze i układy równań liniowych
 Algebra liniowa Macierze i układy równań liniowych Własności wyznaczników det I = 1, det(ab) = det A det B, det(a T ) = det A. Macierz nieosobliwa Niech A będzie macierzą kwadratową wymiaru n n. Mówimy,
Algebra liniowa Macierze i układy równań liniowych Własności wyznaczników det I = 1, det(ab) = det A det B, det(a T ) = det A. Macierz nieosobliwa Niech A będzie macierzą kwadratową wymiaru n n. Mówimy,
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Tematyka egzaminu z Podstaw sterowania
 Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
ELEMENTY AUTOMATYKI PRACA W PROGRAMIE SIMULINK 2013
 SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
Informatyczne Systemy Sterowania
 Adam Wiernasz Nr albumu: 161455 e-mail: 161455@student.pwr.wroc.pl Informatyczne Systemy Sterowania Laboratorium nr 1 Prowadzący: Dr inż. Magdalena Turowska I. Wykaz modeli matematycznych członów dynamicznych
Adam Wiernasz Nr albumu: 161455 e-mail: 161455@student.pwr.wroc.pl Informatyczne Systemy Sterowania Laboratorium nr 1 Prowadzący: Dr inż. Magdalena Turowska I. Wykaz modeli matematycznych członów dynamicznych
1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI
 Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań.
 III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
Porównanie wyników symulacji wpływu kształtu i amplitudy zakłóceń na jakość sterowania piecem oporowym w układzie z regulatorem PID lub rozmytym
 ARCHIVES of FOUNDRY ENGINEERING Published quarterly as the organ of the Foundry Commission of the Polish Academy of Sciences ISSN (1897-3310) Volume 15 Special Issue 4/2015 133 138 28/4 Porównanie wyników
ARCHIVES of FOUNDRY ENGINEERING Published quarterly as the organ of the Foundry Commission of the Polish Academy of Sciences ISSN (1897-3310) Volume 15 Special Issue 4/2015 133 138 28/4 Porównanie wyników
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM
 TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 3 BADANIE CHARAKTERYSTYK CZASOWYCH LINIOWYCH UKŁADÓW RLC. Cel ćwiczenia Celem ćwiczenia są pomiary i analiza
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM AKADEMIA MORSKA Katedra Telekomunikacji Morskiej ĆWICZENIE 3 BADANIE CHARAKTERYSTYK CZASOWYCH LINIOWYCH UKŁADÓW RLC. Cel ćwiczenia Celem ćwiczenia są pomiary i analiza
Regulacja adaptacyjna w anemometrze stałotemperaturowym
 3 Prace Instytutu Mechaniki Górotworu PAN Tom 8, nr 1-4, (2006), s. 3-7 Instytut Mechaniki Górotworu PAN Regulacja adaptacyjna w anemometrze stałotemperaturowym PAWEŁ LIGĘZA Instytut Mechaniki Górotworu
3 Prace Instytutu Mechaniki Górotworu PAN Tom 8, nr 1-4, (2006), s. 3-7 Instytut Mechaniki Górotworu PAN Regulacja adaptacyjna w anemometrze stałotemperaturowym PAWEŁ LIGĘZA Instytut Mechaniki Górotworu
Katedra Automatyzacji Laboratorium Podstaw Automatyzacji Produkcji Laboratorium Podstaw Automatyzacji
 Katedra Automatyzacji Laboratorium Podstaw Automatyzacji Produkcji Laboratorium Podstaw Automatyzacji Opracowanie: mgr inż. Krystian Łygas, inż. Wojciech Danilczuk Na podstawie materiałów Prof. dr hab.
Katedra Automatyzacji Laboratorium Podstaw Automatyzacji Produkcji Laboratorium Podstaw Automatyzacji Opracowanie: mgr inż. Krystian Łygas, inż. Wojciech Danilczuk Na podstawie materiałów Prof. dr hab.
5. Rozwiązywanie układów równań liniowych
 5. Rozwiązywanie układów równań liniowych Wprowadzenie (5.1) Układ n równań z n niewiadomymi: a 11 +a 12 x 2 +...+a 1n x n =a 10, a 21 +a 22 x 2 +...+a 2n x n =a 20,..., a n1 +a n2 x 2 +...+a nn x n =a
5. Rozwiązywanie układów równań liniowych Wprowadzenie (5.1) Układ n równań z n niewiadomymi: a 11 +a 12 x 2 +...+a 1n x n =a 10, a 21 +a 22 x 2 +...+a 2n x n =a 20,..., a n1 +a n2 x 2 +...+a nn x n =a
Procedura modelowania matematycznego
 Procedura modelowania matematycznego System fizyczny Model fizyczny Założenia Uproszczenia Model matematyczny Analiza matematyczna Symulacja komputerowa Rozwiązanie w postaci modelu odpowiedzi Poszerzenie
Procedura modelowania matematycznego System fizyczny Model fizyczny Założenia Uproszczenia Model matematyczny Analiza matematyczna Symulacja komputerowa Rozwiązanie w postaci modelu odpowiedzi Poszerzenie
Spis treści. Przedmowa... XI. Rozdział 1. Pomiar: jednostki miar... 1. Rozdział 2. Pomiar: liczby i obliczenia liczbowe... 16
 Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
POLITECHNIKA ŚLĄSKA WYDZIAŁ GÓRNICTWA I GEOLOGII. Roman Kaula
 POLITECHNIKA ŚLĄSKA WYDZIAŁ GÓRNICTWA I GEOLOGII Roman Kaula ZASTOSOWANIE NOWOCZESNYCH NARZĘDZI INŻYNIERSKICH LabVIEW oraz MATLAB/Simulink DO MODELOWANIA UKŁADÓW DYNAMICZNYCH PLAN WYKŁADU Wprowadzenie
POLITECHNIKA ŚLĄSKA WYDZIAŁ GÓRNICTWA I GEOLOGII Roman Kaula ZASTOSOWANIE NOWOCZESNYCH NARZĘDZI INŻYNIERSKICH LabVIEW oraz MATLAB/Simulink DO MODELOWANIA UKŁADÓW DYNAMICZNYCH PLAN WYKŁADU Wprowadzenie
Technika regulacji automatycznej
 Technika regulacji automatycznej Wykład 1 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 30 Plan wykładu Podstawowe informacje Modele układów elektrycznych
Technika regulacji automatycznej Wykład 1 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 30 Plan wykładu Podstawowe informacje Modele układów elektrycznych
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 9. Dobór nastaw
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 9. Dobór nastaw
Właściwości dynamiczne kolektora słonecznego a efektywność instalacji grzewczej
 Właściwości dynamiczne kolektora słonecznego a efektywność instalacji grzewczej mgr inż. Joanna Aleksiejuk 2016-09-19 Problemy gospodarki energią i środowiskiem w rolnictwie, leśnictwie i przemyśle spożywczym
Właściwości dynamiczne kolektora słonecznego a efektywność instalacji grzewczej mgr inż. Joanna Aleksiejuk 2016-09-19 Problemy gospodarki energią i środowiskiem w rolnictwie, leśnictwie i przemyśle spożywczym
WYKŁAD 9 METODY ZMIENNEJ METRYKI
 WYKŁAD 9 METODY ZMIENNEJ METRYKI Kierunki sprzężone. Metoda Newtona Raphsona daje dobre przybliżenie najlepszego kierunku poszukiwań, lecz jest to okupione znacznym kosztem obliczeniowym zwykle postać
WYKŁAD 9 METODY ZMIENNEJ METRYKI Kierunki sprzężone. Metoda Newtona Raphsona daje dobre przybliżenie najlepszego kierunku poszukiwań, lecz jest to okupione znacznym kosztem obliczeniowym zwykle postać
CHARAKTERYSTYKA I ZASTOSOWANIA ALGORYTMÓW OPTYMALIZACJI ROZMYTEJ. E. ZIÓŁKOWSKI 1 Wydział Odlewnictwa AGH, ul. Reymonta 23, Kraków
 36/3 Archives of Foundry, Year 004, Volume 4, 3 Archiwum Odlewnictwa, Rok 004, Rocznik 4, Nr 3 PAN Katowice PL ISSN 64-5308 CHARAKTERYSTYKA I ZASTOSOWANIA ALGORYTMÓW OPTYMALIZACJI ROZMYTEJ E. ZIÓŁKOWSKI
36/3 Archives of Foundry, Year 004, Volume 4, 3 Archiwum Odlewnictwa, Rok 004, Rocznik 4, Nr 3 PAN Katowice PL ISSN 64-5308 CHARAKTERYSTYKA I ZASTOSOWANIA ALGORYTMÓW OPTYMALIZACJI ROZMYTEJ E. ZIÓŁKOWSKI
1. Podstawowe pojęcia
 1. Podstawowe pojęcia Sterowanie optymalne obiektu polega na znajdowaniu najkorzystniejszej decyzji dotyczącej zamierzonego wpływu na obiekt przy zadanych ograniczeniach. Niech dany jest obiekt opisany
1. Podstawowe pojęcia Sterowanie optymalne obiektu polega na znajdowaniu najkorzystniejszej decyzji dotyczącej zamierzonego wpływu na obiekt przy zadanych ograniczeniach. Niech dany jest obiekt opisany
PRAWO OHMA DLA PRĄDU PRZEMIENNEGO
 ĆWICZENIE 53 PRAWO OHMA DLA PRĄDU PRZEMIENNEGO Cel ćwiczenia: wyznaczenie wartości indukcyjności cewek i pojemności kondensatorów przy wykorzystaniu prawa Ohma dla prądu przemiennego; sprawdzenie prawa
ĆWICZENIE 53 PRAWO OHMA DLA PRĄDU PRZEMIENNEGO Cel ćwiczenia: wyznaczenie wartości indukcyjności cewek i pojemności kondensatorów przy wykorzystaniu prawa Ohma dla prądu przemiennego; sprawdzenie prawa
Dynamiczne badanie wzmacniacza operacyjnego- ćwiczenie 8
 Dynamiczne badanie wzmacniacza operacyjnego- ćwiczenie 8 1. Cel ćwiczenia Celem ćwiczenia jest dynamiczne badanie wzmacniacza operacyjnego, oraz zapoznanie się z metodami wyznaczania charakterystyk częstotliwościowych.
Dynamiczne badanie wzmacniacza operacyjnego- ćwiczenie 8 1. Cel ćwiczenia Celem ćwiczenia jest dynamiczne badanie wzmacniacza operacyjnego, oraz zapoznanie się z metodami wyznaczania charakterystyk częstotliwościowych.
Podstawy Automatyki. Wykład 2 - podstawy matematyczne. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 2 - podstawy matematyczne Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe, n.p. turbulencje, wiele
Wykład 2 - podstawy matematyczne Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe, n.p. turbulencje, wiele
KORELACJE I REGRESJA LINIOWA
 KORELACJE I REGRESJA LINIOWA Korelacje i regresja liniowa Analiza korelacji: Badanie, czy pomiędzy dwoma zmiennymi istnieje zależność Obie analizy się wzajemnie przeplatają Analiza regresji: Opisanie modelem
KORELACJE I REGRESJA LINIOWA Korelacje i regresja liniowa Analiza korelacji: Badanie, czy pomiędzy dwoma zmiennymi istnieje zależność Obie analizy się wzajemnie przeplatają Analiza regresji: Opisanie modelem
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Sterowanie napędów maszyn i robotów
 Wykład 5 - Identyfikacja Instytut Automatyki i Robotyki (IAiR), Politechnika Warszawska Warszawa, 2015 Koncepcje estymacji modelu Standardowe drogi poszukiwania modeli parametrycznych M1: Analityczne określenie
Wykład 5 - Identyfikacja Instytut Automatyki i Robotyki (IAiR), Politechnika Warszawska Warszawa, 2015 Koncepcje estymacji modelu Standardowe drogi poszukiwania modeli parametrycznych M1: Analityczne określenie
WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI
 WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI Stefan WÓJTOWICZ, Katarzyna BIERNAT ZAKŁAD METROLOGII I BADAŃ NIENISZCZĄCYCH INSTYTUT ELEKTROTECHNIKI ul. Pożaryskiego 8, 04-703 Warszawa tel. (0)
WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI Stefan WÓJTOWICZ, Katarzyna BIERNAT ZAKŁAD METROLOGII I BADAŃ NIENISZCZĄCYCH INSTYTUT ELEKTROTECHNIKI ul. Pożaryskiego 8, 04-703 Warszawa tel. (0)
Selection of controller parameters Strojenie regulatorów
 Division of Metrology and Power Processes Automation Selection of controller parameters Strojenie regulatorów A-9 Automatics laboratory Laboratorium automatyki Developed by//opracował: mgr inż. Wojciech
Division of Metrology and Power Processes Automation Selection of controller parameters Strojenie regulatorów A-9 Automatics laboratory Laboratorium automatyki Developed by//opracował: mgr inż. Wojciech
CYFROWE PRZTWARZANIE SYGNAŁÓW (Zastosowanie transformacji Fouriera)
 I. Wprowadzenie do ćwiczenia CYFROWE PRZTWARZANIE SYGNAŁÓW (Zastosowanie transformacji Fouriera) Ogólnie termin przetwarzanie sygnałów odnosi się do nauki analizowania zmiennych w czasie procesów fizycznych.
I. Wprowadzenie do ćwiczenia CYFROWE PRZTWARZANIE SYGNAŁÓW (Zastosowanie transformacji Fouriera) Ogólnie termin przetwarzanie sygnałów odnosi się do nauki analizowania zmiennych w czasie procesów fizycznych.
ZASTOSOWANIE RACHUNKU OPERATORÓW MIKUS- IŃSKIEGO W PEWNYCH ZAGADNIENIACH DYNAMIKI KONSTRUKCJI
 Budownictwo 18 Mariusz Poński ZASTOSOWANIE RACHUNKU OPERATORÓW MIKUS- IŃSKIEGO W PEWNYCH ZAGADNIENIACH DYNAMIKI KONSTRUKCJI 1. Metody transformacji całkowych Najczęściej spotykaną metodą rozwiązywania
Budownictwo 18 Mariusz Poński ZASTOSOWANIE RACHUNKU OPERATORÓW MIKUS- IŃSKIEGO W PEWNYCH ZAGADNIENIACH DYNAMIKI KONSTRUKCJI 1. Metody transformacji całkowych Najczęściej spotykaną metodą rozwiązywania
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa.
 VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania. Podstawy Automatyki
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podsta Automatyki Transmitancja operatorowa i widmowa systemu, znajdowanie odpowiedzi w dziedzinie s i w
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podsta Automatyki Transmitancja operatorowa i widmowa systemu, znajdowanie odpowiedzi w dziedzinie s i w
Podstawy automatyki. Energetyka Sem. V Wykład 1. Sem /17 Hossein Ghaemi
 Podstawy automatyki Energetyka Sem. V Wykład 1 Sem. 1-2016/17 Hossein Ghaemi Hossein Ghaemi Katedra Automatyki i Energetyki Wydział Oceanotechniki i Okrętownictwa Politechnika Gdańska pok. 222A WOiO Tel.:
Podstawy automatyki Energetyka Sem. V Wykład 1 Sem. 1-2016/17 Hossein Ghaemi Hossein Ghaemi Katedra Automatyki i Energetyki Wydział Oceanotechniki i Okrętownictwa Politechnika Gdańska pok. 222A WOiO Tel.:
Laboratorium z podstaw automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Dobór parametrów układu regulacji, Identyfikacja parametrów obiektów dynamicznych Kierunek studiów: Transport, Stacjonarne
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Dobór parametrów układu regulacji, Identyfikacja parametrów obiektów dynamicznych Kierunek studiów: Transport, Stacjonarne
Laboratorium z podstaw automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności, dobór układów i parametrów regulacji, identyfikacja obiektów Kierunek studiów: Transport, Stacjonarne
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności, dobór układów i parametrów regulacji, identyfikacja obiektów Kierunek studiów: Transport, Stacjonarne
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Modele układów dynamicznych - laboratorium. SIMULINK - wprowadzenie
 Modele układów dynamicznych - laboratorium SIMULINK - wprowadzenie SIMULINK Simulink to przybornik (toolbo) pakietu Matlab przeznaczony do symulacji układów dynamicznych w trybie graficznym. Simulink to
Modele układów dynamicznych - laboratorium SIMULINK - wprowadzenie SIMULINK Simulink to przybornik (toolbo) pakietu Matlab przeznaczony do symulacji układów dynamicznych w trybie graficznym. Simulink to
Ważne rozkłady i twierdzenia c.d.
 Ważne rozkłady i twierdzenia c.d. Funkcja charakterystyczna rozkładu Wielowymiarowy rozkład normalny Elipsa kowariacji Sploty rozkładów Rozkłady jednostajne Sploty z rozkładem normalnym Pobieranie próby
Ważne rozkłady i twierdzenia c.d. Funkcja charakterystyczna rozkładu Wielowymiarowy rozkład normalny Elipsa kowariacji Sploty rozkładów Rozkłady jednostajne Sploty z rozkładem normalnym Pobieranie próby
Metoda określania pozycji wodnicy statków na podstawie pomiarów odległości statku od głowic laserowych
 inż. Marek Duczkowski Metoda określania pozycji wodnicy statków na podstawie pomiarów odległości statku od głowic laserowych słowa kluczowe: algorytm gradientowy, optymalizacja, określanie wodnicy W artykule
inż. Marek Duczkowski Metoda określania pozycji wodnicy statków na podstawie pomiarów odległości statku od głowic laserowych słowa kluczowe: algorytm gradientowy, optymalizacja, określanie wodnicy W artykule
Egzamin / zaliczenie na ocenę*
 Zał. nr do ZW /01 WYDZIAŁ / STUDIUM KARTA PRZEDMIOTU Nazwa w języku polskim Identyfikacja systemów Nazwa w języku angielskim System identification Kierunek studiów (jeśli dotyczy): Inżynieria Systemów
Zał. nr do ZW /01 WYDZIAŁ / STUDIUM KARTA PRZEDMIOTU Nazwa w języku polskim Identyfikacja systemów Nazwa w języku angielskim System identification Kierunek studiów (jeśli dotyczy): Inżynieria Systemów
Wprowadzenie do technik regulacji automatycznej. prof nzw. dr hab. inż. Krzysztof Patan
 Wprowadzenie do technik regulacji automatycznej prof nzw. dr hab. inż. Krzysztof Patan Czym jest AUTOMATYKA? Automatyka to dziedzina nauki i techniki zajmująca się teorią i praktycznym zastosowaniem urządzeń
Wprowadzenie do technik regulacji automatycznej prof nzw. dr hab. inż. Krzysztof Patan Czym jest AUTOMATYKA? Automatyka to dziedzina nauki i techniki zajmująca się teorią i praktycznym zastosowaniem urządzeń
Mechatronika i inteligentne systemy produkcyjne. Modelowanie systemów mechatronicznych Platformy przetwarzania danych
 Mechatronika i inteligentne systemy produkcyjne Modelowanie systemów mechatronicznych Platformy przetwarzania danych 1 Sterowanie procesem oparte na jego modelu u 1 (t) System rzeczywisty x(t) y(t) Tworzenie
Mechatronika i inteligentne systemy produkcyjne Modelowanie systemów mechatronicznych Platformy przetwarzania danych 1 Sterowanie procesem oparte na jego modelu u 1 (t) System rzeczywisty x(t) y(t) Tworzenie
Rozdział 1 PROGRAMOWANIE LINIOWE
 Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 1 PROGRAMOWANIE LINIOWE 1.2 Ćwiczenia komputerowe Ćwiczenie 1.1 Wykorzystując
Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 1 PROGRAMOWANIE LINIOWE 1.2 Ćwiczenia komputerowe Ćwiczenie 1.1 Wykorzystując
Monitorowanie i Diagnostyka w Systemach Sterowania na studiach II stopnia specjalności: Systemy Sterowania i Podejmowania Decyzji
 Monitorowanie i Diagnostyka w Systemach Sterowania na studiach II stopnia specjalności: Systemy Sterowania i Podejmowania Decyzji Analiza składników podstawowych - wprowadzenie (Principal Components Analysis
Monitorowanie i Diagnostyka w Systemach Sterowania na studiach II stopnia specjalności: Systemy Sterowania i Podejmowania Decyzji Analiza składników podstawowych - wprowadzenie (Principal Components Analysis
Podstawowe człony dynamiczne
 . Człon proporcjonalny 2. Człony całkujący idealny 3. Człon inercyjny Podstawowe człony dynamiczne charakterystyki czasowe = = = + 4. Człony całkujący rzeczywisty () = + 5. Człon różniczkujący rzeczywisty
. Człon proporcjonalny 2. Człony całkujący idealny 3. Człon inercyjny Podstawowe człony dynamiczne charakterystyki czasowe = = = + 4. Człony całkujący rzeczywisty () = + 5. Człon różniczkujący rzeczywisty
ANALIZA WPŁYWU WYBRANYCH PARAMETRÓW SYGNAŁU WYMUSZAJĄCEGO NA CZAS ODPOWIEDZI OBIEKTU
 II Konferencja Naukowa KNWS'05 "Informatyka- sztuka czy rzemios o" 15-18 czerwca 2005, Z otniki Luba skie ANALIZA WPŁYWU WYBRANYCH PARAMETRÓW SYGNAŁU WYMUSZAJĄCEGO NA CZAS ODPOWIEDZI OBIEKTU Piotr Mróz
II Konferencja Naukowa KNWS'05 "Informatyka- sztuka czy rzemios o" 15-18 czerwca 2005, Z otniki Luba skie ANALIZA WPŁYWU WYBRANYCH PARAMETRÓW SYGNAŁU WYMUSZAJĄCEGO NA CZAS ODPOWIEDZI OBIEKTU Piotr Mróz
Komputerowa Analiza Danych Doświadczalnych
 Komputerowa Analiza Danych Doświadczalnych Prowadząca: dr inż. Hanna Zbroszczyk e-mail: gos@if.pw.edu.pl tel: +48 22 234 58 51 konsultacje: poniedziałek, 10-11; środa: 11-12 www: http://www.if.pw.edu.pl/~gos/students/kadd
Komputerowa Analiza Danych Doświadczalnych Prowadząca: dr inż. Hanna Zbroszczyk e-mail: gos@if.pw.edu.pl tel: +48 22 234 58 51 konsultacje: poniedziałek, 10-11; środa: 11-12 www: http://www.if.pw.edu.pl/~gos/students/kadd
Dynamika procesu zmienna stała. programowalne zmiany parametrów r.
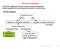 Sterowanie adaptacyjne Sterowanie adaptacyjne polega na dostosowywaniu (adaptacji) nastaw regulatora do zmian parametrów obiektu (w trakcie pracy) Techniki adaptacji Dynamika procesu zmienna stała regulator
Sterowanie adaptacyjne Sterowanie adaptacyjne polega na dostosowywaniu (adaptacji) nastaw regulatora do zmian parametrów obiektu (w trakcie pracy) Techniki adaptacji Dynamika procesu zmienna stała regulator
PRZYKŁAD ZASTOSOWANIA DOKŁADNEGO NIEPARAMETRYCZNEGO PRZEDZIAŁU UFNOŚCI DLA VaR. Wojciech Zieliński
 PRZYKŁAD ZASTOSOWANIA DOKŁADNEGO NIEPARAMETRYCZNEGO PRZEDZIAŁU UFNOŚCI DLA VaR Wojciech Zieliński Katedra Ekonometrii i Statystyki SGGW Nowoursynowska 159, PL-02-767 Warszawa wojtek.zielinski@statystyka.info
PRZYKŁAD ZASTOSOWANIA DOKŁADNEGO NIEPARAMETRYCZNEGO PRZEDZIAŁU UFNOŚCI DLA VaR Wojciech Zieliński Katedra Ekonometrii i Statystyki SGGW Nowoursynowska 159, PL-02-767 Warszawa wojtek.zielinski@statystyka.info
Podstawy Automatyki. Wykład 9 - Dobór regulatorów. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 9 - Dobór regulatorów. Instytut Automatyki i Robotyki Warszawa, 2017 Dobór regulatorów Podstawową przesłanką przy wyborze rodzaju regulatora są właściwości dynamiczne obiektu regulacji. Rysunek:
Wykład 9 - Dobór regulatorów. Instytut Automatyki i Robotyki Warszawa, 2017 Dobór regulatorów Podstawową przesłanką przy wyborze rodzaju regulatora są właściwości dynamiczne obiektu regulacji. Rysunek:
2. Wyznaczenie parametrów dynamicznych obiektu na podstawie odpowiedzi na skok jednostkowy, przy wykorzystaniu metody Küpfmüllera.
 1. Celem projektu jest zaprojektowanie układu regulacji wykorzystującego regulator PI lub regulator PID, dla określonego obiektu składającego się z iloczynu dwóch transmitancji G 1 (s) i G 2 (s). Następnym
1. Celem projektu jest zaprojektowanie układu regulacji wykorzystującego regulator PI lub regulator PID, dla określonego obiektu składającego się z iloczynu dwóch transmitancji G 1 (s) i G 2 (s). Następnym
Automatyka i robotyka
 Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
Teoria sterowania - studia niestacjonarne AiR 2 stopień
 Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Procesy wykładniczego wzrostu i spadku (np populacja bakterii, rozpad radioaktywny, wymiana ciepła) można modelować równaniem
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Procesy wykładniczego wzrostu i spadku (np populacja bakterii, rozpad radioaktywny, wymiana ciepła) można modelować równaniem
SYMULACJA ZAKŁÓCEŃ W UKŁADACH AUTOMATYKI UTWORZONYCH ZA POMOCĄ OBWODÓW ELEKTRYCZNYCH W PROGRAMACH MATHCAD I PSPICE
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 76 Electrical Engineering 2013 Piotr FRĄCZAK* SYMULACJA ZAKŁÓCEŃ W UKŁADACH AUTOMATYKI UTWORZONYCH ZA POMOCĄ OBWODÓW ELEKTRYCZNYCH W PROGRAMACH MATHCAD
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 76 Electrical Engineering 2013 Piotr FRĄCZAK* SYMULACJA ZAKŁÓCEŃ W UKŁADACH AUTOMATYKI UTWORZONYCH ZA POMOCĄ OBWODÓW ELEKTRYCZNYCH W PROGRAMACH MATHCAD
Równania różniczkowe wyższych rzędów
 Równania różniczkowe wyższych rzędów Marcin Orchel Spis treści 1 Wstęp 1 1.1 Istnienie rozwiązań............................... 1 1. Rozwiązanie ogólne............................... 1.3 Obniżanie rzędu
Równania różniczkowe wyższych rzędów Marcin Orchel Spis treści 1 Wstęp 1 1.1 Istnienie rozwiązań............................... 1 1. Rozwiązanie ogólne............................... 1.3 Obniżanie rzędu
Estymacja parametrów Wybrane zagadnienia implementacji i wykorzystania
 Estymacja parametrów Wybrane zagadnienia implementacji i wykorzystania Wykład w ramach przedmiotu Komputerowe systemy sterowania i wspomagania decyzji Plan wykładu Potrzeba estymacji parametrów Estymacja
Estymacja parametrów Wybrane zagadnienia implementacji i wykorzystania Wykład w ramach przedmiotu Komputerowe systemy sterowania i wspomagania decyzji Plan wykładu Potrzeba estymacji parametrów Estymacja
Zastosowanie rachunku wyrównawczego do uwiarygodnienia wyników pomiarów w układzie cieplnym bloku energetycznego siłowni parowej
 Marcin Szega Zastosowanie rachunku wyrównawczego do uwiarygodnienia wyników pomiarów w układzie cieplnym bloku energetycznego siłowni parowej (Monografia habilitacyjna nr 193. Wydawnictwo Politechniki
Marcin Szega Zastosowanie rachunku wyrównawczego do uwiarygodnienia wyników pomiarów w układzie cieplnym bloku energetycznego siłowni parowej (Monografia habilitacyjna nr 193. Wydawnictwo Politechniki
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Komputerowa Analiza Danych Doświadczalnych
 Komputerowa Analiza Danych Doświadczalnych Prowadząca: dr inż. Hanna Zbroszczyk e-mail: gos@if.pw.edu.pl tel: +48 22 234 58 51 konsultacje: poniedziałek, 10-11, środa: 11-12 www: http://www.if.pw.edu.pl/~gos/students/kadd
Komputerowa Analiza Danych Doświadczalnych Prowadząca: dr inż. Hanna Zbroszczyk e-mail: gos@if.pw.edu.pl tel: +48 22 234 58 51 konsultacje: poniedziałek, 10-11, środa: 11-12 www: http://www.if.pw.edu.pl/~gos/students/kadd
Metoda największej wiarygodności
 Rozdział Metoda największej wiarygodności Ogólnie w procesie estymacji na podstawie prób x i (każde x i może być wektorem) wyznaczamy parametr λ (w ogólnym przypadku również wektor) opisujący domniemany
Rozdział Metoda największej wiarygodności Ogólnie w procesie estymacji na podstawie prób x i (każde x i może być wektorem) wyznaczamy parametr λ (w ogólnym przypadku również wektor) opisujący domniemany
Kryteria optymalizacji w systemach sterowania rozmytego piecami odlewniczymi
 A R C H I V E S of F O U N D R Y E N G I N E E R I N G Published quarterly as the organ of the Foundry Commission of the Polish Academy of Sciences ISSN (1897-3310) Volume 14 Special Issue 2/2014 95 100
A R C H I V E S of F O U N D R Y E N G I N E E R I N G Published quarterly as the organ of the Foundry Commission of the Polish Academy of Sciences ISSN (1897-3310) Volume 14 Special Issue 2/2014 95 100
Regulacja dwupołożeniowa.
 Politechnika Krakowska Wydział Inżynierii Elektrycznej i Komputerowej Zakład eorii Sterowania Regulacja dwupołożeniowa. Kraków Zakład eorii Sterowania (E ) Regulacja dwupołożeniowa opis ćwiczenia.. Opis
Politechnika Krakowska Wydział Inżynierii Elektrycznej i Komputerowej Zakład eorii Sterowania Regulacja dwupołożeniowa. Kraków Zakład eorii Sterowania (E ) Regulacja dwupołożeniowa opis ćwiczenia.. Opis
ANALIZA WŁAŚCIWOŚCI FILTRU PARAMETRYCZNEGO I RZĘDU
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 78 Electrical Engineering 2014 Seweryn MAZURKIEWICZ* Janusz WALCZAK* ANALIZA WŁAŚCIWOŚCI FILTRU PARAMETRYCZNEGO I RZĘDU W artykule rozpatrzono problem
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 78 Electrical Engineering 2014 Seweryn MAZURKIEWICZ* Janusz WALCZAK* ANALIZA WŁAŚCIWOŚCI FILTRU PARAMETRYCZNEGO I RZĘDU W artykule rozpatrzono problem
Algorytmy sztucznej inteligencji
 Algorytmy sztucznej inteligencji Dynamiczne sieci neuronowe 1 Zapis macierzowy sieci neuronowych Poniżej omówione zostaną części składowe sieci neuronowych i metoda ich zapisu za pomocą macierzy. Obliczenia
Algorytmy sztucznej inteligencji Dynamiczne sieci neuronowe 1 Zapis macierzowy sieci neuronowych Poniżej omówione zostaną części składowe sieci neuronowych i metoda ich zapisu za pomocą macierzy. Obliczenia
PODSTAWY AUTOMATYKI. MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż.
 Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
Rys 1 Schemat modelu masa- sprężyna- tłumik
 Rys 1 Schemat modelu masa- sprężyna- tłumik gdzie: m-masa bloczka [kg], ẏ prędkośćbloczka [ m s ]. 3. W kolejnym energię potencjalną: gdzie: y- przemieszczenie bloczka [m], k- stała sprężystości, [N/m].
Rys 1 Schemat modelu masa- sprężyna- tłumik gdzie: m-masa bloczka [kg], ẏ prędkośćbloczka [ m s ]. 3. W kolejnym energię potencjalną: gdzie: y- przemieszczenie bloczka [m], k- stała sprężystości, [N/m].
Elementy Modelowania Matematycznego Wykład 7 Programowanie nieliniowe i całkowitoliczbowe
 Spis treści Elementy Modelowania Matematycznego Wykład 7 i całkowitoliczbowe Romuald Kotowski Katedra Informatyki Stosowanej PJWSTK 2009 Spis treści Spis treści 1 Wstęp 2 3 Spis treści Spis treści 1 Wstęp
Spis treści Elementy Modelowania Matematycznego Wykład 7 i całkowitoliczbowe Romuald Kotowski Katedra Informatyki Stosowanej PJWSTK 2009 Spis treści Spis treści 1 Wstęp 2 3 Spis treści Spis treści 1 Wstęp
1. Opis teoretyczny regulatora i obiektu z opóźnieniem.
 Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie:. Opis teoretyczny regulatora i obiektu z opóźnieniem. W regulacji dwupołożeniowej sygnał sterujący przyjmuje dwie wartości: pełne załączenie i wyłączenie...
Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie:. Opis teoretyczny regulatora i obiektu z opóźnieniem. W regulacji dwupołożeniowej sygnał sterujący przyjmuje dwie wartości: pełne załączenie i wyłączenie...
INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki
 Opracowano na podstawie: INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki 1. Kaczorek T.: Teoria sterowania, PWN, Warszawa 1977. 2. Węgrzyn S.: Podstawy automatyki, PWN, Warszawa 1980 3.
Opracowano na podstawie: INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki 1. Kaczorek T.: Teoria sterowania, PWN, Warszawa 1977. 2. Węgrzyn S.: Podstawy automatyki, PWN, Warszawa 1980 3.
Ćwiczenie - 1 OBSŁUGA GENERATORA I OSCYLOSKOPU. WYZNACZANIE CHARAKTERYSTYKI AMPLITUDOWEJ I FAZOWEJ NA PRZYKŁADZIE FILTRU RC.
 Ćwiczenie - 1 OBSŁUGA GENERATORA I OSCYLOSKOPU. WYZNACZANIE CHARAKTERYSTYKI AMPLITUDOWEJ I FAZOWEJ NA PRZYKŁADZIE FILTRU RC. Spis treści 1 Cel ćwiczenia 2 2 Podstawy teoretyczne 2 2.1 Charakterystyki częstotliwościowe..........................
Ćwiczenie - 1 OBSŁUGA GENERATORA I OSCYLOSKOPU. WYZNACZANIE CHARAKTERYSTYKI AMPLITUDOWEJ I FAZOWEJ NA PRZYKŁADZIE FILTRU RC. Spis treści 1 Cel ćwiczenia 2 2 Podstawy teoretyczne 2 2.1 Charakterystyki częstotliwościowe..........................
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: MODELOWANIE I SYMULACJA UKŁADÓW STEROWANIA Kierunek: Mechatronika Rodzaj przedmiotu: Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE C1.
Nazwa przedmiotu: MODELOWANIE I SYMULACJA UKŁADÓW STEROWANIA Kierunek: Mechatronika Rodzaj przedmiotu: Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE C1.
WIELOKRYTERIALNY DOBÓR ROZTRZĄSACZY OBORNIKA
 Inżynieria Rolnicza 7(95)/2007 WIELOKRYTERIALNY DOBÓR ROZTRZĄSACZY OBORNIKA Andrzej Turski, Andrzej Kwieciński Katedra Maszyn i Urządzeń Rolniczych, Akademia Rolnicza w Lublinie Streszczenie: W pracy przedstawiono
Inżynieria Rolnicza 7(95)/2007 WIELOKRYTERIALNY DOBÓR ROZTRZĄSACZY OBORNIKA Andrzej Turski, Andrzej Kwieciński Katedra Maszyn i Urządzeń Rolniczych, Akademia Rolnicza w Lublinie Streszczenie: W pracy przedstawiono
Rola stacji gazowych w ograniczaniu strat gazu w sieciach dystrybucyjnych
 Rola stacji gazowych w ograniczaniu strat gazu w sieciach dystrybucyjnych Politechnika Warszawska Zakład Systemów Ciepłowniczych i Gazowniczych Prof. dr hab. inż. Andrzej J. Osiadacz Dr hab. inż. Maciej
Rola stacji gazowych w ograniczaniu strat gazu w sieciach dystrybucyjnych Politechnika Warszawska Zakład Systemów Ciepłowniczych i Gazowniczych Prof. dr hab. inż. Andrzej J. Osiadacz Dr hab. inż. Maciej
Cyfrowe algorytmy sterowania AR S1 semestr 4 Projekt 4
 Cyfrowe algorytmy sterowania AR S1 semestr 4 Projekt 4 MPC Sterowanie predykcyjne Cel: Poznanie podstaw regulacji predykcyjnej i narzędzi do badań symulacyjnych Wykonali: Konrad Słodowicz Patryk Frankowski
Cyfrowe algorytmy sterowania AR S1 semestr 4 Projekt 4 MPC Sterowanie predykcyjne Cel: Poznanie podstaw regulacji predykcyjnej i narzędzi do badań symulacyjnych Wykonali: Konrad Słodowicz Patryk Frankowski
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Automatyka zastosowania, metody i narzędzia, perspektywy Synteza systemów sterowania z wykorzystaniem regulatorów
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Automatyka zastosowania, metody i narzędzia, perspektywy Synteza systemów sterowania z wykorzystaniem regulatorów
Co to jest wektor? Jest to obiekt posiadający: moduł (długość), kierunek wraz ze zwrotem.
 1 Wektory Co to jest wektor? Jest to obiekt posiadający: moduł (długość), kierunek wraz ze zwrotem. 1.1 Dodawanie wektorów graficzne i algebraiczne. Graficzne - metoda równoległoboku. Sprowadzamy wektory
1 Wektory Co to jest wektor? Jest to obiekt posiadający: moduł (długość), kierunek wraz ze zwrotem. 1.1 Dodawanie wektorów graficzne i algebraiczne. Graficzne - metoda równoległoboku. Sprowadzamy wektory
RÓWNANIA RÓŻNICZKOWE WYKŁAD 2
 RÓWNANIA RÓŻNICZKOWE WYKŁAD 2 Równania różniczkowe o zmiennych rozdzielonych Równania sprowadzalne do równań o zmiennych rozdzielonych Niech f będzie funkcją ciągłą na przedziale (a, b), spełniającą na
RÓWNANIA RÓŻNICZKOWE WYKŁAD 2 Równania różniczkowe o zmiennych rozdzielonych Równania sprowadzalne do równań o zmiennych rozdzielonych Niech f będzie funkcją ciągłą na przedziale (a, b), spełniającą na
Regulatory o działaniu ciągłym P, I, PI, PD, PID
 Regulatory o działaniu ciągłym P, I, PI, PD, PID Regulatory o działaniu ciągłym (analogowym) zmieniają wartość wielkości sterującej obiektem w sposób ciągły, tzn. wielkość ta może przyjmować wszystkie
Regulatory o działaniu ciągłym P, I, PI, PD, PID Regulatory o działaniu ciągłym (analogowym) zmieniają wartość wielkości sterującej obiektem w sposób ciągły, tzn. wielkość ta może przyjmować wszystkie
