Estymacja parametrów Wybrane zagadnienia implementacji i wykorzystania
|
|
|
- Lech Biernacki
- 7 lat temu
- Przeglądów:
Transkrypt
1 Estymacja parametrów Wybrane zagadnienia implementacji i wykorzystania Wykład w ramach przedmiotu Komputerowe systemy sterowania i wspomagania decyzji
2 Plan wykładu Potrzeba estymacji parametrów Estymacja jako etap procesu identyfikacji systemu Estymacja gradientowa Niekrzepka Krzepka Estymacja metodą najmniejszych kwadratów Wsadowa Z przesuwnym oknem Rekursywna (iteracyjna) Z współczynnikiem zapominania
3 Implementacja w Matlabie/Simulinku Mplik Mplik+Simulink Implementacja w języku C Implementacja w PLC (język ST)
4 Przykładowa parametryzacja dla modelu ARMA
5
6 Estymacja gradientowa Dzielenie przez zero, szum pomiarowy może uniemożliwiad wyznaczenie thety
7 Algorytm gradientowy
8 Metoda największego spadku (steepest descent)
9
10
11 M. Gaussa-Seidela
12
13 Regresja liniowa metoda najmniejszych kwadratów Popularna metoda statystyczna Można ją odnaleźd w pracach Gaussa ( ) przy wyznaczaniu orbit planet Wykorzystywana do wyznaczania nieznanych wielkości na podstawie znanych wielkości (oraz wiedzy o strukturze zależności między nimi) Użyteczna w wielu zastosowaniach: opracowaniu wyników pomiarów, modelowaniu, pośrednio sterowaniu
14 Jak na podstawie pomiarów y(t) otrzymad theta?
15 Wektor N x 1 Macierz N x n
16 Metoda najmniejszych kwadratów
17
18 Postad rekurencyjna ze wsp. zapominania
19
20 Dryf parametrów Zjawisko dryftu parametrów może wystąpid, gdy zastosowana zostaje klasyczna metoda estymacji parametrów (np. gradientowa lub najmniejszych kwadratów) dla obiektu posiadającego błędy modelowania nie będące białym szumem. Efektem dryftu parametrów jest to, że estymaty parametrów modeli zmierzają do nieskooczoności przy utrzymywaniu niewielkiego błędu modelowania. Otrzymanie nieograniczonych estymat parametrów uniemożliwia otrzymanie poprawnego sterowania. Istotne jest to, że efekt ten pojawia się nawet w obliczu bardzo korzystnego błędu modelowania addytywnego zakłócenia, które zanika.
21 Dryf parametrów
22 Dryf parametrów
23 Estymacja krzepka błąd modelowania jest ograniczony
24
25
26
27
28
29
30
31
32
33
34 Model parametryczny T y( t) t ( ) y(t) Wielkośd mierzona, najczęściej wyjściowa T (t) Wektor znanych wielkości (regresor, zmienne regresji) Wektor nieznanych (wyznaczanych, estymowanych parametrów)
35 Realizacja w Matlabie Matlab M plik
36 Matlab RLS z FF
37
38
39 u = sign(randn(50,1)); % input e = 0.2*randn(50,1); % noise th0 = idpoly([ ],[ ],[ ]); % a low order idpoly model opt = simoptions('addnoise',true,'noisedata',e); y = sim(th0,u,opt); z = iddata(y,u); plot(z) % analysis data object thm1 = roe(z,[2 2 1],'ff',0.98);
40 ROE Computes estimates recursively for an output error model. [THM,YHAT] = ROE(Z,NN,adm,adg) z : An IDDATA object or the output-input data matrix z = [y u]. The routine is for single input, single output data only. NN : NN = [nb nf nk], The orders and delay of an output error input-output model (see also OE). adm: Adaptation mechanism. adg: Adaptation gain adm='ff', adg=lam: Forgetting factor algorithm, with forgetting factor lam adm='kf', adg=r1: The Kalman filter algorithm with R1 as covariance matrix of the parameter changes per time step adm='ng', adg=gam: A normalized gradient algorithm, with gain gam adm='ug', adg=gam: An unnormalized gradient algorithm with gain gam THM: The resulting estimates. Row k contains the estimates "in alphabetic order" corresponding to data up to time k (row k in Z) YHAT: The predicted values of the outputs. Row k corresponds to time k. Initial value of parameters(th0) and of "P-matrix" (P0) can be given by [THM,YHAT,P] = ROE(Z,NN,adm,adg,TH0,P0) Initial and last values of auxiliary data vectors phi and psi are obtained by [THM,YHAT,P,phi,psi] = ROE(Z,NN,adm,adg,TH0,P0,phi0,psi0).
41 Metoda ruchomego okna dyskusja Układy niestacjonarne Parametry zmienne w czasie Stała liczba danych brana pod uwagę
42
43 Bibliografia Ioannou P., Sun J. (1996) Robust Adaptive Control, PTR Prentice Hall Soderstrom T., Stoica P. (1997) Identyfikacja systemów, Wydawnictwo Naukowe PWN Janiszowski K. (2002) Identyfikacja modeli parametrycznych, Akademicka Oficyna Wydawnicza EXIT Gang T. (2003) Adaptive Control Design and Analysis Wiley-Interscience, A John Wiley & Sons Inc. Publication
44 Bibliografia cd. Astrom K., Wittenmark B. (1995) Adaptive Control Second Edition, Addison-Wesley Publishing Company Niederlioski A., Mościoski J, Ogonowski Z. (1995) Regulacja adaptacyjna, Wydawnictwo Naukowe PWN
Wprowadzenie do sterowania adaptacyjnego
 Wykład w ramach przedmiotu Komputerowe Systemy Sterowania dla sem. VI AiR AiSS WEiA PG Wprowadzenie do sterowania adaptacyjnego Opracował dr inż. Jarosław Tarnawski 1 Plan wykładu Definicja sterowania
Wykład w ramach przedmiotu Komputerowe Systemy Sterowania dla sem. VI AiR AiSS WEiA PG Wprowadzenie do sterowania adaptacyjnego Opracował dr inż. Jarosław Tarnawski 1 Plan wykładu Definicja sterowania
Egzamin / zaliczenie na ocenę*
 Zał. nr do ZW /01 WYDZIAŁ / STUDIUM KARTA PRZEDMIOTU Nazwa w języku polskim Identyfikacja systemów Nazwa w języku angielskim System identification Kierunek studiów (jeśli dotyczy): Inżynieria Systemów
Zał. nr do ZW /01 WYDZIAŁ / STUDIUM KARTA PRZEDMIOTU Nazwa w języku polskim Identyfikacja systemów Nazwa w języku angielskim System identification Kierunek studiów (jeśli dotyczy): Inżynieria Systemów
Automatyka i Robotyka II stopień ogólno akademicki studia niestacjonarne. wszystkie Katedra Automatyki i Robotyki Dr inż.
 KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2013/2014 Identyfikacja obiektów sterowania Identification of Control Systems A.
KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2013/2014 Identyfikacja obiektów sterowania Identification of Control Systems A.
Sterowanie napędów maszyn i robotów
 Wykład 5 - Identyfikacja Instytut Automatyki i Robotyki (IAiR), Politechnika Warszawska Warszawa, 2015 Koncepcje estymacji modelu Standardowe drogi poszukiwania modeli parametrycznych M1: Analityczne określenie
Wykład 5 - Identyfikacja Instytut Automatyki i Robotyki (IAiR), Politechnika Warszawska Warszawa, 2015 Koncepcje estymacji modelu Standardowe drogi poszukiwania modeli parametrycznych M1: Analityczne określenie
KARTA OPISU MODUŁU KSZTAŁCENIA
 Nazwa modułu: Kierunek studiów KARTA OPISU MODUŁU KSZTAŁCENIA Identyfikacja i systemy adaptacyjne Profil kształcenia (ogólnoakademicki, praktyczny) Kod Rok / Semestr Automatyka i Robotyka ogólnoakademicki
Nazwa modułu: Kierunek studiów KARTA OPISU MODUŁU KSZTAŁCENIA Identyfikacja i systemy adaptacyjne Profil kształcenia (ogólnoakademicki, praktyczny) Kod Rok / Semestr Automatyka i Robotyka ogólnoakademicki
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania MODELOWANIE I IDENTYFIKACJA Studia niestacjonarne Estymacja parametrów modeli, metoda najmniejszych kwadratów.
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania MODELOWANIE I IDENTYFIKACJA Studia niestacjonarne Estymacja parametrów modeli, metoda najmniejszych kwadratów.
Dynamika procesu zmienna stała. programowalne zmiany parametrów r.
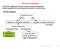 Sterowanie adaptacyjne Sterowanie adaptacyjne polega na dostosowywaniu (adaptacji) nastaw regulatora do zmian parametrów obiektu (w trakcie pracy) Techniki adaptacji Dynamika procesu zmienna stała regulator
Sterowanie adaptacyjne Sterowanie adaptacyjne polega na dostosowywaniu (adaptacji) nastaw regulatora do zmian parametrów obiektu (w trakcie pracy) Techniki adaptacji Dynamika procesu zmienna stała regulator
Wykład 4 Wybór najlepszej procedury. Estymacja parametrów re
 Wykład 4 Wybór najlepszej procedury. Estymacja parametrów regresji z wykorzystaniem metody bootstrap. Wrocław, 22.03.2017r Wybór najlepszej procedury - podsumowanie Co nas interesuje przed przeprowadzeniem
Wykład 4 Wybór najlepszej procedury. Estymacja parametrów regresji z wykorzystaniem metody bootstrap. Wrocław, 22.03.2017r Wybór najlepszej procedury - podsumowanie Co nas interesuje przed przeprowadzeniem
Analityczne metody detekcji uszkodzeń
 Instytut Sterowania i Systemów Informatycznych Universytet Zielonogórski Wykład 5 Model procesu Rozważmy czasowo-dyskretny model liniowy gdzie: k dyskretny czas, x(k) R n wektor stanu, x(k + 1) = Ax(k)
Instytut Sterowania i Systemów Informatycznych Universytet Zielonogórski Wykład 5 Model procesu Rozważmy czasowo-dyskretny model liniowy gdzie: k dyskretny czas, x(k) R n wektor stanu, x(k + 1) = Ax(k)
Podstawy automatyki. Energetyka Sem. V Wykład 1. Sem /17 Hossein Ghaemi
 Podstawy automatyki Energetyka Sem. V Wykład 1 Sem. 1-2016/17 Hossein Ghaemi Hossein Ghaemi Katedra Automatyki i Energetyki Wydział Oceanotechniki i Okrętownictwa Politechnika Gdańska pok. 222A WOiO Tel.:
Podstawy automatyki Energetyka Sem. V Wykład 1 Sem. 1-2016/17 Hossein Ghaemi Hossein Ghaemi Katedra Automatyki i Energetyki Wydział Oceanotechniki i Okrętownictwa Politechnika Gdańska pok. 222A WOiO Tel.:
Ćwiczenie 6 Projektowanie filtrów cyfrowych o skończonej i nieskończonej odpowiedzi impulsowej
 Ćwiczenie 6 Projektowanie filtrów cyfrowych o skończonej i nieskończonej odpowiedzi impulsowej 1. Filtry FIR o skończonej odpowiedzi impulsowej (SOI) Filtracja FIR polega na tym, że sygnał wyjściowy powstaje
Ćwiczenie 6 Projektowanie filtrów cyfrowych o skończonej i nieskończonej odpowiedzi impulsowej 1. Filtry FIR o skończonej odpowiedzi impulsowej (SOI) Filtracja FIR polega na tym, że sygnał wyjściowy powstaje
WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU
 Zał. nr 4 do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim STATYSTYCZNA ANALIZA DANYCH Nazwa w języku angielskim STATISTICAL DATA ANALYSIS Kierunek studiów (jeśli dotyczy):
Zał. nr 4 do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim STATYSTYCZNA ANALIZA DANYCH Nazwa w języku angielskim STATISTICAL DATA ANALYSIS Kierunek studiów (jeśli dotyczy):
Wprowadzenie do teorii ekonometrii. Wykład 1 Warunkowa wartość oczekiwana i odwzorowanie liniowe
 Wprowadzenie do teorii ekonometrii Wykład 1 Warunkowa wartość oczekiwana i odwzorowanie liniowe Zajęcia Wykład Laboratorium komputerowe 2 Zaliczenie EGZAMIN (50%) Na egzaminie obowiązują wszystkie informacje
Wprowadzenie do teorii ekonometrii Wykład 1 Warunkowa wartość oczekiwana i odwzorowanie liniowe Zajęcia Wykład Laboratorium komputerowe 2 Zaliczenie EGZAMIN (50%) Na egzaminie obowiązują wszystkie informacje
Ćwiczenie 6 Projektowanie filtrów cyfrowych o skończonej i nieskończonej odpowiedzi impulsowej
 Ćwiczenie 6 Projektowanie filtrów cyfrowych o skończonej i nieskończonej odpowiedzi impulsowej. Filtry FIR o skończonej odpowiedzi impulsowej (SOI) Filtracja FIR polega na tym, że sygnał wyjściowy powstaje
Ćwiczenie 6 Projektowanie filtrów cyfrowych o skończonej i nieskończonej odpowiedzi impulsowej. Filtry FIR o skończonej odpowiedzi impulsowej (SOI) Filtracja FIR polega na tym, że sygnał wyjściowy powstaje
WSKAZÓWKI DO WYKONANIA SPRAWOZDANIA Z WYRÓWNAWCZYCH ZAJĘĆ LABORATORYJNYCH
 WSKAZÓWKI DO WYKONANIA SPRAWOZDANIA Z WYRÓWNAWCZYCH ZAJĘĆ LABORATORYJNYCH Dobrze przygotowane sprawozdanie powinno zawierać następujące elementy: 1. Krótki wstęp - maksymalnie pół strony. W krótki i zwięzły
WSKAZÓWKI DO WYKONANIA SPRAWOZDANIA Z WYRÓWNAWCZYCH ZAJĘĆ LABORATORYJNYCH Dobrze przygotowane sprawozdanie powinno zawierać następujące elementy: 1. Krótki wstęp - maksymalnie pół strony. W krótki i zwięzły
Automatyka i Robotyka II Stopień ogólno akademicki studia niestacjonarne wszystkie Katedra Automatyki i Robotyki Prof. dr hab. inż.
 Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2013/2014
Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2013/2014
Filtr Kalmana. Struktury i Algorytmy Sterowania Wykład 1-2. prof. dr hab. inż. Mieczysław A. Brdyś mgr inż. Tomasz Zubowicz
 Filtr Kalmana Struktury i Algorytmy Sterowania Wykład 1-2 prof. dr hab. inż. Mieczysław A. Brdyś mgr inż. Tomasz Zubowicz Politechnika Gdańska, Wydział Elektortechniki i Automatyki 2013-10-09, Gdańsk Założenia
Filtr Kalmana Struktury i Algorytmy Sterowania Wykład 1-2 prof. dr hab. inż. Mieczysław A. Brdyś mgr inż. Tomasz Zubowicz Politechnika Gdańska, Wydział Elektortechniki i Automatyki 2013-10-09, Gdańsk Założenia
Egzamin / zaliczenie na ocenę* WYMAGANIA WSTĘPNE W ZAKRESIE WIEDZY, UMIEJĘTNOŚCI I INNYCH KOMPETENCJI
 Zał. nr do ZW 33/01 WYDZIAŁ / STUDIUM KARTA PRZEDMIOTU Nazwa w języku polskim Modele i analiza systemów. Nazwa w języku angielskim Models and system analysis. Kierunek studiów (jeśli dotyczy): Inżynieria
Zał. nr do ZW 33/01 WYDZIAŁ / STUDIUM KARTA PRZEDMIOTU Nazwa w języku polskim Modele i analiza systemów. Nazwa w języku angielskim Models and system analysis. Kierunek studiów (jeśli dotyczy): Inżynieria
Przedmowa Wykaz oznaczeń Wykaz skrótów 1. Sygnały i ich parametry 1 1.1. Pojęcia podstawowe 1 1.2. Klasyfikacja sygnałów 2 1.3.
 Przedmowa Wykaz oznaczeń Wykaz skrótów 1. Sygnały i ich parametry 1 1.1. Pojęcia podstawowe 1 1.2. Klasyfikacja sygnałów 2 1.3. Sygnały deterministyczne 4 1.3.1. Parametry 4 1.3.2. Przykłady 7 1.3.3. Sygnały
Przedmowa Wykaz oznaczeń Wykaz skrótów 1. Sygnały i ich parametry 1 1.1. Pojęcia podstawowe 1 1.2. Klasyfikacja sygnałów 2 1.3. Sygnały deterministyczne 4 1.3.1. Parametry 4 1.3.2. Przykłady 7 1.3.3. Sygnały
Ekonometria. Wprowadzenie do modelowania ekonometrycznego Estymator KMNK. Jakub Mućk. Katedra Ekonomii Ilościowej
 Ekonometria Wprowadzenie do modelowania ekonometrycznego Estymator Jakub Mućk Katedra Ekonomii Ilościowej Jakub Mućk Ekonometria Wykład 1 Estymator 1 / 16 Agenda 1 Literatura Zaliczenie przedmiotu 2 Model
Ekonometria Wprowadzenie do modelowania ekonometrycznego Estymator Jakub Mućk Katedra Ekonomii Ilościowej Jakub Mućk Ekonometria Wykład 1 Estymator 1 / 16 Agenda 1 Literatura Zaliczenie przedmiotu 2 Model
doc. dr Beata Pułska-Turyna Zarządzanie B506 mail: mgr Piotr J. Gadecki Zakład Badań Operacyjnych Zarządzania B 505.
 doc. dr Beata Pułska-Turyna Zakład Badań Operacyjnych Zarządzanie B506 mail: turynab@wz.uw.edu.pl mgr Piotr J. Gadecki Zakład Badań Operacyjnych Zarządzania B 505. Tel.: (22)55 34 144 Mail: student@pgadecki.pl
doc. dr Beata Pułska-Turyna Zakład Badań Operacyjnych Zarządzanie B506 mail: turynab@wz.uw.edu.pl mgr Piotr J. Gadecki Zakład Badań Operacyjnych Zarządzania B 505. Tel.: (22)55 34 144 Mail: student@pgadecki.pl
Praca dyplomowa magisterska
 Praca dyplomowa magisterska Implementacja algorytmów filtracji adaptacyjnej o strukturze transwersalnej na platformie CUDA Dyplomant: Jakub Kołakowski Opiekun pracy: dr inż. Michał Meller Plan prezentacji
Praca dyplomowa magisterska Implementacja algorytmów filtracji adaptacyjnej o strukturze transwersalnej na platformie CUDA Dyplomant: Jakub Kołakowski Opiekun pracy: dr inż. Michał Meller Plan prezentacji
WYDZIAŁ BUDOWNICTWA LĄDOWEGO I WODNEGO
 Zał. nr 4 do ZW WYDZIAŁ BUDOWNICTWA LĄDOWEGO I WODNEGO KARTA PRZEDMIOTU Nazwa w języku polskim STATYSTYKA STOSOWANA Nazwa w języku angielskim APPLIED STATISTICS Kierunek studiów (jeśli dotyczy): Specjalność
Zał. nr 4 do ZW WYDZIAŁ BUDOWNICTWA LĄDOWEGO I WODNEGO KARTA PRZEDMIOTU Nazwa w języku polskim STATYSTYKA STOSOWANA Nazwa w języku angielskim APPLIED STATISTICS Kierunek studiów (jeśli dotyczy): Specjalność
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM. Ćwiczenie 2. Badanie algorytmów adaptacyjnych LMS i RLS
 ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 2 Badanie algorytmów adaptacyjnych LMS i RLS 1. CEL ĆWICZENIA Celem ćwiczenia jest samodzielna implementacja przez studentów dwóch podstawowych
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 2 Badanie algorytmów adaptacyjnych LMS i RLS 1. CEL ĆWICZENIA Celem ćwiczenia jest samodzielna implementacja przez studentów dwóch podstawowych
Projektowanie systemów pomiarowych. 02 Dokładność pomiarów
 Projektowanie systemów pomiarowych 02 Dokładność pomiarów 1 www.technidyneblog.com 2 Jak dokładnie wykonaliśmy pomiar? Czy duża / wysoka dokładność jest zawsze konieczna? www.sparkfun.com 3 Błąd pomiaru.
Projektowanie systemów pomiarowych 02 Dokładność pomiarów 1 www.technidyneblog.com 2 Jak dokładnie wykonaliśmy pomiar? Czy duża / wysoka dokładność jest zawsze konieczna? www.sparkfun.com 3 Błąd pomiaru.
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM. Ćwiczenie 2. Badanie algorytmów adaptacyjnych LMS i RLS
 ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 2 Badanie algorytmów adaptacyjnych LMS i RLS 1. CEL ĆWICZENIA Celem ćwiczenia jest samodzielna implementacja przez studentów dwóch podstawowych
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 2 Badanie algorytmów adaptacyjnych LMS i RLS 1. CEL ĆWICZENIA Celem ćwiczenia jest samodzielna implementacja przez studentów dwóch podstawowych
Identyfikacja obiektów dynamicznych za pomocą sieci neuronowych
 Metody Sztucznej Inteligencji w Sterowaniu Ćwiczenie 3 Identyfikacja obiektów dynamicznych za pomocą sieci neuronowych Przygotował: mgr inż. Marcin Pelic Instytut Technologii Mechanicznej Politechnika
Metody Sztucznej Inteligencji w Sterowaniu Ćwiczenie 3 Identyfikacja obiektów dynamicznych za pomocą sieci neuronowych Przygotował: mgr inż. Marcin Pelic Instytut Technologii Mechanicznej Politechnika
x x 1. Przedmiot identyfikacji System x (1) x (2) : x (s) a 1 a 2 : a s mierzone, a = zestaw współczynników konkretyzujacych F ()
 . Przedmiot identyfikacji System () x (2) x * a z y ( s ) x y = F (x,z)=f(x,z,a ),gdziex = F () znane, a nieznane x () x (2) x (s) mierzone, a = a a 2 a s zestaw współczynników konkretyzujacych F () informacja
. Przedmiot identyfikacji System () x (2) x * a z y ( s ) x y = F (x,z)=f(x,z,a ),gdziex = F () znane, a nieznane x () x (2) x (s) mierzone, a = a a 2 a s zestaw współczynników konkretyzujacych F () informacja
KARTA INFORMACYJNA PRZEDMIOTU
 Uniwersytet Rzeszowski WYDZIAŁ KIERUNEK Matematyczno-Przyrodniczy Fizyka techniczna SPECJALNOŚĆ RODZAJ STUDIÓW stacjonarne, studia pierwszego stopnia KARTA INFORMACYJNA PRZEDMIOTU NAZWA PRZEDMIOTU WG PLANU
Uniwersytet Rzeszowski WYDZIAŁ KIERUNEK Matematyczno-Przyrodniczy Fizyka techniczna SPECJALNOŚĆ RODZAJ STUDIÓW stacjonarne, studia pierwszego stopnia KARTA INFORMACYJNA PRZEDMIOTU NAZWA PRZEDMIOTU WG PLANU
STATYSTYKA MATEMATYCZNA
 Zał. nr 4 do ZW WYDZIAŁ ELEKTRONIKI KARTA PRZEDMIOTU Nazwa w języku polskim STATYSTYKA MATEMATYCZNA Nazwa w języku angielskim Mathematical Statistics Kierunek studiów (jeśli dotyczy): Specjalność (jeśli
Zał. nr 4 do ZW WYDZIAŁ ELEKTRONIKI KARTA PRZEDMIOTU Nazwa w języku polskim STATYSTYKA MATEMATYCZNA Nazwa w języku angielskim Mathematical Statistics Kierunek studiów (jeśli dotyczy): Specjalność (jeśli
KOMPUTEROWY MODEL UKŁADU STEROWANIA MIKROKLIMATEM W PRZECHOWALNI JABŁEK
 Inżynieria Rolnicza 8(117)/2009 KOMPUTEROWY MODEL UKŁADU STEROWANIA MIKROKLIMATEM W PRZECHOWALNI JABŁEK Ewa Wachowicz, Piotr Grudziński Katedra Automatyki, Politechnika Koszalińska Streszczenie. W pracy
Inżynieria Rolnicza 8(117)/2009 KOMPUTEROWY MODEL UKŁADU STEROWANIA MIKROKLIMATEM W PRZECHOWALNI JABŁEK Ewa Wachowicz, Piotr Grudziński Katedra Automatyki, Politechnika Koszalińska Streszczenie. W pracy
Wstęp do sieci neuronowych, wykład 03 Warstwy RBF, jednostka Adaline.
 Wstęp do sieci neuronowych, wykład 3 Warstwy, jednostka Adaline. Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 211-1-18 1 Pomysł Przykłady Zastosowanie 2
Wstęp do sieci neuronowych, wykład 3 Warstwy, jednostka Adaline. Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 211-1-18 1 Pomysł Przykłady Zastosowanie 2
Komputerowa Analiza Danych Doświadczalnych
 Komputerowa Analiza Danych Doświadczalnych dr inż. Adam Kisiel kisiel@if.pw.edu.pl pokój 117b (12b) 1 Materiały do wykładu Transparencje do wykładów: http://www.if.pw.edu.pl/~kisiel/kadd/kadd.html Literatura
Komputerowa Analiza Danych Doświadczalnych dr inż. Adam Kisiel kisiel@if.pw.edu.pl pokój 117b (12b) 1 Materiały do wykładu Transparencje do wykładów: http://www.if.pw.edu.pl/~kisiel/kadd/kadd.html Literatura
Systemy Wspomagania Decyzji
 Regresja Szkoła Główna Służby Pożarniczej Zakład Informatyki i Łączności January 24, 2014 1 Wprowadzenie 2 Regresja liniowa 3 Regresja nieliniowa 4 Regresja logistyczna 5 Estymacja parametrów 6 Podsumowanie
Regresja Szkoła Główna Służby Pożarniczej Zakład Informatyki i Łączności January 24, 2014 1 Wprowadzenie 2 Regresja liniowa 3 Regresja nieliniowa 4 Regresja logistyczna 5 Estymacja parametrów 6 Podsumowanie
Rozpoznawanie obrazów
 Rozpoznawanie obrazów Laboratorium Python Zadanie nr 1 Regresja liniowa autorzy: A. Gonczarek, J.M. Tomczak, S. Zaręba, M. Zięba, J. Kaczmar Cel zadania Celem zadania jest implementacja liniowego zadania
Rozpoznawanie obrazów Laboratorium Python Zadanie nr 1 Regresja liniowa autorzy: A. Gonczarek, J.M. Tomczak, S. Zaręba, M. Zięba, J. Kaczmar Cel zadania Celem zadania jest implementacja liniowego zadania
Algorytmy ze skończoną pamięcią dla przetwarzania sygnałów w diagnostyce procesów.
 Mgr inż. Jędrzej Byrski 28.11.2014 Katedra Informatyki Stosowanej Wydział EAIiIB, AGH 1. Tezy i zakres rozprawy AUTOREFERAT PRACY DOKTORSKIEJ Algorytmy ze skończoną pamięcią dla przetwarzania sygnałów
Mgr inż. Jędrzej Byrski 28.11.2014 Katedra Informatyki Stosowanej Wydział EAIiIB, AGH 1. Tezy i zakres rozprawy AUTOREFERAT PRACY DOKTORSKIEJ Algorytmy ze skończoną pamięcią dla przetwarzania sygnałów
Uczenie ze wzmocnieniem
 Uczenie ze wzmocnieniem Maria Ganzha Wydział Matematyki i Nauk Informatycznych 2018-2019 O projekcie nr 2 roboty (samochody, odkurzacze, drony,...) gry planszowe, sterowanie (optymalizacja; windy,..) optymalizacja
Uczenie ze wzmocnieniem Maria Ganzha Wydział Matematyki i Nauk Informatycznych 2018-2019 O projekcie nr 2 roboty (samochody, odkurzacze, drony,...) gry planszowe, sterowanie (optymalizacja; windy,..) optymalizacja
Metody optymalizacji Optimization methods Forma studiów: stacjonarne Poziom studiów II stopnia. Liczba godzin/tydzień: 1W, 1Ć
 Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: obowiązkowy w ramach treści dodatkowych Rodzaj zajęć: wykład, ćwiczenia Metody Optimization methods Forma studiów: stacjonarne Poziom studiów
Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: obowiązkowy w ramach treści dodatkowych Rodzaj zajęć: wykład, ćwiczenia Metody Optimization methods Forma studiów: stacjonarne Poziom studiów
Optymalizacja ciągła
 Optymalizacja ciągła 5. Metoda stochastycznego spadku wzdłuż gradientu Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 04.04.2019 1 / 20 Wprowadzenie Minimalizacja różniczkowalnej
Optymalizacja ciągła 5. Metoda stochastycznego spadku wzdłuż gradientu Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 04.04.2019 1 / 20 Wprowadzenie Minimalizacja różniczkowalnej
Egzamin / zaliczenie na ocenę*
 Zał. nr do ZW 33/01 WYDZIAŁ / STUDIUM KARTA PRZEDMIOTU Nazwa w języku polskim Optymalizacja systemów Nazwa w języku angielskim System optimization Kierunek studiów (jeśli dotyczy): Inżynieria Systemów
Zał. nr do ZW 33/01 WYDZIAŁ / STUDIUM KARTA PRZEDMIOTU Nazwa w języku polskim Optymalizacja systemów Nazwa w języku angielskim System optimization Kierunek studiów (jeśli dotyczy): Inżynieria Systemów
4. EKSPLOATACJA UKŁADU NAPĘD ZWROTNICOWY ROZJAZD. DEFINICJA SIŁ W UKŁADZIE Siła nastawcza Siła trzymania
 3 SPIS TREŚCI Przedmowa... 11 1. WPROWADZENIE... 13 1.1. Budowa rozjazdów kolejowych... 14 1.2. Napędy zwrotnicowe... 15 1.2.1. Napęd zwrotnicowy EEA-4... 18 1.2.2. Napęd zwrotnicowy EEA-5... 20 1.3. Współpraca
3 SPIS TREŚCI Przedmowa... 11 1. WPROWADZENIE... 13 1.1. Budowa rozjazdów kolejowych... 14 1.2. Napędy zwrotnicowe... 15 1.2.1. Napęd zwrotnicowy EEA-4... 18 1.2.2. Napęd zwrotnicowy EEA-5... 20 1.3. Współpraca
Elektrotechnika II stopień ogólnoakademicki. stacjonarne. przedmiot specjalnościowy. obowiązkowy polski semestr II semestr letni. tak. Laborat. 30 g.
 KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013 Metody estymacji parametrów i sygnałów Estimation methods of parameters
KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013 Metody estymacji parametrów i sygnałów Estimation methods of parameters
Statystyczne Metody Opracowania Wyników Pomiarów
 Statystyczne Metody Opracowania Wyników Pomiarów dla studentów ZMIN Teresa Jaworska-Gołąb 2017/18 Co czytać [1] I Pracownia fizyczna, Andrzej Magiera red., Oficyna Wydawnicza IMPULS, Kraków 2006; http://www.1pf.if.uj.edu.pl/materialy/zalecana-literatura
Statystyczne Metody Opracowania Wyników Pomiarów dla studentów ZMIN Teresa Jaworska-Gołąb 2017/18 Co czytać [1] I Pracownia fizyczna, Andrzej Magiera red., Oficyna Wydawnicza IMPULS, Kraków 2006; http://www.1pf.if.uj.edu.pl/materialy/zalecana-literatura
Estymacja częstotliwości podstawowej sieci energetycznej na podstawie scałkowanego sygnału napięcia
 SIWOŃ Cezary 1 Estymacja częstotliwości podstawowej sieci energetycznej na podstawie scałkowanego sygnału napięcia WSTĘP Utrzymanie stałej częstotliwości napięcia w sieci energetycznej jest jednym z najważniejszych
SIWOŃ Cezary 1 Estymacja częstotliwości podstawowej sieci energetycznej na podstawie scałkowanego sygnału napięcia WSTĘP Utrzymanie stałej częstotliwości napięcia w sieci energetycznej jest jednym z najważniejszych
Komputerowe przetwarzanie obrazu Laboratorium 5
 Komputerowe przetwarzanie obrazu Laboratorium 5 Przykład 1 Histogram obrazu a dobór progu binaryzacji. Na podstawie charakterystyki histogramu wybrano dwa różne progi binaryzacji (120 oraz 180). Proszę
Komputerowe przetwarzanie obrazu Laboratorium 5 Przykład 1 Histogram obrazu a dobór progu binaryzacji. Na podstawie charakterystyki histogramu wybrano dwa różne progi binaryzacji (120 oraz 180). Proszę
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: przedmiot obowiązkowy w ramach treści kierunkowych, moduł kierunkowy ogólny Rodzaj zajęć: wykład, ćwiczenia I KARTA PRZEDMIOTU CEL PRZEDMIOTU
Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: przedmiot obowiązkowy w ramach treści kierunkowych, moduł kierunkowy ogólny Rodzaj zajęć: wykład, ćwiczenia I KARTA PRZEDMIOTU CEL PRZEDMIOTU
WYMAGANIA WSTĘPNE W ZAKRESIE WIEDZY, UMIEJĘTNOŚCI I INNYCH KOMPETENCJI
 WYDZIAŁ GEOINŻYNIERII, GÓRNICTWA I GEOLOGII KARTA PRZEDMIOTU Nazwa w języku polskim: Statystyka matematyczna Nazwa w języku angielskim: Mathematical Statistics Kierunek studiów (jeśli dotyczy): Górnictwo
WYDZIAŁ GEOINŻYNIERII, GÓRNICTWA I GEOLOGII KARTA PRZEDMIOTU Nazwa w języku polskim: Statystyka matematyczna Nazwa w języku angielskim: Mathematical Statistics Kierunek studiów (jeśli dotyczy): Górnictwo
Zał nr 4 do ZW. Dla grupy kursów zaznaczyć kurs końcowy. Liczba punktów ECTS charakterze praktycznym (P)
 Zał nr 4 do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim : Algebra numeryczna Nazwa w języku angielskim : Numerical algebra Kierunek studiów : Informatyka Specjalność
Zał nr 4 do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim : Algebra numeryczna Nazwa w języku angielskim : Numerical algebra Kierunek studiów : Informatyka Specjalność
Estymacja wektora stanu w prostym układzie elektroenergetycznym
 Zakład Sieci i Systemów Elektroenergetycznych LABORATORIUM INFORMATYCZNE SYSTEMY WSPOMAGANIA DYSPOZYTORÓW Estymacja wektora stanu w prostym układzie elektroenergetycznym Autorzy: dr inż. Zbigniew Zdun
Zakład Sieci i Systemów Elektroenergetycznych LABORATORIUM INFORMATYCZNE SYSTEMY WSPOMAGANIA DYSPOZYTORÓW Estymacja wektora stanu w prostym układzie elektroenergetycznym Autorzy: dr inż. Zbigniew Zdun
Stanisław Cichocki. Natalia Nehrebecka
 Stanisław Cichocki Natalia Nehrebecka 1 2 3 1. Wprowadzenie do danych panelowych a) Charakterystyka danych panelowych b) Zalety i ograniczenia 2. Modele ekonometryczne danych panelowych a) Model efektów
Stanisław Cichocki Natalia Nehrebecka 1 2 3 1. Wprowadzenie do danych panelowych a) Charakterystyka danych panelowych b) Zalety i ograniczenia 2. Modele ekonometryczne danych panelowych a) Model efektów
1. Stacjonarnośd i niestacjonarnośd szeregów czasowych 2. Test ADF i test KPSS 3. Budowa modeli ARMA dla zmiennych niestacjonarnych 4.
 1. Stacjonarnośd i niestacjonarnośd szeregów czasowych 2. Test ADF i test KPSS 3. Budowa modeli ARMA dla zmiennych niestacjonarnych 4. Prognozowanie stóp zwrotu na podstawie modeli ARMA 5. Relacje kointegrujące
1. Stacjonarnośd i niestacjonarnośd szeregów czasowych 2. Test ADF i test KPSS 3. Budowa modeli ARMA dla zmiennych niestacjonarnych 4. Prognozowanie stóp zwrotu na podstawie modeli ARMA 5. Relacje kointegrujące
Statystyczne Metody Opracowania Wyników Pomiarów
 Statystyczne Metody Opracowania Wyników Pomiarów dla studentów ZMIN Teresa Jaworska-Gołąb 2018/19 Co czytać [1] I Pracownia fizyczna, Andrzej Magiera red., Oficyna Wydawnicza IMPULS, Kraków 2006; http://www.1pf.if.uj.edu.pl/materialy/zalecana-literatura
Statystyczne Metody Opracowania Wyników Pomiarów dla studentów ZMIN Teresa Jaworska-Gołąb 2018/19 Co czytać [1] I Pracownia fizyczna, Andrzej Magiera red., Oficyna Wydawnicza IMPULS, Kraków 2006; http://www.1pf.if.uj.edu.pl/materialy/zalecana-literatura
Algorytmy sztucznej inteligencji
 Algorytmy sztucznej inteligencji Dynamiczne sieci neuronowe 1 Zapis macierzowy sieci neuronowych Poniżej omówione zostaną części składowe sieci neuronowych i metoda ich zapisu za pomocą macierzy. Obliczenia
Algorytmy sztucznej inteligencji Dynamiczne sieci neuronowe 1 Zapis macierzowy sieci neuronowych Poniżej omówione zostaną części składowe sieci neuronowych i metoda ich zapisu za pomocą macierzy. Obliczenia
Metody systemowe i decyzyjne w informatyce
 Metody systemowe i decyzyjne w informatyce Laboratorium MATLAB Zadanie nr 1 Regresja liniowa autorzy: A. Gonczarek, J.M. Tomczak Cel zadania Celem zadania jest zapoznanie się z liniowym zadaniem najmniejszych
Metody systemowe i decyzyjne w informatyce Laboratorium MATLAB Zadanie nr 1 Regresja liniowa autorzy: A. Gonczarek, J.M. Tomczak Cel zadania Celem zadania jest zapoznanie się z liniowym zadaniem najmniejszych
Statystyka opisowa. Wykład V. Regresja liniowa wieloraka
 Statystyka opisowa. Wykład V. e-mail:e.kozlovski@pollub.pl Spis treści 1 Prosta regresji cechy Y względem cech X 1,..., X k. 2 3 Wyznaczamy zależność cechy Y od cech X 1, X 2,..., X k postaci Y = α 0 +
Statystyka opisowa. Wykład V. e-mail:e.kozlovski@pollub.pl Spis treści 1 Prosta regresji cechy Y względem cech X 1,..., X k. 2 3 Wyznaczamy zależność cechy Y od cech X 1, X 2,..., X k postaci Y = α 0 +
Obserwatory stanu, zasada separowalności i regulator LQG
 Obserwatory stanu, zasada separowalności i regulator LQG Zaawansowane Techniki Sterowania Wydział Mechatroniki Politechniki Warszawskiej Anna Sztyber ZTS (IAiR PW) LQR Anna Sztyber / 29 Plan wykładu Obserwatory
Obserwatory stanu, zasada separowalności i regulator LQG Zaawansowane Techniki Sterowania Wydział Mechatroniki Politechniki Warszawskiej Anna Sztyber ZTS (IAiR PW) LQR Anna Sztyber / 29 Plan wykładu Obserwatory
Wykład 10 Skalowanie wielowymiarowe
 Wykład 10 Skalowanie wielowymiarowe Wrocław, 30.05.2018r Skalowanie wielowymiarowe (Multidimensional Scaling (MDS)) Główne cele MDS: przedstawienie struktury badanych obiektów przez określenie treści wymiarów
Wykład 10 Skalowanie wielowymiarowe Wrocław, 30.05.2018r Skalowanie wielowymiarowe (Multidimensional Scaling (MDS)) Główne cele MDS: przedstawienie struktury badanych obiektów przez określenie treści wymiarów
Wykład 1. Model w badaniach systemowych. Wstęp pojęcia podstawowe
 Wykład 1. Model w badaniach systemowych. Wstęp pojęcia podstawowe Godziny konsultacji 3 Zakładane efekty kształcenia Badania systemowe Model w badaniach systemowych Przegląd treści wykładu Literatura 4
Wykład 1. Model w badaniach systemowych. Wstęp pojęcia podstawowe Godziny konsultacji 3 Zakładane efekty kształcenia Badania systemowe Model w badaniach systemowych Przegląd treści wykładu Literatura 4
Knovel Math: Jakość produktu
 Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
Knovel Math: Jakość produktu Knovel jest agregatorem materiałów pełnotekstowych dostępnych w formacie PDF i interaktywnym. Narzędzia interaktywne Knovel nie są stworzone wokół specjalnych algorytmów wymagających
Filtracja pomiarów z głowic laserowych
 dr inż. st. of. Paweł Zalewsi Filtracja pomiarów z głowic laserowych słowa luczowe: filtracja pomiaru odległości, PNDS Założenia filtracji pomiaru odległości. Problem wyznaczenia odległości i parametrów
dr inż. st. of. Paweł Zalewsi Filtracja pomiarów z głowic laserowych słowa luczowe: filtracja pomiaru odległości, PNDS Założenia filtracji pomiaru odległości. Problem wyznaczenia odległości i parametrów
Wykład wprowadzający
 Monitorowanie i Diagnostyka w Systemach Sterowania na studiach II stopnia specjalności: Systemy Sterowania i Podejmowania Decyzji Wykład wprowadzający dr inż. Michał Grochowski kiss.pg.mg@gmail.com michal.grochowski@pg.gda.pl
Monitorowanie i Diagnostyka w Systemach Sterowania na studiach II stopnia specjalności: Systemy Sterowania i Podejmowania Decyzji Wykład wprowadzający dr inż. Michał Grochowski kiss.pg.mg@gmail.com michal.grochowski@pg.gda.pl
MODEL STRUKTURALNY RELACJI MIĘDZY SATYSFAKCJĄ
 MODEL STRUKTURALNY RELACJI MIĘDZY SATYSFAKCJĄ I LOJALNOŚCIĄ WOBEC MARKI Adam Sagan Akademia Ekonomiczna w Krakowie, Katedra Analizy Rynku i Badań Marketingowych Wstęp Modelowanie strukturalne ma wielorakie
MODEL STRUKTURALNY RELACJI MIĘDZY SATYSFAKCJĄ I LOJALNOŚCIĄ WOBEC MARKI Adam Sagan Akademia Ekonomiczna w Krakowie, Katedra Analizy Rynku i Badań Marketingowych Wstęp Modelowanie strukturalne ma wielorakie
III TUTORIAL Z METOD OBLICZENIOWYCH
 III TUTORIAL Z METOD OBLICZENIOWYCH ALGORYTMY ROZWIĄZYWANIA UKŁADÓW RÓWNAŃ LINIOWYCH Opracowanie: Agata Smokowska Marcin Zmuda Trzebiatowski Koło Naukowe Mechaniki Budowli KOMBO Spis treści: 1. Wstęp do
III TUTORIAL Z METOD OBLICZENIOWYCH ALGORYTMY ROZWIĄZYWANIA UKŁADÓW RÓWNAŃ LINIOWYCH Opracowanie: Agata Smokowska Marcin Zmuda Trzebiatowski Koło Naukowe Mechaniki Budowli KOMBO Spis treści: 1. Wstęp do
Politechnika Gdańska Wydział Elektrotechniki i Automatyki. Automatyka i Robotyka Systemy Sterowania i Wspomagania Decyzji
 Monitorowanie i Diagnostyka w Systemach Sterowania (MiDwSS) Podstawowe sposoby opisu niepewności, wybrane zagadnienia zastosowania estymacji rekursywnej dla potrzeb monitorowania i diagnostyki w systemach
Monitorowanie i Diagnostyka w Systemach Sterowania (MiDwSS) Podstawowe sposoby opisu niepewności, wybrane zagadnienia zastosowania estymacji rekursywnej dla potrzeb monitorowania i diagnostyki w systemach
Podstawy opracowania wyników pomiarów
 Podstawy opracowania wyników pomiarów I Pracownia Fizyczna Chemia C 02. 03. 2017 na podstawie wykładu dr hab. Pawła Koreckiego Katarzyna Dziedzic-Kocurek Instytut Fizyki UJ, Zakład Fizyki Medycznej k.dziedzic-kocurek@uj.edu.pl
Podstawy opracowania wyników pomiarów I Pracownia Fizyczna Chemia C 02. 03. 2017 na podstawie wykładu dr hab. Pawła Koreckiego Katarzyna Dziedzic-Kocurek Instytut Fizyki UJ, Zakład Fizyki Medycznej k.dziedzic-kocurek@uj.edu.pl
Statystyka od podstaw Janina Jóźwiak, Jarosław Podgórski
 Statystyka od podstaw Janina Jóźwiak, Jarosław Podgórski Książka jest nowoczesnym podręcznikiem przeznaczonym dla studentów uczelni i wydziałów ekonomicznych. Wykład podzielono na cztery części. W pierwszej
Statystyka od podstaw Janina Jóźwiak, Jarosław Podgórski Książka jest nowoczesnym podręcznikiem przeznaczonym dla studentów uczelni i wydziałów ekonomicznych. Wykład podzielono na cztery części. W pierwszej
WYMAGANIA WSTĘPNE W ZAKRESIE WIEDZY, UMIEJĘTNOŚCI I INNYCH KOMPETENCJI
 Zał. nr 4 do ZW WYDZIAŁ ELEKTRONIKI KARTA PRZEDMIOTU Nazwa w języku polskim STATYSTYKA MATEMATYCZNA (EiT stopień) Nazwa w języku angielskim Mathematical Statistics Kierunek studiów (jeśli dotyczy): Specjalność
Zał. nr 4 do ZW WYDZIAŁ ELEKTRONIKI KARTA PRZEDMIOTU Nazwa w języku polskim STATYSTYKA MATEMATYCZNA (EiT stopień) Nazwa w języku angielskim Mathematical Statistics Kierunek studiów (jeśli dotyczy): Specjalność
WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI
 WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI Stefan WÓJTOWICZ, Katarzyna BIERNAT ZAKŁAD METROLOGII I BADAŃ NIENISZCZĄCYCH INSTYTUT ELEKTROTECHNIKI ul. Pożaryskiego 8, 04-703 Warszawa tel. (0)
WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI Stefan WÓJTOWICZ, Katarzyna BIERNAT ZAKŁAD METROLOGII I BADAŃ NIENISZCZĄCYCH INSTYTUT ELEKTROTECHNIKI ul. Pożaryskiego 8, 04-703 Warszawa tel. (0)
Filtracja optymalna i adaptacyjna
 Wydział Elektryczny ZMAiPC LABORAORIUM CYFROWEGO PRZEWARZANIA SYGNAŁÓW Ćwiczenie 6 Filtracja optymalna i adaptacyjna 1. Cel ćwiczenia Zapoznanie się z projektowaniem filtrów optymalnych metodą minimalizacji
Wydział Elektryczny ZMAiPC LABORAORIUM CYFROWEGO PRZEWARZANIA SYGNAŁÓW Ćwiczenie 6 Filtracja optymalna i adaptacyjna 1. Cel ćwiczenia Zapoznanie się z projektowaniem filtrów optymalnych metodą minimalizacji
Promotor: dr Marek Pawełczyk. Marcin Picz
 Promotor: dr Marek Pawełczyk Marcin Picz Stosowane metody: - Grupa metod odejmowania widm (subtractive( subtractive-typetype algorithms); - Filtracja Wienera; - Neural networks & Fuzzy logic (sieci neuronowe
Promotor: dr Marek Pawełczyk Marcin Picz Stosowane metody: - Grupa metod odejmowania widm (subtractive( subtractive-typetype algorithms); - Filtracja Wienera; - Neural networks & Fuzzy logic (sieci neuronowe
Modelowanie danych hodowlanych
 Modelowanie danych hodowlanych 1. Wykład wstępny. Algebra macierzowa 3. Wykorzystanie różnych źródeł informacji w predykcji wartości hodowlanej 4. Kowariancja genetyczna pomiędzy spokrewnionymi osobnikami
Modelowanie danych hodowlanych 1. Wykład wstępny. Algebra macierzowa 3. Wykorzystanie różnych źródeł informacji w predykcji wartości hodowlanej 4. Kowariancja genetyczna pomiędzy spokrewnionymi osobnikami
Podstawy Automatyki. Wykład 7 - obiekty regulacji. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Politechnika Gdańska Wydział Oceanotechniki i Okrętownictwa. Marzec Podstawy teorii optymalizacji Oceanotechnika, II stop., sem.
 Politechnika Gdańska Wydział Oceanotechniki i Okrętownictwa St. II stop., sem. I, Kierunek Oceanotechnika, Spec. Okrętowe Podstawy teorii optymalizacji Wykład 1 M. H. Ghaemi Marzec 2016 Podstawy teorii
Politechnika Gdańska Wydział Oceanotechniki i Okrętownictwa St. II stop., sem. I, Kierunek Oceanotechnika, Spec. Okrętowe Podstawy teorii optymalizacji Wykład 1 M. H. Ghaemi Marzec 2016 Podstawy teorii
Podstawy opracowania wyników pomiarów z elementami analizy niepewności pomiarowych
 Podstawy opracowania wyników pomiarów z elementami analizy niepewności pomiarowych dla studentów Chemii 2007 Paweł Korecki 2013 Andrzej Kapanowski Po co jest Pracownia Fizyczna? 1. Obserwacja zjawisk i
Podstawy opracowania wyników pomiarów z elementami analizy niepewności pomiarowych dla studentów Chemii 2007 Paweł Korecki 2013 Andrzej Kapanowski Po co jest Pracownia Fizyczna? 1. Obserwacja zjawisk i
Metody iteracyjne rozwiązywania układów równań liniowych (5.3) Normy wektorów i macierzy (5.3.1) Niech. x i. i =1
 Normy wektorów i macierzy (5.3.1) Niech 1 X =[x x Y y =[y1 x n], oznaczają wektory przestrzeni R n, a yn] niech oznacza liczbę rzeczywistą. Wyrażenie x i p 5.3.1.a X p = p n i =1 nosi nazwę p-tej normy
Normy wektorów i macierzy (5.3.1) Niech 1 X =[x x Y y =[y1 x n], oznaczają wektory przestrzeni R n, a yn] niech oznacza liczbę rzeczywistą. Wyrażenie x i p 5.3.1.a X p = p n i =1 nosi nazwę p-tej normy
//warunki początkowe m=500; T=30; c=0.4; t=linspace(0,t,m); y0=[-2.5;2.5];
![//warunki początkowe m=500; T=30; c=0.4; t=linspace(0,t,m); y0=[-2.5;2.5]; //warunki początkowe m=500; T=30; c=0.4; t=linspace(0,t,m); y0=[-2.5;2.5];](/thumbs/88/115527151.jpg) 4.3. Przykłady wykorzystania funkcji bibliotecznych 73 MATLAB % definiowanie funkcji function [dx]=vderpol(t,y) global c; dx=[y(2); c*(1-y(1)^2)*y(2)-y(1)]; SCILAB // definiowanie układu function [f]=vderpol(t,y,c)
4.3. Przykłady wykorzystania funkcji bibliotecznych 73 MATLAB % definiowanie funkcji function [dx]=vderpol(t,y) global c; dx=[y(2); c*(1-y(1)^2)*y(2)-y(1)]; SCILAB // definiowanie układu function [f]=vderpol(t,y,c)
WPŁYW OPÓŹNIENIA NA DYNAMIKĘ UKŁADÓW Z REGULACJĄ KLASYCZNĄ I ROZMYTĄ
 Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Nr 65 Politechniki Wrocławskiej Nr 65 Studia i Materiały Nr 31 2011 Kinga GÓRNIAK* układy z opóźnieniem, regulacja rozmyta, model Mamdaniego,
Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Nr 65 Politechniki Wrocławskiej Nr 65 Studia i Materiały Nr 31 2011 Kinga GÓRNIAK* układy z opóźnieniem, regulacja rozmyta, model Mamdaniego,
ESTYMACJA PARAMETRÓW TERMOFIZYCZNYCH CIAŁ IZOTROPOWYCH ZA POMOCĄ METODY FILTRACJI DYNAMICZNEJ ORAZ PRZEDZIAŁOWEGO UŚREDNIANIA WYNIKÓW POMIARÓW
 MODELOWANIE INśYNIERSKIE ISSN 896-77X 34, s. 73-78, Gliwice 007 ESTYMACJA PARAMETRÓW TERMOFIZYCZNYCH CIAŁ IZOTROPOWYCH ZA POMOCĄ METODY FILTRACJI DYNAMICZNEJ ORAZ PRZEDZIAŁOWEGO UŚREDNIANIA WYNIKÓW POMIARÓW
MODELOWANIE INśYNIERSKIE ISSN 896-77X 34, s. 73-78, Gliwice 007 ESTYMACJA PARAMETRÓW TERMOFIZYCZNYCH CIAŁ IZOTROPOWYCH ZA POMOCĄ METODY FILTRACJI DYNAMICZNEJ ORAZ PRZEDZIAŁOWEGO UŚREDNIANIA WYNIKÓW POMIARÓW
przedmiot kierunkowy (podstawowy / kierunkowy / inny HES) obieralny (obowiązkowy / nieobowiązkowy) polski semestr VI
 Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2018/2019
Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2018/2019
Wprowadzenie do technik regulacji automatycznej. prof nzw. dr hab. inż. Krzysztof Patan
 Wprowadzenie do technik regulacji automatycznej prof nzw. dr hab. inż. Krzysztof Patan Czym jest AUTOMATYKA? Automatyka to dziedzina nauki i techniki zajmująca się teorią i praktycznym zastosowaniem urządzeń
Wprowadzenie do technik regulacji automatycznej prof nzw. dr hab. inż. Krzysztof Patan Czym jest AUTOMATYKA? Automatyka to dziedzina nauki i techniki zajmująca się teorią i praktycznym zastosowaniem urządzeń
KORELACJA 1. Wykres rozrzutu ocena związku między zmiennymi X i Y. 2. Współczynnik korelacji Pearsona
 KORELACJA 1. Wykres rozrzutu ocena związku między zmiennymi X i Y 2. Współczynnik korelacji Pearsona 3. Siła i kierunek związku między zmiennymi 4. Korelacja ma sens, tylko wtedy, gdy związek między zmiennymi
KORELACJA 1. Wykres rozrzutu ocena związku między zmiennymi X i Y 2. Współczynnik korelacji Pearsona 3. Siła i kierunek związku między zmiennymi 4. Korelacja ma sens, tylko wtedy, gdy związek między zmiennymi
Statystyczne Metody Opracowania Wyników Pomiarów
 Statystyczne Metody Opracowania Wyników Pomiarów dla studentów Ochrony Środowiska Teresa Jaworska-Gołąb 2017/18 Co czytać [1] H. Szydłowski, Pracownia fizyczna, PWN, Warszawa 1999. [2] A. Zięba, Analiza
Statystyczne Metody Opracowania Wyników Pomiarów dla studentów Ochrony Środowiska Teresa Jaworska-Gołąb 2017/18 Co czytać [1] H. Szydłowski, Pracownia fizyczna, PWN, Warszawa 1999. [2] A. Zięba, Analiza
Ekonometria_FIRJK Arkusz1
 Rok akademicki: Grupa przedmiotów Numer katalogowy: Nazwa przedmiotu 1) : łumaczenie nazwy na jęz. angielski 3) : Kierunek studiów 4) : Ekonometria Econometrics Ekonomia ECS 2) Koordynator przedmiotu 5)
Rok akademicki: Grupa przedmiotów Numer katalogowy: Nazwa przedmiotu 1) : łumaczenie nazwy na jęz. angielski 3) : Kierunek studiów 4) : Ekonometria Econometrics Ekonomia ECS 2) Koordynator przedmiotu 5)
Podstawy Sztucznej Inteligencji
 Politechnika Łódzka Katedra Informatyki Stosowanej Podstawy Sztucznej Inteligencji Laboratorium Ćwiczenie 2 Wykorzystanie środowiska Matlab do modelowania sztucznych sieci neuronowych Opracowali: Dr hab
Politechnika Łódzka Katedra Informatyki Stosowanej Podstawy Sztucznej Inteligencji Laboratorium Ćwiczenie 2 Wykorzystanie środowiska Matlab do modelowania sztucznych sieci neuronowych Opracowali: Dr hab
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM. Ćwiczenie 1. Modelowanie i analiza widmowa dyskretnych sygnałów losowych
 ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 1 Modelowanie i analiza widmowa dyskretnych sygnałów losowych 1. CEL ĆWICZENIA Celem ćwiczenia jest zapoznanie studentów z wybranymi algorytmami
ADAPTACYJNE PRZETWARZANIE SYGNAŁÓW LABORATORIUM Ćwiczenie 1 Modelowanie i analiza widmowa dyskretnych sygnałów losowych 1. CEL ĆWICZENIA Celem ćwiczenia jest zapoznanie studentów z wybranymi algorytmami
Diagnostyka procesów przemysłowych Kod przedmiotu
 Diagnostyka procesów przemysłowych - opis przedmiotu Informacje ogólne Nazwa przedmiotu Diagnostyka procesów przemysłowych Kod przedmiotu 06.0-WE-AiRP-DPP Wydział Kierunek Wydział Informatyki, Elektrotechniki
Diagnostyka procesów przemysłowych - opis przedmiotu Informacje ogólne Nazwa przedmiotu Diagnostyka procesów przemysłowych Kod przedmiotu 06.0-WE-AiRP-DPP Wydział Kierunek Wydział Informatyki, Elektrotechniki
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Statystyka komputerowa Computer statistics Zarządzanie i Inżynieria Produkcji Management and Engineering of Production Rodzaj przedmiotu: Fakultatywny - oferta Poziom studiów:
Nazwa przedmiotu: Kierunek: Statystyka komputerowa Computer statistics Zarządzanie i Inżynieria Produkcji Management and Engineering of Production Rodzaj przedmiotu: Fakultatywny - oferta Poziom studiów:
1.1 Klasyczny Model Regresji Liniowej
 1.1 Klasyczny Model Regresji Liniowej Klasyczny model Regresji Liniowej jest bardzo użytecznym narzędziem służącym do analizy danych empirycznych. Analiza regresji zajmuje się opisem zależności między
1.1 Klasyczny Model Regresji Liniowej Klasyczny model Regresji Liniowej jest bardzo użytecznym narzędziem służącym do analizy danych empirycznych. Analiza regresji zajmuje się opisem zależności między
Rozdział 2: Metoda największej wiarygodności i nieliniowa metoda najmniejszych kwadratów
 Rozdział : Metoda największej wiarygodności i nieliniowa metoda najmniejszych kwadratów W tym rozdziale omówione zostaną dwie najpopularniejsze metody estymacji parametrów w ekonometrycznych modelach nieliniowych,
Rozdział : Metoda największej wiarygodności i nieliniowa metoda najmniejszych kwadratów W tym rozdziale omówione zostaną dwie najpopularniejsze metody estymacji parametrów w ekonometrycznych modelach nieliniowych,
Zastosowanie uogólnionych modeli liniowych i uogólnionych mieszanych modeli liniowych do analizy danych dotyczacych występowania zębiniaków
 Zastosowanie uogólnionych modeli liniowych i uogólnionych mieszanych modeli liniowych do analizy danych dotyczacych występowania zębiniaków Wojciech Niemiro, Jacek Tomczyk i Marta Zalewska Uniwersytet
Zastosowanie uogólnionych modeli liniowych i uogólnionych mieszanych modeli liniowych do analizy danych dotyczacych występowania zębiniaków Wojciech Niemiro, Jacek Tomczyk i Marta Zalewska Uniwersytet
Matlab - zastosowania Matlab - applications. Informatyka II stopień (I stopień / II stopień) ogólnoakademicki (ogólno akademicki / praktyczny)
 KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013 Matlab - zastosowania Matlab - applications A. USYTUOWANIE MODUŁU W SYSTEMIE
KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013 Matlab - zastosowania Matlab - applications A. USYTUOWANIE MODUŁU W SYSTEMIE
Machine Learning for Data Science (CS4786) Lecture11. Random Projections & Canonical Correlation Analysis
 Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
POLITECHNIKA ŚLĄSKA WYDZIAŁ GÓRNICTWA I GEOLOGII. Roman Kaula
 POLITECHNIKA ŚLĄSKA WYDZIAŁ GÓRNICTWA I GEOLOGII Roman Kaula ZASTOSOWANIE NOWOCZESNYCH NARZĘDZI INŻYNIERSKICH LabVIEW oraz MATLAB/Simulink DO MODELOWANIA UKŁADÓW DYNAMICZNYCH PLAN WYKŁADU Wprowadzenie
POLITECHNIKA ŚLĄSKA WYDZIAŁ GÓRNICTWA I GEOLOGII Roman Kaula ZASTOSOWANIE NOWOCZESNYCH NARZĘDZI INŻYNIERSKICH LabVIEW oraz MATLAB/Simulink DO MODELOWANIA UKŁADÓW DYNAMICZNYCH PLAN WYKŁADU Wprowadzenie
Tematyka seminariów z informatyki dla studentów I roku kierunku lekarsko-dentystycznego w roku akademickim 2017/2018.
 Tematyka seminariów z informatyki dla studentów I roku kierunku lekarsko-dentystycznego w roku akademickim 2017/2018. 1. Sieci komputerowe rodzaje, budowa, model ISO/OSI. 2. Istota kompresji danych. Zastosowania.
Tematyka seminariów z informatyki dla studentów I roku kierunku lekarsko-dentystycznego w roku akademickim 2017/2018. 1. Sieci komputerowe rodzaje, budowa, model ISO/OSI. 2. Istota kompresji danych. Zastosowania.
Narzędzia matematyczne zastosowane w systemie biomonitoringu wody
 Narzędzia matematyczne zastosowane w systemie biomonitoringu wody Piotr Przymus Krzysztof Rykaczewski Wydział Matematyki i Informatyki Uniwersytet Mikołaja Kopernika Toruń 1 of 24 18 marca 2009 Cel referatu
Narzędzia matematyczne zastosowane w systemie biomonitoringu wody Piotr Przymus Krzysztof Rykaczewski Wydział Matematyki i Informatyki Uniwersytet Mikołaja Kopernika Toruń 1 of 24 18 marca 2009 Cel referatu
Statystyka i Analiza Danych
 Warsztaty Statystyka i Analiza Danych Gdańsk, 20-22 lutego 2014 Zastosowania wybranych technik regresyjnych do modelowania współzależności zjawisk Janusz Wątroba StatSoft Polska Centrum Zastosowań Matematyki
Warsztaty Statystyka i Analiza Danych Gdańsk, 20-22 lutego 2014 Zastosowania wybranych technik regresyjnych do modelowania współzależności zjawisk Janusz Wątroba StatSoft Polska Centrum Zastosowań Matematyki
Nazwa przedmiotu: Informatyczne systemy statystycznej obróbki danych. Informatics systems for the statistical treatment of data Kierunek:
 Nazwa przedmiotu: Informatyczne systemy statystycznej obróbki danych I KARTA PRZEDMIOTU CEL PRZEDMIOTU Informatics systems for the statistical treatment of data Kierunek: Forma studiów Informatyka Stacjonarne
Nazwa przedmiotu: Informatyczne systemy statystycznej obróbki danych I KARTA PRZEDMIOTU CEL PRZEDMIOTU Informatics systems for the statistical treatment of data Kierunek: Forma studiów Informatyka Stacjonarne
WYKŁAD 8 ANALIZA REGRESJI
 WYKŁAD 8 ANALIZA REGRESJI Regresja 1. Metoda najmniejszych kwadratów-regresja prostoliniowa 2. Regresja krzywoliniowa 3. Estymacja liniowej funkcji regresji 4. Testy istotności współczynnika regresji liniowej
WYKŁAD 8 ANALIZA REGRESJI Regresja 1. Metoda najmniejszych kwadratów-regresja prostoliniowa 2. Regresja krzywoliniowa 3. Estymacja liniowej funkcji regresji 4. Testy istotności współczynnika regresji liniowej
Wykład Ćwiczenia Laboratorium Projekt Seminarium Liczba godzin zajęć zorganizowanych w Uczelni
 Zał. nr do ZW 33/01 WYDZIAŁ PODSTAWOWYCH ROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim TEORIA ESTYMACJI Nazwa w języku angielskim ESTIMATION THEORY Kierunek studiów (jeśli dotyczy): MATEMATYKA
Zał. nr do ZW 33/01 WYDZIAŁ PODSTAWOWYCH ROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim TEORIA ESTYMACJI Nazwa w języku angielskim ESTIMATION THEORY Kierunek studiów (jeśli dotyczy): MATEMATYKA
Metody numeryczne Wykład 4
 Metody numeryczne Wykład 4 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Metody skończone rozwiązywania
Metody numeryczne Wykład 4 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Metody skończone rozwiązywania
