E K O N O M E T R I A (kurs 10 godz.)
|
|
|
- Marta Pawlik
- 6 lat temu
- Przeglądów:
Transkrypt
1 E K O N O M E T R I A (kurs 0 godz.) PLAN kursu A. Ekoometra: defcje, pojęca, przkład B. Elemet statstk matematczej (zmea losowa, przedzałowa estmacja parametrów populacj, hpotez parametrcze) C. Model ekoometrcz: budowa modelu, werfkacja, terpretacja parametrów modelu. LITERATURA:. Statstka ekoometra, Brska-Rąpała A., Kozarkewcz A., red. auk. Łuck. Z., Wd. AGH, Kraków, 0.. Ekoometra badaa operacje, [red.] Gruszczńsk M., Kuszewsk T., Podgórska M., PWN, Warszawa, Statstka w zarządzau, Aczel A. D., PWN, Warszawa, 000. Warto dla początkującch:. Zars metod ekoometr, Nowak E., PWN, Warszawa, 997.
2 Ekoometra: defcje, pojęca, przkład auka o merzeu zwązków wstępującch mędz zjawskam lub procesam ekoomczm a m zjawskam (ekoomczm, przrodczm, techczm, demografczm socjologczm) w celach pozawczch dla progozowaa [Bartosewcz S., 978] auka zajmująca sę emprczą werfkacją praw ekoomczch [Thel H., 979] auka pomoccza w ramach ekoom, wkorzstująca arzędza matematk, statstk oraz formatk do badaa loścowch zwązków zachodzącch mędz zjawskam zmem ekoomczm. Jest zborem metod opracowach ajczęścej poza ekoomą, ale wkorzstwach a jej polu. auka zajmująca sę ustalaem, za pomocą metod matematczo-statstczch, loścowch prawdłowośc zachodzącch w żcu gospodarczm [własa] SPECYFICZNE WARUNKI PROWADZENIA BADAŃ EKONOMETRYCZNYCH brak możlwośc powtórzea ekspermetu, badae zjawsko ekoomcze jest stable, tj. ulega jede ewelkm powolm zmaom, zjawsko mus bć merzale, tj. jego cech muszą bć wrażae lczbowo, moża określć czk wpłwające a jego zachowae, dostępe są dae statstcze opsujące zachowae (w sese loścowm) badaego sstemu w przeszłośc, trudośc z dam: dostępość, lość, wargodość, porówwalość.
3 NARZĘDZIEM BADAWCZYM EKONOMETRII JEST MODEL EKONOMETRYCZNY ops fragmetu ekoomczej rzeczwstośc, uwzględając tlko stote jej elemet; kostrukcja mślowa, która w uproszczo sposób przedstawa fukcjoowae lub zachowae gospodark lub jej częśc def. dla ekoom; kostrukcja formala, która za pomocą pewego rówaa lub układu rówań przedstawa zasadcze powązaa wstępujące pomędz rozpatrwam zjawskam ekoomczm [Hellwg Z.]. Model ekoometrcz za pomocą rówaa/rówań przedstawa zależośc wstępujące pomędz zmem. ELEMENTY MODELU: Zmee, Parametr Elemet losowe 0,,...,
4 WŁAŚCIWOŚCI MODELU EKONOMETRYCZNEGO: merzalość zjawsk; jedozaczość formala w zapse, odcztwau terpretacj uzskach wków; jest zasadą, że każde rówae modelu przedstawa mechazm kształtowaa sę jedej tlko jedej zmeej, to zacz wraża relacje, w jakch zmea ta zmea sę w zależośc od wartośc, jake przjmują e zmee odgrwające w dam rówau rolę przcz. Jeżel węc model ma przedstawć mechazm kształtowaa sę jedej tlko zmeej, będze składał sę z jedego rówaa. 0,,...,,, 3, f ( f ( f (,,,,,,,,, 3,- 3,,, ),,,,,,,, 3, 3, ) ) Jeżel atomast celem modelu będze ops mechazmu kształtowaa sę klku zmech (k), to mus składać sę z klku rówań (k).
5 DANE STATYSTYCZNE W MODELU szereg czasow dae przekrojowe dae paelowe Szereg czasow formacje lczbowe przedstawające sta badaego zjawska (procesu) w kolejch mometach (okresach). Zwczajowo zmee przedstawoe w forme szeregu czasowego są zapswae z deksem t: Dae przekrojowe - formacje lczbowe przedstawające sta badaego zjawska w ustalom momece (okrese), ale odoszą sę do różch obektów. Zapsuje sę je z deksem : t Dae paelowe formacje lczbowe dla welu obektów, z którch każd jest obserwowa w co ajmej dwóch okresach., t, t MODELE EKONOMETRYCZNE OPARTE NA RÓŻNYCH DANYCH STATYSTYCZNYCH PRZYKŁADY
6 KLASYFIKACJA MODELI EKONOMETRYCZNYCH I. Klasfkacja według woszoej formacj: modele przczowo-skutkowe skutek X przcz f (,,..., k ) Modele te budujem z dach przekrojowch (róże obekt w tm samm momece) modele tedecj rozwojowej aalzowae zjawsko t czas f (t) Modele te budujem z szeregów czasowch (te sam obekt w różch mometach) II. Klasfkacja według stopa uwzględaa czasu: modele statcze (a podstawe dach przekrojowch) modele damcze (a podstawe szeregów czasowch, dach paelowch) III. Klasfkacja według lowośc: modele lowe modele elowe (koecza trasformacja lowa) 0... k k,,..., 0
7 ETAPY BUDOWY MODELU EKONOMETRYCZNEGO. Sformułowae problemu a. wbór zmech:,,,... b. wbór postac matematczej modelu: lowa, potęgowa,.... Zebrae dach statstczch (róże źródła) 3. Estmacja parametrów modelu: a. parametrów strukturalch: a 0, a, a,... b. parametrów stochastczch: s(a ), s(), R, R 4. Werfkacja modelu (prz użcu hpotez testów statstczch) 6. Iterpretacja modelu MODEL BEZ WERYFIKACJI NIE MA ŻADNEJ WARTOŚCI wcągęce wosków dla celów zarządzaa (przedsęborstwem, gospodarką), stmulowaa procesam gospodarczm (kosumpcj dóbr, tp.), produkcjm (tempo wdobca rop/gazu).
8 ZAŁOŻENIA STANDARDOWEGO MODELU REGRESJI LINIOWEJ Zmea objaśaa - jest zmeą losową; rozkład tej zmeej opsuje zbór wartośc, które może oa przjmować (w dam momece obserwujem tlko jedą wartość). Założee e dotcz tej kokretej wartośc lecz procesu geerującego tę wartość. Wartość oczekwaa rozkładu zmeej dla obserwacj : E( /, ) 0 0,, - ezaeparametr,..., Waracja prz dach, jest stała: var( /, ) - ezaparametr Waracja merz stopeń wpłwu a zmeą czków ch ż (zmee pomęte); stałość waracj mplkuje, że dspersja łączego wpłwu zmech pomętch e zmea sę w czase. Składk losow rówaa Każd składk losow ma (prz ustaloch, ) wartość oczekwaą rówą zero warację. E( /, )
9 PODSTAWOWE POJĘCIA I TERMINY KORELACJA fakt powązaa, współzależośc, zwązku zmech ze sobą WSPÓŁCZYNNIK KORELACJI lczba określająca słę keruek tego zwązku współczk korelacj lowej dwu zmech: r lub r Współczk r ese dwe formacje poprzez swój zak moduł r 0 r r S SS S współczk korelacj lowej welu zmech (korelacj welokrotej lub welorakej): R 0 R KOWARIANCJA Dla dużej prób 30 cov(,) Dla małej prób <30 cov(,) ( ( )( )( ) ) S S Zak kowaracj formuje o charakterze współzmeośc (dodat keruk zma zgode, ujem przecwe keruk zma). Wartość kowaracj w jedostkach, w jakch są zmee dlatego ta mara e może bć wkorzstaa do porówań (jak współczk korelacj) r cov(,) s() s() s() s()
10 REGRESJA statstcza metoda modelowaa zwązków mędz zmem; opsuje ją fukcja odzwercedlająca powązae zmech (czków) Model ekoometrcz za pomocą rówaa przedstawa zależość wstępującą pomędz zmem. ŷ a 0 WSPÓŁCZYNNIK REGRESJI lczba stojąca prz każdej zmeej, określająca jej wpłw a zmeą a a 0 wraz wol (stała), współrzęda puktu przecęca z osą Y a współczk regresj, tages kąta achlea prostej składk losow N(0, ) a 0 Metod estmacj rówaa regresj metoda ajmejszch kwadratów (MNK) podwója MNK regresje specjale: grzbetowa (rdge regresso), odpora (robust) td. metoda ajwększej wargodośc
11 METODA NAJMNIEJSZYCH KWADRATÓW MNK Estmator ˆ wzaczo MNK jest estmatorem zgodm, eobcążom ajefektwejszm. eobcążo wartość oczekwaa estmatora jest rówa szacowaemu parametrow zgod cąg oce uzskach za pomocą tego estmatora jest stochastcze zbeż do szacowaego parametru : E( ) ˆ lm P{ ˆ } ajefektwejsz estmator o ajmejszej waracj ZAŁOŻENIA DLA MNK. Postać modelu jest lowa względem parametrów. Zmee objaśające są welkoścam elosowm 3. Składk losow jest zmeą losową: E()=0; D ()=cost 4. Realzacje zmech są ezależe, co sprawa, że cąg {} jest cągem ezależch zmech losowch 5. Składk losow jest eskorelowa ze zmem objaśającm 6. Zmee objaśające są wole od współlowośc. 7. k< gdze: k lczba zmech objaśającch; lczość prób
12 MNK a przkładze modelu dwóch zmech MNK pozwala wzaczć współczk a 0 a prostej, która ajlepej pasuje do puktów emprczch. 0 0 ) a a ( m SSE a a ŷ 0 0 a a a a Newadome: a 0, a m SSE ) ŷ ( Y ŷ ˆ X a a ) ( ) )( ( a 0
13 MIARY DOBROCI MODELU REGRESJI Y ŷ ˆ ˆ ( ) ( ˆ ) ( ˆ ) SSTO = SSTR + SSE = SSTO (zmeość całkowta) = SSTR (zmeość wjaśoa) = SSE (zmeość ewjaśoa) (SUMOWANIE OD DO ) ŷ a 0 a ) ( ) (ŷ ) ( ŷ X Współczk determacj r SSTR SSTO (ŷ ( ) ) Współczk zbeżośc SSE SSTO ( ( Błąd stadardow reszt (dla modelu z jedą zmeą objaśającą) ŷ ) ) s SSE ( ŷ )
14 STATYSTYKA MATEMATYCZNA W EKONOMETRII
15 WNIOSKOWANIE STATYSTYCZNE Przedmotem tego dzału jest szacowae (estmacja) ezach parametrów populacj; wcągae wosków o rozkładze parametrach populacj geeralej a podstawe badaa próbk (hpotez statstcze). Teora estmacj zajmuje sę szacowaem parametrów populacj geeralej a podstawe próbk statstczej. Rodzaje estmacj puktowa przedzałowa Próbka mus bć pobraa w sposób losow, tz. każd elemet populacj (tj. zborowośc geeralej) mus meć jedakową szasę trafea do próbk.
16 Pojęca z teor estmacj parametr populacj lczbowa charakterstka całej populacj statstka z prób lczbowa charakterstka prób estmator (estmator) parametru populacj statstka z prób użwaa do oszacowaa tego parametru. Oceą lub szacukem parametru jest kokreta wartość lczbowa estmatora z daej prób estmacja - podae wartośc oce ezaego parametru populacj Estmator jest to zmea losowa, której realzacjam są wartośc powstałe przez pobrae z populacj bardzo welu próbek. Estmator jak każda zmea ma swoją wartość oczekwaą odchlee stadardowe. Wartość oszacowaa (estmate) jest to wartość daego parametru wzaczoa a podstawe jedej, rzeczwśce pobraej próbk. eobcążo wartość oczekwaa estmatora jest rówa szacowaemu parametrow zgod (PWL) E( ) ˆ prawdopodobeństwo, że jego wartość jest blska wartośc szacowaego parametru, wzrasta wraz ze wzrostem lczebośc ajefektwejsz estmator o ajmejszej waracj Cech dobrego estmatora
17 CO MOŻE BYĆ PARAMETREM POPULACJI? Nazwa parametru Wartość średa Odchlee stadardowe Waracja Współczk regresj Smbol dla populacj Smbol dla próbk s s a Lczba stop swobod Jest to lczba określająca le dach ze zboru moża zmeć bez zagrożea zmaą wzaczaego parametru (statstk). prz oblczau średej ogóle k
18 ESTYMACJA PRZEDZIAŁOWA PARAMETRU POPULACJI Przedzał ufośc jest to przedzał, w którm z prawdopodobeństwem zajduje sę ezaa wartość parametru populacj Pozom ufośc ( ) jest to prawdopodobeństwo, że ezaa wartość parametru zajduje sę w przedzale ufośc. Pozom stotośc () jest to prawdopodobeństwo, że ezaa wartość parametru e zajduje sę wewątrz przedzału ufośc. e azw: marges błędu, pozom krtcz Wbór wartośc pozomu stotośc zależ od badacza, atur problemu od tego, jak dokłade chce o werfkować swoje przpuszczea o parametrach p. modelu a 0 a (werfkacja hpotez). Najczęścej przjmuje sę α=0,05 (rzadzej 0,, 0,03, 0,0 lub 0,00).
19 ESTYMACJA PRZEDZIAŁOWA a przkładze WARTOŚCI ŚREDNIEJ POPULACJI Celem jest ustalee le wos ezaa wartość : estmacja puktowa: = estmacja przedzałowa: Dla >30 s s P( z z ) Dla <30 s s P( t t ),,
20 Kwatle rzędu / rozkładu t-studeta rozkładu ormalego rozkład Studeta jest bardzej płask, ma dłuższe ogo rozkład Studeta jest określo tlko jedm parametrem Rozkład ormal stadarzowa, z 0,39 0,388 0,38 0,375 0,36 0,34 0,3 0,75 0,4 (lczba stop swobod) Rozkład Studeta, t Parametr rozkładu, Średa 0 0 Waracja / rozkład ormal z rozkład Studeta t =8 tablca rozkładu Studeta pokazuje kwatle rzędu dla daego (wartośc t odpowadające założoemu pozomow stotośc dla daej lczb stop swobod) 0 z / t / ()
21
22 PRZEDZIAŁY UFNOŚCI DLA PARAMETRÓW MODELU REGRESJI P(a t/ ; s(a) a t/ ; s(a) a oszacowaa wartośc współczka regresj s(a ) błąd oszacowaa współczka regresj Iterpretacja przedzału ufośc jest astępująca: Z prawdopodobeństwem rzeczwsta wartość parametru a jest lczbą z przedzału. Im słow, z prawdopodobeństwem wzaczo przedzał e pokrwa rzeczwstej wartośc parametru (może to wkać z ewłaścwe dobraej prób statstczej, a podstawe której szacowao parametr a ).
23 WERYFIKACJA HIPOTEZ STATYSTYCZNYCH Hpoteza statstcza to każde przpuszczee dotczące populacj geeralej wsute a podstawe próbk statstczej: Poeważ prz posługwau sę próbką gd e ma pewośc, stawa sę dwe wkluczające sę hpotez: hpotezę zerową H 0 hpotezę alteratwą H (H a ) Werfkacja: polega a sprawdzeu, która z ch jest prawdzwa, a która fałszwa posługujem sę testam statstczm (z, t,, F e). Sformułowae H 0 H (H 0 : =4,0 H : 4,0; lub >4,0; lub <4,0). Przjęce pozomu błędu I rodzaju ( = 0,05) 3. Dobrae testu werfkującego (statstk, sprawdzau hpotez Z ) w zależośc od rodzaju hpotez 4. Ustalee obszaru krtczego testu (odcztae wartośc krtczej statstk werfkującej z tablc dla przjętego pozomu : z tabl, z kr, z ) 5. Oblczee wartośc statstk a podstawe próbk (z obl ) 6. Porówae dwu statstk podjęce deczj o przjęcu lub odrzuceu hpotez H 0 7. Iterpretacja podjętej deczj Kolejość czośc prz werfkacj hpotez:
24 HIPOTEZY PARAMETRYCZNE dotczą parametrów populacj geeralej, które ozaczm ogólm smbolem hpoteza zerowa polega a przjęcu, że ezae jest rówe 0 werfkacja prawdzwośc tej hpotez polega a sprawdzeu, cz wartość 0 zajduje sę w przedzale ufośc parametru Trz stuacje prz werfkacj hpotez.. H H H : 0 0 : H : 0 0 : H H : 0 0 : 0 Dla przpadku: H H : 0 0 : 0 / / Przedzał przjęca H 0 : z / <z obl < z / Przedzał odrzucea H 0 : z / z / z obl < z / oraz z obl > z / czl z obl > z /
25 HIPOTEZY PARAMETRYCZNE a podstawe ŚREDNIEJ DLA POPULACJI Dla >30 stosujem statstkę z [o rozkładze ormalm N(0;)] Poberam próbkę lczm H 0 : = 0 H : 0 Reguła deczja s z 0 obl Odrzucam H 0, jeżel z obl >z / Dla <30 stosujem statstkę t [o rozkładze Studeta] Poberam próbkę lczm Reguła deczja Odrzucam H 0, jeżel t obl >t /, =- t 0 obl s Przkład. W celu sprawdzea, cz ow lek jest lepsz od dotchczasowego, zbadao jego skuteczość a 6 chorch, merząc współczk odbudow czerwoch całek krw: 6,3; 7,8; 8,; 8,3; 8,7 9,4. Lek użwa dotchczas daje wartość współczka a pozome 8,3. Sprawdź hpotezę prz pozome stotośc 0,0.
26 Przkład Mesąc Wdatk a reklamę (X) (ml zł) Wartość sprzedaż (Y) (ml zł)., 0. 0,8 9 3.,0 0 4., , ,8 8 7., , ,9 9 0., 05 Wpłw wdatków a reklamę a welkość sprzedaż Stadard T Parameter Estmate Error Value Wraz wol Wspł. regresj ŷ = 46,49 + 5,57 + r=0,88 9,88 0,6 6,84 Hpotez: H 0 : = 0 H : 0 Statstka t: t 0,05; (0-) =,306 t obl. = 5,
27 PORÓWNANIE DWÓCH WARIANCJI, test Fshera W ekoometr będze am jeszcze potrzeba statstka Fshera (rozkład Fshera-Sedecora). Porówae dwóch waracj Poberam próbk: s s Statstka Fshera, daa dwoma parametram:, Rozkład F dla f(f) F
28 TEST FISHERA f(f) Próbk: s s / lub F 0 F / lub F Zawsze prawostro obszar krtcz testu Gd s > s = - = - H 0 : = F obl s s H : Reguła deczja Odrzucam H 0, jeżel... Gd s < s = - = - s F obl = s F obl >F /(, )
29 ANALIZA WARIANCYJNA umożlwa badae wpłwu czków emerzalch a zmeą Y (czkem może bć: metoda auczaa, dośwadczee pracowka, metoda sprzedaż, zależość regresja, tp.) Aalza waracj jedoczkowa Badau podlega waracja zmeej Y s ( ) a w szczególośc lczk tego wzoru ( ) zwaa całkowtą sumą kwadratów lub zmeoścą całkowtą SSTO (Sum of Squares Total) SUMY KWADRATÓW SSTO Sum of Squares Total Całkowta suma kwadratów SSTr Sum of Squares/Treatmet Suma kwadratów z dzałaa czka SSE Sum of Squares/Error Suma kwadratów z błędu WARIANCJE MSTr MSE Mea Square/Treatmet Mea Square/Error Śred kwadrat z czka Śred kwadrat z błędu
30 Aalza waracj model regresj Y ŷ ˆ ˆ ( ) = SSTO (zmeość całkowta) ( ˆ ) = SSTR (zmeość wjaśoa rówaem regresj) ( ˆ ) = SSE (zmeość ewjaśoa) ŷ a 0 a SSTO = SSTR + SSE X SSTO: ( ) SSTR: (ŷ ) SSE: ( ŷ ) R SSTR SSTO (ŷ ( ) ) SSE SSTO ( ŷ ) ( )
31 ANALIZA WARIANCJI a testowae hpotez o stotośc współczka regresj H 0 : = 0 Przkład H : 0 TABELKA ANOVY Przcza zmeośc Suma Kwadratów SS (Sum of Squares) Stope swobod ν (Df) Średe kwadrat MS (Mea Squares) Statstka F Regresja 6,9 k-= 6,9 F 0bl =6,5 Błąd 374,0 -k=8 46,7 Razem 600,9 -=9 F 0,05; ; 8 = 5,3 F obl >F (k-, -) k lość parametrów modelu szacowach MNK lczość prób Odrzucam hpotezę zerową współczk regresj jest stot
Wnioskowanie statystyczne dla korelacji i regresji.
 STATYSTYKA MATEMATYCZNA WYKŁAD 6 Woskowae statstcze dla korelacj regresj. Aalza korelacj Założee: zmea losowa dwuwmarowa X, Y) ma rozkład ormal o współczku korelacj ρ. X, Y cech adae rówocześe. X X X...
STATYSTYKA MATEMATYCZNA WYKŁAD 6 Woskowae statstcze dla korelacj regresj. Aalza korelacj Założee: zmea losowa dwuwmarowa X, Y) ma rozkład ormal o współczku korelacj ρ. X, Y cech adae rówocześe. X X X...
opisać wielowymiarową funkcją rozkładu gęstości prawdopodobieństwa f(x 1 , x xn
 ROZKŁAD PRAWDOPODBIEŃSTWA WIELU ZMIENNYCH LOSOWYCH W przpadku gd mam do czea z zmem losowm możem prawdopodobeństwo, ż przjmą oe wartośc,,, opsać welowmarową fukcją rozkładu gęstośc prawdopodobeństwa f(,,,.
ROZKŁAD PRAWDOPODBIEŃSTWA WIELU ZMIENNYCH LOSOWYCH W przpadku gd mam do czea z zmem losowm możem prawdopodobeństwo, ż przjmą oe wartośc,,, opsać welowmarową fukcją rozkładu gęstośc prawdopodobeństwa f(,,,.
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZA 1. Wkład wstęp. Teora prawdopodobeństwa elemet kombatork. Zmee losowe ch rozkład 3. Populacje prób dach, estmacja parametrów 4. Testowae hpotez statstczch 5. Test parametrcze (a
STATYSTYKA MATEMATYCZA 1. Wkład wstęp. Teora prawdopodobeństwa elemet kombatork. Zmee losowe ch rozkład 3. Populacje prób dach, estmacja parametrów 4. Testowae hpotez statstczch 5. Test parametrcze (a
Prawdopodobieństwo i statystyka r.
 Zadae. W ure zajduje sę 5 kul, z których 5 jest bałych czarych. Losujemy bez zwracaa kolejo po jedej kul. Kończymy losowae w momece, kedy wycągęte zostaą wszystke czare kule. Oblcz wartość oczekwaą lczby
Zadae. W ure zajduje sę 5 kul, z których 5 jest bałych czarych. Losujemy bez zwracaa kolejo po jedej kul. Kończymy losowae w momece, kedy wycągęte zostaą wszystke czare kule. Oblcz wartość oczekwaą lczby
Stanisław Cichocki Natalia Nehrebecka. Zajęcia 7-8
 Stasław Cchock Natala Nehreecka Zajęca 7-8 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartość oczekwaa eocążoość estymatora Waracja
Stasław Cchock Natala Nehreecka Zajęca 7-8 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartość oczekwaa eocążoość estymatora Waracja
Materiały do wykładu 7 ze Statystyki
 Materał do wkładu 7 ze Statstk Aalza ZALEŻNOŚCI pomędz CECHAMI (Aalza KORELACJI REGRESJI) korelacj wkres rozrzutu (korelogram) rodzaje zależośc (brak, elowa, lowa) pomar sł zależośc lowej (współczk korelacj
Materał do wkładu 7 ze Statstk Aalza ZALEŻNOŚCI pomędz CECHAMI (Aalza KORELACJI REGRESJI) korelacj wkres rozrzutu (korelogram) rodzaje zależośc (brak, elowa, lowa) pomar sł zależośc lowej (współczk korelacj
Statystyka. Katarzyna Chudy Laskowska
 Statstka Katarza Chud Laskowska http://kc.sd.prz.edu.pl/ Aalza korelacj umożlwa stwerdzee wstępowaa zależośc oraz oceę jej atężea ZALEŻNOŚCI pomędz CECHAMI: CECHY: ILOŚCIOWA ILOŚCIOWA CECHY: JAKOŚCIOWA
Statstka Katarza Chud Laskowska http://kc.sd.prz.edu.pl/ Aalza korelacj umożlwa stwerdzee wstępowaa zależośc oraz oceę jej atężea ZALEŻNOŚCI pomędz CECHAMI: CECHY: ILOŚCIOWA ILOŚCIOWA CECHY: JAKOŚCIOWA
KORELACJA KORELACJA I REGRESJA. X, Y - cechy badane równocześnie. Dane statystyczne zapisujemy w szeregu statystycznym dwóch cech
 KORELACJA I REGRESJA. KORELACJA X, Y - cech badae rówocześe. Dae statstcze zapsujem w szeregu statstczm dwóch cech...... lub w tablc korelacjej. X Y... l.... l.... l................... k k k... kl k..j......l
KORELACJA I REGRESJA. KORELACJA X, Y - cech badae rówocześe. Dae statstcze zapsujem w szeregu statstczm dwóch cech...... lub w tablc korelacjej. X Y... l.... l.... l................... k k k... kl k..j......l
BADANIE WSPÓŁZALEśNOŚCI DWÓCH CECH - ANALIZA KORELACJI PROSTEJ
 Matematka statstka matematcza dla rolków w SGGW Aa Rajfura, KDB WYKŁAD 2 BADANIE WSPÓŁZALEśNOŚCI DWÓCH CECH - ANALIZA KORELACJI PROSTEJ Matematka statstka matematcza dla rolków w SGGW Aa Rajfura, KDB Przkład.
Matematka statstka matematcza dla rolków w SGGW Aa Rajfura, KDB WYKŁAD 2 BADANIE WSPÓŁZALEśNOŚCI DWÓCH CECH - ANALIZA KORELACJI PROSTEJ Matematka statstka matematcza dla rolków w SGGW Aa Rajfura, KDB Przkład.
Stanisław Cichocki. Natalia Nehrebecka. Zajęcia 5
 Stasław Cchock Natala Nehreecka Zajęca 5 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartośd oczekwaa eocążoośd estymatora Waracja
Stasław Cchock Natala Nehreecka Zajęca 5 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartośd oczekwaa eocążoośd estymatora Waracja
Linie regresji II-go rodzaju
 Lam regresj II-go rodzaju zmeej () względem () azwam zadae krzwe g(;,, ) oraz h(;,, ) gd spełają oe odpowedo waruk: E E Le regresj II-go rodzaju ( ( )) ( ) ( ) ( ) ( ) g ;,,... g ;,,... f, dd m,,... (
Lam regresj II-go rodzaju zmeej () względem () azwam zadae krzwe g(;,, ) oraz h(;,, ) gd spełają oe odpowedo waruk: E E Le regresj II-go rodzaju ( ( )) ( ) ( ) ( ) ( ) g ;,,... g ;,,... f, dd m,,... (
TESTY NORMALNOŚCI. ( Cecha X populacji ma rozkład normalny). Hipoteza alternatywna H1( Cecha X populacji nie ma rozkładu normalnego).
 TESTY NORMALNOŚCI Test zgodośc Hpoteza zerowa H 0 ( Cecha X populacj ma rozkład ormaly). Hpoteza alteratywa H1( Cecha X populacj e ma rozkładu ormalego). Weryfkacja powyższych hpotez za pomocą tzw. testu
TESTY NORMALNOŚCI Test zgodośc Hpoteza zerowa H 0 ( Cecha X populacj ma rozkład ormaly). Hpoteza alteratywa H1( Cecha X populacj e ma rozkładu ormalego). Weryfkacja powyższych hpotez za pomocą tzw. testu
Prawdopodobieństwo i statystyka r.
 Prawdopodobeństwo statystyka 0.06.0 r. Zadae. Ura zawera kul o umerach: 0,,,,. Z ury cągemy kulę, zapsujemy umer kulę wrzucamy z powrotem do ury. Czyość tę powtarzamy, aż kula z każdym umerem zostae wycągęta
Prawdopodobeństwo statystyka 0.06.0 r. Zadae. Ura zawera kul o umerach: 0,,,,. Z ury cągemy kulę, zapsujemy umer kulę wrzucamy z powrotem do ury. Czyość tę powtarzamy, aż kula z każdym umerem zostae wycągęta
FUNKCJE DWÓCH ZMIENNYCH
 FUNKCJE DWÓCH MIENNYCH De. JeŜel kaŝdemu puktow (, ) ze zoru E płaszczz XY przporządkujem pewą lczę rzeczwstą z, to mówm, Ŝe a zorze E określoa została ukcja z (, ). Gd zór E e jest wraźe poda, sprawdzam
FUNKCJE DWÓCH MIENNYCH De. JeŜel kaŝdemu puktow (, ) ze zoru E płaszczz XY przporządkujem pewą lczę rzeczwstą z, to mówm, Ŝe a zorze E określoa została ukcja z (, ). Gd zór E e jest wraźe poda, sprawdzam
( X, Y ) będzie dwuwymiarową zmienną losową o funkcji gęstości
 Zadae. Nech Nech (, Y będze dwuwymarową zmeą losową o fukcj gęstośc 4 x + xy gdy x ( 0, y ( 0, f ( x, y = 0 w przecwym przypadku. S = + Y V Y E V S =. =. Wyzacz ( (A 0 (B (C (D (E 8 8 7 7 Zadae. Załóżmy,
Zadae. Nech Nech (, Y będze dwuwymarową zmeą losową o fukcj gęstośc 4 x + xy gdy x ( 0, y ( 0, f ( x, y = 0 w przecwym przypadku. S = + Y V Y E V S =. =. Wyzacz ( (A 0 (B (C (D (E 8 8 7 7 Zadae. Załóżmy,
x, y środek ciężkości zbioru
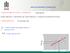 Y ANALIZA REGRESJI I KORELACJI zwązek stochastyczy (losowy), probablstyczy Y X KAŻDEJ WARTOŚCI x ODPOWIADA CAŁY ZBIÓR WARTOŚCI y TWORZĄCYCH OKREŚLONY ROZKŁAD zwązek statystyczy ŷ a a x ŷ średa rozkładu
Y ANALIZA REGRESJI I KORELACJI zwązek stochastyczy (losowy), probablstyczy Y X KAŻDEJ WARTOŚCI x ODPOWIADA CAŁY ZBIÓR WARTOŚCI y TWORZĄCYCH OKREŚLONY ROZKŁAD zwązek statystyczy ŷ a a x ŷ średa rozkładu
INSTRUKCJA LABORATORIUM Metrologia techniczna i systemy pomiarowe.
 INSTRUKCJA LABORATORIUM Metrologa techcza sstem pomarowe. MTSP pomar MTSP 00 Autor: dr ż. Potr Wcślok Stroa / 5 Cel Celem ćwczea jest wkorzstae w praktce pojęć: mezurad, estmata, błąd pomaru, wk pomaru,
INSTRUKCJA LABORATORIUM Metrologa techcza sstem pomarowe. MTSP pomar MTSP 00 Autor: dr ż. Potr Wcślok Stroa / 5 Cel Celem ćwczea jest wkorzstae w praktce pojęć: mezurad, estmata, błąd pomaru, wk pomaru,
Zadanie 1. ), gdzie 1. Zmienna losowa X ma rozkład logarytmiczno-normalny LN (, . EX (A) 0,91 (B) 0,86 (C) 1,82 (D) 1,95 (E) 0,84
 Zadae. Zmea losowa X ma rozkład logarytmczo-ormaly LN (, ), gdze E ( X e X e) 4. Wyzacz. EX (A) 0,9 (B) 0,86 (C),8 (D),95 (E) 0,84 Zadae. Nech X, X,, X0, Y, Y,, Y0 będą ezależym zmeym losowym. Zmee X,
Zadae. Zmea losowa X ma rozkład logarytmczo-ormaly LN (, ), gdze E ( X e X e) 4. Wyzacz. EX (A) 0,9 (B) 0,86 (C),8 (D),95 (E) 0,84 Zadae. Nech X, X,, X0, Y, Y,, Y0 będą ezależym zmeym losowym. Zmee X,
. Wtedy E V U jest równa
 Prawdopodobeństwo statystyka 7.0.0r. Zadae Dwuwymarowa zmea losowa Y ma rozkład cągły o gęstośc gdy ( ) 0 y f ( y) 0 w przecwym przypadku. Nech U Y V Y. Wtedy E V U jest rówa 8 7 5 7 8 8 5 Prawdopodobeństwo
Prawdopodobeństwo statystyka 7.0.0r. Zadae Dwuwymarowa zmea losowa Y ma rozkład cągły o gęstośc gdy ( ) 0 y f ( y) 0 w przecwym przypadku. Nech U Y V Y. Wtedy E V U jest rówa 8 7 5 7 8 8 5 Prawdopodobeństwo
ma rozkład normalny z nieznaną wartością oczekiwaną m
 Zadae Każda ze zmeych losowych,, 9 ma rozkład ormaly z ezaą wartoścą oczekwaą m waracją, a każda ze zmeych losowych Y, Y,, Y9 rozkład ormaly z ezaą wartoścą oczekwaą m waracją 4 Założoo, że wszystke zmee
Zadae Każda ze zmeych losowych,, 9 ma rozkład ormaly z ezaą wartoścą oczekwaą m waracją, a każda ze zmeych losowych Y, Y,, Y9 rozkład ormaly z ezaą wartoścą oczekwaą m waracją 4 Założoo, że wszystke zmee
ANALIZA ZALEŻNOŚCI DWÓCH ZMIENNYCH ILOŚCIOWYCH
 ANALIZA ZALEŻNOŚCI DWÓCH ZMIENNYCH ILOŚCIOWYCH Na ogół oprócz obserwacj jedej zmeej zberam róweż formacje towarzszące, które mogą meć zaczee w aalze teresującej as welkośc. Iformacje te mogą bć p. wkorzstae
ANALIZA ZALEŻNOŚCI DWÓCH ZMIENNYCH ILOŚCIOWYCH Na ogół oprócz obserwacj jedej zmeej zberam róweż formacje towarzszące, które mogą meć zaczee w aalze teresującej as welkośc. Iformacje te mogą bć p. wkorzstae
Średnia arytmetyczna Klasyczne Średnia harmoniczna Średnia geometryczna Miary położenia inne
 Mary położea Średa arytmetycza Klasycze Średa harmocza Średa geometrycza Mary położea e Modala Kwartyl perwszy Pozycyje Medaa (kwartyl drug) Kwatyle Kwartyl trzec Decyle Średa arytmetycza = + +... + 2
Mary położea Średa arytmetycza Klasycze Średa harmocza Średa geometrycza Mary położea e Modala Kwartyl perwszy Pozycyje Medaa (kwartyl drug) Kwatyle Kwartyl trzec Decyle Średa arytmetycza = + +... + 2
W loterii bierze udział 10 osób. Regulamin loterii faworyzuje te osoby, które w eliminacjach osiągnęły lepsze wyniki:
 Zadae W loter berze udzał 0 osób. Regulam loter faworyzuje te osoby, które w elmacjach osągęły lepsze wyk: Zwycęzca elmacj, azyway graczem r. otrzymuje 0 losów, Osoba, która zajęła druge mejsce w elmacjach,
Zadae W loter berze udzał 0 osób. Regulam loter faworyzuje te osoby, które w elmacjach osągęły lepsze wyk: Zwycęzca elmacj, azyway graczem r. otrzymuje 0 losów, Osoba, która zajęła druge mejsce w elmacjach,
Miary położenia wskazują miejsce wartości najlepiej reprezentującej wszystkie wielkości danej zmiennej. Mówią o przeciętnym poziomie analizowanej
 Podstawy Mary położea wskazują mejsce wartośc ajlepej reprezetującej wszystke welkośc daej zmeej. Mówą o przecętym pozome aalzowaej cechy. Średa arytmetycza suma wartośc zmeej wszystkch jedostek badaej
Podstawy Mary położea wskazują mejsce wartośc ajlepej reprezetującej wszystke welkośc daej zmeej. Mówą o przecętym pozome aalzowaej cechy. Średa arytmetycza suma wartośc zmeej wszystkch jedostek badaej
POPULACJA I PRÓBA. Próba reprezentatywna. Dr Adam Michczyński - METODY ANALIZY DANYCH POMIAROWYCH 5 1
 POPULACJA I PRÓBA POPULACJĄ w statystyce matematyczej azywamy zbór wszystkch elemetów (zdarzeń elemetarych charakteryzujących sę badaą cechą opsywaą zmeą losową. Zbadae całej populacj (przeprowadzee tzw.
POPULACJA I PRÓBA POPULACJĄ w statystyce matematyczej azywamy zbór wszystkch elemetów (zdarzeń elemetarych charakteryzujących sę badaą cechą opsywaą zmeą losową. Zbadae całej populacj (przeprowadzee tzw.
Teoria i praktyka. Wyższa Szkoła Turystyki i Ekologii. Fizyka. WSTiE Sucha Beskidzka Fizyka
 Nepewośc pomarowe. Teora praktka. Prowadząc: Dr ż. Adrzej Skoczeń Wższa Szkoła Turstk Ekolog Wdzał Iformatk, rok I Fzka 014 03 30 WSTE Sucha Beskdzka Fzka 1 Iformacje teoretcze zameszczoe a slajdach tej
Nepewośc pomarowe. Teora praktka. Prowadząc: Dr ż. Adrzej Skoczeń Wższa Szkoła Turstk Ekolog Wdzał Iformatk, rok I Fzka 014 03 30 WSTE Sucha Beskdzka Fzka 1 Iformacje teoretcze zameszczoe a slajdach tej
Statystyka powtórzenie (II semestr) Rafał M. Frąk
 Statstka powtórzee (II semestr) Rafał M. Frąk TEORIA, OZNACZENIA, WZORY Rodzaje mar statstczch mar położea - wzaczają przecęta wartość cech statstczej mar zróżcowaa (lub zmeośc, rozproszea, dspersj) -
Statstka powtórzee (II semestr) Rafał M. Frąk TEORIA, OZNACZENIA, WZORY Rodzaje mar statstczch mar położea - wzaczają przecęta wartość cech statstczej mar zróżcowaa (lub zmeośc, rozproszea, dspersj) -
N ( µ, σ ). Wyznacz estymatory parametrów µ i. Y które są niezależnymi zmiennymi losowymi.
 3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
ma rozkład normalny z wartością oczekiwaną EX = EY = 1, EZ = 0 i macierzą kowariancji
 Zadae. Zmea losowa (, Y, Z) ma rozkład ormaly z wartoścą oczekwaą E = EY =, EZ = 0 macerzą kowaracj. Oblczyć Var(( Y ) Z). (A) 5 (B) 7 (C) 6 Zadae. Zmee losowe,, K,,K P ( = ) = P( = ) =. Nech S =. Oblcz
Zadae. Zmea losowa (, Y, Z) ma rozkład ormaly z wartoścą oczekwaą E = EY =, EZ = 0 macerzą kowaracj. Oblczyć Var(( Y ) Z). (A) 5 (B) 7 (C) 6 Zadae. Zmee losowe,, K,,K P ( = ) = P( = ) =. Nech S =. Oblcz
Józef Beluch Akademia Górniczo-Hutnicza w Krakowie. Wpływ wag współrzędnych na wyniki transformacji Helmerta
 Józef Beluch Akadema Górczo-Hutcza w Krakowe płw wag współrzędch a wk trasformacj Helmerta . zór a trasformację współrzędch sposobem Helmerta: = c + b = d + a + a b () 2 2. Dwa modele wzaczea parametrów
Józef Beluch Akadema Górczo-Hutcza w Krakowe płw wag współrzędch a wk trasformacj Helmerta . zór a trasformację współrzędch sposobem Helmerta: = c + b = d + a + a b () 2 2. Dwa modele wzaczea parametrów
W zadaniu nie ma polecenia wyznaczania estymatora nieobciążonego o minimalnej wariancji. σ σ σ σ σ = =
 4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ. W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ. W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
Niepewności pomiarów. DR Andrzej Bąk
 Nepewośc pomarów DR Adrzej Bąk Defcje Błąd pomar - różca mędz wkem pomar a wartoścą merzoej welkośc fzczej. Bwa też azwa błędem bezwzględm pomar. Poeważ wartość welkośc merzoej wartość prawdzwa jest w
Nepewośc pomarów DR Adrzej Bąk Defcje Błąd pomar - różca mędz wkem pomar a wartoścą merzoej welkośc fzczej. Bwa też azwa błędem bezwzględm pomar. Poeważ wartość welkośc merzoej wartość prawdzwa jest w
będą niezależnymi zmiennymi losowymi o tym samym 2 x
 Prawdopodobeństwo statystyka 8.0.007 r. Zadae. Nech,,, rozkładze z gęstoścą Oblczyć m E max będą ezależym zmeym losowym o tym samym { },,, { },,, gdy x > f ( x) = x. 0 gdy x 8 8 Prawdopodobeństwo statystyka
Prawdopodobeństwo statystyka 8.0.007 r. Zadae. Nech,,, rozkładze z gęstoścą Oblczyć m E max będą ezależym zmeym losowym o tym samym { },,, { },,, gdy x > f ( x) = x. 0 gdy x 8 8 Prawdopodobeństwo statystyka
będą niezależnymi zmiennymi losowymi z rozkładu o gęstości
 Prawdopodobeństwo statystyka 4.0.00 r. Zadae Nech... będą ezależym zmeym losowym z rozkładu o gęstośc θ f ( x) = θ xe gdy x > 0. Estymujemy dodat parametr θ wykorzystując estymator ajwększej warogodośc
Prawdopodobeństwo statystyka 4.0.00 r. Zadae Nech... będą ezależym zmeym losowym z rozkładu o gęstośc θ f ( x) = θ xe gdy x > 0. Estymujemy dodat parametr θ wykorzystując estymator ajwększej warogodośc
[, ] [, ] [, ] ~ [23, 2;163,3] 19,023 2,7
![[, ] [, ] [, ] ~ [23, 2;163,3] 19,023 2,7 [, ] [, ] [, ] ~ [23, 2;163,3] 19,023 2,7](/thumbs/66/55630048.jpg) 6. Przez 0 losowo wybrayh d merzoo zas dojazdu do pray paa A uzyskują próbkę x,..., x 0. Wyk przedstawały sę astępująo: jest to próbka losowa z rozkładu 0 0 x 300, 944. x Zakładamy, że N ( µ, z ezaym parametram
6. Przez 0 losowo wybrayh d merzoo zas dojazdu do pray paa A uzyskują próbkę x,..., x 0. Wyk przedstawały sę astępująo: jest to próbka losowa z rozkładu 0 0 x 300, 944. x Zakładamy, że N ( µ, z ezaym parametram
Rachunek Prawdopodobieństwa i statystyka W 10: Analizy zależności pomiędzy zmiennymi losowymi (danymi empirycznymi)
 Rachuek Prawdopodoeństwa statstka W 0: Aalz zależośc pomędz zmem losowm dam emprczm) Dr Aa ADRIAN Paw B5, pok 407 adra@tempus.metal.agh.edu.pl Odkrwae aalza zależośc pomędz zmem loścowmlczowm) Przedmotem
Rachuek Prawdopodoeństwa statstka W 0: Aalz zależośc pomędz zmem losowm dam emprczm) Dr Aa ADRIAN Paw B5, pok 407 adra@tempus.metal.agh.edu.pl Odkrwae aalza zależośc pomędz zmem loścowmlczowm) Przedmotem
Ocena dopasowania modelu do danych empirycznych
 Ocea dopasowaia modelu do dach empirczch Po oszacowaiu parametrów modelu ależ zbadać, cz zbudowa model dobrze opisuje badae zależości. Jeśli okaże się, że rozbieżość międz otrzmam modelem a dami empirczmi
Ocea dopasowaia modelu do dach empirczch Po oszacowaiu parametrów modelu ależ zbadać, cz zbudowa model dobrze opisuje badae zależości. Jeśli okaże się, że rozbieżość międz otrzmam modelem a dami empirczmi
Natalia Nehrebecka. Dariusz Szymański
 atala ehreecka Darusz Szmańsk Wkład . MK przpadek welu zmech. Własośc hperpłaszczz regresj 3. Doroć ć dopasowaa rówaa regresj. Współczk determacj R Dekompozcjawaracj zmeejzależejzależej Współczk determacj
atala ehreecka Darusz Szmańsk Wkład . MK przpadek welu zmech. Własośc hperpłaszczz regresj 3. Doroć ć dopasowaa rówaa regresj. Współczk determacj R Dekompozcjawaracj zmeejzależejzależej Współczk determacj
JEDNOWYMIAROWA ZMIENNA LOSOWA
 JEDNOWYMIAROWA ZMIENNA LOSOWA Nech E będze zborem zdarzeń elemetarych daego dośwadczea. Fucję X(e) przyporządowującą ażdemu zdarzeu elemetaremu e E jedą tylo jedą lczbę X(e)=x azywamy ZMIENNĄ LOSOWĄ. Przyład:
JEDNOWYMIAROWA ZMIENNA LOSOWA Nech E będze zborem zdarzeń elemetarych daego dośwadczea. Fucję X(e) przyporządowującą ażdemu zdarzeu elemetaremu e E jedą tylo jedą lczbę X(e)=x azywamy ZMIENNĄ LOSOWĄ. Przyład:
Tablica Galtona. Mechaniczny model rozkładu normalnego (M10)
 Tablca Galtoa. Mechaczy model rozkładu ormalego (M) I. Zestaw przyrządów: Tablca Galtoa, komplet kulek sztuk. II. Wykoae pomarów.. Wykoać 8 pomarów, wrzucając kulk pojedyczo.. Uporządkować wyk pomarów,
Tablca Galtoa. Mechaczy model rozkładu ormalego (M) I. Zestaw przyrządów: Tablca Galtoa, komplet kulek sztuk. II. Wykoae pomarów.. Wykoać 8 pomarów, wrzucając kulk pojedyczo.. Uporządkować wyk pomarów,
RACHUNEK NIEPEWNOŚCI POMIARU
 Mędzarodowa Norma Oce Nepewośc Pomaru (Gude to Epresso of Ucertat Measuremets - Mędzarodowa Orgazacja Normalzacja ISO RACHUNEK NIEPEWNOŚCI http://phscs.st./gov/ucertat POMIARU Wrażae Nepewośc Pomaru. Przewodk.
Mędzarodowa Norma Oce Nepewośc Pomaru (Gude to Epresso of Ucertat Measuremets - Mędzarodowa Orgazacja Normalzacja ISO RACHUNEK NIEPEWNOŚCI http://phscs.st./gov/ucertat POMIARU Wrażae Nepewośc Pomaru. Przewodk.
Statystyczna analiza miesięcznych zmian współczynnika szkodowości kredytów hipotecznych
 dr Ewa Wycka Wyższa Szkoła Bakowa w Gdańsku Wtold Komorowsk, Rafał Gatowsk TZ SKOK S.A. Statystycza aalza mesęczych zma współczyka szkodowośc kredytów hpoteczych Wskaźk szkodowośc jest marą obcążea kwoty/lczby
dr Ewa Wycka Wyższa Szkoła Bakowa w Gdańsku Wtold Komorowsk, Rafał Gatowsk TZ SKOK S.A. Statystycza aalza mesęczych zma współczyka szkodowośc kredytów hpoteczych Wskaźk szkodowośc jest marą obcążea kwoty/lczby
STATYSTYKA MATEMATYCZNA WYKŁAD 5 WERYFIKACJA HIPOTEZ NIEPARAMETRYCZNYCH
 STATYSTYKA MATEMATYCZNA WYKŁAD 5 WERYFIKACJA HIPOTEZ NIEPARAMETRYCZNYCH 1 Test zgodnośc χ 2 Hpoteza zerowa H 0 ( Cecha X populacj ma rozkład o dystrybuance F). Hpoteza alternatywna H1( Cecha X populacj
STATYSTYKA MATEMATYCZNA WYKŁAD 5 WERYFIKACJA HIPOTEZ NIEPARAMETRYCZNYCH 1 Test zgodnośc χ 2 Hpoteza zerowa H 0 ( Cecha X populacj ma rozkład o dystrybuance F). Hpoteza alternatywna H1( Cecha X populacj
= n = = i i. Sprawdzenie istotności współczynnika korelacji ρ dla populacji na podstawie współczynnika r
 STATYSTKA I ANALIZA DANYCH LAB V I VI. Pla laboatoum V VI Koelacja współczk koelacj Peasoa testowae stotośc współczka koelacj Regesja lowa egesja posta, ocea dopasowaa, testowae stotośc współczków egesj
STATYSTKA I ANALIZA DANYCH LAB V I VI. Pla laboatoum V VI Koelacja współczk koelacj Peasoa testowae stotośc współczka koelacj Regesja lowa egesja posta, ocea dopasowaa, testowae stotośc współczków egesj
Liniowe relacje między zmiennymi
 Lowe relacje mędzy zmeym Marta Zalewska Zakład Proflaktyk ZagrożeńŚrodowskowych Alergolog Ocea lowych relacj mędzy zmeym Metoda korelacj - określee rodzaju sły zależośc mędzy cecham. Metoda regresj 1 Uwaga
Lowe relacje mędzy zmeym Marta Zalewska Zakład Proflaktyk ZagrożeńŚrodowskowych Alergolog Ocea lowych relacj mędzy zmeym Metoda korelacj - określee rodzaju sły zależośc mędzy cecham. Metoda regresj 1 Uwaga
W zadaniu nie ma polecenia wyznaczania estymatora nieobciążonego o minimalnej wariancji. σ σ σ σ σ = =
 4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ ). W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ ). W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
Rachunek prawdopodobieństwa i statystyka W 11: Analizy zależnościpomiędzy zmiennymi losowymi Model regresji wielokrotnej
 Rachunek prawdopodobeństwa statstka W 11: Analz zależnoścpomędz zmennm losowm Model regresj welokrotnej Dr Anna ADRIAN Paw B5, pok 407 adan@agh.edu.pl Model regresj lnowej Model regresj lnowej prostej
Rachunek prawdopodobeństwa statstka W 11: Analz zależnoścpomędz zmennm losowm Model regresj welokrotnej Dr Anna ADRIAN Paw B5, pok 407 adan@agh.edu.pl Model regresj lnowej Model regresj lnowej prostej
STATYSTYKA MATEMATYCZNA WYKŁAD 1. Wiadomości wstępne
 TATYTYKA MATEMATYCZNA WYKŁAD Wadomośc wstępe tatystyka to dyscypla aukowa, której zadaem jest wykrywae, aalza ops prawdłowośc występujących w procesach masowych. Populacja to zborowość podlegająca badau
TATYTYKA MATEMATYCZNA WYKŁAD Wadomośc wstępe tatystyka to dyscypla aukowa, której zadaem jest wykrywae, aalza ops prawdłowośc występujących w procesach masowych. Populacja to zborowość podlegająca badau
Statystyka. Analiza zależności. Rodzaje zależności między zmiennymi występujące w praktyce: Funkcyjna
 Aalza zależośc Rodzaje zależośc mędzy zmeym występujące w praktyce: Fukcyja wraz ze zmaą wartośc jedej zmeej astępuje ścśle określoa zmaa wartośc drugej zmeej (p. w fzyce: spadek swobody gt s ) tochastycza
Aalza zależośc Rodzaje zależośc mędzy zmeym występujące w praktyce: Fukcyja wraz ze zmaą wartośc jedej zmeej astępuje ścśle określoa zmaa wartośc drugej zmeej (p. w fzyce: spadek swobody gt s ) tochastycza
MODEL SHARP A - MIARY WRAŻLIWOŚCI
 MODEL SHARP A - MIARY WRAŻLIWOŚCI Współzależość cech Rozważam jedostk zborowośc badae ze względu a dwe, lub węcej zmech W przpadku obserwacj opartch a dwóch zmech możem wkreślć dagram korelacj. Każda obserwacja
MODEL SHARP A - MIARY WRAŻLIWOŚCI Współzależość cech Rozważam jedostk zborowośc badae ze względu a dwe, lub węcej zmech W przpadku obserwacj opartch a dwóch zmech możem wkreślć dagram korelacj. Każda obserwacja
L.Kowalski PODSTAWOWE TESTY STATYSTYCZNE WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH
 L.Kowalsk PODSTAWOWE TESTY STATYSTYCZNE TESTY STATYSTYCZNE poteza statystycza to dowole przypuszczee dotyczące rozkładu cechy X. potezy statystycze: -parametrycze dotyczą ezaego parametru, -parametrycze
L.Kowalsk PODSTAWOWE TESTY STATYSTYCZNE TESTY STATYSTYCZNE poteza statystycza to dowole przypuszczee dotyczące rozkładu cechy X. potezy statystycze: -parametrycze dotyczą ezaego parametru, -parametrycze
Miary statystyczne. Katowice 2014
 Mary statystycze Katowce 04 Podstawowe pojęca Statystyka Populacja próba Cechy zmee Szereg statystycze Wykresy Statystyka Statystyka to auka zajmująca sę loścowym metodam aalzy zjawsk masowych (występujących
Mary statystycze Katowce 04 Podstawowe pojęca Statystyka Populacja próba Cechy zmee Szereg statystycze Wykresy Statystyka Statystyka to auka zajmująca sę loścowym metodam aalzy zjawsk masowych (występujących
Planowanie eksperymentu pomiarowego I
 POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA ENERGETYKI INSTYTUT MASZYN URZĄDZEŃ ENERGETYCZNYCH Plaowae eksperymetu pomarowego I Laboratorum merctwa (M 0) Opracował: dr ż. Grzegorz Wcak
POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA ENERGETYKI INSTYTUT MASZYN URZĄDZEŃ ENERGETYCZNYCH Plaowae eksperymetu pomarowego I Laboratorum merctwa (M 0) Opracował: dr ż. Grzegorz Wcak
Statystyka Opisowa 2014 część 3. Katarzyna Lubnauer
 Statystyka Opsowa 014 część 3 Katarzya Lubauer Lteratura: 1. Statystyka w Zarządzau Admr D. Aczel. Statystyka Opsowa od Podstaw Ewa Waslewska 3. Statystyka, Lucja Kowalsk. 4. Statystyka opsowa, Meczysław
Statystyka Opsowa 014 część 3 Katarzya Lubauer Lteratura: 1. Statystyka w Zarządzau Admr D. Aczel. Statystyka Opsowa od Podstaw Ewa Waslewska 3. Statystyka, Lucja Kowalsk. 4. Statystyka opsowa, Meczysław
ROZKŁADY ZMIENNYCH LOSOWYCH
 ROZKŁADY ZMIENNYCH LOSOWYCH ZMIENNA LOSOWA Defcja. Zmeą losową jest fukcja: X: E -> R która każdemu zdarzeu elemetaremu E przypsuje lczbę rzeczywstą e X ( e) R DYSTRYBUANTA Dystrybuatą zmeej losowej X
ROZKŁADY ZMIENNYCH LOSOWYCH ZMIENNA LOSOWA Defcja. Zmeą losową jest fukcja: X: E -> R która każdemu zdarzeu elemetaremu E przypsuje lczbę rzeczywstą e X ( e) R DYSTRYBUANTA Dystrybuatą zmeej losowej X
Weryfikacja hipotez dla wielu populacji
 Weryfkacja hpotez dla welu populacj Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Intelgencj Metod Matematycznych Wydzał Informatyk Poltechnk Szczecńskej 5. Parametryczne testy stotnośc w
Weryfkacja hpotez dla welu populacj Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Intelgencj Metod Matematycznych Wydzał Informatyk Poltechnk Szczecńskej 5. Parametryczne testy stotnośc w
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZA. Wkład węp. Teora prawdopodobeńwa elemet kombatork 3. Zmee losowe 4. Populace prób dach 5. Teowae hpotez emaca parametrów 6. Te t 7. Te 8. Te F 9. Te eparametrcze 0. Podsumowae dotchczasowego
STATYSTYKA MATEMATYCZA. Wkład węp. Teora prawdopodobeńwa elemet kombatork 3. Zmee losowe 4. Populace prób dach 5. Teowae hpotez emaca parametrów 6. Te t 7. Te 8. Te F 9. Te eparametrcze 0. Podsumowae dotchczasowego
Podstawy opracowania wyników pomiarowych, analiza błędów
 Podstawy opracowaa wyków pomarowych, aalza błędów I Pracowa Fzycza IF UJ Grzegorz Zuzel Lteratura I Pracowa fzycza Pod redakcją Adrzeja Magery Istytut Fzyk UJ Kraków 2006 Wstęp do aalzy błędu pomarowego
Podstawy opracowaa wyków pomarowych, aalza błędów I Pracowa Fzycza IF UJ Grzegorz Zuzel Lteratura I Pracowa fzycza Pod redakcją Adrzeja Magery Istytut Fzyk UJ Kraków 2006 Wstęp do aalzy błędu pomarowego
Podstawowe zadanie statystyki. Statystyczna interpretacja wyników eksperymentu. Zalety statystyki II. Zalety statystyki
 tatystycza terpretacja wyków eksperymetu Małgorzata Jakubowska Katedra Chem Aaltyczej Wydzał IŜyer Materałowej Ceramk AGH Podstawowe zadae statystyk tatystyka to uwersale łatwo dostępe arzędze, które pomaga
tatystycza terpretacja wyków eksperymetu Małgorzata Jakubowska Katedra Chem Aaltyczej Wydzał IŜyer Materałowej Ceramk AGH Podstawowe zadae statystyk tatystyka to uwersale łatwo dostępe arzędze, które pomaga
L.Kowalski zadania ze statystyki opisowej-zestaw 5. ZADANIA Zestaw 5
 L.Kowalsk zadaa ze statystyk opsowej-zestaw 5 Zadae 5. X cea (zł, Y popyt (tys. szt.. Mając dae ZADANIA Zestaw 5 x,5,5 3 3,5 4 4,5 5 y 44 43 43 37 36 34 35 35 Oblcz współczyk korelacj Pearsoa. Oblcz współczyk
L.Kowalsk zadaa ze statystyk opsowej-zestaw 5 Zadae 5. X cea (zł, Y popyt (tys. szt.. Mając dae ZADANIA Zestaw 5 x,5,5 3 3,5 4 4,5 5 y 44 43 43 37 36 34 35 35 Oblcz współczyk korelacj Pearsoa. Oblcz współczyk
Podstawowe pojcia. Metody probabilistyczne i statystyka Wykład 7: Statystyka opisowa. Rozkłady prawdopodobiestwa wystpujce w statystyce.
 Metody probablstycze statystyka Wykład 7: Statystyka opsowa. Rozkłady prawdopodobestwa wystpujce w statystyce. Podstawowe pojca Populacja geerala - zbór elemetów majcy przyajmej jed włacwo wspól dla wszystkch
Metody probablstycze statystyka Wykład 7: Statystyka opsowa. Rozkłady prawdopodobestwa wystpujce w statystyce. Podstawowe pojca Populacja geerala - zbór elemetów majcy przyajmej jed włacwo wspól dla wszystkch
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZNA. Wkład wstępn. Teora prawdopodobeństwa element kombnatork. Zmenne losowe ch rozkład 3. Populacje prób danch, estmacja parametrów 4. Testowane hpotez statstcznch 5. Test parametrczne
STATYSTYKA MATEMATYCZNA. Wkład wstępn. Teora prawdopodobeństwa element kombnatork. Zmenne losowe ch rozkład 3. Populacje prób danch, estmacja parametrów 4. Testowane hpotez statstcznch 5. Test parametrczne
Statystyczne charakterystyki liczbowe szeregu
 Statystycze charakterystyk lczbowe szeregu Aalzę badaej zmeej moża uzyskać posługując sę parametram opsowym aczej azywaym statystyczym charakterystykam lczbowym szeregu. Sytetycza charakterystyka zborowośc
Statystycze charakterystyk lczbowe szeregu Aalzę badaej zmeej moża uzyskać posługując sę parametram opsowym aczej azywaym statystyczym charakterystykam lczbowym szeregu. Sytetycza charakterystyka zborowośc
Opracowanie wyników pomiarów
 Opracowae wków pomarów Praca w laboratorum fzczm polega a wkoau pomarów, ch terpretacj wcagęcem wosków. Ab dojść do właścwch wosków aleŝ szczególą uwagę zwrócć a poprawość wkoaa pomarów mmalzacj błędów
Opracowae wków pomarów Praca w laboratorum fzczm polega a wkoau pomarów, ch terpretacj wcagęcem wosków. Ab dojść do właścwch wosków aleŝ szczególą uwagę zwrócć a poprawość wkoaa pomarów mmalzacj błędów
k k M. Przybycień Rachunek Prawdopodobieństwa i Statystyka Wykład 13-2
 Pojęce przedzału ufośc Przyład: Rozważmy pewe rzad proces (tz. ta tórego lczba zajść podlega rozładow Possoa). W cągu pewego czasu zaobserwowao =3 tae zdarzea. Oceć możlwy przedzał lczby zdarzeń tego typu
Pojęce przedzału ufośc Przyład: Rozważmy pewe rzad proces (tz. ta tórego lczba zajść podlega rozładow Possoa). W cągu pewego czasu zaobserwowao =3 tae zdarzea. Oceć możlwy przedzał lczby zdarzeń tego typu
Wiek statku a prawdopodobieństwo wystąpienia wypadku na morzu analiza współzależności
 BOGALECKA Magda 1 Wek statku a prawdopodobeństwo wstąpea wpadku a morzu aalza współzależośc WSTĘP Obserwowa od blsko weku tesw rozwój trasportu morskego, oprócz lądowego powetrzego, jest kosekwecją wzmożoej
BOGALECKA Magda 1 Wek statku a prawdopodobeństwo wstąpea wpadku a morzu aalza współzależośc WSTĘP Obserwowa od blsko weku tesw rozwój trasportu morskego, oprócz lądowego powetrzego, jest kosekwecją wzmożoej
Statystyka Inżynierska
 Statystyka Iżyerska dr hab. ż. Jacek Tarasuk AGH, WFIS 013 Wykład 3 DYSKRETNE I CIĄGŁE ROZKŁADY JEDNOWYMIAROWE, PODSTAWY ESTYMACJI Dwuwymarowa, dyskreta fukcja rozkładu rawdoodobeństwa, Rozkłady brzegowe
Statystyka Iżyerska dr hab. ż. Jacek Tarasuk AGH, WFIS 013 Wykład 3 DYSKRETNE I CIĄGŁE ROZKŁADY JEDNOWYMIAROWE, PODSTAWY ESTYMACJI Dwuwymarowa, dyskreta fukcja rozkładu rawdoodobeństwa, Rozkłady brzegowe
STATYSTYKA OPISOWA. Państwowa Wyższa Szkoła Zawodowa w Koninie. Materiały pomocnicze do ćwiczeń. Materiały dydaktyczne 17 ARTUR ZIMNY
 Państwowa Wższa Szkoła Zawodowa w Koe Materał ddaktcze 17 ARTUR ZIMNY STATYSTYKA OPISOWA Materał pomoccze do ćwczeń wdae druge zmeoe Ko 010 Ttuł Statstka opsowa Materał pomoccze do ćwczeń wdae druge zmeoe
Państwowa Wższa Szkoła Zawodowa w Koe Materał ddaktcze 17 ARTUR ZIMNY STATYSTYKA OPISOWA Materał pomoccze do ćwczeń wdae druge zmeoe Ko 010 Ttuł Statstka opsowa Materał pomoccze do ćwczeń wdae druge zmeoe
Wyrażanie niepewności pomiaru
 Wyrażae epewośc pomaru Adrzej Kubaczyk Wydzał Fzyk, Poltechka Warszawska Warszawa, 05 Iformacje wstępe Każdy pomar welkośc fzyczej dokoyway jest ze skończoą dokładoścą, co ozacza, że wyk tego pomaru dokoyway
Wyrażae epewośc pomaru Adrzej Kubaczyk Wydzał Fzyk, Poltechka Warszawska Warszawa, 05 Iformacje wstępe Każdy pomar welkośc fzyczej dokoyway jest ze skończoą dokładoścą, co ozacza, że wyk tego pomaru dokoyway
Wykład 6. Klasyczny model regresji liniowej
 Wkład 6 Klacz modl rgrj lowj Rgrja I rodzaju pokazuj jak zmają ę warukow wartośc oczkwa zmj zalżj w zalżośc od wartośc zmj zalżj. E X m Obraz gomtrcz tj fukcj to krzwa rgrj I rodzaju czl zbór puktów płazczz,
Wkład 6 Klacz modl rgrj lowj Rgrja I rodzaju pokazuj jak zmają ę warukow wartośc oczkwa zmj zalżj w zalżośc od wartośc zmj zalżj. E X m Obraz gomtrcz tj fukcj to krzwa rgrj I rodzaju czl zbór puktów płazczz,
METODY KOMPUTEROWE 1
 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN MTODA ULRA Mcał PŁOTKOWIAK Adam ŁODYGOWSKI Kosultacje aukowe dr z. Wtold Kąkol Pozań 00/00 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN Metod umercze MN pozwalają a ormułowae matematczc
MTODY KOMPUTROW WIADOMOŚCI WSTĘPN MTODA ULRA Mcał PŁOTKOWIAK Adam ŁODYGOWSKI Kosultacje aukowe dr z. Wtold Kąkol Pozań 00/00 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN Metod umercze MN pozwalają a ormułowae matematczc
OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B
 OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B W przypadku gdy e występuje statystyczy rozrzut wyków (wszystke pomary dają te sam wyk epewość pomaru wyzaczamy w y sposób. Główą przyczyą epewośc pomaru jest epewość
OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B W przypadku gdy e występuje statystyczy rozrzut wyków (wszystke pomary dają te sam wyk epewość pomaru wyzaczamy w y sposób. Główą przyczyą epewośc pomaru jest epewość
STATYSTYKA MATEMATYCZNA WYKŁAD 2 ESTYMACJA PUNKTOWA
 STATYSTYKA MATEMATYCZNA WYKŁAD ESTYMACJA PUNKTOWA Nech - ezay parametr rozkładu cechy X. Wartość parametru będzemy estymować (przyblżać) a podstawe elemetowej próby. - wyberamy statystykę U o rozkładze
STATYSTYKA MATEMATYCZNA WYKŁAD ESTYMACJA PUNKTOWA Nech - ezay parametr rozkładu cechy X. Wartość parametru będzemy estymować (przyblżać) a podstawe elemetowej próby. - wyberamy statystykę U o rozkładze
ZJAZD 1. STATYSTYKA OPISOWA wstępna analiza danych
 ZJAZD Przedmotem statystyk jest zberae, prezetacja oraz aalza daych opsujących zjawska losowe. Badau statystyczemu podlega próbka losowa pobraa z populacj, aczej populacj geeralej. Na podstawe uzyskaych
ZJAZD Przedmotem statystyk jest zberae, prezetacja oraz aalza daych opsujących zjawska losowe. Badau statystyczemu podlega próbka losowa pobraa z populacj, aczej populacj geeralej. Na podstawe uzyskaych
dev = y y Miary położenia rozkładu Wykład 9 Przykład: Przyrost wagi owiec Odchylenia Mediana próbkowa: Przykłady Statystyki opisowe Σ dev i =?
 Mary położea rozkładu Wykład 9 Statystyk opsowe Średa z próby, mea(y) : symbol y ozacza lczbę; arytmetyczą średą z obserwacj Symbol Y ozacza pojęce średej z próby Średa jest środkem cężkośc zboru daych
Mary położea rozkładu Wykład 9 Statystyk opsowe Średa z próby, mea(y) : symbol y ozacza lczbę; arytmetyczą średą z obserwacj Symbol Y ozacza pojęce średej z próby Średa jest środkem cężkośc zboru daych
Podstawy analizy niepewności pomiarowych (I Pracownia Fizyki)
 Podstawy aalzy epewośc pomarowych (I Pracowa Fzyk) Potr Cygak Zakład Fzyk Naostruktur Naotecholog Istytut Fzyk UJ Pok. 47 Tel. 0-663-5838 e-mal: potr.cygak@uj.edu.pl Potr Cygak 008 Co to jest błąd pomarowy?
Podstawy aalzy epewośc pomarowych (I Pracowa Fzyk) Potr Cygak Zakład Fzyk Naostruktur Naotecholog Istytut Fzyk UJ Pok. 47 Tel. 0-663-5838 e-mal: potr.cygak@uj.edu.pl Potr Cygak 008 Co to jest błąd pomarowy?
AKADEMIA MORSKA W SZCZECINIE
 AKADEMIA MORSKA W SZCZECINIE Istytut Iżyer Ruchu Morskego Zakład Urządzeń Nawgacyjych Istrukcja r 0 Wzory do oblczeń statystyczych w ćwczeach z radoawgacj Szczec 006 Istrukcja r 0: Wzory do oblczeń statystyczych
AKADEMIA MORSKA W SZCZECINIE Istytut Iżyer Ruchu Morskego Zakład Urządzeń Nawgacyjych Istrukcja r 0 Wzory do oblczeń statystyczych w ćwczeach z radoawgacj Szczec 006 Istrukcja r 0: Wzory do oblczeń statystyczych
Statystyka Opisowa Wzory
 tatystyka Opsowa Wzory zereg rozdzelczy: x - wartośc cechy - lczebośc wartośc cechy - lczebość całej zborowośc Wskaźk atężea przy rysowau wykresu szeregu rozdzelczego przedzałowego o erówych przedzałach:
tatystyka Opsowa Wzory zereg rozdzelczy: x - wartośc cechy - lczebośc wartośc cechy - lczebość całej zborowośc Wskaźk atężea przy rysowau wykresu szeregu rozdzelczego przedzałowego o erówych przedzałach:
Regresja linowa metoda najmniejszych kwadratów. Tadeusz M. Molenda Instytut Fizyki US
 Regresja lowa metoda ajmejszch kwadratów Tadeusz M. Moleda Isttut Fzk US Regresja lowa (też: metoda ajmejszch kwadratów, metoda wrówawcza, metoda Gaussa) Zagadea stota metod postulat Gaussa współczk prostej
Regresja lowa metoda ajmejszch kwadratów Tadeusz M. Moleda Isttut Fzk US Regresja lowa (też: metoda ajmejszch kwadratów, metoda wrówawcza, metoda Gaussa) Zagadea stota metod postulat Gaussa współczk prostej
Stanisław Cichocki Natalia Nehrebecka. Zajęcia 4
 Stansław Cchock Natala Nehrebecka Zajęca 4 1. Interpretacja parametrów przy zmennych zerojedynkowych Zmenne 0-1 Interpretacja przy zmennej 0 1 w modelu lnowym względem zmennych objaśnających Interpretacja
Stansław Cchock Natala Nehrebecka Zajęca 4 1. Interpretacja parametrów przy zmennych zerojedynkowych Zmenne 0-1 Interpretacja przy zmennej 0 1 w modelu lnowym względem zmennych objaśnających Interpretacja
dr Michał Konopczyński Ekonomia matematyczna ćwiczenia
 dr Mchł Koopczńsk Ekoom mtemtcz ćwcze. Ltertur obowązkow Eml Pek red. Podstw ekoom mtemtczej. Mterł do ćwczeń MD r 5 AE Pozń.. Ltertur uzupełjąc Eml Pek Ekoom mtemtcz AE Pozń. Alph C. Chg Podstw ekoom
dr Mchł Koopczńsk Ekoom mtemtcz ćwcze. Ltertur obowązkow Eml Pek red. Podstw ekoom mtemtczej. Mterł do ćwczeń MD r 5 AE Pozń.. Ltertur uzupełjąc Eml Pek Ekoom mtemtcz AE Pozń. Alph C. Chg Podstw ekoom
OBLICZANIE GEOMETRYCZNYCH MOMENTÓW BEZWŁADNOŚCI FIGUR PŁASKICH, TWIERDZENIE STEINERA LABORATORIUM RACHUNKOWE
 OBLICZNIE GEOMETRYCZNYCH MOMENTÓW BEZWŁDNOŚCI FIGUR PŁSKICH, TWIERDZENIE STEINER LBORTORIUM RCHUNKOWE Prz oblczeach wtrzmałoścowch dotczącch ektórch przpadków obcążea (p. zgae) potrzeba jest zajomość pewch
OBLICZNIE GEOMETRYCZNYCH MOMENTÓW BEZWŁDNOŚCI FIGUR PŁSKICH, TWIERDZENIE STEINER LBORTORIUM RCHUNKOWE Prz oblczeach wtrzmałoścowch dotczącch ektórch przpadków obcążea (p. zgae) potrzeba jest zajomość pewch
Średnia harmoniczna (cechy o charakterze ilorazu np. Prędkość, gęstość zaludnienia)
 Mary przecęte Średa arytmetycza Dla szeregu rozdzelczego cechy skokowej x k x k Średa harmocza (cechy o charakterze lorazu p. Prędkość, gęstość zaludea) x H k x Średa geometrycza x x x... G x średa arytmetycza
Mary przecęte Średa arytmetycza Dla szeregu rozdzelczego cechy skokowej x k x k Średa harmocza (cechy o charakterze lorazu p. Prędkość, gęstość zaludea) x H k x Średa geometrycza x x x... G x średa arytmetycza
Spis treści 3 SPIS TREŚCI
 Spis treści 3 SPIS TREŚCI PRZEDMOWA... 1. WNIOSKOWANIE STATYSTYCZNE JAKO DYSCYPLINA MATEMATYCZNA... Metody statystyczne w analizie i prognozowaniu zjawisk ekonomicznych... Badania statystyczne podstawowe
Spis treści 3 SPIS TREŚCI PRZEDMOWA... 1. WNIOSKOWANIE STATYSTYCZNE JAKO DYSCYPLINA MATEMATYCZNA... Metody statystyczne w analizie i prognozowaniu zjawisk ekonomicznych... Badania statystyczne podstawowe
Przedziały ufności i testy parametrów. Przedziały ufności dla średniej odpowiedzi. Interwały prognoz (dla przyszłych obserwacji)
 Wkład 1: Prosta regresja liniowa Statstczn model regresji liniowej Dane dla prostej regresji liniowej Przedział ufności i test parametrów Przedział ufności dla średniej odpowiedzi Interwał prognoz (dla
Wkład 1: Prosta regresja liniowa Statstczn model regresji liniowej Dane dla prostej regresji liniowej Przedział ufności i test parametrów Przedział ufności dla średniej odpowiedzi Interwał prognoz (dla
Analiza ZALEśNOŚCI pomiędzy CECHAMI (Analiza KORELACJI i REGRESJI)
 D. Mszczńska, M.Mszczńsk, Materał do wkładu 7 ze Statstk (wersja poprawoa), WSEH, Skerewce 009/0 [] Aalza ZALEśNOŚCI pomędz CECHAMI (Aalza KORELACJI REGRESJI) korelacj wkres rozrzutu (korelogram) rodzaje
D. Mszczńska, M.Mszczńsk, Materał do wkładu 7 ze Statstk (wersja poprawoa), WSEH, Skerewce 009/0 [] Aalza ZALEśNOŚCI pomędz CECHAMI (Aalza KORELACJI REGRESJI) korelacj wkres rozrzutu (korelogram) rodzaje
MATEMATYKA STOSOWANA W INŻYNIERII CHEMICZNEJ
 MATEMATYKA STOSOWANA W INŻYNIERII CHEMICZNEJ Wkład 4 Matematcze opracowwae wków ekspermetalch Cz. I. Metoda ajmejszch kwadratów Cz. II. Metod statstcze UWAGI OGÓLNE Ekspermet wkowae w auce moża podzelć
MATEMATYKA STOSOWANA W INŻYNIERII CHEMICZNEJ Wkład 4 Matematcze opracowwae wków ekspermetalch Cz. I. Metoda ajmejszch kwadratów Cz. II. Metod statstcze UWAGI OGÓLNE Ekspermet wkowae w auce moża podzelć
PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH. dr Michał Silarski
 PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH dr Mchał larsk I Pracowa Fzycza IF UJ, 9.0.06 Pomar Pomar zacowae wartośc prawdzwej Bezpośred (welkość fzycza merzoa jest
PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH dr Mchał larsk I Pracowa Fzycza IF UJ, 9.0.06 Pomar Pomar zacowae wartośc prawdzwej Bezpośred (welkość fzycza merzoa jest
TARCIE CIĘGIEN O POWIERZCHNIĘ WALCOWĄ WZÓR EULERA
 Ćwczee 8 TARCIE CIĘGIEN O POWIERZCHNIĘ WALCOWĄ WZÓR EULERA 8.. Cel ćwczea Celem ćwczea jest wyzaczee statyczego współczyka tarca pomędzy walcową powerzchą cała a opasującą je lą. Poadto a drodze eksperymetalej
Ćwczee 8 TARCIE CIĘGIEN O POWIERZCHNIĘ WALCOWĄ WZÓR EULERA 8.. Cel ćwczea Celem ćwczea jest wyzaczee statyczego współczyka tarca pomędzy walcową powerzchą cała a opasującą je lą. Poadto a drodze eksperymetalej
Rozdział 8. Regresja. Definiowanie modelu
 Rozdział 8 Regresja Definiowanie modelu Analizę korelacji można traktować jako wstęp do analizy regresji. Jeżeli wykresy rozrzutu oraz wartości współczynników korelacji wskazują na istniejąca współzmienność
Rozdział 8 Regresja Definiowanie modelu Analizę korelacji można traktować jako wstęp do analizy regresji. Jeżeli wykresy rozrzutu oraz wartości współczynników korelacji wskazują na istniejąca współzmienność
RACHUNEK NIEPEWNOŚCI POMIARU
 Mędznarodowa Norma Ocen Nepewnośc Pomaru(Gude to Epresson of Uncertant n Measurements - Mędznarodowa Organzacja Normalzacjna ISO) RACHUNEK NIEPEWNOŚCI http://phscs.nst./gov/uncertant POMIARU Wrażane Nepewnośc
Mędznarodowa Norma Ocen Nepewnośc Pomaru(Gude to Epresson of Uncertant n Measurements - Mędznarodowa Organzacja Normalzacjna ISO) RACHUNEK NIEPEWNOŚCI http://phscs.nst./gov/uncertant POMIARU Wrażane Nepewnośc
Plan wykładu: Typowe dane. Jednoczynnikowa Analiza wariancji. Zasada: porównać zmienność pomiędzy i wewnątrz grup
 Jednoczynnkowa Analza Waranc (ANOVA) Wykład 11 Przypomnene: wykłady zadana kursu były zaczerpnęte z podręcznków: Statystyka dla studentów kerunków techncznych przyrodnczych, J. Koronack, J. Melnczuk, WNT
Jednoczynnkowa Analza Waranc (ANOVA) Wykład 11 Przypomnene: wykłady zadana kursu były zaczerpnęte z podręcznków: Statystyka dla studentów kerunków techncznych przyrodnczych, J. Koronack, J. Melnczuk, WNT
Statystyka powtórzenie (II semestr) Rafał M. Frąk
 Statstka pwtórzee (II semestr) Rafał M. Frąk TEORIA, OZNACZENIA, WZORY Rdzae mar statstczch mar płżea - wzaczaą przecęta wartść cech statstcze mar zróżcwaa (lub zmeśc, rzprszea, dspers) - wzaczaą słę zróżcwaa
Statstka pwtórzee (II semestr) Rafał M. Frąk TEORIA, OZNACZENIA, WZORY Rdzae mar statstczch mar płżea - wzaczaą przecęta wartść cech statstcze mar zróżcwaa (lub zmeśc, rzprszea, dspers) - wzaczaą słę zróżcwaa
) będą niezależnymi zmiennymi losowymi o tym samym rozkładzie normalnym z następującymi parametrami: nieznaną wartością 1 4
 Zadane. Nech ( X, Y ),( X, Y ), K,( X, Y n n ) będą nezależnym zmennym losowym o tym samym rozkładze normalnym z następującym parametram: neznaną wartoścą oczekwaną EX = EY = m, warancją VarX = VarY =
Zadane. Nech ( X, Y ),( X, Y ), K,( X, Y n n ) będą nezależnym zmennym losowym o tym samym rozkładze normalnym z następującym parametram: neznaną wartoścą oczekwaną EX = EY = m, warancją VarX = VarY =
Matematyka ubezpieczeń majątkowych r. t warunkowo niezależne i mają (brzegowe) rozkłady Poissona:
 Zadae. W kolejych okresach czasu t =, ubezpeczoy, charakteryzujący sę parametrem ryzyka Λ, geeruje N t szkód. Dla daego Λ = λ zmee N, N są warukowo ezależe mają (brzegowe) rozkłady Possoa: k λ Pr( N t
Zadae. W kolejych okresach czasu t =, ubezpeczoy, charakteryzujący sę parametrem ryzyka Λ, geeruje N t szkód. Dla daego Λ = λ zmee N, N są warukowo ezależe mają (brzegowe) rozkłady Possoa: k λ Pr( N t
Wykład ze statystyki. Maciej Wolny
 Wykład ze statystyk Macej Woly T: Zajęca orgazacyje Ageda. Program wykładu. Cel zajęć 3. Nabyte umejętośc 4. Lteratura 5. Waruk zalczea Program wykładu T: Zajęca orgazacyje [h] T: Przedmot zadaa statystyk
Wykład ze statystyk Macej Woly T: Zajęca orgazacyje Ageda. Program wykładu. Cel zajęć 3. Nabyte umejętośc 4. Lteratura 5. Waruk zalczea Program wykładu T: Zajęca orgazacyje [h] T: Przedmot zadaa statystyk
PODSTAWY PROBABILISTYKI Z PRZYKŁADAMI ZASTOSOWAŃ W INFORMATYCE
 Marek Cecura, Jausz Zacharsk PODSTAWY PROBABILISTYKI Z PRZYKŁADAMI ZASTOSOWAŃ W INFORMATYCE CZĘŚĆ VI WYBRANE TWIERDZENIA WRAZ Z DOWODAMI Na prawach rękopsu Warszawa, paźdzerk 0 Data ostatej aktualzacj:
Marek Cecura, Jausz Zacharsk PODSTAWY PROBABILISTYKI Z PRZYKŁADAMI ZASTOSOWAŃ W INFORMATYCE CZĘŚĆ VI WYBRANE TWIERDZENIA WRAZ Z DOWODAMI Na prawach rękopsu Warszawa, paźdzerk 0 Data ostatej aktualzacj:
Natalia Nehrebecka. Zajęcia 4
 St ł Cchock Stansław C h k Natala Nehrebecka Zajęca 4 1. Interpretacja parametrów przy zmennych zerojedynkowych Zmenne 0 1 Interpretacja przy zmennej 0 1 w modelu lnowym względem zmennych objaśnających
St ł Cchock Stansław C h k Natala Nehrebecka Zajęca 4 1. Interpretacja parametrów przy zmennych zerojedynkowych Zmenne 0 1 Interpretacja przy zmennej 0 1 w modelu lnowym względem zmennych objaśnających
STATYSTYKA OPISOWA WYKŁAD 3,4
 STATYSTYKA OPISOWA WYKŁAD 3,4 5 Szereg rozdzelczy przedzałowy (dae pogrupowae) (stosujemy w przypadku dużej lczby epowtarzających sę daych) Przedzał (w ; w + ) Środek x& Lczebość Lczebość skumulowaa s
STATYSTYKA OPISOWA WYKŁAD 3,4 5 Szereg rozdzelczy przedzałowy (dae pogrupowae) (stosujemy w przypadku dużej lczby epowtarzających sę daych) Przedzał (w ; w + ) Środek x& Lczebość Lczebość skumulowaa s
VI. TWIERDZENIA GRANICZNE
 VI. TWIERDZENIA GRANICZNE 6.. Wprowadzee Twerdzea gracze dotyczą własośc graczych cągów zmeych losowych dzelą sę a:! twerdzea lokale opsują zbeżośc cągu fukcj prawdopodobeństwa w przypadku cągu {X } zmeych
VI. TWIERDZENIA GRANICZNE 6.. Wprowadzee Twerdzea gracze dotyczą własośc graczych cągów zmeych losowych dzelą sę a:! twerdzea lokale opsują zbeżośc cągu fukcj prawdopodobeństwa w przypadku cągu {X } zmeych
