W-23 (Jaroszewicz) 20 slajdów Na podstawie prezentacji prof. J. Rutkowskiego
|
|
|
- Kamila Witkowska
- 8 lat temu
- Przeglądów:
Transkrypt
1 Bangkok, Thailand, March 011
2 W-3 (Jaroszewicz) 0 slajdów Na odstawie rezentacji rof. J. Rutkowskiego Fizyka kwantowa fale rawdoodobieństwa funkcja falowa aczki falowe materii zasada nieoznaczoności równanie Schrodingera
3 3/0-W3 Fale rawdoodobieństwa Rozkład elektronów na ekranie owinien być sumą rozkładów dla każdej szczeliny oddzielnie - obserwujemy obraz interferencyjny dla dwóch szczelin Do wyjaśnienia tego aradoksu musimy stworzyć nowy formalizm matematyczny: fale materii traktować jako fale rawdoodobieństwa wytwarzającą na ekranie obraz rążków rawdoodobieństwa B P 1 Rozkład obserwowany A r r 1 P Rozkład klasyczny
4 4/0-W3 Funkcja falowa Formalizm matematyczny za omocą którego usuwa się te aradoksy, rzyisuje każdej cząstce materialnej funkcję falową (,y,z,t) będącą funkcją wsółrzędnych i czasu Znajdując rozkład natężenia w obrazie dyfrakcyjnym można określić rawdoodobieństwo, że elektron adnie w określonym miejscu ekranu Kwadrat amlitudy funkcji falowej jest roorcjonalny do gęstości rawdoodobieństwa znalezienia elektronu w danym elemencie obszaru
5 5/0-W3 Właściwości funkcji falowej Prawdoodobieństwo znalezienia się elektronu w objętości dvddydz P ddydz gdzie warunek unormowania funkcji falowej dv 1 zasada suerozycji 1 + funkcja falowa owinna być ograniczona < V funkcja falowa nie stanowi bezośrednio obserwowanej wielkości. Fale klasyczne i fale odowiadające cząstkom odlegają równaniom matematycznym tego samego tyu, lecz w rzyadku klasycznym amlituda fali jest bezośrednio obserwowana, a dla funkcji falowej nie.
6 6/0-W3 h λ h π π λ h k π k h π Funkcja falowa cząstki oruszającej się wzdłuż osi, której długość fali jest równa λ o ( k t ) A cos o ω Stąd widać, iż rzeczywista ostać funkcji falowej jest niewłaściwa bo istniałyby unkty, gdzie nie można jej zaobserwować. Leiej zatem stosować ostać zesoloną i( k o ωt ) Ae ( k t ) A cos o ω ( i( k t )) i( k t ) Ae o ω Ae o ω ( ) A Pokazaliśmy, że jeżeli ęd cząstki osiada określoną wartość, to cząstkę można znaleźć z jednakowym rawdoodobieństwem w dowolnym unkcie rzestrzeni. Inaczej mówiąc, jeżeli ęd cząstki jest dokładnie znany, to nic nie wiemy o jej miejscu ołożenia.
7 7/0-W3 Paczki falowe materii Dla cząstki znajdującej się w t0 w określonym obszarze rzestrzeni kwadrat modułu funkcji falowej rzyjmuje ostać funkcji Gaussa A e σ (, 0) A e e( ik ) 4σ Tak zlokalizowana funkcja nazywana jest aczką falową o
8 8/0-W3 B B Suerozycja fal monochromatycznych Paczka falowa jest suerozycją fal o różnych długościach, odowiadają one różnym wartościom ędu k wsółczynniki Fouriera σ π e e 4σ 4σ ( k) e σ ( k k ) ( ) σ e π e e [ ] ( ) o σ o ( ik ) B e( ik ) o ( ik ) B( k) e( ik) B o ( ) B ( ) σ π n e σ e π n dk ( ) o σ ( ) o σ σ σ
9 9/0-W3 Zasada nieoznaczoności czym węższa jest rzestrzennie aczka falowa tym szerszy rozkład o ędzie σ σσ σ niemożliwe jest jednoczesne dokładne określenie wartości wsółrzędnej i ędu cząstki
10 10/0-W3 Zasada nieoznaczoności w ociągu λ chcemy zmierzyć rędkość ociągu wiedząc, że każdy wagon ma długość λ minęło nas n wagonów w ciągu czasu t okonana rzez ociąg droga wynosi l nλ l λ średnia rędkość ociągu wynosi l nλ v l t nλ t v vλ 4 v l t λ t im większy rzedział czasu tym omiar rędkości dokładniejszy, ale maleje dokładność ołożenia ociągu w chwili omiaru v n w mechanice kwantowej ociąg to aczka falowa o długości fali λ rozciągająca się na obszar l nλ λ h h 4 λ 4
11 11/0-W3 Znaczenie zasady nieoznaczoności Heisenberga szerokość aczki falowej 1/ k t1/ ω k E ω E t S Działanie S można określić z dokładnością stałej Plancka Zasada nieoznaczoności określa granice możliwości naszych omiarów. Jest jednym z fundamentalnych twierdzeń mechaniki kwantowej: wyjaśnia dyfrakcję na szczelinie energie cząstek są zawsze większe od zera elektron nie sada na jądro atomowe
12 1/0-W3 Prędkość gruowa aczki klasycznie v g dω dk k E ( k ω ) ω E m m dω dk k m dω k v g dk m m v v g Paczka falowa rzemieszcza się z rędkością równą rędkości cząstki relatywistycznie E Eo + E de c c d dω de mv v g c c dk d E mc v v
13 13/0-W3 Rozływanie się aczki falowej Udowodnimy, że ojedynczej aczce falowej właściwy jest rozrzut wartości rędkości gruowej v g, który owinien rowadzić do zwiększenia szerokości. ( vg )t dvg 1 v v m o t g d - szerokość aczki falowej rośnie roorcjonalnie do t g m Rozływania się aczki falowej można uniknąć umieszczając cząstkę w studni otencjału o swobodny elektron zlokalizowany w chwili oczątkowej w obszarze o m (tyowy rozmiar atomu) o uływie sekundy będziemy mieć 1100 km
14 14/0-W3 Cząstka w studni otencjału wystęuje nałożenie się dwóch fal rozchodzących się w rzeciwnych kierunkach owstaje fala stojąca E (ev) E E 3 ik iωt ik iωt ( ) ( ik ik ) iωt t Be Be B e e e, iωt iωt (, t) ibe sin( k) Ae sin( k) Z warunków brzegowych n k n E n bo (0,t)0 n sin ( kl) 0 π n m ml kl nπ k n 00 sin 0 ( k) nπ L E E 1 e ik L e i n ik dozwolone wartości liczby falowej i energii cząstki λ
15 15/0-W3 Równanie Schrodingera-jak? E + m A sin k U( ) ( + ϕ) m m( E U 1 ) k ( E U ) k A sin d d d d d d ( k + ϕ) k m [ E U1 ] m [ E U( ) ] 1 (a) (b) (c) E 0 0 E 0 K /m U 1 U U 3 U() Jest to stacjonarne, jednowymiarowe równanie Schrödingera słuszne w układach nierelatywistycznych od warunkiem, że rozkład rawdoodobieństwa nie zmienia się w czasie
16 16/0-W3 Równanie Schrodingera W sytuacjach stacjonarnych, gdy otencjał nie zmienia się w czasie, zmienne rzestrzenne i czas można rozsearować i zaisać funkcję falową w ostaci: iω, y, z, t, y, z e d d ( ) ( ) t Postać rzestrzennej funkcji falowej, dla rzyadku jednowymiarowego, wyznaczamy z równania Schrödingera: m [ E U( ) ] stacjonarne, jednowymiarowe równanie Schrödingera równania Newtona fale dźwiękowe i fale w strunach równania Mawella fale świetlne równanie Schrödingera fale materii (funkcja falowa)
17 17/0-W3 Równanie Schrodingera dla d m cząstki swobodnej E U( ) U( ) 0 d k d d d m E którego rozwiązaniem jest d oznaczając rzyjmując B0 (cząstka orusza się w kierunku dodatnich ) iωt i ( ) ( ) ( k ωt t e Ae ), k m E [ ] tylko kinetyczna E ik ik ( ) Ae + Be m m m k E m π π λ k h funkcją falową cząstki swobodnej jest fala łaska o długości λ określonej zależnością de Broglie a
18 18/0-W3 Równanie Schrodingera dla nieskończonej jamy otencjału U E 3 E E 1 U d d m [ E U( ) ] U( ) 0 k m E 0 L U0 k d ik Ae + d warunki brzegowe ( 0 ) ( L) 0 A + B 0 sin Ae ( kl) 0 ikl ik ( ) Be + Be ikl kl π n E n n n ( ) C sin C Ai ml L wartości energii E n nazywamy wartościami własnymi odowiadające im funkcje falowe n funkcjami własnymi 0 nπ ( ikl ) 0 A e ikl e n1,,3... π
19 19/0-W3 Wnioski energia jest skwantowana, wystęują dyskretne wartości (oziomy) energii (n liczba kwantowa) cząstka nie może osiadać energii zerowej wynika z zasady nieoznaczoności L L E > 0 m stałą C wyznaczamy z warunku unormowania L L * nπ d C sin d L 0 0 L C 1 nπ C L n ( ) sin L L dla obiektów klasycznych oszczególne oziomy są tak bliskie, że nierozróżnialne 1 L 0 sin nπ L L d
20 Bangkok, Thailand, March 011
gęstością prawdopodobieństwa
 Funkcja falowa Zgodnie z hipotezą de Broglie'a, cząstki takie jak elektron czy proton, mają własności falowe. Własności falowe cząstki (lub innego obiektu) w mechanice kwantowej opisuje tzw. funkcja falowa(,t)
Funkcja falowa Zgodnie z hipotezą de Broglie'a, cząstki takie jak elektron czy proton, mają własności falowe. Własności falowe cząstki (lub innego obiektu) w mechanice kwantowej opisuje tzw. funkcja falowa(,t)
PODSTAWY MECHANIKI KWANTOWEJ
 PODSTAWY MECHANIKI KWANTOWEJ De Broglie, na podstawie analogii optycznych, w roku 194 wysunął hipotezę, że cząstki materialne także charakteryzują się dualizmem korpuskularno-falowym. Hipoteza de Broglie
PODSTAWY MECHANIKI KWANTOWEJ De Broglie, na podstawie analogii optycznych, w roku 194 wysunął hipotezę, że cząstki materialne także charakteryzują się dualizmem korpuskularno-falowym. Hipoteza de Broglie
r. akad. 2012/2013 wykład III-IV Mechanika kwantowa Podstawy Procesów i Konstrukcji Inżynierskich Mechanika kwantowa
 r. akad. 01/013 wykład III-IV Podstawy Procesów i Konstrukcji Inżynierskich Mechanika kwantowa Zakład Zakład Biofizyki Biofizyki 1 Falowa natura materii Zarówno fale elektromagnetyczne (fotony) jaki i
r. akad. 01/013 wykład III-IV Podstawy Procesów i Konstrukcji Inżynierskich Mechanika kwantowa Zakład Zakład Biofizyki Biofizyki 1 Falowa natura materii Zarówno fale elektromagnetyczne (fotony) jaki i
Elementy mechaniki kwantowej. Mechanika kwantowa co to jest? Fale materii hipoteza de Broglie'a Funkcja falowa Równanie Schrödingera
 lementy mechaniki kwantowej Mechanika kwantowa co to jest? Fale materii hipoteza de Broglie'a Funkcja falowa Równanie Schrödingera Fale materii de Broglie a (rok 193) De Broglie zaproponował, że każdy
lementy mechaniki kwantowej Mechanika kwantowa co to jest? Fale materii hipoteza de Broglie'a Funkcja falowa Równanie Schrödingera Fale materii de Broglie a (rok 193) De Broglie zaproponował, że każdy
FALE MATERII. De Broglie, na podstawie analogii optycznych, w roku 1924 wysunął hipotezę, że
 FAL MATRII De Broglie, na podstawie analogii optycznych, w roku 194 wysunął hipotezę, że cząstki materialne także charakteryzują się dualizmem korpuskularno-falowym. Hipoteza de Broglie a Cząstce materialnej
FAL MATRII De Broglie, na podstawie analogii optycznych, w roku 194 wysunął hipotezę, że cząstki materialne także charakteryzują się dualizmem korpuskularno-falowym. Hipoteza de Broglie a Cząstce materialnej
Rozwiązania zadań z podstaw fizyki kwantowej
 Rozwiązania zadań z podstaw fizyki kwantowej Jacek Izdebski 5 stycznia roku Zadanie 1 Funkcja falowa Ψ(x) = A n sin( πn x) jest zdefiniowana jedynie w obszarze
Rozwiązania zadań z podstaw fizyki kwantowej Jacek Izdebski 5 stycznia roku Zadanie 1 Funkcja falowa Ψ(x) = A n sin( πn x) jest zdefiniowana jedynie w obszarze
Elementy mechaniki kwantowej. Mechanika kwantowa co to jest? Funkcja falowa Równanie Schrödingera
 lementy mechaniki kwantowej Mechanika kwantowa co to jest? Funkcja falowa Równanie Schrödingera Funkcja falowa Jak matematycznie opisać własności falowe materii? Czym są fale materii? Własności falowe
lementy mechaniki kwantowej Mechanika kwantowa co to jest? Funkcja falowa Równanie Schrödingera Funkcja falowa Jak matematycznie opisać własności falowe materii? Czym są fale materii? Własności falowe
Elementy mechaniki kwantowej. Mechanika kwantowa co to jest? Fale materii hipoteza de Broglie'a Funkcja falowa Równanie Schrödingera
 Elementy mechaniki kwantowej Mechanika kwantowa co to jest? Fale materii hipoteza de Broglie'a Funkcja falowa Równanie Schrödingera Fale materii de Broglie a (rok 1923) De Broglie zaproponował, że każdy
Elementy mechaniki kwantowej Mechanika kwantowa co to jest? Fale materii hipoteza de Broglie'a Funkcja falowa Równanie Schrödingera Fale materii de Broglie a (rok 1923) De Broglie zaproponował, że każdy
Fizyka 3.3 WYKŁAD II
 Fizyka 3.3 WYKŁAD II Promieniowanie elektromagnetyczne Dualizm korpuskularno-falowy światła Fala elektromagnetyczna Strumień fotonów o energii E F : E F = hc λ c = 3 10 8 m/s h = 6. 63 10 34 J s Światło
Fizyka 3.3 WYKŁAD II Promieniowanie elektromagnetyczne Dualizm korpuskularno-falowy światła Fala elektromagnetyczna Strumień fotonów o energii E F : E F = hc λ c = 3 10 8 m/s h = 6. 63 10 34 J s Światło
Mechanika kwantowa. Erwin Schrödinger ( ) Werner Heisenberg
 Mechanika kwantowa Erwin Schrödinger (1887-1961) Werner Heisenberg 1901-1976 Falowe równanie ruchu (uproszczenie: przypadek jednowymiarowy) Dla fotonów Dla cząstek Równanie Schrödingera y x = 1 c y t y(
Mechanika kwantowa Erwin Schrödinger (1887-1961) Werner Heisenberg 1901-1976 Falowe równanie ruchu (uproszczenie: przypadek jednowymiarowy) Dla fotonów Dla cząstek Równanie Schrödingera y x = 1 c y t y(
Dualizm korpuskularno falowy
 Dualizm korpuskularno falowy Fala elektromagnetyczna o długości λ w pewnych zjawiskach zachowuje się jak cząstka (foton) o pędzie p=h/λ i energii E = h = h. c/λ p Cząstki niosą pęd p Cząstce o pędzie p
Dualizm korpuskularno falowy Fala elektromagnetyczna o długości λ w pewnych zjawiskach zachowuje się jak cząstka (foton) o pędzie p=h/λ i energii E = h = h. c/λ p Cząstki niosą pęd p Cząstce o pędzie p
Jak matematycznie opisać własności falowe materii? Czym są fale materii?
 Funkcja falowa Jak matematycznie opisać własności falowe materii? Czym są fale materii? Własności falowe materii (cząstek, układów cząstek) opisuje matematycznie pewna funkcja falowa ( x, Funkcja falowa
Funkcja falowa Jak matematycznie opisać własności falowe materii? Czym są fale materii? Własności falowe materii (cząstek, układów cząstek) opisuje matematycznie pewna funkcja falowa ( x, Funkcja falowa
Ciało doskonale czarne absorbuje całkowicie padające promieniowanie. Parametry promieniowania ciała doskonale czarnego zależą tylko jego temperatury.
 1 Ciało doskonale czarne absorbuje całkowicie padające promieniowanie. Parametry promieniowania ciała doskonale czarnego zależą tylko jego temperatury. natężenie natężenie teoria klasyczna wynik eksperymentu
1 Ciało doskonale czarne absorbuje całkowicie padające promieniowanie. Parametry promieniowania ciała doskonale czarnego zależą tylko jego temperatury. natężenie natężenie teoria klasyczna wynik eksperymentu
Jak matematycznie opisać własności falowe materii? Czym są fale materii?
 Funkcja falowa Jak matematycznie opisać własności falowe materii? Czym są fale materii? Własności falowe materii (cząstek, układów cząstek) opisuje matematycznie pewna funkcja falowa ( x, t ) Tutaj upraszczamy
Funkcja falowa Jak matematycznie opisać własności falowe materii? Czym są fale materii? Własności falowe materii (cząstek, układów cząstek) opisuje matematycznie pewna funkcja falowa ( x, t ) Tutaj upraszczamy
Zjawisko Comptona opis pół relatywistyczny
 FOTON 33, Lato 06 7 Zjawisko Comtona ois ół relatywistyczny Jerzy Ginter Wydział Fizyki UW Zderzenie fotonu ze soczywającym elektronem Przy omawianiu dualizmu koruskularno-falowego jako jeden z ięknych
FOTON 33, Lato 06 7 Zjawisko Comtona ois ół relatywistyczny Jerzy Ginter Wydział Fizyki UW Zderzenie fotonu ze soczywającym elektronem Przy omawianiu dualizmu koruskularno-falowego jako jeden z ięknych
λ(pm) p 1 rozpraszanie bez zmiany λ ze wzrostem λ p e 0,07 0,08 λ (nm) tł o
 W 1916r. Einstein rozszerzył swoją koncepcję kwantów światła, przypisując im pęd. Fotonowi o energii ħω odpowiada pęd p ħω/c /λ Efekt Comptona 193r. - rozpraszanie promieni X 1keV- kilka MeV na elektronac
W 1916r. Einstein rozszerzył swoją koncepcję kwantów światła, przypisując im pęd. Fotonowi o energii ħω odpowiada pęd p ħω/c /λ Efekt Comptona 193r. - rozpraszanie promieni X 1keV- kilka MeV na elektronac
Efekt Comptona. Efektem Comptona nazywamy zmianę długości fali elektromagnetycznej w wyniku rozpraszania jej na swobodnych elektronach
 Efekt Comptona. Efektem Comptona nazywamy zmianę długości fali elektromagnetycznej w wyniku rozpraszania jej na swobodnych elektronach Efekt Comptona. p f Θ foton elektron p f p e 0 p e Zderzenia fotonów
Efekt Comptona. Efektem Comptona nazywamy zmianę długości fali elektromagnetycznej w wyniku rozpraszania jej na swobodnych elektronach Efekt Comptona. p f Θ foton elektron p f p e 0 p e Zderzenia fotonów
VII. CZĄSTKI I FALE VII.1. POSTULAT DE BROGLIE'A (1924) De Broglie wysunął postulat fal materii tzn. małym cząstkom przypisał fale.
 VII. CZĄSTKI I FALE VII.1. POSTULAT DE BROGLIE'A (1924) De Broglie wysunął postulat fal materii tzn. małym cząstkom przypisał fale. Światło wykazuje zjawisko dyfrakcyjne. Rys.VII.1.Światło padające na
VII. CZĄSTKI I FALE VII.1. POSTULAT DE BROGLIE'A (1924) De Broglie wysunął postulat fal materii tzn. małym cząstkom przypisał fale. Światło wykazuje zjawisko dyfrakcyjne. Rys.VII.1.Światło padające na
Zasada nieoznaczoności Heisenberga
 Fale materii paczki falowe o różnej szerokości Dwa gaussowskie rozkład amplitud fal armonicznc o różnc szerokościac σ p i różnc wartościac średnic pędu p. Części rzeczwista ReΨ i urojona mψ funkcji falowc
Fale materii paczki falowe o różnej szerokości Dwa gaussowskie rozkład amplitud fal armonicznc o różnc szerokościac σ p i różnc wartościac średnic pędu p. Części rzeczwista ReΨ i urojona mψ funkcji falowc
Równanie Schrödingera
 Równanie Schrödingera Maciej J. Mrowiński 29 lutego 2012 Zadanie RS1 Funkcja falowa opisująca stan pewnej cząstki w chwili t = 0 ma następującą postać: A(a Ψ(x,0) = 2 x 2 ) gdy x [ a,a] 0 gdy x / [ a,a]
Równanie Schrödingera Maciej J. Mrowiński 29 lutego 2012 Zadanie RS1 Funkcja falowa opisująca stan pewnej cząstki w chwili t = 0 ma następującą postać: A(a Ψ(x,0) = 2 x 2 ) gdy x [ a,a] 0 gdy x / [ a,a]
V. RÓWNANIA MECHANIKI KWANTOWEJ
 V. RÓWNANIA MECHANIKI KWANTOWEJ 1 1 Postulaty mechaniki kwantowej Istota teorii kwantowej może być sformułowana za pomocą postulatów, których spełnienie postulujemy i których nie można wyprowadzić z żadnych
V. RÓWNANIA MECHANIKI KWANTOWEJ 1 1 Postulaty mechaniki kwantowej Istota teorii kwantowej może być sformułowana za pomocą postulatów, których spełnienie postulujemy i których nie można wyprowadzić z żadnych
Równanie Schrödingera
 Fizyka 2 Wykład 3 1 Równanie Schrödingera Chcemy znaleźć dopuszczalne wartości energii układu fizycznego, dla którego znamy energię potencjalną. Z zasady odpowiedniości znamy postać hamiltonianu. Wybieramy
Fizyka 2 Wykład 3 1 Równanie Schrödingera Chcemy znaleźć dopuszczalne wartości energii układu fizycznego, dla którego znamy energię potencjalną. Z zasady odpowiedniości znamy postać hamiltonianu. Wybieramy
FIZYKA 2. Janusz Andrzejewski
 FIZYKA 2 wykład 12 Janusz Andrzejewski Światło Falowa natura Dyfrakcja Interferencja Załamanie i odbicie Korpuskuralna natura Teoria promieniowania ciała doskonale czarnego Zjawisko fotoelekryczne Zjawisko
FIZYKA 2 wykład 12 Janusz Andrzejewski Światło Falowa natura Dyfrakcja Interferencja Załamanie i odbicie Korpuskuralna natura Teoria promieniowania ciała doskonale czarnego Zjawisko fotoelekryczne Zjawisko
Wykład FIZYKA II. 12. Mechanika kwantowa. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA II. Mechanika kwantowa Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/ MECHANIKA KWANTOWA Podstawę mechaniki kwantowej stanowi
Wykład FIZYKA II. Mechanika kwantowa Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/ MECHANIKA KWANTOWA Podstawę mechaniki kwantowej stanowi
Początek XX wieku. Dualizm korpuskularno - falowy
 Początek XX wieku Światło: fala czy cząstka? Kwantowanie energii promieniowania termicznego postulat Plancka efekt fotoelektryczny efekt Comptona Fale materii de Broglie a Dualizm korpuskularno - falowy
Początek XX wieku Światło: fala czy cząstka? Kwantowanie energii promieniowania termicznego postulat Plancka efekt fotoelektryczny efekt Comptona Fale materii de Broglie a Dualizm korpuskularno - falowy
Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie
 napisał Michał Wierzbicki Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie Prędkość grupowa paczki falowej Paczka falowa jest superpozycją fal o różnej częstości biegnących wzdłuż osi z.
napisał Michał Wierzbicki Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie Prędkość grupowa paczki falowej Paczka falowa jest superpozycją fal o różnej częstości biegnących wzdłuż osi z.
Wykład 9 Podstawy teorii kwantów fale materii, dualizm falowo-korpuskularny, funkcja falowa, równanie Schrödingera, stacjonarne równanie
 Wykład 9 Podstawy teorii kwantów fale materii, dualizm falowo-korpuskularny, funkcja falowa, równanie Schrödingera, stacjonarne równanie Schrödingera, zasada nieoznaczoności Heisenberga, ruch cząstki swobodnej,
Wykład 9 Podstawy teorii kwantów fale materii, dualizm falowo-korpuskularny, funkcja falowa, równanie Schrödingera, stacjonarne równanie Schrödingera, zasada nieoznaczoności Heisenberga, ruch cząstki swobodnej,
Fizyka kwantowa. promieniowanie termiczne zjawisko fotoelektryczne. efekt Comptona dualizm korpuskularno-falowy. kwantyzacja światła
 W- (Jaroszewicz) 19 slajdów Na podstawie prezentacji prof. J. Rutkowskiego Fizyka kwantowa promieniowanie termiczne zjawisko fotoelektryczne kwantyzacja światła efekt Comptona dualizm korpuskularno-falowy
W- (Jaroszewicz) 19 slajdów Na podstawie prezentacji prof. J. Rutkowskiego Fizyka kwantowa promieniowanie termiczne zjawisko fotoelektryczne kwantyzacja światła efekt Comptona dualizm korpuskularno-falowy
Chemia ogólna - część I: Atomy i cząsteczki
 dr ab. Wacław Makowski Cemia ogólna - część I: Atomy i cząsteczki 1. Kwantowanie. Atom wodoru 3. Atomy wieloelektronowe 4. Termy atomowe 5. Cząsteczki dwuatomowe 6. Hybrydyzacja 7. Orbitale zdelokalizowane
dr ab. Wacław Makowski Cemia ogólna - część I: Atomy i cząsteczki 1. Kwantowanie. Atom wodoru 3. Atomy wieloelektronowe 4. Termy atomowe 5. Cząsteczki dwuatomowe 6. Hybrydyzacja 7. Orbitale zdelokalizowane
PODSTAWY MECHANIKI KWANTOWEJ
 PODSTAWY MECHANIKI KWANTOWEJ Za dzień narodzenia mechaniki kwantowej jest uważany 14 grudnia roku 1900. Tego dnia, na posiedzeniu Niemieckiego Towarzystwa Fizycznego w Instytucie Fizyki Uniwersytetu Berlińskiego
PODSTAWY MECHANIKI KWANTOWEJ Za dzień narodzenia mechaniki kwantowej jest uważany 14 grudnia roku 1900. Tego dnia, na posiedzeniu Niemieckiego Towarzystwa Fizycznego w Instytucie Fizyki Uniwersytetu Berlińskiego
Rodzaje fal. 1. Fale mechaniczne. 2. Fale elektromagnetyczne. 3. Fale materii. dyfrakcja elektronów
 Wykład VI Fale t t + Dt Rodzaje fal 1. Fale mechaniczne 2. Fale elektromagnetyczne 3. Fale materii dyfrakcja elektronów Fala podłużna v Przemieszczenia elementów spirali ( w prawo i w lewo) są równoległe
Wykład VI Fale t t + Dt Rodzaje fal 1. Fale mechaniczne 2. Fale elektromagnetyczne 3. Fale materii dyfrakcja elektronów Fala podłużna v Przemieszczenia elementów spirali ( w prawo i w lewo) są równoległe
Równanie falowe Schrödingera ( ) ( ) Prostokątna studnia potencjału o skończonej głębokości. i 2 =-1 jednostka urojona. Ψ t. V x.
 Równanie falowe Schrödingera h Ψ( x, t) + V( x, t) Ψ( x, t) W jednym wymiarze ( ) ( ) gdy V x, t = V x x Ψ = ih t Gdy V(x,t)=V =const cząstka swobodna, na którą nie działa siła Fala biegnąca Ψ s ( x, t)
Równanie falowe Schrödingera h Ψ( x, t) + V( x, t) Ψ( x, t) W jednym wymiarze ( ) ( ) gdy V x, t = V x x Ψ = ih t Gdy V(x,t)=V =const cząstka swobodna, na którą nie działa siła Fala biegnąca Ψ s ( x, t)
IX. MECHANIKA (FIZYKA) KWANTOWA
 IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
Podstawy fizyki kwantowej i budowy materii
 Podstawy fizyki kwantowej i budowy materii prof. dr hab. Aleksander Filip Żarnecki Zakład Cząstek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej Wykład 5 7 listopada 2016 A.F.Żarnecki Podstawy
Podstawy fizyki kwantowej i budowy materii prof. dr hab. Aleksander Filip Żarnecki Zakład Cząstek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej Wykład 5 7 listopada 2016 A.F.Żarnecki Podstawy
Mechanika Kwantowa. Maciej J. Mrowiński. 24 grudnia Funkcja falowa opisująca stan pewnej cząstki ma następującą postać: 2 x 2 )
 Mechanika Kwantowa Maciej J. Mrowiński 4 grudnia 11 Zadanie MK1 Funkcja falowa opisująca stan pewnej cząstki w chwili t = ma następującą postać: A(a Ψ(x,) = x ) gdy x [ a,a] gdy x / [ a,a] gdzie a +. Wyznacz
Mechanika Kwantowa Maciej J. Mrowiński 4 grudnia 11 Zadanie MK1 Funkcja falowa opisująca stan pewnej cząstki w chwili t = ma następującą postać: A(a Ψ(x,) = x ) gdy x [ a,a] gdy x / [ a,a] gdzie a +. Wyznacz
Jednowymiarowa mechanika kwantowa Rozpraszanie na potencjale Na początek rozważmy najprostszy przypadek: próg potencjału
 Fizyka 2 Wykład 4 1 Jednowymiarowa mechanika kwantowa Rozpraszanie na potencjale Na początek rozważmy najprostszy przypadek: próg potencjału Niezależne od czasu równanie Schödingera ma postać: 2 d ( x)
Fizyka 2 Wykład 4 1 Jednowymiarowa mechanika kwantowa Rozpraszanie na potencjale Na początek rozważmy najprostszy przypadek: próg potencjału Niezależne od czasu równanie Schödingera ma postać: 2 d ( x)
Stara i nowa teoria kwantowa
 Stara i nowa teoria kwantowa Braki teorii Bohra: - podane jedynie położenia linii, brak natężeń -nie tłumaczy ilości elektronów na poszczególnych orbitach - model działa gorzej dla atomów z więcej niż
Stara i nowa teoria kwantowa Braki teorii Bohra: - podane jedynie położenia linii, brak natężeń -nie tłumaczy ilości elektronów na poszczególnych orbitach - model działa gorzej dla atomów z więcej niż
RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU
 X. RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU Równanie Schrődingera niezależne od czasu to równanie postaci: ħ 2 2m d 2 x dx 2 V xx = E x (X.1) Warunki regularności na x i a) skończone b) ciągłe c) jednoznaczne
X. RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU Równanie Schrődingera niezależne od czasu to równanie postaci: ħ 2 2m d 2 x dx 2 V xx = E x (X.1) Warunki regularności na x i a) skończone b) ciągłe c) jednoznaczne
Podstawy Akustyki. Drgania normalne a fale stojące Składanie fal harmonicznych: Fale akustyczne w powietrzu Efekt Dopplera.
 W-1 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka falowa Fale akustyczne w powietrzu
W-1 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka falowa Fale akustyczne w powietrzu
h 2 h p Mechanika falowa podstawy pˆ 2
 Mechanika falowa podstawy Hipoteza de Broglie a Zarówno promieniowanie jak i cząstki materialne posiadają naturę dwoistą korpuskularno-falową. Z każdą mikrocząstką można związać pewien proces falowy pierwotnie
Mechanika falowa podstawy Hipoteza de Broglie a Zarówno promieniowanie jak i cząstki materialne posiadają naturę dwoistą korpuskularno-falową. Z każdą mikrocząstką można związać pewien proces falowy pierwotnie
Mechanika kwantowa Schrödingera
 Fizyka 2 Wykład 2 1 Mechanika kwantowa Schrödingera Hipoteza de Broglie a wydawała się nie zgadzać z dynamiką Newtona. Mechanika kwantowa Schrödingera zawiera mechanikę kwantową jako przypadek graniczny
Fizyka 2 Wykład 2 1 Mechanika kwantowa Schrödingera Hipoteza de Broglie a wydawała się nie zgadzać z dynamiką Newtona. Mechanika kwantowa Schrödingera zawiera mechanikę kwantową jako przypadek graniczny
Fizyka 3. Konsultacje: p. 329, Mechatronika
 Fizyka 3 Konsultacje: p. 39, Mechatronika marzan@mech.pw.edu.pl Zaliczenie: 1 sprawdzian 30 pkt 15.1 18 3.0 18.1 1 3.5 1.1 4 4.0 4.1 7 4.5 7.1 30 5.0 http:\\adam.mech.pw.edu.pl\~marzan Program: - elementy
Fizyka 3 Konsultacje: p. 39, Mechatronika marzan@mech.pw.edu.pl Zaliczenie: 1 sprawdzian 30 pkt 15.1 18 3.0 18.1 1 3.5 1.1 4 4.0 4.1 7 4.5 7.1 30 5.0 http:\\adam.mech.pw.edu.pl\~marzan Program: - elementy
Doświadczenie Younga Thomas Young. Dyfrakcja światła na dwóch szczelinach Światło zachowuje się jak fala - interferencja
 Doświadczenie Younga 1801 Thomas Young Dyfrakcja światła na dwóch szczelinach Światło zachowuje się jak fala - interferencja Doświadczenie Younga c.d. fotodetektor + głośnik fala ciągły sygnał o zmiennym
Doświadczenie Younga 1801 Thomas Young Dyfrakcja światła na dwóch szczelinach Światło zachowuje się jak fala - interferencja Doświadczenie Younga c.d. fotodetektor + głośnik fala ciągły sygnał o zmiennym
Wykład FIZYKA I. 11. Fale mechaniczne. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA I 11. Fale mechaniczne Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html FALA Falą nazywamy każde rozprzestrzeniające
Wykład FIZYKA I 11. Fale mechaniczne Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html FALA Falą nazywamy każde rozprzestrzeniające
Własności falowe materii
 Część 3 Własności falowe materii 1. Rozpraszanie promieni X 2. Fale De Brogliea 3. Rozpraszanie elektronu 4. Ruch falowy 5. Transformata Fouriera 6. Zasada nieokreśloności 7. Cząsteczka w pudle 8. Prawdopodobieństwo,
Część 3 Własności falowe materii 1. Rozpraszanie promieni X 2. Fale De Brogliea 3. Rozpraszanie elektronu 4. Ruch falowy 5. Transformata Fouriera 6. Zasada nieokreśloności 7. Cząsteczka w pudle 8. Prawdopodobieństwo,
Teorie wiązania chemicznego i podstawowe zasady mechaniki kwantowej Zjawiska, które zapowiadały nadejście nowej ery w fizyce i przybliżały
 WYKŁAD 1 Teorie wiązania chemicznego i podstawowe zasady mechaniki kwantowej Zjawiska, które zapowiadały nadejście nowej ery w fizyce i przybliżały sformułowanie praw fizyki kwantowej: promieniowanie katodowe
WYKŁAD 1 Teorie wiązania chemicznego i podstawowe zasady mechaniki kwantowej Zjawiska, które zapowiadały nadejście nowej ery w fizyce i przybliżały sformułowanie praw fizyki kwantowej: promieniowanie katodowe
Komentarz 3 do fcs. Drgania sieci krystalicznej. I ciepło właściwe ciała stałego.
 Komentarz do fcs. Drgania sieci krystalicznej. I cieło właściwe ciała stałego. Drgania kryształu możemy rozważać z dwóch unktów widzenia. Pierwszy to makroskoowy, gdy długość fali jest znacznie większa
Komentarz do fcs. Drgania sieci krystalicznej. I cieło właściwe ciała stałego. Drgania kryształu możemy rozważać z dwóch unktów widzenia. Pierwszy to makroskoowy, gdy długość fali jest znacznie większa
Promieniowanie X. Jak powstaje promieniowanie rentgenowskie Budowa lampy rentgenowskiej Widmo ciągłe i charakterystyczne promieniowania X
 Promieniowanie X Jak powstaje promieniowanie rentgenowskie Budowa lampy rentgenowskiej Widmo ciągłe i charakterystyczne promieniowania X Lampa rentgenowska Lampa rentgenowska Promieniowanie rentgenowskie
Promieniowanie X Jak powstaje promieniowanie rentgenowskie Budowa lampy rentgenowskiej Widmo ciągłe i charakterystyczne promieniowania X Lampa rentgenowska Lampa rentgenowska Promieniowanie rentgenowskie
Statystyka nieoddziaływujących gazów Bosego i Fermiego
 Statystyka nieoddziaływujących gazów Bosego i Fermiego Bozony: fotony (kwanty pola elektromagnetycznego, których liczba nie jest zachowana mogą być pojedynczo pochłaniane lub tworzone. W konsekwencji,
Statystyka nieoddziaływujących gazów Bosego i Fermiego Bozony: fotony (kwanty pola elektromagnetycznego, których liczba nie jest zachowana mogą być pojedynczo pochłaniane lub tworzone. W konsekwencji,
Zad Sprawdzić, czy dana funkcja jest funkcją własną danego operatora. Jeśli tak, znaleźć wartość własną funkcji.
 Zad. 1.1. Sprawdzić, czy dana funkcja jest funkcją własną danego operatora. Jeśli tak, znaleźć wartość własną funkcji. Zad. 1.1.a. Funkcja: ϕ = sin2x Zad. 1.1.b. Funkcja: ϕ = e x 2 2 Operator: f = d2 dx
Zad. 1.1. Sprawdzić, czy dana funkcja jest funkcją własną danego operatora. Jeśli tak, znaleźć wartość własną funkcji. Zad. 1.1.a. Funkcja: ϕ = sin2x Zad. 1.1.b. Funkcja: ϕ = e x 2 2 Operator: f = d2 dx
Fale materii. gdzie h= 6.6 10-34 J s jest stałą Plancka.
 Fale materii 194- Louis de Broglie teoria fal materii, 199- nagroda Nobla Hipoteza de Broglie głosi, że dwoiste korpuskularno falowe zachowanie jest cechą nie tylko promieniowania, lecz również materii.
Fale materii 194- Louis de Broglie teoria fal materii, 199- nagroda Nobla Hipoteza de Broglie głosi, że dwoiste korpuskularno falowe zachowanie jest cechą nie tylko promieniowania, lecz również materii.
III. EFEKT COMPTONA (1923)
 III. EFEKT COMPTONA (1923) Zjawisko zmiany długości fali promieniowania roentgenowskiego rozpraszanego na swobodnych elektronach. Zjawisko to stoi u podstaw mechaniki kwantowej. III.1. EFEKT COMPTONA Rys.III.1.
III. EFEKT COMPTONA (1923) Zjawisko zmiany długości fali promieniowania roentgenowskiego rozpraszanego na swobodnych elektronach. Zjawisko to stoi u podstaw mechaniki kwantowej. III.1. EFEKT COMPTONA Rys.III.1.
Foton, kwant światła
 015-0- Fizyka kwantowa dotyczy świata mikroskopowego wiele wielkości jest skwantowanyc, tzn. występuje w całkowityc wielokrotnościac pewnyc minimalnyc porcji zwanyc kwantami Foton, kwant światła Zjawiska
015-0- Fizyka kwantowa dotyczy świata mikroskopowego wiele wielkości jest skwantowanyc, tzn. występuje w całkowityc wielokrotnościac pewnyc minimalnyc porcji zwanyc kwantami Foton, kwant światła Zjawiska
Wykład 18: Elementy fizyki współczesnej -2
 Wykład 18: Elementy fizyki współczesnej - Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Efekt fotoelektryczny 1887 Hertz;
Wykład 18: Elementy fizyki współczesnej - Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Efekt fotoelektryczny 1887 Hertz;
Fizyka 12. Janusz Andrzejewski
 Fizyka 1 Janusz Andrzejewski Przypomnienie: Drgania procesy w których pewna wielkość fizyczna na przemian maleje i rośnie Okresowy ruch drgający (periodyczny) - jeżeli wartości wielkości fizycznych zmieniające
Fizyka 1 Janusz Andrzejewski Przypomnienie: Drgania procesy w których pewna wielkość fizyczna na przemian maleje i rośnie Okresowy ruch drgający (periodyczny) - jeżeli wartości wielkości fizycznych zmieniające
Ψ(x, t) punkt zamocowania liny zmienna t, rozkład zaburzeń w czasie. x (lub t)
 RUCH FALOWY 1 Fale sejsmiczne Fale morskie Kamerton Interferencja RÓWNANIE FALI Fala rozchodzenie się zaburzeń w ośrodku materialnym lub próżni: fale podłużne i poprzeczne w ciałach stałych, fale podłużne
RUCH FALOWY 1 Fale sejsmiczne Fale morskie Kamerton Interferencja RÓWNANIE FALI Fala rozchodzenie się zaburzeń w ośrodku materialnym lub próżni: fale podłużne i poprzeczne w ciałach stałych, fale podłużne
Optyka. Wykład V Krzysztof Golec-Biernat. Fale elektromagnetyczne. Uniwersytet Rzeszowski, 8 listopada 2017
 Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
Wykład FIZYKA II. 11. Optyka kwantowa. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA II 11. Optyka kwantowa Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/ FIZYKA KLASYCZNA A FIZYKA WSPÓŁCZESNA Fizyka klasyczna
Wykład FIZYKA II 11. Optyka kwantowa Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/ FIZYKA KLASYCZNA A FIZYKA WSPÓŁCZESNA Fizyka klasyczna
Problemy fizyki początku XX wieku
 Mechanika kwantowa Problemy fizyki początku XX wieku Promieniowanie ciała doskonale czarnego Ciałem doskonale czarnym nazywamy ciało całkowicie pochłaniające na nie promieniowanie elektromagnetyczne, niezależnie
Mechanika kwantowa Problemy fizyki początku XX wieku Promieniowanie ciała doskonale czarnego Ciałem doskonale czarnym nazywamy ciało całkowicie pochłaniające na nie promieniowanie elektromagnetyczne, niezależnie
gdzie λ - długość fali, h - stała Plancka, p - pęd cząstki.
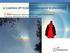 3.7. Model współczesny Louis Victor Pierre Raymond de Broglie (189-1987) (Rysunek 3-35) w swojej pracy doktorskiej z 194 roku, wysunął przypuszczenie, że skoro fale elektromagnetyczne mogą przejawiać naturę
3.7. Model współczesny Louis Victor Pierre Raymond de Broglie (189-1987) (Rysunek 3-35) w swojej pracy doktorskiej z 194 roku, wysunął przypuszczenie, że skoro fale elektromagnetyczne mogą przejawiać naturę
Metody rozwiązania równania Schrödingera
 Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
falowa natura materii
 10 listopada 2016 1 Fale de Broglie a Dyfrakcja promieni X 1895 promieniowanie X dopiero w 1912 dowód na ich falowa naturę - to promieniowanie elektromagnetyczne zjawiska falowe: ugięcia, dyfrakcji - trudne:
10 listopada 2016 1 Fale de Broglie a Dyfrakcja promieni X 1895 promieniowanie X dopiero w 1912 dowód na ich falowa naturę - to promieniowanie elektromagnetyczne zjawiska falowe: ugięcia, dyfrakcji - trudne:
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki
 OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania (3.7), pomimo swojej prostoty, nie posiadają poza nielicznymi przypadkami ścisłych rozwiązań,
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania (3.7), pomimo swojej prostoty, nie posiadają poza nielicznymi przypadkami ścisłych rozwiązań,
Wykład 21: Studnie i bariery cz.1.
 Wyład : Studnie i bariery cz.. Dr inż. Zbigniew Szlarsi Katedra Eletronii, paw. C-, po.3 szla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szlarsi/ 3.6.8 Wydział Informatyi, Eletronii i Równanie Schrödingera
Wyład : Studnie i bariery cz.. Dr inż. Zbigniew Szlarsi Katedra Eletronii, paw. C-, po.3 szla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szlarsi/ 3.6.8 Wydział Informatyi, Eletronii i Równanie Schrödingera
Atom wodoru i jony wodoropodobne
 Atom wodoru i jony wodoropodobne dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Spis treści Spis treści 1. Model Bohra atomu wodoru 2 1.1. Porządek
Atom wodoru i jony wodoropodobne dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Spis treści Spis treści 1. Model Bohra atomu wodoru 2 1.1. Porządek
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 26, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 26, 28.05.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 25 - przypomnienie
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 26, 28.05.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 25 - przypomnienie
Kwantowe własności promieniowania, ciało doskonale czarne, zjawisko fotoelektryczne zewnętrzne.
 Kwantowe własności promieniowania, ciało doskonale czarne, zjawisko fotoelektryczne zewnętrzne. DUALIZM ŚWIATŁA fala interferencja, dyfrakcja, polaryzacja,... kwant, foton promieniowanie ciała doskonale
Kwantowe własności promieniowania, ciało doskonale czarne, zjawisko fotoelektryczne zewnętrzne. DUALIZM ŚWIATŁA fala interferencja, dyfrakcja, polaryzacja,... kwant, foton promieniowanie ciała doskonale
ZASADY PRZEPROWADZANIA EGZAMINU DYPLOMOWEGO KOŃCZĄCEGO STUDIA PIERWSZEGO ORAZ DRUGIEGO STOPNIA NA KIERUNKU FIZYKA
 ZASADY PRZEPROWADZANIA EGZAMINU DYPLOMOWEGO KOŃCZĄCEGO STUDIA PIERWSZEGO ORAZ DRUGIEGO STOPNIA NA KIERUNKU FIZYKA INSTYTUT FIZYKI WYDZIAŁ MATEMATYKI, FIZYKI I TECHNIKI UNIWERSYTET KAZIMIERZA WIELKIEGO
ZASADY PRZEPROWADZANIA EGZAMINU DYPLOMOWEGO KOŃCZĄCEGO STUDIA PIERWSZEGO ORAZ DRUGIEGO STOPNIA NA KIERUNKU FIZYKA INSTYTUT FIZYKI WYDZIAŁ MATEMATYKI, FIZYKI I TECHNIKI UNIWERSYTET KAZIMIERZA WIELKIEGO
Ładunek elektryczny jest skwantowany
 1. WSTĘP DO MECHANIKI KWANTOWEJ 1.1. Budowa materii i kwantowanie ładunku Materia w skali mikroskopowej nie jest ciągła lecz zbudowana z atomów mówimy, że jest skwantowana Powierzchnia platyny Ładunek
1. WSTĘP DO MECHANIKI KWANTOWEJ 1.1. Budowa materii i kwantowanie ładunku Materia w skali mikroskopowej nie jest ciągła lecz zbudowana z atomów mówimy, że jest skwantowana Powierzchnia platyny Ładunek
Światło fala, czy strumień cząstek?
 1 Światło fala, czy strumień cząstek? Teoria falowa wyjaśnia: Odbicie Załamanie Interferencję Dyfrakcję Polaryzację Efekt fotoelektryczny Efekt Comptona Teoria korpuskularna wyjaśnia: Odbicie Załamanie
1 Światło fala, czy strumień cząstek? Teoria falowa wyjaśnia: Odbicie Załamanie Interferencję Dyfrakcję Polaryzację Efekt fotoelektryczny Efekt Comptona Teoria korpuskularna wyjaśnia: Odbicie Załamanie
Nieskończona jednowymiarowa studnia potencjału
 Nieskończona jednowymiarowa studnia potencjału Zagadnienie dane jest następująco: znaleźć funkcje własne i wartości własne operatora energii dla cząstki umieszczonej w nieskończonej studni potencjału,
Nieskończona jednowymiarowa studnia potencjału Zagadnienie dane jest następująco: znaleźć funkcje własne i wartości własne operatora energii dla cząstki umieszczonej w nieskończonej studni potencjału,
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki
 OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania optyki półklasycznej Posłużymy się teraz równaniem (2.4), i Ψ t = ĤΨ ażeby wyprowadzić
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania optyki półklasycznej Posłużymy się teraz równaniem (2.4), i Ψ t = ĤΨ ażeby wyprowadzić
Wykład 17: Optyka falowa cz.1.
 Wykład 17: Optyka falowa cz.1. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Zasada Huyghensa Christian Huygens 1678 r. pierwsza
Wykład 17: Optyka falowa cz.1. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Zasada Huyghensa Christian Huygens 1678 r. pierwsza
Rozdział 4 Równanie Schrödingera
 Rozdział 4 Równanie Schrödingera 4.1 Równanie falowe Schrödingera 4. Obserwable, stany stacjonarne, wartości średnie 4.3 Nieskończona studnia potencjału 4.4 Skończona studnia potencjału 4.5 Trójwymiarowa
Rozdział 4 Równanie Schrödingera 4.1 Równanie falowe Schrödingera 4. Obserwable, stany stacjonarne, wartości średnie 4.3 Nieskończona studnia potencjału 4.4 Skończona studnia potencjału 4.5 Trójwymiarowa
Fale elektromagnetyczne
 Fale elektromagnetyczne dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Plan wykładu Spis treści 1. Analiza pola 2 1.1. Rozkład pola...............................................
Fale elektromagnetyczne dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Plan wykładu Spis treści 1. Analiza pola 2 1.1. Rozkład pola...............................................
Podstawy fizyki kwantowej
 Wykład I Prolog Przy końcu XIX wieku fizyka, którą dzisiaj określamy jako klasyczną, zdawała się być nauką ostateczną w tym sensie, że wszystkie jej podstawowe prawa były już ustanowione, a efektem dalszego
Wykład I Prolog Przy końcu XIX wieku fizyka, którą dzisiaj określamy jako klasyczną, zdawała się być nauką ostateczną w tym sensie, że wszystkie jej podstawowe prawa były już ustanowione, a efektem dalszego
Zasada nieoznaczoności Heisenberga. Konsekwencją tego, Ŝe cząstki mikroświata mają takŝe własności falowe jest:
 Zasada nieoznaczoności Heisenberga Konsekwencją tego, Ŝe cząstki mikroświata mają takŝe własności falowe jest: Pewnych wielkości fizycznych nie moŝna zmierzyć równocześnie z dowolną dokładnością. Iloczyn
Zasada nieoznaczoności Heisenberga Konsekwencją tego, Ŝe cząstki mikroświata mają takŝe własności falowe jest: Pewnych wielkości fizycznych nie moŝna zmierzyć równocześnie z dowolną dokładnością. Iloczyn
Wykład 26. Elementy mechaniki kwantowej.
 1 Wykład 6 Elementy mechaniki kwantowej. 11.1 Modele atomu Thomsona i Rutherforda. Pierwsza próba stworzenia modelu atomu na podstawie zebranych danych doświadczalnych była dokonana przez J.J. Thomsona
1 Wykład 6 Elementy mechaniki kwantowej. 11.1 Modele atomu Thomsona i Rutherforda. Pierwsza próba stworzenia modelu atomu na podstawie zebranych danych doświadczalnych była dokonana przez J.J. Thomsona
Mechanika kwantowa. Jak opisać atom wodoru? Jak opisać inne cząsteczki?
 Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Elektron fala stojąca wokół jądra Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkowy
Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Elektron fala stojąca wokół jądra Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkowy
= sin. = 2Rsin. R = E m. = sin
 Natężenie światła w obrazie dyfrakcyjnym Autorzy: Zbigniew Kąkol, Piotr Morawski Chcemy teraz znaleźć wyrażenie na rozkład natężenia w całym ekranie w funkcji kąta θ. Szczelinę dzielimy na N odcinków i
Natężenie światła w obrazie dyfrakcyjnym Autorzy: Zbigniew Kąkol, Piotr Morawski Chcemy teraz znaleźć wyrażenie na rozkład natężenia w całym ekranie w funkcji kąta θ. Szczelinę dzielimy na N odcinków i
Wykład Budowa atomu 2
 Wykład 7.12.2016 Budowa atomu 2 O atomach cd Model Bohra podsumowanie Serie widmowe O czym nie mówi model Bohra Wzbudzenie, emisja, absorpcja O liniach widmowych Kwantowomechaniczny model atomu sformułowanie
Wykład 7.12.2016 Budowa atomu 2 O atomach cd Model Bohra podsumowanie Serie widmowe O czym nie mówi model Bohra Wzbudzenie, emisja, absorpcja O liniach widmowych Kwantowomechaniczny model atomu sformułowanie
Mechanika klasyczna zasada zachowania energii. W obszarze I cząstka biegnie z prędkością v I, Cząstka przechodzi z obszaru I do II.
 Próg potencjału Mecanika klasyczna zasada zacowania energii mvi mv E + V W obszarze I cząstka biegnie z prędkością v I, E > V w obszarze cząstka biegnie z prędkością v Cząstka przecodzi z obszaru I do.
Próg potencjału Mecanika klasyczna zasada zacowania energii mvi mv E + V W obszarze I cząstka biegnie z prędkością v I, E > V w obszarze cząstka biegnie z prędkością v Cząstka przecodzi z obszaru I do.
WSTĘP DO OPTYKI FOURIEROWSKIEJ
 1100-4BW1, rok akademicki 018/19 WSTĘP DO OPTYKI FOURIEROWSKIEJ dr hab. Rafał Kasztelanic Wykład 4 Przestrzeń swobodna jako filtr częstości przestrzennych Załóżmy, że znamy rozkład pola na fale monochromatyczne
1100-4BW1, rok akademicki 018/19 WSTĘP DO OPTYKI FOURIEROWSKIEJ dr hab. Rafał Kasztelanic Wykład 4 Przestrzeń swobodna jako filtr częstości przestrzennych Załóżmy, że znamy rozkład pola na fale monochromatyczne
Światło ma podwójną naturę:
 Światło ma podwójną naturę: przejawia własności fal i cząstek W. C. Roentgen ( Nobel 1901) Istnieje ciągłe przejście pomiędzy tymi własnościami wzdłuż spektrum fal elektromagnetycznych Dla niskich częstości
Światło ma podwójną naturę: przejawia własności fal i cząstek W. C. Roentgen ( Nobel 1901) Istnieje ciągłe przejście pomiędzy tymi własnościami wzdłuż spektrum fal elektromagnetycznych Dla niskich częstości
2.14. Zasada zachowania energii mechanicznej
 Wykład 6 14 Zasada zachowania energii mechanicznej Informatyka 011/1 Stajesz na szczycie góry Mocujesz deskę, zakładasz gogle i zaczynasz szaleńczy zjazd W miarę jak twoja energia otencjalna zamienia się
Wykład 6 14 Zasada zachowania energii mechanicznej Informatyka 011/1 Stajesz na szczycie góry Mocujesz deskę, zakładasz gogle i zaczynasz szaleńczy zjazd W miarę jak twoja energia otencjalna zamienia się
Wykład 13 Mechanika Kwantowa
 Wykład 13 Mechanika Kwantowa Maciej J. Mrowiński mrow@if.pw.edu.pl Wydział Fizyki Politechnika Warszawska 25 maja 2016 Maciej J. Mrowiński (IF PW) Wykład 13 25 maja 2016 1 / 21 Wprowadzenie Sprawy organizacyjne
Wykład 13 Mechanika Kwantowa Maciej J. Mrowiński mrow@if.pw.edu.pl Wydział Fizyki Politechnika Warszawska 25 maja 2016 Maciej J. Mrowiński (IF PW) Wykład 13 25 maja 2016 1 / 21 Wprowadzenie Sprawy organizacyjne
( n) Łańcuchy Markowa X 0, X 1,...
 Łańcuchy Markowa Łańcuchy Markowa to rocesy dyskretne w czasie i o dyskretnym zbiorze stanów, "bez amięci". Zwykle będziemy zakładać, że zbiór stanów to odzbiór zbioru liczb całkowitych Z lub zbioru {,,,...}
Łańcuchy Markowa Łańcuchy Markowa to rocesy dyskretne w czasie i o dyskretnym zbiorze stanów, "bez amięci". Zwykle będziemy zakładać, że zbiór stanów to odzbiór zbioru liczb całkowitych Z lub zbioru {,,,...}
wykład 1. Fizyka Jądrowa Bogdan Muryn
 wykład 1. Fizyka Jądrowa Bogdan Muryn Jednostki: Podczas tego wykładu obowiązują jednostki układu SI. Przez ładunek będziemy rozumieć (o ile nie zaznaczymy inaczej): Q Q 4 Wtedy ładunek elementarny ma
wykład 1. Fizyka Jądrowa Bogdan Muryn Jednostki: Podczas tego wykładu obowiązują jednostki układu SI. Przez ładunek będziemy rozumieć (o ile nie zaznaczymy inaczej): Q Q 4 Wtedy ładunek elementarny ma
Podstawy Akustyki. Drgania normalne a fale stojące Składanie fal harmonicznych: Fale akustyczne w powietrzu Efekt Dopplera
 Jucatan, Mexico, February 005 W-10 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka
Jucatan, Mexico, February 005 W-10 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka
POSTULATY MECHANIKI KWANTOWEJ cd i formalizm matematyczny
 POSTULATY MECHANIKI KWANTOWEJ cd i formalizm matematyczny Funkcja Falowa Postulat 1 Dla każdego układu istnieje funkcja falowa (funkcja współrzędnych i czasu), która jest ciągła, całkowalna w kwadracie,
POSTULATY MECHANIKI KWANTOWEJ cd i formalizm matematyczny Funkcja Falowa Postulat 1 Dla każdego układu istnieje funkcja falowa (funkcja współrzędnych i czasu), która jest ciągła, całkowalna w kwadracie,
Wykład 26 Wersja robocza Elementy mechaniki kwantowej.
 Piotr Posmykiewicz Wykład z fizyki 1 Wykład 6 Wersja robocza Elementy mechaniki kwantowej. 6.1 Modele atomu Thomsona i Rutherforda. Pierwsza próbę stworzenia modelu atomu na podstawie zebranych danych
Piotr Posmykiewicz Wykład z fizyki 1 Wykład 6 Wersja robocza Elementy mechaniki kwantowej. 6.1 Modele atomu Thomsona i Rutherforda. Pierwsza próbę stworzenia modelu atomu na podstawie zebranych danych
Fale elektromagnetyczne. Gradient pola. Gradient pola... Gradient pola... Notatki. Notatki. Notatki. Notatki. dr inż. Ireneusz Owczarek 2013/14
 dr inż. Ireneusz Owczarek CNMiF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2013/14 1 dr inż. Ireneusz Owczarek Gradient pola Gradient funkcji pola skalarnego ϕ przypisuje każdemu punktowi
dr inż. Ireneusz Owczarek CNMiF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2013/14 1 dr inż. Ireneusz Owczarek Gradient pola Gradient funkcji pola skalarnego ϕ przypisuje każdemu punktowi
Interferometr Macha-Zehndera. Zapis sinusoidalnej siatki dyfrakcyjnej i pomiar jej okresu przestrzennego.
 Ćwiczenie 6 Interferometr Macha-Zehndera. Zapis sinusoidalnej siatki dyfrakcyjnej i pomiar jej okresu przestrzennego. Interferometr Macha-Zehndera Interferometr Macha-Zehndera jest często wykorzystywany
Ćwiczenie 6 Interferometr Macha-Zehndera. Zapis sinusoidalnej siatki dyfrakcyjnej i pomiar jej okresu przestrzennego. Interferometr Macha-Zehndera Interferometr Macha-Zehndera jest często wykorzystywany
Własności falowe cząstek. Zasada nieoznaczoności Heisenberga.
 Własnośi falowe ząstek. Zasada nieoznazonośi Heisenberga. Dlazego ząstka o określonej masie nie moŝe oruszać się z rędkośią równą rędkośi światła? Relatywistyzne równanie określająe energię oruszająego
Własnośi falowe ząstek. Zasada nieoznazonośi Heisenberga. Dlazego ząstka o określonej masie nie moŝe oruszać się z rędkośią równą rędkośi światła? Relatywistyzne równanie określająe energię oruszająego
Podstawy fizyki sezon 1 VIII. Ruch falowy
 Podstawy fizyki sezon 1 VIII. Ruch falowy Agnieszka Obłąkowska-Mucha WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Gdzie szukać fal? W potocznym
Podstawy fizyki sezon 1 VIII. Ruch falowy Agnieszka Obłąkowska-Mucha WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Gdzie szukać fal? W potocznym
WYKŁAD 15. Gęstość stanów Zastosowanie: oscylatory kwantowe (ª bosony bezmasowe) Formalizm dla nieoddziaływujących cząstek Bosego lub Fermiego
 WYKŁAD 15 Gęstość stanów Zastosowanie: oscylatory kwantowe (ª bosony bezmasowe) Formalizm dla nieoddziaływujących cząstek Bosego lub Fermiego 1 Statystyka nieoddziaływujących gazów Bosego i Fermiego Bosony
WYKŁAD 15 Gęstość stanów Zastosowanie: oscylatory kwantowe (ª bosony bezmasowe) Formalizm dla nieoddziaływujących cząstek Bosego lub Fermiego 1 Statystyka nieoddziaływujących gazów Bosego i Fermiego Bosony
Karta (sylabus) modułu/przedmiotu Transport Studia I stopnia
 Karta (sylabus) modułu/przedmiotu Transport Studia I stopnia Przedmiot: Rodzaj przedmiotu: Kod przedmiotu: Rok: I Semestr: I Forma studiów: Rodzaj zajęć i liczba godzin 60 w semestrze: Wykład 30 Ćwiczenia
Karta (sylabus) modułu/przedmiotu Transport Studia I stopnia Przedmiot: Rodzaj przedmiotu: Kod przedmiotu: Rok: I Semestr: I Forma studiów: Rodzaj zajęć i liczba godzin 60 w semestrze: Wykład 30 Ćwiczenia
Mini-quiz 0 Mini-quiz 1
 rawda fałsz Mini-quiz 0.Wielkości ekstensywne to: a rędkość kątowa b masa układu c ilość cząstek d temeratura e całkowity moment magnetyczny.. Układy otwarte: a mogą wymieniać energię z otoczeniem b mogą
rawda fałsz Mini-quiz 0.Wielkości ekstensywne to: a rędkość kątowa b masa układu c ilość cząstek d temeratura e całkowity moment magnetyczny.. Układy otwarte: a mogą wymieniać energię z otoczeniem b mogą
Przedmiot: Fizyka. Światło jako fala. 2016/17, sem. letni 1
 Światło jako fala 1 Fala elektromagnetyczna widmo promieniowania Czułość oka ludzkiego w zakresie widzialnym 2 Wytwarzanie fali elektromagnetycznej o częstościach radiowych H. Hertz (1888) doświadczalne
Światło jako fala 1 Fala elektromagnetyczna widmo promieniowania Czułość oka ludzkiego w zakresie widzialnym 2 Wytwarzanie fali elektromagnetycznej o częstościach radiowych H. Hertz (1888) doświadczalne
Mechanika cieczy. Ciecz jako ośrodek ciągły. 1. Cząsteczki cieczy nie są związane w położeniach równowagi mogą przemieszczać się na duże odległości.
 Mecanika cieczy Ciecz jako ośrodek ciągły. Cząsteczki cieczy nie są związane w ołożeniac równowagi mogą rzemieszczać się na duże odległości.. Cząsteczki cieczy oddziałują ze sobą, lecz oddziaływania te
Mecanika cieczy Ciecz jako ośrodek ciągły. Cząsteczki cieczy nie są związane w ołożeniac równowagi mogą rzemieszczać się na duże odległości.. Cząsteczki cieczy oddziałują ze sobą, lecz oddziaływania te
