Dualizm korpuskularno falowy
|
|
|
- Mariusz Borowski
- 8 lat temu
- Przeglądów:
Transkrypt
1 Dualizm korpuskularno falowy Fala elektromagnetyczna o długości λ w pewnych zjawiskach zachowuje się jak cząstka (foton) o pędzie p=h/λ i energii E = h = h. c/λ p Cząstki niosą pęd p Cząstce o pędzie p można przyporządkować falę o długości λ=h/p λ
2 Postulat o falowej naturze elektronów (1924, Nagroda Nobla 1929) ν Louis-Victor, 7 e duke de Broglie Louis de Broglie ( )
3 Jak jest długość fali elektronu o energii 10 ev? (V= m/s) λ = h p 2 p Ek = p = 2mE 2m K
4 Jak jest długość fali piłki tenisowej? (V=50 km/s) λ = h p = J s kg m s = m
5 Fale ulegają dyfrakcji i interferują Elektrony zachowują się jak fale? Thomas Young ( )
6 Doświadczenie Younga S 2 S 1 θ Δr r 1 θ d r 2 P O y Warunek maksimum d sin θ = mλ Warunek minimum d sin θ = ( m λ) D Δr = r2 -r1 = d sin θ E1 = E0 sin( kr1 ωt) E2 = E0 sin( kr2 ωt) E = E 1 + E 2 = 2E 0 sin(k r - ωt) Warunkiem interferencji jest spójność (koherencja) żródeł światła S 1 i S 2, czyli stałość różnicy faz
7 Postulat o falowej naturze elektronów (1924) Udowodniony już w roku 1927 Clinton Davisson, Lester Germer (nierelatywistyczne elektrony) George Thomson (relatywistyczne elektrony) Ekran, film Wiązka padająca prom. X elektrony Dyfrakcja elektronów niskoenergetycznych na powierzchni kryształu niklu Folia metalowa Pierścień dyfrakcyjny
8 Dualizm korpuskularno falowy Fala elektromagnetyczna o długości λ w pewnych zjawiskach zachowuje się jak cząstka (foton) o pędzie p=h/λ i energii E = h = h. c/λ p Cząstki niosą pęd p Cząstce o pędzie p można przyporządkować falę o długości λ=h/p λ
9 Jak opisać matematycznie fale materii? Równanie klasycznej fali Najprostsze rozwiązanie Fala biegnąca o dokładnie określonej częstotliwości istniejąca w całej przestrzeni
10 = h 2π Jak opisać fale materii? W najprostszym przybliżeniu: 2π k = = λ p ω = E Ψ( x, t) = Asin( kx ω t + ϕ) p E = Asin( x t + ϕ) zbyt szczególne, ogólniej w postaci zespolonej: Ψ( x, t) = A[sin( kx ω t + ϕ) + i cos( kx ωt + ϕ)] Ψ( x, t) = Ae i( kx ωt+ ϕ ) = Ae i( p x E t+ ϕ ) Funkcja falowa opisująca cząstkę o pędzie dokładnie = p O takiej cząstce możemy powiedzieć, że się znajduje wszędzie Uwaga! Liczby zespolone
11 Opis fal przy pomocy liczb zespolonych Pole elektryczne fali świetlnej o częstości ω można opisać: Ψ(x,t) = A cos(kx ωt ϕ) Ponieważ exp(iϕ) = cos(θ) + i sin(θ) (formuła Eulera ): lub Ψ (x,t) = Re { A exp[i(kx ωt ϕ)]} Ψ (x,t) = 1/2 A exp[i(kx ωt ϕ)] + c.c. gdzie + c.c. oznacza plus sprzężenie zespolone wszystkiego, co jest przed plusem.
12 Przypomnienie: liczby zespolone Każdą liczbę zespoloną z, można zapisać: Tak więc: i z = Re{ z } + i Im{ z } Re{ z } = 1/2 ( z + z* ) Im{ z } = 1/2i ( z z* ) gdzie z* jest liczbą sprzężoną liczby z ( i i ) Wielkość z (moduł), liczby zespolonej: z 2 = z z* = Re{ z } 2 + Im{ z } 2 Liczbę z zapisać można w postaci polarnej: A exp(iϕ). z A 2 = Re{ z } 2 + Im{ z } 2 tan(ϕ) = Im{ z } / Re{ z }
13 Fale zapisane przy pomocy zespolonych amplitud W opisie fal wygodnie jest dopuścić zespolone amplitudy: Ψ (x,t) = A exp[i(kx ωt ϕ)] Ψ (x,t) = { Aexp(-i ϕ )} exp[i(kx ωt] Ψ 0 (x,t) = Aexp(-i ϕ) (Stała amplituda zespolona) Ψ (x,t) = Ψ 0 exp [i(kx ωt)] Szybko-zmienne części zostały odseparowane od części stałych
14 Liczby zespolone ułatwiają życie Dodawanie fal o tych samych częstościach i różnych fazach początkowych daje falę o tej samej częstości. Nie jest to takie oczywiste w zapisie z użyciem funkcji trygonometrycznych, a jest natychmiastowe z użyciem funkcji wykładniczych Ψ tot (x,t) = Ψ 1 exp [i(kx ωt)] + Ψ 2 exp [i(kx ωt)]+ Ψ 3 exp [i(kx ωt)]= = (Ψ 1 + Ψ 2 + Ψ 3 ) exp [i(kx ωt)] wszystkie fazy początkowe zostały włączone w E 1, E 2, i E 3. Ψ tot (x,t) Ψ 1 Ψ 2 Ψ 3
15 Interpretacja funkcji falowej Klasyczna fala świetlna Klasyczna fala świetlna f.f. opisuje natężenie pola e-mag, a jej kwadrat natężenie światła. Ale obraz interferencyjny obserwowany jest też jeśli na szczelinę padają pojedyncze fotony. Wtedy: Obraz dyfrakcyjny należy interpretować jako obraz prawdopodobieństwa wykrycia fotonu w danym miejscu Podobnie dla fal materii
16 Interpretacja funkcji falowej Klasyczne cząstki Fale materii Fala materii funkcja falowa związana jest z prawdopodobieństwem tego, że cząstka znajduje się w danym miejscu.
17 Interpretacja funkcji falowej (Max Born, 1926) Przykład: funkcja falowa cząstki o stałym pędzie dokładnie = p (cząstka swobodna poruszająca się w przestrzeni bez żadnych ograniczeń) Ψ p E i( x t) (, ) = x t Ae = Ae ikx e iωt Separacja zmiennych przestrzennych i czasowych = Ψ( x) e iωt Interpretuję się nie funkcję falową (zespolona), ale jej kwadrat P( x) dx = Ψ( x, t) 2 dx P(x) jest gęstością prawdopodobieństwa P(x)dx jest prawdopodobieństwem znalezienia cząstki w obszarze (x, x + dx) Prawdopodobieństwo znalezienia cząstki w skończonym obszarze (x 1, x 2 ) Uwaga! Liczby zespolone * Ψ 2 P x = 2 = Ψ Ψ Ψ ( x, t) x 1 2 dx
18
19 Interpretacja funkcji falowej 2 Dla cząstki swobodnej: p E i( x t) p E i( x t) Ψ( x, t) = Ae Ae = A 2 Gęstość prawdopodobieństwa Ψ( x, t) 2 Dla cząstki swobodnej: Gęstość prawdopodobieństwa jest w przestrzeni stała Warunek normalizacji: prawdopodobieństwo znalezienia cząstki gdziekolwiek = 1 Ψ( x, t) 2 dx = 1
20 Cząstki oddziałują (nie są swobodne) Np. elektrony w krysztale, ale także swobodny elektron który docierając do ekranu zostaje zarejestrowany Jak wygląda funkcja falowa elektronu, którego położenie jest lepiej określone? Na przykład tak: Pakiet falowy (paczka falowa)
21 Pakiet falowy jest wynikiem superpozycji wielu fal o różnych częstościach i długościach Najprostszy przypadek dwie fale Zdudnienia
22 Pakiet falowy jest wynikiem superpozycji wielu fal o różnych częstościach i długościach. Δk Δx Pakiet falowy jest wynikiem superpozycji wielu fal o różnych częstościach i długościach. Im szerszy jest zakres liczb falowych fal składowych (Δk), tym mniejsza jest szerokość pakietu Δx
23 PhET Interactive Simulations Copyright University of Colorado. Some rights reserved. Visit Symulacja
24 Można udowodnić że: k p p p x 1 Zasada nieoznaczoności Heisenberga x y z x y z 2π k = = λ p Iloczyn nieokreśloności pędu cząstki i nieokreśloności jej położenia w danym kierunku równy co najmniej od stałej Plancka. Oznacza to, że im dokładniej mierzymy pęd, to znaczy zmniejszamy np. Δp x, tym bardziej rośnie nieoznaczoność położenia Δx. Podobnie: E t Jeżeli cząstka posiada energię E, to dokładność jej wyznaczenia ΔE zależy od czasu pomiaru Δt. Im dłużej cząstka jest w stanie o energii E tym dokładniej można tę energię wyznaczyć.
25
26
27
28 Mechanika kwantowa Erwin Schrödinger ( ) Werner Heisenberg
PODSTAWY MECHANIKI KWANTOWEJ
 PODSTAWY MECHANIKI KWANTOWEJ De Broglie, na podstawie analogii optycznych, w roku 194 wysunął hipotezę, że cząstki materialne także charakteryzują się dualizmem korpuskularno-falowym. Hipoteza de Broglie
PODSTAWY MECHANIKI KWANTOWEJ De Broglie, na podstawie analogii optycznych, w roku 194 wysunął hipotezę, że cząstki materialne także charakteryzują się dualizmem korpuskularno-falowym. Hipoteza de Broglie
FALE MATERII. De Broglie, na podstawie analogii optycznych, w roku 1924 wysunął hipotezę, że
 FAL MATRII De Broglie, na podstawie analogii optycznych, w roku 194 wysunął hipotezę, że cząstki materialne także charakteryzują się dualizmem korpuskularno-falowym. Hipoteza de Broglie a Cząstce materialnej
FAL MATRII De Broglie, na podstawie analogii optycznych, w roku 194 wysunął hipotezę, że cząstki materialne także charakteryzują się dualizmem korpuskularno-falowym. Hipoteza de Broglie a Cząstce materialnej
Ciało doskonale czarne absorbuje całkowicie padające promieniowanie. Parametry promieniowania ciała doskonale czarnego zależą tylko jego temperatury.
 1 Ciało doskonale czarne absorbuje całkowicie padające promieniowanie. Parametry promieniowania ciała doskonale czarnego zależą tylko jego temperatury. natężenie natężenie teoria klasyczna wynik eksperymentu
1 Ciało doskonale czarne absorbuje całkowicie padające promieniowanie. Parametry promieniowania ciała doskonale czarnego zależą tylko jego temperatury. natężenie natężenie teoria klasyczna wynik eksperymentu
Efekt Comptona. Efektem Comptona nazywamy zmianę długości fali elektromagnetycznej w wyniku rozpraszania jej na swobodnych elektronach
 Efekt Comptona. Efektem Comptona nazywamy zmianę długości fali elektromagnetycznej w wyniku rozpraszania jej na swobodnych elektronach Efekt Comptona. p f Θ foton elektron p f p e 0 p e Zderzenia fotonów
Efekt Comptona. Efektem Comptona nazywamy zmianę długości fali elektromagnetycznej w wyniku rozpraszania jej na swobodnych elektronach Efekt Comptona. p f Θ foton elektron p f p e 0 p e Zderzenia fotonów
Elementy mechaniki kwantowej. Mechanika kwantowa co to jest? Fale materii hipoteza de Broglie'a Funkcja falowa Równanie Schrödingera
 lementy mechaniki kwantowej Mechanika kwantowa co to jest? Fale materii hipoteza de Broglie'a Funkcja falowa Równanie Schrödingera Fale materii de Broglie a (rok 193) De Broglie zaproponował, że każdy
lementy mechaniki kwantowej Mechanika kwantowa co to jest? Fale materii hipoteza de Broglie'a Funkcja falowa Równanie Schrödingera Fale materii de Broglie a (rok 193) De Broglie zaproponował, że każdy
Elementy mechaniki kwantowej. Mechanika kwantowa co to jest? Fale materii hipoteza de Broglie'a Funkcja falowa Równanie Schrödingera
 Elementy mechaniki kwantowej Mechanika kwantowa co to jest? Fale materii hipoteza de Broglie'a Funkcja falowa Równanie Schrödingera Fale materii de Broglie a (rok 1923) De Broglie zaproponował, że każdy
Elementy mechaniki kwantowej Mechanika kwantowa co to jest? Fale materii hipoteza de Broglie'a Funkcja falowa Równanie Schrödingera Fale materii de Broglie a (rok 1923) De Broglie zaproponował, że każdy
Promieniowanie X. Jak powstaje promieniowanie rentgenowskie Budowa lampy rentgenowskiej Widmo ciągłe i charakterystyczne promieniowania X
 Promieniowanie X Jak powstaje promieniowanie rentgenowskie Budowa lampy rentgenowskiej Widmo ciągłe i charakterystyczne promieniowania X Lampa rentgenowska Lampa rentgenowska Promieniowanie rentgenowskie
Promieniowanie X Jak powstaje promieniowanie rentgenowskie Budowa lampy rentgenowskiej Widmo ciągłe i charakterystyczne promieniowania X Lampa rentgenowska Lampa rentgenowska Promieniowanie rentgenowskie
Elementy mechaniki kwantowej. Mechanika kwantowa co to jest? Funkcja falowa Równanie Schrödingera
 lementy mechaniki kwantowej Mechanika kwantowa co to jest? Funkcja falowa Równanie Schrödingera Funkcja falowa Jak matematycznie opisać własności falowe materii? Czym są fale materii? Własności falowe
lementy mechaniki kwantowej Mechanika kwantowa co to jest? Funkcja falowa Równanie Schrödingera Funkcja falowa Jak matematycznie opisać własności falowe materii? Czym są fale materii? Własności falowe
Jak matematycznie opisać własności falowe materii? Czym są fale materii?
 Funkcja falowa Jak matematycznie opisać własności falowe materii? Czym są fale materii? Własności falowe materii (cząstek, układów cząstek) opisuje matematycznie pewna funkcja falowa ( x, Funkcja falowa
Funkcja falowa Jak matematycznie opisać własności falowe materii? Czym są fale materii? Własności falowe materii (cząstek, układów cząstek) opisuje matematycznie pewna funkcja falowa ( x, Funkcja falowa
Własności falowe materii
 Część 3 Własności falowe materii 1. Rozpraszanie promieni X 2. Fale De Brogliea 3. Rozpraszanie elektronu 4. Ruch falowy 5. Transformata Fouriera 6. Zasada nieokreśloności 7. Cząsteczka w pudle 8. Prawdopodobieństwo,
Część 3 Własności falowe materii 1. Rozpraszanie promieni X 2. Fale De Brogliea 3. Rozpraszanie elektronu 4. Ruch falowy 5. Transformata Fouriera 6. Zasada nieokreśloności 7. Cząsteczka w pudle 8. Prawdopodobieństwo,
Jak matematycznie opisać własności falowe materii? Czym są fale materii?
 Funkcja falowa Jak matematycznie opisać własności falowe materii? Czym są fale materii? Własności falowe materii (cząstek, układów cząstek) opisuje matematycznie pewna funkcja falowa ( x, t ) Tutaj upraszczamy
Funkcja falowa Jak matematycznie opisać własności falowe materii? Czym są fale materii? Własności falowe materii (cząstek, układów cząstek) opisuje matematycznie pewna funkcja falowa ( x, t ) Tutaj upraszczamy
FIZYKA 2. Janusz Andrzejewski
 FIZYKA 2 wykład 12 Janusz Andrzejewski Światło Falowa natura Dyfrakcja Interferencja Załamanie i odbicie Korpuskuralna natura Teoria promieniowania ciała doskonale czarnego Zjawisko fotoelekryczne Zjawisko
FIZYKA 2 wykład 12 Janusz Andrzejewski Światło Falowa natura Dyfrakcja Interferencja Załamanie i odbicie Korpuskuralna natura Teoria promieniowania ciała doskonale czarnego Zjawisko fotoelekryczne Zjawisko
Mechanika kwantowa. Erwin Schrödinger ( ) Werner Heisenberg
 Mechanika kwantowa Erwin Schrödinger (1887-1961) Werner Heisenberg 1901-1976 Falowe równanie ruchu (uproszczenie: przypadek jednowymiarowy) Dla fotonów Dla cząstek Równanie Schrödingera y x = 1 c y t y(
Mechanika kwantowa Erwin Schrödinger (1887-1961) Werner Heisenberg 1901-1976 Falowe równanie ruchu (uproszczenie: przypadek jednowymiarowy) Dla fotonów Dla cząstek Równanie Schrödingera y x = 1 c y t y(
Fale materii. gdzie h= 6.6 10-34 J s jest stałą Plancka.
 Fale materii 194- Louis de Broglie teoria fal materii, 199- nagroda Nobla Hipoteza de Broglie głosi, że dwoiste korpuskularno falowe zachowanie jest cechą nie tylko promieniowania, lecz również materii.
Fale materii 194- Louis de Broglie teoria fal materii, 199- nagroda Nobla Hipoteza de Broglie głosi, że dwoiste korpuskularno falowe zachowanie jest cechą nie tylko promieniowania, lecz również materii.
Ładunek elektryczny jest skwantowany
 1. WSTĘP DO MECHANIKI KWANTOWEJ 1.1. Budowa materii i kwantowanie ładunku Materia w skali mikroskopowej nie jest ciągła lecz zbudowana z atomów mówimy, że jest skwantowana Powierzchnia platyny Ładunek
1. WSTĘP DO MECHANIKI KWANTOWEJ 1.1. Budowa materii i kwantowanie ładunku Materia w skali mikroskopowej nie jest ciągła lecz zbudowana z atomów mówimy, że jest skwantowana Powierzchnia platyny Ładunek
Światło fala, czy strumień cząstek?
 1 Światło fala, czy strumień cząstek? Teoria falowa wyjaśnia: Odbicie Załamanie Interferencję Dyfrakcję Polaryzację Efekt fotoelektryczny Efekt Comptona Teoria korpuskularna wyjaśnia: Odbicie Załamanie
1 Światło fala, czy strumień cząstek? Teoria falowa wyjaśnia: Odbicie Załamanie Interferencję Dyfrakcję Polaryzację Efekt fotoelektryczny Efekt Comptona Teoria korpuskularna wyjaśnia: Odbicie Załamanie
Chemia ogólna - część I: Atomy i cząsteczki
 dr ab. Wacław Makowski Cemia ogólna - część I: Atomy i cząsteczki 1. Kwantowanie. Atom wodoru 3. Atomy wieloelektronowe 4. Termy atomowe 5. Cząsteczki dwuatomowe 6. Hybrydyzacja 7. Orbitale zdelokalizowane
dr ab. Wacław Makowski Cemia ogólna - część I: Atomy i cząsteczki 1. Kwantowanie. Atom wodoru 3. Atomy wieloelektronowe 4. Termy atomowe 5. Cząsteczki dwuatomowe 6. Hybrydyzacja 7. Orbitale zdelokalizowane
Fizyka 3.3 WYKŁAD II
 Fizyka 3.3 WYKŁAD II Promieniowanie elektromagnetyczne Dualizm korpuskularno-falowy światła Fala elektromagnetyczna Strumień fotonów o energii E F : E F = hc λ c = 3 10 8 m/s h = 6. 63 10 34 J s Światło
Fizyka 3.3 WYKŁAD II Promieniowanie elektromagnetyczne Dualizm korpuskularno-falowy światła Fala elektromagnetyczna Strumień fotonów o energii E F : E F = hc λ c = 3 10 8 m/s h = 6. 63 10 34 J s Światło
Podstawy fizyki kwantowej i budowy materii
 Podstawy fizyki kwantowej i budowy materii prof. dr hab. Aleksander Filip Żarnecki Zakład Cząstek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej Wykład 5 7 listopada 2016 A.F.Żarnecki Podstawy
Podstawy fizyki kwantowej i budowy materii prof. dr hab. Aleksander Filip Żarnecki Zakład Cząstek i Oddziaływań Fundamentalnych Instytut Fizyki Doświadczalnej Wykład 5 7 listopada 2016 A.F.Żarnecki Podstawy
Fizyka kwantowa. promieniowanie termiczne zjawisko fotoelektryczne. efekt Comptona dualizm korpuskularno-falowy. kwantyzacja światła
 W- (Jaroszewicz) 19 slajdów Na podstawie prezentacji prof. J. Rutkowskiego Fizyka kwantowa promieniowanie termiczne zjawisko fotoelektryczne kwantyzacja światła efekt Comptona dualizm korpuskularno-falowy
W- (Jaroszewicz) 19 slajdów Na podstawie prezentacji prof. J. Rutkowskiego Fizyka kwantowa promieniowanie termiczne zjawisko fotoelektryczne kwantyzacja światła efekt Comptona dualizm korpuskularno-falowy
Światło ma podwójną naturę:
 Światło ma podwójną naturę: przejawia własności fal i cząstek W. C. Roentgen ( Nobel 1901) Istnieje ciągłe przejście pomiędzy tymi własnościami wzdłuż spektrum fal elektromagnetycznych Dla niskich częstości
Światło ma podwójną naturę: przejawia własności fal i cząstek W. C. Roentgen ( Nobel 1901) Istnieje ciągłe przejście pomiędzy tymi własnościami wzdłuż spektrum fal elektromagnetycznych Dla niskich częstości
λ(pm) p 1 rozpraszanie bez zmiany λ ze wzrostem λ p e 0,07 0,08 λ (nm) tł o
 W 1916r. Einstein rozszerzył swoją koncepcję kwantów światła, przypisując im pęd. Fotonowi o energii ħω odpowiada pęd p ħω/c /λ Efekt Comptona 193r. - rozpraszanie promieni X 1keV- kilka MeV na elektronac
W 1916r. Einstein rozszerzył swoją koncepcję kwantów światła, przypisując im pęd. Fotonowi o energii ħω odpowiada pęd p ħω/c /λ Efekt Comptona 193r. - rozpraszanie promieni X 1keV- kilka MeV na elektronac
VII. CZĄSTKI I FALE VII.1. POSTULAT DE BROGLIE'A (1924) De Broglie wysunął postulat fal materii tzn. małym cząstkom przypisał fale.
 VII. CZĄSTKI I FALE VII.1. POSTULAT DE BROGLIE'A (1924) De Broglie wysunął postulat fal materii tzn. małym cząstkom przypisał fale. Światło wykazuje zjawisko dyfrakcyjne. Rys.VII.1.Światło padające na
VII. CZĄSTKI I FALE VII.1. POSTULAT DE BROGLIE'A (1924) De Broglie wysunął postulat fal materii tzn. małym cząstkom przypisał fale. Światło wykazuje zjawisko dyfrakcyjne. Rys.VII.1.Światło padające na
PODSTAWY MECHANIKI KWANTOWEJ
 PODSTAWY MECHANIKI KWANTOWEJ Za dzień narodzenia mechaniki kwantowej jest uważany 14 grudnia roku 1900. Tego dnia, na posiedzeniu Niemieckiego Towarzystwa Fizycznego w Instytucie Fizyki Uniwersytetu Berlińskiego
PODSTAWY MECHANIKI KWANTOWEJ Za dzień narodzenia mechaniki kwantowej jest uważany 14 grudnia roku 1900. Tego dnia, na posiedzeniu Niemieckiego Towarzystwa Fizycznego w Instytucie Fizyki Uniwersytetu Berlińskiego
Zasada nieoznaczoności Heisenberga
 Fale materii paczki falowe o różnej szerokości Dwa gaussowskie rozkład amplitud fal armonicznc o różnc szerokościac σ p i różnc wartościac średnic pędu p. Części rzeczwista ReΨ i urojona mψ funkcji falowc
Fale materii paczki falowe o różnej szerokości Dwa gaussowskie rozkład amplitud fal armonicznc o różnc szerokościac σ p i różnc wartościac średnic pędu p. Części rzeczwista ReΨ i urojona mψ funkcji falowc
Doświadczenie Younga Thomas Young. Dyfrakcja światła na dwóch szczelinach Światło zachowuje się jak fala - interferencja
 Doświadczenie Younga 1801 Thomas Young Dyfrakcja światła na dwóch szczelinach Światło zachowuje się jak fala - interferencja Doświadczenie Younga c.d. fotodetektor + głośnik fala ciągły sygnał o zmiennym
Doświadczenie Younga 1801 Thomas Young Dyfrakcja światła na dwóch szczelinach Światło zachowuje się jak fala - interferencja Doświadczenie Younga c.d. fotodetektor + głośnik fala ciągły sygnał o zmiennym
Początek XX wieku. Dualizm korpuskularno - falowy
 Początek XX wieku Światło: fala czy cząstka? Kwantowanie energii promieniowania termicznego postulat Plancka efekt fotoelektryczny efekt Comptona Fale materii de Broglie a Dualizm korpuskularno - falowy
Początek XX wieku Światło: fala czy cząstka? Kwantowanie energii promieniowania termicznego postulat Plancka efekt fotoelektryczny efekt Comptona Fale materii de Broglie a Dualizm korpuskularno - falowy
Wykład 17: Optyka falowa cz.1.
 Wykład 17: Optyka falowa cz.1. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Zasada Huyghensa Christian Huygens 1678 r. pierwsza
Wykład 17: Optyka falowa cz.1. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Zasada Huyghensa Christian Huygens 1678 r. pierwsza
Wykład I Krzysztof Golec-Biernat Optyka 1 / 16
 Optyka Wykład I Krzysztof Golec-Biernat Fale 1 Uniwersytet Rzeszowski, 4 października 2017 Wykład I Krzysztof Golec-Biernat Optyka 1 / 16 Uwagi wstępne 30 h wykładu wykład przy pomocy transparencji lub
Optyka Wykład I Krzysztof Golec-Biernat Fale 1 Uniwersytet Rzeszowski, 4 października 2017 Wykład I Krzysztof Golec-Biernat Optyka 1 / 16 Uwagi wstępne 30 h wykładu wykład przy pomocy transparencji lub
Równanie falowe Schrödingera ( ) ( ) Prostokątna studnia potencjału o skończonej głębokości. i 2 =-1 jednostka urojona. Ψ t. V x.
 Równanie falowe Schrödingera h Ψ( x, t) + V( x, t) Ψ( x, t) W jednym wymiarze ( ) ( ) gdy V x, t = V x x Ψ = ih t Gdy V(x,t)=V =const cząstka swobodna, na którą nie działa siła Fala biegnąca Ψ s ( x, t)
Równanie falowe Schrödingera h Ψ( x, t) + V( x, t) Ψ( x, t) W jednym wymiarze ( ) ( ) gdy V x, t = V x x Ψ = ih t Gdy V(x,t)=V =const cząstka swobodna, na którą nie działa siła Fala biegnąca Ψ s ( x, t)
Stara i nowa teoria kwantowa
 Stara i nowa teoria kwantowa Braki teorii Bohra: - podane jedynie położenia linii, brak natężeń -nie tłumaczy ilości elektronów na poszczególnych orbitach - model działa gorzej dla atomów z więcej niż
Stara i nowa teoria kwantowa Braki teorii Bohra: - podane jedynie położenia linii, brak natężeń -nie tłumaczy ilości elektronów na poszczególnych orbitach - model działa gorzej dla atomów z więcej niż
WSTĘP DO OPTYKI FOURIEROWSKIEJ
 1100-4BW1, rok akademicki 018/19 WSTĘP DO OPTYKI FOURIEROWSKIEJ dr hab. Rafał Kasztelanic Wykład 4 Przestrzeń swobodna jako filtr częstości przestrzennych Załóżmy, że znamy rozkład pola na fale monochromatyczne
1100-4BW1, rok akademicki 018/19 WSTĘP DO OPTYKI FOURIEROWSKIEJ dr hab. Rafał Kasztelanic Wykład 4 Przestrzeń swobodna jako filtr częstości przestrzennych Załóżmy, że znamy rozkład pola na fale monochromatyczne
IX. MECHANIKA (FIZYKA) KWANTOWA
 IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
gęstością prawdopodobieństwa
 Funkcja falowa Zgodnie z hipotezą de Broglie'a, cząstki takie jak elektron czy proton, mają własności falowe. Własności falowe cząstki (lub innego obiektu) w mechanice kwantowej opisuje tzw. funkcja falowa(,t)
Funkcja falowa Zgodnie z hipotezą de Broglie'a, cząstki takie jak elektron czy proton, mają własności falowe. Własności falowe cząstki (lub innego obiektu) w mechanice kwantowej opisuje tzw. funkcja falowa(,t)
Podstawy fizyki kwantowej
 Wykład I Prolog Przy końcu XIX wieku fizyka, którą dzisiaj określamy jako klasyczną, zdawała się być nauką ostateczną w tym sensie, że wszystkie jej podstawowe prawa były już ustanowione, a efektem dalszego
Wykład I Prolog Przy końcu XIX wieku fizyka, którą dzisiaj określamy jako klasyczną, zdawała się być nauką ostateczną w tym sensie, że wszystkie jej podstawowe prawa były już ustanowione, a efektem dalszego
Rozwiązania zadań z podstaw fizyki kwantowej
 Rozwiązania zadań z podstaw fizyki kwantowej Jacek Izdebski 5 stycznia roku Zadanie 1 Funkcja falowa Ψ(x) = A n sin( πn x) jest zdefiniowana jedynie w obszarze
Rozwiązania zadań z podstaw fizyki kwantowej Jacek Izdebski 5 stycznia roku Zadanie 1 Funkcja falowa Ψ(x) = A n sin( πn x) jest zdefiniowana jedynie w obszarze
RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU
 X. RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU Równanie Schrődingera niezależne od czasu to równanie postaci: ħ 2 2m d 2 x dx 2 V xx = E x (X.1) Warunki regularności na x i a) skończone b) ciągłe c) jednoznaczne
X. RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU Równanie Schrődingera niezależne od czasu to równanie postaci: ħ 2 2m d 2 x dx 2 V xx = E x (X.1) Warunki regularności na x i a) skończone b) ciągłe c) jednoznaczne
Światło jako fala Fala elektromagnetyczna widmo promieniowania Czułość oka ludzkiego w zakresie widzialnym
 Światło jako fala Fala elektromagnetyczna widmo promieniowania ν = c λ Czułość oka ludzkiego w zakresie widzialnym Wytwarzanie fali elektromagnetycznej o częstościach radiowych E(x, t) = Em sin (kx ωt)
Światło jako fala Fala elektromagnetyczna widmo promieniowania ν = c λ Czułość oka ludzkiego w zakresie widzialnym Wytwarzanie fali elektromagnetycznej o częstościach radiowych E(x, t) = Em sin (kx ωt)
Podstawy Akustyki. Drgania normalne a fale stojące Składanie fal harmonicznych: Fale akustyczne w powietrzu Efekt Dopplera.
 W-1 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka falowa Fale akustyczne w powietrzu
W-1 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka falowa Fale akustyczne w powietrzu
Falowa natura materii
 r. akad. 2012/2013 wykład I - II Podstawy Procesów i Konstrukcji Inżynierskich Falowa natura materii 1 r. akad. 2012/2013 Podstawy Procesów i Konstrukcji Inżynierskich Warunki zaliczenia: Aby uzyskać dopuszczenie
r. akad. 2012/2013 wykład I - II Podstawy Procesów i Konstrukcji Inżynierskich Falowa natura materii 1 r. akad. 2012/2013 Podstawy Procesów i Konstrukcji Inżynierskich Warunki zaliczenia: Aby uzyskać dopuszczenie
falowa natura materii
 10 listopada 2016 1 Fale de Broglie a Dyfrakcja promieni X 1895 promieniowanie X dopiero w 1912 dowód na ich falowa naturę - to promieniowanie elektromagnetyczne zjawiska falowe: ugięcia, dyfrakcji - trudne:
10 listopada 2016 1 Fale de Broglie a Dyfrakcja promieni X 1895 promieniowanie X dopiero w 1912 dowód na ich falowa naturę - to promieniowanie elektromagnetyczne zjawiska falowe: ugięcia, dyfrakcji - trudne:
Równanie Schrödingera
 Równanie Schrödingera Maciej J. Mrowiński 29 lutego 2012 Zadanie RS1 Funkcja falowa opisująca stan pewnej cząstki w chwili t = 0 ma następującą postać: A(a Ψ(x,0) = 2 x 2 ) gdy x [ a,a] 0 gdy x / [ a,a]
Równanie Schrödingera Maciej J. Mrowiński 29 lutego 2012 Zadanie RS1 Funkcja falowa opisująca stan pewnej cząstki w chwili t = 0 ma następującą postać: A(a Ψ(x,0) = 2 x 2 ) gdy x [ a,a] 0 gdy x / [ a,a]
W-23 (Jaroszewicz) 20 slajdów Na podstawie prezentacji prof. J. Rutkowskiego
 Bangkok, Thailand, March 011 W-3 (Jaroszewicz) 0 slajdów Na odstawie rezentacji rof. J. Rutkowskiego Fizyka kwantowa fale rawdoodobieństwa funkcja falowa aczki falowe materii zasada nieoznaczoności równanie
Bangkok, Thailand, March 011 W-3 (Jaroszewicz) 0 slajdów Na odstawie rezentacji rof. J. Rutkowskiego Fizyka kwantowa fale rawdoodobieństwa funkcja falowa aczki falowe materii zasada nieoznaczoności równanie
Wykład 9 Podstawy teorii kwantów fale materii, dualizm falowo-korpuskularny, funkcja falowa, równanie Schrödingera, stacjonarne równanie
 Wykład 9 Podstawy teorii kwantów fale materii, dualizm falowo-korpuskularny, funkcja falowa, równanie Schrödingera, stacjonarne równanie Schrödingera, zasada nieoznaczoności Heisenberga, ruch cząstki swobodnej,
Wykład 9 Podstawy teorii kwantów fale materii, dualizm falowo-korpuskularny, funkcja falowa, równanie Schrödingera, stacjonarne równanie Schrödingera, zasada nieoznaczoności Heisenberga, ruch cząstki swobodnej,
h 2 h p Mechanika falowa podstawy pˆ 2
 Mechanika falowa podstawy Hipoteza de Broglie a Zarówno promieniowanie jak i cząstki materialne posiadają naturę dwoistą korpuskularno-falową. Z każdą mikrocząstką można związać pewien proces falowy pierwotnie
Mechanika falowa podstawy Hipoteza de Broglie a Zarówno promieniowanie jak i cząstki materialne posiadają naturę dwoistą korpuskularno-falową. Z każdą mikrocząstką można związać pewien proces falowy pierwotnie
Wykład 13 Mechanika Kwantowa
 Wykład 13 Mechanika Kwantowa Maciej J. Mrowiński mrow@if.pw.edu.pl Wydział Fizyki Politechnika Warszawska 25 maja 2016 Maciej J. Mrowiński (IF PW) Wykład 13 25 maja 2016 1 / 21 Wprowadzenie Sprawy organizacyjne
Wykład 13 Mechanika Kwantowa Maciej J. Mrowiński mrow@if.pw.edu.pl Wydział Fizyki Politechnika Warszawska 25 maja 2016 Maciej J. Mrowiński (IF PW) Wykład 13 25 maja 2016 1 / 21 Wprowadzenie Sprawy organizacyjne
39 DUALIZM KORPUSKULARNO FALOWY.
 Włodzimierz Wolczyński 39 DUALIZM KORPUSKULARNO FALOWY. ZJAWISKO FOTOELEKTRYCZNE. FALE DE BROGILE Fale radiowe Fale radiowe ultrakrótkie Mikrofale Podczerwień IR Światło Ultrafiolet UV Promienie X (Rentgena)
Włodzimierz Wolczyński 39 DUALIZM KORPUSKULARNO FALOWY. ZJAWISKO FOTOELEKTRYCZNE. FALE DE BROGILE Fale radiowe Fale radiowe ultrakrótkie Mikrofale Podczerwień IR Światło Ultrafiolet UV Promienie X (Rentgena)
Rodzaje fal. 1. Fale mechaniczne. 2. Fale elektromagnetyczne. 3. Fale materii. dyfrakcja elektronów
 Wykład VI Fale t t + Dt Rodzaje fal 1. Fale mechaniczne 2. Fale elektromagnetyczne 3. Fale materii dyfrakcja elektronów Fala podłużna v Przemieszczenia elementów spirali ( w prawo i w lewo) są równoległe
Wykład VI Fale t t + Dt Rodzaje fal 1. Fale mechaniczne 2. Fale elektromagnetyczne 3. Fale materii dyfrakcja elektronów Fala podłużna v Przemieszczenia elementów spirali ( w prawo i w lewo) są równoległe
falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi
 Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi stabilne w czasie ich
Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi stabilne w czasie ich
ZADANIE 111 DOŚWIADCZENIE YOUNGA Z UŻYCIEM MIKROFAL
 ZADANIE 111 DOŚWIADCZENIE YOUNGA Z UŻYCIEM MIKROFAL X L Rys. 1 Schemat układu doświadczalnego. Fala elektromagnetyczna (światło, mikrofale) po przejściu przez dwie blisko położone (odległe o d) szczeliny
ZADANIE 111 DOŚWIADCZENIE YOUNGA Z UŻYCIEM MIKROFAL X L Rys. 1 Schemat układu doświadczalnego. Fala elektromagnetyczna (światło, mikrofale) po przejściu przez dwie blisko położone (odległe o d) szczeliny
r. akad. 2012/2013 wykład III-IV Mechanika kwantowa Podstawy Procesów i Konstrukcji Inżynierskich Mechanika kwantowa
 r. akad. 01/013 wykład III-IV Podstawy Procesów i Konstrukcji Inżynierskich Mechanika kwantowa Zakład Zakład Biofizyki Biofizyki 1 Falowa natura materii Zarówno fale elektromagnetyczne (fotony) jaki i
r. akad. 01/013 wykład III-IV Podstawy Procesów i Konstrukcji Inżynierskich Mechanika kwantowa Zakład Zakład Biofizyki Biofizyki 1 Falowa natura materii Zarówno fale elektromagnetyczne (fotony) jaki i
Optyka. Wykład V Krzysztof Golec-Biernat. Fale elektromagnetyczne. Uniwersytet Rzeszowski, 8 listopada 2017
 Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
Cząstki i siły. Piotr Traczyk. IPJ Warszawa
 Cząstki i siły tworzące nasz wszechświat Piotr Traczyk IPJ Warszawa Plan Wstęp Klasyfikacja cząstek elementarnych Model Standardowy 2 Wstęp 3 Jednostki, konwencje Prędkość światła c ~ 3 x 10 8 m/s Stała
Cząstki i siły tworzące nasz wszechświat Piotr Traczyk IPJ Warszawa Plan Wstęp Klasyfikacja cząstek elementarnych Model Standardowy 2 Wstęp 3 Jednostki, konwencje Prędkość światła c ~ 3 x 10 8 m/s Stała
FALOWA NATURA MATERII
 FALOWA NATURA MATERII Zadawniony podział: fizyka klasyczna (do 1900 r.) fizyka współczesna (od 1900 r., prawo Plancka). Przekonanie o falowej naturze materii ugruntowało się w latach dwudziestych XX w.
FALOWA NATURA MATERII Zadawniony podział: fizyka klasyczna (do 1900 r.) fizyka współczesna (od 1900 r., prawo Plancka). Przekonanie o falowej naturze materii ugruntowało się w latach dwudziestych XX w.
Rys. 1 Interferencja dwóch fal sferycznych w punkcie P.
 Ćwiczenie 4 Doświadczenie interferencyjne Younga Wprowadzenie teoretyczne Charakterystyczną cechą fal jest ich zdolność do interferencji. Światło jako fala elektromagnetyczna również może interferować.
Ćwiczenie 4 Doświadczenie interferencyjne Younga Wprowadzenie teoretyczne Charakterystyczną cechą fal jest ich zdolność do interferencji. Światło jako fala elektromagnetyczna również może interferować.
OPTYKA FALOWA. W zjawiskach takich jak interferencja, dyfrakcja i polaryzacja światło wykazuje naturę
 OPTYKA FALOWA W zjawiskach takich jak interferencja, dyfrakcja i polaryzacja światło wykazuje naturę falową. W roku 8 Thomas Young wykonał doświadczenie, które pozwoliło wyznaczyć długość fali światła.
OPTYKA FALOWA W zjawiskach takich jak interferencja, dyfrakcja i polaryzacja światło wykazuje naturę falową. W roku 8 Thomas Young wykonał doświadczenie, które pozwoliło wyznaczyć długość fali światła.
18 K A T E D R A F I ZYKI STOSOWAN E J
 18 K A T E D R A F I ZYKI STOSOWAN E J P R A C O W N I A F I Z Y K I Ćw. 18. Wyznaczanie długości fal świetlnych diody laserowej przy pomocy siatki dyfrakcyjnej Wprowadzenie Światło jest promieniowaniem
18 K A T E D R A F I ZYKI STOSOWAN E J P R A C O W N I A F I Z Y K I Ćw. 18. Wyznaczanie długości fal świetlnych diody laserowej przy pomocy siatki dyfrakcyjnej Wprowadzenie Światło jest promieniowaniem
Fizyka 3. Konsultacje: p. 329, Mechatronika
 Fizyka 3 Konsultacje: p. 39, Mechatronika marzan@mech.pw.edu.pl Zaliczenie: 1 sprawdzian 30 pkt 15.1 18 3.0 18.1 1 3.5 1.1 4 4.0 4.1 7 4.5 7.1 30 5.0 http:\\adam.mech.pw.edu.pl\~marzan Program: - elementy
Fizyka 3 Konsultacje: p. 39, Mechatronika marzan@mech.pw.edu.pl Zaliczenie: 1 sprawdzian 30 pkt 15.1 18 3.0 18.1 1 3.5 1.1 4 4.0 4.1 7 4.5 7.1 30 5.0 http:\\adam.mech.pw.edu.pl\~marzan Program: - elementy
Dyfrakcja. Dyfrakcja to uginanie światła (albo innych fal) przez drobne obiekty (rozmiar porównywalny z długością fali) do obszaru cienia
 Dyfrakcja 1 Dyfrakcja Dyfrakcja to uginanie światła (albo innych fal) przez drobne obiekty (rozmiar porównywalny z długością fali) do obszaru cienia uginanie na szczelinie uginanie na krawędziach przedmiotów
Dyfrakcja 1 Dyfrakcja Dyfrakcja to uginanie światła (albo innych fal) przez drobne obiekty (rozmiar porównywalny z długością fali) do obszaru cienia uginanie na szczelinie uginanie na krawędziach przedmiotów
Wykład FIZYKA II. 11. Optyka kwantowa. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA II 11. Optyka kwantowa Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/ FIZYKA KLASYCZNA A FIZYKA WSPÓŁCZESNA Fizyka klasyczna
Wykład FIZYKA II 11. Optyka kwantowa Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/ FIZYKA KLASYCZNA A FIZYKA WSPÓŁCZESNA Fizyka klasyczna
Metody Optyczne w Technice. Wykład 5 Interferometria laserowa
 Metody Optyczne w Technice Wykład 5 nterferometria laserowa Promieniowanie laserowe Wiązka monochromatyczna Duża koherencja przestrzenna i czasowa Niewielka rozbieżność wiązki Duża moc Największa możliwa
Metody Optyczne w Technice Wykład 5 nterferometria laserowa Promieniowanie laserowe Wiązka monochromatyczna Duża koherencja przestrzenna i czasowa Niewielka rozbieżność wiązki Duża moc Największa możliwa
V. RÓWNANIA MECHANIKI KWANTOWEJ
 V. RÓWNANIA MECHANIKI KWANTOWEJ 1 1 Postulaty mechaniki kwantowej Istota teorii kwantowej może być sformułowana za pomocą postulatów, których spełnienie postulujemy i których nie można wyprowadzić z żadnych
V. RÓWNANIA MECHANIKI KWANTOWEJ 1 1 Postulaty mechaniki kwantowej Istota teorii kwantowej może być sformułowana za pomocą postulatów, których spełnienie postulujemy i których nie można wyprowadzić z żadnych
Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem. S 0 amplituda odkształcenia. f [Hz] -częstotliwość.
![Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem. S 0 amplituda odkształcenia. f [Hz] -częstotliwość. Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem. S 0 amplituda odkształcenia. f [Hz] -częstotliwość.](/thumbs/96/127964376.jpg) Akusto-optyka Fala akustyczna jest falą mechaniczną Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem ( x, t) S cos( Ωt qx) s Częstotliwość kołowa Ω πf Długość fali
Akusto-optyka Fala akustyczna jest falą mechaniczną Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem ( x, t) S cos( Ωt qx) s Częstotliwość kołowa Ω πf Długość fali
Kwantowe własności promieniowania, ciało doskonale czarne, zjawisko fotoelektryczne zewnętrzne.
 Kwantowe własności promieniowania, ciało doskonale czarne, zjawisko fotoelektryczne zewnętrzne. DUALIZM ŚWIATŁA fala interferencja, dyfrakcja, polaryzacja,... kwant, foton promieniowanie ciała doskonale
Kwantowe własności promieniowania, ciało doskonale czarne, zjawisko fotoelektryczne zewnętrzne. DUALIZM ŚWIATŁA fala interferencja, dyfrakcja, polaryzacja,... kwant, foton promieniowanie ciała doskonale
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki
 OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Rezonansowe oddziaływanie układu atomowego z promieniowaniem "! "!! # $%&'()*+,-./-(01+'2'34'*5%.25%&+)*-(6
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Rezonansowe oddziaływanie układu atomowego z promieniowaniem "! "!! # $%&'()*+,-./-(01+'2'34'*5%.25%&+)*-(6
Równanie Schrödingera
 Fizyka 2 Wykład 3 1 Równanie Schrödingera Chcemy znaleźć dopuszczalne wartości energii układu fizycznego, dla którego znamy energię potencjalną. Z zasady odpowiedniości znamy postać hamiltonianu. Wybieramy
Fizyka 2 Wykład 3 1 Równanie Schrödingera Chcemy znaleźć dopuszczalne wartości energii układu fizycznego, dla którego znamy energię potencjalną. Z zasady odpowiedniości znamy postać hamiltonianu. Wybieramy
Wykład 18: Elementy fizyki współczesnej -2
 Wykład 18: Elementy fizyki współczesnej - Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Efekt fotoelektryczny 1887 Hertz;
Wykład 18: Elementy fizyki współczesnej - Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Efekt fotoelektryczny 1887 Hertz;
Podstawy mechaniki kwantowej. Jak opisać świat w małej skali?
 Podstawy mechaniki kwantowej Jak opisać świat w małej skali? 1 Promieniowanie elektromagnetyczne gamma X ultrafiolet podczerwień mikrofale radiowe widzialne Wavelength in meters 10-1 10-10 10-8 4 x 10-7
Podstawy mechaniki kwantowej Jak opisać świat w małej skali? 1 Promieniowanie elektromagnetyczne gamma X ultrafiolet podczerwień mikrofale radiowe widzialne Wavelength in meters 10-1 10-10 10-8 4 x 10-7
Przedmiot: Fizyka. Światło jako fala. 2016/17, sem. letni 1
 Światło jako fala 1 Fala elektromagnetyczna widmo promieniowania Czułość oka ludzkiego w zakresie widzialnym 2 Wytwarzanie fali elektromagnetycznej o częstościach radiowych H. Hertz (1888) doświadczalne
Światło jako fala 1 Fala elektromagnetyczna widmo promieniowania Czułość oka ludzkiego w zakresie widzialnym 2 Wytwarzanie fali elektromagnetycznej o częstościach radiowych H. Hertz (1888) doświadczalne
Problemy fizyki początku XX wieku
 Mechanika kwantowa Problemy fizyki początku XX wieku Promieniowanie ciała doskonale czarnego Ciałem doskonale czarnym nazywamy ciało całkowicie pochłaniające na nie promieniowanie elektromagnetyczne, niezależnie
Mechanika kwantowa Problemy fizyki początku XX wieku Promieniowanie ciała doskonale czarnego Ciałem doskonale czarnym nazywamy ciało całkowicie pochłaniające na nie promieniowanie elektromagnetyczne, niezależnie
= sin. = 2Rsin. R = E m. = sin
 Natężenie światła w obrazie dyfrakcyjnym Autorzy: Zbigniew Kąkol, Piotr Morawski Chcemy teraz znaleźć wyrażenie na rozkład natężenia w całym ekranie w funkcji kąta θ. Szczelinę dzielimy na N odcinków i
Natężenie światła w obrazie dyfrakcyjnym Autorzy: Zbigniew Kąkol, Piotr Morawski Chcemy teraz znaleźć wyrażenie na rozkład natężenia w całym ekranie w funkcji kąta θ. Szczelinę dzielimy na N odcinków i
Własności światła laserowego
 Własności światła laserowego Cechy światła laserowego: rozbieżność (równoległość) wiązki, pasmo spektralne, gęstość mocy oraz spójność (koherencja). Równoległość wiązki Dyfrakcyjną rozbieżność kątową awkącie
Własności światła laserowego Cechy światła laserowego: rozbieżność (równoległość) wiązki, pasmo spektralne, gęstość mocy oraz spójność (koherencja). Równoległość wiązki Dyfrakcyjną rozbieżność kątową awkącie
gdzie λ - długość fali, h - stała Plancka, p - pęd cząstki.
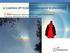 3.7. Model współczesny Louis Victor Pierre Raymond de Broglie (189-1987) (Rysunek 3-35) w swojej pracy doktorskiej z 194 roku, wysunął przypuszczenie, że skoro fale elektromagnetyczne mogą przejawiać naturę
3.7. Model współczesny Louis Victor Pierre Raymond de Broglie (189-1987) (Rysunek 3-35) w swojej pracy doktorskiej z 194 roku, wysunął przypuszczenie, że skoro fale elektromagnetyczne mogą przejawiać naturę
Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem. S 0 amplituda odkształcenia. f [Hz] - częstotliwość.
![Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem. S 0 amplituda odkształcenia. f [Hz] - częstotliwość. Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem. S 0 amplituda odkształcenia. f [Hz] - częstotliwość.](/thumbs/102/155632743.jpg) Akusto-optyka Fala akustyczna jest falą mechaniczną Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem ( x, t) S cos( Ωt qx) s Częstotliwość kołowa Ω πf Długość fali
Akusto-optyka Fala akustyczna jest falą mechaniczną Oscylator wprowadza lokalne odkształcenie s ośrodka propagujące się zgodnie z równaniem ( x, t) S cos( Ωt qx) s Częstotliwość kołowa Ω πf Długość fali
INŻYNIERIA BIOMEDYCZNA. Wykład IX
 INŻYNIERIA BIOMEDYCZNA Wykład IX 01.12.2018 1 PLAN Fizyka około 1900 roku Promieniowanie elektromagnetyczne Natura materii Równanie Schrödingera Struktura elektronowa atomu Oryginalne dokumenty nie pozostawiają
INŻYNIERIA BIOMEDYCZNA Wykład IX 01.12.2018 1 PLAN Fizyka około 1900 roku Promieniowanie elektromagnetyczne Natura materii Równanie Schrödingera Struktura elektronowa atomu Oryginalne dokumenty nie pozostawiają
INŻYNIERIA BIOMEDYCZNA. Wykład IX
 INŻYNIERIA BIOMEDYCZNA Wykład IX 1 PLAN Fizyka około 1900 roku Promieniowanie elektromagnetyczne Natura materii Równanie Schrödingera Struktura elektronowa atomu Oryginalne dokumenty nie pozostawiają wątpliwości,
INŻYNIERIA BIOMEDYCZNA Wykład IX 1 PLAN Fizyka około 1900 roku Promieniowanie elektromagnetyczne Natura materii Równanie Schrödingera Struktura elektronowa atomu Oryginalne dokumenty nie pozostawiają wątpliwości,
Fizyka. dr Bohdan Bieg p. 36A. wykład ćwiczenia laboratoryjne ćwiczenia rachunkowe
 Fizyka dr Bohdan Bieg p. 36A wykład ćwiczenia laboratoryjne ćwiczenia rachunkowe Literatura Raymond A. Serway, John W. Jewett, Jr. Physics for Scientists and Engineers, Cengage Learning D. Halliday, D.
Fizyka dr Bohdan Bieg p. 36A wykład ćwiczenia laboratoryjne ćwiczenia rachunkowe Literatura Raymond A. Serway, John W. Jewett, Jr. Physics for Scientists and Engineers, Cengage Learning D. Halliday, D.
Fala jest zaburzeniem, rozchodzącym się w ośrodku, przy czym żadna część ośrodka nie wykonuje zbyt dużego ruchu
 Ruch falowy Fala jest zaburzeniem, rozchodzącym się w ośrodku, przy czym żadna część ośrodka nie wykonuje zbyt dużego ruchu Fala rozchodzi się w przestrzeni niosąc ze sobą energię, ale niekoniecznie musi
Ruch falowy Fala jest zaburzeniem, rozchodzącym się w ośrodku, przy czym żadna część ośrodka nie wykonuje zbyt dużego ruchu Fala rozchodzi się w przestrzeni niosąc ze sobą energię, ale niekoniecznie musi
Mechanika Kwantowa. Maciej J. Mrowiński. 24 grudnia Funkcja falowa opisująca stan pewnej cząstki ma następującą postać: 2 x 2 )
 Mechanika Kwantowa Maciej J. Mrowiński 4 grudnia 11 Zadanie MK1 Funkcja falowa opisująca stan pewnej cząstki w chwili t = ma następującą postać: A(a Ψ(x,) = x ) gdy x [ a,a] gdy x / [ a,a] gdzie a +. Wyznacz
Mechanika Kwantowa Maciej J. Mrowiński 4 grudnia 11 Zadanie MK1 Funkcja falowa opisująca stan pewnej cząstki w chwili t = ma następującą postać: A(a Ψ(x,) = x ) gdy x [ a,a] gdy x / [ a,a] gdzie a +. Wyznacz
POSTULATY MECHANIKI KWANTOWEJ cd i formalizm matematyczny
 POSTULATY MECHANIKI KWANTOWEJ cd i formalizm matematyczny Funkcja Falowa Postulat 1 Dla każdego układu istnieje funkcja falowa (funkcja współrzędnych i czasu), która jest ciągła, całkowalna w kwadracie,
POSTULATY MECHANIKI KWANTOWEJ cd i formalizm matematyczny Funkcja Falowa Postulat 1 Dla każdego układu istnieje funkcja falowa (funkcja współrzędnych i czasu), która jest ciągła, całkowalna w kwadracie,
Ψ(x, t) punkt zamocowania liny zmienna t, rozkład zaburzeń w czasie. x (lub t)
 RUCH FALOWY 1 Fale sejsmiczne Fale morskie Kamerton Interferencja RÓWNANIE FALI Fala rozchodzenie się zaburzeń w ośrodku materialnym lub próżni: fale podłużne i poprzeczne w ciałach stałych, fale podłużne
RUCH FALOWY 1 Fale sejsmiczne Fale morskie Kamerton Interferencja RÓWNANIE FALI Fala rozchodzenie się zaburzeń w ośrodku materialnym lub próżni: fale podłużne i poprzeczne w ciałach stałych, fale podłużne
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki
 OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania (3.7), pomimo swojej prostoty, nie posiadają poza nielicznymi przypadkami ścisłych rozwiązań,
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania (3.7), pomimo swojej prostoty, nie posiadają poza nielicznymi przypadkami ścisłych rozwiązań,
Wykład 16: Optyka falowa
 Wykład 16: Optyka falowa Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Zasada Huyghensa Christian Huygens 1678 r. pierwsza falowa
Wykład 16: Optyka falowa Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Zasada Huyghensa Christian Huygens 1678 r. pierwsza falowa
Wykład 9: Fale cz. 1. dr inż. Zbigniew Szklarski
 Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Fizyka elektryczność i magnetyzm
 Fizyka elektryczność i magnetyzm W5 5. Wybrane zagadnienia z optyki 5.1. Światło jako część widma fal elektromagnetycznych. Fale elektromagnetyczne, które współczesny człowiek potrafi wytwarzać, i wykorzystywać
Fizyka elektryczność i magnetyzm W5 5. Wybrane zagadnienia z optyki 5.1. Światło jako część widma fal elektromagnetycznych. Fale elektromagnetyczne, które współczesny człowiek potrafi wytwarzać, i wykorzystywać
WŁASNOŚCI FAL (c.d.)
 RUCH FALOWY Własności i rodzaje fal. Prędkość rozchodzenia się fal. Fala harmoniczna płaska. Fala stojąca. Zasada Huygensa. Dyfrakcja fal. Obraz dyfrakcyjny. Kryterium Rayleigha. Interferencja fal. Doświadczenie
RUCH FALOWY Własności i rodzaje fal. Prędkość rozchodzenia się fal. Fala harmoniczna płaska. Fala stojąca. Zasada Huygensa. Dyfrakcja fal. Obraz dyfrakcyjny. Kryterium Rayleigha. Interferencja fal. Doświadczenie
OPTYKA FALOWA I (FTP2009L) Ćwiczenie 2. Dyfrakcja światła na szczelinach.
 OPTYKA FALOWA I (FTP2009L) Ćwiczenie 2. Dyfrakcja światła na szczelinach. Zagadnienia, które należy znać przed wykonaniem ćwiczenia: Dyfrakcja światła to zjawisko fizyczne zmiany kierunku rozchodzenia
OPTYKA FALOWA I (FTP2009L) Ćwiczenie 2. Dyfrakcja światła na szczelinach. Zagadnienia, które należy znać przed wykonaniem ćwiczenia: Dyfrakcja światła to zjawisko fizyczne zmiany kierunku rozchodzenia
Zjawisko interferencji fal
 Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi stabilne w czasie ich
Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi stabilne w czasie ich
Moment pędu fali elektromagnetycznej
 napisał Michał Wierzbicki Moment pędu fali elektromagnetycznej Definicja momentu pędu pola elektromagnetycznego Gęstość momentu pędu pola J w elektrodynamice definuje się za pomocą wzoru: J = r P = ɛ 0
napisał Michał Wierzbicki Moment pędu fali elektromagnetycznej Definicja momentu pędu pola elektromagnetycznego Gęstość momentu pędu pola J w elektrodynamice definuje się za pomocą wzoru: J = r P = ɛ 0
Mechanika klasyczna zasada zachowania energii. W obszarze I cząstka biegnie z prędkością v I, Cząstka przechodzi z obszaru I do II.
 Próg potencjału Mecanika klasyczna zasada zacowania energii mvi mv E + V W obszarze I cząstka biegnie z prędkością v I, E > V w obszarze cząstka biegnie z prędkością v Cząstka przecodzi z obszaru I do.
Próg potencjału Mecanika klasyczna zasada zacowania energii mvi mv E + V W obszarze I cząstka biegnie z prędkością v I, E > V w obszarze cząstka biegnie z prędkością v Cząstka przecodzi z obszaru I do.
Wykład 16: Optyka falowa
 Wykład 16: Optyka falowa Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Zasada Huyghensa Christian Huygens 1678 r. pierwsza
Wykład 16: Optyka falowa Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Zasada Huyghensa Christian Huygens 1678 r. pierwsza
Dyfrakcja. interferencja światła. dr inż. Romuald Kędzierski
 Dyfrakcja i interferencja światła. dr inż. Romuald Kędzierski Zasada Huygensa - przypomnienie Każdy punkt ośrodka, do którego dotarło czoło fali można uważać za źródło nowej fali kulistej. Fale te zwane
Dyfrakcja i interferencja światła. dr inż. Romuald Kędzierski Zasada Huygensa - przypomnienie Każdy punkt ośrodka, do którego dotarło czoło fali można uważać za źródło nowej fali kulistej. Fale te zwane
Fizyka 12. Janusz Andrzejewski
 Fizyka 1 Janusz Andrzejewski Przypomnienie: Drgania procesy w których pewna wielkość fizyczna na przemian maleje i rośnie Okresowy ruch drgający (periodyczny) - jeżeli wartości wielkości fizycznych zmieniające
Fizyka 1 Janusz Andrzejewski Przypomnienie: Drgania procesy w których pewna wielkość fizyczna na przemian maleje i rośnie Okresowy ruch drgający (periodyczny) - jeżeli wartości wielkości fizycznych zmieniające
Falowa natura materii
 r. akad. 2012/2013 wykład I - II Podstawy Procesów i Konstrukcji Inżynierskich Falowa natura materii 1 r. akad. 2012/2013 Podstawy Procesów i Konstrukcji Inżynierskich Warunki zaliczenia: Aby uzyskać dopuszczenie
r. akad. 2012/2013 wykład I - II Podstawy Procesów i Konstrukcji Inżynierskich Falowa natura materii 1 r. akad. 2012/2013 Podstawy Procesów i Konstrukcji Inżynierskich Warunki zaliczenia: Aby uzyskać dopuszczenie
Mechanika kwantowa. Jak opisać atom wodoru? Jak opisać inne cząsteczki?
 Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Elektron fala stojąca wokół jądra Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkowy
Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Elektron fala stojąca wokół jądra Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkowy
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 2, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 17.02.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Równania Maxwella r-nie falowe
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 17.02.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Równania Maxwella r-nie falowe
Zasada nieoznaczoności Heisenberga. Konsekwencją tego, Ŝe cząstki mikroświata mają takŝe własności falowe jest:
 Zasada nieoznaczoności Heisenberga Konsekwencją tego, Ŝe cząstki mikroświata mają takŝe własności falowe jest: Pewnych wielkości fizycznych nie moŝna zmierzyć równocześnie z dowolną dokładnością. Iloczyn
Zasada nieoznaczoności Heisenberga Konsekwencją tego, Ŝe cząstki mikroświata mają takŝe własności falowe jest: Pewnych wielkości fizycznych nie moŝna zmierzyć równocześnie z dowolną dokładnością. Iloczyn
III. EFEKT COMPTONA (1923)
 III. EFEKT COMPTONA (1923) Zjawisko zmiany długości fali promieniowania roentgenowskiego rozpraszanego na swobodnych elektronach. Zjawisko to stoi u podstaw mechaniki kwantowej. III.1. EFEKT COMPTONA Rys.III.1.
III. EFEKT COMPTONA (1923) Zjawisko zmiany długości fali promieniowania roentgenowskiego rozpraszanego na swobodnych elektronach. Zjawisko to stoi u podstaw mechaniki kwantowej. III.1. EFEKT COMPTONA Rys.III.1.
Podstawy mechaniki kwantowej
 Podstawy mechaniki kwantowej Jak opisać świat w małej skali? Czy świat jest realny? 1 Promieniowanie elektromagnetyczne gamma X ultrafiolet podczerwień mikrofale radiowe widzialne Wavelength in meters
Podstawy mechaniki kwantowej Jak opisać świat w małej skali? Czy świat jest realny? 1 Promieniowanie elektromagnetyczne gamma X ultrafiolet podczerwień mikrofale radiowe widzialne Wavelength in meters
o pomiarze i o dekoherencji
 o pomiarze i o dekoherencji Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW pomiar dekoherencja pomiar kolaps nieoznaczoność paradoksy dekoherencja Przykładowy
o pomiarze i o dekoherencji Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW pomiar dekoherencja pomiar kolaps nieoznaczoność paradoksy dekoherencja Przykładowy
