Fale elektromagnetyczne
|
|
|
- Andrzej Michałowski
- 7 lat temu
- Przeglądów:
Transkrypt
1 Fale elektromagnetyczne dr inż. Ireneusz Owczarek CMF PŁ /13 Plan wykładu Spis treści 1. Analiza pola Rozkład pola Dywergencja i rotacja Równania Maxwella Fale elektromagnetyczne Wstęp Modele w optyce Model falowy światła
2 1. Analiza pola 1.1. Rozkład pola Gradient pola Gradient funkcji pola skalarnego ϕ przypisuje każdemu punktowi tego pola określony wektor: grad ϕ = ϕ i + ϕ y j + ϕ z k Wyznacza pole wektorowe, przyporządkowane danemu polu skalarnemu. Wektor grad ϕ: jest prostopadły do powierzchni ekwiskalarnej, ma zwrot skierowany od powierzchni ekwiskalarnej o mniejszej wartości do powierzchni o większej wartości. Gradient pola... Funkcje pola grad ϕ zapisuje się grad ϕ = ϕ gdzie Operator nabla = i + y j + z k, w operacjach matematycznych traktowany jest jak symboliczny wektor. Pozwala zapisać operacje różniczkowe na funkcjach w prostej i zwartej formie działań wektorów. c Ireneusz Owczarek,
3 Gradient pola... Iloczyn skalarny dwóch operatorów nabla: = 2 = ( i + j y + k z ) 2 = y z 2. Operator Laplace a (laplasjan) jest to operator różniczkowy drugiego rzędu = 2 = y z 2. Laplasjan jest operatorem skalarnym działającym na pole skalarne. Operator traktowany jest formalnie jako wektor, można więc utworzyć iloczyn skalarny i wektorowy wektora z dowolnym innym wektorem. Np. pewną funkcja pola wektorowego V (x, y, z) = i V x(x, y, z) + j V y(x, y, z) + k V z(x, y, z) Dywergencja i rotacja Definicje Dywergencja (rozbieżność, źródłowość) pola wektorowego V (x, y, z) to operator różniczkowy przyporządkowujący trójwymiarowemu polu wektorowemu pole skalarne będące formalnym iloczynem skalarnym operatora nabla z polem: V = ( i + j y + k z = Vx + Vy y + Vz z = div V. Pole nazywa się bezźródłowym gdy div V = 0. ) ( i V x + j V y + k V z) = Rotacja (wirowość) pola wektorowego V (x, y, z) to operator różniczkowy działający na pole wektorowe V (x, y, z), tworzy pole wektorowe wskazujące wirowanie (gęstość cyrkulacji) pola wyjściowego ( ) V = i ( i V x + j V y + k V z) = + j y + k z ( ) Vz = i y Vy + j z i j k = y z V x V y V z = rot V. ( Vx z Vz ) + k Pole nazywa się bezwirowym lub zachowawczym gdy rot V = 0. ( Vy Vx y ) = c Ireneusz Owczarek,
4 1.3. Równania Maxwella Wstęp Równania Maxwella stanowią fundamentalną podstawę teorii zjawisk elektromagnetycznych, podobnie jak zasady dynamiki Newtona są podstawą mechaniki. Można znaleźć pola E i B w dowolnym punkcie przestrzeni i w dowolnej chwili czasu, jeżeli znane są współrzędne i prędkości ładunków wytwarzających pola. Równania Maxwella są niesymetryczne względem pól elektrycznego i magnetycznego (istnieją ładunki elektryczne, a brak jest ładunków magnetycznych). Prawa te są słuszne zarówno w przypadku statycznym (pola niezależne od czasu) jak i w przypadku pól zależnych od czasu. Ważną konsekwencją równań Maxwella jest istnienie fali elektromagnetycznej. Prawa Maxwella 1. Prawo Gaussa dla elektryczności. Ładunki są źródłem pola elektrycznego E = ρ ε Prawo Gaussa dla magnetyzmu. Pole magnetyczne jest bezźródłowe B = Prawo Faraday a. Zmienne w czasie pole magnetyczne wytwarza pole elektryczne E = B t. 4. Prawo Ampére a. Przepływający prąd oraz zmienne pole elektryczne wytwarzają pole magnetyczne B = µ 0 J + ε0µ 0 E t. W sposób niejawny równania te zawierają równanie ciągłości J + ρ t = 0. c Ireneusz Owczarek,
5 Dla fal rozchodzących się w próżni Prawo Gaussa dla elektryczności Prawo Gaussa dla magnetyzmu Prawo Faraday a E = 0. B = 0. E = B t. Prawo Ampére a B = ε 0µ 0 E t. c Ireneusz Owczarek,
6 2. Fale elektromagnetyczne 2.1. Wstęp 2.2. Modele w optyce Co to jet światło? Fala elektromagnetyczna jest falą rozchodzącą się w próżni lub ośrodku materialnym wywołaną zmianami rozkładu przestrzennego ładunków elektrycznych. Istotną cechą wszystkich fal elektromagnetycznych jest ta sama wartość prędkości rozchodzenia się fali, tj. c 2, m/s. Światło to promieniowanie elektromagnetyczne o długościach fali, zawierających się w zakresie czułości oka ludzkiego, tj. od 380nm do 760nm. Jest to tzw. zakres widzialny. Największa czułość wypada dla fal o długości ok. 550nm. Porównanie systemów sensorycznych człowieka Model falowy światła Fala elektromagnetyczna płaska Ważne cechy pól: elektrycznego i magnetycznego które występują zawsze, niezależnie od tego jak wytwarzana jest fala: 1. Wektory E i B są zawsze prostopadłe do kierunku rozchodzenia się fal, zatem fala elektromagnetyczna jest falą poprzeczną. c Ireneusz Owczarek,
7 2. Wektor natężenia pola elektrycznego jest zawsze prostopadły do wektora natężenia pola magnetycznego. 3. Iloczyn wektorowy E B zawsze wyznacza kierunek rozchodzenia się fali. 4. Natężenie pola elektrycznego i indukcja pola magnetycznego zmieniają się zawsze sinusoidalnie. Ponadto wektory pól zmieniają się z taką samą częstością, a ich oscylacje są zgodne w fazie. Jaki jest kierunek indukcji magnetycznej? Jeżeli E ma składową w kierunku osi y, a B w kierunku z, to płaską, poprzeczna fala elektromagnetyczna ma postać: { Ey(x, y, z, t) = E m sin(kx ωt), B z(x, y, z, t) = B m sin(kx ωt), c Ireneusz Owczarek,
8 i rozchodzi się wzdłuż osi x to oraz E x = E z = 0 i E y = E y(x, y, z, t), E i j k = y z E x E y E z = ( ) ( ) ( ) = i Ez y E y E + j x z z Ez + Ey k Ex = y = k Ey. Korzystając z prawa Faraday a otrzymuje się B t = k Ey, lub E y = Bz t. (1) Oznacza to, że istnieje tylko jedna składowa wektora B z, czyli pole magnetyczne wskazuje kierunek z (pole indukcji magnetycznej jest prostopadłe do pola elektrycznego). Podobnie można pokazać (dla B z = B z(x, t)), że B = j Bz, i korzystając z prawa Ampére a otrzymuje się B z = ε0µ0 E y t. (2) Prędkość fal elektromagnetycznych Korzystają z równań dla płaskiej fali elektromagnetycznej oraz z tego, że E y = E i B z = B otrzymuje się E y B z t = kem cos(kx ωt), = ωb m cos(kx ωt). Wobec tego równanie ( 1) sprowadza się do postaci Prędkość fali biegnącej zatem iloraz amplitud ke m cos(kx ωt) = ωb m cos(kx ωt). Postępując podobnie w przypadku równania ( 2) można zapisać w postaci z której otrzymuje się c = ω k, (3) E m B m = c. (4) kb m cos(kx ωt) = ε 0µ 0ωE m cos(kx ωt), E m = 1 ω B m µ 0ε 0 k = 1 µ 0ε 0c = c, Prędkości fal elektromagnetycznych w próżni Wszystkie fale elektromagnetyczne, w tym również światło widzialne, rozchodzą się w próżni z tą samą prędkością 1 c =, (5) µ0ε 0 która wynosi ok. 2, m s. c Ireneusz Owczarek,
9 Równanie falowe dla fali elektromagnetycznej Postać równania falowego można uzyskać jeżeli policzy się pochodną cząstkową względem x wyrażenia ( 1) 2 E 2 = 2 B t, oraz pochodną cząstkową względem t wyrażenia ( 2) 2 B t = ε0µ0 2 E t 2. Przyrównanie do siebie tych równań daje równanie które ma postać równania falowego 2 E t 2 = 1 ε 0µ 0 2 E 2, (6) 2 ξ t 2 = v2 2 ξ 2, lub w bardziej zwartej postaci równania różniczkowego ruchu falowego 2 ξ = 1 c 2 2 ξ t 2. (7) Własności fali elektromagnetycznej Źródłem fali elektromagnetycznej jest przyspieszający ładunek. W punkcie, do którego dociera fala, natężenie pola elektrycznego zmienia się zgodnie z relacją E y(x, y, z, t) = E m sin(kx ωt). Drgający ładunek nie promieniuje we wszystkich kierunkach jednakowo. W kierunku, w którym drga ładunek, fala elektromagnetyczna nie rozchodzi się. Fala elektromagnetyczna jest to rozchodzenie się w próżni lub w ośrodku materialnym wzajemnie indukujących się zmiennych pól E i B. Z tego powodu nie wymaga istnienia ośrodka do swego przemieszczania się. Fala elektromagnetyczna jest falą poprzeczną: wektory E i B są wzajemnie do siebie prostopadłe i są też prostopadłe do kierunku rozchodzenia się fali. Prędkość fal elektromagnetycznych zależna jest od własności elektrycznych i magnetycznych ośrodka, w którym się ona rozchodzi Literatura c = 1 = 2, m ε0µ 0 s, [1] Halliday D., Resnick R, Walker J. Podstawy Fizyki t PWN, [2] Praca zbiorowa pod red. A. Justa Wstęp do analizy matematycznej i wybranych zagadnień z fizyki. Wydawnictwo PŁ, Łódź [3] Jaworski B., Dietłaf A. Kurs Fizyki t PWN, [4] Strona internetowa prowadzona przez CMF PŁ e-fizyka. Podstawy fizyki. [5] Kąkol Z. Żukrowski J. kakol/wyklady_pl.htm Wykłady z fizyki. c Ireneusz Owczarek,
Fale elektromagnetyczne. Gradient pola. Gradient pola... Gradient pola... Notatki. Notatki. Notatki. Notatki. dr inż. Ireneusz Owczarek 2013/14
 dr inż. Ireneusz Owczarek CNMiF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2013/14 1 dr inż. Ireneusz Owczarek Gradient pola Gradient funkcji pola skalarnego ϕ przypisuje każdemu punktowi
dr inż. Ireneusz Owczarek CNMiF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2013/14 1 dr inż. Ireneusz Owczarek Gradient pola Gradient funkcji pola skalarnego ϕ przypisuje każdemu punktowi
Fizyka. dr Bohdan Bieg p. 36A. wykład ćwiczenia laboratoryjne ćwiczenia rachunkowe
 Fizyka dr Bohdan Bieg p. 36A wykład ćwiczenia laboratoryjne ćwiczenia rachunkowe Literatura Raymond A. Serway, John W. Jewett, Jr. Physics for Scientists and Engineers, Cengage Learning D. Halliday, D.
Fizyka dr Bohdan Bieg p. 36A wykład ćwiczenia laboratoryjne ćwiczenia rachunkowe Literatura Raymond A. Serway, John W. Jewett, Jr. Physics for Scientists and Engineers, Cengage Learning D. Halliday, D.
Pole elektromagnetyczne. Równania Maxwella
 Pole elektromagnetyczne (na podstawie Wikipedii) Pole elektromagnetyczne - pole fizyczne, za pośrednictwem którego następuje wzajemne oddziaływanie obiektów fizycznych o właściwościach elektrycznych i
Pole elektromagnetyczne (na podstawie Wikipedii) Pole elektromagnetyczne - pole fizyczne, za pośrednictwem którego następuje wzajemne oddziaływanie obiektów fizycznych o właściwościach elektrycznych i
Księgarnia PWN: David J. Griffiths - Podstawy elektrodynamiki
 Księgarnia PWN: David J. Griffiths - Podstawy elektrodynamiki Spis treści Przedmowa... 11 Wstęp: Czym jest elektrodynamika i jakie jest jej miejsce w fizyce?... 13 1. Analiza wektorowa... 19 1.1. Algebra
Księgarnia PWN: David J. Griffiths - Podstawy elektrodynamiki Spis treści Przedmowa... 11 Wstęp: Czym jest elektrodynamika i jakie jest jej miejsce w fizyce?... 13 1. Analiza wektorowa... 19 1.1. Algebra
Podstawy fizyki sezon 2 6. Równania Maxwella
 Podstawy fizyki sezon 2 6. Równania Maxwella Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Dotychczas pokazaliśmy:
Podstawy fizyki sezon 2 6. Równania Maxwella Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Dotychczas pokazaliśmy:
Optyka. Wykład V Krzysztof Golec-Biernat. Fale elektromagnetyczne. Uniwersytet Rzeszowski, 8 listopada 2017
 Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
RÓWNANIA MAXWELLA. Czy pole magnetyczne może stać się źródłem pola elektrycznego? Czy pole elektryczne może stać się źródłem pola magnetycznego?
 RÓWNANIA MAXWELLA Czy pole magnetyczne może stać się źródłem pola elektrycznego? Czy pole elektryczne może stać się źródłem pola magnetycznego? Wykład 3 lato 2012 1 Doświadczenia Wykład 3 lato 2012 2 1
RÓWNANIA MAXWELLA Czy pole magnetyczne może stać się źródłem pola elektrycznego? Czy pole elektryczne może stać się źródłem pola magnetycznego? Wykład 3 lato 2012 1 Doświadczenia Wykład 3 lato 2012 2 1
Analiza wektorowa. Teoria pola.
 Analiza wektorowa. Teoria pola. Pole skalarne Pole wektorowe ϕ = ϕ(x, y, z) A = A x (x, y, z) i x + A y (x, y, z) i y + A z (x, y, z) i z Gradient grad ϕ = ϕ x i x + ϕ y i y + ϕ z i z Jeśli przemieścimy
Analiza wektorowa. Teoria pola. Pole skalarne Pole wektorowe ϕ = ϕ(x, y, z) A = A x (x, y, z) i x + A y (x, y, z) i y + A z (x, y, z) i z Gradient grad ϕ = ϕ x i x + ϕ y i y + ϕ z i z Jeśli przemieścimy
Widmo fal elektromagnetycznych
 Czym są fale elektromagnetyczne? Widmo fal elektromagnetycznych dr inż. Romuald Kędzierski Podstawowe pojęcia związane z falami - przypomnienie pole falowe część przestrzeni objęta w danej chwili falą
Czym są fale elektromagnetyczne? Widmo fal elektromagnetycznych dr inż. Romuald Kędzierski Podstawowe pojęcia związane z falami - przypomnienie pole falowe część przestrzeni objęta w danej chwili falą
Różniczkowe prawo Gaussa i co z niego wynika...
 Różniczkowe prawo Gaussa i co z niego wynika... Niech ładunek będzie rozłożony w objętości V z ciągłą gęstością ρ(x,y,z). Wytworzone przez ten ładunek pole elektryczne będzie również zmieniać się w przestrzeni
Różniczkowe prawo Gaussa i co z niego wynika... Niech ładunek będzie rozłożony w objętości V z ciągłą gęstością ρ(x,y,z). Wytworzone przez ten ładunek pole elektryczne będzie również zmieniać się w przestrzeni
METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ
 METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ Wykład 3 Elementy analizy pól skalarnych, wektorowych i tensorowych Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 1 Analiza
METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ Wykład 3 Elementy analizy pól skalarnych, wektorowych i tensorowych Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 1 Analiza
Podstawy elektrodynamiki / David J. Griffiths. - wyd. 2, dodr. 3. Warszawa, 2011 Spis treści. Przedmowa 11
 Podstawy elektrodynamiki / David J. Griffiths. - wyd. 2, dodr. 3. Warszawa, 2011 Spis treści Przedmowa 11 Wstęp: Czym jest elektrodynamika i jakie jest jej miejsce w fizyce? 13 1. Analiza wektorowa 19
Podstawy elektrodynamiki / David J. Griffiths. - wyd. 2, dodr. 3. Warszawa, 2011 Spis treści Przedmowa 11 Wstęp: Czym jest elektrodynamika i jakie jest jej miejsce w fizyce? 13 1. Analiza wektorowa 19
Teoria pola elektromagnetycznego
 Teoria pola elektromagnetycznego Odpowiedzialny za przedmiot (wykłady): prof. dr hab. inż. Stanisław Gratkowski Ćwiczenia i laboratoria: dr inż. Krzysztof Stawicki ks@zut.edu.pl e-mail: w temacie wiadomości
Teoria pola elektromagnetycznego Odpowiedzialny za przedmiot (wykłady): prof. dr hab. inż. Stanisław Gratkowski Ćwiczenia i laboratoria: dr inż. Krzysztof Stawicki ks@zut.edu.pl e-mail: w temacie wiadomości
Rozważania rozpoczniemy od fal elektromagnetycznych w próżni. Dla próżni równania Maxwella w tzw. postaci różniczkowej są następujące:
 Rozważania rozpoczniemy od fal elektromagnetycznych w próżni Dla próżni równania Maxwella w tzw postaci różniczkowej są następujące:, gdzie E oznacza pole elektryczne, B indukcję pola magnetycznego a i
Rozważania rozpoczniemy od fal elektromagnetycznych w próżni Dla próżni równania Maxwella w tzw postaci różniczkowej są następujące:, gdzie E oznacza pole elektryczne, B indukcję pola magnetycznego a i
Wykład I Krzysztof Golec-Biernat Optyka 1 / 16
 Optyka Wykład I Krzysztof Golec-Biernat Fale 1 Uniwersytet Rzeszowski, 4 października 2017 Wykład I Krzysztof Golec-Biernat Optyka 1 / 16 Uwagi wstępne 30 h wykładu wykład przy pomocy transparencji lub
Optyka Wykład I Krzysztof Golec-Biernat Fale 1 Uniwersytet Rzeszowski, 4 października 2017 Wykład I Krzysztof Golec-Biernat Optyka 1 / 16 Uwagi wstępne 30 h wykładu wykład przy pomocy transparencji lub
Wykład 9: Fale cz. 1. dr inż. Zbigniew Szklarski
 Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Fale elektromagnetyczne
 Rozdział 7 Fale elektromagnetyczne 7.1 Prąd przesunięcia. II równanie Maxwella Poznane dotąd prawa elektrostatyki, magnetostatyki oraz indukcji elektromagnetycznej można sformułować w czterech podstawowych
Rozdział 7 Fale elektromagnetyczne 7.1 Prąd przesunięcia. II równanie Maxwella Poznane dotąd prawa elektrostatyki, magnetostatyki oraz indukcji elektromagnetycznej można sformułować w czterech podstawowych
Fizyka 2 Wróbel Wojciech
 Fizyka w poprzednim odcinku 1 Prawo Faradaya Fizyka B Bd S Strumień magnetyczny Jednostka: Wb (Weber) = T m d SEM B Siła elektromotoryczna Praca, przypadająca na jednostkę ładunku, wykonana w celu wytworzenia
Fizyka w poprzednim odcinku 1 Prawo Faradaya Fizyka B Bd S Strumień magnetyczny Jednostka: Wb (Weber) = T m d SEM B Siła elektromotoryczna Praca, przypadająca na jednostkę ładunku, wykonana w celu wytworzenia
Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie
 napisał Michał Wierzbicki Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie Prędkość grupowa paczki falowej Paczka falowa jest superpozycją fal o różnej częstości biegnących wzdłuż osi z.
napisał Michał Wierzbicki Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie Prędkość grupowa paczki falowej Paczka falowa jest superpozycją fal o różnej częstości biegnących wzdłuż osi z.
PDF stworzony przez wersję demonstracyjną pdffactory
 Promieniowanie elektromagnetyczne (fala elektromagnetyczna) rozchodzące się w przestrzeni zaburzenie pola elektromagnetycznego. Zaburzenie to ma charakter fali poprzecznej, w której składowa elektryczna
Promieniowanie elektromagnetyczne (fala elektromagnetyczna) rozchodzące się w przestrzeni zaburzenie pola elektromagnetycznego. Zaburzenie to ma charakter fali poprzecznej, w której składowa elektryczna
Przedmowa do wydania drugiego Konwencje i ważniejsze oznaczenia... 13
 Przedmowa do wydania drugiego... 11 Konwencje i ważniejsze oznaczenia... 13 1. Rachunek i analiza wektorowa... 17 1.1. Wielkości skalarne i wektorowe... 17 1.2. Układy współrzędnych... 20 1.2.1. Układ
Przedmowa do wydania drugiego... 11 Konwencje i ważniejsze oznaczenia... 13 1. Rachunek i analiza wektorowa... 17 1.1. Wielkości skalarne i wektorowe... 17 1.2. Układy współrzędnych... 20 1.2.1. Układ
cz. 2. dr inż. Zbigniew Szklarski
 Wykład 14: Pole magnetyczne cz.. dr inż. Zbigniew zklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.zklarski/ Prąd elektryczny jako źródło pola magnetycznego - doświadczenie Oersteda Kiedy przez
Wykład 14: Pole magnetyczne cz.. dr inż. Zbigniew zklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.zklarski/ Prąd elektryczny jako źródło pola magnetycznego - doświadczenie Oersteda Kiedy przez
Równania dla potencjałów zależnych od czasu
 Równania dla potencjałów zależnych od czasu Potencjały wektorowy A( r, t i skalarny ϕ( r, t dla zależnych od czasu pola elektrycznego E( r, t i magnetycznego B( r, t definiujemy poprzez następujące zależności
Równania dla potencjałów zależnych od czasu Potencjały wektorowy A( r, t i skalarny ϕ( r, t dla zależnych od czasu pola elektrycznego E( r, t i magnetycznego B( r, t definiujemy poprzez następujące zależności
Równania Maxwella. Wstęp E B H J D
 Równania Maxwella E B t, H J D t, D, B 0 Równania materiałowe B 0 H M, D 0 E P, J E, gdzie: 0 przenikalność elektryczną próżni ( 0 8854 10 1 As/Vm), 0 przenikalność magetyczną próżni ( 0 4 10 7 Vs/Am),
Równania Maxwella E B t, H J D t, D, B 0 Równania materiałowe B 0 H M, D 0 E P, J E, gdzie: 0 przenikalność elektryczną próżni ( 0 8854 10 1 As/Vm), 0 przenikalność magetyczną próżni ( 0 4 10 7 Vs/Am),
Fale cz. 1. dr inż. Ireneusz Owczarek CMF PŁ 2012/13
 Fale cz. 1 dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 01/13 Plan wykładu Spis treści 1. Procesy falowe 1.1. Klasyfikacja fal..............................................
Fale cz. 1 dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 01/13 Plan wykładu Spis treści 1. Procesy falowe 1.1. Klasyfikacja fal..............................................
Wykład 9: Fale cz. 1. dr inż. Zbigniew Szklarski
 Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
Wykład 9: Fale cz. 1 dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Klasyfikacja fal fale mechaniczne zaburzenie przemieszczające się w ośrodku sprężystym, fale elektromagnetyczne
ZESTAW PYTAŃ I ZAGADNIEŃ NA EGZAMIN Z FIZYKI sem /13
 1 ZESTAW PYTAŃ I ZAGADNIEŃ NA EGZAMIN Z FIZYKI sem. 2 2012/13 Ruch falowy 1. Co to jest fala mechaniczna? Podaj warunki niezbędne do zaobserwowania rozchodzenia się fali mechanicznej. 2. Jaka wielkość
1 ZESTAW PYTAŃ I ZAGADNIEŃ NA EGZAMIN Z FIZYKI sem. 2 2012/13 Ruch falowy 1. Co to jest fala mechaniczna? Podaj warunki niezbędne do zaobserwowania rozchodzenia się fali mechanicznej. 2. Jaka wielkość
Ładunek elektryczny. Zastosowanie równania Laplace a w elektro- i magnetostatyce. Joanna Wojtal. Wprowadzenie. Podstawowe cechy pól siłowych
 6 czerwca 2013 Ładunek elektryczny Ciała fizyczne mogą być obdarzone (i w znacznej większości faktycznie są) ładunkiem elektrycznym. Ładunek ten może być dodatni lub ujemny. Kiedy na jednym ciele zgromadzonych
6 czerwca 2013 Ładunek elektryczny Ciała fizyczne mogą być obdarzone (i w znacznej większości faktycznie są) ładunkiem elektrycznym. Ładunek ten może być dodatni lub ujemny. Kiedy na jednym ciele zgromadzonych
Fizyka 2 Podstawy fizyki
 Fizyka Podstawy fizyki dr hab. inż. Wydział Fizyki e-mail: wrobel.studia@gmail.com konsultacje: Gmach Mechatroniki, pok. 34; środa 13-14 i po umówieniu mailowym http://www.if.pw.edu.pl/~wrobel/simr_f_17.html
Fizyka Podstawy fizyki dr hab. inż. Wydział Fizyki e-mail: wrobel.studia@gmail.com konsultacje: Gmach Mechatroniki, pok. 34; środa 13-14 i po umówieniu mailowym http://www.if.pw.edu.pl/~wrobel/simr_f_17.html
Podstawy fizyki wykład 7
 Podstawy fizyki wykład 7 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, W11, PWr Drgania Drgania i fale Drgania harmoniczne Siła sprężysta Energia drgań Składanie drgań Drgania tłumione i wymuszone Fale
Podstawy fizyki wykład 7 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, W11, PWr Drgania Drgania i fale Drgania harmoniczne Siła sprężysta Energia drgań Składanie drgań Drgania tłumione i wymuszone Fale
Z52: Algebra liniowa Zagadnienie: Zastosowania algebry liniowej Zadanie: Operatory różniczkowania, zagadnienie brzegowe.
 Z5: Algebra liniowa Zagadnienie: Zastosowania algebry liniowej Zadanie: Operatory różniczkowania zagadnienie brzegowe Dyskretne operatory różniczkowania Numeryczne obliczanie pochodnych oraz rozwiązywanie
Z5: Algebra liniowa Zagadnienie: Zastosowania algebry liniowej Zadanie: Operatory różniczkowania zagadnienie brzegowe Dyskretne operatory różniczkowania Numeryczne obliczanie pochodnych oraz rozwiązywanie
Równania Maxwella i równanie falowe
 Równania Maxwella i równanie falowe Prezentacja zawiera kopie folii omawianch na wkładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wkorzstanie niekomercjne dozwolone pod warunkiem podania
Równania Maxwella i równanie falowe Prezentacja zawiera kopie folii omawianch na wkładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wkorzstanie niekomercjne dozwolone pod warunkiem podania
Moment pędu fali elektromagnetycznej
 napisał Michał Wierzbicki Moment pędu fali elektromagnetycznej Definicja momentu pędu pola elektromagnetycznego Gęstość momentu pędu pola J w elektrodynamice definuje się za pomocą wzoru: J = r P = ɛ 0
napisał Michał Wierzbicki Moment pędu fali elektromagnetycznej Definicja momentu pędu pola elektromagnetycznego Gęstość momentu pędu pola J w elektrodynamice definuje się za pomocą wzoru: J = r P = ɛ 0
Równania Maxwella. roth t
 , H wektory natężenia pola elektrycznego i magnetycznego D, B wektory indukcji elektrycznej i magnetycznej J gęstość prądu elektrycznego Równania Maxwella D roth t B rot+ t J Dla ośrodka izotropowego D
, H wektory natężenia pola elektrycznego i magnetycznego D, B wektory indukcji elektrycznej i magnetycznej J gęstość prądu elektrycznego Równania Maxwella D roth t B rot+ t J Dla ośrodka izotropowego D
Rozdział 8. Fale elektromagnetyczne
 Rozdział 8. Fale elektromagnetyczne 208 Spis treści Widmo fal elektromagnetycznych Równanie falowe Rozchodzenie się fal elektromagnetycznych Wektor Poyntinga Podsumowanie z indukcji EM i fal EM Zadania
Rozdział 8. Fale elektromagnetyczne 208 Spis treści Widmo fal elektromagnetycznych Równanie falowe Rozchodzenie się fal elektromagnetycznych Wektor Poyntinga Podsumowanie z indukcji EM i fal EM Zadania
- Strumień mocy, który wpływa do obszaru ograniczonego powierzchnią A ( z minusem wpływa z plusem wypływa)
 37. Straty na histerezę. Sens fizyczny. Energia dostarczona do cewki ferromagnetykiem jest znacznie większa od energii otrzymanej. Energia ta jest tworzona w ferromagnetyku opisanym pętlą histerezy, stąd
37. Straty na histerezę. Sens fizyczny. Energia dostarczona do cewki ferromagnetykiem jest znacznie większa od energii otrzymanej. Energia ta jest tworzona w ferromagnetyku opisanym pętlą histerezy, stąd
Rozdział 6. Równania Maxwella. 6.1 Pierwsza para
 Rozdział 6 Równania Maxwella Podstawą elektrodynamiki klasycznej są równania Maxwella, które wiążą pola elektryczne E i magnetyczne B ze sobą oraz z ładunkami i prądami elektrycznymi. Pola E i B są funkcjami
Rozdział 6 Równania Maxwella Podstawą elektrodynamiki klasycznej są równania Maxwella, które wiążą pola elektryczne E i magnetyczne B ze sobą oraz z ładunkami i prądami elektrycznymi. Pola E i B są funkcjami
Elektrodynamika #
 Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Nazwa przedmiotu Elektrodynamika Nazwa jednostki prowadzącej przedmiot Kod ECTS 13.2.0052 Instytut Fizyki Teoretycznej
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Nazwa przedmiotu Elektrodynamika Nazwa jednostki prowadzącej przedmiot Kod ECTS 13.2.0052 Instytut Fizyki Teoretycznej
Fale elektromagnetyczne Katarzyna Weron
 Fale elektromagnetyczne Katarzyna Weron Matematyka Stosowana Kiedy mówimy myślimy Mechanika klasyczna Isaac Newton (1687) Elektrodynamika James Clerk Maxwell (1861) Teoria względności Albert Einstein (1905)
Fale elektromagnetyczne Katarzyna Weron Matematyka Stosowana Kiedy mówimy myślimy Mechanika klasyczna Isaac Newton (1687) Elektrodynamika James Clerk Maxwell (1861) Teoria względności Albert Einstein (1905)
Dr Piotr Sitarek. Instytut Fizyki, Politechnika Wrocławska
 Podstawy fizyki Wykład 11 Dr Piotr Sitarek Instytut Fizyki, Politechnika Wrocławska D. Halliday, R. Resnick, J.Walker: Podstawy Fizyki, tom 3, Wydawnictwa Naukowe PWN, Warszawa 2003. K.Sierański, K.Jezierski,
Podstawy fizyki Wykład 11 Dr Piotr Sitarek Instytut Fizyki, Politechnika Wrocławska D. Halliday, R. Resnick, J.Walker: Podstawy Fizyki, tom 3, Wydawnictwa Naukowe PWN, Warszawa 2003. K.Sierański, K.Jezierski,
Zał nr 4 do ZW. Dla grupy kursów zaznaczyć kurs końcowy. Liczba punktów ECTS charakterze praktycznym (P)
 Zał nr 4 do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim : Fizyka Nazwa w języku angielskim : Physics Kierunek studiów : Informatyka Specjalność (jeśli dotyczy) :
Zał nr 4 do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim : Fizyka Nazwa w języku angielskim : Physics Kierunek studiów : Informatyka Specjalność (jeśli dotyczy) :
1 Płaska fala elektromagnetyczna
 1 Płaska fala elektromagnetyczna 1.1 Fala w wolnej przestrzeni Rozwiązanie równań Maxwella dla zespolonych amplitud pól przemiennych sinusoidalnie, reprezentujące płaską falę elektromagnetyczną w wolnej
1 Płaska fala elektromagnetyczna 1.1 Fala w wolnej przestrzeni Rozwiązanie równań Maxwella dla zespolonych amplitud pól przemiennych sinusoidalnie, reprezentujące płaską falę elektromagnetyczną w wolnej
Promieniowanie dipolowe
 Promieniowanie dipolowe Potencjały opóźnione φ i A dla promieniowanie punktowego dipola elektrycznego wygodnie jest wyrażać przez wektor Hertza Z φ = ϵ 0 Z, spełniający niejednorodne równanie falowe A
Promieniowanie dipolowe Potencjały opóźnione φ i A dla promieniowanie punktowego dipola elektrycznego wygodnie jest wyrażać przez wektor Hertza Z φ = ϵ 0 Z, spełniający niejednorodne równanie falowe A
LASERY I ICH ZASTOSOWANIE
 LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 3 Temat: Efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą modulowania zmiany polaryzacji światła oraz
LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 3 Temat: Efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą modulowania zmiany polaryzacji światła oraz
Podstawy fizyki sezon 2 6. Indukcja magnetyczna
 Podstawy fizyki sezon 2 6. Indukcja magnetyczna Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Dotychczas
Podstawy fizyki sezon 2 6. Indukcja magnetyczna Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Dotychczas
FIZYKA 2. Janusz Andrzejewski
 FIZYKA wykład 7 Janusz Andrzejewski Niedoceniany geniusz Nikola Tesla Nikola Tesla wynalazł (lub znakomicie ulepszył) większość urządzeń, które spowodowały to, że prąd zmienny wyparł z naszych domów prąd
FIZYKA wykład 7 Janusz Andrzejewski Niedoceniany geniusz Nikola Tesla Nikola Tesla wynalazł (lub znakomicie ulepszył) większość urządzeń, które spowodowały to, że prąd zmienny wyparł z naszych domów prąd
Rodzaje fal. 1. Fale mechaniczne. 2. Fale elektromagnetyczne. 3. Fale materii. dyfrakcja elektronów
 Wykład VI Fale t t + Dt Rodzaje fal 1. Fale mechaniczne 2. Fale elektromagnetyczne 3. Fale materii dyfrakcja elektronów Fala podłużna v Przemieszczenia elementów spirali ( w prawo i w lewo) są równoległe
Wykład VI Fale t t + Dt Rodzaje fal 1. Fale mechaniczne 2. Fale elektromagnetyczne 3. Fale materii dyfrakcja elektronów Fala podłużna v Przemieszczenia elementów spirali ( w prawo i w lewo) są równoległe
[ A i ' ]=[ D ][ A i ] (2.3)
![[ A i ' ]=[ D ][ A i ] (2.3) [ A i ' ]=[ D ][ A i ] (2.3)](/thumbs/71/66132002.jpg) . WSTĘP DO TEORII SPRĘŻYSTOŚCI 1.. WSTĘP DO TEORII SPRĘŻYSTOŚCI.1. Tensory macierzy Niech macierz [D] będzie macierzą cosinusów kierunkowych [ D ]=[ i ' j ] (.1) Macierz transformowana jest równa macierzy
. WSTĘP DO TEORII SPRĘŻYSTOŚCI 1.. WSTĘP DO TEORII SPRĘŻYSTOŚCI.1. Tensory macierzy Niech macierz [D] będzie macierzą cosinusów kierunkowych [ D ]=[ i ' j ] (.1) Macierz transformowana jest równa macierzy
Podstawy elektromagnetyzmu. Wykład 2. Równania Maxwella
 Podstawy elektromagnetyzmu Wykład 2 Równania Maxwella Prawa Maxwella opisują pola Pole elektryczne... to zjawisko występujące w otoczeniu naładowanych elektrycznie obiektów lub jest skutkiem zmiennego
Podstawy elektromagnetyzmu Wykład 2 Równania Maxwella Prawa Maxwella opisują pola Pole elektryczne... to zjawisko występujące w otoczeniu naładowanych elektrycznie obiektów lub jest skutkiem zmiennego
Fale elektromagnetyczne w dielektrykach
 Fale elektromagnetyczne w dielektrykach Ryszard J. Barczyński, 2016 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Krótka historia odkrycia
Fale elektromagnetyczne w dielektrykach Ryszard J. Barczyński, 2016 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Krótka historia odkrycia
Ruch drgajacy. Drgania harmoniczne. Drgania harmoniczne... Drgania harmoniczne... Notatki. Notatki. Notatki. Notatki. dr inż.
 Ruch drgajacy dr inż. Ireneusz Owczarek CNMiF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 1 dr inż. Ireneusz Owczarek Ruch drgajacy Drgania harmoniczne Drgania oscylacje to cykliczna
Ruch drgajacy dr inż. Ireneusz Owczarek CNMiF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 1 dr inż. Ireneusz Owczarek Ruch drgajacy Drgania harmoniczne Drgania oscylacje to cykliczna
BADANIE INTERFERENCJI MIKROFAL PRZY UŻYCIU INTERFEROMETRU MICHELSONA
 ZDNIE 11 BDNIE INTERFERENCJI MIKROFL PRZY UŻYCIU INTERFEROMETRU MICHELSON 1. UKŁD DOŚWIDCZLNY nadajnik mikrofal odbiornik mikrofal 2 reflektory płytka półprzepuszczalna prowadnice do ustawienia reflektorów
ZDNIE 11 BDNIE INTERFERENCJI MIKROFL PRZY UŻYCIU INTERFEROMETRU MICHELSON 1. UKŁD DOŚWIDCZLNY nadajnik mikrofal odbiornik mikrofal 2 reflektory płytka półprzepuszczalna prowadnice do ustawienia reflektorów
cz. 2. dr inż. Zbigniew Szklarski
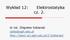 Wykład 2: lektrostatyka cz. 2. dr inż. Zbigniew zklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.zklarski/ Dygresja matematyczna - operatory Operator przyporządkowuje np. polu skalarnemu odpowiednie
Wykład 2: lektrostatyka cz. 2. dr inż. Zbigniew zklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.zklarski/ Dygresja matematyczna - operatory Operator przyporządkowuje np. polu skalarnemu odpowiednie
LASERY I ICH ZASTOSOWANIE W MEDYCYNIE
 LASERY I ICH ZASTOSOWANIE W MEDYCYNIE Laboratorium Instrukcja do ćwiczenia nr 4 Temat: Modulacja światła laserowego: efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą
LASERY I ICH ZASTOSOWANIE W MEDYCYNIE Laboratorium Instrukcja do ćwiczenia nr 4 Temat: Modulacja światła laserowego: efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą
Fala elektromagnetyczna o określonej częstotliwości ma inną długość fali w ośrodku niż w próżni. Jako przykłady policzmy:
 Rozważania rozpoczniemy od ośrodków jednorodnych. W takich ośrodkach zależność między indukcją pola elektrycznego a natężeniem pola oraz między indukcją pola magnetycznego a natężeniem pola opisana jest
Rozważania rozpoczniemy od ośrodków jednorodnych. W takich ośrodkach zależność między indukcją pola elektrycznego a natężeniem pola oraz między indukcją pola magnetycznego a natężeniem pola opisana jest
Podstawy elektromagnetyzmu. Wykład 1. Rachunek wektorowy
 Podstawy elektromagnetyzmu Wykład 1 Rachunek wektorowy Co to jest,,pole? Matematyka: odwzorowanie Rn Rm które przypisuje każdemu punktowi wartość (skalarną lub wektorową). Fizyka: Własność przestrzeni
Podstawy elektromagnetyzmu Wykład 1 Rachunek wektorowy Co to jest,,pole? Matematyka: odwzorowanie Rn Rm które przypisuje każdemu punktowi wartość (skalarną lub wektorową). Fizyka: Własność przestrzeni
Prowadzący: Kamil Fedus pokój nr 569 lub 2.20 COK konsultacje: środy
 Prowadzący: Kamil Fedus pokój nr 569 lub 2.20 COK konsultacje: środy 12 00-14 00 e-mail: kamil@fizyka.umk.pl Istotne informacje 20 spotkań (40 godzin lekcyjnych) wtorki (s. 22, 08:00-10:00), środy (s.
Prowadzący: Kamil Fedus pokój nr 569 lub 2.20 COK konsultacje: środy 12 00-14 00 e-mail: kamil@fizyka.umk.pl Istotne informacje 20 spotkań (40 godzin lekcyjnych) wtorki (s. 22, 08:00-10:00), środy (s.
Fale elektromagnetyczne
 Fale elektromagnetyczne Ryszard J. Barczyński, 2017 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Krótka historia odkrycia fali elektromagnetycznej
Fale elektromagnetyczne Ryszard J. Barczyński, 2017 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Krótka historia odkrycia fali elektromagnetycznej
REZONANSY : IDENTYFIKACJA WŁAŚCIWOŚCI PRZEZ ANALIZĘ FAL PARCJALNYCH, WYKRESY ARGANDA
 REZONANSY : IDENTYFIKACJA WŁAŚCIWOŚCI PRZEZ ANALIZĘ FAL PARCJALNYCH, WYKRESY ARGANDA Opis układu cząsteczek w mechanice kwantowej: 1. Funkcja falowa, 2. Wektora stanu ψ. TRANSFORMACJE UKŁADU CZĄSTEK: 1.
REZONANSY : IDENTYFIKACJA WŁAŚCIWOŚCI PRZEZ ANALIZĘ FAL PARCJALNYCH, WYKRESY ARGANDA Opis układu cząsteczek w mechanice kwantowej: 1. Funkcja falowa, 2. Wektora stanu ψ. TRANSFORMACJE UKŁADU CZĄSTEK: 1.
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 6 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 6 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Wprowadzenie do optyki nieliniowej
 Wprowadzenie do optyki nieliniowej Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone pod warunkiem podania
Wprowadzenie do optyki nieliniowej Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone pod warunkiem podania
Podstawy fizyki sezon 2 8. Fale elektromagnetyczne
 Podstawy fizyki sezon 8. Fale elektromagnetyczne Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Przenoszenie
Podstawy fizyki sezon 8. Fale elektromagnetyczne Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Przenoszenie
Fizyka dla Informatyków Wykład 8 Mechanika cieczy i gazów
 Fizyka dla Informatyków Wykład 8 Katedra Informatyki Stosowanej PJWSTK 2008 Spis treści Spis treści 1 Podstawowe równania hydrodynamiki 2 3 Równanie Bernoulliego 4 Spis treści Spis treści 1 Podstawowe
Fizyka dla Informatyków Wykład 8 Katedra Informatyki Stosowanej PJWSTK 2008 Spis treści Spis treści 1 Podstawowe równania hydrodynamiki 2 3 Równanie Bernoulliego 4 Spis treści Spis treści 1 Podstawowe
Kolokwium 2. Środa 14 czerwca. Zasady takie jak na pierwszym kolokwium
 Fizyka Kolokwium Środa 14 czerwca Zasady takie jak na pierwszym kolokwium 1 Fizyka w poprzednim odcinku Prawo Faradaya Fizyka B Bd S Strumień magnetyczny Jednostka: Wb (Weber) = T m d SEM dt B Siła elektromotoryczna
Fizyka Kolokwium Środa 14 czerwca Zasady takie jak na pierwszym kolokwium 1 Fizyka w poprzednim odcinku Prawo Faradaya Fizyka B Bd S Strumień magnetyczny Jednostka: Wb (Weber) = T m d SEM dt B Siła elektromotoryczna
WYMAGANIA WSTĘPNE W ZAKRESIE WIEDZY, UMIEJĘTNOŚCI I INNYCH KOMPETENCJI
 Zał. nr 4 do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim: Podstawy elektrodynamiki Nazwa w języku angielskim: Introduction to Electrodynamics Kierunek studiów (jeśli
Zał. nr 4 do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim: Podstawy elektrodynamiki Nazwa w języku angielskim: Introduction to Electrodynamics Kierunek studiów (jeśli
ZAGADNIENIA DO EGZAMINU Z FIZYKI W SEMESTRZE LETNIM 2010/11
 ZAGADNIENIA DO EGZAMINU Z FIZYKI W SEMESTRZE LETNIM 2010/11 1. Rachunek niepewności pomiaru 1.1. W jaki sposób podajemy wynik pomiaru? Co jest źródłem rozbieżności pomiędzy wartością uzyskiwaną w eksperymencie
ZAGADNIENIA DO EGZAMINU Z FIZYKI W SEMESTRZE LETNIM 2010/11 1. Rachunek niepewności pomiaru 1.1. W jaki sposób podajemy wynik pomiaru? Co jest źródłem rozbieżności pomiędzy wartością uzyskiwaną w eksperymencie
LABORATORIUM POMIARY W AKUSTYCE. ĆWICZENIE NR 4 Pomiar współczynników pochłaniania i odbicia dźwięku oraz impedancji akustycznej metodą fali stojącej
 LABORATORIUM POMIARY W AKUSTYCE ĆWICZENIE NR 4 Pomiar współczynników pochłaniania i odbicia dźwięku oraz impedancji akustycznej metodą fali stojącej 1. Cel ćwiczenia Celem ćwiczenia jest poznanie metody
LABORATORIUM POMIARY W AKUSTYCE ĆWICZENIE NR 4 Pomiar współczynników pochłaniania i odbicia dźwięku oraz impedancji akustycznej metodą fali stojącej 1. Cel ćwiczenia Celem ćwiczenia jest poznanie metody
Rozkład nauczania fizyki w klasie II liceum ogólnokształcącego w Zespole Szkół nr 53 im. S. Sempołowskiej rok szkolny 2015/2016
 Rozkład nauczania fizyki w klasie II liceum ogólnokształcącego w Zespole Szkół nr 53 im. S. Sempołowskiej rok szkolny 2015/2016 Warszawa, 31 sierpnia 2015r. Zespół Przedmiotowy z chemii i fizyki Temat
Rozkład nauczania fizyki w klasie II liceum ogólnokształcącego w Zespole Szkół nr 53 im. S. Sempołowskiej rok szkolny 2015/2016 Warszawa, 31 sierpnia 2015r. Zespół Przedmiotowy z chemii i fizyki Temat
WYMAGANIA EDUKACYJNE FIZYKA STOSOWANA II Liceum Ogólnokształcące im. Adama Asnyka w Bielsku-Białej
 WYMAGANIA EDUKACYJNE FIZYKA STOSOWANA II Liceum Ogólnokształcące im. Adama Asnyka w Bielsku-Białej OSIĄGNIĘCIA UCZNIÓW Z ZAKRESIE KSZTAŁCENIA W kolumnie "wymagania na poziom podstawowy" opisano wymagania
WYMAGANIA EDUKACYJNE FIZYKA STOSOWANA II Liceum Ogólnokształcące im. Adama Asnyka w Bielsku-Białej OSIĄGNIĘCIA UCZNIÓW Z ZAKRESIE KSZTAŁCENIA W kolumnie "wymagania na poziom podstawowy" opisano wymagania
Struktura pasmowa ciał stałych
 Struktura pasmowa ciał stałych dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Spis treści 1. Pasmowa teoria ciała stałego 2 1.1. Wstęp do teorii..............................................
Struktura pasmowa ciał stałych dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Spis treści 1. Pasmowa teoria ciała stałego 2 1.1. Wstęp do teorii..............................................
Elektrostatyka. Prawo Coulomba Natężenie pola elektrycznego Energia potencjalna pola elektrycznego
 Elektrostatyka Prawo Coulomba Natężenie pola elektrycznego Energia potencjalna pola elektrycznego 1 Prawo Coulomba odpychanie naelektryzowane szkło nie-naelektryzowana miedź F 1 4 0 q 1 q 2 r 2 0 8.85
Elektrostatyka Prawo Coulomba Natężenie pola elektrycznego Energia potencjalna pola elektrycznego 1 Prawo Coulomba odpychanie naelektryzowane szkło nie-naelektryzowana miedź F 1 4 0 q 1 q 2 r 2 0 8.85
Ψ(x, t) punkt zamocowania liny zmienna t, rozkład zaburzeń w czasie. x (lub t)
 RUCH FALOWY 1 Fale sejsmiczne Fale morskie Kamerton Interferencja RÓWNANIE FALI Fala rozchodzenie się zaburzeń w ośrodku materialnym lub próżni: fale podłużne i poprzeczne w ciałach stałych, fale podłużne
RUCH FALOWY 1 Fale sejsmiczne Fale morskie Kamerton Interferencja RÓWNANIE FALI Fala rozchodzenie się zaburzeń w ośrodku materialnym lub próżni: fale podłużne i poprzeczne w ciałach stałych, fale podłużne
1. Podstawy matematyki
 1. Podstawy matematyki 1.1. Pola Pole wiąże wielkość fizyczną z położeniem punktu w przestrzeni W przypadku, gdy pole jest zależne od czasu, możemy je zapisać jako. Najprostszym przykładem pola jest pole
1. Podstawy matematyki 1.1. Pola Pole wiąże wielkość fizyczną z położeniem punktu w przestrzeni W przypadku, gdy pole jest zależne od czasu, możemy je zapisać jako. Najprostszym przykładem pola jest pole
I. PROMIENIOWANIE CIEPLNE
 I. PROMIENIOWANIE CIEPLNE - lata '90 XIX wieku WSTĘP Widmo promieniowania elektromagnetycznego zakres "pokrycia" różnymi rodzajami fal elektromagnetycznych promieniowania zawartego w danej wiązce. rys.i.1.
I. PROMIENIOWANIE CIEPLNE - lata '90 XIX wieku WSTĘP Widmo promieniowania elektromagnetycznego zakres "pokrycia" różnymi rodzajami fal elektromagnetycznych promieniowania zawartego w danej wiązce. rys.i.1.
Fizyka - opis przedmiotu
 Fizyka - opis przedmiotu Informacje ogólne Nazwa przedmiotu Fizyka Kod przedmiotu 06.4-WI-EKP-Fiz-S16 Wydział Kierunek Wydział Budownictwa, Architektury i Inżynierii Środowiska Energetyka komunalna Profil
Fizyka - opis przedmiotu Informacje ogólne Nazwa przedmiotu Fizyka Kod przedmiotu 06.4-WI-EKP-Fiz-S16 Wydział Kierunek Wydział Budownictwa, Architektury i Inżynierii Środowiska Energetyka komunalna Profil
Propagacja fal elektromagnetycznych w różnych ośrodkach optycznych
 Prof. Dr Halina Abramczyk Technical University of Lodz, Faculty of Chemistry Institute of Applied Radiation Chemistry Poland, 93-590 Lodz, Wroblewskiego 15 Phone:(+ 48 42) 631-31-88; fax:(+ 48 42) 684
Prof. Dr Halina Abramczyk Technical University of Lodz, Faculty of Chemistry Institute of Applied Radiation Chemistry Poland, 93-590 Lodz, Wroblewskiego 15 Phone:(+ 48 42) 631-31-88; fax:(+ 48 42) 684
Elektryczność i Magnetyzm
 Elektryczność i Magnetyzm Reinhard Kulessa II semestr r. akademickiego 2006/2007 Literatura E.M. Purcell, Berkeley Physics Course, Elektryczność i Magnetyzm David J. Griffiths:, "Podstawy Eelektrodynamiki",
Elektryczność i Magnetyzm Reinhard Kulessa II semestr r. akademickiego 2006/2007 Literatura E.M. Purcell, Berkeley Physics Course, Elektryczność i Magnetyzm David J. Griffiths:, "Podstawy Eelektrodynamiki",
Dźwięk. Cechy dźwięku, natura światła
 Dźwięk. Cechy dźwięku, natura światła Fale dźwiękowe (akustyczne) - podłużne fale mechaniczne rozchodzące się w ciałach stałych, cieczach i gazach. Zakres słyszalnej częstotliwości f: 20 Hz < f < 20 000
Dźwięk. Cechy dźwięku, natura światła Fale dźwiękowe (akustyczne) - podłużne fale mechaniczne rozchodzące się w ciałach stałych, cieczach i gazach. Zakres słyszalnej częstotliwości f: 20 Hz < f < 20 000
Fizyka dla Informatyki Stosowanej
 Fizyka dla Informatyki Stosowanej Jacek Golak Semestr zimowy 8/9 Wykład nr 5 Fale elektromagnetyczne Punkt wyjścia: równania Maxwella (układ SI!) Najpierw dla próżni ε przenikalność dielektryczna próżni
Fizyka dla Informatyki Stosowanej Jacek Golak Semestr zimowy 8/9 Wykład nr 5 Fale elektromagnetyczne Punkt wyjścia: równania Maxwella (układ SI!) Najpierw dla próżni ε przenikalność dielektryczna próżni
Siły zachowawcze i energia potencjalna. Katarzyna Sznajd-Weron Mechanika i termodynamika dla matematyki stosowanej 2017/18
 Siły zachowawcze i energia potencjalna Katarzyna Sznajd-Weron Mechanika i termodynamika dla matematyki stosowanej 2017/18 Polecana literatura John R Taylor, Mechanika klasyczna, tom1 Wydawnictwo Naukowe
Siły zachowawcze i energia potencjalna Katarzyna Sznajd-Weron Mechanika i termodynamika dla matematyki stosowanej 2017/18 Polecana literatura John R Taylor, Mechanika klasyczna, tom1 Wydawnictwo Naukowe
Spis treści. Tom 1 Przedmowa do wydania polskiego 13. Przedmowa 15. Wstęp 19
 Spis treści Tom 1 Przedmowa do wydania polskiego 13 Przedmowa 15 1 Wstęp 19 1.1. Istota fizyki.......... 1 9 1.2. Jednostki........... 2 1 1.3. Analiza wymiarowa......... 2 3 1.4. Dokładność w fizyce.........
Spis treści Tom 1 Przedmowa do wydania polskiego 13 Przedmowa 15 1 Wstęp 19 1.1. Istota fizyki.......... 1 9 1.2. Jednostki........... 2 1 1.3. Analiza wymiarowa......... 2 3 1.4. Dokładność w fizyce.........
18. Siły bezwładności Siła bezwładności w ruchu postępowych Siła odśrodkowa bezwładności Siła Coriolisa
 Kinematyka 1. Podstawowe własności wektorów 5 1.1 Dodawanie (składanie) wektorów 7 1.2 Odejmowanie wektorów 7 1.3 Mnożenie wektorów przez liczbę 7 1.4 Wersor 9 1.5 Rzut wektora 9 1.6 Iloczyn skalarny wektorów
Kinematyka 1. Podstawowe własności wektorów 5 1.1 Dodawanie (składanie) wektorów 7 1.2 Odejmowanie wektorów 7 1.3 Mnożenie wektorów przez liczbę 7 1.4 Wersor 9 1.5 Rzut wektora 9 1.6 Iloczyn skalarny wektorów
Elektrostatyka, cz. 1
 Podstawy elektromagnetyzmu Wykład 3 Elektrostatyka, cz. 1 Prawo Coulomba F=k q 1 q 2 r 2 1 q1 q 2 Notka historyczna: 1767: John Priestley - sugestia 1771: Henry Cavendish - eksperyment 1785: Charles Augustin
Podstawy elektromagnetyzmu Wykład 3 Elektrostatyka, cz. 1 Prawo Coulomba F=k q 1 q 2 r 2 1 q1 q 2 Notka historyczna: 1767: John Priestley - sugestia 1771: Henry Cavendish - eksperyment 1785: Charles Augustin
Wykład 14: Indukcja cz.2.
 Wykład 14: Indukcja cz.. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. -1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 10.05.017 Wydział Informatyki, Elektroniki i 1 Przykład
Wykład 14: Indukcja cz.. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. -1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 10.05.017 Wydział Informatyki, Elektroniki i 1 Przykład
MECHANIKA 2. Zasady pracy i energii. Wykład Nr 12. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Wykład Nr 12 Zasady pracy i energii Prowadzący: dr Krzysztof Polko WEKTOR POLA SIŁ Wektor pola sił możemy zapisać w postaci: (1) Prawa strona jest gradientem funkcji Φ, czyli (2) POTENCJAŁ
MECHANIKA 2 Wykład Nr 12 Zasady pracy i energii Prowadzący: dr Krzysztof Polko WEKTOR POLA SIŁ Wektor pola sił możemy zapisać w postaci: (1) Prawa strona jest gradientem funkcji Φ, czyli (2) POTENCJAŁ
Literatura. Prowadzący: dr inż. Sławomir Bielecki adiunkt Zakład Racjonalnego Użytkowania Energii ITC PW. Zakres wykładu. Pole pojęcie fizyczne
 Prowadzący: dr inż. Sławomir Bielecki adiunkt Zakład Racjonalnego Użytkowania Energii ITC PW pok. 405A TC slawomir.bielecki@itc.pw.edu.pl http://itc.pw.edu.pl/pracownicy/naukowo-dydaktyczni/bielecki-slawomir
Prowadzący: dr inż. Sławomir Bielecki adiunkt Zakład Racjonalnego Użytkowania Energii ITC PW pok. 405A TC slawomir.bielecki@itc.pw.edu.pl http://itc.pw.edu.pl/pracownicy/naukowo-dydaktyczni/bielecki-slawomir
Fala EM w izotropowym ośrodku absorbującym
 Fala EM w izotropowym ośrodku absorbującym Fala EM powoduje generację zmienne pole elektryczne E Zmienne co do kierunku i natężenia, Pole E Nie wywołuje w ośrodku prądu elektrycznego Powoduje ruch elektronów
Fala EM w izotropowym ośrodku absorbującym Fala EM powoduje generację zmienne pole elektryczne E Zmienne co do kierunku i natężenia, Pole E Nie wywołuje w ośrodku prądu elektrycznego Powoduje ruch elektronów
Elektrodynamika Część 1 Elektrostatyka Ryszard Tanaś Zakład Optyki Nieliniowej, UAM
 Elektrodynamika Część 1 Elektrostatyka Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/\~tanas Spis treści 1 Literatura 3 2 Elektrostatyka 4 2.1 Pole elektryczne......................
Elektrodynamika Część 1 Elektrostatyka Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/\~tanas Spis treści 1 Literatura 3 2 Elektrostatyka 4 2.1 Pole elektryczne......................
Efekt naskórkowy (skin effect)
 Efekt naskórkowy (skin effect) Rozważmy cylindryczny przewód o promieniu a i o nieskończonej długości. Przez przewód płynie prąd I = I 0 cos ωt. Dla niezbyt dużych częstości ω możemy zaniedbać prąd przesunięcia,
Efekt naskórkowy (skin effect) Rozważmy cylindryczny przewód o promieniu a i o nieskończonej długości. Przez przewód płynie prąd I = I 0 cos ωt. Dla niezbyt dużych częstości ω możemy zaniedbać prąd przesunięcia,
Odziaływania fundamentalne
 Odziaływania fundamentalne silne elektromagn. słabe grawitacja Odziaływanie silne krótkozasięgowe (10-15 jadro atomowe), wymiana cięŝkich cząstek (gluony) Yukawa Odziaływania elektromagnetyczne atomy cząsteczki
Odziaływania fundamentalne silne elektromagn. słabe grawitacja Odziaływanie silne krótkozasięgowe (10-15 jadro atomowe), wymiana cięŝkich cząstek (gluony) Yukawa Odziaływania elektromagnetyczne atomy cząsteczki
Fala jest zaburzeniem, rozchodzącym się w ośrodku, przy czym żadna część ośrodka nie wykonuje zbyt dużego ruchu
 Ruch falowy Fala jest zaburzeniem, rozchodzącym się w ośrodku, przy czym żadna część ośrodka nie wykonuje zbyt dużego ruchu Fala rozchodzi się w przestrzeni niosąc ze sobą energię, ale niekoniecznie musi
Ruch falowy Fala jest zaburzeniem, rozchodzącym się w ośrodku, przy czym żadna część ośrodka nie wykonuje zbyt dużego ruchu Fala rozchodzi się w przestrzeni niosąc ze sobą energię, ale niekoniecznie musi
MECHANIKA 2. Zasady pracy i energii. Wykład Nr 12. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Wykład Nr 12 Zasady pracy i energii Prowadzący: dr Krzysztof Polko WEKTOR POLA SIŁ Wektor pola sił możemy zapisać w postaci: (1) Prawa strona jest gradientem funkcji Φ, czyli (2) POTENCJAŁ
MECHANIKA 2 Wykład Nr 12 Zasady pracy i energii Prowadzący: dr Krzysztof Polko WEKTOR POLA SIŁ Wektor pola sił możemy zapisać w postaci: (1) Prawa strona jest gradientem funkcji Φ, czyli (2) POTENCJAŁ
Wprowadzenie do technologii HDR
 Wprowadzenie do technologii HDR Konwersatorium 2 - inspiracje biologiczne mgr inż. Krzysztof Szwarc krzysztof@szwarc.net.pl Sosnowiec, 5 marca 2018 1 / 26 mgr inż. Krzysztof Szwarc Wprowadzenie do technologii
Wprowadzenie do technologii HDR Konwersatorium 2 - inspiracje biologiczne mgr inż. Krzysztof Szwarc krzysztof@szwarc.net.pl Sosnowiec, 5 marca 2018 1 / 26 mgr inż. Krzysztof Szwarc Wprowadzenie do technologii
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 2, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 17.02.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Równania Maxwella r-nie falowe
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 17.02.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Równania Maxwella r-nie falowe
POLE MAGNETYCZNE W PRÓŻNI
 POLE MAGNETYCZNE W PRÓŻNI Oprócz omówionych już oddziaływań grawitacyjnych (prawo powszechnego ciążenia) i elektrostatycznych (prawo Couloma) dostrzega się inny rodzaj oddziaływań, które nazywa się magnetycznymi.
POLE MAGNETYCZNE W PRÓŻNI Oprócz omówionych już oddziaływań grawitacyjnych (prawo powszechnego ciążenia) i elektrostatycznych (prawo Couloma) dostrzega się inny rodzaj oddziaływań, które nazywa się magnetycznymi.
Fotonika. Plan: Wykład 3: Polaryzacja światła
 Fotonika Wykład 3: Polaryzacja światła Plan: Równania Maxwella w ośrodku optycznie liniowym Równania Maxwella dla fal monochromatycznych Polaryzacja światła Fala płaska spolaryzowana Polaryzacje liniowe,
Fotonika Wykład 3: Polaryzacja światła Plan: Równania Maxwella w ośrodku optycznie liniowym Równania Maxwella dla fal monochromatycznych Polaryzacja światła Fala płaska spolaryzowana Polaryzacje liniowe,
MECHANIKA II. Praca i energia punktu materialnego
 MECHANIKA II. Praca i energia punktu materialnego Daniel Lewandowski Politechnika Wrocławska, Wydział Mechaniczny, Katedra Mechaniki i Inżynierii Materiałowej http://kmim.wm.pwr.edu.pl/lewandowski/ daniel.lewandowski@pwr.edu.pl
MECHANIKA II. Praca i energia punktu materialnego Daniel Lewandowski Politechnika Wrocławska, Wydział Mechaniczny, Katedra Mechaniki i Inżynierii Materiałowej http://kmim.wm.pwr.edu.pl/lewandowski/ daniel.lewandowski@pwr.edu.pl
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO. dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury
 KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
Elektrodynamika Część 1 Elektrostatyka Ryszard Tanaś Zakład Optyki Nieliniowej, UAM
 Elektrodynamika Część 1 Elektrostatyka Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 1 Literatura 3 2 Elektrostatyka 4 2.1 Pole elektryczne....................
Elektrodynamika Część 1 Elektrostatyka Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 1 Literatura 3 2 Elektrostatyka 4 2.1 Pole elektryczne....................
