Wykład X. ε, ε, ε = ε oznaczają współrzędne tensora odkształcenia, u i w są współrzędnymi wektora WYBRANE DZIAŁY ANALIZY MATEMATYCZNEJ
|
|
|
- Urszula Krzemińska
- 5 lat temu
- Przeglądów:
Transkrypt
1 Wykład X ROZWIĄZANIE RÓWNAŃ RÓŻNICZKOWYC Z WYKORZYSTANIEM TRANSFORMACJI LAPLACE A i FOURIERA CIĄG DALSZY. Konsolidacja półprzesrzeni konsolidujące pod działaniem ruchomego obciążenia skupionego. Rozważmy półprzesrzeń konsolidującą z powierzchnią brzegową przepuszczalną dla cieczy. Przyjmijmy że w chwili = do powierzchni brzegowej półprzesrzeni zosało nagle przyłożone obciążenie skupione rozłożone wzdłuż linii. Od momenu saru obciążenie porusza się ze sała prędkością v wzdłuż osi x. Schema zagadnienia przedsawiono na rys... Rys... Schema zagadnienia płaskiego. Zakładamy że prędkość v jes mała i zagadnienie możemy rakować jako quasisayczne. Punkem wyjścia rozważań jes układ podsawowych równań porosprężysości Bioa. Zagadnienie będzie rakowane jako płaskie w płaskim sanie odkszałcenia. Równania równowagi wewnęrznej ośrodka dwufazowego z pominięciem sił masowych maja posać nasępującą: ( ( + + = + + =. (. Przy czym = są współrzędnymi ensora naprężenia szkieleu a = pf jes naprężeniem przenoszonym przez ciecz odniesionym do jednoski powierzchni całkowiej elemenu; p oznacza ciśnienie hydrosayczne a f współczynnik porowaości objęościowej ośrodka. Związki geomeryczne w przypadku płaskiego sanu odkszałcenia mają posać: ε = u ; ε = w ; ε = ( u + w ε = ε + ε ; θ = U + W (. ε ε ε = ε oznaczają współrzędne ensora odkszałcenia u i w są współrzędnymi wekora przemieszczenia odpowiednio w kierunku osi x i x a U i W są współrzędnymi wekora
2 przemieszczenia cząsek cieczy odpowiednio w kierunku osi x i x. Związki fizyczne dla rozważanego ośrodka przyjęo w posaci podanej przez [Bioa 956]: = Nε + Qθ + Aε = Nε + Qθ + Aε = Nε = = = Aε + Qθ = Qε + Rθ (. gdzie ANQR są sałymi Bioa rozważanego ośrodka. Równania (. i (. uzupełnia równanie przepływu przez ośrodek poroway równanie Bioa Darcy ego k θ ε = D D ρgf D D (.4 przy czym k jes współczynnikiem przepuszczalności Darcy ego Oznaczając C k ρgf = równanie przepływu możemy zapisać w posaci: ρ g oznacza ciężar właściwy wody. Dθ Dε C =. (.5 D D Należy uaj podkreślić że dylaacja wysępująca w powyższych wzorach jes dylaacja pozorną szkieleu związaną z dylaacją rzeczywisą prosym związkiem: ( f ε = ε. (.6 W dalszych rozważaniach posłużymy się inną posacią równania przepływu. Wyeliminujemy z niego wielkość θ za pomocą osaniego ze związków fizycznych (. i w wyniku orzymamy: D Dε C = (.7 R D R D gdzie = Q + R. Zbiorcze równania eorii konsolidacji wyrazimy w przemieszczeniach. W ym celu w równania równowagi wewnęrznej (. podsawimy związki fizyczne (. wykorzysamy związki geomeryczne (. i po uporządkowaniu wraz równaniem przepływu (.4 napiszemy: N u + ( M + N ε = R N w + ( M + N ε = R D Dε C =. R D R D (.8
3 Równania (.8 sanowią sprzężony układ równań porosprężysości Bioa w przypadku płaskiego sanu odkszałcenia. Wyjściowy układ równań eorii konsolidacji M.A. Bioa (.8 zawiera pierwsze pochodne względem czasu o należy podać warości rozważanych funkcji w chwili =. Warunki począkowe dla ego układu równań sprawiały wielu badaczom poważne problemy. Szereg auorów (np. [Bio 956b] [McNamee i Gibson 96a] sosując do rozwiązania zagadnień ransformację Laplace a przyjmowali że w chwili = poszukiwane funkcje równają się zeru w całym badanym obszarze. Orzymane prze nich rozwiązania nie spełniają warunku począkowego. Podobnie posępowaliśmy w poprzednich rozwiązaniach zagadnień jednowymiarowych. Mówimy w akim przypadku że mamy do czynienia z efekami naychmiasowymi. Temu zagadnieniu poświecona jes praca [Derskiego Kisiela 969]. Auorzy ej pracy przyjęli że w przypadku zagadnień płaskich isnieją odkszałcenia naychmiasowe i ze wraz z nimi wysępuje naychmiasowe naprężenie cieczy różne od zera. Oznaczyli e funkcje wskaźnikiem górnym zero zn.: u w ( ( x y = u x y = = w x y = = = (.9 Warunki e jako funkcje miejsca muszą wg cyowanej pracy [Derskiego Kisiela 969] spełniać układ równań niezależny od czasu: N u + ( M + N ε = R ( N w + ( M + N ε = R C = (. oraz warunki brzegowe. Dalej auorzy ej pracy swierdzają że isnienie ych funkcji można formalnie uwzględnić przy sosowaniu na układzie równań ransformacji Laplace a określonej wzorem: def s u w u w e d = ( ( % % %. (. Zagadnieniem niezgodności przyjęych warunków począkowych z orzymanymi warościami poszukiwanych funkcji w zerze w układach równań różniczkowych zajmował się [Doesch 964. Według Doescha warości począkowe wynikają z przeszłości układu fizycznego opisanego przez równania różniczkowe. Są o warości z kórymi układ przechodząc od ujemnych osiąga chwilę = Są o więc warości: F F F F K. 4 Wyjaśnienie że warości e nie zawsze są równe warościom począkowym: F + F + F + F + K 4 o znaczy że przejście od przeszłości do przyszłości w chwili = może nie być ciągłe jes według Doescha nasępujące: Przyczyna nie leży w warościach począkowych kóre wynikają z układu i działającego w przeszłości wzbudzenia lecz na wzbudzeniu działającym w czasie = kóre w procesie włączenia wybieramy bez wzięcia pod uwagę układu. Gdy nowe funkcje wzbudzające dla nie odpowiadają funkcjom wzbudzającym z przeszłości układu dla < o znaczy gdy w chwili
4 = wysępują skoki nie można się dziwić że również warości F F F F4 K zmieniają się skokowok. Doesch swierdza również że można udowodnić fizyczną poprawność orzymanych warości w czasie = + jeżeli sosujemy na układzie ransformację Laplace a. Opisane niezgodności nie mogą wysępować w dowolnym układzie równań i sosując kryerium Doescha można określić kiedy orzymane rozwiązania na pewno posiadają przyjęe warości począkowe. I ak: K mogą być zadane dowolnie wedy Warości począkowe F F F F 4 gdy wyznacznik ze współczynników przy najwyższych pochodnych po czasie jes różny od zera. Gdy warunek en jes spełniony rozwiązania na pewno przyjmują zadane warości począkowe. Za pomocą ego kryerium ławo swierdzimy że w przypadku układu równań (. kryerium o nie jes spełnione gdyż pochodne po czasie wysępują ylko w rzecim równaniu. Skokowo przyłożone obciążenie do powierzchni brzegowej (funkcja eaviseid a wyjaśnia dlaczego w rozwiązaniach przedsawionych w pracach [Kończaka ] [Sobczyńskiej ] i wielu innych badaczy isnieją osiadania różne od zera wbrew przyjęym począkowo warościom. Przyjmując za auorem pracy [Srzelecki 97] że w chwili = + isnieją osiadania naychmiasowe i funkcja naprężenia hydrosaycznego cieczy różna od zera oznaczymy e funkcje również wskaźnikiem górnym zero. Według mnie funkcje u w powinny spełniać nasępujący układ równań niezależny od czasu: N u + ( M + N ε = R ( N w + ( M + N ε = R = ε. (. Porównując powyższy układ równań z układem równań (. zauważymy że układ równań (. różni się od układu równań wyprowadzonego przez auorów pracy [Derski Kisiel 969] równaniem przepływu. Zajmijmy się bliżej ym równaniem. W posaci zależnej od czasu równanie o ma posać: D D Dε C = (. R D R D przy czym oznacza pochodną masową względem czasu. W ogólnym przypadku funkcje i ε D są zależne od prędkości przyłożenia obciążenia do półprzesrzeni konsolidującej v r. Więc: r przy czym v = ( vx vy vz D = + vx x + vy y + vz z D Dε = ε + vxε x + vy ε y + vzε z D (.4 r oraz v = ( vx vy vz hydrosaycznego - dylaacji pozornej szkieleu ε. Prędkości v r i v r są zależne od prędkości v r są wekorami prędkości zmiany naprężenia zmiany obciążenia na powierzchni półprzesrzeni konsolidującej. Gdy prędkość ruchu obciążenia jes mała (zagadnienie quasi-sayczne i sayczne uważamy że iloczyny: v ; v ; v ; v ε ; v ε ; v ε x x y y z z x x y y z z
5 są małe i przyjmujemy równe zero. W naszym rozparywanym przypadku prędkość v r z jaką przykładamy obciążenie do powierzchni brzegowej w chwili = + jes nieskończenie duża. Uwzględniając pionowy kierunek wekora prędkości v r możemy napisać: v = v = ; v = v = ; v = v =. x x y y z z Równanie (. sprowadza się więc w chwili = + do posaci: gdyż i C ε nie zależą od czasu więc v v R R ε y y = y y (.5 = ε =. Podzielmy obie srony równania (.5 przez vy = vy i obliczmy granicę uzyskanego wyrażenia z v y dążącym do nieskończoności: C y lim = lim y vy v vy y R R sąd równanie filracji sprowadza się w chwili = + do posaci: ε (.6 ε = (.7 y y Układ równań (.8 w ineresującym nas przypadku musi spełniać nasępujące warunki graniczne: Warunki brzegowe. naprężenia pionowe w szkielecie pod poruszająca się siłą skupioną wynoszą: x Pδ ( x v η ( gdzie δ ( oznacza delę Diraca a = ; (.8 η funkcję eaviseide a.. Naprężenia syczne na powierzchni ograniczającej półprzesrzeń konsolidującą są równe zero: = = ; (.9 x. Naprężenia w cieczy na powierzchni ograniczającej półprzesrzeń konsolidującą są równe zero: x = = ; (. 4. Przemieszczenie u w nieskończonej odległości od siły skupionej P jes równe zeru: u x r x v = ; (. 5. Przemieszczenie u w nieskończononej odległości od siły skupionej P jes równe zeru:
6 w x r x v = ; (. 6. Funkcja naprężenia w cieczy w nieskończonej odległości od siły skupionej P jes równe zeru: x r x v =. (. Warunki począkowe. Opierając się na kryerium Doescha [] przyjmiemy warunki począkowe w posaci: ε =. (.4 Rozważane przez nas zagadnienie brzegowe wygodnie rozwiązać jes w ruchomym układzie odniesienia: r ξ = x v ξ = x ξ = x. (.5 Sosując w dalszym ciągu w opisie procesu pełzania zapis Einseina będziemy jednakże pamięać że układ równań przyjęy jes określony równaniami (.8. Układ równań w ruchomym układzie odniesienia sprowadza się do posaci: N u + ( M + N ε = R N w + ( M + N ε = R v v C = & & ε + ε. R R R R (.6 Warunki graniczne naomias mają posać: ξ = ξ = ξ = = = ( = Pδ ξ η (.7 u = w = = ξ ξ ξ ξ ξ ξ ε =. Rozwiązania układu równań (.6 z warunkami granicznymi (.7 przeprowadzimy sosując ransformację Laplace a:
7 ( ε θ ij εij = ( u w % ε % θ ij % εij L u w % % % % (.8 Uwzględniając warunek począkowy w posaci związku (.4 równania wyjściowe liniowej eorii konsolidacji w ruchomym układzie odniesienia po przeprowadzeniu ransformacji Laplace a mają posać: N u% + ( M + N % ε = % R N w% + ( M + N % ε = % R s v s v C % = % % % ε + % ε R R R R (.9 naomias warunki brzegowe po wykonaniu przedsawienia całkowego Fouriera funkcji obciążenia wyrażają się związkami: % % % ξ = ξ = = ξ = π = = p ( α iαξ s e dα (. u% = w% = % = ξ ξ ξ ξ ξ ξ przy czym p( α jes przekszałceniem zespolonym Fouriera funkcji obciążenia. Przejdźmy do rozwiązania układu równań (.9. Zróżniczkujmy pierwsze z równań po ξ m drugie po ξ i dodając sronami po uporządkowaniu orzymujemy równanie: gdzie K = R M ( + N. % ε = % (. K Wykonując nasępnie na równaniu przepływu obusronnie operację Laplace a orzymujemy: s v s v C % = % % % ε + % ε. (. R R R R Korzysając ze związku (. i równania (. rugujemy z ego osaniego funkcje obrazu dylaacji ε% i mamy: ( sk vk % % % (. + = gdzie K = ( ( + R M + N + C M N R Rozwiązanie równania (. ma posać:
8 = % ϕ + % ϕ %. (.4 Przy czym ϕ% jes funkcją harmoniczną spełniającą równanie: % (.5 ϕ = naomias ϕ% jes rozwiązaniem równania: % ϕ % ϕ % ϕ. (.6 sk + vk = Dla zbudowania rozwiązania szczególnego równań przemieszczeniowych (.9 wprowadźmy ransformaę Laplace a funkcji poencjału przemieszczenia Φ % zdefiniowaną związkami: def def u% = Φ % ; w% = Φ %. (.7 Wsawiając związki (.7 do równań przemieszczeniowych (.9 a nasępnie całkując pierwsze z równań względem ξ a drugie po ξ dosajemy po uporządkowaniu równanie Poissona: % %. (.8 Φ = K Z uwagi na związek (.8 i posać rozwiązania (.4 funkcję Φ % zapiszemy w posaci: Φ % = Φ % + Φ% (.9 przy czym Φ % jes funkcją biharmoniczną spełniającą równanie: % % (.4 Φ = Kϕ a Φ % jes rozwiązaniem równania:. (.4 % % Φ = Kϕ Rozwiązania (.9 jak ławo wykazać spełniają równania przemieszczeniowe (.9 i rozprzężone równanie przepływu (. naomias nie spełnia wyjściowego równania filracji. Aby spełnić o równanie należy do rozwiązania poencjalnego dodać rozwiązanie jednorodnego układu równań: N u% M N % + + ε = N w% M N %. + + ε = (.4 Rozwiązanie układu (.4 przyjmiemy w posaci funkcji Galerkina zdefiniowanej związkami: def u % = a % χ def = χ + w % b % a % χ (.4
9 przy czym równanie: + + a = M N b = M N N N naomias χ% jes funkcją biharmoniczną spełniająca χ = %. (.44 Poszukiwane rozwiązania układu równań przemieszczeniowych (.4 wyrażają się przy pomocy sumy: u% = u% + u % ; w% = w% + w %. (.45 Rozwiązania (8.5 musza spełniać równanie przepływu (.9. Prowadzi o do dodakowego warunku wiążącego funkcję ϕ% z funkcją Galerkina χ% mianowicie: KCR % %. (.46 χ = ϕ Funkcje wysępujące w rozwiązaniu przyjmiemy w posaci zespolonych całek Fouriera. Rozpoczniemy od wyznaczenia funkcji %. Zgodnie ze wzorem (.4 funkcja % jes sumą funkcji ϕ% i ϕ%. Funkcję ϕ% przyjmiemy w posaci: a i A( s e ξ αξ ϕ = α e dα π %. (.47 O akim wyborze funkcji zdecydował warunek że przy ξ bez względu na znak parameru całkowania α wszyskie funkcje wchodzące w skład rozwiązania powinny zanikać. Funkcja ϕ% ma spełniać równanie (.6 i wobec ego przyjmujemy ja w posaci: ϕ = B α s α + Kivα + Ksξ iαξ dα ( exp exp %. (.48 π W wyrażeniach (.47 i (.48 A( α s i B( s α są nieznanymi funkcjami parameru α i parameru różniczkowania s. Zgodnie ze wzorem (.4 funkcję naprężenia % wyrazimy nasępująco: = A( α s exp ( α ξ + B α s exp α + ikvα + Ksξ exp( iαξ dα π % (.49 Wykorzysując warunek brzegowy (. orzymujemy związek: ( α ( α B s = A s. (.5 Funkcja % po wyeliminowaniu ze wzoru (.49 funkcji parameru B( s α ma posać: % = A( α s exp( α ξ exp α + ikvα + Ksξ exp( iαξ dα π. (.5
10 Przejdźmy nasępnie do określenia ransformay funkcji poencjału dyfuzyjnego Φ %. Opierając się na wzorze (.9 widzimy że należy uprzednio wyznaczyć funkcje Φ % i Φ %. Funkcja Φ % jes biharmoniczna. Powinna spełniać równanie (.4. Rozwiązanie ego równania ma posać: Φ = αξ C α s αξ iαξ dα ( exp exp %. (.5 π Po podsawieniu funkcji Φ % (.5 do równanie (.4 orzymujemy związek pomiędzy funkcja parameru C ( α s i A( s α w posaci: C ( α s ( α s K A =. (.5 α α Po podsawieniu do (.5 zależności (.5 dosajemy Φ % wyrażone całką: ( α s A ξ Φ % = α ξ αξ dα. (.54 K exp π α exp( i Funkcję Φ % przyjmujemy w posaci zespolonej całki Fouriera: Φ = D α s α + ikvα + Ksξ iαξ dα ( exp exp %. (.55 π Po wykonaniu przepisanych różniczkowań wzorem (.4 dosajemy w wyniku zależność pomiędzy D ( α s i A( α s. Zależność a wyraża się związkiem: D ( α s = ( α s A K K vα i + s. (.56 Funkcję Φ % można już po uwzględnieniu związku (.56 zapisać w nasępujący sposób: ( α s K A Φ % = α + Kviα + Ksξ iαξ dα exp exp α + s π K v i. (.57 Osaecznie ransformaę Laplace a funkcji poencjału dyfuzyjnego możemy zapisać w posaci nasępującej zespolonej całki Fouriera: ( α s KA ξ exp( α ξ α Φ % = π KA( α s + exp ( α + Kviα + Ksξ exp ( iαξ dα. vα i + s (.58 Pozosała do wyznaczenia ransformaa funkcji Galerkina χ%. Przyjmiemy ją w posaci:
11 χ = F ( α s + αξg ( α s exp ( α ξ exp ( iαξ dα π %. (.59 Podsawiając wyrażenia (.59 i (.47 do warunku (.46 orzymamy zależność: G ( α s ( α s RKC A =. (.6 α Funkcja Galerkina po uwzględnieniu relacji (.6 w przesrzeni obrazu wyraża się całką: ( α s RKC A χ = F ( α s exp ( α ξ exp( iαξ dα π + α % (.6 Funkcje Φ % oraz χ% określają składowe sanu odkszałcenia i za ich pośrednicwem funkcje % ij kóre musza spełniać założone warunki brzegowe (.. Rozwiązanie szczególne po wykorzysaniu związków geomerycznych (. fizycznych (. oraz związku (.7 ma nasępująca posać: % % % % MR NQ % % MR NQ % = NΦ%. = NΦ + Φ = NΦ + Φ (.6 Rozwiązanie układu jednorodnego znajdziemy po wykorzysaniu związków (. (. i (.. Maja one posać: % = M % χ M + N % χ % = + 4 % χ + % χ ( M N ( M N % = + % χ + % χ. ( M N ( M N (.6 Rozwiązanie osaeczne ma posać: % = % + % % = % + % % = % + %. (.64 Po podsawieniu wzorów (.6 i (.6 odpowiednio zróżniczkowanych funkcji Φ % i χ% określonych wzorami (.6 oraz podsawiając ξ = orzymamy:
12 ξ= ( iαξ ( α s ( α + NKRC NKA α % ξ = = α + α α α * π A s N F s K v i s *exp dα % ( α s α NKRCA( α s NK A π α α = + + K ( viα s ( a NKA α s α α + Kviα + Ks Naα F ( α s + exp ( iαξ dα. + α (.65 Wykorzysanie warunków brzegowych (.7 oraz wzorów (.65 prowadzi do liniowego układu A s F α s : równań algebraicznych ze względu na ( α i ( ( α. ( α NKRC NKα %p + A( α s Nα α F ( α s = π K ( vα i + s s NKα NKRC α NKα α + Kviα + Ks + ( + a + A( α s + α α K ( viα + s Naα F s = (.66 Po rozwiązaniu układu równań (.66 orzymujemy: przy czym A ( α s π p( α ( vα i + s ( α + + ( α = (.67 s v i s a g s b Funkcję F ( s g α s = a α + Kviα + Ks NKRC a = NK + a NK b =. K α wyrazimy związkiem: (.68 α α α α α α F ( α s = + + a + aα α K ( vα i + s A s K RKC K + Kvi + Ks. (.69 Jak o już wspomniano p( α jes przekszałceniem Fouriera funkcji obciążenia. Korzysając z przekszałcenia całkowego Fouriera funkcji Diraca mamy: P p( α = (.7 π
13 gdzie P - obciążenie na jednoskę długości [ N / m ]. Podsawiając (.7 do wyrażenia (.67 i wykonując prose przekszałcenia algebraiczne funkcję A α s można przedsawić w nasępującej posaci: A ( α s p α α α α α = a s s v i B s + v i + A + A + Kvi + Ks ( + α + α (.7 przy czym b ab b K A = B =. a a Funkcje Φ % (.58 oraz χ% (.59 określają składowe wekora przemieszczenia u% i w%. Korzysając ze związków (.7 znajdziemy ransformay Laplace a funkcji przemieszczenia dyfuzyjnego u% i w%. A mianowicie: ξ α % i K u = ( α exp( α ξ exp ξ α α * π A s + + Kvi + Ks α α K v i *exp dα ( iαξ ( iαξ ( K α + s K ξ α α α % K + Kvi + Ks w = ( α exp ( α ξ exp ξ α α * π A s + Kvi + Ks α α K v i *exp dα. (.7 + s Drugą część rozwiązania u % i w % można wyznaczyć na podsawie zależności (.4. Po wykonaniu przepisanych zależnością (.4 działań ransformay rozwiązań orzymamy w posaci: ( ( i ( α ( α s( α ξ % i RKCa A u = + α α ( α * π a F s α exp α ξ exp αξ dα % RKCb α RKCa α w = ( α ( α ( α ξ + π A s A s α α aα F s + exp ( α ξ exp ( iαξ dα. (.7 Na podsawie związków (.9 i (.5 rozwiązania ogólne układu równań dosajemy w posaci nasępujących zespolonych całek Fouriera:
14 ( α ( α ( α ξ ξ α ( α i RKCa A s K A s u% = α α ( α * π + a F s α α Kα A( α s exp ( α ξ exp ( ξ α + Kviα + Ks exp ( iαξ dα K viα + s K ( α ξ RKC ( a α ξ α w% = ( α ( α + π A s A s α α + ( + ( α + aα F s K exp α ξ α Kviα Ks exp α Kviα Ks exp iαξ dα + ( + + ( K vi s % = ( α exp( α ξ exp( ξ α + α + exp ( αξ α π A s Kvi Ks i d (.74 przy czym A( α s i F ( s α są określone wzorami (.7 i (.69. Obecnie zgodnie z zapowiedzą wykażemy że funkcje (.74 w chwili = spełniają układ równań (.. Wykorzysamy w ym celu wierdzenie Doescha [] kóre mówi: lim F o Jeżeli isnieje sf ( s lim F = lim % ". (.75 s Po wykonaniu przejść granicznych zgodnie z (.75 orzymujemy: p ξ M + N ξξ u = arcg ( ξ K + + K M + N ξ + ξ π ( + + N N K K N p M + N w = ( + K exp ( α ξ exp ( αξ α + + i d M N α 4π ( + N N K + K N M + N ξ + ( + K + K N ξ + ξ p ξ =. M + N ξ + ξ π N ( + K + K N (.76 Jak ławo sprawdzić wypisane wyżej granice ransformay przemieszczeń i funkcji naprężeń hydrosaycznych wyrażone wzorami (.76 isonie spełniają układ równań (. z warunkami brzegowymi (.8 do (.. VIII... Wyznaczenie funkcji osiadań powierzchni półprzesrzeni konsolidującej.
15 Określenie w posaci jawnej wszyskich uzyskanych rozwiązań jes zadaniem rudnym i nie ma moim zadaniem isonego znaczenie w zasosowaniach inżynierskich. Znacznie ławiej jes uzyskać rozwiązania meodami numerycznymi co zosanie przedsawione w rozdziale IX. W dalszym ciągu ineresować nas będzie wyłącznie osiadanie obciążonej powierzchni. Określa je funkcja w% dla y =. Uzyskane rozwiązanie dla funkcji osiadań może pełnić isoną rolę w zakresie weryfikacji procedur numerycznych. Transformaa funkcji osiadań wyraża się wzorem: s + vα i + Aα + A α α + Kviα + Ks D w% = exp( iαξ dα ξ π α s s vα i Bα ( + + = ( (.77 PKRC a przy czym D =. a Aby orzymać poszukiwaną funkcję osiadania wykonamy najpierw odwroną ransformację Laplace a na funkcji w% dla y = określoną wzorem: γ + i w( ξ = w % ( ξ s exp ( s ds. (.78 π i γ i Nasępnie wykonamy przepisane wzorem (.77 całkowanie względem zmiennej α. Jak ławo swierdzić w rozwiązaniu (.77 wysępują całki ypu: exp ( i αξ d α (.79 α kóre jak wiadomo (parz [Sobczyńska 966] dla każdego ograniczonego ξ równają się nieskończoności. Zaem w dalszym posępowaniu zajmiemy się określeniem względnego osiadania powierzchni półprzesrzeni. Orzymamy je poprzez wprowadzenie dodakowego warunku że dla %. Powyższe założenie jes spełnieniem warunku ξ = ± gdzie l jes dowolnie duże w( ± l = l brzegowego (.. Sąd mamy: s + vα i + Aα + A α α + Kviα + Ks D w% = ( exp( iαξ exp( iα l dα ξ π α s s vα i Bα ( + + =. (.8 Dla lepszej przejrzysości przy obliczaniu całek wysępujących we wzorze (.8 zapiszemy go w posaci: przy czym: (% % % % % (.8 w = D I + II + III + IV ξ = gdzie
16 ( exp( αξ exp ( α s i i l I% = π α α α dα s( s + vi + B ( exp( exp( dα s ( s + vi + B ( exp( exp ( dα s( s + vi + B + + ( exp ( exp( s ( s + vi + B vα i iαξ iα l II % = π α α α Aα iαξ iα l III% = π α α α A α α Kviα Ks iαξ iα l IV% = π α α α dα. (.8 Po uwzględnieniu wyników całkowania i uporządkowaniu orzymujemy osaecznie wzór na osiadanie względne półprzesrzeni konsolidującej: ξ ( + ( + pη ξ vτ K l vτ K w( ξ = F ln + exp exp τ + ξ = 8π d Nb l τ 4τ 4τ ' ' ' ' ( A A + ( B B + ( C C D + D } F I I F I I F I I I I przy czym: (.8
17 ' B ( v i π ξ + τ ξ + vτ I A = ( ξ + v τ exp Erf τ 4 τ i d τ τ B Bτ ( l vτ ' i π + l + vτ I A = ( l + vτ exp Erf τ 4 τ i d τ τ B Bτ I I B ( ξ + vτ BK ( τ K = exp dτ BK ( τ + τ τ 4 + τ ( τ ( τ l + v K = exp dτ BK ( τ + τ τ 4 BK + τ ( ξ + v v v v v K IC = + v Erfc d τ B K B τ B K π τ τ exp ( ξ τ ( + v ' v π v τ v v τ K l IC = exp ( l + v Erfc dτ τ B K B τ B K ( ( τ + v π + v v + + I D = exp + v Erfc τ B K B B K BK v BK τ τ BK τ τ K ξ v ( ξ dτ τ ' v π v τ τ τ τ exp BK + v v BK + K l + v I = ( + D l v Erfc dτ τ B K B B K τ + τ BK (.84 gdzie: F = M + N 4( + K F = N M + N ( + K + K N M + N K ( + K N KN 4 K + K M + N F M + N K ( + K N = M N + K + ( + K N K + F = 4K B = ( K 4K ( + K ( + K K K + + ( K M + N N M + N N M + N N M + N N
18 M + N b =. M + N Zajmiemy się badaniem zbieżności całek wysępujących w rozwiązaniu oraz zbadaniem zachowania się funkcji osiadania w przypadkach granicznych. W wymienionym wzorze wysępują czery grupy całek o podobnej budowie. Nie ma porzeby zaem analizować wszyskich całek lecz jedynie reprezenaywne dla grup a mianowicie: A = τ ( ξ + vτ exp dτ 4τ ( τ K ( v ( ξ + vτ ( τ K A = exp dτ τ BK ( τ + τ 4 + τ BK i π ( ξ τ exp 4 τ τ τ B ξ + τ ξ + vτ A = + v Erf i + Bτ l + v l + vτ + ( l + vτ exp Erf τ 4 τ i d B Bτ v π v τ v v τ K ξ + v A 4 = exp ( ξ + vτ Erfc + τ B K B B K τ ( + v v τ v v τ K l exp ( l + vτ Erfc dτ. B K B B K τ (.85 Sprawdźmy najpierw czy wymienione całki są zbieżne przy dowolnych ξ z wyłączeniem punku ξ = zn. punku w kórym znajduje się obciążenie przy τ. Zajmiemy się najpierw badaniem zbieżności całek A i A. W ym celu zapiszmy je w innej posaci. Dokonując w obydwu całkach podsawienia: Orzymamy λ τ =. v ξ + Kλ λ A = exp dλ (.86 λ 4 I
19 v ξ + Kλ λ A = exp dλ. (.87 λ Bkλ + ( BK 4 BKλ + ( BK Do badania zbieżności ych całek zasosujemy kryerium całki niewłaściwej Cauchy ego kóre głosi: Jeżeli isnieje aka warość f λ λ pozosaje ograniczony gdy p > dla kórej iloczyn p λ o badana całka jes bezwzględnie zbieżna. Spełnienie ego warunku gwaranuje isnienie skończonej granicy: lim λ f p λ λ <. (.88 Przyjmując w przypadku całek A i A p = badamy granicę: v ξ + Kλ λ lim λ exp = λ 4 (.89 v ξ + K ξ K lim exp exp λ BK BK 4KB 4 KB BK BK + + λ λ λ = <. (.9 Widzimy zaem że obie całki w badanym obszarze są ograniczone. Zbadamy nasępnie zbieżność całki ' '' A. Dla uławienia dowodu rozbijmy całkę A na dwie całki A i A : ( τ ( v ' i π ( ξ τ exp 4 τ τ τ B ξ + τ ξ + vτ A = + v Erfc i + B l + v l + vτ ( l + vτ exp Erfc τ 4 τ i d B B '' i π ( ξ + vτ ξ + vτ A = ( ξ + vτ exp Erfc + 4 τ i τ τ B B ( τ l + v l + vτ ( l + vτ exp Erfc τ 4 τ i d B B (.9 (.9 przy czym:
20 A = A + A. (.9 ' '' Jeżeli całki ' A i A SA zbieżne o na mocy podsawowego wierdzenia o zbieżności całek []: '' F x dx Jeżeli zbieżne są całki i o zbieżna jes całka ± G x dx ± = ± F x G x dx i: F x G x dx F x dx G x dx. (.94 Do zbadania zbieżności ej całki skorzysamy z kryerium Cauchu ego dla przypadku gdy funkcja podcałkowa posiada osobliwość w jednej z granic całkowania. Kryerium o głosi: g Całka p F x dx dla kórej dolna granica jes punkem osobliwym jes zbieżna bezwzglednie jeżeli isnieje aka liczba α < ze isnieje granica: lim ( p x α F ( x x p <. (.95 ' Zbadajmy najpierw zbieżność całki A. Jeżeli skorzysamy z rozwinięcia asympoycznego funkcji Erfc( z (parz [Riżik Gradsein 964]: Erfc z k ( Γ k + = (.96 π exp( z k + ( z Oraz przyjmiemy że α = o na podsawie wymienionego kryerium należy zbadać granicę: τ Bτ Bτ * 4* B τ Bτ * 4* B τ lim L L = (.97 π τ τ Całka ( ξ + vτ ( ξ + vτ ( l + vτ ( l + vτ 4 4 ' A jes więc bezwzględnie zbieżna. Funkcja podcałkowa całki budowę jak całka ' A. Posępując analogicznie jak z całką '' A ma idenyczna ' '' A ławo wykazać że całka A jes A na podsawie cyowanego również bezwzględnie zbieżna. Z ego wynika że całka wierdzenia (8. jes bezwzględnie zbieżna. Do badania zbieżności całki A 4 skorzysamy z ego samego kryerium co w przypadku całki A. Korzysając z rozwiązania asympoycznego funkcji Erfc( z (8. oraz przyjmując α = o na podsawie wymienionego kryerium (8. należy zbadać granicę:
21 τ ( ξ + vτ K B K lim τ exp + π τ ( ξ τ 4τ v BK + v τ ( ξ + τ v K v B K τ L + 4 τ ( ξ τ v K + v 4 B K τ B K ( l + vτ K exp + + π τ ( τ v BK l + v 4τ τ ( + τ v K l v B K τ L = v τ K l + vτ 4 B K τ 4. (.98 Z ego wynika że funkcja A 4 dla badanego obszaru jes bezwzględnie zbieżna. W en sposób wykazaliśmy że całki wchodzące w skład wzoru są bezwzględnie zbieżne dla ξ. Zbadamy nasępnie jak zachowują się funkcje podcałkowe gdy ξ. Jak ławo swierdzić granica funkcji podcałkowych dla ξ jes skończona. Funkcja osiadań ma jednak w punkcie przyłożenia obciążenia osobliwość ypu logarymicznego. Dla warości ξ różnych od zera w przedziale ( l l osiadania są ograniczone. Zbadamy nasępnie jak zachowuje się funkcja osiadań gdy prędkość przemieszczania się obciążenia dąży do zera. Przechodząc do granicy przy v z wyrażeniem (.98 orzymamy: pη ξ ξ K l K w( ξ ξ = = ln + + = 8π F Ei Ei v Nb l 4 4 / // / // ( a a + ( b b F I I F I I (.99 przy czym
22 Ei ( ς / π i ξ iξ Ia = ξ exp Erf d τ 4Bτ τ Bτ // Ia = l Erf d I I π i l il exp τ 4Bτ τ Bτ K dτ ( + 4 KB ( τ + τ / ξ b = exp τ BK τ τ // b l K = exp dτ τ BK ( τ + τ 4 KB ( τ + τ. oznacza funkcję wykładniczo-całkową kórej przedsawienie całkowe ma posać Ei ( ς ς exp( τ dτ τ =. Porównując orzymany rezula z osiadaniem względnym w( ξ ξ = powierzchni brzegowej półprzesrzeni konsolidującej obliczonym w przypadku działania obciążenia skupionego [Srzelecki 874b] widać że wzory e są idenyczne. Zbadamy nasępnie osiadania półprzesrzeni konsolidującej w chwili = +. Po wykonaniu przejścia granicznego we wzorze Błąd! Nie można odnaleźć źródła odwołania. z orzymujemy: ( ξ ξ = lim ( ξ w = w = + ξ = =+ ( + ( + p M N K ξ ln M + N l π N ( + K + K N. (. Ławo można swierdzić że wzór (. pokrywa się z rozwiązaniem (.77 oczywiście po uwzględnieniu wpięcia dla ξ = ± l w ξ i wykonania całkowania względem α. Zbadajmy nasępnie osiadania dla. Rozparzymy je w ruchomym układzie współrzędnych. Zauważymy że funkcje podcałkowe całek wchodzących w skład wzoru: / / IC IC ID ID zależą w sposób jawny od i przy mają w granicy warość zero. Osaecznie osiadanie po czasie wyraża się wzorem:
23 ( ξ + τ ( + τ p ξ v K l v K lim w( ξ = F ln + exp exp τ + ξ = 8π d Nb l τ 4τ 4τ π i ξ + vτ ξ + vτ l + vτ l + vτ + ( ξ + vτ exp Erf i ( l + vτ exp Erf i dτ 4 τ 4 τ τ τ τ B B B Bτ + lim F (. ( BK ( ξ + vτ K l + vτ K exp exp dτ}. τ BK ( τ + τ 4 τ + τ 4 τ + τ BK Jak wykazano wcześniej wysępujące we wzorze (. całki są zbieżne w całym przedziale więc są zbieżne w przypadku całki: zmiennej ( BK ( ξ + vτ K l + vτ K S = exp exp dτ. τ BK ( τ + τ 4 τ + τ 4 τ + τ BK (. Zauważymy że przy funkcja podcałkowa dąży do zera. Pozosawimy jednak e funkcję w rozwiązaniu (. gdyż w szczególnym przypadku gdy f zn gdy mamy do czynienia z ośrodkiem sprężysym nieporowaym całka S ma warość skończoną. Rozparzmy bliżej en przypadek. Zauważymy że przy f sała B równa się zero i wówczas korzysając z ablic całek [] mamy: ξ K l K ξ lim S = lim exp exp ln f = = τ 4τ 4τ l. (. W przypadku f całka lim S =. Funkcja osiadań Błąd! Nie można odnaleźć źródła odwołania. posiada w punkcie ξ = osobliwość ypu ξ ln. Dla pozosałych l ξ w przedziale ( l l warości funkcji są ograniczone. Opierając się na pracy [Doescha 964] możemy więc swierdzić że orzymane rozwiązanie Błąd! Nie można odnaleźć źródła odwołania. jes saeczne i posiada zw. saeczność niewłaściwą. Zbadamy jeszcze przebieg osiadania gdy i v. W ym przypadku wzór (. przyjmuje posać: w ( ξ π ii p M + N + K ξ = + ln + ξ = π N ( + ( + 4( + v M N K K M N l + lim F I (.4 przy czym:
24 ξ ξ l l I = ξ exp Erf i l exp Erf i dτ 4Bτ 4 τ τ Bτ Bτ Bτ I ξ K l K = exp exp dτ. τ BK ( τ + τ 4 BK ( τ + τ 4 BK ( τ + τ Jak ławo wykazać przy f całka I dąży do zera a całka I jak o wykazano wyżej ma ξ warość ln. Osaecznie wiec osiadanie względne powierzchni wyraża się wówczas l wzorem: w ( ξ ( ν ξ = v f p Gπ ξ l = ln. (.5 Uwzględniono uaj że M odpowiada w ym przypadku sałej Lamego λ a N odpowiada modułowi odkszałcenia posaciowego G. Jak widać osiadania względne wyrażone wzorem (.5 odpowiadają ściśle rozwiązaniu Flamanda z eorii sprężysości [Nowacki 97]. Wykonane przejścia graniczne pod znakiem całki są dopuszczalne z uwagi na fak że badane wyrażenia spełniają wymagane dla akiej operacji warunki co wykazano w pracy [Srzelecki 97c].
2.1 Zagadnienie Cauchy ego dla równania jednorodnego. = f(x, t) dla x R, t > 0, (2.1)
 Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
WYBRANE DZIAŁY ANALIZY MATEMATYCZNEJ. Wykład VII Przekształcenie Fouriera.
 7. Całka Fouriera w posaci rzeczywisej. Wykład VII Przekszałcenie Fouriera. Doychczas rozparywaliśmy szeregi Fouriera funkcji w ograniczonym przedziale [ l, l] lub [ ] Teraz pokażemy analogicznie przedsawienie
7. Całka Fouriera w posaci rzeczywisej. Wykład VII Przekszałcenie Fouriera. Doychczas rozparywaliśmy szeregi Fouriera funkcji w ograniczonym przedziale [ l, l] lub [ ] Teraz pokażemy analogicznie przedsawienie
DYNAMIKA KONSTRUKCJI
 10. DYNAMIKA KONSTRUKCJI 1 10. 10. DYNAMIKA KONSTRUKCJI 10.1. Wprowadzenie Ogólne równanie dynamiki zapisujemy w posaci: M d C d Kd =P (10.1) Zapis powyższy oznacza, że równanie musi być spełnione w każdej
10. DYNAMIKA KONSTRUKCJI 1 10. 10. DYNAMIKA KONSTRUKCJI 10.1. Wprowadzenie Ogólne równanie dynamiki zapisujemy w posaci: M d C d Kd =P (10.1) Zapis powyższy oznacza, że równanie musi być spełnione w każdej
ψ przedstawia zależność
 Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
C d u. Po podstawieniu prądu z pierwszego równania do równania drugiego i uporządkowaniu składników lewej strony uzyskuje się:
 Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
Równania różniczkowe. Lista nr 2. Literatura: N.M. Matwiejew, Metody całkowania równań różniczkowych zwyczajnych.
 Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
ĆWICZENIE 7 WYZNACZANIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA. Wprowadzenie
 ĆWICZENIE 7 WYZNACZIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA Wprowadzenie Ciało drgające w rzeczywisym ośrodku z upływem czasu zmniejsza ampliudę drgań maleje energia mechaniczna
ĆWICZENIE 7 WYZNACZIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA Wprowadzenie Ciało drgające w rzeczywisym ośrodku z upływem czasu zmniejsza ampliudę drgań maleje energia mechaniczna
Całka nieoznaczona Andrzej Musielak Str 1. Całka nieoznaczona
 Całka nieoznaczona Andrzej Musielak Sr Całka nieoznaczona Całkowanie o operacja odwrona do liczenia pochodnych, zn.: f()d = F () F () = f() Z definicji oraz z abeli pochodnych funkcji elemenarnych od razu
Całka nieoznaczona Andrzej Musielak Sr Całka nieoznaczona Całkowanie o operacja odwrona do liczenia pochodnych, zn.: f()d = F () F () = f() Z definicji oraz z abeli pochodnych funkcji elemenarnych od razu
( ) ( ) ( τ) ( t) = 0
 Obliczanie wraŝliwości w dziedzinie czasu... 1 OBLICZANIE WRAśLIWOŚCI W DZIEDZINIE CZASU Meoda układu dołączonego do obliczenia wraŝliwości układu dynamicznego w dziedzinie czasu. Wyznaczane będą zmiany
Obliczanie wraŝliwości w dziedzinie czasu... 1 OBLICZANIE WRAśLIWOŚCI W DZIEDZINIE CZASU Meoda układu dołączonego do obliczenia wraŝliwości układu dynamicznego w dziedzinie czasu. Wyznaczane będą zmiany
Zasada pędu i popędu, krętu i pokrętu, energii i pracy oraz d Alemberta bryły w ruchu postępowym, obrotowym i płaskim
 Zasada pędu i popędu, kręu i pokręu, energii i pracy oraz d Alembera bryły w ruchu posępowym, obroowym i płaskim Ruch posępowy bryły Pęd ciała w ruchu posępowym obliczamy, jak dla punku maerialnego, skupiając
Zasada pędu i popędu, kręu i pokręu, energii i pracy oraz d Alembera bryły w ruchu posępowym, obroowym i płaskim Ruch posępowy bryły Pęd ciała w ruchu posępowym obliczamy, jak dla punku maerialnego, skupiając
Ruch płaski. Bryła w ruchu płaskim. (płaszczyzna kierująca) Punkty bryły o jednakowych prędkościach i przyspieszeniach. Prof.
 Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
Silniki cieplne i rekurencje
 6 FOTO 33, Lao 6 Silniki cieplne i rekurencje Jakub Mielczarek Insyu Fizyki UJ Chciałbym Pańswu zaprezenować zagadnienie, kóre pozwala, rozważając emaykę sprawności układu silników cieplnych, zapoznać
6 FOTO 33, Lao 6 Silniki cieplne i rekurencje Jakub Mielczarek Insyu Fizyki UJ Chciałbym Pańswu zaprezenować zagadnienie, kóre pozwala, rozważając emaykę sprawności układu silników cieplnych, zapoznać
Zagadnienia brzegowe dla równań eliptycznych
 Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Podstawowe wyidealizowane elementy obwodu elektrycznego Rezystor ( ) = ( ) ( ) ( ) ( ) ( ) ( ) ( τ ) i t i t u ( ) u t u t i ( ) i t. dowolny.
 Tema. Opracował: esław Dereń Kaedra Teorii Sygnałów Insyu Telekomunikacji Teleinformayki i Akusyki Poliechnika Wrocławska Prawa auorskie zasrzeżone Podsawowe wyidealizowane elemeny obwodu elekrycznego
Tema. Opracował: esław Dereń Kaedra Teorii Sygnałów Insyu Telekomunikacji Teleinformayki i Akusyki Poliechnika Wrocławska Prawa auorskie zasrzeżone Podsawowe wyidealizowane elemeny obwodu elekrycznego
Wykład 5 Elementy teorii układów liniowych stacjonarnych odpowiedź na dowolne wymuszenie
 Wykład 5 Elemeny eorii układów liniowych sacjonarnych odpowiedź na dowolne wymuszenie Prowadzący: dr inż. Tomasz Sikorski Insyu Podsaw Elekroechniki i Elekroechnologii Wydział Elekryczny Poliechnika Wrocławska
Wykład 5 Elemeny eorii układów liniowych sacjonarnych odpowiedź na dowolne wymuszenie Prowadzący: dr inż. Tomasz Sikorski Insyu Podsaw Elekroechniki i Elekroechnologii Wydział Elekryczny Poliechnika Wrocławska
Równanie przewodnictwa cieplnego (I)
 Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
VII. ZAGADNIENIA DYNAMIKI
 Konderla P. Meoda Elemenów Skończonych, eoria i zasosowania 47 VII. ZAGADNIENIA DYNAMIKI. Równanie ruchu dla zagadnienia dynamicznego Q, (7.) gdzie M NxN macierz mas, C NxN macierz łumienia, K NxN macierz
Konderla P. Meoda Elemenów Skończonych, eoria i zasosowania 47 VII. ZAGADNIENIA DYNAMIKI. Równanie ruchu dla zagadnienia dynamicznego Q, (7.) gdzie M NxN macierz mas, C NxN macierz łumienia, K NxN macierz
Pobieranie próby. Rozkład χ 2
 Graficzne przedsawianie próby Hisogram Esymaory przykład Próby z rozkładów cząskowych Próby ze skończonej populacji Próby z rozkładu normalnego Rozkład χ Pobieranie próby. Rozkład χ Posać i własności Znaczenie
Graficzne przedsawianie próby Hisogram Esymaory przykład Próby z rozkładów cząskowych Próby ze skończonej populacji Próby z rozkładu normalnego Rozkład χ Pobieranie próby. Rozkład χ Posać i własności Znaczenie
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania. Podstawy Automatyki
 Poliechnika Gdańska Wydział Elekroechniki i Auomayki Kaedra Inżynierii Sysemów Serowania Podsawy Auomayki Repeyorium z Podsaw auomayki Zadania do ćwiczeń ermin T15 Opracowanie: Kazimierz Duzinkiewicz,
Poliechnika Gdańska Wydział Elekroechniki i Auomayki Kaedra Inżynierii Sysemów Serowania Podsawy Auomayki Repeyorium z Podsaw auomayki Zadania do ćwiczeń ermin T15 Opracowanie: Kazimierz Duzinkiewicz,
Szeregi Fouriera. Powyższe współczynniki można wyznaczyć analitycznie z następujących zależności:
 Trygonomeryczny szereg Fouriera Szeregi Fouriera Każdy okresowy sygnał x() o pulsacji podsawowej ω, spełniający warunki Dirichlea:. całkowalny w okresie: gdzie T jes okresem funkcji x(), 2. posiadający
Trygonomeryczny szereg Fouriera Szeregi Fouriera Każdy okresowy sygnał x() o pulsacji podsawowej ω, spełniający warunki Dirichlea:. całkowalny w okresie: gdzie T jes okresem funkcji x(), 2. posiadający
Dystrybucje, wiadomości wstępne (I)
 Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Wykład 4 Metoda Klasyczna część III
 Teoria Obwodów Wykład 4 Meoda Klasyczna część III Prowadzący: dr inż. Tomasz Sikorski Insyu Podsaw Elekroechniki i Elekroechnologii Wydział Elekryczny Poliechnika Wrocławska D-, 5/8 el: (7) 3 6 fax: (7)
Teoria Obwodów Wykład 4 Meoda Klasyczna część III Prowadzący: dr inż. Tomasz Sikorski Insyu Podsaw Elekroechniki i Elekroechnologii Wydział Elekryczny Poliechnika Wrocławska D-, 5/8 el: (7) 3 6 fax: (7)
Dynamiczne formy pełzania i relaksacji (odprężenia) górotworu
 Henryk FILCEK Akademia Górniczo-Hunicza, Kraków Dynamiczne formy pełzania i relaksacji (odprężenia) góroworu Sreszczenie W pracy podano rozważania na ema możliwości wzbogacenia reologicznego równania konsyuywnego
Henryk FILCEK Akademia Górniczo-Hunicza, Kraków Dynamiczne formy pełzania i relaksacji (odprężenia) góroworu Sreszczenie W pracy podano rozważania na ema możliwości wzbogacenia reologicznego równania konsyuywnego
1 Relacje i odwzorowania
 Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Krzywe na płaszczyźnie.
 Krzwe na płaszczźnie. Współrzędne paramerczne i biegunowe. Współrzędne biegunowe. Dan jes punk O, zwan biegunem, kór sanowi począek półprosej, zwanej półosią. Dowoln punk P na płaszczźnie można opisać
Krzwe na płaszczźnie. Współrzędne paramerczne i biegunowe. Współrzędne biegunowe. Dan jes punk O, zwan biegunem, kór sanowi począek półprosej, zwanej półosią. Dowoln punk P na płaszczźnie można opisać
Sformułowanie Schrödingera mechaniki kwantowej. Fizyka II, lato
 Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.
Sformułowanie Schrödingera mechaniki kwanowej Fizyka II, lao 018 1 Wprowadzenie Posać funkcji falowej dla fali de Broglie a, sin sin k 1 Jes o przypadek jednowymiarowy Posać a zosała określona meodą zgadywania.
WNIOSKOWANIE STATYSTYCZNE
 Wnioskowanie saysyczne w ekonomerycznej analizie procesu produkcyjnego / WNIOSKOWANIE STATYSTYCZNE W EKONOMETRYCZNEJ ANAIZIE PROCESU PRODUKCYJNEGO Maeriał pomocniczy: proszę przejrzeć srony www.cyf-kr.edu.pl/~eomazur/zadl4.hml
Wnioskowanie saysyczne w ekonomerycznej analizie procesu produkcyjnego / WNIOSKOWANIE STATYSTYCZNE W EKONOMETRYCZNEJ ANAIZIE PROCESU PRODUKCYJNEGO Maeriał pomocniczy: proszę przejrzeć srony www.cyf-kr.edu.pl/~eomazur/zadl4.hml
Lista nr Znaleźć rozwiązania ogólne następujących równań różniczkowych: a) y = y t,
 RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE B Lisa nr 1 1. Napisać równanie różniczkowe, jakie spełnia napięcie u = u() na okładkach kondensaora w obwodzie zawierającym połączone szeregowo oporność R i pojemność C,
RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE B Lisa nr 1 1. Napisać równanie różniczkowe, jakie spełnia napięcie u = u() na okładkach kondensaora w obwodzie zawierającym połączone szeregowo oporność R i pojemność C,
Równania różniczkowe cząstkowe drugiego rzędu
 Równania różniczkowe cząstkowe drugiego rzędu Marcin Orchel Spis treści 1 Wstęp 1 1.1 Metoda faktoryzacji (rozdzielania zmiennych)................ 5 1.2 Metoda funkcji Greena.............................
Równania różniczkowe cząstkowe drugiego rzędu Marcin Orchel Spis treści 1 Wstęp 1 1.1 Metoda faktoryzacji (rozdzielania zmiennych)................ 5 1.2 Metoda funkcji Greena.............................
Praca domowa nr 1. Metodologia Fizyki. Grupa 1. Szacowanie wartości wielkości fizycznych Zad Stoisz na brzegu oceanu, pogoda jest idealna,
 Praca domowa nr. Meodologia Fizyki. Grupa. Szacowanie warości wielkości fizycznych Zad... Soisz na brzegu oceanu, pogoda jes idealna, powierze przeźroczyse; proszę oszacować jak daleko od Ciebie znajduje
Praca domowa nr. Meodologia Fizyki. Grupa. Szacowanie warości wielkości fizycznych Zad... Soisz na brzegu oceanu, pogoda jes idealna, powierze przeźroczyse; proszę oszacować jak daleko od Ciebie znajduje
2. Wprowadzenie. Obiekt
 POLITECHNIKA WARSZAWSKA Insyu Elekroenergeyki, Zakład Elekrowni i Gospodarki Elekroenergeycznej Bezpieczeńswo elekroenergeyczne i niezawodność zasilania laoraorium opracował: prof. dr ha. inż. Józef Paska,
POLITECHNIKA WARSZAWSKA Insyu Elekroenergeyki, Zakład Elekrowni i Gospodarki Elekroenergeycznej Bezpieczeńswo elekroenergeyczne i niezawodność zasilania laoraorium opracował: prof. dr ha. inż. Józef Paska,
Rachunek różniczkowy i całkowy 2016/17
 Rachunek różniczkowy i całkowy 26/7 Zadania domowe w pakietach tygodniowych Tydzień 3-7..26 Zadanie O. Czy dla wszelkich zbiorów A, B i C zachodzą następujące równości: (A B)\C = (A\C) (B\C), A\(B\C) =
Rachunek różniczkowy i całkowy 26/7 Zadania domowe w pakietach tygodniowych Tydzień 3-7..26 Zadanie O. Czy dla wszelkich zbiorów A, B i C zachodzą następujące równości: (A B)\C = (A\C) (B\C), A\(B\C) =
Metody Lagrange a i Hamiltona w Mechanice
 Meody Lagrange a i Hamilona w Mechanice Mariusz Przybycień Wydział Fizyki i Informayki Sosowanej Akademia Górniczo-Hunicza Wykład 7 M. Przybycień (WFiIS AGH) Meody Lagrange a i Hamilona... Wykład 7 1 /
Meody Lagrange a i Hamilona w Mechanice Mariusz Przybycień Wydział Fizyki i Informayki Sosowanej Akademia Górniczo-Hunicza Wykład 7 M. Przybycień (WFiIS AGH) Meody Lagrange a i Hamilona... Wykład 7 1 /
Matematyka ubezpieczeń majątkowych r. ma złożony rozkład Poissona. W tabeli poniżej podano rozkład prawdopodobieństwa ( )
 Zadanie. Zmienna losowa: X = Y +... + Y N ma złożony rozkład Poissona. W abeli poniżej podano rozkład prawdopodobieńswa składnika sumy Y. W ejże abeli podano akże obliczone dla k = 0... 4 prawdopodobieńswa
Zadanie. Zmienna losowa: X = Y +... + Y N ma złożony rozkład Poissona. W abeli poniżej podano rozkład prawdopodobieńswa składnika sumy Y. W ejże abeli podano akże obliczone dla k = 0... 4 prawdopodobieńswa
1.1 Przegląd wybranych równań i modeli fizycznych. , u x1 x 2
 Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
27. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
 27. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE 27.1. Wiadomości wstępne Równaniem różniczkowym cząstkowym nazywamy związek w którym występuje funkcja niewiadoma u dwóch lub większej liczby zmiennych niezależnych i
27. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE 27.1. Wiadomości wstępne Równaniem różniczkowym cząstkowym nazywamy związek w którym występuje funkcja niewiadoma u dwóch lub większej liczby zmiennych niezależnych i
GEOTECHNIKA KIERUNEK GEODEZJA I KARTOGRAFIA. 9. MODELE REOLOGICZNE GRUNTÓW I SKAŁ Monika Bartlewska
 9.. Modele reologiczne 9. MODEE REOOGICZNE GRUNTÓW I KAŁ Monika Barlewska W poprzednim rozdziale przyjęliśmy założenie, że szkiele grunowy jes ciałem nieodkszałcalnym, a jeżeli dopuszczamy jakieś odkszałcenia
9.. Modele reologiczne 9. MODEE REOOGICZNE GRUNTÓW I KAŁ Monika Barlewska W poprzednim rozdziale przyjęliśmy założenie, że szkiele grunowy jes ciałem nieodkszałcalnym, a jeżeli dopuszczamy jakieś odkszałcenia
[ P ] T PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES. [ u v u v u v ] T. wykład 4. Element trójkątny płaski stan (naprężenia lub odkształcenia)
![[ P ] T PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES. [ u v u v u v ] T. wykład 4. Element trójkątny płaski stan (naprężenia lub odkształcenia) [ P ] T PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES. [ u v u v u v ] T. wykład 4. Element trójkątny płaski stan (naprężenia lub odkształcenia)](/thumbs/88/115575588.jpg) PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES wykład 4 Element trójkątny płaski stan (naprężenia lub odkształcenia) Obszar zdyskretyzowany trójkątami U = [ u v u v u v ] T stopnie swobody elementu P = [ P ]
PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES wykład 4 Element trójkątny płaski stan (naprężenia lub odkształcenia) Obszar zdyskretyzowany trójkątami U = [ u v u v u v ] T stopnie swobody elementu P = [ P ]
ROCZNIKI INŻYNIERII BUDOWLANEJ ZESZYT 7/2007 Komisja Inżynierii Budowlanej Oddział Polskiej Akademii Nauk w Katowicach
 ROZNIKI INŻYNIERII BUDOWLANEJ ZESZYT 7/007 Komisja Inżynierii Budowlanej Oddział Polskiej Akademii Nauk w Kaowicach WYZNAZANIE PARAMETRÓW FUNKJI PEŁZANIA DREWNA W UJĘIU LOSOWYM * Kamil PAWLIK Poliechnika
ROZNIKI INŻYNIERII BUDOWLANEJ ZESZYT 7/007 Komisja Inżynierii Budowlanej Oddział Polskiej Akademii Nauk w Kaowicach WYZNAZANIE PARAMETRÓW FUNKJI PEŁZANIA DREWNA W UJĘIU LOSOWYM * Kamil PAWLIK Poliechnika
POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA i ENERGETYKI INSTYTUT MASZYN i URZĄDZEŃ ENERGETYCZNYCH
 POLIECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA i ENERGEYKI INSYU MASZYN i URZĄDZEŃ ENERGEYCZNYCH IDENYFIKACJA PARAMERÓW RANSMIANCJI Laboraorium auomayki (A ) Opracował: Sprawdził: Zawierdził:
POLIECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA i ENERGEYKI INSYU MASZYN i URZĄDZEŃ ENERGEYCZNYCH IDENYFIKACJA PARAMERÓW RANSMIANCJI Laboraorium auomayki (A ) Opracował: Sprawdził: Zawierdził:
Dyskretny proces Markowa
 Procesy sochasyczne WYKŁAD 4 Dyskreny roces Markowa Rozarujemy roces sochasyczny X, w kórym aramer jes ciągły zwykle. Będziemy zakładać, że zbiór sanów jes co najwyżej rzeliczalny. Proces X, jes rocesem
Procesy sochasyczne WYKŁAD 4 Dyskreny roces Markowa Rozarujemy roces sochasyczny X, w kórym aramer jes ciągły zwykle. Będziemy zakładać, że zbiór sanów jes co najwyżej rzeliczalny. Proces X, jes rocesem
1. Liczby zespolone Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą. (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną?
 1. Liczby zespolone 1.1. Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną? 1.2. Doprowadzić do postaci a + ib liczby zespolone (i) (1 13i)/(1 3i),
1. Liczby zespolone 1.1. Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną? 1.2. Doprowadzić do postaci a + ib liczby zespolone (i) (1 13i)/(1 3i),
y 1 y 2 = f 2 (t, y 1, y 2,..., y n )... y n = f n (t, y 1, y 2,..., y n ) f 1 (t, y 1, y 2,..., y n ) y = f(t, y),, f(t, y) =
 Uk lady równań różniczkowych Pojȩcia wsȩpne Uk ladem równań różniczkowych nazywamy uk lad posaci y = f (, y, y 2,, y n ) y 2 = f 2 (, y, y 2,, y n ) y n = f n (, y, y 2,, y n ) () funkcje f j, j =, 2,,
Uk lady równań różniczkowych Pojȩcia wsȩpne Uk ladem równań różniczkowych nazywamy uk lad posaci y = f (, y, y 2,, y n ) y 2 = f 2 (, y, y 2,, y n ) y n = f n (, y, y 2,, y n ) () funkcje f j, j =, 2,,
5 Równania różniczkowe zwyczajne rzędu drugiego
 5 Równania różniczkowe zwyczajne rzędu drugiego Definicja 5.1. Równaniem różniczkowym zwyczajnym rzędu drugiego nazywamy równanie postaci F ( x, y, y, y ) = 0, (12) w którym niewiadomą jest funkcja y =
5 Równania różniczkowe zwyczajne rzędu drugiego Definicja 5.1. Równaniem różniczkowym zwyczajnym rzędu drugiego nazywamy równanie postaci F ( x, y, y, y ) = 0, (12) w którym niewiadomą jest funkcja y =
Wojewódzki Konkurs Matematyczny dla uczniów gimnazjów. Etap szkolny 5 listopada 2013 Czas 90 minut
 Wojewódzki Konkurs Maemayczny dla uczniów gimnazjów. Eap szkolny 5 lisopada 2013 Czas 90 minu ZADANIA ZAMKNIĘTE Zadanie 1. (1 punk) Liczby A = 0, 99, B = 0, 99 2, C = 0, 99 3, D = 0, 99, E=0, 99 1 usawiono
Wojewódzki Konkurs Maemayczny dla uczniów gimnazjów. Eap szkolny 5 lisopada 2013 Czas 90 minu ZADANIA ZAMKNIĘTE Zadanie 1. (1 punk) Liczby A = 0, 99, B = 0, 99 2, C = 0, 99 3, D = 0, 99, E=0, 99 1 usawiono
DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Rys Model układu
 Ćwiczenie 7 DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Cel ćwiczenia Doświadczalne wyznaczenie częstości drgań własnych układu o dwóch stopniach swobody, pokazanie postaci drgań odpowiadających
Ćwiczenie 7 DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Cel ćwiczenia Doświadczalne wyznaczenie częstości drgań własnych układu o dwóch stopniach swobody, pokazanie postaci drgań odpowiadających
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa.
 VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
RÓWNANIA RÓŻNICZKOWE WYKŁAD 13
 RÓWNANIA RÓŻNICZKOWE WYKŁAD 13 Geomeria różniczkowa Geomeria różniczkowa o dział maemayki, w kórym do badania obieków geomerycznych wykorzysuje się meody opare na rachunku różniczkowym. Obieky geomeryczne
RÓWNANIA RÓŻNICZKOWE WYKŁAD 13 Geomeria różniczkowa Geomeria różniczkowa o dział maemayki, w kórym do badania obieków geomerycznych wykorzysuje się meody opare na rachunku różniczkowym. Obieky geomeryczne
Część I. MECHANIKA. Wykład KINEMATYKA PUNKTU MATERIALNEGO. Ruch jednowymiarowy Ruch na płaszczyźnie i w przestrzeni.
 Część I. MECHANIKA Wykład.. KINEMATYKA PUNKTU MATERIALNEGO Ruch jednowymiarowy Ruch na płaszczyźnie i w przesrzeni 1 KINEMATYKA PUNKTU MATERIALNEGO KINEMATYKA zajmuje się opisem ruchu ciał bez rozparywania
Część I. MECHANIKA Wykład.. KINEMATYKA PUNKTU MATERIALNEGO Ruch jednowymiarowy Ruch na płaszczyźnie i w przesrzeni 1 KINEMATYKA PUNKTU MATERIALNEGO KINEMATYKA zajmuje się opisem ruchu ciał bez rozparywania
Układy równań i równania wyższych rzędów
 Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
1. Liczby zespolone Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą. (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną?
 1. Liczby zespolone 1.1. Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną? 1.2. Doprowadzić do postaci a + ib liczby zespolone (i) (1 13i)/(1 3i),
1. Liczby zespolone 1.1. Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną? 1.2. Doprowadzić do postaci a + ib liczby zespolone (i) (1 13i)/(1 3i),
E k o n o m e t r i a S t r o n a 1. Nieliniowy model ekonometryczny
 E k o n o m e r i a S r o n a Nieliniowy model ekonomeryczny Jednorównaniowy model ekonomeryczny ma posać = f( X, X,, X k, ε ) gdzie: zmienna objaśniana, X, X,, X k zmienne objaśniające, ε - składnik losowy,
E k o n o m e r i a S r o n a Nieliniowy model ekonomeryczny Jednorównaniowy model ekonomeryczny ma posać = f( X, X,, X k, ε ) gdzie: zmienna objaśniana, X, X,, X k zmienne objaśniające, ε - składnik losowy,
oznacza przyrost argumentu (zmiennej niezależnej) x 3A82 (Definicja). Granicę (właściwą) ilorazu różnicowego funkcji f w punkcie x x x e x lim x lim
 WYKŁAD 9 34 Pochodna nkcji w pnkcie Inerpreacja geomerczna pochodnej Własności pochodnch Twierdzenia Rolle a Lagrange a Cach ego Regla de lhôspiala Niech ( ) O( ) będzie nkcją określoną w pewnm ooczeni
WYKŁAD 9 34 Pochodna nkcji w pnkcie Inerpreacja geomerczna pochodnej Własności pochodnch Twierdzenia Rolle a Lagrange a Cach ego Regla de lhôspiala Niech ( ) O( ) będzie nkcją określoną w pewnm ooczeni
1. Liczby zespolone Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą. (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną?
 1. Liczby zespolone 1.1. Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną? 1.2. Doprowadzić do postaci a + ib liczby zespolone (i) (1 13i)/(1 3i),
1. Liczby zespolone 1.1. Stwierdzić kiedy kwadrat liczby zespolonej jest liczbą (i) rzeczywistą, (ii) ujemną, (iii) tylko urojoną? 1.2. Doprowadzić do postaci a + ib liczby zespolone (i) (1 13i)/(1 3i),
WYKŁAD FIZYKAIIIB 2000 Drgania tłumione
 YKŁD FIZYKIIIB Drgania łumione (gasnące, zanikające). F siła łumienia; r F r b& b współczynnik łumienia [ Nm s] m & F m & && & k m b m F r k b& opis różnych zjawisk izycznych Niech Ce p p p p 4 ± Trzy
YKŁD FIZYKIIIB Drgania łumione (gasnące, zanikające). F siła łumienia; r F r b& b współczynnik łumienia [ Nm s] m & F m & && & k m b m F r k b& opis różnych zjawisk izycznych Niech Ce p p p p 4 ± Trzy
Definicja i własności wartości bezwzględnej.
 Równania i nierówności z wartością bezwzględną. Rozwiązywanie układów dwóch (trzech) równań z dwiema (trzema) niewiadomymi. Układy równań liniowych z parametrem, analiza rozwiązań. Definicja i własności
Równania i nierówności z wartością bezwzględną. Rozwiązywanie układów dwóch (trzech) równań z dwiema (trzema) niewiadomymi. Układy równań liniowych z parametrem, analiza rozwiązań. Definicja i własności
1 Równania różniczkowe zwyczajne o rozdzielonych zmiennych
 Równania różniczkowe zwyczajne o rozdzielonych zmiennych Definicja. Równaniem różniczkowym o rozdzielonych zmiennych nazywamy równanie postaci p(y) = q() (.) rozwiązanie równania sprowadza się do postaci
Równania różniczkowe zwyczajne o rozdzielonych zmiennych Definicja. Równaniem różniczkowym o rozdzielonych zmiennych nazywamy równanie postaci p(y) = q() (.) rozwiązanie równania sprowadza się do postaci
ANALIZA MATEMATYCZNA Z ELEMENTAMI STATYSTYKI MATEMATYCZNEJ
 ANALIZA MATEMATYCZNA Z ELEMENTAMI STATYSTYKI MATEMATYCZNEJ FUNKCJE DWÓCH ZMIENNYCH RZECZYWISTYCH Definicja 1. Niech A będzie dowolnym niepustym zbiorem. Metryką w zbiorze A nazywamy funkcję rzeczywistą
ANALIZA MATEMATYCZNA Z ELEMENTAMI STATYSTYKI MATEMATYCZNEJ FUNKCJE DWÓCH ZMIENNYCH RZECZYWISTYCH Definicja 1. Niech A będzie dowolnym niepustym zbiorem. Metryką w zbiorze A nazywamy funkcję rzeczywistą
Kinematyka W Y K Ł A D I. Ruch jednowymiarowy. 2-1 Przemieszczenie, prędkość. x = x 2 - x x t
 Wykład z fizyki. Pior Posmykiewicz W Y K Ł A D I Ruch jednowymiarowy Kinemayka Zaczniemy wykład z fizyki od badania przedmioów będących w ruchu. Dział fizyki, kóry zajmuje się badaniem ruchu ciał bez wnikania
Wykład z fizyki. Pior Posmykiewicz W Y K Ł A D I Ruch jednowymiarowy Kinemayka Zaczniemy wykład z fizyki od badania przedmioów będących w ruchu. Dział fizyki, kóry zajmuje się badaniem ruchu ciał bez wnikania
Rozwiązywanie zależności rekurencyjnych metodą równania charakterystycznego
 Rozwiązywanie zależności rekurencyjnych metodą równania charakterystycznego WMS, 2019 1 Wstęp Niniejszy dokument ma na celu prezentację w teorii i na przykładach rozwiązywania szczególnych typów równań
Rozwiązywanie zależności rekurencyjnych metodą równania charakterystycznego WMS, 2019 1 Wstęp Niniejszy dokument ma na celu prezentację w teorii i na przykładach rozwiązywania szczególnych typów równań
Pole magnetyczne magnesu w kształcie kuli
 napisał Michał Wierzbicki Pole magnetyczne magnesu w kształcie kuli Rozważmy kulę o promieniu R, wykonaną z materiału ferromagnetycznego o stałej magnetyzacji M = const, skierowanej wzdłuż osi z. Gęstość
napisał Michał Wierzbicki Pole magnetyczne magnesu w kształcie kuli Rozważmy kulę o promieniu R, wykonaną z materiału ferromagnetycznego o stałej magnetyzacji M = const, skierowanej wzdłuż osi z. Gęstość
Nieskończona jednowymiarowa studnia potencjału
 Nieskończona jednowymiarowa studnia potencjału Zagadnienie dane jest następująco: znaleźć funkcje własne i wartości własne operatora energii dla cząstki umieszczonej w nieskończonej studni potencjału,
Nieskończona jednowymiarowa studnia potencjału Zagadnienie dane jest następująco: znaleźć funkcje własne i wartości własne operatora energii dla cząstki umieszczonej w nieskończonej studni potencjału,
Przekształcenie Laplace a. Definicja i własności, transformaty podstawowych sygnałów
 Przekzałcenie Laplace a Deinicja i właności, ranormay podawowych ygnałów Tranormaą Laplace a unkcji je unkcja S zmiennej zepolonej, kórą oznacza ię naępująco: L[ ] unkcja S nazywana bywa również unkcją
Przekzałcenie Laplace a Deinicja i właności, ranormay podawowych ygnałów Tranormaą Laplace a unkcji je unkcja S zmiennej zepolonej, kórą oznacza ię naępująco: L[ ] unkcja S nazywana bywa również unkcją
Funkcje analityczne. Wykład 12
 Funkcje analityczne. Wykład 2 Szeregi Laurenta. Osobliwości funkcji zespolonych. Twierdzenie o residuach Paweł Mleczko Funkcje analityczne (rok akademicki 206/207) Plan wykładu W czasie wykładu omawiać
Funkcje analityczne. Wykład 2 Szeregi Laurenta. Osobliwości funkcji zespolonych. Twierdzenie o residuach Paweł Mleczko Funkcje analityczne (rok akademicki 206/207) Plan wykładu W czasie wykładu omawiać
Podstawowe przypadki (stany) obciążenia elementów : 1. Rozciąganie lub ściskanie 2. Zginanie 3. Skręcanie 4. Ścinanie
 Podstawowe przypadki (stany) obciążenia elementów : 1. Rozciąganie lub ściskanie 2. Zginanie 3. Skręcanie 4. Ścinanie Rozciąganie lub ściskanie Zginanie Skręcanie Ścinanie 1. Pręt rozciągany lub ściskany
Podstawowe przypadki (stany) obciążenia elementów : 1. Rozciąganie lub ściskanie 2. Zginanie 3. Skręcanie 4. Ścinanie Rozciąganie lub ściskanie Zginanie Skręcanie Ścinanie 1. Pręt rozciągany lub ściskany
KURS EKONOMETRIA. Lekcja 1 Wprowadzenie do modelowania ekonometrycznego ZADANIE DOMOWE. Strona 1
 KURS EKONOMETRIA Lekcja 1 Wprowadzenie do modelowania ekonomerycznego ZADANIE DOMOWE www.erapez.pl Srona 1 Część 1: TEST Zaznacz poprawną odpowiedź (ylko jedna jes prawdziwa). Pyanie 1 Kóre z poniższych
KURS EKONOMETRIA Lekcja 1 Wprowadzenie do modelowania ekonomerycznego ZADANIE DOMOWE www.erapez.pl Srona 1 Część 1: TEST Zaznacz poprawną odpowiedź (ylko jedna jes prawdziwa). Pyanie 1 Kóre z poniższych
ĆWICZENIE NR 43 U R I (1)
 ĆWCZENE N 43 POMY OPO METODĄ TECHNCZNĄ Cel ćwiczenia: wyznaczenie warości oporu oporników poprzez pomiary naężania prądu płynącego przez opornik oraz napięcia na oporniku Wsęp W celu wyznaczenia warości
ĆWCZENE N 43 POMY OPO METODĄ TECHNCZNĄ Cel ćwiczenia: wyznaczenie warości oporu oporników poprzez pomiary naężania prądu płynącego przez opornik oraz napięcia na oporniku Wsęp W celu wyznaczenia warości
Granica i ciągłość funkcji. 1 Granica funkcji rzeczywistej jednej zmiennej rzeczywsitej
 Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus listopada 07r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus listopada 07r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
ANALIZA MATEMATYCZNA
 ANALIZA MATEMATYCZNA TABLICE Spis treści: 1.) Pochodne wzory 2 2.) Całki wzory 3 3.) Kryteria zbieżności szeregów 4 4.) Przybliżona wartość wyrażenia 5 5.) Równanie płaszczyzny stycznej i prostej normalnej
ANALIZA MATEMATYCZNA TABLICE Spis treści: 1.) Pochodne wzory 2 2.) Całki wzory 3 3.) Kryteria zbieżności szeregów 4 4.) Przybliżona wartość wyrażenia 5 5.) Równanie płaszczyzny stycznej i prostej normalnej
SZEREGI LICZBOWE I FUNKCYJNE
 Mając dowolny ciąg można z niego utworzyć nowy ciąg sum częściowych: Ten nowy rodzaj ciągu nazywamy szeregiem liczbowym, a jeśli to mamy do czynienia z nieskończonym szeregiem liczbowym, który oznaczany
Mając dowolny ciąg można z niego utworzyć nowy ciąg sum częściowych: Ten nowy rodzaj ciągu nazywamy szeregiem liczbowym, a jeśli to mamy do czynienia z nieskończonym szeregiem liczbowym, który oznaczany
Równanie przewodnictwa cieplnego (II)
 Wykład 5 Równanie przewodnictwa cieplnego (II) 5.1 Metoda Fouriera dla pręta ograniczonego 5.1.1 Pierwsze zagadnienie brzegowe dla pręta ograniczonego Poszukujemy rozwiązania równania przewodnictwa spełniającego
Wykład 5 Równanie przewodnictwa cieplnego (II) 5.1 Metoda Fouriera dla pręta ograniczonego 5.1.1 Pierwsze zagadnienie brzegowe dla pręta ograniczonego Poszukujemy rozwiązania równania przewodnictwa spełniającego
4.2. Obliczanie przewodów grzejnych metodą dopuszczalnego obciążenia powierzchniowego
 4.. Obliczanie przewodów grzejnych meodą dopuszczalnego obciążenia powierzchniowego Meodą częściej sosowaną w prakyce projekowej niż poprzednia, jes meoda dopuszczalnego obciążenia powierzchniowego. W
4.. Obliczanie przewodów grzejnych meodą dopuszczalnego obciążenia powierzchniowego Meodą częściej sosowaną w prakyce projekowej niż poprzednia, jes meoda dopuszczalnego obciążenia powierzchniowego. W
Przemieszczeniem ciała nazywamy zmianę jego położenia
 1 Przemieszczeniem ciała nazywamy zmianę jego położenia + 0 k k 0 Przemieszczenie jes wekorem. W przypadku jednowymiarowym możliwy jes ylko jeden kierunek, a zwro określamy poprzez znak. Przyjmujemy, że
1 Przemieszczeniem ciała nazywamy zmianę jego położenia + 0 k k 0 Przemieszczenie jes wekorem. W przypadku jednowymiarowym możliwy jes ylko jeden kierunek, a zwro określamy poprzez znak. Przyjmujemy, że
Wojciech Grąziewicz. Skrypt dla studentów politechnik. Centrum Nauczania Matematyki i Kształcenia na Odległość
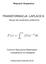 Wojciech Grąziewicz Skryp dla sudenów poliechnik Cenrum Nauczania Maemayki i Kszałcenia na Odległość Poliechnika Gdańska 26 SPIS TREŚCI Skryp przeznaczony jes głównie dla sudenów kierunków elekrycznych,
Wojciech Grąziewicz Skryp dla sudenów poliechnik Cenrum Nauczania Maemayki i Kszałcenia na Odległość Poliechnika Gdańska 26 SPIS TREŚCI Skryp przeznaczony jes głównie dla sudenów kierunków elekrycznych,
PROGNOZOWANIE I SYMULACJE. mgr Żaneta Pruska. Ćwiczenia 2 Zadanie 1
 PROGNOZOWANIE I SYMULACJE mgr Żanea Pruska Ćwiczenia 2 Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X, wyrażona w ysiącach wyprodukowanych i dosarczonych szuk firmie Bea,
PROGNOZOWANIE I SYMULACJE mgr Żanea Pruska Ćwiczenia 2 Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X, wyrażona w ysiącach wyprodukowanych i dosarczonych szuk firmie Bea,
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ
 RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ Wykorzysano: M A T E M A T Y K A Wykład dla sudenów Część Krzyszo KOŁOWROCKI, ZBIÓR ZADAŃ Z RACHUNKU CAŁKOWEGO Krzyszo PISKÓRZ Deinicja CAŁKA NIEOZNACZONA Funkcję
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ Wykorzysano: M A T E M A T Y K A Wykład dla sudenów Część Krzyszo KOŁOWROCKI, ZBIÓR ZADAŃ Z RACHUNKU CAŁKOWEGO Krzyszo PISKÓRZ Deinicja CAŁKA NIEOZNACZONA Funkcję
i j k Oprac. W. Salejda, L. Bujkiewicz, G.Harań, K. Kluczyk, M. Mulak, J. Szatkowski. Wrocław, 1 października 2015
 WM-E; kier. MBM, lisa za. nr. p. (z kary przemiou): Rozwiązywanie zaań z zakresu: ransformacji ukłaów współrzęnych, rachunku wekorowego i różniczkowo-całkowego o kursu Fizyka.6, r. ak. 05/6; po koniec
WM-E; kier. MBM, lisa za. nr. p. (z kary przemiou): Rozwiązywanie zaań z zakresu: ransformacji ukłaów współrzęnych, rachunku wekorowego i różniczkowo-całkowego o kursu Fizyka.6, r. ak. 05/6; po koniec
cx siła z jaką element tłumiący działa na to ciało.
 Drgania układu o jedny sopniu swobody Rozparzy układ składający się z ciała o asie połączonego z nierucoy podłoże za poocą eleenu sprężysego o współczynniku szywności k oraz eleenu łuiącego o współczynniku
Drgania układu o jedny sopniu swobody Rozparzy układ składający się z ciała o asie połączonego z nierucoy podłoże za poocą eleenu sprężysego o współczynniku szywności k oraz eleenu łuiącego o współczynniku
Matematyka II. Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 2018/2019 wykład 13 (27 maja)
 Matematyka II Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 208/209 wykład 3 (27 maja) Całki niewłaściwe przedział nieograniczony Rozpatrujemy funkcje ciągłe określone na zbiorach < a, ),
Matematyka II Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 208/209 wykład 3 (27 maja) Całki niewłaściwe przedział nieograniczony Rozpatrujemy funkcje ciągłe określone na zbiorach < a, ),
Gr.A, Zad.1. Gr.A, Zad.2 U CC R C1 R C2. U wy T 1 T 2. U we T 3 T 4 U EE
 Niekóre z zadań dają się rozwiązać niemal w pamięci, pamięaj jednak, że warunkiem uzyskania różnej od zera liczby punków za każde zadanie, jes przedsawienie, oprócz samego wyniku, akże rozwiązania, wyjaśniającego
Niekóre z zadań dają się rozwiązać niemal w pamięci, pamięaj jednak, że warunkiem uzyskania różnej od zera liczby punków za każde zadanie, jes przedsawienie, oprócz samego wyniku, akże rozwiązania, wyjaśniającego
Równania dla potencjałów zależnych od czasu
 Równania dla potencjałów zależnych od czasu Potencjały wektorowy A( r, t i skalarny ϕ( r, t dla zależnych od czasu pola elektrycznego E( r, t i magnetycznego B( r, t definiujemy poprzez następujące zależności
Równania dla potencjałów zależnych od czasu Potencjały wektorowy A( r, t i skalarny ϕ( r, t dla zależnych od czasu pola elektrycznego E( r, t i magnetycznego B( r, t definiujemy poprzez następujące zależności
Dobór przekroju żyły powrotnej w kablach elektroenergetycznych
 Dobór przekroju żyły powronej w kablach elekroenergeycznych Franciszek pyra, ZPBE Energopomiar Elekryka, Gliwice Marian Urbańczyk, Insyu Fizyki Poliechnika Śląska, Gliwice. Wsęp Zagadnienie poprawnego
Dobór przekroju żyły powronej w kablach elekroenergeycznych Franciszek pyra, ZPBE Energopomiar Elekryka, Gliwice Marian Urbańczyk, Insyu Fizyki Poliechnika Śląska, Gliwice. Wsęp Zagadnienie poprawnego
Jacek Kwiatkowski Magdalena Osińska. Procesy zawierające stochastyczne pierwiastki jednostkowe identyfikacja i zastosowanie.
 DYNAMICZNE MODELE EKONOMETRYCZNE Jacek Kwiakowski Magdalena Osińska Uniwersye Mikołaja Kopernika Procesy zawierające sochasyczne pierwiaski jednoskowe idenyfikacja i zasosowanie.. Wsęp Większość lieraury
DYNAMICZNE MODELE EKONOMETRYCZNE Jacek Kwiakowski Magdalena Osińska Uniwersye Mikołaja Kopernika Procesy zawierające sochasyczne pierwiaski jednoskowe idenyfikacja i zasosowanie.. Wsęp Większość lieraury
Rachunek całkowy - całka oznaczona
 SPIS TREŚCI. 2. CAŁKA OZNACZONA: a. Związek między całką oznaczoną a nieoznaczoną. b. Definicja całki oznaczonej. c. Własności całek oznaczonych. d. Zastosowanie całek oznaczonych. e. Zamiana zmiennej
SPIS TREŚCI. 2. CAŁKA OZNACZONA: a. Związek między całką oznaczoną a nieoznaczoną. b. Definicja całki oznaczonej. c. Własności całek oznaczonych. d. Zastosowanie całek oznaczonych. e. Zamiana zmiennej
Analiza matematyczna 2 Lista zadań
 Analiza maemayczna Lisa zadań Opracowanie: dr Marian Gewer, doc. Zbigniew Skoczylas Lisa. Korzysając z definicji zbadać zbieżność całek niewłaściwych pierwszego rodzaju: d) + ; b) arccg; e) +) ; c) 4+3
Analiza maemayczna Lisa zadań Opracowanie: dr Marian Gewer, doc. Zbigniew Skoczylas Lisa. Korzysając z definicji zbadać zbieżność całek niewłaściwych pierwszego rodzaju: d) + ; b) arccg; e) +) ; c) 4+3
Mechanika. Wykład 2. Paweł Staszel
 Mechanika Wykład 2 Paweł Staszel 1 Przejście graniczne 0 2 Podstawowe twierdzenia o pochodnych: pochodna funkcji mnożonej przez skalar pochodna sumy funkcji pochodna funkcji złożonej pochodna iloczynu
Mechanika Wykład 2 Paweł Staszel 1 Przejście graniczne 0 2 Podstawowe twierdzenia o pochodnych: pochodna funkcji mnożonej przez skalar pochodna sumy funkcji pochodna funkcji złożonej pochodna iloczynu
LABORATORIUM PODSTAWY ELEKTRONIKI Badanie Bramki X-OR
 LORTORIUM PODSTWY ELEKTRONIKI adanie ramki X-OR 1.1 Wsęp eoreyczny. ramka XOR ramka a realizuje funkcję logiczną zwaną po angielsku EXLUSIVE-OR (WYŁĄZNIE LU). Polska nazwa brzmi LO. Funkcję EX-OR zapisuje
LORTORIUM PODSTWY ELEKTRONIKI adanie ramki X-OR 1.1 Wsęp eoreyczny. ramka XOR ramka a realizuje funkcję logiczną zwaną po angielsku EXLUSIVE-OR (WYŁĄZNIE LU). Polska nazwa brzmi LO. Funkcję EX-OR zapisuje
Matematyka A kolokwium: godz. 18:05 20:00, 24 maja 2017 r. rozwiązania. ) zachodzi równość: x (t) ( 1 + x(t) 2)
 Matematyka A kolokwium: godz. 18:05 0:00, 4 maja 017 r. rozwiązania 1. 7 p. Znaleźć wszystkie takie funkcje t xt, że dla każdego t π, π zachodzi równość: x t 1 + xt 1+4t 0. p. Wśród znalezionych w poprzedniej
Matematyka A kolokwium: godz. 18:05 0:00, 4 maja 017 r. rozwiązania 1. 7 p. Znaleźć wszystkie takie funkcje t xt, że dla każdego t π, π zachodzi równość: x t 1 + xt 1+4t 0. p. Wśród znalezionych w poprzedniej
Całka podwójna po prostokącie
 Całka podwójna po prostokącie Rozważmy prostokąt = {(x, y) R : a x b, c y d}, gdzie a, b, c, d R, oraz funkcję dwóch zmiennych f : R ograniczoną w tym prostokącie. rostokąt dzielimy na n prostokątów i
Całka podwójna po prostokącie Rozważmy prostokąt = {(x, y) R : a x b, c y d}, gdzie a, b, c, d R, oraz funkcję dwóch zmiennych f : R ograniczoną w tym prostokącie. rostokąt dzielimy na n prostokątów i
Elementy rachunku różniczkowego i całkowego
 Elementy rachunku różniczkowego i całkowego W paragrafie tym podane zostaną elementarne wiadomości na temat rachunku różniczkowego i całkowego oraz przykłady jego zastosowania w fizyce. Małymi literami
Elementy rachunku różniczkowego i całkowego W paragrafie tym podane zostaną elementarne wiadomości na temat rachunku różniczkowego i całkowego oraz przykłady jego zastosowania w fizyce. Małymi literami
Wykład 4: Transformata Laplace a
 Rachunek prawdopodobieńwa MAP164 Wydział Elekroniki, rok akad. 28/9, em. leni Wykładowca: dr hab. A. Jurlewicz Wykład 4: Tranformaa Laplace a Definicja. Niech f() będzie funkcją określoną na R, przy czym
Rachunek prawdopodobieńwa MAP164 Wydział Elekroniki, rok akad. 28/9, em. leni Wykładowca: dr hab. A. Jurlewicz Wykład 4: Tranformaa Laplace a Definicja. Niech f() będzie funkcją określoną na R, przy czym
( 3 ) Kondensator o pojemności C naładowany do różnicy potencjałów U posiada ładunek: q = C U. ( 4 ) Eliminując U z równania (3) i (4) otrzymamy: =
 ROZŁADOWANIE KONDENSATORA I. el ćwiczenia: wyznaczenie zależności napięcia (i/lub prądu I ) rozładowania kondensaora w funkcji czasu : = (), wyznaczanie sałej czasowej τ =. II. Przyrządy: III. Lieraura:
ROZŁADOWANIE KONDENSATORA I. el ćwiczenia: wyznaczenie zależności napięcia (i/lub prądu I ) rozładowania kondensaora w funkcji czasu : = (), wyznaczanie sałej czasowej τ =. II. Przyrządy: III. Lieraura:
Równania różniczkowe wyższych rzędów
 Równania różniczkowe wyższych rzędów Marcin Orchel Spis treści 1 Wstęp 1 1.1 Istnienie rozwiązań............................... 1 1. Rozwiązanie ogólne............................... 1.3 Obniżanie rzędu
Równania różniczkowe wyższych rzędów Marcin Orchel Spis treści 1 Wstęp 1 1.1 Istnienie rozwiązań............................... 1 1. Rozwiązanie ogólne............................... 1.3 Obniżanie rzędu
Pojęcia podstawowe 1
 Tomasz Lubera Pojęcia podsawowe aa + bb + dd + pp + rr + ss + Kineyka chemiczna dział chemii fizycznej zajmujący się przebiegiem reakcji chemicznych w czasie, ich mechanizmami oraz wpływem różnych czynników
Tomasz Lubera Pojęcia podsawowe aa + bb + dd + pp + rr + ss + Kineyka chemiczna dział chemii fizycznej zajmujący się przebiegiem reakcji chemicznych w czasie, ich mechanizmami oraz wpływem różnych czynników
Badanie funktorów logicznych TTL - ćwiczenie 1
 adanie funkorów logicznych TTL - ćwiczenie 1 1. Cel ćwiczenia Zapoznanie się z podsawowymi srukurami funkorów logicznych realizowanych w echnice TTL (Transisor Transisor Logic), ich podsawowymi paramerami
adanie funkorów logicznych TTL - ćwiczenie 1 1. Cel ćwiczenia Zapoznanie się z podsawowymi srukurami funkorów logicznych realizowanych w echnice TTL (Transisor Transisor Logic), ich podsawowymi paramerami
RÓWNANIA RÓŻNICZKOWE WYKŁAD 2
 RÓWNANIA RÓŻNICZKOWE WYKŁAD 2 Równania różniczkowe o zmiennych rozdzielonych Równania sprowadzalne do równań o zmiennych rozdzielonych Niech f będzie funkcją ciągłą na przedziale (a, b), spełniającą na
RÓWNANIA RÓŻNICZKOWE WYKŁAD 2 Równania różniczkowe o zmiennych rozdzielonych Równania sprowadzalne do równań o zmiennych rozdzielonych Niech f będzie funkcją ciągłą na przedziale (a, b), spełniającą na
II. RÓŻNICZKOWANIE I CAŁKOWANIE NUMERYCZNE Janusz Adamowski
 II. RÓŻNICZKOWANIE I CAŁKOWANIE NUMERYCZNE Janusz Adamowski 1 1 Różniczkowanie numeryczne Rozważmy funkcję f(x) określoną na sieci równoodległyc węzłów. Funkcja f(x) może być dana za pomocą wzoru analitycznego
II. RÓŻNICZKOWANIE I CAŁKOWANIE NUMERYCZNE Janusz Adamowski 1 1 Różniczkowanie numeryczne Rozważmy funkcję f(x) określoną na sieci równoodległyc węzłów. Funkcja f(x) może być dana za pomocą wzoru analitycznego
Przemysław Klęsk. Słowa kluczowe: analiza składowych głównych, rozmaitości algebraiczne
 Przemysław Klęsk O ALGORYTMIE PRINCIPAL MANIFOLDS OPARTYM NA PCA SŁUŻACYM DO ZNAJDOWANIA DZIEDZIN JAKO ROZMAITOŚCI ALGEBRAICZNYCH NA PODSTAWIE ZBIORU DANYCH, PROPOZYCJA MIAR JAKOŚCI ROZMAITOŚCI Sreszczenie
Przemysław Klęsk O ALGORYTMIE PRINCIPAL MANIFOLDS OPARTYM NA PCA SŁUŻACYM DO ZNAJDOWANIA DZIEDZIN JAKO ROZMAITOŚCI ALGEBRAICZNYCH NA PODSTAWIE ZBIORU DANYCH, PROPOZYCJA MIAR JAKOŚCI ROZMAITOŚCI Sreszczenie
WYKŁAD 14. Rozdział 7: Drgania parametryczne
 WYKŁD 4 Rozdział 7: Drgania parameryczne 7.. Isoa drgań paramerycznych Na wsępie przywołajmy klasyfikację drgań ze względu na źródło energii podaną w Wykładzie. W klasyfikacji ej wyodrębnione zosały czery
WYKŁD 4 Rozdział 7: Drgania parameryczne 7.. Isoa drgań paramerycznych Na wsępie przywołajmy klasyfikację drgań ze względu na źródło energii podaną w Wykładzie. W klasyfikacji ej wyodrębnione zosały czery
