Pomiary dawek promieniowania wytwarzanego w liniowych przyspieszaczach na użytek radioterapii

Transkrypt

1 Pomary dawek promenowana wytwarzanego w lnowych przyspeszaczach na użytek radoterap Włodzmerz Łobodzec Zakład Radoterap Szptala m. S. Leszczyńskego w Katowcach

2 Cel radoterap napromenene obszaru PTV zaplanowaną, możlwe jednorodną, dawką z równoczesnym dużym gradentem dawk poza tym obszarem Obszary w planowanu radoterap GTV (Gross Tumour Volume ) CTV (Clncal Target Volume) PTV (Plannng Target Volume ) TV (Treated Volume) obszar leczony IV (Irradated Volume)-obszar napromenany

3 Fantom Woda stanow standardowy materał do pomarów dozymetrycznych zarówno dla wązek fotonów jak elektronów. Stosuje sę równeż fantomy stałe (meszanka odpowednch komponentów). Fantom stały mus mtować wodę pod względem: gęstośc, lczby elektronów w grame materału, efektywnej lczby atomowej Z eff. la promenowana wytwarzanego w lnowych przyspeszaczach Z eff = a a Z A 2 A Z a, Z, A masowy udzał, lczba atomowa, lczba masowa -tego składnka.

4 etektory promenowana dla rutynowej dozymetr w radoterap Cylndryczna (naparstkowa) komora jonzacyjna 0.6 cm 3 typu Farmer 3. Płaska komora jonzacyjna np. typu Markus etektory półprzewodnkowe: ody krzemowe MOSFET Metal-Oxde Semconductor Feld Effect Transstor

5 Cylndryczna komora jonzacyjna typu Farmer Punkt referencyjny komory cylndrycznej jest zlokalzowany na os komory w połowe długośc naparstka komory. W wynku absorpcj fotonów w naparstku komory, we wnęce komory powstaje ładunek elektryczny. pow Q m woda pow swoda, pow s, pow f ( E) woda = Komora wykalbrowana służy do pomaru w fantome dawk absolutnej wązek fotonów oraz elektronów o energ powyżej 10MeV.

6 Płaska komora jonzacyjna 1. elektroda (wejścowa)- polaryzacyjna 2. elektroda zborcza 3.Perśceń ochronny. a-wysokość wnęk powetrznej. d- średnca elektrody (wejścowej) m- średnca elektrody zborczej g- szerokość perścena ochronnego. Punkt referencyjny komory - to środek wewnętrznej powerzchn okna komory Wykalbrowana komora służy do pomaru w fantome dawk absolutnej wązek elektronów. Zalecana także do pomarów PG wązek fotonów zwłaszcza w obszarze buldup.

7 oda krzemowa to detektor, w którym półprzewodnk (krzem) o relatywne małych wymarach używany jest do pomarów dawk promenowana. W wynku współoddzaływana z nm promenowana jonzującego, powstają nośnk ładunku elektrycznego (wolne elektrony dzury z ładunkem dodatnm). Lczba nośnków jest proporcjonalna do energ promenowana jonzującego pochłonętego w materale półprzewodnka. Elektrony przemeszczają sę do obszaru n,, a dzury do obszaru p co powoduje pojawene sę różncy potencjałów czyl napęca elektrycznego o wartośc proporcjonalnej do lczby nośnków elektrycznych. Wartość tego napęca rejestrowana przez odpowedn układ elektronczny jest proporcjonalna do dawk promenowana. ody półprzewodnkowe są użyteczne do pomarów dawk n vvo oraz do pomarów rozkładu dawk względnej w fantome zwłaszcza w obszarach dużego jej gradentu.

8 etektor MOSFET - to mnaturowy detektor półprzewodnkowy, którego objętość aktywna jest mnejsza nż 1 mm 3. Mają zastosowane główne w pomarach dawk n vvo. etektor umocowany jest na cenkm pasku z polamdu, z przewodem umożlwającym podłączene go do zaslacza podczas napromenana. Okładk detektora wykonane są z elementów przewodzących, natomast delektryk stanow dwutlenek krzemu. Na elektrody detektora podaje sę napęce progowe 20 V.

9 W wynku dzałana promenowana jonzującego, w detektorze powstają nośnk ładunku elektrycznego w lczbe proporcjonalnej do pochłonętej energ promenowana. Nośnk, dochodząc do elektrod, zmnejszają różncę napęć o odpowedną wartość. Zmana wartośc różncy napęć jest proporcjonalna do pochłonętej energ promenowana jonzującego. W detektorach używanych w radoterap, w zależnośc od zastosowanego zaslacza, dawka promenowana 1cGy powoduje zmnejszene napęca detektora o 1mV lub 3mV. etektor MOSFET może zatem skumulować dawkę promenowana odpowedno 200Gy lub 70Gy, po czym staje sę bezużyteczny. Procentowe nepewnośc awka [cgy] Standardowy Wysokej czułośc 200 <2 % <0,8% <3% <1,2% 20 <8% <3%

10 Kalbracja komory cylndrycznej Z ref =5 cm lub 10 cm S=10cm x 10cm a>5cm Porównując wskazana kalbrowanego dawkomerza (M Co ) z wartoścam poprawnym dawk w wodze ( w,co ), określa sę współczynnk kalbracyjny badanego dawkomerza w wodze jako: N, w, Co = w, Co M Co [ cgy] [ nc ] M Co skorygowane na cśnene, temperaturę, efekt polaryzacj. Symbol Co można zastąpć ogólnym symbolem Q

11 awka w wodze na głębokośc z ref dla jakośc promenowana Q nnej nż Q 0 użytej do kalbracj komory wynos: = M N w, Q Q, w, Q Q Współczynnk korekcyjny zdefnowany jako: k = Q, Q 0 N N, w, Q, w, Q k 0 Q, 0 0 wnen być wyznaczony dla ndywdualnej komory stosowanej wązk u użytkownka. Oblczone współczynnk korekcyjne dla różnych cylndrycznych komór jonzacyjnych jakośc wązk fotonów podano w tabel 6.III raportu 398 IAEA. Jakość wązk fotonów Q określa sę jako: Q = TPR(20) TPR(10) = 1,2661 P(20) P(10) 0,0595

12 Pomar wydajnośc fotonów awkomerz Kethley nr ser , komora PTW "Farmer" typ 3004 nr 0241 MV M k p,t LJM SS głęb. N,w,Qo TPR 20,10 k Q (*) st XIO % [nc] [cm] [cm] [cgy/nc] [cgy/jm] [cgy/jm] 6 12, ,535 0,671 0,991 0,651 0,653-0, , ,353 0,762 0,975 0,749 0,749 0,1 *) Tabela 6.III str.64 W, Q = M Q N, W, Qo kq, Qo

13 Kalbracja komory płaskej Markus Istneje zwązek empryczny: E 0 = C. R 50, C = 2,33MeV. cm - 1 Jakość wązk elektronów (R 50 ) użytej do kalbracj komór płaskch wynosła 8,74 g cm -2. Q cross jakość wązk użytej do kalbracj Z ref =0,6R 50-0,1 S= 10cm x10cm, R 50 <7gcm 2 S= 20cm x20cm, R 50 >7gcm 2 Porównując wskazana (M Qcross ) kalbrowanego dawkomerza z wartoścam poprawnym dawk w wodze ( w,qcross ), określa sę współczynnk kalbracyjny badanego dawkomerza jako: w, Qcross [ cgy] N, w, Qcross = M [ nc ] M Qcross - skorygowane na cśnene, temperaturę, efekt polaryzacj rekombnacj jonów Qcross

14 awka w wodze na z ref dla jakośc wązk elektronów Q nnej nż Q cross wynos : W, Q = M Q N, W, Q kq, cross Q cross Współczynnk korekcyjny zdefnowany jako: k Q, Qcross = N N, w, Q, w, Q cross wnen być wyznaczony dla ndywdualnej komory stosowanej wązk u użytkownka co jest trudne do wykonana. W tabel 7.IV raportu 398 IAEA podano oblczone współczynnk korekcyjne dla różnych płaskch komór jonzacyjnych jakośc wązk elektronów jednak w stosunku do współczynnka pośrednego Q nt, odpowednego dla jakośc wązk o R 50 = 7,5 g cm -2.

15 Fragment tabel 7.IV IAEA: Oblczone wartośc k Q,Qnt w funkcj jakośc wązk R 50 (Q nt = 7,5 g. cm -2 ) Jakość wązk R 50 [g. cm - 2 ] Komora Markus 1,038 1,028 1,020 1,014 1,008 1,003 0,997 0,988 0,976 0,965 Aby skorzystać z wartośc współczynnków zameszczonych w tabel 7.IV raportu 398, należy je znormalzować do wartośc współczynnka Q cross określonego dla jakośc wązk R 50 =8,74 g. cm -2 użytej do kalbracj zatem: k Q, Qcross = k Q, Qnt k 1 Qcross, Qnt Uwzględnając wartośc zawarte w tabel będze: oraz dawka na z ref będze: k Q k, Q = Q,nt cross 1,006 W, Q = M Q N, W, Q kq, Q cross nt 1,006

16 Pomar wydajnośc elektronów awkomerz Kethley nr ser , Pomar dawk w wodze komorą Markus kalbrowaną w wązce (Q cross ) elektronów o jakośc R 50 =8,74g. cm -2 MeV M k p,t LJM SS z ref (*) N,w,Qcross R 50 k Q,Qcross (**) (max/ref) st XIO % [nc] [cm] [cm] [cgy/nc] [cm] [cgy/jm] [cgy/jm] 6 1,8190 1,3 50,93 2,3 1,043 1,000 0,966 0,962 0,5 9 1,8300 2,1 50,93 3,6 1,028 1,000 0,958 0,959-0,1 12 1,8252 2,8 50,93 4,8 1,021 1,000 0,949 0,956-0,7 15 1,8543 3,6 50,93 6,1 1,014 1,0000 0,958 0,960-0,2 18 1,8364 4,5 50,93 7,7 1,000 1,014 0,948 0,946 0,3 21 1,8066 5,0 50,93 8,5 1,000 1,028 0,946 0,943 0,3 *) z ref = 0,6 R50 0,1 **) kq, Q = kq, Q = k nt Q, Q cross nt kq, Q 1 cross nt 1,006

17 Łączne wartośc procentowej nepewnośc określena dawk w wodze na z ref z uwzględnenem nepewnośc: kalbracj dawkomerza (PSL SSL), stablnośc dawkomerzy (standardowego kalbrowanego), M Q względem merzonej LJM, współczynnka jakośc wązk k Q, współczynnków korekcyjnych kalbrowanego dawkomerza. Promenowane komora Technka kalbracj σ [%] Fotony cylndryczna wązka γ 60 Co 1,5 Elektrony (R 50 >4 g cm -2 ) cylndryczna wązka γ 60 Co 1,6 Elektrony (R 50 >4 g cm -2 ) cylndryczna wązka elektronów Q cross 1,4 Elektrony (R 50 >1 g cm -2 ) płaska wązka γ 60 Co 2,1 Elektrony (R 50 >1 g cm -2 ) płaska wązka elektronów Q cross 1,4

18 Wartośc procentowej nepewnośc oblczonego współczynnka jakośc wązk k Q Promenowane komora Technka kalbracj σ [%] Fotony cylndryczna wązka γ 60 Co 1,0 Elektrony (R 50 >4 g cm -2 ) cylndryczna wązka γ 60 Co 1,2 Elektrony (R 50 >4 g cm -2 ) cylndryczna wązka elektronów Q cross 0,9 Elektrony (R 50 >1 g cm -2 ) płaska wązka γ 60 Co 1,7 Elektrony (R 50 >1 g cm -2 ) płaska wązka elektronów Q cross 0,6

19 etektor półprzewodnkowy Wskazana detektorów półprzewodnkowych są proporcjonalne do pochłonętej energ promenowana: Merzony względny rozkład dawk w fantome PG lub profle można bezpośredno wyrazć poprzez wskazana detektorów. Komora jonzacyjna R R półprzewodnk awk ładunek masa powetrza powetrze powetrze R woda powetrze swoda, powetrze Fotony: s w,p = const, dla z > z max Elektrony: s w,p = s w,p (E)

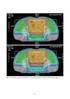
20 [%] Porównane krzywych jonzacj PG wązk elektronów o energ 15MeV. PG % jonzacja Krzywe otrzymano na podstawe pomarów wykonanych płaską komorą jonzacyjna typu Markus 3162 o współczynnku N,W = 50.93cGy. nc. Kalbrowanej w wązce elektronów o jakośc R 50 =8,74 g. cm gł[mm] Warunk pomaru: SS= cm S = 10cmx10cm

21 Wykres zależnośc PG wązk elektronów o energ 15MeV. a) Powerzchna czołowa detektora na powerzchn wody b) Powerzchna czołowa detektora przesunęta 1 mm nad powerzchnę wody

22 awka wejścowa na głębokośc maksymalnej mocy dawk awka w napromenanym środowsku (fantom lub pacjent), pochodząca od pojedynczej stacjonarnej wązk promenowana, w os wązk awka wyjścowa w odległośc od wyjśca wązk ze środowska równej głębokośc maksymalnej dawk danego promenowana. F wej = R kom wej wej = F wej R wej

23 Kalbracje detektora MOSFET w warunkach równowag elektronów F = R kom MOSFET F = R kom MOSFET = F skóra R MOSFET

24 ) ( ) ( / ) ( ) ( ) ( ) ( / ) ( ) ( ) ( ref M ref M ref M ref M d m m m m c c c c = 1) ) ( ( % = d d

25 Tolerancja procentowego odchylena dawk dla różnych obszarów wązk fotonowej Obszar Jednorodne Środowsko, prosta geometra Kompleksowa geometra (fltr klnowy, nejednorodność, asymetra, blok/lmc) Zastosowane co najmnej dwóch kompleksowych geometr Oś centralna -wysoka dawka, mały gradent dawk 2% 3% 4% Narastane dawk w os centralnej wązk, penumbra - wysoka dawka, duży gradent 10% lub 2 mm 15% lub 3 mm 15% lub 3 mm Poza centralną osą wązk wysoka dawka, mały gradent dawk 3% 3% 4% Poza grancą wązk promenowana nska dawka, mały gradent dawk 30% (3%) 40% (4%) 50% (5%)