Wstęp do Robotyki (Zakres materiału na egzamin)
|
|
|
- Kornelia Kowal
- 9 lat temu
- Przeglądów:
Transkrypt
1 Wstęp do Robotyki c W. Szynkiewicz, 9 1 Wstęp do Robotyki (Zakres materiału na egzamin) 1. Podstawowe pojęcia z dziedziny robotyki: krótka historia robotyki, działy robotyki, definicja robota. Elementy składowe systemu robotycznego: efektory(np. układ lokomocji, ramię manipulatora, itp.) czujniki układ sterowania komputerowego Rodzaje robotów i ich charakterystyka oraz zastosowania: roboty mobilne(kołowe, gąsienicowe, kroczące, pływające, latające), roboty manipulacyjne; roboty przemysłowe, usługowe, roboty specjalne.. Budowa i programowanie robotów modułowych- zestawy Lego NXT Mindstorms: budowa i funkcje mikrosterownika NXT, silniki i czujniki. Budowa i funkcje środowiska NBC/NXC do programowania robotów. 3. Opis położenia i orientacji: Podstawowe pojęcia matematyczne: iloczyn skalarny i wektorowy wektorów, układ współrzędnych ortokartezjańskich, wektor przesunięcia, macierz rotacji(obrotu) własności macierzy obrotu, składanie obrotów. Wybrane reprezentacje położenia i orientacji: współrzędne kartezjańskie, obroty wokół osi układu bieżącego kąty Eulera, obroty wokół osi układu ustalonego, np. kąty kołysanie-kiwanie-myszkowanie, reprezentacja obrotu oś-kąt. Wstęp do Robotyki c W. Szynkiewicz, 9 Macierz przekształcenia jednorodnego własności, interpretacja. 4. Zagadnienia kinematyki manipulatorów. Więzy holonomiczne i nieholonomiczne. Kinematyka układu holnomicznego. Struktury geometryczne manipulatorów robotów. Kinematyka manipulatorów z otwartymi łańcuchami kinematycznymi proste zadanie kinematyki. 5. Pojęcie jakobianu w robotyce. Jakobian analityczny i geometryczny manipulatora. Odwrotne zadanie kinematyki manipulatora. 6. Układy lokomocji robotów. Zagadnienia związane z lokomocją: stabilność, charakterystyka kontaktu, rodzaj środowiska. Roboty(maszyny) kroczące(skaczące, dwunożne, cztero-, sześcio-, ośmionożne). Rodzaje chodów i ich opis. Zalety i wady maszyn kroczących. Roboty kołowe. Cechy robotów kołowych. Rodzaje kół i ich charakterystyka. Więzy(ograniczenia) ruchu pojedynczego koła. Więzy ruchu holonomiczne i nieholonomiczne. 7. Podstawowe rodzaje baz jezdnych kołowych robotów mobilnych i ich charakterystyka. Napęd różnicowy, trójkołowy, synchroniczny, wielokierunkowy, Ackermana. Pojęcia mobilności i sterowności i manewrowości robotów kołowych. Roboty kołowe niezdegenerowane warunki. Opis i klasyfikacja robotów kołowych typy robotów trójkołowych.
2 Wstęp do Robotyki c W. Szynkiewicz, Kinematyka robotów mobilnych: równania ruchu prostych robotów kołowych. 9. Percepcja. Klasyfikacja czujników. Podstawowe charakterystyki czujników. Czujniki stosowane w robotach: odometryczne, inercyjne, dotykowe, zbliżeniowe, odległości, orientacji. Metody pomiaru odległości. 1. Problem autonomicznej nawigacji robota mobilnego. Źródła niepewności w nawigacji. Ogólny schemat nawigacji autonomicznej. Samolokalizacja. Podział podejść do problemu samolokalizacji. Metody pomiaru pozycji (samo-lokalizacji) robota. Budowa mapy środowiska reprezentacja otoczenia robota. Podstawowe rodzaje map. Problemy występujące przy budowie map. Planowanie ścieżki. Kryteria podziału metod planowania ścieżek. Metody planowania ścieżek ruchu robotów mobilnych. 11. Struktury i układy sterowania i programowania robotów. Metody i algorytmy sterowania robotów: sterowanie reaktywne, behawioralne, bazujące na modelu, struktury hybrydowe. Wstęp do Robotyki c W. Szynkiewicz, 9 4 Programowe struktury ramowe. Opis robota jako agenta upostaciowionego. Niezależne sterowanie osiami podstawowe struktury regulatorów. Krzywe interpolacja. 1. Systemy wielorobotowe/wieloagentowe. Cele tworzenia, problemy i typowe zadania(np. RoboCup). Podział systemów wielorobotowych ze względu na: strukturę organizacji, sposoby komunikacji oraz stopień współpracy. Sposoby współpracy robotów. 13. Sztuczna inteligencja a robotyka. Uczenie się agentów/robotów. Składniki systemu uczącego się. Cele i rodzaje uczenia się, metody uczenia się. Uczenie się ze wzmocnieniem specyfika.
3 Wstęp do Robotyki c W. Szynkiewicz, 9 5 Reprezentacje obrotów Obrótwprzestrzeni R 3 : z 1 z P y 1 x 1 k j 1 k 1 i 1 j i y x Rys.1:ObrótwR 3 Macierz obrotu macierz kosinusów kierunkowych: 1R= i 1 i j 1 i k 1 i i 1 j j 1 j k 1 j i 1 k j 1 k k 1 k (1) Wstęp do Robotyki c W. Szynkiewicz, 9 6 Własności macierzy obrotu(rotacji): (1)macierzRjestortogonalna:RR T =R T R=I 3 Każda kolumna(wiersz) macierzy R jest wektorem jednostkowym. ()R(u w)=(ru) (Rw) (3)detR=((Ri) (Rj)) ((Rk))= (Rk) =+1(dlaukładówprawoskrętnych) Macierze obrotu R tworzą specjalną grupę obrotów SO(3). Składanie obrotów: p = 1Rp 1, p 1 = 1 Rp, p = Rp Względem osi bieżącego układu(mnożenie prawostronne): stąd p = 1R 1 Rp R= 1R 1 R Względem osi układu ustalonego(mnożenie lewostronne): R= 1 R 1R
4 Wstęp do Robotyki c W. Szynkiewicz, 9 7 Inne wybrane reprezentacje obrotu: reprezentacja oś-kąt(obrót wokół dowolnej osi) kątyeuler a(1zestawów=3xx) obroty wokół osi układu ustalonego (1 zestawów = 3xx) np. kąty roll-pitch-yaw (kołysanie-kiwanie-myszkowanie) Zadanie 1a: Danajestmacierz3 3wykazać,żejesttomacierzobrotu Rozwiązanie: R= Możnatowykazaćprzezpokazanie,żeR T R=I,gdzieIjestmacierząjednostkową R T R= = Wstęp do Robotyki c W. Szynkiewicz, 9 8 Zadanie 1b: Dane są dwie macierze obrotu: Wykazać, że: (a)r 1 SO() (b)r 1 R SO() R 1 = cosθ sinθ sinθ cosθ R = cosϕ sinϕ sinϕ cosϕ (c) R 1 R = cos(θ+ϕ) sin(θ+ϕ) sin(θ+ϕ) cos(θ+ϕ) Rozwiązanie: Ad(a):Należypokazać,żeR 1 R T 1=R T 1R 1 =IorazdetR 1 =+1: R 1 R T 1= cθ sθ sθ cθ cθ sθ = sθ cθ c θ+s θ sθcθ sθcθ sθcθ sθcθ c θ+s θ detr 1 =c θ ( s θ)=+1 Ad(b):Należypokazać,że(R 1 R ) T R 1 R =Iorazdet(R 1 R )=+1: (R 1 R ) T R 1 R =R T R T 1R 1 R =R T R =I = 1 1
5 Wstęp do Robotyki c W. Szynkiewicz, 9 9 Ad(c): R 1 R = det(r 1 R )=det(r 1 )det(r )=1 1=+1 cθ sθ sθ cθ cϕ sϕ sϕ cϕ Wykorzystując tożsamości trygonometryczne = cθcϕ sθsϕ=cos(θ+ϕ) cθcϕ sθsϕ cθsϕ sθcϕ sθcϕ+cθsϕ sθsϕ+cθcϕ otrzymamy rozwiązanie zadania. sθcϕ+cθsϕ=sin(θ+ϕ) Wstęp do Robotyki c W. Szynkiewicz, 9 1 {} z P z 1 k k 1 1d 1 P O 1 j 1 y 1 x 1 i 1 {1} O j i y x Macierze przekształcenia jednorodnego: T= Rys.:PrzesunięcieiobrótwR 3 R 3 3 d 3 1 f 1 3 s 1 1 = obrót przesunięcie perspektywa skalowanie
6 Wstęp do Robotyki c W. Szynkiewicz, 9 11 Macierz odwrotna: T 1 = R d 1 1 = R T R T d 1 Interpretacje macierzy przekształcenia jednorodnego: 1. Opisuje układ{1} względem układu{}. 1T= 1R 1d 1 Kolumnymacierzyrotacji(macierzykosinusówkierunkowych) 1Rsąwersoramiokreślającymikierunki osiukładu{1}wukładzie{}.wektor 1dokreślapołożeniepoczątkuukładu{1}wukładzie{}..Macierzjednorodnajakoprzekształcenieodwzorowujące.Macierz 1Todwzorowuje 1 P P. 3.Macierzjakooperatorprzekształcenia.MacierzTdziałanawektor P 1 tworzącwektor P (przesunięty iobróconywukładzie{}) Wstęp do Robotyki c W. Szynkiewicz, 9 1 Zadanie a: Układortokartezjański{1}=(O 1,x 1,y 1,z 1 )początkowopokrywałsięzukładem{}=(o,x,y,z ), następniezostałobróconyokątϕ= π 6 wokółosiz iprzesuniętyod=6wzdłużosix.punktpma współrzędnewukładzie{1}współrzędne 1 P=[,,3] T.ObliczyćwspółrzędnepunktuPwukładzie{}. Rozwiązanie: Transformacja współrzędnych z układu{1} do{} opisana jest wzorem: Macierz przekształcenia jednorodnego ma postać: 1T= P= 1T 1 P= 3 1 P= 1T 1 P cosϕ sinϕ d sinϕ cosϕ 1 1 Zapisując we współrzędnych jednorodnych współrzędne punktu P, możemy obliczyć = 3 1
7 Wstęp do Robotyki c W. Szynkiewicz, 9 13 Zadanie b: Mającdanąmacierz 1T obliczyćmacierz 1 T. Rozwiązanie: 1T= 1 1 cosϕ sinϕ sinϕ cosϕ 3 1 KorzystajączewzorunaodwrotnośćMPJ 1T 1 = 1 Tobliczamy 1 T== 1T 1 = gdziecϕ=cosϕorazsϕ=sinϕ 1R T 1R T 1d = cϕ sϕ cϕ 3sϕ sϕ cϕ sϕ 3cϕ 1, Wstęp do Robotyki c W. Szynkiewicz, 9 14 Rys. 3: Parametry Denavita-Hartenberga Parametry Denavita-Hartenberga: a i 1 długośćczłonu odległośćosiz i 1 odosiz i mierzonawzdłużosix i 1, α i 1 skręcenieczłonu kątmiędzyosiamiz i 1 iz i mierzonywokółosix i 1, d i odsunięcieprzegubu odległośćosix i 1 odosix i mierzonawzdłużosiz i, θ i kątprzegubu kątmiędzyosiamix i 1 ix i mierzonywokółosiz i.
8 Wstęp do Robotyki c W. Szynkiewicz, 9 15 i 1 i T=Rot x,αi 1 Trans x,ai 1 Rot z,θi Trans z,di = 1 cα i 1 sα i 1 sα i 1 cα i a i cθ i sθ i sθ i cθ i d i 1 () Powymnożeniumacierzypostaćkońcowa i 1 i T jest następująca: i 1 i T= gdzies() sin()orazc() cos(). cθ i sθ i a i 1 sθ i cα i 1 cθ i cα i 1 sα i 1 sα i 1 d i sθ i sα i 1 cθ i sα i 1 cα i 1 cα i 1 d i 1, (3) Wstęp do Robotyki c W. Szynkiewicz, 9 16 Algorytm rozwiązywania prostego zadania kinematyki wykorzystującego notację D-H: 1.Umieśćioznaczosieprzegubówz 1,...,z n.. Przyjmij bazowy układ współrzędnych{}, tak aby dla zerowej wartości współrzędnej konfiguracyjnej osie układów{} oraz{1} pokrywały się. Dlai=1,...,wykonajkrokiod3do8: 3.UmieśćpoczątekukładuO i wpunkcieprzecięciaosiz i przezwspólnąnormalnądoosiz i orazz i+1 lub wpunkcieprzecięciaosiz i orazz i+1 gdyosieteprzecinająsię. 4.Wybierzośx i wzdłużprostejnormalnejdoosiz i orazz i+1,albowkierunkunormalnejdopłaszczyzny obutychosigdyosiez i iz i+1 przecinająsię. 5.Wybierzośy i tak,abyukładbyłprawoskrętny. 6. Wybierz takie usytuowanie układu{n}, aby spowodować zerowanie się jak największej liczby parametrów. 7.UtwórztabelęparametrówD-H(a i 1,α i 1,d i,θ i ). 8.Zbudujmacierzeprzekształceniajednorodnego i 1 i T wstawiając parametry do równania: 9.Obliczmacierz nt= 1T 1 T... n 1 n T
9 Wstęp do Robotyki c W. Szynkiewicz, 9 17 Zadanie 3: Dla manipulatora przestrzennego typu 3R(rys.4) należy: związać z każdym członem układ współrzędnych i przedstawićnarysunku.podaćwtabeliparametryd-hiobliczyćmacierzejednorodne i 1 i T,anastępnie rozwiązać proste zadanie kinematyki dla tego manipulatora i obliczyć położenie i orientację układu{4} w układzie bazowym. x 4 y 4 l 3 3 z l x Rys. 4: Manipulator przestrzenny 3R Wstęp do Robotyki c W. Szynkiewicz, 9 18 Rozwiązanie: x 4 y z, 1 l x x, 1 y 4 l 3 y 3 x 3 3 i α i 1 a i 1 d i θ i 1 θ 1 9 θ 3 l θ 3 4 l 3 Tablica parametrów Denavita-Hartenberga(D-H) dla manipulatora przestrzennego typu 3R Korzystajączwzorunamacierzprzejścia i 1 i Tobliczamy 1T= c 1 s 1 s 1 c T= c s a 1 1 s c 1 Rozwiązaniem prostego zadania kinematyki jest macierz 3T= 4T= 1T 1 T 3T 3 4T c 3 s 3 l s 3 c T= 1 l
10 Wstęp do Robotyki c W. Szynkiewicz, 9 19 Funkcje trygonometryczne sumy i różnicy kątów: cos(θ 1 +θ )=c 1 =c 1 c s 1 s sin(θ 1 +θ )=s 1 =c 1 s +s 1 c cos(θ 1 θ )=c 1 c +s 1 s sin(θ 1 θ )=s 1 c c 1 s Rozwiązanie PZK dla robota typu 3R: 4T= c 1 c 3 c 1 s 3 s 1 l c 1 c +l 3 c 1 c 3 s 1 c 3 s 1 s 3 c 1 l s 1 c +l 3 s 1 c 3 s 3 c 3 l s +l 3 s 3 1 (4) Wstęp do Robotyki c W. Szynkiewicz, 9 Robot Konstrukcja Osie Struktura kinematyczna Przestrzeñ robocza Przyk³ad Typ Kartezjañski PPP Cylindryczny RPP Sferyczny RRP SCARA RRP Stawowy RRR Równoleg³y
11 Wstęp do Robotyki c W. Szynkiewicz, 9 1 Maszyny kroczące: Podział maszyn kroczących ze względu rodzaj stabilności ruchu: statycznie stabilne mają dużo aktywnych stopni swobody, ich postura(konfiguracja) jest stała, ruch opisywany jest za pomocą metod kinematycznych; quasi-statycznie stabilne w porównaniu z pierwszą grupą mają mniejszą liczbę stopni swobody, pomiędzy statycznie stabilnymi fazami ruchu występują fazy utraty stabilności statycznej, maszyna nie przewraca się zachowana jest stabilność dynamiczna(tylko w krótkim czasie); dynamicznie stabilne mają od kilku do kilkudziesięciu stopni swobody, cechują się ciągle zmienną konfiguracją(posturą), wynikiem zmian konfiguracji jest, stabilny dynamicznie, ruch postępowy maszyny. Podział maszyn kroczących ze względu na liczbę nóg: jednonożne(monopedy) maszyny skaczące, typu odwrócone wahadło, w celu zachowania równowagi maszyna musi być dynamicznie stabilna; dwunożne(bipedy) chodzące, skaczące, w tym maszyny humanoidalne, o dużych stopach(stabilne quasi-statycznie), albo maszyny stabilne dynamicznie(robot HONDA); czteronożne zazwyczaj nogi przypominają kończyny owadów, istnieją także urządzenia, których nogi są odwzorowaniem kończyn czworonogów(ssaków, płazów, gadów); sześcionożne z założenia przypominają owady, zarówno posturą kończyn jak i statycznym sposobem chodu; Wstęp do Robotyki c W. Szynkiewicz, 9 wielonożne składające się z wielu segmentów ciała wyposażonych w nogi, poruszają się podobnie jak stonogi, maszyny te są stabilne statycznie. Zalety maszyn kroczących: adaptacja i manewrowość w zróżnicowanym(nierównym) terenie możliwość pokonywania przeszkód(dziury, nierówności) potencjalna możliwość manipulowania obiektami za pomocą kończyn(np. owady) Wady maszyn kroczących: skomplikowana budowa mechaniczna(duża liczba stopni swobody) duże zapotrzebowanie na energię(wiele napędów) złożony układ sterowania
12 Wstęp do Robotyki c W. Szynkiewicz, 9 3 Rodzaje kół: Rys. 5: Podstawowe rodzaje kół: a) koło zwykłe-stałe, b) koło samonastawne, c) koło szwedzkie, d) koło sferyczne. Wstęp do Robotyki c W. Szynkiewicz, 9 4 Zadanie 4: Jaki rodzaj koła przedstawiono na poniższym rysunku. Jakie jest znaczenie parametrów d, l, α, β, ϕ i jakim układzie są one definiowane, które z nich są zmiennymi? y 1 korpus robota l t A d B r x 1 P d Rozwiązanie:?
13 Wstęp do Robotyki c W. Szynkiewicz, 9 5 Podstawowe rodzaje baz jezdnych kołowych robotów mobilnych Napęd różnicowy dwa niezależnie napędzane koła jednej osi, dla zachowania równowagi dodane jest trzecie koło bierne(lub dwa bierne koła) Napęd synchroniczny trzy napędzane koła w układzie trójkątnym, wszystkie skierowane w jednym kierunku z możliwością zmiany kierunku ruchu bez zmiany orientacji bazy Napęd dookólny(wielokierunkowy) podobny do napędu synchronicznego, ale każde koło jest złożonym mechanizmem i może toczyć się w dowolnym kierunku Napęd trójkołowy przednie koło napędowe i kierujące, dwa koła tylnej osi są nie napędzane(są kołami biernymi) Napęd Ackermana(samochód kinematyczny) typowy czterokołowy pojazd, napęd na dwa koła(zazwyczaj przednie) jednej osi i dwa koła drugiej osi nie są napędzane Wstęp do Robotyki c W. Szynkiewicz, 9 6 Zadanie 5: Co to są nie zdegenerowane kołowe roboty mobilne? Rozwiązanie: Roboty niezdegenerowane spełniają następujące założenia: 1.Jeślirobotmawięcejniżjednozwykłestałekoło(tj.N f >1),tokołatemająwspólnąoś,czyli rankc 1f 1.. Środki kół kierujących orientowalnych względem prostej przechodzącej przez środek koła nie są współosiowezkołamistałymi,czylirankc 1 (β s )=rankc 1f +rankc 1s (β s ) 3.LiczbarankC 1s (β s ) jestliczbąkółkierujących,któremogąbyćorientowaneniezależniedla kierowaniarobotem.liczbatajestnazywanastopniemsterowności(kierowalności)robotaδ s : δ s =rankc 1s (β s ) (5) Wpływ sterowności na pozycje robota ξ jest pośredni. Zmiana pozycji nastąpi po zmianie orientacji koła kierowalnego i wykonaniu ruchu przez robota.
14 Wstęp do Robotyki c W. Szynkiewicz, 9 7 Kinematyka mobilnych robotów kołowych Proste zadanie kinematyki: ξ= Odwrotne zadanie kinematyki: Równanie kinematyki prostej w zwartej postaci: ẋ ẏ θ =f(ϕ 1,...,ϕ n,β 1,...,β m, β 1,..., β m ) [ϕ 1,...,ϕ n,β 1,...,β m, β 1,..., β m )] T =f(ẋ,ẏ, θ) q=g(q)u (6) gdzie albo q ξ β s q ξ,g(q) R T (θ)p,u η gdyδ s =,G(q) RT (θ)p(β s ) I,u η µ gdy,δ s 1 Wstęp do Robotyki c W. Szynkiewicz, 9 8 Zadanie 6: Wyprowadź podstawowe równania kinematyki robota o napędzie różnicowym pokazanym na rys. 6 w układzieinercjalnym(x I,Y I ).WyznaczwzórnachwilowypromieńskręturobotaR s. Y I y Y R l V l d P X R d V p p R s O x X I Rys. 6: Robot z napędem różnicowym Rozwiązanie: Prędkość wyrażona w układzie inercjalnym powiązana jest z prędkością w układzie lokalnym robota zależnością: ẋ cosθ sinθ ξ I = ẏ =R 1 (θ) ξ R,gdziemacierzobrotuR(θ)= sinθ cosθ θ 1
15 Wstęp do Robotyki c W. Szynkiewicz, 9 9 Prędkościliniowekółsąodpowiedniorównev l =rω l orazv p =rω p,stądprędkośćliniowapojazdujest średnią arytmetyczną ẋ R =r ω l+ω p Przyjmując, że chwilowy środek obrotu jest w punkcie styku koła z podłożem, prędkość kątowa w układzie lokalnym ω= θ= r d (ω l ω p ) stąd ξ I = Chwilowy promień obrotu obliczany z zależności ẋ ẏ θ =R 1 (θ)r ω l +ω p ω l ω p d ω(r s d )=v p, ω(r s + d )=v l, stąd otrzymujemy R s = d ω l +ω p ω l ω p Wstęp do Robotyki c W. Szynkiewicz, 9 3 Zadanie 7: Wyprowadzić równanie więzów nieholnomicznych(brak poślizgu) dla koła, którego środek leży punkcie P (początekukładurobotax R,Y R )ikierunekruchupokrywasięzosiąy R :a)dlachwilowejprędkościw ξ R wukładzielokalnym,b)dlachwilowejprędkości ξ I wukładzieinercjalnym. Rozwiązanie: a)wukładzielokalnymzwarunkubrakupoślizguwynika,żeruchwzdłużosix R jestniemożliwy,czyli czyli równanie więzów można zapisać ẋ R = [1][ẋ R ;ẏ R θ] T =[1] ξ R = b)ponieważ ξ I =R 1 (θ) ξ R,tozpunktua)wynika,że po pomnożeniu otrzymany [1]R 1 (θ) ξ R = [cosθsinθ] ξ I =[cosθsinθ][ẋ I ẏ I θ] T = lub można to zapisać jako ẋ I cosθ+ẏ I sinθ=
16 Wstęp do Robotyki c W. Szynkiewicz, 9 31 Ogólny podział(typowe zastosowanie) Czujniki PC//P Przełączniki kontaktowe, czułki (anteny), zderzaki(zamykanie EC P Czujniki dotykowe(detekcja fizycznego pętli np. mikrowyłączniki), sztuczna skóra kontaktu) lub zbliżeniowe Bariery optyczne Bezkontaktowe czujniki zbliżeniowe potencjometry PC P Odometryczne(położenie i prędkość kątowa) rezolwery i selsyny PC A enkodery optyczne: przyrostowe i bezwzględne PC A enkodery magnetyczne, indukcyjne, pojemnościowe PC A kompasy(mechaniczno-magnetyczne, magnetyczne, efekt Halla, EC P Kierunku(orientacji robota w układzie magnetorezystywne, magnetoelastyczne) inercjalnym) żyroskopy(mechaniczne i optyczne) PC P inklinometry /P GPS Naziemne latarnie kierunkowe(lokalizacja w Aktywne optyczne lub radiowe latarnie stałym układzie odniesienia) Aktywne ultradźwiękowe latarnie Latarnie odbiciowe Czujniki odbiciowe czujniki ultradźwiękowe sonary Aktywne czujniki pomiaru odległości radary, lidary (odbiciowe, czas-lotu, triangulacja) optyczna triangulacja(1d) światło strukturalne(d) Czujniki ruchu/prędkości(prędkość względna radary dopplerowskie do stacjonarnych lub ruchomych obiektów) sonary dopplerowskie Czujniki wizyjne(odległości, analizy obrazu, Kamery CCD/CMOS EC P segmentacji, rozpoznawania obiektów) układy wizyjne(pomiaru odległości, śledzenia obiektów) Czujniki wielkości fizycznych i chemicznych termometry, termopary, higrometry, tensometry, liczniki /P środowiska(np. temperatury, wilgotności, Geigera-Müllera, itp. ciśnienia, promieniowania radioaktywnego) Tabela 1: Klasyfikacja czujników stosowanych w robotach mobilnych(a-aktywne, P-pasywne, PC-proprioceptywne, EC-eksteroceptywne) Wstęp do Robotyki c W. Szynkiewicz, 9 3 Struktury sterowania: 1. reaktywne nie myśl reaguj. Struktura równoległa złożona z równolegle wykonujących się prostych reguł typu bodziec-reakcja.. behawioralne zastanów się nad sposobem zachowania się i działaj. Struktura równoległa równolegle działające zachowania(mogą być b. złożone). 3. deliberatywne(oparte na modelu) dokładnie planuj i dopiero potem działaj. Struktura sekwencyjna S-P-A. 4. hybrydowe myśl(planuj) i działaj niezależnie/równolegle. Struktura warstwowa układu sterowania zazwyczaj trójwarstwowa warstwa dolna reaktywna, warstwa górna(planowania) wykorzystuje model oraz warstwa pośrednia, łącząca.
17 Wstęp do Robotyki c W. Szynkiewicz, 9 33 Zadanie 8: Obliczyćwielomiantrzeciegostopniabędącytrajektoriąprzejściamiędzykonfiguracjąpoczątkowąq i konfiguracjąkońcowąq f wczasiet f =1s,rozpoczynającikończącruchzprędkościąrównązero.Narysować trajektorięorazprzebiegiprędkościiprzyspieszeniadlaq =1iq f =. Rozwiązanie: Równanie parametryczne wielomianu trzeciego stopnia prędkość q(t)=a +a 1 t+a t +a 3 t 3 q(t)=a 1 +a t+3a 3 t Zwarunkówgranicznychdlat=it=t f wynika,układczterechrównańzczteremaniewiadomymi q =a +a 1 t +a t +a 3 t 3 q f =a +a 1 t f +a t f+a 3 t 3 f q (t)=a 1 +a t +3a 3 t q f (t)=a 1 +a t f +3a 3 t f Wstęp do Robotyki c W. Szynkiewicz, 9 34 Cztery równania można zapisać w postaci równania macierzowego: 1 t t t 3 1 t 3t 1 t f t f t 3 f 1 t f 3t f a a 1 a a 3 Popodstawieniut =it f =1orazq = q f =mamy co jest równoważne równaniom po rozwiązaniu dwóch ostatnich równań mamy a a 1 a a 3 a =q a 1 = = = q q q ḟ q f q q ḟ q f a +a 3 =q f q a +3a 3 = a =3(q f q ) a 3 = (q f q )
18 Wstęp do Robotyki c W. Szynkiewicz, 9 35 zatem wielomian ma postać q(t)=q +3(q f q )t (q f q )t 3 popodstawieniuwartościq =1iq f = mamy q(t)=1 9t +6t 3 q(t)= 18t+18t q(t)= 18+36t 1 Położenie Prędkość Przyspieszenie q q q t t t
Kinematyka manipulatorów robotów
 Wstęp do Robotyki c W. Szynkiewicz, 29 1 Podstawowe pojęcia: Kinematyka manipulatorów robotów Ogniwo(człon, ramię) bryła sztywna(zbiór punktów materialnych, których wzajemne położenie jest stałe). Przegub(złącze)
Wstęp do Robotyki c W. Szynkiewicz, 29 1 Podstawowe pojęcia: Kinematyka manipulatorów robotów Ogniwo(człon, ramię) bryła sztywna(zbiór punktów materialnych, których wzajemne położenie jest stałe). Przegub(złącze)
Rozszerzony konspekt preskryptu do przedmiotu Podstawy Robotyki
 Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Rozszerzony konspekt preskryptu do przedmiotu Podstawy Robotyki dr inż. Marek Wojtyra Instytut Techniki Lotniczej
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Rozszerzony konspekt preskryptu do przedmiotu Podstawy Robotyki dr inż. Marek Wojtyra Instytut Techniki Lotniczej
D l. D p. Rodzaje baz jezdnych robotów mobilnych
 ERO Elementy robotyki 1 Rodzaje baz jezdnych robotów mobilnych Napęd różnicowy dwa niezależnie napędzane koła jednej osi, dla zachowania równowagi dodane jest trzecie koło bierne (lub dwa bierne koła)
ERO Elementy robotyki 1 Rodzaje baz jezdnych robotów mobilnych Napęd różnicowy dwa niezależnie napędzane koła jednej osi, dla zachowania równowagi dodane jest trzecie koło bierne (lub dwa bierne koła)
Kinematyka robotów mobilnych
 Kinematyka robotów mobilnych Maciej Patan Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Adaptacja slajdów do wykładu Autonomous mobile robots R. Siegwart (ETH Zurich Master Course:
Kinematyka robotów mobilnych Maciej Patan Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Adaptacja slajdów do wykładu Autonomous mobile robots R. Siegwart (ETH Zurich Master Course:
Egzamin 1 Strona 1. Egzamin - AR egz Zad 1. Rozwiązanie: Zad. 2. Rozwiązanie: Koła są takie same, więc prędkości kątowe też są takie same
 Egzamin 1 Strona 1 Egzamin - AR egz1 2005-06 Zad 1. Rozwiązanie: Zad. 2 Rozwiązanie: Koła są takie same, więc prędkości kątowe też są takie same Zad.3 Rozwiązanie: Zad.4 Rozwiązanie: Egzamin 1 Strona 2
Egzamin 1 Strona 1 Egzamin - AR egz1 2005-06 Zad 1. Rozwiązanie: Zad. 2 Rozwiązanie: Koła są takie same, więc prędkości kątowe też są takie same Zad.3 Rozwiązanie: Zad.4 Rozwiązanie: Egzamin 1 Strona 2
Wstęp do robotyki. Plan wykładów. Wojciech Szynkiewicz. Plan wykładu... Plan wykładu... Instytut Automatyki i Informatyki Stosowanej PW
 Plan wykładów Wstęp do robotyki Wojciech Szynkiewicz pok.554 e-mail: W.Szynkiewicz@ia.pw.edu.pl Instytut Automatyki i Informatyki Stosowanej PW Podstawowe pojęcia z dziedziny robotyki: krótka historia
Plan wykładów Wstęp do robotyki Wojciech Szynkiewicz pok.554 e-mail: W.Szynkiewicz@ia.pw.edu.pl Instytut Automatyki i Informatyki Stosowanej PW Podstawowe pojęcia z dziedziny robotyki: krótka historia
Notacja Denavita-Hartenberga
 Notacja DenavitaHartenberga Materiały do ćwiczeń z Podstaw Robotyki Artur Gmerek Umiejętność rozwiązywania prostego zagadnienia kinematycznego jest najbardziej bazową umiejętność zakresu Robotyki. Wyznaczyć
Notacja DenavitaHartenberga Materiały do ćwiczeń z Podstaw Robotyki Artur Gmerek Umiejętność rozwiązywania prostego zagadnienia kinematycznego jest najbardziej bazową umiejętność zakresu Robotyki. Wyznaczyć
Podstawy Robotyki Określenie kinematyki oraz dynamiki manipulatora
 Podstawy Robotyki Określenie kinematyki oraz dynamiki manipulatora AiR V sem. Gr. A4/ Wicher Bartłomiej Pilewski Wiktor 9 stycznia 011 1 1 Wstęp Rysunek 1: Schematyczne przedstawienie manipulatora W poniższym
Podstawy Robotyki Określenie kinematyki oraz dynamiki manipulatora AiR V sem. Gr. A4/ Wicher Bartłomiej Pilewski Wiktor 9 stycznia 011 1 1 Wstęp Rysunek 1: Schematyczne przedstawienie manipulatora W poniższym
Kinematyka manipulatora równoległego typu DELTA 106 Kinematyka manipulatora równoległego hexapod 110 Kinematyka robotów mobilnych 113
 Spis treści Wstęp 11 1. Rozwój robotyki 15 Rys historyczny rozwoju robotyki 15 Dane statystyczne ilustrujące rozwój robotyki przemysłowej 18 Czynniki stymulujące rozwój robotyki 23 Zakres i problematyka
Spis treści Wstęp 11 1. Rozwój robotyki 15 Rys historyczny rozwoju robotyki 15 Dane statystyczne ilustrujące rozwój robotyki przemysłowej 18 Czynniki stymulujące rozwój robotyki 23 Zakres i problematyka
Jan Awrejcewicz- Mechanika Techniczna i Teoretyczna. Statyka. Kinematyka
 Jan Awrejcewicz- Mechanika Techniczna i Teoretyczna. Statyka. Kinematyka SPIS TREŚCI Przedmowa... 7 1. PODSTAWY MECHANIKI... 11 1.1. Pojęcia podstawowe... 11 1.2. Zasada d Alemberta... 18 1.3. Zasada prac
Jan Awrejcewicz- Mechanika Techniczna i Teoretyczna. Statyka. Kinematyka SPIS TREŚCI Przedmowa... 7 1. PODSTAWY MECHANIKI... 11 1.1. Pojęcia podstawowe... 11 1.2. Zasada d Alemberta... 18 1.3. Zasada prac
OPISY PRZESTRZENNE I PRZEKSZTAŁCENIA
 OPISY PRZESTRZENNE I PRZEKSZTAŁCENIA Wprowadzenie W robotyce przez pojęcie manipulacji rozumiemy przemieszczanie w przestrzeni przedmiotów i narzędzi za pomocą specjalnego mechanizmu. W związku z tym pojawia
OPISY PRZESTRZENNE I PRZEKSZTAŁCENIA Wprowadzenie W robotyce przez pojęcie manipulacji rozumiemy przemieszczanie w przestrzeni przedmiotów i narzędzi za pomocą specjalnego mechanizmu. W związku z tym pojawia
Jakobiany. Kinematykę we współrzędnych możemy potraktować jako operator przekształcający funkcje czasu
 Wstęp do Robotyki c W. Szynkiewicz, 29 1 Jakobiany Kinematykę we współrzędnych możemy potraktować jako operator przekształcający funkcje czasu ( t )z(t)=k(x(t)) Ponieważ funkcje w powyższym równaniu są
Wstęp do Robotyki c W. Szynkiewicz, 29 1 Jakobiany Kinematykę we współrzędnych możemy potraktować jako operator przekształcający funkcje czasu ( t )z(t)=k(x(t)) Ponieważ funkcje w powyższym równaniu są
Manipulatory i roboty mobilne AR S1 semestr 5
 Manipulatory i roboty mobilne AR S semestr 5 Konrad Słodowicz MN: Zadanie proste kinematyki manipulatora szeregowego - DOF Położenie manipulatora opisać można dwojako w przestrzeni kartezjańskiej lub zmiennych
Manipulatory i roboty mobilne AR S semestr 5 Konrad Słodowicz MN: Zadanie proste kinematyki manipulatora szeregowego - DOF Położenie manipulatora opisać można dwojako w przestrzeni kartezjańskiej lub zmiennych
Rozszerzony konspekt preskryptu do przedmiotu Teoria Maszyn i Mechanizmów
 Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Rozszerzony konspekt preskryptu do przedmiotu Teoria Maszyn i Mechanizmów Prof. dr hab. inż. Janusz Frączek Instytut
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Rozszerzony konspekt preskryptu do przedmiotu Teoria Maszyn i Mechanizmów Prof. dr hab. inż. Janusz Frączek Instytut
Podstawy robotyki - opis przedmiotu
 Podstawy robotyki - opis przedmiotu Informacje ogólne Nazwa przedmiotu Podstawy robotyki Kod przedmiotu 06.9-WE-AiRP-PR Wydział Kierunek Wydział Informatyki, Elektrotechniki i Automatyki Automatyka i robotyka
Podstawy robotyki - opis przedmiotu Informacje ogólne Nazwa przedmiotu Podstawy robotyki Kod przedmiotu 06.9-WE-AiRP-PR Wydział Kierunek Wydział Informatyki, Elektrotechniki i Automatyki Automatyka i robotyka
MECHANIKA 2 KINEMATYKA. Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 KINEMATYKA Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY Prowadzący: dr Krzysztof Polko Określenie położenia ciała sztywnego Pierwszy sposób: Określamy położenia trzech punktów ciała nie leżących
MECHANIKA 2 KINEMATYKA Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY Prowadzący: dr Krzysztof Polko Określenie położenia ciała sztywnego Pierwszy sposób: Określamy położenia trzech punktów ciała nie leżących
i = [ 0] j = [ 1] k = [ 0]
![i = [ 0] j = [ 1] k = [ 0] i = [ 0] j = [ 1] k = [ 0]](/thumbs/70/62901734.jpg) Ćwiczenia nr TEMATYKA: Układy współrzędnych: kartezjański, walcowy (cylindryczny), sferyczny (geograficzny), Przekształcenia: izometryczne, nieizometryczne. DEFINICJE: Wektor wodzący: wektorem r, ρ wodzącym
Ćwiczenia nr TEMATYKA: Układy współrzędnych: kartezjański, walcowy (cylindryczny), sferyczny (geograficzny), Przekształcenia: izometryczne, nieizometryczne. DEFINICJE: Wektor wodzący: wektorem r, ρ wodzącym
Wprowadzenie do robotyki
 Wprowadzenie do robotyki Robotyka to nauka i technologia projektowania, budowy i zastosowania sterowanych komputerowo urządzeń mechanicznych popularnie zwanych robotami. Robot urządzenie mechaniczne, które
Wprowadzenie do robotyki Robotyka to nauka i technologia projektowania, budowy i zastosowania sterowanych komputerowo urządzeń mechanicznych popularnie zwanych robotami. Robot urządzenie mechaniczne, które
2.9. Kinematyka typowych struktur manipulatorów
 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 2.9. Kinematyka typowych struktur manipulatorów 2.9.1. Manipulator planarny 3DOF Notacja DH Rys. 28 Tablica 1 Parametry DH Nr ogniwa
Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 2.9. Kinematyka typowych struktur manipulatorów 2.9.1. Manipulator planarny 3DOF Notacja DH Rys. 28 Tablica 1 Parametry DH Nr ogniwa
MODEL MANIPULATORA O STRUKTURZE SZEREGOWEJ W PROGRAMACH CATIA I MATLAB MODEL OF SERIAL MANIPULATOR IN CATIA AND MATLAB
 Kocurek Łukasz, mgr inż. email: kocurek.lukasz@gmail.com Góra Marta, dr inż. email: mgora@mech.pk.edu.pl Politechnika Krakowska, Wydział Mechaniczny MODEL MANIPULATORA O STRUKTURZE SZEREGOWEJ W PROGRAMACH
Kocurek Łukasz, mgr inż. email: kocurek.lukasz@gmail.com Góra Marta, dr inż. email: mgora@mech.pk.edu.pl Politechnika Krakowska, Wydział Mechaniczny MODEL MANIPULATORA O STRUKTURZE SZEREGOWEJ W PROGRAMACH
PRACA DYPLOMOWA MAGISTERSKA
 KATEDRA WYTRZYMAŁOSCI MATERIAŁÓW I METOD KOMPUTEROWYCH MACHANIKI PRACA DYPLOMOWA MAGISTERSKA Analiza kinematyki robota mobilnego z wykorzystaniem MSC.VisualNastran PROMOTOR Prof. dr hab. inż. Tadeusz Burczyński
KATEDRA WYTRZYMAŁOSCI MATERIAŁÓW I METOD KOMPUTEROWYCH MACHANIKI PRACA DYPLOMOWA MAGISTERSKA Analiza kinematyki robota mobilnego z wykorzystaniem MSC.VisualNastran PROMOTOR Prof. dr hab. inż. Tadeusz Burczyński
MECHANIKA 2. Wykład Nr 3 KINEMATYKA. Temat RUCH PŁASKI BRYŁY MATERIALNEJ. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Wykład Nr 3 KINEMATYKA Temat RUCH PŁASKI BRYŁY MATERIALNEJ Prowadzący: dr Krzysztof Polko Pojęcie Ruchu Płaskiego Rys.1 Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie
MECHANIKA 2 Wykład Nr 3 KINEMATYKA Temat RUCH PŁASKI BRYŁY MATERIALNEJ Prowadzący: dr Krzysztof Polko Pojęcie Ruchu Płaskiego Rys.1 Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI KATEDRA AUTOMATYKI. Robot do pokrycia powierzchni terenu
 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI KATEDRA AUTOMATYKI Robot do pokrycia powierzchni terenu Zadania robota Zadanie całkowitego pokrycia powierzchni na podstawie danych sensorycznych Zadanie unikania przeszkód
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI KATEDRA AUTOMATYKI Robot do pokrycia powierzchni terenu Zadania robota Zadanie całkowitego pokrycia powierzchni na podstawie danych sensorycznych Zadanie unikania przeszkód
Mechanika ogólna / Tadeusz Niezgodziński. - Wyd. 1, dodr. 5. Warszawa, Spis treści
 Mechanika ogólna / Tadeusz Niezgodziński. - Wyd. 1, dodr. 5. Warszawa, 2010 Spis treści Część I. STATYKA 1. Prawa Newtona. Zasady statyki i reakcje więzów 11 1.1. Prawa Newtona 11 1.2. Jednostki masy i
Mechanika ogólna / Tadeusz Niezgodziński. - Wyd. 1, dodr. 5. Warszawa, 2010 Spis treści Część I. STATYKA 1. Prawa Newtona. Zasady statyki i reakcje więzów 11 1.1. Prawa Newtona 11 1.2. Jednostki masy i
Ogłoszenie. Egzaminy z TEORII MASZYN I MECHANIZMÓW dla grup 12A1, 12A2, 12A3 odbędą się w sali A3: I termin 1 lutego 2017 r. godz
 Laboratorium Badań Technoklimatycznych i Maszyn Roboczych Ogłoszenie Egzaminy z TEORII MASZYN I MECHANIZMÓW dla grup 12A1, 12A2, 12A3 odbędą się w sali A3: I termin 1 lutego 2017 r. godz. 9 00 12 00. II
Laboratorium Badań Technoklimatycznych i Maszyn Roboczych Ogłoszenie Egzaminy z TEORII MASZYN I MECHANIZMÓW dla grup 12A1, 12A2, 12A3 odbędą się w sali A3: I termin 1 lutego 2017 r. godz. 9 00 12 00. II
Wprowadzenie do robotyki
 Wprowadzenie do robotyki Robotyka to nauka i technologia projektowania, budowy i zastosowania sterowanych komputerowo urządzeń mechanicznych popularnie zwanych robotami. Robot urządzenie mechaniczne, które
Wprowadzenie do robotyki Robotyka to nauka i technologia projektowania, budowy i zastosowania sterowanych komputerowo urządzeń mechanicznych popularnie zwanych robotami. Robot urządzenie mechaniczne, które
Mechanika Robotów. Wojciech Lisowski. 5 Planowanie trajektorii ruchu efektora w przestrzeni roboczej
 Katedra Robotyki i Mechatroniki Akademia Górniczo-Hutnicza w Krakowie Mechanika Robotów Wojciech Lisowski 5 Planowanie trajektorii ruchu efektora w przestrzeni roboczej Mechanika Robotów KRiM, WIMIR, AGH
Katedra Robotyki i Mechatroniki Akademia Górniczo-Hutnicza w Krakowie Mechanika Robotów Wojciech Lisowski 5 Planowanie trajektorii ruchu efektora w przestrzeni roboczej Mechanika Robotów KRiM, WIMIR, AGH
ZAGADNIENIA PROGRAMOWE I WYMAGANIA EDUKACYJNE DO TESTU PRZYROSTU KOMPETENCJI Z MATEMATYKI DLA UCZNIA KLASY II
 ZAGADNIENIA PROGRAMOWE I WYMAGANIA EDUKACYJNE DO TESTU PRZYROSTU KOMPETENCJI Z MATEMATYKI DLA UCZNIA KLASY II POZIOM ROZSZERZONY Równania i nierówności z wartością bezwzględną. rozwiązuje równania i nierówności
ZAGADNIENIA PROGRAMOWE I WYMAGANIA EDUKACYJNE DO TESTU PRZYROSTU KOMPETENCJI Z MATEMATYKI DLA UCZNIA KLASY II POZIOM ROZSZERZONY Równania i nierówności z wartością bezwzględną. rozwiązuje równania i nierówności
Mechanika. Wykład 2. Paweł Staszel
 Mechanika Wykład 2 Paweł Staszel 1 Przejście graniczne 0 2 Podstawowe twierdzenia o pochodnych: pochodna funkcji mnożonej przez skalar pochodna sumy funkcji pochodna funkcji złożonej pochodna iloczynu
Mechanika Wykład 2 Paweł Staszel 1 Przejście graniczne 0 2 Podstawowe twierdzenia o pochodnych: pochodna funkcji mnożonej przez skalar pochodna sumy funkcji pochodna funkcji złożonej pochodna iloczynu
Mechanika ogólna. Kinematyka. Równania ruchu punktu materialnego. Podstawowe pojęcia. Równanie ruchu po torze (równanie drogi)
 Kinematyka Mechanika ogólna Wykład nr 7 Elementy kinematyki Dział mechaniki zajmujący się matematycznym opisem układów mechanicznych oraz badaniem geometrycznych właściwości ich ruchu, bez wnikania w związek
Kinematyka Mechanika ogólna Wykład nr 7 Elementy kinematyki Dział mechaniki zajmujący się matematycznym opisem układów mechanicznych oraz badaniem geometrycznych właściwości ich ruchu, bez wnikania w związek
Temat 1. Wprowadzenie do nawigacji robotów mobilnych. Dariusz Pazderski Opracowanie w ramach programu ERA Inżyniera
 Kurs: Algorytmy Nawigacji Robotów Mobilnych Temat 1 Wprowadzenie do nawigacji robotów mobilnych 1 Pojęcia podstawowe Dariusz Pazderski Opracowanie w ramach programu ERA Inżyniera Na początku wprowadzimy
Kurs: Algorytmy Nawigacji Robotów Mobilnych Temat 1 Wprowadzenie do nawigacji robotów mobilnych 1 Pojęcia podstawowe Dariusz Pazderski Opracowanie w ramach programu ERA Inżyniera Na początku wprowadzimy
1. STRUKTURA MECHANIZMÓW 1.1. POJĘCIA PODSTAWOWE
 1. STRUKTURA MECHANIZMÓW 1.1. POJĘCIA PODSTAWOWE 1.1.1. Człon mechanizmu Człon mechanizmu to element konstrukcyjny o dowolnym kształcie, ruchomy bądź nieruchomy, zwany wtedy podstawą, niepodzielny w aspekcie
1. STRUKTURA MECHANIZMÓW 1.1. POJĘCIA PODSTAWOWE 1.1.1. Człon mechanizmu Człon mechanizmu to element konstrukcyjny o dowolnym kształcie, ruchomy bądź nieruchomy, zwany wtedy podstawą, niepodzielny w aspekcie
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ
 RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 6 2016/2017, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 6 2016/2017, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
Roboty przemysłowe. Cz. II
 Roboty przemysłowe Cz. II Klasyfikacja robotów Ze względu na rodzaj napędu: - hydrauliczny (duże obciążenia) - pneumatyczny - elektryczny - mieszany Obecnie roboty przemysłowe bardzo często posiadają napędy
Roboty przemysłowe Cz. II Klasyfikacja robotów Ze względu na rodzaj napędu: - hydrauliczny (duże obciążenia) - pneumatyczny - elektryczny - mieszany Obecnie roboty przemysłowe bardzo często posiadają napędy
Roboty przemysłowe. Wprowadzenie
 Roboty przemysłowe Wprowadzenie Pojęcia podstawowe Manipulator jest to mechanizm cybernetyczny przeznaczony do realizacji niektórych funkcji kończyny górnej człowieka. Należy wyróżnić dwa rodzaje funkcji
Roboty przemysłowe Wprowadzenie Pojęcia podstawowe Manipulator jest to mechanizm cybernetyczny przeznaczony do realizacji niektórych funkcji kończyny górnej człowieka. Należy wyróżnić dwa rodzaje funkcji
Spis treści. Przedmowa... 7
 Spis treści SPIS TREŚCI Przedmowa... 7 1. PODSTAWY MECHANIKI... 11 1.1. Pojęcia podstawowe... 11 1.2. Zasada d Alemberta... 18 1.3. Zasada prac przygotowanych... 22 1.4. Przyrost funkcji i wariacja funkcji...
Spis treści SPIS TREŚCI Przedmowa... 7 1. PODSTAWY MECHANIKI... 11 1.1. Pojęcia podstawowe... 11 1.2. Zasada d Alemberta... 18 1.3. Zasada prac przygotowanych... 22 1.4. Przyrost funkcji i wariacja funkcji...
GRAFIKA KOMPUTEROWA podstawy matematyczne. dr inż. Hojny Marcin pokój 406, pawilon B5 E-mail: mhojny@metal.agh.edu.pl Tel.
 GRAFIKA KOMPUTEROWA podstawy matematyczne dr inż. Hojny Marcin pokój 406, pawilon B5 E-mail: mhojny@metal.agh.edu.pl Tel. (12) 617 46 37 Plan wykładu 1/4 ZACZNIEMY OD PRZYKŁADOWYCH PROCEDUR i PRZYKŁADÓW
GRAFIKA KOMPUTEROWA podstawy matematyczne dr inż. Hojny Marcin pokój 406, pawilon B5 E-mail: mhojny@metal.agh.edu.pl Tel. (12) 617 46 37 Plan wykładu 1/4 ZACZNIEMY OD PRZYKŁADOWYCH PROCEDUR i PRZYKŁADÓW
MECHANIKA 2 RUCH POSTĘPOWY I OBROTOWY CIAŁA SZTYWNEGO. Wykład Nr 2. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Wykład Nr 2 RUCH POSTĘPOWY I OBROTOWY CIAŁA SZTYWNEGO Prowadzący: dr Krzysztof Polko WSTĘP z r C C(x C,y C,z C ) r C -r B B(x B,y B,z B ) r C -r A r B r B -r A A(x A,y A,z A ) Ciało sztywne
MECHANIKA 2 Wykład Nr 2 RUCH POSTĘPOWY I OBROTOWY CIAŁA SZTYWNEGO Prowadzący: dr Krzysztof Polko WSTĘP z r C C(x C,y C,z C ) r C -r B B(x B,y B,z B ) r C -r A r B r B -r A A(x A,y A,z A ) Ciało sztywne
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO. dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury
 KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ
 RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 7 2012/2013, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 7 2012/2013, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
Struktura manipulatorów
 Temat: Struktura manipulatorów Warianty struktury manipulatorów otrzymamy tworząc łańcuch kinematyczny o kolejnych osiach par kinematycznych usytuowanych pod kątem prostym. W ten sposób w zależności od
Temat: Struktura manipulatorów Warianty struktury manipulatorów otrzymamy tworząc łańcuch kinematyczny o kolejnych osiach par kinematycznych usytuowanych pod kątem prostym. W ten sposób w zależności od
Równa Równ n a i n e i ru r ch u u ch u po tor t ze (równanie drogi) Prędkoś ędkoś w ru r ch u u ch pros pr t os ol t i ol n i io i wym
 Mechanika ogólna Wykład nr 14 Elementy kinematyki i dynamiki 1 Kinematyka Dział mechaniki zajmujący się matematycznym opisem układów mechanicznych oraz badaniem geometrycznych właściwości ich ruchu, bez
Mechanika ogólna Wykład nr 14 Elementy kinematyki i dynamiki 1 Kinematyka Dział mechaniki zajmujący się matematycznym opisem układów mechanicznych oraz badaniem geometrycznych właściwości ich ruchu, bez
ROZKŁAD MATERIAŁU DO II KLASY LICEUM (ZAKRES ROZSZERZONY) A WYMAGANIA PODSTAWY PROGRAMOWEJ.
 ROZKŁAD MATERIAŁU DO II KLASY LICEUM (ZAKRES ROZSZERZONY) A WYMAGANIA PODSTAWY PROGRAMOWEJ. LICZBA TEMAT GODZIN LEKCYJNYCH Potęgi, pierwiastki i logarytmy (8 h) Potęgi 3 Pierwiastki 3 Potęgi o wykładnikach
ROZKŁAD MATERIAŁU DO II KLASY LICEUM (ZAKRES ROZSZERZONY) A WYMAGANIA PODSTAWY PROGRAMOWEJ. LICZBA TEMAT GODZIN LEKCYJNYCH Potęgi, pierwiastki i logarytmy (8 h) Potęgi 3 Pierwiastki 3 Potęgi o wykładnikach
1) Podaj i opisz znane ci języki programowania sterowników opisanych w normie IEC 61131-3.
 PLC 1) Podaj i opisz znane ci języki programowania sterowników opisanych w normie IEC 61131-3. 1.Ladder Diagram (LD) język graficzny schematów drabinkowych 2. Function Block Diagram (FBD) jezyk bloków
PLC 1) Podaj i opisz znane ci języki programowania sterowników opisanych w normie IEC 61131-3. 1.Ladder Diagram (LD) język graficzny schematów drabinkowych 2. Function Block Diagram (FBD) jezyk bloków
2) R stosuje w obliczeniach wzór na logarytm potęgi oraz wzór na zamianę podstawy logarytmu.
 ZAKRES ROZSZERZONY 1. Liczby rzeczywiste. Uczeń: 1) przedstawia liczby rzeczywiste w różnych postaciach (np. ułamka zwykłego, ułamka dziesiętnego okresowego, z użyciem symboli pierwiastków, potęg); 2)
ZAKRES ROZSZERZONY 1. Liczby rzeczywiste. Uczeń: 1) przedstawia liczby rzeczywiste w różnych postaciach (np. ułamka zwykłego, ułamka dziesiętnego okresowego, z użyciem symboli pierwiastków, potęg); 2)
Sposoby modelowania układów dynamicznych. Pytania
 Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: KINEMATYKA I DYNAMIKA MANIPULATORÓW I ROBOTÓW Kierunek: Mechatronika Rodzaj przedmiotu: obowiązkowy na specjalności: Systemy sterowania Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU
Nazwa przedmiotu: KINEMATYKA I DYNAMIKA MANIPULATORÓW I ROBOTÓW Kierunek: Mechatronika Rodzaj przedmiotu: obowiązkowy na specjalności: Systemy sterowania Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU
WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA POSZCZEGÓLNYCH ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI POLITECHNICZNEJ KLASA 2
 WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA POSZCZEGÓLNYCH ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI POLITECHNICZNEJ KLASA 2 I. GEOMETRIA ANALITYCZNA: Wektor w układzie współrzędnych.
WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA POSZCZEGÓLNYCH ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI POLITECHNICZNEJ KLASA 2 I. GEOMETRIA ANALITYCZNA: Wektor w układzie współrzędnych.
Koncepcje lokomocji. Maciej Patan Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych
 Koncepcje lokomocji Maciej Patan Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Adaptacja slajdów do wykładu Autonomous mobile robots R. Siegwart (ETH Zurich Master Course: 151-0854-00L)
Koncepcje lokomocji Maciej Patan Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Adaptacja slajdów do wykładu Autonomous mobile robots R. Siegwart (ETH Zurich Master Course: 151-0854-00L)
Zastosowanie Robotów. Ćwiczenie 6. Mariusz Janusz-Bielecki. laboratorium
 Zastosowanie Robotów laboratorium Ćwiczenie 6 Mariusz Janusz-Bielecki Zak lad Informatyki i Robotyki Wersja 0.002.01, 7 Listopada, 2005 Wst ep Do zadań inżynierów robotyków należa wszelkie dzia lania
Zastosowanie Robotów laboratorium Ćwiczenie 6 Mariusz Janusz-Bielecki Zak lad Informatyki i Robotyki Wersja 0.002.01, 7 Listopada, 2005 Wst ep Do zadań inżynierów robotyków należa wszelkie dzia lania
Roboty mobilne. Co to jest robot mobilny?
 Co to jest robot mobilny? Roboty mobilne To kompozycja różnorodnych fizycznych i informatycznych składników tworząca 4 podstawowe podsystemy: - Ruchu (locomotion) - Detekcji (sensing) - Wnioskowania (reasoning)
Co to jest robot mobilny? Roboty mobilne To kompozycja różnorodnych fizycznych i informatycznych składników tworząca 4 podstawowe podsystemy: - Ruchu (locomotion) - Detekcji (sensing) - Wnioskowania (reasoning)
Symulacje komputerowe
 Fizyka w modelowaniu i symulacjach komputerowych Jacek Matulewski (e-mail: jacek@fizyka.umk.pl) http://www.fizyka.umk.pl/~jacek/dydaktyka/modsym/ Symulacje komputerowe Dynamika bryły sztywnej Wersja: 8
Fizyka w modelowaniu i symulacjach komputerowych Jacek Matulewski (e-mail: jacek@fizyka.umk.pl) http://www.fizyka.umk.pl/~jacek/dydaktyka/modsym/ Symulacje komputerowe Dynamika bryły sztywnej Wersja: 8
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw udowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2016/2017
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw udowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2016/2017
Zakres na egzaminy poprawkowe w r. szk. 2013/14 /nauczyciel M.Tatar/
 Zakres na egzaminy poprawkowe w r. szk. 2013/14 /nauczyciel M.Tatar/ MATEMATYKA Klasa III ZAKRES PODSTAWOWY Dział programu Temat Wymagania. Uczeń: 1. Miara łukowa kąta zna pojęcia: kąt skierowany, kąt
Zakres na egzaminy poprawkowe w r. szk. 2013/14 /nauczyciel M.Tatar/ MATEMATYKA Klasa III ZAKRES PODSTAWOWY Dział programu Temat Wymagania. Uczeń: 1. Miara łukowa kąta zna pojęcia: kąt skierowany, kąt
Orientacja zewnętrzna pojedynczego zdjęcia
 Orientacja zewnętrzna pojedynczego zdjęcia Proces opracowania fotogrametrycznego zdjęcia obejmuje: 1. Rekonstrukcję kształtu wiązki promieni rzutujących (orientacja wewnętrzna ck, x, y punktu głównego)
Orientacja zewnętrzna pojedynczego zdjęcia Proces opracowania fotogrametrycznego zdjęcia obejmuje: 1. Rekonstrukcję kształtu wiązki promieni rzutujących (orientacja wewnętrzna ck, x, y punktu głównego)
Ćwiczenia nr 7. TEMATYKA: Krzywe Bézier a
 TEMATYKA: Krzywe Bézier a Ćwiczenia nr 7 DEFINICJE: Interpolacja: przybliżanie funkcji za pomocą innej funkcji, zwykle wielomianu, tak aby były sobie równe w zadanych punktach. Poniżej przykład interpolacji
TEMATYKA: Krzywe Bézier a Ćwiczenia nr 7 DEFINICJE: Interpolacja: przybliżanie funkcji za pomocą innej funkcji, zwykle wielomianu, tak aby były sobie równe w zadanych punktach. Poniżej przykład interpolacji
MECHANIKA OGÓLNA (II)
 MECHNIK GÓLN (II) Semestr: II (Mechanika I), III (Mechanika II), rok akad. 2013/2014 Liczba godzin: sem. II *) - wykład 30 godz., ćwiczenia 30 godz. sem. III *) - wykład 30 godz., ćwiczenia 30 godz., ale
MECHNIK GÓLN (II) Semestr: II (Mechanika I), III (Mechanika II), rok akad. 2013/2014 Liczba godzin: sem. II *) - wykład 30 godz., ćwiczenia 30 godz. sem. III *) - wykład 30 godz., ćwiczenia 30 godz., ale
Dynamika manipulatora. Robert Muszyński Janusz Jakubiak Instytut Cybernetyki Technicznej Politechnika Wrocławska. Podstawy robotyki wykład VI
 Podstawy robotyki Wykład VI Robert Muszyński Janusz Jakubiak Instytut Cybernetyki Technicznej Politechnika Wrocławska Dynamika opisuje sposób zachowania się manipulatora poddanego wymuszeniu w postaci
Podstawy robotyki Wykład VI Robert Muszyński Janusz Jakubiak Instytut Cybernetyki Technicznej Politechnika Wrocławska Dynamika opisuje sposób zachowania się manipulatora poddanego wymuszeniu w postaci
Podstawy robotyki wykład VI. Dynamika manipulatora
 Podstawy robotyki Wykład VI Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Dynamika opisuje sposób zachowania się manipulatora poddanego wymuszeniu
Podstawy robotyki Wykład VI Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Dynamika opisuje sposób zachowania się manipulatora poddanego wymuszeniu
Z poprzedniego wykładu:
 Z poprzedniego wykładu: Człon: Ciało stałe posiadające możliwość poruszania się względem innych członów Para kinematyczna: klasy I, II, III, IV i V (względem liczby stopni swobody) Niższe i wyższe pary
Z poprzedniego wykładu: Człon: Ciało stałe posiadające możliwość poruszania się względem innych członów Para kinematyczna: klasy I, II, III, IV i V (względem liczby stopni swobody) Niższe i wyższe pary
dr Mariusz Grządziel 15,29 kwietnia 2014 Przestrzeń R k R k = R R... R k razy Elementy R k wektory;
 Wykłady 8 i 9 Pojęcia przestrzeni wektorowej i macierzy Układy równań liniowych Elementy algebry macierzy dodawanie, odejmowanie, mnożenie macierzy; macierz odwrotna dr Mariusz Grządziel 15,29 kwietnia
Wykłady 8 i 9 Pojęcia przestrzeni wektorowej i macierzy Układy równań liniowych Elementy algebry macierzy dodawanie, odejmowanie, mnożenie macierzy; macierz odwrotna dr Mariusz Grządziel 15,29 kwietnia
MATeMAtyka klasa II poziom rozszerzony
 MATeMAtyka klasa II poziom rozszerzony W klasie drugiej na poziomie rozszerzonym realizujemy materiał z klasy pierwszej tylko z poziomu rozszerzonego (na czerwono) oraz cały materiał z klasy drugiej. Rozkład
MATeMAtyka klasa II poziom rozszerzony W klasie drugiej na poziomie rozszerzonym realizujemy materiał z klasy pierwszej tylko z poziomu rozszerzonego (na czerwono) oraz cały materiał z klasy drugiej. Rozkład
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: MECHANIKA I BUDOWA MASZYN Rodzaj przedmiotu: obowiązkowy na kierunku Rodzaj zajęć: wykład, laboratorium ROBOTYKA Robotics Forma studiów: stacjonarne Poziom przedmiotu: I stopnia
Nazwa przedmiotu: Kierunek: MECHANIKA I BUDOWA MASZYN Rodzaj przedmiotu: obowiązkowy na kierunku Rodzaj zajęć: wykład, laboratorium ROBOTYKA Robotics Forma studiów: stacjonarne Poziom przedmiotu: I stopnia
Zagadnienia do małej matury z matematyki klasa II Poziom podstawowy i rozszerzony
 Zagadnienia do małej matury z matematyki klasa II Poziom podstawowy i rozszerzony Uczeń realizujący zakres rozszerzony powinien również spełniać wszystkie wymagania w zakresie poziomu podstawowego. Zakres
Zagadnienia do małej matury z matematyki klasa II Poziom podstawowy i rozszerzony Uczeń realizujący zakres rozszerzony powinien również spełniać wszystkie wymagania w zakresie poziomu podstawowego. Zakres
ROZKŁAD MATERIAŁU NAUCZANIA KLASA 1, ZAKRES PODSTAWOWY
 ROZKŁAD MATERIAŁU NAUCZANIA KLASA 1, ZAKRES PODSTAWOWY Numer lekcji 1 2 Nazwa działu Lekcja organizacyjna. Zapoznanie z programem nauczania i kryteriami wymagań Zbiór liczb rzeczywistych i jego 3 Zbiór
ROZKŁAD MATERIAŁU NAUCZANIA KLASA 1, ZAKRES PODSTAWOWY Numer lekcji 1 2 Nazwa działu Lekcja organizacyjna. Zapoznanie z programem nauczania i kryteriami wymagań Zbiór liczb rzeczywistych i jego 3 Zbiór
PODSTAWY ROBOTYKI. Opracował: dr hab. inż. Adam Rogowski
 PODSTAWY ROBOTYKI Opracował: dr hab. inż. Adam Rogowski Autor wykładu: dr hab. inż. Adam Rogowski pok. ST 405 adam.rogowski@pw.edu.pl Literatura: - Treść niniejszego wykładu dostępna na www.cim.pw.edu.pl/lzp
PODSTAWY ROBOTYKI Opracował: dr hab. inż. Adam Rogowski Autor wykładu: dr hab. inż. Adam Rogowski pok. ST 405 adam.rogowski@pw.edu.pl Literatura: - Treść niniejszego wykładu dostępna na www.cim.pw.edu.pl/lzp
WYMAGANIA EDUKACYJNE Z MATEMATYKI KLASA III ZAKRES ROZSZERZONY (90 godz.) , x
 WYMAGANIA EDUACYJNE Z MATEMATYI LASA III ZARES ROZSZERZONY (90 godz.) Oznaczenia: wymagania konieczne (dopuszczający); P wymagania podstawowe (dostateczny); R wymagania rozszerzające (dobry); D wymagania
WYMAGANIA EDUACYJNE Z MATEMATYI LASA III ZARES ROZSZERZONY (90 godz.) Oznaczenia: wymagania konieczne (dopuszczający); P wymagania podstawowe (dostateczny); R wymagania rozszerzające (dobry); D wymagania
UKŁADY WIELOCZŁONOWE Z WIĘZAMI JEDNOSTRONNYMI W ZASTOSOWANIU DO MODELOWANIA ZŁOŻONYCH UKŁADÓW MECHANICZNYCH
 POLITECHNIKA GDAŃSKA KRZYSZTOF LIPIŃSKI UKŁADY WIELOCZŁONOWE Z WIĘZAMI JEDNOSTRONNYMI W ZASTOSOWANIU DO MODELOWANIA ZŁOŻONYCH UKŁADÓW MECHANICZNYCH GDAŃSK 2012 PRZEWODNICZĄCY KOMITETU REDAKCYJNEGO WYDAWNICTWA
POLITECHNIKA GDAŃSKA KRZYSZTOF LIPIŃSKI UKŁADY WIELOCZŁONOWE Z WIĘZAMI JEDNOSTRONNYMI W ZASTOSOWANIU DO MODELOWANIA ZŁOŻONYCH UKŁADÓW MECHANICZNYCH GDAŃSK 2012 PRZEWODNICZĄCY KOMITETU REDAKCYJNEGO WYDAWNICTWA
Przedmiotowy system oceniania wraz z określeniem wymagań edukacyjnych klasa druga zakres rozszerzony
 Przedmiotowy system oceniania wraz z określeniem wymagań edukacyjnych klasa druga zakres rozszerzony Wymagania konieczne (K) dotyczą zagadnień elementarnych, stanowiących swego rodzaju podstawę, zatem
Przedmiotowy system oceniania wraz z określeniem wymagań edukacyjnych klasa druga zakres rozszerzony Wymagania konieczne (K) dotyczą zagadnień elementarnych, stanowiących swego rodzaju podstawę, zatem
FIZYKA klasa 1 Liceum Ogólnokształcącego (4 letniego)
 2019-09-01 FIZYKA klasa 1 Liceum Ogólnokształcącego (4 letniego) Treści z podstawy programowej przedmiotu POZIOM ROZSZERZONY (PR) SZKOŁY BENEDYKTA Podstawa programowa FIZYKA KLASA 1 LO (4-letnie po szkole
2019-09-01 FIZYKA klasa 1 Liceum Ogólnokształcącego (4 letniego) Treści z podstawy programowej przedmiotu POZIOM ROZSZERZONY (PR) SZKOŁY BENEDYKTA Podstawa programowa FIZYKA KLASA 1 LO (4-letnie po szkole
Etap 1. Rysunek: Układy odniesienia
 Wprowadzenie. Jaś i Małgosia kręcą się na karuzeli symetrycznej dwuramiennej. Siedzą na karuzeli zwróceni do siebie twarzami, symetrycznie względem osi obrotu karuzeli. Jaś ma dropsa, którego chce dać
Wprowadzenie. Jaś i Małgosia kręcą się na karuzeli symetrycznej dwuramiennej. Siedzą na karuzeli zwróceni do siebie twarzami, symetrycznie względem osi obrotu karuzeli. Jaś ma dropsa, którego chce dać
PRZEKŁADNIE ZĘBATE. Przekł. o osiach stałych. Przekładnie obiegowe. Planetarne: W=1 Różnicowe i sumujące: W>1
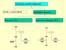 PRZEKŁADNIE ZĘBATE Przekł. o osiach stałych Przekładnie obiegowe Planetarne: W=1 Różnicowe i sumujące: W>1 Przekładnie obiegowe: Planetarne: W=1 2 I II 3 ( j ) 1 I n=3 p 1 =2 p 2 =1 W = 3(n-1) - 2p 1 -
PRZEKŁADNIE ZĘBATE Przekł. o osiach stałych Przekładnie obiegowe Planetarne: W=1 Różnicowe i sumujące: W>1 Przekładnie obiegowe: Planetarne: W=1 2 I II 3 ( j ) 1 I n=3 p 1 =2 p 2 =1 W = 3(n-1) - 2p 1 -
Karta (sylabus) modułu/przedmiotu Mechatronika Studia pierwszego stopnia. Podstawy robotyki Rodzaj przedmiotu: Zaliczenie Język wykładowy:
 Karta (sylabus) modułu/przedmiotu Mechatronika Studia pierwszego stopnia Przedmiot: Podstawy robotyki Rodzaj przedmiotu: obowiązkowy Kod przedmiotu: MT 1 S 0 6 38-0_1 Rok: III Semestr: 6 Forma studiów:
Karta (sylabus) modułu/przedmiotu Mechatronika Studia pierwszego stopnia Przedmiot: Podstawy robotyki Rodzaj przedmiotu: obowiązkowy Kod przedmiotu: MT 1 S 0 6 38-0_1 Rok: III Semestr: 6 Forma studiów:
ROBOTYKA. Odwrotne zadanie kinematyki - projekt. http://www.mbmaster.pl
 ROBOTYKA Odwrotne zadanie kinematyki - projekt Zawartość. Wstęp...... Proste zadanie kinematyki cel...... Odwrotne zadanie kinematyki cel..... Analiza statyczna robota..... Proste zadanie kinematyki....
ROBOTYKA Odwrotne zadanie kinematyki - projekt Zawartość. Wstęp...... Proste zadanie kinematyki cel...... Odwrotne zadanie kinematyki cel..... Analiza statyczna robota..... Proste zadanie kinematyki....
Spis treści. Wstęp Część I STATYKA
 Spis treści Wstęp... 15 Część I STATYKA 1. WEKTORY. PODSTAWOWE DZIAŁANIA NA WEKTORACH... 17 1.1. Pojęcie wektora. Rodzaje wektorów... 19 1.2. Rzut wektora na oś. Współrzędne i składowe wektora... 22 1.3.
Spis treści Wstęp... 15 Część I STATYKA 1. WEKTORY. PODSTAWOWE DZIAŁANIA NA WEKTORACH... 17 1.1. Pojęcie wektora. Rodzaje wektorów... 19 1.2. Rzut wektora na oś. Współrzędne i składowe wektora... 22 1.3.
3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas
 3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas oddziaływanie między ciałami, ani też rola, jaką to
3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas oddziaływanie między ciałami, ani też rola, jaką to
Karta (sylabus) modułu/przedmiotu Mechatronika Studia pierwszego stopnia. Podstawy robotyki Rodzaj przedmiotu: Zaliczenie Język wykładowy:
 Karta (sylabus) modułu/przedmiotu Mechatronika Studia pierwszego stopnia Przedmiot: Podstawy robotyki Rodzaj przedmiotu: obowiązkowy Kod przedmiotu: MT 1 S 0 6 38-0_1 Rok: III Semestr: 6 Forma studiów:
Karta (sylabus) modułu/przedmiotu Mechatronika Studia pierwszego stopnia Przedmiot: Podstawy robotyki Rodzaj przedmiotu: obowiązkowy Kod przedmiotu: MT 1 S 0 6 38-0_1 Rok: III Semestr: 6 Forma studiów:
Modelowanie i symulacja II Modelling and Simulation II. Automatyka i Robotyka II stopień ogólno akademicki studia stacjonarne
 KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2013/2014 Modelowanie i symulacja II Modelling and Simulation II A. USYTUOWANIE
KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2013/2014 Modelowanie i symulacja II Modelling and Simulation II A. USYTUOWANIE
WYMAGANIA Z WIEDZY I UMIEJĘTNOŚCI NA POSZCZEGÓLNE STOPNIE SZKOLNE DLA KLASY CZWARTEJ H. zakres rozszerzony. Wiadomości i umiejętności
 WYMAGANIA Z WIEDZY I UMIEJĘTNOŚCI NA POSZCZEGÓLNE STOPNIE SZKOLNE DLA KLASY CZWARTEJ H. zakres rozszerzony Funkcja wykładnicza i funkcja logarytmiczna. Stopień Wiadomości i umiejętności -definiować potęgę
WYMAGANIA Z WIEDZY I UMIEJĘTNOŚCI NA POSZCZEGÓLNE STOPNIE SZKOLNE DLA KLASY CZWARTEJ H. zakres rozszerzony Funkcja wykładnicza i funkcja logarytmiczna. Stopień Wiadomości i umiejętności -definiować potęgę
PLAN WYNIKOWY Z MATEMATYKI DLA KLASY II TECHNIKUM 5 - LETNIEGO
 Lp. I PLAN WYNIKOWY Z MATEMATYKI DLA KLASY II TECHNIKUM 5 - LETNIEGO Temat lekcji Umiejętności Podstawowe Ponadpodstawowe Funkcja kwadratowa Uczeń: Uczeń: 1 Wykres i własności funkcji y = ax 2. - narysuje
Lp. I PLAN WYNIKOWY Z MATEMATYKI DLA KLASY II TECHNIKUM 5 - LETNIEGO Temat lekcji Umiejętności Podstawowe Ponadpodstawowe Funkcja kwadratowa Uczeń: Uczeń: 1 Wykres i własności funkcji y = ax 2. - narysuje
Rozdział VII. Przekształcenia geometryczne na płaszczyźnie Przekształcenia geometryczne Symetria osiowa Symetria środkowa 328
 Drogi Czytelniku 9 Oznaczenia matematyczne 11 Podstawowe wzory 15 Rozdział I. Zbiory. Działania na zbiorach 21 1. Zbiór liczb naturalnych 22 1.1. Działania w zbiorze liczb naturalnych 22 1.2. Prawa działań
Drogi Czytelniku 9 Oznaczenia matematyczne 11 Podstawowe wzory 15 Rozdział I. Zbiory. Działania na zbiorach 21 1. Zbiór liczb naturalnych 22 1.1. Działania w zbiorze liczb naturalnych 22 1.2. Prawa działań
Próbny egzamin z matematyki dla uczniów klas II LO i III Technikum. w roku szkolnym 2012/2013
 Próbny egzamin z matematyki dla uczniów klas II LO i III Technikum w roku szkolnym 2012/2013 I. Zakres materiału do próbnego egzaminu maturalnego z matematyki: 1) liczby rzeczywiste 2) wyrażenia algebraiczne
Próbny egzamin z matematyki dla uczniów klas II LO i III Technikum w roku szkolnym 2012/2013 I. Zakres materiału do próbnego egzaminu maturalnego z matematyki: 1) liczby rzeczywiste 2) wyrażenia algebraiczne
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw udowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw udowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Efekty kształcenia na kierunku AiR drugiego stopnia - Wiedza Wydziału Elektrotechniki, Automatyki i Informatyki Politechniki Opolskiej
 Efekty na kierunku AiR drugiego stopnia - Wiedza K_W01 K_W02 K_W03 K_W04 K_W05 K_W06 K_W07 K_W08 K_W09 K_W10 K_W11 K_W12 K_W13 K_W14 Ma rozszerzoną wiedzę dotyczącą dynamicznych modeli dyskretnych stosowanych
Efekty na kierunku AiR drugiego stopnia - Wiedza K_W01 K_W02 K_W03 K_W04 K_W05 K_W06 K_W07 K_W08 K_W09 K_W10 K_W11 K_W12 K_W13 K_W14 Ma rozszerzoną wiedzę dotyczącą dynamicznych modeli dyskretnych stosowanych
Funkcje liniowe i wieloliniowe w praktyce szkolnej. Opracowanie : mgr inż. Renata Rzepińska
 Funkcje liniowe i wieloliniowe w praktyce szkolnej Opracowanie : mgr inż. Renata Rzepińska . Wprowadzenie pojęcia funkcji liniowej w nauczaniu matematyki w gimnazjum. W programie nauczania matematyki w
Funkcje liniowe i wieloliniowe w praktyce szkolnej Opracowanie : mgr inż. Renata Rzepińska . Wprowadzenie pojęcia funkcji liniowej w nauczaniu matematyki w gimnazjum. W programie nauczania matematyki w
Więzy i ich klasyfikacja Wykład 2
 Więzy i ich klasyfikacja Wykład 2 Karol Kołodziej (przy współpracy Bartosza Dziewita) Instytut Fizyki Uniwersytet Śląski, Katowice http://kk.us.edu.pl Karol Kołodziej Mechanika klasyczna i relatywistyczna
Więzy i ich klasyfikacja Wykład 2 Karol Kołodziej (przy współpracy Bartosza Dziewita) Instytut Fizyki Uniwersytet Śląski, Katowice http://kk.us.edu.pl Karol Kołodziej Mechanika klasyczna i relatywistyczna
2.12. Zadania odwrotne kinematyki
 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 2.12. Zadania odwrotne kinematyki Określenie zadania odwrotnego kinematyki T 0 N = [ ] n s a p = r 11 r 12 r 13 p x r 21 r 22 r 23
Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 2.12. Zadania odwrotne kinematyki Określenie zadania odwrotnego kinematyki T 0 N = [ ] n s a p = r 11 r 12 r 13 p x r 21 r 22 r 23
Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1
 Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 1. Wiadomości wstępne 1.1. Robotyka Po raz pierwszy terminu robot użył Karel Čapek w sztuce Rossum s Universal Robots w 1921r. Od
Politechnika Poznańska, Katedra Sterowania i Inżynierii Systemów str. 1 1. Wiadomości wstępne 1.1. Robotyka Po raz pierwszy terminu robot użył Karel Čapek w sztuce Rossum s Universal Robots w 1921r. Od
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Propozycja szczegółowego rozkładu materiału dla 4-letniego technikum, zakres podstawowy i rozszerzony. Klasa I (90 h)
 Propozycja szczegółowego rozkładu materiału dla 4-letniego technikum, zakres podstawowy i rozszerzony (według podręczników z serii MATeMAtyka) Klasa I (90 h) Temat Liczba godzin 1. Liczby rzeczywiste 15
Propozycja szczegółowego rozkładu materiału dla 4-letniego technikum, zakres podstawowy i rozszerzony (według podręczników z serii MATeMAtyka) Klasa I (90 h) Temat Liczba godzin 1. Liczby rzeczywiste 15
Sylabus do programu kształcenia obowiązującego od roku akademickiego 2012/13
 Sylabus do programu kształcenia obowiązującego od roku akademickiego 2012/13 (1) Nazwa Algebra liniowa z geometrią (2) Nazwa jednostki prowadzącej Instytut Matematyki przedmiot (3) Kod () Studia Kierunek
Sylabus do programu kształcenia obowiązującego od roku akademickiego 2012/13 (1) Nazwa Algebra liniowa z geometrią (2) Nazwa jednostki prowadzącej Instytut Matematyki przedmiot (3) Kod () Studia Kierunek
TEORIA MECHANIZMÓW I MANIPULATORÓW
 TEORIA MECHANIZMÓW I MANIPULATORÓW TEORIA MECHANIZMÓW I MANIPULATORÓW Dr inż. Artur Handke Katedra Inżynierii Biomedycznej, Mechatroniki i Teorii Mechanizmów Wydział Mechaniczny ul. Łukasiewicza 7/9, 50-371
TEORIA MECHANIZMÓW I MANIPULATORÓW TEORIA MECHANIZMÓW I MANIPULATORÓW Dr inż. Artur Handke Katedra Inżynierii Biomedycznej, Mechatroniki i Teorii Mechanizmów Wydział Mechaniczny ul. Łukasiewicza 7/9, 50-371
T13 Modelowanie zautomatyzowanych procesów wytwórczych, programowanie maszyn CNC
 T13 Modelowanie zautomatyzowanych procesów wytwórczych, programowanie maszyn CNC 1. Wstęp Wg normy ISO ITR 8373, robot przemysłowy jest automatycznie sterowaną, programowalną, wielozadaniową maszyną manipulacyjną
T13 Modelowanie zautomatyzowanych procesów wytwórczych, programowanie maszyn CNC 1. Wstęp Wg normy ISO ITR 8373, robot przemysłowy jest automatycznie sterowaną, programowalną, wielozadaniową maszyną manipulacyjną
Elementy geometrii analitycznej w R 3
 Rozdział 12 Elementy geometrii analitycznej w R 3 Elementy trójwymiarowej przestrzeni rzeczywistej R 3 = {(x,y,z) : x,y,z R} możemy interpretować co najmniej na trzy sposoby, tzn. jako: zbiór punktów (x,
Rozdział 12 Elementy geometrii analitycznej w R 3 Elementy trójwymiarowej przestrzeni rzeczywistej R 3 = {(x,y,z) : x,y,z R} możemy interpretować co najmniej na trzy sposoby, tzn. jako: zbiór punktów (x,
Podstawy robotyki. Wykład II. Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska
 Podstawy robotyki Wykład II Ruch ciała sztywnego w przestrzeni euklidesowej Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Preliminaria matematyczne
Podstawy robotyki Wykład II Ruch ciała sztywnego w przestrzeni euklidesowej Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Preliminaria matematyczne
Kryteria oceniania z matematyki dla klasy M+ (zakres rozszerzony) Klasa II
 Funkcja liniowa Kryteria oceniania z matematyki dla klasy M+ (zakres rozszerzony) Klasa II Zakres Dopuszczający Dostateczny Dobry Bardzo dobry - rozpoznaje funkcję liniową na podstawie wzoru - zna postać
Funkcja liniowa Kryteria oceniania z matematyki dla klasy M+ (zakres rozszerzony) Klasa II Zakres Dopuszczający Dostateczny Dobry Bardzo dobry - rozpoznaje funkcję liniową na podstawie wzoru - zna postać
IV.3 Ruch swobodny i nieswobodny. Więzy. Reakcje więzów
 IV.3 Ruch swobodny i nieswobodny. Więzy. Reakcje więzów Jan Królikowski Fizyka IBC 1 Ruch swobodny i nieswobodny. Stany równowagi Rozważamy ciało w pewnym układzie inercjalnym (UI). Gdy: prędkość tego
IV.3 Ruch swobodny i nieswobodny. Więzy. Reakcje więzów Jan Królikowski Fizyka IBC 1 Ruch swobodny i nieswobodny. Stany równowagi Rozważamy ciało w pewnym układzie inercjalnym (UI). Gdy: prędkość tego
R11. Programowanie robota opartego o kinematykę platformy Sterwarta-Gougha. Pracownia Nauki Programowania i Aplikacji Robotów Przemysłowych
 Pracownia Nauki Programowania i Aplikacji Robotów Przemysłowych Instrukcja laboratoryjna R Programowanie robota opartego o kinematykę platformy Sterwarta-Gougha. Instrukcja dla studentów studiów dziennych.
Pracownia Nauki Programowania i Aplikacji Robotów Przemysłowych Instrukcja laboratoryjna R Programowanie robota opartego o kinematykę platformy Sterwarta-Gougha. Instrukcja dla studentów studiów dziennych.
Podstawy robotyki wykład III. Kinematyka manipulatora
 Podstawy robotyki Wykład III sztywnego Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Manipulator typu PUMA ogniwo 2 ogniwo 3 ogniwo 1 PUMA układy
Podstawy robotyki Wykład III sztywnego Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Manipulator typu PUMA ogniwo 2 ogniwo 3 ogniwo 1 PUMA układy
Zadania kinematyki mechanizmów
 Zadania kinematyki mechanizmów struktura mechanizmu wymiary ogniw ruch ogniw napędowych związki kinematyczne położeń, prędkości, przyspieszeń ogniw zadanie proste kinematyki zadanie odwrotne kinematyki
Zadania kinematyki mechanizmów struktura mechanizmu wymiary ogniw ruch ogniw napędowych związki kinematyczne położeń, prędkości, przyspieszeń ogniw zadanie proste kinematyki zadanie odwrotne kinematyki
