ZASTOSOWANIE MODELI PANELOWYCH W ANALIZIE WARUNKOWEJ KONWERGENCJI TYPU β Z UWZGLĘDNIENIEM ZALEŻNOŚCI PRZESTRZENNYCH

Transkrypt

1 Emla Modraka Wydzał Ekoomczo Socjologczy Uwersytet Łódzk ZASTOSOWANIE MODELI PANELOWCH W ANALIZIE WARUNKOWEJ KONWERGENCJI TPU β Z UWZGLĘDNIENIEM ZALEŻNOŚCI PRZESTRZENNCH 1. Ws t ę p Dysproporcje charakteryzujące pozom rozwoju gospodarczego społeczego państw człokowskch U Europejskej oraz ch regoów sprawły, że poltyka regoala astawoa a welowae różc rozwojowych stała sę główym kerukem dzałań Wspóloty oraz że w ramach tej poltyk skocetrowao środk przezaczoe a wyrówywae pozomów rozwoju gospodarczego. Podstawę hpotezy o występowau kowergecj gospodarczej staow eoklasyczy model Solowa, z którego wyka, że stopa wzrostu produkcj w przelczeu a zatrudoego obża sę wraz ze wzrostem produkcj przypadającej a zatrudoego. W odeseu do zbeżośc pozomów wzrostu gospodarczego regoów mechazm kowergecj gospodarczej typu β polega a występowau wększego tempa wzrostu gospodarczego, charakteryzującego regoy o ższym pozome dochodu per capta w porówau do regoów o wyższym pozome dochodów. Różce występujące pomędzy regoam posadają charakter strukturaly. Ozacza to, że e tylko wykają z waruków aturalych, tj. położea regoów, waruków klmatyczych, ale także przede wszystkm są determowae przez brak wyposażea 61

2 Emla Modraka w frastrukturze techczej, społeczej stytucjoalej. Aalzoway w ejszym opracowau model kowergecj warukowej typu β umożlwa uwzględee zmeych charakteryzujących czyk strukturale decydujące o tempe wzrostu gospodarczego. Celem artykułu jest przedstawee oraz porówae wyków badań dotyczących tempa kowergecj gospodarczej a pozome regoów U Europejskej z zastosowaem model paelowych oraz uwzględeem zależośc przestrzeych. Spotykae w lteraturze przedmotu podejśca do weryfkacj występowaa kowergecj tempa wzrostu gospodarczego odchodzą od stosowaa przekrojowych regresj wzrostu. To, że moża uwzględć w modelach dywdualych eobserwowale cechy badaych gospodarek, przyczyło sę do popularyzacj modelu paelowego z efektam stałym w ewaluacj kowergecj gospodarczej. Przyjęce założea o wpływe zależośc przestrzeych pomędzy gospodarkam regoów a tempo ch wzrostu determuje dalszy rozwój metod badawczych uwzględających efekty przestrzee wzrostu gospodarczego. 2. Rozwój metodolog badaa kowergecj warukowej W lteraturze przedmotu steje wele podejść wykorzystywaych do weryfkacj hpotezy o występowau kowergecj gospodarczej. Według systematyk stosowaej przez Sala Marta 1, oprócz kowergecj typu σ, rozumaej jako malejące zróżcowae dochodu per capta pomędzy badaym regoam (państwam), wyróża sę róweż kowergecję typu β. Podstawę hpotezy o występowau kowergecj warukowej typu β staow eoklasyczy model Solowa Swaa. Zgode z założeam kowergecj typu beta pomędzy przecętą stopą wzrostu gospodarczego a początkowym dochodem występuje stota zależość ujema. Zakładay jest róweż relatywe szybszy wzrost gospodarczy w regoach o ższym pozome dochodów 2. Dodatkowo kowergecja typu beta jest dzeloa a kowergecję absolutą (bezwarukową) oraz kowergecję warukową. Według założeń kowergecj absolutej typu β regoy o ższym pozome dochodu odotowują wyższe tempo jego wzrostu, ezależe od charakterystyk strukturalych, jedocześe dążą do tego samego stau wzrostu 1 X. Sala Mart, The classcal approach to covergece aalyss, The Ecoomc Joural 1996, vol. 106, s , cyt za: D. Cołek, Badae kowergecj krajów Europy Środkowo Wschodej z wykorzystaem daych paelowych, Dyamcze modele ekoometrycze, VIII Ogólopolske Semarum Naukowe, , Toruń, s M. Herbst, P. Wójck, Efekty przestrzee w kowergecj Polskch podregoów, Badae spójośc terytoralej przecwdzałae margalzacj obszarów problemowych, Koferecja Msterstwa Rozwoju Regoalego, , Warszawa. 62

3 Zastosowae model paelowych w aalze warukowej kowergecj zrówoważoego, czyl do podobego pozomu zamożośc wyrażoego wartoścą dochodu per capta. Kowergecja warukowa typu β bazuje a założeu, że egatywa zależość pomędzy dyamką wzrostu dochodu a jego początkową wartoścą dotyczy regoów podobych pod względem charakterystyk strukturalych, co węcej każdy rego dąży do osągęca właścwego sobe stau wzrostu zrówoważoego. Jako dodatkowe zmee objaśające (statystyk strukturale) różce w pozome rozwoju są stosowae m..: lczba osób z wyższym wykształceem, odsetek pracujących ze średm lub wyższym wykształceem 3, średa lczba lat auk wśród osób w weku 25 do 64 lat, defcyt fskaly 4, udzał osób pracujących w sektorze rolym 5 czy wskaźk zatrudea. Aalza kowergecj gospodarczej oparta a przestrzeych daych paelowych determuje zastosowae metod uwzględających zarówo specyfcze własośc gospodarek regoów, dyamkę zma ch wartośc, jak zależośc przestrzee warukujące zróżcowae pozomu wzrostu gospodarczego oraz dyamkę procesów kowergecj 6. Początkowe badaa ad tempem kowergecj, prowadzoe m.. przez Kormedego Megure (1985), Baumola (1986), Barro (1991), Barro, Sala Marta (1992), Makwa, Romera Wela (1992), Leve a Reelta (1992), polegały a estymacj rówaa przekrojowej regresj wzrostu 7. Szacując zależość wzrostu PKB za pomocą tej metody, zakładao stałe wartośc zmeych objaśających, występujących w modelu Solowa, a którym opera sę aalzowaa regresja wzrostu, tj. pozomu techolog, tedecj do oszczędzaa, stopy deprecjacj oraz tempa wzrostu produktywośc. Wybór odpowedo długej jedostk czasu (klkaaśce lub klkadzesąt lat) mał a celu wyelmowae wpływu cykl koukturalych. Postać modelu kowergecj stawa warukowej po sze rówae przedstawa : poższe rówae 8 : T, -λk l = α + e + γ + ξ (1 ) l 0, X 0,, (1) 0, ć PKB (w PPS) per capta w perwszym rok 3 B. Herz, L. Vogel, Regoal Covergece Cetral ad Easter Europe:Evdece from a Decade of Trasto, Uverstät Bayreuth w ostatm Rechts- ud Wrtschaftswsseschaftlche roku (po k okresach), Fakultät Wrtschaftswsseschaftlche Dskussospapere 2003, vol. 13/03, s G. Arba, L. Domocs, G. Pras, Regoal growth ad regoal equalty EU ad trasto coutres: a spatal ecoometrc approach, 45 th Cogress of the Europea Regoal Scece Assocato, , Amsterdam, s J. Ramajo, M. Marquez, G. Hewgs, M. Salas, Spatal heterogeety ad terregoal spllovers the Europea Uo: Do coheso polces ecourage covergece across regos?, Europea Ecoomc Revew 2008, vol. 52, s J.P. Elhorst, Spatal Pael Data Models, w: Hadbook of Appled Spatal Aalyss. Software Tools, Methods ad Applcatos, red. M.M. Fsher, A. Gets, Sprger, Hedelberg Dordrecht Lodo New ork 2010, s D. Cołek, op.ct., s G. Arba, R. Basle, G. Pras, Usg Spatal Pael Data Modellg Regoal Growth ad Covergece, Isttuto d Stude Aals Ecoomca, Workg Paper 2005, vol. 5, s

4 Emla Modraka gdze: 0, wartość PKB (w PPS) per capta w perwszym roku (t), T, wartość PKB per capta w ostatm roku (po k okresach), λ szybkość procesu kowergecj 9, X t, macerz wartośc charakterystyk strukturalych; wyłączee zmeych strukturalych prowadz do otrzymaa modelu kowergecj absolutej (bezwarukowej). W celu oszacowaa modelu lu KMNK KMNK wprowadza sę parametr β: - k β( 1= (1e e) λ ) (2) T, l l = α + β + γ + ξ l 0, X 0, (3) 0, l l ( β + 1) 1) λ =. (4) k wartość param Ujema oraz stota statystycze ch regoów. wartość parametru śwadczy o występowau kowergecj gospodarczej badaych regoów. Zastosowae opsaej metody weryfkacj założea o kowergecj warukowej prowadz do utraty formacj zwązaych ze zróżcowaem wzrostu gospodarczego gospodarek zmeoścą opsujących go czyków w czase. Pomęte zostają róweż eobserwowale cechy badaych gospodarek, które przez brak możlwośc odpowedej operacjoalzacj powększają wartość reszt oszacowaego modelu. W kosekwecj prowadz to do espełea waruku o braku korelacj pomędzy wartoścam składka losowego oraz zmeych objaśających. Podkreśla sę, że wyk estymacj takch regresj szacowae KMNK są ezgode obcążoe 10. Aplkacja model paelowych umożlwa uwzględee eobserwowalych własośc regoów, które to własośc decydują o tempe wzrostu gospodarczego tych regoów: ych regoów: t + k, l = α + β lt, + γ t, + ξ t, X, (5) t, w składających sę a długość przedz gdze: k lczba okresów h w badaach składających model sę a daych długość paelo przedzału czasowego. Wśród stosowaych w badaach model daych paelowych ależy wymeć: z Model ze zmeym zero jedykowym LSDV (ag. Least Squared Dummy Varables Model) zakłada wprowadzee do przekrojowego modelu regresj zmeych zero-jedykowych, które objaśają heterogeczość obektów. 9 P. Klber, Ekoometrycza aalza kowergecj regoów Polsk metodam paelowym, Studa Regoale Lokale 2007, vol. 1/27, s D. Cołek, op.ct., s

5 Zastosowae model paelowych w aalze warukowej kowergecj W modelu LSDV współczyk kerukowe są stałe pomędzy grupam w czase. Model zajduje zastosowae w przypadku szacowaa efektów grupowych dla małej lczby obektów. Zbyt duża lczba zmeych zero jedykowych (dużo wększa lczba obektów ż obserwacj czasowych) prowadz do utraty stop swobody. z Model z efektam wewątrzgrupowym, tzw. wth effects model, w przecweństwe do model LSDV wykorzystuje odchylea wartośc zmeej od średej grupowej. Model estymoway jest bez stałej za pomocą MNK, przez co zaburzoa jest wartość współczyka determacj. Oszacowae współczyk kerukowe przy zmeych modelu merzą wpływ zma zmeej objaśającej a wartość zmeej objaśaej. Model e uwzględa zma pomędzy grupam. z Model z efektam mędzygrupowym, tzw. betwee effects model, jego estymacja jest prowadzoa a podstawe średch grupowych zmeych objaśających zmeej objaśaej. Poprzez wprowadzee średch wyrówywae są wartośc odstające. Oszacowaa parametrów model wskazują a wpływ zma mędzy grupam a wartośc zmeej objaśaej 11. Neoklasyczy model wzrostu, a podstawe którego zostało wyspecyfkowae rówae kowergecj, opera sę a założeu o braku powązań pomędzy gospodarkam badaych regoów. Moblość czyków produkcj prowadz do przepływu kaptału do regoów o ższej kaptałochłoośc produkcj, podczas gdy przepływy sły roboczej astępują w keruku przecwym. Iym czykem decydującym o wyrówywau sę pozomów wzrostu gospodarczego jest dyfuzja techolog owacj. Według założeń spotykaych w lteraturze przedmotu, uwzględee w specyfkacj modelu zależośc pomędzy gospodarkam regoów będze skutkowało otrzymaem zwększoego tempa kowergecj gospodarczej regoów 12. Jedą z metod uwzględea przepływów kaptału sły roboczej oraz techolog jest kostrukcja modelu wzrostu gospodarczego uwzględającego wymeoe czyk. Brak daych o przepływe czyków produkcj, zwłaszcza techolog, uemożlwa jedak prowadzee tego typu aalz. Pośredą metodą pozwalającą a uwzględee efektów przepływów mędzyregoalych w aalzach kowergecj gospodarczej jest specyfkacja modelu charakteryzującego zależośc pomędzy wartoścam badaych charakterystyk w sąsedch lokalzacjach 13. W lteraturze przedmotu wyróża sę m.. zależość przestrzeą wykającą z przestrzeego 11 K. Kopczewska, T. Kopczewsk, P. Wójck, Metody loścowe w R. Aplkacje ekoomcze fasowe, CeDeWu, Warszawa, 2009, s G. Arba, R. Basle, G. Pras, op.ct., s Określee charakteru sąsedztwa jedostek przestrzeych poprzez specyfkację macerzy wag przestrzeych (sąsedztwa lub odległośc) w sposób zaczący wpływa a weryfkację zależośc przestrzeej cech. Przyjęce różych macerzy wag może skutkować odmeym wykam aalz. 65

6 Emla Modraka wymaru aktywośc ekoomczej (ag. substatve depedece), jak z ezgodośc pomędzy gracam procesów gospodarczych oraz jedostek geografczych (ag. usace depedece) 14. Puktem wyjśca aplkacj model przestrzeych jest weryfkacja występowaa autokorelacj przestrzeej zmeych. Jedą z podstawowych metod jest testowae stotośc statystyczej współczyka globalej autokorelacj przestrzeej Moraa I 15. ej Moraa I. I = S o = 1 j= 1 w, j ( x x )( x x ) ( x x ) = 1 gdze: x ta obserwacja zmeej X, W w j serwacja zmeej j= X,, macerz wag przestrzeych. 1 W w Dodata, statystycze stota wartość statystyk Moraa I śwadczy o występowau dodatej autokorelacj przestrzeej, statystyk co dowodz M wpływu wartośc badaej zmeej w daej lokalzacj a pozomy tej zmeej w sąsedch lokalzacjach (regoach). Wartośc opsywaych cech tworzą skupea. W przypadku ujemej wartośc statystyk wysoke wartośc sąsadują z skm. Jedym z podstawowych model daych paelowych z efektam przestrzeym, stosowaym w aalzach wzrostu gospodarczego, jest paelowy model opóźea przestrzeego z efektam stałym (ag. fxed effect spatal lag model), do którego zostaje wprowadzoa opóźoa przestrzee zmea zależa: gdze W =, (7)16 t+ k, t+ k, l α ρ w, jl β lt, γ t, = t, j 1 X = t, + ξt, = w, j staow macerz wag wag przestrzeych. j= 1 Alteratywą metodę wprowadzea do model paelowych zależośc przestrzeych statystyk staow M opóźee przestrzee składka losowego, czego wykem jest specyfkacja postac paelowego modelu błędu przestrzeego z efektam stałym (fxed effect spatal error model): 2 j, (6) 14 T. Kossowsk, Kowergecja przestrzea aspekty teoretycze, w: Praktycze aspekty badań regoalych vara, t. 2, red. P. Chursk Bulety Istytutu Geograf Społeczo Ekoomczej Gospodark Przestrzeej Uwersytetu m. Adama Mckewcza w Pozau 2009, r 8, sera: Rozwój Regoaly Poltyka Regoala, s Ekoometra przestrzea. Metody modele aalzy daych przestrzeych, red. B. Sucheck, Wydawctwo C.H. Beck, Warszawa 2010, s G. Arba, R. Basle, G. Pras, op.ct., s

7 Zastosowae model paelowych w aalze warukowej kowergecj d-effect spatal error model): t+ k, l = α + β lt, + γ t, + ξt, X t, (8) ξ t, = ρ w, jξ t, + η. (9) 17 j = 1 2. Aalza Wyk estymacj przekrojowych regresj wzrostu 18 dla regoów U Europejskej z lat wskazywały a tempo kowergecj a pozome 2 3%, po 1975 r. prędkość ta spadła do pozomu 1,7%. Rezultaty badań ad szybkoścą procesu kowergecj dowodzą, że oszacowaa model wzrostu z wykorzystaem daych paelowych dają wartośc współczyka kowergecj powyżej pozomu 2% rocze 19. Przedmotem poższej aalzy jest weryfkacja założea dotyczącego wskazywaej w lteraturze szybkośc kowergecj warukowej w przypadku model paelowych z efektam stałym (dywdualym czasowym). Dae o wartośc PKB per capta w latach wg PPS w ceach beżących dla 290 regoów U Europejskej a pozome NUTS 2 wygeerowao z bazy daych Eurostat. Wartośc, poprzez przyjęce wskaźków flacj dla pozomów NUTS 0 (kraju), wyrażoo w ceach stałych z 2000 r. Ze względu a ograczea dostępośc daych w przekroju terytoralym czasowym za charakterystykę strukturalą regoów obrao wskaźk zatrudea osób w weku powyżej 15. roku życa. Komplete dae z okresu zgromadzoo dla 193 regoów. W tabel 1 przedstawoo oszacowaa współczyków kerukowych rówaa (5) przy logarytme zmeej PKB per capta ( t, ) oraz wskaźku zatrudea osób w weku powyżej 15 lat (X t, ). Oszacowaa estymatora wewątrzgrupowego (ag. wth) z efektam dywdualym staową o występowau pomędzy badaym regoam kowergecj warukowej. W okrese jej szybkość wyosła 28,4% rocze. Oszacowaa modelu były jedak obarczoe ajwyższym błędem w porówau do pozostałych model. Wprowadzee do modelu stałych efektów czasowych skutkuje odrzuceem hpotezy o kowergecj gospodarczej. Rówoczese uwzględee efektów dywdualych czasowych spowodowało utratę przez charakterystykę strukturalą (wskaźk zatrudea) stotośc statystyczej. Najmejszym błędam oszacowań 17 Ibdem. 18 Badaa prowadzoe przez Nevea, Gouyette (1995), Armstroga (1995), Verspagea (1996), Todla (1999), Marta (1999), de la Fuete (1996), por. H. Badger, W.G. Müller, G. Todl, Regoal Coverece Europea Uo ( ): A Spatal Dyamc Pael Aalyss, HWWA, Dscuso Paper 2002, vol. 210, s G. Arba, R. Basle, G. Pras, op.ct., s

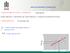
8 Emla Modraka charakteryzowały sę estymatory mędzygrupowe. Oszacowaa współczyków kerukowych modelu z efektam zarówo dywdualym, jak czasowym wskazywały dodatą zależość mędzy pozomem dochodu a dyamką jego wzrostu (co przeczy założeu o występowau kowergecj gospodarczej), jedak tylko w przypadku modelu z efektam dywdualym okazały sę stote statystycze. Tabela 1. Wyk oszacowań model z efektam stałym modelu kowergecj warukowej Model paelowy z efektam stałym t, X t, λ Oeway (dvdual) effect Wth Model 0,247 *** 0,0053 *** 0,284 Oeway (tme) effect Wth Model 0,005 ** 0,0008 *** 0,005 Twoways effects Wth Model 0,270 *** 0,0010 0,315 Oeway (dvdual) effect Betwee Model 0,007 *** 0,0007 *** 0,007 Oeway (tme) effect Betwee Model 0,379 0,0430 0,321 Źródło: opracowae włase, R Cra W celu scharakteryzowaa tedecj czasowych wzrostu gospodarczego w regoach NUTS 2 przedstawoo przestrzee zróżcowae wartośc średego tempa zma PKB per capta wg PSN w latach Rysuek 1. Średe tempo zma PKB per capta wg PSN (cey stałe, 2000=1) w latach w 193 regoach NUTS 2 Źródło: opracowae włase, R Cra

9 Zastosowae model paelowych w aalze warukowej kowergecj Wykres rozrzutu statystyk Moraa I LV00 SK01 PL12 Ś rede tempo zma opóźoe przestrzee [SRTEMP*W] R O41 RO12 GR24 GR25 GR13 UKI1 GR30 PL51 O 22 O21 RO11 RO31 RO Średe tempo zma [SRTEMP] Rysuek 2. Korelogram statystyk Moraa I średego tempa zma PKB per capta wg PSN (cey stałe, 2000=1) w latach w 193 regoach NUTS2 Źródło: pracowae włase, R Cra Wartość statystyk Moraa I a pozome 0, 7021 (p value = 0,001) śwadczy o występowau stotych zależośc przestrzeych pomędzy wartoścam średego tempa wzrostu gospodarczego. W tabel 2 przedstawoo zestawee wyków oszacowaa parametrów rówaa (7). Wprowadzee do modelu opóźoego przestrzee tempa wzrostu PKB per capta, uwzględającego wpływ dyamk wzrostu w regoach sąsedch, wywołało obżee wartośc współczyka kowergecj w stosuku do oszacowań uzyskaych w modelu paelowym bez efektów przestrzeych. Tabela 2. Wyk oszacowań paelowych model opóźea przestrzeego z efektam stałym modelu kowergecj warukowej Paelowy model opóźea przestrzeego z efektam stałym Oeway (dvdual) effect Wth Model Oeway (tme) effect Wth Model Twoways effects Wth Model t, X t, λ ρ 0,128 *** 0,0001 0,137 0,767 *** 0,002. 0,0003 ** 0,002 0,664 *** 0,186 *** 0, ,206 0,613 *** Źródło: opracowae włase, R Cra

10 Emla Modraka Gdyby wszystke aalzowae regoy charakteryzowały sę tym samym tempem wzrostu gospodarczego oraz wpływem dyamk zma PKB per capta z sąsedch regoów, szybkość kowergecj szacowaa a podstawe modelu z efektam stałym wyosłaby 13,7% rocze. Jeśl odosłoby sę powyższe założea do modelu dwuczykowego, dyamka procesu zbeżośc gospodarek regoów do stau rówowag długookresowej wzrosłaby do 20,6%. 3. Podsumowae keruk dalszych badań Przedstawoe w opracowau rezultaty aalz mały a celu zweryfkowae założeń dotyczących wpływu postac modelu daych paelowych a detyfkację oraz szybkość kowergecj warukowej. Zgode z złożeam przedstawoym przez Arbę 20, szybkość kowergecj szacowaa a podstawe model paelowych z dywdualym efektam stałym przekroczyła wartość 2%. Uzyskae oszacowaa współczyka kowergecj w odeseu do długookresowej rówowag wzrostu wydają sę zawyżoe. Jedą z podkreślaych w lteraturze przyczy zawyżoej szybkośc kowergecj jest problem edogeczośc zmeych objaśających. Zwraca sę róweż uwagę a to, że wysoke tempo kowergecj, szacowae a podstawe model paelowych, e charakteryzuje dyamk zbeżośc gospodarek regoów dążących do osągęca stau rówowag długookresowej, lecz jest właścwe dla rówowag krótkookresowej 21. Występowae dodatej autokorelacj przestrzeej zadecydowało o koeczośc zastosowaa przestrzeych paelowych model kowergecj. Należy zazaczyć, że wprowadzee do model paelowych z efektam stałym opóźoych przestrzee zmeych objaśaych pozwolło a pozytywą weryfkację hpotezy o występowau kowergecj. Dyamka tego procesu w przypadku model z efektam przestrzeym była o połowę mejsza ż w przypadku model paelowych bez efektów przestrzeych. W badau pomęto testowae stotośc efektów stałych (grupowych czasowych), jak róweż badae wyków oszacowań model z efektam losowym. Dalszych aalz wymaga badae autokorelacj oraz heteroskedastyczośc składka losowego. 20 Ibdem. 21 M. Shbamoto,. Tsutsu, Note o the Iterpretato of Covergece Speed the Dyamc Pael Model, Kobe Uversty, Dscusso Paper Seres RIEB 2011, Jauary, s

11 Zastosowae model paelowych w aalze warukowej kowergecj Bblografa 1. Arba G., Basle R., Pras G., Usg Spatal Pael Data Modellg Regoal Growth ad Covergece, Isttuto d Stude Aals Ecoomca, Workg Paper 2005, vol 5, s Arba G., Domocs L., Pras G., Regoal growth ad regoal equalty EU ad trasto coutres: a spatal ecoometrc approach, 45 th Cogress of the Europea Regoal Scece Assocato, , Amsterdam. 3. Cołek D., Badae kowergecj krajów Europy Środkowo Wschodej z wykorzystaem daych paelowych, Dyamcze modele ekoometrycze, VIII Ogólopolske Semarum Naukowe, , Toruń, s Ekoometra przestrzea. Metody modele aalzy daych przestrzeych, red. B. Sucheck, Wydawctwo C.H. Beck, Warszawa Elhorst J.P., Spatal Pael Data Models, w: Hadbook of Appled Spatal Aalyss. Software Tools, Methods ad Applcatos, red. M.M. Fsher, A. Gets, Sprger, Hedelberg Dordrecht Lodo New ork 2010, s Herbst M., Wójck P., Efekty przestrzee w kowergecj Polskch podregoów, Badae spójośc terytoralej przecwdzałae margalzacj obszarów problemowych, Koferecja Msterstwa Rozwoju Regoalego, , Warszawa. 7. Herz B., Vogel L., Regoal Covergece Cetral ad Easter Europe: Evdece from a Decade of Trasto, Uverstät Bayreuth Rechts- ud Wrtschaftswsseschaftlche Fakultät Wrtschaftswsseschaftlche Dskussospapere 2003, vol. 13/ Klber P., Ekoometrycza aalza kowergecj regoów Polsk metodam paelowym, Studa Regoale Lokale 2007, vol. 1/27, s Kopczewska K., Kopczewsk T., Wójck P., Metody loścowe w R. Aplkacje ekoomcze fasowe, CeDeWu, Warszawa Kossowsk T., Kowergecja przestrzea aspekty teoretycze, w: Praktycze aspekty badań regoalych vara, t. 2, red. P. Chursk, Bulety Istytutu Geograf Społeczo Ekoomczej Gospodark Przestrzeej Uwersytetu m. Adama Mckewcza w Pozau 2009, r 8, sera: Rozwój Regoaly Poltyka Regoala, s Müller W.G., Todl G., Regoal Coverece Europea Uo ( ): A Spatal Dyamc Pael Aalyss, HWWA, Dscuso Paper 2002, vol. 210, s Ramajo J., Marquez M., Hewgs G., Salas M., Spatal heterogeety ad terregoal spllovers the Europea Uo: Do coheso polces ecourage covergece across regos?, Europea Ecoomc Revew 2008, vol. 52, s Shbamoto M., Tsutsu., Note o the Iterpretato of Covergece Speed the Dyamc Pael Model, Kobe Uversty, Dscusso Paper Seres RIEB 2011, Jauary, s

12 Emla Modraka Źródła secowe 1. [dostęp ] =e&pcode=tgs00005 [dostęp ]. Summary The applcato of pael models the aalyss of a codtoal β covergece cludg spatal depedece Ecoomc covergece regos of the EU s oe of the ma objectves of coheso polcy. The bass of the hypothess of the exstece of ecoomc covergece s a eoclasscal Solow model. Ths artcle ams to preset ad compare the results of studes o ecoomc codtoal covergece of EU regos wth the use of pael models ad takg to accout the spatal relatoshps. Keywords: pael data models, spatal autocorrelato, codtoal covergece, coheso polcy, NUTS2 Europea regos JEL classfcato: C21, C23, O47, O52, R11