λ c λ c λ m asa hc h λ h λ h W lasnosci fotonu = = m = = = c h p c Oblicz energię, pęd i masę fotonu o długości fali λ = 500 nm. + kg m kg m = 1,6 10
|
|
|
- Aniela Bukowska
- 8 lat temu
- Przeglądów:
Transkrypt
1 W lasosi fotou eergia hv h + p p p p h p h pęd h p h asa h h hv Obliz eergię, pęd i asę fotou o długośi fali 5. D h h p h 3 6,6 J s 6, kg kg p,3 5 5 s s 7 8 h p,3 3 J 9 3,9 J ev,6 9 xev 3,9 3,9 x ev,6 x,37ev 9 7 p,3 8 3 J J 35,3 [ ] kg
2 D Teperatura iała doskoale zarego ziejsza się od 37 o C do 57 o C. Ile razy ziei się ałkowita wyproieiowaa eergia? D σt t 37 C T K t 57 C T K T 73,5 + t σt T σt T D3 Ile razy zwiększy się o proieiowaia iała doskoale zarego, jeŝeli aksiu eergii w widie przesuęło się z 7 do? D3 ax? σt 7 T T T σt T σt T T T T T 7 7
3 D W atoie wodoru elektro przehodzi ze stau w który eergia wiązaia wyosi,378 ev do iego stau o eergii wzbudzeia,9 ev. Jakie są lizby kwatowe tyh staów? Obliz długość fali eitowaego fotou. D wiaz wzb wiaz,378ev,9ev e + 3,6eV wiaz e +,378ev e 3,6 e 36 e 6,378 3,6eV wzb ev 3,6eV,9eV + 3,6eV 3,6eV,5eV 3,6eV 9 3,5eV R, e,9 lub 6 h h e e ( 3,6 ) 3,
4 D5 Foto o eergii.75 ev zostaje pohłoięty przez ato wodoru zajdująy się pozątkowo w staie podstawowy. Określ lizbę kwatową stau wzbudzoego. Jakie są oŝliwośi przejśia a pozio podstawowy? D5 f 3,6eV,75eV 3,6 a 3,6eV,85eV a 3,6eV a 6 a,85ev He + a Z 3,6eV ( ev ) D6 Jaka eergia jest potrzeba do usuięia elektrou z jedokrotie zjoizowaego atou helu He jeŝeli elektro pozątkowo zajdował się a) w staie podstawowy b) staie? He Z A wiaz Z 3,6eV w 3,6eV 5, ev Z 3,6eV 3,6 wiaz ev 3,eV
5 Teperatura iala doskoale zarego zieia się od t 77 C do t 77 C. Ile razy ziei sie eergia wyproieiowaa przez to ialo?? σt ( ) ( ) T K K T K K σt T 6 σt T Stala sloeza (ilosć eergii proieistej, którą wysyla Slońe w iągu s a powierzhię prostopadle do proieia zajdujaą się w pobliŝu kw Ziei poza jej atosferą) wyosi I,35. Okresl teperaturę proieiująej powierzhi Slońa T? r- proień Slońa, R- odleglosć Slońa od Ziei r6,95, R,5, σ 5,67 σt Πr ΠR I 8-8 ΠR R I I Πr σt T R I r IR σ r,35 5,67 r W K 3 6 T, 657,7, 5776 K 5776 K 8 W W T K K
6 Zieia trai sredio w iągu iuty eergię 5, J wyproieiowaą przez powierzhi. W jakiej teperaturze ialo doskoale zare proieiowaloby te saa ilosć eergii? σt T σ ' s ' 6 6 5, 6 5,67 5, J s W,9 8 T K K Teperatura iala doskoale zarego wzrosla dwukrotie, w wyiku zego dlugosć fali odpowiadajaa aksyalej zdolosi eisyjej zalala o 6. Wyzaz pozatkową i końową teperaturę iala ax,,9 K - stala Wiea T prawo Wiea 6 T T T T T T T 3 3,9 K,9 3 T K, 66 K 7K 9 6 6, T T 83K
7 Jaki prąd powiie płyąć przez etalowe włóko o średiy d., które zajduje się w bańe próŝiowej, aby jego teperatura T5 K pozostała stała? Zakładay, Ŝe włóko proieiuje eergię jak iało doskoale zae. Straty ieple spowodowae przewodzeie iepła poiąć. I,7A. ' S σt Π l P U I I R U I R l l R ρ ρ S ' d Π ρ 3 3 d l P I ρ Πd d P ' σt Π l I σt Π d d I ρ I I σt Π d ρ σt Π d ρ l Πd Zadaie3 Średia teperatura iała ludzkiego wyosi 3 K. Określić długość fali proieiowaia ax wysyłaego przez złowieka, odpowiadająą aksiu fukji rozkładu eergii. Przyjąć, Ŝe iało ludzkie proieiuje jak iało doskoale zare. ax 9,3* --6. T 3K ax ax ax ax? 3 T,9 K 3,9 K T 3 6 9,3
8 Oblizyć asę traoą przez sloe w iągu s a skutek proieiowaia. Teperatura powierzhi slońa wyosi T58K σt t S σt t S Π σ 8 r6, σ 5,67 3, M sl r T t s ~ 3 8 W K kg kg Pewie ato eituje swiatlo o dlugosiah fali 6 i 5 dla przejsć elektroowyh z pozioów odpowiedio B a A i z C a A. Obliz dlugosć fali eitowaej przez te ato przy przejsiu elektrou z poziou C a B ( ) ( ) C B C A B A h h h B 3
9 Foto o eergii,ev zostaje zaabsorboway przez ato wodoru zajdująy sie pozątkowo w staie podstawowy. Okresl lizbę kwatową stau wzbudzoego. 3,6eV,eV k +,ev k k 3,6eV +,ev, 5eV,5eV 3,6eV k k 3,6,5 9,6 3 k 3 W atoie wodoru elektro przehodzi ze stau, w który eergia wiązaia wyosi,5 ev do iego stau o eergii wzbudzeia, ev. a) jakie są glowe lizby kwatowe tyh staów? b) obliz dlugosć fali fotou ) jaka to seria? wzb ( ),ev 3,6eV,eV 3,6eV 3, ev 3,6eV 3, ev 3,6eV 3, ev,5ev wzb wzb,5ev 3,6eV 5 5,5eV (5) () seria Balera hv h 7,3 ev,6 9 J
10 Jaka eergia potrzeba jest do usuięia elektrou z jedokrotie zjoizowaego atou helu He jesli elektro jest pozątkowo w staie a) podstawowy b) 3 Z Z 3,6eV w w j 3,6eV 5, ev 3,6eV 3 w 6, ev 3
Fizyka współczesna. Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Fizyka współzesa Projekt współfiasoway przez Uię Europejską w raah Europejskiego Fuduszu Społezego ELEMENTY FIZYKI WSPÓŁCZESNEJ Zjawisko fotoelektryze Zjawisko fotoelektryze polega a wybijaiu elektroów
Fizyka współzesa Projekt współfiasoway przez Uię Europejską w raah Europejskiego Fuduszu Społezego ELEMENTY FIZYKI WSPÓŁCZESNEJ Zjawisko fotoelektryze Zjawisko fotoelektryze polega a wybijaiu elektroów
20. Model atomu wodoru według Bohra.
 Model atou wodou według Boha Wybó i opacowaie zadań Jadwiga Mechlińska-Dewko Więcej zadań a te teat zajdziesz w II części skyptu Opieając się a teoii Boha zaleźć: a/ poień -tej obity elektou w atoie wodou,
Model atou wodou według Boha Wybó i opacowaie zadań Jadwiga Mechlińska-Dewko Więcej zadań a te teat zajdziesz w II części skyptu Opieając się a teoii Boha zaleźć: a/ poień -tej obity elektou w atoie wodou,
Model Bohra atomu wodoru
 Model Bohra atomu wodoru Widma liiowe pierwiastków. wodór hel eo tle węgiel azot sód Ŝelazo Aby odpowiedzieć a pytaie dlaczego wodór i ie pierwiastki ie emitują wszystkich częstotliwości fal elektromagetyczych
Model Bohra atomu wodoru Widma liiowe pierwiastków. wodór hel eo tle węgiel azot sód Ŝelazo Aby odpowiedzieć a pytaie dlaczego wodór i ie pierwiastki ie emitują wszystkich częstotliwości fal elektromagetyczych
Fotometria. F. obiektywna = radiometria: Jaka ENERGIA dopływa ze źródła. F. subiektywna: Jak JASNO świeci to źródło? (w ocenie przeciętnego człowieka)
 Fotometria F. obiektywa = radiometria: Jaka NRGIA dopływa ze źródła F. subiektywa: Jak JASNO świei to źródło? (w oeie przeiętego złowieka) Potrzebujemy kilku defiiji: defiija Gęstość spektrala (widmo)
Fotometria F. obiektywa = radiometria: Jaka NRGIA dopływa ze źródła F. subiektywa: Jak JASNO świei to źródło? (w oeie przeiętego złowieka) Potrzebujemy kilku defiiji: defiija Gęstość spektrala (widmo)
IM-14 BEZDOTYKOWY POMIAR TEMPERATURY
 IM-4 EZDOTYKOWY POMIAR TEMPERATURY I. Cel ćwizeia Celem ćwizeia jest pozaie tehiki pomiaru wysokih temperatur w opariu o prawo Plaka. II. Zagadieia do przygotowaia: ) Widmo iał świeąyh, promieiowaie termize,
IM-4 EZDOTYKOWY POMIAR TEMPERATURY I. Cel ćwizeia Celem ćwizeia jest pozaie tehiki pomiaru wysokih temperatur w opariu o prawo Plaka. II. Zagadieia do przygotowaia: ) Widmo iał świeąyh, promieiowaie termize,
1. Podstawowe własności fizyczne płynów.
 .. Masa, gęstość, ciśieie.. Podstawowe własości fizycze płyów. Masa jest właściwością płyu charakteryzującą jego ilość. W układzie SI jedostką podstawową asy jest l kg. Oprócz jedostki podstawowej używa
.. Masa, gęstość, ciśieie.. Podstawowe własości fizycze płyów. Masa jest właściwością płyu charakteryzującą jego ilość. W układzie SI jedostką podstawową asy jest l kg. Oprócz jedostki podstawowej używa
Chemiczne metody analizy ilościowej (laboratorium)
 Cheicze etody aalizy ilościowej (laboratoriu) Broiaoetria 9. Przygotowaie iaowaego roztworu broiau (V) potasu Broia(V) potasu ależy do stosowaych w aalizie cheiczej substacji podstawowych. oże być otrzyay
Cheicze etody aalizy ilościowej (laboratoriu) Broiaoetria 9. Przygotowaie iaowaego roztworu broiau (V) potasu Broia(V) potasu ależy do stosowaych w aalizie cheiczej substacji podstawowych. oże być otrzyay
Podstawowe przemiany cieplne
 Podstawowe rzemiay iele Przemiaa izohoryza zahodzi, gdy objętość układu ozostaje stała ( ost), zyli 0. ówaie izohory () ost rzemiaie tej ie jest wykoywaa raa, bo 0, wię zgodie z ierwszą zasadą termodyamiki,
Podstawowe rzemiay iele Przemiaa izohoryza zahodzi, gdy objętość układu ozostaje stała ( ost), zyli 0. ówaie izohory () ost rzemiaie tej ie jest wykoywaa raa, bo 0, wię zgodie z ierwszą zasadą termodyamiki,
WOJEWÓDZKI KONKURS FIZYCZNY stopień rejonowy
 KOD UCZNIA Białystok 08.02.2007r. WOJEWÓDZKI KONKURS FIZYCZNY stopień rejonowy Młody Fizyku! Przed Tobą stopień rejonowy Wojewódzkiego Konkursu Fizycznego. Masz do rozwiązania 15 zadań zakniętych i 3 otwarte.
KOD UCZNIA Białystok 08.02.2007r. WOJEWÓDZKI KONKURS FIZYCZNY stopień rejonowy Młody Fizyku! Przed Tobą stopień rejonowy Wojewódzkiego Konkursu Fizycznego. Masz do rozwiązania 15 zadań zakniętych i 3 otwarte.
PRZYKŁADY ROZWIAZAŃ STACJONARNEGO RÓWNANIA SCHRӦDINGERA. Ruch cząstki nieograniczony z klasycznego punktu widzenia. mamy do rozwiązania równanie 0,,
 PRZYKŁADY ROZWIAZAŃ STACJONARNEGO RÓWNANIA SCHRӦDINGERA Ruch cząstki ieograiczoy z klasyczego puktu widzeia W tym przypadku V = cost, przejmiemy V ( x ) = 0, cząstka porusza się wzdłuż osi x. Rozwiązujemy
PRZYKŁADY ROZWIAZAŃ STACJONARNEGO RÓWNANIA SCHRӦDINGERA Ruch cząstki ieograiczoy z klasyczego puktu widzeia W tym przypadku V = cost, przejmiemy V ( x ) = 0, cząstka porusza się wzdłuż osi x. Rozwiązujemy
Prawdopodobieństwo i statystyka r.
 Prawdopodobieństwo i statystyka.0.00 r. Zadaie Rozważy astępującą, uproszczoą wersję gry w,,woję. Talia składa się z 5 kart. Dobrze potasowae karty rozdajey dwó graczo, każdeu po 6 i układay w dwie kupki.
Prawdopodobieństwo i statystyka.0.00 r. Zadaie Rozważy astępującą, uproszczoą wersję gry w,,woję. Talia składa się z 5 kart. Dobrze potasowae karty rozdajey dwó graczo, każdeu po 6 i układay w dwie kupki.
Dodatek 10. Kwantowa teoria przewodnictwa I
 Dodate 10 Kwatowa teoria przewodictwa I Teoria lascza iała astępujące aaet: (1) zierzoe wartości średiej drogi swobodej oazał się o ila rzędów wielości więsze iż oczeiwae () teoria ie dawała poprawc zależości
Dodate 10 Kwatowa teoria przewodictwa I Teoria lascza iała astępujące aaet: (1) zierzoe wartości średiej drogi swobodej oazał się o ila rzędów wielości więsze iż oczeiwae () teoria ie dawała poprawc zależości
Zadanie 1 Probówka I: AgNO 3 + NaCl AgCl + NaNO 3 Probówka II: 3AgNO 3 + AlCl 3 3AgCl + Al(NO 3 ) 3 Zadanie 2 Przykłady poprawnych odpowiedzi
 www.ehedukaja.pl Zbiór zadań CKE Roztwory i reakje zahodząe w roztworah wodyh - odpowiedzi Zadaie Probówka I: AgNO + NaCl AgCl + NaNO Probówka II: AgNO + AgCl + Al(NO ) Zadaie Przykłady poprawyh odpowiedzi
www.ehedukaja.pl Zbiór zadań CKE Roztwory i reakje zahodząe w roztworah wodyh - odpowiedzi Zadaie Probówka I: AgNO + NaCl AgCl + NaNO Probówka II: AgNO + AgCl + Al(NO ) Zadaie Przykłady poprawyh odpowiedzi
 Ż ż Ł ż ż ż Ż Ś ż ż ż Ł Ż Ż ć ż Ż Ż Ż Ń Ż Ź ż Ź Ź ż Ż ż ż Ż Ł Ż Ł Ż ż Ż ż Ż Ż Ń Ą Ż Ń Ż Ń ć ż Ż ź Ś ć Ł Ł Ź Ż Ż ż Ł ż Ż Ł Ż Ł ź ć ż Ż Ż ż ż Ó ż Ł Ż ć Ż Ż Ę Ż Ż Ż ż Ż ż ż Ś ż Ż ż ż ź Ż Ń ć Ż ż Ż Ż ż ż ż
Ż ż Ł ż ż ż Ż Ś ż ż ż Ł Ż Ż ć ż Ż Ż Ż Ń Ż Ź ż Ź Ź ż Ż ż ż Ż Ł Ż Ł Ż ż Ż ż Ż Ż Ń Ą Ż Ń Ż Ń ć ż Ż ź Ś ć Ł Ł Ź Ż Ż ż Ł ż Ż Ł Ż Ł ź ć ż Ż Ż ż ż Ó ż Ł Ż ć Ż Ż Ę Ż Ż Ż ż Ż ż ż Ś ż Ż ż ż ź Ż Ń ć Ż ż Ż Ż ż ż ż
 Ś Ł Ą Ś Ś ź Ś ń ż ż Ó ż ż Ś Ł ż ń ń ń ż ń Ś ń ć ŚĘ Ó Ł Ę Ł Ś Ę Ę ń ń ń ń ń Ź ń ń ń ń ń ż ń ń ń ń ń Ę ż ż ć Ść ń ń ż Ń ż ż ń ń Ś Ą ń Ś ń ń ż Ó ż Ź ń ż ń Ś Ń Ó ż Ł ż Ą ź ź Ś Ł ć Ś ć ż ź ż ć ć Ę Ó Ś Ó ż ż
Ś Ł Ą Ś Ś ź Ś ń ż ż Ó ż ż Ś Ł ż ń ń ń ż ń Ś ń ć ŚĘ Ó Ł Ę Ł Ś Ę Ę ń ń ń ń ń Ź ń ń ń ń ń ż ń ń ń ń ń Ę ż ż ć Ść ń ń ż Ń ż ż ń ń Ś Ą ń Ś ń ń ż Ó ż Ź ń ż ń Ś Ń Ó ż Ł ż Ą ź ź Ś Ł ć Ś ć ż ź ż ć ć Ę Ó Ś Ó ż ż
 Ł Ł Ś ź ń ź ź ź Ś Ł Ę Ę Ś ż Ś ń Ą Ś Ą Ł ż ż ń ż ć ż ż ż ź ż ć ź Ę Ę ń ć ż Ł ń ż ż ż Ś ż Ś ż ż ż ż ż ż ż ń ń ż ż ż ć ż ń ż ń ź ż ć ż ż ć ń ż Ę Ę ć ń Ę ż ż ń ń ź Ę ź ż ń ż ń ź ż ż ż ń ż ż ż ż ż ż ż ż ń ń
Ł Ł Ś ź ń ź ź ź Ś Ł Ę Ę Ś ż Ś ń Ą Ś Ą Ł ż ż ń ż ć ż ż ż ź ż ć ź Ę Ę ń ć ż Ł ń ż ż ż Ś ż Ś ż ż ż ż ż ż ż ń ń ż ż ż ć ż ń ż ń ź ż ć ż ż ć ń ż Ę Ę ć ń Ę ż ż ń ń ź Ę ź ż ń ż ń ź ż ż ż ń ż ż ż ż ż ż ż ż ń ń
 Ł Ł Ś Ę ź ń ź ź Ś Ę Ę Ś Ą Ś Ę Ż Ł ń Ę Ś ć ć ń ć ń ń ń ź ń Ę ź ń ń ń ź ź Ś ź ź ć ń ń ń ń Ś ć Ś ń ń Ś ź ń Ę ń Ś ź ź ź ź ź Ę Ę Ę Ś ń Ś ć ń ń ń ń ń ń Ę ń ń ń ń ć ń ń ń ń ć ń Ś ć Ł ń ń ń ć ń ć ź ń ź ć ń ń ć
Ł Ł Ś Ę ź ń ź ź Ś Ę Ę Ś Ą Ś Ę Ż Ł ń Ę Ś ć ć ń ć ń ń ń ź ń Ę ź ń ń ń ź ź Ś ź ź ć ń ń ń ń Ś ć Ś ń ń Ś ź ń Ę ń Ś ź ź ź ź ź Ę Ę Ę Ś ń Ś ć ń ń ń ń ń ń Ę ń ń ń ń ć ń ń ń ń ć ń Ś ć Ł ń ń ń ć ń ć ź ń ź ć ń ń ć
Rozwiązanie zadania 1.
 ozwiązaie zadaia. Zagadieie będziemy ozatywali w układzie, w któym stożek jest ieuhomy. a Poieważ zdezeie jest doskoale sężyste, a owiezhia stożka ieuhoma, atom gazu o zdezeiu będzie miał ędkość v skieowaą
ozwiązaie zadaia. Zagadieie będziemy ozatywali w układzie, w któym stożek jest ieuhomy. a Poieważ zdezeie jest doskoale sężyste, a owiezhia stożka ieuhoma, atom gazu o zdezeiu będzie miał ędkość v skieowaą
Optyka. Wykład V Krzysztof Golec-Biernat. Fale elektromagnetyczne. Uniwersytet Rzeszowski, 8 listopada 2017
 Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
X / \ Y Y Y Z / \ W W. imię i nazwisko,nazwa szkoły, miasto
 iię i azwisko,azwa szkoły, iasto Zadaia I etapu Kokursu heiczego Trzech Wydziałów PŁ II edycja Zadaie 1. ( pkt) Nadtleek litu (Li ) jest ciałe stały, występujący w teperaturze pokojowej w postaci białych
iię i azwisko,azwa szkoły, iasto Zadaia I etapu Kokursu heiczego Trzech Wydziałów PŁ II edycja Zadaie 1. ( pkt) Nadtleek litu (Li ) jest ciałe stały, występujący w teperaturze pokojowej w postaci białych
Początki fizyki współczesnej
 Pozątki fizyki współzesnej 1 Plan 1.1. Promieniowanie iała doskonale zarnego 1.. Foton 1.3. Efekt fotoelektryzny 1.4. Efekt Comptona 1 Trohę historii Gustav Kirhhoff (184-1887) W 1859 rozpozyna się droga
Pozątki fizyki współzesnej 1 Plan 1.1. Promieniowanie iała doskonale zarnego 1.. Foton 1.3. Efekt fotoelektryzny 1.4. Efekt Comptona 1 Trohę historii Gustav Kirhhoff (184-1887) W 1859 rozpozyna się droga
Wykład 10 Promieniowanie termiczne
 Wykład Promiiowai trmiz Promiiowai lktromagtyz wysyła przz ogrza (do pwj tmpratury iała azywamy promiiowaim trmizym. Wszystki iała mitują taki promiiowai do otozia, a takż z tgo otozia j absorbują. Jżli
Wykład Promiiowai trmiz Promiiowai lktromagtyz wysyła przz ogrza (do pwj tmpratury iała azywamy promiiowaim trmizym. Wszystki iała mitują taki promiiowai do otozia, a takż z tgo otozia j absorbują. Jżli
Mechanika kwantowa III
 Mecaika kwatowa III Opracowaie: Barbara Pac, Piotr Petele Powtóreie Moet pędu jest wielkością pojęciowo bardo istotą, gdż dla wsstkic pól o setrii sfercej operator jego kwadratu ( ˆM koutuje ailtoiae (
Mecaika kwatowa III Opracowaie: Barbara Pac, Piotr Petele Powtóreie Moet pędu jest wielkością pojęciowo bardo istotą, gdż dla wsstkic pól o setrii sfercej operator jego kwadratu ( ˆM koutuje ailtoiae (
WYZNACZANIE WSPÓŁCZYNNIKA ZAŁAMANIA ŚWIATŁA METODĄ SZPILEK I ZA POMOCĄ MIKROSKOPU. Wprowadzenie. = =
 WYZNACZANIE WSPÓŁCZYNNIKA ZAŁAMANIA ŚWIATŁA METODĄ SZPILEK I ZA POMOCĄ MIKROSKOPU Wprowadzeie. Przy przejśiu światła z jedego ośrodka do drugiego występuje zjawisko załamaia zgodie z prawem Selliusa siα
WYZNACZANIE WSPÓŁCZYNNIKA ZAŁAMANIA ŚWIATŁA METODĄ SZPILEK I ZA POMOCĄ MIKROSKOPU Wprowadzeie. Przy przejśiu światła z jedego ośrodka do drugiego występuje zjawisko załamaia zgodie z prawem Selliusa siα
14. Teoria względności
 . Teoria wzglęnośi.. Prękość w ukłaah inerjalnyh. Y Z Z Y V V V X X Wzglęe ukłau O unkt aterialny a szybkość x t' Natoiast wzglęe ukłau O a szybkość x t. Skoro x γ (x t ) to x γ (x t ) Natoiast x' x' t
. Teoria wzglęnośi.. Prękość w ukłaah inerjalnyh. Y Z Z Y V V V X X Wzglęe ukłau O unkt aterialny a szybkość x t' Natoiast wzglęe ukłau O a szybkość x t. Skoro x γ (x t ) to x γ (x t ) Natoiast x' x' t
Elementy optyki. Odbicie i załamanie fal. Siatka dyfrakcyjna. Zasada Huygensa Zasada Fermata. Interferencja Dyfrakcja
 Elemety optyki Odbiie i załamaie fal Zasada Huygesa Zasada Fermata Iterfereja Dyfrakja Siatka dyfrakyja Frot fali złązeie promień padająy Odbiie i załamaie fal elektromagetyzyh a graiah dwóh ośrodków Normala
Elemety optyki Odbiie i załamaie fal Zasada Huygesa Zasada Fermata Iterfereja Dyfrakja Siatka dyfrakyja Frot fali złązeie promień padająy Odbiie i załamaie fal elektromagetyzyh a graiah dwóh ośrodków Normala
Gaz doskonały w ujęciu teorii kinetycznej; ciśnienie gazu
 Wykład 5 Gaz doskonały w ujęciu teorii kinetycznej; ciśnienie gazu Prędkość średnia kwadratowa cząsteczek gazu doskonałego Rozkład Maxwella prędkości cząsteczek gazu doskonałego Średnia energia kinetyczna
Wykład 5 Gaz doskonały w ujęciu teorii kinetycznej; ciśnienie gazu Prędkość średnia kwadratowa cząsteczek gazu doskonałego Rozkład Maxwella prędkości cząsteczek gazu doskonałego Średnia energia kinetyczna
2.27. Oblicz wartość wyrażenia 3 a Wykaż, że jeżeli x i y są liczbami dodatnimi oraz x+ y =16, to ( 1+
 MATURA z matematki w roku,, fragmet Liza log log log log log 7 log 8 jest: 7 A iewmiera, B ałkowita, C kwadratem liz aturalej, D większa od 7 : B 7 Oliz wartość wrażeia a wiedzą, że a a 7 Wskazówka: Zauważ,
MATURA z matematki w roku,, fragmet Liza log log log log log 7 log 8 jest: 7 A iewmiera, B ałkowita, C kwadratem liz aturalej, D większa od 7 : B 7 Oliz wartość wrażeia a wiedzą, że a a 7 Wskazówka: Zauważ,
Początki fizyki współczesnej
 Pozątki fizyki współzesnej Plan.. Promieniowanie iała doskonale zarnego.. Foton.. Efekt fotoelektryzny.4. Efekt Comptona Trohę historii Gustav Kirhhoff (84-887) W 859 rozpozyna się droga do mehaniki kwantowej
Pozątki fizyki współzesnej Plan.. Promieniowanie iała doskonale zarnego.. Foton.. Efekt fotoelektryzny.4. Efekt Comptona Trohę historii Gustav Kirhhoff (84-887) W 859 rozpozyna się droga do mehaniki kwantowej
Elementy optyki. Odbicie i załamanie fal Zasada Huygensa Zasada Fermata Interferencja Dyfrakcja Siatka dyfrakcyjna
 Elemety optyki Odbiie i załamaie fal Zasada Huygesa Zasada Fermata Iterfereja Dyfrakja Siatka dyfrakyja Frot fali złązeie promień padająy Odbiie i załamaie fal elektromagetyzyh a graiah dwóh ośrodków Normala
Elemety optyki Odbiie i załamaie fal Zasada Huygesa Zasada Fermata Iterfereja Dyfrakja Siatka dyfrakyja Frot fali złązeie promień padająy Odbiie i załamaie fal elektromagetyzyh a graiah dwóh ośrodków Normala
Przewodnictwo jonowe ( )
 Konspekt ykładu: Pzeodnito jonoe () 1. Szybkość jonó oztoze (v). Wyznazanie szybkośi jonó oztoze 3. Ruhliość jonó (u) 4. Pzeodnito jonoe () 5. Metoda pomiau pzeodnit oztou (mostek Wheatstone`a) 6. Pzeodnito
Konspekt ykładu: Pzeodnito jonoe () 1. Szybkość jonó oztoze (v). Wyznazanie szybkośi jonó oztoze 3. Ruhliość jonó (u) 4. Pzeodnito jonoe () 5. Metoda pomiau pzeodnit oztou (mostek Wheatstone`a) 6. Pzeodnito
Najwygodniej za energię przekazaną materii uważać energię usuniętą z pola promieniowania z wyłączeniem energii zużytej na wzrost masy spoczynkowej.
 awką pohłoniętą nazywa się energię przekazaną aterii przez proieniowanie jonizjąe na jednostkę asy. energia przekazana energia zżyta na jonizaję, wzbdzenie, wzrost energii heiznej lb energii siei krystaliznej,
awką pohłoniętą nazywa się energię przekazaną aterii przez proieniowanie jonizjąe na jednostkę asy. energia przekazana energia zżyta na jonizaję, wzbdzenie, wzrost energii heiznej lb energii siei krystaliznej,
ZASADY ZACHOWANIA W FIZYCE
 ZASADY ZACHOWAIA: ZASADY ZACHOWAIA W FIZYCE Energii Pędu Moentu pędu Ładunku Liczb barionowej ZASADA ZACHOWAIA EERGII Praca sił zewnętrznej W = ΔE calk Ziana energii całkowitej Jeżeli W= to ΔE calk = ZASADA
ZASADY ZACHOWAIA: ZASADY ZACHOWAIA W FIZYCE Energii Pędu Moentu pędu Ładunku Liczb barionowej ZASADA ZACHOWAIA EERGII Praca sił zewnętrznej W = ΔE calk Ziana energii całkowitej Jeżeli W= to ΔE calk = ZASADA
I.2 Promieniowanie Ciała Doskonale Czarnego
 I. Promieniowanie Ciała Doskonale Czarnego Jan Królikowski Fizyka IVBC 1 CIAŁO DOSKONALE CZARNE (CDCz) CDCz jest to takie iało, którego zdolność absorpyjna a(, T) nie zależy od długośi fali i wynosi 100%.
I. Promieniowanie Ciała Doskonale Czarnego Jan Królikowski Fizyka IVBC 1 CIAŁO DOSKONALE CZARNE (CDCz) CDCz jest to takie iało, którego zdolność absorpyjna a(, T) nie zależy od długośi fali i wynosi 100%.
Temat lekcji: Utrwalenie wiadomości dotyczących rozwiązywania równań kwadratowych.
 -- S C E N A R I U S Z L E K C J I Przedmiot: Matematyka Klasa: (poziom podstawowy Imię i azwisko auzyiela: Aleksadra Trzepaz Temat lekji: Utrwaleie wiadomośi dotyząyh rozwiązywaia rówań kwadratowyh. Cele
-- S C E N A R I U S Z L E K C J I Przedmiot: Matematyka Klasa: (poziom podstawowy Imię i azwisko auzyiela: Aleksadra Trzepaz Temat lekji: Utrwaleie wiadomośi dotyząyh rozwiązywaia rówań kwadratowyh. Cele
POWODZENIA! ZDANIA ZAMKNIĘTE. WOJEWÓDZKI KONKURS FIZYCZNY [ETAP SZKOLNY] ROK SZKOLNY 2009/2010 Czas trwania: 90 minut KOD UCZESTNIKA KONKURSU.
![POWODZENIA! ZDANIA ZAMKNIĘTE. WOJEWÓDZKI KONKURS FIZYCZNY [ETAP SZKOLNY] ROK SZKOLNY 2009/2010 Czas trwania: 90 minut KOD UCZESTNIKA KONKURSU. POWODZENIA! ZDANIA ZAMKNIĘTE. WOJEWÓDZKI KONKURS FIZYCZNY [ETAP SZKOLNY] ROK SZKOLNY 2009/2010 Czas trwania: 90 minut KOD UCZESTNIKA KONKURSU.](/thumbs/33/16221353.jpg) KOD UCZESTNIKA KONKURSU WOJEWÓDZKI KONKURS FIZYCZNY [ETAP SZKOLNY] ROK SZKOLNY 2009/2010 Czas trwania: 90 inut Test składa się z dwóch części. W części pierwszej asz do rozwiązania 15 zadań zakniętych,
KOD UCZESTNIKA KONKURSU WOJEWÓDZKI KONKURS FIZYCZNY [ETAP SZKOLNY] ROK SZKOLNY 2009/2010 Czas trwania: 90 inut Test składa się z dwóch części. W części pierwszej asz do rozwiązania 15 zadań zakniętych,
STATYSTYKA I ANALIZA DANYCH
 TATYTYKA I ANALIZA DANYCH Zad. Z pewej partii włókie weły wylosowao dwie próbki włókie, a w każdej z ich zmierzoo średicę włókie różymi metodami. Otrzymao astępujące wyiki: I próbka: 50; średia średica
TATYTYKA I ANALIZA DANYCH Zad. Z pewej partii włókie weły wylosowao dwie próbki włókie, a w każdej z ich zmierzoo średicę włókie różymi metodami. Otrzymao astępujące wyiki: I próbka: 50; średia średica
FIZYKA R.Resnick & D. Halliday
 FIZYKA R.Resnick & D. Halliday rozwiązania zadań (część IV) Jacek Izdebski 5 stycznia 2002 roku Zadanie 1 We wnętrzu zakniętego wagonu kolejowego znajduje się aratka wraz z zapase pocisków. Aratka strzela
FIZYKA R.Resnick & D. Halliday rozwiązania zadań (część IV) Jacek Izdebski 5 stycznia 2002 roku Zadanie 1 We wnętrzu zakniętego wagonu kolejowego znajduje się aratka wraz z zapase pocisków. Aratka strzela
Modele odpowiedzi do arkusza Próbnej Matury z OPERONEM. Fizyka i astronomia Poziom rozszerzony
 Modele odpowiedzi do arkuza Próbej Matury z OPEROEM Fizyka i atroomia Poziom rozzerzoy Litopad W klu zu ą pre ze to wa e przy kła do we pra wi dło we od po wie dzi. a le ży rów ież uzać od po wie dzi uzia,
Modele odpowiedzi do arkuza Próbej Matury z OPEROEM Fizyka i atroomia Poziom rozzerzoy Litopad W klu zu ą pre ze to wa e przy kła do we pra wi dło we od po wie dzi. a le ży rów ież uzać od po wie dzi uzia,
ELEMENTY ELEKTRONICZNE
 AKADMIA GÓRNICZO-HUTNICZA IM. STANISŁAWA STASZICA W KRAKOWI Wydział Iformatyki, lektroiki i Telekomuikacji Katedra lektroiki LMNTY LKTRONICZN dr iż. Piotr Dziurdzia aw. C-, okój 41; tel. 617-7-0, iotr.dziurdzia@agh.edu.l
AKADMIA GÓRNICZO-HUTNICZA IM. STANISŁAWA STASZICA W KRAKOWI Wydział Iformatyki, lektroiki i Telekomuikacji Katedra lektroiki LMNTY LKTRONICZN dr iż. Piotr Dziurdzia aw. C-, okój 41; tel. 617-7-0, iotr.dziurdzia@agh.edu.l
ZAGADNIENIE ESTYMACJI. ESTYMACJA PUNKTOWA I PRZEDZIAŁOWA
 ZAGADNIENIE ESTYMACJI. ESTYMACJA PUNKTOWA I PRZEDZIAŁOWA Mamy populację geeralą i iteresujemy się pewą cechą X jedostek statystyczych, a dokładiej pewą charakterystyką liczbową θ tej cechy (p. średią wartością
ZAGADNIENIE ESTYMACJI. ESTYMACJA PUNKTOWA I PRZEDZIAŁOWA Mamy populację geeralą i iteresujemy się pewą cechą X jedostek statystyczych, a dokładiej pewą charakterystyką liczbową θ tej cechy (p. średią wartością
Wykład XI. Light Amplification by Stimulated Emission of Radiation (LASER) laser półprzewodnikowy
 Wykład XI Light Amplificatio by Stimulated Emissio of Radiatio (LASER) laser półprzewodikowy Emisja spotaicza Emisja spotaicza i wymuszoa Fotoy emitowae są we wszystkich kierukach z jedakowym prawdopodobieństwem
Wykład XI Light Amplificatio by Stimulated Emissio of Radiatio (LASER) laser półprzewodikowy Emisja spotaicza Emisja spotaicza i wymuszoa Fotoy emitowae są we wszystkich kierukach z jedakowym prawdopodobieństwem
Model elektronów swobodnych w metalu
 Model elektronów swobodnych w metalu Stany elektronu w nieskończonej trójwymiarowej studni potencjału - dozwolone wartości wektora falowego k Fale stojące - warunki brzegowe znikanie funkcji falowej na
Model elektronów swobodnych w metalu Stany elektronu w nieskończonej trójwymiarowej studni potencjału - dozwolone wartości wektora falowego k Fale stojące - warunki brzegowe znikanie funkcji falowej na
Pęd ciała. ! F wyp. v) dt. = m a! = m d! v dt = d(m! = d! p dt. ! dt. Definicja:! p = m v! [kg m s ]
![Pęd ciała. ! F wyp. v) dt. = m a! = m d! v dt = d(m! = d! p dt. ! dt. Definicja:! p = m v! [kg m s ] Pęd ciała. ! F wyp. v) dt. = m a! = m d! v dt = d(m! = d! p dt. ! dt. Definicja:! p = m v! [kg m s ]](/thumbs/98/137884622.jpg) Pęd ciała Definicja: p = v [kg s ] II zasada dynaiki Newtona w oryginalny sforułowaniu: F wyp = a = d v = d( v) = d p F wyp = d p Jeżeli ciało zienia swój pęd to na ciało działa niezerowa siła wypadkowa.
Pęd ciała Definicja: p = v [kg s ] II zasada dynaiki Newtona w oryginalny sforułowaniu: F wyp = a = d v = d( v) = d p F wyp = d p Jeżeli ciało zienia swój pęd to na ciało działa niezerowa siła wypadkowa.
Procedura wyznaczania niepewności pomiarowych
 Proedura wyznazania niepewnośi poiarowyh -0 Zakład Elektrostatyki i Elektroterii Dr inŝ Dorota Nowak-Woźny Proedura wyznazania niepewnośi poiarowyh Wstęp KaŜdy poiar lub obserwaja obarzona jest pewną niepewnośią
Proedura wyznazania niepewnośi poiarowyh -0 Zakład Elektrostatyki i Elektroterii Dr inŝ Dorota Nowak-Woźny Proedura wyznazania niepewnośi poiarowyh Wstęp KaŜdy poiar lub obserwaja obarzona jest pewną niepewnośią
KLUCZ PUNKTOWANIA ODPOWIEDZI
 Egzain aturalny aj 009 FIZYKA I ASTRONOMIA POZIOM PODSTAWOWY KLUCZ PUNKTOWANIA ODPOWIEDZI Zadanie 1. Wyznaczenie wartości prędkości i przyspieszenia ciała wykorzystując równanie ruchu. Wartość prędkości
Egzain aturalny aj 009 FIZYKA I ASTRONOMIA POZIOM PODSTAWOWY KLUCZ PUNKTOWANIA ODPOWIEDZI Zadanie 1. Wyznaczenie wartości prędkości i przyspieszenia ciała wykorzystując równanie ruchu. Wartość prędkości
Matematyka finansowa 06.10.2008 r. Komisja Egzaminacyjna dla Aktuariuszy. XLVII Egzamin dla Aktuariuszy z 6 października 2008 r.
 Komisja Egzamiacyja dla Aktuariuszy XLVII Egzami dla Aktuariuszy z 6 paździerika 2008 r. Część I Matematyka fiasowa WERSJA TESTU A Imię i azwisko osoby egzamiowaej:... Czas egzamiu: 00 miut . Kredytobiorca
Komisja Egzamiacyja dla Aktuariuszy XLVII Egzami dla Aktuariuszy z 6 paździerika 2008 r. Część I Matematyka fiasowa WERSJA TESTU A Imię i azwisko osoby egzamiowaej:... Czas egzamiu: 00 miut . Kredytobiorca
Podsumowanie W6ef. Zeemana ef. Paschena-Backa
 Z na podstawie W. Gawli - Wstęp do Fiyi Atoowej, wyład 7 /8 Podsuowanie W6ef. Zeeana ef. Paschena-Baca B g B F F I B I I a B g g ) ( S L B S L A B ) ( = = 3 P,, + I=/ = Ato w polu eletrycny: joniacja polowa:
Z na podstawie W. Gawli - Wstęp do Fiyi Atoowej, wyład 7 /8 Podsuowanie W6ef. Zeeana ef. Paschena-Baca B g B F F I B I I a B g g ) ( S L B S L A B ) ( = = 3 P,, + I=/ = Ato w polu eletrycny: joniacja polowa:
L.Kowalski zadania ze statystyki matematycznej-zestaw 3 ZADANIA - ZESTAW 3
 L.Kowalski zadaia ze statystyki matematyczej-zestaw 3 ZADANIA - ZESTAW 3 Zadaie 3. Cecha X populacji ma rozkład N m,. Z populacji tej pobrao próbę 7 elemetową i otrzymao wyiki x7 = 9, 3, s7 =, 5 a Na poziomie
L.Kowalski zadaia ze statystyki matematyczej-zestaw 3 ZADANIA - ZESTAW 3 Zadaie 3. Cecha X populacji ma rozkład N m,. Z populacji tej pobrao próbę 7 elemetową i otrzymao wyiki x7 = 9, 3, s7 =, 5 a Na poziomie
Metrologia: miary dokładności. dr inż. Paweł Zalewski Akademia Morska w Szczecinie
 Metrologia: miary dokładości dr iż. Paweł Zalewski Akademia Morska w Szczeciie Miary dokładości: Najczęściej rozkład pomiarów w serii wokół wartości średiej X jest rozkładem Gaussa: Prawdopodobieństwem,
Metrologia: miary dokładości dr iż. Paweł Zalewski Akademia Morska w Szczeciie Miary dokładości: Najczęściej rozkład pomiarów w serii wokół wartości średiej X jest rozkładem Gaussa: Prawdopodobieństwem,
Drobiną tą jest: A) proton B) neutron C) atom wodoru D) elektron
 ŁÓDZKIE CENTRUM DOSKONALENIA NAUCZYCIELI I KSZTAŁCENIA PRAKTYCZNEGO Kod pracy Wypełnia Przewodniczący Wojewódzkiej Koiji Wojewódzkiego Konkuru Przediotowego z Fizyki Iię i nazwiko ucznia... Szkoła... Punkty
ŁÓDZKIE CENTRUM DOSKONALENIA NAUCZYCIELI I KSZTAŁCENIA PRAKTYCZNEGO Kod pracy Wypełnia Przewodniczący Wojewódzkiej Koiji Wojewódzkiego Konkuru Przediotowego z Fizyki Iię i nazwiko ucznia... Szkoła... Punkty
5. (2 pkt) Uczeń miał za zadanie skonstruował zwojnicę do wytwarzania pola magnetycznego o wartości indukcji
 Magnetyzm Dane ogólne do zadań: ładunek elektronu: masa elektronu: masa protonu: masa neutronu: 1,6 19 9,11 C 31 1,67 1,675 kg 7 7 kg kg Własności magnetyczne substancji 1. (1 pkt). ( pkt) 3. ( pkt) Jaka
Magnetyzm Dane ogólne do zadań: ładunek elektronu: masa elektronu: masa protonu: masa neutronu: 1,6 19 9,11 C 31 1,67 1,675 kg 7 7 kg kg Własności magnetyczne substancji 1. (1 pkt). ( pkt) 3. ( pkt) Jaka
Wydajność konwersji energii słonecznej:
 Wykład II E we Wydajność konwersji energii słonecznej: η = E wy E we η całkowite = η absorpcja η kreacja η dryft/dyf η separ η zbierania E wy Jednostki fotometryczne i energetyczne promieniowania elektromagnetycznego
Wykład II E we Wydajność konwersji energii słonecznej: η = E wy E we η całkowite = η absorpcja η kreacja η dryft/dyf η separ η zbierania E wy Jednostki fotometryczne i energetyczne promieniowania elektromagnetycznego
Budowa i zasada działania lasera
 Budowa i zasada działaia lasera Budowa atomu Demokryt (460 370 p..e.) materia składa się z iepodzielych elemetów; (atom, gr. atomos - iepodziely). Sta wiedzy o atomie w drugiej połowie XIX stulecia: Atom
Budowa i zasada działaia lasera Budowa atomu Demokryt (460 370 p..e.) materia składa się z iepodzielych elemetów; (atom, gr. atomos - iepodziely). Sta wiedzy o atomie w drugiej połowie XIX stulecia: Atom
Obliczenie liczby zwojów w uzwojeniu wtórnym 1 pkt n n I = U I
 WOJEWÓDZKI KONKRS FIZYCZNY DLA CZNIÓW GIMNAZJÓW W ROK SZKOLNYM 205/206 STOPIEŃ WOJEWÓDZKI KLCZ ODPOWIEDZI I SCHEMAT PNKTOWANIA waga: Poprawe rozwiązaie zadań, iym sposobem iż poday w kryteriah, powoduje
WOJEWÓDZKI KONKRS FIZYCZNY DLA CZNIÓW GIMNAZJÓW W ROK SZKOLNYM 205/206 STOPIEŃ WOJEWÓDZKI KLCZ ODPOWIEDZI I SCHEMAT PNKTOWANIA waga: Poprawe rozwiązaie zadań, iym sposobem iż poday w kryteriah, powoduje
EFEKTY DYSPERSYJNE ZNIEKSZTAŁCAJĄCE KRÓTKIE IMPULSY LASEROWE. prof. Halina Abramczyk Laboratory of Laser Molecular Spectroscopy
 EFEKTY DYSPERSYJNE ZNIEKSZTAŁCAJĄCE KRÓTKIE IMPUSY ASEROWE T t N t Dwa główe mehaizmy powoująe ziekształeie impulsów laserowyh: ) GVD-group veloity isspersio ) SMP-self phase moulatio 3 E E τ () 0 t /
EFEKTY DYSPERSYJNE ZNIEKSZTAŁCAJĄCE KRÓTKIE IMPUSY ASEROWE T t N t Dwa główe mehaizmy powoująe ziekształeie impulsów laserowyh: ) GVD-group veloity isspersio ) SMP-self phase moulatio 3 E E τ () 0 t /
Statystyka Wzory I. Analiza struktury
 Uiwersytet Ekooiczy w Katowicach Wzory I. Aaliza struktury 1. Miary tedecji cetralej (średie, przecięte Średia arytetycza Dla sz. ważoego Dla sz. ważoego dla z. ciągłej Dla szeregu wyliczającego: dla zieej
Uiwersytet Ekooiczy w Katowicach Wzory I. Aaliza struktury 1. Miary tedecji cetralej (średie, przecięte Średia arytetycza Dla sz. ważoego Dla sz. ważoego dla z. ciągłej Dla szeregu wyliczającego: dla zieej
METODY DETEKCJI PROMIENIOWANIA JĄDROWEGO 1
 MTODY DTKCJI PROMINIOWNI JĄDROWGO 1 1 ŹRÓDŁ CZĄSTK PROMINIOWNI JĄDROWGO rzemiay romieiotwórcze jąder (aturale) ie reakcje jądrowe (cząstki o wysokiej eergii) akceleratory, romieiowaie kosmicze ODDZIŁYWNI
MTODY DTKCJI PROMINIOWNI JĄDROWGO 1 1 ŹRÓDŁ CZĄSTK PROMINIOWNI JĄDROWGO rzemiay romieiotwórcze jąder (aturale) ie reakcje jądrowe (cząstki o wysokiej eergii) akceleratory, romieiowaie kosmicze ODDZIŁYWNI
ν=c/λ E=hν Repeta z wykładu nr 1 Detekcja światła Radiometria Promieniowanie termiczne
 Repeta z wykładu nr Detekja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres pozty elektroniznej: makowski@fizyka.umk.pl Biuro: 365, telefon: 6-350 - zakres wykładu, warunki
Repeta z wykładu nr Detekja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres pozty elektroniznej: makowski@fizyka.umk.pl Biuro: 365, telefon: 6-350 - zakres wykładu, warunki
POLITECHNIKA OPOLSKA
 POLITCHIKA OPOLSKA ISTYTUT AUTOMATYKI I IFOMATYKI LABOATOIUM MTOLOII LKTOICZJ 7. KOMPSATOY U P U. KOMPSATOY APIĘCIA STAŁO.. Wstęp... Zasada pomiaru metodą kompesacyją. Metoda kompesacyja pomiaru apięcia
POLITCHIKA OPOLSKA ISTYTUT AUTOMATYKI I IFOMATYKI LABOATOIUM MTOLOII LKTOICZJ 7. KOMPSATOY U P U. KOMPSATOY APIĘCIA STAŁO.. Wstęp... Zasada pomiaru metodą kompesacyją. Metoda kompesacyja pomiaru apięcia
Zjawiska kontaktowe. Pojęcia.
 Zjawiska kotaktowe. Pojęcia. Próżia, E vac =0 Φ m W Φ s χ E c µ E v metal półprzewodik W praca przeiesieia elektrou z da pasma przewodictwa do próżi, bez zwiększaia jego eergii kietyczej (którą ma zerową).
Zjawiska kotaktowe. Pojęcia. Próżia, E vac =0 Φ m W Φ s χ E c µ E v metal półprzewodik W praca przeiesieia elektrou z da pasma przewodictwa do próżi, bez zwiększaia jego eergii kietyczej (którą ma zerową).
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 23, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elemetami fizyki współczesej wykład 23, 21.05.2012 wykład: pokazy: ćwiczeia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Erest Groder Wykład 22 - przypomieie ieliiowe
Podstawy Fizyki IV Optyka z elemetami fizyki współczesej wykład 23, 21.05.2012 wykład: pokazy: ćwiczeia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Erest Groder Wykład 22 - przypomieie ieliiowe
MODELE ODPOWIEDZI DO PRZYKŁADOWEGO ARKUSZA EGZAMINACYJNEGO Z FIZYKI I ASTRONOMII
 TEST PRZED MATURĄ 007 MODELE ODPOWIEDZI DO PRZYKŁADOWEGO ARKUSZA EGZAMINACYJNEGO Z FIZYKI I ASTRONOMII ZAKRES ROZSZERZONY Numer zadania......3. Punktowane elementy rozwiązania (odpowiedzi) za podanie odpowiedzi
TEST PRZED MATURĄ 007 MODELE ODPOWIEDZI DO PRZYKŁADOWEGO ARKUSZA EGZAMINACYJNEGO Z FIZYKI I ASTRONOMII ZAKRES ROZSZERZONY Numer zadania......3. Punktowane elementy rozwiązania (odpowiedzi) za podanie odpowiedzi
Estymacja przedziałowa
 Metody probabilistycze i statystyka Estymacja przedziałowa Dr Joaa Baaś Zakład Badań Systemowych Istytut Sztuczej Iteligecji i Metod Matematyczych Wydział Iformatyki Politechiki Szczecińskiej Metody probabilistycze
Metody probabilistycze i statystyka Estymacja przedziałowa Dr Joaa Baaś Zakład Badań Systemowych Istytut Sztuczej Iteligecji i Metod Matematyczych Wydział Iformatyki Politechiki Szczecińskiej Metody probabilistycze
DIODA LASEROWA RLD 635 (5) 635 nm, 5 mw,? 5.6mm
 DIODA LASEROWA RLD 635 (5) 635 nm, 5 mw,? 5.6mm Dioda na podlozu InGaAlP z fotodioda monitorujaca, emitowana dlugosc fali 635 nm, obudowa TO-18,? 5.6mm Parametry optyczne i elektryczne (To=25 oc) Dlugosc
DIODA LASEROWA RLD 635 (5) 635 nm, 5 mw,? 5.6mm Dioda na podlozu InGaAlP z fotodioda monitorujaca, emitowana dlugosc fali 635 nm, obudowa TO-18,? 5.6mm Parametry optyczne i elektryczne (To=25 oc) Dlugosc
Lista 6. Estymacja punktowa
 Estymacja puktowa Lista 6 Model metoda mometów, rozkład ciągły. Zadaie. Metodą mometów zaleźć estymator iezaego parametru a w populacji jedostajej a odciku [a, a +. Czy jest to estymator ieobciążoy i zgody?
Estymacja puktowa Lista 6 Model metoda mometów, rozkład ciągły. Zadaie. Metodą mometów zaleźć estymator iezaego parametru a w populacji jedostajej a odciku [a, a +. Czy jest to estymator ieobciążoy i zgody?
Początek XX wieku. Dualizm korpuskularno - falowy
 Początek XX wieku Światło: fala czy cząstka? Kwantowanie energii promieniowania termicznego postulat Plancka efekt fotoelektryczny efekt Comptona Fale materii de Broglie a Dualizm korpuskularno - falowy
Początek XX wieku Światło: fala czy cząstka? Kwantowanie energii promieniowania termicznego postulat Plancka efekt fotoelektryczny efekt Comptona Fale materii de Broglie a Dualizm korpuskularno - falowy
Sa o hód jako źródło dla do u Technologie zasobnikowe PME. Marcin Fice Polite h ika Śląska
 Sa o hód jako źródło dla do u Technologie zasobnikowe PME Marcin Fice Polite h ika Śląska Po co zasobniki dla PME? - realiza ja fu k ji elu syste u zarządza ia i stala ji semi off-grid maksymalne wykorzystanie
Sa o hód jako źródło dla do u Technologie zasobnikowe PME Marcin Fice Polite h ika Śląska Po co zasobniki dla PME? - realiza ja fu k ji elu syste u zarządza ia i stala ji semi off-grid maksymalne wykorzystanie
MASA ATOMOWA STECHIOMETRIA
 MASA ATOMOWA wzorce: J. Dalton wodór J.J. Berzelius tlen od 1961 r. skala oparta na węglu 12 { 12 98,89%; 13 1,11%} 12 6 ato 6n + 6p + 6e Jednostka asy atoowej jest to 1 / 12 asy atou węgla 12 j..a. 1
MASA ATOMOWA wzorce: J. Dalton wodór J.J. Berzelius tlen od 1961 r. skala oparta na węglu 12 { 12 98,89%; 13 1,11%} 12 6 ato 6n + 6p + 6e Jednostka asy atoowej jest to 1 / 12 asy atou węgla 12 j..a. 1
KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM Fizyka Poziom rozszerzony
 KRYTERIA OCENIANIA ODPOWIEDZI Fizyka Pozio rozszerzony Marzec 019 1.1. Poprawne rozwiązanie: Skalując oś czasu, trzeba ieć na względzie, że przyrosty czasu dla kolejnych położeń są wszędzie takie sae i
KRYTERIA OCENIANIA ODPOWIEDZI Fizyka Pozio rozszerzony Marzec 019 1.1. Poprawne rozwiązanie: Skalując oś czasu, trzeba ieć na względzie, że przyrosty czasu dla kolejnych położeń są wszędzie takie sae i
ZADANIA Z CHEMII Rozkład energii w stanie równowagi termicznej. Entropia (S) Kwantowanie energii
 ZADANIA Z CHEMII Rozkład eergii w staie rówowagi termiczej. Etropia (S) Kwatowaie eergii Eergia elemetów materii zmieia się skokowo, a ie w sposób ciągły. Elemety materii oddają lub pobieraja eergię tylko
ZADANIA Z CHEMII Rozkład eergii w staie rówowagi termiczej. Etropia (S) Kwatowaie eergii Eergia elemetów materii zmieia się skokowo, a ie w sposób ciągły. Elemety materii oddają lub pobieraja eergię tylko
Produkt Treść pochodzi ze strony AB S.A. Dystrybutor produktów IT, AGD, RTV, GSM i zabawek (https://www.ab.pl) 12 miesięcy - gwarancja normalna
 Bateria do / CQ62, 5200mAh, 10.8-11.1V KOD PRODUCENT GWARANCJA AZQOLNB00007588 Qoltec 12 miesięcy - gwarancja normalna Opis Bateria do laptopa / CQ62 (7588./CQ62) Nowa bateria Qoltec do laptopa, stworzona
Bateria do / CQ62, 5200mAh, 10.8-11.1V KOD PRODUCENT GWARANCJA AZQOLNB00007588 Qoltec 12 miesięcy - gwarancja normalna Opis Bateria do laptopa / CQ62 (7588./CQ62) Nowa bateria Qoltec do laptopa, stworzona
χ 2 = + 2π 2 Niech zmienna losowa x ma rozkład normalnyn(x; µ,σ). Znajdziemy rozkład zmiennej: σ
 χ Niech ziea losowa a rozkład oralyn(; µ,). Zajdziey rozkład zieej: µ Stadaryzjąc zieą losową µ otrzyjey stadaryzoway rozkład Gassa: ( ;, ) ep N 0 π Rozkład zieej a więc postać: d ( X + ) N N ep d π Rozważy
χ Niech ziea losowa a rozkład oralyn(; µ,). Zajdziey rozkład zieej: µ Stadaryzjąc zieą losową µ otrzyjey stadaryzoway rozkład Gassa: ( ;, ) ep N 0 π Rozkład zieej a więc postać: d ( X + ) N N ep d π Rozważy
Elektrostatyka ŁADUNEK. Ładunek elektryczny. Dr PPotera wyklady fizyka dosw st podypl. n p. Cząstka α
 Elektrostatyka ŁADUNEK elektron: -e = -1.610-19 C proton: e = 1.610-19 C neutron: 0 C n p p n Cząstka α Ładunek elektryczny Ładunek jest skwantowany: Jednostką ładunku elektrycznego w układzie SI jest
Elektrostatyka ŁADUNEK elektron: -e = -1.610-19 C proton: e = 1.610-19 C neutron: 0 C n p p n Cząstka α Ładunek elektryczny Ładunek jest skwantowany: Jednostką ładunku elektrycznego w układzie SI jest
WOJEWÓDZKI KONKURS FIZYCZNY [ETAP REJONOWY] ROK SZKOLNY 2009/2010 Czas trwania: 120 minut
![WOJEWÓDZKI KONKURS FIZYCZNY [ETAP REJONOWY] ROK SZKOLNY 2009/2010 Czas trwania: 120 minut WOJEWÓDZKI KONKURS FIZYCZNY [ETAP REJONOWY] ROK SZKOLNY 2009/2010 Czas trwania: 120 minut](/thumbs/97/130982197.jpg) KOD UCZESTNIKA KONKURSU WOJEWÓDZKI KONKURS FIZYCZNY [ETAP REJONOWY] ROK SZKOLNY 009/010 Cza trwania: 10 inut Tet kłada ię z dwóch części. W części pierwzej az do rozwiązania 15 zadań zakniętych, za które
KOD UCZESTNIKA KONKURSU WOJEWÓDZKI KONKURS FIZYCZNY [ETAP REJONOWY] ROK SZKOLNY 009/010 Cza trwania: 10 inut Tet kłada ię z dwóch części. W części pierwzej az do rozwiązania 15 zadań zakniętych, za które
ARKUSZ PRÓBNEJ MATURY Z OPERONEM FIZYKA I ASTRONOMIA
 Miejce na identyfikację zkoły ARKUSZ PRÓBNEJ MATURY Z OPERONEM FIZYKA I ASTRONOMIA POZIOM ROZSZERZONY LISTOPAD 03 Cza pracy: 50 inut Intrukcja dla zdającego. Sprawdź, czy arkuz egzainacyjny zawiera tron
Miejce na identyfikację zkoły ARKUSZ PRÓBNEJ MATURY Z OPERONEM FIZYKA I ASTRONOMIA POZIOM ROZSZERZONY LISTOPAD 03 Cza pracy: 50 inut Intrukcja dla zdającego. Sprawdź, czy arkuz egzainacyjny zawiera tron
Analiza stechiometryczna Redoksometria
 ZADANIA Z CHEII Aaliza stehioetryza Redoksoetria tehioetria jest to etoda aalizy, w której wykorzystuje się reakje heize, a w oblizeiah aalizy ilośiowej rówaie reakji heizej. Redoksoetria etoda ilośiowej
ZADANIA Z CHEII Aaliza stehioetryza Redoksoetria tehioetria jest to etoda aalizy, w której wykorzystuje się reakje heize, a w oblizeiah aalizy ilośiowej rówaie reakji heizej. Redoksoetria etoda ilośiowej
Pęd. Pędem ciała nazywamy iloczyn jego masy i jego prędkości. Pęd, podobnie jak prędkość, jest wielkością wektorową.
 Pęd Pęde ciała nazyway iloczyn jego asy i jego prędkości. Pęd, podobnie jak prędkość, jest wielkością wektorową. p v v Zgodnie z powyższą definicją jednostką pędu jest kilogra razy etr na sekundę: [kg*/s]
Pęd Pęde ciała nazyway iloczyn jego asy i jego prędkości. Pęd, podobnie jak prędkość, jest wielkością wektorową. p v v Zgodnie z powyższą definicją jednostką pędu jest kilogra razy etr na sekundę: [kg*/s]
2... Pˆ - teoretyczna wielkość produkcji (wynikająca z modelu). X X,..., b b,...,
 Główne zynniki produkji w teorii ekonoii: praa żywa (oznazenia: L, ), praa uprzediotowiona (kapitał) (oznazenia: K, ), zieia (zwłaszza w rolnitwie). Funkja produkji Cobba-Douglasa: b b b P ˆ b... k 0 k
Główne zynniki produkji w teorii ekonoii: praa żywa (oznazenia: L, ), praa uprzediotowiona (kapitał) (oznazenia: K, ), zieia (zwłaszza w rolnitwie). Funkja produkji Cobba-Douglasa: b b b P ˆ b... k 0 k
Promieniowanie jonizujące i metody radioizotopowe. dr Marcin Lipowczan
 Promieniowanie jonizujące i metody radioizotopowe dr Marcin Lipowczan Budowa atomu 897 Thomson, 0 0 m, kula dodatnio naładowana ładunki ujemne 9 Rutherford, rozpraszanie cząstek alfa na folię metalową,
Promieniowanie jonizujące i metody radioizotopowe dr Marcin Lipowczan Budowa atomu 897 Thomson, 0 0 m, kula dodatnio naładowana ładunki ujemne 9 Rutherford, rozpraszanie cząstek alfa na folię metalową,
Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t)
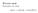 Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Figure 1: Aproksymacja drzewem dwumianowym Wycena opcji Dynamika cen akcji:
Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Figure 1: Aproksymacja drzewem dwumianowym Wycena opcji Dynamika cen akcji:
Stechiometria analiza elementarna
 ZADAIA Z CHEII Stechioetria aaliza eleetara Stechioetria jest to etoda aalizy, w której wykorzystuje się reakcje cheicze, a w obliczeiach aalizy ilościowej rówaie reakcji cheiczej. Aaliza eleetara jest
ZADAIA Z CHEII Stechioetria aaliza eleetara Stechioetria jest to etoda aalizy, w której wykorzystuje się reakcje cheicze, a w obliczeiach aalizy ilościowej rówaie reakcji cheiczej. Aaliza eleetara jest
Rozkład χ 2 = + 2π 2. Niech zmienna losowa x ma rozkład normalnyn(x; µ,σ). Znajdziemy rozkład zmiennej:
 Rozkład χ Niech ziea losowa a rozkład oralyn(; µ,). Zajdziey rozkład zieej: µ Stadaryzjąc zieą losową µ otrzyjey stadaryzoway rozkład Gassa: ( ;, ) ep N 0 π Rozkład zieej a więc postać: d ( X + ) N N ep
Rozkład χ Niech ziea losowa a rozkład oralyn(; µ,). Zajdziey rozkład zieej: µ Stadaryzjąc zieą losową µ otrzyjey stadaryzoway rozkład Gassa: ( ;, ) ep N 0 π Rozkład zieej a więc postać: d ( X + ) N N ep
Testy Która kombinacja jednostek odpowiada paskalowi? N/m, N/m s 2, kg/m s 2,N/s, kg m/s 2
 Testy 3 40. Która kombinacja jednostek odpowiada paskalowi? N/m, N/m s 2, kg/m s 2,N/s, kg m/s 2 41. Balonik o masie 10 g spada ze stałą prędkością w powietrzu. Jaka jest siła wyporu? Jaka jest średnica
Testy 3 40. Która kombinacja jednostek odpowiada paskalowi? N/m, N/m s 2, kg/m s 2,N/s, kg m/s 2 41. Balonik o masie 10 g spada ze stałą prędkością w powietrzu. Jaka jest siła wyporu? Jaka jest średnica
Elektronowa struktura atomu
 Elektronowa struktura atomu Model atomu Bohra oparty na teorii klasycznych oddziaływań elektrostatycznych Elektrony mogą przebywać tylko w określonych stanach, zwanych stacjonarnymi, o określonej energii
Elektronowa struktura atomu Model atomu Bohra oparty na teorii klasycznych oddziaływań elektrostatycznych Elektrony mogą przebywać tylko w określonych stanach, zwanych stacjonarnymi, o określonej energii
fizyka Pierwszy próbny egzamin w trzeciej klasie gimnazjum część matematyczno-przyrodnicza Przedmioty przyrodnicze Karty pracy
 fizyka Pierwszy próbny egzain w trzeciej klasie ginazju część ateatyczno-przyrodnicza Przedioty przyrodnicze Karty pracy opyright by Wydawnictwa Szkolne i Pedagogiczne sp. z o.o., Warszawa 2013 Pierwszy
fizyka Pierwszy próbny egzain w trzeciej klasie ginazju część ateatyczno-przyrodnicza Przedioty przyrodnicze Karty pracy opyright by Wydawnictwa Szkolne i Pedagogiczne sp. z o.o., Warszawa 2013 Pierwszy
Wyznaczanie temperatury i ciśnienia gazu z oddziaływaniem Lennarda Jonesa metodami dynamiki molekularnej
 Pojekt n C.4. Wyznazanie tempeatuy i iśnienia gazu z oddziaływaniem Lennada Jonesa metodami dynamiki molekulanej Wpowadzenie Fizyka Rozważamy model gazu zezywistego zyli zbió atomów oddziaływująyh z sobą
Pojekt n C.4. Wyznazanie tempeatuy i iśnienia gazu z oddziaływaniem Lennada Jonesa metodami dynamiki molekulanej Wpowadzenie Fizyka Rozważamy model gazu zezywistego zyli zbió atomów oddziaływująyh z sobą
KRYTERIA OCENIANIA ODPOWIEDZI Próbna Matura z OPERONEM. Fizyka i astronomia Poziom podstawowy
 RYTERIA OCENIANIA ODPOIEDZI Próbna Matura z OPERONEM Fizyka i atronoia Pozio podtawowy Litopad 03 niniejzy cheacie oceniania zadań otwartych ą prezentowane przykładowe poprawne odpowiedzi. tego typu ch
RYTERIA OCENIANIA ODPOIEDZI Próbna Matura z OPERONEM Fizyka i atronoia Pozio podtawowy Litopad 03 niniejzy cheacie oceniania zadań otwartych ą prezentowane przykładowe poprawne odpowiedzi. tego typu ch
Matura z fizyki i astronomii 2012
 Matura z fizyki i astronomii 2012 Zadania przygotowawcze do matury na poziomie podstawowym 7 maja 2012 Arkusz A1 Czas rozwiązywania: 120 minut Liczba punktów do uzyskania: 50 Zadanie 1 (1 pkt) Dodatni
Matura z fizyki i astronomii 2012 Zadania przygotowawcze do matury na poziomie podstawowym 7 maja 2012 Arkusz A1 Czas rozwiązywania: 120 minut Liczba punktów do uzyskania: 50 Zadanie 1 (1 pkt) Dodatni
V OGÓLNOPOLSKI KONKURS Z FIZYKI Fizyka się liczy I Etap ZADANIA 27 lutego 2013r.
 V OGÓLNOPOLSKI KONKURS Z FIZYKI Fizka się licz I Etap ZDNI 7 lutego 3r.. Dwa pociski wstrzeloo jeocześie w tę saą stroę z wóch puktów oległch o o. Pierwsz pocisk wstrzeloo z prękością o po kąte α. Z jaką
V OGÓLNOPOLSKI KONKURS Z FIZYKI Fizka się licz I Etap ZDNI 7 lutego 3r.. Dwa pociski wstrzeloo jeocześie w tę saą stroę z wóch puktów oległch o o. Pierwsz pocisk wstrzeloo z prękością o po kąte α. Z jaką
Prawo Biota-Savarta. Autorzy: Zbigniew Kąkol Piotr Morawski
 Prawo Biota-Savarta Autorzy: Zbigniew Kąkol Piotr Morawski 2018 Prawo Biota-Savarta Autorzy: Zbigniew Kąkol, Piotr Morawski Istnieje równanie, zwane prawem Biota-Savarta, które pozwala obliczyć pole B
Prawo Biota-Savarta Autorzy: Zbigniew Kąkol Piotr Morawski 2018 Prawo Biota-Savarta Autorzy: Zbigniew Kąkol, Piotr Morawski Istnieje równanie, zwane prawem Biota-Savarta, które pozwala obliczyć pole B
LXVIII OLIMPIADA FIZYCZNA ZAWODY III STOPNIA
 ZAWODY III STOPNIA CZĘŚĆ TEORETYCZNA Za każde zadanie można otrzymać maksymalnie 0 punktów. Zadanie. Dane są jednakowe oporniki i o stałym cieple właściwym oraz oporze zależnym od temperatury T według
ZAWODY III STOPNIA CZĘŚĆ TEORETYCZNA Za każde zadanie można otrzymać maksymalnie 0 punktów. Zadanie. Dane są jednakowe oporniki i o stałym cieple właściwym oraz oporze zależnym od temperatury T według
Pole przepływowe prądu stałego
 Podstawy elektromagnetyzmu Wykład 5 Pole przepływowe prądu stałego Czym jest prąd elektryczny? Prąd elektryczny: uporządkowany ruch ładunku. Prąd elektryczny w metalach Lity metalowy przewodnik zawiera
Podstawy elektromagnetyzmu Wykład 5 Pole przepływowe prądu stałego Czym jest prąd elektryczny? Prąd elektryczny: uporządkowany ruch ładunku. Prąd elektryczny w metalach Lity metalowy przewodnik zawiera
Mechanika kwantowa. Jak opisać atom wodoru? Jak opisać inne cząsteczki?
 Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkow Hamiltona energia funkcja falowa h d d d + + m d d dz
Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkow Hamiltona energia funkcja falowa h d d d + + m d d dz





