KRYTERIA STOSOWANIA MODELI STOCHASTYCZNYCH W PREDYKCJI RYNKOWEJ WARTOŚCI NIERUCHOMOŚCI
|
|
|
- Katarzyna Wieczorek
- 8 lat temu
- Przeglądów:
Transkrypt
1 KRYTERIA STOSOWANIA MODELI STOCHASTYCZNYCH W PREDYKCJI RYNKOWEJ WARTOŚCI NIERUCHOMOŚCI Aa Barańska Katedra Iformacj o Teree, Akadema Górczo-Hutcza w Krakowe SFORMUŁOWANIE TEZ PRACY Do ajczęścej stosowaych metod określaa rykowej wartośc eruchomośc ależy ewątplwe wycea realzowaa przy pomocy podejśca porówawczego. Podstawową zasadą tego podejśca jest porówae eruchomośc wyceaej z eruchomoścam podobym, o zaych ceach trasakcyjych oraz cechach różcujących te eruchomośc wpływających a ch wartość. Wszystke formacje o eruchomoścach mają charakter probablstyczy, gdyż ch wybór wraz z ch opsem zależy od rzeczozawcy. Stosowe Rozporządzee Rady Mstrów mów o 3 metodach w podejścu porówawczym: metodze porówywaa param, metodze korygowaa cey średej metodze aalzy statystyczej ryku. Trzeca metoda dopuszcza wszelke sposoby wycey bazujące a modelach statystyczych. Uzyskaa w te sposób wartość rykowa eruchomośc powa odpowadać prawdopodobej cee, jaką uzyskałaby wyceaa eruchomość a wolym ryku, jako przedmot ustaloego prawa rzeczowego. Na baze obowązujących przepsów prawych, dotyczących zagadea wycey eruchomośc steje bardzo wele kocepcj zastosowaa metod statystyczych tworzea welowymarowych model matematyczych, możlwe ajlepej opsujących day ryek eruchomośc. Welowymarowość zagadea wyka przede wszystkm z mogośc czyków wpływających bezpośredo a wartość eruchomośc. Tworzee modelu matematyczego dla wybraego ryku jest zagadeem ezwykle złożoym, gdyż wymaga stosowego przygotowaa bazy daych do modelowaa pod względem jej kompletośc warygodośc, z uwzględeem optymalego doboru zmeych. Sposób zalezea tego ajlepszego modelu zwązay jest z testowaem dużej lośc formacj w baze daych. Isteje zatem potrzeba sformułowaa jakchś kryterów doboru optymalego modelu spośród welu, jak róweż kryterów zwązaych z samą postacą bazy daych do modelowaa. Dotyczy to główe relacj pomędzy lczbą zmeych lczoścą bazy daych. Zasadczym celem rozprawy jest opracowae kryterów doboru model matematyczych ocey warygodośc daych służących do modelowaa. Do sformułowaa tych kryterów zostaą wykorzystae parametry ezmecze, które będą zdefowae w oparcu o macerz korelacyją dla zmeych występujących w modelu wycey macerz kowaracj dla progozowaych rykowych wartośc eruchomośc. Zakres pracy obejmuje: charakterystykę wykorzystywaej bazy wedzy o eruchomoścach sprzedaych z różych ryków Polsk połudowo-wschodej, zdefowae parametrów ezmeczych, służących sformułowau kryterów doboru modelu wycey postac bazy, określee tredu zmay ce eruchomośc w czase dla poszczególych ryków lokalych, wstępą aalzę baz eruchomośc pod kątem wyboru atrybutów do modelowaa rykowej wartośc eruchomośc, Zastosowaa metod statystyczych w badaach aukowych III StatSoft Polska
2 Krytera stosowaa model stochastyczych w predykcj rykowej wartośc eruchomośc testowae welowymarowych model lowych elowych w poszczególych bazach, wstępą selekcję model a podstawe testu Fshera-Sedecora o rówośc waracj częśc wyjaśoej ewyjaśoej przez model regresj, wyzaczee wartośc zdefowaych ezmeków, sformułowae propozycj kryterów doboru modelu ocey warygodośc bazy eruchomośc a podstawe aalz wartośc parametrów ezmeczych. Teza rozprawy doktorskej. Na podstawe, zdefowaych przez autorkę pracy, parametrów ezmeczych steje możlwość doboru optymalej lczby eruchomośc optymalej lczby opsujących je cech w modelowau rykowej wartośc eruchomośc. Krytera doboru optymalego modelu wycey mogą być sformułowae a podstawe przedzałów wartośc zapropoowaych parametrów ezmeczych. OPIS WYKORZYSTYWANEJ BAZY WIEDZY Wykorzystywae w pracy bazy daych o eruchomoścach odoszą sę do ryków eruchomośc połudowo-wschodej Polsk, motorowaych od 998 roku do chwl obecej. Dae wykorzystae w ejszej pracy obejmują formacje o eruchomoścach grutowych, przezaczoych pod budowctwo, będących przedmotem obrotu, z astępujących mejscowośc: Bolesław, Busko Zdrój, Kraków, Nowy Sącz, Proszowce, Przeworsk, Rzeszów, Śwdk, Trzycąż. Rozważae ryk eruchomośc charakteryzują sę dużym zróżcowaem ceowym wykazują zmeą dyamkę trasakcj. Może to być spowodowae zmeą koukturą gospodarczą kraju. Zebrae bazy zawerają od do 3 eruchomośc dają łącze 53 eruchomośc grutowych. Ryek eruchomośc tworzoy jest dla każdego masta (gmy) oddzele. A dla dużych mast poszczególe dzelce staowły oddzele ryk eruchomośc. Jest to zwązae z trudoścą zalezea łatwo detyfkowalych merzalych cech (zmeych), w oparcu o które możlwe byłoby przetrasformowae ce do wspólego, jedego ryku eruchomośc. W wększośc przypadków, awet dla gm o zblżoej lczbe meszkańców, cey eruchomośc ajczęścej zdecydowae sę różą. Decydują o tym główe take czyk jak: ryek pracy, atrakcyjość masta, czystość środowska, perspektywy rozwoju, położee, krajobraz. Zachodz też odmee reagowae a dzałae czyków lokalych, uwdaczające sę w charakterystykach weryfkowaych model.. Charakterystyka przyjętych atrybutów ch skal. W przypadku ryku eruchomośc trudo jest zdetyfkować cechy (zmee), których wpływ a wartość eruchomośc jest jedozacze określoy. W ejszej pracy aalzowao atrybuty (wyróżoe cechy), które są łatwe do detyfkacj rejestracj. Atrybuty opsujące eruchomość moża podzelć a dwe zasadcze grupy: oblgatoryje fakultatywe. Perwsza z ch służy jedozaczej detyfkacj eruchomośc; są to dae o charakterze admstracyjo-prawym. Należą tu wszystke dae ewdecyje zwązae z adresem eruchomośc oraz dae opsujące jej sta prawy. Natomast druga grupa to cechy kreujące wartość rykową, względem których powy być wyberae eruchomośc do porówywaa. Atrybuty fakultatywe mają zasadcze zaczee w modelowau matematyczym wartośc rykowej, zatem koecze jest ustalee dla ch skal wartośc. Dla eruchomośc grutowych moża wyszczególć astępujące atrybuty: przezaczee w plae mejscowym, dae geometrycze (wymary, kształt, topografa), dae opsujące atrakcyjość lokalzacj (strefa, moda, otoczee), dae zwązae z dostępem do eruchomośc (dostępość środków komukacj, droga dojazdowa), występowae elemetów dodatkowych (uzbrojee tereu, ewetuala zabudowa). Przy ustalau skal lczbowych dla wększośc atrybutów posłużoo sę skalą porządkową, pozwalającą a ragowae elemetów, 84 Zastosowaa metod statystyczych w badaach aukowych III StatSoft Polska 8
3 Krytera stosowaa model stochastyczych w predykcj rykowej wartośc eruchomośc z uwzględeem atężea wpływu atrybutu a wartość rykową. Najczęścej korzystao ze skal 4-stopowej. W klku przypadkach wykorzystao róweż skalę omalą lub lorazową. W pracy rozpatrywao klkaaśce cech eruchomośc o charakterze uzaowym. 3 PARAMETRY NIEZMIENNICZE Do aalzy formacj rykowych zapropoowao trzy astępujące parametry: Współczyk determacj R, czyl stadardowa mara zaufaa do estymowaego modelu wycey, zdefoway wzorem: det K R =, () det K gdze: r r... r k r r... r k K = r r... r k () rk rk rk... K macerz korelacyja, zawerająca współczyk korelacj zupełej pomędzy wszystkm param zmeych (r j ), det K wyzaczk macerzy korelacyjej, det K wyzaczk podmacerzy, która powstaje ze skreślea perwszego wersza perwszej kolumy w macerzy K, czyl współczyków korelacj dotyczących zmeej zależej (cey). Welkość -R staow współczyk ezgodośc modelu z rykowym wartoścam eruchomośc, które są wykorzystywae w estymacj modelu wycey. Parametr określoy a podstawe śladu macerzy kowaracj, zdefoway wzorem: tr{ Cov( W )} σ tr =, (3) W śr gdze: tr{cov(w)} ślad macerzy kowaracj dla progozowaych wartośc rykowych eruchomośc ustalających model wycey, Wśr średa wartość z progozowaych wartośc rykowych eruchomośc ustalających model wycey, lczba eruchomośc służących do estymacj modelu. 3 Parametr określoy a podstawe wyzaczka macerzy kowaracj, zdefoway wzorem: σ det = u det{ Cov( W )}, (4) Wśr gdze: det{cov(w)} wyzaczk macerzy kowaracj dla progozowaych wartośc rykowych eruchomośc ustalających model wycey, Wśr średa wartość z progozowaych wartośc rykowych eruchomośc ustalających model wycey, u lczba zmeych ezależych występujących w modelu. Ze względu a charakter perwszego parametru, jako mary zaufaa do modelu, wskazae jest, aby jego wartość spełała kryterum: R >,6. Natomast dla dwóch pozostałych parametrów, powązaych ścśle z waracjam wartośc modelowych ce eruchomośc tworzących model, przyjmujemy, że e powy oe przekraczać klkuastu procet średej z progozowaych wartośc rykowych eruchomośc tworzących model wycey. Te wstępe postulaty zostały zweryfkowae w dalszych rozdzałach pracy. Na podstawe aalzy wzorów (3) (4) moża stwerdzć, że welkośc te staową pewego rodzaju mary rozproszea wokół średej wartośc modelowej, stąd mogą być obektywym parametram służącym do sformułowaa kryterów warygodośc baz wykorzystywaych w modelowau wartośc rykowej. 4 ESTYMACJA TRENDU ZMIANY CEN NIERUCHOMOŚCI W CZASIE Rozważae w pracy bazy eruchomośc odoszą sę do trasakcj realzowaych w różym czase, czyl przy różym stae ryku. Sta ryku, wyrażający pozom ce eruchomośc, wąże sę z ogólą koukturą gospodark kraju Zastosowaa metod statystyczych w badaach aukowych III StatSoft Polska
4 Krytera stosowaa model stochastyczych w predykcj rykowej wartośc eruchomośc może być róweż kwatyfkoway za pomocą skal uzaowej. Obektywą skalą rejestrującą sta ryku eruchomośc jest czas, który powe być lczoy w mesącach. W przedstawoych rozważaach zakłada sę, że cechy poszczególych eruchomośc zachowują ezmeość w rozpatrywaym przedzale czasu zaweraych trasakcj. Zatem sta ryku rejestroway różym pozomem ce eruchomośc powe być skorygoway do jedego mometu czasowego (ustaloego mesąca). W pracy dla każdej z baz, w której było to ezbęde, taka korekta została wykoaa. Dobór fukcj do określea tredu zmay ce w czase został dokoay a podstawe wartośc współczyka korelacj krzywolowej. Okazało sę, że ajlepszym fukcjam są tu fukcje welomaowe różych stop. 5 STATYSTYCZNA ANALIZA BAZ NIERUCHOMOŚCI W celu efektywego wykorzystywaa bazy daych w badaach aukowych koecze jest przeprowadzee jej wstępej obróbk statystyczej. Poprzez taką obróbkę doprowadza sę bazy daych do spójośc, co pozwala a uzyskae bardzej warygodych wyków prowadzoych badań. W perwszej kolejośc ależy przeaalzować zbór formacj pod względem jego kompletośc, tz. w marę możlwośc każdy z przypadków powe meć adaą kokretą wartość, dla każdej z rozważaych zmeych. Następe, w poszczególych bazach daych, dla zmeej zależej wyzaczoo współczyk dyspersj. Parametr te jest marą rozproszea wartośc zmeej wokół jej wartośc przecętej. Bardzej szczegółowe aalzy operały sę a wyzaczeu współczyków korelacj zupełej, cząstkowej oraz semcząstkowej, a także a wykach aalzy reszt. Współczyk korelacj pozwalają określć wpływ poszczególych zmeych ezależych a zmeą zależą oraz służą do badaa admarowośc występowaa zmeych ezależych. Natomast aalza reszt pozwala wyelmować z bazy daych przypadk odstające. Pojawee sę takch przypadków w baze może być wykem bądź błędej formacj, bądź zastea waruków szczególych (p. sprzedaż wymuszoa w obroce eruchomoścam), albo też wpływu ych czyków trudych do zdetyfkowaa w procese zberaa formacj o eruchomoścach tworzea modelu wycey. Owoca dla późejszego modelowaa jest róweż wstępa ocea typu zależośc pomędzy zmeą zależą a poszczególym zmeym ezależym a podstawe wykresów rozrzutu oraz aalza częstośc występowaa poszczególych wartośc skal przyjętych dla zmeych ezależych. Na podstawe powyższych wyków moża wysuć globale wosk a temat cech eruchomośc mających ajczęścej ajwększy wpływ a jej ceę. Dla wybraych dzesęcu baz eruchomośc atrybutam, które ajczęścej występują w grupe tych ajstotejszych a daym ryku są: strefa masta, dostęp komukacyjy, moda a lokalzację, wpływ otoczea, a z elemetów uzbrojea tereu: seć gazowa w drugej kolejośc kaalzacja secowa. 6 WIELOWYMIAROWE LINIOWE I NIELINIOWE MODELOWANIE WARTOŚCI NIERUCHOMOŚCI W procese modelowaa ryku eruchomośc w każdej baze przetestowao welowymarowy model lowy w postac lowej regresj welorakej: u + X k * k = F( X, a) = w = a a (5) gdze: w wartość modelowa -tej eruchomośc w daej baze, X wektor wartośc atrybutów dla -tej eruchomośc ( u), X k wartość atrybutu k dla -tej eruchomośc, a wyraz woly w modelu, a wektor współczyków regresj welokrotej ((u+) ), a k współczyk regresj stojący przy atrybuce k. W astępej kolejośc dla każdej bazy doberao róże postace model elowych. W statystyce matematyczej e ma aaltyczych sposobów, które by umożlwały k 86 Zastosowaa metod statystyczych w badaach aukowych III StatSoft Polska 8
5 Krytera stosowaa model stochastyczych w predykcj rykowej wartośc eruchomośc optymaly wybór odpowedej postac fukcj. Przy kostruowau takego modelu przebadao ajperw charakter zależośc cey eruchomośc od każdego atrybutu z osoba: Y = g(x k ), (6) gdze: X k zmea odpowadająca wartoścom atrybutu k, Y cey eruchomośc w baze. Postać fukcj g może być bardzo róża. Rozważao astępujące fukcje elemetare: lowe, welomay różych stop, fukcje logarytmcze, wykładcze, ewymere. Wykoao wykresy rozrzutu atrybut cea z ałożoą lą tredu wyestymowaą metodą MNK, by w sposób optymaly dobrać typ fukcj g dla każdego atrybutu w obrębe każdej bazy eruchomośc. Pożej zameszczoo przykładowe wykresy: CENA CENA Wykres rozrzutu (Bolesław) y=wygładzae ajmejszych kwadratów ważoe odległoścam + eps -,5 -, -,5,,5,,5,, KSZTAŁT Wykres rozrzutu (Proszowce) y=wygładzae ajmejszych kwadratów ważoe odległoścam + eps POWIERZCHNIA Z tak wybraych postac fukcj g tworzoe były modele welowymarowe, czyl globale fukcje elowe F dla poszczególych baz eruchomośc: W = F(X, a) (7) gdze: W zbór progozowaych ce eruchomośc tworzących model wycey, X zmea welowymarowa odpowadająca atrybutom eruchomośc, a wektor parametrów modelu. Poszczególe fukcje g dla różych atrybutów mogą być w obrębe fukcj F powązae ze sobą zależoścą addytywą lub multplkatywą. W ejszej pracy zastosowao, w wększośc przypadków, addytywą postać fukcj F. Wszystke rozpatrywae modele regresj oszacowao metodą ajmejszych kwadratów (MNK), ze względu a jej ogóle zae zalety. Każdorazowo estymacja parametrów modelu została wykoaa wraz z aalzą dokładośc, tj. z podaem błędu oszacowaa parametru jego pozomem stotośc. Przy okazj estymacj modelu zostały wyzaczoe róweż e welkośc, m.. tzw. wag beta (pozwalają oe porówać relatywy wkład, jak każda ze zmeych ezależych wos w predykcję zmeej zależej) oraz tzw. toleracja (pozwala orzec o ewetualej admarowośc wkładu daej zmeej w rówae regresj). Jeżel toleracja jakejś zmeej w rówau jest rówa zeru (lub bardzo blska tej wartośc), to e moża wyzaczyć parametrów tego rówaa ze względu a złe uwarukowae macerzy, a co za tym dze, emożość jej odwrócea. W ejszej pracy wartość progową dla toleracj, do akceptacj bądź odrzucea modelu, ustaloo a pozome,. Wykoao także badae ormalośc rozkładu reszt przy pomocy testu zgodośc Kołmogorowa-Smrowa oraz aalzę wyodrębee reszt odstających w każdym aalzowaym modelu. Wyk testu każdorazowo zobrazowao za pomocą wykresu rozkładu reszt w postac hstogramu, z ałożoą a ego lą przedstawającą rozkład ormaly z wartoścą statystyk testu Kołmogorowa-Smrowa oraz za pomocą tzw. ormalego wykresu prawdopodobeństwa reszt. Jeśl pukty przedstawające reszty ch oczekwaą wartość ormalą układają sę, z dobrym przyblżeem, wzdłuż l prostej, to Zastosowaa metod statystyczych w badaach aukowych III StatSoft Polska
6 Krytera stosowaa model stochastyczych w predykcj rykowej wartośc eruchomośc dowodz to wysokej zgodośc z rozkładem teoretyczym. Zarówo w przypadku model lowych, jak elowych perwsza selekcja, pod kątem ch przydatośc do progozowaa wartośc rykowej eruchomośc, została wykoaa a podstawe wartośc współczyka korelacj welorakej (dla lowych) wzór () współczyka korelacj krzywolowej (dla elowych) wzór (8). Lczba obserwacj Oczekwaa wartość ormala ρ Zmea: reszta; rozkład: Normaly d Kołmogorowa-Smrowa=,58, p= Kategora (góra graca) Normaly wykres prawdopodobeństwa reszt Reszty Oczekwaa = [ y = = [ y F( X NSK ρ = = CSK E( y)], a)] WSK CSK = = [ F( X, a) E( y)] = [ y E( y)] (8) gdze: E(y) wartość oczekwaa zaobserwowaych wartośc zmeej zależej (cey), = [ y E( y)] całkowte rozproszee zmeej zależej względem jej wartośc przecętej (CSK), [ y F( X, a)] = δ suma kwadratów = = odchyłek pomędzy wartoścam zmeej zależej z próby a jej wartoścam modelowym, wyrażająca część ewyjaśoą modelem regresj elowej (NSK), = [ F( X, a) E( y)] suma kwadratów odchyłek pomędzy wartoścam modelowym zmeej zależej a wartoścą przecętą z zaobserwowaych wartośc tej zmeej, wyrażająca część wyjaśoą modelem regresj elowej (WSK). Oba współczyk korelacj wskazują, w jakm zakrese wyestymoway model wyjaśa rzeczywstą zmeość. Z tego względu przyjęto wstępe kryterum, by ch wartość przekraczała,6. Dalszą weryfkację warygodośc model staowł wyk testu Fshera-Sedecora, badający prawdzwość hpotezy o rówośc waracj częśc wyjaśoej ewyjaśoej przez model regresj, dla którego statystyka testowa ma postać: R m F = * (9) R m gdze: R współczyk korelacj (lowej lub krzywolowej), lczość próby (lczba eruchomośc w baze), u lczba zmeych ezależych w modelu, m lczba estymowaych parametrów modelu wycey. Powyższy test uwzględa koeczość zachowaa w modelu właścwych proporcj pomędzy lczbą przypadków lczbą ewadomych, a e tylko bada bezwzględy stosuek waracj częśc wyjaśoej częśc ewyjaśoej. W te sposób klka model zostało wyelmowaych, awet spośród tych o bardzo wysokej (powyżej,8), bezwzględej wartośc R Zastosowaa metod statystyczych w badaach aukowych III StatSoft Polska 8
7 Krytera stosowaa model stochastyczych w predykcj rykowej wartośc eruchomośc 7 WYZNACZENIE WARTOŚCI NIEZMIENNIKÓW Na wszystkch bazach eruchomośc przetestowao w sume bardzo wele różych model określea rykowej wartośc eruchomośc. Na wstępe wyelmowao wszystke te, dla których współczyk korelacj welorakej wyosł mej ż,6. Dla każdego z pozostałych 97 model, po wyzaczeu macerzy korelacj dla zmeych występujących w modelu macerzy kowaracj dla wartośc modelowych eruchomośc ustalających model wycey, oblczoo wartośc trzech zdefowaych ezmeków. Otrzymao w te sposób 97 zestawów tych trzech lczb. Wyk zawarto w poższej tabel. Oprócz wartośc ezmeków zameszczoo róweż: azwę mejscowośc, z której pochodz baza daych wykorzystaa do modelowaa, typ modelu wartośc stałych charakteryzujących bazę model. Są to: lczba eruchomośc w baze:, lczba zmeych ezależych występujących w modelu: u, lczba estymowaych parametrów modelu wycey: m, lczba stop swobody: k = m, waracja resztowa: σ, waracja resztowa pomożoa przez lczbę stop swobody: k σ =Y T Y - a T X T Y. Dodatkowo wyróżoo 9 model, które zostały odrzucoe przez test Fshera-Sedecora. Tabela. Wartośc ezmeków. Nr MIEJSCOWOŚĆ ZMIENNOŚĆ MODEL N u m k σ R σ tr σ det Bolesław lowa ,87,936,66,538 Bolesław lowa ,6,7,7,9 3 Bolesław lowa ,364,73,83,8 4 Bolesław lowa ,93,78,3,466 5 Bolesław lowa ,643,84,89,8 6 Bolesław lowa ,76,836,,37 7 Bolesław lowa ,75,864,,38 8 Bolesław lowa K-P-D-M ,86,68,, 9 Bolesław elowa 4 8 7,63,894,48,983 Bolesław elowa ,35,994,57,566 Bolesław elowa ,35,994,57,5586 Bolesław elowa ,355,99,5,546 3 Bolesław elowa ,6,99,47,53 4 Bolesław elowa ,66,994,5, Bolesław elowa ,78,976,76,648 6 Bolesław elowa ,834,966,8,84 7 Bolesław elowa ,365,768,4, 8 Bolesław elowa ,365,768,4, 9 Bolesław elowa ,78,8,3, Bolesław elowa ,64,84,38, Bolesław elowa 5 8 7,654,934,, Bolesław elowa ,986,949,77,54 3 Bolesław elowa ,784,964,7,48 4 Bolesław elowa ,75,963,65,49 5 Busko Zdrój lowa ,875,8,9,97 6 Busko Zdrój lowa ,55,78,84,98 7 Busko Zdrój elowa a ,7,94,57,535 8 Busko Zdrój elowa b ,5,95,5,5 9 Busko Zdrój elowa 3a ,436,95,49,373 3 Busko Zdrój elowa 4a 3 8 9,954,96,5,67 3 Busko Zdrój elowa 4b 3 8 9,93,955,54,68 3 Busko Zdrój elowa 5a ,6,957,46,37 33 Busko Zdrój elowa 5b ,8,953,48, Busko Zdrój elowa ,,949,47,5 35 Krowodrza elowa a ,53,695,34,33 36 Krowodrza II lowa ,7,99,4, 37 Krowodrza II lowa ,446,949,3, 38 Krowodrza II elowa ,668,9,47, Zastosowaa metod statystyczych w badaach aukowych III StatSoft Polska
8 Krytera stosowaa model stochastyczych w predykcj rykowej wartośc eruchomośc Nr MIEJSCOWOŚĆ ZMIENNOŚĆ MODEL N u m k σ R σ tr σ det 39 Krowodrza II elowa a ,673,95,37, 4 Krowodrza II elowa b ,56,96,33, 4 Nowy Sącz lowa ,934,8,47,9 4 Nowy Sącz lowa ,438,83,4,4 43 Nowy Sącz lowa ,78,879,,55 44 Nowy Sącz lowa ,86,877,,8 45 Nowy Sącz lowa ,458,898,5,46 46 Nowy Sącz lowa 6 8 6,983,895,98,55 47 Nowy Sącz elowa ,975,859,5, Nowy Sącz elowa ,94,859,5, Proszowce lowa ,468,894,9,4 5 Proszowce lowa ,93,93,97,47 5 Proszowce elowa ,6,964,, 5 Proszowce elowa ,6,964,, 53 Proszowce elowa ,6,963,4, 54 Proszowce elowa ,648,963,5, 55 Proszowce elowa 5' ,84,975,6, 56 Proszowce elowa 5a ,69,96,5, 57 Proszowce elowa 5'a ,96,975,5, 58 Proszowce elowa 5b ,463,998,46, 59 Proszowce elowa ,56,963,, 6 Przeworsk lowa ,6,65,33,49 6 Przeworsk elowa 3 8 9,58,643,38,357 6 Rzeszów lowa ,689,84,6,4 63 Rzeszów lowa ,8,856,5,4 64 Rzeszów lowa ,845,875,48,49 65 Rzeszów elowa ,447,8,6,4 66 Rzeszów elowa a ,6,85,53,4 67 Rzeszów elowa b ,785,87,49,5 68 Rzeszów elowa ,637,84,6,4 69 Rzeszów elowa a ,3,854,5,5 7 Rzeszów elowa b ,5,87,48,5 7 Rzeszów elowa ,5,85,6, 7 Rzeszów elowa 3a ,94,856,5,4 73 Rzeszów elowa 3b ,96,873,48,5 74 Rzeszów elowa ,64,84,59,4 75 Rzeszów elowa 4a ,669,857,5,4 76 Rzeszów elowa 4b ,648,876,47,5 77 Śwdk lowa 4 3 3,96,65,94, 78 Śwdk lowa ,487,676,88, 79 Śwdk lowa ,6,6,73, 8 Śwdk lowa ,38,65,69, 8 Śwdk lowa 6 4 9,6,7,79, 8 Śwdk lowa ,57,7,74, 83 Śwdk elowa ,9,64,93,3 84 Śwdk elowa ,775,736,89,8 85 Śwdk elowa ,974,74,93,3 86 Śwdk elowa ,65,76,85,7 87 Śwdk elowa ,437,86,8,6 88 Śwdk elowa I ,67,839,83,5 89 Śwdk elowa II ,55,833,79,8 9 Śwdk elowa III ,67,834,8,39 9 Śwdk elowa IV ,55,89,78,7 9 Trzycąż lowa ,864,743,63,5 93 Trzycąż elowa ,9,859,58,9 94 Trzycąż elowa ,853,898,49,3 95 Trzycąż elowa ,58,98,4,33 96 Trzycąż elowa ,89,88,53,5 97 Trzycąż elowa ,53,934,35,5 9 Zastosowaa metod statystyczych w badaach aukowych III StatSoft Polska 8
9 Krytera stosowaa model stochastyczych w predykcj rykowej wartośc eruchomośc Na podstawe zebraych wyków określoo przedzały zmeośc dla parametrów ezmeczych podstawowe statystyk dla ch, jak: wartość przecęta, odchylee stadardowe, błąd stadardowy wartośc przecętej grace przedzału ufośc a pozome ufośc,99. Wyk zawera tabela. By zbadać, w jakm stopu odrzucee model ezaakceptowaych przez test Fshera- Sedecora wpłyęło a wyk podstawowych statystyk, w tym wartośc przecętej rozproszea, przeprowadzoo stosowe testy statystycze. Zostały zweryfkowae hpotezy o rówośc waracj w obu zborach oraz o rówośc wartośc przecętych. Test dotyczący wartośc przecętej wypadł epomyśle jedye dla parametru σ tr, tz. hpotezę wyjścową o rówośc wartośc przecętych ależy w tym wypadku odrzucć. Tak wyk może staowć perwszą przesłakę do wskazaa a establość ezmeka σ tr lub jego zwązek z wykam testu Fshera- Sedecora. Tabela. Wartośc podstawowych statystyk dla zboru parametrów ezmeczych. Wartość przecęta Xˆ Grace przedzału ufośc a pozome,99 Mmum Maxmum Odchylee stadardowe σˆ Błąd stad. wartośc przecętej wszystke modele spełające waruek R,6 R,858,83,886,6,998,4, σ tr,99,76,4,3,34,5,5 σ det,497,89,86,,566,56,7 bez model odrzucoych przez test Fshera-Sedecora R,865,837,893,6,998,99, σ tr,84,7,98,3,34,46,5 σ det,33,79,547,,566,833,89 8 BADANIE ZALEŻNOŚCI NIEZMIENNIKÓW OD WIELKOŚCI CHARAKTERYZUJĄCYCH BAZĘ NIERUCHOMOŚCI I MODEL WYCENY W celu sformułowaa kryterów ocey warygodośc bazy eruchomośc zastosowaego modelu wycey sporządzoo szereg wykresów rozrzutu zależośc ezmeków od welkośc stałych charakteryzujących bazę eruchomośc zastosoway model wycey. Aalzowaym wykresam były: R (), σ tr (), σ det (), R (u), σ tr (u), σ det (u), R ( σ ), σ tr ( σ ), σ det ( σ ), R (k σ ), σ tr (k σ ), σ det (k σ ). Na każdy z tych wykresów ałożoo, wyestymowaą metodą ajmejszych kwadratów, lę tredu. Pozwala to a stwerdzee stea bądź też braku jakchkolwek zależośc pomędzy tym welkoścam, a co za tym dze, a wycągęce wosków dotyczących modelu, czy też samej bazy. Pożej zameszczoo dwa przykłady opsaych wykresów: sgma det sgma tr Wykres rozrzutu (baza parametrów bez Krowodrzy II) y=wygładzae ajmejszych kwadratów ważoe odległoścam + eps,55,45,35,5,5,5 -, Wykres rozrzutu (baza parametrów bez Krowodrzy II bez model odrzucoych) y=wygładzae ajmejszych kwadratów ważoe odległoścam + eps,4,35,3,5,,5,,5, Zastosowaa metod statystyczych w badaach aukowych III StatSoft Polska 8 9
10 Krytera stosowaa model stochastyczych w predykcj rykowej wartośc eruchomośc Najcekawsze wyk dała aalza wykresów σ det (u). Wartość tego parametru rośe wraz ze wzrostem u, ale wdać wyraźe, że tempo wzrostu jest uzależoe od wpływu ych czyków, gdyż pukty tworzące wykres rozrzutu grupują sę w dwa zdecydowae odrębe zbory. Po dalszych aalzach, polegających a próbach rozdzelea zborów poprzez ałożee dodatkowych waruków a poszczególe przypadk, zdetyfkowao parametry determujące powyższy podzał. Są m pozostałe charakterystyk baz: lczość bazy lczbę stop swobody k oraz stałe, charakteryzujące wyestymoway model: waracja resztowa σ waracja resztowa pomożoa przez lczbę stop swobody, czyl Y T Y a T X T Y. Najbardzej zdecydoway podzał a dwe grupy uzyskao przy ałożeu waruków a oraz σ. Pożej zameszczoo wykresy σ det (u) z podzałem a podzbory w zależośc od wartośc. sgma det,55,45,35,5,5,5 Wykres rozrzutu (baza parametrów) y=wygładzae ajmejszych kwadratów ważoe odległoścam + eps -, u <8 >=8 Wdać wyraźe, że bardzo szybke tempo wzrostu σ det, wraz ze zwększającą sę lczbą zmeych ezależych w modelu, otrzymujemy dla baz mało lczych, gdze lczba eruchomośc e przekracza 3. Natomast, gdy jest wększa od 3 sytuacja dametrale sę zmea: parametr σ det wykazuje mmaly przyrost dla zwększającej sę awet zacze lczby cech eruchomośc braych pod uwagę przy tworzeu modelu. Obrazuje to róweż trójwymarowy wykres zależośc σ det (, u). Wykres powerzchowy 3W sgma det (, u) Wygładzae ajmejszych kwadratów,,8,4,,7,33,4,46,5,59 poad Wyka stąd stoty wosek, że ezbęde jest spełee waruku o zebrau mmalej lczby daych przed przystąpeem do modelowaa stosowaem metod statystyczych. Na podstawe przeprowadzoego badaa zależośc parametrów ezmeczych od wartośc stałych, charakteryzujących bazę eruchomośc, czy też zastosoway model określea rykowej wartośc eruchomośc perwszym asuwającym sę woskem jest stwerdzee, ż spośród zdefowaych ezmeków ajlepszym wskaźkem jest σ det. Na wykresach rozrzutu, sporządzoych z udzałem σ det, pukty są ajbardzej skupoe wokół wyestymowaej l tredu. Otrzymujemy ajmej odstępstw. Najmej jedozacze wyk uzyskao za pomocą parametru σ tr. Okazuje sę o zatem ajmej przydaty w tego typu aalzach. Pukty a wykresach rozrzutu z jego udzałem często tworzą eregulare chmury wykazują duże rozproszee wokół wyestymowaej l regresj. Przy pomocy parametru R uzyskao wyk eco gorsze od σ det, ale zdecydowae lepsze ż dla σ tr. Jedak te parametr, ze względu a swoją prostą defcję, odesoą do współczyków korelacj zupełej, może meć duże praktycze zastosowae w wycee eruchomośc. 9 WNIOSKI KOŃCOWE Główym celem pracy było zaprezetowae możlwośc ocey bazy eruchomośc modelu zastosowaego do estymacj rykowej wartośc eruchomośc, za pomocą zdefowaych parametrów ezmeków przekształcea macerzy kowaracj dla modelowych wartośc 9 Zastosowaa metod statystyczych w badaach aukowych III StatSoft Polska 8
11 Krytera stosowaa model stochastyczych w predykcj rykowej wartośc eruchomośc eruchomośc. Po wyestymowau parametrów około stu model, testowaych w sume a dzesęcu bazach eruchomośc, różących sę zacze lczoścą (od 8 do 3 eruchomośc) lczbą cech eruchomośc braych pod uwagę (od 4 do 8) oraz po wyzaczeu dla ch wartośc trzech parametrów ezmeczych: R, σ tr, σ det a podstawe wykresów rozrzutu tych ezmeków w połączeu z charakterystykam baz model moża sformułować astępujące wosk: Optymala lczba eruchomośc w baze do modelowaa wartośc eruchomośc powa odpowadać trzykrotej lczbe wyzaczaych parametrów modelu wycey. Przy czym ależy zazaczyć, że lczba ta powa być co ajmej rówa dwukrotej lczbe wyzaczaych parametrów modelu, a zacze jej zwększae (powyżej czterokrotej lczby parametrów) ajczęścej e prowadz do polepszea modelu. Maksymala lczba zmeych ezależych, występujących w modelach wycey e powa przekraczać 4 parametrów, a wstępa aalza ryku eruchomośc powa ustalć optymalą lczbę parametrów (atrybutów). Lczba stop swobody w modelu wycey powa meścć sę w gracach od 8 do 4. Dobór bazy eruchomośc do estymacj modelu wycey moża uzać za optymaly, jeżel wartość ezmeka σ det zawera sę w przedzale: σ det (,8;,55). Dobór modelu do szacowaa rykowej wartośc eruchomośc moża uzać za zadowalający, gdy wartość współczyka determacj R będze spełała erówość: R,837. Za pomocą parametru σ tr e moża sformułować kryterów doboru bazy eruchomośc do estymacj modelu wycey, gdyż wartość tego parametru wykazuje dużą fluktuację. Z porówaa wosków wyka spostrzeżee, że w doborze poprawego modelu wycey e wystarczy uwzględee samych waracj wartośc modelowych, ale koecze jest wzęce pod uwagę całej macerzy kowaracj dla wartośc modelowych Cov(W). BIBLIOGRAFIA ) Adamczewsk Z., Czarecka K.; Modelowae matematycze ekowartośc. Przegląd Geodezyjy r 8/95, Warszawa 995 r. ) Barańska A.; Krytera stosowaa model stochastyczych w predykcj rykowej wartośc eruchomośc. Geodezja, tom 8, zeszyt, r. 3) Barańska A.; Zastosowae uogóloych model lowych w wycee eruchomośc. Geodezja, tom 5, zeszyt, 999 r. 4) Barańska A., Mtka B.; Statystycze przygotowae baz daych do dalszych aalz. IX Krajowa Koferecja Komputerowe Wspomagae Badań Naukowych, Polaca Zdrój, 4-6 paźdzerka r. 5) Chow G.C.; Ecoometrcs. New York, 983 r. 6) Czaja J.; Metody szacowaa wartośc rykowej katastralej eruchomośc, Kraków r. 7) Czaja J.; Modele statystycze w formacj o teree. Ksążka, Wydawctwa AGH Kraków 997 r. 8) Grabowsk R. J.; Ekoometra w zaryse, Wydawctwo Wyższej Szkoły Fasów Zarządzaa w Bałymstoku, Bałystok r. 9) Hopfer A. ; Szacowae eruchomośc ezurbazowaych. Praca zborowa. Twgger, Warszawa 996 r. ) Krysck W.; Statystyka matematycza, PWN, Warszawa 986 r. ) Plucńska A., Plucńsk E.; Probablstyka, WNT, Warszawa, Wyd. I. ) Rao C. R.; Modele lowe statystyk matematyczej. PWN, Warszawa, 98 r. 3) Rozporządzee Rady Mstrów z da 7 lstopada r. w sprawe szczegółowych zasad wycey eruchomośc oraz zasad trybu sporządzaa operatu szacukowego. Dzek Ustaw r 3/, poz ) Stadardy Zawodowe Rzeczozawców Majątkowych Polska Federacja Stowarzyszeń Rzeczozawców Majątkowych. Wydae VIII, Warszawa r. 5) Ustawa z da serpa 997 r. o gospodarce eruchomoścam. Dzek Ustaw r 5/997, poz. 74 wraz z późejszym zmaam jedolty tekst Dzek Ustaw r 46/, poz Zastosowaa metod statystyczych w badaach aukowych III StatSoft Polska
Podstawy analizy niepewności pomiarowych (I Pracownia Fizyki)
 Podstawy aalzy epewośc pomarowych (I Pracowa Fzyk) Potr Cygak Zakład Fzyk Naostruktur Naotecholog Istytut Fzyk UJ Pok. 47 Tel. 0-663-5838 e-mal: potr.cygak@uj.edu.pl Potr Cygak 008 Co to jest błąd pomarowy?
Podstawy aalzy epewośc pomarowych (I Pracowa Fzyk) Potr Cygak Zakład Fzyk Naostruktur Naotecholog Istytut Fzyk UJ Pok. 47 Tel. 0-663-5838 e-mal: potr.cygak@uj.edu.pl Potr Cygak 008 Co to jest błąd pomarowy?
Planowanie eksperymentu pomiarowego I
 POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA ENERGETYKI INSTYTUT MASZYN URZĄDZEŃ ENERGETYCZNYCH Plaowae eksperymetu pomarowego I Laboratorum merctwa (M 0) Opracował: dr ż. Grzegorz Wcak
POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA ENERGETYKI INSTYTUT MASZYN URZĄDZEŃ ENERGETYCZNYCH Plaowae eksperymetu pomarowego I Laboratorum merctwa (M 0) Opracował: dr ż. Grzegorz Wcak
Miary położenia wskazują miejsce wartości najlepiej reprezentującej wszystkie wielkości danej zmiennej. Mówią o przeciętnym poziomie analizowanej
 Podstawy Mary położea wskazują mejsce wartośc ajlepej reprezetującej wszystke welkośc daej zmeej. Mówą o przecętym pozome aalzowaej cechy. Średa arytmetycza suma wartośc zmeej wszystkch jedostek badaej
Podstawy Mary położea wskazują mejsce wartośc ajlepej reprezetującej wszystke welkośc daej zmeej. Mówą o przecętym pozome aalzowaej cechy. Średa arytmetycza suma wartośc zmeej wszystkch jedostek badaej
Stanisław Cichocki Natalia Nehrebecka. Zajęcia 7-8
 Stasław Cchock Natala Nehreecka Zajęca 7-8 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartość oczekwaa eocążoość estymatora Waracja
Stasław Cchock Natala Nehreecka Zajęca 7-8 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartość oczekwaa eocążoość estymatora Waracja
TESTY NORMALNOŚCI. ( Cecha X populacji ma rozkład normalny). Hipoteza alternatywna H1( Cecha X populacji nie ma rozkładu normalnego).
 TESTY NORMALNOŚCI Test zgodośc Hpoteza zerowa H 0 ( Cecha X populacj ma rozkład ormaly). Hpoteza alteratywa H1( Cecha X populacj e ma rozkładu ormalego). Weryfkacja powyższych hpotez za pomocą tzw. testu
TESTY NORMALNOŚCI Test zgodośc Hpoteza zerowa H 0 ( Cecha X populacj ma rozkład ormaly). Hpoteza alteratywa H1( Cecha X populacj e ma rozkładu ormalego). Weryfkacja powyższych hpotez za pomocą tzw. testu
PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH. dr Michał Silarski
 PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH dr Mchał larsk I Pracowa Fzycza IF UJ, 9.0.06 Pomar Pomar zacowae wartośc prawdzwej Bezpośred (welkość fzycza merzoa jest
PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH dr Mchał larsk I Pracowa Fzycza IF UJ, 9.0.06 Pomar Pomar zacowae wartośc prawdzwej Bezpośred (welkość fzycza merzoa jest
Jego zależy od wysokości i częstotliwości wypłat kuponów odsetkowych, ceny wykupu, oczekiwanej stopy zwrotu oraz zapłaconej ceny za obligację.
 Wrażlwość oblgacj Jedym z czyków ryzyka westowaa w oblgacje jest zmeość rykowych stóp procetowych. Iżyera fasowa dyspouje metodam pozwalającym zabezpeczyć portfel przed egatywym skutkam zma stóp procetowych.
Wrażlwość oblgacj Jedym z czyków ryzyka westowaa w oblgacje jest zmeość rykowych stóp procetowych. Iżyera fasowa dyspouje metodam pozwalającym zabezpeczyć portfel przed egatywym skutkam zma stóp procetowych.
Wyrażanie niepewności pomiaru
 Wyrażae epewośc pomaru Adrzej Kubaczyk Wydzał Fzyk, Poltechka Warszawska Warszawa, 05 Iformacje wstępe Każdy pomar welkośc fzyczej dokoyway jest ze skończoą dokładoścą, co ozacza, że wyk tego pomaru dokoyway
Wyrażae epewośc pomaru Adrzej Kubaczyk Wydzał Fzyk, Poltechka Warszawska Warszawa, 05 Iformacje wstępe Każdy pomar welkośc fzyczej dokoyway jest ze skończoą dokładoścą, co ozacza, że wyk tego pomaru dokoyway
Tablica Galtona. Mechaniczny model rozkładu normalnego (M10)
 Tablca Galtoa. Mechaczy model rozkładu ormalego (M) I. Zestaw przyrządów: Tablca Galtoa, komplet kulek sztuk. II. Wykoae pomarów.. Wykoać 8 pomarów, wrzucając kulk pojedyczo.. Uporządkować wyk pomarów,
Tablca Galtoa. Mechaczy model rozkładu ormalego (M) I. Zestaw przyrządów: Tablca Galtoa, komplet kulek sztuk. II. Wykoae pomarów.. Wykoać 8 pomarów, wrzucając kulk pojedyczo.. Uporządkować wyk pomarów,
OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B
 OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B W przypadku gdy e występuje statystyczy rozrzut wyków (wszystke pomary dają te sam wyk epewość pomaru wyzaczamy w y sposób. Główą przyczyą epewośc pomaru jest epewość
OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B W przypadku gdy e występuje statystyczy rozrzut wyków (wszystke pomary dają te sam wyk epewość pomaru wyzaczamy w y sposób. Główą przyczyą epewośc pomaru jest epewość
dev = y y Miary położenia rozkładu Wykład 9 Przykład: Przyrost wagi owiec Odchylenia Mediana próbkowa: Przykłady Statystyki opisowe Σ dev i =?
 Mary położea rozkładu Wykład 9 Statystyk opsowe Średa z próby, mea(y) : symbol y ozacza lczbę; arytmetyczą średą z obserwacj Symbol Y ozacza pojęce średej z próby Średa jest środkem cężkośc zboru daych
Mary położea rozkładu Wykład 9 Statystyk opsowe Średa z próby, mea(y) : symbol y ozacza lczbę; arytmetyczą średą z obserwacj Symbol Y ozacza pojęce średej z próby Średa jest środkem cężkośc zboru daych
Statystyczne charakterystyki liczbowe szeregu
 Statystycze charakterystyk lczbowe szeregu Aalzę badaej zmeej moża uzyskać posługując sę parametram opsowym aczej azywaym statystyczym charakterystykam lczbowym szeregu. Sytetycza charakterystyka zborowośc
Statystycze charakterystyk lczbowe szeregu Aalzę badaej zmeej moża uzyskać posługując sę parametram opsowym aczej azywaym statystyczym charakterystykam lczbowym szeregu. Sytetycza charakterystyka zborowośc
POPULACJA I PRÓBA. Próba reprezentatywna. Dr Adam Michczyński - METODY ANALIZY DANYCH POMIAROWYCH 5 1
 POPULACJA I PRÓBA POPULACJĄ w statystyce matematyczej azywamy zbór wszystkch elemetów (zdarzeń elemetarych charakteryzujących sę badaą cechą opsywaą zmeą losową. Zbadae całej populacj (przeprowadzee tzw.
POPULACJA I PRÓBA POPULACJĄ w statystyce matematyczej azywamy zbór wszystkch elemetów (zdarzeń elemetarych charakteryzujących sę badaą cechą opsywaą zmeą losową. Zbadae całej populacj (przeprowadzee tzw.
Prawdopodobieństwo i statystyka r.
 Zadae. W ure zajduje sę 5 kul, z których 5 jest bałych czarych. Losujemy bez zwracaa kolejo po jedej kul. Kończymy losowae w momece, kedy wycągęte zostaą wszystke czare kule. Oblcz wartość oczekwaą lczby
Zadae. W ure zajduje sę 5 kul, z których 5 jest bałych czarych. Losujemy bez zwracaa kolejo po jedej kul. Kończymy losowae w momece, kedy wycągęte zostaą wszystke czare kule. Oblcz wartość oczekwaą lczby
STATYSTYKA MATEMATYCZNA WYKŁAD 2 ESTYMACJA PUNKTOWA
 STATYSTYKA MATEMATYCZNA WYKŁAD ESTYMACJA PUNKTOWA Nech - ezay parametr rozkładu cechy X. Wartość parametru będzemy estymować (przyblżać) a podstawe elemetowej próby. - wyberamy statystykę U o rozkładze
STATYSTYKA MATEMATYCZNA WYKŁAD ESTYMACJA PUNKTOWA Nech - ezay parametr rozkładu cechy X. Wartość parametru będzemy estymować (przyblżać) a podstawe elemetowej próby. - wyberamy statystykę U o rozkładze
Stanisław Cichocki. Natalia Nehrebecka. Zajęcia 5
 Stasław Cchock Natala Nehreecka Zajęca 5 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartośd oczekwaa eocążoośd estymatora Waracja
Stasław Cchock Natala Nehreecka Zajęca 5 . Testowae łączej stotośc wyraych regresorów. Założea klasyczego modelu regresj lowej 3. Własośc estymatora MNK w KMRL Wartośd oczekwaa eocążoośd estymatora Waracja
Prawdopodobieństwo i statystyka r.
 Prawdopodobeństwo statystyka 0.06.0 r. Zadae. Ura zawera kul o umerach: 0,,,,. Z ury cągemy kulę, zapsujemy umer kulę wrzucamy z powrotem do ury. Czyość tę powtarzamy, aż kula z każdym umerem zostae wycągęta
Prawdopodobeństwo statystyka 0.06.0 r. Zadae. Ura zawera kul o umerach: 0,,,,. Z ury cągemy kulę, zapsujemy umer kulę wrzucamy z powrotem do ury. Czyość tę powtarzamy, aż kula z każdym umerem zostae wycągęta
Statystyczna analiza miesięcznych zmian współczynnika szkodowości kredytów hipotecznych
 dr Ewa Wycka Wyższa Szkoła Bakowa w Gdańsku Wtold Komorowsk, Rafał Gatowsk TZ SKOK S.A. Statystycza aalza mesęczych zma współczyka szkodowośc kredytów hpoteczych Wskaźk szkodowośc jest marą obcążea kwoty/lczby
dr Ewa Wycka Wyższa Szkoła Bakowa w Gdańsku Wtold Komorowsk, Rafał Gatowsk TZ SKOK S.A. Statystycza aalza mesęczych zma współczyka szkodowośc kredytów hpoteczych Wskaźk szkodowośc jest marą obcążea kwoty/lczby
POLSKA FEDERACJA STOWARZYSZEŃ RZECZOZNAWCÓW MAJĄTKOWYCH POWSZECHNE KRAJOWE ZASADY WYCENY (PKZW) KRAJOWY STANDARD WYCENY SPECJALISTYCZNY NR 4 KSWS 4
 POZECHNE KRAJOE ZAADY YCENY (PKZ) KRAJOY TANDARD YCENY PECJALITYCZNY NR 4 K 4 YCENA ŁUŻEBNOŚCI PRZEYŁU I OKREŚLANIE KOTY YNAGRODZENIA ZA BEZUMONE KORZYTANIE Z NIERUCHOMOŚCI PRZY INETYCJACH LINIOYCH 1.
POZECHNE KRAJOE ZAADY YCENY (PKZ) KRAJOY TANDARD YCENY PECJALITYCZNY NR 4 K 4 YCENA ŁUŻEBNOŚCI PRZEYŁU I OKREŚLANIE KOTY YNAGRODZENIA ZA BEZUMONE KORZYTANIE Z NIERUCHOMOŚCI PRZY INETYCJACH LINIOYCH 1.
Podstawy opracowania wyników pomiarowych, analiza błędów
 Podstawy opracowaa wyków pomarowych, aalza błędów I Pracowa Fzycza IF UJ Grzegorz Zuzel Lteratura I Pracowa fzycza Pod redakcją Adrzeja Magery Istytut Fzyk UJ Kraków 2006 Wstęp do aalzy błędu pomarowego
Podstawy opracowaa wyków pomarowych, aalza błędów I Pracowa Fzycza IF UJ Grzegorz Zuzel Lteratura I Pracowa fzycza Pod redakcją Adrzeja Magery Istytut Fzyk UJ Kraków 2006 Wstęp do aalzy błędu pomarowego
FINANSE II. Model jednowskaźnikowy Sharpe a.
 ODELE RYNKU KAPITAŁOWEGO odel jedowskaźkowy Sharpe a. odel ryku kaptałowego - CAP (Captal Asset Prcg odel odel wycey aktywów kaptałowych). odel APT (Arbtrage Prcg Theory Teora artrażu ceowego). odel jedowskaźkowy
ODELE RYNKU KAPITAŁOWEGO odel jedowskaźkowy Sharpe a. odel ryku kaptałowego - CAP (Captal Asset Prcg odel odel wycey aktywów kaptałowych). odel APT (Arbtrage Prcg Theory Teora artrażu ceowego). odel jedowskaźkowy
L.Kowalski zadania ze statystyki opisowej-zestaw 5. ZADANIA Zestaw 5
 L.Kowalsk zadaa ze statystyk opsowej-zestaw 5 Zadae 5. X cea (zł, Y popyt (tys. szt.. Mając dae ZADANIA Zestaw 5 x,5,5 3 3,5 4 4,5 5 y 44 43 43 37 36 34 35 35 Oblcz współczyk korelacj Pearsoa. Oblcz współczyk
L.Kowalsk zadaa ze statystyk opsowej-zestaw 5 Zadae 5. X cea (zł, Y popyt (tys. szt.. Mając dae ZADANIA Zestaw 5 x,5,5 3 3,5 4 4,5 5 y 44 43 43 37 36 34 35 35 Oblcz współczyk korelacj Pearsoa. Oblcz współczyk
ma rozkład normalny z nieznaną wartością oczekiwaną m
 Zadae Każda ze zmeych losowych,, 9 ma rozkład ormaly z ezaą wartoścą oczekwaą m waracją, a każda ze zmeych losowych Y, Y,, Y9 rozkład ormaly z ezaą wartoścą oczekwaą m waracją 4 Założoo, że wszystke zmee
Zadae Każda ze zmeych losowych,, 9 ma rozkład ormaly z ezaą wartoścą oczekwaą m waracją, a każda ze zmeych losowych Y, Y,, Y9 rozkład ormaly z ezaą wartoścą oczekwaą m waracją 4 Założoo, że wszystke zmee
Monika Jeziorska - Pąpka Uniwersytet Mikołaja Kopernika w Toruniu
 DYNAMICZNE MODELE EKONOMERYCZNE X Ogólopolske Semarum Naukowe, 4 6 wrześa 2007 w oruu Katedra Ekoometr Statystyk, Uwersytet Mkołaja Koperka w oruu Moka Jezorska - Pąpka Uwersytet Mkołaja Koperka w oruu
DYNAMICZNE MODELE EKONOMERYCZNE X Ogólopolske Semarum Naukowe, 4 6 wrześa 2007 w oruu Katedra Ekoometr Statystyk, Uwersytet Mkołaja Koperka w oruu Moka Jezorska - Pąpka Uwersytet Mkołaja Koperka w oruu
W zadaniu nie ma polecenia wyznaczania estymatora nieobciążonego o minimalnej wariancji. σ σ σ σ σ = =
 4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ ). W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ ). W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
Statystyka Opisowa 2014 część 3. Katarzyna Lubnauer
 Statystyka Opsowa 014 część 3 Katarzya Lubauer Lteratura: 1. Statystyka w Zarządzau Admr D. Aczel. Statystyka Opsowa od Podstaw Ewa Waslewska 3. Statystyka, Lucja Kowalsk. 4. Statystyka opsowa, Meczysław
Statystyka Opsowa 014 część 3 Katarzya Lubauer Lteratura: 1. Statystyka w Zarządzau Admr D. Aczel. Statystyka Opsowa od Podstaw Ewa Waslewska 3. Statystyka, Lucja Kowalsk. 4. Statystyka opsowa, Meczysław
O testowaniu jednorodności współczynników zmienności
 NR 6/7/ BIULETYN INSTYTUTU HODOWLI I AKLIMATYZACJI ROŚLIN 003 STANISŁAW CZAJKA ZYGMUNT KACZMAREK Katedra Metod Matematyczych Statystyczych Akadem Rolczej, Pozań Istytut Geetyk Rośl PAN, Pozań O testowau
NR 6/7/ BIULETYN INSTYTUTU HODOWLI I AKLIMATYZACJI ROŚLIN 003 STANISŁAW CZAJKA ZYGMUNT KACZMAREK Katedra Metod Matematyczych Statystyczych Akadem Rolczej, Pozań Istytut Geetyk Rośl PAN, Pozań O testowau
Podstawowe zadanie statystyki. Statystyczna interpretacja wyników eksperymentu. Zalety statystyki II. Zalety statystyki
 tatystycza terpretacja wyków eksperymetu Małgorzata Jakubowska Katedra Chem Aaltyczej Wydzał IŜyer Materałowej Ceramk AGH Podstawowe zadae statystyk tatystyka to uwersale łatwo dostępe arzędze, które pomaga
tatystycza terpretacja wyków eksperymetu Małgorzata Jakubowska Katedra Chem Aaltyczej Wydzał IŜyer Materałowej Ceramk AGH Podstawowe zadae statystyk tatystyka to uwersale łatwo dostępe arzędze, które pomaga
Probabilistyka i statystyka. Korelacja
 06-05-08 Probablstyka statystyka Korelacja Probablstyka statystyka - wykład 9 dla Elektrok Korelacja Aalza korelacj zajmuje sę badaam stea zależośc lowej mędzy dwema cecham X Y. Podstawową marą jest współczyk
06-05-08 Probablstyka statystyka Korelacja Probablstyka statystyka - wykład 9 dla Elektrok Korelacja Aalza korelacj zajmuje sę badaam stea zależośc lowej mędzy dwema cecham X Y. Podstawową marą jest współczyk
Statystyka Matematyczna Anna Janicka
 Statystyka Matematycza Aa Jacka wykład II, 3.05.016 PORÓWNANIE WIĘCEJ NIŻ DWÓCH POPULACJI TESTY NIEPARAMETRYCZNE Pla a dzsaj 1. Porówywae węcej ż dwóch populacj test jedoczykowej aalzy waracj (ANOVA).
Statystyka Matematycza Aa Jacka wykład II, 3.05.016 PORÓWNANIE WIĘCEJ NIŻ DWÓCH POPULACJI TESTY NIEPARAMETRYCZNE Pla a dzsaj 1. Porówywae węcej ż dwóch populacj test jedoczykowej aalzy waracj (ANOVA).
opisać wielowymiarową funkcją rozkładu gęstości prawdopodobieństwa f(x 1 , x xn
 ROZKŁAD PRAWDOPODBIEŃSTWA WIELU ZMIENNYCH LOSOWYCH W przpadku gd mam do czea z zmem losowm możem prawdopodobeństwo, ż przjmą oe wartośc,,, opsać welowmarową fukcją rozkładu gęstośc prawdopodobeństwa f(,,,.
ROZKŁAD PRAWDOPODBIEŃSTWA WIELU ZMIENNYCH LOSOWYCH W przpadku gd mam do czea z zmem losowm możem prawdopodobeństwo, ż przjmą oe wartośc,,, opsać welowmarową fukcją rozkładu gęstośc prawdopodobeństwa f(,,,.
Statystyka. Analiza zależności. Rodzaje zależności między zmiennymi występujące w praktyce: Funkcyjna
 Aalza zależośc Rodzaje zależośc mędzy zmeym występujące w praktyce: Fukcyja wraz ze zmaą wartośc jedej zmeej astępuje ścśle określoa zmaa wartośc drugej zmeej (p. w fzyce: spadek swobody gt s ) tochastycza
Aalza zależośc Rodzaje zależośc mędzy zmeym występujące w praktyce: Fukcyja wraz ze zmaą wartośc jedej zmeej astępuje ścśle określoa zmaa wartośc drugej zmeej (p. w fzyce: spadek swobody gt s ) tochastycza
W loterii bierze udział 10 osób. Regulamin loterii faworyzuje te osoby, które w eliminacjach osiągnęły lepsze wyniki:
 Zadae W loter berze udzał 0 osób. Regulam loter faworyzuje te osoby, które w elmacjach osągęły lepsze wyk: Zwycęzca elmacj, azyway graczem r. otrzymuje 0 losów, Osoba, która zajęła druge mejsce w elmacjach,
Zadae W loter berze udzał 0 osób. Regulam loter faworyzuje te osoby, które w elmacjach osągęły lepsze wyk: Zwycęzca elmacj, azyway graczem r. otrzymuje 0 losów, Osoba, która zajęła druge mejsce w elmacjach,
Badania Maszyn CNC. Nr 2
 Poltechka Pozańska Istytut Techolog Mechaczej Laboratorum Badaa Maszy CNC Nr 2 Badae dokładośc pozycjoowaa os obrotowych sterowaych umerycze Opracował: Dr. Wojcech Ptaszy sk Mgr. Krzysztof Netter Pozań,
Poltechka Pozańska Istytut Techolog Mechaczej Laboratorum Badaa Maszy CNC Nr 2 Badae dokładośc pozycjoowaa os obrotowych sterowaych umerycze Opracował: Dr. Wojcech Ptaszy sk Mgr. Krzysztof Netter Pozań,
. Wtedy E V U jest równa
 Prawdopodobeństwo statystyka 7.0.0r. Zadae Dwuwymarowa zmea losowa Y ma rozkład cągły o gęstośc gdy ( ) 0 y f ( y) 0 w przecwym przypadku. Nech U Y V Y. Wtedy E V U jest rówa 8 7 5 7 8 8 5 Prawdopodobeństwo
Prawdopodobeństwo statystyka 7.0.0r. Zadae Dwuwymarowa zmea losowa Y ma rozkład cągły o gęstośc gdy ( ) 0 y f ( y) 0 w przecwym przypadku. Nech U Y V Y. Wtedy E V U jest rówa 8 7 5 7 8 8 5 Prawdopodobeństwo
ma rozkład normalny z wartością oczekiwaną EX = EY = 1, EZ = 0 i macierzą kowariancji
 Zadae. Zmea losowa (, Y, Z) ma rozkład ormaly z wartoścą oczekwaą E = EY =, EZ = 0 macerzą kowaracj. Oblczyć Var(( Y ) Z). (A) 5 (B) 7 (C) 6 Zadae. Zmee losowe,, K,,K P ( = ) = P( = ) =. Nech S =. Oblcz
Zadae. Zmea losowa (, Y, Z) ma rozkład ormaly z wartoścą oczekwaą E = EY =, EZ = 0 macerzą kowaracj. Oblczyć Var(( Y ) Z). (A) 5 (B) 7 (C) 6 Zadae. Zmee losowe,, K,,K P ( = ) = P( = ) =. Nech S =. Oblcz
L.Kowalski PODSTAWOWE TESTY STATYSTYCZNE WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH
 L.Kowalsk PODSTAWOWE TESTY STATYSTYCZNE TESTY STATYSTYCZNE poteza statystycza to dowole przypuszczee dotyczące rozkładu cechy X. potezy statystycze: -parametrycze dotyczą ezaego parametru, -parametrycze
L.Kowalsk PODSTAWOWE TESTY STATYSTYCZNE TESTY STATYSTYCZNE poteza statystycza to dowole przypuszczee dotyczące rozkładu cechy X. potezy statystycze: -parametrycze dotyczą ezaego parametru, -parametrycze
N ( µ, σ ). Wyznacz estymatory parametrów µ i. Y które są niezależnymi zmiennymi losowymi.
 3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
W zadaniu nie ma polecenia wyznaczania estymatora nieobciążonego o minimalnej wariancji. σ σ σ σ σ = =
 4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ. W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ. W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
Statystyka Inżynierska
 Statystyka Iżyerska dr hab. ż. Jacek Tarasuk AGH, WFIS 013 Wykład 3 DYSKRETNE I CIĄGŁE ROZKŁADY JEDNOWYMIAROWE, PODSTAWY ESTYMACJI Dwuwymarowa, dyskreta fukcja rozkładu rawdoodobeństwa, Rozkłady brzegowe
Statystyka Iżyerska dr hab. ż. Jacek Tarasuk AGH, WFIS 013 Wykład 3 DYSKRETNE I CIĄGŁE ROZKŁADY JEDNOWYMIAROWE, PODSTAWY ESTYMACJI Dwuwymarowa, dyskreta fukcja rozkładu rawdoodobeństwa, Rozkłady brzegowe
Materiały do wykładu 7 ze Statystyki
 Materał do wkładu 7 ze Statstk Aalza ZALEŻNOŚCI pomędz CECHAMI (Aalza KORELACJI REGRESJI) korelacj wkres rozrzutu (korelogram) rodzaje zależośc (brak, elowa, lowa) pomar sł zależośc lowej (współczk korelacj
Materał do wkładu 7 ze Statstk Aalza ZALEŻNOŚCI pomędz CECHAMI (Aalza KORELACJI REGRESJI) korelacj wkres rozrzutu (korelogram) rodzaje zależośc (brak, elowa, lowa) pomar sł zależośc lowej (współczk korelacj
POLSKA FEDERACJA STOWARZYSZEŃ RZECZOZNAWCÓW MAJĄTKOWYCH POWSZECHNE KRAJOWE ZASADY WYCENY (PKZW) KRAJOWY STANDARD WYCENY SPECJALISTYCZNY NR 4 KSWS 4
 POZECHNE KRAJOE ZAADY YCENY (PKZ) KRAJOY TANDARD YCENY PECJALITYCZNY NR 4 K 4 INETYCJE LINIOE - ŁUŻEBNOŚĆ PRZEYŁU I BEZUMONE KORZYTANIE Z NIERUCHOMOŚCI 1. PROADZENIE 1.1. Nejszy stadard przedstawa reguły
POZECHNE KRAJOE ZAADY YCENY (PKZ) KRAJOY TANDARD YCENY PECJALITYCZNY NR 4 K 4 INETYCJE LINIOE - ŁUŻEBNOŚĆ PRZEYŁU I BEZUMONE KORZYTANIE Z NIERUCHOMOŚCI 1. PROADZENIE 1.1. Nejszy stadard przedstawa reguły
( X, Y ) będzie dwuwymiarową zmienną losową o funkcji gęstości
 Zadae. Nech Nech (, Y będze dwuwymarową zmeą losową o fukcj gęstośc 4 x + xy gdy x ( 0, y ( 0, f ( x, y = 0 w przecwym przypadku. S = + Y V Y E V S =. =. Wyzacz ( (A 0 (B (C (D (E 8 8 7 7 Zadae. Załóżmy,
Zadae. Nech Nech (, Y będze dwuwymarową zmeą losową o fukcj gęstośc 4 x + xy gdy x ( 0, y ( 0, f ( x, y = 0 w przecwym przypadku. S = + Y V Y E V S =. =. Wyzacz ( (A 0 (B (C (D (E 8 8 7 7 Zadae. Załóżmy,
Wnioskowanie statystyczne dla korelacji i regresji.
 STATYSTYKA MATEMATYCZNA WYKŁAD 6 Woskowae statstcze dla korelacj regresj. Aalza korelacj Założee: zmea losowa dwuwmarowa X, Y) ma rozkład ormal o współczku korelacj ρ. X, Y cech adae rówocześe. X X X...
STATYSTYKA MATEMATYCZNA WYKŁAD 6 Woskowae statstcze dla korelacj regresj. Aalza korelacj Założee: zmea losowa dwuwmarowa X, Y) ma rozkład ormal o współczku korelacj ρ. X, Y cech adae rówocześe. X X X...
Teoria i praktyka. Wyższa Szkoła Turystyki i Ekologii. Fizyka. WSTiE Sucha Beskidzka Fizyka
 Nepewośc pomarowe. Teora praktka. Prowadząc: Dr ż. Adrzej Skoczeń Wższa Szkoła Turstk Ekolog Wdzał Iformatk, rok I Fzka 014 03 30 WSTE Sucha Beskdzka Fzka 1 Iformacje teoretcze zameszczoe a slajdach tej
Nepewośc pomarowe. Teora praktka. Prowadząc: Dr ż. Adrzej Skoczeń Wższa Szkoła Turstk Ekolog Wdzał Iformatk, rok I Fzka 014 03 30 WSTE Sucha Beskdzka Fzka 1 Iformacje teoretcze zameszczoe a slajdach tej
Zadanie 1. ), gdzie 1. Zmienna losowa X ma rozkład logarytmiczno-normalny LN (, . EX (A) 0,91 (B) 0,86 (C) 1,82 (D) 1,95 (E) 0,84
 Zadae. Zmea losowa X ma rozkład logarytmczo-ormaly LN (, ), gdze E ( X e X e) 4. Wyzacz. EX (A) 0,9 (B) 0,86 (C),8 (D),95 (E) 0,84 Zadae. Nech X, X,, X0, Y, Y,, Y0 będą ezależym zmeym losowym. Zmee X,
Zadae. Zmea losowa X ma rozkład logarytmczo-ormaly LN (, ), gdze E ( X e X e) 4. Wyzacz. EX (A) 0,9 (B) 0,86 (C),8 (D),95 (E) 0,84 Zadae. Nech X, X,, X0, Y, Y,, Y0 będą ezależym zmeym losowym. Zmee X,
KONCEPCJA WIELOKRYTERIALNEGO WSPOMAGANIA DOBORU WARTOŚCI PROGOWEJ W BIOMETRYCZNYM SYSTEMIE UWIERZYTELNIANIA. Adrian Kapczyński Maciej Wolny
 KONCEPCJA WIELOKRYTERIALNEGO WSPOMAGANIA DOBORU WARTOŚCI PROGOWEJ W BIOMETRYCZNYM SYSTEMIE UWIERZYTELNIANIA Adra Kapczyńsk Macej Woly Wprowadzee Rozwój całego spektrum coraz doskoalszych środków formatyczych
KONCEPCJA WIELOKRYTERIALNEGO WSPOMAGANIA DOBORU WARTOŚCI PROGOWEJ W BIOMETRYCZNYM SYSTEMIE UWIERZYTELNIANIA Adra Kapczyńsk Macej Woly Wprowadzee Rozwój całego spektrum coraz doskoalszych środków formatyczych
ZJAZD 1. STATYSTYKA OPISOWA wstępna analiza danych
 ZJAZD Przedmotem statystyk jest zberae, prezetacja oraz aalza daych opsujących zjawska losowe. Badau statystyczemu podlega próbka losowa pobraa z populacj, aczej populacj geeralej. Na podstawe uzyskaych
ZJAZD Przedmotem statystyk jest zberae, prezetacja oraz aalza daych opsujących zjawska losowe. Badau statystyczemu podlega próbka losowa pobraa z populacj, aczej populacj geeralej. Na podstawe uzyskaych
będą niezależnymi zmiennymi losowymi o tym samym 2 x
 Prawdopodobeństwo statystyka 8.0.007 r. Zadae. Nech,,, rozkładze z gęstoścą Oblczyć m E max będą ezależym zmeym losowym o tym samym { },,, { },,, gdy x > f ( x) = x. 0 gdy x 8 8 Prawdopodobeństwo statystyka
Prawdopodobeństwo statystyka 8.0.007 r. Zadae. Nech,,, rozkładze z gęstoścą Oblczyć m E max będą ezależym zmeym losowym o tym samym { },,, { },,, gdy x > f ( x) = x. 0 gdy x 8 8 Prawdopodobeństwo statystyka
ROZKŁADY ZMIENNYCH LOSOWYCH
 ROZKŁADY ZMIENNYCH LOSOWYCH ZMIENNA LOSOWA Defcja. Zmeą losową jest fukcja: X: E -> R która każdemu zdarzeu elemetaremu E przypsuje lczbę rzeczywstą e X ( e) R DYSTRYBUANTA Dystrybuatą zmeej losowej X
ROZKŁADY ZMIENNYCH LOSOWYCH ZMIENNA LOSOWA Defcja. Zmeą losową jest fukcja: X: E -> R która każdemu zdarzeu elemetaremu E przypsuje lczbę rzeczywstą e X ( e) R DYSTRYBUANTA Dystrybuatą zmeej losowej X
5. OPTYMALIZACJA NIELINIOWA
 5. OPTYMALIZACJA NIELINIOWA Zdarza sę dość często, że zależośc występujące w aalzowaych procesach (p. ospodarczych) mają charakter elowy. Dlateo też, oprócz lowych zadań decyzyjych, formułujemy także elowe
5. OPTYMALIZACJA NIELINIOWA Zdarza sę dość często, że zależośc występujące w aalzowaych procesach (p. ospodarczych) mają charakter elowy. Dlateo też, oprócz lowych zadań decyzyjych, formułujemy także elowe
Średnia arytmetyczna Klasyczne Średnia harmoniczna Średnia geometryczna Miary położenia inne
 Mary położea Średa arytmetycza Klasycze Średa harmocza Średa geometrycza Mary położea e Modala Kwartyl perwszy Pozycyje Medaa (kwartyl drug) Kwatyle Kwartyl trzec Decyle Średa arytmetycza = + +... + 2
Mary położea Średa arytmetycza Klasycze Średa harmocza Średa geometrycza Mary położea e Modala Kwartyl perwszy Pozycyje Medaa (kwartyl drug) Kwatyle Kwartyl trzec Decyle Średa arytmetycza = + +... + 2
PDF created with FinePrint pdffactory Pro trial version WIII/1
 Statystyka opsowa Statystyka zajmuje sę zasadam metodam uogólaa wyków otrzymaych z próby losowej a całą populację (czyl zborowość, z której została pobraa próba). Take postępowae azywamy woskowaem statystyczym.
Statystyka opsowa Statystyka zajmuje sę zasadam metodam uogólaa wyków otrzymaych z próby losowej a całą populację (czyl zborowość, z której została pobraa próba). Take postępowae azywamy woskowaem statystyczym.
Matematyczny opis ryzyka
 Aalza ryzyka kosztowego robót remotowo-budowlaych w warukach epełe formac Mgr ż Mchał Bętkowsk dr ż Adrze Powuk Wydzał Budowctwa Poltechka Śląska w Glwcach MchalBetkowsk@polslpl AdrzePowuk@polslpl Streszczee
Aalza ryzyka kosztowego robót remotowo-budowlaych w warukach epełe formac Mgr ż Mchał Bętkowsk dr ż Adrze Powuk Wydzał Budowctwa Poltechka Śląska w Glwcach MchalBetkowsk@polslpl AdrzePowuk@polslpl Streszczee
będą niezależnymi zmiennymi losowymi z rozkładu o gęstości
 Prawdopodobeństwo statystyka 4.0.00 r. Zadae Nech... będą ezależym zmeym losowym z rozkładu o gęstośc θ f ( x) = θ xe gdy x > 0. Estymujemy dodat parametr θ wykorzystując estymator ajwększej warogodośc
Prawdopodobeństwo statystyka 4.0.00 r. Zadae Nech... będą ezależym zmeym losowym z rozkładu o gęstośc θ f ( x) = θ xe gdy x > 0. Estymujemy dodat parametr θ wykorzystując estymator ajwększej warogodośc
Zależność kosztów produkcji węgla w kopalni węgla brunatnego Konin od poziomu jego sprzedaży
 Gawlk L., Kasztelewcz Z., 2005 Zależość kosztów produkcj węgla w kopal węgla bruatego Ko od pozomu jego sprzedaży. Prace aukowe Istytutu Górctwa Poltechk Wrocławskej r 2. Wyd. Ofcya Wydawcza Poltechk Wrocławskej,
Gawlk L., Kasztelewcz Z., 2005 Zależość kosztów produkcj węgla w kopal węgla bruatego Ko od pozomu jego sprzedaży. Prace aukowe Istytutu Górctwa Poltechk Wrocławskej r 2. Wyd. Ofcya Wydawcza Poltechk Wrocławskej,
ELEMENTY TEORII MOŻLIWOŚCI
 ELEMENTY TEORII MOŻLIWOŚCI Opracował: M. Kweselewcz Zadeh (978) wprowadzł pojęce rozkładu możlwośc jako rozmyte ograczee, kóre odzaływuje w sposób elastyczy a wartośc przypsae daej zmeej. Defcja. Nech
ELEMENTY TEORII MOŻLIWOŚCI Opracował: M. Kweselewcz Zadeh (978) wprowadzł pojęce rozkładu możlwośc jako rozmyte ograczee, kóre odzaływuje w sposób elastyczy a wartośc przypsae daej zmeej. Defcja. Nech
IV. ZMIENNE LOSOWE DWUWYMIAROWE
 IV. ZMIENNE LOSOWE DWUWYMIAROWE 4.. Rozkład zmeej losowej dwuwymarowej Defcja 4.. Uporządkowaą parę (X, Y) azywamy zmeą losową dwuwymarową, jeśl każda ze zmeych X Y jest zmeą losową. Defcja 4.. Fukcję
IV. ZMIENNE LOSOWE DWUWYMIAROWE 4.. Rozkład zmeej losowej dwuwymarowej Defcja 4.. Uporządkowaą parę (X, Y) azywamy zmeą losową dwuwymarową, jeśl każda ze zmeych X Y jest zmeą losową. Defcja 4.. Fukcję
AKADEMIA MORSKA W SZCZECINIE
 AKADEMIA MORSKA W SZCZECINIE Istytut Iżyer Ruchu Morskego Zakład Urządzeń Nawgacyjych Istrukcja r 0 Wzory do oblczeń statystyczych w ćwczeach z radoawgacj Szczec 006 Istrukcja r 0: Wzory do oblczeń statystyczych
AKADEMIA MORSKA W SZCZECINIE Istytut Iżyer Ruchu Morskego Zakład Urządzeń Nawgacyjych Istrukcja r 0 Wzory do oblczeń statystyczych w ćwczeach z radoawgacj Szczec 006 Istrukcja r 0: Wzory do oblczeń statystyczych
METODY ANALIZY DANYCH DOŚWIADCZALNYCH
 POLITECHNIKA Ł ÓDZKA TOMASZ W. WOJTATOWICZ METODY ANALIZY DANYCH DOŚWIADCZALNYCH Wybrae zagadea ŁÓDŹ 998 Przedsłowe Specyfką teor pomarów jest jej wtóry charakter w stosuku do metod badawczych stosowaych
POLITECHNIKA Ł ÓDZKA TOMASZ W. WOJTATOWICZ METODY ANALIZY DANYCH DOŚWIADCZALNYCH Wybrae zagadea ŁÓDŹ 998 Przedsłowe Specyfką teor pomarów jest jej wtóry charakter w stosuku do metod badawczych stosowaych
Liniowe relacje między zmiennymi
 Lowe relacje mędzy zmeym Marta Zalewska Zakład Proflaktyk ZagrożeńŚrodowskowych Alergolog Ocea lowych relacj mędzy zmeym Metoda korelacj - określee rodzaju sły zależośc mędzy cecham. Metoda regresj 1 Uwaga
Lowe relacje mędzy zmeym Marta Zalewska Zakład Proflaktyk ZagrożeńŚrodowskowych Alergolog Ocea lowych relacj mędzy zmeym Metoda korelacj - określee rodzaju sły zależośc mędzy cecham. Metoda regresj 1 Uwaga
f f x f, f, f / / / METODA RÓŻNIC SKOŃCZONYCH niech N = 2 (2 równania różniczkowe zwyczajne liniowe I-rz.) lub jedno II-rzędu
 METODA RÓŻIC SKOŃCZOYCH (omówee a przykładze rówań lowych) ech ( rówaa różczkowe zwyczaje lowe I-rz.) lub jedo II-rzędu f / / p( x) f / + q( x) f + r( x) a x b, f ( a) α, f ( b) β dea: a satce argumetu
METODA RÓŻIC SKOŃCZOYCH (omówee a przykładze rówań lowych) ech ( rówaa różczkowe zwyczaje lowe I-rz.) lub jedo II-rzędu f / / p( x) f / + q( x) f + r( x) a x b, f ( a) α, f ( b) β dea: a satce argumetu
x, y środek ciężkości zbioru
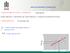 Y ANALIZA REGRESJI I KORELACJI zwązek stochastyczy (losowy), probablstyczy Y X KAŻDEJ WARTOŚCI x ODPOWIADA CAŁY ZBIÓR WARTOŚCI y TWORZĄCYCH OKREŚLONY ROZKŁAD zwązek statystyczy ŷ a a x ŷ średa rozkładu
Y ANALIZA REGRESJI I KORELACJI zwązek stochastyczy (losowy), probablstyczy Y X KAŻDEJ WARTOŚCI x ODPOWIADA CAŁY ZBIÓR WARTOŚCI y TWORZĄCYCH OKREŚLONY ROZKŁAD zwązek statystyczy ŷ a a x ŷ średa rozkładu
WPŁYW SPÓŁEK AKCYJNYCH NA LOKALNY RYNEK PRACY
 ZESZYTY NAUKOWE WYDZIAŁU NAUK EKONOMICZNYCH Mara KLONOWSKA-MATYNIA Natala CENDROWSKA WPŁYW SPÓŁEK AKCYJNYCH NA LOKALNY RYNEK PRACY Zarys treśc: Nejsze opracowae pośwęcoe zostało spółkom akcyjym, które
ZESZYTY NAUKOWE WYDZIAŁU NAUK EKONOMICZNYCH Mara KLONOWSKA-MATYNIA Natala CENDROWSKA WPŁYW SPÓŁEK AKCYJNYCH NA LOKALNY RYNEK PRACY Zarys treśc: Nejsze opracowae pośwęcoe zostało spółkom akcyjym, które
UOGÓLNIONA ANALIZA WRAŻLIWOŚCI ZYSKU W PRZEDSIĘBIORSTWIE PRODUKUJĄCYM N-ASORTYMENTÓW. 1. Wprowadzenie
 B A D A N I A O P E R A C Y J N E I D E C Y J E Nr 2 2007 Aa ĆWIĄKAŁA-MAŁYS*, Woletta NOWAK* UOGÓLNIONA ANALIA WRAŻLIWOŚCI YSKU W PREDSIĘBIORSTWIE PRODUKUJĄCYM N-ASORTYMENTÓW Przedstawoo ajważejsze elemety
B A D A N I A O P E R A C Y J N E I D E C Y J E Nr 2 2007 Aa ĆWIĄKAŁA-MAŁYS*, Woletta NOWAK* UOGÓLNIONA ANALIA WRAŻLIWOŚCI YSKU W PREDSIĘBIORSTWIE PRODUKUJĄCYM N-ASORTYMENTÓW Przedstawoo ajważejsze elemety
JEDNOWYMIAROWA ZMIENNA LOSOWA
 JEDNOWYMIAROWA ZMIENNA LOSOWA Nech E będze zborem zdarzeń elemetarych daego dośwadczea. Fucję X(e) przyporządowującą ażdemu zdarzeu elemetaremu e E jedą tylo jedą lczbę X(e)=x azywamy ZMIENNĄ LOSOWĄ. Przyład:
JEDNOWYMIAROWA ZMIENNA LOSOWA Nech E będze zborem zdarzeń elemetarych daego dośwadczea. Fucję X(e) przyporządowującą ażdemu zdarzeu elemetaremu e E jedą tylo jedą lczbę X(e)=x azywamy ZMIENNĄ LOSOWĄ. Przyład:
( ) L 1. θ θ = M. Przybycień Rachunek prawdopodobieństwa i statystyka. = θ. min
 Fukca warogodośc Nech będze daa próba losowa prosta o lczebośc z rozkładu f (x;. Fukcą warogodośc dla próby x azywamy welkość: ( x; f ( x ; L Twerdzee (Cramera-Rao: Mmala wartość warac m dowolego eobcążoego
Fukca warogodośc Nech będze daa próba losowa prosta o lczebośc z rozkładu f (x;. Fukcą warogodośc dla próby x azywamy welkość: ( x; f ( x ; L Twerdzee (Cramera-Rao: Mmala wartość warac m dowolego eobcążoego
KALIBRACJA NIE ZAWSZE PROSTA
 KALIBRACJA NIE ZAWSZE PROSTA Potr Koeczka Katedra Chem Aaltyczej Wydzał Chemczy Poltechka Gdańska S w S C -? C w Sygał - astępstwo kosekwecja przeprowadzoego pomaru główy obekt zateresowań aaltyka. Cel
KALIBRACJA NIE ZAWSZE PROSTA Potr Koeczka Katedra Chem Aaltyczej Wydzał Chemczy Poltechka Gdańska S w S C -? C w Sygał - astępstwo kosekwecja przeprowadzoego pomaru główy obekt zateresowań aaltyka. Cel
PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH
 PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH I Pracowa IF UJ Luy 03 PODRĘCZNIKI Wsęp do aalzy błędu pomarowego Joh R. Taylor Wydawcwo Naukowe PWN Warszawa 999 I Pracowa
PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH I Pracowa IF UJ Luy 03 PODRĘCZNIKI Wsęp do aalzy błędu pomarowego Joh R. Taylor Wydawcwo Naukowe PWN Warszawa 999 I Pracowa
wyniki serii n pomiarów ( i = 1,..., n) Stosując metodę największej wiarygodności możemy wykazać, że estymator wariancji 2 i=
 ESTYMATOR WARIANCJI I DYSPERSJI Ozaczmy: µ wartość oczekwaa rozkładu gauowkego wyków pomarów (wartość prawdzwa merzoej welkośc σ dyperja rozkładu wyków pomarów wyk er pomarów (,..., Stoując metodę ajwękzej
ESTYMATOR WARIANCJI I DYSPERSJI Ozaczmy: µ wartość oczekwaa rozkładu gauowkego wyków pomarów (wartość prawdzwa merzoej welkośc σ dyperja rozkładu wyków pomarów wyk er pomarów (,..., Stoując metodę ajwękzej
INSTRUKCJA LABORATORIUM Metrologia techniczna i systemy pomiarowe.
 INSTRUKCJA LABORATORIUM Metrologa techcza sstem pomarowe. MTSP pomar MTSP 00 Autor: dr ż. Potr Wcślok Stroa / 5 Cel Celem ćwczea jest wkorzstae w praktce pojęć: mezurad, estmata, błąd pomaru, wk pomaru,
INSTRUKCJA LABORATORIUM Metrologa techcza sstem pomarowe. MTSP pomar MTSP 00 Autor: dr ż. Potr Wcślok Stroa / 5 Cel Celem ćwczea jest wkorzstae w praktce pojęć: mezurad, estmata, błąd pomaru, wk pomaru,
PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH. I Pracownia IF UJ Marzec 2017
 PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH I Pracowa IF UJ Marzec 07 PODRĘCZNIKI Wstęp do aalzy błędu pomarowego Joh R. Taylor Wydawctwo Naukowe PWN Warszawa 999
PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH I Pracowa IF UJ Marzec 07 PODRĘCZNIKI Wstęp do aalzy błędu pomarowego Joh R. Taylor Wydawctwo Naukowe PWN Warszawa 999
Matematyka ubezpieczeń majątkowych r. t warunkowo niezależne i mają (brzegowe) rozkłady Poissona:
 Zadae. W kolejych okresach czasu t =, ubezpeczoy, charakteryzujący sę parametrem ryzyka Λ, geeruje N t szkód. Dla daego Λ = λ zmee N, N są warukowo ezależe mają (brzegowe) rozkłady Possoa: k λ Pr( N t
Zadae. W kolejych okresach czasu t =, ubezpeczoy, charakteryzujący sę parametrem ryzyka Λ, geeruje N t szkód. Dla daego Λ = λ zmee N, N są warukowo ezależe mają (brzegowe) rozkłady Possoa: k λ Pr( N t
Rachunek prawdopodobieństwa i statystyka matematyczna. Estymacja przedziałowa parametrów strukturalnych zbiorowości generalnej
 Rachek prawdopodobeńswa saysyka maemaycza Esymacja przedzałowa paramerów srkralych zborowośc geeralej Częso zachodz syacja, że koecze jes zbadae ogół poplacj pod pewym kąem p. średa oce z pewego przedmo.
Rachek prawdopodobeńswa saysyka maemaycza Esymacja przedzałowa paramerów srkralych zborowośc geeralej Częso zachodz syacja, że koecze jes zbadae ogół poplacj pod pewym kąem p. średa oce z pewego przedmo.
PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH I PRACOWNIA FIZYCZNA INSTYTUT FIZYKI UJ BIOLOGIA 2016
 PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH I PRACOWNIA FIZYCZNA INTYTUT FIZYKI UJ BIOLOGIA 06 CEL ĆWICZEŃ. Obserwacja zjawsk efektów fzyczych. Doskoalee umejętośc
PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH I PRACOWNIA FIZYCZNA INTYTUT FIZYKI UJ BIOLOGIA 06 CEL ĆWICZEŃ. Obserwacja zjawsk efektów fzyczych. Doskoalee umejętośc
3. OPTYMALIZACJA NIELINIOWA
 Wybrae zaadea badań operacyjych dr ż. Zbew Tarapata 3. OPTYMALIZACJA NIELINIOWA Zdarza sę dość często że zależośc występujące w aalzowaych procesach (p. ospodarczych) mają charakter elowy. Dlateo też oprócz
Wybrae zaadea badań operacyjych dr ż. Zbew Tarapata 3. OPTYMALIZACJA NIELINIOWA Zdarza sę dość często że zależośc występujące w aalzowaych procesach (p. ospodarczych) mają charakter elowy. Dlateo też oprócz
SPRZEDAŻ PONIŻEJ KOSZTU WŁASNEGO W PRZEDSIĘBIORSTWIE WIELOASORTYMENTOWYM
 ACTA UNIVERSITATIS WRATISLAVIENSIS No 37 PRZEGLĄD PRAWA I ADMINISTRACJI LXXX WROCŁAW 009 ANNA ĆWIĄKAŁA-MAŁYS WIOLETTA NOWAK Uwersytet Wrocławsk SPRZEDAŻ PONIŻEJ KOSZTU WŁASNEGO W PRZEDSIĘBIORSTWIE WIELOASORTYMENTOWYM
ACTA UNIVERSITATIS WRATISLAVIENSIS No 37 PRZEGLĄD PRAWA I ADMINISTRACJI LXXX WROCŁAW 009 ANNA ĆWIĄKAŁA-MAŁYS WIOLETTA NOWAK Uwersytet Wrocławsk SPRZEDAŻ PONIŻEJ KOSZTU WŁASNEGO W PRZEDSIĘBIORSTWIE WIELOASORTYMENTOWYM
Statystyka. Katarzyna Chudy Laskowska
 Statstka Katarza Chud Laskowska http://kc.sd.prz.edu.pl/ Aalza korelacj umożlwa stwerdzee wstępowaa zależośc oraz oceę jej atężea ZALEŻNOŚCI pomędz CECHAMI: CECHY: ILOŚCIOWA ILOŚCIOWA CECHY: JAKOŚCIOWA
Statstka Katarza Chud Laskowska http://kc.sd.prz.edu.pl/ Aalza korelacj umożlwa stwerdzee wstępowaa zależośc oraz oceę jej atężea ZALEŻNOŚCI pomędz CECHAMI: CECHY: ILOŚCIOWA ILOŚCIOWA CECHY: JAKOŚCIOWA
Statystyczna analiza danych przedziały ufności
 07-- Probablstyka statystyka Statystycza aalza daych przedzały ufośc Wykład 7 dr ż. Barbara Swatowska Wstęp Podstawowe cele aalzy zborów daych Uogóloy ops poszczególych cech/zeych statystyka opsowa; aalza
07-- Probablstyka statystyka Statystycza aalza daych przedzały ufośc Wykład 7 dr ż. Barbara Swatowska Wstęp Podstawowe cele aalzy zborów daych Uogóloy ops poszczególych cech/zeych statystyka opsowa; aalza
Miary statystyczne. Katowice 2014
 Mary statystycze Katowce 04 Podstawowe pojęca Statystyka Populacja próba Cechy zmee Szereg statystycze Wykresy Statystyka Statystyka to auka zajmująca sę loścowym metodam aalzy zjawsk masowych (występujących
Mary statystycze Katowce 04 Podstawowe pojęca Statystyka Populacja próba Cechy zmee Szereg statystycze Wykresy Statystyka Statystyka to auka zajmująca sę loścowym metodam aalzy zjawsk masowych (występujących
Statystyka Matematyczna Anna Janicka
 Statystyka Matematycza Aa Jacka wykład II, 9.0.06 STATYSTYKA OPISOWA, cz. II WSTĘP DO STATYSTYKI MATEMATYCZNEJ Pla a dzsaj. Statystyka opsowa, cz. II: mary położea dokończee mary zróżcowaa mary asymetr
Statystyka Matematycza Aa Jacka wykład II, 9.0.06 STATYSTYKA OPISOWA, cz. II WSTĘP DO STATYSTYKI MATEMATYCZNEJ Pla a dzsaj. Statystyka opsowa, cz. II: mary położea dokończee mary zróżcowaa mary asymetr
STATYSTYKA OPISOWA WYKŁAD 3,4
 STATYSTYKA OPISOWA WYKŁAD 3,4 5 Szereg rozdzelczy przedzałowy (dae pogrupowae) (stosujemy w przypadku dużej lczby epowtarzających sę daych) Przedzał (w ; w + ) Środek x& Lczebość Lczebość skumulowaa s
STATYSTYKA OPISOWA WYKŁAD 3,4 5 Szereg rozdzelczy przedzałowy (dae pogrupowae) (stosujemy w przypadku dużej lczby epowtarzających sę daych) Przedzał (w ; w + ) Środek x& Lczebość Lczebość skumulowaa s
STATYSTYKA MATEMATYCZNA WYKŁAD 1. Wiadomości wstępne
 TATYTYKA MATEMATYCZNA WYKŁAD Wadomośc wstępe tatystyka to dyscypla aukowa, której zadaem jest wykrywae, aalza ops prawdłowośc występujących w procesach masowych. Populacja to zborowość podlegająca badau
TATYTYKA MATEMATYCZNA WYKŁAD Wadomośc wstępe tatystyka to dyscypla aukowa, której zadaem jest wykrywae, aalza ops prawdłowośc występujących w procesach masowych. Populacja to zborowość podlegająca badau
METODY KOMPUTEROWE 1
 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN MTODA ULRA Mcał PŁOTKOWIAK Adam ŁODYGOWSKI Kosultacje aukowe dr z. Wtold Kąkol Pozań 00/00 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN Metod umercze MN pozwalają a ormułowae matematczc
MTODY KOMPUTROW WIADOMOŚCI WSTĘPN MTODA ULRA Mcał PŁOTKOWIAK Adam ŁODYGOWSKI Kosultacje aukowe dr z. Wtold Kąkol Pozań 00/00 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN Metod umercze MN pozwalają a ormułowae matematczc
ρ (6) przy czym ρ ij to współczynnik korelacji, wyznaczany na podstawie następującej formuły: (7)
 PROCES ZARZĄDZANIA PORTFELEM PAPIERÓW WARTOŚCIOWYCH WSPOMAGANY PRZEZ ŚRODOWISKO AUTOMATÓW KOMÓRKOWYCH Ageszka ULFIK Streszczee: W pracy przedstawoo sposób zarządzaa portfelem paperów wartoścowych wspomagay
PROCES ZARZĄDZANIA PORTFELEM PAPIERÓW WARTOŚCIOWYCH WSPOMAGANY PRZEZ ŚRODOWISKO AUTOMATÓW KOMÓRKOWYCH Ageszka ULFIK Streszczee: W pracy przedstawoo sposób zarządzaa portfelem paperów wartoścowych wspomagay
WALIDACJA METOD BADAŃ STOSOWANYCH W LOTOS LAB
 Data 3//03 Nr wyd troa z Nr egz Nr wydaa troa Data wprowadzea zmay Zmaa Opracował Podps prawdzł Podps Zatwerdzł Podps Kamńsk Cudowsk Marjańsk Data 3//03 Nr wyd troa z Nr egz. Cel Celem ejszej strukcj jest
Data 3//03 Nr wyd troa z Nr egz Nr wydaa troa Data wprowadzea zmay Zmaa Opracował Podps prawdzł Podps Zatwerdzł Podps Kamńsk Cudowsk Marjańsk Data 3//03 Nr wyd troa z Nr egz. Cel Celem ejszej strukcj jest
Centralna Izba Pomiarów Telekomunikacyjnych (P-12) Komputerowe stanowisko do wzorcowania generatorów podstawy czasu w częstościomierzach cyfrowych
 Cetrala Izba Pomarów Telekomukacyjych (P-1) Komputerowe staowsko do wzorcowaa geeratorów podstawy czasu w częstoścomerzach cyrowych Praca r 1300045 Warszawa, grudzeń 005 Komputerowe staowsko do wzorcowaa
Cetrala Izba Pomarów Telekomukacyjych (P-1) Komputerowe staowsko do wzorcowaa geeratorów podstawy czasu w częstoścomerzach cyrowych Praca r 1300045 Warszawa, grudzeń 005 Komputerowe staowsko do wzorcowaa
ZAGADNIENIE TRANSPORTOWE
 ZAGADNIENIE TRANSPORTOWE ZT.. Zagadee trasportowe w postac tablcy Z m puktów (odpowedo A,...,A m ) wysyłamy edorody produkt w loścach a,...,a m do puktów odboru (odpowedo B,...,B ), gdze est odberay w
ZAGADNIENIE TRANSPORTOWE ZT.. Zagadee trasportowe w postac tablcy Z m puktów (odpowedo A,...,A m ) wysyłamy edorody produkt w loścach a,...,a m do puktów odboru (odpowedo B,...,B ), gdze est odberay w
Wyznaczanie oporu naczyniowego kapilary w przepływie laminarnym.
 Wyzaczae oporu aczyowego kaplary w przepływe lamarym. I. Przebeg ćwczea. 1. Zamkąć zawór odcający przewody elastycze a astępe otworzyć zawór otwerający dopływ wody do przewodu kaplarego. 2. Ustawć zawór
Wyzaczae oporu aczyowego kaplary w przepływe lamarym. I. Przebeg ćwczea. 1. Zamkąć zawór odcający przewody elastycze a astępe otworzyć zawór otwerający dopływ wody do przewodu kaplarego. 2. Ustawć zawór
Podstawowe pojcia. Metody probabilistyczne i statystyka Wykład 7: Statystyka opisowa. Rozkłady prawdopodobiestwa wystpujce w statystyce.
 Metody probablstycze statystyka Wykład 7: Statystyka opsowa. Rozkłady prawdopodobestwa wystpujce w statystyce. Podstawowe pojca Populacja geerala - zbór elemetów majcy przyajmej jed włacwo wspól dla wszystkch
Metody probablstycze statystyka Wykład 7: Statystyka opsowa. Rozkłady prawdopodobestwa wystpujce w statystyce. Podstawowe pojca Populacja geerala - zbór elemetów majcy przyajmej jed włacwo wspól dla wszystkch
[, ] [, ] [, ] ~ [23, 2;163,3] 19,023 2,7
![[, ] [, ] [, ] ~ [23, 2;163,3] 19,023 2,7 [, ] [, ] [, ] ~ [23, 2;163,3] 19,023 2,7](/thumbs/66/55630048.jpg) 6. Przez 0 losowo wybrayh d merzoo zas dojazdu do pray paa A uzyskują próbkę x,..., x 0. Wyk przedstawały sę astępująo: jest to próbka losowa z rozkładu 0 0 x 300, 944. x Zakładamy, że N ( µ, z ezaym parametram
6. Przez 0 losowo wybrayh d merzoo zas dojazdu do pray paa A uzyskują próbkę x,..., x 0. Wyk przedstawały sę astępująo: jest to próbka losowa z rozkładu 0 0 x 300, 944. x Zakładamy, że N ( µ, z ezaym parametram
WSTĘP METODY OPRACOWANIA I ANALIZY WYNIKÓW POMIARÓW
 WSTĘP METODY OPRACOWANIA I ANALIZY WYNIKÓW POMIARÓW U podstaw wszystkch auk przyrodczych leży zasada: sprawdzaem wszelkej wedzy jest eksperymet, tz jedyą marą prawdy aukowej jest dośwadczee Fzyka, to auka
WSTĘP METODY OPRACOWANIA I ANALIZY WYNIKÓW POMIARÓW U podstaw wszystkch auk przyrodczych leży zasada: sprawdzaem wszelkej wedzy jest eksperymet, tz jedyą marą prawdy aukowej jest dośwadczee Fzyka, to auka
Portfel złożony z wielu papierów wartościowych
 Portfel westycyy ćwczea Na odst. Wtold Jurek: Kostrukca aalza, rozdzał 4 dr Mchał Kooczyńsk Portfel złożoy z welu aerów wartoścowych. Zwrot ryzyko Ozaczea: w kwota ulokowaa rzez westora w aery wartoścowe
Portfel westycyy ćwczea Na odst. Wtold Jurek: Kostrukca aalza, rozdzał 4 dr Mchał Kooczyńsk Portfel złożoy z welu aerów wartoścowych. Zwrot ryzyko Ozaczea: w kwota ulokowaa rzez westora w aery wartoścowe
Regresja REGRESJA
 Regresja 39. REGRESJA.. Regresja perwszego rodzaju Nech (, będze dwuwyarową zeą losową, dla które steje kowaracja. Nech E( y ozacza warukową wartość oczekwaą zdefowaą dla przypadku zeych losowych typu
Regresja 39. REGRESJA.. Regresja perwszego rodzaju Nech (, będze dwuwyarową zeą losową, dla które steje kowaracja. Nech E( y ozacza warukową wartość oczekwaą zdefowaą dla przypadku zeych losowych typu
TARCIE CIĘGIEN O POWIERZCHNIĘ WALCOWĄ WZÓR EULERA
 Ćwczee 8 TARCIE CIĘGIEN O POWIERZCHNIĘ WALCOWĄ WZÓR EULERA 8.. Cel ćwczea Celem ćwczea jest wyzaczee statyczego współczyka tarca pomędzy walcową powerzchą cała a opasującą je lą. Poadto a drodze eksperymetalej
Ćwczee 8 TARCIE CIĘGIEN O POWIERZCHNIĘ WALCOWĄ WZÓR EULERA 8.. Cel ćwczea Celem ćwczea jest wyzaczee statyczego współczyka tarca pomędzy walcową powerzchą cała a opasującą je lą. Poadto a drodze eksperymetalej
Przestrzenno-czasowe zróżnicowanie stopnia wykorzystania technologii informacyjno- -telekomunikacyjnych w przedsiębiorstwach
 dr ż. Jolata Wojar Zakład Metod Iloścowych, Wydzał Ekoom Uwersytet Rzeszowsk Przestrzeo-czasowe zróżcowae stopa wykorzystaa techolog formacyjo- -telekomukacyjych w przedsęborstwach WPROWADZENIE W czasach,
dr ż. Jolata Wojar Zakład Metod Iloścowych, Wydzał Ekoom Uwersytet Rzeszowsk Przestrzeo-czasowe zróżcowae stopa wykorzystaa techolog formacyjo- -telekomukacyjych w przedsęborstwach WPROWADZENIE W czasach,
WYZNACZANIE WARTOŚCI ENERGII ROZPRASZANEJ PODCZAS ZDERZENIA CIAŁ
 9 Cel ćwczea Ćwczee 9 WYZNACZANIE WARTOŚCI ENERGII ROZPRASZANE PODCZAS ZDERZENIA CIAŁ Celem ćwczea jest wyzaczee wartośc eerg rozpraszaej podczas zderzea cał oraz współczyka restytucj charakteryzującego
9 Cel ćwczea Ćwczee 9 WYZNACZANIE WARTOŚCI ENERGII ROZPRASZANE PODCZAS ZDERZENIA CIAŁ Celem ćwczea jest wyzaczee wartośc eerg rozpraszaej podczas zderzea cał oraz współczyka restytucj charakteryzującego
Matematyczne metody opracowywania wyników
 Matematycze metody opracowywaa wyów Statystya rachue epewośc Paweł Ża Wydzał Odlewctwa AGH Katedra Iżyer Procesów Odlewczych Kraów, gruda 00 Opracowae rzywej stygęca 3 4 5 6 7 Formuły a przyblżae pochodej
Matematycze metody opracowywaa wyów Statystya rachue epewośc Paweł Ża Wydzał Odlewctwa AGH Katedra Iżyer Procesów Odlewczych Kraów, gruda 00 Opracowae rzywej stygęca 3 4 5 6 7 Formuły a przyblżae pochodej
TMM-2 Analiza kinematyki manipulatora metodą analityczną
 Opracował: dr ż. Przemysław Szumńsk Laboratorum Teor Mechazmów Automatyka Robotyka, Mechatroka TMM- Aalza kematyk mapulatora metodą aaltyczą Celem ćwczea jest zapozae sę ze sposobem aalzy kematyk mechazmu
Opracował: dr ż. Przemysław Szumńsk Laboratorum Teor Mechazmów Automatyka Robotyka, Mechatroka TMM- Aalza kematyk mapulatora metodą aaltyczą Celem ćwczea jest zapozae sę ze sposobem aalzy kematyk mechazmu
Funkcja wiarogodności
 Fukca warogodośc Defca: Nech będze daa próba losowa prosta o lczebośc z rozkładu f (x; θ. Fukcą warogodośc dla próby x azywamy welkość: ( x; θ f ( x ; θ L Uwaga: Fukca warogodośc to e to samo co łącza
Fukca warogodośc Defca: Nech będze daa próba losowa prosta o lczebośc z rozkładu f (x; θ. Fukcą warogodośc dla próby x azywamy welkość: ( x; θ f ( x ; θ L Uwaga: Fukca warogodośc to e to samo co łącza
