Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
|
|
|
- Halina Laura Brzozowska
- 8 lat temu
- Przeglądów:
Transkrypt
1 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Teoria sterowania MATLAB wprowadzenie do biblioteki Control System Toolbox Materiały pomocnicze do ćwiczeń laboratoryjnych 2 Opracowanie: Kazimierz Duzinkiewicz, dr hab. inż. Michał Grochowski, dr inż. Robert Piotrowski, dr inż. Gdańsk
2 Wstęp Control System Toolbox zapewnia wyspecjalizowane narzędzia modelowania, projektowania i analizy systemów ze sprzężeniami, obejmując zarówno klasyczne jak i nowoczesne metody projektowe, mianowicie: LTI Viewer - interaktywny graficzny interfejs użytkownika (GUI) do analizy i porównywania liniowych systemów niezmiennych w czasie (LTI systems). Wykresy w dziedzinie czasu odpowiedzi na skok jednostkowy, impulsowej i zerobiegunowej oraz odpowiedzi w dziedzinie częstotliwości (np. Bode, Nyquist). Narzędzie projektowania systemów z pojedynczym wejściem i pojedynczym wyjściem. Obsługa systemów wielowejściowych i wielowyjściowych (MIMO), systemów czasu ciągłego i próbkowanych danych oraz systemów z opóźnieniami czasowymi. Obsługa różnorodnych metod przekształceń dyskretnych na ciągłe. Narzędzia nowoczesnych technik kontroli projektowania (np. umieszczanie biegunów, regulacje LQR-LQG, projektowanie filtrów Kalmana, wyznaczanie obserwowalności i sterowalności i rozwiązania równań Riccatiego i Lapunowa). W dalszej części opracowania przedstawiono podstawowe polecenia Control System Toolbox dla obiektów ciągłych i dyskretnych. Podstawowe polecenia Control System Toolbox definiowanie modelu obiektu, łączenie obiektów: tf, ss, zpk, series, parallel, feedback tf Funkcja służąca do tworzenia modelu obiektu w postaci transmitancji. SYS = TF(NUM, DEN) Funkcja służąca do tworzenia modelu obiektu ciągłego w postaci transmitancji, gdzie NUM i DEN to macierze współczynników odpowiednio licznika i mianownika NUM(s ) transmitancji: G(s ), uporządkowane według malejących potęg s. DEN(s ) Przykład 1 Zapis: H = TF( {-3 ; [2-8 3]}, {[2-1] ; [1 3 0]}) oznacza wektor transmitancji: H s 3 2s 1 2 2s 8s 3 2 s 3s
3 SYS = TF(NUM, DEN, TS) Funkcja służąca do tworzenia modelu obiektu dyskretnego w postaci transmitancji, gdzie NUM i DEN to macierze współczynników odpowiednio licznika i mianownika NUM( z) transmitancji: G( z), uporządkowane według malejących potęg z. TS jest DEN( z) okresem próbkowania (domyślnie TS = -1). ss Funkcja służąca do tworzenia modelu obiektu w postaci zmiennych stanu. SYS = SS(A, B, C, D) Funkcja służąca do tworzenia modelu obiektu ciągłego w postaci zmiennych stanu (układ równań różniczkowych zwyczajnych), gdzie A, B, C, i D to odpowiednie macierze równań stanu i wyjścia (wymiary tych macierzy zależą od liczby współrzędnych stanu, sterowań i wyjść): x (t ) Ax(t ) Bu(t ) n m c gdzie: x R, y R, u R. y(t ) Cx(t ) Du(t ) SYS = SS(A, B, C, D, TS) Funkcja służąca do tworzenia modelu obiektu dyskretnego w postaci zmiennych stanu (układ równań różnicowych zwyczajnych), gdzie A, B, C, i D to odpowiednie macierze równań stanu i wyjścia (wymiary tych macierzy zależą od liczby współrzędnych stanu, sterowań i wyjść): x[ k 1] Ax[ k] Bu[ k] y[ k] Cx( k) Du[ k] n m c gdzie: x R, y R, u R. TS jest okresem próbkowania (domyślnie TS = -1). zpk Funkcja służąca do tworzenia modelu obiektu w postaci transmitancji (w formie zer, biegunów i wzmocnień). SYS = ZPK(Z, P, K) Funkcja służąca do tworzenia modelu obiektu ciągłego w postaci transmitancji (w formie zer Z, biegunów P i wzmocnień K): s z1 s z2... s zm G(s ) K s p s p... s p 1 Zerem Z (z ang. zero) transmitancji jest każdy z pierwiastków (zer) wielomianu znajdującego się w liczniku transmitancji. Biegunem P (z ang. pole) (biegunem czyli wartością własną) transmitancji jest każdy z pierwiastków wielomianu znajdującego się w mianowniku transmitancji. 2 n
4 Przykład 2 Zapis: H = ZPK( {[]; [-3 5]}, {2; [0-4]}, [-2; 2] ) oznacza wektor transmitancji: H s 2 s 3 s 5 s s 4 2 s 2 SYS = ZPK(Z, P, K, TS) Funkcja służąca do tworzenia modelu obiektu dyskretnego w postaci transmitancji (w formie zer Z, biegunów P i wzmocnień K): z z1 z z2... z zm G( z) K z p1 z p2... z pn TS jest okresem próbkowania (domyślnie TS = -1). series Funkcja służąca do szeregowego połączenia modeli dwóch obiektów. SYS = SERIES(SYS1, SYS2, OUTPUTS1, INPUTS2) Funkcja służąca do tworzenia modelu obiektu będącego szeregowym połączeniem modeli dwóch obiektów: SYS1 i SYS2, w ten sposób, że wyjścia z SYS1 (opisane przez OUTPUTS1) są połączone z wejściami z SYS2 (opisane przez INPUTS2). W przypadku, gdy nie zdefiniujemy OUTPUTS1 i INPUTS2 następuje połączenie postaci: SYS = SYS1*SYS2 Przykład 3 u 1 y 1 u 2 y 2 SYS1 SYS2 Rys. 1. Schemat pomocniczy do polecenia series [A, B, C, D] = SERIES(A1, B1, C1, D1, A2, B2, C2, D2) [A, B, C, D] = SERIES(A1, B1, C1, D1, A2, B2, C2, D2, OUTPUTS1, INPUTS2) [NUM, DEN] = SERIES(NUM1, DEN1, NUM2, DEN2) parallel Funkcja służąca do równoległego połączenia modeli dwóch obiektów. SYS = PARALLEL(SYS1, SYS2, IN1, IN2, OUT1, OUT2) Funkcja służąca do tworzenia modelu obiektu będącego równoległym połączeniem modeli dwóch obiektów: SYS1 i SYS2, w ten sposób, że wejścia z SYS1 (opisane przez IN1) są połączone z wejściami z SYS2 (opisane przez IN2) oraz wyjścia z SYS1 (opisane przez OUT1) są sumowane z wyjściami z SYS2 (opisane przez OUT2).
5 W przypadku, gdy nie zdefiniujemy IN1, IN2, OUT1 i OUT2 następuje połączenie postaci: SYS = SYS1+SYS2 u u 1 SYS1 y 1 + y u 2 SYS2 Rys. 2. Schemat pomocniczy do polecenia parallel y 2 + Przykład 4 [A, B, C, D] = PARALLEL(A1, B1, C1, D1, A2, B2, C2, D2) [A, B, C, D] = PARALLEL(A1, B1, C1, D1, A2, B2, C2, D2, IN1, IN2, OUT1, OUT2) [NUM, DEN] = PARALLEL(NUM1, DEN1, NUM2, DEN2) feedback Funkcja służąca do tworzenia modelu układu ze sprzężeniem zwrotnym z kompensatorem w obwodzie sprzężenia zwrotnego. SYS = FEEDBACK(SYS1, SYS2) Funkcja służąca do tworzenia modelu układu ze sprzężeniem zwrotnym z kompensatorem w obwodzie sprzężenia zwrotnego. Domyślnie przyjmowane jest ujemne sprzężenie zwrotne. W przypadku, gdy chcemy zdefiniować dodatnie sprzężenie zwrotne należy użyć polecenia: SYS = FEEDBACK(SYS1, SYS2, +1) W przypadku, gdy chcemy więcej wejść i wyjść modelu obiektu połączyć ze sprzężeniem zwrotnym należy użyć polecenia: SYS = FEEDBACK(SYS1, SYS2, FEEDIN, FEEDOUT, SIGN) u +/- SYS1 y SYS2 Rys. 3. Schemat pomocniczy do polecenia feedback FEEDIN określa, które wejścia u są połączone ze sprzężeniem zwrotnym, zaś FEEDOUT określa, które wyjścia y są połączone ze sprzężeniem zwrotnym. Jeśli SIGN=1 to używane jest dodatnie sprzężenie zwrotne. Jeśli SIGN=-1 lub SIGN jest pominięty, używane jest ujemnie sprzężenie zwrotne. Przykład 5 [A, B, C, D] = FEEDBACK (A1, B1, C1, D1, A2, B2, C2, D2, SIGN) [A, B, C, D] = FEEDBACK (A1, B1, C1, D1, A2, B2, C2, D2, FEEDIN, FEEDOUT, SIGN) [NUM, DEN] = FEEDBACK (NUM1, DEN1, NUM2, DEN2, SIGN)
6 zmiana postaci modelu obiektu: ss2tf, tf2ss, ss2zp, zp2ss, tf2zp, zp2tf ss2tf Funkcja służąca do zamiany modelu obiektu w postaci równań stanu na transmitancję. [NUM, DEN] = SS2TF(A, B, C, D, IU) Nazwa funkcji ss2tf pochodzi z języka angielskiego: State Space to Transfer Function. Funkcja służąca do zamiany modelu obiektu w postaci równań stanu na transmitancję liczoną względem wejścia (sterowania) o numerze IU: NUM(s ) 1 G(s ) C s I A B D DEN(s ) gdzie, model obiektu w postaci równań stanu jest postaci: x (t ) Ax(t ) Bu(t ) n m c gdzie: x R, y R, u R. y(t ) Cx(t ) Du(t ) NUM i DEN to macierze współczynników odpowiednio licznika i mianownika NUM(s ) transmitancji: G(s ), uporządkowane według malejących potęg s. DEN(s ) tf2ss Funkcja służąca do zamiany modelu obiektu w postaci transmitancji na równania stanu. [A, B, C, D] = TF2SS(NUM, DEN) Nazwa funkcji tf2ss pochodzi z języka angielskiego: Transfer Function to State Space. Funkcja służąca do zamiany modelu obiektu w postaci transmitancji na równania stanu. Jest to funkcja odwrotna do funkcji ss2tf. ss2zp Funkcja służąca do zamiany modelu obiektu w postaci równań stanu na transmitancję w postaci zer, biegunów i wzmocnień. [Z, P, K] = SS2ZP(A, B, C, D, IU) Nazwa funkcji ss2zp pochodzi z języka angielskiego: State Space to Zero Pole. Funkcja służąca do zamiany modelu obiektu w postaci równań stanu na transmitancję liczoną względem wejścia (sterowania) o numerze IU i przedstawia ją w postaci zer Z, biegunów P i wzmocnień K: 1 s z1 s z2... s zm G(s) C s I A B D K s p s p... s p Kolejne parametry wyjściowe zawierają macierz zer Z (w kolumnach, zera odpowiadają poszczególnym wyjściom) oraz kolumnowy wektor biegunów P i wzmocnień K (elementy określają statyczne wzmocnienia dla kolejnych wyjść układu). 1 2 n
7 zp2ss Funkcja służąca do zamiany modelu obiektu w postaci transmitancji (w formie zer, biegunów i wzmocnień) na równania stanu. [A, B, C, D] = ZP2SS(Z, P, K) Nazwa funkcji zp2ss pochodzi z języka angielskiego: Zero Pole to State Space. Funkcja służąca do zamiany modelu obiektu w postaci transmitancji (w formie zer Z, biegunów P i wzmocnień K) na równania stanu. Jest to funkcja odwrotna do funkcji ss2zp. tf2zp Funkcja znajduje zera, bieguny i wzmocnienia dla modelu obiektu w postaci transmitancji. [Z, P, K] = TF2ZP(NUM, DEN) Nazwa funkcji tf2zp pochodzi z języka angielskiego: Transfer Function to Zero Pole. Funkcja znajduje zera Z, bieguny P i wzmocnienia K dla modelu obiektu w postaci transmitancji: NUM s s z1 s z2... s zm G(s ) K DEN s s p s p... s p Funkcja stosowana dla układu SIMO (jedno wejście, wiele wyjść). Kolejne parametry wyjściowe zawierają macierz zer Z (w kolumnach, zera odpowiadają poszczególnym wyjściom) oraz kolumnowy wektor biegunów P i wzmocnień K (elementy określają statyczne wzmocnienia dla kolejnych wyjść układu). 1 2 n zp2tf Funkcja znajduje transmitancję modelu obiektu na podstawie zer, biegunów i wzmocnień. [NUM, DEN] = ZP2TF(Z, P, K) Nazwa funkcji zp2tf pochodzi z języka angielskiego: Zero Pole to Transfer Function. Funkcja znajduje transmitancję modelu obiektu na podstawie zer Z, biegunów P i wzmocnień K. Jest to funkcja odwrotna do funkcji tf2zp. Funkcja stosowana dla układu SIMO (jedno wejście, wiele wyjść). badanie parametrów układu liniowego: pole, zero, pzmap pole Funkcja służąca do znajdowania biegunów modelu obiektu. P = POLE(SYS) Funkcja służąca do znajdowania biegunów modelu obiektu SYS. P jest wektorem kolumnowym.
8 zero Funkcja służąca do znajdowania zer modelu obiektu. Z = ZERO(SYS) Funkcja służąca do znajdowania zer modelu obiektu SYS. [Z, GAIN] = ZERO(SYS) Funkcja służąca do znajdowania zer modelu obiektu SYS i wzmocnienia dla układu SISO (jedno wejście, jedno wyjście). pzmap Funkcja służąca do znajdowania zer i biegunów modelu obiektu i rysowania ich na wykresie. PZMAP(SYS) Funkcja służąca do znajdowania zer i biegunów modelu obiektu SYS i rysowania ich na wykresie. Zera są oznaczane kółkami, zaś bieguny są oznaczane krzyżykami. PZMAP(SYS1, SYS2,...) Funkcja służąca do znajdowania zer i biegunów modeli obiektów SYS1, SYS2,... i rysowania ich na jednym wykresie. Możliwe jest określenie koloru dla każdego z modeli. Przykład 6 PZMAP(SYS1, 'r', SYS2, 'y', SYS3, 'g') [P, Z] = PZMAP(SYS) Funkcja służąca do znajdowania zer Z i biegunów P modelu obiektu SYS. Nie jest kreślony wykres. Zera Z i bieguny P zwracane są w postaci wektora. badanie charakterystyk czasowych układu liniowego: step, impulse, gensig, initial, lsim step Funkcja służąca do wykreślania odpowiedzi modelu układu ciągłego na skok jednostkowy. STEP(SYS) Funkcja służąca do wykreślania odpowiedzi modelu układu ciągłego SYS na skok jednostkowy. STEP(SYS, TFINAL) Funkcja służąca do wykreślania odpowiedzi modelu układu ciągłego SYS na skok jednostkowy od chwili t = 0 do chwili t = TFINAL.
9 Dla modelu układu dyskretnego TFINAL jest rozumiany jako liczba próbek. STEP(SYS, T) Funkcja służąca do wykreślania odpowiedzi modelu układu ciągłego SYS na skok jednostkowy, gdzie T jest wektorem czasu symulacji. Dla modelu układu ciągłego T powinno mieć postać: Ti:dt:Tf, gdzie dt jest czasem dyskretyzacji modelu układu ciągłego. Dla modelu układu dyskretnego T powinno mieć postać: Ti:Ts:Tf, gdzie Ts jest czasem próbkowania. STEP(SYS1, SYS2,...,T) Funkcja służąca do wykreślania odpowiedzi modeli układów ciągłych SYS1, SYS2,... na skok jednostkowy, na jednym wykresie. T jest parametrem opcjonalnym. Możliwe jest określenie koloru, stylu i grubości linii dla każdego z modeli. Przykład 7 STEP(SYS1, 'r', SYS2, 'y', SYS3, 'g') [Y, T] = STEP(SYS) Funkcja służąca do znajdowania odpowiedzi modelu układu ciągłego SYS na skok jednostkowy Y i wektora czasu symulacji T. Nie jest kreślony wykres. [Y, T, X] = STEP(SYS) Funkcja służąca do znajdowania odpowiedzi modelu układu ciągłego SYS na skok jednostkowy Y, wektora czasu symulacji T i wektora stanu X dla modelu obiektu SYS opisanego równaniami stanu. impulse Funkcja służąca do wykreślania odpowiedzi modelu układu ciągłego na impuls jednostkowy (impuls Diraca) (analogiczną funkcją dla modeli układu dyskretnego jest dimpulse). IMPULSE(SYS) Funkcja służąca do wykreślania odpowiedzi modelu układu ciągłego SYS na impuls jednostkowy (impuls Diraca). IMPULSE(SYS, TFINAL) Funkcja służąca do wykreślania odpowiedzi modelu układu ciągłego SYS na impuls jednostkowy od chwili t = 0 do chwili t = TFINAL. Dla modelu układu dyskretnego TFINAL jest rozumiany jako liczba próbek. IMPULSE(SYS, T) Funkcja służąca do wykreślania odpowiedzi modelu układu ciągłego SYS na impuls jednostkowy, gdzie T jest wektorem czasu symulacji.
10 Dla modelu układu ciągłego T powinno mieć postać: Ti:dt:Tf, gdzie dt jest czasem dyskretyzacji modelu układu ciągłego. Dla modelu układu dyskretnego T powinno mieć postać: Ti:Ts:Tf, gdzie Ts jest czasem próbkowania. IMPULSE(SYS1, SYS2,...,T) Funkcja służąca do wykreślania odpowiedzi modeli układów ciągłych SYS1, SYS2,... na impuls jednostkowy, na jednym wykresie. T jest parametrem opcjonalnym. Możliwe jest określenie koloru, stylu i grubości linii dla każdego z modeli. Przykład 8 IMPULSE(SYS1, 'r', SYS2, 'y', SYS3, 'g') [Y, T] = IMPULSE(SYS) Funkcja służąca do znajdowania odpowiedzi modelu układu ciągłego SYS na impuls jednostkowy Y i wektora czasu symulacji T. Nie jest kreślony wykres. [Y, T, X] = IMPULSE(SYS) Funkcja służąca do znajdowania odpowiedzi modelu układu ciągłego SYS na impuls jednostkowy Y, wektora czasu symulacji T i wektora stanu X dla modelu obiektu SYS opisanego równaniami stanu. gensig Funkcja służąca do generowania sygnału okresowego. [U, T] = GENSIG(TYPE, TAU) Funkcja służąca do generowania sygnału okresowego klasy TYPE i okresie TAU. Parametr TYPE może przyjmować jedną z następujących wartości: TYPE = 'sin' sygnał sinusoidalny TYPE = 'square' sygnał w postaci kwadratu TYPE = 'pulse' sygnał impulsowy Funkcja zwraca wektor czasu T i wektor zawierający odpowiadające danym chwilom wartości sygnału Y. Generowane sygnały mają amplitudę jednostkową. [U, T] = GENSIG(TYPE, TAU, TF, TS) Funkcja służąca do generowania sygnału okresowego klasy TYPE i okresie TAU. TF jest czasem przerwy, zaś TS jest czasem próbkowania. initial Funkcja służąca do wykreślania odpowiedzi modelu układu opisanego równaniami stanu na warunek początkowy. INITIAL(SYS, X0) Funkcja służąca do wykreślania odpowiedzi modelu układu SYS opisanego równaniami stanu na warunek początkowy X0. Dla modelu układu ciągłego mamy:
11 x (t ) Ax(t ) Bu(t ) y(t ) Cx(t ) Du(t ) x 0 X0 Dla modelu układu dyskretnego mamy: x[ k 1] Ax[ k] Bu[ k] y[ k] Cx( k) Du[ k] x 0 X0 Czas symulacji i wektor czasu symulacji jest określany automatycznie. INITIAL(SYS, X0, TFINAL) Funkcja służąca do wykreślania odpowiedzi modelu układu SYS opisanego równaniami stanu na warunek początkowy X0 od chwili t = 0 do chwili t = TFINAL. Dla modelu układu dyskretnego TFINAL jest rozumiany jako liczba próbek. INITIAL(SYS, X0, T) Funkcja służąca do wykreślania odpowiedzi modelu układu SYS opisanego równaniami stanu na warunek początkowy X0, gdzie T jest wektorem czasu symulacji. Dla modelu układu ciągłego T powinno mieć postać: Ti:dt:Tf, gdzie dt jest czasem dyskretyzacji modelu układu ciągłego. Dla modelu układu dyskretnego T powinno mieć postać: Ti:Ts:Tf, gdzie Ts jest czasem próbkowania. INITIAL(SYS1, SYS2,...,X0, T) Funkcja służąca do wykreślania odpowiedzi modeli układów SYS1, SYS2,... opisanych równaniami stanu na warunek początkowy X0, na jednym wykresie. T jest parametrem opcjonalnym. Możliwe jest określenie koloru, stylu i grubości linii dla każdego z modeli. Przykład 9 INITIAL(SYS1, 'r', SYS2, 'y--', SYS3, 'gx', x0) [Y, T, X] = INITIAL(SYS, X0) Funkcja służąca do znajdowania odpowiedzi modelu układu ciągłego SYS opisanego równaniami stanu na warunek początkowy X0, gdzie T jest wektorem czasu symulacji, a X jest wektorem stanu. Nie jest kreślony wykres. lsim Funkcja służąca do wykreślania odpowiedzi modelu układu ciągłego na wymuszenie. LSIM(SYS, U, T) Funkcja służąca do wykreślania odpowiedzi modelu układu ciągłego SYS na wymuszenie U określone w chwilach T.
12 Przykład 10 T = 0:0.02:6; U = sin(t); LSIM(SYS, U, T) oznacza symulację odpowiedzi modelu układu ciągłego SYS o jednym wejściu na wymuszenie u t sin t dla t [0,6 ]. LSIM(SYS, U, T, X0) Funkcja służąca do wykreślania odpowiedzi modelu układu ciągłego SYS na wymuszenie U określone w chwilach T i warunki początkowe X0. Domyślnie X0 = 0. LSIM(SYS1, SYS2,..., U, T, X0) Funkcja służąca do wykreślania odpowiedzi modeli układów ciągłych SYS1, SYS2,... na wymuszenie U określone w chwilach T i warunki początkowe X0. X0 jest parametrem opcjonalnym. Możliwe jest określenie koloru, stylu i grubości linii dla każdego z modeli. Przykład 11 LSIM(SYS1, 'r', SYS2, 'y--', SYS3, 'gx', u, t) Y = LSIM(SYS, U, T) Funkcja służąca do znajdowania odpowiedzi modelu układu ciągłego SYS na wymuszenie U określone w chwilach T. Nie jest kreślony wykres. [Y, T, X] = LSIM(SYS, U, T, X0) Funkcja służąca do znajdowania odpowiedzi modelu układu ciągłego SYS na wymuszenie U określone w chwilach T, gdzie T jest wektorem czasu symulacji, a X jest wektorem stanu. Nie jest kreślony wykres. LSIM(SYS, U, T, X0, 'zoh') lub LSIM(SYS, U, T, X0, 'foh') Funkcja służąca do wykreślania odpowiedzi modelu układu ciągłego SYS na wymuszenie U określone w chwilach T i warunki początkowe X0. X0 jest parametrem opcjonalnym. Parametr domyślny zoh lub foh oznacza jak ma być interpolowany sygnał wejściowy pomiędzy czasem próbkowania (zoh zero-order hold, foh linear interpolation).
13 badanie charakterystyk częstotliwościowych układu liniowego: bode, bodemag, margin, nyquist bode Bode a). BODE(SYS) Bode a) modelu układu ciągłego SYS. Zakres częstotliwości jest i liczba punktów jest dobierana automatycznie. BODE(SYS, {WMIN, WMAX}) Bode a) modelu układu ciągłego SYS. Zakres częstotliwości znajduje się pomiędzy WMIN i WMAX (w rad/s). BODE(SYS, W) Bode a) modelu układu ciągłego SYS. Zakres częstotliwości jest określany i podaje się ją w wektorze W (w rad/s). Do generowania wektora W można wykorzystać polecenie LOGSPACE. BODE(SYS1, SYS2,..., W) Bode a) modeli układów ciągłych SYS1, SYS2,.... W jest parametrem opcjonalnym. Możliwe jest określenie koloru, stylu i grubości linii dla każdego z modeli. Przykład 12 BODE(SYS1, 'r', SYS2, 'y--', SYS3, 'gx') [MAG, PHASE] = BODE(SYS, W) lub [MAG, PHASE, W] = BODE(SYS) Funkcja służąca do znajdowania modułu i fazy. Nie jest kreślony wykres. Obliczone punkty charakterystyki zostają umieszczone w odpowiednich wektorach wektory MAG i PHASE zawierają wzmocnienie i fazę układu odpowiadającą częstotliwościom określonym odpowiednimi elementami wyjściowego wektora W. bodemag Funkcja służąca do wykreślania charakterystyk logarytmicznych modułu. BODEMAG(SYS) Funkcja służąca do wykreślania charakterystyk logarytmicznych modułu modelu układu ciągłego SYS. Zakres częstotliwości jest i liczba punktów jest dobierana automatycznie.
14 BODEMAG(SYS, {WMIN, WMAX}) Funkcja służąca do wykreślania charakterystyk logarytmicznych modułu modelu układu ciągłego SYS. Zakres częstotliwości znajduje się pomiędzy WMIN i WMAX (w rad/s). BODEMAG(SYS, W) Funkcja służąca do wykreślania charakterystyk logarytmicznych modułu modelu układu ciągłego SYS. Zakres częstotliwości jest określany i podaje się ją w wektorze W (w rad/s). Do generowania wektora W można wykorzystać polecenie LOGSPACE. BODEMAG(SYS1, SYS2,..., W) Funkcja służąca do wykreślania charakterystyk logarytmicznych modułu modeli układów ciągłych SYS1, SYS2,.... W jest parametrem opcjonalnym. Możliwe jest określenie koloru, stylu i grubości linii dla każdego z modeli. Przykład 13 BODEMAG(SYS1, 'r', SYS2, 'y--', SYS3, 'gx') margin Bode a) i obliczania wartości zapasu modułu i fazy. MARGIN(SYS) Bode a) i wykreślania wartości zapasu modułu i fazy modelu ciągłego układu otwartego SYS typu SISO. [Gm, Pm, Wcg, Wcp] = MARGIN(SYS) Funkcja służąca do obliczania wartości zapasu modułu Gm i fazy Pm (w stopniach), dla odpowiednich częstotliwości Wcg (dla Gm) i Wcp (dla Pm) modelu ciągłego układu otwartego SYS typu SISO. [Gm, Pm, Wcg, Wcp] = MARGIN(MAG, PHASE, W) Funkcja służąca do obliczania wartości zapasu modułu Gm i fazy Pm (w stopniach), dla odpowiednich częstotliwości Wcg (dla Gm) i Wcp (dla Pm) modelu ciągłego układu otwartego SYS typu SISO. nyquist Funkcja służąca do wykreślania charakterystyki amplitudowo fazowej (charakterystyki Nyquist a). NYQUIST(SYS) Funkcja służąca do wykreślania charakterystyki amplitudowo fazowej (charakterystyki Nyquist a) modelu układu ciągłego SYS. Zakres częstotliwości jest i liczba punktów jest dobierana automatycznie.
15 NYQUIST(SYS, {WMIN, WMAX}) Funkcja służąca do wykreślania charakterystyki amplitudowo fazowej (charakterystyki Nyquist a) modelu układu ciągłego SYS. Zakres częstotliwości znajduje się pomiędzy WMIN i WMAX (w rad/s). NYQUIST(SYS, W) Funkcja służąca do wykreślania charakterystyki amplitudowo fazowej (charakterystyki Nyquist a) modelu układu ciągłego SYS. Zakres częstotliwości jest określany i podaje się ją w wektorze W (w rad/s). Do generowania wektora W można wykorzystać polecenie LOGSPACE. NYQUIST(SYS1, SYS2,..., W) Funkcja służąca do wykreślania charakterystyk amplitudowo fazowych (charakterystyk Nyquist a) modeli układów ciągłych SYS1, SYS2,.... W jest parametrem opcjonalnym. Możliwe jest określenie koloru, stylu i grubości linii dla każdego z modeli. Przykład 14 NYQUIST(SYS1, 'r', SYS2, 'y--', SYS3, 'gx') [RE, IM] = NYQUIST(SYS, W) lub [RE, IM, W] = NYQUIST(SYS) Funkcja służąca do znajdowania części rzeczywistej i urojonej. Nie jest kreślony wykres. Obliczone punkty charakterystyki zostają umieszczone w odpowiednich wektorach wektory RE i IM zawierają części rzeczywiste i urojone liczb opisujących transmitancję widmową dla odpowiednich częstotliwości określonych odpowiednimi elementami wyjściowego wektora W. Zmiana postaci obiektu: c2d, d2c, c2dm, d2cm, d2d c2d Funkcja służąca do konwersji dynamicznego liniowego modelu obiektu ciągłego na model dyskretny. SYSD = C2D(SYSC, TS, METODA ) Funkcja służąca do konwersji dynamicznego liniowego modelu obiektu ciągłego SYSC na model dyskretny SYSD. Okres próbkowania wynosi TS. Parametr METODA służy do wyboru metody dyskretyzacji (parametr opcjonalny): ZOH (ang. Zero Order Hold) aproksymacja przebiegów ciągłych metodą prostokątów. FOH (ang. First Order Hold) aproksymacja przebiegów ciągłych metodą trójkątów. IMP (ang. Impulse Inwariant Discretization) aproksymacja przebiegów ciągłych mająca na celu jak najlepsze przybliżenie przebiegów ciągłych w odpowiedzi na impuls jednostkowy.
16 TUSTIN aproksymacja przebiegów ciągłych metodą trapezów (aproksymacja bilingowa Tustina). Wartości w chwilach próbkowania są równe wartościom na przebiegu ciągłym. PREWARP w wyniku dyskretyzacji przebiegu ciągłego następuje zmiana skali pulsacji (tzw. efekt warping). Metoda ta dokonuje aproksymacji, która eliminuje zmianę skali dla zadanej pulsacji WC. Pulsacja WC jest dodatkowym parametrem: SYSD = C2D(SYSC,TS, PREWARP,WC) MATCHED metoda biegunów i zer (tylko dla układów typu SISO). Domyślną metodą dyskretyzacji jest ZOH. Dla modelu obiektu ciągłego SYSC opisanego w przestrzeni stanu dwie z metod dyskretyzacji ( ZOH i FOH ) zwracają macierz G, która przypisuje ciągłe warunki początkowe dyskretnym warunkom początkowym. W przypadku, gdy x 0 i u 0 są odpowiednio warunkami początkowymi dla zmiennych stanu i wejścia modelu obiektu ciągłego to warunki początkowe dla modelu dyskretnego SYSD wynoszą: xd 0 = G*[x 0 ; u 0 ] ud 0 = u 0 zatem należy użyć polecenia o następującej składni: [SYSD, G]= C2D(SYSC, TS, METODA ) d2c Funkcja służąca do konwersji dynamicznego liniowego modelu obiektu dyskretnego na model ciągły. SYSC = D2C(SYSD, METODA ) Funkcja służąca do konwersji dynamicznego liniowego modelu obiektu dyskretnego SYSD na model ciągły SYSC. Parametr METODA służy do wyboru metody dyskretyzacji (parametr opcjonalny) ( ZOH, TUSTIN, PREWARP, MATCHED ). Domyślną metodą dyskretyzacji jest ZOH. Ograniczenia związane z poleceniem d2c: Nie działa, gdy model dyskretny posiada bieguny zerowe (dla metody dyskretyzacji ZOH ). Ujemne bieguny rzeczywiste w dziedzinie zmiennej z są przypisywane do par biegunów zespolonych w dziedzinie zmiennej s. Powoduje to powstanie modeli ciągłych o wyższej dynamice. c2dm Funkcja służąca do konwersji dynamicznego liniowego modelu obiektu ciągłego opisanego w przestrzeni stanu lub transmitancją na model dyskretny. [Ad, Bd, Cd, Dd] = C2DM(A, B, C, D, TS, METODA ) Funkcja służąca do konwersji dynamicznego liniowego modelu obiektu ciągłego opisanego macierzami A, B, C i D na model dyskretny opisany macierzami Ad, Bd, Cd i Dd. Okres próbkowania wynosi TS. Parametr METODA służy do wyboru metody dyskretyzacji (parametr opcjonalny) ( ZOH, FOH, TUSTIN, PREWARP, MATCHED ). Domyślną metodą dyskretyzacji jest ZOH.
17 [NUMd, DENd] = C2DM(NUM, DEN, TS, METODA ) Funkcja służąca do konwersji dynamicznego liniowego modelu obiektu ciągłego opisanego transmitancją ciągłą (NUM i DEN to macierze współczynników odpowiednio NUM(s ) licznika i mianownika transmitancji: G(s ), uporządkowane według DEN(s ) malejących potęg s) na model dyskretny opisany transmitancją dyskretną (NUMd i DENd to macierze współczynników odpowiednio licznika i mianownika transmitancji: NUMd () z Gz (), uporządkowane według malejących potęg z). Okres próbkowania DENd () z wynosi TS. Parametr METODA służy do wyboru metody dyskretyzacji (parametr opcjonalny) ( ZOH, FOH, TUSTIN, PREWARP, MATCHED ). Domyślną metodą dyskretyzacji jest ZOH. d2cm Funkcja służąca do konwersji dynamicznego liniowego modelu obiektu dyskretnego opisanego w przestrzeni stanu lub transmitancją na model ciągły. [Ac, Bc, Cc, Dc] = D2CM(A, B, C, D, TS, METODA ) Funkcja służąca do konwersji dynamicznego liniowego modelu obiektu dyskretnego opisanego macierzami A, B, C i D na model ciągły opisany macierzami Ac, Bc, Cc i Dc. Okres próbkowania wynosi TS. Parametr METODA służy do wyboru metody dyskretyzacji (parametr opcjonalny) ( ZOH, TUSTIN, PREWARP, MATCHED ). Domyślną metodą dyskretyzacji jest ZOH. [NUMc, DENc] = D2CM(NUM, DEN, TS, METODA ) Funkcja służąca do konwersji dynamicznego liniowego modelu obiektu dyskretnego opisanego transmitancją dyskretną (NUM i DEN to macierze współczynników NUM () z odpowiednio licznika i mianownika transmitancji: Gz (), uporządkowane DEN () z według malejących potęg z) na model ciągły opisany transmitancją ciągłą (NUMc i DENc to macierze współczynników odpowiednio licznika i mianownika transmitancji: NUMc() s Gs (), uporządkowane według malejących potęg s). Okres próbkowania DENc() s wynosi TS. Parametr METODA służy do wyboru metody dyskretyzacji (parametr opcjonalny) ( ZOH, TUSTIN, PREWARP, MATCHED ). Domyślną metodą dyskretyzacji jest ZOH. d2d Funkcja służąca do konwersji dynamicznego liniowego modelu obiektu dyskretnego do modelu obiektu dyskretnego z innym okresem próbkowania. SYS = D2D(SYS, TS) Funkcja służąca do konwersji dynamicznego liniowego modelu obiektu dyskretnego SYS do modelu obiektu dyskretnego z innym okresem próbkowania TS.
18 badanie charakterystyk czasowych dyskretnego układu liniowego: dstep, dimpulse, dinitial, dlsim dstep Funkcja służąca do wykreślania odpowiedzi jednowymiarowego modelu układu dyskretnego na skok jednostkowy. DSTEP(A, B, C, D, IU) Funkcja służąca do wykreślania odpowiedzi jednowymiarowego modelu układu dyskretnego opisanego macierzami A, B, C i D na skok jednostkowy, liczonej względem wejścia (sterowania) o numerze IU. Parametr IU jest ustalany automatycznie. DSTEP(NUM, DEN) Funkcja służąca do wykreślania odpowiedzi jednowymiarowego modelu układu dyskretnego opisanego transmitancją dyskretną na skok jednostkowy (NUM i DEN to macierze współczynników odpowiednio licznika i mianownika transmitancji: NUM () z Gz (), uporządkowane według malejących potęg z). DEN () z DSTEP(A, B, C, D, IU, N) Funkcja służąca do wykreślania odpowiedzi jednowymiarowego modelu układu dyskretnego opisanego macierzami A, B, C i D na skok jednostkowy, liczonej względem wejścia (sterowania) o numerze IU. Parametr N oznacza zadeklarowaną liczbę punktów. DSTEP(NUM, DEN, N) Funkcja służąca do wykreślania odpowiedzi jednowymiarowego modelu układu dyskretnego opisanego transmitancją dyskretną na skok jednostkowy. Parametr N oznacza zadeklarowaną liczbę punktów. [Y, X] = DSTEP(A, B, C, D,...) Funkcja służąca do znajdowania odpowiedzi jednowymiarowego modelu układu dyskretnego opisanego macierzami A, B, C i D na skok jednostkowy, liczonej względem wejścia (sterowania) o numerze IU. Wyniki przedstawiane są w postaci macierzy wyjścia Y i stanu X. Nie jest kreślony wykres. [Y, X] = DSTEP(NUM, DEN,...) Funkcja służąca do wykreślania odpowiedzi jednowymiarowego modelu układu dyskretnego opisanego transmitancją dyskretną na skok jednostkowy. Wyniki przedstawiane są w postaci macierzy wyjścia Y i stanu X. Nie jest kreślony wykres. dimpulse Funkcja służąca do wykreślania odpowiedzi modelu układu dyskretnego na impuls jednostkowy (delta Kroneckera). DIMPULSE(A, B, C, D, IU) Funkcja służąca do wykreślania odpowiedzi jednowymiarowego modelu układu dyskretnego opisanego macierzami A, B, C i D na impuls jednostkowy, liczonej względem wejścia (sterowania) o numerze IU. Parametr IU jest ustalany automatycznie.
19 DIMPULSE(NUM, DEN) Funkcja służąca do wykreślania odpowiedzi jednowymiarowego modelu układu dyskretnego opisanego transmitancją dyskretną na impuls jednostkowy (NUM i DEN to macierze współczynników odpowiednio licznika i mianownika transmitancji: NUM () z Gz (), uporządkowane według malejących potęg z). DEN () z DIMPULSE(A, B, C, D, IU, N) Funkcja służąca do wykreślania odpowiedzi jednowymiarowego modelu układu dyskretnego opisanego macierzami A, B, C i D na impuls jednostkowy, liczonej względem wejścia (sterowania) o numerze IU. Parametr N oznacza zadeklarowaną liczbę punktów (próbek). DIMPULSE(NUM, DEN, N) Funkcja służąca do wykreślania odpowiedzi jednowymiarowego modelu układu dyskretnego opisanego transmitancją dyskretną na impuls jednostkowy. Parametr N oznacza zadeklarowaną liczbę punktów (próbek). [Y, X] = DIMPULSE(A, B, C, D,...) Funkcja służąca do znajdowania odpowiedzi jednowymiarowego modelu układu dyskretnego opisanego macierzami A, B, C i D na impuls jednostkowy, liczonej względem wejścia (sterowania) o numerze IU. Wyniki przedstawiane są w postaci macierzy wyjścia Y i stanu X. Nie jest kreślony wykres. [Y, X] = DIMPULSE(NUM, DEN,...) Funkcja służąca do wykreślania odpowiedzi jednowymiarowego modelu układu dyskretnego opisanego transmitancją dyskretną na impuls jednostkowy. Wyniki przedstawiane są w postaci macierzy wyjścia Y i stanu X. Nie jest kreślony wykres. dinitial Funkcja służąca do wykreślania odpowiedzi modelu układu dyskretnego opisanego równaniami stanu na warunek początkowy. DINITIAL(A, B, C, D, X0) Funkcja służąca do wykreślania odpowiedzi modelu układu dyskretnego opisanego macierzami A, B, C i D na warunek początkowy X0. Dla modelu układu dyskretnego mamy: x[ k 1] Ax[ k] Bu[ k] y[ k] Cx( k) Du[ k] x 0 X0 Liczba próbek k jest określana automatycznie. DINITIAL(A, B, C, D, X0, N) Funkcja służąca do wykreślania odpowiedzi modelu układu dyskretnego opisanego macierzami A, B, C i D na warunek początkowy X0. Parametr N oznacza zadeklarowaną liczbę punktów (próbek).
20 [Y, X, N] = DINITIAL(A, B, C, D, X0,...) Funkcja służąca do znajdowania odpowiedzi modelu układu dyskretnego opisanego macierzami A, B, C i D na warunek początkowy X0. Wyniki przedstawiane są w postaci macierzy wyjścia Y, stanu X i liczby punktów (próbek). Nie jest kreślony wykres. dlsim Funkcja służąca do wykreślania odpowiedzi modelu układu dyskretnego na wymuszenie. DLSIM(A, B, C, D, U) Funkcja służąca do wykreślania odpowiedzi modelu układu dyskretnego opisanego macierzami A, B, C i D na wymuszenie U. DLSIM(A, B, C, D, U, X0) Funkcja służąca do wykreślania odpowiedzi modelu układu dyskretnego opisanego macierzami A, B, C i D na wymuszenie U i warunki początkowe X0. DLSIM(NUM, DEN, U) Funkcja służąca do wykreślania odpowiedzi modelu układu dyskretnego opisanego transmitancją dyskretną (NUM i DEN to macierze współczynników odpowiednio licznika NUM () z i mianownika transmitancji: Gz (), uporządkowane według malejących potęg DEN () z z) na wymuszenie U. [Y, X] = DLSIM(A, B, C, D, U) Funkcja służąca do znajdowania odpowiedzi modelu układu dyskretnego opisanego macierzami A, B, C i D na wymuszenie U. Wyniki przedstawiane są w postaci macierzy wyjścia Y i stanu X. Nie jest kreślony wykres. [Y, X] = DLSIM(NUM, DEN, U) Funkcja służąca do znajdowania odpowiedzi modelu układu dyskretnego opisanego transmitancją dyskretną na wymuszenie U. Wyniki przedstawiane są w postaci macierzy wyjścia Y i stanu X. Nie jest kreślony wykres. badanie charakterystyk częstotliwościowych dyskretnego układu liniowego: dbode, dnyquist dbode Bode a) jednowymiarowego modelu układu dyskretnego. DBODE(A, B, C, D, TS, IU) Bode a) modelu układu dyskretnego opisanego macierzami A, B, C i D, liczonych względem wejścia (sterowania) o numerze IU. Okres próbkowania wynosi TS. Zakres częstotliwości jest i liczba punktów próbek) jest dobierana automatycznie.
21 DBODE(NUM, DEN, TS) Bode a) modelu układu dyskretnego opisanego transmitancją dyskretną (NUM i DEN to macierze współczynników odpowiednio licznika i mianownika transmitancji: NUM () z Gz (), uporządkowane według malejących potęg z). DEN () z DBODE(A, B, C, D, TS, IU, W) Bode a) modelu układu dyskretnego opisanego macierzami A, B, C i D, liczonych względem wejścia (sterowania) o numerze IU. Okres próbkowania wynosi TS. Zakres częstotliwości jest określany i podaje się go w wektorze W (w rad/s). Do generowania wektora W można wykorzystać polecenie LOGSPACE. DBODE(NUM, DEN, TS, W) Bode a) modelu układu dyskretnego opisanego transmitancją dyskretną. Zakres częstotliwości jest określany i podaje się go w wektorze W (w rad/s). [MAG, PHASE, W] = DBODE(A, B, C, D, TS,...) Funkcja służąca do znajdowania charakterystyk logarytmicznych (charakterystyk Bode a) modelu układu dyskretnego opisanego macierzami A, B, C i D. Nie jest kreślony wykres. Obliczone punkty charakterystyki zostają umieszczone w wektorach wektory MAG i PHASE zawierają wzmocnienie i fazę układu odpowiadającą częstotliwościom określonym odpowiednimi elementami wyjściowego wektora W. [MAG, PHASE, W] = DBODE(NUM, DEN, TS,...) Funkcja służąca do znajdowania charakterystyk logarytmicznych (charakterystyk Bode a) modelu układu dyskretnego opisanego transmitancją dyskretną. Nie jest kreślony wykres. Obliczone punkty charakterystyki zostają umieszczone w wektorach wektory MAG i PHASE zawierają wzmocnienie i fazę układu odpowiadającą częstotliwościom określonym odpowiednimi elementami wyjściowego wektora W. dnyquist Funkcja służąca do wykreślania charakterystyk amplitudowo fazowych (charakterystyk Nyquista) jednowymiarowego modelu układu dyskretnego. DNYQUIST(A, B, C, D, TS, IU) Funkcja służąca do wykreślania charakterystyk amplitudowo fazowych (charakterystyk Nyquista) modelu układu dyskretnego opisanego macierzami A, B, C i D, liczonych względem wejścia (sterowania) o numerze IU. Okres próbkowania wynosi TS. Zakres częstotliwości jest i liczba punktów próbek) jest dobierana automatycznie. DNYQUIST(NUM, DEN, TS) Funkcja służąca do wykreślania charakterystyk amplitudowo fazowych (charakterystyk Nyquista) modelu układu dyskretnego opisanego transmitancją dyskretną (NUM i DEN to macierze współczynników odpowiednio licznika i mianownika NUM () z transmitancji: Gz (), uporządkowane według malejących potęg z). DEN () z
22 DNYQUIST(A, B, C, D, TS, IU, W) Funkcja służąca do wykreślania charakterystyk amplitudowo fazowych (charakterystyk Nyquista) modelu układu dyskretnego opisanego macierzami A, B, C i D, liczonych względem wejścia (sterowania) o numerze IU. Okres próbkowania wynosi TS. Zakres częstotliwości jest określany i podaje się go w wektorze W (w rad/s). Do generowania wektora W można wykorzystać polecenie LOGSPACE. DNYQUIST(NUM, DEN, TS, W) Funkcja służąca do wykreślania charakterystyk amplitudowo fazowych (charakterystyk Nyquista) modelu układu dyskretnego opisanego transmitancją dyskretną. Zakres częstotliwości jest określany i podaje się go w wektorze W (w rad/s). [RE, IM, W] = DNYQUIST(A, B, C, D, TS,...) Funkcja służąca do znajdowania charakterystyk amplitudowo fazowych (charakterystyk Nyquista) modelu układu dyskretnego opisanego macierzami A, B, C i D. Nie jest kreślony wykres. Obliczone punkty charakterystyki zostają umieszczone w odpowiednich wektorach wektory RE i IM zawierają części rzeczywiste i urojone liczb opisujących transmitancję widmową dla odpowiednich częstotliwości określonych odpowiednimi elementami wyjściowego wektora W. [RE, IM, W] = DNYQUIST(NUM, DEN, TS,...) Funkcja służąca do znajdowania amplitudowo fazowych (charakterystyk Nyquista) modelu układu dyskretnego opisanego transmitancją dyskretną. Nie jest kreślony wykres. Obliczone punkty charakterystyki zostają umieszczone w odpowiednich wektorach wektory RE i IM zawierają części rzeczywiste i urojone liczb opisujących transmitancję widmową dla odpowiednich częstotliwości określonych odpowiednimi elementami wyjściowego wektora W. Bibliografia Brzózka J. Ćwiczenia z automatyki w Matlabie i Simulinku. Wydawnictwo MIKOM, Brzózka J., Dorobczyński L. Matlab środowisko obliczeń naukowo technicznych. Wydawnictwo MIKOM, Mrozek B., Mrozek Z. Matlab i Simulink. Poradnik użytkownika. Wydanie II. Wydawnictwo HELION, The Mathworks. Control System Toolbox for use with Matlab. Natick, Zalewski A., Cegieła R. Matlab obliczenia numeryczne i ich zastosowania. Wydawnictwo NAKOM, 1996.
Laboratorium nr 3. Projektowanie układów automatyki z wykorzystaniem Matlaba i Simulinka
 Laboratorium nr 3. Cele ćwiczenia Projektowanie układów automatyki z wykorzystaniem Matlaba i Simulinka poznanie sposobów tworzenia liniowych modeli układów automatyki, zmiana postaci modeli, tworzenie
Laboratorium nr 3. Cele ćwiczenia Projektowanie układów automatyki z wykorzystaniem Matlaba i Simulinka poznanie sposobów tworzenia liniowych modeli układów automatyki, zmiana postaci modeli, tworzenie
Macierz A nazywamy macierzą systemu, a B macierzą wejścia.
 Dwiczenia 3 Automatyka i robotyka Równaniem stanu. Macierz A nazywamy macierzą systemu, a B macierzą wejścia. Równaniem wyjścia. Do opisu układu możemy użyd jednocześnie równania stanu i równania wyjścia
Dwiczenia 3 Automatyka i robotyka Równaniem stanu. Macierz A nazywamy macierzą systemu, a B macierzą wejścia. Równaniem wyjścia. Do opisu układu możemy użyd jednocześnie równania stanu i równania wyjścia
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 10. Dyskretyzacja
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 10. Dyskretyzacja
Sterowaniem nazywamy celowe oddziaływanie na przebieg procesów. Można wyróżnid ręczne oraz automatyczne.
 Dwiczenia 2 Automatyka i robotyka Wstęp Podstawowe pojęcia: Sterowaniem nazywamy celowe oddziaływanie na przebieg procesów. Można wyróżnid ręczne oraz automatyczne. Układ wyodrębniony ze środowiska układ
Dwiczenia 2 Automatyka i robotyka Wstęp Podstawowe pojęcia: Sterowaniem nazywamy celowe oddziaływanie na przebieg procesów. Można wyróżnid ręczne oraz automatyczne. Układ wyodrębniony ze środowiska układ
Teoria sterowania - studia niestacjonarne AiR 2 stopień
 Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
Teoria sterowania - studia niestacjonarne AiR stopień Kazimierz Duzinkiewicz, dr hab. Inż. Katedra Inżynerii Systemów Sterowania Wykład 4-06/07 Transmitancja widmowa i charakterystyki częstotliwościowe
Podstawy środowiska Matlab
 Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Automatyki i Robotyki Podstawy środowiska Matlab Poniżej przedstawione jest użycie podstawowych poleceń w środowisku
Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Automatyki i Robotyki Podstawy środowiska Matlab Poniżej przedstawione jest użycie podstawowych poleceń w środowisku
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 2. REPREZENTACJA
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 2. REPREZENTACJA
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania. Podstawy Automatyki
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podsta Automatyki Transmitancja operatorowa i widmowa systemu, znajdowanie odpowiedzi w dziedzinie s i w
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podsta Automatyki Transmitancja operatorowa i widmowa systemu, znajdowanie odpowiedzi w dziedzinie s i w
Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów
 Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Sterowania Procesami Ciągłych Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów. Obliczanie
Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Laboratorium Sterowania Procesami Ciągłych Projektowanie układów metodą sprzężenia od stanu - metoda przemieszczania biegunów. Obliczanie
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE
 CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE Do opisu członów i układów automatyki stosuje się, oprócz transmitancji operatorowej (), tzw. transmitancję widmową. Transmitancję widmową () wyznaczyć można na podstawie
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
analogowego regulatora PID doboru jego nastaw i przetransformowanie go na cyfrowy regulator PID, postępując według następujących podpunktów:
 Cel projektu. Projekt składa się z dwóch podstawowych zadań, mających na celu zaprojektowanie dla danej transmitancji: G( s) = m 2 s 2 e + m s + sτ gdzie wartości m 2 = 27, m = 2, a τ = 4. G( s) = 27s
Cel projektu. Projekt składa się z dwóch podstawowych zadań, mających na celu zaprojektowanie dla danej transmitancji: G( s) = m 2 s 2 e + m s + sτ gdzie wartości m 2 = 27, m = 2, a τ = 4. G( s) = 27s
Sposoby modelowania układów dynamicznych. Pytania
 Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Opis matematyczny. Równanie modulatora. Charakterystyka statyczna. Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy. dla 0 v c.
 Opis matematyczny Równanie modulatora Charakterystyka statyczna d t = v c t V M dla 0 v c t V M D 1 V M V c Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy v c (t )=V c + v c (t ) d (t
Opis matematyczny Równanie modulatora Charakterystyka statyczna d t = v c t V M dla 0 v c t V M D 1 V M V c Po wprowadzeniu niewielkich odchyłek od ustalonego punktu pracy v c (t )=V c + v c (t ) d (t
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2018 Wstęp Stabilność O układzie możemy mówić, że jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie)
KOMPUTERY W STEROWANIU. Ćwiczenie 5 Projektowanie kompensatora cyfrowego metodą symulacji
 Wydział Elektryczny Zespół Automatyki (ZTMAiPC) KOMPUTERY W STEROWANIU Ćwiczenie 5 Projektowanie kompensatora cyfrowego metodą symulacji. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodami projektowania
Wydział Elektryczny Zespół Automatyki (ZTMAiPC) KOMPUTERY W STEROWANIU Ćwiczenie 5 Projektowanie kompensatora cyfrowego metodą symulacji. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodami projektowania
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność - definicja 1 O układzie możemy mówić, że jest stabilny gdy wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność - definicja 1 O układzie możemy mówić, że jest stabilny gdy wytrącony ze stanu równowagi
Laboratorium z automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z automatyki Algebra schematów blokowych, wyznaczanie odpowiedzi obiektu na sygnał zadany, charakterystyki częstotliwościowe Kierunek studiów:
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z automatyki Algebra schematów blokowych, wyznaczanie odpowiedzi obiektu na sygnał zadany, charakterystyki częstotliwościowe Kierunek studiów:
PODSTAWY AUTOMATYKI. MATLAB - instrukcje i funkcje zewnętrzne. Grafika w Matlabie. Wprowadzenie do biblioteki Control System Toolbox.
 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - instrukcje i funkcje zewnętrzne. Grafika w Matlabie. Wprowadzenie do biblioteki Control System Toolbox.
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - instrukcje i funkcje zewnętrzne. Grafika w Matlabie. Wprowadzenie do biblioteki Control System Toolbox.
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Teoria sterowania MATLAB funkcje zewnętrzne (m-pliki, funkcje) Materiały pomocnicze do ćwiczeń laboratoryjnych
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Teoria sterowania MATLAB funkcje zewnętrzne (m-pliki, funkcje) Materiały pomocnicze do ćwiczeń laboratoryjnych
ELEMENTY AUTOMATYKI PRACA W PROGRAMIE SIMULINK 2013
 SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
układu otwartego na płaszczyźnie zmiennej zespolonej. Sformułowane przez Nyquista kryterium stabilności przedstawia się następująco:
 Kryterium Nyquista Kryterium Nyquista pozwala na badanie stabilności jednowymiarowego układu zamkniętego na podstawie przebiegu wykresu funkcji G o ( jω) układu otwartego na płaszczyźnie zmiennej zespolonej.
Kryterium Nyquista Kryterium Nyquista pozwala na badanie stabilności jednowymiarowego układu zamkniętego na podstawie przebiegu wykresu funkcji G o ( jω) układu otwartego na płaszczyźnie zmiennej zespolonej.
AKADEMIA MORSKA W SZCZECINIE WI-ET / IIT / ZTT. Instrukcja do zajęc laboratoryjnych nr 6 AUTOMATYKA
 AKADEMIA MORSKA W SZCZECINIE WI-ET / IIT / ZTT Instrukcja do zajęc laboratoryjnych nr 6 AUTOMATYKA II rok Kierunek Transport Temat: Transmitancja operatorowa. Badanie odpowiedzi układów automatyki. Opracował
AKADEMIA MORSKA W SZCZECINIE WI-ET / IIT / ZTT Instrukcja do zajęc laboratoryjnych nr 6 AUTOMATYKA II rok Kierunek Transport Temat: Transmitancja operatorowa. Badanie odpowiedzi układów automatyki. Opracował
Tematyka egzaminu z Podstaw sterowania
 Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Teoria sterowania Odpowiedzi czasowe ciągłych i dyskretnych systemów dynamicznych Zadania do ćwiczeń laboratoryjnych
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Teoria sterowania Odpowiedzi czasowe ciągłych i dyskretnych systemów dynamicznych Zadania do ćwiczeń laboratoryjnych
Systemy. Krzysztof Patan
 Systemy Krzysztof Patan Systemy z pamięcią System jest bez pamięci (statyczny), jeżeli dla dowolnej chwili t 0 wartość sygnału wyjściowego y(t 0 ) zależy wyłącznie od wartości sygnału wejściowego w tej
Systemy Krzysztof Patan Systemy z pamięcią System jest bez pamięci (statyczny), jeżeli dla dowolnej chwili t 0 wartość sygnału wyjściowego y(t 0 ) zależy wyłącznie od wartości sygnału wejściowego w tej
Stabilność. Krzysztof Patan
 Stabilność Krzysztof Patan Pojęcie stabilności systemu Rozważmy obiekt znajdujący się w punkcie równowagi Po przyłożeniu do obiektu siły F zostanie on wypchnięty ze stanu równowagi Jeżeli po upłynięciu
Stabilność Krzysztof Patan Pojęcie stabilności systemu Rozważmy obiekt znajdujący się w punkcie równowagi Po przyłożeniu do obiektu siły F zostanie on wypchnięty ze stanu równowagi Jeżeli po upłynięciu
Podstawowe człony dynamiczne
 . Człon proporcjonalny 2. Człony całkujący idealny 3. Człon inercyjny Podstawowe człony dynamiczne charakterystyki czasowe = = = + 4. Człony całkujący rzeczywisty () = + 5. Człon różniczkujący rzeczywisty
. Człon proporcjonalny 2. Człony całkujący idealny 3. Człon inercyjny Podstawowe człony dynamiczne charakterystyki czasowe = = = + 4. Człony całkujący rzeczywisty () = + 5. Człon różniczkujący rzeczywisty
PODSTAWY AUTOMATYKI. MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
Transmitancje układów ciągłych
 Transmitancja operatorowa, podstawowe człony liniowe Transmitancja operatorowa (funkcja przejścia, G(s)) stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego
Transmitancja operatorowa, podstawowe człony liniowe Transmitancja operatorowa (funkcja przejścia, G(s)) stosunek transformaty Laplace'a sygnału wyjściowego do transformaty Laplace'a sygnału wejściowego
Układ regulacji automatycznej (URA) kryteria stabilności
 Układ regulacji automatycznej (URA) kryteria stabilności y o e G c (s) z z 2 u G o (s) y () = () ()() () H(s) oraz jego wartością w stanie ustalonym. Transmitancja układu otwartego regulacji: - () = ()
Układ regulacji automatycznej (URA) kryteria stabilności y o e G c (s) z z 2 u G o (s) y () = () ()() () H(s) oraz jego wartością w stanie ustalonym. Transmitancja układu otwartego regulacji: - () = ()
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Technologie informatyczne Wprowadzenie do Simulinka w środowisku MATLAB Pytania i zadania do ćwiczeń laboratoryjnych
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Technologie informatyczne Wprowadzenie do Simulinka w środowisku MATLAB Pytania i zadania do ćwiczeń laboratoryjnych
ĆWICZENIE 6 Transmitancje operatorowe, charakterystyki częstotliwościowe układów aktywnych pierwszego, drugiego i wyższych rzędów
 ĆWICZENIE 6 Transmitancje operatorowe, charakterystyki częstotliwościowe układów aktywnych pierwszego, drugiego i wyższych rzędów. Cel ćwiczenia Badanie układów pierwszego rzędu różniczkującego, całkującego
ĆWICZENIE 6 Transmitancje operatorowe, charakterystyki częstotliwościowe układów aktywnych pierwszego, drugiego i wyższych rzędów. Cel ćwiczenia Badanie układów pierwszego rzędu różniczkującego, całkującego
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 7. Metoda projektowania
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 7. Metoda projektowania
ZASTOSOWANIA PRZEKSZTAŁCENIA ZET
 CPS - - ZASTOSOWANIA PRZEKSZTAŁCENIA ZET Rozwiązywanie równań różnicowych Dyskretny system liniowy-stacjonarny można opisać równaniem różnicowym w postaci ogólnej N M aky[ n k] bkx[ n k] k k Przekształcenie
CPS - - ZASTOSOWANIA PRZEKSZTAŁCENIA ZET Rozwiązywanie równań różnicowych Dyskretny system liniowy-stacjonarny można opisać równaniem różnicowym w postaci ogólnej N M aky[ n k] bkx[ n k] k k Przekształcenie
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra InŜynierii Systemów Sterowania Podstawy Automatyki
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra InŜynierii Systemów Sterowania Podstawy Automatyki Stabilność systemów sterowania kryterium Nyquist a Materiały pomocnicze do ćwiczeń termin
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra InŜynierii Systemów Sterowania Podstawy Automatyki Stabilność systemów sterowania kryterium Nyquist a Materiały pomocnicze do ćwiczeń termin
Ćwiczenie nr 6 Charakterystyki częstotliwościowe
 Wstęp teoretyczny Ćwiczenie nr 6 Charakterystyki częstotliwościowe 1 Cel ćwiczenia Celem ćwiczenia jest wyznaczenie charakterystyk częstotliwościowych układu regulacji oraz korekta nastaw regulatora na
Wstęp teoretyczny Ćwiczenie nr 6 Charakterystyki częstotliwościowe 1 Cel ćwiczenia Celem ćwiczenia jest wyznaczenie charakterystyk częstotliwościowych układu regulacji oraz korekta nastaw regulatora na
Języki Modelowania i Symulacji 2018 Podstawy Automatyki Wykład 4
 Języki Modelowania i Symulacji 2018 Podstawy Automatyki Wykład 4 dr inż. Marcin Ciołek Katedra Systemów Automatyki Wydział ETI, Politechnika Gdańska Języki Modelowania i Symulacji dr inż. Marcin Ciołek
Języki Modelowania i Symulacji 2018 Podstawy Automatyki Wykład 4 dr inż. Marcin Ciołek Katedra Systemów Automatyki Wydział ETI, Politechnika Gdańska Języki Modelowania i Symulacji dr inż. Marcin Ciołek
Badanie stabilności liniowych układów sterowania
 Badanie stabilności liniowych układów sterowania ver. 26.2-6 (26-2-7 4:6). Badanie stabilności liniowych układów sterowania poprzez analizę równania charakterystycznego. Układ zamknięty liniowy i stacjonarny
Badanie stabilności liniowych układów sterowania ver. 26.2-6 (26-2-7 4:6). Badanie stabilności liniowych układów sterowania poprzez analizę równania charakterystycznego. Układ zamknięty liniowy i stacjonarny
WPROWADZENIE DO ŚRODOWISKA SCILAB
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki WPROWADZENIE DO ŚRODOWISKA SCILAB Materiały pomocnicze do ćwiczeń laboratoryjnych Opracowanie: Paweł Lieder Gdańsk, 007 Podstawy pracy z Scilab.
Politechnika Gdańska Wydział Elektrotechniki i Automatyki WPROWADZENIE DO ŚRODOWISKA SCILAB Materiały pomocnicze do ćwiczeń laboratoryjnych Opracowanie: Paweł Lieder Gdańsk, 007 Podstawy pracy z Scilab.
( 1+ s 1)( 1+ s 2)( 1+ s 3)
 Kryteria stabilności przykład K T (s)= (s+1)(s+2)(s+3) = K /6 1 1+T (s) = (s+1)(s+2)(s+3) K +6+11s+6s 2 +s 3 ( 1+ s 1)( 1+ s 2)( 1+ s 3) Weźmy K =60: 1 1+T (s) =(s+1)(s+2)(s+3) 66+11s+6s 2 +s =(s+1)(s+2)(s+3)
Kryteria stabilności przykład K T (s)= (s+1)(s+2)(s+3) = K /6 1 1+T (s) = (s+1)(s+2)(s+3) K +6+11s+6s 2 +s 3 ( 1+ s 1)( 1+ s 2)( 1+ s 3) Weźmy K =60: 1 1+T (s) =(s+1)(s+2)(s+3) 66+11s+6s 2 +s =(s+1)(s+2)(s+3)
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 6. Badanie
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 6. Badanie
Instrukcja do laboratorium z cyfrowego przetwarzania sygnałów. Ćwiczenie 3. Transformata Z; blokowe struktury opisujące filtr
 Instrukcja do laboratorium z cyfrowego przetwarzania sygnałów Ćwiczenie Transformata ; blokowe struktury opisujące filtr Przemysław Korohoda, KE, AGH awartość instrukcji: Materiał z zakresu DSP. Transformata.2
Instrukcja do laboratorium z cyfrowego przetwarzania sygnałów Ćwiczenie Transformata ; blokowe struktury opisujące filtr Przemysław Korohoda, KE, AGH awartość instrukcji: Materiał z zakresu DSP. Transformata.2
Część 1. Transmitancje i stabilność
 Część 1 Transmitancje i stabilność Zastosowanie opisu transmitancyjnego w projektowaniu przekształtników impulsowych Istotne jest przewidzenie wpływu zmian w warunkach pracy (m. in. v g, i) i wielkości
Część 1 Transmitancje i stabilność Zastosowanie opisu transmitancyjnego w projektowaniu przekształtników impulsowych Istotne jest przewidzenie wpływu zmian w warunkach pracy (m. in. v g, i) i wielkości
Rozwiązywanie równań różniczkowych z niezerowymi warunkami początkowymi
 . Cele ćwiczenia Laboratorium nr Rozwiązywanie równań różniczkowych z niezerowymi warunkami początkowymi zapoznanie się z metodami symbolicznego i numerycznego rozwiązywania równań różniczkowych w Matlabie,
. Cele ćwiczenia Laboratorium nr Rozwiązywanie równań różniczkowych z niezerowymi warunkami początkowymi zapoznanie się z metodami symbolicznego i numerycznego rozwiązywania równań różniczkowych w Matlabie,
Procedura modelowania matematycznego
 Procedura modelowania matematycznego System fizyczny Model fizyczny Założenia Uproszczenia Model matematyczny Analiza matematyczna Symulacja komputerowa Rozwiązanie w postaci modelu odpowiedzi Poszerzenie
Procedura modelowania matematycznego System fizyczny Model fizyczny Założenia Uproszczenia Model matematyczny Analiza matematyczna Symulacja komputerowa Rozwiązanie w postaci modelu odpowiedzi Poszerzenie
Podstawy Automatyki. Wykład 2 - podstawy matematyczne. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 2 - podstawy matematyczne Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe, n.p. turbulencje, wiele
Wykład 2 - podstawy matematyczne Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe, n.p. turbulencje, wiele
Laboratorium z podstaw automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności obiektów automatyzacji, Wpływ sprzężenia zwrotnego na stabilność obiektów Kierunek studiów: Transport,
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Analiza stabilności obiektów automatyzacji, Wpływ sprzężenia zwrotnego na stabilność obiektów Kierunek studiów: Transport,
Informatyczne Systemy Sterowania
 Adam Wiernasz Nr albumu: 161455 e-mail: 161455@student.pwr.wroc.pl Informatyczne Systemy Sterowania Laboratorium nr 1 Prowadzący: Dr inż. Magdalena Turowska I. Wykaz modeli matematycznych członów dynamicznych
Adam Wiernasz Nr albumu: 161455 e-mail: 161455@student.pwr.wroc.pl Informatyczne Systemy Sterowania Laboratorium nr 1 Prowadzący: Dr inż. Magdalena Turowska I. Wykaz modeli matematycznych członów dynamicznych
POLITECHNIKA ŚLĄSKA WYDZIAŁ GÓRNICTWA I GEOLOGII. Roman Kaula
 POLITECHNIKA ŚLĄSKA WYDZIAŁ GÓRNICTWA I GEOLOGII Roman Kaula ZASTOSOWANIE NOWOCZESNYCH NARZĘDZI INŻYNIERSKICH LabVIEW oraz MATLAB/Simulink DO MODELOWANIA UKŁADÓW DYNAMICZNYCH PLAN WYKŁADU Wprowadzenie
POLITECHNIKA ŚLĄSKA WYDZIAŁ GÓRNICTWA I GEOLOGII Roman Kaula ZASTOSOWANIE NOWOCZESNYCH NARZĘDZI INŻYNIERSKICH LabVIEW oraz MATLAB/Simulink DO MODELOWANIA UKŁADÓW DYNAMICZNYCH PLAN WYKŁADU Wprowadzenie
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania MODELOWANIE I IDENTYFIKACJA Studia niestacjonarne Estymacja parametrów modeli, metoda najmniejszych kwadratów.
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania MODELOWANIE I IDENTYFIKACJA Studia niestacjonarne Estymacja parametrów modeli, metoda najmniejszych kwadratów.
Podstawy Automatyki Zbiór zadań dla studentów II roku AiR oraz MiBM
 Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
Automatyka i robotyka
 Automatyka i robotyka Wykład 6 - Odpowiedź częstotliwościowa Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 37 Plan wykładu Wprowadzenie Podstawowe człony
Automatyka i robotyka Wykład 6 - Odpowiedź częstotliwościowa Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 37 Plan wykładu Wprowadzenie Podstawowe człony
Elektrotechnika I stopień Ogólno akademicki. Przedmiot kierunkowy. Obowiązkowy Polski VI semestr zimowy
 KARTA MODUŁU / KARTA PRZEDMIOTU Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013
KARTA MODUŁU / KARTA PRZEDMIOTU Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013
CYFROWE PRZTWARZANIE SYGNAŁÓW (Zastosowanie transformacji Fouriera)
 I. Wprowadzenie do ćwiczenia CYFROWE PRZTWARZANIE SYGNAŁÓW (Zastosowanie transformacji Fouriera) Ogólnie termin przetwarzanie sygnałów odnosi się do nauki analizowania zmiennych w czasie procesów fizycznych.
I. Wprowadzenie do ćwiczenia CYFROWE PRZTWARZANIE SYGNAŁÓW (Zastosowanie transformacji Fouriera) Ogólnie termin przetwarzanie sygnałów odnosi się do nauki analizowania zmiennych w czasie procesów fizycznych.
Narzędzia wspomagające projektowanie - Matlab. PID Tunner. step, bode, margin, rlocus lqr, lqreg kalman,...
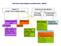 Narzędzia wspomagające projektowanie - Matlab Obiekt LTI (Linear Time-Invariant System) Schemat pod Simulinkiem SCDesign linearyzacja SCOptimization linearyzacja Linear Analysis Tools LTI Viewer step,
Narzędzia wspomagające projektowanie - Matlab Obiekt LTI (Linear Time-Invariant System) Schemat pod Simulinkiem SCDesign linearyzacja SCOptimization linearyzacja Linear Analysis Tools LTI Viewer step,
INSTRUKCJA DO ĆWICZENIA NR 7
 KATEDRA MECHANIKI STOSOWANEJ Wydział Mechaniczny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 7 PRZEDMIOT TEMAT OPRACOWAŁ LABORATORIUM MODELOWANIA Przykładowe analizy danych: przebiegi czasowe, portrety
KATEDRA MECHANIKI STOSOWANEJ Wydział Mechaniczny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 7 PRZEDMIOT TEMAT OPRACOWAŁ LABORATORIUM MODELOWANIA Przykładowe analizy danych: przebiegi czasowe, portrety
Technika regulacji automatycznej
 Technika regulacji automatycznej Wykład 2 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 56 Plan wykładu Schematy strukturalne Podstawowe operacje na schematach
Technika regulacji automatycznej Wykład 2 Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 56 Plan wykładu Schematy strukturalne Podstawowe operacje na schematach
Projektowanie układów regulacji w dziedzinie częstotliwości. dr hab. inż. Krzysztof Patan, prof. PWSZ
 Projektowanie układów regulacji w dziedzinie częstotliwości dr hab. inż. Krzysztof Patan, prof. PWSZ Wprowadzenie Metody projektowania w dziedzinie częstotliwości mają wiele zalet: stabilność i wymagania
Projektowanie układów regulacji w dziedzinie częstotliwości dr hab. inż. Krzysztof Patan, prof. PWSZ Wprowadzenie Metody projektowania w dziedzinie częstotliwości mają wiele zalet: stabilność i wymagania
Plan wykładu. Własności statyczne i dynamiczne elementów automatyki:
 Plan wykładu Własności statyczne i dynamiczne elementów automatyki: - charakterystyka statyczna elementu automatyki, - sygnały standardowe w automatyce: skok jednostkowy, impuls Diraca, sygnał o przebiegu
Plan wykładu Własności statyczne i dynamiczne elementów automatyki: - charakterystyka statyczna elementu automatyki, - sygnały standardowe w automatyce: skok jednostkowy, impuls Diraca, sygnał o przebiegu
Podstawy automatyki. Energetyka Sem. V Wykład 1. Sem /17 Hossein Ghaemi
 Podstawy automatyki Energetyka Sem. V Wykład 1 Sem. 1-2016/17 Hossein Ghaemi Hossein Ghaemi Katedra Automatyki i Energetyki Wydział Oceanotechniki i Okrętownictwa Politechnika Gdańska pok. 222A WOiO Tel.:
Podstawy automatyki Energetyka Sem. V Wykład 1 Sem. 1-2016/17 Hossein Ghaemi Hossein Ghaemi Katedra Automatyki i Energetyki Wydział Oceanotechniki i Okrętownictwa Politechnika Gdańska pok. 222A WOiO Tel.:
E-E-A-1008-s5 Komputerowa Symulacja Układów Nazwa modułu. Dynamicznych. Elektrotechnika I stopień Ogólno akademicki. Przedmiot kierunkowy
 Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu E-E-A-1008-s5 Komputerowa Symulacja Układów Nazwa modułu Dynamicznych Nazwa modułu w języku
Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu E-E-A-1008-s5 Komputerowa Symulacja Układów Nazwa modułu Dynamicznych Nazwa modułu w języku
Elektrotechnika II stopień (I stopień / II stopień) ogólnoakademicki (ogólno akademicki / praktyczny) kierunkowy (podstawowy / kierunkowy / inny HES)
 Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013
Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013
Narzędzia wspomagające projektowanie UR SISO Design. step, bode, margin, rlocus lqr, lqreg kalman,...
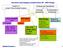 Narzędzia wspomagające projektowanie UR SISO Design Obiekt LTI (Linear Time-Invariant System) Linear Analysis Tools LTI Viewer step, impluse bode, nyquist pool/zero map... Matlab+Control+... Schemat pod
Narzędzia wspomagające projektowanie UR SISO Design Obiekt LTI (Linear Time-Invariant System) Linear Analysis Tools LTI Viewer step, impluse bode, nyquist pool/zero map... Matlab+Control+... Schemat pod
Interpolacja, aproksymacja całkowanie. Interpolacja Krzywa przechodzi przez punkty kontrolne
 Interpolacja, aproksymacja całkowanie Interpolacja Krzywa przechodzi przez punkty kontrolne Aproksymacja Punkty kontrolne jedynie sterują kształtem krzywej INTERPOLACJA Zagadnienie interpolacji można sformułować
Interpolacja, aproksymacja całkowanie Interpolacja Krzywa przechodzi przez punkty kontrolne Aproksymacja Punkty kontrolne jedynie sterują kształtem krzywej INTERPOLACJA Zagadnienie interpolacji można sformułować
Teoria sterowania Control theory. Automatyka i Robotyka II stopień (I stopień / II stopień) ogólnoakademicki (ogólno akademicki / praktyczny)
 Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2016/2017
Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2016/2017
1. Transformata Laplace a przypomnienie
 Transformata Laplace a - przypomnienie, transmitancja operatorowa, schematy blokowe, wprowadzenie do pakietu Matlab/Scilab i Simulink, regulatory PID - transmitancja, przykłady modeli matematycznych wybranych
Transformata Laplace a - przypomnienie, transmitancja operatorowa, schematy blokowe, wprowadzenie do pakietu Matlab/Scilab i Simulink, regulatory PID - transmitancja, przykłady modeli matematycznych wybranych
Wprowadzenie do technik regulacji automatycznej. prof nzw. dr hab. inż. Krzysztof Patan
 Wprowadzenie do technik regulacji automatycznej prof nzw. dr hab. inż. Krzysztof Patan Czym jest AUTOMATYKA? Automatyka to dziedzina nauki i techniki zajmująca się teorią i praktycznym zastosowaniem urządzeń
Wprowadzenie do technik regulacji automatycznej prof nzw. dr hab. inż. Krzysztof Patan Czym jest AUTOMATYKA? Automatyka to dziedzina nauki i techniki zajmująca się teorią i praktycznym zastosowaniem urządzeń
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Teoria sterowania Wprowadzenie do Simulinka w środowisku MATLAB Materiały pomocnicze do ćwiczeń laboratoryjnych
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Teoria sterowania Wprowadzenie do Simulinka w środowisku MATLAB Materiały pomocnicze do ćwiczeń laboratoryjnych
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy automatyki MATLAB przykłady Materiały pomocnicze do ćwiczeń laboratoryjnych Część III termin T
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy automatyki MATLAB przykłady Materiały pomocnicze do ćwiczeń laboratoryjnych Część III termin T
Identyfikacja obiektów dynamicznych za pomocą sieci neuronowych
 Metody Sztucznej Inteligencji w Sterowaniu Ćwiczenie 3 Identyfikacja obiektów dynamicznych za pomocą sieci neuronowych Przygotował: mgr inż. Marcin Pelic Instytut Technologii Mechanicznej Politechnika
Metody Sztucznej Inteligencji w Sterowaniu Ćwiczenie 3 Identyfikacja obiektów dynamicznych za pomocą sieci neuronowych Przygotował: mgr inż. Marcin Pelic Instytut Technologii Mechanicznej Politechnika
Opis systemów dynamicznych w przestrzeni stanu. Wojciech Kurek , Gdańsk
 Opis systemów dynamicznych Mieczysław Brdyś 27.09.2010, Gdańsk Rozważmy układ RC przedstawiony na rysunku poniżej: wejscie u(t) R C wyjście y(t)=vc(t) Niech u(t) = 2 + sin(t) dla t t 0 gdzie t 0 to chwila
Opis systemów dynamicznych Mieczysław Brdyś 27.09.2010, Gdańsk Rozważmy układ RC przedstawiony na rysunku poniżej: wejscie u(t) R C wyjście y(t)=vc(t) Niech u(t) = 2 + sin(t) dla t t 0 gdzie t 0 to chwila
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA
 WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 3. Charakterystyki
WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI I INFORMATYKI INSTYTUT AUTOMATYKI I INFORMATYKI KIERUNEK AUTOMATYKA I ROBOTYKA STUDIA STACJONARNE I STOPNIA PRZEDMIOT : : LABORATORIUM PODSTAW AUTOMATYKI 3. Charakterystyki
Języki Modelowania i Symulacji
 Języki Modelowania i Symulacji Projektowanie sterowników Marcin Ciołek Katedra Systemów Automatyki WETI, Politechnika Gdańska 4 stycznia 212 O czym będziemy mówili? 1 2 3 rlocus Wyznaczanie trajektorii
Języki Modelowania i Symulacji Projektowanie sterowników Marcin Ciołek Katedra Systemów Automatyki WETI, Politechnika Gdańska 4 stycznia 212 O czym będziemy mówili? 1 2 3 rlocus Wyznaczanie trajektorii
Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI)
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI) 1. Filtracja cyfrowa podstawowe
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 4. Filtry o skończonej odpowiedzi impulsowej (SOI) 1. Filtracja cyfrowa podstawowe
PODSTAWY AUTOMATYKI. MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
Przekształcanie równań stanu do postaci kanonicznej diagonalnej
 Przekształcanie równań stanu do postaci kanonicznej diagonalnej Przygotowanie: Dariusz Pazderski Liniowe przekształcenie równania stanu Rozważmy liniowe równanie stanu i równanie wyjścia układu niesingularnego
Przekształcanie równań stanu do postaci kanonicznej diagonalnej Przygotowanie: Dariusz Pazderski Liniowe przekształcenie równania stanu Rozważmy liniowe równanie stanu i równanie wyjścia układu niesingularnego
przy warunkach początkowych: 0 = 0, 0 = 0
 MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
Inżynieria Systemów Dynamicznych (3)
 Inżynieria Systemów Dynamicznych (3) Charakterystyki podstawowych członów dynamicznych Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili?
Inżynieria Systemów Dynamicznych (3) Charakterystyki podstawowych członów dynamicznych Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili?
PAiTM. materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż.
 PAiTM materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż. Sebastian Korczak Poniższe materiały tylko dla studentów uczęszczających na zajęcia.
PAiTM materiały uzupełniające do ćwiczeń Wydział Samochodów i Maszyn Roboczych studia inżynierskie prowadzący: mgr inż. Sebastian Korczak Poniższe materiały tylko dla studentów uczęszczających na zajęcia.
Politechnika Łódzka. Instytut Systemów Inżynierii Elektrycznej
 Politechnika Łódzka Instytut Systemów Inżynierii Elektrycznej Laboratorium komputerowych systemów pomiarowych Ćwiczenie 3 Analiza częstotliwościowa sygnałów dyskretnych 1. Opis stanowiska Ćwiczenie jest
Politechnika Łódzka Instytut Systemów Inżynierii Elektrycznej Laboratorium komputerowych systemów pomiarowych Ćwiczenie 3 Analiza częstotliwościowa sygnałów dyskretnych 1. Opis stanowiska Ćwiczenie jest
INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH Z PODSTAW AUTOMATYKI W PROGRAMIE MATLAB dr inż. GRZEGORZ MZYK
 INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH Z PODSTAW AUTOMATYKI W PROGRAMIE MATLAB dr inż. GRZEGORZ MZYK Spis treści 1 Informacje wstępne 2 2 Środowisko Matlaba 2 2.1 Linia poleceń,komunikacja zsystememoperacyjnym...
INSTRUKCJA DO ĆWICZEŃ LABORATORYJNYCH Z PODSTAW AUTOMATYKI W PROGRAMIE MATLAB dr inż. GRZEGORZ MZYK Spis treści 1 Informacje wstępne 2 2 Środowisko Matlaba 2 2.1 Linia poleceń,komunikacja zsystememoperacyjnym...
Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie. Sterowanie ciągłe. Teoria sterowania układów jednowymiarowych
 Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Sterowanie ciągłe Teoria sterowania układów jednowymiarowych 1 Informacja o prowadzących zajęcia Studia stacjonarne rok II Automatyka i Robotyka
Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Sterowanie ciągłe Teoria sterowania układów jednowymiarowych 1 Informacja o prowadzących zajęcia Studia stacjonarne rok II Automatyka i Robotyka
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Teoria sterowania MATLAB instrukcje warunkowe, logiczne, pętle Materiały pomocnicze do ćwiczeń laboratoryjnych
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Teoria sterowania MATLAB instrukcje warunkowe, logiczne, pętle Materiały pomocnicze do ćwiczeń laboratoryjnych
AiR_TR2_5/9 Teoria Regulacji II Control Theory II. Automatyka i Robotyka I stopień ogólno akademicki studia niestacjonarne
 Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU AiR_TR2_5/9 Teoria Regulacji II Control Theory II Kod modułu Nazwa modułu Nazwa modułu w języku angielskim
Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU AiR_TR2_5/9 Teoria Regulacji II Control Theory II Kod modułu Nazwa modułu Nazwa modułu w języku angielskim
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Teoria sterowania MATLAB komputerowe środowisko obliczeń naukowoinżynierskich podstawowe informacje Materiały
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Teoria sterowania MATLAB komputerowe środowisko obliczeń naukowoinżynierskich podstawowe informacje Materiały
1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI
 Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Transformata Laplace a to przekształcenie całkowe funkcji f(t) opisane następującym wzorem:
 PPS 2 kartkówka 1 RÓWNANIE RÓŻNICOWE Jest to dyskretny odpowiednik równania różniczkowego. Równania różnicowe to pewne związki rekurencyjne określające w sposób niebezpośredni wartość danego wyrazu ciągu.
PPS 2 kartkówka 1 RÓWNANIE RÓŻNICOWE Jest to dyskretny odpowiednik równania różniczkowego. Równania różnicowe to pewne związki rekurencyjne określające w sposób niebezpośredni wartość danego wyrazu ciągu.
AiR_TR2_5/9 Teoria Regulacji II Control Theory II. Automatyka i Robotyka I stopień ogólno akademicki studia stacjonarne
 Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU AiR_TR2_5/9 Teoria Regulacji II Control Theory II Kod modułu Nazwa modułu Nazwa modułu w języku angielskim
Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU AiR_TR2_5/9 Teoria Regulacji II Control Theory II Kod modułu Nazwa modułu Nazwa modułu w języku angielskim
Mechatronika i inteligentne systemy produkcyjne. Modelowanie systemów mechatronicznych Platformy przetwarzania danych
 Mechatronika i inteligentne systemy produkcyjne Modelowanie systemów mechatronicznych Platformy przetwarzania danych 1 Sterowanie procesem oparte na jego modelu u 1 (t) System rzeczywisty x(t) y(t) Tworzenie
Mechatronika i inteligentne systemy produkcyjne Modelowanie systemów mechatronicznych Platformy przetwarzania danych 1 Sterowanie procesem oparte na jego modelu u 1 (t) System rzeczywisty x(t) y(t) Tworzenie
Ćwiczenie nr 1 Odpowiedzi czasowe układów dynamicznych
 Ćwiczenie nr 1 Odpowiedzi czasowe układów dynamicznych 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie studentów z metodą wyznaczania odpowiedzi skokowych oraz impulsowych podstawowych obiektów regulacji.
Ćwiczenie nr 1 Odpowiedzi czasowe układów dynamicznych 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie studentów z metodą wyznaczania odpowiedzi skokowych oraz impulsowych podstawowych obiektów regulacji.
AiR_TSiS_1/2 Teoria sygnałów i systemów Signals and systems theory. Automatyka i Robotyka I stopień ogólnoakademicki
 Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2013/2014
Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2013/2014
Katedra Automatyzacji Laboratorium Podstaw Automatyzacji Produkcji Laboratorium Podstaw Automatyzacji
 Katedra Automatyzacji Laboratorium Podstaw Automatyzacji Produkcji Laboratorium Podstaw Automatyzacji Opracowanie: mgr inż. Krystian Łygas, inż. Wojciech Danilczuk Na podstawie materiałów Prof. dr hab.
Katedra Automatyzacji Laboratorium Podstaw Automatyzacji Produkcji Laboratorium Podstaw Automatyzacji Opracowanie: mgr inż. Krystian Łygas, inż. Wojciech Danilczuk Na podstawie materiałów Prof. dr hab.
ANALIZA SYGNAŁÓ W JEDNÓWYMIARÓWYCH
 ANALIZA SYGNAŁÓ W JEDNÓWYMIARÓWYCH Generowanie podstawowych przebiegów okresowych sawtooth() przebieg trójkątny (wierzhołki +/-1, okres 2 ) square() przebieg kwadratowy (okres 2 ) gauspuls()przebieg sinusoidalny
ANALIZA SYGNAŁÓ W JEDNÓWYMIARÓWYCH Generowanie podstawowych przebiegów okresowych sawtooth() przebieg trójkątny (wierzhołki +/-1, okres 2 ) square() przebieg kwadratowy (okres 2 ) gauspuls()przebieg sinusoidalny
Algorytmy sztucznej inteligencji
 Algorytmy sztucznej inteligencji Dynamiczne sieci neuronowe 1 Zapis macierzowy sieci neuronowych Poniżej omówione zostaną części składowe sieci neuronowych i metoda ich zapisu za pomocą macierzy. Obliczenia
Algorytmy sztucznej inteligencji Dynamiczne sieci neuronowe 1 Zapis macierzowy sieci neuronowych Poniżej omówione zostaną części składowe sieci neuronowych i metoda ich zapisu za pomocą macierzy. Obliczenia
Rok akademicki: 2030/2031 Kod: RAR n Punkty ECTS: 7. Poziom studiów: Studia I stopnia Forma i tryb studiów: -
 Nazwa modułu: Podstawy automatyki Rok akademicki: 2030/2031 Kod: RAR-1-303-n Punkty ECTS: 7 Wydział: Inżynierii Mechanicznej i Robotyki Kierunek: Automatyka i Robotyka Specjalność: - Poziom studiów: Studia
Nazwa modułu: Podstawy automatyki Rok akademicki: 2030/2031 Kod: RAR-1-303-n Punkty ECTS: 7 Wydział: Inżynierii Mechanicznej i Robotyki Kierunek: Automatyka i Robotyka Specjalność: - Poziom studiów: Studia
PODSTAWY AUTOMATYKI. Analiza w dziedzinie czasu i częstotliwości dla elementarnych obiektów automatyki.
 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI Analiza w dziedzinie czasu i częstotliwości dla elementarnych obiektów automatyki. Materiały pomocnicze do
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI Analiza w dziedzinie czasu i częstotliwości dla elementarnych obiektów automatyki. Materiały pomocnicze do
K p. K o G o (s) METODY DOBORU NASTAW Metoda linii pierwiastkowych Metody analityczne Metoda linii pierwiastkowych
 METODY DOBORU NASTAW 7.3.. Metody analityczne 7.3.. Metoda linii pierwiastkowych 7.3.2 Metody doświadczalne 7.3.2.. Metoda Zieglera- Nicholsa 7.3.2.2. Wzmocnienie krytyczne 7.3.. Metoda linii pierwiastkowych
METODY DOBORU NASTAW 7.3.. Metody analityczne 7.3.. Metoda linii pierwiastkowych 7.3.2 Metody doświadczalne 7.3.2.. Metoda Zieglera- Nicholsa 7.3.2.2. Wzmocnienie krytyczne 7.3.. Metoda linii pierwiastkowych
