ĆWICZENIE NR 1 WYŁĄCZANIE PRĄDU STAŁEGO PRZEZ STYCZNIKI
|
|
|
- Witold Wolski
- 8 lat temu
- Przeglądów:
Transkrypt
1 ĆWICZENIE NR 1 WYŁĄCZANIE PRĄDU STAŁEGO PRZEZ STYCZNIKI Autor: mgr inż. Tdeusz Dszczyński Mil: dszczyt@ee.pw.edu.pl SPIS TREŚCI 1. Cel ćwiczeni Wstęp teoretyczny Styczniki Elektryczny łuk prądu stłego Wyłącznie prądu stłego Przebieg ćwiczeni Przykłdowe pytni Sprwozdnie Bibliogrfi
2 1. Cel ćwiczeni Celem ćwiczeni jest zpoznnie się z procesmi złączni i wyłączni prądu stłego, procesmi zchodzącymi w przestrzeni międzystykowej orz budową i dziłniem styczników. W rmch ćwiczeni zostnie przedstwiony i wyjśniony wpływ indukcyjności n procesy łączeniowe. 2. Wstęp teoretyczny 2.1. Styczniki Według normy PN-EN :2010 Aprtur rozdzielcz i sterownicz niskonpięciow Część 1: Postnowieni ogólne stycznik jest określny jko łącznik mechnizmowy przestwiny w inny sposób niż ręcznie, o tylko jednym położeniu spoczynkowym styków ruchomych, zdolny do złączni, przewodzeni i wyłączni prądów w normlnych wrunkch prcy obwodu, tkże przy przeciążenich mogących powstć w roboczych wrunkch prcy. Posid więc zdolności łączeniowe chrkterystyczne dl rozłącznik. Rys. 1. Symbol grficzny stycznik: stycznik zwierny (w stnie niewzbudzonym zestyk otwrty), b stycznik o wyzwlniu smoczynnym, c - stycznik rozwierny (w stnie niewzbudzonym zestyk zmknięty). Wytwórc prtury elektrycznej ustl i podje wielkości i cechy znmionowe prtów chrkteryzujące urządzenie ze względu n jego przeznczenie i zdolność do prcy w określonych wrunkch prcy. Wrtościmi znmionowymi są tkie wrtości wielkości używne do opisu technicznego, które odpowidją określonemu zbiorowi wrunków prcy dl podzespołu, urządzeni, wyposżeni lub ukłdu. Powinny być one dostępne n tbliczce znmionowej prtu. Pozostłe wrtości (np. nie liczbowe) powinn zwierć dokumentcj techniczn (informcyjn) krt ktlogow. Wielkościmi znmionowymi stycznik są: - Znmionowe npięcie izolcji stycznik U ni poziom izolcji torów głównych w stosunku do konstrukcji wsporczej, torów głównych między sobą i w stosunku do torów pomocniczych orz poziom izolcji przerwy biegunowej w kżdym torze głównym. Ozncz to iż znmionowe npięcie sieci nie może przekrczć wrtości U ni stycznik prcującego w tej sieci. 2
3 - Rodzj prądu torów głównych stycznik określ stosowlność prtu w siecich prądu przemiennego lub stłego. - Ktegori użytkowni styczników określ podstwowe njczęstsze przeznczenie styczników. W tbeli nr 1 przedstwiono ktegorie użytkowni styczników ze względu n chrkter obciążeń. Rodzj prądu Chrkterystyk odbiornik Zstosownie stycznik do łączeni: b c d e f g Prąd przemienny - obciążeń młoindukcyjnych i nieindukcyjnych - pieców oporowych - przeciętej sieci przemysłowej AC1 - silników pierścieniowych - rozruch, hmownie przeciwprądem - silników kltkowych - rozruch przełącznikiem Y/ - silników synchronicznych - rozruch przełącznikiem Y/ i utotrnsformtorowy - silników pierścieniowych - rozruch, wyłącznie bez hmowni przeciwprądem - silników kltkowych - rozruch bezpośredni, wyłącznie przy pełnej prędkości obrotowej AC1 AC2 AC3 - j.w. + rozruch przełącznikiem Y/ AC2 AC1 AC1 AC1 AC1 AC1 A1 AC2 AC2 AC2 AC2 AC2 A2 AC3 AC2 AC2 AC2 AC2 AC2 A2 AC3 AC3 AC3 AC3 AC3 A3 Rodzj prądu - silników synchronicznych - rozruch bezpośredni, wyłącznie przy pełnej prędkości obrotowej - silników indukcyjnych kltkowych - rozruch bezpośredni, impulsownie, rewersownie AC3 AC4 AC4 AC4 AC4 AC4 AC4 - j.w. + wyłącznie przy zhmownym lub wolno wirującym silniku Chrkterystyk odbiornik Zstosownie stycznik do łączeni: d e f g h A4 Prąd stły - obciążeń młoindukcyjnych DC1 DC1 DC1 - pieców oporowych i rezystorów - silników bocznikowych - rozruch, wyłącznie przy znmionowej prędkości obrotowej - silników bocznikowych - rozruch, impulsownie, rewersownie - silników szeregowych - wyłącznie przy pełnej prędkości obrotowej - silników szeregowych - rozruch, impulsownie, rewersownie DC1 D1 DC1t DC2 DC2 DC2 DC2 DC2t DC3 DC3 DC3 DC3 DC3t DC4 DC4 DC4 DC4 DC4t DC5 DC+ DC5 DC5 DC5t - rozruch i wyłącznie wirujących silników D2 - rozruch i wyłącznie zhmownych i wolno wirujących silników Tbel 1. Ktegorie użytkowni styczników ze względu n chrkter obciążeń. D3 - Wytrzymłość zwrciow określ się ją z pomocą dwóch wrtości: znmionowy prąd n-sekundowy (wrtość skuteczn prądu krótkotrwłego n- sekundowego, który płynąc n-sekund przez tor prądowy stycznik nie spowoduje ndmiernego ngrzni prtu i uszkodzeni prtu) i prąd szczytowy (szczytow 3
4 wrtość prądu zwrciowego, którą stycznik wytrzymuje bez uszkodzeń w stnie zmknięci). - Czsy włsne otwierni i zmykni, czs wyłączeni chrkteryzują współdziłnie zestyków pomocniczych z zestykmi głównymi i między sobą. Określją możliwości stosowni prtu w różnych ukłdch. Stycznik dokowo może być wyposżony w zestyki pomocnicze, określne wielkościmi: liczbą i rodzj zestyków, rodzj prądu, prąd cieplny ciągły (skuteczn wrtość prądu, który przepływjąc dowolnie długo przez tor prądowy stycznik nie spowoduje przekroczeni ustlonych w normch przyrostów tempertur elementów stycznik), prąd i npięcie łączeniowe, ktegori użytkowni, trwłość łączeniow, wytrzymłość zwrciow jko prąd szczytowy. Styk ruchomy, sprzężony z mechnizmem npędowym stycznik, wrz ze stykiem nieruchomym tworzą zestyk łączeniowy. Dokowo jeden z zestyków posid zwsze sprężynę stykową, służącą do wywierni docisku zestykowego wstępnego (bezpośrednio po zetknięciu się styków) i roboczego (w stnie ustlonym zmknięci). Występują dw położeni wymuszone styku ruchomego zwierne (zmknięty w położeniu wymuszonym) i rozwierne (otwrty w położeniu wymuszonym. Jko prt elektryczny stycznik służy głównie do łączeni silników w wrunkch roboczych. Stycznik może wykonuje prcę przepustową przewodząc prąd elektryczny lub mnewrową, złączjąc i wyłączjąc prąd w wrunkch roboczych. W ćwiczeniu wykorzystuje się jednobiegunowy stycznik prądu stłego typu SE- 310 i SE-410. Budow prtu zostł przedstwion n rys. 2. Rys 2. Budow jednobiegunowego stycznik prądu stłego typu SE: 1 elektromgnes npędowy, 2 styk ruchomy, 3 komor gszeniow z obrysem 3 elektromgnesu wydmuchowego, 4 cewk szeregowego elektromgnesu wydmuchowego, 5 przełącznik obwodów wtórnych, 6 zciski przyłączowe toru prądowego głównego, 7 połączenie pone styku ruchomego, 8 podstw. 4
5 2.2. Elektryczny łuk prądu stłego Przy wyłączniu obwodu zwierjącego SEM, w chwili rozejści się styków orz przy odpowiednich poziomch prądów i npięć, pojwi się łuk elektryczny. Zjwisk zchodzące między elektrodmi po przyłożeniu do nich pewnego npięci zleżą od: - rodzju i ciśnieni gzu w przerwie międzyelektrodowej, - czynników zewnętrznych (joniztory i dejoniztory), - wielkości i zmienności w czsie przyłożonego npięci, - mteriłu i ksztłtu elektrod, - pewnych sprzężeń pojemnościowych posidjących wpływ n rozkłd pol między elektrodmi. Wskutek różnego rodzju promieniowni (np. rdioktywne, kosmiczne, itp.) pewn ilość cząstek gzu może ulegć jonizcji zpewnijąc stły przyrost koncentrcji pr łdunków. Jednocześnie wrz z jonizcją gzu zchodzi tkże łączenie się różnoimiennych łdunków (rekombincj), co powoduje pewien ubytek łdunków. Dzięki tym dwóm zjwiskom otrzymujemy ściśle określony stopień jonizcji gzu. Rozptrując obwód z rys. 3, pole pomiędzy elektrodmi A i K jest przyczyn przepływu łdunków. Łdunki donie podążją do ktody w kierunku spdku potencjłu, ntomist elektrony w kierunku donim grdientu potencjłu. Rys. 3. Obwód prądu stłego - źródło E, rezystncj R orz dwie elektrody A i C. Zmienijąc npięcie pomiędzy elektrodmi dosttecznie wolno, by dl kżdej wrtości pomirowej ustlił się koncentrcj łdunków, możn wykreślić sttyczną chrkterystykę npięciowo-prądową wyłdowń (rys. 4). 5
6 Rys. 4. Chrkterystyk sttyczn wyłdowń w gzie. Pod wpływem pol potencjlnego elektrod odpływją łdunki i zmieni się stn koncentrcji pr łdunków: n = q α (1) R Gdzie: q przyrost koncentrcji pr łdunków wskutek jonizcji nturlnej, α R współczynnik rekombincji. W mirę zwiększni się ntężeni pol, zwiększ się liczb przepływjących do elektrod łdunków, ż do momentu gdy liczb wszystkich generownych pr łdunków będzie przepływł do elektrod. Wystąpi prąd nsyceni, którego gęstość nie wzrst wrz ze wzrostem ntężeni pol (odcinek 1-2). Dlszy wzrost pol będzie wówczs jedynie zwiększł prędkość łdunków, czyli ich energię kinetyczną. W punkcie 2 elektron osiąg energię kinetyczną równą energii jonizcji i nstępują pierwsze wyłdowni Townsend. Zkłdjąc że n pewnej drodze przebiegjący elektron o prędkości v ek spowoduje jonizcję α cząsteczek gzu, wówczs przyrost pr łdunków wskutek elektronowej jonizcji zderzeniowej α w czsie wyniesie: dn K = αn e (2) Gdzie: α pierwszy współczynnik jonizcji zderzeniowej Townsend, n e koncentrcj elektronów. Zgięcie krzywej (rys. 4) w punkcie 3 przypisywne jest jonizcji zderzeniowej, zjwiskom przy ktodzie, elektronowej emisji wtórnej ktody orz elektronowej fotoemisji ktody. Przebieg n odcinku 3-4 określny jest z pomocą drugiego współczynnik Townsend. Przy poziomie npięci określonym w punkcie 4 nstąpi 6
7 zpłon wyłdowń smoistnych, których rozwój jest uzleżniony od prmetrów obwodu orz stnu gzu. Wyłdowni Townsend (niewidoczne) przechodząc pod wpływem przyłożonego npięci do wyłdowń smoistnych mogą się różnorko rozwijć: 1) Z pośrednictwem wyłdowń wrstwowych świetlących (4-5-6), które ngle (6-8) lub stopniowo (6-7) przerdzją się w wyłdownie łukowe (punkt 9) 2) Bezpośrednio (4-8) w wyłdownie łukowe (punkt 9) Chrkterystyk sttyczn łuku stnowi część chrkterystyki sttycznej wyłdowń U=f(i) w zkresie dużych prądów. W zleżności od przebiegu wyłdowń smoistnych chrkterystyk sttyczn może mieć różny przebieg, jednk z uwgi n występownie wyłdowń początkowych przy brdzo młych wrtościch prądu zzwyczj posługujemy się przebiegiem uproszczonym (rys. 5). Npięcie u z przy prądzie i=0 nzywmy npięciem zpłonu. Sttyczną chrkterystyką łuku nzywmy tką zleżność npięci łuku u s =f(i ) przy stłej długości l i w określonych wrunkch zewnętrznych, przy której dl kżdej pry wrtości u (i ) spełniony jest wrunek: dn ( i ) s = dn K dn + T dn + R dn + D = 0 (3) Rys. 5. Chrkterystyki łuku prądu stłego: 1 sttyczn, 2 dynmiczn. 7
8 Wyrz dn K jest pomijlny z uwgi n młą wrtość K. Wyrzy: przyrost koncentrcji pr łdunków wskutek jonizcji cieplnej, dn T dn R określ określ przyrost koncentrcji pr łdunków wskutek rekombincji objętościowej, dn D określ przyrost koncentrcji pr łdunków wskutek dyfuzji mbipolrnej i w niewymuszonym ośrodku jest pomijlny. Przy szybkich zminch prądu stn koncentrcji, tempertur, ciepło i średnic łuku nie odpowidją chwilowym wrtościom prądu obserwownego w stnie ustlonym. Otrzymujemy wtedy nieskończoną liczbę dynmicznych chrkterystyk npięciowo prądowych u =f(i ). Przebieg chrkterystyki dynmicznej zleży tkże od prędkości zmin prądu. Im szybsze są zminy prądu, tym niżej leży chrkterystyk dynmiczn poniżej chrkterystyki sttycznej. Przy mlejącym prądzie, npięcie u w chwili i = 0 nzyw się npięciem gszeni łuku u g Wyłącznie prądu stłego Prktycznie we wszystkich przypdkch wyłączni obwodów silnoprądowych powstje łuk elektryczny. Istotą wszelkich zbiegów konstruktorów prtów elektrycznych, w szczególności ukłdów stykowo-gszeniowych, jest tkie projektownie urządzeń, by możliwie jk njbrdziej ogrniczyć skutki dziłni tego łuku (ngrzewnie komór i styków, zużycie mteriłu styków). Podstwowymi zbiegmi są skrócenie czsu pleni się łuku i zmniejsznie wydzielnej w łuku energii. Prąd stły w sposób nturlny nie przechodzi przez zero i jego wyłączenie wymg pewnych zbiegów wymuszjących przejście do wrtości zerowej. Ogólny wrunek wyłączni prądu o wrtości początkowej I w możn określić jko: I w i = i 0 (4) Gdzie i chwilow wrtość prądu łuku. Funkcj i (t) powinn być mlejąc, le przebieg może posidć różnorki: - bez punktów przegięci wrunek wyłączeni możemy określić jko: di i = 0 i = I w < 0 (5) 8
9 d i - posid zwykłe punkty przegięci ( = 0 d i 2 orz 0 3 ) ogólny wrunek wyłączeni określ się jko: 2 3 i ( t w di ) = 0 i ( t w) < 0 (6) Gdzie t w czs łukowy wyłączeni. Wrunki z nierówności (5) nzyw się dynmicznymi wrunkmi wyłączni. Są one konieczne, lecz nie zwsze wystrczjące do wyłączeni prądu. Z uwgi n chrkter ćwiczeni przedstwione zostnie i omówione dokłdniej wyłącznie prądu stłego przez zwiększnie rezystncji łuku. Anlizując ukłd szeregowy RL (rys. 6) przebieg prądu po złączeniu możn opisć wzorem: E t T i e = I m 1 e R = t T 1 (7) Rys. 6. Schemt zstępczy obwodu szeregowego RL, zsilnego npięciem stłym. Z równni (7) możn wyznczyć przebieg prądu złącznego (rys. 7). Wrtość prądu po jednej stłej czsowej możn określić jko: i =, 632 t= T 0 I (8) m Po czsie równym czterem stłym czsowym T, prąd prktycznie osiąg wrtość ustloną: i =, 98 t= T 0 I (9) m Stłą czsową T możn obliczyć jko: 9
10 L T = (10) R Rys. 7. Przebieg prądu stłego przy złączniu. Otwrcie wyłącznik W z obwodu z rys. 6 może nstąpić w skutek sytucji wryjnej, np. zwrci. Z uwgi n czs włsny wyłącznik, wyłączenie może nstąpić przy ustlonej wrtości prądu zwrciowego lub przed ustleniem się prądu zwrciowego. Stycznik lub wyłącznik prąd stłego mją możliwość tylko wyłączeni po ustleniu się prądu. Zstosownie bezpiecznik topikowego lub wyłącznik szybkiego umożliwi uzysknie wyłączeni przed ustleniem się prądu. Niezleżnie do tego kiedy nstąpi wyłączenie, zdniem prtu elektrycznego jest sprowdzenie prądu do zer. Złóżmy że mmy obwód z rys. 6 orz: - wyłącznik W w stnie zmkniętym nie m wpływu n przebieg prądu zwrciowego, - czs włsny wyłącznik W jest długi, - wrunki chłodzeni łuku są określone i stłe, - styki wyłącznik W rozchodzą się z nieskończenie dużą prędkością n określoną odległość s, - brk oddziływni zewnętrznego pol mgnetycznego i pol temperturowego n łuk (długość łuku równ jest s i jest stł). Uwzględnijąc powyższe złożeni orz korzystjąc z II prw Kirchhoff dl obwodu z rys. 6 otrzymujemy: 10
11 di E = Ri + L + u (11) Gdzie i prąd łuku, u npięcie łuku między stykmi łącznik W. Częścią równni (11), któr pokzuje zminę prądu łuku jest różniczk di cząstkow L, któr przyjmuje wrtość: di L i = I i =0 ł w = E Ri u (12) di Aby spełnić ogólny wrunek wyłączni, różniczk cząstkow L powinn przyjmowć wrtości mniejsze od zer. Otrzymujemy więc nierówność: E Ri u < 0 (13) Npięcie redukujące prąd w obwodzie powinno ztem spełnić nierówność: i = 0 [ u ( E Ri )] > 0 i = 0 u = i = I i = I (14) w w Powyższ nierówność (11) określ wrunek dynmiczny wyłączni prądu stłego. Wrunek ten (l = const) zostnie spełniony jeżeli przebieg chrkterystyki sttycznej będzie określony nierównością: ( E Ri ) i = 0 i =0 u s > i = I i = I (15) w w Nierówność (15) określ konieczny i wystrczjący wrunek sttyczny wyłączni prądu stłego. Wyłączenie obwodu prądu stłego jest możliwe (l = const), jeżeli chrkterystyk sttyczn łuku u s =f(i ) posid dl kżdej wrtości prądu i, wrtości większe, niż chrkterystyk zewnętrzn obwodu E-Ri =f(i ). Dzięki temu zostnie spełnion nierówność (14) orz w obwodzie powstnie donie npięcie redukujące w cłym obwodzie 11
12 Rys. 8. Ilustrcj grficzn wyłączni prądu stłego. Może dojść do sytucji, w której chrkterystyk sttyczn łuku m przebieg jk n rys. 8. Wówczs nie nstąpi wyłączenie. Złożony wrunek wyłączni byłby spełniony w przedzile I w -i 1, w którym prąd łuku mlłby z określoną prędkością decydującą o przebiegu chrkterystyki dynmicznej w tym przedzile: di ( E Ri ) u = (16) L Prędkość zmin prądu mleje w mirę zbliżni się do chrkterystyki zewnętrznej obwodu. W punkcie przecięci się obu chrkterystyk (punkt A) prędkość t osiąg wrtość zero stn równowgi sttycznej, w której brk jest npięci redukującego, łuk będzie się utrzymywł trwle (i =i 1 ): E = Ri + u (17) 1 s1 Wrunek wyłączeni prądu stłego (15) wymg by chrkterystyk sttyczn łuku nie posidł punktów wspólnych z chrkterystyk zewnętrzną obwodu, więc nie m możliwości osiągnięcie równowgi sttycznej łuku. Jeśli zpewnimy dostteczny odbiór mocy z łuku wrunek ten zostnie spełniony. Moc łuku wyłączeniowego wyniesie w powyższym przypdku: 2 di P = u i = Ei Ri i L (18) Energi łuku wyłączeniowego od początku wyłączeni wyniesie: t w A = P = E i R i L i di (19) 0 t w 0 t w 0 2 I 0 w 12
13 Gdzie: I w prąd wyłączeniowy dl t=0, t w czs łukowy. Zmniejszniu się prądu i ł do zer towrzyszy wzrost npięci łuku do wrtości npięci gśnięci u g, które możn wyznczyć jko: u g dił di = ł uł E L = E + L ił 0 = (20) Podczs wyłączni określonego obwodu prądu stłego (dne: E, L i R) wielkość przepięci zleży od zmin prądu w chwili wyłączeni, indukcyjności wyłącznego obwodu orz npięci łuku. Im większ indukcyjność, tym większ energi mgnetyczn n niej zgromdzon i większ wrtość przepięci. Większ indukcyjność powoduje tkże wolniejsze zmniejsznie się wyłączlnego prądu. Wpływ n przepięcie u g m tkże ukłd gszeniowy, kiedy intensywniej odbier ciepło z knłu łukowego, powoduje zwiększenie stromości mleni prądu łuku. 13
14 3. Przebieg ćwiczeni Nleży stosowć się bezwzględnie do poleceń prowdzącego ćwiczenie. Kżdą pierwszą czynność łączeniową i pomir wykonuje njpierw prowdzący ćwiczenie i tylko on dopuszcz grupę do wykonywni ćwiczeni. Grup m z zdnie: 1) Zpoznć się z ukłdem pomirowym nrysowć ukłd pomirowy w protokole, sprwdzić połączeni w stnie beznpięciowym; spisć sensownie tbliczki znmionowe użytych prtów orz zpoznć i zidentyfikowć spisne wrtości; zorientowć się jk mierzony jest prąd i npięcie i do którego knłu oscyloskopu przyłączone są odpowiednie pomiry. 2) Wykonć pomiry prądu i npięci dl różnych nstw indukcyjności nleży bezwzględnie pozostwić nie zmienioną nstwę rezystncji. Nstw indukcyjności Wrtość npięci U [V] Wrtość prądu I [A] R[Ω] ) Wykonć pomiry złączni prądu w ukłdzie z użyciem komputer. 4) Wykonć pomiry wyłączni prądu w ukłdzie z użyciem komputer. 5) Dyskusj dotycząc otrzymnych wyników. 14
15 4. Przykłdowe pytni 1. Jkim prtem elektrycznym jest stycznik i jkimi możliwościmi łączeniowym się chrkteryzuje? 2. Jkim prtem elektrycznym jest odłącznik i jkimi możliwościmi łączeniowym się chrkteryzuje? 3. Jkim prtem elektrycznym jest rozłącznik i jkimi możliwościmi łączeniowym się chrkteryzuje? 4. Jkim prtem elektrycznym jest wyłącznik i jkimi możliwościmi łączeniowym się chrkteryzuje? 5. Jkie są podstwowe prmetry elektryczne styczników? 6. Jkie są metody wyłączni prądu stłego? 7. Czym jest chrkterystyk sttyczn łuku prądu stłego? 8. Czym jest chrkterystyk dynmiczn łuku prądu stłego? 9. Jki jest wpływ indukcyjności n wyłącznie prądu stłego? 10. Wpływ przepięć n izolcję obwodu? 5. Sprwozdnie Sprwozdnie powinno zwierć: 1. Cel ćwiczeni 2. Krótki, zwięzły, n temt wstęp teoretyczny dotyczący temtu ćwiczeni. 3. Opis bdnego ukłdu, rysunek obwodu, dne znmionowe prtów użytych podczs ćwiczeni, oczekiwne wyniki pomirów. 4. Otrzymne opisne przebiegi, opis dotyczący otrzymnych wyników. 5. Chrkterystyk dynmiczn i zewnętrzn obwodu z opisem. 6. Wnioski Wszystkie przebiegi nleży wykonć z użyciem progrmu Mtlb. 15
16 6. Bibliogrfi 1. Jn Mksymiuk, Aprty elektryczne, WNT Jerzy Kryński, Elektryczne prty rozdzielcze, PWN Adm Bóbr, Włdysłw Polowczyk, Jędrzej Tucholski, Styczniki energoelektryczne, WNT PN-EN :2010 Aprtur rozdzielcz i sterownicz niskonpięciow Część 1: Postnowieni ogólne 5. Mteriły z wykłdu. 16
Ćwiczenia laboratoryjne z przedmiotu : Napędy Hydrauliczne i Pneumatyczne
 Lbortorium nr 11 Temt: Elementy elektropneumtycznych ukłdów sterowni 1. Cel ćwiczeni: Opnownie umiejętności identyfikcji elementów elektropneumtycznych n podstwie osprzętu FESTO Didctic. W dużej ilości
Lbortorium nr 11 Temt: Elementy elektropneumtycznych ukłdów sterowni 1. Cel ćwiczeni: Opnownie umiejętności identyfikcji elementów elektropneumtycznych n podstwie osprzętu FESTO Didctic. W dużej ilości
Zastosowanie multimetrów cyfrowych do pomiaru podstawowych wielkości elektrycznych
 Zstosownie multimetrów cyfrowych do pomiru podstwowych wielkości elektrycznych Cel ćwiczeni Celem ćwiczeni jest zpoznnie się z możliwościmi pomirowymi współczesnych multimetrów cyfrowych orz sposobmi wykorzystni
Zstosownie multimetrów cyfrowych do pomiru podstwowych wielkości elektrycznych Cel ćwiczeni Celem ćwiczeni jest zpoznnie się z możliwościmi pomirowymi współczesnych multimetrów cyfrowych orz sposobmi wykorzystni
Grażyna Nowicka, Waldemar Nowicki BADANIE RÓWNOWAG KWASOWO-ZASADOWYCH W ROZTWORACH ELEKTROLITÓW AMFOTERYCZNYCH
 Ćwiczenie Grżyn Nowick, Wldemr Nowicki BDNIE RÓWNOWG WSOWO-ZSDOWYC W ROZTWORC ELETROLITÓW MFOTERYCZNYC Zgdnieni: ktywność i współczynnik ktywności skłdnik roztworu. ktywność jonów i ktywność elektrolitu.
Ćwiczenie Grżyn Nowick, Wldemr Nowicki BDNIE RÓWNOWG WSOWO-ZSDOWYC W ROZTWORC ELETROLITÓW MFOTERYCZNYC Zgdnieni: ktywność i współczynnik ktywności skłdnik roztworu. ktywność jonów i ktywność elektrolitu.
Realizacje zmiennych są niezależne, co sprawia, że ciąg jest ciągiem niezależnych zmiennych losowych,
 Klsyczn Metod Njmniejszych Kwdrtów (KMNK) Postć ć modelu jest liniow względem prmetrów (lbo nleży dokonć doprowdzeni postci modelu do liniowości względem prmetrów), Zmienne objśnijące są wielkościmi nielosowymi,
Klsyczn Metod Njmniejszych Kwdrtów (KMNK) Postć ć modelu jest liniow względem prmetrów (lbo nleży dokonć doprowdzeni postci modelu do liniowości względem prmetrów), Zmienne objśnijące są wielkościmi nielosowymi,
Metody Lagrange a i Hamiltona w Mechanice
 Metody Lgrnge i Hmilton w Mechnice Mriusz Przybycień Wydził Fizyki i Informtyki Stosownej Akdemi Górniczo-Hutnicz Wykłd 3 M. Przybycień (WFiIS AGH) Metody Lgrnge i Hmilton... Wykłd 3 1 / 15 Przestrzeń
Metody Lgrnge i Hmilton w Mechnice Mriusz Przybycień Wydził Fizyki i Informtyki Stosownej Akdemi Górniczo-Hutnicz Wykłd 3 M. Przybycień (WFiIS AGH) Metody Lgrnge i Hmilton... Wykłd 3 1 / 15 Przestrzeń
2. Tensometria mechaniczna
 . Tensometri mechniczn Wstęp Tensometr jk wskzywłby jego nzw to urządzenie służące do pomiru nprężeń. Jk jednk widomo, nprężeni nie są wielkościmi mierzlnymi i stnowią jedynie brdzo wygodne pojęcie mechniki
. Tensometri mechniczn Wstęp Tensometr jk wskzywłby jego nzw to urządzenie służące do pomiru nprężeń. Jk jednk widomo, nprężeni nie są wielkościmi mierzlnymi i stnowią jedynie brdzo wygodne pojęcie mechniki
Wymagania edukacyjne matematyka klasa 2 zakres podstawowy 1. SUMY ALGEBRAICZNE
 Wymgni edukcyjne mtemtyk kls 2 zkres podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych
Wymgni edukcyjne mtemtyk kls 2 zkres podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych
Przetworniki Elektromaszynowe st. n. st. sem. V (zima) 2018/2019
 Kolokwium główne Wrint A Przetworniki lektromszynowe st. n. st. sem. V (zim 018/019 Trnsormtor Trnsormtor trójzowy m nstępujące dne znmionowe: S 00 kva 50 Hz HV / LV 15 ±x5% / 0,4 kv poł. Dyn Pondto widomo,
Kolokwium główne Wrint A Przetworniki lektromszynowe st. n. st. sem. V (zim 018/019 Trnsormtor Trnsormtor trójzowy m nstępujące dne znmionowe: S 00 kva 50 Hz HV / LV 15 ±x5% / 0,4 kv poł. Dyn Pondto widomo,
2. FUNKCJE WYMIERNE Poziom (K) lub (P)
 Kls drug poziom podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych redukuje wyrzy
Kls drug poziom podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych redukuje wyrzy
POLITECHNIKA GDAŃSKA Wydział Elektrotechniki i Automatyki Katedra Energoelektroniki i Maszyn Elektrycznych M O D E L O W A N I E I S Y M U L A C J A
 POLTECHNKA GDAŃSKA Wydził Elektrotechniki i Automtyki Ktedr Energoelektroniki i Mszyn Elektrycznych M O D E L O W A N E S Y M U L A C J A S Y S T E M Ó W M E C H A T O N K Kierunek Automtyk i obotyk Studi
POLTECHNKA GDAŃSKA Wydził Elektrotechniki i Automtyki Ktedr Energoelektroniki i Mszyn Elektrycznych M O D E L O W A N E S Y M U L A C J A S Y S T E M Ó W M E C H A T O N K Kierunek Automtyk i obotyk Studi
KRYTERIA OCENIANIA TECHNOLOGIA NAPRAW ZESPOŁÓW I PODZESPOŁÓW MECHANICZNYCH POJAZDÓW SAMOCHODOWYCH KLASA I TPS
 KRYTRIA OCNIANIA TCHNOLOGIA NAPRAW ZSPOŁÓW I PODZSPOŁÓW MCHANICZNYCH POJAZDÓW SAMOCHODOWYCH KLASA I TPS Temt Klsyfikcj i identyfikcj pojzdów smochodowych Zgdnieni - Rodzje ukłdów, - Zdni i ogóln budow
KRYTRIA OCNIANIA TCHNOLOGIA NAPRAW ZSPOŁÓW I PODZSPOŁÓW MCHANICZNYCH POJAZDÓW SAMOCHODOWYCH KLASA I TPS Temt Klsyfikcj i identyfikcj pojzdów smochodowych Zgdnieni - Rodzje ukłdów, - Zdni i ogóln budow
Ćwiczenie 9. BADANIE UKŁADÓW ZASILANIA I STEROWANIA STANOWISKO I. Badanie modelu linii zasilającej prądu przemiennego
 ortorium elektrotechniki Ćwiczenie 9. BADAIE UKŁADÓ ZASIAIA I STEOAIA STAOISKO I. Bdnie modelu linii zsiljącej prądu przemiennego Ukłd zowy (ez połączeń wrintowych) 30 V~ A A A 3 3 3 A 3 A 6 V 9 0 I A
ortorium elektrotechniki Ćwiczenie 9. BADAIE UKŁADÓ ZASIAIA I STEOAIA STAOISKO I. Bdnie modelu linii zsiljącej prądu przemiennego Ukłd zowy (ez połączeń wrintowych) 30 V~ A A A 3 3 3 A 3 A 6 V 9 0 I A
EUROELEKTRA Ogólnopolska Olimpiada Wiedzy Elektrycznej i Elektronicznej Rok szkolny 2014/2015 Zadania dla grupy elektronicznej na zawody II stopnia
 EOELEKTA Ogólnopolsk Olimpid Wiedzy Elektrycznej i Elektronicznej ok szkolny 204/205 Zdni dl grupy elektronicznej n zwody stopni Zdnie Dl diody półprzewodnikowej, której przeieg chrkterystyki prądowo-npięciowej
EOELEKTA Ogólnopolsk Olimpid Wiedzy Elektrycznej i Elektronicznej ok szkolny 204/205 Zdni dl grupy elektronicznej n zwody stopni Zdnie Dl diody półprzewodnikowej, której przeieg chrkterystyki prądowo-npięciowej
Komisja Egzaminacyjna dla Aktuariuszy LIX Egzamin dla Aktuariuszy z 12 marca 2012 r. Część I Matematyka finansowa
 Mtemtyk finnsow 12.03.2012 r. Komisj Egzmincyjn dl Akturiuszy LIX Egzmin dl Akturiuszy z 12 mrc 2012 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 100 minut
Mtemtyk finnsow 12.03.2012 r. Komisj Egzmincyjn dl Akturiuszy LIX Egzmin dl Akturiuszy z 12 mrc 2012 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 100 minut
Wymagania edukacyjne matematyka klasa 2b, 2c, 2e zakres podstawowy rok szkolny 2015/2016. 1.Sumy algebraiczne
 Wymgni edukcyjne mtemtyk kls 2b, 2c, 2e zkres podstwowy rok szkolny 2015/2016 1.Sumy lgebriczne N ocenę dopuszczjącą: 1. rozpoznje jednominy i sumy lgebriczne 2. oblicz wrtości liczbowe wyrżeń lgebricznych
Wymgni edukcyjne mtemtyk kls 2b, 2c, 2e zkres podstwowy rok szkolny 2015/2016 1.Sumy lgebriczne N ocenę dopuszczjącą: 1. rozpoznje jednominy i sumy lgebriczne 2. oblicz wrtości liczbowe wyrżeń lgebricznych
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE IIc ZAKRES PODSTAWOWY I ROZSZERZONY
 WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE IIc ZAKRES PODSTAWOWY I ROZSZERZONY. JĘZYK MATEMATYKI oblicz wrtość bezwzględną liczby rzeczywistej stosuje interpretcję geometryczną wrtości bezwzględnej liczby
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE IIc ZAKRES PODSTAWOWY I ROZSZERZONY. JĘZYK MATEMATYKI oblicz wrtość bezwzględną liczby rzeczywistej stosuje interpretcję geometryczną wrtości bezwzględnej liczby
Ć W I C Z E N I E N R E-14
 INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII MATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA ELEKTRYCZNOŚCI I MAGNETYZMU Ć W I C Z E N I E N R E-14 WYZNACZANIE SZYBKOŚCI WYJŚCIOWEJ ELEKTRONÓW
INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII MATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA ELEKTRYCZNOŚCI I MAGNETYZMU Ć W I C Z E N I E N R E-14 WYZNACZANIE SZYBKOŚCI WYJŚCIOWEJ ELEKTRONÓW
MATeMAtyka 3 inf. Przedmiotowy system oceniania wraz z określeniem wymagań edukacyjnych. Zakres podstawowy i rozszerzony. Dorota Ponczek, Karolina Wej
 Dorot Ponczek, Krolin Wej MATeMAtyk 3 inf Przedmiotowy system ocenini wrz z określeniem wymgń edukcyjnych Zkres podstwowy i rozszerzony Wyróżnione zostły nstępujące wymgni progrmowe: konieczne (K), podstwowe
Dorot Ponczek, Krolin Wej MATeMAtyk 3 inf Przedmiotowy system ocenini wrz z określeniem wymgń edukcyjnych Zkres podstwowy i rozszerzony Wyróżnione zostły nstępujące wymgni progrmowe: konieczne (K), podstwowe
Układ elektrohydrauliczny do badania siłowników teleskopowych i tłokowych
 TDUSZ KRT TOMSZ PRZKŁD Ukłd elektrohydruliczny do bdni siłowników teleskopowych i tłokowych Wprowdzenie Polsk Norm PN-72/M-73202 Npędy i sterowni hydruliczne. Cylindry hydruliczne. Ogólne wymgni i bdni
TDUSZ KRT TOMSZ PRZKŁD Ukłd elektrohydruliczny do bdni siłowników teleskopowych i tłokowych Wprowdzenie Polsk Norm PN-72/M-73202 Npędy i sterowni hydruliczne. Cylindry hydruliczne. Ogólne wymgni i bdni
Modelowanie i obliczenia techniczne. Metody numeryczne w modelowaniu: Różniczkowanie i całkowanie numeryczne
 Modelownie i obliczeni techniczne Metody numeryczne w modelowniu: Różniczkownie i cłkownie numeryczne Pochodn unkcji Pochodn unkcji w punkcie jest deiniown jko grnic ilorzu różnicowego (jeżeli istnieje):
Modelownie i obliczeni techniczne Metody numeryczne w modelowniu: Różniczkownie i cłkownie numeryczne Pochodn unkcji Pochodn unkcji w punkcie jest deiniown jko grnic ilorzu różnicowego (jeżeli istnieje):
5/28 5/29. Moeller HPL /2005. Moeller HPL /2005
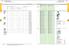 5/8 Aprty kompletne do 75 kw Aprty kompletne do 75 kw 5/9 Znmionowy prąd prcy Mx moc silnik indukcyjnego trójfzowego 50 60 Hz Konw.prąd termiczny Ith = Ie AC- przy 55 C AC-3 AC-3 AC-4 bez obudowy w obudowie
5/8 Aprty kompletne do 75 kw Aprty kompletne do 75 kw 5/9 Znmionowy prąd prcy Mx moc silnik indukcyjnego trójfzowego 50 60 Hz Konw.prąd termiczny Ith = Ie AC- przy 55 C AC-3 AC-3 AC-4 bez obudowy w obudowie
Propozycja przedmiotowego systemu oceniania wraz z określeniem wymagań edukacyjnych (zakres podstawowy)
 Propozycj przedmiotowego systemu ocenini wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Proponujemy, by omwijąc dne zgdnienie progrmowe lub rozwiązując zdnie, nuczyciel określł do jkiego zkresu
Propozycj przedmiotowego systemu ocenini wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Proponujemy, by omwijąc dne zgdnienie progrmowe lub rozwiązując zdnie, nuczyciel określł do jkiego zkresu
cz. 2 dr inż. Zbigniew Szklarski
 Wykłd 11: Elektrosttyk cz. 2 dr inż. Zbigniew Szklrski szkl@gh.edu.pl http://lyer.uci.gh.edu.pl/z.szklrski/ Pole elektryczne przewodnik N powierzchni metlicznej (przewodzącej) cły łdunek gromdzi się n
Wykłd 11: Elektrosttyk cz. 2 dr inż. Zbigniew Szklrski szkl@gh.edu.pl http://lyer.uci.gh.edu.pl/z.szklrski/ Pole elektryczne przewodnik N powierzchni metlicznej (przewodzącej) cły łdunek gromdzi się n
POMIAR MODUŁU SPRĘŻYSTOŚCI STALI PRZEZ POMIAR WYDŁUŻENIA DRUTU
 POMIAR MODUŁU SPRĘŻYSTOŚCI STALI PRZEZ POMIAR WYDŁUŻENIA DRUTU I. Cel ćwiczeni: zpoznnie z teorią odksztłceń sprężystych cił stłych orz z prwem Hooke.Wyzncznie modułu sprężystości (modułu Young) metodą
POMIAR MODUŁU SPRĘŻYSTOŚCI STALI PRZEZ POMIAR WYDŁUŻENIA DRUTU I. Cel ćwiczeni: zpoznnie z teorią odksztłceń sprężystych cił stłych orz z prwem Hooke.Wyzncznie modułu sprężystości (modułu Young) metodą
usuwa niewymierność z mianownika wyrażenia typu
 Wymgni edukcyjne n poszczególne oceny z mtemtyki Kls pierwsz zkres podstwowy. LICZBY RZECZYWISTE podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych i złożonych orz przyporządkowuje
Wymgni edukcyjne n poszczególne oceny z mtemtyki Kls pierwsz zkres podstwowy. LICZBY RZECZYWISTE podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych i złożonych orz przyporządkowuje
WYMAGANIA I KRYTERIA OCENIANIA Z MATEMATYKI W 3 LETNIM LICEUM OGÓLNOKSZTAŁCĄCYM
 WYMAGANIA I KRYTERIA OCENIANIA Z MATEMATYKI W 3 LETNIM LICEUM OGÓLNOKSZTAŁCĄCYM Kls drug A, B, C, D, E, G, H zkres podstwowy 1. FUNKCJA LINIOWA rozpoznje funkcję liniową n podstwie wzoru lub wykresu rysuje
WYMAGANIA I KRYTERIA OCENIANIA Z MATEMATYKI W 3 LETNIM LICEUM OGÓLNOKSZTAŁCĄCYM Kls drug A, B, C, D, E, G, H zkres podstwowy 1. FUNKCJA LINIOWA rozpoznje funkcję liniową n podstwie wzoru lub wykresu rysuje
WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ
 Ćwiczenie 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ 9.. Opis teoretyczny Soczewką seryczną nzywmy przezroczystą bryłę ogrniczoną dwom powierzchnimi serycznymi o promienich R i
Ćwiczenie 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ 9.. Opis teoretyczny Soczewką seryczną nzywmy przezroczystą bryłę ogrniczoną dwom powierzchnimi serycznymi o promienich R i
Analiza matematyczna i algebra liniowa
 Anliz mtemtyczn i lgebr liniow Mteriły pomocnicze dl studentów do wykłdów Mcierze liczbowe i wyznczniki. Ukłdy równń liniowych. Mcierze. Wyznczniki. Mcierz odwrotn. Równni mcierzowe. Rząd mcierzy. Ukłdy
Anliz mtemtyczn i lgebr liniow Mteriły pomocnicze dl studentów do wykłdów Mcierze liczbowe i wyznczniki. Ukłdy równń liniowych. Mcierze. Wyznczniki. Mcierz odwrotn. Równni mcierzowe. Rząd mcierzy. Ukłdy
Aparatura sterująca i sygnalizacyjna Czujniki indukcyjne zbliżeniowe LSI
 Aprtur sterując i sygnlizcyjn Czujniki indukcyjne zbliżeniowe LSI Czujnik indukcyjny zbliżeniowy prcuje n zsdzie tłumionego oscyltor LC: jeżeli w obszr dziłni dostnie się metl, to z ukłdu zostje pobrn
Aprtur sterując i sygnlizcyjn Czujniki indukcyjne zbliżeniowe LSI Czujnik indukcyjny zbliżeniowy prcuje n zsdzie tłumionego oscyltor LC: jeżeli w obszr dziłni dostnie się metl, to z ukłdu zostje pobrn
PROJEKT BUDOWLANY. Obiekt: Budynek istniejący C Na terenie kompleksu szpitalnego Przy ul. Staszica 16 73-110 Stargard Szczeciński
 PROJEKT BUDOWLANY Relizcj etpu przebudowy i modernizcji 3 piętr Oddziłu Rehbilitcyjnego polegjącego n budowie szybu windowego, montżu windy szpitlnej orz niezbędnej rozbudowie obiektu budynku C znjdującego
PROJEKT BUDOWLANY Relizcj etpu przebudowy i modernizcji 3 piętr Oddziłu Rehbilitcyjnego polegjącego n budowie szybu windowego, montżu windy szpitlnej orz niezbędnej rozbudowie obiektu budynku C znjdującego
BADANIE ZALEŻNOŚCI PRZENIKALNOŚCI MAGNETYCZNEJ
 ADANIE ZAEŻNOŚCI PRZENIKANOŚCI MAGNETYCZNEJ FERRIMAGNETYKÓW OD TEMPERATURY 1. Teori Włściwości mgnetyczne sstncji chrkteryzje współczynnik przeniklności mgnetycznej. Dl próżni ten współczynnik jest równy
ADANIE ZAEŻNOŚCI PRZENIKANOŚCI MAGNETYCZNEJ FERRIMAGNETYKÓW OD TEMPERATURY 1. Teori Włściwości mgnetyczne sstncji chrkteryzje współczynnik przeniklności mgnetycznej. Dl próżni ten współczynnik jest równy
Wymagania kl. 2. Uczeń:
 Wymgni kl. 2 Zkres podstwowy Temt lekcji Zkres treści Osiągnięci uczni. SUMY ALGEBRAICZNE. Sumy lgebriczne definicj jednominu pojęcie współczynnik jednominu porządkuje jednominy pojęcie sumy lgebricznej
Wymgni kl. 2 Zkres podstwowy Temt lekcji Zkres treści Osiągnięci uczni. SUMY ALGEBRAICZNE. Sumy lgebriczne definicj jednominu pojęcie współczynnik jednominu porządkuje jednominy pojęcie sumy lgebricznej
Wymagania na ocenę dopuszczającą z matematyki klasa II Matematyka - Babiański, Chańko-Nowa Era nr prog. DKOS 4015-99/02
 Wymgni n ocenę dopuszczjącą z mtemtyki kls II Mtemtyk - Bbiński, Chńko-Now Er nr prog. DKOS 4015-99/02 Temt lekcji Zkres treści Osiągnięci uczni WIELOMIANY 1. Stopień i współczynniki wielominu 2. Dodwnie
Wymgni n ocenę dopuszczjącą z mtemtyki kls II Mtemtyk - Bbiński, Chńko-Now Er nr prog. DKOS 4015-99/02 Temt lekcji Zkres treści Osiągnięci uczni WIELOMIANY 1. Stopień i współczynniki wielominu 2. Dodwnie
Algebra Boola i podstawy systemów liczbowych. Ćwiczenia z Teorii Układów Logicznych, dr inż. Ernest Jamro. 1. System dwójkowy reprezentacja binarna
 lger Bool i podstwy systemów liczowych. Ćwiczeni z Teorii Ukłdów Logicznych, dr inż. Ernest Jmro. System dwójkowy reprezentcj inrn Ukłdy logiczne operują tylko n dwóch stnch ozncznymi jko zero (stn npięci
lger Bool i podstwy systemów liczowych. Ćwiczeni z Teorii Ukłdów Logicznych, dr inż. Ernest Jmro. System dwójkowy reprezentcj inrn Ukłdy logiczne operują tylko n dwóch stnch ozncznymi jko zero (stn npięci
Matematyka finansowa 10.03.2014 r. Komisja Egzaminacyjna dla Aktuariuszy. LXVI Egzamin dla Aktuariuszy z 10 marca 2014 r. Część I
 Mtemtyk finnsow.03.2014 r. Komisj Egzmincyjn dl Akturiuszy LXVI Egzmin dl Akturiuszy z mrc 2014 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 0 minut 1 Mtemtyk
Mtemtyk finnsow.03.2014 r. Komisj Egzmincyjn dl Akturiuszy LXVI Egzmin dl Akturiuszy z mrc 2014 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 0 minut 1 Mtemtyk
Oznaczenia: K wymagania konieczne; P wymagania podstawowe; R wymagania rozszerzające; D wymagania dopełniające; W wymagania wykraczające
 Wymgni edukcyjne z mtemtyki ls 2 b lo Zkres podstwowy Oznczeni: wymgni konieczne; wymgni podstwowe; R wymgni rozszerzjące; D wymgni dopełnijące; W wymgni wykrczjące Temt lekcji Zkres treści Osiągnięci
Wymgni edukcyjne z mtemtyki ls 2 b lo Zkres podstwowy Oznczeni: wymgni konieczne; wymgni podstwowe; R wymgni rozszerzjące; D wymgni dopełnijące; W wymgni wykrczjące Temt lekcji Zkres treści Osiągnięci
Montaż na płycie SPX P (OOC) SPX P SPX P SPX P
 SPX i SPX -V tbel doboru SPX - ROZŁĄCZNIKI BEZPIECZNIKOWE SKRZYNKOWE NH Montż n płycie Typ Nr ref. In (A) Rozmir wkłdki SPX 000 15-P 5 00 15 000 (OOC) SPX 00 1-P 5 0 1 00 SPX 1 -P 5 04 1 SPX 400-P 5 0
SPX i SPX -V tbel doboru SPX - ROZŁĄCZNIKI BEZPIECZNIKOWE SKRZYNKOWE NH Montż n płycie Typ Nr ref. In (A) Rozmir wkłdki SPX 000 15-P 5 00 15 000 (OOC) SPX 00 1-P 5 0 1 00 SPX 1 -P 5 04 1 SPX 400-P 5 0
Aparatura sterująca i sygnalizacyjna Łączniki krańcowe LS-Titan
 Łączniki krńcowe ezpieczeństw LS4 ZB, LS ZB Łączniki krńcowe ezpieczeństw firmy Moeller są wykonne specjlnie do ndzorowni pozycji osłon ochronnych: drzwi, klp, kopuł i sitek ochronnych. Spełniją one wymgni
Łączniki krńcowe ezpieczeństw LS4 ZB, LS ZB Łączniki krńcowe ezpieczeństw firmy Moeller są wykonne specjlnie do ndzorowni pozycji osłon ochronnych: drzwi, klp, kopuł i sitek ochronnych. Spełniją one wymgni
POLITECHNIKA GDAŃSKA Wydział Elektrotechniki i Automatyki Katedra Energoelektroniki i Maszyn Elektrycznych
 POLITECHNIKA GDAŃSKA Wydził Elektrotechniki i Automtyki Ktedr Energoelektroniki i Mszyn Elektrycznych S Y S T E M Y E L E K T R O M E C H A N I C Z N E PROJEKT/LABORATORIUM ĆWICZENIE (SPS) SILNIK PRĄDU
POLITECHNIKA GDAŃSKA Wydził Elektrotechniki i Automtyki Ktedr Energoelektroniki i Mszyn Elektrycznych S Y S T E M Y E L E K T R O M E C H A N I C Z N E PROJEKT/LABORATORIUM ĆWICZENIE (SPS) SILNIK PRĄDU
Zadania. I. Podzielność liczb całkowitych
 Zdni I. Podzielność liczb cłkowitych. Pewn liczb sześciocyfrow kończy się cyfrą 5. Jeśli tę cyfrę przestwimy n miejsce pierwsze ze strony lewej to otrzymmy nową liczbę cztery rzy większą od poprzedniej.
Zdni I. Podzielność liczb cłkowitych. Pewn liczb sześciocyfrow kończy się cyfrą 5. Jeśli tę cyfrę przestwimy n miejsce pierwsze ze strony lewej to otrzymmy nową liczbę cztery rzy większą od poprzedniej.
Opis i analiza metod pomiaru prędkości kątowej. Prądnice tachometryczne.
 Opis i nliz metod pomiru prędkości kątowej. Prądnice tcometryczne. Prądnice tcometryczne są to młe prądnice elektryczne, któryc npięcie wyjściowe zwier informcję o prędkości obrotowej, w niektóryc przypdkc
Opis i nliz metod pomiru prędkości kątowej. Prądnice tcometryczne. Prądnice tcometryczne są to młe prądnice elektryczne, któryc npięcie wyjściowe zwier informcję o prędkości obrotowej, w niektóryc przypdkc
Macierz. Wyznacznik macierzy. Układ równań liniowych
 Temt wykłdu: Mcierz. Wyzncznik mcierzy. Ukłd równń liniowych Kody kolorów: żółty nowe pojęcie pomrńczowy uwg kursyw komentrz * mterił ndobowiązkowy Ann Rjfur, Mtemtyk Zgdnieni. Pojęci. Dziłni n mcierzch.
Temt wykłdu: Mcierz. Wyzncznik mcierzy. Ukłd równń liniowych Kody kolorów: żółty nowe pojęcie pomrńczowy uwg kursyw komentrz * mterił ndobowiązkowy Ann Rjfur, Mtemtyk Zgdnieni. Pojęci. Dziłni n mcierzch.
Wykład 2. Granice, ciągłość, pochodna funkcji i jej interpretacja geometryczna
 1 Wykłd Grnice, ciągłość, pocodn unkcji i jej interpretcj geometryczn.1 Grnic unkcji. Grnic lewostronn i grnic prwostronn unkcji Deinicj.1 Mówimy, że liczb g jest grnicą lewostronną unkcji w punkcie =,
1 Wykłd Grnice, ciągłość, pocodn unkcji i jej interpretcj geometryczn.1 Grnic unkcji. Grnic lewostronn i grnic prwostronn unkcji Deinicj.1 Mówimy, że liczb g jest grnicą lewostronną unkcji w punkcie =,
Bardzo krótki wstęp do elektroniki cyfrowej
 Brdzo krótki wstęp do elektroniki cyfrowej Słwomir Mmic http://min5.mu.edu.pl/~zfp/sm/home.html Pln ) Ukłdy logiczne b) Algebr Boole i jej relizcj sprzętow c) Brmki są dwie? d) Prosty przykłd sumtor e)
Brdzo krótki wstęp do elektroniki cyfrowej Słwomir Mmic http://min5.mu.edu.pl/~zfp/sm/home.html Pln ) Ukłdy logiczne b) Algebr Boole i jej relizcj sprzętow c) Brmki są dwie? d) Prosty przykłd sumtor e)
Wektor kolumnowy m wymiarowy macierz prostokątna o wymiarze n=1 Wektor wierszowy n wymiarowy macierz prostokątna o wymiarze m=1
 Rchunek mcierzowy Mcierzą A nzywmy funkcję 2-zmiennych, któr prze liczb nturlnych (i,j) gdzie i = 1,2,3,4.,m; j = 1,2,3,4,n przyporządkowuje dokłdnie jeden element ij. 11 21 A = m1 12 22 m2 1n 2n mn Wymirem
Rchunek mcierzowy Mcierzą A nzywmy funkcję 2-zmiennych, któr prze liczb nturlnych (i,j) gdzie i = 1,2,3,4.,m; j = 1,2,3,4,n przyporządkowuje dokłdnie jeden element ij. 11 21 A = m1 12 22 m2 1n 2n mn Wymirem
Autor: Zbigniew Tuzimek Opracowanie wersji elektronicznej: Tomasz Wdowiak
 DNIE UKŁDÓW LOKD UTOMTYCZNYCH uor: Zigniew Tuzimek Oprcownie wersji elekronicznej: Tomsz Wdowik 1. Cel i zkres ćwiczeni Celem ćwiczeni jes zpoznnie sudenów z udową orz dziłniem zezpieczeń i lokd sosownych
DNIE UKŁDÓW LOKD UTOMTYCZNYCH uor: Zigniew Tuzimek Oprcownie wersji elekronicznej: Tomsz Wdowik 1. Cel i zkres ćwiczeni Celem ćwiczeni jes zpoznnie sudenów z udową orz dziłniem zezpieczeń i lokd sosownych
Transformatory sterujące ST, DTZ, transformatory wielouzwojeniowe UTI, uniwersalne zasilacze AING
 sterujące ST, DTZ, trnsformtory wielouzwojeniowe UTI, uniwerslne zsilcze AING Wszystkie trnsformtory są budowne i sprwdzne zgodnie z njnowszymi przepismi normy IEC/EN 61558. Dltego w zleżności od wykonni
sterujące ST, DTZ, trnsformtory wielouzwojeniowe UTI, uniwerslne zsilcze AING Wszystkie trnsformtory są budowne i sprwdzne zgodnie z njnowszymi przepismi normy IEC/EN 61558. Dltego w zleżności od wykonni
Wymagania edukacyjne na poszczególne oceny z matematyki w klasie II poziom rozszerzony
 Wymgni edukcyjne n poszczególne oceny z mtemtyki w klsie II poziom rozszerzony N ocenę dopuszczjącą, uczeń: rysuje wykres funkcji f ( x) x i podje jej włsności; sprwdz lgebricznie, czy dny punkt nleży
Wymgni edukcyjne n poszczególne oceny z mtemtyki w klsie II poziom rozszerzony N ocenę dopuszczjącą, uczeń: rysuje wykres funkcji f ( x) x i podje jej włsności; sprwdz lgebricznie, czy dny punkt nleży
DZIAŁ 2. Figury geometryczne
 1 kl. 6, Scenriusz lekcji Pole powierzchni bryły DZAŁ 2. Figury geometryczne Temt w podręczniku: Pole powierzchni bryły Temt jest przeznczony do relizcji podczs 2 godzin lekcyjnych. Zostł zplnowny jko
1 kl. 6, Scenriusz lekcji Pole powierzchni bryły DZAŁ 2. Figury geometryczne Temt w podręczniku: Pole powierzchni bryły Temt jest przeznczony do relizcji podczs 2 godzin lekcyjnych. Zostł zplnowny jko
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY VIII w roku szkolnym 2015/2016
 WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY VIII w roku szkolnym 015/016 oprcowł: Dnut Wojcieszek n ocenę dopuszczjącą rysuje wykres funkcji f ( ) i podje jej włsności sprwdz lgebricznie, czy dny punkt
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY VIII w roku szkolnym 015/016 oprcowł: Dnut Wojcieszek n ocenę dopuszczjącą rysuje wykres funkcji f ( ) i podje jej włsności sprwdz lgebricznie, czy dny punkt
PODSTAWY BAZ DANYCH Wykład 3 2. Pojęcie Relacyjnej Bazy Danych
 PODSTAWY BAZ DANYCH Wykłd 3 2. Pojęcie Relcyjnej Bzy Dnych 2005/2006 Wykłd "Podstwy z dnych" 1 Rozkłdlno dlność schemtów w relcyjnych Przykłd. Relcj EGZ(U), U := { I, N, P, O }, gdzie I 10 10 11 N f f
PODSTAWY BAZ DANYCH Wykłd 3 2. Pojęcie Relcyjnej Bzy Dnych 2005/2006 Wykłd "Podstwy z dnych" 1 Rozkłdlno dlność schemtów w relcyjnych Przykłd. Relcj EGZ(U), U := { I, N, P, O }, gdzie I 10 10 11 N f f
WENTYLACJA PRZESTRZENI POTENCJALNIE ZAGROŻONYCH WYBUCHEM MIESZANIN GAZOWYCH
 Ochron przeciwwybuchow Michł Świerżewski WENTYLACJA PRZESTRZENI POTENCJALNIE ZAGROŻONYCH WYBUCHEM MIESZANIN GAZOWYCH 1. Widomości ogólne Zgodnie z postnowienimi rozporządzeni Ministr Sprw Wewnętrznych
Ochron przeciwwybuchow Michł Świerżewski WENTYLACJA PRZESTRZENI POTENCJALNIE ZAGROŻONYCH WYBUCHEM MIESZANIN GAZOWYCH 1. Widomości ogólne Zgodnie z postnowienimi rozporządzeni Ministr Sprw Wewnętrznych
Proporcjonalny zawór redukcyjny typ 3WZCDE6
 ZSOSOWNIE OIS DZIŁNI roporcjonlny zwór redukcyjny typ 3WZCDE6 WN6 do 10 M 3 do 15 dm /min KR KLOGOW - INSRUKCJ OSŁUGI 3-drogowy zwór redukcyjny sterowny elektrycznie, proporcjonlnie typ 3WZCDE6 stosowny
ZSOSOWNIE OIS DZIŁNI roporcjonlny zwór redukcyjny typ 3WZCDE6 WN6 do 10 M 3 do 15 dm /min KR KLOGOW - INSRUKCJ OSŁUGI 3-drogowy zwór redukcyjny sterowny elektrycznie, proporcjonlnie typ 3WZCDE6 stosowny
Wyrównanie sieci niwelacyjnej
 1. Wstęp Co to jest sieć niwelcyjn Po co ją się wyrównje Co chcemy osiągnąć 2. Metod pośrednicząc Wyrównnie sieci niwelcyjnej Metod pośrednicząc i metod grpow Mmy sieć skłdjącą się z szereg pnktów. Niektóre
1. Wstęp Co to jest sieć niwelcyjn Po co ją się wyrównje Co chcemy osiągnąć 2. Metod pośrednicząc Wyrównnie sieci niwelcyjnej Metod pośrednicząc i metod grpow Mmy sieć skłdjącą się z szereg pnktów. Niektóre
Równania i nierówności kwadratowe z jedną niewiadomą
 50 REPETYTORIUM 31 Równni i nierówności kwdrtowe z jedną niewidomą Równnie wielominowe to równość dwóch wyrżeń lgebricznych Kżd liczb, któr po podstwieniu w miejscu niewidomej w równniu o jednej niewidomej
50 REPETYTORIUM 31 Równni i nierówności kwdrtowe z jedną niewidomą Równnie wielominowe to równość dwóch wyrżeń lgebricznych Kżd liczb, któr po podstwieniu w miejscu niewidomej w równniu o jednej niewidomej
KONKURS MATEMATYCZNY dla uczniów gimnazjów w roku szkolnym 2012/13. Propozycja punktowania rozwiązań zadań
 KONKURS MATEMATYCZNY dl uczniów gimnzjów w roku szkolnym 0/ II etp zwodów (rejonowy) 0 listopd 0 r. Propozycj punktowni rozwiązń zdń Uwg: Z kżde poprwne rozwiąznie inne niż przewidzine w propozycji punktowni
KONKURS MATEMATYCZNY dl uczniów gimnzjów w roku szkolnym 0/ II etp zwodów (rejonowy) 0 listopd 0 r. Propozycj punktowni rozwiązń zdń Uwg: Z kżde poprwne rozwiąznie inne niż przewidzine w propozycji punktowni
KSIĘGA ZNAKU. Znak posiada swój obszar ochronny i w jego obrębie nie mogą się znajdować żadne elementy, nie związane ze znakiem.
 KSIĘGA ZNAKU KSIĘGA ZNAKU Poniżej przedstwion jest chrkterystyk znku 7 lt Uniwersytetu Łódzkiego. Wszystkie proporcje i sposób rozmieszczeni poszczególnych elementów są ściśle określone. Wprowdznie jkichkolwiek
KSIĘGA ZNAKU KSIĘGA ZNAKU Poniżej przedstwion jest chrkterystyk znku 7 lt Uniwersytetu Łódzkiego. Wszystkie proporcje i sposób rozmieszczeni poszczególnych elementów są ściśle określone. Wprowdznie jkichkolwiek
POLITECHNIKA GDAŃSKA
 POLITECHNIKA GDAŃSKA WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI KATEDRA ENERGOELEKTRONIKI I MASZYN ELEKTRYCZNYCH LABORATORIUM MASZYNY ELEKTRYCZNE ĆWICZENIE (MPS) MASZYNY PRĄDU STAŁEGO SILNIK OBCOWZBUDNY BADANIE
POLITECHNIKA GDAŃSKA WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI KATEDRA ENERGOELEKTRONIKI I MASZYN ELEKTRYCZNYCH LABORATORIUM MASZYNY ELEKTRYCZNE ĆWICZENIE (MPS) MASZYNY PRĄDU STAŁEGO SILNIK OBCOWZBUDNY BADANIE
WYKŁAD 7 CYFROWE UKŁADY SCALONE
 65 KŁAD 7 CYFRO UKŁADY SCALONE Ukłdy nlogowe są przystosowne do przetwrzni npięć (lu prądów), których wrtości zwierją się w pewnym przedzile ukłd nlogowy wrtości Ukłdy cyfrowe służą do przetwrzni sygnłów
65 KŁAD 7 CYFRO UKŁADY SCALONE Ukłdy nlogowe są przystosowne do przetwrzni npięć (lu prądów), których wrtości zwierją się w pewnym przedzile ukłd nlogowy wrtości Ukłdy cyfrowe służą do przetwrzni sygnłów
Rozdzielacz suwakowy sterowany elektrycznie typ WE10
 Rozdzielcz suwkowy sterowny elektrycznie typ WE WN do,5 M do dm /min KR KLOGOW - INSRUKCJ OSŁUGI WK 499 78.4 ZSOSOWNIE Rozdzielcz suwkowy sterowny elektrycznie typ WE jest przeznczony do zminy kierunku
Rozdzielcz suwkowy sterowny elektrycznie typ WE WN do,5 M do dm /min KR KLOGOW - INSRUKCJ OSŁUGI WK 499 78.4 ZSOSOWNIE Rozdzielcz suwkowy sterowny elektrycznie typ WE jest przeznczony do zminy kierunku
Praca, potencjał i pojemność
 Prc, potencjł i pojemność Mciej J. Mrowiński 1 listopd 2010 Zdnie PPP1 h Wyzncz wrtość potencjłu elektrycznego w punkcie oddlonym o h od cienkiego, jednorodnie nłdownego łdunkiem Q pierścieni o promieniu.
Prc, potencjł i pojemność Mciej J. Mrowiński 1 listopd 2010 Zdnie PPP1 h Wyzncz wrtość potencjłu elektrycznego w punkcie oddlonym o h od cienkiego, jednorodnie nłdownego łdunkiem Q pierścieni o promieniu.
ĆWICZENIE ANALIZA SITOWA I PODSTAWY OCENY GRANULOMETRYCZNEJ SUROWCÓW I PRODUKTÓW
 1 ĆWICZENIE ANALIZA SITOWA I PODSTAWY OCENY GANULOMETYCZNEJ SUOWCÓW I PODUKTÓW 1. Cel zkres ćwczen Celem ćwczen jest opnowne przez studentów metody oceny mterłu sypkego pod względem loścowej zwrtośc frkcj
1 ĆWICZENIE ANALIZA SITOWA I PODSTAWY OCENY GANULOMETYCZNEJ SUOWCÓW I PODUKTÓW 1. Cel zkres ćwczen Celem ćwczen jest opnowne przez studentów metody oceny mterłu sypkego pod względem loścowej zwrtośc frkcj
Temat lekcji Zakres treści Osiągnięcia ucznia
 ln wynikowy kls 2c i 2e - Jolnt jąk Mtemtyk 2. dl liceum ogólnoksztłcącego, liceum profilownego i technikum. sztłcenie ogólne w zkresie podstwowym rok szkolny 2015/2016 Wymgni edukcyjne określjące oceny:
ln wynikowy kls 2c i 2e - Jolnt jąk Mtemtyk 2. dl liceum ogólnoksztłcącego, liceum profilownego i technikum. sztłcenie ogólne w zkresie podstwowym rok szkolny 2015/2016 Wymgni edukcyjne określjące oceny:
Szczegółowe wymagania edukacyjne z matematyki, klasa 2C, poziom podstawowy
 Szczegółowe wymgni edukcyjne z mtemtyki, kls 2C, poziom podstwowy Wymgni konieczne () dotyczą zgdnieo elementrnych, stnowiących swego rodzju podstwę, ztem powinny byd opnowne przez kżdego uczni. Wymgni
Szczegółowe wymgni edukcyjne z mtemtyki, kls 2C, poziom podstwowy Wymgni konieczne () dotyczą zgdnieo elementrnych, stnowiących swego rodzju podstwę, ztem powinny byd opnowne przez kżdego uczni. Wymgni
Rozwiązania maj 2017r. Zadania zamknięte
 Rozwiązni mj 2017r. Zdni zmknięte Zd 1. 5 16 5 2 5 2 Zd 2. 5 2 27 2 23 2 2 2 2 Zd 3. 2log 3 2log 5log 3 log 5 log 9 log 25log Zd. 120% 8910 1,2 8910 2,2 8910 $%, 050 Zd 5. Njłtwiej jest zuwżyć że dl 1
Rozwiązni mj 2017r. Zdni zmknięte Zd 1. 5 16 5 2 5 2 Zd 2. 5 2 27 2 23 2 2 2 2 Zd 3. 2log 3 2log 5log 3 log 5 log 9 log 25log Zd. 120% 8910 1,2 8910 2,2 8910 $%, 050 Zd 5. Njłtwiej jest zuwżyć że dl 1
Przedmiotowy system oceniania z matematyki wraz z określeniem wymagań edukacyjnych (zakres podstawowy) Klasa II TAK
 I Postnowieni ogólne Przedmiotowy system ocenini z mtemtyki wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Kls II TAK 1. Wrunkiem uzyskni pozytywnej oceny semestrlnej z mtemtyki jest: ) zliczenie
I Postnowieni ogólne Przedmiotowy system ocenini z mtemtyki wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Kls II TAK 1. Wrunkiem uzyskni pozytywnej oceny semestrlnej z mtemtyki jest: ) zliczenie
Podstawy Techniki Cyfrowej Układy komutacyjne
 Podstwy Techniki Cyfrowej Ukłdy komutcyjne Ukłdy kombincyjne, umożliwijące przełącznie (komutcję) sygnłów cyfrowych, nzyw się ukłdmi ukłdmi komutcyjnymi. Do podstwowych ukłdów komutcyjnych zlicz się multipleksery
Podstwy Techniki Cyfrowej Ukłdy komutcyjne Ukłdy kombincyjne, umożliwijące przełącznie (komutcję) sygnłów cyfrowych, nzyw się ukłdmi ukłdmi komutcyjnymi. Do podstwowych ukłdów komutcyjnych zlicz się multipleksery
Katalog wymagań programowych na poszczególne stopnie szkolne. Matematyka. Poznać, zrozumieć
 Ktlog wymgń progrmowych n poszczególne stopnie szkolne Mtemtyk. Poznć, zrozumieć Ksztłcenie w zkresie podstwowym. Kls 2 Poniżej podjemy umiejętności, jkie powinien zdobyć uczeń z kżdego dziłu, by uzyskć
Ktlog wymgń progrmowych n poszczególne stopnie szkolne Mtemtyk. Poznć, zrozumieć Ksztłcenie w zkresie podstwowym. Kls 2 Poniżej podjemy umiejętności, jkie powinien zdobyć uczeń z kżdego dziłu, by uzyskć
Materiały pomocnicze do ćwiczeń z przedmiotu: Ogrzewnictwo, wentylacja i klimatyzacja II. Klimatyzacja
 Mteriły pomocnicze do ćwiczeń z przedmiotu: Orzewnictwo, wentylcj i klimtyzcj II. Klimtyzcj Rozdził 1 Podstwowe włsności powietrz jko nośnik ciepł mr inż. Anieszk Sdłowsk-Słę Mteriły pomocnicze do klimtyzcji.
Mteriły pomocnicze do ćwiczeń z przedmiotu: Orzewnictwo, wentylcj i klimtyzcj II. Klimtyzcj Rozdził 1 Podstwowe włsności powietrz jko nośnik ciepł mr inż. Anieszk Sdłowsk-Słę Mteriły pomocnicze do klimtyzcji.
Wymagania edukacyjne z matematyki FUNKCJE dopuszczającą dostateczną dobrą bardzo dobrą
 Wymgni edukcyjne z mtemtyki Kls IIC. Rok szkolny 013/014 Poziom podstwowy FUNKCJE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje przyporządkowni będące funkcjmi określ funkcję różnymi
Wymgni edukcyjne z mtemtyki Kls IIC. Rok szkolny 013/014 Poziom podstwowy FUNKCJE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje przyporządkowni będące funkcjmi określ funkcję różnymi
Ćwiczenie nr 2-SCO. Warstwa połowiąca WP. Ćwiczenie nr 2. 1 Cel ćwiczenia
 Ćwiczenie nr 2-SCO. Wrstw połowiąc WP 1 Cel ćwiczeni Wyznczenie pierwszej wrstwy połowiącej WP (Hlf Vlue Lyer) dl promieniowni X generownego w prcie rentgenowskim (energi 5-15 kev). Wyzncznie współczynnik
Ćwiczenie nr 2-SCO. Wrstw połowiąc WP 1 Cel ćwiczeni Wyznczenie pierwszej wrstwy połowiącej WP (Hlf Vlue Lyer) dl promieniowni X generownego w prcie rentgenowskim (energi 5-15 kev). Wyzncznie współczynnik
Przedmiotowy system oceniania z matematyki wraz z określeniem wymagań edukacyjnych (zakres podstawowy) Klasa II LO
 I Postnowieni ogólne Przedmiotowy system ocenini z mtemtyki wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Kls II LO 1. Wrunkiem uzyskni pozytywnej oceny semestrlnej z mtemtyki jest: ) zliczenie
I Postnowieni ogólne Przedmiotowy system ocenini z mtemtyki wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Kls II LO 1. Wrunkiem uzyskni pozytywnej oceny semestrlnej z mtemtyki jest: ) zliczenie
Struktura energetyczna ciał stałych-cd. Fizyka II dla Elektroniki, lato
 Struktur energetyczn cił stłych-cd Fizyk II dl Elektroniki, lto 011 1 Fizyk II dl Elektroniki, lto 011 Przybliżenie periodycznego potencjłu sieci krystlicznej model Kronig- Penney potencjł rzeczywisty
Struktur energetyczn cił stłych-cd Fizyk II dl Elektroniki, lto 011 1 Fizyk II dl Elektroniki, lto 011 Przybliżenie periodycznego potencjłu sieci krystlicznej model Kronig- Penney potencjł rzeczywisty
WEKTORY skalary wektory W ogólnym przypadku, aby określić wektor, należy znać:
 WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
Fizyka. Kurs przygotowawczy. na studia inżynierskie. mgr Kamila Haule
 Fizyk Kurs przygotowwczy n studi inżynierskie mgr Kmil Hule Dzień 3 Lbortorium Pomir dlczego mierzymy? Pomir jest nieodłączną częścią nuki. Stopień znjomości rzeczy często wiąże się ze sposobem ich pomiru.
Fizyk Kurs przygotowwczy n studi inżynierskie mgr Kmil Hule Dzień 3 Lbortorium Pomir dlczego mierzymy? Pomir jest nieodłączną częścią nuki. Stopień znjomości rzeczy często wiąże się ze sposobem ich pomiru.
Badanie czasów zamykania i otwierania styków łączników. Badania czasów niejednoczesności zamykania i otwierania styków. Badania odskoków styków
 Badanie czasów zamykania i otwierania styków łączników. Badania czasów niejednoczesności zamykania i otwierania styków Badania odskoków styków 1. Rodzaje styczników. Styczniki można klasyfikować według
Badanie czasów zamykania i otwierania styków łączników. Badania czasów niejednoczesności zamykania i otwierania styków Badania odskoków styków 1. Rodzaje styczników. Styczniki można klasyfikować według
Wymagania na poszczególne oceny z matematyki w Zespole Szkół im. St. Staszica w Pile. Kl. II poziom podstawowy
 Wymgni n poszczególne oceny z mtemtyki w Zespole Szkół im. St. Stszic w Pile 1. SUMY ALGEBRAICZNE Kl. II poziom podstwowy Uczeń otrzymuje ocenę dopuszczjącą, jeśli: rozpoznje jednominy i sumy lgebriczne
Wymgni n poszczególne oceny z mtemtyki w Zespole Szkół im. St. Stszic w Pile 1. SUMY ALGEBRAICZNE Kl. II poziom podstwowy Uczeń otrzymuje ocenę dopuszczjącą, jeśli: rozpoznje jednominy i sumy lgebriczne
Wykład 6 Dyfrakcja Fresnela i Fraunhofera
 Wykłd 6 Dyfrkcj Fresnel i Frunhofer Zjwisko dyfrkcji (ugięci) świtł odkrył Grimldi (XVII w). Poleg ono n uginniu się promieni świetlnych przechodzących w pobliżu przeszkody (np. brzeg szczeliny). Wyjśnienie
Wykłd 6 Dyfrkcj Fresnel i Frunhofer Zjwisko dyfrkcji (ugięci) świtł odkrył Grimldi (XVII w). Poleg ono n uginniu się promieni świetlnych przechodzących w pobliżu przeszkody (np. brzeg szczeliny). Wyjśnienie
Zadanie 5. Kratownica statycznie wyznaczalna.
 dnie 5. Krtownic sttycznie wyznczln. Wyznczyć wrtości sił w prętch krtownicy sttycznie wyznczlnej przedstwionej n Rys.1: ). metodą nlitycznego równowżeni węzłów, ). metodą gricznego równowżeni węzłów;
dnie 5. Krtownic sttycznie wyznczln. Wyznczyć wrtości sił w prętch krtownicy sttycznie wyznczlnej przedstwionej n Rys.1: ). metodą nlitycznego równowżeni węzłów, ). metodą gricznego równowżeni węzłów;
ZJAWISKO TERMOEMISJI ELEKTRONÓW
 Ćwiczenie 49 T. Wiktorczyk ZJAWISKO TERMOEMISJI ELEKTRONÓW Cel ćwiczeni: wyznczenie prcy wyjści elektronów z wolfrmu orz pomir chrkterystyki prądowo npięciowej diody próżniowej Zgdnieni: termoemisj elektronów,
Ćwiczenie 49 T. Wiktorczyk ZJAWISKO TERMOEMISJI ELEKTRONÓW Cel ćwiczeni: wyznczenie prcy wyjści elektronów z wolfrmu orz pomir chrkterystyki prądowo npięciowej diody próżniowej Zgdnieni: termoemisj elektronów,
Technikum Nr 2 im. gen. Mieczysława Smorawińskiego w Zespole Szkół Ekonomicznych w Kaliszu
 Technikum Nr 2 im. gen. Mieczysłw Smorwińskiego w Zespole Szkół Ekonomicznych w Kliszu Wymgni edukcyjne niezbędne do uzyskni poszczególnych śródrocznych i rocznych ocen klsyfikcyjnych z obowiązkowych zjęć
Technikum Nr 2 im. gen. Mieczysłw Smorwińskiego w Zespole Szkół Ekonomicznych w Kliszu Wymgni edukcyjne niezbędne do uzyskni poszczególnych śródrocznych i rocznych ocen klsyfikcyjnych z obowiązkowych zjęć
Wykład 2. Pojęcie całki niewłaściwej do rachunku prawdopodobieństwa
 Wykłd 2. Pojęcie cłki niewłściwej do rchunku prwdopodobieństw dr Mriusz Grządziel 4 mrc 24 Pole trpezu krzywoliniowego Przypomnienie: figurę ogrniczoną przez: wykres funkcji y = f(x), gdzie f jest funkcją
Wykłd 2. Pojęcie cłki niewłściwej do rchunku prwdopodobieństw dr Mriusz Grządziel 4 mrc 24 Pole trpezu krzywoliniowego Przypomnienie: figurę ogrniczoną przez: wykres funkcji y = f(x), gdzie f jest funkcją
symbol dodatkowy element graficzny kolorystyka typografia
 Identyfikcj wizuln Fundcji n rzecz Nuki Polskiej 1/00 Elementy podstwowe symbol dodtkowy element grficzny kolorystyk typogrfi Identyfikcj wizuln Fundcji n rzecz Nuki Polskiej 1/01 Elementy podstwowe /
Identyfikcj wizuln Fundcji n rzecz Nuki Polskiej 1/00 Elementy podstwowe symbol dodtkowy element grficzny kolorystyk typogrfi Identyfikcj wizuln Fundcji n rzecz Nuki Polskiej 1/01 Elementy podstwowe /
Kodowanie liczb. Kodowanie stałopozycyjne liczb całkowitych. Niech liczba całkowita a ma w systemie dwójkowym postać: Kod prosty
 Kodownie licz Kodownie stłopozycyjne licz cłkowitych Niech licz cłkowit m w systemie dwójkowym postć: nn 0 Wtedy może yć on przedstwion w postci ( n+)-itowej przy pomocy trzech niżej zdefiniownych kodów
Kodownie licz Kodownie stłopozycyjne licz cłkowitych Niech licz cłkowit m w systemie dwójkowym postć: nn 0 Wtedy może yć on przedstwion w postci ( n+)-itowej przy pomocy trzech niżej zdefiniownych kodów
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego. Energia aktywacji jodowania acetonu. opracowała dr B. Nowicka, aktualizacja D.
 Ktedr Chemii Fizycznej Uniwersytetu Łódzkiego Energi ktywcji jodowni cetonu oprcowł dr B. Nowick, ktulizcj D. Wliszewski ćwiczenie nr 8 Zkres zgdnień obowiązujących do ćwiczeni 1. Cząsteczkowość i rzędowość
Ktedr Chemii Fizycznej Uniwersytetu Łódzkiego Energi ktywcji jodowni cetonu oprcowł dr B. Nowick, ktulizcj D. Wliszewski ćwiczenie nr 8 Zkres zgdnień obowiązujących do ćwiczeni 1. Cząsteczkowość i rzędowość
PRZEGLĄD FUNKCJI ELEMENTARNYCH. (powtórzenie) y=f(x)=ax+b,
 WYKŁAD 0 PRZEGLĄD FUNKCJI ELEMENTARNYCH (powtórzenie) 1. Funkcje liniowe Funkcją liniową nzywmy funkcję postci y=f()=+b, gdzie, b są dnymi liczbmi zwnymi odpowiednio: - współczynnik kierunkowy, b - wyrz
WYKŁAD 0 PRZEGLĄD FUNKCJI ELEMENTARNYCH (powtórzenie) 1. Funkcje liniowe Funkcją liniową nzywmy funkcję postci y=f()=+b, gdzie, b są dnymi liczbmi zwnymi odpowiednio: - współczynnik kierunkowy, b - wyrz
str. 1 Temat: Sterowanie stycznikami za pomocą przycisków.
 Temat: Sterowanie stycznikami za pomocą przycisków. Na rys. 7.17 przedstawiono układ sterowania silnika o rozruchu bezpośrednim za pomocą stycznika. Naciśnięcie przycisku Z powoduje podanie napięcia na
Temat: Sterowanie stycznikami za pomocą przycisków. Na rys. 7.17 przedstawiono układ sterowania silnika o rozruchu bezpośrednim za pomocą stycznika. Naciśnięcie przycisku Z powoduje podanie napięcia na
wersja podstawowa (gradient)
 księg znku wersj podstwow (grdient) Logo RAKU FILM w wersji podstwowej może występowć w dwóch wrintch, n jsnym (domyślnie - biłe tło) orz n ciemnym (domyślnie - czrne tło). Nleży unikć stosowni logo n
księg znku wersj podstwow (grdient) Logo RAKU FILM w wersji podstwowej może występowć w dwóch wrintch, n jsnym (domyślnie - biłe tło) orz n ciemnym (domyślnie - czrne tło). Nleży unikć stosowni logo n
Zawór regulacyjny ZK210 z wielostopniową dyszą promieniową
 Zwór regulcyjny z wielostopniową dyszą promieniową Zwór regulcyjny Opis Zwór regulcyjny służący do prcy przy wysokich ciśnienich różnicowych. Stosowny jest między innymi, w instlcjch przemysłowych i elektrownich,
Zwór regulcyjny z wielostopniową dyszą promieniową Zwór regulcyjny Opis Zwór regulcyjny służący do prcy przy wysokich ciśnienich różnicowych. Stosowny jest między innymi, w instlcjch przemysłowych i elektrownich,
2. PODSTAWY STATYKI NA PŁASZCZYŹNIE
 M. DSTY STTYKI N ŁSZZYŹNIE. DSTY STTYKI N ŁSZZYŹNIE.. Zsdy dynmiki Newton Siłą nzywmy wektorową wielkość, któr jest mirą mechnicznego oddziływni n ciło ze strony innych cił. dlszej części ędziemy rozptrywć
M. DSTY STTYKI N ŁSZZYŹNIE. DSTY STTYKI N ŁSZZYŹNIE.. Zsdy dynmiki Newton Siłą nzywmy wektorową wielkość, któr jest mirą mechnicznego oddziływni n ciło ze strony innych cił. dlszej części ędziemy rozptrywć
Wymagania na poszczególne oceny z matematyki w Zespole Szkół im. St. Staszica w Pile. Kl. I poziom podstawowy
 Wymgni n poszczególne oceny z mtemtyki w Zespole Szkół im. St. Stszic w Pile. LICZBY RZECZYWISTE Kl. I poziom podstwowy podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych
Wymgni n poszczególne oceny z mtemtyki w Zespole Szkół im. St. Stszic w Pile. LICZBY RZECZYWISTE Kl. I poziom podstwowy podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych
Redukcja układów sił działających na bryły sztywne
 1 Redukcj ukłdów sił dziłjących n bryły sztywne W zdnich tego rozdziłu wykorzystuje się zsdy redukcji ukłdów sił wykłdne w rmch mechniki ogólnej i powtórzone w tomie 1 podręcznik. Zdnie 1 Zredukowć ukłd
1 Redukcj ukłdów sił dziłjących n bryły sztywne W zdnich tego rozdziłu wykorzystuje się zsdy redukcji ukłdów sił wykłdne w rmch mechniki ogólnej i powtórzone w tomie 1 podręcznik. Zdnie 1 Zredukowć ukłd
Uszczelnienie przepływowe w maszyn przepływowych oraz sposób diagnozowania uszczelnienia przepływowego zwłaszcza w maszyn przepływowych
 Uszczelnienie przepływowe w mszyn przepływowych orz sposób dignozowni uszczelnieni przepływowego zwłszcz w mszyn przepływowych Przedmiotem wynlzku jest uszczelnienie przepływowe mszyn przepływowych orz
Uszczelnienie przepływowe w mszyn przepływowych orz sposób dignozowni uszczelnieni przepływowego zwłszcz w mszyn przepływowych Przedmiotem wynlzku jest uszczelnienie przepływowe mszyn przepływowych orz
WYKŁAD 5. Typy macierzy, działania na macierzach, macierz układu równań. Podstawowe wiadomości o macierzach
 Mtemtyk I WYKŁD. ypy mcierzy, dziłni n mcierzch, mcierz ukłdu równń. Podstwowe widomości o mcierzch Ogóln postć ukłdu m równń liniowych lgebricznych z n niewidomymi x x n xn b x x n xn b, niewidome: x,
Mtemtyk I WYKŁD. ypy mcierzy, dziłni n mcierzch, mcierz ukłdu równń. Podstwowe widomości o mcierzch Ogóln postć ukłdu m równń liniowych lgebricznych z n niewidomymi x x n xn b x x n xn b, niewidome: x,
INSTALACJE ELEKTRYCZNE
 PROJEKT BUDOWLANY Remont budynku gospodrczego Adres: Nowe Wrpno dz. 817 obręb Nowe Wrpno 1 72-022 Nowe Wrpno Inwestor: Gmin Nowe Wrpno pl. wycięstw 1 72-022 Nowe Wrpno Autor: Archiplex Prcowni Projektow
PROJEKT BUDOWLANY Remont budynku gospodrczego Adres: Nowe Wrpno dz. 817 obręb Nowe Wrpno 1 72-022 Nowe Wrpno Inwestor: Gmin Nowe Wrpno pl. wycięstw 1 72-022 Nowe Wrpno Autor: Archiplex Prcowni Projektow
Wiedza i doświadczenie ZBUD - Twoja pewność wyboru! PRZECIĄGARKI I WCIAGARKI LINOWE PRZECIĄGARKI I WCIĄGARKI LINOWE
 ZKŁD UDOWY URZĄDZEŃ DŹWIGNIOWYH tel 1 00 tel 1 0 fx 1 mrketing@zbud.com.pl PRZEIĄGRKI I WIĄGRKI LINOWE zbud@zbud.com.pl ul.zbieñsk -00 Dąbrow Trnowsk 017 Wiedz i doświdczenie ZUD - Twoj pewność wyboru!
ZKŁD UDOWY URZĄDZEŃ DŹWIGNIOWYH tel 1 00 tel 1 0 fx 1 mrketing@zbud.com.pl PRZEIĄGRKI I WIĄGRKI LINOWE zbud@zbud.com.pl ul.zbieñsk -00 Dąbrow Trnowsk 017 Wiedz i doświdczenie ZUD - Twoj pewność wyboru!
Mechanika nieba B. Arkusz I i II Czas pracy 90 minut Instrukcja dla zdającego. Aktualizacja Czerwiec ROK Arkusz I i II
 0004 Mechnik nieb B Dne osobowe włściciel rkusz 0004 Mechnik nieb B Czs prcy 90 minut Instrukcj dl zdjącego. Proszę sprwdzić, czy rkusz egzmincyjny zwier 8 stron. Ewentulny brk nleży zgłosić osobie ndzorującej
0004 Mechnik nieb B Dne osobowe włściciel rkusz 0004 Mechnik nieb B Czs prcy 90 minut Instrukcj dl zdjącego. Proszę sprwdzić, czy rkusz egzmincyjny zwier 8 stron. Ewentulny brk nleży zgłosić osobie ndzorującej
KOMPLEKSOWE POMIARY FREZÓW OBWIEDNIOWYCH
 KOMPLEKSOWE POMIARY FREZÓW OBWIEDNIOWYCH Michł PAWŁOWSKI 1 1. WSTĘP Corz większy rozwój przemysłu energetycznego, w tym siłowni witrowych stwi corz większe wymgni woec producentów przekłdni zętych jeśli
KOMPLEKSOWE POMIARY FREZÓW OBWIEDNIOWYCH Michł PAWŁOWSKI 1 1. WSTĘP Corz większy rozwój przemysłu energetycznego, w tym siłowni witrowych stwi corz większe wymgni woec producentów przekłdni zętych jeśli
Materiały szkoleniowe DRGANIA MECHANICZNE ZAGROŻENIA I PROFILAKTYKA. Serwis internetowy BEZPIECZNIEJ CIOP-PIB
 Mteriły szkoleniowe DRGANIA MECHANICZNE ZAGROŻENIA I PROFILAKTYKA Serwis internetowy BEZPIECZNIEJ CIOP-PIB 1. Wprowdzenie Drgnimi nzywne są procesy, w których chrkterystyczne dl nich wielkości fizyczne
Mteriły szkoleniowe DRGANIA MECHANICZNE ZAGROŻENIA I PROFILAKTYKA Serwis internetowy BEZPIECZNIEJ CIOP-PIB 1. Wprowdzenie Drgnimi nzywne są procesy, w których chrkterystyczne dl nich wielkości fizyczne
Prosta metoda sprawdzania fundamentów ze względu na przebicie
 Konstrkcje Elementy Mteriły Prost metod sprwdzni fndmentów ze względ n przebicie Prof dr b inż Micł Knff, Szkoł Główn Gospodrstw Wiejskiego w Wrszwie, dr inż Piotr Knyzik, Politecnik Wrszwsk 1 Wprowdzenie
Konstrkcje Elementy Mteriły Prost metod sprwdzni fndmentów ze względ n przebicie Prof dr b inż Micł Knff, Szkoł Główn Gospodrstw Wiejskiego w Wrszwie, dr inż Piotr Knyzik, Politecnik Wrszwsk 1 Wprowdzenie
