GRK 3. Dr Wojciech Palubicki
|
|
|
- Sebastian Nowicki
- 5 lat temu
- Przeglądów:
Transkrypt
1 GRK 3 Dr Wojciech Palubicki
2 Potok graficzny
3 Potok graficzny World Space View Space Orthographic view Window space Canonincal view
4 Potok graficzny World Space View Space Orthographic view Canonincal view Window space Potok graficzny z ortograficznym rzutem: x y M vp M ort M cam z 1 Potok graficzny z perspektywicznym rzutem: x y M vp M per M cam z 1
5 Wyrównanie systemów współrzędnych v e +y w M cam u w -x + x -y
6 M cam Macierz transformacji z world space na view space jest wtedy: M cam = u x u y u z 0 v x v y v z 0 w y w z w x e x 0 e y 1 e z 0 1
7 Rzutowanie równoległe y g -z
8 Ortograficzna bryła widzenia M orth = 2 r l 0 l+r l+r 2 2 t b 0 0 b+t n f 0 l+r r l b+t t b n+f n f 1
9 Przekształcenie bryły kanonicznej M vp = n x 2 0 n y n x n y n y n x
10 Rzutowania Ortograficzne rzutowanie
11 Rzutowania Perspektywicznie rzutowanie Ortograficzne rzutowanie
12 Macierz P n 0 0 n n + f nf 1 0 x y z 1 = nx z ny z n + f nf z 1
13 Transformacja bryły widzenia Bryla widzenia Ortograficzna bryła widzenia
14 System współrzędnych jednorodnych Nasze multiplikacje macierzami do liniowe transformacje, tzn. tylko mogą wygenerować wartości jak np.: x = a 1 x + b 1 y + c 1 z Wprowadzenie współrzędnych jednorodnych umożliwia reprezentacje punktów (x, y, z) jako (x, y, z, 1) i umożliwia nam skorzystanie z afinicznych transformacji, np.: x = a 1 x + b 1 y + c 1 z + d 1
15 System współrzędnych jednorodnych We współrzędnych jednorodnych wektor: (x, y, z, 1) reprezentuje punkt (x, y, z) Teraz wprowadzamy możliwość reprezentacji punktów za pomocy: (x, y, z, w) co daje nam punkt (x/w, y/w, z/w)
16 Współrzędne jednorodne (x, y)
17 Współrzędne jednorodne (x, y) (x, y, 1)
18 Współrzędne jednorodne (x, y, w) (x, y) (x, y, 1)
19 Współrzędne jednorodne (x, y, w) (x, y) /w (x, y) (x, y, 1)
20 August Möbius
21 System współrzędnych jednorodnych Wtedy transformacja macierzowa staje się: x y z 1 = a 1 b 1 c 1 T x a 2 b 2 c 2 T y a 3 b 3 c 3 T z a 4 b 4 w c 4 x y z 1 = a 1 x + b 1 y + c 1 z + T x a 2 x + b 2 y + c 2 z + T y a 3 x + b 3 y + c 3 z + T z a 4 x + b 4 y + c 4 z + w a 1 x + b 1 y + c 1 z + T x a 2 x + b 2 y + c 2 z + T y a 3 x + b 3 y + c 3 z + T z a 4 x + b 4 y + c 4 z + w homogenizacja a 1 x+b 1 y+c 1 z+t x a 4 x+b 4 y+c 4 z+w a 2 x+b 2 y+c 2 z+t y a 4 x+b 4 y+c 4 z+w a 3 x+b 3 y+c 3 z+t z a 4 x+b 4 y+c 4 z+w 1
22 Transformacja bryły widzenia Kalkulacja: a 1 x + b 1 y + c 1 z + T x a 4 x + b 4 y + c 4 z + w a 2 x + b 2 y + c 2 z + T y a 4 x + b 4 y + c 4 z + w a 3 x + b 3 y + c 3 z + T z a 4 x + b 4 y + c 4 z + w 1 Cel: nx z ny z z 1
23 Transformacja bryły widzenia Kalkulacja: a 1 x + b 1 y + c 1 z + T x a 4 x + b 4 y + c 4 z + w a 2 x + b 2 y + c 2 z + T y a 4 x + b 4 y + c 4 z + w a 3 x + b 3 y + c 3 z + T z a 4 x + b 4 y + c 4 z + w 1 Cel: nx z ny z z x y z 1 Czwarty wiersz
24 Transformacja bryły widzenia Kalkulacja: a 1 x + b 1 y + c 1 z + T x a 4 x + b 4 y + c 4 z + w a 2 x + b 2 y + c 2 z + T y a 4 x + b 4 y + c 4 z + w a 3 x + b 3 y + c 3 z + T z a 4 x + b 4 y + c 4 z + w 1 Cel: nx z ny z z x y z 1 Czwarty wiersz
25 Transformacja bryły widzenia Kalkulacja: a 1 x + b 1 y + c 1 z + T x a 4 x + b 4 y + c 4 z + w a 2 x + b 2 y + c 2 z + T y a 4 x + b 4 y + c 4 z + w a 3 x + b 3 y + c 3 z + T z a 4 x + b 4 y + c 4 z + w 1 Cel: nx z ny z z x y z 1 n 0 0. n x y z 1 Czwarty wiersz Pierwszy i drugi wiersz
26 Transformacja bryły widzenia Kalkulacja: a 1 x + b 1 y + c 1 z + T x a 4 x + b 4 y + c 4 z + w a 2 x + b 2 y + c 2 z + T y a 4 x + b 4 y + c 4 z + w a 3 x + b 3 y + c 3 z + T z a 4 x + b 4 y + c 4 z + w 1 Cel: nx z ny z z x y z 1 n 0 0. n x y z 1 Czwarty wiersz Pierwszy i drugi wiersz
27 Co z trzecim wierszem? nx n 0 0 n x y z ny?? 0 0?? 1 0 z 1 z z 1
28 Macierz P n 0 0 n n + f nf 1 0 x y z 1 = nx z ny z n + f nf z 1
29 Transformacja bryły widzenia e near plane far plane
30 Transformacja bryły widzenia e near plane far plane
31 Uproszczony Potok Graficzny (Rendering) Model Matrix View Matrix Projection Matrix Viewport Transform Object Space World Space View Space Clip Space Screen Space
32 Wektor normalny Wektor normalny jest skierowany prostopadle do płaszczyzny Możemy skorzystać z iloczynu wektorowego żeby obliczyć wartość wektora normalnego n n = a b Konwencją jest podawać wierzchołki w kierunku przeciwnym do zegara n = (V 2 V 1 ) (V 3 V 2 )
33 Skierowanie wielokątów Wielokąt jest skierowany do przodu (front facing) gdy normalna powierzchni jest skierowane do punktu widzenia, w innym przypadku jest skierowany do tylu (back facing)
34 Jakie trójkąty rzutować? Trójkąty które lezą (częściowo) poza bryłą widzenia nie musza być rzutowane i są cięte (clipping/culling)
35 Jakie trójkąty rzutować? CULLING Trójkąty które lezą (częściowo) poza bryłą widzenia nie musza być rzutowane i są cięte (clipping/culling)
36 Jakie trójkąty rzutować? Trójkąty które lezą (częściowo) poza bryłą widzenia nie musza być rzutowane i są cięte (clipping/culling) CLIPPING
37 Jakie trójkąty rzutować? Trójkąty które lezą (częściowo) poza bryłą widzenia nie musza być rzutowane i są cięte (clipping/culling) Pozostałe trójkąty są rzutowane na powierzchnie widzenia
38 Jakie trójkąty rzutować? Trójkąty które lezą (częściowo) poza bryłą widzenia nie musza być rzutowane i są cięte (clipping/culling) Pozostałe trójkąty są rzutowane na powierzchnie widzenia
39 Clipping Żeby zdecydować czy pociąć trójkąt musimy: Sprawdzić czy on przecina hiperpłaszczyznę Stworzyć nowy trójkąt(y)
40 Clipping Żeby zdecydować czy pociąć trójkąt musimy: Sprawdzić czy on przecina hiperpłaszczyznę Stworzyć nowy trójkąt(y)
41 Sprawdzanie przecinania Równanie dla hiperpłaszczyzny przez punkt q i normalną n jest dane przez: f p = n p q = 0 Konwencja: normalne naszych hiperpłaszczyzna są z kierowane na zewnątrz (bryły widzenia), czyli gdy f p < 0 to p jest wewnątrz, a jak f p > 0 to p jest zewnątrz płaszczyzny.
42 3D - iloczyn skalarny a b Definicja 1: a b = a 1 b 1 + a 2 b 2 + a 3 b 3
43 3D - iloczyn skalarny a b Definicja 1: a b = a 1 b 1 + a 2 b 2 + a 3 b 3 Definicja 2: a b = a b cos(θ)
44 Sprawdzanie przecinania Równanie dla hiperpłaszczyzny przez punkt q i normalną n jest dane przez: f p = n p q = 0 Konwencja: normalne naszych hiperpłaszczyzna są z kierowane na zewnątrz (bryły widzenia), czyli gdy f p < 0 to p jest wewnątrz, a jak f p > 0 to p jest zewnątrz płaszczyzny.
45 Sprawdzanie przecinania Równanie dla hiperpłaszczyzny przez punkt q i normalną n jest dane przez: f p = n p q = 0 Konwencja: normalne hiperpłaszczyzn są z kierowane na zewnątrz (bryły widzenia), czyli gdy f p < 0 to p jest wewnątrz, a jak f p > 0 to p jest zewnątrz płaszczyzny.
46 Sprawdzanie przecinania Równanie dla hiperpłaszczyzny przez punkt q i normalną n jest dane przez: f p = n p q = 0 Konwencja: normalne hiperpłaszczyzn są z kierowane na zewnątrz (bryły widzenia), czyli gdy f p < 0 to p jest wewnątrz, a jak f p > 0 to p jest zewnątrz płaszczyzny.
47 Sprawdzanie przecinania Równanie dla hiperpłaszczyzny przez punkt q i normalną n jest dane przez: f p = n p q = 0 Konwencja: normalne hiperpłaszczyzn są z kierowane na zewnątrz (bryły widzenia), czyli gdy f p < 0 to p jest wewnątrz, a jak f p > 0 to p jest zewnątrz płaszczyzny.
48 Sprawdzanie przecinania Równanie dla hiperpłaszczyzny przez punkt q i normalną n jest dane przez: f p = n p q = 0 Konwencja: normalne hiperpłaszczyzn są z kierowane na zewnątrz (bryły widzenia), czyli gdy f p < 0 to p jest wewnątrz, a jak f p > 0 to p jest zewnątrz płaszczyzny.
49 Sprawdzanie przecinania Równanie dla hiperpłaszczyzny przez punkt q i normalną n jest dane przez: f p = n p q = 0 Konwencja: normalne hiperpłaszczyzn są z kierowane na zewnątrz (bryły widzenia), czyli gdy f p < 0 to p jest wewnątrz, a jak f p > 0 to p jest zewnątrz płaszczyzny.
50 Obliczenie punktów przecięcia Jak dwa punkty Ԧa i b są po różnych stronach hiperpłaszczyzny stwarzamy równanie krzywej która przez te punkty przechodzi: Ԧp t = Ԧa + t b Ԧa Podkładając te równanie pod nasze równanie hiperpłaszczyzny daje nam: n Ԧp Ԧq = 0 n Ԧa + t b Ԧa Ԧq = 0 t = n a+n q n (a b)
51 Obliczenie punktów przecięcia Jak dwa punkty Ԧa i b są po różnych stronach hiperpłaszczyzny stwarzamy równanie krzywej która przez te punkty przechodzi: Ԧp t = Ԧa + t b Ԧa Podkładając te równanie pod nasze równanie hiperpłaszczyzny daje nam: n Ԧp Ԧq = 0 n Ԧa + t b Ԧa Ԧq = 0 t = n a+n q n (a b)
52 Obliczenie punktów przecięcia Jak dwa punkty Ԧa i b są po różnych stronach hiperpłaszczyzny stwarzamy równanie krzywej która przez te punkty przechodzi: Ԧp t = Ԧa + t b Ԧa Podkładając te równanie pod nasze równanie hiperpłaszczyzny daje nam: n Ԧp Ԧq = 0 n Ԧa + t b Ԧa Ԧq = 0 t = n a+n q n (a b)
53 Obliczenie punktów przecięcia Jak dwa punkty Ԧa i b są po różnych stronach hiperpłaszczyzny stwarzamy równanie krzywej która przez te punkty przechodzi: Ԧp t = Ԧa + t b Ԧa Podkładając te równanie pod nasze równanie hiperpłaszczyzny daje nam: n Ԧp Ԧq = 0 n Ԧa + t b Ԧa Ԧq = 0 t = n a+n q n (a b)
54 Stwarzanie nowych trójkątów Na podstawie dwóch punktów intersekcji możemy pociąć nasz trójkąt według naszej hiperpłaszczyzny w następujący sposób: Jak dwa wierzchołki są zewnątrz hiperpłaszczyzny dostajemy nowy trójkąt Jak jeden wierzchołek jest zewnątrz hiperpłaszczyzny dostajemy dwa nowe trójkąty
55 Stwarzanie nowych trójkątów Ale co gdy trójkąt jest przecinany przez dwie płaszczyzny?
56 Stwarzanie nowych trójkątów Przecinamy względem jednej
57 Stwarzanie nowych trójkątów Przecinamy względem drugiej
58 x y z 1 Macierz transformacji x y z w Homogenizacja x /w y /w z /w 1 Rasteryzacja
59 Clipping po homogenizacji Proste równania dla hiperpłaszczyzn:
60 Problem z płaszczyzną XY z p = n + f fn z z p ~ 1 z z p z
61 Clipping przed homogenizacją Wierzchołki bryły widzenia da się obliczyć przez M per -1 Wtedy równania płaszczyzn bryły widzenia można wyprowadzić
62 Clipping w systemie współrzędnych jednorodnych Jednak najłatwiej da się wykonać clipping w systemie współrzędnych jednorodnych. To znaczy: ucinamy trójkąty w czterech wymiarach według trójwymiarowych hiperpłaszczyzn.
63 Clipping w systemie współrzędnych jednorodnych Jednak najłatwiej da się wykonać clipping w systemie współrzędnych jednorodnych. To znaczy: ucinamy trójkąty w czterech wymiarach według trójwymiarowych hiperpłaszczyzn.
64 Algorytmy clippingu dla dowolnych wielokątów Greiner-Hormann Sutherland Hodgman Weiler Atherton Vatti
65 Culling Gdy jednak trójkąt leży poza bryłą widzenia usuwamy go całkowicie z dalszych obliczeń Testowanie wierzchołków jest jednak kosztowne
66 Bryły brzegowe (bounding volumes) Używanie brył brzegowych dla skomplikowanych obiektów geometrycznych przyspiesza potok graficzny
67 Bryły brzegowe (bounding volumes) Często kule są używane jako bryły brzegowe Jak płaszczyzna jest dana przez Ԧp Ԧa n = 0 i kula ma środek Ԧc i promień r, wtedy sprawdzamy nierówność Ԧc a n > r n
68 Bryły brzegowe (bounding volumes) Często kule są używane jako bryły brzegowe Jak płaszczyzna jest dana przez Ԧp Ԧa n = 0 i kula ma środek Ԧc i promień r, wtedy sprawdzamy nierówność Ԧc a n > r n n Ԧa Ԧc r
69 Bryły brzegowe (bounding volumes) Często kule są używane jako bryły brzegowe Jak płaszczyzna jest dana przez Ԧp Ԧa n = 0 i kula ma środek Ԧc i promień r, wtedy sprawdzamy nierówność Ԧc a n > r n n Ԧa Ԧc r
70 Culling Frustum culling usuwanie trójkątów poza bryły widzenia Backface culling usuwanie trójkątów orientowane od pozycji kamery
71 Backface culling Gdy modelujemy obiekty geometryczne za pomocy trójkątów to normalna trójkątów jest ustawiona na zewnątrz obiektu Odrzucanie trójkątów których normalna jest skierowana od punktu widzenia nazywamy to backface culling (usuwanie powierzchni tylnych)
72
73
74
75
76
77
78
79 v n = v n cos(θ) Skierowany do przodu gdy θ > π 2, dlatego cos θ < 0 i v n < 0
80 v n = v n cos(θ) Skierowany do przodu gdy θ > π 2, dlatego cos θ < 0 i v n < 0
81
82 wszystkie wielokąty backface culling
83 wszystkie wielokąty backface culling
84 Przykład Bez backface culling Backface culling
85
86 Algorytm malarza (painter s algorithm)
87 Algorytm malarza (painter s algorithm) Algorytm rysuje wielokąty w kolejności odległości od kamery Najmniejsza współrzędna z s od wszystkich wielokątów jest używana żeby odległość obliczyć Bliższe wielokąty zasłaniają te które są dalej
88 Przykład
89 Częściowe pokrywanie wielokątów
90 Z-bufor Algorytm z-buforu jest podobny w koncepcji do algorytmu malarza ale na skali pikseli Dwie tablice są stworzone gdzie każdy piksel koresponduje jednemu elementu tablicy Bufor głębokości (depth buffer) zatrzymuje dystans z od najbliższej powierzchni w ułożonej przestrzeni świata dla każdego pikselu Bufor klatek (frame buffer) zatrzymuje indeksy wielokątów (żeby później wybrać właściwe kolory)
91 Z-bufor
92
93 Z-bufor przyklad
94
95 Jak wewnętrzne punkty są obliczone Przejdź wszystkie horyzontalne wiersze pikseli (scan lines) od góry do dołu Oblicz piksele na lewym i prawym rogu linii skanowania przez interpolacje pomiędzy punktami P Oblicz piksele na linii skanowania C interpolując między nimi A i B
96 Interpolowanie między wierzchołkami: x A, i+1 = x A, i x A x B, i+1 = x B, i x B y A, i+1 = y A, i 1 y B, i+1 = y B, i 1 Gdzie x A = y A y 0 y 2 y 0 x B = y B y 1 y 2 y 1
97 Obliczanie z Używając równanie wektorowe płaszczyzny: N r = s Wartość z i+1 jest z i+1 = z i n x n z Gdzie n x n z jest stała
98 Wymogi pamięciowe Dla wyświetlacza 1920 x 1080 pikseli używając 16b RGB model kolorowy i 24b buforu głębokości zużycie pamięci jest:
99 Wymogi pamięciowe Dla wyświetlacza 1920 x 1080 pikseli używając 16b RGB model kolorowy i 24b buforu głębokości zużycie pamięci jest: pamiec = bufor glebokosci + bufor klatek
100 Wymogi pamięciowe Dla wyświetlacza 1920 x 1080 pikseli używając 16b RGB model kolorowy i 24b buforu głębokości zużycie pamięci jest: pamiec = bufor glebokosci + bufor klatek =
101 Wymogi pamięciowe Dla wyświetlacza 1920 x 1080 pikseli używając 16b RGB model kolorowy i 24b buforu głębokości zużycie pamięci jest: pamiec = bufor glebokosci + bufor klatek = = ,177,600
102 Wymogi pamięciowe Dla wyświetlacza 1920 x 1080 pikseli używając 16b RGB model kolorowy i 24b buforu głębokości zużycie pamięci jest: pamiec = bufor glebokosci + bufor klatek = = ,177,600 = 82,944,000b
103 Wymogi pamięciowe Dla wyświetlacza 1920 x 1080 pikseli używając 16b RGB model kolorowy i 24b buforu głębokości zużycie pamięci jest: pamiec = bufor glebokosci + bufor klatek = = ,177,600 = 82,944,000b = 10,368,600B ~ 10MB
104 CPU GPU
105 CPU GPU Vertex shader Fragment shader
106 GLSL syntaks GLSL jest jak C ale bez Wskaźników Rekursji Dynamicznej alokacji pamięci GLSL jest jak C ale z Domyślną obsługą wektorów i macierzy Bardzo dobrą biblioteką matematyczną
107 GLSL syntaks: in/ out/ uniform Uniform (constant) input Shader Streaming input Shader Shader Shader Output
108 GLSL syntaks: in/ out/ uniform Przykład #version 430 uniform mat4 u_modelview; layout (location = 0) in vec4 Position; layout (location = 1) in vec4 Color; out vec3 fs_color; void main(void) { fs_color = Color; gl_position = u_modelview * Position; } uniform: dane wejściowe które są stałe przez jedne wywołanie gldraw in: dane wejściowe dla poszczególnych shaderow out: dane wyjściowe shadera
109 GLSL syntaks GLSL ma preprocesora #version 330 #ifdef FAST_EXACT_METHOD FastExact(); #else SlowApproximate(); #endif //... many others Wszystkie shadery mają funkcje main() void main(void) { }
110 GLSL: Typy Typy skalarne: float, int, uint, bool Wektory tez są typy domyslne: vec2, vec3, vec4 ivec*, uvec*, bvec* Elementy wektorów można na kilka sposobów wywołać:.x,.y,.z,.w.r,.g,.b,.a.s,.t,.p,.q pozycja lub kierunek kolor współrzędne tekstur mojkolor.xyz mojkolor.xgb
111 GLSL: Wektory Konstruktory: vec3 xyz = vec3(1.0, 2.0, 3.0); vec3 xyz = vec3(1.0); // [1.0, 1.0, 1.0] vec3 xyz = vec3(vec2(1.0, 2.0), 3.0);
112 GLSL: Wektory Swizzle: selekcja lub zamiana elementów vec4 c = vec4(0.5, 1.0, 0.8, 1.0); vec3 rgb = c.rgb; // [0.5, 1.0, 0.8] vec3 bgr = c.bgr; // [0.8, 1.0, 0.5] vec3 rrr = c.rrr; // [0.5, 0.5, 0.5] c.a = 0.5; // [0.5, 1.0, 0.8, 0.5] c.rb = 0.0; // [0.0, 1.0, 0.0, 0.5] float g = rgb[1]; // 1.0, indeksowanie
113 GLSL: Macierze Macierze są typy domyślne: kwadratowa: mat2, mat3, mat4 M x N: matmxn m kolumn, n wierszy Zapisywanie macierzy:
114 GLSL: Macierze Konstruktory mat3 i = mat3(1.0); // 3x3 macierz jednostkowa mat2 m = mat2(1.0, 2.0, // [ ] 3.0, 4.0); // [ ] Elementy macierzy float f = m[kolumna][wiersz]; Macierz jako tablica wektorów float x = m[0].x; // element x pierwszej kolumny vec2 yz = m[1].yz; // elementy yz drugiej kolumny Swizzle
115 GLSL: Wektory i Macierze Macierz wektor operacje: vec3 xyz = //... vec3 v0 = 2.0 * xyz; // skalowanie vec3 v1 = v0 + xyz; // addycja vec3 v2 = v0 * xyz; // iloczyn elementów mat3 m = //... mat3 v = //... mat3 mv = v * m; // macierz * macierz mat3 xyz2 = mv * xyz; // macierz * wektor mat3 xyz3 = xyz * mv; // wektor * macierz
116 GLSL domyślne funkcje Wybrane funkcje trygonometryczne float s = sin(theta); float c = cos(theta); float t = tan(theta); W radianach float theta = asin(s); //... vec3 angles = vec3(/*... */); vec3 vs = sin(angles); Funkcje również obsługują wektory
117 GLSL domyślne funkcje Funkcje nieliniowe float x1 = pow(x, y); float x2 = exp(x); float x3 = exp2(x); float l = log(x); // ln float l2 = log2(x); // log2 float s = sqrt(x); float is = inversesqrt(x);
118 GLSL domyślne funkcje Inne funkcje float ax = abs(x); // wartość absolutna float sx = sign(x); // -1.0, 0.0, 1.0 float m0 = min(x, y); // wartość minimalna float m1 = max(x, y); // wartość maksymalna float c = clamp(x, 0.0, 1.0); // wiele innych: floor(), ceil(), // step(), smoothstep(),...
119 GLSL domyślne funkcje Przykład float x = //... float f; if (x > 0.0) { f = 2.0; } else { f = -2.0; } sign(x)*2.0
120 GLSL domyślne funkcje Wybrane funkcje geometryczne vec3 l = //... vec3 n = //... vec3 p = //... vec3 q = //... float f = length(l); // długość wektora float d = distance(p, q); // dystans pomiędzy dwoma punktami float d2 = dot(l, n); vec3 v2 = cross(l, n); vec3 v3 = normalize(l); // iloczyn skalarny // iloczyn wektorowy // normalizacja vec3 v3 = reflect(l, n); // refleksja
121 GLSL domyślne funkcje reflect(-l, n) Mając l i n, znajdź r. l n r
122 GLSL domyślne funkcje Co jest nie poprawne w tym kodzie? vec3 n = //... normalize(n); normalize() zwraca wartość
123 GLSL domyślne funkcje Wybrane metody numeryczne mat4 m = //... mat4 t = transpose(m); float d = determinant(m); mat4 d = inverse(m); //transpozycja //wyznacznik //macierz odwrotna
GRK 4. dr Wojciech Palubicki
 GRK 4 dr Wojciech Palubicki Uproszczony Potok Graficzny (Rendering) Model Matrix View Matrix Projection Matrix Viewport Transform Object Space World Space View Space Clip Space Screen Space Projection
GRK 4 dr Wojciech Palubicki Uproszczony Potok Graficzny (Rendering) Model Matrix View Matrix Projection Matrix Viewport Transform Object Space World Space View Space Clip Space Screen Space Projection
GRK 2. dr Wojciech Palubicki
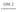 GRK dr Wojciech Palubicki Macierz wektor produkt jako Transformacja T: R n R m T Ԧx = A Ԧx Przemieszczanie wierzchołków - Transformacje Skalowanie Rotacja Translacja -y -y Macierz rotacji M wobec punktu
GRK dr Wojciech Palubicki Macierz wektor produkt jako Transformacja T: R n R m T Ԧx = A Ԧx Przemieszczanie wierzchołków - Transformacje Skalowanie Rotacja Translacja -y -y Macierz rotacji M wobec punktu
GRK 5. dr Wojciech Palubicki
 GRK 5 dr Wojciech Palubicki Uproszczony Potok Graficzny (Rendering) Model Matrix View Matrix Projection Matrix Viewport Transform Object Space World Space View Space Clip Space Screen Space Projection
GRK 5 dr Wojciech Palubicki Uproszczony Potok Graficzny (Rendering) Model Matrix View Matrix Projection Matrix Viewport Transform Object Space World Space View Space Clip Space Screen Space Projection
GRK 5. dr Wojciech Palubicki
 GRK 5 dr Wojciech Palubicki Projekty (dwu-osobowe) Napisać symulacje lotu kosmicznego w OpenGLu: Korzystając tylko z bibliotek które na ćwiczeniach zostały omówione Interaktywna symulacja Wszystkie wielokąty
GRK 5 dr Wojciech Palubicki Projekty (dwu-osobowe) Napisać symulacje lotu kosmicznego w OpenGLu: Korzystając tylko z bibliotek które na ćwiczeniach zostały omówione Interaktywna symulacja Wszystkie wielokąty
Grafika komputerowa i wizualizacja. dr Wojciech Pałubicki
 Grafika komputerowa i wizualizacja dr Wojciech Pałubicki Grafika komputerowa Obrazy wygenerowane za pomocy komputera Na tych zajęciach skupiamy się na obrazach wygenerowanych ze scen 3D do interaktywnych
Grafika komputerowa i wizualizacja dr Wojciech Pałubicki Grafika komputerowa Obrazy wygenerowane za pomocy komputera Na tych zajęciach skupiamy się na obrazach wygenerowanych ze scen 3D do interaktywnych
Transformacje obiektów 3D
 Synteza i obróbka obrazu Transformacje obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Lokalny układ współrzędnych Tworząc model obiektu, zapisujemy
Synteza i obróbka obrazu Transformacje obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Lokalny układ współrzędnych Tworząc model obiektu, zapisujemy
Programowanie Procesorów Graficznych
 Programowanie Procesorów Graficznych Wykład 1 9.10.2012 Prehistoria Zadaniem karty graficznej było sterowanie sygnałem do monitora tak aby wyświetlić obraz zgodnie z zawartościa pamięci. Programiści pracowali
Programowanie Procesorów Graficznych Wykład 1 9.10.2012 Prehistoria Zadaniem karty graficznej było sterowanie sygnałem do monitora tak aby wyświetlić obraz zgodnie z zawartościa pamięci. Programiści pracowali
Animowana grafika 3D. Opracowanie: J. Kęsik.
 Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Rzutowanie Równoległe Perspektywiczne Rzutowanie równoległe Rzutowanie równoległe jest powszechnie używane w rysunku technicznym - umożliwienie
Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Rzutowanie Równoległe Perspektywiczne Rzutowanie równoległe Rzutowanie równoległe jest powszechnie używane w rysunku technicznym - umożliwienie
Grafika Komputerowa Wykład 5. Potok Renderowania Oświetlenie. mgr inż. Michał Chwesiuk 1/38
 Wykład 5 Potok Renderowania Oświetlenie mgr inż. 1/38 Podejście śledzenia promieni (ang. ray tracing) stosuje się w grafice realistycznej. Śledzone są promienie przechodzące przez piksele obrazu wynikowego
Wykład 5 Potok Renderowania Oświetlenie mgr inż. 1/38 Podejście śledzenia promieni (ang. ray tracing) stosuje się w grafice realistycznej. Śledzone są promienie przechodzące przez piksele obrazu wynikowego
Wykład 4. Rendering (1) Informacje podstawowe
 Wykład 4. Rendering (1) Informacje podstawowe Z punktu widzenia dzisiejszego programowania gier: Direct3D jest najczęściej wykorzystywanym przez profesjonalnych deweloperów gier API graficznym na platformie
Wykład 4. Rendering (1) Informacje podstawowe Z punktu widzenia dzisiejszego programowania gier: Direct3D jest najczęściej wykorzystywanym przez profesjonalnych deweloperów gier API graficznym na platformie
Ćwiczenia nr 4. TEMATYKA: Rzutowanie
 TEMATYKA: Rzutowanie Ćwiczenia nr 4 DEFINICJE: Rzut na prostą: rzutem na prostą l (zwaną rzutnią) w kierunku rzutowania k (k l) nazywamy przekształcenie płaszczyzny przyporządkowujące: a) Punktom prostej
TEMATYKA: Rzutowanie Ćwiczenia nr 4 DEFINICJE: Rzut na prostą: rzutem na prostą l (zwaną rzutnią) w kierunku rzutowania k (k l) nazywamy przekształcenie płaszczyzny przyporządkowujące: a) Punktom prostej
Grafika Komputerowa Wykład 4. Synteza grafiki 3D. mgr inż. Michał Chwesiuk 1/30
 Wykład 4 mgr inż. 1/30 Synteza grafiki polega na stworzeniu obrazu w oparciu o jego opis. Synteza obrazu w grafice komputerowej polega na wykorzystaniu algorytmów komputerowych do uzyskania obrazu cyfrowego
Wykład 4 mgr inż. 1/30 Synteza grafiki polega na stworzeniu obrazu w oparciu o jego opis. Synteza obrazu w grafice komputerowej polega na wykorzystaniu algorytmów komputerowych do uzyskania obrazu cyfrowego
Geometria analityczna - przykłady
 Geometria analityczna - przykłady 1. Znaleźć równanie ogólne i równania parametryczne prostej w R 2, któr przechodzi przez punkt ( 4, ) oraz (a) jest równoległa do prostej x + 5y 2 = 0. (b) jest prostopadła
Geometria analityczna - przykłady 1. Znaleźć równanie ogólne i równania parametryczne prostej w R 2, któr przechodzi przez punkt ( 4, ) oraz (a) jest równoległa do prostej x + 5y 2 = 0. (b) jest prostopadła
Elementy geometrii analitycznej w R 3
 Rozdział 12 Elementy geometrii analitycznej w R 3 Elementy trójwymiarowej przestrzeni rzeczywistej R 3 = {(x,y,z) : x,y,z R} możemy interpretować co najmniej na trzy sposoby, tzn. jako: zbiór punktów (x,
Rozdział 12 Elementy geometrii analitycznej w R 3 Elementy trójwymiarowej przestrzeni rzeczywistej R 3 = {(x,y,z) : x,y,z R} możemy interpretować co najmniej na trzy sposoby, tzn. jako: zbiór punktów (x,
SIMR 2016/2017, Analiza 2, wykład 1, Przestrzeń wektorowa
 SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
Z ostatniego wzoru i zależności (3.20) można obliczyć n6. Otrzymujemy (3.23) 3.5. Transformacje geometryczne
 46 III. Przekształcenia w przestrzeni trójwymiarowej Z ostatniego wzoru i zależności (3.20) można obliczyć n6. Otrzymujemy (3.23) 3.5. Transformacje geometryczne Złożone obiekty trójwymiarowe można uważać,
46 III. Przekształcenia w przestrzeni trójwymiarowej Z ostatniego wzoru i zależności (3.20) można obliczyć n6. Otrzymujemy (3.23) 3.5. Transformacje geometryczne Złożone obiekty trójwymiarowe można uważać,
A,B M! v V ; A + v = B, (1.3) AB = v. (1.4)
 Rozdział 1 Prosta i płaszczyzna 1.1 Przestrzeń afiniczna Przestrzeń afiniczna to matematyczny model przestrzeni jednorodnej, bez wyróżnionego punktu. Można w niej przesuwać punkty równolegle do zadanego
Rozdział 1 Prosta i płaszczyzna 1.1 Przestrzeń afiniczna Przestrzeń afiniczna to matematyczny model przestrzeni jednorodnej, bez wyróżnionego punktu. Można w niej przesuwać punkty równolegle do zadanego
Synteza i obróbka obrazu. Tekstury. Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych
 Synteza i obróbka obrazu Tekstury Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Tekstura Tekstura (texture) obraz rastrowy (mapa bitowa, bitmap) nakładany na
Synteza i obróbka obrazu Tekstury Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Tekstura Tekstura (texture) obraz rastrowy (mapa bitowa, bitmap) nakładany na
WEKTORY I MACIERZE. Strona 1 z 11. Lekcja 7.
 Strona z WEKTORY I MACIERZE Wektory i macierze ogólnie nazywamy tablicami. Wprowadzamy je:. W sposób jawny: - z menu Insert Matrix, - skrót klawiszowy: {ctrl}+m, - odpowiedni przycisk z menu paska narzędziowego
Strona z WEKTORY I MACIERZE Wektory i macierze ogólnie nazywamy tablicami. Wprowadzamy je:. W sposób jawny: - z menu Insert Matrix, - skrót klawiszowy: {ctrl}+m, - odpowiedni przycisk z menu paska narzędziowego
GRAFIKA KOMPUTEROWA podstawy matematyczne. dr inż. Hojny Marcin pokój 406, pawilon B5 E-mail: mhojny@metal.agh.edu.pl Tel.
 GRAFIKA KOMPUTEROWA podstawy matematyczne dr inż. Hojny Marcin pokój 406, pawilon B5 E-mail: mhojny@metal.agh.edu.pl Tel. (12) 617 46 37 Plan wykładu 1/4 ZACZNIEMY OD PRZYKŁADOWYCH PROCEDUR i PRZYKŁADÓW
GRAFIKA KOMPUTEROWA podstawy matematyczne dr inż. Hojny Marcin pokój 406, pawilon B5 E-mail: mhojny@metal.agh.edu.pl Tel. (12) 617 46 37 Plan wykładu 1/4 ZACZNIEMY OD PRZYKŁADOWYCH PROCEDUR i PRZYKŁADÓW
FUNKCJA LINIOWA - WYKRES. y = ax + b. a i b to współczynniki funkcji, które mają wartości liczbowe
 FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (postać kierunkowa) Funkcja liniowa to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości liczbowe Szczególnie ważny w postaci
FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (postać kierunkowa) Funkcja liniowa to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości liczbowe Szczególnie ważny w postaci
Algebra liniowa z geometrią
 Algebra liniowa z geometrią Maciej Czarnecki 15 stycznia 2013 Spis treści 1 Geometria płaszczyzny 2 1.1 Wektory i skalary........................... 2 1.2 Macierze, wyznaczniki, układy równań liniowych.........
Algebra liniowa z geometrią Maciej Czarnecki 15 stycznia 2013 Spis treści 1 Geometria płaszczyzny 2 1.1 Wektory i skalary........................... 2 1.2 Macierze, wyznaczniki, układy równań liniowych.........
Geometria w R 3. Iloczyn skalarny wektorów
 Geometria w R 3 Andrzej Musielak Str 1 Geometria w R 3 Działania na wektorach Wektory w R 3 możemy w naturalny sposób dodawać i odejmować, np.: [2, 3, 1] + [ 1, 2, 1] = [1, 5, 2] [2, 3, 1] [ 1, 2, 1] =
Geometria w R 3 Andrzej Musielak Str 1 Geometria w R 3 Działania na wektorach Wektory w R 3 możemy w naturalny sposób dodawać i odejmować, np.: [2, 3, 1] + [ 1, 2, 1] = [1, 5, 2] [2, 3, 1] [ 1, 2, 1] =
0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do
 0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do obserwatora f) w kierunku od obserwatora 1. Obrót dookoła osi
0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do obserwatora f) w kierunku od obserwatora 1. Obrót dookoła osi
Programowanie gier komputerowych Tomasz Martyn Wykład 6. Materiały informacje podstawowe
 Programowanie gier komputerowych Tomasz Martyn Wykład 6. Materiały informacje podstawowe Czym są tekstury? Tekstury są tablicowymi strukturami danych o wymiarze od 1 do 3, których elementami są tzw. teksele.
Programowanie gier komputerowych Tomasz Martyn Wykład 6. Materiały informacje podstawowe Czym są tekstury? Tekstury są tablicowymi strukturami danych o wymiarze od 1 do 3, których elementami są tzw. teksele.
Geometria analityczna
 Geometria analityczna Paweł Mleczko Teoria Informacja (o prostej). postać ogólna prostej: Ax + By + C = 0, A + B 0, postać kanoniczna (kierunkowa) prostej: y = ax + b. Współczynnik a nazywamy współczynnikiem
Geometria analityczna Paweł Mleczko Teoria Informacja (o prostej). postać ogólna prostej: Ax + By + C = 0, A + B 0, postać kanoniczna (kierunkowa) prostej: y = ax + b. Współczynnik a nazywamy współczynnikiem
GEOMETRIA ANALITYCZNA W PRZESTRZENI
 GEOMETRIA ANALITYCZNA W PRZESTRZENI Położenie punktu w przestrzeni określamy za pomocą trzech liczb (x, y, z). Liczby te odpowiadają rzutom na osie układu współrzędnych: każdy rzut wzdłuż płaszczyzny równoległej
GEOMETRIA ANALITYCZNA W PRZESTRZENI Położenie punktu w przestrzeni określamy za pomocą trzech liczb (x, y, z). Liczby te odpowiadają rzutom na osie układu współrzędnych: każdy rzut wzdłuż płaszczyzny równoległej
Przekształcenia geometryczne. Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej
 Przekształcenia geometryczne Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej Akademia Górniczo Hutnicza w Krakowie Przekształcenia elementarne w przestrzeni D Punkty p w E na płaszczyźnie
Przekształcenia geometryczne Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej Akademia Górniczo Hutnicza w Krakowie Przekształcenia elementarne w przestrzeni D Punkty p w E na płaszczyźnie
Zadania egzaminacyjne
 Rozdział 13 Zadania egzaminacyjne Egzamin z algebry liniowej AiR termin I 03022011 Zadanie 1 Wyznacz sumę rozwiązań równania: (8z + 1 i 2 2 7 iz 4 = 0 Zadanie 2 Niech u 0 = (1, 2, 1 Rozważmy odwzorowanie
Rozdział 13 Zadania egzaminacyjne Egzamin z algebry liniowej AiR termin I 03022011 Zadanie 1 Wyznacz sumę rozwiązań równania: (8z + 1 i 2 2 7 iz 4 = 0 Zadanie 2 Niech u 0 = (1, 2, 1 Rozważmy odwzorowanie
Lista. Algebra z Geometrią Analityczną. Zadanie 1 Przypomnij definicję grupy, które z podanych struktur są grupami:
 Lista Algebra z Geometrią Analityczną Zadanie 1 Przypomnij definicję grupy, które z podanych struktur są grupami: (N, ), (Z, +) (Z, ), (R, ), (Q \ {}, ) czym jest element neutralny i przeciwny w grupie?,
Lista Algebra z Geometrią Analityczną Zadanie 1 Przypomnij definicję grupy, które z podanych struktur są grupami: (N, ), (Z, +) (Z, ), (R, ), (Q \ {}, ) czym jest element neutralny i przeciwny w grupie?,
dr Mariusz Grządziel 15,29 kwietnia 2014 Przestrzeń R k R k = R R... R k razy Elementy R k wektory;
 Wykłady 8 i 9 Pojęcia przestrzeni wektorowej i macierzy Układy równań liniowych Elementy algebry macierzy dodawanie, odejmowanie, mnożenie macierzy; macierz odwrotna dr Mariusz Grządziel 15,29 kwietnia
Wykłady 8 i 9 Pojęcia przestrzeni wektorowej i macierzy Układy równań liniowych Elementy algebry macierzy dodawanie, odejmowanie, mnożenie macierzy; macierz odwrotna dr Mariusz Grządziel 15,29 kwietnia
FUNKCJA LINIOWA, RÓWNANIA I UKŁADY RÓWNAŃ LINIOWYCH
 FUNKCJA LINIOWA, RÓWNANIA I UKŁADY RÓWNAŃ LINIOWYCH PROPORCJONALNOŚĆ PROSTA Proporcjonalnością prostą nazywamy zależność między dwoma wielkościami zmiennymi x i y, określoną wzorem: y = a x Gdzie a jest
FUNKCJA LINIOWA, RÓWNANIA I UKŁADY RÓWNAŃ LINIOWYCH PROPORCJONALNOŚĆ PROSTA Proporcjonalnością prostą nazywamy zależność między dwoma wielkościami zmiennymi x i y, określoną wzorem: y = a x Gdzie a jest
ALGEBRA z GEOMETRIA, ANALITYCZNA,
 ALGEBRA z GEOMETRIA, ANALITYCZNA, MAT00405 PRZEKSZTAL CANIE WYRAZ EN ALGEBRAICZNYCH, WZO R DWUMIANOWY NEWTONA Uprościć podane wyrażenia 7; (b) ( 6)( + ); (c) a 5 6 8a ; (d) ( 5 )( 5 + ); (e) ( 45x 4 y
ALGEBRA z GEOMETRIA, ANALITYCZNA, MAT00405 PRZEKSZTAL CANIE WYRAZ EN ALGEBRAICZNYCH, WZO R DWUMIANOWY NEWTONA Uprościć podane wyrażenia 7; (b) ( 6)( + ); (c) a 5 6 8a ; (d) ( 5 )( 5 + ); (e) ( 45x 4 y
Trójwymiarowa grafika komputerowa rzutowanie
 Trójwymiarowa grafika komputerowa rzutowanie Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej Rzutowanie w przestrzeni 3D etapy procesu rzutowania określenie rodzaju rzutu określenie
Trójwymiarowa grafika komputerowa rzutowanie Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej Rzutowanie w przestrzeni 3D etapy procesu rzutowania określenie rodzaju rzutu określenie
RENDERING W CZASIE RZECZYWISTYM. Michał Radziszewski
 RENDERING W CZASIE RZECZYWISTYM Michał Radziszewski Plan wykładu Programy geometrii wprowadzenie Miejsce w potoku graficznym Wejścia i wyjścia programów geometrii Wierzchołki, prymitywy, ich nowe rodzaje
RENDERING W CZASIE RZECZYWISTYM Michał Radziszewski Plan wykładu Programy geometrii wprowadzenie Miejsce w potoku graficznym Wejścia i wyjścia programów geometrii Wierzchołki, prymitywy, ich nowe rodzaje
Bartosz Bazyluk OpenGL Współczesne podejście do programowania grafiki Część II: Programy cieniujące (shadery)
 OpenGL Współczesne podejście do programowania grafiki Część II: Programy cieniujące (shadery) Programowanie Gier Komputerowych, Informatyka S, III Rok PLAN WYKŁADU Transformacje geometryczne Pożegnanie
OpenGL Współczesne podejście do programowania grafiki Część II: Programy cieniujące (shadery) Programowanie Gier Komputerowych, Informatyka S, III Rok PLAN WYKŁADU Transformacje geometryczne Pożegnanie
FUNKCJA LINIOWA - WYKRES
 FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (Postać kierunkowa) Funkcja liniowa jest podstawowym typem funkcji. Jest to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości
FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (Postać kierunkowa) Funkcja liniowa jest podstawowym typem funkcji. Jest to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości
cx cx 1,cx 2,cx 3,...,cx n. Przykład 4, 5
 Matematyka ZLic - 07 Wektory i macierze Wektorem rzeczywistym n-wymiarowym x x 1, x 2,,x n nazwiemy ciąg n liczb rzeczywistych (tzn odwzorowanie 1, 2,,n R) Zbiór wszystkich rzeczywistych n-wymiarowych
Matematyka ZLic - 07 Wektory i macierze Wektorem rzeczywistym n-wymiarowym x x 1, x 2,,x n nazwiemy ciąg n liczb rzeczywistych (tzn odwzorowanie 1, 2,,n R) Zbiór wszystkich rzeczywistych n-wymiarowych
9. Podstawowe narzędzia matematyczne analiz przestrzennych
 Waldemar Izdebski - Wykłady z przedmiotu SIT 75 9. odstawowe narzędzia matematyczne analiz przestrzennych Niniejszy rozdział służy ogólnemu przedstawieniu metod matematycznych wykorzystywanych w zagadnieniu
Waldemar Izdebski - Wykłady z przedmiotu SIT 75 9. odstawowe narzędzia matematyczne analiz przestrzennych Niniejszy rozdział służy ogólnemu przedstawieniu metod matematycznych wykorzystywanych w zagadnieniu
Mapowanie tekstur Mip-mapy (level of detail) Filtrowanie Multiteksturowanie
 Mapowanie tekstur Mip-mapy (level of detail) Filtrowanie Multiteksturowanie Korekcja perspektywy http://en.wikipedia.org/wiki/file:perspective_correct_texture_mapping.jpg GL_TEXTURE_MIN_FILTER Zmniejszanie
Mapowanie tekstur Mip-mapy (level of detail) Filtrowanie Multiteksturowanie Korekcja perspektywy http://en.wikipedia.org/wiki/file:perspective_correct_texture_mapping.jpg GL_TEXTURE_MIN_FILTER Zmniejszanie
3. FUNKCJA LINIOWA. gdzie ; ół,.
 1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
Prosta i płaszczyzna w przestrzeni
 Prosta i płaszczyzna w przestrzeni Wybrane wzory i informacje Równanie prostej przechodzącej przez punkt P 0 = (x 0, y 0, z 0 ) o wektorze wodzącym r 0 i równoległej do wektora v = [a, b, c] : postać parametrycznego
Prosta i płaszczyzna w przestrzeni Wybrane wzory i informacje Równanie prostej przechodzącej przez punkt P 0 = (x 0, y 0, z 0 ) o wektorze wodzącym r 0 i równoległej do wektora v = [a, b, c] : postać parametrycznego
OpenGL : Oświetlenie. mgr inż. Michał Chwesiuk mgr inż. Tomasz Sergej inż. Patryk Piotrowski. Szczecin, r 1/23
 OpenGL : mgr inż. Michał Chwesiuk mgr inż. Tomasz Sergej inż. Patryk Piotrowski 1/23 Folder z plikami zewnętrznymi (resources) Po odpaleniu przykładowego projektu, nie uruchomi się on poprawnie. Powodem
OpenGL : mgr inż. Michał Chwesiuk mgr inż. Tomasz Sergej inż. Patryk Piotrowski 1/23 Folder z plikami zewnętrznymi (resources) Po odpaleniu przykładowego projektu, nie uruchomi się on poprawnie. Powodem
1. PODSTAWY TEORETYCZNE
 1. PODSTAWY TEORETYCZNE 1 1. 1. PODSTAWY TEORETYCZNE 1.1. Wprowadzenie W pierwszym wykładzie przypomnimy podstawowe działania na macierzach. Niektóre z nich zostały opisane bardziej szczegółowo w innych
1. PODSTAWY TEORETYCZNE 1 1. 1. PODSTAWY TEORETYCZNE 1.1. Wprowadzenie W pierwszym wykładzie przypomnimy podstawowe działania na macierzach. Niektóre z nich zostały opisane bardziej szczegółowo w innych
Shadery. Artur Staszczyk Bartłomiej Filipek
 Shadery Artur Staszczyk www.astaszczyk.com Bartłomiej Filipek www.bartlomiejfilipek.pl Bartlomiej.filipek@gmail.com Potok graficzny Vertex shader Fragment shader GLSL Przykłady Inne shadery? Vertex shader
Shadery Artur Staszczyk www.astaszczyk.com Bartłomiej Filipek www.bartlomiejfilipek.pl Bartlomiej.filipek@gmail.com Potok graficzny Vertex shader Fragment shader GLSL Przykłady Inne shadery? Vertex shader
LABORATORIUM 3 ALGORYTMY OBLICZENIOWE W ELEKTRONICE I TELEKOMUNIKACJI. Wprowadzenie do środowiska Matlab
 LABORATORIUM 3 ALGORYTMY OBLICZENIOWE W ELEKTRONICE I TELEKOMUNIKACJI Wprowadzenie do środowiska Matlab 1. Podstawowe informacje Przedstawione poniżej informacje maja wprowadzić i zapoznać ze środowiskiem
LABORATORIUM 3 ALGORYTMY OBLICZENIOWE W ELEKTRONICE I TELEKOMUNIKACJI Wprowadzenie do środowiska Matlab 1. Podstawowe informacje Przedstawione poniżej informacje maja wprowadzić i zapoznać ze środowiskiem
System graficzny. Potok graficzny 3D. Scena 3D Zbiór trójwymiarowych danych wejściowych wykorzystywanych do wygenerowania obrazu wyjściowego 2D.
 System graficzny scena 3D algorytm graficzny obraz 2D Potok graficzny 3D Radosław Mantiuk Dane wejściowe Algorytm tworzący obraz wyjściowy na podstawie sceny 3D Dane wyjściowe Wydział Informatyki Zachodniopomorski
System graficzny scena 3D algorytm graficzny obraz 2D Potok graficzny 3D Radosław Mantiuk Dane wejściowe Algorytm tworzący obraz wyjściowy na podstawie sceny 3D Dane wyjściowe Wydział Informatyki Zachodniopomorski
Implementacja sieci neuronowych na karcie graficznej. Waldemar Pawlaszek
 Implementacja sieci neuronowych na karcie graficznej Waldemar Pawlaszek Motywacja Czyli po co to wszystko? Motywacja Procesor graficzny GPU (Graphics Processing Unit) Wydajność Elastyczność i precyzja
Implementacja sieci neuronowych na karcie graficznej Waldemar Pawlaszek Motywacja Czyli po co to wszystko? Motywacja Procesor graficzny GPU (Graphics Processing Unit) Wydajność Elastyczność i precyzja
gdzie (4.20) (4.21) 4.3. Rzut równoległy
 4.3. Rzut równoległy 75 gdzie (4.20) Punkt zbiegu, określony wzorami (4.19) (4.20), leży na prostej przechodzącej przez środek rzutowania i równoległej do wektora u. Zauważmy, że gdy wektor u jest równoległy
4.3. Rzut równoległy 75 gdzie (4.20) Punkt zbiegu, określony wzorami (4.19) (4.20), leży na prostej przechodzącej przez środek rzutowania i równoległej do wektora u. Zauważmy, że gdy wektor u jest równoległy
ELEKTROTECHNIKA Semestr 1 Rok akad / ZADANIA Z MATEMATYKI Zestaw Przedstaw w postaci algebraicznej liczby zespolone: (3 + 2j)(5 2j),
 ELEKTROTECHNIKA Semestr Rok akad. / 5 ZADANIA Z MATEMATYKI Zestaw. Przedstaw w postaci algebraicznej liczby zespolone: (3 + j)(5 j) 3 j +j (5 + j) (3 + j) 3. Narysuj zbiory punktów na płaszczyźnie: +j
ELEKTROTECHNIKA Semestr Rok akad. / 5 ZADANIA Z MATEMATYKI Zestaw. Przedstaw w postaci algebraicznej liczby zespolone: (3 + j)(5 j) 3 j +j (5 + j) (3 + j) 3. Narysuj zbiory punktów na płaszczyźnie: +j
i = [ 0] j = [ 1] k = [ 0]
![i = [ 0] j = [ 1] k = [ 0] i = [ 0] j = [ 1] k = [ 0]](/thumbs/70/62901734.jpg) Ćwiczenia nr TEMATYKA: Układy współrzędnych: kartezjański, walcowy (cylindryczny), sferyczny (geograficzny), Przekształcenia: izometryczne, nieizometryczne. DEFINICJE: Wektor wodzący: wektorem r, ρ wodzącym
Ćwiczenia nr TEMATYKA: Układy współrzędnych: kartezjański, walcowy (cylindryczny), sferyczny (geograficzny), Przekształcenia: izometryczne, nieizometryczne. DEFINICJE: Wektor wodzący: wektorem r, ρ wodzącym
Geometria analityczna
 Geometria analityczna Wektory Zad Dane są wektory #» a, #» b, #» c Znaleźć długość wektora #» x (a #» a = [, 0, ], #» b = [0,, 3], #» c = [,, ], #» x = #» #» a b + 3 #» c ; (b #» a = [,, ], #» b = [,,
Geometria analityczna Wektory Zad Dane są wektory #» a, #» b, #» c Znaleźć długość wektora #» x (a #» a = [, 0, ], #» b = [0,, 3], #» c = [,, ], #» x = #» #» a b + 3 #» c ; (b #» a = [,, ], #» b = [,,
Potok graficzny i shadery. Hubert Rutkowski
 Potok graficzny i shadery Hubert Rutkowski 1. Coś o mnie Zakład Technologii Gier Uniwerytetu Jagiellońskiego 2. Potok graficzny jak w OpenGL Cry Engine 3 (zródło: CryTek) Vertex specification
Potok graficzny i shadery Hubert Rutkowski 1. Coś o mnie Zakład Technologii Gier Uniwerytetu Jagiellońskiego 2. Potok graficzny jak w OpenGL Cry Engine 3 (zródło: CryTek) Vertex specification
Zajęcia nr 1 (1h) Dwumian Newtona. Indukcja. Zajęcia nr 2 i 3 (4h) Trygonometria
 Technologia Chemiczna 008/09 Zajęcia wyrównawcze. Pokazać, że: ( )( ) n k k l = ( n l )( n l k l Zajęcia nr (h) Dwumian Newtona. Indukcja. ). Rozwiązać ( ) ( równanie: ) n n a) = 0 b) 3 ( ) n 3. Znaleźć
Technologia Chemiczna 008/09 Zajęcia wyrównawcze. Pokazać, że: ( )( ) n k k l = ( n l )( n l k l Zajęcia nr (h) Dwumian Newtona. Indukcja. ). Rozwiązać ( ) ( równanie: ) n n a) = 0 b) 3 ( ) n 3. Znaleźć
Rachunek wektorowy - wprowadzenie. dr inż. Romuald Kędzierski
 Rachunek wektorowy - wprowadzenie dr inż. Romuald Kędzierski Graficzne przedstawianie wielkości wektorowych Długość wektora jest miarą jego wartości Linia prosta wyznaczająca kierunek działania wektora
Rachunek wektorowy - wprowadzenie dr inż. Romuald Kędzierski Graficzne przedstawianie wielkości wektorowych Długość wektora jest miarą jego wartości Linia prosta wyznaczająca kierunek działania wektora
Przegląd architektury PlayStation 3
 Przegląd architektury PlayStation 3 1 Your Name Your Title Your Organization (Line #1) Your Organization (Line #2) Sony PlayStation 3 Konsola siódmej generacji Premiera: listopad 2006 33,5 mln sprzedanych
Przegląd architektury PlayStation 3 1 Your Name Your Title Your Organization (Line #1) Your Organization (Line #2) Sony PlayStation 3 Konsola siódmej generacji Premiera: listopad 2006 33,5 mln sprzedanych
Przekształcenia liniowe
 Przekształcenia liniowe Zadania Które z następujących przekształceń są liniowe? (a) T : R 2 R 2, T (x, x 2 ) = (2x, x x 2 ), (b) T : R 2 R 2, T (x, x 2 ) = (x + 3x 2, x 2 ), (c) T : R 2 R, T (x, x 2 )
Przekształcenia liniowe Zadania Które z następujących przekształceń są liniowe? (a) T : R 2 R 2, T (x, x 2 ) = (2x, x x 2 ), (b) T : R 2 R 2, T (x, x 2 ) = (x + 3x 2, x 2 ), (c) T : R 2 R, T (x, x 2 )
Oświetlenie obiektów 3D
 Synteza i obróbka obrazu Oświetlenie obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Rasteryzacja Spłaszczony po rzutowaniu obraz siatek wielokątowych
Synteza i obróbka obrazu Oświetlenie obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Rasteryzacja Spłaszczony po rzutowaniu obraz siatek wielokątowych
Repetytorium z matematyki ćwiczenia
 Spis treści 1 Liczby rzeczywiste 1 2 Geometria analityczna. Prosta w układzie kartezjańskim Oxy 4 3 Krzywe drugiego stopnia na płaszczyźnie kartezjańskiej 6 4 Dziedzina i wartości funkcji 8 5 Funkcja liniowa
Spis treści 1 Liczby rzeczywiste 1 2 Geometria analityczna. Prosta w układzie kartezjańskim Oxy 4 3 Krzywe drugiego stopnia na płaszczyźnie kartezjańskiej 6 4 Dziedzina i wartości funkcji 8 5 Funkcja liniowa
Geometria Analityczna w Przestrzeni
 Algebra p. 1/25 Algebra Geometria Analityczna w Przestrzeni Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045
Algebra p. 1/25 Algebra Geometria Analityczna w Przestrzeni Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045
Obraz jako funkcja Przekształcenia geometryczne
 Cyfrowe przetwarzanie obrazów I Obraz jako funkcja Przekształcenia geometryczne dr. inż Robert Kazała Definicja obrazu Obraz dwuwymiarowa funkcja intensywności światła f(x,y); wartość f w przestrzennych
Cyfrowe przetwarzanie obrazów I Obraz jako funkcja Przekształcenia geometryczne dr. inż Robert Kazała Definicja obrazu Obraz dwuwymiarowa funkcja intensywności światła f(x,y); wartość f w przestrzennych
Mobilne Aplikacje Multimedialne
 Mobilne Aplikacje Multimedialne Rozszerzona rzeczywistość (AR, Augmented Reality) w Systemie Android Cz.1 Krzysztof Bruniecki Podstawy Algebra liniowa, operacje na wektorach, macierzach, iloczyn skalarny
Mobilne Aplikacje Multimedialne Rozszerzona rzeczywistość (AR, Augmented Reality) w Systemie Android Cz.1 Krzysztof Bruniecki Podstawy Algebra liniowa, operacje na wektorach, macierzach, iloczyn skalarny
FIGURY I PRZEKSZTAŁCENIA GEOMETRYCZNE
 Umiejętności opracowanie: Maria Lampert LISTA MOICH OSIĄGNIĘĆ FIGURY I PRZEKSZTAŁCENIA GEOMETRYCZNE Co powinienem umieć Umiejętności znam podstawowe przekształcenia geometryczne: symetria osiowa i środkowa,
Umiejętności opracowanie: Maria Lampert LISTA MOICH OSIĄGNIĘĆ FIGURY I PRZEKSZTAŁCENIA GEOMETRYCZNE Co powinienem umieć Umiejętności znam podstawowe przekształcenia geometryczne: symetria osiowa i środkowa,
Sphere tracing: integracja z klasycznymi metodami symulacji i renderingu
 Sphere tracing: integracja z klasycznymi metodami symulacji i renderingu IGK 2012 Michał Jarząbek W skrócie Funkcje niejawne opisują powierzchnie niejawne Powierzchnie niejawne metoda reprezentacji "obiektów"
Sphere tracing: integracja z klasycznymi metodami symulacji i renderingu IGK 2012 Michał Jarząbek W skrócie Funkcje niejawne opisują powierzchnie niejawne Powierzchnie niejawne metoda reprezentacji "obiektów"
Algebra z geometrią analityczną zadania z odpowiedziami
 Algebra z geometrią analityczną zadania z odpowiedziami Maciej Burnecki Spis treści strona główna 1 Wyrażenia algebraiczne, indukcja matematyczna 2 2 Geometria analityczna w R 2 Liczby zespolone 4 4 Wielomiany
Algebra z geometrią analityczną zadania z odpowiedziami Maciej Burnecki Spis treści strona główna 1 Wyrażenia algebraiczne, indukcja matematyczna 2 2 Geometria analityczna w R 2 Liczby zespolone 4 4 Wielomiany
Co to jest wektor? Jest to obiekt posiadający: moduł (długość), kierunek wraz ze zwrotem.
 1 Wektory Co to jest wektor? Jest to obiekt posiadający: moduł (długość), kierunek wraz ze zwrotem. 1.1 Dodawanie wektorów graficzne i algebraiczne. Graficzne - metoda równoległoboku. Sprowadzamy wektory
1 Wektory Co to jest wektor? Jest to obiekt posiadający: moduł (długość), kierunek wraz ze zwrotem. 1.1 Dodawanie wektorów graficzne i algebraiczne. Graficzne - metoda równoległoboku. Sprowadzamy wektory
1 Logika. 1. Udowodnij prawa logiczne: 3. (p q) (p q) 2. (p q) ( q p) 2. Sprawdź, czy wyrażenie ((p q) r) (p (q r)) jest tautologią.
 Logika. Udowodnij prawa logiczne:. (p q) ( p q). (p q) ( q p) 3. (p q) (p q). Sprawdź czy wyrażenie ((p q) r) (p (q r)) jest tautologią. 3. Zad 3. Sprawdź czy zdanie: Jeżeli liczba a dzieli się przez i
Logika. Udowodnij prawa logiczne:. (p q) ( p q). (p q) ( q p) 3. (p q) (p q). Sprawdź czy wyrażenie ((p q) r) (p (q r)) jest tautologią. 3. Zad 3. Sprawdź czy zdanie: Jeżeli liczba a dzieli się przez i
Notacja Denavita-Hartenberga
 Notacja DenavitaHartenberga Materiały do ćwiczeń z Podstaw Robotyki Artur Gmerek Umiejętność rozwiązywania prostego zagadnienia kinematycznego jest najbardziej bazową umiejętność zakresu Robotyki. Wyznaczyć
Notacja DenavitaHartenberga Materiały do ćwiczeń z Podstaw Robotyki Artur Gmerek Umiejętność rozwiązywania prostego zagadnienia kinematycznego jest najbardziej bazową umiejętność zakresu Robotyki. Wyznaczyć
Metody i analiza danych
 2015/2016 Metody i analiza danych Macierze Laboratorium komputerowe 2 Anna Kiełbus Zakres tematyczny 1. Funkcje wspomagające konstruowanie macierzy 2. Dostęp do elementów macierzy. 3. Działania na macierzach
2015/2016 Metody i analiza danych Macierze Laboratorium komputerowe 2 Anna Kiełbus Zakres tematyczny 1. Funkcje wspomagające konstruowanie macierzy 2. Dostęp do elementów macierzy. 3. Działania na macierzach
Grafika Komputerowa Wykład 6. Teksturowanie. mgr inż. Michał Chwesiuk 1/23
 Wykład 6 mgr inż. 1/23 jest to technika w grafice komputerowej, której celem jest zwiększenie szczegółowości renderowanych powierzchni za pomocą tekstur. jest to pewna funkcja (najczęściej w formie bitmapy)
Wykład 6 mgr inż. 1/23 jest to technika w grafice komputerowej, której celem jest zwiększenie szczegółowości renderowanych powierzchni za pomocą tekstur. jest to pewna funkcja (najczęściej w formie bitmapy)
Karta przedmiotu. Podstawy programowania procesorów graficznych. realizowanego w ramach projektu PO WER
 Karta przedmiotu Podstawy programowania procesorów graficznych realizowanego w ramach projektu PO WER 2017-2019 Wydział Inżynierii Elektrycznej i Komputerowej Kierunek studiów: Informatyka Profil: Ogólnoakademicki
Karta przedmiotu Podstawy programowania procesorów graficznych realizowanego w ramach projektu PO WER 2017-2019 Wydział Inżynierii Elektrycznej i Komputerowej Kierunek studiów: Informatyka Profil: Ogólnoakademicki
Funkcje liniowe i wieloliniowe w praktyce szkolnej. Opracowanie : mgr inż. Renata Rzepińska
 Funkcje liniowe i wieloliniowe w praktyce szkolnej Opracowanie : mgr inż. Renata Rzepińska . Wprowadzenie pojęcia funkcji liniowej w nauczaniu matematyki w gimnazjum. W programie nauczania matematyki w
Funkcje liniowe i wieloliniowe w praktyce szkolnej Opracowanie : mgr inż. Renata Rzepińska . Wprowadzenie pojęcia funkcji liniowej w nauczaniu matematyki w gimnazjum. W programie nauczania matematyki w
2 Przygotował: mgr inż. Maciej Lasota
 Laboratorium nr 2 1/6 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Manipulowanie przestrzenią 2 Przygotował: mgr inż. Maciej Lasota 1) Manipulowanie przestrzenią Istnieją dwa typy układów współrzędnych:
Laboratorium nr 2 1/6 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Manipulowanie przestrzenią 2 Przygotował: mgr inż. Maciej Lasota 1) Manipulowanie przestrzenią Istnieją dwa typy układów współrzędnych:
Matematyka dla studentów ekonomii : wykłady z ćwiczeniami/ Ryszard Antoniewicz, Andrzej Misztal. Wyd. 4 popr., 6 dodr. Warszawa, 2012.
 Matematyka dla studentów ekonomii : wykłady z ćwiczeniami/ Ryszard Antoniewicz, Andrzej Misztal. Wyd. 4 popr., 6 dodr. Warszawa, 2012 Spis treści Przedmowa 9 CZĘŚĆ I. WSTĘP DO MATEMATYKI 11 Wykład 1. Rachunek
Matematyka dla studentów ekonomii : wykłady z ćwiczeniami/ Ryszard Antoniewicz, Andrzej Misztal. Wyd. 4 popr., 6 dodr. Warszawa, 2012 Spis treści Przedmowa 9 CZĘŚĆ I. WSTĘP DO MATEMATYKI 11 Wykład 1. Rachunek
Grafika komputerowa Wykład 4 Geometria przestrzenna
 Grafika komputerowa Wykład 4 Geometria przestrzenna Instytut Informatyki i Automatyki Państwowa Wyższa Szkoła Informatyki i Przedsiębiorczości w Łomży 2 0 0 9 Spis treści Spis treści 1 Geometria 3D - podstawowe
Grafika komputerowa Wykład 4 Geometria przestrzenna Instytut Informatyki i Automatyki Państwowa Wyższa Szkoła Informatyki i Przedsiębiorczości w Łomży 2 0 0 9 Spis treści Spis treści 1 Geometria 3D - podstawowe
Zestaw Obliczyć objętość równoległościanu zbudowanego na wektorach m, n, p jeśli wiadomo, że objętość równoległościanu zbudowanego na wektorach:
 Zestaw 9. Wykazać, że objętość równoległościanu zbudowanego na przekątnych ścian danego równoległościanu jest dwa razy większa od objętości równoległościanu danego.. Obliczyć objętość równoległościanu
Zestaw 9. Wykazać, że objętość równoległościanu zbudowanego na przekątnych ścian danego równoległościanu jest dwa razy większa od objętości równoległościanu danego.. Obliczyć objętość równoległościanu
ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ
 ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ Lista zadań dla kursów mających ćwiczenia co dwa tygodnie. Zadania po symbolu potrójne karo omawiane są na ćwiczeniach rzadko, ale warto też poświęcić im nieco uwagi. Przy
ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ Lista zadań dla kursów mających ćwiczenia co dwa tygodnie. Zadania po symbolu potrójne karo omawiane są na ćwiczeniach rzadko, ale warto też poświęcić im nieco uwagi. Przy
Wykład 14. Elementy algebry macierzy
 Wykład 14 Elementy algebry macierzy dr Mariusz Grządziel 26 stycznia 2009 Układ równań z dwoma niewiadomymi Rozważmy układ równań z dwoma niewiadomymi: a 11 x + a 12 y = h 1 a 21 x + a 22 y = h 2 a 11,
Wykład 14 Elementy algebry macierzy dr Mariusz Grządziel 26 stycznia 2009 Układ równań z dwoma niewiadomymi Rozważmy układ równań z dwoma niewiadomymi: a 11 x + a 12 y = h 1 a 21 x + a 22 y = h 2 a 11,
Algebra z geometrią analityczną zadania z odpowiedziami
 Algebra z geometrią analityczną zadania z odpowiedziami Maciej Burnecki opracowanie Spis treści I Wyrażenia algebraiczne, indukcja matematyczna 2 II Geometria analityczna w R 2 4 III Liczby zespolone 5
Algebra z geometrią analityczną zadania z odpowiedziami Maciej Burnecki opracowanie Spis treści I Wyrażenia algebraiczne, indukcja matematyczna 2 II Geometria analityczna w R 2 4 III Liczby zespolone 5
Bartosz Bazyluk SYNTEZA GRAFIKI 3D Grafika realistyczna i czasu rzeczywistego. Pojęcie sceny i kamery. Grafika Komputerowa, Informatyka, I Rok
 SYNTEZA GRAFIKI 3D Grafika realistyczna i czasu rzeczywistego. Pojęcie sceny i kamery. Grafika Komputerowa, Informatyka, I Rok Synteza grafiki 3D Pod pojęciem syntezy grafiki rozumiemy stworzenie grafiki
SYNTEZA GRAFIKI 3D Grafika realistyczna i czasu rzeczywistego. Pojęcie sceny i kamery. Grafika Komputerowa, Informatyka, I Rok Synteza grafiki 3D Pod pojęciem syntezy grafiki rozumiemy stworzenie grafiki
Architektura Procesorów Graficznych
 Architektura Procesorów Graficznych Referat: Rendering 3D: potok 3D, możliwości wsparcia sprzętowego, możliwości przyspieszenia obliczeń. Grupa wyrównawcza Cezary Sosnowski 1. Renderowanie Renderowanie
Architektura Procesorów Graficznych Referat: Rendering 3D: potok 3D, możliwości wsparcia sprzętowego, możliwości przyspieszenia obliczeń. Grupa wyrównawcza Cezary Sosnowski 1. Renderowanie Renderowanie
ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ
 ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ Maciej Burnecki opracowanie strona główna Spis treści I Zadania Wyrażenia algebraiczne indukcja matematyczna Geometria analityczna na płaszczyźnie Liczby zespolone 4 Wielomiany
ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ Maciej Burnecki opracowanie strona główna Spis treści I Zadania Wyrażenia algebraiczne indukcja matematyczna Geometria analityczna na płaszczyźnie Liczby zespolone 4 Wielomiany
Ćwiczenia nr 7. TEMATYKA: Krzywe Bézier a
 TEMATYKA: Krzywe Bézier a Ćwiczenia nr 7 DEFINICJE: Interpolacja: przybliżanie funkcji za pomocą innej funkcji, zwykle wielomianu, tak aby były sobie równe w zadanych punktach. Poniżej przykład interpolacji
TEMATYKA: Krzywe Bézier a Ćwiczenia nr 7 DEFINICJE: Interpolacja: przybliżanie funkcji za pomocą innej funkcji, zwykle wielomianu, tak aby były sobie równe w zadanych punktach. Poniżej przykład interpolacji
? 14. Dana jest funkcja. Naszkicuj jej wykres. Dla jakich argumentów funkcja przyjmuje wartości dodatnie? 15. Dana jest funkcja f x 2 a x
 FUNKCE FUNKCJA LINIOWA Sporządź tabelkę i narysuj wykres funkcji ( ) Dla jakich argumentów wartości funkcji są większe od 5 Podaj warunek równoległości prostych Wyznacz równanie prostej równoległej do
FUNKCE FUNKCJA LINIOWA Sporządź tabelkę i narysuj wykres funkcji ( ) Dla jakich argumentów wartości funkcji są większe od 5 Podaj warunek równoległości prostych Wyznacz równanie prostej równoległej do
Podstawy przetwarzania obrazów teledetekcyjnych. Format rastrowy
 Podstawy przetwarzania obrazów teledetekcyjnych Format rastrowy Definicja rastrowego modelu danych - podstawowy element obrazu cyfrowego to piksel, uważany w danym momencie za wewnętrznie jednorodny -
Podstawy przetwarzania obrazów teledetekcyjnych Format rastrowy Definicja rastrowego modelu danych - podstawowy element obrazu cyfrowego to piksel, uważany w danym momencie za wewnętrznie jednorodny -
1 Temat: Vertex Shader
 Instrukcja Architektura procesorów graficznych 1 Temat: Vertex Shader Przygotował: mgr inż. Tomasz Michno 1 Wstęp 1.1 Czym jest shader Shader jest programem (zazwyczaj krótkim), wykonywanym przez kartę
Instrukcja Architektura procesorów graficznych 1 Temat: Vertex Shader Przygotował: mgr inż. Tomasz Michno 1 Wstęp 1.1 Czym jest shader Shader jest programem (zazwyczaj krótkim), wykonywanym przez kartę
Obliczenia iteracyjne
 Lekcja Strona z Obliczenia iteracyjne Zmienne iteracyjne (wyliczeniowe) Obliczenia iteracyjne wymagają zdefiniowania specjalnej zmiennej nazywanej iteracyjną lub wyliczeniową. Zmienną iteracyjną od zwykłej
Lekcja Strona z Obliczenia iteracyjne Zmienne iteracyjne (wyliczeniowe) Obliczenia iteracyjne wymagają zdefiniowania specjalnej zmiennej nazywanej iteracyjną lub wyliczeniową. Zmienną iteracyjną od zwykłej
Wykład 16. P 2 (x 2, y 2 ) P 1 (x 1, y 1 ) OX. Odległość tych punktów wyraża się wzorem: P 1 P 2 = (x 1 x 2 ) 2 + (y 1 y 2 ) 2
 Wykład 16 Geometria analityczna Przegląd wiadomości z geometrii analitycznej na płaszczyźnie rtokartezjański układ współrzędnych powstaje przez ustalenie punktu początkowego zwanego początkiem układu współrzędnych
Wykład 16 Geometria analityczna Przegląd wiadomości z geometrii analitycznej na płaszczyźnie rtokartezjański układ współrzędnych powstaje przez ustalenie punktu początkowego zwanego początkiem układu współrzędnych
GEOMETRIA ANALITYCZNA W PRZESTRZENI
 Wykład z Podstaw matematyki dla studentów Inżynierii Środowiska Wykład 13. Egzaminy I termin wtorek 31.01 14:00 Aula A Wydział Budownictwa II termin poprawkowy czwartek 9.02 14:00 Aula A Wydział Budownictwa
Wykład z Podstaw matematyki dla studentów Inżynierii Środowiska Wykład 13. Egzaminy I termin wtorek 31.01 14:00 Aula A Wydział Budownictwa II termin poprawkowy czwartek 9.02 14:00 Aula A Wydział Budownictwa
Modelowanie i wstęp do druku 3D Wykład 1. Robert Banasiak
 Modelowanie i wstęp do druku 3D Wykład 1 Robert Banasiak Od modelu 3D do wydruku 3D Typowa droga...czasem wyboista... Pomysł!! Modeler 3D Przygotowanie modelu do druku Konfiguracja Programu do drukowania
Modelowanie i wstęp do druku 3D Wykład 1 Robert Banasiak Od modelu 3D do wydruku 3D Typowa droga...czasem wyboista... Pomysł!! Modeler 3D Przygotowanie modelu do druku Konfiguracja Programu do drukowania
Definicja i własności wartości bezwzględnej.
 Równania i nierówności z wartością bezwzględną. Rozwiązywanie układów dwóch (trzech) równań z dwiema (trzema) niewiadomymi. Układy równań liniowych z parametrem, analiza rozwiązań. Definicja i własności
Równania i nierówności z wartością bezwzględną. Rozwiązywanie układów dwóch (trzech) równań z dwiema (trzema) niewiadomymi. Układy równań liniowych z parametrem, analiza rozwiązań. Definicja i własności
= i Ponieważ pierwiastkami stopnia 3 z 1 są (jak łatwo wyliczyć) liczby 1, 1+i 3
 ZESTAW I 1. Rozwiązać równanie. Pierwiastki zaznaczyć w płaszczyźnie zespolonej. z 3 8(1 + i) 3 0, Sposób 1. Korzystamy ze wzoru a 3 b 3 (a b)(a 2 + ab + b 2 ), co daje: (z 2 2i)(z 2 + 2(1 + i)z + (1 +
ZESTAW I 1. Rozwiązać równanie. Pierwiastki zaznaczyć w płaszczyźnie zespolonej. z 3 8(1 + i) 3 0, Sposób 1. Korzystamy ze wzoru a 3 b 3 (a b)(a 2 + ab + b 2 ), co daje: (z 2 2i)(z 2 + 2(1 + i)z + (1 +
1. Równania i nierówności liniowe
 Równania i nierówności liniowe Wykonać działanie: Rozwiązać równanie: ( +x + ) x a) 5x 5x+ 5 = 50 x 0 b) 6(x + x + ) = (x + ) (x ) c) x 0x (0 x) 56 = 6x 5 5 ( x) Rozwiązać równanie: a) x + x = 4 b) x x
Równania i nierówności liniowe Wykonać działanie: Rozwiązać równanie: ( +x + ) x a) 5x 5x+ 5 = 50 x 0 b) 6(x + x + ) = (x + ) (x ) c) x 0x (0 x) 56 = 6x 5 5 ( x) Rozwiązać równanie: a) x + x = 4 b) x x
Bartłomiej Filipek www.ii.uj.edu.pl/~filipek
 Bartłomiej Filipek www.ii.uj.edu.pl/~filipek Nasz Cel Prehistoria krótki wstęp Nowa era! Vertex Shaders Fragment Shaders Podstawy GLSL Obsługa GLSL z API OpenGL Dodajmy parę efektów! Podsumowanie Dodatkowe
Bartłomiej Filipek www.ii.uj.edu.pl/~filipek Nasz Cel Prehistoria krótki wstęp Nowa era! Vertex Shaders Fragment Shaders Podstawy GLSL Obsługa GLSL z API OpenGL Dodajmy parę efektów! Podsumowanie Dodatkowe
Grafika komputerowa Wykład 8 Modelowanie obiektów graficznych cz. II
 Grafika komputerowa Wykład 8 Modelowanie obiektów graficznych cz. II Instytut Informatyki i Automatyki Państwowa Wyższa Szkoła Informatyki i Przedsiębiorczości w Łomży 2 0 0 9 Spis treści Spis treści 1
Grafika komputerowa Wykład 8 Modelowanie obiektów graficznych cz. II Instytut Informatyki i Automatyki Państwowa Wyższa Szkoła Informatyki i Przedsiębiorczości w Łomży 2 0 0 9 Spis treści Spis treści 1
Podłączanie bibliotek Zapis danych do pliku graficznego Generowanie promienia pierwotnego Import sceny z pliku Algorytm ray tracingu
 Ray Tracer cz.1 Michał Chwesiuk Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Wydział Informatyki 4 Kwiecień 2017 Michał Chwesiuk Ray Tracer cz.1 4 Kwiecień 2017 1/21 Plan zajęć laboratoryjnych
Ray Tracer cz.1 Michał Chwesiuk Zachodniopomorski Uniwersytet Technologiczny w Szczecinie Wydział Informatyki 4 Kwiecień 2017 Michał Chwesiuk Ray Tracer cz.1 4 Kwiecień 2017 1/21 Plan zajęć laboratoryjnych
4. Rysowanie krzywych
 1. Operator plot y x \begin{tikzpicture} \draw[->] (-0.2,0) -- (4.2,0) node[right] {$x$}; \draw[->] (0,-1.2) -- (0,4.2) node[above] {$y$}; \draw (3,4) -- (3,3) plot coordinates{(2,3) (3,0) (4,3)}; \end{tikzpicture}
1. Operator plot y x \begin{tikzpicture} \draw[->] (-0.2,0) -- (4.2,0) node[right] {$x$}; \draw[->] (0,-1.2) -- (0,4.2) node[above] {$y$}; \draw (3,4) -- (3,3) plot coordinates{(2,3) (3,0) (4,3)}; \end{tikzpicture}
Julia 4D - raytracing
 i przykładowa implementacja w asemblerze Politechnika Śląska Instytut Informatyki 27 sierpnia 2009 A teraz... 1 Fraktale Julia Przykłady Wstęp teoretyczny Rendering za pomocą śledzenia promieni 2 Implementacja
i przykładowa implementacja w asemblerze Politechnika Śląska Instytut Informatyki 27 sierpnia 2009 A teraz... 1 Fraktale Julia Przykłady Wstęp teoretyczny Rendering za pomocą śledzenia promieni 2 Implementacja
Macierze. Rozdział Działania na macierzach
 Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
PRZYDATNE WZORY SYMBOLE PUNKTY I LINIE
 WZORY PRZYDATNE WZORY SYMBOLE α - często używane do przedstawiania kąta Δ - oznacza "zmiana w" ε - współczynnik restytucji f(t) - funkcja f w odniesieniu do t μ - współczynnik tarcia ω - tu przedstawia
WZORY PRZYDATNE WZORY SYMBOLE α - często używane do przedstawiania kąta Δ - oznacza "zmiana w" ε - współczynnik restytucji f(t) - funkcja f w odniesieniu do t μ - współczynnik tarcia ω - tu przedstawia
