Modern methods of statistical physics
|
|
|
- Katarzyna Janiszewska
- 6 lat temu
- Przeglądów:
Transkrypt
1 Modern methods of statistical physics František Slanina Institute of Physics, Academy of Sciences of the Czech Republic, Prague slanina Ising model Renormalisation group Modern methods of statistical physics p.1/20
2 Ising model spins: S i {+1, 1} H = J <ij> S i S j h i S i < ij >: neighbours on a lattice (graph) Modern methods of statistical physics p.2/20
3 Ising model spins: S i {+1, 1} H = J <ij> S i S j h i S i < ij >: neighbours on a lattice (graph) Linear chain: Modern methods of statistical physics p.2/20
4 Ising model spins: S i {+1, 1} H = J <ij> S i S j h i S i < ij >: neighbours on a lattice (graph) Linear chain: Square lattice Triangular lattice Modern methods of statistical physics p.2/20
5 Ising model spins: S i {+1, 1} H = J <ij> S i S j h i S i < ij >: neighbours on a lattice (graph) Linear chain: Square lattice Triangular lattice Duality Honeycomb lattice Modern methods of statistical physics p.2/20
6 Mean-field solution 1. Naive (Bragg-Wiliams) k neighbours, H eff = J neighbours of 0 S 0S j, Modern methods of statistical physics p.3/20
7 Mean-field solution 1. Naive (Bragg-Wiliams) k neighbours, H eff = J neighbours of 0 S 0S j, neighbours of 0 S j k S m = tanh βjkm Modern methods of statistical physics p.3/20
8 Mean-field solution 1. Naive (Bragg-Wiliams) k neighbours, H eff = J neighbours of 0 S 0S j, neighbours of 0 S j k S m = tanh βjkm βjk = 0.7 βjk = Modern methods of statistical physics p.3/20
9 Mean-field solution 1. Naive (Bragg-Wiliams) k neighbours, H eff = J neighbours of 0 S 0S j, neighbours of 0 S j k S m = tanh βjkm βjk = 0.7 βjk = tanh x = x 1 3 x m = 0 or m = 3 βjk 1 (βjk) 3 Modern methods of statistical physics p.3/20
10 Mean-field solution 1. Naive (Bragg-Wiliams) k neighbours, H eff = J neighbours of 0 S 0S j, neighbours of 0 S j k S m = tanh βjkm βjk = 0.7 βjk = tanh x = x 1 3 x m = 0 or m = 3 βjk 1 (βjk) 3 Critical temperature: β c = 1 Jk, m (T c T ) 1/2 crit. exp.: β = 1 2 Modern methods of statistical physics p.3/20
11 Mean-field solution Sophisticated: Modern methods of statistical physics p.4/20
12 Mean-field solution Sophisticated: Fully connected graph Self-consistent equations for local order parameter. (magnetisation) Modern methods of statistical physics p.4/20
13 Mean-field solution Sophisticated: Fully connected graph Self-consistent equations for local order parameter. (magnetisation) Bethe-Peierls (=Bethe lattice) Recurrent equations for locally conditioned partition function. Modern methods of statistical physics p.4/20
14 Mean-field solution 2. Fully connected H = Jk N Partition function (ij) S i S j h i S i = 1 2 Jk N ( i S i ) 2 h i S i + Jk 2 }{{} we drop Z = {S i } e βh[{s i}] = {S i } e 1 2 β Jk N (P i S i) 2 +βh P i S i Trick: Hubbard-Stratonovich transform e 1 2 A2 = dx 2π e 1 2 x2 +xa Z = N 2π e N [ ( 1 2 x2 ln 2 cosh(x )] βjk+βh) dx Saddle-point method: e Nφ(x) e Nφ(x ) φ(x) has minimum at x = x : φ (x ) = 0, φ (x ) > 0 Modern methods of statistical physics p.5/20
15 Mean-field solution 2. Fully connected H = Jk N Partition function (ij) S i S j h i S i = 1 2 Jk N ( i S i ) 2 h i S i + Jk 2 }{{} we drop Z = {S i } e βh[{s i}] = {S i } e 1 2 β Jk N (P i S i) 2 +βh P i S i Trick: Hubbard-Stratonovich transform e 1 2 A2 = dx 2π e 1 2 x2 +xa Z = N 2π e N [ ( 1 2 x2 ln 2 cosh(x )] βjk+βh) dx Saddle-point method: e Nφ(x) e Nφ(x ) φ(x) has minimum at x = x : φ (x ) = 0, φ (x ) > 0 Modern methods of statistical physics p.5/20
16 Mean-field solution 2. Fully connected H = Jk N Partition function (ij) S i S j h i S i = 1 2 Jk N ( i S i ) 2 h i S i + Jk 2 }{{} we drop Z = {S i } e βh[{s i}] = {S i } e 1 2 β Jk N (P i S i) 2 +βh P i S i Trick: Hubbard-Stratonovich transform e 1 2 A2 = dx 2π e 1 2 x2 +xa Z = N 2π e N [ ( 1 2 x2 ln 2 cosh(x )] βjk+βh) dx Saddle-point method: e Nφ(x) e Nφ(x ) φ(x) has minimum at x = x : φ (x ) = 0, φ (x ) > 0 Modern methods of statistical physics p.5/20
17 Mean-field solution 2. Fully connected H = Jk N Partition function (ij) S i S j h i S i = 1 2 Jk N ( i S i ) 2 h i S i + Jk 2 }{{} we drop Z = {S i } e βh[{s i}] = {S i } e 1 2 β Jk N (P i S i) 2 +βh P i S i Trick: Hubbard-Stratonovich transform e 1 2 A2 = dx 2π e 1 2 x2 +xa Z = N 2π e N [ ( 1 2 x2 ln 2 cosh(x )] βjk+βh) dx Saddle-point method: e Nφ(x) e Nφ(x ) φ(x) has minimum at x = x : φ (x ) = 0, φ (x ) > 0 Modern methods of statistical physics p.5/20
18 Mean-field solution 2. Fully connected H = Jk N Partition function (ij) S i S j h i S i = 1 2 Jk N ( i S i ) 2 h i S i + Jk 2 }{{} we drop Z = {S i } e βh[{s i}] = {S i } e 1 2 β Jk N (P i S i) 2 +βh P i S i Trick: Hubbard-Stratonovich transform e 1 2 A2 = dx 2π e 1 2 x2 +xa Z = N 2π e N [ ( 1 2 x2 ln 2 cosh(x )] βjk+βh) dx Saddle-point method: e Nφ(x) e Nφ(x ) φ(x) has minimum at x = x : φ (x ) = 0, φ (x ) > 0 Modern methods of statistical physics p.5/20
19 φ(x) = 1 2 x2 ln ( 2 cosh(x βjk + βh) ) redefine: m = x βjk. φ (x) = 0 m = tanh(βjkm + βh) (as before) Modern methods of statistical physics p.6/20
20 φ(x) = 1 2 x2 ln ( 2 cosh(x βjk + βh) ) redefine: m = x βjk. φ (x) = 0 m = tanh(βjkm + βh) (as before) susceptibility: χ = lim h 0 dm dh χ (T T c ) 1 γ = 1 Modern methods of statistical physics p.6/20
21 φ(x) = 1 2 x2 ln ( 2 cosh(x βjk + βh) ) redefine: m = x βjk. φ (x) = 0 m = tanh(βjkm + βh) (as before) susceptibility: χ = lim h 0 dm dh χ (T T c ) 1 γ = 1 free energy: substitute minimum into φ(x) φ(x) + ln 2 (T c T ) 2 specific heat C (T c T ) 0 α = 0 Modern methods of statistical physics p.6/20
22 φ(x) = 1 2 x2 ln ( 2 cosh(x βjk + βh) ) redefine: m = x βjk. φ (x) = 0 m = tanh(βjkm + βh) (as before) susceptibility: χ = lim h 0 dm dh χ (T T c ) 1 γ = 1 free energy: substitute minimum into φ(x) φ(x) + ln 2 (T c T ) 2 specific heat C (T c T ) 0 α = 0 Just at critical point: m = tanh(m + βh) h 1 3 δ = 3 Modern methods of statistical physics p.6/20
23 φ(x) = 1 2 x2 ln ( 2 cosh(x βjk + βh) ) redefine: m = x βjk. φ (x) = 0 m = tanh(βjkm + βh) (as before) susceptibility: χ = lim h 0 dm dh χ (T T c ) 1 γ = 1 free energy: substitute minimum into φ(x) φ(x) + ln 2 (T c T ) 2 specific heat C (T c T ) 0 α = 0 Just at critical point: m = tanh(m + βh) h 1 3 δ = 3 Summary of critical exponents β = 1 2 γ = 1 δ = 3 α = 0 Modern methods of statistical physics p.6/20
24 Z (S 0 1) } Bethe-lattice approximation 1 { 2 S 3 0 } Z (S 0 2) Z (S 0 3) Z(S 0 l) = all spins in l-th branch e βh[{s} only l-th branch] Modern methods of statistical physics p.7/20
25 Z (S 0 1) } Bethe-lattice approximation Iterative cutting of k branches { 2 S 3 0 } Z (S 0 2) Z (S 0 3) 1 Z(S 0 1) = Z(S 0 2) = Z(S 0 3) =... = Z(S 0 k) = Z(S 0 ) Z = S 0 Z k (S 0 ) Z(S 0 l) = all spins in l-th branch e βh[{s} only l-th branch] Modern methods of statistical physics p.7/20
26 Z (S 0 1) } Bethe-lattice approximation Iterative cutting of k branches { 2 S 3 0 } Z (S 0 2) Z (S 0 3) Z(S 0 l) = 1 all spins in l-th branch e βh[{s} only l-th branch] Z(S 0 1) = Z(S 0 2) = Z(S 0 3) =... = Z(S 0 k) = Z(S 0 ) Z n (S 0 ) = S 1 Z = S 0 Z k (S 0 ) e βj S 0S 1 [Z n 1 (S 1 )] k 1 Modern methods of statistical physics p.7/20
27 Fixed point for quantity x = Z( 1)/Z(+1) Modern methods of statistical physics p.8/20
28 Fixed point for quantity x = Z( 1)/Z(+1) x = e βj + e βj x k 1 e βj + e βj x k 1 Modern methods of statistical physics p.8/20
29 Fixed point for quantity x = Z( 1)/Z(+1) x = e βj + e βj x k 1 e βj + e βj x k 1 x n e βj = 0.9 e βj = x n Modern methods of statistical physics p.8/20
30 Fixed point for quantity x = Z( 1)/Z(+1) x = e βj + e βj x k 1 e βj + e βj x k 1 x n e βj = 0.9 e βj = x n Magnetisation m = 1 xk 1+x k Modern methods of statistical physics p.8/20
31 Fixed point for quantity x = Z( 1)/Z(+1) x = e βj + e βj x k 1 e βj + e βj x k 1 x n e βj = 0.9 e βj = Magnetisation m = 1 xk 1+x k Critical point tanh β c J = 1 1 k x n Modern methods of statistical physics p.8/20
32 One-dimensional Ising model H = J N 1 i=1 S i S i+1 JS N S 1 h N i=1 S i Modern methods of statistical physics p.9/20
33 One-dimensional Ising model H = J N 1 i=1 S i S i+1 JS N S 1 h N i=1 S i Z = {S i } e βh = {S i } eβ(js 1S 2 +h(s 1 +S 2 )/2) e β(js 3S 3 +h(s 2 +S 3 )/2)... e β(js NS 1 +h(s N +S 1 )/2) Modern methods of statistical physics p.9/20
34 One-dimensional Ising model H = J N 1 i=1 S i S i+1 JS N S 1 h N i=1 S i Z = {S i } e βh = {S i } eβ(js 1S 2 +h(s 1 +S 2 )/2) e β(js 3S 3 +h(s 2 +S 3 )/2)... e β(js NS 1 +h(s N +S 1 )/2) ( ) V (S, S ) = e β(jss +h(s+s )/2), or V = e β(j+h) e βj e βj e β(j h) Modern methods of statistical physics p.9/20
35 One-dimensional Ising model H = J N 1 i=1 S i S i+1 JS N S 1 h N i=1 S i Z = {S i } e βh = {S i } eβ(js 1S 2 +h(s 1 +S 2 )/2) e β(js 3S 3 +h(s 2 +S 3 )/2)... e β(js NS 1 +h(s N +S 1 )/2) ( ) V (S, S ) = e β(jss +h(s+s )/2), or V = e β(j+h) e βj e βj e β(j h) Z = TrV N = λ N 1 + λ N 2 λ N 1 (λ 1 > λ 2 ) Modern methods of statistical physics p.9/20
36 One-dimensional Ising model H = J N 1 i=1 S i S i+1 JS N S 1 h N i=1 S i Z = {S i } e βh = {S i } eβ(js 1S 2 +h(s 1 +S 2 )/2) e β(js 3S 3 +h(s 2 +S 3 )/2)... e β(js NS 1 +h(s N +S 1 )/2) ( ) V (S, S ) = e β(jss +h(s+s )/2), or V = e β(j+h) e βj e βj e β(j h) Z = TrV N = λ N 1 + λ N 2 λ N 1 (λ 1 > λ 2 ) Free energy density: f = β 1 ln λ 1 Modern methods of statistical physics p.9/20
37 One-dimensional Ising model H = J N 1 i=1 S i S i+1 JS N S 1 h N i=1 S i Z = {S i } e βh = {S i } eβ(js 1S 2 +h(s 1 +S 2 )/2) e β(js 3S 3 +h(s 2 +S 3 )/2)... e β(js NS 1 +h(s N +S 1 )/2) ( ) V (S, S ) = e β(jss +h(s+s )/2), or V = e β(j+h) e βj e βj e β(j h) Z = TrV N = λ N 1 + λ N 2 λ N 1 (λ 1 > λ 2 ) Free energy density: f = β 1 ln λ 1 Eigenvalues of V : λ 1,2 = e βj cosh βh ± e 2βJ sinh 2 βh + e 2βJ Modern methods of statistical physics p.9/20
38 Magnetisation: m = f h = e βj sinh βh e 2βJ sinh 2 βh + e 2βJ Modern methods of statistical physics p.10/20
39 Magnetisation: m = f h = e βj sinh βh e 2βJ sinh 2 βh + e 2βJ... no phase transition! Modern methods of statistical physics p.10/20
40 Magnetisation: m = f h = e βj sinh βh e 2βJ sinh 2 βh + e 2βJ Susceptibility:... no phase transition! χ = m h h=0 = βe 2βJ Modern methods of statistical physics p.10/20
41 Magnetisation: m = f h = e βj sinh βh e 2βJ sinh 2 βh + e 2βJ Susceptibility:... no phase transition! Correlation function (h = 0): χ = m h h=0 = βe 2βJ S i S j = 1 Z TrσV j i σv N (j i) = ( ) j i λ2 λ 1 ξ = (ln tanh βj) e2βj diverges for β (or T 0) Modern methods of statistical physics p.10/20
42 Series expansions 1. High-temperature Z = e βh = {S i } {S i } <ij> e βjs is j Modern methods of statistical physics p.11/20
43 Series expansions 1. High-temperature Z = e βh = e βjsisj = (cosh βj) L {S i } {S i } <ij> {S i } <ij> (1 + S i S j tanh βj) Modern methods of statistical physics p.11/20
44 Series expansions 1. High-temperature Z = e βh = e βjsisj = (cosh βj) L {S i } {S i } <ij> {S i } <ij> (1 + S i S j tanh βj) Modern methods of statistical physics p.11/20
45 Series expansions 1. High-temperature Z = e βh = e βjsisj = (cosh βj) L {S i } {S i } <ij> {S i } <ij> (1 + S i S j tanh βj) Modern methods of statistical physics p.11/20
46 Series expansions 1. High-temperature Z = e βh = e βjsisj = (cosh βj) L {S i } {S i } <ij> {S i } <ij> (1 + S i S j tanh βj) 2. Low-temperature Z = 2e βjl e 2βJ l contours Modern methods of statistical physics p.11/20
47 Series expansions 1. High-temperature Z = e βh = e βjsisj = (cosh βj) L {S i } {S i } <ij> {S i } <ij> (1 + S i S j tanh βj) 2. Low-temperature Z = 2e βjl e 2βJ l contours Modern methods of statistical physics p.11/20
48 Series expansions 1. High-temperature Z = e βh = e βjsisj = (cosh βj) L {S i } {S i } <ij> {S i } <ij> (1 + S i S j tanh βj) 2. Low-temperature Z = 2e βjl e 2βJ l contours Modern methods of statistical physics p.11/20
49 Analysis of the series expansions 1. Duality: define tanh β J = e 2βJ low-t Z(βJ) = 2 N (cosh βj) L contours (tanh βj)l high-t Z(βJ) = 2e βjl contours (tanh β J ) l Modern methods of statistical physics p.12/20
50 Analysis of the series expansions 1. Duality: define tanh β J = e 2βJ low-t Z(βJ) = 2 N (cosh βj) L contours (tanh βj)l high-t Z(βJ) = 2e βjl contours (tanh β J ) l }{{} Z(βJ) Z(β J ) = 2N 1 (cosh βj) L e β J L Modern methods of statistical physics p.12/20
51 Analysis of the series expansions 1. Duality: define tanh β J = e 2βJ low-t Z(βJ) = 2 N (cosh βj) L contours (tanh βj)l high-t Z(βJ) = 2e βjl contours (tanh β J ) l }{{} Z(βJ) Z(β J ) = 2N 1 (cosh βj) L e β J L Critical point: β J = βj β c J = Modern methods of statistical physics p.12/20
52 Analysis of the series expansions 1. Duality: define tanh β J = e 2βJ low-t Z(βJ) = 2 N (cosh βj) L contours (tanh βj)l high-t Z(βJ) = 2e βjl contours (tanh β J ) l }{{} Z(βJ) Z(β J ) = 2N 1 (cosh βj) L e β J L Critical point: β J = βj β c J = Compare: mean-field β c J = 0.25, Bethe-Peierls β c J = Modern methods of statistical physics p.12/20
53 Analysis of the series expansions 1. Duality: define tanh β J = e 2βJ low-t Z(βJ) = 2 N (cosh βj) L contours (tanh βj)l high-t Z(βJ) = 2e βjl contours (tanh β J ) l }{{} Z(βJ) Z(β J ) = 2N 1 (cosh βj) L e β J L Critical point: β J = βj β c J = Compare: mean-field β c J = 0.25, Bethe-Peierls β c J = Extraction of exponents: φ(x) = l=0 a l x l A(x x c ) γ Modern methods of statistical physics p.12/20
54 Analysis of the series expansions 1. Duality: define tanh β J = e 2βJ low-t Z(βJ) = 2 N (cosh βj) L contours (tanh βj)l high-t Z(βJ) = 2e βjl contours (tanh β J ) l }{{} Z(βJ) Z(β J ) = 2N 1 (cosh βj) L e β J L Critical point: β J = βj β c J = Compare: mean-field β c J = 0.25, Bethe-Peierls β c J = Extraction of exponents: φ(x) = l=0 a l x l A(x x c ) γ r l (l + 1) a l+1 a l l a l a l 1 1 x c Modern methods of statistical physics p.12/20
55 Analysis of the series expansions 1. Duality: define tanh β J = e 2βJ low-t Z(βJ) = 2 N (cosh βj) L contours (tanh βj)l high-t Z(βJ) = 2e βjl contours (tanh β J ) l }{{} Z(βJ) Z(β J ) = 2N 1 (cosh βj) L e β J L Critical point: β J = βj β c J = Compare: mean-field β c J = 0.25, Bethe-Peierls β c J = Extraction of exponents: φ(x) = l=0 a l x l A(x x c ) γ a l r l (l + 1) a l+1 l 1 a l a l 1 x c ( ) al s l l x c γ a l 1 Modern methods of statistical physics p.12/20
56 Renormalisation group Modern methods of statistical physics p.13/20
57 Renormalisation group Old spins S i New spins S I Projector P ({ S I }, {S i }) Modern methods of statistical physics p.13/20
58 Renormalisation group Old spins S i New spins S I Projector P ({ S I }, {S i }) example: 1D Ising S 1 S 2 S 3 S4 S5 S6 S7 S S S S Modern methods of statistical physics p.13/20
59 Renormalisation group Old spins S i New spins S I Projector P ({ S I }, {S i }) example: 1D Ising S 1 S 2 S 3 S4 S5 S6 S7 S S2 S3 S4 1 P = I δ( S I S 2I 1 ) Modern methods of statistical physics p.13/20
60 Old measure New measure µ({s i }) = e H({S i}) µ({ S I }) = {S i } P ({ S I }, {S i })µ({s i }) = e H({ S I }) Ng Modern methods of statistical physics p.14/20
61 Old measure New measure µ({s i }) = e H({S i}) µ({ S I }) = {S i } P ({ S I }, {S i })µ({s i }) = e H({ S I }) Ng H({S i }) = K 1 H 1 ({S i }) + K 2 H 2 ({S i }) +... H({ S I }) = K 1 H 1 ({ S I }) + K 2 H 2 ({ S I }) +... Modern methods of statistical physics p.14/20
62 Old measure New measure µ({s i }) = e H({S i}) µ({ S I }) = {S i } P ({ S I }, {S i })µ({s i }) = e H({ S I }) Ng H({S i }) = K 1 H 1 ({S i }) + K 2 H 2 ({S i }) +... H({ S I }) = K 1 H 1 ({ S I }) + K 2 H 2 ({ S I }) +... dynamical process (K 1, K 2,...) ( K 1, K 2,...) K i = R i (K 1, K 2,...) Modern methods of statistical physics p.14/20
63 Old measure New measure µ({s i }) = e H({S i}) µ({ S I }) = {S i } P ({ S I }, {S i })µ({s i }) = e H({ S I }) Ng H({S i }) = K 1 H 1 ({S i }) + K 2 H 2 ({S i }) +... H({ S I }) = K 1 H 1 ({ S I }) + K 2 H 2 ({ S I }) +... dynamical process (K 1, K 2,...) ( K 1, K 2,...) Schematically: K i = R i (K 1, K 2,...) one parameter: T c T Modern methods of statistical physics p.14/20
64 Old measure New measure µ({s i }) = e H({S i}) µ({ S I }) = {S i } P ({ S I }, {S i })µ({s i }) = e H({ S I }) Ng H({S i }) = K 1 H 1 ({S i }) + K 2 H 2 ({S i }) +... H({ S I }) = K 1 H 1 ({ S I }) + K 2 H 2 ({ S I }) +... dynamical process (K 1, K 2,...) ( K 1, K 2,...) Schematically: stable K i = R i (K 1, K 2,...) one parameter: T c T K 2 K Modern methods of statistical physics p.14/20
65 Old measure New measure µ({s i }) = e H({S i}) µ({ S I }) = {S i } P ({ S I }, {S i })µ({s i }) = e H({ S I }) Ng H({S i }) = K 1 H 1 ({S i }) + K 2 H 2 ({S i }) +... H({ S I }) = K 1 H 1 ({ S I }) + K 2 H 2 ({ S I }) +... dynamical process (K 1, K 2,...) ( K 1, K 2,...) Schematically: stable K i = R i (K 1, K 2,...) one parameter: unstable T c T K 2 K 2 K K Modern methods of statistical physics p.14/20
66 Old measure New measure µ({s i }) = e H({S i}) µ({ S I }) = {S i } P ({ S I }, {S i })µ({s i }) = e H({ S I }) Ng H({S i }) = K 1 H 1 ({S i }) + K 2 H 2 ({S i }) +... H({ S I }) = K 1 H 1 ({ S I }) + K 2 H 2 ({ S I }) +... dynamical process (K 1, K 2,...) ( K 1, K 2,...) Schematically: stable K i = R i (K 1, K 2,...) one parameter: unstable mixed T c T K 2 K 2 K 2 K K Modern methods of statistical physics p.14/20 K
67 Fixed points: K = R(K ) Modern methods of statistical physics p.15/20
68 Fixed points: K = R(K ) linearisation: δ K i = j R i K j δk j Modern methods of statistical physics p.15/20
69 Fixed points: K = R(K ) linearisation: δ K i = j R i K j δk j diagonalisation: Ū α = λ α U α Modern methods of statistical physics p.15/20
70 Fixed points: K = R(K ) linearisation: δ K i = j R i K j δk j diagonalisation: Ū α = λ α U α semigroup property λ α = b y α λ α > 1 repulsive y α > 0 U α relevant λ α < 1 attractive y α < 0 U α irrelevant Modern methods of statistical physics p.15/20
71 Fixed points: K = R(K ) linearisation: δ K i = j R i K j δk j diagonalisation: Ū α = λ α U α semigroup property λ α = b y α λ α > 1 repulsive y α > 0 U α relevant λ α < 1 attractive y α < 0 U α irrelevant Scaling: f(t c T, h) = b d f((t c T ) b y T, h y h ) Modern methods of statistical physics p.15/20
72 Fixed points: K = R(K ) linearisation: δ K i = j R i K j δk j diagonalisation: Ū α = λ α U α semigroup property λ α = b y α λ α > 1 repulsive y α > 0 U α relevant λ α < 1 attractive y α < 0 U α irrelevant Scaling: f(t c T, h) = b d f((t c T ) b y T, h y h ) α = 2 d y T β = d y h δ = y T y h d y h Modern methods of statistical physics p.15/20
73 Renormalisation group solution of 1D Ising model Modern methods of statistical physics p.16/20
74 Renormalisation group solution of 1D Ising model J = 1 4 ln cosh(2j + h) ln cosh(2j h) 1 2 ln cosh h h = h ln cosh(2j + h) 1 2 ln cosh(2j h) Modern methods of statistical physics p.16/20
75 Renormalisation group solution of 1D Ising model J = 1 4 ln cosh(2j + h) ln cosh(2j h) 1 2 ln cosh h h = h ln cosh(2j + h) 1 2 ln cosh(2j h) 5 4 h J Modern methods of statistical physics p.16/20
76 Scaling relations f(t, h) = b d f(tb y T, hb y h ) ξ(t, h) = bξ(tb y T, hb y h ) C(r, t, h) = b 2yh 2d C(r/b, tb y T, hb y h ) Modern methods of statistical physics p.17/20
77 Scaling relations f(t, h) = b d f(tb y T, hb y h ) ξ(t, h) = bξ(tb y T, hb y h ) C(r, t, h) = b 2yh 2d C(r/b, tb y T, hb y h ) α = 2 d y T ν = 1 y T νd = 2 α Modern methods of statistical physics p.17/20
78 Scaling relations f(t, h) = b d f(tb y T, hb y h ) ξ(t, h) = bξ(tb y T, hb y h ) C(r, t, h) = b 2yh 2d C(r/b, tb y T, hb y h ) α = 2 d y T ν = 1 y T β = d y h δ = y T y h d y h γ = 2y h d y T νd = 2 α γ = β(δ 1) Modern methods of statistical physics p.17/20
79 Scaling relations f(t, h) = b d f(tb y T, hb y h ) ξ(t, h) = bξ(tb y T, hb y h ) C(r, t, h) = b 2yh 2d C(r/b, tb y T, hb y h ) α = 2 d y T ν = 1 y T β = d y h δ = y T y h d y h γ = 2y h d y T νd = 2 α γ = β(δ 1) α + 2β + γ = 2 Modern methods of statistical physics p.17/20
80 Scaling relations f(t, h) = b d f(tb y T, hb y h ) ξ(t, h) = bξ(tb y T, hb y h ) C(r, t, h) = b 2yh 2d C(r/b, tb y T, hb y h ) α = 2 d y T ν = 1 y T β = d y h δ = y T y h d y h γ = 2y h d y T η = 2y h + d + 2 νd = 2 α γ = β(δ 1) α + 2β + γ = 2 γ = ν(2 η) Modern methods of statistical physics p.17/20
81 Overview of Ising critical exponents exponent mean-field d = 2 Onsager d = 3 high-t expansion α discontinuity ± β 1/2 1/ ± γ 1 7/ ± δ η 1/ ± ν 0 1/ ± Modern methods of statistical physics p.18/20
82 Liquid-gas transition Phase diagram of water Modern methods of statistical physics p.19/20
83 Liquid-gas transition V(r) r Lennard-Jones potential ˆ` r0 12 ` r0 6 V (r) = 4 r r Phase diagram of water Modern methods of statistical physics p.19/20
84 Liquid-gas transition V(r) r Lennard-Jones potential ˆ` r0 12 ` r0 6 V (r) = 4 r r V(r) Phase diagram of water r Modern methods of statistical physics p.19/20
85 Lattice gas model Molecules on a lattice. Occupation numbers: n i {0, 1} H = <ij> ɛ n i n j Modern methods of statistical physics p.20/20
86 Lattice gas model Molecules on a lattice. Occupation numbers: n i {0, 1} H = <ij> ɛ n i n j Grand-canonical partition function Z = {n i } e βɛ P <ij> n in j βµ P i n i Modern methods of statistical physics p.20/20
87 Lattice gas model Molecules on a lattice. Occupation numbers: n i {0, 1} H = <ij> ɛ n i n j Grand-canonical partition function Z = {n i } e βɛ P <ij> n in j βµ P i n i Mapping on Ising model in magnetic field: n i = 1 2 (S i + 1), J = 1 4 ɛ, h = 1 2 µ ɛ k magnetisation density: M = 2ρ 1 Modern methods of statistical physics p.20/20
Aerodynamics I Compressible flow past an airfoil
Aerodynamics I Compressible flow past an airfoil transonic flow past the RAE-8 airfoil (M = 0.73, Re = 6.5 10 6, α = 3.19 ) Potential equation in compressible flows Full potential theory Let us introduce
H γ0 - the standard enthalpy of g phase. H β γ - the transition enthalpy of b to g
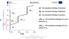H α0 - the standard enthalpy of a phase H β0 - the standard enthalpy of b phase H γ0 - the standard enthalpy of g phase H α β - the transition enthalpy of a to b phase at T t1 H β γ - the transition enthalpy
Model standardowy i stabilność próżni
Model standardowy i stabilność próżni Marek Lewicki Instytut Fizyki teoretycznej, Wydzia l Fizyki, Uniwersytet Warszawski Sympozjum Doktoranckie Warszawa-Fizyka-Kraków, 4 Marca 2016, Kraków Na podstawie:
Granica i ciągłość funkcji. 1 Granica funkcji rzeczywistej jednej zmiennej rzeczywsitej
Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus listopada 07r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Granica i ciągłość funkcji. 1 Granica funkcji rzeczywistej jednej zmiennej rzeczywistej
Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus 3 listopada 06r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Inverse problems - Introduction - Probabilistic approach
Inverse problems - Introduction - Probabilistic approach Wojciech Dȩbski Instytut Geofizyki PAN debski@igf.edu.pl Wydział Fizyki UW, 13.10.2004 Wydział Fizyki UW Warszawa, 13.10.2004 (1) Plan of the talk
Machine Learning for Data Science (CS4786) Lecture11. Random Projections & Canonical Correlation Analysis
Machine Learning for Data Science (CS4786) Lecture11 5 Random Projections & Canonical Correlation Analysis The Tall, THE FAT AND THE UGLY n X d The Tall, THE FAT AND THE UGLY d X > n X d n = n d d The
Convolution semigroups with linear Jacobi parameters
Convolution semigroups with linear Jacobi parameters Michael Anshelevich; Wojciech Młotkowski Texas A&M University; University of Wrocław February 14, 2011 Jacobi parameters. µ = measure with finite moments,
Few-fermion thermometry
Few-fermion thermometry Phys. Rev. A 97, 063619 (2018) Tomasz Sowiński Institute of Physics of the Polish Academy of Sciences Co-authors: Marcin Płodzień Rafał Demkowicz-Dobrzański FEW-BODY PROBLEMS FewBody.ifpan.edu.pl
Az ideális Bose-gáz termodinamikai mennyiségei
Az ideális Bose-gáz termodinamikai mennyiségei Kiegészítés III. éves BsC fizikusok számára Cserti József Eötvös Loránd udományegyetem, Komplex Rendszerek Fizikája anszék 016. február 1. Néhány alapvető
Co to jest model Isinga?
Co to jest model Isinga? Fakty eksperymentalne W pewnych metalach (np. Fe, Ni) następuje spontaniczne ustawianie się spinów wzdłuż pewnego kierunku, powodując powstanie makroskopowego pola magnetycznego.
v = v i e i v 1 ] T v =
![v = v i e i v 1 ] T v =](/thumbs/97/130738346.jpg "v = v i e i v 1 ] T v =")
v U = e i,..., e n ) v = n v i e i i= e i i v T v = = v v n v n U v v v +q 3q +q +q b c d XY X +q Y 3q r +q = r 3q = r +q = r +q = r 3q = r +q = E = E +q + E 3q + E +q = k q r+q 3 + k 3q r 3q 3 b V = kq
Strings on Celestial Sphere. Stephan Stieberger, MPP München
Strings on Celestial Sphere Stephan Stieberger, MPP München String Theory from a Worldsheet Perspective Galileo Galilei Institute, Firenze April 15-19, 2019 based on: St.St., T.R. Taylor: Strings on Celestial
Struktura polimerów i biopolimerów (2)
Struktura polimerów i biopolimerów (2) Andrzej Koliński Pracownia Teorii Biopolimerów Wydział Chemii, Uniwersytet Warszawski kolinski@chem.uw.edu.pl http://www.biocomp.chem.uw.edu.pl Podsumowanie poprzedniego
Unitary representations of SL(2, R)
Unitary representations of SL(, R) Katarzyna Budzik 8 czerwca 018 1/6 Plan 1 Schroedinger operators with inverse square potential Universal cover of SL(, R) x + (m 1 4) 1 x 3 Integrating sl(, R) representations
Metody Obliczeniowe w Nauce i Technice
7. Równania nieliniowe (non-linear equations) Marian Bubak Department of Computer Science AGH University of Science and Technology Krakow, Poland bubak@agh.edu.pl dice.cyfronet.pl Contributors Dawid Prokopek
Krytyczność i przejścia fazowe. Katarzyna Sznajd-Weron
Krytyczność i przejścia fazowe Katarzyna Sznajd-Weron Temperatura Curie Temperatura Curie ciągłe przejście fazowe magnes ferromagnetyk Przejście fazowe Katarzyna Sznajd-Weron Ferromagnetyk T T c Paramagnetyk
T = Z t T t T t T t T t T : Z N (s i ) n i=1 n n S S = {(s i ) n i=1 N n : s j + j s k + k ( n), n N}. 1 j k n (s 1, s 2,..., s n ) s 1 s 2... s n m = s 1 s 2... s n m s i m i = 1,..., n S m S m = {(s
Wielki rozkład kanoniczny
, granica termodynamiczna i przejścia fazowe Instytut Fizyki 2015 Podukład otwarty Podukład otwarty S opisywany układ + rezerwuar R Podukład otwarty S opisywany układ + rezerwuar R układ S + R jest izolowany
Zestaw zadań z Równań różniczkowych cząstkowych I 18/19
Zestaw zadań z Równań różniczkowych cząstkowych I 18/19 Zad 1. Znaleźć rozwiązania ogólne u = u(x, y) następujących równań u x = 1, u y = 2xy, u yy = 6y, u xy = 1, u x + y = 0, u xxyy = 0. Zad 2. Znaleźć
A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations
A sufficient condition of regularity for axially symmetric solutions to the Navier-Stokes equations G. Seregin & W. Zajaczkowski A sufficient condition of regularity for axially symmetric solutions to
Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application
Towards Stability Analysis of Data Transport Mechanisms: a Fluid Model and an Application Gayane Vardoyan *, C. V. Hollot, Don Towsley* * College of Information and Computer Sciences, Department of Electrical
Spektroskopia mionów w badaniach wybranych materiałów magnetycznych. Piotr M. Zieliński NZ35 IFJ PAN
Spektroskopia mionów w badaniach wybranych materiałów magnetycznych Piotr M. Zieliński NZ35 IFJ PAN 1. Fundamenty spektroskopii mionów. Typowy eksperyment 3. Cel i obiekty badań 4. Przykłady otrzymanych
Constructions of Nonequilibrium Statistical Mechanics Piotr Nayar, Seria I
Constructions of onequilibrium Statistical Mechanics Piotr ayar, Seria I Zadanie F Maj c dan sum statystyczn Z H, T mo»emy wyznaczy energi swobodn na jeden spin ukªadu poprzez przej±cie do granicy termodynamicznej
1 Relacje i odwzorowania
Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
PROSTE A POZYTECZNE NIERÓWNOśCI MACIERZOWE
PROSTE A POZYTECZNE NIERÓWNOśCI MACIERZOWE TOMASZ TKOCZ Streszczenie. Tekst zawiera notatki do referatu z Seminarium Fizyki Teoretycznej. Jest to w zasadzie tłumaczenie(z uzupełnionymi pewnymi skrótami
Eksperymenty reaktorowe drugiej generacji wyznaczenie ϑ 13
Eksperymenty reaktorowe drugiej generacji wyznaczenie ϑ 13 v Przypomnienie wyniku eksperymentu KamLAND - weryfikującego oscylacje neutrin słonecznych v Formuły na prawdopodobieństwo disappearance antyneutrin
O problemie sterowania aproksymacyjnego dla semiliniowych inkluzji różniczkowych w przestrzeniach Hilberta
O problemie sterowania aproksymacyjnego dla semiliniowych inkluzji różniczkowych w przestrzeniach Hilberta Krzysztof RYKACZEWSKI Uniwersytet Mikołaja Kopernika w Toruniu SNA 2011 Toruń, 10 września 2011
Dualities and 5-brane webs for 5d rank 2 SCFTs
Dualities and 5-brane webs for 5d rank 2 SCFTs Sung-Soo Kim (UESTC) 2018-11-08 Hirotaka Hayashi (Tokai univ.), Kimyeong Lee (KIAS), Futoshi Yagi (SWJTU) arxiv: 1801.03916, 1806.10569 In this talk, we focus
2.1 Przykład wstępny Określenie i konstrukcja Model dwupunktowy Model gaussowski... 7
Spis treści Spis treści 1 Przedziały ufności 1 1.1 Przykład wstępny.......................... 1 1.2 Określenie i konstrukcja...................... 3 1.3 Model dwupunktowy........................ 5 1.4
STATYSTYKA MATEMATYCZNA WYKŁAD października 2009
STATYSTYKA MATEMATYCZNA WYKŁAD 4 26 października 2009 Rozkład N(µ, σ). Estymacja σ σ 2 = 1 σ 2π + = E µ,σ (X µ) 2 { (x µ) 2 exp 1 ( ) } x µ 2 dx 2 σ Rozkład N(µ, σ). Estymacja σ σ 2 = 1 σ 2π + = E µ,σ
Jądrowe klasyfikatory liniowe
Jądrowe klasyfikatory liniowe Waldemar Wołyński Wydział Matematyki i Informatyki UAM Poznań Wisła, 9 grudnia 2009 Waldemar Wołyński () Jądrowe klasyfikatory liniowe Wisła, 9 grudnia 2009 1 / 19 Zagadnienie
}, gdzie a = t (n) )(f(t(n) k. ) f(t(n) k 1 ) 1+δ = 0,
Zadania z Procesów Stochastycznych II - 1 1. Niech π n = {t (n), t(n) 1,..., t(n) k n }, gdzie a = t (n) < t (n) 1
model isinga 2d ab 10 grudnia 2016
model isinga 2d ab 10 grudnia 2016 tematyka Model spinów Isinga Hamiltonian i suma statystyczna modelu Metoda Monte-Carlo. Algorytm Metropolisa. Obserwable Modelowanie: Model Isinga 1 hamiltonian I Hamiltonian,
Matematyczne Metody Fizyki II
Matematyczne Metody Fizyki II Mariusz Przybycień Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza Wykład 1 M. Przybycień (WFiIS AGH) Matematyczne Metody Fizyki II Wykład 1 1 / 16 Literatura
M W M Z correlation. πα 1 M G F 2 = 2M 2 W 2 W
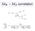M W M Z correlation µ W ν µ e ν e G F 2 = 2M 2 W πα ( 1 M 2 W /MZ) 2 with loop contributions G F 2 = 2M 2 W (1+ r) πα ( 1 M 2 W /MZ) 2 1-loop examples ØÓÔ ÕÙ Ö r : quantum correction r = r(m t,m H ) Ï
Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM
Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................
Przejścia fazowe w 1D modelu Isinga
Przejścia fazowe w 1D modelu Isinga z zero-temperaturową dynamiką Glaubera Rafał Topolnicki rafal.topolnicki@gmail.com Wydział Fizyki i Astronomii Uniwersytet Wrocławski Wydział Podstawowych Problemów
R Z N C. p11. a!b! = b (a b)!b! d n dx n [xn sin x] = x n(n k) (sin x) (n) = n(n 1) (n k + 1) sin(x + kπ. n(n 1) (n k + 1) sin(x + lπ 2 )
![R Z N C. p11. a!b! = b (a b)!b! d n dx n [xn sin x] = x n(n k) (sin x) (n) = n(n 1) (n k + 1) sin(x + kπ. n(n 1) (n k + 1) sin(x + lπ 2 )](/thumbs/102/156200514.jpg "R Z N C. p11. a!b! = b (a b)!b! d n dx n [xn sin x] = x n(n k) (sin x) (n) = n(n 1) (n k + 1) sin(x + kπ. n(n 1) (n k + 1) sin(x + lπ 2 )")
5 Z N p ) a a + b)! b ) a!b! a a! b a b)!b! p n n k nn k) n ) n k) d n d n [n sin ] n nn k) sin ) n) k n nn ) n k + ) sin + lπ ) k d n d n [n sin ] n k ) n n ) n k) sin ) k) k n k ) n nn ) n k + ) sin
DOBÓR FUNKCJI WŁASNEJ PRZEMIESZCZENIA UKŁADÓW DRGAJĄCYCH GIĘTNIE W RUCHU UNOSZENIA
MODELOWANIE INŻYNIERSKIE ISSN 896-77X 33, s. 7-34, Gliwice 007 DOBÓR FUNKCJI WŁASNEJ PRZEMIESZCZENIA UKŁADÓW DRGAJĄCYCH GIĘTNIE W RUCHU UNOSZENIA ANDRZEJ BUCHACZ, SŁAWOMIR ŻÓŁKIEWSKI Instytut Automatyzacji
Metodyki projektowania i modelowania systemów Cyganek & Kasperek & Rajda 2013 Katedra Elektroniki AGH
Kierunek Elektronika i Telekomunikacja, Studia II stopnia Specjalność: Systemy wbudowane Metodyki projektowania i modelowania systemów Cyganek & Kasperek & Rajda 2013 Katedra Elektroniki AGH Zagadnienia
O testach wielowymiarowej normalności opartych na statystyce Shapiro-Wilka
O testach wielowymiarowej normalności opartych na statystyce Shapiro-Wilka Katedra Zastosowań Matematyki i Informatyki Uniwersytet Przyrodniczy w Lublinie Wisła 2012, 7.12.2012 Plan prezentacji 1 Wprowadzenie
n [2, 11] 1.5 ( G. Pick 1899).
![n [2, 11] 1.5 ( G. Pick 1899).](/thumbs/98/135090138.jpg "n [2, 11] 1.5 ( G. Pick 1899).")
1. / / 2. R 4k 3. 4. 5. 6. / 7. /n 8. n 1 / / Z d ( R d ) d P Z d R d R d? n > 0 n 1.1. R 2 6 n 5 n [Scherrer 1946] d 3 R 3 6 1.2 (Schoenberg 1937). d 3 R d n n = 3, 4, 6 1.1. d 3 R d 1.3. θ θ/π 1.4. 0
Metody inwersji Bayesowskiej -L7- IGF PAN, 21.IV.2005
Metody inwersji Bayesowskiej -L7- Podejście optymalizacyjne i probabilistyczne podobieństwa i różnice (C) G(m) d obs + λ m m apr = min d obs m apr d th = d true + ɛ obs = m true + ɛ apr = G(m) + ɛ th G(m)
STATYSTYKA MATEMATYCZNA WYKŁAD 5. 2 listopada 2009
STATYSTYKA MATEMATYCZNA WYKŁAD 5 2 listopada 2009 Poprzedni wykład: przedział ufności dla µ, σ nieznane Rozkład N(µ, σ). Wnioskowanie o średniej µ, gdy σ nie jest znane Testowanie H : µ = µ 0, K : µ
4.1. Lecture 4 & 5. Riemann. f(t)dt. a = t 0 <t 1 < <t n 1 <b= t n (4.1) , n [t i 1,t i ] t i t i 1 (i =1,...,n) f(ξ i )(t i t i 1 ) (4.
![4.1. Lecture 4 & 5. Riemann. f(t)dt. a = t 0 <t 1 < <t n 1 <b= t n (4.1) , n [t i 1,t i ] t i t i 1 (i =1,...,n) f(ξ i )(t i t i 1 ) (4.](/thumbs/99/139565186.jpg "4.1. Lecture 4 & 5. Riemann. f(t)dt. a = t 0 <t 1 < <t n 1 <b= t n (4.1) , n [t i 1,t i ] t i t i 1 (i =1,...,n) f(ξ i )(t i t i 1 ) (4.")
Lecture 4 & 5 4 4.1 Riemnn t f(t) [, b] (Riemnn ) f(t)dt [, b] n 1 t 1,...,t n 1 t 0
Fizyka gwiazd. 1 Budowa gwiazd. 19 maja Stosunek r g R = 2GM
Fizyka gwiazd 19 maja 2004 1 Budowa gwiazd Stosunek r g R = 2GM c 2 R (gdzie M, R jest masa i promieniem gwiazdy) daje nam informację konieczności uwzględnienia poprawek relatywistycznych. 0-0 Rysunek
Dyrektor oraz pracownicy Miejsko - Gminnego Ośrodka Kultury w Kowalewie Pomorskim
Wszystkim Nauczycielom i pracownikom oświaty z okazji Dnia Edukacji Narodowej moc najserdeczniejszych życzeń, spełnienia najskrytszych marzeń oraz byście mogli w pełni realizować swoje plany życiowe i
Porównanie modeli regresji. klasycznymi modelami regresji liniowej i logistycznej
Porównanie modeli logicznej regresji z klasycznymi modelami regresji liniowej i logistycznej Instytut Matematyczny, Uniwersytet Wrocławski Małgorzata Bogdan Instytut Matematyki i Informatyki, Politechnika
Elementy wspo łczesnej teorii inwersji
Elementy wspo łczesnej teorii inwersji Metoda optymalizacyjna (2) W. Debski, 8.01.2015 Liniowy problem odwrotny m est (λ) = m apr + (G T G + λi) 1 G T ( dobs G m apr) +δ d est d o = + λ I ( G T G + λi
Testowanie hipotez. Hipoteza prosta zawiera jeden element, np. H 0 : θ = 2, hipoteza złożona zawiera więcej niż jeden element, np. H 0 : θ > 4.
Testowanie hipotez Niech X = (X 1... X n ) będzie próbą losową na przestrzeni X zaś P = {P θ θ Θ} rodziną rozkładów prawdopodobieństwa określonych na przestrzeni próby X. Definicja 1. Hipotezą zerową Θ
Zespół Szkół Technicznych. Badanie wyświetlaczy LCD
Zespół Szkół Technicznych Badanie wyświetlaczy LCD WYŚWIETLACZE LCD CZĘSC TEORETYCZNA ZALETY: ) mały pobór mocy, 2) ekonomiczność pod względem zużycia energii (pobór prądu przy 5V mniejszy niż 2mA), 3)
O pewnym twierdzeniu S. Łojasiewicza, J. Wloki, Z. Zieleżnego
O pewnym twierdzeniu S. Łojasiewicza, J. Wloki, Z. Zieleżnego Jan Ligęza Instytut Matematyki Wisła Letnia Szkoła Instytutu Matematyki wrzesień 2010 r. [1] S. Łojasiewicz, J. Wloka, Z. Zieleżny; Über eine
Zastosowania metod analitycznej złożoności obliczeniowej do przetwarzania sygnałów cyfrowych oraz w metodach numerycznych teorii aproksymacji
Zastosowania metod analitycznej złożoności obliczeniowej do przetwarzania sygnałów cyfrowych oraz w metodach numerycznych teorii aproksymacji Marek A. Kowalski Uniwersytet Kardynała Stefana Wyszyńskiego
Primal Formulation. Find u h V h such that. A h (u h, v h )= fv h dx v h V h, where. u h v h dx. A h (u h, v h ) = DGFEM Primal Formulation.
aaaftxicbvtnbtnaehzdsov5aqthlimaokskuviowkfs+vekehjfkbapg6znehmvwa9d7zqksvwipa1xeaeuvagnhni1nshou5ll8tcz33w7o+thyjlunc7vtcq16vr1jc0b9s1bt+9sbe/cpzfbhbhajwepok9dlclngvyvu5x+ciok/sgnp8pjs+m/ndjiskb8vbchhfh4lniieaw05oxu6j0mxkjfjgeicthxvbrimhigpkzsws1+7ngn7w1nha8jbyzioeiddyoymhzxhrmg8/myu4bgqyq5zx05wctq2f89glebdsku09n1gzoggftogizzcvkp9bivtytcghv4ydfkaokbqdmwvf2iabcyov4hgec5x8+wjyhgdr3u8qq+hjtqfz9mkn5ceqd7mjutwp0pt3jqttw1gxsfagjrhccytefbhiolawya5kogufle59x8ky6pwvsyq8nkrepyaf7omhnlclq5bbtr3es84varia+kt2l8swbyhpgymznwpc/sfbysspy2s73baxeybzenbmhswsu61po1hdyaxd4vinas5vm3e6pbgipfckepjwjjq0wmeezptcmwpvlbkk10cg814oiej/0ibrm6njfgx8olf6gjfaw8ueoz4fw+s1inng4sjsjyuuhyqqoygwraxa9wwusj4hfawcriwisqd0eykh2jsluei3skhawdjomihx4jszkkaxqlwhkor4nccss2wqjdqsjgjrkljt0rulqfxlj0pnlrsvtoyjoq0hxuwaw3olnxuk5mksialft5mant/usi6uv9aqs5xzwhctrestftsvvw/0xe6yiidnisbwd91gjifmhuj1b3dwaug/399rn29/3+7uglypy2rfvwa6thda0n1qh12jq2+hapfkt8r/yo/kz+qv6p/q3+y0mra0xopau01jf+ayoux6w=
Estymatory regresji rangowej oparte na metodzie LASSO
Estymatory regresji rangowej oparte na metodzie LASSO Wojciech Rejchel UMK Toruń Wisła 2013 Z = (X, Y ), Z = (X, Y ) - niezależne wektory losowe o tym samym rozkładzie P X, X X R m, Y, Y R Z = (X, Y ),
Weryfikacja hipotez statystycznych
Weryfikacja hipotez statystycznych Przykład (wstępny). Producent twierdzi, że wadliwość produkcji wynosi 5%. My podejrzewamy, że rzeczywista wadliwość produkcji wynosi 15%. Pobieramy próbę stuelementową
Podstawowe rozkłady zmiennych losowych typu dyskretnego
Podstawowe rozkłady zmieych losowych typu dyskretego. Zmiea losowa X ma rozkład jedopuktowy, skocetroway w pukcie x 0 (ozaczay przez δ(x 0 )), jeżeli P (X = x 0 ) =. EX = x 0, V arx = 0. e itx0.. Zmiea
Wyk lad z Algebry Liniowej dla studentów WNE UW. Rok akademicki 2017/2018. Przyk lady zadań na ćwiczenia. 1. Które z cia
Wyk lad z Algebry Liniowej dla studentów WNE UW. Rok akademicki 2017/2018. Przyk lady zadań na ćwiczenia. 1. Które z cia gów: ( 1, 1, 1, 1), (2, 3, 1, 4), (4, 3, 2, 1), (4, 0, 3, 1) sa rozwia 2 zaniami
Tryb Matematyczny w L A TEX-u
Tryb Matematyczny w L A TEX-u Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2011-12-13 1 2 Tekst w trybie matematycznym Ściąga z symboli 3 Jak nie pisać pracy magisterskiej
Numeryczne aproksymacje prawdopodobieństwa ruiny
Numeryczne aproksymacje prawdopodobieństwa ruiny Krzysztof Burnecki Aleksander Weron Centrum Metod Stochastycznych im. Hugona Steinhausa Instytut Matematyki i Informatyki Politechnika Wrocławska www.im.pwr.wroc.pl/
Własności estymatorów regresji porządkowej z karą LASSO
Własności estymatorów regresji porządkowej z karą LASSO Uniwersytet Mikołaja Kopernika w Toruniu Uniwersytet Warszawski Badania sfinansowane ze środków Narodowego Centrum Nauki przyznanych w ramach finansowania
n=0 (n + r)a n x n+r 1 (n + r)(n + r 1)a n x n+r 2. Wykorzystując te obliczenia otrzymujemy, że lewa strona równania (1) jest równa
Równanie Bessela Będziemy rozważać następujące równanie Bessela x y xy x ν )y 0 ) gdzie ν 0 jest pewnym parametrem Rozwiązania równania ) nazywamy funkcjami Bessela rzędu ν Sprawdzamy, że x 0 jest regularnym
Prognozowalne kryterium całkowalności według A. N. Shiryaeva i A. S. Cherny ego Joanna Karłowska-Pik. Historia
1 Prognozowalne kryterium całkowalności według A. N. Shiryaeva i A. S. Cherny ego Joanna Karłowska-Pik Całka stochastyczna ( t ) H s dx s = H X. t Historia K. Itô (1944) konstrukcja całki stochastycznej
Różne rozkłady prawdopodobieństwa
Różne rozłady prawdopodobieństwa. Rozład dwupuntowy D(p). Zmienna losowa ξ ma rozład D(p), jeżeli P p {ξ = 0} = p oraz P p {ξ = } = p. Eξ = p D ξ = p( p). Rozład dwumianowy Bin(n, p). Zmienna losowa ξ
THERMODYNAMICS OF OXYGEN IN DILUTE LIQUID SILVER-TELLURIUM ALLOYS
AGH University of Science and Technology Faculty of Non-Ferrous Metals Laboratory of Physical Chemistry and Electrochemistry THERMODYNAMICS OF OXYGEN IN DILUTE LIQUID SILVER-TELLURIUM ALLOYS Justyna Nyk,
2017 R. Robert Gajewski: Mathcad Prime 4. Solution of examples Rozwiązania przykładów
07 R. Robert Gajewski: Mathcad Prime 4 0. Calculate numerically and present results in different formats and precision. 0. Oblicz numerycznie i przedstaw wyniki w różnych formatach i z różną precyzją.
PROJEKT BELKI PODSUWNICOWEJ I SŁUPA W STALOWEJ HALI PRZEMYSŁOWEJ.
PROJEKT BELKI PODSUWNICOWEJ I SŁUPA W STALOWEJ HALI PRZEMYSŁOWEJ. CZĘŚĆ - BELKA PODSUWNICOWA. Założenia. Hala jednonawowa o układzie raowy : - rozstaw ra : L B 6.5 - ilość pół : n 8 - długość hali : L
Komputerowa analiza zagadnień różniczkowych 6. Metoda diagramowa. Obszary stabilności. P. F. Góra
Komputerowa analiza zagadnień różniczkowych 6. Metoda diagramowa. Obszary stabilności. P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2013 Metoda diagramowa Ręczne wyprowadzanie równan wiaż acych współczynniki
Funkcje charakterystyczne zmiennych losowych, linie regresji 1-go i 2-go rodzaju
Funkcje charakterystyczne zmiennych losowych, linie regresji -go i 2-go rodzaju Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Zadania z Rachunku Prawdopodobieństwa III - 1
Zadania z Rachunku Prawdopodobieństwa III - 1 Funkcją tworzącą momenty (transformatą Laplace a) zmiennej losowej X nazywamy funkcję M X (t) := Ee tx, t R. 1. Oblicz funkcję tworzącą momenty zmiennych o
Machine Learning for Data Science (CS4786) Lecture 11. Spectral Embedding + Clustering
Machine Learning for Data Science (CS4786) Lecture 11 Spectral Embedding + Clustering MOTIVATING EXAMPLE What can you say from this network? MOTIVATING EXAMPLE How about now? THOUGHT EXPERIMENT For each
y = The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Explain your answer, write in complete sentences.
The Chain Rule Show all work. No calculator unless otherwise stated. If asked to Eplain your answer, write in complete sentences. 1. Find the derivative of the functions y 7 (b) (a) ( ) y t 1 + t 1 (c)
Elektrostatyka Potencjały I linie sił pola. Symetria cylindryczna Odwzorowania konforemne
Elektrostatyka Potencjały I linie sił pola Symetria cylindryczna Odwzorowania konforemne Metoda rozdzielania zmiennych Dwa wymiary Laplasjan. Symetria cylindryczna. 1 r r V (r r )+ 1 V r ϕ = 0; V = R(
(Slant delay mesoscale functions)
M. Figurski, M. Gałuszkiewicz, P. Kamiński, K. Kroszczyński Mesoscale mapping functions (Slant delay mesoscale functions) M. Figurski, M. Gałuszkiewicz, P. Kamiński, K. Kroszczyński We present a prototype
CAŁKI NIEOZNACZONE C R}.
CAŁKI NIEOZNACZONE Definicja 1 Funkcja F jest funkcją pierwotną funkcji f na przedziale I, jeżeli F (x) = f(x) dla każdego x I. Np. funkcjami pierwotnymi funkcji f(x) = sin x na R są cos x, cos x+1, cos
Identyfikacja cząstek
Określenie masy i ładunku cząstek Pomiar prędkości przy znanym pędzie e/ µ/ π/ K/ p czas przelotu (TOF) straty na jonizację de/dx Promieniowanie Czerenkowa (C) Promieniowanie przejścia (TR) Różnice w charakterze
Kiedy przebiegają reakcje?
Kiedy przebiegają reakcje? Thermodynamics lets us predict whether a process will occur but gives no information about the amount of time required for the process. CH 4(g) + 2O 2(g) substraty 2(g) egzotermiczna
THE RATE OF GW CAPTURE OF STELLAR-MASS BHS IN NUCLEAR STAR CLUSTERS. Alexander Rasskazov & Bence Kocsis Eotvos University
THE RATE OF GW CAPTURE OF STELLAR-MASS BHS IN NUCLEAR STAR CLUSTERS Alexander Rasskazov & Bence Kocsis Eotvos University Merger rate density of events with e>0.1 in the LIGO band (>10 Hz), Gpc -3 yr -1
Obliczeniowa nośność przekroju zbudowanego wyłącznie z efektywnych części pasów. Wartość przybliżona = 0,644. Rys. 25. Obwiednia momentów zginających
Obliczeniowa nośność przekroju zbudowanego wyłącznie z efektywnych części pasów. Wartość przybliżona f y M f,rd b f t f (h γ w + t f ) M0 Interakcyjne warunki nośności η 1 M Ed,385 km 00 mm 16 mm 355 1,0
5 Przegląd najważniejszych rozkładów
5 Przegląd najważniejszych rozkładów 5. Rozkład Bernoulliego W niezmieniających się warunkach wykonujemy n razy pewne doświadczenie. W wyniku każdego doświadczenia może nastąpić zdarzenie A lub A. Zakładamy,
Subdyfuzja w układach membranowych
Subdyfuzja w układach membranowych Tadeusz Kosztołowicz Institute of Physics, Jan Kochanowski University, ul. Świȩtokrzyska 15, 25-406 Kielce, Poland, tadeusz.kosztolowicz@ujk.edu.pl Między teorią a zastosowaniami
Układ okresowy. Przewidywania teorii kwantowej
Przewidywania teorii kwantowej Chemia kwantowa - podsumowanie Cząstka w pudle Atom wodoru Równanie Schroedingera H ˆ = ˆ T e Hˆ = Tˆ e + Vˆ e j Chemia kwantowa - podsumowanie rozwiązanie Cząstka w pudle
Funkcje Analityczne, ćwiczenia i prace domowe
Funkcje Analityczne, ćwiczenia i prace domowe P. Wojtaszczyk 29 maja 22 Ten plik będzie progresywnie modyfikowany. Będzie on zawierał. Zadanie omówione na ćwiczeniach 2. Zadania ćwiczebne do samodzielnego
Symmetry and Geometry of Generalized Higgs Sectors
Symmetry and Geometry of Generalized Higgs Sectors Ryo Nagai Tohoku University in collaboration with M. Tanabashi (Nagoya U.), Y. Uchida (Nagoya U.), and K. Tsumura (Kyoto U.) PPP2018 @ YITP, Aug. 6-10,
Rozpoznawanie obrazów
Rozpoznawanie obrazów Ćwiczenia lista zadań nr 5 autorzy: A. Gonczarek, J.M. Tomczak Przykładowe problemy Klasyfikacja binarna Dla obrazu x zaproponowano dwie cechy φ(x) = (φ 1 (x) φ 2 (x)) T. Na obrazie
Lecture 18 Review for Exam 1
Spring, 2019 ME 323 Mechanics of Materials Lecture 18 Review for Exam 1 Reading assignment: HW1-HW5 News: Ready for the exam? Instructor: Prof. Marcial Gonzalez Announcements Exam 1 - Wednesday February
Jacek Jakubowski, Rafał Sztencel Rachunek prawdopodobieństwa dla (prawie) każdego (wyd. I) Ostatnia aktualizacja: 6 lutego 2004
ERRATA Jacek Jakubowski, Rafał Sztencel Rachunek prawdopodobieństwa dla (prawie) każdego (wyd. I) Ostatnia aktualizacja: 6 lutego 2004 Rozdział 20 2 przykładzie 4 przykładzie 5 Rozdział 2 48 4 P (B 2 B
Programowanie dynamiczne i modele rekurencyjne w ekonomii Wykład 2
Programowanie dynamiczne i modele rekurencyjne w ekonomii Wykład Michał Ramsza października Streszczenie Wykład drugi bazuje głównie na [, roz 6 5, [, roz oraz [ Materiał obejmuje zagadnienie zwiazane
BIOPHYSICS. Politechnika Łódzka, ul. Żeromskiego 116, Łódź, tel. (042)
BIOPHYSICS Prezentacja multimedialna współfinansowana przez Unię Europejską w ramach Europejskiego Funduszu Społecznego w projekcie pt. Innowacyjna dydaktyka bez ograniczeń - zintegrowany rozwój Politechniki
Proposal of thesis topic for mgr in. (MSE) programme in Telecommunications and Computer Science
Proposal of thesis topic for mgr in (MSE) programme 1 Topic: Monte Carlo Method used for a prognosis of a selected technological process 2 Supervisor: Dr in Małgorzata Langer 3 Auxiliary supervisor: 4
Y = α 1 Z α k Z k + e. (1) (k 1)[ktrA2 (tra) 2 ] (4) d = 1 k. (por. np. Kolupa, 2006). Wówczas jak to wynika ze wzorów (2) i (3) mamy:
![Y = α 1 Z α k Z k + e. (1) (k 1)[ktrA2 (tra) 2 ] (4) d = 1 k. (por. np. Kolupa, 2006). Wówczas jak to wynika ze wzorów (2) i (3) mamy:](/thumbs/92/110279918.jpg "Y = α 1 Z α k Z k + e. (1) (k 1)[ktrA2 (tra) 2 ] (4) d = 1 k. (por. np. Kolupa, 2006). Wówczas jak to wynika ze wzorów (2) i (3) mamy:")
PRZEGLĄD STATYSTYCZNY R. LVIII ZESZYT 3-4 2011 MICHAŁ KOLUPA, JOANNA PLEBANIAK KILKA UWAG O WARTOŚCIACH WŁASNYCH MACIERZY KORELACJI W niniejszej pracy, w nawiązaniu do pracy Kolupa, 2006, podajemy konstrukcję
The Lorenz System and Chaos in Nonlinear DEs
The Lorenz System and Chaos in Nonlinear DEs April 30, 2019 Math 333 p. 71 in Chaos: Making a New Science by James Gleick Adding a dimension adds new possible layers of complexity in the phase space of
Dupin cyclides osculating surfaces
Paweł Walczak, Uniwersytet Łódzki, Dijon, 25 stycznia 2012 Colaborators: Remi Langevin (UdeB), Adam Bartoszek, Szymon Walczak (UŁ) What is extrinsic conformal geometry? Conformal transformations = transformations
(4) (b) m. (c) (d) sin α cos α = sin 2 k = sin k sin k. cos 2 m = cos m cos m. (g) (e)(f) sin 2 x + cos 2 x = 1. (h) (f) (i)
(3) (e) sin( θ) sin θ cos( θ) cos θ sin(θ + π/) cos θ cos(θ + π/) sin θ sin(θ π/) cos θ cos(θ π/) sin θ sin(θ ± π) sin θ cos(θ ± π) cos θ sin(θ ± π) sin θ cos(θ ± π) cos θ (f) cos x cos y (g) sin x sin
Mody sprzężone plazmon-fonon w silnych polach magnetycznych
Mody sprzężone plazmon-fonon w silnych polach magnetycznych Mody sprzężone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga,, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Bładzenie przypadkowe i lokalizacja
Bładzenie przypadkowe i lokalizacja Zdzisław Burda Jarosław Duda, Jean-Marc Luck, Bartłomiej Wacław Seminarium Wydziałowe WFiIS AGH, 07/11/2014 Plan referatu Wprowadzenie Zwykłe bładzenie przypadkowe (GRW)
1.1 Przegląd wybranych równań i modeli fizycznych. , u x1 x 2
Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
Elektrodynamika. Część 8. Fale elektromagnetyczne. Ryszard Tanaś. Zakład Optyki Nieliniowej, UAM
Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/\~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................