Elektroniczna aparatura medyczna VII Lasery i technika światłowodowa
|
|
|
- Błażej Feliks Laskowski
- 6 lat temu
- Przeglądów:
Transkrypt
1 lekronina aparaura medna SMSTR V Cłowiek- najlepsa inwesja Projek współfinansowan pre Unię uropejską w ramah uropejskiego Fundusu Społenego lekronina aparaura medna VII Laser i ehnika świałowodowa Kompabilność elekromagnena Bepieeńswo pajena
2 Laser i ehnika świałowodowa w mednie Laser i ehnika świałowodowa w mednie Zasosowania - diagnoska obraowanie pomiar perfuji - erapia bardo seroki akres asosowań - inne świałowod jako elemen orów pomiarowh słabh sgnałów - świałowod jako elemen iolajne Lieraura. K.Paorski M.Kujawińska L.Sałbu Inerferomeria laserowa OWPW 005. Fiedor P e al. red) Zars klininh asosowań laserów Ankar 995
3 Laser w mednie Promieniowanie laserowe Zasada diałania lasera dosarenie energii ak b nasąpiło prejśie aomu na wżs poiom energen 0 >) aki san san wbudon jes nierwał nasępuje powró do sanu 0 i emisja foonu emisja sponanina. Jeśli do aomu w sanie wbudenia dore kolejn kwan energii o warośi równej różni poiomów wmusi prejśie do niżsego poiomu energenego ora emisję kwanów promieniowania o ej samej faie długośi fali polaraji i kierunku propagaji emisja wmusona podsawa diałania lasera. Laser w mednie Promieniowanie laserowe Warunek niebędn dla uskania emisji wmusonej inwersja obsadeń poiomów energenh j. więej aomów ośrodka powinno naleźć się na poiomie. Wprowadenie do akiego ośrodka promieniowania świała) prniesie siln wros emisji ego ośrodka - w porównaniu e sanem be inwersji obsadeń. Inwersję obsadeń uskuje się pre doprowadenie do ośrodka energii np. pre pompowanie opne świało lamp łukowej błskowej) prepłw prądu pre łąe p-n lub ga.
4 Laser w mednie Promieniowanie laserowe Jeśli w ośrodku nasąpi inwersja obsadeń wówas promieniowanie pohodąe emisji sponaninej spowoduje emisję wmusoną kóra będie narasać lawinowo dla fali świała rohodąej się wdłuż ośrodka. Niewkonalne ehninie rowiąanie bardo długim ośrodkiem asąpiono ssemem wieriadeł kórh jedno odbija nieałkowiie ęść energii prehodi pre nie i sanowi wiąkę laserową. Zjawisko o nasąpi pod warunkiem apewnienia warunku fa fala sojąa w reonaore ałkowia liba połówek fali międ wieriadłami) ora ampliud wmonienie promieniowania w ośrodku reonaora prewżsa sra akże wiąka whodąa lasera jes roumiana jako sraa). Laser w mednie Promieniowanie laserowe Właśiwośi promieniowania laserowego - monohromaność - bieżność > wsoka gęsość mo do 0 W/m ) - spójność - sał wiąek fa fali w prekroju wiąki i międ dwoma prekrojami
5 Laser w mednie Oddiałwanie promieniowania lasera na kanki Oddiałwanie wiąki świała lasera na kanki Zależne od rodaju kanki gęsośi mo promieniowania asu oddiałwania i długośi fali a akże rodaju kanki miękka warda). fek: - fooermine - foojoniajne - foohemine - foooksne - foosmulajne.
6 Laser w mednie Oddiałwanie promieniowania lasera na kanki fek fooermine: absorpja promieniowania nagrewanie denauraja koagulaja odparowanie i usunięie. Zakres skuków ależ od dosaronej energii asu dosarania i skuenośi odprowadania iepła pre kankę. Podgranie do 40 C nie powoduje nieodwraalnh mi an powżej 45 C anają się akie mian powżej C koagulaja kanki pow żej 90 C parowanie wod powżej 00 C wrenie rorwanie kanki dalej węglenie. Laser w mednie Oddiałwanie promieniowania lasera na kanki fek foojoniajne: wnik podawania krókorwałh impulsów promieniowania o dużej gęsośi mo ponad 00MW/m) powsanie plam silnie absorbująej promieniowanie laserowe ekspansja plam powsanie fali udereniowej rorwanie kanki. Wkorswane do mikrohirurgii predniej ęśi oka robijania łogów nerkowh i żółiowh i aorów w naniah krwionośnh.
7 Laser w mednie Oddiałwanie promieniowania lasera na kanki fek foohemine/foooksne: wnik selekwnej absorpji promieniowania pre kanki hromofor). DNA absorbuje nadfiole mian hemine. Fooablaja na imno krókorwałe impuls promieniowania laserowego UV o dużej gęsośi mo mogą rorwać wiąania hemine be nagrewania kanki hirurgia rogówki). Laser w mednie Oddiałwanie promieniowania lasera na kanki fek foosmulajne: absorpja promieniowania laserowego o małej mo. Prpusenia promieniowanie laserowe powoduje smulaję ransporu elekronów i angiogene. Zasosowania - erapia bólu uraów
8 Laser w mednie Oddiałwanie promieniowania lasera na kanki Laser w mednie Oddiałwanie promieniowania lasera na kanki Zależność progowej warośi gęsośi energii powodująej erminą eroję kanki od długośi fali lasera ) i współnnik absorpji wod )
9 Laser w mednie Oddiałwanie promieniowania lasera na kanki Uproson model wrosu emperaur podas oddiał- wania erminego lasera ależn od długośi fali i mo promieniowania ora kanki Shema kraeru wworonego pre laser. srefa węglona i koagulaji - mian nieodwraalne; srefa obręku mian na ogół odwraalne mikropęhere wnikłe wrenia wod) Laser w mednie Oddiałwanie promieniowania lasera na kanki Rodaje emisji laserowej Długorwałe diałanie promieniowania laserowego powżej kilku ms) prewodenie iepła pre kanki powięksa obsar eroji i marwi. Wielokrone oddiałwanie krókih impulsów promieniowania o małej ęsoliwośi powarania rośnie głębokość kraeru pole eroji i marwi nie ulega nanemu powiękseniu.
10 Obraowanie opne Opna omografia koherenjna OCT Inerferomeria pomiar/obraowanie wkorsująe nakładanie się inerferenję) dwóh lub więej fal świała kórego wnik ależ od relaji faowh międ mi falami. Fala elekromagnena A - ampliuda ω - pulsaja φ - faa Dwie fale i Suma fal ))] )ep[ ) j A φ ω ))] ) ep[ ) j A φ ω ))] )ep[ ) j A φ ω i i ) ) Inerferenja wnik koherennej superpoji fal Naężenie świała dla sum fal inenswność - warość średniokwadraowa sum fal * onaa wielkość sprężoną) : Dla dwóh fal o h samh pulsajah i równoległh polarajah rokład inenswnośi ma posać: I I - inenswność fal i φ - różnia fa h fal Obraowanie opne Opna omografia koherenjna OCT ) I + * * * * ) I I I )] os[ ) I I I I I φ + + ))] ) ep[ ) j A φ ω ))] )ep[ ) j A φ ω
11 Obraowanie opne Opna omografia koherenjna OCT Inenswność I ) I + I + II os[ φ )] Obra prążkow inenswnośi Maksima inerferogramu wsępują dla różni fa będąej wielokronośią π lub różni długośi dróg opnh równej wielokronośi λ. γ - konras inenswnośi I γ ) I ma ma ) I ) + I min min ) ) Obraowanie opne Opna omografia koherenjna OCT Inerferomeria ehnika pomiarowa wkorsująa inerferenję wiąek świała w najprossm prpadku dwóh) Shema blokow inerferomeru
12 Obraowanie opne Opna omografia koherenjna OCT Paramer źródła laserowego Droga koherenji l : dioda laserowa 6m świało białe.um laser He-Ne 300m as koherenji: l τ τ f f - serokość widmowa wnaana rokładu widmowej gęsośi mo promieniowania WGMf): f WGM f ) df ) 0 WGM f ) df 0 Obraowanie opne Opna omografia koherenjna OCT Zakres jednonanego inerferomernego pomiaru różni dróg fa) ogranion jes do ęśi długośi fali λ /4). Zakres en można roserć sosują dwie długośi fali promieniowania. Wed w. ekwiwalenna długośi fali wnosi λ ekw λ λ / λ - λ. l f Innm skueniejsm rowiąaniem jes śledenie maksimum koherenji asowej korelaji) międ wiąkami predmioową i odniesienia. Wmaga o asosowania źródła o niskiej koherenji asowej li o serokim widmie emiowanej wiąki np. diod laserowej. Wed długość koherenji jes l mała i sgnał inerferenjn ma posać jak na rsunku.
13 Obraowanie opne Opna omografia koherenjna OCT l f Długość koherenji jes mała i sgnał inerferenjn ma posać jak obok. Konras wsokie ampliud) wsępują lko w obsare koherenji. Rodielość wdłużną określa wię długość koherenji pasmo promieniowania) w akim akresie można deekować odbie lub roprosone pre badan obiek promieniowanie skanują głębokość popre mianę położenia wieriadła odniesienia a skanowanie laeralne apewnia inne wieriadło pewna analogia do ulrasonografii). Obraowanie wmaga emisji bardo krókih impulsów świała fs). Obraowanie opne Opna omografia koherenjna OCT Konras wsokie ampliud koherenji) wsępują lko w obsare koherenji. Rodielość wdłużną określa wię długość koherenji pasmo promieniowania) w akim akresie można deekować odbie lub roprosone pre badan obiek promieniowanie skanują głębokość popre mianę położenia wieriadła odniesienia a skanowanie laeralne apewnia odpowiednie wieriadło pewna analogia do ulrasonografii). Obraowanie wmaga emisji bardo krókih impulsów świała fs).
14 Obraowanie opne Opna omografia koherenjna OCT Inerferomerne OCT) obra śian pęhera moowego. pielium w prpadku fijologinm jes nanie iemniejse od kanki łąnej niż w prpadku wsępowania sanu apalnego biała kreska - odinek mm). A.Johansson K.Kromer R.Sroka H. Sepp Clinial opial diagnosis saus and perspeives Medial Laser Appliaion 3 008)55 74 Laser i ehnika świałowodowa w mednie Świałowod w ehnie pomiarowej Prawo Snelliusa n sin Θ n sin Θ Jeśli ośrodek II jes opnie mniej gęs od ośrodka I j. n <n może dojść do ałkowiego odbiia fali świała na grani ośrodków. Ką dla kórego o jawisko ahodi nawan kąem graninm. sin Θ n gr n To właśnie jawisko wkorswane jes w ehnie świałowodowej.
15 Laser i ehnika świałowodowa w mednie Świałowod w ehnie pomiarowej Gęss opnie rdeń ooon jes mniej gęsą powłoką. Sożek akepaji sożek uworon pre krn ka Θa dla kórego promień może wniknąć do świałowodu powiera. n 3 sin Θa n sin Θ b Laser i ehnika świałowodowa w mednie Świałowod w ehnie pomiarowej W obrębie sożka akepaji możliwe są różne warośi kąa Θ o onaa że promienie może mieć różnej długośi drogi w świałowodie. Mówim wed o różnh modah. Drogi modów mogą nanie się różnić o prowadi do dspersji.
16 Laser i ehnika świałowodowa w mednie Świałowod w ehnie pomiarowej dspersja Sgnał wejśiow Skuek dspersji I Skuek dspersji II nakładanie się impulsów świała Laser i ehnika świałowodowa w mednie Świałowod w ehnie pomiarowej Wnikająe uskodeń powłoki Sra Wnikająe odbić ahodąh na połąeniah apewnienie dopasowania
17 Laser i ehnika świałowodowa w mednie Dioda laserowa i jej paramer prkład) Paramer Prąd progow Wjśiowa mo opna Nahlenie h-ki prejśiowej Długość fali Robieżność wiąki podłużna) 50mA p) 0mW min) 0.5mW/mA p) 785nm p) deg p) Robieżność wiąki poprena) 30 deg p) Laser i ehnika świałowodowa w mednie Dioda laserowa i jej paramer prkład)
18 Laser i ehnika świałowodowa w mednie Dioda laserowa Świałowod i diod laserowe w ehnie pomiarowej
19 Świałowod i diod laserowe w ehnie pomiarowej Świałowod i diod laserowe w ehnie pomiarowej Pomiar słuhowh poenjałów wwołanh sanu usalonego Sanowisko do badań - predwmania HS4 i wmania DB4 firm Tuker-Davis Tehnologies uwaga połąenie świałowodowe HS4 i DB4!) - słuhawki audiomerne TDH-39 - kompuer karą dźwiękową
Elektroniczna aparatura medyczna VII
 06-- lekronina aparaura medna SMSTR V Cłowiek- najlepsa inwesja Projek współfinansowan pre Unię uropejską w ramah uropejskiego Fundusu Społenego lekronina aparaura medna V Laser i ehnika świałowodowa 06--
06-- lekronina aparaura medna SMSTR V Cłowiek- najlepsa inwesja Projek współfinansowan pre Unię uropejską w ramah uropejskiego Fundusu Społenego lekronina aparaura medna V Laser i ehnika świałowodowa 06--
Elektroniczna aparatura medyczna VII Lasery i technika światłowodowa
 Elektroniczna aparatura medczna SEMESTR V Człowiek- najlepsza inwestcja Projekt współfinansowan przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Elektroniczna aparatura medczna V Laser
Elektroniczna aparatura medczna SEMESTR V Człowiek- najlepsza inwestcja Projekt współfinansowan przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Elektroniczna aparatura medczna V Laser
ρ - gęstość ładunku j - gęstość prądu FALE ELEKTROMAGNETYCZNE W PRÓŻNI: Równania Maxwella: -przenikalność elektryczna próżni=8,8542x10-12 F/m
 -- G:\AA_Wklad \FIN\DOC\em.do Drgania i fale III rok Fiki C FAL LKTROMAGNTYCZN W PRÓŻNI: Równania Mawella: di ρ ε ρ di j ρ - gęsość ładunku j - gęsość prądu ro di ro j ε ε -prenikalność elekrna próżni8854
-- G:\AA_Wklad \FIN\DOC\em.do Drgania i fale III rok Fiki C FAL LKTROMAGNTYCZN W PRÓŻNI: Równania Mawella: di ρ ε ρ di j ρ - gęsość ładunku j - gęsość prądu ro di ro j ε ε -prenikalność elekrna próżni8854
G:\WYKLAD IIIBC 2001\FIN2001\Ruch falowy2001.doc. Drgania i fale II rok Fizyki BC
 3-- G:\WYKLAD IIIBC \FIN\Ruh falow.do Drgania i fale II ro Fii BC Ruh falow: Fala rohodąe się w presreni aburenie lub odsałenie (pole). - impuls lub drgania. Jeśli rohodi się prędośią o po asie : ( r)
3-- G:\WYKLAD IIIBC \FIN\Ruh falow.do Drgania i fale II ro Fii BC Ruh falow: Fala rohodąe się w presreni aburenie lub odsałenie (pole). - impuls lub drgania. Jeśli rohodi się prędośią o po asie : ( r)
ψ przedstawia zależność
 Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Fale biegnące. y t=0 vt. y = f(x), t = 0 y = f(x - vt), t ogólne równanie fali biegnącej w prawo
 ale (mechaniczne) ala - rozchodzenie się się zaburzenia (w maerii) nie dzięki ruchowi posępowemu samej maerii ale dzięki oddziałwaniu (sprężsemu) Rodzaje i cech fal Rodzaj zaburzenia mechaniczne elekromagneczne
ale (mechaniczne) ala - rozchodzenie się się zaburzenia (w maerii) nie dzięki ruchowi posępowemu samej maerii ale dzięki oddziałwaniu (sprężsemu) Rodzaje i cech fal Rodzaj zaburzenia mechaniczne elekromagneczne
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 7 wykład: Piotr Fita pokazy: Jacek Szczytko ćwiczenia: Aneta Drabińska, Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 7 wykład: Piotr Fita pokazy: Jacek Szczytko ćwiczenia: Aneta Drabińska, Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet
Powierzchnie stopnia drugiego
 Algebra WYKŁAD 3 Powierchnie sopnia drugiego Deinicja Powierchnią sopnia drugiego kwadrką nawam biór punków presreni rójwmiarowej, spełniającch równanie A B C D E F G H I K gdie A, B,, K są sałmi i prnajmniej
Algebra WYKŁAD 3 Powierchnie sopnia drugiego Deinicja Powierchnią sopnia drugiego kwadrką nawam biór punków presreni rójwmiarowej, spełniającch równanie A B C D E F G H I K gdie A, B,, K są sałmi i prnajmniej
Zestaw zadań 12: Przekształcenia liniowe. Macierze przekształceń liniowych. z z + 2 2x + y. x y z. x y + 2t 2x + 3y + 5z t x + z t
 Zesaw adań : Preksałcenia liniowe. Maciere preksałceń liniowch () Kóre podanch niżej preksałceń ϕ : K n K m są preksałceniami liniowmi: a) n = m = 3, ϕ( + ) = +, b) n = m = 3, ϕ( ) = +, 3 + + + +, d) n
Zesaw adań : Preksałcenia liniowe. Maciere preksałceń liniowch () Kóre podanch niżej preksałceń ϕ : K n K m są preksałceniami liniowmi: a) n = m = 3, ϕ( + ) = +, b) n = m = 3, ϕ( ) = +, 3 + + + +, d) n
Zestaw zadań 12: Przekształcenia liniowe. z z + 2 2x + y. x y z. x y + 2t 2x + 3y + 5z t x + z t. x y + 2t 2x 3y + 5z t x z t
 Zesaw adań : Preksałcenia liniowe () Kóre podanch niżej preksałceń ϕ : K n K m są preksałceniami liniowmi: a) n = m = 3, ϕ( + +, b) n = m = 3, ϕ( +, 3 + + + +, d) n = m = 3, ϕ( +, c) n = m = 3, ϕ( e) n
Zesaw adań : Preksałcenia liniowe () Kóre podanch niżej preksałceń ϕ : K n K m są preksałceniami liniowmi: a) n = m = 3, ϕ( + +, b) n = m = 3, ϕ( +, 3 + + + +, d) n = m = 3, ϕ( +, c) n = m = 3, ϕ( e) n
MECHANIKA RELATYWISTYCZNA TRANFORMACJA LORENTZA
 Wdiał EAIiE Kierunek: ELEKTRONIKA I TELEKOMUNIKACJA Predmio: Fika II MECHANIKA RELATYWISTYCZNA TRANFORMACJA LORENTZA 0/0, lao SZCZEGÓLNA TEORIA WZGLĘDNOŚCI Fika relawisna jes wiąana pomiarem miejsa i asu
Wdiał EAIiE Kierunek: ELEKTRONIKA I TELEKOMUNIKACJA Predmio: Fika II MECHANIKA RELATYWISTYCZNA TRANFORMACJA LORENTZA 0/0, lao SZCZEGÓLNA TEORIA WZGLĘDNOŚCI Fika relawisna jes wiąana pomiarem miejsa i asu
G:\AA_Wyklad 2000\FIN\DOC\Fale wodnem.doc. Drgania i fale III rok Fizyki BC. Model: - długi kanał o prostokątnym przekroju i głębokości h,
 13-1-00 G:\AA_Wklad 000\FIN\DOC\Fale Fale wodne: Drgania i fale III rok Fiki BC Model: - długi kanał o prostokątnm prekroju i głębokości h, - ruch fali wdłuż, nieależn od x, wchlenia wdłuż, - woda nieściśliwa
13-1-00 G:\AA_Wklad 000\FIN\DOC\Fale Fale wodne: Drgania i fale III rok Fiki BC Model: - długi kanał o prostokątnm prekroju i głębokości h, - ruch fali wdłuż, nieależn od x, wchlenia wdłuż, - woda nieściśliwa
WSTĘP DO ELEKTRONIKI
 WSTĘP DO ELEKTRONIKI Część I Napięcie, naężenie i moc prądu elekrycznego Sygnały elekryczne i ich klasyfikacja Rodzaje układów elekronicznych Janusz Brzychczyk IF UJ Elekronika Dziedzina nauki i echniki
WSTĘP DO ELEKTRONIKI Część I Napięcie, naężenie i moc prądu elekrycznego Sygnały elekryczne i ich klasyfikacja Rodzaje układów elekronicznych Janusz Brzychczyk IF UJ Elekronika Dziedzina nauki i echniki
Technika laserowa, otrzymywanie krótkich impulsów Praca impulsowa
 Praca impulsowa Impuls trwa określony czas i jest powtarzany z pewną częstotliwością; moc w pracy impulsowej znacznie wyższa niż w pracy ciągłej (pomiędzy impulsami może magazynować się energia) Ablacja
Praca impulsowa Impuls trwa określony czas i jest powtarzany z pewną częstotliwością; moc w pracy impulsowej znacznie wyższa niż w pracy ciągłej (pomiędzy impulsami może magazynować się energia) Ablacja
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 8 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2015/16
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 8 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2015/16
A21, B21, B12 współczynniki wprowadzone przez Einsteina w 1917 r.
 Absorpcja i emisja fotonu przez atom, który ma dwa poziomy energii hν=e2-e1 h=6,63 10-34 J s Emisja spontaniczna A21 prawdopodobieństwo emisji fotonu przez atom w stanie E2 w ciągu sekundy Absorpcja (wymuszona)
Absorpcja i emisja fotonu przez atom, który ma dwa poziomy energii hν=e2-e1 h=6,63 10-34 J s Emisja spontaniczna A21 prawdopodobieństwo emisji fotonu przez atom w stanie E2 w ciągu sekundy Absorpcja (wymuszona)
Energia w ruchu harmonicznym
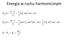 Energia w ruchu haroniczn cos 1 kx x k E p 1 1 kx x v E k k p kx E E E Fale przkład Fala echaniczna poprzeczna Fala echaniczna podłużna Fala echaniczna akusczna Fala elekroagneczna np. radiowa świało Fale:
Energia w ruchu haroniczn cos 1 kx x k E p 1 1 kx x v E k k p kx E E E Fale przkład Fala echaniczna poprzeczna Fala echaniczna podłużna Fala echaniczna akusczna Fala elekroagneczna np. radiowa świało Fale:
i j k Oprac. W. Salejda, L. Bujkiewicz, G.Harań, K. Kluczyk, M. Mulak, J. Szatkowski. Wrocław, 1 października 2015
 WM-E; kier. MBM, lisa za. nr. p. (z kary przemiou): Rozwiązywanie zaań z zakresu: ransformacji ukłaów współrzęnych, rachunku wekorowego i różniczkowo-całkowego o kursu Fizyka.6, r. ak. 05/6; po koniec
WM-E; kier. MBM, lisa za. nr. p. (z kary przemiou): Rozwiązywanie zaań z zakresu: ransformacji ukłaów współrzęnych, rachunku wekorowego i różniczkowo-całkowego o kursu Fizyka.6, r. ak. 05/6; po koniec
Fizyka dla Informatyki Stosowanej
 Fizyka dla Informayki Sosowanej Jacek Golak Semesr zimowy 018/019 Wykład nr 14 Równania Mawella w próżni E 0 B 0 B E B j 0 0 E Uwaga: To są równania w układzie SI! 8.85419 0 4 π 0 10 7 10 T m A 1 C N m
Fizyka dla Informayki Sosowanej Jacek Golak Semesr zimowy 018/019 Wykład nr 14 Równania Mawella w próżni E 0 B 0 B E B j 0 0 E Uwaga: To są równania w układzie SI! 8.85419 0 4 π 0 10 7 10 T m A 1 C N m
Związek między ruchem harmonicznym a ruchem jednostajnym po okręgu
 Związek międz ruchem harmonicznm a ruchem jednosajnm po okręgu Rozważm rzu Q i R punku P na osie i : Q cos v r R sin R Q P δ Q cos ( δ ) R sin ( δ ) Jeżeli punk P porusza się ruchem jednosajnm po okręgu,
Związek międz ruchem harmonicznm a ruchem jednosajnm po okręgu Rozważm rzu Q i R punku P na osie i : Q cos v r R sin R Q P δ Q cos ( δ ) R sin ( δ ) Jeżeli punk P porusza się ruchem jednosajnm po okręgu,
Belki złożone i zespolone
 Belki łożone i espolone efinicja belki łożonej siła rowarswiająca projekowanie połąceń prkła obliceń efinicja belki espolonej ałożenia echnicnej eorii ginania rokła naprężeń normalnch prkła obliceń Belki
Belki łożone i espolone efinicja belki łożonej siła rowarswiająca projekowanie połąceń prkła obliceń efinicja belki espolonej ałożenia echnicnej eorii ginania rokła naprężeń normalnch prkła obliceń Belki
LASERY I ICH ZASTOSOWANIE W MEDYCYNIE
 LASERY I ICH ZASTOSOWANIE W MEDYCYNIE Laboratorium Instrukcja do ćwiczenia nr 4 Temat: Modulacja światła laserowego: efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą
LASERY I ICH ZASTOSOWANIE W MEDYCYNIE Laboratorium Instrukcja do ćwiczenia nr 4 Temat: Modulacja światła laserowego: efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą
WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA
 DROGI i CYKLE HAMILTONA w grfh kierownh Dl grfu kierownego D = ( V, A ) rogą wierhołk 0 V o V nwm iąg (npremienn) wierhołków i łuków grfu: ( 0,,,,...,,, ), pełniją wrunek i = ( i, i ) l i =,..., rogę nwm
DROGI i CYKLE HAMILTONA w grfh kierownh Dl grfu kierownego D = ( V, A ) rogą wierhołk 0 V o V nwm iąg (npremienn) wierhołków i łuków grfu: ( 0,,,,...,,, ), pełniją wrunek i = ( i, i ) l i =,..., rogę nwm
Studia magisterskie ENERGETYKA. Jan A. Szantyr. Wybrane zagadnienia z mechaniki płynów. Ćwiczenia 6. Wyznaczanie przepływu przez rurociągi II
 Sia maiserskie ENERGETYKA Jan A. Sanyr Wyrane aanienia meaniki płynów Ćwienia 6 Wynaanie prepływ pre rroiąi II Prykła W owarym iornik najje się prosokąny owór o serokośi i wysokośi, amykany aswą. Olełość
Sia maiserskie ENERGETYKA Jan A. Sanyr Wyrane aanienia meaniki płynów Ćwienia 6 Wynaanie prepływ pre rroiąi II Prykła W owarym iornik najje się prosokąny owór o serokośi i wysokośi, amykany aswą. Olełość
Metody Optyczne w Technice. Wykład 5 Interferometria laserowa
 Metody Optyczne w Technice Wykład 5 nterferometria laserowa Promieniowanie laserowe Wiązka monochromatyczna Duża koherencja przestrzenna i czasowa Niewielka rozbieżność wiązki Duża moc Największa możliwa
Metody Optyczne w Technice Wykład 5 nterferometria laserowa Promieniowanie laserowe Wiązka monochromatyczna Duża koherencja przestrzenna i czasowa Niewielka rozbieżność wiązki Duża moc Największa możliwa
Wyprowadzenie ogólnej postaci kinematyki z uniwersalnym układem odniesienia
 Wprowadenie ogólnej posai kinemaki uniwersalnm układem odniesienia Karol Sosek Poliehnika Resowska Kaedra Termodnamiki i Mehaniki Płnów al. Powsańów Warsaw, 35-959 Resów, Poland ksosek@pr.edu.pl Roman
Wprowadenie ogólnej posai kinemaki uniwersalnm układem odniesienia Karol Sosek Poliehnika Resowska Kaedra Termodnamiki i Mehaniki Płnów al. Powsańów Warsaw, 35-959 Resów, Poland ksosek@pr.edu.pl Roman
K gęstość widmowa (spektralna) energii: 12 Classical theory (5000 K) 10 Rozbieżność w obszarze krótkich fal (katastrofa w nadfiolecie)
 Opyka kwanowa wprowadzenie Króka (pre-)hisoria foonu (9-93) Począki modelu foonowego Własności świała i jego oddziaływania z maerią, niedające się opisać w ramach fizyki klasycznej Deekcja pojedynczych
Opyka kwanowa wprowadzenie Króka (pre-)hisoria foonu (9-93) Począki modelu foonowego Własności świała i jego oddziaływania z maerią, niedające się opisać w ramach fizyki klasycznej Deekcja pojedynczych
Początek XX wieku. Dualizm korpuskularno - falowy
 Początek XX wieku Światło: fala czy cząstka? Kwantowanie energii promieniowania termicznego postulat Plancka efekt fotoelektryczny efekt Comptona Fale materii de Broglie a Dualizm korpuskularno - falowy
Początek XX wieku Światło: fala czy cząstka? Kwantowanie energii promieniowania termicznego postulat Plancka efekt fotoelektryczny efekt Comptona Fale materii de Broglie a Dualizm korpuskularno - falowy
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 8 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2013/14
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 8 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2013/14
Szkoła z przyszłością. szkolenie współfinansowane przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Szkoła z przyszłośią szkolenie współfinansowane przez Unię Europejską w ramah Europejskiego Funduszu Społeznego Narodowe Cenrum Badań Jądrowyh, ul. Andrzeja Sołana 7, 05-400 Owok-Świerk ĆWICZENIE a L A
Szkoła z przyszłośią szkolenie współfinansowane przez Unię Europejską w ramah Europejskiego Funduszu Społeznego Narodowe Cenrum Badań Jądrowyh, ul. Andrzeja Sołana 7, 05-400 Owok-Świerk ĆWICZENIE a L A
Wyprowadzenie ogólnej postaci kinematyki z uniwersalnym układem odniesienia
 Wprowadenie ogólnej posai kinemaki uniwersalnm układem odniesienia Karol Sosek Poliehnika Resowska Kaedra Termodnamiki i Mehaniki Płnów al. Powsańów Warsaw, 35-959 Resów, Poland ksosek@pr.edu.pl Roman
Wprowadenie ogólnej posai kinemaki uniwersalnm układem odniesienia Karol Sosek Poliehnika Resowska Kaedra Termodnamiki i Mehaniki Płnów al. Powsańów Warsaw, 35-959 Resów, Poland ksosek@pr.edu.pl Roman
Katedra Geotechniki i Budownictwa Drogowego. WYDZIAŁ NAUK TECHNICZNYCH Uniwersytet Warmińsko-Mazurski
 Katedra Geotechniki i Budownictwa Drogowego WYDZIAŁ NAUK TECHNICZNYCH Uniwersytet Warmińsko-Maurski Mechanika Gruntów dr inż. Ireneus Dyka http://pracownicy.uwm.edu.pl/i.dyka e-mail: i.dyka@uwm.edu.pl
Katedra Geotechniki i Budownictwa Drogowego WYDZIAŁ NAUK TECHNICZNYCH Uniwersytet Warmińsko-Maurski Mechanika Gruntów dr inż. Ireneus Dyka http://pracownicy.uwm.edu.pl/i.dyka e-mail: i.dyka@uwm.edu.pl
Krzywe na płaszczyźnie.
 Krzwe na płaszczźnie. Współrzędne paramerczne i biegunowe. Współrzędne biegunowe. Dan jes punk O, zwan biegunem, kór sanowi począek półprosej, zwanej półosią. Dowoln punk P na płaszczźnie można opisać
Krzwe na płaszczźnie. Współrzędne paramerczne i biegunowe. Współrzędne biegunowe. Dan jes punk O, zwan biegunem, kór sanowi począek półprosej, zwanej półosią. Dowoln punk P na płaszczźnie można opisać
LASERY I ICH ZASTOSOWANIE
 LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 3 Temat: Efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą modulowania zmiany polaryzacji światła oraz
LASERY I ICH ZASTOSOWANIE Laboratorium Instrukcja do ćwiczenia nr 3 Temat: Efekt magnetooptyczny 5.1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z metodą modulowania zmiany polaryzacji światła oraz
BEZPIECZE STWO PRACY Z LASERAMI
 BEZPIECZE STWO PRACY Z LASERAMI Szkodliwe dzia anie promieniowania laserowego dotyczy oczu oraz skóry cz owieka, przy czym najbardziej zagro one s oczy. Ze wzgl du na kierunkowo wi zki zagro enie promieniowaniem
BEZPIECZE STWO PRACY Z LASERAMI Szkodliwe dzia anie promieniowania laserowego dotyczy oczu oraz skóry cz owieka, przy czym najbardziej zagro one s oczy. Ze wzgl du na kierunkowo wi zki zagro enie promieniowaniem
Matematyka ubezpieczeń majątkowych r. ma złożony rozkład Poissona. W tabeli poniżej podano rozkład prawdopodobieństwa ( )
 Zadanie. Zmienna losowa: X = Y +... + Y N ma złożony rozkład Poissona. W abeli poniżej podano rozkład prawdopodobieńswa składnika sumy Y. W ejże abeli podano akże obliczone dla k = 0... 4 prawdopodobieńswa
Zadanie. Zmienna losowa: X = Y +... + Y N ma złożony rozkład Poissona. W abeli poniżej podano rozkład prawdopodobieńswa składnika sumy Y. W ejże abeli podano akże obliczone dla k = 0... 4 prawdopodobieńswa
ANEMOMETRIA LASEROWA
 1 Wstęp ANEMOMETRIA LASEROWA Anemometria laserowa pozwala na bezdotykowy pomiar prędkośi zastezek (elementów) rozpraszajayh światło Źródłem światła jest laser, którego wiazka jest dzielona się nadwiewiazki
1 Wstęp ANEMOMETRIA LASEROWA Anemometria laserowa pozwala na bezdotykowy pomiar prędkośi zastezek (elementów) rozpraszajayh światło Źródłem światła jest laser, którego wiazka jest dzielona się nadwiewiazki
Fale elektromagnetyczne spektrum
 Fale elekroagneyczne spekru w próżni wszyskie fale e- rozchodzą się z prędkością c 3. 8 /s Jaes Clerk Mawell (w połowie XIX w.) wykazał, że świało jes falą elekroagneyczną rozprzesrzeniającą się falą ziennego
Fale elekroagneyczne spekru w próżni wszyskie fale e- rozchodzą się z prędkością c 3. 8 /s Jaes Clerk Mawell (w połowie XIX w.) wykazał, że świało jes falą elekroagneyczną rozprzesrzeniającą się falą ziennego
Wymagania przedmiotowe z fizyki - klasa III (obowiązujące w roku szkolnym 2013/2014)
 Wymagania przedmioowe z izyki - klasa III (obowiązujące w roku szkolnym 013/014) 8. Drgania i ale sprężyse!wskazuje w ooczeniu przykłady ciał wykonujących ruch drgający!podaje znaczenie pojęć: położenie
Wymagania przedmioowe z izyki - klasa III (obowiązujące w roku szkolnym 013/014) 8. Drgania i ale sprężyse!wskazuje w ooczeniu przykłady ciał wykonujących ruch drgający!podaje znaczenie pojęć: położenie
Właściwości światła laserowego
 Właściwości światła laserowego Cechy charakterystyczne światła laserowego: rozbieżność (równoległość) wiązki, pasmo spektralne, gęstość mocy spójność (koherencja). Równoległość wiązki Dyfrakcyjną rozbieżność
Właściwości światła laserowego Cechy charakterystyczne światła laserowego: rozbieżność (równoległość) wiązki, pasmo spektralne, gęstość mocy spójność (koherencja). Równoległość wiązki Dyfrakcyjną rozbieżność
PODSTAWY CHEMII KWANTOWEJ. Jacek Korchowiec Wydział Chemii UJ Zakład Chemii Teoretycznej Zespół Chemii Kwantowej Grupa Teorii Reaktywności Chemicznej
 PODSTWY CHEMII KWTOWEJ Jacek Korchowiec Wydział Chemii UJ Zakład Chemii Teoreycznej Zespół Chemii Kwanowej Grupa Teorii Reakywności Chemicznej LITERTUR R. F. alewajski, Podsawy i meody chemii kwanowej:
PODSTWY CHEMII KWTOWEJ Jacek Korchowiec Wydział Chemii UJ Zakład Chemii Teoreycznej Zespół Chemii Kwanowej Grupa Teorii Reakywności Chemicznej LITERTUR R. F. alewajski, Podsawy i meody chemii kwanowej:
Szczególna Teoria Eteru
 Sególna Teoria Eeru dowolnm skróeniem poprenm Karol Sosek Roman Sosek www.se.om.pl Coprigh b Karol Sosek and Roman Sosek Resów wresień 6 Sosek Karol & Sosek Roman Spis reśi. WSTĘP... 3. CZAS I ROGA PRZEPŁYWU
Sególna Teoria Eeru dowolnm skróeniem poprenm Karol Sosek Roman Sosek www.se.om.pl Coprigh b Karol Sosek and Roman Sosek Resów wresień 6 Sosek Karol & Sosek Roman Spis reśi. WSTĘP... 3. CZAS I ROGA PRZEPŁYWU
Ponadto, jeśli fala charakteryzuje się sferycznym czołem falowym, powyższy wzór można zapisać w następujący sposób:
 Zastosowanie laserów w Obrazowaniu Medycznym Spis treści 1 Powtórka z fizyki Zjawisko Interferencji 1.1 Koherencja czasowa i przestrzenna 1.2 Droga i czas koherencji 2 Lasery 2.1 Emisja Spontaniczna 2.2
Zastosowanie laserów w Obrazowaniu Medycznym Spis treści 1 Powtórka z fizyki Zjawisko Interferencji 1.1 Koherencja czasowa i przestrzenna 1.2 Droga i czas koherencji 2 Lasery 2.1 Emisja Spontaniczna 2.2
Przykład 6.3. Uogólnione prawo Hooke a
 Prkład 6 Uogónione prawo Hooke a Zwiąki międ odkstałceniami i naprężeniami w prpadku ciała iotropowego opisuje uogónione prawo Hooke a: ] ] ] a Rowiąując równania a wgędem naprężeń otrmujem wiąki: b W
Prkład 6 Uogónione prawo Hooke a Zwiąki międ odkstałceniami i naprężeniami w prpadku ciała iotropowego opisuje uogónione prawo Hooke a: ] ] ] a Rowiąując równania a wgędem naprężeń otrmujem wiąki: b W
Wyznaczanie reakcji dynamicznych oraz wyważanie ciała w ruchu obrotowym wokół stałej osi 8
 Wnacanie reakcji dnaicnch ora wważanie ciała w ruchu oroow wokół sałej osi 8 Wprowadenie Jeśli dowolne ciało swne o asie jes w ruchu oroow wokół osi, o na podporach powsają reakcje A i B. Składowe ch reakcji
Wnacanie reakcji dnaicnch ora wważanie ciała w ruchu oroow wokół sałej osi 8 Wprowadenie Jeśli dowolne ciało swne o asie jes w ruchu oroow wokół osi, o na podporach powsają reakcje A i B. Składowe ch reakcji
KOHERENCJA ŚWIATŁA PODSTAWY OPTYKI STATYSTYCZNEJ
 KOHERENCJA ŚWIATŁA PODSTAWY OPTYKI STATYSTYCZNEJ prof. dr hab. inż. Krzyszof Paorski 1. WłaściwoW ciwości saysyczne świała a ermicznego ( losowego( losowego ) A. Naęż ężenie (inensywność ść) ) promieniowania
KOHERENCJA ŚWIATŁA PODSTAWY OPTYKI STATYSTYCZNEJ prof. dr hab. inż. Krzyszof Paorski 1. WłaściwoW ciwości saysyczne świała a ermicznego ( losowego( losowego ) A. Naęż ężenie (inensywność ść) ) promieniowania
13. Optyczne łącza analogowe
 TELEKOMUNIKACJA OPTOFALOWA 13. Opyczne łącza analogowe Spis reści: 13.1. Wprowadzenie 13.. Łącza analogowe z bezpośrednią modulacją mocy 13.3. Łącza analogowe z modulacją zewnęrzną 13.4. Paramery łącz
TELEKOMUNIKACJA OPTOFALOWA 13. Opyczne łącza analogowe Spis reści: 13.1. Wprowadzenie 13.. Łącza analogowe z bezpośrednią modulacją mocy 13.3. Łącza analogowe z modulacją zewnęrzną 13.4. Paramery łącz
2. Całkowita liczba modów podłużnych. Dobroć rezonatora. Związek między szerokością linii emisji wymuszonej a dobrocią rezonatora
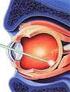 . Całkowita liczba modów podłużnych. Dobroć rezonatora. Związek między szerokością linii emisji wymuszonej a dobrocią rezonatora Gdy na ośrodek czynny, który nie znajduje się w rezonatorze optycznym, pada
. Całkowita liczba modów podłużnych. Dobroć rezonatora. Związek między szerokością linii emisji wymuszonej a dobrocią rezonatora Gdy na ośrodek czynny, który nie znajduje się w rezonatorze optycznym, pada
Techniczne podstawy promienników
 Techniczne podstawy promienników podczerwieni Technical Information,, 17.02.2009, Seite/Page 1 Podstawy techniczne Rozdz. 1 1 Rozdział 1 Zasady promieniowania podczerwonego - Podstawy fizyczne - Widmo,
Techniczne podstawy promienników podczerwieni Technical Information,, 17.02.2009, Seite/Page 1 Podstawy techniczne Rozdz. 1 1 Rozdział 1 Zasady promieniowania podczerwonego - Podstawy fizyczne - Widmo,
Metody Lagrange a i Hamiltona w Mechanice
 Meody Lagrange a i Hamilona w Mechanice Mariusz Przybycień Wydział Fizyki i Informayki Sosowanej Akademia Górniczo-Hunicza Wykład 7 M. Przybycień (WFiIS AGH) Meody Lagrange a i Hamilona... Wykład 7 1 /
Meody Lagrange a i Hamilona w Mechanice Mariusz Przybycień Wydział Fizyki i Informayki Sosowanej Akademia Górniczo-Hunicza Wykład 7 M. Przybycień (WFiIS AGH) Meody Lagrange a i Hamilona... Wykład 7 1 /
Laboratorium techniki światłowodowej. Ćwiczenie 2. Badanie apertury numerycznej światłowodów
 Laboratorium techniki światłowodowej Ćwiczenie 2. Badanie apertury numerycznej światłowodów Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdaoska Gdańsk 2006 1. Wprowadzenie Światłowody
Laboratorium techniki światłowodowej Ćwiczenie 2. Badanie apertury numerycznej światłowodów Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdaoska Gdańsk 2006 1. Wprowadzenie Światłowody
LASERY NA CIELE STAŁYM BERNARD ZIĘTEK
 LASERY NA CIELE STAŁYM BERNARD ZIĘTEK TEK Lasery na ciele stałym lasery, których ośrodek czynny jest: -kryształem i ciałem amorficznym (również proszkiem), - dielektrykiem i półprzewodnikiem. 2 Podział
LASERY NA CIELE STAŁYM BERNARD ZIĘTEK TEK Lasery na ciele stałym lasery, których ośrodek czynny jest: -kryształem i ciałem amorficznym (również proszkiem), - dielektrykiem i półprzewodnikiem. 2 Podział
ĆWICZENIE 4 Badanie stanów nieustalonych w obwodach RL, RC i RLC przy wymuszeniu stałym
 ĆWIZENIE 4 Badanie sanów nieusalonych w obwodach, i przy wymuszeniu sałym. el ćwiczenia Zapoznanie się z rozpływem prądów, rozkładem w sanach nieusalonych w obwodach szeregowych, i Zapoznanie się ze sposobami
ĆWIZENIE 4 Badanie sanów nieusalonych w obwodach, i przy wymuszeniu sałym. el ćwiczenia Zapoznanie się z rozpływem prądów, rozkładem w sanach nieusalonych w obwodach szeregowych, i Zapoznanie się ze sposobami
ZEWNĘTRZNA MODULACJA ŚWIATŁA
 ZWNĘTRZNA MOACJA ŚWATŁA . Wsęp Modulacją świała aywamy miay w casie paramerów fali świelej. Modulaorem jes urądeie, kóre wymusa miay paramerów fali w casie. Płaską falę moochromaycą rochodącą się w ośrodku
ZWNĘTRZNA MOACJA ŚWATŁA . Wsęp Modulacją świała aywamy miay w casie paramerów fali świelej. Modulaorem jes urądeie, kóre wymusa miay paramerów fali w casie. Płaską falę moochromaycą rochodącą się w ośrodku
2.1 Zagadnienie Cauchy ego dla równania jednorodnego. = f(x, t) dla x R, t > 0, (2.1)
 Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
J. Szantyr - Wykład 4 Napór hydrostatyczny Napór hydrostatyczny na ściany płaskie
 J. antr - Wkład Napór hdrostatcn Napór hdrostatcn na ścian płaskie Napór elementarn: d n( p pa ) d nρgd Napór całkowit: ρg nd ρgn d gdie: C Napór hdrostatcn na ścianę płaską predstawia układ elementarnch
J. antr - Wkład Napór hdrostatcn Napór hdrostatcn na ścian płaskie Napór elementarn: d n( p pa ) d nρgd Napór całkowit: ρg nd ρgn d gdie: C Napór hdrostatcn na ścianę płaską predstawia układ elementarnch
EPR. W -1/2 =-1/2 gµ B B
 Hamiltonian spinow Elektronow reonans paramanetcn jest wiąan absorpcją pola wsokiej cęstotliwości, która towars mianie orientacji spin w ewnętrnm polu manetcnm. Niesparowane spinowe moment manetcne µ s
Hamiltonian spinow Elektronow reonans paramanetcn jest wiąan absorpcją pola wsokiej cęstotliwości, która towars mianie orientacji spin w ewnętrnm polu manetcnm. Niesparowane spinowe moment manetcne µ s
BADANIE CYFROWYCH UKŁADÓW ELEKTRONICZNYCH TTL strona 1/7
 BADANIE CYFROWYCH UKŁADÓW ELEKTRONICZNYCH TTL strona 1/7 BADANIE CYFROWYCH UKŁADÓW ELEKTRONICZNYCH TTL 1. Wiadomości wstępne Monolitcne układ scalone TTL ( ang. Trasistor Transistor Logic) stanowią obecnie
BADANIE CYFROWYCH UKŁADÓW ELEKTRONICZNYCH TTL strona 1/7 BADANIE CYFROWYCH UKŁADÓW ELEKTRONICZNYCH TTL 1. Wiadomości wstępne Monolitcne układ scalone TTL ( ang. Trasistor Transistor Logic) stanowią obecnie
Podstawy elektrotechniki
 Wydział Mechaniczno-Energeyczny Podsawy elekroechniki Prof. dr hab. inż. Juliusz B. Gajewski, prof. zw. PWr Wybrzeże S. Wyspiańskiego 27, 5-37 Wrocław Bud. A4 Sara kołownia, pokój 359 Tel.: 71 32 321 Fax:
Wydział Mechaniczno-Energeyczny Podsawy elekroechniki Prof. dr hab. inż. Juliusz B. Gajewski, prof. zw. PWr Wybrzeże S. Wyspiańskiego 27, 5-37 Wrocław Bud. A4 Sara kołownia, pokój 359 Tel.: 71 32 321 Fax:
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 14, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fiyki IV Optyka elementami fiyki współcesnej wykład 4, 30.03.0 wykład: pokay: ćwicenia: Cesław Radewic Radosław Chrapkiewic, Filip Oimek Ernest Grodner Wykład 3 - prypomnienie płasko-równoległy
Podstawy Fiyki IV Optyka elementami fiyki współcesnej wykład 4, 30.03.0 wykład: pokay: ćwicenia: Cesław Radewic Radosław Chrapkiewic, Filip Oimek Ernest Grodner Wykład 3 - prypomnienie płasko-równoległy
Niezwykłe światło. ultrakrótkie impulsy laserowe. Piotr Fita
 Niezwykłe światło ultrakrótkie impulsy laserowe Laboratorium Procesów Ultraszybkich Zakład Optyki Wydział Fizyki Uniwersytetu Warszawskiego Światło Fala elektromagnetyczna Dla światła widzialnego długość
Niezwykłe światło ultrakrótkie impulsy laserowe Laboratorium Procesów Ultraszybkich Zakład Optyki Wydział Fizyki Uniwersytetu Warszawskiego Światło Fala elektromagnetyczna Dla światła widzialnego długość
Ogólne cechy ośrodków laserowych
 Ogólne cechy ośrodków laserowych Gazowe Cieczowe Na ciele stałym Naturalna jednorodność Duże długości rezonatora Małe wzmocnienia na jednostkę długości ośrodka czynnego Pompowanie prądem (wzdłużne i poprzeczne)
Ogólne cechy ośrodków laserowych Gazowe Cieczowe Na ciele stałym Naturalna jednorodność Duże długości rezonatora Małe wzmocnienia na jednostkę długości ośrodka czynnego Pompowanie prądem (wzdłużne i poprzeczne)
n n 1 2 = exp( ε ε ) 1 / kt = exp( hν / kt) (23) 2 to wzór (22) przejdzie w następującą równość: ρ (ν) = B B A / B 2 1 hν exp( ) 1 kt (24)
 n n 1 2 = exp( ε ε ) 1 / kt = exp( hν / kt) (23) 2 to wzór (22) przejdzie w następującą równość: ρ (ν) = B B A 1 2 / B hν exp( ) 1 kt (24) Powyższe równanie określające gęstość widmową energii promieniowania
n n 1 2 = exp( ε ε ) 1 / kt = exp( hν / kt) (23) 2 to wzór (22) przejdzie w następującą równość: ρ (ν) = B B A 1 2 / B hν exp( ) 1 kt (24) Powyższe równanie określające gęstość widmową energii promieniowania
Wykład 17: Optyka falowa cz.1.
 Wykład 17: Optyka falowa cz.1. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Zasada Huyghensa Christian Huygens 1678 r. pierwsza
Wykład 17: Optyka falowa cz.1. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Zasada Huyghensa Christian Huygens 1678 r. pierwsza
Lasery półprzewodnikowe na złączu p-n. Laser półprzewodnikowy a dioda świecąca
 Laser półprzewodnikowy a dioda świecąca Emisja laserowa pojawia się po przekroczeniu progowej wartości natężenia prądu płynącego w kierunku przewodzenia przez heterozłącze p-n w strukturze lasera. Przy
Laser półprzewodnikowy a dioda świecąca Emisja laserowa pojawia się po przekroczeniu progowej wartości natężenia prądu płynącego w kierunku przewodzenia przez heterozłącze p-n w strukturze lasera. Przy
Politechnika Wrocławska Instytut Telekomunikacji, Teleinformatyki i Akustyki. Klucze analogowe. Wrocław 2010
 Poliechnika Wrocławska nsyu elekomunikacji, eleinformayki i Akusyki Klucze analogowe Wrocław 200 Poliechnika Wrocławska nsyu elekomunikacji, eleinformayki i Akusyki Pojęcia podsawowe Podsawą realizacji
Poliechnika Wrocławska nsyu elekomunikacji, eleinformayki i Akusyki Klucze analogowe Wrocław 200 Poliechnika Wrocławska nsyu elekomunikacji, eleinformayki i Akusyki Pojęcia podsawowe Podsawą realizacji
Źródła światła: Lampy (termiczne) na ogół wymagają filtrów. Wojciech Gawlik, Metody Optyczne w Medycynie 2010/11 - wykł. 3 1/18
 Źródła światła: Lampy (termiczne) na ogół wymagają filtrów Wojciech Gawlik, Metody Optyczne w Medycynie 2010/11 - wykł. 3 1/18 Lampy: a) szerokopasmowe, rozkład Plancka 2hc I( λ) = 5 λ 2 e 1 hc λk T B
Źródła światła: Lampy (termiczne) na ogół wymagają filtrów Wojciech Gawlik, Metody Optyczne w Medycynie 2010/11 - wykł. 3 1/18 Lampy: a) szerokopasmowe, rozkład Plancka 2hc I( λ) = 5 λ 2 e 1 hc λk T B
W-9 (Jaroszewicz) 15 slajdów. Równanie fali płaskiej parametry fali Równanie falowe prędkość propagacji, Składanie fal fale stojące
 Jucaan, Meico, Februar 005 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i
Jucaan, Meico, Februar 005 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i
Optyczne elementy aktywne
 Optyczne elementy aktywne Źródła optyczne Diody elektroluminescencyjne Diody laserowe Odbiorniki optyczne Fotodioda PIN Fotodioda APD Generowanie światła kontakt metalowy typ n GaAs podłoże typ n typ n
Optyczne elementy aktywne Źródła optyczne Diody elektroluminescencyjne Diody laserowe Odbiorniki optyczne Fotodioda PIN Fotodioda APD Generowanie światła kontakt metalowy typ n GaAs podłoże typ n typ n
Prognozowanie i symulacje
 Prognozowanie i smulacje Lepiej znać prawdę niedokładnie, niż dokładnie się mlić. J. M. Kenes dr Iwona Kowalska ikowalska@wz.uw.edu.pl Prognozowanie meod naiwne i średnie ruchome Meod naiwne poziom bez
Prognozowanie i smulacje Lepiej znać prawdę niedokładnie, niż dokładnie się mlić. J. M. Kenes dr Iwona Kowalska ikowalska@wz.uw.edu.pl Prognozowanie meod naiwne i średnie ruchome Meod naiwne poziom bez
Ruch falowy, ośrodek sprężysty
 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i pęd przenoszone przez falę
W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i pęd przenoszone przez falę
ZADANIA Z FUNKCJI ANALITYCZNYCH LICZBY ZESPOLONE
 . Oblicyć: ZADANIA Z FUNKCJI ANALITYCZNYCH a) ( 7i) ( 9i); b) (5 i)( + i); c) 4+3i ; LICZBY ZESPOLONE d) 3i 3i ; e) pierwiastki kwadratowe 8 + i.. Narysować biór tych licb espolonych, które spełniają warunek:
. Oblicyć: ZADANIA Z FUNKCJI ANALITYCZNYCH a) ( 7i) ( 9i); b) (5 i)( + i); c) 4+3i ; LICZBY ZESPOLONE d) 3i 3i ; e) pierwiastki kwadratowe 8 + i.. Narysować biór tych licb espolonych, które spełniają warunek:
Przykład 3.7. Naprężenia styczne przy zginaniu belki cienkościennej.
 Prkład.7. Naprężenia tcne pr ginaniu belki cienkościennej. Wnac rokład naprężenia tcnego w prekroju podporowm belki wpornikowej o prekroju cienkościennm obciążonej na wobodnm końcu pionową iłą P. Siła
Prkład.7. Naprężenia tcne pr ginaniu belki cienkościennej. Wnac rokład naprężenia tcnego w prekroju podporowm belki wpornikowej o prekroju cienkościennm obciążonej na wobodnm końcu pionową iłą P. Siła
Transformator Φ M. uzwojenia; siła elektromotoryczna indukowana w i-tym zwoju: dφ. = z1, z2 liczba zwojów uzwojenia pierwotnego i wtórnego.
 Transformator Φ r Φ M Φ r i i u u Φ i strumień magnetycny prenikający pre i-ty wój pierwsego uwojenia; siła elektromotorycna indukowana w i-tym woju: dφ ei, licba wojów uwojenia pierwotnego i wtórnego.
Transformator Φ r Φ M Φ r i i u u Φ i strumień magnetycny prenikający pre i-ty wój pierwsego uwojenia; siła elektromotorycna indukowana w i-tym woju: dφ ei, licba wojów uwojenia pierwotnego i wtórnego.
6. Emisja światła, diody LED i lasery polprzewodnikowe
 6. Emisja światła, diody LED i lasery polprzewodnikowe Typy rekombinacji Rekombinacja promienista Diody LED Lasery półprzewodnikowe Struktury niskowymiarowe OLEDy 1 Promieniowanie termiczne Rozkład Plancka
6. Emisja światła, diody LED i lasery polprzewodnikowe Typy rekombinacji Rekombinacja promienista Diody LED Lasery półprzewodnikowe Struktury niskowymiarowe OLEDy 1 Promieniowanie termiczne Rozkład Plancka
Szczegółowe wymagania edukacyjne z fizyki dla klas drugich i trzecich gimnazjum
 Szczegółowe wymagania edukacyjne z fizyki dla klas drugich i rzecich gimnazjum 5. Siły w przyrodzie Lp. Tema lekcji Wymagania konieczne 44 Rodzaje i skuki oddziaływań wymienia różne rodzaje oddziaływania
Szczegółowe wymagania edukacyjne z fizyki dla klas drugich i rzecich gimnazjum 5. Siły w przyrodzie Lp. Tema lekcji Wymagania konieczne 44 Rodzaje i skuki oddziaływań wymienia różne rodzaje oddziaływania
Lasery. Własności światła laserowego Zasada działania Rodzaje laserów
 Lasery Własności światła laserowego Zasada działania Rodzaje laserów Lasery Laser - nazwa utworzona jako akronim od Light Amplification by Stimulated Emission of Radiation - wzmocnienie światła poprzez
Lasery Własności światła laserowego Zasada działania Rodzaje laserów Lasery Laser - nazwa utworzona jako akronim od Light Amplification by Stimulated Emission of Radiation - wzmocnienie światła poprzez
Wstęp do astrofizyki I
 Wstęp do astrofizyki I Wykład 2 Tomasz Kwiatkowski 12 październik 2009 r. Tomasz Kwiatkowski, Wstęp do astrofizyki I, Wykład 2 1/21 Plan wykładu Promieniowanie ciała doskonale czarnego Związek temperatury
Wstęp do astrofizyki I Wykład 2 Tomasz Kwiatkowski 12 październik 2009 r. Tomasz Kwiatkowski, Wstęp do astrofizyki I, Wykład 2 1/21 Plan wykładu Promieniowanie ciała doskonale czarnego Związek temperatury
Podwaliny szczególnej teorii względności
 W-6 (Jarosewi) 7 slajdów Na podsawie preenaji prof. J. Rukowskiego Podwalin sególnej eorii wględnośi asada wględnośi Galileusa ekspermen Mihelsona i Morle a ransformaja Lorena pierwsa spreność współesnej
W-6 (Jarosewi) 7 slajdów Na podsawie preenaji prof. J. Rukowskiego Podwalin sególnej eorii wględnośi asada wględnośi Galileusa ekspermen Mihelsona i Morle a ransformaja Lorena pierwsa spreność współesnej
Rodzaje fal. 1. Fale mechaniczne. 2. Fale elektromagnetyczne. 3. Fale materii. dyfrakcja elektronów
 Wykład VI Fale t t + Dt Rodzaje fal 1. Fale mechaniczne 2. Fale elektromagnetyczne 3. Fale materii dyfrakcja elektronów Fala podłużna v Przemieszczenia elementów spirali ( w prawo i w lewo) są równoległe
Wykład VI Fale t t + Dt Rodzaje fal 1. Fale mechaniczne 2. Fale elektromagnetyczne 3. Fale materii dyfrakcja elektronów Fala podłużna v Przemieszczenia elementów spirali ( w prawo i w lewo) są równoległe
Fale mechaniczne i akustyczne
 Fale mechaniczne i akusyczne Zadania z rozwiązaniami Projek współfinansowany przez Unię uropejską w ramach uropejskiego Funduszu Społecznego Projek współfinansowany przez Unię uropejską w ramach uropejskiego
Fale mechaniczne i akusyczne Zadania z rozwiązaniami Projek współfinansowany przez Unię uropejską w ramach uropejskiego Funduszu Społecznego Projek współfinansowany przez Unię uropejską w ramach uropejskiego
w diagnostyce medycznej III
 Technika ultradźwiękowa w diagnostyce medycznej SEMESTR VI Człowiek- najlepsza inwestycja Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Technika ultradźwiękowa
Technika ultradźwiękowa w diagnostyce medycznej SEMESTR VI Człowiek- najlepsza inwestycja Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego Technika ultradźwiękowa
WYKŁAD FIZYKAIIIB 2000 Drgania tłumione
 YKŁD FIZYKIIIB Drgania łumione (gasnące, zanikające). F siła łumienia; r F r b& b współczynnik łumienia [ Nm s] m & F m & && & k m b m F r k b& opis różnych zjawisk izycznych Niech Ce p p p p 4 ± Trzy
YKŁD FIZYKIIIB Drgania łumione (gasnące, zanikające). F siła łumienia; r F r b& b współczynnik łumienia [ Nm s] m & F m & && & k m b m F r k b& opis różnych zjawisk izycznych Niech Ce p p p p 4 ± Trzy
Wydajność konwersji energii słonecznej:
 Wykład II E we Wydajność konwersji energii słonecznej: η = E wy E we η całkowite = η absorpcja η kreacja η dryft/dyf η separ η zbierania E wy Jednostki fotometryczne i energetyczne promieniowania elektromagnetycznego
Wykład II E we Wydajność konwersji energii słonecznej: η = E wy E we η całkowite = η absorpcja η kreacja η dryft/dyf η separ η zbierania E wy Jednostki fotometryczne i energetyczne promieniowania elektromagnetycznego
Fizyka elektryczność i magnetyzm
 Fizyka elektryczność i magnetyzm W5 5. Wybrane zagadnienia z optyki 5.1. Światło jako część widma fal elektromagnetycznych. Fale elektromagnetyczne, które współczesny człowiek potrafi wytwarzać, i wykorzystywać
Fizyka elektryczność i magnetyzm W5 5. Wybrane zagadnienia z optyki 5.1. Światło jako część widma fal elektromagnetycznych. Fale elektromagnetyczne, które współczesny człowiek potrafi wytwarzać, i wykorzystywać
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 12, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 1, 3.03.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek rnest Grodner Wykład 11 - przypomnienie superpozycja
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 1, 3.03.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek rnest Grodner Wykład 11 - przypomnienie superpozycja
Podstawy Akustyki. Drgania normalne a fale stojące Składanie fal harmonicznych: Fale akustyczne w powietrzu Efekt Dopplera.
 W-1 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka falowa Fale akustyczne w powietrzu
W-1 (Jaroszewicz) 14 slajdów Podstawy Akustyki Drgania normalne a fale stojące Składanie fal harmonicznych: prędkość grupowa, dyspersja fal, superpozycja Fouriera, paczka falowa Fale akustyczne w powietrzu
SPECYFIKACJA ISTOTNYCH WARUNKÓW ZAMÓWIENIA
 Z a m a w i a j» c y G D Y S K I O R O D E K S P O R T U I R E K R E A C J I J E D N O S T K A B U D E T O W A 8 1 5 3 8 G d y n i a, u l O l i m p i j s k a 5k 9 Z n a k s p r a w y G O S I R D Z P I
Z a m a w i a j» c y G D Y S K I O R O D E K S P O R T U I R E K R E A C J I J E D N O S T K A B U D E T O W A 8 1 5 3 8 G d y n i a, u l O l i m p i j s k a 5k 9 Z n a k s p r a w y G O S I R D Z P I
Głównie występuje w ośrodkach gazowych i ciekłych.
 W/g ermodynamiki - ciepło jes jednym ze sposobów ransporu energii do/z bila, zysy przepływ ciepła może wysąpić jedynie w ciałach sałych pozosających w spoczynku. Proces wymiany ciepla: przejmowanie ciepła
W/g ermodynamiki - ciepło jes jednym ze sposobów ransporu energii do/z bila, zysy przepływ ciepła może wysąpić jedynie w ciałach sałych pozosających w spoczynku. Proces wymiany ciepla: przejmowanie ciepła
ver b drgania harmoniczne
 ver-28.10.11 b drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne N = n=1 A n cos nω n Fig (...) analiza Fouriera małe drgania E p E E k jeden sopień swobody: E p -A E p A 0
ver-28.10.11 b drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne N = n=1 A n cos nω n Fig (...) analiza Fouriera małe drgania E p E E k jeden sopień swobody: E p -A E p A 0
Podstawy Fizyki III Optyka z elementami fizyki współczesnej. wykład 12, Mateusz Winkowski, Łukasz Zinkiewicz
 Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład, 0..07 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład - przypomnienie superpozycja
Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład, 0..07 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład - przypomnienie superpozycja
napór cieczy - wypadkowy ( hydrostatyczny )
 5. apór hdrostatcn i równowaga ciał płwającch Płn najdując się w stanie równowagi oddiałwuje na ścian ogranicające ropatrwaną jego objętość i sił te nawane są naporami hdrostatcnmi. Omawiana problematka
5. apór hdrostatcn i równowaga ciał płwającch Płn najdując się w stanie równowagi oddiałwuje na ścian ogranicające ropatrwaną jego objętość i sił te nawane są naporami hdrostatcnmi. Omawiana problematka
drgania h armoniczne harmoniczne
 ver-8..7 drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne () An cos( nω + ϕ n ) N n Fig (...) analiza Fouriera małe drgania E p E E k E p ( ) jeden sopień swobody: -A A E p
ver-8..7 drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne () An cos( nω + ϕ n ) N n Fig (...) analiza Fouriera małe drgania E p E E k E p ( ) jeden sopień swobody: -A A E p
Zjawisko interferencji fal
 Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi stabilne w czasie ich
Zjawisko interferencji fal Interferencja to efekt nakładania się fal (wzmacnianie i osłabianie się ruchu falowego widoczne w zmianach amplitudy i natęŝenia fal) w którym zachodzi stabilne w czasie ich
Wyprowadzenie wszystkich transformacji liniowych spełniających wyniki eksperymentu Michelsona-Morleya oraz dyskusja o podstawach relatywistyki
 Wprowadenie wsskih ransformaji liniowh spełniająh wniki ekspermenu Mihelsona-Morlea ora dskusja o podsawah relawiski Roman Sosek Poliehnika Resowska, Kaedra Meod Ilośiowh, Resów, Polska rsosek@pr.edu.pl
Wprowadenie wsskih ransformaji liniowh spełniająh wniki ekspermenu Mihelsona-Morlea ora dskusja o podsawah relawiski Roman Sosek Poliehnika Resowska, Kaedra Meod Ilośiowh, Resów, Polska rsosek@pr.edu.pl
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 8 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 8 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Wyprowadzenie ogólnej postaci kinematyki z uniwersalnym układem odniesienia
 Arkuł ukaał się w jęku angielskim w owarm dosępie w asopiśmie Resuls in Phsis Sosek Karol, Sosek Roman 08 The deriaion of he general form of kinemais wih he uniersal referene ssem Resuls in Phsis, Vol.
Arkuł ukaał się w jęku angielskim w owarm dosępie w asopiśmie Resuls in Phsis Sosek Karol, Sosek Roman 08 The deriaion of he general form of kinemais wih he uniersal referene ssem Resuls in Phsis, Vol.
ZASTOSOWANIE WZMACNIACZY OPERACYJNYCH DO LINIOWEGO PRZEKSZTAŁCANIA SYGNAŁÓW. Politechnika Wrocławska
 Poliechnika Wrocławska Insyu elekomunikacji, eleinformayki i Akusyki Zakład kładów Elekronicznych Insrukcja do ćwiczenia laboraoryjnego ZASOSOWANIE WZMACNIACZY OPEACYJNYCH DO LINIOWEGO PZEKSZAŁCANIA SYGNAŁÓW
Poliechnika Wrocławska Insyu elekomunikacji, eleinformayki i Akusyki Zakład kładów Elekronicznych Insrukcja do ćwiczenia laboraoryjnego ZASOSOWANIE WZMACNIACZY OPEACYJNYCH DO LINIOWEGO PZEKSZAŁCANIA SYGNAŁÓW
Pomiar drogi koherencji wybranych źródeł światła
 Politechnika Gdańska WYDZIAŁ ELEKTRONIKI TELEKOMUNIKACJI I INFORMATYKI Katedra Optoelektroniki i Systemów Elektronicznych Pomiar drogi koherencji wybranych źródeł światła Instrukcja do ćwiczenia laboratoryjnego
Politechnika Gdańska WYDZIAŁ ELEKTRONIKI TELEKOMUNIKACJI I INFORMATYKI Katedra Optoelektroniki i Systemów Elektronicznych Pomiar drogi koherencji wybranych źródeł światła Instrukcja do ćwiczenia laboratoryjnego
Wygładzanie metodą średnich ruchomych w procesach stałych
 Wgładzanie meodą średnich ruchomch w procesach sałch Cel ćwiczenia. Przgoowanie procedur Średniej Ruchomej (dla ruchomego okna danch); 2. apisanie procedur do obliczenia sandardowego błędu esmacji;. Wizualizacja
Wgładzanie meodą średnich ruchomch w procesach sałch Cel ćwiczenia. Przgoowanie procedur Średniej Ruchomej (dla ruchomego okna danch); 2. apisanie procedur do obliczenia sandardowego błędu esmacji;. Wizualizacja
