Synteza optymalnego regulatora stanu. Uk lady z czasem ci ag lym.
|
|
|
- Patryk Socha
- 8 lat temu
- Przeglądów:
Transkrypt
1 Synteza optymalnego regulatora stanu. Uk lady z czasem ci ag lym. Po wyznaczeniu optymalnego nominalnego) procesu sterowania x o, u o nasuwa siȩ kwestia podtrzymywania tego procesu w warunkach ma lych fluktuacji parametrów obiektu sterowania. Fluktuacje te powoduj a odchylenie aktualnej trajektorii stanu od jej przebiegu optymalnego nominalnego). Celem zniwelowania tego odchylenia wprowadzamy nowe wspó lrzȩdne stanu i sterowania xt) := xt) x o t), ut) := ut) u o t) i określamy korektȩ sterowania optymalnego nominalnego) na podstawie rozwi azania problemu liniowo-kwadratowego sterowania optymalnego LKSO) aproksymuj acego problem wyjściowy w otoczeniu procesu optymalnego nominalnego). Aproksymuj acy problem LKSO dla procesów z czasem ci ag lym polega na minimalizacji kwadratowego wskaźnika jakości Gx, u) =.5x T t 1 )Qxt 1 ).5 t1 przy ograniczeniu w postaci liniowego równania stanu x T t)p t)xt) u T t)rt)ut))dt ẋt) = At)xt) Bt)ut), t [, t 1 ], z zadanym warunkiem pocz atkowym x) = x. Zak ladamy, że Q R n n jest macierz a symetryczn a dodatnio pó lokreślon a, P t) R n n jest macierz a symetryczn a dodatnio pó lokreślon a dla t [, t 1 ], Rt) R n n jest macierz a symetryczn a dodatnio określon a dla t [, t 1 ]. Sk ladnik wskaźnika jakości.5x T t 1 )Qxt 1 ) stanowi miarȩ odchylenia stanu końcowego trajektorii od jego wartości optymalnej nominalnej). Dla Q = I jest to suma kwadratów wspó lrzȩdnych stanu końcowego. Sk ladnik wskaźnika jakości.5 t 1 xt t)p t)xt) stanowi miarȩ odchylenia aktualnej trajektorii stanu od jej przebiegu optymalnego nominalnego) w przedziale sterowania [, t 1 ]. Dla P t) = I jest to ca lka z kwadratu odchylenia aktualnej trajektorii od jej przebiegu optymalnego nominalnego) w przedziale 1
2 sterowania [, t 1 ]. Sk ladnik wskaźnika jakości.5 t 1 ut t)rt)ut) określa koszty sterowania koryguj acego odchylenie aktualnej trajektorii od jej przebiegu optymalnego nominalnego). Sk ladnik ten ogranicza chwilowe wartości sterowania koryguj acego. Równanie stanu jest linearyzacj a wyjściowych, ogólnie bior ac, nieliniowych równań stanu na procesie optymalnym nominalnym). Oznacza to, że At) = f x x o t), u o t), t), Bt) = f u x o t), u o t), t). Określenie korekty sterowania optymalnego nominalnego) w uk ladzie zamkniȩtym nazywa siȩ syntez a optymalnego regulatora stanu. Do rozwi azania tego zadania zastosujemy zasadȩ maksimum. Zapisujemy hamiltonian problemu Hλt), xt), ut), t) =.5x T t)p t)xt)u T t)rt)ut))λ T t)at)xt)bt)ut)) i wydzielamy czȩść hamiltonianu zależn a od sterowania Hλt), xt), ut), t) =.5u T t)rt)ut) λ T t)bt)ut). Maksymalizuj ac hamiltonian wzglȩdem sterowania korzystamy z warunku H u t) = na sterowanie nie s a na lożone ograniczenia chwilowe) oraz ze wzoru na różniczkowanie formy kwadratowej ϕz) =..5z T Kz ϕ z z) =. z T K. Uzyskujemy wiȩc H u t) = u ot t)rt) λ T t)bt) = Rt)u o t) = B T t)λt) u o t) = R 1 t)b T t)λt). Sprawdzamy warunek wystarczaj acy maksimum hamiltonianu drugiego rzȩdu H uu t) = Rt) H uu t) <, co oznacza, że macierz pochodnych cz astkowych hamiltonianu jest ujemnie określona i że wyznaczone rozwi azanie stanowi maksimum. Jest to maksimum globalne, gdyż jest to jedyne rozwi azanie spe lniaj ace warunki optymalności. 2
3 Określamy uk lad równań kanonicznych zasady maksimum niestacjonarnego problemu LKSO ẋt) = H T λ t), x) = x, λt) = H T x t), λ t1 = Qxt 1 ) tj. ẋt) = At)xt) Bt)R 1 t)b T t)λt), t [, t 1 ], x) = x, λt) = A T t)λt) P t)xt), λ t1 = Qxt 1 ). Tak wiȩc warunki konieczne optymalności rozważanego procesu sterowania sprowadzaj a siȩ do uk ladu niestacjonarnych liniowych równań różniczkowych z warunkami dwugranicznymi. Jeden z efektywnych sposobów rozwi azywania tego uk ladu polega na zastosowaniu tzw. niestacjonarnego liniowego podstawienia Riccatiego λt) = Kt)xt), gdzie Kt) R n n jest macierz a Riccatiego wi aż ac a wektor stanu i wektor zmiennych sprzȩżonych niestacjonarnego problemu LKSO. Przewidywanie powi azania tych wektorów w postaci niestacjonarnej liniowej zależności jest uzasadnione przez fakt, że uk lad równań kanonicznych ma postać niestacjonarn a liniow a. Stosujemy podstawienie Riccatiego do uk ladu równań kanonicznych ẋt) = At)xt) Bt)R 1 t)b T t)kt)xt), Kt)xt) Kt)ẋt) = A T t)kt)xt) P t)xt). Pierwsze z tych równań podstawiamy do drugiego Kt)xt)Kt) At)Bt)R 1 t)b T t)kt) ) xt) = A T t)kt)xt)p t)xt). Równanie to bȩdzie spe lnione dla każdego stanu xt), jeśli macierz Kt) bȩdzie spe lniać nastȩpuj ace macierzowe równanie różniczkowe Riccatiego Kt) = Kt)At) A T t)kt) Kt)Bt)R 1 t)b T t)kt) P t) z warunkiem końcowym Kt 1 ) = Q. Ostatni warunek wynika z warunku końcowego dla zmiennej sprzȩżonej λt1 ) = Qxt 1 ) λt 1 ) = Kt 1 )xt 1 ) ) Kt 1 ) = Q. 3
4 Po wyznaczeniu macierzy Kt) określamy rów nanie optymalnego regulatora stanu u o t) = R 1 t)b T t)kt)xt). Jest to liniowe niestacjonarne równanie macierzowe. Uk lad sterowania z warstw a regulacji sterowanie optymalne Optymalny niestacjonarny regulator stanu R 1 t)b T t)kt) 1 korekta sterowania optymalnego Obiekt sterowania xt) czȩste fluktuacje parametru Macierz Riccatiego posiada nastȩpuj ace w lasności: 1. Macierz Kt) jest symetryczna. 2. Macierz Kt) jest ujemnie określona. Aby wykazać symetryczność macierzy Riccatiego porównamy równanie Riccatiego Kt) = Kt)At) A T t)kt) Kt)Bt)R 1 t)b T t)kt) P t), Kt 1 ) = Q i jego transpozycjȩ K T t) = A T t)k T t) K T t)at) K T t)bt)r 1 t)b T t)k T t) P t), K T t 1 ) = Q. Macierz K T t) jest rozwi azaniem tego samego równania różniczkowego co i macierz Kt) z tym samym warunkiem końcowym. Z twierdzenia o istnieniu 4
5 i jednoznaczności rozwi azań równań różniczkowych wynika, że musi zachodzić równość K T t) = Kt), co oznacza, że macierz Kt) jest symetryczna. Aby wykazać ujemn a określoność macierzy Riccatiego zapisujemy na podstawie równania Riccatiego zależność = x T t) P t) A T t)kt) Kt)At) Kt)Bt)R 1 t)b T t)kt) Kt) ) xt) = x T t) P t)kt)bt)r 1 t)b T t)kt) At)Bt)R 1 t)b T t)kt)) T Kt) Kt) Kt)At) Bt)R 1 t)b T t)kt)) ) xt) = x T t)p t)xt) x T t)kt)bt)r 1 t)rt)r 1 t)b T t)kt)xt) ẋ T t)kt)xt) x T t) Kt)xt) x T t)kt)ẋt) = x T t)p t)xt)u T t)rt)ut) ẋ T t)kt)xt)x T t) Kt)xt)x T t)kt)ẋt)) tj. czyli x T t)p t)xt) u T t)rt)ut)) = d dt xt t)kt)xt)). Ca lkuj ac ostatnie wyrażenie w granicach od t 1 do t uzyskujemy t t x T s)p s)xs) u T d s)rs)us))ds = t 1 t 1 ds xt s)ks)xs))ds t1 t x T s)p s)xs)u T s)rs)us))ds = x T t 1 )t 1 )Kt 1 )xt 1 ) x T t)kt)xt) = x T t 1 )Qxt 1 ) x T t)kt)xt) 5
6 i ostatecznie x T t 1 )Qxt 1 ) t1 t x T s)p s)xs) u T s)rs)us))ds = x T t)kt)xt). Ponieważ macierze Q i P t) s a dodatnio pó lokreślone, a macierz Rt) jest dodatnio określona, wiȩc wyrażenie po lewej stronie ostatniego równania jest zawsze dodatnie. Oznacza to, że macierz Kt) po prawej stronie tego wyrażenia jest ujemnie określona dla wszystkich t [, t 1 ]. Równanie Riccatiego rozwi azywane jest metodami numerycznymi jako równanie różniczkowe z zadanym warunkiem końcowym. Symetryczność macierzy Riccatiego jest wykorzystywana do redukcji zmiennych w równaniu Riccatiego - może być to istotne w przypadku uk ladów o dużej liczbie zmiennych stanu. Ujemna określoność macierzy Riccatiego umożliwia jednoznaczne wyznaczenie optymalnego regulatora stanu dla uk ladów stacjonarnych z nieskończonym horyzontem czasowym sterowania. Jeśli fluktuacje parametru obiektu s a stosunkowo rzadkie, to podstaw a do wyznaczenia sterowanie koryguj acego może być rozwi azanie nastȩpuj acego stacjonarnego problemu LKSO: zminimalizować wskaźnik jakości Gx, u) =.5 x T t)p xt) u T t)rut))dt przy ograniczeniach w postaci liniowego stacjonarnego równania stanu ẋt) = Axt) But), t [, ) z zadanym warunkiem pocz atkowym x) = x i końcowym x ) =. Zak ladamy, że macierze P i R s a dodatnio określone. Macierze A i B mog a być uśrednieniami macierzy Jacobiego f x x o, u o t), t), f u x o, u o t), t) wyjściowego równania stanu na procesie optymalnym tj. 1 A = lim τ τ τ f x x o, u o t), t)dt, 6
7 1 τ B = lim f u x o, u o t), t)dt. τ τ Warunek pocz atkowy x stanowi odchylenie pocz atkowe aktualnego stanu od stanu optymalnego nominalnego). Ponieważ z za lożenia zaburzenia stanu s a stosunkowo rzadkie, wiȩc mamy do dyspozycji d lugi horyzont czasowy dla zregulowania zaistnia lego zaburzenia stanu. Przyjmuj ac idealny przypadek nieskończonego horyzontu czasowego regulacji stanu stawiamy wymaganie pe lnej niwelacji zaburzenia stanu x ) =. Dlatego stan końcowy nie pojawia siȩ we wskaźniku jakości. Stacjonarny problem LKSO rozwi ażemy stosuj ac zasadȩ maksimum. Zapisujemy hamiltonian problemu Hλt), xt), ut)) =.5x T t)p xt) u T t)rut)) λ T t)axt) But)) i wydzielamy jego czȩść zależn a od sterowania Hλt), xt), ut)) =.5u T t)rut) λ T t)but). Maksymalizuj ac hamiltonian wzglȩdem sterowania korzystamy z warunku H u t) = na sterowanie nie s a na lożone ograniczenia chwilowe) oraz ze wzoru na różniczkowanie formy kwadratowej Uzyskujemy wiȩc ϕz). =.5z T Kz ϕ z z). = z T K. H u t) = u ot t)r λ T t)b = Ru o t) = B T λt) i st ad u o t) = R 1 B T λt). Sprawdzamy warunek wystarczaj acy optymalności drugiego rzȩdu H uu t) = R H uu t) <, co oznacza, że macierz pochodnych cz astkowych hamiltonianu jest ujemnie określona i że wyznaczone rozwi azanie stanowi maksimum. Jest to maksimum globalne, gdyż jest to jedyne rozwi azanie spe lniaj ace warunki optymalności. Określamy uk lad równań kanonicznych zasady maksimum stacjonarnego problemu LKSO ẋt) = H T λ t), x) = x, x ) =, λt) = H T x t), 7
8 tj. ẋt) = Axt) BR 1 B T λt), t [, t 1 ], x) = x, x ) =, λt) = A T λt) P xt). Tak wiȩc warunki konieczne optymalności rozważanego procesu sterowania sprowadzaj a siȩ do uk ladu stacjonarnych liniowych równań różniczkowych z warunkami dwugranicznymi. Jeden z efektywnych sposobów rozwi azywania tego uk ladu polega na zastosowaniu tzw. stacjonarnego liniowego podstawienia Riccatiego λt) = Kxt), gdzie K R n n jest macierz a Riccatiego wi aż ac a wektor stanu i wektor zmiennych sprzȩżonych stacjonarnego problemu LKSO. Przewidywanie powi azania tych wektorów w postaci stacjonarnej liniowej zaleṅości jest uzasadnione przez fakt, że uk lad równań kanonicznych ma postać stacjonarn a liniow a. Stosuj ac stacjonarne podstawienie Riccatiego do pierwszego równania kanonicznego zasady maksimum uzyskujemy równanie stanu zamkniȩtego uk ladu jego regulacji ẋt) = A BR 1 B T K)xt). Stosuj ac to podstawienie do drugiego równania kanonicznego zasady maksimum uzyskujemy równanie dla określenia macierzy K Kẋt) = A T Kxt) P xt) tj. KA BR 1 B T K)xt) = A T Kxt) P xt), co oznacza, że macierz K powinna spe lniać macierzowe algebraiczne równanie Riccatiego KA A T K KBR 1 B T K P =. W teorii równań macierzowych dowodzi siȩ, że macierzowe algebraiczne równanie Riccatiego posiada wśród wielu rozwi azań jedno i tylko jedno rozwi azanie ujemnie określone K <. To w laśnie rozwi azanie stosujemy do określenia optymalnego stacjonarnego regulatora stanu u o t) = R 1 B T Kxt). 8
9 Uk lad sterowania z warstw a regulacji sterowanie optymalne Optymalny stacjonarny regulator stanu R 1 B T K 1 korekta sterowania optymalnego Obiekt sterowania xt) sporadyczne fluktuacje parametru Przeprowadzimy analizȩ stabilności optymalnego stacjonarnego uk ladu regulacji stanu. W tym celu zdefiniujemy funkcjȩ Lapunowa tego uk ladu w postaci V x) = x T Kx. Ponieważ K <, wiȩc pierwszy i trzeci postulat definicji funkcji Lapunowa jest spe lniony. Celem weryfikacji drugiego postulatu funkcji Lapunowa obliczymy pochodn a tej funkcji wzd luż trajektorii stanu uk ladu V x) = ẋ T Kx x T Kẋ = x T ABR 1 B T K) T Kx x T KABR 1 B T K)x = x T KA A T K KBR 1 B T K KBR 1 B T K)x x T P KBR 1 B T K)x. Macierz P jest z za lożenia dodatnio określona, a wyrażenie x T KBR 1 B T Kx = z T R 1 z jest nieujemnie określone, gdyż macierz R 1 jest dodatnio określona. Jeśli spe lniony jest dodatkowy warunek x z = B T Kx, to ostatnie wyrażenie jest dodatnio określone nawet jeśli macierz P jest tylko nieujemnie określona. Wynika st ad, że optymalny uk lad regulacji stanu jest asymptotycznie stabilny tj. x ) =. Bȩdzie on również asymptotycznie 9
10 stabilny nawet jeśli macierz P jest tylko nieujemnie określona, jeśli wartości w lasne macierzy zamkniȩtego uk ladu regulacji maj a ujemne czȩści rzeczywiste. Przyk lad: Wyznaczyć optymalny regulator stanu jeśli mamy do czynienia z czȩstymi fluktuacjami parametru obiektu i problem LKSO jest postaci Gx, u) =.5x 2 t 1 ).5 t1 u 2 t)dt, ẋt) = xt) ut), x) = x. Zestawiamy dane dla równania Riccatiego A = 1, B = 1, Q = 1, P =, R = 1 i zapisujemy to równanie Kt) = 2Kt) K 2 t), Kt 1 ) = 1. Dla takiego szczególnego przypadku znane jest analityczne rozwi azanie równania Riccatiego Kt) = 2/1 e 2 t t1) ). Tak wiȩc równanie optymalnego niestacjonarnego ma postać u o t) = R 1 B T Kt)xt) u o t) = 2xt)/1 e 2 t t1) ). Przyk lad: Wyznaczyć optymalny regulator stanu jeśli mamy do czynienia ze sporadycznymi fluktuacjami parametru obiektu i problem LKSO jest postaci Gx, u) =.5 x 2 1t) u 2 t))dt ) ) 1 ẋt) = xt) ut), 1 x) = x. Zapisujemy dane dla zestawienia równania Riccatiego ) ) ) ) A = 1 k 1 k 2, B =, Q =, P =, R = 1, K = 1 1 k 2 k 3. 1
11 To macierzowe równanie jest równoważne trzem skalarnym równaniom postaci Zapisujemy macierzowe równanie Riccatiego ) ) ) ) k 1 k 2 1 k 1 k 2 k 2 k 3 1 k 2 k 3 ) ) k 1 k 2 ) ) ) k 1 k = k 2 k 3 1 k 2 k 3 które maj a rozwi azanie tj. k 2 2 = 1, k 1 k 2 k 3 =, 2k 2 k 2 3 =, k 1 = 2, k 2 = 1, k 3 = 2 K = Macierz K jest ujemnie określona, gdyż jej minory g lówne zmieniaj a znak pocz awszy od znaku ujemnego 1 = 1, 2 = 2 1 = 1. Aby sprawdzić, czy zamkniȩty uk lad regulacji stanu jest asymptotycznie stabilny, wyznaczamy równanie stanu tego uk ladu ẋt) = Ãxt), à = A BR 1 B T K) ) tj. ) 1 2 ẋt) = xt), 2 2 a zatem ) si à = s 1 1 s 2 i wartości w lasne uk ladu regulacji stanu s 1,2 = 1 ± j)/ 2 maj a ujemne czȩści rzeczywiste. Optymalny regulator stanu jest wiȩc asymptotycznie stabilny. 11
12 Przyk lad: Minimalizacja zużycia surowca w chemicznym procesie produkcyjnym. W przep lywowym reaktorze chemicznym zachodzi proces przemiany surowca A w produkt użyteczny B i w produkt uboczny C. Wyróżniamy zmienne stanu x 1 t) - stȩżenie surowca A w reaktorze, x 2 t) - stȩżenie produktu użytecznego B w reaktorze, u 1 t) - stȩżenia surowca A w strumieniu wejściowym reaktora, u 2 t) - natȩżenie przep lywu mieszaniny przez reaktor. Należy minimalizować średnie zużycie surowca Gx, u) = 1 τ uwzglȩdniaj ac równania stanu procesu τ u 1 t)u 2 t)dt ẋt) = u 1 t)u 2 t) u 2 t)x 1 t) 3x 2 1t) ax 1 t), ẋt) = u 2 t)x 2 t) 3x 2 1t), ograniczenia technologiczne w postaci zadanego średniego poziomu nieprzereagowanego surowca i średniego poziomu produkcji sk ladnika użytecznego 1 τ τ x i t)dt = 1/3, i = 1, 2, oraz ograniczenia chwilowe stanu i sterowania x i t), u i t) 2, i = 1, 2, przy czym a jest parametrem o nominalnej wartości a = 1, który jednak podlega czȩstym fluktuacjom. Zak ladamy, że proces należy prowadzić na optymalnym poziomie statycznym x o 1, x o 2, ū o 1, ū 2) = 1/3, 1/3, 1, 1). W zwi azku z potrzeb a niwelowania wp lywu fluktuacji parametru a na przebieg procesu formu lujemy problem LKSO stanowi acy podstawȩ syntezy optymalnego niestacjonarnego regulatora stanu: zminimalizować odchylenie procesu aktualnego od procesu optymalnego w skończonym czasie t 1 skorelowanym z czȩstości a fluktuacji parametru x 2 1t 1 ) x 2 2t 1 ) t1 x 2 1t) x 2 2t) u 2 1t) u 2 2t))dt 12
13 uwzglȩdniaj ac liniow a aproksymacjȩ równań stanu ẋt) = i zaburzenie stanu pocz atkowego ) xt) 1 2/3 1/3 ) ut) x) = x. Celem wyznaczenia optymalnego regulatora stanu należy rozwi azać nastȩpuj ace równanie różniczkowe Riccatiego ) ) ) k1 t) k2 t) k 1 t) k 2 t) 4 k 2 t) k3 t) k 2 t) k 3 t) 2 1 k 1 t) k 2 t) ) ) k 2 t) 1 2/3 1 k 3 t) 1/3 2/3 1/3 4 2 ) k 1 t) z zadanym macierzowym warunkiem końcowym 1 k 2 t) ) ) k 1 t 1 ) k 2 t 1 ) 1 =. k 2 t 1 ) k 3 t 1 ) 1 ) k 1 t) k 2 t) ) k 2 t) k 3 t) ) ) k 2 t) 1 = k 3 t) Macierzowe równanie różniczkowe Riccatiego z zadanym warunkiem końcowym rozwi azujemy za pomoc a metod numerycznych np. NDSolve w systemie Mathematica. przy użyciu procedury Jeśli fluktuacje parametru obiektu s a sporadyczne, to podstawȩ do syntezy optymalnego stacjonarnego regulatora stanu stanowi rozwi azanie nastȩpuj acego problemu LKSO: zminimalizować odchylenie procesu aktualnego od procesu optymalnego w nieskończonym czasie t 1 = x 2 1t) x 2 2t) u 2 1t) u 2 2t))dt uwzglȩdniaj ac liniow a aproksymacjȩ równań stanu ẋt) = i zaburzenie stanu pocz atkowego ) xt) 1 2/3 1/3 ) ut) x) = x. 13
14 Celem syntezy optymalnego stacjonarnego regulatora stanu należy rozwi azać nastȩpuj ace macierzowe algebraiczne równanie Riccatiego ) ) ) ) k 1 k k 1 k 2 k 2 k k 2 k 3 ) ) ) ) ) k 1 k 2 1 2/3 1 k 1 k 2 1 = k 2 k 3 1/3 2/3 1/3 k 2 k 3 1 To macierzowe równanie Riccatiego można również rozwi azywać przy użyciu metod numerycznych np. za pomoc a procedury NSolve w systemie Mathematica. 14
Sterowanie optymalne dla uk ladów nieliniowych. Zasada maksimum Pontriagina.
 Sterowanie optymalne dla uk ladów nieliniowych. Zasada maksimum Pontriagina. Podstawowy problem sterowania optymalnego dla uk ladów nieliniowych W podstawowym problemie sterowania optymalnego minimalizacji
Sterowanie optymalne dla uk ladów nieliniowych. Zasada maksimum Pontriagina. Podstawowy problem sterowania optymalnego dla uk ladów nieliniowych W podstawowym problemie sterowania optymalnego minimalizacji
Sterowalność liniowych uk ladów sterowania
 Sterowalność liniowych uk ladów sterowania W zadaniach sterowania docelowego należy przeprowadzić obiekt opisywany za pomoc a równania stanu z zadanego stanu pocz atkowego ẋ(t) = f(x(t), u(t), t), t [t,
Sterowalność liniowych uk ladów sterowania W zadaniach sterowania docelowego należy przeprowadzić obiekt opisywany za pomoc a równania stanu z zadanego stanu pocz atkowego ẋ(t) = f(x(t), u(t), t), t [t,
Mnożniki funkcyjne Lagrange a i funkcje kary w sterowaniu optymalnym
 Mnożniki funkcyjne Lagrange a i funkcje kary w sterowaniu optymalnym Sprowadzanie zadań sterowania optymalnego do zadań wariacyjnych metod a funkcji kary i mnożników Lagrange a - zadania sterowania optymalnego
Mnożniki funkcyjne Lagrange a i funkcje kary w sterowaniu optymalnym Sprowadzanie zadań sterowania optymalnego do zadań wariacyjnych metod a funkcji kary i mnożników Lagrange a - zadania sterowania optymalnego
Mnożniki funkcyjne Lagrange a i funkcje kary w sterowaniu optymalnym
 Mnożniki funkcyjne Lagrange a i funkcje kary w sterowaniu optymalnym Sprowadzanie zadań sterowania optymalnego do zadań wariacyjnych metod a funkcji kary i mnożników Lagrange a - zadania sterowania optymalnego
Mnożniki funkcyjne Lagrange a i funkcje kary w sterowaniu optymalnym Sprowadzanie zadań sterowania optymalnego do zadań wariacyjnych metod a funkcji kary i mnożników Lagrange a - zadania sterowania optymalnego
Liniowe uk lady sterowania.
 Liniowe uk lady sterowania Rozwi azywanie liniowych rownań stanu Uk lady z czasem ci ag lym Liniowe stacjonarne równania stanu Przyk lad: Uk lad sterowania tarcz a obrotow a prȩt sprȩżysty tarcza obrotowa
Liniowe uk lady sterowania Rozwi azywanie liniowych rownań stanu Uk lady z czasem ci ag lym Liniowe stacjonarne równania stanu Przyk lad: Uk lad sterowania tarcz a obrotow a prȩt sprȩżysty tarcza obrotowa
Sterowanie minimalnoczasowe dla uk ladów liniowych. Krzywe prze l aczeń.
 Sterowanie minimalnoczasowe dla uk ladów liniowych. Krzywe prze l aczeń. Sprowadzanie zadań sterowania optymalnego do zadań wariacyjnych metod a funkcji kary i mnożników Lagrange a - zadania sterowania
Sterowanie minimalnoczasowe dla uk ladów liniowych. Krzywe prze l aczeń. Sprowadzanie zadań sterowania optymalnego do zadań wariacyjnych metod a funkcji kary i mnożników Lagrange a - zadania sterowania
Zagadnienie Dualne Zadania Programowania Liniowego. Seminarium Szkoleniowe Edyta Mrówka
 Zagadnienie Dualne Zadania Programowania Liniowego Seminarium Szkoleniowe Edyta Mrówka Ogólne zagadnienie PL Znajdź taki wektor X = (x 1, x 2,..., x n ), który minimalizuje kombinacje liniow a przy ograniczeniach
Zagadnienie Dualne Zadania Programowania Liniowego Seminarium Szkoleniowe Edyta Mrówka Ogólne zagadnienie PL Znajdź taki wektor X = (x 1, x 2,..., x n ), który minimalizuje kombinacje liniow a przy ograniczeniach
liniowych uk ladów sterowania
 Sterowalność i obserwowalność liniowych uk ladów sterowania W zadaniach sterowania docelowego należy przeprowadzić obiekt opisywany za pomoc a równania stanu z zadanego stanu pocz atkowego ẋ(t) = f(x(t),
Sterowalność i obserwowalność liniowych uk ladów sterowania W zadaniach sterowania docelowego należy przeprowadzić obiekt opisywany za pomoc a równania stanu z zadanego stanu pocz atkowego ẋ(t) = f(x(t),
Sterowanie optymalne
 Sterowanie optymalne Sterowanie Procesami Ciągłymi 2017 Optymalizacja statyczna funkcji Funkcja celu/kryterialna/kosztów Ograniczenie Q(x) min x x = arg min Q(x) x x X, gdzie X zbiór rozwiązań dopuszczalnych
Sterowanie optymalne Sterowanie Procesami Ciągłymi 2017 Optymalizacja statyczna funkcji Funkcja celu/kryterialna/kosztów Ograniczenie Q(x) min x x = arg min Q(x) x x X, gdzie X zbiór rozwiązań dopuszczalnych
Pierwsze kolokwium z Matematyki I 4. listopada 2013 r. J. de Lucas
 Pierwsze kolokwium z Matematyki I 4. listopada 03 r. J. de Lucas Uwagi organizacyjne: Każde zadanie rozwi azujemy na osobnej kartce, opatrzonej imieniem i nazwiskiem w lasnym oraz osoby prowadz acej ćwiczenia,
Pierwsze kolokwium z Matematyki I 4. listopada 03 r. J. de Lucas Uwagi organizacyjne: Każde zadanie rozwi azujemy na osobnej kartce, opatrzonej imieniem i nazwiskiem w lasnym oraz osoby prowadz acej ćwiczenia,
POCHODNA KIERUNKOWA. DEFINICJA Jeśli istnieje granica lim. to granica ta nazywa siȩ pochodn a kierunkow a funkcji f(m) w kierunku osi l i oznaczamy
 POCHODNA KIERUNKOWA Pochodne cz astkowe funkcji f(m) = f(x, y, z) wzglȩdem x, wzglȩdem y i wzglȩdem z wyrażaj a prȩdkość zmiany funkcji w kierunku osi wspó lrzȩdnych; np. f x jest prȩdkości a zmiany funkcji
POCHODNA KIERUNKOWA Pochodne cz astkowe funkcji f(m) = f(x, y, z) wzglȩdem x, wzglȩdem y i wzglȩdem z wyrażaj a prȩdkość zmiany funkcji w kierunku osi wspó lrzȩdnych; np. f x jest prȩdkości a zmiany funkcji
Liczby zespolone, liniowa zależność i bazy Javier de Lucas. a d b c. ad bc
 Liczby zespolone, liniowa zależność i bazy Javier de Lucas Ćwiczenie. Dowieść, że jeśli µ := c d d c, to homografia h(x) = (ax+b)/(cx+d), a, b, c, d C, ad bc, odwzorowuje oś rzeczywist a R C na okr ag
Liczby zespolone, liniowa zależność i bazy Javier de Lucas Ćwiczenie. Dowieść, że jeśli µ := c d d c, to homografia h(x) = (ax+b)/(cx+d), a, b, c, d C, ad bc, odwzorowuje oś rzeczywist a R C na okr ag
Wprowadzenie do teorii sterowania
 Wprowadzenie do teorii sterowania Literatura podstawowa T. Kaczorek i inni, Podstawy teorii sterowania, WNT, Warszawa 2005. T. Kaczorek, Teoria sterowania i systemów, PWN, Warszawa 1996. T. Kaczorek, Teoria
Wprowadzenie do teorii sterowania Literatura podstawowa T. Kaczorek i inni, Podstawy teorii sterowania, WNT, Warszawa 2005. T. Kaczorek, Teoria sterowania i systemów, PWN, Warszawa 1996. T. Kaczorek, Teoria
Zasada optymalności Bellmana. Uogólniony optymalny regulator stanu.
 Zasada optymalności Bellmana. Uogólniony optymalny regulator stanu. Podstawowy problem sterowania optymalnego dla uk ladów nieliniowych z czasem ci ag lym W podstawowym problemie sterowania optymalnego
Zasada optymalności Bellmana. Uogólniony optymalny regulator stanu. Podstawowy problem sterowania optymalnego dla uk ladów nieliniowych z czasem ci ag lym W podstawowym problemie sterowania optymalnego
Suma i przeciȩcie podprzestrzeni, przestrzeń ilorazowa Javier de Lucas
 Suma i przeciȩcie podprzestrzeni, przestrzeń ilorazowa Javier de Lucas Ćwiczenie 1. Dowieść, że jeśli U i V s a podprzestrzeniami n-wymiarowej przestrzeni wektorowej oraz dim U = r i dim V = s, to max(0,
Suma i przeciȩcie podprzestrzeni, przestrzeń ilorazowa Javier de Lucas Ćwiczenie 1. Dowieść, że jeśli U i V s a podprzestrzeniami n-wymiarowej przestrzeni wektorowej oraz dim U = r i dim V = s, to max(0,
Stabilność liniowych uk ladów sterowania
 Stabilność liniowych uk ladów sterowania Stabilność uk ladów z czasem ci ag lym W teorii stabilności uk ladów sterowania badamy wrażliwość trajektorii stanu na zaburzenia stanu pocz atkowego. Interesuje
Stabilność liniowych uk ladów sterowania Stabilność uk ladów z czasem ci ag lym W teorii stabilności uk ladów sterowania badamy wrażliwość trajektorii stanu na zaburzenia stanu pocz atkowego. Interesuje
Równania różniczkowe cz astkowe rzȩdu pierwszego
 Równania różniczkowe cz astkowe rzȩd pierwszego 1 Równania liniowe jednorodne Rozważmy równanie a 1 ( 1,..., n ) 1 +... + a n ( 1,..., n ) n = 0, (1) gdzie a i, i = 1,..., n s a dane, a fnkcja = ( 1,...,
Równania różniczkowe cz astkowe rzȩd pierwszego 1 Równania liniowe jednorodne Rozważmy równanie a 1 ( 1,..., n ) 1 +... + a n ( 1,..., n ) n = 0, (1) gdzie a i, i = 1,..., n s a dane, a fnkcja = ( 1,...,
y 1 y 2 = f 2 (t, y 1, y 2,..., y n )... y n = f n (t, y 1, y 2,..., y n ) f 1 (t, y 1, y 2,..., y n ) y = f(t, y),, f(t, y) =
 Uk lady równań różniczkowych Pojȩcia wsȩpne Uk ladem równań różniczkowych nazywamy uk lad posaci y = f (, y, y 2,, y n ) y 2 = f 2 (, y, y 2,, y n ) y n = f n (, y, y 2,, y n ) () funkcje f j, j =, 2,,
Uk lady równań różniczkowych Pojȩcia wsȩpne Uk ladem równań różniczkowych nazywamy uk lad posaci y = f (, y, y 2,, y n ) y 2 = f 2 (, y, y 2,, y n ) y n = f n (, y, y 2,, y n ) () funkcje f j, j =, 2,,
Wyk lad 14 Formy kwadratowe I
 Wyk lad 14 Formy kwadratowe I Wielomian n-zmiennych x 1,, x n postaci n a ij x i x j, (1) gdzie a ij R oraz a ij = a ji dla wszystkich i, j = 1,, n nazywamy forma kwadratowa n-zmiennych Forme (1) można
Wyk lad 14 Formy kwadratowe I Wielomian n-zmiennych x 1,, x n postaci n a ij x i x j, (1) gdzie a ij R oraz a ij = a ji dla wszystkich i, j = 1,, n nazywamy forma kwadratowa n-zmiennych Forme (1) można
Funkcje wielu zmiennych
 Funkcje wielu zmiennych 13 Zbiory w przestrzeni Definicja Przestrzeni a trójwymiarow a (przestrzeni a) nazywamy zbiór wszystkich trójek uporz adkowanych (x y z) gdzie x y z R. Przestrzeń tȩ oznaczamy symbolem
Funkcje wielu zmiennych 13 Zbiory w przestrzeni Definicja Przestrzeni a trójwymiarow a (przestrzeni a) nazywamy zbiór wszystkich trójek uporz adkowanych (x y z) gdzie x y z R. Przestrzeń tȩ oznaczamy symbolem
Elementy analizy funkcjonalnej PRZESTRZENIE LINIOWE
 Elementy analizy funkcjonalnej PRZESTRZENIE LINIOWE Niech K = R lub K = C oraz X - dowolny zbiór. Określmy dwa dzia lania: dodawanie + : X X X i mnożenie przez liczbȩ : K X X, spe lniaj ace nastȩpuj ace
Elementy analizy funkcjonalnej PRZESTRZENIE LINIOWE Niech K = R lub K = C oraz X - dowolny zbiór. Określmy dwa dzia lania: dodawanie + : X X X i mnożenie przez liczbȩ : K X X, spe lniaj ace nastȩpuj ace
Projektowanie uk ladów sterowania z wykorzystaniem ich postaci kanonicznych
 Projektowanie uk ladów sterowania z wykorzystaniem ich postaci kanonicznych Niech bȩdzie dany uk lad sterowania taki, że nie wszystkie jego zmienne stanu s a bezpośrednio dostȩpne (mierzalne. Uk lad pozwalaj
Projektowanie uk ladów sterowania z wykorzystaniem ich postaci kanonicznych Niech bȩdzie dany uk lad sterowania taki, że nie wszystkie jego zmienne stanu s a bezpośrednio dostȩpne (mierzalne. Uk lad pozwalaj
Metoda Simplex bez użycia tabel simplex 29 kwietnia 2010
 R. Rȩbowski 1 WPROWADZENIE Metoda Simplex bez użycia tabel simplex 29 kwietnia 2010 1 Wprowadzenie Powszechnie uważa siȩ, że metoda simplex, jako uniwersalny algorytm pozwalaj acyznaleźć rozwi azanie optymalne
R. Rȩbowski 1 WPROWADZENIE Metoda Simplex bez użycia tabel simplex 29 kwietnia 2010 1 Wprowadzenie Powszechnie uważa siȩ, że metoda simplex, jako uniwersalny algorytm pozwalaj acyznaleźć rozwi azanie optymalne
Funkcje wielu zmiennych
 Funkcje wielu zmiennych 8 Pochodna kierunkowa funkcji Definicja Niech funkcja f określona bȩdzie w otoczeniu punktu P 0 = (x 0, y 0 ) oraz niech v = [v x, v y ] bȩdzie wektorem. Pochodn a kierunkow a funkcji
Funkcje wielu zmiennych 8 Pochodna kierunkowa funkcji Definicja Niech funkcja f określona bȩdzie w otoczeniu punktu P 0 = (x 0, y 0 ) oraz niech v = [v x, v y ] bȩdzie wektorem. Pochodn a kierunkow a funkcji
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań.
 III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
CHEMIA KWANTOWA MONIKA MUSIA L. Ćwiczenia. mm
 CHEMIA KWANTOWA MONIKA MUSIA L Ćwiczenia METODY PRZYBLIŻONE ROZWIA ZYWANIA RÓWNANIA SCHRÖDINGERA METODA WARIACYJNA metoda wariacyjna ĤΨ n = E n Ψ n Ψ n ortonormalne Szukamy rozwi azań dla stanu podstawowego,
CHEMIA KWANTOWA MONIKA MUSIA L Ćwiczenia METODY PRZYBLIŻONE ROZWIA ZYWANIA RÓWNANIA SCHRÖDINGERA METODA WARIACYJNA metoda wariacyjna ĤΨ n = E n Ψ n Ψ n ortonormalne Szukamy rozwi azań dla stanu podstawowego,
Ekonomia matematyczna i dynamiczna optymalizacja
 Ekonomia matematyczna i dynamiczna optymalizacja Ramy wyk ladu i podstawowe narz edzia matematyczne SGH Semestr letni 2012-13 Uk lady dynamiczne Rozwiazanie modelu dynamicznego bardzo czesto można zapisać
Ekonomia matematyczna i dynamiczna optymalizacja Ramy wyk ladu i podstawowe narz edzia matematyczne SGH Semestr letni 2012-13 Uk lady dynamiczne Rozwiazanie modelu dynamicznego bardzo czesto można zapisać
Wprowadzenie do metod sterowania optymalnego
 Wprowadzenie do metod sterowania optymalnego Pojȩcie procesu sterowania obejmuje zestaw trajektorii stanu i sterowania (x, u) X U, gdzie X jest przestrzeni a trajektorii stanu, a U jest przestrzeni a sterowania.
Wprowadzenie do metod sterowania optymalnego Pojȩcie procesu sterowania obejmuje zestaw trajektorii stanu i sterowania (x, u) X U, gdzie X jest przestrzeni a trajektorii stanu, a U jest przestrzeni a sterowania.
Niesimpleksowe metody rozwia zywania zadań PL. Seminarium Szkoleniowe Edyta Mrówka
 Niesimpleksowe metody rozwia zywania zadań PL Seminarium Szkoleniowe Metoda Simplex: wady i zalety Algorytm SIMPLEX jest szeroko znany i stosowany do rozwi azywania zadań programowania liniowego w praktyce.
Niesimpleksowe metody rozwia zywania zadań PL Seminarium Szkoleniowe Metoda Simplex: wady i zalety Algorytm SIMPLEX jest szeroko znany i stosowany do rozwi azywania zadań programowania liniowego w praktyce.
Po wprowadzeniu zmiennych uzupe lniaj acych otrzymamy równoważny mu problem w postaci kanonicznej:
 ROZDZIA L Metoda sympleksowa Motto: Matematyka nie może wype lnić życia ale jej nieznajomość już niejednemu je wype lni la H Steinhaus Tablica sympleksowa Rozważmy ZPL w postaci klasycznej maksymalizować
ROZDZIA L Metoda sympleksowa Motto: Matematyka nie może wype lnić życia ale jej nieznajomość już niejednemu je wype lni la H Steinhaus Tablica sympleksowa Rozważmy ZPL w postaci klasycznej maksymalizować
Formy kwadratowe. Rozdział 10
 Rozdział 10 Formy kwadratowe Rozważmy rzeczywistą macierz symetryczną A R n n Definicja 101 Funkcję h : R n R postaci h (x) = x T Ax (101) nazywamy formą kwadratową Macierz symetryczną A występującą w
Rozdział 10 Formy kwadratowe Rozważmy rzeczywistą macierz symetryczną A R n n Definicja 101 Funkcję h : R n R postaci h (x) = x T Ax (101) nazywamy formą kwadratową Macierz symetryczną A występującą w
Inżynieria Systemów Dynamicznych (4)
 Inżynieria Systemów Dynamicznych (4) liniowych (układów) Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 2 WE OKREŚLO 3 ASYMPTO 4 DYNAMICZ
Inżynieria Systemów Dynamicznych (4) liniowych (układów) Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 2 WE OKREŚLO 3 ASYMPTO 4 DYNAMICZ
Dyskretne modele populacji
 Dyskretne modele populacji Micha l Machtel Adam Soboczyński 19 stycznia 2007 Typeset by FoilTEX Dyskretne modele populacji [1] Wst ep Dyskretny opis modelu matematycznego jest dobry dla populacji w których
Dyskretne modele populacji Micha l Machtel Adam Soboczyński 19 stycznia 2007 Typeset by FoilTEX Dyskretne modele populacji [1] Wst ep Dyskretny opis modelu matematycznego jest dobry dla populacji w których
Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych
 Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych [ ] e Zadanie 1 Pokazać, że X(t) = 2t cos t sin t e 2t jest specjalną macierzą fundamentalną w sin t cos t [ 2 cos chwili τ = 0 układu
Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych [ ] e Zadanie 1 Pokazać, że X(t) = 2t cos t sin t e 2t jest specjalną macierzą fundamentalną w sin t cos t [ 2 cos chwili τ = 0 układu
ANALIZA II 15 marca 2014 Semestr letni. Ćwiczenie 1. Czy dan a funkcjȩ da siȩ dookreślić w punkcie (0, 0) tak, żeby otrzymana funkcja by la ci ag la?
 Ci ag lość i norma Ćwiczenie. Czy dan a funkcjȩ da siȩ dookreślić w punkcie (0, 0) tak, żeby otrzymana funkcja by la ci ag la? f (x, y) = x2 y 2 x 2 + y 2, f 2(x, y) = x2 y x 2 + y 2 f 3 (x, y) = x2 y
Ci ag lość i norma Ćwiczenie. Czy dan a funkcjȩ da siȩ dookreślić w punkcie (0, 0) tak, żeby otrzymana funkcja by la ci ag la? f (x, y) = x2 y 2 x 2 + y 2, f 2(x, y) = x2 y x 2 + y 2 f 3 (x, y) = x2 y
Stabilność II Metody Lapunowa badania stabilności
 Metody Lapunowa badania stabilności Interesuje nas w sposób szczególny system: Wprowadzamy dla niego pojęcia: - stabilności wewnętrznej - odnosi się do zachowania się systemu przy zerowym wejściu, czyli
Metody Lapunowa badania stabilności Interesuje nas w sposób szczególny system: Wprowadzamy dla niego pojęcia: - stabilności wewnętrznej - odnosi się do zachowania się systemu przy zerowym wejściu, czyli
Asymptota pozioma: oṡ x, gdy y = 0 Asymptota pionowa: oṡ y, gdy x = 0. Hyperbola 1 x
 1 SZKO LA PODSTAWOWA HELIANTUS 02-892 WARSZAWA ul. BAŻANCIA 16 Asymptota pozioma: oṡ x, gdy y = 0 Asymptota pionowa: oṡ y, gdy x = 0 2 1 0 3 1 2 x Hyperbola 1 x FUNKCJE ELEMENTARNE WYMIERNE POTȨGOWE LOGARYTMICZNE
1 SZKO LA PODSTAWOWA HELIANTUS 02-892 WARSZAWA ul. BAŻANCIA 16 Asymptota pozioma: oṡ x, gdy y = 0 Asymptota pionowa: oṡ y, gdy x = 0 2 1 0 3 1 2 x Hyperbola 1 x FUNKCJE ELEMENTARNE WYMIERNE POTȨGOWE LOGARYTMICZNE
Przestrzenie wektorowe, liniowa niezależność wektorów, bazy przestrzeni wektorowych
 Grupa, cia lo Zadanie 1. Jakie w lasności w zbiorze liczb naturalnych, ca lkowitych, wymiernych, rzeczywistych maj dzia lania a b = a b, a b = a 2 + b 2, a b = a+b, a b = b. 2 Zadanie 2. Pokazać, że (R
Grupa, cia lo Zadanie 1. Jakie w lasności w zbiorze liczb naturalnych, ca lkowitych, wymiernych, rzeczywistych maj dzia lania a b = a b, a b = a 2 + b 2, a b = a+b, a b = b. 2 Zadanie 2. Pokazać, że (R
Wyk lad 9 Przekszta lcenia liniowe i ich zastosowania
 Wyk lad 9 Przekszta lcenia liniowe i ich zastosowania 1 Przekszta lcenia liniowe i ich w lasności Definicja 9.1. Niech V i W bed przestrzeniami liniowymi. Przekszta lcenie f : V W spe lniajace warunki:
Wyk lad 9 Przekszta lcenia liniowe i ich zastosowania 1 Przekszta lcenia liniowe i ich w lasności Definicja 9.1. Niech V i W bed przestrzeniami liniowymi. Przekszta lcenie f : V W spe lniajace warunki:
RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE. Marta Zelmańska
 RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE Marta Zelmańska Toruń 009 1 Rozdział 1 Wstęp Definicja 1. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie: F (t, x, x, x,..., x (n) ) = 0 (1.1) Rozwiązaniem równania
RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE Marta Zelmańska Toruń 009 1 Rozdział 1 Wstęp Definicja 1. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie: F (t, x, x, x,..., x (n) ) = 0 (1.1) Rozwiązaniem równania
ci agi i szeregi funkcji Javier de Lucas Ćwiczenie 1. Zbadać zbieżność (punktow a i jednostajn a) ci agu funkcji nx 2 + x
 ci agi i szeregi funkcji Javier de Lucas Ćwiczenie 1 Zbadać zbieżność (punktow a i jednostajn a) ci agu funkcji f n : [, [ x nx + x nx + 1, Rozwi azanie: Mówi siȩ, że ci ag funkcji f n zd aży punktowo
ci agi i szeregi funkcji Javier de Lucas Ćwiczenie 1 Zbadać zbieżność (punktow a i jednostajn a) ci agu funkcji f n : [, [ x nx + x nx + 1, Rozwi azanie: Mówi siȩ, że ci ag funkcji f n zd aży punktowo
SZKO LA PODSTAWOWA HELIANTUS WARSZAWA ul. BAŻANCIA 16. Hyperbola 1 x FUNKCJE ELEMENTARNE WYMIERNE POTȨGOWE LOGARYTMICZNE.
 1 SZKO LA PODSTAWOWA HELIANTUS 0-89 WARSZAWA ul. BAŻANCIA 16 1 0 3 1 x Hyperbola 1 x FUNKCJE ELEMENTARNE WYMIERNE POTȨGOWE LOGARYTMICZNE Prof. dr. Tadeusz STYŠ Warszawa 018 1 1 Projekt dziesi aty Contents
1 SZKO LA PODSTAWOWA HELIANTUS 0-89 WARSZAWA ul. BAŻANCIA 16 1 0 3 1 x Hyperbola 1 x FUNKCJE ELEMENTARNE WYMIERNE POTȨGOWE LOGARYTMICZNE Prof. dr. Tadeusz STYŠ Warszawa 018 1 1 Projekt dziesi aty Contents
Pierwiastki arytmetyczne n a
 Chapter 1 Pierwiastki arytmetyczne n a Operacja wyci aganie pierwiastka stopnia n z liczby a jest odwrotn a operacj a do potȩgowania, jeżeli operacja odwrotna jest wykonalna w liczbach rzeczywistych. Zacznijmy
Chapter 1 Pierwiastki arytmetyczne n a Operacja wyci aganie pierwiastka stopnia n z liczby a jest odwrotn a operacj a do potȩgowania, jeżeli operacja odwrotna jest wykonalna w liczbach rzeczywistych. Zacznijmy
Metody kierunków poprawy dla nieliniowych problemów sterowania optymalnego
 Metody kierunków poprawy dla nieliniowych problemów sterowania optymalnego Problem optymalnego sterowania procesem dynamicznym może polegać na polega na minimalizacji wskaźnika jakości obejmuj acego koszty
Metody kierunków poprawy dla nieliniowych problemów sterowania optymalnego Problem optymalnego sterowania procesem dynamicznym może polegać na polega na minimalizacji wskaźnika jakości obejmuj acego koszty
Wprowadzenie z dynamicznej optymalizacji
 Wprowadzenie z dynamicznej optymalizacji Lukasz Woźny 29 kwietnia 2007 Spis treści 1 Optymalizacja statyczna a optymalizacja dynamiczna 2 1.1 Ekstrema lokalne funkcji wielu zmiennych - statyka...... 2
Wprowadzenie z dynamicznej optymalizacji Lukasz Woźny 29 kwietnia 2007 Spis treści 1 Optymalizacja statyczna a optymalizacja dynamiczna 2 1.1 Ekstrema lokalne funkcji wielu zmiennych - statyka...... 2
Metody Numeryczne Wykład 4 Wykład 5. Interpolacja wielomianowa
 Sformułowanie zadania interpolacji Metody Numeryczne Wykład 4 Wykład 5 Interpolacja wielomianowa Niech D R i niech F bȩdzie pewnym zbiorem funkcji f : D R. Niech x 0, x 1,..., x n bȩdzie ustalonym zbiorem
Sformułowanie zadania interpolacji Metody Numeryczne Wykład 4 Wykład 5 Interpolacja wielomianowa Niech D R i niech F bȩdzie pewnym zbiorem funkcji f : D R. Niech x 0, x 1,..., x n bȩdzie ustalonym zbiorem
Wyk lad 7 Baza i wymiar przestrzeni liniowej
 Wyk lad 7 Baza i wymiar przestrzeni liniowej 1 Baza przestrzeni liniowej Niech V bedzie przestrzenia liniowa. Powiemy, że podzbiór X V jest maksymalnym zbiorem liniowo niezależnym, jeśli X jest zbiorem
Wyk lad 7 Baza i wymiar przestrzeni liniowej 1 Baza przestrzeni liniowej Niech V bedzie przestrzenia liniowa. Powiemy, że podzbiór X V jest maksymalnym zbiorem liniowo niezależnym, jeśli X jest zbiorem
Wprowadzenie do teorii sterowania. Procesy sterowania o parametrach skupionych.
 Dr hab. inż. Krystyn Styczeń, prof. PWr Wprowadzenie do teorii sterowania. Procesy sterowania o parametrach skupionych. http://staff.iiar.pwr.wroc.pl/krystyn.styczen/ http://krystyn.styczen.staff.iiar.pwr.wroc.pl/
Dr hab. inż. Krystyn Styczeń, prof. PWr Wprowadzenie do teorii sterowania. Procesy sterowania o parametrach skupionych. http://staff.iiar.pwr.wroc.pl/krystyn.styczen/ http://krystyn.styczen.staff.iiar.pwr.wroc.pl/
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa.
 VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
Wyk lad 11 1 Wektory i wartości w lasne
 Wyk lad 11 Wektory i wartości w lasne 1 Wektory i wartości w lasne Niech V bedzie przestrzenia liniowa nad cia lem K Każde przekszta lcenie liniowe f : V V nazywamy endomorfizmem liniowym przestrzeni V
Wyk lad 11 Wektory i wartości w lasne 1 Wektory i wartości w lasne Niech V bedzie przestrzenia liniowa nad cia lem K Każde przekszta lcenie liniowe f : V V nazywamy endomorfizmem liniowym przestrzeni V
Podstawy Automatyki. Wykład 2 - podstawy matematyczne. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 2 - podstawy matematyczne Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe, n.p. turbulencje, wiele
Wykład 2 - podstawy matematyczne Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe, n.p. turbulencje, wiele
Metoda Karusha-Kuhna-Tuckera
 Badania operacyjne i teoria optymalizacji Poznań, 2015/2016 Plan 1 Sformułowanie problemu 2 3 Warunki ortogonalności 4 Warunki Karusha-Kuhna-Tuckera 5 Twierdzenia Karusha-Kuhna-Tuckera 6 Ograniczenia w
Badania operacyjne i teoria optymalizacji Poznań, 2015/2016 Plan 1 Sformułowanie problemu 2 3 Warunki ortogonalności 4 Warunki Karusha-Kuhna-Tuckera 5 Twierdzenia Karusha-Kuhna-Tuckera 6 Ograniczenia w
Tematyka egzaminu z Podstaw sterowania
 Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
Tematyka egzaminu z Podstaw sterowania Rafał Trójniak 6 września 2009 Spis treści 1 Rozwiązane tematy 1 1.1 Napisać równanie różniczkowe dla zbiornika z odpływem grawitacyjnym...............................
gdy wielomian p(x) jest podzielny bez reszty przez trójmian kwadratowy x rx q. W takim przypadku (5.10)
 5.5. Wyznaczanie zer wielomianów 79 gdy wielomian p(x) jest podzielny bez reszty przez trójmian kwadratowy x rx q. W takim przypadku (5.10) gdzie stopieñ wielomianu p 1(x) jest mniejszy lub równy n, przy
5.5. Wyznaczanie zer wielomianów 79 gdy wielomian p(x) jest podzielny bez reszty przez trójmian kwadratowy x rx q. W takim przypadku (5.10) gdzie stopieñ wielomianu p 1(x) jest mniejszy lub równy n, przy
Dyskretne modele populacji
 Dyskretne modele populacji Micha l Machtel Adam Soboczyński 17 stycznia 2007 Typeset by FoilTEX Dyskretne modele populacji [1] Wst ep Dyskretny opis modelu matematycznego jest dobry dla populacji w których
Dyskretne modele populacji Micha l Machtel Adam Soboczyński 17 stycznia 2007 Typeset by FoilTEX Dyskretne modele populacji [1] Wst ep Dyskretny opis modelu matematycznego jest dobry dla populacji w których
CHEMIA KWANTOWA MONIKA MUSIA L METODA HÜCKLA. Ćwiczenia. http://zcht.mfc.us.edu.pl/ mm
 CHEMIA KWANTOWA MONIKA MUSIA L METODA HÜCKLA Ćwiczenia Zwi azki organiczne zawieraj ace uk lady π-elektronowe Sprzȩżony uk lad wi azań podwójnych: -C=C-C=C-C=C-C=C- Skumulowany uk lad wi azań podwójnych:
CHEMIA KWANTOWA MONIKA MUSIA L METODA HÜCKLA Ćwiczenia Zwi azki organiczne zawieraj ace uk lady π-elektronowe Sprzȩżony uk lad wi azań podwójnych: -C=C-C=C-C=C-C=C- Skumulowany uk lad wi azań podwójnych:
Uogólnione modele uk ladów sterowania
 Uogólnione modele uk ladów sterowania Różniczkowo-algebraiczne modele uk ladów sterowania Analiza w lasności wielu uk ladów sterowania wymaga uogólnienia modeli procesów zachodz acych w tych uk ladach.
Uogólnione modele uk ladów sterowania Różniczkowo-algebraiczne modele uk ladów sterowania Analiza w lasności wielu uk ladów sterowania wymaga uogólnienia modeli procesów zachodz acych w tych uk ladach.
Zestaw nr 7 Ekstremum funkcji jednej zmiennej. Punkty przegiȩcia wykresu. Asymptoty
 Zestaw nr 7 Ekstremum funkcji jednej zmiennej. Punkty przegiȩcia wykresu. Asymptoty November 20, 2009 Przyk ladowe zadania z rozwi azaniami Zadanie 1. Znajdź równanie asymptot funkcji f jeśli: a) f(x)
Zestaw nr 7 Ekstremum funkcji jednej zmiennej. Punkty przegiȩcia wykresu. Asymptoty November 20, 2009 Przyk ladowe zadania z rozwi azaniami Zadanie 1. Znajdź równanie asymptot funkcji f jeśli: a) f(x)
Metody rzutowania i funkcji barierowych dla problemów sterowania optymalnego
 Metody rzutowania i funkcji barierowych dla problemów sterowania optymalnego Problem optymalnego sterowania procesem dynamicznym z ograniczeniami zasobowymi może polegać na polega na minimalizacji wskaźnika
Metody rzutowania i funkcji barierowych dla problemów sterowania optymalnego Problem optymalnego sterowania procesem dynamicznym z ograniczeniami zasobowymi może polegać na polega na minimalizacji wskaźnika
PROGRAMOWANIE KWADRATOWE
 PROGRAMOWANIE KWADRATOWE Programowanie kwadratowe Zadanie programowania kwadratowego: Funkcja celu lub/i co najmniej jedno z ograniczeń jest funkcją kwadratową. 2 Programowanie kwadratowe Nie ma uniwersalnej
PROGRAMOWANIE KWADRATOWE Programowanie kwadratowe Zadanie programowania kwadratowego: Funkcja celu lub/i co najmniej jedno z ograniczeń jest funkcją kwadratową. 2 Programowanie kwadratowe Nie ma uniwersalnej
Wykład z modelowania matematycznego.
 Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Rodzina funkcji
Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Rodzina funkcji
KOLOKWIUM Z ALGEBRY I R
 Instrucje: Każde zadanie jest za 4 puntów. Rozwi azanie ażdego zadania musi znajdować siȩ na osobnej artce oraz być napisane starannie i czytelnie. W nag lówu ażdego rozwi azania musz a znajdować siȩ dane
Instrucje: Każde zadanie jest za 4 puntów. Rozwi azanie ażdego zadania musi znajdować siȩ na osobnej artce oraz być napisane starannie i czytelnie. W nag lówu ażdego rozwi azania musz a znajdować siȩ dane
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Modelowanie
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Modelowanie Zad Wyznacz transformaty Laplace a poniższych funkcji, korzystając z tabeli transformat: a) 8 3e 3t b) 4 sin 5t 2e 5t + 5 c) e5t e
Funkcje wielu zmiennych
 Funkcje wielu zmiennych Zbiory na p laszczyźnie Przestrzeni a dwuwymiarow a (p laszczyzn a) nazywamy zbiór wszystkich par uporz adkowanych (x, y), gdzie x, y R. Przestrzeń tȩ oznaczamy symbolem R 2 : R
Funkcje wielu zmiennych Zbiory na p laszczyźnie Przestrzeni a dwuwymiarow a (p laszczyzn a) nazywamy zbiór wszystkich par uporz adkowanych (x, y), gdzie x, y R. Przestrzeń tȩ oznaczamy symbolem R 2 : R
Wprowadzenie do teorii sterowania. Procesy o parametrach skupionych
 Politechnika Wroc lawska Wydzia l Elektroniki Katedra K8 Prof. dr hab. inż. Krystyn Styczeń http://staff.iiar.pwr.wroc.pl/krystyn.styczen/ Wprowadzenie do teorii sterowania. Procesy o parametrach skupionych
Politechnika Wroc lawska Wydzia l Elektroniki Katedra K8 Prof. dr hab. inż. Krystyn Styczeń http://staff.iiar.pwr.wroc.pl/krystyn.styczen/ Wprowadzenie do teorii sterowania. Procesy o parametrach skupionych
teoria i przykłady zastosowań
 : teoria i przykłady zastosowań Katedra Sterowania i Pomiarów Zachodniopomorski Uniwersytet Technologiczny w Szczecinie e-mail: emirsaj@zut.edu.pl Zielona Góra, 22 listopada 21 Spis treści 1 O jakie równanie
: teoria i przykłady zastosowań Katedra Sterowania i Pomiarów Zachodniopomorski Uniwersytet Technologiczny w Szczecinie e-mail: emirsaj@zut.edu.pl Zielona Góra, 22 listopada 21 Spis treści 1 O jakie równanie
Programowanie celowe #1
 Programowanie celowe #1 Problem programowania celowego (PC) jest przykładem problemu programowania matematycznego nieliniowego, który można skutecznie zlinearyzować, tzn. zapisać (i rozwiązać) jako problem
Programowanie celowe #1 Problem programowania celowego (PC) jest przykładem problemu programowania matematycznego nieliniowego, który można skutecznie zlinearyzować, tzn. zapisać (i rozwiązać) jako problem
Rozdzia l 11. Przestrzenie Euklidesowe Definicja, iloczyn skalarny i norma. iloczynem skalarnym.
 Rozdzia l 11 Przestrzenie Euklidesowe 11.1 Definicja, iloczyn skalarny i norma Definicja 11.1 Przestrzenia Euklidesowa nazywamy par e { X K,ϕ }, gdzie X K jest przestrzenia liniowa nad K, a ϕ forma dwuliniowa
Rozdzia l 11 Przestrzenie Euklidesowe 11.1 Definicja, iloczyn skalarny i norma Definicja 11.1 Przestrzenia Euklidesowa nazywamy par e { X K,ϕ }, gdzie X K jest przestrzenia liniowa nad K, a ϕ forma dwuliniowa
Wyk lad 5 W lasności wyznaczników. Macierz odwrotna
 Wyk lad 5 W lasności wyznaczników Macierz odwrotna 1 Operacje elementarne na macierzach Bardzo ważne znaczenie w algebrze liniowej odgrywaja tzw operacje elementarne na wierszach lub kolumnach macierzy
Wyk lad 5 W lasności wyznaczników Macierz odwrotna 1 Operacje elementarne na macierzach Bardzo ważne znaczenie w algebrze liniowej odgrywaja tzw operacje elementarne na wierszach lub kolumnach macierzy
Wyk lad 9 Baza i wymiar przestrzeni liniowej
 Wyk lad 9 Baza i wymiar przestrzeni liniowej 1 Operacje elementarne na uk ladach wektorów Niech α 1,..., α n bed dowolnymi wektorami przestrzeni liniowej V nad cia lem K. Wyróżniamy nastepuj ace operacje
Wyk lad 9 Baza i wymiar przestrzeni liniowej 1 Operacje elementarne na uk ladach wektorów Niech α 1,..., α n bed dowolnymi wektorami przestrzeni liniowej V nad cia lem K. Wyróżniamy nastepuj ace operacje
Przestrzenie wektorowe, liniowa niezależność Javier de Lucas
 Przestrzenie wektorowe, liniowa niezależność Javier de Lucas Ćwiczenie 1. W literaturze można znaleźć pojȩcia przestrzeni liniowej i przestrzeni wektorowej. Obie rzeczy maj a tak a sam a znaczenie. Nastȩpuj
Przestrzenie wektorowe, liniowa niezależność Javier de Lucas Ćwiczenie 1. W literaturze można znaleźć pojȩcia przestrzeni liniowej i przestrzeni wektorowej. Obie rzeczy maj a tak a sam a znaczenie. Nastȩpuj
1. Podstawowe pojęcia
 1. Podstawowe pojęcia Sterowanie optymalne obiektu polega na znajdowaniu najkorzystniejszej decyzji dotyczącej zamierzonego wpływu na obiekt przy zadanych ograniczeniach. Niech dany jest obiekt opisany
1. Podstawowe pojęcia Sterowanie optymalne obiektu polega na znajdowaniu najkorzystniejszej decyzji dotyczącej zamierzonego wpływu na obiekt przy zadanych ograniczeniach. Niech dany jest obiekt opisany
Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t)
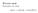 Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Figure 1: Aproksymacja drzewem dwumianowym Wycena opcji Dynamika cen akcji:
Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Figure 1: Aproksymacja drzewem dwumianowym Wycena opcji Dynamika cen akcji:
UKŁADY ALGEBRAICZNYCH RÓWNAŃ LINIOWYCH
 Transport, studia I stopnia rok akademicki 2011/2012 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Uwagi wstępne Układ liniowych równań algebraicznych można
Transport, studia I stopnia rok akademicki 2011/2012 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Uwagi wstępne Układ liniowych równań algebraicznych można
Zadania o liczbach zespolonych
 Zadania o liczbach zespolonych Zadanie 1. Znaleźć takie liczby rzeczywiste a i b, aby zachodzi ly równości: a) a( + i) + b(4 i) 6 i, b) a( + i) + b( + i) 8i, c) a(4 i) + b(1 + i) 7 1i, ( ) a d) i + b +i
Zadania o liczbach zespolonych Zadanie 1. Znaleźć takie liczby rzeczywiste a i b, aby zachodzi ly równości: a) a( + i) + b(4 i) 6 i, b) a( + i) + b( + i) 8i, c) a(4 i) + b(1 + i) 7 1i, ( ) a d) i + b +i
Zestaw nr 6 Pochodna funkcji jednej zmiennej. Styczna do krzywej. Elastyczność funkcji. Regu la de l Hospitala
 Zestaw nr 6 Pochodna funkcji jednej zmiennej. Styczna do krzywej. Elastyczność funkcji. Regu la de l Hospitala November 12, 2009 Przyk ladowe zadania z rozwi azaniami Zadanie 1. Oblicz pochodne nastȩpuj
Zestaw nr 6 Pochodna funkcji jednej zmiennej. Styczna do krzywej. Elastyczność funkcji. Regu la de l Hospitala November 12, 2009 Przyk ladowe zadania z rozwi azaniami Zadanie 1. Oblicz pochodne nastȩpuj
MATEMATYKA DZIELENIE LICZB Z RESZTA CECHY PODZIELNOṠCI
 1 SZKO LA PODSTAWOWA HELIANTUS 02-892 WARSZAWA ul. BAŻANCIA 16 Opercja modulo a b( mod c) MATEMATYKA DZIELENIE LICZB Z RESZTA CECHY PODZIELNOṠCI Prof. dr. Tadeusz STYŠ WARSZAWA 2018 1 1 Projekt pi aty
1 SZKO LA PODSTAWOWA HELIANTUS 02-892 WARSZAWA ul. BAŻANCIA 16 Opercja modulo a b( mod c) MATEMATYKA DZIELENIE LICZB Z RESZTA CECHY PODZIELNOṠCI Prof. dr. Tadeusz STYŠ WARSZAWA 2018 1 1 Projekt pi aty
w = w i ξ i. (1) i=1 w 1 w 2 :
 S. D. G lazek, www.fuw.edu.pl/ stglazek, 11.III.2005 1 I. MACIERZ LINIOWEGO ODWZOROWANIA PRZESTRZENI WEKTOROWYCH Wyobraźmy sobie, że przestrzeń wektorowa W jest zbudowana z kombinacji liniowych n liniowo
S. D. G lazek, www.fuw.edu.pl/ stglazek, 11.III.2005 1 I. MACIERZ LINIOWEGO ODWZOROWANIA PRZESTRZENI WEKTOROWYCH Wyobraźmy sobie, że przestrzeń wektorowa W jest zbudowana z kombinacji liniowych n liniowo
Rozdzia l 10. Najważniejsze normalne logiki modalne
 Rozdzia l 10. Najważniejsze normalne logiki modalne 1. Logiki modalne normalne Definicja. Inwariantny zbiór formu l X jȩzyka modalnego L = (L,,,,, ) nazywamy logik a modaln a zbazowan a na logice klasycznej
Rozdzia l 10. Najważniejsze normalne logiki modalne 1. Logiki modalne normalne Definicja. Inwariantny zbiór formu l X jȩzyka modalnego L = (L,,,,, ) nazywamy logik a modaln a zbazowan a na logice klasycznej
Niech X bȩdzie dowolnym zbiorem. Dobry porz adek to relacja P X X (bȩdziemy pisać x y zamiast x, y P ) o w lasnościach:
 Teoria miary WPPT IIr semestr zimowy 2009 Wyk lad 4 Liczby kardynalne, indukcja pozaskończona DOBRY PORZA DEK 14/10/09 Niech X bȩdzie dowolnym zbiorem Dobry porz adek to relacja P X X (bȩdziemy pisać x
Teoria miary WPPT IIr semestr zimowy 2009 Wyk lad 4 Liczby kardynalne, indukcja pozaskończona DOBRY PORZA DEK 14/10/09 Niech X bȩdzie dowolnym zbiorem Dobry porz adek to relacja P X X (bȩdziemy pisać x
Podstawy Automatyki. Wykład 2 - matematyczne modelowanie układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 2 - matematyczne modelowanie układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2019 Wstęp Obiekty (procesy) rzeczywiste, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
Wykład 2 - matematyczne modelowanie układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2019 Wstęp Obiekty (procesy) rzeczywiste, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
Niezb. ednik matematyczny. Niezb. ednik matematyczny
 Niezb ednik matematyczny Niezb ednik matematyczny Liczby zespolone I Rozważmy zbiór R R (zbiór par liczb rzeczywistych) i wprowadźmy w nim nastepuj ace dzia lania: z 1 + z 2 = (x 1, y 1 ) + (x 2, y 2 )
Niezb ednik matematyczny Niezb ednik matematyczny Liczby zespolone I Rozważmy zbiór R R (zbiór par liczb rzeczywistych) i wprowadźmy w nim nastepuj ace dzia lania: z 1 + z 2 = (x 1, y 1 ) + (x 2, y 2 )
FUNKCJA KWADRATOWA. 1. Definicje i przydatne wzory. lub trójmianem kwadratowym nazywamy funkcję postaci: f(x) = ax 2 + bx + c
 FUNKCJA KWADRATOWA 1. Definicje i przydatne wzory DEFINICJA 1. Funkcja kwadratowa lub trójmianem kwadratowym nazywamy funkcję postaci: f(x) = ax + bx + c taką, że a, b, c R oraz a 0. Powyższe wyrażenie
FUNKCJA KWADRATOWA 1. Definicje i przydatne wzory DEFINICJA 1. Funkcja kwadratowa lub trójmianem kwadratowym nazywamy funkcję postaci: f(x) = ax + bx + c taką, że a, b, c R oraz a 0. Powyższe wyrażenie
wszystkich kombinacji liniowych wektorów układu, nazywa się powłoką liniową uk ładu wektorów
 KOINACJA LINIOWA UKŁADU WEKTORÓW Definicja 1 Niech będzie przestrzenią liniową (wektorową) nad,,,, układem wektorów z przestrzeni, a,, współczynnikami ze zbioru (skalarami). Wektor, nazywamy kombinacją
KOINACJA LINIOWA UKŁADU WEKTORÓW Definicja 1 Niech będzie przestrzenią liniową (wektorową) nad,,,, układem wektorów z przestrzeni, a,, współczynnikami ze zbioru (skalarami). Wektor, nazywamy kombinacją
Wyk lad 8 macierzy i twierdzenie Kroneckera-Capellego
 Wyk lad 8 Rzad macierzy i twierdzenie Kroneckera-Capellego 1 Określenie rz edu macierzy Niech A bedzie m n - macierza Wówczas wiersze macierzy A możemy w naturalny sposób traktować jako wektory przestrzeni
Wyk lad 8 Rzad macierzy i twierdzenie Kroneckera-Capellego 1 Określenie rz edu macierzy Niech A bedzie m n - macierza Wówczas wiersze macierzy A możemy w naturalny sposób traktować jako wektory przestrzeni
RÓŻNICZKOWANIE FUNKCJI WIELU ZMIENNYCH: rachunek pochodnych dla funkcji wektorowych. Pochodne cząstkowe funkcji rzeczywistej wielu zmiennych
 RÓŻNICZKOWANIE FUNKCJI WIELU ZMIENNYCH: rachunek pochodnych dla funkcji wektorowych Pochodne cząstkowe funkcji rzeczywistej wielu zmiennych wyliczamy według wzoru (x, x 2,..., x n ) f(x, x 2,..., x n )
RÓŻNICZKOWANIE FUNKCJI WIELU ZMIENNYCH: rachunek pochodnych dla funkcji wektorowych Pochodne cząstkowe funkcji rzeczywistej wielu zmiennych wyliczamy według wzoru (x, x 2,..., x n ) f(x, x 2,..., x n )
Wyk lad 12. (ii) najstarszy wspó lczynnik wielomianu f jest elementem odwracalnym w P. Dowód. Niech st(f) = n i niech a bedzie
 1 Dzielenie wielomianów Wyk lad 12 Ważne pierścienie Definicja 12.1. Niech P bedzie pierścieniem, który może nie być dziedzina ca lkowitości. Powiemy, że w pierścieniu P [x] jest wykonalne dzielenie z
1 Dzielenie wielomianów Wyk lad 12 Ważne pierścienie Definicja 12.1. Niech P bedzie pierścieniem, który może nie być dziedzina ca lkowitości. Powiemy, że w pierścieniu P [x] jest wykonalne dzielenie z
Rozdzia l 2. Najważniejsze typy algebr stosowane w logice
 Rozdzia l 2. Najważniejsze typy algebr stosowane w logice 1. Algebry Boole a Definicja. Kratȩ dystrybutywn a z zerem i jedynk a, w której dla każdego elementu istnieje jego uzupe lnienie nazywamy algebr
Rozdzia l 2. Najważniejsze typy algebr stosowane w logice 1. Algebry Boole a Definicja. Kratȩ dystrybutywn a z zerem i jedynk a, w której dla każdego elementu istnieje jego uzupe lnienie nazywamy algebr
Podstawy Automatyki. Wykład 2 - modelowanie matematyczne układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 2 - modelowanie matematyczne układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2019 Wstęp Obiekty (procesy) rzeczywiste, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
Wykład 2 - modelowanie matematyczne układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2019 Wstęp Obiekty (procesy) rzeczywiste, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
Funkcje dwóch zmiennych
 Funkcje dwóch zmiennych Je zeli ka zdemu punktowi P o wspó rzednych x; y) z pewnego obszaru D na p aszczyźnie R 2 przyporzadkujemy w sposób jednoznaczny liczb e rzeczywista z, to przyporzadkowanie to nazywamy
Funkcje dwóch zmiennych Je zeli ka zdemu punktowi P o wspó rzednych x; y) z pewnego obszaru D na p aszczyźnie R 2 przyporzadkujemy w sposób jednoznaczny liczb e rzeczywista z, to przyporzadkowanie to nazywamy
Komputerowa analiza zagadnień różniczkowych 10. Dwupunktowe problemy brzegowe (BVP, Boundary Value Problems)
 Komputerowa analiza zagadnień różniczkowych 10. Dwupunktowe problemy brzegowe (BVP, Boundary Value Problems) P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2007/08 Wprowadzenie Rozważmy
Komputerowa analiza zagadnień różniczkowych 10. Dwupunktowe problemy brzegowe (BVP, Boundary Value Problems) P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2007/08 Wprowadzenie Rozważmy
Normy wektorów i macierzy
 Rozdzia l 3 Normy wektorów i macierzy W tym rozdziale zak ladamy, że K C. 3.1 Ogólna definicja normy Niech ψ : K m,n [0, + ) b edzie przekszta lceniem spe lniaj acym warunki: (i) A K m,n ψ(a) = 0 A = 0,
Rozdzia l 3 Normy wektorów i macierzy W tym rozdziale zak ladamy, że K C. 3.1 Ogólna definicja normy Niech ψ : K m,n [0, + ) b edzie przekszta lceniem spe lniaj acym warunki: (i) A K m,n ψ(a) = 0 A = 0,
Równania różniczkowe cząstkowe drugiego rzędu
 Równania różniczkowe cząstkowe drugiego rzędu Marcin Orchel Spis treści 1 Wstęp 1 1.1 Metoda faktoryzacji (rozdzielania zmiennych)................ 5 1.2 Metoda funkcji Greena.............................
Równania różniczkowe cząstkowe drugiego rzędu Marcin Orchel Spis treści 1 Wstęp 1 1.1 Metoda faktoryzacji (rozdzielania zmiennych)................ 5 1.2 Metoda funkcji Greena.............................
Równania różniczkowe. Notatki z wykładu.
 Równania różniczkowe Notatki z wykładu http://robert.brainusers.net 17.06.2009 Notatki własne z wykładu. Są niekompletne, bez bibliografii oraz mogą zawierać błędy i usterki. Z tego powodu niniejszy dokument
Równania różniczkowe Notatki z wykładu http://robert.brainusers.net 17.06.2009 Notatki własne z wykładu. Są niekompletne, bez bibliografii oraz mogą zawierać błędy i usterki. Z tego powodu niniejszy dokument
Podstawy Automatyki. Wykład 2 - modelowanie matematyczne układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 2 - modelowanie matematyczne układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2017 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
Wykład 2 - modelowanie matematyczne układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2017 Wstęp Rzeczywiste obiekty regulacji, a co za tym idzie układy regulacji, mają właściwości nieliniowe,
Opis systemów dynamicznych w przestrzeni stanu. Wojciech Kurek , Gdańsk
 Opis systemów dynamicznych Mieczysław Brdyś 27.09.2010, Gdańsk Rozważmy układ RC przedstawiony na rysunku poniżej: wejscie u(t) R C wyjście y(t)=vc(t) Niech u(t) = 2 + sin(t) dla t t 0 gdzie t 0 to chwila
Opis systemów dynamicznych Mieczysław Brdyś 27.09.2010, Gdańsk Rozważmy układ RC przedstawiony na rysunku poniżej: wejscie u(t) R C wyjście y(t)=vc(t) Niech u(t) = 2 + sin(t) dla t t 0 gdzie t 0 to chwila
Matematyka A kolokwium, 27 maja 2015, godz. 18:15 20:10
 Matematyka A kolokwium, 7 maja, godz 8: : Poprawiłem: godz :, 4 września r 3 p Rozwiazać x t x t xt = x t x t xt = 6 + t cos3t + 36te 3t 7e 3t Pierwiastkami równania charakterystycznego = λ λ = λ + 3λ
Matematyka A kolokwium, 7 maja, godz 8: : Poprawiłem: godz :, 4 września r 3 p Rozwiazać x t x t xt = x t x t xt = 6 + t cos3t + 36te 3t 7e 3t Pierwiastkami równania charakterystycznego = λ λ = λ + 3λ
Pochodne cz ¾astkowe i ich zastosowanie.
 Pochodne cz ¾astkowe i ich zastosowanie. Adam Kiersztyn Lublin 2013 Adam Kiersztyn () Pochodne cz ¾astkowe i ich zastosowanie. maj 2013 1 / 18 Zanim przejdziemy do omawiania pochodnych funkcji wielu zmiennych
Pochodne cz ¾astkowe i ich zastosowanie. Adam Kiersztyn Lublin 2013 Adam Kiersztyn () Pochodne cz ¾astkowe i ich zastosowanie. maj 2013 1 / 18 Zanim przejdziemy do omawiania pochodnych funkcji wielu zmiennych
Regulator liniowo kwadratowy na przykładzie wahadła odwróconego
 Regulator liniowo kwadratowy na przykładzie wahadła odwróconego kwiecień 2012 Sterowanie Teoria Przykład wahadła na wózku Dany jest system dynamiczny postaci: ẋ = f (x, u) (1) y = h(x) (2) Naszym zadaniem
Regulator liniowo kwadratowy na przykładzie wahadła odwróconego kwiecień 2012 Sterowanie Teoria Przykład wahadła na wózku Dany jest system dynamiczny postaci: ẋ = f (x, u) (1) y = h(x) (2) Naszym zadaniem
Równania Naviera-Stokesa
 Równania Naviera-Stokesa Na pograniczu matematyki i fizyki Grzegorz Lukaszewicz (MIM UW) KNFM, 3 listopada 2011 Plan wyk ladu Równania Naviera-Stokesa w R 3. Model a rzeczywistość. Zwi azki. Obecny stan
Równania Naviera-Stokesa Na pograniczu matematyki i fizyki Grzegorz Lukaszewicz (MIM UW) KNFM, 3 listopada 2011 Plan wyk ladu Równania Naviera-Stokesa w R 3. Model a rzeczywistość. Zwi azki. Obecny stan
