Zestawienie symboli matematycznych
|
|
|
- Teresa Sowińska
- 7 lat temu
- Przeglądów:
Transkrypt
1 1 Zestawienie symboli matematycznych W poniższych tabelach zestawiono wszystkie symbole standardowo dostępne w trybie matematycznym. Symbole w tabelach są dostępne, jeżeli mamy zainstalowane dodatkowe fonty matematyczne i do dokumentu dołączymy pakiet amssymb. W razie braku fontów lub pakietu można je odnaleźć w CTAN://macros/latex/required/amslatex. Ponadto dużo bardziej kompletne zestawienie symboli matematycznych można znaleźć w CTAN://info/symbols/comprehensive. Tabela 1: Akcenty matematyczne â \hat{a} ǎ \check{a} ã \tilde{a} á \acute{a} à \grave{a} ȧ \dot{a} ä \ddot{a} ă \breve{a} ā \bar{a} a \vec{a} Â \widehat{a} Ã \widetilde{a} Tabela 2: Litery alfabetu greckiego α \alpha θ \theta o o υ \upsilon β \beta ϑ \vartheta π \pi φ \phi γ \gamma ι \iota ϖ \varpi ϕ \varphi δ \delta κ \kappa ρ \rho χ \chi ɛ \epsilon λ \lambda ϱ \varrho ψ \psi ε \varepsilon µ \mu σ \sigma ω \omega ζ \zeta ν \nu ς \varsigma η \eta ξ \xi τ \tau Γ \Gamma Λ \Lambda Σ \Sigma Ψ \Psi \Delta Ξ \Xi Υ \Upsilon Ω \Omega Θ \Theta Π \Pi Φ \Phi 1 Tabele przygotowano na podstawie pliku symbols.tex (David Carlisle), gruntownie zmodyfikowanego zgodnie z sugestiami Josefa Tkadleca.
2 2 Tabela 3: Symbole relacji Odpowiednie symbole negacji można utworzyć, poprzedzając każde z poniższych poleceń instrukcją \not. < < > > = = \leq lub \le \geq lub \ge \equiv. \ll \gg = \doteq \prec \succ \sim \preceq \succeq \simeq \subset \supset \approx \subseteq \supseteq = \cong \sqsubset a \sqsupset a \Join a \sqsubseteq \sqsupseteq \bowtie \in \ni, \owns \propto \vdash \dashv = \models \mid \parallel \perp \smile \frown \asymp : : / \notin \neq lub \ne a Dostępne po dołączeniu pakietu latexsym. Tabela 4: Symbole operacji dwuargumentowych ± \pm \mp \triangleleft \cdot \div \triangleright \times \ \setminus \star \cup \cap \ast \sqcup \sqcap \circ \vee, \lor \wedge, \land \bullet \oplus \ominus \diamond \odot \oslash \uplus \otimes \bigcirc \amalg \bigtriangleup \bigtriangledown \dagger \lhd a \rhd a \ddagger \unlhd a \unrhd a \wr
3 3 Tabela 5: Symbole zmiennej wielkości \sum \bigcup \bigvee \bigoplus \prod \bigcap \bigwedge \bigotimes \coprod \bigsqcup \bigodot \int \oint \biguplus Tabela 6: Strzałki \leftarrow lub \gets \longleftarrow \uparrow \rightarrow lub \to \longrightarrow \downarrow \leftrightarrow \longleftrightarrow \updownarrow \Leftarrow = \Longleftarrow \Uparrow \Rightarrow = \Longrightarrow \Downarrow \Leftrightarrow \Longleftrightarrow \Updownarrow \mapsto \longmapsto \nearrow \hookleftarrow \hookrightarrow \searrow \leftharpoonup \rightharpoonup \swarrow \leftharpoondown \rightharpoondown \nwarrow \rightleftharpoons \iff \leadsto a a Dostępne po dołączeniu pakietu latexsym. Tabela 7: Ograniczniki ( ( ) ) \uparrow \Uparrow [ [ lub \lbrack \rangle \downarrow \Downarrow { \{ lub \lbrace \langle \updownarrow \Updownarrow ] ] lub \rbrack \rfloor lub \vert \ lub \Vert } \} lub \rbrace \lfloor \lceil \rceil / / \ \backslash Tabela 8: Duże ograniczniki \lmoustache \lgroup \rgroup \arrowvert \Arrowvert \bracevert \rmoustache
4 4 Tabela 9: Różne symbole.... \dots \cdots. \vdots.. \ddots \hbar ı \imath j \jmath l \ell R \Re I \Im ℵ \aleph \wp \forall \exists \mho a \partial \prime \emptyset \infty \nabla \triangle \Box a \Diamond a \bot \top \angle \surd \diamondsuit \heartsuit \clubsuit \spadesuit \neg lub \lnot \flat \natural \sharp a Dostępne po dołączeniu pakietu latexsym. Tabela 10: Symbole niematematyczne \dag \S \copyright \ddag \P \pounds Polecenia te są dostępne również w trybie tekstowym. Tabela 11: Ograniczniki (pakiet AMS) \ulcorner \urcorner \llcorner \lrcorner Tabela 12: Symbole Greckie i Hebrajskie (pakiet AMS) Ϝ \digamma κ \varkappa ℶ \beth ℸ \daleth ג \gimel
5 5 Tabela 13: Symbole relacji (pakiet AMS) \lessdot \gtrdot \doteqdot lub \Doteq \leqslant \geqslant \risingdotseq \eqslantless \eqslantgtr \fallingdotseq \leqq \geqq \eqcirc \lll lub \llless \ggg lub \gggtr \circeq \lesssim \gtrsim \triangleq \lessapprox \gtrapprox \bumpeq \lessgtr \gtrless \Bumpeq \lesseqgtr \gtreqless \thicksim \lesseqqgtr \gtreqqless \thickapprox \preccurlyeq \succcurlyeq \approxeq \curlyeqprec \curlyeqsucc \backsim \precsim \succsim \backsimeq \precapprox \succapprox \vdash \subseteqq \supseteqq \Vdash \Subset \Supset \Vvdash \sqsubset \sqsupset \backepsilon \therefore \because \varpropto \shortmid \shortparallel \between \smallsmile \smallfrown \pitchfork \vartriangleleft \vartriangleright \blacktriangleleft \trianglelefteq \trianglerighteq \blacktriangleright Tabela 14: Strzałki (pakiet AMS) \dashleftarrow \dashrightarrow \multimap \leftleftarrows \rightrightarrows \upuparrows \leftrightarrows \rightleftarrows \downdownarrows \Lleftarrow \Rrightarrow \upharpoonleft \twoheadleftarrow \twoheadrightarrow \upharpoonright \leftarrowtail \rightarrowtail \downharpoonleft \leftrightharpoons \rightleftharpoons \downharpoonright \leftrightsquigarrow \rightsquigarrow \Lsh \looparrowleft \looparrowright \Rsh \curvearrowleft \curvearrowright \circlearrowleft \circlearrowright
6 6 Tabela 15: Negacje symbolów relacji i strzałek (pakiet AMS) \nless \ngtr \varsubsetneqq \lneq \gneq \varsupsetneqq \nleq \ngeq \nsubseteqq \nleqslant \ngeqslant \nsupseteqq \lneqq \gneqq \nmid \lvertneqq \gvertneqq \nparallel \nleqq \ngeqq \nshortmid \lnsim \gnsim \nshortparallel \lnapprox \gnapprox \nsim \nprec \nsucc \ncong \npreceq \nsucceq \nvdash \precneqq \succneqq \nvdash \precnsim \succnsim \nvdash \precnapprox \succnapprox \nvdash \subsetneq \supsetneq \ntriangleleft \varsubsetneq \varsupsetneq \ntriangleright \nsubseteq \nsupseteq \ntrianglelefteq \subsetneqq \supsetneqq \ntrianglerighteq \nleftarrow \nrightarrow \nleftrightarrow \nleftarrow \nrightarrow \nleftrightarrow Tabela 16: Relacje dwuargumentowe (pakiet AMS) \dotplus \centerdot \intercal \ltimes \rtimes \divideontimes \Cup lub \doublecup \veebar \smallsetminus \Cap lub \doublecap \barwedge \doublebarwedge \boxplus \boxminus \circleddash \boxtimes \boxdot \circledcirc \leftthreetimes \curlyvee \circledast \rightthreetimes \curlywedge
7 7 Tabela 17: Różne symbole (pakiet AMS) \hbar ħ \hslash k \Bbbk \square \blacksquare S \circleds \vartriangle \blacktriangle \complement \triangledown \blacktriangledown \Game \lozenge \blacklozenge \bigstar \angle \measuredangle \sphericalangle \diagup \diagdown \backprime \nexists Ⅎ \Finv \varnothing ð \eth \mho Tabela 18: Kroje pisma dostępne w trybie matematycznym Przykład Polecenie Wymagany pakiet ABCdef \mathrm{abcdef} ABCdef \mathit{abcdef} ABCdef \mathnormal{abcdef} ABC \mathcal{abc} A BC \mathcal{abc} mathrsfs ABC \mathcal{abc} eucal z opcją mathcal lub \mathscr{abc} eucal z opcją mathscr ABCdef \mathfrak{abcdef} eufrak ABC \mathbb{abc} amsfonts lub amssymb
Tryb Matematyczny w L A TEX-u
 Tryb Matematyczny w L A TEX-u Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2011-12-13 1 2 Tekst w trybie matematycznym Ściąga z symboli 3 Jak nie pisać pracy magisterskiej
Tryb Matematyczny w L A TEX-u Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2011-12-13 1 2 Tekst w trybie matematycznym Ściąga z symboli 3 Jak nie pisać pracy magisterskiej
Symbole Numer Nazwa Opis Znaczenie Wygląd. Latin small "f" with hook (function, florin) Greek capital letter "alpha"
 Symbole Numer Nazwa Opis Znaczenie Wygląd ƒ Litery greckie ƒ Latin small "f" with hook (function, florin) Łacińskie małe "f" z "haczykiem" (funkcja, floren) Α Α "alpha" Grecka wielka litera "alfa" Α Β
Symbole Numer Nazwa Opis Znaczenie Wygląd ƒ Litery greckie ƒ Latin small "f" with hook (function, florin) Łacińskie małe "f" z "haczykiem" (funkcja, floren) Α Α "alpha" Grecka wielka litera "alfa" Α Β
INFORMATYKA I L A TEX
 Wykład INFORMATYKA I L A TEX Marta Tyran-Kamińska semestr letni 2004/2005 TEX program stworzony przez Donalda Knutha, przeznaczony do składu tekstów w sposób automatyczny, w szczególności tekstów matematycznych.
Wykład INFORMATYKA I L A TEX Marta Tyran-Kamińska semestr letni 2004/2005 TEX program stworzony przez Donalda Knutha, przeznaczony do składu tekstów w sposób automatyczny, w szczególności tekstów matematycznych.
Latex Matematyka. Komputerowy skład tekstu. Akademia im. Jan Długosza. bwozna@gmail.com
 Latex Matematyka dr hab. Bożena Woźna-Szcześniak Akademia im. Jan Długosza bwozna@gmail.com Komputerowy skład tekstu Dwa tryby matematyczne Wyrażenia matematyczne w L A T E X-u można pisać w dwóch trybach:
Latex Matematyka dr hab. Bożena Woźna-Szcześniak Akademia im. Jan Długosza bwozna@gmail.com Komputerowy skład tekstu Dwa tryby matematyczne Wyrażenia matematyczne w L A T E X-u można pisać w dwóch trybach:
Matematyka w AMS-LAT E X
 Matematyka w AMS-L A T E X 16 października 2007 Na poczatek Przed użyciem... Od czego zaczać? Dołaczanie matematycznych elementów Do używania brzydkiej matematyki nie potrzebujemy niczego, jednak taka
Matematyka w AMS-L A T E X 16 października 2007 Na poczatek Przed użyciem... Od czego zaczać? Dołaczanie matematycznych elementów Do używania brzydkiej matematyki nie potrzebujemy niczego, jednak taka
Komputerowy skład w L A T E X
 Komputerowy skład w L A T E X dr hab. Bożena Woźna-Szcześniak, prof. UJD Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie b.wozna@ujd.edu.pl Laboratorium 9 B. Woźna-Szcześniak (UJD)
Komputerowy skład w L A T E X dr hab. Bożena Woźna-Szcześniak, prof. UJD Uniwersytet Humanistyczno-Przyrodniczy im. Jana Długosza w Częstochowie b.wozna@ujd.edu.pl Laboratorium 9 B. Woźna-Szcześniak (UJD)
system opracowywania dokumentów L A T E X
 system opracowywania dokumentów L A T E X 29 października 2007 spis treści 1 polecenia wprowadzające otoczenie math - wzór umieszczony w tekście \begin{math}... \end{math} \(... \) $... $ otoczenie displaymath
system opracowywania dokumentów L A T E X 29 października 2007 spis treści 1 polecenia wprowadzające otoczenie math - wzór umieszczony w tekście \begin{math}... \end{math} \(... \) $... $ otoczenie displaymath
Úvod do TEXu. Brno, L A TEX dokumenty a matematika.
 Úvod do TEXu 3 L A TEX dokumenty a matematika. Matematický mód Matematická prostředí v PlainTEXu a L A TEXu Mezery a písma v matematickém módu Matematické značky a symboly Konstrukce v matematickém módu
Úvod do TEXu 3 L A TEX dokumenty a matematika. Matematický mód Matematická prostředí v PlainTEXu a L A TEXu Mezery a písma v matematickém módu Matematické značky a symboly Konstrukce v matematickém módu
Pracownia przetwarzania dokumentów 3. Matematyka w L A TEX-u
 Bartosz Ziemkiewicz Joanna Karłowska-Pik Pracownia przetwarzania dokumentów 3. Matematyka w L A TEX-u Materiały dydaktyczne do kształcenia na odległość dla studentów matematyki (specjalność: matematyka
Bartosz Ziemkiewicz Joanna Karłowska-Pik Pracownia przetwarzania dokumentów 3. Matematyka w L A TEX-u Materiały dydaktyczne do kształcenia na odległość dla studentów matematyki (specjalność: matematyka
!!! Teoria, która się tutaj znajduje też wchodzi w zakres kolokwium.!!!
 DB WMA(ns) semestr zimowy 2017 rozgrzewka przed kolokwium SPIS TREŚCI Teoria w niniejszym zbiorku została opracowana na podstawie książki: R. Murawski, K. Świrydowicz, Wstęp do teorii mnogości, Wyd. Naukowe
DB WMA(ns) semestr zimowy 2017 rozgrzewka przed kolokwium SPIS TREŚCI Teoria w niniejszym zbiorku została opracowana na podstawie książki: R. Murawski, K. Świrydowicz, Wstęp do teorii mnogości, Wyd. Naukowe
Spis wszystkich symboli
 1 Spis wszystkich symboli Symbole podstawowe - pojedyncze znaki, alfabet grecki α β γ Γ δ ξ η ε ϕ ν ρ τ θ Θ ψ Ψ φ Φ Ω Υ Σ -alfa -beta - gamma - gamma (duże) - delta (małe) - delta (duże) -ksi -eta - epsilon
1 Spis wszystkich symboli Symbole podstawowe - pojedyncze znaki, alfabet grecki α β γ Γ δ ξ η ε ϕ ν ρ τ θ Θ ψ Ψ φ Φ Ω Υ Σ -alfa -beta - gamma - gamma (duże) - delta (małe) - delta (duże) -ksi -eta - epsilon
POLITECHNIKA LUBELSKA KARTA MODUŁU (SYLABUS)
 STOPIEŃ STUDIÓW: RODZAJ STUDIÓW: KIERUNEK STUDIÓW: KARTA MODUŁU (SYLABUS) Studia I stopnia (inżynierskie) studia stacjonarne MECHATRONIKA (MT) PRZEDMIOT: ROK STUDIÓW: SEMESTR: RODZAJ ZAJĘĆ I LICZBA GODZIN:
STOPIEŃ STUDIÓW: RODZAJ STUDIÓW: KIERUNEK STUDIÓW: KARTA MODUŁU (SYLABUS) Studia I stopnia (inżynierskie) studia stacjonarne MECHATRONIKA (MT) PRZEDMIOT: ROK STUDIÓW: SEMESTR: RODZAJ ZAJĘĆ I LICZBA GODZIN:
POLITECHNIKA LUBELSKA KARTA MODUŁU (SYLABUS)
 STOPIEŃ STUDIÓW: RODZAJ STUDIÓW: KIERUNEK STUDIÓW: KARTA MODUŁU (SYLABUS) Studia I stopnia (inżynierskie) studia stacjonarne MECHATRONIKA (MT) PRZEDMIOT: ROK STUDIÓW: SEMESTR: RODZAJ ZAJĘĆ I LICZBA GODZIN:
STOPIEŃ STUDIÓW: RODZAJ STUDIÓW: KIERUNEK STUDIÓW: KARTA MODUŁU (SYLABUS) Studia I stopnia (inżynierskie) studia stacjonarne MECHATRONIKA (MT) PRZEDMIOT: ROK STUDIÓW: SEMESTR: RODZAJ ZAJĘĆ I LICZBA GODZIN:
OpenOffice.org Math dla uczniów i studentów
 OpenOffice.org Math dla uczniów i studentów Paweł Wimmer Darmowa publikacja dostarczona przez ZloteMysli.pl Niniejsza publikacja może być kopiowana, oraz dowolnie rozprowadzana tylko i wyłącznie w formie
OpenOffice.org Math dla uczniów i studentów Paweł Wimmer Darmowa publikacja dostarczona przez ZloteMysli.pl Niniejsza publikacja może być kopiowana, oraz dowolnie rozprowadzana tylko i wyłącznie w formie
Edycja tekstu w programie LATEX - wzory matematyczne
 Edycja tekstu w programie LATEX - wzory matematyczne 8 października 017 1. Liczby należy wpisywać używając trybu matematycznego, tzn. zamiast -314 wpisujemy $-314$. Różnica wygląda tak: -314 oraz 314.
Edycja tekstu w programie LATEX - wzory matematyczne 8 października 017 1. Liczby należy wpisywać używając trybu matematycznego, tzn. zamiast -314 wpisujemy $-314$. Różnica wygląda tak: -314 oraz 314.
1. OPEN OFFICE WZORY
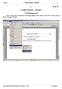 Część 1 1. OPEN OFFICE - WZORY 1 1. 1. OPEN OFFICE WZORY 1.1 Wstawianie wzoru Chcąc wstawić wzór do dokumentu tekstowego programu Writer należy z menu Wstaw wybrać pozycję Obiekt a następnie Formuła. Część
Część 1 1. OPEN OFFICE - WZORY 1 1. 1. OPEN OFFICE WZORY 1.1 Wstawianie wzoru Chcąc wstawić wzór do dokumentu tekstowego programu Writer należy z menu Wstaw wybrać pozycję Obiekt a następnie Formuła. Część
Granica i ciągłość funkcji. 1 Granica funkcji rzeczywistej jednej zmiennej rzeczywsitej
 Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus listopada 07r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus listopada 07r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Fizyka 1(mechanika) AF14. Wykład 1
 Fizyka 1(mechanika) 1100-1AF14 Wykład 1 Jerzy Łusakowski 03.10.2016 Plan wykładu Informacje o wykładzie Przedmiot i metodologia fizyki Fizyka a matematyka Układ jednostek SI, rzędy wielkości Pomiary fizyczne
Fizyka 1(mechanika) 1100-1AF14 Wykład 1 Jerzy Łusakowski 03.10.2016 Plan wykładu Informacje o wykładzie Przedmiot i metodologia fizyki Fizyka a matematyka Układ jednostek SI, rzędy wielkości Pomiary fizyczne
Nadawanie uprawnieo i logowanie
 Nadawanie uprawnieo i logowanie Rejestracja Każdy kierownik jednostki posiada wcześniej założone konto konta zakładane są przez pracownika Działu Informacji Naukowej BG osoba odpowiedzialna: Zofia Kukurowska,
Nadawanie uprawnieo i logowanie Rejestracja Każdy kierownik jednostki posiada wcześniej założone konto konta zakładane są przez pracownika Działu Informacji Naukowej BG osoba odpowiedzialna: Zofia Kukurowska,
L A TEX. czyli czym pisać teksty naukowe. Zbigniew Koza. Uniwersytet Wrocławski Instytut Fizyki Teoretycznej. LATEX p. 1/34
 L A TEX czyli czym pisać teksty naukowe Zbigniew Koza Uniwersytet Wrocławski Instytut Fizyki Teoretycznej LATEX p. 1/34 Trochę historii: TEX W latach 80-tych Donald Knuth opracował zbiór programów do komputerowego
L A TEX czyli czym pisać teksty naukowe Zbigniew Koza Uniwersytet Wrocławski Instytut Fizyki Teoretycznej LATEX p. 1/34 Trochę historii: TEX W latach 80-tych Donald Knuth opracował zbiór programów do komputerowego
Granica i ciągłość funkcji. 1 Granica funkcji rzeczywistej jednej zmiennej rzeczywistej
 Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus 3 listopada 06r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus 3 listopada 06r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
W miarę krótki i praktyczny kurs LATEX-a w π e minut
 W miarę krótki i praktyczny kurs LATEX-a w π e minut wersja 1.52 Ryszard Paweł Kostecki kostecki % fuw.edu.pl http://www.fuw.edu.pl/ kostecki 7 października 2008 Streszczenie Tak, to prawda: masz przed
W miarę krótki i praktyczny kurs LATEX-a w π e minut wersja 1.52 Ryszard Paweł Kostecki kostecki % fuw.edu.pl http://www.fuw.edu.pl/ kostecki 7 października 2008 Streszczenie Tak, to prawda: masz przed
L A TEX- podstawy. Politechnika Wrocławska. Wrocław, 29 listopada 2007
 L A TEX- podstawy Mateusz Kulikowski Adam Ratajczak Politechnika Wrocławska Wrocław, 29 listopada 2007 Plan prezentacji 1 Wprowadzenie 2 Struktura kodu dokumentu 3 Formatowanie tekstu 4 Ilustracje i tabele
L A TEX- podstawy Mateusz Kulikowski Adam Ratajczak Politechnika Wrocławska Wrocław, 29 listopada 2007 Plan prezentacji 1 Wprowadzenie 2 Struktura kodu dokumentu 3 Formatowanie tekstu 4 Ilustracje i tabele
Dyrektor oraz pracownicy Miejsko - Gminnego Ośrodka Kultury w Kowalewie Pomorskim
 Wszystkim Nauczycielom i pracownikom oświaty z okazji Dnia Edukacji Narodowej moc najserdeczniejszych życzeń, spełnienia najskrytszych marzeń oraz byście mogli w pełni realizować swoje plany życiowe i
Wszystkim Nauczycielom i pracownikom oświaty z okazji Dnia Edukacji Narodowej moc najserdeczniejszych życzeń, spełnienia najskrytszych marzeń oraz byście mogli w pełni realizować swoje plany życiowe i
Zespół Szkół Technicznych. Badanie wyświetlaczy LCD
 Zespół Szkół Technicznych Badanie wyświetlaczy LCD WYŚWIETLACZE LCD CZĘSC TEORETYCZNA ZALETY: ) mały pobór mocy, 2) ekonomiczność pod względem zużycia energii (pobór prądu przy 5V mniejszy niż 2mA), 3)
Zespół Szkół Technicznych Badanie wyświetlaczy LCD WYŚWIETLACZE LCD CZĘSC TEORETYCZNA ZALETY: ) mały pobór mocy, 2) ekonomiczność pod względem zużycia energii (pobór prądu przy 5V mniejszy niż 2mA), 3)
STATYSTYKA. Rafał Kucharski. Uniwersytet Ekonomiczny w Katowicach 2015/16 ROND, Finanse i Rachunkowość, rok 2
 STATYSTYKA Rafał Kucharski Uniwersytet Ekonomiczny w Katowicach 2015/16 ROND, Finanse i Rachunkowość, rok 2 Wybrane litery alfabetu greckiego α alfa β beta Γ γ gamma δ delta ɛ, ε epsilon η eta Θ θ theta
STATYSTYKA Rafał Kucharski Uniwersytet Ekonomiczny w Katowicach 2015/16 ROND, Finanse i Rachunkowość, rok 2 Wybrane litery alfabetu greckiego α alfa β beta Γ γ gamma δ delta ɛ, ε epsilon η eta Θ θ theta
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZNA Rafał Kucharski Uniwersytet Ekonomiczny w Katowicach 08/9 Zarządzanie e-mail: www: konsultacje: rafal.kucharski@ue.katowice.pl http://web.ue.katowice.pl/rkucharski/ Piątki, 5:0-6:0,
STATYSTYKA MATEMATYCZNA Rafał Kucharski Uniwersytet Ekonomiczny w Katowicach 08/9 Zarządzanie e-mail: www: konsultacje: rafal.kucharski@ue.katowice.pl http://web.ue.katowice.pl/rkucharski/ Piątki, 5:0-6:0,
Narzędzia informatyczne. Matematyka w L A T E Xu
 Narzędzia informatyczne. Matematyka w L A T E Xu Aleksander Denisiuk Uniwersytet Warmińsko-Mazurski Olsztyn, ul. Słoneczna 54 denisjuk@matman.uwm.edu.pl 1 / 33 Matematyka w L A T E Xu Najnowsza wersja
Narzędzia informatyczne. Matematyka w L A T E Xu Aleksander Denisiuk Uniwersytet Warmińsko-Mazurski Olsztyn, ul. Słoneczna 54 denisjuk@matman.uwm.edu.pl 1 / 33 Matematyka w L A T E Xu Najnowsza wersja
Gazetka Matematyczna Publicznego Gimnazjum nr 3
 Gazetka Matematyczna Publicznego Gimnazjum nr 3 nr 1: IX-X 2017r Witamy serdecznie po wakacjach wszystkich naszych czytelników a w szczególności nowo przybyłych do naszego gimnazjum tj. uczniów klasy szóstej
Gazetka Matematyczna Publicznego Gimnazjum nr 3 nr 1: IX-X 2017r Witamy serdecznie po wakacjach wszystkich naszych czytelników a w szczególności nowo przybyłych do naszego gimnazjum tj. uczniów klasy szóstej
Podstawy LATEX-a. Tomasz Bielaczyc
 Czym jest TEX TEX jest to komputerowy system profesjonalnego składu tekstu. Został stworzony przez Donalda Knutha i od 1982 roku, czyli momentu udostępnienia prawie się nie zmienił. Jest on natomiast intensywnie
Czym jest TEX TEX jest to komputerowy system profesjonalnego składu tekstu. Został stworzony przez Donalda Knutha i od 1982 roku, czyli momentu udostępnienia prawie się nie zmienił. Jest on natomiast intensywnie
Matematyka dyskretna. Andrzej Łachwa, UJ, 2019 Zadania 1-100
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl Zadania 1-100 Udowodnij, że A (B C) = (A B) (A C) za pomocą diagramów Venna. Udowodnij formalnie, że (A B i A C) A B C oraz że (A
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl Zadania 1-100 Udowodnij, że A (B C) = (A B) (A C) za pomocą diagramów Venna. Udowodnij formalnie, że (A B i A C) A B C oraz że (A
Edytor wzorów w OpenOffice Mini podręcznik
 Edytor wzorów w OpenOffice Mini podręcznik Autor: Marcin Klessa Wolsztyn 2012 1. Wprowadzenie Edytor wzorów w pakiecie Open Office różni się od edytora używanego w popularnym MSOffice. Z pozoru wygląda
Edytor wzorów w OpenOffice Mini podręcznik Autor: Marcin Klessa Wolsztyn 2012 1. Wprowadzenie Edytor wzorów w pakiecie Open Office różni się od edytora używanego w popularnym MSOffice. Z pozoru wygląda
Technologie Informacyjne Laboratorium. Ćwiczenie nr 1
 Technologie Informacyjne Laboratorium Ćwiczenie nr 1 Zaawansowana edycja tekstu w programie Word I. Zagadnienia: 1. Automatyczne formatowanie akapitów 2. Tworzenie automatycznego spisu treści 3. Dodawanie
Technologie Informacyjne Laboratorium Ćwiczenie nr 1 Zaawansowana edycja tekstu w programie Word I. Zagadnienia: 1. Automatyczne formatowanie akapitów 2. Tworzenie automatycznego spisu treści 3. Dodawanie
STATYSTYKA MATEMATYCZNA WYKŁAD października 2009
 STATYSTYKA MATEMATYCZNA WYKŁAD 4 26 października 2009 Rozkład N(µ, σ). Estymacja σ σ 2 = 1 σ 2π + = E µ,σ (X µ) 2 { (x µ) 2 exp 1 ( ) } x µ 2 dx 2 σ Rozkład N(µ, σ). Estymacja σ σ 2 = 1 σ 2π + = E µ,σ
STATYSTYKA MATEMATYCZNA WYKŁAD 4 26 października 2009 Rozkład N(µ, σ). Estymacja σ σ 2 = 1 σ 2π + = E µ,σ (X µ) 2 { (x µ) 2 exp 1 ( ) } x µ 2 dx 2 σ Rozkład N(µ, σ). Estymacja σ σ 2 = 1 σ 2π + = E µ,σ
Fizyka 1(mechanika) AF14. Wykład 1
 Fizyka 1(mechanika) 1100-1AF14 Wykład 1 Jerzy Łusakowski 02.10.2017 Plan wykładu Informacje o wykładzie Przedmiot i metodologia fizyki Układ jednostek SI, rzędy wielkości Pomiary fizyczne i niepewności
Fizyka 1(mechanika) 1100-1AF14 Wykład 1 Jerzy Łusakowski 02.10.2017 Plan wykładu Informacje o wykładzie Przedmiot i metodologia fizyki Układ jednostek SI, rzędy wielkości Pomiary fizyczne i niepewności
Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym
 Ćwiczenia ZPI 1 Współczynniki greckie Odpowiadają na pytanie o ile zmieni się wartość opcji w wyniku: Współczynnik Delta (Δ) - zmiany wartości instrumentu bazowego Współczynnik Theta (Θ) - upływu czasu
Ćwiczenia ZPI 1 Współczynniki greckie Odpowiadają na pytanie o ile zmieni się wartość opcji w wyniku: Współczynnik Delta (Δ) - zmiany wartości instrumentu bazowego Współczynnik Theta (Θ) - upływu czasu
Co to są liczby naturalne i czemu ich nie ma?! Adam Kolany
 Co to są liczby naturalne i czemu ich nie ma?! Adam Kolany Co to są liczby naturalne i czemu ich nie ma?! Adam Kolany Załóżmy, że wiemy co to są liczby naturalne... Język (I-go rzędu): V, { F n : n IN
Co to są liczby naturalne i czemu ich nie ma?! Adam Kolany Co to są liczby naturalne i czemu ich nie ma?! Adam Kolany Załóżmy, że wiemy co to są liczby naturalne... Język (I-go rzędu): V, { F n : n IN
Pracownia dyplomowa Przewodnik po LATEXu
 Uniwersytet Technologiczno Przyrodniczy im. Jana i Jędrzeja Śniadeckich w Bydgoszczy Instytut Matematyki i Fizyki Gerard Czajkowski Natalia Kruszewska Pracownia dyplomowa Przewodnik po LATEXu Specjalność:
Uniwersytet Technologiczno Przyrodniczy im. Jana i Jędrzeja Śniadeckich w Bydgoszczy Instytut Matematyki i Fizyki Gerard Czajkowski Natalia Kruszewska Pracownia dyplomowa Przewodnik po LATEXu Specjalność:
Wybrane litery alfabetu greckiego
 Wybrae litery alfabetu greckiego α alfa β beta Γ γ gamma δ delta ɛ, ε epsilo η eta Θ θ theta κ kappa Λ λ lambda µ mi ν i ξ ksi π pi ρ, ϱ ro σ sigma τ tau Φ φ, ϕ fi χ chi Ψ ψ psi Ω ω omega Ozaczeia a i
Wybrae litery alfabetu greckiego α alfa β beta Γ γ gamma δ delta ɛ, ε epsilo η eta Θ θ theta κ kappa Λ λ lambda µ mi ν i ξ ksi π pi ρ, ϱ ro σ sigma τ tau Φ φ, ϕ fi χ chi Ψ ψ psi Ω ω omega Ozaczeia a i
Dokumentacja. Opcje europejskie PDE. Zbigniew Matczak
 Dokumentacja Opcje europejskie PDE Zbigniew Matczak Spis treści 1 Model CEV 2 1.1 Cena opcji w modelu CEV...................... 2 1.2 Poprawność funkcji "option value" na podstawie funkcji delta oraz symulacji
Dokumentacja Opcje europejskie PDE Zbigniew Matczak Spis treści 1 Model CEV 2 1.1 Cena opcji w modelu CEV...................... 2 1.2 Poprawność funkcji "option value" na podstawie funkcji delta oraz symulacji
v = v i e i v 1 ] T v =
![v = v i e i v 1 ] T v = v = v i e i v 1 ] T v =](/thumbs/97/130738346.jpg) v U = e i,..., e n ) v = n v i e i i= e i i v T v = = v v n v n U v v v +q 3q +q +q b c d XY X +q Y 3q r +q = r 3q = r +q = r +q = r 3q = r +q = E = E +q + E 3q + E +q = k q r+q 3 + k 3q r 3q 3 b V = kq
v U = e i,..., e n ) v = n v i e i i= e i i v T v = = v v n v n U v v v +q 3q +q +q b c d XY X +q Y 3q r +q = r 3q = r +q = r +q = r 3q = r +q = E = E +q + E 3q + E +q = k q r+q 3 + k 3q r 3q 3 b V = kq
Greka klasyczna. Greka hellenistyczna. Tło historyczne. VIII w. p.n.e. 700 VII w.p.n.e. 600 VI w.p.n.e V w.p.n.e. IV w.p.n.e.
 Tło historyczne VIII w. p.n.e. 700 VII w.p.n.e. 600 VI w.p.n.e. 500 Homer Sofokles, Eurypides, Herodot, V w.p.n.e. Arystofanes, Tukidydes, Sokrates 400 Platon Greka klasyczna IV w.p.n.e. Ksenofont Arystoteles,
Tło historyczne VIII w. p.n.e. 700 VII w.p.n.e. 600 VI w.p.n.e. 500 Homer Sofokles, Eurypides, Herodot, V w.p.n.e. Arystofanes, Tukidydes, Sokrates 400 Platon Greka klasyczna IV w.p.n.e. Ksenofont Arystoteles,
Numeryczne aproksymacje prawdopodobieństwa ruiny
 Numeryczne aproksymacje prawdopodobieństwa ruiny Krzysztof Burnecki Aleksander Weron Centrum Metod Stochastycznych im. Hugona Steinhausa Instytut Matematyki i Informatyki Politechnika Wrocławska www.im.pwr.wroc.pl/
Numeryczne aproksymacje prawdopodobieństwa ruiny Krzysztof Burnecki Aleksander Weron Centrum Metod Stochastycznych im. Hugona Steinhausa Instytut Matematyki i Informatyki Politechnika Wrocławska www.im.pwr.wroc.pl/
1 Funktory i kwantyfikatory
 Logika, relacje v07 egzamin mgr inf niestacj 1 1 Funktory i kwantyfikatory x X x X Φ(x) dla każdego x X (= dla wszystkich x) zachodzi formuła Φ(x) Φ(x) istnieje x X takie, że (= dla pewnego x) zachodzi
Logika, relacje v07 egzamin mgr inf niestacj 1 1 Funktory i kwantyfikatory x X x X Φ(x) dla każdego x X (= dla wszystkich x) zachodzi formuła Φ(x) Φ(x) istnieje x X takie, że (= dla pewnego x) zachodzi
Testico Edu 2.4 Podręcznik użytkownika
 Testico Edu 2.4 Podręcznik użytkownika Opracowanie: Jakub Jeżyna Spis treści INSTALACJA... 5 OBSŁUGA PILOTÓW... 10 A. Ustawienia pilotów, pierwsze uruchomienie... 10 A.1 Licencja... 13 B. Pilot uczniowski...
Testico Edu 2.4 Podręcznik użytkownika Opracowanie: Jakub Jeżyna Spis treści INSTALACJA... 5 OBSŁUGA PILOTÓW... 10 A. Ustawienia pilotów, pierwsze uruchomienie... 10 A.1 Licencja... 13 B. Pilot uczniowski...
STATYSTYKA MATEMATYCZNA WYKŁAD 5. 2 listopada 2009
 STATYSTYKA MATEMATYCZNA WYKŁAD 5 2 listopada 2009 Poprzedni wykład: przedział ufności dla µ, σ nieznane Rozkład N(µ, σ). Wnioskowanie o średniej µ, gdy σ nie jest znane Testowanie H : µ = µ 0, K : µ
STATYSTYKA MATEMATYCZNA WYKŁAD 5 2 listopada 2009 Poprzedni wykład: przedział ufności dla µ, σ nieznane Rozkład N(µ, σ). Wnioskowanie o średniej µ, gdy σ nie jest znane Testowanie H : µ = µ 0, K : µ
Obrona odcinka. Beata Kraska. Rozprawa doktorska Instytut Matematyki Uniwersytetu Śląskiego w Katowicach Katowice, luty 2013
 Rozprawa doktorska Instytut Matematyki Uniwersytetu Śląskiego w Katowicach Katowice, luty 013 Beata Kraska brona odcinka Rozprawa doktorska napisana pod kierunkiem Prof. dr hab. Witolda Rzymowskiego Spis
Rozprawa doktorska Instytut Matematyki Uniwersytetu Śląskiego w Katowicach Katowice, luty 013 Beata Kraska brona odcinka Rozprawa doktorska napisana pod kierunkiem Prof. dr hab. Witolda Rzymowskiego Spis
Różne rozkłady prawdopodobieństwa
 Różne rozłady prawdopodobieństwa. Rozład dwupuntowy D(p). Zmienna losowa ξ ma rozład D(p), jeżeli P p {ξ = 0} = p oraz P p {ξ = } = p. Eξ = p D ξ = p( p). Rozład dwumianowy Bin(n, p). Zmienna losowa ξ
Różne rozłady prawdopodobieństwa. Rozład dwupuntowy D(p). Zmienna losowa ξ ma rozład D(p), jeżeli P p {ξ = 0} = p oraz P p {ξ = } = p. Eξ = p D ξ = p( p). Rozład dwumianowy Bin(n, p). Zmienna losowa ξ
STATYSTYKA MATEMATYCZNA WYKŁAD grudnia 2009
 STATYSTYKA MATEMATYCZNA WYKŁAD 10 14 grudnia 2009 PARAMETRY POŁOŻENIA Przypomnienie: Model statystyczny pomiaru: wynik pomiaru X = µ + ε 1. ε jest zmienną losową 2. E(ε) = 0 pomiar nieobciążony, pomiar
STATYSTYKA MATEMATYCZNA WYKŁAD 10 14 grudnia 2009 PARAMETRY POŁOŻENIA Przypomnienie: Model statystyczny pomiaru: wynik pomiaru X = µ + ε 1. ε jest zmienną losową 2. E(ε) = 0 pomiar nieobciążony, pomiar
Wprowadzenie do systemu LATEX
 Karol Selwat Wprowadzenie do systemu LATEX Skrypt dla studentów Instytutu Matematycznego Uniwersytetu Wrocławskiego Instytut Matematyczny Uniwersytetu Wrocławskiego Wprowadzenie do systemu L A TEX K. Selwat
Karol Selwat Wprowadzenie do systemu LATEX Skrypt dla studentów Instytutu Matematycznego Uniwersytetu Wrocławskiego Instytut Matematyczny Uniwersytetu Wrocławskiego Wprowadzenie do systemu L A TEX K. Selwat
Światło widzialne a widmo elektromagnetyczne
 Światło widzialne a widmo elektromagnetyczne 10 3 λ [nm] λ 10 6 10 12 fale radiowe 1 mm 10 9 10 12 10 9 10 6 mikrofale 100 µm 10 µm 10 15 10 18 10 21 10 3 1 10 3 widmo optyczne prom. X promienie gamma
Światło widzialne a widmo elektromagnetyczne 10 3 λ [nm] λ 10 6 10 12 fale radiowe 1 mm 10 9 10 12 10 9 10 6 mikrofale 100 µm 10 µm 10 15 10 18 10 21 10 3 1 10 3 widmo optyczne prom. X promienie gamma
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 13, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 13, 6.03.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 1 - przypomnienie stosy
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 13, 6.03.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 1 - przypomnienie stosy
Numeryczne metody optymalizacji Optymalizacja w kierunku. informacje dodatkowe
 Numeryczne metody optymalizacji Optymalizacja w kierunku informacje dodatkowe Numeryczne metody optymalizacji x F x = min x D x F(x) Problemy analityczne: 1. Nieliniowa złożona funkcja celu F i ograniczeń
Numeryczne metody optymalizacji Optymalizacja w kierunku informacje dodatkowe Numeryczne metody optymalizacji x F x = min x D x F(x) Problemy analityczne: 1. Nieliniowa złożona funkcja celu F i ograniczeń
Podstawy Fizyki III Optyka z elementami fizyki współczesnej. wykład 13, Mateusz Winkowski, Łukasz Zinkiewicz
 Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład 13, 16.11.017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład 1 - przypomnienie
Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład 13, 16.11.017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład 1 - przypomnienie
WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 4 - zagadnienie estymacji, metody wyznaczania estymatorów
 WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 4 - zagadnienie estymacji, metody wyznaczania estymatorów Agata Boratyńska Agata Boratyńska Statystyka matematyczna, wykład 4 1 / 23 ZAGADNIENIE ESTYMACJI Zagadnienie
WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 4 - zagadnienie estymacji, metody wyznaczania estymatorów Agata Boratyńska Agata Boratyńska Statystyka matematyczna, wykład 4 1 / 23 ZAGADNIENIE ESTYMACJI Zagadnienie
Algorytm I. Obliczanie wymaganej powierzchni absorpcji
 Algorytm I. Oblcne wymgnej powerchn bsorpcj Wsp. prewodnośc olcj λ Zewnętrny wsp. wnn cepł α Prerój ew. olcj d Prerój wew. olcj d Grubość olcj d r Wsp. prenn cepł r α d π d + * ln λ d + α d Wsp. prenn
Algorytm I. Oblcne wymgnej powerchn bsorpcj Wsp. prewodnośc olcj λ Zewnętrny wsp. wnn cepł α Prerój ew. olcj d Prerój wew. olcj d Grubość olcj d r Wsp. prenn cepł r α d π d + * ln λ d + α d Wsp. prenn
LaTeX wprowadzenie. Piotr Kustra. Faculty of Metals Engineering and Industrial Computer Science. Department of Applied Computer Science and Modelling
 LaTeX wprowadzenie Piotr Kustra Faculty of Metals Engineering and Industrial Computer Science Department of Applied Computer Science and Modelling LaTeX co to jest? LaTeX jest to system składu umoŝliwiający
LaTeX wprowadzenie Piotr Kustra Faculty of Metals Engineering and Industrial Computer Science Department of Applied Computer Science and Modelling LaTeX co to jest? LaTeX jest to system składu umoŝliwiający
Gazetka Matematyczna Publicznego Gimnazjum nr 3
 Gazetka Matematyczna Publicznego Gimnazjum nr 3 nr 1: IX-X 2016r Witamy serdecznie po wakacjach wszystkich naszych czytelników a w szczególności nowo przybyłych do naszego gimnazjum. Kolegom i koleżankom
Gazetka Matematyczna Publicznego Gimnazjum nr 3 nr 1: IX-X 2016r Witamy serdecznie po wakacjach wszystkich naszych czytelników a w szczególności nowo przybyłych do naszego gimnazjum. Kolegom i koleżankom
3. Optymalizacja portfela inwestycyjnego Model Markowitza Model jednowskaźnikowy Sharpe a Model wyceny aktywów kapitałowych CAPM
 3. Optymalizacja portfela inwestycyjnego Model Markowitza Model jednowskaźnikowy Sharpe a Model wyceny aktywów kapitałowych CAPM Oczekiwana stopa zwrotu portfela dwóch akcji: E(r p ) = w 1 E(R 1 ) + w
3. Optymalizacja portfela inwestycyjnego Model Markowitza Model jednowskaźnikowy Sharpe a Model wyceny aktywów kapitałowych CAPM Oczekiwana stopa zwrotu portfela dwóch akcji: E(r p ) = w 1 E(R 1 ) + w
Bezbolesny wstęp do LATEX
 Bezbolesny wstęp do L A TEX 27 kwietnia 2004 Historia Ciekawe informacje o TEX-ie Czym jest L A TEX? jest doskonałym, darmowym (również wolnym) systemem składu tekstu, służącym między innymi do przygotowywania
Bezbolesny wstęp do L A TEX 27 kwietnia 2004 Historia Ciekawe informacje o TEX-ie Czym jest L A TEX? jest doskonałym, darmowym (również wolnym) systemem składu tekstu, służącym między innymi do przygotowywania
O pewnym twierdzeniu S. Łojasiewicza, J. Wloki, Z. Zieleżnego
 O pewnym twierdzeniu S. Łojasiewicza, J. Wloki, Z. Zieleżnego Jan Ligęza Instytut Matematyki Wisła Letnia Szkoła Instytutu Matematyki wrzesień 2010 r. [1] S. Łojasiewicz, J. Wloka, Z. Zieleżny; Über eine
O pewnym twierdzeniu S. Łojasiewicza, J. Wloki, Z. Zieleżnego Jan Ligęza Instytut Matematyki Wisła Letnia Szkoła Instytutu Matematyki wrzesień 2010 r. [1] S. Łojasiewicz, J. Wloka, Z. Zieleżny; Über eine
WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 11 i 12 - Weryfikacja hipotez statystycznych
 WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 11 i 12 - Weryfikacja hipotez statystycznych Agata Boratyńska Agata Boratyńska Statystyka matematyczna, wykład 11 i 12 1 / 41 TESTOWANIE HIPOTEZ - PORÓWNANIE
WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 11 i 12 - Weryfikacja hipotez statystycznych Agata Boratyńska Agata Boratyńska Statystyka matematyczna, wykład 11 i 12 1 / 41 TESTOWANIE HIPOTEZ - PORÓWNANIE
Statystyka matematyczna. Wykład III. Estymacja przedziałowa
 Statystyka matematyczna. Wykład III. e-mail:e.kozlovski@pollub.pl Spis treści Rozkłady zmiennych losowych 1 Rozkłady zmiennych losowych Rozkład χ 2 Rozkład t-studenta Rozkład Fischera 2 Przedziały ufności
Statystyka matematyczna. Wykład III. e-mail:e.kozlovski@pollub.pl Spis treści Rozkłady zmiennych losowych 1 Rozkłady zmiennych losowych Rozkład χ 2 Rozkład t-studenta Rozkład Fischera 2 Przedziały ufności
28 maja, Problem Dirichleta, proces Wienera. Procesy Stochastyczne, wykład 14, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126
 Problem Dirichleta, proces Wienera Procesy Stochastyczne, wykład 14, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 28 maja, 2012 Funkcje harmoniczne Niech będzie operatorem Laplace a w
Problem Dirichleta, proces Wienera Procesy Stochastyczne, wykład 14, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 28 maja, 2012 Funkcje harmoniczne Niech będzie operatorem Laplace a w
Funkcje odpowiedzi dla CCQE i wiązek MiniBooNE (cz. I)
 Funkcje odpowiedzi dla CCQE i wiązek MiniBooNE (cz. I) Marcin Gonera Instytut Fizyki Teoretycznej Uniwersytet Wrocławski 23.05.2011 Oddziaływanie EM Rozpraszanie elastyczne elektron-nukleon Foton opisany
Funkcje odpowiedzi dla CCQE i wiązek MiniBooNE (cz. I) Marcin Gonera Instytut Fizyki Teoretycznej Uniwersytet Wrocławski 23.05.2011 Oddziaływanie EM Rozpraszanie elastyczne elektron-nukleon Foton opisany
Płatew dachowa. Kombinacje przypadków obciążeń ustala się na podstawie wzoru. γ Gi G ki ) γ Q Q k. + γ Qi Q ki ψ ( i ) G ki - obciążenia stałe
 Płatew dachowa Przyjęcie schematu statycznego: - belka wolnopodparta - w halach posadowionych na szkodach górniczych lub w przypadkach, w których przewiduje się nierównomierne osiadanie układów poprzecznych
Płatew dachowa Przyjęcie schematu statycznego: - belka wolnopodparta - w halach posadowionych na szkodach górniczych lub w przypadkach, w których przewiduje się nierównomierne osiadanie układów poprzecznych
Porównanie modeli regresji. klasycznymi modelami regresji liniowej i logistycznej
 Porównanie modeli logicznej regresji z klasycznymi modelami regresji liniowej i logistycznej Instytut Matematyczny, Uniwersytet Wrocławski Małgorzata Bogdan Instytut Matematyki i Informatyki, Politechnika
Porównanie modeli logicznej regresji z klasycznymi modelami regresji liniowej i logistycznej Instytut Matematyczny, Uniwersytet Wrocławski Małgorzata Bogdan Instytut Matematyki i Informatyki, Politechnika
Elektrodynamika. Część 9. Potencjały i pola źródeł zmiennych w czasie. Ryszard Tanaś
 Elektrodynamika Część 9 Potencjały i pola źródeł zmiennych w czasie Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 10 Potencjały i pola źródeł zmiennych w
Elektrodynamika Część 9 Potencjały i pola źródeł zmiennych w czasie Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 10 Potencjały i pola źródeł zmiennych w
Greckie współczynniki kalkulowane są po zamknięciu sesji na podstawie następujących danych:
 Metodologia wyznaczania greckich współczynników. (1) Dane wejściowe. Greckie współczynniki kalkulowane są po zamknięciu sesji na podstawie następujących danych: S wartość zamknięcia indeksu WIG20 (pkt),
Metodologia wyznaczania greckich współczynników. (1) Dane wejściowe. Greckie współczynniki kalkulowane są po zamknięciu sesji na podstawie następujących danych: S wartość zamknięcia indeksu WIG20 (pkt),
Projekt silnika bezszczotkowego z magnesami trwałymi
 Projekt silnika bezszczotkowego z magnesami trwałymi dr inż. Michał Michna michna@pg.gda.pl 01-10-16 1. Dane znamionowe moc znamionowa P n : 10kW napięcie znamionowe U n : 400V prędkość znamionowa n n
Projekt silnika bezszczotkowego z magnesami trwałymi dr inż. Michał Michna michna@pg.gda.pl 01-10-16 1. Dane znamionowe moc znamionowa P n : 10kW napięcie znamionowe U n : 400V prędkość znamionowa n n
1 Relacje i odwzorowania
 Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
2.1 Przykład wstępny Określenie i konstrukcja Model dwupunktowy Model gaussowski... 7
 Spis treści Spis treści 1 Przedziały ufności 1 1.1 Przykład wstępny.......................... 1 1.2 Określenie i konstrukcja...................... 3 1.3 Model dwupunktowy........................ 5 1.4
Spis treści Spis treści 1 Przedziały ufności 1 1.1 Przykład wstępny.......................... 1 1.2 Określenie i konstrukcja...................... 3 1.3 Model dwupunktowy........................ 5 1.4
Rys. 1. Rysunek do zadania testowego
 Test zaliczeniowy Zadanie testowe. Przeanalizuj rysunek 1., przedstawiający odwzorowanie pewnej sytuacji przestrzennej przy pomocy metody Monge a (rzutów prostokątnych na dwie wzajemnie prostopadłe rzutnie
Test zaliczeniowy Zadanie testowe. Przeanalizuj rysunek 1., przedstawiający odwzorowanie pewnej sytuacji przestrzennej przy pomocy metody Monge a (rzutów prostokątnych na dwie wzajemnie prostopadłe rzutnie
Wykład 6 Teoria eksperymentu
 Wykład 6 Teoria eksperymentu Wrocław, 11.04.2018r Kwadrat łaciński Uszeregowanie N = p 2 elementów, które podlegają klasyfikacji podwójnej ze względu na p - bloków I rodzaju (wierszy) i p bloków II rodzaju
Wykład 6 Teoria eksperymentu Wrocław, 11.04.2018r Kwadrat łaciński Uszeregowanie N = p 2 elementów, które podlegają klasyfikacji podwójnej ze względu na p - bloków I rodzaju (wierszy) i p bloków II rodzaju
KATALOG DRZWI PVC I HPL
 KATALOG DRZWI PVC I HPL 2018 KATALOG DRZWI PVC I HPL 2018 1 KOMPLEMENTARNOŚĆ INNOWACYJNOŚĆ DESIGN Nasza rola wykracza poza projektowanie i produkcję okien. Oferujemy również rolę doradcy, architekta wnętrz,
KATALOG DRZWI PVC I HPL 2018 KATALOG DRZWI PVC I HPL 2018 1 KOMPLEMENTARNOŚĆ INNOWACYJNOŚĆ DESIGN Nasza rola wykracza poza projektowanie i produkcję okien. Oferujemy również rolę doradcy, architekta wnętrz,
Przekroje efektywne wyboczenia lokalnego 61,88 28,4 0,81 4 =1,34>0,673. = 28,4 ε k. ρ,, = λ 0,22 λ = 1,34 0,22 1,34 =0,62. = =59,39,
 Przekrój efektywny stalweg dźwigara z zastępczymi płytami rttrpwymi klasy 4 W bustrnnie sztywn umcwanym dźwigarze skrzynkwym długści 15,0 m ze stali S355 usztywnin pasy i śrdniki żebrami pdłużnymi (rys.
Przekrój efektywny stalweg dźwigara z zastępczymi płytami rttrpwymi klasy 4 W bustrnnie sztywn umcwanym dźwigarze skrzynkwym długści 15,0 m ze stali S355 usztywnin pasy i śrdniki żebrami pdłużnymi (rys.
Oddziaływanie procesu informacji na dynamikę cen akcji. Małgorzata Doman Akademia Ekonomiczna w Poznaniu
 Oddziaływanie procesu informacji na dynamikę cen akcji. Małgorzaa Doman Akademia Ekonomiczna w Poznaniu Modele mikrosrukury rynku Bageho (97) informed raders próbują wykorzysać swoją przewagę informacyjną
Oddziaływanie procesu informacji na dynamikę cen akcji. Małgorzaa Doman Akademia Ekonomiczna w Poznaniu Modele mikrosrukury rynku Bageho (97) informed raders próbują wykorzysać swoją przewagę informacyjną
Projekt silnika bezszczotkowego prądu przemiennego. 1. Wstęp. 1.1 Dane wejściowe. 1.2 Obliczenia pomocnicze
 projekt_pmsm_v.xmcd 01-04-1 Projekt silnika bezszczotkowego prądu przemiennego 1. Wstęp Projekt silnika bezszczotkowego prądu przemiennego - z sinusoidalnym rozkładem indukcji w szczelinie powietrznej.
projekt_pmsm_v.xmcd 01-04-1 Projekt silnika bezszczotkowego prądu przemiennego 1. Wstęp Projekt silnika bezszczotkowego prądu przemiennego - z sinusoidalnym rozkładem indukcji w szczelinie powietrznej.
Spektroskopia mionów w badaniach wybranych materiałów magnetycznych. Piotr M. Zieliński NZ35 IFJ PAN
 Spektroskopia mionów w badaniach wybranych materiałów magnetycznych Piotr M. Zieliński NZ35 IFJ PAN 1. Fundamenty spektroskopii mionów. Typowy eksperyment 3. Cel i obiekty badań 4. Przykłady otrzymanych
Spektroskopia mionów w badaniach wybranych materiałów magnetycznych Piotr M. Zieliński NZ35 IFJ PAN 1. Fundamenty spektroskopii mionów. Typowy eksperyment 3. Cel i obiekty badań 4. Przykłady otrzymanych
LATEX system do składu tekstu
 L A TEX system do składu tekstu 4 października 2008 Czym jest L A TEX Informacje wstępne Komendy, argumenty, opcje... L A TEX(wym. latech) jest systemem służącym do składu tekstu. W odróżnieniu od programów
L A TEX system do składu tekstu 4 października 2008 Czym jest L A TEX Informacje wstępne Komendy, argumenty, opcje... L A TEX(wym. latech) jest systemem służącym do składu tekstu. W odróżnieniu od programów
Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM
 Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................
Elektrodynamika Część 8 Fale elektromagnetyczne Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 9 Fale elektromagnetyczne 3 9.1 Fale w jednym wymiarze.................
Zastosowanie techniki μsr w badaniach własności magnetyków molekularnych. Piotr M. Zieliński NZ35 IFJ PAN
 Zastosowanie techniki μsr w badaniach własności magnetyków molekularnych. Piotr M. Zieliński NZ35 IFJ PAN 1. Fundamenty spektroskopii mionów. Typowy eksperyment 3. Zjawiska krytyczne i SR 4. Przykłady
Zastosowanie techniki μsr w badaniach własności magnetyków molekularnych. Piotr M. Zieliński NZ35 IFJ PAN 1. Fundamenty spektroskopii mionów. Typowy eksperyment 3. Zjawiska krytyczne i SR 4. Przykłady
= arc tg - eliptyczność. Polaryzacja światła. Prawo Snelliusa daje kąt. Co z amplitudą i polaryzacją? Drgania i fale II rok Fizyka BC
 4-0-0 G:\AA_Wyklad 000\FIN\DOC\Polar.doc Drgaia i fale II rok Fizyka C Polaryzacja światła ( b a) arc tg - eliptyczość Prawo Selliusa daje kąt. Co z amplitudą i polaryzacją? 4-0-0 G:\AA_Wyklad 000\FIN\DOC\Polar.doc
4-0-0 G:\AA_Wyklad 000\FIN\DOC\Polar.doc Drgaia i fale II rok Fizyka C Polaryzacja światła ( b a) arc tg - eliptyczość Prawo Selliusa daje kąt. Co z amplitudą i polaryzacją? 4-0-0 G:\AA_Wyklad 000\FIN\DOC\Polar.doc
Technika obliczeniowa i symulacyjna (TOiS)
 Technika obliczeniowa i symulacyjna (TOiS) Dr inż. Andrzej Dobrucki, doc PWr andrzej.l.dobrucki@pwr.wroc.pl pok. 239 bud C-4 2 Materiały z laboratorium www.zto.ita.pwr.wroc.pl/~ald 3 Witryna ZTO www.zto.ita.pwr.wroc.pl
Technika obliczeniowa i symulacyjna (TOiS) Dr inż. Andrzej Dobrucki, doc PWr andrzej.l.dobrucki@pwr.wroc.pl pok. 239 bud C-4 2 Materiały z laboratorium www.zto.ita.pwr.wroc.pl/~ald 3 Witryna ZTO www.zto.ita.pwr.wroc.pl
Dokumentacja. Wycena opcji europejskich. w modelu Hestona
 Dokumentacja Wycena opcji europejskich w modelu Hestona Konrad Stawski Spis treści 1 Opis problemu 2 2 Opis dyskretyzacji problemu 3 3 Zmienne wykorzystywane w programie 6 4 Spis wykorzystywanych funkcji
Dokumentacja Wycena opcji europejskich w modelu Hestona Konrad Stawski Spis treści 1 Opis problemu 2 2 Opis dyskretyzacji problemu 3 3 Zmienne wykorzystywane w programie 6 4 Spis wykorzystywanych funkcji
(8) Oblicz wyznacznik dowolnie wybranej macierzy stopnia czwartego. (9) Rozwi aż podany układ równań stosuj ac wzory Cramera:
 Zadania przygotowuj ace do kolokwium (budownictwo, studia niestacjonarne, drugi semestr, 209) [7III] () Podaj przykład dowolnej macierzy A drugiego stopnia Oblicz A A T + A T A (2) Podaj przykład dowolnej
Zadania przygotowuj ace do kolokwium (budownictwo, studia niestacjonarne, drugi semestr, 209) [7III] () Podaj przykład dowolnej macierzy A drugiego stopnia Oblicz A A T + A T A (2) Podaj przykład dowolnej
Rezonanse w deekscytacji molekuł mionowych i rozpraszanie elastyczne atomów mionowych helu. Wilhelm Czapliński Katedra Zastosowań Fizyki Jądrowej
 ezonanse w deekscytacj moekuł monowych ozpaszane eastyczne atomów monowych heu Whem Czapńsk Kateda Zastosowań Fzyk Jądowej . ezonanse w deekscytacj moekuł monowych µ He ++ h ++ Heµ h J ν h p d t otacyjna
ezonanse w deekscytacj moekuł monowych ozpaszane eastyczne atomów monowych heu Whem Czapńsk Kateda Zastosowań Fzyk Jądowej . ezonanse w deekscytacj moekuł monowych µ He ++ h ++ Heµ h J ν h p d t otacyjna
Sekantooptyki owali i ich własności
 Sekantooptyki owali i ich własności Magdalena Skrzypiec Wydział Matematyki, Fizyki i Informatyki Uniwersytet Marii Curie-Skłodowskiej 19 października 2009r. Informacje wstępne Definicja Owalem nazywamy
Sekantooptyki owali i ich własności Magdalena Skrzypiec Wydział Matematyki, Fizyki i Informatyki Uniwersytet Marii Curie-Skłodowskiej 19 października 2009r. Informacje wstępne Definicja Owalem nazywamy
Proces rezerwy w czasie dyskretnym z losową stopą procentową i losową składką
 z losową stopą procentową i losową składką Instytut Matematyki i Informatyki Politechniki Wrocławskiej 10 czerwca 2008 Oznaczenia Wprowadzenie ξ n liczba wypłat w (n 1, n], Oznaczenia Wprowadzenie ξ n
z losową stopą procentową i losową składką Instytut Matematyki i Informatyki Politechniki Wrocławskiej 10 czerwca 2008 Oznaczenia Wprowadzenie ξ n liczba wypłat w (n 1, n], Oznaczenia Wprowadzenie ξ n
ISBN (wersja drukowana) ISBN (ebook)
 Iwona Jażdżewska Instytut Geografii Miast i Turyzmu Wydział Nauk Geograficznych, Uniwersytet Łódzki, 90-323 Łódź, ul. Kopcińskiego 31 RECENZENT Jerzy Runge REDAKTOR WYDAWNICTWA UŁ Danuta Bąk SKŁAD I ŁAMANIE
Iwona Jażdżewska Instytut Geografii Miast i Turyzmu Wydział Nauk Geograficznych, Uniwersytet Łódzki, 90-323 Łódź, ul. Kopcińskiego 31 RECENZENT Jerzy Runge REDAKTOR WYDAWNICTWA UŁ Danuta Bąk SKŁAD I ŁAMANIE
Prawdopodobieństwo i statystyka
 Wykład II: Zmienne losowe i charakterystyki ich rozkładów 13 października 2014 Zmienne losowe Wartość oczekiwana Dystrybuanty Słowniczek teorii prawdopodobieństwa, cz. II Definicja zmiennej losowej i jej
Wykład II: Zmienne losowe i charakterystyki ich rozkładów 13 października 2014 Zmienne losowe Wartość oczekiwana Dystrybuanty Słowniczek teorii prawdopodobieństwa, cz. II Definicja zmiennej losowej i jej
GAL 80 zadań z liczb zespolonych
 GAL 80 zadań z liczb zespolonych Postać algebraiczna liczby zespolonej 1 Sprowadź wyrażenia do postaci algebraicznej: (a) ( + i)(3 i) + ( + 31)(3 + 41), (b) (4 + 3i)(5 i) ( 6i), (5 + i)(7 6i) (c), 3 +
GAL 80 zadań z liczb zespolonych Postać algebraiczna liczby zespolonej 1 Sprowadź wyrażenia do postaci algebraicznej: (a) ( + i)(3 i) + ( + 31)(3 + 41), (b) (4 + 3i)(5 i) ( 6i), (5 + i)(7 6i) (c), 3 +
Zadanie 1. Liczba szkód N w ciągu roku z pewnego ryzyka ma rozkład geometryczny: k =
 Matematyka ubezpieczeń majątkowych 0.0.006 r. Zadanie. Liczba szkód N w ciągu roku z pewnego ryzyka ma rozkład geometryczny: k 5 Pr( N = k) =, k = 0,,,... 6 6 Wartości kolejnych szkód Y, Y,, są i.i.d.,
Matematyka ubezpieczeń majątkowych 0.0.006 r. Zadanie. Liczba szkód N w ciągu roku z pewnego ryzyka ma rozkład geometryczny: k 5 Pr( N = k) =, k = 0,,,... 6 6 Wartości kolejnych szkód Y, Y,, są i.i.d.,
n [2, 11] 1.5 ( G. Pick 1899).
![n [2, 11] 1.5 ( G. Pick 1899). n [2, 11] 1.5 ( G. Pick 1899).](/thumbs/98/135090138.jpg) 1. / / 2. R 4k 3. 4. 5. 6. / 7. /n 8. n 1 / / Z d ( R d ) d P Z d R d R d? n > 0 n 1.1. R 2 6 n 5 n [Scherrer 1946] d 3 R 3 6 1.2 (Schoenberg 1937). d 3 R d n n = 3, 4, 6 1.1. d 3 R d 1.3. θ θ/π 1.4. 0
1. / / 2. R 4k 3. 4. 5. 6. / 7. /n 8. n 1 / / Z d ( R d ) d P Z d R d R d? n > 0 n 1.1. R 2 6 n 5 n [Scherrer 1946] d 3 R 3 6 1.2 (Schoenberg 1937). d 3 R d n n = 3, 4, 6 1.1. d 3 R d 1.3. θ θ/π 1.4. 0
Podstawy robotyki. Wykład II. Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska
 Podstawy robotyki Wykład II Ruch ciała sztywnego w przestrzeni euklidesowej Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Preliminaria matematyczne
Podstawy robotyki Wykład II Ruch ciała sztywnego w przestrzeni euklidesowej Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Preliminaria matematyczne
Równania różniczkowe liniowe rzędu pierwszego
 Katedra Matematyki i Ekonomii Matematycznej SGH 21 kwietnia 2016 Wstęp Definicja Równanie różniczkowe + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to
Katedra Matematyki i Ekonomii Matematycznej SGH 21 kwietnia 2016 Wstęp Definicja Równanie różniczkowe + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to
10.0. Schody górne, wspornikowe.
 10.0. Schody górne, wspornikowe. OBCIĄŻENIA: Grupa: A "obc. stałe - pł. spocznik" Stałe γf= 1,0/0,90 Q k = 0,70 kn/m *1,5m=1,05 kn/m. Q o1 = 0,84 kn/m *1,5m=1,6 kn/m, γ f1 = 1,0, Q o = 0,63 kn/m *1,5m=0,95
10.0. Schody górne, wspornikowe. OBCIĄŻENIA: Grupa: A "obc. stałe - pł. spocznik" Stałe γf= 1,0/0,90 Q k = 0,70 kn/m *1,5m=1,05 kn/m. Q o1 = 0,84 kn/m *1,5m=1,6 kn/m, γ f1 = 1,0, Q o = 0,63 kn/m *1,5m=0,95


 =>?.
=>?.