Krzywe stożkowe. Algebra. Aleksander Denisiuk
|
|
|
- Alojzy Marszałek
- 8 lat temu
- Przeglądów:
Transkrypt
1 Algebra Krzywe stożkowe Aleksander Denisiuk Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi Gdańsk Algebra p. 1
2 Krzywe stożkowe Najnowsza wersja tego dokumentu dostępna jest pod adresem Algebra p. 2
3 Współrzędne biegunowe A ρ O O biegun Oś biegunowa g θ g Kierunek odliczania katów (ρ, θ) współrzędne biegunowe Algebra p. 3
4 Równanie krzywej we współrzędnych biegunowych ϕ(ρ,θ) = 0 Przykład 1 (Okrag). ρ = 2Rcosθ A O θ A 0 Algebra p. 4
5 Współrzędne biegunowe a kartezjańskie x = ρcosθ, y = ρsinθ Algebra p. 5
6 Równanie prostej we współrzędnych biegunowych ax+by +c = 0, c < 0 ρcos(α θ) = ρ 0, gdzie cosα = a a2 +b 2, sinα = b a2 +b 2, ρ 0 = c a2 +b 2, Algebra p. 6
7 Krzywa stożkowa Krzywa stożkowa nazywa się krzywa, powstała na przecięciu stożka i płaszczyzny. Algebra p. 7
8 Ogniska i kierownice Każda krzywa stożkowa, oprócz okręgu, jest miejscem geometrycznym punktów, majacych stały stosunek odległości od pewnego punktu F i pewnej prostej δ Punkt F nazywa się ogniskiem krzywej Prosta δ nazywa się kierownica krzywej Algebra p. 8
9 Ogniska i kierownice, cd FM = BM, AM = h/sinα, BM = h/sinβ FM AM = BM AM = sinα sinβ = λ λ nazywa się mimośrodem Algebra p. 9
10 Klasyfikacja krzywych stożkowych W zależności od mimośrodu λ, krzywa stożkowa nazywa się elipsa λ < 1 parabola λ > 1 hyperbola λ > 1 składa się z dwóch gałęzi Algebra p. 10
11 Równanie we współrzędnych biegunowych Niech biegun pokrywa się z ogniskiem krzywej, a oś biegunowa będzie przecinała prostopadle kierownicę Niech p będzie odległościa ogniska od kierownicy W przypadku elipsy i paraboli W przypadku hiperboli ρ p ρcosθ = λ ρ p ρcosθ = ±λ W postaci rozwiazanej względen ρ: W przypadku elipsy i paraboli ρ = W przypadku hiperboli ρ = ±λp 1±λcosθ λp 1+λcosθ Algebra p. 11
12 Równanie we współrzędnych kartezjańskich ρ 2 = λ 2 (p ρcosθ) 2 x 2 +y 2 = λ 2 (p x) 2 (1 λ) 2 x 2 +2pλ 2 x+y 2 λ 2 p 2 = 0 λ 1 (1 λ 2 ) ( x+ pλ2 1 λ 2 ) 2 +y 2 p2 λ 2 1 λ 2 = 0 Nowe współrzędne: x = x+ pλ2 1 λ 2, y = y Elipsa: x 2 a 2 + y 2 b 2 = 1 Hiperbola: x 2 a 2 y 2 b 2 = 1 gdzie a 2 = λ2 p 2 (1 λ 2 ) 2, b 2 = λ2 p 2 1 λ 2 półosie równanie kanoniczne Algebra p. 12
13 Równanie kanoniczne paraboli (1 λ) 2 x 2 +2pλ 2 x+y 2 λ 2 p 2 = 0 λ = 1 2px+y 2 p 2 = 0 y 2 2p ( x+ p 2) = 0 Nowe współrzędne: x = x+ p 2, y = y y 2 2px = 0 Algebra p. 13
14 Właściwości elipsy x2 a 2 + y2 b 2 = 1, a > b > 0 Symetria względem osi i środka układu współrzędnych Elipsa zawarta jest wewnatrz prostokatu x a, y b a nazywa się większa półosia, b mniejsza półosia. Punkty (±a, 0), (0, ±b) wierzchołki elipsy Algebra p. 14
15 Elipsa a okrag Elipsa może zostać otzrymana z okręgu x2 a 2 + y2 b 2 = 1 poprzez skalowanie w kirunku osi Oy ze współczynnikiem b a < 1 Algebra p. 15
16 Właściwości hiperboli x2 a 2 y2 b 2 = 1, a,b > 0 Symetria względem osi i środka układu współrzędnych Hiperbola znajduje się na zewnatrz od prostokatu x a, y b Hiperbola jest położona poza katem x a < y b a nazywa się rzeczywista półosia, b półosia urojona. Punkty (±a, 0) wierzchołki hiperboli Algebra p. 16
17 Asymptoty hiperboli Proste x a ± y b = 0 s a asymptotami hiperboli Odległość od punktów hiperboli do asymptot dazy do żera przy x 2 +y 2 Niech punkt (x,y) leży na hiperboli Liczby x a + y b odległości oraz x a y b = 1 x a + y x b a y b Załóżmy, że odległości nie d sa proporcjonalne do aza do zera, wtedy istnieje taka liczba ε > 0, że dla wszystkich punktów (x,y) hiperboli spełniono x a + y b > ε oraz x a y b > ε A więc x a + y b < 1 ε oraz x a y b < 1 ε Czyli x2 a a + y2 b 2 < 1 ε 2, co jest sprzeczne z tym, że x 2 +y 2 Algebra p. 17
18 Hiperbola sprzężona Hiperbola x2 a y2 2 b = 1 nazywa się sprzężona do hiperboli 2 x 2 a y2 2 b = 1 2 Hiperbola i hiperbola do niej sprzężona maja wspólne asymptoty Hiperbola sprzężona znajduje się w katach uzupełniajacych Algebra p. 18
19 Parabola y 2 = 2px Parabola jest symetryczna względem osi Ox Oś symetrii nazywa się osia paraboli Przecięcie osi z parabola nazywa się wierzchołkiem paraboli Algebra p. 19
20 Równania parametryczne {x = t2 parabola 2p, y = t { x = acost, elipsa y = bsint { x = acosht, hiperbola y = bsinht cosht = et +e t 2, sinht = et e t 2 Algebra p. 20
21 Styczna do krzywej w punkcie(x 0,y 0 ) Styczna do krzywej stożkowej (x 0,y 0 ) nazywa się prosta, która ma z nia dokładnie jeden punkt przecięcia (i nie jest równoległa do osi dla paraboli) Sens geometryczny stycznej: graniczne położenie siecznych przechodzacych przez punkty (x 0,y 0 ) i (x 1,y 1 ) gdy punkt (x 1,y 1 ) daży do (x 0,y 0 ) Można podstawić równanie parametryczne prostej, wychodzacej z punktu (x 0,y 0 ) do równania krzywej: styczna do paraboli yy 0 = p(x+x 0 ) styczna do elipsy xx 0 a + yy 0 2 b = 1 2 styczna do hiperboli xx 0 a yy 0 2 b = 1 2 Algebra p. 21
22 Właściwości ogniskowe Elipsa i hiperbola maja drugie ognisko i druga kierownicę Suma odległości punktów elipsy od ognisk jest stała Różnica odległości punktów hiperboli od ognisk jest stała Ogniska elipsy maja współrzędne (0,±c), c = a 2 b 2 Ogniska hiperboli maja współrzędne (0,±c), c = a 2 +b 2 Promień świetlny wychodzacy z jednego ogniska elipsy po odbiciu od krawędzi przejdzie przez drugie ognisko Promień świetlny wychodzacy z jednego ogniska hierboli po odbiciu od krawędzi będzie pokrywał się z promieniem, wychodzacycm z drugiego ogniska Promień świetlny wychodzacy z ogniska paraboli po odbiciu od krawędzi będzie równoległy do jej osi Algebra p. 22
23 Średnice krzywej stożkowe Średnica elipsy (hiperboli) nazywamy odcinek, przechodzacy przez jej środek Średnica paraboli jest prosta, równoległa do jej osi. Środki równoległych siecznych znajduja się na średnicy 1. Sieczna jest równoległa do osi współrzędnych 2. y = kx+b, k 0, elipsa (hiperbola) αx 2 +βy 2 = 1 y c = α βk x c średnica y = α βkx jest sprzężona do średnicy y = kx 3. y = kx+b, k 0, parabola y c = p k = const Algebra p. 23
24 Krzywe drugiego stopnia a 11 x 2 +2a 12 xy +a 22 y 2 +2a 1 x+2a 2 y +a = 0, przynajmniej jeden ze współczynników a 11, a 12, a 22 jest niezerowy. Niepusta krzywa drugiego stopnia: krzywa stożkowa dwie proste (być może pokrywajace się) punkt Przykład 3x 2 +3y 3 +10xy +14x 2y 13 = 0 Algebra p. 24
Krzywe stożkowe Lekcja VII: Hiperbola
 Krzywe stożkowe Lekcja VII: Hiperbola Wydział Matematyki Politechniki Wrocławskiej Czym jest hiperbola? Hiperbola jest krzywą stożkową powstałą przez przecięcie stożka płaszczyzną pod kątem 0 β < α (gdzie
Krzywe stożkowe Lekcja VII: Hiperbola Wydział Matematyki Politechniki Wrocławskiej Czym jest hiperbola? Hiperbola jest krzywą stożkową powstałą przez przecięcie stożka płaszczyzną pod kątem 0 β < α (gdzie
Krzywe stożkowe Lekcja VI: Parabola
 Krzywe stożkowe Lekcja VI: Parabola Wydział Matematyki Politechniki Wrocławskiej Czym jest parabola? Parabola jest krzywą stożkową powstałą przez przecięcie stożka płaszczyzną pod kątem β = α (gdzie α
Krzywe stożkowe Lekcja VI: Parabola Wydział Matematyki Politechniki Wrocławskiej Czym jest parabola? Parabola jest krzywą stożkową powstałą przez przecięcie stożka płaszczyzną pod kątem β = α (gdzie α
Rozdział 2. Krzywe stożkowe. 2.1 Elipsa. Krzywe stożkowe są zadane ogólnym równaniem kwadratowym na płaszczyźnie
 Rozdział Krzywe stożkowe Krzywe stożkowe są zadane ogólnym równaniem kwadratowym na płaszczyźnie x + By + Cxy + Dx + Ey + F = 0. (.) W zależności od relacji pomiędzy współczynnikami otrzymujemy elipsę,
Rozdział Krzywe stożkowe Krzywe stożkowe są zadane ogólnym równaniem kwadratowym na płaszczyźnie x + By + Cxy + Dx + Ey + F = 0. (.) W zależności od relacji pomiędzy współczynnikami otrzymujemy elipsę,
Zestaw Obliczyć objętość równoległościanu zbudowanego na wektorach m, n, p jeśli wiadomo, że objętość równoległościanu zbudowanego na wektorach:
 Zestaw 9. Wykazać, że objętość równoległościanu zbudowanego na przekątnych ścian danego równoległościanu jest dwa razy większa od objętości równoległościanu danego.. Obliczyć objętość równoległościanu
Zestaw 9. Wykazać, że objętość równoległościanu zbudowanego na przekątnych ścian danego równoległościanu jest dwa razy większa od objętości równoległościanu danego.. Obliczyć objętość równoległościanu
Geometria Analityczna w Przestrzeni
 Algebra p. 1/25 Algebra Geometria Analityczna w Przestrzeni Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045
Algebra p. 1/25 Algebra Geometria Analityczna w Przestrzeni Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045
- Wydział Fizyki Zestaw nr 2. Krzywe stożkowe
 1 Algebra Liniowa z Geometria - Wydział Fizyki Zestaw nr 2 Krzywe stożkowe 1 Znaleźć współrze dne środka i promień okre gu x 2 8x + y 2 + 6y + 20 = 0 2 Znaleźć zbiór punktów płaszczyzny R 2, których odległość
1 Algebra Liniowa z Geometria - Wydział Fizyki Zestaw nr 2 Krzywe stożkowe 1 Znaleźć współrze dne środka i promień okre gu x 2 8x + y 2 + 6y + 20 = 0 2 Znaleźć zbiór punktów płaszczyzny R 2, których odległość
- Wydział Fizyki Zestaw nr 2. Krzywe stożkowe
 1 Algebra Liniowa z Geometria - Wydział Fizyki Zestaw nr 2 Krzywe stożkowe 1 Znaleźć współrze dne środka i promień okre gu x 2 8x + y 2 + 6y + 20 = 0 2 Znaleźć zbiór punktów płaszczyzny R 2, których odległość
1 Algebra Liniowa z Geometria - Wydział Fizyki Zestaw nr 2 Krzywe stożkowe 1 Znaleźć współrze dne środka i promień okre gu x 2 8x + y 2 + 6y + 20 = 0 2 Znaleźć zbiór punktów płaszczyzny R 2, których odległość
Krzywe stożkowe Lekcja V: Elipsa
 Krzywe stożkowe Lekcja V: Elipsa Wydział Matematyki Politechniki Wrocławskiej Czym jest elipsa? Elipsa jest krzywą stożkową powstałą przez przecięcie stożka płaszczyzną pod kątem α < β < π 2 (gdzie α jest
Krzywe stożkowe Lekcja V: Elipsa Wydział Matematyki Politechniki Wrocławskiej Czym jest elipsa? Elipsa jest krzywą stożkową powstałą przez przecięcie stożka płaszczyzną pod kątem α < β < π 2 (gdzie α jest
Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych
 Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych Wydział Matematyki Politechniki Wrocławskiej Okrąg Okrąg jest szczególną krzywą stożkową. Wyznacza nam koło, które jest podstawą
Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych Wydział Matematyki Politechniki Wrocławskiej Okrąg Okrąg jest szczególną krzywą stożkową. Wyznacza nam koło, które jest podstawą
1 Geometria analityczna
 1 Geometria analityczna 1.1 Wektory na płaszczyźnie Wektor to uporządkowana para punktów, z których pierwszy nazywa się początkiem, a drugi końcem wektora. Jeżeli wprowadzimy prostokątny układ współrzędnych,
1 Geometria analityczna 1.1 Wektory na płaszczyźnie Wektor to uporządkowana para punktów, z których pierwszy nazywa się początkiem, a drugi końcem wektora. Jeżeli wprowadzimy prostokątny układ współrzędnych,
Zadania nadobowiązkowe KRZYWE STOŻKOWE OKRĄG
 OKRĄG Przykład 1. W układzie współrzędnych XOY narysujmy okrąg o środku w punkcie (0,0) i promieniu 1: Współrzędne dowolnego punktu P(x,y) leżącego na okręgu spełniają równanie + y =1, natomiast współrzędne
OKRĄG Przykład 1. W układzie współrzędnych XOY narysujmy okrąg o środku w punkcie (0,0) i promieniu 1: Współrzędne dowolnego punktu P(x,y) leżącego na okręgu spełniają równanie + y =1, natomiast współrzędne
Geometria. Hiperbola
 Geometria. Hiperbola Definicja 1 Dano dwa punkty na płaszczyźnie: F 1 i F 2 oraz taką liczbę d, że F 1 F 2 > d > 0. Zbiór punktów płaszczyzny będących rozwiązaniami równania: XF 1 XF 2 = ±d. nazywamy hiperbolą.
Geometria. Hiperbola Definicja 1 Dano dwa punkty na płaszczyźnie: F 1 i F 2 oraz taką liczbę d, że F 1 F 2 > d > 0. Zbiór punktów płaszczyzny będących rozwiązaniami równania: XF 1 XF 2 = ±d. nazywamy hiperbolą.
11. Znajdż równanie prostej prostopadłej do prostej k i przechodzącej przez punkt A = (2;2).
 1. Narysuj poniższe figury: a), b), c) 2. Punkty A = (0;1) oraz B = (-1;0) należą do okręgu którego środek należy do prostej o równaniu x-2 = 0. Podaj równanie okręgu. 3. Znaleźć równanie okręgu przechodzącego
1. Narysuj poniższe figury: a), b), c) 2. Punkty A = (0;1) oraz B = (-1;0) należą do okręgu którego środek należy do prostej o równaniu x-2 = 0. Podaj równanie okręgu. 3. Znaleźć równanie okręgu przechodzącego
(a) (b) (c) o1" o2" o3" o1'=o2'=o3'
 Zad.0. Odwzorowanie powierzchni stożka, walca, sfery oraz punktów leżących na tych powierzchniach. Przy odwzorowaniu powierzchni stożka, walca, sfery przyjmiemy reprezentację konturową, co oznacza, że
Zad.0. Odwzorowanie powierzchni stożka, walca, sfery oraz punktów leżących na tych powierzchniach. Przy odwzorowaniu powierzchni stożka, walca, sfery przyjmiemy reprezentację konturową, co oznacza, że
Geometria analityczna - przykłady
 Geometria analityczna - przykłady 1. Znaleźć równanie ogólne i równania parametryczne prostej w R 2, któr przechodzi przez punkt ( 4, ) oraz (a) jest równoległa do prostej x + 5y 2 = 0. (b) jest prostopadła
Geometria analityczna - przykłady 1. Znaleźć równanie ogólne i równania parametryczne prostej w R 2, któr przechodzi przez punkt ( 4, ) oraz (a) jest równoległa do prostej x + 5y 2 = 0. (b) jest prostopadła
Wykład 16. P 2 (x 2, y 2 ) P 1 (x 1, y 1 ) OX. Odległość tych punktów wyraża się wzorem: P 1 P 2 = (x 1 x 2 ) 2 + (y 1 y 2 ) 2
 Wykład 16 Geometria analityczna Przegląd wiadomości z geometrii analitycznej na płaszczyźnie rtokartezjański układ współrzędnych powstaje przez ustalenie punktu początkowego zwanego początkiem układu współrzędnych
Wykład 16 Geometria analityczna Przegląd wiadomości z geometrii analitycznej na płaszczyźnie rtokartezjański układ współrzędnych powstaje przez ustalenie punktu początkowego zwanego początkiem układu współrzędnych
A. fałszywa dla każdej liczby x.b. prawdziwa dla C. prawdziwa dla D. prawdziwa dla
 Zadanie 1 Liczba jest równa A. B. C. 10 D. Odpowiedź B. Zadanie 2 Liczba jest równa A. 3 B. 2 C. D. Odpowiedź D. Zadanie 3. Liczba jest równa Odpowiedź D. Zadanie 4. Liczba osobników pewnego zagrożonego
Zadanie 1 Liczba jest równa A. B. C. 10 D. Odpowiedź B. Zadanie 2 Liczba jest równa A. 3 B. 2 C. D. Odpowiedź D. Zadanie 3. Liczba jest równa Odpowiedź D. Zadanie 4. Liczba osobników pewnego zagrożonego
Geometria. Rozwiązania niektórych zadań z listy 2
 Geometria. Rozwiązania niektórych zadań z listy 2 Inne rozwiązanie zadania 2. (Wyznaczyć równanie stycznej do elipsy x 2 a 2 + y2 b 2 = 1 w dowolnym jej punkcie (x 0, y 0 ). ) Przypuśćmy, że krzywa na
Geometria. Rozwiązania niektórych zadań z listy 2 Inne rozwiązanie zadania 2. (Wyznaczyć równanie stycznej do elipsy x 2 a 2 + y2 b 2 = 1 w dowolnym jej punkcie (x 0, y 0 ). ) Przypuśćmy, że krzywa na
Funkcja liniowa i prosta podsumowanie
 Funkcja liniowa i prosta podsumowanie Definicja funkcji liniowej Funkcja liniowa określona jest wzorem postaci: y = ax + b, x R, a R, b R a, b współczynniki funkcji dowolne liczby rzeczywiste a- współczynnik
Funkcja liniowa i prosta podsumowanie Definicja funkcji liniowej Funkcja liniowa określona jest wzorem postaci: y = ax + b, x R, a R, b R a, b współczynniki funkcji dowolne liczby rzeczywiste a- współczynnik
Prosta i płaszczyzna w przestrzeni
 Prosta i płaszczyzna w przestrzeni Wybrane wzory i informacje Równanie prostej przechodzącej przez punkt P 0 = (x 0, y 0, z 0 ) o wektorze wodzącym r 0 i równoległej do wektora v = [a, b, c] : postać parametrycznego
Prosta i płaszczyzna w przestrzeni Wybrane wzory i informacje Równanie prostej przechodzącej przez punkt P 0 = (x 0, y 0, z 0 ) o wektorze wodzącym r 0 i równoległej do wektora v = [a, b, c] : postać parametrycznego
SPIS RZECZY. GEOMETRJA ANALITYCZNA NA PŁASZCZYŹNIE.
 SPIS RZECZY. CZĘŚĆ PIERWSZA. GEOMETRJA ANALITYCZNA NA PŁASZCZYŹNIE. ROZDZIAŁ I. Współrzędne na płaszczyźnie. Wektory. 1. Uwaga wstępna 1 2. Współrzędne punktu 1 3. Położenie wektora na osi 4 4. Kąt między
SPIS RZECZY. CZĘŚĆ PIERWSZA. GEOMETRJA ANALITYCZNA NA PŁASZCZYŹNIE. ROZDZIAŁ I. Współrzędne na płaszczyźnie. Wektory. 1. Uwaga wstępna 1 2. Współrzędne punktu 1 3. Położenie wektora na osi 4 4. Kąt między
Repetytorium z matematyki ćwiczenia
 Spis treści 1 Liczby rzeczywiste 1 2 Geometria analityczna. Prosta w układzie kartezjańskim Oxy 4 3 Krzywe drugiego stopnia na płaszczyźnie kartezjańskiej 6 4 Dziedzina i wartości funkcji 8 5 Funkcja liniowa
Spis treści 1 Liczby rzeczywiste 1 2 Geometria analityczna. Prosta w układzie kartezjańskim Oxy 4 3 Krzywe drugiego stopnia na płaszczyźnie kartezjańskiej 6 4 Dziedzina i wartości funkcji 8 5 Funkcja liniowa
Arkusz 6. Elementy geometrii analitycznej w przestrzeni
 Arkusz 6. Elementy geometrii analitycznej w przestrzeni Zadanie 6.1. Obliczyć długości podanych wektorów a) a = [, 4, 12] b) b = [, 5, 2 2 ] c) c = [ρ cos φ, ρ sin φ, h], ρ 0, φ, h R c) d = [ρ cos φ cos
Arkusz 6. Elementy geometrii analitycznej w przestrzeni Zadanie 6.1. Obliczyć długości podanych wektorów a) a = [, 4, 12] b) b = [, 5, 2 2 ] c) c = [ρ cos φ, ρ sin φ, h], ρ 0, φ, h R c) d = [ρ cos φ cos
Algebra linowa w pigułce
 Algebra Algebra linowa w pigułce Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Algebra
Algebra Algebra linowa w pigułce Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Algebra
ODLEGŁOŚĆ NA PŁASZCZYŹNIE - SPRAWDZIAN
 ODLEGŁOŚĆ NA PŁASZCZYŹNIE - SPRAWDZIAN Gr. 1 Zad. 1. Dane są punkty: P = (-, 1), R = (5, -1), S = (, 3). a) Oblicz odległość między punktami R i S. b) Wyznacz współrzędne środka odcinka PR. c) Napisz równanie
ODLEGŁOŚĆ NA PŁASZCZYŹNIE - SPRAWDZIAN Gr. 1 Zad. 1. Dane są punkty: P = (-, 1), R = (5, -1), S = (, 3). a) Oblicz odległość między punktami R i S. b) Wyznacz współrzędne środka odcinka PR. c) Napisz równanie
PRÓBNA MATURA ZADANIA PRZYKŁADOWE
 ZESPÓŁ SZKÓŁ HOTELARSKO TURYSTYCZNO GASTRONOMICZNYCH NR UL. KRASNOŁĘCKA 3, WARSZAWA Z A D AN I A Z A M K N I Ę T E ) Liczba, której 5% jest równe 6, to : A. 0,3 C. 30. D. 0 5% 6 II sposób: x nieznana liczba
ZESPÓŁ SZKÓŁ HOTELARSKO TURYSTYCZNO GASTRONOMICZNYCH NR UL. KRASNOŁĘCKA 3, WARSZAWA Z A D AN I A Z A M K N I Ę T E ) Liczba, której 5% jest równe 6, to : A. 0,3 C. 30. D. 0 5% 6 II sposób: x nieznana liczba
FUNKCJA LINIOWA, OKRĘGI
 FUNKCJA LINIOWA, OKRĘGI. Napisz równanie prostej przechodzącej przez początek układu i prostopadłej do prostej 3x-y+=0.. Oblicz pole trójkąta ograniczonego osiami układy i prostą x+y-6=0. 3. Odcinek o
FUNKCJA LINIOWA, OKRĘGI. Napisz równanie prostej przechodzącej przez początek układu i prostopadłej do prostej 3x-y+=0.. Oblicz pole trójkąta ograniczonego osiami układy i prostą x+y-6=0. 3. Odcinek o
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 25 MARCA 2017 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Najmniejsza liczba całkowita
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 25 MARCA 2017 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Najmniejsza liczba całkowita
KONKURS ZOSTAŃ PITAGORASEM MUM. Podstawowe własności figur geometrycznych na płaszczyźnie
 KONKURS ZOSTAŃ PITAGORASEM MUM ETAP I TEST II Podstawowe własności figur geometrycznych na płaszczyźnie 1. A. Stosunek pola koła wpisanego w kwadrat o boku długości 6 do pola koła opisanego na tym kwadracie
KONKURS ZOSTAŃ PITAGORASEM MUM ETAP I TEST II Podstawowe własności figur geometrycznych na płaszczyźnie 1. A. Stosunek pola koła wpisanego w kwadrat o boku długości 6 do pola koła opisanego na tym kwadracie
Funkcja liniowa -zadania. Funkcja liniowa jest to funkcja postaci y = ax + b dla x R gdzie a, b R oraz
 Funkcja liniowa jest to funkcja postaci y = ax + b dla x R gdzie a, b R oraz x argumenty funkcji y wartości funkcji a współczynnik kierunkowy prostej ( a = tg, gdzie osi OX) - kąt nachylenia wykresu funkcji
Funkcja liniowa jest to funkcja postaci y = ax + b dla x R gdzie a, b R oraz x argumenty funkcji y wartości funkcji a współczynnik kierunkowy prostej ( a = tg, gdzie osi OX) - kąt nachylenia wykresu funkcji
Geometria analityczna
 Geometria analityczna Wektory Zad Dane są wektory #» a, #» b, #» c Znaleźć długość wektora #» x (a #» a = [, 0, ], #» b = [0,, 3], #» c = [,, ], #» x = #» #» a b + 3 #» c ; (b #» a = [,, ], #» b = [,,
Geometria analityczna Wektory Zad Dane są wektory #» a, #» b, #» c Znaleźć długość wektora #» x (a #» a = [, 0, ], #» b = [0,, 3], #» c = [,, ], #» x = #» #» a b + 3 #» c ; (b #» a = [,, ], #» b = [,,
Blok III: Funkcje elementarne. e) y = 1 3 x. f) y = x. g) y = 2x. h) y = 3x. c) y = 3x + 2. d) y = x 3. c) y = x. d) y = x.
 Blok III: Funkcje elementarne III. Narysuj wykres funkcji: a) y = x y = x y = x y = x III. Narysuj wykres funkcji: a) y = x + y = 4 x III. Znajdź miejsca zerowe funkcji: a) y = 6 x y = x e) y = x f) y
Blok III: Funkcje elementarne III. Narysuj wykres funkcji: a) y = x y = x y = x y = x III. Narysuj wykres funkcji: a) y = x + y = 4 x III. Znajdź miejsca zerowe funkcji: a) y = 6 x y = x e) y = x f) y
Analiza Matematyczna. Zastosowania Całek
 Analiza Matematyczna. Zastosowania Całek Aleksander Denisiuk denisiuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 8-45 Gdańsk 9 maja 217
Analiza Matematyczna. Zastosowania Całek Aleksander Denisiuk denisiuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 8-45 Gdańsk 9 maja 217
Zadania do samodzielnego rozwiązania zestaw 11
 Zadania do samodzielnego rozwiązania zestaw 11 1 Podać definicję pochodnej funkcji w punkcie, a następnie korzystając z tej definicji obliczyć ( ) π (a) f, jeśli f(x) = cos x, (e) f (0), jeśli f(x) = 4
Zadania do samodzielnego rozwiązania zestaw 11 1 Podać definicję pochodnej funkcji w punkcie, a następnie korzystając z tej definicji obliczyć ( ) π (a) f, jeśli f(x) = cos x, (e) f (0), jeśli f(x) = 4
rozwiązanie zadania us. 25-go. 28. Własność czterech punktów na kole, przez które przechodzą promienie pęku harmonicznego, maj%cogo swój wierzchołek
 SPIS RZECZY. PRZEDMOWA Errata Str. XIII XVI ROZDZIAŁ I. POJĘCIA WSTĘPNE slr. 1 6 1. Szereg punktów. 2. Zwykłe wyznaczanie położenia punktu na prostej. 3. Wyznaczenie położenia punktu na prostej przy pomocy
SPIS RZECZY. PRZEDMOWA Errata Str. XIII XVI ROZDZIAŁ I. POJĘCIA WSTĘPNE slr. 1 6 1. Szereg punktów. 2. Zwykłe wyznaczanie położenia punktu na prostej. 3. Wyznaczenie położenia punktu na prostej przy pomocy
PRÓBNA MATURA ZADANIA PRZYKŁADOWE
 ZESPÓŁ SZKÓŁ HOTELARSKO TURYSTYCZNO GASTRONOMICZNYCH NR UL. KRASNOŁĘCKA, WARSZAWA Z A D AN I A Z A M K N I Ę T E ) Liczba, której 5% jest równe 6, to : A. 0, C. 0. D. 0 5% 6 II sposób: x nieznana liczba
ZESPÓŁ SZKÓŁ HOTELARSKO TURYSTYCZNO GASTRONOMICZNYCH NR UL. KRASNOŁĘCKA, WARSZAWA Z A D AN I A Z A M K N I Ę T E ) Liczba, której 5% jest równe 6, to : A. 0, C. 0. D. 0 5% 6 II sposób: x nieznana liczba
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 18 KWIETNIA 2015 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Dla każdej liczby
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 18 KWIETNIA 2015 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Dla każdej liczby
PRZYKŁADOWE ZADANIA Z MATEMATYKI NA POZIOMIE PODSTAWOWYM
 PRZYKŁADOWE ZADANIA Z MATEMATYKI NA POZIOMIE PODSTAWOWYM Zad.1. (0-1) Liczba 3 8 3 3 9 2 A. 3 3 Zad.2. (0-1) jest równa: Liczba log24 jest równa: B. 3 32 9 C. 3 4 D. 3 5 A. 2log2 + log20 B. log6 + 2log2
PRZYKŁADOWE ZADANIA Z MATEMATYKI NA POZIOMIE PODSTAWOWYM Zad.1. (0-1) Liczba 3 8 3 3 9 2 A. 3 3 Zad.2. (0-1) jest równa: Liczba log24 jest równa: B. 3 32 9 C. 3 4 D. 3 5 A. 2log2 + log20 B. log6 + 2log2
GEOMETRIA ANALITYCZNA. Poziom podstawowy
 GEOMETRIA ANALITYCZNA Poziom podstawowy Zadanie (4 pkt.) Dana jest prosta k opisana równaniem ogólnym x + y 6. a) napisz równanie prostej k w postaci kierunkowej. b) podaj współczynnik kierunkowy prostej
GEOMETRIA ANALITYCZNA Poziom podstawowy Zadanie (4 pkt.) Dana jest prosta k opisana równaniem ogólnym x + y 6. a) napisz równanie prostej k w postaci kierunkowej. b) podaj współczynnik kierunkowy prostej
Mini tablice matematyczne. Figury geometryczne
 Mini tablice matematyczne Figury geometryczne Spis treści Własności kwadratu Ciekawostka:Kwadrat magiczny Prostokąt Własności prostokąta Trapez Własności trapezu Równoległobok Własności równoległoboku
Mini tablice matematyczne Figury geometryczne Spis treści Własności kwadratu Ciekawostka:Kwadrat magiczny Prostokąt Własności prostokąta Trapez Własności trapezu Równoległobok Własności równoległoboku
EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY 5 MAJA Godzina rozpoczęcia: 9:00. Czas pracy: 170 minut. Liczba punktów do uzyskania: 50
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 01 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę Instrukcja dla zdającego EGZAMIN MATURALNY Z MATEMATYKI
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 01 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę Instrukcja dla zdającego EGZAMIN MATURALNY Z MATEMATYKI
Zad. 8(3pkt) Na podstawie definicji wykaż, że funkcja y=
 Funkcje, funkcja liniowa, funkcja kwadratowa powt. kl. 3d Zad. 1 (5pkt.) Dana jest funkcja f(x)=. Narysuj wykres funkcji g(x)= -f(x). Rozwiąż nierówność g(x). Podaj liczbę rozwiązań równania g(x)=m w zależności
Funkcje, funkcja liniowa, funkcja kwadratowa powt. kl. 3d Zad. 1 (5pkt.) Dana jest funkcja f(x)=. Narysuj wykres funkcji g(x)= -f(x). Rozwiąż nierówność g(x). Podaj liczbę rozwiązań równania g(x)=m w zależności
Wykład z modelowania matematycznego.
 Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Rodzina funkcji
Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Rodzina funkcji
UZUPEŁNIA ZDAJĄCY miejsce na naklejkę
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 017 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 5 maja 017 r.
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 017 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 5 maja 017 r.
AUTORKA: ELŻBIETA SZUMIŃSKA NAUCZYCIELKA ZESPOŁU SZKÓŁ OGÓLNOKSZTAŁCĄCYCH SCHOLASTICUS W ŁODZI ZNANE RÓWNANIA PROSTEJ NA PŁASZCZYŹNIE I W PRZESTRZENI
 UTORK: ELŻBIET SZUMIŃSK NUCZYCIELK ZESPOŁU SZKÓŁ OGÓLNOKSZTŁCĄCYCH SCHOLSTICUS W ŁODZI ZNNE RÓWNNI PROSTEJ N PŁSZCZYŹNIE I W PRZESTRZENI SPIS TREŚCI: PROST N PŁSZCZYŻNIE Str 1. Równanie kierunkowe prostej
UTORK: ELŻBIET SZUMIŃSK NUCZYCIELK ZESPOŁU SZKÓŁ OGÓLNOKSZTŁCĄCYCH SCHOLSTICUS W ŁODZI ZNNE RÓWNNI PROSTEJ N PŁSZCZYŹNIE I W PRZESTRZENI SPIS TREŚCI: PROST N PŁSZCZYŻNIE Str 1. Równanie kierunkowe prostej
i = [ 0] j = [ 1] k = [ 0]
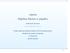
![i = [ 0] j = [ 1] k = [ 0] i = [ 0] j = [ 1] k = [ 0]](/thumbs/70/62901734.jpg) Ćwiczenia nr TEMATYKA: Układy współrzędnych: kartezjański, walcowy (cylindryczny), sferyczny (geograficzny), Przekształcenia: izometryczne, nieizometryczne. DEFINICJE: Wektor wodzący: wektorem r, ρ wodzącym
Ćwiczenia nr TEMATYKA: Układy współrzędnych: kartezjański, walcowy (cylindryczny), sferyczny (geograficzny), Przekształcenia: izometryczne, nieizometryczne. DEFINICJE: Wektor wodzący: wektorem r, ρ wodzącym
Geometria analityczna
 Geometria analityczna Paweł Mleczko Teoria Informacja (o prostej). postać ogólna prostej: Ax + By + C = 0, A + B 0, postać kanoniczna (kierunkowa) prostej: y = ax + b. Współczynnik a nazywamy współczynnikiem
Geometria analityczna Paweł Mleczko Teoria Informacja (o prostej). postać ogólna prostej: Ax + By + C = 0, A + B 0, postać kanoniczna (kierunkowa) prostej: y = ax + b. Współczynnik a nazywamy współczynnikiem
1) 2) 3) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) 18) 19) 20) 21) 22) 23) 24) 25)
 1) Wykresem funkcji kwadratowej f jest parabola o wierzchołku w początku układu współrzędnych i przechodząca przez punkt. Wobec tego funkcja f określona wzorem 2) Punkt należy do paraboli o równaniu. Wobec
1) Wykresem funkcji kwadratowej f jest parabola o wierzchołku w początku układu współrzędnych i przechodząca przez punkt. Wobec tego funkcja f określona wzorem 2) Punkt należy do paraboli o równaniu. Wobec
Arkusz maturalny nr 2 poziom podstawowy ZADANIA ZAMKNIĘTE. Rozwiązania. Wartość bezwzględna jest odległością na osi liczbowej.
 Arkusz maturalny nr 2 poziom podstawowy ZADANIA ZAMKNIĘTE Rozwiązania Zadanie 1 Wartość bezwzględna jest odległością na osi liczbowej. Stop Istnieje wzajemnie jednoznaczne przyporządkowanie między punktami
Arkusz maturalny nr 2 poziom podstawowy ZADANIA ZAMKNIĘTE Rozwiązania Zadanie 1 Wartość bezwzględna jest odległością na osi liczbowej. Stop Istnieje wzajemnie jednoznaczne przyporządkowanie między punktami
FUNKCJA LINIOWA, RÓWNANIA I UKŁADY RÓWNAŃ LINIOWYCH
 FUNKCJA LINIOWA, RÓWNANIA I UKŁADY RÓWNAŃ LINIOWYCH PROPORCJONALNOŚĆ PROSTA Proporcjonalnością prostą nazywamy zależność między dwoma wielkościami zmiennymi x i y, określoną wzorem: y = a x Gdzie a jest
FUNKCJA LINIOWA, RÓWNANIA I UKŁADY RÓWNAŃ LINIOWYCH PROPORCJONALNOŚĆ PROSTA Proporcjonalnością prostą nazywamy zależność między dwoma wielkościami zmiennymi x i y, określoną wzorem: y = a x Gdzie a jest
Równania prostych i krzywych; współrzędne punktu
 Równania prostych i krzywych; współrzędne punktu Zad 1: Na paraboli o równaniu y = 1 x znajdź punkt P leŝący najbliŝej prostej o równaniu x + y = 0 Napisz równanie stycznej do tej paraboli, poprowadzonej
Równania prostych i krzywych; współrzędne punktu Zad 1: Na paraboli o równaniu y = 1 x znajdź punkt P leŝący najbliŝej prostej o równaniu x + y = 0 Napisz równanie stycznej do tej paraboli, poprowadzonej
Przestrzeń liniowa. Algebra. Aleksander Denisiuk
 Algebra Przestrzeń liniowa Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych zamiejscowy ośrodek dydaktyczny w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p.
Algebra Przestrzeń liniowa Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych zamiejscowy ośrodek dydaktyczny w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p.
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH
 STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
Zajęcia nr 1 (1h) Dwumian Newtona. Indukcja. Zajęcia nr 2 i 3 (4h) Trygonometria
 Technologia Chemiczna 008/09 Zajęcia wyrównawcze. Pokazać, że: ( )( ) n k k l = ( n l )( n l k l Zajęcia nr (h) Dwumian Newtona. Indukcja. ). Rozwiązać ( ) ( równanie: ) n n a) = 0 b) 3 ( ) n 3. Znaleźć
Technologia Chemiczna 008/09 Zajęcia wyrównawcze. Pokazać, że: ( )( ) n k k l = ( n l )( n l k l Zajęcia nr (h) Dwumian Newtona. Indukcja. ). Rozwiązać ( ) ( równanie: ) n n a) = 0 b) 3 ( ) n 3. Znaleźć
Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne.
 Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne. Funkcja homograficzna. Definicja. Funkcja homograficzna jest to funkcja określona wzorem f() = a + b c + d, () gdzie współczynniki
Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne. Funkcja homograficzna. Definicja. Funkcja homograficzna jest to funkcja określona wzorem f() = a + b c + d, () gdzie współczynniki
Elementy grafiki komputerowej. Elementy geometrii afinicznej
 Elementy grafiki komputerowej. Elementy geometrii j Aleksander Denisiuk Uniwersytet Warmińsko-Mazurski Olsztyn, ul. Słoneczna 54 denisjuk@matman.uwm.edu.pl 1 / 28 Elementy geometrii j Najnowsza wersja
Elementy grafiki komputerowej. Elementy geometrii j Aleksander Denisiuk Uniwersytet Warmińsko-Mazurski Olsztyn, ul. Słoneczna 54 denisjuk@matman.uwm.edu.pl 1 / 28 Elementy geometrii j Najnowsza wersja
ALGEBRA z GEOMETRIA, ANALITYCZNA,
 ALGEBRA z GEOMETRIA, ANALITYCZNA, MAT00405 PRZEKSZTAL CANIE WYRAZ EN ALGEBRAICZNYCH, WZO R DWUMIANOWY NEWTONA Uprościć podane wyrażenia 7; (b) ( 6)( + ); (c) a 5 6 8a ; (d) ( 5 )( 5 + ); (e) ( 45x 4 y
ALGEBRA z GEOMETRIA, ANALITYCZNA, MAT00405 PRZEKSZTAL CANIE WYRAZ EN ALGEBRAICZNYCH, WZO R DWUMIANOWY NEWTONA Uprościć podane wyrażenia 7; (b) ( 6)( + ); (c) a 5 6 8a ; (d) ( 5 )( 5 + ); (e) ( 45x 4 y
Wektory. Algebra. Aleksander Denisiuk. Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi Gdańsk
 Algebra Wektory Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Wektory Najnowsza wersja
Algebra Wektory Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Wektory Najnowsza wersja
KLASA II TECHNIKUM POZIOM PODSTAWOWY PROPOZYCJA POZIOMÓW WYMAGAŃ
 KLASA II TECHNIKUM POZIOM PODSTAWOWY PROPOZYCJA POZIOMÓW WYMAGAŃ Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i wykraczające (W).
KLASA II TECHNIKUM POZIOM PODSTAWOWY PROPOZYCJA POZIOMÓW WYMAGAŃ Wyróżnione zostały następujące wymagania programowe: konieczne (K), podstawowe (P), rozszerzające (R), dopełniające (D) i wykraczające (W).
Krzywe stożkowe. 1 Powinowactwo prostokątne. 2 Elipsa. Niech l będzie ustaloną prostą i k ustaloną liczbą dodatnią.
 Krzywe stożkowe 1 Powinowatwo prostokątne Nieh l będzie ustaloną prostą i k ustaloną lizbą dodatnią. Definija 1.1. Powinowatwem prostokątnym o osi l i stosunku k nazywamy przekształenie płaszzyzny, które
Krzywe stożkowe 1 Powinowatwo prostokątne Nieh l będzie ustaloną prostą i k ustaloną lizbą dodatnią. Definija 1.1. Powinowatwem prostokątnym o osi l i stosunku k nazywamy przekształenie płaszzyzny, które
= [6; 2]. Wyznacz wierzchołki tego równoległoboku.
![= [6; 2]. Wyznacz wierzchołki tego równoległoboku. = [6; 2]. Wyznacz wierzchołki tego równoległoboku.](/thumbs/74/71133309.jpg) ZADANIE 1 (5 PKT) Wyznacz współrzędne wierzchołków trójkata jeżeli środki jego boków maja współrzędne: P = (1, 3), Q = ( 5, 4), R = ( 6, 7). ZADANIE 2 (5 PKT) Dla jakich wartości parametru α odległość
ZADANIE 1 (5 PKT) Wyznacz współrzędne wierzchołków trójkata jeżeli środki jego boków maja współrzędne: P = (1, 3), Q = ( 5, 4), R = ( 6, 7). ZADANIE 2 (5 PKT) Dla jakich wartości parametru α odległość
TO TRZEBA ROZWIĄZAĆ-(I MNÓSTWO INNYCH )
 Kujawsko-Pomorskie Centrum Edukacji Nauczycieli w Bydgoszczy PLACÓWKA AKREDYTOWANA TO TRZEBA ROZWIĄZAĆ-(I MNÓSTWO INNYCH ) PAKIET ZADAŃ (zadania wybrano ze zbiorów autorów i wydawnictw: Kiełbasa, Res Polona,
Kujawsko-Pomorskie Centrum Edukacji Nauczycieli w Bydgoszczy PLACÓWKA AKREDYTOWANA TO TRZEBA ROZWIĄZAĆ-(I MNÓSTWO INNYCH ) PAKIET ZADAŃ (zadania wybrano ze zbiorów autorów i wydawnictw: Kiełbasa, Res Polona,
Zad.3. Jakub Trojgo i Jakub Wieczorek. 14 grudnia 2013
 Zad.3 Jakub Trojgo i Jakub Wieczorek 14 grudnia 2013 W pierwszej części naszej pracy będziemy chcieli zbadać ciągłość funkcji f(x, y) w przypadku gdy płaszczyzna wyposażona jest w jedną z topologii: a)
Zad.3 Jakub Trojgo i Jakub Wieczorek 14 grudnia 2013 W pierwszej części naszej pracy będziemy chcieli zbadać ciągłość funkcji f(x, y) w przypadku gdy płaszczyzna wyposażona jest w jedną z topologii: a)
PRÓBNY EGZAMIN MATURALNY Z NOWĄ ERĄ
 WPISUJE ZDAJĄCY KOD IMIĘ I NAZWISKO * * nieobowiązkowe PRÓBNY EGZAMIN MATURALNY Z NOWĄ ERĄ MATEMATYKA-POZIOM PODSTAWOWY dysleksja Instrukcja dla zdającego. Sprawdź, czy arkusz egzaminacyjny zawiera 22
WPISUJE ZDAJĄCY KOD IMIĘ I NAZWISKO * * nieobowiązkowe PRÓBNY EGZAMIN MATURALNY Z NOWĄ ERĄ MATEMATYKA-POZIOM PODSTAWOWY dysleksja Instrukcja dla zdającego. Sprawdź, czy arkusz egzaminacyjny zawiera 22
SYLABUS PRZEDMIOTU MATEMATYKA W RAMACH ZAJ
 SYLABUS PRZEDMIOTU MATEMATYKA W RAMACH ZAJĘĆ WYRÓWNAWCZYCH Z MATEMATYKI DLA STUDENTÓW I ROKU BUDOWNICTWA WNT UWM W ROKU AKADEMICKIM 2012/2013 Nazwa przedmiotu: Zajęcia wyrównawcze z matematyki Rodzaj studiów:
SYLABUS PRZEDMIOTU MATEMATYKA W RAMACH ZAJĘĆ WYRÓWNAWCZYCH Z MATEMATYKI DLA STUDENTÓW I ROKU BUDOWNICTWA WNT UWM W ROKU AKADEMICKIM 2012/2013 Nazwa przedmiotu: Zajęcia wyrównawcze z matematyki Rodzaj studiów:
VIII. ZBIÓR PRZYKŁADOWYCH ZADAŃ MATURALNYCH
 VIII. ZIÓR PRZYKŁDOWYCH ZDŃ MTURLNYCH ZDNI ZMKNIĘTE Zadanie. ( pkt) 0 90 Liczba 9 jest równa 0.. 00 C. 0 9 D. 700 7 Zadanie. 8 ( pkt) Liczba 9 jest równa.. 9 C. D. 5 Zadanie. ( pkt) Liczba log jest równa.
VIII. ZIÓR PRZYKŁDOWYCH ZDŃ MTURLNYCH ZDNI ZMKNIĘTE Zadanie. ( pkt) 0 90 Liczba 9 jest równa 0.. 00 C. 0 9 D. 700 7 Zadanie. 8 ( pkt) Liczba 9 jest równa.. 9 C. D. 5 Zadanie. ( pkt) Liczba log jest równa.
3. FUNKCJA LINIOWA. gdzie ; ół,.
 1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
Projekt Era inżyniera pewna lokata na przyszłość jest współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Materiał ddaktczne na zajęcia wrównawcze z matematki dla studentów pierwszego roku kierunku zamawianego Inżnieria Środowiska w ramach projektu Era inżniera pewna lokata na przszłość Projekt Era inżniera
Materiał ddaktczne na zajęcia wrównawcze z matematki dla studentów pierwszego roku kierunku zamawianego Inżnieria Środowiska w ramach projektu Era inżniera pewna lokata na przszłość Projekt Era inżniera
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI LISTOPAD 2010 POZIOM PODSTAWOWY. Czas pracy: 170 minut. Liczba punktów do uzyskania: 50 WPISUJE ZDAJĄCY
 Centralna Komisja Egzaminacyjna Materiał współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego. Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu.
Centralna Komisja Egzaminacyjna Materiał współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego. Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu.
Krzywe i powierzchnie stopnia drugiego
 Krzywe i powierzchnie stopnia drugiego Iwona Malinowska, Zbigniew Šagodowski 25 maja 2015 I. Malinowska, Z. Lagodowski Geometria 25 maja 2015 1 / 30 Rozwa»my dwie proste przecinaj ce si pod k tem α, 0
Krzywe i powierzchnie stopnia drugiego Iwona Malinowska, Zbigniew Šagodowski 25 maja 2015 I. Malinowska, Z. Lagodowski Geometria 25 maja 2015 1 / 30 Rozwa»my dwie proste przecinaj ce si pod k tem α, 0
Projekt Era inżyniera pewna lokata na przyszłość jest współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Materiał ddaktczne na zajęcia wrównawcze z matematki dla studentów pierwszego roku kierunku zamawianego Inżnieria i Gospodarka Wodna w ramach projektu Era inżniera pewna lokata na przszłość Projekt Era
Materiał ddaktczne na zajęcia wrównawcze z matematki dla studentów pierwszego roku kierunku zamawianego Inżnieria i Gospodarka Wodna w ramach projektu Era inżniera pewna lokata na przszłość Projekt Era
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 14 KWIETNIA 2018 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Liczba 5 30 2 3 5
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM PODSTAWOWY 14 KWIETNIA 2018 CZAS PRACY: 170 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Liczba 5 30 2 3 5
Geometria rzutowa - skrypcik
 Geometria rzutowa - skrypcik Dominik Burek, Tomasz Cieśla 13 września 2012 Już niedługo kolejne brakujące rzeczy. 1 Garść twierdzeń i definicji Definicja 1.1. Dane są proste AB, AC, AD. Prosta AE taka,
Geometria rzutowa - skrypcik Dominik Burek, Tomasz Cieśla 13 września 2012 Już niedługo kolejne brakujące rzeczy. 1 Garść twierdzeń i definicji Definicja 1.1. Dane są proste AB, AC, AD. Prosta AE taka,
Ćwiczenia z Geometrii I, czerwiec 2006 r.
 Waldemar ompe echy przystawania trójkątów 1. unkt leży na przekątnej kwadratu (rys. 1). unkty i R są rzutami prostokątnymi punktu odpowiednio na proste i. Wykazać, że = R. R 2. any jest trójkąt ostrokątny,
Waldemar ompe echy przystawania trójkątów 1. unkt leży na przekątnej kwadratu (rys. 1). unkty i R są rzutami prostokątnymi punktu odpowiednio na proste i. Wykazać, że = R. R 2. any jest trójkąt ostrokątny,
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań.
 III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ
 RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 6 2016/2017, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 6 2016/2017, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
Wskazówki do zadań testowych. Matura 2016
 Wskazówki do zadań testowych. Matura 2016 Zadanie 1 la każdej dodatniej liczby a iloraz jest równy.. C.. Korzystamy ze wzoru Zadanie 2 Liczba jest równa.. 2 C.. 3 Zadanie 3 Liczby a i c są dodatnie. Liczba
Wskazówki do zadań testowych. Matura 2016 Zadanie 1 la każdej dodatniej liczby a iloraz jest równy.. C.. Korzystamy ze wzoru Zadanie 2 Liczba jest równa.. 2 C.. 3 Zadanie 3 Liczby a i c są dodatnie. Liczba
Funkcje elementarne. Ksenia Hladysz Własności 2. 3 Zadania 5
 Funkcje elementarne Ksenia Hladysz 16.10.014 Spis treści 1 Funkcje elementarne. 1 Własności 3 Zadania 5 1 Funkcje elementarne. Są to funkcje określone wzorami zawierającymi skończoną ilość operacji algebraicznych
Funkcje elementarne Ksenia Hladysz 16.10.014 Spis treści 1 Funkcje elementarne. 1 Własności 3 Zadania 5 1 Funkcje elementarne. Są to funkcje określone wzorami zawierającymi skończoną ilość operacji algebraicznych
FUNKCJE ZESPOLONE Lista zadań 2005/2006
 FUNKJE ZESPOLONE Lista zadań 25/26 Opracowanie: dr Jolanta Długosz Liczby zespolone. Obliczyć wartości podanych wyrażeń: (2 + ) ( ) 2 4 i (5 + i); b) (3 i)( 4 + 2i); c) 4 + i ; d) ( + i) 4 ; e) ( 2 + 3i)
FUNKJE ZESPOLONE Lista zadań 25/26 Opracowanie: dr Jolanta Długosz Liczby zespolone. Obliczyć wartości podanych wyrażeń: (2 + ) ( ) 2 4 i (5 + i); b) (3 i)( 4 + 2i); c) 4 + i ; d) ( + i) 4 ; e) ( 2 + 3i)
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ
 RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 7 2012/2013, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 7 2012/2013, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
LUBELSKA PRÓBA PRZED MATURA
 NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI LUBELSKA PRÓBA PRZED MATURA DLA KLAS TRZECICH POZIOM PODSTAWOWY GRUPA I 1 STYCZNIA 011 CZAS PRACY: 170 MINUT Zadania zamknięte ZADANIE 1 (1 PKT.) Liczba
NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI LUBELSKA PRÓBA PRZED MATURA DLA KLAS TRZECICH POZIOM PODSTAWOWY GRUPA I 1 STYCZNIA 011 CZAS PRACY: 170 MINUT Zadania zamknięte ZADANIE 1 (1 PKT.) Liczba
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM ROZSZERZONY 28 KWIETNIA 2018 CZAS PRACY: 180 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Liczba 3 3 10 3 2
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW PRZYGOTOWANY PRZEZ SERWIS WWW.ZADANIA.INFO POZIOM ROZSZERZONY 28 KWIETNIA 2018 CZAS PRACY: 180 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Liczba 3 3 10 3 2
Praca kontrolna z matematyki nr 1 Liceum Ogólnokształcące dla Dorosłych Semestr 5 Rok szkolny 2014/2015
 Praca kontrolna z matematyki nr 1 Liceum Ogólnokształcące dla Dorosłych Semestr 5 Rok szkolny 2014/2015 2 6 + 3 1. Oblicz 3. 3 x 1 3x 2. Rozwiąż nierówność > x. 2 3 3. Funkcja f przyporządkowuje każdej
Praca kontrolna z matematyki nr 1 Liceum Ogólnokształcące dla Dorosłych Semestr 5 Rok szkolny 2014/2015 2 6 + 3 1. Oblicz 3. 3 x 1 3x 2. Rozwiąż nierówność > x. 2 3 3. Funkcja f przyporządkowuje każdej
FUNKCJE I RÓWNANIA KWADRATOWE. Lekcja 78. Pojęcie i wykres funkcji kwadratowej str
 FUNKCJE I RÓWNANIA KWADRATOWE Lekcja 78. Pojęcie i wykres funkcji kwadratowej str. 178-180. Funkcja kwadratowa to taka, której wykresem jest parabola. Definicja Funkcją kwadratową nazywamy funkcje postaci
FUNKCJE I RÓWNANIA KWADRATOWE Lekcja 78. Pojęcie i wykres funkcji kwadratowej str. 178-180. Funkcja kwadratowa to taka, której wykresem jest parabola. Definicja Funkcją kwadratową nazywamy funkcje postaci
Podstawowe pojęcia geometryczne
 PLANIMETRIA Podstawowe pojęcia geometryczne Geometria (słowo to pochodzi z języka greckiego i oznacza mierzenie ziemi) jest jednym z działów matematyki, którego przedmiotem jest badanie figur geometrycznych
PLANIMETRIA Podstawowe pojęcia geometryczne Geometria (słowo to pochodzi z języka greckiego i oznacza mierzenie ziemi) jest jednym z działów matematyki, którego przedmiotem jest badanie figur geometrycznych
Weronika Siwek, Układ biegunowy, płaszczyzna Gaussa i nie tylko... 1
 Weronika Siwek, Układ biegunowy, płaszczyzna Gaussa i nie tylko... Spis treści. Badanie przebiegu zmienności funkcji.................. Co i jak, czyli trochę teorii........................ Przykłady................................
Weronika Siwek, Układ biegunowy, płaszczyzna Gaussa i nie tylko... Spis treści. Badanie przebiegu zmienności funkcji.................. Co i jak, czyli trochę teorii........................ Przykłady................................
GEOMETRIA PRZESTRZENNA (STEREOMETRIA)
 GEOMETRIA PRZESTRZENNA (STEREOMETRIA) WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. Na początek omówimy
GEOMETRIA PRZESTRZENNA (STEREOMETRIA) WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. Na początek omówimy
MECHANIKA 2 KINEMATYKA. Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 KINEMATYKA Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY Prowadzący: dr Krzysztof Polko Określenie położenia ciała sztywnego Pierwszy sposób: Określamy położenia trzech punktów ciała nie leżących
MECHANIKA 2 KINEMATYKA Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY Prowadzący: dr Krzysztof Polko Określenie położenia ciała sztywnego Pierwszy sposób: Określamy położenia trzech punktów ciała nie leżących
Układy równań liniowych, macierze, Google
 Układ równań linowych { x+2y = 6, 3x y = 4 (0) Spotkania z Matematyka Układy równań liniowych, macierze, Google Aleksander Denisiuk denisjuk@matman.uwm.edu.pl Uniwersytet Warmińsko-Mazurski w Olsztynie
Układ równań linowych { x+2y = 6, 3x y = 4 (0) Spotkania z Matematyka Układy równań liniowych, macierze, Google Aleksander Denisiuk denisjuk@matman.uwm.edu.pl Uniwersytet Warmińsko-Mazurski w Olsztynie
GEOMETRIA ELEMENTARNA
 Bardo, 7 11 XII A. D. 2016 I Uniwersytecki Obóz Olimpiady Matematycznej GEOMETRIA ELEMENTARNA materiały przygotował Antoni Kamiński na podstawie zbiorów zadań: Przygotowanie do olimpiad matematycznych
Bardo, 7 11 XII A. D. 2016 I Uniwersytecki Obóz Olimpiady Matematycznej GEOMETRIA ELEMENTARNA materiały przygotował Antoni Kamiński na podstawie zbiorów zadań: Przygotowanie do olimpiad matematycznych
NOWA FORMUŁA EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY MMA 2018 UZUPEŁNIA ZDAJĄCY. miejsce na naklejkę UZUPEŁNIA ZESPÓŁ NADZORUJĄCY
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 018 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 5 czerwca 018
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. MMA 018 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z MATEMATYKI POZIOM PODSTAWOWY DATA: 5 czerwca 018
Zad. 1 Liczba jest równa A B C D. Zad. 2 Liczba log16 jest równa A 3log2 + log8 B log4 + 2log3 C 3log4 log4 D log20 log4
 Zad. 1 Liczba jest równa A B C D Zad. Liczba log16 jest równa A 3log + log8 B log4 + log3 C 3log4 log4 D log0 log4 Zad. 3 Rozwiązaniem równania jest liczba A B 18 C 1, D 6 Zad. 4 Większą z dwóch liczb
Zad. 1 Liczba jest równa A B C D Zad. Liczba log16 jest równa A 3log + log8 B log4 + log3 C 3log4 log4 D log0 log4 Zad. 3 Rozwiązaniem równania jest liczba A B 18 C 1, D 6 Zad. 4 Większą z dwóch liczb
ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE II TECHNIKUM.
 I. Funkcje. ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE II TECHNIKUM. 1. Pojęcie funkcji i jej dziedzina. 2. Zbiór wartości funkcji. 3. Wykres funkcji liczbowej i odczytywanie jej własności
I. Funkcje. ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE II TECHNIKUM. 1. Pojęcie funkcji i jej dziedzina. 2. Zbiór wartości funkcji. 3. Wykres funkcji liczbowej i odczytywanie jej własności
MATEMATYKA ZBIÓR ZADAŃ MATURALNYCH. Lata Poziom podstawowy. Uzupełnienie Zadania z sesji poprawkowej z sierpnia 2019 r.
 MATEMATYKA ZBIÓR ZADAŃ MATURALNYH Lata 010 019 Poziom podstawowy Uzupełnienie 019 Zadania z sesji poprawkowej z sierpnia 019 r. Opracował Ryszard Pagacz Spis treści Zadania maturalne.........................................................
MATEMATYKA ZBIÓR ZADAŃ MATURALNYH Lata 010 019 Poziom podstawowy Uzupełnienie 019 Zadania z sesji poprawkowej z sierpnia 019 r. Opracował Ryszard Pagacz Spis treści Zadania maturalne.........................................................
M10. Własności funkcji liniowej
 M10. Własności funkcji liniowej dr Artur Gola e-mail: a.gola@ajd.czest.pl pokój 3010 Definicja Funkcję określoną wzorem y = ax + b, dla x R, gdzie a i b są stałymi nazywamy funkcją liniową. Wykresem funkcji
M10. Własności funkcji liniowej dr Artur Gola e-mail: a.gola@ajd.czest.pl pokój 3010 Definicja Funkcję określoną wzorem y = ax + b, dla x R, gdzie a i b są stałymi nazywamy funkcją liniową. Wykresem funkcji
MATEMATYKA - CYKL 5 GODZINNY. DATA : 8 czerwca 2009
 MATURA EUROPEJSKA 2009 MATEMATYKA - CYKL 5 GODZINNY DATA : 8 czerwca 2009 CZAS TRWANIA EGZAMINU: 4 godziny (240 minut) DOZWOLONE POMOCE : Europejski zestaw wzorów Kalkulator (bez grafiki, bez możliwości
MATURA EUROPEJSKA 2009 MATEMATYKA - CYKL 5 GODZINNY DATA : 8 czerwca 2009 CZAS TRWANIA EGZAMINU: 4 godziny (240 minut) DOZWOLONE POMOCE : Europejski zestaw wzorów Kalkulator (bez grafiki, bez możliwości
FIGURY I PRZEKSZTAŁCENIA GEOMETRYCZNE
 Umiejętności opracowanie: Maria Lampert LISTA MOICH OSIĄGNIĘĆ FIGURY I PRZEKSZTAŁCENIA GEOMETRYCZNE Co powinienem umieć Umiejętności znam podstawowe przekształcenia geometryczne: symetria osiowa i środkowa,
Umiejętności opracowanie: Maria Lampert LISTA MOICH OSIĄGNIĘĆ FIGURY I PRZEKSZTAŁCENIA GEOMETRYCZNE Co powinienem umieć Umiejętności znam podstawowe przekształcenia geometryczne: symetria osiowa i środkowa,
PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 3
 DEFINICJE PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 3 Czworokąt to wielokąt o 4 bokach i 4 kątach. Przekątną czworokąta nazywamy odcinek łączący przeciwległe wierzchołki. Wysokością czworokąta nazywamy
DEFINICJE PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 3 Czworokąt to wielokąt o 4 bokach i 4 kątach. Przekątną czworokąta nazywamy odcinek łączący przeciwległe wierzchołki. Wysokością czworokąta nazywamy
Wielokąty na płaszczyźnie obliczenia z zastosowaniem trygonometrii. Trójkąty. Trójkąt dowolny. Wielokąty trygonometria 1.
 Wielokąty na płaszczyźnie obliczenia z zastosowaniem trygonometrii Wielokąt wypukły miara każdego kąt wewnętrznego jest mniejsza od 180 o. Liczba przekątnych: n*(n-2) Suma kątów wewnętrznych wielokąta
Wielokąty na płaszczyźnie obliczenia z zastosowaniem trygonometrii Wielokąt wypukły miara każdego kąt wewnętrznego jest mniejsza od 180 o. Liczba przekątnych: n*(n-2) Suma kątów wewnętrznych wielokąta
