Marek Miszczyński KBO UŁ. Wybrane elementy teorii grafów 1
|
|
|
- Konrad Szewczyk
- 9 lat temu
- Przeglądów:
Transkrypt
1 Marek Miszczyński KBO UŁ. Wybrane elementy teorii grafów 1 G. Wybrane elementy teorii grafów W matematyce teorię grafów klasyfikuje się jako gałąź topologii. Jest ona jednak ściśle związana z algebrą i teorią macierzy. Grafy są stosowane współcześnie w róŝnych działach nauki i techniki. Za pomocą grafów znakomicie modeluje się i rozwiązuje szeroki wachlarz złoŝonych problemów ekonomicznych, tak w skali mikro- jak i makro zarządzania. Krótki rys historyczny rozwoju teori grafów wygląda następująco: 1736 Leonard Euler (uwaŝany za twórcę teorii grafów) 1847 G.R.Kirchhoff (teoria obwodów elektrycznych) 1857 A.Cayley (chemia: izomery węglowodorów nasyconych) 1859 W.R.Hamilton 1945 i dalsze - intensywny rozwój teorii grafów (N.Deo, F.Harary) i jej zastosowań G.1. Co to jest graf Figura przedstawiona na rysunku G.1. nazywa się grafem 1. WyróŜnione punkty nazywają się wierzchołkami grafu (ang. vertex), zaś linie noszą nazwę krawędzi grafu (ang. edge). Wymagane jest, aby kaŝda krawędź i kaŝdy wierzchołek miały swoją nazwę (etykietę). Rys. G.1. Przykład grafu liniowego Wierzchołki grafu oznaczamy v, v,...,. Zbiór wierzchołków oznaczymy jako { } 1 2 V = v 1, v 2,..., v m i musi to być zbór niepusty (V ). Krawędzie grafu oznaczamy e, e,...,. Zbiór krawędzi oznaczymy jako { } 1 2 E = e 1, e 2,..., e n i moŝe to być zbór pusty. v m e n 1 Ściśle graf liniowy, ale poniewaŝ nie istnieją grafy nieliniowe to mówimy krótko graf.
2 Marek Miszczyński KBO UŁ. Wybrane elementy teorii grafów 2 Gdy nie zachodzi obawa pomyłki, etykiety wierzchołków i krawędzi mogą być V = 12 m E = 12,,..., n. liczbami naturalnymi, tj. {,,..., } oraz { } Dla oznaczenia grafu G moŝemy zapisać krótko G ( V E) składa się ze zbioru wierzchołków V i zbioru krawędzi E. =,, co oznacza, Ŝe graf G Dowolna krawędź e k utoŝsamia się z nieuporządkowaną parą wierzchołków ( vi v j ),. Wierzchołki v i oraz v j związane z krawędzią e k nazywa się wierzchołkami końcowymi krawędzi e k. O krawędzi e k mówimy, Ŝe jest ona incydentna z wierzchołkami v i oraz v j. G.1.1. Definicja grafu V = i i = 12,,..., m będzie dowolnym zbiorem skończonym i Niech { } niech S oznacza zbiór wszystkich (róŝnych) nieuporządkowanych par (i,j) S = i, j i V j V. Pary (i,j) oraz (j,i) elementów zbioru V, to znaczy ( ) { } oznaczają: ten sam element - dla grafu nieskierowanego lub róŝne elementy - dla grafu skierowanego. G = V, E oraz E S nosi nazwę grafu (nieskierowanego lub Para ( ) skierowanego w zaleŝności od definicji zbioru S). G.1.2. Jak rysować grafy 1. kształt linii jest obojętny; graf musi tylko oddawać połączenia (incydencje) pomiędzy wierzchołkami za pomocą krawędzi 2. przecinanie się krawędzi nie jest wierzchołkiem Na przykład grafy na rysunku G.2. są identyczne (izomorficzne) choć na pierwszy rzut oka wydają się róŝne. Rys. G.2. Przykład grafu narysowanego na dwa sposoby Inny przykład to odwzorowanie za pomocą grafu problemu decyzyjnego postawionego przez L.Eulera tzw. problem mostów królewieckich (rysunek G.3.).
3 Marek Miszczyński KBO UŁ. Wybrane elementy teorii grafów 3 "Królewiec połoŝony po obu brzegach rzeki Pregoły i na dwóch wyspach jest połączony siecią siedmiu mostów. NaleŜy wychodząc z dowolnego brzegu (A lub B) odwiedzić obie wyspy (C i D), niekoniecznie raz, i powrócić do punktu wyjścia przechodząc tylko raz przez kaŝdy z 7 mostów." (L.Euler udowodnił, Ŝe problem ten nie ma rozwiązania). Rys. G.3. "Problem mostów królewieckich" G.2. Grafy - wybrane pojęcia G.2.1. Grafy nieskierowane pętla własna - krawędź grafu, której końce są incydentne (związane) z jednym wierzchołkiem (rys. G.1. - krawędź e 1 ) krawędzie równoległe - krawędzie incydentne do tej samej pary wierzchołków (rys. G.1. - krawędzie e 5 i e 6 ) graf prosty - graf bez pętli własnych i krawędzi równoległych. wierzchołek izolowany - nie posiada Ŝadnej krawędzi incydentnej do niego (rys. G.1. - wierzchołek v 6 ) stopień wierzchołka (d) - liczba krawędzi incydentnych z nim (rys. G.1. - stopień wierzchołka v 4 jest równy 3; d=3) graf zerowy - graf bez krawędzi ( E = ) grafy izomorficzne - grafy pokrywające się. Warunkiem koniecznym jest: 1. taka sama liczba wierzchołków 2. taka sama liczba krawędzi 3. taka liczba wierzchołków o danym stopniu Warunku wystarczającego brak w teorii. Przykład grafów, które nie są izomorficzne, a warunek konieczny jest spełniony pokazuje rysunek G.4.. Oba grafy nie są izomorficzne choć mają: po 6 wierzchołków, po 5 krawędzi, po 3
4 Marek Miszczyński KBO UŁ. Wybrane elementy teorii grafów 4 wierzchołki o stopniu 1, po 2 wierzchołki o stopniu 2 oraz po 1 wierzchołku o stopniu 3. Rys. G.4. Grafy pozornie izomorficzne - grafy spełniające tylko warunek konieczny izomorfizmu podgraf - graf g = ( V', E' ) jest podgrafem grafu G ( V E) =, jeŝeli V' V, E' E oraz kaŝda krawędź grafu g ma te same wierzchołki końcowe jak w grafie G. droga (łańcuch) - ciąg (skończony) naprzemienny wierzchołków i krawędzi rozpoczynający się i kończący wierzchołkami, taki Ŝe krawędź jest incydentna do wierzchołków poprzedzających i następujących po niej (rys. G.1. - ciąg {v 3, e 3, v 1, e 4, v 2, e 6, v 4, e 6, v 2, e 5, v 1 }) droga otwarta - droga rozpoczynająca się i kończąca róŝnymi wierzchołkami (rys. G.1. - ciąg {v 5, e 7, v 4, e 2, v 3, e 1, v 3, e 2, v 4 }) droga zamknięta - droga rozpoczynająca się i kończąca tym samym wierzchołkiem (rys. G.1. - ciąg {v 5, e 7, v 4, e 2, v 3, e 1, v 3, e 2, v 4, e 7, v 5 }) droga Eulera - droga przechodząca przez kaŝdą krawędź grafu dokładnie jeden raz (patrz: problem mostów królewieckich) graf Eulera - graf G ( V E) =,, w którym wszystkie wierzchołki są stopnia parzystego (graf dla którego istnieje droga Eulera) ścieŝka - (droga ekstremalna) droga otwarta, w której jeden wierzchołek pojawia się tylko jeden raz; moŝna powiedzieć, Ŝe ścieŝka "nie przecina" samej siebie (rys. G.1. - ciąg {v 3, e 3, v 1, e 5, v 2, e 6, v 4 }) obwód - droga zamknięta, w której tylko wierzchołek początkowy moŝe pojawić się dwa razy (rys. G.1. - ciąg {v 3, e 3, v 1, e 5, v 2, e 6, v 4, e 2, v 3 }) obwód Hamiltona - obwód przechodzący przez wszystkie wierzchołki grafu (graf przykładowy z rys. G.1.. nie ma obwodu poniewaŝ wierzchołek v 6 jest izolowany) ścieŝka Hamiltona - obwód Hamiltona z usuniętą krawędzią graf spójny - graf jest spójny jeŝeli między kaŝdą parą wierzchołków istnieje przynajmniej jedna ścieŝka drzewo - graf spójny bez obwodów przekrój - kaŝdy zbiór krawędzi grafu spójnego, którego usunięcie powoduje, Ŝe graf staje się niespójny. Graf z rys. G.1.. nie jest spójny ze względu na izolowany wierzchołek v 6. Usunięcie wierzchołka v 6 prowadzi do grafu spójnego. W takim
5 Marek Miszczyński KBO UŁ. Wybrane elementy teorii grafów 5 nowym grafie przekrojem jest np. zbiór krawędzi {e 3, e 6 }. Usunięcie krawędzi e 3 oraz e 6 powoduje powstanie niespójności. Inne przekroje to: {e 2, e 6 } oraz {e 2, e 4, e 5 }. G.2.2. Macierzowy zapis grafu nieskierowanego macierz incydencji - grafu G ( V E) = gdzie macierz A mxn [ ] =, o m wierzchołkach i n krawędziach to = 1 jeŝeli krawędź e j jest incydentna z wierzchołkiem v i = 0 w przeciwnym wypadku Własności macierzy incydencji: 1. liczba jedynek w kaŝdej kolumnie = 2 2. liczba jedynek w wierszu = stopień wierzchołka 3. wiersz z zerami to wiersz wierzchołka izolowanego 4. krawędzie równoległe mają identyczne kolumny 5. jeŝeli graf G jest niespójny to moŝna podzielić macierz A na niezaleŝne bloki diagonalne (po odpowiednim uporządkowaniu wierszy i kolumn) 6. rz A=m-1 macierz przyległości - grafu G ( V E) macierz kwadratowa stopnia m A m [ ] =, o m wierzchołkach i n krawędziach to = gdzie = 1 jeŝeli wierzchołki v i oraz v j łączy krawędź = 0 w przeciwnym wypadku Własności macierzy przyległości: 1. liczba jedynek w wierszu (kolumnie) = stopień wierzchołka 2. wiersz (kolumna) z samymi zerami = wierzchołek izolowany 3. a ii 0 ozacza pętlę własną wierzchołka v i
6 Marek Miszczyński KBO UŁ. Wybrane elementy teorii grafów 6 Przykład Rys. G.5. Graf nieskierowany do ilustracji zapisu macierzowego Macierze incydencji i przyległości grafu z rysunku G.5. są następujące A 6x 9 = A 6x 6 = G.2.3. Grafy skierowane i sieci graf skierowany (zorientowany) - graf G ( V E) =,, w którym za pomocą odwzorowania Ψ przekształcić moŝna kaŝdą krawędź e k, związaną z wierzchołkami v i oraz v j, w uporządkowaną parę wierzchołków (v i,v j ). O wierzchołku v i mówimy, Ŝe krawędź e k jest incydentna z wierzchołka v i, natomiast o wierzchołku v j mówimy, Ŝe krawędź e k jest incydentna do wierzchołka v j. krawędź skierowana (łuk) - krawędź w grafie skierowanym wierzchołek początkowy krawędzi (źródło krawędzi) - wierzchołek dla którego krawędź e k = (v i,v j ) jest incydentna z wierzchołka (v i ) wierzchołek końcowy krawędzi (odpływ krawędzi) - wierzchołek dla którego krawędź e k = (v i,v j ) jest incydentna do wierzchołka (v j ) stopień wejściowy wierzchołka ( d v j wierzchołka v j stopień wyjściowy wierzchołka ( d v j wierzchołka v j + ) - liczba krawędzi incydentnych do ) - liczba krawędzi incydentnych z
7 Marek Miszczyński KBO UŁ. Wybrane elementy teorii grafów 7 wierzchołek izolowany - wierzchołek, dla którego stopień wejściowy i stopień wyjściowy są równe zero łuki równoległe (krawędzie skierowane równoległe) - krawędzie grafu skierowanego odwzorowane za pomocą tej samej uporządkowanej pary wierzchołków sieć - graf skierowany (zorientowany), bez pętli własnych i łuków równoległych (tj. graf prosty), bez wierzchołków izolowanych oraz obwodów skierowanych, w którym z kaŝdym łukiem e k związana jest pewna nieujemna liczba zródło sieci - wierzchołek (v j ) o zerowym stopniu wejściowym ( d v j odpływ sieci - wierzchołek (v j ) o zerowym stopniu wyjściowym ( d v j sieć zredukowana - sieć o jednym źródle i jednym odpływie + = 0 ) = 0 ) Pojęcia dróg, ścieŝek, itd. są analogiczne jak w grafie nieskierowanym. Definiując te pojęcia naleŝy pamiętać, Ŝe krawędzie grafu są skierowane, tj. para (v i,v j ) odpowiada zupełnie innej krawędzi niŝ para (v j,v i ) G.2.4. Macierzowy zapis grafu skierowanego G = V, E o m wierzchołkach i n macierz incydencji - grafu skierowanego ( ) krawędziach (łukach) to macierz A mxn [ ] = gdzie = 1 jeŝeli krawędź e j jest incydentna z wierzchołka v i = 1 jeŝeli krawędź e j jest incydentna do wierzchołka v i = 0 w pozostałych przypadkach Własności macierzy incydencji grafu skierowanego: 1. stopień wejściowy wierzchołka jest równy liczbie "-1" w wierszu 2. stopień wyjściowy wierzchołka jest równy liczbie "1" w wierszu 3. liczba jedynek w kaŝdej kolumnie = 2 4. liczba jedynek w wierszu = stopień wierzchołka 5. wiersz z zerami to wiersz wierzchołka izolowanego 6. krawędzie równoległe mają identyczne kolumny 7. jeŝeli graf G jest niespójny to moŝna podzielić macierz A na niezaleŝne bloki diagonalne (po odpowiednim uporządkowaniu wierszy i kolumn) 8. suma elementów w kolumnie jest równa zero 9. rz A=m-1
8 Marek Miszczyński KBO UŁ. Wybrane elementy teorii grafów 8 macierz przyległości - grafu G ( V E) macierz kwadratowa stopnia m A m [ ] =, o m wierzchołkach i n krawędziach to = gdzie = 1 jeŝeli wierzchołki v i oraz v j łączy łuk (v i, v j ) = 0 w przeciwnym wypadku Własności macierzy przyległości: 1. liczba "1" w wierszu = stopień wyjściowy wierzchołka 2. liczba "1" w kolumnie = stopień wejściowy wierzchołka 3. wiersz z samymi zerami = wierzchołek typu odpływ 4. kolumna z samymi zerami = wierzchołek typu źródło 5. wiersz (kolumna) z samymi zerami = wierzchołek izolowany 6. a ii 0 ozacza pętlę własną wierzchołka v i 7. jeŝeli numeracja wierzchołków sieci jest taka, Ŝe dla kaŝdego łuku (v i,v j ) numer wierzchołka v i < v j i jednocześnie macierz przyległości jest macierzą trójkątną dolną, to graf skierowany nie posiada obwodów skierowanych Przykład Rys. G.6. Graf skierowany do ilustracji zapisu macierzowego Macierze incydencji i przyległości grafu z rysunku G.6. są następujące A 6x 9 = A 6x 6 = G.2.5. Numerowanie wierzchołków grafu skierowanego Opisane dalej postępowanie realizuje numerację wierzchołków grafu skierowanego według zasady narastania numerów, tj. dla kaŝdego łuku (v i,v j ) numer wierzchołka v i <v j.opisane postępowanie wykrywa jednocześnie ewentualne obwody skierowane w grafie.
9 Marek Miszczyński KBO UŁ. Wybrane elementy teorii grafów 9 Krok 1 Przyjmij k=1 Krok 2 Znajdź niezaetykietowany wierzchołek o zerowym stopniu wejściowym i przypisz mu etykietę k. JeŜeli taki wierzchołek nie istnieje to idź do kroku 4. Krok 3 Ustaw k=k+1 i przejdź do kroku 2. Krok 4 JeŜeli wszystkie wierzchołki są zaetykietowane to koniec postępowania; jeŝeli nie to idź do kroku 5. Krok 5 JeŜeli stopień wyjściowy kaŝdego zaetykietowanego juŝ wierzchołka nie jest równy zero to usuń wszystkie łuki incydentne z kaŝdego zaetykietowanego wierzchołka i przejdź do kroku 2. JeŜeli są niezaetykietowane wierzchołki i jednocześnie stopień wyjściowy kaŝdego zaetykietowanego wierzchołka jest równy zeru to w sieci istnieje cykl (obwód skierowany) - koniec postępowania. Przykład Rys. G.7. Graf do ilustracji algorytmu numerującego wierzchołki Tabela G.1. Numeracja wierzchołków grafu z rysunku G.7. nadany numer stopień wierzchołka w kolejnych iteracjach e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 wierzchołka I II III IV V VI α x x β x x x γ x x x x x δ Σ x x x x ω x Kolejne iteracje numerowania wierzchołków grafu z rysunku G.7. były następujące. 1. W iteracji I zerowy stopień wejściowy miał wierzchołek γ. Otrzymał on nr 1 i wykreślono kolumny e 1 i e W iteracji II zerowy stopień wejściowy miał wierzchołek Σ. Otrzymał on nr 2 i wykreślono kolumny e 3 i e W iteracji III zerowy stopień wejściowy miał wierzchołek β. Otrzymał on nr 3 i wykreślono kolumny e 5 i e 6.
10 Marek Miszczyński KBO UŁ. Wybrane elementy teorii grafów W iteracji IV zerowy stopień wejściowy miał wierzchołek α. Otrzymał on nr 4 i wykreślono kolumny e 7 i e W iteracji V zerowy stopień wejściowy miał wierzchołek δ. Otrzymał on nr 5 i wykreślono kolumnę e Wierzchołek δ dostał automatycznie nr 6 po wykreśleniu wszystkich kolumn macierzy incydencji A. Literatura [1] Narshing DEO, "Teoria grafów oraz jej zastosowanie w technice i informatyce", PWN, Warszawa, 1980, Seria: Biblioteka Naukowa InŜyniera [2] Robert S.GARFINKEL, George L.NEMHAUSER, "Programowanie całkowitoliczbowe", PWN, Warszawa, 1978, Seria: Biblioteka Naukowa InŜyniera Spis treści dodatku G G. Wybrane elementy teorii grafów... 1 G.1. Co to jest graf... 1 G.1.1. Definicja grafu... 2 G.1.2. Jak rysować grafy... 2 G.2. Grafy - wybrane pojęcia... 3 G.2.1. Grafy nieskierowane... 3 G.2.2. Macierzowy zapis grafu nieskierowanego... 5 G.2.3. Grafy skierowane i sieci... 6 G.2.4. Macierzowy zapis grafu skierowanego... 7 G.2.5. Numerowanie wierzchołków grafu skierowanego... 8 Literatura Spis treści dodatku G... 10
G. Wybrane elementy teorii grafów
 Dorota Miszczyńska, Marek Miszczyński KBO UŁ Wybrane elementy teorii grafów 1 G. Wybrane elementy teorii grafów Grafy są stosowane współcześnie w różnych działach nauki i techniki. Za pomocą grafów znakomicie
Dorota Miszczyńska, Marek Miszczyński KBO UŁ Wybrane elementy teorii grafów 1 G. Wybrane elementy teorii grafów Grafy są stosowane współcześnie w różnych działach nauki i techniki. Za pomocą grafów znakomicie
MATEMATYKA DYSKRETNA - MATERIAŁY DO WYKŁADU GRAFY
 ERIAŁY DO WYKŁADU GRAFY Graf nieskierowany Grafem nieskierowanym nazywamy parę G = (V, E), gdzie V jest pewnym zbiorem skończonym (zwanym zbiorem wierzchołków grafu G), natomiast E jest zbiorem nieuporządkowanych
ERIAŁY DO WYKŁADU GRAFY Graf nieskierowany Grafem nieskierowanym nazywamy parę G = (V, E), gdzie V jest pewnym zbiorem skończonym (zwanym zbiorem wierzchołków grafu G), natomiast E jest zbiorem nieuporządkowanych
Reprezentacje grafów nieskierowanych Reprezentacje grafów skierowanych. Wykład 2. Reprezentacja komputerowa grafów
 Wykład 2. Reprezentacja komputerowa grafów 1 / 69 Macierz incydencji Niech graf G będzie grafem nieskierowanym bez pętli o n wierzchołkach (x 1, x 2,..., x n) i m krawędziach (e 1, e 2,..., e m). 2 / 69
Wykład 2. Reprezentacja komputerowa grafów 1 / 69 Macierz incydencji Niech graf G będzie grafem nieskierowanym bez pętli o n wierzchołkach (x 1, x 2,..., x n) i m krawędziach (e 1, e 2,..., e m). 2 / 69
Matematyczne Podstawy Informatyki
 Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Informacje podstawowe 1. Konsultacje: pokój
Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Informacje podstawowe 1. Konsultacje: pokój
Matematyka dyskretna
 Matematyka dyskretna Wykład 13: Teoria Grafów Gniewomir Sarbicki Literatura R.J. Wilson Wprowadzenie do teorii grafów Definicja: Grafem (skończonym, nieskierowanym) G nazywamy parę zbiorów (V (G), E(G)),
Matematyka dyskretna Wykład 13: Teoria Grafów Gniewomir Sarbicki Literatura R.J. Wilson Wprowadzenie do teorii grafów Definicja: Grafem (skończonym, nieskierowanym) G nazywamy parę zbiorów (V (G), E(G)),
Przykłady grafów. Graf prosty, to graf bez pętli i bez krawędzi wielokrotnych.
 Grafy Graf Graf (ang. graph) to zbiór wierzchołków (ang. vertices), które mogą być połączone krawędziami (ang. edges) w taki sposób, że każda krawędź kończy się i zaczyna w którymś z wierzchołków. Graf
Grafy Graf Graf (ang. graph) to zbiór wierzchołków (ang. vertices), które mogą być połączone krawędziami (ang. edges) w taki sposób, że każda krawędź kończy się i zaczyna w którymś z wierzchołków. Graf
WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA
 DROGI i CYKLE w grafach Dla grafu (nieskierowanego) G = ( V, E ) drogą z wierzchołka v 0 V do v t V nazywamy ciąg (naprzemienny) wierzchołków i krawędzi grafu: ( v 0, e, v, e,..., v t, e t, v t ), spełniający
DROGI i CYKLE w grafach Dla grafu (nieskierowanego) G = ( V, E ) drogą z wierzchołka v 0 V do v t V nazywamy ciąg (naprzemienny) wierzchołków i krawędzi grafu: ( v 0, e, v, e,..., v t, e t, v t ), spełniający
Algorytmy grafowe. Wykład 1 Podstawy teorii grafów Reprezentacje grafów. Tomasz Tyksiński CDV
 Algorytmy grafowe Wykład 1 Podstawy teorii grafów Reprezentacje grafów Tomasz Tyksiński CDV Rozkład materiału 1. Podstawowe pojęcia teorii grafów, reprezentacje komputerowe grafów 2. Przeszukiwanie grafów
Algorytmy grafowe Wykład 1 Podstawy teorii grafów Reprezentacje grafów Tomasz Tyksiński CDV Rozkład materiału 1. Podstawowe pojęcia teorii grafów, reprezentacje komputerowe grafów 2. Przeszukiwanie grafów
Algorytmiczna teoria grafów
 Podstawowe pojęcia i klasy grafów Wykład 1 Grafy nieskierowane Definicja Graf nieskierowany (graf) G = (V,E) jest to uporządkowana para składająca się z niepustego skończonego zbioru wierzchołków V oraz
Podstawowe pojęcia i klasy grafów Wykład 1 Grafy nieskierowane Definicja Graf nieskierowany (graf) G = (V,E) jest to uporządkowana para składająca się z niepustego skończonego zbioru wierzchołków V oraz
TEORIA GRAFÓW I SIECI
 TEORIA GRAFÓW I SIECI Temat nr 3: Marszruty, łańcuchy, drogi w grafach dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 261-83-95-04, p.225/100
TEORIA GRAFÓW I SIECI Temat nr 3: Marszruty, łańcuchy, drogi w grafach dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 261-83-95-04, p.225/100
Teoria grafów podstawy. Materiały pomocnicze do wykładu. wykładowca: dr Magdalena Kacprzak
 Teoria grafów podstawy Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Grafy zorientowane i niezorientowane Przykład 1 Dwa pociągi i jeden most problem wzajemnego wykluczania się Dwa
Teoria grafów podstawy Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Grafy zorientowane i niezorientowane Przykład 1 Dwa pociągi i jeden most problem wzajemnego wykluczania się Dwa
Graf. Definicja marca / 1
 Graf 25 marca 2018 Graf Definicja 1 Graf ogólny to para G = (V, E), gdzie V jest zbiorem wierzchołków (węzłów, punktów grafu), E jest rodziną krawędzi, które mogą być wielokrotne, dokładniej jednoelementowych
Graf 25 marca 2018 Graf Definicja 1 Graf ogólny to para G = (V, E), gdzie V jest zbiorem wierzchołków (węzłów, punktów grafu), E jest rodziną krawędzi, które mogą być wielokrotne, dokładniej jednoelementowych
Algorytmiczna teoria grafów
 Przedmiot fakultatywny 20h wykładu + 20h ćwiczeń 21 lutego 2014 Zasady zaliczenia 1 ćwiczenia (ocena): kolokwium, zadania programistyczne (implementacje algorytmów), praca na ćwiczeniach. 2 Wykład (egzamin)
Przedmiot fakultatywny 20h wykładu + 20h ćwiczeń 21 lutego 2014 Zasady zaliczenia 1 ćwiczenia (ocena): kolokwium, zadania programistyczne (implementacje algorytmów), praca na ćwiczeniach. 2 Wykład (egzamin)
. Podstawy Programowania 2. Grafy i ich reprezentacje. Arkadiusz Chrobot. 9 czerwca 2016
 Podstawy Programowania 2 Grafy i ich reprezentacje Arkadiusz Chrobot Zakład Informatyki 9 czerwca 2016 1 42 Plan 1 Wstęp 2 Teoria grafów 3 Grafy jako struktury danych 4 Zastosowania grafów 2 42 Wstęp Wstęp
Podstawy Programowania 2 Grafy i ich reprezentacje Arkadiusz Chrobot Zakład Informatyki 9 czerwca 2016 1 42 Plan 1 Wstęp 2 Teoria grafów 3 Grafy jako struktury danych 4 Zastosowania grafów 2 42 Wstęp Wstęp
Matematyczne Podstawy Informatyki
 Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Twierdzenie 2.1 Niech G będzie grafem prostym
Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Twierdzenie 2.1 Niech G będzie grafem prostym
Suma dwóch grafów. Zespolenie dwóch grafów
 Suma dwóch grafów G 1 = ((G 1 ), E(G 1 )) G 2 = ((G 2 ), E(G 2 )) (G 1 ) i (G 2 ) rozłączne Suma G 1 G 2 graf ze zbiorem wierzchołków (G 1 ) (G 2 ) i rodziną krawędzi E(G 1 ) E(G 2 ) G 1 G 2 G 1 G 2 Zespolenie
Suma dwóch grafów G 1 = ((G 1 ), E(G 1 )) G 2 = ((G 2 ), E(G 2 )) (G 1 ) i (G 2 ) rozłączne Suma G 1 G 2 graf ze zbiorem wierzchołków (G 1 ) (G 2 ) i rodziną krawędzi E(G 1 ) E(G 2 ) G 1 G 2 G 1 G 2 Zespolenie
Podstawy Programowania 2 Grafy i ich reprezentacje. Plan. Wstęp. Teoria grafów Graf skierowany. Notatki. Notatki. Notatki. Notatki.
 Podstawy Programowania Grafy i ich reprezentacje Arkadiusz Chrobot Zakład Informatyki 7 maja 09 / 4 Plan Wstęp Zastosowania grafów / 4 Wstęp Grafy są w informatyce strukturami danych stosowanymi w wielu
Podstawy Programowania Grafy i ich reprezentacje Arkadiusz Chrobot Zakład Informatyki 7 maja 09 / 4 Plan Wstęp Zastosowania grafów / 4 Wstęp Grafy są w informatyce strukturami danych stosowanymi w wielu
TEORIA GRAFÓW I SIECI
 TEORIA GRAFÓW I SIECI Temat nr 1: Definicja grafu. Rodzaje i części grafów dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 261-83-95-04, p.225/100
TEORIA GRAFÓW I SIECI Temat nr 1: Definicja grafu. Rodzaje i części grafów dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 261-83-95-04, p.225/100
Teoria grafów dla małolatów. Andrzej Przemysław Urbański Instytut Informatyki Politechnika Poznańska
 Teoria grafów dla małolatów Andrzej Przemysław Urbański Instytut Informatyki Politechnika Poznańska Wstęp Matematyka to wiele różnych dyscyplin Bowiem świat jest bardzo skomplikowany wymaga rozważenia
Teoria grafów dla małolatów Andrzej Przemysław Urbański Instytut Informatyki Politechnika Poznańska Wstęp Matematyka to wiele różnych dyscyplin Bowiem świat jest bardzo skomplikowany wymaga rozważenia
Czy istnieje zamknięta droga spaceru przechodząca przez wszystkie mosty w Królewcu dokładnie jeden raz?
 DROGI i CYKLE EULERA w grafach Czy istnieje zamknięta droga spaceru przechodząca przez wszystkie mosty w Królewcu dokładnie jeden raz? Czy można narysować podaną figurę nie odrywając ołówka od papieru
DROGI i CYKLE EULERA w grafach Czy istnieje zamknięta droga spaceru przechodząca przez wszystkie mosty w Królewcu dokładnie jeden raz? Czy można narysować podaną figurę nie odrywając ołówka od papieru
Sortowanie topologiczne skierowanych grafów acyklicznych
 Sortowanie topologiczne skierowanych grafów acyklicznych Metody boolowskie w informatyce Robert Sulkowski http://robert.brainusers.net 23 stycznia 2010 1 Definicja 1 (Cykl skierowany). Niech C = (V, A)
Sortowanie topologiczne skierowanych grafów acyklicznych Metody boolowskie w informatyce Robert Sulkowski http://robert.brainusers.net 23 stycznia 2010 1 Definicja 1 (Cykl skierowany). Niech C = (V, A)
Struktury danych i złożoność obliczeniowa Wykład 5. Prof. dr hab. inż. Jan Magott
 Struktury danych i złożoność obliczeniowa Wykład. Prof. dr hab. inż. Jan Magott Algorytmy grafowe: podstawowe pojęcia, reprezentacja grafów, metody przeszukiwania, minimalne drzewa rozpinające, problemy
Struktury danych i złożoność obliczeniowa Wykład. Prof. dr hab. inż. Jan Magott Algorytmy grafowe: podstawowe pojęcia, reprezentacja grafów, metody przeszukiwania, minimalne drzewa rozpinające, problemy
Gramatyki grafowe. Dla v V, ϕ(v) etykieta v. Klasa grafów nad Σ - G Σ.
 Gramatyki grafowe Def. Nieskierowany NL-graf (etykietowane wierzchołki) jest czwórką g = (V, E, Σ, ϕ), gdzie: V niepusty zbiór wierzchołków, E V V zbiór krawędzi, Σ - skończony, niepusty alfabet etykiet
Gramatyki grafowe Def. Nieskierowany NL-graf (etykietowane wierzchołki) jest czwórką g = (V, E, Σ, ϕ), gdzie: V niepusty zbiór wierzchołków, E V V zbiór krawędzi, Σ - skończony, niepusty alfabet etykiet
0. ELEMENTY LOGIKI. ALGEBRA BOOLE A
 WYKŁAD 5() ELEMENTY LOGIKI ALGEBRA BOOLE A Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek zdań Matematyka zbudowana jest z pierwotnych twierdzeń (nazywamy
WYKŁAD 5() ELEMENTY LOGIKI ALGEBRA BOOLE A Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek zdań Matematyka zbudowana jest z pierwotnych twierdzeń (nazywamy
TEORIA GRAFÓW I SIECI
 TEORIA GRAFÓW I SIECI Temat nr : Grafy Berge a dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 6-83-95-0, p.5/00 Zakład Badań Operacyjnych i
TEORIA GRAFÓW I SIECI Temat nr : Grafy Berge a dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 6-83-95-0, p.5/00 Zakład Badań Operacyjnych i
Drzewa. Jeżeli graf G jest lasem, który ma n wierzchołków i k składowych, to G ma n k krawędzi. Własności drzew
 Drzewa Las - graf, który nie zawiera cykli Drzewo - las spójny Jeżeli graf G jest lasem, który ma n wierzchołków i k składowych, to G ma n k krawędzi. Własności drzew Niech T graf o n wierzchołkach będący
Drzewa Las - graf, który nie zawiera cykli Drzewo - las spójny Jeżeli graf G jest lasem, który ma n wierzchołków i k składowych, to G ma n k krawędzi. Własności drzew Niech T graf o n wierzchołkach będący
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 13/14 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 13/14 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
KURS MATEMATYKA DYSKRETNA
 KURS MATEMATYKA DYSKRETNA LEKCJA 28 Grafy hamiltonowskie ZADANIE DOMOWE www.akademia.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Drogę nazywamy
KURS MATEMATYKA DYSKRETNA LEKCJA 28 Grafy hamiltonowskie ZADANIE DOMOWE www.akademia.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Drogę nazywamy
Elementy teorii grafów Elementy teorii grafów
 Spis tresci 1 Spis tresci 1 Często w zagadnieniach praktycznych rozważa się pewien zbiór obiektów wraz z zależnościami jakie łączą te obiekty. Dla przykładu można badać pewną grupę ludzi oraz strukturę
Spis tresci 1 Spis tresci 1 Często w zagadnieniach praktycznych rozważa się pewien zbiór obiektów wraz z zależnościami jakie łączą te obiekty. Dla przykładu można badać pewną grupę ludzi oraz strukturę
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2012 andrzej.lachwa@uj.edu.pl 13/14 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Matematyka dyskretna Andrzej Łachwa, UJ, 2012 andrzej.lachwa@uj.edu.pl 13/14 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Algorytmy z powracaniem
 Algorytmy z powracaniem Materiały Grafem nazywamy zbiór G = (V, E), gdzie: V jest zbiorem wierzchołków (ang. vertex) E jest zbiorem krawędzi (E można też określić jako podzbiór zbioru nieuporządkowanych
Algorytmy z powracaniem Materiały Grafem nazywamy zbiór G = (V, E), gdzie: V jest zbiorem wierzchołków (ang. vertex) E jest zbiorem krawędzi (E można też określić jako podzbiór zbioru nieuporządkowanych
6. Wstępne pojęcia teorii grafów
 6. Wstępne pojęcia teorii grafów Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2016/2017 rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 6. Wstępne pojęcia teorii grafów zima 2016/2017
6. Wstępne pojęcia teorii grafów Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2016/2017 rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 6. Wstępne pojęcia teorii grafów zima 2016/2017
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 14/15 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 14/15 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Grafy dla każdego. dr Krzysztof Bryś. Wydział Matematyki i Nauk Informacyjnych Politechnika Warszawska.
 Grafy dla każdego dr Krzysztof Bryś brys@mini.pw.edu.pl Wydział Matematyki i Nauk Informacyjnych Politechnika Warszawska www.mini.pw.edu.pl Warszawa, 28 marca 2015 Graf składa się z elementów pewnego zbioru
Grafy dla każdego dr Krzysztof Bryś brys@mini.pw.edu.pl Wydział Matematyki i Nauk Informacyjnych Politechnika Warszawska www.mini.pw.edu.pl Warszawa, 28 marca 2015 Graf składa się z elementów pewnego zbioru
Grafem nazywamy strukturę G = (V, E): V zbiór węzłów lub wierzchołków, Grafy dzielimy na grafy skierowane i nieskierowane:
 Wykład 4 grafy Grafem nazywamy strukturę G = (V, E): V zbiór węzłów lub wierzchołków, E zbiór krawędzi, Grafy dzielimy na grafy skierowane i nieskierowane: Formalnie, w grafach skierowanych E jest podzbiorem
Wykład 4 grafy Grafem nazywamy strukturę G = (V, E): V zbiór węzłów lub wierzchołków, E zbiór krawędzi, Grafy dzielimy na grafy skierowane i nieskierowane: Formalnie, w grafach skierowanych E jest podzbiorem
Digraf. 13 maja 2017
 Digraf 13 maja 2017 Graf skierowany, digraf, digraf prosty Definicja 1 Digraf prosty G to (V, E), gdzie V jest zbiorem wierzchołków, E jest rodziną zorientowanych krawędzi, między różnymi wierzchołkami,
Digraf 13 maja 2017 Graf skierowany, digraf, digraf prosty Definicja 1 Digraf prosty G to (V, E), gdzie V jest zbiorem wierzchołków, E jest rodziną zorientowanych krawędzi, między różnymi wierzchołkami,
Struktury danych i złożoność obliczeniowa Wykład 7. Prof. dr hab. inż. Jan Magott
 Struktury danych i złożoność obliczeniowa Wykład 7 Prof. dr hab. inż. Jan Magott Problemy NP-zupełne Transformacją wielomianową problemu π 2 do problemu π 1 (π 2 π 1 ) jest funkcja f: D π2 D π1 spełniająca
Struktury danych i złożoność obliczeniowa Wykład 7 Prof. dr hab. inż. Jan Magott Problemy NP-zupełne Transformacją wielomianową problemu π 2 do problemu π 1 (π 2 π 1 ) jest funkcja f: D π2 D π1 spełniająca
Podstawowe własności grafów. Wykład 3. Własności grafów
 Wykład 3. Własności grafów 1 / 87 Suma grafów Niech będą dane grafy proste G 1 = (V 1, E 1) oraz G 2 = (V 2, E 2). 2 / 87 Suma grafów Niech będą dane grafy proste G 1 = (V 1, E 1) oraz G 2 = (V 2, E 2).
Wykład 3. Własności grafów 1 / 87 Suma grafów Niech będą dane grafy proste G 1 = (V 1, E 1) oraz G 2 = (V 2, E 2). 2 / 87 Suma grafów Niech będą dane grafy proste G 1 = (V 1, E 1) oraz G 2 = (V 2, E 2).
Algebra liniowa z geometrią
 Algebra liniowa z geometrią Maciej Czarnecki 15 stycznia 2013 Spis treści 1 Geometria płaszczyzny 2 1.1 Wektory i skalary........................... 2 1.2 Macierze, wyznaczniki, układy równań liniowych.........
Algebra liniowa z geometrią Maciej Czarnecki 15 stycznia 2013 Spis treści 1 Geometria płaszczyzny 2 1.1 Wektory i skalary........................... 2 1.2 Macierze, wyznaczniki, układy równań liniowych.........
Algorytmy Równoległe i Rozproszone Część V - Model PRAM II
 Algorytmy Równoległe i Rozproszone Część V - Model PRAM II Łukasz Kuszner pokój 209, WETI http://www.sphere.pl/ kuszner/ kuszner@sphere.pl Oficjalna strona wykładu http://www.sphere.pl/ kuszner/arir/ 2005/06
Algorytmy Równoległe i Rozproszone Część V - Model PRAM II Łukasz Kuszner pokój 209, WETI http://www.sphere.pl/ kuszner/ kuszner@sphere.pl Oficjalna strona wykładu http://www.sphere.pl/ kuszner/arir/ 2005/06
Ogólne wiadomości o grafach
 Ogólne wiadomości o grafach Algorytmy i struktury danych Wykład 5. Rok akademicki: / Pojęcie grafu Graf zbiór wierzchołków połączonych za pomocą krawędzi. Podstawowe rodzaje grafów: grafy nieskierowane,
Ogólne wiadomości o grafach Algorytmy i struktury danych Wykład 5. Rok akademicki: / Pojęcie grafu Graf zbiór wierzchołków połączonych za pomocą krawędzi. Podstawowe rodzaje grafów: grafy nieskierowane,
a) 7 b) 19 c) 21 d) 34
 Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Plan wykładu. Przykład. Przykład 3/19/2011. Przykład zagadnienia transportowego. Optymalizacja w procesach biznesowych Wykład 2 DECYZJA?
 /9/ Zagadnienie transportowe Optymalizacja w procesach biznesowych Wykład --9 Plan wykładu Przykład zagadnienia transportowego Sformułowanie problemu Własności zagadnienia transportowego Metoda potencjałów
/9/ Zagadnienie transportowe Optymalizacja w procesach biznesowych Wykład --9 Plan wykładu Przykład zagadnienia transportowego Sformułowanie problemu Własności zagadnienia transportowego Metoda potencjałów
Podstawowe pojęcia dotyczące drzew Podstawowe pojęcia dotyczące grafów Przykłady drzew i grafów
 Podstawowe pojęcia dotyczące drzew Podstawowe pojęcia dotyczące grafów Przykłady drzew i grafów Drzewa: Drzewo (ang. tree) jest strukturą danych zbudowaną z elementów, które nazywamy węzłami (ang. node).
Podstawowe pojęcia dotyczące drzew Podstawowe pojęcia dotyczące grafów Przykłady drzew i grafów Drzewa: Drzewo (ang. tree) jest strukturą danych zbudowaną z elementów, które nazywamy węzłami (ang. node).
Opracowanie prof. J. Domsta 1
 Opracowanie prof. J. Domsta 1 Algorytm FLEURY'ego: Twierdzenie 6.5 G-graf eulerowski. Wtedy cykl Eulera otrzymujemy nastepująco: a) Start w dowolnym wierzchołku b) Krawędzie w dowolnej kolejności po przebyciu
Opracowanie prof. J. Domsta 1 Algorytm FLEURY'ego: Twierdzenie 6.5 G-graf eulerowski. Wtedy cykl Eulera otrzymujemy nastepująco: a) Start w dowolnym wierzchołku b) Krawędzie w dowolnej kolejności po przebyciu
KURS MATEMATYKA DYSKRETNA
 KURS MATEMATYKA DYSKRETNA LEKCJA 28 Grafy hamiltonowskie Odpowiedzi do zadania domowego www.akademia.etrapez.pl Strona 1 Część 1: TEST 1) b 2) a 3) b 4) d 5) c 6) d 7) b 8) b 9) d 10) a Zad. 1 ODPOWIEDZI
KURS MATEMATYKA DYSKRETNA LEKCJA 28 Grafy hamiltonowskie Odpowiedzi do zadania domowego www.akademia.etrapez.pl Strona 1 Część 1: TEST 1) b 2) a 3) b 4) d 5) c 6) d 7) b 8) b 9) d 10) a Zad. 1 ODPOWIEDZI
Kolorowanie wierzchołków Kolorowanie krawędzi Kolorowanie regionów i map. Wykład 8. Kolorowanie
 Wykład 8. Kolorowanie 1 / 62 Kolorowanie wierzchołków - definicja Zbiory niezależne Niech G będzie grafem bez pętli. Definicja Mówimy, że G jest grafem k kolorowalnym, jeśli każdemu wierzchołkowi możemy
Wykład 8. Kolorowanie 1 / 62 Kolorowanie wierzchołków - definicja Zbiory niezależne Niech G będzie grafem bez pętli. Definicja Mówimy, że G jest grafem k kolorowalnym, jeśli każdemu wierzchołkowi możemy
Układy równań liniowych. Ax = b (1)
 Układy równań liniowych Dany jest układ m równań z n niewiadomymi. Liczba równań m nie musi być równa liczbie niewiadomych n, tj. mn. a a... a b n n a a... a b n n... a a... a b m m mn n m
Układy równań liniowych Dany jest układ m równań z n niewiadomymi. Liczba równań m nie musi być równa liczbie niewiadomych n, tj. mn. a a... a b n n a a... a b n n... a a... a b m m mn n m
Grafy i Zastosowania. 5: Drzewa Rozpinające. c Marcin Sydow. Drzewa rozpinające. Cykle i rozcięcia fundamentalne. Zastosowania
 Grafy i Grafy i 5: Rozpinające Spis zagadnień Grafy i i lasy cykle fundamentalne i własności cykli i rozcięć przestrzenie cykli i rozcięć* : zastosowanie w sieciach elektrycznych minimalne * algorytm Kruskala*
Grafy i Grafy i 5: Rozpinające Spis zagadnień Grafy i i lasy cykle fundamentalne i własności cykli i rozcięć przestrzenie cykli i rozcięć* : zastosowanie w sieciach elektrycznych minimalne * algorytm Kruskala*
Matematyczne Podstawy Informatyki
 Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 03/0 Przeszukiwanie w głąb i wszerz I Przeszukiwanie metodą
Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 03/0 Przeszukiwanie w głąb i wszerz I Przeszukiwanie metodą
WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA
 ELEMENTY TEORII GRAFÓW Literatura: N.Deo Teoria grafów i e zastosowania... PWN (1980) Ross, Wright Matematyka yskretna PWN (199) R.Wilson Wprowazenie o teorii grafów PWN (1999) J.Kulikowski Zarys teorii
ELEMENTY TEORII GRAFÓW Literatura: N.Deo Teoria grafów i e zastosowania... PWN (1980) Ross, Wright Matematyka yskretna PWN (199) R.Wilson Wprowazenie o teorii grafów PWN (1999) J.Kulikowski Zarys teorii
Wykład 10 Grafy, algorytmy grafowe
 . Typy złożoności obliczeniowej Wykład Grafy, algorytmy grafowe Typ złożoności oznaczenie n Jedna operacja trwa µs 5 logarytmiczna lgn. s. s.7 s liniowa n. s.5 s. s Logarytmicznoliniowa nlgn. s.8 s.4 s
. Typy złożoności obliczeniowej Wykład Grafy, algorytmy grafowe Typ złożoności oznaczenie n Jedna operacja trwa µs 5 logarytmiczna lgn. s. s.7 s liniowa n. s.5 s. s Logarytmicznoliniowa nlgn. s.8 s.4 s
ALGORYTMY. 1. Podstawowe definicje Schemat blokowy
 ALGORYTMY 1. Podstawowe definicje Algorytm (definicja nieformalna) to sposób postępowania (przepis) umożliwiający rozwiązanie określonego zadania (klasy zadań), podany w postaci skończonego zestawu czynności
ALGORYTMY 1. Podstawowe definicje Algorytm (definicja nieformalna) to sposób postępowania (przepis) umożliwiający rozwiązanie określonego zadania (klasy zadań), podany w postaci skończonego zestawu czynności
Matematyka dyskretna. Andrzej Łachwa, UJ, B/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 1B/14 Drogi w grafach Marszruta (trasa) w grafie G z wierzchołka w do wierzchołka u to skończony ciąg krawędzi w postaci. W skrócie
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 1B/14 Drogi w grafach Marszruta (trasa) w grafie G z wierzchołka w do wierzchołka u to skończony ciąg krawędzi w postaci. W skrócie
SPÓJNOŚĆ. ,...v k. }, E={v 1. v k. i v k. ,...,v k-1. }. Wierzchołki v 1. v 2. to końce ścieżki.
 SPÓJNOŚĆ Graf jest spójny, gdy dla każdego podziału V na dwa rozłączne podzbiory A i B istnieje krawędź z A do B. Definicja równoważna: Graf jest spójny, gdy każde dwa wierzchołki są połączone ścieżką
SPÓJNOŚĆ Graf jest spójny, gdy dla każdego podziału V na dwa rozłączne podzbiory A i B istnieje krawędź z A do B. Definicja równoważna: Graf jest spójny, gdy każde dwa wierzchołki są połączone ścieżką
ALGORYTMY. 1. Podstawowe definicje Schemat blokowy
 ALGORYTMY 1. Podstawowe definicje Algorytm (definicja nieformalna) to sposób postępowania (przepis) umożliwiający rozwiązanie określonego zadania (klasy zadań), podany w postaci skończonego zestawu czynności
ALGORYTMY 1. Podstawowe definicje Algorytm (definicja nieformalna) to sposób postępowania (przepis) umożliwiający rozwiązanie określonego zadania (klasy zadań), podany w postaci skończonego zestawu czynności
Metody numeryczne Wykład 4
 Metody numeryczne Wykład 4 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Metody skończone rozwiązywania
Metody numeryczne Wykład 4 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Metody skończone rozwiązywania
Podejście zachłanne, a programowanie dynamiczne
 Podejście zachłanne, a programowanie dynamiczne Algorytm zachłanny pobiera po kolei elementy danych, za każdym razem wybierając taki, który wydaje się najlepszy w zakresie spełniania pewnych kryteriów
Podejście zachłanne, a programowanie dynamiczne Algorytm zachłanny pobiera po kolei elementy danych, za każdym razem wybierając taki, który wydaje się najlepszy w zakresie spełniania pewnych kryteriów
Spis treści Podstawowe definicje Wielomian charakterystyczny grafu Grafy silnie regularne
 Spis treści 1 Podstawowe definicje 4 1.1 Grafy................................ 4 1.2 Przykłady grafów......................... 12 1.2.1 Grafy puste i pełne.................... 12 1.2.2 Grafy dwudzielne.....................
Spis treści 1 Podstawowe definicje 4 1.1 Grafy................................ 4 1.2 Przykłady grafów......................... 12 1.2.1 Grafy puste i pełne.................... 12 1.2.2 Grafy dwudzielne.....................
Programowanie liniowe
 Programowanie liniowe Maciej Drwal maciej.drwal@pwr.wroc.pl 1 Problem programowania liniowego min x c T x (1) Ax b, (2) x 0. (3) gdzie A R m n, c R n, b R m. Oznaczmy przez x rozwiązanie optymalne, tzn.
Programowanie liniowe Maciej Drwal maciej.drwal@pwr.wroc.pl 1 Problem programowania liniowego min x c T x (1) Ax b, (2) x 0. (3) gdzie A R m n, c R n, b R m. Oznaczmy przez x rozwiązanie optymalne, tzn.
6a. Grafy eulerowskie i hamiltonowskie
 6a. Grafy eulerowskie i hamiltonowskie Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2016/2017 rzegorz Kosiorowski (Uniwersytet Ekonomiczny6a. w Krakowie) Grafy eulerowskie i hamiltonowskie
6a. Grafy eulerowskie i hamiltonowskie Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2016/2017 rzegorz Kosiorowski (Uniwersytet Ekonomiczny6a. w Krakowie) Grafy eulerowskie i hamiltonowskie
E ' E G nazywamy krawędziowym zbiorem
 Niech G będzie grafem spójnym. Wierzchołek x nazywamy rozcinającym, jeśli G\{x} jest niespójny. Niech G będzie grafem spójnym. V ' V G nazywamy zbiorem rozcinającym jeśli G\V' jest niespójny Niech G będzie
Niech G będzie grafem spójnym. Wierzchołek x nazywamy rozcinającym, jeśli G\{x} jest niespójny. Niech G będzie grafem spójnym. V ' V G nazywamy zbiorem rozcinającym jeśli G\V' jest niespójny Niech G będzie
Złożoność obliczeniowa klasycznych problemów grafowych
 Złożoność obliczeniowa klasycznych problemów grafowych Oznaczenia: G graf, V liczba wierzchołków, E liczba krawędzi 1. Spójność grafu Graf jest spójny jeżeli istnieje ścieżka łącząca każdą parę jego wierzchołków.
Złożoność obliczeniowa klasycznych problemów grafowych Oznaczenia: G graf, V liczba wierzchołków, E liczba krawędzi 1. Spójność grafu Graf jest spójny jeżeli istnieje ścieżka łącząca każdą parę jego wierzchołków.
Wprowadzenie Podstawy Fundamentalne twierdzenie Kolorowanie. Grafy planarne. Przemysław Gordinowicz. Instytut Matematyki, Politechnika Łódzka
 Grafy planarne Przemysław Gordinowicz Instytut Matematyki, Politechnika Łódzka Grafy i ich zastosowania Wykład 12 Plan prezentacji 1 Wprowadzenie 2 Podstawy 3 Fundamentalne twierdzenie 4 Kolorowanie grafów
Grafy planarne Przemysław Gordinowicz Instytut Matematyki, Politechnika Łódzka Grafy i ich zastosowania Wykład 12 Plan prezentacji 1 Wprowadzenie 2 Podstawy 3 Fundamentalne twierdzenie 4 Kolorowanie grafów
WSTĘP DO INFORMATYKI. Grafy i struktury grafowe
 Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej WTĘP DO INFORMATYKI Adrian Horzyk Grafy i struktury grafowe www.agh.edu.pl DEFINICJA GRAFU Graf to
Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej WTĘP DO INFORMATYKI Adrian Horzyk Grafy i struktury grafowe www.agh.edu.pl DEFINICJA GRAFU Graf to
MATEMATYKA DYSKRETNA - KOLOKWIUM 2
 1 MATEMATYKA DYSKRETNA - KOLOKWIUM 2 GRUPA A RACHUNKI+KRÓTKIE WYJAŚNIENIA! NA TEJ KARTCE! KAŻDA DODATKOWA KARTKA TO MINUS 1 PUNKT! Imię i nazwisko...... Nr indeksu... 1. (3p.) Znajdź drzewo o kodzie Prufera
1 MATEMATYKA DYSKRETNA - KOLOKWIUM 2 GRUPA A RACHUNKI+KRÓTKIE WYJAŚNIENIA! NA TEJ KARTCE! KAŻDA DODATKOWA KARTKA TO MINUS 1 PUNKT! Imię i nazwisko...... Nr indeksu... 1. (3p.) Znajdź drzewo o kodzie Prufera
Teoria automatów i języków formalnych. Określenie relacji
 Relacje Teoria automatów i języków formalnych Dr inŝ. Janusz ajewski Katedra Informatyki Określenie relacji: Określenie relacji Relacja R jest zbiorem par uporządkowanych, czyli podzbiorem iloczynu kartezjańskiego
Relacje Teoria automatów i języków formalnych Dr inŝ. Janusz ajewski Katedra Informatyki Określenie relacji: Określenie relacji Relacja R jest zbiorem par uporządkowanych, czyli podzbiorem iloczynu kartezjańskiego
TEORETYCZNE PODSTAWY INFORMATYKI
 1 TEORETYCZNE PODSTAWY INFORMATYKI WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Wykład 14c 2 Definicje indukcyjne Twierdzenia dowodzone przez indukcje Definicje indukcyjne Definicja drzewa
1 TEORETYCZNE PODSTAWY INFORMATYKI WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Wykład 14c 2 Definicje indukcyjne Twierdzenia dowodzone przez indukcje Definicje indukcyjne Definicja drzewa
Zagadnienie transportowe
 9//9 Zagadnienie transportowe Optymalizacja w procesach biznesowych Wykład Plan wykładu Przykład zagadnienia transportowego Sformułowanie problemu Własności zagadnienia transportowego Metoda potencjałów
9//9 Zagadnienie transportowe Optymalizacja w procesach biznesowych Wykład Plan wykładu Przykład zagadnienia transportowego Sformułowanie problemu Własności zagadnienia transportowego Metoda potencjałów
Programowanie dynamiczne i algorytmy zachłanne
 Programowanie dynamiczne i algorytmy zachłanne Tomasz Głowacki tglowacki@cs.put.poznan.pl Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii
Programowanie dynamiczne i algorytmy zachłanne Tomasz Głowacki tglowacki@cs.put.poznan.pl Zajęcia finansowane z projektu "Rozwój i doskonalenie kształcenia na Politechnice Poznańskiej w zakresie technologii
TEORIA GRAFÓW I SIECI
 TEORIA GRAFÓW I SIECI Temat nr 7: Przydziały w grafach i sieciach dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 26-83-95-04, p.225/00 Zakład
TEORIA GRAFÓW I SIECI Temat nr 7: Przydziały w grafach i sieciach dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 26-83-95-04, p.225/00 Zakład
Rozważmy funkcję f : X Y. Dla dowolnego zbioru A X określamy. Dla dowolnego zbioru B Y określamy jego przeciwobraz:
 Rozważmy funkcję f : X Y. Dla dowolnego zbioru A X określamy jego obraz: f(a) = {f(x); x A} = {y Y : x A f(x) = y}. Dla dowolnego zbioru B Y określamy jego przeciwobraz: f 1 (B) = {x X; f(x) B}. 1 Zadanie.
Rozważmy funkcję f : X Y. Dla dowolnego zbioru A X określamy jego obraz: f(a) = {f(x); x A} = {y Y : x A f(x) = y}. Dla dowolnego zbioru B Y określamy jego przeciwobraz: f 1 (B) = {x X; f(x) B}. 1 Zadanie.
Matematyka Dyskretna. Andrzej Szepietowski. 25 czerwca 2002 roku
 Matematyka Dyskretna Andrzej Szepietowski 25 czerwca 2002 roku ( Rozdział 1 Grafy skierowane W tym rozdziale zajmiemy siȩ algorytmami wyszukiwania najkrótszej drogi w grafach skierowanych Każdej krawȩdzi
Matematyka Dyskretna Andrzej Szepietowski 25 czerwca 2002 roku ( Rozdział 1 Grafy skierowane W tym rozdziale zajmiemy siȩ algorytmami wyszukiwania najkrótszej drogi w grafach skierowanych Każdej krawȩdzi
macierze jednostkowe (identyczności) macierze diagonalne, które na przekątnej mają same
 1 Macierz definicja i zapis Macierzą wymiaru m na n nazywamy tabelę a 11 a 1n A = a m1 a mn złożoną z liczb (rzeczywistych lub zespolonych) o m wierszach i n kolumnach (zamiennie będziemy też czasem mówili,
1 Macierz definicja i zapis Macierzą wymiaru m na n nazywamy tabelę a 11 a 1n A = a m1 a mn złożoną z liczb (rzeczywistych lub zespolonych) o m wierszach i n kolumnach (zamiennie będziemy też czasem mówili,
Zofia Kruczkiewicz, Algorytmu i struktury danych, Wykład 14, 1
 Wykład Algorytmy grafowe metoda zachłanna. Właściwości algorytmu zachłannego:. W przeciwieństwie do metody programowania dynamicznego nie występuje etap dzielenia na mniejsze realizacje z wykorzystaniem
Wykład Algorytmy grafowe metoda zachłanna. Właściwości algorytmu zachłannego:. W przeciwieństwie do metody programowania dynamicznego nie występuje etap dzielenia na mniejsze realizacje z wykorzystaniem
D. Miszczyńska, M.Miszczyński KBO UŁ 1 GRY KONFLIKTOWE GRY 2-OSOBOWE O SUMIE WYPŁAT ZERO
 D. Miszczyńska, M.Miszczyński KBO UŁ GRY KONFLIKTOWE GRY 2-OSOBOWE O SUMIE WYPŁAT ZERO Gra w sensie niżej przedstawionym to zasady którymi kierują się decydenci. Zakładamy, że rezultatem gry jest wypłata,
D. Miszczyńska, M.Miszczyński KBO UŁ GRY KONFLIKTOWE GRY 2-OSOBOWE O SUMIE WYPŁAT ZERO Gra w sensie niżej przedstawionym to zasady którymi kierują się decydenci. Zakładamy, że rezultatem gry jest wypłata,
Grafy i Zastosowania. 9: Digrafy (grafy skierowane) c Marcin Sydow
 9: Digrafy (grafy skierowane) Spis zagadnień Digrafy Porządki częściowe Turnieje Przykłady: głosowanie większościowe, ścieżka krytyczna Digraf (graf skierowany) Digraf to równoważny termin z terminem graf
9: Digrafy (grafy skierowane) Spis zagadnień Digrafy Porządki częściowe Turnieje Przykłady: głosowanie większościowe, ścieżka krytyczna Digraf (graf skierowany) Digraf to równoważny termin z terminem graf
(4) x (y z) = (x y) (x z), x (y z) = (x y) (x z), (3) x (x y) = x, x (x y) = x, (2) x 0 = x, x 1 = x
 2. Wykład 2: algebry Boole a, kraty i drzewa. 2.1. Algebra Boole a. 1 Ważnym dla nas przykładem algebr są algebry Boole a, czyli algebry B = (B,,,, 0, 1) typu (2, 2, 1, 0, 0) spełniające własności: (1)
2. Wykład 2: algebry Boole a, kraty i drzewa. 2.1. Algebra Boole a. 1 Ważnym dla nas przykładem algebr są algebry Boole a, czyli algebry B = (B,,,, 0, 1) typu (2, 2, 1, 0, 0) spełniające własności: (1)
Droga i cykl Eulera Przykłady zastosowania drogi i cyku Eulera Droga i cykl Hamiltona. Wykład 4. Droga i cykl Eulera i Hamiltona
 Wykład 4. Droga i cykl Eulera i Hamiltona 1 / 92 Grafy Eulera Droga i cykl Eulera Niech G będzie grafem spójnym. Definicja Jeżeli w grafie G istnieje zamknięta droga prosta zawierająca wszystkie krawędzie
Wykład 4. Droga i cykl Eulera i Hamiltona 1 / 92 Grafy Eulera Droga i cykl Eulera Niech G będzie grafem spójnym. Definicja Jeżeli w grafie G istnieje zamknięta droga prosta zawierająca wszystkie krawędzie
Klasyczne zagadnienie przydziału
 Klasyczne zagadnienie przydziału Można wyodrębnić kilka grup problemów, w których zadaniem jest odpowiednie rozmieszczenie posiadanych zasobów. Najprostszy problem tej grupy nazywamy klasycznym zagadnieniem
Klasyczne zagadnienie przydziału Można wyodrębnić kilka grup problemów, w których zadaniem jest odpowiednie rozmieszczenie posiadanych zasobów. Najprostszy problem tej grupy nazywamy klasycznym zagadnieniem
Ilustracja S1 S2. S3 ściana zewnętrzna
 Grafy płaskie G=(V,E) nazywamy grafem płaskim, gdy V jest skończonym podzbiorem punktów płaszczyzny euklidesowej, a E to zbiór krzywych Jordana (łamanych) o końcach w V i takich, że: 1) rożne krzywe mają
Grafy płaskie G=(V,E) nazywamy grafem płaskim, gdy V jest skończonym podzbiorem punktów płaszczyzny euklidesowej, a E to zbiór krzywych Jordana (łamanych) o końcach w V i takich, że: 1) rożne krzywe mają
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Grafy dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 9 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 1 / 53
Algorytmy i Struktury Danych. Grafy dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 9 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 9 1 / 53
Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA
 Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA Zad. 1 (12p.)Niech n 3k > 0. Zbadać jaka jest najmniejsza możliwa liczba krawędzi w grafie, który ma dokładnie n wierzchołków oraz dokładnie k składowych, z których
Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA Zad. 1 (12p.)Niech n 3k > 0. Zbadać jaka jest najmniejsza możliwa liczba krawędzi w grafie, który ma dokładnie n wierzchołków oraz dokładnie k składowych, z których
Analiza sieci Petriego
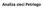 Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Własności behawioralne sieci Petriego
Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Własności behawioralne sieci Petriego
Sieć (graf skierowany)
 Sieci Sieć (graf skierowany) Siecia (grafem skierowanym) G = (V, A) nazywamy zbiór wierzchołków V oraz zbiór łuków A V V. V = {A, B, C, D, E, F}, A = {(A, B), (A, D), (A, C), (B, C),..., } Ścieżki i cykle
Sieci Sieć (graf skierowany) Siecia (grafem skierowanym) G = (V, A) nazywamy zbiór wierzchołków V oraz zbiór łuków A V V. V = {A, B, C, D, E, F}, A = {(A, B), (A, D), (A, C), (B, C),..., } Ścieżki i cykle
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Grafy Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 7 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 7 1 / 43 Grafy -
Algorytmy i Struktury Danych. Grafy Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 7 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 7 1 / 43 Grafy -
Wyznaczniki. Mirosław Sobolewski. Wydział Matematyki, Informatyki i Mechaniki UW. 6. Wykład z algebry liniowej Warszawa, listopad 2013
 Wyznaczniki Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 6. Wykład z algebry liniowej Warszawa, listopad 2013 Mirosław Sobolewski (UW) Warszawa, listopad 2013 1 / 13 Terminologia
Wyznaczniki Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 6. Wykład z algebry liniowej Warszawa, listopad 2013 Mirosław Sobolewski (UW) Warszawa, listopad 2013 1 / 13 Terminologia
Kombinowanie o nieskończoności. 2. Wyspy, mosty, mapy i kredki materiały do ćwiczeń
 Kombinowanie o nieskończoności. 2. Wyspy, mosty, mapy i kredki materiały do ćwiczeń Projekt Matematyka dla ciekawych świata spisał: Michał Korch 15 marzec 2018 Szybkie przypomnienie z wykładu Prezentacja
Kombinowanie o nieskończoności. 2. Wyspy, mosty, mapy i kredki materiały do ćwiczeń Projekt Matematyka dla ciekawych świata spisał: Michał Korch 15 marzec 2018 Szybkie przypomnienie z wykładu Prezentacja
Wykład 8. Drzewo rozpinające (minimum spanning tree)
 Wykład 8 Drzewo rozpinające (minimum spanning tree) 1 Minimalne drzewo rozpinające - przegląd Definicja problemu Własności minimalnych drzew rozpinających Algorytm Kruskala Algorytm Prima Literatura Cormen,
Wykład 8 Drzewo rozpinające (minimum spanning tree) 1 Minimalne drzewo rozpinające - przegląd Definicja problemu Własności minimalnych drzew rozpinających Algorytm Kruskala Algorytm Prima Literatura Cormen,
Matematyka dyskretna - 5.Grafy.
 Matematyka dyskretna - 5.Grafy. W tym rozdziale zajmiemy się grafami. Są to wykresy zawierające rozmaite informacje, przedstawiające połączenia pomiędzy różnymi swoimi elementami. Algorytmy na nich oparte
Matematyka dyskretna - 5.Grafy. W tym rozdziale zajmiemy się grafami. Są to wykresy zawierające rozmaite informacje, przedstawiające połączenia pomiędzy różnymi swoimi elementami. Algorytmy na nich oparte
Wstęp do programowania. Drzewa. Piotr Chrząstowski-Wachtel
 Wstęp do programowania Drzewa Piotr Chrząstowski-Wachtel Drzewa Drzewa definiują matematycy, jako spójne nieskierowane grafy bez cykli. Równoważne określenia: Spójne grafy o n wierzchołkach i n-1 krawędziach
Wstęp do programowania Drzewa Piotr Chrząstowski-Wachtel Drzewa Drzewa definiują matematycy, jako spójne nieskierowane grafy bez cykli. Równoważne określenia: Spójne grafy o n wierzchołkach i n-1 krawędziach
Definicja pochodnej cząstkowej
 1 z 8 gdzie punkt wewnętrzny Definicja pochodnej cząstkowej JeŜeli iloraz ma granicę dla to granicę tę nazywamy pochodną cząstkową funkcji względem w punkcie. Oznaczenia: Pochodną cząstkową funkcji względem
1 z 8 gdzie punkt wewnętrzny Definicja pochodnej cząstkowej JeŜeli iloraz ma granicę dla to granicę tę nazywamy pochodną cząstkową funkcji względem w punkcie. Oznaczenia: Pochodną cząstkową funkcji względem
Kolorowanie wierzchołków
 Kolorowanie wierzchołków Mając dany graf, pokolorować jego wierzchołki w taki sposób, aby każde dwa wierzchołki sąsiednie miały inny kolor. Każda krawędź łączy wierzchołki różnych kolorów. Takie pokolorowanie
Kolorowanie wierzchołków Mając dany graf, pokolorować jego wierzchołki w taki sposób, aby każde dwa wierzchołki sąsiednie miały inny kolor. Każda krawędź łączy wierzchołki różnych kolorów. Takie pokolorowanie
Analiza sieci Petriego
 Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Tomasz Koszlajda Instytut Informatyki
Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Tomasz Koszlajda Instytut Informatyki
Macierze. Rozdział Działania na macierzach
 Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
Procesy stochastyczne WYKŁAD 2-3. Łańcuchy Markowa. Łańcuchy Markowa to procesy "bez pamięci" w których czas i stany są zbiorami dyskretnymi.
 Procesy stochastyczne WYKŁAD 2-3 Łańcuchy Markowa Łańcuchy Markowa to procesy "bez pamięci" w których czas i stany są zbiorami dyskretnymi. Przykład Symetryczne błądzenie przypadkowe na prostej. 1 2 Łańcuchem
Procesy stochastyczne WYKŁAD 2-3 Łańcuchy Markowa Łańcuchy Markowa to procesy "bez pamięci" w których czas i stany są zbiorami dyskretnymi. Przykład Symetryczne błądzenie przypadkowe na prostej. 1 2 Łańcuchem
1 Automaty niedeterministyczne
 Szymon Toruńczyk 1 Automaty niedeterministyczne Automat niedeterministyczny A jest wyznaczony przez następujące składniki: Alfabet skończony A Zbiór stanów Q Zbiór stanów początkowych Q I Zbiór stanów
Szymon Toruńczyk 1 Automaty niedeterministyczne Automat niedeterministyczny A jest wyznaczony przez następujące składniki: Alfabet skończony A Zbiór stanów Q Zbiór stanów początkowych Q I Zbiór stanów
Wykład z modelowania matematycznego. Zagadnienie transportowe.
 Wykład z modelowania matematycznego. Zagadnienie transportowe. 1 Zagadnienie transportowe zostało sformułowane w 1941 przez F.L.Hitchcocka. Metoda rozwiązania tego zagadnienia zwana algorytmem transportowymópracowana
Wykład z modelowania matematycznego. Zagadnienie transportowe. 1 Zagadnienie transportowe zostało sformułowane w 1941 przez F.L.Hitchcocka. Metoda rozwiązania tego zagadnienia zwana algorytmem transportowymópracowana
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Grafy dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 8 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 8 1 / 42
Algorytmy i Struktury Danych. Grafy dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 8 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych. Wykład 8 1 / 42
Ścieżki w grafach. Grafy acykliczne i spójne
 TEORIA GRAFÓW I SIECI - ROZDZIAL II Ścieżki w grafach. Grafy acykliczne i spójne Ścieżka lub droga w grafie [digrafie] G nazywamy dowolny ciag d = (a 0, k 1, a 1,..., k n, a n ), gdzie n N {0}, a i V G,
TEORIA GRAFÓW I SIECI - ROZDZIAL II Ścieżki w grafach. Grafy acykliczne i spójne Ścieżka lub droga w grafie [digrafie] G nazywamy dowolny ciag d = (a 0, k 1, a 1,..., k n, a n ), gdzie n N {0}, a i V G,
