Numerické metody KI/NME. Doc. RNDr. Jiří Felcman, CSc. RNDr. Petr Kubera, Ph.D.
|
|
|
- Małgorzata Wasilewska
- 6 lat temu
- Przeglądów:
Transkrypt
1 Numerické metody KI/NME Doc. RNDr. Jiří Felcman, CSc. RNDr. Petr Kubera, Ph.D. RNDr. Jiří Škvor, Ph.D. Ústí nad Labem 2016
2 Kurz: Obor: Klíčová slova: Anotace: Numerické metody Informační systémy, Informatika (dvouoborové studium). numerické metody, numerická matematika, přibližné řešení Základní kurz numerické matematiky pro informatiky. Záběr tohoto kurzu odpovídá rozsahem základním kurzům matematiky, tj. pokrývá úvod do matematické analýzy a lineární algebry. Konkrétně se jedná o tematiku interpolace, aproximace, integrace a derivace funkce jedné proměnné, řešení lineárních, nelineárních a diferenciálních rovnic a jejich soustav. Autoři by zde chtěli poděkovat Doc. RNDr. Jiřímu Felcmanovi, CSc. za poskytnutí zdrojů jeho přednášek v L A TEXu. Jazyková korektura nebyla provedena, za jazykovou stránku odpovídá autor. Katedra informatiky, PřF, UJEP v Ústí nad Labem, 2016 Autor: Doc. RNDr. Jiří Felcman, CSc., RNDr. Petr Kubera, Ph.D., RNDr. Jiří Škvor, Ph.D.
3 Obsah 1 Aproximace a interpolace v IR Lagrangeův interpolační polynom Kubický spline Konstrukce přirozeného kubického spline Numerická integrace funkcí Newtonovy-Cotesovy vzorce Rombergova a Gaussova kvadratura Rombergova kvadratura Gaussovakvadratura Metody řešení nelineárních rovnic I Řešení jedné nelineární rovnice Metody řešení nelineárních rovnic II Metoda postupných aproximací Hledání kořenů polynomu Řešení soustav lineárních rovnic I Podmíněnost matic Gaußova eliminace Řešení soustav lineárních rovnic II Gaußova eliminace jako faktorizační metoda LU rozklad v obecném případě Choleského rozklad Řešení soustav lineárních rovnic III Odvození klasických iteračních metod Problematika konvergence iteračních metod Řešení soustav lineárních rovnic IV Výpočet vlastních čísel matice Mocninná metoda
4 12 Numerická řešení obyčejných diferenciálních rovnic Jednokrokové metody
5 Úvodní slovo Organizace výuky Tento předmět je ukončem zápočtem a zkouškou. Zápočet je udělen za vypracování seminární práce, která bude zaměřena na praktickou aplikaci probraných úloh. Téma práce bude upřesněno při výuce. Zkouška je ústní a je kladen důraz na porozumnění probírané látce, součástí zkoušky je i rozbor vypracované seminární práce. Numerická matematika je matematická disciplína, která má široké aplikace od předpovědi počasí, informatiky, ekonomie, přes zpracování obrazu až po třeba biologii. Bohužel (pro nás) spektrum jejich nástrojů je velmi široké a navíc celá řada metod vychází z matematického aparátu, který přesahuje Vaše znalosti matematiky. Zde jsou vybrány jen některé metody, které Vám doplňují a rozšiřují Vaše znalosti matematiky a navíc nacházejí i uplatnění v informatice (např. spline křivky). Za klíčové při studiu této disciplíny považujeme pochopení podstaty problému a z něj pramenící schopnost aplikace probraných metod. Za nejméně vhodný způsob považujeme pouhé formální se naučení vět a definic a mechanický způsob použití probraných algoritmů. U studentů informatiky považujeme za důležité i schopnost dané metody implementovat (naprogramovat) se zřetelem, jak k funkčnosti, tak i efektivitě. Text je doplněn otázkami k zamyšlení a úkoly. Otázky k zamyšlení jsou koncipovány tak, aby Vám ukázali daný problém z jiného pohledu a též rozšířili Váš přehled o dané problematice, jsou spíše teoretičtějšího rázu. Úkoly jsou praktické, jsou zaměřeny na aplikaci daných poznatků a implementaci metod. Volbu programovacího jazyka necháváme na Vás. Zde jen poznamenejme, že probírané algoritmy a metody jsou v naprosté většině již implementovány (většinou efektivně) v různých numeckých knihovnách daných jazyků, či nástrojích pro matematické modelovaní MATLAB, Octave, Scilab, A v praxi se spíše jedná o užití těchto knihoven a nástrojů, než o vlastní implementaci daných algoritmů. 5
6 1 Aproximace a interpolace v IR CÍLE KAPITOLY Cílem této kapitoly je seznýmit čtenáře s obecným pohledem na aproximaci funkce v IR. Dále se konkrétně věnujeme jedné z aproximačních metod, konkrétně Lagrangeově interpolaci. KLÍČOVÁ SLOVA Lagrangeova interpolace, chyba interpolace Jedna ze základních úloh numerické matematiky je aproximace dané funkce f jinou funkcí ϕ Zadání aproximované funkce - analyticky, nebo je k dispozici tabulka hodnot (x i, f i ), x i, f i IR, i = 0,..., n, n IN, f i = f(x i ) tabulka hodnot funkce a hodnot derivací funkce do určitého řádu v uzlech x i Pro funkci f definovanou na uzavřeném intervalu [a, b] uvažujeme dělení intervalu[a, b]: a = x 0 < x 1,... < x n = b, n Z + = {0, 1,...} a nazýváme ho sítí. x i, i = 0..., n nazýváme uzly (ekvidistantní, je-li x i = a + ih, kde h IR je krok sítě.) Požadavky na aproximující funkci ϕ: (A) jednoduchý tvar, snadno vyčíslitelná polynom {1, x, x 2, x 3,...} trigonometrický polynom {1, sin x, cos x, sin 2x, cos 2x,...} racionální funkce Pm(x) Q n(x), kde P m(x), resp. Q n (x) jsou polynomy m tého, resp. n tého stupně exponenciální funkce ae bx (B) rovnost hodnot, event. derivací až do řádu m v uzlech: ϕ (j) (x i ) = f (j) (x i ), i = 0,..., n, j = 0,..., m (1.1) (C) ϕ f malá, kde značí normu Poznámka: 1.1. Od požadavku (B, 1.1) někdy upouštíme ( např. proložení přímky třemi body ) Nejčastější způsoby aproximace: 1. Interpolace - k funkci f sestrojíme funkci ϕ z jisté třídy M splňující (B) 6
7 2. Aproximace metodou nejmenších čtverců - k funkci f sestrojíme funkci ϕ z jisté třídy M splňující (B) ve smyslu nejmenších čtverců diskrétní případ n n w i (f(x i ) ϕ(x i )) 2 = min w i (f(x i ) ψ(x i )) 2 ψ M i=0 i=0 kde w i > 0, i = 0,..., n jsou zadaná čísla, zvaná váhy. Název nejmenší čtverce je patrný z následující ukázky: Pro dané dělení intervalu [a, b] a dané kladné váhy w i uvažujme normu funkce f danou vztahem f := n w i (f(x i )) 2 ϕ M se hledá tak, že spojitý případ b a i=0 f ϕ 2 = min f ψ 2 ψ M b w(x)(f(x) ϕ(x)) 2 dx = min w(x)(f(x) ψ(x)) 2 dx ψ M a w je kladná váhová funkce Čebyševova (stejnoměrná) aproximace - k funkci f sestrojíme funkci ϕ z jisté třídy M splňující max ϕ(x) f(x) max ψ(x) f(x) [a,b] [a,b] pro všechny funkce ψ M, kde M je zvolená množina funkcí. 1.1 Lagrangeův interpolační polynom Hledáme polynom L n stupně nejvýše n, píšeme L n Π n, kde Π n značí prostor polynomů stupně nejvýše n. takový že L n (x i ) = f(x i ) i = 0,..., n, (1.2) x i - navzájem různé uzly, obecně neekvidistantní. Takový polynom nazveme Lagrangeovým interpolačním polynomem. Věta 1.1. Necht x 0,..., x n jsou navzájem různé uzly. Pak existuje právě jeden interpolační polynom L n Π n : L n (x i ) = f(x i ) i = 0,..., n. Důkaz. 1. Existence Uvažujme polynomy l i (x) = (x x 0)(x x 1 )... (x x i 1 )(x x i+1 )... (x x n ) (x i x 0 )(x i x 1 )... (x i x i 1 )(x i x i+1 )... (x i x n ) (tzv. Lagrangeovy polynomy). 1 Obecně se stačí, aby existoval její integrál v druhé mocnině na intervalu [a, b], tedy w L 2 (a, b) a kladnost funkce byla porušena v konečném počtu bodů. 7
8 Platí α) l i (x) Π n, β) l i (x j ) = δ ij = 1, i = j, 0, i j. (Kroneckerovo delta). Položme n L n (x) = f(x i )l i (x). i=0 2. Jednoznačnost Necht L 1 n, L 2 n Π n splňují (viz (1.2)) L 1 n(x i ) = L 2 n(x i ) = f(x i ) i = 0,..., n. Potom L 1 n L 2 n Π n je polynom, který má (n+1) různých kořenů. Podle základní věty algebry je L 1 n L 2 n nulový polynom. Poznámka: 1.2. Položme Potom platí ω n+1 (x) = (x x 0 )... (x x n ). l i (x) = kde čárka v ω n+1(x i ) označuje derivaci. ω n+1 (x) (x x i ) ω n+1(x i ), V případě, že potřebujeme vyčíslit Lagrangeův interplační polynom v jednom bodě, je možné použít tzv. Aitken Nevillovo schéma. Věta 1.2. Bud L i0 = f(x i ) hodnoty interpolované funkce v uzlových bodech x i, i = 0,..., n. Označíme-li pomocí L ik Lagrangeův interpolační polynom stupně nejvýše k, který interpoluje funkci f v uzlových bodech x i k,..., x i, 1 k i, i = 1,..., n, pak platí L ik (x) = (x x i k) L i,k 1 (x) (x x i ) L i 1,k 1 (x) x i x i k, i = 1,..., n, 1 k i. (1.3) Při použití Aitkenova Nevillova schématu pomocí rekurentního předpisu (1.3) spočteme hodnotu L nn (x), pro kterou platí L n (x) = L nn (x) Chyba Lagrangeovy interpolace Věta 1.3. Necht f C n+1 (I), kde I je nejmenší interval obsahující x 0,..., x n, x a x 0,..., x n jsou navzájem rùzné uzly,. Necht L n Π n je Lagrangeův interpolační polynom pro funkci f. Pak ξ I f(x ) L n (x ) = f (n+1) (ξ) ω n+1 (x ) (n + 1)! (chyba Lagrangeovy interpolace v bodě x ). 8
9 Důkaz. Pro x = x i je důkaz zřejmý. Pro x x i uvažujeme funkci : kde t IR. Platí: Pro vhodnou volbu F (x) = f(x) L n (x) t ω n+1 (x) F (x i ) = 0 i = 0,..., n. t := f(x ) L n (x ) ω n+1 (x ) platí, že F (x ) = 0. F má tedy n + 2 nulových bodù (uzly x i a bod x ). Podle Rolleovy věty: F. má aspoň n + 1 nulových bodù, F (n+1) má aspoň 1 nulový bod, označme ho ξ. (1.4) F (n+1) (ξ) = 0 = f (n+1) (ξ) 0 t (n + 1)! / ωn+1 (x ) (n + 1)! kde jsme využili toho, že (n+1)-ní derivace L n je nulová a (n+1)-ní derivace ω n+1 je (n+1)!. Dosadíme-li za t ze vztahu (1.4), dostaneme f(x ) L n (x ) = f (n+1) (ξ) ω n+1 (x ). (n + 1)! OTÁZKY K ZAMYŠLENÍ 1. Rozmyslete si případná zjednodušení tvaru Lagrangeových polynomů v případě ekvidistantních uzlů. ÚKOLY 1. Naprogramujte Lagrangeovu interpolační metodu. Vstupem jsou uzlové body a hodnoty funkce v nich, výstupem je graf funkce. 2. Implementujte Aitkenovo Nevillovo schéma. 3. Pomocí Lagrangeovy interpolace interpolujte funkci f(x) = x 2 na intervalu < 1, 1 > v ekvidistantních uzlových bodech. Vyzkoušejte vliv počtu uzlových bodů na kvalitu interpolace. 4. Pomocí Lagrangeovy interpolace se pokuste určit derivaci interpolované funkce f(x), resp. porovnejte derivaci vstupní funkce f (x) s L n(x). Budete tedy muset naprogramovat derivaci L. polynomu, pro její výpočet použijte její aproximaci pomocí diferencí: L n(x) = Ln(x+h) Ln(x h), kde h > 0 je malé. 2h 9
10 2 Kubický spline CÍLE KAPITOLY V této kapitole se budeme věnovat konstrukci přirozeného kubického spline. Cílem je opět navrhnout postup prokládání zadaných bodů, který budeme moci naprogramovat. KLÍČOVÁ SLOVA spline křivky, kubický spline V praktických úlohách jsou poměrně časté situace, kdy máme proložit (interpolovat) velké množství bodů. Použití Lagrangeovy interpolace povede k polynomům vysokých stupňů. Dalším důvodem je to, že i v případě pomerně jednoduchých funkcí, je hodnota interpolované funkce a Lagrangeova interpolačního polynomu značně rozdílná (mimo uzlové body), viz úkol číslo 3 v předchozí kapitole. Nabízí se tedy možnost použití tzv. spline křivek. Definice 2.1. Necht je dáno dělení intervalu [a, b], a = x 0 < x 1 <... < x n = b (x i navzájem různé). Řekneme, že funkce ϕ : [a, b] IR je kubický spline, jestliže 1. ϕ je spojitá (ϕ C 2 [a, b]), 2. ϕ [xi,x i+1 ] je kubický polynom, pro i = 0, 1,..., n 1. Poznámka: 2.1. Spline - elastické pravítko používané při stavbě lodí Poznámka: 2.2. Kubický spline je speciálním případem spline k-tého řádu pro k = 3. Důvodem častého použití kubického spline je fakt, že lidské oko je schopné rozlišit ještě změny 2. derivace. Věta 2.2. Necht f C 2 [a, b]. Pak pro každý kubický spline ϕ splňující platí ϕ(x i ) = f(x i ), i = 0,..., n, ϕ f, kde u 2 := jestliže je splněna některá z následujících třech podmínek: b a u (x) 2 dx, (a) ϕ (a) = 0 = ϕ (b) (b) ϕ (a) = f (a) a ϕ (b) = f (b) (c) ϕ (a) = ϕ (b) a ϕ (a) = ϕ (b) (2.1) Poznámka: 2.3. Ve všech třech případech (a), (b), (c) je kubický spline určen jednoznačně. 10
11 2.1 Konstrukce přirozeného kubického spline V následujícím uvažujme značení: f i := f(x i ) i = 0,..., n, ϕ i := ϕ [xi,x i+1 ] i = 0,..., n 1, h i := x i+1 x i i = 0,..., n 1. Kubický polynom ϕ i je na intervalu [x i, x i+1 ] určen čtyřmi koeficienty (a, b, c, d při kubickém polynomu ϕ(x) = ax 3 + bx 2 + cx + d). Počet intervalů je n, celkem máme tedy pro určení ϕ počet stupňů volnosti 4n. Pro tyto stupně volnosti sestavíme příslušné rovnice. Počet neznámých 4 počet intervalù 4n Počet rovnic ϕ(x i ) = f(x i ), i = 0,..., n n + 1 spojitost ϕ v x i, i = 1,..., n 1 n 1 spojitost ϕ v x i, i = 1,..., n 1 n 1 spojitost ϕ v x i, i = 1,..., n 1 n 1 Počet rovnic je o dvě menší 4n 2 než počet neznámých. Doplníme je proto některou z podmínek (2.1), (a) (b). Uvažujme např. podmínku (2.1), (a), tj. podmínku nulových druhých derivací v krajních bodech. Takový spline nazýváme přirozeným kubickým splinem. Pro určení přirozeného kubického splinu hledáme ϕ i ve vhodném tvaru. Ukazuje se, že efektivní metoda není založena na vyjádření ani na vyjádření ϕ i (x) = a i x 3 + b i x 2 + c i x + d i ϕ i (x) = a i (x x i ) 3 + b i (x x i ) 2 + c i (x x i ) + d i, ale na vyjádření pomocí tzv. momentů, což jsou hodnoty druhé derivace ϕ v uzlech. Označme je M i : M i := ϕ (x i ), i = 0,..., n a předpokládejme, že tyto momenty známe. Později ukážeme, jak je určit. Platí ϕ i kubický polynom ϕ i parabola ϕ i přímka Z předpokladu spojitosti druhé derivace ϕ v uzlech dostáváme M i = ϕ i (x i ), M i+1 = ϕ i (x i+1 ). Je tedy ϕ i přímka, procházející body (x i, M i ) a (x i+1, M i+1 ) (viz obr. 2.1). 11
12 M i+1 ϕ M i i x i x i+1 Obrázek 2.1: Přímka ϕ i ϕ i (x) = (x x i) M i+1 x i+1 x i + M i (x x i+1 ) x i x i+1, Integrací odvodíme ϕ i (x) = M i h i (x x i+1 ) + M i+1 h i (x x i ). ϕ i(x) = M i 2h i (x x i+1 ) 2 + M i+1 2h i (x x i ) 2 + A i, ϕ i (x) = M i 6h i (x x i+1 ) 3 + M i+1 6h i (x x i ) 3 + A i (x x i ) + B i. (2.2) vhodný rozpis integrační konstanty Ve vyjádření ϕ i ve tvaru (2.2) nejprve určíme koeficienty A i, B i, i = 0,..., n 1 pomocí momentů a potom sestavíme rovnice pro momenty. Využijeme k tomu podmínky interpolace ϕ i (x i ) = f i, ϕ i (x i+1 ) = f i+1, i = 0,..., n 1. Což vede na dvě rovnice pro dvě neznámé A i, B i, i = 0,..., n 1. Dostaneme ϕ i (x i ) = M i 6 h2 i + B i = f i, ϕ i (x i+1 ) = M i+1 6 B i =f i M i 6 h2 i, h 2 i + A i h i + f i M i 6 h2 i = f i+1, A i = f i+1 f i + M i M i+1 h i. h i 6 Rovnice pro momenty sestavíme ekvivalentním vyjádřením podmínky spojitosti derivace kubického spline v uzlech: ϕ i 1(x i ) = ϕ i(x i ), i = 1,..., n. Připomeňme si tvar ϕ i ϕ i(x) = M i (x x i+1 ) 2 + M i+1 (x x i ) 2 + A i 2h i 2h i 12
13 resp. ϕ i 1 ϕ i 1(x) = M i 1 (x x i ) 2 + M i (x x i 1 ) 2 + A i 1. 2h i 1 2h i 1 S využitím vyjádření pro A i, resp. A i 1 pomocí momentů dostaneme ϕ i 1(x i ) = 0 + M i h 2 i 1 + f i f i 1 + M i 1 M i h i 1 2h i 1 h i 1 6 = M i h 2 i f i+1 f i + M i M i+1 h i = ϕ 2h i h i 6 i(x i ). Protože konstruujeme přirozený kubický spline, je M 0 = ϕ (x 0 ) = 0 = ϕ (x n ) = M n a dostáváme tak n 1 rovnic (i = 1,..., n 1) pro neznáme momenty M 1, M 2,..., M n 1. Tyto rovnice lze přepsat ve tvaru ( h i 1 6 M hi 1 i h i h i 2 h ) i M i + h i 6 6 M i+1 = f i f i 1 + f i+1 f i. h i 1 h i }{{}}{{} h i 1 +h i g i 3 Maticový zápis vede na soustavu s třídiagonální maticí. h 0 +h 1 3 h h i 1 6 h i 1 +h i 3 h i h n 2 6 h n 2 +h n 1 3 Pro ekvidistantní dělení s krokem h má matice soustavy tvar h M 1 g 1.. M i 1 g i 1 M i = g i M i+1 g i+1.. M n 1 g n 1 Nyní zbývá jen soustavu vyřešit a získat jednotlivé momenty M i, které můžeme použít pro konstrukci spline křivky ve tvaru 2.2. Při vyšetřování řešitelnosti této soustavy lze využít následující definici a větu z algebry: Definice 2.3. Řekneme, že matice A typu n n, n 2 je ostře diagonálně dominantní (ODD), jestliže n a ii > a ij i = 1,..., n. j=1,j i Lemma 2.1. Všechna vlastní čísla matice A typu n n, n leží v komplexní rovině ve sjednocení kruhů (Geršgorinových) z a ii n a ij, i = 1,..., n. (2.3) j=1 j i 13
14 Věta 2.4. Necht A IR nn je ODD. Pak A je nesingulární. Důkaz. pomocí Geršgorinových kruhů A je nesingulární deta 0 rovnice det(a λi) = 0 nemá kořen λ = 0 nula není vlastním číslem matice A. Necht λ je vlastní číslo matice A Ax = λx y := x, x := max x i x i Ay = λy y i 1, i 0 :: y i0 = 1 j i 0 a i0 jy j + a i0 i 0 y i0 = λy i0 j i 0 a i0 jy j = λ a i0 i 0 y i0 λ a i0 i 0 j i 0 a i0 j (Geršgorinův kruh o středu a i0 i 0 a poloměru j i 0 a i0 j ) Kdyby λ = 0 bylo vlastním číslem a i0 i 0 j i 0 a i0 j Spor s ODD λ = 0 tedy není vlastní číslo a matice A je nesingulární. Matice soustavy rovnic pro momenty je ODD, soustava je tedy podle výše uvedené věty jednoznačně řešitelná a protože matice soustavy je třídiagonální, lze pro řešení použít např. Gaußovu eliminaci. OTÁZKY K ZAMYŠLENÍ 1. Rozmyslete si jak implementovat uložení třídiagonální matice soustavy rovnic pro výpočet momentů M i. ÚKOLY 1. Naprogramujte interpolaci pomocí přirozeného kubického spline. Vstup uzlové body a hodnoty funkce v nich, výstupem je graf funkce. 2. Pomocí kubického spline interpolujte funkci f(x) = x 2 na intervalu < 1, 1 > v ekvidistantních uzlových bodech. Porovnejte s Lagrangeovou interpolací. 14
15 3 Numerická integrace funkcí CÍLE KAPITOLY V této kapitole se budem zabývat numerickým výpočtem určitého integrálu (numerickou kvadraturou) funkcí jedné proměnné a ukážeme si základní kvadraturní formule. KLÍČOVÁ SLOVA numerická kvadratura, Newtonovy Cotesovy vzorce, složené Newtonovy Cotesovy vzorce Výpočet určitého integrálu je poměrně obtížná úloha matematické analýzy. Obvykle při ní postupujeme tak, že určíme nejprve primitivní funkci(neurčitý integrál) a poté pomocí Newtonovy- Leibnitzovy formule spočítáme určitý integrál. Bohužel i v případě poměrně jednoduchých funkcí (např. e x2 ) je nalezení primitvní funkce komplikované. A i v případě, že umíme nalézt primitvní funkci, může být velmi komplikovaná a výpočetně náročná, nebo může být integrovaná funkce zadána jen v jistých bodech. Nabízí se tedy provádět výpočet určitého integrálu přibližně, tj. numericky. Necht je dáno dělení intervalu [a, b], a x 0 < x 1 <... < x n b (x i navzájem různé). Označme h = max i {0,...,n 1} x i+1 x i. b n Cíl: I(f) = f(x) dx I h (f) = α i f(x i ). (3.1) a i=0 Vzorec n I h (f) = α i f(x i ) i=0 se nazývá kvadraturní formule, α i jsou koeficienty kvadraturní formule a x i jsou uzly kvadraturní formule. Motivace hledání aproximace určitého integrálu ve tvaru lineární kominace hodnot funkce f v uzlech x i je zřejmá z následujícího odstavce. 3.1 Newtonovy-Cotesovy vzorce Pro dané n IN uvažujme ekvidistantní dělení intervalu [a, b] s krokem h = b a, x n i = a + ih, i = 0,..., n. Aproximujeme-li funkci f Lagrangeovým interpolačním polynomem L n pro uzly x 0,..., x n, lze určitý integrál z funkce f aproximovat následujícím zpùsobem: b n f(x i ) a i=0 b a f(x) dx b a L n (x) dx = l i (x) {}}{ (x x 0 )... (x x i 1 )(x x i+1 )... (x x n ) (x i x 0 )... (x i x i 1 )(x i x i+1 )... (x i x n ) dx = 15
16 n b l i (x) dx f(x i ) (3.1) α i i=0 a } {{ } Tento vzorec nazýváme pro ekvidistantní uzly Newtonův-Cotesův. Pro výpočet koeficientů α i použijeme následující substituci α i := b a subst. x = a + th n j=0,j i x i = a + ih, h = b a n (x x j ) (x i x j ) dx = b a n n (t j) dt (3.2) n 0 (i j) j=0,j i Uved me si příklady některých N-C vzorců. V případě aproximace integrované funkce pomocí lineárního polynomu, mluvíme o tzv. lichoběžníkovém pravidle (n = 1): T h (f) = (b a) f(a) + f(b). (3.3) 2 V případě aproximace integrované funkce pomocí paraboly (n = 2), dostáváme tzv. Simpsonovo pravidlo S h (f) = b a ( ( ) ) a + b f(a) + 4f + f(b). (3.4) 6 2 Z konstrukce Lagrangeovy interpolace L n funkce f Π n plyne, že L n (x) = f(x), a tedy N-C vzorec je přesný pro polynomy stupně nejvýše n. To nás vede k následující definici. Definice 3.1. Řekneme, že kvadraturní formule n i=0 α i f(x i ) má řád přesnosti m, jestliže m IN {0} je maximální číslo takové, že b n p(x) dx = α i p(x i ) p Π m. (3.5) a i=0 Lemma 3.1. Je-li kvadraturní formule n i=0 α i f(x i ) symetrická, t.j. pro i = 0,..., n platí b x n i = x i a, α i = α n i, a je-li její řád n, n sudé, pak je její řád n + 1. Lemma 3.2. Newtonův-Cotesův vzorec je symetrická kvadraturní formule. Důsledek 3.1. Pro n sudé je řád N-C vzorce n + 1. Nyní se budeme zabývat odhadem chyby, které se dopustíme při náhradě přesné hodnoty určitého integrálu I(f) funkce f(x) pomocí N-C vzorců. Definice 3.2. (zbytek kvadraturního vzorce) Rozdíl E h (f) = I(f) I h (f), kde b n I(f) = f(x) dx, I h (f) = α i f(x i ), a i=0 nazýváme zbytek kvadraturního vzorce. 16
17 Pro odhad chyby používáme následující lemata: Lemma 3.3. (Odhad chyby lichoběžníkového pravidla) Necht f C 2 [a, b]. Označme T h (f) N-C vzorec pro n = 1 (lichoběžníkové pravidlo). Pak ξ [a, b]: I(f) T h (f) = f (ξ) 2 Lemma 3.4. (Odhad chyby Simpsonova pravidla) h3, h = (b a). (3.6) 6 Necht f C 3 [a, b]. Označme S h (f) N-C vzorec pro n = 2 (Simpsonovo pravidlo). Pak ξ [a, b]: I(f) S h (f) = h5 90 f (ξ), h = (b a). (3.7) 2 Z výše uvedených lemat vyplývá že chyba, které se dopustíme závisí na jednak na hodnotě derivace integrované funkce a dále též na velikosti kroku h. Při zmenšování kroku h dochází ke zmenšení chyby. Tento fakt je základní myšlenkou pro složené kvadraturní vzorce Složené Newtonovy Cotesovy vzorce Newtonovy Cotesovy vzorce lze také aplikovat tak, že interval [a, b] rozdělíme na n ekvidistantních subintervalù [x i, x i+1 ] velikosti h a na každém z těchto subintervalů použijeme Newtonův Cotesův vzorec pro m + 1 ekvidistantních uzlů x i = x i0 < < x im = x i+1 s krokem H x i = a + ih, h = b a n, i = 0,... n, x i j = x i + jh, H = h m n, m IN I(f) := n 1 i=0 xi+1 x i n 1 f(x) dx IH(f) i = i=0 n 1 m α ij f(x ij ) =: I H (f) i=0 j=0 Věta 3.3. (složené N-C vzorce) Necht f C m+1 [a, b]. Pak pro složené N-C vzorce platí kde c > 0 je konstanta nezávislá na H. I(f) I H (f) ch m+1, (3.8) Důkaz. plyne z odhadu chyby Lagrangeova interpolačního polynomu OTÁZKY K ZAMYŠLENÍ 1. Rozmyslete si jak postupovat v případě určitých integrálů, kde jedna z mezí je nevlastní. 2. Uvažujte složené lichoběžníkové pravidlo s postupným zjemňováním intervalu [a, b] tak, že v každém kroku dochází k rozpůlení dílčích subintervalů: [a, b] na počátku [a, (a + b)/2] a [(a + b/2), b] v druhém kroku [a, (a + b)/4], [(a + b)/4, (a + b)/2)],[(a + b)/2, 3(a + b)/4)] a [3(a + b)/4, b] ve třetím kroku atd. Navrhněte takový postup, kdy se použije pouze hodnota odhadu I h (f) z posledního kroku a hodnoty funkce f v nově přidaných bodech. 17
18 3. Rozmyslete si, jak určit hodnotu m ze vzorce 3.8, viz druhý z praktických úkolů. ÚKOLY 1. Implementujte složené lichoběžníkové a Simpsonovo složené pravidlo. Vstupem je interval, integrovaná funkce a velikost kroku H. 2. Experimentálně určete pro obě složená pravidla závislost chyby které se dopustíme při numerické kvadratuře na velikosti kroku H. Použijte program z předchozího úkolu a funkci pro kterou umíte snadno přesně spočíst její kvadraturu. Zjištěnou závislost zakreslete do grafu, kde jsou obě osy logaritmické. 18
19 4 Rombergova a Gaussova kvadratura CÍLE KAPITOLY V předchozí kapitole jsme se zabývali základními metodami numerické integrace. Postup je sice přímočarý, ale pro dosažení určité přesnosti je potřeba relativně vysokého počtu kroků. Nyní se zaměříme na metody, které tento nedostatek odstraňují. KLÍČOVÁ SLOVA numerická kvadratura, Rombergova kvadratura, Richardsonova extrapolace, Gaussova kvadratura 4.1 Rombergova kvadratura Uvažujme výpočet b a f(x) dx pomocí složeného lichoběžníkového pravidla pro n + 1 uzlù. h = b a n, m = 1, H = h. Věta 4.1. (Eulerova-MacLaurinova) Necht f C 2N+2 [a, b], h = b a, n IN. Potom pro n složené lichoběžníkové pravidlo (označme ho CT h (f)) platí: CT h (f) = p(h 2 ) + O(h 2N+2 ) (4.1) = I(f) + a 1 h 2 + a 2 h a N h 2N + O(h 2N+2 ), (4.2) kde p Π N, p = p(t) = a 0 + a 1 t + + a N t, a 0 = p(0) = b a f(x) dx = I(f). Rombergova kvadratura je založena na tom, že konstruujeme lineární kombinaci vzorců CT h (f) pro vhodné h tak, abychom získali vzorec, který je přesnější. Například uvažujme dvě aproximace b a f(x) dx získané pomocí lichoběžníkového pravidla s krokem h (CT h(f)) a s krokem h/2 (CT h (f)): 2 CT h (f) = I(f) + a 1 h 2 + O(h 4 ) / 1 CT h (f) 2 = h 2 I(f) + a O(h4 ) /4 4CT h (f) CT h (f) 2 3 = I(f) + O(h 4 ) lin. k. = I(f) + chyba (N = 1) 19
20 h 2 16 CT h (f) 4 h 2 4 h 2 CTh (f) 2 CT h (f) Tabulka 4.1: Tabulka hodnot pro Lagrangeovu interpolaci Vhodnou lineární kombinací vzorců, z nichž každý aproximuje integrál I(f) s chybou O(h 2 ), jsme tak odvodili vzorec, který aproximuje integrál I(f) s chybou O(h 4 ). Za předpokladu dostatečné hladkosti funkce f (viz Eulerova MacLaurinova věta) můžeme tímto způsobem odvodit vzorec, který aproximuje integrál I(f) s chybou O(h 2N+2 ). Předpokládejme, že pro tabulku (4.1) máme sestrojen Lagrangeův interpolační polynom v následujícím tvaru L 2 (t) = b 0 }{{} L 2 (0) +b 1 t + b 2 t 2. Všimněme si, jakou roli hraje v tomto postupu vyčíslení Lagrangeova interpolačního polynomu L 2. Protože se jedná o interpolaci, tak na základě Eulerovy MacLaurinovy věty platí následující rovnosti Euler MacLaurin Lagrange CT h (f) = I(f) + a 1 h 2 + a 2 h 4 + O(h 6 ) = L 2 (0) + b 1 h 2 + b 2 h 4 (4.3) h CT h (f) = I(f) + a h4 h 2 16 O(h6 ) = L 2 (0) + b b h (4.4) h CT h (f) = I(f) + a h4 h O(h6 ) = L 2 (0) + b b h (4.5) lin. k. = I(f) O(h 6 ) = L 2 (0) (N = 2) kde rovnost v posledním řádku je získána pomocí lineární kombinace hodnot tak, aby došlo k vzájemné eliminaci členů obsahujících a 1, a 2. Na základě podobnosti polynomů v obou sloupcích, je jasné, ža ta samá lineární kombinace povede k eliminaci členů obsahujících b 1 a b 2. Z výše uvedeného je vidět, že L 2 (0) aproximuje b a f(x) dx s chybou O(h6 ). Při konstrukci L 2 (0) se jedná o tzv. Richardsonovu extrapolaci. Uvedený postup lze provést až do řádu 2N +2 pro uzly ( h ) 2 a hodnoty CT, i = 0,..., N, pomocí nichž konstruujeme L 2 i h N. 2 i Pro vyčíslení Lagrangeova interpolačního polynomu v jediném bodě (zde konkrétně v 0) použijeme Aitkenovo Nevilleovo schéma, viz věta 1.2, kde dosadíme za x = 0 a budeme uvažovat postupné zjemňování kroku h 2, (h/2) 2,..., (h/2 N ) 2 jako ve výše uvedených příkladech. Dostáváme tak následující vzorec T ik = T i,k 1 + T i,k 1 T i 1,k 1, i = 0, 1,..., N, k = 1, 2,..., i, (4.6) 4 k 1 kde hodnoty T i0 jsou dány T i0 = CT h (f). V praxi se používá tak, že inkrementujeme i dokud 2i rozdíl dvou dosud nejpřesnějších hodnot T ik T i 1,k není menší než předepsaná hodnota. 4.2 Gaussova kvadratura Víme, že N-C vzorce (3.1) mají řád aspoň n (pro n sudé dokonce aspoň n + 1). Jakého řádu může být formule typu n i=0 α i f(x i )? Uvažujme pro dané dělení intervalu [a, b], a x 0 <... < x n b kvadraturní formuli n I h (f) = α i f(x i ). (4.7) i=0 20
21 Lemma 4.1. (Řád kvadraturní formule) Řád kvadraturní formule (4.7) je nejvýše 2n + 1. Důkaz. Uvažujme polynom p(x) = n i=0 (x x i ) 2 funkce na intervalu [a, b] a platí pro něj Π 2n+2. Tento polynom je nezáporná b a p(x) > 0. Kvadraturní formule typu (4.7) dává pro tento polynom n α i p(x i ) = 0. i=0 Pro polynom p není tedy kvadraturní formule (4.7) přesná a její řád je tedy nejvýše 2n+1. Gaußova kvadratura je způsob konstrukce vzorce n i=0 α i f(x i ), který je přesný pro všechny polynomy stupně nejvýše 2n + 1. Definice 4.2. Skalární součin v C[a, b] je definován (u, v) = b a u(x)v(x) dx. (4.8) Poznámka: 4.1. Lze snadno ověřit, že takto definovaný součin má obvyklé vlastnosti skalárního součinu, viz otázky a úkoly k této kapitole. Poznámka: 4.2. Podobně jako v definici 4.2 lze definovat skalární součin v C[a, b] (u, v) = b a u(x)v(x)w(x) dx, (4.9) kde w je nezáporná a integrovatelná funkce na intervalu [a, b]. Zde vidět, že výše uvedená definice 4.2 odpovídá volbě váhové funkce w(x) = 1. Definice 4.3. Množina normovaných polynomů Π n = {p Π n ; p(x) = x n + a n 1 x n a 0 }. (4.10) Věta 4.4. (Ortogonální polynomy) Existují jednoznačně určené polynomy p i, pro které platí 1. p i Π i, i IN {0}, (p i, p j ) = 0, i j, 2. Kořeny x 0,..., x n polynomu p n+1, n IN {0}, jsou reálné, jednoduché a leží v (a, b) 3. p 0 (x 0 ) p 0 (x 1 ) p 0 (x n ) p A = 1 (x 0 ) p 1 (x 1 ) p 1 (x n )... p n (x 0 ) p n (x 1 ) p n (x n ) je nesingulární. Poznámka: 4.3. Posloupnost ortogonálních polynomů lze sestrojit pomocí Gramova-Schmidtova ortogonalizačního procesu. V dalším budeme uvažovat skalární součin z definice 4.2 a interval [a, b] = [ 1, 1]. Polynomy, které takto získáme se nazývají Legendrovy polynomy. Platí pro ně následující rekurentní předpis 1 p n+1 (x) = 2n + 1 n + 1 xp n(x) n n + 1 p n 1(x), p 0 (x) = 1, p 1 (x) = x. (4.11) 1 Nemusíme je tedy nutně konstruovat pomocí Gramova-Schmidtova ortogonalizačního procesu. 21
22 Protože v dalším budeme používat Legendrovy polynomy, nazývají se odvozené kvadraturní formule Gaußovy-Legendrovy 2. Myšlenka konstrukce Gaußovy kvadratury: Uzly x i volíme jako kořeny polynomu p n+1 z množiny ortogonálních polynomů {p 0, p 1,..., p n+1 }. S využitím ortogonálních polynomů p 0,..., p n+1 a kořenů x i polynomu p n+1 určíme koeficienty α i Gaußovy kvadraturní formule tak, aby platilo: K tomu vyjádříme polynom q ve tvaru b n q(x) dx = α i q(x i ), q Π 2n+1. (4.12) a i=0 q(x) = r(x)p n+1 (x) + s(x), r, s Π n, (dělení polynomu q polynomem p n+1 ) a polynomy r(x), s(x) Π n vyjádříme jako lineární kombinaci ortogonálních polynomů, specielně necht n s(x) = γ j p j (x). j=0 Na základě tohoto vyjádření má výraz na levé straně v (4.12) tvar b b b q(x) dx = r(x)p n+1 (x) dx + s(x) dx a a } {{ } a =0 =1 b n b n {}}{ = γ j p j (x) dx = γ j p 0 (x) p j (x) dx a j=0 a j=0 n b b b = γ j p 0 (x)p j (x) dx = γ 0 p 0 (x)p 0 (x) dx = γ 0 dx. j=0 a a a Levá strana v (4.12) je tedy rovna γ 0 (b a). Pravá strana v (4.12) má na základě výše uvedených vyjádření tvar n n n α i [r(x i )p n+1 (x i ) +s(x i )] = α i γ j p j (x i ). }{{} i=0 i=0 j=0 =0 Vidíme, že levou a pravou stranu v (4.12) lze tedy vyjádřit jako lineární kombinací jistých výrazů s koeficienty γ j γ 0 (b a) + γ γ n 0 n n = γ 0 p 0 (x i )α i + γ 1 p 1 (x i )α i + + γ n i=0 i=0 n i=0 p n (x i )α i Porovnáním výrazů u koeficientù γ j na levé a pravé straně dostaneme rovnice pro určení hledaných koeficientů α i : ni=0 p 0 (x i )α i = (b a) p 0 (x 0 ) p 0 (x n ) α 0 b a ni=0 p 1 (x i )α i = 0 p 1 (x 0 ) p 1 (x n ) α = 0. (4.13) ni=0 p n (x i )α i = 0 p n (x 0 ) p n (x n ) α n 0 2 Při použití skalárního součinu (4.9), resp. jiných polynomů, dostaneme jinou třídu Gaußových vzorců. 22
23 x 0 = 1 3 x 1 = 1 3 α 0 = 1 α 1 = 1 Tabulka 4.2: Koeficienty a uzly pro n = 1 x 0 = 3 x 5 1 = 0 x 2 = 3 5 α 0 = 5 9 α 1 = 8 9 α 2 = 5 9 Tabulka 4.3: Koeficienty a uzly pro n = 2 Poslední soustava rovnic v (4.13) pro koeficienty α i je jednoznačně řešitelná, viz věta 4.4 a její poslední tvrzení. Nyní si pro ilustraci odvodíme Gaußův kvadraturní vzorec řádu 3 (n = 1) na intervalu [ 1, 1]. Použijeme ortogonální polynomy {1, x, x 2 1}. Poslední z polynomů p 3 2(x) = x 2 1 má dva 3 reálné kořeny x 0,1 = ± 1 3. Dosazením do (4.13) dostáváme následující soustavu rovnic: ( ) ( ) α0 = α 1 ( 2 0 ). Jejím řešením nalezneme hledané koeficienty α 0 = α 1 = 1. Obdobně bychom mohli pokračovat s využitím polynomů vyšších stupňů. Váhy a uzly některých vzorců jsou uvedeny v tabulkách 4.2 a 4.2. Z hlediska stability je výhodné, že koeficienty α i Gaußova kvadraturního vzorce n i=0 α i f(x i ) jsou kladné. Věta 4.5. (pozitivita α i ) Koeficienty α i Gaußova kvadraturního vzorce jsou kladné. Důkaz. Položme: 0 < p k (x) = b a n i=0,i k p k (x) dx = (x x i ) 2 Π 2n n i=0 α i p k (x i ) = α k p k (x k ) }{{} >0 α k kladné k = 0, 1,..., n. Je nutné umět integrovat i přes jiný interval než [ 1, 1] pro který jsme je odvodili. Nabízí se použít větu o substituci a za použití substituce x = 1 ((b a)t + a + b) převést obecný interval 2 [a, b] na interval [ 1, 1] b a f(x)dx = b a f ( 1 2 ((b a)t + a + b) ) dt, (4.14) což aplikací Gaußova kvadraturního vzorce na pravou stranu předešlé rovnice vede na finální kvadraturní vzorec b a f(x)dx = b a 2 n i=0 ( ) 1 α i f 2 ((b a)t i + a + b). (4.15) 23
24 Poznámka: 4.4. Poznamenejme, že je samozřejmě možné používat složené Gaußovy kvadraturní vzorce. OTÁZKY K ZAMYŠLENÍ 1. Vyjděte ze vztahu pro Aitkenovo Nevillovo schéma (1.3) a odvodtě vzorec (4.6) pro Rombergovu kvadraturu. 2. Bud pomocí vztahu (4.11), nebo pomocí Gramova-Schmidtova ortogonalizačního procesu odvod te Legendrovy polynomy pro n = 2, S využitím Legendrových polynomů z předchozího úkolu odvod te Gaußovy kvadraturní vzorce pro n = 2, viz tabulka 4.2. ÚKOLY 1. Implementujte Rombergovu kvadraturu. Vstupem je interval, integrovaná funkce a velikost kroku H. 2. Implementujte složené Gaußovy kvadraturní vzorce. Vstupem je interval, integrovaná funkce a velikost kroku H. 3. Experimentálně určete pro obě metody závislost chyby které se dopustíme při numerické kvadratuře na velikosti kroku H. Použijte programy z předchozích úkolů a funkci pro kterou umíte snadno přesně spočíst její kvadraturu. Zjištěnou závislost zakreslete do grafu, kde jsou obě osy logaritmické. 24
25 5 Metody řešení nelineárních rovnic I CÍLE KAPITOLY V této kapitole si uvedeme základní metody pro řešení jak jedné nelineární rovnice, tak i jejich soustav. KLÍČOVÁ SLOVA metoda půlení intervalu, metoda Regula falsi, Newtonova metoda 5.1 Řešení jedné nelineární rovnice Věnujme se nejprve řešení úlohy f(x) = 0 na intervalu [a, b]. Takové x které tuto rovnici splňuje nazveme kořenem a budeme jej značit α. V dalším předpokládejme, že f C[a, b] a f(a)f(b) < 0 a tedy kořen dané rovnice se opravdu nachází v intervalu [a, b]. Nejprve si uvedeme dvě nejjednodušší vždy konvergentní metody, které se používají jako startovací metody pro metody komplikovanější. Jedná se metodu bisekce a metodu regula falsi Metoda bisekce Metoda bisekce (půlení intervalu) patří mezi nejjednodušší metody pro řešení rovnice f(x) = 0. Její princip spočívá v tom, že postupně půlením počátečního intervalu [a, b] vytváříme posloupnost dílčích subintervalů [a k, b k ] takových, že vždy obsahují kořen α. Položme [a 0, b 0 ]=[a, b], střed intervalu [a k, b k ] je dán c = a + b 2. (5.1) Nový interval [a k+1, b k+1 ] zkonstruujeme tak, aby platilo f(a k+1 )f(b k+1 ) < 0. Což vede na nsledující podmínku [c, b k ], jestliže f(c)f(b k ) < 0 [a k+1, b k+1 ] = [a k, c], jinak. Pokud budeme považovat za odhad kořene střed daného intervalu, tak pro odhad chyby platí (5.2) α c b a 2 k, (5.3) 25
26 kde k je počet iterací. Na základě tohoto vzorce lze odhadnout počet nutných iterací pro dosažení dané přesnosti. Opakované půlení intervalu provádíme tak dlouho, dokud není dosaženo předepsaného počtu iterací, nebo dokud f(c) není dostatečně malá. Poznamenejme, že pokud nastane situace, že f(c) = 0, tak je nalezen kořen a iterační cyklus metody by měl být ukončen Metoda Regula Falsi Nedostatkem metody půlení intervalu bylo to, že při určování bodu c, viz vzorec (5.1), nebylo přihlíženo k průběhu funkce f(x). V metodě regula falsi postupujeme při odhadu kořene následujícím způsobem. Uvažujme dva body (a k, f(a k )) a (b k, f(b k )) a zkonstruujeme sečnu procházející těmito body. Průsečík tečny s osou x prohlásíme za odhad kořene c = a kf(b k ) b k f(a k ). (5.4) f(b k ) f(a k ) Ostatní části výpočetního postupu jsou analogické jako v případě metody půlení intervalu Newtonova metoda Zaměřme se nyní na metodu, která potřebuje silnější podmínky konvergence než předešlé dvě metody, avšak rychlost její konvergence je mnohem vyšší. Metodu budeme rovnou formulovat pro soustavu nelineárních rovnic s tím, že jedna nelineární rovnice je pouze speciálním případem. Necht je dáno nelineární zobrazení F : IR N IR N. Hledáme α :: F (α) = 0. Problém F (x) = 0 nahradíme posloupností lineárních problémů L k (x) = 0, L k : IR N IR N, k = 0, 1,..., takových, že jejich řešení tvoří posloupnost konvergující k řešení problému F (x) = 0. α x (k+1), kde L k (x (k+1) ) = 0. Necht x (0) je dáno. Pro danou aproximaci x (k) uvažujeme L k (x) jako lineární část Taylorova rozvoje zobrazení F v bodě x (k) IR N (J(x) značí Jakobiho matici zobrazení F v bodě x): F (x) = F (x (k) ) + J(x (k) )(x x (k) ) +O( x x (k) 2 ). }{{} L k (x) (za předpokladu dostatečné hladkosti zobrazení F ). Nelineární problém nahradíme problémem lineárním {F (x) = 0} {F (x (k) ) + J(x (k) )(x x (k) ) = 0 }{{} (5.5) L k (x) řešení α nelin. pb. aproximujeme řešením x (k+1) lin. pb. (5.6) α x (k+1) := x (k) J 1 (x (k) )F (x (k) ) (5.7) Vzorec v (5.7), kterým je definována (k+1)-ní aproximace x (k+1) řešení nelineárního problému je formální, ve skutečnosti se inverzní matice nepočítá a algoritmus má následující dva kroky: Algoritmus: 26
27 1. J(x (k) ) (x x k ) = F (x (k) ) - řešíme lineární úlohu pro δx (k) }{{} δx (k) 2. x (k+1) := x (k) + δx (k) - provedeme update předchozí aproximace. Newtonova metoda pro f(x) = 0 Pro N = 1 (nelineární skalární rovnice pro jednu neznámou) má Newtonova metoda názorný geometrický význam. Nelineární funkci f(x) nahradíme lineární funkcí (přímkou), která je tečnou ke grafu funkce f v bodě (x (k), f(x (k) ) (má tedy směrnici f (x (k) ) a prochází bodem (x (k), f(x (k) )). V tomto případě se Newtonova metoda nazývá metodou tečen. V případě jedné dimenze se vzorec (5.7) výrazně zjednoduší (náhrada J 1 (x (k) ) za f (x (k) ) 1 ) x (k+1) = x (k) f(x(k) ) f (x (k) ), x(0) dáno, f (x (k) ) 0. (5.8) Výpočetní schéma se používá tak dlouho, dokud x (k) x (k 1) nedosáhne předepsané hodnoty, nebo dokud není proveden předepsaný počet iterací, případně dokud není fx (k) ) < ɛ. O konvergenci a jejích podmínkách Newtonovy metody pro f(x) = 0 hovoří následující věta. Věta 5.1. Necht f C 2 [a, b], f(a)f(b) < 0, f (x) 0 pro všechna x [a, b] a necht f (x) 0, nebo f (x) 0 (tj. druhá derivace nemění znaménko). Zvolme x 0 [a, b] tak, aby platilo f(x 0 )f (x 0 ) > 0, pak posloupnost x k generovaná předpisem (5.8) je konvergentní. Poznámka: 5.1. Newtonova metoda je speciálním případem náhrady funkce f lineární funkcí l k (x) := f(x (k) ) + (x x (k) )q k, kde směrnice q k se volí q k := f (x (k) ). Věta 5.2. (Konvergence Newtonovy metody pro soustavy) Necht F C(D), D IR N konvexní, otevřená množina, která obsahuje α :: F (α) = 0. Necht J 1 (α), necht R > 0, c > 0, L > 0 takové že: J 1 (α) c, J(x) J(y) }{{} maticová norma L x y }{{} vekt. norma x, y B(α, R), kde B(α, R) je koule o středu α a poloměru R. Potom r, x (0) B(α, r), posloupnost 5.7 je jednoznačně definována a konverguje k α a platí α x (k+1) cl α x (k) 2. (5.9) Výše uvedená věta tedy říká, že pokud jsou v kořeni F (α) = 0 splněny výše uvedené podmínky, tak za předpokladu, že zvolíme x 0 dostatečně blízko kořene α, tak Newtonova metoda konverguje. Tato věta samozřejmě platí i pro jednu nelineární rovnici. Je zde vidět, že Newtonova metoda je citlivá na volbu počáteční iterace, srovnejte s větou 5.1. Dále nás bude zajímat rychlost konvergenčního procesu. 27
28 Řád konvergence Definice 5.3. (Řád konvergence iterační metody pro řešení F (x) = 0) Řekneme, že posloupnost {x (k) } generovaná numerickou metodou konverguje k α s řádem p 1, pokud c > 0 α x (k+1) α x (k) p c k k 0. V takovém případě se numerická metoda nazývá řádu p. Věta 5.2 říká, že Newtonova metoda je kvadraticky konvergentní, α x (k+1) cl α x (k) 2, pokud je x (0) dostatečně blízko α a pokud je J(α) nesingulární. Poznámka: 5.2. Newtonovu metodu je možné modifikovat a tím urychlit, či zjednodušit výpočetní proces, možné modifikace Newtonovy metody: Jacobiho matice se nemění pro p 2 kroků Nepřesné řešení soustavy lin. rovnic Vyčíslení Jacobiho matice pomocí diferencí f (x) f(x+h) f(x). V případě jedné dimenze náhrada derivace f (x (k) ) = f(x(k) ) f(x (k 1) ) h vede na známou metodu sečen. x (k) x (k 1) OTÁZKY K ZAMYŠLENÍ 1. Odvod te vzorec pro odhad chyby pomocí metody bisekce, viz vzorec (5.3). 2. Odvod te vzorec Odvod te dvoubodovou metodu sečen, viz poslední uvedená modifikace Newtonovy metody. 4. Pomocí Newtonovy metody odvod te vzorec pro výpočet odmocniny z čísla c, tj. řešte rovnici x 2 c = 0. ÚKOLY 1. Implementujte metodu půlení intervalu a metodu regula falsi. Vstupem je interval, funkce f(x), maximální počet iterací a velikost chyby. 2. Implementujte Newtonovu metodu pro f(x) = 0. Vstupem je počáteční odhad x (0), funkce f(x) a její derivace, maximální počet iterací a velikost chyby. 3. Pro úlohu se známým řešením porovnejte rychlost konvergence všech tří metod, tj, sledujte chybu jíž se dopustíte v závislosti na iteraci. 4. Implementujte Newtonovu metodu pro soustavu dvou nelineárních rovnic o dvou neznámých. Vstupem je počáteční odhad x (0), funkce F (x) a její Jakobiho matice J(x) (tj. čtyři další funkce), maximální počet iterací a velikost chyby. 28
29 6 Metody řešení nelineárních rovnic II CÍLE KAPITOLY V této kapitole si uvedeme pokročilejší metody řešení nelinerních rovnic a zaměříme se též na speciální případ, a to na řešení algebraických rovnic, tj. hledání kořenů polynomu. KLÍČOVÁ SLOVA metoda postupných aproximací pro nelineární rovnice, kořeny polynomu, Hornerovo schéma 6.1 Metoda postupných aproximací Metoda postupných aproximací je založena na faktu, že pro dané zobrazení F : M IR N IR N je vždy možné transformovat problém F (x) = 0 na ekvivalentní problém x φ(x) = 0, kde pomocná funkce φ je volena tak, aby φ(α) = α právě když F (α) = 0. Bod α, pro který platí φ(α) = α, se nazývá pevným bodem zobrazení φ. Nalezení nulových bodů zobrazení F se tak převede na nalezení pevného bodu zobrazení φ, které se realizuje pomocí následujícího algoritmu: Budiž dáno x (0) x (k+1) := φ(x (k) ), k 0. (6.1) Definice 6.1. (kontrahující zobrazení) Řekneme, že zobrazení G : D IR N IR n je kontrahující na D 0 D, jestliže L < 1 :: G(x) G(y) L x y x, y D 0. Věta 6.2. (Banachova věta o pevném bodě) Necht G : D IR N IR N kontrahující na uzavřené množině D 0 D, G(x) D 0 x D 0. Pak G má právě jeden pevný bod. Tento bod je limitou posloupnosti x (k+1) = φ(x (k) ), x (0) D 0 libovolné. Nyní si ukážeme aplikaci výše uvedeného na řešení rovnice f(x) = 0. Toto rovnici můžeme transformovat do obecného tvaru x = x + ψ(x)f(x) = φ(x), (6.2) kde ψ(x) je vhodně zvolená funkce. Lze vidět, že pokud f(α) = 0 α = φ(α). Příkladem budiž Newtonova metoda, kde funkce ψ je zvolena ψ(x) = 1/f (x) a pak užitím algoritmu (6.1) dostáváme schéma Newtonovy metody (5.8). V dalším zvolme ψ(x) = 1, tj. x = x f(x) = φ(x). Pokud zaručíme, že zobrazení φ(x) bude kontrahující, tak díky předchozí větě o pevném bodě 6.2, získáme užitím schématu (6.1) metodu 29
30 (metoda prosté iterace) pro řešení rovnice f(x) = 0. Kontrakce zobrazení je zde klíčová, pokud zobrazení φ(x) nebude kontrahující, pak iterační schéma nebude fungovat. Jednou z možností jak zaručit konvergenci je splnit podmínky následující věty. Věta 6.3. Necht α je pevný bod zobrazení φ C 1 [a, b] a φ(x) < 1, x [a, b], pak iterační metoda daná schématem (6.1) je konvergentní pro každé x (0) [a, b]. Použití metody je takové, že problém f(x) = 0 převedeme na problém hledání pevného bodu zobrazení x = x f(x) = φ(x) pomocí schématu (6.1), kde φ(x) bude splňovat podmínky věty 6.3. Iterace pak provádíme obdobně jako v případě Newtonovy metody(například tak dlouho, dokud x (k) x (k 1) není menší než předepsaná hodnota). 6.2 Hledání kořenů polynomu Pro nalezení kořenů polynomu p n (x) = a 0 +a 1 x+ +a n x n potřebujeme nejprve lokalizovat jeho kořeny a poté je aproximovat pomocí nějaké vhodné numerické metody z předchozích kapitol. Pro jejich lokalizaci můžeme použít následující věty. Věta 6.4 (Cauchy). Kořeny polynomu leží v kruhu Γ = { z C; z 1 + η, η = } a max k 0 k n 1 a n Věta 6.5 (Budanova-Fourierova). Necht koeficient a n polynomu p n (x) je kladný, krajní body intervalu [a, b] necht nejsou kořeny p n (x). Označme ZZ(x) počet znaménkových změn v posloupnosti p n (x), p n(x),..., p (n) n (x) v bodě x. Počet reálných kořenů (včetně násobnosti) polynomu p n (x) na intervalu [a, b] je dán ZZ(a) ZZ(b), nebo je o sudé číslo menší. Věta 6.6 (Descartes). Počet kladných kořenů (včetně násobnosti) polynomu p n (x) = a 0 + a 1 x + + a n x n je roven počtu znaménkových změn v posloupnosti a 0, a 1,..., a n, nebo je o sudé číslo menší Hornerovo schema V dalším budeme potřebovat vyčíslení hodnoty polynomu p n (x) = a 0 + a 1 x + + a n x n v daném bodě x. Pro vyčíslení polynomu použijeme Hornerovo schema, které je efektivnější než triviální metoda vyhodnocení polynomu. Porovnejme si nyní dva způsoby vyčíslení polynomu: 1. neefektivní r = 1; s = a 0 ; for i = 1 to n do r = r x; s = s + a i r; end for p n (x) = s, počet násobení 2n. 30
31 2. Hornerovo schéma s = a n ; for i = n 1 downto 0 do s = s x + a i ; end for p n (x) = s, počet násobení n. Poznámka: 6.1. Zapišme Hornerovo schéma pro vyčíslení p n (z) takto: b n = a n ; for i = n 1 downto 0 do b i = b i+1 z + a i ; end for p n (z) = b 0. Ukážeme, že tento zápis je vhodný pro vyčíslení derivace p n (a následně použijeme Newtonovu metodu pro určení kořene p n (x)). Pro dělení polynomu polynomem platí (a n x n + a n 1 x n a 0 ) : (x z) = a }{{} n x n 1 + (a n 1 + a n z)x n b 1 + zbytek }{{} b n b n 1 p n (x) = q n 1 (x; z)(x z) + b 0 kde q n 1 (x; z) = b n x n 1 + b n 1 x n b 1 Je-li z kořen, pak b 0 = 0. Nyní aplikujeme Newtonovu metodu pro nalezení kořene polynomu p n. Newtonova metoda: x (k+1) = x (k) Hornerovo sch. {}}{ p n (x (k) ) p n(x (k) ) }{{} Hornerovo sch., x (0) dáno Vzorec, který dostaneme s využitím Hornerova schématu, se nazývá Newtonova-Hornerova metoda: x (k+1) = x (k) p n (x (k) ) q n 1 (x (k) ; x (k) ) Výraz ve jmenovateli dostaneme z následujících vztahů p n(x) = q n 1(x; z)(x z) + q n 1 (x; z), p n(z) = q n 1 (z; z), z := x (k). Algoritmus pro nalezení kořenů polynomu p n : for m = n downto 1 do Najdi kořen r polynomu p m (Newtonova metoda) Vyčísli koeficienty q m 1 (x; r) (pomocí Hornerova schematu) p m 1 := q m 1 end for Poznámka: 6.2. Kvůli zaokrouhlovacím chybám je výhodné začít od kořene nejmenšího v absolutní hodnotě. 31
32 ÚKOLY 1. Implementujte metodu prosté iterace. Vstupem je počáteční odhad x (0), funkce f(x), maximální počet iterací a velikost chyby. 2. Implementujte metodu, která na základě vět odhadne polohy kořenů. Vstupem jsou koeficienty a 0,..., a n. 3. Implementujte Newtonovu metodu pro řešení polynomiální rovnice. Vstupem jsou koeficienty a 0,..., a n, maximální počet iterací a velikost chyby. 32
33 7 Řešení soustav lineárních rovnic I CÍLE KAPITOLY V této kapitole se budeme zabývat matematickým pozadím problematiky řešení soustav linerních rovnic. Dále se zde budeme věnovat některým přímým metodám pro řešení soustav lineárních rovnic. KLÍČOVÁ SLOVA metoda přímé a iterační, vliv zaokrouhlovacích chyb, podmíněnost soustav, Gaußova eliminace Formulace úlohy je následující, hledáme x IR N takové, že Ax = b, A IR NN, A-nesingulární. Protože je daná matice A nesingulární, má úloha právě jedno řešení. Pro řešení výše uvedeného problému rozlišujeme metody: přímé - konečný, předem známý počet kroků pro nalezení řešení iterační - konstruujeme (nekonečnou) posloupnost vektorů konvergujících k řešení Definice 7.1. Necht X je vektorový prostor. Normou. rozumíme zobrazení X R, které pro všechna x, y X splňuje: 1. x 0 x = 0 x = 0, kde 0 rozumíme nulový prvek X, 2. αx = α x, pro všechna α R, 3. x + y x + y. Nejčastěji používané vektorové normy v C N, x C N jsou následující x 1 = x i, i ( ) x 2 = x i 2 x p = ( i i x i p ) 1 p x = max i x i. Euklidova, 1 p <, 33
34 Maticové normy A C NN lze definovat jedním z následujících způsobů Ax A = sup x 0 x, A 1 = max j A 2 = i ρ(a H A) = a ij, }{{} sloupcový součet ρ(aa H ), A H transponovaná a kompl. združená (hermitovská), ρ(b) největší vlastní číslo B v abs. hodnotě (spektrální poloměr), A F = a ij 2 Frobeniova, A = max i i,j Pro vektorové a maticové normy platí 1. I F = N 2. I = 1, Ax A x j a ij řádkový součet. 3. AB A B sub-multiplikativita 7.1 Podmíněnost matic Protože na počítači máme vždy pouze aproximaci vstupních hodnot (např. číslo π je reprezentováno konečným počtem desetiných míst), budeme se též věnovat vlivu zaokrouhlovacích chyb na výpočetní proces. Matice se nazývá dobře podmíněná, jestliže relativně malé změny v koeficientech způsobí relativně malé změny v řešení. Matice se nazývá špatně podmíněná, jestliže relativně malé změny v koeficientech způsobí relativně velké změny v řešení. Analýza zaokrouhlovacích chyb - chyby ve výpočtu se obvykle reprezentují chybami ve vstupních datech. Vzhledem k zaokrouhlovacím chybám poskytuje numerická metoda přibližné řešení, které splňuje perturbovaný systém. Numerická metoda poskytuje (přesné) řešení x + δx perturbovaného systému (A + δa)(x + δx) = b + δb. Z výše uvedené rovnice lze chybu δx lze ( zhruba ) odhadnout následujícím způsobem 1 δx. = A 1 δb A 1 δax, δx A 1 δb + A 1 δa x, δx x A 1 δb x A 1 A x δb x b Dostáváme pak následující nerovnost δx x A A 1 }{{} číslo podmíněnosti K(A). + A 1 δa A A + A 1 δa A A ( δb b + δa ) A 1 Záměrně vynecháváme kroky mezivýpočtu, který je poměrně komplikovaný a pro nás v podstatě nedůležitý. 34
35 Závěr: Velikost relativní chyby δx je závislá na čísle podmíněnosti K(A). Čím je větší číslo podmíněnosti x K(A), tím je úloha hůře podmíněná. 7.2 Gaußova eliminace Gaußova eliminace je přímá metoda, kde je naším cílem převést soustavu Ax = b na tvar Ux = ˆb, kde U je horní trojúhelníková matice. K tomu budeme nad řádky matice provádět ekvivalentní úpravy, tj. úpravy které nemění hodnost matice. Jedná se o násobení řádků rozšířené matice soustavy A b nenulovým číslem, nebo jejich vzájemné sčítání. Celý postup lze popsat pomocí následujícího algoritmu Převod na horní trojúhelníkovou matici for sloupec j = 1 to n 1 do najdi a pj 0, p {j,..., n} if a pj = 0 p then STOP (singularita) else záměna p a j-tého řádku end if for řádek i = j + 1 to n do l ij = a ij a jj ; for k = j + 1 to n do a ik = a ik l ij a jk ; end for b i = b i l ij b j ; end for end for u ij, i j ˆbi jsou pak poslední hodnoty a ij jsou pak poslední hodnoty b i Počet operací v j-tém kroku celkem Hledání a pj 0 n j + 1 nj=2 j = (2+n)(n 1) 2 Výpočet l ij n j n 1 j=1 j = n(n 1) 2 Výpočet a ik 2(n j) 2 2 n 1 j=1 j 2 = 2 2n3 3n 2 +n 6 Výpočet b i 2(n j) 2 n 1 j=1 j = 2 n(n 1) 2 Celkový počet operací: 2 3 n3 + O(n 2 ) Poté, co jsme soustavu převedli do tvaru Ux = ˆb, ji lze snadno řešit pomocí zpětného chodu, tj. nejprve spočteme proměnnou x n z poslední rovnice, poté proměnnou x n 1 z předposlední, atd. Počet operací pro řešení Ux = ˆb : násobení (n+1)n 2 35 sčítání n(n 1) 2
Aproximace funkcí 1,00 0,841 1,10 0,864 1,20 0,885. Body proložíme lomenou čarou.
 Příklad Známe následující hodnoty funkce Φ: u Φ(u) 1,00 0,841 1,10 0,864 1,20 0,885 Odhadněte přibližně hodnoty Φ(1,02) a Φ(1,16). Možnosti: Vezmeme hodnotu v nejbližším bodě. Body proložíme lomenou čarou.
Příklad Známe následující hodnoty funkce Φ: u Φ(u) 1,00 0,841 1,10 0,864 1,20 0,885 Odhadněte přibližně hodnoty Φ(1,02) a Φ(1,16). Možnosti: Vezmeme hodnotu v nejbližším bodě. Body proložíme lomenou čarou.
1 Soustava lineárních rovnic
 Soustavy lineárních rovnic Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Soustava lineárních rovnic 2 Řešitelnost soustavy lineárních rovnic 3 Gaussova eliminační metoda 4 Jordanova eliminační
Soustavy lineárních rovnic Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Soustava lineárních rovnic 2 Řešitelnost soustavy lineárních rovnic 3 Gaussova eliminační metoda 4 Jordanova eliminační
Kristýna Kuncová. Matematika B2 18/19
 (6) Určitý integrál Kristýna Kuncová Matematika B2 18/19 Kristýna Kuncová (6) Určitý integrál 1 / 28 Newtonův integrál Zdroj: https://kwcalculus.wikispaces.com/integral+applications Kristýna Kuncová (6)
(6) Určitý integrál Kristýna Kuncová Matematika B2 18/19 Kristýna Kuncová (6) Určitý integrál 1 / 28 Newtonův integrál Zdroj: https://kwcalculus.wikispaces.com/integral+applications Kristýna Kuncová (6)
Necht je funkce f spojitá v intervalu a, b a má derivaci v (a, b). Pak existuje bod ξ (a, b) tak, že f(b) f(a) b a. Geometricky
 Monotónie a extrémy funkce Diferenciální počet - průběh funkce Věta o střední hodnotě (Lagrange) Necht je funkce f spojitá v intervalu a, b a má derivaci v (a, b). Pak existuje bod ξ (a, b) tak, že f (ξ)
Monotónie a extrémy funkce Diferenciální počet - průběh funkce Věta o střední hodnotě (Lagrange) Necht je funkce f spojitá v intervalu a, b a má derivaci v (a, b). Pak existuje bod ξ (a, b) tak, že f (ξ)
Komplexní analýza. Martin Bohata. Katedra matematiky FEL ČVUT v Praze Martin Bohata Komplexní analýza Mocninné řady 1 / 18
 Komplexní analýza Mocninné řady Martin Bohata Katedra matematiky FEL ČVUT v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Mocninné řady 1 / 18 Posloupnosti komplexních čísel opakování
Komplexní analýza Mocninné řady Martin Bohata Katedra matematiky FEL ČVUT v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Mocninné řady 1 / 18 Posloupnosti komplexních čísel opakování
Numerické metody 8. května FJFI ČVUT v Praze
 Obyčejné diferenciální rovnice Numerické metody 8. května 2018 FJFI ČVUT v Praze 1 Úvod Úvod Základní metody Pokročilejší metody Soustava Vyšší řád Program 1 Úvod Úvod - Úloha Základní úloha, kterou řešíme
Obyčejné diferenciální rovnice Numerické metody 8. května 2018 FJFI ČVUT v Praze 1 Úvod Úvod Základní metody Pokročilejší metody Soustava Vyšší řád Program 1 Úvod Úvod - Úloha Základní úloha, kterou řešíme
Kapitola 4: Soustavy diferenciálních rovnic 1. řádu
 Sbírka příkladů Matematika II pro strukturované studium Kapitola 4: Soustavy diferenciálních rovnic 1 řádu Chcete-li ukončit prohlížení stiskněte klávesu Esc Chcete-li pokračovat stiskněte klávesu Enter
Sbírka příkladů Matematika II pro strukturované studium Kapitola 4: Soustavy diferenciálních rovnic 1 řádu Chcete-li ukončit prohlížení stiskněte klávesu Esc Chcete-li pokračovat stiskněte klávesu Enter
Matematika 2, vzorová písemka 1
 Matematika 2, vzorová písemka Pavel Kreml 9.5.20 Přesun mezi obrazovkami Další snímek: nebo Enter. Zpět: nebo Shift + Enter 2 3 4 Doporučení Pokuste se vyřešit zadané úlohy samostatně. Pokud nebudete vědět
Matematika 2, vzorová písemka Pavel Kreml 9.5.20 Přesun mezi obrazovkami Další snímek: nebo Enter. Zpět: nebo Shift + Enter 2 3 4 Doporučení Pokuste se vyřešit zadané úlohy samostatně. Pokud nebudete vědět
MATEMATIKA 3. Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci
 MATEMATIKA 3 Dana Černá http://www.fp.tul.cz/kmd/ Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci Osnova: Komplexní funkce - definice, posloupnosti, řady Vybrané komplexní funkce
MATEMATIKA 3 Dana Černá http://www.fp.tul.cz/kmd/ Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci Osnova: Komplexní funkce - definice, posloupnosti, řady Vybrané komplexní funkce
5. a 12. prosince 2018
 Integrální počet Neurčitý integrál Seminář 9, 0 5. a. prosince 08 Neurčitý integrál Definice. Necht funkce f (x) je definovaná na intervalu I. Funkce F (x) se nazývá primitivní k funkci f (x) na I, jestliže
Integrální počet Neurčitý integrál Seminář 9, 0 5. a. prosince 08 Neurčitý integrál Definice. Necht funkce f (x) je definovaná na intervalu I. Funkce F (x) se nazývá primitivní k funkci f (x) na I, jestliže
Elementární funkce. Edita Pelantová. únor FJFI, ČVUT v Praze. katedra matematiky, FJFI, ČVUT v Praze
 Elementární funkce Edita Pelantová FJFI, ČVUT v Praze Seminář současné matematiky katedra matematiky, FJFI, ČVUT v Praze únor 2013 c Edita Pelantová (FJFI) Elementární funkce únor 2013 1 / 19 Polynomiální
Elementární funkce Edita Pelantová FJFI, ČVUT v Praze Seminář současné matematiky katedra matematiky, FJFI, ČVUT v Praze únor 2013 c Edita Pelantová (FJFI) Elementární funkce únor 2013 1 / 19 Polynomiální
Numerické metody minimalizace
 Numerické metody minimalizace Než vám klesnou víčka - Stříbrnice 2011 12.2. 16.2.2011 Emu (Brkos 2011) Numerické metody minimalizace 12.2. 16.2.2011 1 / 19 Obsah 1 Úvod 2 Základní pojmy 3 Princip minimalizace
Numerické metody minimalizace Než vám klesnou víčka - Stříbrnice 2011 12.2. 16.2.2011 Emu (Brkos 2011) Numerické metody minimalizace 12.2. 16.2.2011 1 / 19 Obsah 1 Úvod 2 Základní pojmy 3 Princip minimalizace
(1) Derivace. Kristýna Kuncová. Matematika B2 17/18. Kristýna Kuncová (1) Derivace 1 / 35
 (1) Derivace Kristýna Kuncová Matematika B2 17/18 Kristýna Kuncová (1) Derivace 1 / 35 Růst populací Zdroj : https://www.tes.com/lessons/ yjzt-cmnwtvsq/noah-s-ark Kristýna Kuncová (1) Derivace 2 / 35 Růst
(1) Derivace Kristýna Kuncová Matematika B2 17/18 Kristýna Kuncová (1) Derivace 1 / 35 Růst populací Zdroj : https://www.tes.com/lessons/ yjzt-cmnwtvsq/noah-s-ark Kristýna Kuncová (1) Derivace 2 / 35 Růst
Úvodní informace. 18. února 2019
 Úvodní informace Funkce více proměnných Cvičení první 18. února 2019 Obsah 1 Úvodní informace. 2 Funkce více proměnných Definiční obor Úvodní informace. Komunikace: e-mail: olga@majling.eu nebo olga.majlingova@fs.cvut.cz
Úvodní informace Funkce více proměnných Cvičení první 18. února 2019 Obsah 1 Úvodní informace. 2 Funkce více proměnných Definiční obor Úvodní informace. Komunikace: e-mail: olga@majling.eu nebo olga.majlingova@fs.cvut.cz
Edita Pelantová, katedra matematiky / 16
 Edita Pelantová, katedra matematiky seminář současné matematiky, září 2010 Axiomy reálných čísel Axiomy tělesa Axiom 1. x + y = y + x a xy = yx (komutativní zákon). Axiom 2. x + (y + z) = (x + y) + z a
Edita Pelantová, katedra matematiky seminář současné matematiky, září 2010 Axiomy reálných čísel Axiomy tělesa Axiom 1. x + y = y + x a xy = yx (komutativní zákon). Axiom 2. x + (y + z) = (x + y) + z a
Matematika (KMI/PMATE)
 Matematika (KMI/PMATE) Úvod do matematické analýzy Limita a spojitost funkce Matematika (KMI/PMATE) Osnova přednášky lineární funkce y = kx + q definice lineární funkce význam (smysl) koeficientů lineární
Matematika (KMI/PMATE) Úvod do matematické analýzy Limita a spojitost funkce Matematika (KMI/PMATE) Osnova přednášky lineární funkce y = kx + q definice lineární funkce význam (smysl) koeficientů lineární
Funkce zadané implicitně. 4. března 2019
 Funkce zadané implicitně 4. března 2019 Parciální derivace druhého řádu Parciální derivace druhého řádu funkce z = f (x, y) jsou definovány: Parciální derivace 2 f 2 = ( ) f 2 f 2 = ( ) f 2 f a 2 f 2 f
Funkce zadané implicitně 4. března 2019 Parciální derivace druhého řádu Parciální derivace druhého řádu funkce z = f (x, y) jsou definovány: Parciální derivace 2 f 2 = ( ) f 2 f 2 = ( ) f 2 f a 2 f 2 f
Katedra aplikované matematiky FEI VŠB Technická univerzita Ostrava
 Lineární algebra 5. přednáška: Báze a řešitelnost soustav Dalibor Lukáš Katedra aplikované matematiky FEI VŠB Technická univerzita Ostrava email: dalibor.lukas@vsb.cz http://www.am.vsb.cz/lukas/la1 Text
Lineární algebra 5. přednáška: Báze a řešitelnost soustav Dalibor Lukáš Katedra aplikované matematiky FEI VŠB Technická univerzita Ostrava email: dalibor.lukas@vsb.cz http://www.am.vsb.cz/lukas/la1 Text
x2 + 2x 15 x 2 + 4x ) f(x) = x 2 + 2x 15 x2 + x 12 3) f(x) = x 3 + 3x 2 10x. x 3 + 3x 2 10x x 2 + x 12 10) f(x) = log 2.
 Příklady k 1 zápočtové písemce Definiční obor funkce Určete definiční obor funkce: x + x 15 1 f(x x + x 1 ( x + x 1 f(x log x + x 15 x + x 1 3 f(x x 3 + 3x 10x ( x 3 + 3x 10x f(x log x + x 1 x3 + 5x 5
Příklady k 1 zápočtové písemce Definiční obor funkce Určete definiční obor funkce: x + x 15 1 f(x x + x 1 ( x + x 1 f(x log x + x 15 x + x 1 3 f(x x 3 + 3x 10x ( x 3 + 3x 10x f(x log x + x 1 x3 + 5x 5
Kapitola 2. Nelineární rovnice
 Kapitola. Nelineární rovnice Formulace: Je dána funkce f : R! R definovaná na intervalu ha; bi. Hledáme x ha; bi tak, aby f(x) = 0. (x... kořen rovnice) Poznámka: Najít přesné řešení analyticky je možné
Kapitola. Nelineární rovnice Formulace: Je dána funkce f : R! R definovaná na intervalu ha; bi. Hledáme x ha; bi tak, aby f(x) = 0. (x... kořen rovnice) Poznámka: Najít přesné řešení analyticky je možné
Diferenciální rovnice základní pojmy. Rovnice se
 Diferenciální rovnice základní pojmy. Rovnice se separovanými proměnnými. Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské
Diferenciální rovnice základní pojmy. Rovnice se separovanými proměnnými. Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské
Vybrané kapitoly z matematiky
 Vybrané kapitoly z matematiky VŠB-TU Ostrava 2018-2019 Vybrané kapitoly z matematiky 2018-2019 1 / 11 Křivkový integrál Vybrané kapitoly z matematiky 2018-2019 2 / 11 Parametricky zadaná křivka v R 3 :
Vybrané kapitoly z matematiky VŠB-TU Ostrava 2018-2019 Vybrané kapitoly z matematiky 2018-2019 1 / 11 Křivkový integrál Vybrané kapitoly z matematiky 2018-2019 2 / 11 Parametricky zadaná křivka v R 3 :
Cauchyova úloha pro obyčejnou diferenciální rovnici
 Řešení ODR v MATLABu Přednáška 3 15. října 2018 Cauchyova úloha pro obyčejnou diferenciální rovnici y = f (x, y), y(x 0 ) = y 0 Víme, že v intervalu a, b existuje jediné řešení. (f (x, y) a f y jsou spojité
Řešení ODR v MATLABu Přednáška 3 15. října 2018 Cauchyova úloha pro obyčejnou diferenciální rovnici y = f (x, y), y(x 0 ) = y 0 Víme, že v intervalu a, b existuje jediné řešení. (f (x, y) a f y jsou spojité
Linea rnı (ne)za vislost
 [1] Lineární (ne)závislost Skupiny, resp. množiny, vektorů mohou být lineárně závislé nebo lineárně nezávislé... a) zavislost, 3, b) P. Olšák, FEL ČVUT, c) P. Olšák 2010, d) BI-LIN, e) L, f) 2009/2010,
[1] Lineární (ne)závislost Skupiny, resp. množiny, vektorů mohou být lineárně závislé nebo lineárně nezávislé... a) zavislost, 3, b) P. Olšák, FEL ČVUT, c) P. Olšák 2010, d) BI-LIN, e) L, f) 2009/2010,
Komplexní analýza. Martin Bohata. Katedra matematiky FEL ČVUT v Praze Martin Bohata Komplexní analýza Úvod 1 / 32
 Komplexní analýza Úvod Martin Bohata Katedra matematiky FEL ČVUT v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Úvod 1 / 32 Základní informace Stránky předmětu: http://math.feld.cvut.cz/bohata/kan.html
Komplexní analýza Úvod Martin Bohata Katedra matematiky FEL ČVUT v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Úvod 1 / 32 Základní informace Stránky předmětu: http://math.feld.cvut.cz/bohata/kan.html
Metody, s nimiž se seznámíme v této kapitole, lze použít pro libovolnou
 2. Řešení nelineárních rovnic Průvodce studiem Budeme se zabývat výpočtem reálných kořenů nelineární rovnice f(x) =0, (2.0.1) kde f je v jistém smyslu rozumná reálná funkce. Pro některé funkce (kvadratické,
2. Řešení nelineárních rovnic Průvodce studiem Budeme se zabývat výpočtem reálných kořenů nelineární rovnice f(x) =0, (2.0.1) kde f je v jistém smyslu rozumná reálná funkce. Pro některé funkce (kvadratické,
kontaktní modely (Winklerův, Pasternakův)
 TÉMA 7: Pružný poloprostor, modely podloží pružný poloprostor základní předpoklady pružný poloprostor Boussinesqueovo řešení kontaktní modely (Winklerův, Pasternakův) 1 Pružný poloprostor (1) vychází z
TÉMA 7: Pružný poloprostor, modely podloží pružný poloprostor základní předpoklady pružný poloprostor Boussinesqueovo řešení kontaktní modely (Winklerův, Pasternakův) 1 Pružný poloprostor (1) vychází z
Inverzní Z-transformace
 Modelování systémů a procesů (11MSP) Bohumil Kovář, Jan Přikryl, Miroslav Vlček Ústav aplikované matematiky ČVUT v Praze, Fakulta dopravní 9. přednáška 11MSP úterý 16. dubna 2019 verze: 2019-04-15 12:25
Modelování systémů a procesů (11MSP) Bohumil Kovář, Jan Přikryl, Miroslav Vlček Ústav aplikované matematiky ČVUT v Praze, Fakulta dopravní 9. přednáška 11MSP úterý 16. dubna 2019 verze: 2019-04-15 12:25
Stochastické modelování v ekonomii a financích Konzistence odhadu LWS. konzistence OLS odhadu. Předpoklady pro konzistenci LWS
 Whitův pro heteroskedasticitě pro heteroskedasticitě Stochastické modelování v ekonomii a financích 7. 12. 2009 Obsah Whitův pro heteroskedasticitě pro heteroskedasticitě 1 Whitův 2 pro 3 heteroskedasticitě
Whitův pro heteroskedasticitě pro heteroskedasticitě Stochastické modelování v ekonomii a financích 7. 12. 2009 Obsah Whitův pro heteroskedasticitě pro heteroskedasticitě 1 Whitův 2 pro 3 heteroskedasticitě
MATEMATIKA 3 NUMERICKÉ METODY. Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci
 MATEMATIKA 3 NUMERICKÉ METODY Dana Černá http://kmd.fp.tul.cz Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci INFORMACE O PŘEDMĚTU Konzultační hodiny: ÚT 11:00-12:00, budova G,
MATEMATIKA 3 NUMERICKÉ METODY Dana Černá http://kmd.fp.tul.cz Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci INFORMACE O PŘEDMĚTU Konzultační hodiny: ÚT 11:00-12:00, budova G,
podle přednášky doc. Eduarda Fuchse 16. prosince 2010
 Jak souvisí plochá dráha a konečná geometrie? L ubomíra Balková podle přednášky doc. Eduarda Fuchse Trendy současné matematiky 16. prosince 2010 (FJFI ČVUT v Praze) Konečná geometrie 16. prosince 2010
Jak souvisí plochá dráha a konečná geometrie? L ubomíra Balková podle přednášky doc. Eduarda Fuchse Trendy současné matematiky 16. prosince 2010 (FJFI ČVUT v Praze) Konečná geometrie 16. prosince 2010
Lineární algebra - iterační metody
 Lineární algebra - iterační metody Numerické metody 7. dubna 2018 FJFI ČVUT v Praze 1 Úvod Úvod Rozdělení Metody Zastavení SOR Programy 1 Úvod Úvod - LAR Mějme základní úlohu A x = b, (1) kde A R n,n je
Lineární algebra - iterační metody Numerické metody 7. dubna 2018 FJFI ČVUT v Praze 1 Úvod Úvod Rozdělení Metody Zastavení SOR Programy 1 Úvod Úvod - LAR Mějme základní úlohu A x = b, (1) kde A R n,n je
Obsah. Limita posloupnosti a funkce. Petr Hasil. Limita posloupnosti. Pro a R definujeme: Je-li a < 0, pak a =, a ( ) =. vlastní body.
 Obsah a funkce Petr Hasil Přednáška z Matematické analýzy I Úvod 2 c Petr Hasil (MUNI) a funkce Matematická analýza / 90 c Petr Hasil (MUNI) a funkce Matematická analýza 2 / 90 Úvod Úvod Pro a R definujeme:
Obsah a funkce Petr Hasil Přednáška z Matematické analýzy I Úvod 2 c Petr Hasil (MUNI) a funkce Matematická analýza / 90 c Petr Hasil (MUNI) a funkce Matematická analýza 2 / 90 Úvod Úvod Pro a R definujeme:
Průvodce studiem V této kapitole se budeme zabývat diferenciálním počtem pro funkce více
 5 Diferenciální počet funkcí více proměnných Průvodce studiem V této kapitole se budeme zabývat diferenciálním počtem pro funkce více proměnných, především budeme pracovat s funkcemi dvou proměnných Ukážeme
5 Diferenciální počet funkcí více proměnných Průvodce studiem V této kapitole se budeme zabývat diferenciálním počtem pro funkce více proměnných, především budeme pracovat s funkcemi dvou proměnných Ukážeme
Kristýna Kuncová. Matematika B2
 (3) Průběh funkce Kristýna Kuncová Matematika B2 Kristýna Kuncová (3) Průběh funkce 1 / 26 Monotonie (x 2 ) = 2x (sin x) = cos x Jak souvisí derivace funkce a fakt, zda je funkce rostoucí nebo klesající?
(3) Průběh funkce Kristýna Kuncová Matematika B2 Kristýna Kuncová (3) Průběh funkce 1 / 26 Monotonie (x 2 ) = 2x (sin x) = cos x Jak souvisí derivace funkce a fakt, zda je funkce rostoucí nebo klesající?
Obsah. 1 Konstrukce (definice) Riemannova integrálu Výpočet Newtonova Leibnizova věta Aplikace výpočet objemů a obsahů 30
 Určitý integrál Robert Mřík 6. září 8 Obsh 1 Konstrukce (definice) Riemnnov integrálu. Výpočet Newtonov Leibnizov vět. 18 3 Numerický odhd Lichoběžníkové prvidlo 19 4 Aplikce výpočet objemů obshů 3 c Robert
Určitý integrál Robert Mřík 6. září 8 Obsh 1 Konstrukce (definice) Riemnnov integrálu. Výpočet Newtonov Leibnizov vět. 18 3 Numerický odhd Lichoběžníkové prvidlo 19 4 Aplikce výpočet objemů obshů 3 c Robert
Určitý (Riemannův) integrál a aplikace. Nevlastní integrál. 19. prosince 2018
 Určitý (Riemnnův) integrál plikce. Nevlstní integrál Seminář 9. prosince 28 Určitý integrál Existence: Necht funkce f (x) je definovná n uzvřeném intervlu, b. Necht je splněn n tomto intervlu kterákoliv
Určitý (Riemnnův) integrál plikce. Nevlstní integrál Seminář 9. prosince 28 Určitý integrál Existence: Necht funkce f (x) je definovná n uzvřeném intervlu, b. Necht je splněn n tomto intervlu kterákoliv
Co nám prozradí derivace? 21. listopadu 2018
 Co nám prozradí derivace? Seminář sedmý 21. listopadu 2018 Derivace základních funkcí Tečna a normála Tečna ke grafu funkce f v bodě dotyku T = [x 0, f (x 0 )]: y f (x 0 ) = f (x 0 )(x x 0 ) Normála: y
Co nám prozradí derivace? Seminář sedmý 21. listopadu 2018 Derivace základních funkcí Tečna a normála Tečna ke grafu funkce f v bodě dotyku T = [x 0, f (x 0 )]: y f (x 0 ) = f (x 0 )(x x 0 ) Normála: y
GEM a soustavy lineárních rovnic, část 2
 GEM a soustavy lineárních rovnic, část Odpřednesenou látku naleznete v kapitole 6 skript Abstraktní a konkrétní lineární algebra. Jiří Velebil: B6B0LAG 8.3.09: GEM a soustavy, část / Minulá přednáška Gaussova
GEM a soustavy lineárních rovnic, část Odpřednesenou látku naleznete v kapitole 6 skript Abstraktní a konkrétní lineární algebra. Jiří Velebil: B6B0LAG 8.3.09: GEM a soustavy, část / Minulá přednáška Gaussova
Geometrická nelinearita: úvod
 Geometrická nelinearita: úvod Opakování: stabilita prutů Eulerovo řešení s využitím teorie 2. řádu) Stabilita prutů Ritzovou metodou Stabilita tenkých desek 1 Geometrická nelinearita Velké deformace průhyby,
Geometrická nelinearita: úvod Opakování: stabilita prutů Eulerovo řešení s využitím teorie 2. řádu) Stabilita prutů Ritzovou metodou Stabilita tenkých desek 1 Geometrická nelinearita Velké deformace průhyby,
DFT. verze:
 Výpočet spektra signálu pomocí DFT kacmarp@fel.cvut.cz verze: 009093 Úvod Signály můžeme rozdělit na signály spojité v čase nebo diskrétní v čase. Další možné dělení je na signály periodické nebo signály
Výpočet spektra signálu pomocí DFT kacmarp@fel.cvut.cz verze: 009093 Úvod Signály můžeme rozdělit na signály spojité v čase nebo diskrétní v čase. Další možné dělení je na signály periodické nebo signály
Matematika III Stechiometrie stručný
 Matematika III Stechiometrie stručný matematický úvod Miroslava Dubcová, Drahoslava Janovská, Daniel Turzík Ústav matematiky Přednášky LS 2015-2016 Obsah 1 Zápis chemické reakce 2 umožňuje jednotný přístup
Matematika III Stechiometrie stručný matematický úvod Miroslava Dubcová, Drahoslava Janovská, Daniel Turzík Ústav matematiky Přednášky LS 2015-2016 Obsah 1 Zápis chemické reakce 2 umožňuje jednotný přístup
Obsah. 1.2 Integrály typu ( ) R x, s αx+β
 Sbírka úloh z matematické analýzy. Čížek Jiří Kubr Milan. prosince 006 Obsah Neurčitý integrál.. Základní integrály...................................... Integrály typu ) R, s α+β γ+δ d...........................
Sbírka úloh z matematické analýzy. Čížek Jiří Kubr Milan. prosince 006 Obsah Neurčitý integrál.. Základní integrály...................................... Integrály typu ) R, s α+β γ+δ d...........................
Laplaceova transformace
 Laplaceova transformace Modelování systémů a procesů (11MSP) Bohumil Kovář, Jan Přikryl, Miroslav Vlček Ústav aplikované matematiky ČVUT v Praze, Fakulta dopravní 5. přednáška 11MSP 219 verze: 219-3-17
Laplaceova transformace Modelování systémů a procesů (11MSP) Bohumil Kovář, Jan Přikryl, Miroslav Vlček Ústav aplikované matematiky ČVUT v Praze, Fakulta dopravní 5. přednáška 11MSP 219 verze: 219-3-17
(a). Pak f. (a) pro i j a 2 f
 Připomeň: 1. Necht K R n. Pak 1. Funkce více proměnných II 1.1. Parciální derivace vyšších řádů K je kompaktní K je omezená a uzavřená. 2. Necht K R n je kompaktní a f : K R je spojitá. Pak f nabývá na
Připomeň: 1. Necht K R n. Pak 1. Funkce více proměnných II 1.1. Parciální derivace vyšších řádů K je kompaktní K je omezená a uzavřená. 2. Necht K R n je kompaktní a f : K R je spojitá. Pak f nabývá na
Petr Hasil. c Petr Hasil (MUNI) Nekonečné řady MA III (M3100) 1 / 187
 Nekonečné řady Petr Hasil Přednáška z Matematické analýzy III c Petr Hasil (MUNI) Nekonečné řady MA III (M3100) 1 / 187 Obsah 1 Nekonečné číselné řady Základní pojmy Řady s nezápornými členy Řady s libovolnými
Nekonečné řady Petr Hasil Přednáška z Matematické analýzy III c Petr Hasil (MUNI) Nekonečné řady MA III (M3100) 1 / 187 Obsah 1 Nekonečné číselné řady Základní pojmy Řady s nezápornými členy Řady s libovolnými
Katedra aplikované matematiky FEI VŠB Technická univerzita Ostrava
 Lineární algebra 8. přednáška: Kvadratické formy Dalibor Lukáš Katedra aplikované matematiky FEI VŠB Technická univerzita Ostrava email: dalibor.lukas@vsb.cz http://www.am.vsb.cz/lukas/la Text byl vytvořen
Lineární algebra 8. přednáška: Kvadratické formy Dalibor Lukáš Katedra aplikované matematiky FEI VŠB Technická univerzita Ostrava email: dalibor.lukas@vsb.cz http://www.am.vsb.cz/lukas/la Text byl vytvořen
Stavový popis Stabilita spojitých systémů (K611MSAP) Katedra aplikované matematiky Fakulta dopravní ČVUT. čtvrtek 20. dubna 2006
 Modelování systémů a procesů (K611MSAP) Přednáška 4 Katedra aplikované matematiky Fakulta dopravní ČVUT Pravidelná přednáška K611MSAP čtvrtek 20. dubna 2006 Obsah 1 Laplaceova transformace Přenosová funkce
Modelování systémů a procesů (K611MSAP) Přednáška 4 Katedra aplikované matematiky Fakulta dopravní ČVUT Pravidelná přednáška K611MSAP čtvrtek 20. dubna 2006 Obsah 1 Laplaceova transformace Přenosová funkce
Matematika 1 Jiˇr ı Fiˇser 24. z aˇr ı 2013 Jiˇr ı Fiˇser (KMA, PˇrF UP Olomouc) KMA MAT1 24. z aˇr ı / 52
 í150doc-start í251doc-start Jiří Fišer (KMA, PřF UP Olomouc) KMA MAT1 24. září 2013 1 / 52 Matematika 1 Jiří Fišer 24. září 2013 Jiří Fišer (KMA, PřF UP Olomouc) KMA MAT1 24. září 2013 1 / 52 Zimní semestr
í150doc-start í251doc-start Jiří Fišer (KMA, PřF UP Olomouc) KMA MAT1 24. září 2013 1 / 52 Matematika 1 Jiří Fišer 24. září 2013 Jiří Fišer (KMA, PřF UP Olomouc) KMA MAT1 24. září 2013 1 / 52 Zimní semestr
Sb ırka pˇr ıklad u z matematick e anal yzy II Petr Tomiczek
 Sbírka příkladů z matematické analýzy II Petr Tomiczek Obsah 0 Diferenciální rovnice. řádu 0. Separace proměnných Příklad : Najděte obecné řešení (obecný integrál) diferenciální rovnice y = tg x tg y.
Sbírka příkladů z matematické analýzy II Petr Tomiczek Obsah 0 Diferenciální rovnice. řádu 0. Separace proměnných Příklad : Najděte obecné řešení (obecný integrál) diferenciální rovnice y = tg x tg y.
fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného základu (reg. č. CZ.1.07/2.2.00/28.
 Extrémy Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného
Extrémy Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na disciplíny společného
(A B) ij = k. (A) ik (B) jk.
 Příklady z lineární algebry Michael Krbek 1 Opakování 1.1 Matice, determinanty 1. Je dána matice 1 2 0 M = 3 0 1. 1 0 1 Určete M 2, MM T, M T M a vyjádřete M jako součet symetrické a antisymetrické matice!
Příklady z lineární algebry Michael Krbek 1 Opakování 1.1 Matice, determinanty 1. Je dána matice 1 2 0 M = 3 0 1. 1 0 1 Určete M 2, MM T, M T M a vyjádřete M jako součet symetrické a antisymetrické matice!
Funkce více proměnných: limita, spojitost, parciální a směrové derivace, diferenciál
 Matematika III 2. přednáška Funkce více proměnných: limita, spojitost, parciální a směrové derivace, diferenciál Michal Bulant Masarykova univerzita Fakulta informatiky 29. 9. 2010 Obsah přednášky 1 Literatura
Matematika III 2. přednáška Funkce více proměnných: limita, spojitost, parciální a směrové derivace, diferenciál Michal Bulant Masarykova univerzita Fakulta informatiky 29. 9. 2010 Obsah přednášky 1 Literatura
Operace s funkcemi [MA1-18:P2.1] funkční hodnota... y = f(x) (x argument)
![Operace s funkcemi [MA1-18:P2.1] funkční hodnota... y = f(x) (x argument) Operace s funkcemi [MA1-18:P2.1] funkční hodnota... y = f(x) (x argument)](/thumbs/95/126221157.jpg) KAPITOLA : Funkce - úvod [MA-8:P.] reálná funkce (jedné) reálné proměnné... f : A R...... zobrazení množin A R do množin reálných čísel R funkční hodnota... = f() ( argument) ( tj. reálná funkce f : A
KAPITOLA : Funkce - úvod [MA-8:P.] reálná funkce (jedné) reálné proměnné... f : A R...... zobrazení množin A R do množin reálných čísel R funkční hodnota... = f() ( argument) ( tj. reálná funkce f : A
Obsah. Petr Hasil. (konjunkce) (disjunkce) A B (implikace) A je dostačující podmínka pro B; B je nutná podmínka pro A A B: (A B) (B A) A (negace)
 Množiny, číselné obory, funkce Petr Hasil Přednáška z Matematické analýzy I c Petr Hasil (MUNI) Množiny, číselné obory, funkce Matematická analýza / 5 Obsah Množinové operace Operace s funkcemi Definice
Množiny, číselné obory, funkce Petr Hasil Přednáška z Matematické analýzy I c Petr Hasil (MUNI) Množiny, číselné obory, funkce Matematická analýza / 5 Obsah Množinové operace Operace s funkcemi Definice
Petr Beremlijski, Marie Sadowská
 Počítačová cvičení Petr Beremlijski, Marie Sadowská Katedra aplikované matematiky Fakulta elektrotechniky a informatiky VŠB - Technická univerzita Ostrava Cvičení : Matlab nástroj pro matematické modelování
Počítačová cvičení Petr Beremlijski, Marie Sadowská Katedra aplikované matematiky Fakulta elektrotechniky a informatiky VŠB - Technická univerzita Ostrava Cvičení : Matlab nástroj pro matematické modelování
Teorie. kuncova/ Definice 1. Necht f je reálná funkce a a R. Jestliže existuje.
 8. cvičení http://www.karlin.mff.cuni.cz/ kuncova/ kytaristka@gmail.com Teorie Definice. Necht f je reálná funkce a a R. Jestliže eistuje h 0 fa + h) fa), h pak tuto itu nazýváme derivací funkce f v bodě
8. cvičení http://www.karlin.mff.cuni.cz/ kuncova/ kytaristka@gmail.com Teorie Definice. Necht f je reálná funkce a a R. Jestliže eistuje h 0 fa + h) fa), h pak tuto itu nazýváme derivací funkce f v bodě
Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra matematiky
 Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra matematiky bakalářská práce vícebodové okrajové úlohy Plzeň, 18 Hana Levá Prohlášení Prohlašuji, že jsem tuto bakalářskou práci vypracovala
Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra matematiky bakalářská práce vícebodové okrajové úlohy Plzeň, 18 Hana Levá Prohlášení Prohlašuji, že jsem tuto bakalářskou práci vypracovala
Okrajový problém podmínky nejsou zadány v jednom bodu nejčastěji jsou podmínky zadány ve 2 bodech na okrajích, ale mohou být
 Obyčejné diferenciální rovnice 1 Úvod Obyčejnou diferenciální rovnici N-tého řádu f ( x,y,y,y,...,y (N)) = g(x) převádíme na soustavu N diferenciálních rovnic 1. řádu. Provedeme substituce y z 1 y z 2...
Obyčejné diferenciální rovnice 1 Úvod Obyčejnou diferenciální rovnici N-tého řádu f ( x,y,y,y,...,y (N)) = g(x) převádíme na soustavu N diferenciálních rovnic 1. řádu. Provedeme substituce y z 1 y z 2...
Matematika prˇedna sˇka Lenka Prˇibylova 7. u nora 2007 c Lenka Prˇibylova, 200 7
 Matematika přednáška Lenka Přibylová 7. února 2007 Obsah Základy matematické logiky 9 Základní množinové pojmy 13 Množina reálných čísel a její podmnožiny 16 Funkce 18 Složená funkce 20 Vlastnosti funkcí
Matematika přednáška Lenka Přibylová 7. února 2007 Obsah Základy matematické logiky 9 Základní množinové pojmy 13 Množina reálných čísel a její podmnožiny 16 Funkce 18 Složená funkce 20 Vlastnosti funkcí
Euklidovský prostor. Funkce dvou proměnných: základní pojmy, limita a spojitost.
 Euklidovský prostor. Funkce dvou proměnných: základní pojmy, limita a spojitost. Vyšší matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU
Euklidovský prostor. Funkce dvou proměnných: základní pojmy, limita a spojitost. Vyšší matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU
(2) Funkce. Kristýna Kuncová. Matematika B2. Kristýna Kuncová (2) Funkce 1 / 25
 (2) Funkce Kristýna Kuncová Matematika B2 Kristýna Kuncová (2) Funkce 1 / 25 Sudá a lichá funkce Určete, které funkce jsou sudé a které liché: liché: A, D, E sudé: B Kristýna Kuncová (2) Funkce 2 / 25
(2) Funkce Kristýna Kuncová Matematika B2 Kristýna Kuncová (2) Funkce 1 / 25 Sudá a lichá funkce Určete, které funkce jsou sudé a které liché: liché: A, D, E sudé: B Kristýna Kuncová (2) Funkce 2 / 25
Matematická analýza 2. Kubr Milan
 Matematická analýza. Kubr Milan. února 008 Obsah Vektorové funkce jedné reálné proměnné. 3. Základní pojmy...................................... 3. Křivky v R n........................................
Matematická analýza. Kubr Milan. února 008 Obsah Vektorové funkce jedné reálné proměnné. 3. Základní pojmy...................................... 3. Křivky v R n........................................
Matematická analýza II pro kombinované studium. Konzultace první a druhá. RNDr. Libuše Samková, Ph.D. pf.jcu.cz
 Učební texty ke konzultacím předmětu Matematická analýza II pro kombinované studium Konzultace první a druhá RNDr. Libuše Samková, Ph.D. e-mail: lsamkova@ pf.jcu.cz webová stránka: home.pf.jcu.cz/ lsamkova/
Učební texty ke konzultacím předmětu Matematická analýza II pro kombinované studium Konzultace první a druhá RNDr. Libuše Samková, Ph.D. e-mail: lsamkova@ pf.jcu.cz webová stránka: home.pf.jcu.cz/ lsamkova/
MATEMATIKA 1 ALEŠ NEKVINDA. + + pokud x < 0; x. Supremum a infimum množiny.
 MATEMATIKA ALEŠ NEKVINDA DIFERENCIÁLNÍ POČET Přednáška Označíme jako na střední škole N, Z, Q, R a C postupně množinu přirozených, celých, racionálních, reálných a komplexních čísel R = R { } { } Platí:
MATEMATIKA ALEŠ NEKVINDA DIFERENCIÁLNÍ POČET Přednáška Označíme jako na střední škole N, Z, Q, R a C postupně množinu přirozených, celých, racionálních, reálných a komplexních čísel R = R { } { } Platí:
1 Definice. A B A B vlastní podmnožina. 4. Relace R mezi množinami A a B libovolná R A B. Je-li A = B relace na A
 1 Definice 1. Množiny: podmnožina: A B x(x A x B) průnik: A B = {x A x B} sjednocení: A B = {x x A x B} rozdíl: A B = {x A x B} A B A B vlastní podmnožina 2. uspořádaná dvojice: (x, y) = {{x}, {x, y}}
1 Definice 1. Množiny: podmnožina: A B x(x A x B) průnik: A B = {x A x B} sjednocení: A B = {x x A x B} rozdíl: A B = {x A x B} A B A B vlastní podmnožina 2. uspořádaná dvojice: (x, y) = {{x}, {x, y}}
7. Aplikace derivace
 7. Aplikace derivace 7A. Taylorův polynom 7. Aplikace derivace Verze 20. července 207 Derivace funkce se využívá při řešení úloh technické prae i teorie. Uvedeme několik z nich: vyčíslení hodnot funkce,
7. Aplikace derivace 7A. Taylorův polynom 7. Aplikace derivace Verze 20. července 207 Derivace funkce se využívá při řešení úloh technické prae i teorie. Uvedeme několik z nich: vyčíslení hodnot funkce,
algebrou úzce souvisí V druhém tematickém celku se předpokládá základní znalosti z matematické analýzy
 1 Úvodem Prezentace předmětu VMP je vytvořena pro nový předmět, který si klade za cíl seznámit studenty se základy lineární algebry a se základy numerické matematiky. Zejména v prvním tématu budeme pracovat
1 Úvodem Prezentace předmětu VMP je vytvořena pro nový předmět, který si klade za cíl seznámit studenty se základy lineární algebry a se základy numerické matematiky. Zejména v prvním tématu budeme pracovat
Funkce více proměnných: limita, spojitost, derivace
 Matematika III 2. přednáška Funkce více proměnných: limita, spojitost, derivace Michal Bulant Masarykova univerzita Fakulta informatiky 22. 9. 2014 Obsah přednášky 1 Literatura 2 Zobrazení a funkce více
Matematika III 2. přednáška Funkce více proměnných: limita, spojitost, derivace Michal Bulant Masarykova univerzita Fakulta informatiky 22. 9. 2014 Obsah přednášky 1 Literatura 2 Zobrazení a funkce více
Energetické principy a variační metody ve stavební mechanice
 Energetické principy a variační metody ve stavební mechanice Přetvárná práce vnějších sil Přetvárná práce vnitřních sil Potenciální energie Lagrangeův princip Variační metody Ritzova metoda 1 Přetvárná
Energetické principy a variační metody ve stavební mechanice Přetvárná práce vnějších sil Přetvárná práce vnitřních sil Potenciální energie Lagrangeův princip Variační metody Ritzova metoda 1 Přetvárná
Jednoduchá zobrazení. Podpořeno z projektu FRVŠ 584/2011.
 Podpořeno z projektu FRVŠ 584/2011. Obsah 1 2 Obsah 1 2 Společné vlastnosti jednoduchých zobrazení: Zobrazovací ref. plocha je rovina - souřadnice X, Y, případně ρ, ɛ Zobrazovaná ref. plocha je eliposid
Podpořeno z projektu FRVŠ 584/2011. Obsah 1 2 Obsah 1 2 Společné vlastnosti jednoduchých zobrazení: Zobrazovací ref. plocha je rovina - souřadnice X, Y, případně ρ, ɛ Zobrazovaná ref. plocha je eliposid
FAKULTA STAVEBNÍ. Stavební statika. Telefon: WWW:
 VYSOKÁ ŠKOA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA AKUTA STAVEBNÍ Stavební statika Pohyblivé zatížení Jiří Brožovský Kancelář: P H 406/3 Telefon: 597 32 32 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast0.vsb.cz/brozovsky
VYSOKÁ ŠKOA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA AKUTA STAVEBNÍ Stavební statika Pohyblivé zatížení Jiří Brožovský Kancelář: P H 406/3 Telefon: 597 32 32 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast0.vsb.cz/brozovsky
Logika V. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı BI-MLO, ZS 2011/12
 Logika V. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Logika V. RNDr. Kateřina Trlifajová PhD. Katedra teoretické informatiky Fakulta informačních technologíı České vysoké učení technické v Praze c Kateřina Trlifajová, 2010 BI-MLO, ZS 2011/12 Evropský sociální
Jednoduchá zobrazení. Podpořeno z projektu FRVŠ 584/2011.
 Podpořeno z projektu FRVŠ 584/2011. Obsah 1 2 Obsah 1 2 Společné vlastnosti jednoduchých zobrazení: Zobrazovací ref. plocha je rovina - souřadnice X, Y, případně ρ, ɛ Zobrazovaná ref. plocha je eliposid
Podpořeno z projektu FRVŠ 584/2011. Obsah 1 2 Obsah 1 2 Společné vlastnosti jednoduchých zobrazení: Zobrazovací ref. plocha je rovina - souřadnice X, Y, případně ρ, ɛ Zobrazovaná ref. plocha je eliposid
Matematická analýza pro učitele (text je v pracovní verzi)
 Matematická analýza pro učitele (text je v pracovní verzi) Martina Šimůnková 6. června 208 2 Obsah Úvod 7. Co je to funkce.......................... 7.2 Co budeme na funkcích zkoumat................. 9.2.
Matematická analýza pro učitele (text je v pracovní verzi) Martina Šimůnková 6. června 208 2 Obsah Úvod 7. Co je to funkce.......................... 7.2 Co budeme na funkcích zkoumat................. 9.2.
Rovnice proudění Slapový model
 do oceánského proudění Obsah 1 2 3 Co způsobuje proudění v oceánech? vyrovnávání rozdílů v teplotě, salinitě, tlaku, ρ = ρ(p, T, S) vítr - wind stress F wind = ρ air C D AU 2 10 slapy produkují silné proudy,
do oceánského proudění Obsah 1 2 3 Co způsobuje proudění v oceánech? vyrovnávání rozdílů v teplotě, salinitě, tlaku, ρ = ρ(p, T, S) vítr - wind stress F wind = ρ air C D AU 2 10 slapy produkují silné proudy,
Škola matematického modelování 2017
 Počítačová cvičení Škola matematického modelování 2017 Petr Beremlijski, Rajko Ćosić, Marie Sadowská Počítačová cvičení Škola matematického modelování Petr Beremlijski, Rajko Ćosić, Marie Sadowská Katedra
Počítačová cvičení Škola matematického modelování 2017 Petr Beremlijski, Rajko Ćosić, Marie Sadowská Počítačová cvičení Škola matematického modelování Petr Beremlijski, Rajko Ćosić, Marie Sadowská Katedra
Pojem množiny nedefinujeme, pouze připomínáme, že množina je. Nejprve shrneme pojmy a fakta, které znáte ze střední školy.
 1 Kapitola 1 Množiny 1.1 Základní množinové pojmy Pojem množiny nedefinujeme, pouze připomínáme, že množina je souhrn, nebo soubor navzájem rozlišitelných objektů, kterým říkáme prvky. Pro známé množiny
1 Kapitola 1 Množiny 1.1 Základní množinové pojmy Pojem množiny nedefinujeme, pouze připomínáme, že množina je souhrn, nebo soubor navzájem rozlišitelných objektů, kterým říkáme prvky. Pro známé množiny
1 Předmluva Značení... 3
 Sbírka příkladů k předmětu Lineární systémy Jan Krejčí, korektura Martin Goubej 07 Obsah Předmluva. Značení..................................... 3 Lineární obyčejné diferenciální rovnice s konstantními
Sbírka příkladů k předmětu Lineární systémy Jan Krejčí, korektura Martin Goubej 07 Obsah Předmluva. Značení..................................... 3 Lineární obyčejné diferenciální rovnice s konstantními
Periodický pohyb obecného oscilátoru ve dvou dimenzích
 Periodický pohyb obecného ve dvou dimenzích Autor: Šárka Petříčková (A05221, sarpet@students.zcu.cz) Vedoucí: Ing. Petr Nečesal, Ph.D. Matematické metody v aplikovaných vědách a ve vzdělávání, Fakulta
Periodický pohyb obecného ve dvou dimenzích Autor: Šárka Petříčková (A05221, sarpet@students.zcu.cz) Vedoucí: Ing. Petr Nečesal, Ph.D. Matematické metody v aplikovaných vědách a ve vzdělávání, Fakulta
Chyby, podmíněnost a stabilita
 Chyby, podmíněnost a stabilita Numerické metody 4. března 2018 FJFI ČVUT v Praze 1 Úvod Čísla v počítači Chyby Citlivost Stabilita 1 Čísla v počítači Čísla v počítači - Celá čísla jméno bity rozsah typy
Chyby, podmíněnost a stabilita Numerické metody 4. března 2018 FJFI ČVUT v Praze 1 Úvod Čísla v počítači Chyby Citlivost Stabilita 1 Čísla v počítači Čísla v počítači - Celá čísla jméno bity rozsah typy
Ústav teorie informace a automatizace RESEARCH REPORT. Pavel Boček, Karel Vrbenský: Implementace algoritmu MIDIA v prostředí Google Spreadsheets
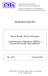 Akademie věd České republiky Ústav teorie informace a automatizace Academy of Sciences of the Czech Republic Institute of Information Theory and Automation RESEARCH REPORT Pavel Boček, Karel Vrbenský:
Akademie věd České republiky Ústav teorie informace a automatizace Academy of Sciences of the Czech Republic Institute of Information Theory and Automation RESEARCH REPORT Pavel Boček, Karel Vrbenský:
Anna Kratochvílová Anna Kratochvílová (FJFI ČVUT) PDR ve zpracování obrazu / 17
 Parciální diferenciální rovnice ve zpracování obrazu Anna Kratochvílová FJFI ČVUT 10. 6. 2009 Anna Kratochvílová (FJFI ČVUT) PDR ve zpracování obrazu 10. 6. 2009 1 / 17 Obsah 1 Motivace 2 Vyšetření pomocí
Parciální diferenciální rovnice ve zpracování obrazu Anna Kratochvílová FJFI ČVUT 10. 6. 2009 Anna Kratochvílová (FJFI ČVUT) PDR ve zpracování obrazu 10. 6. 2009 1 / 17 Obsah 1 Motivace 2 Vyšetření pomocí
Obsah. Aplikovaná matematika I. Vlivem meze Vlivem funkce Bernhard Riemann. Mendelu Brno. 3 Vlastnosti určitého integrálu
 Určitý integrál Aplikovná mtemtik I Dn Říhová Mendelu Brno Obsh Zákldní úloh integrálního počtu Definice určitého integrálu 3 Vlstnosti určitého integrálu 4 Výpočet určitého integrálu 5 Geometrické plikce
Určitý integrál Aplikovná mtemtik I Dn Říhová Mendelu Brno Obsh Zákldní úloh integrálního počtu Definice určitého integrálu 3 Vlstnosti určitého integrálu 4 Výpočet určitého integrálu 5 Geometrické plikce
Univerzita Karlova v Praze Matematicko-fyzikální fakulta
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Lukáš Perůtka Hledání optimálních strategií číselného síta Katedra algebry Vedoucí diplomové práce: Prof. RNDr. Aleš Drápal, CSc.,
Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Lukáš Perůtka Hledání optimálních strategií číselného síta Katedra algebry Vedoucí diplomové práce: Prof. RNDr. Aleš Drápal, CSc.,
TGH01 - Algoritmizace
 TGH01 - Algoritmizace Jan Březina Technical University of Liberec 31. března 2015 Metainformace materiály: jan.brezina.matfyz.cz/vyuka/tgh (./materialy/crls8.pdf - Introduction to algorithms) SPOX: tgh.spox.spoj.pl
TGH01 - Algoritmizace Jan Březina Technical University of Liberec 31. března 2015 Metainformace materiály: jan.brezina.matfyz.cz/vyuka/tgh (./materialy/crls8.pdf - Introduction to algorithms) SPOX: tgh.spox.spoj.pl
Matematický ústav UK Matematicko-fyzikální fakulta. Ukázky aplikací matematiky
 Lineární a nelineární problémy v geometrickém modelování Zbyněk Šír Matematický ústav UK Matematicko-fyzikální fakulta Ukázky aplikací matematiky Zbyněk Šír (MÚ UK) - Lineární a nelineární problémy v geometrickém
Lineární a nelineární problémy v geometrickém modelování Zbyněk Šír Matematický ústav UK Matematicko-fyzikální fakulta Ukázky aplikací matematiky Zbyněk Šír (MÚ UK) - Lineární a nelineární problémy v geometrickém
Paradoxy geometrické pravděpodobnosti
 Katedra aplikované matematiky 1. června 2009 Úvod Cíle práce : Analýza Bertrandova paradoxu. Tvorba simulačního softwaru. Osnova 1 2 3 4 Osnova 1 2 3 4 Osnova 1 2 3 4 Osnova 1 2 3 4 V rovině je zadán kruh
Katedra aplikované matematiky 1. června 2009 Úvod Cíle práce : Analýza Bertrandova paradoxu. Tvorba simulačního softwaru. Osnova 1 2 3 4 Osnova 1 2 3 4 Osnova 1 2 3 4 Osnova 1 2 3 4 V rovině je zadán kruh
Matematika I (KMI/PMATE) Co se naučíme? x = a a x = b. rozumět pojmu střední hodnota funkce na daném intervalu. Obrázek 1.
 Mtemtik I (KMI/PMATE). Integrální počet funkcí jedné proměnné.. Co se nučíme? Po sérii přednášek věnovných integrálům byste měli být schopni: rozumět definici pojmu neurčitý integrál používt metodu přímé
Mtemtik I (KMI/PMATE). Integrální počet funkcí jedné proměnné.. Co se nučíme? Po sérii přednášek věnovných integrálům byste měli být schopni: rozumět definici pojmu neurčitý integrál používt metodu přímé
Fakulta elektrotechnická. Algoritmy pro
 České vysoké učení technické v Praze Fakulta elektrotechnická Katedra řídicí techniky DIPLOMOVÁ PRÁCE Algoritmy pro nelineární prediktivní řízení Praha, 2006 Miroslav Čermák Prohlášení Prohlašuji, že jsem
České vysoké učení technické v Praze Fakulta elektrotechnická Katedra řídicí techniky DIPLOMOVÁ PRÁCE Algoritmy pro nelineární prediktivní řízení Praha, 2006 Miroslav Čermák Prohlášení Prohlašuji, že jsem
Lineární algebra II, přednáška Mgr. Milana Hladíka, Ph.D.
 Lineární algebra II, přednáška Mgr. Milana Hladíka, Ph.D. Poznámky sepsal Robert Husák Letní semestr 29/21 Obsah 1 Permutace 1 2 Determinant 3 3 Polynomy 7 4 Vlastní čísla 9 5 Positivně definitní matice
Lineární algebra II, přednáška Mgr. Milana Hladíka, Ph.D. Poznámky sepsal Robert Husák Letní semestr 29/21 Obsah 1 Permutace 1 2 Determinant 3 3 Polynomy 7 4 Vlastní čísla 9 5 Positivně definitní matice
Kombinatorika a grafy I
 Kombinatorika a grafy I Martin Balko 1. přednáška 19. února 2019 Základní informace Základní informace úvodní kurs, kde jsou probrány základy kombinatoriky a teorie grafů ( pokračování diskrétní matematiky
Kombinatorika a grafy I Martin Balko 1. přednáška 19. února 2019 Základní informace Základní informace úvodní kurs, kde jsou probrány základy kombinatoriky a teorie grafů ( pokračování diskrétní matematiky
Mendelova univerzita v Brně user.mendelu.cz/marik
 INŽNÝRSKÁ MATMATIKA Robert Mařík Mendelova univerzita v Brně marik@mendelu.cz user.mendelu.cz/marik ABSTRAKT. Učební text k mým přednáškám z předmětu Inženýrská matematika. Text je poměrně hutný a není
INŽNÝRSKÁ MATMATIKA Robert Mařík Mendelova univerzita v Brně marik@mendelu.cz user.mendelu.cz/marik ABSTRAKT. Učební text k mým přednáškám z předmětu Inženýrská matematika. Text je poměrně hutný a není
1 Derivace funkce a monotonie
 MA 10. cvičení intervaly monotonie a lokální extrémy Lukáš Pospíšil,2012 1 Derivace funkce a monotonie Jelikož derivace funkce v daném bodě je de-facto směrnice tečny (tangens úhlu, který svírá tečna s
MA 10. cvičení intervaly monotonie a lokální extrémy Lukáš Pospíšil,2012 1 Derivace funkce a monotonie Jelikož derivace funkce v daném bodě je de-facto směrnice tečny (tangens úhlu, který svírá tečna s
Definice Řekneme, že PDA M = (Q,Σ,Γ,δ,q 0,Z 0,F) je. 1. pro všechna q Q a Z Γ platí: kdykoliv δ(q,ε,z), pak δ(q,a,z) = pro všechna a Σ;
 Deterministické zásobníkové automaty Definice 3.72. Řekneme, že PDA M = (Q,Σ,Γ,δ,q 0,Z 0,F) je deterministický (DPDA), jestliže jsou splněny tyto podmínky: 1. pro všechna q Q a Z Γ platí: kdykoliv δ(q,ε,z),
Deterministické zásobníkové automaty Definice 3.72. Řekneme, že PDA M = (Q,Σ,Γ,δ,q 0,Z 0,F) je deterministický (DPDA), jestliže jsou splněny tyto podmínky: 1. pro všechna q Q a Z Γ platí: kdykoliv δ(q,ε,z),
Nekomutativní Gröbnerovy báze
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Bc. Zuzana Požárková Nekomutativní Gröbnerovy báze Katedra algebry Vedoucí diplomové práce: RNDr. Jan Št ovíček, Ph.D. Studijní
Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Bc. Zuzana Požárková Nekomutativní Gröbnerovy báze Katedra algebry Vedoucí diplomové práce: RNDr. Jan Št ovíček, Ph.D. Studijní
Reprezentace dat. BI-PA1 Programování a Algoritmizace I. Ladislav Vagner
 Reprezentace dat BI-PA1 Programování a Algoritmizace I. Ladislav Vagner Katedra teoretické informatiky Fakulta informačních technologíı ČVUT v Praze xvagner@fit.cvut.cz 9., 11. a 12. října 2017 Obsah Dvojková
Reprezentace dat BI-PA1 Programování a Algoritmizace I. Ladislav Vagner Katedra teoretické informatiky Fakulta informačních technologíı ČVUT v Praze xvagner@fit.cvut.cz 9., 11. a 12. října 2017 Obsah Dvojková
TGH01 - Algoritmizace
 TGH01 - Algoritmizace Jan Březina Technical University of Liberec 28. února 2017 Co je to algoritmus? Porovnávání algoritmů Porovnávání algoritmů Co je to algoritmus? Který algoritmus je lepší? Záleží
TGH01 - Algoritmizace Jan Březina Technical University of Liberec 28. února 2017 Co je to algoritmus? Porovnávání algoritmů Porovnávání algoritmů Co je to algoritmus? Který algoritmus je lepší? Záleží
Speciální funkce, Fourierovy řady a Fourierova transformace
 1 Speciální funkce, Fourierovy řady a Fourierova transformace Při studiu mnoha přírodních jevů se setkáváme s veličinami, které jsou všude nulové s výjimkou malého časového intervalu I, ale jejich celková
1 Speciální funkce, Fourierovy řady a Fourierova transformace Při studiu mnoha přírodních jevů se setkáváme s veličinami, které jsou všude nulové s výjimkou malého časového intervalu I, ale jejich celková
x y (A)dy. a) Určete a načrtněte oblasti, ve kterých je funkce diferencovatelná. b) Napište diferenciál funkce v bodě A = [x 0, y 0 ].
![x y (A)dy. a) Určete a načrtněte oblasti, ve kterých je funkce diferencovatelná. b) Napište diferenciál funkce v bodě A = [x 0, y 0 ]. x y (A)dy. a) Určete a načrtněte oblasti, ve kterých je funkce diferencovatelná. b) Napište diferenciál funkce v bodě A = [x 0, y 0 ].](/thumbs/94/121813288.jpg) II.4. Totální diferenciál a tečná rovina Značení pro funkci z = f,: totální diferenciál funkce f v bodě A = 0, 0 ]: dfa = A 0+ A 0 Označme d = 0, d = 0. Pak dfa = A d+ A d Příklad91.Je dána funkce f, =.
II.4. Totální diferenciál a tečná rovina Značení pro funkci z = f,: totální diferenciál funkce f v bodě A = 0, 0 ]: dfa = A 0+ A 0 Označme d = 0, d = 0. Pak dfa = A d+ A d Příklad91.Je dána funkce f, =.
