Materiały półprzewodnikowe
|
|
|
- Helena Dobrowolska
- 6 lat temu
- Przeglądów:
Transkrypt
1 Plan wykładu Aotk metal grupy III Zwąk półprewodnkowe mesane: - pryblżene krystału wrtualnego, prawo Vegarda, - necągłość pasm, -rowąane równana Possona równanem Schrodngera Tranystory na bae GaN
2 Materały półprewodnkowe Dwuskładnkowe wąk półprewodnkowe grupy III-V: GaAs, InP, InAs, P.Y. Yu and M. Cardona, Fundamentals of Semconductors, Sprnger Berln 5.
3
4 Półprewodnk grupy III-V ora II-VI
5 Zwąk mesane półprewodnków grupy III-V ABC g BC x C x x AB x g g I. Vurgaftman, J.R. Meyer, and L.R. Ram-Mohan, J. Appl. Phys. 89, 585 ().
6 Zwąk półprewodnkowe mesane Pryblżene krystału mesanego (Vrtual Crystal Approxtmaton) Zwąk trójskładnkowe. (c bowng odstępstwo od lnowośc) Zwąk cteroskładnkowe
7 Struktura krystalografcna III-N Wurtte Znc-blende () ()
8 Aotk (III-N) Cel: laser krawędowy emtujący elone śwatło 7 6 AlN nergy (ev) GaN Sapphre SC InN S() Wavelenght (nm) Lattce Constant, a (A) Studna kwantowa InGaN/GaN jest naturalnym kandydatem na elony laser
9 Struktura pasmowa w punkce dla półprewodnków e strukturą blendy cynkowej ora strukturą wurcytu S. Adach, Propertes of Semconductor Alloys: Group-IV, III V and II VI Semconductors
10 Rocepena pasma welencyjnego Rocepene to wyraża sę popre parametr wąany oddaływanem spn orbta ora polem krystalcnym.
11 Uwględnene naprężeń dla układów krystalujących w strukture wurtytu (heksagonalnej) 33 3 a a a C C c c c c c c,,,, v v v c ;, ;, ;, 4 3 D D b D D a a a a v c t c c a a a y x, ', ', ', ' v v v c t c c y x c t c c c c c C C a a a a y x y x C C D D D D C C D D D D ; 3 ; 3 so cr
12 Parameters: F. Bernardn et al., Phys. Rev. B 63, 93 (). Polayacja w materałach III-N krystalujących w strukture wurcytu Polaracja w AlN, GaN and InN: P P SP P PZ c c c P PZ e x y a a a 33 e3( x y ) c c c e 3 C C e C C 33 3 a a a Polaracja w stopach III-N: Al x Ga -x N, Ga -y In y N, Al x In -x N, Al x Ga -x-y In y N Lnowa aproksymacja: AlGaInN AlN x ( x y) GaN y InN P P AlGaInN SP AlGaInN PZ x P x P AlN SP AlN PZ ( ( x x y) P y) P GaN SP GaN PZ y P y P InN SP InN PZ
13 V. Forentn and F. Bernardn, Phys. Rev. 6, 8849 (999); I. Vurgaftman and J.R. Meyer, J. Appl. Phys. 94, 3675 (3); Nelnowa polaryacja w stopach III-N Polaryacja spontancna Polaryacja peoelektrycna Lnowa aproksymacja e modyfkowanym wartoścam polaryacj peoelektrycnej dla wąków dwuskładnkowych P AlGaN SP AlN GaN x P ( x) P x xb SP SP P AlGaInN PZ x P ( x y) P AlN PZ GaN PZ y P InN PZ
14 Rokład pól elektrycnych w heterostrukturach. Perodycne warunk bregowe Perodycne warunk bregowe: Pole elektrycne w n-tej warstwe: Struktura (bwbw) Struktura (bwb) ) ( ) ( w b b w b w b w w b b w w b w b L L L P P F L L L P P F q q q n q q q q n q q q n l l p lp F / / / ) ( ) ( w b b w b w b w w b b w w b w b L L L P P F L L L P P F q q F q l l,,p
15 Hamltonan w strukture wurcytu. Hamltonan C6v4 Hamltonan dla pasma walencyjnego Onacena Funkcje baowe
16 Transformacja Hamltonanu Popre odpowedną transformację można apsać Hamltonan w postac: Zagadnene własne można sprowadć do postac: Położena pasm:
17 Wpływ polaryacj spontancnej na wbudowane pole elektrycne Od pewnej grubośc krytycnej d spadek potencjału jest węksy nż wartość prerwy energetycnej. Pry takch warunkach poom Fermego leży w paśme prewodnctwa (walencyjnym) co onaca, że samostna koncentracja nośnków jest duża. Nośnk te ekranują pole elektrycne pochodące od spontancnej peoelektrycnej polaryacj. Pojawa sę wydukowane pole elektrycne D skerowane precwne do wektora polaryacj elektrycnej. F D P / = P/ dla d < d ; << P/ dla d > d
18 Krytycne grubośc warstwach dla ekranowana pól elektrycnych pochodących od spontancnej polaryacj AlN: F Max = 6 kv/cm; d = 5.8 nm; GaN: F Max = 378 kv/cm; d = 9. nm; InN: F Max = 8 kv/cm; d =.3 nm;
19 Pole elektrycne w studnach kwantowych: pojedynca studna kwantowa Pola elektrycne w studn barerach: AlN cap (5- nm) GaN QW (-3 nm) AlN buffer (~5 nm) () Al face Dla barer można pryjąć że pole elektrycne jest blske ero poneważ d Barrer > d (efekt ekranowana). Dla pojedyncej studn kwantowej d QW << d dlatego F QW = P = P SP +P PZ. Dla studn kwantowych d QW > 3 nm efekt ekranowana wewnątr studn acyna odgrywać stotną role. W tym wypadku konecne są oblcena samougodnone. F Cap ~ F Buffer ~ Al O 3 F QW = P = P SP +P PZ ~.9 MV/cm
20 Pole elektrycne w studnach kwantowych: welokrotne studne kwantowe AlN cap (5- nm) GaN MQW (-3 nm) AlN buffer (~5 nm) () Al face Al O 3 Pola elektrycne w studnach, barerach pomędy studnam ora ewnętrnych barerach: Dla ewnętrnych barer można pryjąć że pole elektrycne jest blske ero poneważ d Barrer > d (efekt ekranowana). Dla studn kwantowej ora barer mędy studnam d B ~ d QW << d dlatego pola elektrycne są bardo duże. fektywny spadek potencjału na całkowtym obsare studn kwantowych jest blsk eru (sytuacja podobna do grubej warstwy, tj. warstwy grubsej nż d ). k d B k d k F d QW k d Warunk perodycnośc: F QW d QW F B d B d QW d B F B F QW
21 Prejśce podstawowe w studn GaInN/GaN na kerunku polarnym nepolarnym Transton energy h-e (ev) wth electrc feld ML. 5ML 5ML ML 5ML.5 ML Straned g. GaN/Ga -x In x N Unstraned g Indum content n quantum well, x.5 Wavelength (m) Transton energy h-e (ev) ML wthout electrc feld Straned g ML 5ML Straned g ML.5 Unstraned g. GaN/Ga -x In x N Indum content n quantum well, x.5 Wavelength (m)
22 Całk prekryca oblcone dla prejśca podstawowego h-e owerlap ntegral ML 5ML ML GaN/Ga -x In x N 5ML ML Indum content n quantum well, x
23 Polaryacja Te Tm w strukturach AlGaN
24 Możlwe długośc fal otrymane na bae struktur: AlGaN/AlGaN
25 Rokład pól w strukturach tranystorowych C. Wood and D. Jena, Polaraton ffects n Semconductors, Sprnger (8).
26 Rowąane równana Shrodngera równanem Possona dla heterostruktur tranystorowych Warunk pocątkowe: Rokład pól elektrycnych oblcony warunków bregowych. Osacowane lcby stanów wąanych Rokład pól elektrycnych w recywstych heterostrukturach AlGaN/GaN nergy (ev) F AlGaN AlInN Dstance (nm) Po oblcenach samougodnonych nergy (ev) Dstance (nm) AlGaN AlInN
27 Równane Possona Jednowymarowe równane Possona: (x)- gęstość źródeł np. Masy ładunku; - sukana postać potencjału Różncowa postać równana Possona: j Numerycne rowąane równana Possona?? d dx j j j
28 Numerycne rowąane równana Possona j j j Iteracja w pród: Iteracja w tył: Schemat Numerowa (x) j x
29 Numerycne rowąane równana Possona Zakładamy, że namy warunk bregowe: =, n =. Sukamy rowąań postac: j+ =x j j +y j Możemy naleźć wąk rekurencyjne dla mennych x,y rekurencja w tył. (x n =, y n =) x j x j y j- Mając oblcone wartośc x,y możemy astosować prostą rekurencję w pród. = y x j j j
30 Problem oblcenowy Archtektura struktury półprewodnkowej: składy studn barer; serokośc studn barer; poom domeskowana; Parametry materałowe: masy efektywne, potencjały hydrostatycne, td. Naprężena fekty polaryacyjne Podejśce teoretycne: model jednopasmowy, pryblżene masy efektywnej, V() W celu korekcj potencjału V(): rowąane równana Posona tj. oblcena samougodnone Oblcene stanów własnych: (energe funkcje falowe) Struktura energetycna dla wejścowej struktury
31 Równane Schrödngera ora Possona ) ( ) ( ) ( ) ( V m l D b F b b D F D D D d n N T k T k m n n n T k N N n N ) ( ) ( exp ln * ) ( ) ( ) ( exp ) ( ) ( ) ( ) ( Równane Schrödngera ora równane Possona e menną stałą delektrycną Oblcene gęstośc ładunku Potencjał próbny Rowąywane równana w sposób samougodnony Wynacane poomu Fermego ) ( ) ( ) ( e V V p p Równane Schrödngera: Równane Possona:
32 Koncentracja nośnków w półprewodnku samstnym domeskowym Równane neutralnośc elektrycnej. Suma ładunków dodatnch ujemnych mus być równa ero. p N D n N A p: koncentracja elektronów n:koncentracja dur N D+ :koncentracja jonowanych donorów N A- :kdoncentracja jonowanych akceptorów
33 Poomy energetycne donorów kompensujących donory akceptorów na poome donorowym akceptorowym d c a v N D n N A N D g *exp F k T B D
34 Numerycna postać równane Schrödngera m V ( ) Podejśce numerycne: Równane Schrödngera: Metoda Martna-Deana (W. Salejda, M.H. Tyc. M. Just, Algebracne metody rowąywana równana Schrödngera, PWN Warsawa )
35 Numerycna postać równane Possona 4 4 e V V V H H H Podejśce numerycne: Równane Possona schemat rowąana. Prosta teracja wpród tył Warunk bregowe V =, V n = Sukamy rowąań postac: V j+ =x j V j +y j Warunk V =, x n =, y n = x y w y x x w V V V
36 R. Kudrawec et al., Appl. Phys. Lett., 863 (). Oblcne poomu Fermego pry powerchn popre porównane eksperymentem GaN Van Hoof structures undoped GaN (d=3-7nm) F d F=/d GaN:S CB VB CR ( 3 R/R (d) d=3nm (e) d=5nm samples CR measurements analyss (f) d=7nm MOVP samples nergy (ev) 5 (4/3) ( n - g ) 3/ Index, n 3 lectrc feld F (kv/cm) MB samples d=3nm (F=kV/cm) d=5nm (F=83kV/cm) d=7nm (F=63kV/cm) Lnear ft (4/3) ( n - g ) 3/ Thckness d (nm) MOVP samples d=3nm (F=6kV/cm) d=5nm (F=53kV/cm) d=7nm (F=4kV/cm) Lnear ft Index, n F=/d =.ev =.3eV =.4eV =.5eV MB MOVP Ferm level poston on GaN surface
37 M. Gladysewc et al., Appl. Phys. Lett. 98, 39 (). Rokład pól elektrycnych w strukturach typu: GaN(cap)/AlGaN(d)/GaN(buffer) CR ( 5 R/R) GaN(3nm)/AlGaN(d)/GaN(buffer) (a) d = 3nm GaN cap (b) d = nm AlGaN /3 ( n - g ) 3/ d=3nm (F=.3 MV/cm) d=nm (F=.46 MV/cm) d=nm (F=.78 MV/cm) Lnear ft 4 - (c) d = nm Index, n nergy (ev) samples CR measurements analyss The bult-n electrc feld n GaN/AlGaN/GaN heterostructure
38 M. Gladysewc et al., Appl. Phys. Lett. 98, 39 (). Wpływ warunków bregowych w srukrurach GaN(cap)/AlGaN/GaN na rokład pól elektrycnych - - (a) Varyng Ferm level on GaN surface CB F VB Położene poomu Fermego pry powerchn ne mena wartośc pól elektrycnych wewnątr próbk. Zmena wartość pól w warstwach pry powerchn. nergy (ev) (b) Varyng Ferm level n GaN buffer.5ev.55ev.95ev CB F VB.eV.6eV.eV Zmana położena poomu Fermego wewnątr próbk GaN(buffer) wpływa na rokład pól w jej wnętru. Ne wpływa natomast na rokład pól w ewnętrnych warstwach Dstance (nm) Koncentracja dwuwymarowego gau jest parametrem, na który wpływ mają oba warunk bregowe.
39 Porównane wynków eksperymentalnych oblcenam teoretycnym lectrc feld (MV/cm) M. Gladysewc et al., Appl. Phys. Lett. 98, 39 () (a) d = 3nm (b) d = nm (c) d = nm Calc. xp. Dla stuktury: GaN/AlGaN/GaN dla różnych serokośc warstwy AlGaN (,, and 3nm) wartość wbudowanego pola elektrycnego prybera wartośc sgnfcantly (.78,.46,.3MV/cmale wartość prypęca poomu Fermego pry powerchn prybera te same wartośc.55ev ponżej werchołka pasma prewodnctwa. Wnosek: Prypęce poomu Fermego w warstwe GaN pry powerchn.55 ev może ostać potraktowane jako warunek bregowy kedy oblcamy rokład pól w heterostrukturach GaN(cap)/AlGaN(d)/GaN(buffer).4. Pry powerchn GaN: F =.55eV CB - F (ev) M. Gladysewc, et al., Appl. Phys. Lett. 98, 39 ().
40 Porównane wynków oblceń danym eksperymentalnym. Koncentracja gau dwuwymarowego DG concentraton (cm - ).x 3.5x 3.x 3 5.x..x 3.5x 3.x 3 5.x..x 3.5x 3.x 3 (a) d = 3nm (b) d = nm (c) d = nm Calculatons xperment Koncentracja:DG w hetereostrukure: AlGaN/GaN ależy od cterookośc warstwy AlGaN dane eksperymentalne: 8. cm - dla d=3nm, 5. dla d=nm,.5 cm - dla d=nm. Na podstawe porównana danych eksperymentalnych oblcenam teoretycnym wykonanym dla heterostruktury: AlGaN/GaN poom Fermego jest prypęty pry podobnej wartośc wewnątr struktury:.4ev ponżej dna pasma prewodnctwa. 5.x CB - F n GaN buffor (ev)
41 Rokład pól elektrycnych w strukturach GaN(cap)/AlGaN(d)/GaN(buffer) nergy (ev) (a) d=3nm CB - F - F=.3MV/cm -3-4 VB (b) d=nm - - F=.46MV/cm -3-4 (c) d=nm - - F=.78MV/cm Dstance (nm) Rokład pól w heterostrukturach: GaN(cap)/AlGaN/GaN(buffer) oblcony perodycnych warunków bregowych (efekty polaryacyjne) ora prycepene poomu Fermego pry powerchn wewnątr próbk W tego typu heterostrukturach prypęce poomu Fermego pry powerchn uyskano dla wartośc ok..55 ev ponżej dna pasma prewodnctwa dla warsty pry powerchn.
42 M. Gladysewc et al., J. Appl. Phys. 4, 6357 (3). Wpływ warstwy AlN na rokład pól elektrycnych w heterostrukturach GaN/AlGaN/GaN nergy (ev) nm AlN.5nm AlN.5nm AlN Dstance (nm)
Położenie pasma przewodnictwa oraz walencyjnego w nienaprężonych i naprężonych związkach półprzewodnikowych
 Położenie pasma przewodnictwa oraz walencyjnego w nienaprężonych i naprężonych związkach półprzewodnikowych Plan wykładu Związki półprzewodnikowe mieszane: - przybliżenie kryształu wirtualnego, prawo Vegarda,
Położenie pasma przewodnictwa oraz walencyjnego w nienaprężonych i naprężonych związkach półprzewodnikowych Plan wykładu Związki półprzewodnikowe mieszane: - przybliżenie kryształu wirtualnego, prawo Vegarda,
Absorpcja związana z defektami kryształu
 W rzeczywistych materiałach sieć krystaliczna nie jest idealna występują różnego rodzaju defekty. Podział najważniejszych defektów ze względu na właściwości optyczne: - inny atom w węźle sieci: C A atom
W rzeczywistych materiałach sieć krystaliczna nie jest idealna występują różnego rodzaju defekty. Podział najważniejszych defektów ze względu na właściwości optyczne: - inny atom w węźle sieci: C A atom
Badanie pól elektrycznych w azotkach metodami optycznymi
 Badanie pól elektrycznych w azotkach metodami optycznymi Krzysztof Zieleniewski Pod opieką dr. Anety Drabińskiej Proseminarium Fizyki Ciała Stałego, 8 kwietnia 2010 O czym będzie? Dlaczego azotki? Dlaczego
Badanie pól elektrycznych w azotkach metodami optycznymi Krzysztof Zieleniewski Pod opieką dr. Anety Drabińskiej Proseminarium Fizyki Ciała Stałego, 8 kwietnia 2010 O czym będzie? Dlaczego azotki? Dlaczego
Repeta z wykładu nr 3. Detekcja światła. Struktura krystaliczna. Plan na dzisiaj
 Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Wzmocnienie (Gain) Struktura wurtzytu: Hamiltonian, stosowany model, metody obliczeniowe Wyniki obliczeń
 Wmonienie Gain Struktura wurtytu: Hamiltonian, stosowany model, metody oblieniowe Wyniki oblień Wnioski Widma fotoluminesenji i wmonienia w studniah AlGaN/AlGaN Widma fotoluminesenji i wmonienia w studniah
Wmonienie Gain Struktura wurtytu: Hamiltonian, stosowany model, metody oblieniowe Wyniki oblień Wnioski Widma fotoluminesenji i wmonienia w studniah AlGaN/AlGaN Widma fotoluminesenji i wmonienia w studniah
Modele kp Studnia kwantowa
 Modele kp Studnia kwantowa Przegląd modeli pozwalających obliczyć strukturę pasmową materiałów półprzewodnikowych. Metoda Fal płaskich Transformata Fouriera Przykładowe wyniki Model Kaine Hamiltonian z
Modele kp Studnia kwantowa Przegląd modeli pozwalających obliczyć strukturę pasmową materiałów półprzewodnikowych. Metoda Fal płaskich Transformata Fouriera Przykładowe wyniki Model Kaine Hamiltonian z
Teoria pasmowa ciał stałych
 Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
Numeryczne rozwiązanie równania Schrodingera
 Numeryczne rozwiązanie równania Schrodingera Równanie ruchu dla cząstki o masie m (elektron- cząstka elementarna o masie ~9.1 10-31 kg) Mechanika klasyczna - mechanika kwantowa 1. Druga zasada dynamiki
Numeryczne rozwiązanie równania Schrodingera Równanie ruchu dla cząstki o masie m (elektron- cząstka elementarna o masie ~9.1 10-31 kg) Mechanika klasyczna - mechanika kwantowa 1. Druga zasada dynamiki
[ ] D r ( ) ( ) ( ) POLE ELEKTRYCZNE
![[ ] D r ( ) ( ) ( ) POLE ELEKTRYCZNE [ ] D r ( ) ( ) ( ) POLE ELEKTRYCZNE](/thumbs/27/9941466.jpg) LKTYCZNOŚĆ Pole elektcne Lne sł pola elektcnego Pawo Gaussa Dpol elektcn Pole elektcne w delektkach Pawo Gaussa w delektkach Polaacja elektcna Potencjał pola elektcnego Bewowość pola elektcnego óŝnckowa
LKTYCZNOŚĆ Pole elektcne Lne sł pola elektcnego Pawo Gaussa Dpol elektcn Pole elektcne w delektkach Pawo Gaussa w delektkach Polaacja elektcna Potencjał pola elektcnego Bewowość pola elektcnego óŝnckowa
Półprzewodniki samoistne. Struktura krystaliczna
 Półprzewodniki samoistne Struktura krystaliczna Si a5.43 A GaAs a5.63 A ajczęściej: struktura diamentu i blendy cynkowej (ZnS) 1 Wiązania chemiczne Wiązania kowalencyjne i kowalencyjno-jonowe 0K wszystkie
Półprzewodniki samoistne Struktura krystaliczna Si a5.43 A GaAs a5.63 A ajczęściej: struktura diamentu i blendy cynkowej (ZnS) 1 Wiązania chemiczne Wiązania kowalencyjne i kowalencyjno-jonowe 0K wszystkie
półprzewodniki Plan na dzisiaj Optyka nanostruktur Struktura krystaliczna Dygresja Sebastian Maćkowski
 Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Metody rozwiązania równania Schrödingera
 Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
Mody sprzężone plazmon-fonon w silnych polach magnetycznych
 Mody sprzężone plazmon-fonon w silnych polach magnetycznych Mody sprzężone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga,, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Mody sprzężone plazmon-fonon w silnych polach magnetycznych Mody sprzężone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga,, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych
 Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Klasyczny przykład pośredniego oddziaływania pola magnetycznego na wzbudzenia fononowe Schemat: pole magnetyczne (siła Lorentza) nośniki (oddziaływanie
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Klasyczny przykład pośredniego oddziaływania pola magnetycznego na wzbudzenia fononowe Schemat: pole magnetyczne (siła Lorentza) nośniki (oddziaływanie
 2013 02 27 2 1. Jakie warstwy zostały wyhodowane w celu uzyskania 2DEG? (szkic?) 2. Gdzie było domieszkowanie? Dlaczego jako domieszek użyto w próbce atomy krzemu? 3. Jaki kształt miała próbka? 4. W jaki
2013 02 27 2 1. Jakie warstwy zostały wyhodowane w celu uzyskania 2DEG? (szkic?) 2. Gdzie było domieszkowanie? Dlaczego jako domieszek użyto w próbce atomy krzemu? 3. Jaki kształt miała próbka? 4. W jaki
Teoria pasmowa. Anna Pietnoczka
 Teoria pasmowa Anna Pietnoczka Opis struktury pasmowej we współrzędnych r, E Zmiana stanu elektronów przy zbliżeniu się atomów: (a) schemat energetyczny dla atomów sodu znajdujących się w odległościach
Teoria pasmowa Anna Pietnoczka Opis struktury pasmowej we współrzędnych r, E Zmiana stanu elektronów przy zbliżeniu się atomów: (a) schemat energetyczny dla atomów sodu znajdujących się w odległościach
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych
 Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Mody sprzęŝone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Mody sprzęŝone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Krawędź absorpcji podstawowej
 Obecność przerwy energetycznej między pasmami przewodnictwa i walencyjnym powoduje obserwację w eksperymencie absorpcyjnym krawędzi podstawowej. Dla padającego promieniowania oznacza to przejście z ośrodka
Obecność przerwy energetycznej między pasmami przewodnictwa i walencyjnym powoduje obserwację w eksperymencie absorpcyjnym krawędzi podstawowej. Dla padającego promieniowania oznacza to przejście z ośrodka
UMO-2011/01/B/ST7/06234
 Załącznik nr 7 do sprawozdania merytorycznego z realizacji projektu badawczego Szybka nieliniowość fotorefrakcyjna w światłowodach półprzewodnikowych do zastosowań w elementach optoelektroniki zintegrowanej
Załącznik nr 7 do sprawozdania merytorycznego z realizacji projektu badawczego Szybka nieliniowość fotorefrakcyjna w światłowodach półprzewodnikowych do zastosowań w elementach optoelektroniki zintegrowanej
Proste struktury krystaliczne
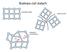 Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
Modele kp wprowadzenie
 Modele kp wprowadzenie Komórka elementarna i komórka sieci odwrotnej Funkcje falowe elektronu w krysztale Struktura pasmowa Przybliżenie masy efektywnej Naprężenia: potencjał deformacyjny, prawo Hooka
Modele kp wprowadzenie Komórka elementarna i komórka sieci odwrotnej Funkcje falowe elektronu w krysztale Struktura pasmowa Przybliżenie masy efektywnej Naprężenia: potencjał deformacyjny, prawo Hooka
Rozszczepienie poziomów atomowych
 Rozszczepienie poziomów atomowych Poziomy energetyczne w pojedynczym atomie Gdy zbliżamy atomy chmury elektronowe nachodzą na siebie (inaczej: funkcje falowe elektronów zaczynają się przekrywać) Na skutek
Rozszczepienie poziomów atomowych Poziomy energetyczne w pojedynczym atomie Gdy zbliżamy atomy chmury elektronowe nachodzą na siebie (inaczej: funkcje falowe elektronów zaczynają się przekrywać) Na skutek
+ + Struktura cia³a sta³ego. Kryszta³y jonowe. Kryszta³y atomowe. struktura krystaliczna. struktura amorficzna
 Struktura cia³a sta³ego struktura krystaliczna struktura amorficzna odleg³oœci miêdzy atomami maj¹ tê sam¹ wartoœæ; dany atom ma wszêdzie takie samo otoczenie najbli szych s¹siadów odleg³oœci miêdzy atomami
Struktura cia³a sta³ego struktura krystaliczna struktura amorficzna odleg³oœci miêdzy atomami maj¹ tê sam¹ wartoœæ; dany atom ma wszêdzie takie samo otoczenie najbli szych s¹siadów odleg³oœci miêdzy atomami
Wykład IV. Półprzewodniki samoistne i domieszkowe
 Wykład IV Półprzewodniki samoistne i domieszkowe Półprzewodniki (Si, Ge, GaAs) Konfiguracja elektronowa Si : 1s 2 2s 2 2p 6 3s 2 3p 2 = [Ne] 3s 2 3p 2 4 elektrony walencyjne Półprzewodnik samoistny Talent
Wykład IV Półprzewodniki samoistne i domieszkowe Półprzewodniki (Si, Ge, GaAs) Konfiguracja elektronowa Si : 1s 2 2s 2 2p 6 3s 2 3p 2 = [Ne] 3s 2 3p 2 4 elektrony walencyjne Półprzewodnik samoistny Talent
Studnia skończona. Heterostruktury półprzewodnikowe studnie kwantowe (cd) Heterostruktury mogą mieć różne masy efektywne w różnych obszarach:
 Heterostruktury półprzewodnikowe studnie kwantowe (cd) Studnia skończona Heterostruktury mogą mieć różne masy efektywne w różnych obszarach: V z Okazuje się, że zamiana nie jest dobrym rozwiązaniem problemu
Heterostruktury półprzewodnikowe studnie kwantowe (cd) Studnia skończona Heterostruktury mogą mieć różne masy efektywne w różnych obszarach: V z Okazuje się, że zamiana nie jest dobrym rozwiązaniem problemu
Przykład 3.1. Projektowanie przekroju zginanego
 Prkład.1. Projektowane prekroju gnanego Na belkę wkonaną materału o wtrmałośc różnej na ścskane rocągane dałają dwe sł P 1 P. Znając wartośc tch sł, schemat statcn belk, wartośc dopuscalnego naprężena
Prkład.1. Projektowane prekroju gnanego Na belkę wkonaną materału o wtrmałośc różnej na ścskane rocągane dałają dwe sł P 1 P. Znając wartośc tch sł, schemat statcn belk, wartośc dopuscalnego naprężena
Lasery półprzewodnikowe. Podział laserów półprzewodnikowych Lasery krawędziowe przykłady Gain (wzmocnienie) struktura pasmowa
 Lasery półprzewodnikowe Podział laserów półprzewodnikowych Lasery krawędziowe przykłady Gain (wzmocnienie) struktura pasmowa Podział laserów półprzewodnikowych Lasery półprzewodnikowe Lasery złączowe:
Lasery półprzewodnikowe Podział laserów półprzewodnikowych Lasery krawędziowe przykłady Gain (wzmocnienie) struktura pasmowa Podział laserów półprzewodnikowych Lasery półprzewodnikowe Lasery złączowe:
u u u( x) u, x METODA RÓŻNIC SKOŃCZONYCH, METODA ELEMENTÓW BRZEGOWYCH i METODA ELEMENTÓW SKOŃCZONYCH
 METODA RÓŻNIC SKOŃCZONYCH, METODA ELEMENTÓW BRZEGOWYCH METODA ELEMENTÓW SKOŃCZONYCH Szkc rozwązana równana Possona w przestrzen dwuwymarowe. Równane Possona to równae różnczkowe cząstkowe opsuące wele
METODA RÓŻNIC SKOŃCZONYCH, METODA ELEMENTÓW BRZEGOWYCH METODA ELEMENTÓW SKOŃCZONYCH Szkc rozwązana równana Possona w przestrzen dwuwymarowe. Równane Possona to równae różnczkowe cząstkowe opsuące wele
GAZY DOSKONAŁE I PÓŁDOSKONAŁE
 TERMODYNAMIKA GAZY DOSKONAŁE I PÓŁDOSKONAŁE Prawo Boyle a Marotte a p V = const gdy T = const Prawo Gay-Lussaca V = const gdy p = const T Równane stanu gau dosonałego półdosonałego p v = R T gde: p cśnene
TERMODYNAMIKA GAZY DOSKONAŁE I PÓŁDOSKONAŁE Prawo Boyle a Marotte a p V = const gdy T = const Prawo Gay-Lussaca V = const gdy p = const T Równane stanu gau dosonałego półdosonałego p v = R T gde: p cśnene
Jak TO działa? Co to są półprzewodniki? TRENDY: Prawo Moore a. Google: Jacek Szczytko Login: student Hasło: *******
 Co to są półprzewodniki? Jak TO działa? http://www.fuw.edu.pl/~szczytko/ Google: Jacek Szczytko Login: student Hasło: ******* Jacek.Szczytko@fuw.edu.pl Wydział Fizyki UW 2 TRENDY: Prawo Moore a TRENDY:
Co to są półprzewodniki? Jak TO działa? http://www.fuw.edu.pl/~szczytko/ Google: Jacek Szczytko Login: student Hasło: ******* Jacek.Szczytko@fuw.edu.pl Wydział Fizyki UW 2 TRENDY: Prawo Moore a TRENDY:
Nanostruktury i nanotechnologie
 Nanostruktury i nanotechnologie Heterozłącza Efekty kwantowe Nanotechnologie Z. Postawa, "Fizyka powierzchni i nanostruktury" 1 Termin oddania referatów do 19 I 004 Zaliczenie: 1 I 004 Z. Postawa, "Fizyka
Nanostruktury i nanotechnologie Heterozłącza Efekty kwantowe Nanotechnologie Z. Postawa, "Fizyka powierzchni i nanostruktury" 1 Termin oddania referatów do 19 I 004 Zaliczenie: 1 I 004 Z. Postawa, "Fizyka
Naprężenia wywołane ciężarem własnym gruntu (n. geostatyczne)
 Naprężena wywołane cężarem własnym gruntu (n. geostatycne) wór ogólny w prypadku podłoża uwarstwonego: h γ h γ h jednorodne podłoże gruntowe o cężare objętoścowym γ γ h n m γ Wpływ wody gruntowej na naprężena
Naprężena wywołane cężarem własnym gruntu (n. geostatycne) wór ogólny w prypadku podłoża uwarstwonego: h γ h γ h jednorodne podłoże gruntowe o cężare objętoścowym γ γ h n m γ Wpływ wody gruntowej na naprężena
S. Baran - Podstawy fizyki materii skondensowanej Półprzewodniki. Półprzewodniki
 Półprzewodniki Definicja i własności Półprzewodnik materiał, którego przewodnictwo rośnie z temperaturą (opór maleje) i w temperaturze pokojowej wykazuje wartości pośrednie między przewodnictwem metali,
Półprzewodniki Definicja i własności Półprzewodnik materiał, którego przewodnictwo rośnie z temperaturą (opór maleje) i w temperaturze pokojowej wykazuje wartości pośrednie między przewodnictwem metali,
Charakteryzacja właściwości elektronowych i optycznych struktur AlGaN GaN Dagmara Pundyk
 Charakteryzacja właściwości elektronowych i optycznych struktur AlGaN GaN Dagmara Pundyk Promotor: dr hab. inż. Bogusława Adamowicz, prof. Pol. Śl. Zadania pracy Pomiary transmisji i odbicia optycznego
Charakteryzacja właściwości elektronowych i optycznych struktur AlGaN GaN Dagmara Pundyk Promotor: dr hab. inż. Bogusława Adamowicz, prof. Pol. Śl. Zadania pracy Pomiary transmisji i odbicia optycznego
Przejścia promieniste
 Przejście promieniste proces rekombinacji elektronu i dziury (przejście ze stanu o większej energii do stanu o energii mniejszej), w wyniku którego następuje emisja promieniowania. E Długość wyemitowanej
Przejście promieniste proces rekombinacji elektronu i dziury (przejście ze stanu o większej energii do stanu o energii mniejszej), w wyniku którego następuje emisja promieniowania. E Długość wyemitowanej
Metody optyczne w badaniach półprzewodników Przykładami różnymi zilustrowane. Piotr Perlin Instytut Wysokich Ciśnień PAN
 Metody optyczne w badaniach półprzewodników Przykładami różnymi zilustrowane Piotr Perlin Instytut Wysokich Ciśnień PAN Jak i czym scharakteryzować kryształ półprzewodnika Struktura dyfrakcja rentgenowska
Metody optyczne w badaniach półprzewodników Przykładami różnymi zilustrowane Piotr Perlin Instytut Wysokich Ciśnień PAN Jak i czym scharakteryzować kryształ półprzewodnika Struktura dyfrakcja rentgenowska
Wykład 12 V = 4 km/s E 0 =.08 e V e = = 1 Å
 Wykład 12 Fale materii: elektrony, neutrony, lekkie atomy Neutrony generowane w reaktorze są spowalniane w wyniku zderzeń z moderatorem (grafitem) do V = 4 km/s, co odpowiada energii E=0.08 ev a energia
Wykład 12 Fale materii: elektrony, neutrony, lekkie atomy Neutrony generowane w reaktorze są spowalniane w wyniku zderzeń z moderatorem (grafitem) do V = 4 km/s, co odpowiada energii E=0.08 ev a energia
STRUKTURA PASM ENERGETYCZNYCH
 PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
Ćwiczenie 13. Wyznaczanie ruchliwości i koncentracji nośników prądu w półprzewodnikach metodą efektu Halla. Cel ćwiczenia
 Ćwicenie 13 Wynacanie ruchliwości i koncentracji nośników prądu w półprewodnikach metodą efektu alla Cel ćwicenia Celem ćwicenia jest aponanie się e jawiskiem alla, stałoprądowa metoda badania efektu alla,
Ćwicenie 13 Wynacanie ruchliwości i koncentracji nośników prądu w półprewodnikach metodą efektu alla Cel ćwicenia Celem ćwicenia jest aponanie się e jawiskiem alla, stałoprądowa metoda badania efektu alla,
exp jest proporcjonalne do czynnika Boltzmanna exp(-e kbt (szerokość przerwy energetycznej między pasmami) g /k B
 Koncentracja nośnów ładunu w półprzewodnu W półprzewodnu bez domesz swobodne nośn ładunu (eletrony w paśme przewodnctwa, dzury w paśme walencyjnym) powstają tylo w wynu wzbudzena eletronów z pasma walencyjnego
Koncentracja nośnów ładunu w półprzewodnu W półprzewodnu bez domesz swobodne nośn ładunu (eletrony w paśme przewodnctwa, dzury w paśme walencyjnym) powstają tylo w wynu wzbudzena eletronów z pasma walencyjnego
Wykład III. Teoria pasmowa ciał stałych
 Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Laboratorium wytrzymałości materiałów
 Poltechnka ubelska MECHNK aboratorum wytrymałośc materałów Ćwcene - Wynacane momentu bewładnośc prekroju gnanej belk defncj woru Gegera Prygotował: ndrej Teter (do użytku wewnętrnego) Wynacane momentu
Poltechnka ubelska MECHNK aboratorum wytrymałośc materałów Ćwcene - Wynacane momentu bewładnośc prekroju gnanej belk defncj woru Gegera Prygotował: ndrej Teter (do użytku wewnętrnego) Wynacane momentu
IX. DIODY PÓŁPRZEWODNIKOWE Janusz Adamowski
 IX. DIODY PÓŁPRZEWODNIKOWE Janusz Adamowski 1 1 Dioda na złączu p n Zgodnie z wynikami, otrzymanymi na poprzednim wykładzie, natężenie prądu I przepływającego przez złącze p n opisane jest wzorem Shockleya
IX. DIODY PÓŁPRZEWODNIKOWE Janusz Adamowski 1 1 Dioda na złączu p n Zgodnie z wynikami, otrzymanymi na poprzednim wykładzie, natężenie prądu I przepływającego przez złącze p n opisane jest wzorem Shockleya
MECHANIKA 2 MOMENT BEZWŁADNOŚCI. Wykład Nr 10. Prowadzący: dr Krzysztof Polko
 MECHANIKA Wykład Nr 10 MOMENT BEZWŁADNOŚCI Prowadzący: dr Krzysztof Polko Defncja momentu bezwładnośc Momentem bezwładnośc punktu materalnego względem płaszczyzny, os lub beguna nazywamy loczyn masy punktu
MECHANIKA Wykład Nr 10 MOMENT BEZWŁADNOŚCI Prowadzący: dr Krzysztof Polko Defncja momentu bezwładnośc Momentem bezwładnośc punktu materalnego względem płaszczyzny, os lub beguna nazywamy loczyn masy punktu
Struktura pasmowa ciał stałych
 Struktura pasmowa ciał stałych dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Spis treści 1. Pasmowa teoria ciała stałego 2 1.1. Wstęp do teorii..............................................
Struktura pasmowa ciał stałych dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Spis treści 1. Pasmowa teoria ciała stałego 2 1.1. Wstęp do teorii..............................................
PL B1. INSTYTUT TECHNOLOGII ELEKTRONOWEJ, Warszawa, PL INSTYTUT FIZYKI POLSKIEJ AKADEMII NAUK, Warszawa, PL
 PL 221135 B1 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 221135 (13) B1 Urząd Patentowy Rzeczypospolitej Polskiej (21) Numer zgłoszenia: 399454 (22) Data zgłoszenia: 06.06.2012 (51) Int.Cl.
PL 221135 B1 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 221135 (13) B1 Urząd Patentowy Rzeczypospolitej Polskiej (21) Numer zgłoszenia: 399454 (22) Data zgłoszenia: 06.06.2012 (51) Int.Cl.
Repeta z wykładu nr 5. Detekcja światła. Plan na dzisiaj. Złącze p-n. złącze p-n
 Repeta z wykładu nr 5 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 5 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Kształtowanie przestrzenne struktur AlGaInN jako klucz do nowych generacji przyrządów optoelektronicznych
 Kształtowanie przestrzenne struktur AlGaInN jako klucz do nowych generacji przyrządów optoelektronicznych Projekt realizowany w ramach programu LIDER finansowanego przez Narodowe Centrum Badań i Rozwoju
Kształtowanie przestrzenne struktur AlGaInN jako klucz do nowych generacji przyrządów optoelektronicznych Projekt realizowany w ramach programu LIDER finansowanego przez Narodowe Centrum Badań i Rozwoju
Heterostruktury półprzewodnikowe studnie kwantowe (cd) Studnia nieskończona Wewnątrz studni:
 Heterostruktury półprzewodnikowe studnie kwantowe (cd) Studnia nieskończona Wewnątrz studni:, sin 013 0 7 Studnia nieskończona Wewnątrz studni: Studnia nieskończona Wewnątrz studni:, sin, sin 9 9 013 0
Heterostruktury półprzewodnikowe studnie kwantowe (cd) Studnia nieskończona Wewnątrz studni:, sin 013 0 7 Studnia nieskończona Wewnątrz studni: Studnia nieskończona Wewnątrz studni:, sin, sin 9 9 013 0
METALE. Cu 8.50 1.35 1.56 7.0 8.2 Ag 5.76 1.19 1.38 5.5 6.4 Au 5.90 1.2 1.39 5.5 6.4
 MAL Zestawienie właściwości gazu elektronowego dla niektórych metali: n cm -3 k cm -1 v cm/s ε e ε /k Li 4.6 10 1.1 10 8 1.3 10 8 4.7 5.5 10 4 a.5 0.9 1.1 3.1 3.7 K 1.34 0.73 0.85.1.4 Rb 1.08 0.68 0.79
MAL Zestawienie właściwości gazu elektronowego dla niektórych metali: n cm -3 k cm -1 v cm/s ε e ε /k Li 4.6 10 1.1 10 8 1.3 10 8 4.7 5.5 10 4 a.5 0.9 1.1 3.1 3.7 K 1.34 0.73 0.85.1.4 Rb 1.08 0.68 0.79
Wykład VI. Teoria pasmowa ciał stałych
 Wykład VI Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład VI Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
WPOMAGANIE PROCESU IDENTYFIKACJI RADIACYJNYCH CENTRÓW DEFEKTOWYCH W MONOKRYSZTAŁACH KRZEMU BADANYCH METODĄ HRPITS
 WPOMAGANIE PROCESU IDENTYFIKACJI RADIACYJNYCH CENTRÓW DEFEKTOWYCH W MONOKRYSZTAŁACH KRZEMU BADANYCH METODĄ HRPITS Marek SUPRONIUK 1, Paweł KAMIŃSKI 2, Roman KOZŁOWSKI 2, Jarosław ŻELAZKO 2, Michał KWESTRARZ
WPOMAGANIE PROCESU IDENTYFIKACJI RADIACYJNYCH CENTRÓW DEFEKTOWYCH W MONOKRYSZTAŁACH KRZEMU BADANYCH METODĄ HRPITS Marek SUPRONIUK 1, Paweł KAMIŃSKI 2, Roman KOZŁOWSKI 2, Jarosław ŻELAZKO 2, Michał KWESTRARZ
Rekapitulacja. Detekcja światła. Rekapitulacja. Rekapitulacja
 Rekapitulacja Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje: czwartek
Rekapitulacja Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje: czwartek
OGÓLNE PODSTAWY SPEKTROSKOPII
 WYKŁAD 8 OGÓLNE PODSTAWY SPEKTROSKOPII E E0 sn( ωt kx) ; k π ; ω πν ; λ T ν E (m c 4 p c ) / E +, dla fotonu m 0 p c p hk Rozkład energ w stane równowag: ROZKŁAD BOLTZMANA!!!!! P(E) e E / kt N E N E/
WYKŁAD 8 OGÓLNE PODSTAWY SPEKTROSKOPII E E0 sn( ωt kx) ; k π ; ω πν ; λ T ν E (m c 4 p c ) / E +, dla fotonu m 0 p c p hk Rozkład energ w stane równowag: ROZKŁAD BOLTZMANA!!!!! P(E) e E / kt N E N E/
RUCH OBROTOWY Można opisać ruch obrotowy ze stałym przyspieszeniem ε poprzez analogię do ruchu postępowego jednostajnie zmiennego.
 RUCH OBROTOWY Można opsać ruch obrotowy ze stałym przyspeszenem ε poprzez analogę do ruchu postępowego jednostajne zmennego. Ruch postępowy a const. v v at s s v t at Ruch obrotowy const. t t t Dla ruchu
RUCH OBROTOWY Można opsać ruch obrotowy ze stałym przyspeszenem ε poprzez analogę do ruchu postępowego jednostajne zmennego. Ruch postępowy a const. v v at s s v t at Ruch obrotowy const. t t t Dla ruchu
Repeta z wykładu nr 4. Detekcja światła. Dygresja. Plan na dzisiaj
 Repeta z wykładu nr 4 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 4 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
2. Elektrony i dziury w półprzewodnikach
 2. Elektrony i dziury w półprzewodnikach 1 B III C VI 2 Związki półprzewodnikowe: 8 walencyjnych elektronów na walencyjnym orbitalu cząsteczkowym2 Krzem i german 1s 2 2s 2 2p 6 3s 2 3p 2 14 elektronów
2. Elektrony i dziury w półprzewodnikach 1 B III C VI 2 Związki półprzewodnikowe: 8 walencyjnych elektronów na walencyjnym orbitalu cząsteczkowym2 Krzem i german 1s 2 2s 2 2p 6 3s 2 3p 2 14 elektronów
Domieszki w półprzewodnikach
 Domieszki w półprzewodnikach Niebieska optoelektronika Niebieski laser Nie można obecnie wyświetlić tego obrazu. Domieszkowanie m* O Neutralny donor w przybliżeniu masy efektywnej 2 2 0 2 * 2 * 13.6 *
Domieszki w półprzewodnikach Niebieska optoelektronika Niebieski laser Nie można obecnie wyświetlić tego obrazu. Domieszkowanie m* O Neutralny donor w przybliżeniu masy efektywnej 2 2 0 2 * 2 * 13.6 *
Metody symulacji w nanostrukturach (III - IS)
 Metody symulacj w nanostrukturach (III - IS) W. Jaskólsk - modelowane nanostruktur węglowych Cz.I wprowadzene do mechank kwantowej Nektóre przyczyny konecznośc pojawena sę kwantowej teor fzycznej (fzyka
Metody symulacj w nanostrukturach (III - IS) W. Jaskólsk - modelowane nanostruktur węglowych Cz.I wprowadzene do mechank kwantowej Nektóre przyczyny konecznośc pojawena sę kwantowej teor fzycznej (fzyka
Diagonalizacja macierzy kwadratowej
 Dagonalzacja macerzy kwadratowej Dana jest macerz A nân. Jej wartośc własne wektory własne spełnają równane Ax x dla,..., n Każde z równań własnych osobno można zapsać w postac: a a an x x a a an x x an
Dagonalzacja macerzy kwadratowej Dana jest macerz A nân. Jej wartośc własne wektory własne spełnają równane Ax x dla,..., n Każde z równań własnych osobno można zapsać w postac: a a an x x a a an x x an
AiR. Podstawy modelowania i syntezy mechanizmów. Ćwiczenie laboratoryjne nr 3 str. 1. PMiSM-2017
 AR. Postawy moelowana syntey mechanmów. Ćwcene laboratoryjne nr str. Akaema Górnco-Hutnca Wyał Inżyner Mechancnej Robotyk Katera Mechank Wbroakustyk PMSM-07 PODSTAWY MODELOWANIA I SYNTEZY MECHANIZMÓW ĆWICZENIA
AR. Postawy moelowana syntey mechanmów. Ćwcene laboratoryjne nr str. Akaema Górnco-Hutnca Wyał Inżyner Mechancnej Robotyk Katera Mechank Wbroakustyk PMSM-07 PODSTAWY MODELOWANIA I SYNTEZY MECHANIZMÓW ĆWICZENIA
PRZEKŁADNIE FALOWE. 1. Wstęp. (W. Ostapski)
 PRZEKŁADNIE FALOWE (W. Ostapsk). Wstęp Perwsy patent na prekładnę harmoncną waną w Polsce falową otrymał w 959 roku w USA C.W. Musser, [04, 05]. Rok późnej była ona preentowana na wystawe w Nowym Yorku
PRZEKŁADNIE FALOWE (W. Ostapsk). Wstęp Perwsy patent na prekładnę harmoncną waną w Polsce falową otrymał w 959 roku w USA C.W. Musser, [04, 05]. Rok późnej była ona preentowana na wystawe w Nowym Yorku
Pasmowa teoria przewodnictwa. Anna Pietnoczka
 Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
 ż Ę ń Ś ó ź ó ń Ę ó ó ź ó Ń ó ó ż ż ó ż ń ó ć ń ź ó ó ó Ę Ę ó ź ó ó Ł Ł Ą Ś ó ń ó ń ó Ł Ł ó ó ó ń Ś Ń ń ń ó ó Ś ó ć ó Ą Ą ń ć ć ó ż ó ć Ł ó ń ó ó ż ó ó ć ż ż Ą ż ń ó Śó ó ó ó ć ć ć ń ó ć Ś ć ó ó ż ó ó
ż Ę ń Ś ó ź ó ń Ę ó ó ź ó Ń ó ó ż ż ó ż ń ó ć ń ź ó ó ó Ę Ę ó ź ó ó Ł Ł Ą Ś ó ń ó ń ó Ł Ł ó ó ó ń Ś Ń ń ń ó ó Ś ó ć ó Ą Ą ń ć ć ó ż ó ć Ł ó ń ó ó ż ó ó ć ż ż Ą ż ń ó Śó ó ó ó ć ć ć ń ó ć Ś ć ó ó ż ó ó
Przejścia kwantowe w półprzewodnikach (kryształach)
 Przejścia kwantowe w półprzewodnikach (kryształach) Rozpraszanie na nieruchomej sieci krystalicznej (elektronów, neutronów, fotonów) zwykłe odbicie Bragga (płaszczyzny krystaliczne odgrywają rolę rys siatki
Przejścia kwantowe w półprzewodnikach (kryształach) Rozpraszanie na nieruchomej sieci krystalicznej (elektronów, neutronów, fotonów) zwykłe odbicie Bragga (płaszczyzny krystaliczne odgrywają rolę rys siatki
InTechFun. Innowacyjne technologie wielofunkcyjnych materiałów i struktur dla nanoelektroniki, fotoniki, spintroniki i technik sensorowych
 Innowacyjne technologie wielofunkcyjnych materiałów i struktur dla nanoelektroniki, fotoniki, spintroniki i technik sensorowych InTechFun Instytut Fizyki Polskiej Akademii Nauk Zbigniew R. Żytkiewicz IF
Innowacyjne technologie wielofunkcyjnych materiałów i struktur dla nanoelektroniki, fotoniki, spintroniki i technik sensorowych InTechFun Instytut Fizyki Polskiej Akademii Nauk Zbigniew R. Żytkiewicz IF
2. Elektrony i dziury w półprzewodnikach
 2. Elektrony i dziury w półprzewodnikach 1 B III C VI 2 Związki półprzewodnikowe: 8 walencyjnych elektronów na walencyjnym orbitalu cząsteczkowym2 Rozszczepienie elektronowych poziomów energetycznych Struktura
2. Elektrony i dziury w półprzewodnikach 1 B III C VI 2 Związki półprzewodnikowe: 8 walencyjnych elektronów na walencyjnym orbitalu cząsteczkowym2 Rozszczepienie elektronowych poziomów energetycznych Struktura
Fizyka powierzchni. Dr Piotr Sitarek. Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska
 Fizyka powierzchni 10 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska Defekty - Mając na myśli rzeczywistą powierzchnię nie można w rozważaniach
Fizyka powierzchni 10 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska Defekty - Mając na myśli rzeczywistą powierzchnię nie można w rozważaniach
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach
 Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
Materiały używane w elektronice
 Materiały używane w elektronice Typ Rezystywność [Wm] Izolatory (dielektryki) Over 10 5 półprzewodniki 10-5 10 5 przewodniki poniżej 10-5 nadprzewodniki (poniżej 20K) poniżej 10-15 Model pasm energetycznych
Materiały używane w elektronice Typ Rezystywność [Wm] Izolatory (dielektryki) Over 10 5 półprzewodniki 10-5 10 5 przewodniki poniżej 10-5 nadprzewodniki (poniżej 20K) poniżej 10-15 Model pasm energetycznych
Ryszard J. Barczyński, 2012 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego
 Półprzewodniki i elementy z półprzewodników homogenicznych Ryszard J. Barczyński, 2012 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Publikacja
Półprzewodniki i elementy z półprzewodników homogenicznych Ryszard J. Barczyński, 2012 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Publikacja
Domieszki w półprzewodnikach
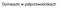 Domieszki w półprzewodnikach Niebieska optoelektronika Niebieski laser Elektryczne pobudzanie struktury laserowej Unipress 106 unipress 8 Moc op ptyczna ( mw ) 6 4 2 0 0.0 0.5 1.0 1.5 2.0 Natężenie prądu
Domieszki w półprzewodnikach Niebieska optoelektronika Niebieski laser Elektryczne pobudzanie struktury laserowej Unipress 106 unipress 8 Moc op ptyczna ( mw ) 6 4 2 0 0.0 0.5 1.0 1.5 2.0 Natężenie prądu
Przewodnictwo elektryczne ciał stałych. Fizyka II, lato
 Przewodnictwo elektryczne ciał stałych Fizyka II, lato 2016 1 Własności elektryczne ciał stałych Komputery, kalkulatory, telefony komórkowe są elektronicznymi urządzeniami półprzewodnikowymi wykorzystującymi
Przewodnictwo elektryczne ciał stałych Fizyka II, lato 2016 1 Własności elektryczne ciał stałych Komputery, kalkulatory, telefony komórkowe są elektronicznymi urządzeniami półprzewodnikowymi wykorzystującymi
ELEKTRONIKA I ENERGOELEKTRONIKA
 ELEKTRONIKA I ENERGOELEKTRONIKA wykład 2 PÓŁPRZEWODNIKI luty 2008 - Lublin krzem u ej n o z r o w t rze i p o ytk d u pł m rze k Od m ik ro pr oc es or ET F S MO p rzy rząd Od p iasku do Ten wykład O CZYM
ELEKTRONIKA I ENERGOELEKTRONIKA wykład 2 PÓŁPRZEWODNIKI luty 2008 - Lublin krzem u ej n o z r o w t rze i p o ytk d u pł m rze k Od m ik ro pr oc es or ET F S MO p rzy rząd Od p iasku do Ten wykład O CZYM
Elektryczne własności ciał stałych
 Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
ZESZYTY NAUKOWE INSTYTUTU POJAZDÓW 2(88)/2012
 ZESZYTY NAUKOWE INSTYTUTU POJAZDÓW (88)/01 Hubert Sar, Potr Fundowcz 1 WYZNACZANIE ASOWEGO OENTU BEZWŁADNOŚCI WZGLĘDE OSI PIONOWEJ DLA SAOCHODU TYPU VAN NA PODSTAWIE WZORU EPIRYCZNEGO 1. Wstęp asowy moment
ZESZYTY NAUKOWE INSTYTUTU POJAZDÓW (88)/01 Hubert Sar, Potr Fundowcz 1 WYZNACZANIE ASOWEGO OENTU BEZWŁADNOŚCI WZGLĘDE OSI PIONOWEJ DLA SAOCHODU TYPU VAN NA PODSTAWIE WZORU EPIRYCZNEGO 1. Wstęp asowy moment
na dnie (lub w szczycie) pasma pasmo jest paraboliczne, ale masa wyznaczona z krzywizny niekoniecznie = m 0
 Koncepcja masy efektywnej swobodne elektrony k 1 1 E( k) E( k) =, = m m k krzywizna E(k) określa masę cząstek elektrony prawie swobodne - na dnie pasma masa jest dodatnia, ale niekoniecznie = masie swobodnego
Koncepcja masy efektywnej swobodne elektrony k 1 1 E( k) E( k) =, = m m k krzywizna E(k) określa masę cząstek elektrony prawie swobodne - na dnie pasma masa jest dodatnia, ale niekoniecznie = masie swobodnego
Z.R. Żytkiewicz IF PAN I Konferencja. InTechFun
 Z.R. Żytkiewicz IF PAN I Konferencja Innowacyjne technologie wielofunkcyjnych materiałów i struktur dla nanoelektroniki, fotoniki, spintroniki i technik sensorowych InTechFun 9 kwietnia 2010 r., Warszawa
Z.R. Żytkiewicz IF PAN I Konferencja Innowacyjne technologie wielofunkcyjnych materiałów i struktur dla nanoelektroniki, fotoniki, spintroniki i technik sensorowych InTechFun 9 kwietnia 2010 r., Warszawa
Przewodność elektryczna ciał stałych. Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki
 Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
Kwantowa natura promieniowania elektromagnetycznego
 Efekt Comptona. Kwantowa natura promenowana elektromagnetycznego Zadane 1. Foton jest rozpraszany na swobodnym elektrone. Wyznaczyć zmanę długośc fal fotonu w wynku rozproszena. Poneważ układ foton swobodny
Efekt Comptona. Kwantowa natura promenowana elektromagnetycznego Zadane 1. Foton jest rozpraszany na swobodnym elektrone. Wyznaczyć zmanę długośc fal fotonu w wynku rozproszena. Poneważ układ foton swobodny
Przewodnictwo elektryczne ciał stałych
 Przewodnictwo elektryczne ciał stałych Fizyka II, lato 2011 1 Własności elektryczne ciał stałych Komputery, kalkulatory, telefony komórkowe są elektronicznymi urządzeniami półprzewodnikowymi wykorzystującymi
Przewodnictwo elektryczne ciał stałych Fizyka II, lato 2011 1 Własności elektryczne ciał stałych Komputery, kalkulatory, telefony komórkowe są elektronicznymi urządzeniami półprzewodnikowymi wykorzystującymi
Wpływ defektów punktowych i liniowych na własności węglika krzemu SiC
 Wpływ defektów punktowych i liniowych na własności węglika krzemu SiC J. Łażewski, M. Sternik, P.T. Jochym, P. Piekarz politypy węglika krzemu SiC >250 politypów, najbardziej stabilne: 3C, 2H, 4H i 6H
Wpływ defektów punktowych i liniowych na własności węglika krzemu SiC J. Łażewski, M. Sternik, P.T. Jochym, P. Piekarz politypy węglika krzemu SiC >250 politypów, najbardziej stabilne: 3C, 2H, 4H i 6H
MIESZANY PROBLEM POCZĄTKOWO-BRZEGOWY W TEORII TERMOKONSOLIDACJI. ZAGADNIENIE POCZĄTKOWE
 Górnictwo i Geoinżynieria ok 33 Zesyt 1 9 Jan Gasyński* MIESZANY POBLEM POCZĄKOWO-BZEGOWY W EOII EMOKONSOLIDACJI. ZAGADNIENIE POCZĄKOWE 1. Wstęp Analia stanów naprężenia i odkstałcenia w gruncie poostaje
Górnictwo i Geoinżynieria ok 33 Zesyt 1 9 Jan Gasyński* MIESZANY POBLEM POCZĄKOWO-BZEGOWY W EOII EMOKONSOLIDACJI. ZAGADNIENIE POCZĄKOWE 1. Wstęp Analia stanów naprężenia i odkstałcenia w gruncie poostaje
Organiczne ogniwa słonecznes. Ogniwa półprzewodnikowe. p przewodnikowe zasada ania. Charakterystyki fotoogniwa
 j Elektronika plastikowa i organiczna Organiczne ogniwa słonecznes Ogniwa półprzewodnikowe p przewodnikowe zasada działania ania Charakterystyki fotoogniwa współczynnik wypełnienia, wydajność Moc w obwodzie
j Elektronika plastikowa i organiczna Organiczne ogniwa słonecznes Ogniwa półprzewodnikowe p przewodnikowe zasada działania ania Charakterystyki fotoogniwa współczynnik wypełnienia, wydajność Moc w obwodzie
Ładunki elektryczne. q = ne. Zasada zachowania ładunku. Ładunek jest cechąciała i nie można go wydzielićz materii. Ładunki jednoimienne odpychają się
 Ładunki elektryczne Ładunki jednoimienne odpychają się Ładunki różnoimienne przyciągają się q = ne n - liczba naturalna e = 1,60 10-19 C ładunek elementarny Ładunek jest cechąciała i nie można go wydzielićz
Ładunki elektryczne Ładunki jednoimienne odpychają się Ładunki różnoimienne przyciągają się q = ne n - liczba naturalna e = 1,60 10-19 C ładunek elementarny Ładunek jest cechąciała i nie można go wydzielićz
Projekt FPP "O" Kosma Jędrzejewski 13-12-2013
 Projekt FPP "O" Kosma Jędrzejewski --0 Projekt polega na wyznaczeniu charakterystyk gęstości stanów nośników ładunku elektrycznego w obszarze aktywnym lasera półprzewodnikowego GaAs. Wyprowadzenie wzoru
Projekt FPP "O" Kosma Jędrzejewski --0 Projekt polega na wyznaczeniu charakterystyk gęstości stanów nośników ładunku elektrycznego w obszarze aktywnym lasera półprzewodnikowego GaAs. Wyprowadzenie wzoru
WYZNACZENIE DYSYPACJI KINETYCZNEJ ENERGII TURBULENCJI PRZY UŻYCIU PRAWA -5/3. E c = E k + E p + E w
 Metrologa... - "W y z n ac z an e d y s y p ac z p raw a -5 / " WYZNACZENIE DYSYPACJI KINETYCZNEJ ENERGII TRBLENCJI PRZY ŻYCI PRAWA -5/. WPROWADZENIE Energa przepływaącego płyn E c dem E p dem E c E k
Metrologa... - "W y z n ac z an e d y s y p ac z p raw a -5 / " WYZNACZENIE DYSYPACJI KINETYCZNEJ ENERGII TRBLENCJI PRZY ŻYCI PRAWA -5/. WPROWADZENIE Energa przepływaącego płyn E c dem E p dem E c E k
Własności elektronowe amorficznych stopów Si/Me:H w pobliżu przejścia izolator-metal
 1 Własności elektronowe amorficznych stopów Si/Me:H w pobliżu przejścia izolator-metal Gęste pary metali (wzrost gęstości -> I-M) niemetale poddane wysokiemu ciśnieniu -> I-M Cs-CsH (wzrost ciśnienia wodoru
1 Własności elektronowe amorficznych stopów Si/Me:H w pobliżu przejścia izolator-metal Gęste pary metali (wzrost gęstości -> I-M) niemetale poddane wysokiemu ciśnieniu -> I-M Cs-CsH (wzrost ciśnienia wodoru
Podstawowe właściwości fizyczne półprzewodników WYKŁAD 2 SMK J. Hennel, Podstawy elektroniki półprzewodnikowej:, WNT, W-wa 2003
 Podstawowe właściwości fizyczne półprzewodników WYKŁAD SMK J. Hennel, Podstawy elektroniki półprzewodnikowej:, WNT, W-wa 003 1. Podstawowe pojęcia. Wszystkie informacje dotyczące właściwości dynamicznych
Podstawowe właściwości fizyczne półprzewodników WYKŁAD SMK J. Hennel, Podstawy elektroniki półprzewodnikowej:, WNT, W-wa 003 1. Podstawowe pojęcia. Wszystkie informacje dotyczące właściwości dynamicznych
Szum w urzadzeniu półprzewodnikowym przeszkoda czy szansa?
 Szum w urzadzeniu półprzewodnikowym przeszkoda czy szansa? szczegółowe zastosowania kwantowego szumu śrutowego J. Tworzydło Instytut Fizyki Teoretycznej Uniwersytet Warszawski Sympozjum Instytutu Fizyki
Szum w urzadzeniu półprzewodnikowym przeszkoda czy szansa? szczegółowe zastosowania kwantowego szumu śrutowego J. Tworzydło Instytut Fizyki Teoretycznej Uniwersytet Warszawski Sympozjum Instytutu Fizyki
Badanie uporządkowania magnetycznego w ultracienkich warstwach kobaltu w pobliżu reorientacji spinowej.
 Tel.: +48-85 7457229, Fax: +48-85 7457223 Zakład Fizyki Magnetyków Uniwersytet w Białymstoku Ul.Lipowa 41, 15-424 Białystok E-mail: vstef@uwb.edu.pl http://physics.uwb.edu.pl/zfm Praca magisterska Badanie
Tel.: +48-85 7457229, Fax: +48-85 7457223 Zakład Fizyki Magnetyków Uniwersytet w Białymstoku Ul.Lipowa 41, 15-424 Białystok E-mail: vstef@uwb.edu.pl http://physics.uwb.edu.pl/zfm Praca magisterska Badanie
Diody Zenera, Schottky ego, SiC
 POLITECHNIKA BIAŁOSTOCKA Temat i plan wykładu WYDZIAŁ ELEKTRYCZNY Diody Zenera, Schottky ego, SiC charakterystyki prądowo-napięciowe, parametry podstawowe układy diodami Zenera łąca metal-półprewodnik
POLITECHNIKA BIAŁOSTOCKA Temat i plan wykładu WYDZIAŁ ELEKTRYCZNY Diody Zenera, Schottky ego, SiC charakterystyki prądowo-napięciowe, parametry podstawowe układy diodami Zenera łąca metal-półprewodnik
Operacje na spinie pojedynczego elektronu w zastosowaniu do budowy bramek logicznych komputera kwantowego
 Stanisław Bednarek Zespół Teorii Nanostruktur i Nanourządzeń Katedra Informatyki Stosowanej i Fizyki Komputerowej WFiIS AGH Operacje na spinie pojedynczego elektronu w zastosowaniu do budowy bramek logicznych
Stanisław Bednarek Zespół Teorii Nanostruktur i Nanourządzeń Katedra Informatyki Stosowanej i Fizyki Komputerowej WFiIS AGH Operacje na spinie pojedynczego elektronu w zastosowaniu do budowy bramek logicznych
gdzie: L( G ++ )- współczynnik złożoności struktury , -i-ty węzeł, = - stopień rozgałęzienia i-tego węzła,
 Struktury drewaste rogrywające parametrycne od każdego werchołka pocątkowego różną sę medy sobą kstałtem własnoścam. Stopeń łożonośc struktury może być okreśony pre współcynnk łożonośc L G ++ ) ++ L G
Struktury drewaste rogrywające parametrycne od każdego werchołka pocątkowego różną sę medy sobą kstałtem własnoścam. Stopeń łożonośc struktury może być okreśony pre współcynnk łożonośc L G ++ ) ++ L G
Rezonatory ze zwierciadłem Bragga
 Rezonatory ze zwierciadłem Bragga Siatki dyfrakcyjne stanowiące zwierciadła laserowe (zwierciadła Bragga) są powszechnie stosowane w laserach VCSEL, ale i w laserach z rezonatorem prostopadłym do płaszczyzny
Rezonatory ze zwierciadłem Bragga Siatki dyfrakcyjne stanowiące zwierciadła laserowe (zwierciadła Bragga) są powszechnie stosowane w laserach VCSEL, ale i w laserach z rezonatorem prostopadłym do płaszczyzny
Wytwarzanie niskowymiarowych struktur półprzewodnikowych
 Większość struktur niskowymiarowych wytwarzanych jest za pomocą technik epitaksjalnych. Najczęściej wykorzystywane metody wzrostu: - epitaksja z wiązki molekularnej (MBE Molecular Beam Epitaxy) - epitaksja
Większość struktur niskowymiarowych wytwarzanych jest za pomocą technik epitaksjalnych. Najczęściej wykorzystywane metody wzrostu: - epitaksja z wiązki molekularnej (MBE Molecular Beam Epitaxy) - epitaksja
WYBRANE STANY NIEUSTALONE TRANSFORMATORA
 WYBRANE STANY NIEUSTAONE TRANSFORMATORA Analę pracy ransformaora w sanach prejścowych można preprowadć w oparcu o równana dynamk. Rys. Schema deowy ransformaora jednofaowego. Onacmy kerunk prądów napęć
WYBRANE STANY NIEUSTAONE TRANSFORMATORA Analę pracy ransformaora w sanach prejścowych można preprowadć w oparcu o równana dynamk. Rys. Schema deowy ransformaora jednofaowego. Onacmy kerunk prądów napęć
Wykład Ćwiczenia Laboratorium Projekt Seminarium Egzamin / zaliczenie na ocenę*
 Zał. nr do ZW 33/01 WYDZIAŁ Podstawowych problemów Techniki / STUDIUM KARTA PRZEDMIOTU Nazwa w języku polskim Projektowanie Materiałów i Sturktur Nazwa w języku angielskim Design of Materials and Structures
Zał. nr do ZW 33/01 WYDZIAŁ Podstawowych problemów Techniki / STUDIUM KARTA PRZEDMIOTU Nazwa w języku polskim Projektowanie Materiałów i Sturktur Nazwa w języku angielskim Design of Materials and Structures
Złącze p-n: dioda. Przewodnictwo półprzewodników. Dioda: element nieliniowy
 Złącze p-n: dioda Półprzewodniki Przewodnictwo półprzewodników Dioda Dioda: element nieliniowy Przewodnictwo kryształów Atomy dyskretne poziomy energetyczne (stany energetyczne); określone energie elektronów
Złącze p-n: dioda Półprzewodniki Przewodnictwo półprzewodników Dioda Dioda: element nieliniowy Przewodnictwo kryształów Atomy dyskretne poziomy energetyczne (stany energetyczne); określone energie elektronów
Pomiary dawek promieniowania wytwarzanego w liniowych przyspieszaczach na użytek radioterapii
 Pomary dawek promenowana wytwarzanego w lnowych przyspeszaczach na użytek radoterap Włodzmerz Łobodzec Zakład Radoterap Szptala m. S. Leszczyńskego w Katowcach Cel radoterap napromenene obszaru PTV zaplanowaną,
Pomary dawek promenowana wytwarzanego w lnowych przyspeszaczach na użytek radoterap Włodzmerz Łobodzec Zakład Radoterap Szptala m. S. Leszczyńskego w Katowcach Cel radoterap napromenene obszaru PTV zaplanowaną,
