2. Elektrony i dziury w półprzewodnikach
|
|
|
- Alina Rosińska
- 8 lat temu
- Przeglądów:
Transkrypt
1 2. Elektrony i dziury w półprzewodnikach 1
2 B III C VI 2 Związki półprzewodnikowe: 8 walencyjnych elektronów na walencyjnym orbitalu cząsteczkowym2
3 Krzem i german 1s 2 2s 2 2p 6 3s 2 3p 2 14 elektronów 1s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 2 4p 2 32 elektrony 3
4 Pasma energetyczne w ciałach stałych Poziomy energetyczne w pojedynczym atomie oddziaływanie z elektronami na sąsiednich atomach (zakaz Pauliego) rozszczepienie poziomów w pasma liczba poziomów w paśmie: (2l+1)*N atomów 4
5 Rozszczepienie poziomów energetycznych w ciele stałym cd puste pasmo przewodnictwa energia poziomy energetyczne w atomie wypełnione pasmo walencyjne wypełnione pasma w ciele stałym 5
6 Związki półprzewodnikowe III-V E g [ev] GaN 3.4 GaP 2.25 GaAs 1.52 GaSb 0.81 II-VI E g [ev] ZnS 3.54 ZnSe 2.7 ZnTe 2.25 CdTe 1.56 HgTe Zamknieta powłoka walencyjna Małe atomy mniejsza stała sieci silniejsze oddziaływanie większa przerwa energetyczna 6
7 Rodzaje struktury ciał stałych 7
8 Symetria translacyjna R n 1 a 1 + n 2 a 2 + n 3 a 3 Komórka elementarna podstawowa cegiełka, może zawierać więcej niż jeden atom Komórka prosta wyznaczona przez wektory a 1, a 2, a 3 Np. sieć regularna przestrzennie centrowana 8
9 2 2 h 2m Opis kwantowy elektronu w sieci periodycznej Elektron w pustej przestrzeni ΔΨ EΨ Ψ k Ae 2 h 2 ΔΨ + UΨ EΨ 2m r r Ψ(r) Ψ(R + r) r r ikr k p r r r U(r) U(R + ) r r ikr 2π λ h λ hk hk 2π Elektron w potencjale periodycznym Ψ Funkcja Blocha funkcja falowa opisująca elektron w polu periodycznym, wektor k określa stan elektronu k u k (r)e u k (r) u k (r+r) relacja de Broghlie a k - wektor quasi-falowy odpowiada quasi-pędowi elektronu pħk W idealnej sieci bez zewnętrznych zaburzeń elektron ma stały quasi-pęd: kconst 9
10 Periodyczność w przestrzeni: xx+a: Ψ u k (x)e ikx u k (x+a)e ik(x+a) periodyczność quasi-pędu: kk+2π/a Ψ u k (x)e ikx u k+2π/a (x)e i(k+2π/a)x Zależność E(k) to ekwiwalent zależności E(p)! E(k) dla swobodnego elektronu E(k) dla elektronu w periodycznej sieci E(k)E(k+2π/a) Energia elektronu w periodycznej sieci jest periodyczną funkcją pędu (czyli k) Ograniczony zakres quasi-pędu (-π/a, π/a) wystarczy żeby w pełni opisać elektron I strefa Brillouine a -π/a 0 π/a -π/a π/a k 10
11 Struktura elektronowa półprzewodników 2 p swobodny elektron w próżni: E(p) 2m elektron w sieci periodycznej w pobliżu ekstremów E(p) 2 p 2m * 2 2 h k 2m * E(k) Pasmo przew m* - masa efektywna elektronu w pasmie r r hk Prędkość translacyjna elektronu v m* k Pasmo walenc Dynamika elektronu: r dp dt r dk h m * dt r dv dt r F zew m* m e - uwzględnia odziaływanie elektronu z siecią 11
12 Model Kroniga-Penneya (słabo związany elektron) h 2m m h 2m 2 2 ΔΨ ΔΨ EΨ + UΨ o 0 < r < a EΨ b < r < 0 Ψ 1 Ae ikx + Be ikx, k 2mE 2 h Ψ 1 Ψ( x ) Ae κx + Be U ( x ) e κx ikx, κ 2m( U h o 2 E ) U o i b 0 tak, że U o b const 12
13 Model Kroniga-Penney a - rozwiązania jeśli U o i b 0 tak, że U o b const warunek na dozwolone poziomy energetyczne P P sin ka ka ma h + cos ka cos Ka 2 bu o P3 ka
14 Elektrony i dziury generacja termiczna pary elektron-dziura - pasmo przewodnictwa E F + pasmo walencyjne CB VB CB CB VB CB VB VB 14
15 Dziura w pasmie walencyjnym E E e h 2 2 h k E c + 2m e * ładunek dziury -(ładunek elektronu) k 2 2 h -k ev h k E v + E h -E ev 2m * h 15
16 Przerwa prosta i przerwa skośna przerwa prosta GaAs, CdS, CdSe, ZnS, InSb, HgTe, GaN przerwa skośna Si, Ge, GaP, AlAs 16
17 Struktura pasmowa - przykłady Si GaAs K Przerwa prosta k Przerwa skośna wave vector k k 17
18 Półprzewodniki mieszane (roztwory stałe) Hg 1-x Cd x Te Zastąpienie części atomów związku atomami o tej samej liczbie elektronów walencyjnych regulacja szerokości przerwy energetycznej 18
19 Półprzewodniki mieszane Al x Ga 1-x As GaAs Al 0.5 Ga 0.5 As AlAs 19
20 Koncentracja swobodnych elektronów w paśmie przewodnictwa i dziur w pasmie walencyjnym Zależy od tego ile jest stanów w paśmie - gęstość stanów - g(e) jakie jest prawdopodobieństwo że elektron ma energię E - f(e) 20
21 Prawdopodobieństwo - rozkład Fermiego-Diraca prawdopodobienstwo f(e) k B T T0 T 1 >0 T 2 >T 1 E F energia E E F - poziom Fermiego, f(e F ) ½ T f f e e (E) 1dla E < (E) 0 K : T > 0 K f e (E) E 0 dla E > E 1 E E 1+ exp kbt F F F 21
22 Koncentracja elektronów w paśmie przewodnictwa n(e)de f e (E)g e (E)dE n n( E) de E c 22
23 Koncentracja swobodnych elektronów i dziur w równowadze termodynamicznej, półprzewodnik samoistny Pasmo Walencyjne Pasmo Walencyjne Pasmo Walencyjn T0 K brak elektronów w paśmie przewodnictwa i dziur w p. walencyjnym T>0 Im wyższa temperatura, tym większe prawdopodobieństwo pojawienia się swobodnego elektronu w pasmie przew. i dziury w pasmie walencyjnym - (Ec E n Ncexp kbt F ) p - (EF E Nvexp kbt v ) N c, N v efektywne gęstości stanów w pasmach ~10 19 cm -3 23
24 Półprzewodnik samoistny Poziom Fermiego w półprzewodniku samoistnym: n p E F ½E 2 E g np n i N c N v exp kb T g + ¾k B m * Tln m * h e ½E g n i - koncentracja nośników samoistnych np n i2 zawsze w warunkach równowagi termodynamicznej! i E g n i (300 K) ~0.25 ev cm -3 InSb,PbSe ~1 ev cm -3 Ge, Si, GaAs ~4 ev <10 10 cm -3 ZnS, SiC, GaN 24
25 Swobodne elektrony i dziury Półprzewodnik samoistny T 0 K T > 0 K np: poziom E F w srodku przerwy energetycznej Samoistna koncentracja swobodnych nosników zalezy od T i Eg n p n i N c N v Eg exp Nc, kbt v Eg exp 2kBT E g 1 ev : n i cm -3 ( j nev Α/mm 2 ) 25
26 Domieszkowanie typ p i n Przykład - krzem Sb donor (5 elektronów walencyjnych) B akceptor (3 elektrony walencyjne) 26
27 Donory i akceptory poziom donorowy E a poziom akceptorowy Żeby zjonizować atom domieszki i stworzyc elektron swobodny wystarczy znacznie mniejsza energia w stosunku do energii potrzebnej do uwolnienia elektronów tworzących wiazania kowalencyjne. Energia jonizacji donora lub akceptora płytki poziom energetyczny E d, E a < 100 mev, zwykle mev 27
28 Typ n Temperatura pokojowa Typ p E d E F swobodne elektrony zjonizowane donory E F E a zjon. akceptory swobodne dziury nn d nn c exp{-(e c -E F )/k B T} Nośniki większościowe pn a pn V exp{-(e F -E V )/k B T} E F blisko krawedzi p. przew pn i2 /N d << n Nośniki mniejszościowe E F blisko krawedzi p. walenc. nn i2 /N a << p 1 atom na milion zastapiony przez domieszkę koncentracja nośników wiekszościowych cm -3 >> n i koncentracja nośników mniejszościowych 10 4 cm -3 << n i 28
29 Koncentracja elektronów w pasmie przewodnictwa w funkcji temperatury (półprzewodnik domieszkowany) niskie T stopniowa jonizacja domieszek n NcN 2 d exp( E d /2k B T) pośrednie T wszystkie domieszki zjonizowane nn d wysokie T dominuje uwalnianie elektronów z wiązań kowalencyjnych N d <<n, E F E g /2 nośniki mniejszościowe: tgα 1 tgα 2 E 2k E d B g 2k B pn i2 /n<<n i 29
30 Kryształ idealny a kryształ realny Kryształ idealny: quasi-pęd elektronu hkconst F 0 vhk/m* const dla małych k (prędkość translacyjna) V sr (3k B T/m*) 1/2 Zaburzenia idealnej sieci: drgania sieci (fonony optyczne i akustyczne) defekty punktowe a) samoistne (luki, atomy międzywęzłowe defekty przestawieniowe np. Ga As ) b) domieszki intencjonalne i zanieczyszczenia defekty liniowe - dyslokacje 30
31 Swobodne elektrony i dziury w polu elektrycznym r F r eε r d( hk) dt h r dk dt m * r dv dt Zderzenia z niedoskonałościami sieci średnia droga swobodna l średni czas pomiędzy zderzeniami τ v av F ee τ v(t) eet/m* prędkość dryfu v d <v>ee τ /m* µe µ v d /E e τ /m* ruchliwość V d <<V T 31
32 Gęstość prądu j e nv d mikroskopowe prawo Ohma: jσe (porównaj IU/R) Przewodnictwo: σ enµ e µ e v d /E stała materiałowa przewodnictwo bipolarne: σe(nµ e +pµ h ) 32
33 Prąd unoszenia i prąd dyfuzji Stała dyfuzji j neμe + k BT D μ e ed n wzór Einsteina t o t o E n(x) t > t o n(x) t > t o x dyfuzja x dryf (unoszenie) -elektrony 33
34 Generacja i rekombinacja G - szybkość generacji nośników (termiczna, optyczna) R - szybkość rekombinacji (promienista, niepromienista) wzrost i zanik nierównowagowej koncentracji elektronów i dziur pod wpływem np. oświetlenia: n n p n p dn dt 0 p 0 + n + p dp dt G R Δn(t) Δn(t) Gτ n p R τ τ τ tu czas życia nierównowagowych nośników (a nie czas pomiedzy zderzeniami jak w µ) [ 1 exp( t/τ) ] Gτ exp( t/τ) 34
35 Droga dyfuzji E 0 : Δn n droga dyfuzji o exp L n D x L n n τ n L D odległość na jaką może przemieścić się nierównowagowy nośnik swobodny w nieobecności ci pola elektrycznego zanim ulegnie rekombinacji 35
36 Ważne atomowe (cząsteczkowe) poziomy energetyczne rozszczepiają się w pasma w ciele stałym najwyższe obsadzone pasmo w półprzewodnikach pasmo walencyjne, najniższe puste pasmo przewodnictwa półprzewodnikowe roztwory stałe sposób na regulację Eg wektor falowy k jest wprost proporcjonalny do quasi-pędu elektronu (dziury); w idealnym krysztale wektor falowy elektronu i jego energia jest funkcją periodyczną. Okres periodyczności wektora k to 2π/a (I strefa Brillouine a) nośniki prądu swobodne elektrony w pasmie przewodnictwa i dziury w pasmie walencyjnym w okolicach ekstremów E(k) energia kinetyczne w funkcji pędu - jest parabolą jak dla elektronu swobodnego, ale masa różna od masy elektronu swobodnego masa efektywna, ta masa charakteryzuje elektron (dziurę) pod działaniem siły zewnętrznej przerwa prosta ((GaAs, InP) max pasma walenc i minimum przew dla k0; skośna (Si, Ge) minimum p.przew dla k 0 koncentracja swobodnych dziur i elektronów w warunkach równowagi termodynamicznej jest określona funkcją Fermiego-Diraca - w półprzew. samoistnym zalezy od Eg i temperatury i jest b mała - w półprzew domieszkowanym powyżej K jest równa konc. donorów (akceptorów) przewodnictwo elektryczne zależy od koncentracji swobodnych nośników i ich ruchliwosci; ruchliwość elektronu (dziury) zależy od średniego czasu między zderzeniami z niedoskonałościami sieci (defekty, fonony) nierównowagowa koncentracja nośników zależy od szybkości generacji (np. optycznej) i rekombinacji (zależnej od czasu życia nierównowagowych nośników) prąd dyfuzji i unoszenia jeden związany z nierównomiernym rozkładem koncentracji n i p, drugi z polem elektrycznym
2. Elektrony i dziury w półprzewodnikach
 2. Elektrony i dziury w półprzewodnikach 1 B III C VI 2 Związki półprzewodnikowe: 8 walencyjnych elektronów na walencyjnym orbitalu cząsteczkowym2 Rozszczepienie elektronowych poziomów energetycznych Struktura
2. Elektrony i dziury w półprzewodnikach 1 B III C VI 2 Związki półprzewodnikowe: 8 walencyjnych elektronów na walencyjnym orbitalu cząsteczkowym2 Rozszczepienie elektronowych poziomów energetycznych Struktura
1. Struktura pasmowa from bonds to bands
 . Strutura pasmowa from bonds to bands Wiązania owalencyjne w cząsteczach Pasma energetyczne w ciałach stałych Przerwa energetyczna w półprzewodniach Dziura w paśmie walencyjnym Przybliżenie prawie swobodnego
. Strutura pasmowa from bonds to bands Wiązania owalencyjne w cząsteczach Pasma energetyczne w ciałach stałych Przerwa energetyczna w półprzewodniach Dziura w paśmie walencyjnym Przybliżenie prawie swobodnego
Rozszczepienie poziomów atomowych
 Rozszczepienie poziomów atomowych Poziomy energetyczne w pojedynczym atomie Gdy zbliżamy atomy chmury elektronowe nachodzą na siebie (inaczej: funkcje falowe elektronów zaczynają się przekrywać) Na skutek
Rozszczepienie poziomów atomowych Poziomy energetyczne w pojedynczym atomie Gdy zbliżamy atomy chmury elektronowe nachodzą na siebie (inaczej: funkcje falowe elektronów zaczynają się przekrywać) Na skutek
Repeta z wykładu nr 3. Detekcja światła. Struktura krystaliczna. Plan na dzisiaj
 Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Teoria pasmowa. Anna Pietnoczka
 Teoria pasmowa Anna Pietnoczka Opis struktury pasmowej we współrzędnych r, E Zmiana stanu elektronów przy zbliżeniu się atomów: (a) schemat energetyczny dla atomów sodu znajdujących się w odległościach
Teoria pasmowa Anna Pietnoczka Opis struktury pasmowej we współrzędnych r, E Zmiana stanu elektronów przy zbliżeniu się atomów: (a) schemat energetyczny dla atomów sodu znajdujących się w odległościach
Półprzewodniki samoistne. Struktura krystaliczna
 Półprzewodniki samoistne Struktura krystaliczna Si a5.43 A GaAs a5.63 A ajczęściej: struktura diamentu i blendy cynkowej (ZnS) 1 Wiązania chemiczne Wiązania kowalencyjne i kowalencyjno-jonowe 0K wszystkie
Półprzewodniki samoistne Struktura krystaliczna Si a5.43 A GaAs a5.63 A ajczęściej: struktura diamentu i blendy cynkowej (ZnS) 1 Wiązania chemiczne Wiązania kowalencyjne i kowalencyjno-jonowe 0K wszystkie
Elektryczne własności ciał stałych
 Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Pasmowa teoria przewodnictwa. Anna Pietnoczka
 Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Wykład IV. Półprzewodniki samoistne i domieszkowe
 Wykład IV Półprzewodniki samoistne i domieszkowe Półprzewodniki (Si, Ge, GaAs) Konfiguracja elektronowa Si : 1s 2 2s 2 2p 6 3s 2 3p 2 = [Ne] 3s 2 3p 2 4 elektrony walencyjne Półprzewodnik samoistny Talent
Wykład IV Półprzewodniki samoistne i domieszkowe Półprzewodniki (Si, Ge, GaAs) Konfiguracja elektronowa Si : 1s 2 2s 2 2p 6 3s 2 3p 2 = [Ne] 3s 2 3p 2 4 elektrony walencyjne Półprzewodnik samoistny Talent
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach
 Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
Przewodność elektryczna ciał stałych. Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki
 Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
Wykład VI. Teoria pasmowa ciał stałych
 Wykład VI Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład VI Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Absorpcja związana z defektami kryształu
 W rzeczywistych materiałach sieć krystaliczna nie jest idealna występują różnego rodzaju defekty. Podział najważniejszych defektów ze względu na właściwości optyczne: - inny atom w węźle sieci: C A atom
W rzeczywistych materiałach sieć krystaliczna nie jest idealna występują różnego rodzaju defekty. Podział najważniejszych defektów ze względu na właściwości optyczne: - inny atom w węźle sieci: C A atom
Wykład III. Teoria pasmowa ciał stałych
 Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
STRUKTURA PASM ENERGETYCZNYCH
 PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
Zaburzenia periodyczności sieci krystalicznej
 Zaburzenia periodyczności sieci krystalicznej Defekty liniowe dyslokacja krawędziowa dyslokacja śrubowa dyslokacja mieszana Defekty punktowe obcy atom w węźle luka w sieci (defekt Schottky ego) obcy atom
Zaburzenia periodyczności sieci krystalicznej Defekty liniowe dyslokacja krawędziowa dyslokacja śrubowa dyslokacja mieszana Defekty punktowe obcy atom w węźle luka w sieci (defekt Schottky ego) obcy atom
Podstawy fizyki ciała stałego półprzewodniki domieszkowane
 Podstawy fizyki ciała stałego półprzewodniki domieszkowane Półprzewodnik typu n IV-Ge V-As Jeżeli pięciowartościowy atom V-As zastąpi w sieci atom IV-Ge to cztery elektrony biorą udział w wiązaniu kowalentnym,
Podstawy fizyki ciała stałego półprzewodniki domieszkowane Półprzewodnik typu n IV-Ge V-As Jeżeli pięciowartościowy atom V-As zastąpi w sieci atom IV-Ge to cztery elektrony biorą udział w wiązaniu kowalentnym,
Teoria pasmowa ciał stałych
 Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
Ryszard J. Barczyński, 2012 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego
 Półprzewodniki i elementy z półprzewodników homogenicznych Ryszard J. Barczyński, 2012 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Publikacja
Półprzewodniki i elementy z półprzewodników homogenicznych Ryszard J. Barczyński, 2012 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Publikacja
Ciała stałe. Literatura: Halliday, Resnick, Walker, t. 5, rozdz. 42 Orear, t. 2, rozdz. 28 Young, Friedman, rozdz
 Ciała stałe Podstawowe własności ciał stałych Struktura ciał stałych Przewodnictwo elektryczne teoria Drudego Poziomy energetyczne w krysztale: struktura pasmowa Metale: poziom Fermiego, potencjał kontaktowy
Ciała stałe Podstawowe własności ciał stałych Struktura ciał stałych Przewodnictwo elektryczne teoria Drudego Poziomy energetyczne w krysztale: struktura pasmowa Metale: poziom Fermiego, potencjał kontaktowy
3. Struktura pasmowa
 3. Strutura pasmowa Funcja Blocha Quasi-pęd, sić odwrotna Przybliżni prawi swobodngo ltronu Dziura w paśmi walncyjnym Masa ftywna Strutura pasmowa (), przyłady Półprzwodnii miszan ltron w rysztal sformułowani
3. Strutura pasmowa Funcja Blocha Quasi-pęd, sić odwrotna Przybliżni prawi swobodngo ltronu Dziura w paśmi walncyjnym Masa ftywna Strutura pasmowa (), przyłady Półprzwodnii miszan ltron w rysztal sformułowani
Przewodnictwo elektryczne ciał stałych
 Przewodnictwo elektryczne ciał stałych Fizyka II, lato 2011 1 Własności elektryczne ciał stałych Komputery, kalkulatory, telefony komórkowe są elektronicznymi urządzeniami półprzewodnikowymi wykorzystującymi
Przewodnictwo elektryczne ciał stałych Fizyka II, lato 2011 1 Własności elektryczne ciał stałych Komputery, kalkulatory, telefony komórkowe są elektronicznymi urządzeniami półprzewodnikowymi wykorzystującymi
Przewodnictwo elektryczne ciał stałych. Fizyka II, lato
 Przewodnictwo elektryczne ciał stałych Fizyka II, lato 2016 1 Własności elektryczne ciał stałych Komputery, kalkulatory, telefony komórkowe są elektronicznymi urządzeniami półprzewodnikowymi wykorzystującymi
Przewodnictwo elektryczne ciał stałych Fizyka II, lato 2016 1 Własności elektryczne ciał stałych Komputery, kalkulatory, telefony komórkowe są elektronicznymi urządzeniami półprzewodnikowymi wykorzystującymi
W1. Właściwości elektryczne ciał stałych
 W1. Właściwości elektryczne ciał stałych Względna zmiana oporu właściwego przy wzroście temperatury o 1 0 C Materiał Opór właściwy [m] miedź 1.68*10-8 0.0061 żelazo 9.61*10-8 0.0065 węgiel (grafit) 3-60*10-3
W1. Właściwości elektryczne ciał stałych Względna zmiana oporu właściwego przy wzroście temperatury o 1 0 C Materiał Opór właściwy [m] miedź 1.68*10-8 0.0061 żelazo 9.61*10-8 0.0065 węgiel (grafit) 3-60*10-3
S. Baran - Podstawy fizyki materii skondensowanej Półprzewodniki. Półprzewodniki
 Półprzewodniki Definicja i własności Półprzewodnik materiał, którego przewodnictwo rośnie z temperaturą (opór maleje) i w temperaturze pokojowej wykazuje wartości pośrednie między przewodnictwem metali,
Półprzewodniki Definicja i własności Półprzewodnik materiał, którego przewodnictwo rośnie z temperaturą (opór maleje) i w temperaturze pokojowej wykazuje wartości pośrednie między przewodnictwem metali,
GAZ ELEKTRONÓW SWOBODNYCH POWYŻEJ ZERA BEZWZGLĘDNEGO.
 GAZ ELEKTRONÓW SWOBODNYCH POWYŻEJ ZERA BEZWZGLĘDNEGO. Funkcja rozkładu Fermiego-Diraca T=0K T>0K 1 f ( E ) = 0 dla dla E E F E > EF f ( E, T ) 1 = E E F kt e + 1 1 T>0K Funkcja rozkładu Fermiego-Diraca
GAZ ELEKTRONÓW SWOBODNYCH POWYŻEJ ZERA BEZWZGLĘDNEGO. Funkcja rozkładu Fermiego-Diraca T=0K T>0K 1 f ( E ) = 0 dla dla E E F E > EF f ( E, T ) 1 = E E F kt e + 1 1 T>0K Funkcja rozkładu Fermiego-Diraca
Struktura pasmowa ciał stałych
 Struktura pasmowa ciał stałych dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Spis treści 1. Pasmowa teoria ciała stałego 2 1.1. Wstęp do teorii..............................................
Struktura pasmowa ciał stałych dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Spis treści 1. Pasmowa teoria ciała stałego 2 1.1. Wstęp do teorii..............................................
Przejścia promieniste
 Przejście promieniste proces rekombinacji elektronu i dziury (przejście ze stanu o większej energii do stanu o energii mniejszej), w wyniku którego następuje emisja promieniowania. E Długość wyemitowanej
Przejście promieniste proces rekombinacji elektronu i dziury (przejście ze stanu o większej energii do stanu o energii mniejszej), w wyniku którego następuje emisja promieniowania. E Długość wyemitowanej
Złącze p-n: dioda. Przewodnictwo półprzewodników. Dioda: element nieliniowy
 Złącze p-n: dioda Półprzewodniki Przewodnictwo półprzewodników Dioda Dioda: element nieliniowy Przewodnictwo kryształów Atomy dyskretne poziomy energetyczne (stany energetyczne); określone energie elektronów
Złącze p-n: dioda Półprzewodniki Przewodnictwo półprzewodników Dioda Dioda: element nieliniowy Przewodnictwo kryształów Atomy dyskretne poziomy energetyczne (stany energetyczne); określone energie elektronów
Przejścia kwantowe w półprzewodnikach (kryształach)
 Przejścia kwantowe w półprzewodnikach (kryształach) Rozpraszanie na nieruchomej sieci krystalicznej (elektronów, neutronów, fotonów) zwykłe odbicie Bragga (płaszczyzny krystaliczne odgrywają rolę rys siatki
Przejścia kwantowe w półprzewodnikach (kryształach) Rozpraszanie na nieruchomej sieci krystalicznej (elektronów, neutronów, fotonów) zwykłe odbicie Bragga (płaszczyzny krystaliczne odgrywają rolę rys siatki
Krawędź absorpcji podstawowej
 Obecność przerwy energetycznej między pasmami przewodnictwa i walencyjnym powoduje obserwację w eksperymencie absorpcyjnym krawędzi podstawowej. Dla padającego promieniowania oznacza to przejście z ośrodka
Obecność przerwy energetycznej między pasmami przewodnictwa i walencyjnym powoduje obserwację w eksperymencie absorpcyjnym krawędzi podstawowej. Dla padającego promieniowania oznacza to przejście z ośrodka
elektryczne ciał stałych
 Wykład 23: Przewodnictwo elektryczne ciał stałych Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 08.06.2017 1 2 Własności elektryczne
Wykład 23: Przewodnictwo elektryczne ciał stałych Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 08.06.2017 1 2 Własności elektryczne
na dnie (lub w szczycie) pasma pasmo jest paraboliczne, ale masa wyznaczona z krzywizny niekoniecznie = m 0
 Koncepcja masy efektywnej swobodne elektrony k 1 1 E( k) E( k) =, = m m k krzywizna E(k) określa masę cząstek elektrony prawie swobodne - na dnie pasma masa jest dodatnia, ale niekoniecznie = masie swobodnego
Koncepcja masy efektywnej swobodne elektrony k 1 1 E( k) E( k) =, = m m k krzywizna E(k) określa masę cząstek elektrony prawie swobodne - na dnie pasma masa jest dodatnia, ale niekoniecznie = masie swobodnego
METALE. Cu 8.50 1.35 1.56 7.0 8.2 Ag 5.76 1.19 1.38 5.5 6.4 Au 5.90 1.2 1.39 5.5 6.4
 MAL Zestawienie właściwości gazu elektronowego dla niektórych metali: n cm -3 k cm -1 v cm/s ε e ε /k Li 4.6 10 1.1 10 8 1.3 10 8 4.7 5.5 10 4 a.5 0.9 1.1 3.1 3.7 K 1.34 0.73 0.85.1.4 Rb 1.08 0.68 0.79
MAL Zestawienie właściwości gazu elektronowego dla niektórych metali: n cm -3 k cm -1 v cm/s ε e ε /k Li 4.6 10 1.1 10 8 1.3 10 8 4.7 5.5 10 4 a.5 0.9 1.1 3.1 3.7 K 1.34 0.73 0.85.1.4 Rb 1.08 0.68 0.79
Elektryczne własności ciał stałych
 Elektryczne własności ciał stałych Izolatory (w temperaturze pokojowej) w praktyce - nie przewodzą prądu elektrycznego. Ich oporność jest b. duża. Np. diament ma oporność większą od miedzi 1024 razy Metale
Elektryczne własności ciał stałych Izolatory (w temperaturze pokojowej) w praktyce - nie przewodzą prądu elektrycznego. Ich oporność jest b. duża. Np. diament ma oporność większą od miedzi 1024 razy Metale
ELEKTRONIKA I ENERGOELEKTRONIKA
 ELEKTRONIKA I ENERGOELEKTRONIKA wykład 2 PÓŁPRZEWODNIKI luty 2008 - Lublin krzem u ej n o z r o w t rze i p o ytk d u pł m rze k Od m ik ro pr oc es or ET F S MO p rzy rząd Od p iasku do Ten wykład O CZYM
ELEKTRONIKA I ENERGOELEKTRONIKA wykład 2 PÓŁPRZEWODNIKI luty 2008 - Lublin krzem u ej n o z r o w t rze i p o ytk d u pł m rze k Od m ik ro pr oc es or ET F S MO p rzy rząd Od p iasku do Ten wykład O CZYM
TEORIA PASMOWA CIAŁ STAŁYCH
 TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
Repeta z wykładu nr 5. Detekcja światła. Plan na dzisiaj. Złącze p-n. złącze p-n
 Repeta z wykładu nr 5 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 5 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Model elektronów swobodnych w metalu
 Model elektronów swobodnych w metalu Stany elektronu w nieskończonej trójwymiarowej studni potencjału - dozwolone wartości wektora falowego k Fale stojące - warunki brzegowe znikanie funkcji falowej na
Model elektronów swobodnych w metalu Stany elektronu w nieskończonej trójwymiarowej studni potencjału - dozwolone wartości wektora falowego k Fale stojące - warunki brzegowe znikanie funkcji falowej na
W5. Rozkład Boltzmanna
 W5. Rozkład Boltzmanna Podstawowym rozkładem w klasycznej fizyce statystycznej jest rozkład Boltzmanna E /( kt ) f B ( E) Ae gdzie: A jest stałą normalizacyjną, k stałą Boltzmanna 5 k 8.61710 ev / K Został
W5. Rozkład Boltzmanna Podstawowym rozkładem w klasycznej fizyce statystycznej jest rozkład Boltzmanna E /( kt ) f B ( E) Ae gdzie: A jest stałą normalizacyjną, k stałą Boltzmanna 5 k 8.61710 ev / K Został
półprzewodniki Plan na dzisiaj Optyka nanostruktur Struktura krystaliczna Dygresja Sebastian Maćkowski
 Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Przerwa energetyczna w germanie
 Ćwiczenie 1 Przerwa energetyczna w germanie Cel ćwiczenia Wyznaczenie szerokości przerwy energetycznej przez pomiar zależności oporu monokryształu germanu od temperatury. Wprowadzenie Eksperymentalne badania
Ćwiczenie 1 Przerwa energetyczna w germanie Cel ćwiczenia Wyznaczenie szerokości przerwy energetycznej przez pomiar zależności oporu monokryształu germanu od temperatury. Wprowadzenie Eksperymentalne badania
Prawo Ohma. qnv. E ρ U I R U>0V. v u E +
 Prawo Ohma U>0V J v u J qnv u - E + J qne d J gęstość prądu [A/cm 2 ] n koncentracja elektronów [cm -3 ] ρ rezystywność [Ωcm] σ - przewodność [S/cm] E natężenie pola elektrycznego [V/cm] I prąd [A] R rezystancja
Prawo Ohma U>0V J v u J qnv u - E + J qne d J gęstość prądu [A/cm 2 ] n koncentracja elektronów [cm -3 ] ρ rezystywność [Ωcm] σ - przewodność [S/cm] E natężenie pola elektrycznego [V/cm] I prąd [A] R rezystancja
VI. POMIAR ZALEŻNOŚCI OPORNOŚCI METALI I PÓŁPRZEWODNIKÓW OD TEMPERATURY
 Oporność właściwa (Ωm) 1 VI. POMIAR ZALEŻNOŚCI OPORNOŚCI METALI I PÓŁPRZEWODNIKÓW OD TEMPERATURY Cel ćwiczenia: pomiar zależności oporności elektrycznej (rezystancji) metalu i półprzewodnika od temperatury,
Oporność właściwa (Ωm) 1 VI. POMIAR ZALEŻNOŚCI OPORNOŚCI METALI I PÓŁPRZEWODNIKÓW OD TEMPERATURY Cel ćwiczenia: pomiar zależności oporności elektrycznej (rezystancji) metalu i półprzewodnika od temperatury,
Dr inż. Zbigniew Szklarski
 Wykład 1: Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
Wykład 1: Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
Repeta z wykładu nr 4. Detekcja światła. Dygresja. Plan na dzisiaj
 Repeta z wykładu nr 4 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 4 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
2. Półprzewodniki. Istnieje duża jakościowa różnica między właściwościami elektrofizycznymi półprzewodników, przewodników i dielektryków.
 2. Półprzewodniki 1 Półprzewodniki to materiały, których rezystywność jest większa niż rezystywność przewodników (metali) oraz mniejsza niż rezystywność izolatorów (dielektryków). Przykłady: miedź - doskonały
2. Półprzewodniki 1 Półprzewodniki to materiały, których rezystywność jest większa niż rezystywność przewodników (metali) oraz mniejsza niż rezystywność izolatorów (dielektryków). Przykłady: miedź - doskonały
elektryczne ciał stałych
 Wykład 23: Przewodnictwo elektryczne ciał stałych Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Własności elektryczne ciał
Wykład 23: Przewodnictwo elektryczne ciał stałych Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Własności elektryczne ciał
Rekapitulacja. Detekcja światła. Rekapitulacja. Rekapitulacja
 Rekapitulacja Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje: czwartek
Rekapitulacja Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje: czwartek
Proste struktury krystaliczne
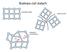 Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
III.4 Gaz Fermiego. Struktura pasmowa ciał stałych
 III.4 Gaz Fermiego. Struktura pasmowa ciał stałych Jan Królikowski Fizyka IVBC 1 Gaz Fermiego Gaz Fermiego to gaz swobodnych, nie oddziałujących, identycznych fermionów w objętości V=a 3. Poszukujemy N(E)dE
III.4 Gaz Fermiego. Struktura pasmowa ciał stałych Jan Królikowski Fizyka IVBC 1 Gaz Fermiego Gaz Fermiego to gaz swobodnych, nie oddziałujących, identycznych fermionów w objętości V=a 3. Poszukujemy N(E)dE
Wykład V Wiązanie kowalencyjne. Półprzewodniki
 Wykład V Wiązanie kowalencyjne. Półprzewodniki Wiązanie kowalencyjne molekuła H 2 Tworzenie wiązania kowalencyjnego w molekule H 2 : elektron w jednym atomie przyciągany jest przez jądro drugiego. Wiązanie
Wykład V Wiązanie kowalencyjne. Półprzewodniki Wiązanie kowalencyjne molekuła H 2 Tworzenie wiązania kowalencyjnego w molekule H 2 : elektron w jednym atomie przyciągany jest przez jądro drugiego. Wiązanie
Zjawiska zachodzące w półprzewodnikach Przewodniki samoistne i niesamoistne
 Zjawiska zachodzące w półprzewodnikach Przewodniki samoistne i niesamoistne Materiały dydaktyczne dla kierunku Technik Optyk (W12) Kwalifikacyjnego kursu zawodowego. Zadania elektroniki: Urządzenia elektroniczne
Zjawiska zachodzące w półprzewodnikach Przewodniki samoistne i niesamoistne Materiały dydaktyczne dla kierunku Technik Optyk (W12) Kwalifikacyjnego kursu zawodowego. Zadania elektroniki: Urządzenia elektroniczne
ELEKTRONIKA ELM001551W
 ELEKTRONIKA ELM001551W Podstawy elektrotechniki i elektroniki Budowa materii fizyka półprzewodników Zakres: Sieć krystaliczna, Rodzaje wiązań chemicznych, Struktura pasmowa półprzewodników Rys historyczny
ELEKTRONIKA ELM001551W Podstawy elektrotechniki i elektroniki Budowa materii fizyka półprzewodników Zakres: Sieć krystaliczna, Rodzaje wiązań chemicznych, Struktura pasmowa półprzewodników Rys historyczny
Dr inż. Zbigniew Szklarski
 Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 08.06.017 Wydział Informatyki, Elektroniki i 1 Struktura
Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 08.06.017 Wydział Informatyki, Elektroniki i 1 Struktura
Przyrządy i układy półprzewodnikowe
 Przyrządy i układy półprzewodnikowe Prof. dr hab. Ewa Popko ewa.popko@pwr.edu.pl www.if.pwr.wroc.pl/~popko p.231a A-1 Zawartość wykładu Wy1, Wy2 Wy3 Wy4 Wy5 Wy6 Wy7 Wy8 Wy9 Wy10 Wy11 Wy12 Wy13 Wy14 Wy15
Przyrządy i układy półprzewodnikowe Prof. dr hab. Ewa Popko ewa.popko@pwr.edu.pl www.if.pwr.wroc.pl/~popko p.231a A-1 Zawartość wykładu Wy1, Wy2 Wy3 Wy4 Wy5 Wy6 Wy7 Wy8 Wy9 Wy10 Wy11 Wy12 Wy13 Wy14 Wy15
3. Struktura pasmowa
 3. Stutua pasmowa Funcja Blocha Quasi-pęd, sić odwotna Pzybliżni pawi swobodngo ltonu Dziua w paśmi walncyjnym Masa ftywna Stutua pasmowa (), pzyłady Półpzwodnii miszan lton w ysztal sfomułowani poblmu
3. Stutua pasmowa Funcja Blocha Quasi-pęd, sić odwotna Pzybliżni pawi swobodngo ltonu Dziua w paśmi walncyjnym Masa ftywna Stutua pasmowa (), pzyłady Półpzwodnii miszan lton w ysztal sfomułowani poblmu
Elektryczne własności ciał stałych
 Elektryczne własności ciał stałych Izolatory (w temperaturze pokojowej) w praktyce - nie przewodzą prądu elektrycznego. Ich oporność jest b. duża. Np. diament ma oporność większą od miedzi 1024 razy Metale
Elektryczne własności ciał stałych Izolatory (w temperaturze pokojowej) w praktyce - nie przewodzą prądu elektrycznego. Ich oporność jest b. duża. Np. diament ma oporność większą od miedzi 1024 razy Metale
Podstawowe właściwości fizyczne półprzewodników WYKŁAD 2 SMK J. Hennel, Podstawy elektroniki półprzewodnikowej:, WNT, W-wa 2003
 Podstawowe właściwości fizyczne półprzewodników WYKŁAD SMK J. Hennel, Podstawy elektroniki półprzewodnikowej:, WNT, W-wa 003 1. Podstawowe pojęcia. Wszystkie informacje dotyczące właściwości dynamicznych
Podstawowe właściwości fizyczne półprzewodników WYKŁAD SMK J. Hennel, Podstawy elektroniki półprzewodnikowej:, WNT, W-wa 003 1. Podstawowe pojęcia. Wszystkie informacje dotyczące właściwości dynamicznych
POLITECHNIKA GDAŃSKA WYDZIAŁ FIZYKI TECHNICZNEJ I MATEMATYKI STOSOWANEJ EKSCYTONY. Seminarium z Molekularnego Ciała a Stałego Jędrzejowski Jaromir
 POLITECHNIKA GDAŃSKA WYDZIAŁ FIZYKI TECHNICZNEJ I MATEMATYKI STOSOWANEJ EKSCYTONY W CIAŁACH ACH STAŁYCH Seminarium z Molekularnego Ciała a Stałego Jędrzejowski Jaromir Co to sąs ekscytony? ekscyton to
POLITECHNIKA GDAŃSKA WYDZIAŁ FIZYKI TECHNICZNEJ I MATEMATYKI STOSOWANEJ EKSCYTONY W CIAŁACH ACH STAŁYCH Seminarium z Molekularnego Ciała a Stałego Jędrzejowski Jaromir Co to sąs ekscytony? ekscyton to
3.4 Badanie charakterystyk tranzystora(e17)
 152 Elektryczność 3.4 Badanie charakterystyk tranzystora(e17) Celem ćwiczenia jest wyznaczenie charakterystyk tranzystora npn w układzie ze wspólnym emiterem W E. Zagadnienia do przygotowania: półprzewodniki,
152 Elektryczność 3.4 Badanie charakterystyk tranzystora(e17) Celem ćwiczenia jest wyznaczenie charakterystyk tranzystora npn w układzie ze wspólnym emiterem W E. Zagadnienia do przygotowania: półprzewodniki,
Fizyka i technologia złącza PN. Adam Drózd 25.04.2006r.
 Fizyka i technologia złącza P Adam Drózd 25.04.2006r. O czym będę mówił: Półprzewodnik definicja, model wiązań walencyjnych i model pasmowy, samoistny i niesamoistny, domieszki donorowe i akceptorowe,
Fizyka i technologia złącza P Adam Drózd 25.04.2006r. O czym będę mówił: Półprzewodnik definicja, model wiązań walencyjnych i model pasmowy, samoistny i niesamoistny, domieszki donorowe i akceptorowe,
Kryształy, półprzewodniki, nanotechnologie. Dr inż. KAROL STRZAŁKOWSKI Instytut Fizyki UMK w Toruniu
 Kryształy, półprzewodniki, nanotechnologie. Dr inż. KAROL STRZAŁKOWSKI Instytut Fizyki UMK w Toruniu skaroll@fizyka.umk.pl Plan ogólny Kryształy, półprzewodniki, nanotechnologie, czyli czym będziemy się
Kryształy, półprzewodniki, nanotechnologie. Dr inż. KAROL STRZAŁKOWSKI Instytut Fizyki UMK w Toruniu skaroll@fizyka.umk.pl Plan ogólny Kryształy, półprzewodniki, nanotechnologie, czyli czym będziemy się
Dr inż. Zbigniew Szklarski
 Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
Dr inż. Zbigniew Szklarski
 Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 19.06.018 Wydział Informatyki, Elektroniki i 1 Struktura
Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 19.06.018 Wydział Informatyki, Elektroniki i 1 Struktura
elektryczne ciał stałych
 Wykład 22: Przewodnictwo elektryczne ciał stałych Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Własności elektryczne ciał
Wykład 22: Przewodnictwo elektryczne ciał stałych Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Własności elektryczne ciał
elektryczne ciał stałych
 Wykład 24: Przewodnictwo elektryczne ciał stałych Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 19.06.2018 1 2 Własności elektryczne
Wykład 24: Przewodnictwo elektryczne ciał stałych Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 19.06.2018 1 2 Własności elektryczne
Podstawowe właściwości fizyczne półprzewodników WYKŁAD 1 SMK J. Hennel: Podstawy elektroniki półprzewodnikowej, WNT, W-wa 2003
 Podstawowe właściwości fizyczne półprzewodników WYKŁAD 1 SMK J. Hennel: Podstawy elektroniki półprzewodnikowej, WNT, W-wa 003 1. Wiązania atomów w krysztale Siły wiążące atomy w kryształ mają charakter
Podstawowe właściwości fizyczne półprzewodników WYKŁAD 1 SMK J. Hennel: Podstawy elektroniki półprzewodnikowej, WNT, W-wa 003 1. Wiązania atomów w krysztale Siły wiążące atomy w kryształ mają charakter
Część 2. Przewodzenie silnych prądów i blokowanie wysokich napięć przy pomocy przyrządów półprzewodnikowych
 Część 2 Przewodzenie silnych prądów i blokowanie wysokich napięć przy pomocy przyrządów półprzewodnikowych Łukasz Starzak, Przyrządy i układy mocy, studia niestacjonarne, lato 2018/19 23 Półprzewodniki
Część 2 Przewodzenie silnych prądów i blokowanie wysokich napięć przy pomocy przyrządów półprzewodnikowych Łukasz Starzak, Przyrządy i układy mocy, studia niestacjonarne, lato 2018/19 23 Półprzewodniki
Ćwiczenie 243 4.2. Badanie zależności temperaturowej oporu elektrycznego metalu i półprzewodnika
 Nazwisko... Data... Nr na liście... Imię... Wydział... Dzień tyg.... Godzina... Ćwiczenie 243 4.2. Badanie zależności temperaturowej oporu elektrycznego metalu i półprzewodnika Tabela I. Metal Nazwa próbki:
Nazwisko... Data... Nr na liście... Imię... Wydział... Dzień tyg.... Godzina... Ćwiczenie 243 4.2. Badanie zależności temperaturowej oporu elektrycznego metalu i półprzewodnika Tabela I. Metal Nazwa próbki:
S. Baran - Podstawy fizyki materii skondensowanej Pasma energetyczne. Pasma energetyczne
 Pasma energetyczne Niedostatki modelu gazu Fermiego elektronów swobodnych Pomimo wielu sukcesów model nie jest w stanie wyjaśnić następujących zagadnień: 1. różnica między metalami, półmetalami, półprzewodnikami
Pasma energetyczne Niedostatki modelu gazu Fermiego elektronów swobodnych Pomimo wielu sukcesów model nie jest w stanie wyjaśnić następujących zagadnień: 1. różnica między metalami, półmetalami, półprzewodnikami
ZALEŻNOŚĆ OPORU ELEKTRYCZNEGO 57 METALU I PÓŁPRZEWODNIKA OD TEMPERATURY
 ZALEŻNOŚĆ OPORU ELEKTRYCZNEGO 57 METALU I PÓŁPRZEWODNIKA OD TEMPERATURY I.. Prąd elektryczny Dla dużej grupy przewodników prądu elektrycznego (metale, półprzewodniki i inne) spełnione jest prawo Ohma,
ZALEŻNOŚĆ OPORU ELEKTRYCZNEGO 57 METALU I PÓŁPRZEWODNIKA OD TEMPERATURY I.. Prąd elektryczny Dla dużej grupy przewodników prądu elektrycznego (metale, półprzewodniki i inne) spełnione jest prawo Ohma,
Chemia nieorganiczna. Copyright 2000 by Harcourt, Inc. All rights reserved.
 Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Pierwiastki 1 1 H 3 Li 11
Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Pierwiastki 1 1 H 3 Li 11
Elementy teorii powierzchni metali
 prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład 4 v.16 Wiązanie metaliczne Wiązanie metaliczne Zajmujemy się tylko metalami dlatego w zasadzie interesuje nas tylko wiązanie metaliczne.
prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład 4 v.16 Wiązanie metaliczne Wiązanie metaliczne Zajmujemy się tylko metalami dlatego w zasadzie interesuje nas tylko wiązanie metaliczne.
Lasery półprzewodnikowe. przewodnikowe. Bernard Ziętek
 Lasery półprzewodnikowe przewodnikowe Bernard Ziętek Plan 1. Rodzaje półprzewodników 2. Parametry półprzewodników 3. Złącze p-n 4. Rekombinacja dziura-elektron 5. Wzmocnienie 6. Rezonatory 7. Lasery niskowymiarowe
Lasery półprzewodnikowe przewodnikowe Bernard Ziętek Plan 1. Rodzaje półprzewodników 2. Parametry półprzewodników 3. Złącze p-n 4. Rekombinacja dziura-elektron 5. Wzmocnienie 6. Rezonatory 7. Lasery niskowymiarowe
S. Baran - Podstawy fizyki materii skondensowanej Gaz Fermiego elektronów swobodnych. Gaz Fermiego elektronów swobodnych
 Gaz Fermiego elektronów swobodnych charakter idea Teoria metali Paula Drudego Teoria metali Arnolda (1900 r.) Sommerfelda (1927 r.) klasyczna kwantowa elektrony przewodnictwa elektrony przewodnictwa w
Gaz Fermiego elektronów swobodnych charakter idea Teoria metali Paula Drudego Teoria metali Arnolda (1900 r.) Sommerfelda (1927 r.) klasyczna kwantowa elektrony przewodnictwa elektrony przewodnictwa w
Elementy elektroniczne Wykłady 3: Półprzewodniki. Teoria złącza PN
 Elementy elektroniczne Wykłady 3: Półprzewodniki. Teoria złącza PN Budowa i właściwości elektryczne ciał stałych - wprowadzenie Budowa atomu: a) model starożytny b) model J.J. Thompsona c) model E. Rutherforda
Elementy elektroniczne Wykłady 3: Półprzewodniki. Teoria złącza PN Budowa i właściwości elektryczne ciał stałych - wprowadzenie Budowa atomu: a) model starożytny b) model J.J. Thompsona c) model E. Rutherforda
Skończona studnia potencjału
 Skończona studnia potencjału U = 450 ev, L = 100 pm Fala wnika w ściany skończonej studni długość fali jest większa (a energia mniejsza) Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach
Skończona studnia potencjału U = 450 ev, L = 100 pm Fala wnika w ściany skończonej studni długość fali jest większa (a energia mniejsza) Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach
+ + Struktura cia³a sta³ego. Kryszta³y jonowe. Kryszta³y atomowe. struktura krystaliczna. struktura amorficzna
 Struktura cia³a sta³ego struktura krystaliczna struktura amorficzna odleg³oœci miêdzy atomami maj¹ tê sam¹ wartoœæ; dany atom ma wszêdzie takie samo otoczenie najbli szych s¹siadów odleg³oœci miêdzy atomami
Struktura cia³a sta³ego struktura krystaliczna struktura amorficzna odleg³oœci miêdzy atomami maj¹ tê sam¹ wartoœæ; dany atom ma wszêdzie takie samo otoczenie najbli szych s¹siadów odleg³oœci miêdzy atomami
Nanostruktury i nanotechnologie
 Nanostruktury i nanotechnologie Heterozłącza Efekty kwantowe Nanotechnologie Z. Postawa, "Fizyka powierzchni i nanostruktury" 1 Termin oddania referatów do 19 I 004 Zaliczenie: 1 I 004 Z. Postawa, "Fizyka
Nanostruktury i nanotechnologie Heterozłącza Efekty kwantowe Nanotechnologie Z. Postawa, "Fizyka powierzchni i nanostruktury" 1 Termin oddania referatów do 19 I 004 Zaliczenie: 1 I 004 Z. Postawa, "Fizyka
P R A C O W N I A
 P R A C O W N I A www.tremolo.pl M E T O D Y B A D A Ń M A T E R I A Ł Ó W (WŁAŚCIWOŚCI ELEKTRYCZNE, MAGNETYCZNE I AKUSTYCZNE) Ewelina Broda Robert Gabor ĆWICZENIE NR 3 WYZNACZANIE ENERGII AKTYWACJI I
P R A C O W N I A www.tremolo.pl M E T O D Y B A D A Ń M A T E R I A Ł Ó W (WŁAŚCIWOŚCI ELEKTRYCZNE, MAGNETYCZNE I AKUSTYCZNE) Ewelina Broda Robert Gabor ĆWICZENIE NR 3 WYZNACZANIE ENERGII AKTYWACJI I
Wykład IV. Dioda elektroluminescencyjna Laser półprzewodnikowy
 Wykład IV Dioda elektroluminescencyjna Laser półprzewodnikowy Półprzewodniki - diagram pasmowy Kryształ Si, Ge, GaAs Struktura krystaliczna prowadzi do relacji dyspersji E(k). Krzywizna pasm decyduje o
Wykład IV Dioda elektroluminescencyjna Laser półprzewodnikowy Półprzewodniki - diagram pasmowy Kryształ Si, Ge, GaAs Struktura krystaliczna prowadzi do relacji dyspersji E(k). Krzywizna pasm decyduje o
Chemia nieorganiczna. Pierwiastki. niemetale Be. 27 Co. 28 Ni. 26 Fe. 29 Cu. 45 Rh. 44 Ru. 47 Ag. 46 Pd. 78 Pt. 76 Os.
 Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Copyright 2000 by Harcourt,
Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Copyright 2000 by Harcourt,
Przyrządy półprzewodnikowe część 2
 Przyrządy półprzewodnikowe część 2 Prof. Zbigniew Lisik Katedra Przyrządów Półprzewodnikowych i Optoelektronicznych pokój: 110 e-mail: zbigniew.lisik@p.lodz.pl wykład 30 godz. laboratorium 30 godz WEEIiA
Przyrządy półprzewodnikowe część 2 Prof. Zbigniew Lisik Katedra Przyrządów Półprzewodnikowych i Optoelektronicznych pokój: 110 e-mail: zbigniew.lisik@p.lodz.pl wykład 30 godz. laboratorium 30 godz WEEIiA
PÓŁPRZEWODNIKI W ELEKTRONICE. Powszechnie uważa się, że współczesna elektronika jest elektroniką półprzewodnikową.
 PÓŁPRZEWODNIKI W ELEKTRONICE Powszechnie uważa się, że współczesna elektronika jest elektroniką półprzewodnikową. 1 Półprzewodniki Półprzewodniki to ciała stałe nieorganiczne lub organiczne o przewodnictwie
PÓŁPRZEWODNIKI W ELEKTRONICE Powszechnie uważa się, że współczesna elektronika jest elektroniką półprzewodnikową. 1 Półprzewodniki Półprzewodniki to ciała stałe nieorganiczne lub organiczne o przewodnictwie
Modele kp wprowadzenie
 Modele kp wprowadzenie Komórka elementarna i komórka sieci odwrotnej Funkcje falowe elektronu w krysztale Struktura pasmowa Przybliżenie masy efektywnej Naprężenia: potencjał deformacyjny, prawo Hooka
Modele kp wprowadzenie Komórka elementarna i komórka sieci odwrotnej Funkcje falowe elektronu w krysztale Struktura pasmowa Przybliżenie masy efektywnej Naprężenia: potencjał deformacyjny, prawo Hooka
POMIAR ZALEŻNOŚCI OPORU METALI I PÓŁPRZEWODNIKÓW OD TEMPERATURY
 ĆWICZENIE 44 POMIAR ZALEŻNOŚCI OPORU METALI I PÓŁPRZEWODNIKÓW OD TEMPERATURY Cel ćwiczenia: Pomiar zależności oporu elektrycznego (rezystancji) metalu i półprzewodnika od temperatury oraz wyznaczenie temperaturowego
ĆWICZENIE 44 POMIAR ZALEŻNOŚCI OPORU METALI I PÓŁPRZEWODNIKÓW OD TEMPERATURY Cel ćwiczenia: Pomiar zależności oporu elektrycznego (rezystancji) metalu i półprzewodnika od temperatury oraz wyznaczenie temperaturowego
Podstawy krystalografii
 Podstawy krystalografii Kryształy Pojęcie kryształu znane było już w starożytności. Nazywano tak ciała o regularnych kształtach i gładkich ścianach. Już wtedy podejrzewano, że te cechy związane są ze szczególną
Podstawy krystalografii Kryształy Pojęcie kryształu znane było już w starożytności. Nazywano tak ciała o regularnych kształtach i gładkich ścianach. Już wtedy podejrzewano, że te cechy związane są ze szczególną
Projekt FPP "O" Kosma Jędrzejewski 13-12-2013
 Projekt FPP "O" Kosma Jędrzejewski --0 Projekt polega na wyznaczeniu charakterystyk gęstości stanów nośników ładunku elektrycznego w obszarze aktywnym lasera półprzewodnikowego GaAs. Wyprowadzenie wzoru
Projekt FPP "O" Kosma Jędrzejewski --0 Projekt polega na wyznaczeniu charakterystyk gęstości stanów nośników ładunku elektrycznego w obszarze aktywnym lasera półprzewodnikowego GaAs. Wyprowadzenie wzoru
E3. Badanie temperaturowej zależności oporu elektrycznego ciał stałych 1/5
 1/5 Celem ćwiczenia jest poznanie temperaturowej zależności przepływu prądu elektrycznego przez przewodnik i półprzewodnik oraz doświadczalne wyznaczenie energii aktywacji przewodnictwa dla półprzewodnika
1/5 Celem ćwiczenia jest poznanie temperaturowej zależności przepływu prądu elektrycznego przez przewodnik i półprzewodnik oraz doświadczalne wyznaczenie energii aktywacji przewodnictwa dla półprzewodnika
ZADANIE Co się dzieje z elektronami w atomie, a co w krysztale?
 1. Wstęp teoretyczny ZADANIE 108 WYZNACZANIE PRZERWY ENERGETYCZNEJ INSB. W ćwiczeniu tym wyznaczymy przerwę energetyczną E G materiału półprzewodnikowego mierząc opór elektryczny próbki w funkcji temperatury.
1. Wstęp teoretyczny ZADANIE 108 WYZNACZANIE PRZERWY ENERGETYCZNEJ INSB. W ćwiczeniu tym wyznaczymy przerwę energetyczną E G materiału półprzewodnikowego mierząc opór elektryczny próbki w funkcji temperatury.
Cel ćwiczenia: Wyznaczenie szerokości przerwy energetycznej przez pomiar zależności oporności elektrycznej monokryształu germanu od temperatury.
 WFiIS PRACOWNIA FIZYCZNA I i II Imię i nazwisko: 1. 2. TEMAT: ROK GRUPA ZESPÓŁ NR ĆWICZENIA Data wykonania: Data oddania: Zwrot do poprawy: Data oddania: Data zliczenia: OCENA Cel ćwiczenia: Wyznaczenie
WFiIS PRACOWNIA FIZYCZNA I i II Imię i nazwisko: 1. 2. TEMAT: ROK GRUPA ZESPÓŁ NR ĆWICZENIA Data wykonania: Data oddania: Zwrot do poprawy: Data oddania: Data zliczenia: OCENA Cel ćwiczenia: Wyznaczenie
Fizyka Ciała Stałego. Struktura krystaliczna. Struktura amorficzna
 Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Struktura energetyczna ciał stałych. Fizyka II dla EiT oraz E, lato
 Struktura energetyczna ciał stałych Fizyka II dla EiT oraz E, lato 016 1 Struktura kryształu Doskonały kryształ składa się z uporządkowanych atomów w sieci krystalicznej, opisanej przez trzy podstawowe
Struktura energetyczna ciał stałych Fizyka II dla EiT oraz E, lato 016 1 Struktura kryształu Doskonały kryształ składa się z uporządkowanych atomów w sieci krystalicznej, opisanej przez trzy podstawowe
Złożone struktury diod Schottky ego mocy
 Złożone struktury diod Schottky ego mocy Diody JBS (Junction Barrier Schottky) złącze blokujące na powierzchni krzemu obniżenie krytycznego natężenia pola (Ubr 50 V) Diody MPS (Merged PINSchottky) struktura
Złożone struktury diod Schottky ego mocy Diody JBS (Junction Barrier Schottky) złącze blokujące na powierzchni krzemu obniżenie krytycznego natężenia pola (Ubr 50 V) Diody MPS (Merged PINSchottky) struktura
Instytut Systemów Inżynierii Elektrycznej Wydział Elektrotechniki, Elektroniki Informatyki i Automatyki Politechnika Łódzka
 Zakład Inżynierii Materiałowej i Systemów Pomiarowych Instytut Systemów Inżynierii Elektrycznej Wydział Elektrotechniki, Elektroniki Informatyki i Automatyki Politechnika Łódzka LABORATORIUM INŻYNIERII
Zakład Inżynierii Materiałowej i Systemów Pomiarowych Instytut Systemów Inżynierii Elektrycznej Wydział Elektrotechniki, Elektroniki Informatyki i Automatyki Politechnika Łódzka LABORATORIUM INŻYNIERII
Część 2. Przewodzenie silnych prądów i blokowanie wysokich napięć przy pomocy przyrządów półprzewodnikowych
 Część 2 Przewodzenie silnych prądów i blokowanie wysokich napięć przy pomocy przyrządów półprzewodnikowych Łukasz Starzak, Przyrządy półprzewodnikowe mocy, zima 2015/16 20 Półprzewodniki Materiały, w których
Część 2 Przewodzenie silnych prądów i blokowanie wysokich napięć przy pomocy przyrządów półprzewodnikowych Łukasz Starzak, Przyrządy półprzewodnikowe mocy, zima 2015/16 20 Półprzewodniki Materiały, w których
Układy nieliniowe. Stabilizator - dioda Zenera. Dioda LED. Prostownik na diodach (Graetza) Logiczna bramka NAND. w.7, p.1
 Układy nieliniowe Układy nieliniowe odgrywają istotną rolę w nowoczesnej elektronice, np.: generatory sygnałów, stabilizatory, odbiorniki i nadajniki w telekomunikacji, zasialcze impulsowe stałego napięcia
Układy nieliniowe Układy nieliniowe odgrywają istotną rolę w nowoczesnej elektronice, np.: generatory sygnałów, stabilizatory, odbiorniki i nadajniki w telekomunikacji, zasialcze impulsowe stałego napięcia
Fizyka Ciała Stałego. Struktura krystaliczna. Struktura amorficzna
 Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Repeta z wykładu nr 6. Detekcja światła. Plan na dzisiaj. Metal-półprzewodnik
 Repeta z wykładu nr 6 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 - kontakt omowy
Repeta z wykładu nr 6 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 - kontakt omowy
