Wprowadzenie. 3 m 3 m LAYOUT A. 3 m 3 m LAYOUT B
|
|
|
- Aleksandra Kowal
- 6 lat temu
- Przeglądów:
Transkrypt
1 Problemy rozmieszczania obiektów w projektowaniu ergonomicznym J. Grobelny and W. Karwowski (International Encyclopedia of Ergonomics and Human Factors, Taylor and Francis 2000) Wprowadzenie Wiele sporód projektowanych stanowisk pracy wymaga podjcia decyzji dotyczcej lokalizacji duej liczby urzdze, obsługiwanych póniej przez człowieka. Sposób lokalizacji powinien zapewni efektywne funkcjonowanie przyszłego systemu człowiek-maszyna. Istot problemu rozmieszczania mona pokaza na prostym przykładzie. Załómy e w pewnym budynku biurowym trzeba codziennie przenosi róne rodzaje dokumentów pomidzy trzema rodzajami komórek (A,B,C). rednio dziennie trzeba w zwizku z tym przej 10 razy pomidzy A i B (w jedn lub drug stron), 5 razy midzy B i C oraz 20 razy midzy A i C. Na rys 1 pokazano schemat korytarza, w którym mieszcz si pokoje (1,2 i 3) z komórkami A, B, C. Jeeli przyj pierwsze rozmieszczenie komórek z rys 1 (LAYOUT_A) wówczas łatwo obliczy e w trakcie dnia trzeba przej 10*3 + 5*3 + 20*6 = 165m. Przyjmujc, e w tych samych pokojach rozmieszczono komórki tak jak w (LAYOUT_B) te same czynnoci przenoszenia wymagaj przejcia 10*6 + 5*3 + 20*3 = 135m A B C 3 m 3 m LAYOUT A A C B 3 m 3 m LAYOUT B
2 Rys.1. Przykład zadania rozmieszczania Wida zatem e w drugim przypadku mona zrealizowa zdefiniowany proces mniejszym wysiłkiem. Przykład biura jest problemem współpracy kilku stanowisk roboczych ale zupełnie analogicznie mona analizowa pojedynczy układ człowiek- maszyna chocia kryterium fizycznego przemieszczania si nie jest oczywicie jedynym sposobem oceny jakoci rozmieszczenia elementów sygnalizacyjnych i sterowniczych w takim układzie. Klasyczny przykład ergonomicznego zagadnienia rozmieszczenia opisywany midzy innymi w podrczniku McCormicka (1976) to problem projektowania kokpitu samolotu. Jednym z podzada jest umieszczenie urzdze sterowniczych które musz by obsługiwane na lepo. W takim przypadku rozsdne podejcie polega na takiej aranacji która gwarantuje najwiksz niezawodno łczn trafiania do odpowiednich urzdze. Podstaw takiej aranacji s podane przez Fitts a (1947) wyniki bada nad celnoci ruchów lepych, które w zalenoci od połoenia celu wzgldem operatora liczbowo ujmuj rednie błdy w trafianiu do celu. Dysponujc informacj o czstoci uycia poszczególnych elementów (urzdze sterowniczych) mona obliczy łczny redni błd trafie dla danego rozmieszczenia sumujc dla kadego urzdzenia iloczyn czstoci uycia i redniego błdu dla miejsca jego umieszczenia. Tradycyjnie jako podstaw do oceny rozmieszczenia urzdze w układzie człowiek praca (człowiek-maszyna) stosuje si wiele rónych zasad i kryteriów. Na przykład Bonney i Wiliams (1977) wymieniaj: typ populacji uytkowników, komfort obsługi, bezpieczestwo, estetyk i mod, blisko urzdze dla ułatwienia obsługi, odpowiedni odległo urzdze w celu unikania pomyłek, rozłoenie pracy na odpowiednie koczyny, wymiary antropometryczne oraz funkcjonalne zalenoci obsługiwanych urzdze. W podrcznikach (np. Proctor i Van Zandt 1994) zwraca si uwag przede wszystkim na grupowanie funkcjonalne urzdze, czstotliwo uywania oraz kolejno uywania. Uwzgldnianie tych (i wielu innych) czynników przez projektanta pracujcego w sposób "tradycyjny" odbywa si intuicyjnie i jest tym lepsze, im szersza jest jego wiedza i wiksze dowiadczenie. Próby formalizacji i obiektywizacji procesu podejmowania tego typu decyzji s prowadzone od wczesnych lat szedziesitych (Mc Cormick E. J. 1976). Ze wzgldu na natur wielu z wymienionych czynników nie mona ich wszystkich włcza do modeli o charakterze matematycznym, operujcych na wielkociach mierzalnych (lub dajcych si rozsdnie skwantyfikowa). W wielu przypadkach formalne modele mog mie jedynie znaczenie narzdzi wspomagajcych proces projektowania. Istnieje jednak w literaturze ergonomicznej wiele przykładów, w których modele formalne w zupełnoci wystarczaj, generujc ostateczn decyzj
3 lokalizacyjn. Modele ergonomiczne rozmieszczania obiektów Nieformalne reguły aranacji urzdze, jak zaznaczono wyej, s znane w ergonomii od dawna. Zestawione jeszcze w latach 60-tych najczciej przywoływane reguły zalecaj stosowanie nastpujcych kryteriów (McCormick, 1976): a) wano rozumiane w ten sposób, e urzdzenia najwaniejsze (z punktu widzenia celów projektowanego układu) powinny by umieszczone w miejscach najwaniejszych (najwygodniejszych z punktu widzenia ich obsługi) b) czsto uycia najczciej uywane elementy naley lokowa w miejscach najkorzystniejszych (jak poprzednio chodzi o obsług tych elementów) c) kolejno uycia urzdzenia uywane jedno po drugim powinny ssiadowa ze sob d) spełniane funkcje urzdzenia zwizane z t sam funkcj projektowanego systemu powinny by łczone w bloki (grupy) Łatwo zauway, e poszczególne kryteria mog w rónych sytuacjach dawa sprzeczne rozwizania. Na przykład element wany (powiedzmy wyłcznik zwizany z bezpieczestwem) moe by uywany niezmiernie rzadko. Poza tym mona sobie wyobrazi take wikszy lub/i inny zestaw zasad w szczególnych przypadkach. Nie mona jednak jednoznacznie okreli hierarchii poszczególnych kryteriów gdy bdzie ona zawsze bardzo mocno zalee od konkretnych uwarunkowa danego przypadku. Mc Cormick (1976) sugeruje jednak i kryteria a) i b) s szczególnie przydatne w rozmieszczaniu paneli (grup narzdzi itp.) w przestrzeni pracy, natomiast c) i d) w aranacji pojedynczych paneli. Rzeczywicie kryteria a) i b) w istocie odnosz si do relacji pomidzy pojedynczymi urzdzeniami a miejscami w przestrzeni a właciwie relacji pomidzy miejscem w przestrzeni a operatorem podczas gdy c) i d) analizuj jedynie wzajemne relacje przestrzenne urzdze midzy sob. Wierwille (1980) budujc formalne modele zaproponował okrelenie kryteriów typu a) i b) kryteriami pierwszego rzdu (first order) (relacje mierzone przez to kryterium dotycz pojedynczych urzdze) a pozostałe dwa kryteriami drugiego rzdu (relacje dotycz par urzdze). W myl przedstawionych reguł ogólny problem ergonomicznego rozmieszczenia elementów stanowiska pracy mona sformalizowa nastpujco:
4 Naley rozmieci N urzdze w przestrzeni pracy w taki sposób aby w maksymalnym stopniu spełni zestaw kryteriów a)-d). Formalny model tego zadania wymaga oczywicie zdefiniowania odpowiedniej skali pomiaru stopnia spełniania zestawu kryteriów a)-d). To z kolei prowadzi do koniecznoci okrelenia metod liczbowego pomiaru wartoci kadego z kryteriów. Taki model jest niezbdny aby mona było odróni jedno rozwizanie od drugiego. Typowe podejcia do operacjonalizacji kryteriów pierwszego rzdu polegaj na konstruowaniu prostych skal kilkupunktowych wag oceniajcych urzdzenia i miejsca ich lokalizacji. Ocena wanoci czy czstoci uycia jest formułowana przez ekspertów w oparciu o wiedz o zadaniach jakie bdzie spełnia projektowane stanowisko pracy. Ocena jakoci danego miejsca musi bazowa na wiedzy ergonomicznej i zaley od typu analizowanego elementu. Dane rozwizanie mona w takiej sytuacji ocenia na przykład za pomoc formuły: Q1= i W i *I p(i) (1) Gdzie W i oznacza wano urzdzenia i dla kryterium a), czsto uycia urzdzenia i dla kryterium b) natomiast I p(i) jest wanoci (jakoci) miejsca umieszczenia elementu i ocenion ergonomicznie a p(i) jest indeksem miejsca umieszczenia i-tego elementu. Jeeli skala W jest uporzdkowana malejco (tzn. urzdzenia waniejsze maj wysze oceny) a skala I odwrotnie wówczas lepsze rozwizanie bdzie miało mniejsz warto Q1. Jeli obie skale bd malejce wówczas lepsze bd rozwizania o wikszej wartoci Q1. Poniej pokazano przykład moliwego zastosowania kryterium 1 rzdu do analizy jakoci rozmieszczenia pojemników, do których trzeba siga w trakcie pracy z okrelon czstotliwoci. Strefy pracy oceniono zgodnie z ogólnymi zasadami ergonomii zasigów - przypisujc im wagi od 1 - najlepszej do 4 - najgorszej.
5 Dane czstoci sigania do pojemników: w procentach wszystkich czynnoci Jako rozwizania (liczymy strefami) Q=10*1 + 5*1 + 40*3 + 25*3 + 20*4 Jako rozwizania Q= 1*( ) + 3*(10+5) Rys.2. Przykład zadania rozmieszczania 1 rzdu Kryteria drugiego rzdu najczciej modeluje si za pomoc sumy iloczynów wskaników powiza i odległoci: Q2= i j>i L ij * D p(i)p(j) (2) L ij jest stopniem powizania obiektów ij i dla kryterium c) oznacza na przykład jak czsto obsługa i wystpuje przed obsług j (lub odwrotnie). Dla kryterium d) wskanik L moe wyraa stopie powizania funkcjonalnego (zadaniowego) obu elementów ij. D p(i)p(j) oznacza odległo miejsc p(i) i p(j) w których odpowiednio umieszczono elementy i j. Podwójna suma oznacza e w ocenie bierze si wszystkie pary urzdze j>i w drugiej sumie ogranicza obliczenia do jednokrotnego uwzgldnienia kadej pary. L ij mona zestawi w macierzy, w której na przeciciu wiersza i z kolumn j umieszcza si stopie powizania obiektów i j. Wówczas najczciej wypełnia si macierze tylko nad główn przektn bo tylko te wielkoci uwzgldnia wzór (2). Dla
6 przykładu z rysunku 1 na przykład bdzie to Komórka organizacyjna A B C A Powizania L B - 5 W tym przypadku, poniewa moliwe miejsca lokalizacji s ograniczone do konkretnych pokojów mona podobnie zestawi odległoci midzy miejscami Pokój odległo (w metrach) 2-3 Poniewa ocena wg wzoru (2) wyraa ogólnie rzecz ujmujc pewn waon odległo naturalne bdzie jeli powizania kadej pary obiektów bd wyznaczane tak, aby wikszej intensywnoci powizania odpowiadała wysza ocena liczbowa a wtedy lepsze rozwizania bdzie cechowa nisza ocena według wzoru (2). Naturaln ocen otrzymuje si dla sytuacji podobnych do tej z rys.1 gdzie ocena (2) jest po prostu długoci drogi jak musz przej pracownicy. Poniej pokazano przykład zastosowania kryterium 2-rzdu do analizy stanowiska pracy z poprzedniego rysunku. Załoono tutaj e siganie do pojemników odbywa si w znanych sekwencjach o ustalonej czstotliwoci. Optymalizacja rozmieszczenia ma za zadanie minimalizowa drog rki - zakładajc, e w sekwencji operator siga kolejno do potrzebnych pojemników.
7 Dane do analizy: Opis czynnosci np w formie sekwencji ruchów:! " # $% $% $% $% $ #& # $% $% $% $% $ #&' Rys.3. Przykład zadania rozmieszczania 2 rzdu Wzory (1) i (2) nie s jedynymi moliwymi modelami kryteriów rozmieszczania. W pracach Karwowskiego i in (1999) oraz Grobelnego i in (1995) zaproponowano na przykład zastosowanie teorii zbiorów rozmytych do konstrukcji metryk oceniajcych rozmieszczenie. Podejcia tego typu maj szczególne znaczenie w analizach ergonomicznych poniewa pozwalaj uj w modelowaniu czsto znaczny stopie nieprecyzyjnoci zwizanej z opisem układu człowiek obiekt techniczny. Opis lingwistyczny jest czsto bardziej naturalny zwłaszcza dla wyraenia stopnia powizania czy wanoci od sztucznych skal liczbowych. Kryteria pierwszego i drugiego rzdu mona wyrazi jzykiem logiki w sposób bardzo zbliony do wyraenia w naturalnym jzyku. Na przykład reguła a) moe by okrelona nastpujco:
8 IF Importance_level (of a given facility) is GREAT THEN Location_place (of a given facility) is PROMINENT (3) Natomiast reguł c) mona wyrazi nastpujco: IF facilities pair ij is USED IN SEQUENCE THEN ij are ADJACENT in the layout (4) Podkrelone wyraenia s w tych okreleniach konkretnymi realizacjami zmiennych lingwistycznych to znaczy takich, których wartociami s słowa. W regule (3) zmienne te to Importance level i prominency of a location place. Reguła (4) operuje na zmiennych które mona by okreli jako sekwencyjno uycia i ssiedztwo. Tak sformułowane wyraenia wyraaj ide odpowiednich reguł w nieco bardziej sformalizowany sposób ale sens wyraanych zalenoci jest wyrany. S to opisy podanego stanu pewnego wzorca z jakim naley porównywa rzeczywiste rozwizania. Operacjonalizacja reguł (3) i (4) musi polega na dostarczeniu mechanizmów wartociowania tak aby jak w przypadku reguł (1) i (2) mona było porówna kade 2 rozwizania (i wybra lepsze). Poniewa reguły s wyraeniami logicznymi najbardziej naturalny sposób wartociowania polega na zastosowaniu reguł logicznych do ich wartociowania. Idea linguistic patterns (Grobelny i in 1995, Karwowski i in, 1999) polega na obliczeniu stopnia spełniania wzorców typu (3) i (4) przez badane rozwizania. Mona tego dokona wykorzystujc jedno z uogólnie klasycznej tablicy implikacji, która okrela prawdziwo zdania IF a THEN b w zalenoci od prawdziwoci składowych (poprzednika a i nastpnika b). Jedno z takich uogólnie to wzór Łukasiewicza : Tr(IF a THEN b) = min ( 1, 1 Tr(a) + Tr(b)) (5) gdzie Tr(...) oznacza stopie prawdziwoci wyraenia(...). Łatwo zauway, e (5) działa jak klasyczna tablica prawdy implikacji jeli za Tr(a) i Tr(b) przyj 0 i/lub 1 to znaczy wyraenia s prawdziwe lub fałszywe. Stopie prawdy równy zero (czyli fałsz) zdanie osiga wtedy kiedy a jest prawdziwe i b fałszywe. Rzeczywiste sytuacje oceny s jednak znacznie blisze stopniowaniu prawdziwoci i wówczas wzór (5) pozwala okreli stopie prawdy implikacji na podstawie stopni prawdy członów a i b. Stopnie prawdy definiuje si w skali od 0 do 1. Wygodnym aparatem dostarczajcym narzdzi formalnego budowania ocen stopnia prawdy jest teoria zbiorów rozmytych (...). Przedstawiane podejcie moe jednak by uywane take w mniej formalny sposób poprzez wykorzystanie subiektywnych ocen
9 prawdziwoci na przykład wyraanych przez ekspertów. Dla przykładu rozpatrzymy sytuacj z rys. 1. w dyskutowanych kategoriach. Najpierw zauwamy, e do problemu przypisania czynnoci do pokoju w powyszym przykładzie nie da si bezporednio zastosowa ocen pierwszego rzdu bo nic nie wiadomo o cennoci poszczególnych pomieszcze ani wadze czynnoci. Natomiast problem iloci przej midzy pokojami mona ocenia za pomoc wzorca typu (4). Do tego konkretnego przykładu wzorzec (4) moe by nieco zmodyfikowany tak aby uyte sformułowania nie budziły wtpliwoci. Mona na przykład zaproponowa nastpujce wyraenie: IF czsto_przej_pomidzy_komórkami_i_j jest DU A THEN pokoje (w których umieszczono ij) SSIADUJ (ze sob) (6) Załómy, e sytuacj ocenia maj ortodoksyjni eksperci uznajcy tylko logik dwuwartociow (prawda, fałsz). Jeeli znaj dane z macierzy przedstawionych wyej i akceptuj wzorzec (6) to w oparciu o sw wiedz i dowiadczenie mog na przykład zawyrokowa e czsto przej równa 20 jest dua a pozostałe nie. Natomiast ssiaduj ze sob tylko pokoje majce wspóln cian a wic 1z2 i 2z3. Te oceny mona równie zestawi w macierzach przez analogi do wczeniejszych: Komórka organizacyjna A B C A Stopie spełnienia lewej strony wzorca (6) B - 0 Pokój Stopie spełnienia prawej strony wzorca (6) 2-1 Majc te dane i rysunek 1 mona teraz dokona dla kadej pary komórek organizacyjnych oceny spełnienia wzorca stosujc reguł (5). Komórki Layout a Layout b AB min (1, 1-0+1) = 1 min (1, 1-0+1) = 1
10 AC min (1, 1-1+0) = 0 min (1, 1-1+1) = 1 BC min (1, 1-0+1) = 1 min (1, 1-0+1) = 1 Jak wida w pierwszym rozmieszczeniu wzorzec nie jest spełniony przez par AC i jej rozmieszczenie. Ocena ta jest logiczna take ze zdroworozsdkowego punktu widzenia ilo przej midzy komórkami AC jest dua (wg oceny ekspertów) a pokoje gdzie je umieszczono nie ssiaduj ze sob. W przypadku drugim wszystkie pary spełniaj wzorzec. Poniewa oceny według reguły Łukasiewicza wyraaj stopie prawdy i 1 oznacza pełn prawd nie mona tak jak we wzorze (2) sumowa tych ocen dla poszczególnych rozmieszcze raczej redni stopie prawdy jest w tej sytuacji bardziej adekwatnym rozwizaniem. A zatem layout spełnia wzorzec (6) w stopniu 2/3 layout b w stopniu 1 a wic całkowicie. Próba klasyfikacji zada rozmieszczania i algorytmy optymalizacji W dotychczasowych rozwaaniach przedstawilimy kilka sposobów konstrukcji miar oceniajcych dane rozwizania. Miary te w sposób liczbowy pozwalaj porówna i wybra rozwizania najlepsze ze zbioru dostpnych. Osobnym problemem jest sposób racjonalnego poszukiwania dobrych rozwiza w rónych przypadkach projektowych. Poniewa owe sposoby bardzo mocno s uwarunkowane niektórymi cechami projektów najpierw spróbujemy dokona pewnej typologii zada a nastpnie przypiszemy sposoby postpowania do typów zada. W poprzedniej sekcji poznalimy pierwszy wyrónik zadania rozmieszczania obiektów. Jest nim rzd przyjtego kryterium. Kryteria pierwszego rzdu jak wskazano sugeruj sposób lokalizacji pojedynczych obiektów w przestrzeni pracy. Kryteria rzdu drugiego oceniaj wzajemne relacje par obiektów. W rozpatrywanym przykładzie logiczne było stosowanie tylko reguły drugiego rzdu. Jak wspomniano tego typu reguły s przydatne take w projektowaniu paneli sterowniczych. W tego typu sytuacjach kryteria pierwszego rzdu s czsto nieprzydatne. Z drugiej strony wiele zada projektowych moe wykorzystywa tylko kryteria pierwszego rzdu. Jak wspomniano wczeniej rozmieszczenie gotowych paneli sterowniczych w przestrzeni moe by oceniane za pomoc zasad pierwszego rzdu zwłaszcza gdy kady panel obsługuje inn funkcj. Mona take wyobrazi sobie sytuacje (zwłaszcza złoonych stanowisk operatorskich), w których jednoczenie trzeba szuka kompromisu midzy zasadami obu rzdów. Niewtpliwie zatem sytuacje projektowe w dziedzinie rozmieszczania obiektów mog by (w uproszczeniu) sklasyfikowane jako zadania pierwszego rzdu, drugiego rzdu i złoone w których oba typy kryteriów trzeba uwzgldnia jednoczenie.
11 Podejcia zwizane z rozwizywaniem zada optymalizacj rozmieszcze poza rzdem kryterium zale take od sposobu ograniczania dostpnych miejsc lokalizacji. Przykład rozpatrzony wyej jest reprezentantem zadania ograniczonego miejsca lokalizacji komórek s zdeterminowane. Take wiadomo, e tylko jedna komórka ma mieci si w jednym pokoju. Wyobraajc sobie jednak projektowanie nowego panelu sterowniczego łatwo zauwaymy, e projektant moe czsto decydowa zarówno o rozmieszczeniu pojedynczych elementów na panelu, jak i o kształcie i rozmiarach samego panelu. Takie zadanie mona okreli mianem otwartego. Przyjmujc przedstawione cechy zada jako kryteria podziału otrzymamy sytuacj przedstawion w tablicy 1. Typ kryterium 1-rzdu 2-rzdu oba jednoczenie miejsca dostpne zadanie ograniczone zadanie ograniczone zadanie ograniczone okrelone 1 rzdu 2 rzdu złoone miejsca dostpne zadanie otwarte zadanie otwarte zadanie otwarte dowolne 1 - rzdu 2 rzdu złoone Tab. 1.Propozycja uproszczonej klasyfikacji zada rozmieszczenia ze wzgldu na typ kryterium i dostpno miejsc. Wprowadzona klasyfikacja pozwala przypisa poszczególnym rodzajom zada metody i algorytmy ich rozwizywania prowadzce do uzyskania optymalnych lub suboptymalnych rozmieszcze. Zadanie ograniczone 1 rzdu modeluje do powszechn sytuacj projektow, w której znamy hierarchi ocen z jednej strony obiektów rozmieszczanych z drugiej strony oceny przydatnoci zdefiniowanych miejsc lokalizacji. Typowy przykład to rozmieszczanie elementów w polu widzenia. Nawet jeli miejsca dostpne nie s fizycznie zdeterminowane to oceny mog by wyznaczone na podstawie wiedzy o polu widzenia człowieka i cała dostpna strefa moe by odpowiednio oceniona na przykład poprzez przypisanie wzgldnych ocen ostroci widzenia. Sytuacja tego typu jest prosta z punktu widzenia formalnej optymalizacji. Oczywiste rozwizanie polega na kolejnym przydzielaniu najwaniejszych obiektów do najlepszych dostpnych miejsc.
12 Jest to rozwizanie optymalne a odpowiednie twierdzenie z algebry przytoczono np. w pracy Grobelnego (1988). Praktyczne wykorzystanie tego typu podejcia opisano w podrczniku McCormick (1976). Rozmieszczenie urzdze sterowniczych w kokpicie samolotu zoptymalizowano szeregujc urzdzenia ze wzgldu na czsto uycia a ocen dostpnych miejsc oparto na znanych wynikach bada Fitts a nad precyzj ruchów lepych. Kolejno umieszczano najczciej uywane elementy w dostpnych strefach o najwikszej precyzji ruchów lepych (zmysłu kinestetycznego). Zadania rozmieszczenia elementów stanowiska pracy oparte o kryteria 1 rzdu otwarte w zasadzie rozwizuje si tak jak zadania zamknite tego samego typu. To znaczy podstaw oceny miejsc s zawsze cechy psychofizyczne człowieka. Jeli dostpne miejsca nie s fizycznie wyznaczone to projektant ma wiksz swobod ale pewne strefy o okrelonych cennociach mog i tak by wyznaczane obiektywnymi własnociami organizmu człowieka, a opisany sposób postpowania daje optymalne (formalnie) rozwizania. Znacznie bardziej złoona sytuacja dotyczy zada opisywanych kryteriami drugiego rzdu. Klasyczne podejcia optymalizacyjne pozwalaj poszukiwa rozwiza tylko dla zada ograniczonych (o okrelonych precyzyjnie miejscach). Zadanie tego typu jest ostatecznie najczciej formułowane jako: rozmieci N urzdze w M dostpnych miejscach (M>=N) tak aby warto funkcji typu (2) była minimalna (lub rednia prawda liczona wg wzorca 4 była maksymalna). Optymalne rozwizania mona osign metod przegldania wszystkich moliwych rozmieszcze oraz metod podziału i ogranicze zaproponowan przez Gavetta i Plytera (1966). Efektywno takiego postpowania pozwala rozwizywa zadania do rozmiaru kilkunastu elementów. Dlatego przy zadaniach wikszych konieczne jest uywanie algorytmów heurystycznych. Poniewa klasyczne algorytmy wymagaj precyzyjnego okrelenia miejsc potencjalnej lokalizacji zadania rozmieszczania otwarte musz by odpowiednio przetransponowane na zadania ograniczone. Najczciej dokonuje si tego poprzez wprowadzenie siatek modułowych ograniczajcych dostpn przestrze do wzłów lub oczek siatki. Sears (1993) zaproponował takie podejcie do optymalizacji okien dialogowych interfejsu komputerowego. Podstaw do budowy kryterium optymalizacji była droga kursora jak trzeba było pokona w podstawowych zadaniach realizowanych przez dane okno dialogu. Znajdujc optymalne rozwizania metod podziału i ogranicze autor wykazał w badaniach empirycznych e rozwizania optymalne uzyskane t metod rzeczywicie poprawiaj efektywno pracy w oknie dialogowym. Drezner (1988) jako pierwszy zaproponował metodyk realizacji zada rozmieszczenia otwartych drugiego rzdu na płaszczynie bez adnych ogranicze w formie tzw szkiców rozproszonych (
13 scattered plots). Sprawny algorytm heurystyczny opiera si na własnociach wektorów własnych i wartoci własnych macierzy (eigen vectors, eigen values). Autor pokazał, e jeli przyj jako kryterium typu (2) formuł: Q2 = c ij d ij 2 /d ij 2 (7) w której c odpowiada czstoci interakcji (L ze wzoru (2) ) d odległo odpowiedniej pary obiektów. Minimalizacja (7) jest moliwa do uzyskania metod analityczn, ale obiekty musz by umieszczone na linii prostej. Współrzdne takiego rozwizania (dla x i y te same) to kolejne elementy wektora własnego zwizanego z drug najmniejsz wartoci własn macierzy S, w której s ij = -c ij dla i j oraz s ii = j c ij dla wszystkich i. Dobre rozwizanie na płaszczynie uzyska mona biorc jako współrzdne y elementy wektora własnego zwizanego z trzeci najmniejsz wartoci własn macierzy S. S to bowiem współrzdne najlepszego rozwizania na linii ortogonalnego wzgldem wektora współrzdnych x. Wprawdzie teoria wektorów własnych i wartoci własnych macierzy jest do skomplikowana ale algorytm generujcy rozwizania w myl tej idei jest bardzo prosty i mona go wykorzysta bez znajomoci tych skomplikowanych poj. Majc dane powizania c ij wystarczy: a) skonstruowa macierz S b) Obliczy wartoci własne i wektory własne c) wybra dwa wektory zwizane z drug i trzeci najmniejsz wartoci własn traktujc je odpowiednio jako zestawy kolejnych współrzdnych odpowiednio x i y rozwizania na płaszczynie. Punkt b) musi by oczywicie zrealizowany w odpowiednim programie komputerowym ale wikszo programów wspomagajcych obliczenia matematyczne zawiera odpowiednie procedury (np. MathematicaTM). Na rys. 2 pokazano przykładowy wykres rozproszony dla przykładu w którym wielkoci c zestawiono w formie 0-1 to znaczy elementy s powizane lub nie w nastpujcy sposób: Na pierwszym miejscu podano numer urzdzenia a na kolejnych numery urzdze powizanych z tym pierwszym.
14 Fig.2. Scatter plot for a data given above. Łatwo zauway, e w wikszoci odpowiadajce elementom powizanym gwiazdki s rozmieszczone blisko siebie w schemacie rozproszonym. Elastyczn metod komputerowego generowania szkiców rozproszonych o zrónicowanych parametrach zaproponowano w pracy Grobelnego(1999).
15 Schemat rozproszony jest bardzo uniwersaln form wspomagania projektowania rozmieszczenia. Zwłaszcza jeli bdzie traktowany jako swoista podpowied słuca projektantowi ale nie zastpujca jego wiedzy umiejtnoci i intuicji. Najbardziej złoone problemy rozmieszczania dotycz sytuacji uycia obu typów kryteriów jednoczenie czyli oceny rozwiza zada złoonych. Klasycznym algorytmem stworzonym dla tego typu sytuacji w inynierii przemysłowej (industrial engineering) jest algorytm Hilliera i Connorsa (1966). Algorytm jest jednak przeznaczony tylko dla zada ograniczonych (ilo miejsc lokalizacji musi by równa iloci rozmieszczanych urzdze). Kryterium typu (1) interpretowali autorzy jako ocen kosztu instalacji maszyn w danych miejscach. Kryterium typu (2) było metryk kosztów transportu w trakcie funkcjonowania układu. Algorytm działa w kierunku minimalizacji sumy obu kryteriów. Wykorzystanie do celów projektowania ergonomicznego wymaga sprowadzenia zadania do ograniczonego oraz wyznaczenia macierzy kosztów instalacji poprzez wyznaczenie wartoci funkcji (1) dla kadego elementu w kadym miejscu. Trzeba pamita take e skale ocen musz by odpowiednio zdefiniowane poniewa algorytm poszukuje kompromisu minimalizujcego sum wartoci kryteriów (1) i (2). Jak dotd nie przedstawiono w literaturze algorytmów rozwizujcych zadanie złoone otwarte w podobny sposób jak podejcie Dreznera rozwizuje zadanie otwarte drugiego rzdu. Osobnym problemem wystpujcym w praktyce projektowania ergonomicznego jest kształt i wielko obiektów które maj tworzy stanowisko pracy. Dyskutowana, z koniecznoci uproszczona klasyfikacja nie ujmuje tego zagadnienia, bowiem klasyczne podejcia algorytmiczne omówione tutaj s w znacznym stopniu niezalene od geometrycznych własnoci obiektów. Jednak wprowadzanie siatek modułowych nasunło pomysł definiowania wymiarów i przyblionych kształtów za pomoc modułów siatki. Pierwsze takie podejcia zastosowano w inynierii przemysłowej ju w latach 60-tych. Przykładem metody tego typu jest CORELAP (...). Scharakteryzowany wczeniej algorytm Searsa (1993) wykorzystuje moduły do podziału miejsc w oknie dialogu ale take do symulowania zarysów funkcjonalnych obiektów rozmieszczanych w projektowanych oknach. Dyskusja i podsumowanie Rozmieszczanie elementów jest wanym procesem projektowania złoonych struktur. Ergonomiczne rozmieszczenie powinno by oparte na optymalizacji kryteriów ergonomicznych.
16 W tym celu trzeba sformułowa mniej lub bardziej precyzyjnie mierzalne funkcje kryteria adekwatne do danej sytuacji. Owe funkcje musz pozwoli odróni lepsze projekty od gorszych. Algorytmy i metody optymalizacyjne w wielu wypadkach pozwalaj znale rozwizania najlepsze lub bardzo dobre. W tym miejscu powstaje pytanie na ile takie, teoretycznie poprawne ergonomicznie rozwizania sprawdzaj si w praktyce. To znaczy czy znalezione przy uyciu dyskutowanych metod rozwizania poprawiaj funkcjonowanie rzeczywistych systemów człowiek maszyna? Niektóre sytuacje s oczywiste i nie wymagaj dodatkowych dowodów czy weryfikacji. Do takich nale problemy o wymiernych fizycznie lub/i ekonomicznie funkcjach (obu rzdów). Podany na pocztku przykład uzmysławia jednoznacznie e ruch w urzdzie zaprojektowanym wg rozmieszczenia b) bdzie mniejszy ni przy rozmieszczeniu a). Wiele problemów ergonomicznych nie ma jednak tak jednoznacznie wymiernych wskaników albo te wskaniki nie s jedynymi wyznacznikami poprawnoci projektu. Do tego typu problemów naley niewtpliwie sfera interakcji człowiek-komputer. Poprawnie zaprojektowane okno dialogowe czy struktura menu niekoniecznie musi wpłyn na dobr jako interfejsu bo czynniki wpływajce na subiektywne i obiektywne oceny oprogramowania s skomplikowane i nie do koca zidentyfikowane. Eksperymenty laboratoryjne Searsa (1993) a take Grobelnego (1998) wskazuj jednak e zoptymalizowane (ze wzgldu na drog kursora w procesie obsługi) okna dialogowe s obsługiwane sprawniej i/lub oceniane subiektywnie lepiej ni okna zaprojektowane bez formalnej analizy rozmieszczenia obiektów. Literatura Bonney M.C., Wiliams R.W.,1977, A computer program to layout controls and panels, Ergonomics, 20, McCormick E.J.,1976, Human factors in engineering and design, Mc Graw Hill, Inc. Fitts P.M.,1947, Psychological research on equipment design, Army Air Forces Aviation Psychology Program Research Reports, REPORT 19. Drezner Z., 1988, A Heuristic Procedure for the Layout of a Large Number of Facilities, Management Sci., 33, Gavett J.W., Plyter N.V., 1966, The optimal assignment of facilities to locations by branch and bound, Oper. Res., 14, Grobelny J., 1988, The "linguistic pattern" method for a workstation layout analysis, Int.J.of Prod.Res. 26, 11 / /.
17 Grobelny J., 1998., Index of difficulty (ID) as a quality factor for a graphical man-machine interfaces. In: Manufacturing agility and hybrid automation-ii. Proceedings of the Sixth International Conference on Human Aspects of Advanced Manufacturing: Agility & Hybrid Automation. Ed. by Waldemar Karwowski and Ravindra Goonetilleke. Santa Monica, CA: IEA Press Grobelny, J., 1999, Some remarks on scatter plots generation procedures for facility layout. Int. J. Prod. Res., 37, Grobelny J., Karwowski W., Zurada J., 1995, Applications of fuzzy-based linguistic patterns for the assessment of computer screen design quality, International Journal of Human-Computer Interaction 7(3) Hillier F.S., Connors M.M., 1966, Quadratic assignment problem algorithm and the location of indivisible facilities, Management Sci., 13, Karwowski W., Lee W., Grobelny J.,1999, Applications fuzzy system methodologies in human factors and ergonomics, submitted for publication in Zimmermann H. (ed.) Handbook of Fuzzy Sets and Systems. Lee, R.C. and Moore, J.M., 1967, CORELAP-computerized relationship layout planning. Journal of Industrial Engineering,18, Proctor R.W., Van Zandt T., 1994, Human Factors in Simple and Complex Systems,Allyn and Bacon. Sears A., 1993, Layout appropriateness: A metric for evaluating user interface widget layout, IEEE Transactions on Software Engineering, 19, Wierwille W.W.,1980, Statistical techniques for instrument panel arrangement, Virginia Polytechnic Inst. and State University.
Projektowanie i analiza zadaniowa interfejsu na przykładzie okna dialogowego.
 Projektowanie i analiza zadaniowa interfejsu na przykładzie okna dialogowego. Jerzy Grobelny Politechnika Wrocławska Projektowanie zadaniowe jest jednym z podstawowych podej do racjonalnego kształtowania
Projektowanie i analiza zadaniowa interfejsu na przykładzie okna dialogowego. Jerzy Grobelny Politechnika Wrocławska Projektowanie zadaniowe jest jednym z podstawowych podej do racjonalnego kształtowania
Planowanie adresacji IP dla przedsibiorstwa.
 Planowanie adresacji IP dla przedsibiorstwa. Wstp Przy podejciu do planowania adresacji IP moemy spotka si z 2 głównymi przypadkami: planowanie za pomoc adresów sieci prywatnej przypadek, w którym jeeli
Planowanie adresacji IP dla przedsibiorstwa. Wstp Przy podejciu do planowania adresacji IP moemy spotka si z 2 głównymi przypadkami: planowanie za pomoc adresów sieci prywatnej przypadek, w którym jeeli
Konspekt lekcji matematyki klasa 4e Liceum Ogólnokształcce
 mgr Tomasz Grbski Konspekt lekcji matematyki klasa 4e Liceum Ogólnokształcce Temat: Dyskusja nad liczb rozwiza równania liniowego i kwadratowego z wartoci bezwzgldn i parametrem. Czas trwania: 45 minut.
mgr Tomasz Grbski Konspekt lekcji matematyki klasa 4e Liceum Ogólnokształcce Temat: Dyskusja nad liczb rozwiza równania liniowego i kwadratowego z wartoci bezwzgldn i parametrem. Czas trwania: 45 minut.
Wspomaganie analizy obcie posturalnych w projektowaniu stanowisk pracy w technologii CAD.
 Wspomaganie analizy obcie posturalnych w projektowaniu stanowisk pracy w technologii CAD. Jerzy Grobelny Instytut Organizacji i Zarzdzania Politechniki Wrocławskiej Wprowadzenie. Obcienia układu ruchu
Wspomaganie analizy obcie posturalnych w projektowaniu stanowisk pracy w technologii CAD. Jerzy Grobelny Instytut Organizacji i Zarzdzania Politechniki Wrocławskiej Wprowadzenie. Obcienia układu ruchu
IV Powiatowy Konkurs Matematyka, Fizyka i Informatyka w Technice Etap finałowy 1 kwietnia 2016
 IV Powiatowy Konkurs Matematyka, Fizyka i Informatyka w Technice Etap finałowy 1 kwietnia 2016 (imi i nazwisko uczestnika) (nazwa szkoły) Arkusz zawiera 8 zada. Zadania 1 i 2 bd oceniane dla kadego uczestnika,
IV Powiatowy Konkurs Matematyka, Fizyka i Informatyka w Technice Etap finałowy 1 kwietnia 2016 (imi i nazwisko uczestnika) (nazwa szkoły) Arkusz zawiera 8 zada. Zadania 1 i 2 bd oceniane dla kadego uczestnika,
Projekt okablowania strukturalnego dla I semestru Akademii CISCO we WSIZ Copernicus we Wrocławiu
 Przygotował: mgr in. Jarosław Szybiski Projekt okablowania strukturalnego dla I semestru Akademii CISCO we WSIZ Copernicus we Wrocławiu 1. Wstp Okablowanie strukturalne to pojcie, którym okrela si specyficzne
Przygotował: mgr in. Jarosław Szybiski Projekt okablowania strukturalnego dla I semestru Akademii CISCO we WSIZ Copernicus we Wrocławiu 1. Wstp Okablowanie strukturalne to pojcie, którym okrela si specyficzne
Izolacja Anteny szerokopasmowe i wskopasmowe
 Izolacja Anteny szerokopasmowe i wskopasmowe W literaturze technicznej mona znale róne opinie, na temat okrelenia, kiedy antena moe zosta nazwana szerokopasmow. Niektórzy producenci nazywaj anten szerokopasmow
Izolacja Anteny szerokopasmowe i wskopasmowe W literaturze technicznej mona znale róne opinie, na temat okrelenia, kiedy antena moe zosta nazwana szerokopasmow. Niektórzy producenci nazywaj anten szerokopasmow
Zastosowanie programu Microsoft Excel do analizy wyników nauczania
 Grayna Napieralska Zastosowanie programu Microsoft Excel do analizy wyników nauczania Koniecznym i bardzo wanym elementem pracy dydaktycznej nauczyciela jest badanie wyników nauczania. Prawidłow analiz
Grayna Napieralska Zastosowanie programu Microsoft Excel do analizy wyników nauczania Koniecznym i bardzo wanym elementem pracy dydaktycznej nauczyciela jest badanie wyników nauczania. Prawidłow analiz
PREZENTACJA DZIAŁANIA KLASYCZNEGO ALGORYTMU GENETYCZNEGO
 Piotr Borowiec PREZENTACJA DZIAŁANIA KLASYCZNEGO ALGORYTMU GENETYCZNEGO Sporód wielu metod sztucznej inteligencji obliczeniowej algorytmy genetyczne doczekały si wielu implementacji. Mona je wykorzystywa
Piotr Borowiec PREZENTACJA DZIAŁANIA KLASYCZNEGO ALGORYTMU GENETYCZNEGO Sporód wielu metod sztucznej inteligencji obliczeniowej algorytmy genetyczne doczekały si wielu implementacji. Mona je wykorzystywa
Cash flow projektu zakładajcego posiadanie własnego magazynu oraz posiłkowanie si magazynem obcym w przypadku sezonowych zwyek
 Optymalizacja zaangaowania kapitałowego 4.01.2005 r. w decyzjach typu make or buy. Magazyn czy obcy cz. 2. Cash flow projektu zakładajcego posiadanie własnego magazynu oraz posiłkowanie si magazynem obcym
Optymalizacja zaangaowania kapitałowego 4.01.2005 r. w decyzjach typu make or buy. Magazyn czy obcy cz. 2. Cash flow projektu zakładajcego posiadanie własnego magazynu oraz posiłkowanie si magazynem obcym
Zarzdzanie i inynieria produkcji Studia II stopnia o profilu: A x P
 Specjalno: Inynieria produkcji w przemyle maszynowym Zintegrowane systemy (CIM) WM Zarzdzanie i inynieria produkcji Studia II stopnia o profilu: A x P Przedmiot: Zintegrowane systemy (CIM) Status przedmiotu:
Specjalno: Inynieria produkcji w przemyle maszynowym Zintegrowane systemy (CIM) WM Zarzdzanie i inynieria produkcji Studia II stopnia o profilu: A x P Przedmiot: Zintegrowane systemy (CIM) Status przedmiotu:
Program do konwersji obrazu na cig zero-jedynkowy
 Łukasz Wany Program do konwersji obrazu na cig zero-jedynkowy Wstp Budujc sie neuronow do kompresji znaków, na samym pocztku zmierzylimy si z problemem przygotowywania danych do nauki sieci. Przyjlimy,
Łukasz Wany Program do konwersji obrazu na cig zero-jedynkowy Wstp Budujc sie neuronow do kompresji znaków, na samym pocztku zmierzylimy si z problemem przygotowywania danych do nauki sieci. Przyjlimy,
Plan wykładu. Reguły asocjacyjne. Przykłady asocjacji. Reguły asocjacyjne. Jeli warunki to efekty. warunki efekty
 Plan wykładu Reguły asocjacyjne Marcin S. Szczuka Wykład 6 Terminologia dla reguł asocjacyjnych. Ogólny algorytm znajdowania reguł. Wyszukiwanie czstych zbiorów. Konstruowanie reguł - APRIORI. Reguły asocjacyjne
Plan wykładu Reguły asocjacyjne Marcin S. Szczuka Wykład 6 Terminologia dla reguł asocjacyjnych. Ogólny algorytm znajdowania reguł. Wyszukiwanie czstych zbiorów. Konstruowanie reguł - APRIORI. Reguły asocjacyjne
Temat: Technika zachłanna. Przykłady zastosowania. Własno wyboru zachłannego i optymalnej podstruktury.
 Temat: Technika zachłanna. Przykłady zastosowania. Własno wyboru zachłannego i optymalnej podstruktury. Algorytm zachłanny ( ang. greedy algorithm) wykonuje zawsze działanie, które wydaje si w danej chwili
Temat: Technika zachłanna. Przykłady zastosowania. Własno wyboru zachłannego i optymalnej podstruktury. Algorytm zachłanny ( ang. greedy algorithm) wykonuje zawsze działanie, które wydaje si w danej chwili
Ustalenie optymalnego układu lokalizacyjnodystrybucyjnego
 10.02.2005 r. Optymalizacja lokalizacji i rejonizacji w sieciach dystrybucji. cz. 2. Ustalenie optymalnego układu lokalizacyjnodystrybucyjnego dla wielu uczestników Przyczyn rozwizywania problemu wielu
10.02.2005 r. Optymalizacja lokalizacji i rejonizacji w sieciach dystrybucji. cz. 2. Ustalenie optymalnego układu lokalizacyjnodystrybucyjnego dla wielu uczestników Przyczyn rozwizywania problemu wielu
Temat: Problem minimalnego drzewa Steinera. Definicja problemu. Zastosowania. Algorytm dokładny Hakimi. Algorytmy aproksymacyjne.
 Temat: Problem minimalnego drzewa Steinera. Definicja problemu. Zastosowania. Algorytm dokładny Hakimi. Algorytmy aproksymacyjne. 1. Definicja problemu Wejcie: Graf spójny niezorientowany G =
Temat: Problem minimalnego drzewa Steinera. Definicja problemu. Zastosowania. Algorytm dokładny Hakimi. Algorytmy aproksymacyjne. 1. Definicja problemu Wejcie: Graf spójny niezorientowany G =
Programowanie Obiektowe
 Programowanie Obiektowe dr in. Piotr Zabawa IBM/Rational Certified Consultant pzabawa@pk.edu.pl WYKŁAD 1 Wstp, jzyki, obiektowo Cele wykładu Zaznajomienie słuchaczy z głównymi cechami obiektowoci Przedstawienie
Programowanie Obiektowe dr in. Piotr Zabawa IBM/Rational Certified Consultant pzabawa@pk.edu.pl WYKŁAD 1 Wstp, jzyki, obiektowo Cele wykładu Zaznajomienie słuchaczy z głównymi cechami obiektowoci Przedstawienie
Temat: Problem najkrótszych cieek w grafach waonych, cz. I: Algorytmy typu label - setting.
 Temat: Problem najkrótszych cieek w grafach waonych, cz. I: Algorytmy typu label - setting.. Oznaczenia i załoenia Oznaczenia G = - graf skierowany z funkcj wagi s wierzchołek ródłowy t wierzchołek
Temat: Problem najkrótszych cieek w grafach waonych, cz. I: Algorytmy typu label - setting.. Oznaczenia i załoenia Oznaczenia G = - graf skierowany z funkcj wagi s wierzchołek ródłowy t wierzchołek
KARTA OCENY MERYTORYCZNEJ W RAMACH PROJEKTU PIERWSZY BIZNES AKTYWIZACJA LOKALNEJ SPOŁECZNOCI. Deklaracja bezstronnoci i poufnoci
 Owiadczam, e: Nr wniosku Imi i nazwisko Kandydata/tki Imi i nazwisko Oceniajcego Imi i nazwisko Kandydata/tki Załcznik nr 5 do Regulaminu rekrutacji do Projektu PIERWSZY BIZNES aktywizacja lokalnej społecznoci
Owiadczam, e: Nr wniosku Imi i nazwisko Kandydata/tki Imi i nazwisko Oceniajcego Imi i nazwisko Kandydata/tki Załcznik nr 5 do Regulaminu rekrutacji do Projektu PIERWSZY BIZNES aktywizacja lokalnej społecznoci
Projektowanie ergonomicznego rozmieszczenia obiektów z uyciem programu Links
 Projektowanie ergonomicznego rozmieszczenia obiektów z uyciem programu Links Jerzy Grobelny Politechnika Wrocławska 1. Zapoznaj si moliwie szeroko z problemem rozmieszczania obiektów (Facilities Layout
Projektowanie ergonomicznego rozmieszczenia obiektów z uyciem programu Links Jerzy Grobelny Politechnika Wrocławska 1. Zapoznaj si moliwie szeroko z problemem rozmieszczania obiektów (Facilities Layout
Podstawowe obiekty AutoCAD-a
 LINIA Podstawowe obiekty AutoCAD-a Zad1: Narysowa lini o pocztku w punkcie o współrzdnych (100, 50) i kocu w punkcie (200, 150) 1. Wybierz polecenie rysowania linii, np. poprzez kilknicie ikony. W wierszu
LINIA Podstawowe obiekty AutoCAD-a Zad1: Narysowa lini o pocztku w punkcie o współrzdnych (100, 50) i kocu w punkcie (200, 150) 1. Wybierz polecenie rysowania linii, np. poprzez kilknicie ikony. W wierszu
Temat: Geometria obliczeniowa cz II. Para najmniej odległych punktów. Sprawdzenie, czy istnieje para przecinajcych si odcinków.
 Temat: Geometria obliczeniowa cz II. Para najmniej odległych punktów. Sprawdzenie, czy istnieje para przecinajcych si odcinków. 1. Para najmniej odległych punktów WP: Dany jest n - elementowy zbiór punktów
Temat: Geometria obliczeniowa cz II. Para najmniej odległych punktów. Sprawdzenie, czy istnieje para przecinajcych si odcinków. 1. Para najmniej odległych punktów WP: Dany jest n - elementowy zbiór punktów
Instrukcja dla pracowników Uniwersytetu Rzeszowskiego.
 Dost p!do!infrastruktury!informatycznej. Instrukcja dla pracowników Uniwersytetu Rzeszowskiego. Wersja dokumentu: 1.0.0 Rzeszów: 23.10.2009 OPTeam S.A. 35-032 Rzeszów, ul. Lisa Kuli 3 INFORMACJA O NOWYCH
Dost p!do!infrastruktury!informatycznej. Instrukcja dla pracowników Uniwersytetu Rzeszowskiego. Wersja dokumentu: 1.0.0 Rzeszów: 23.10.2009 OPTeam S.A. 35-032 Rzeszów, ul. Lisa Kuli 3 INFORMACJA O NOWYCH
Kod pocztowy 00-928. Województwo Mazowieckie. Faks 630-10-19. Adres internetowy (URL) www.mi.gov.pl
 OGŁOSZE O ZAMÓWIENIU Roboty budowlane Dostawy Usługi Wypełnia Urzd Zamówie Publicznych Data otrzymania ogłoszenia Numer identyfikacyjny SEKCJA I: ZAMAWIAJCY I.1) OFICJALNA NAZWA I ADRES ZAMAWIAJCEGO Ministerstwo
OGŁOSZE O ZAMÓWIENIU Roboty budowlane Dostawy Usługi Wypełnia Urzd Zamówie Publicznych Data otrzymania ogłoszenia Numer identyfikacyjny SEKCJA I: ZAMAWIAJCY I.1) OFICJALNA NAZWA I ADRES ZAMAWIAJCEGO Ministerstwo
Uywanie licencji typu On-Demand. Using an On-Demand License Japanese. Language. Contents
 Uywanie licencji typu On-Demand Language Using an On-Demand License Japanese Contents Logowanie do konta Altium Dostpne portale Dostpno licencji Tryb licencji On-Demand Roaming Praca bez dostpu do Internetu
Uywanie licencji typu On-Demand Language Using an On-Demand License Japanese Contents Logowanie do konta Altium Dostpne portale Dostpno licencji Tryb licencji On-Demand Roaming Praca bez dostpu do Internetu
PROBLEM ROZMIESZCZENIA MASZYN LICZĄCYCH W DUŻYCH SYSTEMACH PRZEMYSŁOWYCH AUTOMATYCZNIE STEROWANYCH
 CZESŁAW KULIK PROBLEM ROZMIESZCZENIA MASZYN LICZĄCYCH W DUŻYCH SYSTEMACH PRZEMYSŁOWYCH AUTOMATYCZNIE STEROWANYCH Duże systemy przemysłowe, jak kopalnie, kombinaty metalurgiczne, chemiczne itp., mają złożoną
CZESŁAW KULIK PROBLEM ROZMIESZCZENIA MASZYN LICZĄCYCH W DUŻYCH SYSTEMACH PRZEMYSŁOWYCH AUTOMATYCZNIE STEROWANYCH Duże systemy przemysłowe, jak kopalnie, kombinaty metalurgiczne, chemiczne itp., mają złożoną
Sterowanie prac plotera w układach logiki programowalnej
 LABORATORIUM TECHNIKI CYFROWEJ Sterowanie prac plotera w układach logiki programowalnej Opracowali: mgr in. Rafał Sokół dr in. Krystyna Maria Noga Akademia Morska Wydział Elektryczny Katedra Automatyki
LABORATORIUM TECHNIKI CYFROWEJ Sterowanie prac plotera w układach logiki programowalnej Opracowali: mgr in. Rafał Sokół dr in. Krystyna Maria Noga Akademia Morska Wydział Elektryczny Katedra Automatyki
Metody Informatyczne w Budownictwie Metoda Elementów Skoczonych ZADANIE NR 1
 Metody Informatyczne w Budownictwie Metoda Elementów Skoczonych ZADANIE NR 1 Wyznaczy wektor sił i przemieszcze wzłowych dla układu elementów przedstawionego na rysunku poniej (rysunek nie jest w skali!).
Metody Informatyczne w Budownictwie Metoda Elementów Skoczonych ZADANIE NR 1 Wyznaczy wektor sił i przemieszcze wzłowych dla układu elementów przedstawionego na rysunku poniej (rysunek nie jest w skali!).
1) Grafy eulerowskie własnoci algorytmy. 2) Problem chiskiego listonosza
 165 1) Grafy eulerowskie własnoci algorytmy 2) Problem chiskiego listonosza 166 Grafy eulerowskie Def. Graf (multigraf, niekoniecznie spójny) jest grafem eulerowskim, jeli zawiera cykl zawierajcy wszystkie
165 1) Grafy eulerowskie własnoci algorytmy 2) Problem chiskiego listonosza 166 Grafy eulerowskie Def. Graf (multigraf, niekoniecznie spójny) jest grafem eulerowskim, jeli zawiera cykl zawierajcy wszystkie
Rezonans szeregowy (E 4)
 POLITECHNIKA LSKA WYDZIAŁINYNIERII RODOWISKA I ENERGETYKI INSTYTT MASZYN I RZDZE ENERGETYCZNYCH Rezonans szeregowy (E 4) Opracował: mgr in. Janusz MDRYCH Zatwierdził: W.O. . Cel wiczenia. Celem wiczenia
POLITECHNIKA LSKA WYDZIAŁINYNIERII RODOWISKA I ENERGETYKI INSTYTT MASZYN I RZDZE ENERGETYCZNYCH Rezonans szeregowy (E 4) Opracował: mgr in. Janusz MDRYCH Zatwierdził: W.O. . Cel wiczenia. Celem wiczenia
LOGISTYKA ZAOPATRZENIA I PRODUKCJI ĆWICZENIA 13 ROZMIESZCZENIE STANOWISK (LAYOUT)
 1 LOGISTYKA ZAOPATRZENIA I PRODUKCJI ĆWICZENIA 13 ROZMIESZCZENIE STANOWISK (LAYOUT) Autor: dr inż. Roman DOMAŃSKI 2 LITERATURA Marek Fertsch, Danuta Głowacka-Fertsch Zarządzanie produkcją, WSL Poznań 2004
1 LOGISTYKA ZAOPATRZENIA I PRODUKCJI ĆWICZENIA 13 ROZMIESZCZENIE STANOWISK (LAYOUT) Autor: dr inż. Roman DOMAŃSKI 2 LITERATURA Marek Fertsch, Danuta Głowacka-Fertsch Zarządzanie produkcją, WSL Poznań 2004
w sprawie wprowadzenia procedury naboru pracowników na kierownicze stanowiska urzdnicze i stanowiska urzdnicze w Starostwie Powiatowym w Krasnymstawie
 ZARZDZENIE Nr 13/2005 STAROSTY KRASNOSTAWSKIEGO z dnia 29 sierpnia 2005 roku w sprawie wprowadzenia procedury naboru pracowników na kierownicze stanowiska urzdnicze i stanowiska urzdnicze w Starostwie
ZARZDZENIE Nr 13/2005 STAROSTY KRASNOSTAWSKIEGO z dnia 29 sierpnia 2005 roku w sprawie wprowadzenia procedury naboru pracowników na kierownicze stanowiska urzdnicze i stanowiska urzdnicze w Starostwie
stopie szaro ci piksela ( x, y)
 I. Wstp. Jednym z podstawowych zada analizy obrazu jest segmentacja. Jest to podział obrazu na obszary spełniajce pewne kryterium jednorodnoci. Jedn z najprostszych metod segmentacji obrazu jest progowanie.
I. Wstp. Jednym z podstawowych zada analizy obrazu jest segmentacja. Jest to podział obrazu na obszary spełniajce pewne kryterium jednorodnoci. Jedn z najprostszych metod segmentacji obrazu jest progowanie.
PROWIZJE Menad er Schematy rozliczeniowe
 W nowej wersji systemu pojawił si specjalny moduł dla menaderów przychodni. Na razie jest to rozwizanie pilotaowe i udostpniono w nim jedn funkcj, która zostanie przybliona w niniejszym biuletynie. Docelowo
W nowej wersji systemu pojawił si specjalny moduł dla menaderów przychodni. Na razie jest to rozwizanie pilotaowe i udostpniono w nim jedn funkcj, która zostanie przybliona w niniejszym biuletynie. Docelowo
Rys1 Rys 2 1. metoda analityczna. Rys 3 Oznaczamy prdy i spadki napi jak na powyszym rysunku. Moemy zapisa: (dla wzłów A i B)
 Zadanie Obliczy warto prdu I oraz napicie U na rezystancji nieliniowej R(I), której charakterystyka napiciowo-prdowa jest wyraona wzorem a) U=0.5I. Dane: E=0V R =Ω R =Ω Rys Rys. metoda analityczna Rys
Zadanie Obliczy warto prdu I oraz napicie U na rezystancji nieliniowej R(I), której charakterystyka napiciowo-prdowa jest wyraona wzorem a) U=0.5I. Dane: E=0V R =Ω R =Ω Rys Rys. metoda analityczna Rys
Gramatyki regularne i automaty skoczone
 Gramatyki regularne i automaty skoczone Alfabet, jzyk, gramatyka - podstawowe pojcia Co to jest gramatyka regularna, co to jest automat skoczony? Gramatyka regularna Gramatyka bezkontekstowa Translacja
Gramatyki regularne i automaty skoczone Alfabet, jzyk, gramatyka - podstawowe pojcia Co to jest gramatyka regularna, co to jest automat skoczony? Gramatyka regularna Gramatyka bezkontekstowa Translacja
SZTUCZNA INTELIGENCJA
 SZTUCZNA INTELIGENCJA WYKŁAD 10. WNIOSKOWANIE W LOGICE ROZMYTEJ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska WNIOSKOWANIE W LOGICE DWUWARTOŚCIOWEJ W logice
SZTUCZNA INTELIGENCJA WYKŁAD 10. WNIOSKOWANIE W LOGICE ROZMYTEJ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska WNIOSKOWANIE W LOGICE DWUWARTOŚCIOWEJ W logice
Bazy danych. Plan wykładu. Zalenoci funkcyjne. Wykład 4: Relacyjny model danych - zalenoci funkcyjne. SQL - podzapytania A B
 Plan wykładu Bazy danych Wykład 4: Relacyjny model danych - zalenoci funkcyjne. SQL - podzapytania Definicja zalenoci funkcyjnych Klucze relacji Reguły dotyczce zalenoci funkcyjnych Domknicie zbioru atrybutów
Plan wykładu Bazy danych Wykład 4: Relacyjny model danych - zalenoci funkcyjne. SQL - podzapytania Definicja zalenoci funkcyjnych Klucze relacji Reguły dotyczce zalenoci funkcyjnych Domknicie zbioru atrybutów
MATEMATYCZNE MODELE PRZESTRZENNEJ ORGANIZACJI STANOWISK PRACY
 MATEMATYCZE MODELE PRZESTRZEEJ ORGAIZACJI STAOWISK PRACY GARIK Igor Politechnika Gdańska, Wydział Zarządzania i Ekonomii Streszczenie: Opracowanie zawiera opis niektórych modeli matematycznych, stosowanych
MATEMATYCZE MODELE PRZESTRZEEJ ORGAIZACJI STAOWISK PRACY GARIK Igor Politechnika Gdańska, Wydział Zarządzania i Ekonomii Streszczenie: Opracowanie zawiera opis niektórych modeli matematycznych, stosowanych
Zarzdzanie i Inynieria Produkcji Studia II stopnia o profilu: A P
 Technologiczne i organizacyjne przygotowanie produkcji WM Zarzdzanie i Inynieria Produkcji Studia II stopnia o profilu: A P Przedmiot: Technologiczne i organizacyjne przygotowanie produkcji Kod przedmiotu
Technologiczne i organizacyjne przygotowanie produkcji WM Zarzdzanie i Inynieria Produkcji Studia II stopnia o profilu: A P Przedmiot: Technologiczne i organizacyjne przygotowanie produkcji Kod przedmiotu
Projektowanie algorytmów rekurencyjnych
 C9 Projektowanie algorytmów rekurencyjnych wiczenie 1. Przeanalizowa działanie poniszego algorytmu dla parametru wejciowego n = 4 (rysunek 9.1): n i i
C9 Projektowanie algorytmów rekurencyjnych wiczenie 1. Przeanalizowa działanie poniszego algorytmu dla parametru wejciowego n = 4 (rysunek 9.1): n i i
PROCEDURY REGULACYJNE STEROWNIKÓW PROGRAMOWALNYCH (PLC)
 PROCEDURY REGULACYJNE STEROWNIKÓW PROGRAMOWALNYCH (PLC) W dotychczasowych systemach automatyki przemysłowej algorytm PID był realizowany przez osobny regulator sprztowy - analogowy lub mikroprocesorowy.
PROCEDURY REGULACYJNE STEROWNIKÓW PROGRAMOWALNYCH (PLC) W dotychczasowych systemach automatyki przemysłowej algorytm PID był realizowany przez osobny regulator sprztowy - analogowy lub mikroprocesorowy.
Poprawa efektywnoci metody wstecznej propagacji bdu. Jacek Bartman
 Poprawa efektywnoci metody wstecznej propagac bdu Algorytm wstecznej propagac bdu. Wygeneruj losowo wektory wag. 2. Podaj wybrany wzorzec na wejcie sieci. 3. Wyznacz odpowiedzi wszystkich neuronów wyjciowych
Poprawa efektywnoci metody wstecznej propagac bdu Algorytm wstecznej propagac bdu. Wygeneruj losowo wektory wag. 2. Podaj wybrany wzorzec na wejcie sieci. 3. Wyznacz odpowiedzi wszystkich neuronów wyjciowych
Zadania do wykonaj przed przyst!pieniem do pracy:
 wiczenie 3 Tworzenie bazy danych Biblioteka tworzenie kwerend, formularzy Cel wiczenia: Zapoznanie si ze sposobami konstruowania formularzy operujcych na danych z tabel oraz metodami tworzenia kwerend
wiczenie 3 Tworzenie bazy danych Biblioteka tworzenie kwerend, formularzy Cel wiczenia: Zapoznanie si ze sposobami konstruowania formularzy operujcych na danych z tabel oraz metodami tworzenia kwerend
Metodydowodzenia twierdzeń
 1 Metodydowodzenia twierdzeń Przez zdanie rozumiemy dowolne stwierdzenie, które jest albo prawdziwe, albo faªszywe (nie mo»e by ono jednocze±nie prawdziwe i faªszywe). Tradycyjnie b dziemy u»ywali maªych
1 Metodydowodzenia twierdzeń Przez zdanie rozumiemy dowolne stwierdzenie, które jest albo prawdziwe, albo faªszywe (nie mo»e by ono jednocze±nie prawdziwe i faªszywe). Tradycyjnie b dziemy u»ywali maªych
Multipro GbE. Testy RFC2544. Wszystko na jednej platformie
 Multipro GbE Testy RFC2544 Wszystko na jednej platformie Interlab Sp z o.o, ul.kosiarzy 37 paw.20, 02-953 Warszawa tel: (022) 840-81-70; fax: 022 651 83 71; mail: interlab@interlab.pl www.interlab.pl Wprowadzenie
Multipro GbE Testy RFC2544 Wszystko na jednej platformie Interlab Sp z o.o, ul.kosiarzy 37 paw.20, 02-953 Warszawa tel: (022) 840-81-70; fax: 022 651 83 71; mail: interlab@interlab.pl www.interlab.pl Wprowadzenie
Instrukcja obsługi programu MechKonstruktor
 Instrukcja obsługi programu MechKonstruktor Opracował: Sławomir Bednarczyk Wrocław 2002 1 1. Opis programu komputerowego Program MechKonstruktor słuy do komputerowego wspomagania oblicze projektowych typowych
Instrukcja obsługi programu MechKonstruktor Opracował: Sławomir Bednarczyk Wrocław 2002 1 1. Opis programu komputerowego Program MechKonstruktor słuy do komputerowego wspomagania oblicze projektowych typowych
Wymierne korzyci wynikajce z analizy procesów
 Wymierne korzyci wynikajce z analizy procesów Analiza procesu jest narzdziem do osignicia wyszej efektywnoci organizacji (midzy innymi). Wymaga ona zbudowania modelu procesu biznesowego bdcego opisem funkcjonowania
Wymierne korzyci wynikajce z analizy procesów Analiza procesu jest narzdziem do osignicia wyszej efektywnoci organizacji (midzy innymi). Wymaga ona zbudowania modelu procesu biznesowego bdcego opisem funkcjonowania
Komputerowe wspomaganie prac inynierskich CAE
 Komputerowe wspomaganie prac inynierskich CAE Karta (sylabus) przedmiotu WM Zarzdzanie i inynieria produkcji Studia I stopnia o profilu: A x P Przedmiot: Komputerowe wspomaganie prac inynierskich CAE Kod
Komputerowe wspomaganie prac inynierskich CAE Karta (sylabus) przedmiotu WM Zarzdzanie i inynieria produkcji Studia I stopnia o profilu: A x P Przedmiot: Komputerowe wspomaganie prac inynierskich CAE Kod
Instrukcja obsługi programu CalcuLuX 4.0
 Instrukcja obsługi programu CalcuLuX 4.0 Katarzyna Jach Marcin Kuliski Politechnika Wrocławska Program CalcuLuX jest narzdziem wspomagajcym proces projektowania owietlenia, opracowanym przez Philips Lighting.
Instrukcja obsługi programu CalcuLuX 4.0 Katarzyna Jach Marcin Kuliski Politechnika Wrocławska Program CalcuLuX jest narzdziem wspomagajcym proces projektowania owietlenia, opracowanym przez Philips Lighting.
Instrukcja obsługi dodatku InsERT GT Smart Documents
 Instrukcja obsługi dodatku InsERT GT Smart Documents InsERT, grudzie 2003 http://www.insert.com.pl/office2003 InsERT GT Smart Documents to przygotowany przez firm InsERT specjalny dodatek, umoliwiajcy
Instrukcja obsługi dodatku InsERT GT Smart Documents InsERT, grudzie 2003 http://www.insert.com.pl/office2003 InsERT GT Smart Documents to przygotowany przez firm InsERT specjalny dodatek, umoliwiajcy
WYKŁAD 12. Wzorce projektowe czynnociowe State Mediator
 WYKŁAD 12 Wzorce projektowe czynnociowe State Mediator Behavioral Design Pattern: State [obj] Umoliwia obiektowi zmian zachowania gdy zmienia si jego stan wewntrzny. Dzieki temu obiekt zdaje si zmienia
WYKŁAD 12 Wzorce projektowe czynnociowe State Mediator Behavioral Design Pattern: State [obj] Umoliwia obiektowi zmian zachowania gdy zmienia si jego stan wewntrzny. Dzieki temu obiekt zdaje si zmienia
Laboratorium elektryczne. Falowniki i przekształtniki - I (E 14)
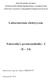 POLITECHNIKA LSKA WYDZIAŁINYNIERII RODOWISKA I ENERGETYKI INSTYTUT MASZYN I URZDZE ENERGETYCZNYCH Laboratorium elektryczne Falowniki i przekształtniki - I (E 14) Opracował: mgr in. Janusz MDRYCH Zatwierdził:
POLITECHNIKA LSKA WYDZIAŁINYNIERII RODOWISKA I ENERGETYKI INSTYTUT MASZYN I URZDZE ENERGETYCZNYCH Laboratorium elektryczne Falowniki i przekształtniki - I (E 14) Opracował: mgr in. Janusz MDRYCH Zatwierdził:
KOSZTY PLANOWEJ OBSŁUGI TECHNICZNEJ CIGNIKÓW ROLNICZYCH NOWEJ GENERACJI
 Technica Agraria 2(2) 2003, 53-57 KOSZTY PLANOWEJ OBSŁUGI TECHNICZNEJ CIGNIKÓW ROLNICZYCH NOWEJ GENERACJI Zenon Grze Streszczenie. W pracy dokonano analizy kosztów planowej obsługi technicznej cigników
Technica Agraria 2(2) 2003, 53-57 KOSZTY PLANOWEJ OBSŁUGI TECHNICZNEJ CIGNIKÓW ROLNICZYCH NOWEJ GENERACJI Zenon Grze Streszczenie. W pracy dokonano analizy kosztów planowej obsługi technicznej cigników
PODSTAWY DIAGNOSTYKI MASZYN
 *************************************************************** Bogdan ÓŁTOWSKI PODSTAWY DIAGNOSTYKI MASZYN ************************************************* BYDGOSZCZ - 1996 motto : na wielkie kłopoty
*************************************************************** Bogdan ÓŁTOWSKI PODSTAWY DIAGNOSTYKI MASZYN ************************************************* BYDGOSZCZ - 1996 motto : na wielkie kłopoty
REGULAMIN KONKURSU OFERT NA WYBÓR BROKERA UBEZPIECZENIOWEGO DLA MIASTA ZIELONA GÓRA, JEGO JEDNOSTEK ORGANIZACYJNYCH ORAZ SPÓŁEK KOMUNALNYCH.
 REGULAMIN KONKURSU OFERT NA WYBÓR BROKERA UBEZPIECZENIOWEGO DLA MIASTA ZIELONA GÓRA, JEGO JEDNOSTEK ORGANIZACYJNYCH ORAZ SPÓŁEK KOMUNALNYCH. I. INFORMACJE PODSTAWOWE Prezydent Miasta Zielona góra ogłasza
REGULAMIN KONKURSU OFERT NA WYBÓR BROKERA UBEZPIECZENIOWEGO DLA MIASTA ZIELONA GÓRA, JEGO JEDNOSTEK ORGANIZACYJNYCH ORAZ SPÓŁEK KOMUNALNYCH. I. INFORMACJE PODSTAWOWE Prezydent Miasta Zielona góra ogłasza
Poradnik korzystania z serwisu UNET: Konfiguracja programu pocztowego
 Poradnik korzystania z serwisu UNET: Konfiguracja programu pocztowego Niniejszy opis dotyczy konfiguracji programu pocztowego Outlook Express z pakietu Internet Explorer, pracujcego pod kontrol systemu
Poradnik korzystania z serwisu UNET: Konfiguracja programu pocztowego Niniejszy opis dotyczy konfiguracji programu pocztowego Outlook Express z pakietu Internet Explorer, pracujcego pod kontrol systemu
DECYZJA. odmawiam uwzgldnienia wniosku. Uzasadnienie
 Decyzja Generalnego Inspektora Ochrony Danych Osobowych z dnia 21 marca 2005 r. odmawiajca uwzgldnienia wniosku o zobowizanie Zarzdu Banku, do wykrelenia danych osobowych dotyczcych Skarcego z Bankowego
Decyzja Generalnego Inspektora Ochrony Danych Osobowych z dnia 21 marca 2005 r. odmawiajca uwzgldnienia wniosku o zobowizanie Zarzdu Banku, do wykrelenia danych osobowych dotyczcych Skarcego z Bankowego
Komputerowa Ksiga Podatkowa Wersja 11.4 ZAKOCZENIE ROKU
 Komputerowa Ksiga Podatkowa Wersja 11.4 ZAKOCZENIE ROKU Przed przystpieniem do liczenia deklaracji PIT-36, PIT-37, PIT-O i zestawienia PIT-D naley zapozna si z objanieniami do powyszych deklaracji. Uwaga:
Komputerowa Ksiga Podatkowa Wersja 11.4 ZAKOCZENIE ROKU Przed przystpieniem do liczenia deklaracji PIT-36, PIT-37, PIT-O i zestawienia PIT-D naley zapozna si z objanieniami do powyszych deklaracji. Uwaga:
ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR 2 POZIOM PODSTAWOWY. 1. x y x y
 Nr zadania Nr czynnoci Przykadowy zestaw zada nr z matematyki ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR POZIOM PODSTAWOWY Etapy rozwizania zadania. Podanie dziedziny funkcji f: 6, 8.. Podanie wszystkich
Nr zadania Nr czynnoci Przykadowy zestaw zada nr z matematyki ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR POZIOM PODSTAWOWY Etapy rozwizania zadania. Podanie dziedziny funkcji f: 6, 8.. Podanie wszystkich
Program SMS4 Monitor
 Program SMS4 Monitor INSTRUKCJA OBSŁUGI Wersja 1.0 Spis treci 1. Opis ogólny... 2 2. Instalacja i wymagania programu... 2 3. Ustawienia programu... 2 4. Opis wskaników w oknie aplikacji... 3 5. Opcje uruchomienia
Program SMS4 Monitor INSTRUKCJA OBSŁUGI Wersja 1.0 Spis treci 1. Opis ogólny... 2 2. Instalacja i wymagania programu... 2 3. Ustawienia programu... 2 4. Opis wskaników w oknie aplikacji... 3 5. Opcje uruchomienia
System midzybankowej informacji gospodarczej Dokumenty Zastrzeone MIG DZ ver. 2.0. Aplikacja WWW ver. 2.1 Instrukcja Obsługi
 System midzybankowej informacji gospodarczej Dokumenty Zastrzeone MIG DZ ver. 2.0. Aplikacja WWW ver. 2.1 Instrukcja Obsługi 1.Wymagania techniczne 1.1. Wymagania sprztowe - minimalne : komputer PC Intel
System midzybankowej informacji gospodarczej Dokumenty Zastrzeone MIG DZ ver. 2.0. Aplikacja WWW ver. 2.1 Instrukcja Obsługi 1.Wymagania techniczne 1.1. Wymagania sprztowe - minimalne : komputer PC Intel
Specjalno techniczna 2. Inynieria produkcji w przemyle maszynowym. Zarzdzanie i inynieria produkcji Studia II stopnia o profilu: A x P
 Specjalno techniczna. Inynieria produkcji w przemyle maszynowym Zintegrowane systemy (CIM) WM Zarzdzanie i inynieria produkcji Studia II stopnia o profilu: A x P Przedmiot: Zintegrowane systemy (CIM) Status
Specjalno techniczna. Inynieria produkcji w przemyle maszynowym Zintegrowane systemy (CIM) WM Zarzdzanie i inynieria produkcji Studia II stopnia o profilu: A x P Przedmiot: Zintegrowane systemy (CIM) Status
Metody oceny uytecznoci
 Metody oceny uytecznoci Z UYTKOWNIKAMI (ocena interpretacyjna) BEZ UYTKOWNIKÓW (ocena predyktywna) OCENA ILOCIOWA OCENA JAKOCIOWA JAKOCIOWA ILOCIOWA Badania laboratoryjne Obserwacje na stanowiskach pracy
Metody oceny uytecznoci Z UYTKOWNIKAMI (ocena interpretacyjna) BEZ UYTKOWNIKÓW (ocena predyktywna) OCENA ILOCIOWA OCENA JAKOCIOWA JAKOCIOWA ILOCIOWA Badania laboratoryjne Obserwacje na stanowiskach pracy
VPN Virtual Private Network. Uycie certyfikatów niekwalifikowanych w sieciach VPN. wersja 1.1 UNIZETO TECHNOLOGIES SA
 VPN Virtual Private Network Uycie certyfikatów niekwalifikowanych w sieciach VPN wersja 1.1 Spis treci 1. CO TO JEST VPN I DO CZEGO SŁUY... 3 2. RODZAJE SIECI VPN... 3 3. ZALETY STOSOWANIA SIECI IPSEC
VPN Virtual Private Network Uycie certyfikatów niekwalifikowanych w sieciach VPN wersja 1.1 Spis treci 1. CO TO JEST VPN I DO CZEGO SŁUY... 3 2. RODZAJE SIECI VPN... 3 3. ZALETY STOSOWANIA SIECI IPSEC
Temat: Algorytmy zachłanne
 Temat: Algorytmy zachłanne Algorytm zachłanny ( ang. greedy algorithm) wykonuje zawsze działanie, które wydaje si w danej chwili najkorzystniejsze. Wybiera zatem lokalnie optymaln moliwo w nadziei, e doprowadzi
Temat: Algorytmy zachłanne Algorytm zachłanny ( ang. greedy algorithm) wykonuje zawsze działanie, które wydaje si w danej chwili najkorzystniejsze. Wybiera zatem lokalnie optymaln moliwo w nadziei, e doprowadzi
SUPLEMENT SM-BOSS WERSJA 6.15
 SUPLEMENT SM-BOSS WERSJA 6.15 Spis treci Wstp...2 Pierwsza czynno...3 Szybka zmiana stawek VAT, nazwy i PKWiU dla produktów...3 Szeroki wydruk rejestru VAT...4 Filtry wydruków dotyczcych VAT...5 Kontrola
SUPLEMENT SM-BOSS WERSJA 6.15 Spis treci Wstp...2 Pierwsza czynno...3 Szybka zmiana stawek VAT, nazwy i PKWiU dla produktów...3 Szeroki wydruk rejestru VAT...4 Filtry wydruków dotyczcych VAT...5 Kontrola
DECYZJA. Warszawa, dnia 31 marca 2006 r. GI-DEC-DS-106/06
 Decyzja Generalnego Inspektora Ochrony Danych Osobowych nakazujca Spółce usunicie uchybie w procesie przetwarzania danych osobowych osób biorcych udział w organizowanych przez t Spółk konkursach, poprzez
Decyzja Generalnego Inspektora Ochrony Danych Osobowych nakazujca Spółce usunicie uchybie w procesie przetwarzania danych osobowych osób biorcych udział w organizowanych przez t Spółk konkursach, poprzez
Temat: Struktury danych do reprezentacji grafów. Wybrane algorytmy grafowe.
 Temat: Struktury danych do reprezentacji grafów. Wybrane algorytmy grafowe. Oznaczenia G = V, E - graf bez wag, gdzie V - zbiór wierzchołków, E- zbiór krawdzi V = n - liczba wierzchołków grafu G E = m
Temat: Struktury danych do reprezentacji grafów. Wybrane algorytmy grafowe. Oznaczenia G = V, E - graf bez wag, gdzie V - zbiór wierzchołków, E- zbiór krawdzi V = n - liczba wierzchołków grafu G E = m
Problem decyzyjny naley do klasy NP. (Polynomial), jeeli moe by rozwizany w czasie conajwyej wielomianowym przez algorytm A dla DTM.
 WYKŁAD : Teoria NP-zupełnoci. Problem decyzyjny naley do klasy P (Polynomial), jeeli moe by rozwizany w czasie conajwyej wielomianowym przez algorytm A dla DTM. (przynaleno ta jest zachowana równie dla
WYKŁAD : Teoria NP-zupełnoci. Problem decyzyjny naley do klasy P (Polynomial), jeeli moe by rozwizany w czasie conajwyej wielomianowym przez algorytm A dla DTM. (przynaleno ta jest zachowana równie dla
Bazy danych. Plan wykładu. Proces modelowania i implementacji bazy danych. Elementy ERD. Wykład 2: Diagramy zwizków encji (ERD)
 Plan wykładu Bazy danych Wykład 2: Diagramy zwizków encji (ERD) Diagramy zwizków encji elementy ERD licznoci zwizków podklasy klucze zbiory słabych encji Małgorzata Krtowska Katedra Oprogramowania e-mail:
Plan wykładu Bazy danych Wykład 2: Diagramy zwizków encji (ERD) Diagramy zwizków encji elementy ERD licznoci zwizków podklasy klucze zbiory słabych encji Małgorzata Krtowska Katedra Oprogramowania e-mail:
1. Klasa typu sealed. Przykład 1. sealed class Standard{ class NowyStandard:Standard{ // błd!!!
 Temat: Klasy typu sealed. Klasy abstrakcyjne. Deklaracja i implementacja interfejsu. Typ Object i operatory is oraz as. Czas ycia obiektu. Destruktory. 1. Klasa typu sealed Przykład 1 Klasa typu sealed
Temat: Klasy typu sealed. Klasy abstrakcyjne. Deklaracja i implementacja interfejsu. Typ Object i operatory is oraz as. Czas ycia obiektu. Destruktory. 1. Klasa typu sealed Przykład 1 Klasa typu sealed
Wojciech Drzewiecki SYSTEMY INFORMACJI GEOGRAFICZNEJ
 Wojciech Drzewiecki SYSTEMY INFORMACJI GEOGRAFICZNEJ Systemem Informacji Geograficznej (Systemem Informacji Przestrzennej, GIS, SIP) nazywamy skomputeryzowany system pozyskiwania, przechowywania, przetwarzania,
Wojciech Drzewiecki SYSTEMY INFORMACJI GEOGRAFICZNEJ Systemem Informacji Geograficznej (Systemem Informacji Przestrzennej, GIS, SIP) nazywamy skomputeryzowany system pozyskiwania, przechowywania, przetwarzania,
budowlanymi - WAP Aleksandra Radziejowska
 budowlanymi - WAP Aleksandra Radziejowska Co to jest optymalizacja wielokryterialna? ustalenie kryterium poszukiwania i oceny optymalnego. Co to jest optymalizacja wielokryterialna? pod zakup maszyny budowlanej
budowlanymi - WAP Aleksandra Radziejowska Co to jest optymalizacja wielokryterialna? ustalenie kryterium poszukiwania i oceny optymalnego. Co to jest optymalizacja wielokryterialna? pod zakup maszyny budowlanej
Matematyka wykªad 1. Macierze (1) Andrzej Torój. 17 wrze±nia 2011. Wy»sza Szkoªa Zarz dzania i Prawa im. H. Chodkowskiej
 Matematyka wykªad 1 Macierze (1) Andrzej Torój Wy»sza Szkoªa Zarz dzania i Prawa im. H. Chodkowskiej 17 wrze±nia 2011 Plan wykªadu 1 2 3 4 5 Plan prezentacji 1 2 3 4 5 Kontakt moja strona internetowa:
Matematyka wykªad 1 Macierze (1) Andrzej Torój Wy»sza Szkoªa Zarz dzania i Prawa im. H. Chodkowskiej 17 wrze±nia 2011 Plan wykªadu 1 2 3 4 5 Plan prezentacji 1 2 3 4 5 Kontakt moja strona internetowa:
M.11.01.04 ZASYPANIE WYKOPÓW WRAZ Z ZAGSZCZENIEM
 ZASYPANIE WYKOPÓW WRAZ Z ZAGSZCZENIEM 1. WSTP 1.1. Przedmiot ST Przedmiotem niniejszej ST s wymagania szczegółowe dotyczce wykonania i odbioru Robót zwizanych z zasypywaniem wykopów z zagszczeniem dla
ZASYPANIE WYKOPÓW WRAZ Z ZAGSZCZENIEM 1. WSTP 1.1. Przedmiot ST Przedmiotem niniejszej ST s wymagania szczegółowe dotyczce wykonania i odbioru Robót zwizanych z zasypywaniem wykopów z zagszczeniem dla
Komputerowy system SWPK do wspomagania procesu koncepcyjnego projektowania chwytaków mechanicznych
 AMME 2003 12th Komputerowy system SWPK do wspomagania procesu koncepcyjnego projektowania chwytaków mechanicznych P. Ociepka, J. wider Katedra Automatyzacji Procesów Technologicznych i Zintegrowanych Systemów
AMME 2003 12th Komputerowy system SWPK do wspomagania procesu koncepcyjnego projektowania chwytaków mechanicznych P. Ociepka, J. wider Katedra Automatyzacji Procesów Technologicznych i Zintegrowanych Systemów
Standardy danych w tagu EPC
 Standardy danych w EPC Strona: 1 Standardy danych w tagu EPC W elektronicznym noniku danych, jakim jest tag EPC (Electronic Produkt Code), bdzie zapisany tylko numer identyfikacyjny. Bdzie to jeden z poniszych
Standardy danych w EPC Strona: 1 Standardy danych w tagu EPC W elektronicznym noniku danych, jakim jest tag EPC (Electronic Produkt Code), bdzie zapisany tylko numer identyfikacyjny. Bdzie to jeden z poniszych
Bazy danych Podstawy teoretyczne
 Pojcia podstawowe Baza Danych jest to zbiór danych o okrelonej strukturze zapisany w nieulotnej pamici, mogcy zaspokoi potrzeby wielu u!ytkowników korzystajcych z niego w sposóbs selektywny w dogodnym
Pojcia podstawowe Baza Danych jest to zbiór danych o okrelonej strukturze zapisany w nieulotnej pamici, mogcy zaspokoi potrzeby wielu u!ytkowników korzystajcych z niego w sposóbs selektywny w dogodnym
SUPLEMENT SM-BOSS WERSJA 6.15
 SUPLEMENT SM-BOSS WERSJA 6.15 Spis treci Wstp...2 Pierwsza czynno...3 Szybka zmiana stawek VAT, nazwy i PKWiU dla produktów...3 Zamiana PKWiU w tabeli PKWiU oraz w Kartotece Produktów...4 VAT na fakturach
SUPLEMENT SM-BOSS WERSJA 6.15 Spis treci Wstp...2 Pierwsza czynno...3 Szybka zmiana stawek VAT, nazwy i PKWiU dla produktów...3 Zamiana PKWiU w tabeli PKWiU oraz w Kartotece Produktów...4 VAT na fakturach
Szukanie najkrótszych dróg z jednym ródłem
 Szukanie najkrótszych dróg z jednym ródłem Algorytm Dijkstry Załoenia: dany jest spójny graf prosty G z wagami na krawdziach waga w(e) dla kadej krawdzi e jest nieujemna dany jest wyróniony wierzchołek
Szukanie najkrótszych dróg z jednym ródłem Algorytm Dijkstry Załoenia: dany jest spójny graf prosty G z wagami na krawdziach waga w(e) dla kadej krawdzi e jest nieujemna dany jest wyróniony wierzchołek
ZARZDZENIE Nr 14/2005. STAROSTY KRASNOSTAWSKIEGO z dnia 29 sierpnia 2005 roku
 ZARZDZENIE Nr 14/2005 STAROSTY KRASNOSTAWSKIEGO z dnia 29 sierpnia 2005 roku w sprawie wprowadzenia procedury naboru pracowników na stanowiska pomocnicze, stanowiska obsługi, stanowiska w ramach robót
ZARZDZENIE Nr 14/2005 STAROSTY KRASNOSTAWSKIEGO z dnia 29 sierpnia 2005 roku w sprawie wprowadzenia procedury naboru pracowników na stanowiska pomocnicze, stanowiska obsługi, stanowiska w ramach robót
I Powiatowy Konkurs Matematyka, Fizyka i Informatyka w Technice Etap finałowy 10 kwietnia 2013 grupa elektryczno-elektroniczna
 I Powiatowy Konkurs Matematyka, Fizyka i Informatyka w Technice Etap finałowy 10 kwietnia 2013 grupa elektryczno-elektroniczna (imi i nazwisko uczestnika) (nazwa szkoły) Arkusz zawiera 6 zada. Zadania
I Powiatowy Konkurs Matematyka, Fizyka i Informatyka w Technice Etap finałowy 10 kwietnia 2013 grupa elektryczno-elektroniczna (imi i nazwisko uczestnika) (nazwa szkoły) Arkusz zawiera 6 zada. Zadania
Bazy danych. Plan wykładu. Podzapytania - wskazówki. Podzapytania po FROM. Wykład 5: Zalenoci wielowartociowe. Sprowadzanie do postaci normalnych.
 Plan wykładu azy danych Wykład 5: Zalenoci wielowartociowe. Sprowadzanie do postaci normalnych. Dokoczenie SQL Zalenoci wielowartociowe zwarta posta normalna Dekompozycja do 4NF Przykład sprowadzanie do
Plan wykładu azy danych Wykład 5: Zalenoci wielowartociowe. Sprowadzanie do postaci normalnych. Dokoczenie SQL Zalenoci wielowartociowe zwarta posta normalna Dekompozycja do 4NF Przykład sprowadzanie do
Klub Paragraf 34, Bronisławów 2006. dr in. Marek Dwiarek. Centralny Instytut Ochrony Pracy Pastwowy Instytut Badawczy
 Klub Paragraf 34, Bronisławów 2006 dr in. Marek Dwiarek Centralny Instytut Ochrony Pracy Pastwowy Instytut Badawczy Tematyka dyskusji Klub Paragraf 34, Bronisławów 2006 Wymagania dotyczce bezpieczestwa
Klub Paragraf 34, Bronisławów 2006 dr in. Marek Dwiarek Centralny Instytut Ochrony Pracy Pastwowy Instytut Badawczy Tematyka dyskusji Klub Paragraf 34, Bronisławów 2006 Wymagania dotyczce bezpieczestwa
6.2. Baza i wymiar. V nazywamy baz-
 62 Baza i wymiar V nazywamy baz- Definicja 66 Niech V bdzie przestrzeni, liniow, nad cia/em F Podzbiór B przestrzeni V, je2eli: () B jest liniowo niezale2ny, (2) B jest generuj,cy, tzn lin(b) =V Przyk/ady:
62 Baza i wymiar V nazywamy baz- Definicja 66 Niech V bdzie przestrzeni, liniow, nad cia/em F Podzbiór B przestrzeni V, je2eli: () B jest liniowo niezale2ny, (2) B jest generuj,cy, tzn lin(b) =V Przyk/ady:
KARTA OCENY JEDNOSTKI NAUKOWEJ
 ZAŁACZNIK nr 2 KARTA OCENY JEDNOSTKI NAUKOWEJ Cz A dla dyscyplin: nauki humanistyczne i społeczne Zespół roboczy Komisji Bada na Rzecz Rozwoju... NAZWA JEDNOSTKI I. WYNIKI DZIAŁALNOCI NAUKOWEJ 1. Publikacje
ZAŁACZNIK nr 2 KARTA OCENY JEDNOSTKI NAUKOWEJ Cz A dla dyscyplin: nauki humanistyczne i społeczne Zespół roboczy Komisji Bada na Rzecz Rozwoju... NAZWA JEDNOSTKI I. WYNIKI DZIAŁALNOCI NAUKOWEJ 1. Publikacje
Tworzenie bazy danych Biblioteka tworzenie tabel i powiza, manipulowanie danymi. Zadania do wykonani przed przystpieniem do pracy:
 wiczenie 2 Tworzenie bazy danych Biblioteka tworzenie tabel i powiza, manipulowanie danymi. Cel wiczenia: Zapoznanie si ze sposobami konstruowania tabel, powiza pomidzy tabelami oraz metodami manipulowania
wiczenie 2 Tworzenie bazy danych Biblioteka tworzenie tabel i powiza, manipulowanie danymi. Cel wiczenia: Zapoznanie si ze sposobami konstruowania tabel, powiza pomidzy tabelami oraz metodami manipulowania
Algorytmy kodowania predykcyjnego
 Algorytmy kodowania predykcyjnego 1. Zasada kodowania 2. Algorytm JPEG-LS 3. Algorytmy CALIC, LOCO-I 4. Algorytmy z wielokrotn rozdzielczoci. Progresywna transmisja obrazów Kompresja obrazów - zestawienie
Algorytmy kodowania predykcyjnego 1. Zasada kodowania 2. Algorytm JPEG-LS 3. Algorytmy CALIC, LOCO-I 4. Algorytmy z wielokrotn rozdzielczoci. Progresywna transmisja obrazów Kompresja obrazów - zestawienie
SIEMENS GIGASET REPEATER
 SIEMENS GIGASET REPEATER Wane wskazówki Wane wskazówki Wskazówki bezpieczestwa Gigaset repeater nie jest urzdzeniem wodoodpornym, nie naley wic umieszcza go w wilgotnych pomieszczeniach. Tylko dostarczony
SIEMENS GIGASET REPEATER Wane wskazówki Wane wskazówki Wskazówki bezpieczestwa Gigaset repeater nie jest urzdzeniem wodoodpornym, nie naley wic umieszcza go w wilgotnych pomieszczeniach. Tylko dostarczony
Ocena obcienia prac fizyczn dynamiczn na stanowisku pracy
 Ocena obcienia prac fizyczn dynamiczn na stanowisku pracy dr med. Joanna Bugajska - Centralny Instytut Ochrony Pracy (artykuł z pakietu edukacyjnego Nauka o pracy - bezpieczestwo, higiena, ergonomia CIOP)
Ocena obcienia prac fizyczn dynamiczn na stanowisku pracy dr med. Joanna Bugajska - Centralny Instytut Ochrony Pracy (artykuł z pakietu edukacyjnego Nauka o pracy - bezpieczestwo, higiena, ergonomia CIOP)
Sposoby przekazywania parametrów w metodach.
 Temat: Definiowanie i wywoływanie metod. Zmienne lokalne w metodach. Sposoby przekazywania parametrów w metodach. Pojcia klasy i obiektu wprowadzenie. 1. Definiowanie i wywoływanie metod W dotychczas omawianych
Temat: Definiowanie i wywoływanie metod. Zmienne lokalne w metodach. Sposoby przekazywania parametrów w metodach. Pojcia klasy i obiektu wprowadzenie. 1. Definiowanie i wywoływanie metod W dotychczas omawianych
LOGIKA I TEORIA ZBIORÓW
 LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
SPECYFIKACJA ISTOTNYCH WARUNKÓW ZAMÓWIENIA (SIWZ)
 SPECYFIKACJA ISTOTNYCH WARUNKÓW ZAMÓWIENIA (SIWZ) I. NAZWA I ADRES ZAMAWIAJCEGO Zamawiajcy: Urzd Skarbowy Pozna-Jeyce Adres: ul. Słowackiego 22, 60-823 Pozna Adres do korespondencji: ul. Słowackiego 22,
SPECYFIKACJA ISTOTNYCH WARUNKÓW ZAMÓWIENIA (SIWZ) I. NAZWA I ADRES ZAMAWIAJCEGO Zamawiajcy: Urzd Skarbowy Pozna-Jeyce Adres: ul. Słowackiego 22, 60-823 Pozna Adres do korespondencji: ul. Słowackiego 22,
ARKUSZ OCENY PRACOWNIKA zatrudnionego na podstawie umowy o prac za okres od... do...
 Załcznik Nr 2 do Zarzdzenia Nr 8/06 Burmistrza Miasta Bukowno z dnia 26.01.2006r. ARKUSZ OCENY PRACOWNIKA zatrudnionego na podstawie umowy o prac za okres od... do... Imi i nazwisko... Stanowisko... Komórka
Załcznik Nr 2 do Zarzdzenia Nr 8/06 Burmistrza Miasta Bukowno z dnia 26.01.2006r. ARKUSZ OCENY PRACOWNIKA zatrudnionego na podstawie umowy o prac za okres od... do... Imi i nazwisko... Stanowisko... Komórka
ELEMENT SYSTEMU BIBI.NET. Instrukcja Obsługi
 ELEMENT SYSTEMU BIBI.NET Instrukcja Obsługi Copyright 2005 by All rights reserved Wszelkie prawa zastrzeone!"# $%%%&%'(%)* +(+%'(%)* Wszystkie nazwy i znaki towarowe uyte w niniejszej publikacji s własnoci
ELEMENT SYSTEMU BIBI.NET Instrukcja Obsługi Copyright 2005 by All rights reserved Wszelkie prawa zastrzeone!"# $%%%&%'(%)* +(+%'(%)* Wszystkie nazwy i znaki towarowe uyte w niniejszej publikacji s własnoci
Poznanie i przyswojenie przez studentów podstawowych poj z zakresu organizacji i zarzdzania C2
 Podstawy zarzdzania WZ Zarzdzanie i inynieria produkcji Studia I stopnia o profilu: A P Przedmiot: Podstawy zarzdzania Status : Jzyk wykładowy: Rok: I Nazwa specjalnoci: Rodzaj zaj i liczba godzin: Studia
Podstawy zarzdzania WZ Zarzdzanie i inynieria produkcji Studia I stopnia o profilu: A P Przedmiot: Podstawy zarzdzania Status : Jzyk wykładowy: Rok: I Nazwa specjalnoci: Rodzaj zaj i liczba godzin: Studia
POWIATOWY URZD PRACY W RADZIEJOWIE ul. Kociuszki 20/22, 88-200 Radziejów,
 POWIATOWY URZD PRACY W RADZIEJOWIE ul. Kociuszki 20/22, 88-200 Radziejów, tel. (054) 285 29 91, fax. (054) 285 29 91, mail: tora@praca.gov.pl Znak sprawy: KO.KŁ-343/11/2010 SPECYFIKACJA ISTOTNYCH WARUNKÓW
POWIATOWY URZD PRACY W RADZIEJOWIE ul. Kociuszki 20/22, 88-200 Radziejów, tel. (054) 285 29 91, fax. (054) 285 29 91, mail: tora@praca.gov.pl Znak sprawy: KO.KŁ-343/11/2010 SPECYFIKACJA ISTOTNYCH WARUNKÓW
Temat: Liniowe uporzdkowane struktury danych: stos, kolejka. Specyfikacja, przykładowe implementacje i zastosowania. Struktura słownika.
 Temat: Liniowe uporzdkowane struktury danych: stos, kolejka. Specyfikacja, przykładowe implementacje i zastosowania. Struktura słownika. 1. Pojcie struktury danych Nieformalnie Struktura danych (ang. data
Temat: Liniowe uporzdkowane struktury danych: stos, kolejka. Specyfikacja, przykładowe implementacje i zastosowania. Struktura słownika. 1. Pojcie struktury danych Nieformalnie Struktura danych (ang. data
POBÓR MOCY MASZYN I URZDZE ODLEWNICZYCH
 Eugeniusz ZIÓŁKOWSKI, 1 Roman WRONA 2 Wydział Odlewnictwa AGH 1. Wprowadzenie. Monitorowanie poboru mocy maszyn i urzdze odlewniczych moe w istotny sposób przyczyni si do oceny technicznej i ekonomicznej
Eugeniusz ZIÓŁKOWSKI, 1 Roman WRONA 2 Wydział Odlewnictwa AGH 1. Wprowadzenie. Monitorowanie poboru mocy maszyn i urzdze odlewniczych moe w istotny sposób przyczyni si do oceny technicznej i ekonomicznej
