SZTUCZNA INTELIGENCJA
|
|
|
- Edyta Czajka
- 5 lat temu
- Przeglądów:
Transkrypt
1 SZTUCZNA INTELIGENCJA WYKŁAD 10. WNIOSKOWANIE W LOGICE ROZMYTEJ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska
2 WNIOSKOWANIE W LOGICE DWUWARTOŚCIOWEJ W logice tradycyjnej (dwuwartościowej, boolowskiej) prawdziwość pewnych zdań jest wnioskowana na podstawie prawdziwości innych zdań. Przez regułę wnioskowania rozumiemy sposób wyprowadzania ze zdań prawdziwych, zwanych przesłankami, zdań prawdziwych, zwanych wnioskami. Regułę wnioskowania modus ponens określa następujący schemat wnioskowania: Przesłanka 1 (fakt) p Przesłanka 2 (reguła, implikacja) p q Wniosek q p i q oznaczają zdania prawdziwe; p jest poprzednikiem, a q następnikiem implikacji. Regułę tę odczytujemy: Jeżeli poprzednik prawdziwej implikacji jest prawdziwy, to następnik jest również prawdziwy. Np. Jeśli prawdą jest p "Jan jest kierowcą" i prawdą jest p q "JEŻELI Z jest kierowcą, TO Z ma prawo jazdy", to prawdą jest q "Jan ma prawo jazdy". 2
3 WNIOSKOWANIE W LOGICE ROZMYTEJ W logice klasycznej zdanie p postaci "x A", gdzie A jest klasycznym zbiorem, może przyjmować dwie wartości logiczne: prawdę lub fałsz. W logice rozmytej zdanie to może przyjmować różne stopnie prawdy (stopnie przynależności elementu x do zbioru A). W logice rozmytej regułę modus ponens odczytujemy: Jeżeli poprzednik implikacji jest prawdziwy w stopniu A i ta implikacja jest prawdziwa w stopniu A B, to następnik jest prawdziwy w stopniu B. Uogólniona reguła modus ponens: Przesłanka 1 (fakt) x jest A' Przesłanka 2 (reguła, implikacja) x jest A y jest B Wniosek y jest B' gdzie: A, A' X i B, B' Y są zbiorami rozmytymi, x i y są zmiennymi lingwistycznymi. Zbiory A i A' oraz B i B' są do siebie podobne. 3
4 WNIOSKOWANIE W LOGICE ROZMYTEJ Np. Jeśli zdanie "Jan jest bardzo bystry" jest prawdą w stopniu A i reguła "JEŻELI Z jest bystry, TO oceny Z są dobre" jest prawdziwa w stopniu A B, to zdanie "Oceny Jana są bardzo dobre" jest prawdziwe w stopniu B. x Jan, Z; y oceny Jana, oceny Z; A bystry; A' bardzo bystry; B dobre; B' bardzo dobre Wynikowy zbiór rozmyty B' wynika ze złożenia zbioru A' i relacji rozmytej A B: B' ( A' x X y) = sup{ t[ ( x), A B ( x, y)]} Relacja rozmyta A B może być zdefiniowana na wiele sposobów. Przyjmijmy definicję Mamdaniego: ( x, y) = min( ( x), ( y)). Stosując operacje min jako t-normę powyższy wzór zapiszemy: A B A B B '( y) = sup{min[ A' ( x),min( A( x), B( y))]} = min{supmin[ A' ( x), A( x)], B x X x X ( y)} 4
5 WNIOSKOWANIE W LOGICE ROZMYTEJ Metodę wyznaczania ( ) możemy zapisać w krokach: B' y 1. Przyjmujemy pewne funkcje przynależności ( x), ( x) i ( y). 2. Znajdujemy przecięcie min[ '( x), ( x)]. A A A ' A B 3. Znajdujemy największą wartość funkcji przynależności tego przecięcia h= sup min[ '( x), ( x)]. x X A A 4. Znajdujemy przecięcie stałej h z B(y), które przyjmujemy jako B' ( y). 5
6 WNIOSKOWANIE W LOGICE ROZMYTEJ UWAGI Zbiór A reprezentuje aktualną/zaobserwowaną wartość zmiennej wejściowej x. Jeśli zmienna ta jest dokładna, jako ( ) stosujemy tzw. singleton: A' x 1, A' ( x) = 0, jeżeli x = x jeżeli x x Jeśli chcemy uwzględnić niepewność pomiaru zmienną x opisujemy pewną funkcją przynależności, jak na rysunku powyżej. Jako t-normę we wzorach powyżej zamiast min możemy zastosować inne rozwiązania. Jeśli zmienna wejściowa x jest wektorem x = [x 1, x 2,, x n ] otrzymamy: B ( y) = min{supmin[ A '( x1), A ( x1)],...,supmin[ A '( xn), A ( xn)], B( y)} ' 1 1 x1 X Tzn. B' ( y) powstaje w wyniku przecięcia B(y) z najmniejszą spośród wartości h wyznaczanych dla każdej współrzędnej x. x X n n n 6
7 ROZMYTE SYSTEMY WNIOSKUJĄCE Rozmyte systemy wnioskujące (RSW) znajdują zastosowanie do modelowania złożonych zjawisk, których modele matematyczne są nieznane lub gdy chcemy uwzględnić informacje nieprecyzyjne lub wieloznaczne. Poniżej opisano tzw. system Mamdaniego. W RSW wiedza jest reprezentowana w postaci symbolicznej rozmytych reguł decyzyjnych. Zastosowanie klasyfikacja, regresja, sterowniki. 7
8 BAZA REGUŁ Baza reguł zwana modelem lingwistycznym, stanowi zbiór N reguł rozmytych R k postaci: Reguła wyraża rozmytą implikację A k B k. R k : JEŻELI x 1 jest A 1 k I I x n jest A n k TO y jest B k Reguły ustalane są przez ekspertów lub tworzone są w procesie uczenia (sieci neuronowo-rozmyte) Każda reguła wyraża pewien związek pomiędzy x i y i ma charakter lokalny Baza reguł jako całość powinna modelować całe zjawisko (globalnie) Większa liczba reguł zapewnia dokładniejsze modelowanie 8
9 BLOK ROZMYWANIA Wartości zmiennych wejściowych x i są rozmywane, tzn. wartości rzeczywiste przekształcane są na zbiór rozmyty A i. Pozwala to uwzględniać niepewność co do wartości zmiennej wejściowej. Jeśli wartość zmiennej jest dokładna stosujemy singleton. 9
10 BLOK WNIOSKOWANIA Wejściem bloku wnioskowania jest zbiór rozmyty A' = A 1 ' A 2 ' A n '. Na wyjściu k-tej reguły otrzymujemy zbiór rozmyty B k '. Wynikowy zbiór rozmyty zbioru reguł B' powstaje poprzez zsumowanie (agregację) zbiorów rozmytych B k '. Funkcja przynależności tego zbioru: y) = max[ 1 ( y), ( y),..., N ( y)] ( B ' 2 B ' B ' B ' Zamiast max możemy użyć innej postaci s-normy. 10
11 BLOK WNIOSKOWANIA PRZYKŁAD Dana jest baza reguł: R 1 : JEŻELI x 1 jest A 1 1 I x 2 jest A 2 1 TO y jest B 1 R 2 : JEŻELI x 1 jest A 1 2 I x 2 jest A 2 2 TO y jest B 2 Na wejście systemu podano przykład: x = T x, x ]. Dla przyjętych funkcji przynależności zbiorów [ 1 2 A 1 1, A 1 2, A 2 1, A 2 2, B 1 i B 2 wyznacz zbiór B'. Jako operatora przecięcia B(y) z h 1 i h 2 zastosuj (a) min, (b) iloczyn. Przy zastosowaniu rozmywania typu singleton otrzymamy: a) b) 11
12 BLOK WNIOSKOWANIA PRZYKŁAD Analogiczny przykład z rozmyciem x za pomocą trójkątnych funkcji przynależności. 12
13 BLOK WNIOSKOWANIA PRZYKŁAD Przykład ze spójnikiem LUB w trzeciej regule. R 1 : JEŻELI x 1 jest A 1 1 I x 2 jest A 2 1 TO y jest B 1 R 2 : JEŻELI x 1 jest A 1 2 I x 2 jest A 2 2 TO y jest B 2 R 3 : JEŻELI x 1 jest A 1 3 LUB x 2 jest A 2 3 TO y jest B 2 13
14 BLOK WYOSTRZANIA Wejście zbiór rozmyty B', wyjście wartość ostra y. Metody wyostrzania: Metoda środka obszaru środek ciężkości figury geometrycznej opisanej funkcją przynależności ( ). B' y y = Y Y y ( y) dy B' ( y) dy B' 14
15 BLOK WYOSTRZANIA Metoda środka obszaru z wartością progową środek ciężkości figury geometrycznej opisanej funkcją przynależności ( ) leżącą powyżej wartości progowej α: y = Yα Yα B' y y ( y) dy B' ( y) dy B', = { y Y : '( y) α} Yα B Metoda wysokości suma argumentów poszczególnych składowych funkcji przynależności, przy których występują ich wartości szczytowe ważonych ich "poziomami odcięcia": y N h k k= 1 = N k= 1 y k max h k 15
16 ROZMYTY SYSTEM WNIOSKUJĄCY PRZYKŁAD Należy ustalić wielkość napiwku w zależności od jakości obsługi i jakości jedzenia. 1. Ustalamy, że zmienne wejściowe obsługa i jedzenie przyjmują wartości od 0 do 10 (nasze oceny). Zmienna wyjściowa napiwek przyjmuje wartości od 0 do 30 (procent od wysokości rachunku). 2. Zmienne obsługa i jedzenie rozmywamy za pomocą singletonu. 3. Ustalamy sposoby realizacji funkcji: I, LUB, implikacja, agregacja, wyostrzanie. 16
17 ROZMYTY SYSTEM WNIOSKUJĄCY PRZYKŁAD 4. Definiujemy zbiory rozmyte dla każdej zmiennej. 17
18 ROZMYTY SYSTEM WNIOSKUJĄCY PRZYKŁAD 5. Wprowadzamy reguły. 18
19 ROZMYTY SYSTEM WNIOSKUJĄCY PRZYKŁAD 6. Zadajemy konkretne wartości zmiennych wejściowych i odczytujemy rezultat. 19
20 ROZMYTY SYSTEM WNIOSKUJĄCY PRZYKŁAD 7. Funkcja zamodelowana przez system. 20
STANDARDOWE FUNKCJE PRZYNALEŻNOŚCI. METODY HEURYSTYCZNE wykład 6. (alternatywa dla s) (zdef. poprzez klasę s) GAUSSOWSKA F.
 METODY HEURYSTYCZNE wykład 6 STANDARDOWE FUNKCJE PRZYNALEŻNOŚCI 2 GAUSSOWSKA F. PRZYNALEŻNOŚCI F. PRZYNALEŻNOŚCI KLASY s środek; a określa szerokość krzywej 3 4 F. PRZYNALEŻNOŚCI KLASY π F. PRZYNALEŻNOŚCI
METODY HEURYSTYCZNE wykład 6 STANDARDOWE FUNKCJE PRZYNALEŻNOŚCI 2 GAUSSOWSKA F. PRZYNALEŻNOŚCI F. PRZYNALEŻNOŚCI KLASY s środek; a określa szerokość krzywej 3 4 F. PRZYNALEŻNOŚCI KLASY π F. PRZYNALEŻNOŚCI
Inżynieria Wiedzy i Systemy Ekspertowe. Logika rozmyta. dr inż. Michał Bereta Politechnika Krakowska
 Inżynieria Wiedzy i Systemy Ekspertowe Logika rozmyta dr inż. Michał Bereta Politechnika Krakowska http://torus.uck.pk.edu.pl/~beretam/ beretam@torus.uck.pk.edu.pl 1 Wyostrzanie Ostateczna, ostra wartość
Inżynieria Wiedzy i Systemy Ekspertowe Logika rozmyta dr inż. Michał Bereta Politechnika Krakowska http://torus.uck.pk.edu.pl/~beretam/ beretam@torus.uck.pk.edu.pl 1 Wyostrzanie Ostateczna, ostra wartość
SZTUCZNA INTELIGENCJA
 SZTUCZNA INTELIGENCJA SYSTEMY ROZMYTE Adrian Horzyk Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Katedra Automatyki i Inżynierii Biomedycznej Laboratorium
SZTUCZNA INTELIGENCJA SYSTEMY ROZMYTE Adrian Horzyk Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Katedra Automatyki i Inżynierii Biomedycznej Laboratorium
Podstawy sztucznej inteligencji
 wykład 4 (Fuzzy logic) 23 listopad 2011 Plan wykładu 1 Systemy wnioskowania z danymi niepewnymi 2 3 Inteligentne systemy z wiedzą Systemy z wiedzą składają się z dwóch części: 1 Baza wiedzy (KB): zbioru
wykład 4 (Fuzzy logic) 23 listopad 2011 Plan wykładu 1 Systemy wnioskowania z danymi niepewnymi 2 3 Inteligentne systemy z wiedzą Systemy z wiedzą składają się z dwóch części: 1 Baza wiedzy (KB): zbioru
Zasada rozszerzania. A U A jest zbiorem rozmytym, B jest obrazem zbioru A Przeniesienie rozmytości A w odwzorowaniu f na zbiór B. sup.
 Zasada rozszerzania f U V U jest zbiorem rozmytym V = f( ), jest obrazem zbioru Przeniesienie rozmytości w odwzorowaniu f na zbiór v) = ( v)? ( f ( ) = sup ( u) gdy ( v) 0 1 = 1 u f ( v) f( ) ( v) 1 0
Zasada rozszerzania f U V U jest zbiorem rozmytym V = f( ), jest obrazem zbioru Przeniesienie rozmytości w odwzorowaniu f na zbiór v) = ( v)? ( f ( ) = sup ( u) gdy ( v) 0 1 = 1 u f ( v) f( ) ( v) 1 0
Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych
 Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych ELEMENTY SZTUCZNEJ INTELIGENCJI Laboratorium nr 6 SYSTEMY ROZMYTE TYPU MAMDANIEGO
Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych ELEMENTY SZTUCZNEJ INTELIGENCJI Laboratorium nr 6 SYSTEMY ROZMYTE TYPU MAMDANIEGO
METODY INTELIGENCJI OBLICZENIOWEJ wykład 6
 METODY INTELIGENCJI OBLICZENIOWEJ wykład 6 2 ZBIORY ROZMYTE I WNIOSKOWANIE PRZYBLIŻONE 965 Lotfi A. Zadeh: : Fuzzy sets In almost every case you can build the same product without fuzzy logic, but fuzzy
METODY INTELIGENCJI OBLICZENIOWEJ wykład 6 2 ZBIORY ROZMYTE I WNIOSKOWANIE PRZYBLIŻONE 965 Lotfi A. Zadeh: : Fuzzy sets In almost every case you can build the same product without fuzzy logic, but fuzzy
Rozmyte systemy doradcze
 Systemy ekspertowe Rozmyte systemy doradcze Plan. Co to jest myślenie rozmyte? 2. Teoria zbiorów rozmytych. 3. Zmienne lingwistyczne. 4. Reguły rozmyte. 5. Wnioskowanie rozmyte (systemy doradcze). typu
Systemy ekspertowe Rozmyte systemy doradcze Plan. Co to jest myślenie rozmyte? 2. Teoria zbiorów rozmytych. 3. Zmienne lingwistyczne. 4. Reguły rozmyte. 5. Wnioskowanie rozmyte (systemy doradcze). typu
Inżynieria Wiedzy i Systemy Ekspertowe. Niepewność wiedzy. dr inż. Michał Bereta Politechnika Krakowska
 Inżynieria Wiedzy i Systemy Ekspertowe Niepewność wiedzy dr inż. Michał Bereta Politechnika Krakowska http://torus.uck.pk.edu.pl/~beretam/ beretam@torus.uck.pk.edu.pl 1 Logika Rozmyta (Fuzzy Logic) Mimo
Inżynieria Wiedzy i Systemy Ekspertowe Niepewność wiedzy dr inż. Michał Bereta Politechnika Krakowska http://torus.uck.pk.edu.pl/~beretam/ beretam@torus.uck.pk.edu.pl 1 Logika Rozmyta (Fuzzy Logic) Mimo
Wnioskowanie rozmyte. Krzysztof Patan
 Wnioskowanie rozmyte Krzysztof Patan Wprowadzenie Informacja precyzyjna jest to jedyna postać informacji akceptowanej przez konwencjonalne metody matematyczne, najczęściej dostarczana jest przez precyzyjne
Wnioskowanie rozmyte Krzysztof Patan Wprowadzenie Informacja precyzyjna jest to jedyna postać informacji akceptowanej przez konwencjonalne metody matematyczne, najczęściej dostarczana jest przez precyzyjne
ZBIORY ROZMYTE I WNIOSKOWANIE PRZYBLIŻONE
 SYSTEMY ROZMYTE ZBIORY ROZMYTE I WNIOSKOWANIE PRZYBLIŻONE 2 965 Lotfi A. Zadeh: Fuzzy sets Metoda reprezentacji wiedzy wyrażonej w języku naturalnym: Temperatura wynosi 29 o C informacja liczbowa - naturalna
SYSTEMY ROZMYTE ZBIORY ROZMYTE I WNIOSKOWANIE PRZYBLIŻONE 2 965 Lotfi A. Zadeh: Fuzzy sets Metoda reprezentacji wiedzy wyrażonej w języku naturalnym: Temperatura wynosi 29 o C informacja liczbowa - naturalna
Jeśli X jest przestrzenią o nieskończonej liczbie elementów:
 Logika rozmyta 2 Zbiór rozmyty może być formalnie zapisany na dwa sposoby w zależności od tego z jakim typem przestrzeni elementów mamy do czynienia: Jeśli X jest przestrzenią o skończonej liczbie elementów
Logika rozmyta 2 Zbiór rozmyty może być formalnie zapisany na dwa sposoby w zależności od tego z jakim typem przestrzeni elementów mamy do czynienia: Jeśli X jest przestrzenią o skończonej liczbie elementów
INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE
 Temat: Podstawowe pojęcia z logiki rozmytej Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1 Wprowadzenie Sterowanie
Temat: Podstawowe pojęcia z logiki rozmytej Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1 Wprowadzenie Sterowanie
6. Zagadnienie parkowania ciężarówki.
 6. Zagadnienie parkowania ciężarówki. Sterowniki rozmyte Aby móc sterować przebiegiem pewnych procesów lub też pracą urządzeń niezbędne jest stworzenie odpowiedniego modelu, na podstawie którego można
6. Zagadnienie parkowania ciężarówki. Sterowniki rozmyte Aby móc sterować przebiegiem pewnych procesów lub też pracą urządzeń niezbędne jest stworzenie odpowiedniego modelu, na podstawie którego można
Temat: Model SUGENO. Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE
 Temat: Model SUGENO Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1 Wprowadzenie Pierwszym rodzajem modelowania
Temat: Model SUGENO Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1 Wprowadzenie Pierwszym rodzajem modelowania
Inteligencja obliczeniowa
 Ćwiczenie nr 3 Zbiory rozmyte logika rozmyta Sterowniki wielowejściowe i wielowyjściowe, relacje rozmyte, sposoby zapisu reguł, aproksymacja funkcji przy użyciu reguł rozmytych, charakterystyki przejściowe
Ćwiczenie nr 3 Zbiory rozmyte logika rozmyta Sterowniki wielowejściowe i wielowyjściowe, relacje rozmyte, sposoby zapisu reguł, aproksymacja funkcji przy użyciu reguł rozmytych, charakterystyki przejściowe
Metody i techniki sztucznej inteligencji / Leszek Rutkowski. wyd. 2, 3 dodr. Warszawa, Spis treści
 Metody i techniki sztucznej inteligencji / Leszek Rutkowski. wyd. 2, 3 dodr. Warszawa, 2012 Spis treści Przedmowa do wydania drugiego Przedmowa IX X 1. Wstęp 1 2. Wybrane zagadnienia sztucznej inteligencji
Metody i techniki sztucznej inteligencji / Leszek Rutkowski. wyd. 2, 3 dodr. Warszawa, 2012 Spis treści Przedmowa do wydania drugiego Przedmowa IX X 1. Wstęp 1 2. Wybrane zagadnienia sztucznej inteligencji
WYKŁAD 10 Rozmyta reprezentacja danych (modelowanie i wnioskowanie rozmyte)
 WYKŁAD 10 Rozmyta reprezentacja danych (modelowanie i wnioskowanie rozmyte) Motywacje:! przezwyciężenie wad tradycyjnych algorytmów komputerowych, które zawodzą zwłaszcza w sytuacjach, w których człowiek
WYKŁAD 10 Rozmyta reprezentacja danych (modelowanie i wnioskowanie rozmyte) Motywacje:! przezwyciężenie wad tradycyjnych algorytmów komputerowych, które zawodzą zwłaszcza w sytuacjach, w których człowiek
Piotr Sobolewski Krzysztof Skorupski
 Plan prezentacji Logika rodzaje Logika klasyczna Logika wielowartościowa Logika rozmyta Historia powstania Definicje Zbiory rozmyte Relacje rozmyte Systemy rozmyte Modele Zastosowanie w optymalizacji przykłady
Plan prezentacji Logika rodzaje Logika klasyczna Logika wielowartościowa Logika rozmyta Historia powstania Definicje Zbiory rozmyte Relacje rozmyte Systemy rozmyte Modele Zastosowanie w optymalizacji przykłady
Zadanie 0 gdy nie mamy logiki rozmytej. Zadanie 1- gdy już mamy logikę rozmytą
 Zadanie 0 gdy nie mamy logiki rozmytej Wyobraźmy sobie, że chcemy oceniad czy dana temperatura świadczy o tym, że jest gorąco czy raczej zimno. A więc znając wartośd liczbową temperatury chcemy oceniad
Zadanie 0 gdy nie mamy logiki rozmytej Wyobraźmy sobie, że chcemy oceniad czy dana temperatura świadczy o tym, że jest gorąco czy raczej zimno. A więc znając wartośd liczbową temperatury chcemy oceniad
7. Zagadnienie parkowania ciężarówki.
 7. Zagadnienie parkowania ciężarówki. Sterowniki rozmyte Aby móc sterować przebiegiem pewnych procesów lub też pracą urządzeń niezbędne jest stworzenie odpowiedniego modelu, na podstawie którego można
7. Zagadnienie parkowania ciężarówki. Sterowniki rozmyte Aby móc sterować przebiegiem pewnych procesów lub też pracą urządzeń niezbędne jest stworzenie odpowiedniego modelu, na podstawie którego można
Inteligencja obliczeniowa
 Ćwiczenie nr 1 Zbiory rozmyte logika rozmyta Tworzenie: termów zmiennej lingwistycznej o różnych kształtach, modyfikatorów, zmiennych o wielu termach; operacje przecięcia, połączenia i dopełnienia 1. Wprowadzenie
Ćwiczenie nr 1 Zbiory rozmyte logika rozmyta Tworzenie: termów zmiennej lingwistycznej o różnych kształtach, modyfikatorów, zmiennych o wielu termach; operacje przecięcia, połączenia i dopełnienia 1. Wprowadzenie
Cel projektu: Wymogi dotyczące sprawozdania:
 W ramach zajęć proszę wykonać sprawozdanie z logiki rozmytej. Sprawozdanie powinno realizować zadanie wnioskowania rozmytego. Cel projektu: Student projektuje bazę wiedzy wnioskowania rozmytego (kilka,
W ramach zajęć proszę wykonać sprawozdanie z logiki rozmytej. Sprawozdanie powinno realizować zadanie wnioskowania rozmytego. Cel projektu: Student projektuje bazę wiedzy wnioskowania rozmytego (kilka,
Technologie i systemy oparte na logice rozmytej
 Zagadnienia I Technologie i systemy oparte na logice rozmytej Mają zastosowania w sytuacjach kiedy nie posiadamy wystarczającej wiedzy o modelu matematycznym rządzącym danym zjawiskiem oraz tam gdzie zbudowanie
Zagadnienia I Technologie i systemy oparte na logice rozmytej Mają zastosowania w sytuacjach kiedy nie posiadamy wystarczającej wiedzy o modelu matematycznym rządzącym danym zjawiskiem oraz tam gdzie zbudowanie
Sztuczna inteligencja : Zbiory rozmyte cz. III
 Instytut Informatyki Uniwersytetu Śląskiego lab 3 Notacja Zadeha: symboliczny zapis zbioru rozmytego dla przestrzeni dyskretnej. Dla X jest przestrzenią o skończonej liczbie elementów X = {x 1, x 2,...,
Instytut Informatyki Uniwersytetu Śląskiego lab 3 Notacja Zadeha: symboliczny zapis zbioru rozmytego dla przestrzeni dyskretnej. Dla X jest przestrzenią o skończonej liczbie elementów X = {x 1, x 2,...,
Np. Olsztyn leży nad Łyną - zdanie prawdziwe, wartość logiczna 1 4 jest większe od 5 - zdanie fałszywe, wartość logiczna 0
 ĆWICZENIE 1 Klasyczny Rachunek Zdań (KRZ): zdania w sensie logicznym, wartości logiczne, spójniki logiczne, zmienne zdaniowe, tabele prawdziwościowe dla spójników logicznych, formuły, wartościowanie zbioru
ĆWICZENIE 1 Klasyczny Rachunek Zdań (KRZ): zdania w sensie logicznym, wartości logiczne, spójniki logiczne, zmienne zdaniowe, tabele prawdziwościowe dla spójników logicznych, formuły, wartościowanie zbioru
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania MODELOWANIE I IDENTYFIKACJA Logika rozmyta podstawy wnioskowania w GUI Fuzzy. Materiały pomocnicze do laboratorium
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania MODELOWANIE I IDENTYFIKACJA Logika rozmyta podstawy wnioskowania w GUI Fuzzy. Materiały pomocnicze do laboratorium
Układy logiki rozmytej. Co to jest?
 PUAV Wykład 14 Co to jest? Co to jest? Logika rozmyta (fuzzy logic) jest to dział matematyki precyzyjnie formalizujący nieprecyzyjne, nieformalne ludzkie rozumowanie. Co to jest? Logika rozmyta (fuzzy
PUAV Wykład 14 Co to jest? Co to jest? Logika rozmyta (fuzzy logic) jest to dział matematyki precyzyjnie formalizujący nieprecyzyjne, nieformalne ludzkie rozumowanie. Co to jest? Logika rozmyta (fuzzy
Problemy złożone trudno jest analizować precyzyjnie Wiedza eksperta w złożonych przypadkach daje się opisać tylko w sposób nieprecyzyjny, np.
 ZBIORY ROZMYTE Problemy złożone trudno jest analizować precyzyjnie Wiedza eksperta w złożonyc przypadkac daje się opisać tylko w sposób nieprecyzyjny, np. W dużym mieście, powinien istnieć regionalny port
ZBIORY ROZMYTE Problemy złożone trudno jest analizować precyzyjnie Wiedza eksperta w złożonyc przypadkac daje się opisać tylko w sposób nieprecyzyjny, np. W dużym mieście, powinien istnieć regionalny port
Sieci Neuronowe - Rok III - kierunek IS w IFAiIS UJ 2008/2009. Sieci Neuronowe. Wykład 11 Algorytmy genetyczne; Systemy rozmyte
 Sieci Neuronowe Wykład 11 Algorytmy genetyczne; Systemy rozmyte wykład przygotowany na podstawie. S. Osowski, Sieci Neuronowe w ujęciu algorytmicznym, Rozdz. 4, PWNT, Warszawa 1996. W. Duch, J. Korbicz,
Sieci Neuronowe Wykład 11 Algorytmy genetyczne; Systemy rozmyte wykład przygotowany na podstawie. S. Osowski, Sieci Neuronowe w ujęciu algorytmicznym, Rozdz. 4, PWNT, Warszawa 1996. W. Duch, J. Korbicz,
Sztuczna inteligencja : Zbiory rozmyte cz. 2
 Sztuczna inteligencja : Zbiory rozmyte cz. 2 Przemysław Juszczuk Instytut Informatyki Uniwersytetu Śląskiego 1 marca 2012 Funkcja trójkątna: Funkcja trójkątna: Funkcja przynależności γ (gamma): Rysunek:
Sztuczna inteligencja : Zbiory rozmyte cz. 2 Przemysław Juszczuk Instytut Informatyki Uniwersytetu Śląskiego 1 marca 2012 Funkcja trójkątna: Funkcja trójkątna: Funkcja przynależności γ (gamma): Rysunek:
Tworzenie rozmytego systemu wnioskowania
 Tworzenie rozmytego systemu wnioskowania Wstęp W odróżnieniu od klasycznych systemów regałowych modele rozmyte pozwalają budowad modele wnioskujące oparte o język naturalny, dzieki czemu inżynierom wiedzy
Tworzenie rozmytego systemu wnioskowania Wstęp W odróżnieniu od klasycznych systemów regałowych modele rozmyte pozwalają budowad modele wnioskujące oparte o język naturalny, dzieki czemu inżynierom wiedzy
SYSTEMY UCZĄCE SIĘ WYKŁAD 4. DRZEWA REGRESYJNE, INDUKCJA REGUŁ. Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska
 SYSTEMY UCZĄCE SIĘ WYKŁAD 4. DRZEWA REGRESYJNE, INDUKCJA REGUŁ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska DRZEWO REGRESYJNE Sposób konstrukcji i przycinania
SYSTEMY UCZĄCE SIĘ WYKŁAD 4. DRZEWA REGRESYJNE, INDUKCJA REGUŁ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska DRZEWO REGRESYJNE Sposób konstrukcji i przycinania
Logika rozmyta. Agnieszka Nowak - Brzezińska
 Logika rozmyta Agnieszka Nowak - Brzezińska Geneza Logiki rozmytej Za twórcę teorii zbiorów rozmytych i logiki rozmytej uważa się Lotfiego A. Zadeha, który w 1965 roku opublikował artykuł Fuzzy Sets (Information
Logika rozmyta Agnieszka Nowak - Brzezińska Geneza Logiki rozmytej Za twórcę teorii zbiorów rozmytych i logiki rozmytej uważa się Lotfiego A. Zadeha, który w 1965 roku opublikował artykuł Fuzzy Sets (Information
ELEMENTY SZTUCZNEJ INTELIGENCJI. Wstęp do logiki rozmytej
 ELEMENTY SZTUCZNEJ INTELIGENCJI 1 Wstęp do logiki rozmytej PLN 1. Co to jest myślenie rozmyte? 2. Teoria zbiorów rozmytych. 3. Zmienne lingwistyczne. 4. Reguły rozmyte. 5. Wnioskowanie rozmyte: 1. typu
ELEMENTY SZTUCZNEJ INTELIGENCJI 1 Wstęp do logiki rozmytej PLN 1. Co to jest myślenie rozmyte? 2. Teoria zbiorów rozmytych. 3. Zmienne lingwistyczne. 4. Reguły rozmyte. 5. Wnioskowanie rozmyte: 1. typu
Temat: Model TS + ANFIS. Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE
 Temat: Model TS + ANFIS Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1 Wprowadzenie Pierwszym rodzajem modelowania
Temat: Model TS + ANFIS Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1 Wprowadzenie Pierwszym rodzajem modelowania
Sterowanie z wykorzystaniem logiki rozmytej
 Sterowanie z wykorzystaniem logiki rozmytej konspekt seminarium Paweł Szołtysek 24 stycznia 2009 1 Wstęp 1.1 Podstawy logiki rozmytej Logika rozmyta jest rodzajem logiki wielowartościowej, stanowi uogólnienie
Sterowanie z wykorzystaniem logiki rozmytej konspekt seminarium Paweł Szołtysek 24 stycznia 2009 1 Wstęp 1.1 Podstawy logiki rozmytej Logika rozmyta jest rodzajem logiki wielowartościowej, stanowi uogólnienie
Reprezentacja rozmyta - zastosowania logiki rozmytej
 17.06.2009 Wrocław Bartosz Chabasinski 148384 Reprezentacja rozmyta - zastosowania logiki rozmytej 1. Wstęp Celem wprowadzenia pojęcia teorii zbiorów rozmytych była potrzeba matematycznego opisania tych
17.06.2009 Wrocław Bartosz Chabasinski 148384 Reprezentacja rozmyta - zastosowania logiki rozmytej 1. Wstęp Celem wprowadzenia pojęcia teorii zbiorów rozmytych była potrzeba matematycznego opisania tych
Logika Stosowana. Wykład 7 - Zbiory i logiki rozmyte Część 3 Prawdziwościowa logika rozmyta. Marcin Szczuka. Instytut Informatyki UW
 Logika Stosowana Wykład 7 - Zbiory i logiki rozmyte Część 3 Prawdziwościowa logika rozmyta Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika
Logika Stosowana Wykład 7 - Zbiory i logiki rozmyte Część 3 Prawdziwościowa logika rozmyta Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika
Implementacja rozmytych systemów wnioskujących w zdaniach regulacji
 Metody Sztucznej Inteligencji w Sterowaniu Ćwiczenie 5 Implementacja rozmytych systemów wnioskujących w zdaniach regulacji Przygotował: mgr inż. Marcin Pelic Instytut Technologii Mechanicznej Politechnika
Metody Sztucznej Inteligencji w Sterowaniu Ćwiczenie 5 Implementacja rozmytych systemów wnioskujących w zdaniach regulacji Przygotował: mgr inż. Marcin Pelic Instytut Technologii Mechanicznej Politechnika
Elementy logiki. Wojciech Buszkowski Wydział Matematyki i Informatyki UAM Zakład Teorii Obliczeń
 Elementy logiki Wojciech Buszkowski Wydział Matematyki i Informatyki UAM Zakład Teorii Obliczeń 1 Klasyczny Rachunek Zdań 1.1 Spójniki logiczne Zdaniem w sensie logicznym nazywamy wyrażenie, które jest
Elementy logiki Wojciech Buszkowski Wydział Matematyki i Informatyki UAM Zakład Teorii Obliczeń 1 Klasyczny Rachunek Zdań 1.1 Spójniki logiczne Zdaniem w sensie logicznym nazywamy wyrażenie, które jest
Sztuczna inteligencja: zbiory rozmyte
 Instytut Informatyki Uniwersytetu Śląskiego lab 1 1 Klasyczna teoria zbiorów 2 Teoria zbiorów rozmytych 3 Zmienne lingwistyczne i funkcje przynależności 4 System rozmyty 5 Preprocesing danych Każdy element
Instytut Informatyki Uniwersytetu Śląskiego lab 1 1 Klasyczna teoria zbiorów 2 Teoria zbiorów rozmytych 3 Zmienne lingwistyczne i funkcje przynależności 4 System rozmyty 5 Preprocesing danych Każdy element
PODSTAWY INŻYNIERI WIEDZY
 Z1-PU7 WYDANIE N1 Strona 1 z 4 (pieczęć wydziału) KARTA PRZEDMIOTU 1. Nazwa przedmiotu: PODSTAWY INŻYNIERI WIEDZY 2. Kod przedmiotu: PIW 3. Karta przedmiotu ważna od roku akademickiego: 2012/2013 4. Forma
Z1-PU7 WYDANIE N1 Strona 1 z 4 (pieczęć wydziału) KARTA PRZEDMIOTU 1. Nazwa przedmiotu: PODSTAWY INŻYNIERI WIEDZY 2. Kod przedmiotu: PIW 3. Karta przedmiotu ważna od roku akademickiego: 2012/2013 4. Forma
SID Wykład 7 Zbiory rozmyte
 SID Wykład 7 Zbiory rozmyte Wydział Matematyki, Informatyki i Mechaniki UW slezak@mimuw.edu.pl Wstęp Language Ontological Commitment Epistemological Commitment (What exists in the world) (What an agent
SID Wykład 7 Zbiory rozmyte Wydział Matematyki, Informatyki i Mechaniki UW slezak@mimuw.edu.pl Wstęp Language Ontological Commitment Epistemological Commitment (What exists in the world) (What an agent
1 Podstawowe oznaczenia
 Poniżej mogą Państwo znaleźć skondensowane wiadomości z wykładu. Należy je traktować jako przegląd pojęć, które pojawiły się na wykładzie. Materiały te nie są w pełni tożsame z tym co pojawia się na wykładzie.
Poniżej mogą Państwo znaleźć skondensowane wiadomości z wykładu. Należy je traktować jako przegląd pojęć, które pojawiły się na wykładzie. Materiały te nie są w pełni tożsame z tym co pojawia się na wykładzie.
Piegat A.: Modelowanie i sterowanie rozmyte, Akademicka Oficyna Wydawnicza EXIT, Warszawa 1999 r.
 Metody prognozowania: Podstawy logiki rozmytej Literatura do wykładu: Piegat A.: Modelowanie i sterowanie rozmyte, Akademicka Oficyna Wydawnicza EXIT, Warszawa 1999 r. D. Rutkowska, M. Pilinski, L. Rutkowski,
Metody prognozowania: Podstawy logiki rozmytej Literatura do wykładu: Piegat A.: Modelowanie i sterowanie rozmyte, Akademicka Oficyna Wydawnicza EXIT, Warszawa 1999 r. D. Rutkowska, M. Pilinski, L. Rutkowski,
W narzędziu typu Excel, Calc czy Gnumeric napisz formułę logiczną która wyznaczy wartośd przynależności dla podanej temperatury do zbioru gorąco.
 Zadanie 0 Wyobraźmy sobie, że chcemy oceniad czy dana temperatura świadczy o tym, że jest gorąco czy raczej zimno. A więc znając wartośd liczbową temperatury chcemy oceniad wartośd funkcji przynależności
Zadanie 0 Wyobraźmy sobie, że chcemy oceniad czy dana temperatura świadczy o tym, że jest gorąco czy raczej zimno. A więc znając wartośd liczbową temperatury chcemy oceniad wartośd funkcji przynależności
Rachunek zdań i predykatów
 Rachunek zdań i predykatów Agnieszka Nowak 14 czerwca 2008 1 Rachunek zdań Do nauczenia :! 1. ((p q) p) q - reguła odrywania RO 2. reguła modus tollens MT: ((p q) q) p ((p q) q) p (( p q) q) p (( p q)
Rachunek zdań i predykatów Agnieszka Nowak 14 czerwca 2008 1 Rachunek zdań Do nauczenia :! 1. ((p q) p) q - reguła odrywania RO 2. reguła modus tollens MT: ((p q) q) p ((p q) q) p (( p q) q) p (( p q)
Logika rozmyta. Agnieszka Nowak - Brzezińska
 Logika rozmyta Agnieszka Nowak - Brzezińska Geneza Logiki rozmytej Za twórcę teorii zbiorów rozmytych i logiki rozmytej uważa się Lotfiego A. Zadeha, który w 1965 roku opublikował artykuł Fuzzy Sets (Information
Logika rozmyta Agnieszka Nowak - Brzezińska Geneza Logiki rozmytej Za twórcę teorii zbiorów rozmytych i logiki rozmytej uważa się Lotfiego A. Zadeha, który w 1965 roku opublikował artykuł Fuzzy Sets (Information
Systemy rozmyte i ich zastosowania. Krzysztof Rykaczewski
 Systemy rozmyte i ich zastosowania Krzysztof Rykaczewski 21 czerwca 2006 SPIS TREŚCI Spis treści 1 Wstęp 1 2 Podstawowe pojęcia i definicje logiki rozmytej 1 2.1 Przykłady funkcji przynależności..................
Systemy rozmyte i ich zastosowania Krzysztof Rykaczewski 21 czerwca 2006 SPIS TREŚCI Spis treści 1 Wstęp 1 2 Podstawowe pojęcia i definicje logiki rozmytej 1 2.1 Przykłady funkcji przynależności..................
LOGIKA MATEMATYCZNA. Poziom podstawowy. Zadanie 2 (4 pkt.) Jeśli liczbę 3 wstawisz w miejsce x, to które zdanie będzie prawdziwe:
 LOGIKA MATEMATYCZNA Poziom podstawowy Zadanie ( pkt.) Która koniunkcja jest prawdziwa: a) Liczba 6 jest niewymierna i 6 jest liczbą dodatnią. b) Liczba 0 jest wymierna i 0 jest najmniejszą liczbą całkowitą.
LOGIKA MATEMATYCZNA Poziom podstawowy Zadanie ( pkt.) Która koniunkcja jest prawdziwa: a) Liczba 6 jest niewymierna i 6 jest liczbą dodatnią. b) Liczba 0 jest wymierna i 0 jest najmniejszą liczbą całkowitą.
Myślenie w celu zdobycia wiedzy = poznawanie. Myślenie z udziałem rozumu = myślenie racjonalne. Myślenie racjonalne logiczne statystyczne
 Literatura: podstawowa: C. Radhakrishna Rao, Statystyka i prawda, 1994. G. Wieczorkowska-Wierzbińska, J. Wierzbiński, Statystyka. Od teorii do praktyki, 2013. A. Aczel, Statystyka w zarządzaniu, 2002.
Literatura: podstawowa: C. Radhakrishna Rao, Statystyka i prawda, 1994. G. Wieczorkowska-Wierzbińska, J. Wierzbiński, Statystyka. Od teorii do praktyki, 2013. A. Aczel, Statystyka w zarządzaniu, 2002.
Tautologia (wyrażenie uniwersalnie prawdziwe - prawo logiczne)
 Tautologia (wyrażenie uniwersalnie prawdziwe - prawo logiczne) Definicja 1: Tautologia jest to takie wyrażenie, którego wartość logiczna jest prawdą przy wszystkich możliwych wartościowaniach zmiennych
Tautologia (wyrażenie uniwersalnie prawdziwe - prawo logiczne) Definicja 1: Tautologia jest to takie wyrażenie, którego wartość logiczna jest prawdą przy wszystkich możliwych wartościowaniach zmiennych
Ziemia obraca się wokół Księżyca, bo posiadając odpowiednią wiedzę można stwierdzić, czy są prawdziwe, czy fałszywe. Zdaniami nie są wypowiedzi:
 1 Elementy logiki W logice zdaniem nazywamy wypowiedź oznajmującą, która (w ramach danej nauki) jest albo prawdziwa, albo fałszywa. Tak więc zdanie może mieć jedną z dwóch wartości logicznych. Prawdziwość
1 Elementy logiki W logice zdaniem nazywamy wypowiedź oznajmującą, która (w ramach danej nauki) jest albo prawdziwa, albo fałszywa. Tak więc zdanie może mieć jedną z dwóch wartości logicznych. Prawdziwość
Logika rozmyta typu 2
 Logika rozmyta typu 2 Zbiory rozmyte Funkcja przynależności Interwałowe zbiory rozmyte Funkcje przynależności przedziałów Zastosowanie.9.5 Francuz Polak Niemiec Arytmetyka przedziałów Operacje zbiorowe
Logika rozmyta typu 2 Zbiory rozmyte Funkcja przynależności Interwałowe zbiory rozmyte Funkcje przynależności przedziałów Zastosowanie.9.5 Francuz Polak Niemiec Arytmetyka przedziałów Operacje zbiorowe
Kurs logiki rozmytej - zadania. Wojciech Szybisty
 Kurs logiki rozmytej - zadania Wojciech Szybisty 2009 Spis treści 1 Zadania - zbiory rozmyte 3 2 Zadania - relacje rozmyte 6 3 Zadania - logika rozmyta 11 1 Zadania - zbiory rozmyte 3 Przykłady rozwiązywania
Kurs logiki rozmytej - zadania Wojciech Szybisty 2009 Spis treści 1 Zadania - zbiory rozmyte 3 2 Zadania - relacje rozmyte 6 3 Zadania - logika rozmyta 11 1 Zadania - zbiory rozmyte 3 Przykłady rozwiązywania
Wstęp do logiki. Klasyczny Rachunek Zdań III
 Wstęp do logiki Klasyczny Rachunek Zdań III Przypomnijmy: Logika: = Teoria form (schematów, reguł) poprawnych wnioskowań. Wnioskowaniem nazywamy jakąkolwiek skończoną co najmniej dwuwyrazową sekwencję
Wstęp do logiki Klasyczny Rachunek Zdań III Przypomnijmy: Logika: = Teoria form (schematów, reguł) poprawnych wnioskowań. Wnioskowaniem nazywamy jakąkolwiek skończoną co najmniej dwuwyrazową sekwencję
ĆWICZENIE 4 ZASTOSOWANIE METOD I NARZĘDZI LOGIKI ROZMYTEJ DO KLASYFIKACJI DANYCH I APROKSYMACJI ODWZOROWAŃ STATYCZNYCH
 Politechnika Białostocka Wydział Elektryczny Katedra Automatyki i Elektroniki ĆWICZENIE 4 ZASTOSOWANIE METOD I NARZĘDZI LOGIKI ROZMYTEJ DO KLASYFIKACJI DANYCH I APROKSYMACJI ODWZOROWAŃ STATYCZNYCH Pracownia
Politechnika Białostocka Wydział Elektryczny Katedra Automatyki i Elektroniki ĆWICZENIE 4 ZASTOSOWANIE METOD I NARZĘDZI LOGIKI ROZMYTEJ DO KLASYFIKACJI DANYCH I APROKSYMACJI ODWZOROWAŃ STATYCZNYCH Pracownia
Systemy uczące się wykład 1
 Systemy uczące się wykład 1 dr Przemysław Juszczuk Katedra Inżynierii Wiedzy, Uniwersytet Ekonomiczny 5 X 2018 e-mail: przemyslaw.juszczuk@ue.katowice.pl Konsultacje: na stronie katedry + na stronie domowej
Systemy uczące się wykład 1 dr Przemysław Juszczuk Katedra Inżynierii Wiedzy, Uniwersytet Ekonomiczny 5 X 2018 e-mail: przemyslaw.juszczuk@ue.katowice.pl Konsultacje: na stronie katedry + na stronie domowej
Zadanie 0 gdy nie mamy logiki rozmytej
 Zadanie 0 gdy nie mamy logiki rozmytej Wyobraźmy sobie, że chcemy oceniad czy dana temperatura świadczy o tym, że jest gorąco czy raczej zimno. A więc znając wartośd liczbową temperatury chcemy oceniad
Zadanie 0 gdy nie mamy logiki rozmytej Wyobraźmy sobie, że chcemy oceniad czy dana temperatura świadczy o tym, że jest gorąco czy raczej zimno. A więc znając wartośd liczbową temperatury chcemy oceniad
Wstęp do logiki. Klasyczny Rachunek Zdań II
 Wstęp do logiki Klasyczny Rachunek Zdań II DEF. 1 (Słownik). Następujące znaki tworzą słownik języka KRZ: p 1, p 2, p 3, (zmienne zdaniowe) ~,,,, (spójniki) ), ( (nawiasy). DEF. 2 (Wyrażenie). Wyrażeniem
Wstęp do logiki Klasyczny Rachunek Zdań II DEF. 1 (Słownik). Następujące znaki tworzą słownik języka KRZ: p 1, p 2, p 3, (zmienne zdaniowe) ~,,,, (spójniki) ), ( (nawiasy). DEF. 2 (Wyrażenie). Wyrażeniem
Temat: ANFIS + TS w zadaniach. Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE
 Temat: ANFIS + TS w zadaniach Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1. Systemy neuronowo - rozmyte Systemy
Temat: ANFIS + TS w zadaniach Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1. Systemy neuronowo - rozmyte Systemy
Wykład z Technologii Informacyjnych. Piotr Mika
 Wykład z Technologii Informacyjnych Piotr Mika Uniwersalna forma graficznego zapisu algorytmów Schemat blokowy zbiór bloków, powiązanych ze sobą liniami zorientowanymi. Jest to rodzaj grafu, którego węzły
Wykład z Technologii Informacyjnych Piotr Mika Uniwersalna forma graficznego zapisu algorytmów Schemat blokowy zbiór bloków, powiązanych ze sobą liniami zorientowanymi. Jest to rodzaj grafu, którego węzły
Logika Stosowana. Wykład 1 - Logika zdaniowa. Marcin Szczuka. Instytut Informatyki UW. Wykład monograficzny, semestr letni 2016/2017
 Logika Stosowana Wykład 1 - Logika zdaniowa Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika Stosowana 2017 1 / 30 Plan wykładu 1 Język
Logika Stosowana Wykład 1 - Logika zdaniowa Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika Stosowana 2017 1 / 30 Plan wykładu 1 Język
MATEMATYKA DYSKRETNA, PODSTAWY LOGIKI I TEORII MNOGOŚCI
 MATEMATYKA DYSKRETNA, PODSTAWY LOGIKI I TEORII MNOGOŚCI Program wykładów: dr inż. Barbara GŁUT Wstęp do logiki klasycznej: rachunek zdań, rachunek predykatów. Elementy semantyki. Podstawy teorii mnogości
MATEMATYKA DYSKRETNA, PODSTAWY LOGIKI I TEORII MNOGOŚCI Program wykładów: dr inż. Barbara GŁUT Wstęp do logiki klasycznej: rachunek zdań, rachunek predykatów. Elementy semantyki. Podstawy teorii mnogości
Zagadnienia AI wykład 1
 Zagadnienia AI wykład Podręcznik do wykładu: Leszek Rutkowski Metody i techniki sztucznej inteligencji Wydawnictwo Naukowe PWN Prezentacje do wykładu będą sukcesywnie umieszczane na stronie: http://merlin.fic.uni.lodz.pl/mskulimowski/
Zagadnienia AI wykład Podręcznik do wykładu: Leszek Rutkowski Metody i techniki sztucznej inteligencji Wydawnictwo Naukowe PWN Prezentacje do wykładu będą sukcesywnie umieszczane na stronie: http://merlin.fic.uni.lodz.pl/mskulimowski/
SYSTEMY UCZĄCE SIĘ WYKŁAD 10. PRZEKSZTAŁCANIE ATRYBUTÓW. Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska.
 SYSTEMY UCZĄCE SIĘ WYKŁAD 10. PRZEKSZTAŁCANIE ATRYBUTÓW Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska INFORMACJE WSTĘPNE Hipotezy do uczenia się lub tworzenia
SYSTEMY UCZĄCE SIĘ WYKŁAD 10. PRZEKSZTAŁCANIE ATRYBUTÓW Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska INFORMACJE WSTĘPNE Hipotezy do uczenia się lub tworzenia
Interwałowe zbiory rozmyte
 Interwałowe zbiory rozmyte 1. Wprowadzenie. Od momentu przedstawienia koncepcji klasycznych zbiorów rozmytych (typu 1), były one krytykowane za postać jaką przybiera funkcja przynależności. W przypadku
Interwałowe zbiory rozmyte 1. Wprowadzenie. Od momentu przedstawienia koncepcji klasycznych zbiorów rozmytych (typu 1), były one krytykowane za postać jaką przybiera funkcja przynależności. W przypadku
I. Podstawowe pojęcia i oznaczenia logiczne i mnogościowe. Elementy teorii liczb rzeczywistych.
 I. Podstawowe pojęcia i oznaczenia logiczne i mnogościowe. Elementy teorii liczb rzeczywistych. 1. Elementy logiki matematycznej. 1.1. Rachunek zdań. Definicja 1.1. Zdaniem logicznym nazywamy zdanie gramatyczne
I. Podstawowe pojęcia i oznaczenia logiczne i mnogościowe. Elementy teorii liczb rzeczywistych. 1. Elementy logiki matematycznej. 1.1. Rachunek zdań. Definicja 1.1. Zdaniem logicznym nazywamy zdanie gramatyczne
Metoda zaburz-obserwuj oraz metoda wspinania
 Metoda zaburz-obserwuj oraz metoda wspinania Algorytm zaburz-obserwuj mierzy się moc (zwykle modułu) przed i po zmianie na tej podstawie podejmuje się decyzję o kierunku następnej zmiany Metoda wspinania
Metoda zaburz-obserwuj oraz metoda wspinania Algorytm zaburz-obserwuj mierzy się moc (zwykle modułu) przed i po zmianie na tej podstawie podejmuje się decyzję o kierunku następnej zmiany Metoda wspinania
Rachunek zdao i logika matematyczna
 Rachunek zdao i logika matematyczna Pojęcia Logika - Zajmuje się badaniem ogólnych praw, według których przebiegają wszelkie poprawne rozumowania, w szczególności wnioskowania. Rachunek zdao - dział logiki
Rachunek zdao i logika matematyczna Pojęcia Logika - Zajmuje się badaniem ogólnych praw, według których przebiegają wszelkie poprawne rozumowania, w szczególności wnioskowania. Rachunek zdao - dział logiki
ZASTOSOWANIE LOGIKI ROZMYTEJ W ZARZĄDZANIU ZAPASAMI THE USE OF FUZZY LOGIC IN INVENTORY MANAGEMENT
 orota Rogowska ZASTOSOWANIE LOGIKI ROZYTEJ W ZARZĄZANIU ZAPASAI Streszczenie Zagadnienie zarządzania zapasami zajmuje ważne miejsce w każdym przedsiębiorstwie. Zapasy stanowią bowiem podstawę zapewnienia
orota Rogowska ZASTOSOWANIE LOGIKI ROZYTEJ W ZARZĄZANIU ZAPASAI Streszczenie Zagadnienie zarządzania zapasami zajmuje ważne miejsce w każdym przedsiębiorstwie. Zapasy stanowią bowiem podstawę zapewnienia
ALGORYTM PROJEKTOWANIA ROZMYTYCH SYSTEMÓW EKSPERCKICH TYPU MAMDANI ZADEH OCENIAJĄCYCH EFEKTYWNOŚĆ WYKONANIA ZADANIA BOJOWEGO
 Szybkobieżne Pojazdy Gąsienicowe (2) Nr 2, 24 Mirosław ADAMSKI Norbert GRZESIK ALGORYTM PROJEKTOWANIA CH SYSTEMÓW EKSPERCKICH TYPU MAMDANI ZADEH OCENIAJĄCYCH EFEKTYWNOŚĆ WYKONANIA ZADANIA BOJOWEGO. WSTĘP
Szybkobieżne Pojazdy Gąsienicowe (2) Nr 2, 24 Mirosław ADAMSKI Norbert GRZESIK ALGORYTM PROJEKTOWANIA CH SYSTEMÓW EKSPERCKICH TYPU MAMDANI ZADEH OCENIAJĄCYCH EFEKTYWNOŚĆ WYKONANIA ZADANIA BOJOWEGO. WSTĘP
Logika Stosowana. Wykład 2 - Logika modalna Część 2. Marcin Szczuka. Instytut Informatyki UW. Wykład monograficzny, semestr letni 2016/2017
 Logika Stosowana Wykład 2 - Logika modalna Część 2 Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika Stosowana 2017 1 / 27 Plan wykładu
Logika Stosowana Wykład 2 - Logika modalna Część 2 Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika Stosowana 2017 1 / 27 Plan wykładu
Temat: Sterowanie mobilnością robota z wykorzystaniem algorytmu logiki rozmytej
 Wrocław, 13.01.2016 Metody sztucznej inteligencji Prowadzący: Dr hab. inż. Ireneusz Jabłoński Temat: Sterowanie mobilnością robota z wykorzystaniem algorytmu logiki rozmytej Wykonał: Jakub Uliarczyk, 195639
Wrocław, 13.01.2016 Metody sztucznej inteligencji Prowadzący: Dr hab. inż. Ireneusz Jabłoński Temat: Sterowanie mobilnością robota z wykorzystaniem algorytmu logiki rozmytej Wykonał: Jakub Uliarczyk, 195639
LOGIKA I TEORIA ZBIORÓW
 LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
Logika formalna wprowadzenie. Ponieważ punkty 10.i 12. nie były omawiane na zajęciach, dlatego można je przeczytać fakultatywnie.
 Logika formalna wprowadzenie Ponieważ punkty 10.i 12. nie były omawiane na zajęciach, dlatego można je przeczytać fakultatywnie. 1. Zdanie logicznie prawdziwe (Prawda logiczna) Zdanie, którego analityczność
Logika formalna wprowadzenie Ponieważ punkty 10.i 12. nie były omawiane na zajęciach, dlatego można je przeczytać fakultatywnie. 1. Zdanie logicznie prawdziwe (Prawda logiczna) Zdanie, którego analityczność
KOMPUTERY W STEROWANIU. Ćwiczenie 6 Projektowanie układu regulacji rozmytej
 Wydział Elektryczny Zespół Automatyki (ZTMAiPC) KOMPUTERY W STEROWANIU Ćwiczenie 6 Projektowanie układu regulacji rozmytej 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z procedurą projektowania
Wydział Elektryczny Zespół Automatyki (ZTMAiPC) KOMPUTERY W STEROWANIU Ćwiczenie 6 Projektowanie układu regulacji rozmytej 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z procedurą projektowania
Wiedza niepewna i wnioskowanie (c.d.)
 Wiedza niepewna i wnioskowanie (c.d.) Dariusz Banasiak Katedra Informatyki Technicznej Wydział Elektroniki Wnioskowanie przybliżone Wnioskowanie w logice tradycyjnej (dwuwartościowej) polega na stwierdzeniu
Wiedza niepewna i wnioskowanie (c.d.) Dariusz Banasiak Katedra Informatyki Technicznej Wydział Elektroniki Wnioskowanie przybliżone Wnioskowanie w logice tradycyjnej (dwuwartościowej) polega na stwierdzeniu
BADANIE GOTOWOŚCI PRZEDSIĘBIORSTW DO ZARZĄDZANIA STRATEGICZNEGO Z WYKORZYSTANIEM ROZMYTEGO RACHUNKU ZDAŃ
 BADANIE GOTOWOŚCI PRZEDSIĘBIORSTW DO ZARZĄDZANIA STRATEGICZNEGO Z WYKORZYSTANIEM ROZMYTEGO RACHUNKU ZDAŃ Agata SZEPTUCH, Marcin ADAM Streszczenie: W artykule podjęto problem badania gotowości przedsiębiorstw
BADANIE GOTOWOŚCI PRZEDSIĘBIORSTW DO ZARZĄDZANIA STRATEGICZNEGO Z WYKORZYSTANIEM ROZMYTEGO RACHUNKU ZDAŃ Agata SZEPTUCH, Marcin ADAM Streszczenie: W artykule podjęto problem badania gotowości przedsiębiorstw
Wstęp do sieci neuronowych, wykład 02 Perceptrony c.d. Maszyna liniowa.
 Wstęp do sieci neuronowych, wykład 02 Perceptrony c.d. Maszyna liniowa. Maja Czoków, Jarosław Piersa, Andrzej Rutkowski Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2018-10-15 Projekt
Wstęp do sieci neuronowych, wykład 02 Perceptrony c.d. Maszyna liniowa. Maja Czoków, Jarosław Piersa, Andrzej Rutkowski Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 2018-10-15 Projekt
KARTA PRZEDMIOTU. 17. Efekty kształcenia:
 Z1-PU7 WYDANIE N1 Strona 1 z 4 (pieczęć wydziału) KARTA PRZEDMIOTU 1. Nazwa przedmiotu: CYBERNETYKA 2. Kod przedmiotu: CYB 3. Karta przedmiotu ważna od roku akademickiego: 2012/2013 4. Forma kształcenia:
Z1-PU7 WYDANIE N1 Strona 1 z 4 (pieczęć wydziału) KARTA PRZEDMIOTU 1. Nazwa przedmiotu: CYBERNETYKA 2. Kod przedmiotu: CYB 3. Karta przedmiotu ważna od roku akademickiego: 2012/2013 4. Forma kształcenia:
Sterownik (regulator) rozmyty przykład [1]
![Sterownik (regulator) rozmyty przykład [1] Sterownik (regulator) rozmyty przykład [1]](/thumbs/53/31458927.jpg) Sterownik (regulator) rozmyty przykład [1] zadanie: przywracanie ustalonej pozycji wózka na platformie masa siła siła -2 m 0 m 2 m tarcie 1 Sterownik (regulator) rozmyty przykład (2) zmienne: x pozycja
Sterownik (regulator) rozmyty przykład [1] zadanie: przywracanie ustalonej pozycji wózka na platformie masa siła siła -2 m 0 m 2 m tarcie 1 Sterownik (regulator) rozmyty przykład (2) zmienne: x pozycja
WNIOSKOWANIE ROZMYTE FUZZY INFERENCE
 Dominik Ziajka WNIOSKOWANIE ROZMYTE FUZZY INFERENCE Celem artykułu jest przedstawienie teorii zbiorów rozmytych, wnioskowania rozmytego oraz porównania ich ze zbiorami przybliżonymi. Wprowadzenie do zbiorów
Dominik Ziajka WNIOSKOWANIE ROZMYTE FUZZY INFERENCE Celem artykułu jest przedstawienie teorii zbiorów rozmytych, wnioskowania rozmytego oraz porównania ich ze zbiorami przybliżonymi. Wprowadzenie do zbiorów
Jeśli przeszkoda jest blisko to przyhamuj
 Rozmyte systemy regułowe Informacja, którą przetwarzają ludzie często (prawie zawsze) jest nieprecyzyjna, a mimo to potrafimy poprawnie wnioskować i podejmować decyzję, czego klasyczne komputery nie potrafią.
Rozmyte systemy regułowe Informacja, którą przetwarzają ludzie często (prawie zawsze) jest nieprecyzyjna, a mimo to potrafimy poprawnie wnioskować i podejmować decyzję, czego klasyczne komputery nie potrafią.
0.1. Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek zdań.
 Wykłady z Analizy rzeczywistej i zespolonej w Matematyce stosowanej Wykład ELEMENTY LOGIKI ALGEBRA BOOLE A Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek
Wykłady z Analizy rzeczywistej i zespolonej w Matematyce stosowanej Wykład ELEMENTY LOGIKI ALGEBRA BOOLE A Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek
Kurs logiki rozmytej - pomoc. Wojciech Szybisty
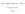 Kurs logiki rozmytej - pomoc Wojciech Szybisty 2009 Spis treści 1 Wymagania 3 2 Zawartość strony internetowej 3 3 Obsługa apletów 6 3.1 Aplet Rodzaje funkcji przynależności...................... 6 3.2
Kurs logiki rozmytej - pomoc Wojciech Szybisty 2009 Spis treści 1 Wymagania 3 2 Zawartość strony internetowej 3 3 Obsługa apletów 6 3.1 Aplet Rodzaje funkcji przynależności...................... 6 3.2
Sztuczna Inteligencja Projekt
 Sztuczna Inteligencja Projekt Temat: Algorytm LEM2 Liczba osób realizujących projekt: 2 1. Zaimplementować algorytm LEM 2. 2. Zaimplementować klasyfikator Classif ier. 3. Za pomocą algorytmu LEM 2 wygenerować
Sztuczna Inteligencja Projekt Temat: Algorytm LEM2 Liczba osób realizujących projekt: 2 1. Zaimplementować algorytm LEM 2. 2. Zaimplementować klasyfikator Classif ier. 3. Za pomocą algorytmu LEM 2 wygenerować
PODSTAWY BAZ DANYCH. 19. Perspektywy baz danych. 2009/2010 Notatki do wykładu "Podstawy baz danych"
 PODSTAWY BAZ DANYCH 19. Perspektywy baz danych 1 Perspektywy baz danych Temporalna baza danych Temporalna baza danych - baza danych posiadająca informację o czasie wprowadzenia lub czasie ważności zawartych
PODSTAWY BAZ DANYCH 19. Perspektywy baz danych 1 Perspektywy baz danych Temporalna baza danych Temporalna baza danych - baza danych posiadająca informację o czasie wprowadzenia lub czasie ważności zawartych
THE PART OF FUZZY SYSTEMS ASSISTING THE DECISION IN DI- AGNOSTICS OF FUEL ENGINE SUBASSEMBLIES DEFECTS
 Journal of KONES Internal Combustion Engines 2005, vol. 12, 3-4 THE PART OF FUZZY SYSTEMS ASSISTING THE DECISION IN DI- AGNOSTICS OF FUEL ENGINE SUBASSEMBLIES DEFECTS Mariusz Topolski Politechnika Wrocławska,
Journal of KONES Internal Combustion Engines 2005, vol. 12, 3-4 THE PART OF FUZZY SYSTEMS ASSISTING THE DECISION IN DI- AGNOSTICS OF FUEL ENGINE SUBASSEMBLIES DEFECTS Mariusz Topolski Politechnika Wrocławska,
Wykład 6. Reguły inferencyjne systemu aksjomatycznego Klasycznego Rachunku Zdań
 Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki Wykład 6. Reguły inferencyjne systemu aksjomatycznego Klasycznego Rachunku Zdań System aksjomatyczny logiki Budując logikę
Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki Wykład 6. Reguły inferencyjne systemu aksjomatycznego Klasycznego Rachunku Zdań System aksjomatyczny logiki Budując logikę
Logika Stosowana Ćwiczenia
 Logika Stosowana Ćwiczenia Systemy sterowania wykorzystujące zbiory rozmyte Marcin Szczuka Instytut Matematyki, Uniwersytet Warszawski Semestr letni 2014/15 Marcin Szczuka (MIMUW) Logika Stosowana 2014/15
Logika Stosowana Ćwiczenia Systemy sterowania wykorzystujące zbiory rozmyte Marcin Szczuka Instytut Matematyki, Uniwersytet Warszawski Semestr letni 2014/15 Marcin Szczuka (MIMUW) Logika Stosowana 2014/15
Logika Stosowana. Wykład 5 - Zbiory i logiki rozmyte Część 1. Marcin Szczuka. Instytut Informatyki UW. Wykład monograficzny, semestr letni 2016/2017
 Logika Stosowana Wykład 5 - Zbiory i logiki rozmyte Część 1 Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika Stosowana 2017 1 / 36 Plan
Logika Stosowana Wykład 5 - Zbiory i logiki rozmyte Część 1 Marcin Szczuka Instytut Informatyki UW Wykład monograficzny, semestr letni 2016/2017 Marcin Szczuka (MIMUW) Logika Stosowana 2017 1 / 36 Plan
1. Wstęp do logiki. Matematyka jest nauką dedukcyjną. Nowe pojęcia definiujemy za pomocą pojęć pierwotnych lub pojęć uprzednio wprowadzonych.
 Elementy logiki i teorii zbiorów. 1. Wstęp do logiki. Matematyka jest nauką dedukcyjną. Nowe pojęcia definiujemy za pomocą pojęć pierwotnych lub pojęć uprzednio wprowadzonych. Pojęcia pierwotne to najprostsze
Elementy logiki i teorii zbiorów. 1. Wstęp do logiki. Matematyka jest nauką dedukcyjną. Nowe pojęcia definiujemy za pomocą pojęć pierwotnych lub pojęć uprzednio wprowadzonych. Pojęcia pierwotne to najprostsze
Kurs logiki rozmytej. Wojciech Szybisty
 Kurs logiki rozmytej Wojciech Szybisty 2009 Spis treści 1 Co to jest logika rozmyta 3 1.1 Podstawy teorii zbiorów rozmytych........................ 3 1.2 Historia.......................................
Kurs logiki rozmytej Wojciech Szybisty 2009 Spis treści 1 Co to jest logika rozmyta 3 1.1 Podstawy teorii zbiorów rozmytych........................ 3 1.2 Historia.......................................
Przykłady zdań w matematyce. Jeśli a 2 + b 2 = c 2, to trójkąt o bokach długości a, b, c jest prostokątny (a, b, c oznaczają dane liczby dodatnie),
 Elementy logiki 1 Przykłady zdań w matematyce Zdania prawdziwe: 1 3 + 1 6 = 1 2, 3 6, 2 Q, Jeśli x = 1, to x 2 = 1 (x oznacza daną liczbę rzeczywistą), Jeśli a 2 + b 2 = c 2, to trójkąt o bokach długości
Elementy logiki 1 Przykłady zdań w matematyce Zdania prawdziwe: 1 3 + 1 6 = 1 2, 3 6, 2 Q, Jeśli x = 1, to x 2 = 1 (x oznacza daną liczbę rzeczywistą), Jeśli a 2 + b 2 = c 2, to trójkąt o bokach długości
5. Rozwiązywanie układów równań liniowych
 5. Rozwiązywanie układów równań liniowych Wprowadzenie (5.1) Układ n równań z n niewiadomymi: a 11 +a 12 x 2 +...+a 1n x n =a 10, a 21 +a 22 x 2 +...+a 2n x n =a 20,..., a n1 +a n2 x 2 +...+a nn x n =a
5. Rozwiązywanie układów równań liniowych Wprowadzenie (5.1) Układ n równań z n niewiadomymi: a 11 +a 12 x 2 +...+a 1n x n =a 10, a 21 +a 22 x 2 +...+a 2n x n =a 20,..., a n1 +a n2 x 2 +...+a nn x n =a
Podstawy Sztucznej Inteligencji (PSZT)
 Podstawy Sztucznej Inteligencji (PSZT) Paweł Wawrzyński Wnioskowanie logiczne i systemy eksperckie Systemy posługujące się logiką predykatów: część 3/3 Dzisiaj Uogólnienie Poprawność i pełność wnioskowania
Podstawy Sztucznej Inteligencji (PSZT) Paweł Wawrzyński Wnioskowanie logiczne i systemy eksperckie Systemy posługujące się logiką predykatów: część 3/3 Dzisiaj Uogólnienie Poprawność i pełność wnioskowania
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Reguły gry zaliczenie przedmiotu wymaga zdania dwóch testów, z logiki (za ok. 5 tygodni) i z filozofii (w sesji); warunkiem koniecznym podejścia do
 Reguły gry zaliczenie przedmiotu wymaga zdania dwóch testów, z logiki (za ok. 5 tygodni) i z filozofii (w sesji); warunkiem koniecznym podejścia do testu z filozofii jest zaliczenie testu z logiki i zaliczenie
Reguły gry zaliczenie przedmiotu wymaga zdania dwóch testów, z logiki (za ok. 5 tygodni) i z filozofii (w sesji); warunkiem koniecznym podejścia do testu z filozofii jest zaliczenie testu z logiki i zaliczenie
