14. PODSTAWY TECHNIKI CYFROWEJ
|
|
|
- Bartłomiej Małecki
- 7 lat temu
- Przeglądów:
Transkrypt
1 14. PODSTAWY TECHNIKI CYFROWEJ UKŁADY CYFROWE Układam cyfrowym (zwanym też układam logcznym) nazywamy układy elektronczne, których zarówno sygnały wejścowe jak wyjścowe są sygnałam bnarnym. Sygnały bnarne (naczej dwójkowe) składają sę z cągów znaków, z których każdy odpowada cyfrze 0 lub 1. Sygnały bnarne tworzą słowa. Najkrótsze słowo zawerające tylko jeden znak (0 lub 1) określa sę jako bt (bnary dgt). Jest to elementarna jednostka nformacj. Słowo o czterech btach nazywamy tetradą (nbble). Słowo o ośmu btach nazywamy bajtem (byte). Osem btów bajtu ponumerowane są od 7 do 0. Wyróżna sę tam tetradę starszą, którą stanową bty z zakresu 7-4 tetradę młodszą, którą stanową bty z zakresu 3-0. Słowa o lczbe btów wększej nż osem ne mają już nazw własnych. Używa sę określeń np. słowo szesnastobtowe lub słowo dwubajtowe, słowo trzydzestodwubtowe lub słowo czterobajtowe td. Przyjmuje sę umowne, że stan logczny wyróżna dwa przecwstawne pozomy welkośc fzycznej: pozom bardzej dodatn, określany jako pozom wysok H (Hgh) oraz pozom mnej dodatn, określany jako pozom nsk oznaczany lterą L (Low). Ops układów logcznych może być możlwy, gdy zostaną określone w sposób jednoznaczny zwązk mędzy abstrakcyjnym stanam 0 1 stanowącym zbór algebry Boole ' a (o czym będze mowa dalej), a realnym pozomam L H. Istneją w tym względze dwe konwencje, które określane są jako logka dodatna logka ujemna. Logka dodatna oznacza, że na wszystkch końcówkach układów stan 1 jest równoważny pozomow wysokemu H, a stan 0 jest równoważny pozomow nskemu L. Logka ujemna oznacza, że na wszystkch końcówkach układów stan 1 jest równoważny pozomow nskemu L, a stan 0 jest równoważny pozomow wysokemu H. W dalszej częśc materału przyjęto, że stosowana jest logka dodatna. Układy cyfrowe wykorzystują operacje oparte na algebrze Boole a 1. Zerojedynkowa algebra Boole'a sygnałów bnarnych jest opsana przez system: B,,, (14.1) gdze: B jest zborem dwuelementowym B={0,1}, w którym są określone operacje dwuargumentowe + operacja jednoargumentowa. Znak + w tym zapse jest operatorem sumy logcznej oznaczanej też przez symbol (alternatywa). Znak jest operatorem loczynu logcznego oznaczanego też przez symbol (konunkcja). Znak oznacza negację. Dla dowolnych zmennych boolowskch x, y, z, to jest zmennych przyjmujących wartośc ze zboru B stneją następujące prawa algebry Boole'a opsane w tabel George Boole ( ) angelsk logk matematyk, profesor matematyk w Queen s College w Cork (Irlanda), twórca algebry logk. W 1854 roku napsał Prawa myślena gdze zawarł podstawowe reguły logk. Istotą jego ujęca były dzałana na obektach, które mogą przyjmować tylko dwe wartośc: prawdę fałsz. Wojcech Wawrzyńsk Podstawy Elektronk Podstawy technk cyfrowej 1
2 Tabela Prawa algebry Boole a lp postać loczynu logcznego (konunkcj) postać sumy logcznej (alternatywy) nazwa prawa 1 xx=x x+x=x dempotentność 2 xy=yx x+y=y+x przemenność 3 x(yz)=(xy)z x +(y+z)=(x+y)+z łączność 4 x+(yz)= (x+y)(x+z) x(y+z)= (xy)+(xz) rozdzelczość 5 x(x+y)=x x+(xy)=x pochłanane 6 x1=x x+0=x własność stałych (element neutralny) 7 x0=0 x+1=1 własność stałych (własnośc zera jedynk ) 8 x x 0 x x 1 własność negacj 9 x x podwójna negacja 10 x y x y x y x y de Morgana Omówene praw algebry Boole a Indempotentność (1) stwerdza, że w wynku mnożena zmennej samej przez sebe lub sumowana zmennej z ną samą otrzymujemy wartość perwotną tej zmennej. Przemenność (2) łączność (3) oznaczają, że można zmenać kolejnośc łączyć zmenne boolowske, a operacja taka ne wpłyne na wynk dzałana. Prawo rozdzelczośc (4) pokazuje jak zapsać konunkcję w postac alternatywy odwrotne. Prawo pochłanana (5) ukazuje jake dzałana mogą doprowadzć do elmnowana jednej zmennej. Prawo własnośc stałych (6) określa, że elementem neutralnym dla mnożena logcznego jest 1, a elementem neutralnym dla dodawana logcznego jest zero. Oznacza to, że odpowedno mnożene przez element neutralny dodawane elementu neutralnego ne zmena wartośc perwotnej wyrażena. Prawo własnośc stałych (7) wyraża zasadę, że każda zmenna pomnożona przez 0 daje w rezultace 0, a każda zmenna zsumowana z 1 daje w rezultace 1. Własność negacj (8) wyraża zasadę, że loczyn logczny zmennej jej negacj (zaprzeczena) jest 0, albowem któraś z nch mus być zerem a wynk mnożena przez 0 jest oczywsty. Natomast suma zmennej jej negacj (zaprzeczena) wynos 1, albowem któraś ze zmennych mus meć wartość 1, a wynk sumowana w tym przypadku jest też jednoznaczny. Prawo podwójnej negacj (9) wyraża sens, że neprawda neprawdy jest prawdą. Zatem podwójna negacja zmennej boolowskej ne zmena jej wartośc perwotnej. Prawa de Morgana 2 (10) ne są już tak całkem oczywste. Można je udowodnć tworząc odpowedne tablce przechodząc z postac po lewej strone równana do postac po prawej jego strone. Rola tych równań w praktyce analzy układów logcznych jest znacząca. Perwsze z nch mów (postać konunkcj), że negacja loczynu jest równa sume negacj. Druge (postać alternatywy) stwerdza, że negacja sumy jest równa loczynow negacj. Umożlwa to przechodzene od postac loczynu logcznego do postac sumy logcznej odwrotne. 2 Właścwe Augustus de Morgan ( , angelsk matematyk logk) podał w roku 1858 jedyne jedno z tych praw - postać alternatywną. Postać konunkcj podał w roku 1867 amerykańsk flozof, logk matematyk Charles Sanders Perce ( ), który w dzejach flozof zapsał sę jako twórca popularnego w USA kerunku flozofcznego zwanego pragmatyzmem. Wojcech Wawrzyńsk Podstawy Elektronk Podstawy technk cyfrowej 2
3 X. REPREZENTACJA DANYCH W SYSTEMACH CYFROWYCH - WYBRANE ZAGADNIENIA X.1. POZYCYJNE SYSTEMY LICZBOWE Zaps pozycyjny lczb oznacza, że w cągu cyfr reprezentującym lczbę znak każdej cyfry zajmuje ścśle określoną pozycję, przy czym tej pozycj przyporządkowana jest odpowedna waga będąca potęgą podstawy. Ilość znaków stosowanych w każdym pozycyjnym systeme lczbowym jest taka sama jak jego podstawa. W słowe A o długośc n (czyl lośc cyfr równej n) reprezentującym lczbę L(A)=an-1...a1a0 każdy znak a zajmuje określoną pozycję tej pozycj przyporządkowana jest waga p. Stała p jest podstawą przyjętego zapsu lczbowego. Można wyrazć to w postac matematycznej: n 1 L a p (X.1) (A) Od welu weków zaps nformacj lczbowych przez człoweka realzowany jest w systeme dzesętnym 3. Zaps ten poparty jest tradycją, popularnoścą zrozumałoścą jak ne trudno sę domyślć podstawa kodu równa sę lczbe palców obu rąk człoweka 4. Podstawą systemu jest lczba dzesęć (p=10) dlatego używane jest dzesęć symbol cyfr, a manowce 0, 1, 2, 3, 4, 5, 6, 7, 8 9. Każdą lczbę w kodze dzesętnym można przedstawć jako sumę składnków: na przykład: (a n 1...a 1a 0 ) a n 1 L = a n-110 n a a (X.2) 3 L (2578) a 10 = = gdze rodzaj zapsu zaznaczany jest przez dolny ndeks przy lczbe 5. 3 Termny system lczbowy dalej stosowany kod lczbowy są tu utożsamane. Take podejśce spotykane jest w lteraturze przedmotu poneważ kod jest umownym systemem znaków umożlwającym przekazywane nformacj. 4 Zaps dzesętny jest w powszechnym użycu dopero od dzesęcu weków. Został on opracowany w Indach około pątego weku n.e. udostępnony cywlzacj europejskej przez Arabów. W starożytnym Rzyme też był stosowany kod dzesętny, lecz ne był to kod pozycyjny. Stosowane były wtedy ( do dzś są stosowane w wybranych sytuacjach) następujące symbole I=1 10, V=5 10, X=10 10, L=50 10, C=100 10, D=500 10, M= Tylko dwa spośród tych symbol można skojarzyć z perwszym lteram łacńskch nazw lczebnków: C-centum M-mlle. Pozostałe oznaczena wynkają z przyjętej konwencj. W kodze tym brak było symbolu zera, a odczyt poprzedzony być musał analzą względnego rozmeszczena poszczególnych symbol reprezentujących określone cyfry (do cekawostek zalczyć należy modyfkację zapsu rzymskego cyfr dokonanego przez króla Francj Ludwka XIV; otóż kazał on sę psać Ludwk XIIII żądał by zegary w Wersalu o godzne czwartej wskazywały na cyfrę IIII, co zostało do dzsaj na tarczach zegarowych wykorzystujących cyfry rzymske [3]). Koncepcja zera była jednak znana w starożytnej Mezopotam, gdze był stosowany pozycyjny kod lczbowy o 60-cu symbolach. Kod ten został zarzucony ok r p.n.e., ale wpływ tego rozwązana trwa do dzsaj albowem godzna ma 60 mnut, mnuta ma 60 sekund, koło ma 6x60=360 stopn [4]. 5 Indeksy dolne oznaczają: 10 kod dzesętny, 2 naturalny kod dwójkowy, 16 kod heksadecymalny, BCD kod dwójkowo-dzesętny, 1z10 kod jeden z dzesęcu, ZM kod znak-moduł, U1 kod uzupełnena do jednego, U2 kod uzupełnena do dwóch. Wojcech Wawrzyńsk Podstawy Elektronk Podstawy technk cyfrowej 3
4 System dwójkowy (bnarny) posada tylko dwe cyfry 0 1 podstawą zapsu jest lczba 2 (p=2). Już od dawna budzł on zanteresowane flozofów matematyków 6. W tym systeme najpopularnejszym zapsem jest naturalny kod dwójkowy. W naturalnym kodze dwójkowym w słowe B o długośc n reprezentującym lczbę L(B)=bn-1...b1b0 każdy znak b zajmuje określoną pozycję tej pozycj przyporządkowana jest odpowedna waga p, gdze podstawą przyjętego tego zapsu jest lczba 2 (p=2). na przykład: n 1 n 1...b1b 0 ) b 2 0 L (b = b n-12 n b b 02 0 (X.3) 3 L (1101) b 2 = = W słowe dwójkowym bt zwązany z najwększą wagą (skrajny z lewej strony w ww. zapse) jest btem najbardzej znaczącym (najstarszym) zwanym btem MSB (Most Sgnfcant Bt). Bt zwązany z najmnejszą wagą (skrajny z prawej strony) jest btem najmnej znaczącym (najmłodszym) LSB (Least Sgnfcant Bt). Zamana odwrotna tj. lczby dzesętnej na dwójkową następuje poprzez kolejne dzelene lczby dzesętnej przez 2 stwerdzene czy jest reszta (1) czy jej ne ma (0). Przykład Rozważmy zamanę lczby dzesętnej 1310 na postać w naturalnym kodze dwójkowym. W tym celu należy dokonać następujących dzeleń obserwacj czy w wynku pozostaje reszta: 13/2=6 jest reszta 1 LSB 6/2 = 3 ne ma reszty 0 3/2 = 1 jest reszta 1 1/2 = 0 jest reszta 1 MSB co daje = Zauważmy, że wynk otrzymujemy w kolejnośc od btu najmnej znaczącego (LSB) do najbardzej znaczącego (MSB). Konec przykładu. Dla lczb ułamkowych wyrażanych w naturalnym kodze dwójkowym stosuje sę przy poszczególnych cyfrach z prawej strony symbolu częśc ułamkowej (kropk) wag o wykładnkach ujemnych zależnych od umejscowena cyfry w częśc ułamkowej. Na przykład: = = Gottfred Lebntz ( ) - nemeck flozof, matematyk fzyk. Jako perwszy zaproponował rozszerzene założeń obowązujących w systeme dzesętnym na systemy lczbowe o nnych podstawach. Był on człowekem bardzo relgjnym uduchowonym dlatego przypsywał systemow dwójkowemu nezwykłe znaczene. Fakt, że każdą lczbę można przedstawć za pomocą zer jedynek wązał z tym, że Bóg (1) stworzył śwat z nczego (0). Warto pamętać, że Lebntz jest twórcą rachunku różnczkowego całkowego, choć do końca życa sperał sę o perwszeństwo w tej dzedzne z Izaakem Newton em. Jednak Lebntz ne szedł drogą Newton a streszczającą sę w słowach: zrobć co trzeba, a potem unkać dyskusj na temat zastosowanych metod - podał uzasadnene metod oblczana pochodnej całkowana oraz wprowadzł formalzm zapsu stosowany do dzsaj (symbole pochodnej df/dx f/ x symbol całk pochodzący z maneryczne napsanego wyrazu umma). Pochodzł prawdopodobne z rodzny Lubeneckch - polskch Aran, którzy wyemgrowal do Nemec [1]. Wojcech Wawrzyńsk Podstawy Elektronk Podstawy technk cyfrowej 4
5 Zamana częśc ułamkowej lczby dzesętnej na dwójkową polega na powtarzanu mnożena przez dwa jeśl wynk jest wększy lub równy jednośc to bt o odpowednej wadze ma wartość 1. Wtedy to dalszemu mnożenu podlega część pomnejszona o 1. Gdy natomast w wynku mnożena przez dwa otrzymuje sę lczbę mnejszą od jednośc to bt o odpowadającej jej wadze ma wartość 0 ponowne wykonuje sę mnożene otrzymanego wynku. Dzałane prowadz sę do wyczerpana możlwośc mnożena lub gdy dojdze sę do dopuszczalnej lośc btów określających część ułamkową. Przykład Zamenć lczbę ułamkową dzesętną na postać ułamkową w naturalnym kodze dwójkowym. W tym celu dokonujemy następujących dzałań: lczba ułamkowa dzesętne lczba pomnożona przez 2 czy wynk mnożena wększy lub równy 1 bt częśc ułamkowej w naturalnym kodze dwójkowym tak ne tak ne tak tak 1 td. w zależnośc od tego le btów mamy do dyspozycj w zapse bnarnym częśc ułamkowej W wynku otrzymujemy = Wynk przekształcena jest przyblżony co łatwo sprawdzć, gdyż = Dysponując bowem sześcoma btam ne można uzyskać dla tej lczby wększej dokładnośc. Konec przykładu. Zaps lczb w naturalnym kodze dwójkowym powoduje koneczność operowana stosunkowo długm cągam znaków, co sprzyja popełnanu błędów. Zaps ten jest nezbyt poręczny z punktu wdzena programstów wykorzystujących język maszynowy komputerów 7. Dla uproszczena notacj jej skrócena wprowadzono kod heksadecymalny naczej zwany szesnastkowym. Cyfry bnarne są grupowane w tym kodze w zespoły po 4 (grupowane w tetrady). Każda możlwa kombnacja czterech cyfr bnarnych otrzymuje symbol jak w tabel X.1. Dla oznaczena perwszych dzesęcu grup lczb bnarnych wykorzystano cyfry systemu dzesętnego, a pozostałym przypsano symbole lterowe odpowedno A, B, C, D, E F. Tabela X.1. Kod heksadecymalny = = = =C = = = =D = = =A =E = = =B =F 16 W kodze heksadecymalnym w słowe H o długośc n reprezentującym lczbę L(H)=hn-1...h1h0 każdy znak h zajmuje określoną pozycję tej pozycj przyporządkowana jest odpowedna waga p, gdze podstawą przyjętego zapsu lczbowego jest 16 (p=16). 7 Symbolcznym zapsem nstrukcj danych, które odpowadają zapsow bnarnemu języka maszynowego komputera jest język nskego pozomu zwany asemblerem. Wojcech Wawrzyńsk Podstawy Elektronk Podstawy technk cyfrowej 5
6 na przykład: n 1 L = h n-116 n h h (X.4) (h n 1...h 1h 0 ) h L (2C3) h 16 = C = = Notacja heksadecymalna jest używana szczególne do zapsu dowolnego cągu cyfr bnarnych (cągów bnarnych) nezależne od tego czy reprezentują one lczby, tekst czy nny rodzaj danych. Wynka to z tego, że jest ona bardzej zwarta nż notacja bnarna. Ponadto w wększośc komputerów dane bnarne reprezentowane są jako welokrotność czterech btów (tetrady) co oznacza, ż w zapse można je zastąpć pojedynczym znakam kodu heksadecymalnego. Zwększa to zwęzłość zapsu zmnejsza prawdopodobeństwo popełnena błędów przez programstę. Istotne też jest, że konwersja mędzy notacją bnarną a heksadecymalną jest bardzo łatwa. Na przykład cąg bnarny jest równoważny zapsow DE116, a dośwadczony programsta może w myśl przetwarzać zaps bnarny na heksadecymalny heksadecymalny na bnarny w postac cągu tetrad oznaczanych pojedynczym symbolam kodu szesnastkowego. X.2. KODY DWÓJKOWO DZIESIĘTNE W kodach dwójkowo dzesętnych BCD (Bnary Coded Decmal) każda cyfra lczby dzesętnej jest osobno kodowana dwójkowo w postac odpowednego słowa. W kodze dwójkowo dzesętnym BCD 8421 każda cyfra lczby dzesętnej jest oddzelne kodowana dwójkowo w postac czterobtowego słowa w naturalnym kodze dwójkowym = = BCD naturalny kod dwójkowy dla poszczególnych cyfr dzesętnych Cała lczba dzesętna jest przedstawana jako złożene słów dwójkowych reprezentujących wszystke kolejne cyfry tej lczby. Dla zapsu dzesęcu cyfr kodu dzesętnego potrzebne jest czterobtowe słowo w kodze dwójkowym. Z kole słowo take umożlwa zaps szesnastu lczb, czyl sześć z nch jest po prostu zbędne. Oznacza to, że kod BCD jest kodem nadmarowym. Kod BCD stosowany jest w bardzo wydajnych jednostkach komputerowych typu manframe. Komputery tego typu posadają duże zasoby oblczenowe z zaps ten mmo nadmarowośc umożlwa osągnęce wysokej precyzj oblczeń. Specjalnym rodzajem kodu dwójkowo dzesętnego jest kod 1 z 10 zwany też kodem perścenowym (tab.x.2). Kod ten posada słowo dzesęcobtowe w którym zawsze dzewęć btów zajmują zera, a jeden bt przeznaczony jest dla jedynk. Położene jedynk decyduje o tym, jakej lczbe dzesętnej odpowada zaps bnarny w tym kodze. Wojcech Wawrzyńsk Podstawy Elektronk Podstawy technk cyfrowej 6
7 Tab.X.2. Kod 1z = z = z = z = z = z = z = z = z = z = z10 Kod ten jest najprostszym koncepcyjne kodem do wprowadzana do układu cyfrowego cyfr kodu dzesętnego z klawatury urządzena cyfrowego, której poszczególne klawsze reprezentują lczby od zera do dzewęcu (ne dotyczy to klawatury komputera, o czym będze mowa dalej). [1] Kordos M.: Wykłady z hstor matematyk. SCRIPT, Warszawa 2006 [2] Clark Scott H.A.: W sercu PC. Helon. Glwce 2003 [3] Crlly T.: 50 teor matematyk. PWN, Warszawa 2009 [4] Kalsz J.: Postawy elektronk cyfrowej. WKŁ, Warszawa 2007 Lteratura przedmotu Horowtz P., Hll W.: Sztuka elektronk, tom I. WKŁ, Warszawa 1997 Horowtz P., Hll W.: Sztuka elektronk, tom II. WKŁ, Warszawa 1997 Kaźmerkowsk M.P., Matysk J.T.: Wprowadzene do elektronk energoelektronk. Ofcyna Wydawncza PW, Warszawa 2005 Łuba T., Zberzchowsk B.: Układy logczne. Wydawnctwo WIT, Warszawa 2005 Mano M.M., Kme Ch.R.: Podstawy projektowana układów logcznych komputerów. WNT, Warszawa 2007 Null L., Labur J.: Struktura organzacyjna archtektura systemów komputerowych. Helon, Glwce 2004 Stallngs W. Organzacja archtektura systemu komputerowego. WNT, Warszawa 2004 Skorupsk A. Podstawy technk cyfrowej. WKŁ, Warszawa 2001 Tanenbaum A.S.: Struktura organzacyjna systemów komputerowych. Helon, Glwce 2006 Ttze U., Schenk Ch.: Układy półprzewodnkowe. WNT, Warszawa 2009 Watson J. Elektronka. WKŁ, Warszawa 1999 Wojcech Wawrzyńsk Podstawy Elektronk Podstawy technk cyfrowej 7
8 14.2. KLUCZ TRANZYSTOROWY POJĘCIE KLUCZA Klucz (naczej przełącznk) jest elementem umożlwającym naprzemenne zwerane rozwerane wybranej częśc obwodu elektrycznego. Jest on podstawowym elementem wykonawczym technk cyfrowej. W najprostszej postac kojarzony jest on z dwupołożenowym przełącznkem mechancznym (rys.14.1a). Jego charakterystykę prądowo-napęcową przedstawono na (rys. 14.1b). Jest to charakterystyka klucza dealnego, gdyż w stane włączena (zwarca) pokrywa sę ona z osą rzędnych (napęce na kluczu ma wtedy wartość zerową), a w stane wyłączena (rozwarca) pokrywa sę z osą odcętych (prąd w tym stane ma wartość zerową). Charakterystyka ta prezentuje zależność prądowo-napęcową, do której dąży sę przy projektowanu kluczy, ale z uwag na właścwośc rzeczywstych elementów wykonawczych jest ona praktyczne neosągalna. Rys Modele klucza: a) klucz dealny, b) charakterystyka prądowo-napęcowa klucza dealnego, c) klucz rzeczywsty, d) charakterystyka prądowo-napęcowa klucza rzeczywstego Bardzej realnym modelem klucza jest układ przedstawony na rys.14.1c. Jego charakterystykę prądowo-napęcową pokazano na rys.14.1d. Jak wdać, w stane włączena (zwarca) prąd płyne przez rezystor RF, dealny przełącznk S oraz źródło UF. Źródło to symbolzuje spadek napęca na zwartym kluczu, który w warunkach rzeczywstych ne jest zerowy. W stane wyłączena (rozwarca) jedyną drogą przepływu prądu jest rezystor RR. Poneważ rezystancja RR jest znaczne wększa od RF, węc przebeg charakterystyk w obu stanach różn sę od sebe kątem pochylena względem os odcętych 8. Jako elementy przełącznkowe są powszechne używane elementy półprzewodnkowe jakm są tranzystory bpolarne unpolarne (polowe). Przez przełączane elementu półprzewodnkowego rozume sę take welkosygnałowe oddzaływane (najczęścej wymuszenem mpulsowym) na wejśce danego elementu, że pod tym wpływem zachodz na jego wyjścu szybke przejśce ze stanu neprzewodzena do stanu przewodzena lub odwrotne. 8 Kąt pochylena charakterystyk na rys.14.1d wynos odpowedno dla stanu włączena arcctg R F a dla stanu wyłączena arcctg R R Wojcech Wawrzyńsk Podstawy Elektronk Podstawy technk cyfrowej 8
9 TRANZYSTOR BIPOLARNY JAKO KLUCZ Cecham dobrego klucza (przełącznka) są, jak wspomnano, dobre zwerane w stane włączena dobre rozwerane w stane wyłączena. Ponadto oczekuje sę, że stan włączena będze sę charakteryzował dużą wartoścą prądu dopuszczalnego, jak może popłynąć przez zwarty klucz, a stan wyłączena dużą wartoścą dopuszczalnego napęca, jake może sę pojawć po obu stronach rozwartego przełącznka. Rozpatrzmy klucz tranzystorowy narysowany na rys.14.2a. Jest to tranzystor bpolarny n-p-n pracujący w konfguracj wspólnego emtera z rezystorem RC w obwodze kolektora rezystorem RB w obwodze bazy. Jest on sterowany przebegem prostokątnym doprowadzanym do bazy poprzez wspomnany rezystor RB. Przy napęcu bazy eg=-er tranzystor jest zatkany, a punkt pracy znajduje sę w punkce QR (rys. 14.2b). W obwodze wyjścowym płyne newelk prąd zerowy ICE0, który dla uproszczena można w dalszych rozważanach pomnąć. W obwodze wejścowym płyne z kole newelk prąd zerowy zaporowo spolaryzowanego złącza kolektorbaza. Jest to prąd ICB0. Jego wartość jest newelka, ale poneważ slne zależy on od temperatury (podwaja sę co dzesęć stopn), mus być brany pod uwagę przy oblczenach warunków sterowana. Zatkane tranzystora następuje przy spełnenu warunku zatkana, który można zapsać nerównoścą: UBE 0,5V. Warunek zatkana jest napęcowy dotyczy takego obszaru pracy tranzystora, w którym praktyczne przestaje płynąć prąd bazy sterujący wejścem tranzystora. Powoduje to, że ne płyne też prąd kolektora ne ma spadku napęca na rezystorze kolektorowym RC (rys. 14.3a). Można zatem stwerdzć, że z obu stron rezystora RC jest taka sama wartość napęca, które jest napęcem zaslana UCC. Zatem napęce wyjścowe tranzystora jest równe napęcu zaslana UCC. Klucz z tranzystorem w stane zatkana odpowada stanow wyłączena (rozwarca) w modelu klucza omawanym w poprzednm podrozdzale. Rys Przełączane tranzystora bpolarnego: a) typowy układ klucza sterowanego przebegem prostokątnym, b) charakterystyk wyjścowe z zaznaczenem zman położeń punktu pracy Wojcech Wawrzyńsk Podstawy Elektronk Podstawy technk cyfrowej 9
10 Rys Klucz tranzystorowy: a) tranzystor w stane zatkana, b) tranzystor w stane nasycena Przy napęcu bazy eg=+ef tranzystor jest nasycony (rys. 14.3b). Punkt pracy znajduje sę w punkce QF (rys. 14.2b). Zarówno złącze baza emter jak baza kolektor tranzystora bpolarnego w stane nasycena są spolaryzowane w kerunku przewodzena. Oba napęca przewodzena złączy występują szeregowo przecwstawne. Napęce przewodzena złącza baza-emter UBEP jest neco wększe nż napęce przewodzena złącza baza-kolektor UBCP. Na wyjścu tranzystora utrzymuje sę napęca nasycena UCEsat=UBEP-UBCP, które ma wartość dodatną wynos dla tranzystorów małej mocy około 0,2 V. Zatem w tych warunkach napęce wyjścowe ma małą wartość określaną sę jako Uwy=UCEsat=0,2V (rys.14.3b). Klucz z tranzystorem w stane nasycena odpowada stanow włączena (zwarca) w modelu klucza omawanym w poprzednm podrozdzale. Aby włączyć klucz, czyl wprowadzć tranzystor w stan nasycena, trzeba w obwodze wejścowym spełnć warunek nasycena. Warunek nasycena tranzystora bpolarnego jest prądowy określa sę go jako IB β0>icm. Prąd ICM jest maksymalnym prądem kolektora określanym jako: I CM = U CC + U CEsat R C (4.2) Z warunku nasycena wypływa wnosek, że wartość prądu bazy mus być na tyle duża, aby loczyn tego prądu współczynnka wzmocnena prądowego β0 był wększy od wartośc maksymalnego prądu kolektora. Ze wzoru (14.2) wynka, że maksymalny prąd kolektora zależy od napęca zaslana welkośc rezystancj kolektorowej. Zmany bowem samego UCEsat w funkcj prądu są newelke. Po osągnęcu warunku nasycena dalsze zwększane prądu bazy ne ma wpływu na prąd kolektora a w obwodze wyjścowym nasyconego tranzystora ne popłyne wększy prąd nż ta jego wartość wynkająca z równana (14.2) TRANZYSTOR UNIPOLARNY JAKO KLUCZ Praca tranzystora unpolarnego z zolowaną bramką jako klucza (przełącznka) jest rozpatrywana w konfguracj wspólnego źródła. Na rys.14.4a przedstawono klucz z wykorzystanem tranzystora MOSFET z kanałem typu n normalne wyłączonym. Rezystor RD jest rezystorem drenu decydującym o nachylenu prostej obcążena. Wojcech Wawrzyńsk Podstawy Elektronk Podstawy technk cyfrowej 10
11 Rys Przełączane tranzystora unpolarnego (MOSFET z kanałem typu n normalne wyłączony): a) układ klucza, b) charakterystyk z zaznaczenem trajektor zmany punktów pracy przy przełączanu tranzystora Na rys.14.4b przedstawono charakterystykę wyjścową z zaznaczenem zmany punktu pracy w trakce przełączana. Przełączane tranzystora unpolarnego polega na możlwe szybkm przesunęcu punktu pracy z obszaru odcęca (punkt pracy QR) przez obszar nasycena do zakresu lnowego charakterystyk wyjścowej (punkt pracy QF) oraz gdy wymuszene wejścowe zmen sę na przecwne powroce punktu pracy do zakresu odcęca. Komentarz dotyczący nazewnctwa Nazwa obszar nasycena w przypadku tranzystorów bpolarnego unpolarnego dotyczy nnych częśc charakterystyk wyjścowych. W tranzystorze bpolarnym rozróżnamy trzy obszary: obszar nasycena, gdy złącza baza emter baza kolektor są spolaryzowane w kerunku przewodzena - dotyczy to częśc charakterystyk wyjścowej dla małych wartośc napęca UCE blskej napęcu UCEsat, obszar zatkana, gdy wymenone złącza są spolaryzowane w kerunku zaporowym - dotyczy to zakresu charakterystyk wyjścowej blskego os odcętych a węc wtedy, gdy ne płyne prąd bazy obszar aktywny, gdy złącze baza emter jest spolaryzowane w kerunku przewodzena a złącze baza kolektor w kerunku zaporowym - obszar charakterystyk wyjścowej rozcągający sę pomędzy nasycenem zatkanem. W tranzystorze unpolarnym wyróżnamy obszar nasycena (naczej pentodowy), gdy charakterystyk wyjścowe są zblżone do ln równoległych do os odcętych (powyżej kolana charakterystyk), obszar odcęca, gdy prąd drenu praktyczne ne płyne, zakres lnowy (zwany też zakresem nenasycena lub trodowym), gdy przyrost prądu drenu dla zwększającego sę napęca dren-źródło jest prawe lnowy (ponżej kolana charakterystyk). W rozpatrywanym przypadku napęce sterujące doprowadzane do bramk zmena sę w grancach od zera (ER = 0V) do wartośc dodatnej +EF, dla której następuje całkowte otwarce kanału mędzy drenem a źródłem. Poneważ tranzystor jest normalne wyłączony, zatem brak wysterowana bramk powoduje brak możlwośc przepływu prądu mędzy elektrodam drenu źródła, zatem ne przepływa prąd przez rezystor drenu RD. Z obu stron rezystora jest wtedy to samo napęce równe napęcu zaslana +UDD, które jest też podawane na wyjśce. Klucz jest w stane wyłączena, a na charakterystyce wyjścowej odpowada to osągnęcu punktu pracy QR. Przy wysterowanu bramk odpowedną wartoścą napęca dodatnego +EF następuje całkowte otwarce kanału. Rezystancja kanału spada wówczas do najnższej możlwej wartośc Wojcech Wawrzyńsk Podstawy Elektronk Podstawy technk cyfrowej 11
12 płyne duży prąd drenu: od źródła +UDD przez rezystor RD, elektrody dren źródło tranzystora do drugej elektrody zaslana (masy). Napęce wyjścowe osąga wtedy wartość określoną zależnoścą na dzelnk napęcowy złożony z ww. elementów obwodu tak: U DS = U DD (14.3) r D +R D gdze: UDD - napęce zaslana, rd - rezystancja kanału w stane włączena klucza, RD1 - rezystancja rezystora drenu. Poneważ wartość rezystancj kanału jest znaczne mnejsza od wartośc rezystancj rezystora drenu, napęce wyjścowe ma nską wartość. Klucz jest w stane włączena osąga punkt pracy QF na charakterystyce wyjścowej (rys.14.5b). r D Wojcech Wawrzyńsk Podstawy Elektronk Podstawy technk cyfrowej 12
Zapis informacji, systemy pozycyjne 1. Literatura Jerzy Grębosz, Symfonia C++ standard. Harvey M. Deitl, Paul J. Deitl, Arkana C++. Programowanie.
 Zaps nformacj, systemy pozycyjne 1 Lteratura Jerzy Grębosz, Symfona C++ standard. Harvey M. Detl, Paul J. Detl, Arkana C++. Programowane. Zaps nformacj w komputerach Wszystke elementy danych przetwarzane
Zaps nformacj, systemy pozycyjne 1 Lteratura Jerzy Grębosz, Symfona C++ standard. Harvey M. Detl, Paul J. Detl, Arkana C++. Programowane. Zaps nformacj w komputerach Wszystke elementy danych przetwarzane
Ćwiczenie 2. Parametry statyczne tranzystorów bipolarnych
 Ćwczene arametry statyczne tranzystorów bpolarnych el ćwczena odstawowym celem ćwczena jest poznane statycznych charakterystyk tranzystorów bpolarnych oraz metod dentyfkacj parametrów odpowadających m
Ćwczene arametry statyczne tranzystorów bpolarnych el ćwczena odstawowym celem ćwczena jest poznane statycznych charakterystyk tranzystorów bpolarnych oraz metod dentyfkacj parametrów odpowadających m
Zestaw zadań 4: Przestrzenie wektorowe i podprzestrzenie. Liniowa niezależność. Sumy i sumy proste podprzestrzeni.
 Zestaw zadań : Przestrzene wektorowe podprzestrzene. Lnowa nezależność. Sumy sumy proste podprzestrzen. () Wykazać, że V = C ze zwykłym dodawanem jako dodawanem wektorów operacją mnożena przez skalar :
Zestaw zadań : Przestrzene wektorowe podprzestrzene. Lnowa nezależność. Sumy sumy proste podprzestrzen. () Wykazać, że V = C ze zwykłym dodawanem jako dodawanem wektorów operacją mnożena przez skalar :
TRANZYSTOR BIPOLARNY CHARAKTERYSTYKI STATYCZNE
 POLITHNIKA RZSZOWSKA Katedra Podstaw lektronk Instrkcja Nr4 F 00/003 sem. letn TRANZYSTOR IPOLARNY HARAKTRYSTYKI STATYZN elem ćwczena jest pomar charakterystyk statycznych tranzystora bpolarnego npn lb
POLITHNIKA RZSZOWSKA Katedra Podstaw lektronk Instrkcja Nr4 F 00/003 sem. letn TRANZYSTOR IPOLARNY HARAKTRYSTYKI STATYZN elem ćwczena jest pomar charakterystyk statycznych tranzystora bpolarnego npn lb
architektura komputerów w. 3 Arytmetyka komputerów
 archtektura komputerów w. 3 Arytmetyka komputerów Systemy pozycyjne - dodawane w systeme dwójkowym 100101011001110010101 100111101000001000 0110110011101 1 archtektura komputerów w 3 1 Arytmetyka bnarna.
archtektura komputerów w. 3 Arytmetyka komputerów Systemy pozycyjne - dodawane w systeme dwójkowym 100101011001110010101 100111101000001000 0110110011101 1 archtektura komputerów w 3 1 Arytmetyka bnarna.
XXX OLIMPIADA FIZYCZNA ETAP III Zadanie doświadczalne
 XXX OLIMPIADA FIZYCZNA ETAP III Zadane dośwadczalne ZADANIE D Nazwa zadana: Maszyna analogowa. Dane są:. doda półprzewodnkowa (krzemowa) 2. opornk dekadowy (- 5 Ω ), 3. woltomerz cyfrowy, 4. źródło napęca
XXX OLIMPIADA FIZYCZNA ETAP III Zadane dośwadczalne ZADANIE D Nazwa zadana: Maszyna analogowa. Dane są:. doda półprzewodnkowa (krzemowa) 2. opornk dekadowy (- 5 Ω ), 3. woltomerz cyfrowy, 4. źródło napęca
Laboratorium ochrony danych
 Laboratorum ochrony danych Ćwczene nr Temat ćwczena: Cała skończone rozszerzone Cel dydaktyczny: Opanowane programowej metody konstruowana cał skończonych rozszerzonych GF(pm), poznane ch własnośc oraz
Laboratorum ochrony danych Ćwczene nr Temat ćwczena: Cała skończone rozszerzone Cel dydaktyczny: Opanowane programowej metody konstruowana cał skończonych rozszerzonych GF(pm), poznane ch własnośc oraz
3. ŁUK ELEKTRYCZNY PRĄDU STAŁEGO I PRZEMIENNEGO
 3. ŁUK ELEKTRYCZNY PRĄDU STŁEGO I PRZEMIENNEGO 3.1. Cel zakres ćwczena Celem ćwczena jest zapoznane sę z podstawowym właścwoścam łuku elektrycznego palącego sę swobodne, w powetrzu o cśnentmosferycznym.
3. ŁUK ELEKTRYCZNY PRĄDU STŁEGO I PRZEMIENNEGO 3.1. Cel zakres ćwczena Celem ćwczena jest zapoznane sę z podstawowym właścwoścam łuku elektrycznego palącego sę swobodne, w powetrzu o cśnentmosferycznym.
Stan wysoki (H) i stan niski (L)
 PODSTAWY Przez układy cyfrowe rozumiemy układy, w których w każdej chwili występują tylko dwa (zwykle) możliwe stany, np. tranzystor, jako element układu cyfrowego, może być albo w stanie nasycenia, albo
PODSTAWY Przez układy cyfrowe rozumiemy układy, w których w każdej chwili występują tylko dwa (zwykle) możliwe stany, np. tranzystor, jako element układu cyfrowego, może być albo w stanie nasycenia, albo
Metody analizy obwodów
 Metody analzy obwodów Metoda praw Krchhoffa, która jest podstawą dla pozostałych metod Metoda transfguracj, oparte na przekształcenach analzowanego obwodu na obwód równoważny Metoda superpozycj Metoda
Metody analzy obwodów Metoda praw Krchhoffa, która jest podstawą dla pozostałych metod Metoda transfguracj, oparte na przekształcenach analzowanego obwodu na obwód równoważny Metoda superpozycj Metoda
Zaawansowane metody numeryczne
 Wykład 9. jej modyfkacje. Oznaczena Będzemy rozpatrywać zagadnene rozwązana następującego układu n równań lnowych z n newadomym x 1... x n : a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x
Wykład 9. jej modyfkacje. Oznaczena Będzemy rozpatrywać zagadnene rozwązana następującego układu n równań lnowych z n newadomym x 1... x n : a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x
I. Elementy analizy matematycznej
 WSTAWKA MATEMATYCZNA I. Elementy analzy matematycznej Pochodna funkcj f(x) Pochodna funkcj podaje nam prędkość zman funkcj: df f (x + x) f (x) f '(x) = = lm x 0 (1) dx x Pochodna funkcj podaje nam zarazem
WSTAWKA MATEMATYCZNA I. Elementy analzy matematycznej Pochodna funkcj f(x) Pochodna funkcj podaje nam prędkość zman funkcj: df f (x + x) f (x) f '(x) = = lm x 0 (1) dx x Pochodna funkcj podaje nam zarazem
EUROELEKTRA. Ogólnopolska Olimpiada Wiedzy Elektrycznej i Elektronicznej. Rok szkolny 2013/2014
 EUROELEKTRA Ogólnopolska Olmpada Wedzy Elektrycznej Elektroncznej Rok szkolny 232 Zadana z elektronk na zawody III stopna (grupa elektronczna) Zadane. Oblczyć wzmocnene napęcowe, rezystancję wejścową rezystancję
EUROELEKTRA Ogólnopolska Olmpada Wedzy Elektrycznej Elektroncznej Rok szkolny 232 Zadana z elektronk na zawody III stopna (grupa elektronczna) Zadane. Oblczyć wzmocnene napęcowe, rezystancję wejścową rezystancję
Projekt 6 6. ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH CAŁKOWANIE NUMERYCZNE
 Inormatyka Podstawy Programowana 06/07 Projekt 6 6. ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH CAŁKOWANIE NUMERYCZNE 6. Równana algebraczne. Poszukujemy rozwązana, czyl chcemy określć perwastk rzeczywste równana:
Inormatyka Podstawy Programowana 06/07 Projekt 6 6. ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH CAŁKOWANIE NUMERYCZNE 6. Równana algebraczne. Poszukujemy rozwązana, czyl chcemy określć perwastk rzeczywste równana:
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 1. Układy równań liniowych
 Zaawansowane metody numeryczne Komputerowa analza zagadneń różnczkowych 1. Układy równań lnowych P. F. Góra http://th-www.f.uj.edu.pl/zfs/gora/ semestr letn 2006/07 Podstawowe fakty Równane Ax = b, x,
Zaawansowane metody numeryczne Komputerowa analza zagadneń różnczkowych 1. Układy równań lnowych P. F. Góra http://th-www.f.uj.edu.pl/zfs/gora/ semestr letn 2006/07 Podstawowe fakty Równane Ax = b, x,
SZACOWANIE NIEPEWNOŚCI POMIARU METODĄ PROPAGACJI ROZKŁADÓW
 SZACOWANIE NIEPEWNOŚCI POMIARU METODĄ PROPAGACJI ROZKŁADÓW Stefan WÓJTOWICZ, Katarzyna BIERNAT ZAKŁAD METROLOGII I BADAŃ NIENISZCZĄCYCH INSTYTUT ELEKTROTECHNIKI ul. Pożaryskego 8, 04-703 Warszawa tel.
SZACOWANIE NIEPEWNOŚCI POMIARU METODĄ PROPAGACJI ROZKŁADÓW Stefan WÓJTOWICZ, Katarzyna BIERNAT ZAKŁAD METROLOGII I BADAŃ NIENISZCZĄCYCH INSTYTUT ELEKTROTECHNIKI ul. Pożaryskego 8, 04-703 Warszawa tel.
LABORATORIUM PODSTAW ELEKTROTECHNIKI Badanie obwodów prądu sinusoidalnie zmiennego
 Ćwczene 1 Wydzał Geonżyner, Górnctwa Geolog ABORATORUM PODSTAW EEKTROTECHNK Badane obwodów prądu snusodalne zmennego Opracował: Grzegorz Wśnewsk Zagadnena do przygotowana Ops elementów RC zaslanych prądem
Ćwczene 1 Wydzał Geonżyner, Górnctwa Geolog ABORATORUM PODSTAW EEKTROTECHNK Badane obwodów prądu snusodalne zmennego Opracował: Grzegorz Wśnewsk Zagadnena do przygotowana Ops elementów RC zaslanych prądem
Stanisław Cichocki. Natalia Nehrebecka. Wykład 6
 Stansław Cchock Natala Nehrebecka Wykład 6 1 1. Zastosowane modelu potęgowego Przekształcene Boxa-Coxa 2. Zmenne cągłe za zmenne dyskretne 3. Interpretacja parametrów przy zmennych dyskretnych 1. Zastosowane
Stansław Cchock Natala Nehrebecka Wykład 6 1 1. Zastosowane modelu potęgowego Przekształcene Boxa-Coxa 2. Zmenne cągłe za zmenne dyskretne 3. Interpretacja parametrów przy zmennych dyskretnych 1. Zastosowane
Diagnostyka układów kombinacyjnych
 Dagnostyka układów kombnacyjnych 1. Wprowadzene Dagnostyka obejmuje: stwerdzene stanu układu, systemu lub ogólne sec logcznej. Jest to tzw. kontrola stanu wykrywająca czy dzałane sec ne jest zakłócane
Dagnostyka układów kombnacyjnych 1. Wprowadzene Dagnostyka obejmuje: stwerdzene stanu układu, systemu lub ogólne sec logcznej. Jest to tzw. kontrola stanu wykrywająca czy dzałane sec ne jest zakłócane
Za: Stanisław Latoś, Niwelacja trygonometryczna, [w:] Ćwiczenia z geodezji II [red.] J. Beluch
![Za: Stanisław Latoś, Niwelacja trygonometryczna, [w:] Ćwiczenia z geodezji II [red.] J. Beluch Za: Stanisław Latoś, Niwelacja trygonometryczna, [w:] Ćwiczenia z geodezji II [red.] J. Beluch](/thumbs/25/5046464.jpg) Za: Stansław Latoś, Nwelacja trygonometryczna, [w:] Ćwczena z geodezj II [red.] J. eluch 6.1. Ogólne zasady nwelacj trygonometrycznej. Wprowadzene Nwelacja trygonometryczna, zwana równeż trygonometrycznym
Za: Stansław Latoś, Nwelacja trygonometryczna, [w:] Ćwczena z geodezj II [red.] J. eluch 6.1. Ogólne zasady nwelacj trygonometrycznej. Wprowadzene Nwelacja trygonometryczna, zwana równeż trygonometrycznym
Stanisław Cichocki. Natalia Nehrebecka. Wykład 6
 Stansław Cchock Natala Nehrebecka Wykład 6 1 1. Interpretacja parametrów przy zmennych objaśnających cągłych Semelastyczność 2. Zastosowane modelu potęgowego Model potęgowy 3. Zmenne cągłe za zmenne dyskretne
Stansław Cchock Natala Nehrebecka Wykład 6 1 1. Interpretacja parametrów przy zmennych objaśnających cągłych Semelastyczność 2. Zastosowane modelu potęgowego Model potęgowy 3. Zmenne cągłe za zmenne dyskretne
Przedmiot: Układy Logiczne Literatura:
 Przedmot: Układy Logczne Lteratura:. Halna Kamonka-Mkuła, n.: Synteza analza ukłaów cyfrowych. Wydawnctwo Pracown Komputerowej Jacka Skalmerskego, Glwce 6.. Władysław Majewsk: Układy logczne. Wydawnctwa
Przedmot: Układy Logczne Lteratura:. Halna Kamonka-Mkuła, n.: Synteza analza ukłaów cyfrowych. Wydawnctwo Pracown Komputerowej Jacka Skalmerskego, Glwce 6.. Władysław Majewsk: Układy logczne. Wydawnctwa
Stanisław Cichocki. Natalia Nehrebecka. Wykład 7
 Stansław Cchock Natala Nehrebecka Wykład 7 1 1. Zmenne cągłe a zmenne dyskretne 2. Interpretacja parametrów przy zmennych dyskretnych 1. Zmenne cągłe a zmenne dyskretne 2. Interpretacja parametrów przy
Stansław Cchock Natala Nehrebecka Wykład 7 1 1. Zmenne cągłe a zmenne dyskretne 2. Interpretacja parametrów przy zmennych dyskretnych 1. Zmenne cągłe a zmenne dyskretne 2. Interpretacja parametrów przy
Urządzenia wejścia-wyjścia
 Urządzena wejśca-wyjśca Klasyfkacja urządzeń wejśca-wyjśca. Struktura mechanzmu wejśca-wyjśca (sprzętu oprogramowana). Interakcja jednostk centralnej z urządzenam wejśca-wyjśca: odpytywane, sterowane przerwanam,
Urządzena wejśca-wyjśca Klasyfkacja urządzeń wejśca-wyjśca. Struktura mechanzmu wejśca-wyjśca (sprzętu oprogramowana). Interakcja jednostk centralnej z urządzenam wejśca-wyjśca: odpytywane, sterowane przerwanam,
Pokazać, że wyżej zdefiniowana struktura algebraiczna jest przestrzenią wektorową nad ciałem
 Zestaw zadań : Przestrzene wektorowe. () Wykazać, że V = C ze zwykłym dodawanem jako dodawanem wektorów operacją mnożena przez skalar : C C C, (z, v) z v := z v jest przestrzeną lnową nad całem lczb zespolonych
Zestaw zadań : Przestrzene wektorowe. () Wykazać, że V = C ze zwykłym dodawanem jako dodawanem wektorów operacją mnożena przez skalar : C C C, (z, v) z v := z v jest przestrzeną lnową nad całem lczb zespolonych
Kodowanie informacji. Kody liczbowe
 Wykład 2 2-1 Kodowanie informacji PoniewaŜ komputer jest urządzeniem zbudowanym z układów cyfrowych, informacja przetwarzana przez niego musi być reprezentowana przy pomocy dwóch stanów - wysokiego i niskiego,
Wykład 2 2-1 Kodowanie informacji PoniewaŜ komputer jest urządzeniem zbudowanym z układów cyfrowych, informacja przetwarzana przez niego musi być reprezentowana przy pomocy dwóch stanów - wysokiego i niskiego,
RODZAJE INFORMACJI. Informacje analogowe. Informacje cyfrowe. U(t) U(t) Umax. Umax. R=(0,Umax) nieskończony zbiór możliwych wartości. Umax.
 RODZAJE INFORMACJI Informacje analogowe U(t) Umax Umax 0 0 R=(0,Umax) nieskończony zbiór możliwych wartości WE MASZYNA ANALOGOWA WY Informacje cyfrowe U(t) Umaxq Umax R=(U, 2U, 3U, 4U) # # MASZYNA # CYFROWA
RODZAJE INFORMACJI Informacje analogowe U(t) Umax Umax 0 0 R=(0,Umax) nieskończony zbiór możliwych wartości WE MASZYNA ANALOGOWA WY Informacje cyfrowe U(t) Umaxq Umax R=(U, 2U, 3U, 4U) # # MASZYNA # CYFROWA
MATEMATYKA POZIOM ROZSZERZONY Kryteria oceniania odpowiedzi. Arkusz A II. Strona 1 z 5
 MATEMATYKA POZIOM ROZSZERZONY Krytera ocenana odpowedz Arkusz A II Strona 1 z 5 Odpowedz Pytane 1 2 3 4 5 6 7 8 9 Odpowedź D C C A B 153 135 232 333 Zad. 10. (0-3) Dana jest funkcja postac. Korzystając
MATEMATYKA POZIOM ROZSZERZONY Krytera ocenana odpowedz Arkusz A II Strona 1 z 5 Odpowedz Pytane 1 2 3 4 5 6 7 8 9 Odpowedź D C C A B 153 135 232 333 Zad. 10. (0-3) Dana jest funkcja postac. Korzystając
SZTUCZNA INTELIGENCJA
 SZTUCZNA INTELIGENCJA WYKŁAD 15. ALGORYTMY GENETYCZNE Częstochowa 014 Dr hab. nż. Grzegorz Dudek Wydzał Elektryczny Poltechnka Częstochowska TERMINOLOGIA allele wartośc, waranty genów, chromosom - (naczej
SZTUCZNA INTELIGENCJA WYKŁAD 15. ALGORYTMY GENETYCZNE Częstochowa 014 Dr hab. nż. Grzegorz Dudek Wydzał Elektryczny Poltechnka Częstochowska TERMINOLOGIA allele wartośc, waranty genów, chromosom - (naczej
płytka montażowa z tranzystorami i rezystorami, pokazana na rysunku 1. płytka montażowa do badania przerzutnika astabilnego U CC T 2 masa
 Tranzystor jako klucz elektroniczny - Ćwiczenie. Cel ćwiczenia Zapoznanie się z podstawowymi układami pracy tranzystora bipolarnego jako klucza elektronicznego. Bramki logiczne realizowane w technice RTL
Tranzystor jako klucz elektroniczny - Ćwiczenie. Cel ćwiczenia Zapoznanie się z podstawowymi układami pracy tranzystora bipolarnego jako klucza elektronicznego. Bramki logiczne realizowane w technice RTL
Analiza rodzajów skutków i krytyczności uszkodzeń FMECA/FMEA według MIL STD - 1629A
 Analza rodzajów skutków krytycznośc uszkodzeń FMECA/FMEA według MIL STD - 629A Celem analzy krytycznośc jest szeregowane potencjalnych rodzajów uszkodzeń zdentyfkowanych zgodne z zasadam FMEA na podstawe
Analza rodzajów skutków krytycznośc uszkodzeń FMECA/FMEA według MIL STD - 629A Celem analzy krytycznośc jest szeregowane potencjalnych rodzajów uszkodzeń zdentyfkowanych zgodne z zasadam FMEA na podstawe
± Δ. Podstawowe pojęcia procesu pomiarowego. x rzeczywiste. Określenie jakości poznania rzeczywistości
 Podstawowe pojęca procesu pomarowego kreślene jakośc poznana rzeczywstośc Δ zmerzone rzeczywste 17 9 Zalety stosowana elektrycznych przyrządów 1/ 1. możlwość budowy czujnków zamenających werne każdą welkość
Podstawowe pojęca procesu pomarowego kreślene jakośc poznana rzeczywstośc Δ zmerzone rzeczywste 17 9 Zalety stosowana elektrycznych przyrządów 1/ 1. możlwość budowy czujnków zamenających werne każdą welkość
Komputer kwantowy Zasady funkcjonowania. Dr hab. inż. Krzysztof Giaro Politechnika Gdańska Wydział ETI
 Komputer kwantowy Zasady funkcjonowana Dr hab. nż. Krzysztof Garo Poltechnka Gdańska Wydzał ETI Oblczena kwantowe. R. Feynman [985] symulację zachowana układu kwantowego należy przeprowadzć na "maszyne"
Komputer kwantowy Zasady funkcjonowana Dr hab. nż. Krzysztof Garo Poltechnka Gdańska Wydzał ETI Oblczena kwantowe. R. Feynman [985] symulację zachowana układu kwantowego należy przeprowadzć na "maszyne"
W praktyce często zdarza się, że wyniki obu prób możemy traktować jako. wyniki pomiarów na tym samym elemencie populacji np.
 Wykład 7 Uwaga: W praktyce często zdarza sę, że wynk obu prób możemy traktować jako wynk pomarów na tym samym elemence populacj np. wynk x przed wynk y po operacj dla tego samego osobnka. Należy wówczas
Wykład 7 Uwaga: W praktyce często zdarza sę, że wynk obu prób możemy traktować jako wynk pomarów na tym samym elemence populacj np. wynk x przed wynk y po operacj dla tego samego osobnka. Należy wówczas
STATYSTYKA MATEMATYCZNA WYKŁAD 5 WERYFIKACJA HIPOTEZ NIEPARAMETRYCZNYCH
 STATYSTYKA MATEMATYCZNA WYKŁAD 5 WERYFIKACJA HIPOTEZ NIEPARAMETRYCZNYCH 1 Test zgodnośc χ 2 Hpoteza zerowa H 0 ( Cecha X populacj ma rozkład o dystrybuance F). Hpoteza alternatywna H1( Cecha X populacj
STATYSTYKA MATEMATYCZNA WYKŁAD 5 WERYFIKACJA HIPOTEZ NIEPARAMETRYCZNYCH 1 Test zgodnośc χ 2 Hpoteza zerowa H 0 ( Cecha X populacj ma rozkład o dystrybuance F). Hpoteza alternatywna H1( Cecha X populacj
1.1. Pozycyjne systemy liczbowe
 1.1. Pozycyjne systemy liczbowe Systemami liczenia nazywa się sposób tworzenia liczb ze znaków cyfrowych oraz zbiór reguł umożliwiających wykonywanie operacji arytmetycznych na liczbach. Dla dowolnego
1.1. Pozycyjne systemy liczbowe Systemami liczenia nazywa się sposób tworzenia liczb ze znaków cyfrowych oraz zbiór reguł umożliwiających wykonywanie operacji arytmetycznych na liczbach. Dla dowolnego
12. Wprowadzenie Sygnały techniki cyfrowej Systemy liczbowe. Matematyka: Elektronika:
 PRZYPOMNIJ SOBIE! Matematyka: Dodawanie i odejmowanie "pod kreską". Elektronika: Sygnały cyfrowe. Zasadę pracy tranzystorów bipolarnych i unipolarnych. 12. Wprowadzenie 12.1. Sygnały techniki cyfrowej
PRZYPOMNIJ SOBIE! Matematyka: Dodawanie i odejmowanie "pod kreską". Elektronika: Sygnały cyfrowe. Zasadę pracy tranzystorów bipolarnych i unipolarnych. 12. Wprowadzenie 12.1. Sygnały techniki cyfrowej
Badanie współzależności dwóch cech ilościowych X i Y. Analiza korelacji prostej
 Badane współzależnośc dwóch cech loścowych X Y. Analza korelacj prostej Kody znaków: żółte wyróżnene nowe pojęce czerwony uwaga kursywa komentarz 1 Zagadnena 1. Zwązek determnstyczny (funkcyjny) a korelacyjny.
Badane współzależnośc dwóch cech loścowych X Y. Analza korelacj prostej Kody znaków: żółte wyróżnene nowe pojęce czerwony uwaga kursywa komentarz 1 Zagadnena 1. Zwązek determnstyczny (funkcyjny) a korelacyjny.
Systemy liczbowe używane w technice komputerowej
 Systemy liczbowe używane w technice komputerowej Systemem liczenia nazywa się sposób tworzenia liczb ze znaków cyfrowych oraz zbiór reguł umożliwiających wykonywanie operacji arytmetycznych na liczbach.
Systemy liczbowe używane w technice komputerowej Systemem liczenia nazywa się sposób tworzenia liczb ze znaków cyfrowych oraz zbiór reguł umożliwiających wykonywanie operacji arytmetycznych na liczbach.
Statystyka. Zmienne losowe
 Statystyka Zmenne losowe Zmenna losowa Zmenna losowa jest funkcją, w której każdej wartośc R odpowada pewen podzbór zboru będący zdarzenem losowym. Zmenna losowa powstaje poprzez przyporządkowane każdemu
Statystyka Zmenne losowe Zmenna losowa Zmenna losowa jest funkcją, w której każdej wartośc R odpowada pewen podzbór zboru będący zdarzenem losowym. Zmenna losowa powstaje poprzez przyporządkowane każdemu
Stanisław Cichocki. Natalia Nehrebecka. Wykład 6
 Stansław Cchock Natala Nehrebecka Wykład 6 1 1. Zastosowane modelu potęgowego Model potęgowy Przekształcene Boxa-Coxa 2. Zmenne cągłe za zmenne dyskretne 3. Interpretacja parametrów przy zmennych dyskretnych
Stansław Cchock Natala Nehrebecka Wykład 6 1 1. Zastosowane modelu potęgowego Model potęgowy Przekształcene Boxa-Coxa 2. Zmenne cągłe za zmenne dyskretne 3. Interpretacja parametrów przy zmennych dyskretnych
Podstawy Automatyki. Wykład 9 - Podstawy matematyczne automatyki procesów dyskretnych. dr inż. Jakub Możaryn. Instytut Automatyki i Robotyki
 Wykład 9 - Podstawy matematyczne automatyki procesów dyskretnych Instytut Automatyki i Robotyki Warszawa, 2015 Kody liczb całkowitych nieujemnych Kody liczbowe dzielimy na analityczne nieanalityczne (symboliczne)
Wykład 9 - Podstawy matematyczne automatyki procesów dyskretnych Instytut Automatyki i Robotyki Warszawa, 2015 Kody liczb całkowitych nieujemnych Kody liczbowe dzielimy na analityczne nieanalityczne (symboliczne)
Podstawowe operacje arytmetyczne i logiczne dla liczb binarnych
 1 Podstawowe operacje arytmetyczne i logiczne dla liczb binarnych 1. Podstawowe operacje logiczne dla cyfr binarnych Jeśli cyfry 0 i 1 potraktujemy tak, jak wartości logiczne fałsz i prawda, to działanie
1 Podstawowe operacje arytmetyczne i logiczne dla liczb binarnych 1. Podstawowe operacje logiczne dla cyfr binarnych Jeśli cyfry 0 i 1 potraktujemy tak, jak wartości logiczne fałsz i prawda, to działanie
KRZYWA BÉZIERA TWORZENIE I WIZUALIZACJA KRZYWYCH PARAMETRYCZNYCH NA PRZYKŁADZIE KRZYWEJ BÉZIERA
 KRZYWA BÉZIERA TWORZENIE I WIZUALIZACJA KRZYWYCH PARAMETRYCZNYCH NA PRZYKŁADZIE KRZYWEJ BÉZIERA Krzysztof Serżęga Wyższa Szkoła Informatyk Zarządzana w Rzeszowe Streszczene Artykuł porusza temat zwązany
KRZYWA BÉZIERA TWORZENIE I WIZUALIZACJA KRZYWYCH PARAMETRYCZNYCH NA PRZYKŁADZIE KRZYWEJ BÉZIERA Krzysztof Serżęga Wyższa Szkoła Informatyk Zarządzana w Rzeszowe Streszczene Artykuł porusza temat zwązany
Natalia Nehrebecka. Zajęcia 3
 St ł Cchock Stansław C h k Natala Nehrebecka Zajęca 3 1. Dobroć dopasowana równana regresj. Współczynnk determnacj R Dk Dekompozycja warancj zmennej zależnej ż Współczynnk determnacj R. Zmenne cągłe a
St ł Cchock Stansław C h k Natala Nehrebecka Zajęca 3 1. Dobroć dopasowana równana regresj. Współczynnk determnacj R Dk Dekompozycja warancj zmennej zależnej ż Współczynnk determnacj R. Zmenne cągłe a
Diagonalizacja macierzy kwadratowej
 Dagonalzacja macerzy kwadratowej Dana jest macerz A nân. Jej wartośc własne wektory własne spełnają równane Ax x dla,..., n Każde z równań własnych osobno można zapsać w postac: a a an x x a a an x x an
Dagonalzacja macerzy kwadratowej Dana jest macerz A nân. Jej wartośc własne wektory własne spełnają równane Ax x dla,..., n Każde z równań własnych osobno można zapsać w postac: a a an x x a a an x x an
Cyfrowy zapis informacji. 5 grudnia 2013 Wojciech Kucewicz 2
 Cyfrowy zapis informacji 5 grudnia 2013 Wojciech Kucewicz 2 Bit, Bajt, Słowo 5 grudnia 2013 Wojciech Kucewicz 3 Cyfrowy zapis informacji Bit [ang. binary digit] jest elementem zbioru dwuelementowego używanym
Cyfrowy zapis informacji 5 grudnia 2013 Wojciech Kucewicz 2 Bit, Bajt, Słowo 5 grudnia 2013 Wojciech Kucewicz 3 Cyfrowy zapis informacji Bit [ang. binary digit] jest elementem zbioru dwuelementowego używanym
Procedura normalizacji
 Metody Badań w Geograf Społeczno Ekonomcznej Procedura normalzacj Budowane macerzy danych geografcznych mgr Marcn Semczuk Zakład Przedsęborczośc Gospodark Przestrzennej Instytut Geograf Unwersytet Pedagogczny
Metody Badań w Geograf Społeczno Ekonomcznej Procedura normalzacj Budowane macerzy danych geografcznych mgr Marcn Semczuk Zakład Przedsęborczośc Gospodark Przestrzennej Instytut Geograf Unwersytet Pedagogczny
Analiza danych OGÓLNY SCHEMAT. http://zajecia.jakubw.pl/ Dane treningowe (znana decyzja) Klasyfikator. Dane testowe (znana decyzja)
 Analza danych Dane trenngowe testowe. Algorytm k najblższych sąsadów. Jakub Wróblewsk jakubw@pjwstk.edu.pl http://zajeca.jakubw.pl/ OGÓLNY SCHEMAT Mamy dany zbór danych podzelony na klasy decyzyjne, oraz
Analza danych Dane trenngowe testowe. Algorytm k najblższych sąsadów. Jakub Wróblewsk jakubw@pjwstk.edu.pl http://zajeca.jakubw.pl/ OGÓLNY SCHEMAT Mamy dany zbór danych podzelony na klasy decyzyjne, oraz
Modele wieloczynnikowe. Modele wieloczynnikowe. Modele wieloczynnikowe ogólne. α β β β ε. Analiza i Zarządzanie Portfelem cz. 4.
 Modele weloczynnkowe Analza Zarządzane Portfelem cz. 4 Ogólne model weloczynnkowy można zapsać jako: (,...,,..., ) P f F F F = n Dr Katarzyna Kuzak lub (,...,,..., ) f F F F = n Modele weloczynnkowe Można
Modele weloczynnkowe Analza Zarządzane Portfelem cz. 4 Ogólne model weloczynnkowy można zapsać jako: (,...,,..., ) P f F F F = n Dr Katarzyna Kuzak lub (,...,,..., ) f F F F = n Modele weloczynnkowe Można
Model IS-LM-BP. Model IS-LM-BP jest wersją modelu ISLM w gospodarce otwartej. Pokazuje on zatem jak
 Ćwczena z Makroekonom II Model IS-LM- Model IS-LM- jest wersją modelu ISLM w gospodarce otwartej. Pokazuje on zatem jak gospodarka taka zachowuje sę w krótkm okrese, w efekce dzałań podejmowanych w ramach
Ćwczena z Makroekonom II Model IS-LM- Model IS-LM- jest wersją modelu ISLM w gospodarce otwartej. Pokazuje on zatem jak gospodarka taka zachowuje sę w krótkm okrese, w efekce dzałań podejmowanych w ramach
SYSTEMY LICZBOWE 275,538 =
 SYSTEMY LICZBOWE 1. Systemy liczbowe Najpopularniejszym systemem liczenia jest system dziesiętny, który doskonale sprawdza się w życiu codziennym. Jednak jego praktyczna realizacja w elektronice cyfrowej
SYSTEMY LICZBOWE 1. Systemy liczbowe Najpopularniejszym systemem liczenia jest system dziesiętny, który doskonale sprawdza się w życiu codziennym. Jednak jego praktyczna realizacja w elektronice cyfrowej
Pracownia Automatyki i Elektrotechniki Katedry Tworzyw Drzewnych Ćwiczenie 3. Analiza obwodów RLC przy wymuszeniach sinusoidalnych w stanie ustalonym
 ĆWCZENE 3 Analza obwodów C przy wymszenach snsodalnych w stane stalonym 1. CE ĆWCZENA Celem ćwczena jest praktyczno-analtyczna ocena obwodów elektrycznych przy wymszenach snsodalne zmennych.. PODSAWY EOEYCZNE
ĆWCZENE 3 Analza obwodów C przy wymszenach snsodalnych w stane stalonym 1. CE ĆWCZENA Celem ćwczena jest praktyczno-analtyczna ocena obwodów elektrycznych przy wymszenach snsodalne zmennych.. PODSAWY EOEYCZNE
Teoretyczne Podstawy Informatyki
 Teoretyczne Podstawy Informatyki cel zajęć Celem kształcenia jest uzyskanie umiejętności i kompetencji w zakresie budowy schematów blokowych algor ytmów oraz ocenę ich złożoności obliczeniowej w celu optymizacji
Teoretyczne Podstawy Informatyki cel zajęć Celem kształcenia jest uzyskanie umiejętności i kompetencji w zakresie budowy schematów blokowych algor ytmów oraz ocenę ich złożoności obliczeniowej w celu optymizacji
STANDARDOWE TECHNIKI KOMPRESJI SYGNAŁÓW
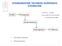 STANDARDOWE TECHNIKI KOMPRESJI SYGNAŁÓW Źródło Kompresja Kanał transmsj sek wdeo 60 Mbt 2 mn muzyk (44 00 próbek/sek, 6 btów/próbkę) 84 Mbt Dekompresja Odborca. Metody bezstratne 2. Metody stratne 2 Kodowane
STANDARDOWE TECHNIKI KOMPRESJI SYGNAŁÓW Źródło Kompresja Kanał transmsj sek wdeo 60 Mbt 2 mn muzyk (44 00 próbek/sek, 6 btów/próbkę) 84 Mbt Dekompresja Odborca. Metody bezstratne 2. Metody stratne 2 Kodowane
Budowa. Metoda wytwarzania
 Budowa Tranzystor JFET (zwany też PNFET) zbudowany jest z płytki z jednego typu półprzewodnika (p lub n), która stanowi tzw. kanał. Na jego końcach znajdują się styki źródła (ang. source - S) i drenu (ang.
Budowa Tranzystor JFET (zwany też PNFET) zbudowany jest z płytki z jednego typu półprzewodnika (p lub n), która stanowi tzw. kanał. Na jego końcach znajdują się styki źródła (ang. source - S) i drenu (ang.
RUCH OBROTOWY Można opisać ruch obrotowy ze stałym przyspieszeniem ε poprzez analogię do ruchu postępowego jednostajnie zmiennego.
 RUCH OBROTOWY Można opsać ruch obrotowy ze stałym przyspeszenem ε poprzez analogę do ruchu postępowego jednostajne zmennego. Ruch postępowy a const. v v at s s v t at Ruch obrotowy const. t t t Dla ruchu
RUCH OBROTOWY Można opsać ruch obrotowy ze stałym przyspeszenem ε poprzez analogę do ruchu postępowego jednostajne zmennego. Ruch postępowy a const. v v at s s v t at Ruch obrotowy const. t t t Dla ruchu
SYSTEMY LICZBOWE. SYSTEMY POZYCYJNE: dziesiętny (arabski): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 rzymski: I, II, III, V, C, M
 SYSTEMY LICZBOWE SYSTEMY POZYCYJNE: dziesiętny (arabski):,, 2, 3, 4, 5, 6, 7, 8, 9 rzymski: I, II, III, V, C, M System pozycyjno wagowy: na przykład liczba 444 4 4 4 4 4 4 Wagi systemu dziesiętnego:,,,,...
SYSTEMY LICZBOWE SYSTEMY POZYCYJNE: dziesiętny (arabski):,, 2, 3, 4, 5, 6, 7, 8, 9 rzymski: I, II, III, V, C, M System pozycyjno wagowy: na przykład liczba 444 4 4 4 4 4 4 Wagi systemu dziesiętnego:,,,,...
SYSTEMY LICZBOWE. Zapis w systemie dziesiętnym
 SYSTEMY LICZBOWE 1. Systemy liczbowe Najpopularniejszym systemem liczenia jest system dziesiętny, który doskonale sprawdza się w życiu codziennym. Jednak jego praktyczna realizacja w elektronice cyfrowej
SYSTEMY LICZBOWE 1. Systemy liczbowe Najpopularniejszym systemem liczenia jest system dziesiętny, który doskonale sprawdza się w życiu codziennym. Jednak jego praktyczna realizacja w elektronice cyfrowej
Architektura komputerów Wykład 2
 Architektura komputerów Wykład 2 Jan Kazimirski 1 Elementy techniki cyfrowej 2 Plan wykładu Algebra Boole'a Podstawowe układy cyfrowe bramki Układy kombinacyjne Układy sekwencyjne 3 Algebra Boole'a Stosowana
Architektura komputerów Wykład 2 Jan Kazimirski 1 Elementy techniki cyfrowej 2 Plan wykładu Algebra Boole'a Podstawowe układy cyfrowe bramki Układy kombinacyjne Układy sekwencyjne 3 Algebra Boole'a Stosowana
Urządzenia Techniki. Klasa I TI. System dwójkowy (binarny) -> BIN. Przykład zamiany liczby dziesiętnej na binarną (DEC -> BIN):
 1. SYSTEMY LICZBOWE UŻYWANE W TECHNICE KOMPUTEROWEJ System liczenia - sposób tworzenia liczb ze znaków cyfrowych oraz zbiór reguł umożliwiających wykonywanie operacji arytmetycznych na liczbach. Do zapisu
1. SYSTEMY LICZBOWE UŻYWANE W TECHNICE KOMPUTEROWEJ System liczenia - sposób tworzenia liczb ze znaków cyfrowych oraz zbiór reguł umożliwiających wykonywanie operacji arytmetycznych na liczbach. Do zapisu
Stanisław Cichocki Natalia Nehrebecka. Zajęcia 4
 Stansław Cchock Natala Nehrebecka Zajęca 4 1. Interpretacja parametrów przy zmennych zerojedynkowych Zmenne 0-1 Interpretacja przy zmennej 0 1 w modelu lnowym względem zmennych objaśnających Interpretacja
Stansław Cchock Natala Nehrebecka Zajęca 4 1. Interpretacja parametrów przy zmennych zerojedynkowych Zmenne 0-1 Interpretacja przy zmennej 0 1 w modelu lnowym względem zmennych objaśnających Interpretacja
Zjawiska masowe takie, które mogą wystąpid nieograniczoną ilośd razy. Wyrazów Obcych)
 Statystyka - nauka zajmująca sę metodam badana przedmotów zjawsk w ch masowych przejawach ch loścową lub jakoścową analzą z punktu wdzena nauk, do której zakresu należą.
Statystyka - nauka zajmująca sę metodam badana przedmotów zjawsk w ch masowych przejawach ch loścową lub jakoścową analzą z punktu wdzena nauk, do której zakresu należą.
KURS STATYSTYKA. Lekcja 6 Regresja i linie regresji ZADANIE DOMOWE. www.etrapez.pl Strona 1
 KURS STATYSTYKA Lekcja 6 Regresja lne regresj ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowedź (tylko jedna jest prawdzwa). Pytane 1 Funkcja regresj I rodzaju cechy Y zależnej
KURS STATYSTYKA Lekcja 6 Regresja lne regresj ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowedź (tylko jedna jest prawdzwa). Pytane 1 Funkcja regresj I rodzaju cechy Y zależnej
Natalia Nehrebecka. Zajęcia 4
 St ł Cchock Stansław C h k Natala Nehrebecka Zajęca 4 1. Interpretacja parametrów przy zmennych zerojedynkowych Zmenne 0 1 Interpretacja przy zmennej 0 1 w modelu lnowym względem zmennych objaśnających
St ł Cchock Stansław C h k Natala Nehrebecka Zajęca 4 1. Interpretacja parametrów przy zmennych zerojedynkowych Zmenne 0 1 Interpretacja przy zmennej 0 1 w modelu lnowym względem zmennych objaśnających
Twierdzenie Bezouta i liczby zespolone Javier de Lucas. Rozwi azanie 2. Z twierdzenia dzielenia wielomianów, mamy, że
 Twerdzene Bezouta lczby zespolone Javer de Lucas Ćwczene 1 Ustal dla których a, b R można podzelć f 1 X) = X 4 3X 2 + ax b przez f 2 X) = X 2 3X+2 Oblcz a b Z 5 jeżel zak ladamy, że f 1 f 2 s a welomanam
Twerdzene Bezouta lczby zespolone Javer de Lucas Ćwczene 1 Ustal dla których a, b R można podzelć f 1 X) = X 4 3X 2 + ax b przez f 2 X) = X 2 3X+2 Oblcz a b Z 5 jeżel zak ladamy, że f 1 f 2 s a welomanam
Sprawozdanie powinno zawierać:
 Sprawozdane pownno zawerać: 1. wypełnoną stronę tytułową (gotowa do ćw. nr 0 na strone drugej, do pozostałych ćwczeń zameszczona na strone 3), 2. krótk ops celu dośwadczena, 3. krótk ops metody pomaru,
Sprawozdane pownno zawerać: 1. wypełnoną stronę tytułową (gotowa do ćw. nr 0 na strone drugej, do pozostałych ćwczeń zameszczona na strone 3), 2. krótk ops celu dośwadczena, 3. krótk ops metody pomaru,
STARE A NOWE KRAJE UE KONKURENCYJNOŚĆ POLSKIEGO EKSPORTU
 Ewa Szymank Katedra Teor Ekonom Akadema Ekonomczna w Krakowe ul. Rakowcka 27, 31-510 Kraków STARE A NOWE KRAJE UE KONKURENCYJNOŚĆ POLSKIEGO EKSPORTU Abstrakt Artykuł przedstawa wynk badań konkurencyjnośc
Ewa Szymank Katedra Teor Ekonom Akadema Ekonomczna w Krakowe ul. Rakowcka 27, 31-510 Kraków STARE A NOWE KRAJE UE KONKURENCYJNOŚĆ POLSKIEGO EKSPORTU Abstrakt Artykuł przedstawa wynk badań konkurencyjnośc
Wykład Turbina parowa kondensacyjna
 Wykład 9 Maszyny ceplne turbna parowa Entropa Równane Claususa-Clapeyrona granca równowag az Dośwadczena W. Domnk Wydzał Fzyk UW ermodynamka 08/09 /5 urbna parowa kondensacyjna W. Domnk Wydzał Fzyk UW
Wykład 9 Maszyny ceplne turbna parowa Entropa Równane Claususa-Clapeyrona granca równowag az Dośwadczena W. Domnk Wydzał Fzyk UW ermodynamka 08/09 /5 urbna parowa kondensacyjna W. Domnk Wydzał Fzyk UW
Dla człowieka naturalnym sposobem liczenia jest korzystanie z systemu dziesiętnego, dla komputera natomiast korzystanie z zapisu dwójkowego
 Arytmetyka cyfrowa Dla człowieka naturalnym sposobem liczenia jest korzystanie z systemu dziesiętnego, dla komputera natomiast korzystanie z zapisu dwójkowego (binarnego). Zapis binarny - to system liczenia
Arytmetyka cyfrowa Dla człowieka naturalnym sposobem liczenia jest korzystanie z systemu dziesiętnego, dla komputera natomiast korzystanie z zapisu dwójkowego (binarnego). Zapis binarny - to system liczenia
Technologie Informacyjne
 System binarny Szkoła Główna Służby Pożarniczej Zakład Informatyki i Łączności October 7, 26 Pojęcie bitu 2 Systemy liczbowe 3 Potęgi dwójki 4 System szesnastkowy 5 Kodowanie informacji 6 Liczby ujemne
System binarny Szkoła Główna Służby Pożarniczej Zakład Informatyki i Łączności October 7, 26 Pojęcie bitu 2 Systemy liczbowe 3 Potęgi dwójki 4 System szesnastkowy 5 Kodowanie informacji 6 Liczby ujemne
WSTĘP. Budowa bramki NAND TTL, ch-ka przełączania, schemat wewnętrzny, działanie 2
 WSTĘP O liczbie elementów użytych do budowy jakiegoś urządzenia elektronicznego, a więc i o możliwości obniżenia jego ceny, decyduje dzisiaj liczba zastosowanych w nim układów scalonych. Najstarszą rodziną
WSTĘP O liczbie elementów użytych do budowy jakiegoś urządzenia elektronicznego, a więc i o możliwości obniżenia jego ceny, decyduje dzisiaj liczba zastosowanych w nim układów scalonych. Najstarszą rodziną
Rozwiązywanie zadań optymalizacji w środowisku programu MATLAB
 Rozwązywane zadań optymalzacj w środowsku programu MATLAB Zagadnene optymalzacj polega na znajdowanu najlepszego, względem ustalonego kryterum, rozwązana należącego do zboru rozwązań dopuszczalnych. Standardowe
Rozwązywane zadań optymalzacj w środowsku programu MATLAB Zagadnene optymalzacj polega na znajdowanu najlepszego, względem ustalonego kryterum, rozwązana należącego do zboru rozwązań dopuszczalnych. Standardowe
Systemy liczbowe. 1. Przedstawić w postaci sumy wag poszczególnych cyfr liczbę rzeczywistą R = (10).
 Wprowadzenie do inżynierii przetwarzania informacji. Ćwiczenie 1. Systemy liczbowe Cel dydaktyczny: Poznanie zasad reprezentacji liczb w systemach pozycyjnych o różnych podstawach. Kodowanie liczb dziesiętnych
Wprowadzenie do inżynierii przetwarzania informacji. Ćwiczenie 1. Systemy liczbowe Cel dydaktyczny: Poznanie zasad reprezentacji liczb w systemach pozycyjnych o różnych podstawach. Kodowanie liczb dziesiętnych
Prąd elektryczny U R I =
 Prąd elektryczny porządkowany ruch ładunków elektrycznych (nośnków prądu). Do scharakteryzowana welkośc prądu służy natężene prądu określające welkość ładunku przepływającego przez poprzeczny przekrój
Prąd elektryczny porządkowany ruch ładunków elektrycznych (nośnków prądu). Do scharakteryzowana welkośc prądu służy natężene prądu określające welkość ładunku przepływającego przez poprzeczny przekrój
Minister Edukacji Narodowej Pani Katarzyna HALL Ministerstwo Edukacji Narodowej al. J. Ch. Szucha 25 00-918 Warszawa Dnia 03 czerwca 2009 r.
 Mnster Edukacj arodowej Pan Katarzyna HALL Mnsterstwo Edukacj arodowej al. J. Ch. Szucha 25 00-918 arszawa Dna 03 czerwca 2009 r. TEMAT: Propozycja zmany art. 30a ustawy Karta auczycela w forme lstu otwartego
Mnster Edukacj arodowej Pan Katarzyna HALL Mnsterstwo Edukacj arodowej al. J. Ch. Szucha 25 00-918 arszawa Dna 03 czerwca 2009 r. TEMAT: Propozycja zmany art. 30a ustawy Karta auczycela w forme lstu otwartego
Realizacja logiki szybkiego przeniesienia w prototypie prądowym układu FPGA Spartan II
 obert Berezowsk Natala Maslennkowa Wydzał Elektronk Poltechnka Koszalńska ul. Partyzantów 7, 75-4 Koszaln Mchał Bałko Przemysław Sołtan ealzacja logk szybkego przenesena w prototype prądowym układu PG
obert Berezowsk Natala Maslennkowa Wydzał Elektronk Poltechnka Koszalńska ul. Partyzantów 7, 75-4 Koszaln Mchał Bałko Przemysław Sołtan ealzacja logk szybkego przenesena w prototype prądowym układu PG
Weryfikacja hipotez dla wielu populacji
 Weryfkacja hpotez dla welu populacj Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Intelgencj Metod Matematycznych Wydzał Informatyk Poltechnk Szczecńskej 5. Parametryczne testy stotnośc w
Weryfkacja hpotez dla welu populacj Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Intelgencj Metod Matematycznych Wydzał Informatyk Poltechnk Szczecńskej 5. Parametryczne testy stotnośc w
Systemy liczbowe. Bibliografia: Urządzenia techniki komputerowej, K. Wojtuszkiewicz
 PODSTAWY TEORII UKŁADÓW CYFROWYCH Systemy liczbowe Opracował: Andrzej Nowak Bibliografia: Urządzenia techniki komputerowej, K. Wojtuszkiewicz http://pl.wikipedia.org/ System liczbowy zbiór reguł jednolitego
PODSTAWY TEORII UKŁADÓW CYFROWYCH Systemy liczbowe Opracował: Andrzej Nowak Bibliografia: Urządzenia techniki komputerowej, K. Wojtuszkiewicz http://pl.wikipedia.org/ System liczbowy zbiór reguł jednolitego
Określanie mocy cylindra C w zaleŝności od ostrości wzroku V 0 Ostrość wzroku V 0 7/5 6/5 5/5 4/5 3/5 2/5 Moc cylindra C 0,5 0,75 1,0 1,25 1,5 > 2
 T A R C Z A Z E G A R O W A ASTYGMATYZM 1.Pojęca ogólne a) astygmatyzm prosty (najbardzej zgodny z pozomem) - najbardzej płask połudnk tzn. o najmnejszej mocy jest pozomy b) astygmatyzm odwrotny (najbardzej
T A R C Z A Z E G A R O W A ASTYGMATYZM 1.Pojęca ogólne a) astygmatyzm prosty (najbardzej zgodny z pozomem) - najbardzej płask połudnk tzn. o najmnejszej mocy jest pozomy b) astygmatyzm odwrotny (najbardzej
ĆWICZENIE NR 2 POMIARY W OBWODACH RLC PRĄDU PRZEMIENNEGO
 ĆWENE N POMAY W OBWODAH PĄD PEMENNEGO el ćwczena: dośwadczalne sprawdzene prawa Oha, praw Krchhoffa zależnośc fazowych ędzy snsodalne zenny przebega prądów napęć w obwodach zawerających eleenty,,, oraz
ĆWENE N POMAY W OBWODAH PĄD PEMENNEGO el ćwczena: dośwadczalne sprawdzene prawa Oha, praw Krchhoffa zależnośc fazowych ędzy snsodalne zenny przebega prądów napęć w obwodach zawerających eleenty,,, oraz
Rachunek niepewności pomiaru opracowanie danych pomiarowych
 Rachunek nepewnośc pomaru opracowane danych pomarowych Mędzynarodowa Norma Oceny Nepewnośc Pomaru (Gude to Epresson of Uncertanty n Measurements - Mędzynarodowa Organzacja Normalzacyjna ISO) http://physcs.nst./gov/uncertanty
Rachunek nepewnośc pomaru opracowane danych pomarowych Mędzynarodowa Norma Oceny Nepewnośc Pomaru (Gude to Epresson of Uncertanty n Measurements - Mędzynarodowa Organzacja Normalzacyjna ISO) http://physcs.nst./gov/uncertanty
Stanisław Cichocki. Natalia Nehrebecka. Wykład 7
 Stansław Cchock Natala Nehrebecka Wykład 7 1 1. Interakcje 2. Przyblżane model nelnowych 3. Założena KMRL 1. Interakcje 2. Przyblżane model nelnowych 3. Założena KMRL W standardowym modelu lnowym zakładamy,
Stansław Cchock Natala Nehrebecka Wykład 7 1 1. Interakcje 2. Przyblżane model nelnowych 3. Założena KMRL 1. Interakcje 2. Przyblżane model nelnowych 3. Założena KMRL W standardowym modelu lnowym zakładamy,
Systemy zapisu liczb.
 Systemy zapisu liczb. Cele kształcenia: Zapoznanie z systemami zapisu liczb: dziesiętny, dwójkowy, ósemkowy, szesnastkowy. Zdobycie umiejętności wykonywania działań na liczbach w różnych systemach. Zagadnienia:
Systemy zapisu liczb. Cele kształcenia: Zapoznanie z systemami zapisu liczb: dziesiętny, dwójkowy, ósemkowy, szesnastkowy. Zdobycie umiejętności wykonywania działań na liczbach w różnych systemach. Zagadnienia:
Stanisław Cichocki. Natalia Nehrebecka Katarzyna Rosiak-Lada. Zajęcia 3
 Stansław Cchock Natala Nehrebecka Katarzyna Rosak-Lada Zajęca 3 1. Dobrod dopasowana równana regresj. Współczynnk determnacj R 2 Dekompozycja warancj zmennej zależnej Współczynnk determnacj R 2 2. Zmenne
Stansław Cchock Natala Nehrebecka Katarzyna Rosak-Lada Zajęca 3 1. Dobrod dopasowana równana regresj. Współczynnk determnacj R 2 Dekompozycja warancj zmennej zależnej Współczynnk determnacj R 2 2. Zmenne
Arytmetyka liczb binarnych
 Wartość dwójkowej liczby stałoprzecinkowej Wartość dziesiętna stałoprzecinkowej liczby binarnej Arytmetyka liczb binarnych b n-1...b 1 b 0,b -1 b -2...b -m = b n-1 2 n-1 +... + b 1 2 1 + b 0 2 0 + b -1
Wartość dwójkowej liczby stałoprzecinkowej Wartość dziesiętna stałoprzecinkowej liczby binarnej Arytmetyka liczb binarnych b n-1...b 1 b 0,b -1 b -2...b -m = b n-1 2 n-1 +... + b 1 2 1 + b 0 2 0 + b -1
PODSTAWY DZIAŁANIA UKŁADÓW CYFROWYCH
 PODSTAWY DZIAŁANIA UKŁADÓW CYFROWYCH 110001010001010001011100111000011100 11000101000101000101110011100001110001001100011 1 Podstawy dzałana układów cyfrowych Sygnał analogowy przyjmuje dowolne wartośc
PODSTAWY DZIAŁANIA UKŁADÓW CYFROWYCH 110001010001010001011100111000011100 11000101000101000101110011100001110001001100011 1 Podstawy dzałana układów cyfrowych Sygnał analogowy przyjmuje dowolne wartośc
5. Pochodna funkcji. lim. x c x c. (x c) = lim. g(c + h) g(c) = lim
 5. Pocodna funkcj Defncja 5.1 Nec f: (a, b) R nec c (a, b). Jeśl stneje granca lm x c x c to nazywamy ją pocodną funkcj f w punkce c oznaczamy symbolem f (c) Twerdzene 5.1 Jeśl funkcja f: (a, b) R ma pocodną
5. Pocodna funkcj Defncja 5.1 Nec f: (a, b) R nec c (a, b). Jeśl stneje granca lm x c x c to nazywamy ją pocodną funkcj f w punkce c oznaczamy symbolem f (c) Twerdzene 5.1 Jeśl funkcja f: (a, b) R ma pocodną
Stanisław Cichocki. Natalia Nehrebecka. Wykład 7
 Stansław Cchock Natala Nehrebecka Wykład 7 . Zmenne dyskretne Kontrasty: efekty progowe, kontrasty w odchylenach Interakcje. Przyblżane model nelnowych Stosowane do zmennych dyskretnych o uporządkowanych
Stansław Cchock Natala Nehrebecka Wykład 7 . Zmenne dyskretne Kontrasty: efekty progowe, kontrasty w odchylenach Interakcje. Przyblżane model nelnowych Stosowane do zmennych dyskretnych o uporządkowanych
 Zadane 1: Wyznacz średne ruchome 3-okresowe z następujących danych obrazujących zużyce energ elektrycznej [kwh] w pewnym zakładze w mesącach styczeń - lpec 1998 r.: 400; 410; 430; 40; 400; 380; 370. Zadane
Zadane 1: Wyznacz średne ruchome 3-okresowe z następujących danych obrazujących zużyce energ elektrycznej [kwh] w pewnym zakładze w mesącach styczeń - lpec 1998 r.: 400; 410; 430; 40; 400; 380; 370. Zadane
Proces narodzin i śmierci
 Proces narodzn śmerc Jeżel w ewnej oulacj nowe osobnk ojawają sę w sosób losowy, rzy czym gęstość zdarzeń na jednostkę czasu jest stała w czase wynos λ, oraz lczba osobnków n, które ojawły sę od chwl do
Proces narodzn śmerc Jeżel w ewnej oulacj nowe osobnk ojawają sę w sosób losowy, rzy czym gęstość zdarzeń na jednostkę czasu jest stała w czase wynos λ, oraz lczba osobnków n, które ojawły sę od chwl do
Proste modele ze złożonym zachowaniem czyli o chaosie
 Proste modele ze złożonym zachowanem czyl o chaose 29 kwetna 2014 Komputer jest narzędzem coraz częścej stosowanym przez naukowców do ukazywana skrzętne ukrywanych przez naturę tajemnc. Symulacja, obok
Proste modele ze złożonym zachowanem czyl o chaose 29 kwetna 2014 Komputer jest narzędzem coraz częścej stosowanym przez naukowców do ukazywana skrzętne ukrywanych przez naturę tajemnc. Symulacja, obok
Tranzystor JFET i MOSFET zas. działania
 Tranzystor JFET i MOSFET zas. działania brak kanału v GS =v t (cutoff ) kanał otwarty brak kanału kanał otwarty kanał zamknięty w.2, p. kanał zamknięty Co było na ostatnim wykładzie? Układy cyfrowe Najczęściej
Tranzystor JFET i MOSFET zas. działania brak kanału v GS =v t (cutoff ) kanał otwarty brak kanału kanał otwarty kanał zamknięty w.2, p. kanał zamknięty Co było na ostatnim wykładzie? Układy cyfrowe Najczęściej
ALGEBRY HALLA DLA POSETÓW SKOŃCZONEGO TYPU PRINJEKTYWNEGO
 ALGEBRY HALLA DLA POSETÓW SKOŃCZONEGO TYPU PRINJEKTYWNEGO NA PODSTAWIE REFERATU JUSTYNY KOSAKOWSKIEJ. Moduły prnjektywne posety skończonego typu prnjektywnego Nech I będze skończonym posetem. Przez max
ALGEBRY HALLA DLA POSETÓW SKOŃCZONEGO TYPU PRINJEKTYWNEGO NA PODSTAWIE REFERATU JUSTYNY KOSAKOWSKIEJ. Moduły prnjektywne posety skończonego typu prnjektywnego Nech I będze skończonym posetem. Przez max
Rozkład dwupunktowy. Rozkład dwupunktowy. Rozkład dwupunktowy x i p i 0 1-p 1 p suma 1
 Rozkład dwupunktowy Zmenna losowa przyjmuje tylko dwe wartośc: wartość 1 z prawdopodobeństwem p wartość 0 z prawdopodobeństwem 1- p x p 0 1-p 1 p suma 1 Rozkład dwupunktowy Funkcja rozkładu prawdopodobeństwa
Rozkład dwupunktowy Zmenna losowa przyjmuje tylko dwe wartośc: wartość 1 z prawdopodobeństwem p wartość 0 z prawdopodobeństwem 1- p x p 0 1-p 1 p suma 1 Rozkład dwupunktowy Funkcja rozkładu prawdopodobeństwa
Statystyka Inżynierska
 Statystyka Inżynerska dr hab. nż. Jacek Tarasuk AGH, WFIS 013 Wykład DYSKRETNE I CIĄGŁE ROZKŁADY JEDNOWYMIAROWE Zmenna losowa, Funkcja rozkładu, Funkcja gęstośc, Dystrybuanta, Charakterystyk zmennej, Funkcje
Statystyka Inżynerska dr hab. nż. Jacek Tarasuk AGH, WFIS 013 Wykład DYSKRETNE I CIĄGŁE ROZKŁADY JEDNOWYMIAROWE Zmenna losowa, Funkcja rozkładu, Funkcja gęstośc, Dystrybuanta, Charakterystyk zmennej, Funkcje
SYSTEM ZALICZEŃ ĆWICZEŃ
 AMI, zma 010/011 mgr Krzysztof Rykaczewsk System zalczeń Wydzał Matematyk Informatyk UMK SYSTEM ZALICZEŃ ĆWICZEŃ z Analzy Matematycznej I, 010/011 (na podst. L.G., K.L., J.M., K.R.) Nnejszy dokument dotyczy
AMI, zma 010/011 mgr Krzysztof Rykaczewsk System zalczeń Wydzał Matematyk Informatyk UMK SYSTEM ZALICZEŃ ĆWICZEŃ z Analzy Matematycznej I, 010/011 (na podst. L.G., K.L., J.M., K.R.) Nnejszy dokument dotyczy
Cyfrowy zapis informacji
 F1-1 Cyfrowy zapis informacji Alfabet: uporządkowany zbiór znaków, np. A = {a,b,..., z} Słowa (ciągi) informacyjne: łańcuchy znakowe, np. A i = gdtr Długość słowa n : liczba znaków słowa, np. n(sbdy) =
F1-1 Cyfrowy zapis informacji Alfabet: uporządkowany zbiór znaków, np. A = {a,b,..., z} Słowa (ciągi) informacyjne: łańcuchy znakowe, np. A i = gdtr Długość słowa n : liczba znaków słowa, np. n(sbdy) =
Wstęp do informatyki- wykład 1
 MATEMATYKA 1 Wstęp do informatyki- wykład 1 Systemy liczbowe Treści prezentowane w wykładzie zostały oparte o: S. Prata, Język C++. Szkoła programowania. Wydanie VI, Helion, 2012 www.cplusplus.com Jerzy
MATEMATYKA 1 Wstęp do informatyki- wykład 1 Systemy liczbowe Treści prezentowane w wykładzie zostały oparte o: S. Prata, Język C++. Szkoła programowania. Wydanie VI, Helion, 2012 www.cplusplus.com Jerzy
EKONOMETRIA I Spotkanie 1, dn. 05.10.2010
 EKONOMETRIA I Spotkane, dn. 5..2 Dr Katarzyna Beń Program ramowy: http://www.sgh.waw.pl/nstytuty/e/oferta_dydaktyczna/ekonometra_stacjonarne_nest acjonarne/ Zadana, dane do zadań, ważne nformacje: http://www.e-sgh.pl/ben/ekonometra
EKONOMETRIA I Spotkane, dn. 5..2 Dr Katarzyna Beń Program ramowy: http://www.sgh.waw.pl/nstytuty/e/oferta_dydaktyczna/ekonometra_stacjonarne_nest acjonarne/ Zadana, dane do zadań, ważne nformacje: http://www.e-sgh.pl/ben/ekonometra
