Szybkość reakcji chemicznej jest proporcjonalna do iloczynu stężeń. reagentów w danej chwili. n A + m B +... p C + r D +... v = k 1 C A n C B m...
|
|
|
- Bogna Kucharska
- 8 lat temu
- Przeglądów:
Transkrypt
1 9 KINETYKA CHEMICZNA Zagadnienia eoreyczne Prawo działania mas. Szybość reacji chemicznych. Reacje zerowego, pierwszego i drugiego rzędu. Cząseczowość i rzędowość reacji chemicznych. Czynnii wpływające na szybość reacji (sężenie, emperaura). Energia aywacji. Równanie Arrheniusa. Kaaliza homogeniczna i heerogeniczna. Kaalizaory i inhibiory. Auoaaliza. Izobara Van Hoffa. Hydroliza sacharozy. Pomiar sałej szybości reacji I rzędu. Sprawdzono w rou 204 przez A. Chomiciego Teoria mułowaniu można przedsawić nasępująco: Dla reacji odwracalnej: zapisujemy prawo działania mas: Podsawowym prawem ineyi chemicznej jes prawo działania mas, óre w najprosszym sfor- Szybość reacji chemicznej jes proporcjonalna do iloczynu sężeń n A + m B +... p C + r D +... v = C A n C B m... dc gdzie v - szybość reacji - sała szybości reacji, d C A, C B - sężenia subsancji A, B w M/dm 3. Dla reacji odwronej (przebiegającej od prawej do lewej srony): i wg ego samego prawa szybość reacji: pc + rd +... na + mb +... v = 2 C C p C D r... W sanie równowagi chemicznej szybości ych reacji są sobie równe i wówczas: C A n C B m... = 2 C C p C D r... Dzieląc obie srony równania przez 2 C A C B orzymamy: 2 C C gdzie / 2 = K (sała równowagi reacji) reagenów w danej chwili p C m A C C r D n B Ta posać prawa działania mas jes najczęściej używana w rozważaniach chemii analiycznej pod nazwą prawa Guldberga - Waage go. Gdy w ażdym elemenarnym acie rea
2 Kineya 2 cji bierze udział ylo jedna cząsecza, reacja nosi nazwę jednocząseczowej. Jeżeli w elemenarnym acie reacji biorą udział dwie cząseczi - reacja jes dwucząseczowa, jeśli reagują rzy cząseczi - reacja jes rójcząseczowa, id. Prawo działania mas zapisujemy wówczas (C - sężenia molowe reagujących subsancji): V = C V = C C 2 V = C C 2 C 3 (dla reacji jednocząseczowej) (dla reacji dwucząseczowej) (dla reacji rójcząseczowej) Doświadczalnie powierdzono, że równania np. reacji jednocząseczowych spełniane są również przez inne, nieoniecznie jednocząseczowe reacje. Z ego względu rozróżnia się reacje pierwszego rzędu spełniające równania reacji jednocząseczowych, reacje drugiego rzędu spełniające równania reacji dwucząseczowych i reacje rzeciego rzędu spełniające równania reacji rójcząseczowych. Reacje pierwszego rzędu Ponieważ szybość reacji definiujemy jao zmianę sężenia subsancji w jednosce czasu, równanie na szybość reacji można napisać nasępująco: dc dc c ponieważ v d d Minus w wyrażeniu szybości reacji wysępuje wówczas, gdy sężenie subsancji reagujących maleje, j. gdy dc 0. Równanie powyższe jes równaniem różniczowym, dla scałowania go należy rozdzielić zmienne: dc d c podzielić sronami przez d c orzymując dc d c i dc c a po scałowaniu orzymujemy ln c = - + cons. ( ). Sałą cons. wyznaczamy z warunów począowych gdy = 0 i c = a (sężenie począowe), podsawiając nasępnie e waruni do równania ln c = - + cons. orzymujemy ln c = cons. Po wyznaczeniu sałej całowania (cons.) równanie ( ) przybiera posać: ln c = - + ln a lub inaczej ln c - ln a = -, i po podzieleniu sron przez - ln a - ln c =, a w ońcu: ln a c, (2a), a aże inaczej a ln a x, (2b) gdzie a - sężenie począowe, c - sężenie po upływie czasu, a - x spade sężenia po upływie czasu. Wsawmy do równania ( 2b ) x = a - c. Wymiar sałej zależy ylo od d
3 Kineya 3 obranej jednosi czasu (w równaniu wysępuje iloraz sężenia, więc wymiary sężeń srócą się dając w efecie liczbę niemianowaną). Podsawiając do równania ( 2a ) zamias a/c = 2, j. c = a/2, orzymujemy czas po jaim przereaguje połowa począowej ilości subsancji czyli czas zwany czasem półrwania reacji /2 ( - au). ln2 / 2, a ponieważ ln 2 = / 2 Czas półrwania w reacjach I rzędu w odróżnieniu od reacji wyższych rzędów nie zależy od sężenia począowego i charaeryzuje szybość reacji I - rzędowych, podobnie, ja sała szybości (por. reację rozpadu pierwiasów promieniowórczych). Hydroliza sacharozy Hydroliza sacharozy przebiega wg równania : H + C 2 H 22 O + H 2 O C 6 H 2 O 6 + C 6 H 2 O 6 sacharoza emperaura glioza fruoza jes o więc reacja dwucząseczowa, dla órej prawo działania mas wyraża się wzorem: v = C sacharoza C woda (3) W rozcieńczonych rozworach sacharozy zmiana sężenia wody będzie bardzo mała, można więc przyjąć, że warość C woda = cons, sąd równanie (3), przy wyrażeniu C woda = przyjmie posać: v = C sacharoza i wobec ego, można przyjąć, że reacja hydrolizy (inwersji) jes reacją I-rzędową (pseudo pierwszorzędowa). Chcąc nasępnie wyznaczyć warość (sałą inwersji) musimy znać sężenie począowe a i sężenie c - po czasie. ln a c i ( ln Po zmianie logarymów nauralnych na dziesięne, orzymujemy: a log (ponieważ ln x = log x ) (4) c Zmiany sężenia sacharozy wyznaczamy meodą polarymeryczną. Glioza jes prawosręna, naomias cuier zinwerowany jes lewosręny, ponieważ powsająca w wyniu hydrolizy fruoza sręca płaszczyznę świała spolaryzowanego w lewo w więszym sopniu niż wynosi sręcalność gliozy w prawo. a c )
4 Kineya 4 Jeżeli na począu pomiaru rozwór sręca płaszczyznę polaryzacji o ą o, a po całowiej inwersji o ą, sężenie począowe będzie proporcjonalne do różnicy sręceń: a = ( o - ), gdzie oznacza - współczynni proporcjonalności. Podobnie w dowolnej chwili, mierzonej od momenu rozpoczęcia reacji, sężenie nie zinwerowanego curu będzie równe c = ( - ), po podsawieniu do wzoru ( 4 ) wyrażenia a = ( o - ), oraz c = ( - ), orzymujemy w ońcu: log 0 (5) lub jeszcze inaczej: log (6) 2 2 gdzie oraz 2 są ąami mierzonymi po czasie i 2. Z powyższego wynia, że równania ( 4 ), ( 5 ) i ( 6 ) są równocenne dla reacji inwersji sacharozy jao reacji I-rzędowej. W ym przypadu, w ych równaniach sężenia a oraz c zasąpiono ąami, 2 i. Wyznaczenie sałej inwersji sprowadza się więc do prosych pomiarów ąów sręcenia płaszczyzny świała spolaryzowanego przechodzącego przez rozwór, w órym a reacja zachodzi. Podczas wyliczenia należy pamięać, aby odczyywać ąy sręcenia z odpowiednimi znaami (sręcalność w prawo +, zaś w lewo - ). Podczas doonywania pomiarów należy urzymywać sałą emperaurę, ponieważ szybość reacji bardzo zależy od emperaury. Zasosowanie w farmacji Obliczanie sężenia leu w organizmie Prawidłowości ineyi chemicznej znalazły szeroie zasosowanie w opisie procesów związanych z przemieszczaniem się cząsecze leu po jego wprowadzeniu do organizmu i obejmujących aie eapy ja : wchłanianie leu z miejsca podania do rążenia, dysrybucję (rozmieszczenie w płynach i anach) oraz eliminację leu. Dziedzina zajmująca się ym nazywa się farmaoineyą, w przeciwieńswie do farmaodynamii, óra zajmuje się wpływem leu na organizm. Jednym z przyładów zasosowania farmaoineyi w farmacji może być obliczanie sężenia leu w organizmie człowiea po podaniu dożylnym. W ym uproszczonym modelu organizmu załada się isnienie jednego omparmenu (grupa ane usroju w órych le i jego meaboliy podlegają aim samym prawom ineycznym) o objęości V, do órego podaje się za pomocą szybiej iniecji dożylnej dawę leu Q, óra nasępnie podlega meabolizmowi i wydalaniu. Sężenie począowe leu C 0 będzie wynosiło Q/V. Sężenie C () po
5 Kineya 5 czasie będzie zależne od sopnia eliminacji leu. Więszość leów wyazuje farmaoineyę pierwszorzędową, w órej sopień eliminacji leu jes proporcjonalny do jego sężenia. Szybość ę zgodnie z ineya reacji I rzędu zapisujemy: lnc=lnc 0 -K Przeszałcając o równanie możemy obliczyć sałą szybości eliminacji leu: K=/ *ln C 0 /C Im wyższą warość ma sała eliminacji ym szybciej le jes usuwany z usroju. Podsawiając do równania zamias C wyrażenie C 0 /2 możemy obliczyć biologiczny ores półrwania leu. Biologiczny ores półrwania nie zależy od podanej dawi leu a jes odwronie proporcjonalny do sałej szybości eliminacji. Oznacza o ze im mniejsza warość sałej szybości eliminacji, ym więsza jes warość biologicznego oresu półrwania, czyli ym wolniej zachodzi eliminacja leu z organizmu. Wiedza a pozwala na odpowiednie dobranie częsoliwości podania leu. Badanie rwałości leu meoda przyśpieszonego sarzenia Przechowywaniu leów mogą owarzyszyć nieodwracalne zmiany, powsałe w wyniu reacji chemicznych, zjawis fizycznych i procesów biologicznych. Niezwyle isone jes więc usalenie oresów rwałości preparaów farmaceuycznych, wprowadzanych do obrou. Przyjęo, że posać leu uznaje się za rwałą wówczas, gdy zawarość subsancji leczniczej wynosi ponad 90% delarowanej ilości w danej emperaurze przechowywania, przy czym produy rozładu są nieosyczne, ich wygląd oraz zapach nie uległy zmianie. Oresem rwałości preparau nazywa się czas, w órym zawarość subsancji leczniczej nie zmniejszyła się więcej niż o 0% od momenu wyproduowania. Powszechnie znaną meoda badania rwałości leu jes meoda sezonowania. Polega ona na przechowywaniu preparau w oryginalnym opaowaniu przez co najmniej ro w warunach oreślonej srefy limaycznej. W ym czasie w odsępach 3-miesięcznych oznacza się zawarość badanych subsancji, ocenia się prepara wizualnie bada właściwości fizyochemiczne i czysość mirobiologiczną. Zaleą ej meody jes analiza procesów rozładu subsancji w warunach idenycznych, w jaich prepara będzie przechowywany. Jednaże jes ona bardzo czasochłonna. Tes przyspieszonego sarzenia pozwala znacznie srócić czas rwania analiz. Wyorzysuje się uaj podwyższoną emperaurę, odgrywającą rolę czynnia przyspieszającego szybość reacji rozładu badanych subsancji.
6 Kineya 6 Meoda a sprowadza się do wyznaczenia sałej szybości dla procesu rozładu w ilu wyższych emperaurach. Nasępnie znajduje się zależność sałej szybości od emperaury, zgodnie z równaniem Arrheniusa i doonuje esrapolacji, np. graficznej, jej warości (log ) do emperaury poojowej. Rzędowość reacji usala się na podsawie wyniów oznaczeń analiycznych w pobranych próbach po eście przyśpieszonego sarzenia- zazwyczaj sosując meodę graficzną. W ym celu na podsawie orzymanych warości sporządza się wyresy zależności logarymu sężenia (logc) w funcji czasu (dla reacji pierwszego rzędu) lub odwroności sężenia (dla reacji drugiego rzędu). Ponieważ więszość reacji rozładu przebiega zgodnie z ineyą reacji pierwszego rzędu, o sałe szybości rozładu () oblicza się na podsawie wzoru: = 2,303 * lg [C 0 /(C 0 C x )]/ [min ] gdzie: C 0 o sężenie wyjściowe subsancji oznaczanej w czasie = 0, naomias C x o sężenie subsancji przereagowanej (produu) po oreślonym czasie. Na podsawie orzymanych wyniów sporządza się wyresy zależności ln od odwroności emperaury bezwzględnej. Dla liniowej zależności ln = f (/T) meodą regresji liniowej wyznacza się współczynni nachylenia prosej oraz pun przecięcia z osią rzędnych, a nasępnie na ich podsawie energię aywacji (Ea) oraz współczynni częsoliwości (A): Sałą szybości reacji w emperaurze przechowywania T wylicza się, orzysając z wyznaczonych wcześniej warości Ea oraz A. Czas, w órym rozładowi ulegnie 0% badanej subsancji w emperaurze przechowywania T oblicza się według wzoru: 0% = 0,053/ T Badanie ineyi procesu rozpuszczania ciał sałych Szybość rozpuszczania odgrywa isoną rolę w przypadu leów sosowanych w posaci sałej (ablei, apsułi, proszi). Dobór odpowiedniej wielości cząse subsancji leczniczej decydujący o szybości rozpuszczanie będzie decydował o szybości pojawiania się leu we rwi oraz wpływał na warość osiąganych sężeń. Jeżeli szybość rozpuszczania jes mniejsza od szybości wchłaniania, o rozpuszczanie będzie procesem onrolującym wchłanianie subsancji, co dla nieórych leów może mieć onsewencje w zapocząowaniu oraz inensywności działania. Badanie szybości rozpuszczania leów odbywa się według sandardowych procedur, órych podsawą jes oznaczanie ilości rozpuszczonej subsancji w
7 Kineya 7 czasie. Oznaczanie ego parameru pozwala wychwycić wiele z ewenualnych błędów óre mogłyby wysąpić w procesie wywarzania ablee- np. użycie nieodpowiedniej odmiany polimorficznej, zby mała zawarość subsancji leczniczej, nieprawidłowości przy powleaniu. Do pomiarów sosuje się różne ypy aparaów. Najpopularniejszym jes apara łopaowy, sładający się z orągłodennej zlewi przyryej przyrywą, mieszadła łopaowego oraz łaźni wodnej urzymującej sałą emperaurę 37 o C +/- 0,5 o C. Badany le umieszcza się w aparacie z płynem symulującym so żołądowy lub jeliowy (np. 0, mol/dm 3 HCl, bufor fosforanowy o ph 6,8). Dodaowo czasem sosuje się płyny fizjologiczne. W czasie rwania esperymenu pobiera się próbi w órych oznacza się sężenie badanej subsancji. Na podsawie orzymanych danych wyreśla się rzywe uwalniania leu, odczyując z nich warość Q - sopień uwalniania subsancji leczniczej (wyrażona w % ilość subsancji leczniczej uwolnionej do rozworu w oreślonym czasie w sosunu do dawi zawarej w ablece).farmaopea Polsa oreśla warości Q dla ablee o niemodyfiowanej szybości uwalniania, ablee dojeliowych i ablee o modyfiowanej szybości uwalniania.
8 Kineya 8 Wyonanie ćwiczenia 9. KINETYKA CHEMICZNA WYZNACZANIE STAŁEJ SZYBKOŚCI REAKCJI HYDROLIZY (INWERSJI) SACHAROZY Zadania:. Wyznaczyć sałą hydrolizy sacharozy w obecności wasu solnego sężeniu 2,6 mol dm Wyznaczyć czas półrwania ej reacji ( /2 ) z wyresu = f ( ) i załączonego wyresu pomocniczego. Wzory pomocnicze: Wyonanie ćwiczenia: a log a x () / 2 (2) A. Przygoowanie Polarymeru. Napełnić rurę polarymeryczną woda desylowaną, sprawdzić szczelność połączeń 2. Włączyć polarymer aby lampa osiągnęła prawidłową emperaurę pracy. B. Przygoowanie próbi 3. Do olbi miarowej pojemności 00 cm 3 odmierzyć cylindrem miarowym 25 cm 3 rozworu wodnego sacharozy, dodać 40 cm 3 HCl (2,6 mol dm -3 ), dodać wody desylowanej do resi i doładnie wymieszać. Należy pamięać że po zmieszaniu wszysich sładniów rozworu, zaczyna się reacja hydrolizy (inwersji) sacharozy. C. Pomiar 4. Przemyć dwuronie rurę polarymeryczną małą ilością orzymanego rozworu sacharozy. Podczas przemywania zwrócić uwagę na o, czy połączenie ruri polarymerycznej z płyą szlaną jes szczelne. Jeżeli wysępuje przecie, należy doręcić naręę, aby przecie en wyeliminować. 5. Rurę polarymeryczną napełnić orzymanym rozworem sacharozy (cała rura polarymeryczna musi być wypełniona rozworem sacharozy). UWAGA: Polarymer powinien być włączony 5 minu przed pomiarem! Pomiędzy olejnymi pomiarami należy wyłączyć polarymer aby zapobiec przegrzaniu lampy. 6. Po upewnieniu się, że rozwór nie wyciea z ruri polarymerycznej, niezwłocznie umieścić ją w polarymerze i odczyać ą sręcenia płaszczyzny świała spolaryzowanego ( 0 ).
9 Kineya 9 7. Pomiary należy przeprowadzić na yle szybo, by pozwoliły na uzysanie rzyronego odczyu warości ąa sręcenia w ciągu o. min. Do abeli (wzór abeli ) zapisać średnią warość odczyu z rzech pomiarów. 8. Dalsze pomiary wyonać olejno w nasępujących odsępach czasowych: 0 min (0 min od począu esperymenu), 5 min (25 min od począu esperymenu), 20 min (45 min od począu esperymenu), 30 min (75 min od począu esperymenu), 30 min (05 min od począu esperymenu). Czasy e są również podane w Tabeli. 9. Pozosały rozwór curu w olbie miarowej należy umieścić w łaźni wodnej, órą należy włączyć przy olejnym, piąym pomiarze (po upływie 75 min od począu esperymenu). 0. Rozwór sacharozy powinien być ogrzewany w emperaurze 70 C przez 30 min.. Po ym czasie rozwór w olbie oziębić do emperaury poojowej i napełnić nim rurę polarymeryczną, opróżnioną po doonaniu 6 pomiaru (05 min od począu esperymenu). 2. Teraz zmierzony ą,, będzie mieć warość ujemną, odpowiadającą warości, gdy proces inwersji przebiega niesończenie długo. Warość ego ąa należy obliczyć (ponieważ nie można odczyać jej bezpośrednio ze sali polarymeru) odejmując 80 od warości ąa odczyanej ze sali, np. odczyany ą ma warość 76,7 O, zaem do abeli należy wsawić obliczoną warość: 76,7-80 = - 3, Orzymane wynii zamieścić w Tabeli. Pomiar między pomiarami Czas [min] Od począu Ką Tabela /min - Sałą wylicza się ze wzoru:
10 Kineya 0 lub [log( 0 ) log( )] (3) [log ( ) log ( )] (4) 2 2 Do obliczania sałej szybości na podsawie dwóch olejnych odczyów wyorzysuje się równanie (4). Podczas obliczania należy zwracać uwagę, aby warość ąa sręcenia płaszczyzny świała spolaryzowanego zasosować z właściwym znaiem. Z załączonego wyresu pomocniczego = f ( ) wyznaczyć począowe sężenie sacharozy (np., dla ąa sręcenia 0 = 2.2 z rzywej można odczyać, że c 0 = 8.4 g sacharozy/00 g rozworu. Nasępnie wyznaczyć ą sręcenia, jai będzie miała mieszanina po czasie /2, wiedząc, że wedy sężenie poszczególnych sładniów wynosi: c /2 (sacharozy) = c 0 / 2; c /2 (gliozy) = c 0 / 4,025; c /2 (fruozy) = c 0 / 4,025 Z wyresu pomocniczego (zależność ąa sręcenia płaszczyzny świała spolaryzowanego od sężenia sacharozy, fruozy i gluozy) odczyać ąy sręcenia płaszczyzny świała spolaryzowanego ( ½(sacharozy), ½(gliozy), ½(fruozy) odpowiadające poszczególnym rozworom sacharozy, gliozy i fruozy (rzywe, 2, 3 ) odpowiednio dla sężeń: c /2 (sacharozy), c /2 (gliozy) i c /2 (fruozy) (zn. gdy proces inwersji sacharozy przebiegł do połowy). Orzymane warości ąów sręcenia płaszczyzny świała spolaryzowanego zsumować zgodnie poniższym równaniem: /2 = ½(sacharozy) + ½(gliozy) - ½(fruozy) Orzymana warość jes oznaczona symbolem: ½. Oreśla ona a sręcenia płaszczyzny świała spolaryzowanego rozworu, w órym inwersja sacharozy przebiegła do połowy. Na podsawie wyliczonej warości /2 i sporządzonego, na podsawie własnych wyniów, wyresu, = f ( ), wyznaczyć warość czasu, /2, po órym proces inwersji sacharozy przebiegł do polowy (czas półrwania inwersji sacharozy).
11 Kineya Wynii obliczeń podać w Tabeli 2. Sężenie curu w g/00 cm 3 rozworu po czasie /2 Ką sręcenia płaszczyzny świała spolaryzowanego odczyany z wyresu pomocniczego, = f ( c ) Ką sręcenia płaszczyzny świała spolaryzowanego rozworu sacharozy po czasie /2 Tabela 2 Czas, /2, odczyany z wyresu (min) Sacharoza, c 0 / 2 = ½ (sacharozy) = Glioza, c/4,025 = ½ (gliozy) = Fruoza, c/4,025 = ½ (fruozy) = UWAGA: Lampę polarymeru należy wyłączyć po pomiarze i ponownie włączać na 5 minu przed ażdym nasępnym pomiarem.
12 Wyres pomocniczy Kineya 2
13 Kineya 3 9.KINETYKA CHEMICZNA WYZNACZANIE STAŁEJ SZYBKOŚCI REAKCJI HYDROLIZY (INWERSJI) SACHAROZY (schema formularza do opracowania wyniów ćwiczenia) Daa wyonania ćwiczenia: Imię i nazwiso sudena: GS: Imię i nazwiso asysena: Zadania do wyonania: Sosowane wzory: Tabela. Wyres. Zależność ąa sręcenia płaszczyzny świała spolaryzowanego od czasu dla rozworu sacharozy, = f ( ) Wyres 2. log ( - ) = f ( ) Tabela 2. Obliczenia (przyłady sosowanych obliczeń). Omówienie wyniów i wniosi. Obliczyć czas półrwania reacji wyorzysując wyliczoną średnią warość, na podsawie danych z abeli oraz równania (2). Podpis sudena: Podpis opieuna: Daa
reagentów w danej chwili n A + m B +... p C + r D +... v = k 1 C A n C B m...
 9 KINETYKA CHEMICZNA Zagadnienia eoreyczne Prawo działania mas. Szybość reacji chemicznych. Reacje zerowego, pierwszego i drugiego rzędu. Cząseczowość i rzędowość reacji chemicznych. Czynnii wpływające
9 KINETYKA CHEMICZNA Zagadnienia eoreyczne Prawo działania mas. Szybość reacji chemicznych. Reacje zerowego, pierwszego i drugiego rzędu. Cząseczowość i rzędowość reacji chemicznych. Czynnii wpływające
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego. Skręcalność właściwa sacharozy. opiekun ćwiczenia: dr A. Pietrzak
 Kaedra Chemii Fizycznej Uniwersyeu Łódzkiego Skręcalność właściwa sacharozy opiekun ćwiczenia: dr A. Pierzak ćwiczenie nr 19 Zakres zagadnień obowiązujących do ćwiczenia 1. Akywność opyczna a srukura cząseczki.
Kaedra Chemii Fizycznej Uniwersyeu Łódzkiego Skręcalność właściwa sacharozy opiekun ćwiczenia: dr A. Pierzak ćwiczenie nr 19 Zakres zagadnień obowiązujących do ćwiczenia 1. Akywność opyczna a srukura cząseczki.
9 k KINETYKA CHEMICZNA
 9 k KINETYKA CHEMICZNA Zagadnienia teoretyczne Prawo działania mas. Szybkość reakcji chemicznych. Reakcje zerowego, pierwszego i drugiego rzędu. Cząsteczkowość i rzędowość reakcji chemicznych. Czynniki
9 k KINETYKA CHEMICZNA Zagadnienia teoretyczne Prawo działania mas. Szybkość reakcji chemicznych. Reakcje zerowego, pierwszego i drugiego rzędu. Cząsteczkowość i rzędowość reakcji chemicznych. Czynniki
Szybkość reakcji chemicznej jest proporcjonalna do iloczynu stężeń. reagentów w danej chwili. n A + m B +... p C + r D +... v = k1 CA n CB m...
 9 KINETYKA CHEMICZNA Zagadnienia teoretyczne Prawo działania mas. Szybkość reakcji chemicznych. Reakcje zerowego, pierwszego i drugiego rzędu. Cząsteczkowość i rzędowość reakcji chemicznych. Czynniki wpływające
9 KINETYKA CHEMICZNA Zagadnienia teoretyczne Prawo działania mas. Szybkość reakcji chemicznych. Reakcje zerowego, pierwszego i drugiego rzędu. Cząsteczkowość i rzędowość reakcji chemicznych. Czynniki wpływające
Analiza popytu. Ekonometria. Metody i analiza problemów ekonomicznych. (pod red. Krzysztofa Jajugi), Wydawnictwo AE Wrocław, 1999.
 Analiza popyu Eonomeria. Meody i analiza problemów eonomicznych (pod red. Krzyszofa Jajugi) Wydawnicwo AE Wrocław 1999. Popy P = f ( X X... X ε ) 1 2 m Zmienne onrolowane: np.: cena (C) nałady na relamę
Analiza popyu Eonomeria. Meody i analiza problemów eonomicznych (pod red. Krzyszofa Jajugi) Wydawnicwo AE Wrocław 1999. Popy P = f ( X X... X ε ) 1 2 m Zmienne onrolowane: np.: cena (C) nałady na relamę
Całka nieoznaczona Andrzej Musielak Str 1. Całka nieoznaczona
 Całka nieoznaczona Andrzej Musielak Sr Całka nieoznaczona Całkowanie o operacja odwrona do liczenia pochodnych, zn.: f()d = F () F () = f() Z definicji oraz z abeli pochodnych funkcji elemenarnych od razu
Całka nieoznaczona Andrzej Musielak Sr Całka nieoznaczona Całkowanie o operacja odwrona do liczenia pochodnych, zn.: f()d = F () F () = f() Z definicji oraz z abeli pochodnych funkcji elemenarnych od razu
Ćwiczenie 13. Stanisław Lamperski WYZNACZANIE STAŁEJ SZYBKOŚCI REAKCJI ORAZ ENTROPII I ENTALPII AKTYWACJI
 Ćwiczenie 3 Sanisław Lampersi WYZNACZANIE SAŁEJ SZYBKOŚCI REAKCJI ORAZ ENROPII I ENALPII AKYWACJI Zagadnienia: Pojęcie szybości reacji, liczby posępu reacji. Równanie ineyczne, rzędowość a cząseczowość
Ćwiczenie 3 Sanisław Lampersi WYZNACZANIE SAŁEJ SZYBKOŚCI REAKCJI ORAZ ENROPII I ENALPII AKYWACJI Zagadnienia: Pojęcie szybości reacji, liczby posępu reacji. Równanie ineyczne, rzędowość a cząseczowość
Temat 6. ( ) ( ) ( ) k. Szeregi Fouriera. Własności szeregów Fouriera. θ możemy traktować jako funkcje ω, których dziedziną jest dyskretny zbiór
 ema 6 Opracował: Lesław Dereń Kaedra eorii Sygnałów Insyu eleomuniacji, eleinformayi i Ausyi Poliechnia Wrocławsa Prawa auorsie zasrzeżone Szeregi ouriera Jeżeli f ( ) jes funcją oresową o oresie, czyli
ema 6 Opracował: Lesław Dereń Kaedra eorii Sygnałów Insyu eleomuniacji, eleinformayi i Ausyi Poliechnia Wrocławsa Prawa auorsie zasrzeżone Szeregi ouriera Jeżeli f ( ) jes funcją oresową o oresie, czyli
Ćwiczenie XII: PRAWO PODZIAŁU NERNSTA
 Ćwiczenie XII: PRAWO PODZIAŁU NERNSTA opracowanie: Wojciech Solarski Wprowadzenie Prawo podziału sformułowane przez Walera H. Nensa opisuje układ rójskładnikowy, z czego dwa składniki o rozpuszczalniki
Ćwiczenie XII: PRAWO PODZIAŁU NERNSTA opracowanie: Wojciech Solarski Wprowadzenie Prawo podziału sformułowane przez Walera H. Nensa opisuje układ rójskładnikowy, z czego dwa składniki o rozpuszczalniki
KINETYKA INWERSJI SACHAROZY
 Dorota Warmińska, Maciej Śmiechowski Katedra Chemii Fizycznej, Wydział Chemiczny, Politechnika Gdańska KINETYKA INWERSJI SACHAROZY Wstęp teoretyczny Kataliza kwasowo-zasadowa Kataliza kwasowo-zasadowa
Dorota Warmińska, Maciej Śmiechowski Katedra Chemii Fizycznej, Wydział Chemiczny, Politechnika Gdańska KINETYKA INWERSJI SACHAROZY Wstęp teoretyczny Kataliza kwasowo-zasadowa Kataliza kwasowo-zasadowa
DYNAMIKA KONSTRUKCJI
 10. DYNAMIKA KONSTRUKCJI 1 10. 10. DYNAMIKA KONSTRUKCJI 10.1. Wprowadzenie Ogólne równanie dynamiki zapisujemy w posaci: M d C d Kd =P (10.1) Zapis powyższy oznacza, że równanie musi być spełnione w każdej
10. DYNAMIKA KONSTRUKCJI 1 10. 10. DYNAMIKA KONSTRUKCJI 10.1. Wprowadzenie Ogólne równanie dynamiki zapisujemy w posaci: M d C d Kd =P (10.1) Zapis powyższy oznacza, że równanie musi być spełnione w każdej
1 Kinetyka reakcji chemicznych
 Podstawy obliczeń chemicznych 1 1 Kinetyka reakcji chemicznych Szybkość reakcji chemicznej definiuje się jako ubytek stężenia substratu lub wzrost stężenia produktu w jednostce czasu. ν = c [ ] 2 c 1 mol
Podstawy obliczeń chemicznych 1 1 Kinetyka reakcji chemicznych Szybkość reakcji chemicznej definiuje się jako ubytek stężenia substratu lub wzrost stężenia produktu w jednostce czasu. ν = c [ ] 2 c 1 mol
Pojęcia podstawowe 1
 Tomasz Lubera Pojęcia podsawowe aa + bb + dd + pp + rr + ss + Kineyka chemiczna dział chemii fizycznej zajmujący się przebiegiem reakcji chemicznych w czasie, ich mechanizmami oraz wpływem różnych czynników
Tomasz Lubera Pojęcia podsawowe aa + bb + dd + pp + rr + ss + Kineyka chemiczna dział chemii fizycznej zajmujący się przebiegiem reakcji chemicznych w czasie, ich mechanizmami oraz wpływem różnych czynników
Ćwiczenie VI KATALIZA HOMOGENICZNA: ESTRYFIKACJA KWASÓW ORGANICZNYCH ALKOHOLAMI
 Zjawisa powierzchniowe i ataliza Ćwiczenie VI ATALIZA HMGNIZNA: STYFIAJA WASÓW GANIZNYH ALHLAMI WPWADZNI stry wasów organicznych stanowią jedną z ważniejszych grup produtów przemysłu chemicznego, ta pod
Zjawisa powierzchniowe i ataliza Ćwiczenie VI ATALIZA HMGNIZNA: STYFIAJA WASÓW GANIZNYH ALHLAMI WPWADZNI stry wasów organicznych stanowią jedną z ważniejszych grup produtów przemysłu chemicznego, ta pod
( 3 ) Kondensator o pojemności C naładowany do różnicy potencjałów U posiada ładunek: q = C U. ( 4 ) Eliminując U z równania (3) i (4) otrzymamy: =
 ROZŁADOWANIE KONDENSATORA I. el ćwiczenia: wyznaczenie zależności napięcia (i/lub prądu I ) rozładowania kondensaora w funkcji czasu : = (), wyznaczanie sałej czasowej τ =. II. Przyrządy: III. Lieraura:
ROZŁADOWANIE KONDENSATORA I. el ćwiczenia: wyznaczenie zależności napięcia (i/lub prądu I ) rozładowania kondensaora w funkcji czasu : = (), wyznaczanie sałej czasowej τ =. II. Przyrządy: III. Lieraura:
LABORATORIUM PODSTAWY ELEKTRONIKI Badanie Bramki X-OR
 LORTORIUM PODSTWY ELEKTRONIKI adanie ramki X-OR 1.1 Wsęp eoreyczny. ramka XOR ramka a realizuje funkcję logiczną zwaną po angielsku EXLUSIVE-OR (WYŁĄZNIE LU). Polska nazwa brzmi LO. Funkcję EX-OR zapisuje
LORTORIUM PODSTWY ELEKTRONIKI adanie ramki X-OR 1.1 Wsęp eoreyczny. ramka XOR ramka a realizuje funkcję logiczną zwaną po angielsku EXLUSIVE-OR (WYŁĄZNIE LU). Polska nazwa brzmi LO. Funkcję EX-OR zapisuje
( ) ( ) ( τ) ( t) = 0
 Obliczanie wraŝliwości w dziedzinie czasu... 1 OBLICZANIE WRAśLIWOŚCI W DZIEDZINIE CZASU Meoda układu dołączonego do obliczenia wraŝliwości układu dynamicznego w dziedzinie czasu. Wyznaczane będą zmiany
Obliczanie wraŝliwości w dziedzinie czasu... 1 OBLICZANIE WRAśLIWOŚCI W DZIEDZINIE CZASU Meoda układu dołączonego do obliczenia wraŝliwości układu dynamicznego w dziedzinie czasu. Wyznaczane będą zmiany
C d u. Po podstawieniu prądu z pierwszego równania do równania drugiego i uporządkowaniu składników lewej strony uzyskuje się:
 Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
POMIAR PARAMETRÓW SYGNAŁOW NAPIĘCIOWYCH METODĄ PRÓKOWANIA I CYFROWEGO PRZETWARZANIA SYGNAŁU
 Pomiar paramerów sygnałów napięciowych. POMIAR PARAMERÓW SYGNAŁOW NAPIĘCIOWYCH MEODĄ PRÓKOWANIA I CYFROWEGO PRZEWARZANIA SYGNAŁU Cel ćwiczenia Poznanie warunków prawidłowego wyznaczania elemenarnych paramerów
Pomiar paramerów sygnałów napięciowych. POMIAR PARAMERÓW SYGNAŁOW NAPIĘCIOWYCH MEODĄ PRÓKOWANIA I CYFROWEGO PRZEWARZANIA SYGNAŁU Cel ćwiczenia Poznanie warunków prawidłowego wyznaczania elemenarnych paramerów
WNIOSKOWANIE STATYSTYCZNE
 Wnioskowanie saysyczne w ekonomerycznej analizie procesu produkcyjnego / WNIOSKOWANIE STATYSTYCZNE W EKONOMETRYCZNEJ ANAIZIE PROCESU PRODUKCYJNEGO Maeriał pomocniczy: proszę przejrzeć srony www.cyf-kr.edu.pl/~eomazur/zadl4.hml
Wnioskowanie saysyczne w ekonomerycznej analizie procesu produkcyjnego / WNIOSKOWANIE STATYSTYCZNE W EKONOMETRYCZNEJ ANAIZIE PROCESU PRODUKCYJNEGO Maeriał pomocniczy: proszę przejrzeć srony www.cyf-kr.edu.pl/~eomazur/zadl4.hml
Teoria sterowania 1 Temat ćwiczenia nr 7a: Synteza parametryczna układów regulacji.
 eoria serowania ema ćwiczenia nr 7a: Syneza parameryczna uładów regulacji. Celem ćwiczenia jes orecja zadanego uładu regulacji wyorzysując nasępujące meody: ryerium ampliudy rezonansowej, meodę ZiegleraNicholsa
eoria serowania ema ćwiczenia nr 7a: Syneza parameryczna uładów regulacji. Celem ćwiczenia jes orecja zadanego uładu regulacji wyorzysując nasępujące meody: ryerium ampliudy rezonansowej, meodę ZiegleraNicholsa
Kinetyka chemiczna jest działem fizykochemii zajmującym się szybkością i mechanizmem reakcji chemicznych w różnych warunkach. a RT.
 Ćwiczenie 12, 13. Kinetyka chemiczna. Kinetyka chemiczna jest działem fizykochemii zajmującym się szybkością i mechanizmem reakcji chemicznych w różnych warunkach. Szybkość reakcji chemicznej jest związana
Ćwiczenie 12, 13. Kinetyka chemiczna. Kinetyka chemiczna jest działem fizykochemii zajmującym się szybkością i mechanizmem reakcji chemicznych w różnych warunkach. Szybkość reakcji chemicznej jest związana
ĆWICZENIE NR 43 U R I (1)
 ĆWCZENE N 43 POMY OPO METODĄ TECHNCZNĄ Cel ćwiczenia: wyznaczenie warości oporu oporników poprzez pomiary naężania prądu płynącego przez opornik oraz napięcia na oporniku Wsęp W celu wyznaczenia warości
ĆWCZENE N 43 POMY OPO METODĄ TECHNCZNĄ Cel ćwiczenia: wyznaczenie warości oporu oporników poprzez pomiary naężania prądu płynącego przez opornik oraz napięcia na oporniku Wsęp W celu wyznaczenia warości
Dobór przekroju żyły powrotnej w kablach elektroenergetycznych
 Dobór przekroju żyły powronej w kablach elekroenergeycznych Franciszek pyra, ZPBE Energopomiar Elekryka, Gliwice Marian Urbańczyk, Insyu Fizyki Poliechnika Śląska, Gliwice. Wsęp Zagadnienie poprawnego
Dobór przekroju żyły powronej w kablach elekroenergeycznych Franciszek pyra, ZPBE Energopomiar Elekryka, Gliwice Marian Urbańczyk, Insyu Fizyki Poliechnika Śląska, Gliwice. Wsęp Zagadnienie poprawnego
ψ przedstawia zależność
 Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Akademia Morska w Szczecinie. Laboratorium paliw, olejów i smarów
 Akademia Morska w Szczecinie Wydział Mechaniczny Kaedra Fizyki i Chemii Laboraorium paliw, olejów i smarów Ćwiczenie laboraoryjne Pomiar gęsości oraz wyznaczanie emperaurowego współczynnika gęsości produków
Akademia Morska w Szczecinie Wydział Mechaniczny Kaedra Fizyki i Chemii Laboraorium paliw, olejów i smarów Ćwiczenie laboraoryjne Pomiar gęsości oraz wyznaczanie emperaurowego współczynnika gęsości produków
Równania różniczkowe. Lista nr 2. Literatura: N.M. Matwiejew, Metody całkowania równań różniczkowych zwyczajnych.
 Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
2.1 Zagadnienie Cauchy ego dla równania jednorodnego. = f(x, t) dla x R, t > 0, (2.1)
 Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Katedra Systemów Przetwarzania Sygnałów SZEREGI FOURIERA
 Ćwiczenie Zmodyfiowano 7..5 Prawa auorsie zasrzeżone: Kaedra Sysemów Przewarzania Sygnałów PWr SZEREGI OURIERA Celem ćwiczenia jes zapoznanie się z analizą i synezą sygnałów oresowych w dziedzinie częsoliwości.
Ćwiczenie Zmodyfiowano 7..5 Prawa auorsie zasrzeżone: Kaedra Sysemów Przewarzania Sygnałów PWr SZEREGI OURIERA Celem ćwiczenia jes zapoznanie się z analizą i synezą sygnałów oresowych w dziedzinie częsoliwości.
3. EKSPERYMENTALNE METODY WYZNACZANIA MODELI MATEMATYCZNYCH Sposób wyznaczania charakterystyki czasowej
 3. Esperymenalne meody wyznaczania modeli maemaycznych 3. EKSPERYMENALNE MEODY WYZNACZANIA MODELI MAEMAYCZNYCH 3.. Sposób wyznaczania charaerysyi czasowej Charaerysyę czasową orzymuje się na wyjściu obieu,
3. Esperymenalne meody wyznaczania modeli maemaycznych 3. EKSPERYMENALNE MEODY WYZNACZANIA MODELI MAEMAYCZNYCH 3.. Sposób wyznaczania charaerysyi czasowej Charaerysyę czasową orzymuje się na wyjściu obieu,
KINETYKA REAKCJI CHEMICZNYCH I KATALIZA
 ĆWICZENIE NR KINETYKA REAKCJI CHEMICZNYCH I KATALIZA Cel ćwiczenia Badanie wpływu temperatury i atalizatora na szybość reacji. Zares wymaganych wiadomość. Szybość reacji chemicznych definicja, jednosti..
ĆWICZENIE NR KINETYKA REAKCJI CHEMICZNYCH I KATALIZA Cel ćwiczenia Badanie wpływu temperatury i atalizatora na szybość reacji. Zares wymaganych wiadomość. Szybość reacji chemicznych definicja, jednosti..
4.2. Obliczanie przewodów grzejnych metodą dopuszczalnego obciążenia powierzchniowego
 4.. Obliczanie przewodów grzejnych meodą dopuszczalnego obciążenia powierzchniowego Meodą częściej sosowaną w prakyce projekowej niż poprzednia, jes meoda dopuszczalnego obciążenia powierzchniowego. W
4.. Obliczanie przewodów grzejnych meodą dopuszczalnego obciążenia powierzchniowego Meodą częściej sosowaną w prakyce projekowej niż poprzednia, jes meoda dopuszczalnego obciążenia powierzchniowego. W
Przedmiot: Chemia budowlana Zakład Materiałoznawstwa i Technologii Betonu
 Przedmiot: Chemia budowlana Zakład Materiałoznawstwa i Technologii Betonu Ćw. 4 Kinetyka reakcji chemicznych Zagadnienia do przygotowania: Szybkość reakcji chemicznej, zależność szybkości reakcji chemicznej
Przedmiot: Chemia budowlana Zakład Materiałoznawstwa i Technologii Betonu Ćw. 4 Kinetyka reakcji chemicznych Zagadnienia do przygotowania: Szybkość reakcji chemicznej, zależność szybkości reakcji chemicznej
ZESZYT DO ĆWICZEŃ Z BIOFIZYKI
 ZESZYT DO ĆWCZEŃ Z BOFZYK mię i nazwisko:. Kierunek:.. 1 Regulamin zajęć dydakycznych z biofizyki Wydział Nauk o Zdrowiu UMB, kierunek zdrowie publiczne Sprawy ogólne 1. Zajęcia dydakyczne z biofizyki
ZESZYT DO ĆWCZEŃ Z BOFZYK mię i nazwisko:. Kierunek:.. 1 Regulamin zajęć dydakycznych z biofizyki Wydział Nauk o Zdrowiu UMB, kierunek zdrowie publiczne Sprawy ogólne 1. Zajęcia dydakyczne z biofizyki
ĆWICZENIE 4 Badanie stanów nieustalonych w obwodach RL, RC i RLC przy wymuszeniu stałym
 ĆWIZENIE 4 Badanie sanów nieusalonych w obwodach, i przy wymuszeniu sałym. el ćwiczenia Zapoznanie się z rozpływem prądów, rozkładem w sanach nieusalonych w obwodach szeregowych, i Zapoznanie się ze sposobami
ĆWIZENIE 4 Badanie sanów nieusalonych w obwodach, i przy wymuszeniu sałym. el ćwiczenia Zapoznanie się z rozpływem prądów, rozkładem w sanach nieusalonych w obwodach szeregowych, i Zapoznanie się ze sposobami
Ćwiczenie 14. Maria Bełtowska-Brzezinska KINETYKA REAKCJI ENZYMATYCZNYCH
 Ćwiczenie 14 aria Bełtowska-Brzezinska KINETYKA REAKCJI ENZYATYCZNYCH Zagadnienia: Podstawowe pojęcia kinetyki chemicznej (szybkość reakcji, reakcje elementarne, rząd reakcji). Równania kinetyczne prostych
Ćwiczenie 14 aria Bełtowska-Brzezinska KINETYKA REAKCJI ENZYATYCZNYCH Zagadnienia: Podstawowe pojęcia kinetyki chemicznej (szybkość reakcji, reakcje elementarne, rząd reakcji). Równania kinetyczne prostych
dr inż. MARCIN MAŁACHOWSKI Instytut Technik Innowacyjnych EMAG
 dr inż. MARCIN MAŁACHOWSKI Insyu Technik Innowacyjnych EMAG Wykorzysanie opycznej meody pomiaru sężenia pyłu do wspomagania oceny paramerów wpływających na możliwość zaisnienia wybuchu osiadłego pyłu węglowego
dr inż. MARCIN MAŁACHOWSKI Insyu Technik Innowacyjnych EMAG Wykorzysanie opycznej meody pomiaru sężenia pyłu do wspomagania oceny paramerów wpływających na możliwość zaisnienia wybuchu osiadłego pyłu węglowego
Laboratorium 5. Wpływ temperatury na aktywność enzymów. Inaktywacja termiczna
 Laboratorium 5 Wpływ temperatury na aktywność enzymów. Inaktywacja termiczna Prowadzący: dr inż. Karolina Labus 1. CZĘŚĆ TEORETYCZNA Szybkość reakcji enzymatycznej zależy przede wszystkim od stężenia substratu
Laboratorium 5 Wpływ temperatury na aktywność enzymów. Inaktywacja termiczna Prowadzący: dr inż. Karolina Labus 1. CZĘŚĆ TEORETYCZNA Szybkość reakcji enzymatycznej zależy przede wszystkim od stężenia substratu
Ćwiczenie IX KATALITYCZNY ROZKŁAD WODY UTLENIONEJ
 Wprowadzenie Ćwiczenie IX KATALITYCZNY ROZKŁAD WODY UTLENIONEJ opracowanie: Barbara Stypuła Celem ćwiczenia jest poznanie roli katalizatora w procesach chemicznych oraz prostego sposobu wyznaczenia wpływu
Wprowadzenie Ćwiczenie IX KATALITYCZNY ROZKŁAD WODY UTLENIONEJ opracowanie: Barbara Stypuła Celem ćwiczenia jest poznanie roli katalizatora w procesach chemicznych oraz prostego sposobu wyznaczenia wpływu
(Ćwiczenie nr 4) Wpływ siły jonowej roztworu na stałą szybkości reakcji.
 (Ćwiczenie nr 4) Wpływ siły jonowej roztworu na stałą szybości reacji Wstęp Rozpatrzmy reację zachodzącą w roztworze pomiędzy jonami i w wyniu tórej powstaje produt D: D stała szybości reacji () Gdy reacja
(Ćwiczenie nr 4) Wpływ siły jonowej roztworu na stałą szybości reacji Wstęp Rozpatrzmy reację zachodzącą w roztworze pomiędzy jonami i w wyniu tórej powstaje produt D: D stała szybości reacji () Gdy reacja
POMIARY CZĘSTOTLIWOŚCI I PRZESUNIĘCIA FAZOWEGO SYGNAŁÓW OKRESOWYCH. Cel ćwiczenia. Program ćwiczenia
 Pomiary częsoliwości i przesunięcia fazowego sygnałów okresowych POMIARY CZĘSOLIWOŚCI I PRZESUNIĘCIA FAZOWEGO SYGNAŁÓW OKRESOWYCH Cel ćwiczenia Poznanie podsawowych meod pomiaru częsoliwości i przesunięcia
Pomiary częsoliwości i przesunięcia fazowego sygnałów okresowych POMIARY CZĘSOLIWOŚCI I PRZESUNIĘCIA FAZOWEGO SYGNAŁÓW OKRESOWYCH Cel ćwiczenia Poznanie podsawowych meod pomiaru częsoliwości i przesunięcia
ĆWICZENIE 7 WYZNACZANIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA. Wprowadzenie
 ĆWICZENIE 7 WYZNACZIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA Wprowadzenie Ciało drgające w rzeczywisym ośrodku z upływem czasu zmniejsza ampliudę drgań maleje energia mechaniczna
ĆWICZENIE 7 WYZNACZIE LOGARYTMICZNEGO DEKREMENTU TŁUMIENIA ORAZ WSPÓŁCZYNNIKA OPORU OŚRODKA Wprowadzenie Ciało drgające w rzeczywisym ośrodku z upływem czasu zmniejsza ampliudę drgań maleje energia mechaniczna
Układy sekwencyjne asynchroniczne Zadania projektowe
 Układy sekwencyjne asynchroniczne Zadania projekowe Zadanie Zaprojekować układ dwusopniowej sygnalizacji opycznej informującej operaora procesu o przekroczeniu przez konrolowany paramer warości granicznej.
Układy sekwencyjne asynchroniczne Zadania projekowe Zadanie Zaprojekować układ dwusopniowej sygnalizacji opycznej informującej operaora procesu o przekroczeniu przez konrolowany paramer warości granicznej.
Badanie kinetyki inwersji sacharozy
 Badanie kinetyki inwersji sacharozy Cel ćwiczenia: Celem ćwiczenia jest wyznaczenie stałej szybkości, energii aktywacji oraz czynnika przedwykładniczego reakcji inwersji sacharozy. Opis metody: Roztwory
Badanie kinetyki inwersji sacharozy Cel ćwiczenia: Celem ćwiczenia jest wyznaczenie stałej szybkości, energii aktywacji oraz czynnika przedwykładniczego reakcji inwersji sacharozy. Opis metody: Roztwory
Wyznaczanie temperatury i wysokości podstawy chmur
 Wyznaczanie emperaury i wysokości podsawy chmur Czas rwania: 10 minu Czas obserwacji: dowolny Wymagane warunki meeorologiczne: pochmurnie lub umiarkowane zachmurzenie Częsoliwość wykonania: 1 raz w ciągu
Wyznaczanie emperaury i wysokości podsawy chmur Czas rwania: 10 minu Czas obserwacji: dowolny Wymagane warunki meeorologiczne: pochmurnie lub umiarkowane zachmurzenie Częsoliwość wykonania: 1 raz w ciągu
3. Badanie kinetyki enzymów
 3. Badanie kinetyki enzymów Przy stałym stężeniu enzymu, a przy zmieniającym się początkowym stężeniu substratu, zmiany szybkości reakcji katalizy, wyrażonej jako liczba moli substratu przetworzonego w
3. Badanie kinetyki enzymów Przy stałym stężeniu enzymu, a przy zmieniającym się początkowym stężeniu substratu, zmiany szybkości reakcji katalizy, wyrażonej jako liczba moli substratu przetworzonego w
Politechnika Częstochowska Wydział Inżynierii Mechanicznej i Informatyki. Sprawozdanie #2 z przedmiotu: Prognozowanie w systemach multimedialnych
 Poliechnika Częsochowska Wydział Inżynierii Mechanicznej i Informayki Sprawozdanie #2 z przedmiou: Prognozowanie w sysemach mulimedialnych Andrzej Siwczyński Andrzej Rezler Informayka Rok V, Grupa IO II
Poliechnika Częsochowska Wydział Inżynierii Mechanicznej i Informayki Sprawozdanie #2 z przedmiou: Prognozowanie w sysemach mulimedialnych Andrzej Siwczyński Andrzej Rezler Informayka Rok V, Grupa IO II
POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA i ENERGETYKI INSTYTUT MASZYN i URZĄDZEŃ ENERGETYCZNYCH
 POLIECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA i ENERGEYKI INSYU MASZYN i URZĄDZEŃ ENERGEYCZNYCH IDENYFIKACJA PARAMERÓW RANSMIANCJI Laboraorium auomayki (A ) Opracował: Sprawdził: Zawierdził:
POLIECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA i ENERGEYKI INSYU MASZYN i URZĄDZEŃ ENERGEYCZNYCH IDENYFIKACJA PARAMERÓW RANSMIANCJI Laboraorium auomayki (A ) Opracował: Sprawdził: Zawierdził:
Inżynieria Środowiska
 ROZTWORY BUFOROWE Roztworami buforowymi nazywamy takie roztwory, w których stężenie jonów wodorowych nie ulega większym zmianom ani pod wpływem rozcieńczania wodą, ani pod wpływem dodatku nieznacznych
ROZTWORY BUFOROWE Roztworami buforowymi nazywamy takie roztwory, w których stężenie jonów wodorowych nie ulega większym zmianom ani pod wpływem rozcieńczania wodą, ani pod wpływem dodatku nieznacznych
PRZEDMIOTOWY SYSTEM OCENIANIA Z FIZYKI WYMAGANIA EDUKACYJNE DLA UCZNIÓW KLAS I
 PRZEDMIOTOWY SYSTEM OCENIANIA Z FIZYKI WYMAGANIA EDUKACYJNE DLA UCZNIÓW KLAS I Wymagania konieczne ocena dopuszczająca wie że długość i odległość mierzymy w milimerach cenymerach merach lub kilomerach
PRZEDMIOTOWY SYSTEM OCENIANIA Z FIZYKI WYMAGANIA EDUKACYJNE DLA UCZNIÓW KLAS I Wymagania konieczne ocena dopuszczająca wie że długość i odległość mierzymy w milimerach cenymerach merach lub kilomerach
Ćwiczenie 8 Wyznaczanie stałej szybkości reakcji utleniania jonów tiosiarczanowych
 CHEMI FIZYCZN Ćwiczenie 8 Wyznaczanie stałej szybkości reakcji utleniania jonów tiosiarczanowych W ćwiczeniu przeprowadzana jest reakcja utleniania jonów tiosiarczanowych za pomocą jonów żelaza(iii). Przebieg
CHEMI FIZYCZN Ćwiczenie 8 Wyznaczanie stałej szybkości reakcji utleniania jonów tiosiarczanowych W ćwiczeniu przeprowadzana jest reakcja utleniania jonów tiosiarczanowych za pomocą jonów żelaza(iii). Przebieg
DOBÓR PRZEKROJU ŻYŁY POWROTNEJ W KABLACH ELEKTROENERGETYCZNYCH
 Franciszek SPYRA ZPBE Energopomiar Elekryka, Gliwice Marian URBAŃCZYK Insyu Fizyki Poliechnika Śląska, Gliwice DOBÓR PRZEKROJU ŻYŁY POWROTNEJ W KABLACH ELEKTROENERGETYCZNYCH. Wsęp Zagadnienie poprawnego
Franciszek SPYRA ZPBE Energopomiar Elekryka, Gliwice Marian URBAŃCZYK Insyu Fizyki Poliechnika Śląska, Gliwice DOBÓR PRZEKROJU ŻYŁY POWROTNEJ W KABLACH ELEKTROENERGETYCZNYCH. Wsęp Zagadnienie poprawnego
Zasada pędu i popędu, krętu i pokrętu, energii i pracy oraz d Alemberta bryły w ruchu postępowym, obrotowym i płaskim
 Zasada pędu i popędu, kręu i pokręu, energii i pracy oraz d Alembera bryły w ruchu posępowym, obroowym i płaskim Ruch posępowy bryły Pęd ciała w ruchu posępowym obliczamy, jak dla punku maerialnego, skupiając
Zasada pędu i popędu, kręu i pokręu, energii i pracy oraz d Alembera bryły w ruchu posępowym, obroowym i płaskim Ruch posępowy bryły Pęd ciała w ruchu posępowym obliczamy, jak dla punku maerialnego, skupiając
E k o n o m e t r i a S t r o n a 1. Nieliniowy model ekonometryczny
 E k o n o m e r i a S r o n a Nieliniowy model ekonomeryczny Jednorównaniowy model ekonomeryczny ma posać = f( X, X,, X k, ε ) gdzie: zmienna objaśniana, X, X,, X k zmienne objaśniające, ε - składnik losowy,
E k o n o m e r i a S r o n a Nieliniowy model ekonomeryczny Jednorównaniowy model ekonomeryczny ma posać = f( X, X,, X k, ε ) gdzie: zmienna objaśniana, X, X,, X k zmienne objaśniające, ε - składnik losowy,
Ćwiczenie 7. Wyznaczanie stałej szybkości oraz parametrów termodynamicznych reakcji hydrolizy aspiryny.
 1 Ćwiczenie 7. Wyznaczanie stałej szybkości oraz parametrów termodynamicznych reakcji hydrolizy aspiryny. Chemiczna stabilność leków jest ważnym terapeutycznym problemem W przypadku chemicznej niestabilności
1 Ćwiczenie 7. Wyznaczanie stałej szybkości oraz parametrów termodynamicznych reakcji hydrolizy aspiryny. Chemiczna stabilność leków jest ważnym terapeutycznym problemem W przypadku chemicznej niestabilności
PROJEKT nr 1 Projekt spawanego węzła kratownicy. Sporządził: Andrzej Wölk
 PROJEKT nr 1 Projek spawanego węzła kraownicy Sporządził: Andrzej Wölk Projek pojedynczego węzła spawnego kraownicy Siły: 1 = 10 3 = -10 Kąy: α = 5 o β = 75 o γ = 75 o Schema węzła kraownicy Dane: Grubość
PROJEKT nr 1 Projek spawanego węzła kraownicy Sporządził: Andrzej Wölk Projek pojedynczego węzła spawnego kraownicy Siły: 1 = 10 3 = -10 Kąy: α = 5 o β = 75 o γ = 75 o Schema węzła kraownicy Dane: Grubość
WYKŁAD 1 ZASADY ELEKTROMECHANICZNEGO PRZETWARZANIA ENERGII
 WYKŁAD 1 ZASADY ELEKTROMECHANICZNEGO RZETWARZANIA ENERGII 1.1. Zasada zachowania energii. unem wyjściowym dla analizy przewarzania energii i mocy w pewnym przedziale czasu jes zasada zachowania energii
WYKŁAD 1 ZASADY ELEKTROMECHANICZNEGO RZETWARZANIA ENERGII 1.1. Zasada zachowania energii. unem wyjściowym dla analizy przewarzania energii i mocy w pewnym przedziale czasu jes zasada zachowania energii
Silniki cieplne i rekurencje
 6 FOTO 33, Lao 6 Silniki cieplne i rekurencje Jakub Mielczarek Insyu Fizyki UJ Chciałbym Pańswu zaprezenować zagadnienie, kóre pozwala, rozważając emaykę sprawności układu silników cieplnych, zapoznać
6 FOTO 33, Lao 6 Silniki cieplne i rekurencje Jakub Mielczarek Insyu Fizyki UJ Chciałbym Pańswu zaprezenować zagadnienie, kóre pozwala, rozważając emaykę sprawności układu silników cieplnych, zapoznać
Badanie funktorów logicznych TTL - ćwiczenie 1
 adanie funkorów logicznych TTL - ćwiczenie 1 1. Cel ćwiczenia Zapoznanie się z podsawowymi srukurami funkorów logicznych realizowanych w echnice TTL (Transisor Transisor Logic), ich podsawowymi paramerami
adanie funkorów logicznych TTL - ćwiczenie 1 1. Cel ćwiczenia Zapoznanie się z podsawowymi srukurami funkorów logicznych realizowanych w echnice TTL (Transisor Transisor Logic), ich podsawowymi paramerami
Matematyka ubezpieczeń majątkowych r. ma złożony rozkład Poissona. W tabeli poniżej podano rozkład prawdopodobieństwa ( )
 Zadanie. Zmienna losowa: X = Y +... + Y N ma złożony rozkład Poissona. W abeli poniżej podano rozkład prawdopodobieńswa składnika sumy Y. W ejże abeli podano akże obliczone dla k = 0... 4 prawdopodobieńswa
Zadanie. Zmienna losowa: X = Y +... + Y N ma złożony rozkład Poissona. W abeli poniżej podano rozkład prawdopodobieńswa składnika sumy Y. W ejże abeli podano akże obliczone dla k = 0... 4 prawdopodobieńswa
POMIARY CZĘSTOTLIWOŚCI I PRZESUNIĘCIA FAZOWEGO SYGNAŁÓW OKRESOWYCH
 Program ćwiczeń: Pomiary częsoliwości i przesunięcia fazowego sygnałów okresowych POMIARY CZĘSTOTLIWOŚCI I PRZESUNIĘCIA FAZOWEGO SYGNAŁÓW OKRESOWYCH Cel ćwiczenia Celem ćwiczenia jes poznanie: podsawowych
Program ćwiczeń: Pomiary częsoliwości i przesunięcia fazowego sygnałów okresowych POMIARY CZĘSTOTLIWOŚCI I PRZESUNIĘCIA FAZOWEGO SYGNAŁÓW OKRESOWYCH Cel ćwiczenia Celem ćwiczenia jes poznanie: podsawowych
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM
 EORI OBWODÓW I SYGNŁÓW LBORORIUM KDEMI MORSK Katedra eleomuniacji Morsiej Ćwiczenie nr 2: eoria obwodów i sygnałów laboratorium ĆWICZENIE 2 BDNIE WIDM SYGNŁÓW OKRESOWYCH. Cel ćwiczenia Celem ćwiczenia
EORI OBWODÓW I SYGNŁÓW LBORORIUM KDEMI MORSK Katedra eleomuniacji Morsiej Ćwiczenie nr 2: eoria obwodów i sygnałów laboratorium ĆWICZENIE 2 BDNIE WIDM SYGNŁÓW OKRESOWYCH. Cel ćwiczenia Celem ćwiczenia
Wygładzanie metodą średnich ruchomych w procesach stałych
 Wgładzanie meodą średnich ruchomch w procesach sałch Cel ćwiczenia. Przgoowanie procedur Średniej Ruchomej (dla ruchomego okna danch); 2. apisanie procedur do obliczenia sandardowego błędu esmacji;. Wizualizacja
Wgładzanie meodą średnich ruchomch w procesach sałch Cel ćwiczenia. Przgoowanie procedur Średniej Ruchomej (dla ruchomego okna danch); 2. apisanie procedur do obliczenia sandardowego błędu esmacji;. Wizualizacja
Szeregi Fouriera (6 rozwiązanych zadań +dodatek)
 PWR I Załad eorii Obwodów Szeregi ouriera (6 rozwiązanych zadań +dodae) Opracował Dr Czesław Michali Zad Znaleźć ores nasępujących sygnałów: a) y 3cos(ω ) + 5cos(7ω ) + cos(5ω ), b) y cos(ω ) + 5cos(ω
PWR I Załad eorii Obwodów Szeregi ouriera (6 rozwiązanych zadań +dodae) Opracował Dr Czesław Michali Zad Znaleźć ores nasępujących sygnałów: a) y 3cos(ω ) + 5cos(7ω ) + cos(5ω ), b) y cos(ω ) + 5cos(ω
DYNAMICZNE MODELE EKONOMETRYCZNE
 DYNAMICZNE MODELE EKONOMETRYCZNE IX Ogólnopolskie Seminarium Naukowe, 6 8 września 005 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Pior Fiszeder Uniwersye Mikołaja Kopernika
DYNAMICZNE MODELE EKONOMETRYCZNE IX Ogólnopolskie Seminarium Naukowe, 6 8 września 005 w Toruniu Kaedra Ekonomerii i Saysyki, Uniwersye Mikołaja Kopernika w Toruniu Pior Fiszeder Uniwersye Mikołaja Kopernika
20. Wyznaczanie ciepła właściwego lodu c pl i ciepła topnienia lodu L
 20. Wyznaczanie ciepła właściwego lodu c pl i ciepła opnienia lodu L I. Wprowadzenie 1. Ciepło właściwe lodu i ciepło opnienia lodu wyznaczymy meodą kalorymeryczną sporządzając odpowiedni bilans cieplny.
20. Wyznaczanie ciepła właściwego lodu c pl i ciepła opnienia lodu L I. Wprowadzenie 1. Ciepło właściwe lodu i ciepło opnienia lodu wyznaczymy meodą kalorymeryczną sporządzając odpowiedni bilans cieplny.
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego. Wpływ stężenia kwasu na szybkość hydrolizy estru
 Katedra Chemii Fizycznej Uniwersytetu Łódzkiego Wpływ stężenia kwasu na szybkość hydrolizy estru ćwiczenie nr 25 opracowała dr B. Nowicka, aktualizacja D. Waliszewski Zakres zagadnień obowiązujących do
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego Wpływ stężenia kwasu na szybkość hydrolizy estru ćwiczenie nr 25 opracowała dr B. Nowicka, aktualizacja D. Waliszewski Zakres zagadnień obowiązujących do
PROGNOZOWANIE I SYMULACJE. mgr Żaneta Pruska. Ćwiczenia 2 Zadanie 1
 PROGNOZOWANIE I SYMULACJE mgr Żanea Pruska Ćwiczenia 2 Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X, wyrażona w ysiącach wyprodukowanych i dosarczonych szuk firmie Bea,
PROGNOZOWANIE I SYMULACJE mgr Żanea Pruska Ćwiczenia 2 Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X, wyrażona w ysiącach wyprodukowanych i dosarczonych szuk firmie Bea,
A B Skąd wiadomo, że reakcja zachodzi? Co jest miarą szybkości reakcji?
 Kinetya chemiczna 3.1.1. Pojęcie szybości reacji chemicznej 3.1.. Ilościowe miary szybości 3.1.3. Reacje pierwszego rzędu 3.1.4. Reacje zerowego rzędu 3.1.5. Przyłady SZYBKOŚĆ REAKCJI HOMOGENICZNEJ A B
Kinetya chemiczna 3.1.1. Pojęcie szybości reacji chemicznej 3.1.. Ilościowe miary szybości 3.1.3. Reacje pierwszego rzędu 3.1.4. Reacje zerowego rzędu 3.1.5. Przyłady SZYBKOŚĆ REAKCJI HOMOGENICZNEJ A B
oznacza przyrost argumentu (zmiennej niezależnej) x 3A82 (Definicja). Granicę (właściwą) ilorazu różnicowego funkcji f w punkcie x x x e x lim x lim
 WYKŁAD 9 34 Pochodna nkcji w pnkcie Inerpreacja geomerczna pochodnej Własności pochodnch Twierdzenia Rolle a Lagrange a Cach ego Regla de lhôspiala Niech ( ) O( ) będzie nkcją określoną w pewnm ooczeni
WYKŁAD 9 34 Pochodna nkcji w pnkcie Inerpreacja geomerczna pochodnej Własności pochodnch Twierdzenia Rolle a Lagrange a Cach ego Regla de lhôspiala Niech ( ) O( ) będzie nkcją określoną w pewnm ooczeni
Analiza rynku projekt
 Analiza rynku projek A. Układ projeku 1. Srona yułowa Tema Auor 2. Spis reści 3. Treść projeku 1 B. Treść projeku 1. Wsęp Po co? Na co? Dlaczego? Dlaczego robię badania? Jakimi meodami? Dla Kogo o jes
Analiza rynku projek A. Układ projeku 1. Srona yułowa Tema Auor 2. Spis reści 3. Treść projeku 1 B. Treść projeku 1. Wsęp Po co? Na co? Dlaczego? Dlaczego robię badania? Jakimi meodami? Dla Kogo o jes
d[a] = dt gdzie: [A] - stężenie aspiryny [OH - ] - stężenie jonów hydroksylowych - ] K[A][OH
![d[a] = dt gdzie: [A] - stężenie aspiryny [OH - ] - stężenie jonów hydroksylowych - ] K[A][OH d[a] = dt gdzie: [A] - stężenie aspiryny [OH - ] - stężenie jonów hydroksylowych - ] K[A][OH](/thumbs/48/24702101.jpg) 1 Ćwiczenie 7. Wyznaczanie stałej szybkości oraz parametrów termodynamicznych reakcji hydrolizy aspiryny. Chemiczna stabilność leków jest ważnym terapeutycznym problemem W przypadku chemicznej niestabilności
1 Ćwiczenie 7. Wyznaczanie stałej szybkości oraz parametrów termodynamicznych reakcji hydrolizy aspiryny. Chemiczna stabilność leków jest ważnym terapeutycznym problemem W przypadku chemicznej niestabilności
KI + Pb(NO 3 ) 2 PbI 2 + KNO 3. fermentacja alkoholowa
 Kinetyka chemiczna KI + Pb(NO 3 ) 2 PbI 2 + KNO 3 fermentacja alkoholowa czynniki wpływaj ywające na szybkość reakcji chemicznych stęż ężenie reagentów w (lub ciśnienie gazów w jeżeli eli reakcja przebiega
Kinetyka chemiczna KI + Pb(NO 3 ) 2 PbI 2 + KNO 3 fermentacja alkoholowa czynniki wpływaj ywające na szybkość reakcji chemicznych stęż ężenie reagentów w (lub ciśnienie gazów w jeżeli eli reakcja przebiega
LABORATORIUM Z KATALIZY HOMOGENICZNEJ I HETEROGENICZNEJ WYZNACZANIE STAŁEJ SZYBKOŚCI REAKCJI UTLENIANIA POLITECHNIKA ŚLĄSKA WYDZIAŁ CHEMICZNY
 POLITECHNIKA ŚLĄSKA WYDZIAŁ CHEMICZNY KATEDRA FIZYKOCHEMII I TECHNOLOGII POLIMERÓW WYZNACZANIE STAŁEJ SZYBKOŚCI REAKCJI UTLENIANIA JONÓW TIOSIARCZANOWYCH Miejsce ćwiczenia: Zakład Chemii Fizycznej, sala
POLITECHNIKA ŚLĄSKA WYDZIAŁ CHEMICZNY KATEDRA FIZYKOCHEMII I TECHNOLOGII POLIMERÓW WYZNACZANIE STAŁEJ SZYBKOŚCI REAKCJI UTLENIANIA JONÓW TIOSIARCZANOWYCH Miejsce ćwiczenia: Zakład Chemii Fizycznej, sala
LABORATORIUM PODSTAW ELEKTRONIKI PROSTOWNIKI
 ZESPÓŁ LABORATORIÓW TELEMATYKI TRANSPORTU ZAKŁAD TELEKOMUNIKJI W TRANSPORCIE WYDZIAŁ TRANSPORTU POLITECHNIKI WARSZAWSKIEJ LABORATORIUM PODSTAW ELEKTRONIKI INSTRUKCJA DO ĆWICZENIA NR 5 PROSTOWNIKI DO UŻYTKU
ZESPÓŁ LABORATORIÓW TELEMATYKI TRANSPORTU ZAKŁAD TELEKOMUNIKJI W TRANSPORCIE WYDZIAŁ TRANSPORTU POLITECHNIKI WARSZAWSKIEJ LABORATORIUM PODSTAW ELEKTRONIKI INSTRUKCJA DO ĆWICZENIA NR 5 PROSTOWNIKI DO UŻYTKU
Chemia Analityczna. Autor: prof. dr hab. inż Marek Biziuk
 Cheia Analiyczna Auor: pro. dr hab. inż Marek Biziuk Kaedra Cheii Analiycznej Wydział Cheiczny Poliechnika Gdańska 21 ANALIZA MIARECZKOWA (dział analizy objęościowej - woluerii) Meody iareczkowe służą
Cheia Analiyczna Auor: pro. dr hab. inż Marek Biziuk Kaedra Cheii Analiycznej Wydział Cheiczny Poliechnika Gdańska 21 ANALIZA MIARECZKOWA (dział analizy objęościowej - woluerii) Meody iareczkowe służą
Przybliżenie elektronów prawie swobodnych; metoda pseudopotencjału
 Przybliżenie eleronów prawie swobodnych; meoda pseudopoencjału Sieć pusa gdzie: Weor G gra uaj role indesu pasma. Warosci własne energii wyrażają się wzorem: Przybliżenie eleronów prawie swobodnych Ażeby
Przybliżenie eleronów prawie swobodnych; meoda pseudopoencjału Sieć pusa gdzie: Weor G gra uaj role indesu pasma. Warosci własne energii wyrażają się wzorem: Przybliżenie eleronów prawie swobodnych Ażeby
ANALIZA, PROGNOZOWANIE I SYMULACJA / Ćwiczenia 1
 ANALIZA, PROGNOZOWANIE I SYMULACJA / Ćwiczenia 1 mgr inż. Żanea Pruska Maeriał opracowany na podsawie lieraury przedmiou. Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X,
ANALIZA, PROGNOZOWANIE I SYMULACJA / Ćwiczenia 1 mgr inż. Żanea Pruska Maeriał opracowany na podsawie lieraury przedmiou. Zadanie 1 Firma Alfa jes jednym z głównych dosawców firmy Bea. Ilość produku X,
Wyznaczanie stałej dysocjacji pk a słabego kwasu metodą konduktometryczną CZĘŚĆ DOŚWIADCZALNA. Tabela wyników pomiaru
 Wyznaczanie stałej dysocjacji pk a słabego kwasu metodą konduktometryczną Cel ćwiczenia Celem ćwiczenia jest wyznaczenie stałej dysocjacji pk a słabego kwasu metodą konduktometryczną. Zakres wymaganych
Wyznaczanie stałej dysocjacji pk a słabego kwasu metodą konduktometryczną Cel ćwiczenia Celem ćwiczenia jest wyznaczenie stałej dysocjacji pk a słabego kwasu metodą konduktometryczną. Zakres wymaganych
PROGNOZOWANIE. Ćwiczenia 2. mgr Dawid Doliński
 Ćwiczenia 2 mgr Dawid Doliński Modele szeregów czasowych sały poziom rend sezonowość Y Y Y Czas Czas Czas Modele naiwny Modele średniej arymeycznej Model Browna Modele ARMA Model Hola Modele analiyczne
Ćwiczenia 2 mgr Dawid Doliński Modele szeregów czasowych sały poziom rend sezonowość Y Y Y Czas Czas Czas Modele naiwny Modele średniej arymeycznej Model Browna Modele ARMA Model Hola Modele analiyczne
Opracował dr inż. Tadeusz Janiak
 Opracował dr inż. Tadeusz Janiak 1 Uwagi dla wykonujących ilościowe oznaczanie metodami spektrofotometrycznymi 3. 3.1. Ilościowe oznaczanie w metodach spektrofotometrycznych Ilościowe określenie zawartości
Opracował dr inż. Tadeusz Janiak 1 Uwagi dla wykonujących ilościowe oznaczanie metodami spektrofotometrycznymi 3. 3.1. Ilościowe oznaczanie w metodach spektrofotometrycznych Ilościowe określenie zawartości
LABORATORIUM Z ELEKTRONIKI
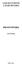 LABORAORIM Z ELEKRONIKI PROSOWNIKI Józef Boksa WA 01 1. PROSOWANIKI...3 1.1. CEL ĆWICZENIA...3 1.. WPROWADZENIE...3 1..1. Prosowanie...3 1.3. PROSOWNIKI NAPIĘCIA...3 1.4. SCHEMAY BLOKOWE KŁADÓW POMIAROWYCH...5
LABORAORIM Z ELEKRONIKI PROSOWNIKI Józef Boksa WA 01 1. PROSOWANIKI...3 1.1. CEL ĆWICZENIA...3 1.. WPROWADZENIE...3 1..1. Prosowanie...3 1.3. PROSOWNIKI NAPIĘCIA...3 1.4. SCHEMAY BLOKOWE KŁADÓW POMIAROWYCH...5
KINETYKA HYDROLIZY SACHAROZY
 Ćwiczenie nr 2 KINETYKA HYDROLIZY SACHAROZY I. Kinetyka hydrolizy sacharozy reakcja chemiczna Zasada: Sacharoza w środowisku kwaśnym ulega hydrolizie z wytworzeniem -D-glukozy i -D-fruktozy. Jest to reakcja
Ćwiczenie nr 2 KINETYKA HYDROLIZY SACHAROZY I. Kinetyka hydrolizy sacharozy reakcja chemiczna Zasada: Sacharoza w środowisku kwaśnym ulega hydrolizie z wytworzeniem -D-glukozy i -D-fruktozy. Jest to reakcja
EFEKT SOLNY BRÖNSTEDA
 EFEKT SLNY RÖNSTED Pojęcie eektu solnego zostało wprowadzone przez rönsteda w celu wytłumaczenia wpływu obojętnego elektrolitu na szybkość reakcji zachodzących między jonami. Założył on, że reakcja pomiędzy
EFEKT SLNY RÖNSTED Pojęcie eektu solnego zostało wprowadzone przez rönsteda w celu wytłumaczenia wpływu obojętnego elektrolitu na szybkość reakcji zachodzących między jonami. Założył on, że reakcja pomiędzy
Chemia - laboratorium
 Chemia - laboratorium Wydział Geologii, Geofizyki i Ochrony Środowiska Studia stacjonarne, Rok I, Semestr zimowy 013/14 Dr hab. inż. Tomasz Brylewski e-mail: brylew@agh.edu.pl tel. 1-617-59 Katedra Fizykochemii
Chemia - laboratorium Wydział Geologii, Geofizyki i Ochrony Środowiska Studia stacjonarne, Rok I, Semestr zimowy 013/14 Dr hab. inż. Tomasz Brylewski e-mail: brylew@agh.edu.pl tel. 1-617-59 Katedra Fizykochemii
Ocena płynności wybranymi metodami szacowania osadu 1
 Bogdan Ludwiczak Wprowadzenie Ocena płynności wybranymi meodami szacowania osadu W ubiegłym roku zaszły znaczące zmiany doyczące pomiaru i zarządzania ryzykiem bankowym. Są one konsekwencją nowowprowadzonych
Bogdan Ludwiczak Wprowadzenie Ocena płynności wybranymi meodami szacowania osadu W ubiegłym roku zaszły znaczące zmiany doyczące pomiaru i zarządzania ryzykiem bankowym. Są one konsekwencją nowowprowadzonych
Kombinowanie prognoz. - dlaczego należy kombinować prognozy? - obejmowanie prognoz. - podstawowe metody kombinowania prognoz
 Noaki do wykładu 005 Kombinowanie prognoz - dlaczego należy kombinować prognozy? - obejmowanie prognoz - podsawowe meody kombinowania prognoz - przykłady kombinowania prognoz gospodarki polskiej - zalecenia
Noaki do wykładu 005 Kombinowanie prognoz - dlaczego należy kombinować prognozy? - obejmowanie prognoz - podsawowe meody kombinowania prognoz - przykłady kombinowania prognoz gospodarki polskiej - zalecenia
Przemieszczeniem ciała nazywamy zmianę jego położenia
 1 Przemieszczeniem ciała nazywamy zmianę jego położenia + 0 k k 0 Przemieszczenie jes wekorem. W przypadku jednowymiarowym możliwy jes ylko jeden kierunek, a zwro określamy poprzez znak. Przyjmujemy, że
1 Przemieszczeniem ciała nazywamy zmianę jego położenia + 0 k k 0 Przemieszczenie jes wekorem. W przypadku jednowymiarowym możliwy jes ylko jeden kierunek, a zwro określamy poprzez znak. Przyjmujemy, że
Ruch płaski. Bryła w ruchu płaskim. (płaszczyzna kierująca) Punkty bryły o jednakowych prędkościach i przyspieszeniach. Prof.
 Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
Modelowanie i obliczenia techniczne. Równania różniczkowe Numeryczne rozwiązywanie równań różniczkowych zwyczajnych
 Moelowanie i obliczenia echniczne Równania różniczowe Numeryczne rozwiązywanie równań różniczowych zwyczajnych Przyła ułau ynamicznego E Uła ynamiczny R 0 Zachozi porzeba wyznaczenia: C u C () i() ur ir
Moelowanie i obliczenia echniczne Równania różniczowe Numeryczne rozwiązywanie równań różniczowych zwyczajnych Przyła ułau ynamicznego E Uła ynamiczny R 0 Zachozi porzeba wyznaczenia: C u C () i() ur ir
KI + Pb(NO 3 ) 2 PbI 2 + KNO 3. fermentacja alkoholowa
 Kinetyka chemiczna KI + Pb(NO 3 ) 2 PbI 2 + KNO 3 fermentacja alkoholowa czynniki wpływaj ywające na szybkość reakcji chemicznych stęż ężenie reagentów w (lub ciśnienie gazów w jeżeli eli reakcja przebiega
Kinetyka chemiczna KI + Pb(NO 3 ) 2 PbI 2 + KNO 3 fermentacja alkoholowa czynniki wpływaj ywające na szybkość reakcji chemicznych stęż ężenie reagentów w (lub ciśnienie gazów w jeżeli eli reakcja przebiega
Algebra liniowa z geometrią analityczną
 WYKŁAD. Własności zbiorów liczbowych. Podzielność liczb całowitych, relacja przystawania modulo, twierdzenie chińsie o resztach. Liczby całowite Liczby 0,±,±,±3,... nazywamy liczbami całowitymi. Zbiór
WYKŁAD. Własności zbiorów liczbowych. Podzielność liczb całowitych, relacja przystawania modulo, twierdzenie chińsie o resztach. Liczby całowite Liczby 0,±,±,±3,... nazywamy liczbami całowitymi. Zbiór
Wymagania konieczne i podstawowe Uczeń: 1. Wykonujemy pomiary
 ocena dopuszczająca Wymagania podsawowe ocena dosaeczna ocena dobra Wymagania dopełniające ocena bardzo dobra 1 Lekcja wsępna 1. Wykonujemy pomiary 2 3 Wielkości fizyczne, kóre mierzysz na co dzień wymienia
ocena dopuszczająca Wymagania podsawowe ocena dosaeczna ocena dobra Wymagania dopełniające ocena bardzo dobra 1 Lekcja wsępna 1. Wykonujemy pomiary 2 3 Wielkości fizyczne, kóre mierzysz na co dzień wymienia
Wyznaczanie ciepła topnienia lodu lub ciepła właściwego wybranego ciała
 dla specjalnośći Biofizya moleularna Wyznaczanie ciepła topnienia lodu lub ciepła właściwego wybranego ciała I. WSTĘP C 1 C 4 Ciepło jest wielością charateryzującą przepływ energii (analogiczną do pracy
dla specjalnośći Biofizya moleularna Wyznaczanie ciepła topnienia lodu lub ciepła właściwego wybranego ciała I. WSTĘP C 1 C 4 Ciepło jest wielością charateryzującą przepływ energii (analogiczną do pracy
Dr inŝ. Janusz Eichler Dr inŝ. Jacek Kasperski. ODSTĘPSTWA RZECZYWISTEGO OBIEGU ABSORPCYJNO-DYFUZYJNEGO OD OBIEGU TEORETYCZNEGO (część I).
 Dr inŝ Janusz Eichler Dr inŝ Jacek Kasperski Zakład Chłodnicwa i Kriogeniki Insyu echniki Cieplnej i Mechaniki Płynów I-20 Poliechnika Wrocławska ODSĘPSWA RZECZYWISEGO OBIEGU ABSORPCYJNO-DYFUZYJNEGO OD
Dr inŝ Janusz Eichler Dr inŝ Jacek Kasperski Zakład Chłodnicwa i Kriogeniki Insyu echniki Cieplnej i Mechaniki Płynów I-20 Poliechnika Wrocławska ODSĘPSWA RZECZYWISEGO OBIEGU ABSORPCYJNO-DYFUZYJNEGO OD
Ćwiczenie 6. Symulacja komputerowa wybranych procesów farmakokinetycznych z uwzględnieniem farmakokinetyki bezmodelowej
 Ćwiczenie 6. Symulacja komputerowa wybranych procesów farmakokinetycznych z uwzględnieniem farmakokinetyki bezmodelowej Celem ćwiczenia jest wyznaczenie podstawowych parametrów farmakokinetycznych paracetamolu
Ćwiczenie 6. Symulacja komputerowa wybranych procesów farmakokinetycznych z uwzględnieniem farmakokinetyki bezmodelowej Celem ćwiczenia jest wyznaczenie podstawowych parametrów farmakokinetycznych paracetamolu
Wrocław, DIALIZA 1. OPIS PROCESU
 Wrocław, 24.11.15 DIALIZA 1. OPIS PROCESU Do procesów membranowych służących do rozdzielania układów ciekłych należy akże dializa. Jes o izobaryczny i izoermiczny proces membranowy, w kórym siłą napędową
Wrocław, 24.11.15 DIALIZA 1. OPIS PROCESU Do procesów membranowych służących do rozdzielania układów ciekłych należy akże dializa. Jes o izobaryczny i izoermiczny proces membranowy, w kórym siłą napędową
LABORATORIUM TECHNIKI CIEPLNEJ INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ
 INSTTUTU TECHNIKI CIEPLNEJ WDZIAŁ INŻNIERII ŚRODOWISKA I ENERGETKI POLITECHNIKI ŚLĄSKIEJ INSTRUKCJA LABORATORJNA Tema ćwiczenia: WZNACZANIE WSPÓŁCZNNIKA PRZEWODZENIA CIEPŁA CIAŁ STAŁCH METODĄ STANU UPORZĄDKOWANEGO
INSTTUTU TECHNIKI CIEPLNEJ WDZIAŁ INŻNIERII ŚRODOWISKA I ENERGETKI POLITECHNIKI ŚLĄSKIEJ INSTRUKCJA LABORATORJNA Tema ćwiczenia: WZNACZANIE WSPÓŁCZNNIKA PRZEWODZENIA CIEPŁA CIAŁ STAŁCH METODĄ STANU UPORZĄDKOWANEGO
Kinetyka chemiczna kataliza i reakcje enzymatyczne
 inetya chemiczna ataliza i reacje enzymatyczne Wyład z Chemii Fizycznej str. 3.3 / 1 Ilościowy opis mechanizm działania atalizatorów Wyład z Chemii Fizycznej str. 3.3 / 2 Ilościowy opis mechanizm działania
inetya chemiczna ataliza i reacje enzymatyczne Wyład z Chemii Fizycznej str. 3.3 / 1 Ilościowy opis mechanizm działania atalizatorów Wyład z Chemii Fizycznej str. 3.3 / 2 Ilościowy opis mechanizm działania
EKONOMETRIA wykład 2. Prof. dr hab. Eugeniusz Gatnar.
 EKONOMERIA wykład Prof. dr hab. Eugeniusz Ganar eganar@mail.wz.uw.edu.pl Przedziały ufności Dla paramerów srukuralnych modelu: P bˆ j S( bˆ z prawdopodobieńswem parameru b bˆ S( bˆ, ( m j j j, ( m j b
EKONOMERIA wykład Prof. dr hab. Eugeniusz Ganar eganar@mail.wz.uw.edu.pl Przedziały ufności Dla paramerów srukuralnych modelu: P bˆ j S( bˆ z prawdopodobieńswem parameru b bˆ S( bˆ, ( m j j j, ( m j b
