Modelowanie niepewności
|
|
|
- Beata Marszałek
- 5 lat temu
- Przeglądów:
Transkrypt
1 Modelowanie niepewności rzetwarzanie numerczne informacji niepewnej niepełnej nej i niepreczjnej lan władu Źródła a niepewności informacji odejście probabilistczne do modelowania niepewności - twierdzenie aesa Współcznni niepewności Teoria Dempstera-Shafera Zbior rozmte
2 3 Źródła a niepewności Niepewność samej wiedz zapisanej w bazie wiedz zasad zapisane np. w postaci reguł nie muszą bć uniwersalne Niedoładne/niepreczjne obserwacje Źródło o pochodzenia danch może e bć niepewne Uzsane sposobem tór nie jest pewn błą łąd metod sończona doładno adność przrządów w itp. Niepreczjne pojęcia Jęz opisu mało o preczjn niejednoznaczn 4 Źródła a niepewności - przład IF smptomxból_z l_zęba TN chorobaxpróchnica chnica Reguła a jest nieompletna bo nie wszsc pacjenci z objawami bólu b mają próchnic chnicę Istnieje wiele często nieograniczona liczba przczn z powodu tórch obserwujem ból b l np.: IF smptomxból_z l_zęba TN chorobaxpróchnica chnica chorobaxparadontoza chorobaxnowa_ósema
3 5 Źródła a niepewności - przład IF smptomxból_z l_zęba TN chorobaxpróchnica chnica Reguła a nie odzwierciedla fatcznego związu zu przcznowo-sutowego abducja więc c może: IF chorobaxpróchnica chnica TN smptomxból_z l_zęba Reguła a deducjna równier wnież nie jest ompletna mogą istnieć pacjenci tórz mimo próchnic nie będąb odczuwali bólub Kompletność reguł wmagałab ab podania wszstich szczegółowch warunów w w tórch próchnica powoduje ból. b 6 Źródła a niepewności - przład IF smptomxból_z l_zęba smptomxopuchlizna smptomzębina bina ubti rtgstan_zapaln TN chorobaxpróchnica chnica Doładno adność reguł wmagałab ab często ogromnej liczb warunów zdefiniowanie ich wszstich często jest niemożliwe ze względu na ograniczoną wiedzę w danej dziedzinie albo niepratczne nie wszstie waruni mogłb zawsze bć sprawdzone!
4 7 Źródła a niepewności - przład IF smptomxból_z l_zęba TN chorobaxpróchnica chnica Reguła a nie reprezentuje zatem onsewencji w sensie logicznm lecz jest wrazem przeonania esperta obarczonm zawsze pewną dozą niepewności rawdopodobieństwo jao pewna miara pozwala na opis niepewności tego co ma swoje źródło o w naszej ignorancji i niewiedz rzpisanie prawdopodobieństwa regule będzie b oznaczać w jaim procencie przpadów nierozróżnialnch nialnch od wsazanch w regule espert uznał to stwierdzenie za prawdziwe spet numercznego przetwarzania niepewności 8 Numerczne przetwarzanie niepewności obejmuje: Matematczn model reprezentacji informacji niepewnej pozwalając przdzielać niepewność fatom i regułom wniosowania Mechanizm łączenia niepewnch informacji pochodzącch cch z różnch r źródeł Mechanizm propagacji niepewności w tracie procesu wniosowania
5 9 odejście probabilistczne Sąd d się bierze prawdopodobieństwo? odejście tradcjne historczne naliza szans na uzsanie oreślonego wniu w grach losowch np. prawdopodobieństwo trafienia szósti w tota wnosi / odejście statstczne zęstotliwościowe prawdopodobieństwo zdarzenia jest często stością wstępowania tego zdarzenia w bardzo dużej liczbie identcznch prób odejście subietwne Miara racjonalnego przeonania obserwatora esperta że zdarzenie wstąpi
6 sjomat rachunu prawdopodobieństwa sjomat : Każde zdarzenie losowe charaterzuje pewna liczba zwana prawdopodobieństwem zdarzenia spełniaj niająca nierówno wność. sjomat : rawdopodobieństwo zdarzenia pewnego równa się zaś zdarzenia niemożliwego wnosi. sjomat 3: rawdopodobieństwo sum zdarzeń parami włą łączającch cch się równe sumie prawdopodobieństw tch zdarzeń sjomat sąs podstawą wznaczania miar niepewności jaą jest prawdopodobieństwo w podejściu subietwnm 3 Rodzaje prawdopodobieństwa rawdopodobieństwo bezwarunowe wraża a stopień niepewności w stuacji brau jaicholwie innch informacji oznaczane przez jao miara przeonania o prawdziwości prz zupełnm brau innch obserwacji nazwane prawdopodobieństwem a priori rawdopodobieństwo warunowe wraża a stopień niepewności po zaobserwowaniu fatów dotczącch cch zdarzenia oznaczane przez jao miara przeonania o prawdziwości prz założeniu że z pewności cią zaszło nazwane prawdopodobieństwem a posteriori
7 4 rawdopodobieństwo warunowe Jeżeli eli uzsano informacje odnośnie nie nieznanch wcześniej fatów prawdopodobieństwo a priori musim zastąpi pić prawdopodobieństwem a posteriori warunowm zapiswanm wg notacji: tóra oznacza prawdopodobieństwo gd zaszło o. Wartość prawdopodobieństwa warunowego wnosi: = / bo w zbiorze wszstich zdarzeń w tórch zaobserwowano jest tąt częś ęścią z nich w tórch zaobserwowano równier wnież 5 Twierdzenia aesa rawdopodobieństwo ażdej hipotez można zdefiniować opierając c się na dowodach za lub przeciw tej hipotezie: Reguła a powższa wnia z prawdopod.. warunowch: po porównaniu ich stronami i podzieleniu przez >
8 Twierdzenia aesa jao reguła wniosowania 6 Twierdzenie aesa: odnosi się do zależno ności międz obserwacją a hipotezą reprezentowanej w postaci reguł: IF TN Ocenianie szans potencjalnch wniosów w hipoteza na podstawie danch obserwacja jest zatem zależne od fatcznego związu zu przcznowo-suto suto- wego międz nimi wartość oraz naszej wiedz niewiedz przjętej a priori oraz. Twierdzenia aesa - normalizacja 7 Możem uninąć onieczności ci szacowania prawdo- podobieństwa a priori wstąpienia obserwacji orzstając c z normalizacji będącej b onsewencją asjomatów w rachunu prawdopodobieństwa: a z twierdzenia aesa wiem że: dodając c obustronnie i wstawiając c otrzmane do w mianowniu otrzmam:
9 Twierdzenia aesa - marginalizacja 8 W pratce mam zazwczaj nie jedną hipotezę lecz zbiór r hipotez m m i jeżeli eli spełniaj niają one waruni: i j False i True i i j i to normalizacja opiera się na regule tzw.marginalizacji marginalizacji: i i i i twierdzenie aesa przjmuje wted postać: j i j j i i i m i o w stuacji gd mam wiele obserwacji? 9 Załóżm że e mam dwie reguł: IF smptomxból TN chorobaxpróchnica chnica IF smptomxubti TN chorobaxpróchnica chnica Ja wznaczć prawdopodobieństwo próchnic jeśli wstąpi pił obdwa objaw? Załadaj adając że e znam wartość próchniaból oraz próchnicaubti cz możem sorzstać z tw.aesa i asjomatów w prawdopodobieństwa? ból ubti próchnica próchnica próchnica ból ubti ból ubti
10 roblem z łączeniem obserwacji orządowanie obserwacji Zazwczaj onieczne jest uwzględnianie więszej liczb równoczesnch obserwacji n n w celu ustalania prawdopodobieństwa hipotez: n n n Zastosowanie powższego równania r w pratce dla dużej liczb obserwacji jest jedna bardzo trudne niezbędna jest bowiem znajomość prawdo- podobieństw dla wszstich ombinacji par i j tróje i j czwóre i j m itd. Liczba potrzebnch wartości prawdopodobieństw rośnie zatem władniczo z liczbą obserwacji!!! W wielu dziedzinach równoczesne r przetwarzanie obserwacji n n prz ustalaniu prawdopodo- bieństwa hipotez nie jest onieczne dane mogą bć przetwarzanie sewencjnie np. zgodnie z olejności cią ich uzsiwania rzetwarzanie obserwacji jedna po drugiej jest możliwe o ile uwzględnim że e hipoteza i olejna obserwacja warunowane są bazową wcześniejsz niejszą obserwacją :
11 Uogólnienie twierdzenia aesa Międz uwarunowaniem od obserwacji a uwarunowaniem od istnieje ścisła a zależno ność: z tórej wnia uogólniona postać twierdzenia aesa: bo: = na podstawie = oraz zależno ności wprowadzonej powżej. Zastosowanie uogólnionego twierdzenie aesa 3 Opierając c sewencjną atualizację prawdopodo- bieństw na uogólnionm twierdzeniu aesa zauważm że e dotchczasowe prawdopodobieństwo jest zawsze salowane przez cznni zależn od olejnej obserwacji: Duża a liczba obserwacji nadal jedna impliuje znaczną złożoność procesu atualizacji prawdopodobieństw
12 Założenie o warunowej niezależno ność obserwacji 4 Dalsze reduowanie wmagań dotczącch cch procesu atualizacja prawdopodobieństw możliwe jest jednie po przjęciu bardzo istotnego założenia o warunowej niezależno ności obserwacji n tórego spełnienie oznacza iż i : = oraz = a w onsewencji: = bo wiedząc że = z war. niezależno ności mam: = a po podzieleniu stronami przez i zastosowaniu tw.aesa otrzmam: = odobnie: = Twierdzenie aesa i założenie o warunowej niezależno ność 5 Założenie o warunowej niezależno ności obserwacji oznacza że e bez względu na liczbę obserwacji n spełnione sąs zależno ności: i n = i i j = i i j wówczas wczas tw.aesa przjmie postać: n n n Założenie o warunowej niezależno ności informacji jest luczowe bo dopiero wted możliwe jest efetwne worzstanie tw. aesa w pratce
13 Marginalizacja i założenie o warunowej niezależno ność 6 Wiem że e uwzględnienie zamiast jednej wielu hipotez m m wmaga użcia u reguł marginalizacji tóra wartości prawdopodobieństw pozwala wznaczć na podstawie łącznch rozład adów w hipotez i obserwacji: jej zastosowanie do wszstich obserwacji n pozwala wprowadzić najogólniejsz lniejszą postać tw. aesa: j i j i n i m n j j n i i i i i 8 Zalet podejścia baesowsiego Worzstuje technię opartą na ugruntowanej teorii prawdopodobieństwa Opiera się na danch deducjnch tóre uzsać dużo o prościej niż dane z abducji Worzstuje podejście subietwne do prawdopodobieństwa ale wsparte obecności cią danch rawdopodobieństwo hipotez zawsze może e zostać zatualizowane po zaobserwowaniu olejnch fatów Uzsane prawdopodobieństwa nie zależą od olejności napłwu informacji
14 9 Wad podejścia baesowsiego 3 Wad podejścia baesowsiego Założenia na tórch jest oparte asjomat rachunu prawdopodobieństwa sąs w pratce zazwczaj niespełnione nione Ignorancja niewiedza jest urta w prawdopodobieństwach a priori i nie jest przetwarzania bezpośrednio rawdopodobieństwa można oreśli lić jednie dla zdarzeń elementarnch a nie dla ich alternatw pod- zbiorów Informacje onflitowe nie sąs wrwane lecz propagowane przez reguł wniosowania Zawsze jest onieczna jest znajomość prawdopodo- bieństw a priori ojawienie się nowej hipotez wmaga zawsze atualizacji pozostałch prawdopodobieństw Założenie o warunowej niezależno ności w realnm świecie rzado jest spełnione ojedncze prawdopodobieństwo hipotez mówi m nam niewiele na temat jego preczji doładno adności
15 Wniosowanie w logice a wniosowanie baesowsie 3 MODULRNOŚĆ ŚĆ: W sstemach wniosowania logicznego do wprowadze- nia ze zdefiniowanej reguł IF TN wstarcz tlo ang.localit ang.localit Jeśli raz ważem prawdzi- wość jaiejś tez to można z niej sorzstać w olejnch dowodach bez potrzeb ponownego jej dowodzenia ang.detachment W logice prawdziwość zdań złożonch onch można wznaczć opierając c się na wartości logicznej ich sładowch NIMODULRNOŚĆ ŚĆ: W sstemach probabilist- cznch trzeba brać pod uwagę od razu wszstie dostępne przesłani Każda zmiana przesłane zmienia stopień przeonania o prawdziwość wprowadzonego twierdzenia Ogólnie w probabilistce nie jest spełniona ta własnow asność chba że e wprowadzim silne założenie o warunowej niezależno ności 3 Współcznni pewności
16 33 Model współcznnia pewności utorz: Shortliffe i uchanan 973 sstem MYIN Motwacją bła reducja danch potrzebna do wznaczania niepewności w stosunu do podejścia baesowsiego Uproszczenie obliczeń w stosunu do podejścia opartego na twierdzeniu aesa Interpretacja współcznnia pewności jao przrostu prawdopodobieństw warunowch Współcznni pewności F sojarzon jest z regułą postaci przesłana - hipoteza: IF TN Współcznni pewności ang.certaint factor 34 Współcznni pewności F to wielość liczbowa przpiswana regule o wartościach z przedziału [- ] reprezentująca zmianę wiargodności hipotez po zaobserwowaniu fatu. Współcznni oreśla zmianę ilościow ciową stopnia wiargodności hipotez jego atualizację po wstąpieniu obserwacji Dodatnie wartości F oznaczają wzrost wiargodności hipotez Ujemne wartości F oznaczają wzrost niewiargodności hipotez spade wiargodności
17 Reguł i współcznnii pewności 35 aza wiedz słada się z reguł tórm esperci przpisują współcznnii pewności postaci: Kluczowm elementem wniosowania w zbiorze reguł jest mechanizm propagacji niepewności przez sieć wniosowania na tór sładaj adają się funcje: Łączenia równolegr wnoległego ego informacji Łączenia szeregowego informacji ropagacja niepewności: połą łączenie równolegr wnoległe 36 Równoległe e połą łączenie: : dwie różne r obserwacje potwierdzają tę samą hipotezę F F F& & Wniow współcznni: F F F F & F F F F F min{ F F } F F F F F F
18 ropagacja niepewności: połą łączenie szeregowe 37 Szeregowe połą łączenie: : hipoteza jednej reguł staje się przesłan aną olejnej reguł F F F Wniow współcznni: F F F F F F F jeżeli eli nic nie wiadomo o F przjmujem że jest on równ r. Zmodfiowan model współcznnia pewności 38 W bazie wiedz oprócz reguł zazwczaj mam równier wnież fat tórm przpisujem tzw. miarę pewności ci: jest prawdziwe nic nie wiem o jest fałszwe rzpisanie miar pewności fatom wmaga zmian reprezentacji reguł: F Nowa postać reguł wmaga równier wnież zmian metod propagacji szeregowej i równolegr wnoległej ej
19 Zmodfiowana propagacja niepewności 39 ropagacja oreśla nową wartość miar pewności hipotez po ostatnio wonanej regule: F F F min{ F } gdzie F = F F F F prz czm jeśli jest negatwne to reguła a nie może bć odpalona co możem zapisać : F F ma{ } Miara pewności dla warunów w złożonchz onch 4 Jeżeli eli część warunowa reguł odwołuj uję się do więcej niż jednej obserwacji to onieczne jest wznaczenie miar pewności dla warunu złożonegoz onego wg zasad: min ma
20 odstawowe własnow asności współcznnia pewności 4 Funcja pewności jest odwzorowaniem ciągłm Nigd nie wchodzi poza zares [-;[ ] Gd albo albo F równe sąs to również wnosi Gd albo albo F równe sąs - to również wnosi - Gd mam sprzeczność reguł i hipotez czli F = to zawsze = Gd nic nie wiadomo o czli = to = F Gd obserwacja jest pewna czli = to F = F Współcznni pewności - przład 4 Rozważm przładow zbiór r fatów w o następuj pującch początowch miarach pewności: =.5 =.6 D= = = = F=. oraz zbiór r reguł: IF TN WIT F=.8 IF D TN WIT F=.7 IF TN F WIT F=.9
21 Współcznni pewności - przład 43 F F=. F=.9 = = F=.8 =.8 F=.7 D D= =.5 =.6 Współcznni pewności - przład 44 F F=. F=.9 = = F=.8 F=.7 =ma{.5.6}=.6 D D= =.5 =.6
22 45 Wsp Współcznni pewno cznni pewności ci - prz przład ad =.5 =.5 D F =.6 =.6 = = D= = = = F=. =. F F =.8*.6=.48 =.8*.6=.48 F F=.7 =.7 F F=.9 =.9 =.6 =.6 46 Wsp Współcznni pewno cznni pewności ci - prz przład ad =.5 =.5 D F =.6 =.6 =+ =+-*.48=.48 *.48=.48 D= = = = F=. =. F F =.48 =.48 F F=.7 =.7 F F=.9 =.9 =.6 =.6
23 47 Wsp Współcznni pewno cznni pewności ci - prz przład ad =.5 =.5 D F =.6 =.6 = = D= = =.48 =.48 F=. =. F F =.48 =.48 F F=F F =.7 =.7 F F=.9 =.9 =.6 =.6 48 Wsp Współcznni pewno cznni pewności ci - prz przład ad =.5 =.5 D F =.6 =.6 =+ =+-*.7=.7 *.7=.7 D= = F=. =. F F =.48 =.48 F F =.7 =.7 F F=.9 =.9 =.6 =.6 =.48 =.48
24 49 Wsp Współcznni pewno cznni pewności ci - prz przład ad =.5 =.5 D F =.6 =.6 =.7 =.7 D= = F=. =. F F =.48 =.48 F F =.7 =.7 F F=.9 =.9 =.6 =.6 =.48 =.48 =min{.48.7}=.48 =min{.48.7}=.48 5 Wsp Współcznni pewno cznni pewności ci - prz przład ad =.5 =.5 D F =.6 =.6 =.7 =.7 D= = F=. =. F F =.48 =.48 F F =.7 =.7 F F =.9*.48=.43 =.9*.48=.43 =.6 =.6 =.48 =.48 =.48 =.48
25 Współcznni pewności - przład 5 F F=.+-.*.43=.546.*.43=.546 F =.43 =.48 =.48 F =.48 =.6 D =.7 F =.7 D= =.5 =.6 Interpretacja probabilistczna współcznnia pewności ecerman 986 podał interpretację probabilistczną współcznnia pewności: F Wazał również że e orginalna interpretacja podana prze Shortliffe a i uchanana bła a błęb łędna Sformułowa ował asjomat dla współcznnia pewności i wazał iżi złożenie o modularności localit and detachment reguł ze współcznniiem pewności jest niezgodne z możliw liwą interpretacją probabilistczną 5
26 Słabości modelu opartego na współcznniach pewności 53 ecerman dowiódł że e gwarancja modularność reguł sprowadza się w gruncie rzecz do założenia o warunowej niezależno ności obserwacji i hipotez ja w podejściu baesowsim Wazał taże że e założenia sąs nawet mocniejsze warunowa niezależno ność obserwacji od hipotez ale również od negacji hipotez ecerman udowodnił również że e niezależnie od interpretacji nie można spełni nić wszstich asjomatów dotczącch cch propagacji współcznnia jeżeli eli sieć wniosowania nie ma strutur drzewa o z modelem współcznnia pewności? 54 omimo zarzutów ecermana współcznni pewności sprawdził się dobrze w pratcznch sstemach regułowch gdż wiedza w nich zawarta ma dużo więsz wpłw na jaość wniosowania niż sam mechanizm propagacji pewności rowadzono równier wnież prace zaończone sucesem w tórch wazano bra onieczności ci probabilistcznej interpretacji współcznnia pewności [maa ruz G.. eliaovg. 996]
27 55 Teoria Dempstera-Shafera 56 Teoria Dempstera-Shafera Model dopuszczając c częś ęściowe spełnienie asjomati probabilistcznej Wznacza prawdopodobieństwa z jaimi można udowodnić dane hipotez na podstawie posiadanch informacji ang. provabilit Wiedza jest reprezentowana w postaci funcji przeonania ang. belief oraz funcji wobrażalno alności ang. plausibilit
28 Teoria Dempstera-Shafera a probabilista 57 Teoria Dempstera-Shafera Shafera model częś ęściow bo: Zdarzenia nie muszą bć elementarne i wzajemnie wluczające ce się tlo taie o jaich posiadam informacje jest zbiór r tzw. elementów w ognisowch rzeonanie o prawdziwości hipotez i jej negacji nie muszą sumować się do Obie te wartości mogą wnosić zero ied bra dowodów zarówno za ja i przeciw hipotezie Teoria Dempstera-Shafera a twierdzenie aesa 59 Dla zbioru zdarzeń ={ ={... n } Twierdzenie aesa dotcz obserwacji wspierającch pojedncze hipotez ażda obserwacja ażdą hipotezę w zbiorze np.: Teoria Dempstera-Shafera dotcz obserwacji tóre wspierają podzbior hipotez np.: { 4 5 }
29 Funcja mas prawdopodobieństw 6 azow rozład prawdopodobieństwa dla tch zdarzeń dla tórch posiadam informację elementów ognisowch T musi spełnia niać waruni: m T : m [ ] m dla wszstich pozostałch T mam m=. Rozład ten reprezentuje częś ęściowe przeonania tórch nie musim bo bra wiedz! rozdzielać na elementarne zdarzenia 6 Funcja przeonania Funcja przeonania oznaczana w srócie el [ ] mierz siłę pozsanch informacji wspierającch przeonanie o prawdziwości rozważanego anego zbioru hipotez: el m Zależno ności dla el : el el el el el el
30 6 Funcja wobrażalno alności Funcja wobrażalno alności oznaczana w srócie l [] oreśla siłę informacji mającch jaiolwie związe ze ze zbiorem hipotez: l m Funcja l jest dualna względem el i można wazać że e zachodzi zależno ność: l el l oznacza zatem na ile przeonanie o prawdziwości jest ograniczone przez obserwacje wspierające Inne zależno ności: l l l l l l 63 rzeonanie i wobrażalno alność ewności niepewność ść oreślonej hipotez jest reprezentowana przez przedział: [el l ] el l Teoria Dempstera-Shafera pozwala wniosować o stopniu naszej pewności co do hipotez cz też pewności naszch przeonań co do hipotez Im szersz przedział tm więsza niepewność hipotez więsza ignorancja związana zana z hipotezą rzedział zerowej szeroości nie oznacza hipotez pewnej lecz preczjną wiedzę na temat prawdopodobieństwa hipotez
31 65 rzład Załóżm że e zmienna losowa może e przjmować wartości ze zbioru {abc}. Zbiór r wszstich możliwch podzbiorów w hipotez będzie zatem równ: r ={{ {{a} {b}{ {c}{ {ab}{ } {bc}{ {ac}{ {abc}}{ rzjmijm rozład bazow prawdopodobieństwa hipotez: m {a}. {b}. {c}. Zbiór r elementów w ognisowch: {ab} {ac} {bc} {abc}..3. T={{ {{a} {b}{ {c}{ {ab}{ } {bc}{ {abc}}{ 66 rzład Mając c rozład bazow prawdopodobieństwa: m {a}. {b}. {c}. {ab} {ac} {bc} {abc}..3. możem obliczć wartości funcji przeonania: el{b}= {b}=m{b}=.{b}=. el{ab}= {ab}=m{a}+m{b}+m{ab}=.+.+.=.5{ab}=.+.+.=.5 Rezultat: {a} m. el. {b}.. {c}.. {ab}..5 {ac}.3 {bc} {abc}.3..5
32 67 rzład Mając c rozład bazow prawdopodobieństwa: m {a}. {b}. {c}. {ab} {ac} {bc} {abc}..3. możem obliczć wartości funcji wobrażalno alności: l{a}= {a}=m{a}+m{ab}+m{abc}=.+.+.=.5{abc}=.+.+.=.5 Rezultat: m el l {a}...5 {b}...7 {c}...5 {ab}..5.9 {ac}.3.7 {bc} {abc} Łączenie obserwacji z różnch źródeł 68 Łączenie niepewności z różnch r źródeł opiera się na znajomości rozład adów w bazowch ażdego źródła W przpadu dwóch źródeł o rozładach m oraz m połą łączenie obserwacji pozwala wznaczć nową wartość m 3 wg wzoru: m 3 m m F m m F Każda olejna obserwacja może e bć łączona z wpadowm rozładem poprzednich obserwacji i prowadzić do następnego nowego rozładu
33 69 rzład łączenia obserwacji Załóżm że e zmienna losowa może e przjmować wartości ze zbioru {abc}. Zbiór r wszstich możliwch podzbiorów w hipotez będzie zatem równ: r ={{ {{a} {b}{ {c}{ {ab}{ } {bc}{ {ac}{ {abc}}{ rzjmijm że e mam dwa alternatwne źródła a obserwacji: m m {a}.. {b}.. {c}.. {ab}..3 {bc}.3. {abc}.. m {ac}= Mechanizm łączenia obserwacji opiera się na poszuiwaniu elementów w wspólnch tch obserwacji 7 rzład łączenia obserwacji {abc}. {bc}. {ab}.3 {c}. {b}. {a}. m m {a}. {b}. {c}. {ab}. {bc}.3 {abc}. rostoąt reprezen- tuje przecięcie cie zb. hipotez {b} oraz {ab} więc sprowadza się do {b} Wiedza o hipotezie jest rozproszona międz obserwa- cjami musim uwzględni dnić wszelie dane wspierające {b}
34 7 rzład łączenia obserwacji {abc}. {bc}. Suma wszelich danch wspierają- cch hipotezę {b} : {ab}.3 m m { b} { b} m m {c}. {b}. {a}. m m {a}. {b}. {c}. {ab}. {bc}.3 {abc}. le łączna suma nowch wartości wpadowch wszstich hipotez nie jest równa r bo mam puste przecięcia cia 7 rzład łączenia obserwacji {abc}. {bc}. {ab}.3 {c}. {b}. Konieczna jest normalizacja dzielim ażdą nową wartość przez łączn czną sumę nowch wartości wpado- wch wszstich hipotez: m m {a}. m m {a}. {b}. {c}. {ab}. {bc}.3 {abc}. czli pomniejszone o obszar wszstich pustch przecięć
35 73 rzład łączenia obserwacji {abc}. {bc}. {ab}.3 {c}. {b}. {a}. m m {a}. {b}. {c}. {ab}. {bc}.3 {abc}. Obszar pustch przecięć ęć: m m obszar {b}: { b} m m po normalizacji: rzład łączenia obserwacji {abc}. {bc}. Każdej hipotezie odpowiada pewien sumarczn obszar: {ab}.3 m { m a}.3 m { m b}.33 {c}. m { m c}.8 m { m ab}. {b}. {a}. m m {a}. {b}. {c}. {ab}. {bc}.3 {abc}. m { m bc}. m { m abc}.
36 75 rzład Mając c wpadow rozład bazow : m m el l {a} {b} 3/77 33/77 {a} {b} 3/77 33/77 3/77 5/77 33/77 56/77 {c} 8/77 {c} 8/77 8/77 /77 {ab} {ac} {bc} {abc} /77 /77 /77 możem obliczć wartości funcji przeonania i wobrażalno alności: Rezultat: {ab} {ac} {bc} {abc} /77 /77 /77 57/77 69/77 /77 33/77 5/77 64/77 77/77 77/77 8 Teoria zbiorów w rozmtch
37 Teoria zbiorów w rozmtch ang. fuzz set tpu 8 Opracowana przez L.. Zadeha w 965 owstała a w celu reprezentacji niepreczjności ci jęza j naturalnego ang. vagueness i jego pojęć Nie ma związu zu z żadnmi miarami prawdopodobieństwa Nie jest pojednczą teorią lecz raczej rodziną teorii 8 Zbiór r lasczn W lascznej teorii mnogości zbiór r jest charaterzo- wan przez binarną funcję prznależno ności elementów: : : U { } Funcja ta pozwala wtczć wraźną granicę międz tmi elementami przestrzeni/uniwersum tóre ang. universe of discource do zbioru należą i nie należą żą: U =
38 83 Zbiór r rozmt W przpadu oreśle leń jęzowch i smbolicznch! postaci wsoi wzrost nisa temperatura itp. podział elementów w na te należą żące do zbioru oraz te tóre nie należą nie jest preczjn Naturalnm wdaje się zatem rozszerzenie wartości jaie może e przjąć funcja prznależno ności do przedziału: : U [ ] zatem zbiór r rozmt w przestrzeni U gdzie U to zbiór r par: = { /:: } inaczej: = / w tórm : U [ ] 84 rzład zbiorów w rozmtch rzład W przestrzeni cfr dziesiętnch U={ 8 9} zdefiniujem w postaci zbioru rozmtego pojęcie cfra mała : = = =.9 3=.6 4=.3 5= 6= 7= 8= 9= inn zapis zbioru rozmtego : = / + / +.9/ +.6/3 +.3/4 + + /5 + /6 + /7 + /8 + /9 prz czm zna / nie oznacza dzielenia a + nie oznacza sum algebraicznej lecz teoriomnogościow ciową
39 85 rzład zbiorów w rozmtch Funcja prznależno ności może e bć również zdefiniowana dla zbioru o niesończonej liczbie elementów wted stosujem notację: = U / rzład W przestrzeni liczb rzeczwistch zdefiniujem w postaci zbioru rozmtego pojęcie liczba blisa 7 : 7 = + -7 = [+-7 ] - / Rozmte funcje prznależno ności Funcja singleton przjmuje postać: gd gd i reprezentuje ona doładnie jeden punt w przestrzeni rozważań tór w pełni należ do zbioru rozmtego; w pozostałch puntach przestrzeni jej wartość wnosi
40 87 Rozmte funcje prznależno ności Funcja las jest zdefiniowana przez funcję prznależno ności postaci: dla a a ; a b dla a b b a dla b gdzie a i b są parametrami funcji a b 88 Rozmte funcje prznależno ności Funcja las t jest zdefiniowana przez funcję prznależno ności postaci: dla a a dla a b t ; a b c b a c dla b c c b dla c a b c
41 89 Rozmte funcje prznależno ności Funcja las L jest zdefiniowana przez funcję prznależno ności postaci: b L ; a b c b a dla a dla a b dla b a b odstawowe pojęcia teorii zbiorów w rozmtch 9 Nośniiem zbioru rozmtego nazwam zbiór r tch elementów w przestrzeni U dla tórch > co zapisujem: supp = {{ U: > } Wsoość zbioru rozmtego oznaczam h i oreślam jao res górn g funcji : h sup U prz czm dla zbioru sończonego: h ma U
42 odstawowe pojęcia teorii zbiorów w rozmtch 9 Zbiór r rozmt nazwam normalnm jeżeli eli jego wsoość wnosi tzn. h = Zbiór r rozmt tór nie jest normaln możem zawsze znormalizować przez operację: norm h Zbiór r rozmt zawiera się w zbiorze rozmtm co zapisujem wted i tlo wted gd: UU 9 Operacje na zbiorach rozmtch Sumą zbiorów w rozmtch U nazwam zbiór rozmt o funcji prznależno ności = ma { { } rzecięciem ciem zbiorów w rozmtch U nazwam zbiór r rozmt o funcji prznależno ności = min { { } Uzupełnieniem dopełnieniem zbioru rozmtego U nazwam zbiór r rozmt ~ ~ o funcji prznależno ności ~ =
43 93 Operacje na zbiorach rozmtch Sumą zbiorów w rozmtch U nazwam zbiór rozmt o funcji prznależno ności = ma { { } Operacje na zbiorach rozmtch rzecięciem ciem zbiorów w rozmtch U nazwam zbiór r rozmt o funcji prznależno ności = min { { }
44 95 Operacje na zbiorach rozmtch Uzupełnieniem dopełnieniem zbioru rozmtego U nazwam zbiór r rozmt ~ ~ o funcji prznależno ności ~ = rzład operacji na zbiorach rozmtch 96 rzład Załóżm że U={3456} oraz =.9/3 + /4 +.6/6 =.7/3 + /5 +.4/6 Zgodnie z definicją mam: =.9/3 + /4 + /5 +.6/6 =.7/3 +.4/6 ~ = / + / +./3 + /5 +.4/6 Należ zauważć że: ~ = / + / +.9/3 + /4 + /5 +.6/6 U ~ =./3 +.4/6
45 97 Operacje na zbiorach rozmtch Ilocznem artezjańsim zbiorów w rozmtch U nazwam zbiór r rozmt o funcji prznależno ności = min { { } rzład Załóżm że e mam: =.5/ +.9/4 =.3/ +.7/4 +./6 Zgodnie z definicją mam: =.3/ +.5/4 +./ /4 +.7/44 +./46 98 Zasada rozszerzania Załóżm że e dane jest nierozmte odwzorowanie f przestrzeni U w przestrzeń Y : f : U Y oraz zbiór r rozmt U : = / Zbiór r rozmt induowan przez to odwzorowanie i oreślon w przestrzeni Y jest postaci: = f = f /f gdzie: sup gd f f f gd f
46 rzład zastosowania zasad rozszerzania 99 rzład Załóżm że =./3 +.4/ +.7/5 oraz f = + wted zgodnie z definicją mam: = f =./7 +.4/5 +.7/ rzład ied odwzorowanie f nie jest wzajemnie jednoznaczne! Załóżm że =.3/- +.5/3 +.7/ oraz f = wted zgodnie z definicją mam: = f =.5/9 + ma.3;.7/4 = =.5/9 +.7/4 rzład zastosowania zasad rozszerzania rzład Załóżm że e przestrzeń U jest postaci U U i zbiór r rozmt U reprezentuje liczb blisie liczbie =.7/ + / +.8/3 zaś zbiór U liczb blisie liczbie 3 3 =.8/ + /3 +.6/4 oraz = f = wted zbiór będzie zbiorem rozmtm liczb blisich liczbie 6 6 postaci: = f = min.7;.8/ + min.7;/3 + + mamin.7;.6;min;.8/4+ + mamin;;min.8;.8/6+ + min;.6/8 + min.8;/9 + min.8;.6/ = =.7/ +.7/3 +.8/4 + /6 +.6/8 +.8/9 +.6/
47 Liczb rozmte Zbiór r rozmt oreślon na zbiorze liczb rzeczwistch tai tórego funcja prznależno ności: : [; ] spełnia waruni: zbiór jest normaln tzn. h= zbiór jest wpuł 3 funcja jest przedziałami ami ciągła nazwam liczbą rozmtą Liczb rozmte Liczba rozmta jest dodatnia jeżeli eli = Liczba rozmta jest ujemna jeżeli eli = Liczba ujemna Liczba ani ujemna ani dodatnia Liczba dodatnia
48 odstawowe operacje na liczbach rozmtch 3 Definicja wszstich operacji na liczbach rozmtch jest onsewencją zastosowania zasad rozszerzania dla operatorów w unarnch mam: = / gdzie = a dla operatorów w binarnch: = z/ gdzie z sup min{ ; } z oraz oznacza operator np. +-/ / itp. rzład operacji na liczbach rozmtch 4 rzład Załóżm że e dane sąs dwie liczb rozmte =.7/ + /3 +.6/4 =.8/3 + /4 +.5/6 tóre należ dodać do siebie co oznaczm operatorem rozmtm. Zgodnie z definicją otrzmam: = min.7;.8/5 + mamin.7;;min;.8/6 + + mamin;;min.6;.8/7+ + mamin.7;.5;min.6;/8+ + min;.5/9 + min.6;.5/ = =.7/5 +.8/6 + /7 +.6/8 +.5/9 +.5/
49 5 Relacja rozmta Relacją rozmtą R międz dwoma niepustmi zbiorami nierozmtmi z przestrzeni X i Y nazwam dowoln zbiór r rozmt oreślon na ilocznie artezjańsim X Y tzn. R X Y = {: X Y} czli relacja rozmta jest zbiorem par: R = {: R } X Y gdzie R : X Y [; ] jest funcją prznależno ności Należ podreśli lić że e relacja rozmta jest zbiorem rozmtm więc c obowiązuj zują dla niej podane wcześniej definicje przecięcia cia sum i dopełnienia 7 rzład relacji rozmtej rzład Załóżm że X = Y = [; ] oznacza długod ugość żcia człowiea wówczas w wczas relacja R o funcji prznależno ności: R 3 dla dla 3 dla 3 może e bć uznana za reprezentację niepreczjnego porównania w postaci sformułowania owania osoba jest dużo o starsza od osob.
50 8 Złożenie zbioru i relacji rozmtej Złożenie relacji rozmtej R X Y i relacji rozmtej S Y Z tóre oznaczam RS jest relacją rozmtą RS X Z o funcji prznależno ności postaci: R S z sup min{ R ; S z } Złożenie zbioru rozmtego X i relacji rozmtej R X Y tóre oznaczam R jest zbiorem rozmtm Y o funcji prznależno ności postaci: sup min{ ; } Y X W teorii zbiorów w rozmtch znane sąs też inne alternatwne definicje złożenia z relacji rozmtej R 9 rzład relacji rozmtej rzład Załóżm że e dane sąs dwie relacje rozmte R i S reprezentowane przez macierze: R S złożenie Q tch relacji będzie b miało o postać:. Q R S.6 gdzie: q.4 q q q q q 3 3
51 rzład relacji rozmtej ciąg g dalsz przładu zatem: q = mamin.;.3; min.5;.7 =.5 q = mamin.;.6; min.5;.9 =.5 q = mamin.;.8; min.5;.4 =.4 q = mamin.6;.3; min;.7 =.7 q = mamin.6;.6; min;.9 =.9 q = mamin.6;.8; min;.4 =.6.5 Q Wniosowania rozmte Rozmtą regułą odrwania nazwam regułę o następuj pującm schemacie wniosowania is przesłana impliacja IF is TN is wniose is gdzie X oraz Y są zbiorami rozmtmi natomiast są tzw. zmiennmi lingwistcznmi Zmienne lingwistczne to taie zmienne tóre przjmują jao wartość słowa lub zdania z jęza j naturalnego tórm odpowiadają zbior rozmte np. zmienna hałas as może e przjmować wartości { mał średni średniowsoi wsoi }
52 Wniosowania rozmte W rozmtej regule odrwania w przeciwieństwie do tradcjnej reguł modus ponens przesłana nie odnosi się do zbioru tór wstępuje w warunu impliacji lecz do innego zbioru odobnie wniose nie odnosi się do wniu impliacji lecz do innego zbioru tór oreślon jest przez złożenie zbioru rozmtego i rozmtej impliacji tzn. = Impliacja rozmta jest zatem rodzajem relacji rozmtej R X Y o funcji prznależno ności R= więc c z definicji złożenia z relacji rozmtch mam: sup min{ ; } X 3 Impliacja jao relacja rozmta Funcja prznależno ności onluzji rozmtej reguł odrwania zależ od funcji prznależno ności impliacji tóra może e bć definiowana w różn r sposób Najczęś ęściej worzstwan jest tzw. model Mamdaniego w tórm wróżniam dwie definicje: reguła a tpu minimum = = min { { } reguła a tpu iloczn Larsena Larsena =
53 4 Impliacja jao relacja rozmta Należ podreśli lić że e reguł tpu Mamdaniego nie sąs impliacjami w sensie logicznm co ilustruje tabela: min { { } Istnieje szereg definicji impliacji rozmtej tóre w przeciwieństwie do reguł Mamdaniego są impliacjami logicznmi model logiczn ale nie znalazł one za- stosowania pratcznego np. impliacja Łuasiewicza: = min {; - + } rchitetura rozmtego sstemu wniosowania 5 aza reguł lo rozmwania X Mechanizm wniosowania Y lo wostrzania
54 6 Rozmta baza reguł aza reguł rozmtch oreślana równier wnież mianem modelu lingwistcznego słada się z reguł rozmtch następuj pującej postaci: IF is ND is ND ND n is n TN is gdzie i X oraz Y są zbiorami rozmtmi natomiast i zmiennmi wejściowmi modelu lingwistcznmi zmienną wjściow ciową modelu lingwistcznego Załadam adam że e reguł z bazie wiedz sąs powiązane operatorem logicznm dsjuncji oraz zmienne wjściowe sąs wzajemnie niezależne ne 7 Rozmta reguła Regułę rozmtą postaci: IF is ND is ND ND n is n TN is przjmując c oznaczenie: = n oraz odpowiednio X = X X X n możem przedstawić jao rozmtą impliację R: gdzie R jest rodzajem relacji rozmtej oreślonej na zbiorze X Y tzn. R X Y jest zbiorem rozmtm o funcji prznależno ności: R = gdzie = [[ n ] T
55 8 lo rozmwania lo rozmwania X Na wejściu rozmtego sstemu wniosującego podawan jest nierozmt sgnał: T... X tór podlega operacji rozmwania ang. fuzzifica- tion w celu odwzorowania na zbiór r rozmt X = X X X n Najczęś ęściej worzstwaną operacją rozmwania jest rozmwanie tpu singleton: gd gd n 9 lo wniosowania Na wejściu blou rozmtego wniosowania mam zbiór r rozmt X = X X X n Na wjściu blou wniosowania otrzmujem jeden zbiór r rozmt Y oreślon zależno nością: N N N R X Mechanizm wniosowania Y gdzie N jest liczbą reguł rozmtch oraz X Y zaś jego funcja prznależno ności przjmuje postać: ma sup min{ ; }... N X
56 rz rzład wniosowania ad wniosowania Niech dane b Niech dane będą dwie regu dwie reguł rozmte: rozmte: a sgna a sgnał wj wjściow blou wniosowania b ciow blou wniosowania będzie wnosi dzie wnosił: } ; ma{ } ; ma{ is is is : is is is : R R TN ND IF TN ND IF is is is : is is is : R R TN ND IF TN ND IF na wej na wejście sstemu podano sgna cie sstemu podano sgnał. Dla operacji rozmwania tpu Dla operacji rozmwania tpu singleton singleton wej wejście blou cie blou wniosowania to wniosowania to zb zb. rozmte z funcjami prznale. rozmte z funcjami prznależno ności: ci: T T gdzie: gdzie: }] ; [min{ sup X X }] ; [min{ sup X X rz rzład wniosowania ad wniosowania oniewa onieważ: } ; min{ } ; min{ } ; min{ } ; min{ } ; ; min{ sup X X } ; ; min{ sup X X to: to: Dla Dla regu reguł minimum minimum tpu tpu Mamdaniego Mamdaniego otrzmam: otrzmam: } ; ; min{ } }; ; min{min{ } ; min{ } ; ; min{ } }; ; min{min{ } ; min{ Ostatecznie: Ostatecznie: }} ; ; ma{min{ }} ; ; ma{min{
57 Graficzna interpretacja przładu dla reguł minimum min min ma 3 rzład wniosowania Jeżeli eli dla impliacji zastosujem regułę tpu iloczn Larsena otrzmam: min{ ; min{ Ostatecznie: } ; } ma{ min{ ; }}
58 Graficzna interpretacja przładu dla ilocznu Larsena Larsena 4 min min ma 5 rzład wniosowania Jeśli użjem u innej niż singleton operacji rozmwania na wejściu blou wniosowania pojawią się liczb rozmte oraz o funcjach prznależno ności oraz. W efecie: sup X X sup X X min X X min sup X sup X X [min{min[ [min{ sup [min{ min{ ; ; ; ; }] ; ; ; }] min{ ; } ; sup min{ ; } ma min sup X X ];min[ ; ; ; ; } ; ]}] ; min{ ; ; sup min{ ; ; X
59 Graficzna interpretacja przładu dla reguł minimum 6 sup ix i min{ i ; i i i min ma 7 lo wostrzania Y lo wostrzania Na wejściu blou wostrzania mam zbiór r rozmt Y z funcją prznależno ności tór trzeba odwzorować w jedną wartość Y Najczęś ęściej worzstwana jest metoda środa cięż ężości funcji prznależno ności postaci gdzie tzn. N N jest nazwane środiem zbioru rozmtego arg ma{ }
60 9 Interpretacja graficzna operacji Interpretacja graficzna operacji wostrzania wostrzania is is is : is is is : R R TN ND IF TN ND IF is is is : is is is : R R TN ND IF TN ND IF Dla prz Dla przładu z adu z dwoma regu dwoma regułami: ami:
Wstęp do Sztucznej Inteligencji: Laboratorium Sterownik rozmyty
 Wstęp do Sztucznej Inteligencji: Laboratorium Sterowni rozmt Zbior rozmte pozwalają w sposób usstematzowan modelować pojęcia niepreczjne, jaimi ludzie posługują się na co dzień. Przładem może bć wrażenie
Wstęp do Sztucznej Inteligencji: Laboratorium Sterowni rozmt Zbior rozmte pozwalają w sposób usstematzowan modelować pojęcia niepreczjne, jaimi ludzie posługują się na co dzień. Przładem może bć wrażenie
Definicja. Złożenie zbioru rozmytego i relacji rozmytej. Rozważmy. zbiór rozmyty A X z funkcją przynależności
 Zagadnienia I Złożenie zbioru rozmtego i relacji rozmtej Rozważm zbiór rozmt X z funcją prznależności relację rozmtą RX Y z funcją prznależności Definicja R Złożenie zbioru rozmtego i relacji rozmtej R
Zagadnienia I Złożenie zbioru rozmtego i relacji rozmtej Rozważm zbiór rozmt X z funcją prznależności relację rozmtą RX Y z funcją prznależności Definicja R Złożenie zbioru rozmtego i relacji rozmtej R
ELEMENTY TEORII ZBIORÓW ROZMYTYCH
 ELEMENTY TEORII ZBIORÓW ROZMYTYCH OPRACOWAŁ: M. KWIESIELEWICZ POJĘCIA NIEPRECYZYJNE ODDZIAŁYWANIA CZŁOWIEK-OBIEKT TECHNICZNY OTOCZENIE (Hoang 990: człowieka na otoczenie, np.: ergonomiczna konstrukcja
ELEMENTY TEORII ZBIORÓW ROZMYTYCH OPRACOWAŁ: M. KWIESIELEWICZ POJĘCIA NIEPRECYZYJNE ODDZIAŁYWANIA CZŁOWIEK-OBIEKT TECHNICZNY OTOCZENIE (Hoang 990: człowieka na otoczenie, np.: ergonomiczna konstrukcja
Zmienna losowa. M. Przybycień Rachunek prawdopodobieństwa i statystyka
 Zmienna losowa ozszerzenie znaczenia funcji zmiennej rzeczwistej na przpadi, ied zmienna niezależna nie jest liczbą rzeczwistą: odległość to funcja par puntów, obwód trójąta, to funcja oreślona na zbiorze
Zmienna losowa ozszerzenie znaczenia funcji zmiennej rzeczwistej na przpadi, ied zmienna niezależna nie jest liczbą rzeczwistą: odległość to funcja par puntów, obwód trójąta, to funcja oreślona na zbiorze
Teoria zbiorów w rozmytych
 8 Teori ziorów w rozmtch Teori ziorów w rozmtch ng. fuzz set tpu 8 Oprcown przez L.. Zdeh w 965 Powstł w celu reprezentcji niepreczj ci jęz j nturlnego ng. vgueness i jego pojęć Nie m związu zu z Ŝdnmi
8 Teori ziorów w rozmtch Teori ziorów w rozmtch ng. fuzz set tpu 8 Oprcown przez L.. Zdeh w 965 Powstł w celu reprezentcji niepreczj ci jęz j nturlnego ng. vgueness i jego pojęć Nie m związu zu z Ŝdnmi
Logika klasyczna i rozmyta. Rozmyte złożenie relacji (ang. fuzzy composition) Złożenie relacji (ang. composition)
 Złożenie relacji ang. compoition) Niech X Y, Y Z. Ptanie: X Z? Cz można znaleźć taą relację, tóra wiąże te ame element z X, tóre zawiera z tmi ammi elementami z Z, tóre zawiera? Czli cz zuam X Z. Przład
Złożenie relacji ang. compoition) Niech X Y, Y Z. Ptanie: X Z? Cz można znaleźć taą relację, tóra wiąże te ame element z X, tóre zawiera z tmi ammi elementami z Z, tóre zawiera? Czli cz zuam X Z. Przład
RÓWNANIA RÓŻNICZKOWE WYKŁAD 3
 RÓWNANIA RÓŻNICZKOWE WYKŁAD 3 Równania różniczkowe liniowe Metoda przewidwań Metoda przewidwań całkowania równania niejednorodnego ' p( x) opiera się na następującm twierdzeniu. Twierdzenie f ( x) Suma
RÓWNANIA RÓŻNICZKOWE WYKŁAD 3 Równania różniczkowe liniowe Metoda przewidwań Metoda przewidwań całkowania równania niejednorodnego ' p( x) opiera się na następującm twierdzeniu. Twierdzenie f ( x) Suma
A i A j lub A j A i. Operator γ : 2 X 2 X jest ciągły gdy
 3. Wyład 7: Inducja i reursja struturalna. Termy i podstawianie termów. Dla uninięcia nieporozumień notacyjnych wprowadzimy rozróżnienie między funcjami i operatorami. Operatorem γ w zbiorze X jest funcja
3. Wyład 7: Inducja i reursja struturalna. Termy i podstawianie termów. Dla uninięcia nieporozumień notacyjnych wprowadzimy rozróżnienie między funcjami i operatorami. Operatorem γ w zbiorze X jest funcja
Podstawy rachunku prawdopodobieństwa (przypomnienie)
 . Zdarzenia odstawy rachunu prawdopodobieństwa (przypomnienie). rawdopodobieństwo 3. Zmienne losowe 4. rzyład rozładu zmiennej losowej. Zdarzenia (events( events) Zdarzenia elementarne Ω - zbiór zdarzeń
. Zdarzenia odstawy rachunu prawdopodobieństwa (przypomnienie). rawdopodobieństwo 3. Zmienne losowe 4. rzyład rozładu zmiennej losowej. Zdarzenia (events( events) Zdarzenia elementarne Ω - zbiór zdarzeń
Wektory. P. F. Góra. rok akademicki
 Wektor P. F. Góra rok akademicki 009-0 Wektor zwiazan. Wektorem zwiazanm nazwam parę punktów. Jeżeli parę tę stanowią punkt,, wektor przez nie utworzon oznaczm. Graficznie koniec wektora oznaczam strzałką.
Wektor P. F. Góra rok akademicki 009-0 Wektor zwiazan. Wektorem zwiazanm nazwam parę punktów. Jeżeli parę tę stanowią punkt,, wektor przez nie utworzon oznaczm. Graficznie koniec wektora oznaczam strzałką.
Całkowanie przez podstawianie i dwa zadania
 Całkowanie przez podstawianie i dwa zadania Antoni Kościelski Funkcje dwóch zmiennch i podstawianie Dla funkcji dwóch zmiennch zachodzi następując wzór na całkowanie przez podstawianie: f(x(a, b), (a,
Całkowanie przez podstawianie i dwa zadania Antoni Kościelski Funkcje dwóch zmiennch i podstawianie Dla funkcji dwóch zmiennch zachodzi następując wzór na całkowanie przez podstawianie: f(x(a, b), (a,
Matematyka dyskretna. Wykład 2: Kombinatoryka. Gniewomir Sarbicki
 Matematya dysretna Wyład 2: Kombinatorya Gniewomir Sarbici Kombinatorya Definicja Kombinatorya zajmuje się oreślaniem mocy zbiorów sończonych, w szczególności mocy zbiorów odwzorowań jednego zbioru w drugi
Matematya dysretna Wyład 2: Kombinatorya Gniewomir Sarbici Kombinatorya Definicja Kombinatorya zajmuje się oreślaniem mocy zbiorów sończonych, w szczególności mocy zbiorów odwzorowań jednego zbioru w drugi
14. Grupy, pierścienie i ciała.
 4. Grup, pierścienie i ciała. Definicja : Zbiór A nazwam grupą jeśli jest wposaŝon w działanie wewnętrzne łączne, jeśli to działanie posiada element neutraln i kaŝd element zbioru A posiada element odwrotn.
4. Grup, pierścienie i ciała. Definicja : Zbiór A nazwam grupą jeśli jest wposaŝon w działanie wewnętrzne łączne, jeśli to działanie posiada element neutraln i kaŝd element zbioru A posiada element odwrotn.
Ekstrema funkcji dwóch zmiennych
 Wkład z matematki inżnierskiej Ekstrema funkcji dwóch zmiennch JJ, IMiF UTP 18 JJ (JJ, IMiF UTP) EKSTREMA 18 1 / 47 Ekstrema lokalne DEFINICJA. Załóżm, że funkcja f (, ) jest określona w pewnm otoczeniu
Wkład z matematki inżnierskiej Ekstrema funkcji dwóch zmiennch JJ, IMiF UTP 18 JJ (JJ, IMiF UTP) EKSTREMA 18 1 / 47 Ekstrema lokalne DEFINICJA. Załóżm, że funkcja f (, ) jest określona w pewnm otoczeniu
L.Kowalski zadania z rachunku prawdopodobieństwa-zestaw 4 ZADANIA - ZESTAW 4
 ZADANIA - ZESTAW 4 Zadanie 4. 0-0,4 c 0 0, 0, Wznacz c. Wznacz rozkład brzegowe. Cz, są niezależne? (odp. c = 0,3 Zadanie 4.- 0-0,4 0,3 0 0, 0, Wznaczć macierz kowariancji i korelacji. Cz, są skorelowane?
ZADANIA - ZESTAW 4 Zadanie 4. 0-0,4 c 0 0, 0, Wznacz c. Wznacz rozkład brzegowe. Cz, są niezależne? (odp. c = 0,3 Zadanie 4.- 0-0,4 0,3 0 0, 0, Wznaczć macierz kowariancji i korelacji. Cz, są skorelowane?
STANDARDOWE FUNKCJE PRZYNALEŻNOŚCI. METODY HEURYSTYCZNE wykład 6. (alternatywa dla s) (zdef. poprzez klasę s) GAUSSOWSKA F.
 METODY HEURYSTYCZNE wykład 6 STANDARDOWE FUNKCJE PRZYNALEŻNOŚCI 2 GAUSSOWSKA F. PRZYNALEŻNOŚCI F. PRZYNALEŻNOŚCI KLASY s środek; a określa szerokość krzywej 3 4 F. PRZYNALEŻNOŚCI KLASY π F. PRZYNALEŻNOŚCI
METODY HEURYSTYCZNE wykład 6 STANDARDOWE FUNKCJE PRZYNALEŻNOŚCI 2 GAUSSOWSKA F. PRZYNALEŻNOŚCI F. PRZYNALEŻNOŚCI KLASY s środek; a określa szerokość krzywej 3 4 F. PRZYNALEŻNOŚCI KLASY π F. PRZYNALEŻNOŚCI
Sterowanie rozmyte. mgr inż. Piotr Fiertek p. 544
 Sterowanie rozmte mgr inż. Piotr iertek p. 544 Literatura do wkładu: D. Driankov H. Hellendoorn M. einfrank Wprowadzenie do sterowania ozmtego Wdawnictwo Naukowo-Techniczne Warszawa 996 Piegat A.: Modelowanie
Sterowanie rozmte mgr inż. Piotr iertek p. 544 Literatura do wkładu: D. Driankov H. Hellendoorn M. einfrank Wprowadzenie do sterowania ozmtego Wdawnictwo Naukowo-Techniczne Warszawa 996 Piegat A.: Modelowanie
Zagadnienia AI wykład 3
 Zagadnienia I wyład 3 Rozmyte systemy wniosujące by móc sterować pewnym procesem technologicznym lub tez pracą urządzeń onieczne jest zbudowanie modelu, na podstawie tórego można będzie podejmować decyzje
Zagadnienia I wyład 3 Rozmyte systemy wniosujące by móc sterować pewnym procesem technologicznym lub tez pracą urządzeń onieczne jest zbudowanie modelu, na podstawie tórego można będzie podejmować decyzje
Metoda podziału zbioru obiektów na wielokryterialne klastry jakościowe
 BIULET ISTTUTU SSTEMÓW IFOMATCZCH (03) Metoda podziału zbioru obietów na wielorterialne lastr jaościowe A. AMELJAŃCZK aameljancz@wat.edu.pl Insttut Sstemów Informatcznch Wdział Cberneti WAT ul. S. Kalisiego,
BIULET ISTTUTU SSTEMÓW IFOMATCZCH (03) Metoda podziału zbioru obietów na wielorterialne lastr jaościowe A. AMELJAŃCZK aameljancz@wat.edu.pl Insttut Sstemów Informatcznch Wdział Cberneti WAT ul. S. Kalisiego,
Zasada rozszerzania. A U A jest zbiorem rozmytym, B jest obrazem zbioru A Przeniesienie rozmytości A w odwzorowaniu f na zbiór B. sup.
 Zasada rozszerzania f U V U jest zbiorem rozmytym V = f( ), jest obrazem zbioru Przeniesienie rozmytości w odwzorowaniu f na zbiór v) = ( v)? ( f ( ) = sup ( u) gdy ( v) 0 1 = 1 u f ( v) f( ) ( v) 1 0
Zasada rozszerzania f U V U jest zbiorem rozmytym V = f( ), jest obrazem zbioru Przeniesienie rozmytości w odwzorowaniu f na zbiór v) = ( v)? ( f ( ) = sup ( u) gdy ( v) 0 1 = 1 u f ( v) f( ) ( v) 1 0
σ-ciało zdarzeń Niech Ω będzie niepustym zbiorem zdarzeń elementarnych, a zbiór F rodziną podzbiorów zbioru Ω spełniającą warunki: jeśli A F, to A F;
 Zdarzenie losowe i zdarzenie elementarne Zdarzenie (zdarzenie losowe) - wyni pewnej obserwacji lub doświadczenia; może być ilościowy lub jaościowy. Zdarzenie elementarne - najprostszy wyni doświadczenia
Zdarzenie losowe i zdarzenie elementarne Zdarzenie (zdarzenie losowe) - wyni pewnej obserwacji lub doświadczenia; może być ilościowy lub jaościowy. Zdarzenie elementarne - najprostszy wyni doświadczenia
Wykład 4 Testy zgodności. dystrybuanta rozkładu populacji dystrybuanty rozkładów dwóch populacji rodzaj rozkładu wartości parametrów.
 Wkład Test zgodności. Test zgodności służą do werikacji hipotez mówiącch, że a dstrbuanta rozkładu populacji ma określoną z gór postać unkcjną b dstrbuant rozkładów dwóch populacji nie różnią się w sposób
Wkład Test zgodności. Test zgodności służą do werikacji hipotez mówiącch, że a dstrbuanta rozkładu populacji ma określoną z gór postać unkcjną b dstrbuant rozkładów dwóch populacji nie różnią się w sposób
Technologie i systemy oparte na logice rozmytej
 Zagadnienia I Technologie i systemy oparte na logice rozmytej Mają zastosowania w sytuacjach kiedy nie posiadamy wystarczającej wiedzy o modelu matematycznym rządzącym danym zjawiskiem oraz tam gdzie zbudowanie
Zagadnienia I Technologie i systemy oparte na logice rozmytej Mają zastosowania w sytuacjach kiedy nie posiadamy wystarczającej wiedzy o modelu matematycznym rządzącym danym zjawiskiem oraz tam gdzie zbudowanie
Pierwiastki kwadratowe z liczby zespolonej
 Pierwiastki kwadratowe z liczb zespolonej Pierwiastkiem kwadratowm z liczb w C nazwam każdą liczbę zespoloną z C, dla której z = w. Zbiór wszstkich pierwiastków oznaczam smbolem w. Innmi słow w = {z C
Pierwiastki kwadratowe z liczb zespolonej Pierwiastkiem kwadratowm z liczb w C nazwam każdą liczbę zespoloną z C, dla której z = w. Zbiór wszstkich pierwiastków oznaczam smbolem w. Innmi słow w = {z C
Rozkład normalny (Gaussa)
 Rozład ormal (Gaussa Wprowadzeie rozładu Gaussa w modelu Laplace a błędów pomiarowch. Rozważm pomiar wielości, tór jest zaburza przez losowch efetów o wielości ε ażd, zarówo zaiżającch ja i zawżającch
Rozład ormal (Gaussa Wprowadzeie rozładu Gaussa w modelu Laplace a błędów pomiarowch. Rozważm pomiar wielości, tór jest zaburza przez losowch efetów o wielości ε ażd, zarówo zaiżającch ja i zawżającch
25. RÓWNANIA RÓŻNICZKOWE PIERWSZEGO RZĘDU. y +y tgx=sinx
 5. RÓWNANIA RÓŻNICZKOWE PIERWSZEGO RZĘDU 5.1. Pojęcia wstępne. Klasfikacja równań i rozwiązań Rozróżniam dwa zasadnicze tp równań różniczkowch: równania różniczkowe zwczajne i równania różniczkowe cząstkowe.
5. RÓWNANIA RÓŻNICZKOWE PIERWSZEGO RZĘDU 5.1. Pojęcia wstępne. Klasfikacja równań i rozwiązań Rozróżniam dwa zasadnicze tp równań różniczkowch: równania różniczkowe zwczajne i równania różniczkowe cząstkowe.
SKRYPT Z MATEMATYKI. Wstęp do matematyki. Rafał Filipów Piotr Szuca
 Publikacja współfinansowana przez Unię Europejską w ramach Europejskiego Funduszu Społecznego SKRYPT Z MATEMATYKI Wstęp do matematki Rafał Filipów Piotr Szuca Publikacja współfinansowana przez Unię Europejską
Publikacja współfinansowana przez Unię Europejską w ramach Europejskiego Funduszu Społecznego SKRYPT Z MATEMATYKI Wstęp do matematki Rafał Filipów Piotr Szuca Publikacja współfinansowana przez Unię Europejską
Rysunek 1-1. Przykładowy zbiór klasyczny (nierozmyty) oraz jego funkcja przynale żności.
 Podstaw logiki rozmtej i regulatorów rozmtch. Zbiór rozmt Pojęcie zbioru rozmtego zostało wprowadzone przez L. A. Zadeha w 965. Celem wprowadzenia tego pojęcia bła chęć modelowania procesów złożonch, w
Podstaw logiki rozmtej i regulatorów rozmtch. Zbiór rozmt Pojęcie zbioru rozmtego zostało wprowadzone przez L. A. Zadeha w 965. Celem wprowadzenia tego pojęcia bła chęć modelowania procesów złożonch, w
4. Schematy blokowe; algebra schematów blokowych
 57. Schemat bloowe; algebra chematów bloowch W ażdm złożonm ładzie atomati można wodrębnić wpółpracjące ze obą element protze, tórch właściwości ą znane i formłowane np. w potaci tranmitancji operatorowej.
57. Schemat bloowe; algebra chematów bloowch W ażdm złożonm ładzie atomati można wodrębnić wpółpracjące ze obą element protze, tórch właściwości ą znane i formłowane np. w potaci tranmitancji operatorowej.
Zadania do rozdziału 10.
 Zadania do rozdziału 0. Zad.0.. Jaką wsokość musi mieć pionowe zwierciadło ab osoba o wzroście.80 m mogła się w nim zobaczć cała. Załóżm, że ocz znajdują się 0 cm poniżej czubka głow. Ab prawidłowo rozwiązać
Zadania do rozdziału 0. Zad.0.. Jaką wsokość musi mieć pionowe zwierciadło ab osoba o wzroście.80 m mogła się w nim zobaczć cała. Załóżm, że ocz znajdują się 0 cm poniżej czubka głow. Ab prawidłowo rozwiązać
Rozkład normalny (Gaussa)
 Rozład ormal (Gaussa Wprowadzeie rozładu Gaussa w modelu Laplace a błędów pomiarowch. Rozważm pomiar wielości, tór jest zaburza przez losowch efetów o wielości ε ażd, zarówo zaiżającch ja i zawżającch
Rozład ormal (Gaussa Wprowadzeie rozładu Gaussa w modelu Laplace a błędów pomiarowch. Rozważm pomiar wielości, tór jest zaburza przez losowch efetów o wielości ε ażd, zarówo zaiżającch ja i zawżającch
Metody numeryczne. Wykład nr 2. dr hab. Piotr Fronczak
 Metod numerczne Wład nr dr hab. Piotr Froncza Przbliżone rozwiązwanie równań nieliniowch Jedno równanie z jedną niewiadomą Szuam pierwiastów rzeczwistch równania =. zwle jest uncją nieliniową zatem orzstam
Metod numerczne Wład nr dr hab. Piotr Froncza Przbliżone rozwiązwanie równań nieliniowch Jedno równanie z jedną niewiadomą Szuam pierwiastów rzeczwistch równania =. zwle jest uncją nieliniową zatem orzstam
Programowanie nieliniowe optymalizacja funkcji wielu zmiennych
 Ekonomia matematczna II Ekonomia matematczna II Prowadząc ćwiczenia Programowanie nieliniowe optmalizacja unkcji wielu zmiennch Modele programowania liniowego często okazują się niewstarczające w modelowaniu
Ekonomia matematczna II Ekonomia matematczna II Prowadząc ćwiczenia Programowanie nieliniowe optmalizacja unkcji wielu zmiennch Modele programowania liniowego często okazują się niewstarczające w modelowaniu
12. FUNKCJE WIELU ZMIENNYCH. z = x + y jest R 2, natomiast jej
 1. FUNKCJE WIELU ZMIENNYCH 1.1. FUNKCJE DWÓCH ZMIENNYCH Funkcją dwóch zmiennch określoną w zbiorze D R nazwam przporządkowanie każdej parze liczb () D dokładnie jednej liczb rzeczwistej z. Piszem prz tm
1. FUNKCJE WIELU ZMIENNYCH 1.1. FUNKCJE DWÓCH ZMIENNYCH Funkcją dwóch zmiennch określoną w zbiorze D R nazwam przporządkowanie każdej parze liczb () D dokładnie jednej liczb rzeczwistej z. Piszem prz tm
MODYFIKACJE ALGORYTMU UŚREDNIANIA WYKŁADNICZEGO DO USUWANIA ZAKŁÓCENIA ADDYTYWNEGO
 POZA UIVE RSITY OF TE COLOGY ACADE MIC JOURALS o 80 Electrical Engineering 04 Grzegorz MIKOŁAJCZAK* Jaub PĘKSIŃSKI* Janusz KOWALSKI** MODYFIKACJE ALGORYTMU UŚREDIAIA WYKŁADICZEGO DO USUWAIA ZAKŁÓCEIA ADDYTYWEGO
POZA UIVE RSITY OF TE COLOGY ACADE MIC JOURALS o 80 Electrical Engineering 04 Grzegorz MIKOŁAJCZAK* Jaub PĘKSIŃSKI* Janusz KOWALSKI** MODYFIKACJE ALGORYTMU UŚREDIAIA WYKŁADICZEGO DO USUWAIA ZAKŁÓCEIA ADDYTYWEGO
Algebra liniowa z geometrią analityczną
 WYKŁAD. Własności zbiorów liczbowych. Podzielność liczb całowitych, relacja przystawania modulo, twierdzenie chińsie o resztach. Liczby całowite Liczby 0,±,±,±3,... nazywamy liczbami całowitymi. Zbiór
WYKŁAD. Własności zbiorów liczbowych. Podzielność liczb całowitych, relacja przystawania modulo, twierdzenie chińsie o resztach. Liczby całowite Liczby 0,±,±,±3,... nazywamy liczbami całowitymi. Zbiór
FINAŁ 10 marca 2007 r. KLASA PIERWSZA - POZIOM PODSTAWOWY Czas pisania 90 minut. x +
 FINAŁ 0 marca 007 r. KLASA PIERWSZA - POZIOM PODSTAWOWY Czas pisania 90 minut ZADANIE Największ wspóln dzielnik dwóch liczb naturalnch wnosi 6, a ich najmniejsza wspólna wielokrotność tch liczb równa jest
FINAŁ 0 marca 007 r. KLASA PIERWSZA - POZIOM PODSTAWOWY Czas pisania 90 minut ZADANIE Największ wspóln dzielnik dwóch liczb naturalnch wnosi 6, a ich najmniejsza wspólna wielokrotność tch liczb równa jest
Pomiar bezpośredni przyrządem wskazówkowym elektromechanicznym
 . Rodzaj poiaru.. Poiar bezpośredni (prost) W przpadku poiaru pojednczej wielkości przrząde wskalowan w jej jednostkach wartość niedokładności ± określa graniczn błąd przrządu analogowego lub cfrowego
. Rodzaj poiaru.. Poiar bezpośredni (prost) W przpadku poiaru pojednczej wielkości przrząde wskalowan w jej jednostkach wartość niedokładności ± określa graniczn błąd przrządu analogowego lub cfrowego
SZTUCZNA INTELIGENCJA
 SZTUCZNA INTELIGENCJA WYKŁAD 10. WNIOSKOWANIE W LOGICE ROZMYTEJ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska WNIOSKOWANIE W LOGICE DWUWARTOŚCIOWEJ W logice
SZTUCZNA INTELIGENCJA WYKŁAD 10. WNIOSKOWANIE W LOGICE ROZMYTEJ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska WNIOSKOWANIE W LOGICE DWUWARTOŚCIOWEJ W logice
RACHUNEK CAŁKOWY FUNKCJI DWÓCH ZMIENNYCH
 RACHUNEK CAŁKOWY FUNKCJI WÓCH ZMIENNYCH einicja całki podwójnej po prostokącie einicja Podziałem prostokąta R ={ : a b c d} inaczej: R = [a b] [c d] nazwam zbiór Pn złożon z prostokątów R R... Rn które
RACHUNEK CAŁKOWY FUNKCJI WÓCH ZMIENNYCH einicja całki podwójnej po prostokącie einicja Podziałem prostokąta R ={ : a b c d} inaczej: R = [a b] [c d] nazwam zbiór Pn złożon z prostokątów R R... Rn które
METODY INTELIGENCJI OBLICZENIOWEJ wykład 6
 METODY INTELIGENCJI OBLICZENIOWEJ wykład 6 2 ZBIORY ROZMYTE I WNIOSKOWANIE PRZYBLIŻONE 965 Lotfi A. Zadeh: : Fuzzy sets In almost every case you can build the same product without fuzzy logic, but fuzzy
METODY INTELIGENCJI OBLICZENIOWEJ wykład 6 2 ZBIORY ROZMYTE I WNIOSKOWANIE PRZYBLIŻONE 965 Lotfi A. Zadeh: : Fuzzy sets In almost every case you can build the same product without fuzzy logic, but fuzzy
A. Cel ćwiczenia. B. Część teoretyczna
 A. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z wsaźniami esploatacyjnymi eletronicznych systemów bezpieczeństwa oraz wyorzystaniem ich do alizacji procesu esplatacji z uwzględnieniem przeglądów
A. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z wsaźniami esploatacyjnymi eletronicznych systemów bezpieczeństwa oraz wyorzystaniem ich do alizacji procesu esplatacji z uwzględnieniem przeglądów
Równania różniczkowe cząstkowe
 Równania różniczkowe cząstkowe Definicja: Równaniem różniczkowm cząstkowm nazwam takie równanie różniczkowe w którm wstępuje co najmniej jedna pochodna cząstkowa niewiadomej funkcji dwóch lub więcej zmiennch
Równania różniczkowe cząstkowe Definicja: Równaniem różniczkowm cząstkowm nazwam takie równanie różniczkowe w którm wstępuje co najmniej jedna pochodna cząstkowa niewiadomej funkcji dwóch lub więcej zmiennch
1 Działania na zbiorach
 M. Beśka, Wstęp do teorii miary, rozdz. 1 1 1 Działania na zbiorach W rozdziale tym przypomnimy podstawowe działania na zbiorach koncentrując się na własnościach tych działań, które będą przydatne w dalszej
M. Beśka, Wstęp do teorii miary, rozdz. 1 1 1 Działania na zbiorach W rozdziale tym przypomnimy podstawowe działania na zbiorach koncentrując się na własnościach tych działań, które będą przydatne w dalszej
P k k (n k) = k {O O O} = ; {O O R} =
 Definicja.5 (Kombinacje bez powtórzeń). Każdy -elementowy podzbiór zbioru A wybrany (w dowolnej olejności) bez zwracania nazywamy ombinacją bez powtórzeń. Twierdzenie.5 (Kombinacje bez powtórzeń). Liczba
Definicja.5 (Kombinacje bez powtórzeń). Każdy -elementowy podzbiór zbioru A wybrany (w dowolnej olejności) bez zwracania nazywamy ombinacją bez powtórzeń. Twierdzenie.5 (Kombinacje bez powtórzeń). Liczba
Badanie zależności cech
 PODSTAWY STATYSTYKI 1. Teoria prawdopodobieństwa i element kombinatorki. Zmienne losowe i ich rozkład 3. Populacje i prób danch, estmacja parametrów 4. Testowanie hipotez 5. Test parametrczne (na przkładzie
PODSTAWY STATYSTYKI 1. Teoria prawdopodobieństwa i element kombinatorki. Zmienne losowe i ich rozkład 3. Populacje i prób danch, estmacja parametrów 4. Testowanie hipotez 5. Test parametrczne (na przkładzie
Jest to zasadniczo powtórka ze szkoły średniej, być może z niektórymi rzeczami nowymi.
 Logika Jest to zasadniczo powtórka ze szkoły średniej, być może z niektórymi rzeczami nowymi. Często słowu "logika" nadaje się szersze znaczenie niż temu o czym będzie poniżej: np. mówi się "logiczne myślenie"
Logika Jest to zasadniczo powtórka ze szkoły średniej, być może z niektórymi rzeczami nowymi. Często słowu "logika" nadaje się szersze znaczenie niż temu o czym będzie poniżej: np. mówi się "logiczne myślenie"
Rozwiązywanie układu równań metodą przeciwnych współczynników
 Rozwiązwanie układu równań metodą przeciwnch współcznników Sposob postępowania krok po kroku: I. przgotowanie równań. pozbwam się ułamków mnoŝąc kaŝd jednomian równania równań przez najmniejszą wspólną
Rozwiązwanie układu równań metodą przeciwnch współcznników Sposob postępowania krok po kroku: I. przgotowanie równań. pozbwam się ułamków mnoŝąc kaŝd jednomian równania równań przez najmniejszą wspólną
Realizacja funkcji przełączających
 Realizacja funkcji przełączającch. Wprowadzenie teoretczne.. Podstawowe funkcje logiczne Funkcja logiczna NOT AND OR Zapis = x x = = x NAND NOR.2. Metoda minimalizacji funkcji metodą tablic Karnaugha Metoda
Realizacja funkcji przełączającch. Wprowadzenie teoretczne.. Podstawowe funkcje logiczne Funkcja logiczna NOT AND OR Zapis = x x = = x NAND NOR.2. Metoda minimalizacji funkcji metodą tablic Karnaugha Metoda
Równania różniczkowe cząstkowe
 Równania różniczkowe cząstkowe Definicja Równaniem różniczkowm cząstkowm nazwam takie równanie różniczkowe w którm wstępuje co najmniej jedna pochodna cząstkowa niewiadomej funkcji dwóch lub więcej zmiennch
Równania różniczkowe cząstkowe Definicja Równaniem różniczkowm cząstkowm nazwam takie równanie różniczkowe w którm wstępuje co najmniej jedna pochodna cząstkowa niewiadomej funkcji dwóch lub więcej zmiennch
Liczby zespolone. Niech C = R 2. Zdefiniujmy dwa działania w C. Dodawanie + : C 2 C zdefiniowane jest przez
 Liczb zespolone Ciało liczb zespolonch Niech C = R. Zdefiniujm dwa działania w C. Dodawanie + : C C zdefiniowane jest przez (, ) + (, ) = ( +, + ). Ćwiczenie. Obliczm (, ) + (, 0) =.................................................
Liczb zespolone Ciało liczb zespolonch Niech C = R. Zdefiniujm dwa działania w C. Dodawanie + : C C zdefiniowane jest przez (, ) + (, ) = ( +, + ). Ćwiczenie. Obliczm (, ) + (, 0) =.................................................
FUNKCJE. (odwzorowania) Funkcje 1
 FUNKCJE (odwzorowania) Funkcje 1 W matematyce funkcja ze zbioru X w zbiór Y nazywa się odwzorowanie (przyporządkowanie), które każdemu elementowi zbioru X przypisuje jeden, i tylko jeden element zbioru
FUNKCJE (odwzorowania) Funkcje 1 W matematyce funkcja ze zbioru X w zbiór Y nazywa się odwzorowanie (przyporządkowanie), które każdemu elementowi zbioru X przypisuje jeden, i tylko jeden element zbioru
Macierze normalne. D : Dowolną macierz kwadratową można zapisać w postaci A = B + ic gdzie ( ) B = A + A B = A + A = ( A + A)
 Macierze normalne Twierdzenie: Macierz można zdiagonalizować za pomocą unitarnej transformacji podobieństwa wted i tlko wted gd jest normalna (AA A A). ( ) D : Dowolną macierz kwadratową można zapisać
Macierze normalne Twierdzenie: Macierz można zdiagonalizować za pomocą unitarnej transformacji podobieństwa wted i tlko wted gd jest normalna (AA A A). ( ) D : Dowolną macierz kwadratową można zapisać
TEORETYCZNE PODSTAWY INFORMATYKI
 1 TEORETYCZNE PODSTAWY INFORMATYKI 16/01/2017 WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Repetytorium złożoność obliczeniowa 2 Złożoność obliczeniowa Notacja wielkie 0 Notacja Ω i Θ Rozwiązywanie
1 TEORETYCZNE PODSTAWY INFORMATYKI 16/01/2017 WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Repetytorium złożoność obliczeniowa 2 Złożoność obliczeniowa Notacja wielkie 0 Notacja Ω i Θ Rozwiązywanie
Pochodna funkcji wykład 5
 Pochodna funkcji wkład 5 dr Mariusz Grządziel 8 listopada 2010 Funkcja logistczna 40 Rozważm funkcję logistczną = f 0 (t) = 1+5e 0,5t Funkcja f może bć wkorzstana np. do modelowania wzrostu mas ziaren
Pochodna funkcji wkład 5 dr Mariusz Grządziel 8 listopada 2010 Funkcja logistczna 40 Rozważm funkcję logistczną = f 0 (t) = 1+5e 0,5t Funkcja f może bć wkorzstana np. do modelowania wzrostu mas ziaren
Rozwiązywanie belek prostych i przegubowych wyznaczanie reakcji i wykresów sił przekrojowych 6
 ozwiązwanie beek prostch i przegubowch wznaczanie reakcji i wkresów sił przekrojowch 6 Obciążenie beki mogą stanowić sił skupione, moment skupione oraz obciążenia ciągłe q rs. 6.. s. 6. rzed przstąpieniem
ozwiązwanie beek prostch i przegubowch wznaczanie reakcji i wkresów sił przekrojowch 6 Obciążenie beki mogą stanowić sił skupione, moment skupione oraz obciążenia ciągłe q rs. 6.. s. 6. rzed przstąpieniem
Projekt Era inżyniera pewna lokata na przyszłość jest współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Materiał ddaktczne na zajęcia wrównawcze z matematki dla studentów pierwszego roku kierunku zamawianego Inżnieria Środowiska w ramach projektu Era inżniera pewna lokata na przszłość Projekt Era inżniera
Materiał ddaktczne na zajęcia wrównawcze z matematki dla studentów pierwszego roku kierunku zamawianego Inżnieria Środowiska w ramach projektu Era inżniera pewna lokata na przszłość Projekt Era inżniera
Indukcja matematyczna. Zasada minimum. Zastosowania.
 Indukcja matematyczna. Zasada minimum. Zastosowania. Arkadiusz Męcel Uwagi początkowe W trakcie zajęć przyjęte zostaną następujące oznaczenia: 1. Zbiory liczb: R - zbiór liczb rzeczywistych; Q - zbiór
Indukcja matematyczna. Zasada minimum. Zastosowania. Arkadiusz Męcel Uwagi początkowe W trakcie zajęć przyjęte zostaną następujące oznaczenia: 1. Zbiory liczb: R - zbiór liczb rzeczywistych; Q - zbiór
1 Podstawowe oznaczenia
 Poniżej mogą Państwo znaleźć skondensowane wiadomości z wykładu. Należy je traktować jako przegląd pojęć, które pojawiły się na wykładzie. Materiały te nie są w pełni tożsame z tym co pojawia się na wykładzie.
Poniżej mogą Państwo znaleźć skondensowane wiadomości z wykładu. Należy je traktować jako przegląd pojęć, które pojawiły się na wykładzie. Materiały te nie są w pełni tożsame z tym co pojawia się na wykładzie.
Zbiory rozmyte. Teoria i zastosowania we wnioskowaniu aproksymacyjnym
 Zior rozmte Teori i zstosowni we wniosowniu prosmcjnm PODSTWOWE POJĘCI Motwcje Potrze opisni zjwis i pojęć wielozncznch i niepreczjnch użwnch swoodnie w jęzu nturlnm np. wso tempertur młod człowie średni
Zior rozmte Teori i zstosowni we wniosowniu prosmcjnm PODSTWOWE POJĘCI Motwcje Potrze opisni zjwis i pojęć wielozncznch i niepreczjnch użwnch swoodnie w jęzu nturlnm np. wso tempertur młod człowie średni
3.2. Podstawowe własności funkcji. Funkcje cyklometryczne, hiperboliczne. Definicję funkcji f o dziedzinie X i przeciwdziedzinie Y mamy w 3A5.
 WYKŁAD 7 3 Podstawowe własności unkcji Funkcje cklometrczne, hiperboliczne Deinicję unkcji o dziedzinie X i przeciwdziedzinie Y mam w 3A5 3A37 (Uwaga: dziedzina naturalna) Często się zdarza, że unkcja
WYKŁAD 7 3 Podstawowe własności unkcji Funkcje cklometrczne, hiperboliczne Deinicję unkcji o dziedzinie X i przeciwdziedzinie Y mam w 3A5 3A37 (Uwaga: dziedzina naturalna) Często się zdarza, że unkcja
Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne.
 Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne. Funkcja homograficzna. Definicja. Funkcja homograficzna jest to funkcja określona wzorem f() = a + b c + d, () gdzie współczynniki
Funkcje wymierne. Funkcja homograficzna. Równania i nierówności wymierne. Funkcja homograficzna. Definicja. Funkcja homograficzna jest to funkcja określona wzorem f() = a + b c + d, () gdzie współczynniki
Indukcja. Materiały pomocnicze do wykładu. wykładowca: dr Magdalena Kacprzak
 Indukcja Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Charakteryzacja zbioru liczb naturalnych Arytmetyka liczb naturalnych Jedną z najważniejszych teorii matematycznych jest arytmetyka
Indukcja Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Charakteryzacja zbioru liczb naturalnych Arytmetyka liczb naturalnych Jedną z najważniejszych teorii matematycznych jest arytmetyka
Zmienne losowe typu ciągłego. Parametry zmiennych losowych. Izolda Gorgol wyciąg z prezentacji (wykład III)
 Zmienne losowe tpu ciągłego. Parametr zmiennch losowch. Izolda Gorgol wciąg z prezentacji (wkład III) Zmienna losowa tpu ciągłego Zmienna losowa X o ciągłej dstrbuancie F nazwa się zmienną losową tpu ciągłego,
Zmienne losowe tpu ciągłego. Parametr zmiennch losowch. Izolda Gorgol wciąg z prezentacji (wkład III) Zmienna losowa tpu ciągłego Zmienna losowa X o ciągłej dstrbuancie F nazwa się zmienną losową tpu ciągłego,
Warsztat pracy matematyka
 Warsztat prac matematka Izabela Bondecka-Krzkowska Marcin Borkowski Jęzk matematki Teoria Jednm z podstawowch pojęc matematki jest pojęcie zbioru. Teorię opisującą zbior nazwa sie teorią mnogości. Definicja
Warsztat prac matematka Izabela Bondecka-Krzkowska Marcin Borkowski Jęzk matematki Teoria Jednm z podstawowch pojęc matematki jest pojęcie zbioru. Teorię opisującą zbior nazwa sie teorią mnogości. Definicja
Wnioskowanie rozmyte. Krzysztof Patan
 Wnioskowanie rozmyte Krzysztof Patan Wprowadzenie Informacja precyzyjna jest to jedyna postać informacji akceptowanej przez konwencjonalne metody matematyczne, najczęściej dostarczana jest przez precyzyjne
Wnioskowanie rozmyte Krzysztof Patan Wprowadzenie Informacja precyzyjna jest to jedyna postać informacji akceptowanej przez konwencjonalne metody matematyczne, najczęściej dostarczana jest przez precyzyjne
LOGIKA I TEORIA ZBIORÓW
 LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
Systemy ekspertowe - wiedza niepewna
 Instytut Informatyki Uniwersytetu Śląskiego lab 8 Rozpatrzmy następujący przykład: Miażdżyca powoduje często zwężenie tętnic wieńcowych. Prowadzi to zazwyczaj do zmniejszenia przepływu krwi w tych naczyniach,
Instytut Informatyki Uniwersytetu Śląskiego lab 8 Rozpatrzmy następujący przykład: Miażdżyca powoduje często zwężenie tętnic wieńcowych. Prowadzi to zazwyczaj do zmniejszenia przepływu krwi w tych naczyniach,
6. Liczby wymierne i niewymierne. Niewymierność pierwiastków i logarytmów (c.d.).
 6. Liczby wymierne i niewymierne. Niewymierność pierwiastków i logarytmów (c.d.). 0 grudnia 008 r. 88. Obliczyć podając wynik w postaci ułamka zwykłego a) 0,(4)+ 3 3,374(9) b) (0,(9)+1,(09)) 1,() c) (0,(037))
6. Liczby wymierne i niewymierne. Niewymierność pierwiastków i logarytmów (c.d.). 0 grudnia 008 r. 88. Obliczyć podając wynik w postaci ułamka zwykłego a) 0,(4)+ 3 3,374(9) b) (0,(9)+1,(09)) 1,() c) (0,(037))
Zasada indukcji matematycznej
 Sławomir Jemielity Zasada inducji matematycznej Są różne sformułowania tej zasady, mniej lub bardziej abstracyjne My będziemy się posługiwać taą: Niech T(n) oznacza twierdzenie dotyczące liczby naturalnej
Sławomir Jemielity Zasada inducji matematycznej Są różne sformułowania tej zasady, mniej lub bardziej abstracyjne My będziemy się posługiwać taą: Niech T(n) oznacza twierdzenie dotyczące liczby naturalnej
WIELOMIANY I FUNKCJE WYMIERNE
 WIELOMIANY I FUNKCJE WYMIERNE. RozwiąŜ nierówność.. Dla jakiej wartości parametru a R wielomian W() = ++ a dzieli się bez reszty przez +?. Rozwiązać nierówność: a) 5 b) + 4. Wyznaczyć wartości parametru
WIELOMIANY I FUNKCJE WYMIERNE. RozwiąŜ nierówność.. Dla jakiej wartości parametru a R wielomian W() = ++ a dzieli się bez reszty przez +?. Rozwiązać nierówność: a) 5 b) + 4. Wyznaczyć wartości parametru
Inteligencja obliczeniowa
 Ćwiczenie nr 1 Zbiory rozmyte logika rozmyta Tworzenie: termów zmiennej lingwistycznej o różnych kształtach, modyfikatorów, zmiennych o wielu termach; operacje przecięcia, połączenia i dopełnienia 1. Wprowadzenie
Ćwiczenie nr 1 Zbiory rozmyte logika rozmyta Tworzenie: termów zmiennej lingwistycznej o różnych kształtach, modyfikatorów, zmiennych o wielu termach; operacje przecięcia, połączenia i dopełnienia 1. Wprowadzenie
Elementy logiki matematycznej
 Elementy logiki matematycznej Przedmiotem logiki matematycznej jest badanie tzw. wyrażeń logicznych oraz metod rozumowania i sposobów dowodzenia używanych w matematyce, a także w innych dziedzinach, w
Elementy logiki matematycznej Przedmiotem logiki matematycznej jest badanie tzw. wyrażeń logicznych oraz metod rozumowania i sposobów dowodzenia używanych w matematyce, a także w innych dziedzinach, w
Arytmetyka liczb binarnych
 Wartość dwójkowej liczby stałoprzecinkowej Wartość dziesiętna stałoprzecinkowej liczby binarnej Arytmetyka liczb binarnych b n-1...b 1 b 0,b -1 b -2...b -m = b n-1 2 n-1 +... + b 1 2 1 + b 0 2 0 + b -1
Wartość dwójkowej liczby stałoprzecinkowej Wartość dziesiętna stałoprzecinkowej liczby binarnej Arytmetyka liczb binarnych b n-1...b 1 b 0,b -1 b -2...b -m = b n-1 2 n-1 +... + b 1 2 1 + b 0 2 0 + b -1
Zbiory, relacje i funkcje
 Zbiory, relacje i funkcje Zbiory będziemy zazwyczaj oznaczać dużymi literami A, B, C, X, Y, Z, natomiast elementy zbiorów zazwyczaj małymi. Podstawą zależność między elementem zbioru a zbiorem, czyli relację
Zbiory, relacje i funkcje Zbiory będziemy zazwyczaj oznaczać dużymi literami A, B, C, X, Y, Z, natomiast elementy zbiorów zazwyczaj małymi. Podstawą zależność między elementem zbioru a zbiorem, czyli relację
System hilbertowski. Plan wykładu. hilbertowskiego. Definicja systemu hilbertowskiego. Podstawowe twierdzenie systemu. Podstawowe twierdzenie systemu
 Plan wykładu System hilbertowski Wykład 2 Definicja Definicja systemu Reguły y pochodne Twierdzenia dla innych operatorów Porównanie z systemem gentzenowskim Definicja systemu System H jest systemem dowodzenia
Plan wykładu System hilbertowski Wykład 2 Definicja Definicja systemu Reguły y pochodne Twierdzenia dla innych operatorów Porównanie z systemem gentzenowskim Definicja systemu System H jest systemem dowodzenia
Rachunek różniczkowy funkcji jednej zmiennej
 Rachunek różniczkow funkcji jednej zmiennej wkład z MATEMATYKI Budownictwo, studia niestacjonarne sem. I, rok ak. 2008/2009 Katedra Matematki Wdział Informatki Politechnika Białostocka 1 Iloraz różnicow
Rachunek różniczkow funkcji jednej zmiennej wkład z MATEMATYKI Budownictwo, studia niestacjonarne sem. I, rok ak. 2008/2009 Katedra Matematki Wdział Informatki Politechnika Białostocka 1 Iloraz różnicow
i = n = n 1 + n 2 1 i 2 n 1. n(n + 1)(2n + 1) n (n + 1) =
 Druga zasada inducji matematycznej Niech m będzie liczbą całowitą, niech p(n) będzie ciągiem zdań zdefiniowanych na zbiorze {n Z: n m} oraz niech l będzie nieujemną liczbą całowitą. Jeśli (P) wszystie
Druga zasada inducji matematycznej Niech m będzie liczbą całowitą, niech p(n) będzie ciągiem zdań zdefiniowanych na zbiorze {n Z: n m} oraz niech l będzie nieujemną liczbą całowitą. Jeśli (P) wszystie
( ) σ v. Adam Bodnar: Wytrzymałość Materiałów. Analiza płaskiego stanu naprężenia.
 Adam Bdnar: Wtrzmałść Materiałów Analiza płaskieg stanu naprężenia 5 ANALIZA PŁASKIEGO STANU NAPRĘŻENIA 5 Naprężenia na dwlnej płaszczźnie Jak pamiętam płaski stan naprężenia w punkcie cechuje t że wektr
Adam Bdnar: Wtrzmałść Materiałów Analiza płaskieg stanu naprężenia 5 ANALIZA PŁASKIEGO STANU NAPRĘŻENIA 5 Naprężenia na dwlnej płaszczźnie Jak pamiętam płaski stan naprężenia w punkcie cechuje t że wektr
Systemy ekspertowe. Reprezentacja wiedzy niepewnej i wnioskowanie w warunkach niepewności. Model współczynników pewności.
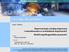 Część siódma Reprezentacja wiedzy niepewnej i wnioskowanie w warunkach niepewności Autor Roman Simiński Model współczynników pewności Kontakt siminski@us.edu.pl www.us.edu.pl/~siminski Niniejsze opracowanie
Część siódma Reprezentacja wiedzy niepewnej i wnioskowanie w warunkach niepewności Autor Roman Simiński Model współczynników pewności Kontakt siminski@us.edu.pl www.us.edu.pl/~siminski Niniejsze opracowanie
Optymalizacja harmonogramów budowlanych - problem szeregowania zadań
 Mieczysław OŁOŃSI Wydział Budownictwa i Inżynierii Środowisa, Szoła Główna Gospodarstwa Wiejsiego, Warszawa, ul. Nowoursynowsa 159 e-mail: mieczyslaw_polonsi@sggw.pl Założenia Optymalizacja harmonogramów
Mieczysław OŁOŃSI Wydział Budownictwa i Inżynierii Środowisa, Szoła Główna Gospodarstwa Wiejsiego, Warszawa, ul. Nowoursynowsa 159 e-mail: mieczyslaw_polonsi@sggw.pl Założenia Optymalizacja harmonogramów
Układy równań i nierówności liniowych
 Układy równań i nierówności liniowych Wiesław Krakowiak 1 grudnia 2010 1 Układy równań liniowych DEFINICJA 11 Układem równań m liniowych o n niewiadomych X 1,, X n, nazywamy układ postaci: a 11 X 1 + +
Układy równań i nierówności liniowych Wiesław Krakowiak 1 grudnia 2010 1 Układy równań liniowych DEFINICJA 11 Układem równań m liniowych o n niewiadomych X 1,, X n, nazywamy układ postaci: a 11 X 1 + +
Kratownice Wieża Eiffel a
 Kratownice Wieża Eiffel a Kratownica jest to konstrukcja nośna, składająca się z prętów połączonch ze sobą w węzłach. Kratownica może bć: 1) płaska, gd wszstkie pręt leżą w jednej płaszczźnie, 2) przestrzenna,
Kratownice Wieża Eiffel a Kratownica jest to konstrukcja nośna, składająca się z prętów połączonch ze sobą w węzłach. Kratownica może bć: 1) płaska, gd wszstkie pręt leżą w jednej płaszczźnie, 2) przestrzenna,
Z funkcji zdaniowej x + 3 = 7 można otrzymać zdania w dwojaki sposób:
 Z funkcji zdaniowej + 3 = 7 można otrzmać zdania w dwojaki sposób: podstawiając w tej funkcji zdaniowej za stałe będące nazwami liczb np. 4 2 itp. poprzedzając tę funkcję zdaniową zwrotami: dla każdego
Z funkcji zdaniowej + 3 = 7 można otrzmać zdania w dwojaki sposób: podstawiając w tej funkcji zdaniowej za stałe będące nazwami liczb np. 4 2 itp. poprzedzając tę funkcję zdaniową zwrotami: dla każdego
Metody probabilistyczne Rozwiązania zadań
 Metody robabilistyczne Rozwiązania zadań 6. Momenty zmiennych losowych 8.11.2018 Zadanie 1. Poaż, że jeśli X Bn, to EX n. Odowiedź: X rzyjmuje wartości w zbiorze {0, 1,..., n} z rawdoodobieństwami zadanymi
Metody robabilistyczne Rozwiązania zadań 6. Momenty zmiennych losowych 8.11.2018 Zadanie 1. Poaż, że jeśli X Bn, to EX n. Odowiedź: X rzyjmuje wartości w zbiorze {0, 1,..., n} z rawdoodobieństwami zadanymi
EGZAMIN GIMNAZJALNY W ROKU SZKOLNYM 2011/2012
 Centralna Komisja Egzaminacjna EGZAMIN GIMNAZJALNY W ROKU SZKOLNYM 2011/2012 CZĘŚĆ MATEMATYCZNO-PRZYRODNICZA MATEMATYKA ODPOWIEDZI I PROPOZYCJE OCENIANIA PRZYKŁADOWEGO ZESTAWU ZADAŃ PAŹDZIERNIK 2011 Zadania
Centralna Komisja Egzaminacjna EGZAMIN GIMNAZJALNY W ROKU SZKOLNYM 2011/2012 CZĘŚĆ MATEMATYCZNO-PRZYRODNICZA MATEMATYKA ODPOWIEDZI I PROPOZYCJE OCENIANIA PRZYKŁADOWEGO ZESTAWU ZADAŃ PAŹDZIERNIK 2011 Zadania
0.1. Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek zdań.
 Wykłady z Analizy rzeczywistej i zespolonej w Matematyce stosowanej Wykład ELEMENTY LOGIKI ALGEBRA BOOLE A Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek
Wykłady z Analizy rzeczywistej i zespolonej w Matematyce stosowanej Wykład ELEMENTY LOGIKI ALGEBRA BOOLE A Logika podstawowe pojęcia: zdania i funktory, reguły wnioskowania, zmienne zdaniowe, rachunek
Projekt 4: Programowanie w logice
 Języki Programowania Projekt 4: Programowanie w logice Środowisko ECL i PS e W projekcie wykorzystane będzie środowisko ECL i PS e. Dostępne jest ono pod adresem http://eclipseclp.org/. Po zainstalowaniu
Języki Programowania Projekt 4: Programowanie w logice Środowisko ECL i PS e W projekcie wykorzystane będzie środowisko ECL i PS e. Dostępne jest ono pod adresem http://eclipseclp.org/. Po zainstalowaniu
L.Kowalski zadania z rachunku prawdopodobieństwa-zestaw 1 ZADANIA - ZESTAW 1. . (odp. a)
 ZADANIA - ZESTAW 1 Zadanie 11 Rzucamy trzy razy monetą A i - zdarzenie polegające na tym, że otrzymamy orła w i - tym rzucie Oreślić zbiór zdarzeń elementarnych Wypisać zdarzenia elementarne sprzyjające
ZADANIA - ZESTAW 1 Zadanie 11 Rzucamy trzy razy monetą A i - zdarzenie polegające na tym, że otrzymamy orła w i - tym rzucie Oreślić zbiór zdarzeń elementarnych Wypisać zdarzenia elementarne sprzyjające
F t+ := s>t. F s = F t.
 M. Beśka, Całka Stochastyczna, wykład 1 1 1 Wiadomości wstępne 1.1 Przestrzeń probabilistyczna z filtracją Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną i niech F = {F t } t 0 będzie rodziną
M. Beśka, Całka Stochastyczna, wykład 1 1 1 Wiadomości wstępne 1.1 Przestrzeń probabilistyczna z filtracją Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną i niech F = {F t } t 0 będzie rodziną
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 5.
 RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 5. PODSTAWOWE ROZKŁADY PRAWDOPODOBIEŃSTWA Rozłady soowe Rozład jednopuntowy Oreślamy: P(X c) 1 gdzie c ustalona liczba. 1 EX c, D 2 X 0 (tylo ten rozład ma zerową wariancję!!!)
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 5. PODSTAWOWE ROZKŁADY PRAWDOPODOBIEŃSTWA Rozłady soowe Rozład jednopuntowy Oreślamy: P(X c) 1 gdzie c ustalona liczba. 1 EX c, D 2 X 0 (tylo ten rozład ma zerową wariancję!!!)
1. Liczby naturalne, podzielność, silnie, reszty z dzielenia
 1. Liczby naturalne, podzielność, silnie, reszty z dzielenia kwadratów i sześcianów przez małe liczby, cechy podzielności przez 2, 4, 8, 5, 25, 125, 3, 9. 26 września 2009 r. Uwaga: Przyjmujemy, że 0 nie
1. Liczby naturalne, podzielność, silnie, reszty z dzielenia kwadratów i sześcianów przez małe liczby, cechy podzielności przez 2, 4, 8, 5, 25, 125, 3, 9. 26 września 2009 r. Uwaga: Przyjmujemy, że 0 nie
Uwaga 1.1 Jeśli R jest relacją w zbiorze X X, to mówimy, że R jest relacją w zbiorze X. Rozważmy relację R X X. Relację R nazywamy zwrotną, gdy:
 Matematya dysretna - wyład 1. Relacje Definicja 1.1 Relacją dwuargumentową nazywamy podzbiór produtu artezjańsiego X Y, tórego elementami są pary uporządowane (x, y), taie, że x X i y Y. Uwaga 1.1 Jeśli
Matematya dysretna - wyład 1. Relacje Definicja 1.1 Relacją dwuargumentową nazywamy podzbiór produtu artezjańsiego X Y, tórego elementami są pary uporządowane (x, y), taie, że x X i y Y. Uwaga 1.1 Jeśli
Motto. Czy to nie zabawne, że ci sami ludzie, którzy śmieją się z science fiction, słuchają prognoz pogody oraz ekonomistów? (K.
 Motto Cz to nie zabawne, że ci sami ludzie, którz śmieją się z science fiction, słuchają prognoz pogod oraz ekonomistów? (K. Throop III) 1 Specfika szeregów czasowch Modele szeregów czasowch są alternatwą
Motto Cz to nie zabawne, że ci sami ludzie, którz śmieją się z science fiction, słuchają prognoz pogod oraz ekonomistów? (K. Throop III) 1 Specfika szeregów czasowch Modele szeregów czasowch są alternatwą
Logika binarna. Prawo łączności mówimy, że operator binarny * na zbiorze S jest łączny gdy (x * y) * z = x * (y * z) dla każdego x, y, z S.
 Logika binarna Logika binarna zajmuje się zmiennymi mogącymi przyjmować dwie wartości dyskretne oraz operacjami mającymi znaczenie logiczne. Dwie wartości jakie mogą te zmienne przyjmować noszą przy tym
Logika binarna Logika binarna zajmuje się zmiennymi mogącymi przyjmować dwie wartości dyskretne oraz operacjami mającymi znaczenie logiczne. Dwie wartości jakie mogą te zmienne przyjmować noszą przy tym
Inżynieria Wiedzy i Systemy Ekspertowe. Logika rozmyta. dr inż. Michał Bereta Politechnika Krakowska
 Inżynieria Wiedzy i Systemy Ekspertowe Logika rozmyta dr inż. Michał Bereta Politechnika Krakowska http://torus.uck.pk.edu.pl/~beretam/ beretam@torus.uck.pk.edu.pl 1 Wyostrzanie Ostateczna, ostra wartość
Inżynieria Wiedzy i Systemy Ekspertowe Logika rozmyta dr inż. Michał Bereta Politechnika Krakowska http://torus.uck.pk.edu.pl/~beretam/ beretam@torus.uck.pk.edu.pl 1 Wyostrzanie Ostateczna, ostra wartość
Metody prognozowania: Jakość prognoz Wprowadzenie (1) 6. Oszacowanie przypuszczalnej trafności prognozy
 Metod prognozowania: Jakość prognoz Dr inż. Sebastian Skoczpiec ver. 03.2012 Wprowadzenie (1) 1. Sformułowanie zadania prognostcznego: 2. Określenie przesłanek prognostcznch: 3. Zebranie danch 4. Określenie
Metod prognozowania: Jakość prognoz Dr inż. Sebastian Skoczpiec ver. 03.2012 Wprowadzenie (1) 1. Sformułowanie zadania prognostcznego: 2. Określenie przesłanek prognostcznch: 3. Zebranie danch 4. Określenie
5. Relacja prawostronnie jednoznaczna (jednoznaczna, inaczej: jest funkcją), jeżeli
 ELJE EF. elacją w produkcie podzbiór n. n (relacją n-argumentową) zwam dowoln EF. elację zbioru. EF. elację zwam relacją międz elementami zbioru a elementami 2 zwam relacją w () zbiorze. EF. la dowolnej
ELJE EF. elacją w produkcie podzbiór n. n (relacją n-argumentową) zwam dowoln EF. elację zbioru. EF. elację zwam relacją międz elementami zbioru a elementami 2 zwam relacją w () zbiorze. EF. la dowolnej
Baza w jądrze i baza obrazu ( )
 Przykład Baza w jądrze i baza obrazu (839) Znajdź bazy jądra i obrazu odwzorowania α : R 4 R 3, gdzie α(x, y, z, t) = (x + 2z + t, 2x + y 3z 5t, x y + z + 4t) () zór ten oznacza, że α jest odwzorowaniem
Przykład Baza w jądrze i baza obrazu (839) Znajdź bazy jądra i obrazu odwzorowania α : R 4 R 3, gdzie α(x, y, z, t) = (x + 2z + t, 2x + y 3z 5t, x y + z + 4t) () zór ten oznacza, że α jest odwzorowaniem
ROZWIĄZANIA I ODPOWIEDZI
 Zastosowania matematki w analitce medcznej zestaw do kol. semestr. - rozwiązania i odpowiedzi (część I). ROZWIĄZANIA I ODPOWIEDZI Zadanie A1. a) Rozważając dwa przpadki ze względu na moduł mam: skąd ostatecznie,3>.
Zastosowania matematki w analitce medcznej zestaw do kol. semestr. - rozwiązania i odpowiedzi (część I). ROZWIĄZANIA I ODPOWIEDZI Zadanie A1. a) Rozważając dwa przpadki ze względu na moduł mam: skąd ostatecznie,3>.
