SKOMPLIKOWANYCH INSTRUMENTÓW
|
|
|
- Dominika Kosińska
- 7 lat temu
- Przeglądów:
Transkrypt
1 wstęp aproksymacja ścisłe wyniki inne metody ZMIENNOŚĆ IMPLIKOWANA W WYCENIE SKOMPLIKOWANYCH INSTRUMENTÓW Andrzej Palczewski Instytut Matematyki Stosowanej i Mechaniki, Uniwersytet Warszawski Warszawa 25 kwietnia 2014 Andrzej Palczewski ( UW) Zmienność implikowana 1 / 35
2 wstęp aproksymacja ścisłe wyniki inne metody Plan wystapienia 1 Wprowadzenie. Praktycy lubia proste wzory. Zmienność implikowana (implied volatility) a zmienność lokalna. 2 Jak przybliżać zmienność implikowana? Model Berestycki-Busca-Florent. Rozwinięcia asymptotyczne. 3 Ścisłe wyniki dla rozwinięć asymptotycznych. 4 Inne metody przybliżania zmienności implikowanej. Andrzej Palczewski ( UW) Zmienność implikowana 2 / 35
3 wstęp aproksymacja ścisłe wyniki inne metody proste wzory zmienność implikowana Dlaczego proste wzory sa ważne? Cytat z artykułu Mike Giles & Ronnie Sircar Siam NEWS, October 2007: The major challenges in computational finance arise not from difficult geometries, as in many physical problems, but from the need for rapid calculation of an EXPECTATION or the solution of its associated Kolmogorov partial differential equation. Efficiency is at the forefront, because models are re-estimated as new market data arrives and calibration (or marking to market ) embeds the expectation/pde calculation in an iterative solution to an inverse problem. Andrzej Palczewski ( UW) Zmienność implikowana 3 / 35
4 wstęp aproksymacja ścisłe wyniki inne metody proste wzory zmienność implikowana Najlepszy jest wzór Blacka (Blacka-Scholesa) W log-normalnym modelu cen instrumentów finansowych cena opcji (call lub put) dana jest zamkniętym wzorem (wzorem Blacka): V call = V call (F 0, K, T, σ B ), gdzie F 0 cena forward instrumentu, K cena realizacji (strike), T czas do zapadalności (expiry) a σ B zmienność. Z wyjatkiem σ B wszystkie parametry wyznaczajace cenę opcji sa znane! σ B można wyznaczyć z cen opcji kwotowanych na rynku. Taka σ B nazywa się zmiennościa implikowana. Andrzej Palczewski ( UW) Zmienność implikowana 4 / 35
5 wstęp aproksymacja ścisłe wyniki inne metody proste wzory zmienność implikowana Problem ze zmiennościa implikowana Ceny instrumentów maja rzadko rozkład log-normalny. W efekcie σ B nie jest stała dla danego instrumentu, ale zmienia się z K oraz T. Otrzymujemy tzw. uśmiech zmienności Andrzej Palczewski ( UW) Zmienność implikowana 5 / 35
6 wstęp aproksymacja ścisłe wyniki inne metody proste wzory zmienność implikowana Zmienność implikowana dla portfela instrumentów Zmiana σ B w zależności od K i T oznacza, że praktycznie dla każdego K i T mamy inny model rynku. To sprawia ogromne problemy przy zarzadzaniu ryzykiem dużych portfeli opcyjnych. Jakie σ B użyć przy wyliczaniu pozycji zabezpieczajacych? (liczenie Delta lub Vega portfela) Należy wyjść poza model log-normalny (model Blacka-Scholesa) rynku. Andrzej Palczewski ( UW) Zmienność implikowana 6 / 35
7 wstęp aproksymacja ścisłe wyniki inne metody proste wzory zmienność implikowana Rozszerzenie modelu Blacka-Scholesa Model log-normalny (model Blacka-Scholesa) W tym modelu σ B jest stałe. df t = σ B F t dw t, F(t 0 ) = F 0. Model lokalnej (stochastycznej) zmienności df t = σ(t, F t, y t )F t dw t, F(t 0 ) = F 0. W tym modelu σ(t, F t, y t ) jest funkcja czasu, ceny instrumentu bazowego, ale także zmiennej y t, która może być innym procesem stochastycznym. Andrzej Palczewski ( UW) Zmienność implikowana 7 / 35
8 wstęp aproksymacja ścisłe wyniki inne metody proste wzory zmienność implikowana Problemy obliczeniowe Model lokalnej (stochastycznej) zmienności df t = σ(t, F t, y t )F t dw t, F(t 0 ) = F 0 (1) nastręcza poważne problemy obliczeniowe. Aby znaleźć cenę opcji należy znaleźć rozwiazanie równania (1) metoda symulacji Monte Carlo (to może być poważne wyzwanie, jeśli proces y t jest wielowymiarowy); albo rozwiazać numerycznie równanie różniczkowe czastkowe odpowiadajace modelowi (1) (odpowiednik równania Blacka-Scholesa); to także może być poważne zadanie numeryczne, jeśli problem jest wielowymiarowy. Andrzej Palczewski ( UW) Zmienność implikowana 8 / 35
9 wstęp aproksymacja ścisłe wyniki inne metody proste wzory zmienność implikowana Problemy obliczeniowe c.d. Opisane metody obliczeniowe na pewno nie daja możliwości wykonywania szybkich obliczeń, o których była mowa na poczatku. Praktycy najchętniej używaja wzoru Blacka, do którego chcieliby wstawić właściwa wartość zmienności implikowanej. Problem: Jak z modelu lokalnej (stochastycznej) zmienności wyznaczyć zmienność implikowana? Odpowiedź na to pytanie zajmuje teoretyków przez ostatnie 15 lat. Andrzej Palczewski ( UW) Zmienność implikowana 9 / 35
10 wstęp aproksymacja ścisłe wyniki inne metody model BBF rozwinięcia asymptotyczne Model Berestycki-Busca-Florent Zróbmy pewne uproszczenie modelu zakładajac, że σ(t, F, y) = σ(t, F), tzn. pozbywamy się dodatkowego procesu stochastycznego y t. Niech C loc (t, F) będzie cena opcji call w modelu (1) po tym uproszczeniu. Funkcja ta spełnia następujace równanie C loc t σ2 (t, F)F 2 C loc FF = 0, Cloc (T, F) = (F K ) +. (2) Rozwiazanie to będziemy oznaczać C loc (t 0, F 0 ; T, K ) aby podkreślić zależność od wszystkich istotnych parametrów. Andrzej Palczewski ( UW) Zmienność implikowana 10 / 35
11 wstęp aproksymacja ścisłe wyniki inne metody model BBF rozwinięcia asymptotyczne Model Berestycki-Busca-Florent c.d. Jeśli w równaniu poprzedniego slajdu wstawimy zamiast funkcji σ(t, F) stała θ, to otrzymamy rozwiazanie dane wzorem Blacka. To rozwiazanie będziemy oznaczać C BS (t 0, F 0 ; T, K, θ). Zmiennośc implikowana możemy teraz zdefiniować jako funkcję θ = θ(t 0, F 0 ; T, K ), taka że C loc (t 0, F 0 ; T, K ) = C BS (t 0, F 0 ; T, K, θ) (3) Wykorzystujac równość (3) oraz równanie (2), które spełniaja funkcje C loc (t 0, F 0 ; T, K ) i C BS (t 0, F 0 ; T, K, θ), możemy znaleźć równanie, jakie spełnia funkcja θ(t 0, F 0 ; T, K ). Andrzej Palczewski ( UW) Zmienność implikowana 11 / 35
12 wstęp aproksymacja ścisłe wyniki inne metody model BBF rozwinięcia asymptotyczne Model Berestycki-Busca-Florent c.d. Ponieważ równanie jest skomplikowane, napiszemy je w nowych zmiennych, które nieco upraszczaja zapis. Nowe zmienne niezależne: x = log(f/k ), τ = T t. W nowych zmiennych równanie dla funkcji θ(τ, x) ma postać 2τθθ τ σ 2( x θ x θ 1 ) τ 2 σ 2 θ 2 θ 2 x τσ 2 θθ xx + θ 2 = 0. (4) W tym wzorze σ = σ(τ, x) jest oczywiście zmiennościa lokalna z modelu (1). Andrzej Palczewski ( UW) Zmienność implikowana 12 / 35
13 wstęp aproksymacja ścisłe wyniki inne metody model BBF rozwinięcia asymptotyczne Model Berestycki-Busca-Florent c.d Równanie (4) jest jeszcze bardziej skomplikowane niż równanie (2), nie widać więc zalet wprowadzania takiego modelu. Na dodatek rozwiazanie równania (4) interesuje nas w przedziale τ [0, T ] a dla τ = 0 równanie (4) staje się osobliwe. Z drugiej strony, gdyby interesować się jedynie rozwiazaniem dla małych wartości τ, to równanie (4) możnaby traktować jako zaburzenie dużo prostszego równania σ 2( x θ x θ 1 ) 2 + θ 2 = 0. Czy takie postępowanie można sformalizować matematycznie? Andrzej Palczewski ( UW) Zmienność implikowana 13 / 35
14 wstęp aproksymacja ścisłe wyniki inne metody model BBF rozwinięcia asymptotyczne Metoda rozwinięć asymptotycznych Odpowiedź na postawione pytanie jest pozytywna! Poczatek tego typu badaniom dał Euler, który zajmował się problemem sumowalności szeregów potęgowych. W przypadku rozwiazań równań różniczkowych teoria ta nazywa się metoda rozwinięć asymptotycznych. Polega ona na poszukiwaniu rozwiazania równania w postaci szeregu potęgowego (względem małego parametru). Taki szereg potęgowy nie musi oczywiście być zbieżny (najczęściej nie jest!), ale można starać się pokazać, że skończona suma częściowa takiego szeregu przybliża właściwe rozwiazanie. Dla naszego problemu poszukiwać będziemy rozwiazania równania (4) w postaci szeregu θ(τ, x) = θ 0 (x) + τθ 1 (x) + τ 2 θ 2 (x) Andrzej Palczewski ( UW) Zmienność implikowana 14 / 35
15 wstęp aproksymacja ścisłe wyniki inne metody model BBF rozwinięcia asymptotyczne Przybliżenie zerowego rzędu Robimy dalsze uproszczenie zakładajac, że lokalna zmienność σ(τ, x) jest jednorodna w czasie, czyli σ = σ(x). Wstawiajac szereg potęgowy z poprzedniego slajdu do równania (4) oraz grupujac wyrazy odpowiadajace różnym potęgom τ dostajemy jako współczynnik przy zerowej potędze równość σ 2 (x) ( xθx 0 θ 0) 2 (θ 0 ) 4 = 0. (5) To jest równanie przybliżenia zerowego rzędu. Andrzej Palczewski ( UW) Zmienność implikowana 15 / 35
16 wstęp aproksymacja ścisłe wyniki inne metody model BBF rozwinięcia asymptotyczne Rozwiazanie zerowego rzędu Przy odpowiednich założeniach na temat gładkości funkcji σ(x) rozwiazanie równania (5) dane jest wyrażeniem ( θ 0 x (x) = x 0 du ) 1. (6) σ(u) Przy tym funkcja θ 0 (x) jest klasy C 2 (R) i jest ograniczona razem ze swoimi pochodnymi. Andrzej Palczewski ( UW) Zmienność implikowana 16 / 35
17 wstęp aproksymacja ścisłe wyniki inne metody model BBF rozwinięcia asymptotyczne Przybliżenie pierwszego rzędu Jako współczynnik przy pierwszej potędze τ dostajemy wyrażenie σ ( xθ 1 x θ 1) + 3θ 0 θ σ2 θ 0 θ 0 xx = 0. (7) To jest równanie przybliżenia pierwszego rzędu. Zauważmy, że jest to liniowe równanie różniczkowe pierwszego rzędu, łatwo więc powinno być znaleźć jego rozwiazanie. Uwaga Równania na przybliżenia wszystkich wyższych rzędów sa też liniowymi równaniami pierwszego rzędu. Andrzej Palczewski ( UW) Zmienność implikowana 17 / 35
18 wstęp aproksymacja ścisłe wyniki inne metody model BBF rozwinięcia asymptotyczne Rozwiazanie pierwszego rzędu Przy odpowiednich założeniach na temat gładkości funkcji σ(x) rozwiazanie równania (7) dane jest wyrażeniem θ 1 (x) = (θ0 (x)) 3 σ(0)σ(x) x 2 ln θ 0. (8) (x) Przy tym funkcja θ 1 (x) jest klasy C 2 (R) i jest ograniczona razem ze swoimi pochodnymi. Andrzej Palczewski ( UW) Zmienność implikowana 18 / 35
19 wstęp aproksymacja ścisłe wyniki inne metody rzad zerowy rzad pierwszy Wyniki BBF dla przybliżenia zerowego rzędu zależność od czasu Twierdzenie (Berestycki, Busca, Florent 2002) W granicy τ 0 mamy zbieżność lim θ(τ, x) = τ 0 θ0 (x), przy czym zbieżność jest jednostajna dla x R. Analogiczny wynik został udowodniony także bez upraszczajacego założenia, że σ jest jednorodna w czasie, tj. dla przypadku, gdy σ = σ(τ, x) (Berestycki, Busca, Florent 2004). Andrzej Palczewski ( UW) Zmienność implikowana 19 / 35
20 wstęp aproksymacja ścisłe wyniki inne metody rzad zerowy rzad pierwszy zależność od czasu Nowe wyniki dla przybliżenia zerowego rzędu Twierdzenie Załóżmy, że funkcja σ(x) jest klasy C 2 (R) i ma ograniczone pochodne. Dodatkowo niech będa spełnione oszacowania 0 < σ L σ(x) σ U <, gdzie σ L, σ U sa stałe. Wtedy istnieja stałe κ > 0 i τ 0 > 0, takie że dla rozwiazania równania (4) dla zmienności implikowanej zachodzi oszacowanie θ(τ, x) θ 0 (x) κτ θ 0 (x). Oszacowanie to zachodzi dla wszystkich τ < τ 0. Andrzej Palczewski ( UW) Zmienność implikowana 20 / 35
21 wstęp aproksymacja ścisłe wyniki inne metody rzad zerowy rzad pierwszy Wyniki dla przybliżenia pierwszego rzędu zależność od czasu Twierdzenie Niech spełnione będa założenia poprzedniego twierdzenia wzmocnione założeniem, że funkcja σ(x) jest klasy C 4 (R) i ma ograniczone pochodne. Wtedy istnieja stałe κ > 0 i τ 0 > 0, takie że dla rozwiazania równania (4) dla zmienności implikowanej zachodzi oszacowanie θ(τ, x) θ 0 (x) τθ 1 (x) κτ 2 θ 0 (x). Oszacowanie to zachodzi dla wszystkich τ < τ 0. Andrzej Palczewski ( UW) Zmienność implikowana 21 / 35
22 wstęp aproksymacja ścisłe wyniki inne metody rzad zerowy rzad pierwszy zależność od czasu Rozwiazanie dla zmienności zależnej od czasu Jak postępować w przypadku, gdy σ = σ(τ, x)? Wtedy należy także funkcję σ rozwinać w szereg potęgowy względem τ σ(τ, x) = σ 0 (x) + τσ 1 (x) (9) Wstawiajac to rozwinięcie oraz rozwinięcie θ do równania dla zmienności implikowanej oraz grupujac wyrazy z odpowiednimi potęgami τ dostaniemy w przybliżeniu zerowego rzędu analogiczne równanie jak w przypadku jednorodnym (jedynie funkcję σ(x) zastapi funkcja σ 0 (x)). Rozwiazanie zerowego rzędu będzie miało wtedy postać ( θ 0 x (x) = x 0 du ) 1. (10) σ 0 (u) Andrzej Palczewski ( UW) Zmienność implikowana 22 / 35
23 wstęp aproksymacja ścisłe wyniki inne metody rzad zerowy Przybliżenie pierwszego rzędu rzad pierwszy zależność od czasu W przybliżeniu pierwszego rzędu dostajemy równanie istotnie różne niż w przypadku jednorodnym w czasie σ 0( xθ 1 x θ 1) + 3θ 0 θ 1 = 1 2 (σ0 ) 2 θ 0 θ 0 xx + σ1 σ 0 (θ0 ) 2. (11) Rozwiazanie tego równania dane jest wzorem θ 1 (x) = (θ0 (x)) 3 ( σ x 2 ln 0 (0)σ 0 (x) x uσ 1 ) (u) θ 0 + (x) 0 (σ 0 (u)) 2 θ 0 (u) du. (12) Andrzej Palczewski ( UW) Zmienność implikowana 23 / 35
24 wstęp aproksymacja ścisłe wyniki inne metody rzad zerowy rzad pierwszy Wyniki dla przybliżenia pierwszego rzędu zależność od czasu Twierdzenie Niech dla funkcji σ 0 (x) spełnione będa założenia analogiczne jak w przypadku jednorodnym w czasie spełniała funkcja σ(x). Dodakowo załóżmy, że funkcja σ 0 (x) jest klasy C 4 (R) a funkcja σ 1 (x) jest klasy C 2 (R) i obie maja ograniczone pochodne. Wtedy istnieja stałe κ > 0 i τ 0 > 0, takie że dla rozwiazania równania (4) dla zmienności implikowanej zachodzi oszacowanie θ(τ, x) θ 0 (x) τθ 1 (x) κτ 2 θ 0 (x), gdzie θ 0 dana jest wzorem (10) a θ 1 wzorem (12) przy czym oszacowanie to zachodzi dla wszystkich τ < τ 0. Andrzej Palczewski ( UW) Zmienność implikowana 24 / 35
25 wstęp aproksymacja ścisłe wyniki inne metody metody geometrii różniczkowej Cena opcji ze wzoru Tanaki Wracamy do poczatkowego modelu rynku z lokalna zmiennościa (deterministyczna a nie stochastyczna dla uproszczenia prezentacji). df t = σ(t, F)F t dw t, F(0) = F 0. (13) Zastosowanie formuły Tanaki prowadzi do następujacego wzoru na cenę opcji C loc (0, F 0 ; T, K ) = ( P(0, T ) (F 0 K ) T 0 ) σ(t, K ) 2 K 2 p(t, K F 0 )dt. (14) p(t, K F 0 ) jest tu rozkładem prawdopodobieństwa dla procesu (13) warunkowanego na F 0. Andrzej Palczewski ( UW) Zmienność implikowana 25 / 35
26 wstęp aproksymacja ścisłe wyniki inne metody metody geometrii różniczkowej Równanie wsteczne Kołmogorowa Funkcja p(t, F F 0 ) spełnia wsteczne równanie Kołmogorowa t p(t, F F 0 ) = 1 ( 2 2 F σ(t, F ) 2 F 2 p(t, F F 0 ) ) = 1 2 σ(t, F)2 F 2 2 F p(t, F F 0) + 2σ(t, F)F F ( σ(t, F)F ) F p(t, F F 0 ) + σ(t, F)F F 2 ( ) σ(t, F)F p(t, F F0 ) ( + F 2 ( ) ) 2 σ(t, F)F p(t, F F0 ). (15) Andrzej Palczewski ( UW) Zmienność implikowana 26 / 35
27 wstęp aproksymacja ścisłe wyniki inne metody metody geometrii różniczkowej Uogólnienie Rozważmy wielowymiarowy proces stochastyczny X t spełniajacy układ równań dx i t = j σ i j (X t)dw j t, d W i t, W j t = ρi,j dt. Prawdopodobieństwo przejścia dla tego procesu G T,X (t, x) spełnia wsteczne równanie Kołmogorowa t G T,X (t, x) + i,j G T,X (T, x) = δ(x X), g i,j (x) 2 x i,x j G T,X (t, x) = 0, gdzie macierz g i,j jest dodatnio określona i dana wzorem g i,j (x) = 1 ρ k,l σk i 2 (x)σj l (x). k,l Andrzej Palczewski ( UW) Zmienność implikowana 27 / 35
28 wstęp aproksymacja ścisłe wyniki inne metody metody geometrii różniczkowej Uogólnienie c.d. Dokonujac zamiany zmiennych τ = T t sprowadzamy równanie Kołmogorowa do równania przewodnictwa cieplnego τ G X (τ, x) = i,j g i,j (x) 2 x i,x j G X (τ, x), G X (0, x) = δ(x X). Andrzej Palczewski ( UW) Zmienność implikowana 28 / 35
29 wstęp aproksymacja ścisłe wyniki inne metody metody geometrii różniczkowej Uogólnienie c.d. Niech M oznacza przestrzeń stanów procesu X t. M jest rozmaitościa Riemanna, jeśli metrykę Riemanna zdefiniujemy przez podanie wzoru na element długości ds 2 = i,j g i,j (x)dx i dx j, gdzie g i,j (x) = 2 k,l ρ k,l σ k i (x)σ l j (x) a ρ k,l jest odwrotnościa ρ k,l. Andrzej Palczewski ( UW) Zmienność implikowana 29 / 35
30 wstęp aproksymacja ścisłe wyniki inne metody metody geometrii różniczkowej Uogólnienie c.d. Twierdzenie (Varadhan 1967) lim 2τ ln G X (τ, x) = d 2 (x, X). τ 0 d(x, y) jest odległościa geodezyjna punktów x i y na rozmaitości Riemanna M wyznaczona przez ds d(x, y) = inf z(t):z(0)=x,z(1)=y 1 0 i,j g i,j (z(t)) dzi dt dz j dt dt. Uwaga Asymptotyczna zbieżność z pracy Berestycki, Busca, Florent (2002) pokrywa się z twierdzeniem Varadhana (należy tylko zdefiniować właściwa strukturę riemannowska). Andrzej Palczewski ( UW) Zmienność implikowana 30 / 35
31 wstęp aproksymacja ścisłe wyniki inne metody metody geometrii różniczkowej Uogólnienie c.d. Równanie Kołmogorowa dla rozkładu prawdopodobieństwa p(t, F F 0 ) jest bardziej skomplikowane niż równanie przewodnictwa cieplnego t p F0 (t, F) = i,j g i,j (F ) 2 F i,f j p F0 (t, F) + i b i (F) F i p F0 (t, F) + q(f)p F0 (t, F), p F0 (0, F) =δ(f F 0 ). (16) Aby badać takie równania na rozmaitości Riemanna należy zdefiniować wiazkę liniowa nad rozmaitościa M, a następnie koneksję w tej wiazce A oraz przekroje wiazki Q. Andrzej Palczewski ( UW) Zmienność implikowana 31 / 35
32 wstęp aproksymacja ścisłe wyniki inne metody metody geometrii różniczkowej Uogólnienie c.d. Wtedy równanie takiego typu jak równanie (16) można zapisać w postaci inwariantnej t p(t, x y) = Dp(t, x y), gdzie D jest operatorem eliptycznym na rozmaitości Riemanna D = g 1/2 i,j g 1/2 g i,j ( i + A i )( j + A j ) + Q a g = det(g i,j ). Andrzej Palczewski ( UW) Zmienność implikowana 32 / 35
33 wstęp aproksymacja ścisłe wyniki inne metody metody geometrii różniczkowej Uogólnienie c.d. W przypadku deterministycznej lokalnej zmienności równanie (16) jest jednowymiarowe. Można więc łatwo znaleźć koneksję A (jednowymiarowa) oraz przekrój Q oraz wykorzystać pochodzace od Yosidy (1953) rozwinięcie asymptotyczne rozwiazania równania (16). W przybliżeniu pierwszego rzędu daje to nastepujacy wzór na cenę opcji call σ(0, K )σ(0, P(0, T ) 1 C loc (0, F 0 ; T, K ) = (F 0 K ) + F0 )T + 2 2π ( ( H 1 (ω) + Q(F av ) + 3 ) ) 4 G(F av) TH 2 (ω), gdzie H 1, H 2, Q i G sa znanymi funkcjami a F av = (F 0 + K )/2, ω = K F 0 dx 2T xσ(0, x). Andrzej Palczewski ( UW) Zmienność implikowana 33 / 35
34 wstęp aproksymacja ścisłe wyniki inne metody metody geometrii różniczkowej Uogólnienie c.d. Wykonujac analogiczne obliczenia dla modelu Blacka (stała zmienność) oraz porównujac otrzymane wzory możemy wyprowadzić przybliżenie pierwszego rzędu dla zmienności implikowanej θ(k, T ) σ(0, K )σ(0, F0 ) H θ(k, T ) = 1 (ω) F0 K H 1 ( ω) ( ( H 1 (ω) + Q(F av ) G(F av) + θ(k, T )2 8 ) H 2 ( ω), H 1 ( ω) ) T H 2(ω) H 1 (ω) gdzie ω = ln(k /F 0) 2T θ(k, T ). Andrzej Palczewski ( UW) Zmienność implikowana 34 / 35
35 wstęp aproksymacja ścisłe wyniki inne metody metody geometrii różniczkowej DZIEKUJ E Andrzej Palczewski ( UW) Zmienność implikowana 35 / 35
Stochastyczne równania różniczkowe, model Blacka-Scholesa
 Stochastyczne równania różniczkowe, model Blacka-Scholesa Marcin Orchel Spis treści 1 Wstęp 1 1.1 Błądzenie losowe................................ 1 1. Proces Wienera................................. 1.3
Stochastyczne równania różniczkowe, model Blacka-Scholesa Marcin Orchel Spis treści 1 Wstęp 1 1.1 Błądzenie losowe................................ 1 1. Proces Wienera................................. 1.3
Dystrybucje, wiadomości wstępne (I)
 Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Temat 8 Dystrybucje, wiadomości wstępne (I) Wielkości fizyczne opisujemy najczęściej przyporządkowując im funkcje (np. zależne od czasu). Inną drogą opisu tych wielkości jest przyporządkowanie im funkcjonałów
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne
 Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Wstęp
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Wstęp
Wstęp do analitycznych i numerycznych metod wyceny opcji
 Wstęp do analitycznych i numerycznych metod wyceny opcji Jan Palczewski Wydział Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski Warszawa, 16 maja 2008 Jan Palczewski Wycena opcji Warszawa, 2008
Wstęp do analitycznych i numerycznych metod wyceny opcji Jan Palczewski Wydział Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski Warszawa, 16 maja 2008 Jan Palczewski Wycena opcji Warszawa, 2008
Komputerowa analiza zagadnień różniczkowych 10. Dwupunktowe problemy brzegowe (BVP, Boundary Value Problems)
 Komputerowa analiza zagadnień różniczkowych 10. Dwupunktowe problemy brzegowe (BVP, Boundary Value Problems) P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2007/08 Wprowadzenie Rozważmy
Komputerowa analiza zagadnień różniczkowych 10. Dwupunktowe problemy brzegowe (BVP, Boundary Value Problems) P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2007/08 Wprowadzenie Rozważmy
Dokumentacja. Portal Mathfinance Wycena opcji paryskich metoda. Wiktor Madejski
 Dokumentacja Portal Mathfinance Wycena opcji paryskich metoda PDE Wiktor Madejski Spis treści 1 Wstęp 2 2 Opcje paryskie 2 2.1 Układ PDE dla opcji paryskich..................... 2 2.2 Schemat numeryczny..........................
Dokumentacja Portal Mathfinance Wycena opcji paryskich metoda PDE Wiktor Madejski Spis treści 1 Wstęp 2 2 Opcje paryskie 2 2.1 Układ PDE dla opcji paryskich..................... 2 2.2 Schemat numeryczny..........................
Definicje i przykłady
 Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Prawa wielkich liczb, centralne twierdzenia graniczne
 , centralne twierdzenia graniczne Katedra matematyki i ekonomii matematycznej 17 maja 2012, centralne twierdzenia graniczne Rodzaje zbieżności ciągów zmiennych losowych, centralne twierdzenia graniczne
, centralne twierdzenia graniczne Katedra matematyki i ekonomii matematycznej 17 maja 2012, centralne twierdzenia graniczne Rodzaje zbieżności ciągów zmiennych losowych, centralne twierdzenia graniczne
Zagadnienia brzegowe dla równań eliptycznych
 Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Metoda rozdzielania zmiennych
 Rozdział 12 Metoda rozdzielania zmiennych W tym rozdziale zajmiemy się metodą rozdzielania zmiennych, którą można zastosować, aby wyrazić jawnymi wzorami rozwiązania pewnych konkretnych równań różniczkowych
Rozdział 12 Metoda rozdzielania zmiennych W tym rozdziale zajmiemy się metodą rozdzielania zmiennych, którą można zastosować, aby wyrazić jawnymi wzorami rozwiązania pewnych konkretnych równań różniczkowych
Układy równań liniowych
 Układy równań liniowych Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 1. wykład z algebry liniowej Warszawa, październik 2015 Mirosław Sobolewski (UW) Warszawa, wrzesień 2015 1 / 1
Układy równań liniowych Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 1. wykład z algebry liniowej Warszawa, październik 2015 Mirosław Sobolewski (UW) Warszawa, wrzesień 2015 1 / 1
Metody iteracyjne dla hiperbolicznych równań różniczkowo-funkcyjnych
 Metody iteracyjne dla hiperbolicznych równań różniczkowo-funkcyjnych Instytut Matematyki Uniwersytet Gdański 6 Wrzesień 2016 Zastosowania równań hiperbolicznych Nieliniowe równania hiperboliczne wykorzystywane
Metody iteracyjne dla hiperbolicznych równań różniczkowo-funkcyjnych Instytut Matematyki Uniwersytet Gdański 6 Wrzesień 2016 Zastosowania równań hiperbolicznych Nieliniowe równania hiperboliczne wykorzystywane
Szeregi funkcyjne. Szeregi potęgowe i trygonometryczne. Katedra Matematyki Wydział Informatyki Politechnika Białostocka
 Szeregi funkcyjne Szeregi potęgowe i trygonometryczne Małgorzata Wyrwas Katedra Matematyki Wydział Informatyki Politechnika Białostocka Szeregi funkcyjne str. 1/36 Szereg potęgowy Szeregiem potęgowym o
Szeregi funkcyjne Szeregi potęgowe i trygonometryczne Małgorzata Wyrwas Katedra Matematyki Wydział Informatyki Politechnika Białostocka Szeregi funkcyjne str. 1/36 Szereg potęgowy Szeregiem potęgowym o
Wstęp do metod numerycznych Uwarunkowanie Eliminacja Gaussa. P. F. Góra
 Wstęp do metod numerycznych Uwarunkowanie Eliminacja Gaussa P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2012 Uwarunkowanie zadania numerycznego Niech ϕ : R n R m będzie pewna funkcja odpowiednio wiele
Wstęp do metod numerycznych Uwarunkowanie Eliminacja Gaussa P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2012 Uwarunkowanie zadania numerycznego Niech ϕ : R n R m będzie pewna funkcja odpowiednio wiele
1 Szeregi potęgowe. 1.1 Promień zbieżności szeregu potęgowego. Wydział Informatyki, KONWERSATORIUM Z MATEMATYKI, 2008/2009.
 Szeregi potęgowe Definicja.. Szeregiem potęgowym o środku w punkcie R nazywamy szereg postaci: gdzie x R oraz c n R dla n = 0,, 2,... c n (x ) n, Przyjmujemy, że 0 0 def =. Liczby c n nazywamy współczynnikami
Szeregi potęgowe Definicja.. Szeregiem potęgowym o środku w punkcie R nazywamy szereg postaci: gdzie x R oraz c n R dla n = 0,, 2,... c n (x ) n, Przyjmujemy, że 0 0 def =. Liczby c n nazywamy współczynnikami
Informacja o przestrzeniach Sobolewa
 Wykład 11 Informacja o przestrzeniach Sobolewa 11.1 Definicja przestrzeni Sobolewa Niech R n będzie zbiorem mierzalnym. Rozważmy przestrzeń Hilberta X = L 2 () z iloczynem skalarnym zdefiniowanym równością
Wykład 11 Informacja o przestrzeniach Sobolewa 11.1 Definicja przestrzeni Sobolewa Niech R n będzie zbiorem mierzalnym. Rozważmy przestrzeń Hilberta X = L 2 () z iloczynem skalarnym zdefiniowanym równością
1 Równania różniczkowe zwyczajne o rozdzielonych zmiennych
 Równania różniczkowe zwyczajne o rozdzielonych zmiennych Definicja. Równaniem różniczkowym o rozdzielonych zmiennych nazywamy równanie postaci p(y) = q() (.) rozwiązanie równania sprowadza się do postaci
Równania różniczkowe zwyczajne o rozdzielonych zmiennych Definicja. Równaniem różniczkowym o rozdzielonych zmiennych nazywamy równanie postaci p(y) = q() (.) rozwiązanie równania sprowadza się do postaci
Z52: Algebra liniowa Zagadnienie: Zastosowania algebry liniowej Zadanie: Operatory różniczkowania, zagadnienie brzegowe.
 Z5: Algebra liniowa Zagadnienie: Zastosowania algebry liniowej Zadanie: Operatory różniczkowania zagadnienie brzegowe Dyskretne operatory różniczkowania Numeryczne obliczanie pochodnych oraz rozwiązywanie
Z5: Algebra liniowa Zagadnienie: Zastosowania algebry liniowej Zadanie: Operatory różniczkowania zagadnienie brzegowe Dyskretne operatory różniczkowania Numeryczne obliczanie pochodnych oraz rozwiązywanie
Rachunek różniczkowy i całkowy w przestrzeniach R n
 Rachunek różniczkowy i całkowy w przestrzeniach R n Na dzisiejszym wykładzie rozważać będziemy funkcje f : R m R n Każda taka funkcję f można przedstawić jako wektor funkcji (f 1, f 2,, f n ), gdzie każda
Rachunek różniczkowy i całkowy w przestrzeniach R n Na dzisiejszym wykładzie rozważać będziemy funkcje f : R m R n Każda taka funkcję f można przedstawić jako wektor funkcji (f 1, f 2,, f n ), gdzie każda
Modele zapisane w przestrzeni stanów
 Modele zapisane w przestrzeni stanów Modele Przestrzeni Stanów (State Space Models) sa to modele, w których część parametrów jest nieobserwowalna i losowa. Zachowanie wielowymiarowej zmiennej y t zależy
Modele zapisane w przestrzeni stanów Modele Przestrzeni Stanów (State Space Models) sa to modele, w których część parametrów jest nieobserwowalna i losowa. Zachowanie wielowymiarowej zmiennej y t zależy
ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH
 Transport, studia I stopnia Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Postać ogólna równania nieliniowego Często występującym, ważnym problemem obliczeniowym
Transport, studia I stopnia Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Postać ogólna równania nieliniowego Często występującym, ważnym problemem obliczeniowym
13 Równanie struny drgającej. Równanie przewodnictwa ciepła.
 Równanie struny drgającej. Równanie przewodnictwa ciepła 13 1 13 Równanie struny drgającej. Równanie przewodnictwa ciepła. 13.1 Równanie struny drgającej Równanie różniczkowe liniowe drugiego rzędu typu
Równanie struny drgającej. Równanie przewodnictwa ciepła 13 1 13 Równanie struny drgającej. Równanie przewodnictwa ciepła. 13.1 Równanie struny drgającej Równanie różniczkowe liniowe drugiego rzędu typu
Funkcje dwóch zmiennych
 Funkcje dwóch zmiennych Andrzej Musielak Str Funkcje dwóch zmiennych Wstęp Funkcja rzeczywista dwóch zmiennych to funkcja, której argumentem jest para liczb rzeczywistych, a wartością liczba rzeczywista.
Funkcje dwóch zmiennych Andrzej Musielak Str Funkcje dwóch zmiennych Wstęp Funkcja rzeczywista dwóch zmiennych to funkcja, której argumentem jest para liczb rzeczywistych, a wartością liczba rzeczywista.
Inżynieria Finansowa: 9. Wartość opcji i model Blacka-Scholesa w praktyce
 Inżynieria Finansowa: 9. Wartość opcji i model Blacka-Scholesa w praktyce Piotr Bańbuła atedra Ekonomii Ilościowej, AE Czerwiec 2017 r. Warszawa, Szkoła Główna Handlowa Wypłata Wypłata Opcja binarna 0
Inżynieria Finansowa: 9. Wartość opcji i model Blacka-Scholesa w praktyce Piotr Bańbuła atedra Ekonomii Ilościowej, AE Czerwiec 2017 r. Warszawa, Szkoła Główna Handlowa Wypłata Wypłata Opcja binarna 0
Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa. Diagnostyka i niezawodność robotów
 Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa Diagnostyka i niezawodność robotów Laboratorium nr 6 Model matematyczny elementu naprawialnego Prowadzący: mgr inż. Marcel Luzar Cele ćwiczenia:
Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa Diagnostyka i niezawodność robotów Laboratorium nr 6 Model matematyczny elementu naprawialnego Prowadzący: mgr inż. Marcel Luzar Cele ćwiczenia:
Analiza matematyczna dla informatyków 3 Zajęcia 14
 Analiza matematyczna dla informatyków 3 Zajęcia 14 Metoda rozwiązywania (Jednorodne równanie różniczkowe liniowe rzędu n o stałych współczynnikach). gdzie a 0,..., a n 1 C. Wielomian charakterystyczny:
Analiza matematyczna dla informatyków 3 Zajęcia 14 Metoda rozwiązywania (Jednorodne równanie różniczkowe liniowe rzędu n o stałych współczynnikach). gdzie a 0,..., a n 1 C. Wielomian charakterystyczny:
Metody numeryczne rozwiązywania równań różniczkowych
 Metody numeryczne rozwiązywania równań różniczkowych Marcin Orchel Spis treści Wstęp. Metody przybliżone dla równań pierwszego rzędu................ Metoda kolejnych przybliżeń Picarda...................2
Metody numeryczne rozwiązywania równań różniczkowych Marcin Orchel Spis treści Wstęp. Metody przybliżone dla równań pierwszego rzędu................ Metoda kolejnych przybliżeń Picarda...................2
RÓWNANIA RÓŻNICZKOWE WYKŁAD 2
 RÓWNANIA RÓŻNICZKOWE WYKŁAD 2 Równania różniczkowe o zmiennych rozdzielonych Równania sprowadzalne do równań o zmiennych rozdzielonych Niech f będzie funkcją ciągłą na przedziale (a, b), spełniającą na
RÓWNANIA RÓŻNICZKOWE WYKŁAD 2 Równania różniczkowe o zmiennych rozdzielonych Równania sprowadzalne do równań o zmiennych rozdzielonych Niech f będzie funkcją ciągłą na przedziale (a, b), spełniającą na
IX. MECHANIKA (FIZYKA) KWANTOWA
 IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
Zastosowania wyznaczników
 Zastosowania wyznaczników Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 7.wykład z algebry liniowej Warszawa, listopad 2012 Mirosław Sobolewski (UW) Warszawa, listopad 2012 1 / 17
Zastosowania wyznaczników Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 7.wykład z algebry liniowej Warszawa, listopad 2012 Mirosław Sobolewski (UW) Warszawa, listopad 2012 1 / 17
Metody numeryczne. materiały do wykładu dla studentów
 Metody numeryczne materiały do wykładu dla studentów 5. Przybliżone metody rozwiązywania równań 5.1 Lokalizacja pierwiastków 5.2 Metoda bisekcji 5.3 Metoda iteracji 5.4 Metoda stycznych (Newtona) 5.5 Metoda
Metody numeryczne materiały do wykładu dla studentów 5. Przybliżone metody rozwiązywania równań 5.1 Lokalizacja pierwiastków 5.2 Metoda bisekcji 5.3 Metoda iteracji 5.4 Metoda stycznych (Newtona) 5.5 Metoda
Rozdział 1. Wektory losowe. 1.1 Wektor losowy i jego rozkład
 Rozdział 1 Wektory losowe 1.1 Wektor losowy i jego rozkład Definicja 1 Wektor X = (X 1,..., X n ), którego każda współrzędna jest zmienną losową, nazywamy n-wymiarowym wektorem losowym (krótko wektorem
Rozdział 1 Wektory losowe 1.1 Wektor losowy i jego rozkład Definicja 1 Wektor X = (X 1,..., X n ), którego każda współrzędna jest zmienną losową, nazywamy n-wymiarowym wektorem losowym (krótko wektorem
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa.
 VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
Proces Poissona. Proces {N(t), t 0} nazywamy procesem zliczającym jeśli N(t) oznacza całkowitą liczbę badanych zdarzeń zaobserwowanych do chwili t.
 Procesy stochastyczne WYKŁAD 5 Proces Poissona. Proces {N(t), t } nazywamy procesem zliczającym jeśli N(t) oznacza całkowitą liczbę badanych zdarzeń zaobserwowanych do chwili t. Proces zliczający musi
Procesy stochastyczne WYKŁAD 5 Proces Poissona. Proces {N(t), t } nazywamy procesem zliczającym jeśli N(t) oznacza całkowitą liczbę badanych zdarzeń zaobserwowanych do chwili t. Proces zliczający musi
Równania różniczkowe. Notatki z wykładu.
 Równania różniczkowe Notatki z wykładu http://robert.brainusers.net 17.06.2009 Notatki własne z wykładu. Są niekompletne, bez bibliografii oraz mogą zawierać błędy i usterki. Z tego powodu niniejszy dokument
Równania różniczkowe Notatki z wykładu http://robert.brainusers.net 17.06.2009 Notatki własne z wykładu. Są niekompletne, bez bibliografii oraz mogą zawierać błędy i usterki. Z tego powodu niniejszy dokument
Stopę zbieżności ciagu zmiennych losowych a n, takiego, że E (a n ) < oznaczamy jako a n = o p (1) prawdopodobieństwa szybciej niż n α.
 Stopy zbieżności Stopę zbieżności ciagu zmiennych losowych a n, takiego, że a n oznaczamy jako a n = o p (1 p 0 a Jeśli n p n α 0, to a n = o p (n α i mówimy a n zbiega według prawdopodobieństwa szybciej
Stopy zbieżności Stopę zbieżności ciagu zmiennych losowych a n, takiego, że a n oznaczamy jako a n = o p (1 p 0 a Jeśli n p n α 0, to a n = o p (n α i mówimy a n zbiega według prawdopodobieństwa szybciej
Informacja o przestrzeniach Hilberta
 Temat 10 Informacja o przestrzeniach Hilberta 10.1 Przestrzenie unitarne, iloczyn skalarny Niech dana będzie przestrzeń liniowa X. Załóżmy, że każdej parze elementów x, y X została przyporządkowana liczba
Temat 10 Informacja o przestrzeniach Hilberta 10.1 Przestrzenie unitarne, iloczyn skalarny Niech dana będzie przestrzeń liniowa X. Załóżmy, że każdej parze elementów x, y X została przyporządkowana liczba
Pochodne cząstkowe i ich zastosowanie. Ekstrema lokalne funkcji
 Pochodne cząstkowe i ich zastosowanie. Ekstrema lokalne funkcji Adam Kiersztyn Lublin 2014 Adam Kiersztyn () Pochodne cząstkowe i ich zastosowanie. Ekstrema lokalne funkcji maj 2014 1 / 24 Zanim przejdziemy
Pochodne cząstkowe i ich zastosowanie. Ekstrema lokalne funkcji Adam Kiersztyn Lublin 2014 Adam Kiersztyn () Pochodne cząstkowe i ich zastosowanie. Ekstrema lokalne funkcji maj 2014 1 / 24 Zanim przejdziemy
Modelowanie rynków finansowych z wykorzystaniem pakietu R
 Modelowanie rynków finansowych z wykorzystaniem pakietu R Metody numeryczne i symulacje stochastyczne Mateusz Topolewski woland@mat.umk.pl Wydział Matematyki i Informatyki UMK Plan działania 1 Całkowanie
Modelowanie rynków finansowych z wykorzystaniem pakietu R Metody numeryczne i symulacje stochastyczne Mateusz Topolewski woland@mat.umk.pl Wydział Matematyki i Informatyki UMK Plan działania 1 Całkowanie
Ciągi liczbowe wykład 3
 Ciągi liczbowe wykład 3 dr Mariusz Grządziel 3 kwietnia 203 Definicja (ciągu liczbowego). Ciagiem liczbowym nazywamy funkcję odwzorowuja- ca zbiór liczb naturalnych w zbiór liczb rzeczywistych. Wartość
Ciągi liczbowe wykład 3 dr Mariusz Grządziel 3 kwietnia 203 Definicja (ciągu liczbowego). Ciagiem liczbowym nazywamy funkcję odwzorowuja- ca zbiór liczb naturalnych w zbiór liczb rzeczywistych. Wartość
O pewnych klasach funkcji prawie okresowych (niekoniecznie ograniczonych)
 (niekoniecznie ograniczonych) Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza, Poznań Będlewo, 25-30 maja 2015 Funkcje prawie okresowe w sensie Bohra Definicja Zbiór E R nazywamy względnie
(niekoniecznie ograniczonych) Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza, Poznań Będlewo, 25-30 maja 2015 Funkcje prawie okresowe w sensie Bohra Definicja Zbiór E R nazywamy względnie
Wykład 3 Jednowymiarowe zmienne losowe
 Wykład 3 Jednowymiarowe zmienne losowe Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną Definicja 1 Jednowymiarowa zmienna losowa (o wartościach rzeczywistych), określoną na przestrzeni probabilistycznej
Wykład 3 Jednowymiarowe zmienne losowe Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną Definicja 1 Jednowymiarowa zmienna losowa (o wartościach rzeczywistych), określoną na przestrzeni probabilistycznej
Równanie przewodnictwa cieplnego (I)
 Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
SZEREGI LICZBOWE I FUNKCYJNE
 Mając dowolny ciąg można z niego utworzyć nowy ciąg sum częściowych: Ten nowy rodzaj ciągu nazywamy szeregiem liczbowym, a jeśli to mamy do czynienia z nieskończonym szeregiem liczbowym, który oznaczany
Mając dowolny ciąg można z niego utworzyć nowy ciąg sum częściowych: Ten nowy rodzaj ciągu nazywamy szeregiem liczbowym, a jeśli to mamy do czynienia z nieskończonym szeregiem liczbowym, który oznaczany
Oznacza to, że chcemy znaleźć minimum, a właściwie wartość najmniejszą funkcji
 Wykład 11. Metoda najmniejszych kwadratów Szukamy zależności Dane są wyniki pomiarów dwóch wielkości x i y: (x 1, y 1 ), (x 2, y 2 ),..., (x n, y n ). Przypuśćmy, że nanieśliśmy je na wykres w układzie
Wykład 11. Metoda najmniejszych kwadratów Szukamy zależności Dane są wyniki pomiarów dwóch wielkości x i y: (x 1, y 1 ), (x 2, y 2 ),..., (x n, y n ). Przypuśćmy, że nanieśliśmy je na wykres w układzie
I. Pochodna i różniczka funkcji jednej zmiennej. 1. Definicja pochodnej funkcji i jej interpretacja fizyczna. Istnienie pochodnej funkcji.
 I. Pochodna i różniczka funkcji jednej zmiennej. 1. Definicja pochodnej funkcji i jej interpretacja fizyczna. Istnienie pochodnej funkcji. Niech x 0 R i niech f będzie funkcją określoną przynajmniej na
I. Pochodna i różniczka funkcji jednej zmiennej. 1. Definicja pochodnej funkcji i jej interpretacja fizyczna. Istnienie pochodnej funkcji. Niech x 0 R i niech f będzie funkcją określoną przynajmniej na
Procesy stochastyczne 2.
 Procesy stochastyczne 2. Listy zadań 1-3. Autor: dr hab.a. Jurlewicz WPPT Matematyka, studia drugiego stopnia, I rok, rok akad. 211/12 1 Lista 1: Własność braku pamięci. Procesy o przyrostach niezależnych,
Procesy stochastyczne 2. Listy zadań 1-3. Autor: dr hab.a. Jurlewicz WPPT Matematyka, studia drugiego stopnia, I rok, rok akad. 211/12 1 Lista 1: Własność braku pamięci. Procesy o przyrostach niezależnych,
Zaawansowane metody numeryczne
 Wykład 11 Ogólna postać metody iteracyjnej Definicja 11.1. (metoda iteracyjna rozwiązywania układów równań) Metodą iteracyjną rozwiązywania { układów równań liniowych nazywamy ciąg wektorów zdefiniowany
Wykład 11 Ogólna postać metody iteracyjnej Definicja 11.1. (metoda iteracyjna rozwiązywania układów równań) Metodą iteracyjną rozwiązywania { układów równań liniowych nazywamy ciąg wektorów zdefiniowany
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. - funkcja dwóch zmiennych,
 IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
Spis treści. Rozdział I. Wstęp do matematyki Rozdział II. Ciągi i szeregi... 44
 Księgarnia PWN: Ryszard Rudnicki, Wykłady z analizy matematycznej Spis treści Rozdział I. Wstęp do matematyki... 13 1.1. Elementy logiki i teorii zbiorów... 13 1.1.1. Rachunek zdań... 13 1.1.2. Reguły
Księgarnia PWN: Ryszard Rudnicki, Wykłady z analizy matematycznej Spis treści Rozdział I. Wstęp do matematyki... 13 1.1. Elementy logiki i teorii zbiorów... 13 1.1.1. Rachunek zdań... 13 1.1.2. Reguły
Matematyka II. Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 2018/2019 wykład 13 (27 maja)
 Matematyka II Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 208/209 wykład 3 (27 maja) Całki niewłaściwe przedział nieograniczony Rozpatrujemy funkcje ciągłe określone na zbiorach < a, ),
Matematyka II Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 208/209 wykład 3 (27 maja) Całki niewłaściwe przedział nieograniczony Rozpatrujemy funkcje ciągłe określone na zbiorach < a, ),
Ważną rolę odgrywają tzw. funkcje harmoniczne. Przyjmujemy następującą definicję. u = 0, (6.1) jest operatorem Laplace a. (x,y)
 Wykład 6 Funkcje harmoniczne Ważną rolę odgrywają tzw. funkcje harmoniczne. Przyjmujemy następującą definicję. e f i n i c j a Funkcję u (x 1, x 2,..., x n ) nazywamy harmoniczną w obszarze R n wtedy i
Wykład 6 Funkcje harmoniczne Ważną rolę odgrywają tzw. funkcje harmoniczne. Przyjmujemy następującą definicję. e f i n i c j a Funkcję u (x 1, x 2,..., x n ) nazywamy harmoniczną w obszarze R n wtedy i
Tydzień nr 9-10 (16 maja - 29 maja), Równania różniczkowe, wartości własne, funkcja wykładnicza od operatora - Matematyka II 2010/2011L
 Tydzień nr 9-10 (16 maja - 29 maja) Równania różniczkowe wartości własne funkcja wykładnicza od operatora - Matematyka II 2010/2011L Wszelkie pytania oraz uwagi o błędach proszę kierować na przemek.majewski@gmail.com
Tydzień nr 9-10 (16 maja - 29 maja) Równania różniczkowe wartości własne funkcja wykładnicza od operatora - Matematyka II 2010/2011L Wszelkie pytania oraz uwagi o błędach proszę kierować na przemek.majewski@gmail.com
Ciagi liczbowe wykład 4
 Ciagi liczbowe wykład 4 dr Mariusz Grzadziel Katedra Matematyki, Uniwersytet Przyrodniczy we Wrocławiu semestr zimowy, r. akad. 2016/2017 Definicja (ciagu liczbowego) Ciagiem liczbowym nazywamy funkcję
Ciagi liczbowe wykład 4 dr Mariusz Grzadziel Katedra Matematyki, Uniwersytet Przyrodniczy we Wrocławiu semestr zimowy, r. akad. 2016/2017 Definicja (ciagu liczbowego) Ciagiem liczbowym nazywamy funkcję
Kryptografia - zastosowanie krzywych eliptycznych
 Kryptografia - zastosowanie krzywych eliptycznych 24 marca 2011 Niech F będzie ciałem doskonałym (tzn. każde rozszerzenie algebraiczne ciała F jest rozdzielcze lub równoważnie, monomorfizm Frobeniusa jest
Kryptografia - zastosowanie krzywych eliptycznych 24 marca 2011 Niech F będzie ciałem doskonałym (tzn. każde rozszerzenie algebraiczne ciała F jest rozdzielcze lub równoważnie, monomorfizm Frobeniusa jest
Całki niewłaściwe. Całki w granicach nieskończonych
 Całki niewłaściwe Całki w granicach nieskończonych Wiemy, co to jest w przypadku skończonego przedziału i funkcji ograniczonej. Okazuje się potrzebne uogólnienie tego pojęcia w różnych kierunkach (przedział
Całki niewłaściwe Całki w granicach nieskończonych Wiemy, co to jest w przypadku skończonego przedziału i funkcji ograniczonej. Okazuje się potrzebne uogólnienie tego pojęcia w różnych kierunkach (przedział
Układy równań liniowych
 Układy równań liniowych Niech K będzie ciałem. Niech n, m N. Równanie liniowe nad ciałem K z niewiadomymi (lub zmiennymi) x 1, x 2,..., x n K definiujemy jako formę zdaniową zmiennej (x 1,..., x n ) K
Układy równań liniowych Niech K będzie ciałem. Niech n, m N. Równanie liniowe nad ciałem K z niewiadomymi (lub zmiennymi) x 1, x 2,..., x n K definiujemy jako formę zdaniową zmiennej (x 1,..., x n ) K
Prawdopodobieństwo i statystyka
 Wykład XIV: Metody Monte Carlo 19 stycznia 2016 Przybliżone obliczanie całki oznaczonej Rozważmy całkowalną funkcję f : [0, 1] R. Chcemy znaleźć przybliżoną wartość liczbową całki 1 f (x) dx. 0 Jeden ze
Wykład XIV: Metody Monte Carlo 19 stycznia 2016 Przybliżone obliczanie całki oznaczonej Rozważmy całkowalną funkcję f : [0, 1] R. Chcemy znaleźć przybliżoną wartość liczbową całki 1 f (x) dx. 0 Jeden ze
XI Konferencja Metody Ilościowe w Badaniach Ekonomicznych
 Rafał M. Łochowski Szkoła Główna Handlowa w Warszawie O górnym ograniczeniu zysku ze strategii handlowej opartej na kointegracji XI Konferencja Metody Ilościowe w Badaniach Ekonomicznych Zależność kointegracyjna
Rafał M. Łochowski Szkoła Główna Handlowa w Warszawie O górnym ograniczeniu zysku ze strategii handlowej opartej na kointegracji XI Konferencja Metody Ilościowe w Badaniach Ekonomicznych Zależność kointegracyjna
Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t)
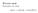 Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Figure 1: Aproksymacja drzewem dwumianowym Wycena opcji Dynamika cen akcji:
Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Wycena opcji Dynamika cen akcji: ds(t) = as(t)dt + σs(t)dw (t) Figure 1: Aproksymacja drzewem dwumianowym Wycena opcji Dynamika cen akcji:
Równania różniczkowe cząstkowe drugiego rzędu
 Równania różniczkowe cząstkowe drugiego rzędu Marcin Orchel Spis treści 1 Wstęp 1 1.1 Metoda faktoryzacji (rozdzielania zmiennych)................ 5 1.2 Metoda funkcji Greena.............................
Równania różniczkowe cząstkowe drugiego rzędu Marcin Orchel Spis treści 1 Wstęp 1 1.1 Metoda faktoryzacji (rozdzielania zmiennych)................ 5 1.2 Metoda funkcji Greena.............................
ZASTOSOWANIE RACHUNKU OPERATORÓW MIKUS- IŃSKIEGO W PEWNYCH ZAGADNIENIACH DYNAMIKI KONSTRUKCJI
 Budownictwo 18 Mariusz Poński ZASTOSOWANIE RACHUNKU OPERATORÓW MIKUS- IŃSKIEGO W PEWNYCH ZAGADNIENIACH DYNAMIKI KONSTRUKCJI 1. Metody transformacji całkowych Najczęściej spotykaną metodą rozwiązywania
Budownictwo 18 Mariusz Poński ZASTOSOWANIE RACHUNKU OPERATORÓW MIKUS- IŃSKIEGO W PEWNYCH ZAGADNIENIACH DYNAMIKI KONSTRUKCJI 1. Metody transformacji całkowych Najczęściej spotykaną metodą rozwiązywania
2. Definicja pochodnej w R n
 2. Definicja pochodnej w R n Niech będzie dana funkcja f : U R określona na zbiorze otwartym U R n. Pochodną kierunkową w punkcie a U w kierunku wektora u R n nazywamy granicę u f(a) = lim t 0 f(a + tu)
2. Definicja pochodnej w R n Niech będzie dana funkcja f : U R określona na zbiorze otwartym U R n. Pochodną kierunkową w punkcie a U w kierunku wektora u R n nazywamy granicę u f(a) = lim t 0 f(a + tu)
Stabilność II Metody Lapunowa badania stabilności
 Metody Lapunowa badania stabilności Interesuje nas w sposób szczególny system: Wprowadzamy dla niego pojęcia: - stabilności wewnętrznej - odnosi się do zachowania się systemu przy zerowym wejściu, czyli
Metody Lapunowa badania stabilności Interesuje nas w sposób szczególny system: Wprowadzamy dla niego pojęcia: - stabilności wewnętrznej - odnosi się do zachowania się systemu przy zerowym wejściu, czyli
Układy liniowo niezależne
 Układy liniowo niezależne Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 3.wykład z algebry liniowej Warszawa, październik 2016 Mirosław Sobolewski (UW) Warszawa, październik 2016 1
Układy liniowo niezależne Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 3.wykład z algebry liniowej Warszawa, październik 2016 Mirosław Sobolewski (UW) Warszawa, październik 2016 1
Programowanie celowe #1
 Programowanie celowe #1 Problem programowania celowego (PC) jest przykładem problemu programowania matematycznego nieliniowego, który można skutecznie zlinearyzować, tzn. zapisać (i rozwiązać) jako problem
Programowanie celowe #1 Problem programowania celowego (PC) jest przykładem problemu programowania matematycznego nieliniowego, który można skutecznie zlinearyzować, tzn. zapisać (i rozwiązać) jako problem
Wstęp do metod numerycznych Faktoryzacja QR i SVD. P. F. Góra
 Wstęp do metod numerycznych Faktoryzacja QR i SVD P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2012 Transformacja Householdera Niech u R N, u 0. Tworzymy macierz W sposób oczywisty P T = P. Obliczmy
Wstęp do metod numerycznych Faktoryzacja QR i SVD P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2012 Transformacja Householdera Niech u R N, u 0. Tworzymy macierz W sposób oczywisty P T = P. Obliczmy
Logarytmy. Funkcje logarytmiczna i wykładnicza. Równania i nierówności wykładnicze i logarytmiczne.
 Logarytmy. Funkcje logarytmiczna i wykładnicza. Równania i nierówności wykładnicze i logarytmiczne. Definicja. Niech a i b będą dodatnimi liczbami rzeczywistymi i niech a. Logarytmem liczby b przy podstawie
Logarytmy. Funkcje logarytmiczna i wykładnicza. Równania i nierówności wykładnicze i logarytmiczne. Definicja. Niech a i b będą dodatnimi liczbami rzeczywistymi i niech a. Logarytmem liczby b przy podstawie
Całkowanie numeryczne
 Całkowanie numeryczne Poniżej omówione zostanie kilka metod przybliżania operacji całkowania i różniczkowania w szczególności uzależnieniu pochodnej od jej różnic skończonych gdy równanie różniczkowe mamy
Całkowanie numeryczne Poniżej omówione zostanie kilka metod przybliżania operacji całkowania i różniczkowania w szczególności uzależnieniu pochodnej od jej różnic skończonych gdy równanie różniczkowe mamy
Rynek, opcje i równania SDE
 Rynek, opcje i równania SDE Adam Majewski Uniwersytet Gdański kwiecień 2009 Adam Majewski (Uniwersytet Gdański) Rynek, opcje i równania SDE kwiecień 2009 1 / 16 1 Rynek, portfel inwestycyjny, arbitraż
Rynek, opcje i równania SDE Adam Majewski Uniwersytet Gdański kwiecień 2009 Adam Majewski (Uniwersytet Gdański) Rynek, opcje i równania SDE kwiecień 2009 1 / 16 1 Rynek, portfel inwestycyjny, arbitraż
Pojęcie szeregu nieskończonego:zastosowania do rachunku prawdopodobieństwa wykład 1
 Pojęcie szeregu nieskończonego:zastosowania do rachunku prawdopodobieństwa wykład dr Mariusz Grządziel 5 lutego 04 Paradoks Zenona z Elei wersja uwspółcześniona Zenek goni Andrzeja; prędkość Andrzeja:
Pojęcie szeregu nieskończonego:zastosowania do rachunku prawdopodobieństwa wykład dr Mariusz Grządziel 5 lutego 04 Paradoks Zenona z Elei wersja uwspółcześniona Zenek goni Andrzeja; prędkość Andrzeja:
19 marzec, Łańcuchy Markowa z czasem dyskretnym. Procesy Stochastyczne, wykład 6, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1136
 Procesy Stochastyczne, wykład 6, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1136 19 marzec, 2012 Przykłady procesów Markowa (i). P = (p ij ) - macierz stochastyczna, tzn. p ij 0, j p ij =
Procesy Stochastyczne, wykład 6, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1136 19 marzec, 2012 Przykłady procesów Markowa (i). P = (p ij ) - macierz stochastyczna, tzn. p ij 0, j p ij =
Rozwiązywanie równań nieliniowych
 Rozwiązywanie równań nieliniowych Marcin Orchel 1 Wstęp Przykłady wyznaczania miejsc zerowych funkcji f : f(ξ) = 0. Wyszukiwanie miejsc zerowych wielomianu n-tego stopnia. Wymiar tej przestrzeni wektorowej
Rozwiązywanie równań nieliniowych Marcin Orchel 1 Wstęp Przykłady wyznaczania miejsc zerowych funkcji f : f(ξ) = 0. Wyszukiwanie miejsc zerowych wielomianu n-tego stopnia. Wymiar tej przestrzeni wektorowej
1 Wykład 4. Proste Prawa wielkich liczb, CTG i metody Monte Carlo
 1 Wykład 4. Proste Prawa wielkich liczb, CTG i metody Monte Carlo 1.1 Rodzaje zbieżności ciagów zmiennych losowych Niech (Ω, F, P ) będzie przestrzenia probabilistyczna na której określony jest ciag {X
1 Wykład 4. Proste Prawa wielkich liczb, CTG i metody Monte Carlo 1.1 Rodzaje zbieżności ciagów zmiennych losowych Niech (Ω, F, P ) będzie przestrzenia probabilistyczna na której określony jest ciag {X
26 marzec, Łańcuchy Markowa z czasem ciągłym. Procesy Stochastyczne, wykład 7, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1136
 Procesy Stochastyczne, wykład 7, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1136 26 marzec, 212 Łańcuchy z czasem ciągłym S = {, 1,..., }, B S = 2 S, ale T = [, ) lub T = (, ). Gdy S skończone,
Procesy Stochastyczne, wykład 7, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1136 26 marzec, 212 Łańcuchy z czasem ciągłym S = {, 1,..., }, B S = 2 S, ale T = [, ) lub T = (, ). Gdy S skończone,
Równania różniczkowe liniowe wyższych rzędów o stałych współcz
 Równania różniczkowe liniowe wyższych rzędów o stałych współczynnikach Katedra Matematyki i Ekonomii Matematycznej SGH 12 maja 2016 Równanie liniowe n-tego rzędu Definicja Równaniem różniczkowym liniowym
Równania różniczkowe liniowe wyższych rzędów o stałych współczynnikach Katedra Matematyki i Ekonomii Matematycznej SGH 12 maja 2016 Równanie liniowe n-tego rzędu Definicja Równaniem różniczkowym liniowym
Jak trudne jest numeryczne całkowanie (O złożoności zadań ciągłych)
 Jak trudne jest numeryczne całkowanie (O złożoności zadań ciągłych) Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki leszekp@mimuw.edu.pl Horyzonty 2014 17-03-2014 Będlewo Zadania numeryczne
Jak trudne jest numeryczne całkowanie (O złożoności zadań ciągłych) Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki leszekp@mimuw.edu.pl Horyzonty 2014 17-03-2014 Będlewo Zadania numeryczne
Układy równań i równania wyższych rzędów
 Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
Wykład 6 Centralne Twierdzenie Graniczne. Rozkłady wielowymiarowe
 Wykład 6 Centralne Twierdzenie Graniczne. Rozkłady wielowymiarowe Nierówność Czebyszewa Niech X będzie zmienną losową o skończonej wariancji V ar(x). Wtedy wartość oczekiwana E(X) też jest skończona i
Wykład 6 Centralne Twierdzenie Graniczne. Rozkłady wielowymiarowe Nierówność Czebyszewa Niech X będzie zmienną losową o skończonej wariancji V ar(x). Wtedy wartość oczekiwana E(X) też jest skończona i
Metody numeryczne w przykładach
 Metody numeryczne w przykładach Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK, Toruń Regionalne Koło Matematyczne 8 kwietnia 2010 r. Bartosz Ziemkiewicz (WMiI UMK) Metody numeryczne w przykładach
Metody numeryczne w przykładach Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK, Toruń Regionalne Koło Matematyczne 8 kwietnia 2010 r. Bartosz Ziemkiewicz (WMiI UMK) Metody numeryczne w przykładach
Quantile hedging. czyli jak tanio i dobrze zabezpieczyć opcję. Michał Krawiec, Piotr Piestrzyński
 czyli jak tanio i dobrze zabezpieczyć opcję Michał Krawiec Piotr Piestrzyński Koło Naukowe Probabilistyki i Statystyki Matematycznej Uniwersytet Wrocławski Niedziela, 19 kwietnia 2015 Przykład (opis problemu)
czyli jak tanio i dobrze zabezpieczyć opcję Michał Krawiec Piotr Piestrzyński Koło Naukowe Probabilistyki i Statystyki Matematycznej Uniwersytet Wrocławski Niedziela, 19 kwietnia 2015 Przykład (opis problemu)
Matematyka z el. statystyki, # 4 /Geodezja i kartografia I/
 Matematyka z el. statystyki, # 4 /Geodezja i kartografia I/ dr n. mat. Zdzisław Otachel Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Akademicka 15, p.211a, bud. Agro
Matematyka z el. statystyki, # 4 /Geodezja i kartografia I/ dr n. mat. Zdzisław Otachel Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Akademicka 15, p.211a, bud. Agro
Całka podwójna po prostokącie
 Całka podwójna po prostokącie Rozważmy prostokąt = {(x, y) R : a x b, c y d}, gdzie a, b, c, d R, oraz funkcję dwóch zmiennych f : R ograniczoną w tym prostokącie. rostokąt dzielimy na n prostokątów i
Całka podwójna po prostokącie Rozważmy prostokąt = {(x, y) R : a x b, c y d}, gdzie a, b, c, d R, oraz funkcję dwóch zmiennych f : R ograniczoną w tym prostokącie. rostokąt dzielimy na n prostokątów i
y + p(t)y + q(t)y = 0. (1) Z rozwiązywaniem równań przez szeregi potęgowe związane są pewne definicje.
 1 Szeregi potęgowe Poszukiwanie rozwiązań równań różniczkowych zwyczajnych w postaci szeregów potęgowych, zwane metodą Frobeniusa, jest bardzo ogólną metodą. Rozważmy równanie y + p(t)y + q(t)y = 0. (1)
1 Szeregi potęgowe Poszukiwanie rozwiązań równań różniczkowych zwyczajnych w postaci szeregów potęgowych, zwane metodą Frobeniusa, jest bardzo ogólną metodą. Rozważmy równanie y + p(t)y + q(t)y = 0. (1)
1 Relacje i odwzorowania
 Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
WYKŁAD 3. Witold Bednorz, Paweł Wolff. Rachunek Prawdopodobieństwa, WNE, Uniwersytet Warszawski. 1 Instytut Matematyki
 WYKŁAD 3 Witold Bednorz, Paweł Wolff 1 Instytut Matematyki Uniwersytet Warszawski Rachunek Prawdopodobieństwa, WNE, 2010-2011 Schemmat Bernouliego Rzucamy 10 razy moneta, próba Bernouliego jest pojedynczy
WYKŁAD 3 Witold Bednorz, Paweł Wolff 1 Instytut Matematyki Uniwersytet Warszawski Rachunek Prawdopodobieństwa, WNE, 2010-2011 Schemmat Bernouliego Rzucamy 10 razy moneta, próba Bernouliego jest pojedynczy
Metoda Monte Carlo i jej zastosowania
 i jej zastosowania Tomasz Mostowski Zajęcia 31.03.2008 Plan 1 PWL 2 3 Plan PWL 1 PWL 2 3 Przypomnienie PWL Istnieje wiele wariantów praw wielkich liczb. Wspólna ich cecha jest asymptotyczne zachowanie
i jej zastosowania Tomasz Mostowski Zajęcia 31.03.2008 Plan 1 PWL 2 3 Plan PWL 1 PWL 2 3 Przypomnienie PWL Istnieje wiele wariantów praw wielkich liczb. Wspólna ich cecha jest asymptotyczne zachowanie
Wykład 11: Martyngały: Twierdzenie o zbieżności i Hoeffdinga
 RAP 412 21.01.2009 Wykład 11: Martyngały: Twierdzenie o zbieżności i Hoeffdinga Wykładowca: Andrzej Ruciński Pisarz: Łukasz Waszak 1 Wstęp Na ostatnim wykładzie przedstawiliśmy twierdzenie o zbieżności
RAP 412 21.01.2009 Wykład 11: Martyngały: Twierdzenie o zbieżności i Hoeffdinga Wykładowca: Andrzej Ruciński Pisarz: Łukasz Waszak 1 Wstęp Na ostatnim wykładzie przedstawiliśmy twierdzenie o zbieżności
Równania różniczkowe cząstkowe. Wojciech Szewczuk
 Równania różniczkowe cząstkowe Równania różniczkowe cząstkowe - wstęp u x = lim x u(x + x, y) u(x, y) x u u(x, y + y) u(x, y) y = lim y y () (2) 2 u x 2 + 2xy 2 u y 2 + u = 3 u x 2 y + x 2 u + 8u = 5y
Równania różniczkowe cząstkowe Równania różniczkowe cząstkowe - wstęp u x = lim x u(x + x, y) u(x, y) x u u(x, y + y) u(x, y) y = lim y y () (2) 2 u x 2 + 2xy 2 u y 2 + u = 3 u x 2 y + x 2 u + 8u = 5y
Konstrukcja uśmiechu zmienności. Dr Piotr Zasępa
 Konstrukcja uśmiechu zmienności Dr Piotr Zasępa Rynek opcji FX Rynek Międzybankowy Market Makerów Klientowski (bank/klient) (bank makler/bank user) Rynek opcji waniliowych Opcje egzotyczne I generacji
Konstrukcja uśmiechu zmienności Dr Piotr Zasępa Rynek opcji FX Rynek Międzybankowy Market Makerów Klientowski (bank/klient) (bank makler/bank user) Rynek opcji waniliowych Opcje egzotyczne I generacji
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 7/15 Rachunek różnicowy Dobrym narzędziem do obliczania skończonych sum jest rachunek różnicowy. W rachunku tym odpowiednikiem operatora
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 7/15 Rachunek różnicowy Dobrym narzędziem do obliczania skończonych sum jest rachunek różnicowy. W rachunku tym odpowiednikiem operatora
Układy równań nieliniowych (wielowymiarowa metoda Newtona-Raphsona) f(x) = 0, gdzie. dla n=2 np.
 Układy równań nieliniowych (wielowymiarowa metoda Newtona-Raphsona f(x 0, f ( f, f,..., f n gdzie 2 x ( x, x 2,..., x n dla n2 np. f ( x, y 0 g( x, y 0 dla każdej wielowymiarowej rozwinięcie w szereg Taylora
Układy równań nieliniowych (wielowymiarowa metoda Newtona-Raphsona f(x 0, f ( f, f,..., f n gdzie 2 x ( x, x 2,..., x n dla n2 np. f ( x, y 0 g( x, y 0 dla każdej wielowymiarowej rozwinięcie w szereg Taylora
1.1 Przegląd wybranych równań i modeli fizycznych. , u x1 x 2
 Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
1 Metody rozwiązywania równań nieliniowych. Postawienie problemu
 1 Metody rozwiązywania równań nieliniowych. Postawienie problemu Dla danej funkcji ciągłej f znaleźć wartości x, dla których f(x) = 0. (1) 2 Przedział izolacji pierwiastka Będziemy zakładać, że równanie
1 Metody rozwiązywania równań nieliniowych. Postawienie problemu Dla danej funkcji ciągłej f znaleźć wartości x, dla których f(x) = 0. (1) 2 Przedział izolacji pierwiastka Będziemy zakładać, że równanie
Pochodna funkcji: zastosowania przyrodnicze wykłady 7 i 8
 Pochodna funkcji: zastosowania przyrodnicze wykłady 7 i 8 dr Mariusz Grzadziel Katedra Matematyki, Uniwersytet Przyrodniczy we Wrocławiu sem. zimowy, r. akad. 2016/2017 Funkcja logistyczna 40 Rozważmy
Pochodna funkcji: zastosowania przyrodnicze wykłady 7 i 8 dr Mariusz Grzadziel Katedra Matematyki, Uniwersytet Przyrodniczy we Wrocławiu sem. zimowy, r. akad. 2016/2017 Funkcja logistyczna 40 Rozważmy
Dokumentacja. Opcje europejskie PDE. Michał Grzelak
 Dokumentacja Opcje europejskie PDE Michał Grzelak Spis treści 1 Ceny opcji z local volatility 2 1.1 Opcje plain vanilla z local volatility................. 2 1.2 Parametry greckie..........................
Dokumentacja Opcje europejskie PDE Michał Grzelak Spis treści 1 Ceny opcji z local volatility 2 1.1 Opcje plain vanilla z local volatility................. 2 1.2 Parametry greckie..........................
Równanie przewodnictwa cieplnego (II)
 Wykład 5 Równanie przewodnictwa cieplnego (II) 5.1 Metoda Fouriera dla pręta ograniczonego 5.1.1 Pierwsze zagadnienie brzegowe dla pręta ograniczonego Poszukujemy rozwiązania równania przewodnictwa spełniającego
Wykład 5 Równanie przewodnictwa cieplnego (II) 5.1 Metoda Fouriera dla pręta ograniczonego 5.1.1 Pierwsze zagadnienie brzegowe dla pręta ograniczonego Poszukujemy rozwiązania równania przewodnictwa spełniającego
13. Równania różniczkowe - portrety fazowe
 13. Równania różniczkowe - portrety fazowe Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie rzegorz Kosiorowski (Uniwersytet Ekonomiczny 13. wrównania Krakowie) różniczkowe - portrety fazowe 1 /
13. Równania różniczkowe - portrety fazowe Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie rzegorz Kosiorowski (Uniwersytet Ekonomiczny 13. wrównania Krakowie) różniczkowe - portrety fazowe 1 /
KADD Minimalizacja funkcji
 Minimalizacja funkcji Poszukiwanie minimum funkcji Foma kwadratowa Metody przybliżania minimum minimalizacja Minimalizacja w n wymiarach Metody poszukiwania minimum Otaczanie minimum Podział obszaru zawierającego
Minimalizacja funkcji Poszukiwanie minimum funkcji Foma kwadratowa Metody przybliżania minimum minimalizacja Minimalizacja w n wymiarach Metody poszukiwania minimum Otaczanie minimum Podział obszaru zawierającego
Transformaty. Kodowanie transformujace
 Transformaty. Kodowanie transformujace Kodowanie i kompresja informacji - Wykład 10 10 maja 2009 Szeregi Fouriera Każda funkcję okresowa f (t) o okresie T można zapisać jako f (t) = a 0 + a n cos nω 0
Transformaty. Kodowanie transformujace Kodowanie i kompresja informacji - Wykład 10 10 maja 2009 Szeregi Fouriera Każda funkcję okresowa f (t) o okresie T można zapisać jako f (t) = a 0 + a n cos nω 0
