Matematyka dyskretna. Andrzej Łachwa, UJ, /15
|
|
|
- Helena Wróblewska
- 8 lat temu
- Przeglądów:
Transkrypt
1 Matematyka dyskretna Andrzej Łachwa, UJ, /15
2 TWIERDZENIE HALLA Twierdzenie o kojarzeniu małżeństw rozważa dwie grupy dziewcząt i chłopców, oraz podgrupy dziewczyn i podgrupy chłopców. Kiedy każdej dziewczynie można przyporządkować jednego kandydata na męża? Okazuje się, że warunkiem koniecznym i wystarczającym na to, by istniało takie skojarzenie par, jest to, by każda podgrupa dziewcząt, licząca k osób, znała co najmniej k chłopców. Jedną z wersji tego twierdzenia jest wersja dla grafów dwudzielnych, gdzie mężczyzn i kobiety interpretuje się jako zbiory wierzchołków grafu dwudzielnego, a krawędzie łączą "mężczyznę" z "kobietą", jeśli się znają.
3 Skojarzenie w grafie dwudzielnym G(V 1 V 2, E) to podzbiór krawędzi, w którym żadne dwie krawędzie nie wychodzą z tego samego wierzchołka. Powiemy, że wierzchołek v V i jest skojarzony, jeśli istnieje w V 3 i taki, że krawędź vw należy do skojarzenia. Pełne skojarzenie V 1 z V 2 w grafie dwudzielnym G(V 1 V 2, E) to skojarzenie, w którym każdy wierzchołek z V 1 jest skojarzony. Hall wprowadza funkcję (A) zwracającą dla A V 1 zbiór tych wierzchołków V 2, które są sąsiednie z przynajmniej jednym wierzchołkiem w zbiorze A.
4 Twierdzenie Halla (1935) Niech G(V 1 V 2, E) będzie grafem dwudzielnym. Wówczas pełne skojarzenie V 1 z V 2 istnieje wtedy i tylko wtedy, gdy A (A) dla każdego podzbioru A zbioru V 1. Przeczytaj dowód w wykładach [4]
5 Algorytm Halla, wersja 1 Niech A i B będą zbiorami dziewcząt i chłopców, A B. Warunek, że każde r dziewcząt zna w sumie co najmniej r chłopców, jest warunkiem koniecznym i wystarczającym na to, by każda z dziewczyn z A znalazła sobie męża wśród znanych jej chłopców z B. Algorytm znajdowania męża Niech B i to zbiór chłopców, które zna dziewczyna a i. Dopóki jest to możliwe dobieramy kolejnym dziewczynom a 1, a 2, a 3 a j chłopców b 1, b 2, b 3 b j, przy czym b 1 B 1 b 2 B 2 \{b 1 }, b 3 B 3 \{b 1, b 2 } itd. Jeżeli uda się to zrobić dla wszystkich dziewczyn, to algorytm znajdowania mężów zakończy się.
6 Jeżeli jednak dla pewnej dziewczyny a j zbiór znanych jej chłopców B j \{b 1, b 2 b j 1 } jest już pusty, to trzeba zerwać przynajmniej jedne zaręczyny. W tym celu dziewczyna a j urządza przyjęcie, na które zaprasza wszystkich znanych jej chłopców (B j ). Chłopcy ci przychodzą ze swoimi narzeczonymi, ale te na wszelki wypadek zabierają ze sobą swoich znajomych chłopców, a ci swoje narzeczone itd, aż do momentu gdy na przyjęcie zostanie zaproszony chłopiec, który nie jest jeszcze zaręczony. Musi się taki znaleźć, bo każda grupa r dziewcząt zna w sumie co najmniej r chłopców, czyli dziewczyny zaproszone na przyjęcie znają w sumie co najmniej tyle samo chłopców, a ponadto dziewczyna a j nie jest zaręczona.
7 Ów niezaręczony chłopiec będzie tańczył z dziewczyną, która go zaprosiła, jej narzeczony z dziewczyną która go zaprosiła, itd. aż na parkiecie znajdzie się chłopiec tańczący z gospodynią przyjęcia. Pary na parkiecie będą to nowe pary narzeczonych, a te, które nie tańczą pozostaną niezmienione. Po przyjęciu wszystkie dziewczyny a 1, a 2, a 3 a j mają narzeczonych i możemy kontynuować dobieranie narzeczonych dla kolejnych dziewczyn.
8 Przykład Niech A={a, b, c, d, e}, B={A, B, C, D, E, F, G, H} oraz a zna A i B b zna A, B, D c zna A, B, C d zna A i C e zna D, E, F, G, H Łączymy (a, A), (b, B), (c, C) i dla d brakuje narzeczonego. Na przyjęcie d zaprasza chłopców A, C, ci swoje narzeczone a, c, te swoich znajomych A, B, C. Chłopiec B zaprasza narzeczoną b, a ona swoich znajomych A, B, D, z których tylko ostatni nie był jeszcze zaproszony (a ponadto nie ma narzeczonej). Pary na parkiecie: (D, b), (B, c), (C, d). Nie tańczą (A, a). Na koniec dobieramy narzeczonego dla e, np. G.
9 Algorytm Halla, wersja 3 Niech G(V 1 V 2, E) będzie grafem dwudzielnym, a funkcja (A) zwraca dla A V 1 zbiór tych wierzchołków z V 2, które są sąsiednie z przynajmniej jednym wierzchołkiem w zbiorze A. Skojarzenie w grafie dwudzielnym G nazwiemy podzbiór krawędzi, w którym żadne dwie krawędzie nie wychodzą z tego samego wierzchołka. Powiemy, że wierzchołek v V i jest skojarzony, jeśli istnieje w V 3 i taki, że krawędź vw należy do skojarzenia. Pełne skojarzenie V 1 z V 2 w grafie dwudzielnym G to skojarzenie, w którym każdy wierzchołek z V 1 jest skojarzony. Pełne skojarzenie V 1 z V 2 istnieje wtedy i tylko wtedy, gdy A (A) dla każdego podzbioru A zbioru V 1.
10 Algorytm znajdowania męża przedstawimy w wersji z losowym doborem narzeczonych. Oznacza to zbudowanie dowolnego skojarzenia w grafie G. Mamy wtedy podzbiór krawędzi M E i podzbiór dziewcząt (podzbiór V 1 ) ze skojarzonymi narzeczonymi z V 2. Jeżeli wylosowane skojarzenie nie jest pełne (i nie da się rozszerzyć do pełnego) to musimy znaleźć dla M tzw. ścieżkę alternującą i zastąpić M skojarzeniem M opartym na tej ścieżce. Skojarzenie M ma moc większą o 1 od mocy M. Jeżeli M nie jest pełne to tworzymy ścieżkę alternującą dla M i zastępujemy M skojarzeniem M opartym na tej ostatniej ścieżce. Postępujemy tak aż do otrzymania skojarzenia pełnego.
11
12 Pytania na egzamin licencjacki z zakresu matematyki dyskretnej Omów metody obliczania sum skończonych Liczby Fibonacciego a "złoty podział"; wniosek Keplera Twierdzenie Halla i algorytm łączenia w pary Trójkąt Stirlinga (dla podziałów) i liczby Bella Zasada szufladkowa Dirichleta
13 Terminy egzaminów z matematyki dyskretnej 18 czerwca 2014, godz sale 055,056, września 2014, godz sale 055, 056 (albo już na nowym kampusie; w takim przypadku informacja o salach ukaże się na stronie Zakładu)
14 Omówienie zadań egzaminacyjnych
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 14/14 TWIERDZENIE HALLA Twierdzenie o kojarzeniu małżeństw rozważa dwie grupy - dziewcząt i chłopców, oraz podgrupy dziewczyn i podgrupy
Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 14/14 TWIERDZENIE HALLA Twierdzenie o kojarzeniu małżeństw rozważa dwie grupy - dziewcząt i chłopców, oraz podgrupy dziewczyn i podgrupy
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 15/15 Twierdzenie Dla grafu prostego następujące warunki są równoważne: 1) jest drzewem, 2) nie zawiera cykli i ma krawędzi, 3)
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 15/15 Twierdzenie Dla grafu prostego następujące warunki są równoważne: 1) jest drzewem, 2) nie zawiera cykli i ma krawędzi, 3)
Wykłady z Matematyki Dyskretnej
 Wykłady z Matematyki Dyskretnej dla kierunku Informatyka dr Instytut Informatyki Politechnika Krakowska Wykłady na bazie materiałów: dra hab. Andrzeja Karafiata dr hab. Joanny Kołodziej, prof. PK Kolorowanie
Wykłady z Matematyki Dyskretnej dla kierunku Informatyka dr Instytut Informatyki Politechnika Krakowska Wykłady na bazie materiałów: dra hab. Andrzeja Karafiata dr hab. Joanny Kołodziej, prof. PK Kolorowanie
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 13/14 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 13/14 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Matematyka dyskretna. Andrzej Łachwa, UJ, A/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 1A/14 Literatura obowiązkowa [1] K.A.Ross, Ch.R.B.Wright: Matematyka Dyskretna. Wydawnictwo Naukowe PWN, Warszawa 1996 [2] R.L.Graham,
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 1A/14 Literatura obowiązkowa [1] K.A.Ross, Ch.R.B.Wright: Matematyka Dyskretna. Wydawnictwo Naukowe PWN, Warszawa 1996 [2] R.L.Graham,
Twierdzenie Halla o małżeństwach
 Twierdzenie Halla o małżeństwach Tomasz Tkocz Streszczenie. Notatki te, przygotowane do referatu wygłoszonego na kółku w II LO w Rybniku, pokazują jak można rozwiązywać życiowe problemy oraz te bardziej
Twierdzenie Halla o małżeństwach Tomasz Tkocz Streszczenie. Notatki te, przygotowane do referatu wygłoszonego na kółku w II LO w Rybniku, pokazują jak można rozwiązywać życiowe problemy oraz te bardziej
Kolorowanie wierzchołków
 Kolorowanie wierzchołków Mając dany graf, pokolorować jego wierzchołki w taki sposób, aby każde dwa wierzchołki sąsiednie miały inny kolor. Każda krawędź łączy wierzchołki różnych kolorów. Takie pokolorowanie
Kolorowanie wierzchołków Mając dany graf, pokolorować jego wierzchołki w taki sposób, aby każde dwa wierzchołki sąsiednie miały inny kolor. Każda krawędź łączy wierzchołki różnych kolorów. Takie pokolorowanie
TEORIA GRAFÓW I SIECI
 TEORIA GRAFÓW I SIECI Temat nr 7: Przydziały w grafach i sieciach dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 26-83-95-04, p.225/00 Zakład
TEORIA GRAFÓW I SIECI Temat nr 7: Przydziały w grafach i sieciach dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 26-83-95-04, p.225/00 Zakład
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 14/15 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 14/15 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA
 DRZEWA i LASY Drzewem nazywamy graf spójny nie zawierający cykli elementarnych. Lasem nazywamy graf nie zawierający cykli elementarnych. Przykłady drzew i lasów takie krawędzie są wykluczone drzewo las
DRZEWA i LASY Drzewem nazywamy graf spójny nie zawierający cykli elementarnych. Lasem nazywamy graf nie zawierający cykli elementarnych. Przykłady drzew i lasów takie krawędzie są wykluczone drzewo las
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 9/14 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 9/14 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Matematyka dyskretna. Andrzej Łachwa, UJ, A/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 9A/14 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 9A/14 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2012 andrzej.lachwa@uj.edu.pl 13/14 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Matematyka dyskretna Andrzej Łachwa, UJ, 2012 andrzej.lachwa@uj.edu.pl 13/14 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Matematyka dyskretna. Andrzej Łachwa, UJ, A/10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 8A/10 Zbiory przeliczalne Przyjmujemy, że Zn = {0, 1, 2, 3, n-1} dla n>0 oraz Zn = przy n=0. Zbiór skończony to zbiór bijektywny z
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 8A/10 Zbiory przeliczalne Przyjmujemy, że Zn = {0, 1, 2, 3, n-1} dla n>0 oraz Zn = przy n=0. Zbiór skończony to zbiór bijektywny z
Podstawowe własności grafów. Wykład 3. Własności grafów
 Wykład 3. Własności grafów 1 / 87 Suma grafów Niech będą dane grafy proste G 1 = (V 1, E 1) oraz G 2 = (V 2, E 2). 2 / 87 Suma grafów Niech będą dane grafy proste G 1 = (V 1, E 1) oraz G 2 = (V 2, E 2).
Wykład 3. Własności grafów 1 / 87 Suma grafów Niech będą dane grafy proste G 1 = (V 1, E 1) oraz G 2 = (V 2, E 2). 2 / 87 Suma grafów Niech będą dane grafy proste G 1 = (V 1, E 1) oraz G 2 = (V 2, E 2).
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 6/10 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 6/10 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Teoria grafów podstawy. Materiały pomocnicze do wykładu. wykładowca: dr Magdalena Kacprzak
 Teoria grafów podstawy Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Grafy zorientowane i niezorientowane Przykład 1 Dwa pociągi i jeden most problem wzajemnego wykluczania się Dwa
Teoria grafów podstawy Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Grafy zorientowane i niezorientowane Przykład 1 Dwa pociągi i jeden most problem wzajemnego wykluczania się Dwa
Matematyka dyskretna. Andrzej Łachwa, UJ, B/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 1B/14 Drogi w grafach Marszruta (trasa) w grafie G z wierzchołka w do wierzchołka u to skończony ciąg krawędzi w postaci. W skrócie
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 1B/14 Drogi w grafach Marszruta (trasa) w grafie G z wierzchołka w do wierzchołka u to skończony ciąg krawędzi w postaci. W skrócie
SKOJARZENIA i ZBIORY WEWN. STABILNE WIERZCH. Skojarzeniem w grafie G nazywamy dowolny podzbiór krawędzi parami niezależnych.
 SKOJARZENIA i ZBIORY WEWN. STABILNE WIERZCH. Rozważamy graf G = (V, E) Dwie krawędzie e, e E nazywamy niezależnymi, jeśli nie są incydentne ze wspólnym wierzchołkiem. Skojarzeniem w grafie G nazywamy dowolny
SKOJARZENIA i ZBIORY WEWN. STABILNE WIERZCH. Rozważamy graf G = (V, E) Dwie krawędzie e, e E nazywamy niezależnymi, jeśli nie są incydentne ze wspólnym wierzchołkiem. Skojarzeniem w grafie G nazywamy dowolny
Digraf. 13 maja 2017
 Digraf 13 maja 2017 Graf skierowany, digraf, digraf prosty Definicja 1 Digraf prosty G to (V, E), gdzie V jest zbiorem wierzchołków, E jest rodziną zorientowanych krawędzi, między różnymi wierzchołkami,
Digraf 13 maja 2017 Graf skierowany, digraf, digraf prosty Definicja 1 Digraf prosty G to (V, E), gdzie V jest zbiorem wierzchołków, E jest rodziną zorientowanych krawędzi, między różnymi wierzchołkami,
Algorytmiczna teoria grafów
 18 maja 2013 Twierdzenie Halla o maª»e«stwach Problem Wyobra¹my sobie,»e mamy m dziewczyn i pewn liczb chªopców. Ka»da dziewczyna chce wyj± za m», przy czym ka»da z nich godzi si po±lubi tylko pewnych
18 maja 2013 Twierdzenie Halla o maª»e«stwach Problem Wyobra¹my sobie,»e mamy m dziewczyn i pewn liczb chªopców. Ka»da dziewczyna chce wyj± za m», przy czym ka»da z nich godzi si po±lubi tylko pewnych
WITAMY SERDECZNIE NA MIĘDZYSZKOLNYCH WARSZTATACH MATEMATYCZNYCH 12
 Dobry matematyk potrafi dostrzegać fakty, matematyk wybitny analogie między faktami, zaś matematyk genialny analogie między analogiami. Stefan Banach WITAMY SERDECZNIE NA MIĘDZYSZKOLNYCH WARSZTATACH MATEMATYCZNYCH
Dobry matematyk potrafi dostrzegać fakty, matematyk wybitny analogie między faktami, zaś matematyk genialny analogie między analogiami. Stefan Banach WITAMY SERDECZNIE NA MIĘDZYSZKOLNYCH WARSZTATACH MATEMATYCZNYCH
MATEMATYKA DYSKRETNA - MATERIAŁY DO WYKŁADU GRAFY
 ERIAŁY DO WYKŁADU GRAFY Graf nieskierowany Grafem nieskierowanym nazywamy parę G = (V, E), gdzie V jest pewnym zbiorem skończonym (zwanym zbiorem wierzchołków grafu G), natomiast E jest zbiorem nieuporządkowanych
ERIAŁY DO WYKŁADU GRAFY Graf nieskierowany Grafem nieskierowanym nazywamy parę G = (V, E), gdzie V jest pewnym zbiorem skończonym (zwanym zbiorem wierzchołków grafu G), natomiast E jest zbiorem nieuporządkowanych
Rachunek podziałów i elementy teorii grafów będą stosowane w procedurach redukcji argumentów i dekompozycji funkcji boolowskich.
 Pojęcia podstawowe c.d. Rachunek podziałów Elementy teorii grafów Klasy zgodności Rachunek podziałów i elementy teorii grafów będą stosowane w procedurach redukcji argumentów i dekompozycji funkcji boolowskich.
Pojęcia podstawowe c.d. Rachunek podziałów Elementy teorii grafów Klasy zgodności Rachunek podziałów i elementy teorii grafów będą stosowane w procedurach redukcji argumentów i dekompozycji funkcji boolowskich.
Matematyka dyskretna. Andrzej Łachwa, UJ, A/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 9A/14 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 9A/14 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
51. Wykorzystywanie sumy, iloczynu i różnicy zdarzeń do obliczania prawdopodobieństw zdarzeń.
 Matematyka lekcja 5 5. Wykorzystywanie sumy, iloczynu i różnicy zdarzeń do obliczania prawdopodobieństw zdarzeń. I. rzypomnij sobie:. Jak rysujemy drzewo stochastyczne i przy jego pomocy obliczamy prawdopodobieństwo
Matematyka lekcja 5 5. Wykorzystywanie sumy, iloczynu i różnicy zdarzeń do obliczania prawdopodobieństw zdarzeń. I. rzypomnij sobie:. Jak rysujemy drzewo stochastyczne i przy jego pomocy obliczamy prawdopodobieństwo
Algorytmiczna teoria grafów
 Przedmiot fakultatywny 20h wykładu + 20h ćwiczeń 21 lutego 2014 Zasady zaliczenia 1 ćwiczenia (ocena): kolokwium, zadania programistyczne (implementacje algorytmów), praca na ćwiczeniach. 2 Wykład (egzamin)
Przedmiot fakultatywny 20h wykładu + 20h ćwiczeń 21 lutego 2014 Zasady zaliczenia 1 ćwiczenia (ocena): kolokwium, zadania programistyczne (implementacje algorytmów), praca na ćwiczeniach. 2 Wykład (egzamin)
Zadania z ćwiczeń #18 (pon. 7 maja) Matematyka Dyskretna
 Zadania z ćwiczeń #18 (pon. 7 maja) Matematyka Dyskretna Q1.: Mamy dany zbiór artykułów, z których każdy ma co najmniej k z n możliwych tagów. Chcemy bardzo z grubsza pokategoryzować artykuły w jak najmniejszą
Zadania z ćwiczeń #18 (pon. 7 maja) Matematyka Dyskretna Q1.: Mamy dany zbiór artykułów, z których każdy ma co najmniej k z n możliwych tagów. Chcemy bardzo z grubsza pokategoryzować artykuły w jak najmniejszą
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 7/15 Rachunek różnicowy Dobrym narzędziem do obliczania skończonych sum jest rachunek różnicowy. W rachunku tym odpowiednikiem operatora
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 7/15 Rachunek różnicowy Dobrym narzędziem do obliczania skończonych sum jest rachunek różnicowy. W rachunku tym odpowiednikiem operatora
Kolorowanie wierzchołków Kolorowanie krawędzi Kolorowanie regionów i map. Wykład 8. Kolorowanie
 Wykład 8. Kolorowanie 1 / 62 Kolorowanie wierzchołków - definicja Zbiory niezależne Niech G będzie grafem bez pętli. Definicja Mówimy, że G jest grafem k kolorowalnym, jeśli każdemu wierzchołkowi możemy
Wykład 8. Kolorowanie 1 / 62 Kolorowanie wierzchołków - definicja Zbiory niezależne Niech G będzie grafem bez pętli. Definicja Mówimy, że G jest grafem k kolorowalnym, jeśli każdemu wierzchołkowi możemy
WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA
 DROGI i CYKLE w grafach Dla grafu (nieskierowanego) G = ( V, E ) drogą z wierzchołka v 0 V do v t V nazywamy ciąg (naprzemienny) wierzchołków i krawędzi grafu: ( v 0, e, v, e,..., v t, e t, v t ), spełniający
DROGI i CYKLE w grafach Dla grafu (nieskierowanego) G = ( V, E ) drogą z wierzchołka v 0 V do v t V nazywamy ciąg (naprzemienny) wierzchołków i krawędzi grafu: ( v 0, e, v, e,..., v t, e t, v t ), spełniający
Graf. Definicja marca / 1
 Graf 25 marca 2018 Graf Definicja 1 Graf ogólny to para G = (V, E), gdzie V jest zbiorem wierzchołków (węzłów, punktów grafu), E jest rodziną krawędzi, które mogą być wielokrotne, dokładniej jednoelementowych
Graf 25 marca 2018 Graf Definicja 1 Graf ogólny to para G = (V, E), gdzie V jest zbiorem wierzchołków (węzłów, punktów grafu), E jest rodziną krawędzi, które mogą być wielokrotne, dokładniej jednoelementowych
KURS MATEMATYKA DYSKRETNA
 KURS MATEMATYKA DYSKRETNA LEKCJA 28 Grafy hamiltonowskie ZADANIE DOMOWE www.akademia.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Drogę nazywamy
KURS MATEMATYKA DYSKRETNA LEKCJA 28 Grafy hamiltonowskie ZADANIE DOMOWE www.akademia.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Drogę nazywamy
E ' E G nazywamy krawędziowym zbiorem
 Niech G będzie grafem spójnym. Wierzchołek x nazywamy rozcinającym, jeśli G\{x} jest niespójny. Niech G będzie grafem spójnym. V ' V G nazywamy zbiorem rozcinającym jeśli G\V' jest niespójny Niech G będzie
Niech G będzie grafem spójnym. Wierzchołek x nazywamy rozcinającym, jeśli G\{x} jest niespójny. Niech G będzie grafem spójnym. V ' V G nazywamy zbiorem rozcinającym jeśli G\V' jest niespójny Niech G będzie
Matematyka dyskretna
 Matematyka dyskretna Wykład 13: Teoria Grafów Gniewomir Sarbicki Literatura R.J. Wilson Wprowadzenie do teorii grafów Definicja: Grafem (skończonym, nieskierowanym) G nazywamy parę zbiorów (V (G), E(G)),
Matematyka dyskretna Wykład 13: Teoria Grafów Gniewomir Sarbicki Literatura R.J. Wilson Wprowadzenie do teorii grafów Definicja: Grafem (skończonym, nieskierowanym) G nazywamy parę zbiorów (V (G), E(G)),
Ilustracja S1 S2. S3 ściana zewnętrzna
 Grafy płaskie G=(V,E) nazywamy grafem płaskim, gdy V jest skończonym podzbiorem punktów płaszczyzny euklidesowej, a E to zbiór krzywych Jordana (łamanych) o końcach w V i takich, że: 1) rożne krzywe mają
Grafy płaskie G=(V,E) nazywamy grafem płaskim, gdy V jest skończonym podzbiorem punktów płaszczyzny euklidesowej, a E to zbiór krzywych Jordana (łamanych) o końcach w V i takich, że: 1) rożne krzywe mają
Teoria grafów. Magdalena Lemańska
 Teoria grafów Magdalena Lemańska Literatura Aspekty kombinatoryki Victor Bryant Graph Theory V.K. Balakrishnan Fundamentals of domination in graphs T. Haynes, S. Hedetniemi, P. Slater Wstęp Graf Grafem
Teoria grafów Magdalena Lemańska Literatura Aspekty kombinatoryki Victor Bryant Graph Theory V.K. Balakrishnan Fundamentals of domination in graphs T. Haynes, S. Hedetniemi, P. Slater Wstęp Graf Grafem
Suma dwóch grafów. Zespolenie dwóch grafów
 Suma dwóch grafów G 1 = ((G 1 ), E(G 1 )) G 2 = ((G 2 ), E(G 2 )) (G 1 ) i (G 2 ) rozłączne Suma G 1 G 2 graf ze zbiorem wierzchołków (G 1 ) (G 2 ) i rodziną krawędzi E(G 1 ) E(G 2 ) G 1 G 2 G 1 G 2 Zespolenie
Suma dwóch grafów G 1 = ((G 1 ), E(G 1 )) G 2 = ((G 2 ), E(G 2 )) (G 1 ) i (G 2 ) rozłączne Suma G 1 G 2 graf ze zbiorem wierzchołków (G 1 ) (G 2 ) i rodziną krawędzi E(G 1 ) E(G 2 ) G 1 G 2 G 1 G 2 Zespolenie
Grafy (3): drzewa. Wykłady z matematyki dyskretnej dla informatyków i teleinformatyków. UTP Bydgoszcz
 Grafy (3): drzewa Wykłady z matematyki dyskretnej dla informatyków i teleinformatyków UTP Bydgoszcz 13 (Wykłady z matematyki dyskretnej) Grafy (3): drzewa 13 1 / 107 Drzewo Definicja. Drzewo to graf acykliczny
Grafy (3): drzewa Wykłady z matematyki dyskretnej dla informatyków i teleinformatyków UTP Bydgoszcz 13 (Wykłady z matematyki dyskretnej) Grafy (3): drzewa 13 1 / 107 Drzewo Definicja. Drzewo to graf acykliczny
Matematyka dyskretna. Andrzej Łachwa, UJ, A/15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2015 andrzej.lachwa@uj.edu.pl 10A/15 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Matematyka dyskretna Andrzej Łachwa, UJ, 2015 andrzej.lachwa@uj.edu.pl 10A/15 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Drzewa spinające MST dla grafów ważonych Maksymalne drzewo spinające Drzewo Steinera. Wykład 6. Drzewa cz. II
 Wykład 6. Drzewa cz. II 1 / 65 drzewa spinające Drzewa spinające Zliczanie drzew spinających Drzewo T nazywamy drzewem rozpinającym (spinającym) (lub dendrytem) spójnego grafu G, jeżeli jest podgrafem
Wykład 6. Drzewa cz. II 1 / 65 drzewa spinające Drzewa spinające Zliczanie drzew spinających Drzewo T nazywamy drzewem rozpinającym (spinającym) (lub dendrytem) spójnego grafu G, jeżeli jest podgrafem
Matematyczne Podstawy Informatyki
 Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Twierdzenie 2.1 Niech G będzie grafem prostym
Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Twierdzenie 2.1 Niech G będzie grafem prostym
Algorytmiczna teoria grafów
 Podstawowe pojęcia i klasy grafów Wykład 1 Grafy nieskierowane Definicja Graf nieskierowany (graf) G = (V,E) jest to uporządkowana para składająca się z niepustego skończonego zbioru wierzchołków V oraz
Podstawowe pojęcia i klasy grafów Wykład 1 Grafy nieskierowane Definicja Graf nieskierowany (graf) G = (V,E) jest to uporządkowana para składająca się z niepustego skończonego zbioru wierzchołków V oraz
Matematyka od zaraz zatrudnię
 Uniwersytet Jagielloński Gdzie jest matematyka? Soczewka, 26-28 listopada 2010 Kolorowanie grafów Dobre kolorowanie wierzchołków grafu, to nadanie im kolorów w taki sposób, że każde dwa wierzchołki połaczone
Uniwersytet Jagielloński Gdzie jest matematyka? Soczewka, 26-28 listopada 2010 Kolorowanie grafów Dobre kolorowanie wierzchołków grafu, to nadanie im kolorów w taki sposób, że każde dwa wierzchołki połaczone
6d. Grafy dwudzielne i kolorowania
 6d. Grafy dwudzielne i kolorowania Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2016/2017 rzegorz Kosiorowski (Uniwersytet Ekonomiczny w6d. Krakowie) Grafy dwudzielne i kolorowania zima
6d. Grafy dwudzielne i kolorowania Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2016/2017 rzegorz Kosiorowski (Uniwersytet Ekonomiczny w6d. Krakowie) Grafy dwudzielne i kolorowania zima
Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle
 Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle Paweł Szołtysek 12 czerwca 2008 Streszczenie Planowanie produkcji jest jednym z problemów optymalizacji dyskretnej,
Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle Paweł Szołtysek 12 czerwca 2008 Streszczenie Planowanie produkcji jest jednym z problemów optymalizacji dyskretnej,
E: Rekonstrukcja ewolucji. Algorytmy filogenetyczne
 E: Rekonstrukcja ewolucji. Algorytmy filogenetyczne Przypominajka: 152 drzewo filogenetyczne to drzewo, którego liśćmi są istniejące gatunki, a węzły wewnętrzne mają stopień większy niż jeden i reprezentują
E: Rekonstrukcja ewolucji. Algorytmy filogenetyczne Przypominajka: 152 drzewo filogenetyczne to drzewo, którego liśćmi są istniejące gatunki, a węzły wewnętrzne mają stopień większy niż jeden i reprezentują
Ciągi Podzbiory Symbol Newtona Zasada szufladkowa Dirichleta Zasada włączania i wyłączania. Ilość najkrótszych dróg. Kombinatoryka. Magdalena Lemańska
 Kombinatoryka Magdalena Lemańska Literatura Matematyka Dyskretna Andrzej Szepietowski http://wazniak.mimuw.edu.pl/ Discrete Mathematics Seymour Lipschutz, Marc Lipson Aspekty kombinatoryki Victor Bryant
Kombinatoryka Magdalena Lemańska Literatura Matematyka Dyskretna Andrzej Szepietowski http://wazniak.mimuw.edu.pl/ Discrete Mathematics Seymour Lipschutz, Marc Lipson Aspekty kombinatoryki Victor Bryant
Matematyka dyskretna. Andrzej Łachwa, UJ, A/15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 4A/15 Liczby Fibonacciego Spośród ciągów zdefiniowanych rekurencyjnie, jednym z najsłynniejszych jest ciąg Fibonacciego (z roku 1202)
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 4A/15 Liczby Fibonacciego Spośród ciągów zdefiniowanych rekurencyjnie, jednym z najsłynniejszych jest ciąg Fibonacciego (z roku 1202)
Matematyka dyskretna. Andrzej Łachwa, UJ, 2019 Zadania 1-100
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl Zadania 1-100 Udowodnij, że A (B C) = (A B) (A C) za pomocą diagramów Venna. Udowodnij formalnie, że (A B i A C) A B C oraz że (A
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl Zadania 1-100 Udowodnij, że A (B C) = (A B) (A C) za pomocą diagramów Venna. Udowodnij formalnie, że (A B i A C) A B C oraz że (A
Matematyka dyskretna. Andrzej Łachwa, UJ, a/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 8a/14 Zbiory przeliczalne Przyjmujemy, że = {0, 1, 2, 3, n-1} dla n>0 oraz = przy n=0. Zbiór skończony to zbiór bijektywny z pewnym
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 8a/14 Zbiory przeliczalne Przyjmujemy, że = {0, 1, 2, 3, n-1} dla n>0 oraz = przy n=0. Zbiór skończony to zbiór bijektywny z pewnym
Elementy statystyki opisowej, teoria prawdopodobieństwa i kombinatoryka
 Wymagania egzaminacyjne: a) oblicza średnią arytmetyczną, średnią ważoną, medianę i odchylenie standardowe danych; interpretuje te parametry dla danych empirycznych, b) zlicza obiekty w prostych sytuacjach
Wymagania egzaminacyjne: a) oblicza średnią arytmetyczną, średnią ważoną, medianę i odchylenie standardowe danych; interpretuje te parametry dla danych empirycznych, b) zlicza obiekty w prostych sytuacjach
WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA Pod auspicjami Polskiej Akademii Nauk Warszawa, ul. Newelska 6, tel.
 WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA Pod auspicjami Polskiej Akademii Nauk 01-447 Warszawa, ul. Newelska 6, tel. 22 3486544 Wydział Informatyki Kierunek studiów Profil Stopień studiów Forma
WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA Pod auspicjami Polskiej Akademii Nauk 01-447 Warszawa, ul. Newelska 6, tel. 22 3486544 Wydział Informatyki Kierunek studiów Profil Stopień studiów Forma
Reprezentacje grafów nieskierowanych Reprezentacje grafów skierowanych. Wykład 2. Reprezentacja komputerowa grafów
 Wykład 2. Reprezentacja komputerowa grafów 1 / 69 Macierz incydencji Niech graf G będzie grafem nieskierowanym bez pętli o n wierzchołkach (x 1, x 2,..., x n) i m krawędziach (e 1, e 2,..., e m). 2 / 69
Wykład 2. Reprezentacja komputerowa grafów 1 / 69 Macierz incydencji Niech graf G będzie grafem nieskierowanym bez pętli o n wierzchołkach (x 1, x 2,..., x n) i m krawędziach (e 1, e 2,..., e m). 2 / 69
Matematyka dyskretna - 5.Grafy.
 Matematyka dyskretna - 5.Grafy. W tym rozdziale zajmiemy się grafami. Są to wykresy zawierające rozmaite informacje, przedstawiające połączenia pomiędzy różnymi swoimi elementami. Algorytmy na nich oparte
Matematyka dyskretna - 5.Grafy. W tym rozdziale zajmiemy się grafami. Są to wykresy zawierające rozmaite informacje, przedstawiające połączenia pomiędzy różnymi swoimi elementami. Algorytmy na nich oparte
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: MATEMATYKA DYSKRETNA Discrete mathematics Forma studiów: Stacjonarne Poziom kwalifikacji: Kod przedmiotu: A_06 Rok: I obowiązkowy w ramach treści
Nazwa przedmiotu: Kierunek: Informatyka Rodzaj przedmiotu: MATEMATYKA DYSKRETNA Discrete mathematics Forma studiów: Stacjonarne Poziom kwalifikacji: Kod przedmiotu: A_06 Rok: I obowiązkowy w ramach treści
Systemy operacyjne 14. Co to jest system operacyjny i jakie są jego podstawowe zadania? Scharakteryzować podstawowe struktury systemów operacyjnych i
 Uniwersytet Jagielloński Wydział Fizyki, Astronomii i Informatyki Stosowanej pytania na egzamin licencjacki 2011/12 pytania te mogą być stosowane także w czasie egzaminu magisterskiego Wstęp do architektury
Uniwersytet Jagielloński Wydział Fizyki, Astronomii i Informatyki Stosowanej pytania na egzamin licencjacki 2011/12 pytania te mogą być stosowane także w czasie egzaminu magisterskiego Wstęp do architektury
Matematyka dyskretna. Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl. Przykłady zadań egzaminacyjnych (do liczenia lub dowodzenia)
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl Przykłady zadań egzaminacyjnych (do liczenia lub dowodzenia) 1. Ile układów kart w pokerze to Dwie pary? Dwie pary to układ 5 kart
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl Przykłady zadań egzaminacyjnych (do liczenia lub dowodzenia) 1. Ile układów kart w pokerze to Dwie pary? Dwie pary to układ 5 kart
ZLICZANIE REKURENCYJNE
 ZLICZANIE REKURENCYJNE Andrzej Sendlewski Wydział Matematyki i Informatyki UMK w Toruniu MA-TA II, Ciechanów 22 maja 2010 Liczby figuralne jako jeden z najprostszych sposobów wprowadzenia w myślenie rekurencyjne
ZLICZANIE REKURENCYJNE Andrzej Sendlewski Wydział Matematyki i Informatyki UMK w Toruniu MA-TA II, Ciechanów 22 maja 2010 Liczby figuralne jako jeden z najprostszych sposobów wprowadzenia w myślenie rekurencyjne
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2014 andrzej.lachwa@uj.edu.pl 8/15 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Matematyka dyskretna Andrzej Łachwa, UJ, 2014 andrzej.lachwa@uj.edu.pl 8/15 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Sprzedaż online. Piotr Sankowski Uniwersytet Warszawski Warszawa p. 1/40
 Sprzedaż online Piotr Sankowski Uniwersytet Warszawski Warszawa 18.04.2013 - p. 1/40 Plan wykładu Problem skojarzeń online Algorytm zachłanny Algorytm losowo rankujacy Dolne ograniczenie Problem aukcji
Sprzedaż online Piotr Sankowski Uniwersytet Warszawski Warszawa 18.04.2013 - p. 1/40 Plan wykładu Problem skojarzeń online Algorytm zachłanny Algorytm losowo rankujacy Dolne ograniczenie Problem aukcji
MATEMATYKA DYSKRETNA - KOLOKWIUM 2
 1 MATEMATYKA DYSKRETNA - KOLOKWIUM 2 GRUPA A RACHUNKI+KRÓTKIE WYJAŚNIENIA! NA TEJ KARTCE! KAŻDA DODATKOWA KARTKA TO MINUS 1 PUNKT! Imię i nazwisko...... Nr indeksu... 1. (3p.) Znajdź drzewo o kodzie Prufera
1 MATEMATYKA DYSKRETNA - KOLOKWIUM 2 GRUPA A RACHUNKI+KRÓTKIE WYJAŚNIENIA! NA TEJ KARTCE! KAŻDA DODATKOWA KARTKA TO MINUS 1 PUNKT! Imię i nazwisko...... Nr indeksu... 1. (3p.) Znajdź drzewo o kodzie Prufera
Matematyka dyskretna zestaw II ( )
 Matematyka dyskretna zestaw II (17-18.10.2016) Uwaga: Część z zadań z tego zestawu opiera się na zasadzie szufladkowej Dirichleta. Zadanie 1. Na ile sposobów można umieścić w 7 szufladach 3 koszule tak,
Matematyka dyskretna zestaw II (17-18.10.2016) Uwaga: Część z zadań z tego zestawu opiera się na zasadzie szufladkowej Dirichleta. Zadanie 1. Na ile sposobów można umieścić w 7 szufladach 3 koszule tak,
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
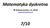 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 7/10 Generowanie podzbiorów Weźmy n-elementowy zbiór X={x 1, x 2 x n }. Każdemu podzbiorowi YX przyporządkujemy ciąg binarny b 0 b
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 7/10 Generowanie podzbiorów Weźmy n-elementowy zbiór X={x 1, x 2 x n }. Każdemu podzbiorowi YX przyporządkujemy ciąg binarny b 0 b
Matematyka ubezpieczeń majątkowych 1.10.2012 r.
 Zadanie. W pewnej populacji każde ryzyko charakteryzuje się trzema parametrami q, b oraz v, o następującym znaczeniu: parametr q to prawdopodobieństwo, że do szkody dojdzie (może zajść co najwyżej jedna
Zadanie. W pewnej populacji każde ryzyko charakteryzuje się trzema parametrami q, b oraz v, o następującym znaczeniu: parametr q to prawdopodobieństwo, że do szkody dojdzie (może zajść co najwyżej jedna
Matematyka dyskretna dla informatyków
 Matematyka dyskretna dla informatyków Część I: Elementy kombinatoryki Jerzy Jaworski Zbigniew Palka Jerzy Szymański Uniwersytet im. Adama Mickiewicza Poznań 2007 4 Zależności rekurencyjne Wiele zależności
Matematyka dyskretna dla informatyków Część I: Elementy kombinatoryki Jerzy Jaworski Zbigniew Palka Jerzy Szymański Uniwersytet im. Adama Mickiewicza Poznań 2007 4 Zależności rekurencyjne Wiele zależności
Funkcja. x X! y Y : x, y f. f : X Y f x = y f : x y. Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje:
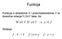 Funkcja Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje: x X! y Y : x, y f f : X Y f x = y f : x y Przykłady f: N N, f(n) = 2n f: N R, f(n) = n/2 f: N {13}, f(n)
Funkcja Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje: x X! y Y : x, y f f : X Y f x = y f : x y Przykłady f: N N, f(n) = 2n f: N R, f(n) = n/2 f: N {13}, f(n)
KOMBINATORYKA OBIEKTY KOMBINATORYCZNE MATEMATYKA DYSKRETNA (2014/2015)
 MATEMATYKA DYSKRETNA (2014/2015) dr hab. inż. Małgorzata Sterna malgorzata.sterna@cs.put.poznan.pl www.cs.put.poznan.pl/msterna/ KOMBINATORYKA OBIEKTY KOMBINATORYCZNE TEORIA ZLICZANIA Teoria zliczania
MATEMATYKA DYSKRETNA (2014/2015) dr hab. inż. Małgorzata Sterna malgorzata.sterna@cs.put.poznan.pl www.cs.put.poznan.pl/msterna/ KOMBINATORYKA OBIEKTY KOMBINATORYCZNE TEORIA ZLICZANIA Teoria zliczania
Problemy Decyzyjne dla Systemów Nieskończonych
 Problemy Decyzyjne dla Systemów Nieskończonych Ćwiczenia 1 17 lutego 2012 Na tych ćwiczeniach zajmiemy się pojęciem well quasi-ordering (WQO) bardzo przydatnym do analizy nieskończonych ciągów. Definicja
Problemy Decyzyjne dla Systemów Nieskończonych Ćwiczenia 1 17 lutego 2012 Na tych ćwiczeniach zajmiemy się pojęciem well quasi-ordering (WQO) bardzo przydatnym do analizy nieskończonych ciągów. Definicja
Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA
 Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA Zad. 1 (12p.)Niech n 3k > 0. Zbadać jaka jest najmniejsza możliwa liczba krawędzi w grafie, który ma dokładnie n wierzchołków oraz dokładnie k składowych, z których
Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA Zad. 1 (12p.)Niech n 3k > 0. Zbadać jaka jest najmniejsza możliwa liczba krawędzi w grafie, który ma dokładnie n wierzchołków oraz dokładnie k składowych, z których
Struktury danych i złożoność obliczeniowa Wykład 7. Prof. dr hab. inż. Jan Magott
 Struktury danych i złożoność obliczeniowa Wykład 7 Prof. dr hab. inż. Jan Magott Problemy NP-zupełne Transformacją wielomianową problemu π 2 do problemu π 1 (π 2 π 1 ) jest funkcja f: D π2 D π1 spełniająca
Struktury danych i złożoność obliczeniowa Wykład 7 Prof. dr hab. inż. Jan Magott Problemy NP-zupełne Transformacją wielomianową problemu π 2 do problemu π 1 (π 2 π 1 ) jest funkcja f: D π2 D π1 spełniająca
Matematyczne Podstawy Informatyki
 Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 03/0 Przeszukiwanie w głąb i wszerz I Przeszukiwanie metodą
Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 03/0 Przeszukiwanie w głąb i wszerz I Przeszukiwanie metodą
Moneta 1 Moneta 2 Kostka O, R O,R 1,2,3,4,5, Moneta 1 Moneta 2 Kostka O O ( )
 Nowa matura kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo
Nowa matura kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo
Grafy dla każdego. dr Krzysztof Bryś. Wydział Matematyki i Nauk Informacyjnych Politechnika Warszawska.
 Grafy dla każdego dr Krzysztof Bryś brys@mini.pw.edu.pl Wydział Matematyki i Nauk Informacyjnych Politechnika Warszawska www.mini.pw.edu.pl Warszawa, 28 marca 2015 Graf składa się z elementów pewnego zbioru
Grafy dla każdego dr Krzysztof Bryś brys@mini.pw.edu.pl Wydział Matematyki i Nauk Informacyjnych Politechnika Warszawska www.mini.pw.edu.pl Warszawa, 28 marca 2015 Graf składa się z elementów pewnego zbioru
(4) x (y z) = (x y) (x z), x (y z) = (x y) (x z), (3) x (x y) = x, x (x y) = x, (2) x 0 = x, x 1 = x
 2. Wykład 2: algebry Boole a, kraty i drzewa. 2.1. Algebra Boole a. 1 Ważnym dla nas przykładem algebr są algebry Boole a, czyli algebry B = (B,,,, 0, 1) typu (2, 2, 1, 0, 0) spełniające własności: (1)
2. Wykład 2: algebry Boole a, kraty i drzewa. 2.1. Algebra Boole a. 1 Ważnym dla nas przykładem algebr są algebry Boole a, czyli algebry B = (B,,,, 0, 1) typu (2, 2, 1, 0, 0) spełniające własności: (1)
Przykłady grafów. Graf prosty, to graf bez pętli i bez krawędzi wielokrotnych.
 Grafy Graf Graf (ang. graph) to zbiór wierzchołków (ang. vertices), które mogą być połączone krawędziami (ang. edges) w taki sposób, że każda krawędź kończy się i zaczyna w którymś z wierzchołków. Graf
Grafy Graf Graf (ang. graph) to zbiór wierzchołków (ang. vertices), które mogą być połączone krawędziami (ang. edges) w taki sposób, że każda krawędź kończy się i zaczyna w którymś z wierzchołków. Graf
Wprowadzenie Podstawy Fundamentalne twierdzenie Kolorowanie. Grafy planarne. Przemysław Gordinowicz. Instytut Matematyki, Politechnika Łódzka
 Grafy planarne Przemysław Gordinowicz Instytut Matematyki, Politechnika Łódzka Grafy i ich zastosowania Wykład 12 Plan prezentacji 1 Wprowadzenie 2 Podstawy 3 Fundamentalne twierdzenie 4 Kolorowanie grafów
Grafy planarne Przemysław Gordinowicz Instytut Matematyki, Politechnika Łódzka Grafy i ich zastosowania Wykład 12 Plan prezentacji 1 Wprowadzenie 2 Podstawy 3 Fundamentalne twierdzenie 4 Kolorowanie grafów
Zał nr 4 do ZW. Dla grupy kursów zaznaczyć kurs końcowy. Liczba punktów ECTS charakterze praktycznym (P)
 Zał nr 4 do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim : Matematyka Dyskretna Nazwa w języku angielskim : Discrete Mathematics Kierunek studiów : Informatyka Specjalność
Zał nr 4 do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim : Matematyka Dyskretna Nazwa w języku angielskim : Discrete Mathematics Kierunek studiów : Informatyka Specjalność
SPÓJNOŚĆ. ,...v k. }, E={v 1. v k. i v k. ,...,v k-1. }. Wierzchołki v 1. v 2. to końce ścieżki.
 SPÓJNOŚĆ Graf jest spójny, gdy dla każdego podziału V na dwa rozłączne podzbiory A i B istnieje krawędź z A do B. Definicja równoważna: Graf jest spójny, gdy każde dwa wierzchołki są połączone ścieżką
SPÓJNOŚĆ Graf jest spójny, gdy dla każdego podziału V na dwa rozłączne podzbiory A i B istnieje krawędź z A do B. Definicja równoważna: Graf jest spójny, gdy każde dwa wierzchołki są połączone ścieżką
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 6/15 Sumy Oto dwie konwencje zapisu skończonych sum wyrazów: (notacja Sigma, Fourier, 1820) Czasami stosowana jest ogólniejsza notacja,
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 6/15 Sumy Oto dwie konwencje zapisu skończonych sum wyrazów: (notacja Sigma, Fourier, 1820) Czasami stosowana jest ogólniejsza notacja,
Problem straŝaka w drzewach. Agnieszka Skorupka Matematyka Stosowana FTiMS
 Problem straŝaka w drzewach Agnieszka Skorupka Matematyka Stosowana FTiMS Problem StraŜaka: Co to jest? Problem StraŜaka: Co to jest? Problem StraŜaka: Co to jest? Problem StraŜaka: Co to jest? Problem
Problem straŝaka w drzewach Agnieszka Skorupka Matematyka Stosowana FTiMS Problem StraŜaka: Co to jest? Problem StraŜaka: Co to jest? Problem StraŜaka: Co to jest? Problem StraŜaka: Co to jest? Problem
KARTA MODUŁU KSZTAŁCENIA
 KARTA MODUŁU KSZTAŁCENIA I. 1 Nazwa modułu kształcenia I. Informacje ogólne Matematyka dyskretna 2 Nazwa jednostki prowadzącej moduł Instytut Informatyki, Zakład Informatyki Stosowanej 3 Kod modułu (wypełnia
KARTA MODUŁU KSZTAŁCENIA I. 1 Nazwa modułu kształcenia I. Informacje ogólne Matematyka dyskretna 2 Nazwa jednostki prowadzącej moduł Instytut Informatyki, Zakład Informatyki Stosowanej 3 Kod modułu (wypełnia
Wykłady z Matematyki Dyskretnej
 Wykłady z Matematyki Dyskretnej dla kierunku Informatyka dr Instytut Informatyki Politechnika Krakowska Wykłady na bazie materiałów: dra hab. Andrzeja Karafiata dr hab. Joanny Kołodziej, prof. PK Informacje
Wykłady z Matematyki Dyskretnej dla kierunku Informatyka dr Instytut Informatyki Politechnika Krakowska Wykłady na bazie materiałów: dra hab. Andrzeja Karafiata dr hab. Joanny Kołodziej, prof. PK Informacje
Znajdowanie skojarzeń na maszynie równoległej
 11 grudnia 2008 Spis treści 1 Skojarzenia w różnych klasach grafów Drzewa Grafy gęste Grafy regularne dwudzielne Claw-free graphs 2 Drzewa Skojarzenia w drzewach Fakt Wybierajac krawędź do skojarzenia
11 grudnia 2008 Spis treści 1 Skojarzenia w różnych klasach grafów Drzewa Grafy gęste Grafy regularne dwudzielne Claw-free graphs 2 Drzewa Skojarzenia w drzewach Fakt Wybierajac krawędź do skojarzenia
Plan wynikowy klasa 3
 Plan wynikowy klasa 3 Przedmiot: matematyka Klasa 3 liceum (technikum) Rok szkolny:........................ Nauczyciel:........................ zakres podstawowy: 28 tyg. 3 h = 84 h (78 h + 6 h do dyspozycji
Plan wynikowy klasa 3 Przedmiot: matematyka Klasa 3 liceum (technikum) Rok szkolny:........................ Nauczyciel:........................ zakres podstawowy: 28 tyg. 3 h = 84 h (78 h + 6 h do dyspozycji
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 6/14 Sumy Oto dwie konwencje zapisu skończonych sum wyrazów: (notacja Sigma, Fourier, 1820) Czasami stosowana jest ogólniejsza notacja,
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 6/14 Sumy Oto dwie konwencje zapisu skończonych sum wyrazów: (notacja Sigma, Fourier, 1820) Czasami stosowana jest ogólniejsza notacja,
Wymagania na poszczególne oceny szkolne z. matematyki. dla uczniów klasy IIIa i IIIb. Gimnazjum im. Jana Pawła II w Mętowie. w roku szkolnym 2015/2016
 Wymagania na poszczególne oceny szkolne z matematyki dla uczniów klasy IIIa i IIIb Gimnazjum im. Jana Pawła II w Mętowie w roku szkolnym 2015/2016 DZIAŁ 1. FUNKCJE (11h) Uczeń: poda definicję funkcji (2)
Wymagania na poszczególne oceny szkolne z matematyki dla uczniów klasy IIIa i IIIb Gimnazjum im. Jana Pawła II w Mętowie w roku szkolnym 2015/2016 DZIAŁ 1. FUNKCJE (11h) Uczeń: poda definicję funkcji (2)
Wstęp do sieci neuronowych, wykład 12 Łańcuchy Markowa
 Wstęp do sieci neuronowych, wykład 12 Łańcuchy Markowa M. Czoków, J. Piersa 2012-01-10 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego 3 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego
Wstęp do sieci neuronowych, wykład 12 Łańcuchy Markowa M. Czoków, J. Piersa 2012-01-10 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego 3 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego
Matematyka dyskretna. Andrzej Łachwa, UJ, B/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 2B/14 Relacje Pojęcia: relacja czyli relacja dwuargumentowa relacja w zbiorze A relacja n-argumentowa Relacja E = {(x, x): x S} jest
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 2B/14 Relacje Pojęcia: relacja czyli relacja dwuargumentowa relacja w zbiorze A relacja n-argumentowa Relacja E = {(x, x): x S} jest
Instytut Informatyki Uniwersytet Wrocławski. Dane w sieciach. (i inne historie) Marcin Bieńkowski
 Dane w sieciach (i inne historie) Marcin Bieńkowski Jak przechowywać dane w sieciach (strony WWW, bazy danych, ) tak, żeby dowolne ciągi odwołań do (części) tych obiektów mogły być obsłużone małym kosztem?
Dane w sieciach (i inne historie) Marcin Bieńkowski Jak przechowywać dane w sieciach (strony WWW, bazy danych, ) tak, żeby dowolne ciągi odwołań do (części) tych obiektów mogły być obsłużone małym kosztem?
Kombinowanie o nieskończoności. 2. Wyspy, mosty, mapy i kredki materiały do ćwiczeń
 Kombinowanie o nieskończoności. 2. Wyspy, mosty, mapy i kredki materiały do ćwiczeń Projekt Matematyka dla ciekawych świata spisał: Michał Korch 15 marzec 2018 Szybkie przypomnienie z wykładu Prezentacja
Kombinowanie o nieskończoności. 2. Wyspy, mosty, mapy i kredki materiały do ćwiczeń Projekt Matematyka dla ciekawych świata spisał: Michał Korch 15 marzec 2018 Szybkie przypomnienie z wykładu Prezentacja
Lista 4. Kamil Matuszewski 22 marca 2016
 Lista 4 Kamil Matuszewski 22 marca 2016 1 2 3 4 5 6 7 8 9 10 Zadanie 2 Ułóż algorytm który dla danego n-wierzchołkowego drzewa i liczby k pokoloruje jak najwięcej wierzchołków tak, by na każdej ścieżce
Lista 4 Kamil Matuszewski 22 marca 2016 1 2 3 4 5 6 7 8 9 10 Zadanie 2 Ułóż algorytm który dla danego n-wierzchołkowego drzewa i liczby k pokoloruje jak najwięcej wierzchołków tak, by na każdej ścieżce
TEORETYCZNE PODSTAWY INFORMATYKI
 1 TEORETYCZNE PODSTAWY INFORMATYKI WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Wykład 14c 2 Definicje indukcyjne Twierdzenia dowodzone przez indukcje Definicje indukcyjne Definicja drzewa
1 TEORETYCZNE PODSTAWY INFORMATYKI WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Wykład 14c 2 Definicje indukcyjne Twierdzenia dowodzone przez indukcje Definicje indukcyjne Definicja drzewa
Matematyka dyskretna
 Matematyka dyskretna Wykład 12: Krzywe eliptyczne Gniewomir Sarbicki Rozważać będziemy przestrzeń K n Definicja: x y λ K x = λy. Relację nazywamy różnieniem się o skalar Przykład: [4, 10, 6, 14] [6, 15,
Matematyka dyskretna Wykład 12: Krzywe eliptyczne Gniewomir Sarbicki Rozważać będziemy przestrzeń K n Definicja: x y λ K x = λy. Relację nazywamy różnieniem się o skalar Przykład: [4, 10, 6, 14] [6, 15,
Algorytmy i struktury danych. Co dziś? Tytułem przypomnienia metoda dziel i zwyciężaj. Wykład VIII Elementarne techniki algorytmiczne
 Algorytmy i struktury danych Wykład VIII Elementarne techniki algorytmiczne Co dziś? Algorytmy zachłanne (greedyalgorithms) 2 Tytułem przypomnienia metoda dziel i zwyciężaj. Problem można podzielić na
Algorytmy i struktury danych Wykład VIII Elementarne techniki algorytmiczne Co dziś? Algorytmy zachłanne (greedyalgorithms) 2 Tytułem przypomnienia metoda dziel i zwyciężaj. Problem można podzielić na
Minimalne drzewa rozpinające
 KNM UŚ 26-28 listopada 2010 Ostrzeżenie Wprowadzenie Motywacja Definicje Niektóre pojęcia pojawiające się podczas tego referatu są naszymi autorskimi tłumaczeniami z języka angielskiego. Nie udało nam
KNM UŚ 26-28 listopada 2010 Ostrzeżenie Wprowadzenie Motywacja Definicje Niektóre pojęcia pojawiające się podczas tego referatu są naszymi autorskimi tłumaczeniami z języka angielskiego. Nie udało nam
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: MATEMATYKA DYSKRETNA Discrete mathematics Kierunek: Rodzaj przedmiotu: obowiązkowy w ramach treści wspólnych z kierunkiem Informatyka Rodzaj zajęć: wykład, ćwiczenia Matematyka Poziom
Nazwa przedmiotu: MATEMATYKA DYSKRETNA Discrete mathematics Kierunek: Rodzaj przedmiotu: obowiązkowy w ramach treści wspólnych z kierunkiem Informatyka Rodzaj zajęć: wykład, ćwiczenia Matematyka Poziom
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2015 andrzej.lachwa@uj.edu.pl 3/15 Indukcja matematyczna Poprawność indukcji matematycznej wynika z dobrego uporządkowania liczb naturalnych, czyli z następującej
Matematyka dyskretna Andrzej Łachwa, UJ, 2015 andrzej.lachwa@uj.edu.pl 3/15 Indukcja matematyczna Poprawność indukcji matematycznej wynika z dobrego uporządkowania liczb naturalnych, czyli z następującej
LXIII Egzamin dla Aktuariuszy z 25 marca 2013 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXIII Egzamin dla Aktuariuszy z 25 marca 2013 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy LXIII Egzamin dla Aktuariuszy z 25 marca 2013 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
