Instytut Informatyki Uniwersytet Wrocławski. Dane w sieciach. (i inne historie) Marcin Bieńkowski
|
|
|
- Anna Sobolewska
- 9 lat temu
- Przeglądów:
Transkrypt
1 Dane w sieciach (i inne historie) Marcin Bieńkowski
2 Jak przechowywać dane w sieciach (strony WWW, bazy danych, ) tak, żeby dowolne ciągi odwołań do (części) tych obiektów mogły być obsłużone małym kosztem? Znany problem, wiele wariantów. Najbardziej klasyczny i podstawowy z wariantów: Page Migration Dane w sieciach / Marcin Bienkowski 2/18
3 Page Migration (model) Sieć komputerów v 3 v 2 v 4 v 5 v 1 v 6 v 7 Jedna kopia jednego niepodzielnego obiektu (strona pamięci) o rozmiarze w lokalnej pamięci jednego z komputerów Koszt komunikacji pomiędzy parą komputerów = = koszt najtańszej ścieżki pomiędzy nimi Dane w sieciach / Marcin Bienkowski 3/18
4 Page Migration (model cd.) Problem: komputery chcą dostępu do danych ze strony W jednym kroku chce odczytać lub zapisać jednostkę danych ze strony v 3 koszt = v 2 v 4 v 5 v 1 v 6 v 7 Koszt migracji = Po obsłudze żądania algorytm może przenieść stronę do nowego komputera Dane w sieciach / Marcin Bienkowski 4/18
5 Problem online WEJŚCIE: ciąg WYJŚCIE: ciąg migracji strony minimalizujący całkowity koszt Problem: przyszłość jest nieznana Nie mamy szansy wyliczyć optymalnego rozwiązania Ale możemy się do niego zbliżyć! Istnieją algorytmy (online), które osiągają koszt zaledwie o stałą większy od rozwiązania optymalnego (OPT) Dane w sieciach / Marcin Bienkowski 5/18
6 Mój wkład w tematykę Sieci rzadko są stabilne, zazwyczaj przepustowości łącz zmieniają się w nieprzewidywalny sposób. Koszty przesyłania danych również ulegają zmianom. Założenie: Koszty przypisane do krawędzi sieci mogą zmieniać się w dowolny sposób, ale powoli. Dane w sieciach / Marcin Bienkowski 6/18
7 Ta wersja problemu okazuje się bardzo trudna Każdy algorytm deterministyczny jest co najmniej razy gorszy od OPT Dla algorytmów zrandomizowanych: razy Umiemy pokazać algorytmy osiągające te współczynniki Dane w sieciach / Marcin Bienkowski 7/18
8 Algorytm dla dwóch wierzchołków Algorytm EDGE W każdym kroku przenieś stronę do wierzchołka, który żądał przed chwilą dostępu do niej, z ppb. wykres : Dane w sieciach / Marcin Bienkowski 8/18
9 Algorytm dla n wierzchołków Algorytm DISTRIBUTE Żądanie w wierzchołku Przenosimy się z ppb. Docelowy wierzchołek wybieramy losowo (im dalej od, tym ppb. mniejsze Dane w sieciach / Marcin Bienkowski 9/18
10 Dygresja Strategię leżącą u podstaw algorytmu DISTRIBUTE da się lekko zmodyfikować i otrzymać: Algorytm dla problemu k-setcover, będący -aproksymacją Dane w sieciach / Marcin Bienkowski 10/18
11 Inne spojrzenie Dlaczego przegraliśmy? Bardzo silny model: adwersarz kontroluje jednocześnie dostęp do strony pamięci jak i zmiany sieci! Rzeczywistość nie jest tak brutalna (miejmy nadzieję) Z drugiej strony: model całkowicie stochastyczny jest zbyt łatwy Dane w sieciach / Marcin Bienkowski 11/18
12 Modyfikacje modelu Zamieńmy część adwersarza przez proces stochastyczny Scenariusz A: Niech fluktuacje sieci będą losowe, a odwołania do strony najgorsze z możliwych. Scenariusz B: Niech zmiany w sieci będą dyktowane przez adwersarza, a komputer czytający ze strony wybierany losowo. Dane w sieciach / Marcin Bienkowski 12/18
13 Modyfikacje modelu Scenariusz A: sieć losowo, żądania adwersarz algorytm który jest co najwyżej razy gorszy od OPT Scenariusz B: sieć adwersarz, żądania losowo algorytm który jest co najwyżej o stały czynnik gorszy od OPT Wyniki osiągane są z dużym prawdopodobieństwem Dane w sieciach / Marcin Bienkowski 13/18
14 Co teraz? Chciałem zająć się czymś zupełnie innym ale minister miał inne zdanie na ten temat Dane w sieciach / Marcin Bienkowski 14/18
15 Rozszerzenia page migration Możliwość replikacji danych (przydatne zwłaszcza przy niemodyfikowalnych obiektach, np. stronach WWW) Wiele obiektów w sieci -- komputery mają ograniczoną przestrzeń dyskową Dane w sieciach / Marcin Bienkowski 15/18
16 Na szczęście są też inne problemy (choć z podobnej dziedziny) (1) Eksploracja terenu grupą robotów robotów Komunikacja między robotami Każdy wierzchołek grafu musi zostać odwiedzony przez przynajmniej jednego robota Chcemy to zrobić jak najszybciej lub też używając jak najmniej energii Dane w sieciach / Marcin Bienkowski 16/18
17 Na szczęście są też inne problemy (choć z podobnej dziedziny) (2) Bufory w routerach kolejek wejściowych o rozmiarze Jedno wyjście Pakiety przychodzące do pełnego bufora są gubione Algorytm decyduje, z której kolejki przekazać pakiet na wyjście Chcemy zminimalizować liczbę straconych pakietów Dane w sieciach / Marcin Bienkowski 17/18
18 Dziękuję za uwagę!
Wykładnicze grafy przypadkowe: teoria i przykłady zastosowań do analizy rzeczywistych sieci złożonych
 Gdańsk, Warsztaty pt. Układy Złożone (8 10 maja 2014) Agata Fronczak Zakład Fizyki Układów Złożonych Wydział Fizyki Politechniki Warszawskiej Wykładnicze grafy przypadkowe: teoria i przykłady zastosowań
Gdańsk, Warsztaty pt. Układy Złożone (8 10 maja 2014) Agata Fronczak Zakład Fizyki Układów Złożonych Wydział Fizyki Politechniki Warszawskiej Wykładnicze grafy przypadkowe: teoria i przykłady zastosowań
Programowanie sieciowe. Tadeusz Trzaskalik
 Programowanie Tadeusz Trzaskalik 8.1. Wprowadzenie Słowa kluczowe Drzewo rozpinające Minimalne drzewo rozpinające Najkrótsza droga w sieci Wierzchołek początkowy Maksymalny przepływ w sieci Źródło Ujście
Programowanie Tadeusz Trzaskalik 8.1. Wprowadzenie Słowa kluczowe Drzewo rozpinające Minimalne drzewo rozpinające Najkrótsza droga w sieci Wierzchołek początkowy Maksymalny przepływ w sieci Źródło Ujście
Metody teorii gier. ALP520 - Wykład z Algorytmów Probabilistycznych p.2
 Metody teorii gier ALP520 - Wykład z Algorytmów Probabilistycznych p.2 Metody teorii gier Cel: Wyprowadzenie oszacowania dolnego na oczekiwany czas działania dowolnego algorytmu losowego dla danego problemu.
Metody teorii gier ALP520 - Wykład z Algorytmów Probabilistycznych p.2 Metody teorii gier Cel: Wyprowadzenie oszacowania dolnego na oczekiwany czas działania dowolnego algorytmu losowego dla danego problemu.
AiSD zadanie trzecie
 AiSD zadanie trzecie Gliwiński Jarosław Marek Kruczyński Konrad Marek Grupa dziekańska I5 5 czerwca 2008 1 Wstęp Celem postawionym przez zadanie trzecie było tzw. sortowanie topologiczne. Jest to typ sortowania
AiSD zadanie trzecie Gliwiński Jarosław Marek Kruczyński Konrad Marek Grupa dziekańska I5 5 czerwca 2008 1 Wstęp Celem postawionym przez zadanie trzecie było tzw. sortowanie topologiczne. Jest to typ sortowania
Wykorzystanie algorytmów mrówkowych w dynamicznym problem
 Wykorzystanie algorytmów mrówkowych w dynamicznym problemie marszrutyzacji Promotor: dr inż. Aneta Poniszewska-Marańda Współpromotor: mgr inż. Łukasz Chomątek 14 czerwca 2013 Przedmiot i cele pracy dyplomowej
Wykorzystanie algorytmów mrówkowych w dynamicznym problemie marszrutyzacji Promotor: dr inż. Aneta Poniszewska-Marańda Współpromotor: mgr inż. Łukasz Chomątek 14 czerwca 2013 Przedmiot i cele pracy dyplomowej
Algorytmy aproksymacyjne i parametryzowane
 Algorytmy aproksymacyjne i parametryzowane Marek Cygan Uniwersytet Warszawski 18 października 2012 Marek Cygan Algorytmy aproksymacyjne i parametryzowane 1/22 Wstęp W algorytmice problemy dzielimy na obliczeniowo
Algorytmy aproksymacyjne i parametryzowane Marek Cygan Uniwersytet Warszawski 18 października 2012 Marek Cygan Algorytmy aproksymacyjne i parametryzowane 1/22 Wstęp W algorytmice problemy dzielimy na obliczeniowo
Algorytmy aproksymacyjne dla problemów stochastycznych
 Algorytmy aproksymacyjne dla problemów stochastycznych Piotr Sankowski Uniwersytet Warszawski PhD Open, 5-6 grudzień, 2008 - p. 1/47 Plan - Wykład III Aproksymacyjne algorytmy online Aproksymacyjne stochastyczne
Algorytmy aproksymacyjne dla problemów stochastycznych Piotr Sankowski Uniwersytet Warszawski PhD Open, 5-6 grudzień, 2008 - p. 1/47 Plan - Wykład III Aproksymacyjne algorytmy online Aproksymacyjne stochastyczne
Algorytmika Problemów Trudnych
 Algorytmika Problemów Trudnych Wykład 9 Tomasz Krawczyk krawczyk@tcs.uj.edu.pl Kraków, semestr letni 2016/17 plan wykładu Algorytmy aproksymacyjne: Pojęcie algorytmu aproksymacyjnego i współczynnika aproksymowalności.
Algorytmika Problemów Trudnych Wykład 9 Tomasz Krawczyk krawczyk@tcs.uj.edu.pl Kraków, semestr letni 2016/17 plan wykładu Algorytmy aproksymacyjne: Pojęcie algorytmu aproksymacyjnego i współczynnika aproksymowalności.
Ustawienia widoku ikon
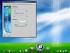 Ustawienia widoku ikon Ikony w oknie możemy wyświetlić w różny sposób. Aby zmienić wygląd wyświetlanych ikon wybieramy ikonę więcej opcji Z otwartego menu wybieramy pasujący nam widok (wielkość) wyświetlanych
Ustawienia widoku ikon Ikony w oknie możemy wyświetlić w różny sposób. Aby zmienić wygląd wyświetlanych ikon wybieramy ikonę więcej opcji Z otwartego menu wybieramy pasujący nam widok (wielkość) wyświetlanych
Sieci komputerowe. Wykład 8: Wyszukiwarki internetowe. Marcin Bieńkowski. Instytut Informatyki Uniwersytet Wrocławski
 Sieci komputerowe Wykład 8: Wyszukiwarki internetowe Marcin Bieńkowski Instytut Informatyki Uniwersytet Wrocławski Sieci komputerowe (II UWr) Wykład 8 1 / 37 czyli jak znaleźć igłę w sieci Sieci komputerowe
Sieci komputerowe Wykład 8: Wyszukiwarki internetowe Marcin Bieńkowski Instytut Informatyki Uniwersytet Wrocławski Sieci komputerowe (II UWr) Wykład 8 1 / 37 czyli jak znaleźć igłę w sieci Sieci komputerowe
Wstęp do programowania
 Wstęp do programowania Algorytmy zachłanne, algoritme Dijkstry Paweł Daniluk Wydział Fizyki Jesień 2013 P. Daniluk(Wydział Fizyki) WP w. XI Jesień 2013 1 / 25 Algorytmy zachłanne Strategia polegająca na
Wstęp do programowania Algorytmy zachłanne, algoritme Dijkstry Paweł Daniluk Wydział Fizyki Jesień 2013 P. Daniluk(Wydział Fizyki) WP w. XI Jesień 2013 1 / 25 Algorytmy zachłanne Strategia polegająca na
Modele i narzędzia optymalizacji w systemach informatycznych zarządzania
 Politechnika Poznańska Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Joanna Józefowska POZNAŃ 2010/11 Spis treści Rozdział 1. Metoda programowania dynamicznego........... 5
Politechnika Poznańska Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Joanna Józefowska POZNAŃ 2010/11 Spis treści Rozdział 1. Metoda programowania dynamicznego........... 5
Algorytmy i Struktury Danych, 2. ćwiczenia
 Algorytmy i Struktury Danych, 2. ćwiczenia 2017-10-13 Spis treści 1 Optymalne sortowanie 5 ciu elementów 1 2 Sortowanie metodą Shella 2 3 Przesunięcie cykliczne tablicy 3 4 Scalanie w miejscu dla ciągów
Algorytmy i Struktury Danych, 2. ćwiczenia 2017-10-13 Spis treści 1 Optymalne sortowanie 5 ciu elementów 1 2 Sortowanie metodą Shella 2 3 Przesunięcie cykliczne tablicy 3 4 Scalanie w miejscu dla ciągów
Asocjacyjna reprezentacja danych i wnioskowanie
 Asocjacyjna reprezentacja danych i wnioskowanie Wykorzystane technologie JetBrains PyCharm 504 Python 35 Struktura drzewa GRAPH PARAM PARAM ID1 ID2 ID_N params params params param_name_1: param_value_1
Asocjacyjna reprezentacja danych i wnioskowanie Wykorzystane technologie JetBrains PyCharm 504 Python 35 Struktura drzewa GRAPH PARAM PARAM ID1 ID2 ID_N params params params param_name_1: param_value_1
Schemat programowania dynamicznego (ang. dynamic programming)
 Schemat programowania dynamicznego (ang. dynamic programming) Jest jedną z metod rozwiązywania problemów optymalizacyjnych. Jej twórcą (1957) był amerykański matematyk Richard Ernest Bellman. Schemat ten
Schemat programowania dynamicznego (ang. dynamic programming) Jest jedną z metod rozwiązywania problemów optymalizacyjnych. Jej twórcą (1957) był amerykański matematyk Richard Ernest Bellman. Schemat ten
komputery? Andrzej Skowron, Hung Son Nguyen Instytut Matematyki, Wydział MIM, UW
 Czego moga się nauczyć komputery? Andrzej Skowron, Hung Son Nguyen son@mimuw.edu.pl; skowron@mimuw.edu.pl Instytut Matematyki, Wydział MIM, UW colt.tex Czego mogą się nauczyć komputery? Andrzej Skowron,
Czego moga się nauczyć komputery? Andrzej Skowron, Hung Son Nguyen son@mimuw.edu.pl; skowron@mimuw.edu.pl Instytut Matematyki, Wydział MIM, UW colt.tex Czego mogą się nauczyć komputery? Andrzej Skowron,
Ataki na serwery Domain Name System (DNS Cache Poisoning)
 Ataki na serwery Domain Name System (DNS Cache Poisoning) Jacek Gawrych semestr 9 Teleinformatyka i Zarządzanie w Telekomunikacji jgawrych@elka.pw.edu.pl Plan prezentacji Pytania Phishing -> Pharming Phishing
Ataki na serwery Domain Name System (DNS Cache Poisoning) Jacek Gawrych semestr 9 Teleinformatyka i Zarządzanie w Telekomunikacji jgawrych@elka.pw.edu.pl Plan prezentacji Pytania Phishing -> Pharming Phishing
Drzewa spinające MST dla grafów ważonych Maksymalne drzewo spinające Drzewo Steinera. Wykład 6. Drzewa cz. II
 Wykład 6. Drzewa cz. II 1 / 65 drzewa spinające Drzewa spinające Zliczanie drzew spinających Drzewo T nazywamy drzewem rozpinającym (spinającym) (lub dendrytem) spójnego grafu G, jeżeli jest podgrafem
Wykład 6. Drzewa cz. II 1 / 65 drzewa spinające Drzewa spinające Zliczanie drzew spinających Drzewo T nazywamy drzewem rozpinającym (spinającym) (lub dendrytem) spójnego grafu G, jeżeli jest podgrafem
Lista 4. Kamil Matuszewski 22 marca 2016
 Lista 4 Kamil Matuszewski 22 marca 2016 1 2 3 4 5 6 7 8 9 10 Zadanie 2 Ułóż algorytm który dla danego n-wierzchołkowego drzewa i liczby k pokoloruje jak najwięcej wierzchołków tak, by na każdej ścieżce
Lista 4 Kamil Matuszewski 22 marca 2016 1 2 3 4 5 6 7 8 9 10 Zadanie 2 Ułóż algorytm który dla danego n-wierzchołkowego drzewa i liczby k pokoloruje jak najwięcej wierzchołków tak, by na każdej ścieżce
Stronicowanie w systemie pamięci wirtualnej
 Pamięć wirtualna Stronicowanie w systemie pamięci wirtualnej Stronicowanie z wymianą stron pomiędzy pamięcią pierwszego i drugiego rzędu. Zalety w porównaniu z prostym stronicowaniem: rozszerzenie przestrzeni
Pamięć wirtualna Stronicowanie w systemie pamięci wirtualnej Stronicowanie z wymianą stron pomiędzy pamięcią pierwszego i drugiego rzędu. Zalety w porównaniu z prostym stronicowaniem: rozszerzenie przestrzeni
Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle
 Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle Paweł Szołtysek 12 czerwca 2008 Streszczenie Planowanie produkcji jest jednym z problemów optymalizacji dyskretnej,
Badania operacyjne: Wykład Zastosowanie kolorowania grafów w planowaniu produkcji typu no-idle Paweł Szołtysek 12 czerwca 2008 Streszczenie Planowanie produkcji jest jednym z problemów optymalizacji dyskretnej,
POTRZEBY A B C D E P P P P P
 1. (2p.) Narysuj przykładowy graf przydziału (jednokrotnych) zasobów (bez zakleszczenia) i sprawdź, jakie przykładowe żądania przydzielenia zasobów spowodują powstanie zakleszczenia, a jakie nie. W przypadku
1. (2p.) Narysuj przykładowy graf przydziału (jednokrotnych) zasobów (bez zakleszczenia) i sprawdź, jakie przykładowe żądania przydzielenia zasobów spowodują powstanie zakleszczenia, a jakie nie. W przypadku
Dokumentacja wstępna TIN. Rozproszone repozytorium oparte o WebDAV
 Piotr Jarosik, Kamil Jaworski, Dominik Olędzki, Anna Stępień Dokumentacja wstępna TIN Rozproszone repozytorium oparte o WebDAV 1. Wstęp Celem projektu jest zaimplementowanie rozproszonego repozytorium
Piotr Jarosik, Kamil Jaworski, Dominik Olędzki, Anna Stępień Dokumentacja wstępna TIN Rozproszone repozytorium oparte o WebDAV 1. Wstęp Celem projektu jest zaimplementowanie rozproszonego repozytorium
Algorytmiczna teoria grafów Przepływy w sieciach.
 Algorytmiczna teoria grafów Sieć przepływowa Siecią przepływową S = (V, E, c) nazywamy graf zorientowany G = (V,E), w którym każdy łuk (u, v) E ma określoną przepustowość c(u, v) 0. Wyróżniamy dwa wierzchołki:
Algorytmiczna teoria grafów Sieć przepływowa Siecią przepływową S = (V, E, c) nazywamy graf zorientowany G = (V,E), w którym każdy łuk (u, v) E ma określoną przepustowość c(u, v) 0. Wyróżniamy dwa wierzchołki:
Akademickie Centrum Informatyki PS. Wydział Informatyki PS
 Akademickie Centrum Informatyki PS Wydział Informatyki PS Akademickie Centrum Informatyki Wydział Informatyki P.S. Warstwy transmisyjne Krzysztof Bogusławski tel. 449 41 82 kbogu@man.szczecin.pl Agenda
Akademickie Centrum Informatyki PS Wydział Informatyki PS Akademickie Centrum Informatyki Wydział Informatyki P.S. Warstwy transmisyjne Krzysztof Bogusławski tel. 449 41 82 kbogu@man.szczecin.pl Agenda
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2014 andrzej.lachwa@uj.edu.pl 15/15 TWIERDZENIE HALLA Twierdzenie o kojarzeniu małżeństw rozważa dwie grupy dziewcząt i chłopców, oraz podgrupy dziewczyn i podgrupy
Matematyka dyskretna Andrzej Łachwa, UJ, 2014 andrzej.lachwa@uj.edu.pl 15/15 TWIERDZENIE HALLA Twierdzenie o kojarzeniu małżeństw rozważa dwie grupy dziewcząt i chłopców, oraz podgrupy dziewczyn i podgrupy
Algorytm Dijkstry znajdowania najkrótszej ścieżki w grafie
 Algorytm Dijkstry znajdowania najkrótszej ścieżki w grafie Używane struktury danych: V - zbiór wierzchołków grafu, V = {1,2,3...,n} E - zbiór krawędzi grafu, E = {(i,j),...}, gdzie i, j Î V i istnieje
Algorytm Dijkstry znajdowania najkrótszej ścieżki w grafie Używane struktury danych: V - zbiór wierzchołków grafu, V = {1,2,3...,n} E - zbiór krawędzi grafu, E = {(i,j),...}, gdzie i, j Î V i istnieje
Struktury danych i złożoność obliczeniowa Wykład 7. Prof. dr hab. inż. Jan Magott
 Struktury danych i złożoność obliczeniowa Wykład 7 Prof. dr hab. inż. Jan Magott Problemy NP-zupełne Transformacją wielomianową problemu π 2 do problemu π 1 (π 2 π 1 ) jest funkcja f: D π2 D π1 spełniająca
Struktury danych i złożoność obliczeniowa Wykład 7 Prof. dr hab. inż. Jan Magott Problemy NP-zupełne Transformacją wielomianową problemu π 2 do problemu π 1 (π 2 π 1 ) jest funkcja f: D π2 D π1 spełniająca
Problem straŝaka w drzewach. Agnieszka Skorupka Matematyka Stosowana FTiMS
 Problem straŝaka w drzewach Agnieszka Skorupka Matematyka Stosowana FTiMS Problem StraŜaka: Co to jest? Problem StraŜaka: Co to jest? Problem StraŜaka: Co to jest? Problem StraŜaka: Co to jest? Problem
Problem straŝaka w drzewach Agnieszka Skorupka Matematyka Stosowana FTiMS Problem StraŜaka: Co to jest? Problem StraŜaka: Co to jest? Problem StraŜaka: Co to jest? Problem StraŜaka: Co to jest? Problem
Laboratorium - Migracja danych w Windows Vista
 5.0 5.1.4.5 Laboratorium - Migracja danych w Windows Vista Wprowadzenie Wydrukuj i uzupełnij to laboratorium. W tym laboratorium używaj systemu Windows Vista. Zalecany sprzęt Do tego ćwiczenia wymagany
5.0 5.1.4.5 Laboratorium - Migracja danych w Windows Vista Wprowadzenie Wydrukuj i uzupełnij to laboratorium. W tym laboratorium używaj systemu Windows Vista. Zalecany sprzęt Do tego ćwiczenia wymagany
Materiały dla finalistów
 Materiały dla finalistów Malachoviacus Informaticus 2016 11 kwietnia 2016 Wprowadzenie Poniższy dokument zawiera opisy zagadnień, które będą niezbędne do rozwiązania zadań w drugim etapie konkursu. Polecamy
Materiały dla finalistów Malachoviacus Informaticus 2016 11 kwietnia 2016 Wprowadzenie Poniższy dokument zawiera opisy zagadnień, które będą niezbędne do rozwiązania zadań w drugim etapie konkursu. Polecamy
Problemy Decyzyjne dla Systemów Nieskończonych
 Problemy Decyzyjne dla Systemów Nieskończonych Ćwiczenia 1 17 lutego 2012 Na tych ćwiczeniach zajmiemy się pojęciem well quasi-ordering (WQO) bardzo przydatnym do analizy nieskończonych ciągów. Definicja
Problemy Decyzyjne dla Systemów Nieskończonych Ćwiczenia 1 17 lutego 2012 Na tych ćwiczeniach zajmiemy się pojęciem well quasi-ordering (WQO) bardzo przydatnym do analizy nieskończonych ciągów. Definicja
Sprzedaż online. Piotr Sankowski Uniwersytet Warszawski Warszawa p. 1/40
 Sprzedaż online Piotr Sankowski Uniwersytet Warszawski Warszawa 18.04.2013 - p. 1/40 Plan wykładu Problem skojarzeń online Algorytm zachłanny Algorytm losowo rankujacy Dolne ograniczenie Problem aukcji
Sprzedaż online Piotr Sankowski Uniwersytet Warszawski Warszawa 18.04.2013 - p. 1/40 Plan wykładu Problem skojarzeń online Algorytm zachłanny Algorytm losowo rankujacy Dolne ograniczenie Problem aukcji
dr inż. Jarosław Forenc
 Informatyka 2 Politechnika Białostocka - Wydział Elektryczny Elektrotechnika, semestr III, studia stacjonarne I stopnia Rok akademicki 2010/2011 Wykład nr 7 (24.01.2011) dr inż. Jarosław Forenc Rok akademicki
Informatyka 2 Politechnika Białostocka - Wydział Elektryczny Elektrotechnika, semestr III, studia stacjonarne I stopnia Rok akademicki 2010/2011 Wykład nr 7 (24.01.2011) dr inż. Jarosław Forenc Rok akademicki
Algorytmy wyznaczania centralności w sieci Szymon Szylko
 Algorytmy wyznaczania centralności w sieci Szymon Szylko Zakład systemów Informacyjnych Wrocław 10.01.2008 Agenda prezentacji Cechy sieci Algorytmy grafowe Badanie centralności Algorytmy wyznaczania centralności
Algorytmy wyznaczania centralności w sieci Szymon Szylko Zakład systemów Informacyjnych Wrocław 10.01.2008 Agenda prezentacji Cechy sieci Algorytmy grafowe Badanie centralności Algorytmy wyznaczania centralności
a) 7 b) 19 c) 21 d) 34
 Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Spacery losowe generowanie realizacji procesu losowego
 Spacery losowe generowanie realizacji procesu losowego Michał Krzemiński Streszczenie Omówimy metodę generowania trajektorii spacerów losowych (błądzenia losowego), tj. szczególnych procesów Markowa z
Spacery losowe generowanie realizacji procesu losowego Michał Krzemiński Streszczenie Omówimy metodę generowania trajektorii spacerów losowych (błądzenia losowego), tj. szczególnych procesów Markowa z
Rachunek prawdopodobieństwa Rozdział 3. Prawdopodobieństwo warunkowe i niezależność zdarzeń.
 Rachunek prawdopodobieństwa Rozdział 3. Prawdopodobieństwo warunkowe i niezależność zdarzeń. 3.2. Niezależność zdarzeń Katarzyna Rybarczyk-Krzywdzińska Niezależność dwóch zdarzeń Intuicja Zdarzenia losowe
Rachunek prawdopodobieństwa Rozdział 3. Prawdopodobieństwo warunkowe i niezależność zdarzeń. 3.2. Niezależność zdarzeń Katarzyna Rybarczyk-Krzywdzińska Niezależność dwóch zdarzeń Intuicja Zdarzenia losowe
51. Wykorzystywanie sumy, iloczynu i różnicy zdarzeń do obliczania prawdopodobieństw zdarzeń.
 Matematyka lekcja 5 5. Wykorzystywanie sumy, iloczynu i różnicy zdarzeń do obliczania prawdopodobieństw zdarzeń. I. rzypomnij sobie:. Jak rysujemy drzewo stochastyczne i przy jego pomocy obliczamy prawdopodobieństwo
Matematyka lekcja 5 5. Wykorzystywanie sumy, iloczynu i różnicy zdarzeń do obliczania prawdopodobieństw zdarzeń. I. rzypomnij sobie:. Jak rysujemy drzewo stochastyczne i przy jego pomocy obliczamy prawdopodobieństwo
Działanie algorytmu oparte jest na minimalizacji funkcji celu jako suma funkcji kosztu ( ) oraz funkcji heurystycznej ( ).
 Algorytm A* Opracowanie: Joanna Raczyńska 1.Wstęp Algorytm A* jest heurystycznym algorytmem służącym do znajdowania najkrótszej ścieżki w grafie. Jest to algorytm zupełny i optymalny, co oznacza, że zawsze
Algorytm A* Opracowanie: Joanna Raczyńska 1.Wstęp Algorytm A* jest heurystycznym algorytmem służącym do znajdowania najkrótszej ścieżki w grafie. Jest to algorytm zupełny i optymalny, co oznacza, że zawsze
Algorytmy genetyczne
 Algorytmy genetyczne Motto: Zamiast pracowicie poszukiwać najlepszego rozwiązania problemu informatycznego lepiej pozwolić, żeby komputer sam sobie to rozwiązanie wyhodował! Algorytmy genetyczne służą
Algorytmy genetyczne Motto: Zamiast pracowicie poszukiwać najlepszego rozwiązania problemu informatycznego lepiej pozwolić, żeby komputer sam sobie to rozwiązanie wyhodował! Algorytmy genetyczne służą
Losowość w rozproszonym modelu
 Losowość w rozproszonym modelu Model: ALP520 - Wykład z Algorytmów Probabilistycznych p.2 Losowość w rozproszonym modelu Model: zbiór procesorów, które moga pracować jednocześnie, połaczonych w sieć ALP520
Losowość w rozproszonym modelu Model: ALP520 - Wykład z Algorytmów Probabilistycznych p.2 Losowość w rozproszonym modelu Model: zbiór procesorów, które moga pracować jednocześnie, połaczonych w sieć ALP520
NAT (Network Address Translation)
 NAT usługa translacji adresów realizowana w celu: - umożliwienia dostępu do sieci większej ilości hostów niz ilość dostępnych adresów IP - podniesienia poziomu bezpieczeństwa sieci prywatnej - uproszczenia
NAT usługa translacji adresów realizowana w celu: - umożliwienia dostępu do sieci większej ilości hostów niz ilość dostępnych adresów IP - podniesienia poziomu bezpieczeństwa sieci prywatnej - uproszczenia
Wykorzystanie algorytmów mrówkowych w dynamicznym problem
 Wykorzystanie algorytmów mrówkowych w dynamicznym problemie marszrutyzacji Promotor: dr inż. Aneta Poniszewska-Marańda Współpromotor: mgr inż. Łukasz Chomątek 18 stycznia 2013 Przedmiot i cele pracy dyplomowej
Wykorzystanie algorytmów mrówkowych w dynamicznym problemie marszrutyzacji Promotor: dr inż. Aneta Poniszewska-Marańda Współpromotor: mgr inż. Łukasz Chomątek 18 stycznia 2013 Przedmiot i cele pracy dyplomowej
Reprezentacje grafów nieskierowanych Reprezentacje grafów skierowanych. Wykład 2. Reprezentacja komputerowa grafów
 Wykład 2. Reprezentacja komputerowa grafów 1 / 69 Macierz incydencji Niech graf G będzie grafem nieskierowanym bez pętli o n wierzchołkach (x 1, x 2,..., x n) i m krawędziach (e 1, e 2,..., e m). 2 / 69
Wykład 2. Reprezentacja komputerowa grafów 1 / 69 Macierz incydencji Niech graf G będzie grafem nieskierowanym bez pętli o n wierzchołkach (x 1, x 2,..., x n) i m krawędziach (e 1, e 2,..., e m). 2 / 69
Modele Obliczeń. Wykład 1 - Wprowadzenie. Marcin Szczuka. Instytut Matematyki, Uniwersytet Warszawski
 Modele Obliczeń Wykład 1 - Wprowadzenie Marcin Szczuka Instytut Matematyki, Uniwersytet Warszawski Wykład fakultatywny w semestrze zimowym 2014/2015 Marcin Szczuka (MIMUW) Modele Obliczeń 2014/2015 1 /
Modele Obliczeń Wykład 1 - Wprowadzenie Marcin Szczuka Instytut Matematyki, Uniwersytet Warszawski Wykład fakultatywny w semestrze zimowym 2014/2015 Marcin Szczuka (MIMUW) Modele Obliczeń 2014/2015 1 /
WOJSKOWA AKADEMIA TECHNICZNA WYDZIAŁ CYBERNETYKI
 WOJSKOWA AKADEMIA TECHNICZNA WYDZIAŁ CYBERNETYKI Analiza i modelowanie Systemów Teleinformatycznych Sprawozdanie z ćwiczenia laboratoryjnego nr 6 Temat ćwiczenia: Modelowanie systemów równoległych z zastosowaniem
WOJSKOWA AKADEMIA TECHNICZNA WYDZIAŁ CYBERNETYKI Analiza i modelowanie Systemów Teleinformatycznych Sprawozdanie z ćwiczenia laboratoryjnego nr 6 Temat ćwiczenia: Modelowanie systemów równoległych z zastosowaniem
Algorytmy Równoległe i Rozproszone Część X - Algorytmy samostabilizujące.
 Algorytmy Równoległe i Rozproszone Część X - Algorytmy samostabilizujące. Łukasz Kuszner pokój 209, WETI http://www.sphere.pl/ kuszner/ kuszner@sphere.pl Oficjalna strona wykładu http://www.sphere.pl/
Algorytmy Równoległe i Rozproszone Część X - Algorytmy samostabilizujące. Łukasz Kuszner pokój 209, WETI http://www.sphere.pl/ kuszner/ kuszner@sphere.pl Oficjalna strona wykładu http://www.sphere.pl/
5c. Sieci i przepływy
 5c. Sieci i przepływy Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2016/2017 rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 5c. Sieci i przepływy zima 2016/2017 1 / 40 1 Definicje
5c. Sieci i przepływy Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2016/2017 rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 5c. Sieci i przepływy zima 2016/2017 1 / 40 1 Definicje
dr inż. Jarosław Forenc
 Informatyka 2 Politechnika Białostocka - Wydział Elektryczny Elektrotechnika, semestr III, studia stacjonarne I stopnia Rok akademicki 2009/2010 Wykład nr 8 (29.01.2009) dr inż. Jarosław Forenc Rok akademicki
Informatyka 2 Politechnika Białostocka - Wydział Elektryczny Elektrotechnika, semestr III, studia stacjonarne I stopnia Rok akademicki 2009/2010 Wykład nr 8 (29.01.2009) dr inż. Jarosław Forenc Rok akademicki
Instytut Mechaniki i Inżynierii Obliczeniowej Wydział Mechaniczny Technologiczny Politechnika Śląska
 Instytut Mechaniki i Inżynierii Obliczeniowej www.imio.polsl.pl fb.com/imiopolsl @imiopolsl Wydział Mechaniczny Technologiczny Politechnika Śląska Języki programowania z programowaniem obiektowym Laboratorium
Instytut Mechaniki i Inżynierii Obliczeniowej www.imio.polsl.pl fb.com/imiopolsl @imiopolsl Wydział Mechaniczny Technologiczny Politechnika Śląska Języki programowania z programowaniem obiektowym Laboratorium
dr inŝ. Jarosław Forenc
 Rok akademicki 2009/2010, Wykład nr 8 2/19 Plan wykładu nr 8 Informatyka 2 Politechnika Białostocka - Wydział Elektryczny Elektrotechnika, semestr III, studia stacjonarne I stopnia Rok akademicki 2009/2010
Rok akademicki 2009/2010, Wykład nr 8 2/19 Plan wykładu nr 8 Informatyka 2 Politechnika Białostocka - Wydział Elektryczny Elektrotechnika, semestr III, studia stacjonarne I stopnia Rok akademicki 2009/2010
Algorytmy dynamiczne. Piotr Sankowski. - p. 1/14
 Algorytmy dynamiczne Piotr Sankowski - p. 1/14 Dynamiczne: drzewa wyszukiwanie wzorca w tekście spójność grafu problemy algebraiczne (FFT i inne) domknięcie przechodnie oraz dynamiczne macierze najkrótsze
Algorytmy dynamiczne Piotr Sankowski - p. 1/14 Dynamiczne: drzewa wyszukiwanie wzorca w tekście spójność grafu problemy algebraiczne (FFT i inne) domknięcie przechodnie oraz dynamiczne macierze najkrótsze
OSTASZEWSKI Paweł (55566) PAWLICKI Piotr (55567) Algorytmy i Struktury Danych PIŁA
 OSTASZEWSKI Paweł (55566) PAWLICKI Piotr (55567) 16.01.2003 Algorytmy i Struktury Danych PIŁA ALGORYTMY ZACHŁANNE czas [ms] Porównanie Algorytmów Rozwiązyjących problem TSP 100 000 000 000,000 10 000 000
OSTASZEWSKI Paweł (55566) PAWLICKI Piotr (55567) 16.01.2003 Algorytmy i Struktury Danych PIŁA ALGORYTMY ZACHŁANNE czas [ms] Porównanie Algorytmów Rozwiązyjących problem TSP 100 000 000 000,000 10 000 000
Quantile hedging. czyli jak tanio i dobrze zabezpieczyć opcję. Michał Krawiec, Piotr Piestrzyński
 czyli jak tanio i dobrze zabezpieczyć opcję Michał Krawiec Piotr Piestrzyński Koło Naukowe Probabilistyki i Statystyki Matematycznej Uniwersytet Wrocławski Niedziela, 19 kwietnia 2015 Przykład (opis problemu)
czyli jak tanio i dobrze zabezpieczyć opcję Michał Krawiec Piotr Piestrzyński Koło Naukowe Probabilistyki i Statystyki Matematycznej Uniwersytet Wrocławski Niedziela, 19 kwietnia 2015 Przykład (opis problemu)
Sieci komputerowe. Wykład 5: Warstwa transportowa: TCP i UDP. Marcin Bieńkowski. Instytut Informatyki Uniwersytet Wrocławski
 Sieci komputerowe Wykład 5: Warstwa transportowa: TCP i UDP Marcin Bieńkowski Instytut Informatyki Uniwersytet Wrocławski Sieci komputerowe (II UWr) Wykład 5 1 / 22 Warstwa transportowa Cechy charakterystyczne:
Sieci komputerowe Wykład 5: Warstwa transportowa: TCP i UDP Marcin Bieńkowski Instytut Informatyki Uniwersytet Wrocławski Sieci komputerowe (II UWr) Wykład 5 1 / 22 Warstwa transportowa Cechy charakterystyczne:
Elementy modelowania matematycznego
 Elementy modelowania matematycznego Łańcuchy Markowa: zagadnienia graniczne. Ukryte modele Markowa. Jakub Wróblewski jakubw@pjwstk.edu.pl http://zajecia.jakubw.pl/ KLASYFIKACJA STANÓW Stan i jest osiągalny
Elementy modelowania matematycznego Łańcuchy Markowa: zagadnienia graniczne. Ukryte modele Markowa. Jakub Wróblewski jakubw@pjwstk.edu.pl http://zajecia.jakubw.pl/ KLASYFIKACJA STANÓW Stan i jest osiągalny
Algorytmy aproksymacyjne dla problemów stochastycznych
 Algorytmy aproksymacyjne dla problemów stochastycznych Marcin Mucha Uniwersytet Warszawski Warszawa 29.04.2011 - p. 1/44 Plan - Wykład II Boosted sampling: drzewo Steinera, problemy addytywne: lokalizacja
Algorytmy aproksymacyjne dla problemów stochastycznych Marcin Mucha Uniwersytet Warszawski Warszawa 29.04.2011 - p. 1/44 Plan - Wykład II Boosted sampling: drzewo Steinera, problemy addytywne: lokalizacja
Drzewa rozpinajace, zbiory rozłaczne, czas zamortyzowany
 , 1 2 3, czas zamortyzowany zajęcia 3. Wojciech Śmietanka, Tomasz Kulczyński, Błażej Osiński rozpinajace, 1 2 3 rozpinajace Mamy graf nieskierowany, ważony, wagi większe od 0. Chcemy wybrać taki podzbiór
, 1 2 3, czas zamortyzowany zajęcia 3. Wojciech Śmietanka, Tomasz Kulczyński, Błażej Osiński rozpinajace, 1 2 3 rozpinajace Mamy graf nieskierowany, ważony, wagi większe od 0. Chcemy wybrać taki podzbiór
Sieci komputerowe. Tadeusz Kobus, Maciej Kokociński Instytut Informatyki, Politechnika Poznańska
 Sieci komputerowe Tadeusz Kobus, Maciej Kokociński Instytut Informatyki, Politechnika Poznańska Translacja adresów w Linuksie Sieci Komputerowe, T. Kobus, M. Kokociński 2 Network Address Translation (NAT)
Sieci komputerowe Tadeusz Kobus, Maciej Kokociński Instytut Informatyki, Politechnika Poznańska Translacja adresów w Linuksie Sieci Komputerowe, T. Kobus, M. Kokociński 2 Network Address Translation (NAT)
Klasyfikacja metodą Bayesa
 Klasyfikacja metodą Bayesa Tadeusz Pankowski www.put.poznan.pl/~tadeusz.pankowski warunkowe i bezwarunkowe 1. Klasyfikacja Bayesowska jest klasyfikacją statystyczną. Pozwala przewidzieć prawdopodobieństwo
Klasyfikacja metodą Bayesa Tadeusz Pankowski www.put.poznan.pl/~tadeusz.pankowski warunkowe i bezwarunkowe 1. Klasyfikacja Bayesowska jest klasyfikacją statystyczną. Pozwala przewidzieć prawdopodobieństwo
Matematyka od zaraz zatrudnię
 Uniwersytet Jagielloński Gdzie jest matematyka? Soczewka, 26-28 listopada 2010 Kolorowanie grafów Dobre kolorowanie wierzchołków grafu, to nadanie im kolorów w taki sposób, że każde dwa wierzchołki połaczone
Uniwersytet Jagielloński Gdzie jest matematyka? Soczewka, 26-28 listopada 2010 Kolorowanie grafów Dobre kolorowanie wierzchołków grafu, to nadanie im kolorów w taki sposób, że każde dwa wierzchołki połaczone
WOJSKOWA AKADEMIA TECHNICZNA WYDZIAŁ CYBERNETYKI
 WOJSKOWA AKADEMIA TECHNICZNA WYDZIAŁ CYBERNETYKI Modelowanie Systemów Teleinformatycznych Sprawozdanie z ćwiczenia laboratoryjnego nr 6 Temat ćwiczenia: Modelowanie systemów równoległych z zastosowaniem
WOJSKOWA AKADEMIA TECHNICZNA WYDZIAŁ CYBERNETYKI Modelowanie Systemów Teleinformatycznych Sprawozdanie z ćwiczenia laboratoryjnego nr 6 Temat ćwiczenia: Modelowanie systemów równoległych z zastosowaniem
Stochastyczne zagadnienie rozdziału z dyskretnym rozkładem popytu
 Stochastyczne zagadnienie rozdziału z dyskretnym rozkładem popytu Marcin Anholcer Uniwersytet Ekonomiczny w Poznaniu 19 marca 2013, Ustroń Marcin Anholcer Stochastyczne zagadnienie rozdziału 1/ 15 1 Zagadnienie
Stochastyczne zagadnienie rozdziału z dyskretnym rozkładem popytu Marcin Anholcer Uniwersytet Ekonomiczny w Poznaniu 19 marca 2013, Ustroń Marcin Anholcer Stochastyczne zagadnienie rozdziału 1/ 15 1 Zagadnienie
Elementy Modelowania Matematycznego
 Elementy Modelowania Matematycznego Wykład 9 Systemy kolejkowe Spis treści Wstęp Systemy masowej obsługi (SMO) Notacja Kendalla Schemat systemu masowej obsługi Przykład systemu M/M/1 Założenia modelu matematycznego
Elementy Modelowania Matematycznego Wykład 9 Systemy kolejkowe Spis treści Wstęp Systemy masowej obsługi (SMO) Notacja Kendalla Schemat systemu masowej obsługi Przykład systemu M/M/1 Założenia modelu matematycznego
Zarządzanie projektami. Tadeusz Trzaskalik
 Zarządzanie projektami Tadeusz Trzaskalik 7.1. Wprowadzenie Słowa kluczowe Projekt Sieć czynności zynność bezpośrednio poprzedzająca Zdarzenie, zdarzenie początkowe, zdarzenie końcowe Właściwa numeracja
Zarządzanie projektami Tadeusz Trzaskalik 7.1. Wprowadzenie Słowa kluczowe Projekt Sieć czynności zynność bezpośrednio poprzedzająca Zdarzenie, zdarzenie początkowe, zdarzenie końcowe Właściwa numeracja
Algorytmiczna teoria grafów
 Przedmiot fakultatywny 20h wykładu + 20h ćwiczeń 21 lutego 2014 Zasady zaliczenia 1 ćwiczenia (ocena): kolokwium, zadania programistyczne (implementacje algorytmów), praca na ćwiczeniach. 2 Wykład (egzamin)
Przedmiot fakultatywny 20h wykładu + 20h ćwiczeń 21 lutego 2014 Zasady zaliczenia 1 ćwiczenia (ocena): kolokwium, zadania programistyczne (implementacje algorytmów), praca na ćwiczeniach. 2 Wykład (egzamin)
Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA
 Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA Zad. 1 (12p.)Niech n 3k > 0. Zbadać jaka jest najmniejsza możliwa liczba krawędzi w grafie, który ma dokładnie n wierzchołków oraz dokładnie k składowych, z których
Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA Zad. 1 (12p.)Niech n 3k > 0. Zbadać jaka jest najmniejsza możliwa liczba krawędzi w grafie, który ma dokładnie n wierzchołków oraz dokładnie k składowych, z których
Metody Programowania
 POLITECHNIKA KRAKOWSKA - WIEiK KATEDRA AUTOMATYKI i TECHNIK INFORMACYJNYCH Metody Programowania www.pk.edu.pl/~zk/mp_hp.html Wykładowca: dr inż. Zbigniew Kokosiński zk@pk.edu.pl Wykład 8: Wyszukiwanie
POLITECHNIKA KRAKOWSKA - WIEiK KATEDRA AUTOMATYKI i TECHNIK INFORMACYJNYCH Metody Programowania www.pk.edu.pl/~zk/mp_hp.html Wykładowca: dr inż. Zbigniew Kokosiński zk@pk.edu.pl Wykład 8: Wyszukiwanie
Przykładowe rozwiązania
 Przykładowe rozwiązania Poniższy dokument zawiera przykładowe rozwiązania zadań z I etapu I edycji konkursu (2014 r.). Rozwiązania w formie takiej jak przedstawiona niżej uzyskałyby pełną liczbę punktów
Przykładowe rozwiązania Poniższy dokument zawiera przykładowe rozwiązania zadań z I etapu I edycji konkursu (2014 r.). Rozwiązania w formie takiej jak przedstawiona niżej uzyskałyby pełną liczbę punktów
Przykład planowania sieci publicznego transportu zbiorowego
 TRANSPORT PUBLICZNY Przykład planowania sieci publicznego transportu zbiorowego Źródło: Bieńczak M., 2015 Politechnika Poznańska, Wydział Maszyn Roboczych i Transportu 1 METODYKA ZAŁOśENIA Dostarczanie
TRANSPORT PUBLICZNY Przykład planowania sieci publicznego transportu zbiorowego Źródło: Bieńczak M., 2015 Politechnika Poznańska, Wydział Maszyn Roboczych i Transportu 1 METODYKA ZAŁOśENIA Dostarczanie
Metody przeszukiwania
 Metody przeszukiwania Co to jest przeszukiwanie Przeszukiwanie polega na odnajdywaniu rozwiązania w dyskretnej przestrzeni rozwiązao. Zwykle przeszukiwanie polega na znalezieniu określonego rozwiązania
Metody przeszukiwania Co to jest przeszukiwanie Przeszukiwanie polega na odnajdywaniu rozwiązania w dyskretnej przestrzeni rozwiązao. Zwykle przeszukiwanie polega na znalezieniu określonego rozwiązania
Temat: Sieci neuronowe oraz technologia CUDA
 Elbląg, 27.03.2010 Temat: Sieci neuronowe oraz technologia CUDA Przygotował: Mateusz Górny VIII semestr ASiSK Wstęp Sieci neuronowe są to specyficzne struktury danych odzwierciedlające sieć neuronów w
Elbląg, 27.03.2010 Temat: Sieci neuronowe oraz technologia CUDA Przygotował: Mateusz Górny VIII semestr ASiSK Wstęp Sieci neuronowe są to specyficzne struktury danych odzwierciedlające sieć neuronów w
Wyznaczanie optymalnej trasy problem komiwojażera
 Wyznaczanie optymalnej trasy problem komiwojażera Optymalizacja w podejmowaniu decyzji Opracowała: mgr inż. Natalia Malinowska Wrocław, dn. 28.03.2017 Wydział Elektroniki Politechnika Wrocławska Plan prezentacji
Wyznaczanie optymalnej trasy problem komiwojażera Optymalizacja w podejmowaniu decyzji Opracowała: mgr inż. Natalia Malinowska Wrocław, dn. 28.03.2017 Wydział Elektroniki Politechnika Wrocławska Plan prezentacji
Problem skoczka szachowego i inne cykle Hamiltona na szachownicy n x n
 i inne cykle Hamiltona na szachownicy n x n Uniwersytet Warszawski 15 marca 2007 Agenda 1 2 naiwne Prosty algorytm liniowy 3 Problem znany był już od bardzo dawna, jako łamigłówka logiczna. Był też stosowany
i inne cykle Hamiltona na szachownicy n x n Uniwersytet Warszawski 15 marca 2007 Agenda 1 2 naiwne Prosty algorytm liniowy 3 Problem znany był już od bardzo dawna, jako łamigłówka logiczna. Był też stosowany
Badania operacyjne egzamin
 Imię i nazwisko:................................................... Nr indeksu:............ Zadanie 1 Załóżmy, że Tablica 1 reprezentuje jeden z kroków algorytmu sympleks dla problemu (1)-(4). Tablica
Imię i nazwisko:................................................... Nr indeksu:............ Zadanie 1 Załóżmy, że Tablica 1 reprezentuje jeden z kroków algorytmu sympleks dla problemu (1)-(4). Tablica
Sieci komputerowe. Wykład 12: Sieci peer-to-peer. Marcin Bieńkowski. Instytut Informatyki Uniwersytet Wrocławski
 Sieci komputerowe Wykład 12: Sieci peer-to-peer Marcin Bieńkowski Instytut Informatyki Uniwersytet Wrocławski Sieci komputerowe (II UWr) Wykład 12 1 / 36 Wprowadzenie Do tej pory mówiliśmy o architekturze
Sieci komputerowe Wykład 12: Sieci peer-to-peer Marcin Bieńkowski Instytut Informatyki Uniwersytet Wrocławski Sieci komputerowe (II UWr) Wykład 12 1 / 36 Wprowadzenie Do tej pory mówiliśmy o architekturze
TESTOWANIE HIPOTEZ STATYSTYCZNYCH Hipotezą statystyczną nazywamy, najogólniej mówiąc, pewną wypowiedź na temat rozkładu interesującej nas cechy.
 TESTOWANIE HIPOTEZ STATYSTYCZNYCH Hipotezą statystyczną nazywamy, najogólniej mówiąc, pewną wypowiedź na temat rozkładu interesującej nas cechy. Hipotezy dzielimy na parametryczne i nieparametryczne. Zajmiemy
TESTOWANIE HIPOTEZ STATYSTYCZNYCH Hipotezą statystyczną nazywamy, najogólniej mówiąc, pewną wypowiedź na temat rozkładu interesującej nas cechy. Hipotezy dzielimy na parametryczne i nieparametryczne. Zajmiemy
Generowanie ciągów bitów losowych z wykorzystaniem sygnałów pochodzących z komputera
 Generowanie ciągów bitów losowych z wykorzystaniem sygnałów pochodzących z komputera Praca dyplomowa magisterska Opiekun: prof. nzw. Zbigniew Kotulski Andrzej Piasecki apiaseck@mion.elka.pw.edu.pl Plan
Generowanie ciągów bitów losowych z wykorzystaniem sygnałów pochodzących z komputera Praca dyplomowa magisterska Opiekun: prof. nzw. Zbigniew Kotulski Andrzej Piasecki apiaseck@mion.elka.pw.edu.pl Plan
Plan wykładu. Wyznaczanie tras. Podsieci liczba urządzeń w klasie C. Funkcje warstwy sieciowej
 Wyznaczanie tras (routing) 1 Wyznaczanie tras (routing) 2 Wyznaczanie tras VLSM Algorytmy rutingu Tablica rutingu CIDR Ruting statyczny Plan wykładu Wyznaczanie tras (routing) 3 Funkcje warstwy sieciowej
Wyznaczanie tras (routing) 1 Wyznaczanie tras (routing) 2 Wyznaczanie tras VLSM Algorytmy rutingu Tablica rutingu CIDR Ruting statyczny Plan wykładu Wyznaczanie tras (routing) 3 Funkcje warstwy sieciowej
Bioinformatyka. Ocena wiarygodności dopasowania sekwencji.
 Bioinformatyka Ocena wiarygodności dopasowania sekwencji www.michalbereta.pl Załóżmy, że mamy dwie sekwencje, które chcemy dopasować i dodatkowo ocenić wiarygodność tego dopasowania. Interesujące nas pytanie
Bioinformatyka Ocena wiarygodności dopasowania sekwencji www.michalbereta.pl Załóżmy, że mamy dwie sekwencje, które chcemy dopasować i dodatkowo ocenić wiarygodność tego dopasowania. Interesujące nas pytanie
Wstęp do sieci neuronowych, wykład 12 Łańcuchy Markowa
 Wstęp do sieci neuronowych, wykład 12 Łańcuchy Markowa M. Czoków, J. Piersa 2012-01-10 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego 3 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego
Wstęp do sieci neuronowych, wykład 12 Łańcuchy Markowa M. Czoków, J. Piersa 2012-01-10 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego 3 1 Łańcucha Markowa 2 Istnienie Szukanie stanu stacjonarnego
DataGuide w półstrukturalnych bazach danych
 DataGuide p. 1/1 DataGuide w półstrukturalnych bazach danych Marcin Jakubek DataGuide p. 2/1 Plan prezentacji Schemat a dane Kilka słów o Lore DataGuide Silny" DataGuide DataGuide a interakcja z użytkownikiem
DataGuide p. 1/1 DataGuide w półstrukturalnych bazach danych Marcin Jakubek DataGuide p. 2/1 Plan prezentacji Schemat a dane Kilka słów o Lore DataGuide Silny" DataGuide DataGuide a interakcja z użytkownikiem
Ćwiczenie 1 Planowanie trasy robota mobilnego w siatce kwadratów pól - Algorytm A
 Ćwiczenie 1 Planowanie trasy robota mobilnego w siatce kwadratów pól - Algorytm A Zadanie do wykonania 1) Utwórz na pulpicie katalog w formacie Imię nazwisko, w którym umieść wszystkie pliki związane z
Ćwiczenie 1 Planowanie trasy robota mobilnego w siatce kwadratów pól - Algorytm A Zadanie do wykonania 1) Utwórz na pulpicie katalog w formacie Imię nazwisko, w którym umieść wszystkie pliki związane z
Grafy Alberta-Barabasiego
 Spis treści 2010-01-18 Spis treści 1 Spis treści 2 Wielkości charakterystyczne 3 Cechy 4 5 6 7 Wielkości charakterystyczne Wielkości charakterystyczne Rozkład stopnie wierzchołków P(deg(x) = k) Graf jest
Spis treści 2010-01-18 Spis treści 1 Spis treści 2 Wielkości charakterystyczne 3 Cechy 4 5 6 7 Wielkości charakterystyczne Wielkości charakterystyczne Rozkład stopnie wierzchołków P(deg(x) = k) Graf jest
Ćwiczenie 1 Automatyczna animacja ruchu
 Automatyczna animacja ruchu Celem ćwiczenia jest poznanie procesu tworzenia automatycznej animacji ruchu, która jest podstawą większości projektów we Flashu. Ze względu na swoją wszechstronność omawiana
Automatyczna animacja ruchu Celem ćwiczenia jest poznanie procesu tworzenia automatycznej animacji ruchu, która jest podstawą większości projektów we Flashu. Ze względu na swoją wszechstronność omawiana
Od czego zacząć przy budowaniu środowisk wysokiej dostępności?
 Budowanie środowisk wysokiej dostępności w oparciu o nową wersję IDS 11 Artur Wroński IBM Information Management Technical Team Leader artur.wronski@pl.ibm.com Od czego zacząć przy budowaniu środowisk
Budowanie środowisk wysokiej dostępności w oparciu o nową wersję IDS 11 Artur Wroński IBM Information Management Technical Team Leader artur.wronski@pl.ibm.com Od czego zacząć przy budowaniu środowisk
Sieć Hopfielda. Sieci rekurencyjne. Ewa Adamus. ZUT Wydział Informatyki Instytut Sztucznej Inteligencji i Metod Matematycznych.
 Sieci rekurencyjne Ewa Adamus ZUT Wydział Informatyki Instytut Sztucznej Inteligencji i Metod Matematycznych 7 maja 2012 Jednowarstwowa sieć Hopfielda, z n neuronami Bipolarna funkcja przejścia W wariancie
Sieci rekurencyjne Ewa Adamus ZUT Wydział Informatyki Instytut Sztucznej Inteligencji i Metod Matematycznych 7 maja 2012 Jednowarstwowa sieć Hopfielda, z n neuronami Bipolarna funkcja przejścia W wariancie
Wstęp do programowania
 Wstęp do programowania Algorytmy zachłanne, programowanie dynamiczne Paweł Daniluk Wydział Fizyki Jesień 2014 P. Daniluk(Wydział Fizyki) WP w. IX Jesień 2014 1 / 26 Algorytmy zachłanne Strategia polegająca
Wstęp do programowania Algorytmy zachłanne, programowanie dynamiczne Paweł Daniluk Wydział Fizyki Jesień 2014 P. Daniluk(Wydział Fizyki) WP w. IX Jesień 2014 1 / 26 Algorytmy zachłanne Strategia polegająca
1. Czym jest Wirtualny Serwer?
 Wirtualny Serwer 1. Czym jest Wirtualny Serwer? 2. Rejestrowanie Wirtualnego Serwera. 3. Praca z Wirtualnym Serwerem. 4. Dlaczego usługa Wirtualny Serwer jest warta uwagi? 1 1. Czym jest Wirtualny Serwer?
Wirtualny Serwer 1. Czym jest Wirtualny Serwer? 2. Rejestrowanie Wirtualnego Serwera. 3. Praca z Wirtualnym Serwerem. 4. Dlaczego usługa Wirtualny Serwer jest warta uwagi? 1 1. Czym jest Wirtualny Serwer?
Charakterystyka sieci klient-serwer i sieci równorzędnej
 Charakterystyka sieci klient-serwer i sieci równorzędnej Sieć klient-serwer Zadaniem serwera w sieci klient-serwer jest: przechowywanie plików i programów systemu operacyjnego; przechowywanie programów
Charakterystyka sieci klient-serwer i sieci równorzędnej Sieć klient-serwer Zadaniem serwera w sieci klient-serwer jest: przechowywanie plików i programów systemu operacyjnego; przechowywanie programów
Modyfikacja algorytmów retransmisji protokołu TCP.
 Modyfikacja algorytmów retransmisji protokołu TCP. Student Adam Markowski Promotor dr hab. Michał Grabowski Cel pracy Celem pracy było przetestowanie i sprawdzenie przydatności modyfikacji klasycznego
Modyfikacja algorytmów retransmisji protokołu TCP. Student Adam Markowski Promotor dr hab. Michał Grabowski Cel pracy Celem pracy było przetestowanie i sprawdzenie przydatności modyfikacji klasycznego
Algorytmy i str ruktury danych. Metody algorytmiczne. Bartman Jacek
 Algorytmy i str ruktury danych Metody algorytmiczne Bartman Jacek jbartman@univ.rzeszow.pl Metody algorytmiczne - wprowadzenia Znamy strukturę algorytmów Trudność tkwi natomiast w podaniu metod służących
Algorytmy i str ruktury danych Metody algorytmiczne Bartman Jacek jbartman@univ.rzeszow.pl Metody algorytmiczne - wprowadzenia Znamy strukturę algorytmów Trudność tkwi natomiast w podaniu metod służących
Znajdowanie wyjścia z labiryntu
 Znajdowanie wyjścia z labiryntu Zadanie to wraz z problemem pakowania najcenniejszego plecaka należy do problemów optymalizacji, które dotyczą znajdowania najlepszego rozwiązania wśród wielu możliwych
Znajdowanie wyjścia z labiryntu Zadanie to wraz z problemem pakowania najcenniejszego plecaka należy do problemów optymalizacji, które dotyczą znajdowania najlepszego rozwiązania wśród wielu możliwych
Równoległy algorytm wyznaczania bloków dla cyklicznego problemu przepływowego z przezbrojeniami
 Równoległy algorytm wyznaczania bloków dla cyklicznego problemu przepływowego z przezbrojeniami dr inż. Mariusz Uchroński Wrocławskie Centrum Sieciowo-Superkomputerowe Agenda Cykliczny problem przepływowy
Równoległy algorytm wyznaczania bloków dla cyklicznego problemu przepływowego z przezbrojeniami dr inż. Mariusz Uchroński Wrocławskie Centrum Sieciowo-Superkomputerowe Agenda Cykliczny problem przepływowy
Płatność tylko za faktycznie zużyte zasoby Zero barier wejścia (opłat minimalnych) Najniższa cena na rynku od 0,06 zł/h za serwer w chmurze i 0,0001
 Kasa z chmury Dlaczego e24cloud? Płatność tylko za faktycznie zużyte zasoby Zero barier wejścia (opłat minimalnych) Najniższa cena na rynku od 0,06 zł/h za serwer w chmurze i 0,0001 PLN/godz z 1 GB plików
Kasa z chmury Dlaczego e24cloud? Płatność tylko za faktycznie zużyte zasoby Zero barier wejścia (opłat minimalnych) Najniższa cena na rynku od 0,06 zł/h za serwer w chmurze i 0,0001 PLN/godz z 1 GB plików
1 Automaty niedeterministyczne
 Szymon Toruńczyk 1 Automaty niedeterministyczne Automat niedeterministyczny A jest wyznaczony przez następujące składniki: Alfabet skończony A Zbiór stanów Q Zbiór stanów początkowych Q I Zbiór stanów
Szymon Toruńczyk 1 Automaty niedeterministyczne Automat niedeterministyczny A jest wyznaczony przez następujące składniki: Alfabet skończony A Zbiór stanów Q Zbiór stanów początkowych Q I Zbiór stanów
Programowanie dynamiczne cz. 2
 Programowanie dynamiczne cz. 2 Wykład 7 16 kwietnia 2019 (Wykład 7) Programowanie dynamiczne cz. 2 16 kwietnia 2019 1 / 19 Outline 1 Mnożenie ciągu macierzy Konstruowanie optymalnego rozwiązania 2 Podstawy
Programowanie dynamiczne cz. 2 Wykład 7 16 kwietnia 2019 (Wykład 7) Programowanie dynamiczne cz. 2 16 kwietnia 2019 1 / 19 Outline 1 Mnożenie ciągu macierzy Konstruowanie optymalnego rozwiązania 2 Podstawy
Analiza Algorytmów 2018/2019 (zadania na laboratorium)
 Analiza Algorytmów 2018/2019 (zadania na laboratorium) Wybór lidera (do 9 III) Zadanie 1 W dowolnym języku programowania zaimplementuj symulator umożliwiający przetestowanie algorytmu wyboru lidera ELECT
Analiza Algorytmów 2018/2019 (zadania na laboratorium) Wybór lidera (do 9 III) Zadanie 1 W dowolnym języku programowania zaimplementuj symulator umożliwiający przetestowanie algorytmu wyboru lidera ELECT
