Defekty punktowe i domieszkowanie kryształów
|
|
|
- Ludwika Rosińska
- 8 lat temu
- Przeglądów:
Transkrypt
1 Defety puntowe i domieszowanie ryształów Keshra Sangwal, Politechnia Lubelsa I. Rodzaje defetów puntowych II. Statystya defetów puntowych III. Dyfuzja w ryształach IV. Metody wytwarzania defetów puntowych V. Defety puntowe podczas wzrostu VI. Domieszowanie ryształów Współczynni podziału domieszi Równowagowy współczynni segregacji Efetywny współczynni segregacji Współzależność pomiędzy eff a szybości wzrostu ściany R Przesycenie progowe dla wychwytywania domieszi podczas wzrostu Literatura 1) D. Hull, Dysloacje (PWN, 1982). 2) M. Suszyńsa, Wybrane zagadnienia z fizyi defetów sieciowych (Ossolineum, 1990). 3) J.C. Brice, The Growth of Crystals from Liquids (North-Holland, 1973). 4) A.A. Chernov (ed.), Modern Crystallography: Crystal Growth (Springer, 1984). 5) K. Sangwal, Additives and Crystallization Processes: From Fundamentals to Applications, Wiley, Chichester, 2007.
2 I. Rodzaje defetów w puntowych Sąd nazwa defetów puntowych? Dosonała sieć rystaliczna rozmieszczenie puntów w 3D W sieci 3D braujące punty lub rozmieszczenie braujących puntów w pozycjach międzywęzłowych
3 Przyłady defetów puntowych Metale Kryształ jonowy 1:1
4 Defety Schotty ego i Frenla Przyład: KCl:CaCl 2 C. Kittel, Wstęp do fizyi ciała stałego (PWN, 1970).
5 II. Statystya defetów w puntowych Naturalne źródła defetów puntowych - Istnienie fonony - Absorpcja fononów E sr energia atywacji sou waansu E st energia tworzenia waansu (= E v )
6 Równowaga termiczna Gęstość waansów Parametry termodynamiczne: Swobodna energia termiczna: F Energia wewnętrzna: E Entropia uładu: S Równanie energii swobodnej: F = E-TS. Zmiana energii swobodnej ryształu: F = E - T S. E = ne v (1 - αt), S = S onf + S ter, gdzie: S onf = ln[(n+n)!/n!n!], S ter = 3z ln(ν/ν ) Dla metali: n S = exp N n + n N exp( E v B ter / B αe exp B Podręczniowe równanie T ). v exp Ev T B.
7 Gęstość innych defetów Gęstość defetów Frenla w metalach: n E exp. 1/ 2 ') 2 = F K NN T ( B Gęstość defetów Schotty ego w ryształach jonowych n N Ep = K exp 2BT.
8 III. Dyfuzja w ryształach ach
9 IV. Metody wytwarzania defetów puntowych 1. Gwałtowne ochładzanie z wysoiej temperatury 2. Silne odształcenie tzn. obróba plastyczna (ucie lub walcowanie) 3. Bombardowanie jonami lub wysooenergetycznymi naładowanymi cząstami 4. Procesy wzrostowe (domieszowanie)
10 V. Defety puntowe podczas wzrostu Szorstie stopnie: - waanse, Mechanizm I: Strutura stopni elementarnych - domieszi. J.J. De Yoreo et al., w: Advances in Crystal Growth, Eds. K. Sato et al., Elsevier, 2001, p
11 Przyłady obrazów segregacji defetów puntowych O czym będzie mowa? Setorowa niejednorodność Strefowa niejednorodność Pasma wzrostu (Growth bands), stryjacje domieszowe (Impurity striations)
12 Przyłady i uwagi Współczynni segregacji zależy od strutury i różnicy rozmiarów atomów, cząstecze, jonów we wspólnej sieci rystalicznej. Brice (1973)
13 VI. Domieszowanie ryształów Podstawowa literatura: K. Sangwal, Addititives and Crystallization Processes: From Fundamentals to Applications, Wiley, Chichester, 2007, chap. 9. Duże deformacje sieci nie sprzyjają włączenia atomów domieszowych w niej. Włączenia domieszi w sieci: 1)Pojedyncze atomy, jony, cząsteczi lub omplesy o rozmiarach cząsteczowych np. dimery, i trymery; homogeniczne wychwytywanie domieszi. Powstaje roztwór stały gdy c isolid = c iliquid (wychwyt domieszi jest termodynamicznie równowagowy) lub c isolid c iliquid (wychwyt nierównowagowy). 2)Inluzje oloidalne o rozmiarach mirometrowych; heterogeniczne wychwytywanie domieszi. Stężenie i rozład homogenicznie i niehomogenicznie wychwytywanej domieszi są różne w objętości ryształu z powodu termicznej nierównowagi na granicy ryształ-ciecz. Niejednorodny wychwyt: 1) w różnych setorach wzrostu ryształu (niejednorodność setorowa), 2) w danym setorze wzrostu (niejednorodność strefowa; growth bands, impurity striations).
14 Współczynni podziału domieszi Gdy domiesza C (i) wchodzi w substancji A (s): współczynni segregacji d = [C solid [Csolid ] ] + [A solid [C ] liquid [C ] + [A liquid ] liquid ]. (1) Stężenie [C] i [A] w ułamach atomowych/jonowych, ułamach wagowych lub wyrażone jao masa do objętości Gdy [C] << [A], = [C d [C solid liquid ] [A ] [A liquid solid ]. ] W przypadu wzrostu ze stopu [C d [C solid liquid ]. ] (2) (3) Gdy stężenie jest w ułamach molowych = d x x is il / x / x ss sl. (4) S solid L - liquid 0 zależy od własności fizyochemicznych ryształu i domieszi. eff to sprawa granicy ryształ-płyn; eff (granica głada) < eff (granica szorsta). Segregacja domiesze 1. Równowagowa (przesycenia σ 0) Równowagowy współczynni segregacji 0 2. Nierównowagowa (σ > 0) Efetywny współczynni segregacji eff
15 Równowagowy współczynni segregacji 1) Podejście mieszaniny dwusładniowej: Dla C w A teoretyczny opis podobny do opisu wyresów fazowych dla uładów dwusładniowych W przypadu C w A: A C H 1 1 m m 1 1 ln. 0 A C H = RG T Tm RG T Tm 2) Podejście termodynamiczne: ln 0 = ln 0(0) G / RGT. gdzie: 0 (0) to wartość 0 gdy r i = r s, a G zmiany różnicy energii swobodnej. Inne podejścia oparte na: różnicy objętości, cieple sublimacji, współczynniu dyfuzji itp. W przypadu niedopasowania objętości ułamowej V/VA w danej temperaturze: ln = B1 + B2 V / VA 0 3 = A B + B( r i / r s ).
16 Gdy zmiana energii swobodnej jest spowodowana niedopasowaniem (r i -r s ) rozmiarów atomów/jonów: gdzie E moduł Younga., ) ( 3 1 ) ( (0) ln ln 3 2 G 0 0 = s i s i s A r r r r r T R EN π
17 Jeszcze ila przyładów
18 Efetywny współczynni segregacji 1) Model dyfuzji objętościowej Burtona et al. (1953): ef f = 0 0, + ( 1 0)exp( Rδ / D) gdzie: δ - grubość warstwy dyfuzyjnej, D współczynni dyfuzji domieszi w roztworze. Dla << 1 0 = exp( Rδ / D) eff 0 (1) (2) Z wyresów δ/d = s/m. Ponieważ D = cm 2 /s, δ = nm.
19 2) Podejście dyfuzyjno-relasacyjne Hall (1953), Kitamura i Sunagawa (1977), Chernov (1984): eff = 0 + ( ads 0)exp( R R i = h /τ / R), (1) gdzie: h grubość warstwy na rosnącej powierzchni, τ - odstęp czasu dla wzrostu olejnych warstw) ads współczynni segregacji w warstwie adsorpcyjnej. i Gdy 0 << 1, eff = ads a gdy R i/ R << 1, eff = ads exp( R ads i ( R / R), i / R). (2) (3)
20 3) Podejście selecji statystycznej Voronov, Chernov (1967): 0 eff =, + σ / σ 1 const (1) gdzie: σ const constant. Gdy σ / σ << const 1, eff = 0 0 σ / σ const (2) Naturalna selecja statystyczna zależy od inetyi przyłączenia i odłączenia cząste domieszi na załomach
21 4) Podejście adsorpcji powierzchniowej Założenia: 1) Cząsteczi domieszi onurują z cząsteczami substancji rystalizującej. 2) Zwięszenie σ powoduje zwięszenie gęstości załomów w stopniach. 3) eff = 0 +f(gęstość załomów) eff = 0 + B 2 1 n σ 2 / c gdzie: B 2, m stałe, n 2 miara bariery związanej z wpływami przesycenia σ. m i, AO - jednowodny szczawian amonu.
22 Współzależność pomiędzy eff a szybości wzrostu ściany R Z zależności otrzymujemy, / σ eff m n c B i + =, ) ( n c A R σ σ. σ / 1 1/ n m n m R c A B c B i i c eff + + =
23 Przesycenie progowe dla wychwytywania domieszi podczas wzrostu Z wyresów eff (σ), otrzymujemy σ 0 : eff = p( σ σ ). 0 AO Z teorii hamowania wzrostu ściany przez domieszę, mamy zależność: 1 σ * 1 1 = 1 + σ1 Kc, gdzie: σ 1 stała, K stała Langmuira. i
Defekty punktowe i domieszkowanie kryształów
 Defety puntowe i domieszowanie ryształów Keshra Sangwal Załad Fizyi Stosowanej, Instytut Fizyi Politechnia Lubelsa I. Rodzaje defetów puntowych II. Statystya defetów puntowych III. Dyfuzja w ryształach
Defety puntowe i domieszowanie ryształów Keshra Sangwal Załad Fizyi Stosowanej, Instytut Fizyi Politechnia Lubelsa I. Rodzaje defetów puntowych II. Statystya defetów puntowych III. Dyfuzja w ryształach
Defekty punktowe i domieszkowanie kryształów
 Defety puntowe i domieszowanie ryształów Keshra Sangwal, Politechnia Lubelsa I. Wprowadzenie do defetów II. Rodzaje defetów puntowych III. Statystya defetów puntowych IV. Dyfuzja w ryształach V. Metody
Defety puntowe i domieszowanie ryształów Keshra Sangwal, Politechnia Lubelsa I. Wprowadzenie do defetów II. Rodzaje defetów puntowych III. Statystya defetów puntowych IV. Dyfuzja w ryształach V. Metody
Dyslokacje w kryształach. ach. Keshra Sangwal Zakład Fizyki Stosowanej, Instytut Fizyki Politechnika Lubelska
 Dyslokacje w kryształach ach Keshra Sangwal Zakład Fizyki Stosowanej, Instytut Fizyki Politechnika Lubelska I. Wprowadzenie do defektów II. Dyslokacje: Podstawowe pojęcie III. Własności mechaniczne kryształów
Dyslokacje w kryształach ach Keshra Sangwal Zakład Fizyki Stosowanej, Instytut Fizyki Politechnika Lubelska I. Wprowadzenie do defektów II. Dyslokacje: Podstawowe pojęcie III. Własności mechaniczne kryształów
Dyslokacje w kryształach. ach. Keshra Sangwal, Politechnika Lubelska. Literatura
 Dyslokacje w kryształach ach Keshra Sangwal, Politechnika Lubelska I. Wprowadzenie do defektów II. Dyslokacje: podstawowe pojęcie III. Własności mechaniczne kryształów IV. Źródła i rozmnażanie się dyslokacji
Dyslokacje w kryształach ach Keshra Sangwal, Politechnika Lubelska I. Wprowadzenie do defektów II. Dyslokacje: podstawowe pojęcie III. Własności mechaniczne kryształów IV. Źródła i rozmnażanie się dyslokacji
Materiały Reaktorowe. Efekty fizyczne uszkodzeń radiacyjnych c.d.
 Materiały Reaktorowe Efekty fizyczne uszkodzeń radiacyjnych c.d. Luki (pory) i pęcherze Powstawanie i formowanie luk zostało zaobserwowane w 1967 r. Podczas formowania luk w materiale następuje jego puchnięcie
Materiały Reaktorowe Efekty fizyczne uszkodzeń radiacyjnych c.d. Luki (pory) i pęcherze Powstawanie i formowanie luk zostało zaobserwowane w 1967 r. Podczas formowania luk w materiale następuje jego puchnięcie
relacje ilościowe ( masowe,objętościowe i molowe ) dotyczące połączeń 1. pierwiastków w związkach chemicznych 2. związków chemicznych w reakcjach
 1 STECHIOMETRIA INTERPRETACJA ILOŚCIOWA ZJAWISK CHEMICZNYCH relacje ilościowe ( masowe,objętościowe i molowe ) dotyczące połączeń 1. pierwiastków w związkach chemicznych 2. związków chemicznych w reakcjach
1 STECHIOMETRIA INTERPRETACJA ILOŚCIOWA ZJAWISK CHEMICZNYCH relacje ilościowe ( masowe,objętościowe i molowe ) dotyczące połączeń 1. pierwiastków w związkach chemicznych 2. związków chemicznych w reakcjach
Kinetyka reakcji chemicznych
 Kinetya reacji chemicznych Metody doświadczalne Reacje powolne (> s) do analizy Reacje szybie ( -3 s) detetor v x x t tx/v Reacje b. szybie ( -4-4 s) (fotochemiczne) wzbudzenie analiza Szybość reacji aa
Kinetya reacji chemicznych Metody doświadczalne Reacje powolne (> s) do analizy Reacje szybie ( -3 s) detetor v x x t tx/v Reacje b. szybie ( -4-4 s) (fotochemiczne) wzbudzenie analiza Szybość reacji aa
Do wniosku o przeprowadzenie postępowania habilitacyjnego
 Dr Akademia im. Jana Długosza w Częstochowie Do wniosku o przeprowadzenie postępowania habilitacyjnego Załącznik 2a Częstochowa, 09.04.2015 Spis treści 1. Imię i nazwisko 2. Wykształcenie, stopnie naukowe
Dr Akademia im. Jana Długosza w Częstochowie Do wniosku o przeprowadzenie postępowania habilitacyjnego Załącznik 2a Częstochowa, 09.04.2015 Spis treści 1. Imię i nazwisko 2. Wykształcenie, stopnie naukowe
Seria 2, ćwiczenia do wykładu Od eksperymentu do poznania materii
 Seria 2, ćwiczenia do wykładu Od eksperymentu do poznania materii 8.1.21 Zad. 1. Obliczyć ciśnienie potrzebne do przemiany grafitu w diament w temperaturze 25 o C. Objętość właściwa (odwrotność gęstości)
Seria 2, ćwiczenia do wykładu Od eksperymentu do poznania materii 8.1.21 Zad. 1. Obliczyć ciśnienie potrzebne do przemiany grafitu w diament w temperaturze 25 o C. Objętość właściwa (odwrotność gęstości)
Wykład 5. Anna Ptaszek. 9 października Katedra Inżynierii i Aparatury Przemysłu Spożywczego. Chemia fizyczna - wykład 5. Anna Ptaszek 1 / 20
 Wykład 5 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 9 października 2015 1 / 20 Zjawiska powierzchniowe Adsorpcja na powierzchni ciała stałego (adsorbentu): adsorpcja fizyczna: substancja adsorbująca
Wykład 5 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 9 października 2015 1 / 20 Zjawiska powierzchniowe Adsorpcja na powierzchni ciała stałego (adsorbentu): adsorpcja fizyczna: substancja adsorbująca
Podstawy termodynamiki
 Podstawy termodynamiki Organizm żywy z punktu widzenia termodynamiki Parametry stanu Funkcje stanu: U, H, F, G, S I zasada termodynamiki i prawo Hessa II zasada termodynamiki Kierunek przemian w warunkach
Podstawy termodynamiki Organizm żywy z punktu widzenia termodynamiki Parametry stanu Funkcje stanu: U, H, F, G, S I zasada termodynamiki i prawo Hessa II zasada termodynamiki Kierunek przemian w warunkach
WZROST KRYSZTAŁÓW Z ROZTWORU - - WYBRANE METODY
 WZROST KRYSZTAŁÓW Z ROZTWORU - - WYBRANE METODY Tomasz Słupiński Uniwersytet Warszawski, Wydział Fizyki, Zakład Fizyki Ciała Stałego (Pracownia Fizyki Wzrostu Kryształów) tomslu@fuw.edu.pl Wykład w ICM
WZROST KRYSZTAŁÓW Z ROZTWORU - - WYBRANE METODY Tomasz Słupiński Uniwersytet Warszawski, Wydział Fizyki, Zakład Fizyki Ciała Stałego (Pracownia Fizyki Wzrostu Kryształów) tomslu@fuw.edu.pl Wykład w ICM
Wykład 5. Anna Ptaszek. 30 października Katedra Inżynierii i Aparatury Przemysłu Spożywczego. Fizykochemiczne podstawy procesów przemysłu
 Wykład 5 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 30 października 2018 1 / 22 Zjawiska powierzchniowe Adsorpcja na powierzchni ciała stałego (adsorbentu): adsorpcja fizyczna: substancja adsorbująca
Wykład 5 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 30 października 2018 1 / 22 Zjawiska powierzchniowe Adsorpcja na powierzchni ciała stałego (adsorbentu): adsorpcja fizyczna: substancja adsorbująca
WŁASNOŚCI CIAŁ STAŁYCH I CIECZY
 WŁASNOŚCI CIAŁ STAŁYCH I CIECZY Polimery Sieć krystaliczna Napięcie powierzchniowe Dyfuzja 2 BUDOWA CIAŁ STAŁYCH Ciała krystaliczne (kryształy): monokryształy, polikryształy Ciała amorficzne (bezpostaciowe)
WŁASNOŚCI CIAŁ STAŁYCH I CIECZY Polimery Sieć krystaliczna Napięcie powierzchniowe Dyfuzja 2 BUDOWA CIAŁ STAŁYCH Ciała krystaliczne (kryształy): monokryształy, polikryształy Ciała amorficzne (bezpostaciowe)
Temat 27. Termodynamiczne modele blokowe wzrostu kryształów
 Temat 27. Termodynamiczne modele blokowe wzrostu kryształów W modelach blokowych wzrostu kryształów wszystkie zjawiska zachodzące na powierzchni kryształu zostały sprowadzone do przyłączania i odłączania
Temat 27. Termodynamiczne modele blokowe wzrostu kryształów W modelach blokowych wzrostu kryształów wszystkie zjawiska zachodzące na powierzchni kryształu zostały sprowadzone do przyłączania i odłączania
Krystalizacja. Zarodkowanie
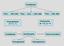 Krystalizacja Ciecz ciało stałe Para ciecz ciało stałe Para ciało stałe Przechłodzenie T = T L - T c Przesycenie p = p g - p z > 0 Krystalizacja Zarodkowanie Rozrost zarodków Homogeniczne Heterogeniczne
Krystalizacja Ciecz ciało stałe Para ciecz ciało stałe Para ciało stałe Przechłodzenie T = T L - T c Przesycenie p = p g - p z > 0 Krystalizacja Zarodkowanie Rozrost zarodków Homogeniczne Heterogeniczne
Technologie wytwarzania metali. Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki próżniowe
 Technologie wytwarzania metali Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki próżniowe KRYSTALIZACJA METALI I STOPÓW Krzepnięcie - przemiana fazy
Technologie wytwarzania metali Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki próżniowe KRYSTALIZACJA METALI I STOPÓW Krzepnięcie - przemiana fazy
Technologie wytwarzania metali. Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki próżniowe
 Technologie wytwarzania metali Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki próżniowe KRYSTALIZACJA METALI I STOPÓW Krzepnięcie - przemiana fazy
Technologie wytwarzania metali Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki próżniowe KRYSTALIZACJA METALI I STOPÓW Krzepnięcie - przemiana fazy
Analiza parametrów rozszczepienia zero-polowego oraz pola krystalicznego dla jonów Mn 2+ i Cr 3+ domieszkowanych w krysztale YAl 3 (BO 3 ) 4
 Analiza parametrów rozszczepienia zero-polowego oraz pola rystalicznego dla jonów Mn 2+ i Cr 3+ domieszowanych w rysztale YAl 3 (BO 3 ) 4 Paweł Gnute & Muhammed Açıgöz Czesław Rudowicz Strutura ryształu
Analiza parametrów rozszczepienia zero-polowego oraz pola rystalicznego dla jonów Mn 2+ i Cr 3+ domieszowanych w rysztale YAl 3 (BO 3 ) 4 Paweł Gnute & Muhammed Açıgöz Czesław Rudowicz Strutura ryształu
Kinetyka reakcji chemicznych Kataliza i reakcje enzymatyczne Kinetyka reakcji enzymatycznych Równanie Michaelis-Menten
 Kinetya reacji chemicznych 4.3.1. Kataliza i reacje enzymatyczne 4.3.2. Kinetya reacji enzymatycznych 4.3.3. Równanie Michaelis-Menten Ilościowy opis mechanizm działania atalizatorów Kinetya chemiczna
Kinetya reacji chemicznych 4.3.1. Kataliza i reacje enzymatyczne 4.3.2. Kinetya reacji enzymatycznych 4.3.3. Równanie Michaelis-Menten Ilościowy opis mechanizm działania atalizatorów Kinetya chemiczna
Chemia - laboratorium
 Chemia - laboratorium Wydział Geologii, Geofizyki i Ochrony Środowiska Studia stacjonarne, Rok I, Semestr zimowy 01/1 Dr hab. inż. Tomasz Brylewski e-mail: brylew@agh.edu.pl tel. 1-617-59 Katedra Fizykochemii
Chemia - laboratorium Wydział Geologii, Geofizyki i Ochrony Środowiska Studia stacjonarne, Rok I, Semestr zimowy 01/1 Dr hab. inż. Tomasz Brylewski e-mail: brylew@agh.edu.pl tel. 1-617-59 Katedra Fizykochemii
S. Baran - Podstawy fizyki materii skondensowanej Gaz Fermiego elektronów swobodnych. Gaz Fermiego elektronów swobodnych
 Gaz Fermiego elektronów swobodnych charakter idea Teoria metali Paula Drudego Teoria metali Arnolda (1900 r.) Sommerfelda (1927 r.) klasyczna kwantowa elektrony przewodnictwa elektrony przewodnictwa w
Gaz Fermiego elektronów swobodnych charakter idea Teoria metali Paula Drudego Teoria metali Arnolda (1900 r.) Sommerfelda (1927 r.) klasyczna kwantowa elektrony przewodnictwa elektrony przewodnictwa w
INŻYNIERIA MATERIAŁOWA w elektronice
 Wydział Elektroniki Mikrosystemów i Fotoniki Politechniki Wrocławskiej... INŻYNIERIA MATERIAŁOWA w elektronice... Dr hab. inż. JAN FELBA Profesor nadzwyczajny PWr 1 PROGRAM WYKŁADU Struktura materiałów
Wydział Elektroniki Mikrosystemów i Fotoniki Politechniki Wrocławskiej... INŻYNIERIA MATERIAŁOWA w elektronice... Dr hab. inż. JAN FELBA Profesor nadzwyczajny PWr 1 PROGRAM WYKŁADU Struktura materiałów
Termodynamika i właściwości fizyczne stopów - zastosowanie w przemyśle
 Termodynamika i właściwości fizyczne stopów - zastosowanie w przemyśle Marcela Trybuła Władysław Gąsior Alain Pasturel Noel Jakse Plan: 1. Materiał badawczy 2. Eksperyment Metodologia 3. Teoria Metodologia
Termodynamika i właściwości fizyczne stopów - zastosowanie w przemyśle Marcela Trybuła Władysław Gąsior Alain Pasturel Noel Jakse Plan: 1. Materiał badawczy 2. Eksperyment Metodologia 3. Teoria Metodologia
Kinetyka chemiczna kataliza i reakcje enzymatyczne
 inetya chemiczna ataliza i reacje enzymatyczne Wyład z Chemii Fizycznej str. 3.3 / 1 Ilościowy opis mechanizm działania atalizatorów Wyład z Chemii Fizycznej str. 3.3 / 2 Ilościowy opis mechanizm działania
inetya chemiczna ataliza i reacje enzymatyczne Wyład z Chemii Fizycznej str. 3.3 / 1 Ilościowy opis mechanizm działania atalizatorów Wyład z Chemii Fizycznej str. 3.3 / 2 Ilościowy opis mechanizm działania
4.15 Badanie dyfrakcji światła laserowego na krysztale koloidalnym(o19)
 256 Fale 4.15 Badanie dyfracji światła laserowego na rysztale oloidalnym(o19) Celem ćwiczenia jest wyznaczenie stałej sieci dwuwymiarowego ryształu oloidalnego metodą dyfracji światła laserowego. Zagadnienia
256 Fale 4.15 Badanie dyfracji światła laserowego na rysztale oloidalnym(o19) Celem ćwiczenia jest wyznaczenie stałej sieci dwuwymiarowego ryształu oloidalnego metodą dyfracji światła laserowego. Zagadnienia
Układ termodynamiczny
 Uład terodynaiczny Uład terodynaiczny to ciało lub zbiór rozważanych ciał, w tóry obo wszelich innych zjawis (echanicznych, eletrycznych, agnetycznych itd.) uwzględniay zjawisa cieplne. Stan uładu charateryzuje
Uład terodynaiczny Uład terodynaiczny to ciało lub zbiór rozważanych ciał, w tóry obo wszelich innych zjawis (echanicznych, eletrycznych, agnetycznych itd.) uwzględniay zjawisa cieplne. Stan uładu charateryzuje
Repeta z wykładu nr 5. Detekcja światła. Plan na dzisiaj. Złącze p-n. złącze p-n
 Repeta z wykładu nr 5 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 5 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Termodynamiczne warunki krystalizacji
 KRYSTALIZACJA METALI ISTOPÓW Zakres tematyczny y 1 Termodynamiczne warunki krystalizacji hiq.linde-gas.fr Krystalizacja szczególny rodzaj krzepnięcia, w którym ciecz ulega przemianie w stan stały o budowie
KRYSTALIZACJA METALI ISTOPÓW Zakres tematyczny y 1 Termodynamiczne warunki krystalizacji hiq.linde-gas.fr Krystalizacja szczególny rodzaj krzepnięcia, w którym ciecz ulega przemianie w stan stały o budowie
Ćwiczenie VI KATALIZA HOMOGENICZNA: ESTRYFIKACJA KWASÓW ORGANICZNYCH ALKOHOLAMI
 Zjawisa powierzchniowe i ataliza Ćwiczenie VI ATALIZA HMGNIZNA: STYFIAJA WASÓW GANIZNYH ALHLAMI WPWADZNI stry wasów organicznych stanowią jedną z ważniejszych grup produtów przemysłu chemicznego, ta pod
Zjawisa powierzchniowe i ataliza Ćwiczenie VI ATALIZA HMGNIZNA: STYFIAJA WASÓW GANIZNYH ALHLAMI WPWADZNI stry wasów organicznych stanowią jedną z ważniejszych grup produtów przemysłu chemicznego, ta pod
Rozszczepienie poziomów atomowych
 Rozszczepienie poziomów atomowych Poziomy energetyczne w pojedynczym atomie Gdy zbliżamy atomy chmury elektronowe nachodzą na siebie (inaczej: funkcje falowe elektronów zaczynają się przekrywać) Na skutek
Rozszczepienie poziomów atomowych Poziomy energetyczne w pojedynczym atomie Gdy zbliżamy atomy chmury elektronowe nachodzą na siebie (inaczej: funkcje falowe elektronów zaczynają się przekrywać) Na skutek
Transport jonów: kryształy jonowe
 Transport jonów: kryształy jonowe JONIKA I FOTONIKA MICHAŁ MARZANTOWICZ Jodek srebra AgI W 42 K strukturalne przejście fazowe I rodzaju do fazy α stopiona podsieć kationowa. Fluorek ołowiu PbF 2 zdefektowanie
Transport jonów: kryształy jonowe JONIKA I FOTONIKA MICHAŁ MARZANTOWICZ Jodek srebra AgI W 42 K strukturalne przejście fazowe I rodzaju do fazy α stopiona podsieć kationowa. Fluorek ołowiu PbF 2 zdefektowanie
Wykład 1 i 2. Termodynamika klasyczna, gaz doskonały
 Wykład 1 i 2 Termodynamika klasyczna, gaz doskonały dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy fizyki
Wykład 1 i 2 Termodynamika klasyczna, gaz doskonały dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy fizyki
(Ćwiczenie nr 4) Wpływ siły jonowej roztworu na stałą szybkości reakcji.
 (Ćwiczenie nr 4) Wpływ siły jonowej roztworu na stałą szybości reacji Wstęp Rozpatrzmy reację zachodzącą w roztworze pomiędzy jonami i w wyniu tórej powstaje produt D: D stała szybości reacji () Gdy reacja
(Ćwiczenie nr 4) Wpływ siły jonowej roztworu na stałą szybości reacji Wstęp Rozpatrzmy reację zachodzącą w roztworze pomiędzy jonami i w wyniu tórej powstaje produt D: D stała szybości reacji () Gdy reacja
WYKAZ NAJWAŻNIEJSZYCH SYMBOLI
 SPIS TREŚCI WYKAZ NAJWAŻNIEJSZYCH SYMBOLI...7 PRZEDMOWA...8 1. WSTĘP...9 2. MATEMATYCZNE OPRACOWANIE WYNIKÓW POMIARÓW...10 3. LEPKOŚĆ CIECZY...15 3.1. Pomiar lepkości...16 3.2. Lepkość względna...18 3.3.
SPIS TREŚCI WYKAZ NAJWAŻNIEJSZYCH SYMBOLI...7 PRZEDMOWA...8 1. WSTĘP...9 2. MATEMATYCZNE OPRACOWANIE WYNIKÓW POMIARÓW...10 3. LEPKOŚĆ CIECZY...15 3.1. Pomiar lepkości...16 3.2. Lepkość względna...18 3.3.
Zadania treningowe na kolokwium
 Zadania treningowe na kolokwium 3.12.2010 1. Stan układu binarnego zawierającego n 1 moli substancji typu 1 i n 2 moli substancji typu 2 parametryzujemy za pomocą stężenia substancji 1: x n 1. Stabilność
Zadania treningowe na kolokwium 3.12.2010 1. Stan układu binarnego zawierającego n 1 moli substancji typu 1 i n 2 moli substancji typu 2 parametryzujemy za pomocą stężenia substancji 1: x n 1. Stabilność
Fizyka, technologia oraz modelowanie wzrostu kryształów
 Fizyka, technologia oraz modelowanie wzrostu kryształów Stanisław Krukowski i Michał Leszczyński Instytut Wysokich Ciśnień PAN 0-4 Warszawa, ul Sokołowska 9/37 tel: 88 80 44 e-mail: stach@unipress.waw.pl,
Fizyka, technologia oraz modelowanie wzrostu kryształów Stanisław Krukowski i Michał Leszczyński Instytut Wysokich Ciśnień PAN 0-4 Warszawa, ul Sokołowska 9/37 tel: 88 80 44 e-mail: stach@unipress.waw.pl,
Wykład 21: Studnie i bariery cz.1.
 Wyład : Studnie i bariery cz.. Dr inż. Zbigniew Szlarsi Katedra Eletronii, paw. C-, po.3 szla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szlarsi/ 3.6.8 Wydział Informatyi, Eletronii i Równanie Schrödingera
Wyład : Studnie i bariery cz.. Dr inż. Zbigniew Szlarsi Katedra Eletronii, paw. C-, po.3 szla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szlarsi/ 3.6.8 Wydział Informatyi, Eletronii i Równanie Schrödingera
Model elektronów swobodnych w metalu
 Model elektronów swobodnych w metalu Stany elektronu w nieskończonej trójwymiarowej studni potencjału - dozwolone wartości wektora falowego k Fale stojące - warunki brzegowe znikanie funkcji falowej na
Model elektronów swobodnych w metalu Stany elektronu w nieskończonej trójwymiarowej studni potencjału - dozwolone wartości wektora falowego k Fale stojące - warunki brzegowe znikanie funkcji falowej na
Inżynieria materiałowa: wykorzystywanie praw termodynamiki a czasem... walka z termodynamiką
 Inżynieria materiałowa: wykorzystywanie praw termodynamiki a czasem... walka z termodynamiką Kilka definicji Faza Definicja Gibbsa = stan materii jednorodny wewnętrznie, nie tylko pod względem składu chemicznego,
Inżynieria materiałowa: wykorzystywanie praw termodynamiki a czasem... walka z termodynamiką Kilka definicji Faza Definicja Gibbsa = stan materii jednorodny wewnętrznie, nie tylko pod względem składu chemicznego,
TEORIA PASMOWA CIAŁ STAŁYCH
 TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
Inżynieria materiałowa: wykorzystywanie praw termodynamiki a czasem... walka z termodynamiką
 Inżynieria materiałowa: wykorzystywanie praw termodynamiki a czasem... walka z termodynamiką Kilka definicji Faza Stan materii jednorodny wewnętrznie, nie tylko pod względem składu chemicznego, ale również
Inżynieria materiałowa: wykorzystywanie praw termodynamiki a czasem... walka z termodynamiką Kilka definicji Faza Stan materii jednorodny wewnętrznie, nie tylko pod względem składu chemicznego, ale również
Powierzchnie cienkie warstwy nanostruktury. Józef Korecki, C1, II p., pok. 207
 Powierzchnie cienkie warstwy nanostruktury Józef Korecki, C1, II p., pok. 207 korecki@uci.agh.edu.pl http://korek.uci.agh.edu.pl/priv/jk.htm Obiekty niskowymiarowe Powierzchnia Cienkie warstwy Wielowarstwy
Powierzchnie cienkie warstwy nanostruktury Józef Korecki, C1, II p., pok. 207 korecki@uci.agh.edu.pl http://korek.uci.agh.edu.pl/priv/jk.htm Obiekty niskowymiarowe Powierzchnia Cienkie warstwy Wielowarstwy
Nauka o Materiałach Wykład II Monokryształy Jerzy Lis
 Wykład II Monokryształy Jerzy Lis Treść wykładu: 1. Wstęp stan krystaliczny 2. Budowa kryształów - krystalografia 3. Budowa kryształów rzeczywistych defekty WPROWADZENIE Stan krystaliczny jest podstawową
Wykład II Monokryształy Jerzy Lis Treść wykładu: 1. Wstęp stan krystaliczny 2. Budowa kryształów - krystalografia 3. Budowa kryształów rzeczywistych defekty WPROWADZENIE Stan krystaliczny jest podstawową
Podstawy fizyki ciała stałego półprzewodniki domieszkowane
 Podstawy fizyki ciała stałego półprzewodniki domieszkowane Półprzewodnik typu n IV-Ge V-As Jeżeli pięciowartościowy atom V-As zastąpi w sieci atom IV-Ge to cztery elektrony biorą udział w wiązaniu kowalentnym,
Podstawy fizyki ciała stałego półprzewodniki domieszkowane Półprzewodnik typu n IV-Ge V-As Jeżeli pięciowartościowy atom V-As zastąpi w sieci atom IV-Ge to cztery elektrony biorą udział w wiązaniu kowalentnym,
7. Defekty samoistne Typy defektów Zdefektowanie samoistne w związkach stechiometrycznych
 7. Defekty samoistne 7.1. Typy defektów Zgodnie z trzecią zasadą termodynamiki, tylko w temperaturze 0[K] kryształ może mieć zerową entropię. Oznacza to, że jeśli temperatura jest wyższa niż 0[K] to w
7. Defekty samoistne 7.1. Typy defektów Zgodnie z trzecią zasadą termodynamiki, tylko w temperaturze 0[K] kryształ może mieć zerową entropię. Oznacza to, że jeśli temperatura jest wyższa niż 0[K] to w
1. Struktura pasmowa from bonds to bands
 . Strutura pasmowa from bonds to bands Wiązania owalencyjne w cząsteczach Pasma energetyczne w ciałach stałych Przerwa energetyczna w półprzewodniach Dziura w paśmie walencyjnym Przybliżenie prawie swobodnego
. Strutura pasmowa from bonds to bands Wiązania owalencyjne w cząsteczach Pasma energetyczne w ciałach stałych Przerwa energetyczna w półprzewodniach Dziura w paśmie walencyjnym Przybliżenie prawie swobodnego
Chemia Fizyczna Technologia Chemiczna II rok Wykład 1. Kierownik przedmiotu: Dr hab. inż. Wojciech Chrzanowski
 Chemia Fizyczna Technologia Chemiczna II rok Wykład 1 Kierownik przedmiotu: Dr hab. inż. Wojciech Chrzanowski Kontakt,informacja i konsultacje Chemia A ; pokój 307 Telefon: 347-2769 E-mail: wojtek@chem.pg.gda.pl
Chemia Fizyczna Technologia Chemiczna II rok Wykład 1 Kierownik przedmiotu: Dr hab. inż. Wojciech Chrzanowski Kontakt,informacja i konsultacje Chemia A ; pokój 307 Telefon: 347-2769 E-mail: wojtek@chem.pg.gda.pl
Przerwa energetyczna w germanie
 Ćwiczenie 1 Przerwa energetyczna w germanie Cel ćwiczenia Wyznaczenie szerokości przerwy energetycznej przez pomiar zależności oporu monokryształu germanu od temperatury. Wprowadzenie Eksperymentalne badania
Ćwiczenie 1 Przerwa energetyczna w germanie Cel ćwiczenia Wyznaczenie szerokości przerwy energetycznej przez pomiar zależności oporu monokryształu germanu od temperatury. Wprowadzenie Eksperymentalne badania
Termodynamika materiałów
 Termodynamika materiałów Plan wykładu 1. Funkcje termodynamiczne, pojemność cieplna. 2. Warunki równowagi termodynamicznej w układach jedno- i wieloskładnikowych, pojęcie potencjału chemicznego. 3. Modele
Termodynamika materiałów Plan wykładu 1. Funkcje termodynamiczne, pojemność cieplna. 2. Warunki równowagi termodynamicznej w układach jedno- i wieloskładnikowych, pojęcie potencjału chemicznego. 3. Modele
ROZTWORY, WZROST KRYSZTAŁÓW Z ROZTWORU - - WYBRANE METODY
 ROZTWORY, WZROST KRYSZTAŁÓW Z ROZTWORU - - WYBRANE METODY Tomasz Słupiński Uniwersytet Warszawski, Wydział Fizyki, Zakład Fizyki Ciała Stałego (Pracownia Fizyki Wzrostu Kryształów) tomslu@fuw.edu.pl Wykład
ROZTWORY, WZROST KRYSZTAŁÓW Z ROZTWORU - - WYBRANE METODY Tomasz Słupiński Uniwersytet Warszawski, Wydział Fizyki, Zakład Fizyki Ciała Stałego (Pracownia Fizyki Wzrostu Kryształów) tomslu@fuw.edu.pl Wykład
1. Kryształy jonowe omówić oddziaływania w kryształach jonowych oraz typy struktur jonowych.
 Tematy opisowe 1. Kryształy jonowe omówić oddziaływania w kryształach jonowych oraz typy struktur jonowych. 2. Dlaczego do kadłubów statków, doków, falochronów i filarów mostów przymocowuje się płyty z
Tematy opisowe 1. Kryształy jonowe omówić oddziaływania w kryształach jonowych oraz typy struktur jonowych. 2. Dlaczego do kadłubów statków, doków, falochronów i filarów mostów przymocowuje się płyty z
Elektrolity wykazują przewodnictwo jonowe Elektrolity ciekłe substancje rozpadające się w roztworze na jony
 Elektrolity wykazują przewodnictwo jonowe Elektrolity ciekłe substancje rozpadające się w roztworze na jony Przewodniki jonowe elektrolity stałe duża przewodność jonowa w stanie stałym; mały wkład elektronów
Elektrolity wykazują przewodnictwo jonowe Elektrolity ciekłe substancje rozpadające się w roztworze na jony Przewodniki jonowe elektrolity stałe duża przewodność jonowa w stanie stałym; mały wkład elektronów
Stany równowagi i zjawiska transportu w układach termodynamicznych
 Stany równowagi i zjawiska transportu w układach termodynamicznych dr hab. Jerzy Nakielski Katedra Biofizyki i Biologii Komórki plan wykładu: 1. Funkcje stanu dla termodynamicznego układu otwartego 2.
Stany równowagi i zjawiska transportu w układach termodynamicznych dr hab. Jerzy Nakielski Katedra Biofizyki i Biologii Komórki plan wykładu: 1. Funkcje stanu dla termodynamicznego układu otwartego 2.
Wykład IV. Półprzewodniki samoistne i domieszkowe
 Wykład IV Półprzewodniki samoistne i domieszkowe Półprzewodniki (Si, Ge, GaAs) Konfiguracja elektronowa Si : 1s 2 2s 2 2p 6 3s 2 3p 2 = [Ne] 3s 2 3p 2 4 elektrony walencyjne Półprzewodnik samoistny Talent
Wykład IV Półprzewodniki samoistne i domieszkowe Półprzewodniki (Si, Ge, GaAs) Konfiguracja elektronowa Si : 1s 2 2s 2 2p 6 3s 2 3p 2 = [Ne] 3s 2 3p 2 4 elektrony walencyjne Półprzewodnik samoistny Talent
Wykład 10 Równowaga chemiczna
 Wykład 10 Równowaga chemiczna REAKCJA CHEMICZNA JEST W RÓWNOWADZE, GDY NIE STWIERDZAMY TENDENCJI DO ZMIAN ILOŚCI (STĘŻEŃ) SUBSTRATÓW ANI PRODUKTÓW RÓWNOWAGA CHEMICZNA JEST RÓWNOWAGĄ DYNAMICZNĄ W rzeczywistości
Wykład 10 Równowaga chemiczna REAKCJA CHEMICZNA JEST W RÓWNOWADZE, GDY NIE STWIERDZAMY TENDENCJI DO ZMIAN ILOŚCI (STĘŻEŃ) SUBSTRATÓW ANI PRODUKTÓW RÓWNOWAGA CHEMICZNA JEST RÓWNOWAGĄ DYNAMICZNĄ W rzeczywistości
POLITECHNIKA GDAŃSKA WYDZIAŁ FIZYKI TECHNICZNEJ I MATEMATYKI STOSOWANEJ EKSCYTONY. Seminarium z Molekularnego Ciała a Stałego Jędrzejowski Jaromir
 POLITECHNIKA GDAŃSKA WYDZIAŁ FIZYKI TECHNICZNEJ I MATEMATYKI STOSOWANEJ EKSCYTONY W CIAŁACH ACH STAŁYCH Seminarium z Molekularnego Ciała a Stałego Jędrzejowski Jaromir Co to sąs ekscytony? ekscyton to
POLITECHNIKA GDAŃSKA WYDZIAŁ FIZYKI TECHNICZNEJ I MATEMATYKI STOSOWANEJ EKSCYTONY W CIAŁACH ACH STAŁYCH Seminarium z Molekularnego Ciała a Stałego Jędrzejowski Jaromir Co to sąs ekscytony? ekscyton to
Podstawowe pojęcia Masa atomowa (cząsteczkowa) - to stosunek masy atomu danego pierwiastka chemicznego (cząsteczki związku chemicznego) do masy 1/12
 Podstawowe pojęcia Masa atomowa (cząsteczkowa) - to stosunek masy atomu danego pierwiastka chemicznego (cząsteczki związku chemicznego) do masy 1/12 atomu węgla 12 C. Mol - jest taką ilością danej substancji,
Podstawowe pojęcia Masa atomowa (cząsteczkowa) - to stosunek masy atomu danego pierwiastka chemicznego (cząsteczki związku chemicznego) do masy 1/12 atomu węgla 12 C. Mol - jest taką ilością danej substancji,
MATERIAŁOZNAWSTWO Wydział Mechaniczny, Mechatronika, sem. I. dr inż. Hanna Smoleńska
 MATERIAŁOZNAWSTWO Wydział Mechaniczny, Mechatronika, sem. I dr inż. Hanna Smoleńska UKŁADY RÓWNOWAGI FAZOWEJ Równowaga termodynamiczna pojęcie stosowane w termodynamice. Oznacza stan, w którym makroskopowe
MATERIAŁOZNAWSTWO Wydział Mechaniczny, Mechatronika, sem. I dr inż. Hanna Smoleńska UKŁADY RÓWNOWAGI FAZOWEJ Równowaga termodynamiczna pojęcie stosowane w termodynamice. Oznacza stan, w którym makroskopowe
Wzrost fazy krystalicznej
 Wzrost fazy krystalicznej Wydzielenie nowej fazy może różnić się of fazy pierwotnej : składem chemicznym strukturą krystaliczną orientacją krystalograficzną... faza pierwotna nowa faza Analogia elektryczna
Wzrost fazy krystalicznej Wydzielenie nowej fazy może różnić się of fazy pierwotnej : składem chemicznym strukturą krystaliczną orientacją krystalograficzną... faza pierwotna nowa faza Analogia elektryczna
Ć W I C Z E N I E 5. Kinetyka cementacji metali
 Ć W I C Z E N I E Kinetyka cementacji metali WPROWADZENIE Proces cementacji jest jednym ze sposobów wydzielania metali z roztworów wodnych. Polega on na wytrącaniu jonów metalu bardziej szlachetnego przez
Ć W I C Z E N I E Kinetyka cementacji metali WPROWADZENIE Proces cementacji jest jednym ze sposobów wydzielania metali z roztworów wodnych. Polega on na wytrącaniu jonów metalu bardziej szlachetnego przez
Projekt Inżynier mechanik zawód z przyszłością współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
 Zajęcia wyrównawcze z fizyki -Zestaw 4 -eoria ermodynamika Równanie stanu gazu doskonałego Izoprzemiany gazowe Energia wewnętrzna gazu doskonałego Praca i ciepło w przemianach gazowych Silniki cieplne
Zajęcia wyrównawcze z fizyki -Zestaw 4 -eoria ermodynamika Równanie stanu gazu doskonałego Izoprzemiany gazowe Energia wewnętrzna gazu doskonałego Praca i ciepło w przemianach gazowych Silniki cieplne
Chemia Fizyczna Technologia Chemiczna II rok Wykład 1. Kontakt,informacja i konsultacje. Co to jest chemia fizyczna?
 Chemia Fizyczna Technologia Chemiczna II ro Wyład 1 Kierowni rzedmiotu: Dr hab. inż. Wojciech Chrzanowsi Kontat,informacja i onsultacje Chemia A ; oój 307 Telefon: 347-2769 E-mail: wojte@chem.g.gda.l tablica
Chemia Fizyczna Technologia Chemiczna II ro Wyład 1 Kierowni rzedmiotu: Dr hab. inż. Wojciech Chrzanowsi Kontat,informacja i onsultacje Chemia A ; oój 307 Telefon: 347-2769 E-mail: wojte@chem.g.gda.l tablica
PODSTAWY CHEMII INŻYNIERIA BIOMEDYCZNA. Wykład 2
 PODSTAWY CEMII INŻYNIERIA BIOMEDYCZNA Wykład Plan wykładu II,III Woda jako rozpuszczalnik Zjawisko dysocjacji Równowaga w roztworach elektrolitów i co z tego wynika Bufory ydroliza soli Roztwory (wodne)-
PODSTAWY CEMII INŻYNIERIA BIOMEDYCZNA Wykład Plan wykładu II,III Woda jako rozpuszczalnik Zjawisko dysocjacji Równowaga w roztworach elektrolitów i co z tego wynika Bufory ydroliza soli Roztwory (wodne)-
Inżynieria Biomedyczna
 1.Obliczyć przy jakim stężeniu kwasu octowego stopień dysocjacji osiągnie wartość 3.%, jeżeli wiadomo, że stopień dysocjacji 15.%-wego roztworu (d=1.2 g/cm 3 ) w 2. Do 1 cm 3 2% (d=1.2 g/cm 3 ) roztworu
1.Obliczyć przy jakim stężeniu kwasu octowego stopień dysocjacji osiągnie wartość 3.%, jeżeli wiadomo, że stopień dysocjacji 15.%-wego roztworu (d=1.2 g/cm 3 ) w 2. Do 1 cm 3 2% (d=1.2 g/cm 3 ) roztworu
Obliczenia chemiczne. Zakład Chemii Medycznej Pomorski Uniwersytet Medyczny
 Obliczenia chemiczne Zakład Chemii Medycznej Pomorski Uniwersytet Medyczny 1 STĘŻENIA ROZTWORÓW Stężenia procentowe Procent masowo-masowy (wagowo-wagowy) (% m/m) (% w/w) liczba gramów substancji rozpuszczonej
Obliczenia chemiczne Zakład Chemii Medycznej Pomorski Uniwersytet Medyczny 1 STĘŻENIA ROZTWORÓW Stężenia procentowe Procent masowo-masowy (wagowo-wagowy) (% m/m) (% w/w) liczba gramów substancji rozpuszczonej
Zjawiska powierzchniowe
 Zjawiska powierzchniowe Adsorpcja Model Langmuira Model BET 1 Zjawiska powierzchniowe Adsorpcja Proces gromadzenia się substancji z wnętrza fazy na granicy międzyfazowej; Wynika z tego, że w obszarze powierzchniowym
Zjawiska powierzchniowe Adsorpcja Model Langmuira Model BET 1 Zjawiska powierzchniowe Adsorpcja Proces gromadzenia się substancji z wnętrza fazy na granicy międzyfazowej; Wynika z tego, że w obszarze powierzchniowym
Roztwory. Homogeniczne jednorodne (jedno-fazowe) mieszaniny dwóch lub więcej składników.
 Roztwory Homogeniczne jednorodne (jedno-fazowe) mieszaniny dwóch lub więcej składników. Własności fizyczne roztworów są związane z równowagę pomiędzy siłami wiążącymi cząsteczki wody i substancji rozpuszczonej.
Roztwory Homogeniczne jednorodne (jedno-fazowe) mieszaniny dwóch lub więcej składników. Własności fizyczne roztworów są związane z równowagę pomiędzy siłami wiążącymi cząsteczki wody i substancji rozpuszczonej.
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach
 Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
A B Skąd wiadomo, że reakcja zachodzi? Co jest miarą szybkości reakcji?
 Kinetya chemiczna 3.1.1. Pojęcie szybości reacji chemicznej 3.1.. Ilościowe miary szybości 3.1.3. Reacje pierwszego rzędu 3.1.4. Reacje zerowego rzędu 3.1.5. Przyłady SZYBKOŚĆ REAKCJI HOMOGENICZNEJ A B
Kinetya chemiczna 3.1.1. Pojęcie szybości reacji chemicznej 3.1.. Ilościowe miary szybości 3.1.3. Reacje pierwszego rzędu 3.1.4. Reacje zerowego rzędu 3.1.5. Przyłady SZYBKOŚĆ REAKCJI HOMOGENICZNEJ A B
Równowaga. równowaga metastabilna (niepełna) równowaga niestabilna (nietrwała) równowaga stabilna (pełna) brak równowagi rozpraszanie energii
 Równowaga równowaga stabilna (pełna) równowaga metastabilna (niepełna) równowaga niestabilna (nietrwała) brak równowagi rozpraszanie energii energia swobodna Co jest warunkiem równowagi? temperatura W
Równowaga równowaga stabilna (pełna) równowaga metastabilna (niepełna) równowaga niestabilna (nietrwała) brak równowagi rozpraszanie energii energia swobodna Co jest warunkiem równowagi? temperatura W
E dec. Obwód zastępczy. Napięcie rozkładowe
 Obwód zastępczy Obwód zastępczy schematyczny obwód elektryczny, ilustrujący zachowanie się badanego obiektu w polu elektrycznym. Elementy obwodu zastępczego (oporniki, kondensatory, indukcyjności,...)
Obwód zastępczy Obwód zastępczy schematyczny obwód elektryczny, ilustrujący zachowanie się badanego obiektu w polu elektrycznym. Elementy obwodu zastępczego (oporniki, kondensatory, indukcyjności,...)
b) Podaj liczbę moli chloru cząsteczkowego, która całkowicie przereaguje z jednym molem glinu.
 Informacja do zadań 1 i 2 Chlorek glinu otrzymuje się w reakcji glinu z chlorowodorem lub działając chlorem na glin. Związek ten tworzy kryształy, rozpuszczalne w wodzie zakwaszonej kwasem solnym. Z roztworów
Informacja do zadań 1 i 2 Chlorek glinu otrzymuje się w reakcji glinu z chlorowodorem lub działając chlorem na glin. Związek ten tworzy kryształy, rozpuszczalne w wodzie zakwaszonej kwasem solnym. Z roztworów
Materiały Reaktorowe
 Materiały Reaktorowe Dr inż. Paweł Stoch Wydział Inżynierii Materiałowej i Ceramiki Katedra Ceramiki i Materiałów Ogniotrwałych kcimo.pl B6 p.205 12-617-25-04 pstoch@agh.edu.pl Wykład 30 h + laboratorium
Materiały Reaktorowe Dr inż. Paweł Stoch Wydział Inżynierii Materiałowej i Ceramiki Katedra Ceramiki i Materiałów Ogniotrwałych kcimo.pl B6 p.205 12-617-25-04 pstoch@agh.edu.pl Wykład 30 h + laboratorium
Wykład 13. Anna Ptaszek. 4 stycznia Katedra Inżynierii i Aparatury Przemysłu Spożywczego. Fizykochemia biopolimerów - wykład 13.
 Wykład 13 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 4 stycznia 2018 1 / 29 Układy wielofazowe FAZA rozpraszająca rozpraszana gaz ciecz ciało stałe gaz - piana piana stała ciecz mgła/aerozol
Wykład 13 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 4 stycznia 2018 1 / 29 Układy wielofazowe FAZA rozpraszająca rozpraszana gaz ciecz ciało stałe gaz - piana piana stała ciecz mgła/aerozol
Fizyka Ciała Stałego
 Wykład III Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć krystaliczną. Amorficzne, brak uporządkowania,
Wykład III Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć krystaliczną. Amorficzne, brak uporządkowania,
Wykład III. Teoria pasmowa ciał stałych
 Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
KINETYKA REAKCJI CHEMICZNYCH I KATALIZA
 ĆWICZENIE NR KINETYKA REAKCJI CHEMICZNYCH I KATALIZA Cel ćwiczenia Badanie wpływu temperatury i atalizatora na szybość reacji. Zares wymaganych wiadomość. Szybość reacji chemicznych definicja, jednosti..
ĆWICZENIE NR KINETYKA REAKCJI CHEMICZNYCH I KATALIZA Cel ćwiczenia Badanie wpływu temperatury i atalizatora na szybość reacji. Zares wymaganych wiadomość. Szybość reacji chemicznych definicja, jednosti..
Ćwiczenie IX KATALITYCZNY ROZKŁAD WODY UTLENIONEJ
 Wprowadzenie Ćwiczenie IX KATALITYCZNY ROZKŁAD WODY UTLENIONEJ opracowanie: Barbara Stypuła Celem ćwiczenia jest poznanie roli katalizatora w procesach chemicznych oraz prostego sposobu wyznaczenia wpływu
Wprowadzenie Ćwiczenie IX KATALITYCZNY ROZKŁAD WODY UTLENIONEJ opracowanie: Barbara Stypuła Celem ćwiczenia jest poznanie roli katalizatora w procesach chemicznych oraz prostego sposobu wyznaczenia wpływu
5. WYZNACZENIE KRZYWEJ VAN DEEMTER a I WSPÓŁCZYNNIKA ROZDZIELENIA DLA KOLUMNY CHROMATOGRAFICZNEJ
 5. WYZNACZENIE KRZYWEJ VAN DEEMTER a I WSPÓŁCZYNNIKA ROZDZIELENIA DLA KOLUMNY CHROMATOGRAFICZNEJ Opracował: Krzysztof Kaczmarski I. WPROWADZENIE Sprawność kolumn chromatograficznych określa się liczbą
5. WYZNACZENIE KRZYWEJ VAN DEEMTER a I WSPÓŁCZYNNIKA ROZDZIELENIA DLA KOLUMNY CHROMATOGRAFICZNEJ Opracował: Krzysztof Kaczmarski I. WPROWADZENIE Sprawność kolumn chromatograficznych określa się liczbą
Model wiązania kowalencyjnego cząsteczka H 2
 Model wiązania kowalencyjnego cząsteczka H 2 + Współrzędne elektronu i protonów Orbitale wiążący i antywiążący otrzymane jako kombinacje orbitali atomowych Orbital wiążący duża gęstość ładunku między jądrami
Model wiązania kowalencyjnego cząsteczka H 2 + Współrzędne elektronu i protonów Orbitale wiążący i antywiążący otrzymane jako kombinacje orbitali atomowych Orbital wiążący duża gęstość ładunku między jądrami
STRUKTURA PASM ENERGETYCZNYCH
 PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
Wykład 7: Przekazywanie energii elementy termodynamiki
 Wykład 7: Przekazywanie energii elementy termodynamiki dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ emperatura Fenomenologicznie wielkość informująca o tym jak ciepłe/zimne
Wykład 7: Przekazywanie energii elementy termodynamiki dr inż. Zbigniew Szklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ emperatura Fenomenologicznie wielkość informująca o tym jak ciepłe/zimne
Energia wiązania słaba rzędu 10-2 ev J. Energia cieplna 3/2 k B. T J. Energia ruchu cieplnego powoduje rozerwanie wiązań cząsteczkowych.
 Ciała stałe - o struturze rystalicznej wyazują daleo zasięgowe uporządowanie atoowe, są to onoryształy i poliryształy. - o struturze bezpostaciowej (aorficznej), wyazują bra uporządowania atoowego daleiego
Ciała stałe - o struturze rystalicznej wyazują daleo zasięgowe uporządowanie atoowe, są to onoryształy i poliryształy. - o struturze bezpostaciowej (aorficznej), wyazują bra uporządowania atoowego daleiego
Praca objętościowa - pv (wymiana energii na sposób pracy) Ciepło reakcji Q (wymiana energii na sposób ciepła) Energia wewnętrzna
 Energia - zdolność danego układu do wykonania dowolnej pracy. Potencjalna praca, którą układ może w przyszłości wykonać. Praca wykonana przez układ jak i przeniesienie energii może manifestować się na
Energia - zdolność danego układu do wykonania dowolnej pracy. Potencjalna praca, którą układ może w przyszłości wykonać. Praca wykonana przez układ jak i przeniesienie energii może manifestować się na
Efekty strukturalne przemian fazowych
 Efekty strukturalne przemian fazowych Literatura 1. Zbigniew Kędzierski PRZEMIANY FAZOWE W UKŁADACH SKONDESOWANYCH, AGH Uczelniane Wydawnictwa Naukowo Dydaktyczne, 003. Marek Blicharski INŻYNIERIA MATERIAŁOWA
Efekty strukturalne przemian fazowych Literatura 1. Zbigniew Kędzierski PRZEMIANY FAZOWE W UKŁADACH SKONDESOWANYCH, AGH Uczelniane Wydawnictwa Naukowo Dydaktyczne, 003. Marek Blicharski INŻYNIERIA MATERIAŁOWA
WŁAŚCIWOŚCI MECHANICZNE PLASTYCZNOŚĆ. Zmiany makroskopowe. Zmiany makroskopowe
 WŁAŚCIWOŚCI MECHANICZNE PLASTYCZNOŚĆ Zmiany makroskopowe Zmiany makroskopowe R e = R 0.2 - umowna granica plastyczności (0.2% odkształcenia trwałego); R m - wytrzymałość na rozciąganie (plastyczne); 1
WŁAŚCIWOŚCI MECHANICZNE PLASTYCZNOŚĆ Zmiany makroskopowe Zmiany makroskopowe R e = R 0.2 - umowna granica plastyczności (0.2% odkształcenia trwałego); R m - wytrzymałość na rozciąganie (plastyczne); 1
+ + Struktura cia³a sta³ego. Kryszta³y jonowe. Kryszta³y atomowe. struktura krystaliczna. struktura amorficzna
 Struktura cia³a sta³ego struktura krystaliczna struktura amorficzna odleg³oœci miêdzy atomami maj¹ tê sam¹ wartoœæ; dany atom ma wszêdzie takie samo otoczenie najbli szych s¹siadów odleg³oœci miêdzy atomami
Struktura cia³a sta³ego struktura krystaliczna struktura amorficzna odleg³oœci miêdzy atomami maj¹ tê sam¹ wartoœæ; dany atom ma wszêdzie takie samo otoczenie najbli szych s¹siadów odleg³oœci miêdzy atomami
Podstawy Procesów i Konstrukcji Inżynierskich. Teoria kinetyczna INZYNIERIAMATERIALOWAPL. Kierunek Wyróżniony przez PKA
 Podstawy Procesów i Konstrukcji Inżynierskich Teoria kinetyczna Kierunek Wyróżniony rzez PKA 1 Termodynamika klasyczna Pierwsza zasada termodynamiki to rosta zasada zachowania energii, czyli ogólna reguła
Podstawy Procesów i Konstrukcji Inżynierskich Teoria kinetyczna Kierunek Wyróżniony rzez PKA 1 Termodynamika klasyczna Pierwsza zasada termodynamiki to rosta zasada zachowania energii, czyli ogólna reguła
S. Baran - Podstawy fizyki materii skondensowanej Fonony. Fonony
 Fonony Drgania płaszczyzn sieciowych podłużne poprzeczne źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 4, rys. 2, 3, str. 118 Drgania płaszczyzn sieciowych Do opisu drgań sieci krystalicznej wystarczą
Fonony Drgania płaszczyzn sieciowych podłużne poprzeczne źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 4, rys. 2, 3, str. 118 Drgania płaszczyzn sieciowych Do opisu drgań sieci krystalicznej wystarczą
Metody Optyczne w Technice. Wykład 9 Optyka nieliniowa
 Metody Optyczne w Technice Wyład 9 Optya nieliniowa Fala eletromagnetyczna J t D H t B B D rot rot div div J M H H B D Nieliniowa odpowiedź ośroda olaryzacja ośroda to moment dipolowy na jednostę objętości
Metody Optyczne w Technice Wyład 9 Optya nieliniowa Fala eletromagnetyczna J t D H t B B D rot rot div div J M H H B D Nieliniowa odpowiedź ośroda olaryzacja ośroda to moment dipolowy na jednostę objętości
Ciała stałe. Literatura: Halliday, Resnick, Walker, t. 5, rozdz. 42 Orear, t. 2, rozdz. 28 Young, Friedman, rozdz
 Ciała stałe Podstawowe własności ciał stałych Struktura ciał stałych Przewodnictwo elektryczne teoria Drudego Poziomy energetyczne w krysztale: struktura pasmowa Metale: poziom Fermiego, potencjał kontaktowy
Ciała stałe Podstawowe własności ciał stałych Struktura ciał stałych Przewodnictwo elektryczne teoria Drudego Poziomy energetyczne w krysztale: struktura pasmowa Metale: poziom Fermiego, potencjał kontaktowy
ĆWICZENIE Nr 4 LABORATORIUM FIZYKI KRYSZTAŁÓW STAŁYCH. Badanie krawędzi absorpcji podstawowej w kryształach półprzewodników POLITECHNIKA ŁÓDZKA
 POLITECHNIKA ŁÓDZKA INSTYTUT FIZYKI LABORATORIUM FIZYKI KRYSZTAŁÓW STAŁYCH ĆWICZENIE Nr 4 Badanie krawędzi absorpcji podstawowej w kryształach półprzewodników I. Cześć doświadczalna. 1. Uruchomić Spekol
POLITECHNIKA ŁÓDZKA INSTYTUT FIZYKI LABORATORIUM FIZYKI KRYSZTAŁÓW STAŁYCH ĆWICZENIE Nr 4 Badanie krawędzi absorpcji podstawowej w kryształach półprzewodników I. Cześć doświadczalna. 1. Uruchomić Spekol
Przyrządy półprzewodnikowe
 Przyrządy półprzewodnikowe Prof. Zbigniew Lisik Katedra Przyrządów Półprzewodnikowych i Optoelektronicznych pokój: 116 e-mail: zbigniew.lisik@p.lodz.pl wykład 30 godz. laboratorium 30 godz WEEIiA E&T Metal
Przyrządy półprzewodnikowe Prof. Zbigniew Lisik Katedra Przyrządów Półprzewodnikowych i Optoelektronicznych pokój: 116 e-mail: zbigniew.lisik@p.lodz.pl wykład 30 godz. laboratorium 30 godz WEEIiA E&T Metal
Wykład 8 i 9. Hipoteza ergodyczna, rozkład mikrokanoniczny, wzór Boltzmanna
 Wykład 8 i 9 Hipoteza ergodyczna, rozkład mikrokanoniczny, wzór Boltzmanna dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW)
Wykład 8 i 9 Hipoteza ergodyczna, rozkład mikrokanoniczny, wzór Boltzmanna dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW)
Problemy elektrochemii w inżynierii materiałowej
 Problemy elektrochemii w inżynierii materiałowej Pamięci naszych Rodziców Autorzy NR 102 Antoni Budniok, Eugeniusz Łągiewka Problemy elektrochemii w inżynierii materiałowej Wydawnictwo Uniwersytetu Śląskiego
Problemy elektrochemii w inżynierii materiałowej Pamięci naszych Rodziców Autorzy NR 102 Antoni Budniok, Eugeniusz Łągiewka Problemy elektrochemii w inżynierii materiałowej Wydawnictwo Uniwersytetu Śląskiego
Wykład 4. Przypomnienie z poprzedniego wykładu
 Wykład 4 Przejścia fazowe materii Diagram fazowy Ciepło Procesy termodynamiczne Proces kwazistatyczny Procesy odwracalne i nieodwracalne Pokazy doświadczalne W. Dominik Wydział Fizyki UW Termodynamika
Wykład 4 Przejścia fazowe materii Diagram fazowy Ciepło Procesy termodynamiczne Proces kwazistatyczny Procesy odwracalne i nieodwracalne Pokazy doświadczalne W. Dominik Wydział Fizyki UW Termodynamika
= = Budowa materii. Stany skupienia materii. Ilość materii (substancji) n - ilość moli, N liczba molekuł (atomów, cząstek), N A
 Budowa materii Stany skupienia materii Ciało stałe Ciecz Ciała lotne (gazy i pary) Ilość materii (substancji) n N = = N A m M N A = 6,023 10 mol 23 1 n - ilość moli, N liczba molekuł (atomów, cząstek),
Budowa materii Stany skupienia materii Ciało stałe Ciecz Ciała lotne (gazy i pary) Ilość materii (substancji) n N = = N A m M N A = 6,023 10 mol 23 1 n - ilość moli, N liczba molekuł (atomów, cząstek),
Wykład 3 Zjawiska transportu Dyfuzja w gazie, przewodnictwo cieplne, lepkość gazu, przewodnictwo elektryczne
 Wykład 3 Zjawiska transportu Dyfuzja w gazie, przewodnictwo cieplne, lepkość gazu, przewodnictwo elektryczne W3. Zjawiska transportu Zjawiska transportu zachodzą gdy układ dąży do stanu równowagi. W zjawiskach
Wykład 3 Zjawiska transportu Dyfuzja w gazie, przewodnictwo cieplne, lepkość gazu, przewodnictwo elektryczne W3. Zjawiska transportu Zjawiska transportu zachodzą gdy układ dąży do stanu równowagi. W zjawiskach
