ROCZNIKI INŻYNIERII BUDOWLANEJ

Transkrypt

1 POLSKA AKADEMIA NAUK ODDZIAŁ W KATOWICACH KOMISJA INŻYNIERII BUDOWLANEJ ISSN ROCZNIKI INŻYNIERII BUDOWLANEJ ZESZYT Wydawntwo współfnansowane ze środów Europejsego Funduszu Rozwoju Regonalnego w ramah Programu Operayjnego Współpray Transgranznej Republa Czesa Rzezpospolta Polsa 7-3 Projet nr rej.: CZ.3./.3./8.635 Współpraa transgranzna szół wyższyh w zarese ohrony nad zabytam ultury wyorzystana opuszzonyh obetów przemysłowyh KATOWICE OPOLE

2 ROCZNIKI INŻYNIERII BUDOWLANEJ zawerają orygnalne prae teoretyzne dośwadzalne z zaresu nżyner budowlanej powstałe w wynu współpray regonalnej praownów nau wydzałów budowntwa uzeln polsh zesh prowadzonej przez Komsję Inżyner Budowlanej Oddzału Polsej Aadem Nau w Katowah. SIEDZIBA KOMISJI INŻYNIERII BUDOWLANEJ O/PAN W KATOWICACH Poltehna Śląsa Wydzał Budowntwa 44- Glwe ul. Aadema 5 KOMITET REDAKCYJNY Przewodnząy Józef GŁOMB (Glwe) Członowe Ján BUJŇÁK (Žlna) Robert ČERNÝ (Praha) Stefana GRZESZCZYK (Opole) Jan KUBIK (Opole) Alos MATERNA (Ostrava) Jř ŠEJNOHA (Praha) Adam ZYBURA (Glwe) Reenzen Prof. S. Grzeszzy Prof. J. Gołaś Prof. R. Janowa Prof. P. Klemm Prof. T. Łagoda Prof. H. Nowa Prof. P. Obraaj Prof. J. Sładzeń Prof. A. Zybura Prof. J. Żmuda Prof. J. Mal Adres Redaj Poltehna Opolsa Wydzał Budowntwa Katedra Fzy Materałów 45-6 Opole ul. Katowa 48 po. nr 8

3 3 Sps treś Jan KUBIK Problemy utrzymana zabytów tehn Problems of preservaton of tehnal monuments..... Paweł FEDCZUK Zastosowane próbnego obążena w projee posadowena reonstruowanego obetu przemysłowego Applaton of load test n the foundaton desgn of reonstruted ndustry buldng. Potr GORECKI Jerzy WYRWAŁ Relaja wzajemnoś w zagadnenu pozątowo-brzegowej lnowej termopezoeletryznoś Reproty relaton n boundary ntal value problem of lnear thermopezoeletrty. Elżbeta JANOWSKA-RENKAS Wpływ mąz grantowej jao wypełnaza w emene na właśwoś betonu. The nfluene of grante powder fller on onrete propertes.... Potr GORECKI Jerzy WYRWAŁ Proes nszzena murów eglanyh w zabytowyh budynah obetah przemysłowyh Degradaton proess of old br walls n monumental and ndustral buldng. Jan KUBIK Dzałana śwatła lasera na powerzhnę ała stałego..... Laser lght mpat on a surfae of sold body Andrzej KUCHARCZYK Wyorzystane metod analzy yfrowej obrazu do oreślana powerzhnowego zasolena Use of dgtal mage analyss methods to determnng surfae salnty... Jan KUBIK Funjonał Lagrange a gradentowej termomehan..... Lagrange funtonal n gradent thermomehans..... Edward MAŁEK Oblzane przerojów żelbetowyh elementów prętowyh z uwzględnenem nelnowoś fzyznej geometryznej Calulaton of renfored onrete setons of rod members tang nto onsderaton physal and geometral nonlnearty Petr MARTINEC Lue AUGUSTINKOÁ Jří ŠČUČKA Martna PEŘINKOÁ Malty na fragmenteh gotého zdva ze Staříče Mortars n fragments of goth masonry from Staříč

4 4 Andrzej MARYNOWICZ Wpływ gradentu temperatury na współzynn przewodzena epła... Temperature gradent nfuene on nsulatng materals thermal ondutvty.. Aradusz MORDAK Zbgnew MAŃKO Analyss of post-tensoned onrete road brdge grders strengthened by frp strps usng FEM under stat load Analza MES bele mostu sprężonego wzmononyh taśmam frp pod obążenem statyznym Potr OPAŁKA Adaptaja hstoryznego obetu poprzemysłowego do nowej funj... Adaptaton of hstoral post-ndustral buldng nto the new funton... Kaml PAWLIK Proes pełzana drewna zaataowanego przez mroorganzmy.... The reep proess of wood attaed by mroorgansms..... Zbgnew PERKOWSKI Metoda wyznazana dyfuzyjnoś eplnej na podstawe pomarów termowzyjnyh. Podstwy teoretyzne A method of determnng of thermal dffusvty based on thermograph measurements. Theoretal baground Jadwga ŚWIRSKA-PERKOWSKA Model matematyzno-fzyzny rury eplnej ze struturą aplarną... Mathematal-physal model of heat ppe wth apllary struture... Martn ARO Jana BOHÁČOÁ Davd BUJDOŠ Jaroslav NOÁČEK álava TOMKOÁ Jozef LČEK Flp OČAČÍK Prmární ohrana povrhu betonu pomoí alaly atvovanýh materálů.. Prmary proteton of onrete surfae usng alal atvated materals... Barbara OJODÍKOÁ Plohy brownfelds verzus loalty staré eologé zátěže a jejh evdene.. Brownfeld and ontamnated stes and ther databases..... Jan KUBIK Joahm RZEPKA Oena uszodzeń onstruj Estmaton of strutures damage

5 ROCZNIKI INŻYNIERII BUDOWLANEJ ZESZYT / Komsja Inżyner Budowlanej Oddzał Polsej Aadem Nau w Katowah PROBLEMY UTRZYMANIA ZABYTKÓW TECHNIKI Jan KUBIK Poltehna Opolsa Opole. Wprowadzene Wraz z odejśem od zasad ustroju sojalstyznego w Polse tóry faworyzował przemysł wydobywzy ęż została w spuśźne poaźna lość opuszzonyh obetów przemysłowyh. W przypadu Opolszzyzny były to główne ementowne pee wapennze oraz przemysł le. W welu przypadah obety te były esploatowane ponad lat a w przypadu wapennów ementown prawe 5 lat. Nezynne załady są wę śwadetwem mnonej przemysłowej epo naszego raju jao tae pownny podlegać ohrone onserwatorsej. Było jedna nazej o wynało ze stosunu społezeństwa regonu do zastanej nfrastrutury materalnej a w tym pozostałoś po przemyśle. Było to przeeż to samo społezeństwo tóre długo ne dentyfowało sę z zastanym zabytam arhtetury śląsej. Trudno wę od nego wymagać szaunu do pozostałoś epo postndustralnej na Śląsu. Tymzasem bogate społezeństwa zahodne najperw dojrzały do łożena na zabyt arhtetury sztu a następne poolena dopero dostrzegały zabyt tehn gotowe były je onserwować utrzymywać. Jeżel te prawdłowoś postrzegane we Franj Nemzeh zy w rajah Sandynaw sę sprawdzają to na aeptaję ratowana zabytów tehn jest u nas za wześne. Istotne na Opolszzyźne znnęły ementowne a la z nh zawerało elementy tehn tehnolog godne zahowana. Zostały jedna rozebrane trudno uwerzyć ż w Opolu praowały przed 3 laty 4 ementowne a dzsaj pozostała tylo ementowna Odra. Ih odejśe jao pozostałoś nnego społezeństwa jest naturalne ale nezahowane orygnalnyh rozwązań XIX-weznej tehn już ne. Nasze społezeństwo zostało zubożone przez bra typowej dla ntelgenj reflesj na temat relaj przeszłoś z teraźnejszośą. Ten bra wystąpł szzególne w przypadu tehn. Co eawsze rozwązana tehnzne tworzone w XIX-weznyh ementownah wapennah mały dużą wartość poznawzą bezpowrotne straoną. Króto mówą za pozostałośam ery poprzemysłowej jao zabytam tehn ne stał prawe nt może tylo urzędowo onserwator zabytów oraz nezauważony zmargnalzowany społezny ruh ohrony zabytów. Natomast dla admnstratorów oraz samorządu stotny był wyrównany teren po zabytah pod przyszłe nwestyje. Obene zmany naszyh postaw wymusza główne Una Europejsa dotują różne przedsęwzęa zwązane z zahowanem naszego rajobrazu ulturowego. To o jest obowązem państwa zahowane tożsamoś ulturowej tehnznej rob podobno

6 6 antynarodowa Una Europejsa. To parados typowy dla rajów postomunstyznyh w tóryh najzęśej na perwszy plan wysuwa sę postulat obrony tożsamoś narodu zagrożonej przez Bruselę ale za hasłam ne podążają zyny. Podobna sytuaja dotyzy zresztą ałej ultury zy nau.. Konserwaja zabytów Rozważana rozpoznemy od przypomnena typowyh etapów pra onserwatorsh dotyząyh zabytów w ogólnoś. Następne spreyzujemy odmennoś tyh pozynań wynająyh ze speyf zabytów tehn zawerająyh unatowe rozwązana tehnzne tehnologzne. Perwszym etapem pra onserwatorsh jest przygotowane doumentaj dotyząej zastanego stanu zabytu. Następnym elementem jest wyonane doumentaj fotografznej obetu oraz szów stanowąyh podstawę przeprowadzena lasyznej nwentaryzaj arhtetonznej. Inwentaryzaja ta stanow zaps stanu materalnego zabytu bez rozróżnana wnana w zasową olejność narastana strutury zabytu. Zwyzajowo ten etap obejmuje rzuty przeroje elewaje oraz detale zabytu. W przypadu zabytów tehn należy równolegle znwentaryzować wyposażene tehnologzne zabytu. Przedstawony tutaj wstępny etap opraowana doumentaj zabytu jest w stoe neo rozszerzoną nwentaryzają arhtetonzną tóra ne zawera jeszze elementów onserwatorsh. 3. Inwentaryzaja onstruyjna Po otrzymanu nwentaryzaj arhtetonznej tehnologznej zabytu przystępujemy do nwentaryzaj onstruyjnej. Wyonujemy tu pomary elementów onstruyjnyh zabytu wraz z nwentaryzają fotografzną h stanu. Na nwentaryzaję arhtetonzną nanosmy wymary ustroju nośnego zabytu. Ze szzególną starannośą pownny być analzowane elementy onstruyjne w najbardzej wytężonyh mejsah oraz mejsa przeazu sł na olejne elementy onstruj. Osobną uwagę pośwęamy zarysowanom wraz z pomarem rozwara rys łązne z wyjaśnenem przyzyn h powstawana. Dotyzy to szzególne slepeń łuów śan flarów. Generalne szzególne doładne analzuje sę tu elementy onstruj tóre deydują o jej stablnoś. Osobną grupę zagadneń stanową problemy posadoweń zabytu odształeń podłoża zman pozomu wód gruntowyh tp. Zwyzajowo do tego opraowana dołązamy nwentaryzaję sutów zawlgoeń wywtów solnyh pudrowana sę wystroju tp. Przeprowadzona nwentaryzaja zaońzona jest spreyzowanem zman onstruyjnyh prowadząyh do zapewnena stablnoś deformaj zabytu. Podane stwerdzena pownny poprzedzć wnos onserwatorse poneważ podają stotne ogranzena na dalsze dzałana onserwatorse. Należy zwróć uwagę na odmenność metod postępowana przy statyznej nwentaryzaj arhtetonznej od nwentaryzaj onstruyjnej tóra zwyle ońzy sę prognozą nety narastana znszzeń oraz sposobam h powstrzymywana. Istotne rozwój fzy budowl pozwala na oraz bardzej obetywną oenę postępu znszzeń elementów materalnyh zabytu deydująyh o jego trwałoś.

7 7 4. Inwentaryzaja onserwatorsa Badana onserwatorse rozpozynamy od ustalena źródeł hstoryznyh zabytu tóre znajdują sę najzęśej w arhwah bbloteah doumentajah onserwatora admnstratora obetu. Dużą wartość posadają stare zdjęa ryny tp. Badana Inwentaryzaja arhtetonzna ) Doumentaja fotografzna Inwentaryzaja tehnologzna ) Urządzena tehn (fotografa) Inwentaryzaja lasyzna ) Pomary zabytu w naturze 3) Doumentaja detal ) Pomary detal tehnolog 4) Inwentaryzaja arhtetonzna zabytu Inwentaryzaja onstruj 5)Pomary elementów onstruj 6) Pomary zarysowań 7) Sanaja elementów onstruj Źródła uszodzeń 8) Badane źródeł hstoryznyh 5 ) Hstora tehn wytwarzana Inwentaryzaja onserwatorsa 9) Ustalene nawarstweń zabytu ) Loalzaja nawarstweń 6 ) Zmany tehnolog ) Wnos onserwatorse Rys.. Shemat dzałań onserwatorsh Fg.. Sheme of onservaton wors

8 8 te pownny prowadzć do ustalena hstor zabytu oreślena jego nawarstweń. Natomast w przypadu zabytów tehn należy dodatowo spreyzować zmany w tehnolog wytwarzana tóre prowadzą do analogznyh nawarstweń modyfaj tehnolog. Typowym są tu zmany wynająe z zastępowana slnów parowyh przez sln spalnowe zy też eletryzne. Podobne uwag dotyzą przeazu napędu z slna na urządzene produyjne. Natomast w przypadu przemysłu ementowego zasadnze zmany wywoływało przejśe z węgla na os oraz zastosowane dmuhaw ntensyfująyh wypał. Z tym zmanam podążały modyfaje proesu tehnologznego tóre pownny być ujęte w doumentaj onserwatorsej. Koneznym elementem jest też doumentaja fotografzna zman ubytów w urządzenah tehnznyh podobne ja lasyzne oenamy stan znszzeń zaeów w zabytah arhtetury. Zauważmy tutaj typową dla zabytów tehn dualność postępowana zwązaną z osobną oeną wartoś samego zabytu ja też jego wyposażena tehnznego. Proes ten shematyzne przedstawony jest na rysunu gdze równolegle wyonujemy lasyzną nwentaryzaję arhtetonzną ()-(4) oraz tehnologzną w zarese wyposażena zabytów tehn. Ten etap pra ońzy sę nwentaryzają materalną zabytu. Inwentaryzaja onserwatorsa zawera olejne etapy (5)-(7) ońząe sę opsem loalzają nawarstweń w budynu. 5. Wnos onserwatorse Po wyonanu nwentaryzaj badań zabytu przystępujemy do h syntezy tóra prowadz do wnosów onserwatorsh zawerająyh fnalne deyzje dotyząe dzałań onserwatorsh przy zabytu etapy (8)-(). W następstwe otrzymamy propozyję dzałań onserwatorsh prowadząyh do: ntegraj odtworzena reonstruj lub restauraj zabytu. Równolegle do tyh tradyyjnyh dzałań onserwatora pownny postępować zynnoś zmerzająe do ntegraj tehnolog lub też odtworzena w ałoś lub zęś ągów tehnologznyh. Ten etap dzałań pownen być podporządowany dydatyznemu aspetow prezentaj zabytu. Lteratura [] Borusewz W.: Konserwaja zabytów budowntwa murowanego Arady Warszawa 985. [] Kub J.: Trwałość zabytów Studa z zaresu Fzy Budowl KILW PAN Łódź 6. PROBLEMS OF PRESERATION OF TECHNICAL MONUMENTS Summary Tehnques sghts lead to new onservaton problems. In the paper new elements of tehnques sghts onservaton are presented.

9 ROCZNIKI INŻYNIERII BUDOWLANEJ ZESZYT / Komsja Inżyner Budowlanej Oddzał Polsej Aadem Nau w Katowah ZASTOSOWANIE PRÓBNEGO OBCIĄŻENIA W PROJEKCIE POSADOWIENIA REKONSTRUOWANEGO OBIEKTU PRZEMYSŁOWEGO Paweł FEDCZUK Poltehna Opolsa Opole. Wprowadzene Konezność przystosowana staryh obetów przemysłowyh do nowyh elów wymaga zwyle wzmonena ( modyfaj) onstruj wymuszają pełnejsze wyorzystane rezerw twąyh w jej nośnoś a w szzególnoś uładu fundamentpodłoże. Dzałane tae poprzedza zwyle projet reonstruj obetu stosująy bardzej złożone modele ośrodów lepej opsująyh rzezywste zahowane materałów onstruyjnyh gruntu. W lasyznym podejśu projetowym zares geotehnzny zgodny z obowązująą normą [] obejmuje sprawdzene warunów stanu granznego nośnoś podłoża jego osadana oraz stateznoś uładu fundament-podłoże. Sprowadza sę to w pratye do weryfaj ompletu nerównoś wyorzystująyh zamnęte rozwązana dla potratowanyh oddzelne warunów. I ta nośność ustala sę ze zmodyfowanego rozwązana Terzaghego [ 3 ] dla modelu Coulomba-Mohra osadane podłoża metodam teor sprężystoś [] (wyorzystująym rozwązana dla jednorodnej półprzestrzen sprężystej obążonej równomerne) z ewentualnym uwzględnenem jednoosowej onsoldaj [] a statezność lasyznym lub uproszzonym metodam sprawdzająym możlwość obrotu sztywnego fundamentu [3 ]. Zastosowane różnyh model ośroda gruntowego unemożlwa w pratye pełne wyorzystane nośnoś gdyż wtedy rzezywste osadana są zdeydowane węsze (nawet larotne) od prognozowanyh. Stwarza to problemy z doładnym ustalenem bezpeznyh rezerw w nośnoś rehabltowanego obetu. Próbne obążene fundamentu w rzezywstyh warunah przyjęte do ustalena realnej bezpeznej nośnoś (z użyem opsująej ten test haraterysty obążene fundamentu osadane podłoża ) pozwala unnąć tyh nedogodnoś. Nnejsze opraowane prezentuje w zaryse spójną onepję taego postępowana umożlwająego w marę poprawne ustalene rzezywstej nośnoś podłoża pod fundamentam rehabltowanego starego obetu przemysłowego. Istotą jej jest próbne obążene wybranego (zmodyfowanego lub nowo wyonanego) fundamentu reonstruowanego obetu w zarese prognozowanego przyrostu obążena pomar jego osadań (w elu wyonana analzy haraterysty obążene fundamentu osadane podłoża ). Postępowane tae pozwala ustalć rzezywste zahowane podłoża

10 w otozenu modyfowanej budowl trudne do oszaowana metodam oblzenowym (nawet numeryznym) uwzględnene: rzezywstej nejednorodnoś podłoża złożonego zahowane gruntu oraz hstor obążena.. Konepja postępowana Zgodne z [] sprawdzene prawdłowoś posadowena reonstruowanego obetu wymaga spełnena trzeh warunów stanu granznego: () nośnoś podłoża gruntowego () osadań (użytowalnoś) (3) stateznoś tworząyh uład 3 nerównoś d R s s E E () d d dst:b stb:b w tóryh: d R d oznazają wartoś oblzenowe obążena ponowego (lub sładowej dzałająej prostopadle do podstawy fundamentu) oporu przew temu oddzaływanu s s d osadane masymalne osadane dopuszzalne E dst:b E stb:b wartoś oblzenowe efetu oddzaływań destablzująyh stablzująyh. W stane granznym użytowalnoś wyróżna sę 5 przypadów przemeszzena fundamentów: (a) osadane masymalne (b) osadane średne () przehylene pojedynzego fundamentu lub grupy fundamentów (d) ugęe fundamentów (f) różnę osadań sprawdzanyh opjonalne dla oreślonyh budowl. Weryfaja stanu granznego stateznoś wymaga sprawdzena możlwoś obrotu uładu fundament-podłoże (z wyorzystanem metody analzy stateznoś ogólnej). Proponowana onepja wyorzystana wynów próbnego obążena fundamentu (lub grupy fundamentów) modyfowanyh obetów przemysłowyh bazuje na analze uzysanej dośwadzalne haraterysty obążene fundamentu osadane podłoża. To postępowana obejmuje: a) oszaowane rzezywstyh wartoś obążena dla modernzowanego obetu jao różny pomędzy dzałająym na obet przed reonstrują po jej wyonanu b) ustalene najneorzystnejszyh warantów pray onstruj (shematów osadana nośnoś) z wyborem zmodernzowanyh fundamentów do próbnego obążena ) modernzaję wybranyh fundamentów d) poddane wyselejonowanyh fundamentów próbnemu obążenu (w zarese neznazene przerazająym oszaowany przyrost obążena) po reonstruj obetu wyreślene zestawu haraterysty obążene fundamentu osadane podłoża e) analzę uzysanyh wynów oraz odzytane z wyresów wartoś osadana dla szaowanego pozomu obążena f) sprawdzene granznyh warunów: nośnoś osadana (odpowednh jego przypadów) stateznoś dla ustalonego pozomu obążena. Ta shematyzne sformułowany to postępowana wymaga dopreyzowana. Oszaowane rzezywstyh wartoś obążena (a) fundamentów starego zmodernzowanego obetu wymaga wyonana poszerzonego projetu wstępnego obejmująego zaresem zestawene obążeń dla budowl przed po modernzaj. W oblzenah najlepej jest posłużyć sę programem omputerowym metody elementów sońzonyh umożlwająym modelowane zahowana gruntu nnyh materałów zwązam nelnowym. Następny ro (b) wyorzystuje omplesowy projet modernzaj onstruj rehabltowanej budowl oraz zatualzowaną doumentaję

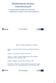
11 geologzną gruntów podłoża. Wybór właśwyh fundamentów do sprawdzena posadowena poprzedza szzegółowa analza możlwyh shematów obążena budowl fundamentów oraz przypadów osadana. Dobera sę estremalne obążone fundamenty występująe w oneznyh do sprawdzena warantah osadana oraz nośnoś. I na nh (po odpowednej modernzaj uwzględnająej ewentualne h powęszene wzmonene lub przebudowę) wyonuje sę próbne obążene w neznazne przerozonym (o 5-%) prognozowanym przedzale obążena. W przypadu nemożnoś poddana h tam badanom zastępuje sę je nowym fundamentam (o dentyznej onstruj posadowenu w blsm otozenu właśwyh) uwzględnają hstorę obążena (wstępne doążają je do pozomu nasu ja panował pod stnejąym fundamentam starej budowl). Ze sporządzonyh haraterysty odzytuje sę rzezywste wartoś osadań obążena wylza nezbędne weloś sprawdza warun zdefnowane nerównośam (). Możlwość utraty stateznoś weryfuje sę oblzenowo wyorzystują odpowedne metody analzy [ 3]. Pratyzne zasady postępowana wyjaśna przyład podany ponżej. 3. Przyład zastosowana Do prezentaj opsanej onepj postępowana (umożlwająej ustalene realnej nośnoś zmodyfowanego fundamentu) wyorzystuje sę teoretyzny przyład reonstruj dwunawowej hal przemysłowej o onstruj ramowej (rys. ). (I) =3N sd=mm SIŁA PIONOWA [N] WYBRANA STOPA FUNDAMENTOWA ANALIZA MES (LxB=5m x 5m MODEL COULOMBA-MOHRA) (II) =35N PRÓBNE OBCIĄśENIE NOWEJ STOPY (LxB=5m x 5m) s=7mm OSIADANIE s [x- m] Rys.. Shemat przyładu zastosowana próbnego obążena fundamentu Fg.. The sheme of example of usng the load test of foundaton Załada sę że w tym budynu środowy ąg stóp fundamentowyh o wadratowej podstawe (mająej długość L szeroość B równą m) wymaga jej powęszena do rozmarów 5m x 5m. Możlwy prognozowany wzrost wartoś oblzenowego obążena osowego wynese N (powęszy sę z N do 3N) nadal spełnają lasyzny warune nośnoś podłoża [] zdefnowany zależnośą (.a). Sła

12 = 3N ne przeraza dopuszzalnej weloś oporu R d (oszaowanej numeryzne z wyorzystanem omputerowego programu metody elementów sońzonyh). Ze względu na tehnzną trudność realzaj próbnego obążena na najneorzystnejszej wyselejonowanej stope (spozywająej na najsłabszej zęś podłoża) badane wyonano na nowej dentyznej stope posadowonej obo wybranej. Poddano ją próbnemu obążenu w przedzale obążena (powęszonemu o 5% wartoś tj. do przyrostu na pozome 5N). Ze względu na zęśowo już wyorzystane osadane podłoża przez stary obet (przed modernzają) przyjęte zostało ogranzene na dodatowy przyrost osadana natyhmastowego s d równy mm. Rezultat wyonanego teoretyzne badana ujęto w formę haraterysty obążene fundamentu osadane podłoża. Analza wyresu poazuje że ta przyrost obążena zostane osągnęty na pozome osadana równym s = 7mm o spełna warun prawdłowoś posadowena spreyzowane nerównośam (.a)-(.b). Poneważ dzałane sły ponowej ne powoduje utraty stateznoś stopy fundamentowej to weryfaja warunu (.) ne jest onezna. 4. Podsumowane Przedstawona onepja zastosowana próbnego obążena pozwala na zblżone do rzezywstoś oszaowane nośnoś podłoża pod fundamentem zahowana uładu fundament-podłoże. Postępowane tae ogranzają jedna warun tehnzne jego realzaj rzezywsty stan rehabltowanego obetu oraz pomnęta strona tehnzna realzaj badana (uwzględnająa ogranzena o do sposobu jej wyonana wytrzymałoś badanyh fragmentów onstruj rehabltowanego obetu przemysłowego). Tym nemnej przewaga opsanego postępowana w stosunu do lasyznyh onepj oblzenowyh polega na możlwoś uwzględnena rzezywstego zahowana gruntu w podłożu realnego wpływu jego własnoś na zahowane uładu fundament-podłoże. Lteratura [] Eurood 7. Projetowane geotehnzne. Część : Zasady ogólne PN-EN 997- Pols Komtet Normalzayjny Warszawa 8. [] Włun Z.: Zarys geotehn WKŁ Warszawa 987. [3] Mota E.: Fundamenty bezpośredne. Wzory table przyłady Arady Warszawa 988. APPLICATION OF LOAD TEST IN THE FOUNDATION DESIGN OF RECONSTRUCTED INDUSTRY BUILDING Summary The followng paper presents the onept of usng the load test and foundaton loadng subsol settlement haraterst n desgn to establsh orretly the real bearng apaty subsol under fundatons of revtalzed old ndustry buldng.

13 ROCZNIKI INŻYNIERII BUDOWLANEJ ZESZYT / Komsja Inżyner Budowlanej Oddzał Polsej Aadem Nau w Katowah RELACJA WZAJEMNOŚCI W ZAGADNIENIU POCZĄTKOWO-BRZEGOWYM LINIOWEJ TERMOPIEZOELEKTRYCZNOŚCI Potr GORECKI Jerzy WYRWAŁ Poltehna Opolsa Opole. Wprowadzene W nżyner budowlanej materały pezoeletryzne znalazły swoje zastosowane główne w nenszząej oene stanu wyrobów onstruj budowlanyh [9]. Czujn pezoeletryzne pozwalają na badane pray budowl w sposób ągły (strutural health montorng). Seć zujnów merzy tae weloś ja deformaje zy atywność sejsmzną. Otrzymane dane pozwalają na szybą reaję na ewentualne uszodzena onstruj. Coraz zęstsze zastosowane materałów pezoeletryznyh w warunah zmennej temperatury spowodowało wzrost zanteresowana zjawsem sprzężena pola termznego z efetem pezoeletryznym [5 6]. Zasady wzajemnoś w przypadu zagadneń pezoeletryznoś eletrostryj były analzowane wyorzystywane przez autorów opraowań [ 7 8]. W nnejszej pray wyprowadzono relaje wzajemnoś w przypadu ompletu równań zagadnena pozątowo-brzegowego lnowej termopezoletryznoś.. Zagadnene pozątowo-brzegowe lnowej termopezoeletryznoś Podstawowe równana lnowej termopezoeletryznoś w przypadu materału anzotropowego przedstawają ponższe równana [ 5] a jl e u Φ β θ f = () lj ej j j j u j j Φ b θ h = () j j β ju& j b Φ& θ& jθ j =. (3) T W powyższyh zależnośah weloś a jl j e j j b β j są współzynnam materałowym przene w dolnym ndese oznaza pohodną ząstową względem danej zmennej (np. u j= u/ x j ) zaś ropa nad daną welośą oznaza pohodną po zase.

14 4 Występująe w powyższyh zależnośah współzynn materałowe harateryzują sę następująym symetram [6]: a jl = a lj j j = a jl = a jl = ajl e j = ej β j = β j. (4) Zjawso pezoeletryznoś opsują zatem 3 równana tensorowe z 3 newadomym ( u Φ θ ). Do powyższyh równań należy dołązyć warun brzegowe: gdze: u= uˆ na Bu (5) σ n a u e Φ β Θ n = p = pˆ na B B B = (6) B j D n ( ) B j = jl l j j j σ u σ Φ = Φ ˆ na B (7) Φ Φ p Θ n = D = Dˆ nab B B = (8) ( e u ) B = j j j j D Φ q n ( = u p Φ DΘ q) θ = ˆ θ na B Θ (9) θ n = q = qˆ na B B B = B () = j j q θ powerzhna do tórej jest przyłożona odpowedna welość wynająa z warunu brzegowego uˆ pˆ Φ ˆ DΘ ˆ ˆ qˆ to olejno zadane na brzegu ała: odształene sła powerzhnowa potenjał eletryzny ładune eletryzny temperatura prostopadła do brzegu sładowa wetora natężena strumena epła. Komplet równań zagadnena uzupełnają warun pozątowe j ( x t = ) = ε j ( x t = ) = ε j w B ( ( x t = ) = E ( x t = ) = E w B ( θ ( t = ) = θ w B ( u () Φ () x q (3) ( ( ( gdze: ε j E θ wartoś pozątowe odształena potenjału eletryznego temperatury. 3. Operatorowa postać zagadnena pozątowo-brzegowego W elu uproszzena dalszyh rozważań uzynena h bardzej larownym równana (-3) (5-3) zostaną przedstawone w następująej zwartej posta operatorowej (maerzowej): A u f = A : E E' u E f E' (4) gdze wetory (maerze olumnowe) weloś poszuwanyh danyh zdefnowane są jao: [ u Φ θ ; u p Φ D θ q; u θ Φ θ θ θ ] T u = (5) ( ( ( f = f h pˆ uˆ Dˆ Φ ˆ qˆ / T ˆ θ / T β ε b E θ (6) [ ] T o o j j D

15 5 zaś nezerowe elementy operatora (maerzy wadratowej) A mają postać: A = ajlδ xlx j A A = ej x jx 3 = βj t x j A = ej xx j A A = j x jx 3 = b t x A = A A = A A = ( )() = βj x j = A 33 A A 3 = βj x j 3 = b x = j (7) t T x x A 89 = A98 = T A( 3)() = b A (5)(4) = x przy zym E oznaza przestrzeń Hlberta zaś E jest przestrzeną sprzężoną z E. 4. Symetra operatora zagadnena pozątowo-brzegowego lnowej termopezoeletryznoś W elu wyazana symetr operatora równana (4) należy go zapsać w następująej alternatywnej posta: Au v f v = (8) j gdze ałe: oznaza dwulnową formę E ' E przedstawoną jao suma następująyh E f u E = I = B f du d I I B f u d I I 9 I I = 4 B f du da I 5 I = B f I ( x ) u d I. (9) W powyższym wzorze symbole f dg f g oznazają odpowedno splot Steltesa splot funj f g zdefnowane jao: t ( t τ ) dg( τ ) f dg = f () f g t = f ( t τ ) g( τ ) dτ () przy zym właśwoś mnożena splotowego opsane są w [3]. Zdefnowany wyżej operator maerzowy A będze symetryzny jeśl spełn następująą relaję: A u u = Au u. () E E

16 6 Aby to wyazać należy wyorzystać twerdzene o dywergenj z tórego wyna że [ ( ) ( ) ] [ ( ) ( ) ] da d q T d D du p d T d b u e du d e u a d T d b u e du e u a B j j j j j j j j j l jl B j j B j j j j j j j j lj jl Φ Φ Φ Φ = Φ Φ Φ θ θ θ θ θ β θ θ θ θ β (3) oraz właśwoś mnożena splotowego tóre poągają za sobą następująą zależność: ( ) ( ) θ θ θ εθ β θ θ β θ θ β ( ( ( & & & Φ = Φ E b d d b du b u j j j j j. (4) Ja łatwo sprawdzć z formuł (5-7) (9) oraz zależnoś (3) (4) wyna że [ ] ( ) ( ) ( ) u Au u Au = Φ Φ Φ Φ Φ Φ Φ Φ = Φ da q q T da d D dd da du p dp u T d d b d b d d u du d u e du e du u a B B B j j j j j j j j j j j j j l jl B u θ θ θ θ θ θ θ θ θ β θ β θ (5) o dowodz symetr zdefnowanego wyżej relajam (7) operatora (maerzy) zadana pozątowo-brzegowego lnowej termopezoeletryznoś zapsanego w alternatywnej posta (8). 5. Relaja wzajemnoś w zagadnenu pozątowo-brzegowe lnowej termopezoeletryznoś Aby wyazać relaję wzajemnoś jaa występuje w zagadnenu pozątowo brzegowym lnowej termopezoeletryznoś oreślonym uładem równań (-3) (5-3) należy rozważyć dwa nezależne od sebe ułady: zdefnowanyh formułą (6) przyzyn { f f } oraz oreślonyh wzorem (5) sutów { u u }. Oba ułady przyzyn sutów pownny spełnać równane (8) a zatem:. = = u f u Au u f u Au (6)

17 7 Odjęe obu powyższyh równań stronam prowadz do zależnoś: u f u f u Au u Au =. (7) Poneważ rozważany operator zagadnena pozątowo brzegowego jest symetryzny zyl spełna warune (5) zatem symetra ta poąga za sobą następująą relaję: u f u f = (8) zwaną też relają (zasadą) wzajemnoś. Relaja ta w posta jawnej przedstawa sę następująo: ( ) ( ) ( ) ( ). ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ d E b da dq T da d q T da dd da d D da dp u da du p d d h du f d E b da dq T da d q T da dd da d D da dp u da du p d d h du f B j j B B B B B B B B j j B B B B B B B q D u q D u Φ Φ Φ = = Φ Φ Φ Θ Φ Θ Φ θ θ θ θ ε β θ θ θ θ θ θ ε β θ θ σ σ ( ( ( ( ( ( (9) 6. Podsumowane W prezentowanym artyule wyprowadzono relaję wzajemnoś w przypadu ompletu równań zagadnena pozątowo-brzegowego lnowej termopezoletryznoś. Otrzymana relaja może zostać wyorzystana do poszuwana analtyznyh numeryznyh rozwązań (np. z wyorzystanem metody elementów brzegowyh [4]) welu problemów nauowyh nżynersh zwązanyh z wyorzystanem materałów pezoeletryznyh. Oznazena symbol D wetor nduj eletryznej eletr dsplaement vetor [C m -3 ] E wetor natężena pola eletryznego eletr feld vetor [ m - ] f wetor sły objętośowej mehanal body fore [N m -3 ] h ładune eletryzny [C m -3 ] n wetor normalny do brzegu unt outward normal vetor q wetor natężena strumena epła heat flux vetor [W m - ]

18 8 t zmenna przestrzenna tme [s] T temperatura pozątowa referene temperature [K] u wetor przemeszzena elast dsplaement vetor [m] x współrzędna przestrzenna spatal poston [m] ε j tensor odształena symmetr stran tensor [-] Φ potenjał eletryzny eletr potental [] η gęstość entrop entropy densty [JK - m -3 ] Θ przyrost temperatury temperature nrement [K] σ j tensor naprężena symmetr stress tensor [Pa]. Lteratura [] Gülay A. Döme M. C. The onsstent Mdln s thermopezoeletr equatons and the prnple of vrtual wor Mehans Researh Communatons [] Iesan D. On the mrostreth pezoeletrty Internatonal Journal of Engneerng Senes [3] Korn G. A. Korn T. M. Mathematal Handboo for Sentsts and Engneers MGraw-Hll New Yor 986. [4] Kögl M. Gaul L. A boundary element method for transent pezoeletr analyss Engneerng Analyss wth Boundary Elements [5] Mndln R. D. On the equatons of moton of pezoeletr rystals n: N. I. Muslshvl Problems of ontnuum Mehans 7th Brthday olume SIAM Phladelpha [6] Nowa W. Some general theorems of thermo-pezoeletrty Journal of Thermal Stress [7] Pan E. Tonon F. Three-dmensonal Green s funtons n ansotrop pezoeletr solds Internatonal Journal of Solds and Strutures [8] Rzepa J. Teoretyzne podstawy zastosowana pezopolmerów do dagnosty onstruj nżynersh (rozprawa dotorsa) Opole 9. [9] Tressler J.F. Aloy S. Newham E. Pezoeletr Sensors and Sensor Materals Journal of Eletroerams RECIPROCITY RELATION IN BOUNDARY INITIAL ALUE PROBLEM OF LINEAR THERMOPIEZOELECTRICITY Summary The paper ontans dervaton of reproty theorem for ntal-boundary value problem of lnear thermopezoeletrty. The results obtaned n ths wor an beome the theoretal bass to formulate the numeral solutons of dfferent sentf and engneerng problems onneted wth pezoeletr materals.

19 ROCZNIKI INŻYNIERII BUDOWLANEJ ZESZYT / Komsja Inżyner Budowlanej Oddzał Polsej Aadem Nau w Katowah WPŁYW MĄCZKI GRANITOWEJ JAKO WYPEŁNIACZA W CEMENCIE NA WŁAŚCIWOŚCI BETONU Elżbeta JANOWSKA-RENKAS Poltehna Opolsa Opole. Wprowadzene Rozwój tehnolog betonu na przestrzen ostatnh ludzesęu lat jest mponująy zwłaszza w rajah wysoo uprzemysłowonyh tóre prześgają sę w realzajah oraz to dosonalszyh onstruj betonowyh [-3]. Betony najnowszej generaj harateryzująe sę wysoą wytrzymałośą na śsane po 8 dnah (6 - MPa) dużą trwałośą pod względem szzelnoś zyl nsą przepuszzalnośą medów ełyh gazowyh ja równeż wysoą odpornośą na śerane [4-7]. Osągnęe tah parametrów możlwe jest dzę zastosowanu dodatów mneralnyh [4-7] domesze hemznyh [8-9] tóre wpływają na poprawę właśwoś śweżej meszan betonowej ja stwardnałego betonu. Jednym z tah materałów może być mąza grantowa. Rozdrobnona do powerzhn właśwej wg Blne a o. 4 m /g może stanowć sładn betonu w posta wypełnaza wpływająego na urabalność śweżej meszan betonowej właśwoś stwardnałego betonu. Mąza grantowa jao sładn odpadowy jest pozyswana przy ozyszzanu ruszywa grantowego wyorzystywanego w produj masy asfaltowej w drogowntwe. Do tej pory ne była wyorzystywana do produj betonów ze względu na obeność zanezyszzeń organznyh w wydobywanym grane. Jedna ozyszzona z zanezyszzeń rozdrobnona do powerzhn porównywalnej bądź węszej od powerzhn właśwej ementu w przyszłoś może stanowć tan eologzny eonomzny sładn betonów XXI weu. W pray wyonano badana oreślająe wpływ rozdrobnonej mąz grantowej na właśwoś betonów modyfowanyh udzałem superpastyfatora najnowszej generaj.. Materały do badań Do wyonana meszane betonowyh zastosowano następująe sładn: ement portlandz wapenny CEM II/A-LL 45R ruszywo naturalne o masymalnym uzarnenu do 8 mm. Kruszywo dobrano metodą gran rzywyh przesewu zgodne z normą DIN 45 o pune pasowym równym 4 %. Proentowy udzał ruszywa dla poszzególnyh fraj wynosł odpowedno: pase drobny / mm % pase średn / mm 5% żwr /4 mm 5 % natomast żwr o fraj 4/8 mm 4 %. Dla ażdej z fraj gęstość stosowanego ruszywa wynosła ρ=3 g/dm 3 superplastyfator socrete HE stosowano w loś % mas. w stosunu do masy ementu

20 mąza mneralna grantowa (bez zanezyszzeń) rozmelona do powerzhn właśwej wg Blane a 4 m /g stosowana w loś 5% mas w stosunu do masy ementu. Sład meszan betonowej podano w tabel. Tabela. Sład meszan betonowej Ilość sładnów Sładn na m 3 w stane suhym [g] Cement CEM II/A-LL 45 R 36 Mąza mneralna grantowa 8 Pase drobny - mm 73 Pase średn - mm 433 Żwr -4 mm 433 Żwr 4-8 mm 693 Woda 6 l Superplastyfator so Crete HE % m.. 36 Razem 4356 W pray wyonano 4 sere betonów: B - na baze ementu portlandzego wapennego CEM II/A-LL 45R B - na baze ementu portlandzego wapennego CEM II/A-LL 45R z dodatem % mas. superplastyfatora A B3 - na baze ementu portlandzego wapennego CEM II/A-LL 45R z dodatem 5 % mas. mąz mneralnej grantowej B4 - na baze ementu portlandzego wapennego CEM II/A-LL 45R z dodatem 5 % mas. mąz mneralnej grantowej oraz % mas. superplastyfatora A. 3. Metody badań Badana wyonano dla śweżyh meszane betonowyh stwardnałego betonu. Dla śweżej meszan betonowej wyonano badana onsystenj metodą ebe zgodne z PN-EN 35-3 Badana meszan betonowej. Część 3: Badane onsystenj metodą ebe. Meszan betonowe dla 4 ser betonu harateryzowały sę jednaową - wlgotną onsystenją (). Dla stwardnałego betonu przeprowadzono badana: wytrzymałoś na śsane po dnah dojrzewana betonu zgodne z PN-EN39-3 Badane betonu. Część 3: Wytrzymałość na śsane ; badana penetraj wody pod śnenem zgodne z PN-EN39-8 Badane betonu. Część 8: Głęboość penetraj pod śnenem. Badana mrozoodpornoś przeprowadzono metoda polsą zgodne z normą PN-88/B-65 po 8 dnah dojrzewana betonów. 4. Wyn badań h nterpretaja Wyn badań wytrzymałoś na śsane próbe betonowyh B B B3 B4 przedstawono w tabel. Na podstawe uzysanyh wynów badań betonów B B B3 B4 można stwerdzć że zastosowane domesz hemznej nowej generaj mąz grantowej znazne zwęsza wytrzymałość betonu w ałym zarese badanej wytrzymałoś oreślonej od 3 do 9 dn (tab. ). Jest to wzrost rzędu 5% w porównanu do betonu B tóry po 3 dnah dojrzewana osągnął wytrzymałość 7 MPa. Natomast w późnejszym orese zasu (po 9 dnah 59 MPa. Najnższą wytrzymałość uzysano dla betonu bez dodatów (B) wytrzymałość po 8 dnah wynosła 5 MPa. Pozostałe betony uzysały wyższe wytrzymałoś od

21 betonu B o 3 % dla betonu B - z udzałem superplastyfatora oraz o. 3 % dla betonu B3 - z dodatem mąz grantowej. Tabela. Wytrzymałość na śsane badanyh betonów Wytrzymałość na śsane [MPa] po dnah: Rodzaj betonu B B B B Badana wyazały że mąza grantowa wpływa na przyrost wytrzymałoś betonów z jej udzałem (tab. ) oraz na zmnejszene wodoprzepuszzalnoś (tab. 3). Tabela. 3. Wyn badana wodoprzepuszzalnoś badanyh betonów Przepuszzalność Rodzaj betonu wody przez beton B B B3 B4 Głęboość penetraj wody [m] Głęboość penetraj wody w głąb betonu B4 była ponad dwurotne mnejsza (5 m) od głębooś wody tóra wnnęła w głąb betonu B na baze zystego ementu. Głęboość wody tóra wnnęła w wewnętrzną struturę betonu B wynosła 45 m. Znazne mnejszą lość wody stwerdzono w wewnętrznyh struturah betonu B3 z udzałem mąz grantowej (4 m) a taże betonu B z dodatem superplastyfatora (39 m). Najbardzej szzelny oazał sę beton B4 z udzałem mąz grantowej superplastyfatora. Dzę zastosowanej do betonu mąze zmnejszyła sę głęboość penetraj wody w głąb betonu B4). Uzysane wyn badań wytrzymałoś na śsane oraz penetraj wody w głąb betonu śwadzą o wytworzenu bardzo szzelnej mrostrutury w betonah z jej udzałem. Tabela 4. Masa złuszzonego materału przed po badanu mrozoodpornoś betonów Rodzaj betonu B B B3 B4 Ubyte masy [g] Spade masy [%] Wyn badań mrozoodpornoś betonów (B B4) oreślone masą złuszzonego materału z betonów poddawanyh zamrażanu zestawono w tabel 4. Natomast wyn badań wytrzymałoś na śsane betonów poddanyh badanu mrozoodpornoś próbe śwadów przedstawono w tabel 5.

22 Wyn badań odpornoś badanyh betonów na dzałane mrozu wyazały że masa próbe po zamrażanu neznazne różn sę od masy próbe przed badanem odpornoś na dzałane mrozu a różna wynos zaledwe % w przypadu betonu B4 zarówno z dodatem superplastyfatora ja mąz grantowej 4-5% dla betonu B3 z dodatem mąz grantowej 8 % dla betonu B z udzałem superplastyfatora oraz -4% dla betonu B z zystego ementu. Tabela 5. Wyn badań wytrzymałoś na śsane betonów po badanu mrozoodpornoś próbe śwadów Rodzaj betonu B B B3 B4 Wytrzymałość na śsane po badanu mrozoodpornoś [MPa] Wytrzymałość na śsane próbe śwadów [MPa] Betony z dodatem superplastyfatora po 5 ylah zamrażana odmrażana wyazały nemalże taą samą wytrzymałość na śsane ja prób śwad. Zgodne z wytyznym normy PN-88/B-65 beton można zalasyfować do danego stopna mrozoodpornoś jeżel po oreślonej lzbe yl zamrażana odmrażana spełna następująe warun : oględzny wyazują bra pęnęć utraty monoltyznoś prób łązna masa ubytów betonu ne przeraza 5% masy próbe ne zamrażanyh obnżene wytrzymałoś na śsane w porównanu do wytrzymałoś próbe ne zamrażanyh ne jest węsza nż %. Betony B B B3 B4 spełnły powyższe warun osągają lasę mrozoodpornoś F5. Badana wyazały orzystny wpływ melonej mąz grantowej na właśwoś betonu o zyn ten sładn porównywalnym nawet ze stosowanym w tehnolog betonu dodatam mneralnym (popoły lotne żużle welopeowe). Dlatego zastosowane mąz grantowej stanowąej materał odpadowy do produj betonu mogłaby znazne obnżyć oszty jego produj przy jednozesnym zwęszenu trwałoś stwardnałego betonu. 5. Wnos Na podstawe uzysanyh wynów badań można stwerdzć że mąza grantowa obo superplastyfatora wpływa na: znazny wzrost wytrzymałoś na śsane betonu zarówno pozątowej ja ońowej (po upływe 9 dn) w porównanu do betonu z zystego ementu CEM II zwęszene wodoszzelnoś głęboość penetraj wody w betone z jej udzałem była dwurotne mnejsza nż dla betonu z zystego ementu zwęszene odpornoś na dzałane mrozu. Prób ne wyazały pęnęć ubytów masy oraz utraty monoltyznoś. Badane wytrzymałoś na śsane wyazało że betony poddane 5 ylom zamrażana rozmrażana uzysały wyn prawe dentyzne ja dla próbe śwadów (ne poddanyh zamrażanu).

23 3 Lteratura [] Atn P.-C.: Cements of yesterday and today: Conrete of tomorrow. Cem. Conr. Res [] Nevlle A.M.: Właśwoś betonu. Pols Cement Kraów. [3] Oamura H. Ozawa K. Ouh M.: Self-Compatng Conrete. Strutural Conrete 3-7. [4] Kurdows W.: Chema ementu PWN Warszawa 99. [5] Peuert S. Garba A.: Cementy rajowe na progu XXI weu-stan atualny perspetywy. Mlenum Kraów [6] Janowsa-Renas E. Srzypzy T.: Trwałość betonu z ementu CEM II/A-LL 45 R Rozn Inżyner Budowlanej Zeszyt [7] Ludwg H.M. Wese F. Hemrh W. Ehrlh N.: Self-Compatng Conrete- Prnples and Prate. Investgaton nto the as Mx Formulaton Comparson of SCC and arous brated Conretes SCC wth Dfferent Fller Components SCC wth Ar Pores Stablzaton of SCC. BFT [8] Borso A. Collepard S Copolla L. Trol R.Collepard E.M.: Advanes n superplastzers for onrete mxtures. Il Cemento 999 t [9] Malhotra.M.: Innovatve applatons of superplatzers n onrete-a revew. Il emento (74) THE INFLUENCE OF GRANITE POWDER FILLER ON CONCRETE PROPERTIES Summary The paper presents the results of studes onernng nfluene of grante powder fller and a superplastzer of the newest generaton on onrete s propertes. An mprovement of propertes of onrete usng both: the powder and superplastzer was show n the artle. Inreasng strength frost resstane and redung permeablty one for the onrete wth grante powder fller and ompared to the pure ement onretes ontanng CEM II A / LL.

24 ROCZNIKI INŻYNIERII BUDOWLANEJ ZESZYT / Komsja Inżyner Budowlanej Oddzał Polsej Aadem Nau w Katowah PROCES NISZCZENIA MURÓW CEGLANYCH W ZABYTKOWYCH BUDYNKACH I OBIEKTACH PRZEMYSŁOWYCH Potr GORECKI Jerzy WYRWAŁ Poltehna Opolsa Opole. Wprowadzene W prezentowanym artyule przedstawono podstawowe zagadnena zwązane z trwałośą nszzenem murów eglanyh staryh zabytowyh budynów obetów przemysłowyh. Omówono wpływ jaoś egeł spajająyh je zapraw wapennyh na tempo nszzena murów a taże h odpornoś na dzałane różnorodnyh zynnów agresywnyh tah ja woda rozpuszzone w nej sole substanje zanezyszzająe atmosferę mroorganzmy zmany temperatury zynn mehanzne.. Trwałość zabytowyh murów eglanyh Trwałość murów eglanyh staryh zabytowyh budynów obetów przemysłowyh a taże tempo h nszzena zależą w głównej merze od jaoś egeł spajająyh je zapraw wapennyh a taże h odpornoś na dzałane różnorodnyh zynnów agresywnyh... Trwałość egeł w staryh murah Cegły w zabytowyh murah różną sę od sebe weloma eham fzyznym mehanznym a taże odpornośą na dzałane wody zynnów atmosferyznyh (np. waśnyh deszzów). Warto przypomneć że właśwoś egły zależą w głównej merze od: sładu jaoś glny oraz sposobu jej przygotowana domesze naturalnyh zawartyh w glne bądź też stosowanyh w proese produj warunów temperatury zasu suszena temperatury warunów wypalana a taże warunów hłodzena. Neodporne na dzałane wody rystalzująyh sol są egły źle wypalone zawerająe nedoładne wymeszane grubozarnste domesz margla zy też prytu oraz domesz sol rozpuszzalnyh w wodze. Cegły tae łatwo pęzneją pod wpływem wody ulegają nszząemu dzałanu wasów zasad. Nasąlwość tah egeł jest duża ształtuje sę od lu do ludzesęu proent. Cegły o nsh parametrah mehanznyh odznazają sę nejednorodną struturą olorem występują w nh rysy a taże rozwarstwają sę łatwo pęają. Artyuł opraowano na podstawe referatu wygłoszonego na polso-zesej onferenj Kulturní památy a opuštěné objety Hrade nad Moraví

25 6 Poneważ w dawnyh zasah ne było możlwoś preyzyjnego sterowana proesem produj egły ja to ma mejse obene dlatego też w staryh budynah budowlah obo egeł o dobryh parametrah mehanznyh fzyznyh spotya sę dość zęsto egły o nsej jaoś. Jeśl egły tae znajdują sę w murah zewnętrznyh główne narażonyh na dzałane zynnów atmosferyznyh to ulegają z begem zasu znaznej lub ałowtej destruj prowadzą do stotnego zmnejszena sę trwałoś murów w tóre są wbudowane. Na przyład z badań egeł gotyh pobranyh z budynów zabytowyh w Torunu wyna [ 3] że egły te harateryzowały sę stosunowo małą wytrzymałośą na śsane (od 6 do 9MPa) zaś h nasąlwość była stosunowo duża (po 4 godznah wynosła od 9 do 6%) natomast właśwoś aplarne były dobre (zas aplarnego podągana wody do wysooś 5m meśł sę w przedzale od do 6mn.). Konsewenją tah podobnyh właśwoś staryh egeł jest nsa odporność welu zabytowyh murów na dzałane zynnów zewnętrznyh a w szzególnoś wody rozpuszzalnyh w wodze sol oraz zman temperatury (zamarzane odmarzane wody)... Trwałość zapraw wapennyh w staryh murah Wadomo że właśwoś fzyzne mehanzne zapraw wapennyh zależą od welu zynnów. Deydująy wpływ na jaość zaprawy murarsej ma przede wszystm jaość wapna lość rodzaj ruszywa oraz jego granulaja a taże warun w jah zahodz proes wązana zaprawy (sprzyja temu powolne jej wysyhane). Jeśl proes ten zahodz w dobryh warunah a tae na przyład panują we wnętrzah budynów to zaprawy wapenne uzysują dobrą jaość tóra polepsza sę z begem zasu. Należy jedna pamętać o tym że nawet najlepsze zaprawy wapenne mają nsą wytrzymałość mehanzną a taże małą odporność na dzałane wody nnyh zynnów atmosferyznyh dlatego też spony z zaprawy wapennej ulegają w staryh murah stosunowo łatwemu nszzenu. 3. Nszzene zabytowyh murów eglanyh Stare mury z upływem zasu zawsze ulegają szybszemu lub wolnejszemu nszzenu Do głównyh zynnów powodująyh obnżene h trwałoś należy zalzyć wodę rozpuszzone w nej sole substanje agresywne zanezyszzająe atmosferę mroorganzmy a taże zmany temperatury zynn mehanzne. 3.. Nszzene murów przez wodę zynn atmosferyzne Mury eglane są nszzone przez wody opadowe (deszz śneg grad) gruntowe a taże sondensowaną w h wnętrzu parę wodną. Każde z wymenonyh rodzajów wody może taże zawerać sładn agresywne (sole wasy). Do szzególne zanezyszzonyh należą wody gruntowe oraz śneg mgła (szzególne w poblżu ośrodów przemysłowyh). Woda zawarta w murah eglanyh powoduje h nszzene hemzne fzyzne bologzne. Warto podreślć że zynn hemzne bologzne ne wywołują proesów destruyjnyh w murah suhyh dlatego ta ważnym jest osuszene murów nadmerne zawlgoonyh (jest to zazwyzaj proes długotrwały osztowny). Nszząe dzałane wody na sładn materałów murów jest spowodowane h rozpuszzanem pęznenem wymywanem a taże rozładem hemznym fzyznym.

26 Klasyfaję stopn zawlgoena murów eglanyh zawera tabla zaś rozład wlgotnoś masowej po gruboś muru przedstawa rys.. Z rysunu tego wyna że najbardzej zawlgoone są wewnętrzne warstwy muru szzególne w przypadu h znaznej gruboś. Tabla. Stopne zawlgoena murów [4] Stopeń Wlgotność masowa [%] Mur I -3 o dopuszzalnej wlgotnoś II 3-5 o podwyższonej wlgotnoś III 5-8 średno zawlgoony I 8- mono zawlgoony > mory Znajdująe sę w wodze zawartej w murah wasy: węglowy (słaby) oraz solny azotowy sarowy (mone) powstają wsute rozpuszzana sę w nej zawartego w powetrzu dwutlenu węgla oraz nnyh gazów je zanezyszzająyh (główne tlenów sar azotu hlorowodoru fluorowodoru). Wszyste wymenone wyżej wasy dzałają destruyjne na mury eglane. W przypadu wasów solnego azotowego jest to destruja natyhmastowa polegająa na rozładanu węglanów znajdująyh sę na powerzhn muru a następne nszzenu oraz głębszyh jego warstw. Poneważ wasy te dzałają wyłązne w środowsu wodnym to rozmary destruj muru zależą od h stężena zęstotlwoś oddzaływana tóre są prostą onsewenją zęstotlwoś długoś oresów występowana zawlgoena murów. 7 Wlgotność masowa Rozład wlgotnoś względnej powetrza otazająego mur Grubość muru Rys.. Rozład wlgotnoś masowej na gruboś muru [4] Fg.. Mosture mass ontent n a br wall [4] Obeność wasu węglowego sprzyja tworzenu sę nawarstweń węglanowyh. Wydawać by sę mogło że proes ten wpływa na zwęszene trwałoś wytrzymałoś muru a tym samym jego odpornoś na zynn mehanzne. Jedna powstawane tyh nawarstweń ma śsły zwąze z osłabenem wytrzymałoś wewnętrznyh part muru wsute mgraj węglanu wapna (w forme waśnego węglanu) ze strefy zawlgoena do porów powerzhnowyh. Z upływem zasu następuje wę oraz węsze osłabene part wewnętrznyh zapraw a taże egeł (jeśl występuje w nh węglan wapna w posta margla) oraz węsze uszzelnene powerzhn murów. W efee ońowym na sute: rystalzaj sol rozpuszzonyh w wodze pod nawarstwenam

27 8 zamarzana wody uwęzonej w warstwah wewnętrznyh w onsewenj uszzelnena powerzhn muru naprężeń śnająyh mędzy nawarstwenam a murem spowodowanyh różnym współzynnam rozszerzalnoś eplnej obserwuje sę pęane złuszzane sę warstw powerzhnowyh (nawarstweń) oraz odsłanane znszzonyh wewnętrznyh part muru []. W przypadu dzałana wasu sarowego proes powstawana nawarstweń na powerzhn muru zahodz szzególne łatwo poneważ przemane węglanu wapna w sarzan wapna (gps) towarzyszy ooło dwurotne zwęszene jego objętoś. 3.. Nszzene murów przez sole rozpuszzalne w wodze Rozpuszzalne w wodze sole nszzą zabytowe mury eglane główne w rezultae h rystalzaj powęszana sę ryształów. Sole slnyh wasów słabyh zasad mogą je taże nszzyć na drodze hemznej (np. hlore sarzan azotan amonu wapna żelaza nne) poneważ w wynu h hydrolzy tworzą sę wasy: solny sarowy azotowy tóryh nszząe dzałane na mury zostało opsane wyżej. Głównym źródłam zasolena murów są: woda gruntowa sól wyorzystywana w orese zmowym do posypywana nawerzhn zanezyszzena przemysłowe nawozy sztuzne oraz zahodząe w murah proesy hemzne. Rozpuszzone w wodze sole przemeszzają sę wraz z roztworem z głębszyh warstw muru do jego obszarów przypowerzhnowyh gdze wsute odparowana wody ulegają rystalzaj osadzają sę na powerzhn muru bądź w jego porah przypowerzhnowyh. Najwęsze supsa sol tworzą sę tam gdze odparowywane wody jest najbardzej ntensywne dlatego też tae zęś muru są najbardzej narażone na znszzene. Zależne od właśwoś strutury muru rodzajów sol h stężena a taże warunów wysyhana (temperatury wlgotnoś) sole mogą tworzyć plamy zae wywty a taże matowe szlste nawarstwena o różnej struturze właśwośah []. Stopne zasolena murów eglanyh zawera tabla zaś rozład zasolena po gruboś muru przedstawa rys.. Z rysunu tego wyna że najwęsze stężene sol występuje w warstwah przypowerzhnowyh muru tam gdze odparowywane wody jest najwęsze a tym samym zawlgoene najmnejsze (por. rys. ). Tabla. Stopne zasolena murów [5] Rodzaj sol Zawartość masowa sol [%] Chlor <..-.5 >.5 Azotany <..-.3 >.3 Sarzany < >.5 Stopeń zasolena ns średn wyso Zatem rystalzaja sol występują główne w przypowerzhnowyh porah szzelnah murów gdze stężene roztworów sol jest najwęsze (rys. ). Cśnene rystalzayjne jest wystarzająo duże aby przy powtarzająyh sę ylah rozpuszzana sol jej rystalzaj doprowadzć stopnowo do znszzena tyh zęś muru. Bardzo nebezpezne dla murów są łatwo rozpuszzalne w wodze sarzany sodu magnezu oraz węglan sodu []. Zwęszane sę stopna uwodnena wypełnająyh pory szzelny muru bezwodnyh posta tyh sol lub h hydratów o nsm stopnu uwodnena sutuje znaznym zwęszenem h objętoś. Warto zaznazyć że śnene hydratayjne wywerane na śan porów materału muru może osągać ta znazne

28 wartoś że przy powtarzająym sę (larotnym) proese hydrataj dehydrataj sol może ono doprowadzć do ałowtego znszzena jego strutury wewnętrznej. Warto zaznazyć że znajdująe sę w murze sole (zarówno w posta roztworów ja ryształów) zmenają też jego efetywną przewodność eplną o należy uwzględnć przy oblzanu strat epła z pomeszzeń budynów zabytowyh [6]. 9 Zawartość sol Sty powerzhn muru z otazająym powetrzem Grubość muru Rys.. Rozład zawartoś sol rozpuszzalnyh na gruboś muru [4] Fg.. Soluble salts ontent n a br wall [4] 3.3. Nszzene murów przez zynn bologzne Głównym zynnam bologznym nszząym mury są drobnoustroje (glony porosty grzyby oraz batere) oraz roślnność zelona. Mehanzm nszząy wydzelanyh w wynu proesów metabolznyh wasów organznyh (np. mleowego szzawowego otowego) jest podobny do opsanego wyżej dzałana wasów neorganznyh []. Natomast dzałane mehanzne roślnnoś zelonej zyl wrastane orzonów hwytnów (np. mhów) w pory szzelny muru powoduje jego osłabene nszzene pęane oraz rozpad egeł zapraw. Dlatego też należy staranne usuwać z powerzhn zabytowyh budynów wszelego rodzaju drobnoustroje roślnność zeloną Nszzene murów przez zmany temperatury Istotnym zynnem nszząym mury są gwałtowne wahana temperatury szzególne o dużej ampltudze przy jej spadu ponżej puntu zamarzana wody w porah materału. W tah warunah woda znajdująa sę w porah aplarah oraz szzelnah zamarza doprowadzają stopnowo do rozsadzana mur. Nszząe dzałane lodu na mur zmnejsza do pewnego stopna zjawso przemeszzana sę wody zamarzająej w materale do porów newypełnonyh wodą a taże jej przehłodzene w aplarah o małyh średnah. Powoduje to znaząe obnżene temperatury zamarzana wody w materałah o struturze porowatej [7]. Z uwag na powyższe zjawsa przyjmuje sę że nszząe dzałane lodu na mury jest w pratye znazne mnej groźne nż dzałane sol rozpuszzalnyh w wodze [] Nszzene murów przez zynn mehanzne Duże znszzena mehanzne murów może spowodować watr tóry porywają pyły drobny pase nne rozdrobnone materały może śerać słabe powerzhn zaorąglać