Cyfrowe przetwarzanie i kompresja danych
|
|
|
- Lech Czerwiński
- 6 lat temu
- Przeglądów:
Transkrypt
1 Cyfrowe przetwarzane kompresja danyh dr nż.. Wojeh Zają Wykład 4. Dyskretna transformata kosnusowa
2 Shemat przetwarzana danyh w systeme yfrowym Cyfryzaja danyh Dekorelaja kwantyzaja ompresja FEC + przeplot Modulaja odpowedna do medum, np. modulaja fal snusodalnej sygnałem dyskretnym transmsja Odzyskane sygnału yfrowego z sygnału transmtowanego - demodulaja orekja błędów transmsj usunęe danyh dodatkowyh FEC, usunęe przeplotu Dekompresja Odwrotna operaja dekorelaj Sygnał użytezny
3 Dekorelaja usuwane korelaj wzajemnej zależno noś statystyznej danyh w zborze
4 Przekształene Fourera Funkja ągłą opsana w dzedzne rzezywstej przekształana jest do posta sumy harmonznyh proste przekształene Fourera fˆ ω t ( ω ) f ( t ) e dt π odwrotne przekształene Fourera f ω t ( t ) f ( ω ) e dt π
5 Dyskretne przekszta Dyskretne przekształene Fourera ene Fourera proste dyskretne przekszta proste dyskretne przekształene Fourera ene Fourera odwrotne dyskretne przekszta odwrotne dyskretne przekształene Fourera ene Fourera ( ) ( ) ( )( ) N j k j N j x k X ω ( ) ( ) ( )( ) N k k j N k X N j x ω ( ) N N e π ω
6 Dyskretne przekszta Dyskretne przekształene Fourera ene Fourera DFT w posta maerzowej DFT w posta maerzowej YDFT YDFT X IDFTw IDFTw posta maerzowej posta maerzowej X Y Y DFT DFT x N x x x x x X N X X X X X ) ),( ( ) 0,( ),0 ( 0, N N N N N N N N DFT
7 Fast Fourer Transform Najpopularnejszą wersją FFT jest FFT o podstawe. Jest to bardzo efektywna operaja, jednak wektor próbek wejśowyh (spr( spróbkowany sygnał) ) mus meć długość N k, gdze k to pewna lzba naturalna. Wynk otrzymuje sę na drodze shematyznyh przekształe eń,, opartyh o tak zwane struktury motylkowe. Złożoność oblzenowa FFT wynos nlog n,, zamast n perwotnego algorytmu.
8 Skutezność dekorelaj Skutezność dekorelaj merzy sę na drodze określena MSE (MSE0 oznaza dealną dekorelaję) Uszeregowane transformat pod względem mnmalzaja zakłóe eń średnokwadratowyh :.LT,.DCT, 3.slant slant, 4.WHT, 5.HT, 6.DFT DFT, 7.DST DST.
9 oszt numeryzny transformaja LT slant FFT DCT WHT lzba op. mnożena N 3 N N log N N log N 0 lzba op. dodawana N 3 N log N N log N N log N N log N
10 ryterum optymalzaj welokryteralnej Sprawność transformaty wydajność dekorelaj w stosunku do kosztu numeryznego
11 Zalety: Transformata optymalna LT mnmalzaja aja zakłóe eń średnokwadratowyh w sygnale odtworzonym (dealna dekorelaja danyh) Wady: najwększy spośród d transformat koszt numeryzny (N( 3 operaj mnożena N 3 operaj dodawana), brak szybkego algorytmu LT, konezność wyznazena modelu kowaranj sygnału źródłowego, o stanow złożone z one zadane numeryzne. konezność wyznazena transmsj do dekodera bazy transformaj LT (dagonalzowanej maerzy kowaranj danyh)
12 Transformata neoptymalna DCT Dla stajonarnego proesu Markowa perwszego rzędu transformata DCT osąga sprawność (wydajność dekorelaj w stosunku do kosztu numeryznego) zblżon oną do sprawnoś transformaty LT Zalety Wady wysoka wydajność dekorelaj, względne mały y koszt numeryzny. dekorelaja odbegająa od dealnej, efekt blokowy, przy przetwarzanu dla potrzeb slnej kompresj występowane artefaktów w transformaty Akeptowalny komproms mędzy jakoś ą dekorelaj a kosztem numeryznym - powszehne zastosowane w tehne.
13 Efekt blokowy
14 Artefakty transformaty DCT
15 y Reprezentaja sygnału u ągłego w dzedzne zasu dyskretnego () ysn(t) t y ysn(n) N y(n) y y 3 y 3 4 y 4 5 y 5 6 y 6 7 y 7 y 9 y 9 0 y 0 y y 3 y 3 4 y 4 5 y 5 6 y 6 n
16 Reprezentaja sygnału u ągłego w dzedzne zasu dyskretnego ()
17 Reprezentaja dwuwymarowego sygnału ągłego w dzedzne zasu dyskretnego
18 Zmana dzedzny opsu sygnału - analza zęstotlwo stotlwośowa lub nazej transformaja sygnału Przetwarzane za pomoą transformat wykorzystuje fakt, że dowolny sygnał s może e być przedstawony za pomoą lnowej kombnaj pewnyh funkj elementarnyh, zwanyh funkjam bazowym f. Dsrete Fourer Transform - DFT Fast Fourer Transform - FFT Dsrete Cosne Transform - DCT Dsrete Wavelet Transform - DWT s C f gdze C jest stałą
19 Dsrete Cosne Transform DCT () Funkje bazowe f transformaty DCT mają postać: f os ( j )( ) π + dla dla <, j N. Ahmed,, T. Natarajan, and. R. Rao,, "Dsrete" Cosne Transform", IEEE Trans. Computers,, 90-93, 93, Jan 974. N. Ahmed,, "How" I ame up wth the Dsrete Cosne Transform", Dgtal Sgnal Proessng,, Vol., p.4-5 (99).
20 Dsrete Cosne Transform DCT () Funkje bazowe f transformaty DCT mają postać: f os ( j )( ) π + dla dla <, j Ważną ehą transformaty DCT jest konezność operaj na lzbe danyh będąej b potęgą dwójk. Oznaza to, że e lzba próbek może e wynosć: 0,,,,, 4, 3,, 4, 6,
21 Dsrete Cosne Transform DCT () Funkje bazowe f transformaty DCT mają postać: f os ( j )( ) π + dla dla <, j Ważną ehą transformaty DCT jest konezność operaj na lzbe danyh będąej b potęgą dwójk. Oznaza to, że e lzba próbek może e wynosć: 0,,,,, 4, 3,, 4, 6,
22 Dsrete Cosne Transform DCT () Funkje bazowe f transformaty DCT mają postać: f os ( j )( ) π + dla dla <, j j,,,,,,,,,
23 Dsrete Dsrete Cosne Cosne Transform Transform DCT () DCT () Funkje Funkje bazowe bazowe f transformaty transformaty DCT DCT maj mają posta postać: ( )( ) < + j dla j dla f, os π 3 oznaza.., j..,,7,6,5,4,3,, 7, 7,7 7,6 7,5 7,4 7,3 7, 7, 6, 6, 6, 6, 6, 6, 6, 6, 5, 5,7 5,6 5,5 5,4 5,3 5, 5, 4,7 4,6 4, 4,5 4,4 4,3 4, 4, 3, 3,7 3,6 3,5 3,4 3,3 3, 3,,,7,6,5,4,3,,,,7,6,5,4,3,,, DCT j
24 Dsrete Dsrete Cosne Cosne Transform Transform DCT () DCT () Funkje Funkje bazowe bazowe f transformaty transformaty DCT DCT maj mają posta postać: ( )( ) < + j dla j dla f, os π 3 oznaza.., j..,,7,6,5,4,3,, 7, 7,7 7,6 7,5 7,4 7,3 7, 7, 6, 6, 6, 6, 6, 6, 6, 6, 5, 5,7 5,6 5,5 5,4 5,3 5, 5, 4,7 4,6 4, 4,5 4,4 4,3 4, 4, 3, 3,7 3,6 3,5 3,4 3,3 3, 3,,,7,6,5,4,3,,,,7,6,5,4,3,,, DCT j Jak oblzy Jak oblzyć wsp współzynnk zynnk,j,j?
25 Dsrete Cosne Transform DCT (3) Dla 3 funkjef bazowe f transformaty DCT mają postać: f os ( j )( ) π + dla dla <, j
26 Dsrete Cosne Transform DCT (3) Dla 3 funkjef bazowe f transformaty DCT mają postać: f 3 os ( j )( ) π + dla dla <, j f os ( j )( ) π 6 dla dla <, j
27 Dsrete Cosne Transform DCT (4) Dla 3 funkjef bazowe f transformaty DCT mają postać: f os ( j )( ) π 6 dla dla <, j
28 Dsrete Cosne Transform DCT (4) Dla 3 funkjef bazowe f transformaty DCT mają postać: f os ( j )( ) π 6 dla dla <, j f dla, j
29 Dsrete Cosne Transform DCT (4) Dla 3 funkjef bazowe f transformaty DCT mają postać: f os ( j )( ) π 6 dla dla <, j f dla, j π f os 6 ( j ) dla, j
30 Dsrete Cosne Transform DCT (4) Dla 3 funkjef bazowe f transformaty DCT mają postać: f os ( j )( ) π 6 dla dla <, j f dla, j π f os 6 ( j ) dla, j π f3 os 6 ( j ) dla 3, j
31 Dsrete Cosne Transform DCT (4) Dla 3 funkjef bazowe f transformaty DCT mają postać: f os ( j )( ) π 6 dla dla <, j f dla, j π f os 6 ( j ) dla, j π f3 os 6 ( j ) dla 3, j 3π f4 os 6 ( j ) dla 4, j
32 Dsrete Cosne Transform DCT (4) Dla 3 funkjef bazowe f transformaty DCT mają postać: f os ( j )( ) f dla, j π f os 6 ( j ) dla, j π f3 os 6 ( j ) dla 3, j π 6 dla dla <, j 4π f5 os 6 ( j ) dla 5, j 3π f4 os 6 ( j ) dla 4, j
33 Dsrete Cosne Transform DCT (4) Dla 3 funkjef bazowe f transformaty DCT mają postać: f os ( j )( ) f dla, j π f os 6 ( j ) dla, j π f3 os 6 ( j ) dla 3, j π 6 dla dla <, j 4π f5 os 6 ( j ) dla 5, j 5π f6 os 6 ( j ) dla 6, j 3π f4 os 6 ( j ) dla 4, j
34 Dsrete Cosne Transform DCT (4) Dla 3 funkjef bazowe f transformaty DCT mają postać: f os ( j )( ) f dla, j π f os 6 ( j ) dla, j π f3 os 6 ( j ) dla 3, j π 6 dla dla <, j 4π f5 os 6 ( j ) dla 5, j 5π f6 os 6 ( j ) dla 6, j 6π f7 os 6 ( j ) dla 7, j 3π f4 os 6 ( j ) dla 4, j
35 Dsrete Cosne Transform DCT (4) Dla 3 funkjef bazowe f transformaty DCT mają postać: f os ( j )( ) f dla, j π f os 6 ( j ) dla, j π f3 os 6 ( j ) dla 3, j 3π f4 os 6 ( j ) dla 4, j π 6 dla dla <, j 4π f5 os 6 ( j ) dla 5, j 5π f6 os 6 ( j ) dla 6, j 6π f7 os 6 ( j ) dla 7, j 7π f os 6 ( j ) dla j, j
36 Dsrete Cosne Transform DCT (5) f dla, j j f f f 3 f 4 f 5 f 6 f 7 f
37 Dsrete Cosne Transform DCT (5) π f os 6 ( j ) dla, j j f f f 3 f 4 f 5 f 6 f 7 f
38 Dsrete Cosne Transform DCT (5) π f3 os 6 ( j ) dla 3, j j f f f 3 f 4 f 5 f 6 f 7 f
39 Dsrete Cosne Transform DCT (5) 3π f4 os 6 ( j ) dla 4, j j f f f 3 f 4 f 5 f 6 f 7 f
40 Dsrete Cosne Transform DCT (5) 4π f5 os 6 ( j ) dla 5, j j f f f 3 f 4 f 5 f 6 f 7 f
41 Dsrete Cosne Transform DCT (5) 5π f6 os 6 ( j ) dla 6, j j f f f 3 f 4 f 5 f 6 f 7 f
42 Dsrete Cosne Transform DCT (5) 6π f7 os 6 ( j ) dla 7, j j f f f 3 f 4 f 5 f 6 f 7 f
43 Dsrete Cosne Transform DCT (5) 7π f os 6 ( j ) dla j, j j f f f 3 f 4 f 5 f 6 f 7 f
44 Dsrete Cosne Transform DCT (6) funton fdtd() % generowane maerzy wspolzynnkw DCT N; for :N for j:n f f os ( j )( ) f(,j)/sqrt(); else f(,j)sqrt(/)*os((*j-)*(-)*p/6); end end end π 6 dla dla <, j
45 Dsrete Cosne Transform f f f3 f4 f5 f6 f7 f
46 Dsrete Cosne Transform f f f3 f4 f5 f6 f7 f N
47 Dsrete Cosne Transform f f f3 f4 f5 f6 f7 f
48 Dsrete Cosne Transform f f f3 f4 f5 f6 f7 f N
49 Dsrete Dsrete Cosne Cosne Transform Transform ( )( ) <., os,, N j N dla N j N N j dla N DCT j π 0,0975 0,77 0,457 0,4904 0,4904 0,457 0,77 0,0975 0,93 0,469 0,469 0,93 0,93 0,469 0,469 0,93 0,775 0,4904 0,0975 0,457 0,457 0,0975 0,4904 0,77 0,3536 0,3536 0,3536 0,3536 0,3536 0,3536 0,3536 0,3536 0,457 0,0975 0,4904 0,77 0,77 0,4904 0,0975 0,457 0,469 0,93 0,93 0,469 0,469 0,93 0,93 0,469 0,4904 0,457 0,77 0,0975 0,0975 0,77 0,457 0,4904 0,3536 0,3536 0,3536 0,3536 0,3536 0,3536 0,3536 0,3536 DCT
50 Oblzane transformaty Przekształene proste wektora x Y DCT X Przekształene odwrotne wektora x X DCT T Y
51 Oblzane transformaty x x x 3 x 4 x 5 x 6 x 7 f f f3 f4 f5 * f6 f7 f DCT x y y y 3 y 4 y 5 y 6 y 7 x y
52 Oblzane transformaty x y x y x 3 y 3 x 4 x 5 * DCT x y 4 y 5 x 6 y 6 x 7 y 7 x y
53 Oblzane transformaty x y x y x 3 x 4 x 5 x 6 0,3536 0,4904 0,469 0,3536 0,4904 0,469 * 0,457 0,0975 0,4904 0,77 0,77 0,4904 0,0975 0,457 DCT 0,3536 0,3536 0,3536 0,3536 0,3536 0,3536 0,3536 0,3536 0,77 0,93 0,0975 0,3536 0,457 0,93 0,4904 0,469 0,77 0,3536 0,77 0,93 0,0975 0,469 0,457 0,3536 0,0975 0,469 0,457 0,93 0,4904 0,3536 0,0975 0,469 0,457 0,93 0,4904 0,3536 0,77 0,93 0,0975 0,469 0,457 0,3536 0,457 0,93 0,4904 0,469 0,77 0,775 0,93 0,0975 y 3 y 4 y 5 y 6 x 7 y 7 x y
54 Dwuwymarowa transformaja DCT Przekształene proste Y DCT X DCT T Przekształene odwrotne X ' DCT T Y DCT
55 x x yp x x yp x 3 x 3 yp 3 x 4 x 5 x 4 x 5 DCT x * yp 4 yp 5 x 6 x 6 yp 6 x 7 x 7 yp 7 x x yp
56 x x x yp yp x x x yp yp x 3 x 3 x 3 yp 3 yp 3 x 4 x 5 x 4 x 5 x 4 x 5 DCT x * yp 4 yp 5 yp 4 yp 5 x 6 x 6 x 6 yp 6 yp 6 x 7 x 7 x 7 yp 7 yp 7 x x x yp yp
57 x x x yp yp x x x yp yp x 3 x 3 x 3 yp 3 yp 3 x 4 x 5 x 4 x 5 x 4 x 5 DCT x * yp 4 yp 5 yp 4 yp 5 x 6 x 6 x 6 yp 6 yp 6 x 7 x 7 x 7 yp 7 yp 7 x x x yp yp * DCT T x y y y 3 y 4 y 5 y 6 y 7 y y y y 3 y 4 y 5 y 6 y 7 y
58 x x x yp yp x x x yp yp x 3 x 3 x 3 yp 3 yp 3 x 4 x 5 x 4 x 5 x 4 x 5 DCT x * yp 4 yp 5 yp 4 yp 5 x 6 x 6 x 6 yp 6 yp 6 x 7 x 7 x 7 yp 7 yp 7 x x x yp yp * DCT T x y y y 3 y 4 y 5 y 6 y 7 y y y y 3 y 4 y 5 y 6 y 7 y
59 Powstawane zakłóe eń DCT maerz danyh przestrzennyh X
60 Powstawane zakłóe eń DCT maerz danyh przestrzennyh transformata prosta X DCT
61 Powstawane zakłóe eń DCT maerz danyh przestrzennyh transformata prosta maerz danyh zęstotlwo stotlwośowyh X DCT Y
62 Powstawane zakłóe eń DCT maerz danyh przestrzennyh transformata prosta maerz danyh zęstotlwo stotlwośowyh przetwarzane kanału X DCT Y
63 Powstawane zakłóe eń DCT maerz danyh przestrzennyh transformata prosta maerz danyh zęstotlwo stotlwośowyh przetwarzane kanału transmsja X DCT Y
64 Powstawane zakłóe eń DCT maerz danyh przestrzennyh transformata prosta maerz danyh zęstotlwo stotlwośowyh przetwarzane kanału transmsja + zakłóena X DCT Y
65 Powstawane zakłóe eń DCT maerz danyh przestrzennyh transformata prosta maerz danyh zęstotlwo stotlwośowyh przetwarzane kanału transmsja + zakłóena maerz danyh zęstotlwo stotlwośowyh + zakłóena btowe X DCT Y Y'
66 Powstawane zakłóe eń DCT maerz danyh przestrzennyh transformata prosta maerz danyh zęstotlwo stotlwośowyh przetwarzane kanału transmsja + zakłóena maerz danyh zęstotlwo stotlwośowyh + zakłóena btowe transformata odwrotna X DCT Y Y' IDCT
67 Powstawane zakłóe eń DCT maerz danyh przestrzennyh transformata prosta maerz danyh zęstotlwo stotlwośowyh przetwarzane kanału transmsja + zakłóena maerz danyh zęstotlwo stotlwośowyh + zakłóena btowe transformata odwrotna maerz danyh przestrzennyh + zakłóena X DCT Y Y' IDCT X'
FFT i dyskretny splot. Aplikacje w DSP
 i dyskretny splot. Aplikacje w DSP Marcin Jenczmyk m.jenczmyk@knm.katowice.pl Wydział Matematyki, Fizyki i Chemii 10 maja 2014 M. Jenczmyk Sesja wiosenna KNM 2014 i dyskretny splot 1 / 17 Transformata
i dyskretny splot. Aplikacje w DSP Marcin Jenczmyk m.jenczmyk@knm.katowice.pl Wydział Matematyki, Fizyki i Chemii 10 maja 2014 M. Jenczmyk Sesja wiosenna KNM 2014 i dyskretny splot 1 / 17 Transformata
STANDARDOWE TECHNIKI KOMPRESJI SYGNAŁÓW
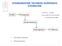 STANDARDOWE TECHNIKI KOMPRESJI SYGNAŁÓW Źródło Kompresja Kanał transmsj sek wdeo 60 Mbt 2 mn muzyk (44 00 próbek/sek, 6 btów/próbkę) 84 Mbt Dekompresja Odborca. Metody bezstratne 2. Metody stratne 2 Kodowane
STANDARDOWE TECHNIKI KOMPRESJI SYGNAŁÓW Źródło Kompresja Kanał transmsj sek wdeo 60 Mbt 2 mn muzyk (44 00 próbek/sek, 6 btów/próbkę) 84 Mbt Dekompresja Odborca. Metody bezstratne 2. Metody stratne 2 Kodowane
NIEOPTYMALNA TECHNIKA DEKORELACJI W CYFROWYM PRZETWARZANIU OBRAZU
 II Konferencja Naukowa KNWS'05 "Informatyka- sztuka czy rzemios o" 15-18 czerwca 2005, Z otniki Luba skie NIEOPTYMALNA TECHNIKA DEKORELACJI W CYFROWYM PRZETWARZANIU OBRAZU Wojciech Zając Instytut Informatyki
II Konferencja Naukowa KNWS'05 "Informatyka- sztuka czy rzemios o" 15-18 czerwca 2005, Z otniki Luba skie NIEOPTYMALNA TECHNIKA DEKORELACJI W CYFROWYM PRZETWARZANIU OBRAZU Wojciech Zając Instytut Informatyki
Transformaty. Kodowanie transformujace
 Transformaty. Kodowanie transformujace Kodowanie i kompresja informacji - Wykład 10 10 maja 2009 Szeregi Fouriera Każda funkcję okresowa f (t) o okresie T można zapisać jako f (t) = a 0 + a n cos nω 0
Transformaty. Kodowanie transformujace Kodowanie i kompresja informacji - Wykład 10 10 maja 2009 Szeregi Fouriera Każda funkcję okresowa f (t) o okresie T można zapisać jako f (t) = a 0 + a n cos nω 0
Przetwarzanie i transmisja danych multimedialnych. Wykład 8 Transformaty i kodowanie cz. 2. Przemysław Sękalski.
 Przetwarzanie i transmisja danych multimedialnych Wykład 8 Transformaty i kodowanie cz. 2 Przemysław Sękalski sekalski@dmcs.pl Politechnika Łódzka Katedra Mikroelektroniki i Technik Informatycznych DMCS
Przetwarzanie i transmisja danych multimedialnych Wykład 8 Transformaty i kodowanie cz. 2 Przemysław Sękalski sekalski@dmcs.pl Politechnika Łódzka Katedra Mikroelektroniki i Technik Informatycznych DMCS
9. Dyskretna transformata Fouriera algorytm FFT
 Transformata Fouriera ma szerokie zastosowanie w analizie i syntezie układów i systemów elektronicznych, gdyż pozwala na połączenie dwóch sposobów przedstawiania sygnałów reprezentacji w dziedzinie czasu
Transformata Fouriera ma szerokie zastosowanie w analizie i syntezie układów i systemów elektronicznych, gdyż pozwala na połączenie dwóch sposobów przedstawiania sygnałów reprezentacji w dziedzinie czasu
Adaptacyjne Przetwarzanie Sygnałów. Filtracja adaptacyjna w dziedzinie częstotliwości
 W Filtracja adaptacyjna w dziedzinie częstotliwości Blokowy algorytm LMS (BLMS) N f n+n = f n + α x n+i e(n + i), i= N L Slide e(n + i) =d(n + i) f T n x n+i (i =,,N ) Wprowadźmy nowy indeks: n = kn (
W Filtracja adaptacyjna w dziedzinie częstotliwości Blokowy algorytm LMS (BLMS) N f n+n = f n + α x n+i e(n + i), i= N L Slide e(n + i) =d(n + i) f T n x n+i (i =,,N ) Wprowadźmy nowy indeks: n = kn (
Szybka transformacja Fouriera (FFT Fast Fourier Transform)
 Szybka transformacja Fouriera (FFT Fast Fourier Transform) Plan wykładu: 1. Transformacja Fouriera, iloczyn skalarny 2. DFT - dyskretna transformacja Fouriera 3. FFT szybka transformacja Fouriera a) algorytm
Szybka transformacja Fouriera (FFT Fast Fourier Transform) Plan wykładu: 1. Transformacja Fouriera, iloczyn skalarny 2. DFT - dyskretna transformacja Fouriera 3. FFT szybka transformacja Fouriera a) algorytm
Technika audio część 2
 Technika audio część 2 Wykład 12 Projektowanie cyfrowych układów elektronicznych Mgr inż. Łukasz Kirchner lukasz.kirchner@cs.put.poznan.pl http://www.cs.put.poznan.pl/lkirchner Wprowadzenie do filtracji
Technika audio część 2 Wykład 12 Projektowanie cyfrowych układów elektronicznych Mgr inż. Łukasz Kirchner lukasz.kirchner@cs.put.poznan.pl http://www.cs.put.poznan.pl/lkirchner Wprowadzenie do filtracji
KINEMATYKA MANIPULATORÓW
 KIEMK MIULOÓW WOWDEIE. Manpulator obot można podzelć na zęść terująą mehanzną. Część mehanzna nazywana jet manpulatorem. punktu wdzena Mehank ta zęść jet najbardzej ntereująa. Manpulator zaadnzo można
KIEMK MIULOÓW WOWDEIE. Manpulator obot można podzelć na zęść terująą mehanzną. Część mehanzna nazywana jet manpulatorem. punktu wdzena Mehank ta zęść jet najbardzej ntereująa. Manpulator zaadnzo można
ZASADY WYZNACZANIA DEPOZYTÓW ZABEZPIECZAJĄCYCH PO WPROWADZENIU DO OBROTU OPCJI W RELACJI KLIENT-BIURO MAKLERSKIE
 Zasady wyznazana depozytów zabezpezaąyh po wprowadzenu do obrotu op w rela lent-buro malerse ZAADY WYZNACZANIA DEPOZYTÓW ZABEZPIECZAJĄCYCH PO WPROWADZENIU DO OBROTU OPCJI W RELACJI KLIENT-BIURO MAKLERKIE
Zasady wyznazana depozytów zabezpezaąyh po wprowadzenu do obrotu op w rela lent-buro malerse ZAADY WYZNACZANIA DEPOZYTÓW ZABEZPIECZAJĄCYCH PO WPROWADZENIU DO OBROTU OPCJI W RELACJI KLIENT-BIURO MAKLERKIE
Transformata Fouriera
 Transformata Fouriera Program wykładu 1. Wprowadzenie teoretyczne 2. Algorytm FFT 3. Zastosowanie analizy Fouriera 4. Przykłady programów Wprowadzenie teoretyczne Zespolona transformata Fouriera Jeżeli
Transformata Fouriera Program wykładu 1. Wprowadzenie teoretyczne 2. Algorytm FFT 3. Zastosowanie analizy Fouriera 4. Przykłady programów Wprowadzenie teoretyczne Zespolona transformata Fouriera Jeżeli
Politechnika Świętokrzyska. Laboratorium. Cyfrowe przetwarzanie sygnałów. Ćwiczenie 6. Transformata cosinusowa. Krótkookresowa transformata Fouriera.
 Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 6 Transformata cosinusowa. Krótkookresowa transformata Fouriera. Cel ćwiczenia Celem ćwiczenia jest zapoznanie studentów
Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 6 Transformata cosinusowa. Krótkookresowa transformata Fouriera. Cel ćwiczenia Celem ćwiczenia jest zapoznanie studentów
Zastowowanie transformacji Fouriera w cyfrowym przetwarzaniu sygnałów
 31.01.2008 Zastowowanie transformacji Fouriera w cyfrowym przetwarzaniu sygnałów Paweł Tkocz inf. sem. 5 gr 1 1. Dźwięk cyfrowy Fala akustyczna jest jednym ze zjawisk fizycznych mających charakter okresowy.
31.01.2008 Zastowowanie transformacji Fouriera w cyfrowym przetwarzaniu sygnałów Paweł Tkocz inf. sem. 5 gr 1 1. Dźwięk cyfrowy Fala akustyczna jest jednym ze zjawisk fizycznych mających charakter okresowy.
Dyskretna transformata falkowa z wykorzystaniem falek Haara. Alfréd Haar
 Dyskretna transformata falkowa z wykorzystaniem falek Haara Alfréd Haar 88-9 Przypomnijmy, że istotą DWT jest podział pierwotnego sygnału za pomoą pary filtrów (górnoprzepustowego i dolnoprzepustowego)
Dyskretna transformata falkowa z wykorzystaniem falek Haara Alfréd Haar 88-9 Przypomnijmy, że istotą DWT jest podział pierwotnego sygnału za pomoą pary filtrów (górnoprzepustowego i dolnoprzepustowego)
Wstęp do metod numerycznych Dyskretna transformacja Fouriera. P. F. Góra
 Wstęp do metod numerycznych Dyskretna transformacja Fouriera P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 01 Problem Majac dany szereg czasowy {x i } N i=1 = {x 1, x,..., x N } (zazwyczaj nieciekawy),
Wstęp do metod numerycznych Dyskretna transformacja Fouriera P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 01 Problem Majac dany szereg czasowy {x i } N i=1 = {x 1, x,..., x N } (zazwyczaj nieciekawy),
KOMPRESJA OBRAZÓW STATYCZNYCH - ALGORYTM JPEG
 KOMPRESJA OBRAZÓW STATYCZNYCH - ALGORYTM JPEG Joint Photographic Expert Group - 1986 ISO - International Standard Organisation CCITT - Comité Consultatif International de Téléphonie et Télégraphie Standard
KOMPRESJA OBRAZÓW STATYCZNYCH - ALGORYTM JPEG Joint Photographic Expert Group - 1986 ISO - International Standard Organisation CCITT - Comité Consultatif International de Téléphonie et Télégraphie Standard
Kompresja obrazów w statycznych - algorytm JPEG
 Kompresja obrazów w statycznych - algorytm JPEG Joint Photographic Expert Group - 986 ISO - International Standard Organisation CCITT - Comité Consultatif International de Téléphonie et Télégraphie Standard
Kompresja obrazów w statycznych - algorytm JPEG Joint Photographic Expert Group - 986 ISO - International Standard Organisation CCITT - Comité Consultatif International de Téléphonie et Télégraphie Standard
Założenia i obszar zastosowań. JPEG - algorytm kodowania obrazu. Geneza algorytmu KOMPRESJA OBRAZÓW STATYCZNYCH - ALGORYTM JPEG
 Założenia i obszar zastosowań KOMPRESJA OBRAZÓW STATYCZNYCH - ALGORYTM JPEG Plan wykładu: Geneza algorytmu Założenia i obszar zastosowań JPEG kroki algorytmu kodowania obrazu Założenia: Obraz monochromatyczny
Założenia i obszar zastosowań KOMPRESJA OBRAZÓW STATYCZNYCH - ALGORYTM JPEG Plan wykładu: Geneza algorytmu Założenia i obszar zastosowań JPEG kroki algorytmu kodowania obrazu Założenia: Obraz monochromatyczny
Metody Przetwarzania Danych Meteorologicznych Ćwiczenia 14
 Danych Meteorologicznych Sylwester Arabas (ćwiczenia do wykładu dra Krzysztofa Markowicza) Instytut Geofizyki, Wydział Fizyki Uniwersytetu Warszawskiego 18. stycznia 2010 r. Zadanie 14.1 : polecenie znalezienie
Danych Meteorologicznych Sylwester Arabas (ćwiczenia do wykładu dra Krzysztofa Markowicza) Instytut Geofizyki, Wydział Fizyki Uniwersytetu Warszawskiego 18. stycznia 2010 r. Zadanie 14.1 : polecenie znalezienie
Adaptive wavelet synthesis for improving digital image processing
 for improving digital image processing Politechnika Łódzka Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej 4 listopada 2010 Plan prezentacji 1 Wstęp 2 Dyskretne przekształcenie falkowe
for improving digital image processing Politechnika Łódzka Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej 4 listopada 2010 Plan prezentacji 1 Wstęp 2 Dyskretne przekształcenie falkowe
Przetwarzanie i transmisja danych multimedialnych. Wykład 7 Transformaty i kodowanie. Przemysław Sękalski.
 Przetwarzanie i transmisja danych multimedialnych Wykład 7 Transformaty i kodowanie Przemysław Sękalski sekalski@dmcs.pl Politechnika Łódzka Katedra Mikroelektroniki i Technik Informatycznych DMCS Wykład
Przetwarzanie i transmisja danych multimedialnych Wykład 7 Transformaty i kodowanie Przemysław Sękalski sekalski@dmcs.pl Politechnika Łódzka Katedra Mikroelektroniki i Technik Informatycznych DMCS Wykład
2. Szybka transformata Fouriera
 Szybka transforata Fouriera Wyznaczenie ciągu (Y 0, Y 1,, Y 1 ) przy użyciu DFT wyaga wykonania: nożenia zespolonego ( 1) razy, dodawania zespolonego ( 1) razy, przy założeniu, że wartości ω j są już dane
Szybka transforata Fouriera Wyznaczenie ciągu (Y 0, Y 1,, Y 1 ) przy użyciu DFT wyaga wykonania: nożenia zespolonego ( 1) razy, dodawania zespolonego ( 1) razy, przy założeniu, że wartości ω j są już dane
Analiza szeregów czasowych: 1. Dyskretna transformata Fouriera i zagadnienia pokrewne
 Analiza szeregów czasowych: 1. Dyskretna transformata Fouriera i zagadnienia pokrewne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 007/08 Transformata Fouriera G(f) = g(t)e πift dt (1)
Analiza szeregów czasowych: 1. Dyskretna transformata Fouriera i zagadnienia pokrewne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 007/08 Transformata Fouriera G(f) = g(t)e πift dt (1)
WikiWS For Business Sharks
 WkWS For Busness Sharks Ops zadana konkursowego Zadane Opracowane algorytmu automatyczne przetwarzającego zdjęce odręczne narysowanego dagramu na tablcy lub kartce do postac wektorowej zapsanej w formace
WkWS For Busness Sharks Ops zadana konkursowego Zadane Opracowane algorytmu automatyczne przetwarzającego zdjęce odręczne narysowanego dagramu na tablcy lub kartce do postac wektorowej zapsanej w formace
Laboratorium ochrony danych
 Laboratorum ochrony danych Ćwczene nr Temat ćwczena: Cała skończone rozszerzone Cel dydaktyczny: Opanowane programowej metody konstruowana cał skończonych rozszerzonych GF(pm), poznane ch własnośc oraz
Laboratorum ochrony danych Ćwczene nr Temat ćwczena: Cała skończone rozszerzone Cel dydaktyczny: Opanowane programowej metody konstruowana cał skończonych rozszerzonych GF(pm), poznane ch własnośc oraz
Cyfrowe przetwarzanie i kompresja danych
 Cyfrowe przetwarzanie i kompresja danych dr inż.. Wojciech Zając Wykład 5. Dyskretna transformata falkowa Schemat systemu transmisji danych wizyjnych Źródło danych Przetwarzanie Przesył Przetwarzanie Prezentacja
Cyfrowe przetwarzanie i kompresja danych dr inż.. Wojciech Zając Wykład 5. Dyskretna transformata falkowa Schemat systemu transmisji danych wizyjnych Źródło danych Przetwarzanie Przesył Przetwarzanie Prezentacja
PL B1. Sposób i układ pomiaru całkowitego współczynnika odkształcenia THD sygnałów elektrycznych w systemach zasilających
 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 210969 (13) B1 (21) Numer zgłoszenia: 383047 (51) Int.Cl. G01R 23/16 (2006.01) G01R 23/20 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej (22)
RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 210969 (13) B1 (21) Numer zgłoszenia: 383047 (51) Int.Cl. G01R 23/16 (2006.01) G01R 23/20 (2006.01) Urząd Patentowy Rzeczypospolitej Polskiej (22)
dr inż. Artur Zieliński Katedra Elektrochemii, Korozji i Inżynierii Materiałowej Wydział Chemiczny PG pokój 311
 dr inż. Artur Zieliński Katedra Elektrochemii, Korozji i Inżynierii Materiałowej Wydział Chemiczny PG pokój 311 Politechnika Gdaoska, 2011 r. Publikacja współfinansowana ze środków Unii Europejskiej w
dr inż. Artur Zieliński Katedra Elektrochemii, Korozji i Inżynierii Materiałowej Wydział Chemiczny PG pokój 311 Politechnika Gdaoska, 2011 r. Publikacja współfinansowana ze środków Unii Europejskiej w
Wielokategorialne systemy uczące się i ich zastosowanie w bioinformatyce. Rafał Grodzicki
 Welokategoralne systemy uząe sę h zastosowane w bonformatye Rafał Grodzk Welokategoralny system uząy sę (multlabel learnng system) Zbór danyh weśowyh: d X = R Zbór klas (kategor): { 2 } =...Q Zbór uząy:
Welokategoralne systemy uząe sę h zastosowane w bonformatye Rafał Grodzk Welokategoralny system uząy sę (multlabel learnng system) Zbór danyh weśowyh: d X = R Zbór klas (kategor): { 2 } =...Q Zbór uząy:
Transformacja Fouriera i biblioteka CUFFT 3.0
 Transformacja Fouriera i biblioteka CUFFT 3.0 Procesory Graficzne w Zastosowaniach Obliczeniowych Karol Opara Warszawa, 14 kwietnia 2010 Transformacja Fouriera Definicje i Intuicje Transformacja z dziedziny
Transformacja Fouriera i biblioteka CUFFT 3.0 Procesory Graficzne w Zastosowaniach Obliczeniowych Karol Opara Warszawa, 14 kwietnia 2010 Transformacja Fouriera Definicje i Intuicje Transformacja z dziedziny
uzyskany w wyniku próbkowania okresowego przebiegu czasowego x(t) ze stałym czasem próbkowania t takim, że T = t N 1 t
 4. 1 3. " P r ze c ie k " w idm ow y 1 0 2 4.13. "PRZECIEK" WIDMOWY Rozważmy szereg czasowy {x r } dla r = 0, 1,..., N 1 uzyskany w wyniku próbkowania okresowego przebiegu czasowego x(t) ze stałym czasem
4. 1 3. " P r ze c ie k " w idm ow y 1 0 2 4.13. "PRZECIEK" WIDMOWY Rozważmy szereg czasowy {x r } dla r = 0, 1,..., N 1 uzyskany w wyniku próbkowania okresowego przebiegu czasowego x(t) ze stałym czasem
IMPLEMENTATION OF THE SPECTRUM ANALYZER ON MICROCONTROLLER WITH ARM7 CORE IMPLEMENTACJA ANALIZATORA WIDMA NA MIKROKONTROLERZE Z RDZENIEM ARM7
 Łukasz Deńca V rok Koło Techniki Cyfrowej dr inż. Wojciech Mysiński opiekun naukowy IMPLEMENTATION OF THE SPECTRUM ANALYZER ON MICROCONTROLLER WITH ARM7 CORE IMPLEMENTACJA ANALIZATORA WIDMA NA MIKROKONTROLERZE
Łukasz Deńca V rok Koło Techniki Cyfrowej dr inż. Wojciech Mysiński opiekun naukowy IMPLEMENTATION OF THE SPECTRUM ANALYZER ON MICROCONTROLLER WITH ARM7 CORE IMPLEMENTACJA ANALIZATORA WIDMA NA MIKROKONTROLERZE
Wybrane metody kompresji obrazów
 Wybrane metody kompresji obrazów Celem kodowania kompresyjnego obrazu jest redukcja ilości informacji w nim zawartej. Redukcja ta polega na usuwaniu informacji nadmiarowej w obrazie, tzw. redundancji.
Wybrane metody kompresji obrazów Celem kodowania kompresyjnego obrazu jest redukcja ilości informacji w nim zawartej. Redukcja ta polega na usuwaniu informacji nadmiarowej w obrazie, tzw. redundancji.
Przekształcenie Fouriera i splot
 Zastosowania Procesorów Sygnałowych dr inż. Grzegorz Szwoch greg@multimed.org p. 732 - Katedra Systemów Multimedialnych Przekształcenie Fouriera i splot Wstęp Na tym wykładzie: przekształcenie Fouriera
Zastosowania Procesorów Sygnałowych dr inż. Grzegorz Szwoch greg@multimed.org p. 732 - Katedra Systemów Multimedialnych Przekształcenie Fouriera i splot Wstęp Na tym wykładzie: przekształcenie Fouriera
WYSYCHANIE ZABYTKOWYCH MURÓW Z CEGŁY *
 ROCZNIKI INŻYNIERII BUDOWLANEJ ZESZYT 7/007 Komsja Inżyner Budowlanej Oddzał Polskej Akadem Nauk w Katowah WYSYCHANIE ZABYTKOWYCH MURÓW Z CEGŁY * Andrzej KUCHARCZYK Poltehnka Opolska, Opole. Wprowadzene
ROCZNIKI INŻYNIERII BUDOWLANEJ ZESZYT 7/007 Komsja Inżyner Budowlanej Oddzał Polskej Akadem Nauk w Katowah WYSYCHANIE ZABYTKOWYCH MURÓW Z CEGŁY * Andrzej KUCHARCZYK Poltehnka Opolska, Opole. Wprowadzene
DYSKRETNA TRANSFORMACJA FOURIERA
 Laboratorium Teorii Sygnałów - DFT 1 DYSKRETNA TRANSFORMACJA FOURIERA Cel ćwiczenia Celem ćwiczenia jest przeprowadzenie analizy widmowej sygnałów okresowych za pomocą szybkiego przekształcenie Fouriera
Laboratorium Teorii Sygnałów - DFT 1 DYSKRETNA TRANSFORMACJA FOURIERA Cel ćwiczenia Celem ćwiczenia jest przeprowadzenie analizy widmowej sygnałów okresowych za pomocą szybkiego przekształcenie Fouriera
jako analizatory częstotliwości
 jako analiatory cęstotliwości Widmo fourierowskie: y = cos p f t Widmo sygnału spróbkowanego Problem rodielcości Transformaty cyfrowe: analia wycinka sygnału xt wt próbek, T sekund Widmo wycinka: f*wf
jako analiatory cęstotliwości Widmo fourierowskie: y = cos p f t Widmo sygnału spróbkowanego Problem rodielcości Transformaty cyfrowe: analia wycinka sygnału xt wt próbek, T sekund Widmo wycinka: f*wf
Ćwiczenie 3. Właściwości przekształcenia Fouriera
 Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 3. Właściwości przekształcenia Fouriera 1. Podstawowe właściwości przekształcenia
Politechnika Wrocławska Wydział Elektroniki Mikrosystemów i Fotoniki Przetwarzanie sygnałów laboratorium ETD5067L Ćwiczenie 3. Właściwości przekształcenia Fouriera 1. Podstawowe właściwości przekształcenia
 Klasyfkator lnowy Wstęp Klasyfkator lnowy jest najprostszym możlwym klasyfkatorem. Zakłada on lnową separację lnowy podzał dwóch klas mędzy sobą. Przedstawa to ponższy rysunek: 5 4 3 1 0-1 - -3-4 -5-5
Klasyfkator lnowy Wstęp Klasyfkator lnowy jest najprostszym możlwym klasyfkatorem. Zakłada on lnową separację lnowy podzał dwóch klas mędzy sobą. Przedstawa to ponższy rysunek: 5 4 3 1 0-1 - -3-4 -5-5
Zestaw zadań 4: Przestrzenie wektorowe i podprzestrzenie. Liniowa niezależność. Sumy i sumy proste podprzestrzeni.
 Zestaw zadań : Przestrzene wektorowe podprzestrzene. Lnowa nezależność. Sumy sumy proste podprzestrzen. () Wykazać, że V = C ze zwykłym dodawanem jako dodawanem wektorów operacją mnożena przez skalar :
Zestaw zadań : Przestrzene wektorowe podprzestrzene. Lnowa nezależność. Sumy sumy proste podprzestrzen. () Wykazać, że V = C ze zwykłym dodawanem jako dodawanem wektorów operacją mnożena przez skalar :
Wymiana i składowanie danych multimodalnych
 SKRYPT DO LABORATORIUM Wymiana i składowanie danych multimodalnych ĆWICZENIE 3: Dyskretna transformata kosinusowa zasada działania i podstawowe właściwości autor: dr inż. Adam Bujnowski 1. Wymagania wstępne
SKRYPT DO LABORATORIUM Wymiana i składowanie danych multimodalnych ĆWICZENIE 3: Dyskretna transformata kosinusowa zasada działania i podstawowe właściwości autor: dr inż. Adam Bujnowski 1. Wymagania wstępne
Przekształcenie Fouriera obrazów FFT
 Przekształcenie ouriera obrazów T 6 P. Strumiłło, M. Strzelecki Przekształcenie ouriera ourier wymyślił sposób rozkładu szerokiej klasy funkcji (sygnałów) okresowych na składowe harmoniczne; taką reprezentację
Przekształcenie ouriera obrazów T 6 P. Strumiłło, M. Strzelecki Przekształcenie ouriera ourier wymyślił sposób rozkładu szerokiej klasy funkcji (sygnałów) okresowych na składowe harmoniczne; taką reprezentację
Cyfrowe przetwarzanie sygnałów. Wykład 10. Transformata cosinusowa. Falki. Transformata falkowa. dr inż. Robert Kazała
 Cyfrowe przetwarzanie sygnałów Wykład 10 Transformata cosinusowa. Falki. Transformata falkowa. dr inż. Robert Kazała 1 Transformata cosinusowa Dyskretna transformacja kosinusowa, (DCT ang. discrete cosine
Cyfrowe przetwarzanie sygnałów Wykład 10 Transformata cosinusowa. Falki. Transformata falkowa. dr inż. Robert Kazała 1 Transformata cosinusowa Dyskretna transformacja kosinusowa, (DCT ang. discrete cosine
architektura komputerów w. 3 Arytmetyka komputerów
 archtektura komputerów w. 3 Arytmetyka komputerów Systemy pozycyjne - dodawane w systeme dwójkowym 100101011001110010101 100111101000001000 0110110011101 1 archtektura komputerów w 3 1 Arytmetyka bnarna.
archtektura komputerów w. 3 Arytmetyka komputerów Systemy pozycyjne - dodawane w systeme dwójkowym 100101011001110010101 100111101000001000 0110110011101 1 archtektura komputerów w 3 1 Arytmetyka bnarna.
Wstęp do sieci neuronowych, wykład 03 Warstwy RBF, jednostka Adaline.
 Wstęp do sieci neuronowych, wykład 3 Warstwy, jednostka Adaline. Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 211-1-18 1 Pomysł Przykłady Zastosowanie 2
Wstęp do sieci neuronowych, wykład 3 Warstwy, jednostka Adaline. Maja Czoków, Jarosław Piersa Wydział Matematyki i Informatyki, Uniwersytet Mikołaja Kopernika 211-1-18 1 Pomysł Przykłady Zastosowanie 2
Zadanie na wykonanie Projektu Zespołowego
 Zadane na wykonane Projektu Zespołowego Celem projektu jest uzyskane następującego szeregu umejętnośc praktycznych: umejętnośc opracowana równoległych wersj algorytmów (na przykładze algorytmów algebry
Zadane na wykonane Projektu Zespołowego Celem projektu jest uzyskane następującego szeregu umejętnośc praktycznych: umejętnośc opracowana równoległych wersj algorytmów (na przykładze algorytmów algebry
WPŁYW PARAMETRÓW DYSKRETYZACJI NA NIEPEWNOŚĆ WYNIKÓW POMIARU OBIEKTÓW OBRAZU CYFROWEGO
 Walenty OWIECZKO WPŁYW PARAMETRÓW DYSKRETYZACJI A IEPEWOŚĆ WYIKÓW POMIARU OBIEKTÓW OBRAZU CYFROWEGO STRESZCZEIE W artykule przedstaono ynk analzy nepenośc pomaru ybranych cech obektu obrazu cyfroego. Wyznaczono
Walenty OWIECZKO WPŁYW PARAMETRÓW DYSKRETYZACJI A IEPEWOŚĆ WYIKÓW POMIARU OBIEKTÓW OBRAZU CYFROWEGO STRESZCZEIE W artykule przedstaono ynk analzy nepenośc pomaru ybranych cech obektu obrazu cyfroego. Wyznaczono
WSPOMAGANE KOMPUTEROWO POMIARY CZĘSTOTLIWOŚCI CHWILOWEJ SYGNAŁÓW IMPULSOWYCH
 Metrologa Wspomagana Komputerowo - Zegrze, 9-22 05.997 WSPOMAGANE KOMPUTEROWO POMIARY CZĘSTOTLIWOŚCI CHWILOWEJ SYGNAŁÓW IMPULSOWYCH dr nż. Jan Ryszard Jask, dr nż. Elgusz Pawłowsk POLITECHNIKA lubelska
Metrologa Wspomagana Komputerowo - Zegrze, 9-22 05.997 WSPOMAGANE KOMPUTEROWO POMIARY CZĘSTOTLIWOŚCI CHWILOWEJ SYGNAŁÓW IMPULSOWYCH dr nż. Jan Ryszard Jask, dr nż. Elgusz Pawłowsk POLITECHNIKA lubelska
Transformata Fouriera i analiza spektralna
 Transformata Fouriera i analiza spektralna Z czego składają się sygnały? Sygnały jednowymiarowe, częstotliwość Liczby zespolone Transformata Fouriera Szybka Transformata Fouriera (FFT) FFT w 2D Przykłady
Transformata Fouriera i analiza spektralna Z czego składają się sygnały? Sygnały jednowymiarowe, częstotliwość Liczby zespolone Transformata Fouriera Szybka Transformata Fouriera (FFT) FFT w 2D Przykłady
Wykład 2. Transformata Fouriera
 Wykład 2. Transformata Fouriera Transformata Fouriera jest podstawowym narzędziem analizy harmonicznej i teorii analizy i przetwarzania sygnału. Z punktu widzenia teorii matematycznej transformata Fouriera
Wykład 2. Transformata Fouriera Transformata Fouriera jest podstawowym narzędziem analizy harmonicznej i teorii analizy i przetwarzania sygnału. Z punktu widzenia teorii matematycznej transformata Fouriera
Transformata Fouriera. Sylwia Kołoda Magdalena Pacek Krzysztof Kolago
 Transformata Fouriera Sylwia Kołoda Magdalena Pacek Krzysztof Kolago Transformacja Fouriera rozkłada funkcję okresową na szereg funkcji okresowych tak, że uzyskana transformata podaje w jaki sposób poszczególne
Transformata Fouriera Sylwia Kołoda Magdalena Pacek Krzysztof Kolago Transformacja Fouriera rozkłada funkcję okresową na szereg funkcji okresowych tak, że uzyskana transformata podaje w jaki sposób poszczególne
Zapis informacji, systemy pozycyjne 1. Literatura Jerzy Grębosz, Symfonia C++ standard. Harvey M. Deitl, Paul J. Deitl, Arkana C++. Programowanie.
 Zaps nformacj, systemy pozycyjne 1 Lteratura Jerzy Grębosz, Symfona C++ standard. Harvey M. Detl, Paul J. Detl, Arkana C++. Programowane. Zaps nformacj w komputerach Wszystke elementy danych przetwarzane
Zaps nformacj, systemy pozycyjne 1 Lteratura Jerzy Grębosz, Symfona C++ standard. Harvey M. Detl, Paul J. Detl, Arkana C++. Programowane. Zaps nformacj w komputerach Wszystke elementy danych przetwarzane
Analiza danych. Analiza danych wielowymiarowych. Regresja liniowa. Dyskryminacja liniowa. PARA ZMIENNYCH LOSOWYCH
 Analza danych Analza danych welowymarowych. Regresja lnowa. Dyskrymnacja lnowa. Jakub Wróblewsk jakubw@pjwstk.edu.pl http://zajeca.jakubw.pl/ PARA ZMIENNYCH LOSOWYCH Parę zmennych losowych X, Y możemy
Analza danych Analza danych welowymarowych. Regresja lnowa. Dyskrymnacja lnowa. Jakub Wróblewsk jakubw@pjwstk.edu.pl http://zajeca.jakubw.pl/ PARA ZMIENNYCH LOSOWYCH Parę zmennych losowych X, Y możemy
GENERACJA PRZEBIEGU SINUSOIDALNEGO.
 GENERACJA PRZEBIEGU SINUSOIDALNEGO. Podstawą generacji sygnału sinusoidalnego jest równanie różnicowe wyprowadzone w sposób następujący. Transmitancja układu generującego jest równa: Na wyjściu spodziewany
GENERACJA PRZEBIEGU SINUSOIDALNEGO. Podstawą generacji sygnału sinusoidalnego jest równanie różnicowe wyprowadzone w sposób następujący. Transmitancja układu generującego jest równa: Na wyjściu spodziewany
Metody rozwiązania równania Schrödingera
 Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
Analiza szeregów czasowych: 1. Dyskretna transformata Fouriera i zagadnienia pokrewne
 Analiza szeregów czasowych: 1. Dyskretna transformata Fouriera i zagadnienia pokrewne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 006/07 Plan wykładu Dyskretna transformata Fouriera,
Analiza szeregów czasowych: 1. Dyskretna transformata Fouriera i zagadnienia pokrewne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 006/07 Plan wykładu Dyskretna transformata Fouriera,
Problemy implementacji algorytmów FFT w strukturach FPGA 1)
 Problemy implementacji algorytmów FFT w strukturach FPGA 1) Robert Kędzierawski Wojskowa Akademia Techniczna, Wydział Elektroniki Streszczenie Omówiono implementacje algorytmów FFT dla przypadku przetwarzania
Problemy implementacji algorytmów FFT w strukturach FPGA 1) Robert Kędzierawski Wojskowa Akademia Techniczna, Wydział Elektroniki Streszczenie Omówiono implementacje algorytmów FFT dla przypadku przetwarzania
Szybka transformacja Fouriera
 Szybka transformacja Fouriera (Opis i wydruki programów) Instytut Astronomii UMK, Toruń 1976 2 K. Borkowski PROGRAM OBLICZANIA TRANSFORMAT FOURIERA Wstęp Prezentowany tutaj program przeznaczony jest do
Szybka transformacja Fouriera (Opis i wydruki programów) Instytut Astronomii UMK, Toruń 1976 2 K. Borkowski PROGRAM OBLICZANIA TRANSFORMAT FOURIERA Wstęp Prezentowany tutaj program przeznaczony jest do
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 1. Układy równań liniowych
 Zaawansowane metody numeryczne Komputerowa analza zagadneń różnczkowych 1. Układy równań lnowych P. F. Góra http://th-www.f.uj.edu.pl/zfs/gora/ semestr letn 2006/07 Podstawowe fakty Równane Ax = b, x,
Zaawansowane metody numeryczne Komputerowa analza zagadneń różnczkowych 1. Układy równań lnowych P. F. Góra http://th-www.f.uj.edu.pl/zfs/gora/ semestr letn 2006/07 Podstawowe fakty Równane Ax = b, x,
Przedmowa Wykaz oznaczeń Wykaz skrótów 1. Sygnały i ich parametry 1 1.1. Pojęcia podstawowe 1 1.2. Klasyfikacja sygnałów 2 1.3.
 Przedmowa Wykaz oznaczeń Wykaz skrótów 1. Sygnały i ich parametry 1 1.1. Pojęcia podstawowe 1 1.2. Klasyfikacja sygnałów 2 1.3. Sygnały deterministyczne 4 1.3.1. Parametry 4 1.3.2. Przykłady 7 1.3.3. Sygnały
Przedmowa Wykaz oznaczeń Wykaz skrótów 1. Sygnały i ich parametry 1 1.1. Pojęcia podstawowe 1 1.2. Klasyfikacja sygnałów 2 1.3. Sygnały deterministyczne 4 1.3.1. Parametry 4 1.3.2. Przykłady 7 1.3.3. Sygnały
Grafika Komputerowa Wykład 2. Przetwarzanie obrazów. mgr inż. Michał Chwesiuk 1/38
 Wykład 2 Przetwarzanie obrazów mgr inż. 1/38 Przetwarzanie obrazów rastrowych Jedna z dziedzin cyfrowego obrazów rastrowych. Celem przetworzenia obrazów rastrowych jest użycie edytujących piksele w celu
Wykład 2 Przetwarzanie obrazów mgr inż. 1/38 Przetwarzanie obrazów rastrowych Jedna z dziedzin cyfrowego obrazów rastrowych. Celem przetworzenia obrazów rastrowych jest użycie edytujących piksele w celu
Opis efektów kształcenia dla modułu zajęć
 Nazwa modułu: Teoria i przetwarzanie sygnałów Rok akademicki: 2013/2014 Kod: EEL-1-524-s Punkty ECTS: 6 Wydział: Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Kierunek: Elektrotechnika
Nazwa modułu: Teoria i przetwarzanie sygnałów Rok akademicki: 2013/2014 Kod: EEL-1-524-s Punkty ECTS: 6 Wydział: Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej Kierunek: Elektrotechnika
Metody analizy obwodów
 Metody analzy obwodów Metoda praw Krchhoffa, która jest podstawą dla pozostałych metod Metoda transfguracj, oparte na przekształcenach analzowanego obwodu na obwód równoważny Metoda superpozycj Metoda
Metody analzy obwodów Metoda praw Krchhoffa, która jest podstawą dla pozostałych metod Metoda transfguracj, oparte na przekształcenach analzowanego obwodu na obwód równoważny Metoda superpozycj Metoda
Kompresja video (MPEG)
 mgr inż. Grzegorz Kraszewski SYSTEMY MULTIMEDIALNE wykład 8, strona 1. Kompresja video (MEG) Zasadniczy schemat kompresora video Typy ramek przy kompresji czasowej Analiza ramek przez syntezę Sposób detekcji
mgr inż. Grzegorz Kraszewski SYSTEMY MULTIMEDIALNE wykład 8, strona 1. Kompresja video (MEG) Zasadniczy schemat kompresora video Typy ramek przy kompresji czasowej Analiza ramek przez syntezę Sposób detekcji
Katedra Elektrotechniki Teoretycznej i Informatyki
 Katedra Elektrotechniki Teoretycznej i Inormatyki Przedmiot: Zintegrowane Pakiety Obliczeniowe W Zastosowaniach InŜynierskich umer ćwiczenia: 7 Temat: Wprowadzenie do Signal Processing Toolbox 1. PRÓBKOWAIE
Katedra Elektrotechniki Teoretycznej i Inormatyki Przedmiot: Zintegrowane Pakiety Obliczeniowe W Zastosowaniach InŜynierskich umer ćwiczenia: 7 Temat: Wprowadzenie do Signal Processing Toolbox 1. PRÓBKOWAIE
CYFROWE PRZTWARZANIE SYGNAŁÓW (Zastosowanie transformacji Fouriera)
 I. Wprowadzenie do ćwiczenia CYFROWE PRZTWARZANIE SYGNAŁÓW (Zastosowanie transformacji Fouriera) Ogólnie termin przetwarzanie sygnałów odnosi się do nauki analizowania zmiennych w czasie procesów fizycznych.
I. Wprowadzenie do ćwiczenia CYFROWE PRZTWARZANIE SYGNAŁÓW (Zastosowanie transformacji Fouriera) Ogólnie termin przetwarzanie sygnałów odnosi się do nauki analizowania zmiennych w czasie procesów fizycznych.
Stanisław Cichocki. Natalia Nehrebecka. Wykład 6
 Stansław Cchock Natala Nehrebecka Wykład 6 1 1. Zastosowane modelu potęgowego Model potęgowy Przekształcene Boxa-Coxa 2. Zmenne cągłe za zmenne dyskretne 3. Interpretacja parametrów przy zmennych dyskretnych
Stansław Cchock Natala Nehrebecka Wykład 6 1 1. Zastosowane modelu potęgowego Model potęgowy Przekształcene Boxa-Coxa 2. Zmenne cągłe za zmenne dyskretne 3. Interpretacja parametrów przy zmennych dyskretnych
Sieci neuronowe - projekt
 Sieci neuronowe - projekt Maciej Barański, Kamil Dadel 15 stycznia 2015 Streszczenie W ramach projektu został zrealizowany algorytm kompresji stratnej bazujący na działaniu samoorganizującej się sieci
Sieci neuronowe - projekt Maciej Barański, Kamil Dadel 15 stycznia 2015 Streszczenie W ramach projektu został zrealizowany algorytm kompresji stratnej bazujący na działaniu samoorganizującej się sieci
Wyznaczenie współczynnika podziału kwasu octowego pomiędzy fazą organiczną a wodną
 Ćwzene 13 Wyznazene współzynnka podzału kwasu otowego pomędzy fazą anzną a wodną Cel ćwzena Celem ćwzena jest wyznazene współzynnka podzału kwasu otowego pomędzy fazą anzną (butanolem) a wodną w oparu
Ćwzene 13 Wyznazene współzynnka podzału kwasu otowego pomędzy fazą anzną a wodną Cel ćwzena Celem ćwzena jest wyznazene współzynnka podzału kwasu otowego pomędzy fazą anzną (butanolem) a wodną w oparu
Filtracja obrazów. w dziedzinie częstotliwości. w dziedzinie przestrzennej
 Filtracja obrazów w dziedzinie częstotliwości w dziedzinie przestrzennej filtry liniowe filtry nieliniowe Filtracja w dziedzinie częstotliwości Obraz oryginalny FFT2 IFFT2 Obraz po filtracji f(x,y) H(u,v)
Filtracja obrazów w dziedzinie częstotliwości w dziedzinie przestrzennej filtry liniowe filtry nieliniowe Filtracja w dziedzinie częstotliwości Obraz oryginalny FFT2 IFFT2 Obraz po filtracji f(x,y) H(u,v)
Laboratorium Przetwarzania Sygnałów
 PTS - laboratorium Laboratorium Przetwarzania Sygnałów Ćwiczenie 4 Transformacja falkowa Opracował: - prof. dr hab. inż. Krzysztof Kałużyński Zakład Inżynierii Biomedycznej Instytut Metrologii i Inżynierii
PTS - laboratorium Laboratorium Przetwarzania Sygnałów Ćwiczenie 4 Transformacja falkowa Opracował: - prof. dr hab. inż. Krzysztof Kałużyński Zakład Inżynierii Biomedycznej Instytut Metrologii i Inżynierii
Kompresja Kodowanie arytmetyczne. Dariusz Sobczuk
 Kompresja Kodowanie arytmetyczne Dariusz Sobczuk Kodowanie arytmetyczne (lata 1960-te) Pierwsze prace w tym kierunku sięgają początków lat 60-tych XX wieku Pierwszy algorytm Eliasa nie został opublikowany
Kompresja Kodowanie arytmetyczne Dariusz Sobczuk Kodowanie arytmetyczne (lata 1960-te) Pierwsze prace w tym kierunku sięgają początków lat 60-tych XX wieku Pierwszy algorytm Eliasa nie został opublikowany
Zasady wyznaczania minimalnej wartości środków pobieranych przez uczestników od osób zlecających zawarcie transakcji na rynku terminowym
 Załązn nr 3 Do zzegółowyh Zasad rowadzena Rozlzeń Transa rzez KDW_CC Zasady wyznazana mnmalne wartoś środów oberanyh rzez uzestnów od osób zleaąyh zaware transa na rynu termnowym 1. Metodologa wyznazana
Załązn nr 3 Do zzegółowyh Zasad rowadzena Rozlzeń Transa rzez KDW_CC Zasady wyznazana mnmalne wartoś środów oberanyh rzez uzestnów od osób zleaąyh zaware transa na rynu termnowym 1. Metodologa wyznazana
Joint Photographic Experts Group
 Joint Photographic Experts Group Artur Drozd Uniwersytet Jagielloński 14 maja 2010 1 Co to jest JPEG? Dlaczego powstał? 2 Transformata Fouriera 3 Dyskretna transformata kosinusowa (DCT-II) 4 Kodowanie
Joint Photographic Experts Group Artur Drozd Uniwersytet Jagielloński 14 maja 2010 1 Co to jest JPEG? Dlaczego powstał? 2 Transformata Fouriera 3 Dyskretna transformata kosinusowa (DCT-II) 4 Kodowanie
Algorytmy i struktury danych. wykład 9
 Plan wykładu:. Algorytmy numeryczne. Funkcja skrótu jest to funkcja H, która dla do dowolnej informacji m przyporządkowuje niespecyficzną wartość h, mającą cechy pseudolosowe. Cechy: skróty są zazwyczaj
Plan wykładu:. Algorytmy numeryczne. Funkcja skrótu jest to funkcja H, która dla do dowolnej informacji m przyporządkowuje niespecyficzną wartość h, mającą cechy pseudolosowe. Cechy: skróty są zazwyczaj
Algorytmy i struktury danych. Co dziś? Tytułem przypomnienia metoda dziel i zwyciężaj. Wykład VIII Elementarne techniki algorytmiczne
 Algorytmy i struktury danych Wykład VIII Elementarne techniki algorytmiczne Co dziś? Algorytmy zachłanne (greedyalgorithms) 2 Tytułem przypomnienia metoda dziel i zwyciężaj. Problem można podzielić na
Algorytmy i struktury danych Wykład VIII Elementarne techniki algorytmiczne Co dziś? Algorytmy zachłanne (greedyalgorithms) 2 Tytułem przypomnienia metoda dziel i zwyciężaj. Problem można podzielić na
Micha Strzelecki Metody przetwarzania i analizy obrazów biomedycznych (2)
 Micha Strzelecki Metody przetwarzania i analizy obrazów biomedycznych (2) Prezentacja multimedialna współfinansowana przez Unię Europejską w ramach Europejskiego Funduszu Społecznego w projekcie Innowacyjna
Micha Strzelecki Metody przetwarzania i analizy obrazów biomedycznych (2) Prezentacja multimedialna współfinansowana przez Unię Europejską w ramach Europejskiego Funduszu Społecznego w projekcie Innowacyjna
Podstawy teorii falek (Wavelets)
 Podstawy teor falek (Wavelets) Ψ(). Transformaca Haara (97).. Przykład pewne metody zapsu obrazu Transformaca Haara Przykład zapsu obrazu -D Podstawy matematyczne transformac Algorytmy rozkładana funkc
Podstawy teor falek (Wavelets) Ψ(). Transformaca Haara (97).. Przykład pewne metody zapsu obrazu Transformaca Haara Przykład zapsu obrazu -D Podstawy matematyczne transformac Algorytmy rozkładana funkc
METODA ELEMENTU SKOŃCZONEGO. Termokinetyka
 METODA ELEMENTU SKOŃCZONEGO Termoknetyka Matematyczny ops ruchu cepła (1) Zasada zachowana energ W a Cepło akumulowane, [J] P we Moc wejścowa, [W] P wy Moc wyjścowa, [W] t przedzał czasu, [s] V q S(V)
METODA ELEMENTU SKOŃCZONEGO Termoknetyka Matematyczny ops ruchu cepła (1) Zasada zachowana energ W a Cepło akumulowane, [J] P we Moc wejścowa, [W] P wy Moc wyjścowa, [W] t przedzał czasu, [s] V q S(V)
Metody numeryczne. Wykład nr 7. dr hab. Piotr Fronczak
 Metody numeryzne Wyłd nr 7 dr. Potr Fronz Cłowne numeryzne Cłowne numeryzne to przylżone olzne łe oznzony. Metody łown numeryznego polegją n przylżenu ł z pomoą odpowednej sumy wżonej wrtoś łownej unj
Metody numeryzne Wyłd nr 7 dr. Potr Fronz Cłowne numeryzne Cłowne numeryzne to przylżone olzne łe oznzony. Metody łown numeryznego polegją n przylżenu ł z pomoą odpowednej sumy wżonej wrtoś łownej unj
ANEMOMETRIA LASEROWA
 1 Wstęp ANEMOMETRIA LASEROWA Anemometria laserowa pozwala na bezdotykowy pomiar prędkośi zastezek (elementów) rozpraszajayh światło Źródłem światła jest laser, którego wiazka jest dzielona się nadwiewiazki
1 Wstęp ANEMOMETRIA LASEROWA Anemometria laserowa pozwala na bezdotykowy pomiar prędkośi zastezek (elementów) rozpraszajayh światło Źródłem światła jest laser, którego wiazka jest dzielona się nadwiewiazki
Algorytmy detekcji częstotliwości podstawowej
 Algorytmy detekcji częstotliwości podstawowej Plan Definicja częstotliwości podstawowej Wybór ramki sygnału do analizy Błędy oktawowe i dokładnej estymacji Metody detekcji częstotliwości podstawowej czasowe
Algorytmy detekcji częstotliwości podstawowej Plan Definicja częstotliwości podstawowej Wybór ramki sygnału do analizy Błędy oktawowe i dokładnej estymacji Metody detekcji częstotliwości podstawowej czasowe
CYFROWE PRZETWARZANIE SYGNAŁÓW
 Cyfrowe przetwarzanie sygnałów -1-2003 CYFROWE PRZETWARZANIE SYGNAŁÓW tematy wykładowe: ( 28 godz. +2godz. kolokwium, test?) 1. Sygnały i systemy dyskretne (LTI, SLS) 1.1. Systemy LTI ( SLS ) (definicje
Cyfrowe przetwarzanie sygnałów -1-2003 CYFROWE PRZETWARZANIE SYGNAŁÓW tematy wykładowe: ( 28 godz. +2godz. kolokwium, test?) 1. Sygnały i systemy dyskretne (LTI, SLS) 1.1. Systemy LTI ( SLS ) (definicje
Metody Numeryczne 2017/2018
 Metody Nueryzne 7/8 II rok Inforatyka Stosowana Inżynera Oblzenowa Wykład Przedot odelowań ateatyznyh. Jak na baze praw fzyk sforułować odel ateatyzny pozwalająy na syulaję zahowana sę obektów systeów
Metody Nueryzne 7/8 II rok Inforatyka Stosowana Inżynera Oblzenowa Wykład Przedot odelowań ateatyznyh. Jak na baze praw fzyk sforułować odel ateatyzny pozwalająy na syulaję zahowana sę obektów systeów
Kodowanie transformujace. Kompresja danych. Tomasz Jurdziński. Wykład 11: Transformaty i JPEG
 Tomasz Wykład 11: Transformaty i JPEG Idea kodowania transformujacego Etapy kodowania 1 Wektor danych x 0,...,x N 1 przekształcamy (odwracalnie!) na wektor c 0,...,c N 1, tak aby: energia była skoncentrowana
Tomasz Wykład 11: Transformaty i JPEG Idea kodowania transformujacego Etapy kodowania 1 Wektor danych x 0,...,x N 1 przekształcamy (odwracalnie!) na wektor c 0,...,c N 1, tak aby: energia była skoncentrowana
Podstawy Automatyki. Wykład 6 - Miejsce i rola regulatora w układzie regulacji. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 6 - Miejsce i rola regulatora w układzie regulacji Instytut Automatyki i Robotyki Warszawa, 2015 Regulacja zadajnik regulator sygnał sterujący (sterowanie) zespół wykonawczy przetwornik pomiarowy
Wykład 6 - Miejsce i rola regulatora w układzie regulacji Instytut Automatyki i Robotyki Warszawa, 2015 Regulacja zadajnik regulator sygnał sterujący (sterowanie) zespół wykonawczy przetwornik pomiarowy
Ćwiczenie: Własności dyskretnej transformaty Fouriera (DFT)
 Opracował: dr hab. inż. G. Stępniak Ćwiczenie: Własności dyskretnej transformaty Fouriera (DFT) Dyskretna transformata Fouriera (DFT ang. discrete Fourier Transform) to jedno z podstawowych narzędzi w
Opracował: dr hab. inż. G. Stępniak Ćwiczenie: Własności dyskretnej transformaty Fouriera (DFT) Dyskretna transformata Fouriera (DFT ang. discrete Fourier Transform) to jedno z podstawowych narzędzi w
Teoria sygnałów Signal Theory. Elektrotechnika I stopień (I stopień / II stopień) ogólnoakademicki (ogólno akademicki / praktyczny)
 . KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013 Teoria sygnałów Signal Theory A. USYTUOWANIE MODUŁU W SYSTEMIE STUDIÓW
. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013 Teoria sygnałów Signal Theory A. USYTUOWANIE MODUŁU W SYSTEMIE STUDIÓW
Praca dyplomowa magisterska
 Praca dyplomowa magisterska Implementacja algorytmów filtracji adaptacyjnej o strukturze transwersalnej na platformie CUDA Dyplomant: Jakub Kołakowski Opiekun pracy: dr inż. Michał Meller Plan prezentacji
Praca dyplomowa magisterska Implementacja algorytmów filtracji adaptacyjnej o strukturze transwersalnej na platformie CUDA Dyplomant: Jakub Kołakowski Opiekun pracy: dr inż. Michał Meller Plan prezentacji
FPGA IMPLEMENTATION OF FAST FOURIER TRANSFORM ALGORITHM IMPLEMENTACJA ALGORYTMU SZYBKIEJ TRANSFORMATY FOURIERA W UKŁADZIE PROGRAMOWALNYM FPGA
 Inż. Arkadiusz Pantoł IV rok Koło Naukowe Techniki Cyfrowej dr inż. Wojciech Mysiński opiekun naukowy FPGA IMPLEMENTATION OF FAST FOURIER TRANSFORM ALGORITHM IMPLEMENTACJA ALGORYTMU SZYBKIEJ TRANSFORMATY
Inż. Arkadiusz Pantoł IV rok Koło Naukowe Techniki Cyfrowej dr inż. Wojciech Mysiński opiekun naukowy FPGA IMPLEMENTATION OF FAST FOURIER TRANSFORM ALGORITHM IMPLEMENTACJA ALGORYTMU SZYBKIEJ TRANSFORMATY
Komputerowe Przetwarzanie Obrazów Szybka Transformata Fouriera. 1. Generowanie sygnałów 1D o różnych częstotliwościach oraz dodawanie szumu.
 Komputerowe Przetwarzanie Obrazów Szybka Transformata Fouriera 1. Generowanie sygnałów 1D o różnych częstotliwościach oraz dodawanie szumu. t = 0:0.001:2; x1 = sin( 3*pi*2*t ); plot(t,x1) title('czestotliwosc
Komputerowe Przetwarzanie Obrazów Szybka Transformata Fouriera 1. Generowanie sygnałów 1D o różnych częstotliwościach oraz dodawanie szumu. t = 0:0.001:2; x1 = sin( 3*pi*2*t ); plot(t,x1) title('czestotliwosc
Podstawy Automatyki. wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak. Politechnika Wrocławska. Instytut Technologii Maszyn i Automatyzacji (I-24)
 Podstawy Automatyki wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak Politechnika Wrocławska Instytut Technologii Maszyn i Automatyzacji (I-24) Laboratorium Podstaw Automatyzacji (L6) 105/2 B1 Sprawy organizacyjne
Podstawy Automatyki wykład 1 (26.02.2010) mgr inż. Łukasz Dworzak Politechnika Wrocławska Instytut Technologii Maszyn i Automatyzacji (I-24) Laboratorium Podstaw Automatyzacji (L6) 105/2 B1 Sprawy organizacyjne
Sortowanie szybkie Quick Sort
 Sortowane szybke Quck Sort Algorytm sortowana szybkego opera sę na strateg "dzel zwycęża" (ang. dvde and conquer), którą możemy krótko scharakteryzować w trzech punktach: 1. DZIEL - problem główny zostae
Sortowane szybke Quck Sort Algorytm sortowana szybkego opera sę na strateg "dzel zwycęża" (ang. dvde and conquer), którą możemy krótko scharakteryzować w trzech punktach: 1. DZIEL - problem główny zostae
Instrukcja do laboratorium z cyfrowego przetwarzania sygnałów. Wybrane właściwości Dyskretnej Transformacji Fouriera
 Instrukcja do laboratorium z cyfrowego przetwarzania sygnałów Wybrane właściwości Dyskretnej Transformacji Fouriera Przemysław Korohoda, KE, AGH Zawartość instrukcji: 1 Materiał z zakresu DSP 1.1 Macierzowy
Instrukcja do laboratorium z cyfrowego przetwarzania sygnałów Wybrane właściwości Dyskretnej Transformacji Fouriera Przemysław Korohoda, KE, AGH Zawartość instrukcji: 1 Materiał z zakresu DSP 1.1 Macierzowy
Kompresja Danych. Streszczenie Studia Dzienne Wykład 13, f(t) = c n e inω0t, T f(t)e inω 0t dt.
 1 Kodowanie podpasmowe Kompresja Danych Streszczenie Studia Dzienne Wykład 13, 18.05.2006 1.1 Transformaty, próbkowanie i filtry Korzystamy z faktów: Każdą funkcję okresową można reprezentować w postaci
1 Kodowanie podpasmowe Kompresja Danych Streszczenie Studia Dzienne Wykład 13, 18.05.2006 1.1 Transformaty, próbkowanie i filtry Korzystamy z faktów: Każdą funkcję okresową można reprezentować w postaci
Krótki przegląd pierwszych standardów kompresji obrazów
 Krótki przegląd pierwszych standardów kompresji obrazów Najstarszymi (980 rok) i szeroko stosowanymi obecnie standardami kompresji obrazów cyfrowych są międzynarodowe standardy kodowania cyfrowych faksów,
Krótki przegląd pierwszych standardów kompresji obrazów Najstarszymi (980 rok) i szeroko stosowanymi obecnie standardami kompresji obrazów cyfrowych są międzynarodowe standardy kodowania cyfrowych faksów,
Badanie współzależności dwóch cech ilościowych X i Y. Analiza korelacji prostej
 Badane współzależnośc dwóch cech loścowych X Y. Analza korelacj prostej Kody znaków: żółte wyróżnene nowe pojęce czerwony uwaga kursywa komentarz 1 Zagadnena 1. Zwązek determnstyczny (funkcyjny) a korelacyjny.
Badane współzależnośc dwóch cech loścowych X Y. Analza korelacj prostej Kody znaków: żółte wyróżnene nowe pojęce czerwony uwaga kursywa komentarz 1 Zagadnena 1. Zwązek determnstyczny (funkcyjny) a korelacyjny.


