Nr3 JEDNOPŁASZCZYZNOWY
|
|
|
- Magda Sowa
- 8 lat temu
- Przeglądów:
Transkrypt
1 Ruch obrotwy południkowy kul widocznych FRAKTALA KULOWEGO, jednopłaszczyznowego - z pliku B.Zeszyt.030. pł.(yz) pł.(yz) pł.(yz) FRAKTAL KULOWY Nr2 FRAKTAL KULOWY Nr3 FRAKTAL KULOWY JEDNOPŁASZCZYZNOWY JEDNOPŁASZCZYZNOWY JEDNOPŁASZCZYZNOWY 24h 0h 24h 0h 1h 24h 0h Nr1 str.1 14h 13h Nr3 pł.(yz) pł.(yz) pł.(yz) FRAKTAL KULOWY Nr4 FRAKTAL KULOWY Nr5 FRAKTAL KULOWY JEDNOPŁASZCZYZNOWY JEDNOPŁASZCZYZNOWY JEDNOPŁASZCZYZNOWY 3h 4h 14h 1 15h Nr5 pł.(yz) pł.(yz) (24h) pł.(yz) FRAKTAL KULOWY Nr6 FRAKTAL KULOWY Nr7 FRAKTAL KULOWY JEDNOPŁASZCZYZNOWY JEDNOPŁASZCZYZNOWY JEDNOPŁASZCZYZNOWY 4h 5h 1 17h liniał poziomy Wykonałem ruch obrotowy południkowego fraktala kulowego w technice (). Fraktal kulowy powstał w pliku: Zeszyt.030. Jest tam "fraktalem martwym" opisanym ciągiem liczbowym rosnącym i malejącym. Zapisany: 13^n, gdzie n=0; 1; 2; 3 (rosnący) i n=0; -1; ; -2; -3 (malejący). Jedynie, co zasługuje na uwagę, powiązałem go z fraktalem sześciennym. To wszystko. Zatem uważam taki fraktal, za "martwy fraktal". Fraktal wg mnie powinien być pokazany w różnych pozycjach. Wtedy będzie "fraktalem żywym" łatwiej kojarzonym. Przy ruchu obrotowym południkowym korzystałem z przy T rządów, w tym z choinek. To dzięki choinkom udało mi się wykonać ruch obrotowy południkowy w godz. od do (24h). Romana - imię mojej małżonki Koszalin dnia r
2 Ruch obrotowy równoleżnikowy kul FRAKTALA KULOWEGO, po ruchu południkowym na największym przekroju kuli. str.2 pł.(yz) pł.(yz) Nr1a Największa płaszczyzna w kuli Nr1b Po obrocie o kąt 90 w osi pion.(z) pojedyńcza 1 Pięć kul na tej samej płaszczyźnie w dużej kuli. Nr kula pojed. Nr2 pł.(yz) pł.(yz) Nr2a Ruch równoleżnikowy Nr2b 1 Największa płaszczyzna w kuli 24h 0h 1h 24h 0h 1 24h 0h 1h kula kula h 13h Nr3 pł.(yz) pł.(yz) Nr3a Ruch równoleżnikowy 1 24h 0h 24h 0h 1 24h 0h kula h h T Koszalin dnia r
3 Ruch obrotowy równoleżnikowy kul FRAKTALA KULOWEGO, po ruchu południkowym na największym przekroju kuli. pł.(yz) pł.(yz) Nr4a Ruch równoleżnikowy Nr4b Nr4 1 zakryta 24h 0h 8 24h 0h 1 24h 0h 9 6 3h 3h 7 str h h Nr5 pł.(yz) pł.(yz) Nr5a Ruch równoleżnikowy Nr5b 2 24h 0h 24h 0h 1 24h 0h h 4h zakryta Nr6 pł.(yz) pł.(yz) Nr6a Ruch równoleżnikowy Nr6b 1 24h 0h 24h 0h 1 24h 0h h 5h 17h 17h 17h T Koszalin dnia r
4 Ruch obrotowy równoleżnikowy kul FRAKTALA KULOWEGO, po ruchu południkowym na największym przekroju kuli. (24h) pł.(yz) (24h) pł.(yz) (24h) Nr7a Ruch równoleżnikowy Nr7b Nr7 Na pierwszy rzut oka, mogło by się wydawać, iż pokazanie w ruchu fraktala kulowego nie powinno mi sprawiać problemów. Okazało się jednak, że jest to zadanie nieco skomplikowane. Przede wszystkim chodzi o to, że są rozmieszczone w trzech płaszczyznach. Najwięcej, bo aż pięć kul znajduje się na płaszczyźnie średnicy kuli dużej (rys.nr1b). Poza tym są dwie inne płasz- czyzny, które są do siebie równolegle położone. Każda z płaszczyzn ma po cztery. Kule są rozmieszczone na przemian parami. Za niebieską kulą ukryta jest zielona kula (rysunki: od Nr1 do Nr7). Z kolei za zieloną kulą ukryta jest niebieska kula. W tym momencie muszę się zastanowić, jak wprowadzić rysunki ruchu równoleżnikowego bocznych płaszczyzn kul, w nawiązaniu do ich położenia przestrzennego, uzależnych od koleinych godzin na tarczy zegara (24h). W związku z tym problemem, będę się posługiwał logiką i analizą wyżej wykonanych rysunków. Być może stanie się tak, że w pewnym momencie sposób wrysowania po cztery w obu płaszczyznach stanie się jasne i oczywiste. Bo jak Państwo wiecie, wszystko, co znajdziecie w plikach wykonuję pierwszy raz. Jedyne wyjątki, to prace nad usunięciem błędów lub ewentualne uzupełnienia, komentarze. Przechodząc do sedna, muszę zauważyć, iż do tej pory to opracowanie przebiega sprawnie i klarownie. Wydaje mi się, że jest dla wszystkich zrozumiałe. RUCH RÓWNOLEŻNIKOWY (Będę posługiwał się numerami rysunków) ; str zakryta Dygresja. Przykład wynikający z logicznego myślenia. Stół czworonożny kwadratowy, czy prostokątny ma zawsze cztery nogi (podparcia). Co się stanie, gdy zabraknie jednej nogi? Odpowiedź prosta. Musimy ją dorobić i wstawić we właściwym miejscu. Tak też zamierzam zrobić z obu pł. Po obrocie o kąt 90 w osi pion.(z) Nr1b Nr1b Pięć kul na tej samej płaszczyźnie w dużej kuli. Cztery punkty centralne kul dla ośmiu kul. Nr1b kula ; ; ; T Koszalin dnia r
5 Nr2b RUCH RÓWNOLEŻNIKOWY (Będę posługiwał się numerami rysunków) Nr2b Nr2b str h 0h 1h 24h 0h 1h 24h 0h 1h 3 4 kula h 13h 13h ; ; ; h h h Nr4b Nr4b Nr4b 1 24h 0h 1 24h 0h 1 24h 0h 3h 3h 3h 3 15h h h T Koszalin dnia r
6 Nr5b RUCH RÓWNOLEŻNIKOWY (Będę posługiwał się numerami rysunków) Nr5b Nr5b 1 24h 0h 1 24h 0h 1 24h 0h str.6 4h 4h 4h Nr6b Nr6b Nr6b 1 24h 0h 1 24h 0h 1 24h 0h 5h 5h 5h 17h 17h 17h Nr7b (24h) Nr7b (24h) Nr7b (24h) ; ; ; zasłania kulę 8, a kula zasłania kulę 10 itd. Podobnie dotyczy to rys.nr1b. Kula 6 zasłania kulę 7, a kula a kula zasłania kulę 13. Teraz tylne. Kula 8 zasłania kulę 9, a kula 10 zasłania kulę 11. Proszę korzystać z tej instrukcji, bo łatwo się Państwo pogubicie. T dot.rys. (Nr1-Nr7) dot.rys. (Nr1b-Nr7b) To jedna z najtrudniejszych lekcji. dot.:str.7.rysunek poglądowy (oriętacyjny) do zrozumienia położenia rysunków kul w rzucie na pł.(xy) i na MAPĘ pł.(yz). Rys.pomocniczy A. Rys.pomocniczy B. Na rys.pomocniczym dot.rys.nr1 są zasłonięte : 6 8; 10; 7 9; To oznacza, że kula Koszalin dnia r
7 RUCH OBROTOWY WOKÓŁ OSI (Z).POZYCJA WYJŚCIOWA FRAKTALA KULOWEGO PRZESTEN. oś (Z) oś (Z) oś (Z) Nr1 Nr2 Nr3 Ruch obrot.płaszczyzn wokół osi (Z). Ruch obrot.płaszczyzn wokół osi (Z). Ruch obrot.płaszczyzn wokół osi (Z) h 0h h 0h h 0h str Nr1b pł.(xy) MAPA oś (Z) Nr2b pł.(xy) MAPA oś (Z) pł.(xy) MAPA oś (Z) Ruch obrot.płaszczyzn wokół osi (Z). Ruch obrot.płaszczyzn wokół osi (Z). Ruch obrot.płaszczyzn wokół osi (Z). 8 24h; h; 1h h; h h INSTRUKCJA pokazująca zasłonięte przez pierwsze. Rys.pomocniczy A. Rys.pomocniczy B pł.(yz) 8 10 pł.(xy) MAPA 7 13 dot.rys. (Nr1-Nr7) dot.rys. (Nr1b-Nr7b) A.Gdy patrzymy w poziomie. B.Gdy patrzymy pionowo z góry. Mając na względzie duże trudności z pokazaniem obrotu fraktala kulowego,przestrzennego wokół osi (Z), wprowadziłem rys.pomocnicze, które powinny ułatwić prace nad tego radzaju rysunkami. Nie znam przyszłości moich opracowań, związane z ruchem. Bo gdyby stały się popularne, wtedy trzeba opracować program, który byłby nieomylnie wskazywał miejsce posadowienia i kolejność kul. W podobny sposób, dla ułatwienia i przyspieszenia pracy, opracowałem "ZESTAW MIŁOSZA" do kosztorysowania izolacji termicznych pod blachę na rurociągach; zbiornikach; armaturze itd. Cel był zawsze ten sam, UPROŚCIĆ SOBIE ROBOTĘ, by się NIE NAROBIĆ. Postanowiłem zakończyć ten plik, ponieważ jest dla mnie zbyt męczący i wymaga niesamowitego skupienia. Jest po prostu trudny. Nawet dla mnie. Jednak, warto go poznać. To nie sztuka wykonać kreskówkę geometryczną, gdy jest często powielana. Sztuką jest pokazanie czegoś nowatorskiego z dostosowaniem odpowiedniej techniki T rysowania obrazów. Uprościłem tę wypowiedź, jako sztuka przekazu. Nieraz mówiłem, że wszystko robię pierwszy raz. Dodatkowo muszę wspomnieć o nowych elementach techniki opartej na przyrządach. Często roszerzam temat moich opracowań, gdy uznam, że może wzbudzić zainteresowanie pasjonatów. Dla młodych chcę pokazać samą puszkę (walec), która ma na swojej powierzchni cztery kropki. Po dwie w kolorze czerwonym i dwie w kolorze niebieskim. Oczywiście, puszka ma być przezroczysta. A teraz zwrócę się do Państwa. Jaką techniką należy się posłużyć, by narysować ruch obrotowy owej puszki (walca z naklejoną elipsą), wobec własnej osi pionowej (Z)? Kolejne pytanie. Jakie należy zastosować przyrządy stosowane w (), by praca była dobrze wykonana? PAŃSTWO MAJĄ JUŻ RYS.; ;, RESZTĘ TRZEBA DORYSOWAĆ. ŻYCZĘ CIERPLIWOŚCI. T Koszalin dnia r
Rys.5a. Grot stożka widziany jako trójkąt równoram. Dwa rysunki w jednym. W' 1h na kole Pkt W najbardziej. 23h na kole w4 2h na kole Ø3
 BRÓT KÓŁ SI (Z) GRTA STŻKEG SKRĘTNEG Z PLIKU SKRYPT (R).009.N NA GDZINIE (24h). Grot turbiny stożkowo-skrętny, ośmiołukowy.rys.powiększony 2*.Ruch obrotowy równoleżnikowy grota wokół osi (X) Rys.6a Rys.5a
BRÓT KÓŁ SI (Z) GRTA STŻKEG SKRĘTNEG Z PLIKU SKRYPT (R).009.N NA GDZINIE (24h). Grot turbiny stożkowo-skrętny, ośmiołukowy.rys.powiększony 2*.Ruch obrotowy równoleżnikowy grota wokół osi (X) Rys.6a Rys.5a
Rys.1 pomocniczy. Okrąg z którego powstały łuki na rys.1b.
 OBRÓT OKÓŁ OSI (Z) GROTA STOŻKOEGO SKRĘTNEGO Z PLIKU SKRYPT (R).9.N NA GOZINIE h(24h). str.1 Grot skrętny turbiny, ośmiołukowy, powiększony 2*. Rysunki pokazują wcześniej poznane metody przekazu wiedzy,
OBRÓT OKÓŁ OSI (Z) GROTA STOŻKOEGO SKRĘTNEGO Z PLIKU SKRYPT (R).9.N NA GOZINIE h(24h). str.1 Grot skrętny turbiny, ośmiołukowy, powiększony 2*. Rysunki pokazują wcześniej poznane metody przekazu wiedzy,
gk T Jak wykorzystać poznaną wiedzę na przyrządach geometrii kulowej (gk), w sposób praktyczny. Rys.2a
 Jak wykorzystać poznaną wiedzę na przyrządach geometrii kulowej (), w sposób praktyczny. str.1 Wpadłem na pomysł, by opracować schemat bryły biurowieca o ciekawej konstrukcji architektonicznej. Najciekawszą
Jak wykorzystać poznaną wiedzę na przyrządach geometrii kulowej (), w sposób praktyczny. str.1 Wpadłem na pomysł, by opracować schemat bryły biurowieca o ciekawej konstrukcji architektonicznej. Najciekawszą
400% Rys.2a Negatyw *** ZASADA *** Rys.1a Pozytyw pł.(yz) Zabawa "włosem" musi być oparta na OPIS WYKONYWANYCH CZYNNOŚCI.
 Szkic 1. `````2 2 str.1 PWIĘKSZ! 00% Rys.2a *** ZSD *** Rys.1a Pozytyw pł.(yz) Zabawa "włosem" musi być oparta na 0h() 12 dwóch rzutach prostokątnych, na dwie 12 płaszczyzny tj. MPĘ (XY) i pł.(yz). Powyższe
Szkic 1. `````2 2 str.1 PWIĘKSZ! 00% Rys.2a *** ZSD *** Rys.1a Pozytyw pł.(yz) Zabawa "włosem" musi być oparta na 0h() 12 dwóch rzutach prostokątnych, na dwie 12 płaszczyzny tj. MPĘ (XY) i pł.(yz). Powyższe
TABELA PRZELICZENIOWA
 Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował: inż. Kazimierz arski Romana - imię
Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował: inż. Kazimierz arski Romana - imię
gk T Rozwiązanie Zadania nr1 - uzupełnienie
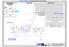 TRÓJKĄT LGICZNY - W NAWIĄZANIU D PLIKU: Skrypt (R).009.02. str.1 SZKIC RIENTACJI Rys.1 pł.(xz) PRZYKŁAD Nr 1 PRZESTRZENNEJ Moim celem jest pokazanie Państwu w jaki sposó zmienię położenie odcylone stożka
TRÓJKĄT LGICZNY - W NAWIĄZANIU D PLIKU: Skrypt (R).009.02. str.1 SZKIC RIENTACJI Rys.1 pł.(xz) PRZYKŁAD Nr 1 PRZESTRZENNEJ Moim celem jest pokazanie Państwu w jaki sposó zmienię położenie odcylone stożka
gk T GEOMETRIA WYKREŚLNA PRZESTRZENNA T (GK) W PRAKTYCE. SZTUKA TRASOWANIA CZ.1. Rys.3. Rys.4. Rysunek jest zbyt duży, zmniejszę go na str.2.
 GEOMERIA WYKREŚLNA PRZESRZENNA (GK) W PRAKYCE. SZUKA RASOWANIA CZ.1. str.1 Kiedyś od jakiegoś gościa otrzymałem emaila. Pytał mnie jakie należy stosować linie i jakie grubości tych linii. W końcu zapytał
GEOMERIA WYKREŚLNA PRZESRZENNA (GK) W PRAKYCE. SZUKA RASOWANIA CZ.1. str.1 Kiedyś od jakiegoś gościa otrzymałem emaila. Pytał mnie jakie należy stosować linie i jakie grubości tych linii. W końcu zapytał
23h 24h;0h(koła) 24[h]*15[ /h]=360[ ]
![23h 24h;0h(koła) 24[h]*15[ /h]=360[ ] 23h 24h;0h(koła) 24[h]*15[ /h]=360[ ]](/thumbs/53/31835593.jpg) Dla młodzieży. brót w kole dużych kropek w prawo, po jego obwodzie. Koło jest odchylone od pionu. W tym opracowaniu będę posługiwał się swoimi przyrządami stosowanymi w geometrii kulowej (). Nabyłem na
Dla młodzieży. brót w kole dużych kropek w prawo, po jego obwodzie. Koło jest odchylone od pionu. W tym opracowaniu będę posługiwał się swoimi przyrządami stosowanymi w geometrii kulowej (). Nabyłem na
TABELA PRZELICZENIOWA
 Romana - imię mojej małżonki Nr 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
Romana - imię mojej małżonki Nr 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
MAGAZYN WIEDZY NR 1 O GEOMETRII KULOWEJ. PROJEKT TWÓRCY (gk). PRZYPOMINA POMNIK. WALEC TRAPEZOWY Z KORYTEM KOŁO. Nr2 6h(48h) ELIPSA pionowa O
 MAGAZYN WIEDZY NR 1 GEMETRII KULWEJ. PRJEKT TWÓRCY (). PRZYPMINA PMNIK. str.1 Rys.1 Widziane KŁ Nr3 Widziana ELIPSA przy kierunku patrzenia 90 na jej centrum. Nr2 6h() ELIPSA pionowa WALEC TRAPEZWY Z KRYTEM
MAGAZYN WIEDZY NR 1 GEMETRII KULWEJ. PRJEKT TWÓRCY (). PRZYPMINA PMNIK. str.1 Rys.1 Widziane KŁ Nr3 Widziana ELIPSA przy kierunku patrzenia 90 na jej centrum. Nr2 6h() ELIPSA pionowa WALEC TRAPEZWY Z KRYTEM
Rys.1. str.1. 48h;0h 18h 19h 20h 21h 22h 46h. 44h r1 4h. 10h. 38h. 34h 14h. 32h 16h. 24h jest linią do przenoszenia szablonów
 Moje własne opracowanie torusa na przyrządach: tarczy zegara (48h); szablonu listwowego A. en rysunek ORUSA, będzie miał ostatecznie 48 promieni. str.1 Rys.1 N 48h;0h 18h 19h 20h 21h 22h 46h 2h 4h 6h 8h
Moje własne opracowanie torusa na przyrządach: tarczy zegara (48h); szablonu listwowego A. en rysunek ORUSA, będzie miał ostatecznie 48 promieni. str.1 Rys.1 N 48h;0h 18h 19h 20h 21h 22h 46h 2h 4h 6h 8h
Pokrywka. Rysunek 1. Projekt - wynik końcowy. Rysunek 2. Pierwsza linia łamana szkicu
 Pokrywka Rysunek 1. Projekt - wynik końcowy Projekt rozpoczynamy od narysowania zamkniętego szkicu. 1. Narysujemy i zwymiarujmy linię łamaną jako część szkicu (nie zamknięty), rys. 2. Uwaga: a) Dodajmy
Pokrywka Rysunek 1. Projekt - wynik końcowy Projekt rozpoczynamy od narysowania zamkniętego szkicu. 1. Narysujemy i zwymiarujmy linię łamaną jako część szkicu (nie zamknięty), rys. 2. Uwaga: a) Dodajmy
Własności walca, stożka i kuli.
 Własności walca, stożka i kuli. 1. Cele lekcji a) Wiadomości Uczeń: - zna pojęcie bryły obrotowej, - zna definicje: walca, stożka, kuli, - zna budowę brył obrotowych, - zna pojęcia związane z symetrią
Własności walca, stożka i kuli. 1. Cele lekcji a) Wiadomości Uczeń: - zna pojęcie bryły obrotowej, - zna definicje: walca, stożka, kuli, - zna budowę brył obrotowych, - zna pojęcia związane z symetrią
gk T Okrąg z punktami wg tarczy zegara (24h), przerobiony na turbinę obrotową. Uruchomienie fantazji. Rys.1 Rys.2
 krąg z punktami wg tarczy zegara (24h), przerobiony na turbinę obrotową. Uruchomienie fantazji. Rys.1 23h 1h 22h 2h str.1 21h 3h 20h 4h 19h 5h 18h 6h 17h 7h 16h 8h 15h 9h 14h 10h 13h 11h Rys.2 Szablon
krąg z punktami wg tarczy zegara (24h), przerobiony na turbinę obrotową. Uruchomienie fantazji. Rys.1 23h 1h 22h 2h str.1 21h 3h 20h 4h 19h 5h 18h 6h 17h 7h 16h 8h 15h 9h 14h 10h 13h 11h Rys.2 Szablon
RZUTOWANIE PROSTOKĄTNE
 RZUTOWANIE PROSTOKĄTNE wg PN-EN ISO 5456-2 rzutowanie prostokątne (przedstawienie prostokątne) stanowi odwzorowanie geometrycznej postaci konstrukcji w postaci rysunków dwuwymiarowych. Jest to taki rodzaj
RZUTOWANIE PROSTOKĄTNE wg PN-EN ISO 5456-2 rzutowanie prostokątne (przedstawienie prostokątne) stanowi odwzorowanie geometrycznej postaci konstrukcji w postaci rysunków dwuwymiarowych. Jest to taki rodzaj
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH
 STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
gk T Rys.5 pionowa oś WYDRĄŻONE KORYTO Rys.6 symetrii Ł łuk kąta 90 &1k &1p pionowa oś Cięciwa=2* 3= 83, [mm] symetrii
![gk T Rys.5 pionowa oś WYDRĄŻONE KORYTO Rys.6 symetrii Ł łuk kąta 90 &1k &1p pionowa oś Cięciwa=2* 3= 83, [mm] symetrii gk T Rys.5 pionowa oś WYDRĄŻONE KORYTO Rys.6 symetrii Ł łuk kąta 90 &1k &1p pionowa oś Cięciwa=2* 3= 83, [mm] symetrii](/thumbs/103/159774468.jpg) Należy się Państwu wyjaśnienie dotyczące znaku: literki C w kółeczku. Jest to znak certyfikatu. Na ten znak zapracowałem od momentu, gdy ponownie, tym razem ja, odkryłem KOŁO. Na początku była to nowa
Należy się Państwu wyjaśnienie dotyczące znaku: literki C w kółeczku. Jest to znak certyfikatu. Na ten znak zapracowałem od momentu, gdy ponownie, tym razem ja, odkryłem KOŁO. Na początku była to nowa
w jednym kwadrat ziemia powietrze równoboczny pięciobok
 Wielościany Definicja 1: Wielościanem nazywamy zbiór skończonej ilości wielokątów płaskich spełniających następujące warunki: 1. każde dwa wielokąty mają bok lub wierzchołek wspólny albo nie mają żadnego
Wielościany Definicja 1: Wielościanem nazywamy zbiór skończonej ilości wielokątów płaskich spełniających następujące warunki: 1. każde dwa wielokąty mają bok lub wierzchołek wspólny albo nie mają żadnego
COMENIUS PROJEKT ROZWOJU SZKOŁY. Sezamie, otwórz się! - rozwijanie zdolności uczenia i myślenia uczniów.
 COMENIUS PROJEKT ROZWOJU SZKOŁY Sezamie, otwórz się! - rozwijanie zdolności uczenia i myślenia uczniów. GIMNAZJUM 20 GDAŃSK POLSKA Maj 2007 SCENARIUSZ LEKCJI MATEMATYKI Z WYKORZYSTANIEM METODY STOLIKÓW
COMENIUS PROJEKT ROZWOJU SZKOŁY Sezamie, otwórz się! - rozwijanie zdolności uczenia i myślenia uczniów. GIMNAZJUM 20 GDAŃSK POLSKA Maj 2007 SCENARIUSZ LEKCJI MATEMATYKI Z WYKORZYSTANIEM METODY STOLIKÓW
Katalog wymagań programowych na poszczególne stopnie szkolne. Matematyka. Poznać, zrozumieć
 Katalog wymagań programowych na poszczególne stopnie szkolne Matematyka. Poznać, zrozumieć Kształcenie w zakresie rozszerzonym. Klasa 4 Poniżej podajemy umiejętności, jakie powinien zdobyć uczeń z każdego
Katalog wymagań programowych na poszczególne stopnie szkolne Matematyka. Poznać, zrozumieć Kształcenie w zakresie rozszerzonym. Klasa 4 Poniżej podajemy umiejętności, jakie powinien zdobyć uczeń z każdego
RZUTOWANIE PROSTOKĄTNE
 RZUTOWANIE PROSTOKĄTNE WPROWADZENIE Wykonywanie rysunku technicznego - zastosowanie Rysunek techniczny przedmiotu jest najczęściej podstawą jego wykonania, dlatego odwzorowywany przedmiot nie powinien
RZUTOWANIE PROSTOKĄTNE WPROWADZENIE Wykonywanie rysunku technicznego - zastosowanie Rysunek techniczny przedmiotu jest najczęściej podstawą jego wykonania, dlatego odwzorowywany przedmiot nie powinien
Rok akademicki 2005/2006
 GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2005/2006 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2005/2006 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
24h MAPA MAPA MAPA MAPA
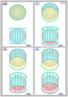 24h 1h str.1 2h 3h 4h 5h str.2 6h 7h 8h 9h str.3 10h 11h 12h 13h str.4 14h 15h 16h 17h str.5 18h 19h 20h 21h str.6 22h 23h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.7 gk
24h 1h str.1 2h 3h 4h 5h str.2 6h 7h 8h 9h str.3 10h 11h 12h 13h str.4 14h 15h 16h 17h str.5 18h 19h 20h 21h str.6 22h 23h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.7 gk
Geometria wykreślna. 5. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław. Politechnika Gdańska, Wydział Architektury
 Geometria wykreślna 5. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Architektura, semestr I 1 5. Obroty i
Geometria wykreślna 5. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Architektura, semestr I 1 5. Obroty i
MECHANIKA 2. Wykład Nr 3 KINEMATYKA. Temat RUCH PŁASKI BRYŁY MATERIALNEJ. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Wykład Nr 3 KINEMATYKA Temat RUCH PŁASKI BRYŁY MATERIALNEJ Prowadzący: dr Krzysztof Polko Pojęcie Ruchu Płaskiego Rys.1 Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie
MECHANIKA 2 Wykład Nr 3 KINEMATYKA Temat RUCH PŁASKI BRYŁY MATERIALNEJ Prowadzący: dr Krzysztof Polko Pojęcie Ruchu Płaskiego Rys.1 Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie
PUNKT PROSTA. Przy rysowaniu rzutów prostej zaczynamy od rzutowania punktów przebicia rzutni prostą (śladów). Następnie łączymy rzuty na π 1 i π 2.
 WYKŁAD 1 Wprowadzenie. Różne sposoby przedstawiania przedmiotu. Podstawy teorii zapisu konstrukcji w grafice inżynierskiej. Zasady rzutu prostokątnego. PUNKT Punkt w odwzorowaniach Monge a rzutujemy prostopadle
WYKŁAD 1 Wprowadzenie. Różne sposoby przedstawiania przedmiotu. Podstawy teorii zapisu konstrukcji w grafice inżynierskiej. Zasady rzutu prostokątnego. PUNKT Punkt w odwzorowaniach Monge a rzutujemy prostopadle
Zadanie I. 2. Gdzie w przestrzeni usytuowane są punkty (w której ćwiartce leży dany punkt): F x E' E''
 GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2012/2013 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2012/2013 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
WIDOKI I PRZEKROJE PRZEDMIOTÓW LINIE PRZENIKANIA BRYŁ
 Zapis i Podstawy Konstrukcji Widoki i przekroje przedmiotów 1 WIDOKI I PRZEKROJE PRZEDMIOTÓW LINIE PRZENIKANIA BRYŁ Rzutami przedmiotów mogą być zarówno widoki przestawiające zewnętrzne kształty przedmiotów
Zapis i Podstawy Konstrukcji Widoki i przekroje przedmiotów 1 WIDOKI I PRZEKROJE PRZEDMIOTÓW LINIE PRZENIKANIA BRYŁ Rzutami przedmiotów mogą być zarówno widoki przestawiające zewnętrzne kształty przedmiotów
Nie tylko wynik Plan wynikowy dla klasy 3 gimnazjum
 Poziomy wymagań edukacyjnych: K konieczny P podstawowy R rozszerzający D dopełniający W wykraczający Nie tylko wynik Plan wynikowy dla klasy 3 gimnazjum Statystyka opisowa i elementy rachunku prawdopodobieństwa
Poziomy wymagań edukacyjnych: K konieczny P podstawowy R rozszerzający D dopełniający W wykraczający Nie tylko wynik Plan wynikowy dla klasy 3 gimnazjum Statystyka opisowa i elementy rachunku prawdopodobieństwa
gk T Zadania nr 2. opracował: inż. Kazimierz Barski dla wszystkich ludzi świata TECHNIKA Koszalin dnia r
 ZNI O ROZWIĄZ. Z WOM UKŁMI PLNT, W KTÓRYH 7 ZY 8 PLNT KRĄŻY WOKÓŁ WÓH WIZ W WÓH PŁSZZYZNH. str.1 PYTNI Z INORMJMI: 1). dzie należy umieścić dwie gwiazdy, by odróżnić oba układy planetarne? 2). Pokazane
ZNI O ROZWIĄZ. Z WOM UKŁMI PLNT, W KTÓRYH 7 ZY 8 PLNT KRĄŻY WOKÓŁ WÓH WIZ W WÓH PŁSZZYZNH. str.1 PYTNI Z INORMJMI: 1). dzie należy umieścić dwie gwiazdy, by odróżnić oba układy planetarne? 2). Pokazane
Skrypt 20. Bryły: 24. Obliczanie pól powierzchni walców w sytuacjach praktycznych. 26. Zastosowanie tw. Pitagorasa do obliczania objętości walców
 Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 20 Bryły: 21. Przykłady brył obrotowych 22.
Projekt Innowacyjny program nauczania matematyki dla gimnazjów współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 20 Bryły: 21. Przykłady brył obrotowych 22.
1. Potęgi. Logarytmy. Funkcja wykładnicza
 1. Potęgi. Logarytmy. Funkcja wykładnicza Tematyka zajęć: WYMAGANIA EDUKACYJNE NA POSZCZEGÓLNE OCENY KL. 3 POZIOM PODSTAWOWY Potęga o wykładniku rzeczywistym powtórzenie Funkcja wykładnicza i jej własności
1. Potęgi. Logarytmy. Funkcja wykładnicza Tematyka zajęć: WYMAGANIA EDUKACYJNE NA POSZCZEGÓLNE OCENY KL. 3 POZIOM PODSTAWOWY Potęga o wykładniku rzeczywistym powtórzenie Funkcja wykładnicza i jej własności
Tomasz Tobiasz PLAN WYNIKOWY (zakres podstawowy)
 Tomasz Tobiasz PLAN WYNIKOWY (zakres podstawowy) klasa 3. PAZDRO Plan jest wykazem wiadomości i umiejętności, jakie powinien mieć uczeń ubiegający się o określone oceny na poszczególnych etapach edukacji
Tomasz Tobiasz PLAN WYNIKOWY (zakres podstawowy) klasa 3. PAZDRO Plan jest wykazem wiadomości i umiejętności, jakie powinien mieć uczeń ubiegający się o określone oceny na poszczególnych etapach edukacji
Numer artykułu: Zestaw do gry w bule. Instrukcja gry. Tchibo GmbH D Hamburg 95091AB2X3VIII
 Numer artykułu: 358 480 Zestaw do gry w bule pl Instrukcja gry Tchibo GmbH D-22290 Hamburg 950912X3VIII 2017-10 Drodzy Klienci! Gra w bule (boule) zwana również petanką jest jedną z najpopularniejszych
Numer artykułu: 358 480 Zestaw do gry w bule pl Instrukcja gry Tchibo GmbH D-22290 Hamburg 950912X3VIII 2017-10 Drodzy Klienci! Gra w bule (boule) zwana również petanką jest jedną z najpopularniejszych
Opis postępowania przy eksportowaniu geometrii z systemu Unigraphics NX do pakietu PANUKL (ver. A)
 1 Opis postępowania przy eksportowaniu geometrii z systemu Unigraphics NX do pakietu PANUKL (ver. A) Przedstawiony poniżej schemat przygotowania geometrii w systemie Unigraphics NX na potrzeby programu
1 Opis postępowania przy eksportowaniu geometrii z systemu Unigraphics NX do pakietu PANUKL (ver. A) Przedstawiony poniżej schemat przygotowania geometrii w systemie Unigraphics NX na potrzeby programu
PRZEKROJE RYSUNKOWE CZ.1 PRZEKROJE PROSTE. Opracował : Robert Urbanik Zespół Szkół Mechanicznych w Opolu
 PRZEKROJE RYSUNKOWE CZ.1 PRZEKROJE PROSTE Opracował : Robert Urbanik Zespół Szkół Mechanicznych w Opolu IDEA PRZEKROJU stosujemy, aby odzwierciedlić wewnętrzne, niewidoczne z zewnątrz, kształty przedmiotu.
PRZEKROJE RYSUNKOWE CZ.1 PRZEKROJE PROSTE Opracował : Robert Urbanik Zespół Szkół Mechanicznych w Opolu IDEA PRZEKROJU stosujemy, aby odzwierciedlić wewnętrzne, niewidoczne z zewnątrz, kształty przedmiotu.
WOJEWÓDZKI KONKURS MATEMATYCZNY
 Kod ucznia Liczba punktów WOJEWÓDZKI KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJÓW W ROKU SZKOLNYM 016/017 0.0.017 1. Test konkursowy zawiera zadania. Są to zadania zamknięte i otwarte. Na ich rozwiązanie
Kod ucznia Liczba punktów WOJEWÓDZKI KONKURS MATEMATYCZNY DLA UCZNIÓW GIMNAZJÓW W ROKU SZKOLNYM 016/017 0.0.017 1. Test konkursowy zawiera zadania. Są to zadania zamknięte i otwarte. Na ich rozwiązanie
Wykorzystanie programu Paint na lekcjach matematyki w nauczaniu zintegrowanym
 Hanna Łukasiewicz HaniaLukasiewicz@interia.pl. Wykorzystanie programu Paint na lekcjach matematyki w nauczaniu zintegrowanym "Technologia informacyjna może wspomagać i wzbogacać wszechstronny rozwój uczniów,
Hanna Łukasiewicz HaniaLukasiewicz@interia.pl. Wykorzystanie programu Paint na lekcjach matematyki w nauczaniu zintegrowanym "Technologia informacyjna może wspomagać i wzbogacać wszechstronny rozwój uczniów,
Co należy zauważyć Rzuty punktu leżą na jednej prostej do osi rzutów x 12, którą nazywamy prostą odnoszącą Wysokość punktu jest odległością rzutu
 Oznaczenia A, B, 1, 2, I, II, punkty a, b, proste α, β, płaszczyzny π 1, π 2, rzutnie k kierunek rzutowania d(a,m) odległość punktu od prostej m(a,b) prosta przechodząca przez punkty A i B α(1,2,3) płaszczyzna
Oznaczenia A, B, 1, 2, I, II, punkty a, b, proste α, β, płaszczyzny π 1, π 2, rzutnie k kierunek rzutowania d(a,m) odległość punktu od prostej m(a,b) prosta przechodząca przez punkty A i B α(1,2,3) płaszczyzna
Ćwiczenie nr 5 i 6 Przygotowanie dokumentacji technicznej dla brył
 Ćwiczenie nr 5 i 6 Przygotowanie dokumentacji technicznej dla brył Zadanie A Celem będzie wykonanie rysunku pokazanego NA KOŃCU zadania. Rysując proszę się posłużyć podanymi tam wymiarami. Pamiętajmy o
Ćwiczenie nr 5 i 6 Przygotowanie dokumentacji technicznej dla brył Zadanie A Celem będzie wykonanie rysunku pokazanego NA KOŃCU zadania. Rysując proszę się posłużyć podanymi tam wymiarami. Pamiętajmy o
Test na koniec nauki w klasie trzeciej gimnazjum
 8 Test na koniec nauki w klasie trzeciej gimnazjum imię i nazwisko ucznia...... data klasa Test 2 1 Na przeciwległych ścianach każdej z pięciu sześciennych kostek umieszczono odpowiednio liczby: 1 i 1,
8 Test na koniec nauki w klasie trzeciej gimnazjum imię i nazwisko ucznia...... data klasa Test 2 1 Na przeciwległych ścianach każdej z pięciu sześciennych kostek umieszczono odpowiednio liczby: 1 i 1,
RZUT CECHOWANY DACHY, NASYPY, WYKOPY
 WYZNACZANIE DACHÓW: RZUT CECHOWANY DACHY, NASYPY, WYKOPY Ograniczymy się do dachów złożonych z płaskich wielokątów nazywanych połaciami, z linią okapu (linią utworzoną przez swobodne brzegi połaci) w postaci
WYZNACZANIE DACHÓW: RZUT CECHOWANY DACHY, NASYPY, WYKOPY Ograniczymy się do dachów złożonych z płaskich wielokątów nazywanych połaciami, z linią okapu (linią utworzoną przez swobodne brzegi połaci) w postaci
Nauka, poprzez zabawę w swoim domu. Rodzice z dziećmi. Rzutowanie bryły geometrycznej. Format ark.a4 12,75*1,75 str.1. "TABLICZKA MNOśENIA AWERS * A
 dla wszystkich ludzi świata Nauka, poprzez zabawę w swoim domu. odzice z dziećmi. zutowanie bryły geometrycznej. Format ark.4 1,7*1,7 str.1 "TBLICZK MNOśENI Podgląd układu (XYZ) DEPT GEOMETII" WES * zutnie:
dla wszystkich ludzi świata Nauka, poprzez zabawę w swoim domu. odzice z dziećmi. zutowanie bryły geometrycznej. Format ark.4 1,7*1,7 str.1 "TBLICZK MNOśENI Podgląd układu (XYZ) DEPT GEOMETII" WES * zutnie:
Geometria. Hiperbola
 Geometria. Hiperbola Definicja 1 Dano dwa punkty na płaszczyźnie: F 1 i F 2 oraz taką liczbę d, że F 1 F 2 > d > 0. Zbiór punktów płaszczyzny będących rozwiązaniami równania: XF 1 XF 2 = ±d. nazywamy hiperbolą.
Geometria. Hiperbola Definicja 1 Dano dwa punkty na płaszczyźnie: F 1 i F 2 oraz taką liczbę d, że F 1 F 2 > d > 0. Zbiór punktów płaszczyzny będących rozwiązaniami równania: XF 1 XF 2 = ±d. nazywamy hiperbolą.
Zasady rzutowania prostokątnego. metodą europejską. Opracował: Robert Urbanik Zespół Szkół Mechanicznych w Opolu. Zasady rzutowania prostokątnego
 Zasady rzutowania prostokątnego metodą europejską Opracował: Robert Urbanik Zespół Szkół Mechanicznych w Opolu Wiadomości ogólne Rzutem nazywamy rysunkowe odwzorowanie przedmiotu lub bryły geometrycznej
Zasady rzutowania prostokątnego metodą europejską Opracował: Robert Urbanik Zespół Szkół Mechanicznych w Opolu Wiadomości ogólne Rzutem nazywamy rysunkowe odwzorowanie przedmiotu lub bryły geometrycznej
WIDOKI I PRZEKROJE PRZEDMIOTÓW
 WIDOKI I PRZEKROJE PRZEDMIOTÓW Rzutami przedmiotów mogą być zarówno widoki przedstawiające zewnętrzne kształty przedmiotów jak i przekroje, które pokazują budowę wewnętrzną przedmiotów wydrążonych. Rys.
WIDOKI I PRZEKROJE PRZEDMIOTÓW Rzutami przedmiotów mogą być zarówno widoki przedstawiające zewnętrzne kształty przedmiotów jak i przekroje, które pokazują budowę wewnętrzną przedmiotów wydrążonych. Rys.
Wymagania edukacyjne z matematyki w klasie III gimnazjum
 Wymagania edukacyjne z matematyki w klasie III gimnazjum - nie potrafi konstrukcyjnie podzielić odcinka - nie potrafi konstruować figur jednokładnych - nie zna pojęcia skali - nie rozpoznaje figur jednokładnych
Wymagania edukacyjne z matematyki w klasie III gimnazjum - nie potrafi konstrukcyjnie podzielić odcinka - nie potrafi konstruować figur jednokładnych - nie zna pojęcia skali - nie rozpoznaje figur jednokładnych
TABELA PRZELICZENIOWA
 Romana - imię mojej małżonki 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
Romana - imię mojej małżonki 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
Widoki WPROWADZENIE. Rzutowanie prostokątne - podział Rzuty prostokątne dzieli się na trzy rodzaje: widoki,.przekroje, kłady.
 Widoki WPROWADZENIE Rzutowanie prostokątne - podział Rzuty prostokątne dzieli się na trzy rodzaje: widoki, przekroje, kłady Widoki obrazują zewnętrzną czyli widoczną część przedmiotu Przekroje przedstawiają
Widoki WPROWADZENIE Rzutowanie prostokątne - podział Rzuty prostokątne dzieli się na trzy rodzaje: widoki, przekroje, kłady Widoki obrazują zewnętrzną czyli widoczną część przedmiotu Przekroje przedstawiają
Podstawowe [P] zna przedmiotowe zasady oceniania omawia regulamin pracowni. omawia wyposażenie apteczki i sprzęt ppoż.
![Podstawowe [P] zna przedmiotowe zasady oceniania omawia regulamin pracowni. omawia wyposażenie apteczki i sprzęt ppoż. Podstawowe [P] zna przedmiotowe zasady oceniania omawia regulamin pracowni. omawia wyposażenie apteczki i sprzęt ppoż.](/thumbs/26/9172034.jpg) WYMAGANIA Z ZAJĘĆ TECHNICZNYCH W GIMNAZJUM NR 4 GLIWICE Osiągnięcia szczegółowe uczniów Dział podręcznika Temat lekcji Treści nauczania Wiadomości Umiejętności Podstawowe [P] Ponadpodstawowe [PP] Podstawowe
WYMAGANIA Z ZAJĘĆ TECHNICZNYCH W GIMNAZJUM NR 4 GLIWICE Osiągnięcia szczegółowe uczniów Dział podręcznika Temat lekcji Treści nauczania Wiadomości Umiejętności Podstawowe [P] Ponadpodstawowe [PP] Podstawowe
OBLICZENIE PRZEKROJU WALCA PO CIĘCIU SKOŚNYM. Rysunki i obliczenia dotyczą walca
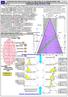 Kolejna metoda obliczania rzędnych i odciętych także obrazowa, przy stosowaniu tzw.przyrostów (trójkątów prostokątnych) różniącymi się kolorami żółtym i zielonym. Przy każdym poziomie koła jest mała tabelka
Kolejna metoda obliczania rzędnych i odciętych także obrazowa, przy stosowaniu tzw.przyrostów (trójkątów prostokątnych) różniącymi się kolorami żółtym i zielonym. Przy każdym poziomie koła jest mała tabelka
Katedra Zarządzania i Inżynierii Produkcji 2013r. Materiały pomocnicze do zajęć laboratoryjnych
 Materiały pomocnicze do zajęć laboratoryjnych 1 Używane w trakcie ćwiczeń moduły programu Autodesk Inventor 2008 Tworzenie złożenia Tworzenie dokumentacji płaskiej Tworzenie części Obserwacja modelu/manipulacja
Materiały pomocnicze do zajęć laboratoryjnych 1 Używane w trakcie ćwiczeń moduły programu Autodesk Inventor 2008 Tworzenie złożenia Tworzenie dokumentacji płaskiej Tworzenie części Obserwacja modelu/manipulacja
I. Potęgi. Logarytmy. Funkcja wykładnicza.
 WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY TRZECIEJ LICEUM OGÓLNOKSZTAŁCĄCEGO ZAKRES PODSTAWOWY I. Potęgi. Logarytmy. Funkcja wykładnicza. dobrą, bardzo - oblicza potęgi o wykładnikach wymiernych; - zna
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY TRZECIEJ LICEUM OGÓLNOKSZTAŁCĄCEGO ZAKRES PODSTAWOWY I. Potęgi. Logarytmy. Funkcja wykładnicza. dobrą, bardzo - oblicza potęgi o wykładnikach wymiernych; - zna
PRZYKŁADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI
 PRZYKŁADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI P-1 POZIOM PODSTAWOWY Czas pracy: 170 minut Za rozwiązanie wszystkich zadań można uzyskać łącznie 50 punktów BRUDNOPIS Zadanie 1. (1 pkt) ZADANIA ZAMKNIĘTE
PRZYKŁADOWY ARKUSZ EGZAMINACYJNY Z MATEMATYKI P-1 POZIOM PODSTAWOWY Czas pracy: 170 minut Za rozwiązanie wszystkich zadań można uzyskać łącznie 50 punktów BRUDNOPIS Zadanie 1. (1 pkt) ZADANIA ZAMKNIĘTE
GRAFIKA KOMPUTEROWA Przekroje Kłady
 Przekroje Przekroje służą do przedstawiania wewnętrznej budowy obiektów. Wybór odpowiedniego przekroju zależy od stopnia złożoności wewnętrznej budowy przedmiotu.. Przekroje całkowite to rzuty przedstawiające
Przekroje Przekroje służą do przedstawiania wewnętrznej budowy obiektów. Wybór odpowiedniego przekroju zależy od stopnia złożoności wewnętrznej budowy przedmiotu.. Przekroje całkowite to rzuty przedstawiające
1/4(koła; okrągu) A A' P'(x)
 skrypt Romany (R) 18h gk dla wszystkich ludzi świata Romana - imię mojej małżonki Nr 19h 17h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. Motto: Patrzymy na to samo, widzimy coś
skrypt Romany (R) 18h gk dla wszystkich ludzi świata Romana - imię mojej małżonki Nr 19h 17h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. Motto: Patrzymy na to samo, widzimy coś
przecięcie graniastosłupa płaszczyzną, przenikanie graniastosłupa z ostrosłupem
 przebicie ostrosłupa prostą, przecięcie graniastosłupa płaszczyzną, przenikanie graniastosłupa z ostrosłupem WSA - wykład VII w dn. 12. I. 2014 r: Przenikanie wzajemne brył nieobrotowych (graniastosłupów,
przebicie ostrosłupa prostą, przecięcie graniastosłupa płaszczyzną, przenikanie graniastosłupa z ostrosłupem WSA - wykład VII w dn. 12. I. 2014 r: Przenikanie wzajemne brył nieobrotowych (graniastosłupów,
Definicja obrotu: Definicja elementów obrotu:
 5. Obroty i kłady Definicja obrotu: Obrotem punktu A dookoła prostej l nazywamy ruch punktu A po okręgu k zawartym w płaszczyźnie prostopadłej do prostej l w kierunku zgodnym lub przeciwnym do ruchu wskazówek
5. Obroty i kłady Definicja obrotu: Obrotem punktu A dookoła prostej l nazywamy ruch punktu A po okręgu k zawartym w płaszczyźnie prostopadłej do prostej l w kierunku zgodnym lub przeciwnym do ruchu wskazówek
Grafika inżynierska geometria wykreślna. 5a. Obroty i kłady. Rozwinięcie wielościanu.
 Grafika inżynierska geometria wykreślna 5a. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Gospodarka przestrzenna,
Grafika inżynierska geometria wykreślna 5a. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Gospodarka przestrzenna,
Politechnika Warszawska Wydział Mechatroniki Instytut Automatyki i Robotyki
 Politechnika Warszawska Wydział Mechatroniki Instytut Automatyki i Robotyki Ćwiczenie laboratoryjne 2 Temat: Modelowanie powierzchni swobodnych 3D przy użyciu programu Autodesk Inventor Spis treści 1.
Politechnika Warszawska Wydział Mechatroniki Instytut Automatyki i Robotyki Ćwiczenie laboratoryjne 2 Temat: Modelowanie powierzchni swobodnych 3D przy użyciu programu Autodesk Inventor Spis treści 1.
Płaszczyzny, Obrót, Szyk
 Płaszczyzny, Obrót, Szyk Zagadnienia. Szyk kołowy, tworzenie brył przez Obrót. Geometria odniesienia, Płaszczyzna. Wykonajmy model jak na rys. 1. Wykonanie korpusu pokrywki Rysunek 1. Model pokrywki (1)
Płaszczyzny, Obrót, Szyk Zagadnienia. Szyk kołowy, tworzenie brył przez Obrót. Geometria odniesienia, Płaszczyzna. Wykonajmy model jak na rys. 1. Wykonanie korpusu pokrywki Rysunek 1. Model pokrywki (1)
Stożkiem nazywamy bryłę obrotową, która powstała przez obrót trójkąta prostokątnego wokół jednej z jego przyprostokątnych.
 1.4. Stożek W tym temacie dowiesz się: jak obliczać pole powierzchni bocznej i pole powierzchni całkowitej stożka, jak obliczać objętość stożka, jak wykorzystywać własności stożków w zadaniach praktycznych.
1.4. Stożek W tym temacie dowiesz się: jak obliczać pole powierzchni bocznej i pole powierzchni całkowitej stożka, jak obliczać objętość stożka, jak wykorzystywać własności stożków w zadaniach praktycznych.
ZADANIE.Nr 1. Z GEOMETRII KULOWEJ (SFERYCZNEJ) W PRAKTYCE (gk).
 ZADANIE.Nr 1. Z GEOMETRII KULOWEJ (SFERYCZNEJ) W PRAKTYCE (). str.1 patrzymy Stożek prosty nr1 Rys.1 m k ELIPSA jest cieniem, czyli rzutem prostopadłym na. Zatem nie podlega odchyleniom od pionu. Co nie
ZADANIE.Nr 1. Z GEOMETRII KULOWEJ (SFERYCZNEJ) W PRAKTYCE (). str.1 patrzymy Stożek prosty nr1 Rys.1 m k ELIPSA jest cieniem, czyli rzutem prostopadłym na. Zatem nie podlega odchyleniom od pionu. Co nie
Gwint gubiony na wale
 Gwint gubiony na wale Zagadnienia. Wyciągnięcie przez wyciągnięcie po ścieżce. Helisa i Spirala. Linia śrubowa (helisa) to krzywa trójwymiarowa zakreślona przez punkt poruszający się ze stałą prędkością
Gwint gubiony na wale Zagadnienia. Wyciągnięcie przez wyciągnięcie po ścieżce. Helisa i Spirala. Linia śrubowa (helisa) to krzywa trójwymiarowa zakreślona przez punkt poruszający się ze stałą prędkością
(a) (b) (c) o1" o2" o3" o1'=o2'=o3'
 Zad.0. Odwzorowanie powierzchni stożka, walca, sfery oraz punktów leżących na tych powierzchniach. Przy odwzorowaniu powierzchni stożka, walca, sfery przyjmiemy reprezentację konturową, co oznacza, że
Zad.0. Odwzorowanie powierzchni stożka, walca, sfery oraz punktów leżących na tych powierzchniach. Przy odwzorowaniu powierzchni stożka, walca, sfery przyjmiemy reprezentację konturową, co oznacza, że
Grafika inżynierska geometria wykreślna. 4. Wielościany. Budowa. Przekroje.
 Grafika inżynierska geometria wykreślna 4. Wielościany. Budowa. Przekroje. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Gospodarka przestrzenna, semestr
Grafika inżynierska geometria wykreślna 4. Wielościany. Budowa. Przekroje. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Gospodarka przestrzenna, semestr
Pochylenia, Lustro. Modelowanie ramienia. Zagadnienia. Wyciągnięcie/dodania/bazy, Pochylenia ścian, Lustro (ewent. wstawianie części, łączenie części)
 Pochylenia, Lustro Zagadnienia. Wyciągnięcie/dodania/bazy, Pochylenia ścian, Lustro (ewent. wstawianie części, łączenie części) Wykonajmy model korbowodu jak na rys. 1 (zobacz też rys. 29, str. 11). Rysunek
Pochylenia, Lustro Zagadnienia. Wyciągnięcie/dodania/bazy, Pochylenia ścian, Lustro (ewent. wstawianie części, łączenie części) Wykonajmy model korbowodu jak na rys. 1 (zobacz też rys. 29, str. 11). Rysunek
PRÓBNY EGZAMIN MATURALNY
 PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW NR 64130 WYGENEROWANY AUTOMATYCZNIE W SERWISIE WWW.ZADANIA.INFO POZIOM ROZSZERZONY CZAS PRACY: 180 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Wielomian P(x)
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI ZESTAW NR 64130 WYGENEROWANY AUTOMATYCZNIE W SERWISIE WWW.ZADANIA.INFO POZIOM ROZSZERZONY CZAS PRACY: 180 MINUT 1 Zadania zamknięte ZADANIE 1 (1 PKT) Wielomian P(x)
WIELOKĄTY FOREMNE I ICH PRZEKĄTNE
 WIELOKĄTY FOREMNE I ICH PRZEKĄTNE Krzysztof Lisiecki Kl. V a SP nr 6 im. Unii Europejskiej w Kłodzku Praca pod kierunkiem: mgr Moniki Chosińskiej Spis treści Lp. Tytuł Str. 1. Wstęp. 2 2. Pojęcia używane
WIELOKĄTY FOREMNE I ICH PRZEKĄTNE Krzysztof Lisiecki Kl. V a SP nr 6 im. Unii Europejskiej w Kłodzku Praca pod kierunkiem: mgr Moniki Chosińskiej Spis treści Lp. Tytuł Str. 1. Wstęp. 2 2. Pojęcia używane
V Konkurs Matematyczny Politechniki Białostockiej
 V Konkurs Matematyczny Politechniki iałostockiej Rozwiązania - klasy pierwsze 27 kwietnia 2013 r. 1. ane są cztery liczby dodatnie a b c d. Wykazać że przynajmniej jedna z liczb a + b + c d b + c + d a
V Konkurs Matematyczny Politechniki iałostockiej Rozwiązania - klasy pierwsze 27 kwietnia 2013 r. 1. ane są cztery liczby dodatnie a b c d. Wykazać że przynajmniej jedna z liczb a + b + c d b + c + d a
Scenariusz lekcji wykorzystujący elementy metody CLIL
 Scenariusz lekcji wykorzystujący elementy metody CLIL Przedmiot: matematyka Etap edukacyjny: II, klasa 4 Temat zajęć: Rozpoznawanie i rysowanie prostych i odcinków równoległych i prostopadłych Realizowane
Scenariusz lekcji wykorzystujący elementy metody CLIL Przedmiot: matematyka Etap edukacyjny: II, klasa 4 Temat zajęć: Rozpoznawanie i rysowanie prostych i odcinków równoległych i prostopadłych Realizowane
Ćwiczenie 9. Rzutowanie i wymiarowanie Strona 1 z 5
 Ćwiczenie 9. Rzutowanie i wymiarowanie Strona 1 z 5 Problem I. Model UD Dana jest bryła, której rzut izometryczny przedstawiono na rysunku 1. (W celu zwiększenia poglądowości na rysunku 2. przedstawiono
Ćwiczenie 9. Rzutowanie i wymiarowanie Strona 1 z 5 Problem I. Model UD Dana jest bryła, której rzut izometryczny przedstawiono na rysunku 1. (W celu zwiększenia poglądowości na rysunku 2. przedstawiono
Π 1 O Π 3 Π Rzutowanie prostokątne Wiadomości wstępne
 2. Rzutowanie prostokątne 2.1. Wiadomości wstępne Rzutowanie prostokątne jest najczęściej stosowaną metodą rzutowania w rysunku technicznym. Reguły nim rządzące zaprezentowane są na rysunkach 2.1 i 2.2.
2. Rzutowanie prostokątne 2.1. Wiadomości wstępne Rzutowanie prostokątne jest najczęściej stosowaną metodą rzutowania w rysunku technicznym. Reguły nim rządzące zaprezentowane są na rysunkach 2.1 i 2.2.
Cenne informacje dla rodziców
 Cenne informacje dla rodziców Rok szkolny 2014/2015 Co trzylatek umieć powinien -Posługuje się określeniami odnoszącymi się do kierunków w przestrzeni (na, pod, za, przed). -Klasyfikuje przedmioty ze względu
Cenne informacje dla rodziców Rok szkolny 2014/2015 Co trzylatek umieć powinien -Posługuje się określeniami odnoszącymi się do kierunków w przestrzeni (na, pod, za, przed). -Klasyfikuje przedmioty ze względu
WYKŁAD IV BRYŁY OBROTOWE PRZEKROJE BRYŁ OBROTOWYCH DR INŻ. ELŻBIETA RUDCZYK-MALIJEWSKA
 WYKŁAD IV BRYŁY OBROTOWE PRZEKROJE BRYŁ OBROTOWYCH DR INŻ. ELŻBIETA RUDCZYK-MALIJEWSKA WALEC powstaje w wyniku obrotu prostokąta wokół prostej zawierającej jeden z jego boków WALEC oś obrotu podstawa wysokość
WYKŁAD IV BRYŁY OBROTOWE PRZEKROJE BRYŁ OBROTOWYCH DR INŻ. ELŻBIETA RUDCZYK-MALIJEWSKA WALEC powstaje w wyniku obrotu prostokąta wokół prostej zawierającej jeden z jego boków WALEC oś obrotu podstawa wysokość
GEOMETRIA PRZESTRZENNA (STEREOMETRIA)
 GEOMETRIA PRZESTRZENNA (STEREOMETRIA) WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. Na początek omówimy
GEOMETRIA PRZESTRZENNA (STEREOMETRIA) WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. Na początek omówimy
Przekazywanie i zdobywanie informacji jest ważne! opracowanie Dorota Tłoczkowska, Warszawa luty 2007 r.
 Przekazywanie i zdobywanie informacji jest ważne! Zdobywanie informacji Wszyscy potrzebujemy różnych informacji. Osoby z niepełnosprawnością intelektualną mają większa trudność, żeby zdobyć potrzebne im
Przekazywanie i zdobywanie informacji jest ważne! Zdobywanie informacji Wszyscy potrzebujemy różnych informacji. Osoby z niepełnosprawnością intelektualną mają większa trudność, żeby zdobyć potrzebne im
Kryteria oceniania z matematyki Klasa III poziom rozszerzony
 Kryteria oceniania z matematyki Klasa III poziom rozszerzony Zakres Dopuszczający Dostateczny Dobry Bardzo dobry Funkcja potęgowa - zna i stosuje tw. o potęgach - zna wykresy funkcji potęgowej o dowolnym
Kryteria oceniania z matematyki Klasa III poziom rozszerzony Zakres Dopuszczający Dostateczny Dobry Bardzo dobry Funkcja potęgowa - zna i stosuje tw. o potęgach - zna wykresy funkcji potęgowej o dowolnym
Rozkład materiału nauczania
 Dział/l.p. Ilość godz. Typ szkoły: TECHNIKUM Zawód: TECHNIK USŁUG FRYZJERSKICH Rok szkolny 2016/2017 Przedmiot: MATEMATYKA Klasa: IV 67 godzin numer programu T5/O/5/12 Rozkład materiału nauczania Temat
Dział/l.p. Ilość godz. Typ szkoły: TECHNIKUM Zawód: TECHNIK USŁUG FRYZJERSKICH Rok szkolny 2016/2017 Przedmiot: MATEMATYKA Klasa: IV 67 godzin numer programu T5/O/5/12 Rozkład materiału nauczania Temat
WYMAGANIA EDUKACYJNE NA POSZCZEGÓLNE OCENY KL. 3 POZIOM ROZSZERZONY
 WYMAGANIA EDUKACYJNE NA POSZCZEGÓLNE OCENY KL. 3 POZIOM ROZSZERZONY 1. Funkcja wykładnicza i logarytmiczna Tematyka zajęć: Potęga o wykładniku rzeczywistym - powtórzenie Funkcja wykładnicza i jej własności
WYMAGANIA EDUKACYJNE NA POSZCZEGÓLNE OCENY KL. 3 POZIOM ROZSZERZONY 1. Funkcja wykładnicza i logarytmiczna Tematyka zajęć: Potęga o wykładniku rzeczywistym - powtórzenie Funkcja wykładnicza i jej własności
aksonometrie trójosiowe odmierzalne odwzorowania na płaszczyźnie
 aksonometrie trójosiowe odmierzalne odwzorowania na płaszczyźnie Przykładowy rzut (od lewej) izometryczny, dimetryczny ukośny i dimetryczny prostokątny Podział aksonometrii ze względu na kierunek rzutowania:
aksonometrie trójosiowe odmierzalne odwzorowania na płaszczyźnie Przykładowy rzut (od lewej) izometryczny, dimetryczny ukośny i dimetryczny prostokątny Podział aksonometrii ze względu na kierunek rzutowania:
Mechanika ogólna. Kinematyka. Równania ruchu punktu materialnego. Podstawowe pojęcia. Równanie ruchu po torze (równanie drogi)
 Kinematyka Mechanika ogólna Wykład nr 7 Elementy kinematyki Dział mechaniki zajmujący się matematycznym opisem układów mechanicznych oraz badaniem geometrycznych właściwości ich ruchu, bez wnikania w związek
Kinematyka Mechanika ogólna Wykład nr 7 Elementy kinematyki Dział mechaniki zajmujący się matematycznym opisem układów mechanicznych oraz badaniem geometrycznych właściwości ich ruchu, bez wnikania w związek
Ćwiczenie nr 3 Edycja modeli bryłowych
 Ćwiczenie nr 3 Edycja modeli bryłowych 1. Fazowanie oraz zaokrąglanie. Wykonaj element pokazany na rys. 1a. Wymiary elementu: średnice 100 i 40. Długość wałków 30 i 100 odpowiednio. Następnie wykonaj fazowanie
Ćwiczenie nr 3 Edycja modeli bryłowych 1. Fazowanie oraz zaokrąglanie. Wykonaj element pokazany na rys. 1a. Wymiary elementu: średnice 100 i 40. Długość wałków 30 i 100 odpowiednio. Następnie wykonaj fazowanie
PL B1. Sposób walcowania poprzecznego dwoma walcami wyrobów typu kula metodą wgłębną. POLITECHNIKA LUBELSKA, Lublin, PL
 PL 218597 B1 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 218597 (13) B1 Urząd Patentowy Rzeczypospolitej Polskiej (21) Numer zgłoszenia: 394836 (22) Data zgłoszenia: 11.05.2011 (51) Int.Cl.
PL 218597 B1 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 218597 (13) B1 Urząd Patentowy Rzeczypospolitej Polskiej (21) Numer zgłoszenia: 394836 (22) Data zgłoszenia: 11.05.2011 (51) Int.Cl.
Przekształcanie wykresów.
 Sławomir Jemielity Przekształcanie wykresów. Pokażemy tu, jak zmiana we wzorze funkcji wpływa na wygląd jej wykresu. A. Mamy wykres funkcji f(). Jak będzie wyglądał wykres f ( ) + a, a stała? ( ) f ( )
Sławomir Jemielity Przekształcanie wykresów. Pokażemy tu, jak zmiana we wzorze funkcji wpływa na wygląd jej wykresu. A. Mamy wykres funkcji f(). Jak będzie wyglądał wykres f ( ) + a, a stała? ( ) f ( )
Rzuty, przekroje i inne przeboje
 Rzuty, przekroje i inne przeboje WYK - Grafika inżynierska Piotr Ciskowski, Sebastian Sobczyk Wrocław, 2015-2016 Rzuty prostokątne Rzuty prostokątne pokazują przedmiot z kilku stron 1. przedmiot ustawiamy
Rzuty, przekroje i inne przeboje WYK - Grafika inżynierska Piotr Ciskowski, Sebastian Sobczyk Wrocław, 2015-2016 Rzuty prostokątne Rzuty prostokątne pokazują przedmiot z kilku stron 1. przedmiot ustawiamy
FUNKCJA LINIOWA, RÓWNANIA I UKŁADY RÓWNAŃ LINIOWYCH
 FUNKCJA LINIOWA, RÓWNANIA I UKŁADY RÓWNAŃ LINIOWYCH PROPORCJONALNOŚĆ PROSTA Proporcjonalnością prostą nazywamy zależność między dwoma wielkościami zmiennymi x i y, określoną wzorem: y = a x Gdzie a jest
FUNKCJA LINIOWA, RÓWNANIA I UKŁADY RÓWNAŃ LINIOWYCH PROPORCJONALNOŚĆ PROSTA Proporcjonalnością prostą nazywamy zależność między dwoma wielkościami zmiennymi x i y, określoną wzorem: y = a x Gdzie a jest
MATERIAŁ DIAGNOSTYCZNY Z MATEMATYKI
 Miejsce na naklejkę z kodem szkoły dysleksja MATERIAŁ DIAGNOSTYCZNY Z MATEMATYKI POZIOM PODSTAWOWY Czas pracy 120 minut Instrukcja dla zdającego 1. Sprawdź, czy arkusz zawiera 13 stron (zadania 1 11).
Miejsce na naklejkę z kodem szkoły dysleksja MATERIAŁ DIAGNOSTYCZNY Z MATEMATYKI POZIOM PODSTAWOWY Czas pracy 120 minut Instrukcja dla zdającego 1. Sprawdź, czy arkusz zawiera 13 stron (zadania 1 11).
WYMAGANIA EDUKACYJNE Rok szkolny 2018/2019
 WYMAGANIA EDUKACYJNE Rok szkolny 2018/2019 Przedmiot Klasa Nauczyciele uczący Poziom matematyka 4e Łukasz Jurczak rozszerzony 2. Elementy analizy matematycznej ocena dopuszczająca ocena dostateczna ocena
WYMAGANIA EDUKACYJNE Rok szkolny 2018/2019 Przedmiot Klasa Nauczyciele uczący Poziom matematyka 4e Łukasz Jurczak rozszerzony 2. Elementy analizy matematycznej ocena dopuszczająca ocena dostateczna ocena
Plan wynikowy, klasa 3 ZSZ
 Plan wynikowy, klasa 3 ZSZ Nazwa działu Temat Liczba godzin 1. Trójkąty prostokątne powtórzenie 1. Trygonometria (10 h) 2. Funkcje trygonometryczne kąta ostrego 3. 4. Trygonometria zastosowania 5. 6. Związki
Plan wynikowy, klasa 3 ZSZ Nazwa działu Temat Liczba godzin 1. Trójkąty prostokątne powtórzenie 1. Trygonometria (10 h) 2. Funkcje trygonometryczne kąta ostrego 3. 4. Trygonometria zastosowania 5. 6. Związki
Wojewódzki Konkurs Matematyczny dla uczniów gimnazjów. Etap Wojewódzki 16 lutego 2018 Czas 90 minut Rozwiązania i punktacja
 Wojewódzki Konkurs Matematyczny dla uczniów gimnazjów. Etap Wojewódzki 6 lutego 208 Czas 90 minut Rozwiązania i punktacja ZADANIA ZAMKNIĘTE Zadanie. ( punkt) Odległość między miastami A i B na mapie wynosi
Wojewódzki Konkurs Matematyczny dla uczniów gimnazjów. Etap Wojewódzki 6 lutego 208 Czas 90 minut Rozwiązania i punktacja ZADANIA ZAMKNIĘTE Zadanie. ( punkt) Odległość między miastami A i B na mapie wynosi
WYMAGANIA EDUKACYJNE Z MATEMATYKI 2016/2017 (zakres podstawowy) klasa 3abc
 WYMAGANIA EDUKACYJNE Z MATEMATYKI 2016/2017 (zakres podstawowy) klasa 3abc 1, Ciągi zna definicję ciągu (ciągu liczbowego); potrafi wyznaczyć dowolny wyraz ciągu liczbowego określonego wzorem ogólnym;
WYMAGANIA EDUKACYJNE Z MATEMATYKI 2016/2017 (zakres podstawowy) klasa 3abc 1, Ciągi zna definicję ciągu (ciągu liczbowego); potrafi wyznaczyć dowolny wyraz ciągu liczbowego określonego wzorem ogólnym;
dla symboli graficznych O bardzo dużej liczbie szczegółów 0,18 0,35 0,70 0,25 A3 i A4 O dużej liczbie szczegółów
 6/ LINIE RYSUNKOWE Normy rysunkowe PN-EN ISO 128-20:2002 Rysunek techniczny. Zasady ogólne przedstawiania Część 20: Wymagania podstawowe dotyczące linii PN-ISO 128-23:2002 Rysunek techniczny. Ogólne zasady
6/ LINIE RYSUNKOWE Normy rysunkowe PN-EN ISO 128-20:2002 Rysunek techniczny. Zasady ogólne przedstawiania Część 20: Wymagania podstawowe dotyczące linii PN-ISO 128-23:2002 Rysunek techniczny. Ogólne zasady
WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI W KLASIE III GIMNAZJUM
 WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI W KLASIE III GIMNAZJUM OCENA ŚRÓDROCZNA: NIEDOSTATECZNY ocenę niedostateczny otrzymuje uczeń, który
WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI W KLASIE III GIMNAZJUM OCENA ŚRÓDROCZNA: NIEDOSTATECZNY ocenę niedostateczny otrzymuje uczeń, który
Wymiarowanie. Wymiary normalne. Elementy wymiaru rysunkowego Znak ograniczenia linii wymiarowej
 Wymiary normalne Wymiarowanie Elementy wymiaru rysunkowego Znak ograniczenia linii wymiarowej 1. Linia wymiarowa 2. Znak ograniczenia linii wymiarowej 3. Liczba wymiarowa 4. Pomocnicza linia wymiarowa
Wymiary normalne Wymiarowanie Elementy wymiaru rysunkowego Znak ograniczenia linii wymiarowej 1. Linia wymiarowa 2. Znak ograniczenia linii wymiarowej 3. Liczba wymiarowa 4. Pomocnicza linia wymiarowa
SZa 98 strona 1 Rysunek techniczny
 Wstęp Wymiarowanie Rodzaje linii rysunkowych i ich przeznaczenie 1. linia ciągła cienka linie pomocnicze, kreskowanie przekrojów, linie wymiarowe, 2. linia ciągła gruba krawędzie widoczne 3. linia kreskowa
Wstęp Wymiarowanie Rodzaje linii rysunkowych i ich przeznaczenie 1. linia ciągła cienka linie pomocnicze, kreskowanie przekrojów, linie wymiarowe, 2. linia ciągła gruba krawędzie widoczne 3. linia kreskowa
Osiągnięcia ponadprzedmiotowe
 Osiągnięcia ponadprzedmiotowe W rezultacie kształcenia matematycznego w klasie 3 gimnazjum uczeń potrafi: Umiejętności konieczne i podstawowe czytać teksty w stylu matematycznym wykorzystywać słownictwo
Osiągnięcia ponadprzedmiotowe W rezultacie kształcenia matematycznego w klasie 3 gimnazjum uczeń potrafi: Umiejętności konieczne i podstawowe czytać teksty w stylu matematycznym wykorzystywać słownictwo
G T. Przyrząd graficzny o średnicy [KS] 48h w (gks). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. ϕ 7,00 cm ϕ 5,00 cm ϕ 3,00 cm
![G T. Przyrząd graficzny o średnicy [KS] 48h w (gks). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. ϕ 7,00 cm ϕ 5,00 cm ϕ 3,00 cm G T. Przyrząd graficzny o średnicy [KS] 48h w (gks). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. ϕ 7,00 cm ϕ 5,00 cm ϕ 3,00 cm](/thumbs/71/64805542.jpg) Przyrząd graficzny o średnicy [KS] 48h w (). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. Rys.1 Nie określona płaszczyzna rzutu Kuli [K]. 354,375 358,125 1,875 5,625 356,25 48h ; 0h 3,75 Format
Przyrząd graficzny o średnicy [KS] 48h w (). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. Rys.1 Nie określona płaszczyzna rzutu Kuli [K]. 354,375 358,125 1,875 5,625 356,25 48h ; 0h 3,75 Format
ZAPIS UKŁADU WYMIARÓW. RODZAJE RYSUNKÓW
 Zapis i Podstawy Konstrukcji Wymiarowanie. Rodzaje rysunków 1 ZAPIS UKŁADU WYMIARÓW. RODZAJE RYSUNKÓW Rysunek przedmiotu wykonany w rzutach prostokątnych lub aksonometrycznych przedstawia jedynie jego
Zapis i Podstawy Konstrukcji Wymiarowanie. Rodzaje rysunków 1 ZAPIS UKŁADU WYMIARÓW. RODZAJE RYSUNKÓW Rysunek przedmiotu wykonany w rzutach prostokątnych lub aksonometrycznych przedstawia jedynie jego
Materiały pomocnicze z programu AutoCAD 2014.
 Materiały pomocnicze z programu AutoCAD 2014. Poniżej przedstawiony zostanie przykładowy rysunek wykonany w programie AutoCAD 2014. Po uruchomieniu programu należy otworzyć szablon KKM, w którym znajdują
Materiały pomocnicze z programu AutoCAD 2014. Poniżej przedstawiony zostanie przykładowy rysunek wykonany w programie AutoCAD 2014. Po uruchomieniu programu należy otworzyć szablon KKM, w którym znajdują
