gk T Rzutowanie walców w geometrii wykreśl.wg (gk).

Transkrypt

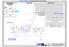
1 Dodatkowe przyrządy stosow.w (), do przyspieszenia prac kreślarskich rzutowania walców. Format ark. A4 : 14,25*1,75 str.1 Rys.1 Sprawdzenie średnicy KULI ϕ13,12 cm, na podstawie okrągłej linijki. UWAGA: wszystkie wymiary liniowe będą podawane w [cm]. 23h 24h ; 0h 1h 22h 2h 21h 3h 20h 4h 19h 5h 17h 7h 1 8h 15h 9h 14h 10h 13h 11h Rys.2 pł.( X Z ) pionowa rzenikanie walców. Ten rys.2 wykonałem w 12 minutach na swoich przyrządach Rys.3 Ustawienie pionowe przyrządów do rys.promieni dla stoŝków lub innych brył owalnych, jak teŝ brył nieobrotowych np. stoŝek z odchyl.wierzchołkiem od centrum podstawy. owyŝsze przyrządy są moją własnością inte- lektualną z racji moje- T owanie walców w geometrii wykreśl.wg (). go autorstwa. Romana - imię mojej małŝonki TECHNIKA Koszalin dnia: 22 września 2016r

2 Dodatkowe przyrządy stosowane w (), do przyspieszenia prac kreślarskich - rzutowania walców. Rys.4 pł.( X Z ) pionowa Nie moŝna tak sobie rys.dowolnie elipsy kół. Rys.5 pł.(xz) pionowa str.2 0h KULA 0h 0h 0h 0h 0h 21h 3h 21h 3h 21h 3h 4,00 cm " 15h 9h 15h 9h 15h 9h Rys.6 pł.( X Y ) pozioma Rys.A pł.( X Y ) pozioma rzeniesiona kopia rys.6. 5' 5" 4' 4" Błękitne linie przechodzą przez 3 pkt.(h) parzyste i nieparzyste. α wys.dowolna r 1 α 1 x 1 =0,75cm 6 α 1 ' "' α ' 15" Kierunek osi obrot. Są dwa najwaŝniejsze walca "konus-konserwa" elementy rzutni kaŝdego 0,48cm rzy kolejności wykon. walca na pł.poziomej: odczas rysowania 14' 14" operacji, naleŝy pomi- element nr 2 wykonałem 21 ope- 21 jać kąty wraz z ich (oś obrot.walca) racji - cyfry(4) czer oznaczeniami i przyrzą- element nr 1 wone, małe wg ko- 19 α 2 90 x 2 =1,665 cm dami (czarno- niebiesk. ) α 90 (kierunek z ϕ walca) lejności działania. 17 α 2 α kątα 1 = ATAN ( x 1 / r ) r = 2,00 cm omimo zagęszczenia logikę konstrukcji kątα 1 = 0,35877 [rad] elem. rys.2 nie mogłem kaŝdego walca. kątα 1 = [ ] 20,5560 sobie odmówić nanie- Rys.zawiera całą kątα 2 = ACOS( x 2 / r ) Rys.6a 0,48cm sienia krzywych elipsy Rys.B Kopia kątα 2 = 0,58719 [rad] k. Niestety,część krzy- Dotyczy rys.a kopii dłuŝszego walca. Kopię wzbogaciłem promieniami kątα 2 = 33,6436 [ ] wych będzie zasłonię- błękitnymi związanymi ze średnicą KULI ( ϕ ). KULA jest w pozycji pionota (w klamerkach). wej, więc ma inne rozmieszczenie pkt. okrągłej linijki, niŝ kierunki osi obrotowych walców. Zatem mam do czynienie z dodatkowymi promieniami. Rys.A Konstrukcja przyrządów rzyrządy :elipsa koła i promienie walca do skopiowania. Na razie nie wiem, jak je wykorzystam, ale na pewno to zrobię. 0h 21h 3h 21h 3h 0h odgląd układu (XYZ) nie: (XZ); (YZ); (XY). E (XZ) F A B O kula (YZ) G Hściany 15h 9h 15h 9h C (XY) D sześciana To nie jest stal zbrojeniowa, to są przyrządy. romienie: czarne parzyste i niebieskie nieparzyste. T owanie walców w geometrii wykreśl.wg (). TECHNIKA Koszalin dnia: 26 września 2016r

3 Dodatkowe przyrządy stosowane w (), do przyspieszenia prac kreślarskich - rzutowania walców. str.3 Rys.4 pł.( X Z ) pionowa Nie moŝna tak sobie rys.dowolnie elipsy kół. Rys.5 pł.( X Z ) pionowa atrzymy 0h KULA 0h 0h 0h 0h 0h 0h 0h 21h 3h 21h 3h 21h 3h 4,00 cm " 15h 9h 15h 9h 15h 9h 6,55 cm Rys.6 pł.( X Y ) pozioma Rys.7 pł.( X Y ) pozioma g= 4,00 cm α 1 4,00 cm r α 1 x 1 =0,75cm α 1 ' α h= 2,15 cm '" f = 7,04723 cm dług.rzeczywista h T owanie walców w geometrii wykreśl.wg (). TECHNIKA Koszalin dnia: 27 września 2016r

4 Dodatkowe przyrządy stosowane w (), do przyspieszenia prac kreślarskich - rzutowania i interpretacji walców. str.4 Rys.4 pł.( X Z ) pionowa Nie moŝna tak sobie rys.dowolnie elipsy kół. Rys.5 pł.( X Z ) pionowa atrzymy 0h KULA 0h 0h 0h 0h 0h 0h 0h 21h 3h 21h 3h 21h 3h 4,00 cm " 15h 9h 15h 9h 15h 9h 6,55 cm Rys.6 pł.( X Y ) pozioma Rys.7 pł.( X Y ) pozioma g= 4,00 cm α 1 4,00 cm r α 1 x 1 =0,75cm α 1 ' α 1 90 h= 2,15 cm '" f = 7,04723 cm dług.rzeczywista h Tylko z pozoru wydawało się, Ŝe to zadanie będzie proste i łatwe do rozwiązania. W rzeczywistości okazało się zadaniem trudniejszym. śeby być pewny, wykonałem dodatkowy rzut prostokątny na pł. ( X Z )poziomą, lecz od strony bocznej AWERS - u (ś ciana pionowa zielo - na ). Właśnie dzięki temu rzutowi uporządkowałem w swojej wyobraźni, jak przebiega przenikanie obu brył obrotowych. W pierwszej wersji tego pliku było kilka błędów merytorycznych. Dlatego, natychmiast dokonałem modyfikacji tego pliku T owanie walców w geometrii wykreśl.wg (). TECHNIKA Koszalin dnia: 28 września 2016r

5 Dodatkowe przyrządy stosowane w (), do przyspieszenia prac kreślarskich - rzutowania walców. Rys.4 pł.( X Z ) pionowa Nie moŝna tak sobie rys.dowolnie elipsy kół. Rys.5 pł.( X Z ) pionowa str.5 Rys.6 pł.( X Y ) pozioma Narysowałem krzywą, przerywaną czerwoną 0,5 ukrytą za krawędzią podstawy walca konusa - konserwa. Rys.7 pł.( X Y ) pozioma atrzymy na pł. ( X Z ) pionową atrzymy na pł. ( Y Z ) pionową T owanie walców w geometrii wykreśl.wg (). TECHNIKA Koszalin dnia: 29 września 2016r

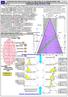
6 Nie moŝe być tak, by 2 razy 2 było 4 i 5. rawda jest tylko jedna w rzutowowaniu brył. Zgodna z moją (). str.6 Za czym powiem o co chodzi, chcę powołać się na mój plik B.Skrypt (R) Cz.I. str.3. Rysunek dotyczący TEORII w ().Jak się zmienia rzut prostokatny figury ELISY KOŁA, przy jej zmianie połoŝenia w pasie ruchu równoleŝnikowego wokół KULI. Skrypt opracowałem w kwietniu 2016r. O błędach w Internecie poinformowałem zainteresowanych em dnia 31 kwietnia 2016r.Hasło w Internt.: "Zadania do samodzielnego opracowania". rzenikanie brył obrotowych. Rys.1 pł.( X Z )pionowa Długość tej bryły ma średnicę KULI, ϕ 13,12cm, a średnica KULI bryły ma ϕ4,00cm.należy zaprojektować 4 bryły. Nr2 : Elipsa koła (4,00cm*2,45cm) Nr3 : Elipsa koła (4,00cm*3,48cm) Nr4 : Elipsa koła (4,00cm*3,55cm) 23h 24h ; 0h 1h 22h Korbka do obracania bryły 2h Stojak Nr1 :Ślad b=4,0cm Strona lewa zamknięcia bryły, która nie jest bryłą obrotową. ELISY KÓŁ w pasie jasnoniebieskim. b=4,00cm 21h 3h 90 Nr2 Nr1 20h Nr2 Nr3 Nr4 4h em zamknięcia jest tylko ślad. 19h 5h Nie trzyma średnicy. ϕ 4,00cm Trzyma za to inną, a=1,00cm ϕ3,55cm mniejszą średnicę: ϕ 3,55cm a=1,00cm śebym stał się przekonu- Gdyby odciąć kawa- jący muszę wykonać łki i je wstawić w 17h 7h pewną czynność. Muszę miejsca puste byłby c=5,87cm tę bryłę o rzucie równolewtedy walec na 100%. N r1 głoboku, przewiercić by b=4,00cm 1 8h zamontować w niej pręt. Operator tego przyrządu Wiercenie wyk.w pł.pion. jest z zawodu korbowniczym. przez pkt.centr. osi owinien mieć pełny etat pracy. 15h 9h bryły, Ŝeby móc bryłę MoŜe zorganizować zw.zawodowe obracać w pł.poziomej. korbowniczych i starać się załoŝyć 14h 10h W rzeczywistości wykowłasną partię korbowniczych. U nas 13h 11h nam to na tym rysunku. jest wszystko moŝliwe np.. wg (). Rys.2 pł.( X Y )poziomy K 1 = 11,67 cm Rys.2 przedstawia rzut bryły nieobrotowej na pł.poziomą.wewnątrz bryły pokazuję średnicę KULI, która jest jednocześnie średnicą bryły. Dobrałem kolor pn. "BRZASK" dnia. T Nie moŝe tak być by 2*2=4, a nawet 5 w (). Romana - imię mojej małŝonki TECHNIKA Koszalin dnia: 22 września 2016r

7 Nie moŝe być tak, by 2 razy 2 było 4 i 5. rawda jest tylko jedna w rzutowowaniu brył. Zgodna z moją (). str.7 Rys.3 pł.( X Z )pionowa Długość tej bryły ma średnicę KULI, ϕ 13,12cm, a średnica KULI bryły ma ϕ4,00cm. Należy zaprojektować 4 bryły. Nr2 : Elipsa koła (4,00cm*2,45cm) 24h ; 0h 23h 1h L 1 =2,55cm 22h 2h 21h 3h Nr2 20h Nr3 Nr4 4h 19h 5h ϕ 4,00cm ϕ3,55cm 17h 7h 1 8h 15h 9h 14h 10h 13h 11h Rys.2 pł.( X Y )poziomy KaŜdy rzut bryły na pł.poziomą będzie prostokątem. Bryły będą się róŝniły połoŝeniem od kaŝdej kolejnej bryły. Łuk z okrągłej linijki. R = 13,1330 cm Rys.2a Bez skali: R owinno być: R = 13,12 cm, a jest: R = 13,04005 cm RóŜnica: 0,07995 cm K 1= 2*a+2*0,5*b=6,00 cm K 2= 11,5777 cm z odczytu K 2= 11,5777 cm 90 Rys.2b c=5,87cm RóŜnica: ϕkoła - L = -0,013 cm wynik z odczytu Łuk Małe kółeczka do oznaczenia punktów proszę wykonywać uŝywaz okrągłej linijki. Sprawdzenie zgodności połoŝenia bryły na rysunku: rzy tych skaczących "pchłach"- (elem.rysunku), wynik wydaje się niezły. śaden element rysunku nie trzyma swoich wymiarów i samoistnie się przesuwa. WaŜne. jąc nie funkcji elipsa, lecz z schematu blokowego.ostatnio wykonuję np.punkty central- ne elips kół o wym.0,08cm*0,08cm (białe tło) z linii grub.0,75. Natomiast punkty do linii na krzywych mają wym.0,06cm*0,06cm. Z tym, Ŝe kolor dla [h] promieni nieparzystych mają niebieskie tło (wypełnienie), a parzyste mają czarne. Grubość linii kółeczek 0,75. Stosuję takŝe takie same punkty, gdy chcę pokazać punkty na wierzchu, czyli widoczne. Wtedy punkty mają tło czerwone, a linia koła jest z jasnej czerwieni. W przypadku punktów niewidocznych, bo zakrytych uŝy- T Nie moŝe tak być by 2*2=4, a nawet 5 w (). wam tło czarne z linią koła lekko szarą. Rysunki są wtedy w miarę czytelne. TECHNIKA Koszalin dnia: 24 września 2016r

8 Nie moŝe być tak, by 2 razy 2 było 4 i 5. rawda jest tylko jedna w rzutowowaniu brył. Zgodna z moją (). str.8 Rys.3 pł.( X Z )pionowa Długość tej bryły ma średnicę KULI ϕ 13,12cm, a średnica KULI bryły ma ϕ4,00cm.należy zaprojektować 4 bryły. Nr3 : Elipsa koła (4,00cm*3,48cm) 23h 24h ; 0h 1h 22h 2h 21h 3h Nr2 Nr3 20h Nr4 4h 19h 5h ϕ 4,00cm ϕ3,55cm 17h 7h 1 8h 15h 9h 14h 10h 13h 11h Rys.4 pł.( X Y )poziomy KaŜdy rzut bryły na pł.poziomą będzie prostokątem. Bryły będą się róŝniły połoŝeniem od kaŝdej kolejnej bryły. Rys.4a Bez skali: R owinno być: R = 13,12cm, a jest: R = 13,02948 cm RóŜnica:R - R = 0,09052 cm K 1= 2*a+2*0,5*b=6,00 cm K 3= 11,5658 cm 90 K 3= 11,5658 cm z odczutu T Nie moŝe tak być by 2*2=4, a nawet 5 w (). TECHNIKA Koszalin dnia: 25 września 2016r

9 Nie moŝe być tak, by 2 razy 2 było 4 i 5. rawda jest tylko jedna w rzutowowaniu brył. Zgodna z moją (). str.9 Rys.5 pł.( X Z )pionowa Długość tej bryły ma średnicę KULI ϕ 13,12cm, a średnica KULI bryły ma ϕ4,00cm.należy zaprojektować 4 bryły. Nr4 : Elipsa koła (4,00cm*3,55cm) 23h 24h ; 0h 1h 22h 2h 21h 3h 20h Nr4 4h 19h 5h ϕ 4,00cm ϕ3,55cm 17h 7h 1 8h 15h 9h 14h 10h 13h 11h Rys.6 pł.( X Y )poziomy K 1= 11,67 cm Nr4 Dlaczego K 1 ma wym.= 11,72 cm? Nr3 Odp.przeciwprostok. R = 13,12 cm przeciwprostok.l 1=(2*a+2*0,5*b)= 6,00 cm Nr2 Z wzoru itagorasa obl. K 1: K 1= 11,67 cm Nr1 Cieszę się, Ŝe udało mi się w tym przykładzie na stronach (4-7) połączyć ruch równoleŝnikowy, wirowy przy rzutowaniu prostokątnym brył na płasz- T Nie moŝe tak być by 2*2=4, a nawet 5 w (). czyznę poziomą ( X Y ).Wkrótce stanie się to normą. TECHNIKA Koszalin dnia: 26 września 2016r

10 Dodatkowy RZYKŁAD. Dla treningu wyobraźni. Ten produkt trzeba uznać jako ściągawkę. str.10 Dwie piłki. KaŜda do połowy niebieska po drugiej Ŝółta, na czterech rzutniach, pod kontrolą podglądu układu ( X Y Z ), zapakowane w prostopadłościanie. Rys.1 pł.( X Z ) pionowa AWERS () Rys.2 pł.( Y Z ) pionowa AWERS () odgląd układu (XYZ) 0h 0h 0h atrzymy nie: (XZ); (YZ); (XY). E (XZ) F A B C O kula (YZ) G Hściany (XY) D sześciana Rys.3 pł.( X Y ) pozioma REWERS () Rys.4 pł.( X Y ) pozioma REWERS () Na podglądzie kostki sześ- Jeśli strzałki są równoległe do krawędzi ścianek, to są w poziomie. cianu są pokazane 3 ściany kolorowe: AWERSY. Z przodu błękina pł.( X Z ) 0h 0h 0h pionowa, z boku pł.( Y Z ), po obejściu o 90 teŝ pionowa w kolorze zielonym. U dołu na pł.( X Y )poziomej w kolorze jasnoczerwonej. atrzymy Same rysunki piłek niewie- Na rysunkach pokazuję zielone, duŝe strzałki. One poka- le mówią,bez tarczy zegara zują na którą płaszczyznę będzie wykonywany rzut prostok. 24h. O poprawności wyko- 0h urpurowa strzałka wskazuje kierunek patrzenia naszych nywanej pracy decydują oczy na pł.( X Z )pionową.kolory niebieski i Ŝółty są sobie właściwie oznakowane przeciwstawne (zimno - ciepło) i wskazują (przód i tył). punkty z których wychodzą śółty tył jest z reguły zasłonięty, ale nie przy piłkach. promienie niebieskie i czar- Rys.5 pł.( X Z )pionowa AWERS Rys.6 pł.( X Z )pionowa AWERS ne. Mam świadomość, Ŝe 0h 0h 0h ludzie lubią rzeczy proste, nieskomplikowane.właśnie cały czas do tego dąŝe. Rys.7 pł.( X Y )pozioma AWERS atrzymy od spodu. Rys.8 pł.( X Y )pozioma AWERS atrzymy od spodu 0h 0h 0h Oficjalnie rysunki rzutów prostokątnych wykonuje się zgodnie z tym schematem. Wydaje mi się, iŝ przez te 8 lat pracy nad () i swoją 0h wyobraźnią,potrafię znaleźć lepsze i łatwiejsze rozwiązania rzutów. Właśnie moŝna je zobaczyć na rys.1 ; rys.2 ; rys.3 i rys.4. rzy moich rzutach na pł.poziomą korzystam z REWERSÓW. To tak, jakbym wszedł na kostkę sześcianu i patrzył na rysunek z góry, a nie od dołu. rzez to nie mam kłopotu z rzut.interpr.i przenik. Ten plik doskonale wpływa na rozwój wyobraźni, sprawności umysłowej kaŝdego człowieka, niezaleŝnie od jego wieku. Za 1,5 m-ca kończę 71 lat i będę dalej tworzył (). T RZYKŁAD.Dwie piłki dwukolorowe (). Romana - imię mojej małŝonki TECHNIKA Koszalin dnia: 26 września 2016r