Matematyka dyskretna. Andrzej Łachwa, UJ, 2019 Zadania
|
|
|
- Zuzanna Lipińska
- 6 lat temu
- Przeglądów:
Transkrypt
1 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 Zadania
2 101. Oblicz postać zwartą symbolu { n 4} Udowodnij, że n k =1 ( 1) k ( n k) = Ile może być 4-cyfrowych kodów PIN, w których nie powtarza się żadna cyfra? 104. Alfabet Morse'a składa się z dwóch znaków: kreski i kropki. Ilu znakowe alfabety możemy zakodować słowami alfabetu Morse'a o długości nie większej niż k? Policz dla k=5, 6, Udowodnij, że 2 n jest O(n!) Udowodnij, że 5n 4 +7n 2 3n 12 jest O(n 4 ) 107. Co oznacza napis 5n 6 + ln(n) + O(n 4 ) = O(n 6 )?
3 108. Napisz tożsamość Couchyego dla współczynników dwumianowych i omów ją na przykładzie grupy m mężczyzn i k kobiet Ile jest różnych układów kart w pokerze określanych jako kolor? 110. Ile rozwiązań w dziedzinie naturalnej ma równanie x 0 +x 1 +x 2 +x 3 +x 4 =7? 111. Policz x 3 x n Ile jest liczb naturalnych nie większych od 300, podzielnych przez 2 lub przez 3, lub przez 5 (wykorzystaj zasadę włączania i wyłączania)? 113. Ile transpozycji ma dowolna permutacja typu [ ]? 114. Co oznacza współczynnik 6 0, 3, 0,0, 4? Ile wynosi?
4 115. Osiemnaście osób uczestniczy w grze polegającej na wylosowaniu 2 kart z talii 52 kart. Każda osoba losuje karty z całej talii. Wynik losowania to suma uzyskanych punktów (za dwójkę mamy 2 punkty, za trójkę 3 punkty, itd., aż do dziesiątki za 10 punktów; za figury otrzymujemy także po 10 punktów). Wygrywają te osoby, które mają taki sam wynik. Czy zdarzy się gra w której nikt nie wygra (odpowiedź uzasadnij)? Jakie jest prawdopodobieństwo wyniku 20 punktów? 116. Jaka jest średnia liczba cykli permutacji zbioru 5-elementowego. Zanim zaczniesz, policz w pamięci jaka jest średnia liczba zeszytów przypadająca na plecak, jeżeli w 10 plecakach są po 2 zeszyty i w 20 plecakach po 3 zeszyty? 117. Policz czego jest więcej: (a) rozmieszczeń uporządkowanych 3 elementów w 4 pudełkach czy (b) 4 elementów w 3 pudełkach?
5 118. W sklepie 5 klientów i są 3 kasy. Jaka jest szansa, że osoba nr 4 będzie pierwsza przy kasie nr kule (nierozróżnialne) wkładam do czapki i do skarpety. Na ile sposobów mogę to zrobić? A jeśli 52 kule (nierozróżnialne) wkładam do czapki i do dwóch skarpet (nierozróżnialnych), to na ile sposobów mogę to zrobić? 120. Policz różnicę z funkcji f(x) = 2 x x 2 3 x x 3. Wynik przedstaw w najprost-szej formie i bez potęg dolnych. Zastosuj dwukrotnie wzór na różnicę iloczynu. x 121. Policz różnicę z funkcji f(x) = 3 i 2 7. i=0
6 122. Ile różnych słów 5-literowych można utworzyć ze słowa LALKA (tzn. z pięciu klocków z literami L, L, A, A, K)? Ile różnych słów 4-literowych można utworzyć ze słowa LALKA? Ile różnych słów 3-literowych można utworzyć ze słowa LALKA? 123. Sprawdź, czy jest podzielna przez 17 (wykorzystaj małe twierdzenie Fermata). n 124. Udowodnij, że k k =1 ( n. k) =n 2n Rozwiąż metodą czynnika sumacyjnego rekurencję P 0 = 0 P n = 3P n-1 +3 n n 2 dla n > 0.
7 126. Oblicz różnicę wielomianu p(x)=2x 3 3x 2 +4x, zamieniając ten wielomian na wielomian potęg dolnych i różnicując potęgi dolne. n 127. Policz k =0 zwykłych. (k 3 + 3k 2 ). Wynik przedstaw w postaci wielomianu potęg 128. Mamy klocki z literami AABBCCDEF. Ile różnych napisów możemy utworzyć wykorzystując w każdym napisie wszystkie klocki? 129. Na ile sposobów można wybrać w pokerze figurę zwaną dwie pary? Użyj pojęcia typu dwóch par oznaczanego jako X,Y (na przykład typ 5,W oznacza, że mamy parę piątek, parę waletów i coś, co nie jest ani piątką ani waletem). Kolejność kart nie ma znaczenia Rozwiązać równanie: ( 3) x ( x =0, dla naturalnej liczby x>2. 2)
8 131. W sklepie są piłki w siedmiu kolorach. Klient wybrał 3 piłki, każdą w innym kolorze. Na ile sposobów mógł kupić te piłki? Kolejność nie ma znaczenia W sklepie są jabłka, gruszki i pomarańcze. Klient kupił 7 owoców. Na ile sposobów mógł kupić owoce? Kolejność nie ma znaczenia studentów zostało zapytanych, jaki przedmiot dodatkowy chcieliby wybrać w następnym semestrze, spośród trzech: historii, geografii i socjologii. 45 studentów wybrało tylko historię, 38 tylko geografię, 21 tylko socjologię. Ponadto 18 wybrało historię i geografię (i być może trzeci przedmiot), 9 historię i socjologię (i być może trzeci przedmiot), 4 geografię i socjologię (i być może trzeci przedmiot), oraz 23 nie wybrało żadnego przedmiotu. Ilu studentów wybrało wszystkie trzy przedmioty? W rozwiązaniu użyj diagramów Venna i zasady włączaniawyłączania.
9 134. Czy prawdą jest, że ? Czy prawda jest, że ? Czy zamiast wykonywania obliczeń możemy zastosować tu małe twierdzenie Fermata? 135. Udowodnij, że x 1 δ x = H x +C. n 136. Oblicz sumę skończonego ciągu geometrycznego a q i (q 1) i=0 wykorzystując metodę sumy nieoznaczonej Cztery osoby grają w karty. Po przerwie zmieniają zajmowane przy stole miejsca w ten sposób, by żadna z nich nie usiadła na tym samym krześle na którym siedziała wcześniej. Na ile sposobów mogą to zrobić?
10 138. Pięć osób (każda ma jeden samochód) wymieniają się na weekend swoimi samochodami. W tym celu wrzucają do urny kluczyki do samochodów i kolejno je losują. Jeżeli ktoś wylosuje kluczyki do swojego samochodu, to losuje ponownie, a następnie zwraca swoje kluczki do urny. Może się zdarzyć, że po wylosowaniu swojego samochodu urna będzie pusta (pozostałe cztery osoby już się wymieniły samochodami) - wtedy osoba ta zostanie na weekend ze swoim samochodem. Ile może być różnych wyników takiego losowania, gdzie będzie dokładnie jedna para osób taka, że jedna z nich wylosowała samochód drugiej, a druga tej pierwszej? Kolejność nie ma znaczenia. Nie wypisuj wyników losowań (chyba że dla przykładu). Użyj odpowiedniej konstrukcji matematycznej.
11 139. Ile może być różnych wyników losowania opisanego wyżej, że będą dokładnie dwie pary osób takie, że w każdej parze jedna z osób wylosowała samochód drugiej, a druga tej pierwszej? Kolejność nie ma znaczenia. Nie wypisuj wyników losowań (chyba że dla przykładu). Użyj odpowiedniej konstrukcji matematycznej Zapisz wielomian (1+x) 7 w zwykłej postaci (jako suma jednomianów) Siedem identycznych ołówków wkładamy do trzech pudełek: białego, czerwonego i czarnego. Żadne pudełko nie może być puste. Na ile sposobów można to zrobić? Użyj odpowiedniej konstrukcji matematycznej Mamy 10 różnych słów. Z trzech układamy pierwsze zdanie, z innych czterech drugie zdanie i z pozostałych trzech trzecie zdanie. Ile różnych 3- zdaniowych tekstów możemy zbudować?
12 143. Ile różnych liczb 9-cyfrowych można utworzyć z cyfr 1,2,...,9 tak, aby żadna cyfra w liczbie nie powtarzała się? Oszacuj tę liczbę Grający w totolotka stawia na wylosowanie sześciu liczb, które wybiera się spośród liczb od 1 do 49. Ile zakładów należy zawrzeć, aby zagwarantować sobie sześć trafień? Oszacuj tę liczbę. Ile jest takich zakładów, w których żadna liczba nie jest przewidziana trafnie? Oszacuj prawdopodobieństwo takiego zdarzenia. A ile jest takich, w których co najwyżej jedna liczba jest przewidziana trafnie?
13 145. Uczestnik zakładów totalizatora piłkarskiego przepowiada wyniki 12 różnych spotkań piłkarskich. Jako wyniki spotkań w grę wchodzą: remis, zwycięstwo gospodarzy, zwycięstwo gości. Ile co najmniej kuponów należy oddać, aby mieć 12 trafień, tzn. przewidzieć właściwe wyniki wszystkich dwunastu spotkań? Oszacuj tę liczbę Ile jest sposobów ustawienia 5 mężczyzn i 4 kobiet w szeregu tak aby z obu stron każdej kobiety stali mężczyźni? 147. W kiosku mamy do wyboru 9 rodzajów różnych widokówek. Ile jest sposobów wysłania po jednej kartce do czterech znajomych? 148. Ile różnych wyrazów można utworzyć ze słowa MATEMATYKA?
14 149. Ile prób trzeba podjąć w najbardziej niesprzyjającym przypadku, aby otworzyć zamek szyfrowy, który ma 4 współosiowe pierścienie, a na każdym z nich znajduje się po sześć cyfr? 150. Policz różnicę z funkcji g(x) = n k =1 3 x k Ile różnych sznurów złożonych z 11 korali można zbudować mając do dyspozycji dowolną liczbę koralików czerwonych, białych, niebieskich i zielonych Rzucamy jednocześnie kostką czarną i kostką białą. Wyznaczyć liczbę rzutów, w których a) liczba oczek, które ukazały się na białej kostce jest mniejsza od liczby oczek, które wypadły na czarnej kostce; b) liczba oczek, które ukazały się na czarnej kostce nie jest mniejsza od liczby oczek, które wypadły na białej kostce.
15 153. Ile jest różnych wyników rzucając (a) trzema jednakowymi kostkami jednocześnie? (b) trzema różnokolorowymi kostkami jednocześnie? (c) rzucając jedną kostką 3 razy? 154. Ile różnych dzielników naturalnych ma liczba a) 2310 ; b) 65536; c) ; d) n Czy prawdą jest, że dla n>0 zachodzi (2i+1)=3 n 2? i=n 156. Wśród 9 osób są dwie rodziny: 3-osobowa i 4-osobowa. Na ile sposobów można ustawić te 9 osób w szereg tak, aby przynajmniej jedna z tych rodzin stała w szeregu razem (tworzyła zwarty podszereg, zwartą grupę)?
16 157. Na koncercie ma wystąpić 10 osób: 4 piosenkarzy i 6 piosenkarek. Na ile sposobów można ustalić przebieg koncertu tak, aby występy kobiet i mężczyzn przeplatały się? 158. Niech 0 r<m<n. Ile jest takich rozmieszczeń n rozróżnialnych kul w m rozróżnialnych szufladach, że co najmniej r szuflad pozostaje pustych? Kolejność kul w szufladzie nie ma znaczenia Posługując się interpretacją kombinatoryczną pokaż, że.
17 160. Napisać na ile różnych sposobów można k przedmiotów rozmieścić w n pudełkach uwzględniając wszystkie możliwe zestawiania następujących warunków: a) przedmioty są rozróżnialne lub nierozróżnialne. b) pudełka są rozróżnialne lub nierozróżnialne. c) każde pudełko może zawierać co najwyżej jeden przedmiot lub może zawierać dowolną liczbę przedmiotów Ile układów kart w pokerze to Trójka? Trójka to układ 5 kart wylosowanych z talii 52 kart, w którym występują trzy karty tej samej wysokości (np. trzy walety) i dwie karty różnej wysokości między sobą i różnej od tamtych trzech Policz czego jest więcej: (a) rozmieszczeń uporządkowanych 3 elementów w 5 pudełkach czy (b) 4 elementów w 4 pudełkach?
18 163. Po nocy spędzonej na nauce matematyki dyskretnej każdą ze 100 osób bolała głowa lub bolał brzuch lub miała wzmożone pragnienie. 60 osób bolała głowa, 35 osób bolał brzuch, 10 osób nie bolała ani głowa ani brzuch. Spośród 26 osób, które miały wzmożone pragnienie, 6 bolała głowa a 11 brzuch. Ile osób miało wszystkie wymienione wyżej objawy przeuczenia matematyki dyskretnej? 164. Na prywatce jest 5 par małżeńskich. Po zakończeniu każdy mężczyzna wychodzi z losowo wybraną kobietą. a) Ile jest wszystkich możliwości doboru takich par? b) W ilu przypadkach żaden mężczyzna nie wyjdzie ze swoją żoną? Podaj obie liczby Ile jest permutacji liczb 1; 2; 3;... n, w których liczby 1; 2; 3 nie tworzą trzech kolejnych wyrazów (niezależnie od porządku). Podaj wzór.
19 166. Narysuj trójkąt Stirlinga dla cykli Spośród 20 pracowników pewnej firmy 5 jest na urlopie. Spośród wszystkich 8, którzy mają zostać zwolnieni na urlopie jest 4. Ilu jest takich, którzy ani nie są na urlopie ani nie zostaną zwolnieni? 168. Narysuj trójkąt Stirlinga dla podziałów Wieczorem, po zajęciach, każdy 6 z pozostałych do końca studentów wychodzi w losowo wybranej kurtce. Na ile sposobów mogą ubrać kurtki tak, aby żaden nie wyszedł w swojej? 170. W skład 5-osobowej komisji mogą wejść przedstawiciele 10 narodowości. Na ile sposobów można wybrać komisje tak, aby nie składała się z przedstawicieli tylko jednej narodowości? Podaj liczbę.
Matematyka dyskretna. Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl. Przykłady zadań egzaminacyjnych (do liczenia lub dowodzenia)
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl Przykłady zadań egzaminacyjnych (do liczenia lub dowodzenia) 1. Ile układów kart w pokerze to Dwie pary? Dwie pary to układ 5 kart
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl Przykłady zadań egzaminacyjnych (do liczenia lub dowodzenia) 1. Ile układów kart w pokerze to Dwie pary? Dwie pary to układ 5 kart
Moneta 1 Moneta 2 Kostka O, R O,R 1,2,3,4,5, Moneta 1 Moneta 2 Kostka O O ( )
 Nowa matura kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo
Nowa matura kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo
Prawdopodobieństwo
 Prawdopodobieństwo http://www.matemaks.pl/ Wstęp do rachunku prawdopodobieństwa http://www.matemaks.pl/wstep-do-rachunku-prawdopodobienstwa.html Rachunek prawdopodobieństwa pomaga obliczyć szansę zaistnienia
Prawdopodobieństwo http://www.matemaks.pl/ Wstęp do rachunku prawdopodobieństwa http://www.matemaks.pl/wstep-do-rachunku-prawdopodobienstwa.html Rachunek prawdopodobieństwa pomaga obliczyć szansę zaistnienia
Zadanie 1. Oblicz prawdopodobieństwo, że rzucając dwiema kostkami do gry otrzymamy:
 Zadanie 1. Oblicz prawdopodobieństwo, że rzucając dwiema kostkami do gry otrzymamy: a) sumę oczek równą 6, b) iloczyn oczek równy 6, c) sumę oczek mniejszą niż 11, d) iloczyn oczek będący liczbą parzystą,
Zadanie 1. Oblicz prawdopodobieństwo, że rzucając dwiema kostkami do gry otrzymamy: a) sumę oczek równą 6, b) iloczyn oczek równy 6, c) sumę oczek mniejszą niż 11, d) iloczyn oczek będący liczbą parzystą,
Matematyka podstawowa X. Rachunek prawdopodobieństwa
 Matematyka podstawowa X Rachunek prawdopodobieństwa Zadania wprowadzające: 1. Rzucasz trzy razy monetą a) Napisz zbiór wszystkich wyników tego doświadczenia losowego. Ile ich jest? Wyrzuciłeś większą liczbę
Matematyka podstawowa X Rachunek prawdopodobieństwa Zadania wprowadzające: 1. Rzucasz trzy razy monetą a) Napisz zbiór wszystkich wyników tego doświadczenia losowego. Ile ich jest? Wyrzuciłeś większą liczbę
c) Zaszły oba zdarzenia A i B; d) Zaszło zdarzenie A i nie zaszło zdarzenie B;
 Rachunek prawdopodobieństwa rozwiązywanie zadań 1. Rzucamy dwa razy symetryczną sześcienną kostką do gry. Zapisujemy liczbę oczek, jakie wypadły w obu rzutach. Wypisz zdarzenia elementarne tego doświadczenia.
Rachunek prawdopodobieństwa rozwiązywanie zadań 1. Rzucamy dwa razy symetryczną sześcienną kostką do gry. Zapisujemy liczbę oczek, jakie wypadły w obu rzutach. Wypisz zdarzenia elementarne tego doświadczenia.
R_PRACA KLASOWA 1 Statystyka i prawdopodobieństwo.
 R_PRACA KLASOWA 1 Statystyka i prawdopodobieństwo. Zadanie 1. Wyznacz średnią arytmetyczną, dominantę i medianę zestawu danych: 1, 5, 3, 2, 2, 4, 4, 6, 7, 1, 1, 4, 5, 5, 3. Zadanie 2. W zestawie danych
R_PRACA KLASOWA 1 Statystyka i prawdopodobieństwo. Zadanie 1. Wyznacz średnią arytmetyczną, dominantę i medianę zestawu danych: 1, 5, 3, 2, 2, 4, 4, 6, 7, 1, 1, 4, 5, 5, 3. Zadanie 2. W zestawie danych
Matematyka dyskretna. Andrzej Łachwa, UJ, A/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 9A/14 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 9A/14 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Lista zadania nr 2 Metody probabilistyczne i statystyka studia I stopnia informatyka (rok 2) Wydziału Ekonomiczno-Informatycznego Filia UwB w Wilnie
 Lista zadania nr 2 Metody probabilistyczne i statystyka studia I stopnia informatyka (rok 2) Wydziału Ekonomiczno-Informatycznego Filia UwB w Wilnie Jarosław Kotowicz Instytut Matematyki Uniwersytet w
Lista zadania nr 2 Metody probabilistyczne i statystyka studia I stopnia informatyka (rok 2) Wydziału Ekonomiczno-Informatycznego Filia UwB w Wilnie Jarosław Kotowicz Instytut Matematyki Uniwersytet w
Matematyka dyskretna zestaw II ( )
 Matematyka dyskretna zestaw II (17-18.10.2016) Uwaga: Część z zadań z tego zestawu opiera się na zasadzie szufladkowej Dirichleta. Zadanie 1. Na ile sposobów można umieścić w 7 szufladach 3 koszule tak,
Matematyka dyskretna zestaw II (17-18.10.2016) Uwaga: Część z zadań z tego zestawu opiera się na zasadzie szufladkowej Dirichleta. Zadanie 1. Na ile sposobów można umieścić w 7 szufladach 3 koszule tak,
PRAWDOPODOBIEŃSTWO I KOMBINATORYKA
 PRAWDOPODOBIEŃSTWO I KOMBINATORYKA ZADANIE ( PKT) Z urny zawierajacej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej kuli białej jest równe 8, a prawdopodobieństwo
PRAWDOPODOBIEŃSTWO I KOMBINATORYKA ZADANIE ( PKT) Z urny zawierajacej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej kuli białej jest równe 8, a prawdopodobieństwo
Kombinatoryka. Jerzy Rutkowski. Teoria. P n = n!. (1) Zadania obowiązkowe
 Kombinatoryka Jerzy Rutkowski 2. Elementy kombinatoryki 2.1. Permutacje Definicja 1. Niech n N. Permutacją n-elementowego zbioru A nazywamy dowolną funkcję różnowartościową f : {1,..., n} A. Innymi słowy:
Kombinatoryka Jerzy Rutkowski 2. Elementy kombinatoryki 2.1. Permutacje Definicja 1. Niech n N. Permutacją n-elementowego zbioru A nazywamy dowolną funkcję różnowartościową f : {1,..., n} A. Innymi słowy:
L.Kowalski zadania z rachunku prawdopodobieństwa-zestaw 1 ZADANIA - ZESTAW 1. (odp. a) B A C, b) A, c) A B, d) Ω)
 ZADANIA - ZESTAW 1 Zadanie 1.1 Rzucamy trzy razy monetą. A i - zdarzenie polegające na tym, że otrzymamy orła w i - tym rzucie. Określić zbiór zdarzeń elementarnych. Wypisać zdarzenia elementarne sprzyjające
ZADANIA - ZESTAW 1 Zadanie 1.1 Rzucamy trzy razy monetą. A i - zdarzenie polegające na tym, że otrzymamy orła w i - tym rzucie. Określić zbiór zdarzeń elementarnych. Wypisać zdarzenia elementarne sprzyjające
RACHUNEK PRAWDOPODOBIEŃSTWA I KOMBINATORYKA
 RACHUNEK PRAWDOPODOBIEŃSTWA I KOMBINATORYKA Doświadczenia losowe Rachunek prawdopodobieństwa zajmuje się zdarzeniami jakie zachodzą, gdy przeprowadzamy doświadczenia losowe. Mówimy, że doświadczenie jest
RACHUNEK PRAWDOPODOBIEŃSTWA I KOMBINATORYKA Doświadczenia losowe Rachunek prawdopodobieństwa zajmuje się zdarzeniami jakie zachodzą, gdy przeprowadzamy doświadczenia losowe. Mówimy, że doświadczenie jest
Matematyka dyskretna. Andrzej Łachwa, UJ, A/15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2015 andrzej.lachwa@uj.edu.pl 10A/15 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Matematyka dyskretna Andrzej Łachwa, UJ, 2015 andrzej.lachwa@uj.edu.pl 10A/15 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Doświadczenie i zdarzenie losowe
 Doświadczenie i zdarzenie losowe Doświadczenie losowe jest to takie doświadczenie, które jest powtarzalne w takich samych warunkach lub zbliżonych, a którego wyniku nie można przewidzieć jednoznacznie.
Doświadczenie i zdarzenie losowe Doświadczenie losowe jest to takie doświadczenie, które jest powtarzalne w takich samych warunkach lub zbliżonych, a którego wyniku nie można przewidzieć jednoznacznie.
NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI ZADANIE 1 oczka. ZADANIE 2 iloczynu oczek równego 12.
 IMIE I NAZWISKO ZADANIE 1 Rzucamy sześcienna kostka do gry. Jakie jest prawdopodobieństwo, że wypadna co najmniej dwa oczka. ZADANIE 2 Rzucamy trzy razy symetryczna sześcienna kostka do gry. Oblicz prawdopodobieństwo
IMIE I NAZWISKO ZADANIE 1 Rzucamy sześcienna kostka do gry. Jakie jest prawdopodobieństwo, że wypadna co najmniej dwa oczka. ZADANIE 2 Rzucamy trzy razy symetryczna sześcienna kostka do gry. Oblicz prawdopodobieństwo
= 10 9 = Ile jest wszystkich dwucyfrowych liczb naturalnych podzielnych przez 3? A. 12 B. 24 C. 29 D. 30. Sposób I = 30.
 Kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Flagę, taką jak pokazano na rysunku, należy zszyć z trzech jednakowej szerokości pasów kolorowej tkaniny. Oba pasy zewnętrzne
Kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Flagę, taką jak pokazano na rysunku, należy zszyć z trzech jednakowej szerokości pasów kolorowej tkaniny. Oba pasy zewnętrzne
Rachunek prawdopodobieństwa
 Rachunek prawdopodobieństwa Sebastian Rymarczyk srymarczyk@afm.edu.pl Tematyka zajęć 1. Elementy kombinatoryki. 2. Definicje prawdopodobieństwa. 3. Własności prawdopodobieństwa. 4. Zmienne losowe, parametry
Rachunek prawdopodobieństwa Sebastian Rymarczyk srymarczyk@afm.edu.pl Tematyka zajęć 1. Elementy kombinatoryki. 2. Definicje prawdopodobieństwa. 3. Własności prawdopodobieństwa. 4. Zmienne losowe, parametry
Zdarzenie losowe (zdarzenie)
 Zdarzenie losowe (zdarzenie) Ćw. 1. Ze zbioru cyfr (l, 2,3,..., 9} losowo wybieramy jedną. a) Wypisz zdarzenia elementarne, sprzyjające: zdarzeniu A, że wybrano liczbę parzystą zdarzeniu B, że wybrano
Zdarzenie losowe (zdarzenie) Ćw. 1. Ze zbioru cyfr (l, 2,3,..., 9} losowo wybieramy jedną. a) Wypisz zdarzenia elementarne, sprzyjające: zdarzeniu A, że wybrano liczbę parzystą zdarzeniu B, że wybrano
Z4. Ankieta złożona ma być z trzech pytań: A, B i C. Na ile sposobów można ją ułożyć zmieniając tylko kolejność pytań? ODP. Jest 6 możliwych sposobów.
 PERMUTACJE Z1. Oblicz: Z2. Doprowadź do najprostszej postaci wyrażenia: Z3. Sprawdź czy prawdziwa jest równość: Dana równość jest prawdziwa. Z4. Ankieta złożona ma być z trzech pytań: A, B i C. Na ile
PERMUTACJE Z1. Oblicz: Z2. Doprowadź do najprostszej postaci wyrażenia: Z3. Sprawdź czy prawdziwa jest równość: Dana równość jest prawdziwa. Z4. Ankieta złożona ma być z trzech pytań: A, B i C. Na ile
KURS PRAWDOPODOBIEŃSTWO
 KURS PRAWDOPODOBIEŃSTWO Lekcja 2 Klasyczna definicja prawdopodobieństwa ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Według klasycznej
KURS PRAWDOPODOBIEŃSTWO Lekcja 2 Klasyczna definicja prawdopodobieństwa ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Według klasycznej
01DRAP - klasyczna definicja prawdopodobieństwa
 01DRAP - klasyczna definicja prawdopodobieństwa Ω zbiór zdarzeń elementarnych. Gdy Ω < oraz P({ω} = 1 Ω, dla każdego ω Ω (tzn. każde zdarzenie elementarne jest równo prawdopodobne, to P (A = A Ω Przydatne
01DRAP - klasyczna definicja prawdopodobieństwa Ω zbiór zdarzeń elementarnych. Gdy Ω < oraz P({ω} = 1 Ω, dla każdego ω Ω (tzn. każde zdarzenie elementarne jest równo prawdopodobne, to P (A = A Ω Przydatne
01DRAP - klasyczna definicja prawdopodobieństwa
 01DRAP - klasyczna definicja prawdopodobieństwa Ω zbiór zdarzeń elementarnych. Gdy Ω < oraz P({ω} = 1 Ω, dla każdego ω Ω (tzn. każde zdarzenie elementarne jest równo prawdopodobne, to P (A = A Ω Przydatne
01DRAP - klasyczna definicja prawdopodobieństwa Ω zbiór zdarzeń elementarnych. Gdy Ω < oraz P({ω} = 1 Ω, dla każdego ω Ω (tzn. każde zdarzenie elementarne jest równo prawdopodobne, to P (A = A Ω Przydatne
01DRAP - klasyczna definicja prawdopodobieństwa
 01DRAP - klasyczna definicja prawdopodobieństwa Ω zbiór zdarzeń elementarnych. Gdy Ω < oraz P({ω} = 1 Ω, dla każdego ω Ω (tzn. każde zdarzenie elementarne jest równo prawdopodobne, to P (A = A Ω Przydatne
01DRAP - klasyczna definicja prawdopodobieństwa Ω zbiór zdarzeń elementarnych. Gdy Ω < oraz P({ω} = 1 Ω, dla każdego ω Ω (tzn. każde zdarzenie elementarne jest równo prawdopodobne, to P (A = A Ω Przydatne
PRAWDOPODOBIEŃSTWO CZAS PRACY: 180 MIN. ZADANIE 1 (5 PKT) NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI
 IMIE I NAZWISKO PRAWDOPODOBIEŃSTWO PRAWDOPODOBIEŃSTWO CZAS PRACY: 180 MIN. SUMA PUNKTÓW: 100 ZADANIE 1 (5 PKT) Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia A na każdej kostce wypadła
IMIE I NAZWISKO PRAWDOPODOBIEŃSTWO PRAWDOPODOBIEŃSTWO CZAS PRACY: 180 MIN. SUMA PUNKTÓW: 100 ZADANIE 1 (5 PKT) Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia A na każdej kostce wypadła
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) PRAWDOPODOBIEŃSTWO ZAJŚCIA ZDARZENIA A POD WARUNKIEM, ŻE ZASZŁO ZDARZENIE B
 KLASYCZ NA DEFINICJA PRAW DOPOD OBIEŃSTWA ( ) PRAWDOPOD OBIEŃSTW O W A RUNKOWE PRAWDOPODOBIEŃSTWO ZAJŚCIA ZDARZENIA A POD WARUNKIEM, ŻE ZASZŁO ZDARZENIE B ( ) WIĘC CO OZNACZA, ŻE ZDARZENIE B NIE MA WPŁYWU
KLASYCZ NA DEFINICJA PRAW DOPOD OBIEŃSTWA ( ) PRAWDOPOD OBIEŃSTW O W A RUNKOWE PRAWDOPODOBIEŃSTWO ZAJŚCIA ZDARZENIA A POD WARUNKIEM, ŻE ZASZŁO ZDARZENIE B ( ) WIĘC CO OZNACZA, ŻE ZDARZENIE B NIE MA WPŁYWU
Elementy statystyki opisowej, teoria prawdopodobieństwa i kombinatoryka
 Wymagania egzaminacyjne: a) oblicza średnią arytmetyczną, średnią ważoną, medianę i odchylenie standardowe danych; interpretuje te parametry dla danych empirycznych, b) zlicza obiekty w prostych sytuacjach
Wymagania egzaminacyjne: a) oblicza średnią arytmetyczną, średnią ważoną, medianę i odchylenie standardowe danych; interpretuje te parametry dla danych empirycznych, b) zlicza obiekty w prostych sytuacjach
Obliczanie prawdopodobieństwa za pomocą metody drzew metoda drzew. Drzewem Reguła iloczynów. Reguła sum.
 Obliczanie prawdopodobieństwa za pomocą metody drzew Jeżeli doświadczenie losowe składa się z więcej niż jednego etapu, takich jak serie rzutów kostką lub monetą, zastosowanie klasycznej definicji prawdopodobieństwa
Obliczanie prawdopodobieństwa za pomocą metody drzew Jeżeli doświadczenie losowe składa się z więcej niż jednego etapu, takich jak serie rzutów kostką lub monetą, zastosowanie klasycznej definicji prawdopodobieństwa
Metody probabilistyczne
 Metody probabilistyczne 1. Prawdopodobieństwo klasyczne Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 03.10.2017 1 / 19 Rys historyczny Francja, XVII w.: gry hazardowe
Metody probabilistyczne 1. Prawdopodobieństwo klasyczne Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 03.10.2017 1 / 19 Rys historyczny Francja, XVII w.: gry hazardowe
Matematyka dyskretna. Andrzej Łachwa, UJ, A/10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 8A/10 Zbiory przeliczalne Przyjmujemy, że Zn = {0, 1, 2, 3, n-1} dla n>0 oraz Zn = przy n=0. Zbiór skończony to zbiór bijektywny z
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 8A/10 Zbiory przeliczalne Przyjmujemy, że Zn = {0, 1, 2, 3, n-1} dla n>0 oraz Zn = przy n=0. Zbiór skończony to zbiór bijektywny z
KOMBINATORYKA. Problem przydziału prac
 KOMBINATORYKA Dział matematyki zajmujący się badaniem różnych możliwych zestawień i ugrupowań, jakie można tworzyć z dowolnego zbioru skończonego. Zbiory skończone, najczęściej wraz z pewną relacją obiekty
KOMBINATORYKA Dział matematyki zajmujący się badaniem różnych możliwych zestawień i ugrupowań, jakie można tworzyć z dowolnego zbioru skończonego. Zbiory skończone, najczęściej wraz z pewną relacją obiekty
RACHUNEK PRAWDOPODOBIEŃSTWA
 RACHUNEK PRAWDOPODOBIEŃSTWA Zadanie 1. W urnie jest 1000 kartoników będących losami loterii pieniężnej. Cztery z kartoników wygrywają po 100 zł i szesnaście po 10 zł. Reszta kartoników to losy puste. Pierwszy
RACHUNEK PRAWDOPODOBIEŃSTWA Zadanie 1. W urnie jest 1000 kartoników będących losami loterii pieniężnej. Cztery z kartoników wygrywają po 100 zł i szesnaście po 10 zł. Reszta kartoników to losy puste. Pierwszy
P r a w d o p o d o b i eństwo Lekcja 1 Temat: Lekcja organizacyjna. Program. Kontrakt.
 P r a w d o p o d o b i eństwo Lekcja 1 Temat: Lekcja organizacyjna. Program. Kontrakt. Lekcja 2 Temat: Podstawowe pojęcia związane z prawdopodobieństwem. Str. 10-21 1. Doświadczenie losowe jest to doświadczenie,
P r a w d o p o d o b i eństwo Lekcja 1 Temat: Lekcja organizacyjna. Program. Kontrakt. Lekcja 2 Temat: Podstawowe pojęcia związane z prawdopodobieństwem. Str. 10-21 1. Doświadczenie losowe jest to doświadczenie,
Zestaw 1-1 Organizacja plików: Oddajemy tylko źródła programów (pliki o rozszerzeniach.cpp)!!!
 Zestaw 1-1 1. Napisz program pobierający od użytkownika liczbę całkowitą R (R>1) i liczbę rzeczywistą dodatnią S, a następnie informujący ile kolejnych liczb z ciągu 1, R-1, R 2-2, R 3-3, R 4-4, należy
Zestaw 1-1 1. Napisz program pobierający od użytkownika liczbę całkowitą R (R>1) i liczbę rzeczywistą dodatnią S, a następnie informujący ile kolejnych liczb z ciągu 1, R-1, R 2-2, R 3-3, R 4-4, należy
ZAGADANIENIA NA EGZAMIN USTNY Z MATEMATYKI
 ZAGADANIENIA NA EGZAMIN USTNY Z MATEMATYKI SEMESTR I ZESTAW. Podaj liczbę przeciwną i odwrotną do liczby 2 2. Jak zmieniła się cena wyrobu po podwyżce o 20%, a następnie po obniżeniu otrzymanej ceny o
ZAGADANIENIA NA EGZAMIN USTNY Z MATEMATYKI SEMESTR I ZESTAW. Podaj liczbę przeciwną i odwrotną do liczby 2 2. Jak zmieniła się cena wyrobu po podwyżce o 20%, a następnie po obniżeniu otrzymanej ceny o
Kombinatoryka i rachunek prawdopodobieństwa
 Kombinatoryka i rachunek prawdopodobieństwa Jerzy Rutkowski Kombinatoryka i rachunek prawdopodobieństwa 2. Elementy kombinatoryki 2.1. Permutacje Definicja 1. Niech n N. Permutacją n-elementowego zbioru
Kombinatoryka i rachunek prawdopodobieństwa Jerzy Rutkowski Kombinatoryka i rachunek prawdopodobieństwa 2. Elementy kombinatoryki 2.1. Permutacje Definicja 1. Niech n N. Permutacją n-elementowego zbioru
RACHUNEK PRAWDOPODOBIEŃSTWA ZADANIA Z ROZWIĄZANIAMI. Uwaga! Dla określenia liczebności zbioru (mocy zbioru) użyto zamiennie symboli: Ω lub
 RACHUNEK PRAWDOPODOBIEŃSTWA ZADANIA Z ROZWIĄZANIAMI Uwaga! Dla określenia liczebności zbioru (mocy zbioru) użyto zamiennie symboli: Ω lub 1. W grupie jest 15 kobiet i 18 mężczyzn. Losujemy jedną osobę
RACHUNEK PRAWDOPODOBIEŃSTWA ZADANIA Z ROZWIĄZANIAMI Uwaga! Dla określenia liczebności zbioru (mocy zbioru) użyto zamiennie symboli: Ω lub 1. W grupie jest 15 kobiet i 18 mężczyzn. Losujemy jedną osobę
12DRAP - parametry rozkładów wielowymiarowych
 DRAP - parametry rozkładów wielowymiarowych Definicja.. Jeśli h : R R, a X, Y ) jest wektorem losowym o gęstości fx, y) to EhX, Y ) = hx, y)fx, y)dxdy. Jeśli natomiast X, Y ) ma rozkład dyskretny skupiony
DRAP - parametry rozkładów wielowymiarowych Definicja.. Jeśli h : R R, a X, Y ) jest wektorem losowym o gęstości fx, y) to EhX, Y ) = hx, y)fx, y)dxdy. Jeśli natomiast X, Y ) ma rozkład dyskretny skupiony
Matematyka dyskretna. Andrzej Łachwa, UJ, a/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 8a/14 Zbiory przeliczalne Przyjmujemy, że = {0, 1, 2, 3, n-1} dla n>0 oraz = przy n=0. Zbiór skończony to zbiór bijektywny z pewnym
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 8a/14 Zbiory przeliczalne Przyjmujemy, że = {0, 1, 2, 3, n-1} dla n>0 oraz = przy n=0. Zbiór skończony to zbiór bijektywny z pewnym
02DRAP - Aksjomatyczna definicja prawdopodobieństwa, zasada w-w
 02DRAP - Aksjomatyczna definicja prawdopodobieństwa, zasada w-w A Zadania na ćwiczenia Zadanie A.1. Niech Ω = R oraz F będzie σ-ciałem generowanym przez rodzinę wszystkich przedziałów otwartych typu (,
02DRAP - Aksjomatyczna definicja prawdopodobieństwa, zasada w-w A Zadania na ćwiczenia Zadanie A.1. Niech Ω = R oraz F będzie σ-ciałem generowanym przez rodzinę wszystkich przedziałów otwartych typu (,
Zadanie 1. Na diagramie Venna dla 3 zbiorów zaznacz:
 Zadanie 1 Na diagramie Venna dla 3 zbiorów zaznacz: A B C Zadanie 1 Na diagramie Venna dla 3 zbiorów zaznacz: A B C A B C Zadanie 1 Na diagramie Venna dla 3 zbiorów zaznacz: A B C A B C A B C Zadanie 1
Zadanie 1 Na diagramie Venna dla 3 zbiorów zaznacz: A B C Zadanie 1 Na diagramie Venna dla 3 zbiorów zaznacz: A B C A B C Zadanie 1 Na diagramie Venna dla 3 zbiorów zaznacz: A B C A B C A B C Zadanie 1
Matematyka dyskretna. Andrzej Łachwa, UJ, A/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 9A/14 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 9A/14 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Matematyka dyskretna. Andrzej Łachwa, UJ, 2019 Zadania 1-100
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl Zadania 1-100 Udowodnij, że A (B C) = (A B) (A C) za pomocą diagramów Venna. Udowodnij formalnie, że (A B i A C) A B C oraz że (A
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl Zadania 1-100 Udowodnij, że A (B C) = (A B) (A C) za pomocą diagramów Venna. Udowodnij formalnie, że (A B i A C) A B C oraz że (A
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 14/14 TWIERDZENIE HALLA Twierdzenie o kojarzeniu małżeństw rozważa dwie grupy - dziewcząt i chłopców, oraz podgrupy dziewczyn i podgrupy
Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 14/14 TWIERDZENIE HALLA Twierdzenie o kojarzeniu małżeństw rozważa dwie grupy - dziewcząt i chłopców, oraz podgrupy dziewczyn i podgrupy
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE III TECHNIKUM.
 ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE III TECHNIKUM. I GEOMETRIA ANALITYCZNA 1. Równanie prostej w postaci ogólnej i kierunkowej powtórzenie 2. Wzajemne położenie dwóch prostych powtórzenie
ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE III TECHNIKUM. I GEOMETRIA ANALITYCZNA 1. Równanie prostej w postaci ogólnej i kierunkowej powtórzenie 2. Wzajemne położenie dwóch prostych powtórzenie
Kurs ZDAJ MATURĘ Z MATEMATYKI MODUŁ 14 Zadania statystyka, prawdopodobieństwo i kombinatoryka
 1 TEST WSTĘPNY 1. (1p) Zestaw danych 3, 5, x, 7, 10, 12 jest uporządkowany niemalejąco. Mediana tego zestawu jest równa 6, więc liczba x jest równa A. 7 B. 6 C. 5 D. 4 2. (2p) Średnia arytmetyczna liczb:
1 TEST WSTĘPNY 1. (1p) Zestaw danych 3, 5, x, 7, 10, 12 jest uporządkowany niemalejąco. Mediana tego zestawu jest równa 6, więc liczba x jest równa A. 7 B. 6 C. 5 D. 4 2. (2p) Średnia arytmetyczna liczb:
KOMBINATORYKA I P-WO CZ.1 PODSTAWA
 KOMBINATORYKA I P-WO CZ.1 PODSTAWA ZADANIE 1 (1 PKT) Pan Jakub ma marynarki, 7 par różnych spodni i 10 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i
KOMBINATORYKA I P-WO CZ.1 PODSTAWA ZADANIE 1 (1 PKT) Pan Jakub ma marynarki, 7 par różnych spodni i 10 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i
Ćw,1. Wypisz wszystkie k-wyrazowe wariacje bez powtórzeń zbioru A = {1, 2,3 }, gdy: a) k = l, b) k = 2, c) k = 3. Wariacje 1 z 6
 Wariacje bez powtórzeń Jeśli w doświadczeniu losowym ze zbioru n-elementowego wybieramy k elementów w ten sposób, że: wybrane elementy nie mogą się powtarzać kolejność wybranych elementów jest istotna
Wariacje bez powtórzeń Jeśli w doświadczeniu losowym ze zbioru n-elementowego wybieramy k elementów w ten sposób, że: wybrane elementy nie mogą się powtarzać kolejność wybranych elementów jest istotna
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 10/15 WARIACJE Liczba wariacji, czyli różnych ciągów k-elementowych o wyrazach ze zbioru n-elementowego, wynosi n k. Ciąg k-elementowy,
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 10/15 WARIACJE Liczba wariacji, czyli różnych ciągów k-elementowych o wyrazach ze zbioru n-elementowego, wynosi n k. Ciąg k-elementowy,
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 6/10 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 6/10 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Prawdopodobieństwo. Prawdopodobieństwo. Jacek Kłopotowski. Katedra Matematyki i Ekonomii Matematycznej SGH. 16 października 2018
 Katedra Matematyki i Ekonomii Matematycznej SGH 16 października 2018 Definicja σ-algebry Definicja Niech Ω oznacza zbiór niepusty. Rodzinę M podzbiorów zbioru Ω nazywamy σ-algebrą (lub σ-ciałem) wtedy
Katedra Matematyki i Ekonomii Matematycznej SGH 16 października 2018 Definicja σ-algebry Definicja Niech Ω oznacza zbiór niepusty. Rodzinę M podzbiorów zbioru Ω nazywamy σ-algebrą (lub σ-ciałem) wtedy
Kombinatoryka i rachunek prawdopodobieństwa (rozszerzenie)
 Kombinatoryka i rachunek prawdopodobieństwa (rozszerzenie) (1) Ile liczb czterocyfrowych można utworzyć używając jedynie cyfr 1,2,3,4,5,6,7,8? (2) Ile liczb czterocyfrowych o różnych cyfrach można utworzyć
Kombinatoryka i rachunek prawdopodobieństwa (rozszerzenie) (1) Ile liczb czterocyfrowych można utworzyć używając jedynie cyfr 1,2,3,4,5,6,7,8? (2) Ile liczb czterocyfrowych o różnych cyfrach można utworzyć
KOMBINATORYKA OBIEKTY KOMBINATORYCZNE MATEMATYKA DYSKRETNA (2014/2015)
 MATEMATYKA DYSKRETNA (2014/2015) dr hab. inż. Małgorzata Sterna malgorzata.sterna@cs.put.poznan.pl www.cs.put.poznan.pl/msterna/ KOMBINATORYKA OBIEKTY KOMBINATORYCZNE TEORIA ZLICZANIA Teoria zliczania
MATEMATYKA DYSKRETNA (2014/2015) dr hab. inż. Małgorzata Sterna malgorzata.sterna@cs.put.poznan.pl www.cs.put.poznan.pl/msterna/ KOMBINATORYKA OBIEKTY KOMBINATORYCZNE TEORIA ZLICZANIA Teoria zliczania
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 7/10 Generowanie podzbiorów Weźmy n-elementowy zbiór X={x 1, x 2 x n }. Każdemu podzbiorowi YX przyporządkujemy ciąg binarny b 0 b
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 7/10 Generowanie podzbiorów Weźmy n-elementowy zbiór X={x 1, x 2 x n }. Każdemu podzbiorowi YX przyporządkujemy ciąg binarny b 0 b
SPRAWDZIAN KOMBINATORYKA
 www.zadania.info NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI SPRAWDZIAN KOMBINATORYKA 12 GRUDNIA 2011 CZAS PRACY: 45 MIN. ZADANIE 1 Spośród liczb {1, 2, 3,..., 1000} losujemy jednocześnie dwie, które
www.zadania.info NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI SPRAWDZIAN KOMBINATORYKA 12 GRUDNIA 2011 CZAS PRACY: 45 MIN. ZADANIE 1 Spośród liczb {1, 2, 3,..., 1000} losujemy jednocześnie dwie, które
Typy zadań kombinatorycznych:
 Typy zadań kombinatorycznych: I. Ustawianie wszystkich elementów zbioru w pewnej kolejności Przestawieniem nazywamy ustawienie elementów danego zbioru w pewnej kolejności. Liczba przestawień określa na
Typy zadań kombinatorycznych: I. Ustawianie wszystkich elementów zbioru w pewnej kolejności Przestawieniem nazywamy ustawienie elementów danego zbioru w pewnej kolejności. Liczba przestawień określa na
Skrypt 30. Prawdopodobieństwo
 Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 30 Prawdopodobieństwo 5.
Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 30 Prawdopodobieństwo 5.
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Zadanie PP RP 1. Z pojemnika, w którym znajdują się cztery losy z numerami 112, 121, 211, 212 losujemy trzy razy po jednym losie, po każdym losowaniu zwracając wylosowany los do pojemnika. Oblicz prawdopodobieństwo,
Zadanie PP RP 1. Z pojemnika, w którym znajdują się cztery losy z numerami 112, 121, 211, 212 losujemy trzy razy po jednym losie, po każdym losowaniu zwracając wylosowany los do pojemnika. Oblicz prawdopodobieństwo,
Matematyka dyskretna
 Matematyka dyskretna Zbiór zadań kolekcjonowanych w ciągu semestralnego kursu Matematyka dyskretna prof. dr hab. M. Morayne dla studentów informatyki magisterskiej WPPT PWr wiosna-lato 2005 UWAGA: Zadania
Matematyka dyskretna Zbiór zadań kolekcjonowanych w ciągu semestralnego kursu Matematyka dyskretna prof. dr hab. M. Morayne dla studentów informatyki magisterskiej WPPT PWr wiosna-lato 2005 UWAGA: Zadania
KURS PRAWDOPODOBIEŃSTWO
 KURS PRAWDOPODOBIEŃSTWO Lekcja 3 Definicja prawdopodobieństwa Kołmogorowa. Prawdopodobieństwa warunkowe i niezależne. ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko
KURS PRAWDOPODOBIEŃSTWO Lekcja 3 Definicja prawdopodobieństwa Kołmogorowa. Prawdopodobieństwa warunkowe i niezależne. ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko
Rachunek prawdopodobieństwa Rozdział 1. Wstęp
 Rachunek prawdopodobieństwa Rozdział 1. Wstęp 1.1. Prawdopodobieństwo klasyczne Katarzyna Rybarczyk-Krzywdzińska Definicja Zadaliśmy pytanie. Bolek, Lolek i Tola wstąpili do kasyna. Dla każdego z nich
Rachunek prawdopodobieństwa Rozdział 1. Wstęp 1.1. Prawdopodobieństwo klasyczne Katarzyna Rybarczyk-Krzywdzińska Definicja Zadaliśmy pytanie. Bolek, Lolek i Tola wstąpili do kasyna. Dla każdego z nich
Statystyka matematyczna
 Statystyka matematyczna Wykład 2 Magdalena Alama-Bućko 5 marca 2018 Magdalena Alama-Bućko Statystyka matematyczna 5 marca 2018 1 / 14 Prawdopodobieństwo klasyczne Ω - zbiór wszystkich zdarzeń elementarnych
Statystyka matematyczna Wykład 2 Magdalena Alama-Bućko 5 marca 2018 Magdalena Alama-Bućko Statystyka matematyczna 5 marca 2018 1 / 14 Prawdopodobieństwo klasyczne Ω - zbiór wszystkich zdarzeń elementarnych
liczb naturalnych czterocyfrowych. Mamy do dyspozycji następujące cyfry: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. g) Ile jest liczb czterocyfrowych parzystych?
 KOMBINATORYKA ZADANIA Z ROZWIĄZANIAMI 1. Udziel odpowiedzi na poniższe pytania: a) Ile jest możliwych wyników w rzucie jedną kostką? W rzucie jedną kostką możemy otrzymać jeden spośród następujących wyników:
KOMBINATORYKA ZADANIA Z ROZWIĄZANIAMI 1. Udziel odpowiedzi na poniższe pytania: a) Ile jest możliwych wyników w rzucie jedną kostką? W rzucie jedną kostką możemy otrzymać jeden spośród następujących wyników:
ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE III TECHNIKUM.
 ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE III TECHNIKUM. I. Trygonometria. 1. Definicje funkcji trygonometrycznych kąta ostrego w trójkącie prostokątnym. 2. Rozwiązywanie trójkątów prostokątnych
ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE III TECHNIKUM. I. Trygonometria. 1. Definicje funkcji trygonometrycznych kąta ostrego w trójkącie prostokątnym. 2. Rozwiązywanie trójkątów prostokątnych
( ) ( ) Przykład: Z trzech danych elementów: a, b, c, można utworzyć trzy następujące 2-elementowe kombinacje: ( ) ( ) ( ).
 KOMBINATORYKA Kombinatoryka zajmuje się wyznaczaniem liczby elementów zbiorów skończonych utworzonych zgodnie z określonymi zasadami. Do podstawowych pojęć kombinatorycznych należą: PERMUTACJE Silnia.
KOMBINATORYKA Kombinatoryka zajmuje się wyznaczaniem liczby elementów zbiorów skończonych utworzonych zgodnie z określonymi zasadami. Do podstawowych pojęć kombinatorycznych należą: PERMUTACJE Silnia.
KURS PRAWDOPODOBIEŃSTWO
 KURS PRAWDOPODOBIEŃSTWO Lekcja 4 Prawdopodobieństwo całkowite i twierdzenie Bayesa. Drzewko stochastyczne. Schemat Bernoulliego. ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź
KURS PRAWDOPODOBIEŃSTWO Lekcja 4 Prawdopodobieństwo całkowite i twierdzenie Bayesa. Drzewko stochastyczne. Schemat Bernoulliego. ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź
12. RACHUNEK PRAWDOPODOBIEŃSTWA I STATYSTYKA zadania
 2. RACHUNEK PRAWDOPODOBIEŃSTWA I STATYSTYKA zadania Zad.2.. Oblicz ile moŝna utworzyć z cyfr 0,, 2, liczb: a) dwucyfrowych, których cyfry mogą się powtarzać; b) trzycyfrowych o niepowtarzających się cyfrach;
2. RACHUNEK PRAWDOPODOBIEŃSTWA I STATYSTYKA zadania Zad.2.. Oblicz ile moŝna utworzyć z cyfr 0,, 2, liczb: a) dwucyfrowych, których cyfry mogą się powtarzać; b) trzycyfrowych o niepowtarzających się cyfrach;
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 9/14 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
Matematyka dyskretna Andrzej Łachwa, UJ, 2017 andrzej.lachwa@uj.edu.pl 9/14 Zasada Dirichleta 1 ZASADA SZUFLADKOWA DIRICHLETA (1ZSD) Jeśli n obiektów jest rozmieszczonych w m szufladach i n > m > 0, to
ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE III TECHNIKUM.
 ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE III TECHNIKUM. I Geometria analityczna 1. Równanie prostej w postaci ogólnej i kierunkowej powtórzenie 2. Wzajemne położenie dwóch prostych powtórzenie
ZAGADNIENIA NA EGZAMIN POPRAWKOWY Z MATEMATYKI W KLASIE III TECHNIKUM. I Geometria analityczna 1. Równanie prostej w postaci ogólnej i kierunkowej powtórzenie 2. Wzajemne położenie dwóch prostych powtórzenie
Prawdopodobieństwo Warunkowe Prawdopodobieństwo Całkowite Niezależność Stochastyczna Zdarzeń
 Prawdopodobieństwo Warunkowe Prawdopodobieństwo Całkowite Niezależność Stochastyczna Zdarzeń Zadanie 1 Po potasowaniu sześciu kart: asa, dwójki, trójki, czwórki, piątki i szóstki wyłożono na stół w rzędzie
Prawdopodobieństwo Warunkowe Prawdopodobieństwo Całkowite Niezależność Stochastyczna Zdarzeń Zadanie 1 Po potasowaniu sześciu kart: asa, dwójki, trójki, czwórki, piątki i szóstki wyłożono na stół w rzędzie
c) ( 13 (1) (2) Zadanie 2. Losując bez zwracania kolejne litery ze zbioru AAAEKMMTTY, jakie jest prawdopodobieństwo Odp.
 Zadania na kolokwium nr Zadanie. Spośród kart w tali wylosowano. Jakie jest prawdopodobieństwo: pików, kierów, trefli i karo otrzymania wszystkich kolorów otrzymania dokładnie pików a ( b ( ( c ( ( ( (
Zadania na kolokwium nr Zadanie. Spośród kart w tali wylosowano. Jakie jest prawdopodobieństwo: pików, kierów, trefli i karo otrzymania wszystkich kolorów otrzymania dokładnie pików a ( b ( ( c ( ( ( (
Rachunek prawdopodobieństwa- wykład 2
 Rachunek prawdopodobieństwa- wykład 2 Pojęcie dyskretnej przestrzeni probabilistycznej i określenie prawdopodobieństwa w tej przestrzeni dr Marcin Ziółkowski Instytut Matematyki i Informatyki Uniwersytet
Rachunek prawdopodobieństwa- wykład 2 Pojęcie dyskretnej przestrzeni probabilistycznej i określenie prawdopodobieństwa w tej przestrzeni dr Marcin Ziółkowski Instytut Matematyki i Informatyki Uniwersytet
Temat 18: Statystyka i prawdopodobieństwo w naszym życiu.
 Temat 8: Statystyka i prawdopodobieństwo w naszym życiu. Jakie są miary statystyczne? Średnia arytmetyczna. Średnia arytmetyczna dwóch liczb a i b to połowa ich sumy Średnia arytmetyczna trzech liczb a,
Temat 8: Statystyka i prawdopodobieństwo w naszym życiu. Jakie są miary statystyczne? Średnia arytmetyczna. Średnia arytmetyczna dwóch liczb a i b to połowa ich sumy Średnia arytmetyczna trzech liczb a,
PRAWDOPODOBIEOSTWO ZAJŚCIA ZDARZENIA A POD WARUNKIEM, ŻE ZASZŁO ZDARZENIE B
 KLASYCZ NA DEFINICJA PRAW DOPOD OBIEŃSTWA P A = A Ω PRAWDOPOD OBIEŃSTW O W A RUNKOWE P(A B) P A B =, P B 0 PRAWDOPODOBIEOSTWO ZAJŚCIA ZDARZENIA A POD WARUNKIEM, ŻE ZASZŁO ZDARZENIE B P A B = P A B = P
KLASYCZ NA DEFINICJA PRAW DOPOD OBIEŃSTWA P A = A Ω PRAWDOPOD OBIEŃSTW O W A RUNKOWE P(A B) P A B =, P B 0 PRAWDOPODOBIEOSTWO ZAJŚCIA ZDARZENIA A POD WARUNKIEM, ŻE ZASZŁO ZDARZENIE B P A B = P A B = P
Prawdopodobieństwo zadania na sprawdzian
 Prawdopodobieństwo zadania na sprawdzian Zad. 1. Zdarzenia A, B, C oznaczają, że wzięto co najmniej po jednej książce odpowiednio z pierwszych, drugich i trzecich dzieł zebranych. Każde z dzieł zebranych
Prawdopodobieństwo zadania na sprawdzian Zad. 1. Zdarzenia A, B, C oznaczają, że wzięto co najmniej po jednej książce odpowiednio z pierwszych, drugich i trzecich dzieł zebranych. Każde z dzieł zebranych
a. zbiór wszystkich potasowań talii kart (w którym S dostaje 13 pierwszych kart, W - 13 kolejnych itd.);
 03DRAP - Przykłady przestrzeni probabilistycznych Definicja 1 Przestrzeń probabilistyczna to trójka (Ω, F, P), gdzie Ω zbiór zdarzeń elementarnych, F σ ciało zdarzeń (podzbiorów Ω), P funkcja prawdopodobieństwa/miara
03DRAP - Przykłady przestrzeni probabilistycznych Definicja 1 Przestrzeń probabilistyczna to trójka (Ω, F, P), gdzie Ω zbiór zdarzeń elementarnych, F σ ciało zdarzeń (podzbiorów Ω), P funkcja prawdopodobieństwa/miara
Podstawy nauk przyrodniczych Matematyka
 Podstawy nauk przyrodniczych Matematyka Elementy rachunku prawdopodobieństwa dr inż. Małgorzata Szeląg Zakład Genetyki Molekularnej Człowieka tel. 61 829 59 04 malgorzata.szelag@amu.edu.pl Pokój 1.118
Podstawy nauk przyrodniczych Matematyka Elementy rachunku prawdopodobieństwa dr inż. Małgorzata Szeląg Zakład Genetyki Molekularnej Człowieka tel. 61 829 59 04 malgorzata.szelag@amu.edu.pl Pokój 1.118
Lista 1. Prawdopodobieństwo klasyczne i geometryczne
 Metody statystyczne. Lista 1. 1 Lista 1. Prawdopodobieństwo klasyczne i geometryczne 1. Jakie jest prawdopodobieństwo, że (a) z talii zawierającej 52 karty wybierzemy losowo asa? (b) z talii zawierającej
Metody statystyczne. Lista 1. 1 Lista 1. Prawdopodobieństwo klasyczne i geometryczne 1. Jakie jest prawdopodobieństwo, że (a) z talii zawierającej 52 karty wybierzemy losowo asa? (b) z talii zawierającej
Temat: Statystyka i prawdopodobieństwo w naszym życiu.
 Dla nauczyciela Spotkanie 9 Temat: Statystyka i prawdopodobieństwo w naszym życiu. Na zajęcia potrzebne będą pomoce tzn. kostki do gry, talia kart, monety lub inne. Przy omawianiu doświadczeń losowych
Dla nauczyciela Spotkanie 9 Temat: Statystyka i prawdopodobieństwo w naszym życiu. Na zajęcia potrzebne będą pomoce tzn. kostki do gry, talia kart, monety lub inne. Przy omawianiu doświadczeń losowych
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 7/15 Rachunek różnicowy Dobrym narzędziem do obliczania skończonych sum jest rachunek różnicowy. W rachunku tym odpowiednikiem operatora
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 7/15 Rachunek różnicowy Dobrym narzędziem do obliczania skończonych sum jest rachunek różnicowy. W rachunku tym odpowiednikiem operatora
Funkcja. x X! y Y : x, y f. f : X Y f x = y f : x y. Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje:
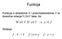 Funkcja Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje: x X! y Y : x, y f f : X Y f x = y f : x y Przykłady f: N N, f(n) = 2n f: N R, f(n) = n/2 f: N {13}, f(n)
Funkcja Funkcja o dziedzinie X i przeciwdziedzinie Y to dowolna relacja f XxY taka, że: Notacje: x X! y Y : x, y f f : X Y f x = y f : x y Przykłady f: N N, f(n) = 2n f: N R, f(n) = n/2 f: N {13}, f(n)
Zadania z Zasad planowania eksperymentu i opracowania wyników pomiarów. Zestaw 1.
 Zestaw 1. Zadanie. 1. Wyobraźnia jest ważniejsza od wiedzy A.Einstein Czy zdarzenia polegające na wyciągnięciu z talii liczącej 52 karty dowolnej karty pik (zdarzenie A) i wyciągnięciu asa (zdarzenie B)
Zestaw 1. Zadanie. 1. Wyobraźnia jest ważniejsza od wiedzy A.Einstein Czy zdarzenia polegające na wyciągnięciu z talii liczącej 52 karty dowolnej karty pik (zdarzenie A) i wyciągnięciu asa (zdarzenie B)
I. FUNKCJA WYKŁADNICZA I LOGARYTMY 1. POTĘGI Zad.1. Zapisz za pomocą potęgi o podanej podstawie:
 Strona 1 z 9 I. FUNKCJA WYKŁADNICZA I LOGARYTMY 1. POTĘGI Zapisz za pomocą potęgi o podanej podstawie: 5 4 ( 27) ( ) a), podstawa : ( ) b) 6 ( 9) c), podstawa: (5) d) Oblicz: a) 1 6 4 2 1 1 1 2 (0,25)
Strona 1 z 9 I. FUNKCJA WYKŁADNICZA I LOGARYTMY 1. POTĘGI Zapisz za pomocą potęgi o podanej podstawie: 5 4 ( 27) ( ) a), podstawa : ( ) b) 6 ( 9) c), podstawa: (5) d) Oblicz: a) 1 6 4 2 1 1 1 2 (0,25)
Propozycje rozwiązań zadań otwartych z próbnej matury rozszerzonej przygotowanej przez OPERON.
 Propozycje rozwiązań zadań otwartych z próbnej matury rozszerzonej przygotowanej przez OPERON. Zadanie 6. Dane są punkty A=(5; 2); B=(1; -3); C=(-2; -8). Oblicz odległość punktu A od prostej l przechodzącej
Propozycje rozwiązań zadań otwartych z próbnej matury rozszerzonej przygotowanej przez OPERON. Zadanie 6. Dane są punkty A=(5; 2); B=(1; -3); C=(-2; -8). Oblicz odległość punktu A od prostej l przechodzącej
Rzucamy dwa razy sprawiedliwą, sześcienną kostką do gry. Oblicz prawdopodobieństwo otrzymania:
 Statystyka Ubezpieczeniowa Część 1. Rachunek prawdopodobieństwa: - prawdopodobieństwo klasyczne - zdarzenia niezależne - prawdopodobieństwo warunkowe - prawdopodobieństwo całkowite - wzór Bayesa Schemat
Statystyka Ubezpieczeniowa Część 1. Rachunek prawdopodobieństwa: - prawdopodobieństwo klasyczne - zdarzenia niezależne - prawdopodobieństwo warunkowe - prawdopodobieństwo całkowite - wzór Bayesa Schemat
Matematyka Dyskretna Rozgrzewka I test semestr letni 2012/2013
 Matematyka Dyskretna Rozgrzewka I test semestr letni 2012/2013 Zadanie 1. Dla n naturalnego mamy zdanie: Jeżeli n jest liczbą pierwszą, to n jest równa 2 lub jest liczbą nieparzystą. Możemy je zapisać
Matematyka Dyskretna Rozgrzewka I test semestr letni 2012/2013 Zadanie 1. Dla n naturalnego mamy zdanie: Jeżeli n jest liczbą pierwszą, to n jest równa 2 lub jest liczbą nieparzystą. Możemy je zapisać
BAZA ZADAŃ KLASA 3 Ha 2014/2015
 BAZA ZADAŃ KLASA 3 Ha 2014/2015 GEOMETRIA 1 W trójkącie prostokątnym wysokość poprowadzona na przeciwprostokątną ma długość 10 cm, a promień okręgu opisanego ma długość 19 cm Oblicz pole tego trójkąta
BAZA ZADAŃ KLASA 3 Ha 2014/2015 GEOMETRIA 1 W trójkącie prostokątnym wysokość poprowadzona na przeciwprostokątną ma długość 10 cm, a promień okręgu opisanego ma długość 19 cm Oblicz pole tego trójkąta
Ćwiczenia z metodyki nauczania rachunku prawdopodobieństwa
 Ćwiczenia z metodyki nauczania rachunku prawdopodobieństwa 25 marca 209 Zadanie. W urnie jest b kul białych i c kul czarnych. Losujemy n kul bez zwracania. Jakie jest prawdopodobieństwo, że pierwsza kula
Ćwiczenia z metodyki nauczania rachunku prawdopodobieństwa 25 marca 209 Zadanie. W urnie jest b kul białych i c kul czarnych. Losujemy n kul bez zwracania. Jakie jest prawdopodobieństwo, że pierwsza kula
Wersja testu A 18 czerwca 2012 r. x 2 +x dx
 1. Funkcja f : R R jest różniczkowalna na całej prostej, a ponadto dla każdej liczby rzeczywistej x zachodzi nierówność f x
1. Funkcja f : R R jest różniczkowalna na całej prostej, a ponadto dla każdej liczby rzeczywistej x zachodzi nierówność f x
a. zbiór wszystkich potasowań talii kart (w którym S dostaje 13 pierwszych kart, W - 13 kolejnych itd.);
 03DRAP - Przykłady przestrzeni probabilistycznych A Zadania na ćwiczenia Zadanie A1 (wskazówka: pierwsze ćwicznia i rozdział 23 przykł 1 i 2) Zbuduj model przestrzeni klasycznej (czyli takiej, w której
03DRAP - Przykłady przestrzeni probabilistycznych A Zadania na ćwiczenia Zadanie A1 (wskazówka: pierwsze ćwicznia i rozdział 23 przykł 1 i 2) Zbuduj model przestrzeni klasycznej (czyli takiej, w której
Matematyczne Podstawy Kognitywistyki
 Matematyczne Podstawy Kognitywistyki Dorota Leszczyńska-Jasion Kombinatoryka, ci agi liczbowe, skończone przestrzenie probabilistyczne Przykłady zagadnień kombinatorycznych Rozważmy układ n miast o bardzo
Matematyczne Podstawy Kognitywistyki Dorota Leszczyńska-Jasion Kombinatoryka, ci agi liczbowe, skończone przestrzenie probabilistyczne Przykłady zagadnień kombinatorycznych Rozważmy układ n miast o bardzo
ZADANIE 1 ZADANIE 2. NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI A) 5,5 B) 8 C) 5,75 D) 4. nie wygramy nagrody jest równe A)
 ZADANIE 1 Średnia arytmetyczna licz 5,5,7,3,9,9,4,4 jest liczba A) 5,5 B) 8 C) 5,75 D) 4 ZADANIE 2 Na loterii jest 10 losów, z których 4 sa wygrywajace. Kupujemy jeden los. Prawdopodobieństwo zdarzenia,
ZADANIE 1 Średnia arytmetyczna licz 5,5,7,3,9,9,4,4 jest liczba A) 5,5 B) 8 C) 5,75 D) 4 ZADANIE 2 Na loterii jest 10 losów, z których 4 sa wygrywajace. Kupujemy jeden los. Prawdopodobieństwo zdarzenia,
Matematyka dyskretna. Andrzej Łachwa, UJ, A/15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 4A/15 Liczby Fibonacciego Spośród ciągów zdefiniowanych rekurencyjnie, jednym z najsłynniejszych jest ciąg Fibonacciego (z roku 1202)
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 4A/15 Liczby Fibonacciego Spośród ciągów zdefiniowanych rekurencyjnie, jednym z najsłynniejszych jest ciąg Fibonacciego (z roku 1202)
Laboratorium nr 1. Kombinatoryka
 Laboratorium nr 1. Kombinatoryka 1. Spośród n różnych elementów wybieramy k elementów. Na ile sposobów możemy to uczynić? Wypisać wszystkie możliwe wybory w przypadku gdy n=3 i k=2. Wykonać obliczenia
Laboratorium nr 1. Kombinatoryka 1. Spośród n różnych elementów wybieramy k elementów. Na ile sposobów możemy to uczynić? Wypisać wszystkie możliwe wybory w przypadku gdy n=3 i k=2. Wykonać obliczenia
Zestaw 2: Zmienne losowe. 0, x < 1, 2, 2 x, 1 1 x, 1 x, F 9 (x) =
 Zestaw : Zmienne losowe. Które z poniższych funkcji są dystrybuantami? Odpowiedź uzasadnij. Wskazówka: naszkicuj wykres. 0, x 0,, x 0, F (x) = x, F (x) = x, 0 x
Zestaw : Zmienne losowe. Które z poniższych funkcji są dystrybuantami? Odpowiedź uzasadnij. Wskazówka: naszkicuj wykres. 0, x 0,, x 0, F (x) = x, F (x) = x, 0 x
ZBIÓR ZADAŃ MATURALNYCH Z MATEMATYKI
 ZBIÓR ZADAŃ MATURALNYCH Z MATEMATYKI AUTORZY: Zespół w12i SPIS TREŚCI LICZBY RZECZYWISTE.2 FUNKCJE 11 CIĄGI...27 GEOMETRIA ANALITYCZNA.36 RACHUNEK PRAWDOPODOBIEŃSTWA, STATYSTYKA.44 1 LICZBY RZECZYWISTE
ZBIÓR ZADAŃ MATURALNYCH Z MATEMATYKI AUTORZY: Zespół w12i SPIS TREŚCI LICZBY RZECZYWISTE.2 FUNKCJE 11 CIĄGI...27 GEOMETRIA ANALITYCZNA.36 RACHUNEK PRAWDOPODOBIEŃSTWA, STATYSTYKA.44 1 LICZBY RZECZYWISTE
KURS PRAWDOPODOBIEŃSTWO
 KURS PRAWDOPODOBIEŃSTWO Lekcja 1 Elementy kombinatoryki ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Kombinatorykę można określić
KURS PRAWDOPODOBIEŃSTWO Lekcja 1 Elementy kombinatoryki ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). Pytanie 1 Kombinatorykę można określić
ELEMENTY KOMBINATORYKI
 ELEMENTY KOMBINATORYKI Kombinatoryka to dział matematyki, który zajmuje się zliczaniem, na ile sposobów może zajść jakieś zjawisko. Powstała dzięki grom hazardowym a dopiero później rozwinęła się w gałąź
ELEMENTY KOMBINATORYKI Kombinatoryka to dział matematyki, który zajmuje się zliczaniem, na ile sposobów może zajść jakieś zjawisko. Powstała dzięki grom hazardowym a dopiero później rozwinęła się w gałąź
