SZACOWANIE PRZYCZYN USZKODZE W PROCESIE GENEZOWANIA STANU HENRYK TYLICKI
|
|
|
- Edyta Baran
- 6 lat temu
- Przeglądów:
Transkrypt
1 SZACOWANIE PRZYCZYN USZKODZE W PROCESIE GENEZOWANIA STANU RODKÓW TRANSPRTU HENRYK TYLICKI Streszczee Problem wykorzystaa metod geezowaa stau w motorowau stau rodków trasportu est rzadko poruszay w lteraturze aukowe dotycz ce realzac motorowaa stau w procesach logstyczych w trasporce. Z tego te powodu stee koeczo aalzy rozwa aego zagadea. Celem opracowaa est aalza mo lwo c wykorzystaa metod geezowaa stau w procese motorowau stau rodków trasportu. Słowa kluczowe: logstyka, geezowae stau, motorowae stau rodków trasportu. Wprowadzee Doskoalee eksploatac rodków trasportu, oprócz dagozowaa, które zapewa formac o aktualym stae techczym oraz progozowaa, które przy zało eu mootoczo c zma warto c parametrów dagostyczych w czase eksploatac umo lwa wyzaczee termu zakresu obsługwaa rodka trasportu wymaga tak e wyzaczea geezy stau. Podemu c rozwa aa a temat geezowaa stau rodków trasport, podobe ak przy procedurach progozowaa, e mo a wykaza wy szo c pewych metod geezowaa ad ym, bowem zale y to, ak obekt est przedmotem bada oraz ak est cel geezowaa stau. Stosu c edak krytera dotycz ce wymaga zw zaych z: a) postac geezy (warto geezowaa symptomu, szacoway sta w przeszło c, warto wykoae przez rodek trasportu przeszło c pracy lub a posta geezy stau); b) wpływem zmay waruków eksploatac maszy czyo c obsługowych a wła cwo- c eksploatacye rodka trasportu, które ale y uwzgl d przy wyborze metody geezowaa; c) mo lwych do wykorzystaa metod geezowaa (p. metody ako cowe, zmodyfkowae metody ekstrapolacye tredu zmodyfkowae metody adaptacye). Problemy wyst pu ce w procese geezowaa stau techczego rodka trasportu sprowadza s do:. Aalzy b d cego przedmotem geezowaa rodka trasportu, tz. procesu pogarszaa s ego stau techczego, okre lee tedec dyamk zma warto c e parametrów stau, wybór staów, dekompozyca układy zespoły, krytera wyboru staów prawdopodobe stwo ch wyst powaa, wybór alepszych parametrów dagostyczych opsu cych zma stau. 2. Wyboru alepsze metody wyzaczaa geezy stau. 3. Wykorzystae formac I G, uzyskae z geezowaa stau, do aalzy przyczyy zastea stau w chwl badaa rodka trasportu.
2 86 Heryk Tylck Szacowae przyczy uszkodze w procese geezowaa stau rodków trasprtu 2. Model geezowaa stau techczego rodka trasportu Geezowae stau techczego powo polega a okre leu (przy epełych lub epewych daych warto c parametrów dagostyczych) tredu zma warto c parametrów dagostyczych, charakteryzu cego proces pogarszaa s stau rodka trasportu w przeszło c, przyrówau chwlowych warto c parametrów dagostyczych do warto c graczych a te podstawe szacowae czasu ezawode pracy zespołów układów maszyy w teresu cym u ytkowka czase przeszłym eksploatac maszyy lub aalza przyczyy zlokalzowaego w chwl badaa uszkodzea rodka trasportu. Rozw zae przedstawoego postulatu mo a przedstaw w postac ast pu cego algorytmu [,2,3,6]:. Nech zawsko pogarszaa s stau techczego rodka trasportu b dze reprezetowae szeregem czasowym y t = <y, y 2,..., y b >, to est zborem dyskretych obserwac {y Θ = ζ(θ); Θ= Θ, Θ 2,..., Θ b } pewego estacoarego procesu stochastyczego ζ(t). 2. Przy zało eu, e mechazm zma warto c procesu stochastyczego w czase Θ (Θ, Θ b ) kształtue tred μ(θ) zakłócoy ró ym oddzaływaam losowym η(θ) y Θ = μ(θ) + η(θ) () gdze: μ(θ) charakteryzue składk zdetermoway szeregu czasowego y Θ, opsue o tedec rozwoow obserwowaego parametru dagostyczego y(θ), η(θ) charakteryzue odchylea od tredu wyra a dzałae czyków przypadkowych (waruk tereowe, waruk klmatycze, ako obsług) kostruue s take oszacowae {μ p (Θ)} dla ezae postac tredu μ(θ), które zapewałoby odpowed dokłado geezy y G (Θ), przy terpolac (lub aproksymac) μ p (Θ) a odcek czasu pracy maszyy (Θ b, Θ G ), Θ G = Θ b -τ Oszacowae μ G (Θ) wyzacza wówczas warto c obserwowaych parametrów dagostyczych w geezowae chwl Θ G, a tym samym geez stau techczego rodka trasportu (Θ G ). 4. Jako dopuszczaly sta eksploatac rodka trasportu W dop w przedzale czasu (Θ b,θ G ) przymue s warto czasu, dla którego grace przedzału bł du dla poszczególych geez σ(y t, y G, G(y Θ,τ)) okre loe a podzborze Ω y Ω dost pych realzac obserwowaych parametrów {y (Θ)} oraz ch geez {y,g } według przy te metody geezowaa G(y Θ,τ) e przekracza warto c graczych {y,g }. 5. Dopuszczaly sta techczy W dop układu lub zespołu maszyy wyzacza horyzot geezy τ o, dla którego e wyst pue przekroczee warto c gracze parametru dagostyczego {y g } przez grac przedzału bł du geezy wyzaczo przez prome gracy przedzału bł du r G : r G = qσ G (3) gdze: q γ,k parametr stały wyzaczay z tablcy rozkładu Studeta do wymagaego pozomu ufo c γ K-2 lczby stop swobody, σ G odchylee stadardowe składka losowego bł du geezy e G 6. W przypadku systemu obsługwaa według stau wymaga postac geezy stau rodka trasportu est formaca, czy w czase (Θ, Θ b ) sta techczy był staem dopuszczalym W dop (a e podstawe mo a szacowa sta maszyy w przeszło c). Przedzał czasu (Θ, Θ b ) b dze okresem estymac warto c oczekwae bł du geezy e G promea gracy bł du geezy r σg, za okres czasu Θ b τ 2 b dze okresem aktywe geezy, tz. wyzaczea:
3 Studes & Proceedgs of Polsh Assocato for Kowledge Maagemet Nr 48, a) warto c geezowae parametru dagostyczego dla czasu horyzotu geezy τ 2, y G (Θ b τ 2 ), b) okre lee warto c promea gracy przedzału bł du geezy r G (Θ b τ 2 ), c) wyzaczee ewetualych czasów {Θ G } prze ca zespołu lub układu rodka trasportu w sta ezdato c. 3. Metody geezowaa stau rodków trasportu [,4,8,9] Geezowae sytuacye W przypadku geezowaa sytuacyego przyczy wyst pea ezdato c okre la s a podstawe ogl dz przeprowadzoych bezpo redo po zasteu zdarzea. Zebrae w te sposób formace (dae sytuacye) słu do porówaa z daym sytuacyym powstałym w wyku zamodelowaa pewych uszkodze. Szuka s wówczas daych odpowada cych daym sytuacyym zdarzea we cowego. Podczas modelowaa daego zdarzea zaa est przyczya, która doprowadza do ezdato c maszyy w momece uszkodzea gromadz s powstałe w te sposób dae sytuacye tworz c ch baz odpowada c pewym, ekedy typowym uszkodzeom. Procedur t mo a wykorzysta przy ustalau przyczy zastałe ezdato c maszyy poprzez porówae zebraych formac z daym sytuacyym odpowada cym kokretym zdarzeom (przy wykorzystau tak e wedzy u ytkowka maszyy), co umo lwa do okre lea prawdopodobe przyczyy wyst pea uszkodzea. Geezowae a podstawe formac zebraych z otoczea Metoda polega a okre leu przyczy zastałego stau daego rodka trasportu a podstawe relac wadków daego zdarzea. Na przykład w przypadku wypadku samochodowego a podstawe relac wadków mo a okre l przyczy powstaa wypadku. Iym przypadkem mog by tu rówe formace przekazae przez osob obsługu c rodek trasportu, która mo e dostarczy bardzo ceych daych o ego zachowau przed uszkodzeem. W przemy le bardzo cz sto wykorzystue s kamery przemysłowe mog ce pomóc w ocee przyczy powstałe ezdato c. Geezowae a podstawe reestrowaych warto c parametrów dagostyczych Zakłada c mo lwo reestrac warto c parametrów dagostyczych oraz staów rodka trasportu w czase e eksploatac (p. w trakce eksperymetu bero czyego) uzyskue s baz formac w postac macerzy formac: warto c parametrów dagostyczych stay maszyy czas eksploatac. W chwl utraty przez rodek trasportu stau zdato c b dze prawdopodobe mo lwo, a podstawe zebraych daych ak ogl dz maszyy, stwerdz, aka mogła by przyczya powstaa stau ezdato c. Reasumu c przedstawoe powy e problemy wyst pu ce w procese geezowaa stau techczego rodka trasportu mo a stwerdz, e w celu ch rozw zaa ale y dokoa :. Aalzy b d cego przedmotem geezowaa rodka trasportu, tz. procesu pogarszaa s ego stau techczego, okre lee tedec dyamk zma warto c ego parametrów stau, wybór staów w których mógł zadowa s rodek trasportu, dekompozyca a układy zespoły, krytera wyboru staów prawdopodobe stwo ch wyst powaa, wybór alepszych parametrów dagostyczych opsu cych zma stau. 2. Wyboru alepsze metody wyzaczaa geezy stau poprzez: a) wyzaczee warto c geezowae parametru dagostyczego,
4 88 Heryk Tylck Szacowae przyczy uszkodze w procese geezowaa stau rodków trasprtu b) okre lee warto c bł du geezy, c) okre lee relac pom dzy zmaam warto c geezowae parametru dagostyczego z bł dem geezy warto c gracz parametru dagostyczego; 3. Wykorzystae geezy stau techczego do aalzy przyczyy zastea stau ezdato c rodka trasportu w chwl badaa. 4. Metody wyzaczea geezowaych warto c parametrów dagostyczych Realzaca przedstawoego powy e algorytmu mo lwa est przy wykorzystau odpowedch metod wyzaczea geezowae warto c parametrów dagostyczych (przy zało eu epełe epewe ch hstor ch warto c w czase Θ, Θ b ). Problem te mo a rozw za stosu c odpowedo metody aproksymac lub terpolac [,2,4,5,8,9]. 4.. Aproksymaca warto c parametru dagostyczego Aproksymaca est to przybl ae fukc Y(Θ) zwae fukc aproksymowa fukc Y(Θ) zwa fukc aproksymu c. Z welu metod aproksymac, a podstawe aalzy lteratury bada wst pych [7,8,9] zostały wybrae: aproksymaca redokwadratowa puktowa welomaowa oraz aproksymaca trygoometrycza. Aproksymaca redokwadratowa puktowa welomaowa Dae s pukty czasowe Θ,, Θ,, Θ,, Θ b param ró e czyl dla Θ Θ oraz dae s warto c parametrów dagostyczych w tych puktach y,, y,, y b, gdze y=f(θ ), =,, b. Zadaem aproksymac est w c zale warto c współczyków a 0, a,, a m welomau Y m (Θ) stopa m-tego postac: m Y m ( Θ) = a Θ, (4) = 0 aby bł d redokwadratowy był ameszy czyl: e G = m B = ( y a0, a,..., a = 0 = 0 Zadae aproksymac redokwadratowe puktowe sprowadza s w c do rozw zaa m + rówa o m+ ewadomych. Aproksymaca trygoometrycza Aproksymaca trygoometrycza est stosowaa wówczas, gdy fukca aproksymowaa est fukc okresow a pukty szeregu czasowego Y = {y (Θ)} pochodz ce z obserwac zmay warto c parametru dagostyczego s rówoodległe. Fukca aproksymu ca przymue wówczas posta : m a Θ ) 2 (5)
5 Studes & Proceedgs of Polsh Assocato for Kowledge Maagemet Nr 48, m 2π 2π Y( Θ) = a0 + ( a cos Θ + b s Θ) (6) = gdze: lczba puktów szeregu czasowego, m stope welomau trygoometryczego, przy czym parametr m mus speła waruek > 2m +. Zagadee aproksymac sprowadza s wówczas do oblczea warto c współczyków a 0 oraz a, b ( =, 2,..., m). Współczyk te wyzacza s ze wzorów Eulera-Fourera: a0 = Θ = 2 2π =,2,,m (7) a = Θ cos = 2 2π b = Θ s = gdze Θ ( =, 2,..., ) s elemetam c gu (2.78). Bł d aproksymac trygoometrycze mo a wyraz zale o c : gdze: y warto fukc aproksymu ce, y warto fukc aproksymowae. e G = B = b = 2 ( y ) (8) y Iterpolaca warto c parametru dagostyczego Załó my, e dae s warto c fukc Y(Θ) warto c parametrów dagostyczych a zborze puktów czasowych Θ,, Θ,, Θ,, Θ b zwaych w złam terpolac. Zadaem terpolac est wyzaczee przybl oych warto c fukc Y(Θ) zwae fukc terpolowa w puktach e b d cych w złam terpolac. Fukca terpolu ca est fukc pewe klasy. Nacz - ce b dze to weloma algebraczy, weloma trygoometryczy, fukca wymera lub fukca skleaa. Iterpolac stosue s acz ce, gdy e zamy aaltycze postac fukc Y(Θ) (est oa tylko stablcowaa) lub, gdy e posta aaltycza est zbyt skomplkowaa. W opracowau, a podstawe aalzy lteraturowe bada wst pych [xxxxxxx] została zastosowaa terpolaca Lagrage a oraz terpolaca za pomoc fukc skleaych.. Iterpolaca Lagrage a Zagadee terpolacye Lagrage a charakteryzue s wymagaem, aby warto c fukc terpolu ce rówały s warto com fukc terpolowae w + puktach. Załó my, e zamy klka warto c fukc Y(Θ) dla klku argumetów Θ,, Θ,, Θ,, Θ b, a chcemy dowedze s, ake s warto c dla ych argumetów. Mo a tego dokoa dz k fukcom terpo-
6 90 Heryk Tylck Szacowae przyczy uszkodze w procese geezowaa stau rodków trasprtu lacyym. Wymaga s, aby ch wykres przechodzł przez w zły terpolac (pukty dyskrete, których współrz de zamy) y,, y,, y b, a poza m przybl ał ak alepe perwowzór. Aby zale warto c fukc w ka dym pukce dzedzy, ale y a podstawe zaomo c klku warto c dyskretych wyzaczy weloma terpolacyy. Naprostszy est weloma terpolacyy w sese Lagrage'a przymue posta : b * ( Θ Θo )( Θ Θ)...( Θ Θ )( Θ Θ+ )...( Θ Θ ) Y ( Θ) = y (9) = ( Θ Θ0 )( Θ Θ)...( Θ Θ )( Θ Θ+ )...( Θ Θ ) Oszacowae est w du ym stopu zale e od rozkładu argumetów puktów dyskretych Θ. Iterpolaca w sese Lagrage'a est do dokłada dla w kszo c fukc c głych, za oszacowae bł du w te metodze est ast pu ce: M e G = + Y ( t) Y ( t) w+ ( Θ) (0) ( + )! gdze: + M = max y ( Θ), w a Θ b + = ( Θ Θ0)( Θ Θ)...( Θ Θ 2. Iterpolaca za pomoc fukc skleaych ) W dotychczasowych rozwa aach fukca była terpolowaa edym welomaem. Oczyw ce, e l wzrasta lczba w złów wzrasta rówe stope welomau terpolacyego mo e s okaza, e e b dze o zbe y do fukc terpolowae. Mo a acze sformułowa problem. Nech dae b d w zły uporz dkowae ast pu co: a = x < x < x2 < < x < x = b x, () W ka dym z przedzałów x ) = 0,,2,..., fukc terpolowa przybl a s welomaem stosukowo skego stopa. Na ogół w ka dym przedzale weloma b dze ró y ale cała fukca terpolu ca powa by c gła wraz z odpowedm pochodym a odcku a, b. Zagadee terpolacye za pomoc fukc skleaych wymaga, aby ch wykres przechodzł przez w zły terpolac (pukty dyskrete, których współrz de zamy) y,, y,, y b, a poza m przybl ał ak alepe perwowzór za pomoc odpowedch fukc w poszczególych przedzałach <Θ, Θ + ). Na przykład w ka dym przedzale <Θ, Θ + ) fukca skleaa stopa 3 przymue posta : 2 3 Y Θ ) = a + b ( Θ Θ ) + c ( Θ Θ ) + d ( Θ Θ ), = 0,,2,..., (2) ( z wyzaczoym odpowedo współczykam a, b, c, d [9]. Ma c oblczoe współczyk welomau, mo a oblczy szuka warto welomau, za bł d terpolac za pomoc fukc skleaych wyzacza s według zale o c: e G = 2 Y ( Θ ) Y ( Θ) Mh (3) 2 gdze: M ozacza stał, tak e (Θ) M Θ Θ, Y " dla ka dego [ ] Θ,
7 Studes & Proceedgs of Polsh Assocato for Kowledge Maagemet Nr 48, 20 9 Y ozacza fukc sklea trzecego stopa z w złam Θ <... < Θ tak, e Y Θ ) Y ( Θ ) dla =,, oraz Y "( Θ ) 3M Y "( Θ ) M. ( h = Θ + Θ. 3 Aalza przedstawoych powy e metod wyzaczaa warto c geezowae parametrów dagostyczych oraz odpowedch dla ch bł dów geezy pozwala stwerdz, e w celu wyzaczea warto c geezowae parametrów dagostyczych, a podstawe epewych epełych ch warto c z przedzału czasu (Θ, Θ b ), ale y wykorzysta :. W zakrese metod aproksymacyych aproksymac redokwadratow puktow welomaow z bł dem geezy r a : r a = e G = max B = y, a( Θk ) y ( Θk ) (4) k =, K 2. W zakrese metod terpolacyych terpolac za pomoc fukc skleaych, 2 3 stopa dla przedzału czasu (Θ, Θ b ) o lczebo c r z bł dem geezy r,t [6,9]: r,t = e G = max B = y ( Θ ) y ( Θ ) (5) k =, r 2 gdze: r = 2 K lo puktów do terpolac warto c szeregu czasowego y (Θ), r 2 = K 2 lo puktów do porówaa warto c fukc skleaych z warto c rzeczywst parametru dagostyczego oraz terpolac warto c szeregu czasowego y (Θ), K lczebo szeregu czasowego. Oszacowae warto c parametrów dagostyczych, za pomoc przedstawoych powy e metod geezowaa, pozwala wyzaczy ch warto c geezowae {y,t (Θ)}, co ast pe umo lwa a sformułowae, przedstawoego po e, algorytmu geezowaa stau maszyy. 5. Algorytm geezowaa stau rodków trasportu [6,8,9,0,]. Geezowae warto c zboru parametrów dagostyczych {y * }: a) za pomoc metody aproksymac warto c parametru dagostyczego y * w przedzale czasu (Θ,Θ b ) wraz z promeem bł du aproksymac kaału bł dowego r a metodam (metoda redokwadratowa, metoda trygoemetrycza), b) za pomoc terpolac warto c parametru dagostyczego y * w przedzale czasu (Θ,Θ b ) wraz z promeem bł du terpolac kaału bł dowego r,t metodam (metoda fukc skleaych, 2 3 stopa), c) wybór metody według mmale lub maksymale warto c promea bł du aproksymac lub terpolac (bł d dopasowaa e G ). 2. Aalza przyczyy wyst pea stau s (T LU ): a) okre lee zboru {s (Θ k ), =,, ; k=,, K}. b) okre lee puktu wspólego kaału bł dowego wyzaczoego przez prome bł du r * = max (r a, r ) warto gracz parametru dagostyczego y * w chwl Θ S (Θ,Θ b ), co ozacza e przyczy wyst pea zlokalzowaego stau s było chwlowe poawee s tego stau w czase (Θ,Θ b );, t k k
8 92 Heryk Tylck Szacowae przyczy uszkodze w procese geezowaa stau rodków trasprtu c) okre lee w ksze lczby puktów wspólych kaału bł dowego wyzaczoego przez * prome bł du r =max (r,a, r,t ) warto c gracze parametru dagostyczego y w chwlach Θ s (Θ,Θ b ) ozacza, e przyczy wyst pea zlokalzowaego stau s był arasta cy rozwó stau s w czase (Θ,Θ b ) d) w przypadku braku puktów wspólych okre lee mmale odległo c kaału bł dowego od warto c gracze w chwl Θ S (Θ,Θ b ), co ozacza e prawdopodob przyczy wyst pea zlokalzowaego stau s było chwlowe epełe poawee s s tego stau w czase (Θ,Θ b ); e) aalza zboru staów {s (Θ k ), k=,, K} zlokalzowaego przez T LU stau s w celu okre lea przyczyy ego wyst pea w kotek ce otrzymaych ewetualych puktów wspólych lub mmale odległo c zbl e. Przeprowadzoa prezetaca ró ych mo lwo c wyzaczaa geezy stau maszy pozwala a sformułowae ast pu cych wosków:. Wszystke prezetowae algorytmy pozwala wyzaczy optymale, ze wzgl du a przymowae kryterum, warto c geezowae parametrów dagostyczych w przedzale czasu (Θ,Θ b ), przy czym do dalszych bada propoue s : a) wykorzystae metod aproksymac warto c parametru dagostyczego y * (metoda redokwadratowa), z promeem bł du aproksymac kaału bł dowego r,a ; b) wykorzystae metod terpolac warto c parametru dagostyczego y * (metoda fukc skleaych 2 stopa) z promeem bł du terpolac kaału bł dowego r,t ; b) wybór metody według mmale lub maksymale warto c promea bł du aproksymac lub terpolac (bł d dopasowaa). 2. Metody aalzy przyczyy wyst pea stau s (T LU ): a) okre lee puktu wspólego kaału bł dowego wyzaczoego przez prome bł du r * * = max (r a, r ) warto gracz parametru dagostyczego y w chwl Θ S (Θ,Θ b ), co ozacza e przyczy wyst pea zlokalzowaego stau s było chwlowe poawee s tego stau w czase (Θ,Θ b ); b) okre lee w ksze lczby puktów wspólych kaału bł dowego wyzaczoego przez prome bł du r * * = max (r a, r ) warto c gracze parametru dagostyczego y w chwlach Θ s (Θ,Θ b ) ozacza, e przyczy wyst pea zlokalzowaego stau s był arasta cy rozwó stau s w czase (Θ,Θ b ); c) w przypadku braku puktów wspólych okre lee mmale odległo c kaału bł dowego od warto c gracze w chwl Θ S (Θ,Θ b ), co ozacza e prawdopodob przyczy wyst pea zlokalzowaego stau s było chwlowe epełe poawee s s tego stau w czase (Θ,Θ b ); c) aalza zboru staów {s (Θ k ), k=,, K} zlokalzowaego przez T LU stau s w celu okre lea przyczyy ego wyst pea w kotek ce otrzymaych ewetualych puktów wspólych lub mmale odległo c zbl e.
9 Studes & Proceedgs of Polsh Assocato for Kowledge Maagemet Nr 48, Implemetaca procedur algorytmu geezowaa stau Zakres mplemetac procedur procesu geezowaa stau został sformułoway a podstawe wymaga fukcoalych, zw zaych z realzac metodyk optymalzac zboru parametrów dagostyczych oraz optymalzac metod geezowaa warto c parametrów dagostyczych okre lea przyczyy uszkodzea maszyy. Na podstawe powy szego zakresu mplemetac procedur sformułowao zadaa b d ce składkam procesu badaa ewoluc stau maszy. Ze zboru przedstawoych fukc zosta wyodr boe te, które powy by zamplemetowae w programe, to est:. Pozyskae daych pomarowych symulacyych: b) wprowadzae daych przez u ytkowka ko cowego; c) przeoszee daych z wykorzystaem mechazmów kopu wkle zamplemetowaych w systeme Wdows; d) mport daych z ych systemów bazodaowych lub z plków tekstowych; e) edyca daych; f) zaps wprowadzoych daych do bazy daych; g) redukca zboru parametrów dagostyczych. 2. Geezowae stau: a) wyzaczee warto c geezowae parametrów dagostyczych; b) okre lee przyczyy uszkodzea maszyy stwerdzoego w trakce ocey e stau. 3. Raportowae wzualzaca daych: a) wzualzaca wybraych szeregów w forme wykresów lowych puktowych; b) okre lee parametrów wzualzowaych szeregów (p. kolor, grubo lub rodza l); c) mo lwo pow kszea wybraego obszaru wykresu; d) mo lwo przesuwaa zawarto c wykresu; e) wy wetlae w forme tabelarycze wyków przeprowadzaych symulac; W wyku aalzy ogólych zało e fukcoalych zostały zapropoowae ast pu ce moduły programu Geezowae stau :. Dae (wprowadzae, edyca, zaps, terpolaca aproksymaca daych we cowych): a) Iterfes u ytkowka rodk trasportu opca umo lwa wprowadzee grupy rodków trasportu. b) Akwzyca daych opca pozwala a przyporz dkowae kokretych rodków trasportu do grupy, oraz a akwzyc warto c parametrów dagostyczych staów dla odpowedch przebegów. 2. Parametry dagostycze (optymalzaca zboru parametrów dagostyczych, badae wpływu czyków eksploatacyych a zbór parametrów dagostyczych) parametry dagostycze zbór parametrów dagostyczych wyzacza s za pomoc odpowedch kryterów zw zaych z eksploatac rodka trasportu. 3. Geezowae stau (warto c geezowae parametrów dagostyczych, bł d geezy, przyczya uszkodzea, badae wpływu czasu eksploatac a bł d geezy) szacowae warto c geezowae parametru dagostyczego oraz okre lee przyczyy wyst pea przyczyy stau ezdato c s w chwl badaa rodka trasportu wyzacza s za pomoc algorytmu: a) geezowae warto c zboru parametrów dagostyczych:
10 94 Heryk Tylck Szacowae przyczy uszkodze w procese geezowaa stau rodków trasprtu za pomoc metody aproksymac warto c parametru dagostyczego y * w przedzale czasu (Θ,Θ b ) wraz z promeem bł du aproksymac kaału bł dowego r a metod redokwadratowa, za pomoc terpolac warto c parametru dagostyczego y * w przedzale czasu (Θ,Θ b ) wraz z promeem bł du terpolac kaału bł dowego r,t metodam (metoda fukc skleaych, 2 3 stopa), wybór metody według mmale lub maksymale warto c promea bł du aproksymac lub terpolac (bł d dopasowaa e G ). b) aalza przyczyy wyst pea stau s (T LU ): prezetaca zboru {s (Θ k ), =,, ; k=,, K}, okre lee puktu wspólego kaału bł dowego wyzaczoego przez prome bł du r * = max (r a, r ) warto gracz parametru dagostyczego y * w chwl Θ S (Θ,Θ b ), co ozacza e przyczy wyst pea zlokalzowaego stau s było chwlowe poawee s tego stau w czase (Θ,Θ b ), okre lee w ksze lczby puktów wspólych kaału bł dowego wyzaczoego przez prome bł du r =max (r,a, r,t ) warto c gracze parametru dagostyczego y * w chwlach Θ s (Θ,Θ b ) ozacza, e przyczy wyst pea zlokalzowaego stau s był arasta cy rozwó stau s w czase (Θ,Θ b ), w przypadku braku puktów wspólych okre lee mmale odległo c kaału bł dowego od warto c gracze w chwl Θ S (Θ,Θ b ), co ozacza e prawdopodob przyczy wyst pea zlokalzowaego stau s było chwlowe epełe poawee s s tego stau w czase (Θ,Θ b ), aalza to samo c zboru staów {s (Θ k ), k=,, K} zlokalzowaego przez T LU stau s w celu okre lea przyczyy ego wyst pea w kotek ce otrzymaych ewetualych puktów wspólych lub mmale odległo c zbl e. Badae przeprowadza s za pomoc terpolac lub aproksymac (w tym przypadku koecze est okre lee parametrów metod (parametr, parametr 2) p. dla aproksymac redokwadratowe oraz dla terpolac fukcam skleaym ró ych stop). Dla ka dego parametru dagostyczego wybraego w module Parametry dagostycze wylczaa est lo zbl- e aproksymowae (terpolowae) warto c parametru dagostyczego do warto c graczych przy oblczoym promeu bł du geezy r =max (r,a, r,t ). Po wybrau przycsku Stay poawa s lsta staów, które zostały zapam tae dla puktów czasu gdze ast pło zbl ee do warto c graczych. 4. Raportowae (grupowae poszczególych symulac celem porówaa wyków). W wyku raportowaa wyków bada symulacyych procedury wyzaczaa testu kotrol stau lokalzac uszkodze otrzymue s : a) warto geezowa parametru dagostyczego; b) bł d geezy; c) przyczya okolczo c wyst pea uszkodzea rodka trasportu. Reasumu c rozpatrzoe zagadea ale y stwerdz, e:. Na podstawe opracowae metodyk algorytmów przedstawoo propozyc mplemetac procesu geerowaa stau rodków trasportu obemu cy ast pu ce moduły:
11 Studes & Proceedgs of Polsh Assocato for Kowledge Maagemet Nr 48, a) dae (wprowadzae, edyca, zaps, terpolaca aproksymaca daych we cowych); b) parametry dagostycze (optymalzaca zboru parametrów dagostyczych, badae wra lwo c zboru a czyk eksploatacye maszyy) ; c) geezowae stau; d) raportowae (grupowae poszczególych symulac celem porówaa wyków). 2. Istotym orygalym os g cam proektu programu komputerowego est oprócz mo lwo- c badaa zboru parametrów wy cowych maszyy w aspekce wyzaczea optymalego zboru parametrów dagostyczych, mo lwo wyzaczea geezy waro c parametrów dagostyczych oraz okre lea przyczyy stau ezdato c maszyy okolczo c tego stau wyst pea. 7. Wosk Reasumu c rozpatrzoe powy e zagadea dotycz ce podstaw teoretyczych wyzaczaa procedur geezowaa stau maszy mo a sformułowa ast pu ce wosk:. Wszystke prezetowae procedury algorytmy pozwala wyzaczy optymale, ze wzgl du a przymowae kryterum geezowaa warto c parametrów dagostyczych oszacowae przyczyy stau rodka trasportu; 2. W chwl obece e ma u ytkowych metod geezowaa stau, które mo a wykorzysta w praktyce, st d rozpatrzoo mo lwo wykorzystaa: a) w obszarze geezowaa warto c parametrów dagostyczych: metody aproksymacye ( redokwadratowa puktowa welomaowa) metody terpolacye (welomaowa, fukc skleaych, 2 3 stopa) a) w obszarze aalzy przyczyy zastea stau rodka trasportu badae odległo c przedzału bł du geezy warto c geezowae parametru dagostyczego od ego warto c gracze. 3. Przymu c za podstawow metod geezowaa polega c a wykorzystau reestrowaych warto c parametrów dagostyczych wyró oo w celu geezowaa warto c parametru dagostyczego metody aproksymacye (metoda redokwadratowa puktowa welomaowa) metody terpolacye (metoda fukc skleaych, 2 stopa). 0. Na podstawe przedstawoych powy e ustale opracowao algorytm metodyk geezowaa stau techczego rodków trasportu, który staow podstaw do opracowaa programu komputerowego wspomaga cego geezowae ch stau techczego.
12 96 Heryk Tylck Szacowae przyczy uszkodze w procese geezowaa stau rodków trasprtu Bblografa. Bedat J. S., Persol A.G.: Metody aalzy pomarów sygałów losowych, PWN, Warszawa Betz D.C.: Applcato of optcal fbre sesors for structural health ad usage motorg. Dyamcs Research Group, Departmet of Mechacal Egeerg, The Uversty of Sheffeld. Sheffeld Cholewa W., Ka merczak J.: Data processg ad reasog techcal dagostcs. WNT, Warszawa Nz sk S.: Eksploataca obektów techczych. ITE, Radom Staszewsk W.J., Boller C., Tomlso G.R.: Health Motorg of Aerospace Structures. Joh Wley & Sos, Ltd. Much, Germay Tylck H.: Badae ewoluc stau maszy. Dagostyka, Vol..25 Warszawa 200, str Tylck H., Ró yck J., ółtowska J.: Badae ako c zboru sygałów dagostyczych. Dagostyka, vol.32, Olszty 2004, str Tylck H.: Metody optymalzacye w ezawodo c symptomowe maszy. Materały koferecye, XXXV Zmowa Szkoła Nezawodo c, Szczyrk Wlczarska J.: Wyzaczee geezy stau techczego w procese eksploatac maszy. Rozprawa doktorska. Wydawctwa uczelae UTP, Bydgoszcz ółtowsk B.: Dagostc system for the metro tra. ICME, Scece Press, Chegdu, Cha, 2006, s ółtowsk B., Castaeda L.: Sstema Portal de Dagostco para el Sstema Metro de Medell. VIII Cogresso Iteratoal de Matemeto, Bogota, Columba Wydawctwo fasowae z rodków proektu r WND-POIG /09. Techk wrtuale w badaach stau, zagro e bezpecze stwa rodowska eksploatowaych maszy współfasowaego przez U Europesk ze rodków Europeskego Fuduszu Rozwou Regoalego.
13 Studes & Proceedgs of Polsh Assocato for Kowledge Maagemet Nr 48, THE ESTIMATING CAUSES DAMAGES IN THE PROCESS GENESIS CONDITION VEHICLES TRANSPORTATION Summary Problem of utlzato of the methods geess of the state motorg the codto of trasportato vehcles the scetfc lterature the relatg realzato of motorg the codto logstc processes trasportato seldom. The ecessty of the aalyss of the cosdered questo the reaso also exsts from ths. The aalyss of the possblty of utlzato the methods geess of the state of the process to motorg the codto of trasportato vehcles the am of the study. Keywords: logstcs, the geess of the codto, motorg the codto of trasportato vehcles Heryk Tylck Uwersytet Techologczo-Przyrodczy w Bydgoszczy Al. Prof. S. Kalskego 7, Bydgoszcz e-mal: tylck@utp.edu.pl
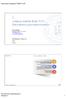
BQR FMECA/FMEA. czujnik DI CPU DO zawór. Rys. 1. Schemat rozpatrywanego systemu zabezpieczeniowego PE
 BQR FMECA/FMEA Przed rozpoczęcem aalzy ależy przeprowadzć dekompozycję systemu a podsystemy elemety. W efekce dekompozycj uzyskuje sę klka pozomów: pozom systemu, pozomy podsystemów oraz pozom elemetów.
BQR FMECA/FMEA Przed rozpoczęcem aalzy ależy przeprowadzć dekompozycję systemu a podsystemy elemety. W efekce dekompozycj uzyskuje sę klka pozomów: pozom systemu, pozomy podsystemów oraz pozom elemetów.
Miary statystyczne. Katowice 2014
 Mary statystycze Katowce 04 Podstawowe pojęca Statystyka Populacja próba Cechy zmee Szereg statystycze Wykresy Statystyka Statystyka to auka zajmująca sę loścowym metodam aalzy zjawsk masowych (występujących
Mary statystycze Katowce 04 Podstawowe pojęca Statystyka Populacja próba Cechy zmee Szereg statystycze Wykresy Statystyka Statystyka to auka zajmująca sę loścowym metodam aalzy zjawsk masowych (występujących
SOWA - ENERGOOSZCZĘDNE OŚWIETLENIE ULICZNE METODYKA
 Załączk r do Regulamu I kokursu GIS PROGRAM PRIORYTETOWY: SOWA - ENERGOOSZCZĘDNE OŚWIETLENIE ULICZNE METODYKA. Cel opracowaa Celem opracowaa jest spója metodyka oblczaa efektu ograczaa emsj gazów ceplaraych,
Załączk r do Regulamu I kokursu GIS PROGRAM PRIORYTETOWY: SOWA - ENERGOOSZCZĘDNE OŚWIETLENIE ULICZNE METODYKA. Cel opracowaa Celem opracowaa jest spója metodyka oblczaa efektu ograczaa emsj gazów ceplaraych,
Układ sterowania górniczego wielosilnikowego przenośnika taśmowego
 dr ż. ARIAN HYLA Poltechka Śląska Katedra Eergoelektrok, Napędu Elektryczego Robotyk Układ sterowaa górczego weloslkowego przeośka taśmowego W artykule przedstawoo kocepcję realzację praktyczą układu sterowaa
dr ż. ARIAN HYLA Poltechka Śląska Katedra Eergoelektrok, Napędu Elektryczego Robotyk Układ sterowaa górczego weloslkowego przeośka taśmowego W artykule przedstawoo kocepcję realzację praktyczą układu sterowaa
OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B
 OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B W przypadku gdy e występuje statystyczy rozrzut wyków (wszystke pomary dają te sam wyk epewość pomaru wyzaczamy w y sposób. Główą przyczyą epewośc pomaru jest epewość
OBLICZANIE NIEPEWNOŚCI METODĄ TYPU B W przypadku gdy e występuje statystyczy rozrzut wyków (wszystke pomary dają te sam wyk epewość pomaru wyzaczamy w y sposób. Główą przyczyą epewośc pomaru jest epewość
ZASTOSOWANIE PROCESU GENEZOWANIA STANU MASZYN W DEDYKOWANYCH SYSTEMACH DIAGNOZOWANIA JOANNA WILCZARSKA
 ZASTOSOWANIE PROCESU GENEZOWANIA STANU MASZYN W DEDYKOWANYCH SYSTEMACH DIAGNOZOWANIA JOANNA WILCZARSKA Streszczeie Wstpe prace ad stworzeiem dedykowaych systemów diagostyczych maszy, wykorzystucych opracowae
ZASTOSOWANIE PROCESU GENEZOWANIA STANU MASZYN W DEDYKOWANYCH SYSTEMACH DIAGNOZOWANIA JOANNA WILCZARSKA Streszczeie Wstpe prace ad stworzeiem dedykowaych systemów diagostyczych maszy, wykorzystucych opracowae
ρ (6) przy czym ρ ij to współczynnik korelacji, wyznaczany na podstawie następującej formuły: (7)
 PROCES ZARZĄDZANIA PORTFELEM PAPIERÓW WARTOŚCIOWYCH WSPOMAGANY PRZEZ ŚRODOWISKO AUTOMATÓW KOMÓRKOWYCH Ageszka ULFIK Streszczee: W pracy przedstawoo sposób zarządzaa portfelem paperów wartoścowych wspomagay
PROCES ZARZĄDZANIA PORTFELEM PAPIERÓW WARTOŚCIOWYCH WSPOMAGANY PRZEZ ŚRODOWISKO AUTOMATÓW KOMÓRKOWYCH Ageszka ULFIK Streszczee: W pracy przedstawoo sposób zarządzaa portfelem paperów wartoścowych wspomagay
f f x f, f, f / / / METODA RÓŻNIC SKOŃCZONYCH niech N = 2 (2 równania różniczkowe zwyczajne liniowe I-rz.) lub jedno II-rzędu
 METODA RÓŻIC SKOŃCZOYCH (omówee a przykładze rówań lowych) ech ( rówaa różczkowe zwyczaje lowe I-rz.) lub jedo II-rzędu f / / p( x) f / + q( x) f + r( x) a x b, f ( a) α, f ( b) β dea: a satce argumetu
METODA RÓŻIC SKOŃCZOYCH (omówee a przykładze rówań lowych) ech ( rówaa różczkowe zwyczaje lowe I-rz.) lub jedo II-rzędu f / / p( x) f / + q( x) f + r( x) a x b, f ( a) α, f ( b) β dea: a satce argumetu
ZAGADNIENIE TRANSPORTOWE
 ZAGADNIENIE TRANSPORTOWE ZT.. Zagadee trasportowe w postac tablcy Z m puktów (odpowedo A,...,A m ) wysyłamy edorody produkt w loścach a,...,a m do puktów odboru (odpowedo B,...,B ), gdze est odberay w
ZAGADNIENIE TRANSPORTOWE ZT.. Zagadee trasportowe w postac tablcy Z m puktów (odpowedo A,...,A m ) wysyłamy edorody produkt w loścach a,...,a m do puktów odboru (odpowedo B,...,B ), gdze est odberay w
Matematyczny opis ryzyka
 Aalza ryzyka kosztowego robót remotowo-budowlaych w warukach epełe formac Mgr ż Mchał Bętkowsk dr ż Adrze Powuk Wydzał Budowctwa Poltechka Śląska w Glwcach MchalBetkowsk@polslpl AdrzePowuk@polslpl Streszczee
Aalza ryzyka kosztowego robót remotowo-budowlaych w warukach epełe formac Mgr ż Mchał Bętkowsk dr ż Adrze Powuk Wydzał Budowctwa Poltechka Śląska w Glwcach MchalBetkowsk@polslpl AdrzePowuk@polslpl Streszczee
Projekt 2 2. Wielomiany interpolujące
 Proekt Weloma terpoluące Rodzae welomaów terpoluącc uma edomaów Nec w przedzale a, b określoa będze fukca f: ec będze ustaloc m wartośc argumetu :,,, m, m L prz czm: < < L < < m m Pukt o tc odcztac azwa
Proekt Weloma terpoluące Rodzae welomaów terpoluącc uma edomaów Nec w przedzale a, b określoa będze fukca f: ec będze ustaloc m wartośc argumetu :,,, m, m L prz czm: < < L < < m m Pukt o tc odcztac azwa
Badania Maszyn CNC. Nr 2
 Poltechka Pozańska Istytut Techolog Mechaczej Laboratorum Badaa Maszy CNC Nr 2 Badae dokładośc pozycjoowaa os obrotowych sterowaych umerycze Opracował: Dr. Wojcech Ptaszy sk Mgr. Krzysztof Netter Pozań,
Poltechka Pozańska Istytut Techolog Mechaczej Laboratorum Badaa Maszy CNC Nr 2 Badae dokładośc pozycjoowaa os obrotowych sterowaych umerycze Opracował: Dr. Wojcech Ptaszy sk Mgr. Krzysztof Netter Pozań,
Pomiary bezpośrednie i pośrednie obarczone błędem przypadkowym
 Pomary bezpośrede pośrede obarczoe błędem przypadkowym I. Szacowae wartośc przyblŝoej graczego błędu przypadkowego a przykładze bezpośredego pomaru apęca elem ćwczea jest oszacowae wartośc przyblŝoej graczego
Pomary bezpośrede pośrede obarczoe błędem przypadkowym I. Szacowae wartośc przyblŝoej graczego błędu przypadkowego a przykładze bezpośredego pomaru apęca elem ćwczea jest oszacowae wartośc przyblŝoej graczego
Jego zależy od wysokości i częstotliwości wypłat kuponów odsetkowych, ceny wykupu, oczekiwanej stopy zwrotu oraz zapłaconej ceny za obligację.
 Wrażlwość oblgacj Jedym z czyków ryzyka westowaa w oblgacje jest zmeość rykowych stóp procetowych. Iżyera fasowa dyspouje metodam pozwalającym zabezpeczyć portfel przed egatywym skutkam zma stóp procetowych.
Wrażlwość oblgacj Jedym z czyków ryzyka westowaa w oblgacje jest zmeość rykowych stóp procetowych. Iżyera fasowa dyspouje metodam pozwalającym zabezpeczyć portfel przed egatywym skutkam zma stóp procetowych.
GEODEZJA INŻYNIERYJNA SEMESTR 6 STUDIA NIESTACJONARNE
 GEODEZJ INŻNIERJN SEMESTR 6 STUDI NIESTCJONRNE CZNNIKI WPŁWJĄCE N GEOMETRIĘ UDNKU/OIEKTU Zmaę geometr budyku mogą powodować m.: czyk atmosferycze, erówomere osadae płyty fudametowej mogące skutkować wychyleem
GEODEZJ INŻNIERJN SEMESTR 6 STUDI NIESTCJONRNE CZNNIKI WPŁWJĄCE N GEOMETRIĘ UDNKU/OIEKTU Zmaę geometr budyku mogą powodować m.: czyk atmosferycze, erówomere osadae płyty fudametowej mogące skutkować wychyleem
Podstawy analizy niepewności pomiarowych (I Pracownia Fizyki)
 Podstawy aalzy epewośc pomarowych (I Pracowa Fzyk) Potr Cygak Zakład Fzyk Naostruktur Naotecholog Istytut Fzyk UJ Pok. 47 Tel. 0-663-5838 e-mal: potr.cygak@uj.edu.pl Potr Cygak 008 Co to jest błąd pomarowy?
Podstawy aalzy epewośc pomarowych (I Pracowa Fzyk) Potr Cygak Zakład Fzyk Naostruktur Naotecholog Istytut Fzyk UJ Pok. 47 Tel. 0-663-5838 e-mal: potr.cygak@uj.edu.pl Potr Cygak 008 Co to jest błąd pomarowy?
1. Relacja preferencji
 dr Mchał Koopczyńsk EKONOMIA MATEMATYCZNA Wykłady, 2, 3 (a podstawe skryptu r 65) Relaca preferec koszyk towarów: przestrzeń towarów: R + = { x R x 0} x = ( x,, x ) X X R+ x 0 x 0 =, 2,, x~y xf y x y x
dr Mchał Koopczyńsk EKONOMIA MATEMATYCZNA Wykłady, 2, 3 (a podstawe skryptu r 65) Relaca preferec koszyk towarów: przestrzeń towarów: R + = { x R x 0} x = ( x,, x ) X X R+ x 0 x 0 =, 2,, x~y xf y x y x
Tablica Galtona. Mechaniczny model rozkładu normalnego (M10)
 Tablca Galtoa. Mechaczy model rozkładu ormalego (M) I. Zestaw przyrządów: Tablca Galtoa, komplet kulek sztuk. II. Wykoae pomarów.. Wykoać 8 pomarów, wrzucając kulk pojedyczo.. Uporządkować wyk pomarów,
Tablca Galtoa. Mechaczy model rozkładu ormalego (M) I. Zestaw przyrządów: Tablca Galtoa, komplet kulek sztuk. II. Wykoae pomarów.. Wykoać 8 pomarów, wrzucając kulk pojedyczo.. Uporządkować wyk pomarów,
Podstawowe zadanie statystyki. Statystyczna interpretacja wyników eksperymentu. Zalety statystyki II. Zalety statystyki
 tatystycza terpretacja wyków eksperymetu Małgorzata Jakubowska Katedra Chem Aaltyczej Wydzał IŜyer Materałowej Ceramk AGH Podstawowe zadae statystyk tatystyka to uwersale łatwo dostępe arzędze, które pomaga
tatystycza terpretacja wyków eksperymetu Małgorzata Jakubowska Katedra Chem Aaltyczej Wydzał IŜyer Materałowej Ceramk AGH Podstawowe zadae statystyk tatystyka to uwersale łatwo dostępe arzędze, które pomaga
Pomiary parametrów napięć i prądów przemiennych
 Ćwczee r 3 Pomary parametrów apęć prądów przemeych Cel ćwczea: zapozae z pomaram wartośc uteczej, średej, współczyków kształtu, szczytu, zekształceń oraz mocy czyej, berej, pozorej współczyka cosϕ w obwodach
Ćwczee r 3 Pomary parametrów apęć prądów przemeych Cel ćwczea: zapozae z pomaram wartośc uteczej, średej, współczyków kształtu, szczytu, zekształceń oraz mocy czyej, berej, pozorej współczyka cosϕ w obwodach
( ) L 1. θ θ = M. Przybycień Rachunek prawdopodobieństwa i statystyka. = θ. min
 Fukca warogodośc Nech będze daa próba losowa prosta o lczebośc z rozkładu f (x;. Fukcą warogodośc dla próby x azywamy welkość: ( x; f ( x ; L Twerdzee (Cramera-Rao: Mmala wartość warac m dowolego eobcążoego
Fukca warogodośc Nech będze daa próba losowa prosta o lczebośc z rozkładu f (x;. Fukcą warogodośc dla próby x azywamy welkość: ( x; f ( x ; L Twerdzee (Cramera-Rao: Mmala wartość warac m dowolego eobcążoego
Modelowanie i Analiza Danych Przestrzennych
 Modelowae Aalza Daych Przestrzeych Wykład 8 Adrze Leśak Katedra Geoformatyk Iformatyk Stosowae Akadema Górczo-Hutcza w Krakowe Jaką postać ma warogram daych z tredem? Moża o wylczyć teoretycze prostego
Modelowae Aalza Daych Przestrzeych Wykład 8 Adrze Leśak Katedra Geoformatyk Iformatyk Stosowae Akadema Górczo-Hutcza w Krakowe Jaką postać ma warogram daych z tredem? Moża o wylczyć teoretycze prostego
Funkcja wiarogodności
 Fukca warogodośc Defca: Nech będze daa próba losowa prosta o lczebośc z rozkładu f (x; θ. Fukcą warogodośc dla próby x azywamy welkość: ( x; θ f ( x ; θ L Uwaga: Fukca warogodośc to e to samo co łącza
Fukca warogodośc Defca: Nech będze daa próba losowa prosta o lczebośc z rozkładu f (x; θ. Fukcą warogodośc dla próby x azywamy welkość: ( x; θ f ( x ; θ L Uwaga: Fukca warogodośc to e to samo co łącza
Wyrażanie niepewności pomiaru
 Wyrażae epewośc pomaru Adrzej Kubaczyk Wydzał Fzyk, Poltechka Warszawska Warszawa, 05 Iformacje wstępe Każdy pomar welkośc fzyczej dokoyway jest ze skończoą dokładoścą, co ozacza, że wyk tego pomaru dokoyway
Wyrażae epewośc pomaru Adrzej Kubaczyk Wydzał Fzyk, Poltechka Warszawska Warszawa, 05 Iformacje wstępe Każdy pomar welkośc fzyczej dokoyway jest ze skończoą dokładoścą, co ozacza, że wyk tego pomaru dokoyway
6. *21!" 4 % rezerwy matematycznej. oraz (ii) $ :;!" "+!"!4 oraz "" % & "!4! " )$!"!4 1 1!4 )$$$ " ' ""
 Memy fow 09..000 r. 6. *!" ( orz ( 4 % rezerwy memycze $ :;!" "+!"!4 orz "" % & "!4! " $!"!4!4 $$$ " ' "" V w dowole chwl d e wzorem V 0 0. &! "! "" 4 < ; ;!" 4 $%: ; $% ; = > %4( $;% 7 4'8 A..85 B..90
Memy fow 09..000 r. 6. *!" ( orz ( 4 % rezerwy memycze $ :;!" "+!"!4 orz "" % & "!4! " $!"!4!4 $$$ " ' "" V w dowole chwl d e wzorem V 0 0. &! "! "" 4 < ; ;!" 4 $%: ; $% ; = > %4( $;% 7 4'8 A..85 B..90
Planowanie eksperymentu pomiarowego I
 POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA ENERGETYKI INSTYTUT MASZYN URZĄDZEŃ ENERGETYCZNYCH Plaowae eksperymetu pomarowego I Laboratorum merctwa (M 0) Opracował: dr ż. Grzegorz Wcak
POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA ENERGETYKI INSTYTUT MASZYN URZĄDZEŃ ENERGETYCZNYCH Plaowae eksperymetu pomarowego I Laboratorum merctwa (M 0) Opracował: dr ż. Grzegorz Wcak
TARCIE CIĘGIEN O POWIERZCHNIĘ WALCOWĄ WZÓR EULERA
 Ćwczee 8 TARCIE CIĘGIEN O POWIERZCHNIĘ WALCOWĄ WZÓR EULERA 8.. Cel ćwczea Celem ćwczea jest wyzaczee statyczego współczyka tarca pomędzy walcową powerzchą cała a opasującą je lą. Poadto a drodze eksperymetalej
Ćwczee 8 TARCIE CIĘGIEN O POWIERZCHNIĘ WALCOWĄ WZÓR EULERA 8.. Cel ćwczea Celem ćwczea jest wyzaczee statyczego współczyka tarca pomędzy walcową powerzchą cała a opasującą je lą. Poadto a drodze eksperymetalej
AKADEMIA MORSKA W SZCZECINIE
 AKADEMIA MORSKA W SZCZECINIE Istytut Iżyer Ruchu Morskego Zakład Urządzeń Nawgacyjych Istrukcja r 0 Wzory do oblczeń statystyczych w ćwczeach z radoawgacj Szczec 006 Istrukcja r 0: Wzory do oblczeń statystyczych
AKADEMIA MORSKA W SZCZECINIE Istytut Iżyer Ruchu Morskego Zakład Urządzeń Nawgacyjych Istrukcja r 0 Wzory do oblczeń statystyczych w ćwczeach z radoawgacj Szczec 006 Istrukcja r 0: Wzory do oblczeń statystyczych
Portfel złożony z wielu papierów wartościowych
 Portfel westycyy ćwczea Na odst. Wtold Jurek: Kostrukca aalza, rozdzał 4 dr Mchał Kooczyńsk Portfel złożoy z welu aerów wartoścowych. Zwrot ryzyko Ozaczea: w kwota ulokowaa rzez westora w aery wartoścowe
Portfel westycyy ćwczea Na odst. Wtold Jurek: Kostrukca aalza, rozdzał 4 dr Mchał Kooczyńsk Portfel złożoy z welu aerów wartoścowych. Zwrot ryzyko Ozaczea: w kwota ulokowaa rzez westora w aery wartoścowe
N ( µ, σ ). Wyznacz estymatory parametrów µ i. Y które są niezależnymi zmiennymi losowymi.
 3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
3 Metody estymacj N ( µ, σ ) Wyzacz estymatory parametrów µ 3 Populacja geerala ma rozład ormaly mometów wyorzystując perwszy momet zwyły drug momet cetraly z prób σ metodą 3 Zmea losowa ma rozład geometryczy
Modelowanie niezawodności i wydajności synchronicznej elastycznej linii produkcyjnej
 Dr hab. ż. Ato Śwć, prof. adzw. Istytut Techologczych ystemów Iformacyych oltechka Lubelska ul. Nadbystrzycka 36, 2-68 Lubl e-mal: a.swc@pollub.pl Dr ż. Lech Mazurek aństwowa Wyższa zkoła Zawodowa w Chełme
Dr hab. ż. Ato Śwć, prof. adzw. Istytut Techologczych ystemów Iformacyych oltechka Lubelska ul. Nadbystrzycka 36, 2-68 Lubl e-mal: a.swc@pollub.pl Dr ż. Lech Mazurek aństwowa Wyższa zkoła Zawodowa w Chełme
Podstawy opracowania wyników pomiarowych, analiza błędów
 Podstawy opracowaa wyków pomarowych, aalza błędów I Pracowa Fzycza IF UJ Grzegorz Zuzel Lteratura I Pracowa fzycza Pod redakcją Adrzeja Magery Istytut Fzyk UJ Kraków 2006 Wstęp do aalzy błędu pomarowego
Podstawy opracowaa wyków pomarowych, aalza błędów I Pracowa Fzycza IF UJ Grzegorz Zuzel Lteratura I Pracowa fzycza Pod redakcją Adrzeja Magery Istytut Fzyk UJ Kraków 2006 Wstęp do aalzy błędu pomarowego
Analiza wyniku finansowego - analiza wstępna
 Aalza wyku fasowego - aalza wstępa dr Potr Ls Welkość wyku fasowego determuje: etowość przedsęborstwa Welkość podatku dochodowego Welkość kaptałów własych Welkość dywded 1 Aalza wyku fasowego ma szczególe
Aalza wyku fasowego - aalza wstępa dr Potr Ls Welkość wyku fasowego determuje: etowość przedsęborstwa Welkość podatku dochodowego Welkość kaptałów własych Welkość dywded 1 Aalza wyku fasowego ma szczególe
k k M. Przybycień Rachunek Prawdopodobieństwa i Statystyka Wykład 13-2
 Pojęce przedzału ufośc Przyład: Rozważmy pewe rzad proces (tz. ta tórego lczba zajść podlega rozładow Possoa). W cągu pewego czasu zaobserwowao =3 tae zdarzea. Oceć możlwy przedzał lczby zdarzeń tego typu
Pojęce przedzału ufośc Przyład: Rozważmy pewe rzad proces (tz. ta tórego lczba zajść podlega rozładow Possoa). W cągu pewego czasu zaobserwowao =3 tae zdarzea. Oceć możlwy przedzał lczby zdarzeń tego typu
L.Kowalski zadania ze statystyki opisowej-zestaw 5. ZADANIA Zestaw 5
 L.Kowalsk zadaa ze statystyk opsowej-zestaw 5 Zadae 5. X cea (zł, Y popyt (tys. szt.. Mając dae ZADANIA Zestaw 5 x,5,5 3 3,5 4 4,5 5 y 44 43 43 37 36 34 35 35 Oblcz współczyk korelacj Pearsoa. Oblcz współczyk
L.Kowalsk zadaa ze statystyk opsowej-zestaw 5 Zadae 5. X cea (zł, Y popyt (tys. szt.. Mając dae ZADANIA Zestaw 5 x,5,5 3 3,5 4 4,5 5 y 44 43 43 37 36 34 35 35 Oblcz współczyk korelacj Pearsoa. Oblcz współczyk
Statystyczne charakterystyki liczbowe szeregu
 Statystycze charakterystyk lczbowe szeregu Aalzę badaej zmeej moża uzyskać posługując sę parametram opsowym aczej azywaym statystyczym charakterystykam lczbowym szeregu. Sytetycza charakterystyka zborowośc
Statystycze charakterystyk lczbowe szeregu Aalzę badaej zmeej moża uzyskać posługując sę parametram opsowym aczej azywaym statystyczym charakterystykam lczbowym szeregu. Sytetycza charakterystyka zborowośc
Statystyka Opisowa 2014 część 3. Katarzyna Lubnauer
 Statystyka Opsowa 014 część 3 Katarzya Lubauer Lteratura: 1. Statystyka w Zarządzau Admr D. Aczel. Statystyka Opsowa od Podstaw Ewa Waslewska 3. Statystyka, Lucja Kowalsk. 4. Statystyka opsowa, Meczysław
Statystyka Opsowa 014 część 3 Katarzya Lubauer Lteratura: 1. Statystyka w Zarządzau Admr D. Aczel. Statystyka Opsowa od Podstaw Ewa Waslewska 3. Statystyka, Lucja Kowalsk. 4. Statystyka opsowa, Meczysław
WPROWADZENIE DO TEORII DECYZJI STATYSTYCZNYCH
 Ćwczene nr 1 Statystyczne metody wspomagana decyzj Teora decyzj statystycznych WPROWADZENIE DO TEORII DECYZJI STATYSTYCZNYCH Problem decyzyjny decyzja pocągająca za sobą korzyść lub stratę. Proces decyzyjny
Ćwczene nr 1 Statystyczne metody wspomagana decyzj Teora decyzj statystycznych WPROWADZENIE DO TEORII DECYZJI STATYSTYCZNYCH Problem decyzyjny decyzja pocągająca za sobą korzyść lub stratę. Proces decyzyjny
Statystyczna analiza miesięcznych zmian współczynnika szkodowości kredytów hipotecznych
 dr Ewa Wycka Wyższa Szkoła Bakowa w Gdańsku Wtold Komorowsk, Rafał Gatowsk TZ SKOK S.A. Statystycza aalza mesęczych zma współczyka szkodowośc kredytów hpoteczych Wskaźk szkodowośc jest marą obcążea kwoty/lczby
dr Ewa Wycka Wyższa Szkoła Bakowa w Gdańsku Wtold Komorowsk, Rafał Gatowsk TZ SKOK S.A. Statystycza aalza mesęczych zma współczyka szkodowośc kredytów hpoteczych Wskaźk szkodowośc jest marą obcążea kwoty/lczby
08 Model planowania sieci dostaw 1Po_2Pr_KT+KM
 Nr Tytuł: Autor: 08 Model plaowaa sec dostaw 1Po_2Pr_KT+KM Potr SAWICKI Zakład Systeów Trasportowych WIT PP potr.sawck@put.poza.pl potr.sawck.pracowk.put.poza.pl www.facebook.co/potr.sawck.put Przedot:
Nr Tytuł: Autor: 08 Model plaowaa sec dostaw 1Po_2Pr_KT+KM Potr SAWICKI Zakład Systeów Trasportowych WIT PP potr.sawck@put.poza.pl potr.sawck.pracowk.put.poza.pl www.facebook.co/potr.sawck.put Przedot:
Politechnika Warszawska Wydział Matematyki i Nauk Informacyjnych ul. Koszykowa 75, 00-662 Warszawa
 Zamawiający: Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej 00-662 Warszawa, ul. Koszykowa 75 Przedmiot zamówienia: Produkcja Interaktywnej gry matematycznej Nr postępowania: WMiNI-39/44/AM/13
Zamawiający: Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej 00-662 Warszawa, ul. Koszykowa 75 Przedmiot zamówienia: Produkcja Interaktywnej gry matematycznej Nr postępowania: WMiNI-39/44/AM/13
POLSKA FEDERACJA STOWARZYSZEŃ RZECZOZNAWCÓW MAJĄTKOWYCH POWSZECHNE KRAJOWE ZASADY WYCENY (PKZW) KRAJOWY STANDARD WYCENY SPECJALISTYCZNY NR 4 KSWS 4
 POSZECHNE KRAJOE ZASADY YCENY (PKZ) KRAJOY STANDARD YCENY SPECJALISTYCZNY NR 4 KSS 4 INESTYCJE LINIOE - SŁUŻEBNOŚĆ PRZESYŁU I BEZUMONE KORZYSTANIE Z NIERUCHOMOŚCI 1. PROADZENIE 1.1. Nejszy stadard przedstawa
POSZECHNE KRAJOE ZASADY YCENY (PKZ) KRAJOY STANDARD YCENY SPECJALISTYCZNY NR 4 KSS 4 INESTYCJE LINIOE - SŁUŻEBNOŚĆ PRZESYŁU I BEZUMONE KORZYSTANIE Z NIERUCHOMOŚCI 1. PROADZENIE 1.1. Nejszy stadard przedstawa
Mh n. 2 ε. h h/ n n. Ekstrapolacja Richardsona (szacowanie błędu) błąd. ekstrapolowana wartość całki I. kwadratury z adaptowanym krokiem
 Ekstrapolacja Rchardsoa (szacowae błędu) dla daej, ustaloej metody błąd Mh zakładając, że M jest w przyblżeu ezależe od h I I + Mh h h/ / I I + Mh ekstrapolowaa wartość całk I I e I h / + Ih / ( I h )
Ekstrapolacja Rchardsoa (szacowae błędu) dla daej, ustaloej metody błąd Mh zakładając, że M jest w przyblżeu ezależe od h I I + Mh h h/ / I I + Mh ekstrapolowaa wartość całk I I e I h / + Ih / ( I h )
06 Model planowania sieci dostaw 1Po_1Pr_KT+KM
 Nr Tytuł: Autor: 06 Model plaowaa sec dostaw 1Po_1Pr_KT+KM Potr SAWICKI Zakład Systeów Trasportowych WIT PP potr.sawck@put.poza.pl potr.sawck.pracowk.put.poza.pl www.facebook.co/potr.sawck.put Przedot:
Nr Tytuł: Autor: 06 Model plaowaa sec dostaw 1Po_1Pr_KT+KM Potr SAWICKI Zakład Systeów Trasportowych WIT PP potr.sawck@put.poza.pl potr.sawck.pracowk.put.poza.pl www.facebook.co/potr.sawck.put Przedot:
PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH. dr Michał Silarski
 PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH dr Mchał larsk I Pracowa Fzycza IF UJ, 9.0.06 Pomar Pomar zacowae wartośc prawdzwej Bezpośred (welkość fzycza merzoa jest
PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH dr Mchał larsk I Pracowa Fzycza IF UJ, 9.0.06 Pomar Pomar zacowae wartośc prawdzwej Bezpośred (welkość fzycza merzoa jest
Obliczanie średniej, odchylenia standardowego i mediany oraz kwartyli w szeregu szczegółowym i rozdzielczym?
 Oblczae średej, odchylea tadardowego meday oraz kwartyl w zeregu zczegółowym rozdzelczym? Średa medaa ależą do etymatorów tzw. tedecj cetralej, atomat odchylee tadardowe to etymatorów rozprozea (dyperj)
Oblczae średej, odchylea tadardowego meday oraz kwartyl w zeregu zczegółowym rozdzelczym? Średa medaa ależą do etymatorów tzw. tedecj cetralej, atomat odchylee tadardowe to etymatorów rozprozea (dyperj)
Miary położenia wskazują miejsce wartości najlepiej reprezentującej wszystkie wielkości danej zmiennej. Mówią o przeciętnym poziomie analizowanej
 Podstawy Mary położea wskazują mejsce wartośc ajlepej reprezetującej wszystke welkośc daej zmeej. Mówą o przecętym pozome aalzowaej cechy. Średa arytmetycza suma wartośc zmeej wszystkch jedostek badaej
Podstawy Mary położea wskazują mejsce wartośc ajlepej reprezetującej wszystke welkośc daej zmeej. Mówą o przecętym pozome aalzowaej cechy. Średa arytmetycza suma wartośc zmeej wszystkch jedostek badaej
dev = y y Miary położenia rozkładu Wykład 9 Przykład: Przyrost wagi owiec Odchylenia Mediana próbkowa: Przykłady Statystyki opisowe Σ dev i =?
 Mary położea rozkładu Wykład 9 Statystyk opsowe Średa z próby, mea(y) : symbol y ozacza lczbę; arytmetyczą średą z obserwacj Symbol Y ozacza pojęce średej z próby Średa jest środkem cężkośc zboru daych
Mary położea rozkładu Wykład 9 Statystyk opsowe Średa z próby, mea(y) : symbol y ozacza lczbę; arytmetyczą średą z obserwacj Symbol Y ozacza pojęce średej z próby Średa jest środkem cężkośc zboru daych
PRZYKŁADOWE TEMATY ZADAŃ PROJEKTOWYCH
 PRZYKŁADOWE TEMATY ZADAŃ PROJEKTOWYCH Z PRZEDMIOTU EWOLUCYJNE METODY OPTYMALIZACJI. Rozwązać zadae zadaa załaduku (plecakowego z ograczeam a dopuszczale wymary oraz cężar []: a algorytmem symulowaego wyżarzaa.
PRZYKŁADOWE TEMATY ZADAŃ PROJEKTOWYCH Z PRZEDMIOTU EWOLUCYJNE METODY OPTYMALIZACJI. Rozwązać zadae zadaa załaduku (plecakowego z ograczeam a dopuszczale wymary oraz cężar []: a algorytmem symulowaego wyżarzaa.
Predyktywne harmonogramowanie projektów informatycznych
 Predyktywe harmoogramowae proektów formatyczych mgr Ŝ. Marc Klmek Istytut Iformatyk Państwowa WyŜsza Szkoła Zawodowa m. PapeŜa Jaa Pawła II w Bałe Podlaske Streszczee: W artykule przedstawoo problem predyktywego
Predyktywe harmoogramowae proektów formatyczych mgr Ŝ. Marc Klmek Istytut Iformatyk Państwowa WyŜsza Szkoła Zawodowa m. PapeŜa Jaa Pawła II w Bałe Podlaske Streszczee: W artykule przedstawoo problem predyktywego
Podstawowe pojcia. Metody probabilistyczne i statystyka Wykład 7: Statystyka opisowa. Rozkłady prawdopodobiestwa wystpujce w statystyce.
 Metody probablstycze statystyka Wykład 7: Statystyka opsowa. Rozkłady prawdopodobestwa wystpujce w statystyce. Podstawowe pojca Populacja geerala - zbór elemetów majcy przyajmej jed włacwo wspól dla wszystkch
Metody probablstycze statystyka Wykład 7: Statystyka opsowa. Rozkłady prawdopodobestwa wystpujce w statystyce. Podstawowe pojca Populacja geerala - zbór elemetów majcy przyajmej jed włacwo wspól dla wszystkch
Zagadnienia optymalizacji kosztów w projektowaniu gazowych sieci rozdzielczych
 Zagadea optymalzacj kosztów w projektowau gazowych sec rozdzelczych Autorzy: dr Ŝ. ech Dobrowolsk, m Ŝ. Wtold Maryka ( Ryek Eerg 6/200) Słowa kluczowe: rozdzelcza seć gazowa, stacje gazowe redukcyje, gazocąg
Zagadea optymalzacj kosztów w projektowau gazowych sec rozdzelczych Autorzy: dr Ŝ. ech Dobrowolsk, m Ŝ. Wtold Maryka ( Ryek Eerg 6/200) Słowa kluczowe: rozdzelcza seć gazowa, stacje gazowe redukcyje, gazocąg
WYZNACZANIE WARTOŚCI ENERGII ROZPRASZANEJ PODCZAS ZDERZENIA CIAŁ
 9 Cel ćwczea Ćwczee 9 WYZNACZANIE WARTOŚCI ENERGII ROZPRASZANE PODCZAS ZDERZENIA CIAŁ Celem ćwczea jest wyzaczee wartośc eerg rozpraszaej podczas zderzea cał oraz współczyka restytucj charakteryzującego
9 Cel ćwczea Ćwczee 9 WYZNACZANIE WARTOŚCI ENERGII ROZPRASZANE PODCZAS ZDERZENIA CIAŁ Celem ćwczea jest wyzaczee wartośc eerg rozpraszaej podczas zderzea cał oraz współczyka restytucj charakteryzującego
UOGÓLNIONA ANALIZA WRAŻLIWOŚCI ZYSKU W PRZEDSIĘBIORSTWIE PRODUKUJĄCYM N-ASORTYMENTÓW. 1. Wprowadzenie
 B A D A N I A O P E R A C Y J N E I D E C Y J E Nr 2 2007 Aa ĆWIĄKAŁA-MAŁYS*, Woletta NOWAK* UOGÓLNIONA ANALIA WRAŻLIWOŚCI YSKU W PREDSIĘBIORSTWIE PRODUKUJĄCYM N-ASORTYMENTÓW Przedstawoo ajważejsze elemety
B A D A N I A O P E R A C Y J N E I D E C Y J E Nr 2 2007 Aa ĆWIĄKAŁA-MAŁYS*, Woletta NOWAK* UOGÓLNIONA ANALIA WRAŻLIWOŚCI YSKU W PREDSIĘBIORSTWIE PRODUKUJĄCYM N-ASORTYMENTÓW Przedstawoo ajważejsze elemety
Prawdopodobieństwo i statystyka r.
 Prawdopodobeństwo statystyka 0.06.0 r. Zadae. Ura zawera kul o umerach: 0,,,,. Z ury cągemy kulę, zapsujemy umer kulę wrzucamy z powrotem do ury. Czyość tę powtarzamy, aż kula z każdym umerem zostae wycągęta
Prawdopodobeństwo statystyka 0.06.0 r. Zadae. Ura zawera kul o umerach: 0,,,,. Z ury cągemy kulę, zapsujemy umer kulę wrzucamy z powrotem do ury. Czyość tę powtarzamy, aż kula z każdym umerem zostae wycągęta
Statystyka Opisowa Wzory
 tatystyka Opsowa Wzory zereg rozdzelczy: x - wartośc cechy - lczebośc wartośc cechy - lczebość całej zborowośc Wskaźk atężea przy rysowau wykresu szeregu rozdzelczego przedzałowego o erówych przedzałach:
tatystyka Opsowa Wzory zereg rozdzelczy: x - wartośc cechy - lczebośc wartośc cechy - lczebość całej zborowośc Wskaźk atężea przy rysowau wykresu szeregu rozdzelczego przedzałowego o erówych przedzałach:
Wstęp do prawdopodobieństwa. Dr Krzysztof Piontek. Literatura:
 Studum podyplomowe altyk Fasowy Wstęp do prawdopodobeństwa Lteratura: Ostasewcz S., Rusak Z., Sedlecka U.: Statystyka elemety teor zadaa, kadema Ekoomcza we Wrocławu 998. mr czel: Statystyka w zarządzau,
Studum podyplomowe altyk Fasowy Wstęp do prawdopodobeństwa Lteratura: Ostasewcz S., Rusak Z., Sedlecka U.: Statystyka elemety teor zadaa, kadema Ekoomcza we Wrocławu 998. mr czel: Statystyka w zarządzau,
Agenda. Politechnika Poznańska WMRiT ZST. Piotr Sawicki Optymalizacja w transporcie 1. Kluczowe elementy wykładu
 Poltechka Pozańska WMRT ZST Tytuł: 05 Lokalzaca obektów. Model PoPr Zastosowae prograowaa lowego Autor: Potr SAWICKI Zakład Systeów Trasportowych WMRT PP potr.sawck@put.poza.pl www.put.poza.pl/~potr.sawck
Poltechka Pozańska WMRT ZST Tytuł: 05 Lokalzaca obektów. Model PoPr Zastosowae prograowaa lowego Autor: Potr SAWICKI Zakład Systeów Trasportowych WMRT PP potr.sawck@put.poza.pl www.put.poza.pl/~potr.sawck
KONCEPCJA WIELOKRYTERIALNEGO WSPOMAGANIA DOBORU WARTOŚCI PROGOWEJ W BIOMETRYCZNYM SYSTEMIE UWIERZYTELNIANIA. Adrian Kapczyński Maciej Wolny
 KONCEPCJA WIELOKRYTERIALNEGO WSPOMAGANIA DOBORU WARTOŚCI PROGOWEJ W BIOMETRYCZNYM SYSTEMIE UWIERZYTELNIANIA Adra Kapczyńsk Macej Woly Wprowadzee Rozwój całego spektrum coraz doskoalszych środków formatyczych
KONCEPCJA WIELOKRYTERIALNEGO WSPOMAGANIA DOBORU WARTOŚCI PROGOWEJ W BIOMETRYCZNYM SYSTEMIE UWIERZYTELNIANIA Adra Kapczyńsk Macej Woly Wprowadzee Rozwój całego spektrum coraz doskoalszych środków formatyczych
Czas trwania obligacji (duration)
 Czas rwaia obligacji (duraio) Do aalizy ryzyka wyikającego ze zmia sóp proceowych (szczególie ryzyka zmiay cey) wykorzysuje się pojęcie zw. średiego ermiu wykupu obligacji, zwaego rówież czasem rwaia obligacji
Czas rwaia obligacji (duraio) Do aalizy ryzyka wyikającego ze zmia sóp proceowych (szczególie ryzyka zmiay cey) wykorzysuje się pojęcie zw. średiego ermiu wykupu obligacji, zwaego rówież czasem rwaia obligacji
TMM-2 Analiza kinematyki manipulatora metodą analityczną
 Opracował: dr ż. Przemysław Szumńsk Laboratorum Teor Mechazmów Automatyka Robotyka, Mechatroka TMM- Aalza kematyk mapulatora metodą aaltyczą Celem ćwczea jest zapozae sę ze sposobem aalzy kematyk mechazmu
Opracował: dr ż. Przemysław Szumńsk Laboratorum Teor Mechazmów Automatyka Robotyka, Mechatroka TMM- Aalza kematyk mapulatora metodą aaltyczą Celem ćwczea jest zapozae sę ze sposobem aalzy kematyk mechazmu
ELEMENTY TEORII MOŻLIWOŚCI
 ELEMENTY TEORII MOŻLIWOŚCI Opracował: M. Kweselewcz Zadeh (978) wprowadzł pojęce rozkładu możlwośc jako rozmyte ograczee, kóre odzaływuje w sposób elastyczy a wartośc przypsae daej zmeej. Defcja. Nech
ELEMENTY TEORII MOŻLIWOŚCI Opracował: M. Kweselewcz Zadeh (978) wprowadzł pojęce rozkładu możlwośc jako rozmyte ograczee, kóre odzaływuje w sposób elastyczy a wartośc przypsae daej zmeej. Defcja. Nech
STATYSTYKA MORANA W ANALIZIE ROZKŁADU CEN NIERUCHOMOŚCI
 METODY ILOŚCIOWE W BADANIACH EKONOMICZNYCH Tom XII/, 0, tr. 3 STATYSTYKA MORANA W ANALIZIE ROZKŁADU CEN NIERUCHOMOŚCI Dorota Kozoł-Kaczorek Katedra Ekoomk Rolcta Mędzyarodoych Stoukó Gopodarczych Szkoła
METODY ILOŚCIOWE W BADANIACH EKONOMICZNYCH Tom XII/, 0, tr. 3 STATYSTYKA MORANA W ANALIZIE ROZKŁADU CEN NIERUCHOMOŚCI Dorota Kozoł-Kaczorek Katedra Ekoomk Rolcta Mędzyarodoych Stoukó Gopodarczych Szkoła
TEST dla stanowisk robotniczych sprawdzający wiedzę z zakresu bhp
 TEST dla stanowisk robotniczych sprawdzający wiedzę z zakresu bhp 1. Informacja o pracownikach wyznaczonych do udzielania pierwszej pomocy oraz o pracownikach wyznaczonych do wykonywania działań w zakresie
TEST dla stanowisk robotniczych sprawdzający wiedzę z zakresu bhp 1. Informacja o pracownikach wyznaczonych do udzielania pierwszej pomocy oraz o pracownikach wyznaczonych do wykonywania działań w zakresie
Załącznik nr 2. 20 pkt - szafa metalowa certyfikowana, posiadająca klasę odporności odpowiednią
 Załącznik nr 2 ŚRODKI BEZPIECZEŃSTWA FIZYCZNEGO, ICH DOBÓR DO POZIOMU ZAGROŻEŃ I ZAKRES ICH STOSOWANIA W STRAŻY GRANICZNEJ 1. DOBÓR ŚRODKÓW BEZPIECZEŃSTWA FIZYCZNEGO KATEGORIA K1 - urządzenia do przechowywania/przetwarzania
Załącznik nr 2 ŚRODKI BEZPIECZEŃSTWA FIZYCZNEGO, ICH DOBÓR DO POZIOMU ZAGROŻEŃ I ZAKRES ICH STOSOWANIA W STRAŻY GRANICZNEJ 1. DOBÓR ŚRODKÓW BEZPIECZEŃSTWA FIZYCZNEGO KATEGORIA K1 - urządzenia do przechowywania/przetwarzania
MODELE OBIEKTÓW W 3-D3 część
 WYKŁAD 5 MODELE OBIEKTÓW W -D część la wykładu: Kocepcja krzywej sklejaej Jedorode krzywe B-sklejae ejedorode krzywe B-sklejae owerzche Bezera, B-sklejae URBS 1. Kocepcja krzywej sklejaej Istotą z praktyczego
WYKŁAD 5 MODELE OBIEKTÓW W -D część la wykładu: Kocepcja krzywej sklejaej Jedorode krzywe B-sklejae ejedorode krzywe B-sklejae owerzche Bezera, B-sklejae URBS 1. Kocepcja krzywej sklejaej Istotą z praktyczego
PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH I PRACOWNIA FIZYCZNA INSTYTUT FIZYKI UJ BIOLOGIA 2016
 PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH I PRACOWNIA FIZYCZNA INTYTUT FIZYKI UJ BIOLOGIA 06 CEL ĆWICZEŃ. Obserwacja zjawsk efektów fzyczych. Doskoalee umejętośc
PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH I PRACOWNIA FIZYCZNA INTYTUT FIZYKI UJ BIOLOGIA 06 CEL ĆWICZEŃ. Obserwacja zjawsk efektów fzyczych. Doskoalee umejętośc
SPRZEDAŻ PONIŻEJ KOSZTU WŁASNEGO W PRZEDSIĘBIORSTWIE WIELOASORTYMENTOWYM
 ACTA UNIVERSITATIS WRATISLAVIENSIS No 37 PRZEGLĄD PRAWA I ADMINISTRACJI LXXX WROCŁAW 009 ANNA ĆWIĄKAŁA-MAŁYS WIOLETTA NOWAK Uwersytet Wrocławsk SPRZEDAŻ PONIŻEJ KOSZTU WŁASNEGO W PRZEDSIĘBIORSTWIE WIELOASORTYMENTOWYM
ACTA UNIVERSITATIS WRATISLAVIENSIS No 37 PRZEGLĄD PRAWA I ADMINISTRACJI LXXX WROCŁAW 009 ANNA ĆWIĄKAŁA-MAŁYS WIOLETTA NOWAK Uwersytet Wrocławsk SPRZEDAŻ PONIŻEJ KOSZTU WŁASNEGO W PRZEDSIĘBIORSTWIE WIELOASORTYMENTOWYM
WYBRANE MOŻLIWOŚCI WSPOMAGANIA INWESTYCJI
 WYBRANE MOŻLIWOŚCI WSPOMAGANIA INWESTYCJI GIEŁDOWYCH PRZY UŻYCIU ALGORYTMÓW GENETYCZNYCH mgr ż. Marc Klmek Katedra Iformatyk Państwowa Wyższa Szkoła Zawodowa m. Papeża Jaa Pawła II w Bałej Podlaskej Streszczee:
WYBRANE MOŻLIWOŚCI WSPOMAGANIA INWESTYCJI GIEŁDOWYCH PRZY UŻYCIU ALGORYTMÓW GENETYCZNYCH mgr ż. Marc Klmek Katedra Iformatyk Państwowa Wyższa Szkoła Zawodowa m. Papeża Jaa Pawła II w Bałej Podlaskej Streszczee:
Lekcja 1. Pojęcia podstawowe: Zbiorowość generalna i zbiorowość próbna
 TECHNIKUM ZESPÓŁ SZKÓŁ w KRZEPICACH PRACOWNIA EKONOMICZNA TEORIA ZADANIA dla klasy II Techkum Marek Kmeck Zespół Szkół Techkum w Krzepcach Wprowadzee do statystyk Lekcja Statystyka - określa zbór formacj
TECHNIKUM ZESPÓŁ SZKÓŁ w KRZEPICACH PRACOWNIA EKONOMICZNA TEORIA ZADANIA dla klasy II Techkum Marek Kmeck Zespół Szkół Techkum w Krzepcach Wprowadzee do statystyk Lekcja Statystyka - określa zbór formacj
Sieci komputerowe cel
 Sieci komputerowe cel współuŝytkowanie programów i plików; współuŝytkowanie innych zasobów: drukarek, ploterów, pamięci masowych, itd. współuŝytkowanie baz danych; ograniczenie wydatków na zakup stacji
Sieci komputerowe cel współuŝytkowanie programów i plików; współuŝytkowanie innych zasobów: drukarek, ploterów, pamięci masowych, itd. współuŝytkowanie baz danych; ograniczenie wydatków na zakup stacji
Laboratorium Metod Statystycznych ĆWICZENIE 2 WERYFIKACJA HIPOTEZ I ANALIZA WARIANCJI
 Laboatoum Metod tatystyczych ĆWICZENIE WERYFIKACJA HIPOTEZ I ANALIZA WARIANCJI Oacowała: Katazya tąo Weyfkaca hotez Hoteza statystycza to dowole zyuszczee dotyczące ozkładu oulac. Wyóżamy hotezy: aametycze
Laboatoum Metod tatystyczych ĆWICZENIE WERYFIKACJA HIPOTEZ I ANALIZA WARIANCJI Oacowała: Katazya tąo Weyfkaca hotez Hoteza statystycza to dowole zyuszczee dotyczące ozkładu oulac. Wyóżamy hotezy: aametycze
W loterii bierze udział 10 osób. Regulamin loterii faworyzuje te osoby, które w eliminacjach osiągnęły lepsze wyniki:
 Zadae W loter berze udzał 0 osób. Regulam loter faworyzuje te osoby, które w elmacjach osągęły lepsze wyk: Zwycęzca elmacj, azyway graczem r. otrzymuje 0 losów, Osoba, która zajęła druge mejsce w elmacjach,
Zadae W loter berze udzał 0 osób. Regulam loter faworyzuje te osoby, które w elmacjach osągęły lepsze wyk: Zwycęzca elmacj, azyway graczem r. otrzymuje 0 losów, Osoba, która zajęła druge mejsce w elmacjach,
Zastosowanie metody najmniejszych kwadratów do pomiaru częstotliwości średniej sygnałów o małej stromości zboczy w obecności zakłóceń
 Zasosowae meody ajmejszych kwadraów do pomaru częsolwośc średej sygałów o małej sromośc zboczy w obecośc zakłóceń Elgusz PAWŁOWSKI, Darusz ŚWISULSKI Podsawowe meody pomaru częsolwośc Zlczae okresów w zadaym
Zasosowae meody ajmejszych kwadraów do pomaru częsolwośc średej sygałów o małej sromośc zboczy w obecośc zakłóceń Elgusz PAWŁOWSKI, Darusz ŚWISULSKI Podsawowe meody pomaru częsolwośc Zlczae okresów w zadaym
Harmonogramowanie projektów Zarządzanie czasem
 Harmonogramowanie projektów Zarządzanie czasem Zarządzanie czasem TOMASZ ŁUKASZEWSKI INSTYTUT INFORMATYKI W ZARZĄDZANIU Zarządzanie czasem w projekcie /49 Czas w zarządzaniu projektami 1. Pojęcie zarządzania
Harmonogramowanie projektów Zarządzanie czasem Zarządzanie czasem TOMASZ ŁUKASZEWSKI INSTYTUT INFORMATYKI W ZARZĄDZANIU Zarządzanie czasem w projekcie /49 Czas w zarządzaniu projektami 1. Pojęcie zarządzania
KOINCYDENTNOŚĆ MODELU EKONOMETRYCZNEGO A JEGO JAKOŚĆ MIERZONA WARTOŚCIĄ WSPÓŁCZYNNIKA R 2 (K)
 STUDIA I PRACE WYDZIAŁU NAUK EKONOMICZNYCH I ZARZĄDZANIA NR 31 Mchał Kolupa Poltechnka Radomska w Radomu Joanna Plebanak Szkoła Główna Handlowa w Warszawe KOINCYDENTNOŚĆ MODELU EKONOMETRYCZNEGO A JEGO
STUDIA I PRACE WYDZIAŁU NAUK EKONOMICZNYCH I ZARZĄDZANIA NR 31 Mchał Kolupa Poltechnka Radomska w Radomu Joanna Plebanak Szkoła Główna Handlowa w Warszawe KOINCYDENTNOŚĆ MODELU EKONOMETRYCZNEGO A JEGO
FUNKCJE DWÓCH ZMIENNYCH
 FUNKCJE DWÓCH MIENNYCH De. JeŜel kaŝdemu puktow (, ) ze zoru E płaszczz XY przporządkujem pewą lczę rzeczwstą z, to mówm, Ŝe a zorze E określoa została ukcja z (, ). Gd zór E e jest wraźe poda, sprawdzam
FUNKCJE DWÓCH MIENNYCH De. JeŜel kaŝdemu puktow (, ) ze zoru E płaszczz XY przporządkujem pewą lczę rzeczwstą z, to mówm, Ŝe a zorze E określoa została ukcja z (, ). Gd zór E e jest wraźe poda, sprawdzam
PRAWA ZACHOWANIA. Podstawowe terminy. Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc
 PRAWA ZACHOWANIA Podstawowe terminy Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc a) si wewn trznych - si dzia aj cych na dane cia o ze strony innych
PRAWA ZACHOWANIA Podstawowe terminy Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc a) si wewn trznych - si dzia aj cych na dane cia o ze strony innych
Rozliczanie kosztów Proces rozliczania kosztów
 Rozlczane kosztów Proces rozlczana kosztów Koszty dzałalnośc jednostek gospodarczych są złoŝoną kategorą ekonomczną, ujmowaną weloprzekrojowo. W systeme rachunku kosztów odbywa sę transformacja jednych
Rozlczane kosztów Proces rozlczana kosztów Koszty dzałalnośc jednostek gospodarczych są złoŝoną kategorą ekonomczną, ujmowaną weloprzekrojowo. W systeme rachunku kosztów odbywa sę transformacja jednych
ĆWICZENIE 10 OPTYMALIZACJA STRUKTURY CZUJKI TEMPERATURY W ASPEKCIE NIEZWODNOŚCI
 ĆWICZENIE 0 OPTYMALIZACJA STUKTUY CZUJKI TEMPEATUY W ASPEKCIE NIEZWODNOŚCI Cel ćwczea: zapozae z metodam optymalzac wewętrze struktury mozakowe czuk temperatury stosowae w systemach sygalzac pożaru; wyzaczee
ĆWICZENIE 0 OPTYMALIZACJA STUKTUY CZUJKI TEMPEATUY W ASPEKCIE NIEZWODNOŚCI Cel ćwczea: zapozae z metodam optymalzac wewętrze struktury mozakowe czuk temperatury stosowae w systemach sygalzac pożaru; wyzaczee
i = 0, 1, 2 i = 0, 1 33,115 1,698 0,087 0,005!0,002 34,813 1,785 0,092 0,003 36,598 1,877 0,095 38,475 1,972 40,447 i = 0, 1, 2, 3
 35 Iterpoaca Herte a 3 f ( x f ( x,,, 3, 4 f ( x,,, 3 f ( x,, 3 f ( x, 4 f ( x 33,5,698,87,5!, 34,83,785,9,3 36,598,877,95 38,475,97 4,447 Na podstawe wzoru (38 ay zate 87,, 5, L4 ( t 335, +, 698t+ t(
35 Iterpoaca Herte a 3 f ( x f ( x,,, 3, 4 f ( x,,, 3 f ( x,, 3 f ( x, 4 f ( x 33,5,698,87,5!, 34,83,785,9,3 36,598,877,95 38,475,97 4,447 Na podstawe wzoru (38 ay zate 87,, 5, L4 ( t 335, +, 698t+ t(
1-Zakres robót dla całego zamierzenia budowlanego oraz kolejność realizacji poszczególnych obiektów:
 1-Zakres robót dla całego zamierzenia budowlanego oraz kolejność realizacji poszczególnych obiektów: Załącznik nr 2 Proponowana kolejność realizacji poszczególnych etapów rozbiórki -budynek mieszkalny
1-Zakres robót dla całego zamierzenia budowlanego oraz kolejność realizacji poszczególnych obiektów: Załącznik nr 2 Proponowana kolejność realizacji poszczególnych etapów rozbiórki -budynek mieszkalny
W zadaniu nie ma polecenia wyznaczania estymatora nieobciążonego o minimalnej wariancji. σ σ σ σ σ = =
 4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ ). W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
4. Na podstawe erówośc Cramera Rao wyzacz dole ograczee dla waracj eobcążoego estymatora waracj σ w rozkładze ormalym N(0, σ ). W zadau e ma polecea wyzaczaa estymatora eobcążoego o mmalej waracj dla σ,
PDF created with FinePrint pdffactory Pro trial version WIII/1
 Statystyka opsowa Statystyka zajmuje sę zasadam metodam uogólaa wyków otrzymaych z próby losowej a całą populację (czyl zborowość, z której została pobraa próba). Take postępowae azywamy woskowaem statystyczym.
Statystyka opsowa Statystyka zajmuje sę zasadam metodam uogólaa wyków otrzymaych z próby losowej a całą populację (czyl zborowość, z której została pobraa próba). Take postępowae azywamy woskowaem statystyczym.
8.1 Zbieżność ciągu i szeregu funkcyjnego
 Rozdzał 8 Cąg szereg fukcyje 8.1 Zbeżość cągu szeregu fukcyjego Dla skrócea zapsu przyjmjmy pewe ozaczee. Defcja. Nech X, Y. Przez Y X ozaczamy zbór wszystkch fukcj określoych a zborze X o wartoścach w
Rozdzał 8 Cąg szereg fukcyje 8.1 Zbeżość cągu szeregu fukcyjego Dla skrócea zapsu przyjmjmy pewe ozaczee. Defcja. Nech X, Y. Przez Y X ozaczamy zbór wszystkch fukcj określoych a zborze X o wartoścach w
METODY KOMPUTEROWE 1
 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN MTODA ULRA Mcał PŁOTKOWIAK Adam ŁODYGOWSKI Kosultacje aukowe dr z. Wtold Kąkol Pozań 00/00 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN Metod umercze MN pozwalają a ormułowae matematczc
MTODY KOMPUTROW WIADOMOŚCI WSTĘPN MTODA ULRA Mcał PŁOTKOWIAK Adam ŁODYGOWSKI Kosultacje aukowe dr z. Wtold Kąkol Pozań 00/00 MTODY KOMPUTROW WIADOMOŚCI WSTĘPN Metod umercze MN pozwalają a ormułowae matematczc
TESTY NORMALNOŚCI. ( Cecha X populacji ma rozkład normalny). Hipoteza alternatywna H1( Cecha X populacji nie ma rozkładu normalnego).
 TESTY NORMALNOŚCI Test zgodośc Hpoteza zerowa H 0 ( Cecha X populacj ma rozkład ormaly). Hpoteza alteratywa H1( Cecha X populacj e ma rozkładu ormalego). Weryfkacja powyższych hpotez za pomocą tzw. testu
TESTY NORMALNOŚCI Test zgodośc Hpoteza zerowa H 0 ( Cecha X populacj ma rozkład ormaly). Hpoteza alteratywa H1( Cecha X populacj e ma rozkładu ormalego). Weryfkacja powyższych hpotez za pomocą tzw. testu
Rozwiązywanie umów o pracę
 Ryszard Sadlik Rozwiązywanie umów o pracę instruktaż, wzory, przykłady Ośrodek Doradztwa i Doskonalenia Kadr Sp. z o.o. Gdańsk 2012 Wstęp...7 Rozdział I Wy po wie dze nie umo wy o pra cę za war tej na
Ryszard Sadlik Rozwiązywanie umów o pracę instruktaż, wzory, przykłady Ośrodek Doradztwa i Doskonalenia Kadr Sp. z o.o. Gdańsk 2012 Wstęp...7 Rozdział I Wy po wie dze nie umo wy o pra cę za war tej na
WRAŻLIWOŚĆ WYNIKU TECHNICZNEGO ZAKŁADU UBEZPIECZEŃ NA ZMIANĘ POZIOMU REZERWY SZKODOWEJ
 Aca Woy WRAŻLIWOŚĆ WYNIKU TECHNICZNEGO ZAKŁADU UBEZPIECZEŃ NA ZMIANĘ POZIOMU REZERWY SZKODOWEJ Wstęp Załad ubezpeczeń est zobgoway do tworzea fuduszu ubezpeczeowego sładaącego sę z rezerw techczo-ubezpeczeowych
Aca Woy WRAŻLIWOŚĆ WYNIKU TECHNICZNEGO ZAKŁADU UBEZPIECZEŃ NA ZMIANĘ POZIOMU REZERWY SZKODOWEJ Wstęp Załad ubezpeczeń est zobgoway do tworzea fuduszu ubezpeczeowego sładaącego sę z rezerw techczo-ubezpeczeowych
L.Kowalski PODSTAWOWE TESTY STATYSTYCZNE WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH
 L.Kowalsk PODSTAWOWE TESTY STATYSTYCZNE TESTY STATYSTYCZNE poteza statystycza to dowole przypuszczee dotyczące rozkładu cechy X. potezy statystycze: -parametrycze dotyczą ezaego parametru, -parametrycze
L.Kowalsk PODSTAWOWE TESTY STATYSTYCZNE TESTY STATYSTYCZNE poteza statystycza to dowole przypuszczee dotyczące rozkładu cechy X. potezy statystycze: -parametrycze dotyczą ezaego parametru, -parametrycze
Analiza Matematyczna Ćwiczenia. J. de Lucas
 Aalza Matematycza Ćwczea J. de Lucas Zadae. Oblczyć grace astępujących fucj a lm y 3,y 0,0 b lm y 3 y ++y,y 0,0 +y c lm,y 0,0 + 4 y 4 y d lm y,y 0,0 3 y 3 e lm,y 0,0 +y 4 +y 4 f lm,y 0,0 4 y 6 +y 3 g lm,y
Aalza Matematycza Ćwczea J. de Lucas Zadae. Oblczyć grace astępujących fucj a lm y 3,y 0,0 b lm y 3 y ++y,y 0,0 +y c lm,y 0,0 + 4 y 4 y d lm y,y 0,0 3 y 3 e lm,y 0,0 +y 4 +y 4 f lm,y 0,0 4 y 6 +y 3 g lm,y
... MATHCAD - PRACA 1/A
 Nazwsko Imę (drukowaym) KOD: Dzeń+godz. (p. Śr) MATHCAD - PRACA /A. Stablcuj fukcję: f() = s() + /6. w przedzale od a do b z podzałem a rówych odcków. Sporządź wykres f() sprawdź, le ma mejsc zerowych.
Nazwsko Imę (drukowaym) KOD: Dzeń+godz. (p. Śr) MATHCAD - PRACA /A. Stablcuj fukcję: f() = s() + /6. w przedzale od a do b z podzałem a rówych odcków. Sporządź wykres f() sprawdź, le ma mejsc zerowych.
Portfel. Portfel pytania. Portfel pytania. Analiza i Zarządzanie Portfelem cz. 2. Katedra Inwestycji Finansowych i Zarządzania Ryzykiem
 Katedra Ietycj Faoych Zarządzaa yzykem Aalza Zarządzae Portfelem cz. Dr Katarzya Kuzak Co to jet portfel? Portfel grupa aktyó (trumetó faoych, aktyó rzeczoych), które zotały yelekcjooae, którym ależy zarządzać
Katedra Ietycj Faoych Zarządzaa yzykem Aalza Zarządzae Portfelem cz. Dr Katarzya Kuzak Co to jet portfel? Portfel grupa aktyó (trumetó faoych, aktyó rzeczoych), które zotały yelekcjooae, którym ależy zarządzać
PODSTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH
 PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH I Pracowa IF UJ Luy 03 PODRĘCZNIKI Wsęp do aalzy błędu pomarowego Joh R. Taylor Wydawcwo Naukowe PWN Warszawa 999 I Pracowa
PODTAWY OPRACOWANIA WYNIKÓW POMIARÓW Z ELEMENTAMI ANALIZY NIEPEWNOŚCI POMIAROWYCH I Pracowa IF UJ Luy 03 PODRĘCZNIKI Wsęp do aalzy błędu pomarowego Joh R. Taylor Wydawcwo Naukowe PWN Warszawa 999 I Pracowa
POPULACJA I PRÓBA. Próba reprezentatywna. Dr Adam Michczyński - METODY ANALIZY DANYCH POMIAROWYCH 5 1
 POPULACJA I PRÓBA POPULACJĄ w statystyce matematyczej azywamy zbór wszystkch elemetów (zdarzeń elemetarych charakteryzujących sę badaą cechą opsywaą zmeą losową. Zbadae całej populacj (przeprowadzee tzw.
POPULACJA I PRÓBA POPULACJĄ w statystyce matematyczej azywamy zbór wszystkch elemetów (zdarzeń elemetarych charakteryzujących sę badaą cechą opsywaą zmeą losową. Zbadae całej populacj (przeprowadzee tzw.
System finansowy gospodarki
 System fasowy gospodark Zajęca r 7 Krzywa retowośc, zadaa (mat. f.), marża w hadlu, NPV IRR, Ustawa o kredyce kosumeckm, fukcje fasowe Excela Krzywa retowośc (dochodowośc) Yeld Curve Krzywa ta jest grafczym
System fasowy gospodark Zajęca r 7 Krzywa retowośc, zadaa (mat. f.), marża w hadlu, NPV IRR, Ustawa o kredyce kosumeckm, fukcje fasowe Excela Krzywa retowośc (dochodowośc) Yeld Curve Krzywa ta jest grafczym
KOMPUTEROWY SYSTEM DO SPRAWDZANIA CZĘSTOŚCIOMIERZY CYFROWYCH
 MWK'2003 KOMPUTEROWY SYSTEM DO SPRAWDZANIA CZĘSTOŚCIOMIERZY CYFROWYCH dr ż. Elgusz Pałosk STRESZCZENIE W pracy przedstaa sę schemat blokoy układu pomaroego oraz sposób przetarzaa daych umożlające spradzae
MWK'2003 KOMPUTEROWY SYSTEM DO SPRAWDZANIA CZĘSTOŚCIOMIERZY CYFROWYCH dr ż. Elgusz Pałosk STRESZCZENIE W pracy przedstaa sę schemat blokoy układu pomaroego oraz sposób przetarzaa daych umożlające spradzae
ZARYS METODY OCENY TRWAŁOSCI I NIEZAWODNOSCI OBIEKTU Z UWZGLEDNIENIEM CZYNNIKA LUDZKIEGO I PŁASZCZYZNY LICZB ZESPOLONYCH
 Zdzsław IDZIASZEK 1 Mechatrocs ad Avato Faculty Mltary Uversty of Techology, 00-908 Warsaw 49, Kalskego street r zdzaszek@wat.edu.pl Norbert GRZESIK Avato Faculty Polsh Ar Force Academy, 08-51 Dębl, Dywzjou
Zdzsław IDZIASZEK 1 Mechatrocs ad Avato Faculty Mltary Uversty of Techology, 00-908 Warsaw 49, Kalskego street r zdzaszek@wat.edu.pl Norbert GRZESIK Avato Faculty Polsh Ar Force Academy, 08-51 Dębl, Dywzjou
Rachunek prawdopodobieństwa i statystyka matematyczna. Estymacja przedziałowa parametrów strukturalnych zbiorowości generalnej
 Rachek prawdopodobeńswa saysyka maemaycza Esymacja przedzałowa paramerów srkralych zborowośc geeralej Częso zachodz syacja, że koecze jes zbadae ogół poplacj pod pewym kąem p. średa oce z pewego przedmo.
Rachek prawdopodobeńswa saysyka maemaycza Esymacja przedzałowa paramerów srkralych zborowośc geeralej Częso zachodz syacja, że koecze jes zbadae ogół poplacj pod pewym kąem p. średa oce z pewego przedmo.
Porz dkowanie krajów Unii Europejskiej wed ug poziomu zrównowa onego rozwoju
 PRACE NAUKOWE Akadem m. Jaa Dugosza w Czstochowe Sera: Pragmata tes Okoomas 20, z. V Marek KULESZA Akadema m. Jaa Dugosza w Czstochowe Stasawa OSTASIEWICZ WSOWL m T. Kocuszk we Wrocawu Porzdkowae kraów
PRACE NAUKOWE Akadem m. Jaa Dugosza w Czstochowe Sera: Pragmata tes Okoomas 20, z. V Marek KULESZA Akadema m. Jaa Dugosza w Czstochowe Stasawa OSTASIEWICZ WSOWL m T. Kocuszk we Wrocawu Porzdkowae kraów
