ANALIZA PROCESU REFORMINGU METANU PARĄ WODNĄ PRZY POMOCY UOGÓLNIONEJ METODY NAJMNIEJSZYCH KWADRATÓW
|
|
|
- Kamil Piotrowski
- 6 lat temu
- Przeglądów:
Transkrypt
1 ZESZYTY NAUKOWE POLITECHNIKI RZESZOWSKIEJ 290, Mechanika 86 RUTMech, t. XXXI, z. 86 (1/14), styczeń-marzec 2014, s Anna ŚCIĄŻKO 1,3 Yosuke KOMATSU 3 Grzegorz BRUS 2 Shinji KIMIJIMA 3 Janusz S. SZMYD 2 ANALIZA PROCESU REORMINGU METANU PARĄ WODNĄ PRZY POMOCY UOGÓLNIONEJ METODY NAJMNIEJSZYCH KWADRATÓW Matematyczny model zjawiska fizycznego obarczony jest niepewnością, wynikającą z niedokładności pomiarów eksperymentalnych, wartości przyjętych parametrów oraz założonych uproszczeń modelowych. Artykuł przedstawia eksperymentalną oraz numeryczną analizę procesu parowego reforming metanu za pomocą Uogólnionej Metody Najmniejszych Kwadratów (GLS). Opublikowane dotychczas równania kinetyki procesu reformingu różnią się znacznie między sobą oraz nie zawierają analizy niepewności przedstawionych rezultatów. Algorytm GLS pozwala na wyznaczenia najbardziej prawdopodobnych wartości empirycznych parametrów definiujących szybkość reakcji reformingu oraz umożliwia obiektywną weryfikację przygotowanego modelu matematycznego. Analiza numeryczna została przeprowadzona w oparciu o badania eksperymentalne z wykorzystaniem 0.3 g próbki katalizatora Ni/YSZ 60:40%v. Pokazano, że metoda GLS zapewnia poprawę dokładności zmiennych mierzonych oraz pozwala na wyznaczenie najbardziej prawdopodobnych wartości niewiadomych oraz niepewności charakteryzujących otrzymane wyniki. Słowa kluczowe: katalizator Ni/YSZ, reforming parowy metanu, analiza błędów pomiarowych 1. Wstęp W klasycznym podejściu do modelowania numerycznego, uproszczenia i niepewność modelu, wynikające z niepewności pomiarów eksperymentalnych, założonych wartości parametrów fizykochemicznych czy uproszczeń modelowych, są pomijane bądź nie są dyskutowane w wystarczającym stopniu. Bada- 1 Autor do korespondencji/corresponding author: Anna Ściążko, Akademia Górniczo-Hutnicza w Krakowie, al. Mickiewicza 30, Kraków, sciazko@agh.edu.pl 2 Akademia Górniczo-Hutnicza w Krakowie, al. Mickiewicza 30, Kraków 3 Shibaura Institute of Technology, Saitama, Japan
2 96 A. Ściążko, Y. Komatsu, G. Brus, S. Kimijima, J. S. Szmyd nia dotyczące kinetyki procesu reformingu metanu można znaleźć w wielu opracowaniach [1,2,4-6], jednak opisy reakcji znacznie odbiegają od siebie. Ponadto, przedstawione rezultaty nie zawierają analizy niepewności uzyskanych wyników. W niemniejszej pracy przedstawiono eksperymentalną oraz numeryczną analizę procesu parowego reforming metanu za pomocą Uogólnionej Metody Najmniejszych Kwadratów (GLS), mającą na celu ocenę wybranych matematycznych modeli omawianego procesu. Metoda GLS zakłada wykorzystanie wszystkich zebranych wyników pomiarów bezpośrednio w modelu, co prowadzi do utworzenia nadokreślonego układu równań modelowych. Układ taki posiada większą liczbę równań niż niewiadomych, oraz ze względu na niepewności pomiarowe, staje się układem sprzecznym. Jak pokazano w [6] algorytm GLS pozwala na wyznaczenia najbardziej prawdopodobnych wartości niewiadomych parametrów definiujących szybkość reakcji reformingu: współczynników rzędu reakcji i energii aktywacji. Oprócz powyższych korzyści, proponowana metoda, dzięki obliczeniu macierzy kowariancji rezultatów, umożliwia walidację przygotowanych modeli procesu oraz obiektywny, z matematycznego punktu widzenia, wybór najdokładniejszego z nich [7]. Analiza numeryczna procesu reformingu parowego metanu została przeprowadzona w oparciu o badania eksperymentalne z wykorzystaniem katalizatora Ni/YSZ, będącego popularnym materiałem dla wysokotemperaturowych ogniw paliwowych SOC [2]. Reforming metanu jest rozważany w kontekście możliwego zastosowania w ogniwach SOC w ramach wewnętrznego połączenia pośredniego lub reakcji zachodzącej bezpośrednio na anodzie. Zaprojektowanie i optymalizacja modelu układu przygotowania paliwa wymaga szczegółowej wiedzy na temat procesu reformingu [3]. W wykorzystanych modelach reformingu zaimplementowano nie tylko równania definiujące szybkość procesu, ale wprowadzono także równania wymuszające spełnienie podstawowych praw fizycznych. Zostało pokazane, że ich wprowadzenie znacznie poprawia jakość uzyskanych rezultatów. Metoda GLS została wykorzystana do wyznaczenia parametrów szybkości reformingu oraz obiektywnej walidacji przygotowanych matematycznych modeli procesu Reforming parowy metanu Reakcjami chemicznymi dominującymi w rozważanym procesie są reforming metanu: CH4 + H2O 3H2 + CO oraz reakcja pary wodnej z tlenkiem węgla: CO + H2O H2 + CO2 [5]. Druga z reakcji jest reakcją słabo egzotermiczną oraz szybką zakłada się, że spełnia ona równanie równowagi [1]. Szybkość procesu jest determinowana przez kinetykę procesu reformingu: E a Rst = wcat Aexp pch p RT b H O 4 2 (1)
3 Analiza procesu reformingu metanu 97 gdzie R st - szybkość reakcji [mol s -1 m -3 ], p - ciśnienie parcjalne [atm], R= uniwersalna stała gazowa [J mol -1 K -1 ], T - temperatura procesu [K], w cat - gęstość katalizatora [g m -3 ], A - stała Arrheniusa [mol min -1 g -1 atm -(a+b) ], E - energia aktywacji [J mol -1 ], a, b - rzędy reakcji [-]. W celu przygotowania modelu procesu oraz wyznaczenia opisu reakcji, niezbędne jest wyznaczenie empirycznych parametrów procesu: rzędów reakcji a oraz b, energii aktywacji E oraz współczynnika A Uogólniona metoda najmniejszych kwadratów Metoda Najmniejszych Kwadratów jest jedną z metod przybliżonego rozwiązywania nadokreślonych układów równań. Nadokreślone układy równań charakteryzują się większą liczbą równań niż zmiennych. Szczegóły metody oraz jej wykorzystanie w problemach związanych z energetyką opisano w [7]. Uogólniona Metoda Najmniejszych Kwadratów (Generalized Least Squares - GLS) zakłada, że wszystkie zmienne występujące w modelu (zarówno wyniki pomiarów u jak i niewiadome x) są traktowane z matematycznego puntu widzenia jako wyniki bezpośrednich pomiarów u. Dla wartości będących niewiadomymi przyjmuje się, że ich błędy s k są duże w porównaniu z błędami bezpośrednich pomiarów s n. Metoda GLS zakłada minimalizację funkcji: 2 2 N y n K v k Φ ( v, y ) = + min k = 1 sk n= 1 s (2) n przy jednoczesnym spełnieniu układu równań ograniczeń modelu. Wektory poprawek pomiarów oraz niewiadomych oznaczono jako v oraz y (V B =[v,y]). Po linearyzacji równań modelu oraz zastosowaniu metody mnożników Lagrange a otrzymuje się następujące rozwiązanie: V = C A W, gdzie = A C A (3) T 1 T B B B B B B B B B gdzie C B - macierz kowariancji a priori, A B blokowa macierz Jackobi ego, W B wektor residuów równań. Macierz kowariancji po procesie uzgadniania C VB, definiująca jakość modelu: T 1 CU CUX CVB = CB CBABB ABCB = T CUX CX (4) By wykorzystać algorytm GLS konieczne jest zdefiniowanie zbioru równań ograniczeń, wektora zmiennych zawierającego parametry mierzone oraz niewiadome, a także macierzy kowariancji a priori, która jest określona przez niepewności charakteryzujące poszczególne pomiary bezpośrednie oraz założone błędy niewiadomych. Preliminarna inicjalizacja wartości niewiadomych
4 98 A. Ściążko, Y. Komatsu, G. Brus, S. Kimijima, J. S. Szmyd następuje na podstawie przeprowadzonej wstępnej analizy procesu. Następnie algorytm rozpoczyna iteracyjne obliczenia, mające na celu spełnienie warunku zbieżności: linearyzację równań ograniczeń poprzez obliczenie macierzy Jacobi ego oraz obliczenie wektorów poprawek V B oraz macierzy kowariancji a posteriori C VB. 2. Badania eksperymentalne oraz wstępna analiza W badaniach doświadczalnych wykorzystano 0.3 [g] próbkę katalizatora niklowego (Ni/YSZ 60:40%vol). Cermet niklowy został wybrany ze względu na możliwość wykorzystania w anodach wysokotemperaturowych ogniw paliwowych typu SOC [2]. Ponadto, jako popularny materiał katalityczny reakcji reformingu [4], zapewnia on możliwość szerokich analiz porównawczych z danymi literaturowymi oraz ewaluację różnych modeli procesu. Schemat układu pomiarowego przedstawiono na Rys. 1. Do reaktora dostarczano wodę, azot oraz metan, natomiast skład osuszonych spalin (ułamki molowe CH 4, H 2, N 2, CO oraz CO 2 ) badano metodą chromatografii gazowej. Rys. 1. Schemat układu pomiarowego: 1- podgrzewacz/parownik, 2 piec, 3 reaktor, 4 tlenek glinu, 5 katalizator, 6 wełna, 7 pogrzewacz/skraplacz, 8 separator pary, 9 - chromatograf gazowy, 10 spaliny, T termopara, przepływomierz masowy ig. 1. Schema of the experimental set-up: 1 - evaporator/preheater, 2 furnace, 3 reformer, 4 alumina balls, 5 catalyst, 6 wool, 7 afterheater/condenser, 8 gas-liquid separator, 9 gas chromatograph, 10 exhaust, T thermocouples, mass flow controller Wartości inicjalizujące parametrów dla algorytmu GLS wyznaczono przez przeprowadzenie wstępnej analizy procesu według metodologii zaproponowanej przez Brusa i in. [2]. Wyniki poszczególnych etapów obliczeń: analizy odchylenia standardowego oraz wykresu Arrheniusa, pokazane na Rys. 2 posłużyły do wyznaczenia wstępnej formy równania kinetyki procesu: Rst = wcat 7.37 exp p p RT CH H O 4 2 (5) gdzie: w cat waga katalizatora [g], R=8.314 [J mol -1 K -1 ] - uniwersalna stała gazowa, T - temperatura [K], p CH4 i p H2O - ciśnienia parcjalne CH 4 i H 2 O [atm].
5 Analiza procesu reformingu metanu 99 A B Rys. 2. A) Wyznaczenie współczynników rzędu reakcji oraz B) wykres Arrheniusa ig. 2. A) Calculation of reaction orders and B) Arrhenius plot 3. Aplikacja Uogólnionej Metody Najmniejszych Kwadratów W celu wyznaczenia parametrów matematycznego opisu procesu refor- mingu metanu przy występującym nadmiarze informacji obarczonych błędami wykorzystano Uogólnioną Metodę Najmniejszych Kwadratów. Przedstawione przykłady pokazują zastosowania metody do wyznaczenia wartości poprawek wielkości mierzonych v i niewiadomych y a także do wyznaczenia macierzy kowariancji wynikóww po uzgadnianiu C VB. Analiza numeryczna zawiera warianty uwzględniające różną ilość równań warunków oraz różne ich typy. W modelach wykorzystano równania opisujące szybkość reakcji (6), liniową zależność Arheniusa (7), bilanse pierwiastków w systemie (8-11) oraz bilans wyjściowy (12): i( j ) o( j) CH 4 CH4 w ( j ) 3 E 10 a b ( j ) ( j ) A exp ( ) ( pch ) ( p ) 0 j = 4 H2O RT 3 E ln A exp ( j ) m + n = 0 line ( j) line RT T ( o( j) o( j) + + = i( j) o( j) CH 4 CH i( j ) i( j) o( j) o( j ) o( j) CH H2O CH H2O H ( o( j) o( j ) = 0 i( j) o( j ) H2O CO i( j ) o( j ) = 0 N 2 N 2 o( j ) o( j) ALL ( CH 4 0 CO2 CO o( j ) o( j) o( j ) o( j) = ) ( ) = 0 CO2 H2O ) H2O H CO CO ) (6) (7) (8) (9) (10) (11) (12)
6 100 A. Ściążko, Y. Komatsu, G. Brus, S. Kimijima, J. S. Szmyd gdzie - przepływ molowy [mol s -1 ], indeksy i oraz o - strumień wejściowy oraz wyjściowy, m line i n line - współczynniki prostej Arrheniusa [-]. Wszystkie z powyższych równań zostały wykorzystane do obliczeń każdego z pomiarów eksperymentalnych - indeks j odnosi się do j-tego punktu pomiarowego. Opis matematyczny wymaga wprowadzenia dodatkowych niewiadomych definiujących prostą Arrheniusa oraz niemierzone przepływy pierwiastków (m.in. azotu). Wektor zmiennych zbudowano z wielkości mierzonych oraz niewiadomych inicjalizowanych na podstawie wstępnej analizy (Rozdział 2). Tabela 1 przedstawia szczegóły pięciu modeli reformingu zaimplementowanych w algorytmie GLS. Kolejne przypadki modelowe zawierają zwiększoną liczbę równań ograniczeń. Przypadek referencyjny (Test 5) zawiera równania jednakowe z Testem 4 oraz zmniejszoną liczbę punktów pomiarowych. Tabela 1. Opis przeprowadzonych testów wraz z liczbą zmiennych i równań Table 1. Description of conducted tests and a number of variables and equations Szybkość reformingu Równanie Arrheniusa Bilans wyjściowy Wartości mierzone Bilanse pierwiastków Niewiadome Test 1 X Test 2 X X Test 3 X X X Test 4 X X X X Test 5 X X X X Zmienne Równania Tabela 2. Rezultaty wartości parametrów a, b, A, E wraz z ich niepewnościami Table 2. Results values of parameters a, b, A, E with their uncertainties Test a b A E ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ±2.27 Zadaniem analizy było oszacowanie wartości parametrów określających szybkość badanego procesu: a, b, A, E. Ich wartości wraz z charakteryzującymi je niepewnościami zebrano w Tab. 2. Suma elementów diagonalnych macierzy kowariancji C VB, przedstawiona na Rys. 3B oraz 3C, może służyć za miarę jakości uzyskanego rezultatu czym mniejsza uzyskana wartość, tym model dokładniej opisuje proces. Na Rys. 3A pokazano wyznaczone w poszczególnych testach rzędy reakcji wraz z ich niepewnościami. Pokazano, że zwiększenie liczby równań modelowych, nakłada dodatkowe warunki, usztywniające uzyskane rezultaty. Szczególnie znaczące jest wymuszenie spełnienia równań
7 Analiza procesu reformingu metanu 101 bilansowych - powoduje to efektywne wykorzystanie wszystkich mierzonych wielkości, co zmniejsza niepewność końcowych rezultatów. Zgodnie z przewi- cha- dywaniami, Test 5, analizujący zmniejszoną liczbę danych pomiarowych rakteryzuje się niewielkim pogorszeniem rezultatu względem Testu 4. Rys. 3. A) Wyznaczone wartości parametrów a i b wraz z niepewnościami oraz suma elementów diagonalnych macierzy C VB dla: B) pomiarów i C) niewiadomych ig. 3. Calculated values of both a and b parameters with their uncertainties and sum of diagonal elements of C VB matrix for: B) measurements and C) unknowns 4. Wnioski W pracy przedstawiono analizę procesu reformingu parowego metanu za pomocą Uogólnionej Metody Najmniejszych Kwadratów. Metoda ta jest stosouzyskania wana, gdy model numeryczny zawiera większą niż niezbędna dla jednoznacznego rozwiązania ilość pomiarów, jednak uzyskane wyniki pomia- jest rowe są obarczone błędami eksperymentalnymi. W takiej sytuacji możliwe uzyskanie skończonego zbioru rozwiązań prawdopodobnych. Metoda GLS po- zwala na wybranie rozwiązania najbardziej prawdopodobnego oraz wyznacze- poprawę nie określającej je niedokładności. Algorytm GLS zapewnia ponadtoo dokładności oszacowania wielkości mierzonych eksperymentalnie. W pracy omówiono przeprowadzone badania eksperymentalnee oraz ich wstępną analizę, którą następnie wykorzystano do inicjalizacji wektorów zmiennych w metodzie GLS. Przedstawiono ponadto wpływ wyboru równań modelowych na jakość uzyskiwanych rezultatów oraz wybrano zbór równań ograniczeń najlepiej opisujące badany przypadek. Najbardziej precyzyjny mo- zależność Arrheniusa, bilanse pierwiastków w strumieniach wejściowym i wyj- del składał się z równań określających kinetykę badanej reakcji, prostoliniową ściowym oraz bilanse udziałów molowych w strumieniu wyjściowym. Dokład- metody GLS, jest kluczowy z punktu widzenia modelowania i optymalizacji systemów ogniw paliwowych SOC. ny opis reakcji reformingu metanu, który można uzyskać dzięki zastosowaniu Literatura [1] Achenbach E., Riensche E.: Methane/steam reforming kinetics for solid oxide fuel cells, J. Power Sources, 52 (1994)
8 102 A. Ściążko, Y. Komatsu, G. Brus, S. Kimijima, J. S. Szmyd [2] Brus G., Komatsu Y., Kimijima S., Szmyd J.S.: An Analysis of Biogas Reforming Process on Ni/YSZ and Ni/SDC Catalysts, Int. J. Thermodyn., 15 (2012) [3] Komatsu Y., Kimijima S., Szmyd J.S.: Numerical analysis on dynamic behavior of solid oxide fuel cell with power output control scheme, J. Power Sources, 223 (2013) [4] Mogensen D., Grunwaldt J.-D., Hendriksen P.V., Dam-Johansen K., Nielsen J.U.: Internal steam reforming in solid oxide fuel cells: Status and opportunities of kinetic studies and their impact on modelling, J. Power Sources. 196 (2011) [5] Odegard R., Johnsen E., Karoliussen H.: Methane reforming on Ni/Zirconia SOC anodes, Solid Oxide uel Cells IV, The Electrochemical Society, Pennington, New York 1995, pp [6] Sciazko A., Komatsu Y., Brus G., Kimijima S.,. Szmyd J.S.: A novel approach to the experimental study on methane/steam reforming kinetics using the Orthogonal Least Squares method, J. Power Sources, 262 (2014) [7] Szargut J.: Rachunek wyrównawczy w technice cieplnej, PAN, Komisja Energetyki, Wrocław Prace były finansowane przez Narodowe Centrum Badań i Rozwoju (Projekt HTRPL, Kontrakt nr SP/J/1/166183/12) oraz Precise Measurement Technology Promotion oundation of Japan. METHANE STEAM REORMING PROCESS ANALYSIS WITH GERERALIZED LEAST SQUARES ALGORITHM S u m m a r y Mathematical model of the physical phenomena contains the uncertainties resulted from the inaccuracy of the measurements, assumed values of parameters and model simplifications. The article presents the experimental and numerical analysis of methane steam reforming process with Generalized Least Squares Method (GLS). Published in the literature equations about kinetics of reforming process are different and they do not contain the uncertainty analysis of the obtained results. The GLS algorithm is adopted to select the most probable values of reforming kinetics parameters and to objectively validate proposed mathematical models. The numerical analysis was conducted on the basis of the experimental measurements of 0.3 g Ni/YSZ 60:40vol catalyst sample. It was proven that GLS method is useful in securing higher accuracy of measured variables, finding the most probable values of unknowns and simultaneously determining the uncertainty coupled with all the variables in the system. Keywords: Ni/YSZ catalyst, steam methane reforming, analysis of measuring errors DOI: /rm Otrzymano/received: Zaakceptowano/accepted:
Zastosowanie rachunku wyrównawczego do uwiarygodnienia wyników pomiarów w układzie cieplnym bloku energetycznego siłowni parowej
 Marcin Szega Zastosowanie rachunku wyrównawczego do uwiarygodnienia wyników pomiarów w układzie cieplnym bloku energetycznego siłowni parowej (Monografia habilitacyjna nr 193. Wydawnictwo Politechniki
Marcin Szega Zastosowanie rachunku wyrównawczego do uwiarygodnienia wyników pomiarów w układzie cieplnym bloku energetycznego siłowni parowej (Monografia habilitacyjna nr 193. Wydawnictwo Politechniki
KINETYKA REAKCJI CO 2 Z WYBRANYMI TYPAMI AMIN W ROZTWORACH WODNYCH
 XXI Ogólnopolska Konferencja Inżynierii Chemicznej i Procesowej Kołobrzeg, 2-6 września 213 ANDRZEJ CHACUK, HANNA KIERZKOWSKA PAWLAK, MARTA SIEMIENIEC KINETYKA REAKCJI CO 2 Z WYBRANYMI TYPAMI AMIN W ROZTWORACH
XXI Ogólnopolska Konferencja Inżynierii Chemicznej i Procesowej Kołobrzeg, 2-6 września 213 ANDRZEJ CHACUK, HANNA KIERZKOWSKA PAWLAK, MARTA SIEMIENIEC KINETYKA REAKCJI CO 2 Z WYBRANYMI TYPAMI AMIN W ROZTWORACH
Numeryczna symulacja rozpływu płynu w węźle
 231 Prace Instytutu Mechaniki Górotworu PAN Tom 7, nr 3-4, (2005), s. 231-236 Instytut Mechaniki Górotworu PAN Numeryczna symulacja rozpływu płynu w węźle JERZY CYGAN Instytut Mechaniki Górotworu PAN,
231 Prace Instytutu Mechaniki Górotworu PAN Tom 7, nr 3-4, (2005), s. 231-236 Instytut Mechaniki Górotworu PAN Numeryczna symulacja rozpływu płynu w węźle JERZY CYGAN Instytut Mechaniki Górotworu PAN,
ĆWICZENIE 3 REZONANS AKUSTYCZNY
 ĆWICZENIE 3 REZONANS AKUSTYCZNY W trakcie doświadczenia przeprowadzono sześć pomiarów rezonansu akustycznego: dla dwóch różnych gazów (powietrza i CO), pięć pomiarów dla powietrza oraz jeden pomiar dla
ĆWICZENIE 3 REZONANS AKUSTYCZNY W trakcie doświadczenia przeprowadzono sześć pomiarów rezonansu akustycznego: dla dwóch różnych gazów (powietrza i CO), pięć pomiarów dla powietrza oraz jeden pomiar dla
WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI
 WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI Stefan WÓJTOWICZ, Katarzyna BIERNAT ZAKŁAD METROLOGII I BADAŃ NIENISZCZĄCYCH INSTYTUT ELEKTROTECHNIKI ul. Pożaryskiego 8, 04-703 Warszawa tel. (0)
WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI Stefan WÓJTOWICZ, Katarzyna BIERNAT ZAKŁAD METROLOGII I BADAŃ NIENISZCZĄCYCH INSTYTUT ELEKTROTECHNIKI ul. Pożaryskiego 8, 04-703 Warszawa tel. (0)
WPŁYW SZYBKOŚCI STYGNIĘCIA NA WŁASNOŚCI TERMOFIZYCZNE STALIWA W STANIE STAŁYM
 2/1 Archives of Foundry, Year 200, Volume, 1 Archiwum Odlewnictwa, Rok 200, Rocznik, Nr 1 PAN Katowice PL ISSN 1642-308 WPŁYW SZYBKOŚCI STYGNIĘCIA NA WŁASNOŚCI TERMOFIZYCZNE STALIWA W STANIE STAŁYM D.
2/1 Archives of Foundry, Year 200, Volume, 1 Archiwum Odlewnictwa, Rok 200, Rocznik, Nr 1 PAN Katowice PL ISSN 1642-308 WPŁYW SZYBKOŚCI STYGNIĘCIA NA WŁASNOŚCI TERMOFIZYCZNE STALIWA W STANIE STAŁYM D.
ESTYMACJA PARAMETRÓW TERMOFIZYCZNYCH CIAŁ IZOTROPOWYCH ZA POMOCĄ METODY FILTRACJI DYNAMICZNEJ ORAZ PRZEDZIAŁOWEGO UŚREDNIANIA WYNIKÓW POMIARÓW
 MODELOWANIE INśYNIERSKIE ISSN 896-77X 34, s. 73-78, Gliwice 007 ESTYMACJA PARAMETRÓW TERMOFIZYCZNYCH CIAŁ IZOTROPOWYCH ZA POMOCĄ METODY FILTRACJI DYNAMICZNEJ ORAZ PRZEDZIAŁOWEGO UŚREDNIANIA WYNIKÓW POMIARÓW
MODELOWANIE INśYNIERSKIE ISSN 896-77X 34, s. 73-78, Gliwice 007 ESTYMACJA PARAMETRÓW TERMOFIZYCZNYCH CIAŁ IZOTROPOWYCH ZA POMOCĄ METODY FILTRACJI DYNAMICZNEJ ORAZ PRZEDZIAŁOWEGO UŚREDNIANIA WYNIKÓW POMIARÓW
7.1. Modelowanie fizyczne 7.2. Modelowanie matematyczne 7.3. Kategorie modelowania matematycznego 7.4. Kategorie modelowania matematycznego 7.5.
 7.. Modelowanie fizyczne 7.2. Modelowanie matematyczne 7.3. Kategorie modelowania matematycznego 7.4. Kategorie modelowania matematycznego 7.5. Kategorie modelowania matematycznego 7.6. Symulatory niestacjonarne
7.. Modelowanie fizyczne 7.2. Modelowanie matematyczne 7.3. Kategorie modelowania matematycznego 7.4. Kategorie modelowania matematycznego 7.5. Kategorie modelowania matematycznego 7.6. Symulatory niestacjonarne
BŁĘDY OKREŚLANIA MASY KOŃCOWEJ W ZAKŁADACH SUSZARNICZYCH WYKORZYSTUJĄC METODY LABORATORYJNE
 Inżynieria Rolnicza 5(103)/2008 BŁĘDY OKREŚLANIA MASY KOŃCOWEJ W ZAKŁADACH SUSZARNICZYCH WYKORZYSTUJĄC METODY LABORATORYJNE Zbigniew Zdrojewski, Stanisław Peroń, Mariusz Surma Instytut Inżynierii Rolniczej,
Inżynieria Rolnicza 5(103)/2008 BŁĘDY OKREŚLANIA MASY KOŃCOWEJ W ZAKŁADACH SUSZARNICZYCH WYKORZYSTUJĄC METODY LABORATORYJNE Zbigniew Zdrojewski, Stanisław Peroń, Mariusz Surma Instytut Inżynierii Rolniczej,
Mgr inż. Marta DROSIŃSKA Politechnika Gdańska, Wydział Oceanotechniki i Okrętownictwa
 MECHANIK 7/2014 Mgr inż. Marta DROSIŃSKA Politechnika Gdańska, Wydział Oceanotechniki i Okrętownictwa WYZNACZENIE CHARAKTERYSTYK EKSPLOATACYJNYCH SIŁOWNI TURBINOWEJ Z REAKTOREM WYSOKOTEMPERATUROWYM W ZMIENNYCH
MECHANIK 7/2014 Mgr inż. Marta DROSIŃSKA Politechnika Gdańska, Wydział Oceanotechniki i Okrętownictwa WYZNACZENIE CHARAKTERYSTYK EKSPLOATACYJNYCH SIŁOWNI TURBINOWEJ Z REAKTOREM WYSOKOTEMPERATUROWYM W ZMIENNYCH
Porównanie wyników symulacji wpływu kształtu i amplitudy zakłóceń na jakość sterowania piecem oporowym w układzie z regulatorem PID lub rozmytym
 ARCHIVES of FOUNDRY ENGINEERING Published quarterly as the organ of the Foundry Commission of the Polish Academy of Sciences ISSN (1897-3310) Volume 15 Special Issue 4/2015 133 138 28/4 Porównanie wyników
ARCHIVES of FOUNDRY ENGINEERING Published quarterly as the organ of the Foundry Commission of the Polish Academy of Sciences ISSN (1897-3310) Volume 15 Special Issue 4/2015 133 138 28/4 Porównanie wyników
Spis treści. Przedmowa... XI. Rozdział 1. Pomiar: jednostki miar... 1. Rozdział 2. Pomiar: liczby i obliczenia liczbowe... 16
 Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Zagadnienia do pracy klasowej: Kinetyka, równowaga, termochemia, chemia roztworów wodnych
 Zagadnienia do pracy klasowej: Kinetyka, równowaga, termochemia, chemia roztworów wodnych 1. Równanie kinetyczne, szybkość reakcji, rząd i cząsteczkowość reakcji. Zmiana szybkości reakcji na skutek zmiany
Zagadnienia do pracy klasowej: Kinetyka, równowaga, termochemia, chemia roztworów wodnych 1. Równanie kinetyczne, szybkość reakcji, rząd i cząsteczkowość reakcji. Zmiana szybkości reakcji na skutek zmiany
OPTYMALIZACJA STEROWANIA MIKROKLIMATEM W PIECZARKARNI
 Inżynieria Rolnicza 6(131)/2011 OPTYMALIZACJA STEROWANIA MIKROKLIMATEM W PIECZARKARNI Leonard Woroncow, Ewa Wachowicz Katedra Automatyki, Politechnika Koszalińska Streszczenie. W pracy przedstawiono wyniki
Inżynieria Rolnicza 6(131)/2011 OPTYMALIZACJA STEROWANIA MIKROKLIMATEM W PIECZARKARNI Leonard Woroncow, Ewa Wachowicz Katedra Automatyki, Politechnika Koszalińska Streszczenie. W pracy przedstawiono wyniki
Nowoczesne narzędzia obliczeniowe do projektowania i optymalizacji kotłów
 Nowoczesne narzędzia obliczeniowe do projektowania i optymalizacji kotłów Mateusz Szubel, Mariusz Filipowicz Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie AGH University of Science and
Nowoczesne narzędzia obliczeniowe do projektowania i optymalizacji kotłów Mateusz Szubel, Mariusz Filipowicz Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie AGH University of Science and
BADANIA SYMULACYJNE I EKSPERYMENTALNE UTLENIAJĄCEGO REAKTORA KATALITYCZNEGO SYSTEMU FILTRA CZĄSTEK STAŁYCH W PROGRAMIE AVL BOOST
 Stanisław Kruczyński 1, Wojciech Kamela 2, Kamil Duniec 2 BADANIA SYMULACYJNE I EKSPERYMENTALNE UTLENIAJĄCEGO REAKTORA KATALITYCZNEGO SYSTEMU FILTRA CZĄSTEK STAŁYCH W PROGRAMIE AVL BOOST Streszczenie.
Stanisław Kruczyński 1, Wojciech Kamela 2, Kamil Duniec 2 BADANIA SYMULACYJNE I EKSPERYMENTALNE UTLENIAJĄCEGO REAKTORA KATALITYCZNEGO SYSTEMU FILTRA CZĄSTEK STAŁYCH W PROGRAMIE AVL BOOST Streszczenie.
Wykład 4. Anna Ptaszek. 9 października Katedra Inżynierii i Aparatury Przemysłu Spożywczego. Chemia fizyczna - wykład 4. Anna Ptaszek 1 / 29
 Wykład 4 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 9 października 2015 1 / 29 Podstawy kinetyki chemicznej pochodna funkcji i jej interpretacja, pojęcie szybkości i prędkości, stechiometria
Wykład 4 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 9 października 2015 1 / 29 Podstawy kinetyki chemicznej pochodna funkcji i jej interpretacja, pojęcie szybkości i prędkości, stechiometria
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż.
 Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
Estymacja wektora stanu w prostym układzie elektroenergetycznym
 Zakład Sieci i Systemów Elektroenergetycznych LABORATORIUM INFORMATYCZNE SYSTEMY WSPOMAGANIA DYSPOZYTORÓW Estymacja wektora stanu w prostym układzie elektroenergetycznym Autorzy: dr inż. Zbigniew Zdun
Zakład Sieci i Systemów Elektroenergetycznych LABORATORIUM INFORMATYCZNE SYSTEMY WSPOMAGANIA DYSPOZYTORÓW Estymacja wektora stanu w prostym układzie elektroenergetycznym Autorzy: dr inż. Zbigniew Zdun
Automatyka i pomiary wielkości fizykochemicznych. Instrukcja do ćwiczenia III. Pomiar natężenia przepływu za pomocą sondy poboru ciśnienia
 Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia III Pomiar natężenia przepływu za pomocą sondy poboru ciśnienia Sonda poboru ciśnienia Sonda poboru ciśnienia (Rys. ) jest to urządzenie
Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia III Pomiar natężenia przepływu za pomocą sondy poboru ciśnienia Sonda poboru ciśnienia Sonda poboru ciśnienia (Rys. ) jest to urządzenie
NIEPEWNOŚĆ POMIARÓW POZIOMU MOCY AKUSTYCZNEJ WEDŁUG ZNOWELIZOWANEJ SERII NORM PN-EN ISO 3740
 PRACE INSTYTUTU TECHNIKI BUDOWLANEJ - KWARTALNIK BUILDING RESEARCH INSTITUTE - QUARTERLY 2 (162) 2012 ARTYKUŁY - REPORTS Anna Iżewska* NIEPEWNOŚĆ POMIARÓW POZIOMU MOCY AKUSTYCZNEJ WEDŁUG ZNOWELIZOWANEJ
PRACE INSTYTUTU TECHNIKI BUDOWLANEJ - KWARTALNIK BUILDING RESEARCH INSTITUTE - QUARTERLY 2 (162) 2012 ARTYKUŁY - REPORTS Anna Iżewska* NIEPEWNOŚĆ POMIARÓW POZIOMU MOCY AKUSTYCZNEJ WEDŁUG ZNOWELIZOWANEJ
FIZYKA LABORATORIUM prawo Ohma
 FIZYKA LABORATORIUM prawo Ohma dr hab. inż. Michał K. Urbański, Wydział Fizyki Politechniki Warszawskiej, pok 18 Gmach Fizyki, murba@if.pw.edu.pl www.if.pw.edu.pl/ murba strona Wydziału Fizyki www.fizyka.pw.edu.pl
FIZYKA LABORATORIUM prawo Ohma dr hab. inż. Michał K. Urbański, Wydział Fizyki Politechniki Warszawskiej, pok 18 Gmach Fizyki, murba@if.pw.edu.pl www.if.pw.edu.pl/ murba strona Wydziału Fizyki www.fizyka.pw.edu.pl
ZADANIE 1 W temperaturze 700 K gazowa mieszanina dwutlenku węgla i wodoru reaguje z wytworzeniem pary wodnej i tlenku węgla. Stała równowagi reakcji
 ZADANIE 1 W temperaturze 700 K gazowa mieszanina dwutlenku węgla i wodoru reaguje z wytworzeniem pary wodnej i tlenku węgla. Stała równowagi reakcji w tej temperaturze wynosi K p = 0,11. Reaktor został
ZADANIE 1 W temperaturze 700 K gazowa mieszanina dwutlenku węgla i wodoru reaguje z wytworzeniem pary wodnej i tlenku węgla. Stała równowagi reakcji w tej temperaturze wynosi K p = 0,11. Reaktor został
OPTYMALIZACJA PARAMETRÓW PRACY PNEUMATYCZNEGO SEPARATORA KASKADOWEGO
 InŜynieria Rolnicza 7/2006 Zbigniew Oszczak Katedra InŜynierii i Maszyn SpoŜywczych Akademia Rolnicza w Lublinie OPTYMALIZACJA PARAMETRÓW PRACY PNEUMATYCZNEGO SEPARATORA KASKADOWEGO Streszczenie W pracy
InŜynieria Rolnicza 7/2006 Zbigniew Oszczak Katedra InŜynierii i Maszyn SpoŜywczych Akademia Rolnicza w Lublinie OPTYMALIZACJA PARAMETRÓW PRACY PNEUMATYCZNEGO SEPARATORA KASKADOWEGO Streszczenie W pracy
Analiza składowych głównych. Wprowadzenie
 Wprowadzenie jest techniką redukcji wymiaru. Składowe główne zostały po raz pierwszy zaproponowane przez Pearsona(1901), a następnie rozwinięte przez Hotellinga (1933). jest zaliczana do systemów uczących
Wprowadzenie jest techniką redukcji wymiaru. Składowe główne zostały po raz pierwszy zaproponowane przez Pearsona(1901), a następnie rozwinięte przez Hotellinga (1933). jest zaliczana do systemów uczących
PORÓWNANIE WYBRANYCH SCHEMATÓW RÓŻNICO- WYCH NA PRZYKŁADZIE RÓWNANIA SELECTED DIFFERENTIAL SCHEMES COMPARISON BY MEANS OF THE EQUATION
 Mirosław GUZIK Grzegorz KOSZŁKA PORÓWNANIE WYBRANYCH SCHEMATÓW RÓŻNICO- WYCH NA PRZYKŁADZIE RÓWNANIA SELECTED DIFFERENTIAL SCHEMES COMPARISON BY MEANS OF THE EQUATION W artykule przedstawiono niektóre
Mirosław GUZIK Grzegorz KOSZŁKA PORÓWNANIE WYBRANYCH SCHEMATÓW RÓŻNICO- WYCH NA PRZYKŁADZIE RÓWNANIA SELECTED DIFFERENTIAL SCHEMES COMPARISON BY MEANS OF THE EQUATION W artykule przedstawiono niektóre
Sterowanie napędów maszyn i robotów
 Wykład 5 - Identyfikacja Instytut Automatyki i Robotyki (IAiR), Politechnika Warszawska Warszawa, 2015 Koncepcje estymacji modelu Standardowe drogi poszukiwania modeli parametrycznych M1: Analityczne określenie
Wykład 5 - Identyfikacja Instytut Automatyki i Robotyki (IAiR), Politechnika Warszawska Warszawa, 2015 Koncepcje estymacji modelu Standardowe drogi poszukiwania modeli parametrycznych M1: Analityczne określenie
Wykład 4. Anna Ptaszek. 27 października Katedra Inżynierii i Aparatury Przemysłu Spożywczego. Chemia fizyczna - wykład 4. Anna Ptaszek 1 / 31
 Wykład 4 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 27 października 2015 1 / 31 Podstawy kinetyki chemicznej pochodna funkcji i jej interpretacja, pojęcie szybkości i prędkości, stechiometria
Wykład 4 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 27 października 2015 1 / 31 Podstawy kinetyki chemicznej pochodna funkcji i jej interpretacja, pojęcie szybkości i prędkości, stechiometria
Definicje. Najprostszy schemat blokowy. Schemat dokładniejszy
 Definicje owanie i symulacja owanie zastosowanie określonej metodologii do stworzenia i weryfikacji modelu dla danego rzeczywistego Symulacja zastosowanie symulatora, w którym zaimplementowano model, do
Definicje owanie i symulacja owanie zastosowanie określonej metodologii do stworzenia i weryfikacji modelu dla danego rzeczywistego Symulacja zastosowanie symulatora, w którym zaimplementowano model, do
KI + Pb(NO 3 ) 2 PbI 2 + KNO 3. fermentacja alkoholowa
 Kinetyka chemiczna KI + Pb(NO 3 ) 2 PbI 2 + KNO 3 fermentacja alkoholowa czynniki wpływaj ywające na szybkość reakcji chemicznych stęż ężenie reagentów w (lub ciśnienie gazów w jeżeli eli reakcja przebiega
Kinetyka chemiczna KI + Pb(NO 3 ) 2 PbI 2 + KNO 3 fermentacja alkoholowa czynniki wpływaj ywające na szybkość reakcji chemicznych stęż ężenie reagentów w (lub ciśnienie gazów w jeżeli eli reakcja przebiega
DIGITALIZACJA GEOMETRII WKŁADEK OSTRZOWYCH NA POTRZEBY SYMULACJI MES PROCESU OBRÓBKI SKRAWANIEM
 Dr inż. Witold HABRAT, e-mail: witekhab@prz.edu.pl Politechnika Rzeszowska, Wydział Budowy Maszyn i Lotnictwa Dr hab. inż. Piotr NIESŁONY, prof. PO, e-mail: p.nieslony@po.opole.pl Politechnika Opolska,
Dr inż. Witold HABRAT, e-mail: witekhab@prz.edu.pl Politechnika Rzeszowska, Wydział Budowy Maszyn i Lotnictwa Dr hab. inż. Piotr NIESŁONY, prof. PO, e-mail: p.nieslony@po.opole.pl Politechnika Opolska,
Ćwiczenie 1 Metody pomiarowe i opracowywanie danych doświadczalnych.
 Ćwiczenie 1 Metody pomiarowe i opracowywanie danych doświadczalnych. Ćwiczenie ma następujące części: 1 Pomiar rezystancji i sprawdzanie prawa Ohma, metoda najmniejszych kwadratów. 2 Pomiar średnicy pręta.
Ćwiczenie 1 Metody pomiarowe i opracowywanie danych doświadczalnych. Ćwiczenie ma następujące części: 1 Pomiar rezystancji i sprawdzanie prawa Ohma, metoda najmniejszych kwadratów. 2 Pomiar średnicy pręta.
KORELACJE I REGRESJA LINIOWA
 KORELACJE I REGRESJA LINIOWA Korelacje i regresja liniowa Analiza korelacji: Badanie, czy pomiędzy dwoma zmiennymi istnieje zależność Obie analizy się wzajemnie przeplatają Analiza regresji: Opisanie modelem
KORELACJE I REGRESJA LINIOWA Korelacje i regresja liniowa Analiza korelacji: Badanie, czy pomiędzy dwoma zmiennymi istnieje zależność Obie analizy się wzajemnie przeplatają Analiza regresji: Opisanie modelem
ZESZYTY NAUKOWE INSTYTUTU POJAZDÓW 1(97)/2014
 ZESZYTY NAUKOWE INSTYTUTU POJAZDÓW 1(97)/2014 Władysław Mitianiec 1 MODELOWANIE I SYMULACJA REDUKCJI NO X W SELEKTYWNYM REAKTORZE KATALITYCZNYM l. Wstęp Jednymi z najbardziej szkodliwych składników spalin
ZESZYTY NAUKOWE INSTYTUTU POJAZDÓW 1(97)/2014 Władysław Mitianiec 1 MODELOWANIE I SYMULACJA REDUKCJI NO X W SELEKTYWNYM REAKTORZE KATALITYCZNYM l. Wstęp Jednymi z najbardziej szkodliwych składników spalin
Ćwiczenie IX KATALITYCZNY ROZKŁAD WODY UTLENIONEJ
 Wprowadzenie Ćwiczenie IX KATALITYCZNY ROZKŁAD WODY UTLENIONEJ opracowanie: Barbara Stypuła Celem ćwiczenia jest poznanie roli katalizatora w procesach chemicznych oraz prostego sposobu wyznaczenia wpływu
Wprowadzenie Ćwiczenie IX KATALITYCZNY ROZKŁAD WODY UTLENIONEJ opracowanie: Barbara Stypuła Celem ćwiczenia jest poznanie roli katalizatora w procesach chemicznych oraz prostego sposobu wyznaczenia wpływu
Inżynieria procesów przetwórstwa węgla, zima 15/16
 Inżynieria procesów przetwórstwa węgla, zima 15/16 Ćwiczenia 1 7.10.2015 1. Załóżmy, że balon ma kształt sfery o promieniu 3m. a. Jaka ilość wodoru potrzebna jest do jego wypełnienia, aby na poziomie morza
Inżynieria procesów przetwórstwa węgla, zima 15/16 Ćwiczenia 1 7.10.2015 1. Załóżmy, że balon ma kształt sfery o promieniu 3m. a. Jaka ilość wodoru potrzebna jest do jego wypełnienia, aby na poziomie morza
Ćw. nr 1. Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła prostego
 2019/02/14 13:21 1/5 Ćw. nr 1. Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła prostego Ćw. nr 1. Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła prostego 1. Cel ćwiczenia Wyznaczenie przyspieszenia
2019/02/14 13:21 1/5 Ćw. nr 1. Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła prostego Ćw. nr 1. Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła prostego 1. Cel ćwiczenia Wyznaczenie przyspieszenia
WYKŁAD 8 ANALIZA REGRESJI
 WYKŁAD 8 ANALIZA REGRESJI Regresja 1. Metoda najmniejszych kwadratów-regresja prostoliniowa 2. Regresja krzywoliniowa 3. Estymacja liniowej funkcji regresji 4. Testy istotności współczynnika regresji liniowej
WYKŁAD 8 ANALIZA REGRESJI Regresja 1. Metoda najmniejszych kwadratów-regresja prostoliniowa 2. Regresja krzywoliniowa 3. Estymacja liniowej funkcji regresji 4. Testy istotności współczynnika regresji liniowej
Najprostszy schemat blokowy
 Definicje Modelowanie i symulacja Modelowanie zastosowanie określonej metodologii do stworzenia i weryfikacji modelu dla danego układu rzeczywistego Symulacja zastosowanie symulatora, w którym zaimplementowano
Definicje Modelowanie i symulacja Modelowanie zastosowanie określonej metodologii do stworzenia i weryfikacji modelu dla danego układu rzeczywistego Symulacja zastosowanie symulatora, w którym zaimplementowano
Materiałowe i technologiczne uwarunkowania stanu naprężeń własnych i anizotropii wtórnej powłok cylindrycznych wytłaczanych z polietylenu
 POLITECHNIKA ŚLĄSKA ZESZYTY NAUKOWE NR 1676 SUB Gottingen 7 217 872 077 Andrzej PUSZ 2005 A 12174 Materiałowe i technologiczne uwarunkowania stanu naprężeń własnych i anizotropii wtórnej powłok cylindrycznych
POLITECHNIKA ŚLĄSKA ZESZYTY NAUKOWE NR 1676 SUB Gottingen 7 217 872 077 Andrzej PUSZ 2005 A 12174 Materiałowe i technologiczne uwarunkowania stanu naprężeń własnych i anizotropii wtórnej powłok cylindrycznych
Wstęp do teorii niepewności pomiaru. Danuta J. Michczyńska Adam Michczyński
 Wstęp do teorii niepewności pomiaru Danuta J. Michczyńska Adam Michczyński Podstawowe informacje: Strona Politechniki Śląskiej: www.polsl.pl Instytut Fizyki / strona własna Instytutu / Dydaktyka / I Pracownia
Wstęp do teorii niepewności pomiaru Danuta J. Michczyńska Adam Michczyński Podstawowe informacje: Strona Politechniki Śląskiej: www.polsl.pl Instytut Fizyki / strona własna Instytutu / Dydaktyka / I Pracownia
METODA MACIERZOWA OBLICZANIA OBWODÓW PRĄDU PRZEMIENNEGO
 POZNAN UNIVERSITY OF TECHNOLOGY ACADEMIC JOURNALS No 93 Electrical Engineering 2018 DOI 10.21008/j.1897-0737.2018.93.0026 Piotr FRĄCZAK METODA MACIERZOWA OBLICZANIA OBWODÓW PRĄDU PRZEMIENNEGO W pracy przedstawiono
POZNAN UNIVERSITY OF TECHNOLOGY ACADEMIC JOURNALS No 93 Electrical Engineering 2018 DOI 10.21008/j.1897-0737.2018.93.0026 Piotr FRĄCZAK METODA MACIERZOWA OBLICZANIA OBWODÓW PRĄDU PRZEMIENNEGO W pracy przedstawiono
Edward Sawiłow Analiza dokładności określenia jednostkowej wartości nieruchomości metodą korygowania ceny średniej
 Edward Sawiłow Analiza dokładności określenia jednostkowej wartości nieruchomości metodą korygowania ceny średniej Acta Scientiarum Polonorum. Administratio Locorum 5/1/2, 63-71 2006 .J jm rot ł? J2 %
Edward Sawiłow Analiza dokładności określenia jednostkowej wartości nieruchomości metodą korygowania ceny średniej Acta Scientiarum Polonorum. Administratio Locorum 5/1/2, 63-71 2006 .J jm rot ł? J2 %
ANALIZA OBCIĄŻEŃ JEDNOSTEK NAPĘDOWYCH DLA PRZESTRZENNYCH RUCHÓW AGROROBOTA
 Inżynieria Rolnicza 7(105)/2008 ANALIZA OBCIĄŻEŃ JEDNOSTEK NAPĘDOWYCH DLA PRZESTRZENNYCH RUCHÓW AGROROBOTA Katedra Podstaw Techniki, Uniwersytet Przyrodniczy w Lublinie Streszczenie. W pracy przedstawiono
Inżynieria Rolnicza 7(105)/2008 ANALIZA OBCIĄŻEŃ JEDNOSTEK NAPĘDOWYCH DLA PRZESTRZENNYCH RUCHÓW AGROROBOTA Katedra Podstaw Techniki, Uniwersytet Przyrodniczy w Lublinie Streszczenie. W pracy przedstawiono
METODY CHEMOMETRYCZNE W IDENTYFIKACJI ŹRÓDEŁ POCHODZENIA
 METODY CHEMOMETRYCZNE W IDENTYFIKACJI ŹRÓDEŁ POCHODZENIA AMFETAMINY Waldemar S. Krawczyk Centralne Laboratorium Kryminalistyczne Komendy Głównej Policji, Warszawa (praca obroniona na Wydziale Chemii Uniwersytetu
METODY CHEMOMETRYCZNE W IDENTYFIKACJI ŹRÓDEŁ POCHODZENIA AMFETAMINY Waldemar S. Krawczyk Centralne Laboratorium Kryminalistyczne Komendy Głównej Policji, Warszawa (praca obroniona na Wydziale Chemii Uniwersytetu
KI + Pb(NO 3 ) 2 PbI 2 + KNO 3. fermentacja alkoholowa
 Kinetyka chemiczna KI + Pb(NO 3 ) 2 PbI 2 + KNO 3 fermentacja alkoholowa czynniki wpływaj ywające na szybkość reakcji chemicznych stęż ężenie reagentów w (lub ciśnienie gazów w jeżeli eli reakcja przebiega
Kinetyka chemiczna KI + Pb(NO 3 ) 2 PbI 2 + KNO 3 fermentacja alkoholowa czynniki wpływaj ywające na szybkość reakcji chemicznych stęż ężenie reagentów w (lub ciśnienie gazów w jeżeli eli reakcja przebiega
PRACA DYPLOMOWA Magisterska
 POLITECHNIKA WARSZAWSKA Wydział Samochodów i Maszyn Roboczych PRACA DYPLOMOWA Magisterska Studia stacjonarne dzienne Semiaktywne tłumienie drgań w wymuszonych kinematycznie układach drgających z uwzględnieniem
POLITECHNIKA WARSZAWSKA Wydział Samochodów i Maszyn Roboczych PRACA DYPLOMOWA Magisterska Studia stacjonarne dzienne Semiaktywne tłumienie drgań w wymuszonych kinematycznie układach drgających z uwzględnieniem
WYBÓR PUNKTÓW POMIAROWYCH
 Scientific Bulletin of Che lm Section of Technical Sciences No. 1/2008 WYBÓR PUNKTÓW POMIAROWYCH WE WSPÓŁRZĘDNOŚCIOWEJ TECHNICE POMIAROWEJ MAREK MAGDZIAK Katedra Technik Wytwarzania i Automatyzacji, Politechnika
Scientific Bulletin of Che lm Section of Technical Sciences No. 1/2008 WYBÓR PUNKTÓW POMIAROWYCH WE WSPÓŁRZĘDNOŚCIOWEJ TECHNICE POMIAROWEJ MAREK MAGDZIAK Katedra Technik Wytwarzania i Automatyzacji, Politechnika
Podstawowe prawa opisujące właściwości gazów zostały wyprowadzone dla gazu modelowego, nazywanego gazem doskonałym (idealnym).
 Spis treści 1 Stan gazowy 2 Gaz doskonały 21 Definicja mikroskopowa 22 Definicja makroskopowa (termodynamiczna) 3 Prawa gazowe 31 Prawo Boyle a-mariotte a 32 Prawo Gay-Lussaca 33 Prawo Charlesa 34 Prawo
Spis treści 1 Stan gazowy 2 Gaz doskonały 21 Definicja mikroskopowa 22 Definicja makroskopowa (termodynamiczna) 3 Prawa gazowe 31 Prawo Boyle a-mariotte a 32 Prawo Gay-Lussaca 33 Prawo Charlesa 34 Prawo
O 2 O 1. Temat: Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego
 msg M 7-1 - Temat: Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego Zagadnienia: prawa dynamiki Newtona, moment sił, moment bezwładności, dynamiczne równania ruchu wahadła fizycznego,
msg M 7-1 - Temat: Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego Zagadnienia: prawa dynamiki Newtona, moment sił, moment bezwładności, dynamiczne równania ruchu wahadła fizycznego,
WPŁYW GĘSTOŚCI SUROWCA NA BILANSOWANIE PRODUKTÓW KLASYFIKACJI HYDRAULICZNEJ W HYDROCYKLONACH W OPARCIU O WYNIKI LASEROWYCH ANALIZ UZIARNIENIA**
 Górnictwo i Geoinżynieria Rok 34 Zeszyt 4/1 2010 Damian Krawczykowski*, Aldona Krawczykowska* WPŁYW GĘSTOŚCI SUROWCA NA BILANSOWANIE PRODUKTÓW KLASYFIKACJI HYDRAULICZNEJ W HYDROCYKLONACH W OPARCIU O WYNIKI
Górnictwo i Geoinżynieria Rok 34 Zeszyt 4/1 2010 Damian Krawczykowski*, Aldona Krawczykowska* WPŁYW GĘSTOŚCI SUROWCA NA BILANSOWANIE PRODUKTÓW KLASYFIKACJI HYDRAULICZNEJ W HYDROCYKLONACH W OPARCIU O WYNIKI
ZASTOSOWANIE METOD NUMERYCZNEGO ODWRÓCENIA PRZEKSZTAŁCENIA LAPLACE A W MODELOWANIU MATEMATYCZNYM WYBRANYCH PROCESÓW INŻYNIERII CHEMICZNEJ
 Technical Issues 3/05 pp. 56-6 ISS 39-395 ZASTOSOWAIE METOD UMERYCZEGO ODWRÓCEIA PRZEKSZTAŁCEIA LAPLACE A W MODELOWAIU MATEMATYCZYM WYBRAYCH PROCESÓW IŻYIERII CHEMICZEJ APPLICATIO OF UMERICAL LAPLACE IVERSIO
Technical Issues 3/05 pp. 56-6 ISS 39-395 ZASTOSOWAIE METOD UMERYCZEGO ODWRÓCEIA PRZEKSZTAŁCEIA LAPLACE A W MODELOWAIU MATEMATYCZYM WYBRAYCH PROCESÓW IŻYIERII CHEMICZEJ APPLICATIO OF UMERICAL LAPLACE IVERSIO
Zadanie 2. (1 pkt) Uzupełnij tabelę, wpisując wzory sumaryczne tlenków w odpowiednie kolumny. CrO CO 2 Fe 2 O 3 BaO SO 3 NO Cu 2 O
 Test maturalny Chemia ogólna i nieorganiczna Zadanie 1. (1 pkt) Uzupełnij zdania. Pierwiastek chemiczny o liczbie atomowej 16 znajduje się w.... grupie i. okresie układu okresowego pierwiastków chemicznych,
Test maturalny Chemia ogólna i nieorganiczna Zadanie 1. (1 pkt) Uzupełnij zdania. Pierwiastek chemiczny o liczbie atomowej 16 znajduje się w.... grupie i. okresie układu okresowego pierwiastków chemicznych,
ANALiZA WPŁYWU PARAMETRÓW SAMOLOTU NA POZiOM HAŁASU MiERZONEGO WEDŁUG PRZEPiSÓW FAR 36 APPENDiX G
 PRACE instytutu LOTNiCTWA 221, s. 115 120, Warszawa 2011 ANALiZA WPŁYWU PARAMETRÓW SAMOLOTU NA POZiOM HAŁASU MiERZONEGO WEDŁUG PRZEPiSÓW FAR 36 APPENDiX G i ROZDZiAŁU 10 ZAŁOżEń16 KONWENCJi icao PIotr
PRACE instytutu LOTNiCTWA 221, s. 115 120, Warszawa 2011 ANALiZA WPŁYWU PARAMETRÓW SAMOLOTU NA POZiOM HAŁASU MiERZONEGO WEDŁUG PRZEPiSÓW FAR 36 APPENDiX G i ROZDZiAŁU 10 ZAŁOżEń16 KONWENCJi icao PIotr
3. Równania konstytutywne
 3. Równania konstytutywne 3.1. Strumienie w zjawiskach transportowych Podczas poprzednich zajęć wprowadziliśmy pojęcie strumienia masy J. W większości zjawisk transportowych występuje analogiczna wielkość
3. Równania konstytutywne 3.1. Strumienie w zjawiskach transportowych Podczas poprzednich zajęć wprowadziliśmy pojęcie strumienia masy J. W większości zjawisk transportowych występuje analogiczna wielkość
Zadanie ChemCad - Batch Reaktor
 Zadanie ChemCad - Batch Reaktor Opracowanie: dr inŝ. E.Wolak Treść zadania: Octan sodu powstaje w wyniku reakcji: NaOH + C2 H5COOCH3 C2H5OH + CH3COONa Wodorotlenek sodu i octan etylu zasilają reaktor okresowy
Zadanie ChemCad - Batch Reaktor Opracowanie: dr inŝ. E.Wolak Treść zadania: Octan sodu powstaje w wyniku reakcji: NaOH + C2 H5COOCH3 C2H5OH + CH3COONa Wodorotlenek sodu i octan etylu zasilają reaktor okresowy
Programowanie celowe #1
 Programowanie celowe #1 Problem programowania celowego (PC) jest przykładem problemu programowania matematycznego nieliniowego, który można skutecznie zlinearyzować, tzn. zapisać (i rozwiązać) jako problem
Programowanie celowe #1 Problem programowania celowego (PC) jest przykładem problemu programowania matematycznego nieliniowego, który można skutecznie zlinearyzować, tzn. zapisać (i rozwiązać) jako problem
PROFIL PRĘDKOŚCI W RURZE PROSTOLINIOWEJ
 LABORATORIUM MECHANIKI PŁYNÓW Ćwiczenie N 7 PROFIL PRĘDKOŚCI W RURZE PROSTOLINIOWEJ . Cel ćwiczenia Doświadczalne i teoretyczne wyznaczenie profilu prędkości w rurze prostoosiowej 2. Podstawy teoretyczne:
LABORATORIUM MECHANIKI PŁYNÓW Ćwiczenie N 7 PROFIL PRĘDKOŚCI W RURZE PROSTOLINIOWEJ . Cel ćwiczenia Doświadczalne i teoretyczne wyznaczenie profilu prędkości w rurze prostoosiowej 2. Podstawy teoretyczne:
Komputerowa Analiza Danych Doświadczalnych
 Komputerowa Analiza Danych Doświadczalnych dr inż. Adam Kisiel kisiel@if.pw.edu.pl pokój 117b (12b) 1 Materiały do wykładu Transparencje do wykładów: http://www.if.pw.edu.pl/~kisiel/kadd/kadd.html Literatura
Komputerowa Analiza Danych Doświadczalnych dr inż. Adam Kisiel kisiel@if.pw.edu.pl pokój 117b (12b) 1 Materiały do wykładu Transparencje do wykładów: http://www.if.pw.edu.pl/~kisiel/kadd/kadd.html Literatura
Regulacja adaptacyjna w anemometrze stałotemperaturowym
 3 Prace Instytutu Mechaniki Górotworu PAN Tom 8, nr 1-4, (2006), s. 3-7 Instytut Mechaniki Górotworu PAN Regulacja adaptacyjna w anemometrze stałotemperaturowym PAWEŁ LIGĘZA Instytut Mechaniki Górotworu
3 Prace Instytutu Mechaniki Górotworu PAN Tom 8, nr 1-4, (2006), s. 3-7 Instytut Mechaniki Górotworu PAN Regulacja adaptacyjna w anemometrze stałotemperaturowym PAWEŁ LIGĘZA Instytut Mechaniki Górotworu
Analiza korelacyjna i regresyjna
 Podstawy Metrologii i Technik Eksperymentu Laboratorium Analiza korelacyjna i regresyjna Instrukcja do ćwiczenia nr 5 Zakład Miernictwa i Ochrony Atmosfery Wrocław, kwiecień 2014 Podstawy Metrologii i
Podstawy Metrologii i Technik Eksperymentu Laboratorium Analiza korelacyjna i regresyjna Instrukcja do ćwiczenia nr 5 Zakład Miernictwa i Ochrony Atmosfery Wrocław, kwiecień 2014 Podstawy Metrologii i
Materiały pomocnicze do laboratorium z przedmiotu Metody i Narzędzia Symulacji Komputerowej
 Materiały pomocnicze do laboratorium z przedmiotu Metody i Narzędzia Symulacji Komputerowej w Systemach Technicznych Symulacja prosta dyszy pomiarowej Bendemanna Opracował: dr inż. Andrzej J. Zmysłowski
Materiały pomocnicze do laboratorium z przedmiotu Metody i Narzędzia Symulacji Komputerowej w Systemach Technicznych Symulacja prosta dyszy pomiarowej Bendemanna Opracował: dr inż. Andrzej J. Zmysłowski
1. Zaproponuj doświadczenie pozwalające oszacować szybkość reakcji hydrolizy octanu etylu w środowisku obojętnym
 1. Zaproponuj doświadczenie pozwalające oszacować szybkość reakcji hydrolizy octanu etylu w środowisku obojętnym 2. W pewnej chwili szybkość powstawania produktu C w reakcji: 2A + B 4C wynosiła 6 [mol/dm
1. Zaproponuj doświadczenie pozwalające oszacować szybkość reakcji hydrolizy octanu etylu w środowisku obojętnym 2. W pewnej chwili szybkość powstawania produktu C w reakcji: 2A + B 4C wynosiła 6 [mol/dm
ANALIZA ROZKŁADU CIŚNIEŃ I PRĘDKOŚCI W PRZEWODZIE O ZMIENNYM PRZEKROJU
 Dr inż. Paweł PIETKIEWICZ Dr inż. Wojciech MIĄSKOWSKI Dr inż. Krzysztof NALEPA Piotr LESZCZYŃSKI Uniwersytet Warmińsko-Mazurski w Olsztynie DOI: 10.17814/mechanik.2015.7.283 ANALIZA ROZKŁADU CIŚNIEŃ I
Dr inż. Paweł PIETKIEWICZ Dr inż. Wojciech MIĄSKOWSKI Dr inż. Krzysztof NALEPA Piotr LESZCZYŃSKI Uniwersytet Warmińsko-Mazurski w Olsztynie DOI: 10.17814/mechanik.2015.7.283 ANALIZA ROZKŁADU CIŚNIEŃ I
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego. Temperaturowa charakterystyka termistora typu NTC
 Katedra Chemii Fizycznej Uniwersytetu Łódzkiego Temperaturowa charakterystyka termistora typu NTC ćwiczenie nr 37 Opracowanie ćwiczenia: dr J. Woźnicka, dr S. elica Zakres zagadnień obowiązujących do ćwiczenia
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego Temperaturowa charakterystyka termistora typu NTC ćwiczenie nr 37 Opracowanie ćwiczenia: dr J. Woźnicka, dr S. elica Zakres zagadnień obowiązujących do ćwiczenia
SYMULACJA ZAKŁÓCEŃ W UKŁADACH AUTOMATYKI UTWORZONYCH ZA POMOCĄ OBWODÓW ELEKTRYCZNYCH W PROGRAMACH MATHCAD I PSPICE
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 76 Electrical Engineering 2013 Piotr FRĄCZAK* SYMULACJA ZAKŁÓCEŃ W UKŁADACH AUTOMATYKI UTWORZONYCH ZA POMOCĄ OBWODÓW ELEKTRYCZNYCH W PROGRAMACH MATHCAD
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 76 Electrical Engineering 2013 Piotr FRĄCZAK* SYMULACJA ZAKŁÓCEŃ W UKŁADACH AUTOMATYKI UTWORZONYCH ZA POMOCĄ OBWODÓW ELEKTRYCZNYCH W PROGRAMACH MATHCAD
WSKAZÓWKI DO WYKONANIA SPRAWOZDANIA Z WYRÓWNAWCZYCH ZAJĘĆ LABORATORYJNYCH
 WSKAZÓWKI DO WYKONANIA SPRAWOZDANIA Z WYRÓWNAWCZYCH ZAJĘĆ LABORATORYJNYCH Dobrze przygotowane sprawozdanie powinno zawierać następujące elementy: 1. Krótki wstęp - maksymalnie pół strony. W krótki i zwięzły
WSKAZÓWKI DO WYKONANIA SPRAWOZDANIA Z WYRÓWNAWCZYCH ZAJĘĆ LABORATORYJNYCH Dobrze przygotowane sprawozdanie powinno zawierać następujące elementy: 1. Krótki wstęp - maksymalnie pół strony. W krótki i zwięzły
REPREZENTACJA LICZBY, BŁĘDY, ALGORYTMY W OBLICZENIACH
 REPREZENTACJA LICZBY, BŁĘDY, ALGORYTMY W OBLICZENIACH Transport, studia I stopnia rok akademicki 2012/2013 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Pojęcie
REPREZENTACJA LICZBY, BŁĘDY, ALGORYTMY W OBLICZENIACH Transport, studia I stopnia rok akademicki 2012/2013 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Pojęcie
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania MODELOWANIE I IDENTYFIKACJA Studia niestacjonarne Estymacja parametrów modeli, metoda najmniejszych kwadratów.
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania MODELOWANIE I IDENTYFIKACJA Studia niestacjonarne Estymacja parametrów modeli, metoda najmniejszych kwadratów.
PRÓBA WERYFIKACJI WYNIKÓW SYMULACJI PROCESU WTRYSKIWANIA W WARUNKACH RZECZYWISTYCH
 DARIUSZ SYKUTERA * PRÓBA WERYFIKACJI WYNIKÓW SYMULACJI PROCESU WTRYSKIWANIA W WARUNKACH RZECZYWISTYCH THE ATTEMPTION OF THE VERYFICATION RESULTS OF THE INJECTION MOULDING SYMULATION IN REAL ENVIROMENT
DARIUSZ SYKUTERA * PRÓBA WERYFIKACJI WYNIKÓW SYMULACJI PROCESU WTRYSKIWANIA W WARUNKACH RZECZYWISTYCH THE ATTEMPTION OF THE VERYFICATION RESULTS OF THE INJECTION MOULDING SYMULATION IN REAL ENVIROMENT
BADANIA WYBRANYCH CZUJNIKÓW TEMPERATURY WSPÓŁPRACUJĄCYCH Z KARTAMI POMIAROWYMI W LabVIEW
 Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Nr 63 Politechniki Wrocławskiej Nr 63 Studia i Materiały Nr 29 2009 Krzysztof PODLEJSKI* czujniki temperatury, LabVIEW BADANIA WYBRANYCH
Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Nr 63 Politechniki Wrocławskiej Nr 63 Studia i Materiały Nr 29 2009 Krzysztof PODLEJSKI* czujniki temperatury, LabVIEW BADANIA WYBRANYCH
Dynamika procesu zmienna stała. programowalne zmiany parametrów r.
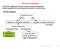 Sterowanie adaptacyjne Sterowanie adaptacyjne polega na dostosowywaniu (adaptacji) nastaw regulatora do zmian parametrów obiektu (w trakcie pracy) Techniki adaptacji Dynamika procesu zmienna stała regulator
Sterowanie adaptacyjne Sterowanie adaptacyjne polega na dostosowywaniu (adaptacji) nastaw regulatora do zmian parametrów obiektu (w trakcie pracy) Techniki adaptacji Dynamika procesu zmienna stała regulator
LABORATORIUM Z FIZYKI
 LABORATORIUM Z FIZYKI LABORATORIUM Z FIZYKI I PRACOWNIA FIZYCZNA C w Gliwicach Gliwice, ul. Konarskiego 22, pokoje 52-54 Regulamin pracowni i organizacja zajęć Sprawozdanie (strona tytułowa, karta pomiarowa)
LABORATORIUM Z FIZYKI LABORATORIUM Z FIZYKI I PRACOWNIA FIZYCZNA C w Gliwicach Gliwice, ul. Konarskiego 22, pokoje 52-54 Regulamin pracowni i organizacja zajęć Sprawozdanie (strona tytułowa, karta pomiarowa)
Niepewności pomiarów
 Niepewności pomiarów Międzynarodowa Organizacja Normalizacyjna (ISO) w roku 1995 opublikowała normy dotyczące terminologii i sposobu określania niepewności pomiarów [1]. W roku 1999 normy zostały opublikowane
Niepewności pomiarów Międzynarodowa Organizacja Normalizacyjna (ISO) w roku 1995 opublikowała normy dotyczące terminologii i sposobu określania niepewności pomiarów [1]. W roku 1999 normy zostały opublikowane
MODELOWANIE POŁĄCZEŃ TYPU SWORZEŃ OTWÓR ZA POMOCĄ MES BEZ UŻYCIA ANALIZY KONTAKTOWEJ
 Jarosław MAŃKOWSKI * Andrzej ŻABICKI * Piotr ŻACH * MODELOWANIE POŁĄCZEŃ TYPU SWORZEŃ OTWÓR ZA POMOCĄ MES BEZ UŻYCIA ANALIZY KONTAKTOWEJ 1. WSTĘP W analizach MES dużych konstrukcji wykonywanych na skalę
Jarosław MAŃKOWSKI * Andrzej ŻABICKI * Piotr ŻACH * MODELOWANIE POŁĄCZEŃ TYPU SWORZEŃ OTWÓR ZA POMOCĄ MES BEZ UŻYCIA ANALIZY KONTAKTOWEJ 1. WSTĘP W analizach MES dużych konstrukcji wykonywanych na skalę
Kinetyka. Kinetyka. Stawia dwa pytania: 1)Jak szybko biegną reakcje? 2) W jaki sposób przebiegają reakcje? energia swobodna, G. postęp reakcji.
 Kinetyka energia swobodna, G termodynamika stan 1 kinetyka termodynamika stan 2 postęp reakcji 1 Kinetyka Stawia dwa pytania: 1)Jak szybko biegną reakcje? 2) W jaki sposób przebiegają reakcje? 2 Jak szybko
Kinetyka energia swobodna, G termodynamika stan 1 kinetyka termodynamika stan 2 postęp reakcji 1 Kinetyka Stawia dwa pytania: 1)Jak szybko biegną reakcje? 2) W jaki sposób przebiegają reakcje? 2 Jak szybko
Analiza możliwości szacowania parametrów mieszanin rozkładów prawdopodobieństwa za pomocą sztucznych sieci neuronowych 4
 Wojciech Sikora 1 AGH w Krakowie Grzegorz Wiązania 2 AGH w Krakowie Maksymilian Smolnik 3 AGH w Krakowie Analiza możliwości szacowania parametrów mieszanin rozkładów prawdopodobieństwa za pomocą sztucznych
Wojciech Sikora 1 AGH w Krakowie Grzegorz Wiązania 2 AGH w Krakowie Maksymilian Smolnik 3 AGH w Krakowie Analiza możliwości szacowania parametrów mieszanin rozkładów prawdopodobieństwa za pomocą sztucznych
PARAMETRY EUTEKTYCZNOŚCI ŻELIWA CHROMOWEGO Z DODATKAMI STOPOWYMI Ni, Mo, V i B
 45/44 Solidification of Metals and Alloys, Year 2000, Volume 2, Book No. 44 Krzepnięcie Metali i Stopów, Rok 2000, Rocznik 2, Nr 44 PAN Katowice PL ISSN 0208-9386 PARAMETRY EUTEKTYCZNOŚCI ŻELIWA CHROMOWEGO
45/44 Solidification of Metals and Alloys, Year 2000, Volume 2, Book No. 44 Krzepnięcie Metali i Stopów, Rok 2000, Rocznik 2, Nr 44 PAN Katowice PL ISSN 0208-9386 PARAMETRY EUTEKTYCZNOŚCI ŻELIWA CHROMOWEGO
Badanie zależności temperatury wrzenia wody od ciśnienia
 Ćwiczenie C2 Badanie zależności temperatury wrzenia wody od ciśnienia C2.1. Cel ćwiczenia Celem ćwiczenia jest pomiar zależności temperatury wrzenia wody od ciśnienia (poniżej ciśnienia atmosferycznego),
Ćwiczenie C2 Badanie zależności temperatury wrzenia wody od ciśnienia C2.1. Cel ćwiczenia Celem ćwiczenia jest pomiar zależności temperatury wrzenia wody od ciśnienia (poniżej ciśnienia atmosferycznego),
Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności. dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl
 Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl Statystyczna teoria korelacji i regresji (1) Jest to dział statystyki zajmujący
Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl Statystyczna teoria korelacji i regresji (1) Jest to dział statystyki zajmujący
WSPÓŁCZYNNIK NIEPEWNOŚCI MODELU OBLICZENIOWEGO NOŚNOŚCI KONSTRUKCJI - PROPOZYCJA WYZNACZANIA
 PRACE INSTYTUTU TECHNIKI BUDOWLANEJ - KWARTALNIK nr 3 (131) 2004 BUILDING RESEARCH INSTITUTE - QUARTERLY No 3 (131) 2004 BADANIA l STUDIA - RESEARCH AND STUDIES Bohdan Lewicki* WSPÓŁCZYNNIK NIEPEWNOŚCI
PRACE INSTYTUTU TECHNIKI BUDOWLANEJ - KWARTALNIK nr 3 (131) 2004 BUILDING RESEARCH INSTITUTE - QUARTERLY No 3 (131) 2004 BADANIA l STUDIA - RESEARCH AND STUDIES Bohdan Lewicki* WSPÓŁCZYNNIK NIEPEWNOŚCI
MATEMATYCZNY MODEL PĘTLI HISTEREZY MAGNETYCZNEJ
 ELEKTRYKA 014 Zeszyt 1 (9) Rok LX Krzysztof SZTYMELSKI, Marian PASKO Politechnika Śląska w Gliwicach MATEMATYCZNY MODEL PĘTLI ISTEREZY MAGNETYCZNEJ Streszczenie. W artykule został zaprezentowany matematyczny
ELEKTRYKA 014 Zeszyt 1 (9) Rok LX Krzysztof SZTYMELSKI, Marian PASKO Politechnika Śląska w Gliwicach MATEMATYCZNY MODEL PĘTLI ISTEREZY MAGNETYCZNEJ Streszczenie. W artykule został zaprezentowany matematyczny
Jak poprawnie napisać sprawozdanie z ćwiczeń laboratoryjnych z fizyki?
 1 Jak poprawnie napisać sprawozdanie z ćwiczeń laboratoryjnych z fizyki? Sprawozdania należny oddać na kolejnych zajęciach laboratoryjnych. Każde opóźnienie powoduje obniżenie oceny za sprawozdanie o 0,
1 Jak poprawnie napisać sprawozdanie z ćwiczeń laboratoryjnych z fizyki? Sprawozdania należny oddać na kolejnych zajęciach laboratoryjnych. Każde opóźnienie powoduje obniżenie oceny za sprawozdanie o 0,
ROZWIĄZYWANIE UKŁADÓW RÓWNAŃ NIELINIOWYCH PRZY POMOCY DODATKU SOLVER PROGRAMU MICROSOFT EXCEL. sin x2 (1)
 ROZWIĄZYWANIE UKŁADÓW RÓWNAŃ NIELINIOWYCH PRZY POMOCY DODATKU SOLVER PROGRAMU MICROSOFT EXCEL 1. Problem Rozważmy układ dwóch równań z dwiema niewiadomymi (x 1, x 2 ): 1 x1 sin x2 x2 cos x1 (1) Nie jest
ROZWIĄZYWANIE UKŁADÓW RÓWNAŃ NIELINIOWYCH PRZY POMOCY DODATKU SOLVER PROGRAMU MICROSOFT EXCEL 1. Problem Rozważmy układ dwóch równań z dwiema niewiadomymi (x 1, x 2 ): 1 x1 sin x2 x2 cos x1 (1) Nie jest
Kinetyka. energia swobodna, G. postęp reakcji. stan 1 stan 2. kinetyka
 Kinetyka postęp reakcji energia swobodna, G termodynamika kinetyka termodynamika stan 1 stan 2 Kinetyka Stawia dwa pytania: 1) Jak szybko biegną reakcje? 2) W jaki sposób przebiegają reakcje? 1) Jak szybko
Kinetyka postęp reakcji energia swobodna, G termodynamika kinetyka termodynamika stan 1 stan 2 Kinetyka Stawia dwa pytania: 1) Jak szybko biegną reakcje? 2) W jaki sposób przebiegają reakcje? 1) Jak szybko
BADANIA SYMULACYJNE PROCESU HAMOWANIA SAMOCHODU OSOBOWEGO W PROGRAMIE PC-CRASH
 BADANIA SYMULACYJNE PROCESU HAMOWANIA SAMOCHODU OSOBOWEGO W PROGRAMIE PC-CRASH Dr inż. Artur JAWORSKI, Dr inż. Hubert KUSZEWSKI, Dr inż. Adam USTRZYCKI W artykule przedstawiono wyniki analizy symulacyjnej
BADANIA SYMULACYJNE PROCESU HAMOWANIA SAMOCHODU OSOBOWEGO W PROGRAMIE PC-CRASH Dr inż. Artur JAWORSKI, Dr inż. Hubert KUSZEWSKI, Dr inż. Adam USTRZYCKI W artykule przedstawiono wyniki analizy symulacyjnej
57 Zjazd PTChem i SITPChem Częstochowa, Promotowany miedzią niklowy katalizator do uwodornienia benzenu
 57 Zjazd PTChem i SITPChem Częstochowa, 14-18.09.2014 Promotowany miedzią niklowy katalizator do uwodornienia benzenu Kamila Michalska Kazimierz Stołecki Tadeusz Borowiecki Uwodornienie benzenu do cykloheksanu
57 Zjazd PTChem i SITPChem Częstochowa, 14-18.09.2014 Promotowany miedzią niklowy katalizator do uwodornienia benzenu Kamila Michalska Kazimierz Stołecki Tadeusz Borowiecki Uwodornienie benzenu do cykloheksanu
EFEKTY KSZTAŁCENIA DLA KIERUNKU STUDIÓW ENERGETYKA
 Załącznik do uchwały Nr 000-8/4/2012 Senatu PRad. z dnia 28.06.2012r. EFEKTY KSZTAŁCENIA DLA KIERUNKU STUDIÓW ENERGETYKA Nazwa wydziału: Mechaniczny Obszar kształcenia w zakresie: Nauk technicznych Dziedzina
Załącznik do uchwały Nr 000-8/4/2012 Senatu PRad. z dnia 28.06.2012r. EFEKTY KSZTAŁCENIA DLA KIERUNKU STUDIÓW ENERGETYKA Nazwa wydziału: Mechaniczny Obszar kształcenia w zakresie: Nauk technicznych Dziedzina
pętla nastrzykowa gaz nośny
 METODA POPRAWY PRECYZJI ANALIZ CHROMATOGRAFICZNYCH GAZÓW ZIEMNYCH POPRZEZ KONTROLOWANY SPOSÓB WPROWADZANIA PRÓBKI NA ANALIZATOR W WARUNKACH BAROSTATYCZNYCH Pracownia Pomiarów Fizykochemicznych (PFC), Centralne
METODA POPRAWY PRECYZJI ANALIZ CHROMATOGRAFICZNYCH GAZÓW ZIEMNYCH POPRZEZ KONTROLOWANY SPOSÓB WPROWADZANIA PRÓBKI NA ANALIZATOR W WARUNKACH BAROSTATYCZNYCH Pracownia Pomiarów Fizykochemicznych (PFC), Centralne
POD- I NADOKREŚLONE UKŁADY ALGEBRAICZNYCH RÓWNAŃ LINIOWYCH
 POD- I NADOKREŚLONE UKŁADY ALGEBRAICZNYCH RÓWNAŃ LINIOWYCH Transport, studia I stopnia rok akademicki 2011/2012 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko
POD- I NADOKREŚLONE UKŁADY ALGEBRAICZNYCH RÓWNAŃ LINIOWYCH Transport, studia I stopnia rok akademicki 2011/2012 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko
Algorytm hybrydowy dla alokacji portfela inwestycyjnego przy ograniczonych zasobach
 Adam Stawowy Algorytm hybrydowy dla alokacji portfela inwestycyjnego przy ograniczonych zasobach Summary: We present a meta-heuristic to combine Monte Carlo simulation with genetic algorithm for Capital
Adam Stawowy Algorytm hybrydowy dla alokacji portfela inwestycyjnego przy ograniczonych zasobach Summary: We present a meta-heuristic to combine Monte Carlo simulation with genetic algorithm for Capital
Wprowadzenie do rachunku niepewności pomiarowej. Jacek Pawlyta
 Wprowadzenie do rachunku niepewności pomiarowej Jacek Pawlyta Fizyka Teorie Obserwacje Doświadczenia Fizyka Teorie Przykłady Obserwacje Przykłady Doświadczenia Przykłady Fizyka Potwierdzanie bądź obalanie
Wprowadzenie do rachunku niepewności pomiarowej Jacek Pawlyta Fizyka Teorie Obserwacje Doświadczenia Fizyka Teorie Przykłady Obserwacje Przykłady Doświadczenia Przykłady Fizyka Potwierdzanie bądź obalanie
fermentacja alkoholowa erozja skał lata dni KI + Pb(NO 3 ) 2 PbI 2 + KNO 3 min Karkonosze Pielgrzymy (1204 m n.p.m.)
 Kinetyka chemiczna lata erozja skał Karkonosze Pielgrzymy (1204 m n.p.m.) fermentacja alkoholowa dni min KI + Pb(NO 3 ) 2 PbI 2 + KNO 3 s ms fs http://www2.warwick.ac.uk/fac/sci/chemistry/research/stavros/stavrosgroup/overview/
Kinetyka chemiczna lata erozja skał Karkonosze Pielgrzymy (1204 m n.p.m.) fermentacja alkoholowa dni min KI + Pb(NO 3 ) 2 PbI 2 + KNO 3 s ms fs http://www2.warwick.ac.uk/fac/sci/chemistry/research/stavros/stavrosgroup/overview/
dr inż. Łukasz Słupik, dr inż. Ludwik Kosyrczyk 1/28
 dr inż. Łukasz Słupik, dr inż. Ludwik Kosyrczyk 1/28 PLAN PREZENTACJI 1. Wstęp 2. Cele pracy 3. Struktura modelu 4. Eksperymenty i pomiary 5. Rezultaty wybranych symulacji 6. Wybrane zastosowania modelu:
dr inż. Łukasz Słupik, dr inż. Ludwik Kosyrczyk 1/28 PLAN PREZENTACJI 1. Wstęp 2. Cele pracy 3. Struktura modelu 4. Eksperymenty i pomiary 5. Rezultaty wybranych symulacji 6. Wybrane zastosowania modelu:
ZMIANA PARAMETRÓW TERMODYNAMICZNYCH POWIETRZA W PAROWNIKU CHŁODZIARKI GÓRNICZEJ Z CZYNNIKIEM R407C***
 Górnictwo i Geoinżynieria Rok 30 Zeszyt 1 2006 Krzysztof Filek*, Piotr Łuska**, Bernard Nowak* ZMIANA PARAMETRÓW TERMODYNAMICZNYCH POWIETRZA W PAROWNIKU CHŁODZIARKI GÓRNICZEJ Z CZYNNIKIEM R407C*** 1. Wstęp
Górnictwo i Geoinżynieria Rok 30 Zeszyt 1 2006 Krzysztof Filek*, Piotr Łuska**, Bernard Nowak* ZMIANA PARAMETRÓW TERMODYNAMICZNYCH POWIETRZA W PAROWNIKU CHŁODZIARKI GÓRNICZEJ Z CZYNNIKIEM R407C*** 1. Wstęp
Odwracalność przemiany chemicznej
 Odwracalność przemiany chemicznej Na ogół wszystkie reakcje chemiczne są odwracalne, tzn. z danych substratów tworzą się produkty, a jednocześnie produkty reakcji ulegają rozkładowi na substraty. Fakt
Odwracalność przemiany chemicznej Na ogół wszystkie reakcje chemiczne są odwracalne, tzn. z danych substratów tworzą się produkty, a jednocześnie produkty reakcji ulegają rozkładowi na substraty. Fakt
Zrównoleglona optymalizacja stochastyczna na dużych zbiorach danych
 Zrównoleglona optymalizacja stochastyczna na dużych zbiorach danych mgr inż. C. Dendek prof. nzw. dr hab. J. Mańdziuk Politechnika Warszawska, Wydział Matematyki i Nauk Informacyjnych Outline 1 Uczenie
Zrównoleglona optymalizacja stochastyczna na dużych zbiorach danych mgr inż. C. Dendek prof. nzw. dr hab. J. Mańdziuk Politechnika Warszawska, Wydział Matematyki i Nauk Informacyjnych Outline 1 Uczenie
4. EKSPLOATACJA UKŁADU NAPĘD ZWROTNICOWY ROZJAZD. DEFINICJA SIŁ W UKŁADZIE Siła nastawcza Siła trzymania
 3 SPIS TREŚCI Przedmowa... 11 1. WPROWADZENIE... 13 1.1. Budowa rozjazdów kolejowych... 14 1.2. Napędy zwrotnicowe... 15 1.2.1. Napęd zwrotnicowy EEA-4... 18 1.2.2. Napęd zwrotnicowy EEA-5... 20 1.3. Współpraca
3 SPIS TREŚCI Przedmowa... 11 1. WPROWADZENIE... 13 1.1. Budowa rozjazdów kolejowych... 14 1.2. Napędy zwrotnicowe... 15 1.2.1. Napęd zwrotnicowy EEA-4... 18 1.2.2. Napęd zwrotnicowy EEA-5... 20 1.3. Współpraca
Procedura szacowania niepewności
 DOKUMENTACJA SYSTEMU ZARZĄDZANIA LABORATORIUM Procedura szacowania niepewności Stron 7 Załączniki Nr 1 Nr Nr 3 Stron Symbol procedury PN//xyz Data Imię i Nazwisko Podpis Opracował Sprawdził Zatwierdził
DOKUMENTACJA SYSTEMU ZARZĄDZANIA LABORATORIUM Procedura szacowania niepewności Stron 7 Załączniki Nr 1 Nr Nr 3 Stron Symbol procedury PN//xyz Data Imię i Nazwisko Podpis Opracował Sprawdził Zatwierdził
DOKUMENTACJA SYSTEMU ZARZĄDZANIA LABORATORIUM. Procedura szacowania niepewności
 DOKUMENTACJA SYSTEMU ZARZĄDZANIA LABORATORIUM Procedura szacowania niepewności Szacowanie niepewności oznaczania / pomiaru zawartości... metodą... Data Imię i Nazwisko Podpis Opracował Sprawdził Zatwierdził
DOKUMENTACJA SYSTEMU ZARZĄDZANIA LABORATORIUM Procedura szacowania niepewności Szacowanie niepewności oznaczania / pomiaru zawartości... metodą... Data Imię i Nazwisko Podpis Opracował Sprawdził Zatwierdził
