Model Lee i Cartera a wysokość świadczeń dożywotnich wyniki dla Polski
|
|
|
- Agnieszka Zakrzewska
- 7 lat temu
- Przeglądów:
Transkrypt
1 Model Lee i Cartera a wysokość świadczeń dożywotnich wyniki dla Polski Jakub Bijak Środkowoeuropejskie Forum Badań Migracyjnych i Ludnościowych, Warszawa Barbara Więckowska Katedra Ubezpieczenia Społecznego Szkoła Główna Handlowa w Warszawie Praca powstała w ramach badania przeprowadzanego na zlecenie Polskiej Izby Ubezpieczeń (PIU), koordynowanego przez Prof. Tadeusza Szumlicza Ogólnopolska Konferencja Naukowa Zagadnienia Aktuarialne Teoria i praktyka Warszawa, 9 11 czerwca 2008 r.
2 Wprowadzenie Plan prezentacji Estymacja parametrów modelu Lee i Cartera Ilustracja: prognoza umieralności dla Polski do 2050 roku Błędy szacunku i prosta analiza wrażliwości wyników Ubezpieczeniowe implikacje wyników prognozy Podsumowanie i wnioski 2
3 Wprowadzenie Motywacja Do określenia wysokości świadczeń emerytalnych w systemie o zdefiniowanej składce wymagane jest określenie długości wypłat Problem Przekrojowe tablice trwania życia przeszacowują rzeczywistą umieralność poszczególnych kohort (grup urodzonych w tym samym roku) Cele pracy Przedstawienie metody prognozowania trwania życia w oparciu o zmodyfikowany model Lee i Cartera Ilustracja dla Polski - prognoza na lata Wybrane implikacje ubezpieczeniowe wyników 3
4 Model Zmodyfikowana wersja modelu Lee i Cartera: liczba zgonów - zmienna losowa o rozkładzie Poissona D ( x, t ) ~ Poisson ( E( x, t ) µ ( x, t )) ln µ ( x, t ) = a x + b x κ t κ + + = κ c ε t t 1 t Taki model dopuszcza heteroskedastyczność reszt między oszacowaną a zaobserwowaną liczbą zgonów Brouhns, N., M. Denuit, J. Vermunt (2002). A Poisson log-linear regression approach to the construction of projected life tables. Insurance: Math. Econ. 31 (3):
5 Model Metody estymacji: Lee i Carter zaproponowali metodę rozkładu wartości osobliwych (SVD), odpowiadającą KMNK Krytyka: metoda nieodpowiednia w przypadku heteroskedastycznych reszt Proponowane alternatywy: ważona MNK lub MNW Źródła niepewności prognozy z modelu L-C: 1. Losowa liczba zgonów D x (rozkład Poissona) 2. Niepewność oszacowań parametrów a x, b x i κ t 3. Ekstrapolacja komponentu κ t Alho, J. (2000). Discussion of Lee (2000). North American Actuarial Journal, 4 (1): Keilman, N., D.Q. Pham (2006), Prediction intervals for Lee-Carter-based mortality forecasts. Referat na European Population Conference 2006, Liverpool,
6 Estymacja współczynników Założenia (podejście kohortowe): Spełnione są równania bilansowe ludności (rysunek) Natężenie umieralności jest przedziałami stałe Migracje równomiernie rozłożone w ciągu roku Wiek x+1 x D (x, t) + I (x, t) P (x, t+1) Wiek ω x max P (x max, t) D (x max, t) +I (x max, t) P (x max, t+1) x 1 P (x 1, t) x max 1 P (x max 1, t) 1 B (t) P (0, t+1) D (0, t) 0 +I (0, t) t t t+1 Rok t t t+1 Rok P liczba ludności B urodzenia I saldo migracji D zgony 6
7 Ilustracja: prognoza dla Polski Dane wyjściowe (GUS) - jednoroczne grupy wieku, w latach osiągniętych - zgony według wieku i kohort (D), lata liczba ludności na początku roku (P), liczba urodzeń w ciągu roku (B), dane oczyszczone; próba ograniczona do Obliczenia Estymacja parametrów: MNW dla rozkładu Poissona Niepewność estymacji: metoda bootstrap (100 prób) x Niepewność ekstrapolacji κ t : Monte Carlo (1000 prób) Oprogramowanie: własny kod w R ( Procedura dość czasochłonna (55 h) 7
8 Ilustracja: prognoza dla Polski Obserwowane i prognozowane ln[µ(x,t)] dla obu płci Polska, (obserwacje do 2005 roku) 8
9 Ilustracja: prognoza dla Polski Wzorce ln[µ(x,t)] według wieku dla obu płci Polska, 1961, 1990, 2005 i 2050 (prognoza) 9
10 Przeciętne dalsze trwanie życia Przekrojowe e(0) dla obu płci, Polska, % przedziały predykcyjne dla różnych źródeł niepewności
11 Przeciętne dalsze trwanie życia Przekrojowe e(0) dla kobiet, Polska, % przedziały predykcyjne dla różnych źródeł niepewności
12 Przeciętne dalsze trwanie życia Przekrojowe e(0) dla mężczyzn, Polska, % przedziały predykcyjne dla różnych źródeł niepewności
13 Przeciętne dalsze trwanie życia Przekrojowe i kohortowe e(60) dla Polski , M + K 80% przedziały predykcyjne dla różnych źródeł niepewności
14 Przeciętne dalsze trwanie życia Przekrojowe i kohortowe e(60) dla Polski , kobiety 80% przedziały predykcyjne dla różnych źródeł niepewności
15 Przeciętne dalsze trwanie życia Przekrojowe i kohortowe e(60) dla Polski , mężczyźni 80% przedziały predykcyjne dla różnych źródeł niepewności
16 Przeciętne dalsze trwanie życia Przekrojowe i kohortowe e(65) dla Polski, 1990, 2005, 2015; 80% przedziały predykcyjne dla różnych źródeł niepewności Wariant 1990 Kobiety Mężczyźni Razem Wskaźniki przekrojowe, e p (65, t) 10% Średnia % Wskaźniki kohortowe, e c (65, t) 10% Średnia %
17 Błędy szacunku Reszty dla µ(x,t): przekrój przez lata kalendarzowe 17
18 Błędy szacunku Reszty dla µ(x,t): przekrój przez grupy wieku 18
19 Analiza wrażliwości wyników Przekrojowe e(0) dla obu płci, Polska : prognozy punktowe dla prób o różnej długości
20 Analiza wrażliwości wyników Przekrojowe e(0) dla obu płci, Polska : porównanie wyników estymacji MNW i SVD
21 Warunki brzegowe kapitał emerytalny zł, płeć kobieta, mężczyzna, bez rozróżniania okres gwarantowany brak <0,10> techniczna stopa zwrotu - 4% <0%, 5%>, wiek emerytalny - 60/65 <60, 70>, narzuty związane z działalnością zakładu ubezpieczeń (emerytalnego) - 7% wartości świadczenia miesięcznie zastosowano kohortowe tablice trwania życia 21
22 Wpływ czynników na wysokość świadczeń płeć ariant Kobiety Mężczyźni Razem 10% średnia 90% 10% średnia 90% 10% średnia 90% iek przejścia na emeryturę , , , , , , , , , , , , , , , , , ,5 Rozróżnianie płci: znaczne różnice pomiędzy świadczeniami mężczyzn i kobiet 18,3% (dla 60-latków) i 19,4% (dla 65-latków) Bez rozróżniania płci: mężczyźni tracą 11% (10,3% vs. 12,6%) kobiety zyskują 8% (8% vs. 9%) 22
23 Wpływ czynników na wysokość świadczeń wiek Wariant wiek przejścia na emeryturę Kobiety Razem 10% Średnia 90% 10% Średnia 90% , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,55 Rozróżniając płeć: przesunięcie decyzji emerytalnych o 1 rok (ceteris paribus) - zwiększenie świadczenia o 2,6% (2,57% vs. 2,77%) łącznie w ciągu 5 lat wzrost o 13,7% (13,5% vs. 14,7%) Bez rozróżniania płci: przyrost 2,64% (2,65% vs. 2,78%) rocznie łącznie w ciągu 5 lat wzrost o 13,9% (13,96% vs. 14,7%) 23
24 Wpływ czynników na wysokość świadczeń wiek Wariant wiek przejścia na emeryturę Mężczyźni Razem 10% Średnia 90% 10% Średnia 90% , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,01 Rozróżniając płeć: przesunięcie decyzji emerytalnych o 1 rok (ceteris paribus) - zwiększenie świadczenia o 3,5% (3,45% vs. 3,59%) łącznie w ciągu 5 lat wzrost o 18,48% (18,5% vs. 19,26%) Bez rozróżniania płci: przyrost 3,32% (3,30% vs. 3,41%) rocznie łącznie w ciągu 5 lat wzrost o 17,74% (17,60% vs. 18,25%) 24
25 Wpływ czynników na wysokość świadczeń wysokość zebranego kapitału analiza dotyczy zebranego kapitału w OFE wzrost funduszu płac 4% stopa zwrotu z OFE 7% okres składkowy 10 lat, 35 lat, 40 lat badana jest stopa zastąpienia w zależności od horyzontu inwestycyjnego Okres Kobiety Mężczyźni Razem składkowy 10 lat 35 lat 40 lat 10 lat 35 lat 40 lat 10 lat 35 lat 40 lat wiek przejścia na emeryturę 60 4,87% 25,59% 31,82% 5,96% 31,31% 38,93% 5,11% 26,87% 33,40% 65 5,54% 29,11% 36,18% 6,88% 36,13% 44,91% 5,71% 29,98% 37,27% analiza dynamiczna: kobieta przesuwając decyzję emerytalną o 5 lat zyskuje świadczenie wyższe o ponad 41% (7% średniorocznie) 25
26 Wpływ czynników na wysokość świadczeń okres gwarantowany Wariant długość okresu gwarantowanego Kobiety (60 lat) Mężczyźni (65 lat) 10% Średnia 90% 10% Średnia 90% , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,07 Kobiety: 10-letni okres gwarantowany kosztuje 1,90% (1,64% vs. 2,20% Mężczyźni: 10-letni okres gwarantowany kosztuje 9,0% (8,28% vs. 10,28% Bez rozróżniania płci: osoba w wieku 60 lat koszt 3,54% (3,25% vs. 4,01%) osoba w wieku 65 lat koszt 5,5% (5,20% vs. 6,46%) 26
27 Wpływ czynników na wysokość świadczeń techniczna stopa zwrotu Kobiety (60 lat) Mężczyźni (65 lat) Wariant 10% Średnia 90% 10% Średnia 90% techniczna stopa procentowa , , , , , , , , , , , , , , , , , , , , , , , ,02 Kobiety: wprowadzenie stopy na poziomie 3% wzrost o 49,6% (52,5% vs. 46,2%) podwyższanie stopy o 1 punkt wzrost o 11,75% (12,25% vs. 11,14%) Mężczyźni: wprowadzenie stopy na poziomie 3% wzrost o 33,3% (34,9% vs. 31,0%) podwyższanie stopy o 1 punkt wzrost świadczenia o 8,51% (8,84% vs. 8,03%) 27
28 Wpływ czynników na wysokość świadczeń Metodologia tworzenia tablic trwania życia Kobiety Mężczyźni Razem Wariant 10% Średnia 90% 10% Średnia 90% 10% Średnia 90% tablice kohortowe , , , , , , , , , , , , , , , , , ,55 tablice przekrojowe , , , , , , , , , , , , , , , , , ,74 rozróżniając płeć: największe różnice pomiędzy wysokościami świadczeń dochodzą nawet do 8% (kobiety dolne granice przedziałów) najmniejsze różnice pomiędzy wysokościami świadczeń to 3,69% (dla 65-letnich mężczyzn) bez rozróżniania płci: różnica w wysokości świadczeń ok.6% deficyt funduszu średnio na beneficjenta w wieku 60 lat 1,46 rocznych wypłat, w wieku 65 lat 1,2 rocznych wypłat 28
29 Podsumowanie i wnioski: metodologia Dwa podstawowe wnioski metodologiczne: 1. Prognozowanie natężenia umieralności w oparciu o odpowiednie dane pozwala obliczyć prawdziwe (kohortowe) dalsze trwanie życia 2. Zmodyfikowany model Lee i Cartera pozwala na formalną analizę różnych źródeł niepewności, co może pomóc ocenić antyselekcję ryzyka Optymistyczny akcent na zakończenie: Najprawdopodobniej będziemy żyć dłużej, niż wynika z prognozy przekrojowych wartości e(x) 29
30 Podsumowanie i wnioski: ubezpieczenia Wnioski ubezpieczeniowe 1. Zastosowanie tablic Unisex wpływa na istotne obniżenie wysokości świadczeń u mężczyzn, jednocześnie powoduje zmniejszenie kosztu okresu gwarantowanego 2. Ze względu na znaczną wrażliwość świadczeń na wysokość technicznej stopy zwrotu należałoby odrzucić możliwość wypłacania świadczeń w formule = kapitał/ przeciętne dalsze trwanie życia (wprowadzenie do analiz stopy procentowej na poziomie 3% wpływa na 50% zwiększenie świadczeń u kobiet) 3. Stosowanie tablic przekrojowych wiąże się z deficytem funduszu emerytalnego na poziomie średnio na beneficjenta w wieku 60 lat 1,46 rocznych wypłat, w wieku 65 lat 1,2 rocznych wypłat 30
31 Model Lee i Cartera a wysokość świadczeń dożywotnich wyniki dla Polski Dziękujemy za uwagę! 31
Wydłużanie wieku emerytalnego w kontekście poprawy wskaźników. Warszawa, 14.05.2012 Arkadiusz Filip
 Wydłużanie wieku emerytalnego w kontekście poprawy wskaźników umieralności w Polsce Warszawa, 14.05.2012 Arkadiusz Filip Plan 1. Wprowadzenie 2. Model Lee-Cartera metoda estymacji poprawy wskaźników umieralności
Wydłużanie wieku emerytalnego w kontekście poprawy wskaźników umieralności w Polsce Warszawa, 14.05.2012 Arkadiusz Filip Plan 1. Wprowadzenie 2. Model Lee-Cartera metoda estymacji poprawy wskaźników umieralności
Wpływ kohortowych tablic trwania życia y na wysokość świadczeń emerytalnych
 Wpływ kohorowych ablic rwania życia y na wysokość świadczeń emeryalnych Kaedra Ubezpieczenia Społecznego Szkoła Główna Handlowa w Warszawie Warszawa, 27 października 2010 r. Plan prezenacji Wprowadzenie
Wpływ kohorowych ablic rwania życia y na wysokość świadczeń emeryalnych Kaedra Ubezpieczenia Społecznego Szkoła Główna Handlowa w Warszawie Warszawa, 27 października 2010 r. Plan prezenacji Wprowadzenie
Stochastyczne modelowanie intensywności zgonów na przykładzie Polski
 Roczniki Kolegium Analiz Ekonomicznych Zeszyt 31/2013 Kamil Jodź Stochastyczne modelowanie intensywności zgonów na przykładzie Polski Streszczenie W artykule zostaną przedstawione różne sposoby stochastycznego
Roczniki Kolegium Analiz Ekonomicznych Zeszyt 31/2013 Kamil Jodź Stochastyczne modelowanie intensywności zgonów na przykładzie Polski Streszczenie W artykule zostaną przedstawione różne sposoby stochastycznego
Prognoza demograficzna dla gmin województwa dolnośląskiego do 2035 roku
 Prognoza demograficzna dla gmin województwa dolnośląskiego do 2035 roku Stanisława Górecka Robert Szmytkie Samorządowa Jednostka Organizacyjna Województwa Dolnośląskiego 1 UWAGI WSTĘPNE Prognoza została
Prognoza demograficzna dla gmin województwa dolnośląskiego do 2035 roku Stanisława Górecka Robert Szmytkie Samorządowa Jednostka Organizacyjna Województwa Dolnośląskiego 1 UWAGI WSTĘPNE Prognoza została
STOCHASTYCZNE MODELOWANIE UMIERALNOŚCI. Kamil Jodź. 1. Wstęp
 STOCHASTYCZNE MODELOWANIE UMIERALNOŚCI Kamil Jodź Uniwersytet Przyrodniczy we Wrocławiu ISSN 1644-6739 Streszczenie: W artykule została przedstawiona metodologia stochastycznego modelowania intensywności
STOCHASTYCZNE MODELOWANIE UMIERALNOŚCI Kamil Jodź Uniwersytet Przyrodniczy we Wrocławiu ISSN 1644-6739 Streszczenie: W artykule została przedstawiona metodologia stochastycznego modelowania intensywności
Ćwiczenia 2. Tablice trwania życia. (life tables)
 Ćwiczenia 2 Tablice trwania życia (life tables) Rodzaje tablic: kohortowa (wzdłużna), która obrazuje rzeczywisty proces wymierania wybranej generacji, przekrojowa, która przedstawia hipotetyczny proces
Ćwiczenia 2 Tablice trwania życia (life tables) Rodzaje tablic: kohortowa (wzdłużna), która obrazuje rzeczywisty proces wymierania wybranej generacji, przekrojowa, która przedstawia hipotetyczny proces
Prognoza demograficzna dla gmin województwa dolnośląskiego do 2035 roku
 Prognoza demograficzna dla gmin województwa dolnośląskiego do 2035 roku dr Stanisława Górecka dr Robert Szmytkie Uniwersytet Wrocławski Prognoza demograficzna to przewidywanie przyszłej liczby i struktury
Prognoza demograficzna dla gmin województwa dolnośląskiego do 2035 roku dr Stanisława Górecka dr Robert Szmytkie Uniwersytet Wrocławski Prognoza demograficzna to przewidywanie przyszłej liczby i struktury
MIĘDZY I WEWNĄTRZPOKOLENIOWA REDYSTRYBUCJA DOCHODOWA W POLSKIM SYSTEMIE EMERYTALNYM
 MIĘDZY I WEWNĄTRZPOKOLENIOWA REDYSTRYBUCJA DOCHODOWA W POLSKIM SYSTEMIE EMERYTALNYM III Międzynarodowa Konferencja Naukowa SYSTEMY ZABEZPIECZENIA SPOŁECZNEGO WOBEC WYZWAŃ DEMOGRAFICZNYCH Poznań, 16-17
MIĘDZY I WEWNĄTRZPOKOLENIOWA REDYSTRYBUCJA DOCHODOWA W POLSKIM SYSTEMIE EMERYTALNYM III Międzynarodowa Konferencja Naukowa SYSTEMY ZABEZPIECZENIA SPOŁECZNEGO WOBEC WYZWAŃ DEMOGRAFICZNYCH Poznań, 16-17
K wartość kapitału zaangażowanego w proces produkcji, w tys. jp.
 Sprawdzian 2. Zadanie 1. Za pomocą KMNK oszacowano następującą funkcję produkcji: Gdzie: P wartość produkcji, w tys. jp (jednostek pieniężnych) K wartość kapitału zaangażowanego w proces produkcji, w tys.
Sprawdzian 2. Zadanie 1. Za pomocą KMNK oszacowano następującą funkcję produkcji: Gdzie: P wartość produkcji, w tys. jp (jednostek pieniężnych) K wartość kapitału zaangażowanego w proces produkcji, w tys.
MODELOWANIE STRUKTURY PROBABILISTYCZNEJ UBEZPIECZEŃ ŻYCIOWYCH Z OPCJĄ ADBS JOANNA DĘBICKA 1, BEATA ZMYŚLONA 2
 JOANNA DĘBICKA 1, BEATA ZMYŚLONA 2 MODELOWANIE STRUKTURY PROBABILISTYCZNEJ UBEZPIECZEŃ ŻYCIOWYCH Z OPCJĄ ADBS X OGÓLNOPOLSKA KONFERENCJA AKTUARIALNA ZAGADNIENIA AKTUARIALNE TEORIA I PRAKTYKA WARSZAWA,
JOANNA DĘBICKA 1, BEATA ZMYŚLONA 2 MODELOWANIE STRUKTURY PROBABILISTYCZNEJ UBEZPIECZEŃ ŻYCIOWYCH Z OPCJĄ ADBS X OGÓLNOPOLSKA KONFERENCJA AKTUARIALNA ZAGADNIENIA AKTUARIALNE TEORIA I PRAKTYKA WARSZAWA,
Model generyczny prognozujący zapotrzebowanie na usługi edukacyjne w jednostkach samorządu terytorialnego. Warszawa-Poznań, 18 grudnia 2012
 Model generyczny prognozujący zapotrzebowanie na usługi edukacyjne w jednostkach samorządu terytorialnego Warszawa-Poznań, 18 grudnia 2012 Budowa modelu Agenda Wprowadzenie do problematyki modelowania
Model generyczny prognozujący zapotrzebowanie na usługi edukacyjne w jednostkach samorządu terytorialnego Warszawa-Poznań, 18 grudnia 2012 Budowa modelu Agenda Wprowadzenie do problematyki modelowania
Wpływ zmiany systemowej na wysokość świadczeń emerytalnych w Polsce
 Barbara Więckowska Katedra Ubezpieczenia Społecznego, Szkoła Główna Handlowa w Warszawie Jakub Bijak School of Social Sciences, University of Southampton Wpływ zmiany systemowej na wysokość świadczeń emerytalnych
Barbara Więckowska Katedra Ubezpieczenia Społecznego, Szkoła Główna Handlowa w Warszawie Jakub Bijak School of Social Sciences, University of Southampton Wpływ zmiany systemowej na wysokość świadczeń emerytalnych
Zakład Ubezpieczeń Społecznych 13 lipca 2018 r. Departament Statystyki i Prognoz Aktuarialnych
 Zakład Ubezpieczeń Społecznych 13 lipca 2018 r. Departament Statystyki i Prognoz Aktuarialnych Szacunkowe skutki finansowe podwyższenia do wysokości emerytury najniższej emerytur z Funduszu Ubezpieczeń
Zakład Ubezpieczeń Społecznych 13 lipca 2018 r. Departament Statystyki i Prognoz Aktuarialnych Szacunkowe skutki finansowe podwyższenia do wysokości emerytury najniższej emerytur z Funduszu Ubezpieczeń
Ewolucja rozwoju ludności Polski: przeszłość i perspektywy
 Rządowa Rada Ludnościowa Ewolucja rozwoju ludności Polski: przeszłość i perspektywy Zbigniew Strzelecki Janusz Witkowski Warszawa 1. 10. 2009 r. Od przyspieszonego rozwoju do ubytku liczby ludności spowolnienie
Rządowa Rada Ludnościowa Ewolucja rozwoju ludności Polski: przeszłość i perspektywy Zbigniew Strzelecki Janusz Witkowski Warszawa 1. 10. 2009 r. Od przyspieszonego rozwoju do ubytku liczby ludności spowolnienie
Wykład 8,
 Wykład 8, 13-05-2016 Metody prognozowania demograficznego. Metody prognozowania ludności (metoda składnikowa, modele wielostanowe, metody prognozowania stochastycznego). PRZEDMIOT PROGNOZOWANIA ludność,
Wykład 8, 13-05-2016 Metody prognozowania demograficznego. Metody prognozowania ludności (metoda składnikowa, modele wielostanowe, metody prognozowania stochastycznego). PRZEDMIOT PROGNOZOWANIA ludność,
Prognozy demograficzne
 Prognozy demograficzne Zadaniem prognoz demograficznych jest ustalenie przyszłego stanu i struktury ludności zarówno dla całego kraju jak i jego regionów. Jednostkami badania które dotyczą prognozy mogą
Prognozy demograficzne Zadaniem prognoz demograficznych jest ustalenie przyszłego stanu i struktury ludności zarówno dla całego kraju jak i jego regionów. Jednostkami badania które dotyczą prognozy mogą
SIGMA KWADRAT. Syntetyczne miary reprodukcji ludności. Statystyka i demografia CZWARTY LUBELSKI KONKURS STATYSTYCZNO-DEMOGRAFICZNY
 SIGMA KWADRAT CZWARTY LUBELSKI KONKURS STATYSTYCZNO-DEMOGRAFICZNY Syntetyczne miary reprodukcji ludności Statystyka i demografia PROJEKT DOFINANSOWANY ZE ŚRODKÓW NARODOWEGO BANKU POLSKIEGO URZĄD STATYSTYCZNY
SIGMA KWADRAT CZWARTY LUBELSKI KONKURS STATYSTYCZNO-DEMOGRAFICZNY Syntetyczne miary reprodukcji ludności Statystyka i demografia PROJEKT DOFINANSOWANY ZE ŚRODKÓW NARODOWEGO BANKU POLSKIEGO URZĄD STATYSTYCZNY
4. Ubezpieczenie Życiowe
 4. Ubezpieczenie Życiowe Składka ubezpieczeniowa musi brać pod uwagę następujące czynniki: 1. Kwotę wypłaconą przy śmierci ubezpieczonego oraz jej wartość aktualną. 2. Rozkład czasu do śmierci ubezpieczonego
4. Ubezpieczenie Życiowe Składka ubezpieczeniowa musi brać pod uwagę następujące czynniki: 1. Kwotę wypłaconą przy śmierci ubezpieczonego oraz jej wartość aktualną. 2. Rozkład czasu do śmierci ubezpieczonego
PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTALNEGO
 ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTALNEGO DO 2060 ROKU WARSZAWA, MAJ 2013 SPIS TREŚCI Spis treści...2 Wstęp...3 Najważniejsze
ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTALNEGO DO 2060 ROKU WARSZAWA, MAJ 2013 SPIS TREŚCI Spis treści...2 Wstęp...3 Najważniejsze
PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTALNEGO
 ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTALNEGO DO 2050 ROKU WARSZAWA, LISTOPAD 2003 SPIS TREŚCI Spis treści...2 Wstęp...3 Najważniejsze zmiany wprowadzone
ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTALNEGO DO 2050 ROKU WARSZAWA, LISTOPAD 2003 SPIS TREŚCI Spis treści...2 Wstęp...3 Najważniejsze zmiany wprowadzone
Ćwiczenia 3. Współczynnik przyrostu naturalnego. Koncepcja ludności zastojowej i ustabilizowanej. Prawo Lotki.
 Ćwiczenia 3 Współczynnik przyrostu naturalnego. Koncepcja ludności zastojowej i ustabilizowanej. Prawo Lotki. Współczynnik przyrostu naturalnego r = U t Z t L t gdzie: U t - urodzenia w roku t Z t - zgony
Ćwiczenia 3 Współczynnik przyrostu naturalnego. Koncepcja ludności zastojowej i ustabilizowanej. Prawo Lotki. Współczynnik przyrostu naturalnego r = U t Z t L t gdzie: U t - urodzenia w roku t Z t - zgony
Ćwiczenia 3. Współczynnik przyrostu naturalnego. Koncepcja ludności zastojowej i ustabilizowanej. Prawo Lotki.
 Ćwiczenia 3 Współczynnik przyrostu naturalnego. Koncepcja ludności zastojowej i ustabilizowanej. Prawo Lotki. Współczynnik przyrostu naturalnego gdzie: U t - urodzenia w roku t Z t - zgony w roku t L t
Ćwiczenia 3 Współczynnik przyrostu naturalnego. Koncepcja ludności zastojowej i ustabilizowanej. Prawo Lotki. Współczynnik przyrostu naturalnego gdzie: U t - urodzenia w roku t Z t - zgony w roku t L t
Polityka społeczna (9): Zabezpieczenie emerytalne II i III filar
 Polityka społeczna (9): Zabezpieczenie emerytalne II i III filar Literatura I. Jędrasik-Jankowska, Pojęcie i konstrukcje prawne ubezpieczenia społecznego, LexisNexis, Warszawa, 2007, s.266-275. 2 Składki
Polityka społeczna (9): Zabezpieczenie emerytalne II i III filar Literatura I. Jędrasik-Jankowska, Pojęcie i konstrukcje prawne ubezpieczenia społecznego, LexisNexis, Warszawa, 2007, s.266-275. 2 Składki
Ćwiczenia 3 ( ) Współczynnik przyrostu naturalnego. Koncepcja ludności zastojowej i ustabilizowanej. Prawo Lotki.
 Ćwiczenia 3 (16.05.2014) Współczynnik przyrostu naturalnego. Koncepcja ludności zastojowej i ustabilizowanej. Prawo Lotki. Współczynnik przyrostu naturalnego gdzie: U t - urodzenia w roku t Z t - zgony
Ćwiczenia 3 (16.05.2014) Współczynnik przyrostu naturalnego. Koncepcja ludności zastojowej i ustabilizowanej. Prawo Lotki. Współczynnik przyrostu naturalnego gdzie: U t - urodzenia w roku t Z t - zgony
Syntetyczne miary reprodukcji ludności
 Trzeci Lubelski Konkurs Statystyczno-Demograficzny z okazji Dnia Statystyki Polskiej Syntetyczne miary reprodukcji ludności Statystyka i Demografia Projekt dofinansowany ze środków Narodowego Banku Polskiego
Trzeci Lubelski Konkurs Statystyczno-Demograficzny z okazji Dnia Statystyki Polskiej Syntetyczne miary reprodukcji ludności Statystyka i Demografia Projekt dofinansowany ze środków Narodowego Banku Polskiego
U z a s a d n i e n i e
 U z a s a d n i e n i e Projekt nowelizacji ustawy z dnia 17 grudnia 1998 r. o emeryturach i rentach z Funduszu Ubezpieczeń Społecznych (Dz. U. z 2004 r. Nr 39, poz. 353, Nr 64, poz. 593, Nr 99, poz. 1001,
U z a s a d n i e n i e Projekt nowelizacji ustawy z dnia 17 grudnia 1998 r. o emeryturach i rentach z Funduszu Ubezpieczeń Społecznych (Dz. U. z 2004 r. Nr 39, poz. 353, Nr 64, poz. 593, Nr 99, poz. 1001,
Zmiany demograficzne w świetle wyników prognozy ludności Polski do 2050 r.
 Zmiany demograficzne w świetle wyników prognozy ludności Polski do 2050 r. "Wpływ zmian demograficznych na stan finansów publicznych Seminarium SGH Małgorzata Waligórska Główny Urząd Statystyczny Warszawa,
Zmiany demograficzne w świetle wyników prognozy ludności Polski do 2050 r. "Wpływ zmian demograficznych na stan finansów publicznych Seminarium SGH Małgorzata Waligórska Główny Urząd Statystyczny Warszawa,
Zakres badań demograficznych
 Zakres badań demograficznych wskaźnik rodności wskaźnik dzietności RUCH NATURALNY STAN I STRUKTURA LUDNOŚCI wskaźniki umieralności wskaźniki zgonów przeciętny dalszy czas trwania życia wskaźnik małżeństw
Zakres badań demograficznych wskaźnik rodności wskaźnik dzietności RUCH NATURALNY STAN I STRUKTURA LUDNOŚCI wskaźniki umieralności wskaźniki zgonów przeciętny dalszy czas trwania życia wskaźnik małżeństw
PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTUR POMOSTOWYCH
 ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTUR POMOSTOWYCH NA LATA 2015 2019 WARSZAWA, MAJ 2013 SPIS TREŚCI Spis treści...2
ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTUR POMOSTOWYCH NA LATA 2015 2019 WARSZAWA, MAJ 2013 SPIS TREŚCI Spis treści...2
Wyniki analizy statystycznej opartej na metodzie modelowania miękkiego
 Wyniki analizy statystycznej opartej na metodzie modelowania miękkiego Dorota Perło Uniwersytet w Białymstoku Wydział Ekonomii i Zarządzania Plan prezentacji. Założenia metodologiczne 2. Specyfikacja modelu
Wyniki analizy statystycznej opartej na metodzie modelowania miękkiego Dorota Perło Uniwersytet w Białymstoku Wydział Ekonomii i Zarządzania Plan prezentacji. Założenia metodologiczne 2. Specyfikacja modelu
PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTALNEGO
 ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTALNEGO DO 2060 ROKU WARSZAWA, MARZEC 2010 SPIS TREŚCI Spis treści...2 Wstęp...3 Najważniejsze zmiany w porównaniu
ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTALNEGO DO 2060 ROKU WARSZAWA, MARZEC 2010 SPIS TREŚCI Spis treści...2 Wstęp...3 Najważniejsze zmiany w porównaniu
Emerytury nowosystemowe wypłacone w grudniu 2018 r. w wysokości niższej niż wysokość najniższej emerytury (tj. niższej niż 1029,80 zł)
 Emerytury nowosystemowe wypłacone w grudniu 18 r. w wysokości niższej niż wysokość najniższej emerytury (tj. niższej niż 9,8 zł) DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH Warszawa 19 1 Zgodnie z art.
Emerytury nowosystemowe wypłacone w grudniu 18 r. w wysokości niższej niż wysokość najniższej emerytury (tj. niższej niż 9,8 zł) DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH Warszawa 19 1 Zgodnie z art.
PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTUR POMOSTOWYCH
 ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTUR POMOSTOWYCH NA LATA 2017 2021 WARSZAWA, GRUDZIEŃ 2015 SPIS TREŚCI Spis treści...2
ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTUR POMOSTOWYCH NA LATA 2017 2021 WARSZAWA, GRUDZIEŃ 2015 SPIS TREŚCI Spis treści...2
Perspektywy rozwoju demograficznego
 Perspektywy rozwoju demograficznego Czy liczba urodzeń w Polsce musi spadać? Seminarium otwarte organizowane przez GUS Lucyna Nowak Departament Badań Demograficznych Źródła informacji wykorzystywanych
Perspektywy rozwoju demograficznego Czy liczba urodzeń w Polsce musi spadać? Seminarium otwarte organizowane przez GUS Lucyna Nowak Departament Badań Demograficznych Źródła informacji wykorzystywanych
Spis treści. Przedmowa... XI. Rozdział 1. Pomiar: jednostki miar... 1. Rozdział 2. Pomiar: liczby i obliczenia liczbowe... 16
 Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Zadanie 1. a) Przeprowadzono test RESET. Czy model ma poprawną formę funkcyjną? 1
 Zadanie 1 a) Przeprowadzono test RESET. Czy model ma poprawną formę funkcyjną? 1 b) W naszym przypadku populacja są inżynierowie w Tajlandii. Czy można jednak przypuszczać, że na zarobki kobiet-inżynierów
Zadanie 1 a) Przeprowadzono test RESET. Czy model ma poprawną formę funkcyjną? 1 b) W naszym przypadku populacja są inżynierowie w Tajlandii. Czy można jednak przypuszczać, że na zarobki kobiet-inżynierów
Ćwiczenia 2. Tablice trwania życia. (life tables)
 Ćwiczenia 2 Tablice trwania życia (life tables) 1. Historia 2. Zasady budowy przekrojowych tablic trwania życia 3. Parametr e(0): zróżnicowanie według płci, zmiany w czasie e(0) w Polsce 4. Przykłady alternatywnych
Ćwiczenia 2 Tablice trwania życia (life tables) 1. Historia 2. Zasady budowy przekrojowych tablic trwania życia 3. Parametr e(0): zróżnicowanie według płci, zmiany w czasie e(0) w Polsce 4. Przykłady alternatywnych
Zastosowanie modelu regresji logistycznej w ocenie ryzyka ubezpieczeniowego. Łukasz Kończyk WMS AGH
 Zastosowanie modelu regresji logistycznej w ocenie ryzyka ubezpieczeniowego Łukasz Kończyk WMS AGH Plan prezentacji Model regresji liniowej Uogólniony model liniowy (GLM) Ryzyko ubezpieczeniowe Przykład
Zastosowanie modelu regresji logistycznej w ocenie ryzyka ubezpieczeniowego Łukasz Kończyk WMS AGH Plan prezentacji Model regresji liniowej Uogólniony model liniowy (GLM) Ryzyko ubezpieczeniowe Przykład
Prognozy demograficzne
 Trzeci Lubelski Konkurs Statystyczno-Demograficzny z okazji Dnia Statystyki Polskiej Prognozy demograficzne Demografia Projekt dofinansowany ze środków Narodowego Banku Polskiego Urząd Statystyczny w Lublinie
Trzeci Lubelski Konkurs Statystyczno-Demograficzny z okazji Dnia Statystyki Polskiej Prognozy demograficzne Demografia Projekt dofinansowany ze środków Narodowego Banku Polskiego Urząd Statystyczny w Lublinie
PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTUR POMOSTOWYCH
 ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTUR POMOSTOWYCH NA LATA 2018 2022 WARSZAWA, MARZEC 2017 SPIS TREŚCI Spis treści...2
ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTUR POMOSTOWYCH NA LATA 2018 2022 WARSZAWA, MARZEC 2017 SPIS TREŚCI Spis treści...2
Zakład Ubezpieczeń Społecznych Departament Statystyki i Prognoz Aktuarialnych
 Zakład Ubezpieczeń Społecznych Departament Statystyki i Prognoz Aktuarialnych Struktura wysokości emerytur i rent wypłacanych przez ZUS po waloryzacji w marcu 2015 roku. Warszawa 2015 Opracowała: Ewa Karczewicz
Zakład Ubezpieczeń Społecznych Departament Statystyki i Prognoz Aktuarialnych Struktura wysokości emerytur i rent wypłacanych przez ZUS po waloryzacji w marcu 2015 roku. Warszawa 2015 Opracowała: Ewa Karczewicz
4. Ubezpieczenie Życiowe
 4. Ubezpieczenie Życiowe Składka ubezpieczeniowa musi brać pod uwagę następujące czynniki: 1. Kwotę wypłaconą przy śmierci ubezpieczonego oraz jej wartość aktualną. 2. Rozkład czasu do śmierci ubezpieczonego
4. Ubezpieczenie Życiowe Składka ubezpieczeniowa musi brać pod uwagę następujące czynniki: 1. Kwotę wypłaconą przy śmierci ubezpieczonego oraz jej wartość aktualną. 2. Rozkład czasu do śmierci ubezpieczonego
Badanie ewolucji tablic trwania życia: Modyfikacje modelu Lee-Cartera Wojciech Otto Wydział Nauk Ekonomicznych Uniwersytetu Warszawskiego
 Badanie ewolucji tablic trwania życia: Modyfikacje modelu Lee-Cartera Wojciech Otto Wydział Nauk Ekonomicznych Uniwersytetu Warszawskiego!! Konferencja Studenckiego Koła Naukowego Finansów i ubezpieczeń
Badanie ewolucji tablic trwania życia: Modyfikacje modelu Lee-Cartera Wojciech Otto Wydział Nauk Ekonomicznych Uniwersytetu Warszawskiego!! Konferencja Studenckiego Koła Naukowego Finansów i ubezpieczeń
SIGMA KWADRAT. Prognozy demograficzne. Statystyka i demografia CZWARTY LUBELSKI KONKURS STATYSTYCZNO-DEMOGRAFICZNY POLSKIE TOWARZYSTWO STATYSTYCZNE
 SIGMA KWADRAT CZWARTY LUBELSKI KONKURS STATYSTYCZNO-DEMOGRAFICZNY Prognozy demograficzne Statystyka i demografia PROJEKT DOFINANSOWANY ZE ŚRODKÓW NARODOWEGO BANKU POLSKIEGO URZĄD STATYSTYCZNY W LUBLINIE
SIGMA KWADRAT CZWARTY LUBELSKI KONKURS STATYSTYCZNO-DEMOGRAFICZNY Prognozy demograficzne Statystyka i demografia PROJEKT DOFINANSOWANY ZE ŚRODKÓW NARODOWEGO BANKU POLSKIEGO URZĄD STATYSTYCZNY W LUBLINIE
PROGNOZA DEMOGRAFICZNA NA LATA DLA WOJEWÓDZTWA WARMIŃSKO-MAZURSKIEGO
 PROGNOZA DEMOGRAFICZNA NA LATA 214-25 DLA WOJEWÓDZTWA WARMIŃSKO-MAZURSKIEGO Niniejsza informacja została opracowana na podstawie prognozy ludności na lata 214 25 dla województw (w podziale na część miejską
PROGNOZA DEMOGRAFICZNA NA LATA 214-25 DLA WOJEWÓDZTWA WARMIŃSKO-MAZURSKIEGO Niniejsza informacja została opracowana na podstawie prognozy ludności na lata 214 25 dla województw (w podziale na część miejską
PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTUR POMOSTOWYCH
 ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTUR POMOSTOWYCH NA LATA 2016 2020 WARSZAWA, LISTOPAD 2014 SPIS TREŚCI Spis treści...2
ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTUR POMOSTOWYCH NA LATA 2016 2020 WARSZAWA, LISTOPAD 2014 SPIS TREŚCI Spis treści...2
płodność, umieralność
 Konferencja naukowa Społeczno-ekonomiczne następstwa rozwoju procesów demograficznych do 2035 roku Biuro Rzecznika Praw Obywatelskich Założenia prognozy ludności płodność, umieralność Warszawa, 25 czerwca
Konferencja naukowa Społeczno-ekonomiczne następstwa rozwoju procesów demograficznych do 2035 roku Biuro Rzecznika Praw Obywatelskich Założenia prognozy ludności płodność, umieralność Warszawa, 25 czerwca
Mapowanie potrzeb zdrowotnych zakres merytoryczny
 1 Mapowanie potrzeb zdrowotnych zakres merytoryczny dr n. ekon. Barbara Więckowska Departament Analiz i Strategii, Ministerstwo Zdrowia Katedra Ubezpieczenia Społecznego, Szkoła Główna Handlowa w Warszawie
1 Mapowanie potrzeb zdrowotnych zakres merytoryczny dr n. ekon. Barbara Więckowska Departament Analiz i Strategii, Ministerstwo Zdrowia Katedra Ubezpieczenia Społecznego, Szkoła Główna Handlowa w Warszawie
Propozycje dodatkowych form oszczędzania na emeryturę
 Propozycje dodatkowych form oszczędzania na emeryturę Zabezpieczenie emerytalne Uniwersytet Wrocławski, Wrocław 3-4 listopad 2016 r. Agnieszka Pobłocka Uniwersytet Gdański a.poblocka@ug.edu.pl Celem prezentacji
Propozycje dodatkowych form oszczędzania na emeryturę Zabezpieczenie emerytalne Uniwersytet Wrocławski, Wrocław 3-4 listopad 2016 r. Agnieszka Pobłocka Uniwersytet Gdański a.poblocka@ug.edu.pl Celem prezentacji
Ubez piecz enie ersalne saln D am a en e t n ow o a a S t S rat ra eg e i g a
 Ubezpieczenie Uniwersalne Diamentowa Strategia 17 październik 2012 Diamentowa Strategia pozwoli Ci zabezpieczyć finansowo rodzinę przed utratą głównych dochodów w przypadku: inwalidztwa, poważnego zachorowania,
Ubezpieczenie Uniwersalne Diamentowa Strategia 17 październik 2012 Diamentowa Strategia pozwoli Ci zabezpieczyć finansowo rodzinę przed utratą głównych dochodów w przypadku: inwalidztwa, poważnego zachorowania,
MINISTER PRACY I POLITYKI SPOŁECZNEJ
 MINISTER PRACY I POLITYKI SPOŁECZNEJ Warszawa, dnia 10 września 2015 r. DUS-0700.245.2015.AS dot. K7INT34097 Pani Małgorzata Kidawa-Błońska Marszałek Sejmu RP Szanowna Pani Marszałek, W odpowiedzi na przekazaną
MINISTER PRACY I POLITYKI SPOŁECZNEJ Warszawa, dnia 10 września 2015 r. DUS-0700.245.2015.AS dot. K7INT34097 Pani Małgorzata Kidawa-Błońska Marszałek Sejmu RP Szanowna Pani Marszałek, W odpowiedzi na przekazaną
ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH ANALIZA WYNIKÓW BADANIA OKRESÓW POBIERANIA EMERYTUR
 ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH ANALIZA WYNIKÓW BADANIA OKRESÓW POBIERANIA EMERYTUR Warszawa 2012 Opracował: Akceptowała: Andrzej Kania Specjalista Izabela
ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH ANALIZA WYNIKÓW BADANIA OKRESÓW POBIERANIA EMERYTUR Warszawa 2012 Opracował: Akceptowała: Andrzej Kania Specjalista Izabela
Ocena prognozy ludności GUS 2003 z perspektywy aglomeracji warszawskiej. Marek Kupiszewski i Jakub Bijak
 Ocena prognozy ludności GUS 2003 z perspektywy aglomeracji warszawskiej Marek Kupiszewski i Jakub Bijak Uwagi ogólne Nie można ocenić prognozy ludności Warszawy bez oceny prognozy ludności Polski, gdyż
Ocena prognozy ludności GUS 2003 z perspektywy aglomeracji warszawskiej Marek Kupiszewski i Jakub Bijak Uwagi ogólne Nie można ocenić prognozy ludności Warszawy bez oceny prognozy ludności Polski, gdyż
PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU UBEZPIECZEŃ SPOŁECZNYCH
 ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU UBEZPIECZEŃ SPOŁECZNYCH NA LATA 2013 2017 WARSZAWA, WRZESIEŃ 2011 SPIS TREŚCI Spis treści...2
ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU UBEZPIECZEŃ SPOŁECZNYCH NA LATA 2013 2017 WARSZAWA, WRZESIEŃ 2011 SPIS TREŚCI Spis treści...2
INDYWIDUALNE EMERYTALNE
 INDYWIDUALNE KONTO EMERYTALNE DLACZEGO WARTO MIEĆ IKE? Rok Źródło Wysokość emertury stopa zastąpienia 1997 Bezpieczeństwo dzięki różnorodności opracowanie Pełnomocnika Rządu ds. Reformy Zabezpieczenia
INDYWIDUALNE KONTO EMERYTALNE DLACZEGO WARTO MIEĆ IKE? Rok Źródło Wysokość emertury stopa zastąpienia 1997 Bezpieczeństwo dzięki różnorodności opracowanie Pełnomocnika Rządu ds. Reformy Zabezpieczenia
Mikroekonometria 3. Mikołaj Czajkowski Wiktor Budziński
 Mikroekonometria 3 Mikołaj Czajkowski Wiktor Budziński Zadanie 1. Wykorzystując dane me.hedonic.dta przygotuj model oszacowujący wartość kosztów zewnętrznych rolnictwa 1. Przeprowadź regresję objaśniającą
Mikroekonometria 3 Mikołaj Czajkowski Wiktor Budziński Zadanie 1. Wykorzystując dane me.hedonic.dta przygotuj model oszacowujący wartość kosztów zewnętrznych rolnictwa 1. Przeprowadź regresję objaśniającą
Zakład Ubezpieczeń Społecznych Departament Statystyki i Prognoz Aktuarialnych
 Zakład Ubezpieczeń Społecznych Departament Statystyki i Prognoz Aktuarialnych Struktura wysokości emerytur i rent wypłacanych przez ZUS po waloryzacji w marcu 2014 roku. Warszawa 2014 Opracowała: Ewa Karczewicz
Zakład Ubezpieczeń Społecznych Departament Statystyki i Prognoz Aktuarialnych Struktura wysokości emerytur i rent wypłacanych przez ZUS po waloryzacji w marcu 2014 roku. Warszawa 2014 Opracowała: Ewa Karczewicz
Ćwiczenia 2. Tablice trwania życia. (life tables)
 Ćwiczenia 2 Tablice trwania życia (life tables) 1. Historia 2. Zasady budowy przekrojowych tablic trwania życia 3. Parametr e(0): zróżnicowanie według płci, zmiany w czasie e(0) w Polsce 4. Przykłady alternatywnych
Ćwiczenia 2 Tablice trwania życia (life tables) 1. Historia 2. Zasady budowy przekrojowych tablic trwania życia 3. Parametr e(0): zróżnicowanie według płci, zmiany w czasie e(0) w Polsce 4. Przykłady alternatywnych
Warszawa, dnia 11 stycznia 2011 r. MINISTERSTWO PRACY I POLITYKI SPOŁECZNEJ PODSEKRETARZ STANU Marek Bucior DUS MJ/10
 MINISTERSTWO PRACY I POLITYKI SPOŁECZNEJ PODSEKRETARZ STANU Marek Bucior DUS-0210-8-MJ/10 Warszawa, dnia 11 stycznia 2011 r. Pani Irena Wójcicka Podsekretarz Stanu Kancelaria Prezydenta Rzeczypospolitej
MINISTERSTWO PRACY I POLITYKI SPOŁECZNEJ PODSEKRETARZ STANU Marek Bucior DUS-0210-8-MJ/10 Warszawa, dnia 11 stycznia 2011 r. Pani Irena Wójcicka Podsekretarz Stanu Kancelaria Prezydenta Rzeczypospolitej
LIV Egzamin dla Aktuariuszy z 4 października 2010 r.
 Komisja Egzaminacyjna dla Aktuariuszy LIV Egzamin dla Aktuariuszy z 4 października 2010 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:...klucz odpowiedzi... Czas egzaminu:
Komisja Egzaminacyjna dla Aktuariuszy LIV Egzamin dla Aktuariuszy z 4 października 2010 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:...klucz odpowiedzi... Czas egzaminu:
LXXIV Egzamin dla Aktuariuszy z 23 maja 2016 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXXIV Egzamin dla Aktuariuszy z 23 maja 2016 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy LXXIV Egzamin dla Aktuariuszy z 23 maja 2016 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Ukryty dług na liczniku długu publicznego. 30 IX 2013 Aleksander Łaszek
 Ukryty dług na liczniku długu publicznego Aleksander Łaszek Ukryty dług na liczniku długu publicznego 1. Dlaczego dług ukryty jest ważny? 2. Zakres ukrytego długu, różne metodologie 3. Metodologia ESA
Ukryty dług na liczniku długu publicznego Aleksander Łaszek Ukryty dług na liczniku długu publicznego 1. Dlaczego dług ukryty jest ważny? 2. Zakres ukrytego długu, różne metodologie 3. Metodologia ESA
Zakład Ubezpieczeń Społecznych Departament Statystyki i Prognoz Aktuarialnych
 Zakład Ubezpieczeń Społecznych Departament Statystyki i Prognoz Aktuarialnych Struktura wysokości emerytur i rent wypłacanych przez ZUS po waloryzacji w marcu 2013 roku. Warszawa 2013 Opracowała: Ewa Karczewicz
Zakład Ubezpieczeń Społecznych Departament Statystyki i Prognoz Aktuarialnych Struktura wysokości emerytur i rent wypłacanych przez ZUS po waloryzacji w marcu 2013 roku. Warszawa 2013 Opracowała: Ewa Karczewicz
Ekonometria. Modelowanie zmiennej jakościowej. Jakub Mućk. Katedra Ekonomii Ilościowej
 Ekonometria Modelowanie zmiennej jakościowej Jakub Mućk Katedra Ekonomii Ilościowej Jakub Mućk Ekonometria Ćwiczenia 8 Zmienna jakościowa 1 / 25 Zmienna jakościowa Zmienna ilościowa może zostać zmierzona
Ekonometria Modelowanie zmiennej jakościowej Jakub Mućk Katedra Ekonomii Ilościowej Jakub Mućk Ekonometria Ćwiczenia 8 Zmienna jakościowa 1 / 25 Zmienna jakościowa Zmienna ilościowa może zostać zmierzona
FORECASTING THE DISTRIBUTION OF AMOUNT OF UNEMPLOYED BY THE REGIONS
 FOLIA UNIVERSITATIS AGRICULTURAE STETINENSIS Folia Univ. Agric. Stetin. 007, Oeconomica 54 (47), 73 80 Mateusz GOC PROGNOZOWANIE ROZKŁADÓW LICZBY BEZROBOTNYCH WEDŁUG MIAST I POWIATÓW FORECASTING THE DISTRIBUTION
FOLIA UNIVERSITATIS AGRICULTURAE STETINENSIS Folia Univ. Agric. Stetin. 007, Oeconomica 54 (47), 73 80 Mateusz GOC PROGNOZOWANIE ROZKŁADÓW LICZBY BEZROBOTNYCH WEDŁUG MIAST I POWIATÓW FORECASTING THE DISTRIBUTION
Metody probabilistyczne
 Metody probabilistyczne Teoria estymacji Jędrzej Potoniec Bibliografia Bibliografia Próba losowa (x 1, x 2,..., x n ) Próba losowa (x 1, x 2,..., x n ) (X 1, X 2,..., X n ) Próba losowa (x 1, x 2,...,
Metody probabilistyczne Teoria estymacji Jędrzej Potoniec Bibliografia Bibliografia Próba losowa (x 1, x 2,..., x n ) Próba losowa (x 1, x 2,..., x n ) (X 1, X 2,..., X n ) Próba losowa (x 1, x 2,...,
System emerytalny problemy na przyszłość
 Zakład Ubezpieczeń Społecznych System emerytalny problemy na przyszłość Materiały z seminariów ZUS Warszawa 2011 ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH System emerytalny problemy na przyszłość Materiały z seminariów
Zakład Ubezpieczeń Społecznych System emerytalny problemy na przyszłość Materiały z seminariów ZUS Warszawa 2011 ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH System emerytalny problemy na przyszłość Materiały z seminariów
Wykład 2. Wybrane zjawiska demograficzne i sposoby ich pomiaru
 Wykład 2. Wybrane zjawiska demograficzne i sposoby ich pomiaru Dlaczego demografia? Rozumienie pojęć z zakresu demografii, wiedza o zjawiskach demograficznych jest istotna, ponieważ: żyjemy w czasach,
Wykład 2. Wybrane zjawiska demograficzne i sposoby ich pomiaru Dlaczego demografia? Rozumienie pojęć z zakresu demografii, wiedza o zjawiskach demograficznych jest istotna, ponieważ: żyjemy w czasach,
Scenariusze zmian płodności i umieralności dla 27 krajów europejskich na lata 2002 2052
 Scenariusze zmian płodności i umieralności dla 27 krajów europejskich na lata 2002 2052 Jakub Bijak Środkowoeuropejskie Forum Badań Migracyjnych Konferencja Perspektywy demograficzne Europy Instytut Statystyki
Scenariusze zmian płodności i umieralności dla 27 krajów europejskich na lata 2002 2052 Jakub Bijak Środkowoeuropejskie Forum Badań Migracyjnych Konferencja Perspektywy demograficzne Europy Instytut Statystyki
Syntetyczne miary reprodukcji ludności
 Syntetyczne miary reprodukcji ludności Wprowadzenie Reprodukcja ludności (population reproduction) jest to odtwarzanie (w czasie) liczby i struktury ludności pod wpływem ruchu naturalnego i ruchu wędrówkowego.
Syntetyczne miary reprodukcji ludności Wprowadzenie Reprodukcja ludności (population reproduction) jest to odtwarzanie (w czasie) liczby i struktury ludności pod wpływem ruchu naturalnego i ruchu wędrówkowego.
METODY STATYSTYCZNE W BIOLOGII
 METODY STATYSTYCZNE W BIOLOGII 1. Wykład wstępny 2. Populacje i próby danych 3. Testowanie hipotez i estymacja parametrów 4. Planowanie eksperymentów biologicznych 5. Najczęściej wykorzystywane testy statystyczne
METODY STATYSTYCZNE W BIOLOGII 1. Wykład wstępny 2. Populacje i próby danych 3. Testowanie hipotez i estymacja parametrów 4. Planowanie eksperymentów biologicznych 5. Najczęściej wykorzystywane testy statystyczne
Model MULTIPOLES - narzędzie do prognozowania, projekcji i symulacji stanu i struktury ludności
 Model MULTIPOLES - narzędzie do prognozowania, projekcji i symulacji stanu i struktury ludności Dorota Kupiszewska i Marek Kupiszewski Konferencja Perspektywy demograficzne Europy Instytut Statystyki i
Model MULTIPOLES - narzędzie do prognozowania, projekcji i symulacji stanu i struktury ludności Dorota Kupiszewska i Marek Kupiszewski Konferencja Perspektywy demograficzne Europy Instytut Statystyki i
Wprowadzenie do teorii ekonometrii. Wykład 1 Warunkowa wartość oczekiwana i odwzorowanie liniowe
 Wprowadzenie do teorii ekonometrii Wykład 1 Warunkowa wartość oczekiwana i odwzorowanie liniowe Zajęcia Wykład Laboratorium komputerowe 2 Zaliczenie EGZAMIN (50%) Na egzaminie obowiązują wszystkie informacje
Wprowadzenie do teorii ekonometrii Wykład 1 Warunkowa wartość oczekiwana i odwzorowanie liniowe Zajęcia Wykład Laboratorium komputerowe 2 Zaliczenie EGZAMIN (50%) Na egzaminie obowiązują wszystkie informacje
EKONOMETRIA STOSOWANA PRZYKŁADOWE ZADANIA EGZAMINACYJNE
 EKONOMETRIA STOSOWANA PRZYKŁADOWE ZADANIA EGZAMINACYJNE ZADANIE 1 Oszacowano zależność między luką popytowa a stopą inflacji dla gospodarki niemieckiej. Wyniki estymacji są następujące: Estymacja KMNK,
EKONOMETRIA STOSOWANA PRZYKŁADOWE ZADANIA EGZAMINACYJNE ZADANIE 1 Oszacowano zależność między luką popytowa a stopą inflacji dla gospodarki niemieckiej. Wyniki estymacji są następujące: Estymacja KMNK,
LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Kobiety w zachodniopomorskim - aspekt demograficzny
 Urząd Marszałkowski Województwa Zachodniopomorskiego Regionalny Ośrodek Polityki Społecznej Kobiety w zachodniopomorskim - aspekt demograficzny Szczecin 2012 Obserwatorium Integracji Społecznej, Projekt
Urząd Marszałkowski Województwa Zachodniopomorskiego Regionalny Ośrodek Polityki Społecznej Kobiety w zachodniopomorskim - aspekt demograficzny Szczecin 2012 Obserwatorium Integracji Społecznej, Projekt
Zróżnicowanie umieralności spowodowanej chorobami układu krążenia w Polsce w 2007 roku.
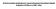 Zróżnicowanie umieralności spowodowanej chorobami układu krążenia w Polsce w 2007 roku. Objaśnienia. Materiałem badawczym były informacje zawarte w kartach zgonów, które przeniesione zostały na komputerowy
Zróżnicowanie umieralności spowodowanej chorobami układu krążenia w Polsce w 2007 roku. Objaśnienia. Materiałem badawczym były informacje zawarte w kartach zgonów, które przeniesione zostały na komputerowy
Wprowadzenie. Pojęcie i ewolucja ryzyka starości. Metody zabezpieczenia ryzyka starości w prawie polskim
 Wprowadzenie Pojęcie i ewolucja ryzyka starości Metody zabezpieczenia ryzyka starości w prawie polskim Przemiany gospodarczo polityczne, a reformy systemów emerytalnych. Reformy systemów emerytalnych :
Wprowadzenie Pojęcie i ewolucja ryzyka starości Metody zabezpieczenia ryzyka starości w prawie polskim Przemiany gospodarczo polityczne, a reformy systemów emerytalnych. Reformy systemów emerytalnych :
4. Średnia i autoregresja zmiennej prognozowanej
 4. Średnia i autoregresja zmiennej prognozowanej 1. Średnia w próbie uczącej Własności: y = y = 1 N y = y t = 1, 2, T s = s = 1 N 1 y y R = 0 v = s 1 +, 2. Przykład. Miesięczna sprzedaż żelazek (szt.)
4. Średnia i autoregresja zmiennej prognozowanej 1. Średnia w próbie uczącej Własności: y = y = 1 N y = y t = 1, 2, T s = s = 1 N 1 y y R = 0 v = s 1 +, 2. Przykład. Miesięczna sprzedaż żelazek (szt.)
Zmiany w liczbie ludności w Polsce w latach
 Zmiany w liczbie ludności w Polsce w latach 1946-2010 Tabela 1 Stan w dniu 31 XII Ludność w tys. Zmiany przyrost, ubytek w okresie tendencje w tys. w % 1946 23 640 - - - - 1966 31 811 1946-1966 rosnąca
Zmiany w liczbie ludności w Polsce w latach 1946-2010 Tabela 1 Stan w dniu 31 XII Ludność w tys. Zmiany przyrost, ubytek w okresie tendencje w tys. w % 1946 23 640 - - - - 1966 31 811 1946-1966 rosnąca
2015-12-16. Wyliczanie emerytury na zasadach zbliżonych do tych panujących przed 1.01.1999 r. Emerytura. Do kiedy stare emerytury?
 Emerytura Zasady wyliczania wysokości emerytury to suma pieniędzy, którą będzie comiesięcznie otrzymywał ubezpieczony z ZUS w momencie, gdy nabędzie status emeryta. Wyliczanie emerytury na zasadach zbliżonych
Emerytura Zasady wyliczania wysokości emerytury to suma pieniędzy, którą będzie comiesięcznie otrzymywał ubezpieczony z ZUS w momencie, gdy nabędzie status emeryta. Wyliczanie emerytury na zasadach zbliżonych
Omówienie regulacji wynikających z ustawy obniżającej wiek emerytalny
 Gdańsk, 2 października 2017 r. Omówienie regulacji wynikających z ustawy obniżającej wiek emerytalny Agnieszka Kurczewska-Stanisławowicz Naczelnik Wydziału Zakład Ubezpieczeń Społecznych Oddział w Gdańsku
Gdańsk, 2 października 2017 r. Omówienie regulacji wynikających z ustawy obniżającej wiek emerytalny Agnieszka Kurczewska-Stanisławowicz Naczelnik Wydziału Zakład Ubezpieczeń Społecznych Oddział w Gdańsku
Oszczędności gospodarstw domowych Analiza przekrojowa i analiza kohort
 Oszczędności gospodarstw domowych Analiza przekrojowa i analiza kohort Barbara Liberda prof. zw. Uniwersytetu Warszawskiego Wydział Nauk Ekonomicznych Konferencja Długoterminowe oszczędzanie Szkoła Główna
Oszczędności gospodarstw domowych Analiza przekrojowa i analiza kohort Barbara Liberda prof. zw. Uniwersytetu Warszawskiego Wydział Nauk Ekonomicznych Konferencja Długoterminowe oszczędzanie Szkoła Główna
Modele DSGE. Jerzy Mycielski. Maj Jerzy Mycielski () Modele DSGE Maj / 11
 Modele DSGE Jerzy Mycielski Maj 2008 Jerzy Mycielski () Modele DSGE Maj 2008 1 / 11 Modele DSGE DSGE - Dynamiczne, stochastyczne modele równowagi ogólnej (Dynamic Stochastic General Equilibrium Model)
Modele DSGE Jerzy Mycielski Maj 2008 Jerzy Mycielski () Modele DSGE Maj 2008 1 / 11 Modele DSGE DSGE - Dynamiczne, stochastyczne modele równowagi ogólnej (Dynamic Stochastic General Equilibrium Model)
Sterowanie wielkością zamówienia w Excelu - cz. 3
 Sterowanie wielkością zamówienia w Excelu - cz. 3 21.06.2005 r. 4. Planowanie eksperymentów symulacyjnych Podczas tego etapu ważne jest określenie typu rozkładu badanej charakterystyki. Dzięki tej informacji
Sterowanie wielkością zamówienia w Excelu - cz. 3 21.06.2005 r. 4. Planowanie eksperymentów symulacyjnych Podczas tego etapu ważne jest określenie typu rozkładu badanej charakterystyki. Dzięki tej informacji
Ukryty dług na liczniku długu publicznego. 30 IX 2013 Aleksander Łaszek
 Ukryty dług na liczniku długu publicznego Aleksander Łaszek Ukryty dług na liczniku długu publicznego 1. Dlaczego dług ukryty jest ważny? 2. Zakres ukrytego długu, różne metodologie 3. Metodologia ESA
Ukryty dług na liczniku długu publicznego Aleksander Łaszek Ukryty dług na liczniku długu publicznego 1. Dlaczego dług ukryty jest ważny? 2. Zakres ukrytego długu, różne metodologie 3. Metodologia ESA
PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTALNEGO DO 2060 ROKU
 ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTALNEGO DO 2060 ROKU WARSZAWA, MARZEC 2016 SPIS TREŚCI Spis treści...2 Wstęp...3
ZAKŁAD UBEZPIECZEŃ SPOŁECZNYCH DEPARTAMENT STATYSTYKI I PROGNOZ AKTUARIALNYCH PROGNOZA WPŁYWÓW I WYDATKÓW FUNDUSZU EMERYTALNEGO DO 2060 ROKU WARSZAWA, MARZEC 2016 SPIS TREŚCI Spis treści...2 Wstęp...3
Warszawa, marzec 2017 r. FUS, FEP i FRD. Jakub Sarbiński, Naczelnik Wydziału Planowania. Departament Finansów Funduszy
 Warszawa, marzec 2017 r. FUS, FEP i FRD Jakub Sarbiński, Naczelnik Wydziału Planowania Departament Finansów Funduszy 2 Plan wykładu: 1. Co to jest FUS? 2. Dochody i wydatki FUS coś o kwotach 3. Wydolność
Warszawa, marzec 2017 r. FUS, FEP i FRD Jakub Sarbiński, Naczelnik Wydziału Planowania Departament Finansów Funduszy 2 Plan wykładu: 1. Co to jest FUS? 2. Dochody i wydatki FUS coś o kwotach 3. Wydolność
Wojciech Bijak. Dynamiczna analiza finansowa minimalnego wymogu kapitałowego (MCR) kalibracja modelu rozszerzonego marginesu wypłacalności
 Dynamiczna analiza finansowa minimalnego wymogu kapitałowego () kalibracja modelu rozszerzonego marginesu wypłacalności Wojciech Bijak Instytut Ekonometrii SGH 8.6.28 1 Plan prezentacji Wymogi kapitałowe
Dynamiczna analiza finansowa minimalnego wymogu kapitałowego () kalibracja modelu rozszerzonego marginesu wypłacalności Wojciech Bijak Instytut Ekonometrii SGH 8.6.28 1 Plan prezentacji Wymogi kapitałowe
Analiza wyników badania okresów pobierania emerytur
 Analiza wyników badania okresów pobierania emerytur Departament Statystyki i Prognoz Aktuarialnych Warszawa 2019 Opracował: Andrzej Kania Wydział Badań Statystycznych Akceptowała: Hanna Zalewska Dyrektor
Analiza wyników badania okresów pobierania emerytur Departament Statystyki i Prognoz Aktuarialnych Warszawa 2019 Opracował: Andrzej Kania Wydział Badań Statystycznych Akceptowała: Hanna Zalewska Dyrektor
Polityka gospodarcza i społeczna (zabezpieczenie emerytalne)
 prof. dr hab. Tadeusz Szumlicz Polityka gospodarcza i społeczna (zabezpieczenie emerytalne) Zakres przedmiotowy systemu zabezpieczenia społecznego wyznacza katalog ryzyk społecznych: choroby macierzyństwa
prof. dr hab. Tadeusz Szumlicz Polityka gospodarcza i społeczna (zabezpieczenie emerytalne) Zakres przedmiotowy systemu zabezpieczenia społecznego wyznacza katalog ryzyk społecznych: choroby macierzyństwa
Ocena realizacji celów RPO WP w roku 2008 za pomocą modelu HERMIN
 Ocena realizacji celów RPO WP w roku 2008 za pomocą modelu HERMIN dr Instytut Wiedzy i Innowacji 2 września 2009 r. Projekt finansowany ze środków Unii Europejskiej z Europejskiego Funduszu Rozwoju Regionalnego
Ocena realizacji celów RPO WP w roku 2008 za pomocą modelu HERMIN dr Instytut Wiedzy i Innowacji 2 września 2009 r. Projekt finansowany ze środków Unii Europejskiej z Europejskiego Funduszu Rozwoju Regionalnego
Wszystko, czego nie wiesz o emeryturach. Ekspert: Dariusz Noszczak, wicedyrektor, Departament Świadczeń Emerytalno-Rentowych, Centrala ZUS
 Wszystko, czego nie wiesz o emeryturach Ekspert: Dariusz Noszczak, wicedyrektor, Departament Świadczeń Emerytalno-Rentowych, Centrala ZUS 2 Ustalanie wysokości emerytur ze starego systemu Ustalanie wysokości
Wszystko, czego nie wiesz o emeryturach Ekspert: Dariusz Noszczak, wicedyrektor, Departament Świadczeń Emerytalno-Rentowych, Centrala ZUS 2 Ustalanie wysokości emerytur ze starego systemu Ustalanie wysokości
Współzależność między migracjami międzynarodowymi a dynamiką ludności i zasobami siły roboczej w Europie,
 Współzależność między migracjami międzynarodowymi a dynamiką ludności i zasobami siły roboczej w Europie, 22 252 Jakub Bijak, Dorota Kupiszewska Marek Kupiszewski, Katarzyna Saczuk Środkowoeuropejskie
Współzależność między migracjami międzynarodowymi a dynamiką ludności i zasobami siły roboczej w Europie, 22 252 Jakub Bijak, Dorota Kupiszewska Marek Kupiszewski, Katarzyna Saczuk Środkowoeuropejskie
Wprowadzenie Model ARMA Sezonowość Prognozowanie Model regresji z błędami ARMA. Modele ARMA
 Ważną klasę modeli dynamicznych stanowią modele ARMA(p, q) Ważną klasę modeli dynamicznych stanowią modele ARMA(p, q) Modele tej klasy są modelami ateoretycznymi Ważną klasę modeli dynamicznych stanowią
Ważną klasę modeli dynamicznych stanowią modele ARMA(p, q) Ważną klasę modeli dynamicznych stanowią modele ARMA(p, q) Modele tej klasy są modelami ateoretycznymi Ważną klasę modeli dynamicznych stanowią
XXXVIII Egzamin dla Aktuariuszy z 20 marca 2006 r.
 Komisja Egzaminacyjna dla Aktuariuszy XXXVIII Egzamin dla Aktuariuszy z 20 marca 2006 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy XXXVIII Egzamin dla Aktuariuszy z 20 marca 2006 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Zakład Ubezpieczeń Społecznych Departament Statystyki i Prognoz Aktuarialnych
 Zakład Ubezpieczeń Społecznych Departament Statystyki i Prognoz Aktuarialnych Struktura wysokości emerytur i rent wypłacanych przez ZUS po waloryzacji i podwyższeniu świadczeń najniższych w marcu 2017
Zakład Ubezpieczeń Społecznych Departament Statystyki i Prognoz Aktuarialnych Struktura wysokości emerytur i rent wypłacanych przez ZUS po waloryzacji i podwyższeniu świadczeń najniższych w marcu 2017
Świadomość emerytalna. Jak żyć, aby otrzymać adekwatną emeryturę?
 Świadomość emerytalna. Jak żyć, aby otrzymać adekwatną emeryturę? Alicja Jajko-Siwek Konferencja Naukowa EDUKACJA FINANSOWA Warszawa 28.09.2017 Wprowadzenie Adekwatne świadczenie emerytalne a świadomość
Świadomość emerytalna. Jak żyć, aby otrzymać adekwatną emeryturę? Alicja Jajko-Siwek Konferencja Naukowa EDUKACJA FINANSOWA Warszawa 28.09.2017 Wprowadzenie Adekwatne świadczenie emerytalne a świadomość
PRZECIĘTNE DALSZE TRWANIE ŻYCIA OSÓB W STARSZYM WIEKU W POLSCE W LATACH I PRÓBA SZACUNKU DO 2012 ROKU
 CZESŁAWA STĘPIEŃ Uniwersytet Łódzki PRZECIĘTNE DALSZE TRWANIE ŻYCIA OSÓB W STARSZYM WIEKU W POLSCE W LATACH 1950 2002 I PRÓBA SZACUNKU DO 2012 ROKU Demograficzne starzenie się społeczeństw staje się coraz
CZESŁAWA STĘPIEŃ Uniwersytet Łódzki PRZECIĘTNE DALSZE TRWANIE ŻYCIA OSÓB W STARSZYM WIEKU W POLSCE W LATACH 1950 2002 I PRÓBA SZACUNKU DO 2012 ROKU Demograficzne starzenie się społeczeństw staje się coraz
21 marca 2013 r. Główne zalety rozwiązania:
 21 marca 2013 r. Stanowisko Izby Gospodarczej Towarzystw Emerytalnych w kwestii wypłat świadczeń z kapitałowego systemu emerytalnego Rozwiązanie wypłat z korzyścią dla gospodarki i klientów Główne zalety
21 marca 2013 r. Stanowisko Izby Gospodarczej Towarzystw Emerytalnych w kwestii wypłat świadczeń z kapitałowego systemu emerytalnego Rozwiązanie wypłat z korzyścią dla gospodarki i klientów Główne zalety
